lOMoARcPSD|47207367 lOMoARcPSD|47207367
A. Danh sách thành viên :
B. Nội dung câu hỏi :
1) (2đ) Tìm hiểu về đường cong tham số trong phần 9.2, Soo T. Tan Single
variable - Calculus early transcendentals.
2) (2đ) Làm các bài tập 40, 41, 42, 43 phần 9.2 nói trên.
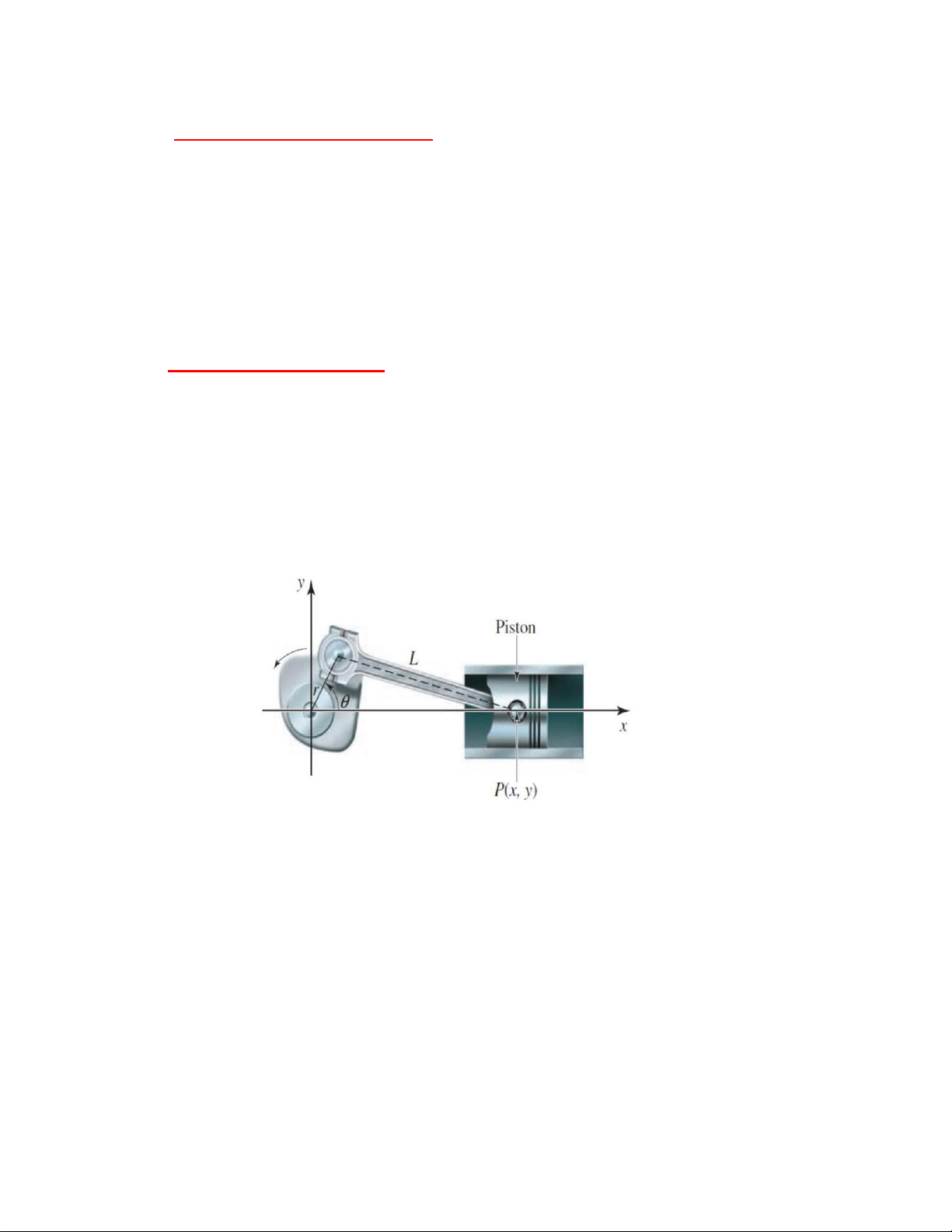
3) (2đ) A piston is attached to a crankshaft by means of a connecting rod of
length , as shown in the figure. If the disk is of radius , find the parametric
equations giving the position of the point P using the angle θ as a parameter.
4) (2đ) Cho đường cong tham số (C) : x = 3t2,y = 3t − t3. • ẽ đườ
• Vng cong (C).
• Tìm điểm tự cắt của (C).
• Vẽ các tiếp tuyến với đường cong tại điểm tự cắt.
Tìm diện tích giới hạn bởi đường cong này (do phần tự cắt tạo ra). age | 1 lOMoARcPSD|47207367
5) (2đ)Một nhà đầu tư cùng lúc đầu tư vào 2 lĩnh vực A và B. Tốc độ tăng lợi
nhuận sau t năm tính từ thời điểm hiện tại đối với các đầu tư A và B theo thứ
tự cho bởi hàm fA(t) = 50 + t2 fB(t) = 200 + 15t (USD/năm).
Đến năm nào thì tốc độ tăng lợi nhuận đối với đầu tư A vượt qua tốc độ
tăng lợi nhuận đối với đầu tư B.
Tính độ chênh lệch lợi nhuận của 2 đầu tư đến thời điểm tìm được ở câu trên.
Biều diễn bằng đồ thị độ chênh lệch này. Page | 2 lOMoARcPSD|47207367
NHẬN XÉT CỦA GIÁO VIÊN HƯỚNG DẪN Page | 3 lOMoARcPSD|47207367 BÀI LÀM
Câu 1 : Đường cong phẳng và hàm tham số : 
Tại sao chúng ta cần sử dụng hàm tham số?
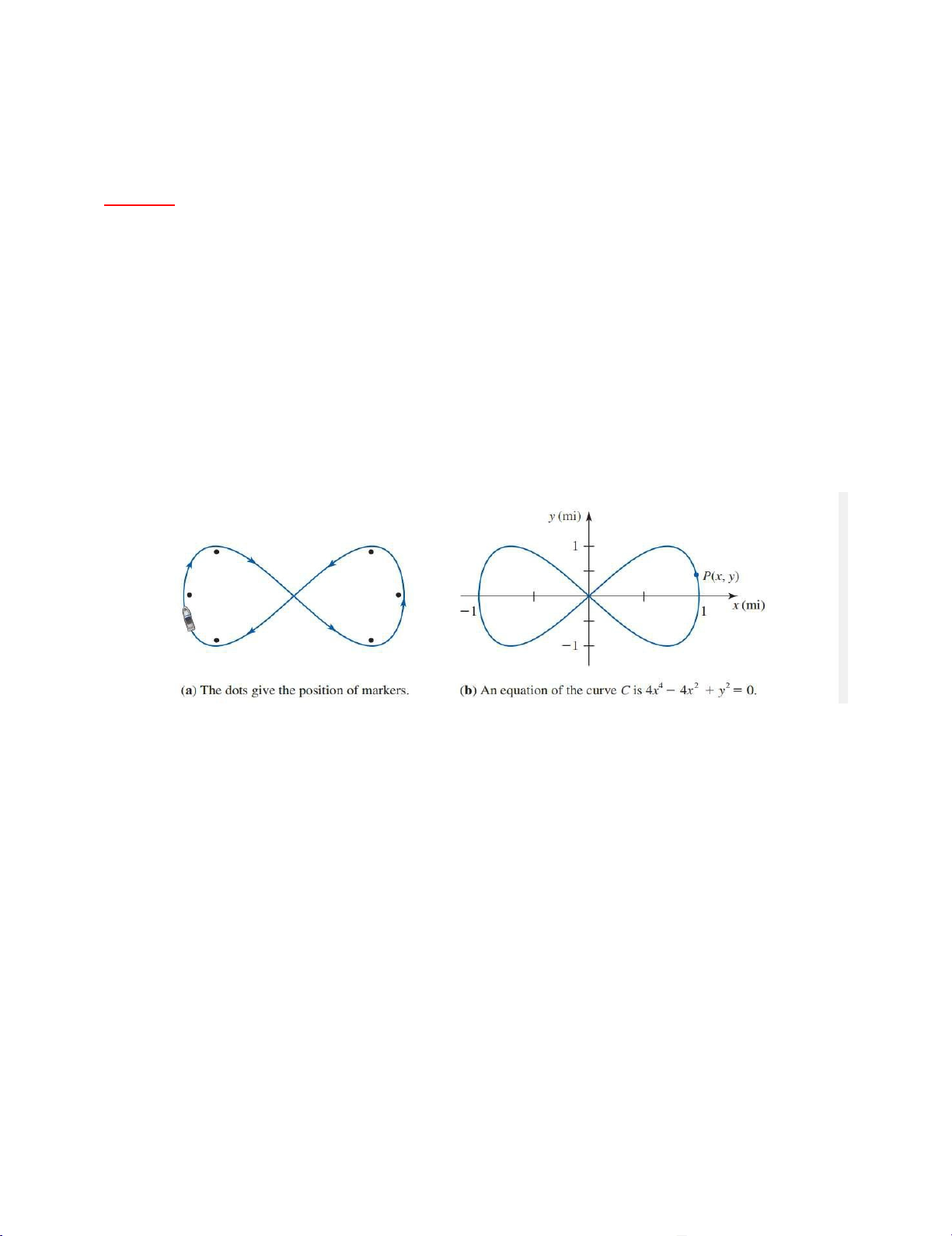
-Hình 1a cho ta một cái nhìn bao quát về lộ trình được định sẵn của một chiếc du thuyền.
-Hình 1b chúng ta được giới thiệu một hệ trục tọa độ xy trong không gian để
diễn tả vị trí của chiếc du thuyền. Theo như hệ tọa độ thì vị trí của chiếc thuyền được
cho bởi điểm P(x;y) và lộ trình của nó có dạng của đồ thị hàm số 4x4 – 4x2 + y2 = 0 ,
được gọi là đường lemniscate. 
Nhưng việc biểu diễn đường lemniscate trong trường hợp này gặp phải 3
nhược điểm lớn.
Đầu tiên, phương trình không được định nghĩa một cách rõ rang rằng y làm hàm
của x hay x là hàm của y. bạn cũng có thể cho rằng đó không phải là đồ thị của hàm số
bằng cách áp dụng các đường tiệm cận đứng và ngang trên hình phẳng ở hình 1b (xem
phần 0.2). vì vậy mà chúng ta không thể sử dụng trực tiếp các kết quả cho những hàm
số được xây dựng từ trước. thứ hai, phương trình không cho chúng ta biết được
khi nào con thuyền sẽ ở tọa độ cho trước (x;y). thứ ba, phương trình không đưa ra
sự nghi hoặc về hướng chuyển động của chiếc du thuyền.
Để khắc phục những nhược điểm khi chung sta xem xét sự chuyển động của
một vật thể trong mặt phẳng hoặc trên những đường cong phẳng không phải là đồ thị
của các hàm số, chúng ta chuyển sang phương án sau. Page | 4 lOMoARcPSD|47207367
Nếu (x,y) là một điểm trên đườ=ng cong() thid trong= ( )mặt phẳng tọa độ xy, chúng ta viết
Mà tại đó f và g là những hàm số của một biến phụ t với với một số miền chung I.
những hàm số đó được gọi là hàm tham số, t được gọi là tham số, và miền chung I ể ải thích đượ [ , ]
được gọi là khoảng tham số.
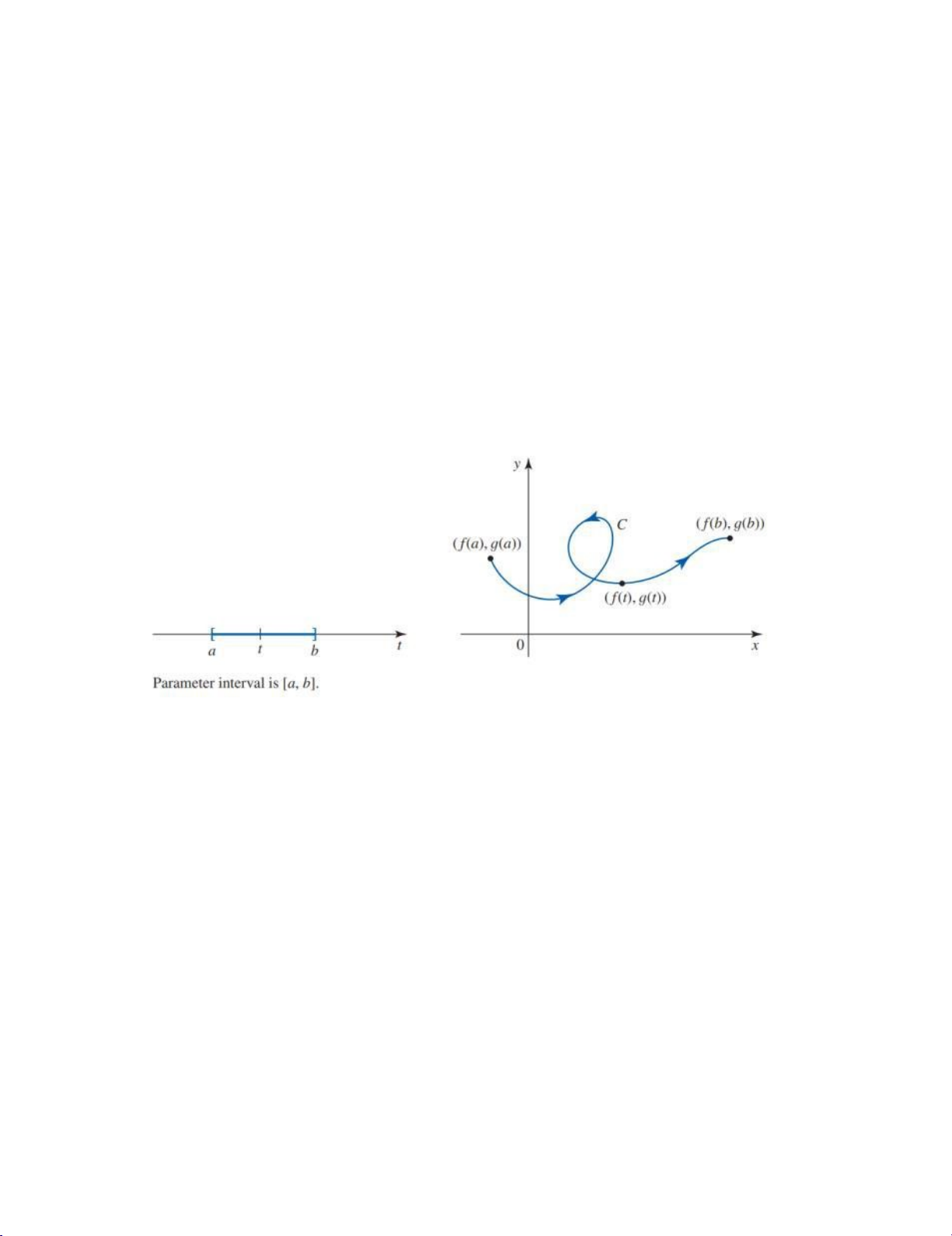
Nếu giả sử rằng thuộc đoạn
đại diện cho thời gian thì chúng ta hoàn toàn có tăng = ( ( ), ( )) th gi
c các hàm tham số theo sự chuyển động của một hạt như sau: tại thời ự điểm
thì hạt ở điểm ban đầu
trên đường cong hay quỹ đạo C. khi
từ đến , hạt này di chuyển theo đường cong theo một hướng cụ thể được gọi là
cuối( ( ), ( )) của đường cong. (xem hình 2) s
định hướng của đường cong, cuối cùng
hạt kết thúc chuyển động tại điểm
Chúng ta cũng có thể giải thích các phương trình tham số b[ằng , ]phương pháp hình
học như sau: ta lấy một đoạn thẳng, có chiều dài bằng với đoạn , sau đó thực hiện các
công đoạn như kéo dài, uốn và xoắn để tạo ra một đường cong C hoàn chỉnh.
 Phác thảo đường cong theo định nghĩa bởi phương trình tham số : 
Trước khi đọc các ví dụ, hãy định nghĩa các thuậ(t ,ngữ)
Mặt phẳng đường cong là tập hợp C gồm các cặp s sau đây: ố
phương trình tham số : = ( ) và = ( )
được xác định bởi các
Trong đó f và g là những hàm số liên tục trên tập xác định. Page | 5 lOMoARcPSD|47207367
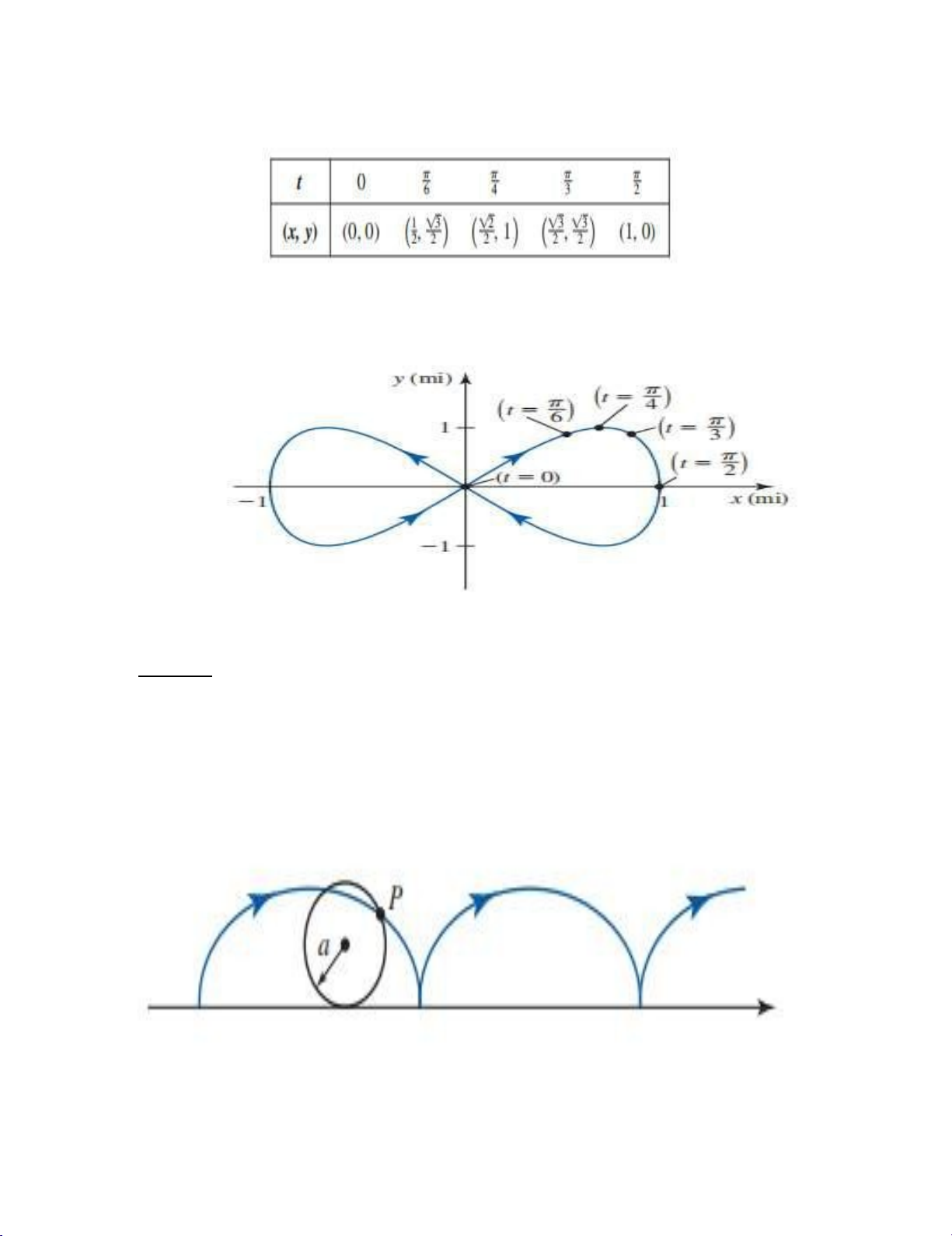
 −Ví1d≤ụ 1:≤V2ẽ đường: cong được mô tả bởi hàm tham số = 2 − 4 và = 2 với
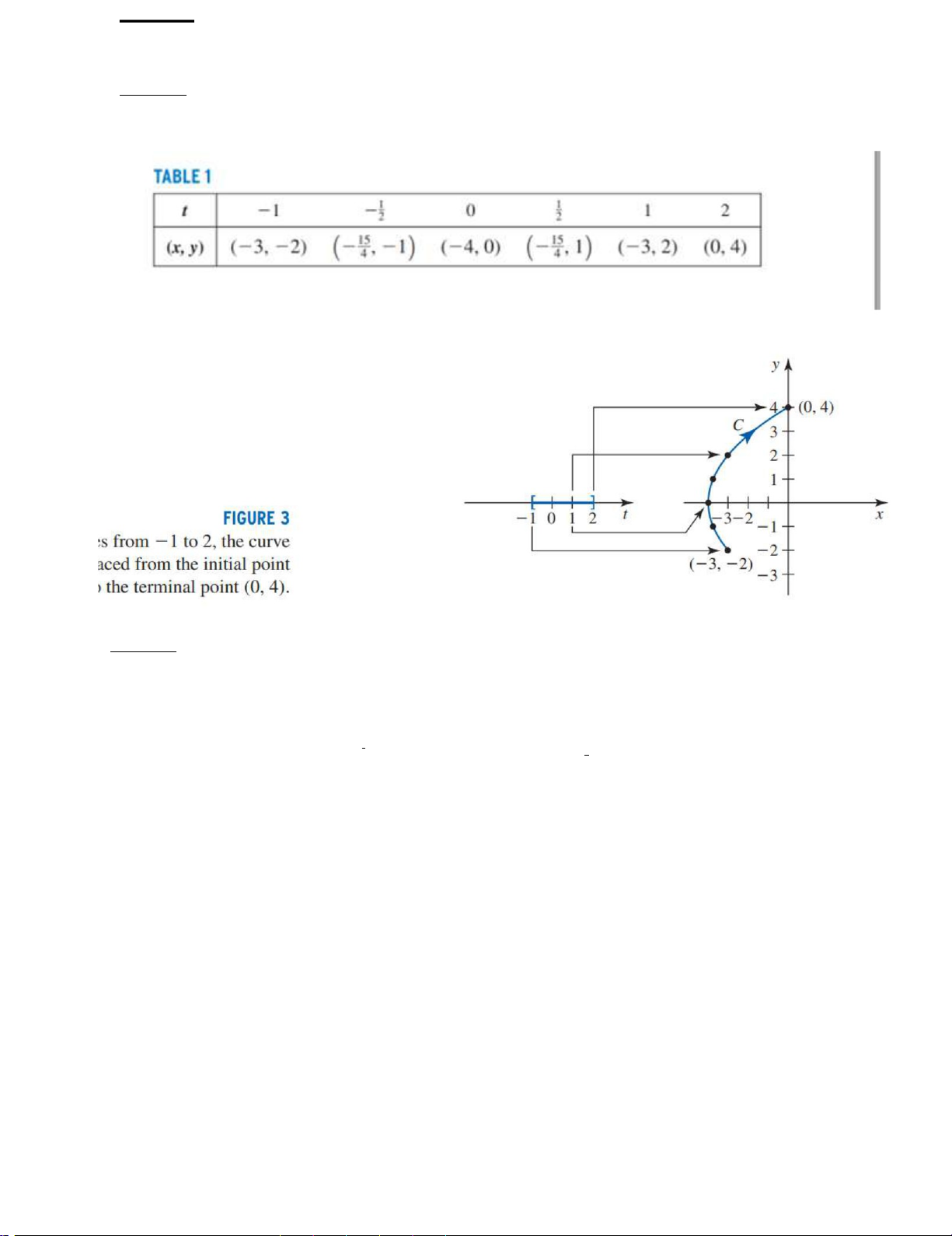
Cách 1: Nối các điểm (x, y) được xác định bởi các giá trị t chọn sẵn ( bảng 1),
chúng ta thu được đường cong như hình 3: cong HÌNH 3
Khi tăng từ -1 đến 2, đường
(−3, −2) đến điểm cuối (0,4) C được nối từ điểm đầu
Cách 2: Chúng ta rút tham số t từ hàm y= 2t đã cho và sau đó thay t vào hàm x, ta được: = ( 2 ) − 4 hay = 2 − 4 1 2 41
ở đầ ủa (−4 , 0) (−3, −2) = −1
ệ Đó chính là phương trình của một đường parabol mà có trục
là trục đối xứng và ối các điể ừ điểm đầu = 2 (0,4) đỉnh là điểm
. Lúc này, nhận thấy tại ta được điể , là điể m m m u c
đường cong thì tại hay điểm
ta có điểm kết thúc đường cong. Vi c n m t
đến điểm cuối cho ta một đường cong như mong muốn. ị ủ ( ) ở ố ( ) đề = ( ) = ( )
*Chúng ta sẽ phải chấp nhận quy ước này, cũng như những gì chúng ta đã làm miền
xác định của hàm số, rằng khoảng tham số của và
sẽ bao gồm tất cả các giá tr c a b i vì và
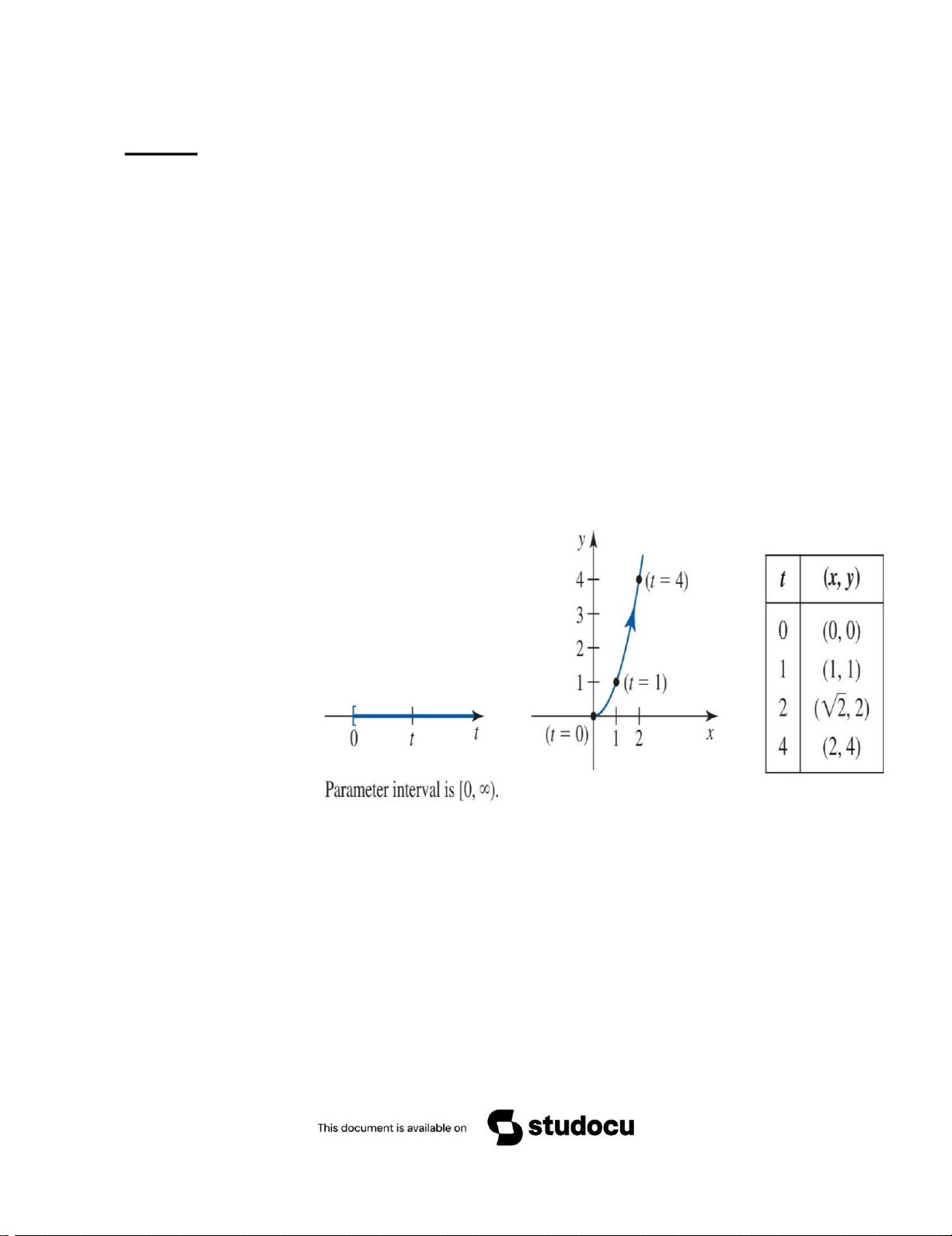
u là s thực, trừ một vài ngoại lệ. Page | 6 lOMoARcPSD|47207367  Ví d ụ 2 :
Phác thảo đường cong tham số cho bởi : b) = ** = a) a)
Chúng ta sẽ rút biến t bằng cách bình phương hàm để được 2 . sau đó thay giá tr c
trình của một ủa ≥ 0
ị đó của t vào hàm y, ta đượ 2, đây là phương = u ki
n của phương trình thứ nhất là
đường parabol. Nhưng lưu ý rằng điề ệ = ≥ả0 nên
. Vì vậy, đường cong mong muốn của chúng ta nằm ở phía bên ph i
c đường parabol như hình 4. Cuối cùng, lưu ý rằng khoảng tham số là , và b b ng cong c b đầu tại (0,0) ở
ắt đầu tăng từ 0 nên đườ
ủa chúng ta cũng sẽ ắt [0, ∞) điểm
và đi dọc theo đường parabol nói trên. HÌNH 4
Do t bắt đầu tăng từ 0, nên đường
cong bắt đầu tại gốc tọa độ và đi
dọc theo toàn bộ nhánh phảicủa đường parabol
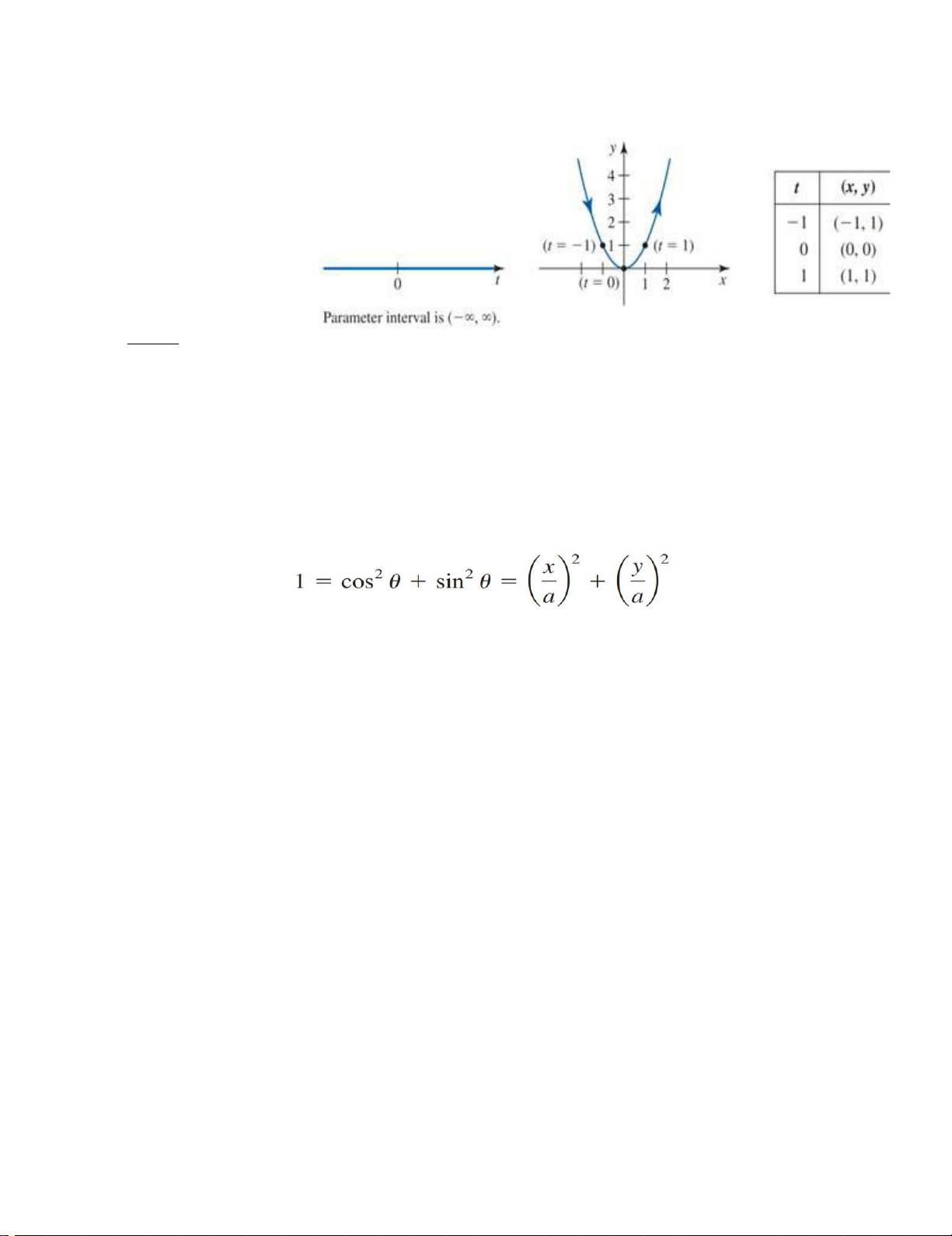
b) m Thay hàm thứ nhất vào hàm số thứ hai, ta được
2. Như chúng ta thấy, ng v ới câu a, nhưng
đường cong được biể u diễ n bởi
ặc dù phương trình này giố = theo đườ ừ ả (−∞, ∞) 2 −∞ ∞
phương trình parabol có phần khác so với câu a. trong trường hợp này, khoảng ẽ điểm = tham số là tới
, đường cong sẽ chạy dọc ả
. hơn nữa, bởi vì t tăng từ ằ = −1,0 à1 ng parabol
t trái sang ph i, bạn có thể kiểm chứng điều đó bằng cách v các
tương ứng, tại
. Bạn cũng có thể nhận ra điều đó
b ng cách kh o sát phuông trình tham số
, phương trình này cho chúng ta bi c khi thì xem hình 5). = ết đượ tăng cũng tăng theo ( Page | 7 lOMoARcPSD|47207367 HÌNH 5 −∞ ∞ Vì t tăng từ lên
toàn bộ đường parabol
được vẽ ra, theo chiều
từ trái sang phải.
Đối với các vấn đề liên quan đến sự chuyển động, việc dùng tham số t là điều hiển
nhiên. Nhưng đối với các trường hợp khác yêu cầu biểu dienx sự khác nhau của các
tham số, như 2 ví dụ sắp được giới thiệu tới đây, chúng ta dùng góc như một tham số.  V
í dụ 3 : Biểu diễn đườ=ng cong àcho b=ởi phương( trình> 0)tham số :
Với các khoảng tham số sau: a) [0,0, 2 ] [ ] b) 0, 4 c) [ ] ** = = và Ta có : Mà 2+ 2= 2
cho chúng ta thấy rằng mỗi đường cong đang xét thuộc một hình
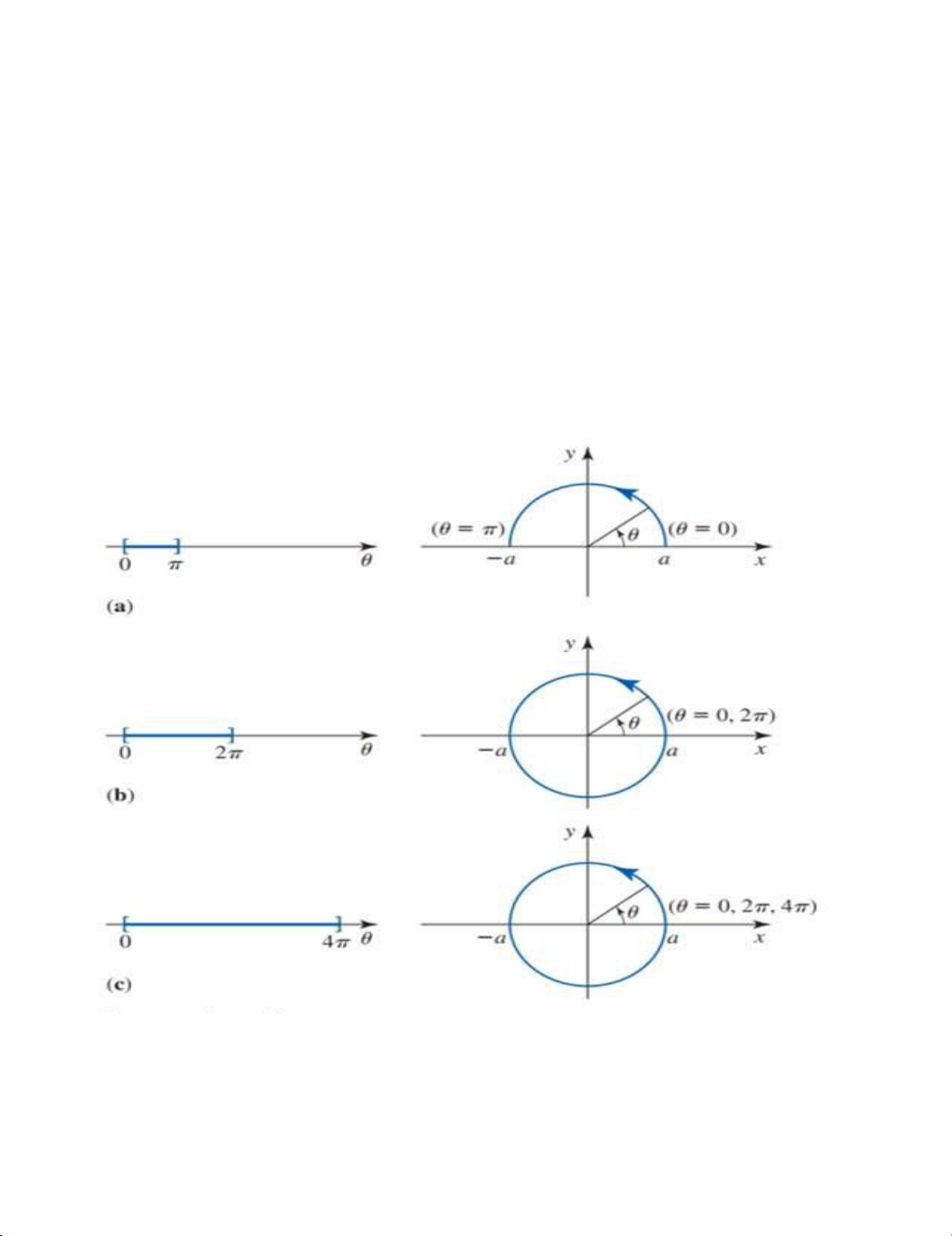
tròn , có tâm tại gốc tọa độ. Suy ra : Điều này với bán kính Page | 8 lOMoARcPSD|47207367 a) Nếu , thì và
, điểm ( , là điểm đầu của đường cong. Do tăng = 0 = = 0 0) Lúc này, đườ (− , 0) từ 0 đến
nên đường cong được vạch ra theo chiều ngược chiều kim
đồng hồ và kết thúc tại điểm . (hình 6a) (hình 6b) ( , 0) b)
ng cong là một vòng tròn hoàn chỉnh được vẽ ra theo chiều
ngược chiều kim đồng hồ, bắt đầu tại điểm
và kết thúc tại chính điểm đó. ( , 0) ( , 0) c)
Đường cong ở đây là một đường tròn được vạch ra 2 lần, theo chiều ngược
chiều kim đồng hồ, bắt đầu tại điểm
và cũng kết thúc tại . (hình 6c) Hình 6 HÌNH 6
Đường cong a tạo ra một hình bán nguyệt, đường cong b vẽ ra một hình tròn
hoàn chỉnh, và đường cong c tạo ra một hình tròn hoàn chỉnh được vẽ 2 lần. tất
cả các đường cong đều được vẽ theo chiều ngược chiều kim đồng hồ. Page | 9 lOMoARcPSD|47207367
 Ví dd d d dô{xtd=dddndddos dond(dddddd ddo d ddddd ≤ ≤ d = d sdn (dd
Giải phương trình (1) theo cos(θ) và phương trình (2) theo sin(θ), cho ta: ** cos = 4 { 3
trình và cộng lại vế theo vế, ta được: sin =
Bình phương mỗi phương x 2 y 2 2 2 COS ) + SIN + Mà SIN (θ) + cos (θ) = 1 θ θ 2 2 4 3
Ta được phương trình: 2 2 x + y = 1 16 9
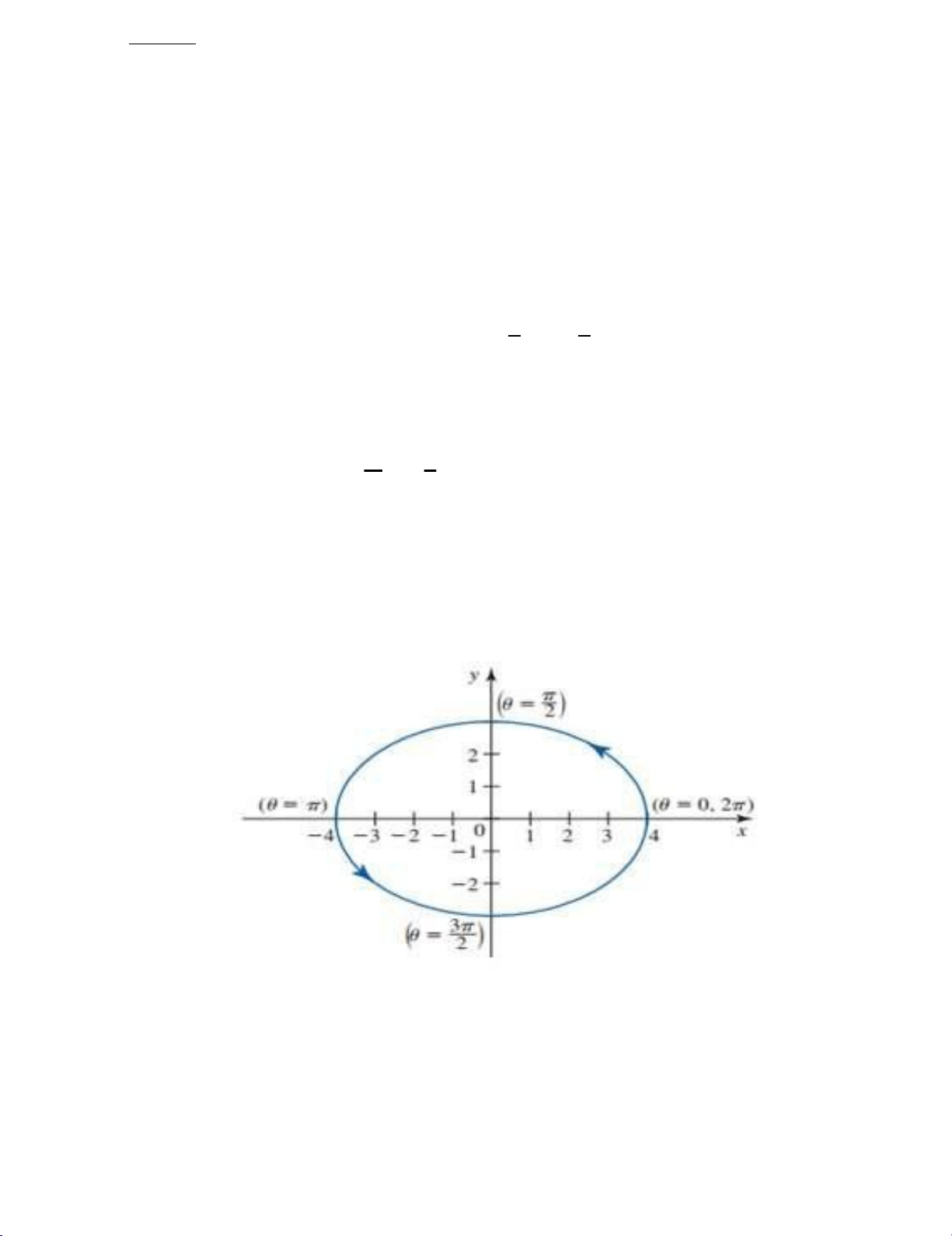
Từ đây, chúng ta thấy rằng tập hợp các điểm trên đường cong trên lập thành một
hình elip. Nếu θ = 0 thì tọa độ (4,0) làm điểm ban đầu của đường cong. Khi θ tăng từ
0 đến 2 , đường cong elip được vạch ra theo hướng ngược chiều kim đồng hồ, kết thúc
tại (4,0). (Hình 7.) Page | 10 lOMoARcPSD|47207367  V
í dụ 5 : Một khoá đào tạo được đề xuất cho 1 du thuyền được thể hiện qua xtham số
=sin : ớ 0 ≤ ≤ 2 = sin 2 ữngphươngtrình
Trong đó x và y được tính bằng dặm.
a) Chứng minh rằng phương trình của khóa học có dạng: 4x4 4x2 y2 0
b) Vẽ đồ thị mô tả khóa học. ** A)
Áp dụng công thức lượng giác: SIN2T = 2 SINT COST x = sin
Phương trình viết lại dưới dạ g: (∗) { = 2 sin cos = 2 cos (∗ ) ⇒ cos = 2 + cos = 1 2 y sin2 2
Áp dụng công thức lượng giác: 2 , ta được: x 1 2 x x2 y2 1 4x2
Với x 0 , quy đồng rút gọn 2 vế ta được: 4x4 4x2 y2 0 (đpcm)
b) Từ kết quả của phần (a), chúng ta thấy rằng đường cong chúng ta cần mô tả có
tính đối xứng qua trục x, trục y và gốc tọa độ. Do đó, chúng ta chỉ cần vẽ một
phần của đường cong nằm trong góc phần tư thứ nhất và sau đó sử dụng tính đối t ,
xứng để hoàn thành đường cong. Vì SINT và SIN2T đều không âm với 0 2
trước tiên chúng ta phác họa đường cong với các giá trị của t 0, , ta có bảng 2 sau : Page | 11 lOMoARcPSD|47207367
Ta thu được đường cong như hình 8. Hướng của du thuyền là hướng của các mũi tên  V
í dụ 6 : Gọi P là một điểm cố định trên vành bánh xe. Nếu bánh xe được lăn
dọc theo một đường thẳng mà không bị trượt, thì điểm P vạch ra một đường
cong gọi là cycloid (Hình 9.). Giả sử bánh xe có bán kính R=a và lăn dọc theo
trục x. Tìm phương trình tham số cho cycloid. Page | 12 lOMoARcPSD|47207367
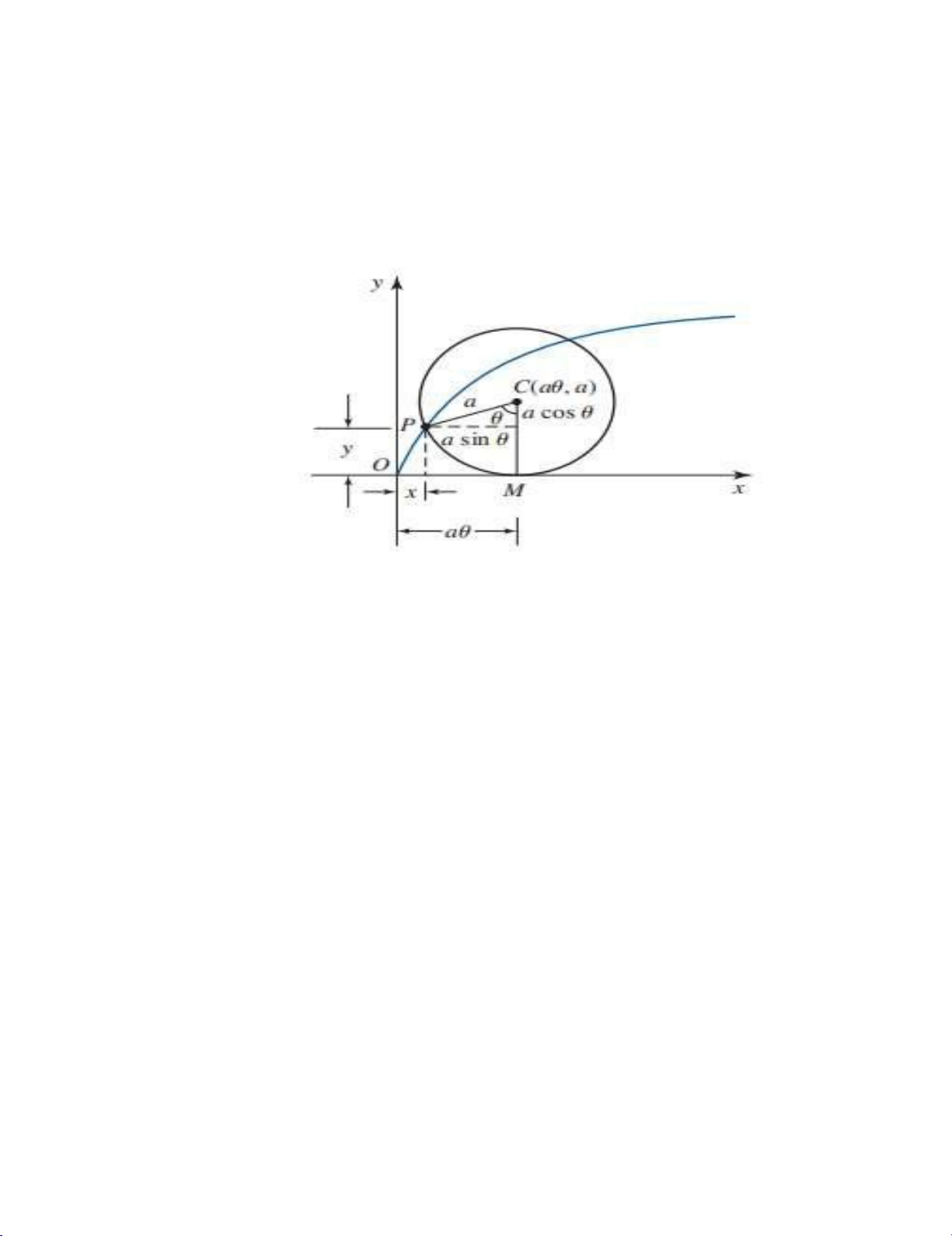
Giả sử bánh xe lăn theo chiều dương với điểm P ban đầu tại điểm gốc tọa độ.
Hình 10. cho thấy vị trí của bánh xe sau khi nó quay qua θ radian. Do không có
trượt, khoảng cách bánh xe lăn từ gốc tọa độ là:
d(O, M) = độ dài cung PM = a.θ
Cho tâm C(aθ, a),{ ngoài ra tọa độ củ P(x, y), thỏa mãn:
xy == d(O,R−M)acosθ−asinθ=a(1= −a(θcosθ−)sinθ)
Ta có thể ngầm hiểu điều kiện của θ là 0 θ
, nhưng thực tế có thể chứng 2
minh rằng chúng có giá trị đối với các giá trị khác của θ. Do đó, phương trình tham số
của cycloid là: { = ( − sin ) ớ − ∞ < < ∞ = (1 − cos )
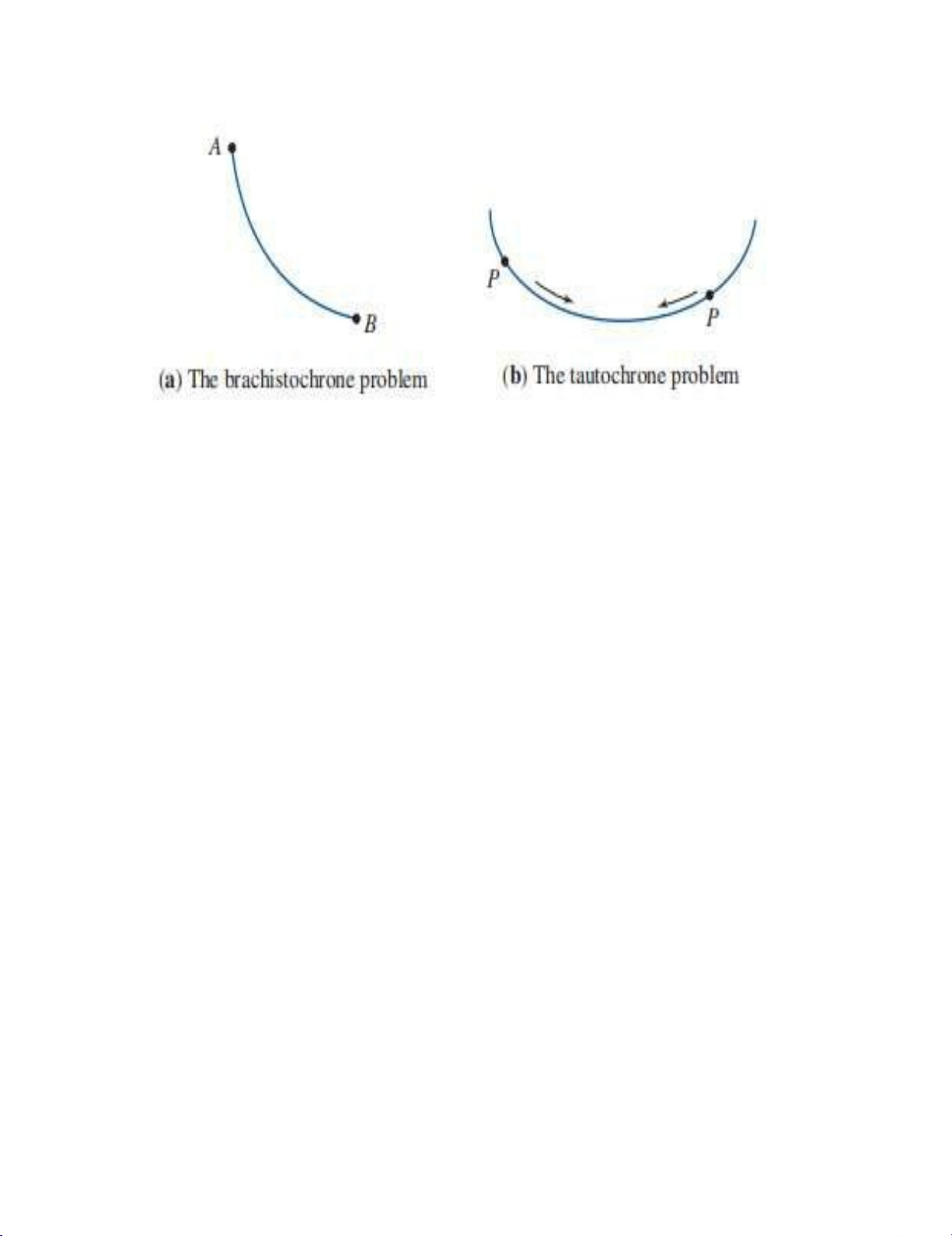
 Cycloid ứng dụng cho hai bài toán nổi tiếng trong toán học: 1)
Bài toán Brachistochrone: Tìm đường cong mà một chất điểm chuyển động
( dưới tác dụng của trong lực) sẽ trượt từ điểm A sang điểm B khác ( không
trùng A), trong thời gian ngắn nhất (Hình 11a.)
2) Bài toán Tautochrone: Tìm đường cong có thuộc tính là phải mất cùng thời
gian để một chất điểm trượt xuống đáy đường cong bất kể hạt đó được đặt ở
đâu trên đường cong (Hình 11b.) Page | 13 lOMoARcPSD|47207367
Bài toán Brachistochrone - bài toán tìm đường cong h ạ xuống nhanh nhất đã
được tiến hành vào năm 1696 bởi nhà toán học người Thụy Sĩ Johann Bernoulli. Mặt
khác, người ta có thể xem rằng một đường cong như vậy là một đường thẳng, nếu ta
xét hai điểm có khoảng cách rất ngắn. Nhưng vận tốc trên đường thẳng sẽ tăng lên
tương đối chậm, trong khi đó nếu chúng ta đi một đường cong gần A hơn, mặc dù
đường đi trở nên dài hơn, chất điểm đi với tốc độ lớn hơn. Bài toán này đã được giải
quyết bởi Johann Bernoulli, anh trai của ông Jacob Bernoulli, Leibniz, Newton và
L’Hoopital. Họ phát hiện ra rằng đường cong đi xuống nhanh nhất là một vòng cung
ngược của một cycloid (hình 11a). Hóa ra, chính đường cong này cũng là lời giải đáp
cho bài toán Tautochrone. lOMoARcPSD|47207367
Câu 2 : Bài tập phương trình tham số : 40)
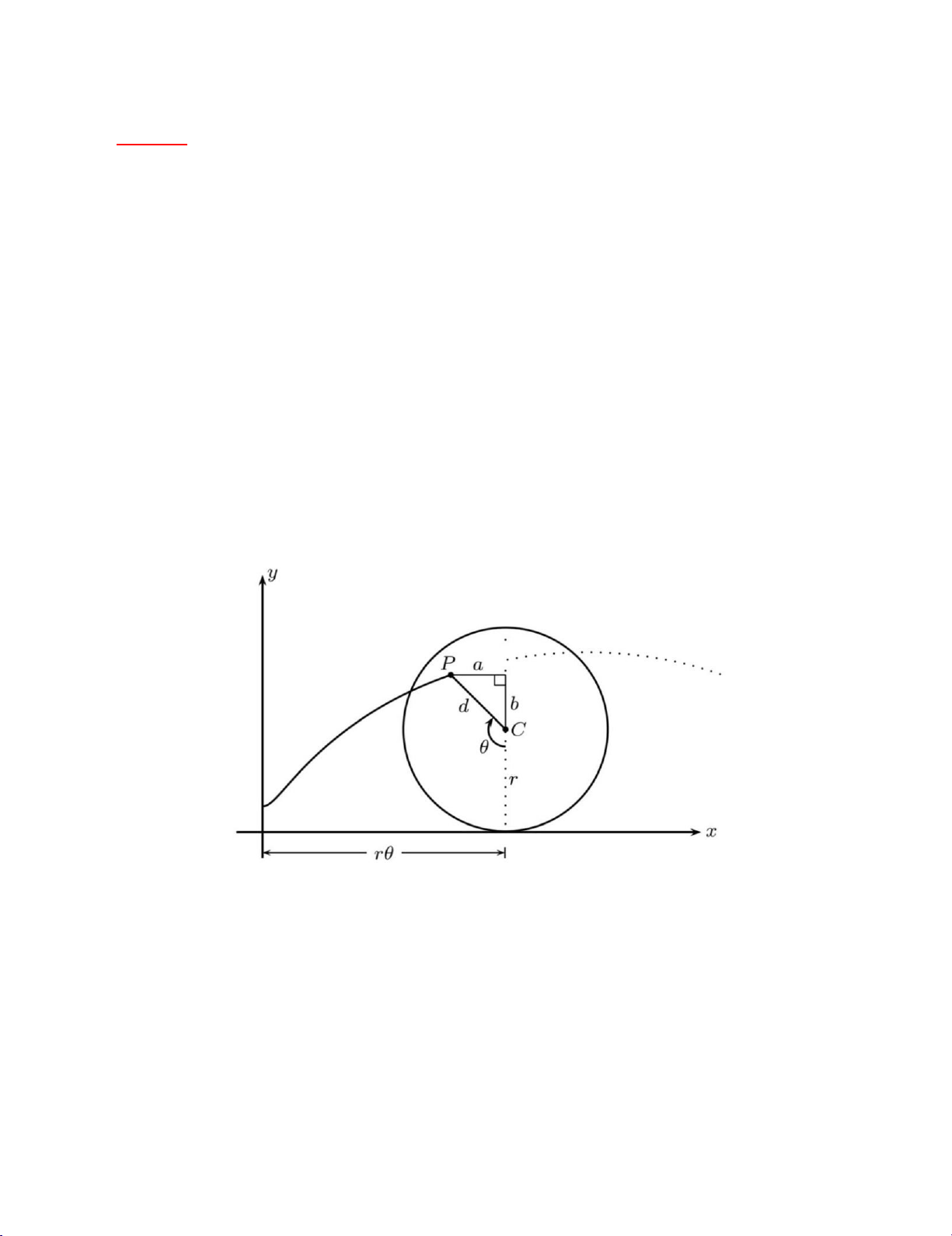
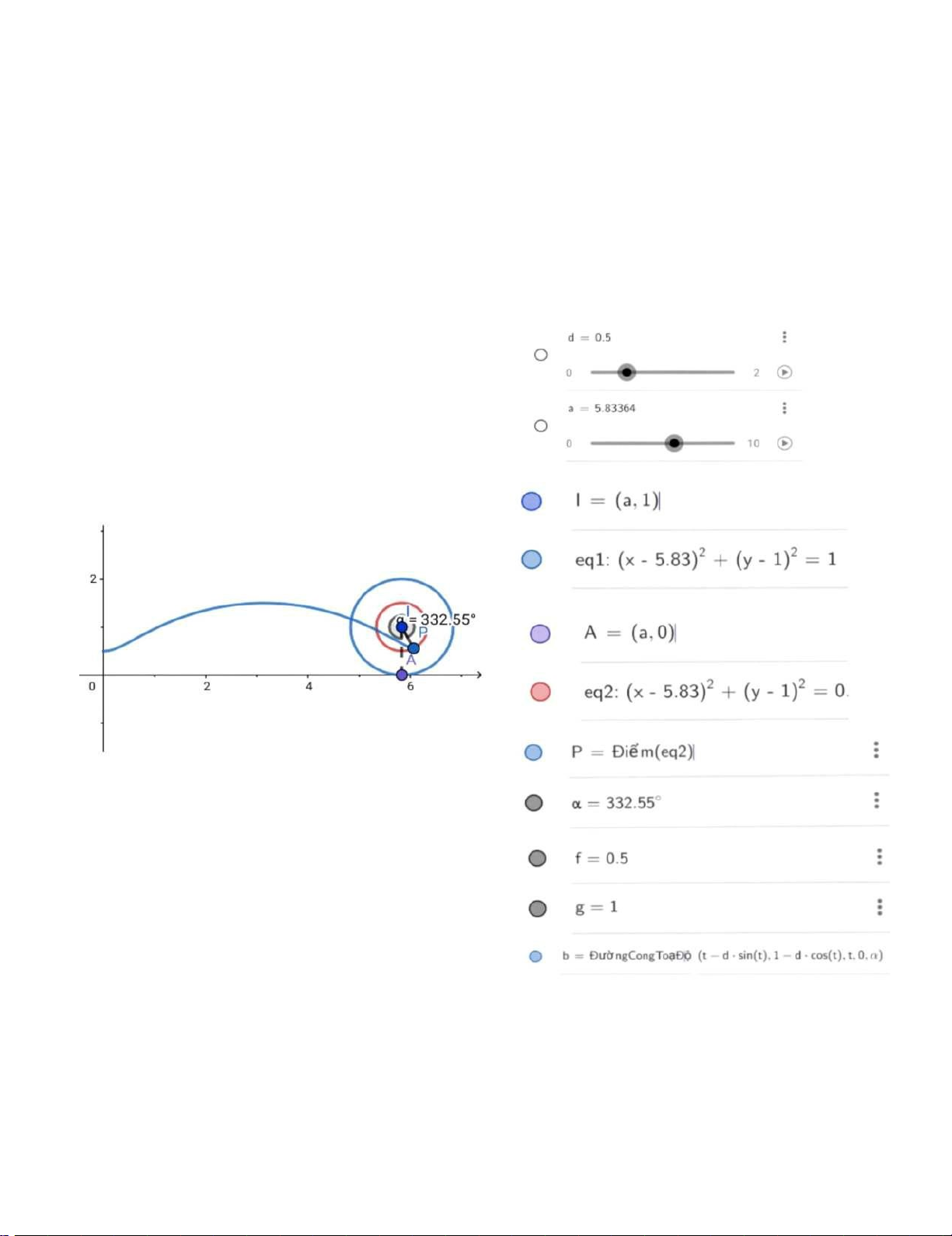
Gọi P là một điểm nằm cách đường tròn (I,r) một đoạn d. Trochoid là
đường cong mà P vạch ra khi đường tròn lăn không trượt dọc theo một đường thẳng ( đường cong cycloid là
trường hợp đặc biệt của đường cong trochoid =v ớ0i d=r ). Giả sử rằng đường tròn lăn dọc theo chiều dương của trục Ox với
khi điểm P nằm tại một trong những điểm thấp nhất trên đường cong trochoid. { = − s in
Hãy chứng minh rằng đường cong trochoid có phương trình tham số như sau: = − cos Trong đó, ọa
là tham số tương tự như trong đường cong cycloid. Hãy phác h
đường cong trochoid trong các trường hợp: dr . **
a) Chứng minh phường trình tham số của đường cong trochoid: = − (1)
Dựa vào đồ thị trên, ta có: (2) { = + = sin = sin( − ) { = cos( − ) { = − cos ⇔ Page | 15 lOMoARcPSD|47207367
Từ (1) và (2) suy ra : − sin (đpcm) { = − cos
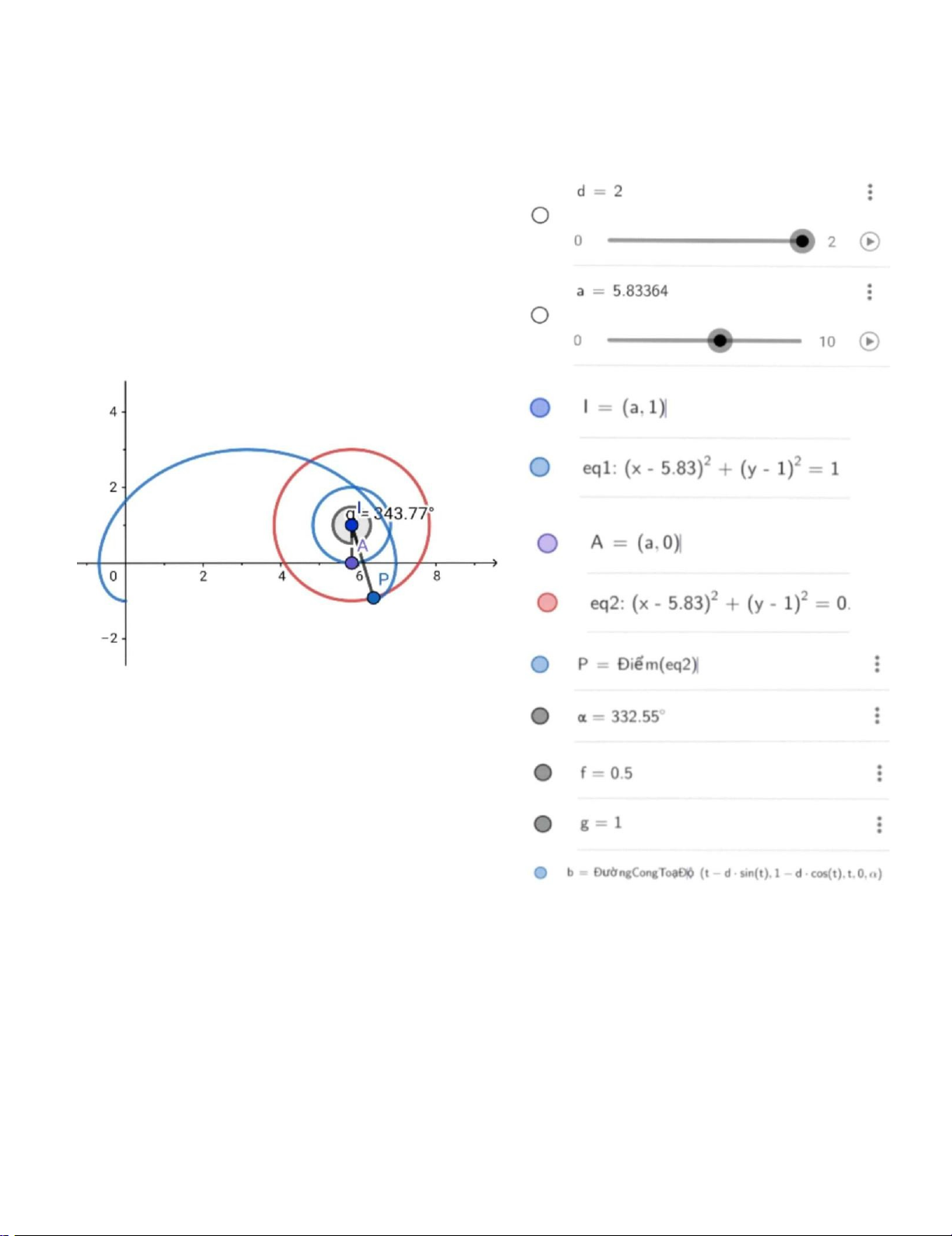
b) Đường cong trochoid với: dPage | 16 lOMoARcPSD|47207367 d>r :
* Sử dụng phần mềm vẽ đồ thị GeoGebra Graphing Calculator* Page | 17 lOMoARcPSD|47207367 41)
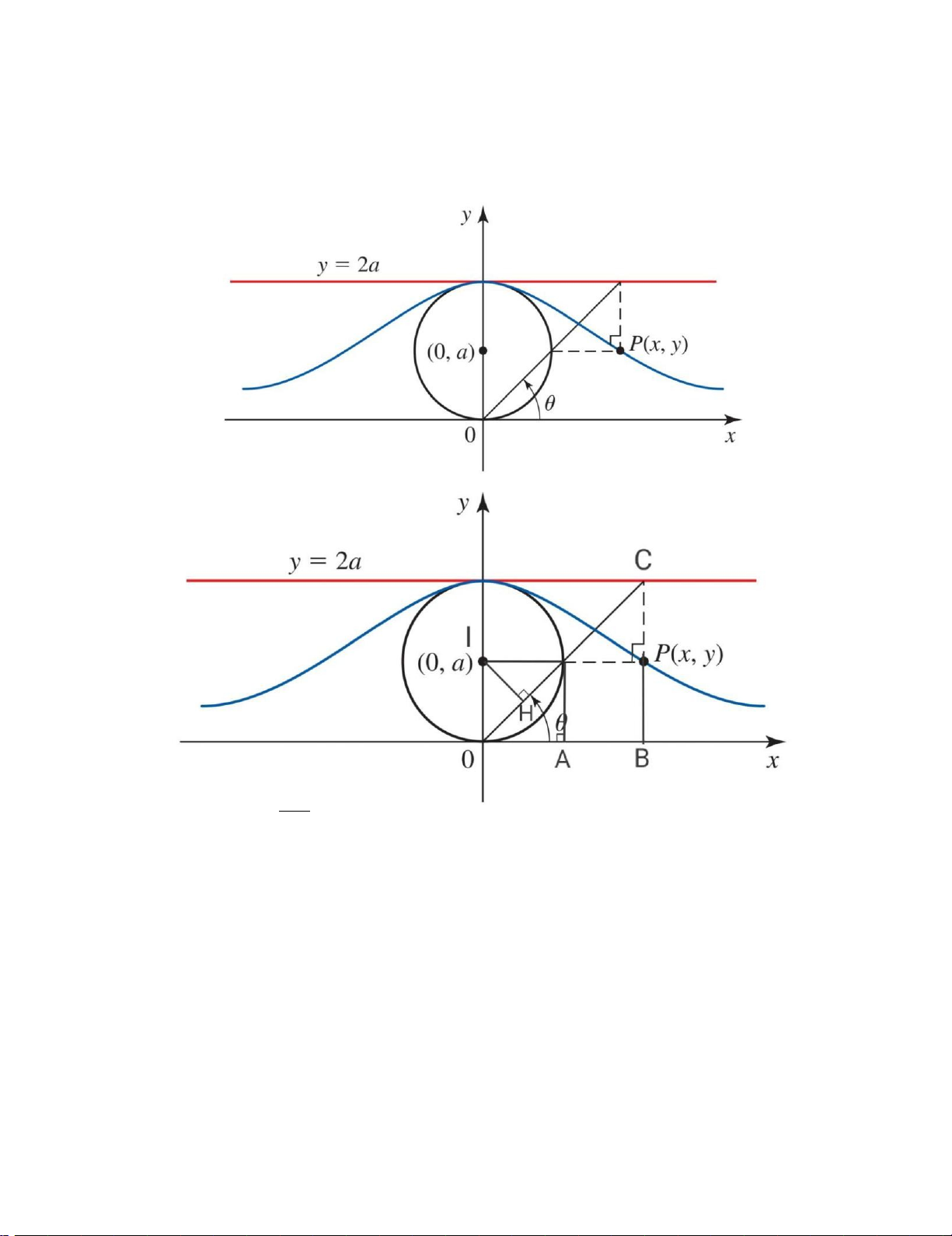
“ Witch of Agnesi ” là đường cong được biểu diễn trong hình minh họa dưới đây:
Chứng minh rằng đường cong= 2 có phươngcot trình tham số là: { = 2 sin2 ** = = tan = cot = 2 cot (1) Ta có : = = = 2 sin Page | 18 lOMoARcPSD|47207367 − ) = sin = cos (2 Mà⇒ = 2 sin (2) 2
Từ (1) và (2) suy ra : { = 2 cot = 2 sin2 (đpcm) 42)
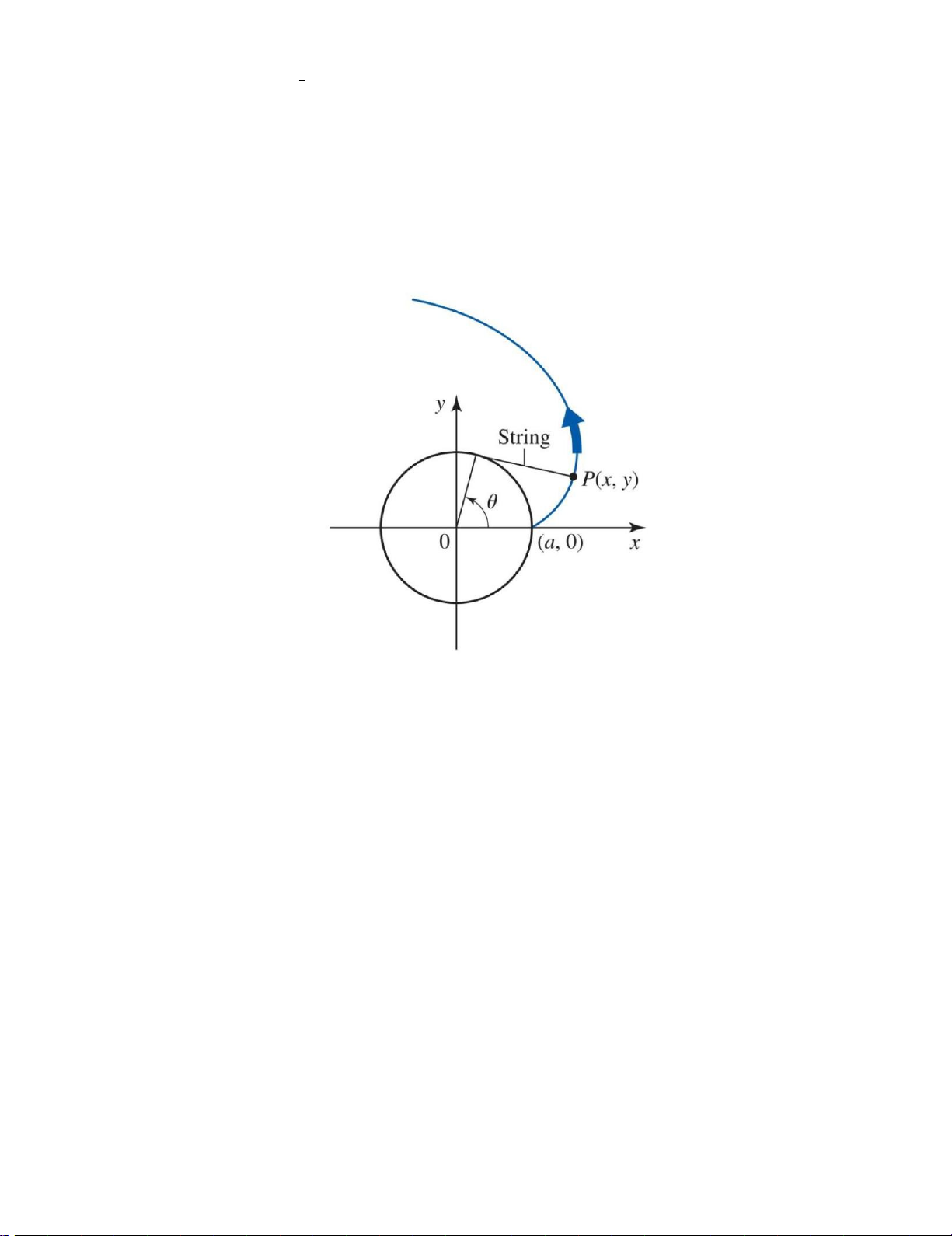
Nếu một sợi dây được gỡ ra từ một vòng tròn (I,a) theo cách mà nó được
giữ trong mặt phẳng của vòng tròn thì điểm P sẽ chạy dọc theo đường cong được
gọi là “ Involute of the circle ” ( Đường thân khai ). Cho hình minh họa dưới đây:
Hãy chứng minh rằng đường= cong (costrên+có sinphương ) trình tham số là: { = (sin − cos ) ** Page | 19