Báo cáo Xây dựng mô hình dự đoán thời tiết của Sapa Việt Nam năm 2025 môn Công nghệ thông tin | Trường Đại học Thủy Lợi

lOMoAR cPSD| 45734214
TRƯỜNG ĐẠI HỌC THỦY LỢI
KHOA CÔNG NGHỆ THÔNG TIN
BÁO CÁO BÀI TẬP LỚN HỌC PHẦN HỌC MÁY
XÂY DỰNG MÔ HÌNH DỰ ĐOÁN THỜI TIẾT CỦA SAPA
VIỆT NAM NĂM 2025 SỬ DỤNG THUẬT TOÁN NAIVE BAYES VÀ KNN.
GIÁO VIÊN HƯỚNG DẪN: PGS.TS NGUYỄN QUANG HOAN NHÓM THỰC HIỆN: NHÓM 1 - 64HTTT1 THÀNH VIÊN: TRẦN QUANG VINH NGUYỄN THANH THỦY PHẠM TIẾN ĐẠT ĐINH QUỐC NGUYÊN Hà nội, năm 2024 lOMoAR cPSD| 45734214 Mục Lục lOMoAR cPSD| 45734214 Lời nói đầu
Sapa, một thị trấn nằm ở vùng núi Tây Bắc Việt Nam, nổi tiếng với vẻ đẹp thiên
nhiên hùng vĩ, khí hậu mát mẻ quanh năm và các nền văn hóa đa dạng của các dân
tộc thiểu số. Tuy nhiên, với đặc điểm địa hình núi cao và khí hậu thay đổi theo
mùa, Sapa cũng phải đối mặt với các hiện tượng thời tiết cực đoan và thiên tai như
mưa lớn, lũ quét, sạt lở đất, và tuyết rơi, gây ảnh hưởng không nhỏ đến đời sống và
sự phát triển kinh tế – xã hội của khu vực.
Trong bối cảnh biến đổi khí hậu toàn cầu đang ngày càng diễn ra phức tạp, việc dự
đoán thời tiết và mức độ thiên tai tại Sapa trở nên quan trọng hơn bao giờ hết. Việc
có thể dự đoán chính xác thời tiết sẽ giúp người dân chủ động ứng phó và giảm
thiểu thiệt hại từ các hiện tượng thiên tai, đồng thời tạo điều kiện thuận lợi cho
ngành du lịch phát triển bền vững.
Bài tập lớn này được thực hiện với mục tiêu xây dựng mô hình dự đoán thời tiết tại
Sapa, Việt Nam, trong năm 2025, sử dụng hai thuật toán học máy phổ biến là
Naive Bayes và K-Nearest Neighbors (KNN). Các thuật toán này sẽ giúp phân tích
dữ liệu thời tiết lịch sử để dự báo những biến động thời tiết trong tương lai, từ đó
cung cấp thông tin hỗ trợ cho việc phòng chống thiên tai, bảo vệ môi trường và đời sống cộng đồng.
Thông qua việc nghiên cứu và phát triển mô hình này, nhóm chúng tôi hy vọng sẽ
đóng góp một phần nhỏ vào việc ứng dụng công nghệ trong công tác phòng chống
và giảm nhẹ thiên tai tại Sapa, đồng thời nâng cao nhận thức và hiểu biết về các
phương pháp học máy, đặc biệt là Naive Bayes và KNN trong lĩnh vực dự báo thời tiết. lOMoAR cPSD| 45734214 Phần 1: Tổng quan
1. Giới thiệu về học máy a. Định nghĩa:
- Học máy (Machine Learning) là một chương trình máy tính được gọi là
học từ kinh nghiệm (thể hiện bằng dữ liệu) E đối với một lớp các nhiệm
vụ T (Task) và thực hiện phép đo (Performance Measure) P, nếu việc
thực hiện các nhiệm vụ tại nhiệm vụ T của nó (của chương trình máy
tính) cũng như được đánh giá bằng phép đo P được cải thiện với kinh nghiệm E.
- Học có giám sát là một phương pháp trong machine learning mà mô
hình học từ dữ liệu huấn luyện (training data) đã được gắn nhãn.
Đây là một trong những loại học máy phổ biến nhất, nơi mỗi điểm dữ
liệu đầu vào có một đầu ra mong muốn tương ứng. Mục tiêu là huấn
luyện mô hình để nó có thể dự đoán chính xác đầu ra cho dữ liệu chưa thấy.
b. Tổng quan về bài toán:
- Giới thiệu đề tài:
Sapa, nằm ở vùng núi phía Bắc Việt Nam, có đặc điểm khí hậu nhiệt
đới gió mùa với mùa hè mưa nhiều và mùa đông lạnh giá. Đặc biệt, với độ
cao và địa hình đồi núi, thời tiết tại Sapa thay đổi nhanh chóng, thường
xuyên có sương mù dày đặc vào mùa đông. Việc dự đoán thời tiết tại Sapa
trở nên vô cùng quan trọng, nhất là trong bối cảnh các hiện tượng khí hậu
cực đoan ngày càng gia tăng. Đề tài này nhằm xây dựng mô hình dự đoán
thời tiết cho Sapa vào năm 2025, sử dụng hai thuật toán học máy nổi bật:
Naive Bayes và K-Nearest Neighbors (KNN), với mục tiêu cung cấp thông
tin dự báo chính xác, hỗ trợ cộng đồng địa phương trong công tác ứng phó
với biến động thời tiết.
- Mục tiêu nghiên cứu:
● Mục tiêu chính: Xây dựng mô hình dự đoán thời tiết cho Sapa, Việt
Nam vào năm 2025, sử dụng thuật toán Bayes và KNN để đưa ra dự
báo chính xác về các yếu tố như nhiệt độ, độ ẩm, mưa, gió trong từng giai đoạn của năm.
● Ứng dụng thuật toán học máy: Sử dụng các mô hình học máy như lOMoAR cPSD| 45734214
Bayes và KNN để phân tích và dự đoán thời tiết cho Sapa dựa trên dữ
liệu lịch sử về khí hậu và thời tiết, giúp đưa ra các dự báo về nhiệt độ,
độ ẩm, mưa và gió trong các mùa và giai đoạn khác nhau trong năm 2025.
● Đánh giá mô hình: So sánh độ chính xác và hiệu quả của từng mô
hình trong việc dự báo thời tiết cho Sapa, từ đó chọn lựa phương pháp
tối ưu dựa trên các chỉ số đánh giá như độ chính xác và độ tin cậy của các kết quả.
- Phương pháp nghiên cứu:
● Thu thập dữ liệu: Sử dụng các dữ liệu khí tượng lịch sử từ các trạm
quan trắc tại Sapa, bao gồm các yếu tố như nhiệt độ, độ ẩm, lượng
mưa, tốc độ gió và các yếu tố khí tượng khác.
● Tiền xử lý dữ liệu: Xử lý dữ liệu thô để chuẩn hóa và chuẩn bị cho
việc huấn luyện mô hình. Các bước tiền xử lý bao gồm làm sạch dữ
liệu, loại bỏ các giá trị thiếu và chuẩn hóa các giá trị đầu vào.
● Áp dụng thuật toán Bayes: Thuật toán Bayes sẽ giúp xây dựng mô
hình xác suất dựa trên dữ liệu lịch sử của Sapa để dự đoán các điều
kiện thời tiết trong tương lai.
● Áp dụng thuật toán KNN: KNN là một thuật toán học máy dựa trên
khoảng cách, dùng để tìm ra các điểm dữ liệu gần nhất và đưa ra dự
đoán cho các điểm mới dựa trên sự tương đồng với các điểm đã biết. -
Các hiện tượng khí hậu và thời tiết quan trọng:
● Nhiệt độ: Nhiệt độ là yếu tố quan trọng trong việc dự đoán các hiện
tượng thời tiết. Việc dự đoán chính xác nhiệt độ tại Sapa sẽ giúp xác
định các đợt lạnh hoặc nóng bất thường, ảnh hưởng đến du lịch và nông nghiệp.
● Lượng mưa: Lượng mưa là yếu tố quan trọng trong việc dự đoán các
trận mưa lớn hoặc lũ lụt ở khu vực Sapa, nơi có địa hình dốc và dễ bị sạt lở đất.
● Tốc độ gió:Gió mạnh có thể tạo ra các cơn bão hoặc làm tăng mức độ
thiệt hại của các hiện tượng thiên tai khác tại Sapa, đặc biệt trong mùa đông và mùa xuân.
- Kết quả dự báo và ứng dụng: lOMoAR cPSD| 45734214
Mô hình dự đoán thời tiết này không chỉ giúp dự báo các điều kiện
thời tiết tại Sapa cho năm 2025 mà còn hỗ trợ các hoạt động nông nghiệp, du
lịch, và công nghiệp tại địa phương. Hơn nữa, việc dự đoán thời tiết chính
xác sẽ giúp các cơ quan chức năng chuẩn bị ứng phó với các hiện tượng thời
tiết cực đoan, giảm thiểu thiệt hại và bảo vệ cuộc sống của cộng đồng. - Kết luận:
Đề tài này không chỉ nhằm dự đoán thời tiết cho Sapa vào năm 2025
mà còn đóng góp vào việc ứng dụng các thuật toán học máy trong dự báo
khí tượng, cung cấp các dự báo chính xác và kịp thời cho công tác phòng
chống thiên tai tại khu vực miền núi này. Mô hình Bayes và KNN sẽ là công
cụ quan trọng hỗ trợ việc ứng phó với biến đổi khí hậu và quản lý thiên tai.
Phần 2: Cơ sở của các thuật toán KNN, Bayes. 1. Giới thiệu:
Trong phần này, sẽ khám phá hai thuật toán học máy mạnh mẽ và phổ biến,
bao gồm K-Nearest Neighbors (KNN) và Naive Bayes. Cả hai thuật toán này đều
là những công cụ quan trọng trong các bài toán phân loại và dự đoán, đặc biệt hữu
ích khi áp dụng vào các lĩnh vực như dự báo thời tiết. Những thuật toán này không
chỉ giúp cải thiện độ chính xác của các mô hình học máy mà còn mở ra khả năng
ứng dụng rộng rãi trong việc xử lý và phân tích dữ liệu phức tạp, chẳng hạn như dự
đoán các yếu tố khí hậu và thiên tai.
2. K-Nearest Neighbors (KNN):
- Giới thiệu: K-Nearest Neighbors (KNN) là một thuật toán học máy đơn
giản nhưng mạnh mẽ, được sử dụng rộng rãi trong các bài toán phân loại
và hồi quy. Thuật toán này hoạt động dựa trên nguyên lý so sánh điểm dữ
liệu mới với các điểm dữ liệu đã có, xác định số lượng k điểm gần nhất
(neighbors) trong không gian đặc trưng và đưa ra dự đoán dựa trên các
nhãn của những điểm này.
- Lý do chọn: KNN được chọn trong bài toán này vì tính đơn giản và hiệu
quả của nó trong việc phân loại các mẫu dữ liệu không cần quá nhiều giả lOMoAR cPSD| 45734214
thuyết về phân phối dữ liệu. Thuật toán có khả năng hoạt động tốt với các
dữ liệu có quan hệ gần gũi về không gian đặc trưng và rất hữu ích trong
các bài toán dự đoán như dự báo thời tiết, nơi các mẫu dữ liệu có thể có sự tương đồng rõ rệt.
3. Gaussian Naive Bayes:
- Giới thiệu: Naive Bayes là một thuật toán học máy dựa trên lý thuyết xác
suất Bayes, với giả định "naive" rằng các đặc trưng (features) của dữ liệu
là độc lập với nhau, tức là mỗi đặc trưng không bị ảnh hưởng bởi các đặc
trưng khác. Điều này đơn giản hóa tính toán, giúp thuật toán hoạt động
hiệu quả ngay cả với lượng dữ liệu lớn. Thuật toán này đặc biệt hiệu quả
trong các bài toán phân loại, đặc biệt khi dữ liệu có tính chất phân lớp rõ ràng. - Lý do chọn:
+ Gaussian Naive Bayes được chọn trong các bài toán phân loại, đặc biệt
là khi dữ liệu có nhiều đặc trưng độc lập và các đặc trưng này có phân
phối gần với phân phối chuẩn. Trong dự đoán thời tiết, có thể có sự
kết hợp của nhiều yếu tố khí hậu như nhiệt độ, độ ẩm, tốc độ gió,
v.v. Gaussian Naive Bayes có thể xử lý tốt các yếu tố này bằng cách
ước tính xác suất cho từng lớp (ví dụ: các tình trạng thời tiết như
nắng, mưa, bão...) dựa trên các đặc trưng này.
+ Một trong những ưu điểm lớn của Gaussian Naive Bayes là khả năng
xử lý rất nhanh và dễ dàng khi dữ liệu có tính chất phân lớp rõ ràng.
Hơn nữa, nó không yêu cầu phải làm quá nhiều tiền xử lý dữ liệu, và
thuật toán có thể đưa ra kết quả dự báo ngay cả khi các đặc trưng
không hoàn toàn độc lập.
4. Các thuật toán được sử dụng:
4.1 K-Nearest Neighbors (KNN):
- Lý thuyết: K-láng giềng gần nhất (K-Nearest Neighbors
Algorithm: KNN) là thuật toán được sử dụng để phân lớp đối
tượng dựa vào khoảng cách gần nhất giữa các đối tượng cần
xếp lớp và tất cả các đối tượng trong dữ liệu huấn luyện và dự báo lOMoAR cPSD| 45734214
- Công thức tính khoảng cách:
Hình 4.1 Công thức tính khoảng cách Euclid Trong đó:
- d là khoảng cách Euclid.
- i = (xi1, xi2, …, xip) và j = (xj1, xj2, …, xjp) là 2 phần tử dữ liệu
- Các bước thực hiện:
B1. Xác định k láng giềng gần nhất, k=5 (K số lượng mẫu có khoảng
cách gần điểm cần tìm xq (Query Point). k nên chọn số lẻ.
B2. Tính khoảng cách giữa các đối tượng hay điểm hỏi (Query Point)
cần tìm cần phân lớp với tất cả các đối tượng trong dữ liệu huấn luyện
(thường sử dụng khoảng cách Euclid)
B3. Sắp xếp khoảng cách theo thứ tự tăng hoặc giảm dần và xác định
k láng giềng gần nhất với đối tượng cần phân lớp
B4. Lấy tất cả các lớp của k láng giềng gần nhất đã xác định
B5. Dựa vào phần lớn lớp của láng giềng gần nhất để xác định lớp cho
các đối tượng cần phân lớp theo quy tắc suy diễn số lớn
- Chuẩn bị dữ liệu:
+ Tách biến đầu vào và đầu ra từ tập dữ liệu, với các biến đầu vào
(precipitation, temp_max, temp_min, wind) và biến đầu ra (weather).
- Xây dựng hàm K-Nearest Neighbors: lOMoAR cPSD| 45734214
+ Chúng ta sẽ triển khai thuật toán K-Nearest Neighbors để dự
đoán nhãn lớp cho tập kiểm thử và đánh giá kết quả.
- Dự đoán và đánh giá trên tập kiểm thử:
+ Cập nhật mô hình KNN để sử dụng trọng số tối ưu.
+ Dự đoán trên tập kiểm thử với trọng số.
⇒ Trong trường hợp này, chúng ta sẽ sử dụng trọng số tỷ lệ nghịch với
khoảng cách Euclidean (trọng số cao cho các điểm gần). Trọng số này sẽ giúp
mô hình đánh giá các mẫu gần hơn có tầm quan trọng lớn hơn khi dự đoán.
4.2 Gaussian Naive Bayes: lOMoAR cPSD| 45734214
- Lý thuyết: Gaussian Naive Bayes là một biến thể của thuật toán Naive
Bayes, trong đó giả định rằng các đặc trưng liên tục của dữ liệu tuân theo
phân phối chuẩn (Gaussian). Mặc dù Naive Bayes nói chung giả định rằng
các đặc trưng là độc lập với nhau, Gaussian Naive Bayes thêm giả định rằng
các đặc trưng liên tục có phân phối chuẩn (Gaussian) trong mỗi lớp của dữ liệu.
- Công thức của định lý Bayes:
Hình 4.3 Công thức của định lý Bayes. Trong đó:
- P(C|X) là xác suất của lớp C khi biết giá trị đặc trưng X (xác suất posterior).
- P(X|C) là xác suất của đặc trưng X khi lớp là C (xác suất likelihood).
- P(C) là xác suất của lớp C (xác suất prior). - P(X) là xác suất của đặc trưng X.
- Công thức phân phối chuẩn được sử dụng trong Gaussian Naive Bayes - :
- Chuẩn bị dữ liệu: lOMoAR cPSD| 45734214
+ Tách các biến đầu vào (features) và biến đầu ra (labels). Trong
trường hợp này, các biến đầu vào có thể là precipitation,
temp_max, temp_min, wind, và biến đầu ra là weather.
- Dự đoán và đánh giá trên tập kiểm thử:
Để dự đoán và đánh giá mô hình Gaussian Naive Bayes trên tập
kiểm thử, ta sẽ tính toán xác suất P(C X) cho từng lớp C và mẫu∣ dữ
liệu X. Lớp có xác suất cao nhất sẽ là lớp dự đoán cho mẫu đó. Sau đó,
chúng ta sẽ tính các chỉ số đánh giá như độ chính xác (accuracy) để
đo lường hiệu quả của mô hình.
Độ chính xác (Accuracy): Đo lường tỷ lệ số dự đoán đúng trên
tổng số mẫu kiểm thử:
Phần 3:DỮ LIỆU VÀ QUY TRÌNH THỰC HIỆN 3.1 Dữ liệu
3.1.1 Mô tả tập dữ liệu lOMoAR cPSD| 45734214
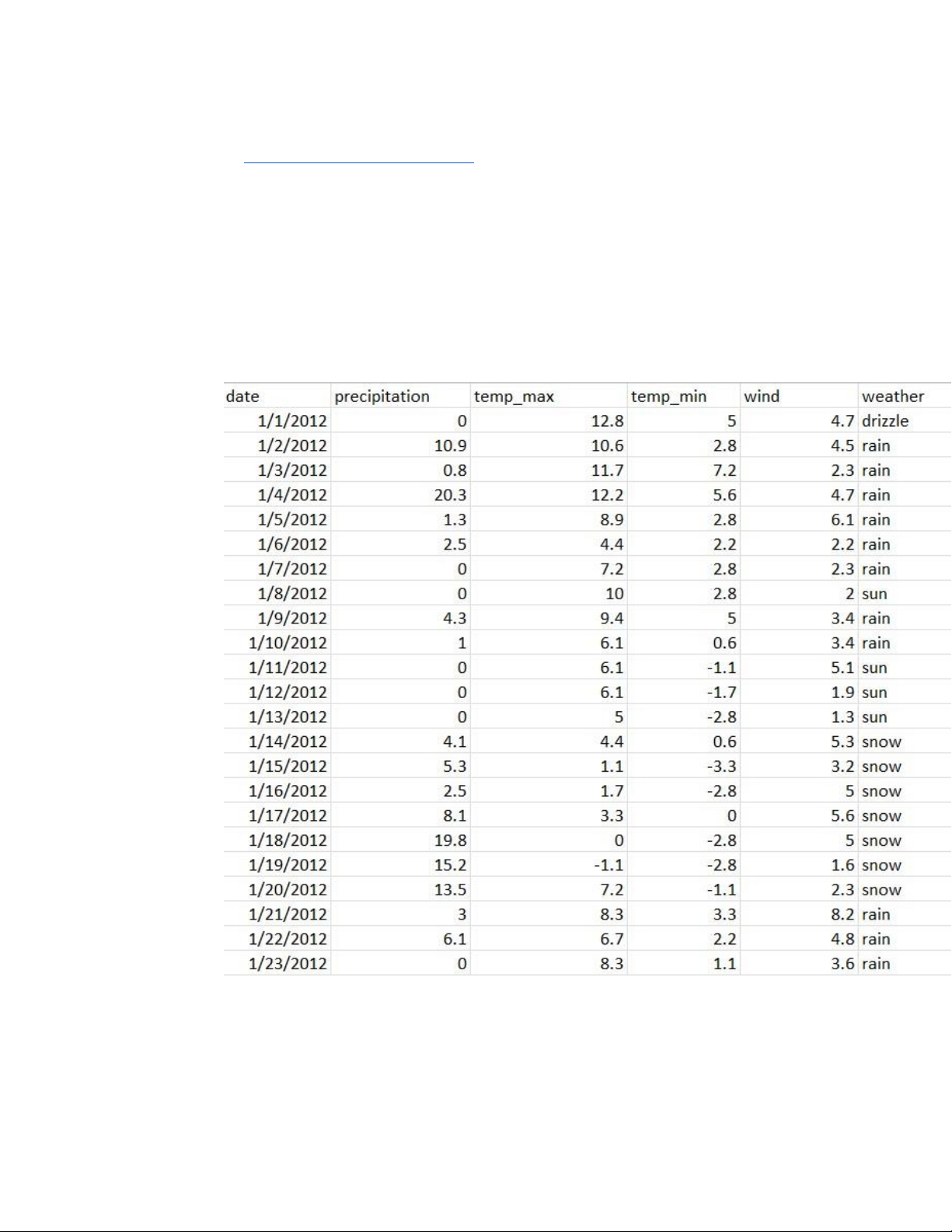
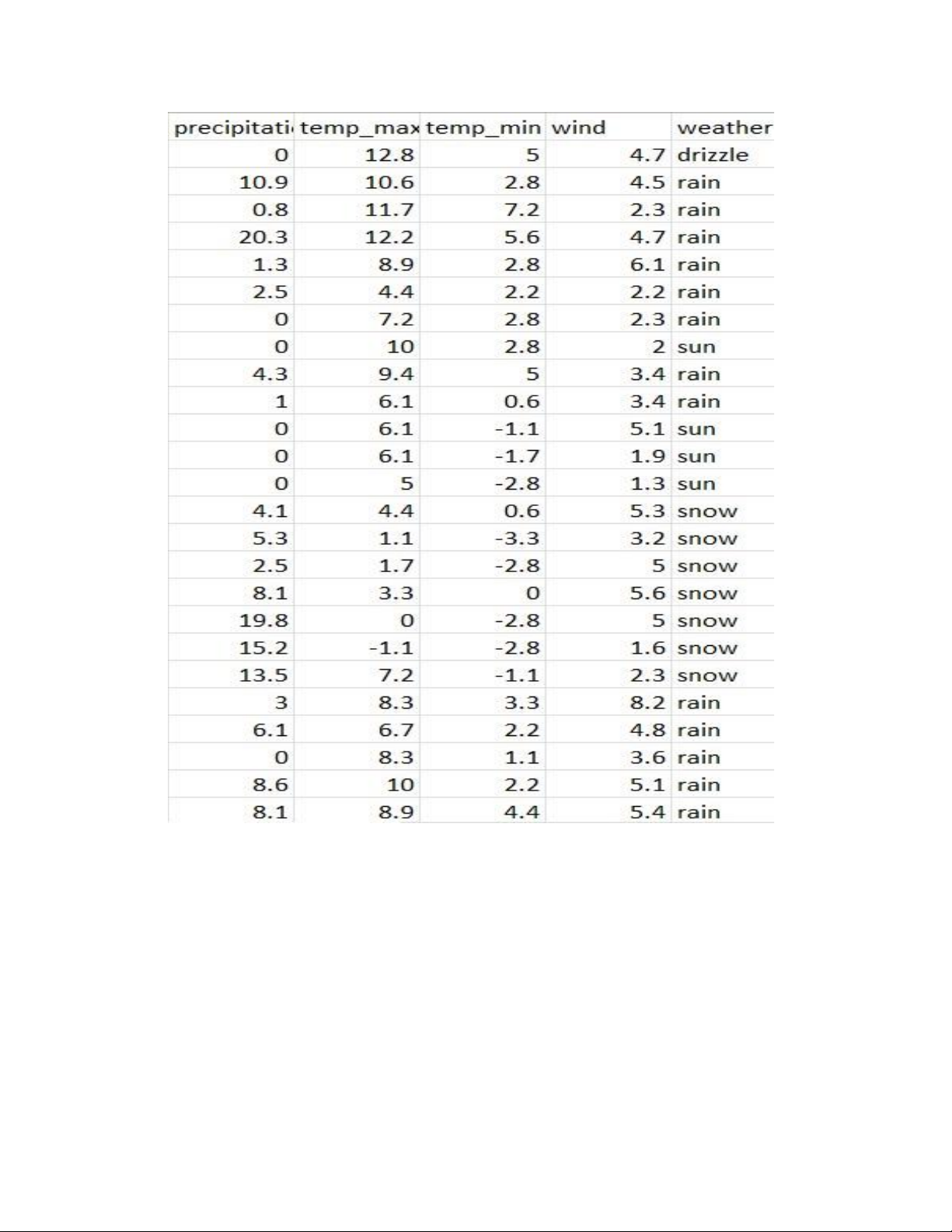
- Nguồn dữ liệu: Tập dữ liệu được sử dụng trong dự án này được thu thập từ
Kaggle (Nhấn vào đây xem dữ liệu) [1], với tổng cộng 1.461 bản ghi. Dữ
liệu ban đầu đã được chuẩn hóa và có thể đưa vào xử lý Dữ liệu bao gồm:
- Date (Ngày tháng): Đây là ngày xảy ra sự kiện thời tiết, trong bài toán dự
đoán, cột này thường không mang ý nghĩa trực tiếp và có thể được loại bỏ
- precipitation (Lượng mưa, mm): Giá trị số đo lượng mưa trong ngày, Đây là
một đặc trưng số liên tục.
- temp_max (Nhiệt độ cao nhất, °C): Giá trị nhiệt độ cao nhất đo được trong
ngày, Đây là một đặc trưng số liên tục.
- temp_min (Nhiệt độ thấp nhất, °C): Giá trị nhiệt độ thấp nhất đo được trong
ngày, Đây là một đặc trưng số liên tục. lOMoAR cPSD| 45734214
- wind (Tốc độ gió, m/s): Tốc độ gió trung bình trong ngày, Đây là một đặc trưng số liên tục
- weather (Loại thời tiết): Đây là nhãn lớp (dữ liệu đầu ra) dùng để dự đoán Nhận xét :
- Mặc dù tập dữ liệu chứa nhiều thông tin nhưng không phải tất cả các thuộc
tính đều liên quan đến bài toán dự đoán thời tiết.
- Các đặc trưng cần thiết cho bài toán này chỉ bao gồm: precipitation , temp_max, temp_min , wind
- Các đặc trưng khác như Date không ảnh hưởng trực tiếp đến khả năng dự
đoán, vì vậy sẽ được loại bỏ trong quá trình tiền xử lý.
3.1.2 Tiền xử lý dữ liệu:
3.1.2.1 Chuẩn hóa dữ liệu:
- Dữ liệu ban đầu bao gồm các cột như: Data, precipitation , temp_max,
temp_min , wind, weather . Tuy nhiên, chỉ các cột precipitation , temp_max,
temp_min , wind, weather là liên quan trực tiếp đến bài toán dự đoán thời
tiết. Do đó, các đặc trưng không liên quan đã bị loại bỏ. lOMoAR cPSD| 45734214 -
3.2 Cài đặt mô hình
3.2.1 Cài đặt chung
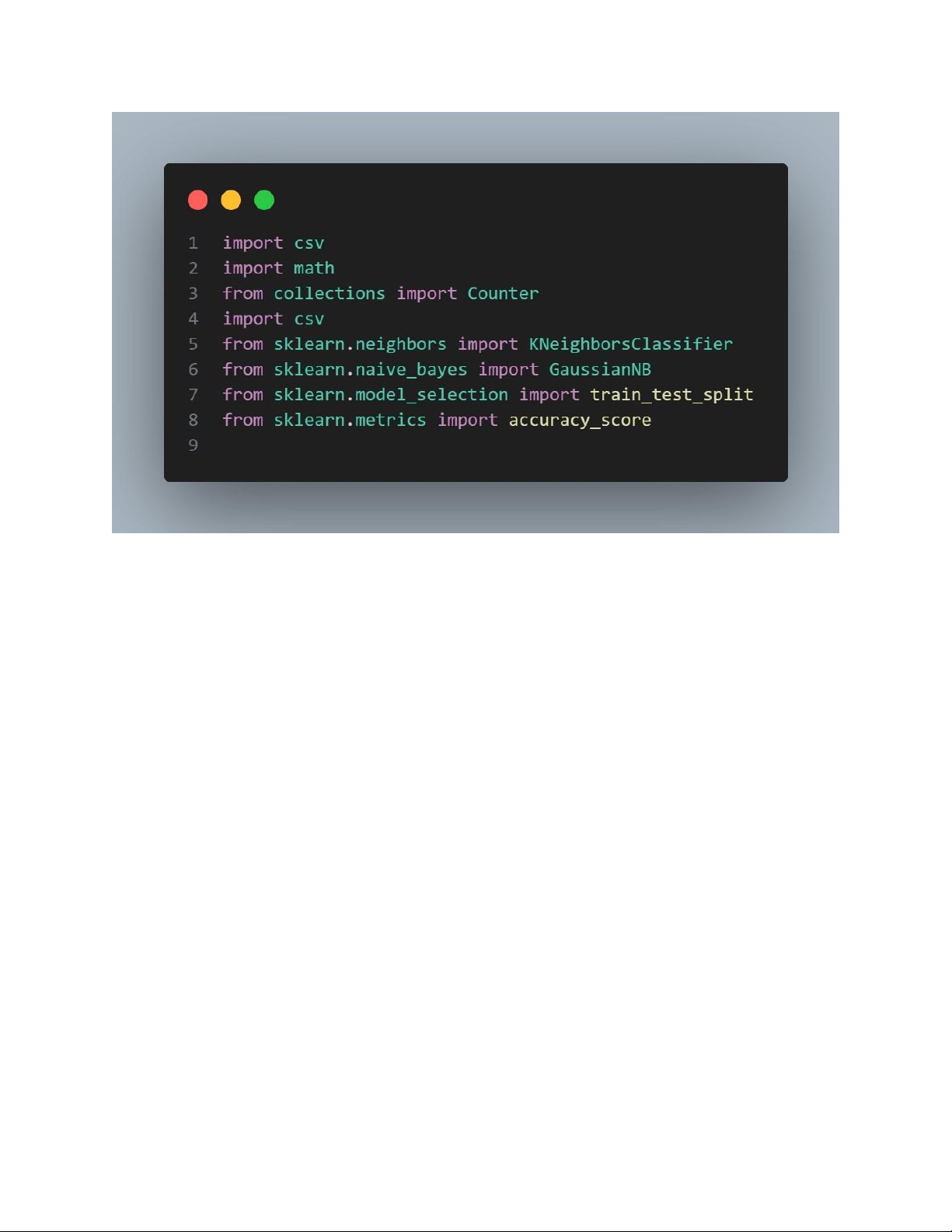
3.2.1.1 Cài đặt thư viện lOMoAR cPSD| 45734214
- csv: Dùng để làm việc với các tệp CSV (Comma-Separated Values), thường
được sử dụng để lưu trữ dữ liệu dạng bảng.
- math: Hỗ trợ các phép toán học, ví dụ: tính căn bậc hai.
- collections.Counter: Cung cấp các công cụ để đếm tần suất xuất hiện của
các phần tử trong một danh sách.
- sklearn (Scikit-learn): Thư viện học máy phổ biến với các công cụ để xây
dựng và đánh giá các mô hình.
3.2.1.2 Đọc và xử lý dữ liệu
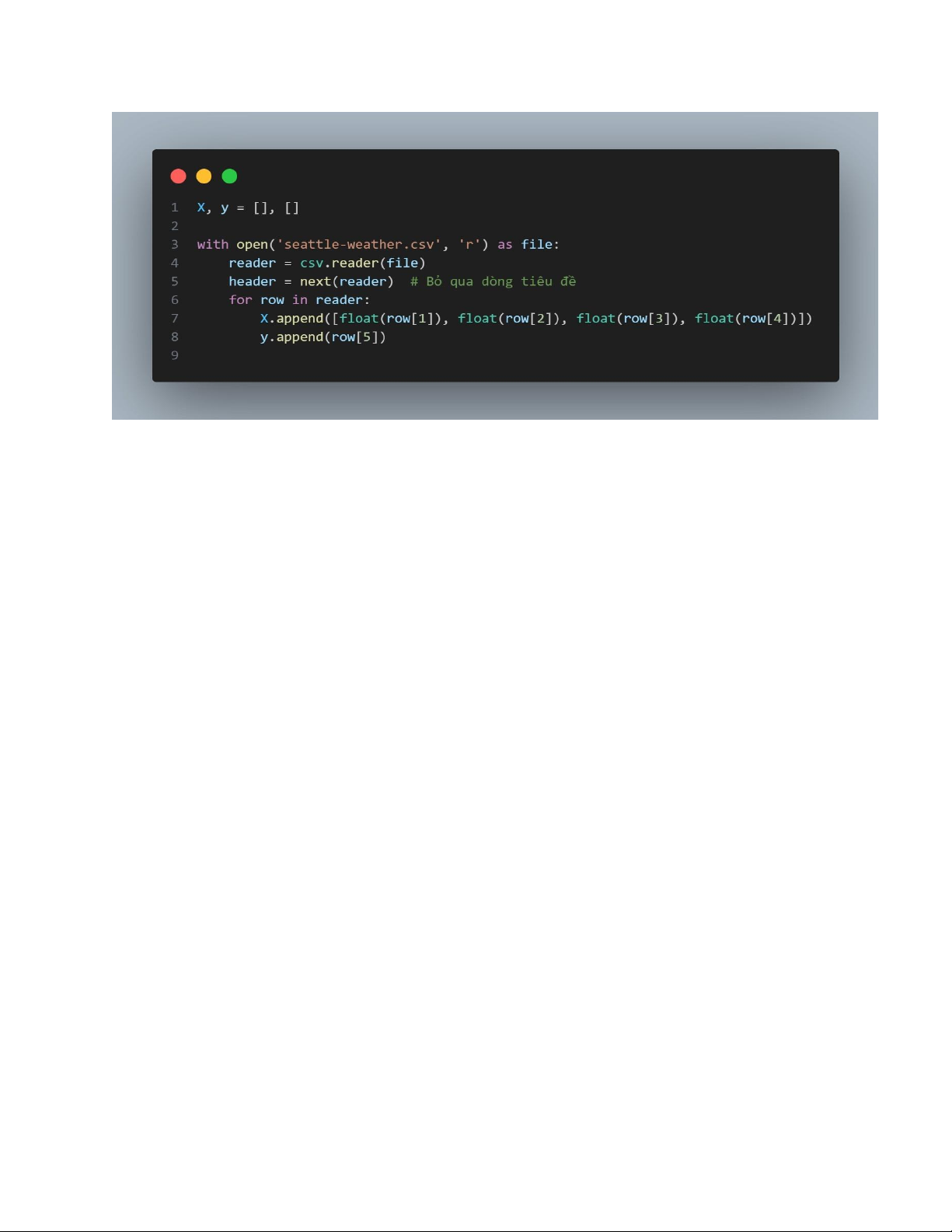
Bước 1 : Đọc dữ liệu lOMoAR cPSD| 45734214
- Mục đích: Khởi tạo hai danh sách rỗng:
+ X: Dùng để lưu trữ các đặc trưng (features) của dữ liệu.
+ y: Dùng để lưu trữ nhãn (labels) tương ứng của mỗi dòng dữ liệu.
- with open('seattle-weather.csv', 'r') as file: Mở tệp dữ liệu CSV có tên
seattle-weather.csv ở chế độ đọc ('r').
- reader = csv.reader(file): Tạo một đối tượng đọc (reader) để duyệt qua từng dòng của tệp CSV.
- header = next(reader):
+ next(reader) đọc dòng đầu tiên từ tệp CSV.
+ Lưu dòng này vào biến header. Dòng đầu tiên này thường chứa tiêu đề các cột (column headers).
+ Sau khi đọc xong dòng tiêu đề, con trỏ sẽ chuyển đến dòng tiếp theo,
giúp bỏ qua tiêu đề khi xử lý dữ liệu.
- for row in reader: Duyệt qua từng dòng dữ liệu (bỏ qua tiêu đề) trong tệp CSV.
- X.append([float(row[1]), float(row[2]), float(row[3]), float(row[4])])
+ Mục đích: Thêm các giá trị từ các cột 1, 2, 3, và 4 (index từ 1 đến 4)
của mỗi dòng vào danh sách X. + Chi tiết:
● float(row[i]): Chuyển đổi giá trị chuỗi từ cột i thành số thực để
thuận tiện cho việc tính toán.
● Lý do chọn các cột này: Đây có thể là các cột chứa đặc trưng (features) như: lOMoAR cPSD| 45734214
○ precipitation: Lượng mưa.
○ temp_max: Nhiệt độ tối đa.
○ temp_min: Nhiệt độ tối thiểu. ○ wind: Tốc độ gió.
- y.append(row[5]):
+ Thêm giá trị từ cột 5 của mỗi dòng vào danh sách y.
+ Là nhãn (label) hoặc biến mục tiêu cần dự đoán (output).
+ Có thể là một cột chứa thông tin thời tiết, ví dụ: weather với các giá trị
như "rainy", "sunny", "foggy",...
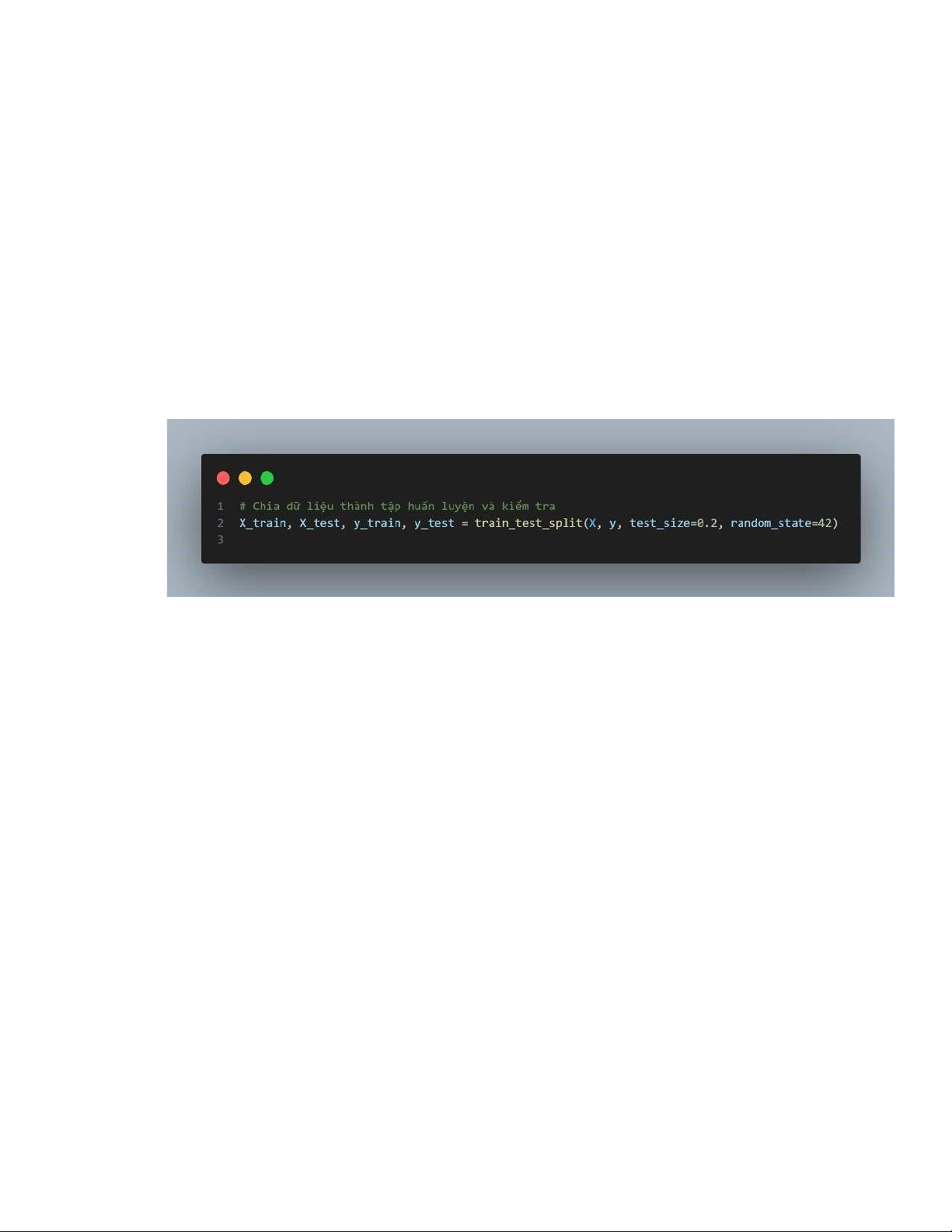
Bước 2: Chia dữ liệu thành tập huấn luyện và kiểm tra (train/test split) - X:
+ Danh sách (hoặc mảng) chứa các đặc trưng đầu vào (features).
+ Đây là dữ liệu đã được chuẩn bị ở đoạn trước. - y:
+ Danh sách (hoặc mảng) chứa nhãn (labels) tương ứng với các dòng trong X.
- test_size=0.2:
+ Tỷ lệ dữ liệu được sử dụng làm tập kiểm tra (testing set).
+ 0.2 có nghĩa là 20% dữ liệu sẽ được dùng làm tập kiểm tra, và 80% dữ
liệu sẽ dùng để huấn luyện mô hình.
- random_state=42:
+ Xác định hạt giống ngẫu nhiên (random seed) để bảo đảm kết quả chia
dữ liệu luôn giống nhau khi chạy lại mã.
+ Lý do sử dụng:
● Để tái hiện kết quả (reproducibility), đặc biệt trong quá trình thử nghiệm và phân tích.
3.1.2.3 Đưa dữ liệu đầu vào lOMoAR cPSD| 45734214
- data_input = [] : Thử nghiệm với một mẫu đầu vào là 1 mảng các giá trị
của các thuộc tính đầu vào
3.2.2 Cài đặt thuật toán
3.2.2.1 Không ứng dụng thư viện vào thuật toán
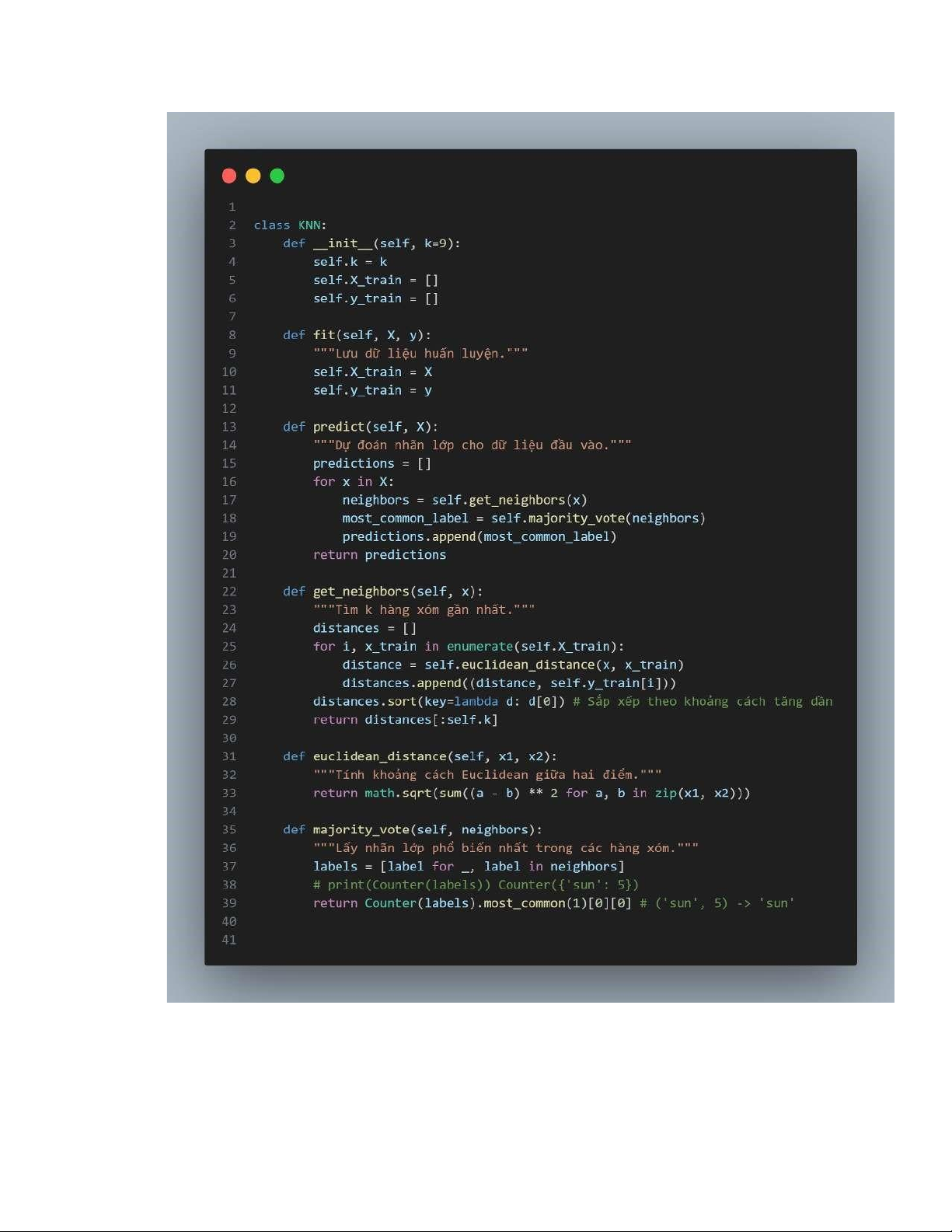
- Thuật toán KNN + Thiết lập lớp KNN:
Lớp KNN (K-Nearest Neighbors) cung cấp các phương thức lưu trữ
dữ liệu, tính khoảng cách giữa các bản ghi với giá trị đầu vào, chọn ra
những nhãn phổ biến nhất trong k điểm, và tìm ra giá trị đầu ra dựa trên dữ
liệu đã được huấn luyện và dữ liệu đầu vào lOMoAR cPSD| 45734214
+ Tạo mô hình KNN và huấn luyện
● Tạo 1 đối tượng có tên knn từ lớp KNN có tham số truyền vào là k =9 lOMoAR cPSD| 45734214
● Từ đối tượng knn gọi phương thức fit gồm 2 tham số: Mảng giá trị đầu
vào của dữ liệu học, và mảng giá trị nhãn của dữ liệu học. Câu lệnh này
sẽ lưu dữ liệu vào đối tượng bước này gọi là huấn luyện mô hình
● Từ đối tượng knn đã được huấn luyện, gọi phương thức predict có tham
số là Mảng giá trị đầu vào của dữ liệu kiểm tra, câu lệnh sẽ trả về 1
mảng các giá trị đầu ra dựa trên các dữ liệu đã được học, mục đích của
câu lệnh này để so sánh với mảng giá trị đầu ra của dữ liệu kiểm tra để
đưa ra độ chính xác của mô hình
+ Tính toán và đưa ra kết quả từ giá trị đầu vào
● Dự đoán nhãn lớp cho đầu vào mới (dữ liệu mẫu) bằng mô hình KNN đã
được huấn luyện. Hàm này sẽ dự đoán nhãn lớp của mẫu dựa trên k láng giềng gần nhất.
+ Đánh giá độ chính xác mô hình