lOMoAR cPSD| 39651089
Biểu diễn số chấm động
Vì bộ nhớ máy tính có giới hạn, chúng ta không thể lưu trữ 1 con số
với ộ chính xác vô hạn bất chấp chúng ta dùng kiểu nhị phân hay
thập phân. Tại một mức nào ó thì ta cần phải cắt giảm bớt. Nhưng ộ
chính xác ến bao nhiêu là ủ? Bao nhiêu chữ số nguyên và bao nhiêu chữ số phần thực?
• Với một công nhân xây dựng, 10 met hay 10.0001 met là như
nhau, phép tính của anh ta không quan tâm ến ộ chính xác quá nhỏ như vậy
• Nhưng với 1 người thiết kế microchip, 0.0001 met ã là 1 sự khác biệt rất lớn.
• Trong vật lý người ta cần tốc ộ ánh sáng (3*109) và hằng số hấp
dẫn newton (0.0000000000667) ể tính toán cùng nhau
Có thể thấy ể có thể áp ứng nhu cầu tính toán a dạng và cả yêu cầu
ộ chính xác người ta ưa ra số chấm ộng. 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 35 lOMoAR cPSD| 39651089 Biểu diễn số chấm ộng
Ta sẽ chuẩn hóa về dạng: ±1.F * 2E
• F: Significand ( Phần thập phân không dấu)
• E: Exponent (Phần số mũ)
Ví dụ:+0.0937510 = +1.1 * 2-4
Có nhiều chuẩn nhưng hiện nay chuẩn IEEE 754 ược dùng nhiều nhất ể lưu trữ số
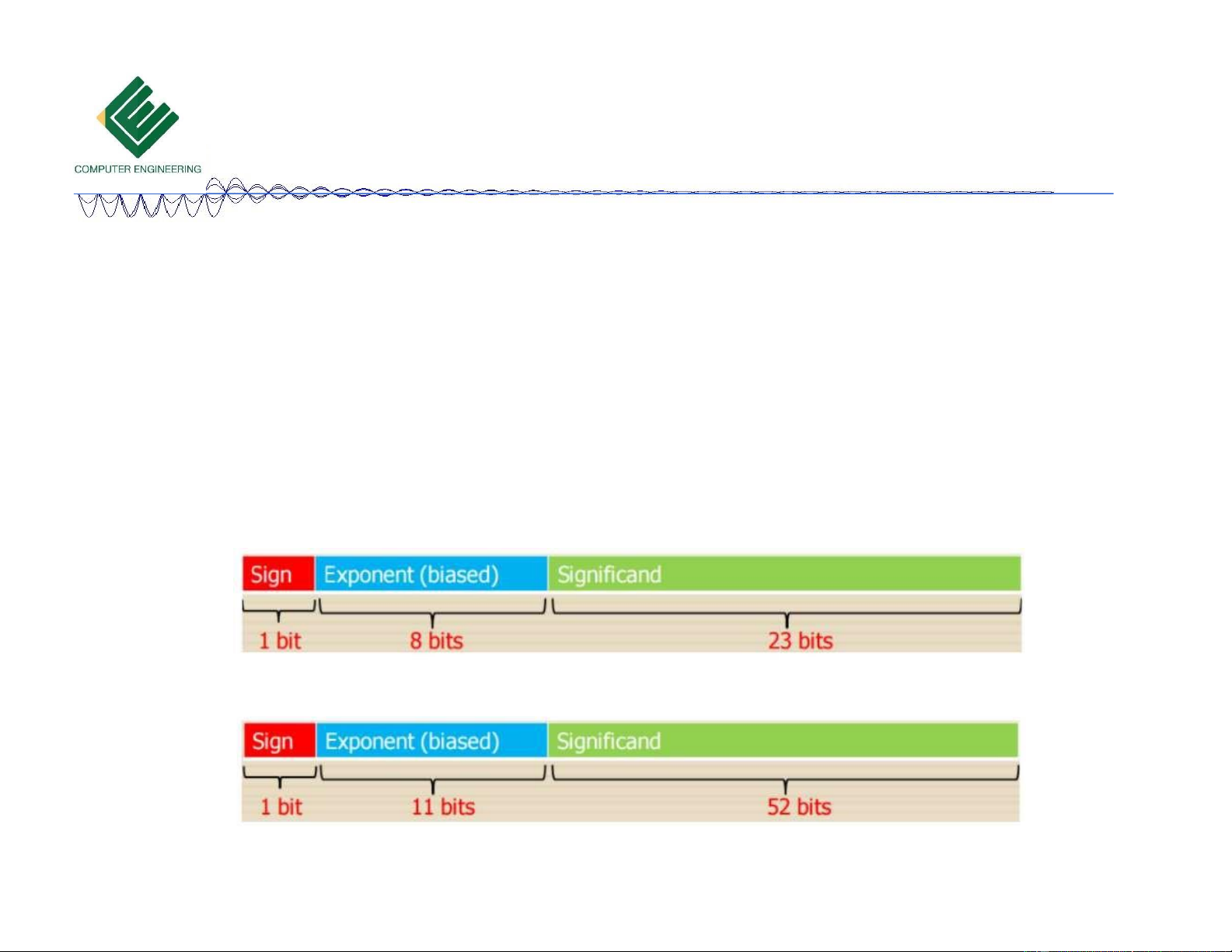
thập phân theo dấu chấm ộng trong máy tính, gồm 2 dạng Số chấm ộng chính xác ơn (32 bits):
Số chấm ộng chính xác kép (64 bits): 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 36 lOMoAR cPSD| 39651089
Biểu diễn số chấm động
Sign: Bit dấu (1: số âm, 0: số dương)
Exponent: Số mũ (Biểu diễn với dạng số quá K (Biased) với: •
Chính xác ơn: K = 127 (2n-1 -1 = 28-1 -1 = 128-1 = 127) với n là số bit lưu trữ Exponent •
Chính xác kép: K = 1023 (2n-1 -1 = 211-1 -1 = 1024-1 = 1023)
Significand (Fraction): Phần ịnh trị (phần lẻ sau dấu chấm)
Ví dụ: Biểu diễn số thực sau theo dạng số chấm ộng chính xác ơn (32 bit): X = 5.25 •
Bước 1: Đổi X sang hệ nhị phânX = -5.2510 = -101.012 •
Bước 2: Chuẩn hóa theo dạng ±1.F * 2E; X = -5.251 = -101.01 = -1.0101 * 22 •
Bước 3: Biểu diễn Floating Point Số âm: bit dấu Sign = 1 Số mũ E = 2
→ Phần mũ exponent với số thừa K=127 ược biểu diễn: Exponent = E +
127 = 2 + 127 = 12910 = 1000 00012
Phần ịnh trị = 0101 0000 0000 0000 0000 000 (Thêm 19 số 0 cho ủ 23 bit)
→ Kết quả nhận ược: 1 1000 0001 0101 0000 0000 0000 0000 000
Biểu diễn số dấu chấm động 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 37 lOMoAR cPSD| 39651089
Số dấu chấm ộng có dạng: S E M Chuyển ổi thuận:
B1: Chuyển ổi số trên ra hệ hai
-2345,125 = -1001 0010 1001.001 (dãy số nhị phân ược biểu diễn bình thường)
B2: Chuẩn hoá theo IEEE 32bit -1001 0010 1001.001
=> -1.001 0010 1001 001 x 2^11
(tức là lùi dấu chấm ra trước kế bên số ầu tiên, bao nhiêu số thì mũ mấy)
B3: Xác ịnh các thông số biểu diễn S,E,M
S: phần ịnh trị là số âm, nên s là 1
E : phần mũ ược xác ịnh E = 11+127=138=10001010
M: phần ịnh trị ược xác ịnh là 001 0010 1001 0010 0000 0000 (23 số) (tức là M =
dãy số sau dấu chấm sau khi chuẩn hóa, còn lại ghi số 0 cho ủ 23 số) Dãy số là: S E M
1 10001010 00100101001001000000000
Biểu diễn số dấu chấm ộng- chuyển ổi nghịch 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 38 lOMoAR cPSD| 39651089 Chuyển ổi nghịch:
1 10001010 00100101001001000000000 B1: Coi số ầu tiên: Số 1: dấu Số 0: dấu +
B2: Lấy dãy tiếp theo 10001010 chuyển về thập phân -> lấy số vừa chuyển về trừ 127 ra số phần mũ 10001010 = 138 138-127 = 11 -> Số mũ 11
B3: Lấy dãy tiếp theo 00100101001001 ếm ủ 11 số ngăn vô dấu phẩy 00100101001.001
B4: Thêm số 1 (bài nào cũng thêm số 1, số 1 này không phải là số 1 ở B1) và dấu ở B1 vào dãy vừa ngăn làm và
ổi sang thập phân => - 100100101001.001 = - 2345.125 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 39