Phương pháp rút gọn bìa Karnaugh - Tổ chức và Cấu trúc Máy tính II | Trường Đại học CNTT Thành Phố Hồ Chí Minh

lOMoAR cPSD| 39651089 Bìa Karnaugh
M. Karnaugh, “The Map Method for Synthesis of
combinatorial Logic Circuits”, Transactions of the
American Institute of Electrical Engineers,
Communications and Electronics, Vol. 72, pp. 593599, November 1953.
Bìa Karnaugh là một công cụ hình học ể ơn giản hóa các biểu thức logic 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 3 lOMoAR cPSD| 39651089 Bìa Karnaugh
Bìa Karnaugh là biểu diễn của bảng sự thật dưới dạng
một ma trận các ô (matrix of squares/cells) trong ó
mỗi ô tương ứng với dạng tích chuẩn (Minterm) hay
dạng tổng chuẩn (Maxterm).
Với một hàm có n biến (literal), chúng ta cần một bảng
sự thật có 2n hàng, tương ứng bìa Karnaugh có 2n ô (cell).
Để biểu diễn một hàm logic, một giá trị ngõ ra trong
bảng sự thật sẽ là một giá trị tương ứng trong một ô (cell) trong bìa Karnaugh 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 4 lOMoAR cPSD| 39651089
Phương pháp rút gọn bìa Karnaugh
Bước 1: Vẽ bìa Karnaugh gồm 2n ô có hàm logic có n biến ngõ vào
Bước 2: Đặt giá trị ngõ vào/ngõ ra lên bìa Karnaugh
Giá trị ngõ vào giữa 2 ô liên tiếp chỉ ược khác nhau một bit.
Giá trị ngõ ra ặt trong ô tương ứng với ngõ vào.
Phương pháp rút gọn bìa Karnaugh Bước 3: Gom nhóm
Gom nhóm các ô liên kề nhau có giá trị ngõ ra giống nhau.
Các ô ược xem là liền kề nhau khi ngõ vào của nó chỉ khác
nhau 1 bit. Có 2 phương pháp: 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 5 lOMoAR cPSD| 39651089
Gom nhóm theo Minterm: gom nhóm các ô có giá trị “1”
Gom nhóm theo Maxterm: gom nhóm các ô có giá trị “0”
Mỗi nhóm có thể có 2i ô (32, 16, 8, 4, 2, 1 ô tương ứng với i là 5, 4, 3, 2, 1, 0)
Nhóm lớn hơn cần ược ưu tiên thực hiện gom trước. Một ô
có thể ược gom bởi nhiều nhóm khác nhau.
Gom nhóm kết thúc khi tất cả các giá trị “1” trong bìa
Karnaugh ã ược gom (theo Minterm), hoặc các giá trị “0”
trong bìa ã ược gom (theo Maxterm)
Phương pháp rút gọn bìa Karnaugh
Bước 4: Rút gọn biểu thức
Nhóm có 2n ô liền kề nhau sẽ rút gọn ược n biến. 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 6 lOMoAR cPSD| 39651089
Mỗi một nhóm sẽ ược biểu diễn thành một term
của biểu thức rút gọn (theo Minterm hoặc Maxterm)
Trong một nhóm, nếu biến ngõ vào nào thay ổi thì
ược bỏ i khỏi term ó, nếu biến ngõ vào nào giữ nguyên thì sẽ
ược giữ lại trong term ó, theo quy tắc:
• Gom nhóm theo Minterm: biến ngõ vào giữ nguyên
nếu giá trị “1”, mang dấu bù nếu giá trị “0”.
• Gom nhóm theo Maxterm: biến ngõ vào giữ
nguyên nếu nó mang giá trị “0”, mang dấu bù nếu giá trị “1”. 10/18/2023
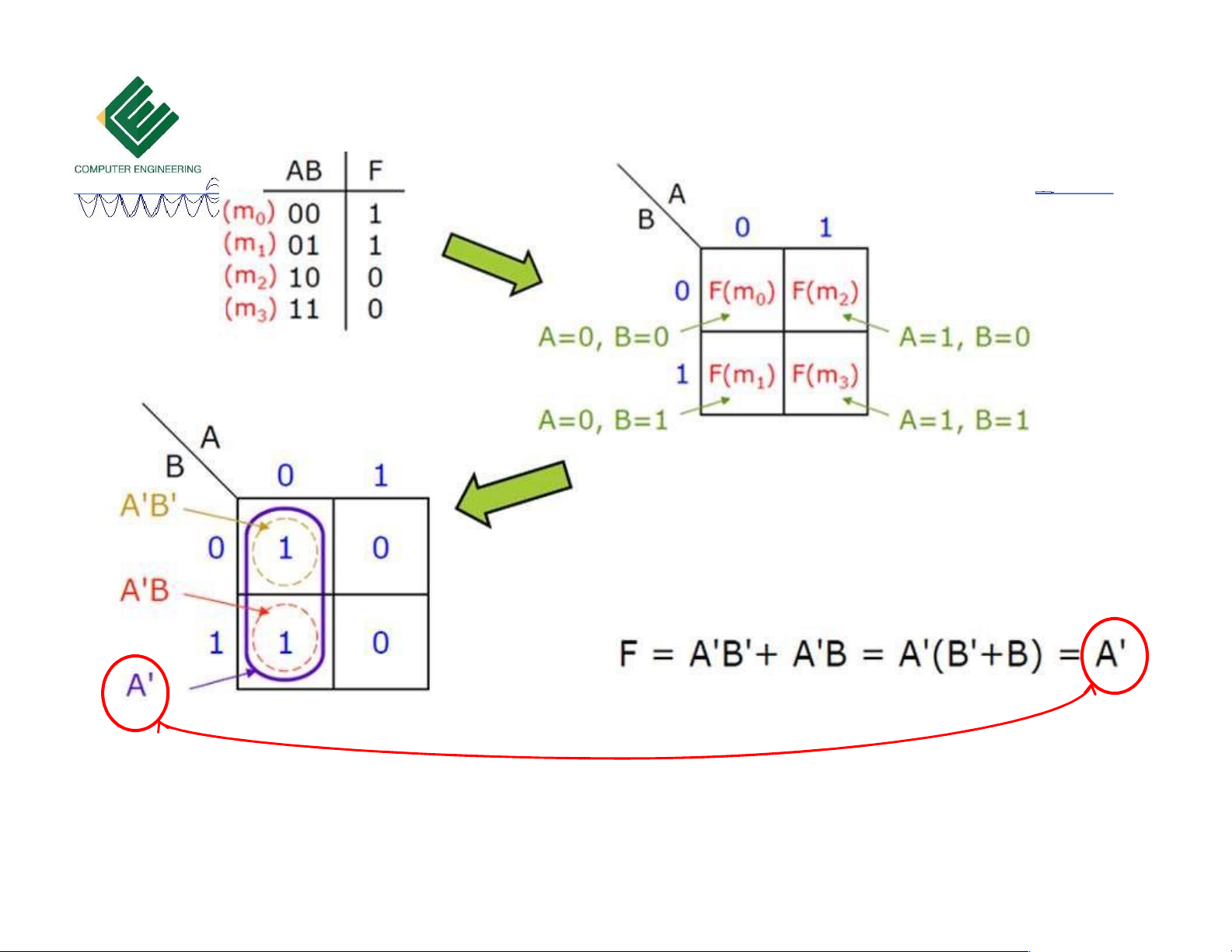
Copyrights 2016 UIT-CE. All Rights Reserved. 7 lOMoAR cPSD| 39651089 Bìa Karnaugh 2 biến 10/18/2023
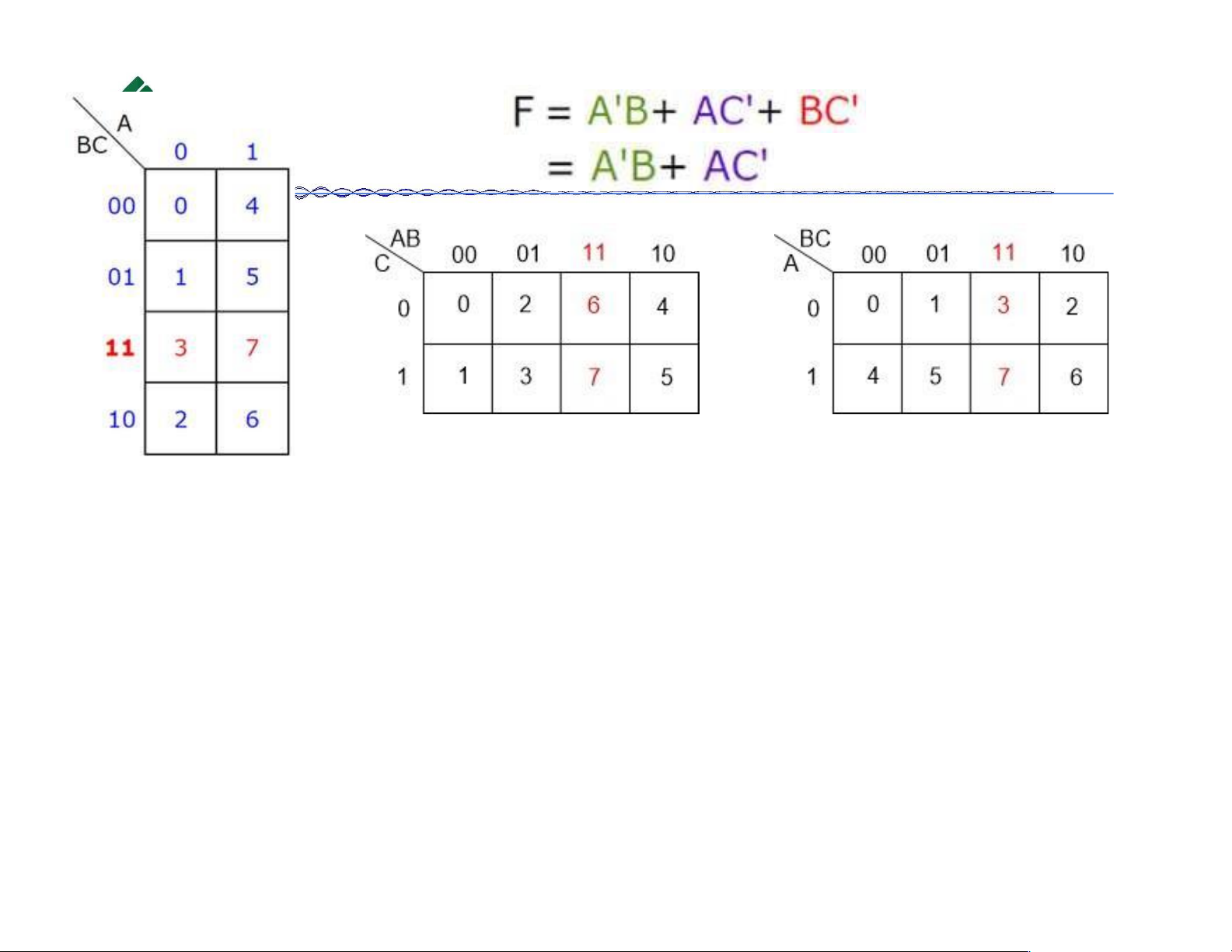
Copyrights 2016 UIT-CE. All Rights Reserved. 8 lOMoAR cPSD| 39651089 Bìa Karnaugh 3 biến Thiết lập bảng K: ại số 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 9 lOMoAR cPSD| 39651089 (chưa tối ưu) (tối ưu) Bìa Karnaugh 3 biến Cách 2 Cách 3 Cách 1 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 10 lOMoAR cPSD| 39651089
Lưu ý: có thể sử dụng cách nào ể biểu diễn bìa-K cũng ược, nhưng
phải lưu ý trọng số của các biến thì mới ảm bảo thứ tự các ô theo giá trị thập phân. 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 11 lOMoAR cPSD| 39651089 Bìa Karnaugh 3 biến 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 12 lOMoAR cPSD| 39651089 Bìa Karnaugh 3 biến 10/18/2023
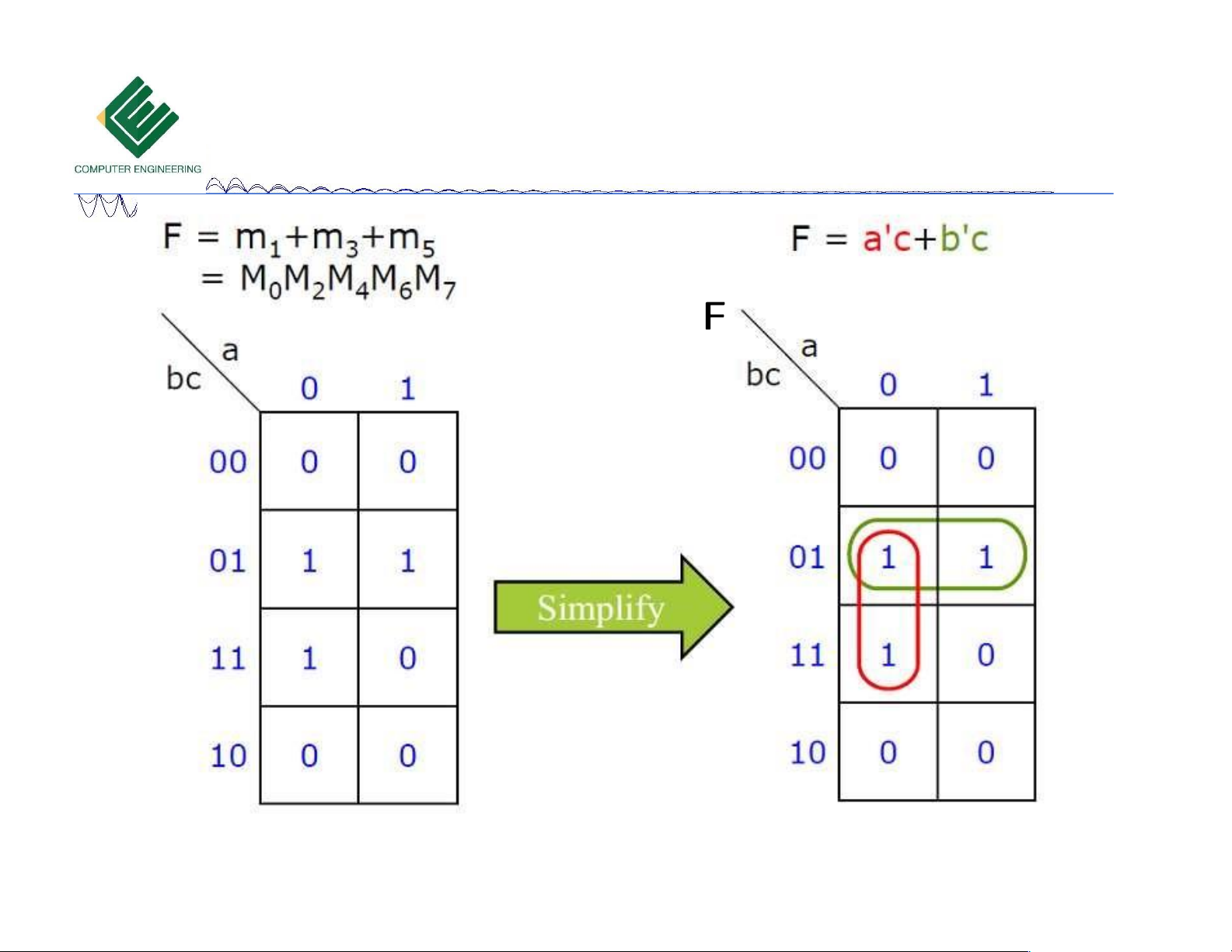
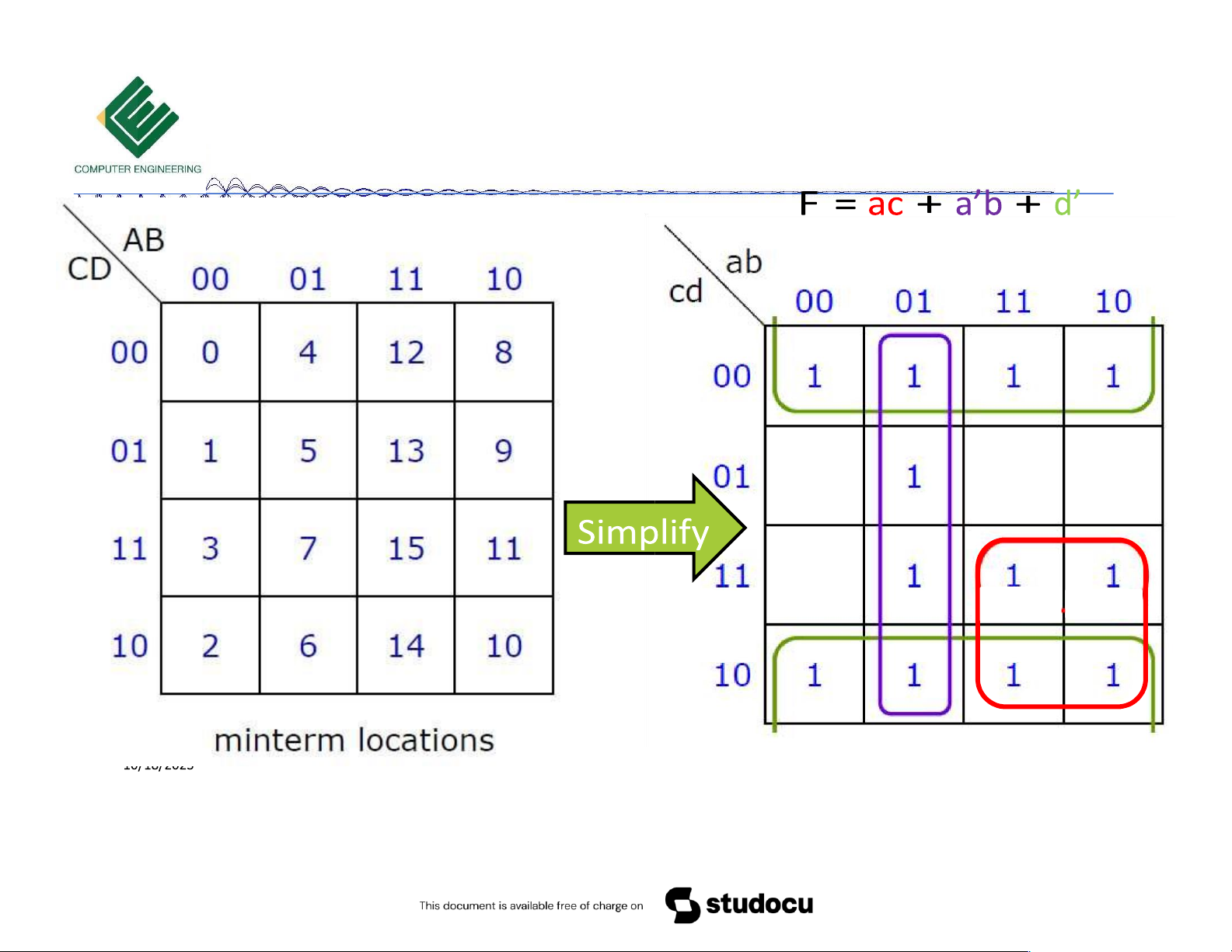
Copyrights 2016 UIT-CE. All Rights Reserved. 13 lOMoAR cPSD| 39651089 Bìa Karnaugh 3 biến F 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 14 lOMoAR cPSD| 39651089 Bìa Karnaugh 3 biến
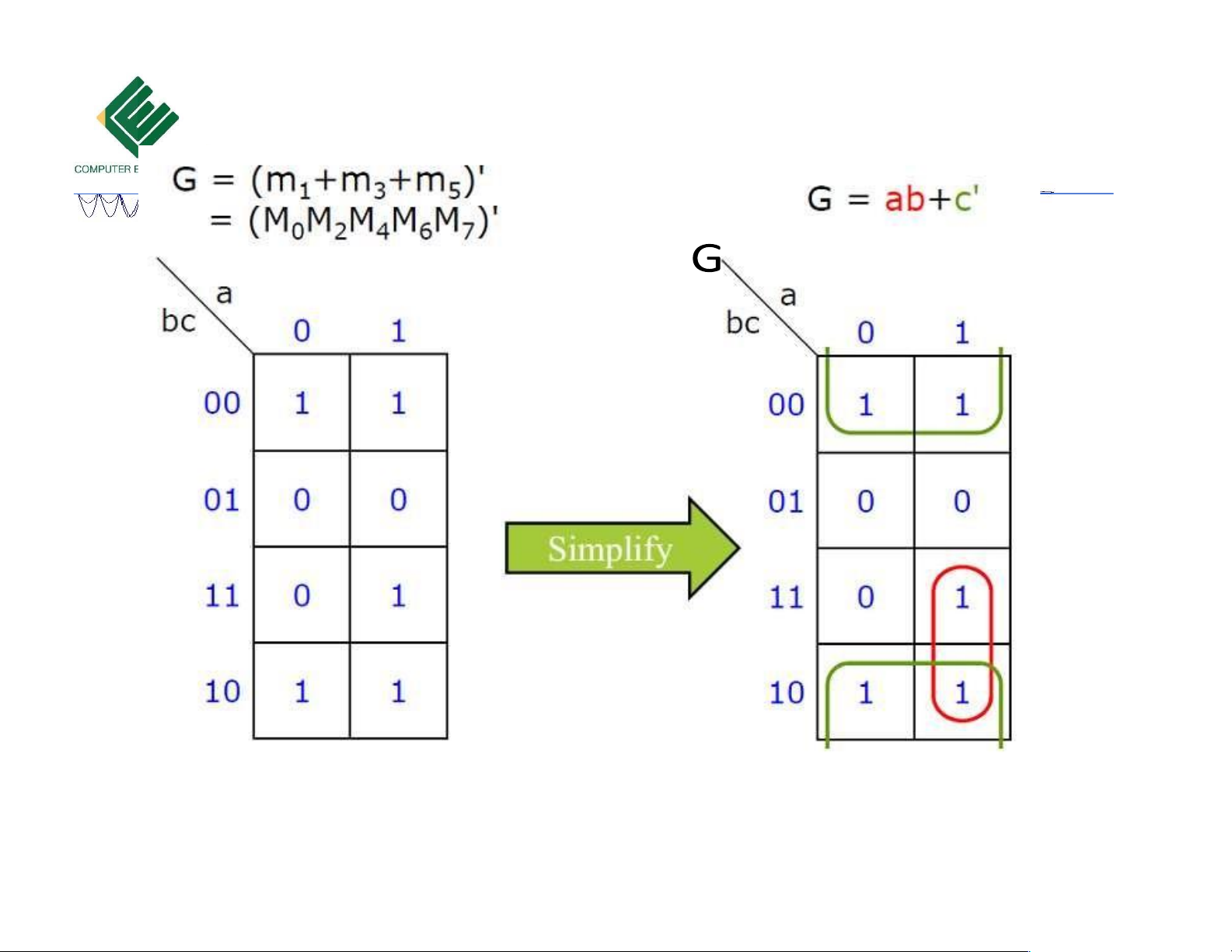
Copyrights 2016 UIT-CE. All Rights Reserved. 15 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 G 10/18/2023
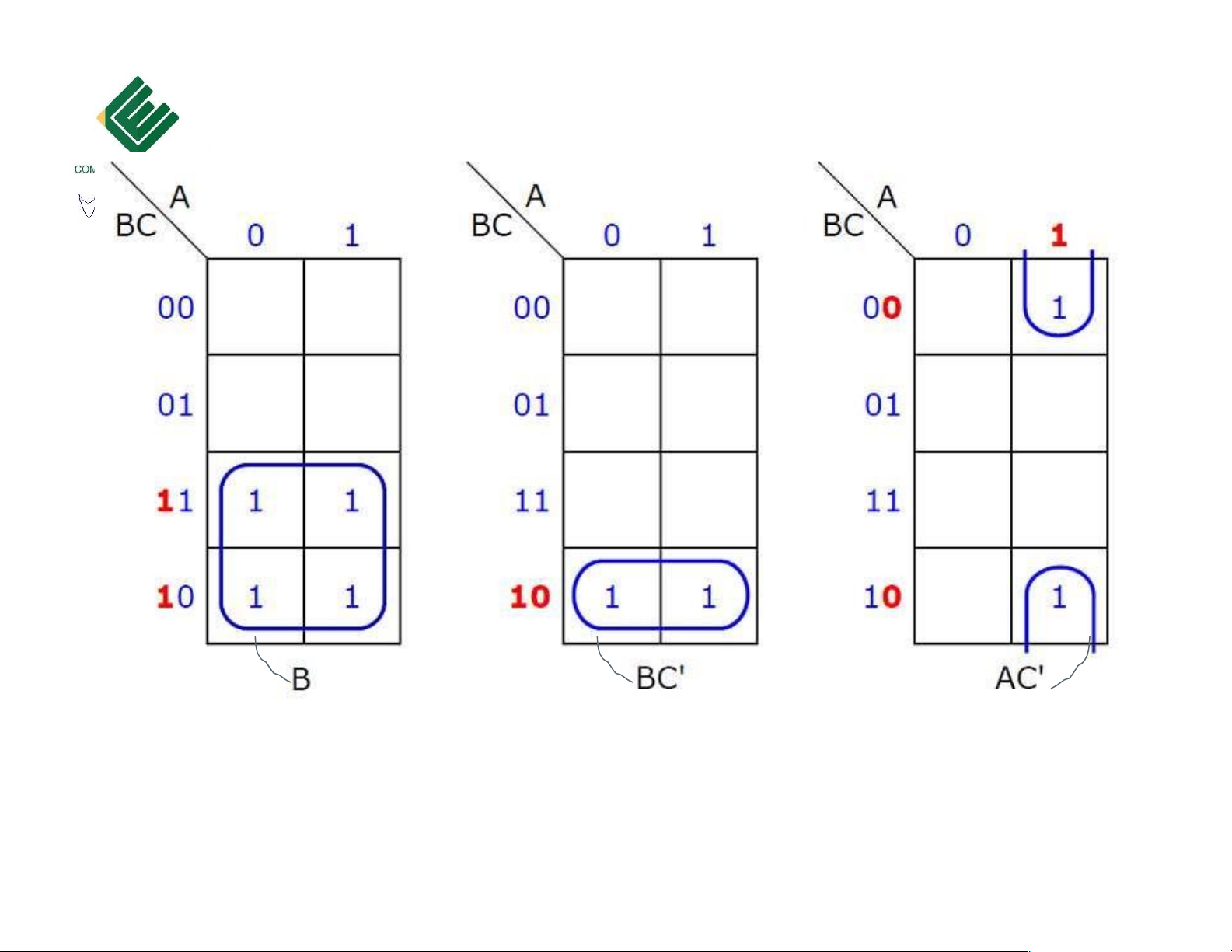
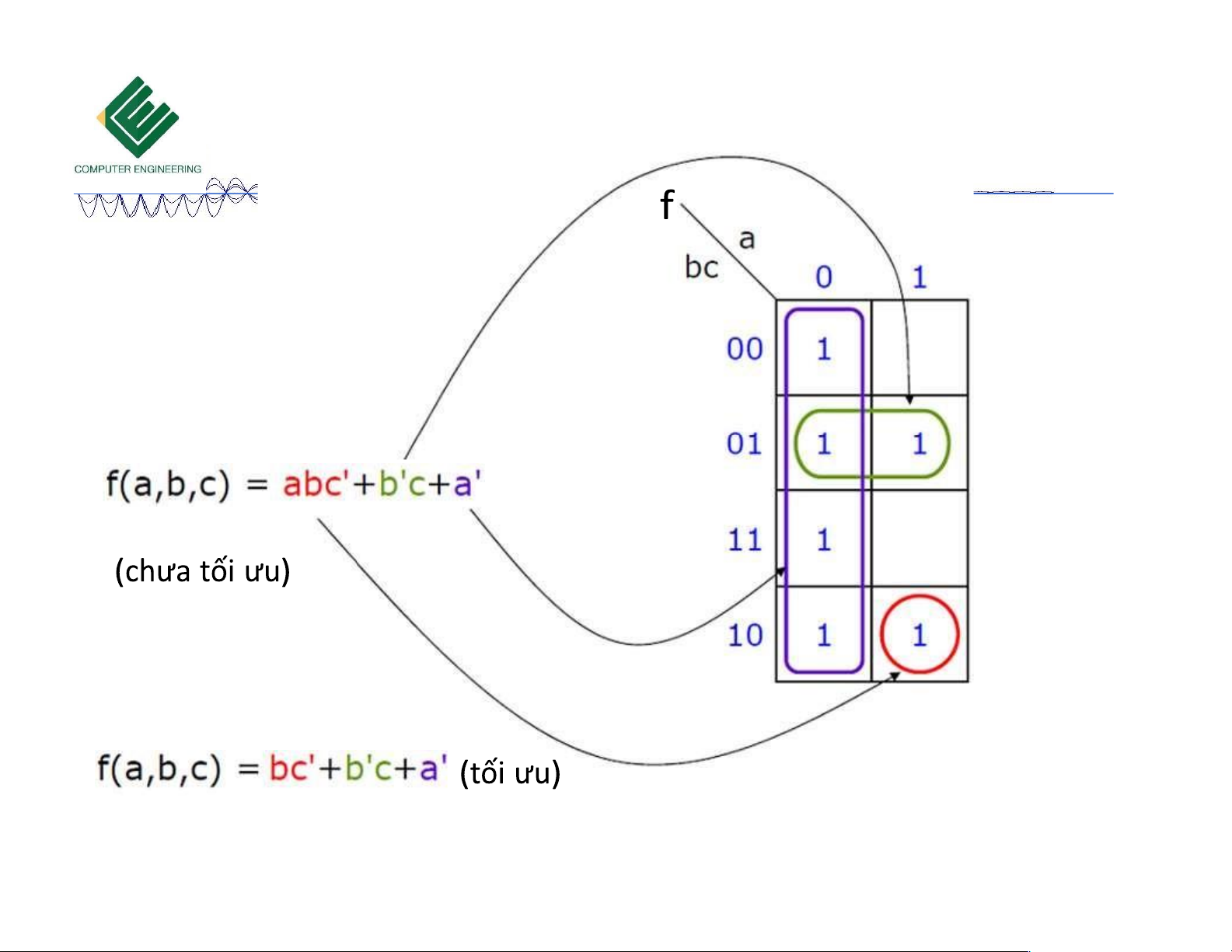
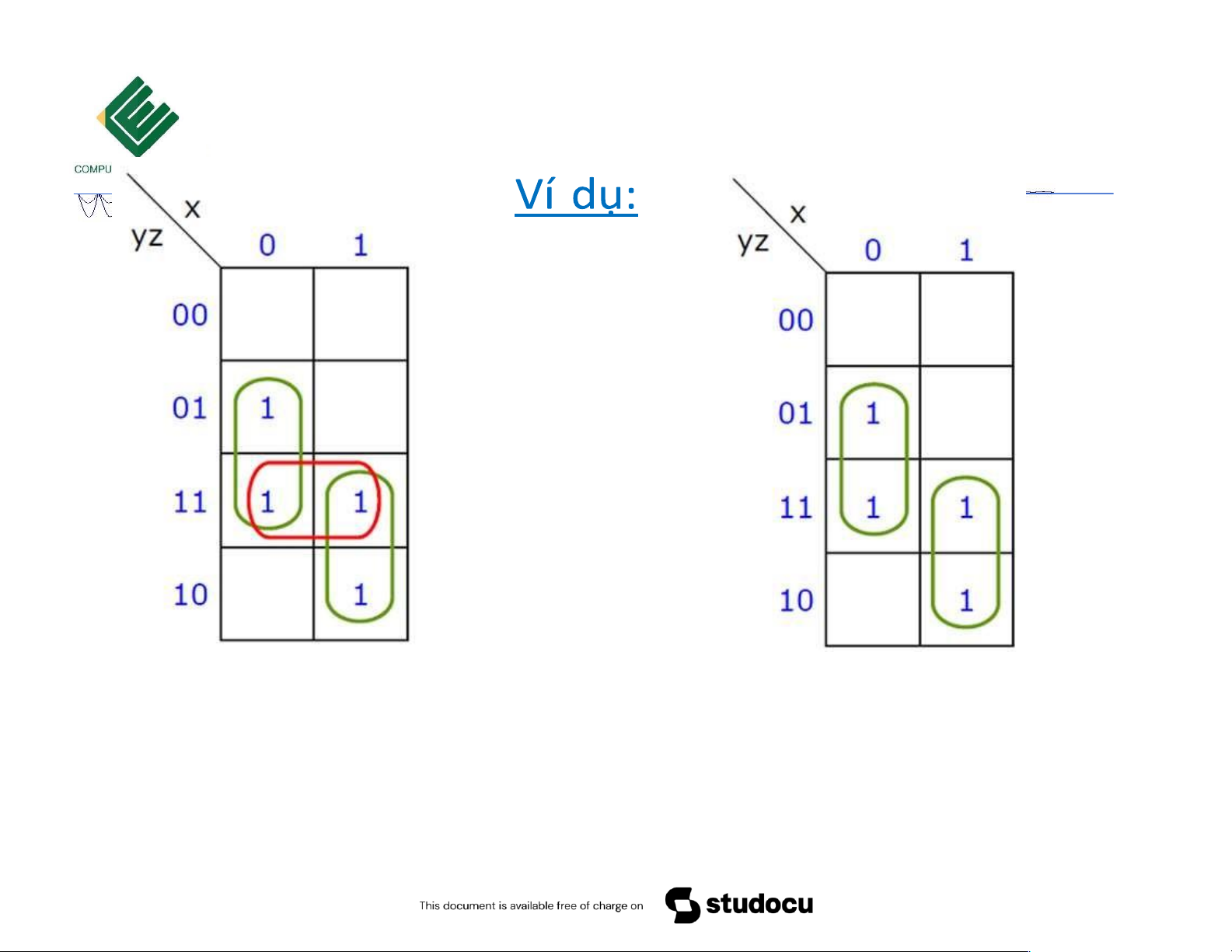
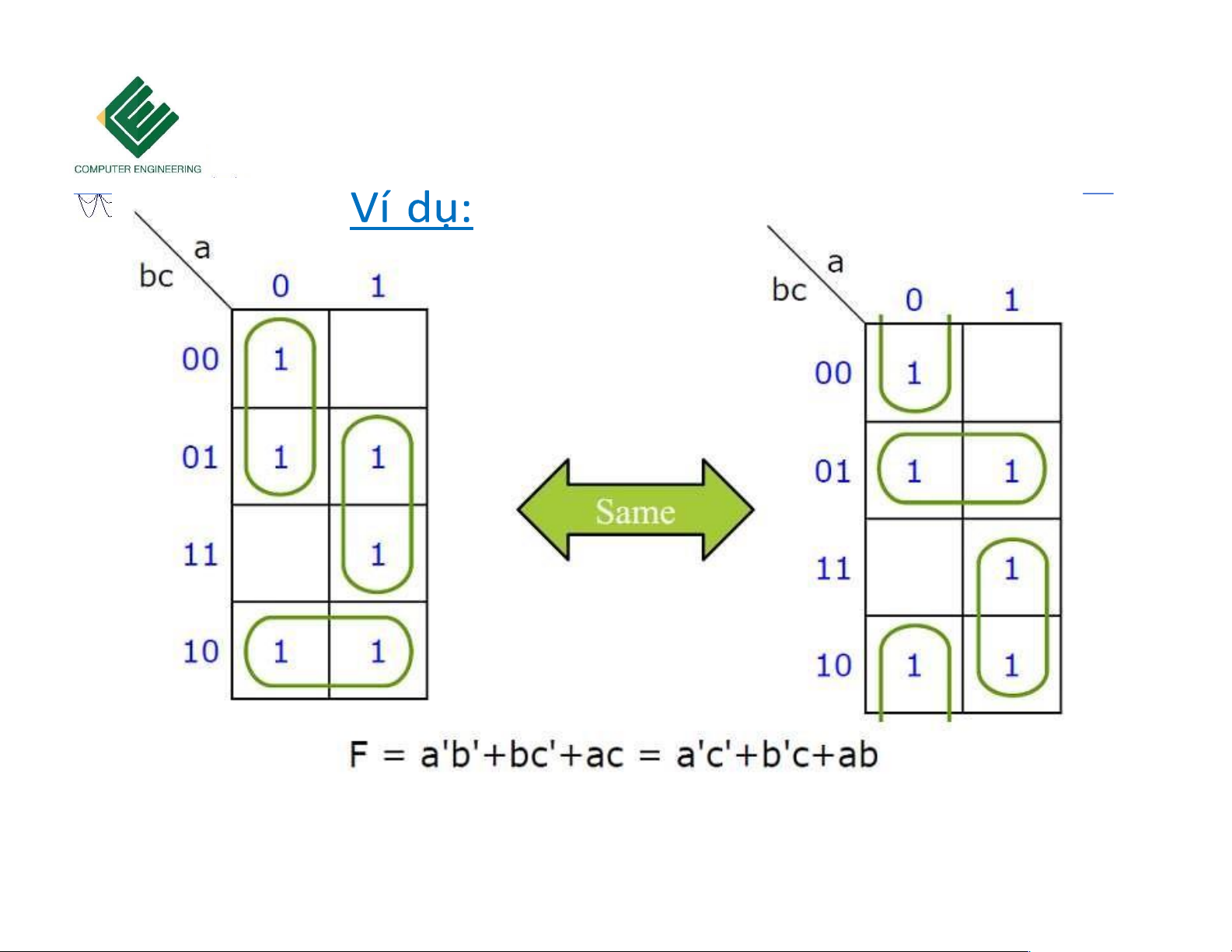
Copyrights 2016 UIT-CE. All Rights Reserved. 16 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bìa Karnaugh 3 biến F = x’z + xy + yz F = x’z + xy Rút gọn chưa tối ưu Rút gọn tối ưu
Copyrights 2016 UIT-CE. All Rights Reserved. 17 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 10/18/2023 Bìa Karnaugh 3 biến 10/18/2023
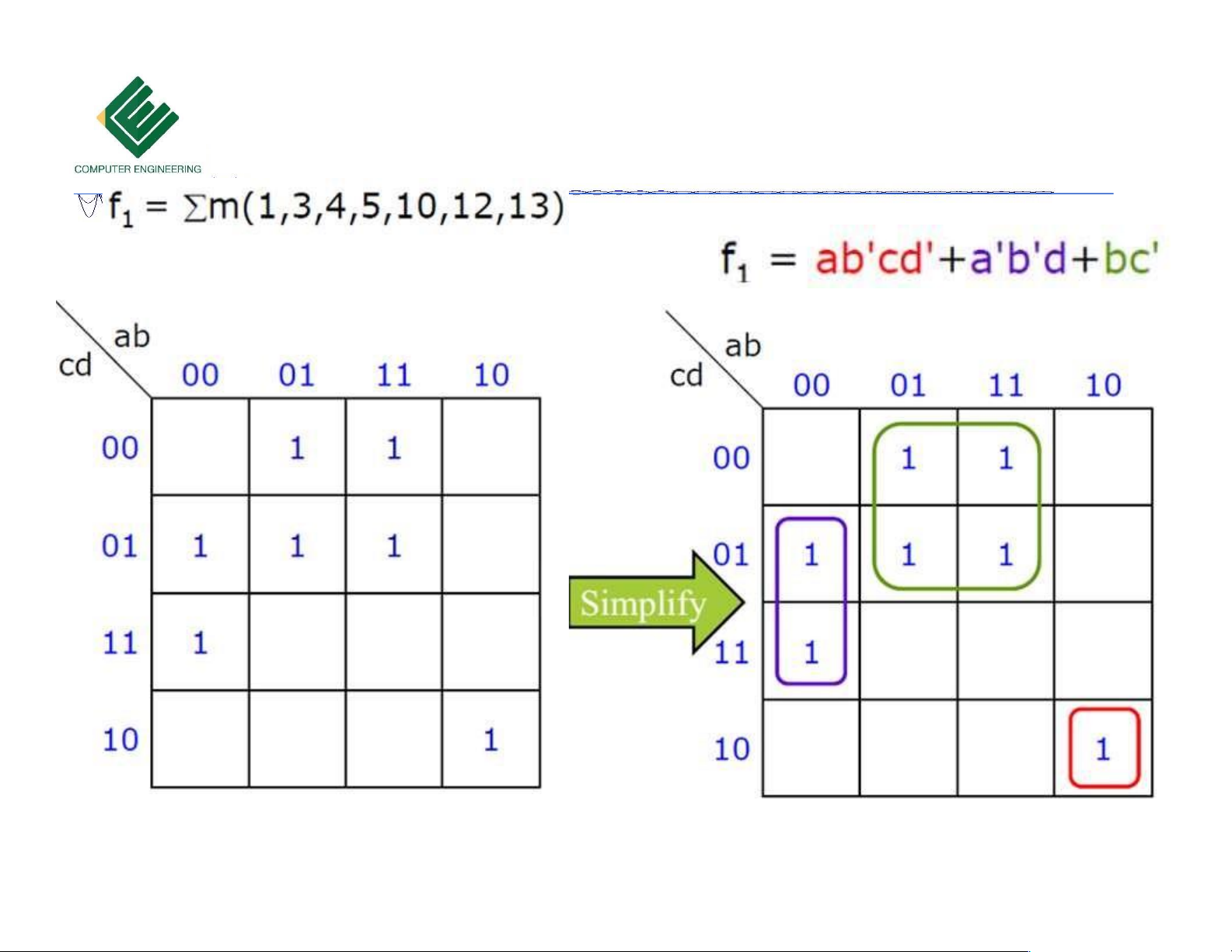
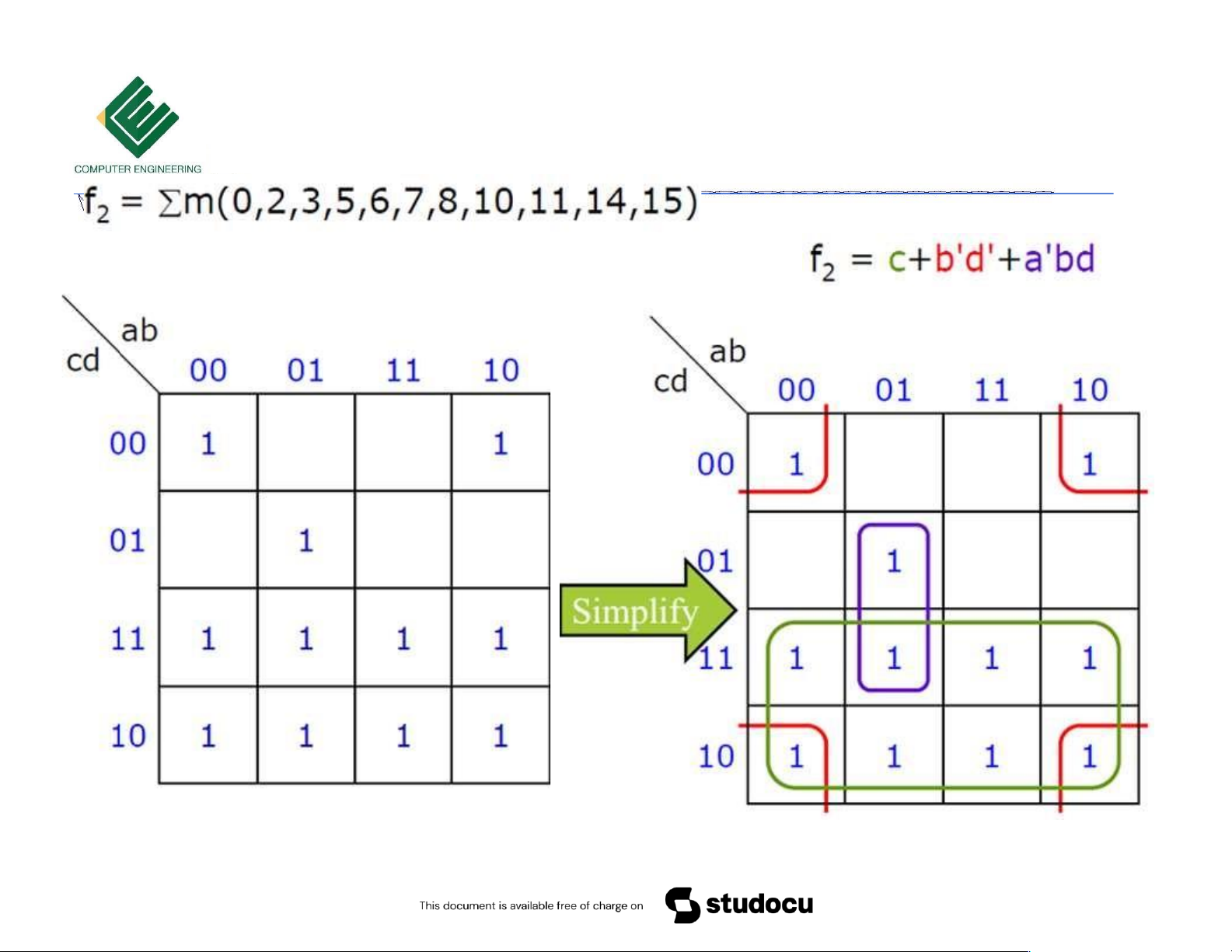
Copyrights 2016 UIT-CE. All Rights Reserved. 18 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bìa Karnaugh 4 biến
Copyrights 2016 UIT-CE. All Rights Reserved. 19 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bìa Karnaugh 4 biến 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved.
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bìa Karnaugh 4 biến 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bìa Karnaugh 5 biến Ví dụ:
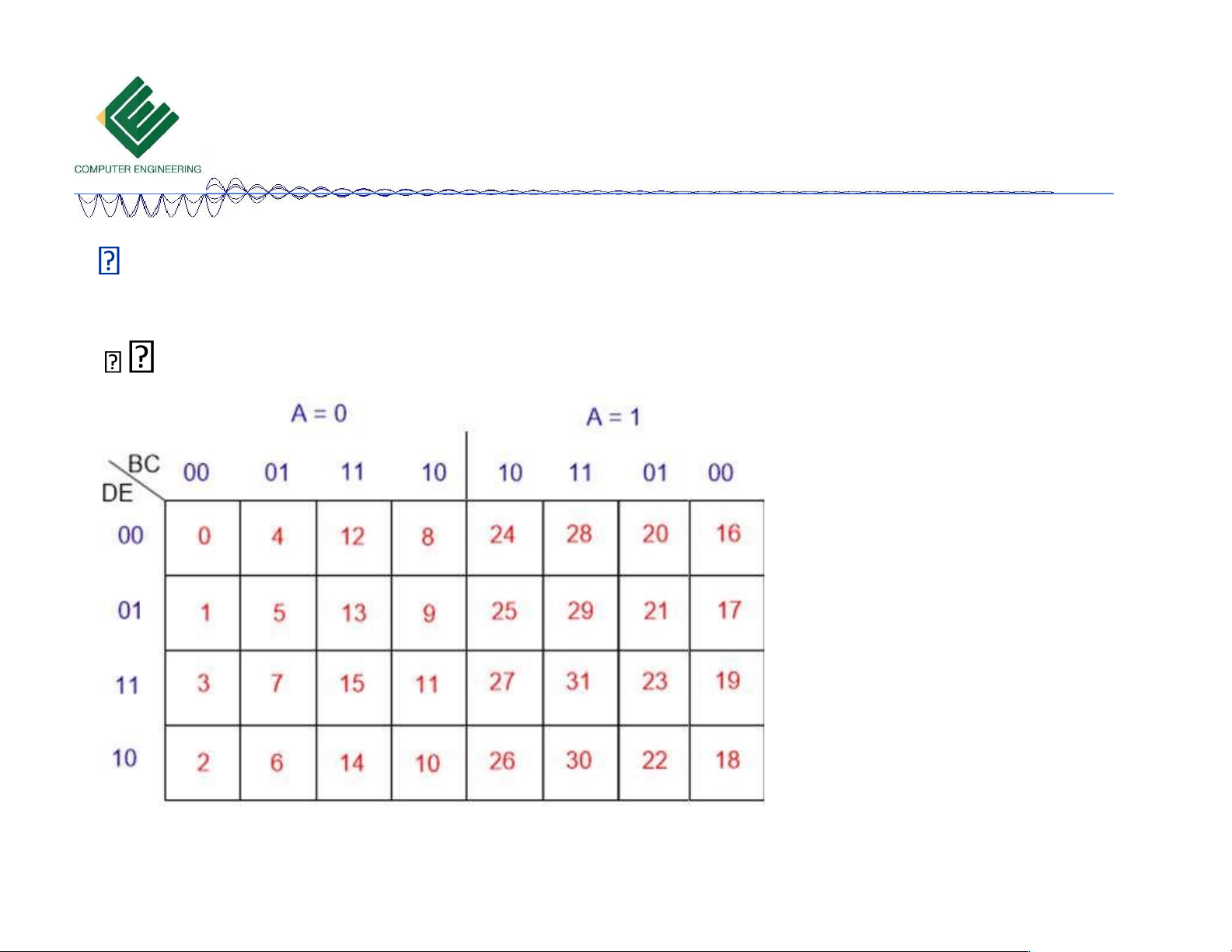
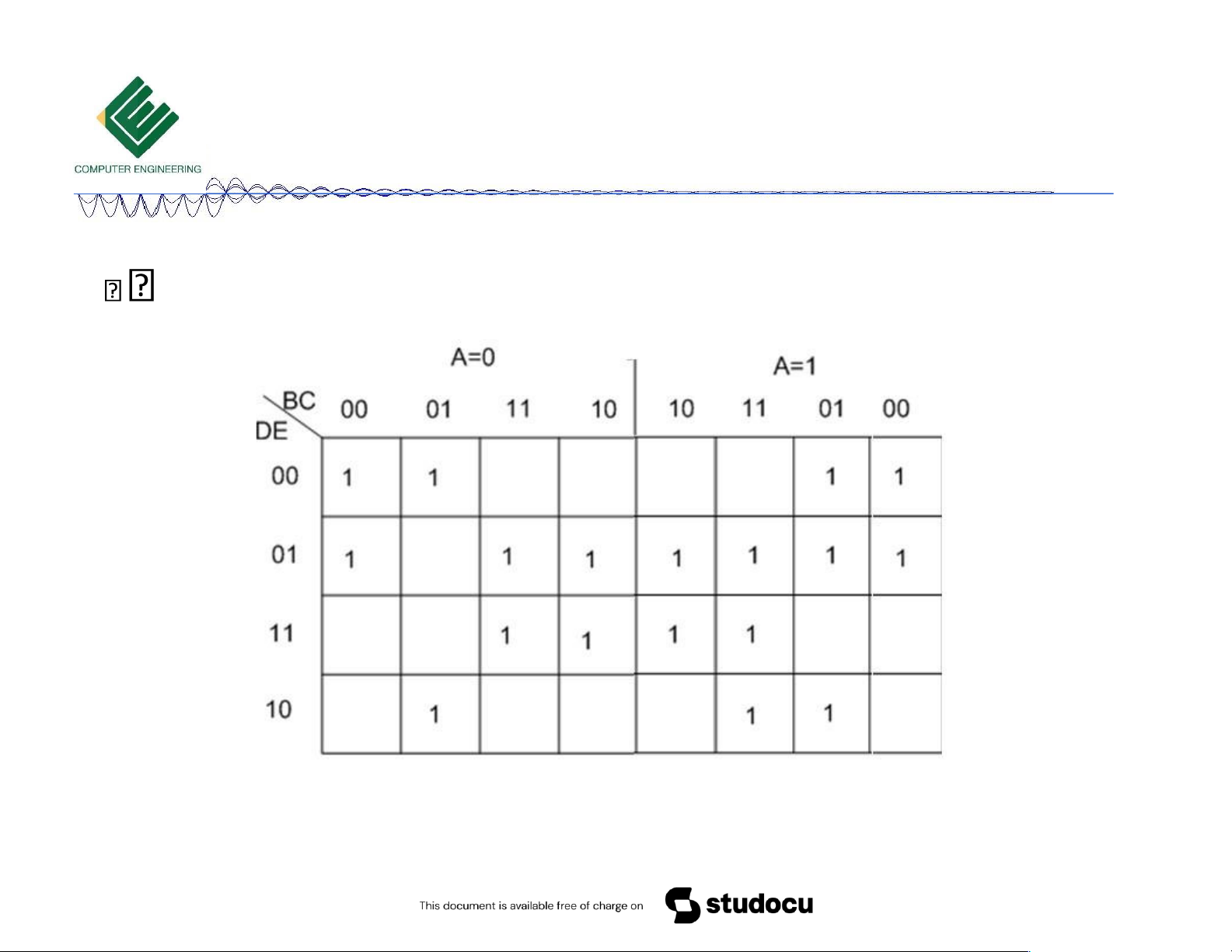
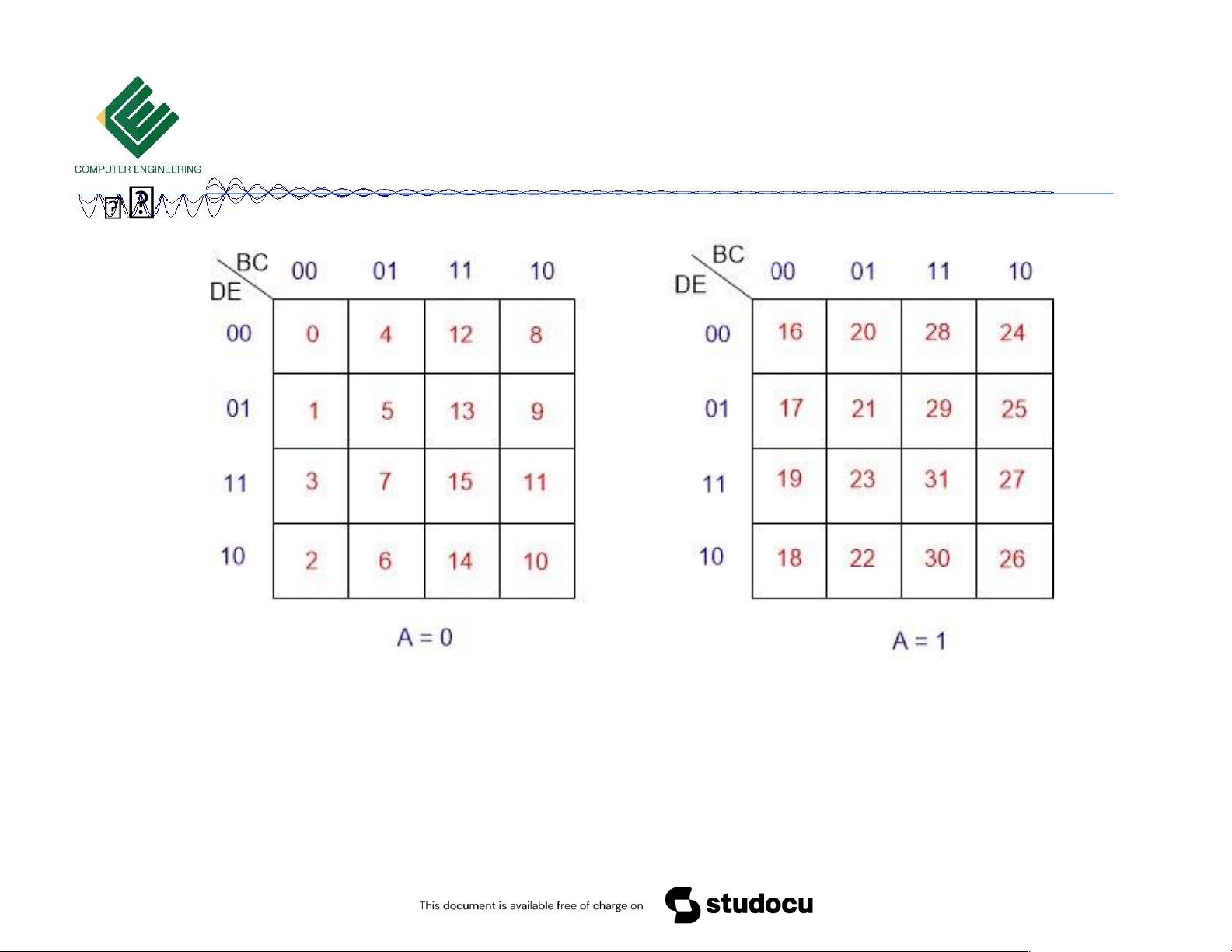
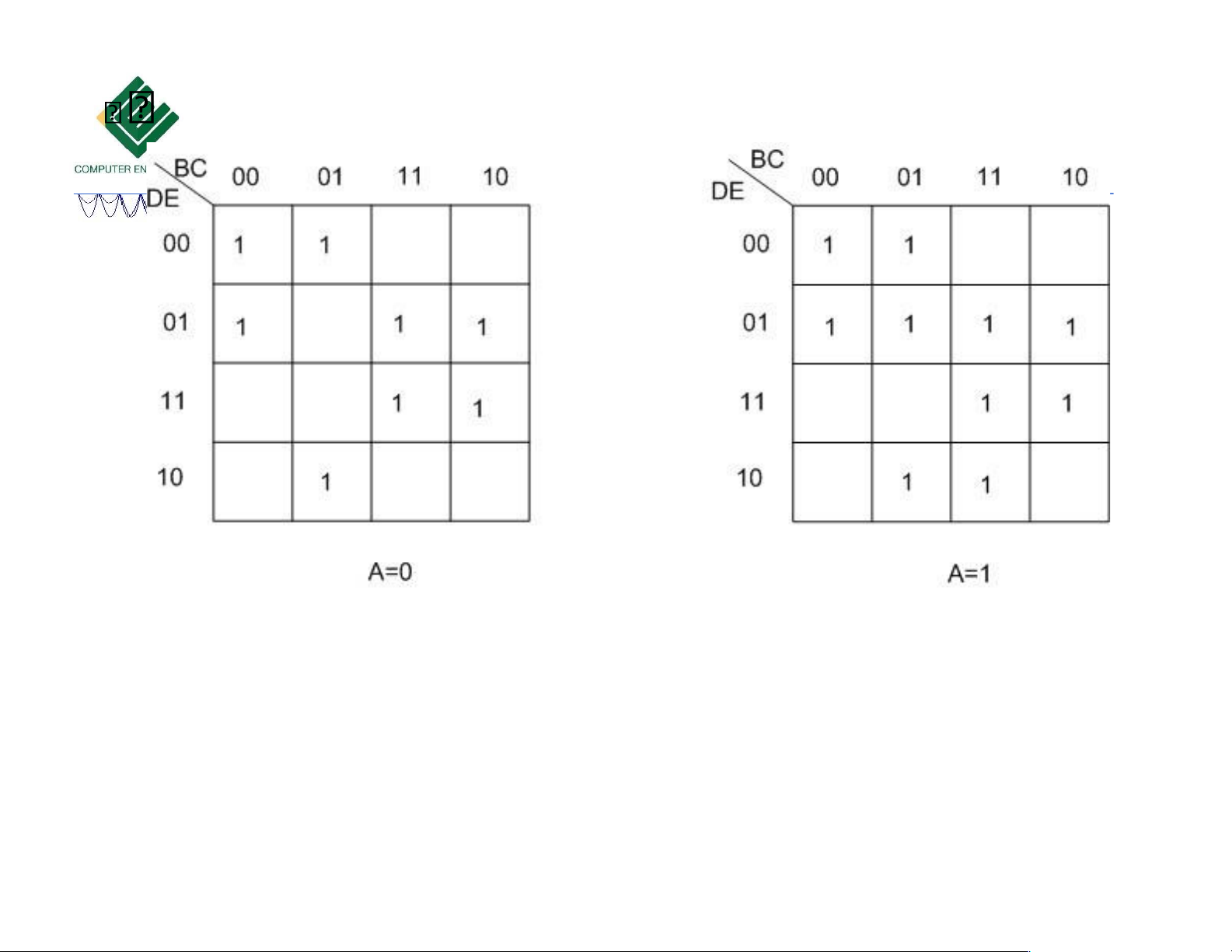
F (31, 30, 29, 27, 25, 2 2, 21, 20,17,16,15,13,11, 9, 6, 4,1, 0)
Vẽ bìa Karnaugh như hình bên
ể vẫn ảm bảo quy tắc: hai ô liên
kề nhau chỉ ược khác nhau 1 bit giá trị ngõ vào 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 22
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bìa Karnaugh 5 biến
F (31, 30, 29, 27, 25, 2 2, 21, 20,17,16,15,13,11, 9, 6, 4,1, 0) Bìa Karnaugh 5 biến 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 23 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
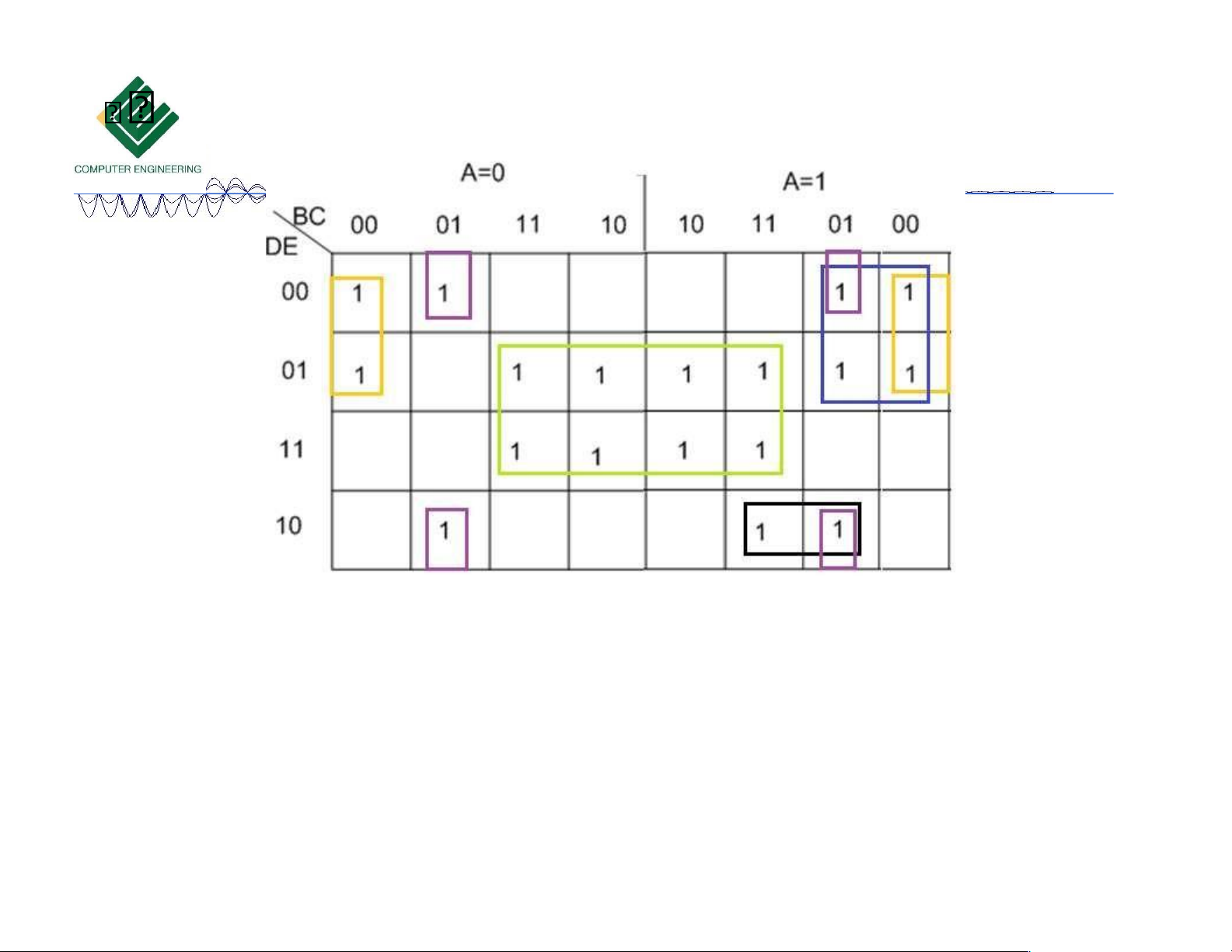
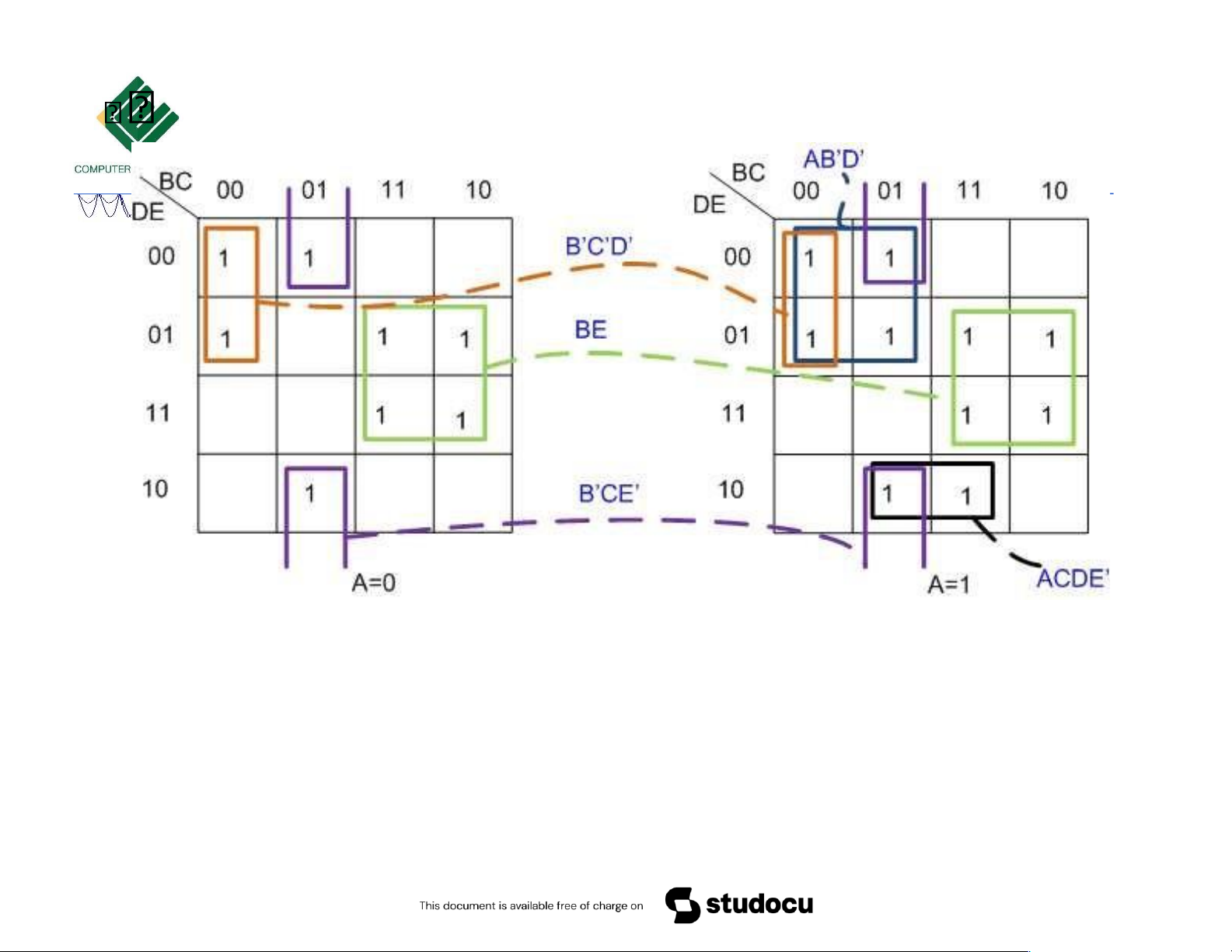
F (31, 30, 29, 27, 25, 2 2, 21, 20,17,16,15,13,11, 9, 6, 4,1, 0)
F = BE + B’CE’ + B’C’D’ + AB’D’ + ACDE’ Bìa Karnaugh 5 biến 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 24
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Phương pháp khác
F (31, 30, 29, 27, 25, 2 2, 21, 20,17,16,15,13,11, 9, 6, 4,1, 0) Bìa Karnaugh 5 biến 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 25 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
F (31, 30, 29, 27, 25, 2 2, 21, 20,17,16,15,13,11, 9, 6, 4,1, 0) Bìa Karnaugh 5 biến 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 26
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
F (31, 30, 29, 27, 25, 2 2, 21, 20,17,16,15,13,11, 9, 6, 4,1, 0)
F = BE + B’CE’ + B’C’D’ + AB’D’ + ACDE’ 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 27 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 28
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
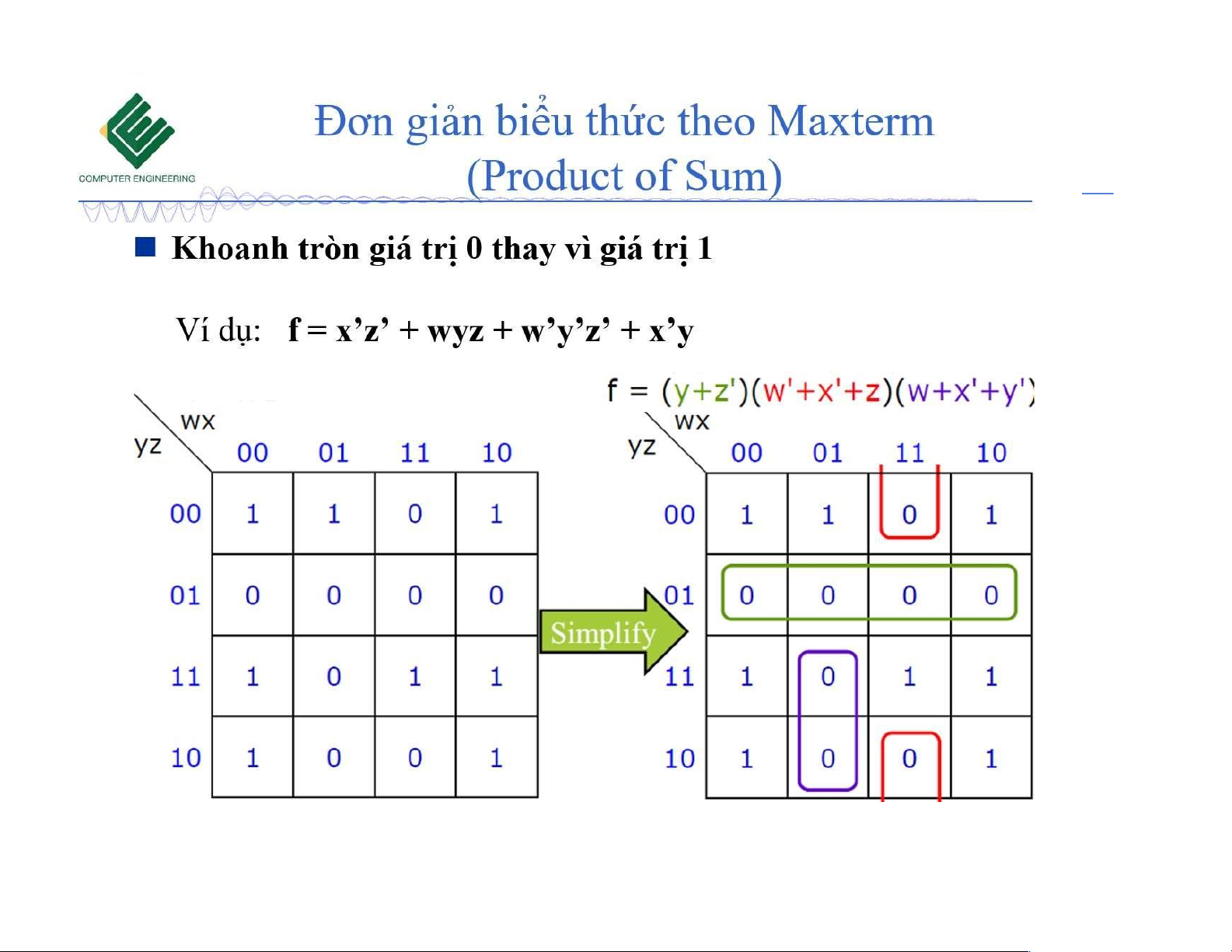
Biểu thức mang giá trị tùy ịnh
Giả thuyết: N1 không bao giờ cho kết quả ABC = 001 và ABC = 110
Câu hỏi : F cho ra giá trị gì trong trường hợp ABC = 001 và ABC = 110 ? 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 29 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Biểu thức mang giá trị tùy ịnh
Trong trường hợp trên thì chúng ta phải làm thế nào ể ơn giản N2 ?
Giả sử F(0,0,1) = 0 và F(1,1,0)=0, ta có biểu thức A B C F 0 0 0 1 sau: 0 0 1 X 0 0 1 0 1 0 1 1 1
F(A,B,C) = A’B’C’ + A’BC’ + A’BC + ABC 1 0 0 0 1 0 1 0
= A’C’(B’ + B) + (A’ + A)BC 0 = 1 1 0 X A’C’·1 + 1·BC + 1 1 1 1 = A’C’ + BC 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 30
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Biểu thức mang giá trị tùy ịnh
Tuy nhiên, nếu giả sử F(0,0,1)=1 và F(1,1,0)=1, ta có biểu thức sau:
F(A,B,C) = A’B’C’ + A’B’C + A’BC’ + A’BC + ABC’ + ABC = A’B’(C’ + C) + A’B(C’ + C) + A B C
F AB(C’ + C) 1 = A’B’ ·1 + A’B ·1 + AB ·1 = A’B’ + A’B + AB = A’B’ + 0 0 0 1 0 0 1 X A’B + A’B + AB 1
= A’(B’ + B) + (A’ + A)B = A’·1 + 1·B = A’ + + 0 1 0 1 B 0 1 1 1 1 0 0 0 1 0 1 0
So sánh với giả thuyết trước ó: 1 1 0 X 1 1 1 1
F(A,B,C) = A’C’ + BC, giải pháp nào chi phí ít hơn (tốt hơn)? 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 31 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
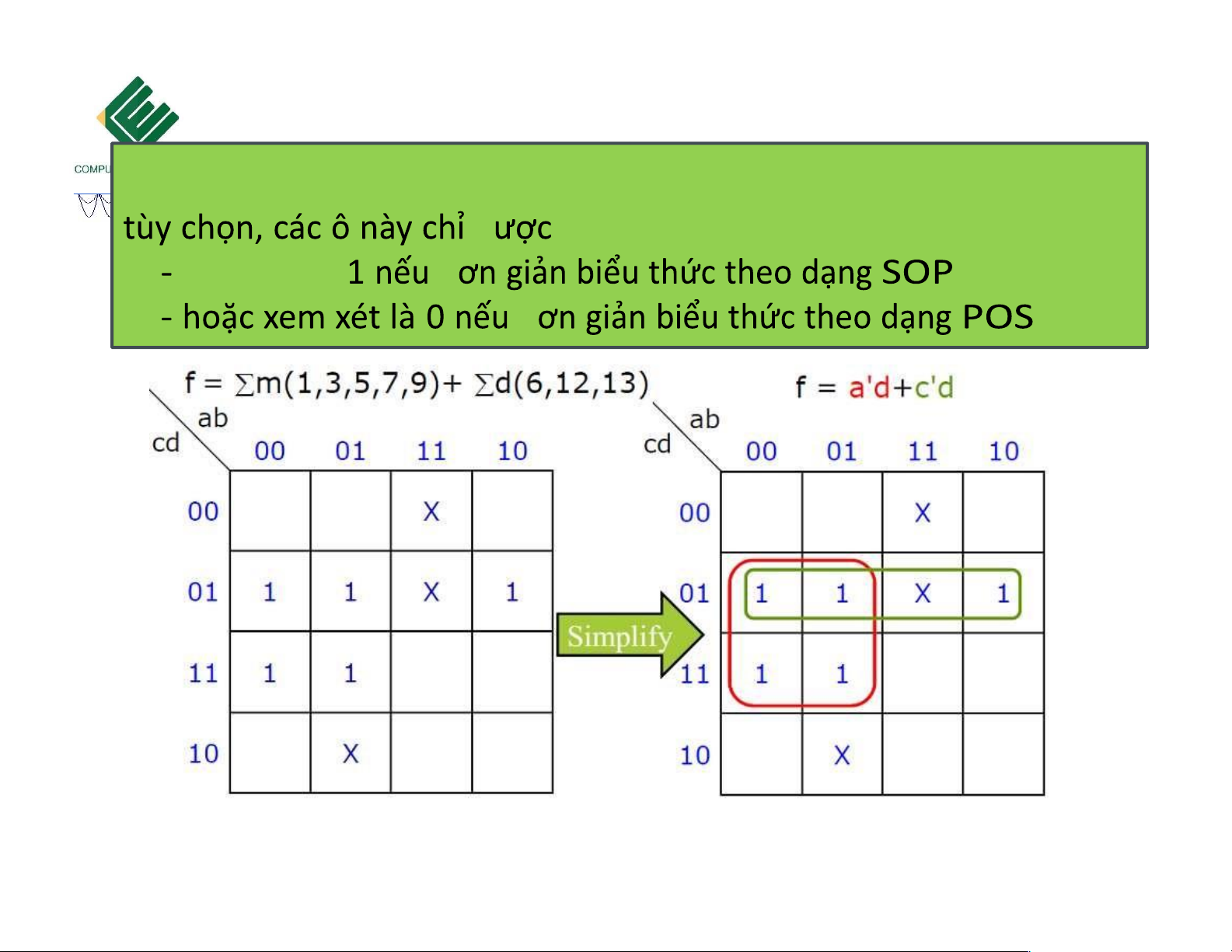
Biểu thức mang giá trị tùy ịnh xem xét là
Tất cả các ô 1 phải ược khoanh tròn, nhưng với ô có giá trị X thì 10/18/2023
Copyrights 2016 UIT-CE. All Rights Reserved. 32
Downloaded by Mai Mai (haumainbyma@gmail.com)