Mạch logic số - Tổ chức và Cấu trúc Máy tính II | Trường Đại học CNTT Thành Phố Hồ Chí Minh
Mạch logic số - Tổ chức và Cấu trúc Máy tính II | Trường Đại học CNTT Thành Phố Hồ Chí Minh được được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Tổ chức và cấu trúc máy tính
Trường: Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 39651089 CẤU TRÚC MÁY TÍNH Mạch Logic số 1 lOMoAR cPSD| 39651089 1
Cổng v Đại số Boole 1.1 Cổng
1.2 Đại số Boole 2
Biểudiễnmạch số qua hmBoole 3
Bản đồ Karnaugh 4
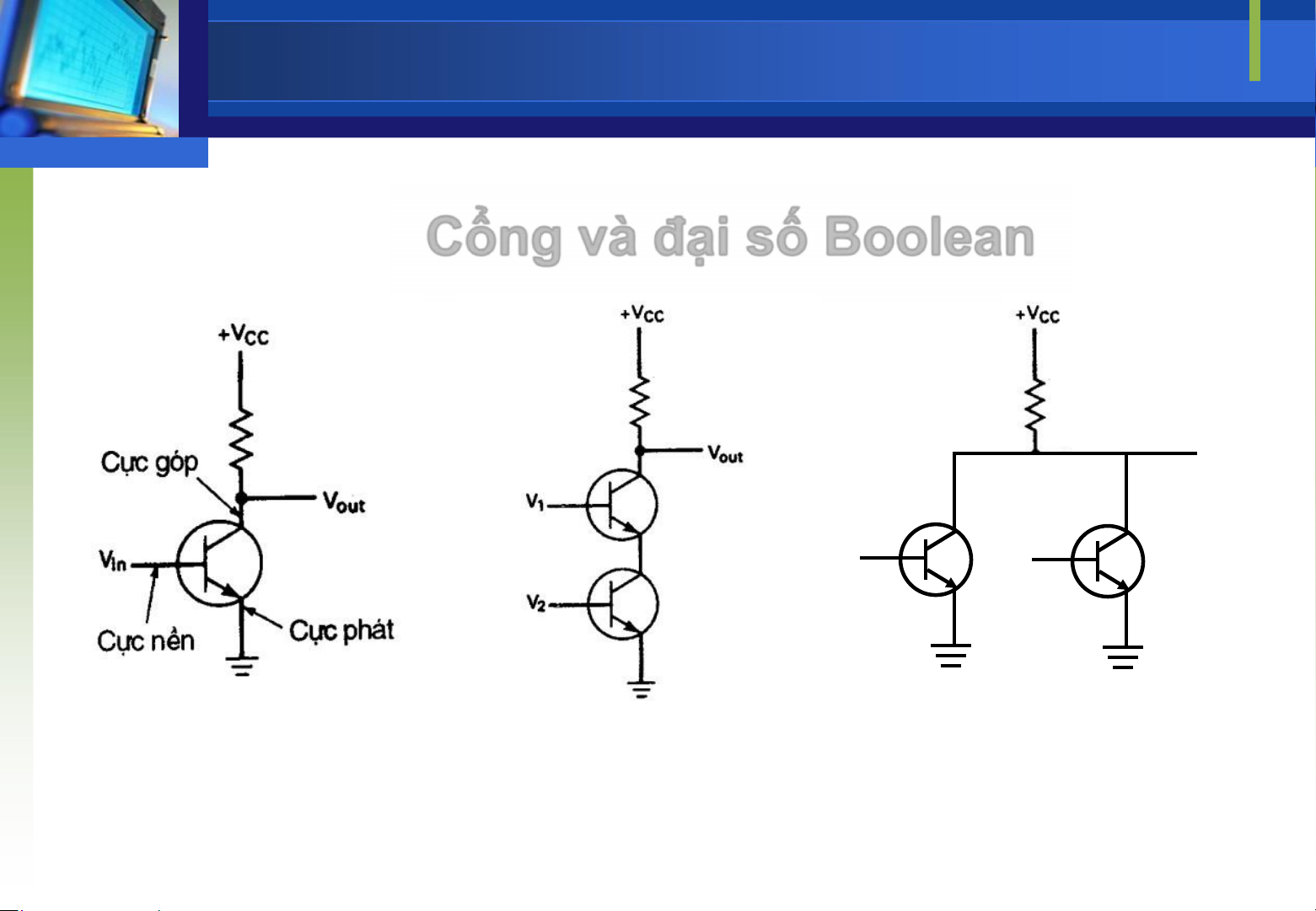
Nhữngmạch Logic số c ơbản Khoa CNTT Nội dung chi tiết 2 lOMoAR cPSD| 39651089 Cổng mộtmạch số g C ồm ổ m ng v ột à nhiềuạ i s hiệố u Boolea một n Là hiệu hay tín vào và tín ra . V out V 1 V 2
Mạchsố ược tạo ra từ cổngcơ hiệu tập hợp các bản, mỗicổngcơbản cóký riêngvà hoạt ộng của ược tả một bảng trị nó mô qua bảng gọi là chân lOMoAR cPSD| 39651089 A X
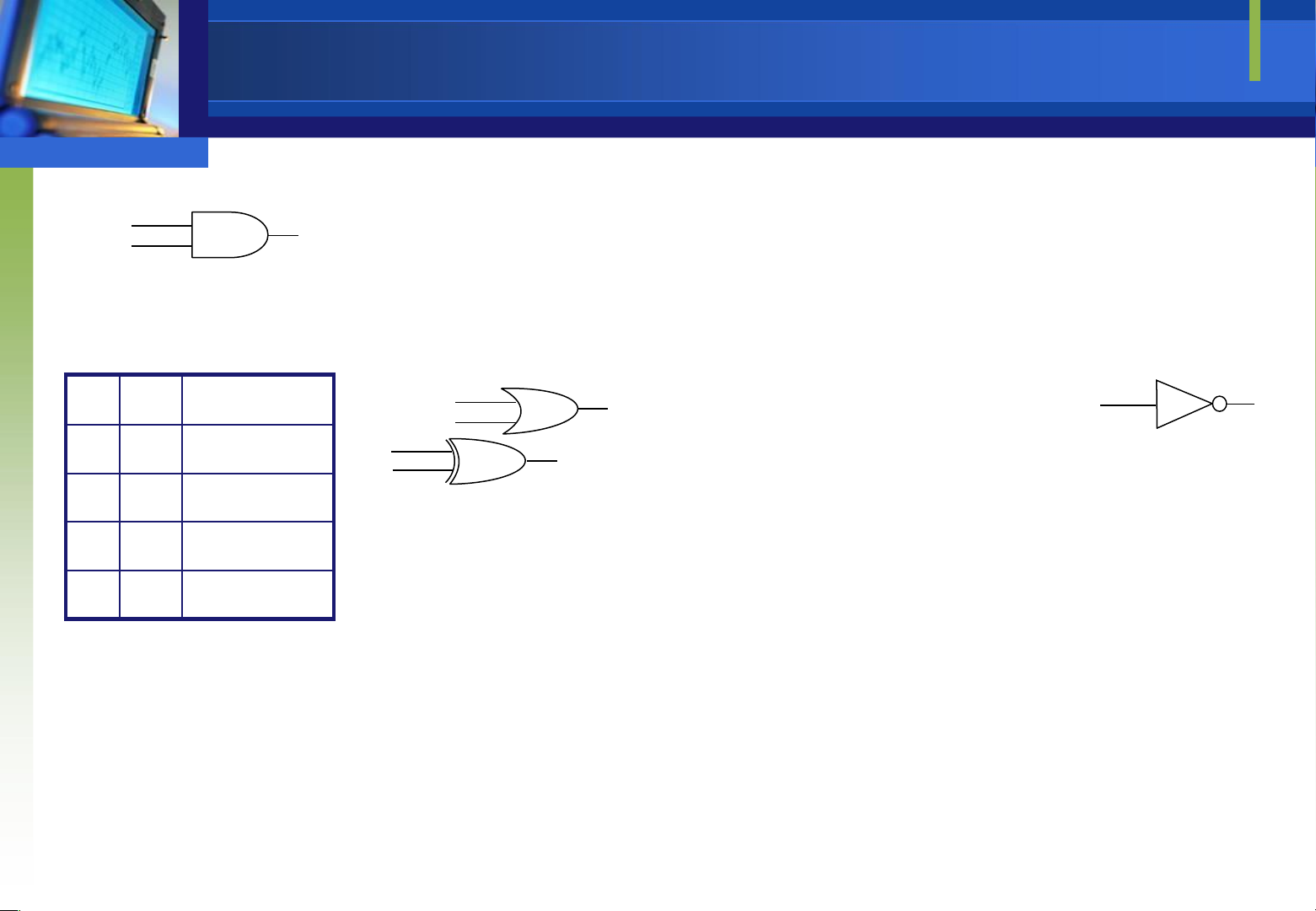
Các cổng cơ bản của logic số B AND A B A AND B A X A X 0 0 0 AB X 0 1 0 B 1 0 0 1 1 1 X=A.B lOMoAR cPSD| 39651089 OR N XOR O T A B A OR B A NOT A A B A XOR B 0 0 0 0 1 0 0 0 0 1 1 1 0 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 X=A+B X=A B X=A lOMoAR cPSD| 39651089 A
Các cổng cơ bản của logic số B A B A NAND B X AB X AB 0 0 1 0 1 1 X 1 0 1 NAND NOR NXOR 1 1 0 lOMoAR cPSD| 39651089 A B A NOR B A B A NXOR B 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 0 0 0 1 1 1 0 1 1
Các cổng NAND, NOR, NXOR là các cổng bù của các cổng
AND, OR, XOR tương ứng. Đây là các cổng cơ bản có ầu ra
nghịch ảo biểu diễn thêm một vòng tròn nhỏ ở ầu ra lOMoAR cPSD| 39651089 Đại số Boolean
Đại số Boolean là môn toán nghiên cứu các mệnh ề luận lý và
là công cụ toán học ể phân tích và tổng hợp các thiết bị mạch số.
Các biến và hàm trong ại số Boolean chỉ có thể nhận giá trị 1 hay 0.
Biến Boolean là biến biểu thị trạng thái của một giá trị iện thế
ta gọi là mức logic. Những trạng thái ó có thể biểu thị bằng các thuật ngữ: lOMoAR cPSD| 39651089 Logic 0 Logic 1 Sai Đúng Tắt Mở Không Có Thấp Cao Công tắc mở Công tắt óng 6
Các phép tính cơ bản của ại số Boolean
Hàm Boolean là hàm của các biến Logic và bản thân cũng chỉ nhận
các giá trị 0 hoặc 1. Thường chúng ta dùng hàm boolean ể biểu diễn
ầu ra của mạch số và các biến logic của hàm ó ể biểu diễn các ầu vào của mạch. lOMoAR cPSD| 39651089
Ba phép tính cơ bản của ại số Boolean
Phép phủ ịnh logic: NOT A
Ví dụ: phủ ịnh của A: NOT A hay Phép cộng logic: OR
Ví dụ: A cộng B ta ký hiệu: A OR B hay A+B Phép nhân logic: AND
Ví dụ: A nhân B ta ký hiệu AAND B hay A.B Các qui tắc Logic lOMoAR cPSD| 39651089
Qui tắc về phép cộng:
A+0 = A A+1 = 1 A+A = A A + = 1A
Qui tắc về phép nhân:
A.0 = 0 A.1 = A A.A = A A. = 0A
Qui tắc về phủ ịnh: A A= lOMoAR cPSD| 39651089 Hàm Logic lOMoAR cPSD| 39651089
Thường ta dùng hàm Boolean ể biểu diễn ầu ra của mạch
số, các biến logic chỉ cho ầu vào của mạch số
Bảng chân trị dùng ể biểu diễn mối quan hệ giữa hàm
Boolean và các biến logic của hàm ó. Ví dụ
Hàm y = A OR B hay y = A + B
Bảng liệt kê mọi tổ hợp có thể có của các A B y
biến logic A và B tượng trưng cho ầu vào 0 0 0
mạch số và các giá trị tương ứng ở ầu ra 0 1 1 y 1 0 1 1 1 1 lOMoAR cPSD| 39651089 Hàm Logic lOMoAR cPSD| 39651089 180ns lOMoAR cPSD| 39651089 Hàm Logic
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
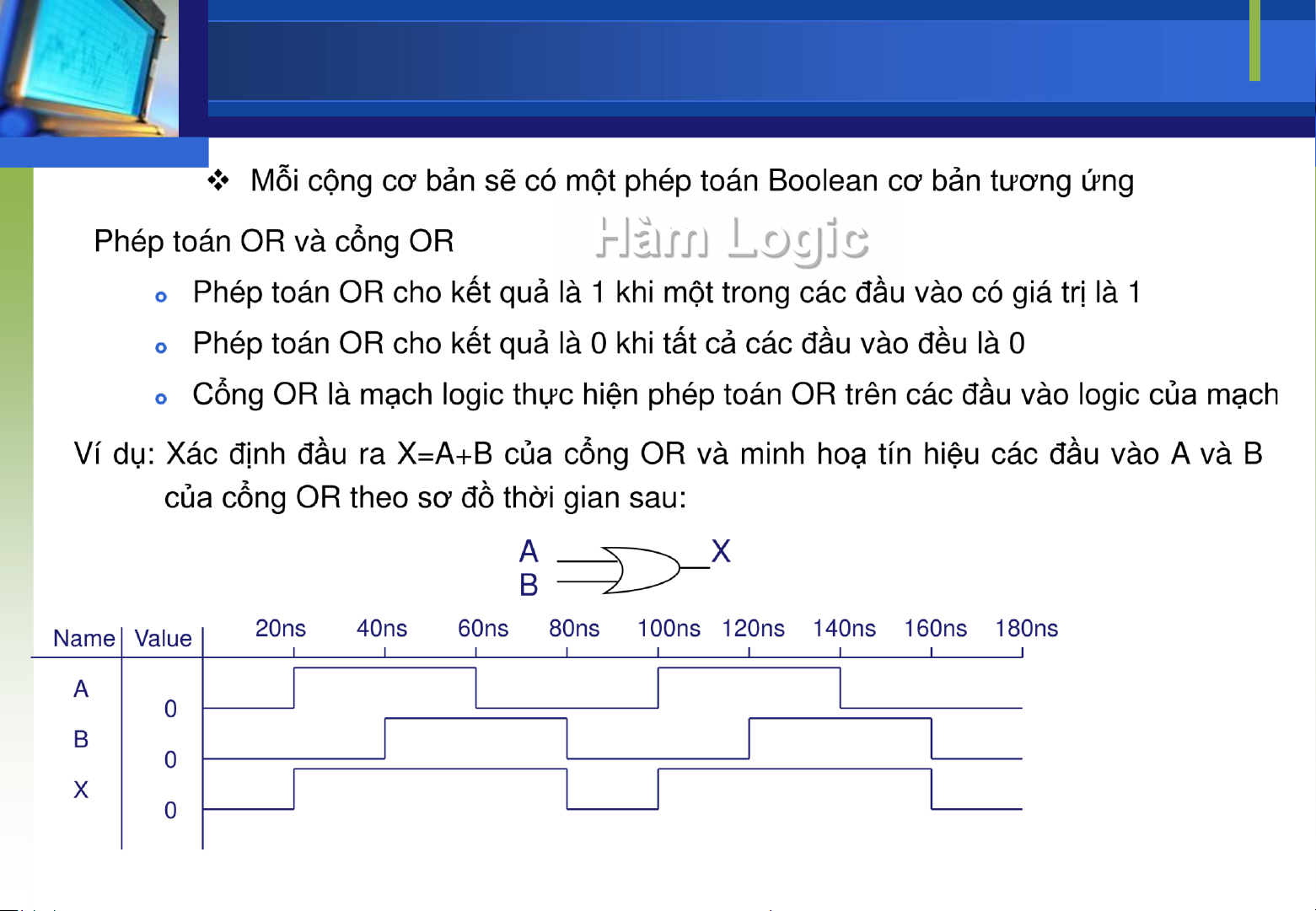
Mỗi cộng cơ bản sẽ có một phép toán Boolean cơ bản tương ứng
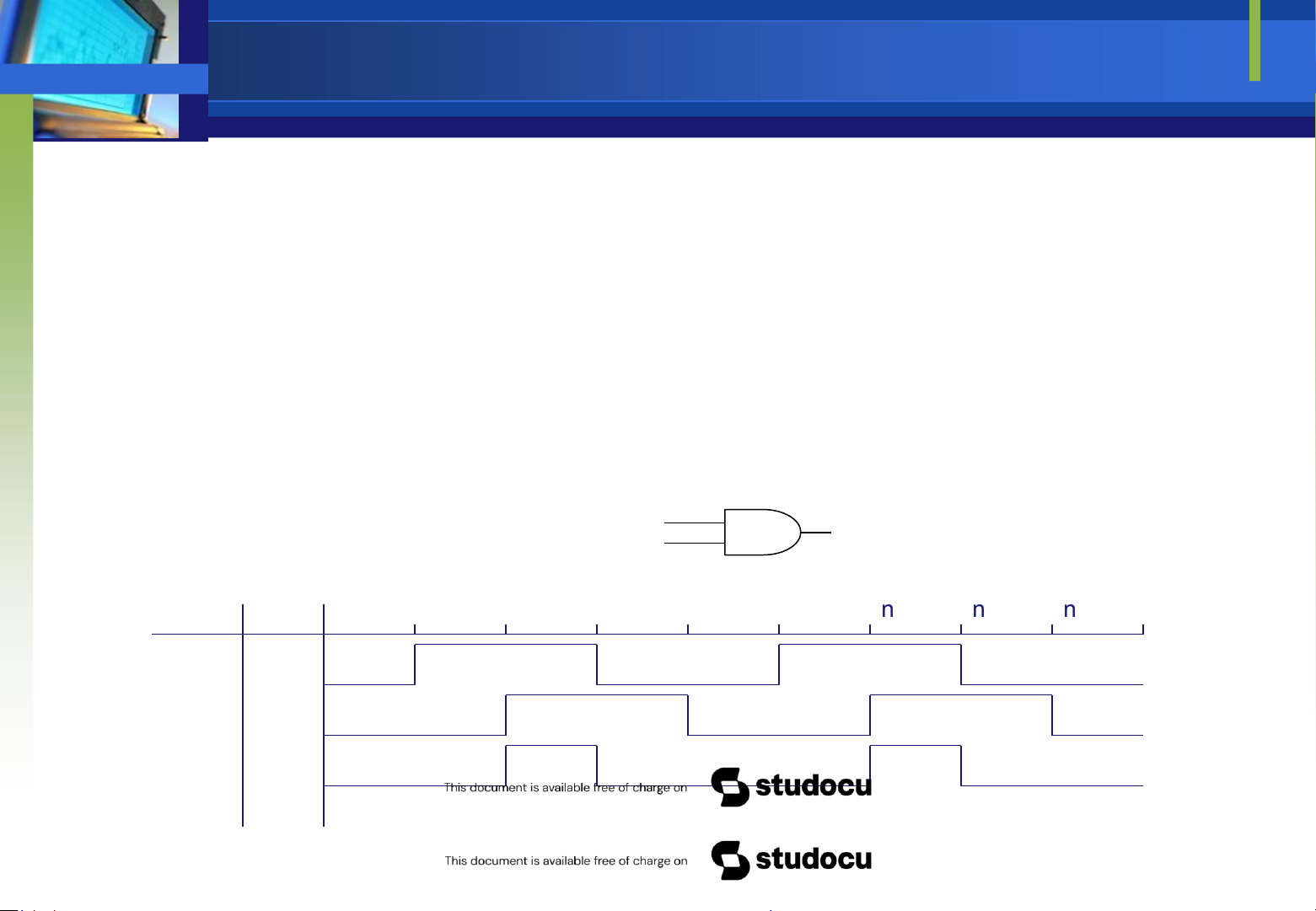
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Phép toán AND cho kết tất cả ầu ều trị quả là 1 khi các vào có giá là1 Phép toán AND cho kết một ầu trị quả là 0 khi trong các vào có giá bằng 0 Cổng AND là mạch thực hiện ầu của logic phép toán AND trên các vàologic Ví dụ ịnh của cổng hoạ hiệu ầu : Xác ầu ra X=A.B AND và minh tín các vàoAvàB Name 20 ns 40 ns 60 ns 80 ns 100 ns ns 120 ns 140 ns 160 180 ns Value A 0 B 0 X 0 Phép toán AND và Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 cổng AND mạch
của cổng AND theo sơ ồ thời gian sau: A X B
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Tên Dạng AND Dạng OR Định luật thống nhất 1A = A 0+A = A Định luật không 0.A = 0 1+A = 1 Định luật Idempotent A.A = A A + A = A Định luật nghịch ảo AA. = 0 A A + = 1 Định luật giao hoán A.B = B.A A+B = B+A Định luật kết hợp (AB).C = A.(BC) (A+B)+C = A+(B+C) Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Định luật phân bố
A+ B.C = (A+B)(A+C) A(B+C) = AB + AC Định luật hấp thụ A(A+B)= A A+AB = A Định luật De Morgan AB = A B+ A B AB+ = .
Các ịnh luật
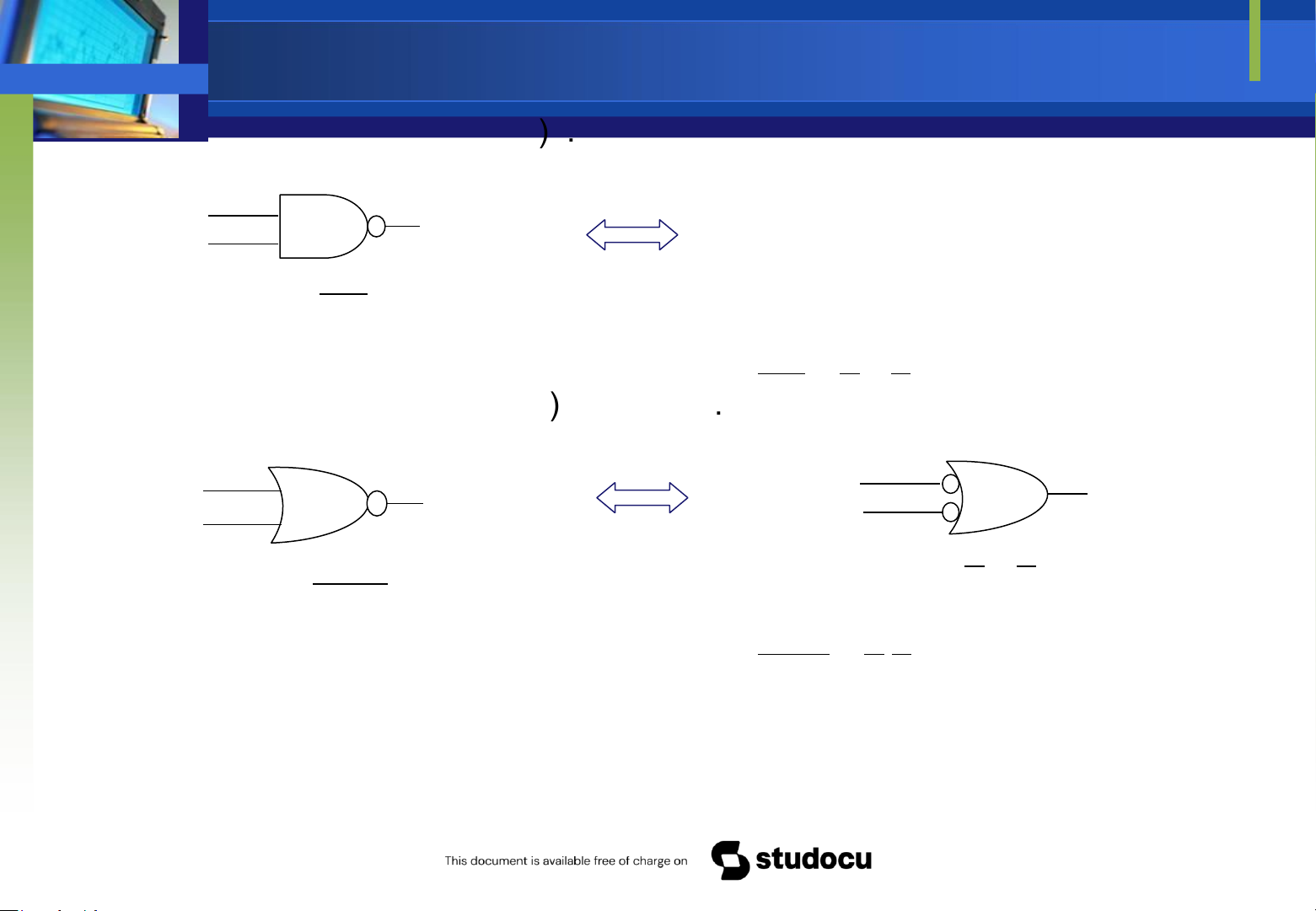
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 ) =+ . aABAB A X B Các cổng tương ương từ ịnh luật De Morgan ) += bABAB . A AX X B B
X AB= . X A B= + AX Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 B X AB= . X A B= +
Rút gọn mạch số bằng
ại số Boolean
Dùng ại số Boolean ơn giản các biểu thức sau
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 a)
Y=A+ABf) 𝑌=(𝐴+𝐵)(𝐴+𝐵)ҧ b Y ABD ABD) =
+ g) 𝑌 = 𝐴+𝐵 𝐵+𝐶 (𝐴+𝐶)ത
c) Y = (A B A B+ )( + )h) 𝑌 =𝐴𝐵𝐶+𝐴𝐵𝐶ҧ +𝐴𝐵𝐶+ത 𝐴𝐵𝐶ҧ d) Y= (BC AD AB
CD+ )( + ) i) 𝑌 =𝐴𝐵𝐶+𝐴𝐵𝐶+𝐴ҧ 𝐵𝐶𝐷ത
j) 𝑌 =𝐴𝐵+𝐴𝐶+𝐵𝐶ത
e) 𝑌 =𝐴+𝐴𝐵ҧ Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
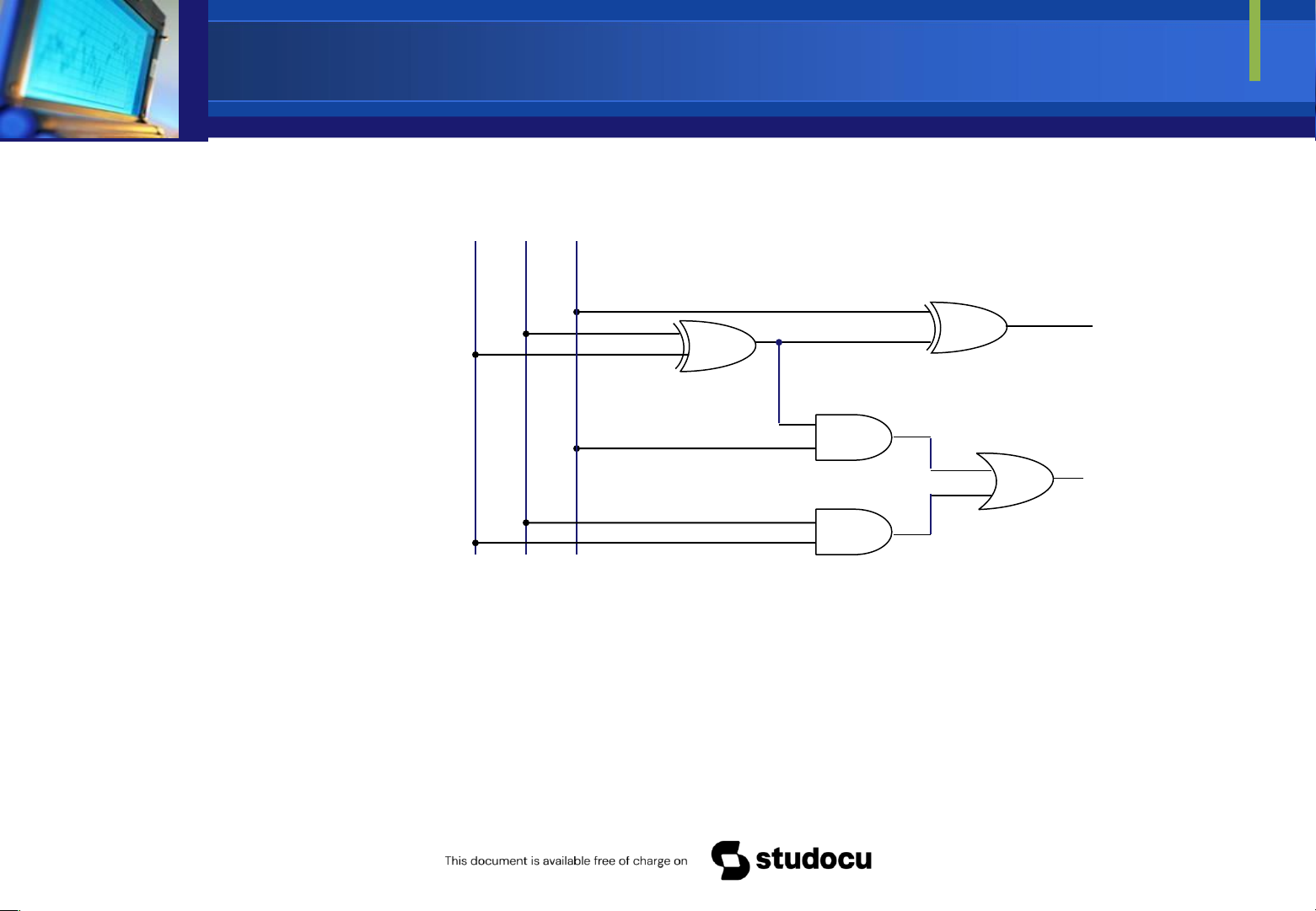
Rút gọn mạch số bằng ại số Boolean A B C D
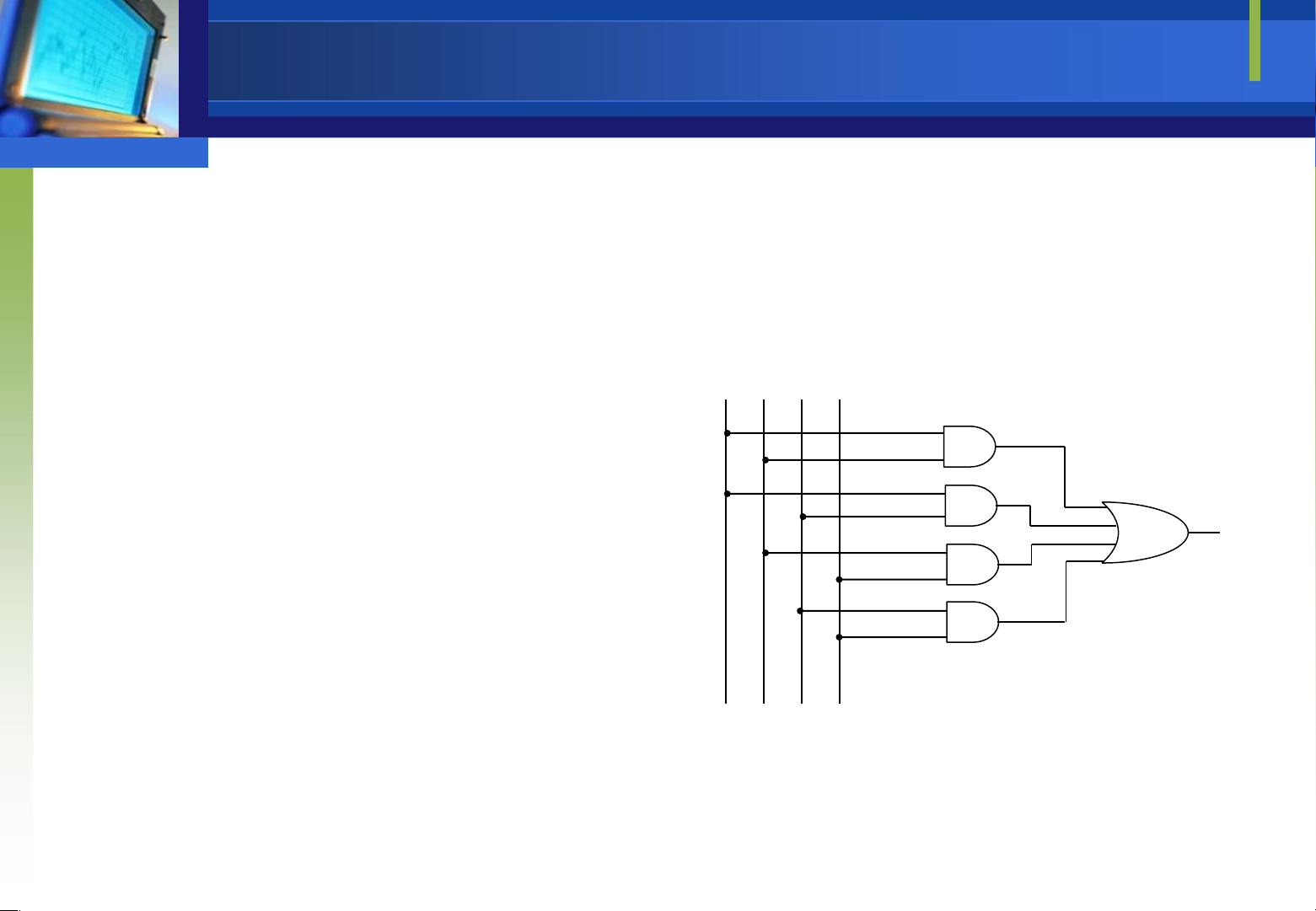
Ví dụ 3: Cho hàm như sau Y = AB + AC + DB + DC. Ta có mạch số sauY thể
Dùng ại số Boolean ta có
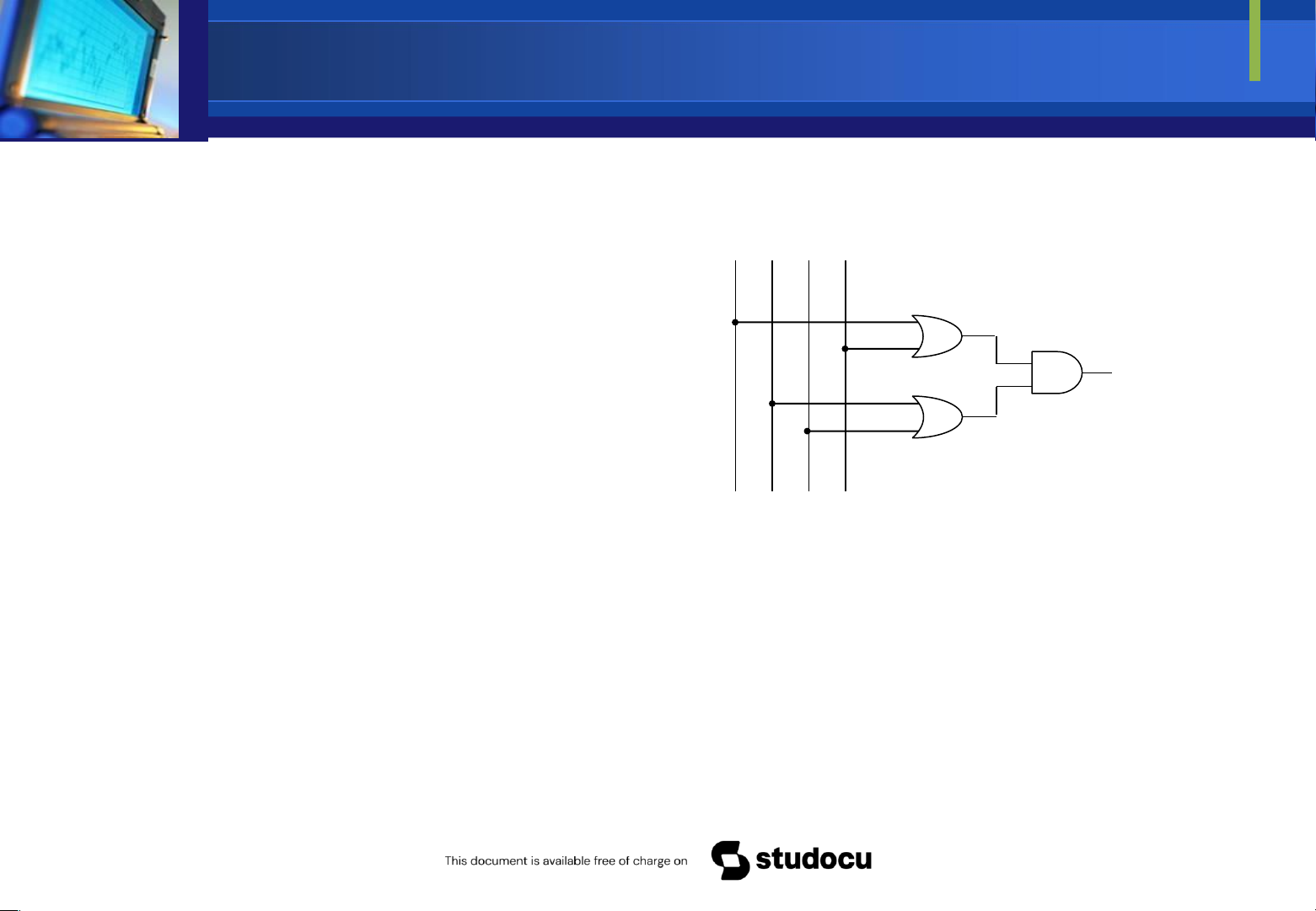
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 ơn giản hàm ã cho A B C D trên thành Y= (A+D)(B+C).
Biễu diễn thành mạch số sau: Y Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Biể
u diễn bằng phưng pháp ại số :
Sử dụng các biến Boolean và các phép toán + (or), . (nhân) , phép not, phép ( xor) ể biểu diễn Ví dụ = + + : FABCABCAC
Biểu diễn bằng bảng chân trị
Liệt kê một danh sách 2n tổ hợp các giá trị 0 và 1 của các biến Boolean
và một cột chỉ ra giá trị của hàm A B C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0
Biễu diễn mạch số1 qua 1 hàm 0 B 1 oolean 1 1 1 1
Downloaded by Mai Mai (haumainbyma@gmail.com) 16 lOMoAR cPSD| 39651089
Biểu diễn bằng hàm Boolean dạng chuẩn 1 n Tích chuẩn m 1): i (0<=i<2 -
là tích số ầy ủ của n biến mà hàm Boolean phụ thuộc
với qui ước biến ó ở dạng bù nếu nó là 0 và không bù nếu nó là 1.
Với hàm có n biến có thể tạo ra 2n tích A B C Minterms chuẩn 0 0 0 m = 0 ABC 0 0 1 mABC = 1
Ví dụ : Hàm Boolean với 3 biến 0 1 0 mA2 BC = 0 1 1 m = 3 ABC 1 0 0 mAB C = 4 1 0 1 m = 5 ABC 1 = 1 0 m 6 ABC 1 = 1 1 mABC 7
Biễu diễn mạch số qua hàm Boole an Downloaded by Mai Mai (haumainbyma@gmail.com) 17 lOMoAR cPSD| 39651089
Biểu diễn bằng hàm Boolean dạng chuẩn 1 HàmBoolean dạng ượcbiểu chuẩn 1 làhàm
diễn dạng tổng cácminterm mà tại trị ó hàmcógiá 1. Viếttổng 21n − quát dạng chuẩn 1: F mF = i . i i= 0 Trong ó - là minterm thứ i m i -
là giá trị của hàm F tương ứng với minterm thứ i F i
Biễu diễn mạch số qua hàm Boolean
Downloaded by Mai Mai (haumainbyma@gmail.com) 18 lOMoAR cPSD| 39651089
Ví dụ biểu diễn bằng hàm Boolean dạng chuẩn 1 Ch
o hàm Boolean có bảng chân trị sau
Hàm F dạng chuẩn 1 ược viết : A B C F = + + 0 FABCABCABCABCA BCABC + + ( ,, ) 0 0 1 0 0 1 0
Hoặc ược viết dạng khác là: 0 1 0 1 F(A,B,C)=m 0 m + + + + 2 m 3 m 6 m 7 0 1 1 1 1
Hoặc ược viết dạng ơn giản hơn là: 0 0 0 1 0 1 0 F ( , ABC , ) = (0,2,3,6,7) 1 1 0 1 1 1 1 1
Biễu diễn mạch số qua hàm Boolean Downloaded by Mai Mai (haumainbyma@gmail.com) 19 lOMoAR cPSD| 39651089
Biểu diễn bằng hàm Boolean dạng chuẩn 2 Tổng chuẩn n M 1): i (0<=i<2 -
là tổng số ầy ủ của n biến mà hàm Boolean phụ thuộc
với qui ước biến ó ở dạng bù nếu nó là 1 và không bù nếu nó là 0.
Với hàm có n biến có thể tạo ra 2n tổng A B C Maxterms chuẩn 0 0 0 MABC =++ 0 0 0 1 MABC =++ 1 0 1 0 MABC =++ 2
Ví dụ : Hàm Boolean với 3 biến 0 1 1 M =++ ABC 3 1 0 0 MABC =++ 4 1 0 1 M =++ ABC 5 1 1 0 M =++ ABC 6 1 1 1 MABC =++ 7
Downloaded by Mai Mai (haumainbyma@gmail.com)
Biễu diễn mạch số qua hàm Boolean 20 lOMoAR cPSD| 39651089
Biểu diễn bằng hàm Boolean dạng chuẩn 2 HàmBoolean dạng ượcbiểu chuẩn 2 làhàm
diễn dạng tíchcácmaxterm mà tại trị ó hàmcógiá 0. Viếttổng quát dạng chuẩn 2: 21n − F = ( MF + i i ) i= 0 Trong ó - là maxterm thứ i M i -
là giá trị của hàm F tương ứng với maxterm thứ i F i 21 Biễu
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
diễn mạch số qua hàm Boolean
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Ví dụ biểu diễn bằng hàm Boolean dạng chuẩn 2
Cho hàm Boolean có bảng chân trị sau
Hàm F dạng chuẩn 2 ược viết : A B C F F( =++ ++ ++ 0 A ,, B CAB ) C ( ABCABC )( )( ) 0 0 1 0
Hoặc ược viết dạng khác là: 0 1 0 0 1 0 1 F(A,B,C)= M 1.M .M 4 5 0 1 1 1
Hoặc ược viết dạng ơn giản hơn là: 1 0 0 0 1 0 1 0 F ( , ABC , ) = ,4, (1 5) 1 1 0 1 1 1 1 1 22 Biễu
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
diễn mạch số qua hàm Boolean
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Trường hợp tuỳ ịnh (don’t care)
Là trường hợp mà tại tổ hợp biến ó giá trị của hàm không xác
ịnh. Trong trường hợp này ở dạng chuẩn 1 ta dùng ký hiệu d, còn ABC F
dạng chuẩn 2 ta dùng ký hiệu D 000 X 001 0
Ví dụ: Hàm F ược cho dưới dạng bảng chân trị sau: 010 1 011 1
Hàm F có bảng chân trị bên sẽ ược biểu diễn 100 0 theo 2 dạng chuẩn: 101 1 110 0 F = (2,3,5)+d(0,7) 111 X Hay
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 F = (1,4,6).D(0,7)
Biểu diễn mạch số logic của hàm Boolean
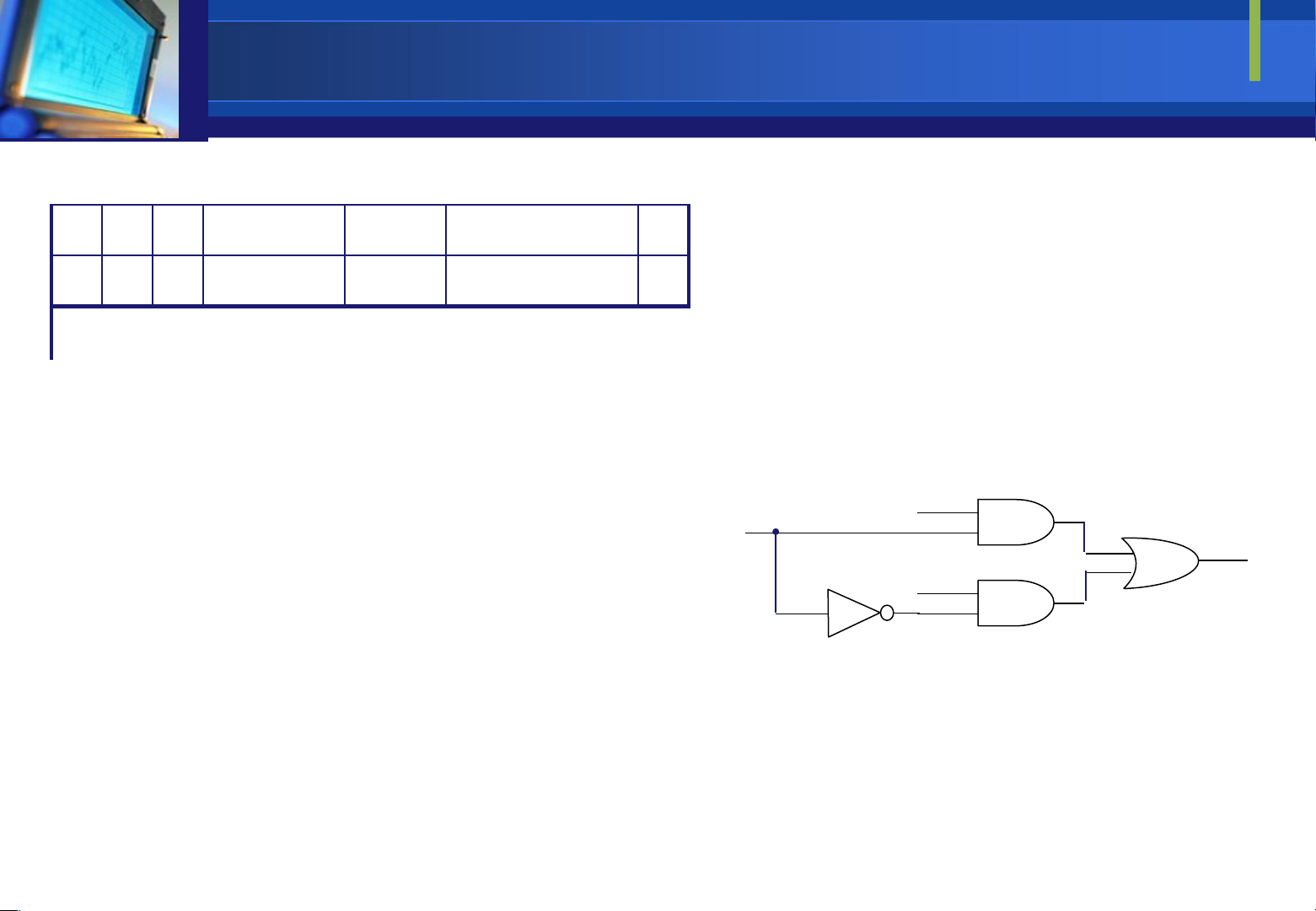
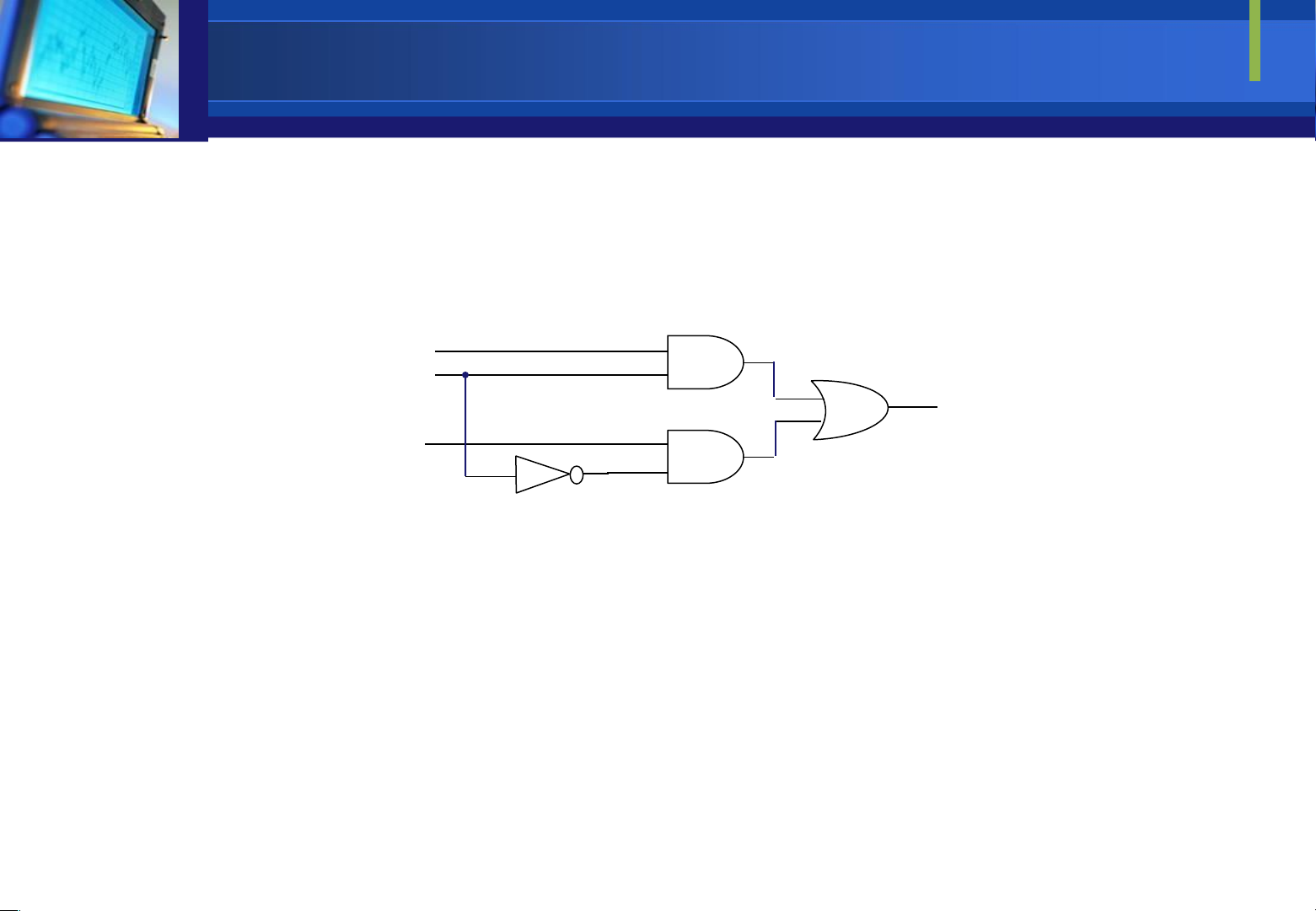
Ví dụ 1: Dùng bảng chân trị ể biểu diễn hàm f = (A and B) or
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 (
A B C A and B Not B C and not B f 0 0 0 0 1 0 0 0 0 1 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 1 1 1
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 1 1 0 1 0 0
1 C and not B). Vẽ sơ ồ mạch số 1 1 1 1 0 0 1 cho hàm
Ta thấy hàm f có các biến ầu
vào là A,B và C. Do ó ta có bảng chân trị 8 dòng cho tổ hợp biến như sau: A C B f
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Biểu diễn mạch số logic của hàm Boolean
Ví dụ 2: Để làm bộ báo biểu cho lái xe biết một số iều kiện người ta thiết kế 1 mạch báo ộng như sau: Cửa lái Tín hiệu: Báo ộng Cửa lái A: 1-mở, 0-óng Mạch Bộ phận ánh lửa logic
Bộ phận ánh lửa B: 1-bật, 0-tắt Đèn pha Đèn pha C: 1-bật, 0-tắt
Hãy thiết kế mạch logic với 3 ầu vào và 1 ầu ra sao cho bộ phận báo ộng hoạt
ộng (báo ộng=1) khi tồn tại 1 trong 2 trạng thái sau:
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
-Đèn pha sáng trong lúc bộ phận ánh lửa tắt
-Cửa mở trong lúc bộ phận ánh lửa hoạt ộng A B f C
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh
Ý nghĩa của bản ồ Karnaugh
Bản ồ Karnaugh là phương tiện biểu diễn mối quan hệ giữa các giá trị logic của biến
ầu vào và giá trị ầu ra tương ứng của hàm Boolean
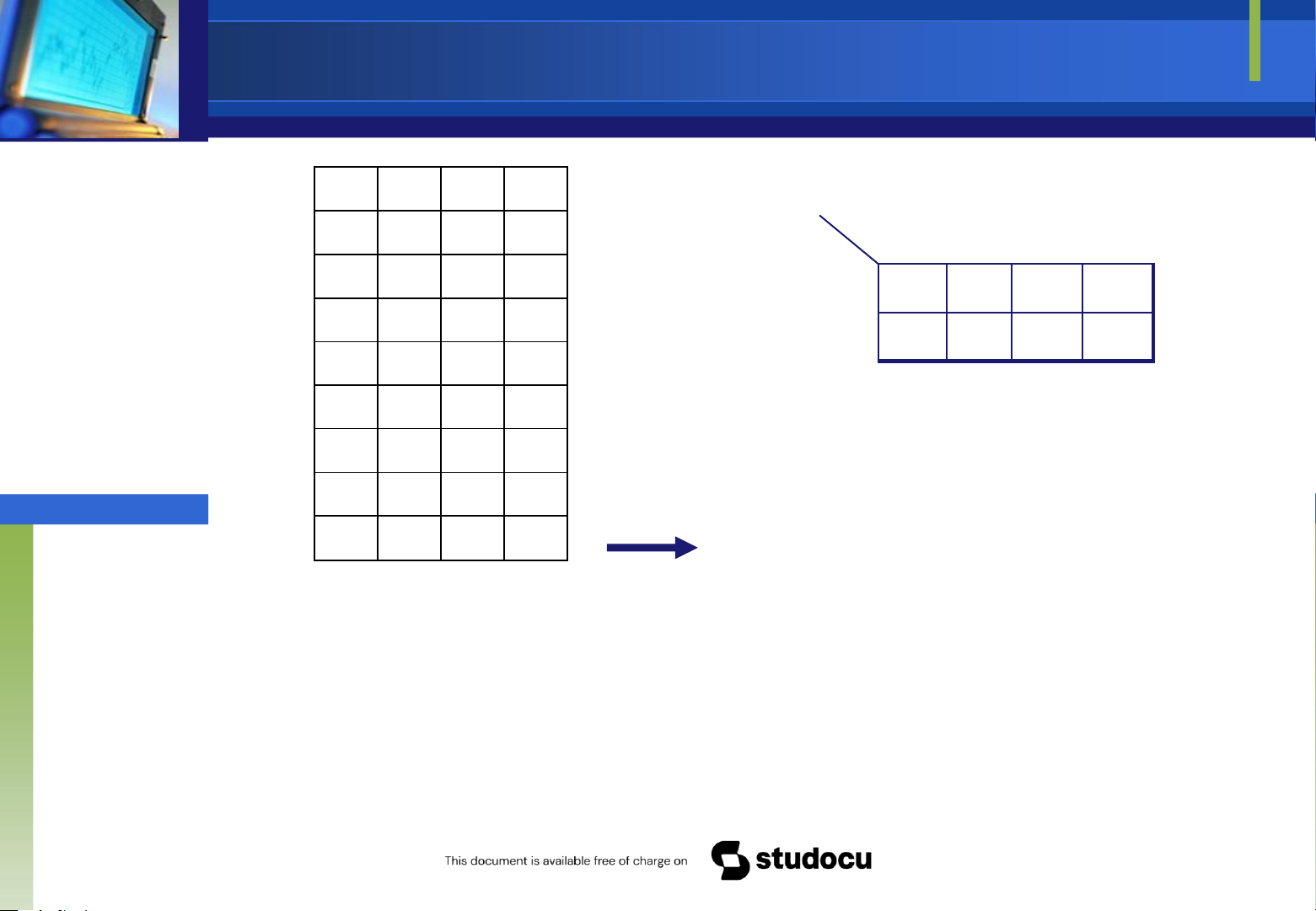
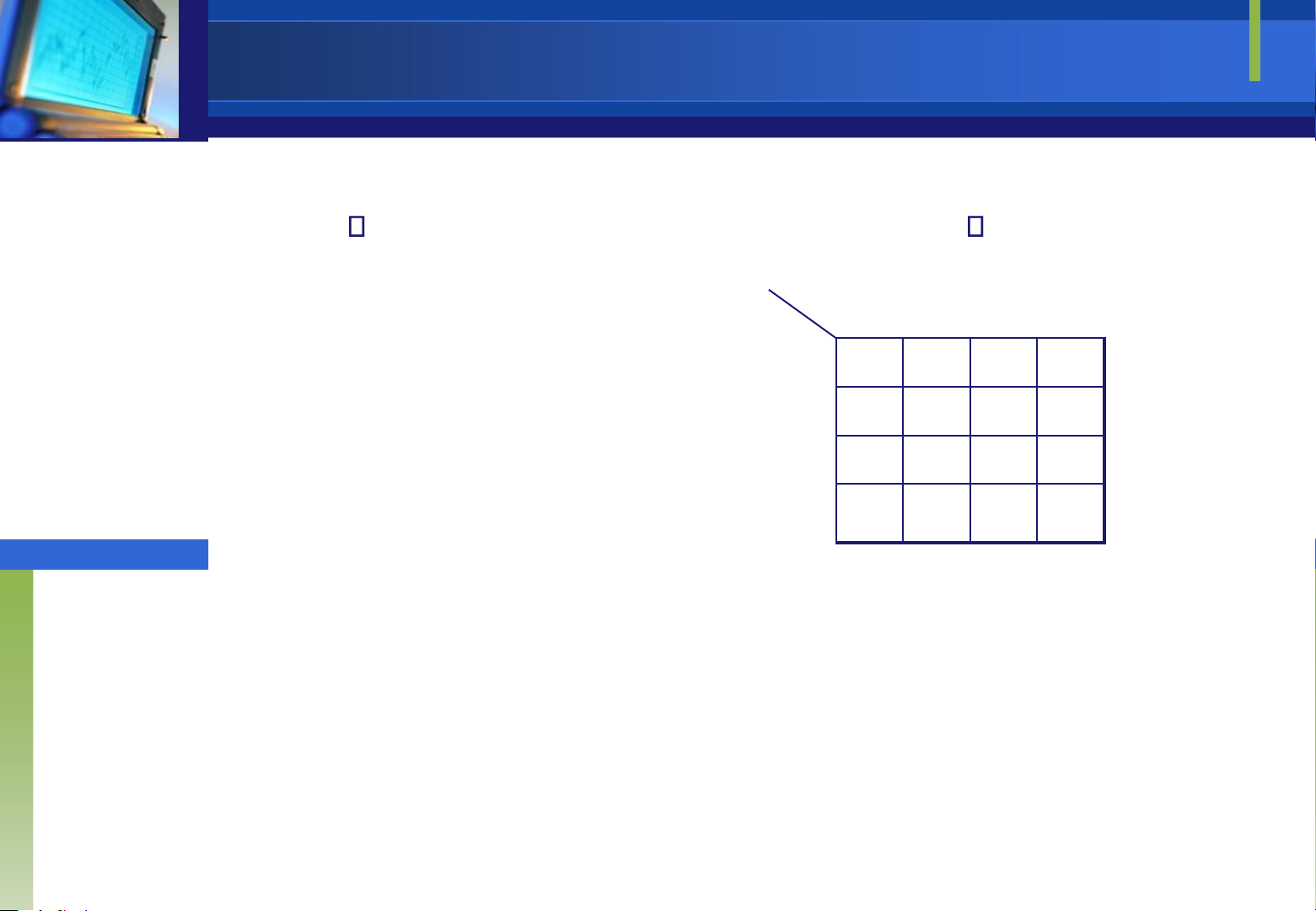
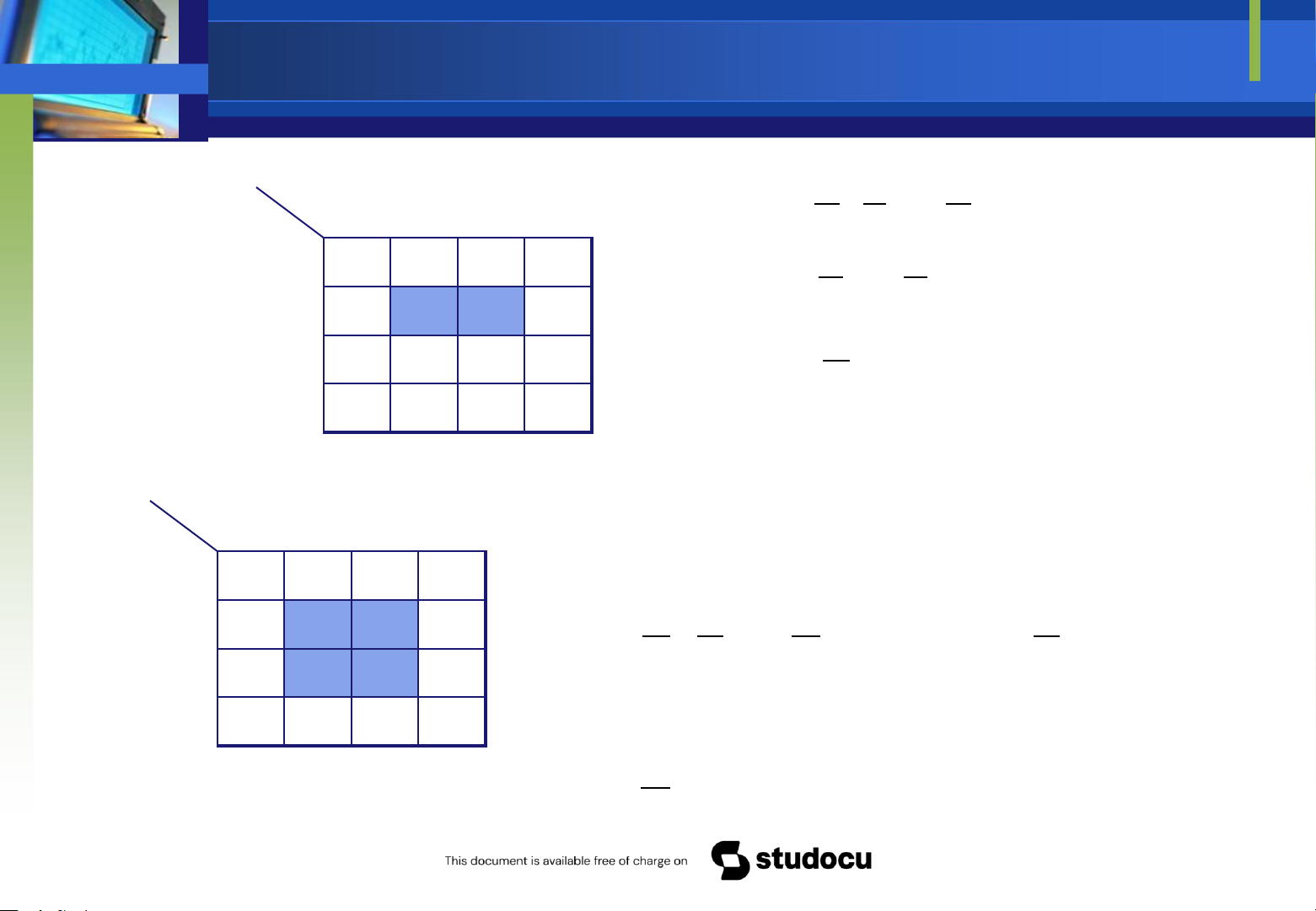
Các dạng bản ồ Karnaugh ơn giản Bản ồ K 2 biến Bản ồ K 3 biến Bản ồ K 4 biến CD 00 01 11 10 AB 00 0 1 3 2 BC A 01 00 01 11 10 4 5 7 6 0 0 1 3 2 11 12 13 15 14 1 10 8 F 4 5 7 6 F 9 11 10
Downloaded by Mai Mai (haumainbyma@gmail.com) 0 lOMoAR cPSD| 39651089 0 1 1 2 3 Bản ồ Karnaugh
Bản ồ Karnaugh là phương pháp biểu diễn hàm Boolean thích hợp cho
việc rút gọn hàm. Mỗi ô của bản ồ biểu diễn một giá trị của hàm (0,1,X) tương
ứng với giá trị 1 hàng trong bảng chân trị
Biểu diễn hàm Boolean trên bản ồ Karnaugh
Chuyển từ bảng chân trị sang bản ồ Karnaugh Giả sử hàm Y bảng chân trị sau: Y A B Y B 0 0 1 A 0 0 0 0 0 1 1 1 0 1 1 1 0 0 1 1 1
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh A B C F 0 BC 0 0 0 A 00 01 11 10 0 0 1 0 0 0 0 1 1 0 1 0 1 1 0 F 0 0 0 1 1 1 1 1 0 0 0 Biểu 1
diễn hàm Boolean trên bản ồ 0 1 0 Karnaugh 1 1 0 1 1 1 1 0 Biểu diễn
hàm F dạng chuẩn 1 vào bản ồ Karnaugh
Nếu cho một hàm F dạng chuẩn 1 thì iền 1 vào các ô có số thứ tự tương ứng với
các tích chuẩn, iền x vào các ô ứng với trường hợp tuỳ ịnh và iền 0 cho các ô còn lại. Ví dụ
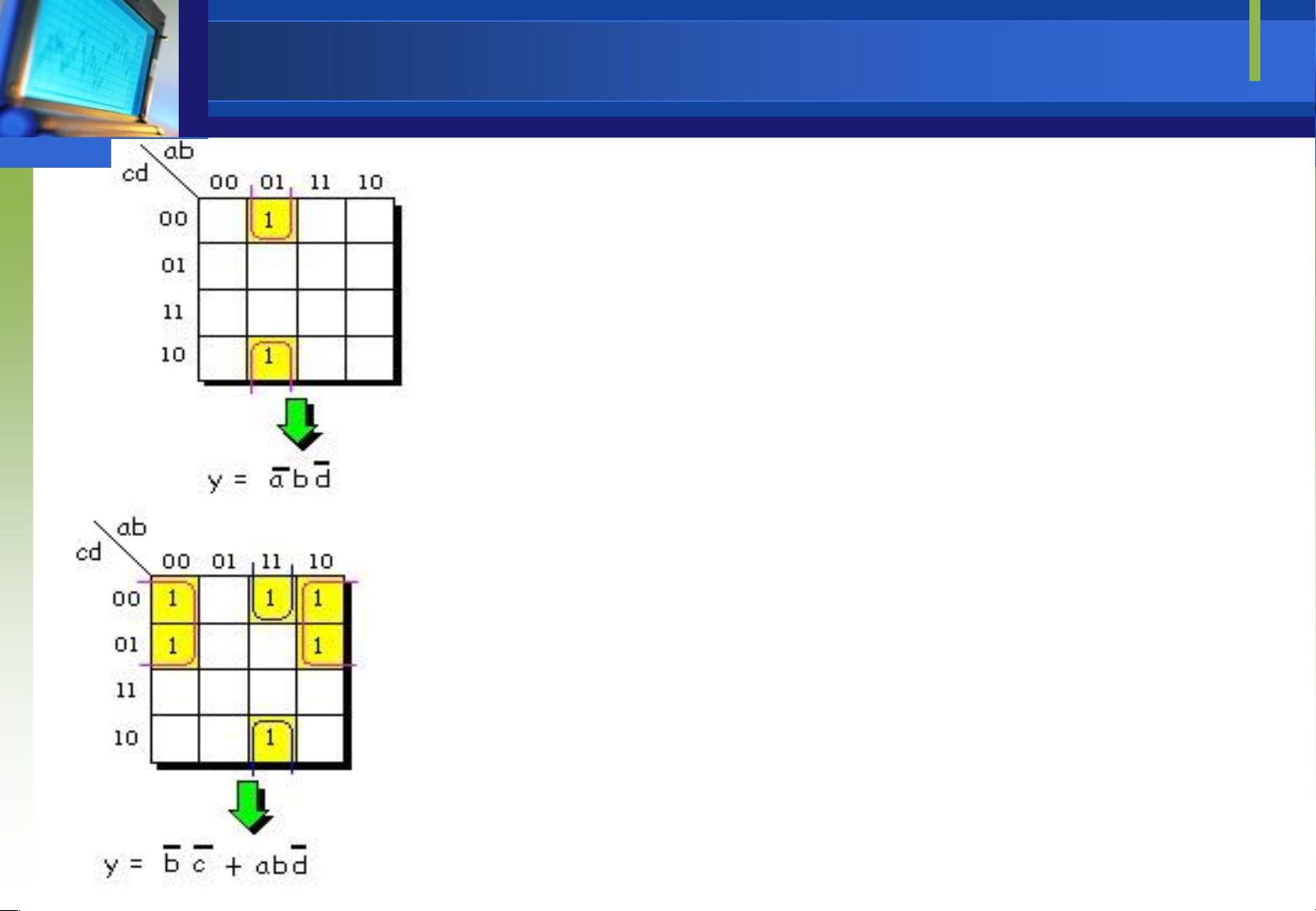
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh
Cho hàm F(A,B,C,D)= (0,2,3,4,6,7,9,13)
Cho hàm F(A,B,C,D)= (0,1,3,4,7,9,10)+d(2,5) F CD AB 00 01 11 10 00 1 1 1 x 01 1 x 1 0 11 0 0 0 0 10 0 1 0 1
Biểu diễn hàm Boolean trên bản ồ Karnaugh
Biểu diễn hàm F dạng chuẩn 2 vào bản ồ Karnaugh
Nếu cho một hàm F dạng chuẩn 2 thì iền 0 vào các ô có số thứ tự tương ứng với
các tổng chuẩn, iền X vào các ô ứng với trường hợp tuỳ ịnh và iền 1 vào các ô còn lại Ví dụ
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh
Cho hàm F(A,B,C,D)= (3,4,5,7,12,13) F CD 00 01 11 10
Cho hàm F(A,B,C,D)= (2,4,6,7,12)+D(0,3) AB 00 0 0 0 0 F CD 01 0 1 1 0 00 01 11 10 AB 11 0 0 0 0 00 X 1 X 0 10 0 0 0 0 01 0 1 0 0 11 0 1 1 1 F CD 10 1 1 1 1 00 01 11 10 AB Ô kế cận 00 0 0 0 0
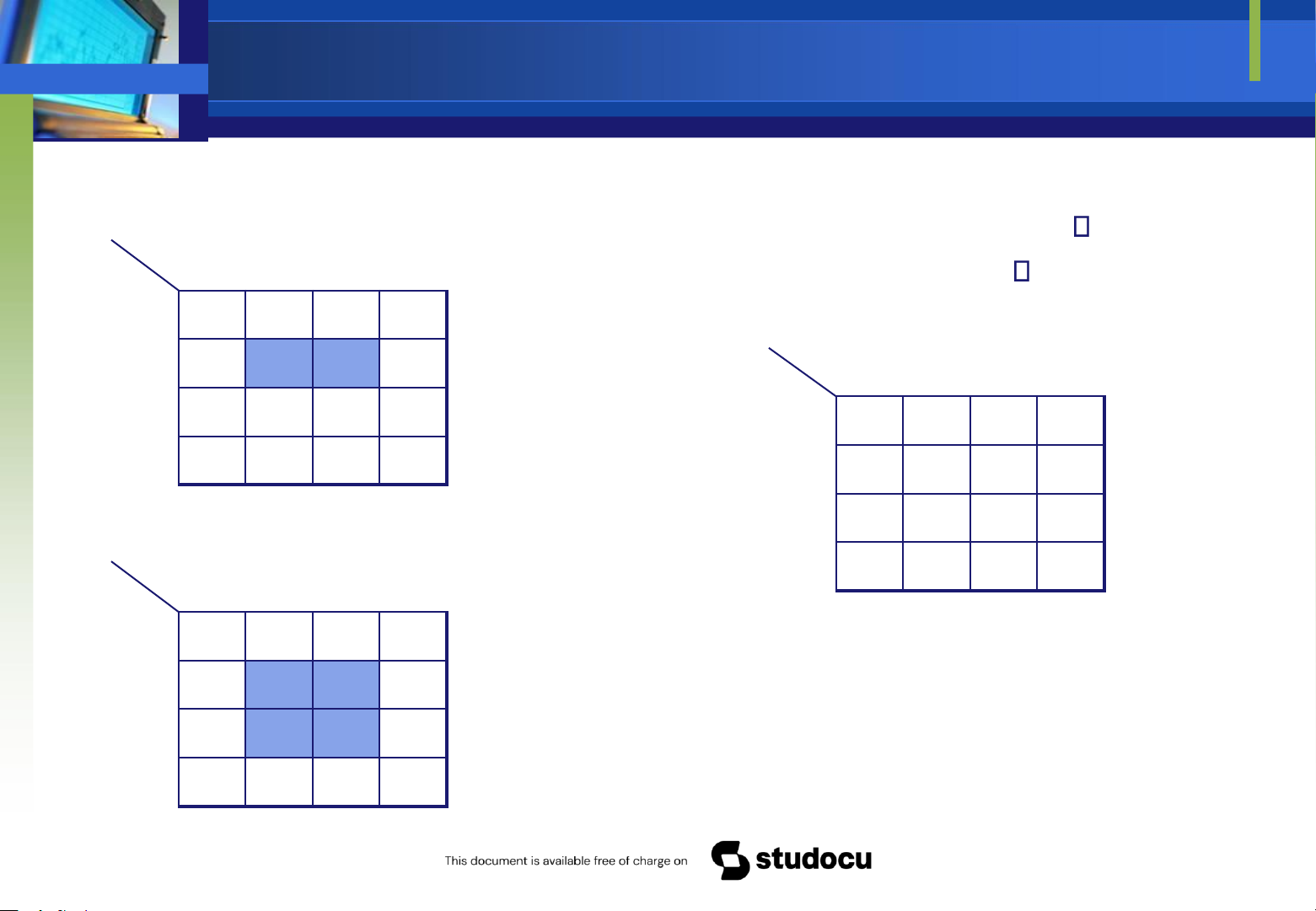
Hai ô ược gọi kế cận nhau là hai ô mà khi ta chuyển từ 01 0 1 1 0
ô này sang ô kia chỉ làm thay ổi giá trị của một biến 11 0 1 1 0 10 0 0 0 0
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh F CD F CD 00 01 11 10 AB 00 01 11 10 AB 00 1 0 0 0 00 0 0 0 0 01 0 1 1 0 01 1 1 1 0 11 0 0 0 0 11 1 0 0 0 10 1 0 0 0 10 0 0 0 0 F F CD CD 00 01 11 10 AB 00 01 11 10 AB 00 0 0 0 0 00 1 0 0 1 01 0 1 1 0 01 0 1 1 0 11 1 1 1 1 11 0 1 1 0 10 0 0 0 0 10 1 0 0 1
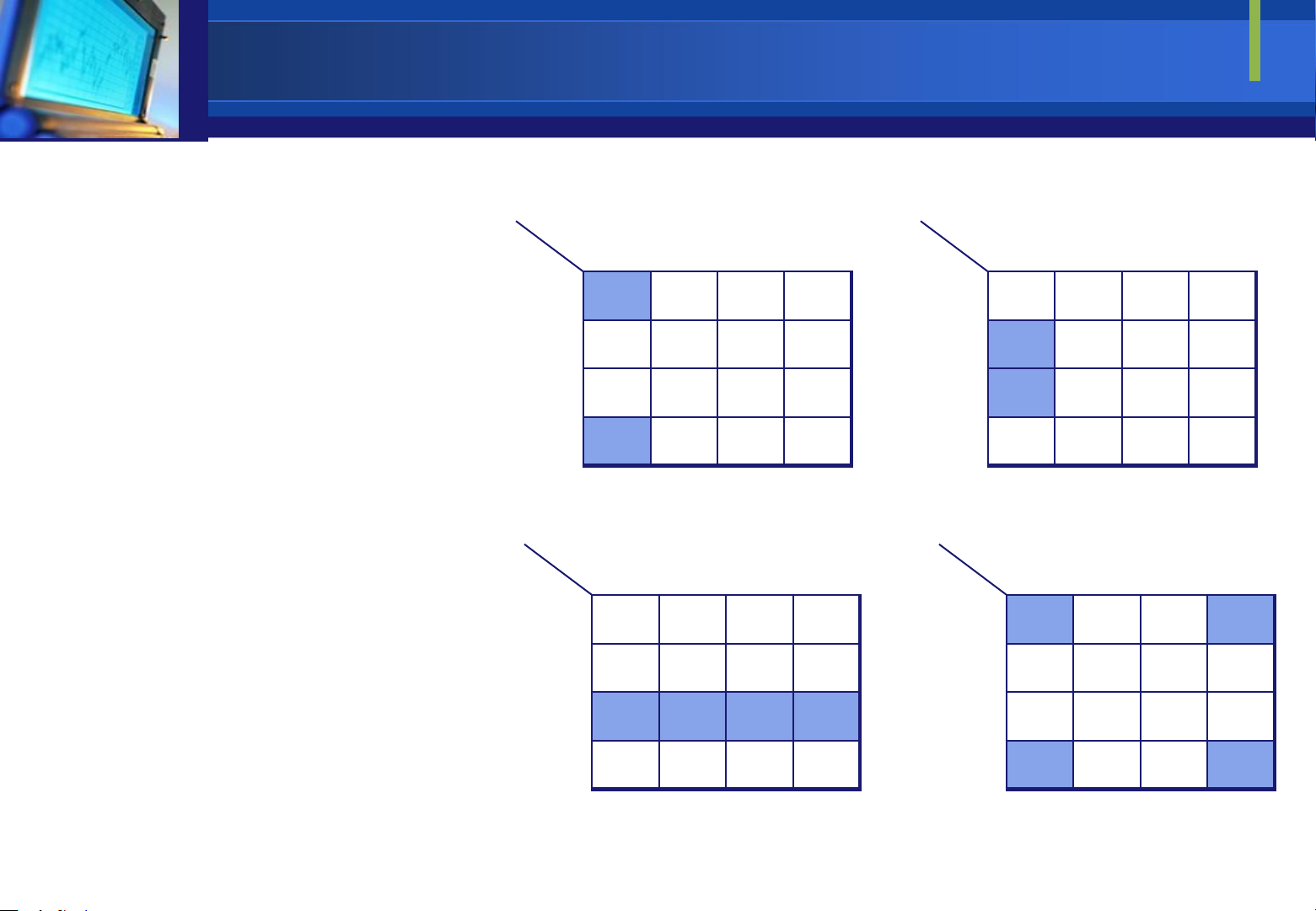
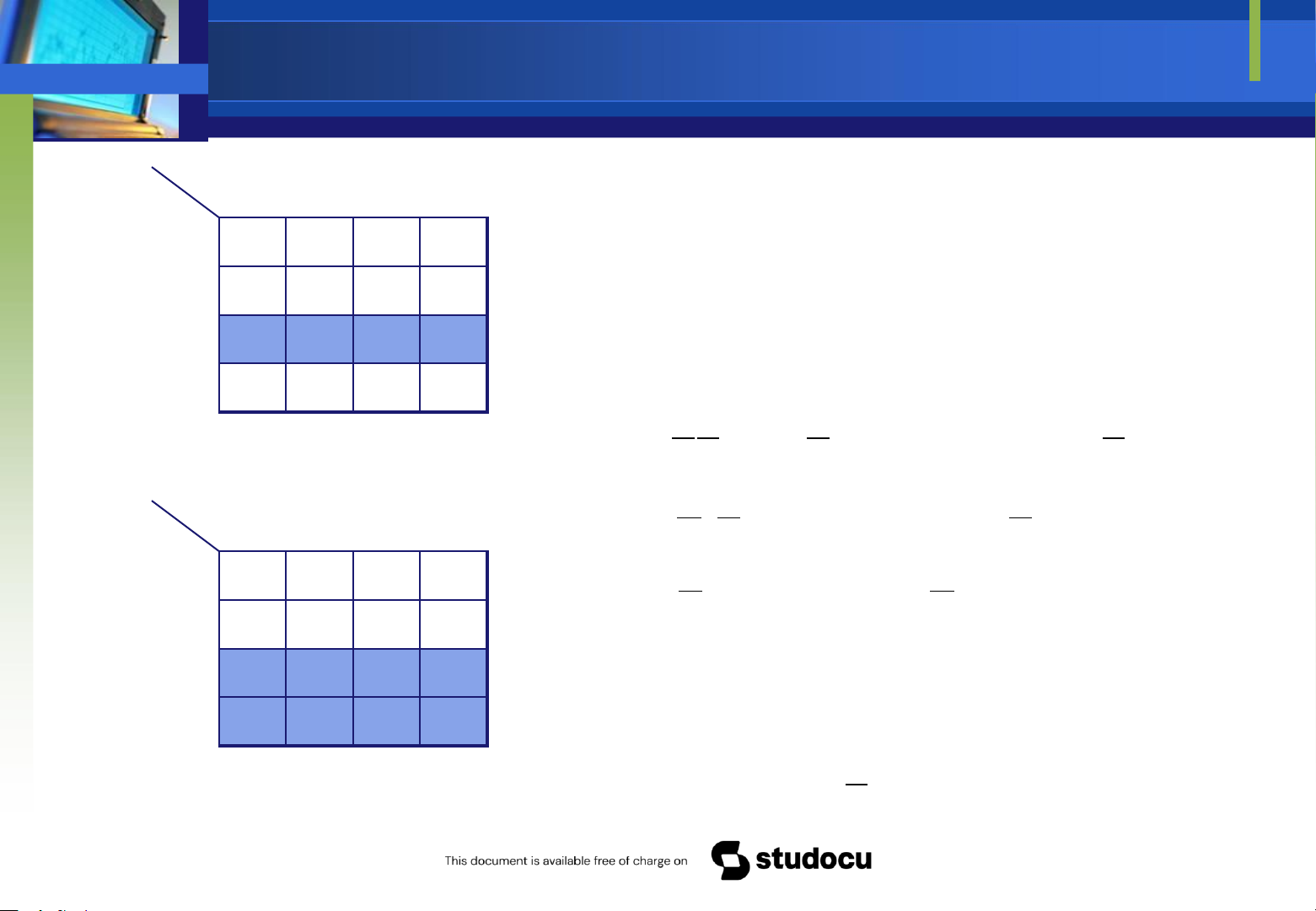
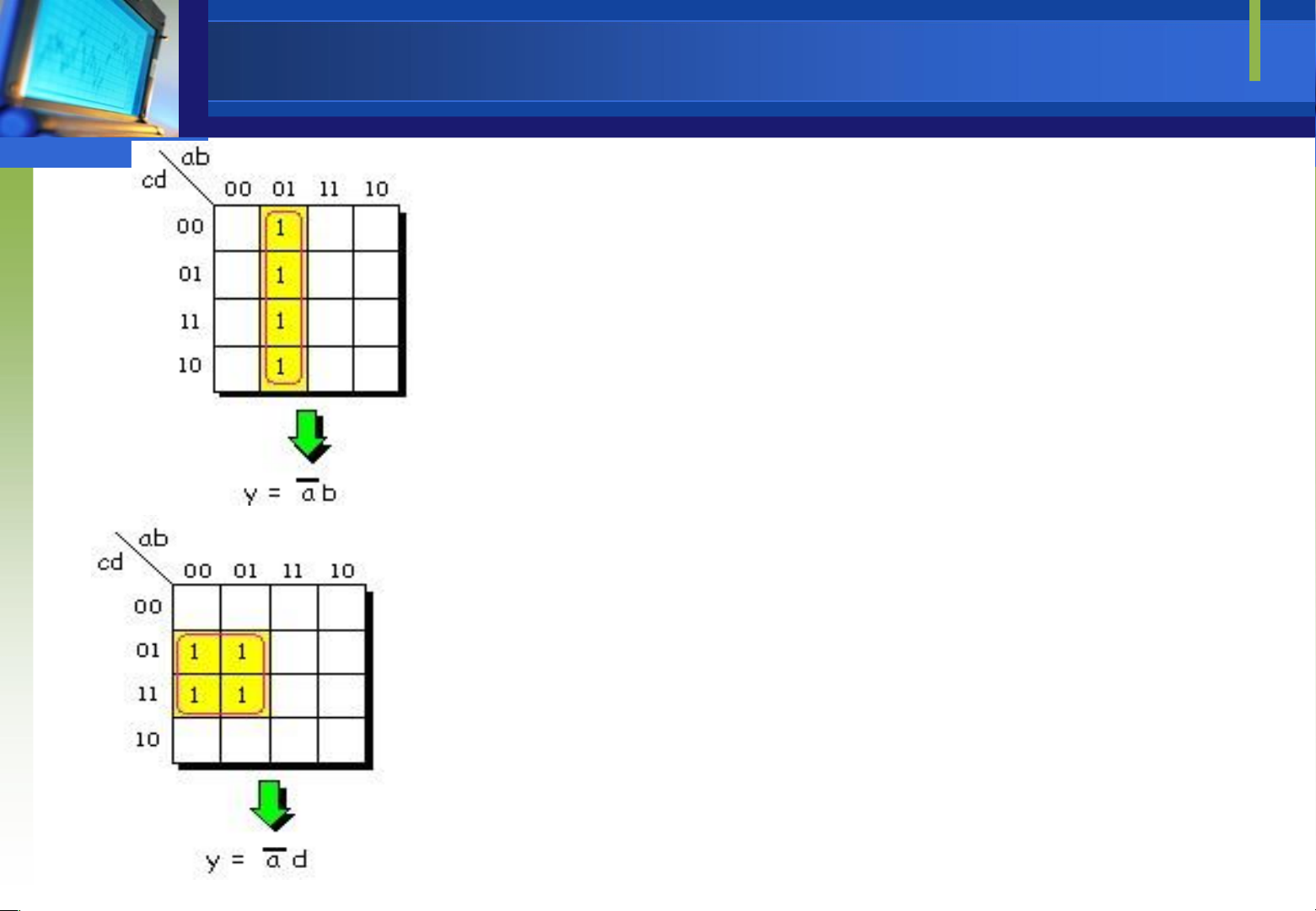
Qui tắc gom ô kế cận
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh F CD 00 01 11 10 AB F ABCD ABCD= + 00 0 0 0 0 01 0 1 1 0 = ABD(C C)+ 11 0 0 0 0 = ABD 10 0 0 0 0 F CD 00 01 11 10 AB 00 0 0 0 0 F F F= +1 2 01 0 1 1 0 11 0 1 1 0 =(ABCD ABCD) (ABCD ABCD+ + 10 0 0 0 0 +)
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh =ABD ABD BD+ =
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 F CD 00 01 11 10 AB Bản ồ Karnaugh 00 0 0 0 0 01 0 1 1 0
Qui tắc gom ô kế cận 11 1 1 1 1 10 0 0 0 0 F ABCD ABCD ABCD ABCD= + + + F CD 00 01 11 10 AB = ABC(D D) ABC(D D)+ + + 00 0 0 0 0 01 0 1 1 0 = ABC ABC AB(C C) AB+ = + = 11 1 1 1 1 10 1 1 1 1 F AB AB= + Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 = A(B B) A+ = Bản ồ Karnaugh
Qui tắc gom ô kế cận
Các ô kế cận ược gom lại thành một nhóm nếu chúng có cùng giá trị 0
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 hay 1
Khi gom các ô kế cận có cùng giá trị 1 ta ược 1 tích các biến có giá trị giống
nhau: 0 tương ứng với bù, 1 tương ứng với không bù, các biến có giá trị khác
nhau thì loại bỏ Khi gom các ô kế cận có cùng giá trị 0 ta ược 1 tổng các
biến có giá trị giống nhau: 1 tương ứng với bù, 0 tương ứng với không bù,
các biến có giá trị khác nhau thì loại bỏ
Hai ô kế cận có tổ hợp nhị phân khác nhau tại 1 biến nên khi gom 2 ô kế cận
thì loại bỏ ược 1 biến. Tương tự gom 4 ô loại bỏ 2 biến, gom 8 ô loại bỏ 3
biến. Một cách tổng quát: khi gom 2n ô kế cận sẽ loại ược n biến, những
biến bị loại là những biến khi ta i vòng qua các ô kế cận mà giá trị của chúng thay ổi Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh
Qui tắc gom ô kế cận
Những iều cần lưu ý khi gom ô:
Vòng gom hợp lệ khi trong vòng gom ó có ít nhất 1 ô chưa thuộc vòng gom nào
Việc kết hợp những ô kế cận tuỳ thuộc vào việc biểu diễn hàm
Boolean theo dạng chuẩn 1 hay chuẩn 2. Nghĩa là nếu biểu diễn theo
dạng chuẩn 1 thì chỉ quan tâm ến những ô kế cận nào có giá trị 1,
ngược lại nếu biểu diễn theo dạng chuẩn 2 thì chỉ quan tâm ến những ô kế cận nào có giá trị 0
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Các vòng phải ược gom sao cho số ô có thể vào trong vòng là lớn nhất
và nhớ là ể ạt iều ó thường ta phải gom những ô ã gom vào trong các vòng khác Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Downloaded by Mai Mai (haumainbyma@gmail.com)
Các ví dụ về gom ô lOMoAR cPSD| 39651089 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Downloaded by Mai Mai (haumainbyma@gmail.com)
Các ví dụ về gom ô lOMoAR cPSD| 39651089 Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bản ồ Karnaugh
Rút gọn hàm bằng bản ồ Karnaugh Qui tắc :
Bước 1: Biểu diễn hàm trên bản ồ Karnaugh
Bước 2: Thực hiện gom các ô kế cận tạo thành các vòng gom, liệt kê tất cả các
vòng gom theo thứ tự vòng 8 ô, vòng 4 ô, vòng 2 ô, vòng 1 ô chú ý vòng gomi
không là tập con của vòng gomj và viết dạng rút gọn của mỗi vòng gom
Bước 3: Loại bỏ những vòng gom không hợp lệ là những vòng gom mà tất cả
các ô của nó ều thuộc về các vòng gom khác
Bước 4: Viết công thức hàm rút gọn dựa vào dạng chuẩn 1 hay chuẩn 2
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Các ví dụ dùng bản ồ Karnaugh ể ơn giản Ví dụ 1:
Dùng bản ồ Karnaugh ể ơn giản hàm f(A,B,C)= (0,2,4,5,6)
Bước 1: Vẽ bản ồ Karnaugh 3 biến BC A 00 01 11 10 1 1 0 1 1 1 1 F
Bước 2: gom các ô kế cận: 1 vòng gom 4 ô: C 1 vòng gom 2 ô: AB
Bước 3: Không có vòng gom không hợp lệ
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Các ví dụ dùng bản ồ Karnaugh ể ơn giản
Bước 4: Viết lại hàm dạng chuẩn 1 theo
các vòng gom trên bản ồ f A B C( , , ) = +AB C
Ví dụ 2: Dùng bản ồ Karnaugh ể F CD ơn giản hàm AB 00 01 11 10 00 1 1 1 f(A,B,C,D)= 01 1 1 1
(0,2,3,4,6,7,9,12,13) và vẽ sơ ồ mạch 11 1 1 10 1
B1:Vẽ bản ồ Karnaugh 4 biến B2: Gom các ô kế cận 2 vòng gom 4 ô : AC, AD
3 vòng gom 2 ô : BCD, ABC, ACD
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Các ví dụ dùng bản ồ Karnaugh ể ơn giản
B3: Loại bỏ những vòng gom không hợp lệ
vòng gom không hợp lệ BCD Viết hàm
B4: Viết hàm dạng chuẩn 1
f A B C( , , ) =AC + AD + ACD + ABC
Ví dụ 2: Dùng bản ồ Karnaugh ể ơn giản hàm
f(A,B,C,D)= (0,2,3,4,6,7,9,12,13) và vẽ sơ ồ mạch
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Các ví dụ dùng bản ồ Karnaugh ể ơn giản ( = + AD + + ,, fABC ) AC A CD ABC A B f C D
Ví dụ 3: Dùng bản ồ Karnaugh ể ơn giản hàm
f(A,B,C,D)= (3,4,5,7,10,12,13).D(8,9,11)
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Các ví dụ dùng bản ồ Karnaugh ể ơn giản
Vẽ bản ồ Karnaugh 4 biến F CD
Gom các ô kế cận theo các ô giá trị 0 00 01 11 10 AB
Viết lại hàm theo các nhóm ã gom trên bản ồ 00 0 01 0 0 0
f A B C( , ,) = +(B C)(A B+ )(A C D+ + ) 11 0 0 10 X X X 0
Khi dùng bản ồ Karnaugh ở các vị trí không xác ịnh thì ta biểu diễn bằng Chú ý:
chữ X và các ô này có thể coi là “1” hay “0” tuỳ thuộc vào trường hợp bản ồ
Karnaugh ể có thể gom số ô lại ược nhiều nhất
Nếu xét gom theo giá trị bằng 0 thì ta chỉ xét các ô có giá trị không, những ô
có giá trị X không cầ xét nhưng có thể gom chung vào các ô có giá trị 0 ể ược hàm tối giản
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Những mạch logic số cơ bản
Mạch Tích hợp IC (Intergrated Circuit)
Mạch kết hợp (Combinational Circuit Mạch tuần tự
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Mạch tích hợp IC
Các cổng logic không chế tạo riêng lẻ mà theo ơn vị mạch tích hợp thường gọi là
IC hay vi mạch (chip) Các IC có ưu iểm :
Kích thước nhỏ gọn, trọng lượng bé
Tiêu thụ năng lượng thấp Tốc ộ hoạt ộng cao
Chịu ược nhiệt cao, ít chịu tác ộng của môi trường Giá thành hạ
Tuỳ thuộc vào khả năng chứa và sắp xếp các cổng trên cùng 1 chip gọi là mức
tích hợp mà IC ược chia thành các loại :
Mạch SSI (cỡ nhỏ): 1-10cổng
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Định nghĩa:
Mạch MSI (cỡ trung bình): 10-100cổng
Mạch LSI (cỡ lớn): 100-100000cổng
Mạch VLSI (cỡ rất lớn): >100000cổng Mạch kết hợp
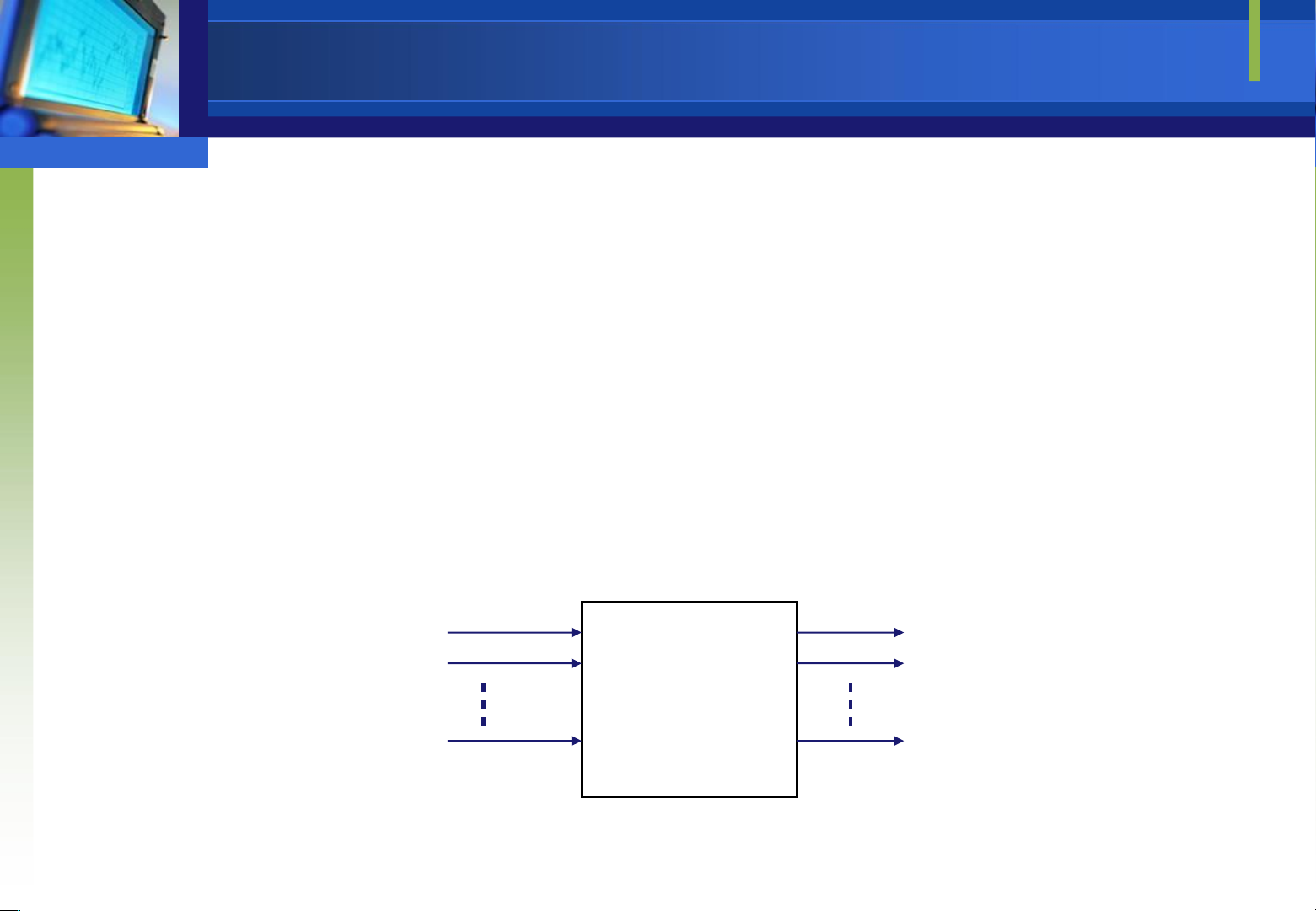
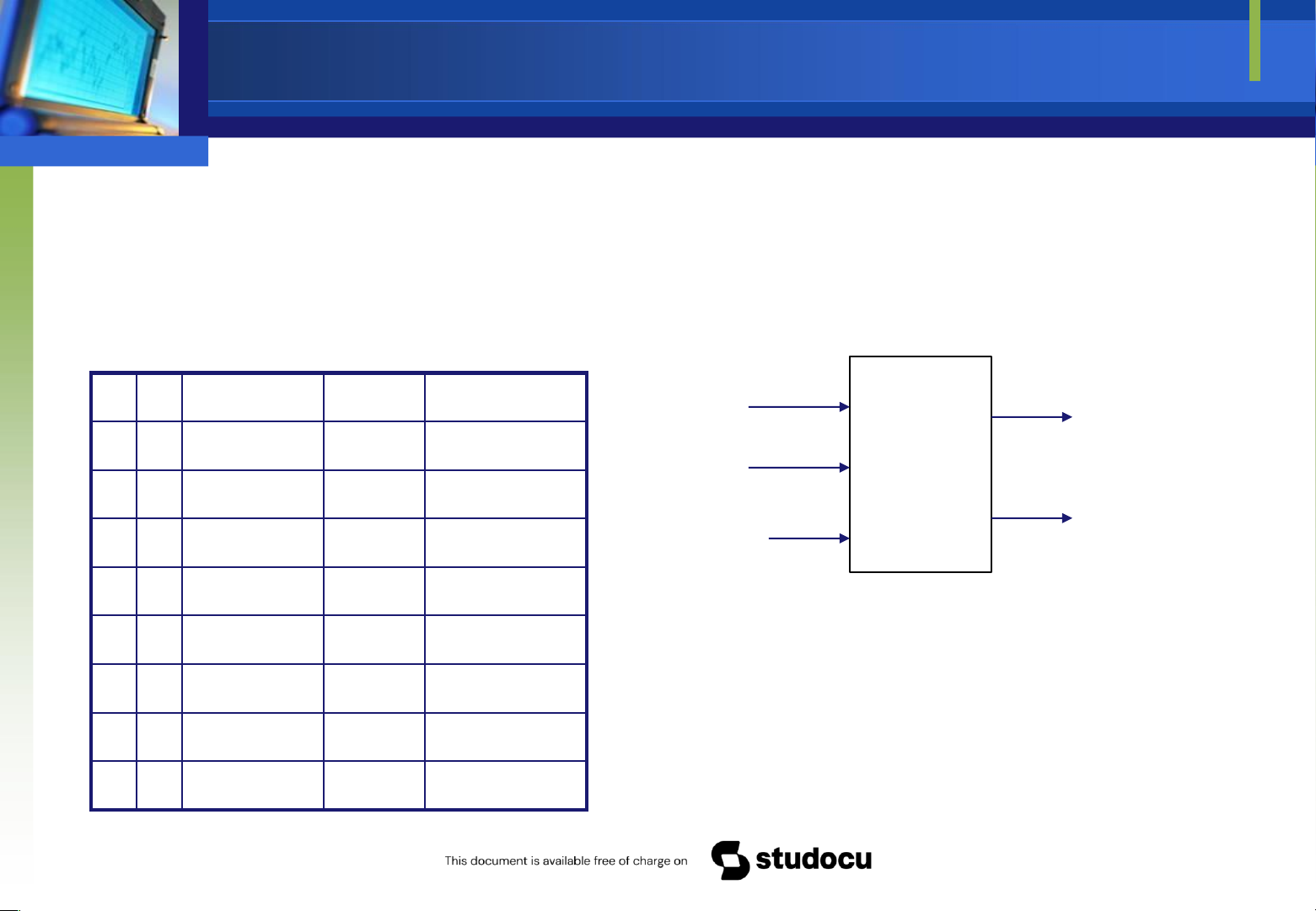
Là tổ hợp các cổng luận lý kết nối với nhau tạo thành một bản mạch
có chung một tập các ngõ vào và ra n input Combinational m output variables circuit variables
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Các bước thiết kế mạch kết hợp:
Xác ịnh bài toán ể i ến kết luận có những ầu nhập, ầu xuất nào
Lập bảng chân trị xác ịnh mối quan hệ giữa nhập và xuất
Dựa vào bảng chân trị xác ịnh hàm cho từng ngõ ra
Dùng ại số Boolean hay bản ồ Karnaugh ể ơn giản các hàm ngõ ra
Vẽ sơ ồ mạch theo các hàm ã cho Bộ dồn kênh
Bộ dồn kênh số là mạch có chức năng chọn lần lượt 1 trong N kênh ưa
vào ể ưa ến ngõ ra duy nhất
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Bộ dồn kênh số là mạch có
2n ường dữ liệu vào (input)
1 ường dữ liệu ra (output)
n ngõ vào iều khiển lựa chọn
Các ngõ vào iều khiển lựa chọn sẽ
ường dữ liệu vào nào ược xuất ra ường dữ liệu ra
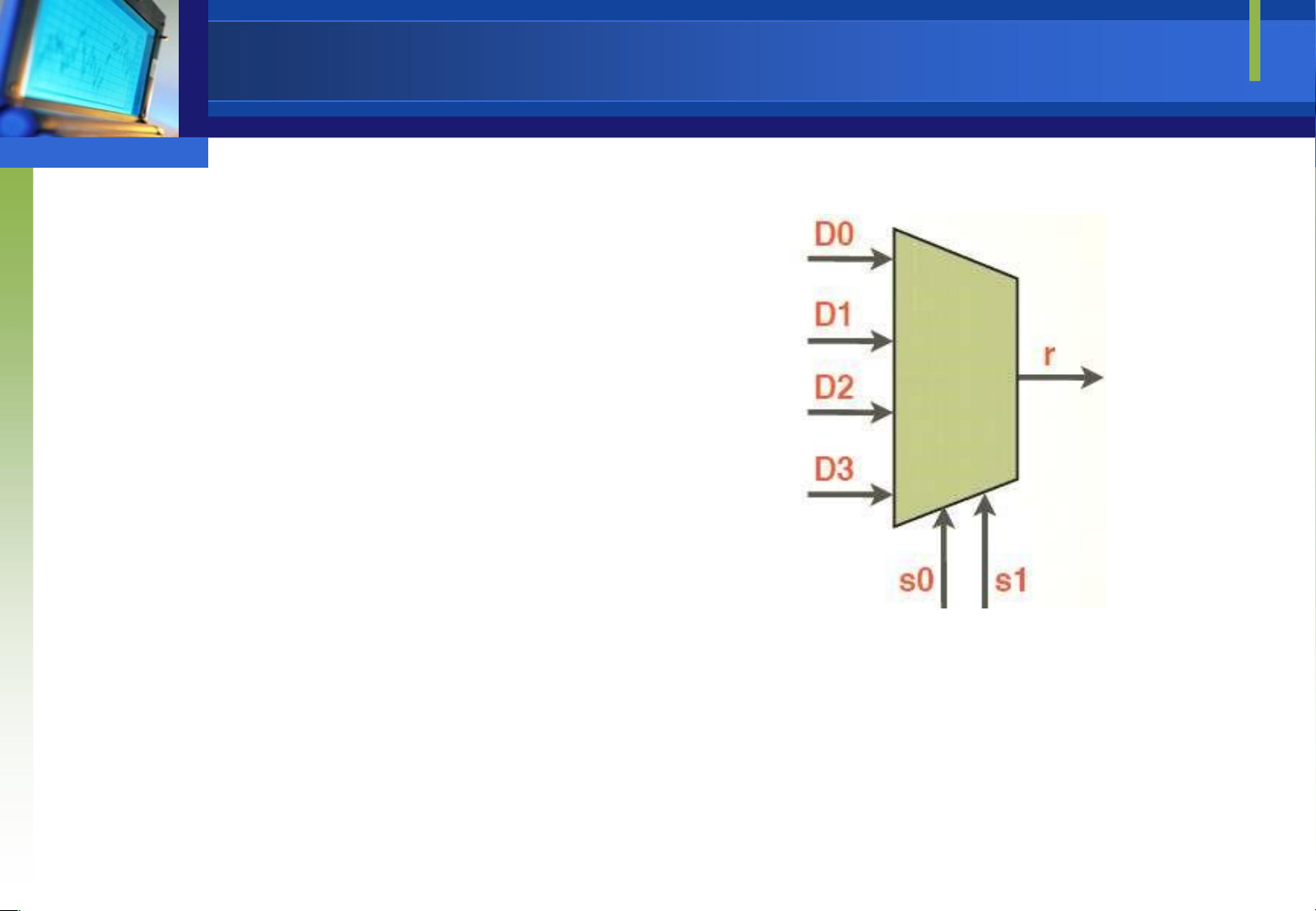
chọn Ví dụ bộ dồn kênh với n = 2
D0,D1,D2,D3: các kênh dữ liệu vào
Ngõ ra r: ường truyền chung
s0,s1: các ngõ vào iều khiển lựa chọn
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bộ dồn kênh 4-1
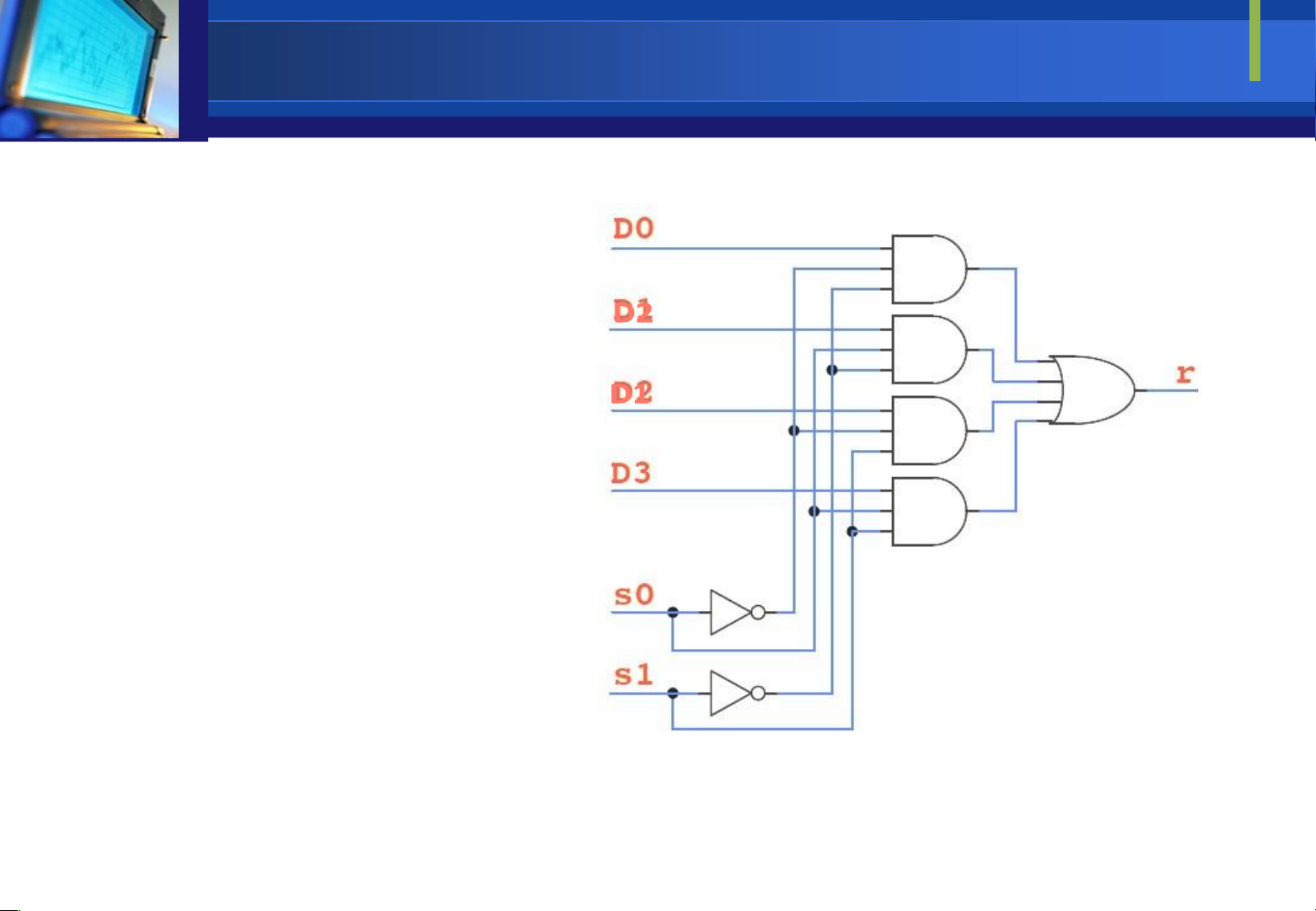
Việc chọn dữ liệu từ 1 trong 4 kênh D0,D1,D2,D3 ể ưa ến s0 s1 r
ường truyền chung tuỳ thuộc vào tổ hợp tín hiệu iều khiển lựa 0 0 D0 chọn s0,s1 theo bảng sau: 0 1 D1 1 0 D2 1 1 D3
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 a a Bộ dồn kênh 8-1
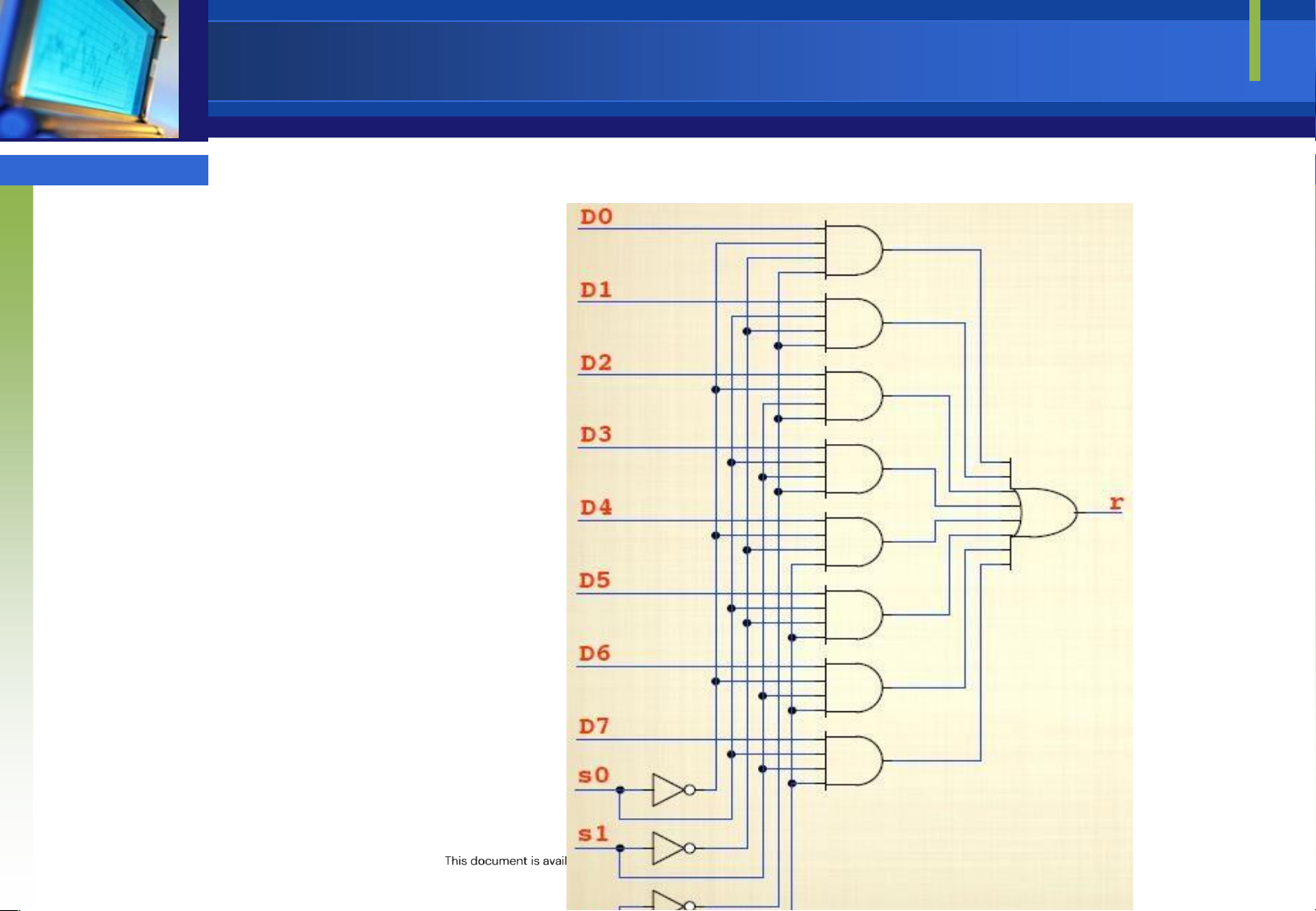
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 nằm trên Bộ dồn kênh 8 ầu vào
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
có 3 ường iều khiển lựa chọn qui ịnh 1 trong 8 ường dữ liệu vào nào sẽ ịnh
tuyến tới cổng OR rồi ra. Bất luận giá trị nào ường iều khiển, 7 cổng AND sẽ
luôn xuất 0, cổng còn lại xuất 0 hay 1 tuỳ thuộc vào giá trị ường vào ược chọn Bộ phân kênh
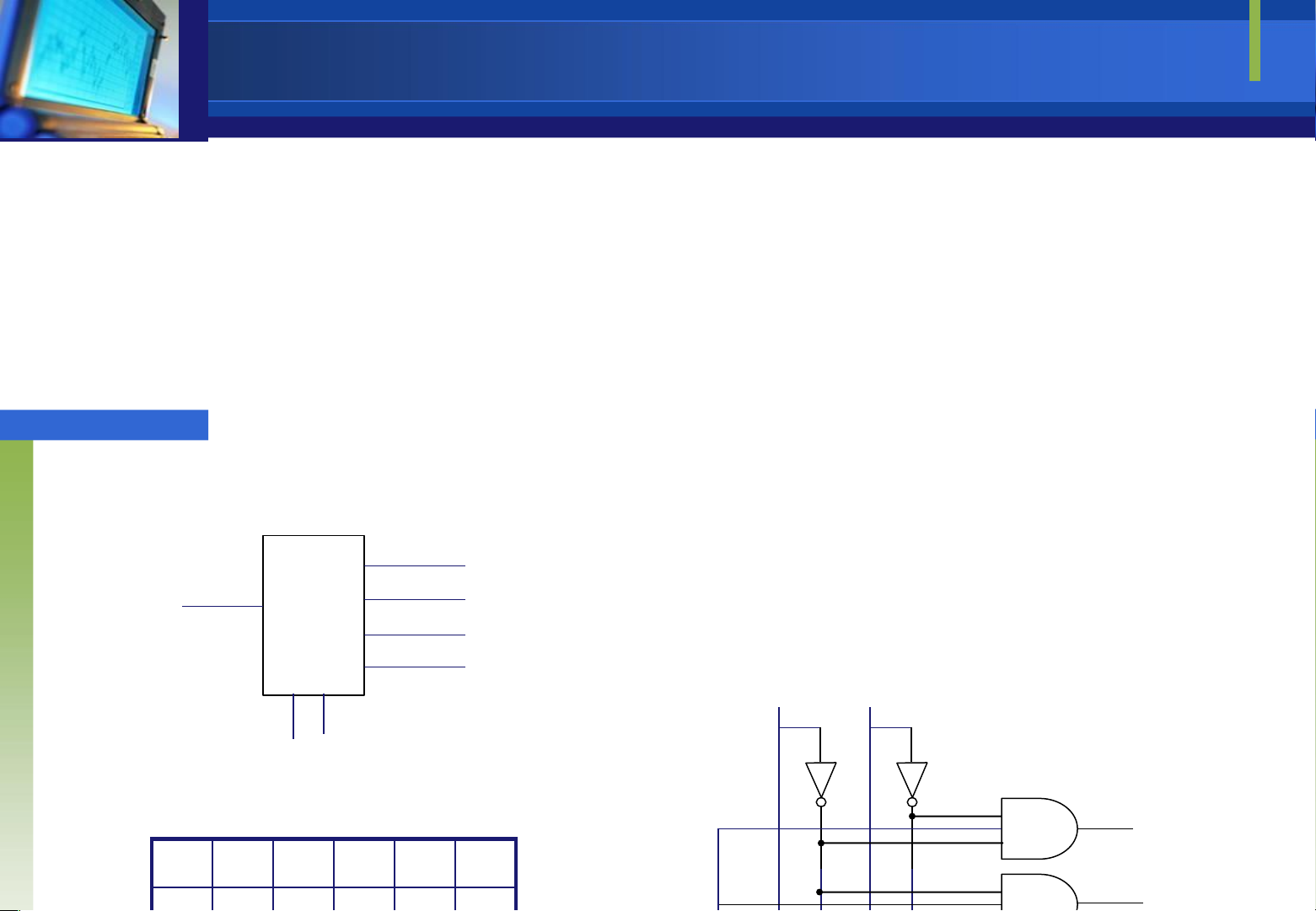
Bộ phân kênh số là mạch có chức năng tách 1 nguồn dữ liệu ở ầu vào ể rẽ ra N ngõ
khác nhau. Xét bộ phân kênh cơ bản có 1 ngõ vào và 4 ngõ ra ký hiệu như sau: y1 x: kênh dữ liệu vào x 1-4 y2
y1,y2,y3,y4: các ngõ ra dữ liệu y3 x
c1,c2: các ngõ vào iều khiển y4 c1 c2 c1 c2 y1
c1 c2 y1 y2 y3 y4 Downloaded by Mai Mai (haumainbyma@gmail.com) y2 0 0 x 0 0 0 lOMoAR cPSD| 39651089
Bảng trạng thái mô tả hoạt ộng mạch
Sơ ồ mạch phân kênh 1-4
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Mạch cộng Mạch nửa cộng
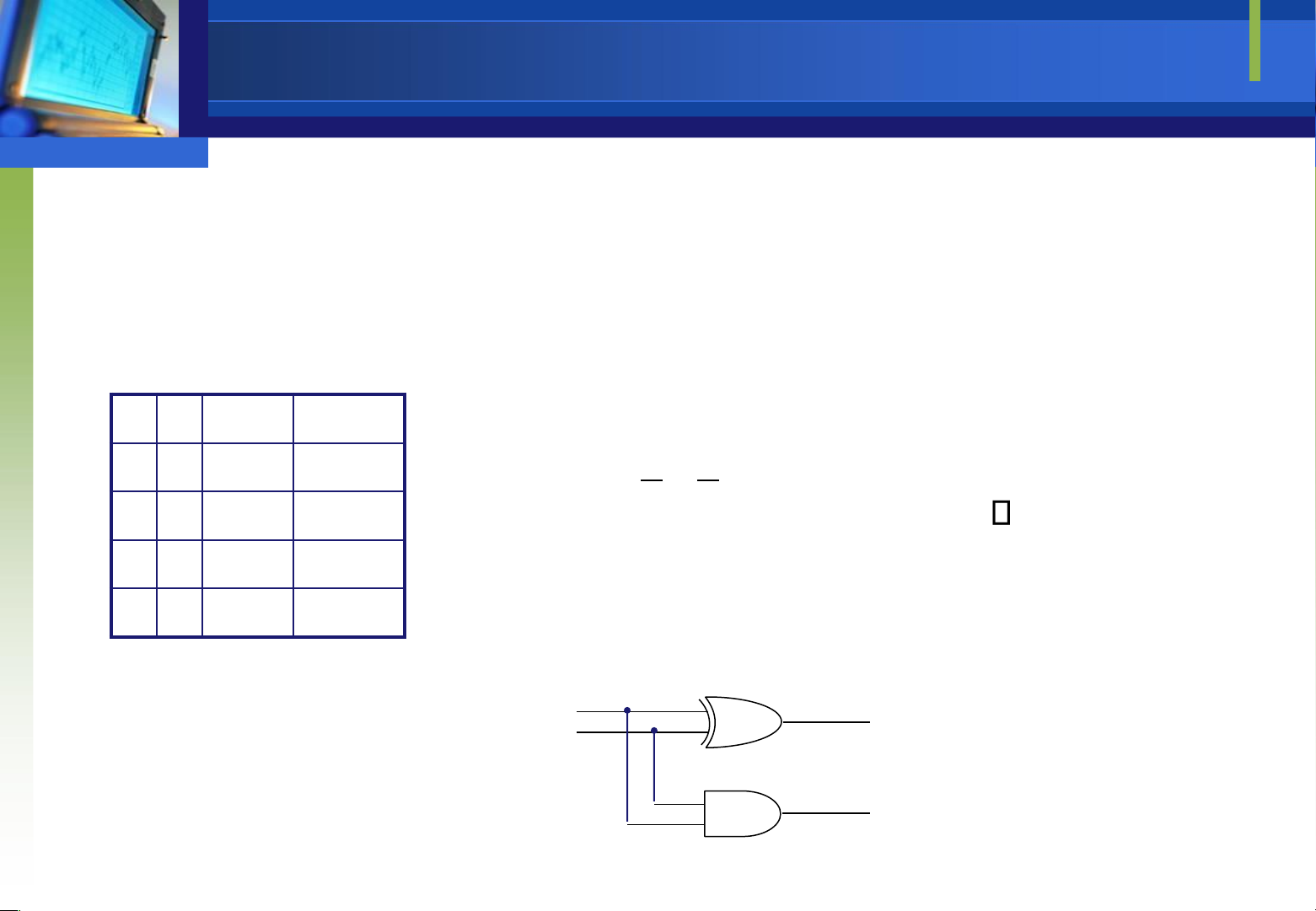
Mạch nửa cộng là mạch cộng 2 số nhị phân 1 bit tạo ra một
bit tổng S và một bit nhớ C
Bảng trạng thái mô tả hoạt ộng của mạch và phương trình logic như sau A B Sum Carry 0 0 0 0 S AB AB A B= . + . = 0 1 1 0 1 0 1 0 C = A.B 1 1 0 1 ASum B Carry Mạch cộng toàn phần
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Mạch cộng
Mạch cộng toàn phần là mạch cộng 2 số nhị phân 1 bit A, B với 1 bit nhớ ược tạo ra
từ bit thấp hơn Carry_in( Cn-1). Mạch tạo ra một bit tổng Sum (S) và một bit nhớ
Carry_out (Cn). Mạch này chính là mạch cộng 3 số nhị phân 1 bit A,B,Cn-1 A A B C S C n-1 n Sum 0 0 0 0 0 Full B 0 Adder 0 1 1 0 Carry_out Carry_in 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0
Carry_in: số nhớ của lần cộng trước 1 0 1 0 1
Carry_out: số nhớ của lần cộng hiện tại 1 1 0 0 1 Sum: Tổng hiện tại 1 1 1 1 1
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Mạch cộng
Bảng trạng thái mô tả hoạt ộng của mạch = Mạch cộng toàn phần SABC
Từ bảng trạng thái ta có hàm logic biễu diễn: = n CABC
n−1 +ABCn−1 +ABCn−1 +ABCn−1 =A B C = C n−1
n−1 ABCn−1 +ABCn−1 +ABCn−1 + = C
n−1(AB AB ABC C+ )+ ( n−1 +
n−1) n−1(A B AB +)
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Mạch cộng A B C n-1 S C n
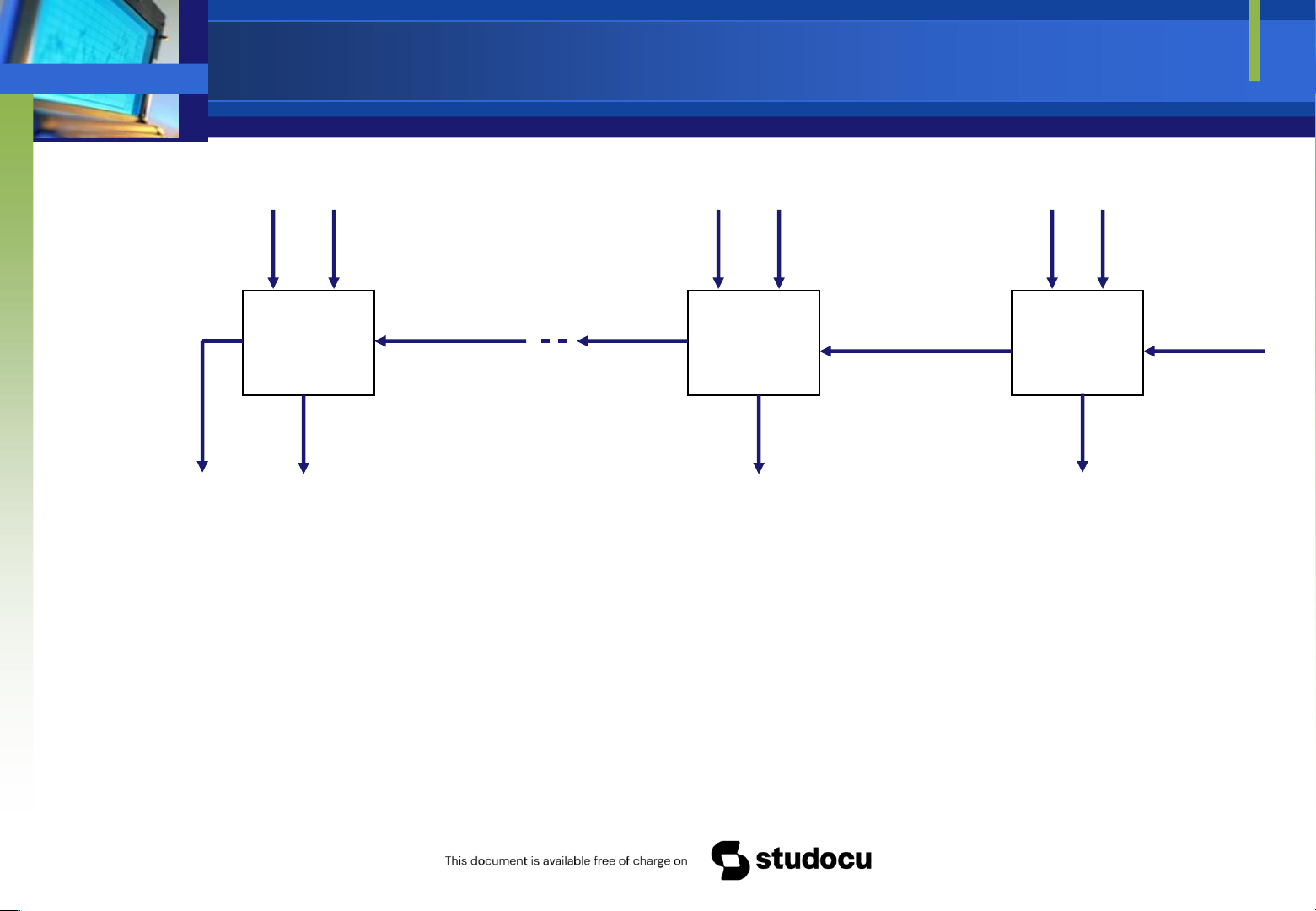
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Bộ cộng n bit
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Carry Carry Carry Carry Carry Full in n-1 out 1 Full Full in 1 out in 0 0 Adder Adder Adder S n An-1 Bn-1
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 A1 B1 A0 B0 Sn-1 S1 S0
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Mạch giải mã và mã hoá Khái niệm
Mạch mã hoá là mạch có nhiệm vụ biến ổi những ký hiệu quen thuộc của con người
sang những ký hiệu không quen thuộc con người
Mạch giải mã là mạch làm nhiệm vụ ngược lại mạch mã hoá, biến ổi những ký hiệu
không quen thuộc với con người sang ký hiệu quen thuộc Mạch mã hoá
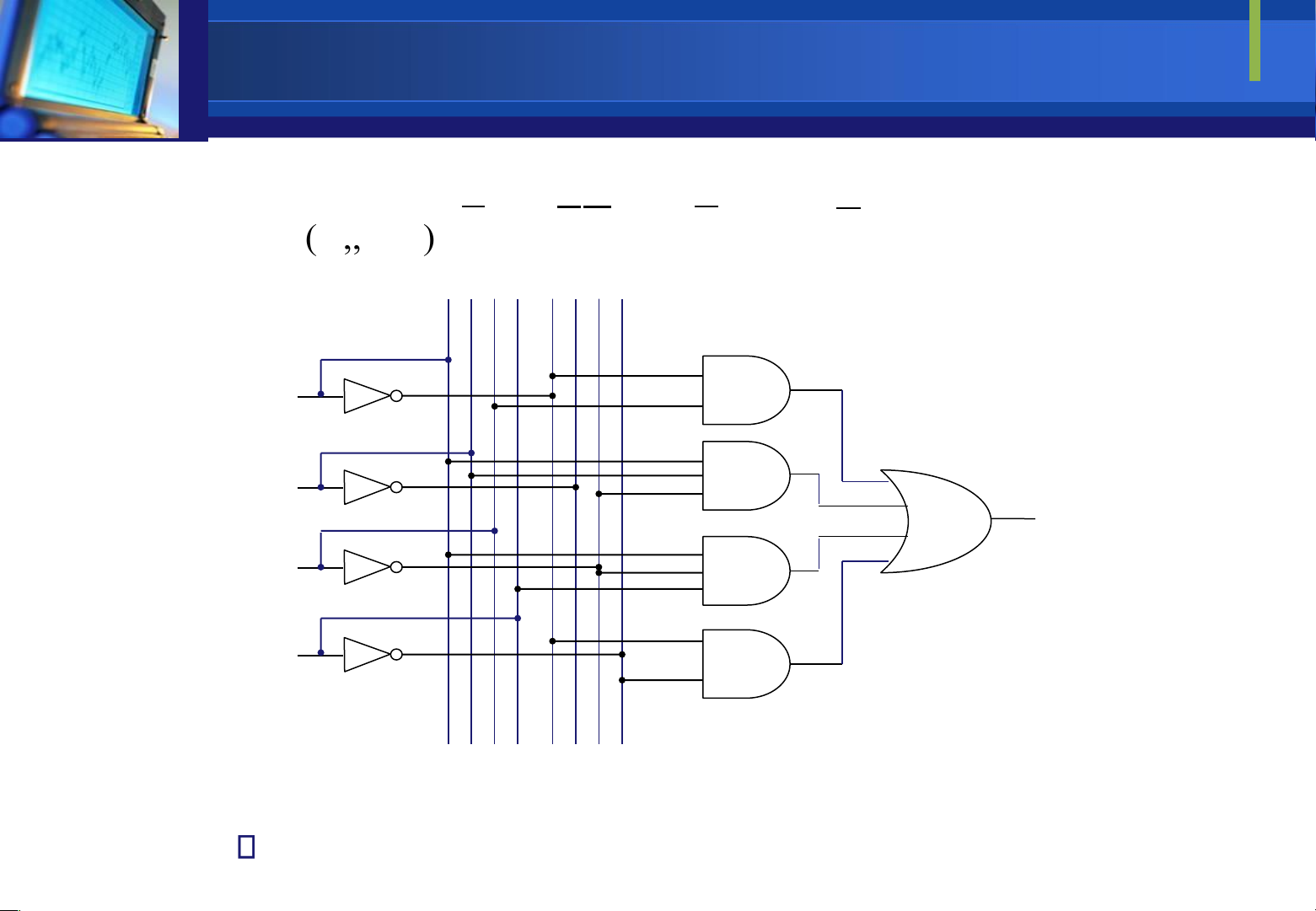
Xét mạch mã hoá nhị phân từ 8 sang 3 (8 ngõ vào và 3 ngõ ra). Sơ ồ khối như sau: x0 A0 Trong ó: x1 Encoder A1
x0,x1,…,x7: là các ngõ vào tín hiệu 8 3 x7 A0,A1,A2: là các ngõ ra
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 A2
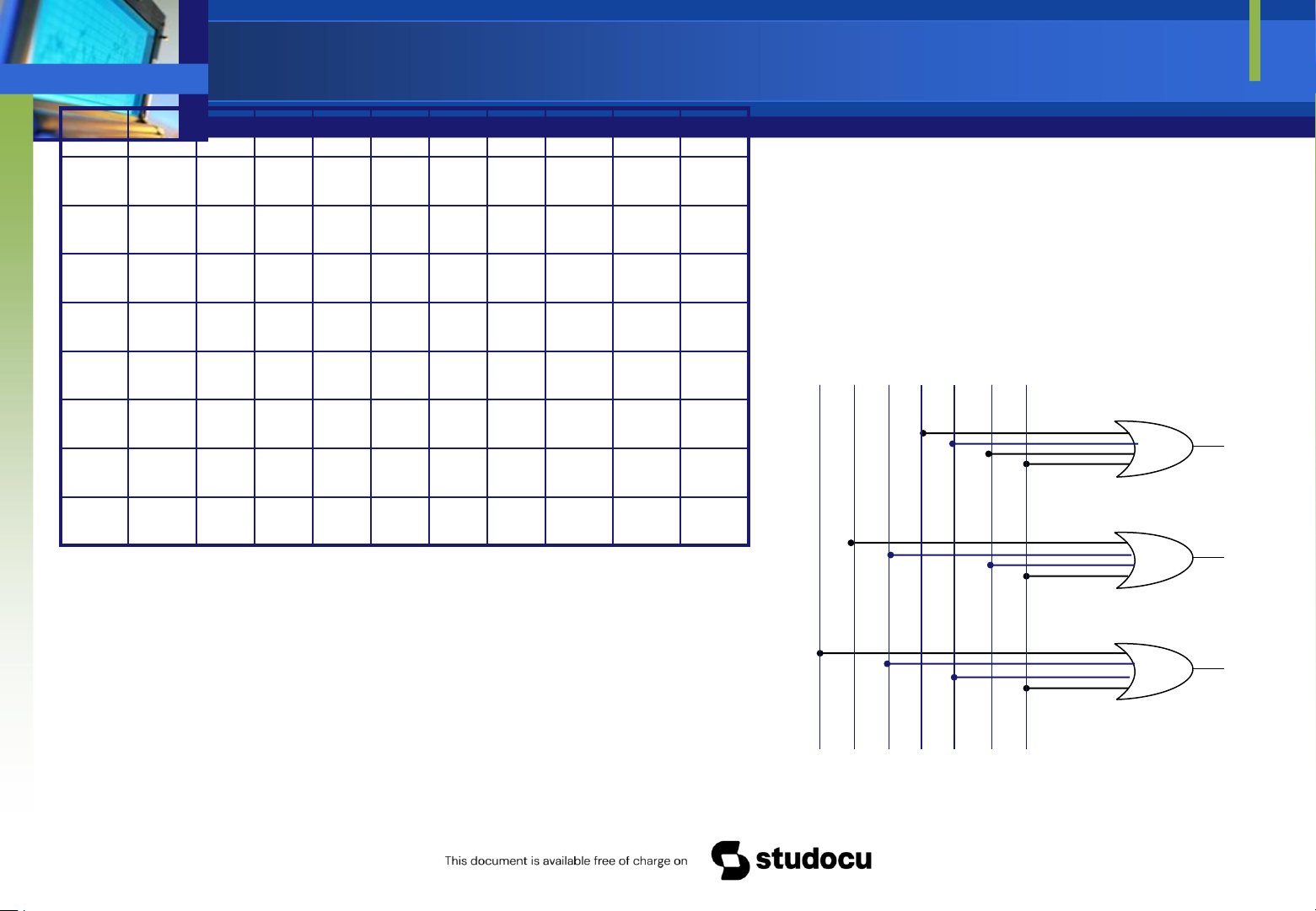
Mạch mã hoá nhị phân 83 thực hiện biến ổi tín hiệu ngõ vào thành 1 từ mã nhị phân
tương ứng ở ngõ ra. Cụ thể 0000, 1001, 2010, 3011, 4100, 5101, 6110,
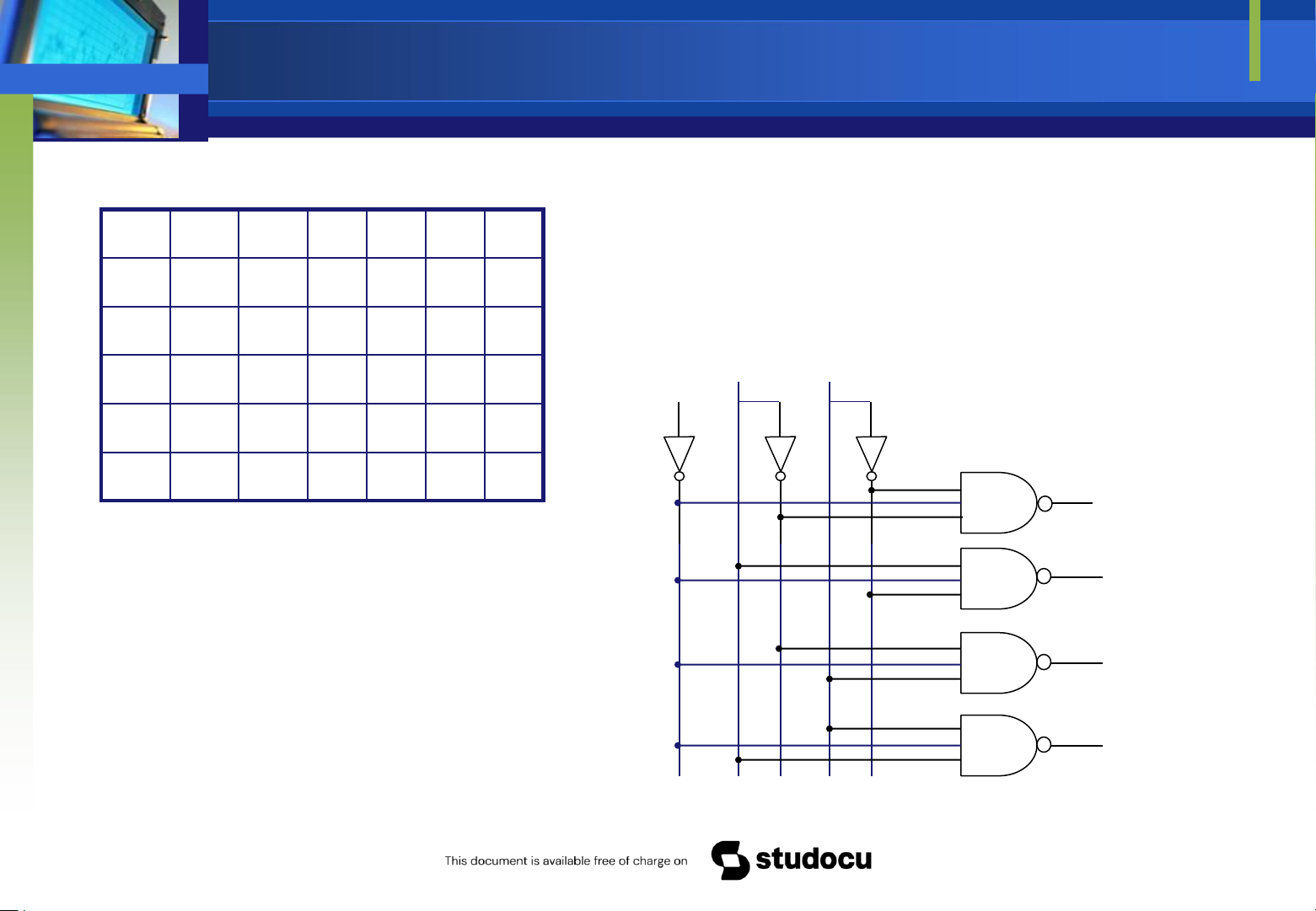
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 x7 x6 x5 Phương tốigiản x4 x2 x1 x0 trìnhlogic : x3 A2 A1 A0 0 0 0 0 0 0 0 1 0 0 0 A0=x1+x3+x5+x7 0 0 0 0 0 0 1 0 0 0 1 A1=x2+x3+x6+x7 0 0 0 0 0 1 0 0 0 1 0 A2=x4+x5+x6+x7 0 0 0 0 1 0 0 0 0 1 1 0 x1 x3x4 x5 x7 0 0 1 0 0 0 0 1 0 0 x2 x6 0 A2 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 1 1 1 A1 Khi một ở trạng ( ngõ vào thái cao mức logic 1) và
các ngõ còn lại thấp (mức xuất A0 logic 0) thì ngõ ra hiện từ mã tương ở mức ứng . Ngõ vào nào logic 1 tương số thì ứng với con ó ở hệ thập phân. M
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 ạch mã hoá 83
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Mạch giải mã
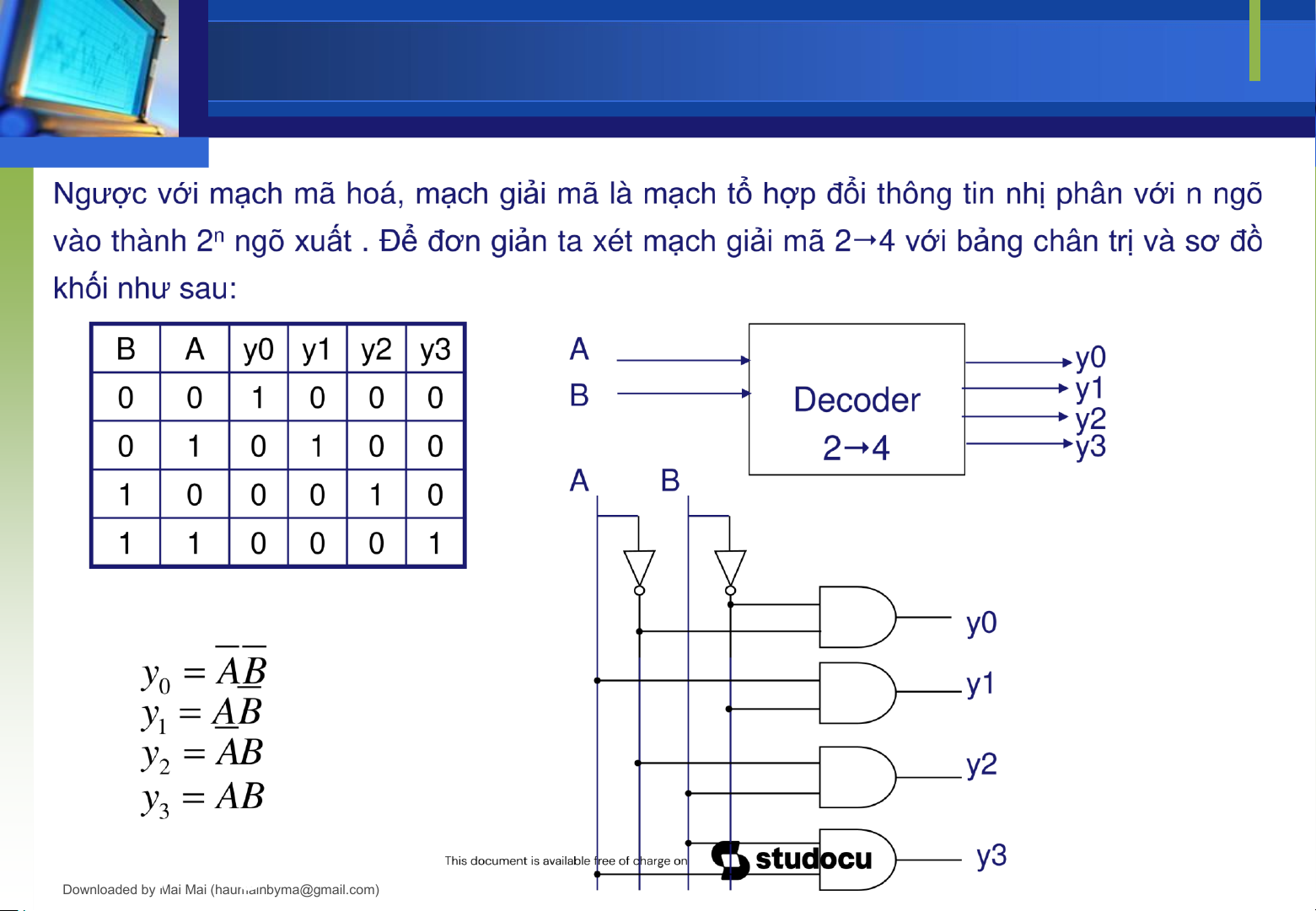
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Phương trình logic tối giản:
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
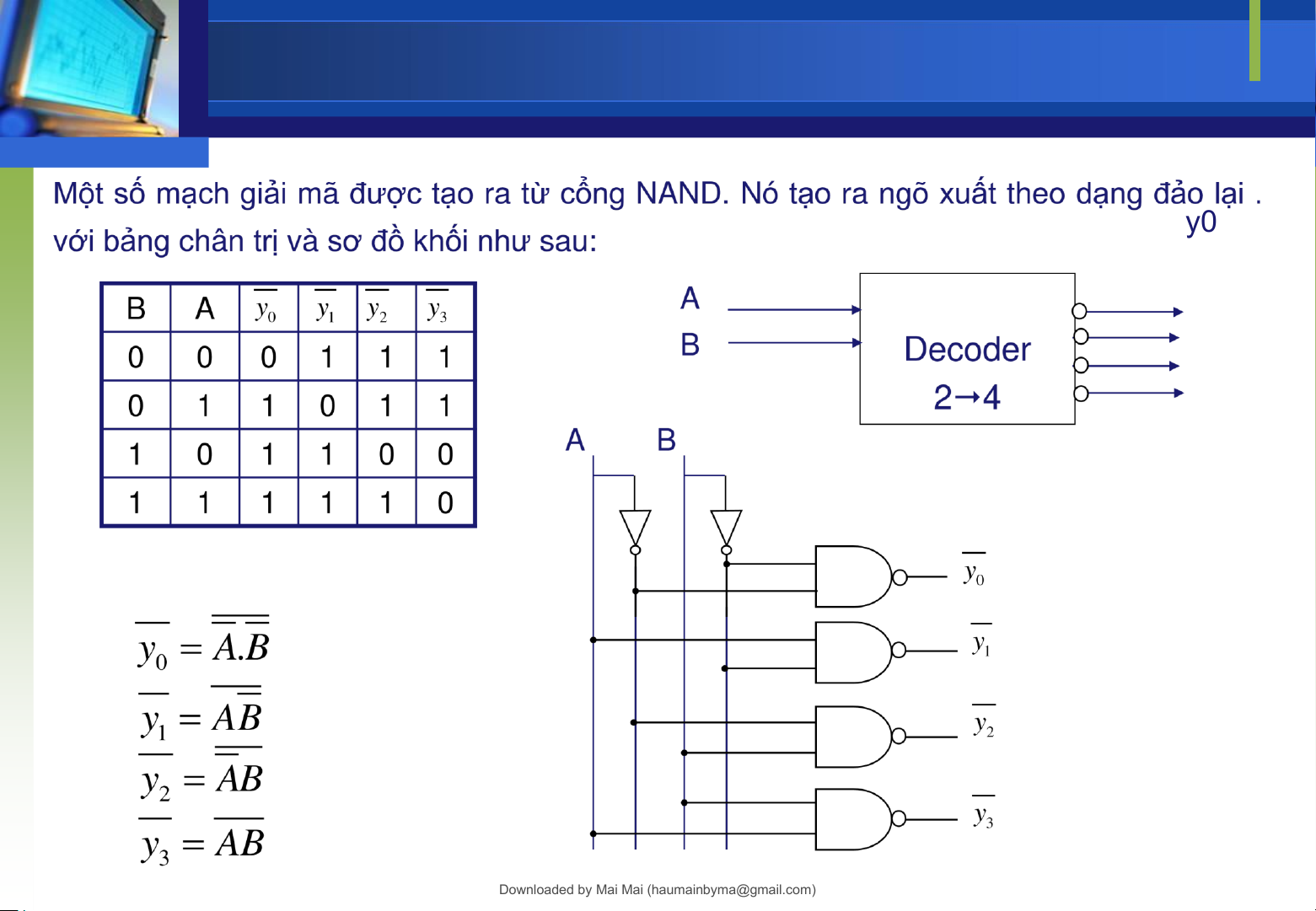
Mạch giải mã với cổng NAND
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 y0
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 y1 y2 y3
Phương trình logic tối giản:
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
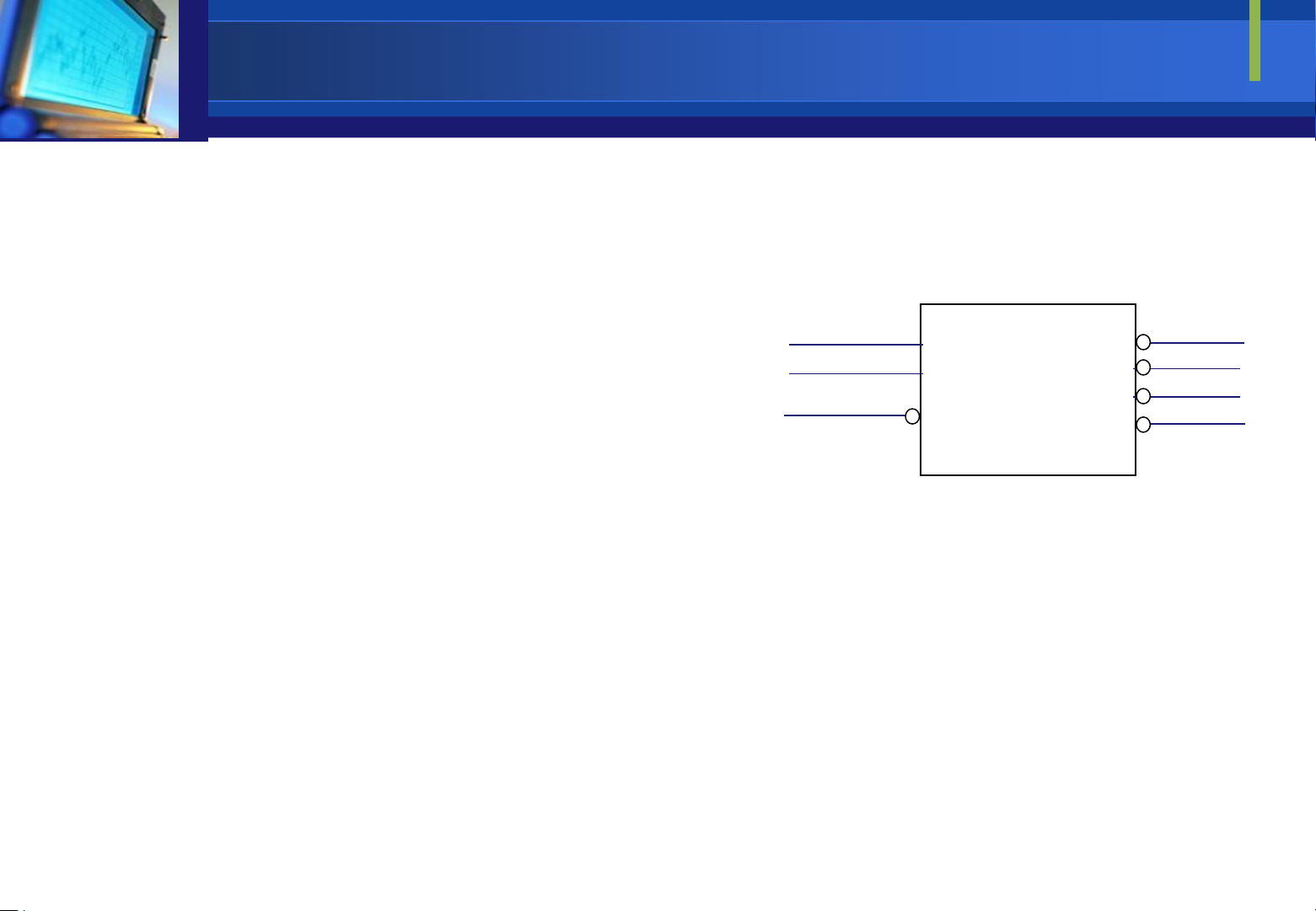
Mạch giải mã với cổng NAND có ường vào iều khiển
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089 Một E B A y0 y1 y2 y3 số 0 0 0 0 1 1 1 mạch 0 0 1 1 0 1 1 giải 0 1 0 1 1 0 1 mã 0 1 1 1 1 1 0 ược 1 X X 1 1 1 1 y0 tạo ra y1 từ cổng với số nhị phân ở cácngõvào.KhiE=1 y2 là không phụ thuộc trị vào các giá ầu y3 vào, ầu ra luôn =1
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
NAND. Nó tạo ra ngõ xuất theo dạng ảo lại với 1 ường vào iều khiển E có bảng chân trị và sơ ồ khối như sau: A y0 B y1 Decoder y2 E 2 4 y3 E A B
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
Mạch hoạt ộng khi tín hiệu
iều khiển E=0 và ngõ ra sẽ
có giá trị 0 tương ứng thì
không cho phép mạch hoạt ộng tức Mở rộng mạch giải mã
Trong một số trường hợp cần giải mã với kích thước lớn mà ta chỉ có mạch
kích thước nhỏ thì có thể ghép hai hay nhiều hơn các mạch ể tạo một mạch
Downloaded by Mai Mai (haumainbyma@gmail.com) lOMoAR cPSD| 39651089
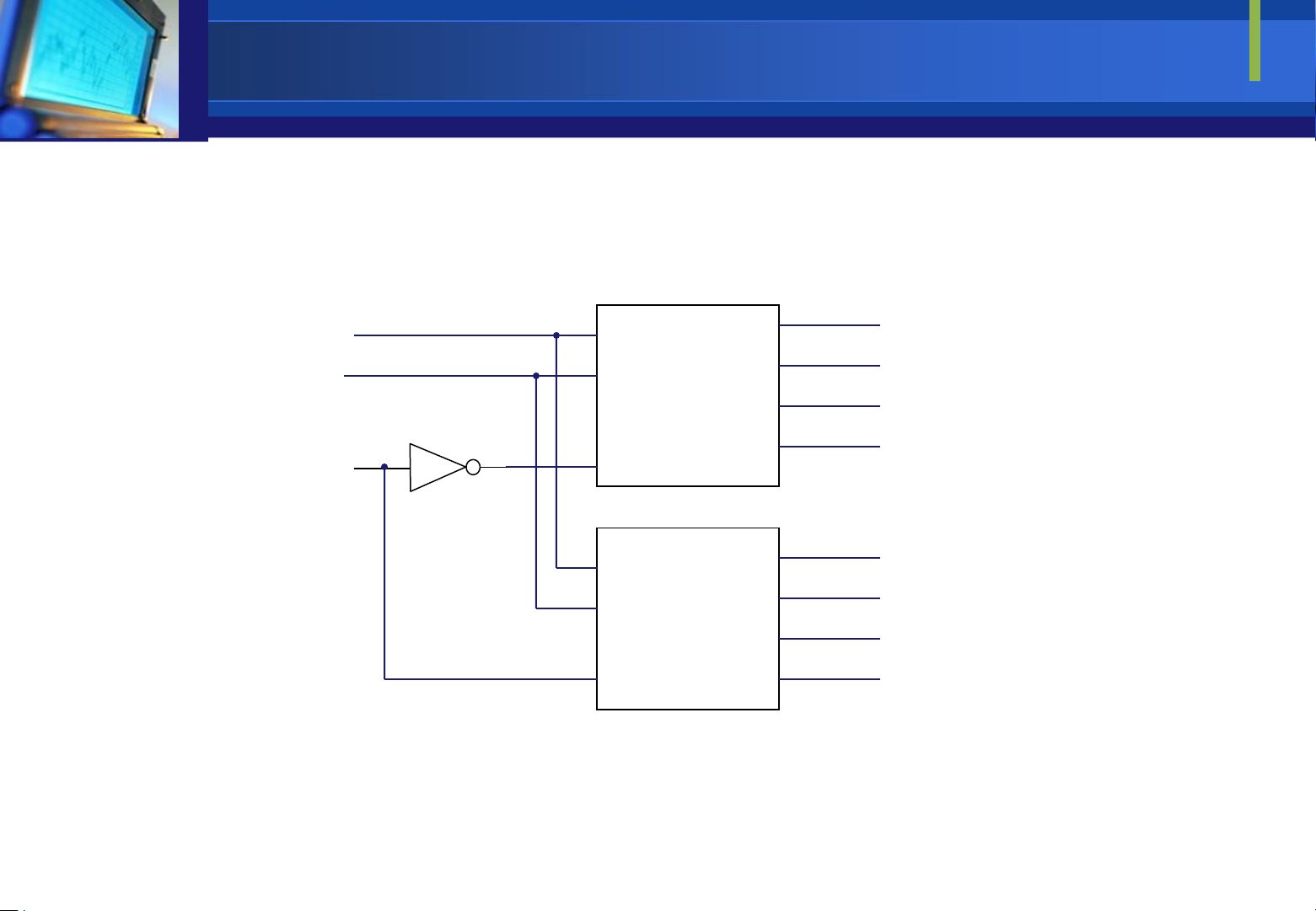
lớn hơn. Ví dụ ta có thể tạo mạch giải mã 38 bằng cách ghép 2 mạch 24. Khi ó ta tận
dụng ngõ vào iều khiển E ể làm ngõ nhập thứ 3 A0 D0 decode A1 D1 2 D2 4 E D3 A2 D4 decode D5 2 D6 4 E D7
Downloaded by Mai Mai (haumainbyma@gmail.com)