Bộ 1: Tổng ôn 12 câu cuối môn Toán – Chinh phục điểm 9+ và 10 kỳ thi THPT
Bộ 1: Tổng ôn 12 câu cuối môn Toán – Chinh phục điểm 9+ và 10 kỳ thi THPT. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.
Chủ đề: Tài liệu ôn thi THPTQG môn Toán 335 tài liệu
Môn: Toán 2.3 K tài liệu
Tác giả:
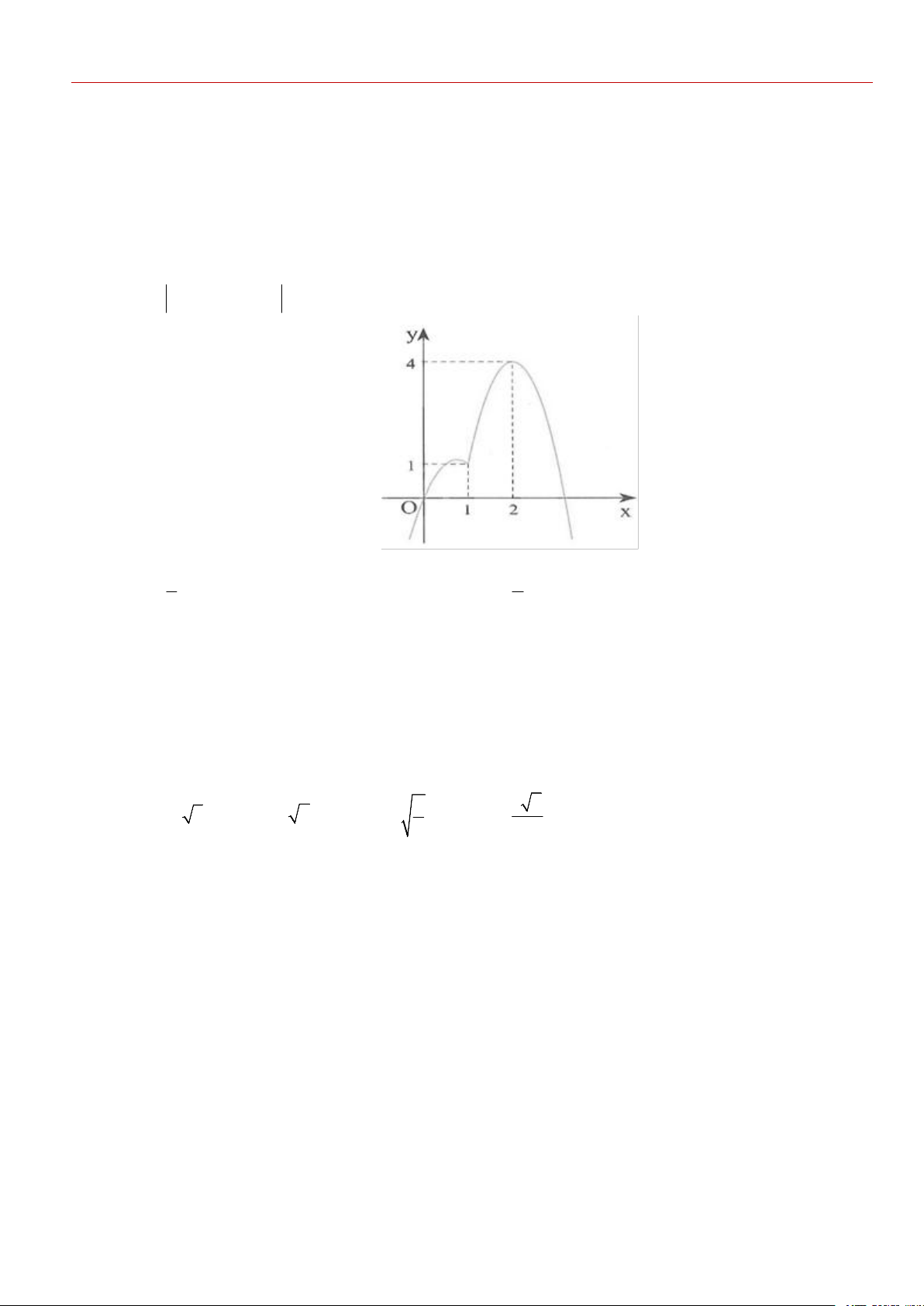
Preview text:
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
BỘ MIX 12 CÂU CUỐI VỀ ĐÍCH 02
(7 NGÀY BỨT PHÁ VỀ ĐÍCH) CA SÁNG : 4H45 SÁNG
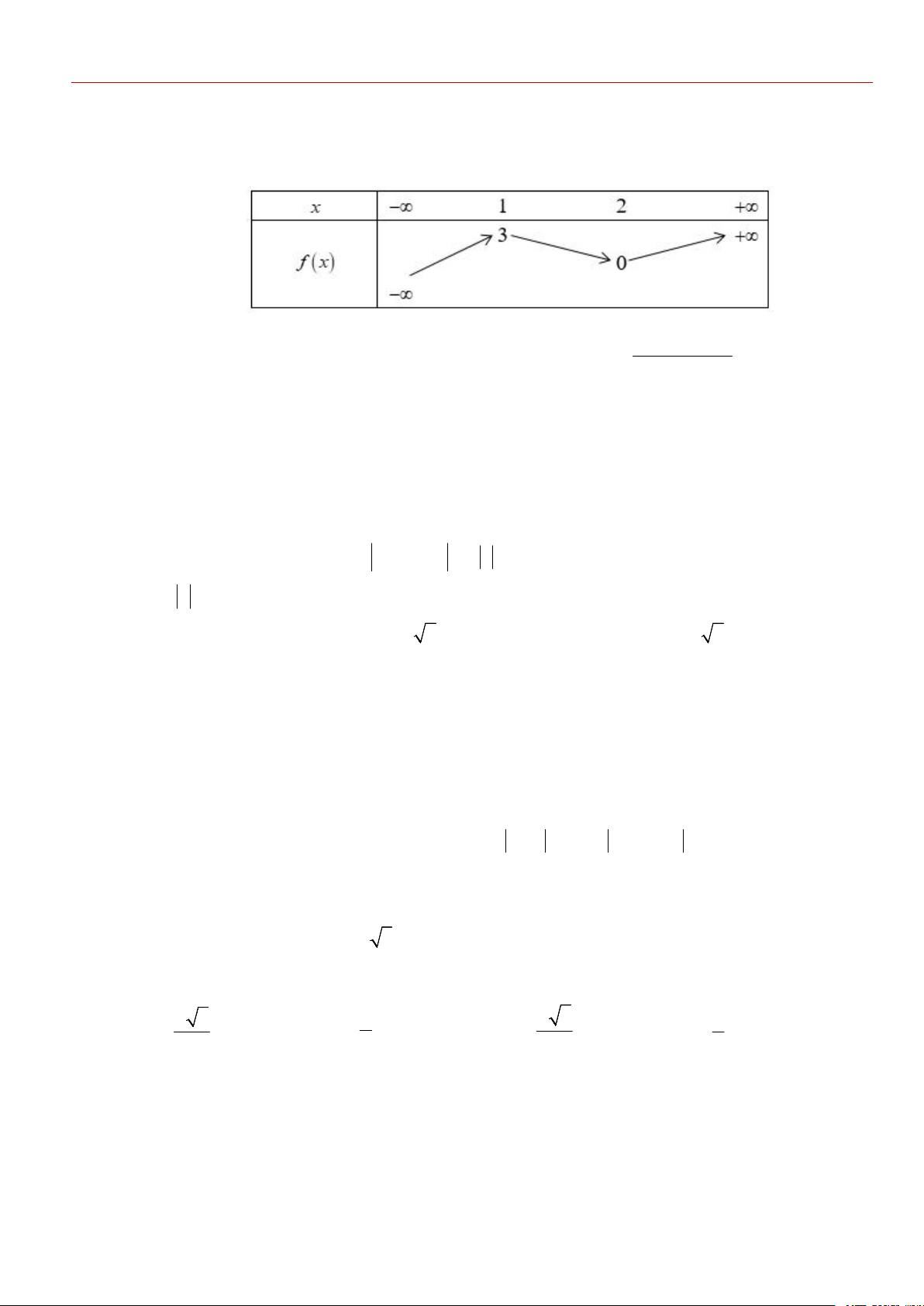
Câu 1: Cho hai số phức z và w thỏa mãn z 4, w 2 . Khi z w 512i đạt giá trị lớn nhất, phần
thực của z iw bằng A. 30 . B. 4 . C. 44 . D. 58 . 13 13 13 13 Câu 2:
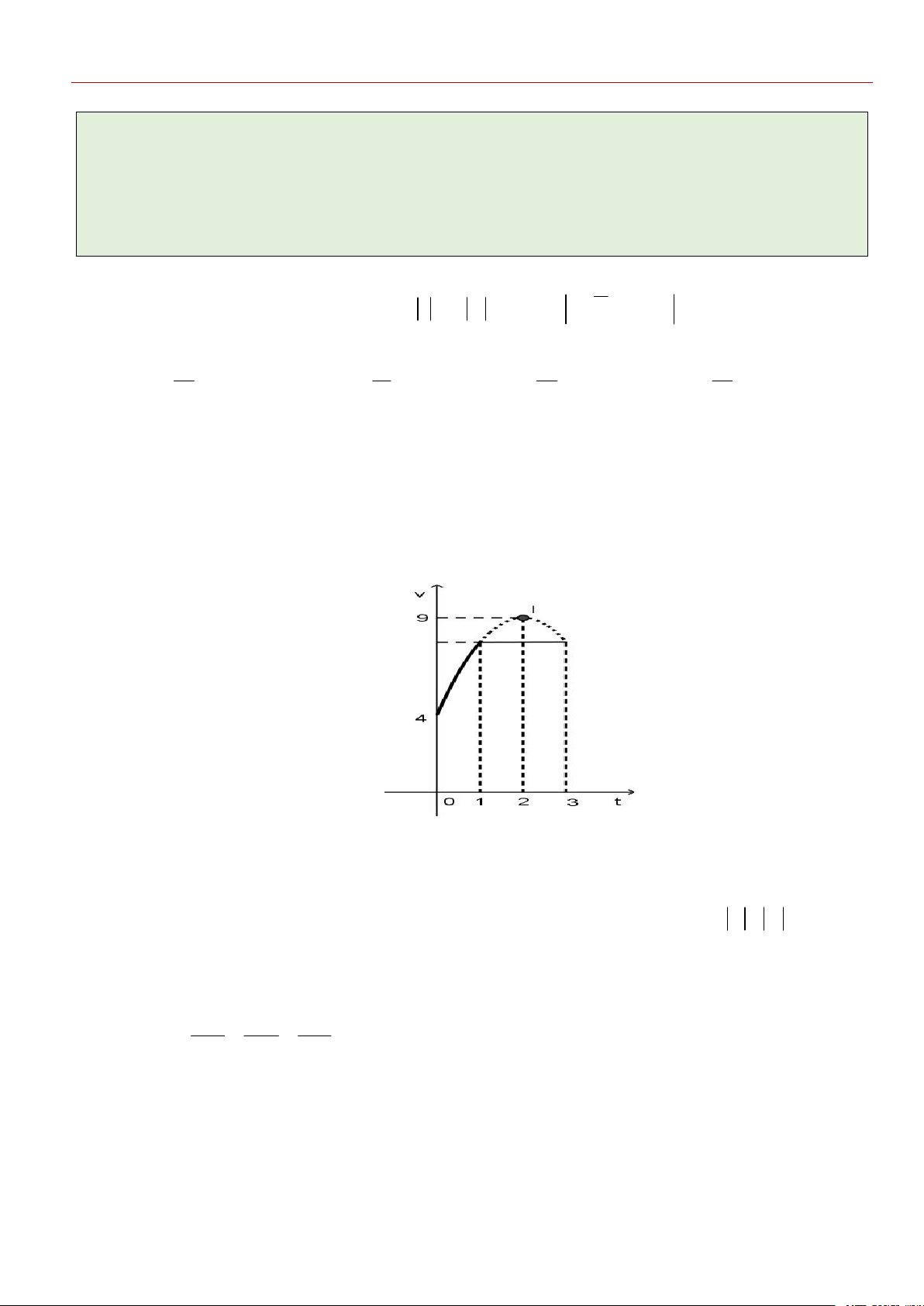
Một vật chuyển động trong 3 giờ với vận tốc (
v km / h) phụ thuộc vào thời gian t(h) có đồ thị
vận tốc như hình bên. Trong thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần
của đường parabol có đỉnh I(2;9) và trục đối xứng song song với trục tung, khoảng thời gian
còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật chuyển
động được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A. s 21,58(km)
B. s 23,25(km)
C. s 13,83(km)
D. s 15,50(km)
Câu 3: Trên tập hợp các số phức, xét phương trình 2
z 2mz 8m 12 0 ( m là tham số thực). Có bao
nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z , z thỏa mãn z z 4? 1 2 1 2 A. 1. B. 2 . C. 3. D. 4 .
Câu 4: Trong không gian với hệ tọa độ Oxyz cho điểm A2;1;2 và đường thẳng d có phương
trình x 1 y 1 z 1
. Gọi P là mặt phẳng đi qua điểm A , song song với đường thẳng d 1 1 1
và khoảng cách từ d tới mặt phẳng P là lớn nhất. Khi đó mặt phẳng P vuông góc với mặt phẳng nào sau đây?
A. x y 6 0.
B. x 3y 2z 10 0 .
C. x 2y 3z 1 0.
D. 3x z 2 0 .
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52 x
Câu 5: Có bao nhiêu cặp số nguyên ; x y thỏa mãn 2 1
0 y 2020 và log 1 2 x y ? 3 y A. 2019. B. 11. C. 2020. D. 4 .
Câu 6: Cho lăng trụ đứng ABC.A B C
. Biết rằng góc giữa hai mặt phẳng A B
C và ABC là 30 , tam giác A B
C đều và diện tích bằng 3 . Thể tích khối lăng trụ ABC.A B C bằng 3 3 A. 2 3 . B. 6 . C. . D. 3 4 4
Câu 7: Cắt hình nón N bởi mặt phẳng đi qua đỉnh S và tạo với trục của N một góc bằng 30° , ta
được thiết diện là tam giác SAB vuông và có diện tích bằng 2
4a . Chiều cao của hình nón bằng Câu 8:
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A2;0;0 , B0;2;0 , C 0;0;2 .
Gọi D là điểm khác O sao cho DA , DB , DC đôi một vuông góc nhau và I a;b;c là
tâm mặt cầu ngoại tiếp tứ diện ABCD . Tính S a b c . A. S 4 B. S 1 C. S 2 D. S 3
Câu 9: Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích
V của khối chóp có thể tích lớn nhất. A. V 144 B. V 576 C. V 576 2 D. V 144 6
Câu 10: Cho mặt cầu S tâm O, bán kính R 3. Mặt phăng P cách O một khoảng bằng 1 và
căt S theo giao tuyến là đương tron C có tâm H . Gọi T là giao điểm của tia HO
với S , tính thể tích V của khối nón có đinh T và đáy là hình tron C . A. 32 V B. V 16 C. 16 V D. V 32 3 3
Câu 11: Tìm tất cả các giá tri thưc của tham số m để đô thi của hàm số 3 2 3
y x 3mx 4m có hai
điểm cưc tri A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ. A. 1 m ; 1 m B. m 1 ; m 1 4 2 4 2 C. m 1 D. m 0
Câu 12: Xét các số phức w z, (
w w 2) thỏa mãn | z | 1 và
2 là số thuần ảo. Khi | z w| 3 , giá trị w 2
của | 2z w | bằng 9 7 3 7 2 3 A. . B. . C. . D. 2 3 . 2 2 3
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
BỘ MIX 12 CÂU CUỐI VỀ ĐÍCH 03
(7 NGÀY BỨT PHÁ VỀ ĐÍCH) CA SÁNG : 4H45 SÁNG
Câu 1: Có bao nhiêu giá trị m nguyên và m 2 022;2022 để phương trình 2
z 2z 1 3m 0 có hai nghiệm phức thỏa mãn z .z z .z . 1 1 2 2 A. 4045 . B. 2021. C. 2022 . D. 2023
Câu 2: Trong không gian với hệ toạ độ Oxyz , gọi P là mặt phẳng đi qua hai điểm A1;7;8 ,
B 2;5;9 sao cho khoảng cách từ điểm M 7;1;2 đến P đạt giá trị lớn nhất. Biết
P có một véctơ pháp tuyến là n a;b;4, khi đó giá trị của tổng a b là A. 1 . B. 3 . C. 6 . D. 2 .
Câu 3: Cho khối nón tròn xoay có đường cao h 5a và bán kính đáy r 4a . Một mặt phẳng
P đi qua đỉnh của khối nón và có khoảng cách đến tâm O của đáy bằng 3a. Diện tích
thiết diện tạo bởi P và hình nón là 25 31 5 31 5 41 25 41 A. 2 a . B. 2 a . C. 2 a . D. 2 a . 16 8 16 32
Câu 4: Cho số phức z thỏa mãn z 1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P z 1 z z 1 . Giá trị của M .m bằng A. 13 3 . B. 13 3 . C. 3 . D. 3 3 . 4 8 3 8 Câu 5:
Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 3 2
y 3x 4x 12x m có 7 điểm cực trị? A. 3 B. 5 C. 6 D. 4 Câu 6:
Trong không gian Oxyz , cho ba điểm A1;2; 1 , B3; 1 ; 1 và C 1 ; 1 ; 1 . Gọi S1 là
mặt cầu có tâm A , bán kính bằng 2 ; S S
2 và 3 là hai mặt cầu có tâm lần lượt là B ,
C và bán kính đều bằng 1. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu S1 , S S 2 , 3 . A. 5 B. 7 C. 6 D. 8
Câu 7: Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3
m 3 m 3sin x sin x có nghiệm thực A. 5 B. 2 C. 4 C. 3
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
Câu 8: Xét số phức z thỏa mãn z 2 i z 4 7i 6 2. Gọi m, M lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của z 1 i . Tính P m M. A. 5 2 2 73 P
B. P 5 2 73 C. 5 2 73 P
D. P 13 73 2 2 Câu 9:
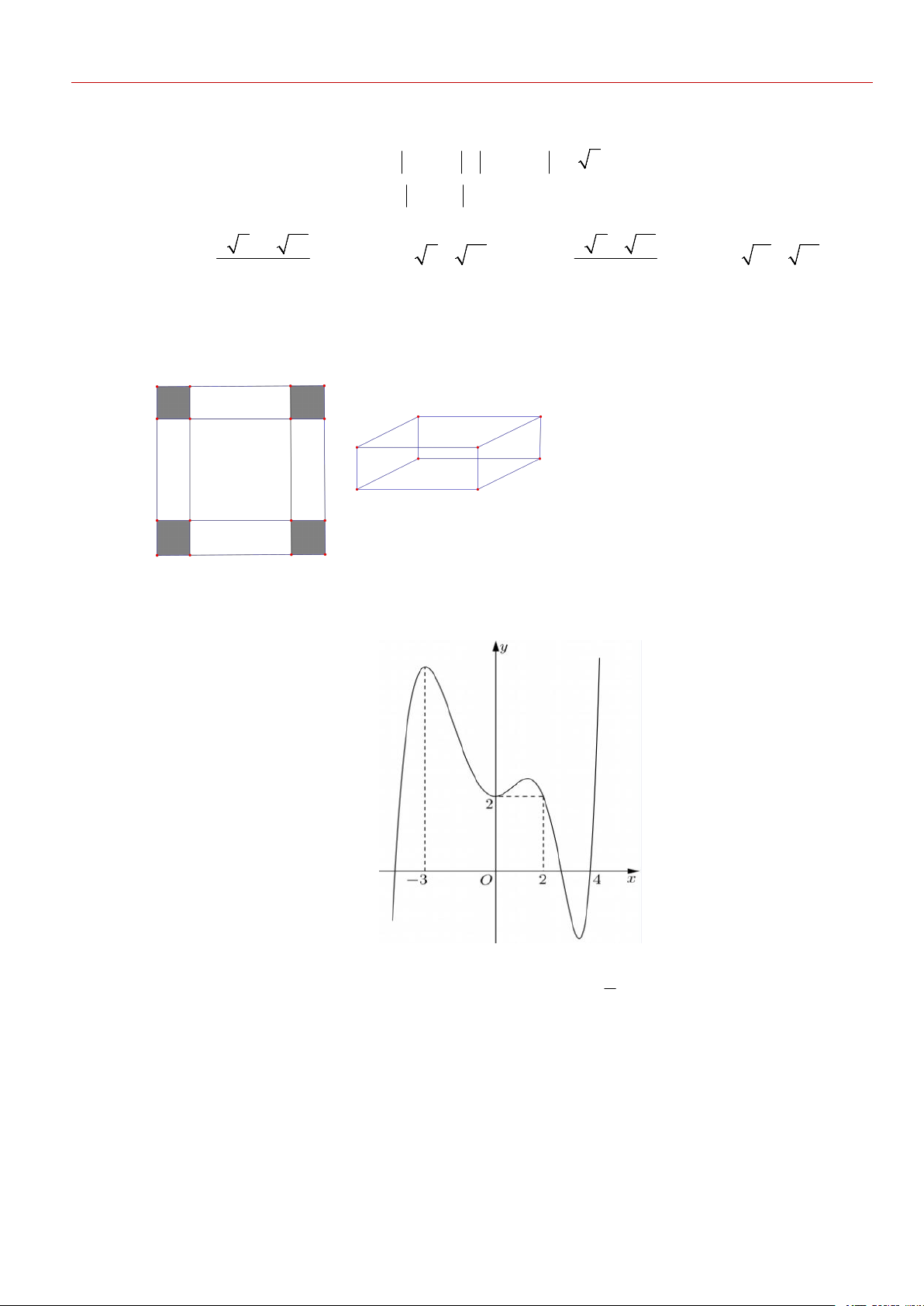
Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó
bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại
như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. x 3 B. x 2 C. x 4 D. x 6
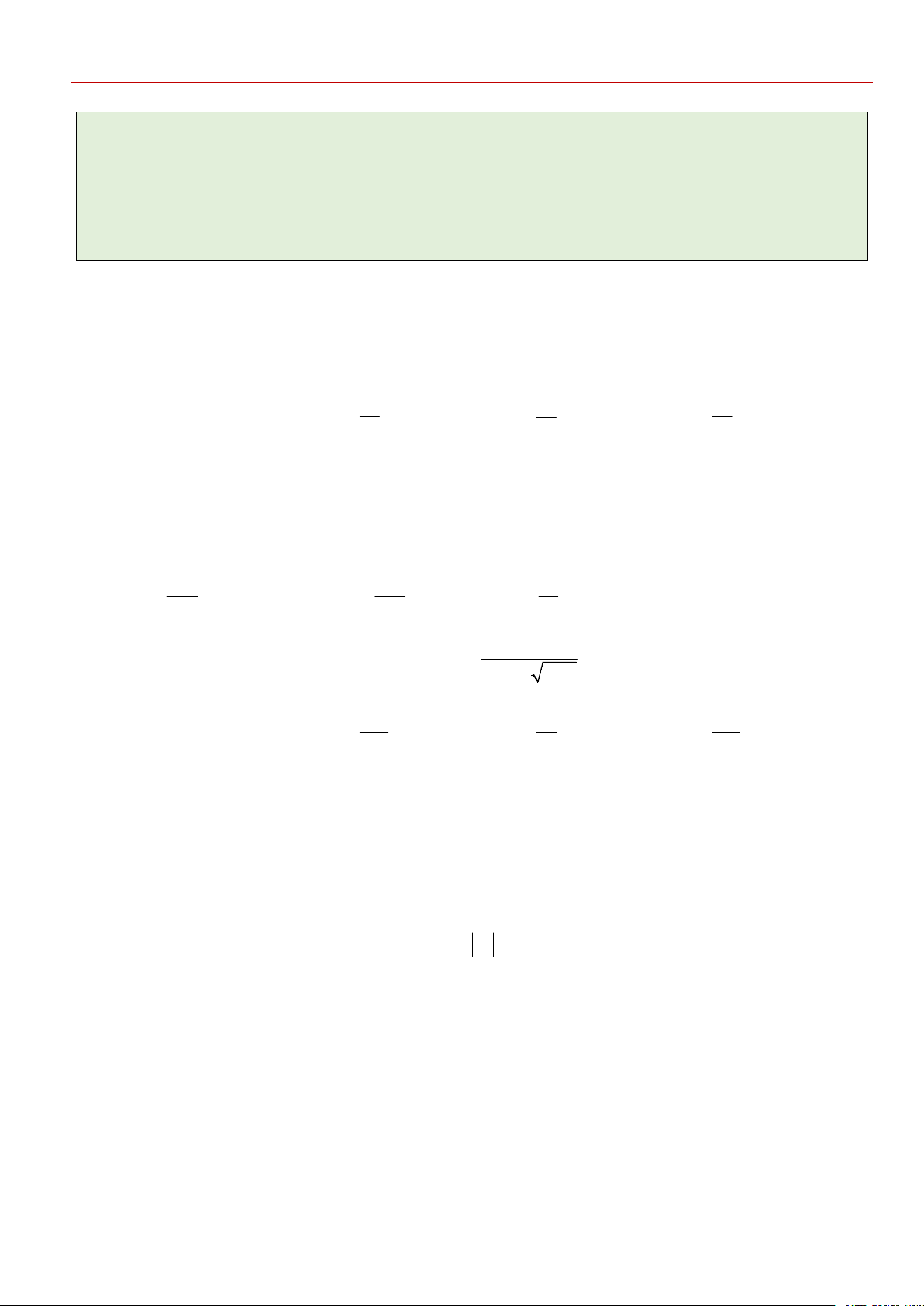
Câu 10: Cho hàm số f x , đồ thị của hàm số y f x là đường cong trong hình bên.
Giá trị lớn nhất của hàm số g x f 2x 4x trên đoạn 3 ;2 bằng 2
A. f 0 . B. f 3 6 . C. f 2 4 . D. f 4 8 .
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
x 3 y 3 z 2
Câu 11: Trong không gian Oxyz , cho hai đường thẳng d : 1 ; 1 2 1
x 5 y 1 z 2 d : 2
và mặt phẳng P: x 2y 3z 5 0 . Đường thẳng vuông góc 3 2 1
với P , cắt d và d có phương trình là 1 2
x 1 y 1 z
x 2 y 3 z 1 A. B. 1 2 3 1 2 3
x 3 y 3 z 2
x 1 y 1 z C. D. 1 2 3 3 2 1
Câu 12: Gọi S là tập tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số 1 4 2
y x 14x 48x m 30 trên đoạn 0;2 không vượt quá 30 . Tổng tất cả 4
các giá trị của S là A. 180. B. 136. C. 120. D. 210 .
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
BỘ MIX 12 CÂU CUỐI VỀ ĐÍCH 04
(7 NGÀY BỨT PHÁ VỀ ĐÍCH) CA SÁNG : 4H45 SÁNG
Câu 1. Xét số phức z a bi
a,b thỏa mãn z 43i 5 . Tính P a b khi
z 13i z 1 i đạt giá trị lớn nhất. A. P 8 B. P 10 C. P 4 D. P 6
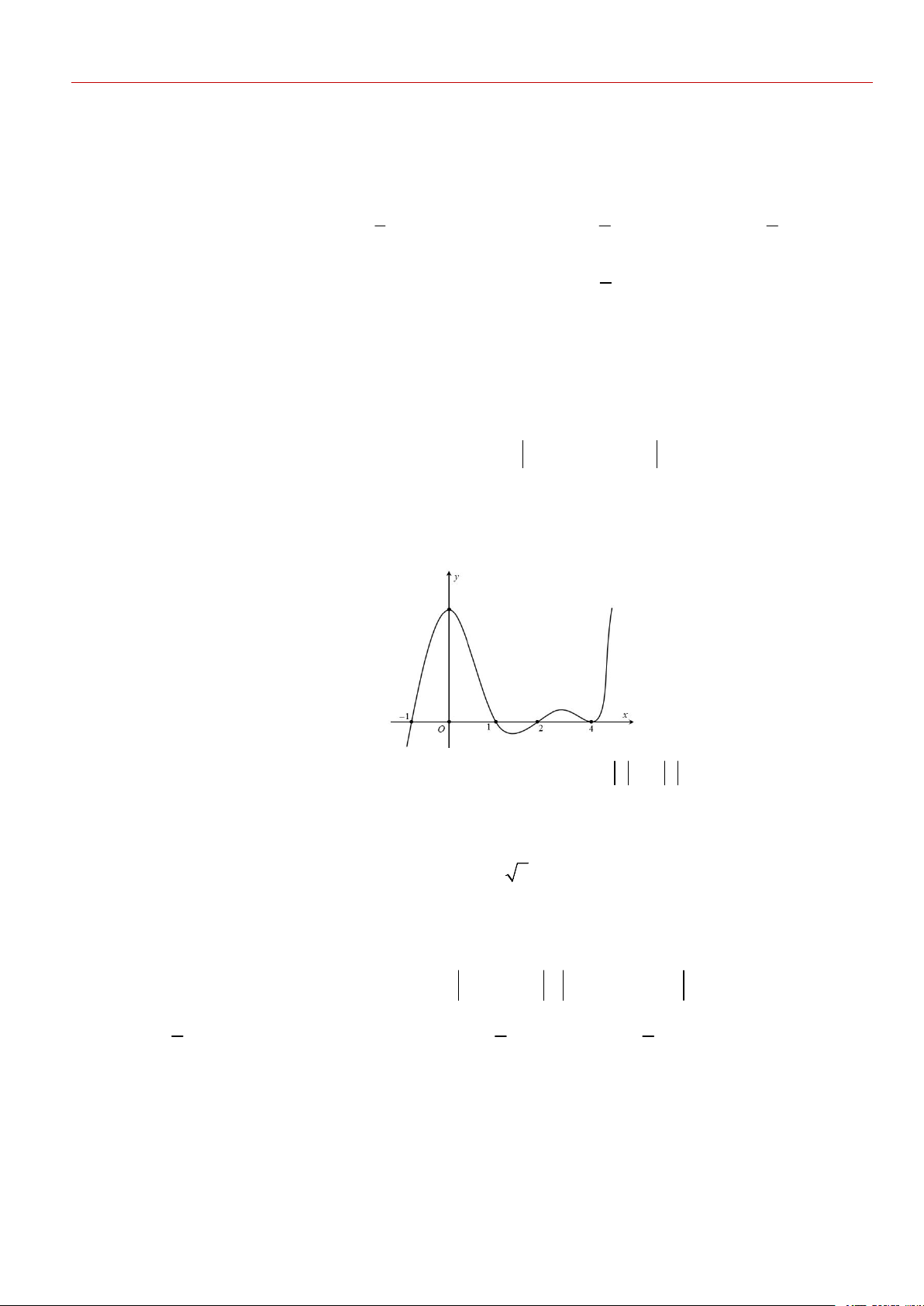
Câu 2. Cho hàm số f x 4 3 2
mx nx px qx r , (với m,n, p,q,r R ). Hàm số y f x có đồ thị như hình vẽ bên dưới: y 1 O 5 x 3 4
Tập nghiệm của phương trình f x r có số phần tử là A. 4 . B. 3. C. 1. D. 2 .
Câu 3. Cho số phức z thỏa mãn z z z z 4. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của P z 2 2i . Đặt A M .
m Mệnh đề nào sau đây là đúng?
A. A 34;6.
B. A6; 42 .
C. A2 7; 33. D. A4;3 3 .
Câu 4. Cho hai số phức z , w thỏa mãn z 3 2 2 , w 4 2i 2 2 . Biết rằng z w đạt giá trị
nhỏ nhất khi z z , w w . Tính 3z w . 0 0 0 0 A. 2 2 . B. 4 2 . C. 1. D. 6 2 . Câu 5. Gọi S
là tập hợp tất cả các giá trị của tham số m để bất phương trình 2 m 4
x m 2 1
x 1 6x 1 0 đúng với mọi xR . Tổng giá trị của tất cả các phần tử thuộc S bằng A. 3 . B. 1. C. 1 . D. 1 . 2 2 2
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
Câu 6. Cho khối lăng trụ ABC.
A BC có thể tích bằng 1. Gọi M , N lần lượt là trung điểm của các đoạn thẳng A
A và BB . Đường thẳng CM cắt đường thẳng C
A tại P , đường thẳng CN cắt
đường thẳng CB tại Q . Thể tích khối đa diện lồi
A MPBNQ bằng A. 1. B. 1 . C. 1 . D. 2 . 3 2 3 1
Câu 7. Cho hàm số f x liên tục trên 1 ;
1 thoả f x 3
2 x t f t dt, x 1;1 . Tính 2 1 1 I f xdx ? 1 A. I 4 . B. I 3. C. I 2 . D. I 1.
Câu 8. Có bao nhiêu số nguyên dương m để hàm số 2 2
y x mx m 4 3mx 19 có 3 điểm cực trị? A. 3. B. 5. C. 1. D. 2.
Câu 9. . Cho hàm số f x có đạo hàm liên tục trên , đồ thị hàm số y f x có đúng 4 điểm
chung với trục hoành như hình vẽ bên dưới:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y f 3
x x m 3 3 2021 2022m có
đúng 11 điểm cực trị ? A.0 B. 2 . C. 5 . D. 1.
Câu 10. Có bao nhiêu số phức z thỏa mãn | z 2 i | 2 2 và z 2 1 là số thuần ảo? A. 0 B. 2 C. 4 D. 3
Câu 11. Trong không gian với hệ tọa độ Oxyz , cho A2;3;
1 , B 2;3;2 , C 1;0;2 .Tìm tọa độ
điểm M thuộc mặt phẳng Oxz để S MA 4MC MA MB MC nhỏ nhất. A. 7 M 1;0; .
B. M 0;3;0 . C. 7 M 1;0; . D. 1 M ;0;2 . 3 3 2
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
Câu 12. Trong không gian Oxyz
cho mặt cầu x 2 y 2 2 3 1 z 4 và đường thẳng x 1 2t
d : y 1
t ,t R . Mặt phẳng chứa d và cắt ( S ) theo một đường tròn có bán kính nhỏ nhất z t có phương trình là
A. y z 1 0 .
B. x 3 y 5z 2 0 . C. x 2 y 3 0 .
D. 3x 2 y 4z 8 0 .
BỘ MIX 12 CÂU CUỐI VỀ ĐÍCH 05
(7 NGÀY BỨT PHÁ VỀ ĐÍCH) CA SÁNG : 4H45 SÁNG
Câu 1. Trên tập hợp các số phức, xét phương trình 2
z a 2 2
3 z 2a 2a 16 0 ( a là tham số
thực). Có bao nhiêu giá trị nguyên của a để phương trình đó có hai nghiệm phân biệt z , z thỏa mãn 1 2
2 z z z z ? 1 2 2 1 A. 2 . B. 1. C. 3. D. 4 .
Câu 2. Trên tập hợp các số phức, xét phương trình 2 2
z 2az b 2b 0(a,b là các tham số thực. Gọi
S là tập hợp các cặp (a;b) sao cho phương trình đó có hai nghiệm z , z thỏa mãn 3z 2iz 3 6i . Số 1 2 1 2
phần tử thuộc S bằng A. 1. B. 3. C. 2. D. 4.
Câu 3. Trong không gian với hệ tọa độ Oxyz
cho điểm A2;1;3 và mặt phẳng
P: x my 2m
1 z m 2 0 , m là tham số. Gọi H a;b;c là hình chiếu vuông góc của điểm A
trên P . Tính a b khi khoảng cách từ điểm A đến P lớn nhất ? A. 1
a b .
B. a b 2 .
C. a b 0. D. 3 a b . 2 2
Câu 4. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 x 2020 và log 512 768 2 1 2 16y x x y ? 4 A. 2019 B. 0 C. 2020 D. 1
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
Câu 5. Cho khối nón đỉnh S có bán kính đáy bằng 2 3a . Gọi A và B là hai điểm thuộc đáy sao cho
AB 4a . Biết khoảng cách từ tâm của đáy đến mặt phẳng SAB bằng 2a , thể tích của khối nón đã cho bằng 8 2 3 a 16 3 3 a A. 3 . B. 3 4 6 a . C. 3 . D. 3 8 2 a .
Câu 6. Trong không gian Oxyz , cho hai điểm A 1
;2;3 và B3;2;5 . Xét hai điểm M và N thay đổi
thuộc mặt phẳng Oxy sao cho MN 2023. Tìm giá trị nhỏ nhất của AM BN . A. 2 17 . B. 65 . C. 25 97 . D. 205 97 .
Câu 7. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số 4 3 2
y = 3x -4x 1 - 2x +m
nghịch biến trến khoảng ; 1 ? A. 5 . B. 4. C. 6. D. 3.
Câu 8. Cho y f xlà hàm số bậc ba và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên m 5
;5 để hàm số g x f f x m có 4 điểm cực trị? A. 5. B. 6. C. 7. D. 8
Câu 9. Trong không gian với hệ trục Oxyz , cho điểm A2; 2
;2 và mặt cầu S x y z 2 2 2 : 2 1.
Điểm M di chuyển trên mặt cầu S đồng thời thỏa mãn OM.AM 6. Điểm M luôn thuộc mặt phẳng nào dưới đây?
A. 2x 2y 6z 9 0 .
B. 2x 2y 6z 9 0 .
C. 2x 2y 6z 9 0 .
D. 2x 2y 6z 9 0 .
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho điểm H 1;2; 2 . Mặt phẳng đi qua H và cắt
các trục Ox,Oy,Oz lần lượt tại các điểm , A ,
B C sao cho H là trực tâm của tam giác ABC. Tính diện tích
mặt cầu ngoại tiếp tứ diện OABC. A. 243 .
B. 81 . C. 81 . D. 243 . 2 2
Câu 11. Cho hàm số y f x có đạo hàm f x x 2 2
1 x 2x với x . Có bao nhiêu
giá trị nguyên dương của tham số m để hàm số f 2x 8x m có 5 điểm cực trị? A. 15. B. 17 . C. 16 D. 18
Câu 12. Cho A0;8;2 và mặt cầu S x 2 y 2 z 2 : 5 3
7 72 và điểm A9; 7;23 . Viết
phương trình mặt phẳng P đi qua A và tiếp xúc với mặt cầu S sao cho khoảng cách từ B đến mặt
phẳng P là lớn nhất. Giải sử n 1; ;
m n là một vectơ pháp tuyến của P . Lúc đó A. . m n 4 . B. . m n 2 . C. . m n 4 . D. . m n 2 .
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
BỘ MIX 12 CÂU CUỐI VỀ ĐÍCH 06
(7 NGÀY BỨT PHÁ VỀ ĐÍCH) CA SÁNG : 4H45 SÁNG
Câu 1. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB a , 0 SBA SCA 90 ,
góc giữa hai mặt phẳng SAB và SAC bằng 0
60 . Thể tích của khối đã cho bằng 3 a 3 3 a A. 3 a . B. . C. a . D. . 3 2 6 Câu 2.
Cho hàm số f x liên tục trên thảo mãn xf 3 x f 2 x 10 6 1
x x 2x, x . Khi đó 0 f xdx ? 1 A. 1 7 . B. 1 3 . C. 17 . D. 1. 20 4 4 8 Câu 3. Cho hàm số x
f x có f 3 3 và f x
, x 0 . Khi đó f xdx bằng x 1 x 1 3 A. 7 . B. 197 . C. 29 . D. 181 . 6 2 6
Câu 4. Có bao nhiêu số nguyên x thoả mãn log
2x 1log x2 1 . x 1 16 2 0? 3 3 A. 17 . B. 18 . C. 16. D. Vô số.
Câu 5. Trên tập hợp các số phức, gọi S là tổng các giá trị thực của m để phương trình 2
mz 2m
1 z m 6 0 có nghiệm z z 1 0 thỏa mãn 0 . Tính S. A. 3 . B. 4 . C. 1. D. 2 .
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
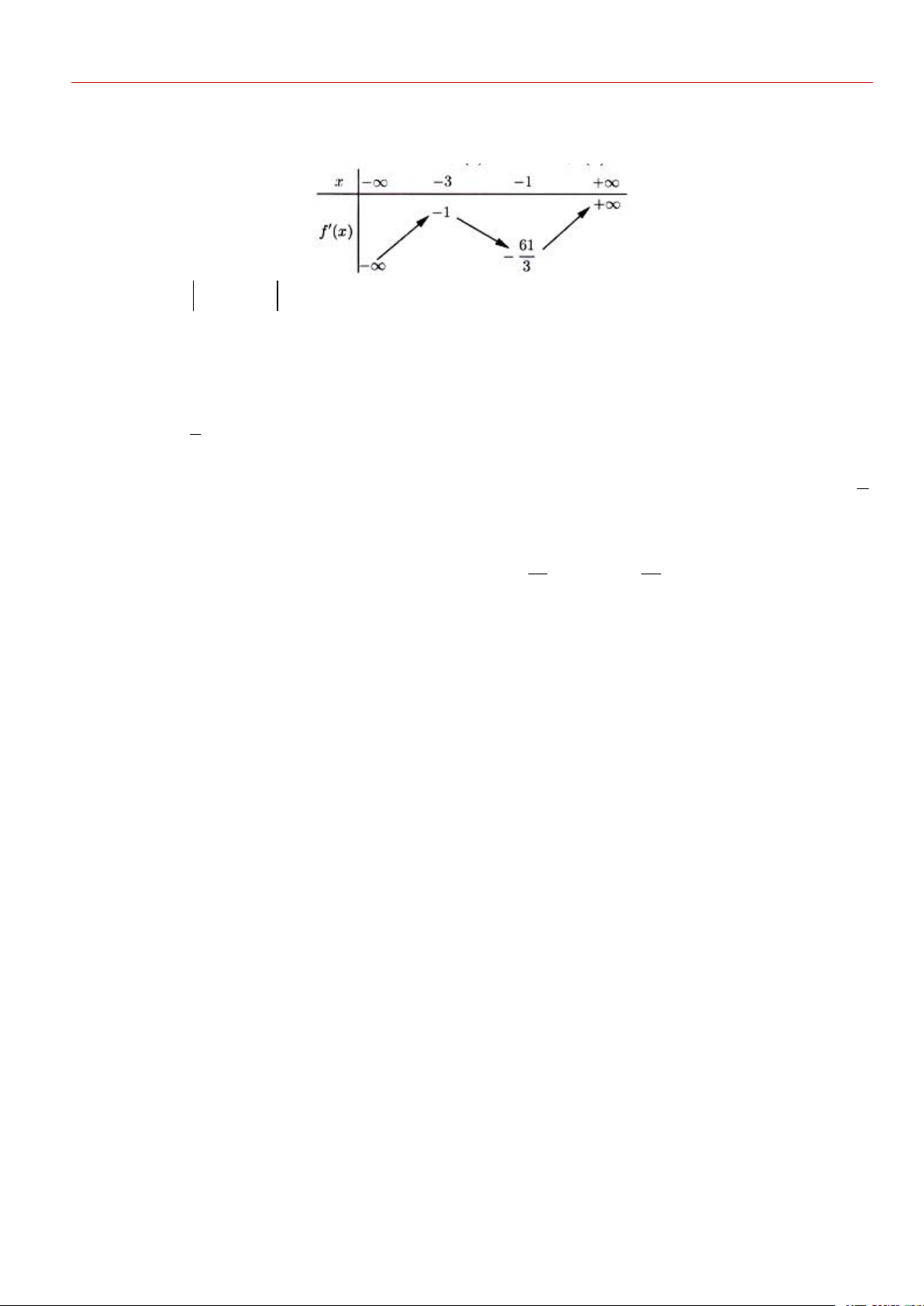
Câu 6. Cho hàm số bậc ba 3 2
f x ax bx cx d có đồ thị như hình vẽ sau.
2x 3x2 x1
Hỏi đồ thị hàm số g x
có bao nhiêu tiệm cận đứng? x 2
1 f x f x A. 5. B. 4 . C. 6 . D. 3.
Câu 7. Trong không gian Oxyz , cho hai điểm A3; 2;3 ; B1;0;5 . Tìm tọa độ điểm M Oxy sao
cho MA MB đạt giá trị nhỏ nhất: A. 9 5 ; ;0 . B. 9 5 ; ;0 . C. 9 5 ; ;0 . D. 9 5 ; ;0 . 4 4 4 4 4 4 4 4
Câu 8. Trong không gian Oxyz, cho hai điểm A2;1;3 và B6;5;5. Xét khối nón N có đỉnh , A
đường tròn đáy nằm trên mặt cầu đường kính A .
B Khi N có thể tích lớn nhất thì mặt phẳng chứa đường
tròn đáy của N có phương trình dạng 2x by cz d 0. Giá trị của b c d bằng A. 21. B. 12. C. 18. D. 15.
Câu 9. Trong không gian Oxyz , cho hai điểm A1;3;2 và B2;1; 4 . Xét hai điểm M và N thay
đổi thuộc mặt phẳng Oxy sao cho MN 4. Giá trị lớn nhất của AM BN bằng A. 5 2 . B. 3 13 . C. 61 . D. 85 . Câu 10.
Trong không gian Oxyz, cho mặt phẳng P : 2x 2y z 3 0 và hai đường thẳng x 1 y z 1 x 2 y z 1 d : ,d :
. Đường thẳng vuông góc với P, đồng thời cắt cả d và d có 1 2 2 2 2 1 2 1 1 2 phương trình là
A. x 3 y 2 z 2 .
B. x 2 y 2 z 1 . 2 2 1 3 2 2 C. x 1 y z 1 .
D. x 2 y 1 z 2 . 2 2 1 2 2 1
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52 Câu 11.
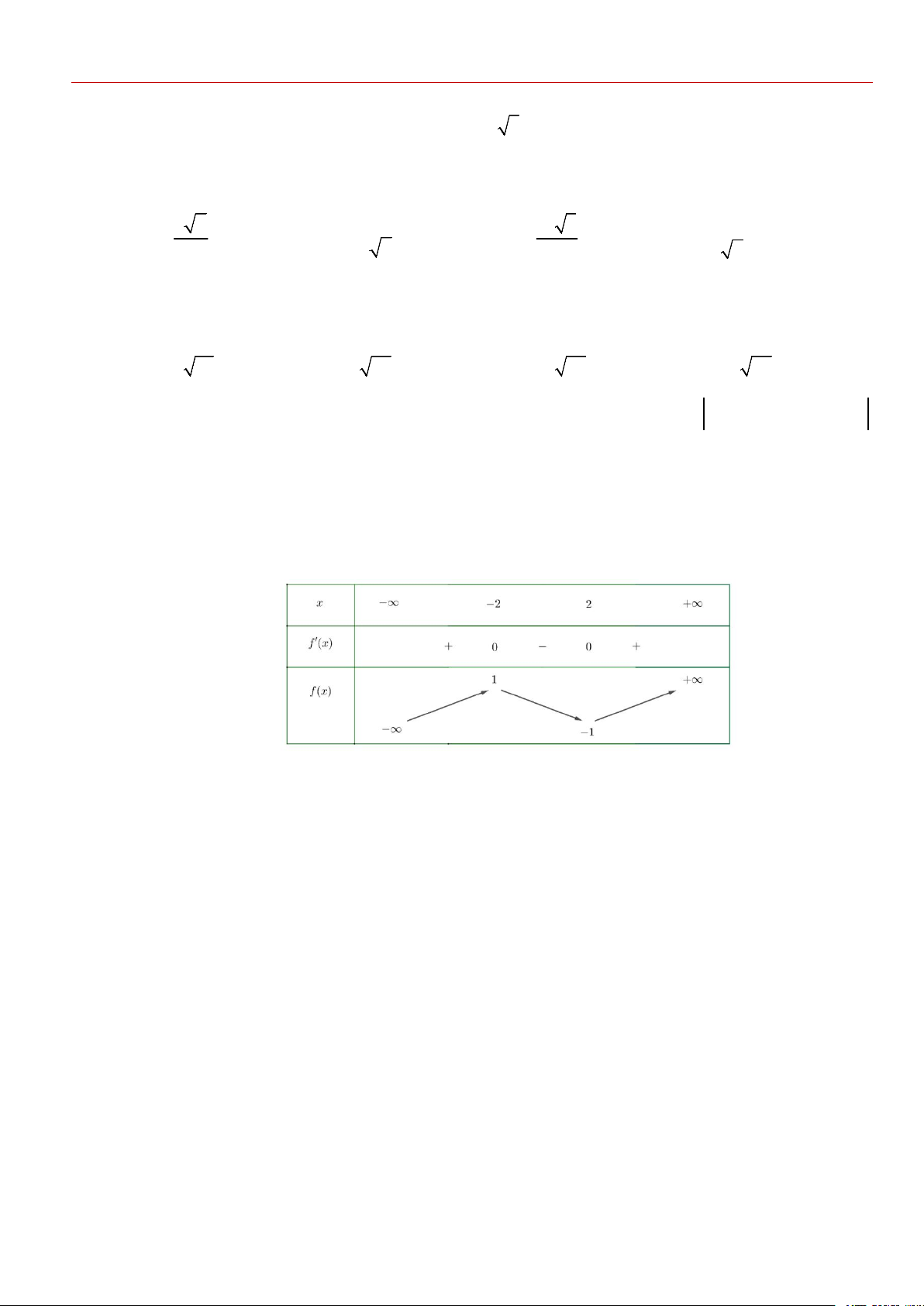
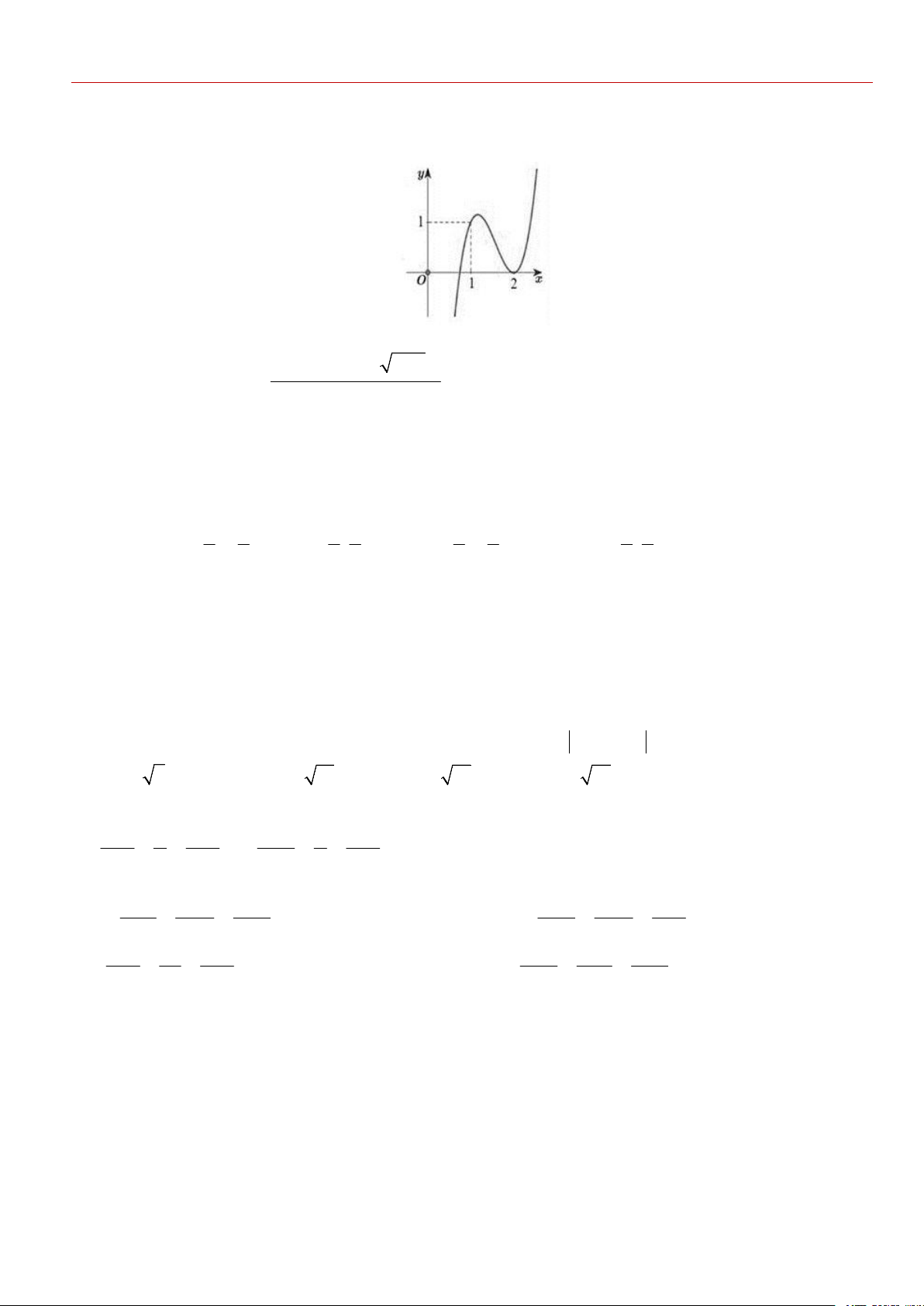
Cho f x là hàm số bậc bốn thỏa mãn f 0 0. Hàm số f 'x có bảng biến thiên như sau:
Hàm số g x f 3
x 3x có bao nhiêu điểm cực trị? A. 3. B. 5. C. 4. D. 2.
Câu 12. Xét f x 4 2
ax bx c(a,b,c R,a 0) sao cho đồ thị hàm số y f x có ba điểm cực trị là , A B và 3 C 1;
. Gọi y g x là hàm số bậc hai có đồ thị đi qua ba điểm ,
A B và C . Khi hình phẳng 5
giới hạn bởi đồ thị của hai hàm số y f x, y g x và hai đường thẳng x 0, x 1 có diện tích bằng 2 , 5
tích phân 1 f x dx bằng 0 A. 1. B. -1. C. 17 . . D. 17 . . 15 15
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
BỘ MIX 12 CÂU CUỐI VỀ ĐÍCH 07 - CUỐI
(7 NGÀY BỨT PHÁ VỀ ĐÍCH) CA SÁNG : 4H45 SÁNG Câu 1.
Trong hệ trục Oxyz, cho điểm A1;3;5, B2;6;
1 , C 4;12;5 và mặt phẳng
P: x 2y 2z 5 0. Gọi M là điểm di động trên P. Gía trị nhỏ nhất của biểu thức S MA MB MC là A. 42. B. 14. C. 14 3. D. 14 . 3 Câu 2. 4
Cho hàm số y f (x) có đạo hàm trên 4 ; 4 , có các điểm cực trị trên 4 ; 4 là 3 ; ; 3
0 ; 2 và có đồ thị như hình vẽ. Đặt hàm số 3
y g(x) f (x 3x) m với m là tham số. Gọi m là giá trị 1
của m để max g(x) 4, m là giá trị của m để min g(x) 2
. Giá trị của m m bằng. 0; 1 2 1 ; 0 1 2 A. 2 . B. 0 . C. 2 . D. 1.
Câu 3. Cho khối lăng trụ ABC A B C
có đáy ABC là tam giác vuông cân tại A , A A A B A C a .
Biết góc giữa hai mặt phẳng BCC B
và ABC bằng 30.Thể tích của khối lăng trụ đã cho bằng 3 3 3 3 A. 3 . a . B. 3 . a . C. 3 . a . D. . a . 24 8 8 8
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
Câu 4. (Chuyên Bắc Giang 2019) Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên như hình bên dưới.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y là f 3 x x 3 A. 2. B. 4. C. 3. D. 1.
Câu 5. Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 2
y x 6x mx có ba điểm cực trị? A. 17 . B. 15. C. 3. D. 7 . Câu 6.
Xét các số phức z thỏa mãn 2
z 3 4i 2 z . Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của z . Giá trị của 2 2 M m bằng A. 28 . B. 18 4 6 . C. 14. D. 11 4 6 . Câu 7.
Trong không gian Oxyz , xét mặt cầu S có tâm I 3;7;12 và bán kính R thay đổi. Có bao
nhiêu giá trị nguyên của R sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của S trong mặt phẳng
Oyz mà hai tiếp tuyến đó cùng đi qua O và góc giữa chúng không nhỏ hơn 60? A. 11. B. 7 . C. 5. D. 3. Câu 8.
Trên tập số phức, xét phương trình 2
z az b 0 a,b . Có bao nhiêu cặp số a,b để
phương trình đó có hai nghiệm phân biệt z , z thỏa mãn z 1 2 và z 3 2i 4 ? 1 2 1 2 A. 2 . B. 4 . C. 6 . D. 5 .
Câu 9. Cho hình trụ có O,O là tâm hai đáy. Xét hình chữ nhật ABCD có ,
A B cùng thuộc O và
C, D cùng thuộc O sao cho AB a 3 , BC 2a đồng thời ABCD tạo với mặt phẳng đáy hình trụ
góc 60. Khoảng cách từ điểm O đến mặt phẳng ABCD bằng a a 3 A. a 3 . B. . C. . D. a . 4 4 2 2
Page: Thầy Nguyễn Chí - Luyện Thi Thương Trò - Zalo : 0971.23.24.52
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3;2;6, B 0;1;0 và mặt cầu
S x 2 y 2 z 2 : 1 2
3 25 . Mặt phẳng P : ax by cz 2 0 đi qua ,
A B và cắt S theo
giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T a b c A. T 3 B. T 4 C. T 5 D. T 2
Câu 11. Cho hàm số y f x liên tục trên có f 0 1 và đồ thị hàm số y f ' x như hình vẽ bên.
Hàm số y f x 3
3 9x 1 đồng biến trên khoảng: A. 1 ; B. ;0 C. 0;2 D. 2 0; 3 3 Câu 12.
Trong không gian Oxyz , cho các mặt phẳng P: x y 2z 1 0 , Q: 2x y z 1 0 .
Gọi S là mặt cầu có tâm thuộc trục hoành, đồng thời S cắt mặt phẳng P theo giao tuyến là một
đường tròn có bán kính 2 và S cắt mặt phẳng Q theo giao tuyến là một đường tròn có bán kính r .
Xác định r sao cho chỉ có đúng một mặt cầu S thỏa mãn yêu cầu. A. r 3 . B. r 2 . C. 3 r . D. 3 2 r . 2 2
