


Preview text:
ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. 2x − 3
Câu 1. Đồ thị hàm số y =
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là x −1
A. x =1 và y = 2 .
B. x =1 và y = −3 .
C. x = 2 và y = 1. D. x = 1 − và y = 2 .
Câu 2. Tìm giá trị nhỏ nhất của hàm số 3 2
y = x - 3x - 9x + 2 = 0 trên đoạn [- 2;0].
A. min y = 0 .
B. min y = 7 .
C. min y = - 20 .
D. min y = 2 . [- 2;0] [- 2;0] [- 2;0] [- 2;0]
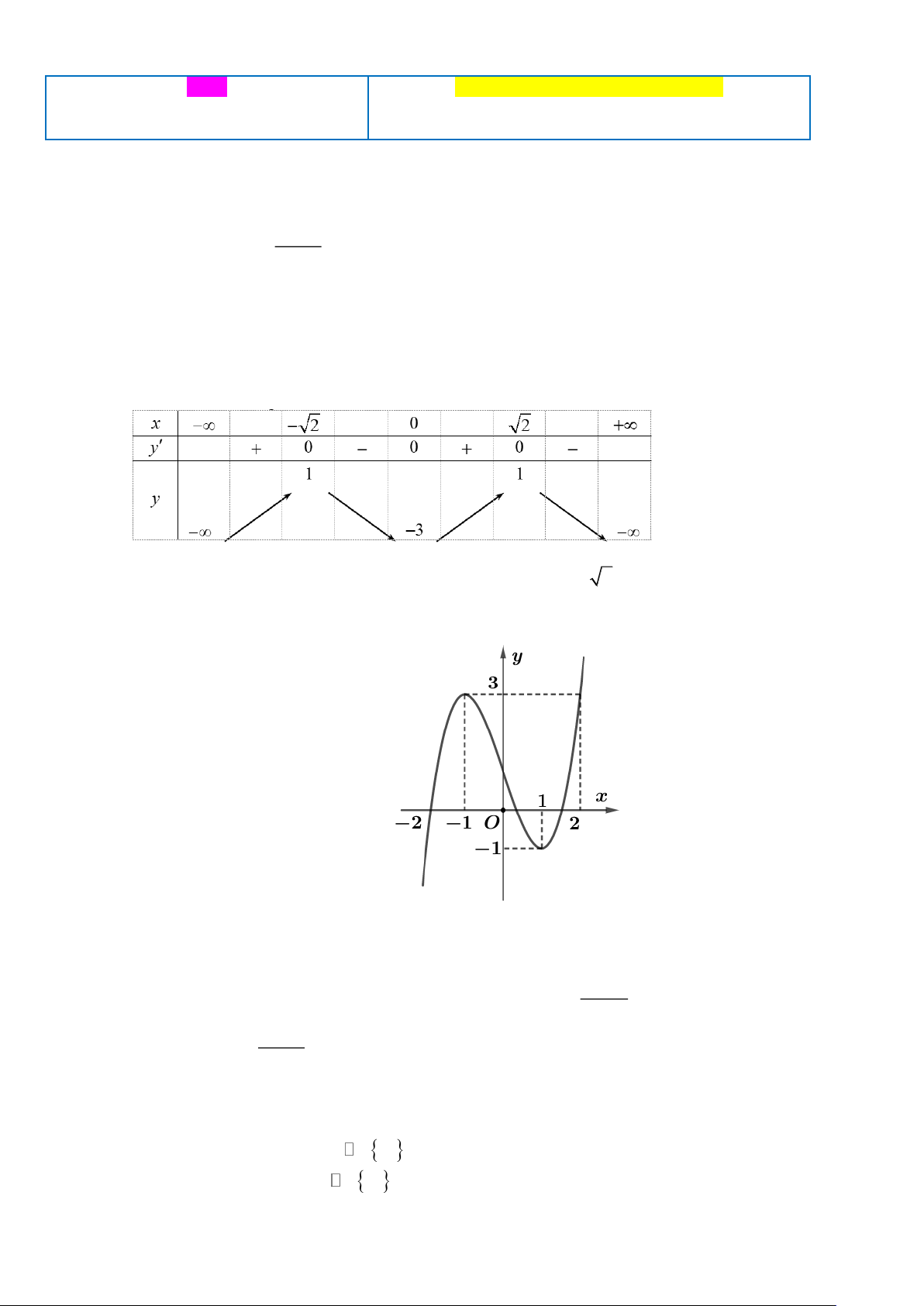
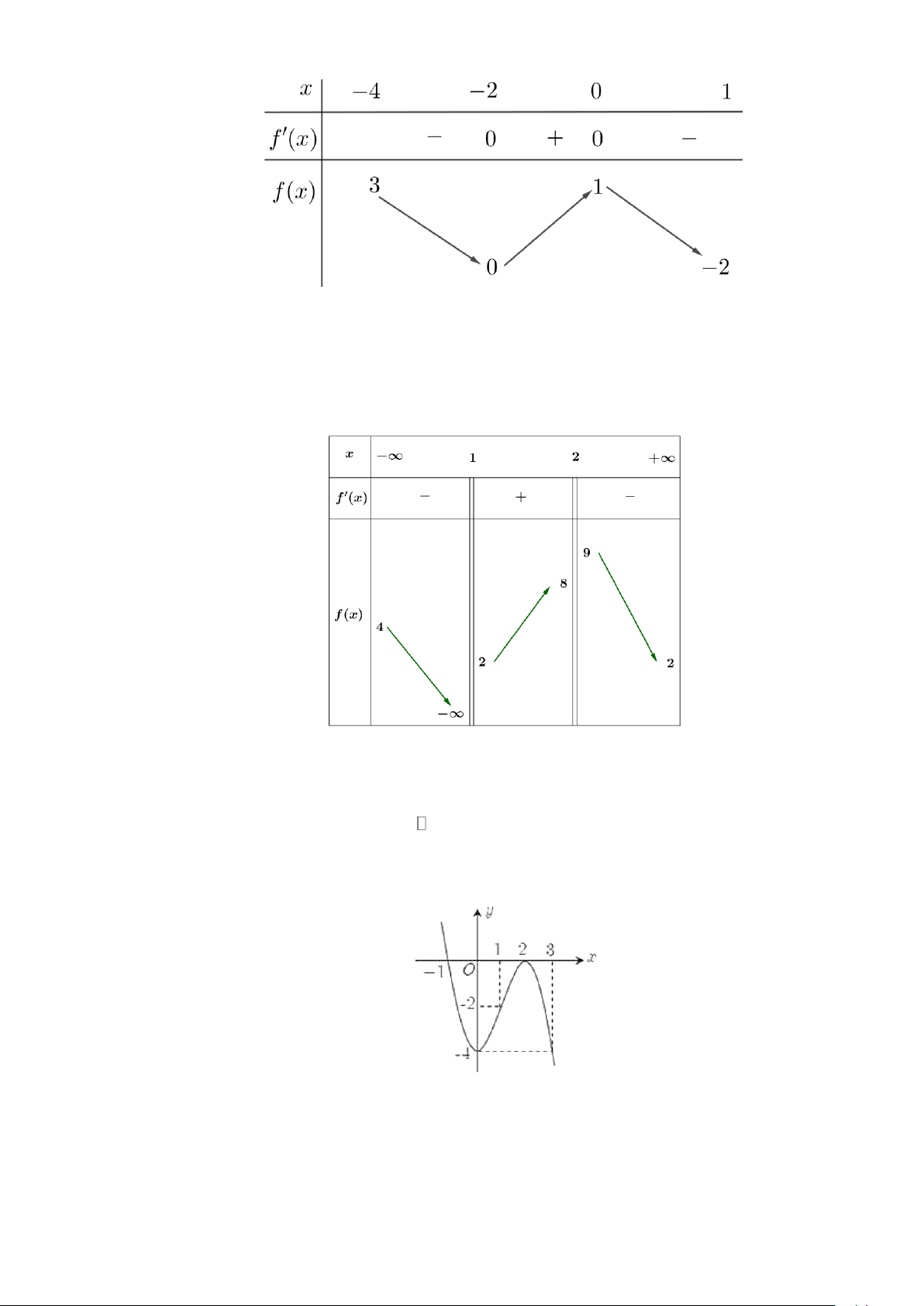
Câu 3. Cho hàm số có bảng biến thiên như sau
Hàm số đạt cực tiểu tại điểm
A. x = 0 . B. x =1.
C. x = 2 . D. x = 3 − .
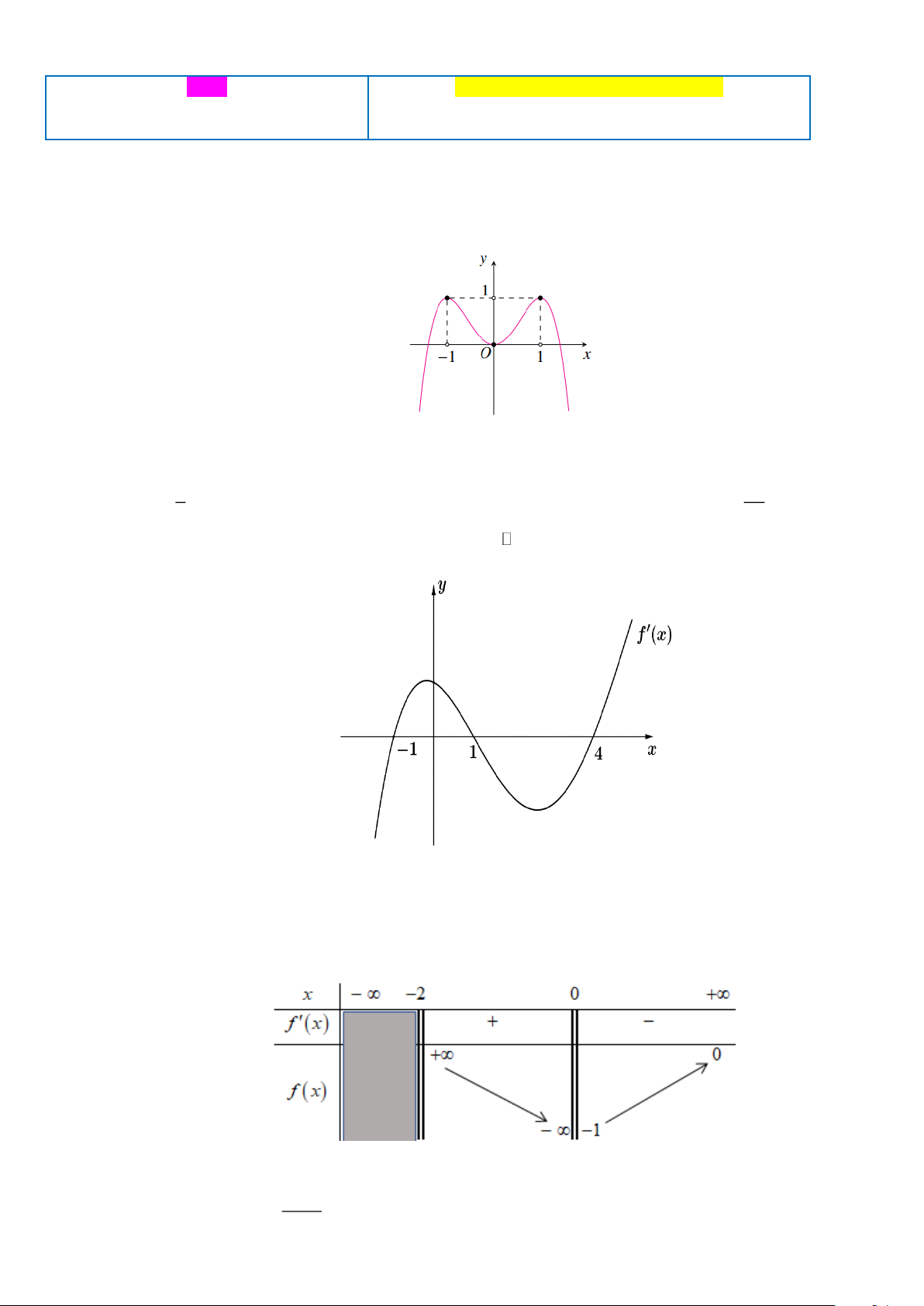
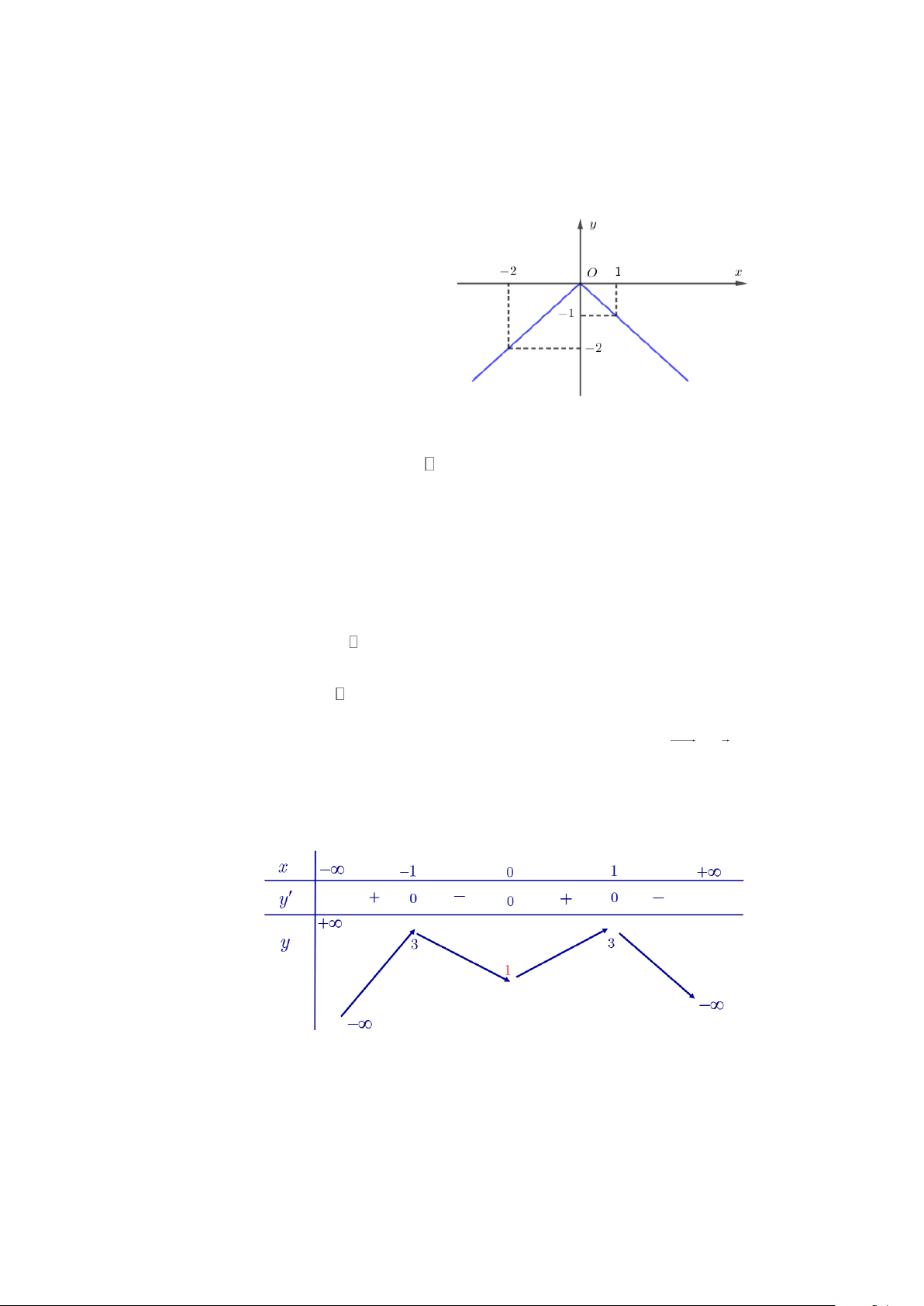
Câu 4. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Gọi M , N lần lượt là giá trị lớn nhất, giá trị nhỏ
nhất của hàm số trên đoạn 2 − ;
2 . Tính giá trị biểu thức P = 3M − 2N . A. 5 . B. 3 . C. 11. D. 2 .
Câu 5. Hàm số nào sau đây có ba điểm cực trị? A. 4 2
y = 3x − x + 2019 . B. 4 2
y = −x − 4x + 2020 . 2x − 4 C. 3 2
y = x − 3x + 5 . D. y = . x +1 2x + 5
Câu 6. Cho hàm số y =
. Khẳng định nào sau đây đúng? x +1
A. Hàm số đồng biến trên các khoảng (− ; − ) 1 ; ( 1 − ;+).
B. Hàm số nghịch biến trên các khoảng (− ; − ) 1 ; ( 1 − ;+).
C. Hàm số nghịch biến trên \ 1 − .
D. Hàm số đồng biến trên \ 1 − .
Câu 7. Trong không gian Oxyz cho điểm A thỏa mãn OA = 2i + j với i, j là hai vectơ đơn vị trên hai trục
Ox , Oy . Tọa độ điểm A là A. A(0;1; ) 1 . B. A(1;1; ) 1 . C. A(0;2; ) 1 .
D. A(2;1;0) .
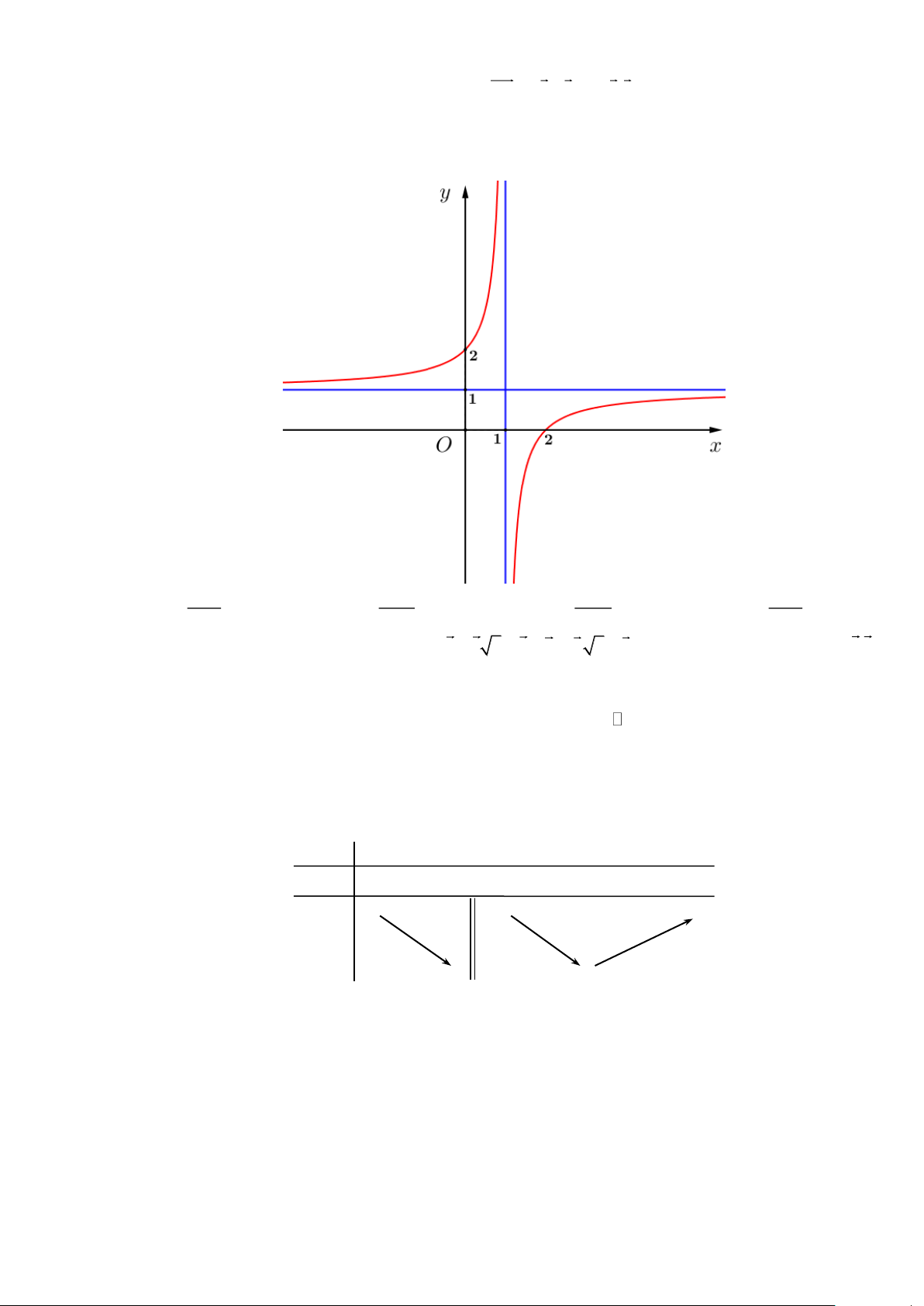
Câu 8. Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ? x −1 x + 2 x − 2 x +1 A. y = . B. y = . C. y = . D. y = . x +1 x −1 x −1 x −1
Câu 9. Trong không gian Oxyz , cho hai véc tơ u = i 3 + k , v = j 3 + k . Khi đó tích vô hướng của . u v bằng A. 2 . B. 1. C. 3 . D. 3 − .
Câu 10. Cho hàm số y = f (x) có đạo hàm y = f (x) = x(x − 2), x
. Hàm số y = f (x) nghịch biến
trên khoảng nào dưới đây? A. (−;0) . B. (2;+) . C. (0;+) . D. (0;2) .
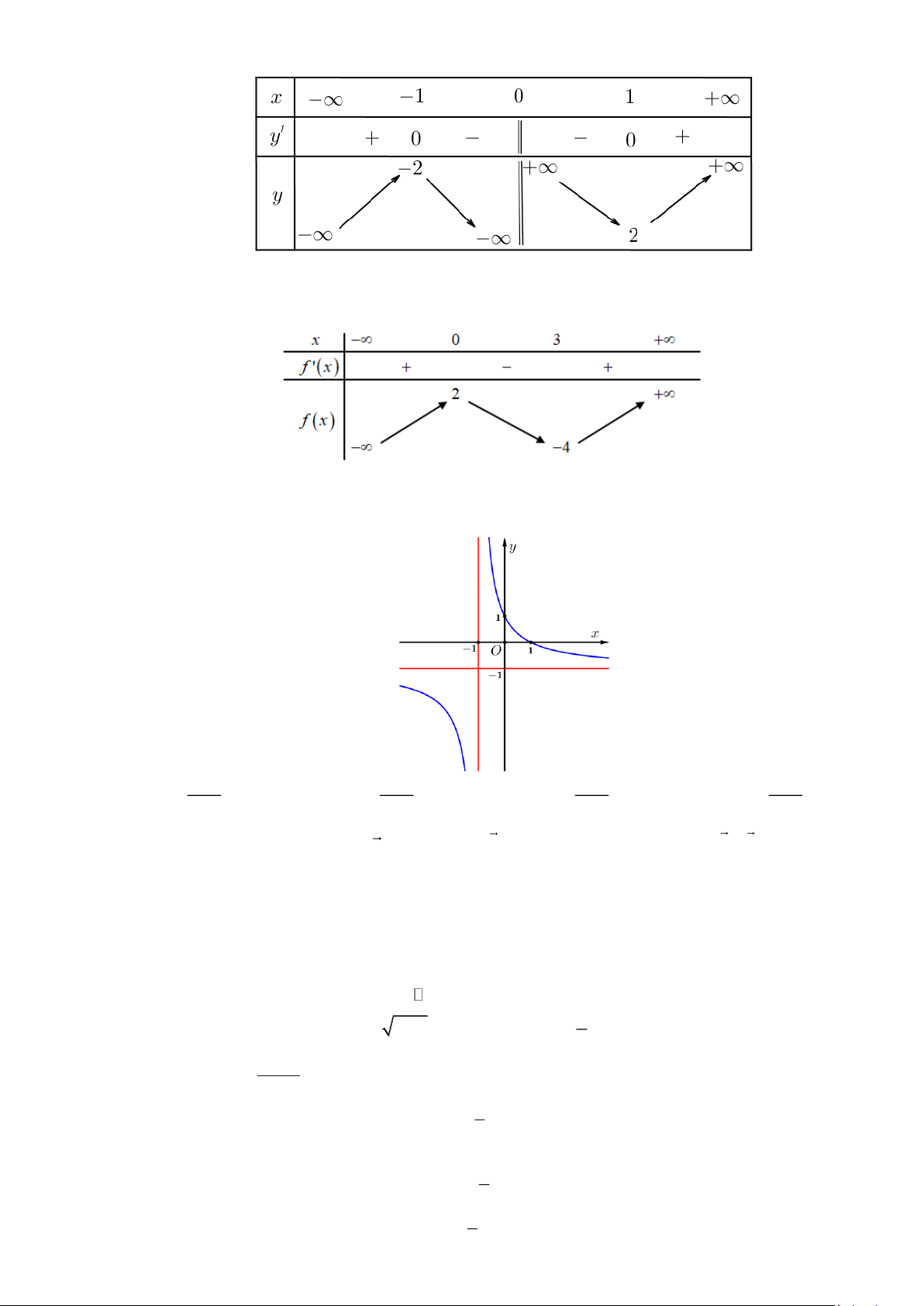
Câu 11. Cho hàm số y = f (x) xác định và liên tục trên (−;0) và (0;+ ) có bảng biến thiên như hình bên. x − 0 3 + f (x) − 0 − 0 + 2 + + f (x) − 2
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng ( 2;+ ).
B. Hàm số có giá trị nhỏ nhất bằng 2 .
C. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số. D. f (− ) 3 f ( 2 − ) .
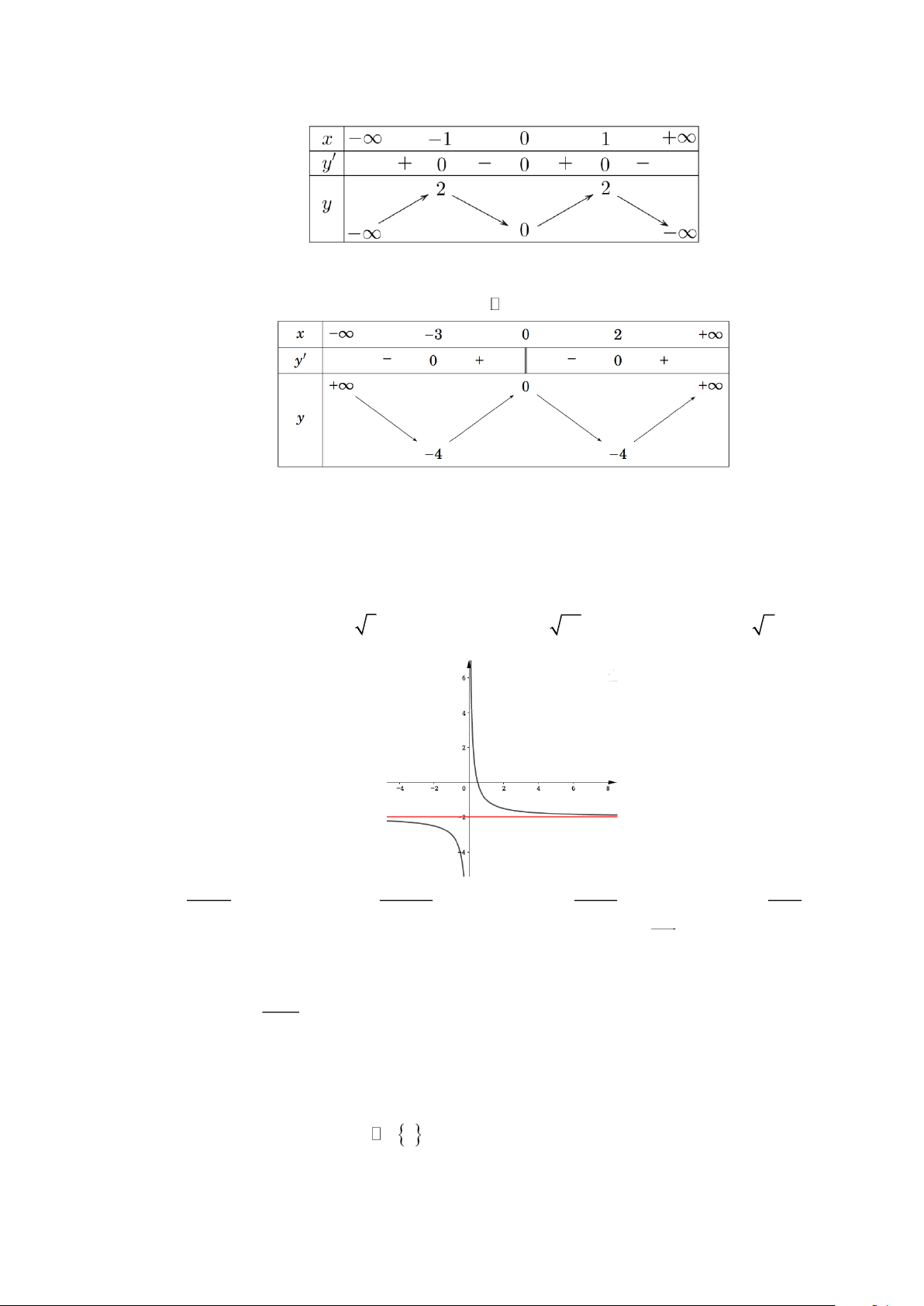
Câu 12. Cho hàm số y = f (x ) có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào dưới đây? A. ( 3 − ;4). B. (1;3). C. (− ; 2 − ). D. (5;7).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một doanh nghiệp sản xuất xe máy có hàm sản xuất là hàm CobbDouglas: 𝑄 = √
3 𝐾2 ⋅ 𝐿, trong đó, 𝐾 và 𝐿 lần lượt kí hiệu số đơn vị vốn tư bản và số đơn vị lao
động mà doanh nghiệp thuê được, còn 𝑄 kí hiệu số xe máy sản xuất ra được.
Giả sử giá thuê một đơn vị vốn tư bản là 𝑐𝐾, giá thuê một đơn vị lao động là 𝑐𝐿, ngoài chi
phí thuê lao động và vốn tư bản, doanh nghiệp còn phải chịu một chi phí cố định là 𝐶0.
Khi đó, hàm số 𝐹 = 𝑐𝐾 ⋅ 𝐾 + 𝑐𝐿 ⋅ 𝐿 + 𝐶0 mô tả tổng chi phí mà doanh nghiệp phải bỏ ra,
thường được gọi là hàm chi phí sản xuất.
Năm 2025 có các hằng số 𝐶0 = 60, 𝑐𝐾 = 12, 𝑐𝐿 = 6 và năm 2026 doanh nghiệp dự định
sản xuất 2500 chiếc xe máy.
Xét tính đúng sai của các khẳng định sau.
a) 𝐹 = 12 ⋅ 𝐾 + 6 ⋅ 25003 + 60. 𝐾2
b) Tổng chi phí tối thiểu doanh nghiệp chi ra để sản xuất 2500 chiếc xe máy là 45060 (đơn vị vốn). c) 𝐿 = 25003. 𝐾2
d) 𝐹′(𝐾) = 12 − 6 ⋅ 25003. 𝐾3
Câu 2. Trong không gian Oxyz cho 3 điểm (
A 1;2; )
3 ,B(- 3;4;- )
1 ,C(2;0;- ) 2 .
a) Gọi D( ; a ;
b c) là điểm thỏa mãn: AD = 2AB −3AC . Khi đó a +b+ 2c = 22 .
b) Gọi G là trọng tâm tam giác ABC , I là trung điểm của AB . Khi đó IG = ( 1 − ;1; ) 1 . c) Góc
ABC là góc lớn hơn 60.
d) Gọi E là điểm thuộc mặt phẳng Oxy để ,
A B, E thẳng hàng. Khi đó tổng hoành độ, tung độ, 3
cao độ của điểm E bằng . 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
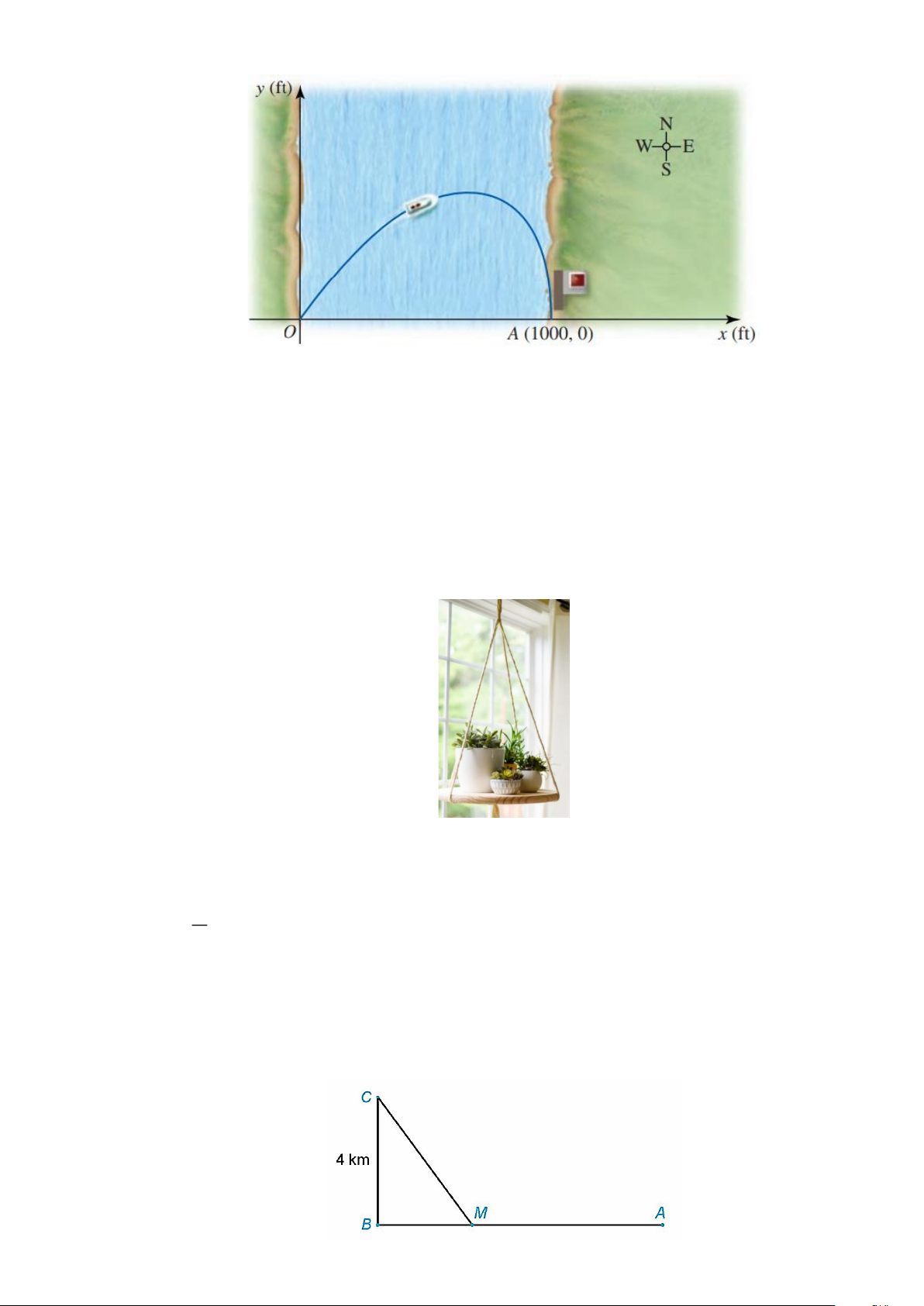
Câu 1. Một con thuyền rời bến O(0,0) trên một bờ sông, luôn đi với vận tốc không đổi 20 dặm/giờ hướng về bến (
A 1000, 0) (phía đông của O ); đồng thời nước sông chảy ngược lên phía bắc với tốc độ 5 dặm/giờ. Người ta cho rằng đường đi của thuyền là 3/4 5/4 1000 − x 1000 − x y = 500 −
, 0 x 1000 1000 1000
Tìm độ lệch bắc lớn nhất mà thuyền đạt được trong suốt hành trình.
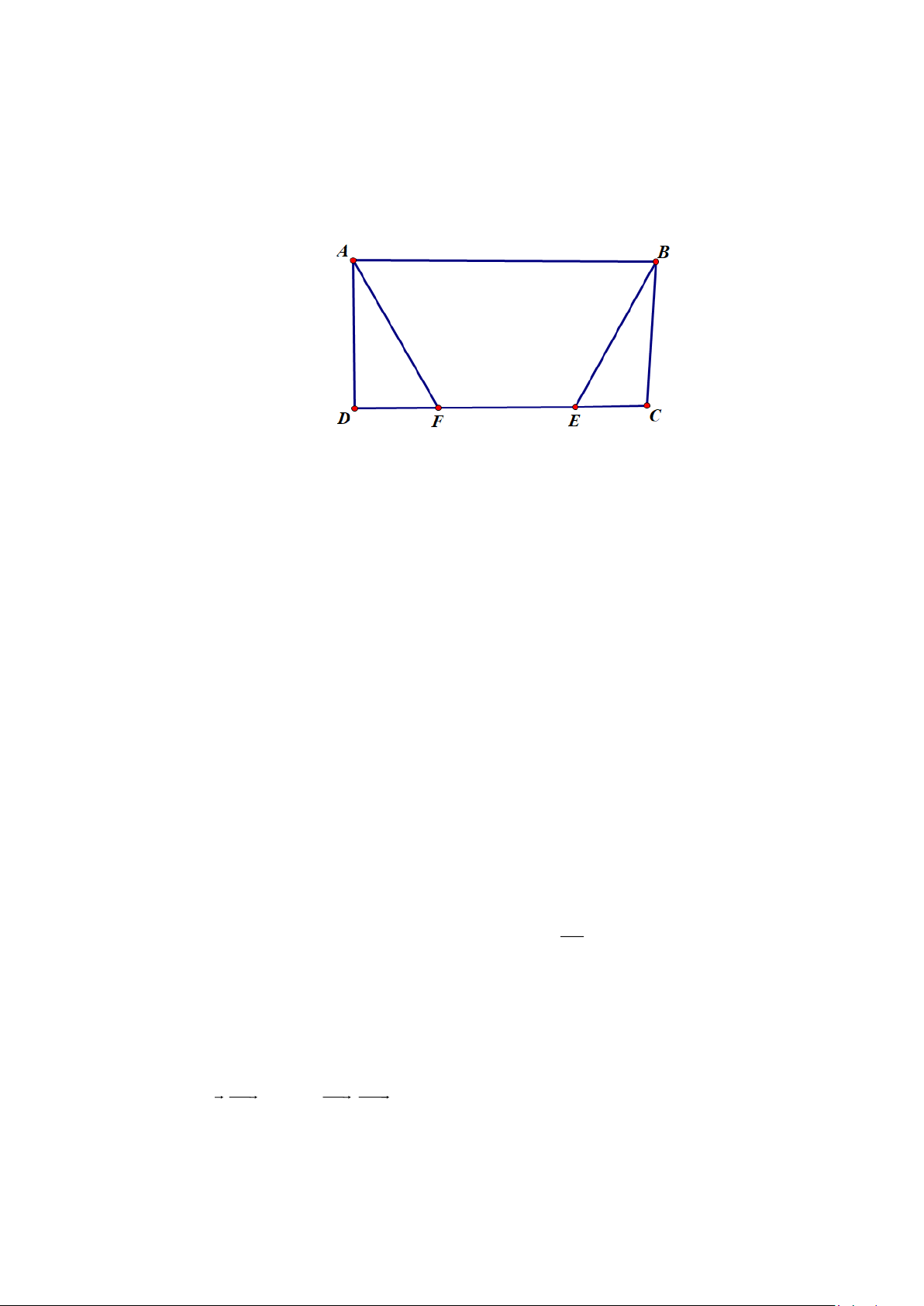
Câu 2. Chọn hệ trục Oxyz với (Oxy ) là mặt đất. Hai khinh khí cầu cùng bay lên tại O. Sau nửa giờ bay,
chiếc khinh khí cầu thứ nhất cách điểm xuất phát về phía Đông 11 và về phía Nam 8 , đồng thời
cách mặt đất 1,3 . Chiếc khinh khí cầu thứ hai cách điểm xuất phát về phía Bắc 8 và về phía Tây 8 ,
đồng thời cách mặt đất 900. Xác định khoảng cách giữa hai chiếc khinh khí cầu sau một giờ bay,
biết rằng mỗi khinh khí cầu bay với vận tốc và phương không đổi.
Câu 4. Một giỏ hoa treo trong nhà làm bằng 3 sợi dây không giãn, mỗi sợi dài 60(cm) miếng kê là một
miếng gỗ cân đối hình tròn bán kính 20(cm) , ba sợi dây được thắt một đầu bên trên và đỡ giá gỗ
tại 3 điểm tạo thành tam giác đều. Biết lực chịu đựng của mỗi sợi dây bằng nhau và mỗi sợi chịu
không quá 15N trọng lượng của miếng giá gỗ là 5N . Tính trọng lượng tối đa của các chậu hoa để dây treo không bị đứt.
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài. ur
Câu 1. Một vật có khối lượng m(kg) khi chịu tác dụng của một lực F thì vật đó sẽ chuyển động với gia ur r F tốc a =
. Tính lực tác dụng lên vật có khối lượng m = 6(kg) khi vật đó chuyển động trên mặt m
phẳng nằm ngang, nhẵn với gia tốc 2
a = 3m / s ?
Câu 2. Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình. Khoảng
cách từ C đến B là 4 km . Bờ biển chạy thẳng từ A đến B với khoảng cách là 10 km . Tổng chi
phí lắp đặt cho 1 km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng.
Xác định vị trí điểm M trên đoạn AB (điểm nối dây từ đất liền ra đảo) để tổng chi phí lắp đặt là nhỏ nhất.
Câu 3. Để thiết kế một chiếc bể cá hình hộp chữ nhật không nắp có chiều cao là 60cm , thể tích 3 96000cm .
Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70000 2
VNĐ / m và loại kính để
làm mặt đáy có giá thành 100000 2
VNĐ / m . Tính chi phí thấp nhất để hoàn thành bể cá.
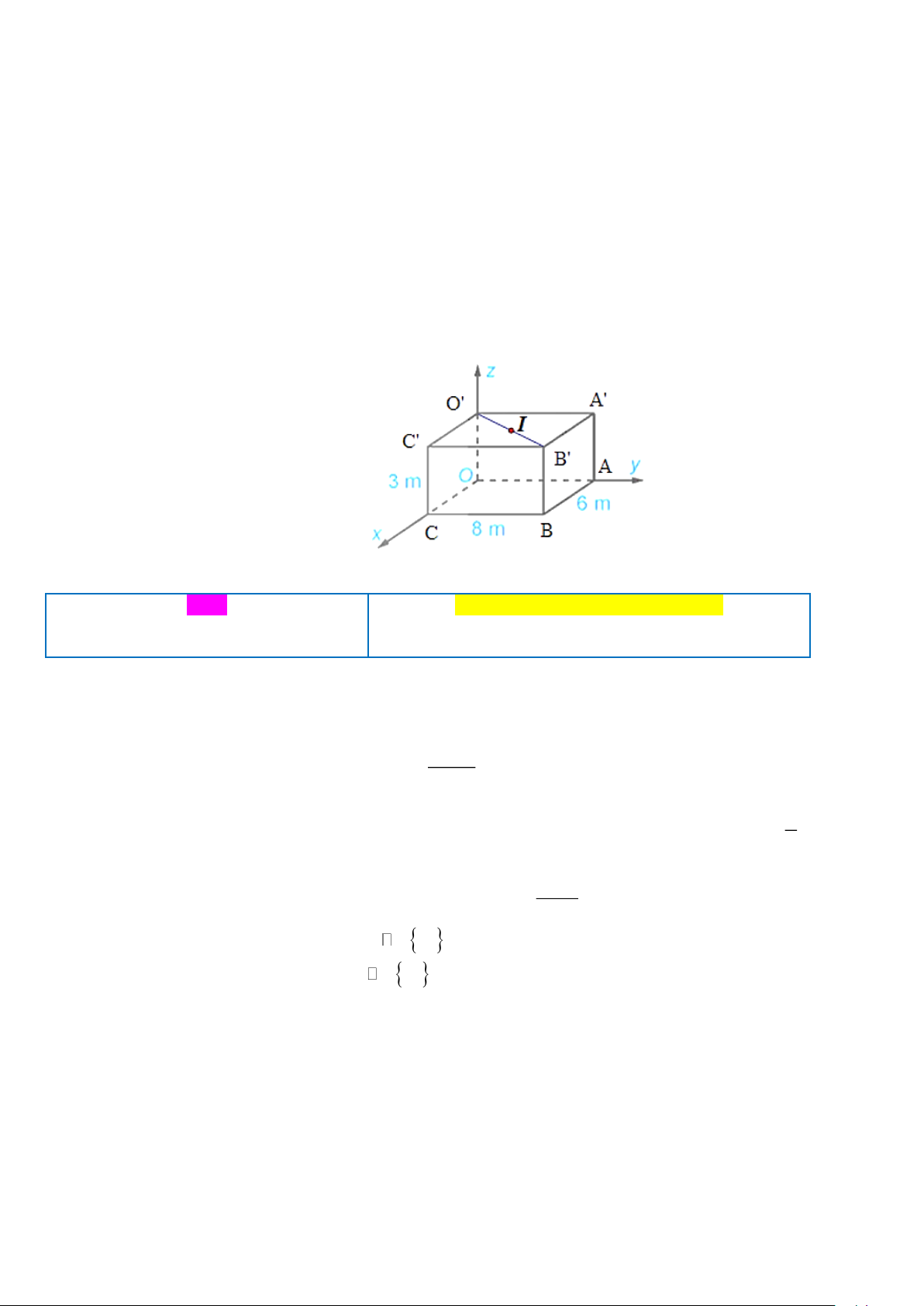
Câu 4. Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8 m , chiều rộng là 6 m và chiều
cao là 3 m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ
Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được
lấy theo mét. Hãy tìm tọa độ của điểm treo đèn. ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. 1− 2x
Câu 1. Tiệm cận ngang của đồ thị hàm số y = là? x − 2 1
A. y = −2 .
B. y = 1.
C. y = 2 . D. y = − . 2 2x +1
Câu 2. Kết luận nào sau đây về tính đơn điệu của hàm số y = là đúng? x +1
A. Hàm số luôn nghịch biến trên \ − 1 .
B. Hàm số luôn đồng biến trên \ − 1 .
C. Hàm số đồng biến trên các khoảng (− ; − ) 1 và (−1;+).
D. Hàm số nghịch biến trên các khoảng (− ; − ) 1 và (−1;+) .
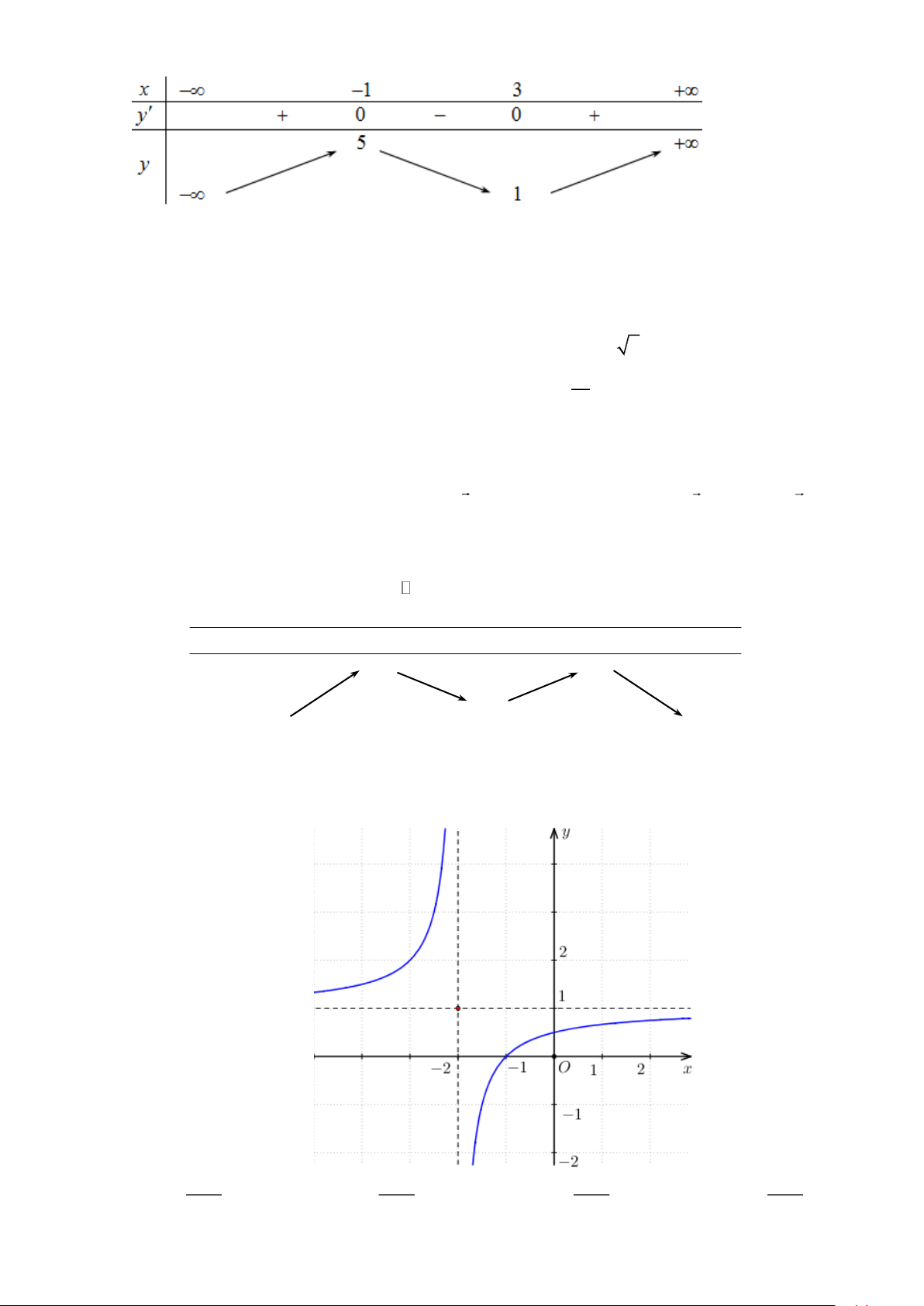
Câu 3. Cho hàm số y = f (x) có bảng biến thiên trên đoạn 4 − ; 1 như sau
Khi đó, mệnh đề nào sau đây đúng?
A. max f ( x) = 1 max f ( x) = 3 . B. . 4 − ; 1 2 − ; 1
C. min f ( x) = 0
min f ( x) = −2 . D. . 2 − ; 1 −4; 1
Câu 4. Cho hàm số y = f (x) có bảng biến thiên được cho như hình bên dưới. Hãy chọn phát biểu đúng
về số đường tiệm cận đứng và ngang của đồ thị hàm số.
A. Đồ thị hàm số có một đường tiệm cận ngang và một đường tiệm cận đứng.
B. Đồ thị hàm số có hai đường tiệm cận ngang và một đường tiệm cận đứng.
C. Đồ thị hàm số có một đường tiệm cận ngang và hai đường tiệm cận đứng.
D. Đồ thị hàm số có hai đường tiệm cận ngang và hai đường tiệm cận đứng.
Câu 5. Cho hàm số y = f (x) xác định trên và có đồ thị hàm số y = f (x) là đường cong trong hình
vẽ, hàm số y = f (x) đã cho đồng biến trên khoảng nào dưới đây? A. (− ; − ) 1 . B. (0;2) . C. (2;+) . D. ( 4 − ;0) .
Câu 6. Cho hàm số y = f (x) có bảng biến thiên như hình bên. Giá trị cực tiểu của hàm số bằng A. 1. B. −1. C. 5 . D. 3 .
Câu 7. Trong không gian Oxyz , cho hai điểm A(1;3;5) và B(1;−1; )
1 . Trung điểm của đoạn thẳng AB có tọa độ là A. (2;2;6). B. (1;1; ) 3 .
C. (0;− 2;− 2) .
D. (0;− 4;− 4) .
Câu 8. Trong các hàm số sau, hàm số nào có 2 điểm cực tiểu: A. 2
y = x − 2x +3. B. 4 2
y = − x + 2x +1 . 3 x C. 4 2
y = x − x . D. 2 y = − x +1. 3 Câu 9. Cho hàm số 3 2
y = x − 3x có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn 2 −
;1 lần lượt là M và
m . Tính T = M + m .
A. T = 2 . B. T = 22 − . C. T = 20 − . D. T = 4 − .
Câu 10. Trong không gian Oxyz , tọa độ một vectơ n vuông góc với cả hai vectơ a = (1;1; 2 − ) , b = (1;0;3) là A. (2;3; ) 1 − . B. (3; 5 − ;− ) 1 . C. (3;5; 2 − ) . D. (2; 3 − ;− ) 1 .
Câu 11. Cho hàm số y = f (x) liên tục trên và có bảng biến thiên như hình vẽ bên dưới. x − −1 0 1 + y + 0 − 0 + 0 − −1 −1 y 2 − − −
Hàm số y = f (x) đồng bi
ến trên khoảng nào dưới đây? A. ( 1 − ;0) . B. (0; ) 1 . C. ( ;0 − ). D. (0;+).
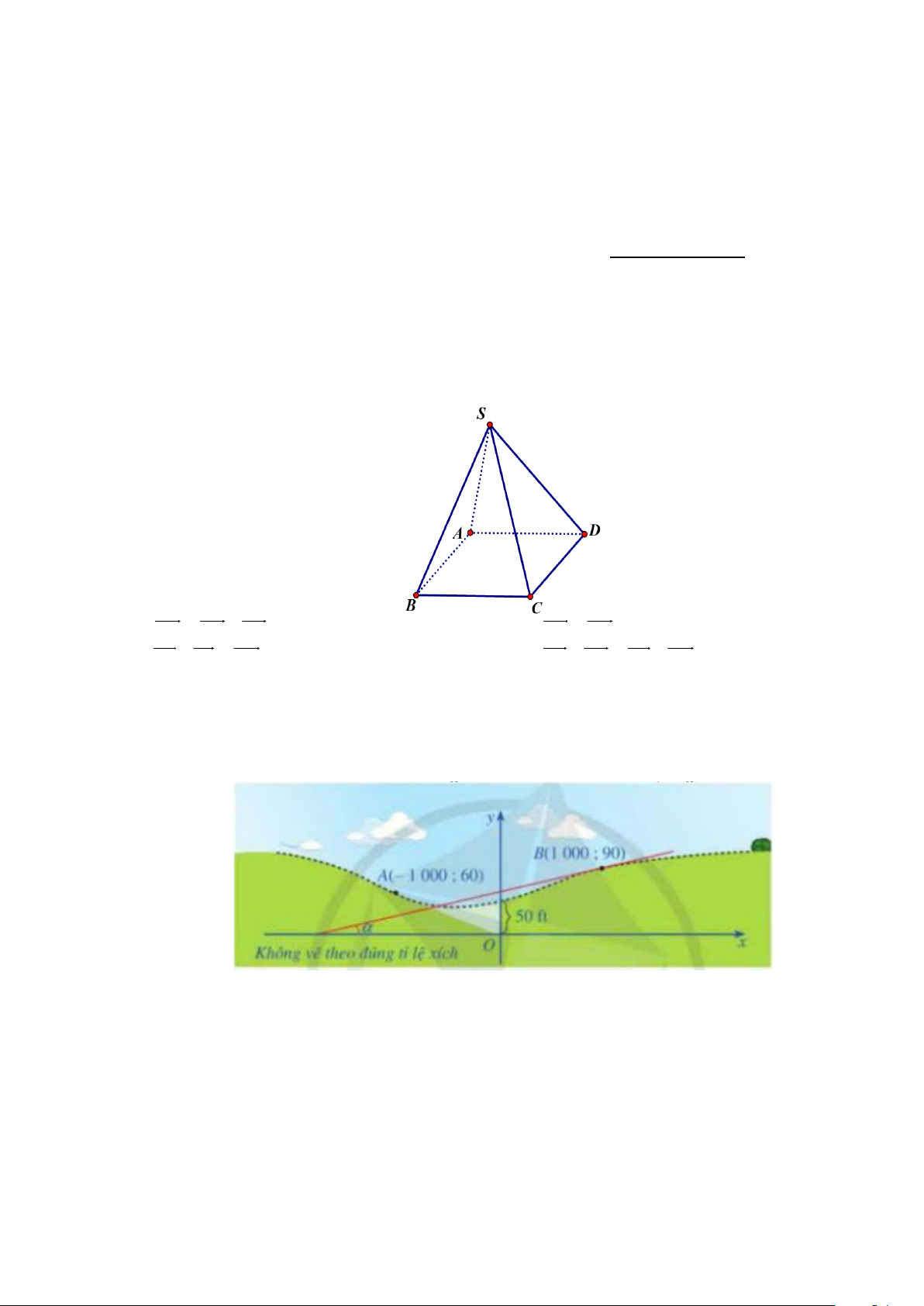
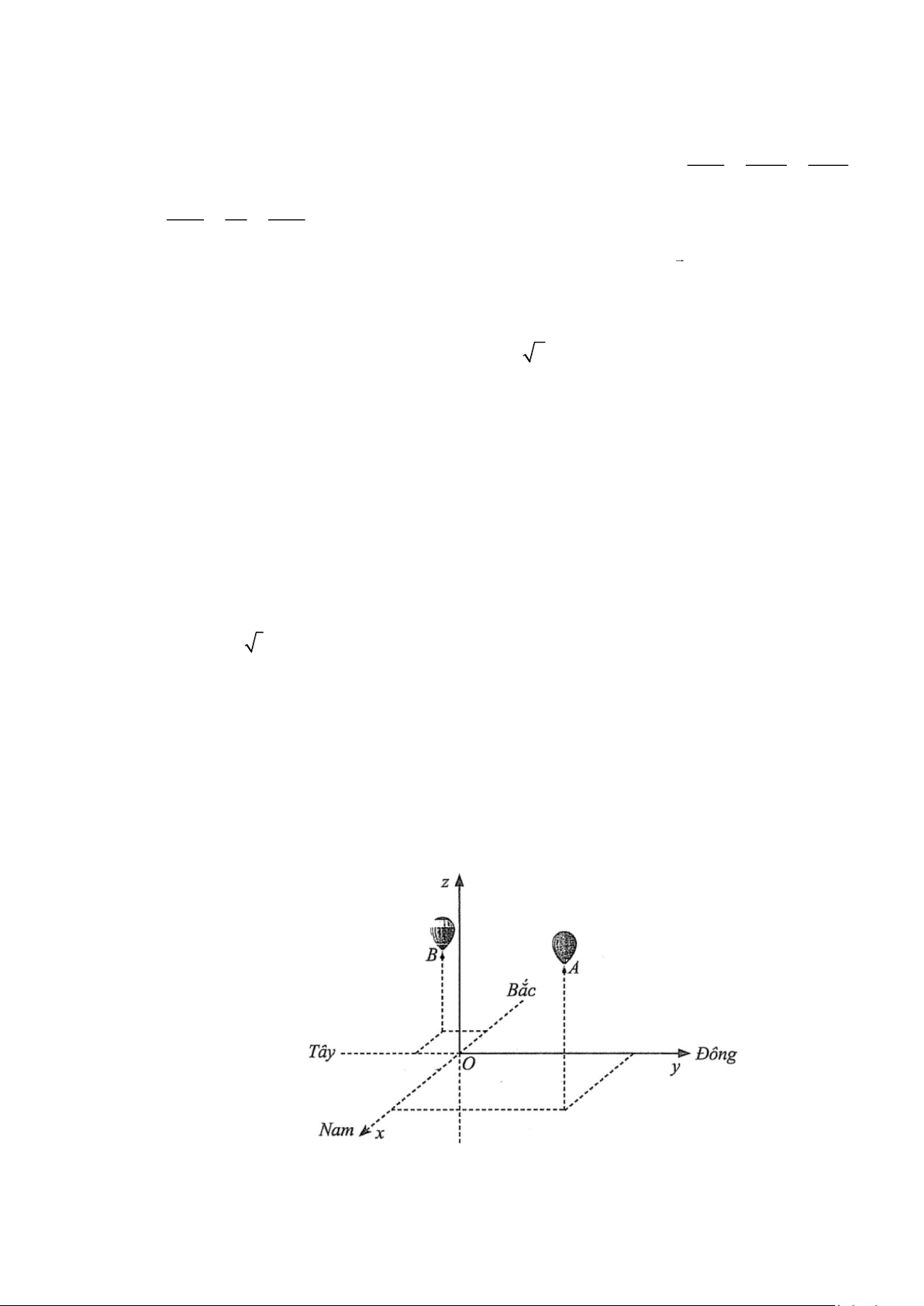
Câu 12. Đường cong của hình vẽ bên là đồ thị của hàm số nào dưới đây? x −1 x +1 x −1 x +1 A. y = . B. y = . C. y = . D. y = . x − 2 x + 2 x + 2 x − 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Những ngày giáp Tết Nguyên Đán cũng là dịp bước vào vụ Đông Xuân, bà con nông dân tích cực
xuống đồng cấy lúa. Cây lúa sau khi được cấy trải qua quá trình tăng trưởng để nhanh và phát triển
chiều cao trước khi làm đòng, trổ bông. Qua nghiên cứu một giống lúa mới, các nhà khoa học nhận
thấy một cây lúa tính từ lúc được cấy bằng một cây mạ với chiều cao 20cm có tốc độ tăng trưởng
chiều cao cho bởi hàm số 3 2 v(t) = 0
− ,1t +1,1t , trong đó t tính theo tuần, v(t) tính bằng cm/tuần.
Gọi h(t) là chiều cao của cây lúa ở tuần thứ t (t 0) .
a) Giai đoạn tăng trưởng chiều cao của cây lúa kéo dài 12 tuần.
b) Chiều cao tối đa của cây lúa là 150cm . c) 1 4 11 3 h(t) = − t + t + 20 . 40 30
d) Vào thời điểm cây lúa phát triển nhanh nhất, chiều cao của cây đã lớn hơn 80cm .
Câu 2. Trong không gian Oxyz , cho điểm A (1;2;- 4),B (1;2;0),C (0;2;0).
a) Nếu điểm D(x;y;z) thỏa mãn DA = DB = DC .vàOD song song với mặt phẳng (A BC ) thì tổng
2x + y - 3z = 6.
A, B,C ,O
b) Gọi (H )là khối hộp nhận các điểm
làm đỉnhvà có một đỉnhthuộc trục Ox khác O.Thể
tích khối hộp(H )bằng 4.
c) Không tồn tại điểm M thuộc mặt phẳng (Oyz )sao choMA = MB = MC .
d) B là hình chiếu vuông góc của A lên mặt phẳng (Oxy ).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Trong không gian chọn hẹ trục toạ độ cho trước, đơn vị đo là kilômet, một rada phát hiện một máy
bay chiến đấu di chuyển với vận tốc và hướng không đổi từ điểm M (1100;650;14) đến điểm N
trong 20 phút. Nếu đến N máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy
bay trong 10 phút tiếp theo là Q(1500;860;16) . Biết một khẩu pháo ở toạ độ vị trí điểm 1700 34 E ;370;
được bắn ra với vận tốc không đổi gấp 5 lần vận tốc máy bay nhằm bắn trúng 3 3
máy bay tại vị trí N . Sau bao nhiêu phút khi máy bay bay từ M thì người điều khiển pháo phải bắn.
Câu 2. Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ
toạ độ Oxyz như hình vẽ dưới với độ dài đơn vị trên các trục tọa độ bằng 1 m . Tìm được tọa độ của vectơ AB = ( ; a ;
b c) . Khi đó tính a + c
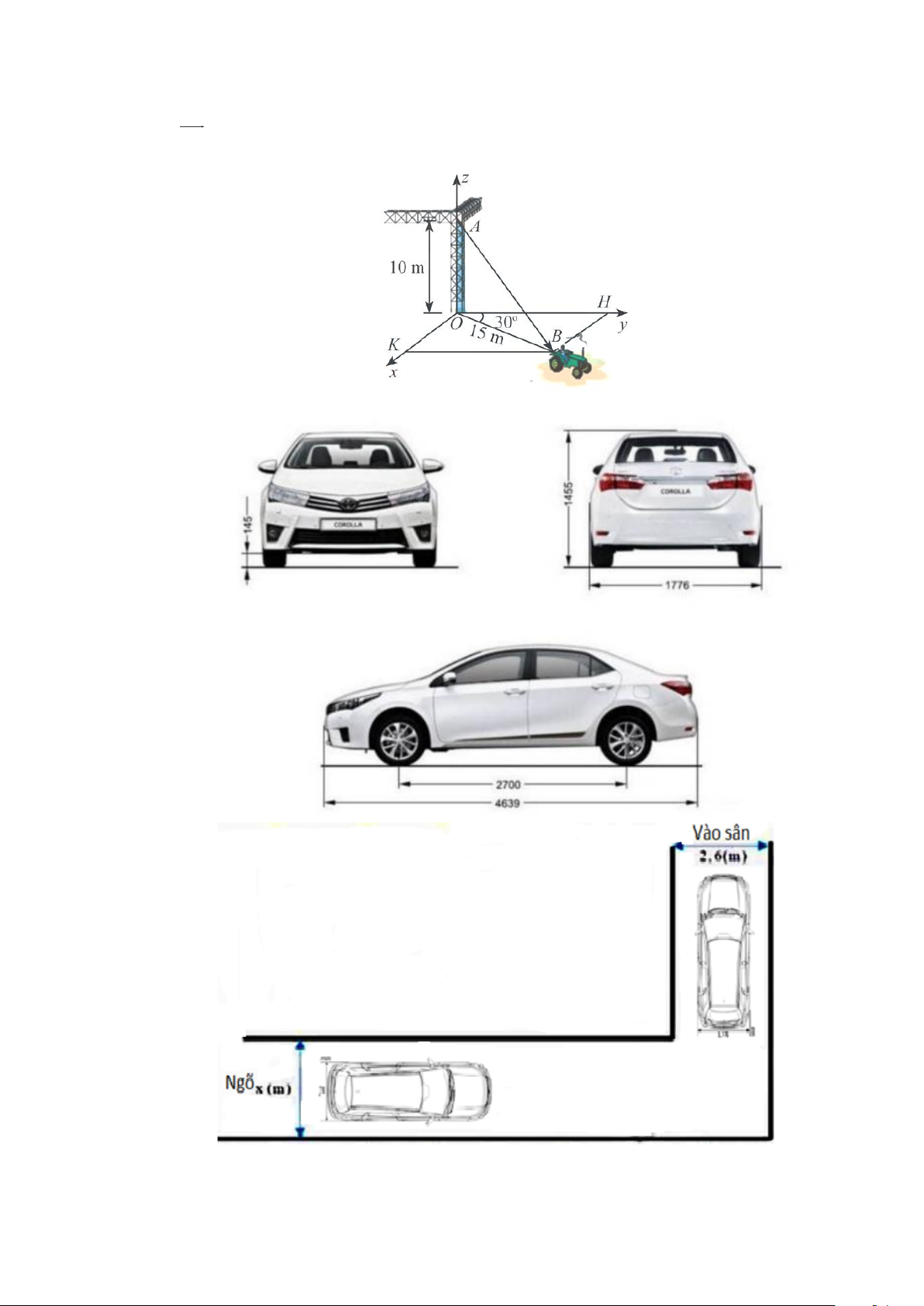
Câu 3. Ông An muốn mua một chiếc ôtô. Ngõ từ đường vào sân nhà ông An hình chữ L.
Đoạn đường đầu tiên có chiều rộng bằng (
x m) , đoạn đường thẳng vào sân chiều rộng 2,6( m) .
Biết kích thước xe ôtô như hình vẽ trên và để ôtô đi qua an toàn thì chiều rộng và chiều dài tương ứng của
đoạn đường phải lớn hơn kích thước thiết kế của ô tô một khoảng, cụ thể là 5m x
1,9m . Để tính toán và thiết
kế đường đi cho ôtô từ ngõ vào sân, ông An coi ôtô như một khối hộp chữ nhật có kích thước chiều dài là ( p
5 m), chiều rộng 1,9(m) . Chiều rộng nhỏ nhất của đoạn đường đầu tiên là x = (m) để ôtô của ông An có q
thể đi vào được sân. Khi đó 2
p − q bằng bao nhiêu?
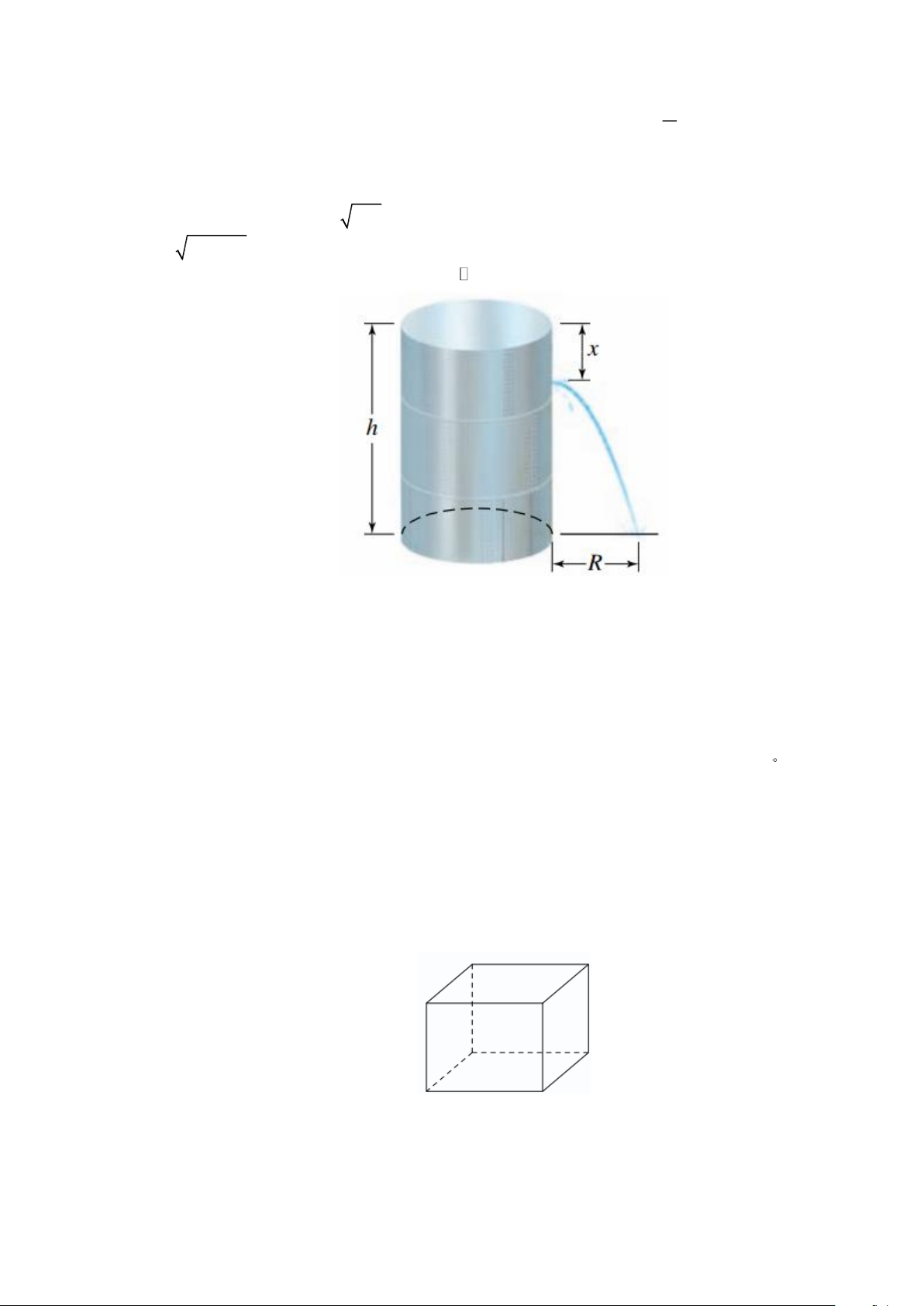
Câu 4. Một bồn hình trụ cao h chứa nước. Theo định luật Torricelli, vận tốc tia nước chảy qua lỗ ở độ sâu
x so với mặt nước là V = 2gx . Người ta cho rằng tầm xa R (feet) của tia nước được cho bởi
R = 2 x(h − x)
Biết lỗ phun nên đặt ở độ cao x = K.h,(K ) so với mặt bồn thì tầm xa R đạt cực đại. Tìm K ?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Thể tích V (đơn vị: centimét khối) của 1 kg nước tại nhiệt độ T (0C T 30
C ) được tính bởi công thức sau: 2 3
V (T ) = 999,87 − 0,06426T + 0,0085043T − 0,0000679T .
Hỏi thể tích V (T),0C T 30
C , giảm trong khoảng nhiệt độ nào?
Câu 2. Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc 100 và có độ lớn
lần lượt là 25 N và 12 N . Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn
4 N . Tính độ lớn của hợp lực của ba lực trên.
Câu 3. Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng 3
288dm dm3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để
xây bể là 500000 đồng/ 2
m . Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí
thuê nhân công sẽ thấp nhất. Hỏi người đó trả chi phí thấp nhất để thuê nhân công xây dựng bể đó là bao nhiêu?
Câu 4. Trong không gian với hệ trục toạ độ cho trước (đơn vị đo lấy theo kilomet), ra đa phát hiện một
máy bay di chuyển với vận tốc và hướng không đổi từ điểm (
A 750; 450;7) đến điểm
B(950;550;9) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của
máy bay sau 10 phút tiếp theo là gì? ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f (x) có đồ thị như hình vẽ. Hàm số y = f (x) nghịch biến trên khoảng nào sau đây? A. ( 1 − ; 0).
B. (0 ; + ) .
C. (− ; 0) . D. (0 ; ) 1 .
Câu 2. Giá trị cực đại của hàm số 3 2
y = x + 2x + x + 3bằng 1 77 A. − . B. 3 . C. −1. D. . 3 27
Câu 3. Cho hàm số y = f (x) xác định, có đạo hàm trên và f ( x) có đồ thị như hình vẽ bên dưới :
Hàm số y = g (x) = f (1− x) đồng biến trên khoảng. A. (−; 2 − ). B. (1;+) . C. (1; ) 3 . D. ( 3 − ;0) .
4. Cho hàm số f ( x) có bảng biến thiên như sau: Câu
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là A. 3. B. 2 . C. 0 . D. 1. 11
Câu 5. Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? x − 3 A. 1 . B. 0 . C. 2 . D. 3.
Câu 6. Cho hàm số y = f (x) có bảng biến thiên như hình bên dưới
Hàm số đạt cực tiểu tại điểm nào? A. x =1 B. x = 1 −
C. x = 2 D. x = 0
Câu 7. Cho hàm số y = f (x) xác định và liên tục trên và có bảng biến thiên như sau
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị cực tiểu bằng 3 − hoặc 2 .
B. Đồ thị của hàm số có đúng 2 điểm cực trị.
C. Hàm số đạt cực đại tại x = 0 .
D. Hàm số có giá trị lớn nhất bằng 0 và có giá trị nhỏ nhất bằng 4 − .
Câu 8. Trong không gian Oxyz , cho hai điểm A(2;1;− )
1 , B(1;2;3). Độ dài đoạn thẳng AB bằng A. 18. B. 3 . C. 22 . D. 3 2 .
Câu 9. Đường cong hình bên là đồ thị hàm số nào dưới đây −x +1 2 − x +1 2x +1 2x A. y = . B. y = . C. y = . D. y = . 2x x x x +1
Câu 10. Trong không gian Oxyz , cho hai điểm A(1;1;− )
1 và B(2;3;2). Véctơ AB có tọa độ là A. (1;2; ) 3 . B. ( 1 − ;− 2;3). C. (3;4; ) 1 . D. (3;5; ) 1 . x −1
Câu 11. Cho hàm số y =
. Chọn khẳng định đúng trong các khẳng định sau; x − 2
A. Hàm số nghịch biến trên các khoảng mà hàm số xác định.
B. Hàm số đồng biến trên khoảng (2;+) .
C. Hàm số nghịch biến trên khoảng (− ; 2)(2;+) .
D. Hàm số nghịch biến trên tập \ 2 .
Câu 12. Tìm giá trị lớn nhất của hàm số f (x) 3 2
= x −3x −9x +10 trên 2 − ;2 .
A. max f ( x) = 5 .
B. max f ( x) = 15 .
C. max f ( x) = 17 .
D. max f ( x) = 12 − . 2 − ;2 2 − ;2 2 − ;2 2 − ;2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một công ty phát triển giáo dục dự định in 𝑎(𝑎 ∈ ℕ) cuốn sách luyện đề minh họa cho học sinh.
Công ty đã khảo sát và tính được chi phí để xuất bản 𝑎 cuốn sách này được biểu diễn bởi hàm số:
𝐶(𝑎) = 𝑎2 − 2000𝑎 + 25000000 (đồng) và chi phí phát hành cho mỗi cuốn sách là 5000 đồng.
a) Chi phí xuất bản và phát hành cho 2000 cuốn sách luyện đề là 33 triệu đồng.
b) Chi phí xuất bản và phát hành cho mỗi cuốn sách là: 𝑇(𝑎) = 𝑎2−2000𝑎+25000000. 𝑎
c) Nếu công ty xuất bản số sách luyện đề lớn hơn 5000 cuốn thì chi phí xuất bản và phát hành cho
mỗi cuốn sách sẽ giảm.
d) Chi phí xuất bản và phát hành cho mỗi cuốn sách luyện đề thấp nhất là 12000 đồng.
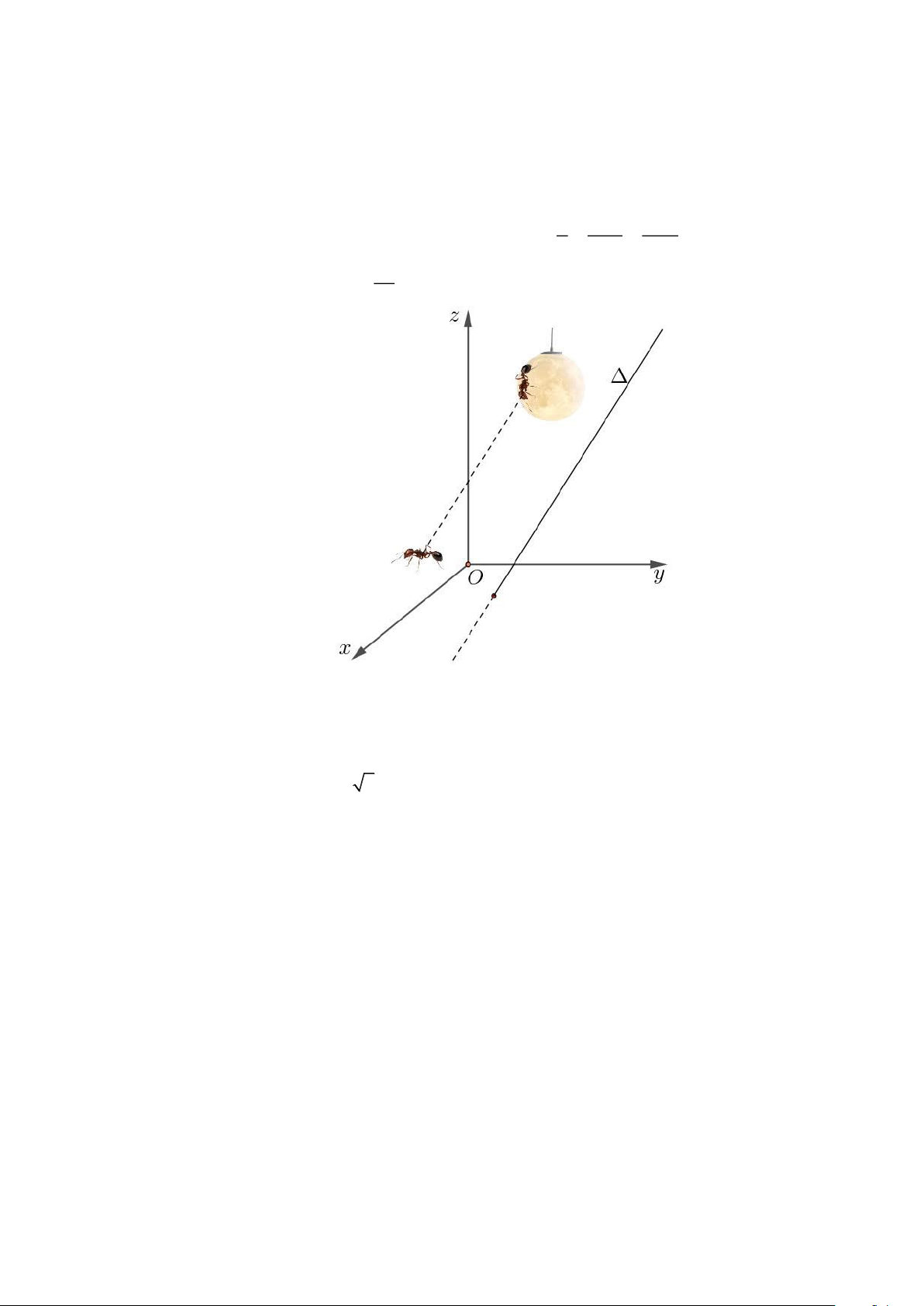
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành như hình vẽ bên dưới. Các mệnh đề sau đúng hay sai?
a) BD = BC − AB .
b) AB = CD .
c) SC − SB = A . D
d) SC + BD = SD + A . D
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Để thiết kế mô hình của một đoạn đường cao tốc nối hai sườn đồi với sự khác biệt về độ cao ở vị trí
hai sườn đồi giao nhau là 50 feet, người ta có thể làm như sau:
Chọn hệ trục tọa độ Oxy với O là vị trí hai sườn đồi giao nhau, phương nằm ngang là trục
Ox , đơn vị trên mỗi trục tọa độ là feet. Chọn hai vị trí ,
A B lần lượt trên hai sườn đồi. Bằng
cách đo đạc tại thực địa, ta xác định được tọa độ hai điểm ,
A B và góc dốc tại điểm B A( 1 − 000;60), B(1000;90)
của sườn đồi. Giả sử ta có
và tan = 0,04 . Trong hệ trục tọa độ
Oxy , quan sát đường cong mô phỏng đoạn đường cao tốc nối hai sườn đồi, đường cong đó
gợi nên hình ảnh đồ thị của hàm số bậc ba. Vì thế ta có thể chọn hàm số bậc ba 3 2
f (x) = ax + bx + cx + d (a 0) sao cho trong hệ trục tọa độ Oxy , đồ thị hàm số đó trên đoạn 1 − 000; 100
0 mô phỏng đoạn đường cao tốc cần thiết kế. Ta chọn theo nguyên tắc: là góc tạo bởi tiếp
tuyến tại B của đồ thị hàm số đó và chiều dương của trục Ox . Tính khoảng cách từ điểm thấp nhất của đoạn
đường đến vị trí hai sườn đồi giao nhau (làm tròn đến hàng đơn vị).
Câu 2. Trong không gian với hệ trục Oxyz, giả sử mặt đất trùng với mặt phẳng (Oxy). Một bóng đèn trang
trí dạng khối cầu có tâm I ( 1
− ;2;4) và bán kính R được treo cố định lên trần nhà. Một con kiến bò
tùy ý trên bóng đèn và một con kiến khác bò tùy ý trên mặt đất, giả sử vectơ tạo bởi tọa độ vị trí x y +1 z − 2
của 2 con kiến luôn cùng phương với đường thẳng : = =
. Biết lúc 2 con kiến gần 1 2 2 57
nhau nhất có khoảng cách bằng
(m) . Bán khối cầu có độ dài bao nhiêu cm . 10
Câu 3. Trong không gian Oxyz , có 3 diễn viên xiếc nhào lộn đang ở 3 vị trí (
A 1; −2;3) , B(3; 4;1) , C( 5
− ;2;1) . Gọi () là một mặt phẳng lưới bảo hộ di động luôn chứa trục hoành sao cho ; A ; B C
nằm cùng phía với () và d ;d ;d lần lượt là khoảng cách từ ; A ;
B C đến () . Tiết mục xiếc sẽ 1 2 3
được bắt đầu khi mặt phẳng () được điều chỉnh để biểu thức T = d + 2.d + 3.d đạt giá trị lớn 1 2 3
nhất. Biết T lớn nhất bằng a b . Hãy tính S = 2a +3b .
Câu 4. Xí nghiệp A sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là 3 2
TC = x − 77x +1000x + 40000 và hàm doanh thu là 2 TR = 2
− x +1312x , với x là số sản phẩm.
Lợi nhuận của xí nghiệp A được xác định bằng hàm số f (x) = TR −TC , cực đại lợi nhuận của xí
nghiệp A khi đó đạt bao nhiêu sản phẩm?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng
không đổi và có độ lớn bằng nhau. Hai tàu luôn giữ được lái sao cho chúng tạo với bờ cùng một
góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc
dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu
nào sang bờ bên kia trước?(Học sinh ghi số 1 hoặc số 2 vào ô đáp án)
Câu 2. Một trang trại rau sạch ở Đà Lạt mỗi ngày thu hoạch được 1 tấn rau. Mỗi ngày, nếu giá bán rau là
30000 đồng/ kg thì bán hết rau, nếu giá bán rau tăng 1000đồng/kg thì số rau thừa tăng 20 kg. Số
rau thừa này được thu mua hết để làm thức ăn chăn nuôi với giá 2000 đồng /kg . Hỏi để mỗi ngày
thu được số tiền bán rau lớn nhất thì trang trại đó nên bán rau với giá bao nhiêu nghìn đồng?
Câu 3. Trong hóa học, cấu tạo của phân tử ammoniac ( NH ) có dạng hình chóp tam giác đều mà đỉnh là 3
nguyên tử nitrogen ( N ) và đáy là tam giác H H H với H , H , H là vị trí của ba nguyên tử 1 2 3 1 2 3
hydrogen (H ) . Góc tạo bởi liên kết H − N − H , có hai cạnh là hai đoạn thẳng nối N với hai trong
ba điểm H , H , H (chẳng hạn
H NH ), gọi là góc liên kết của phân tử NH . Góc này xấp xỉ 1 2 3 1 2 3
107 . Trong không gian Oxyz , cho một phân tử NH được biểu diễn bởi hình chóp tam giác đều 3
N.H H H với O là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm N thuộc trục Oz , 1 2 3
ba nguyên tử hydrogen ở các vị trí H , H , H trong đó H 0;− 2;0 và H H song song với trục 1 ( ) 1 2 3 2 3
Ox như hình vẽ minh hoạ:
Tính khoảng cách giữa hai nguyên tử hdrogen;
Câu 4. Một vật chuyển động theo quy luật 3 2
S = −t +18t , với t (giây) là khoảng thời
gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó.
Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? ĐỀ 4
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Tìm giá trị lớn nhất của hàm số f (x) 3 2
= 2x +3x −12x + 2 trên đoạn 1 − ;2. A. 6 . B. 15. C. 10. D. 11.
Câu 2. Hàm số y = f (x) có đồ thị như hình vẽ:
Mệnh đề nào sau đây đúng?
A. Hàm số không có cực trị.
B. Hàm số nhận giá trị âm với mọi x .
C. Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f ( x) trên đoạn 2 − ;
1 lần lượt là f ( 2 − ) và f ( ) 1 .
D. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f (x) trên đoạn 2 − ;
1 lần lượt là f (0) và f ( 2 − ).
Câu 3. Hàm số y = f (x) có đạo hàm 2
y = x . Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên .
B. Hàm số nghịch biến trên (− ;0
)và đồng biến trên (0;+).
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên (− ;0
)và nghịch biến trên (0;+).
Câu 4. Trong không gian Oxyz, cho hai điểm P(0;0;− ) 3 và Q(1;1;− )
3 . Vectơ PQ + 3 j có tọa độ là A. ( 1 − ; 1 − ;0) . B. (2;1;0) . C. (1;4;0) . D. (1;1; ) 1 .
Câu 5. Trong một hộp đựng 4 quả cầu màu trắng và 9 quả cầu màu đỏ. Hỏi có bao nhiêu cách lấy một quả cầu trong hộp nói trên?
Hàm số y = f (x) đồng biến trên khoảng nào sau đây? A. 9 . B. 36. C. 13. D. 4 .
Câu 6. Với bảng biến thiên sau đây. Khẳng định nào đúng?
A. Đồ thị hàm số có 3 tiệm cận đứng.
B. Đồ thị hàm số có 2 tiệm cận ngang.
C. Đồ thị hàm số có 1 tiệm cận đứng.
D. Đồ thị hàm số có 1 tiệm cận ngang.
Câu 7. Cho hàm số y = f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 3 . C. 0 . D. 4 − .
Câu 8. Đồ thị của hình vẽ bên là đồ thị của hàm số nào trong các hàm số sau: x −1 1− x x +1 x +1 A. y = . B. y = . C. y = . D. y = . x +1 x +1 x −1 1− x
Câu 9. Trong không gian Oxyz , cho a = (1;2; ) 1 và b = ( ; m n )
;1 . Biết rằng vectơ a = b , khi đó giá trị m + 2n bằng A. 5 . B. 4 . C. 2 . D. 3 . Câu 10. Hàm số 3
y = −x +1 có bao nhiêu điểm cực trị? A. 2 . B. 1. C. 3 . D. 0 .
Câu 11. Hàm số nào sau đây nghịch biến trên ? 1
A. y = sin x .
B. y = 1- x . C. y = . D. 3
y = 1- x . x Câu 12. Cho hàm số 3x +1 y =
. Khẳng định nào sau đây đúng? 2x −1
A. Đồ thị có hàm số có tiệm cận ngang là 3 y = . 2
B. Đồ thị có hàm số không có tiệm cận.
C. Đồ thị có hàm số có tiệm cận đứng là 1 x = − . 2
D. Đồ thị có hàm số có tiệm cận đứng là 3 y = . 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. x −1 y − 3 z − 2
Câu 1. Trong không gian với với hệ tọa độ Oxyz , cho hai đường thẳng d : = = và 1 1 1 2 − x −1 y z +1 d : = = . 2 2 1 − 1 −
a) Đường thẳng vuông góc với cả d và d có một véctơ chỉ phương là u = (1;1; ). 1 2 1
b) Đường thẳng d đi qua điểm A(2;4;4). 1
c) Khoảng cách giữa hai đường thẳng d và d là 3 2 . 1 2
d) Đường thẳng d và đường thẳng d chéo nhau. 1 2
Câu 2. Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ
của hạt (đơn vị: mét) tại thời điểm 𝑡 (giây) là 𝑦 = 𝑡3 − 12𝑡 + 3, (𝑡 ≥ 0).
a) Quãng đường hạt đi được trong khoảng thời gian 0 < 𝑡 < 3 là 9 m.
b) Hạt tăng tốc khi 𝑡 > 2 và hạt giảm tốc 0 < 𝑡 < 2.
c) Hạt chuyển động lên trên khi 𝑡 > 2 và hạt chuyển động xuống dưới khi 𝑡 < 2.
d) Hàm vận tốc là: 𝑣(𝑡) = 𝑦′ = 3𝑡2 − 12, (𝑡 ≥ 0) và hàm gia tốc là 𝑎(𝑡) = 6𝑡, (𝑡 ≥ 0).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Vận tốc trung bình của dòng xe trên đoạn đường 124 từ 6#A.M. đến 10#A.M. được xấp xỉ bởi
f (t) = 20t − 40 t + 50, 0 t 4 trong đó t tính bằng giờ kể từ 6 A.M. và f (t) tính bằng km/giờ.
Hỏi vào thời điểm mấy giờ trong buổi sáng (giữa 6#A.M. và 10#A.M.) thì vận tốc trung bình thấp nhất?
Câu 2. Hai chiếc kinh khí cầu A và B bay lên từ cùng một vị trí O trên mặt đất. Sau một khoảng thời gian,
kinh khí cầu A nằm cách điểm xuất phát 4 km về phía Đông và 3km về phía Nam, đồng thời cách
mặt đất 1km ; kinh khí cầu B nằm cách điểm xuất phát 1km về phía Bắc và 1,5km về phía Tây,
đồng thời cách mặt đất 0,8 km . Cùng thời điểm đó, một người đứng trên mặt đất và nhìn thấy hai
kinh khí cầu nói trên. Biết rằng, so với các vị trí quan sát khác trên mặt đất, vị trí người đó đứng có
tổng khoảng cách đến hai kinh khí cầu là nhỏ nhất. Hỏi tổng khoảng cách nhỏ nhất ấy bằng bao nhiêu kilômét?.
Câu 3. Một khu đất trống bằng phẳng hình chữ nhật ABCD như hình vẽ. Từ vị trí A, anh An chạy bộ theo
đường gấp khúc ABEFA để quay lại vị trí A. Vận tốc của anh
An trên đoạn AB và EF bằng 10km / h , vận tốc của anh An trên đoạn BE và AF là 6km / h . Thời gian ngắn
nhất mà anh An di chuyển từ A theo cách trên rồi quay lại A là bao nhiêu phút, biết khoảng cách AB =1km và AD = 0,6km
Câu 4. Khi khắc phục hậu quả của thiên tai, bão lũ, một trong những giải pháp nhằm tiếp tế hàng cứu trợ
đến những nơi khó tiếp cận là sử dụng flycam để xác định vị trí chính xác của người cần cứu trợ,
sau đó sử dụng drone để vận chuyển các vật dụng thiết yếu thả xuống cho người này, giúp họ có thể
cầm cự trong khi chờ đợi lực lượng cứu hộ đến nơi. Hai chiếc drone làm nhiệm vụ chuyển hàng
cứu trợ bay lên từ cùng một địa điểm. Chiếc thứ nhất bay đến điểm cách điểm xuất phát 2,5km về
phía nam và 1,5km về phía đông, đồng thời cách mặt đất 60m. Chiếc thứ hai bay đến điểm cách
điểm xuất phát 3km về phía bắc và 2,5km về phía tây, đồng thời cách mặt đất 40m.Trong không
gian, xét hệ tọa độ Oxyz với gốc tọa độ O đặt tại điểm xuất phát của hai chiếc drone, mặt phẳng
(Oxy) trùng với mặt đất. Giả sử trong trường hợp khẩn cấp cần tìm một vị trí trên mặt đất để tiếp
nhiên liệu và các vật dụng cứu trợ cho hai drone sao cho tổng khoảng cách từ vị trí tiếp nhiên liệu
tới hai drone nhỏ nhất. Vị trí cần tìm cách gốc tọa độ a km theo hướng bắc và b km theo hướng tây.
Khi đó a + b bằng bao nhiêu?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài. ur
Câu 1. Nếu vật chuyển động thẳng đều dưới tác dụng của một lực F thì vật đó đang chịu tác dụng của lực uuur ur ur
ma sát F có độ lớn bằng lực tác dụng F và có hướng ngược với hướng của F . Công thức tính ms
lực ma sát F = , trong đó là hệ số ma sát, N là độ lớn của áp lực. Giả sử một thùng gỗ ms
đang chuyển động thẳng đều trên mặt phẳng nằm ngang có trọng lượng N =150(N ) , hệ số ma sát
giữa vật và mặt phẳng là = 0, 25. Tính lực tác dụng lên thùng gỗ để thùng chuyển động thẳng đều? 2 Q
Câu 2. Hàm chi phí của một nhà máy được cho bởi C = C(Q) =
+ 3Q + 400 trong đó C là tổng chi phí 4
sản xuất Q đơn vị sản phẩm. Với mức sản lượng là bao nhiêu thì chi phí trung bình tính trên mỗi
đơn vị sản phẩm là thấp nhất? Khi đó chi phí trung bình tối thiểu bằng bao nhiêu?
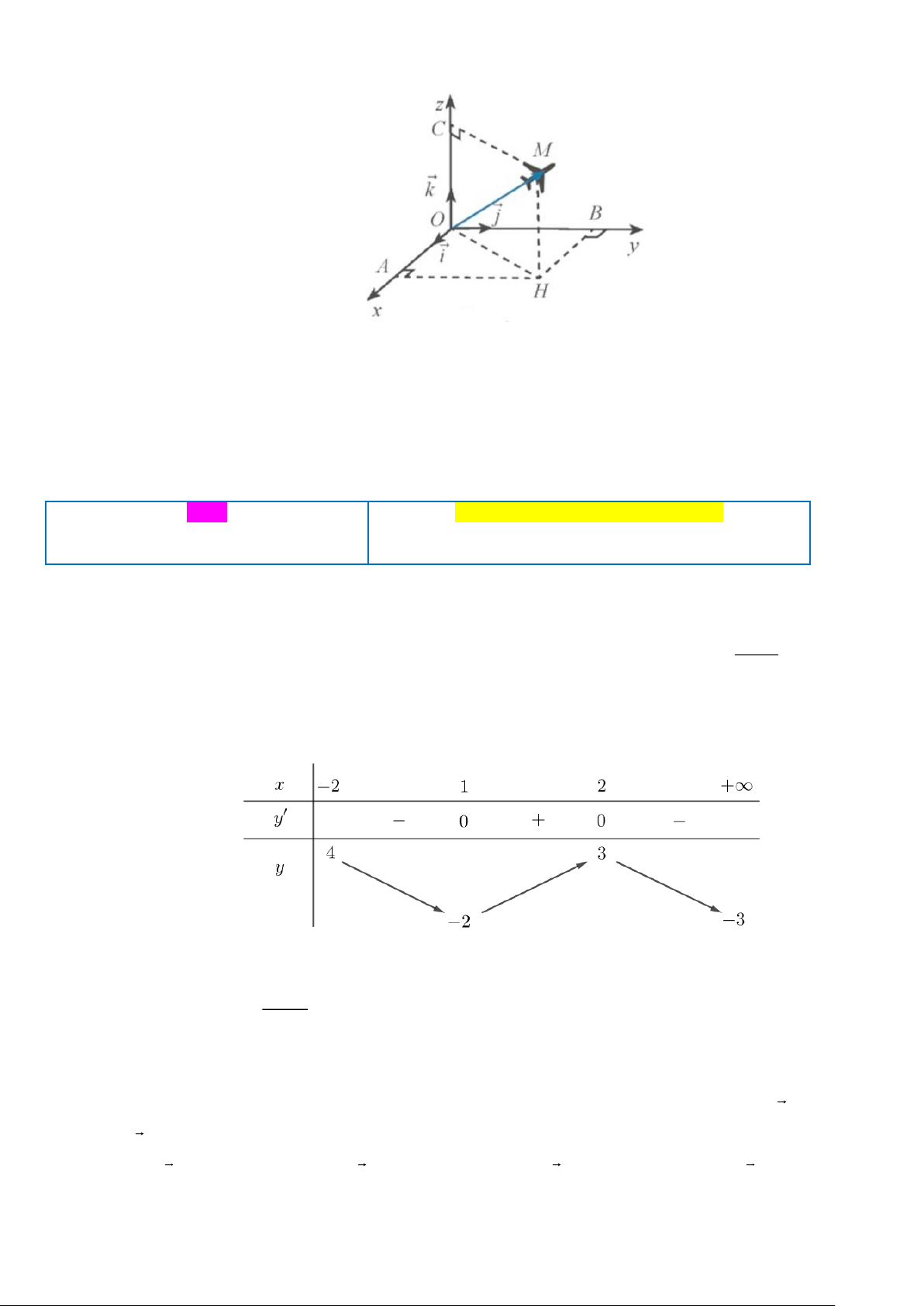
Câu 3. Ở một sân bay, vị trí của máy bay được xác định bởi điểm M trong không gian Oxyz như hình vẽ. Gọi
H là hình chiếu vuông góc của
M xuống mặt phẳng (Oxy). Biết
OM = 79;(i,OH ) = 68 ;(OH,OM ) = 50 . Gọi toạ độ điểm M ( ; a ;
b c) . Giá trị của a +b + c là bao
nhiêu? (làm tròn đến hàng phần mười).
Câu 4. Ho ép khí quản co lại, ảnh hưởng đến tốc độ không khí đi vào khí quản. Tốc độ của không khí đi
váo khí quản khi ho đo được bởi công thức 2
V = k(R - r)r với 0 £ r < R ,
trong đó k là hằng số, R là bán kính bình thường của khí quản, r là bán kính khí quản khi ho.
Hỏi bán kính khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi váo khí quản là lớn nhất? ĐỀ 5
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. 1− 3x
Câu 1. Phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = lần lượt là: x + 2 A. x = 2 − và y = 1.
B. x = 2 và y = 1
C. y = −2 và x = 3 − . D. x = 2 − và y = 3 − .
Câu 2. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ
Khẳng định nào sau đây đúng ? A. y = 3 − . B. y = 3 . C. y = 4 . D. y =1 . CT CD CD CT 5x − 2
Câu 3. Cho hàm số y =
.Mệnh đề nào dưới đây đúng? x + 2
A. Hàm số đồng biến trên khoảng (− ; − 2).
B. Hàm số nghịch biến trên khoảng (− ; − 2).
C. Hàm số đồng biến trên khoảng (− ; + ).
D. Hàm số nghịch biến trên khoảng ( 2; − + ).
Câu 4. Trong không gian Oxyz , véctơ nào dưới đây vuông góc với cả hai véctơ u = ( 1 − ;0;2) ,
v=(4;0;− )1? A. w = (0;7; ) 1 . B. w = (0; 1 − ;0) . C. w = (1;7; ) 1 . D. w = ( 1 − ;7;− ) 1 .
Câu 5. Cho hàm số f ( x) có đạo hàm f ( x) = ( x + )2 ( x − )3 1
1 (2 − x) . Hàm số f ( x) đồng biến
trong khoảng nào dưới đây?




