
Preview text:
ĐỀ 1
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Trong không gian Oxyz , cho hai điểm A(1; 1 − ;2) và B(2;1; )
1 . Độ dài đoạn AB bằng A. 2 . B. 6 . C. 6 . D. 2 .
Câu 2. Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ u = (1; 2 − ; ) 1 và v = (2;1;− ) 1 . Véctơ nào
dưới đây vuông góc với cả hai véctơ u và v ? A. w = 1; 4 − ;7 .
B. w = 1;4;7 . C. w = 1; 3 − ;5 .
D. w = 1;3;5 . 2 ( ) 1 ( ) 4 ( ) 3 ( )
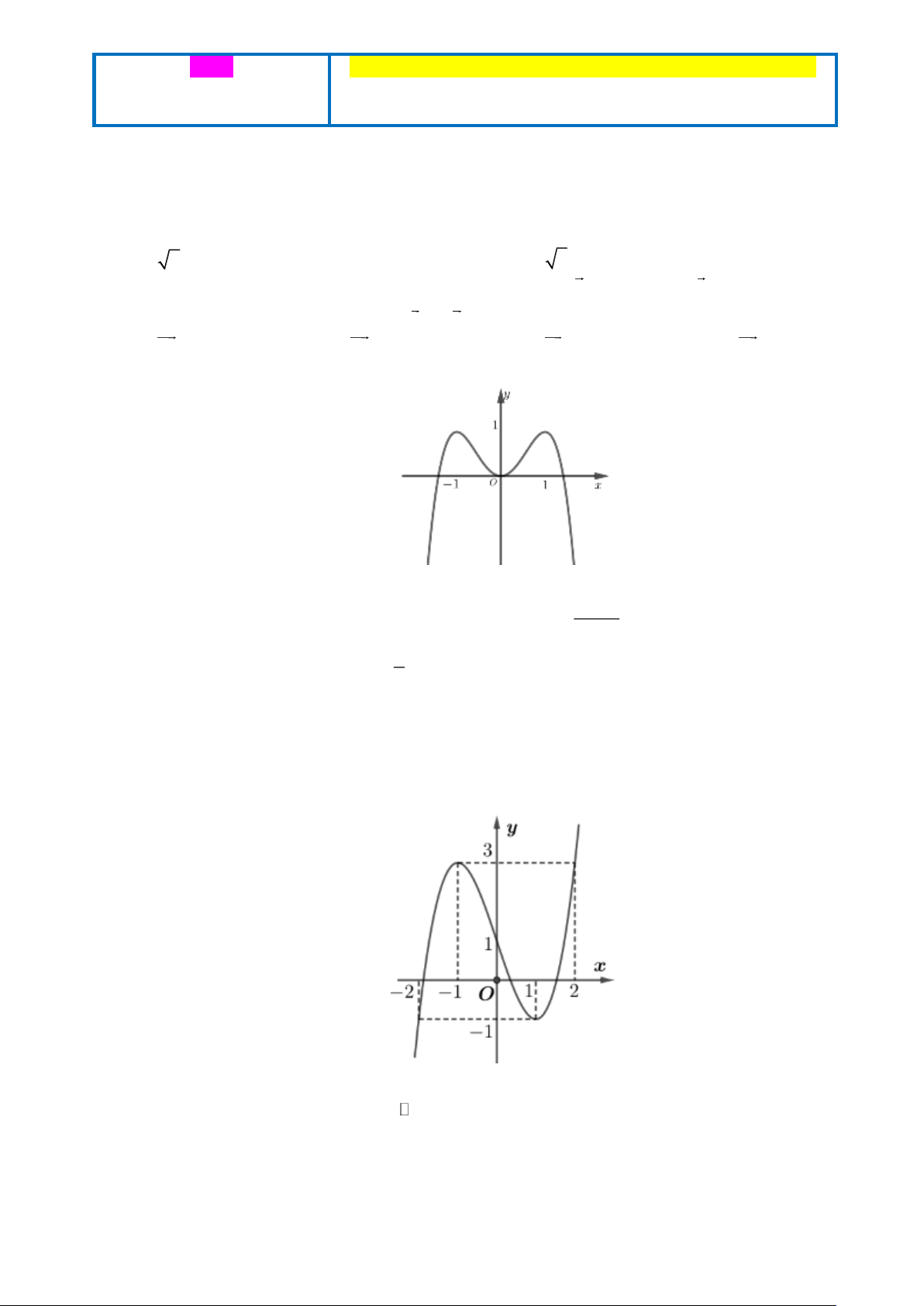
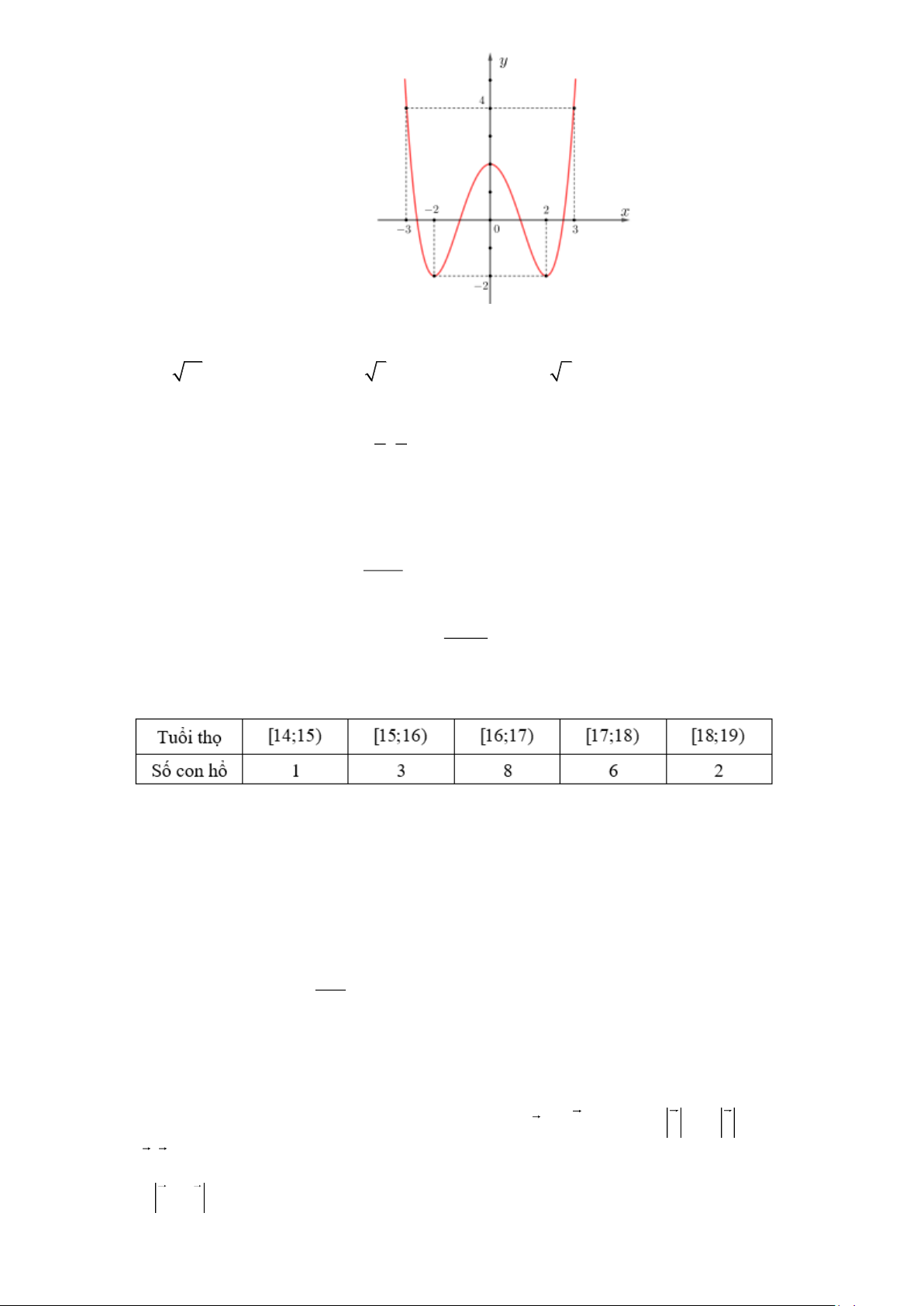
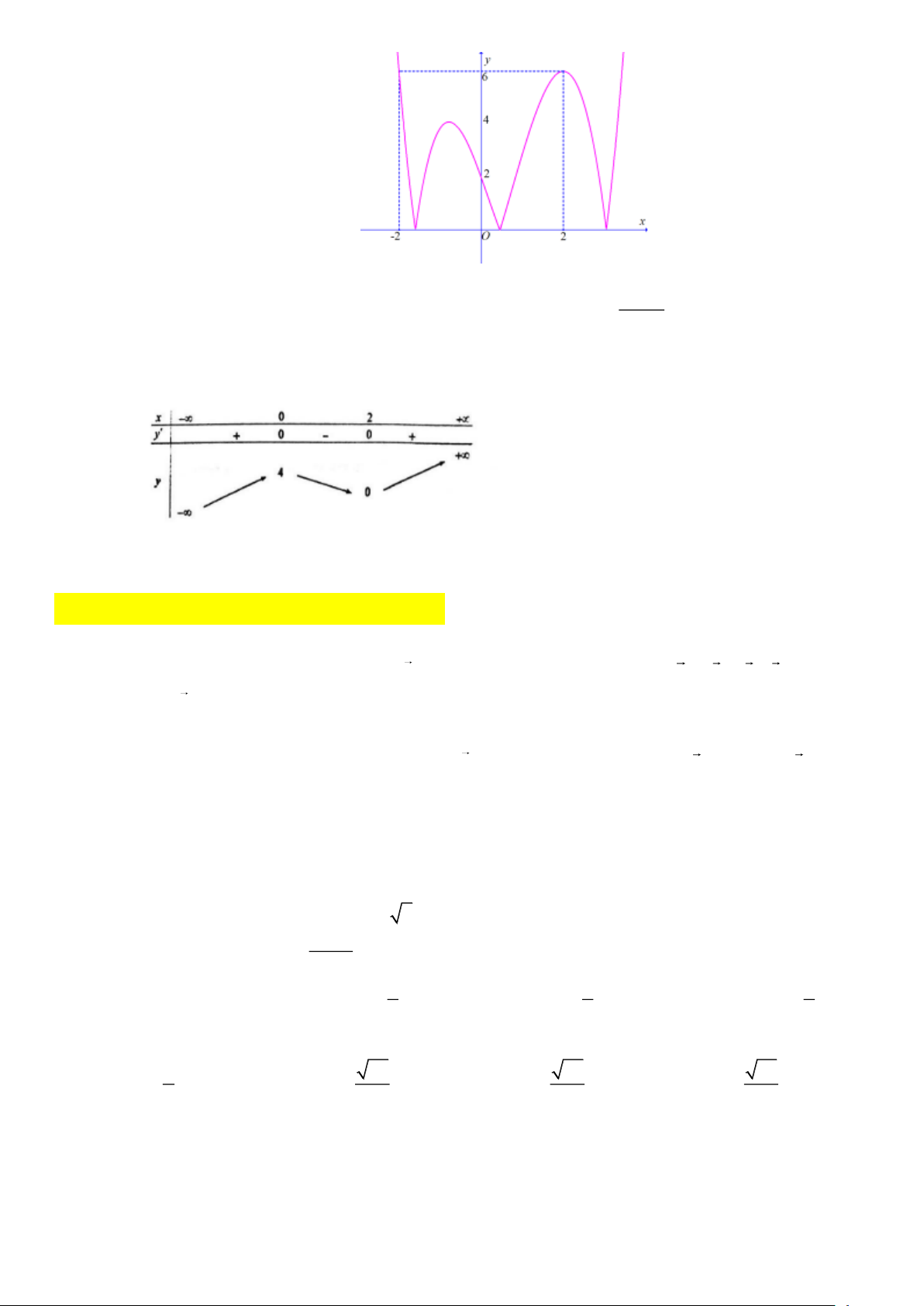
Câu 3. Đồ thị sau đây là đồ thị của hàm số nào? A. 4 2
y = x − 2x +1. B. 4 2
y = −x + 2x +1. C. 4 2
y = x − 2x . D. 4 2
y = −x + 2x . 6x − 5
Câu 4. Phương trình đường tiệm cận ngang của đồ thị hàm số y = là x + 6 5 A. x = 6 − .
B. y = − .
C. x = 6 .
D. y = 6 6
Câu 5. Trong không gian Oxyz , cho 2 điểm M (1;− 2;2) và N (1;0;4) . Toạ độ trung điểm của đoạn thẳng MN là: A. (0;2;2) . B. (1;−1; ) 3 . C. (1;0;3) . D. (2;− 2;6) .
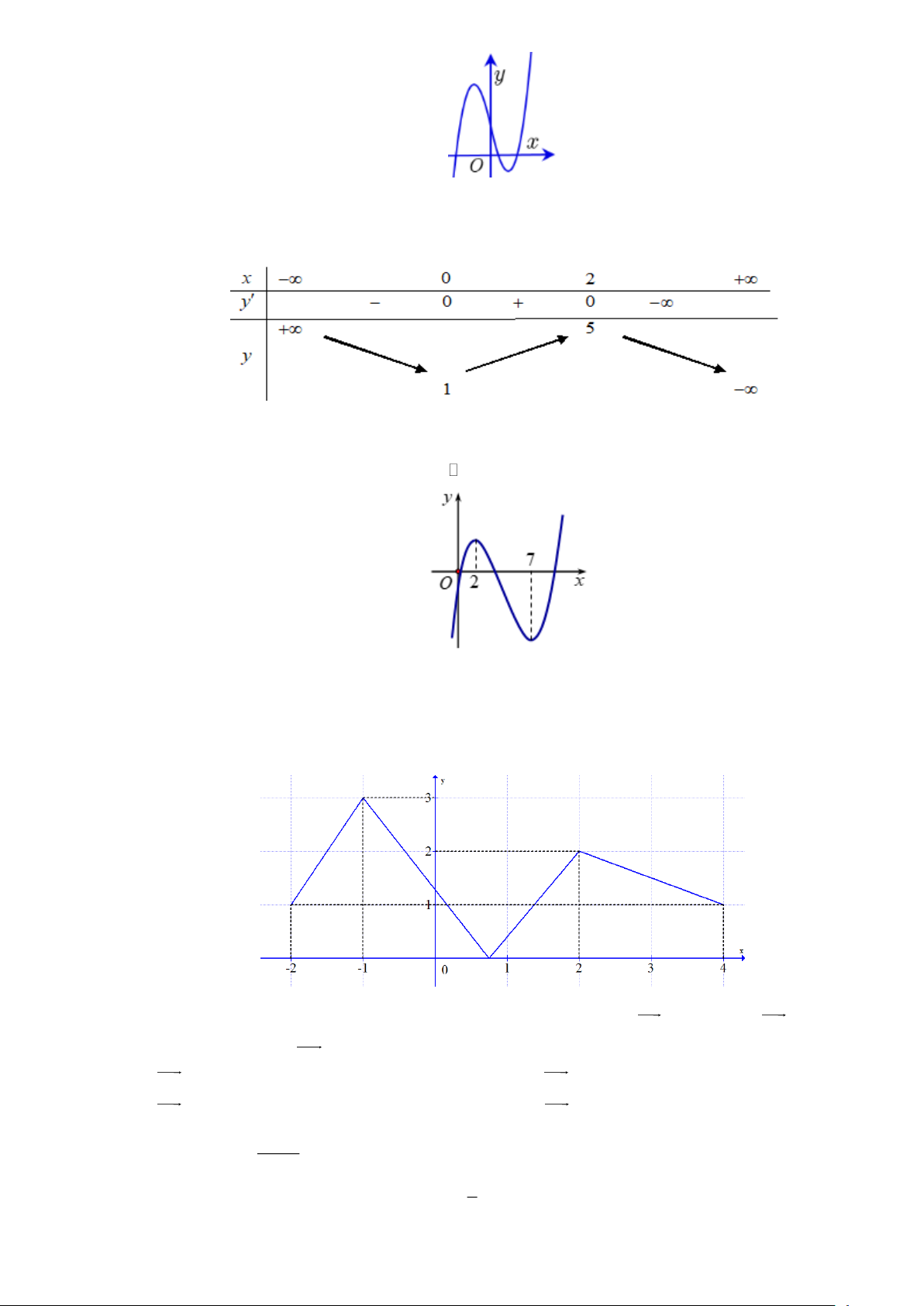
Câu 6. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số y = f (x) đồng biến trên khoảng A. ( 1 − ;+ ). B. (− ; − ) 1 . C. ( ) ;1 − . D. ( 1 − ; ) 1 .
Câu 7. Cho hàm số y = f (x) liên tục trên và có bảng biến thiên (như hình vẽ). Khẳng định nào sau đây sai? Trang 1
A. Hàm số có giá trị lớn nhất bằng 5 .
B. Hàm số có giá trị nhỏ nhất bằng 2 − .
C. Hàm số có hai điểm cực trị.
D. Đồ thị hàm số có hai tiệm cận ngang.
Câu 8. Cho hàm số y = f (x) có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho bằng A. 2 . B. 0 . C. 4 − . D. 3 . 3x +1
Câu 9. Tọa độ điểm M thuộc đồ thị hàm số y =
cách đường tiệm cận đứng của đồ thị hàm số một x −1 khoảng bằng 1là A. (0;− ) 1 ; ( 2 − ;7) . B. ( 1 − ;0); (2;7). C. (0; ) 1 ; (2; 7 − ) . D. (0;− ) 1 ; (2;7) .
(m+ )1 x + 4m+10
Câu 10. Số các giá trị m nguyên để hàm số y =
nghịch biến trên khoảng (− ; 2 − ) là: x + m A. 3 . B. 5 . C. 4 . D. 6 .
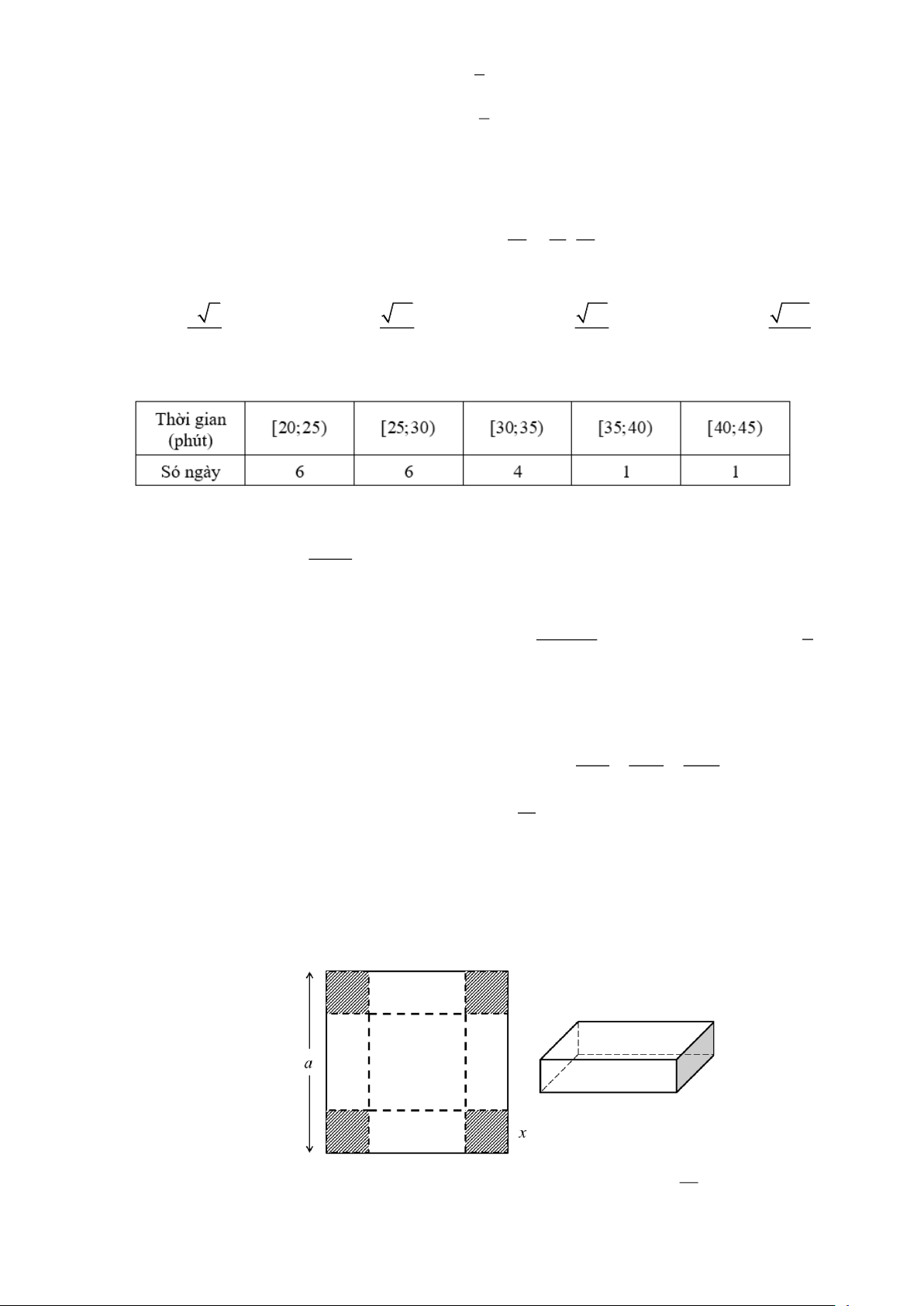
Câu 11. Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm này là A. 20. B. 12. C. 15. D. 26.
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho u = (1;1;2),v = ( 1 − ; ;
m m − 2) . Khi u ,v = 14 thì 11 A. m = 1 − B. m = 1 − hoặc m = − 3 11
C. m =1 hoặc m = −
D. m =1 hoặc m = 3 − 5
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá 30 000 đồng một chiếc và mỗi tháng
cơ sở bán được trung bình 3000 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có
lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 30 000
đồng mà cứ tăng giá thêm 1000 đồng thì mỗi tháng sẽ bán ít hơn 100 chiếc. Biết vốn sản xuất một
chiếc khăn không thay đổi là 18000 .
a) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần tăng thêm 10000 đồng
b) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá 39000 đồng
c) Để đạt lợi nhuận lớn nhất thì sau khi tăng giá mỗi chiếc khăn lãi 21000 đồng
d) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm 800 chiếc
Câu 2. Trong không gian với hệ trục tọa độ Oxyz , cho hình hộp ABC . D A B C D có A(1;2; ) 3 ; B(4;5;6) ; C( 3 − ;2;− ) 1 và D (0; 3
− ;5) . M là trung điểm CC. Khi đó
a) Tọa độ điểm C(9;4;10). Trang 2 11
b) Tọa độ tâm của hình hộp là 2;1; . 2
c) B
D = BA+ AD + CC . 1
d) AM = AB + AD + A A . 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) mà bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
Hãy xác định độ lệch chuẩn của mẫu số liệu trên? (Nếu kết quả là số thập phân thì làm tròn đến hàng đơn vị)
Câu 2. Bộ phận sản xuất của một công ty xác định chi phí để sản xuất x sản phẩm được cho bởi biểu thức 2
T(x) = x + 20x + 4000 (nghìn đồng). Nếu x sản phẩm đều được bán hết và giá bán mỗi sản phẩm
là 150 nghìn đồng thì lợi nhuận lớn nhất mà công ty thu được là bao nhiêu?
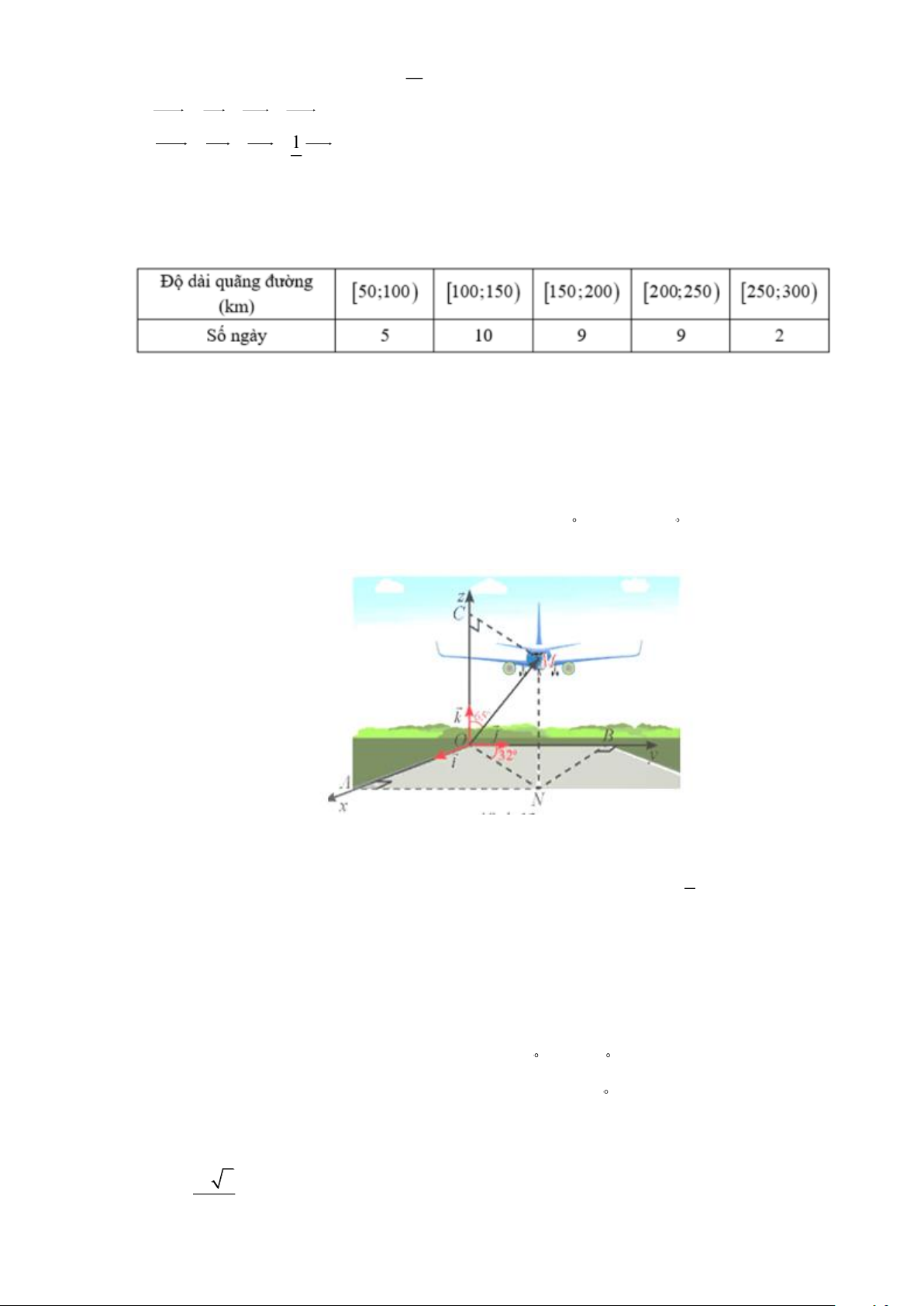
Câu 3. Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như hình vẽ bên dưới,
cho biết M là vị trí của máy bay, OM =14 , NOB = 32 , MOC = 65 . Giả sử M ( ; x y; z) .Tính
S = x + y + z (làm tròn , x ,
y z đến chữ số thập phân thứ nhất).
Câu 4. Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa và các
suối nước đổ về hồ. Tính từ thời điểm 8 giờ sáng, độ sâu của mực nước trong hồ tính theo mét và 1
lên xuống theo thời gian t (giờ) trong ngày cho bởi công thức: h(t ) 3 2
= − t + 5t + 24t (t 0) . 3
Biết rằng phải thông báo cho các hộ dân phải di dời trước khi xả nước theo quy định trước 5 giờ.
Hỏi cần thông báo cho hộ dân di dời trước khi xả nước mấy giờ. Biết rằng mực nước trong hồ phải
lên cao nhất mới xả nước.
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
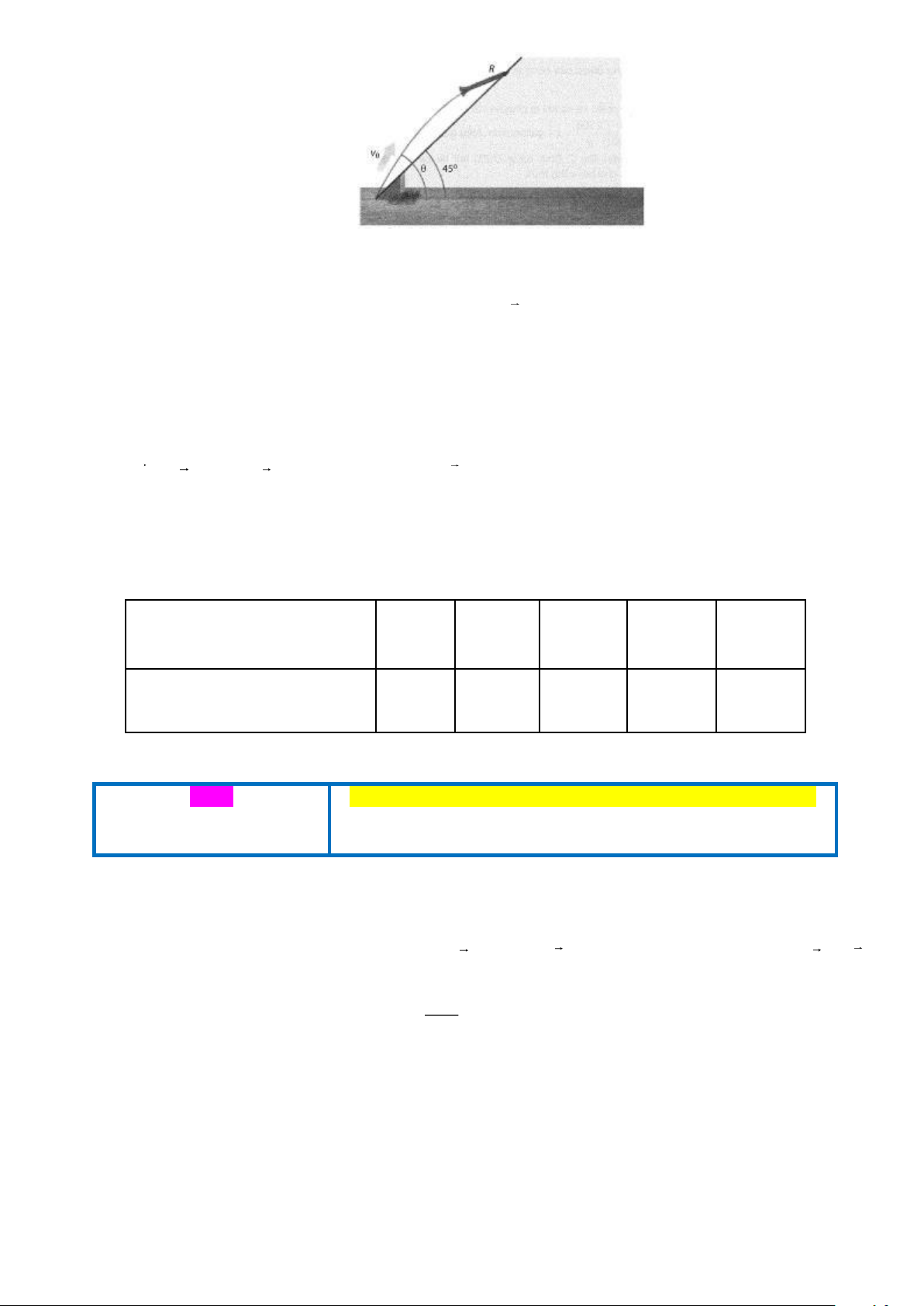
Câu 1. Một vật được phóng lên trời theo một góc xiên (45
90 ) so với phương ngang với vận tốc
ban đầu là v tính từ chân mặt phẳng nghiêng tạo một góc 45 so với phương ngang. Nếu bỏ qua 0
sức cản của không khí thì quãng đường R mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số 2 R ( ) v 2 0 = cos (sin − cos ) 16
Góc ném nào làm cho quãng đường R lớn nhất? Giá trị iớn nhất của R là bao nhiêu? Trang 3
Câu 2. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là 1m ), một cabin cáp treo xuất
phát từ điểm A(10;3;0) và chuyển động đều theo đường cáp thẳng đến vị trí D cách A 4050 m .
Biết đường đi của cabin cùng phương với vectơ u (2; 2 − )
;1 và sau 3 phút kể từ khi xuất phát thì
cabin đến vị trí B có hoành độ x = 550 B
. Hỏi thời gian di chuyển của cabin trên quãng đường AD là bao nhiêu phút?
Câu 3. Theo định luật II Newton (Vật lí 10 - Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023,
trang 60): Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận
với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật:
F = ma trong đó a là vectơ gia tốc m/s 2, F là vectơ lực (N).
Hình 20 tác dụng lên vật, m (kg) là khối lượng của vật.
Muốn truyền cho quả bóng có khối lượng 0,5 kg một gia tốc 50 m/s 2 thì cần một lực đá có độ lớn là bao nhiêu?
Câu 4. Thống kê mức thu nhập theo tháng của một số hộ gia đình ở một khu dân cư cho kết quả như sau: 5;10) Mức thu nhập
10;15) 15;20) 20;25) 25;30) 1 Số hộ gia đình 5 8 15 12 0
Tìm phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm này. ĐỀ 2
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho u = ( ;
x 2;1), v = (1; 1
− ;2x) . Tích vô hướng của u và v .
A. 3x + 2.
B. 3x − 2 . C. 2 − − x . D. x + 2 . 5
Câu 2. Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình? x −1 A. x =1.
B. x = 0 .
C. y = 0 .
D. y = 5 .
Câu 3. Hàm số y = f (x) liên tục và có bảng biến thiên như hình bên. Gọi M là giá trị lớn nhất của hàm
số y = f (x) trên nữa khoảng 0; ) 3 . Tìm mệnh đề đúng. Trang 4
A. M = f (0) .
B. M = f (2).
C. M = f ( ) 3 .
D. M = f (5).
Câu 4. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng A. (1; ) 3 . B. (2;+ ) . C. (0; ) 1 . D. (−;0) .
Câu 5. Đường cong ở hình vẽ
là đồ thị của hàm số nào sau đây? A. 3 2
y = x - 2x + 3 . B. 3 2
y = - x + 2x + 3 . C. 3 2
y = - x + 2x - 3 . D. 4 2
y = x - 3x + 3 .
Câu 6. Mặt cầu (S ) ( x − )2 + ( y + )2 2 : 1
2 + z = 9 có tâm là: A. I ( 1 − ;− 2;0) .
B. I (1;− 2;0) . C. I ( 1 − ;2;0) .
D. I (1;2;0) .
Câu 7. Trong không gian Oxyz , hình chiếu vuông góc của điểm M (3; 5 − ; )
1 trên mặt phẳng (Oyz) có tọa độ là: A. (0; 5 − ; ) 1 . B. (0; 5 − ;0) . C. (0;0; ) 1 . D. (3;0; ) 1 .
Câu 8. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
A. Hàm số f (x) đồng biến trên (−;4) . Trang 5
B. Hàm số f (x) đồng biến trên (−;0)(2;+ ).
C. Hàm số f (x) đồng biến trên (−;0) .
D. Hàm số f (x) đồng biến trên (0;+ ) . ax + b
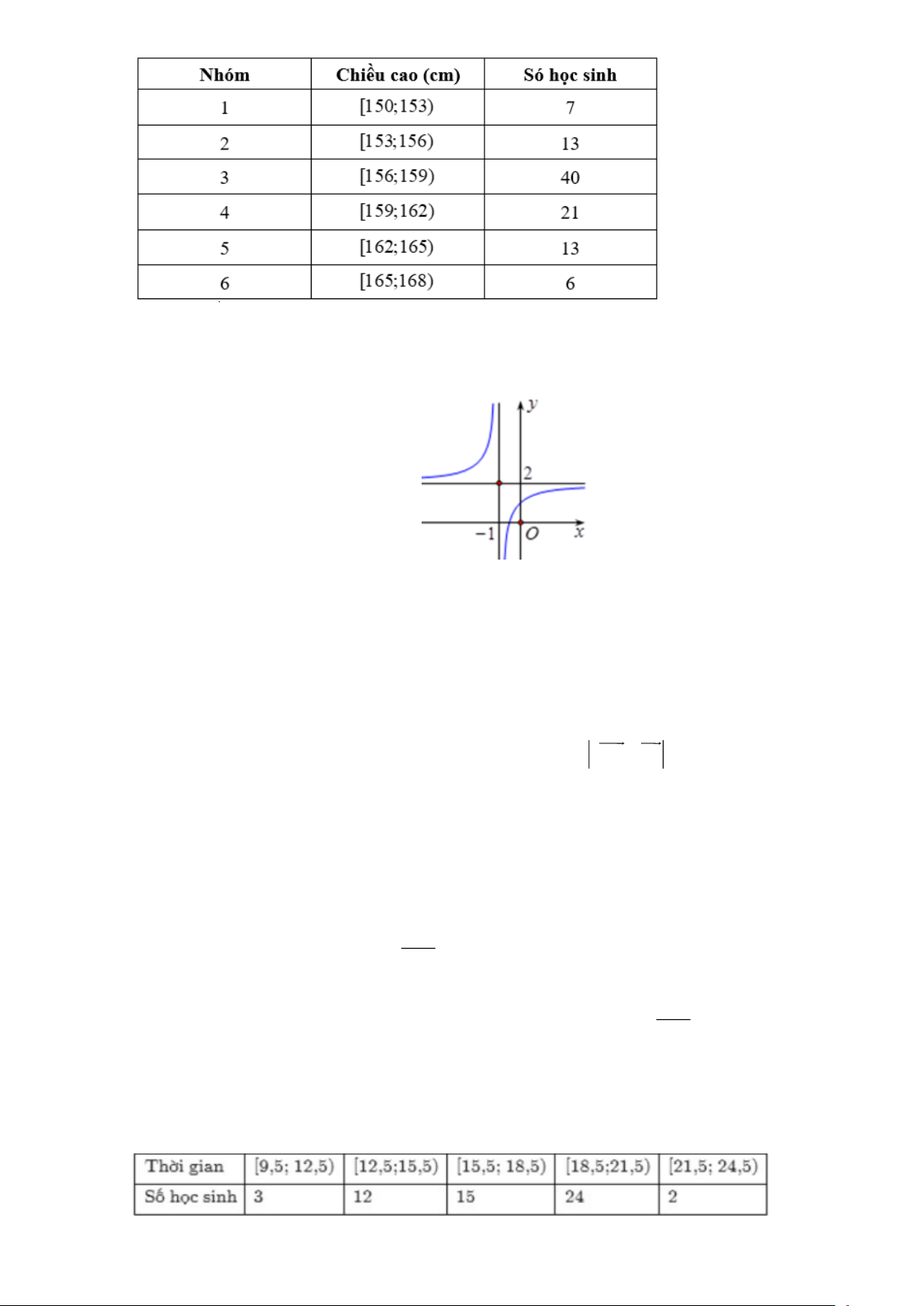
Câu 9. Cho hàm số y =
có đồ thị như hình vẽ bên. x +1 y 1 1 O x
Tìm khẳng định đúng trong các khẳng định sau
A. 0 a b.
B. 0 b a .
C. b 0 a .
D. a b 0.
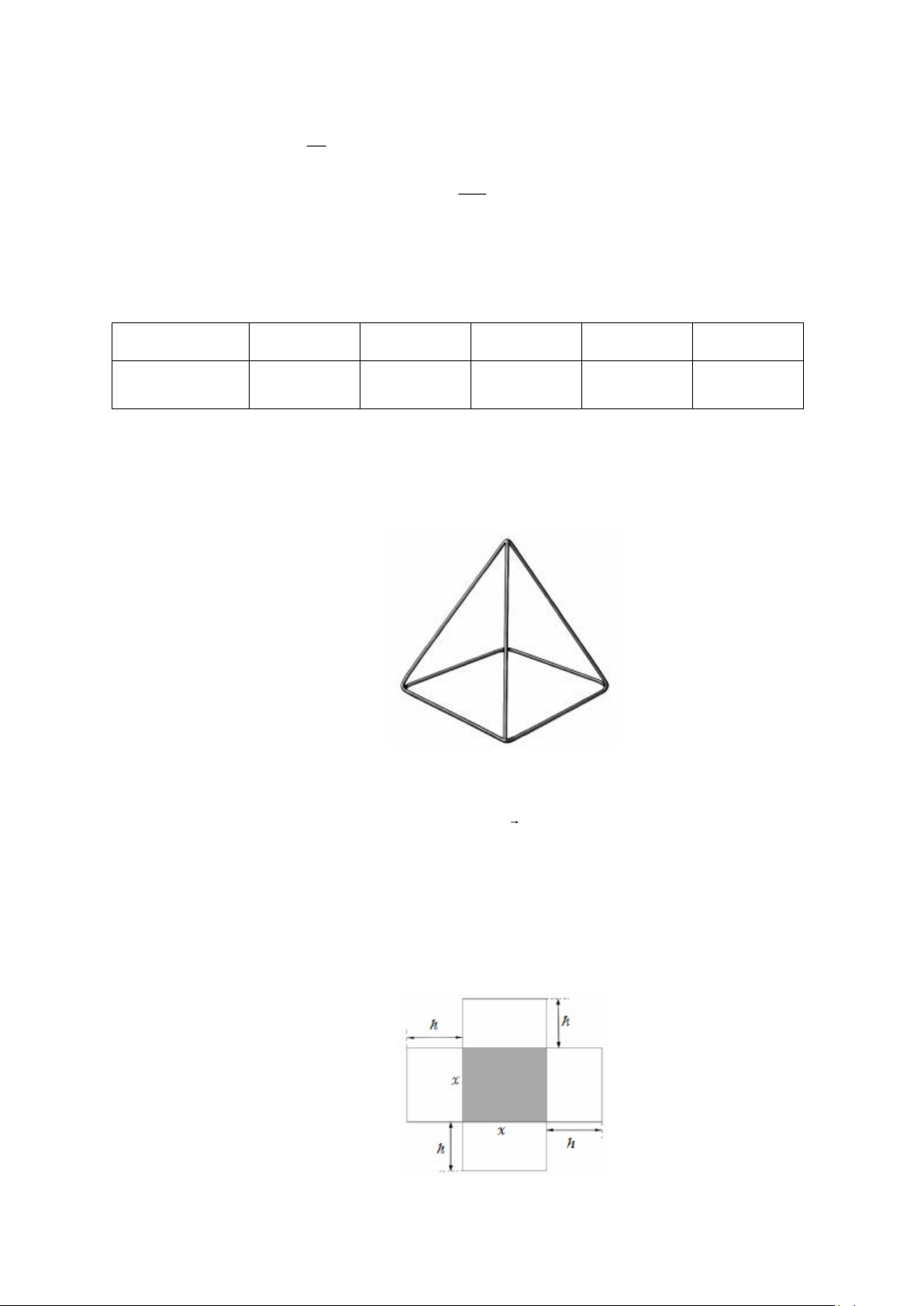
Câu 10. Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau.
Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên. A. 69,8. B. 30. C. 25. D. 6. mx + 2
Câu 11. Cho hàm số y =
, m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham 2x + m
số m để hàm số nghịch biến trên khoảng (0; )
1 . Tìm số phần tử của S . A. 2 . B. 1. C. 5 . D. 3 .
Câu 12. Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm tạo thành tứ giác lồi A(2;0;− ) 1 , B( 2 − ;1;− )
3 , C (1;2;2), D(0; 1 − ; 5
− ). Diện tích của tứ giác này có giá trị bằng 13 6 A. . B. 7 6 . C. 13 6 . D. 4 7 . 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Trong không gian Oxyz, cho điểm A( 2 − ;3; )
1 , B(5;−3;2) và C( 2
− ;2;4) . Đường thẳng AB cắt
mặt phẳng (Oyz) tại điểm M . a) AB = ( 7 − ;− 6; ) 1 . 9 9
b) Tọa độ của điểm M là 0; ; . 7 7
c) Tam giác ABC vuông tại A . 1 2 7
d) Tọa độ trọng tâm của tam giác ABC là G ; ; . 3 3 3
Câu 2. Ông Nam cần xây dựng một bể chứa nước có dạng hình hộp chữ nhật không có nắp đậy để phục vụ
cho việc tưới cây trong vườn. Do các điều kiện về diện tích vườn, ông Nam cần bể có thể tích là 3
36 m , đáy bể có chiều dài gấp hai lần chiều rộng và chiều rộng không quá 4 m , biết rằng chi phí
vật liệu xây dựng mỗi mét vuông diện tích bề mặt là như nhau. Trang 6
Gọi x(m) là chiều rộng của bể, ta có 0 x 4. Khi đó
a) Chiều dài của bể là 2x (m) 18
b) Chiều cao của bể là ( m) . 2 x
c) Tổng diện tích các mặt cần xây là: 2 108 2x + . x
d) Chiều cao bể nước bằng 3(m) thì tổng chi phí vật liệu là nhỏ nhất.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Bảng phân bố sau đây cho biết chiều cao (tính bằng cm) của 500 học sinh trong một trường THCS Chiều cao 150;154) 154;158) 158;162) 162;166) 166;170) 50 Tần số 25 50 200 175
Tính độ lệch chuẩn (làm tròn 2 chữ số thập phân).
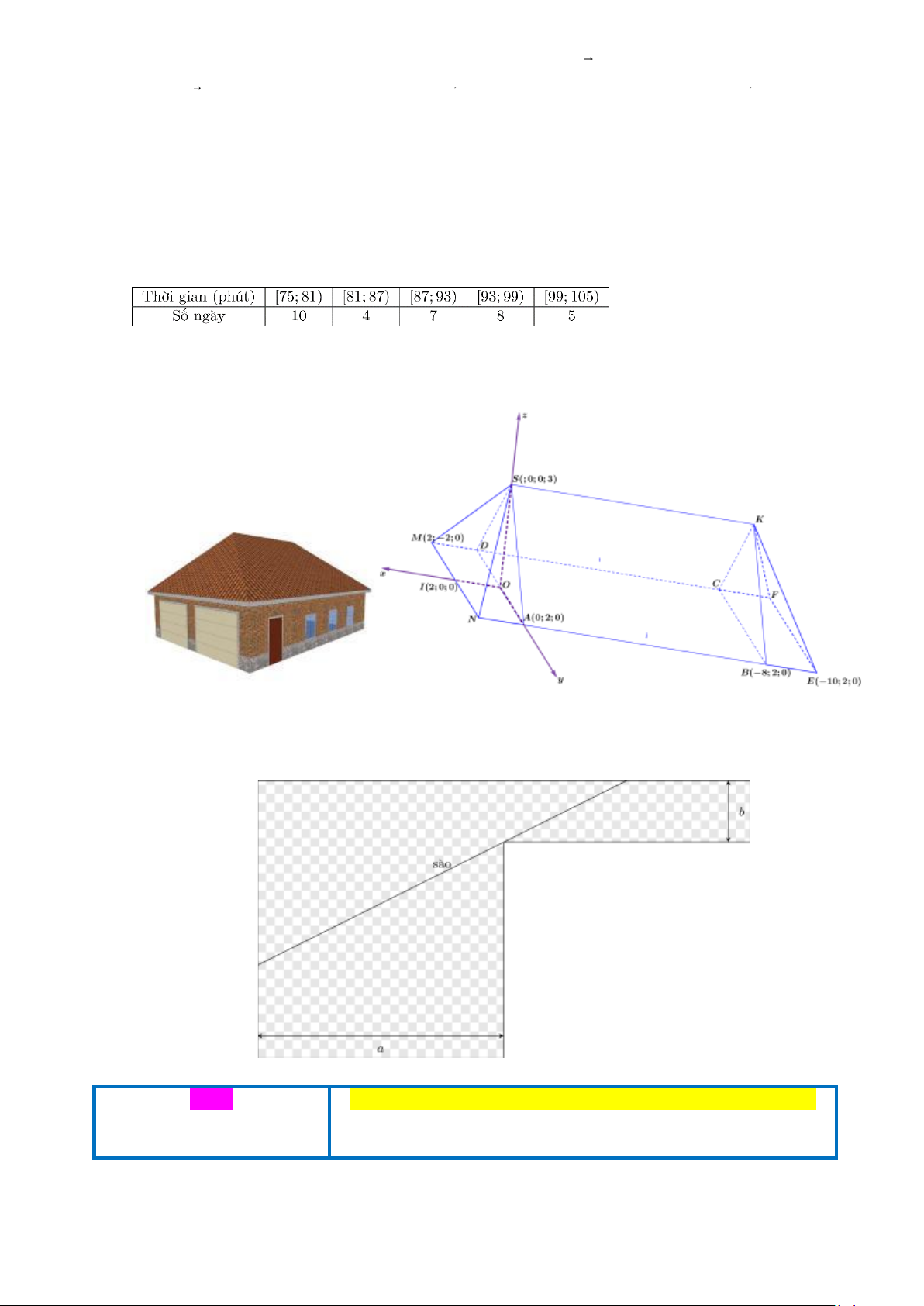
Câu 2. Bạn An có một đoạn dây thép dài 16 dm muốn uốn thành một kim tự tháp có dạng chóp tứ giác
đều (đoạn dây thép được uốn thành 4 cạnh bên và 4 cạnh đáy của kim tự tháp). Hỏi thể tích lớn
nhất của kim tự tháp bạn An có thể làm được là bao nhiêu? (đơn vị: 3
dm , kết quả làm tròn đến hàng phần trăm).
Câu 3. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là 1m ), một cabin cáp treo xuất
phát từ điểm A(10;3;0) và chuyển động đều theo đường cáp thẳng đến vị trí D cách A 4050 m .
Biết đường đi của cabin cùng phương với vectơ u (2; 2 − )
;1 và sau 3 phút kể từ khi xuất phát thì
cabin đến vị trí B có hoành độ x = 550 . Hỏi thời gian di chuyển của cabin trên quãng đường B AD là bao nhiêu phút?
Câu 4. Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông
cạnh x(cm), chiều cao là h(cm) và thể tích là 3
4000cm . Tìm x(cm) sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài. Trang 7
Câu 1. Nếu vật chuyển động thẳng đều dưới tác dụng của một lực F thì vật đó đang chịu tác dụngcủa lực
ma sát F có độ lớn bằng lực tác dụng F và có hướng ngược với hướng của F . Côngthức tính ms
lực ma sát F = N , trong đó là hệ số ma sát, N là độ lớn của áp lực. Giả sử mộtthùng gỗ ms
đang chuyển động thẳng đều trên mặt phẳng nằm ngang có trọng lượng N =128 (N), hệsố ma sát
giữa vật và mặt phẳng là = 0,15. Lực tác dụng lên thùng gỗ để thùng chuyển động thẳng đều là
bao nhiêu? (làm tròn kết quả đến hàng phần chục).
Câu 2. Thống kê thời gian tập thể dục (phút) của một người trong một số ngày được cho trong bảng số liệu sau
Độ lệch chuẩn của mẫu số liệu là bao nhiêu? (làm tròn kết quả đến hàng phần chục).
Câu 3. Phần mái của một căn nhà có dạng là khối đa diện được mô tả và gắn trên hệ trục tọa độ Oxyz như
hình vẽ. Tính thể tích khối đa diện của mái nhà.
Câu 4. Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm
chạm với hành lang (như hình vẽ). Biết a = 24 và b = 3 , hỏi cái sào thỏa mãn điều kiện trên có
chiều dài tối thiểu là bao nhiêu? (làm tròn kết quả đến hàng phần mười) ĐỀ 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. Trang 8
Câu 1. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án ,
A B,C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 4 2
y = x − x +1. B. 2
y = −x + x −1. C. 3
y = −x + 3x +1. D. 3
y = x − 3x +1
Câu 2. Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x + y + z + 2y − 2z − 7 = 0. Bán kính của mặt cầu đã cho bằng A. 9. B. 7 . C. 15 . D. 3 .
Câu 3. Cho hàm số y = f (x) có bảng biến thiên như sau.
Hàm số đạt cực tiểu tại điểm
A. x = 5.
B. x = 0 . C. x =1.
D. x = 2 . 2x −1
Câu 4. Cho hàm số y =
. Khẳng định nào sau đây đúng? −x + 3
A. Đồ thị hàm số có tiệm cận đứng x = 3, tiệm cận ngang y = 2 .
B. Đồ thị hàm số có tiệm cận đứng x = 3
− , tiệm cận ngang y = 2 .
C. Đồ thị hàm số có tiệm cận đứng x = 3, tiệm cận ngang y = −2 .
D. Đồ thị hàm số có tiệm cận đứng x = 3
− , tiệm cận ngang y = −2 .
Câu 5. Cho hàm số y = f (x) liên tục trên các khoảng (− ;
0),(0;+) và có bảng biến thiên dưới đây
Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng ( 1 − ;0).
B. Hàm số đồng biến trên ( ; − 0).
C. Hàm số đồng biến trên (1;+).
D. Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 .
Câu 6. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số này trên đoạn 2 − ; 3 bằng Trang 9 A. 4. B. 5. C. 2. D. 3.
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1; 2 − ;− ) 1 và B(1;4; )
3 . Độ dài đoạn AB là A. 2 13 . B. 2 3 . C. 6 . D. 3 .
Câu 8. Trong không gian Oxyz , cho điểm A(2;1; ) 3 , B(0;3; )
1 . Trung điểm AB có tọa độ là 3 1 A. (2;4;4) . B. 1; ; . C. (2;1;2) . D. (1;2;2) . 2 2
Câu 9. Trong không gian Oxyz , cho bốn điểm A(1;1;4) , B(5; 1
− ;3), C(2;2;m), D(3;1;5) . Tìm tất cả giá
trị thực của tham số m để A , B , C , D là bốn đỉnh của một hình tứ diện.
A. m 6.
B. m 6 .
C. m = 6. D. m 6 .
Câu 10. Kết quả của x + m
m để hàm số y =
đồng biến trên từng khoảng xác định là x + 2
A. m 2.
B. m 2.
C. m 2.
D. m 2 . 2x −1 y = −
Câu 11. Tâm đối xứng I của đồ thị hàm số x +1 là A. I ( 1 − ; 2). B. I ( 1 − ; − 2) .
C. I (1; − 2) .
D. I (1; 2).
Câu 12. Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:
Nhóm chứa tứ phân vị thứ nhất là A. [16;17) . B. [17;18) . C. [15;16) . D. [14;15) .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 12 triệu đồng
một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng
ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần. Khi đó
a) Hàm cầu là p ( x) 1 = −
x +17 (triệu đồng). 200
b) Nếu giá bán là 9 triệu đồng trên mỗi chiếc ti vi thì nhà sản xuất trung bình bán được 1500 ti vi mỗi tuần.
c) Nếu bán được trung bình 1500 ti vi mỗi tuần thì doanh thu là 14 tỉ đồng.
d) Nếu nhà sản suất giảm giá bán 3,5 triệu đồng trên mỗi chiếc ti vi thì doanh thu là lớn nhất.
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a và b thỏa mãn a = 2, b = 3 và (
a,b) = 60 .
a) a − 2b = 28. Trang 10
b) a − b = 7
c) ab = 3 .
d) a + b = 19 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Ở một vịnh biển, ngoài xa có một hòn đảo nhỏ. Người ta tiến hành lấn biển để xây một khu đô thị
và làm một tuyến cáp treo nối khu đô thị với hòn đảo để phát triển du lịch. Xét trong hệ tọa độ Oxy
với đơn vị đo tương ứng 1km có hòn đảo ở O thì đương bao của phần đất lấn biển có dạng là một 2 x +1
phần của đồ thị hàm số y =
. Giả sử tuyến cáp treo được thiết kế nối đảo với đường bao của x
khu đô thị với độ dài ngắn nhất. Độ dài của tuyến cáp treo là bao nhiêu km (làm tròn kết quả đến hàng phần mười)?
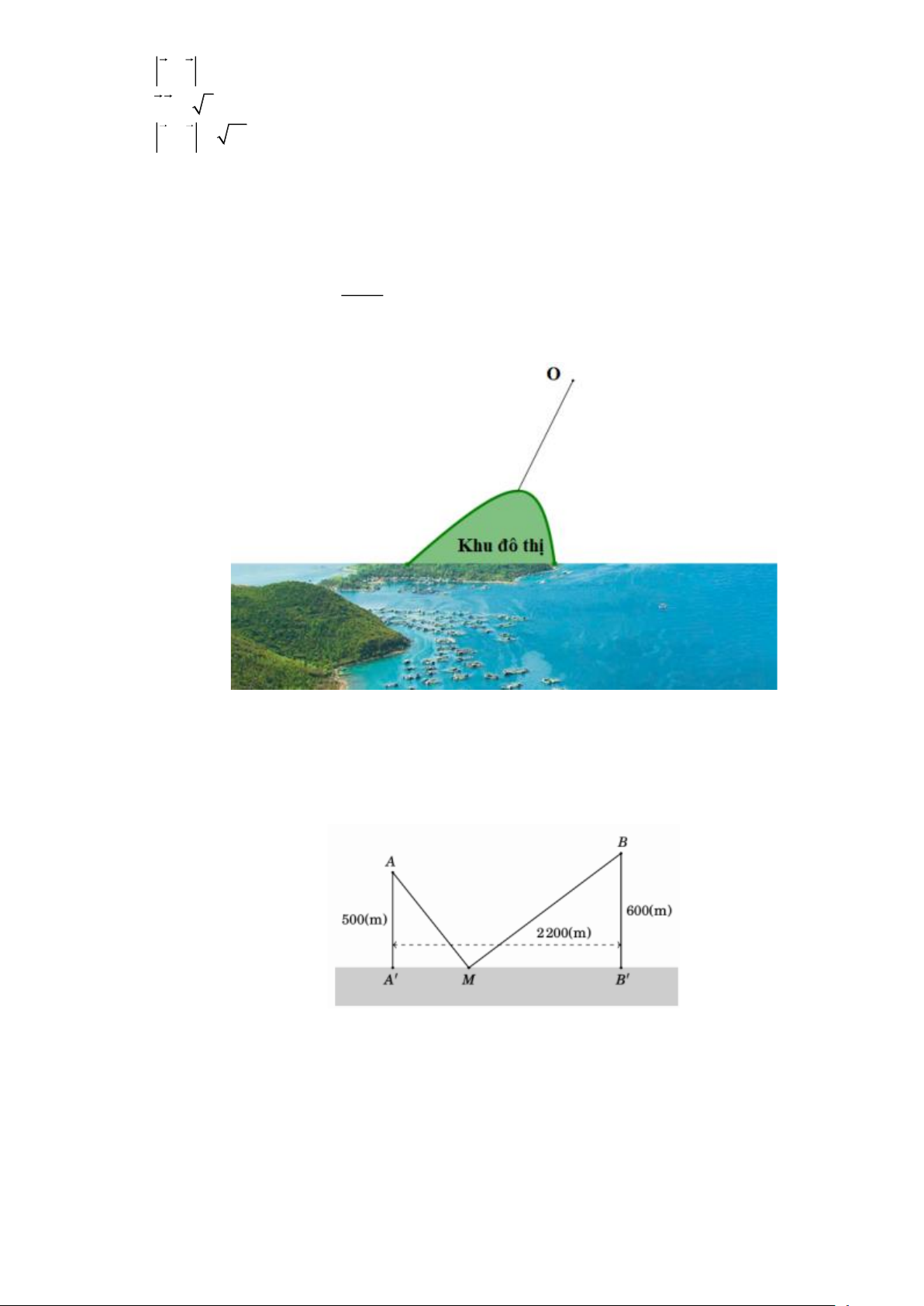
Câu 2. Kết Có hai xã ,
A B cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần lượt là
AA = 550m, BB = 600 m. Người ta đo được A B
= 2200 m như hình vẽ dưới đây. Các kỹ sư
muốn xây dựng một trạm cung cấp nước sạch nằm cạnh bên bờ sông cho người dân của hai xã sử
dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí M của trạm cung cấp nước sạch đó trên
đoạn AB sao cho tổng khoảng cách từ hai xã đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất
của tổng khoảng cách đó.
Câu 3. Trượt nước là một trò chơi vận động được nhiều người yêu thích trong các công viên nước. Một cái
máng trượt nước có thiết kế dạng cung tròn với hai đầu mút là A và B . Chọn hệ trục tọa độ Oxyz
với gốc O đặt tại hình chiếu của A trên mặt đất, mặt phẳng (Oxy) trùng với mặt đất và trục Oz
hướng thẳng đứng lên trời, đơn vị đo lấy theo mét (tham khảo hình vẽ dưới đây). Biết các điểm
A, B và một điểm C nằm trên máng trượt lần lượt có tọa độ là (0;0; ) 5 ,(6;7; ) 1 và (5;0; ) 2 . Độ dài
máng trượt nước đó bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét)? Trang 11
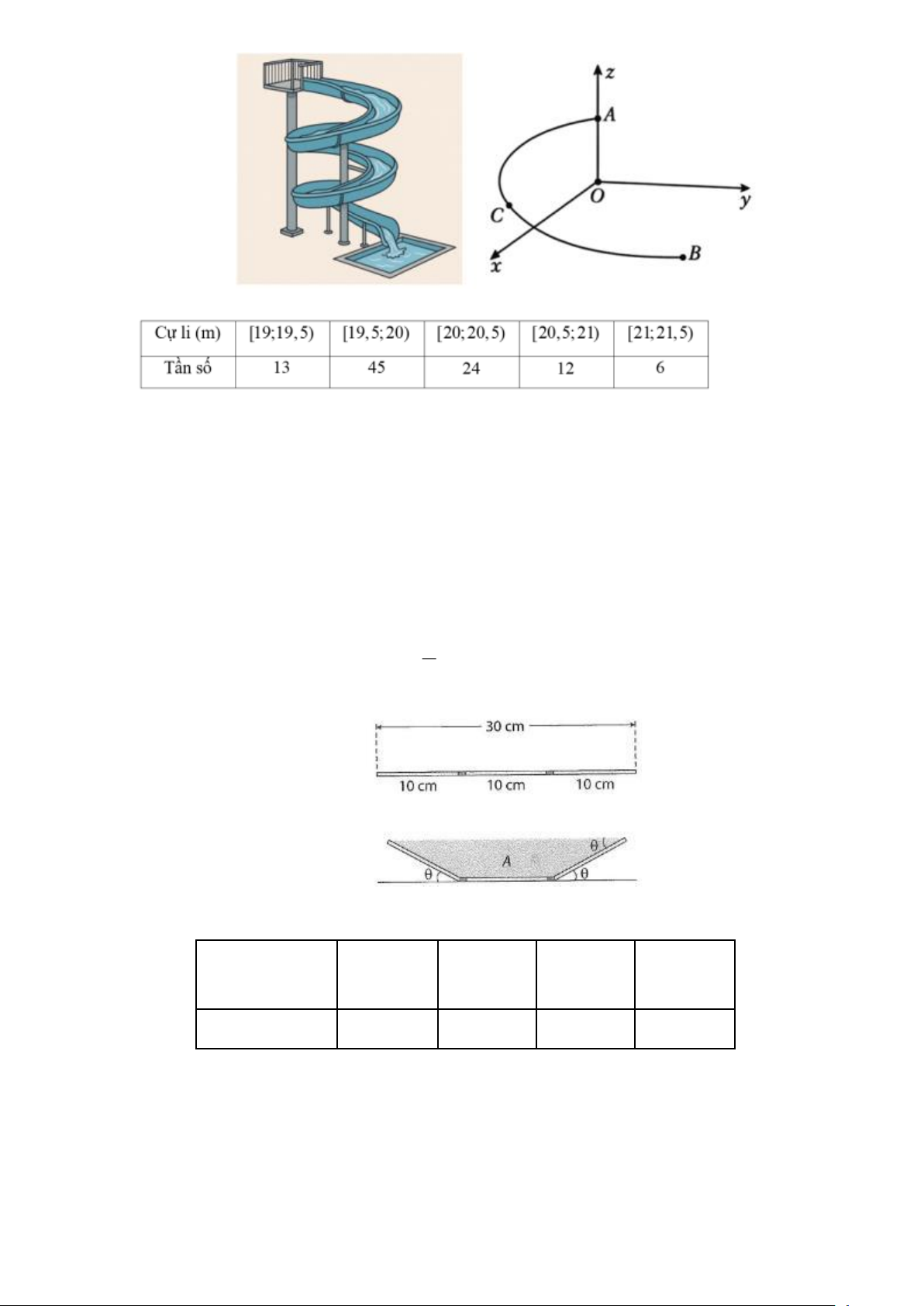
Câu 4. Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
Phương sai của mẫu số liệu ghép nhóm trên bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Máng xối nước mưa được làm bằng một miếng nhôm rộng 30 cm. Sau khi đánh dấu chiều dài 10
cm từ mỗi cạnh, miếng nhôm được gập lên một góc . Diện tích S ( 2
cm ) của mặt cắt ngang của
máng được biểu thị dưới dạng một hàm số của như sau:
S = S ( ) =100sin (cos + ) 1 ,0 . 2
Tìm góc để diện tích S là lớn nhất.
Câu 2. Thầy giáo cho các bạn học sinh lớp 8 vận dụng khái niệm tam giác đồng dạng để thực hành đo
chiều cao của cột cờ. Kết quả đo của các bạn trong lớp được biểu diễn ở bảng sau: 5,0;5, ) 1 5,1;5,2) Chiều cao (m) 4,9;5,0) 5,2;5,3) Số học sinh 9 15 12 4
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Câu 3. Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc 120 và có độ lớn
lần lượt là 20 N và 15 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn
10 N. Tính độ lớn hợp lực của ba lực trên (làm tròn kết quả đến hàng phần mười).
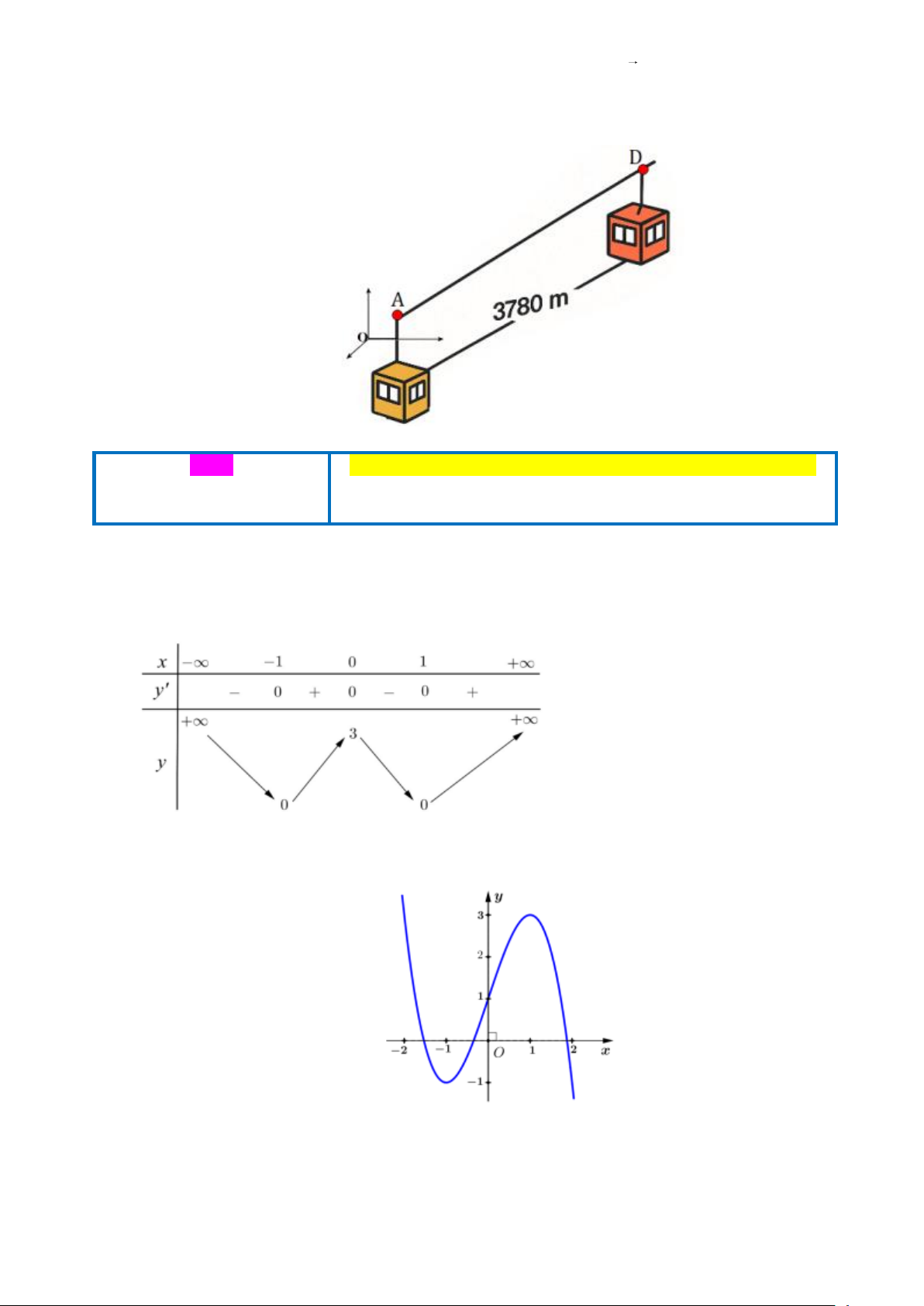
Câu 4. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là 1m ), một cabin cáp treo xuất
phát từ điểm A(10;3;0) và chuyển động đều theo đường cáp thẳng đến vị trí D cách điểm A một Trang 12
khoảng 3780 m . Biết đường đi của cabin cùng phương với vectơ u = (2;− 2; ) 1 và sau 3 phút kể từ
khi xuất phát thì cabin đi đến vị trí B có hoành độ x = 550 . Hỏi thời gian di chuyển của cabin B
trên quãng đường AD là bao nhiêu giây? ĐỀ 4
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ dưới đây
Hàm số có giá trị cực tiểu bằng A. 3 . B. 0 . C. −1 D. 1.
Câu 2. Trong các hàm số sau đây, hàm số nào có đồ thị như hình vẽ. A. 3
y = −x + 3x +1. B. 3 y = −x + 3 . x C. 3
y = −x + 2. D. 3
y = x − 3x +1.
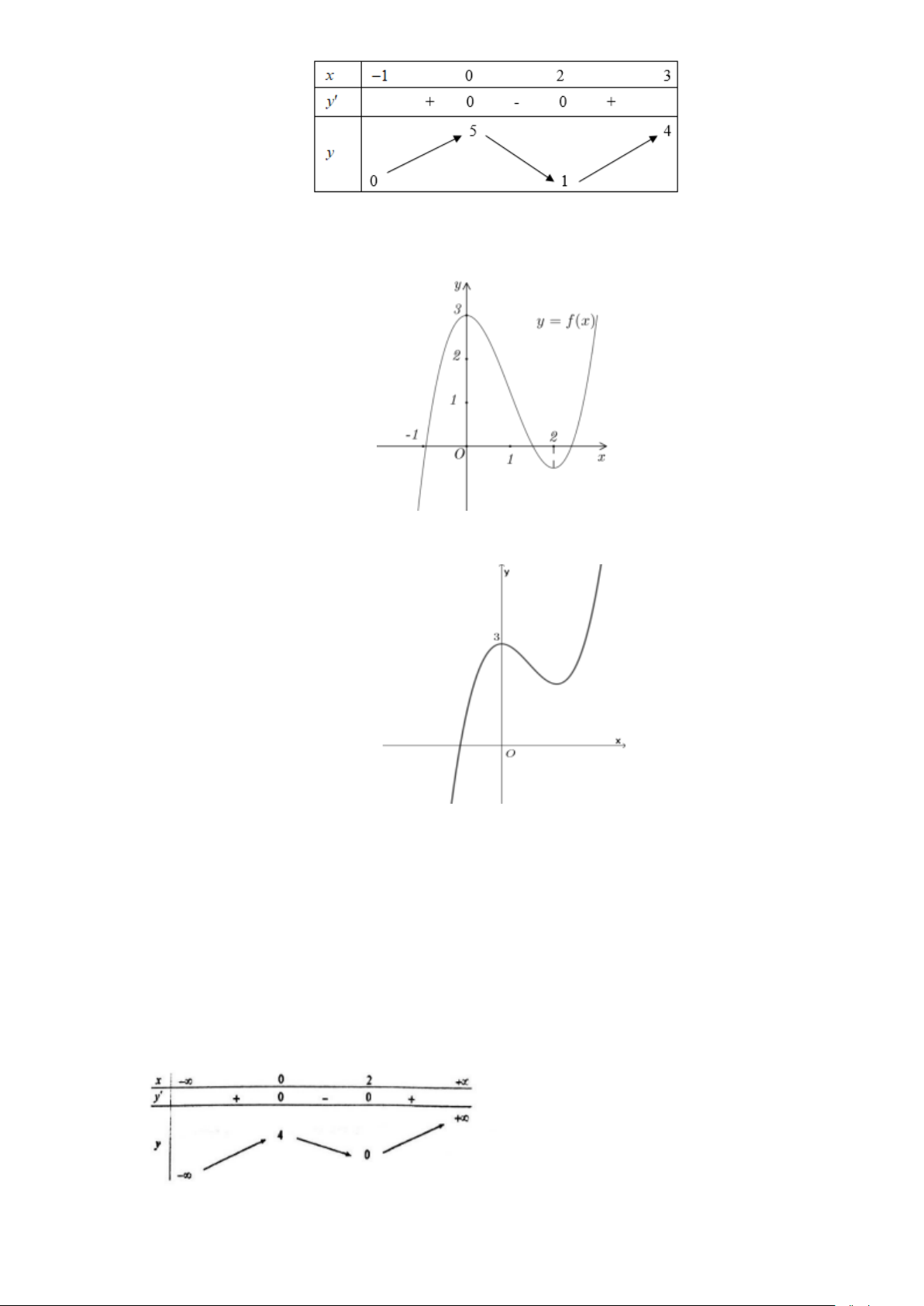
Câu 3. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của hàm số y = f (x) trên đoạn 2 − ;
2 . Giá trị M + m bằng Trang 13 A. 6. B. 9. C. 4. D. 8. 3x − 7
Câu 4. Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số y = là x + 2 A. (3;− 2). B. ( 2 − ;3). C. ( 3 − ;2) . D. (2;−3).
Câu 5. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
A. Hàm số f (x) đồng biến trên (−;4) .
B. Hàm số f (x) đồng biến trên (−;0)(2;+ ).
C. Hàm số f (x) đồng biến trên (−;0) .
D. Hàm số f (x) đồng biến trên (0;+ ).
Câu 6. Trong không gian Oxyz , cho vectơ a biểu diễn của các vectơ đơn vị là a = 2i − 3 j + k . Tọa độ của vectơ a là A. (1;2; ) 3 − . B. (2;1; ) 3 − . C. (2; 3 − ; ) 1 . D. (1; 3 − ;2).
Câu 7. Trong không gian Oxyz , tọa độ một vectơ n vuông góc với cả hai vectơ a = (1;1; 2 − ) , b = (1;0;3) là A. (3; 5 − ;− ) 1 . B. (2;3; ) 1 − . C. (3;5; 2 − ) . D. (2; 3 − ;− ) 1 .
Câu 8. Trong không gian Oxyz, mặt cầu (S ) có phương trình: 2 2 2
x + y + z − 2x − 4y + 6z +10 = 0. Bán
kính của mặt cầu (S ) bằng:
A. R = 2 .
B. R = 3 2 .
C. R = 1 .
D. R = 4 . 2x −1
Câu 9. Tìm m để hàm số y =
đồng biến trên (0;+). x − m 1 1 1
A. m 0.
B. m .
C. m .
D. 0 m . 2 2 2
Câu 10. Trong không gian Oxyz , cho A(1;2;− ) 1 , B(0; 2 − ; )
3 . Tính diện tích tam giác OAB . 7 29 29 78 A. . B. . C. . D. . 2 6 2 2
Câu 11. Cho bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây. Trang 14
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là A. 156,25. B. 157,5. C. 157,54. D. 156,38.
Câu 12. Cho hàm số y = f (x) có đồ thị như đường cong ở hình bên. Xác định tọa độ tâm đối xứng I của đồ thị. A. I (0;2). B. I (-1;0). C. I (-1;2). D. I (2;-1).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Trong không gian Oxyz , cho hai điểm M (2;3;− ) 1 , N ( 1 − ;1; ) 1 .
a) Hình chiếu của điểm M trên trục Oy có tọa độ là ( 2 − ;3; ) 1 .
b) Cho P(1;m −1; )
3 . Tam giác MNP vuông tại N khi và chỉ khi m =1. c) Điểm I ( ; a ;
b c) nằm trên mặt phẳng (Oxy) thỏa mãn T = 3IM − IN đạt giá trị nhỏ nhất. Khi đó
2a +b + c = 9 .
d) Gọi E là điểm đối xứng của điểm M qua N . Tọa độ của điểm E là ( 4 − ; 1 − ;3) .
Câu 2. Anh B chế tạo một bể cá có dạng khối hình hộp chữ nhật không nắp có thể tích 3 0,096m , chiều
cao h = 0,6 m , chiều rộng x , chiều dài y , với x 0, y 0 . Anh B dùng loại kính để làm các mặt
bên có giá 70.000 đồng/ 2
m và loại kính để làm mặt đáy có giá 100.000 đồng/ 2 m . Mọi chi phí
khác xem như không đáng kể. Khi đó 0,16
a) Hàm số biểu thị y theo x là y = . x
b) Chi phí mua kính để làm đáy bể là 11200 đồng. 0,16
c) Biểu thức tính chi phí làm các mặt xung quanh là C = 84000. x + . xq x
d) Chi phí làm bể cá thấp nhất là 100000 đồng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Thời gian truy cập internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm. Trang 15
Câu 2. Một công ty sản xuất mỗi ngày được x sản phẩm (1 x 18). Tổng chi phí sản xuất x sản phẩm
tính bằng nghìn đồng cho bởi hàm chi phí C (x) 3 2
= x −3x +80x +500. Giả sử công ty này bán hết
sản phẩm mỗi ngày với giá 320 nghìn đồng/sản phẩm. Gọi B ( x) là số tiền bán được và L(x) là
lợi nhuận thu được khi bán x sản phẩm. Lợi nhuận (đơn vị tính triệu đồng) tối đa mà công ty có được là bao nhiêu?
Câu 3. Một nhà máy dự định sản xuất không quá 900 sản phẩm. Nếu nhà máy sản xuất x sản phẩm
(1 x 900) thì lợi nhuận nhận được khi bán hết số sản phẩm đó là f (x) 3 2
= −x +900x +56700x + 450000 (đồng). Nhà máy cần sản xuất bao nhiêu sản phẩm để lợi
nhuận thu được là lớn nhất ?
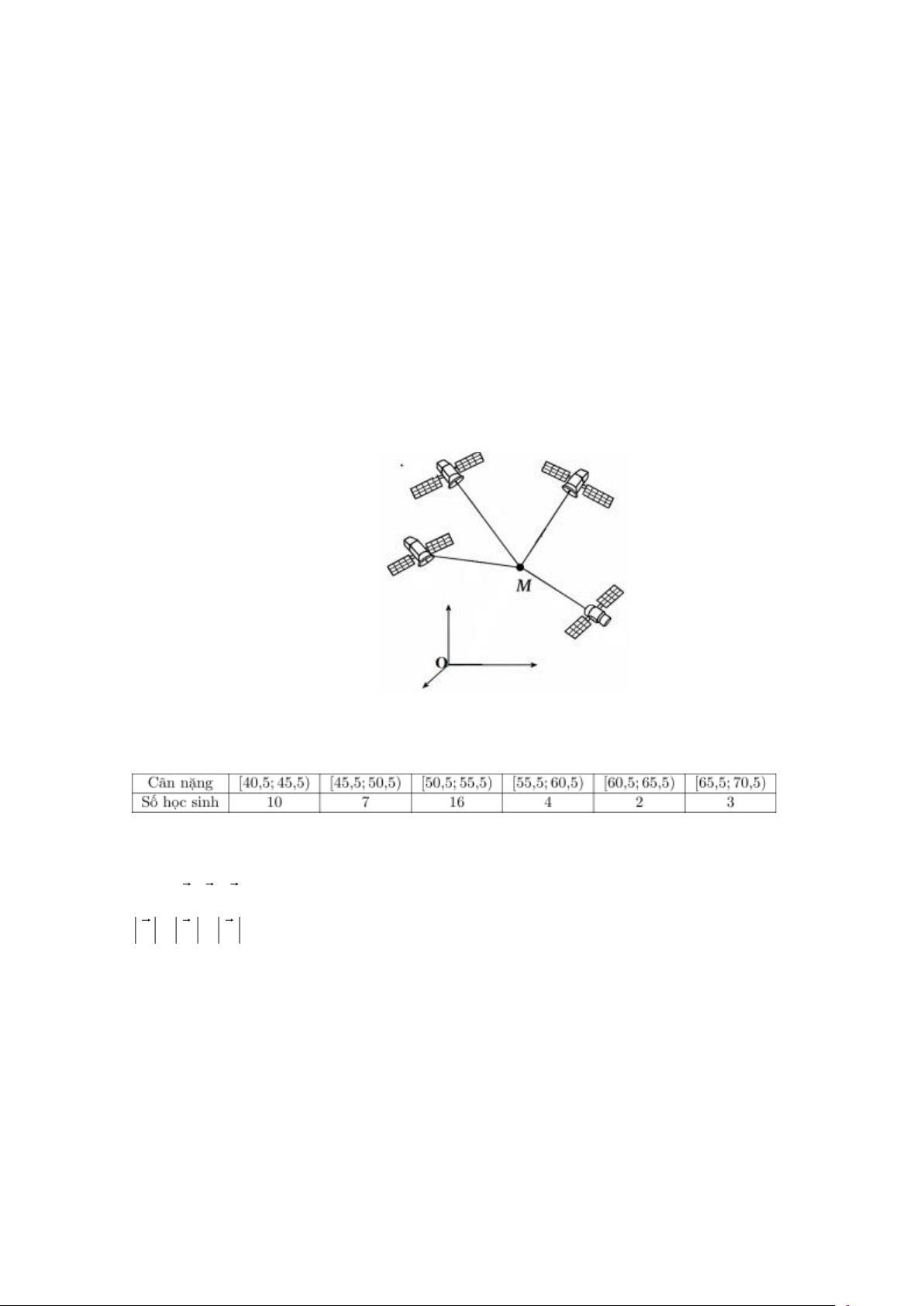
Câu 4. Hệ thống định vị toàn cầu GPS là một hệ thống cho phép xác định vị trí của một vật thể trong
không gian. Trong cùng một thời điểm, vị trí của một điểm M trong không gian sẽ được xác định
bởi bốn vệ tinh cho trước nhờ các bộ thu phát tín hiệu đặt trên các vệ tinh. Giả sử trong không gian
với hệ tọa độ Oxyz , có bốn vệ tinh lần lượt đặt tại các điểm (3
A ;1;0) , B(3;6;6) , C(4;6; 2) ,
D(6; 2;14) ; vị trí M (a; ;
b c) thỏa mãn MA = 3, MB = 6, MC = 5 , MD =13. Khoảng cách từ điểm
M đến điểm O bằng bao nhiêu?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Tìm cân nặng trung bình của học sinh lớp 11D cho trong bảng sau:
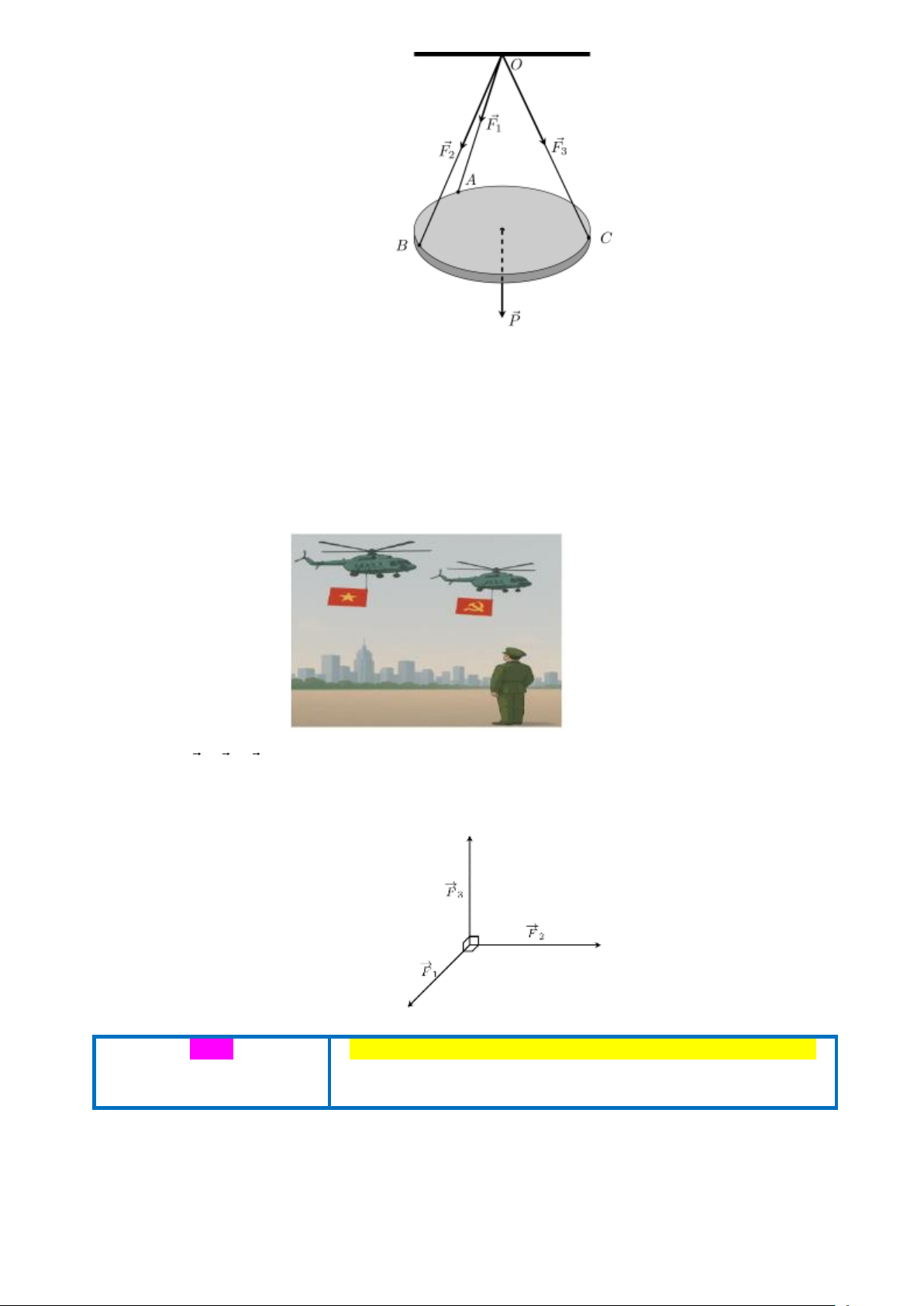
Câu 2. Một tấm gỗ tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không giãn xuất
phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm ,
A B,C trên tấm gỗ tròn sao cho các lực
căng F , F , F lần lượt trên mỗi dây O ,
A OB,OC đôi một vuông góc với nhau và có độ lớn 1 2 3
F = F = F = 25(N) (xem hình vẽ). Tính trọng lượng P của tấm gỗ tròn đó (tính chính xác đến 1 2 3 hàng phần mười). Trang 16
Câu 3. Nhân dịp lễ 30/4/2025, tại Quảng trường trung tâm TP. Hồ Chí Minh diễn ra màn trình diễn máy
bay trực thăng kéo cờ Tổ quốc và cờ Đảng. Hai máy bay cất cánh cùng lúc từ một địa điểm. Sau
một thời gian chiếc thứ nhất cách điểm xuất phát 3 km về phía Nam và 1 km về phía Đông, đồng
thời cách mặt đất 1 km. Chiếc thứ hai nằm cách điểm xuất phát 2 km về phía Bắc và 1 km về phía
Tây, đồng thời cách mặt đất 500m. Cùng thời điểm đó, một chiến sĩ công an đứng trên mặt đất quan
sát thấy hai chiếc máy bay nói trên. Biết rằng, so với các vị trí quan sát trên mặt đất, vị trí chiến sĩ
công an đứng có tổng khoảng cách đến hai chiếc máy bay là nhỏ nhất. Khoảng cách từ vị trí chiến
sĩ công an quan sát đến địa điểm xuất phát của hai chiếc máy bay là bao nhiêu km (kết quả làm tròn đến hàng phần trăm).
Câu 4. Ba lực F , F , F cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 1 2 3
2 ; 3 ; 4 . Hợp lực của ba lực đã cho có độ lớn bao nhiêu Niu-tơn ({\it kết quả làm tròn đến một chữ số thập phân})? ĐỀ 5
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Hàm số nào dưới đây có đồ thị như trong hình vẽ? Trang 17 A. 3
y = - x + 3x + 1. B. 3
y = x - 3x + 1. C. 4 2
y = x - 2x + 1. D. 4 2
y = - x + 2x + 1.
Câu 2. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ sau:
Hàm số y = f (x) đạt cực tiểu tại điểm nào trong các điểm sau?
A. x = 5.
B. x = 2 . C. x =1.
D. x = 0 .
Câu 3. Cho đồ thị hàm số y = f (x) liên tục trên và có đồ thị như hình vẽ bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng (3;6) .
B. Hàm số nghịch biến trên khoảng (6;+).
C. Hàm số đồng biến trên khoảng ( ;3 − ) .
D. Hàm số đồng biến trên khoảng (1;3) .
Câu 4. Cho hàm số y = f (x) có đồ thị trên 2
− ;4 như hình vẽ, giá trị lớn nhất của f (x) trên 2 − ; 4 là A. −1. B. 2 . C. 4. D. 3 .
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A , B với OA = (2;−1;3) , OB = (5;2;− ) 1 .
Tìm tọa độ của vectơ AB . A. AB = ( 3 − ; 3 − ;4) . B. AB = (2; 1 − ;3). C. AB = (3;3; 4 − ) .
D. AB = (7;1;2). Câu 6. Cho hàm số 3x +1 y =
. Khẳng định nào sau đây đúng? 2x −1
A. Đồ thị có hàm số có tiệm cận đứng là 3 y = . 2
B. Đồ thị có hàm số không có tiệm cận. Trang 18
C. Đồ thị có hàm số có tiệm cận ngang là 3 y = . 2
D. Đồ thị có hàm số có tiệm cận đứng là 1 x = − . 2
Câu 7. Trong không gian Oxyz , cho mặt cầu (S) 2 2 2
: x + y + z + 4x − 2y + 6z + 5 = 0. Mặt cầu (S ) có bán kính là ? A. 3. B. 5. C. 2. D. 7. 17 11 17
Câu 8. Trong không gian Oxyz , cho hình nón đỉnh S ; − ;
có đường tròn đáy đi qua ba điểm 18 9 18 A(1;0;0), B(0; 2 − ;0), C(0;0; )
1 . Tính độ dài đường sinh l của hình nón đã cho. 5 2 94 86 194 A. l = . B. l = . C. l = . D. l = . 6 6 6 6
Câu 9. Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Chi
được thống kê lại ở bảng sau:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là A. 31,88. B. 8,125. C. 27,5. D. 23,75. 2x +1
Câu 10. Đồ thị của hàm số y = có tâm đối xứng là: 3 − x A. I (3;− ) 1 .
B. I (3;2) . C. I ( 2 − ; ) 3 . D. I (3; 2 − ). mx − 2 1
Câu 11. Số giá trị nguyên của tham số thực m để hàm số y =
nghịch biến trên khoảng ;+ − 2x + m 2 là A. 4 . B. 2 . C. 5 . D. 3 .
Câu 12. Trong không gian Oxyz , cho các điểm A(2;1;0) , B(0;4;0) ,C(0;2;− )
1 . Biết đường thẳng x −1 y +1 z − 2
vuông góc với mặt phẳng ( ABC) và cắt đường thẳng d : = = tại điểm D( ; a ; b c) 2 1 3 17
thỏa mãn a 0 và tứ diện ABCD có thể tích bằng
. Tổng a +b + c bằng 6 A. 6 . B. 5 . C. 7 . D. 4 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho một tấm nhôm hình vuông cạnh#a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi gập tấm
nhôm lại để được một cái hộp không nắp. a
a) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng . 12 Trang 19 a
b) Thể tích của khối hộp là lớn nhất khi cạnh của hình vuông bị cắt bằng . 6 3 2a
c) Thể tích của khối hộp lớn nhất bằng . 27 3 a
d) Thể tích hộp lớn nhất bằng . 27
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD biết A(2;3;2), B(6; 1 − ; 2 − ), C ( 1 − ; 4 − ;3), D(1;6; 5
− ). Xét tính đúng sai của các mệnh đề sau a) A . B AC = 4 − .
b) Tổng chu vi các mặt của tứ diện gần bằng 106,95 .
c) Tọa độ điểm M trên CD sao cho tam giác AMB có chu vi nhỏ nhất là M (0;1;− ) 1 . d) AB = (1; 1 − ;− ) 1 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Bảng sau cho ta cân nặng của 40 học sinh một lớp 11: Cân nặng
40,5 ; 45,5) 45,5 ; 50,5) 50,5 ; 55,5) 55,5 ; 60,5) 60,5 ; 65,5) (kg) Số học sinh 10 7 16 4 3
Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười)
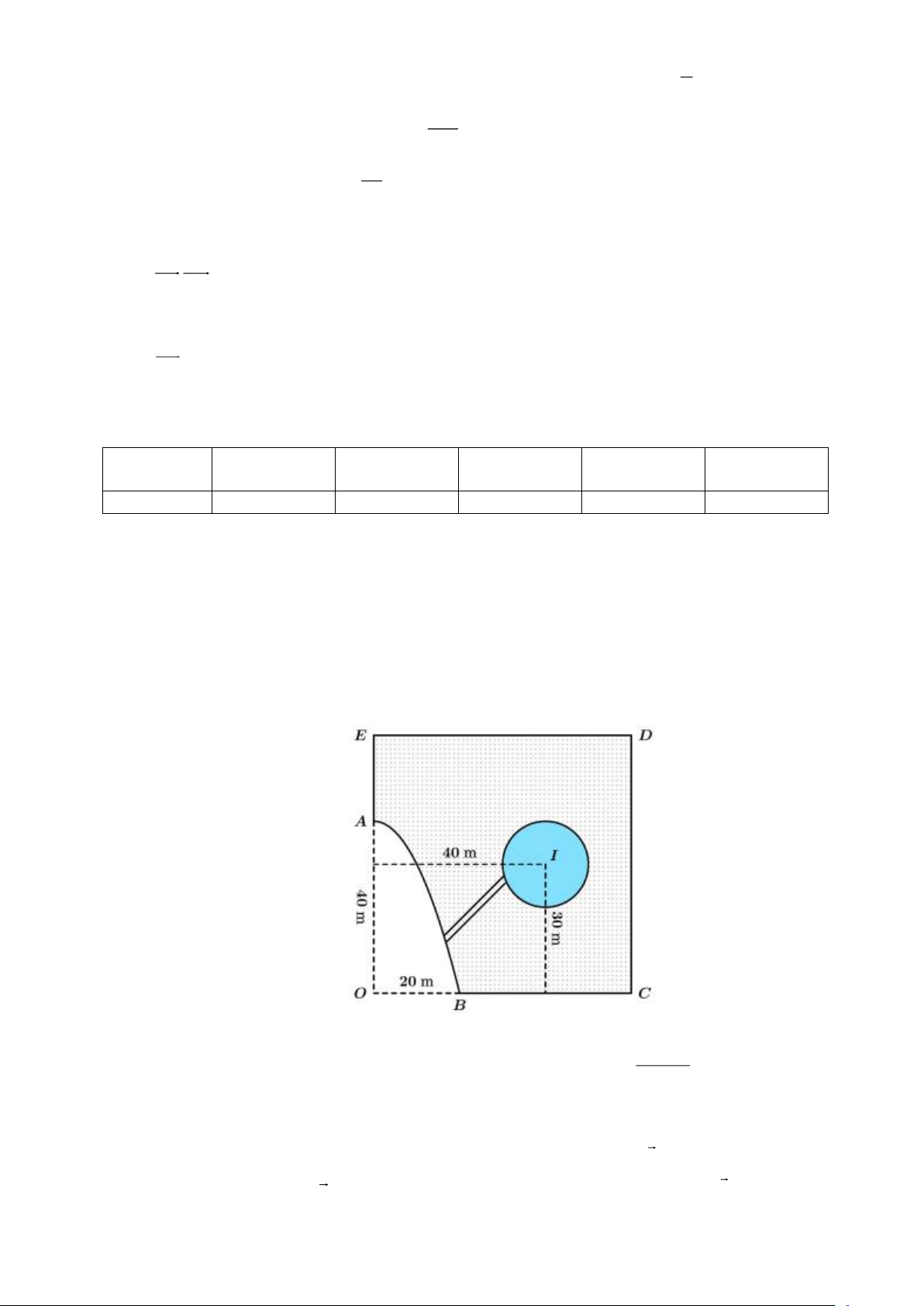
Câu 2. Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m,
người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l (đơn vị mét) của
cây cầu là bao nhiêu (làm tròn đến chữ số hàng phần chục), biết:
- Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O;
- Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ;
- Độ dài đoạn OA và OB lần lượt là 40m và 20m;
- Tâm I của mảnh vườn cách đường thẳng AE và BC lần lượt là 40m và 30m.
Câu 3. Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định)
tuân theo quy luật logistic được mô hình hoá bằng hàm số f (t) 5000 =
,t 0 trong đó thời gian 1+ 5 t e−
t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f (t) sẽ biểu thị tốc độ
bán hàng. Hỏi sau khi phát hành thì tốc độ bán hàng đạt lớn nhất bằng bao nhiêu?
Câu 4. Một thiết bị thăm dò đáy biển như hình vẽ được đẩy bởi một lực f = (5;4; 2 − ) (đơn vị: N) giúp
thiết bị thực hiện độ dời a = (70;20; 4
− 0) (đơn vị: m). Tính công sinh bởi lực f . Trang 20




