









Preview text:
ĐỀ 1
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Trong không gian với hệ trục tọa độ Oxyz, cho A(0;−1; ) 1 , B( 2 − ;1;− ) 1 , C ( 1 − ;3;2). Biết rằng
ABCDlà hình bình hành, khi đó tọa độ điểm D là 2 A. D 1 − ;1; . B. D( 1 − ;−3;− 2).
C. D(1;3;4).
D. D(1;1;4). 3
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(1;0;0), B(0;0; ) 1 , C (2;1; ) 1 . Diện
tích tam giác ABC bằng 6 5 7 11 A. . B. . C. . D. . 2 2 2 2
Câu 3. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi G là điểm thỏa mãn:
GS +GA+GB + GC + GD = 0. Trong các khẳng định sau, khẳng định nào đúng:
A. GS = 4OG .
B. GS = 3OG .
C. G, S, O không thẳng hàng.
D. GS = 5OG .
Câu 4. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm này là A. 12 . B. 60 . C. 100. D. 80 .
Câu 5. Cho hàm số f ( x) liên tục trên và có đạo hàm f (x) thỏa mãn
f (x) = (1− x)(x + 2) g (x)+ 2018 với g (x) 0, x
. Hàm số y = f (1− x)+ 2018x +2019
nghịch biến trên khoảng nào? A. ( ;3 − ). B. (4;+) . C. (1;+). D. (0; ) 3 . 4x − 3
Câu 6. Cho hàm số y =
có đồ thị (C). Biết đồ thị (C) có hai điểm phân biệt M , N và tổng x − 3
khoảng cách từ M hoặc N tới hai tiệm cận là nhỏ nhất. Khi đó MN có giá trị bằng
A. MN = 6.
B. MN = 4 2 .
C. MN = 4 3 . D. MN = 6 2 .
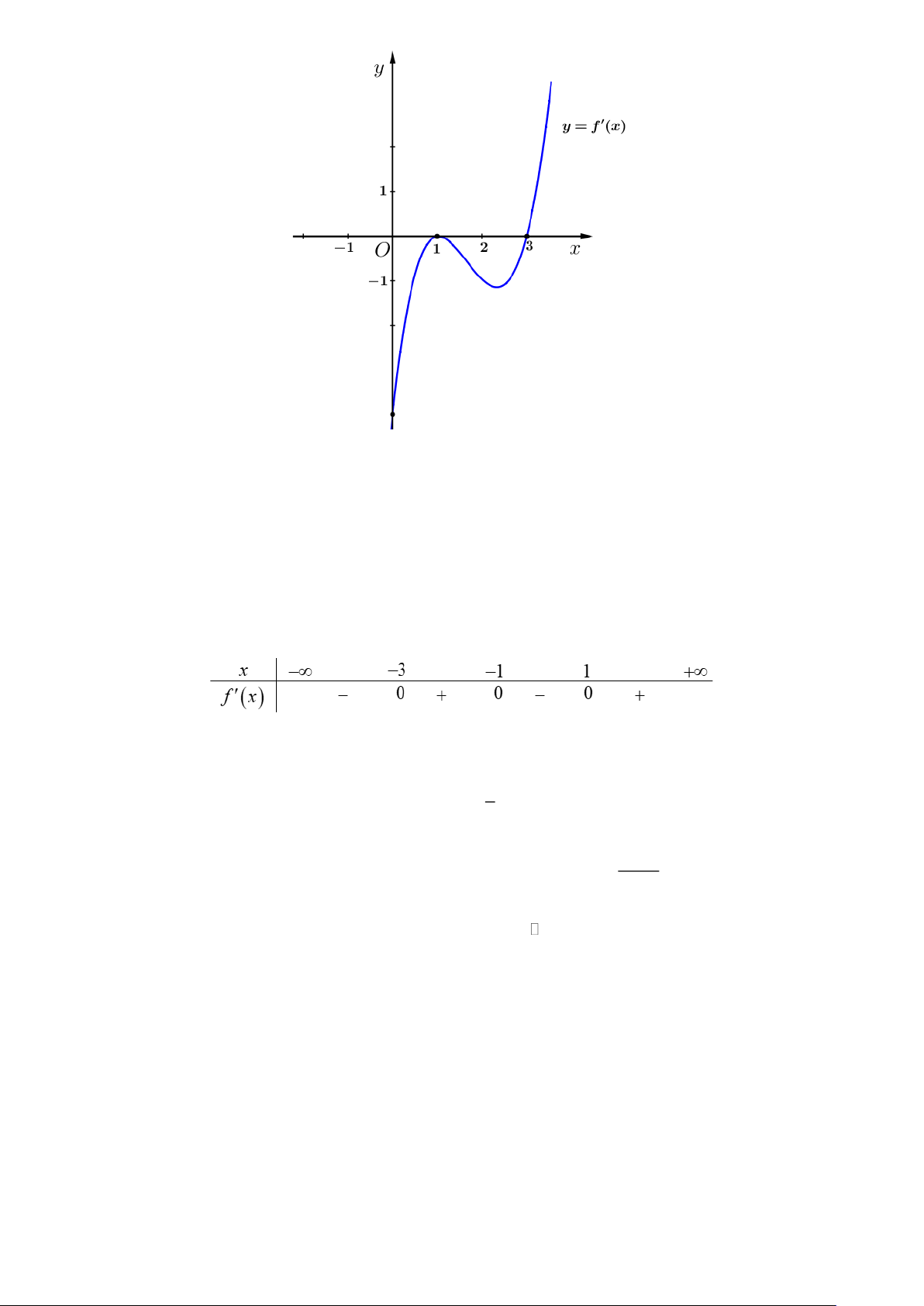
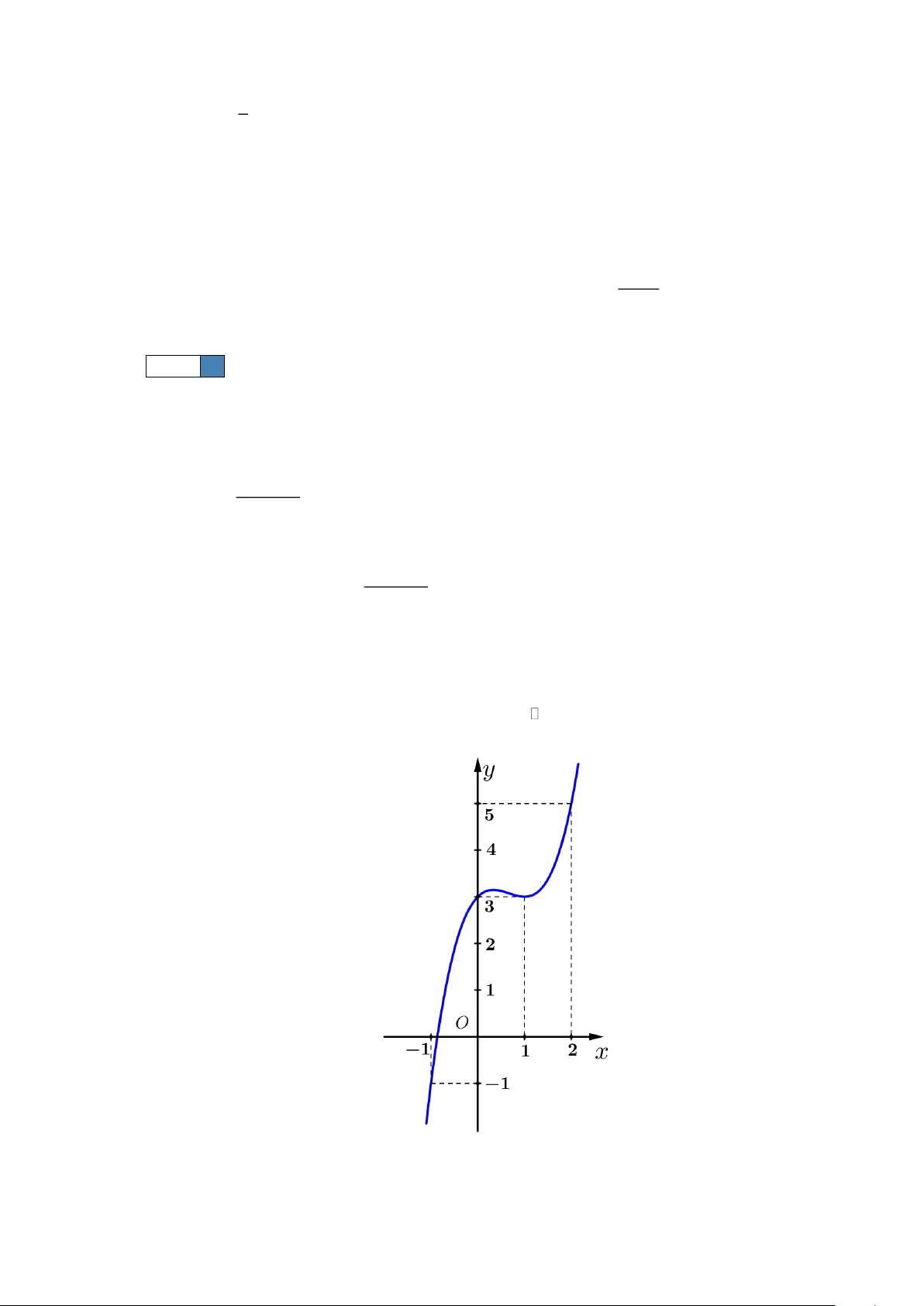
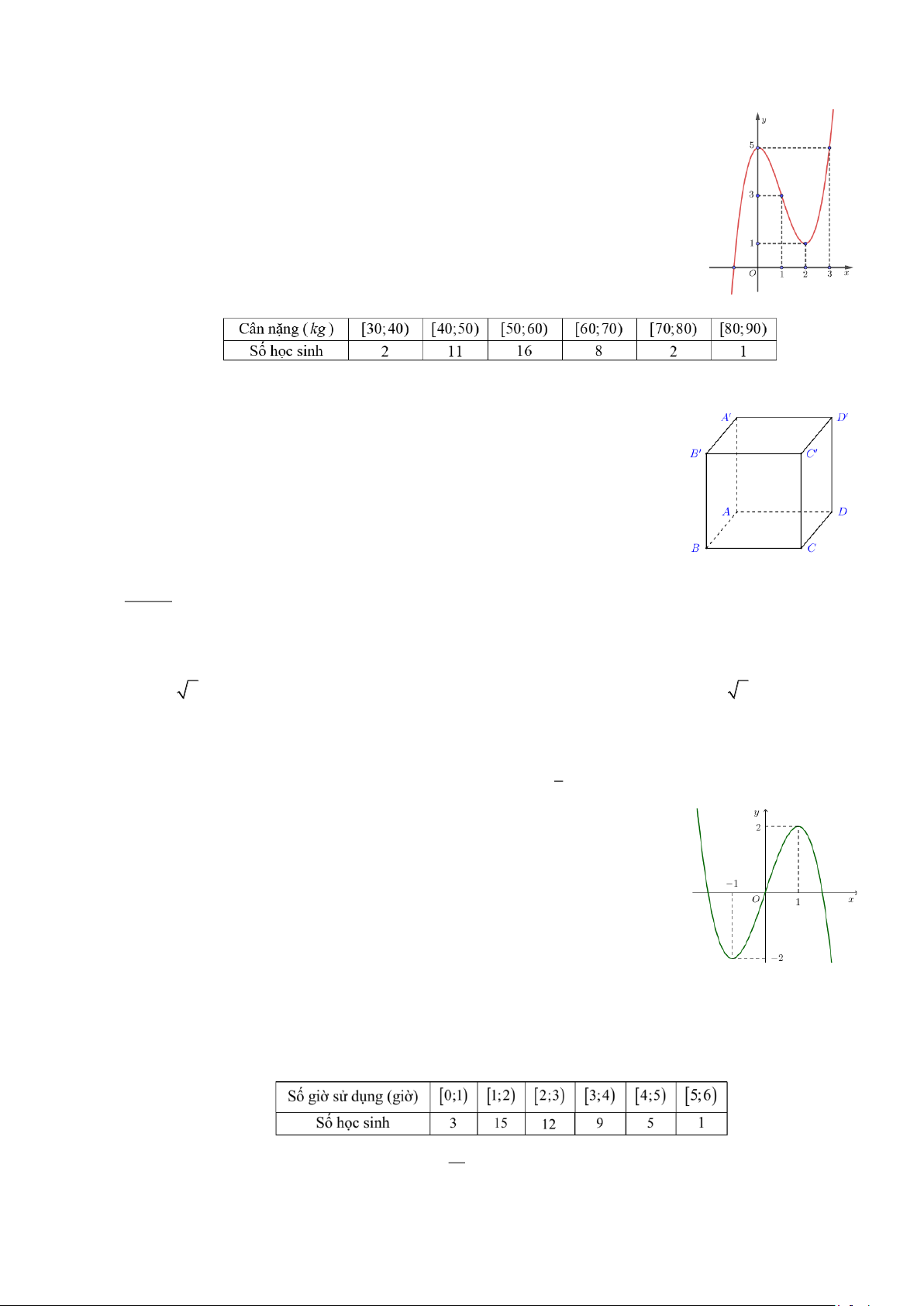
Câu 7. Cho hàm số y = f (x) . Hàm số y = f (x) có đồ thị như hình vẽ dưới đây. Khẳng định nào sau
đây là khẳng định đúng? Trang 1
A. Hàm số y = f (x) đạt cực đại tại x =1.
B. Đồ thị hàm số y = f (x) có một điểm cực tiểu.
C. Đồ thị hàm số y = f (x) có hai điểm cực trị.
D. Hàm số y = f (x) đồng biến trong khoảng ( ) ;1 − .
Câu 8. Tìm giá trị thực của tham số m để đồ thị hàm số 3 2
y = x − 3x + 2 cắt đường thẳng
d : y = m(x − )
1 tại ba điểm phân biệt có hoành độ x , x , x thỏa mãn 2 2 2
x + x + x 5 . 1 2 3 1 2 3 A. m 3 − . B. m 2 − . C. m 2 − . D. m 3 − .
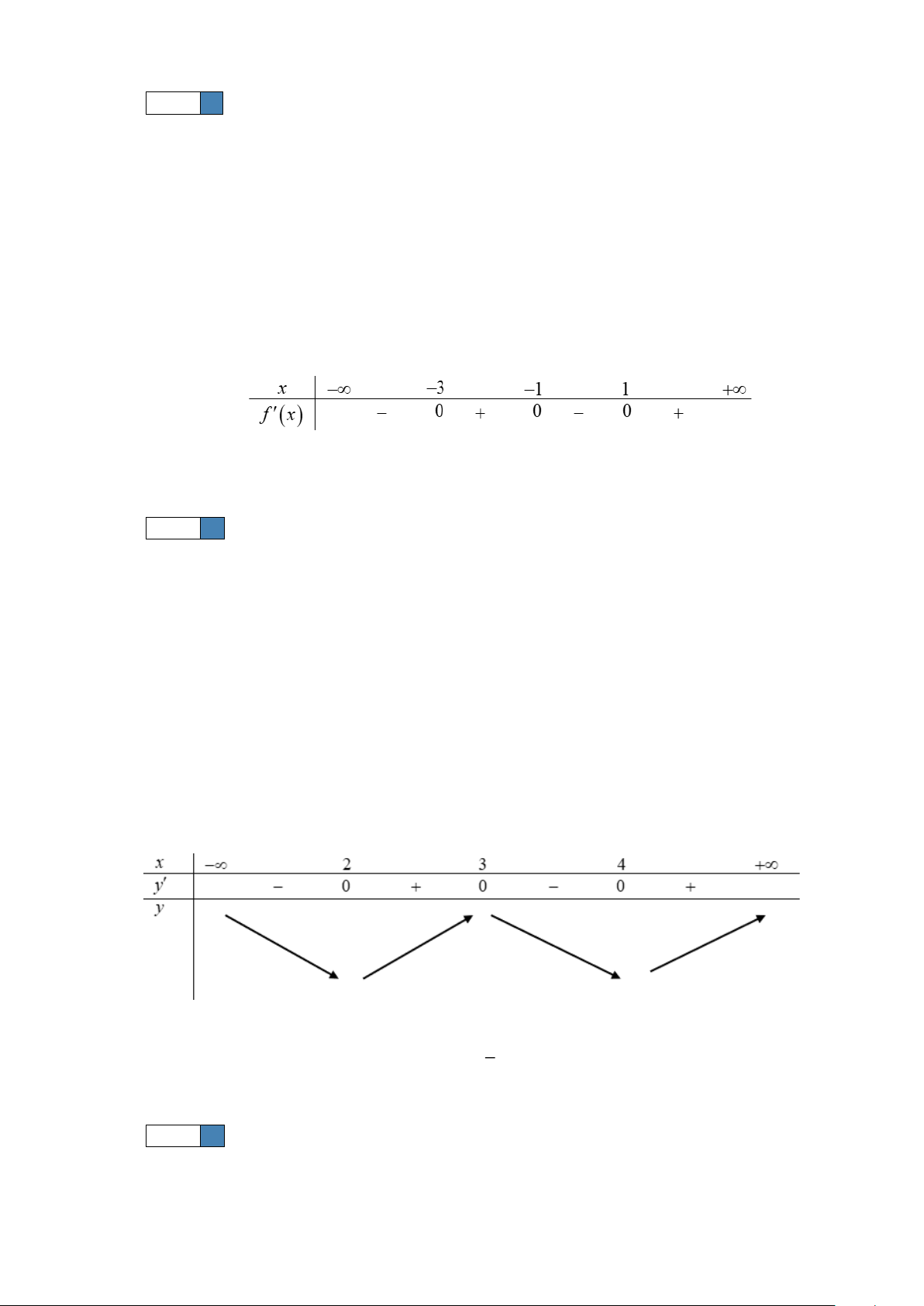
Câu 9. Cho hàm số f ( x) , bảng xét dấu của f ( x) như sau:
Hàm số y = f (5− 2x) đồng biến trên khoảng nào dưới đây? A. (−;− ) 3 . B. (3;4) . C. (1; ) 3 . D. (4;5) . 1
Câu 10. Tìm giá trị thực của tham số m để hàm số 3 2
y = x − mx + ( 2
m − 4) x + 3 đạt cực đại tại x = 3. 3 A. m = 1 − .
B. m =1. C. m = 7 − .
D. m = 5 . x − 2
Câu 11. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = đồng biến trên ( ;0 − )? x − m A. Vô số.
B. 1. C. 2. D. 3.
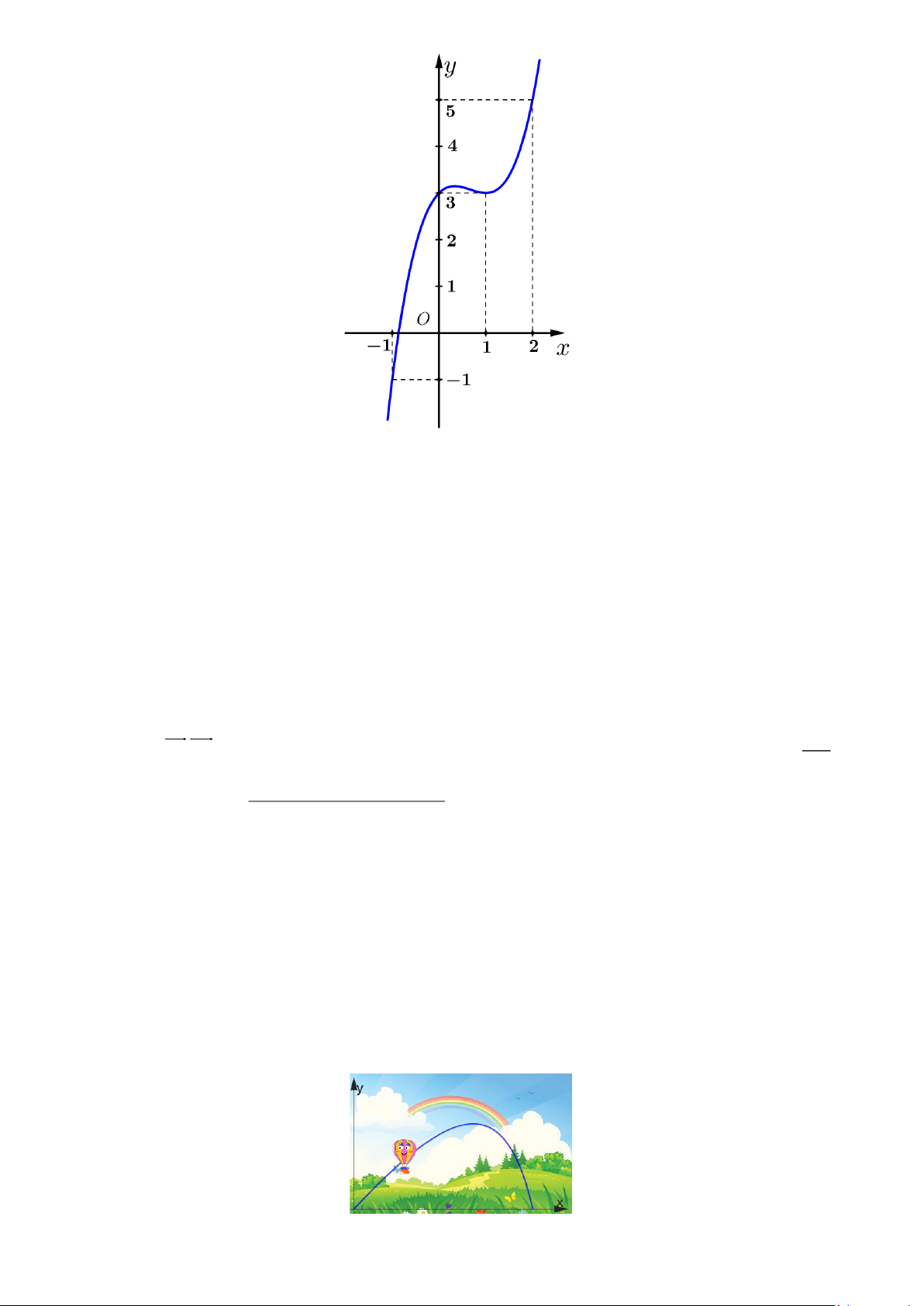
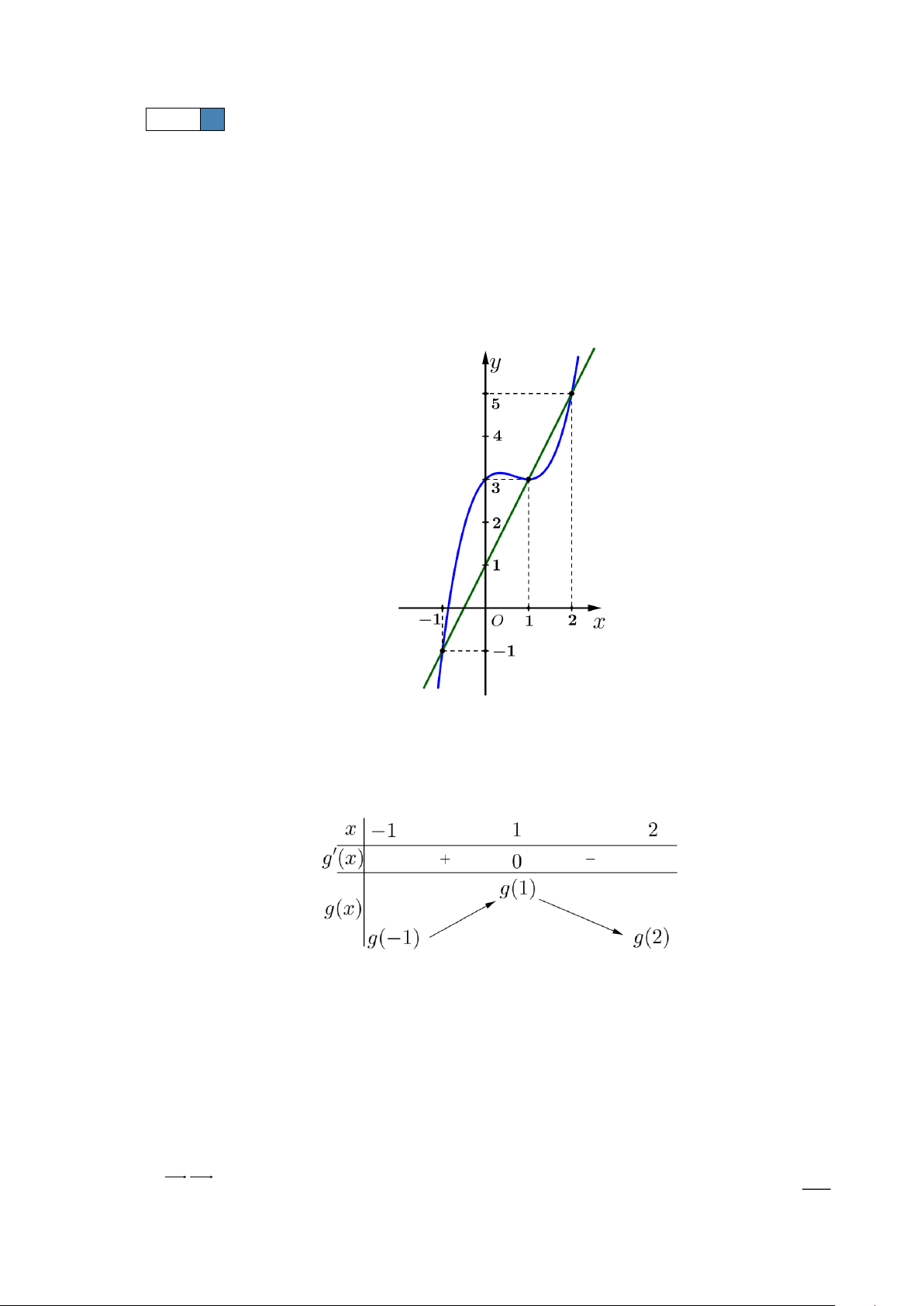
Câu 12. Cho hàm số y = f (x) có đạo hàm và liên tục trên . Biết rằng đồ thị hàm số y = f (x) như dưới đây Trang 2
Tìm giá trị lớn nhất max g ( x) của hàm số g ( ) = ( ) 2 x
f x − x − x trên đoạn 1 − ;2. 1 − ;2
A. max g ( x) = g (2) .
B. max g ( x) = g (0) . 1 − ;2 1 − ;2
C. max g ( x) = g ( ) 1 .
D. max g ( x) = g (− ) 1 . 1 − ;2 1 − ;2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Trong không gian Oxyz , cho S (1;2;3) và các điểm A , B , C thuộc các trục Ox , Oy , Oz sao
cho hình chóp S.ABC có các cạnh SA, SB , SC đôi một vuông góc với nhau. Xét tính đúng sai của các mệnh đề sau
a) Toạ độ điểm C là C (7,0,0) .
b) Tam giác ABC là tam giác vuông. 343 c) S . B SC = 0.
d) Thể tích khối chóp S.ABC bằng . 36 2
−mx + (4 m − 2)x +1− 4 m
Câu 2. Cho hàm số y = x −1 a) Khi m 1
− thì hàm số đạt cực đại và cực tiểu trong miền x 0
b) Khi m =1 đồ thị hàm số không cắt trục Ox
c) Có 2 phương trình tiếp tuyến của (C) song song với đường thẳng x − y = 0
d) Khi m =1 đồ thị hàm số có 2 điểm cực trị
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Đường đi của một khinh khí cầu được gắn trong hệ trục tọa độ là một đường cong bậc hai trên bậc
nhất có đồ thị cắt trục hoành tại hai điểm có tọa độ là (1;0) và (8;0) với đơn vị trên hệ trục tọa độ là
1 (km) . Biết rằng điểm cực đại của đồ thị hàm số là điểm (6;5). Hỏi khi khí cầu đi qua điểm cực đại và
cách mặt đất 3875 (m) thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km ) Trang 3
Câu 2. Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
Hãy tính phương sai của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến chữ số hàng phần trăm).
Câu 3. Cho biết máy bay A đang bay với vectơ vận tốc a = (300;200;400) (đơn vị: km/h). Máy bay B
bay cùng hướng và có tốc độ gấp ba lần tốc độ của máy bay A . (làm tròn đến hàng đơn vị)
Tính tốc độ của máy bay B .
Câu 4. Một cửa hàng kinh doanh trung bình bán được 700 máy điều hòa mỗi tháng với giá 15 triệu đồng
một máy. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 1 triệu đồng, số lượng máy điều
hòa bán ra sẽ tăng thêm khoảng 100 máy mỗi tháng. Biết hàm chi phí hàng tháng là C(x) = 14000− 3x
(triệu đồng), trong đó x là số máy điều hòa bán ra trong tháng, cửa hàng nên đặt giá bán bao nhiêu để lợi
nhuận là lớn nhất? (đơn vị là triệu đồng).
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Một doanh nghiệp cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai máy A và
B . Máy A làm việc trong x ngày cho số tiền lãi là 2
x + 2x (triệu đồng), máy B làm việc trong y ngày cho số tiền lãi là 2 2
− 7y + 326y (triệu đồng). Hỏi doanh nghiệp đó cần sử dụng máy A làm việc trong bao
nhiêu ngày để số tiền lãi thu được nhiều nhất? Biết rằng hai máy A và B không đồng thời làm việc và
máy B làm việc không quá 6 ngày.
Câu 2. Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống
kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu A và B trong 50 ngày giao dịch liên tiếp.
Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro của các loại cổ phiếu có giá
trị trung bình gần bằng nhau. Cổ phiếu nào có phương sai, độ lệch chuẩn cao hơn thì được coi là có độ rủi ro lớn hơn.
Theo quan điểm trên, hãy so sánh độ rủi ro của cổ phiếu A và cổ phiếu B .
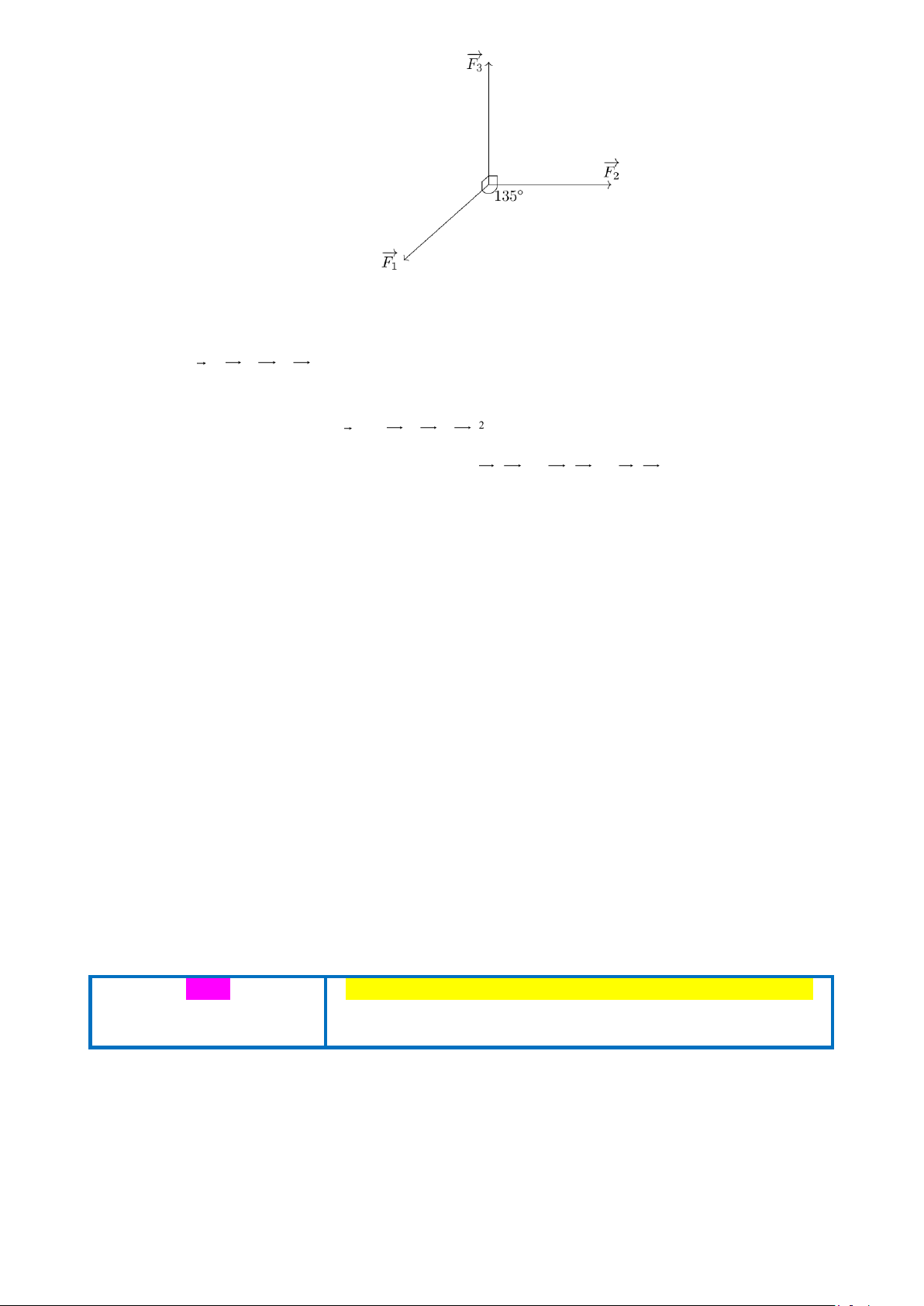
Câu 3. Một chất điểm A nằm trên mặt phẳng nằm ngang ( ) , chịu tác động bởi ba lực F , F , F . Các 1 2 3
lực F , F có giá nằm trong ( ) và (F , F 135 =
, còn lực F có giá vuông góc với ( ) và hướng lên 1 2 ) 1 2 3
trên. Xác định tổng hợp lực của các lực trên, biết rằng độ lớn của ba lực đó lần lượt là 20 N, 15 N và 10
N. (Kết quả làm tròn đến hàng phần chục). Trang 4
Câu 4. Số giá trị nguyên thuộc khoảng ( 2
− 020;2020) của tham số m để hàm số 3 2
y = x − 3x − mx + 2019 đồng biến trên (0;+) là -------- HẾT-------- LỜI GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Trong không gian với hệ trục tọa độ Oxyz, cho A(0;−1; ) 1 , B( 2 − ;1;− ) 1 , C ( 1 − ;3;2). Biết rằng
ABCDlà hình bình hành, khi đó tọa độ điểm D là 2 A. D 1 − ;1; . B. D( 1 − ;−3;− 2).
C. D(1;3;4).
D. D(1;1;4). 3 Lời giải Chọn D x +1 = 2 Gọi D( ; x ;
y z), ta có ABCDlà hình bình hành nên BA = CD y − 3 = 2 − z − 2 = 2 x =1
y =1. Vậy D(1;1;4). z = 4
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A(1;0;0), B(0;0; ) 1 , C (2;1; ) 1 . Diện
tích tam giác ABC bằng 6 5 7 11 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn A AB = ( 1 − ;0 ) ;1 , AC = (1;1 ) ;1 A ; B AC = ( 1 − ;2;− ) 1 . 1 6 S
= AB; AC = . ABC 2 2
Câu 3. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi G là điểm thỏa mãn:
GS +GA+GB + GC + GD = 0. Trong các khẳng định sau, khẳng định nào đúng:
A. GS = 4OG .
B. GS = 3OG . Trang 5
C. G, S, O không thẳng hàng.
D. GS = 5OG . Lời giải Chọn A
GS +GA+GB + GC + GD = 0 GS + 4GO + OA+ OB + OC + OD GS + 4GO = 0 GS = 4OG .
Câu 4. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm này là A. 12 . B. 60 . C. 100. D. 80 . Lời giải Chọn C
Khoảng biến thiên: 100 − 0 =100
Câu 5. Cho hàm số f ( x) liên tục trên và có đạo hàm f (x) thỏa mãn
f (x) = (1− x)(x + 2) g (x)+ 2018 với g (x) 0, x
. Hàm số y = f (1− x)+ 2018x +2019
nghịch biến trên khoảng nào? A. ( ;3 − ). B. (4;+) . C. (1;+). D. (0; ) 3 . Lời giải Chọn B
Đặt: y = h(x) = f (1− x) + 2018x + 2019.
Ta có: h(x) = − f '(1− x) + 2018 = −x(3− x) g (1− x).
Xét h(x) 0 x(3− x) 0 x ( − x) x 0 3 0 . x 3 x = Xét h( x) 0 = 0 . x = 3
Vậy hàm số h( x) nghịch biến trên ( ;0
− ) và (3;+) nên đáp án đúng là đáp án D 4x − 3
Câu 6. Cho hàm số y =
có đồ thị (C). Biết đồ thị (C) có hai điểm phân biệt M , N và tổng x − 3
khoảng cách từ M hoặc N tới hai tiệm cận là nhỏ nhất. Khi đó MN có giá trị bằng
A. MN = 6.
B. MN = 4 2 .
C. MN = 4 3 . D. MN = 6 2 . Lời giải Chọn D 4m − 3 - Giả sử M = ; m
(C ), với m 3. m − 3 Trang 6
- Tiệm cận đứng là đường thẳng x = 3, tiệm cận ngang là đường thẳng y = 4 .
Do đó tổng khoảng cách từ M đến hai tiệm cận là 4m − 3 9 9 d = m − 3 + − 4 = m − 3 + 2. m − 3 . = 6 m − 3 m − 3 m − 3 9 m − 3 = 3 m = 6
Dấu ”= ” xảy ra khi và chỉ khi m − 3 = (m − )2 3 = 9 m − 3 m − 3 = 3 − m = 0 M = (6;7) N = (6;7)
. Một cách tương tự ta có các điểm . M = (0 ) ;1 N = (0; )1
Do M , N phân biệt nên MN = 6 2 .
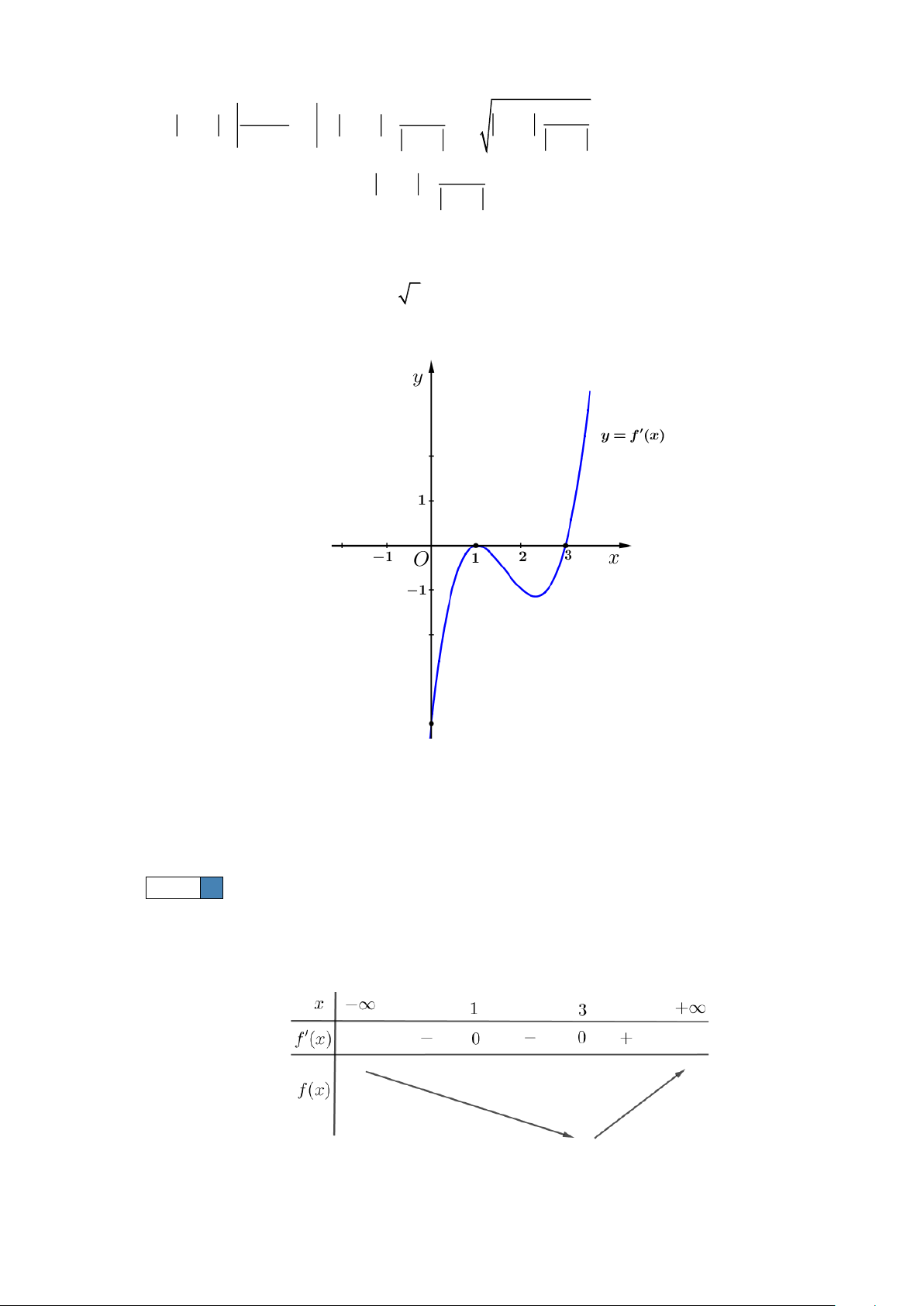
Câu 7. Cho hàm số y = f (x) . Hàm số y = f (x) có đồ thị như hình vẽ dưới đây. Khẳng định nào sau
đây là khẳng định đúng?
A. Hàm số y = f (x) đạt cực đại tại x =1.
B. Đồ thị hàm số y = f (x) có một điểm cực tiểu.
C. Đồ thị hàm số y = f (x) có hai điểm cực trị.
D. Hàm số y = f (x) đồng biến trong khoảng ( ) ;1 − . Lời giải Chọn B
Từ đồ thị hàm số y = f (x) ta có bảng biến thiên của hàm số y = f (x)
Quan sát bảng biến thiên ta thấy đồ thị hàm số y = f (x) có một điểm cực tiểu.
Câu 8. Tìm giá trị thực của tham số m để đồ thị hàm số 3 2
y = x − 3x + 2 cắt đường thẳng
d : y = m(x − )
1 tại ba điểm phân biệt có hoành độ x , x , x thỏa mãn 2 2 2
x + x + x 5 . 1 2 3 1 2 3 Trang 7 A. m 3 − . B. m 2 − . C. m 2 − . D. m 3 − . Lời giải Chọn B
PT hoành độ giao điểm: 3 2
x − 3x + 2 = m(x − ) 1 ( − ) x = x 1 ( 1 2
x − 2x − 2 − m) 1 = 0 . 2
x − 2x − 2 − m = 0 (1)
Cần (1) có hai nghiệm phân biệt x , x khác x = 1 và thỏa mãn 2 2 1+ x + x 5 2 3 1 2 3 = m + 3 0 m + 3 0 1
− 2 − 2 − m 0 3 − − m 0 m 2 − . 2 1
+ S − 2P 5 1 + 4+ 4+ 2m 5
Câu 9. Cho hàm số f ( x) , bảng xét dấu của f ( x) như sau:
Hàm số y = f (5− 2x) đồng biến trên khoảng nào dưới đây? A. (−;− ) 3 . B. (3;4) . C. (1; ) 3 . D. (4;5) . Lời giải Chọn D
Ta có y = f (5− 2x) = 2
− f (5−2x) . 5 − 2x = 3 − x = 4 y = 0 2
− f (5−2x) = 0 5 − 2x = 1 − x = 3 . 5 − 2x =1 x = 2 5 − 2x 3 − x 4 5 − 2x 1
f (5− 2x) 0
; f (5− 2x) 0 1 − 5 − 2x 1 2 x 3 3 − 5 − 2x 1 − x 2 . 3 x 4 Bảng biến thiên
Dựa vào bảng biến thiên hàm số y = f (5− 2x) đồng biến trên khoảng (4;5) . 1
Câu 10. Tìm giá trị thực của tham số m để hàm số 3 2
y = x − mx + ( 2
m − 4) x + 3 đạt cực đại tại x = 3. 3 A. m = 1 − .
B. m =1. C. m = 7 − .
D. m = 5 . Lời giải Chọn D Trang 8 Ta có 2
y = x − mx + ( 2 2
m − 4) ; y = 2x − 2m . 1 y (3) = 0 Hàm số 3 2
y = x − mx + ( 2
m − 4) x + 3 đạt cực đại tại x = 3 khi và chỉ khi: 3 y (3) 0 m =1(L) 2 9
− 6m + m − 4 = 0 2
m − 6m + 5 = 0 m = 5 (TM ). 6 − 2m 0 m 3 m 3
Vậy m = 5 là giá trị cần tìm. x − 2
Câu 11. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = đồng biến trên ( ;0 − )? x − m A. Vô số.
B. 1. C. 2. D. 3. Lời giải Chọn C
Ta có TXĐ: D = R \ m . −m + 2 Khi đó y = . (x − m)2
Hàm số đồng biến trên ( ;0 − ) −m +
y 0 x (− ; 0) 2 0 x − ; 0 2 ( ) m (x − m) − + 2 0 m m ( − ;0 ) 0 2. m 0 m 0
Do mZ m0; 1 .
Vậy có 2 giá trị của m thỏa mãn yêu cầu.
Câu 12. Cho hàm số y = f (x) có đạo hàm và liên tục trên . Biết rằng đồ thị hàm số y = f (x) như dưới đây
Tìm giá trị lớn nhất max g ( x) của hàm số g ( ) = ( ) 2 x
f x − x − x trên đoạn 1 − ;2. 1 − ;2
A. max g ( x) = g (2) .
B. max g ( x) = g (0) . 1 − ;2 1 − ;2 Trang 9
C. max g ( x) = g ( ) 1 .
D. max g ( x) = g (− ) 1 . 1 − ;2 1 − ;2 Lời giải Chọn C
Xét hàm số g ( ) = ( ) 2 x
f x − x − x trên đoạn 1 − ;2.
Ta có g(x) = f (x) − 2x −1.
Cho g(x) = 0 f (x) = 2x +1.
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f (x) với đường thẳng y = 2x +1. x = 1 −
Dựa vào đồ thị hàm số ta thấy
f (x) = 2x +1 x =1 . x = 2 Bảng biến thiên
Dựa vào bảng biến thiên ta thấy max g ( x) = g ( ) 1 . 1 − ;2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Trong không gian Oxyz , cho S (1;2;3) và các điểm A , B , C thuộc các trục Ox , Oy , Oz sao
cho hình chóp S.ABC có các cạnh SA, SB , SC đôi một vuông góc với nhau. Xét tính đúng
sai của các mệnh đề sau
a) Toạ độ điểm C là C (7,0,0) .
b) Tam giác ABC là tam giác vuông. 343 c) S . B SC = 0.
d) Thể tích khối chóp S.ABC bằng . 36 Lời giải Trang 10 a) S b) S c) Đ d) Đ Ta đặt (
A a;0;0) , B(0; ;
b 0) , C(0;0;c) . SA = (a −1; 2 − ; 3 − ) ; SB = ( 1 − ;b − 2; 3 − ) ; SC = ( 1 − ; 2 − ;c − 3) .
Vì SA, SB , SC đôi một vuông góc nên
SA ⊥ SB S . A SB = 0 a = 7 + = a 2b 14
7
SB ⊥ SC S .
B SC = 0 2b + 3c =14 b = .
2 SA ⊥ SC S . A SC = 0 a + 3c = 14 7 c = 3 1 1 7 7 343
Do SA, SB , SC đôi một vuông góc, nên: V = . SA . SB SC = .7. . = . SABC 6 6 2 3 36 2
−mx + (4 m − 2)x +1− 4 m
Câu 2. Cho hàm số y = x −1 a) Khi m 1
− thì hàm số đạt cực đại và cực tiểu trong miền x 0
b) Khi m =1 đồ thị hàm số không cắt trục Ox
c) Có 2 phương trình tiếp tuyến của (C) song song với đường thẳng x − y = 0
d) Khi m =1 đồ thị hàm số có 2 điểm cực trị Lời giải
a) Đ b) Đ c) Đ d) Đ 2 −x + 2x − 3 2
(a)(b) Khi m = 1: y = = −x +1− x −1 x −1
Tập xác định: D = \{1} 2 − + + = − = x 2x 1 x 1 2 y 2 2 2 y =
= 0 −x + 2x +1 = 0 2 (x −1)
x =1+ 2 y = 2 − 2
lim y = : x = 1là tiệm cận đứng x 1 →
lim y = −x +1: y = −x +1là tiệm cận xiên x→ x Bảng biến thiên: x = 0 y = 3 2
y = 0 −x + 2x − 3 = 0 (vô nghiệm), đồ thị hàm số không cắt trục Ox 2 2
−mx + (4m − 2)x +1− 4m
−mx + 2mx − 4m + 2 −1+ 4m (c) y = y = 2 x −1 (x −1) 2 −mx + 2mx +1 Suy ra y = 2 (x −1)
Dấu y là dấu của tam thức 2
g(x) = −mx + 2mx +1 2
g(x) có = m + m
g(1) = −m + 2m +1 = m +1 Trang 11 0 m 1 −
Để hàm số có cực đại và cực tiểu thì m +1 0 m 0 x + x = 2 1 2
Lúc này, hàm số đạt cực đại, cực tiểu tại x = x , x = x và . 1 2 1 x x = − 1 2 m
Giả sử x x 1 2 Theo yêu cầu bài toán: 2 0 (luôn dúng) x 0 x + x 0 1 1 2 1 m 0 x 0 x x 0 − 0 2 1 2 m Giao với điều kiện
0 được m 1 − 2 −x + 2x +1 (d) y = x 2 (x −1)
Đường thẳng x − y = 0 có hệ số góc k =1
Để tiếp tuyến của (C) song song với đường thẳng y = x , cần và đủ là x 1 x 1 2 y = 1 − + + x x 2x 1 2 2 = 1
−x + 2x +1 = x − 2x +1 2 (x −1) x 1
x = 0 y = 3 2 2x 4x 0 − =
x = 2 y = −3
Có hai tiếp tuyến thỏa yêu cầu bài toán:
(T : y =1(x −0) +3 y = x +3 1 ) (
T : y = 1(x − 2) − 3 y = x − 5 2 )
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Đường đi của một khinh khí cầu được gắn trong hệ trục tọa độ là một đường cong bậc hai trên bậc
nhất có đồ thị cắt trục hoành tại hai điểm có tọa độ là (1;0) và (8;0) với đơn vị trên hệ trục tọa
độ là 1 (km) . Biết rằng điểm cực đại của đồ thị hàm số là điểm (6;5). Hỏi khi khí cầu đi qua
điểm cực đại và cách mặt đất 3875 (m) thì khí cầu cách gốc tọa độ theo phương ngang bao
nhiêu? (đơn vị: km ) Lời giải Trả lời 7 , 2 2
x + bx + c
Không mất tính tổng quát, ta giả sử phương trình của đường cong là y = dx + e
Vì đồ thị hàm số cắt trục hoành tại 2 điểm có tọa độ là (1;0) và (8;0) nên Trang 12 2
x + bx + c = (x − )(x − ) 2 1 8 = x −9x +8 2 2 − + − + − − + Suy ra x 9x 8 (2x 9)(dx ) e d(x 9x 8) y = y = 2 dx + e (dx + ) e
Vì đồ thị hàm số có điểm cực đại là (6;5) nên suy ra 3
(6d + e) +10d = 0 y (6) = 0 28d + 3e = 0 3 28 10 − d = ;e = − y(6) = 5 = 5 30 d + 5e = 10 − 5 5 6d + e 2 5(x − 9x + 8)
Vậy phương trình của hàm số là: y =
. Kiểm tra lại điểm cực trị của hàm số này 3x − 28
ta thấy điểm (6;5) là điểm cực đại của đồ thị hàm số.
Yêu cầu bài toán tìm nghiệm x 6 của phương trình 2 5(x − 9x + 8) x = 7,2 2
= 3,875 5x −56,625x +148,5 = 0 3x − 28 x = 4,125 (L)
Vậy khi khí cầu đi qua điểm cực đại và cách mặt đất 3875 (m) thì khí cầu cách gốc tọa độ theo phương ngang là 7,2 km.
Câu 2. Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
Hãy tính phương sai của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến chữ số hàng phần trăm). Lời giải Trả lời 0 , 2 8
Ta có bảng số liệu với đại diện: Cự li (mm) 19, 25 19, 75 20, 25 20, 75 21, 25 Tần số 13 45 24 12 6 n =100
Số trung bình cộng của mẫu số ghép nhóm trên là:
19, 25.13 +19,75.45 + 20, 25.24 + 20,75.12 + 21, 25.6 x = = 20,015 100
Suy ra, phương sai của mẫu số liệu trên là: 1 s =
(13.(19,25 − 20,015)2 + 45.(19,75 − 20,015)2 + 24.(20,25− 20,015)2 2 100
+12.(20,75− 20,015)2 + 6.(21,25− 20,015)2) 0,28.
Câu 3. Cho biết máy bay A đang bay với vectơ vận tốc a = (300;200;400) (đơn vị: km/h). Máy bay B
bay cùng hướng và có tốc độ gấp ba lần tốc độ của máy bay A . (làm tròn đến hàng đơn vị) Trang 13
Tính tốc độ của máy bay B . Lời giải Trả lời 1 6 1 5 3.300 = x x = 900
Ta có: 3a = b 3.200
= y y = 600 b = (900;600;1200) 3.400 z = z = 1200
Tốc độ của máy bay B là: 2 2 2
b = 900 + 600 +1200 1615,55 (km/h)
Câu 4. Một cửa hàng kinh doanh trung bình bán được 700 máy điều hòa mỗi tháng với giá 15 triệu đồng
một máy. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 1 triệu đồng, số lượng
máy điều hòa bán ra sẽ tăng thêm khoảng 100 máy mỗi tháng. Biết hàm chi phí hàng tháng là
C(x) = 14000− 3x (triệu đồng), trong đó x là số máy điều hòa bán ra trong tháng, cửa hàng
nên đặt giá bán bao nhiêu để lợi nhuận là lớn nhất? (đơn vị là triệu đồng). Lời giải Trả lời 9 , 5
Gọi p (triệu đồng) là giá của một máy điều hòa và x là số máy điều hòa bán ra trong tháng.
Ta có hàm cầu p = ax + b đi qua các điểm (700;15) và (800;14) Suy ra 1 p = − x + 22 100
Ta có hàm doanh thu trong tháng là: R ( x) 1 2 = px = − x + 22x 100
Suy ra hàm lợi nhuận của cửa hàng trong tháng là:
L ( x) = R( x) − C ( x) 1 2 = −
x + 22x − (14000 − 3x) 100 L(x) 1 2 = − x + 25x −140 0 0 100
Ta có L(x) đạt GTLN bằng 1625 (triệu đồng) khi x =1250
Vậy cửa hàng nên đặt giá bán để lợi nhuận lớn nhất là: 1 p = −
.1250 + 22 = 9,5 (triệu đồng) 100
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Một doanh nghiệp cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai máy A và
B . Máy A làm việc trong x ngày cho số tiền lãi là 2
x + 2x (triệu đồng), máy B làm việc
trong y ngày cho số tiền lãi là 2 2
− 7y + 326y (triệu đồng). Hỏi doanh nghiệp đó cần sử dụng
máy A làm việc trong bao nhiêu ngày để số tiền lãi thu được nhiều nhất? Biết rằng hai máy A
và B không đồng thời làm việc và máy B làm việc không quá 6 ngày. Lời giải Trang 14
Theo đề x + y = 10 y = 10 − x .
Bài toán trở thành tìm x để hàm số f (x) đạt giá trị lớn nhất với 2 2 2 nf (x) = 2
− 7(10 − x) + 326(10 − x) + x + 2x = 2
− 6x + 216x + 6 5 . 0 54
Vì f (x) là hàm bậc hai có a 0 nên đạt giá trị lớn nhất tại x = 4 do ( y 6 ). 13
Vậy máy A cần được sử dụng trong 4 ngày, máy B cần được sử dụng trong 6 ngày.
Câu 2. Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống
kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu A và B trong 50 ngày giao dịch liên tiếp.
Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro của các loại cổ
phiếu có giá trị trung bình gần bằng nhau. Cổ phiếu nào có phương sai, độ lệch chuẩn cao hơn thì được
coi là có độ rủi ro lớn hơn.
Theo quan điểm trên, hãy so sánh độ rủi ro của cổ phiếu A và cổ phiếu B . Lời giải
Ta có bảng thống kê giá đóng cửa theo giá trị đại diện
• Xét mẫu số liệu của cổ phiếu A
Số trung bình của mẫu số liệu ghép nhóm là
8121+ 9123 +12125 +10127 +11129 x = =125, 28. 1 50
Phương sai của mẫu số liệu ghép nhóm là 2 1 S = ( 2 2 2 2 2
8121 + 9123 +12125 +10127 +11129 ) 2 −125, 28 = 7,5216. 1 50
Độ lệch chuẩn của mẫu số liệu ghép nhóm là S = 7,5216. 1
• Xét mẫu số liệu của cổ phiếu B
Số trung bình của mẫu số liệu ghép nhóm là
16121+ 4123 + 3125 + 6127 + 21129 x = =125, 48. 2 50
Phương sai của mẫu số liệu ghép nhóm là 2 1 S = ( 2 2 2 2 2
16121 + 4123 + 3125 + 6127 + 21129 ) 2 −125, 48 = 12, 4096. 2 50
Độ lệch chuẩn của mẫu số liệu ghép nhóm là S = 12, 4096. 2
Vậy nếu đánh giá độ rủi ro theo phương sai và độ lệch chuẩn thì cổ phiếu A có độ rủi ro thấp hơn cổ phiếu B .
Câu 3. Một chất điểm A nằm trên mặt phẳng nằm ngang ( ) , chịu tác động bởi ba lực F , F , F . Các 1 2 3
lực F , F có giá nằm trong ( ) và (F , F 135 =
, còn lực F có giá vuông góc với ( ) và 1 2 ) 1 2 3
hướng lên trên. Xác định tổng hợp lực của các lực trên, biết rằng độ lớn của ba lực đó lần lượt
là 20 N, 15 N và 10 N. (Kết quả làm tròn đến hàng phần chục). Trang 15 Lời giải
Ta có F = F + F + F . 1 2 3 Suy ra
F = (F + F + F )2 2 1 2
3 2 2 2
= F + F + F + 2F F + 2F F + 2F F 1 2 3 1 2 2 3 1 3 2 2 2
= 20 +15 +10 + 22015cos135 17,3.
Vậy độ lớn của tổng hợp lực là 17,3 N.
Câu 4. Số giá trị nguyên thuộc khoảng ( 2
− 020;2020) của tham số m để hàm số 3 2
y = x − 3x − mx + 2019 đồng biến trên (0;+) là Lời giải Ta có 2
y = 3x − 6x − m .
Hàm số đồng biến trên khi y x ( +) 2 0, 0;
3x −6x − m 0, x (0;+) 2
3x −6x , m x (0;+) ( ) 1
Xét hàm số f (x) 2
= 3x − 6x trên (0;+)
Ta có f (x) = 6x −6, f (x) = 0 x =1. Do đó min f ( x) = f ( ) 1 = 3 − (0;+) ( )1 m 3
− .Kết hợp với giả thiết ta được m( 2 − 020;−
3 . Nên có 2017 số nguyên thỏa mãn -------- HẾT-------- ĐỀ 2
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
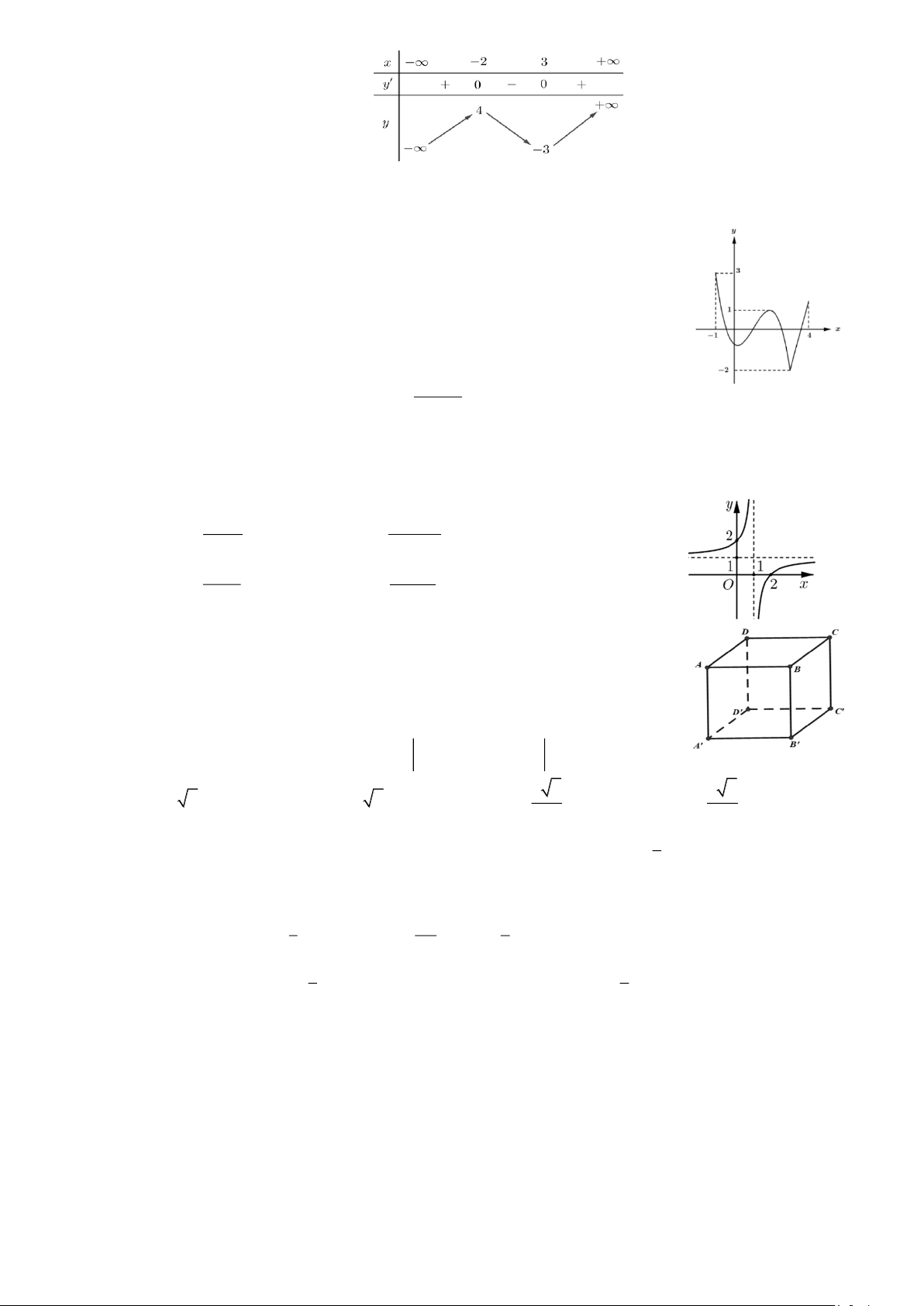
Câu 1: Cho hàm số y = f (x ) xác định trên ¡ và có bảng biến thiên như hình bên dưới Trang 16
Hàm số y = f (x ) đồng biến trên khoảng nào dưới đây? A. (- ¥ ;0). B. (- 2;3). C. (1;+ ¥ ). D. (3;+ ¥ ).
Câu 2: Cho hàm số y = f (x ) xác định, liên tục trên é- 1;4ù ë
û và có đồ thị như hình vẽ
Giá trị lớn nhất của hàm số y = f (x ) trên é- 1;4ù ë û là A. - 1 . B. 3 . C. 1 . D. - 2 .
Câu 3: Tiệm cận đứng của đồ thị hàm số 2x + 3 y =
là đường thẳng có phương x - 1 trình
A. y = 5 .
B. x = 0 .
C. x = 1. D. y = 0 .
Câu 4: Hình dưới đây là đồ thị của hàm số nào? x - 2 - 2 + x A. y = . B. y = . x - 1 x + 1 x - 1 1 - 2x C. y = . D. y = . x - 1 x + 1
Câu 5: Cho hình hộp ABC . D A B ¢ C ¢ D
¢ .¢ Khẳng định nào dưới đây là sai? uuur uuuur uuuur uuuuur uuuur uuuur
A. A D = B C ¢ .¢ B. D A ¢ ¢+ D C ¢ ¢- DD¢= D B ¢ . uuuur uuuur uuur uuur uuur uuur uuur C. A D ¢ ¢+ A B
¢ ¢= A C . D. A B + A D + A A ¢ = A C . uuur uuur uuur
Câu 6: Cho tứ diện đều ABCD cạnh a. Tính AB + AC + AD theo a ? a 6 a 3 A. a 6. B. a 3. C. . D. . 2 2 uuur 1 uuuur
Câu 7: Cho lăng trụ đứng ABC.A B ¢ C
¢ ¢, điểm M trên CC ¢ sao cho MC = - MC .¢ Đặt 3 uuur r uuur r uuur r
A B = a, A C = ,
b A A¢= c. Khẳng định nào dưới đây là đúng ? uuuur r r 1 r uuuur - 3 r r 3 r A. A M ¢ = a - b +
c. B. A M ¢ = a + b - c. 2 2 4 uuuur r r 2 r uuuur r 3 r C. A M ¢ = - a + 2b - c. D. A M ¢ = b - c. 3 4
Câu 8: Trong không gian với hệ tọa độ Oxyz , cho điểm A (- 1;2;0),B (3;4;- 2) và C (1;0;- 3). Biết tọa
độ điểm D (x ;y ;z để tứ giác BACD là hình bình hành. Tính x + y + z ? 0 0 0 ) 0 0 0 A. 12. B. 2. C. - 5. D. - 8.
Câu 9: Trong không gian Oxyz , điểm đối xứng của điểm M (1;2;3)qua trục Ox có tọa độ là A. (1;- 2;- 3). B. (1;0;0). C. (0;2;3). D. (- 1;- 2;- 3). r r
Câu 10: Trong không gian với hệ trục tọa độ Oxyz , cho hai véc tơ u = (- 3;0;1) và v = (0;2;- 2). Tọa ur r r
độ của véc tơ w = 2u - v tương ứng là: Trang 17 A. (- 6;- 2;4). B. (- 6;2;0). C. (- 2;1;3). D. (1;- 2;5).
Câu 11: Một hãng xe ôtô thống kê lại số lần gặp sự cố về động cơ của 100 chiếc xe cùng loại sau 2 năm
sử dụng đầu tiên ở bảng sau. Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm này? (Làm tròn các
kết quả đến hàng phần trăm).
Số lần gặp sự cố 0 é , 5;2, 5 é é é é ê ) 2, 5; 4, 5 ê ) 4, 5; 6, 5 ê ) 6, 5; 8, 5 ê ) 8,5;10,5 ê ) ë ë ë ë ë Số xe 17 33 25 20 5 A. 5, 32 . B. 3, 52 . C. 2, 53 . D. 5, 23 .
Câu 12: Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị:
km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau: Quãng đường (km) 2 é , 7;3, 0 é é é é ê ) 3,0;3,3 ê ) 3,3;3,6 ê ) 3,6;3,9 ê ) 3,9;4,2 ê ) ë ë ë ë ë Số ngày 3 6 5 4 2
Phương sai của mẫu số liệu ghép nhóm là (làm tròn đến hàng phần trăm)
A. 3,39. B. 11,62. C. 0,13. D. 0,36.
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời câu hỏi. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh chọn đúng hoặc sai. Câu 1: Cho hàm số 3 2
y = - x + 2x - 3 có đồ thị (C ).
a) Hàm số có 2 điểm cực trị.
b) Giá trị cực đại của hàm số là 4 . 3
c) f ( 79 ) < f ( 80 10 10 ) 4 145
d) Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số là . 27
Câu 2: Trong không gian Oxyz , cho hai điểm A (1;- 1;2),B (- 2;0;3). uuur r r r
a) OA = i + j + 2k . uuur
b) Tọa độ của vectơ AB = (- 3;1;1). uuuur
c) Điểm A ' là hình chiếu của điểm A trên mặt phẳng tọa độ (Oxy ) thì AA ' = (0;0;2)
d) Tọa độ điểm C để tứ giác OABC là hình bình hành là C (1;1;- 3)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4. 2 3x + 2x
Câu 1: Cho hàm số y =
. Khoảng cách từ điểm M (3;- 2) đến đường tiệm cận xiên của đồ thị 4x + 4 hàm số này bằng
Câu 2: Cho hình lập phương A BCD.A B ¢ C ¢ D
¢ ¢ có cạnh bằng a. Gọi M, N lần lượt là trung điểm của uuuur uuuur A D ¢ ¢ và C D ¢ ¢ Tích vô hướng 2 MN .C B
¢ = na (n là số thập phân). Giá trị của n bằng bao nhiêu?
Câu 3: Một công ty sản xuất bóng đèn LED đã kiểm tra chất lượng sản phẩm của một lô hàng và ghi
nhận thời gian sử dụng của 250 bóng đèn như sau:
Khoảng thời gian (giờ)
Giá trị đại diện
Số lượng bóng đèn [0, 1000) 500 5 [1000, 2000) 1500 46 [2000, 3000) 2500 162 [3000, 4000) 3500 25 [4000, 5000) 4500 12 N = 250
Nếu độ lệch chuẩn của của bảng số liệu trên vượt quá 500 thì lô hàng không đạt tiêu chuẩn.
Qua tính toán người ta thấy lô hàng đã không đạt tiêu chuẩn để đưa ra thị trường. Hỏi độ lệch
chuẩn của lô hàng trên đã vượt qua tiêu chuẩn là bao nhiêu? (kết quả làm tròn đến hàng đơn vị). Trang 18
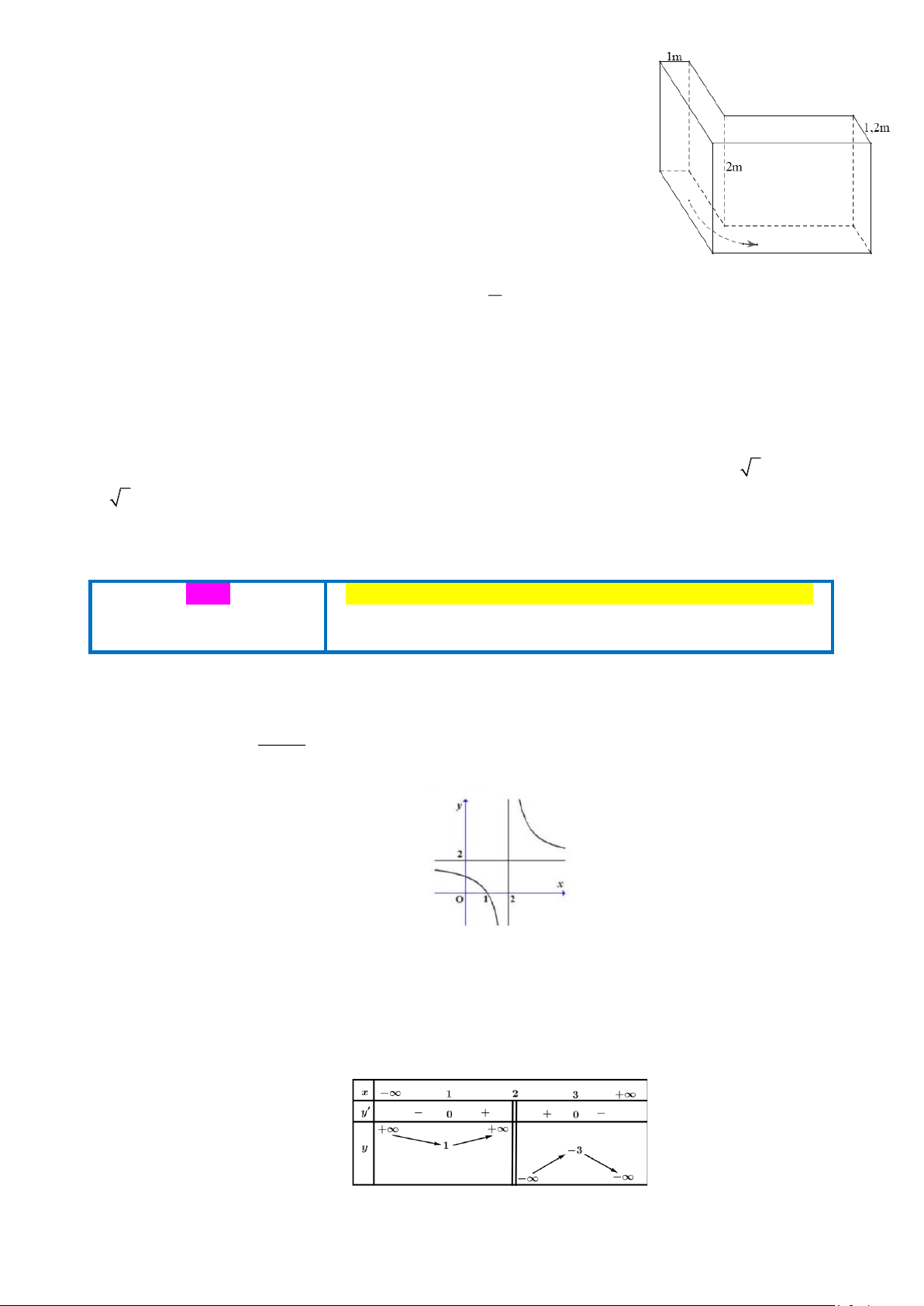
Câu 4: Hành lang trong một tòa nhà có dạng chữ L (hình vẽ) có chiều cao 2
m, một phía rộng 1 m, một phía rộng 1, 2 m. Một người thợ cần mang một số
ống thép cứng các loại có độ dài 2 m, 2, 5 m, 3 m, 3, 5 m, 4 m, từ bên này qua
bên kia. Hỏi có thể mang được mấy loại qua lối đi đó? IV. Tự luận
Câu 1: Một công ty phát động một chiến dịch quảng bá sản phẩm mới và số
lượng người biết đến sản phẩm này tại thời điểm t ngày sau khi bắt đầu 4
chiến dịch được ước tính theo công thức N (t ) t 3 = 10t -
(người). Khi đó N (
¢ t ) là tốc độ lan truyền 2
thông tin (người/ngày) tại thời điểm t với t Î 1 é ;14ù ë
û. Hỏi tốc độ lan truyền thông tin chiến dịch quảng bá
sản phẩm đạt giá trị lớn nhất vào ngày thứ mấy (tính bắt đầu từ ngày phát động chiến dịch)?
Câu 2: Một công ty du lịch tổ chức các tour khám phá vào mỗi cuối tuần, với tối đa 120 khách tham gia
mỗi tour. Nếu giá vé là 400 nghìn đồng/người, toàn bộ số vé đều được bán hết. Tuy nhiên, cứ mỗi khi
tăng giá vé thêm 50 nghìn đồng, số lượng khách đăng ký giảm đi 10 người. Để doanh thu từ mỗi tour đạt
mức cao nhất, công ty nên bán với giá bao nhiêu nghìn đồng mỗi vé (làm tròn đến hàng đơn vị)?
Câu 3: Trong hệ trục toạ độ Oxyz , cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2 , cạnh bên
bằng 5 và O là tâm của đáy. Gọi I (a; ;
b c) là điểm cách đều các đỉnh A, B,C, ,
D S . Biết rằng S thuộc tia
Oz . Tính a + b + c .
---------- HẾT ---------- ĐỀ 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án. ax + b
Câu 1: Cho hàm số y = ( , a ,
b c là các hằng số thực) có đồ thị như hình vẽ bên. Hai đường tiệm x + c
cận của đồ thị hàm số cắt nhau tại I .
Tọa độ của điểm I là A. (0;0). B. (1;2). C. (2;1). D. (2;2). Câu 2: Hàm số 4 2
y = x + 8x đồng biến trên khoảng nào sau đây? A. (0;+ ¥ ). B. (- 2;0). C. (- ¥ ;- 2). D. (- ¥ ;+ ¥ ).
Câu 3: Cho hàm số có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A. 3. B. 1. C. 2. D. - 3 . Trang 19
Câu 4: Giá trị nhỏ nhất của hàm số 4 2
y = x - 2x - 1 trên đoạn 0 é ;2ù ë û bằng
A. 7. B. 1. C. - 1 . D. - 2 .
Câu 5: Cho y = f (x) là hàm số bậc ba có đồ thị như hình vẽ sau: Hàm số đã cho
nghịch biến trên khoảng nào sau đây? A. (- ¥ ;0). B. (1;3). C. (0;1). D. (3;5).
Câu 6: Điều tra cân nặng các học sinh (tính theo đơn vị kilôgram) ở một lớp 12 của
một trường học người ta thu được mẫu số liệu như sau:
Phương sai của mẫu số liệu trên bằng A. 111 . B. 113 . C. 112 . D. 110 .
Câu 7: Xét hình hộp tùy ý AB . CD A B ¢ C ¢ D
¢ ¢ (tham khảo hình vẽ bên).
Khẳng định nào sau đây đúng? uuur uuur uuur uuuur uuur uuur uuur uuuur
A. A B + A D + A A¢= A B ¢. B. A B + A D + A A¢= BD ¢. uuur uuur uuur uuuur uuur uuur uuur uuuur
C. A B + A D + A A ¢= A D ¢. D. A B + A D + A A ¢= A C ¢.
Câu 8: Tổng số lượng đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm 2 số y = là 2 x - x A. 3 . B. 0 . C. 1 . D. 2 . uuur uuur
Câu 9: Cho tứ diện đều ABCD có độ dài mỗi cạnh bằng 2 . Giá trị của DA.DB bằng A. 2 3 . B. 2 . C. - 2 . D. - 2 3 .
Câu 10: Trong không gian Oxyz , cho tam giác A BC có A (1;0;2), B (2;1;4) và trọng tâm là G (- 1;2;0).
Tìm tọa độ của đỉnh C . 2 æ ö
A. C (- 6;5;- 6). B. C (2;3;6).
C. C çç ;1;2÷÷ ç . D. C (6;- 5;6). 3 ÷ è ø
Câu 11: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây? A. 3
y = - x + 3x . B. 3 2
y = x - 3x . C. 3
y = x - 3x . D. 3 2
y = - x + 3x . r r
Câu 12: Trong không gian Oxyz , cho hai vectơ u (- 1;1;3) và v (1;- 1;0). Giá trị r r
của u.v bằng A. - 2 . B. 2 . C. 1 . D. - 1 .
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời câu hỏi. Trong mỗi ý a), b), c), d) ở mỗi câu, thí
sinh chọn đúng hoặc sai.
Câu 1: Số giờ sử dụng smartphone trong 1 ngày nghỉ của học sinh lớp 12A7 được thống kê trong bảng sau 19
a) Số trung vị của mẫu số liệu trên bằng . 8
b) Khoảng biến thiên của mẫu số liệu trên bằng 6. Trang 20




