

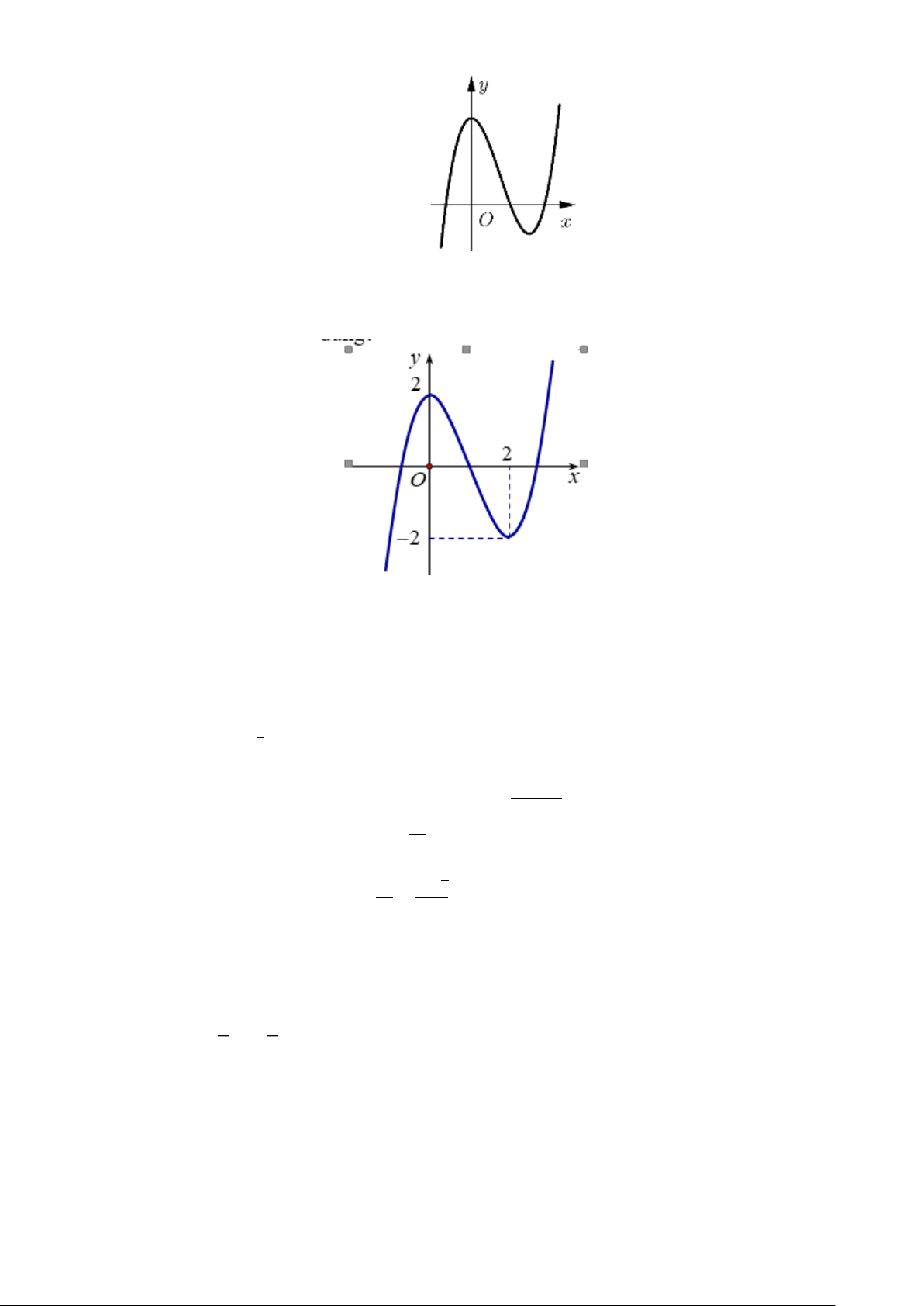



Preview text:
ĐỀ 1
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. x −1
Câu 1. Cho hàm số y =
. Mệnh đề nào sau đây là đúng ? x
A. Hàm số đã cho đồng biến trên R \{0} .
B. Hàm số đã cho chỉ đồng biến trên khoảng ( ;0 − ).
C. Hàm số đã cho đồng biến trên mỗi khoảng xác định.
D. Hàm số đã cho chỉ đồng biến trên khoảng (0;+). 1− 2x
Câu 2. Tiệm cận ngang của đồ thị hàm số y = là x +1
A. y = 1.
B. y = 2 .
C. y = −2 . D. x = 1 − . Câu 3. Hàm số 3 2
y = 2x − x + 5 có điểm cực đại là 1
A. y = 5 .
B. x = 0 .
C. M (0;5) . D. x = . 3
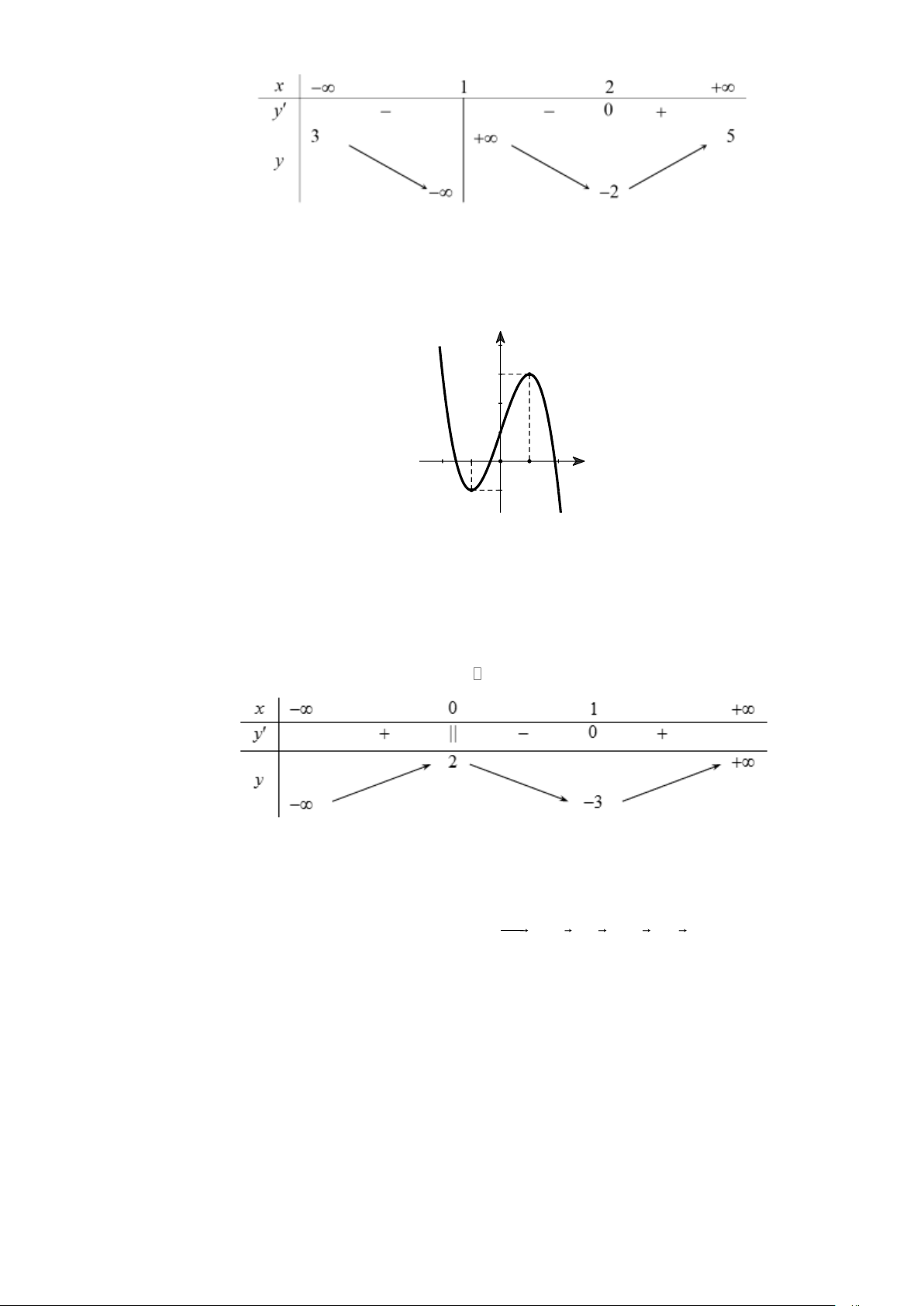
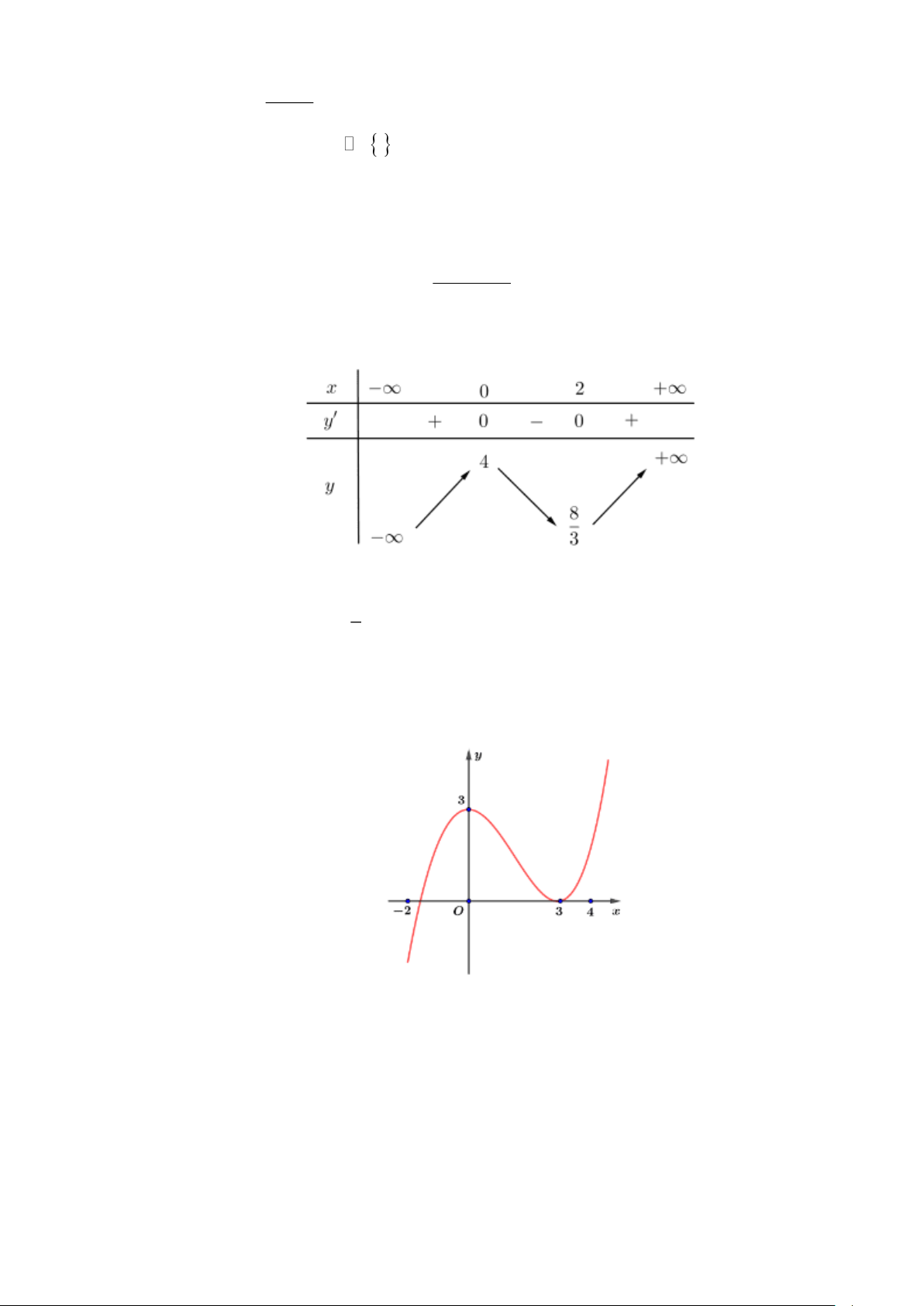
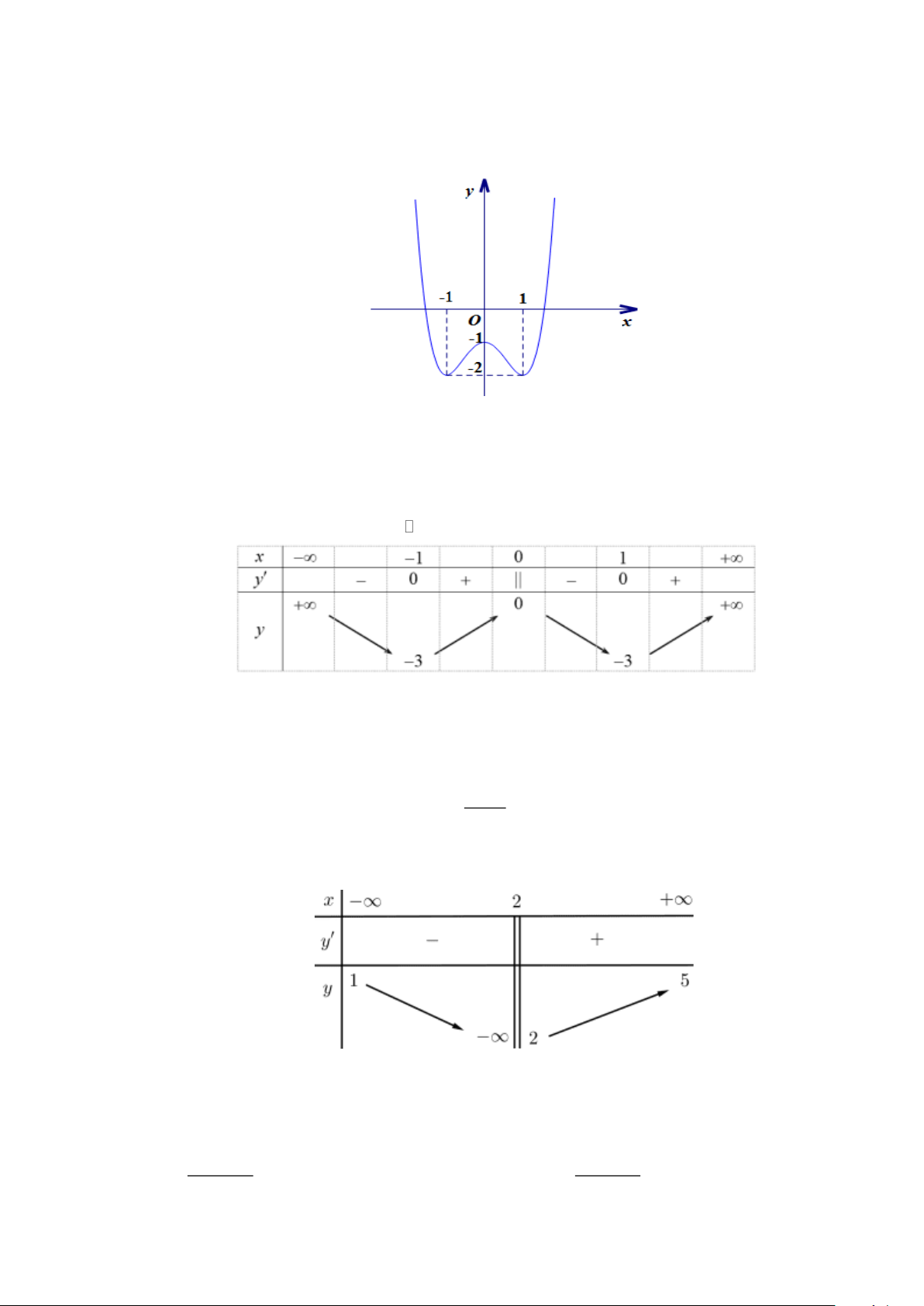
Câu 4. Đường cong trong hình dưới là đồ thị của một hàm số được liệt kê ở bốn phương án ,
A B,C, D dưới
đây. Hỏi hàm số đó là hàm số nào? A. 4 2
y = x − x +1. B. 3
y = −x + 3x +1. C. 2
y = −x + x −1. D. 3
y = x − 3x +1.
Câu 5. Cho hàm số y = f (x) xác định trên nửa khoảng 1
− ;3) có bảng biến thiên như hình vẽ.
Khẳng định nào sau đây đúng?
A. min f ( x) = 2 − .
B. max f ( x) = 2 . x 1 − ;3) x 1 − ;3)
C. min f ( x) = 1 − .
D. max f ( x) = 1. x 1 − ;3) x 1 − ;3) Câu 6.
Cho hàm số y = f (x) xác định trên \
1 , liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình bên. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? Trang 1 A. 2 . B. 3 . C. 4 . D. 1.
Câu 7. Giá trị lớn nhất của hàm số 4 2
f (x) = x − 4x + 5 trên đoạn 2 − ; 3 bằng A. 1. B. 50. C. 5 . D. 122 .
Câu 8. Cho hàm số y = f (x) có đồ thị như hình vẽ y 3 -1 O 1 x -1
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (− ; − ) 1 và (1;+).
B. Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 .
C. Hàm số đồng biến trên khoảng ( 1 − ; ) 3 .
D. Hàm số đồng biến trên khoảng ( 1 − ; ) 1 . Câu 9.
Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên như hình vẽ
Mệnh đề nào dưới đây đúng?
A. Hàm số chỉ có giá trị nhỏ nhất không có giá trị lớn nhất.
B. Hàm số có hai điểm cực trị.
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 3. −
D. Hàm số có một điểm cực trị.
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho vectơ AO = 3(i + 4 j) − 2k +5 j . Tọa độ của điểm A là: A. A(3;5; 2 − ).
B. A(3;17;2). C. A(3; 2 − ;5). D. A( 3 − ; 1 − 7;2).
Câu 11. Cho hàm số y = f (x) có đồ thị như hình vẽ. Hàm số y = f (x) đồng biến trên khoảng nào dưới đây? Trang 2 A. ( 2 − ; 2) . B. ( ; − 0) . C. (2; + ) . D. (0; 2) .
Câu 12. Trong không gian với hệ trục tọa độ Oxyz , cho u = ( 1
− ;1;0) , v = (0;−1;0) . Góc giữa hai véc-tơ u và v là
A. 135o .
B. 120o . C. 60o . D. 45o .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Trong không gian Oxyz , cho hình bình hành ABCD có A(1;2;− ) 3 ,B( 2 − ;3; )
1 ,C (0;2; ) 3 và
D = (x ; y ;z .Khi đó : D D D )
a) Tọa độ điểm D là (3 1 ; ;− ) 1 .
b) DC = ( x ; y − 2;2z − 3 . D D D )
c) AB = CD. d) AB = ( 3 − 1 ; ;4).
Câu 2. Bác Lâm muốn gò một cái thùng bằng tôn dạng hình hộp chữ nhật không nắp có đáy là hình vuông
và đựng đầy được 32 lít nước. Gọi độ dài cạnh đáy của thùng là x (dm), chiều cao của thùng là h(dm).
a) Tổng diện tích xung quanh và diện tích đáy của thùng là: 2
S = xh + x ( 2 4 dm ) . 128 128
b) Đạo hàm của hàm số S ( x) 2 =
+ x là S(x) = + 2x . x 2 x
c) Thể tích của thùng là 2 V = x h ( 3 . dm ) .
d) Để làm được cái thùng mà tốn ít nguyên liệu nhất thì độ dài cạnh đáy của thùng là 4dm .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
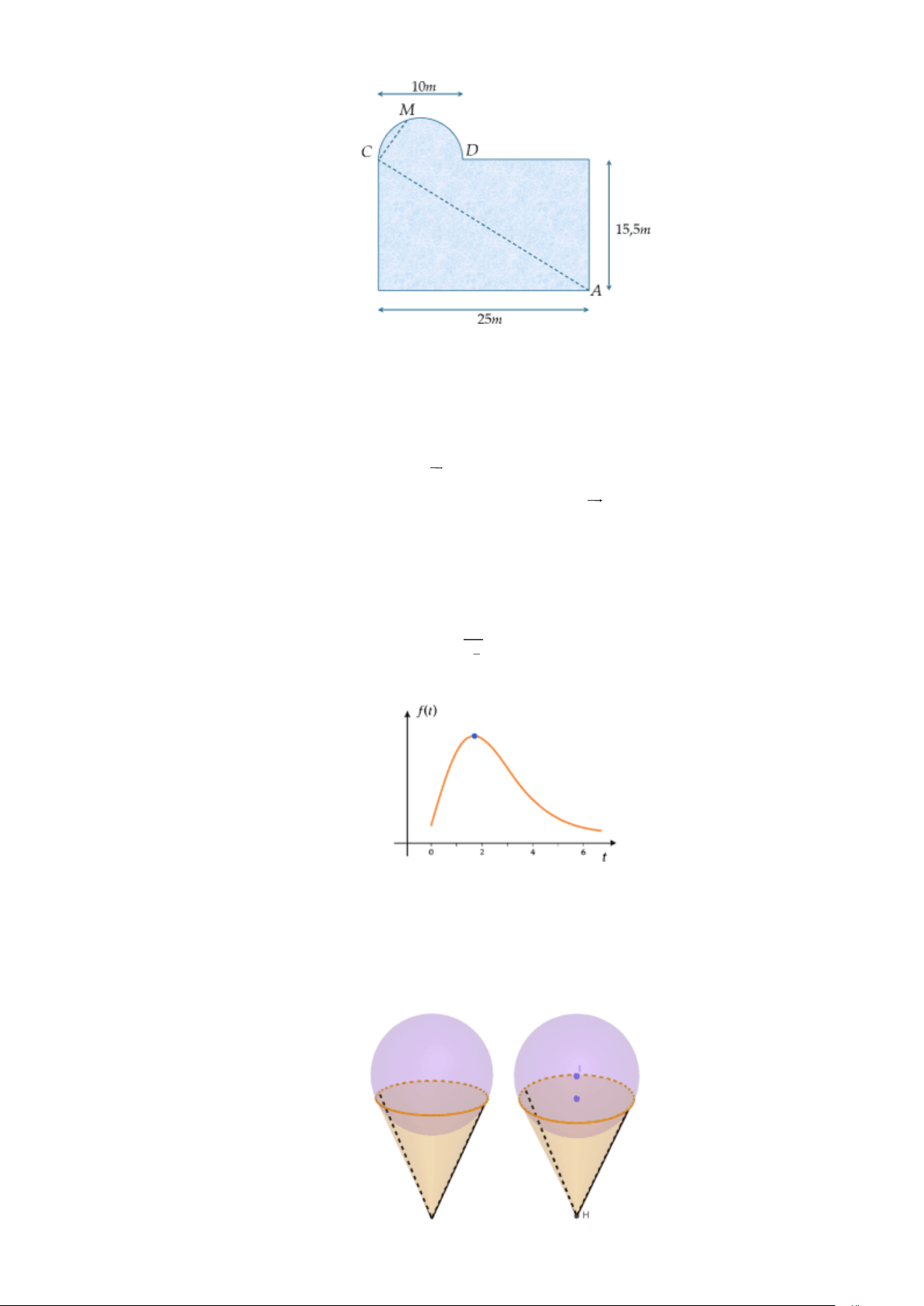
Câu 1. Bạn Hoa thường đi bơi ở hồ Sky Garden cạnh nhà, hồ bơi có thiết kế là một hình chữ nhật với
chiều dài 25 m, chiều rộng 15,5 m và bên cạnh đó là một hình bán nguyệt đường kính 10 m.
Trong một lần bể bơi vắng người nên Hoa đã thực hiện một chu trình là bơi theo đoạn thẳng AC
rồi bơi tiếp đoạn thẳng CM , với M là một vị trí bất kỳ trên hình bán nguyệt. Ngay sau đó bạn đi
bộ theo một hướng qua điểm D dọc bờ của hồ bơi để quay lại vị trí A và kết thúc chu trình.. Trang 3
Biết rằng vận tốc bơi của Hoa là 2,4 km/h, vận tốc đi bộ là 4,8 km/h và tốc độ bơi, vận tốc đi bộ
không thay đổi trong một chu trình. Hỏi thời gian chậm nhất để Hoa thực hiện xong chu trình trên là bao nhiêu phút?.
Câu 2. Trạm kiểm soát không lưu đang theo dõi hai máy bay. Giả sử trong không gian với hệ trục tọa độ
Oxyz , đơn vị đo lấy theo kilomet, tại cùng một thời điểm theo dõi ban đầu: máy bay thứ nhất ở tọa độ (
A 0;35;10) , bay theo hướng vectơ v = 3;4;0 với tốc độ không đổi 900(km / h) và máy bay 1 ( )
thứ hai ở tọa độ B(31;10;1 )
1 , bay theo hướng vectơ v = 5;12;0 với tốc độ không đổi 2 ( )
910(km / h) . Biết rằng khoảng cách an toàn tối thiểu giữa hai máy bay là 5 hải lý. Nếu hai máy bay
tiếp tục duy trì hướng và tốc độ bay như trên thì sau ít nhất bao nhiêu phút, hai máy bay vi phạm khoảng cách an toàn ?
Câu 3. Doanh số bán hàng của một loại sản phẩm (chục triệu đồng) trong một phiên livestream bán hàng 3t
kéo dài sáu giờ theo quy luật hàm số f (t) =
,0 t 6 trong đó thời gian t được tính bằng giờ kể t 2 e
từ khi bắt đầu livestream.
Khi đó, đạo hàm f (
t) sẽ biểu thị tốc độ bán hàng. Hỏi sau bao nhiêu giờ kể từ khi bắt đầu phiên
livestream thì doanh số bán hàng là lớn nhất?
Câu 4. Một cơ sở sản xuất Kem làm một mô hình Kem ốc quế lớn gồm 2 phần: Phần Kem có dạng hình
cầu, phần ốc quế có dạng hình nón. Chủ cơ sở sản xuất muốn gắn một chiếc đèn Led lớn chiếu
thẳng cây kem vào buổi tối, biết rằng chiếc đèn nằm trên mặt phẳng chứa đường tròn (C) là phần
tiếp xúc giữa phần Kem và phần ốc quế. Chọn hệ trục tọa độ Oxyz trong không gian thỏa mãn Trang 4
phần Kem hình cầu có tâm I (1; 2;3) , bán kính R = 3 và phần đỉnh của hình nón là điểm H (0;1; 2) − c
đáy là đường tròn có bán kính R = 6 . Để tối ưu hóa lượng ánh sáng chiếc đèn có thể chiếu vào cây kem N
người ta tính toán rằng chiếc đèn Led sẽ phải ở vị trí M ( ; a ;
b 2), a và từ điểm M kẻ được 2 tiếp tuyến với
đường tròn (C) sao cho góc giữa 2 tiếp tuyến đó không bé hơn 60 . Có bao nhiêu vị trí đặt chiếc đèn Led thỏa
mãn yêu cầu của chủ cơ sở.
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài. ur
Câu 1. Một vật có khối lượng m(kg) khi chịu tác dụng của một lực F thì vật đó sẽ chuyển động với gia ur r F tốc a =
. Tính lực tác dụng lên vật có khối lượng m = 6(kg) khi vật đó chuyển động trên mặt m
phẳng nằm ngang, nhẵn với gia tốc 2
a = 3m / s ?
Câu 2. Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz , một đội gồm ba drone giao hàng ,
A B,C đang có tọa độ là A(1; 3 − ;2), B( ;
m m − 2;6) , C (m − 2; ; m 5) , trong đó
m là tham số, đơn vị đo độ dài tính bằng kilomet. Biết kho hàng đang ở tại điểm I (1;1;0) . Vì lý do
nhiên liệu nên các drone không được di chuyển quá xa kho hàng, cụ thể là các drone không được
cách kho hành quá 100 km. Xác định giá trị của tham số m để các drone cách kho hàng không quá 100km.
Câu 3. Từ một tấm tôn có kích thước 90cm x 300cm , người ta làm một máng thoát nước, mặt cắt ngang
của máng là hình thang cân ABCD có đáy lớn AD , AB = BC = CD = 30c ,
m minh họa hình bên.
Thể tích lớn nhất của máng bằng
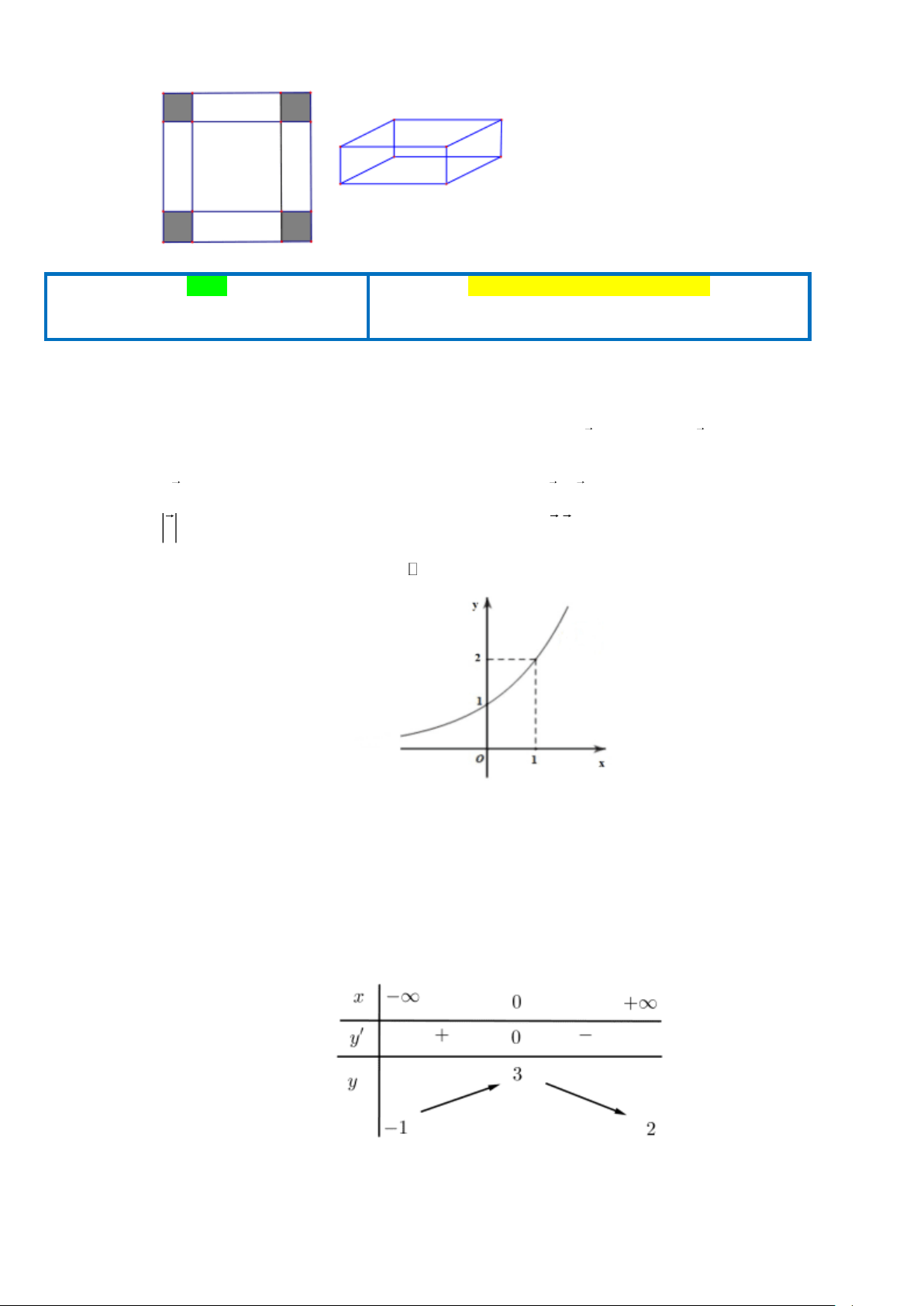
Câu 4. Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh bằng x , rồi gập tấm nhôm lại như hình vẽ dưới đây để
được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. Trang 5 ĐỀ 2
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Trong không gian với hệ trục tọa độ Oxyz , cho hai vec tơ a(1; − 2; 0) và b( 2 − ; 3; ) 1 . Khẳng định
nào sau đây là sai?
A. 2a = (2; − 4; 0) .
B. a + b = ( 1 − ; 1; − ) 1 .
C. b = 14 . D. . a b = 8 − .
Câu 2. Cho hàm số y = f (x) xác định trên , có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch trên trên (0 ) ;1 .
B. Hàm số nghịch trên trên ¡ .
C. Hàm số đồng biến trên ¡ .
D. Hàm số nghịch trên trên (- ¥ ) ;0 .
Câu 3. Giá trị nhỏ nhất của hàm số 3
y = x − 3x + 5 trên đoạn 2;4bằng
A. min y = 7 .
B. min y = 0.
C. min y = 5.
D. min y = 3. 2; 4 2; 4 2; 4 2; 4
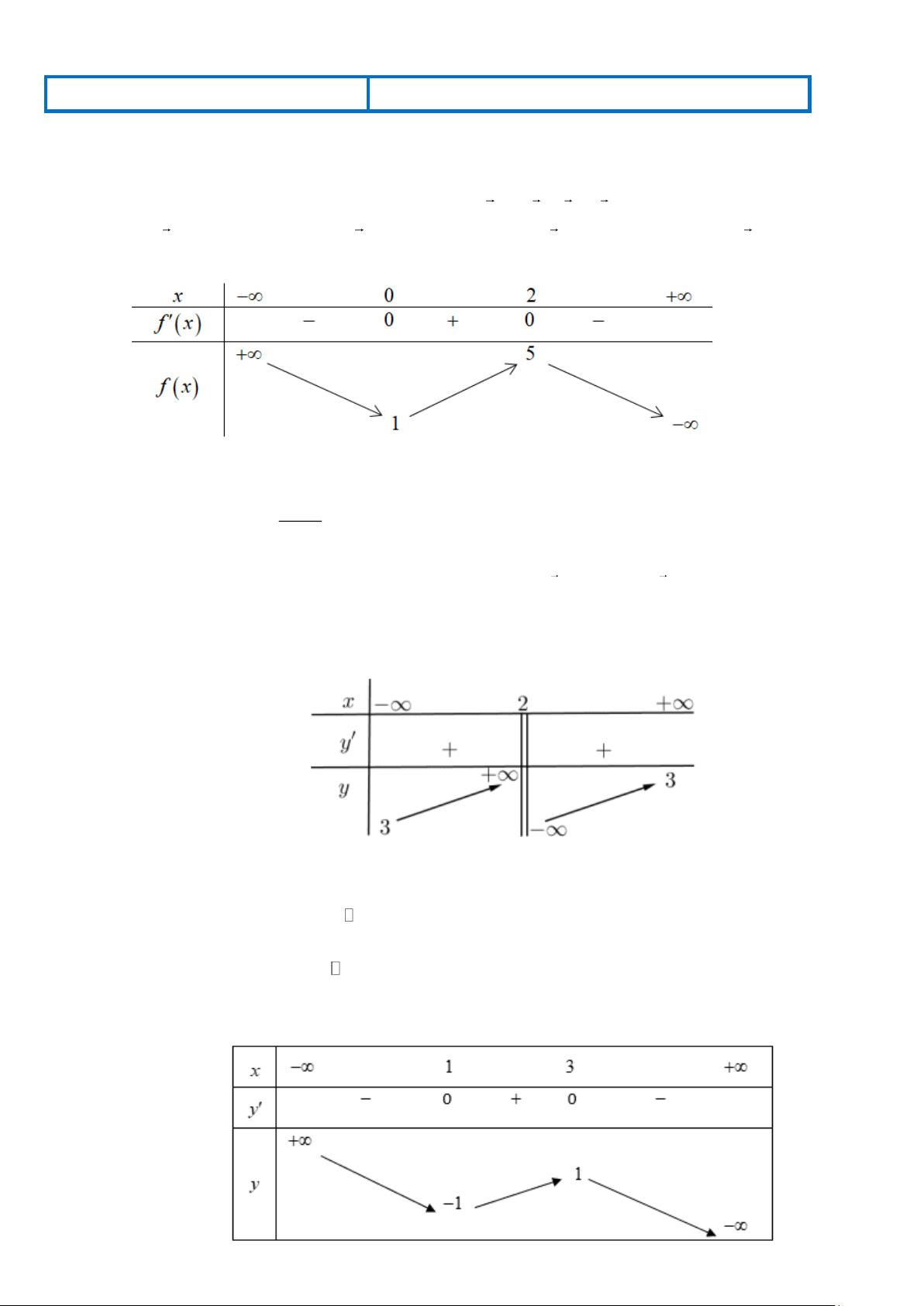
Câu 4. Cho hàm số có bảng biến thiên dưới đây. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có hai đường tiệm cận ngang là y = 1 − ; y = 2.
B. Đồ thị hàm số không có tiệm cận ngang.
C. Đồ thị hàm số có đường tiệm cận đứng x = 1,
− tiệm cận ngang y = 2.
D. Đồ thị hàm số có hai đường tiệm cận đứng. Trang 6 2x +1
Câu 5. Cho hàm số y =
. Khẳng định nào sau đây là ĐÚNG? x −1
A. Hàm số nghịch biến trên \ 1 .
B. Hàm số nghịch biến trên các khoảng ( ) ;1
− và (1;+).
C. Hàm số đồng biến trên các khoảng ( ) ;1
− và (1;+).
D. Hàm số nghịch biến trên ( 1
− ;+)(1;+) . 2x + 2019
Câu 6. Tìm số tiệm cận của đồ thị hàm số y = . x + 1 A. 0 . B. 1. C. 3 . D. 2 .
Câu 7. Cho hàm số y = f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số y = f (x) là 8 A. 4 . B. . C. 2 . D. 0 . 3 → →
Câu 8. Tích vô hướng của hai vectơ a ( 2
− ;2;5) , b(0;1;2) trong không gian bằng A. 12 . B. 13. C. 10. D. 14 .
Câu 9. Cho hàm số y = f (x) có đồ thị như hình vẽ. Tìm khoảng đồng biến của hàm số đã cho. A. (0;4). B. ( 2 − ;3). C. (0; ) 3 . D. ( 2 − ;0) . Câu 10. Hàm số 4 2
y = x + x − 4 có bao nhiêu điểm cực trị? A. 3. B. 0. C. 1. D. 2.
Câu 11. Đồ thị của hàm số nào dưới đây có dạng như đường cong hình vẽ bên? Trang 7 A. 3 2
y = −x + 3x + 3 . B. 3 2
y = x − 3x + 3 . C. 4 2
y = x − 2x + 3 . D. 4 2
y = −x + 2x + 3 .
Câu 12. Cho hàm số y = f (x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số có giá trị cực tiểu bằng 2 .
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 2 − .
D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Xét hàm số 𝑦 = 𝑥 − sin2𝑥 trên khoảng (0; 𝜋). 2
Xét tính đúng sai của các mệnh đề sau:
a) Đồ thị hàm số 𝑦 = 𝑓′(𝑥) cắt đồ thị hàm số 𝑦 = −sin22𝑥 tại 2 nghiệm trên khoảng (0; 𝜋). 2
b) Hàm số nghịch biến trên khoảng (5𝜋 ; 𝜋). 12
c) Hàm số có 2 điểm cực trị.
d) Giá trị cực tiểu của hàm số là 5𝜋 − 2+√3. 24 4
Câu 2. Trong không gian Oxyz , cho ba điểm A(1;2; ) 3 , B(0;1; ) 1 ,C (1;0; 2 − ) .
a) Trung điểm I của đoạn AC có tọa độ I (1;1; ) 1 .
b) Có 2 điểm trong 3 điểm đã cho nằm trong mặt phẳng (Oxz) . 2 1 c) Với M ;0; −
nằm trên mặt phẳng Oxz thì tổng 2 2 2
MA + 2MB + 3MC đạt giá trị nhỏ nhất. 3 6
d) Mặt phẳng ( ABC) có phương trình tổng quát x − 5y + 2z + 3 = 0.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
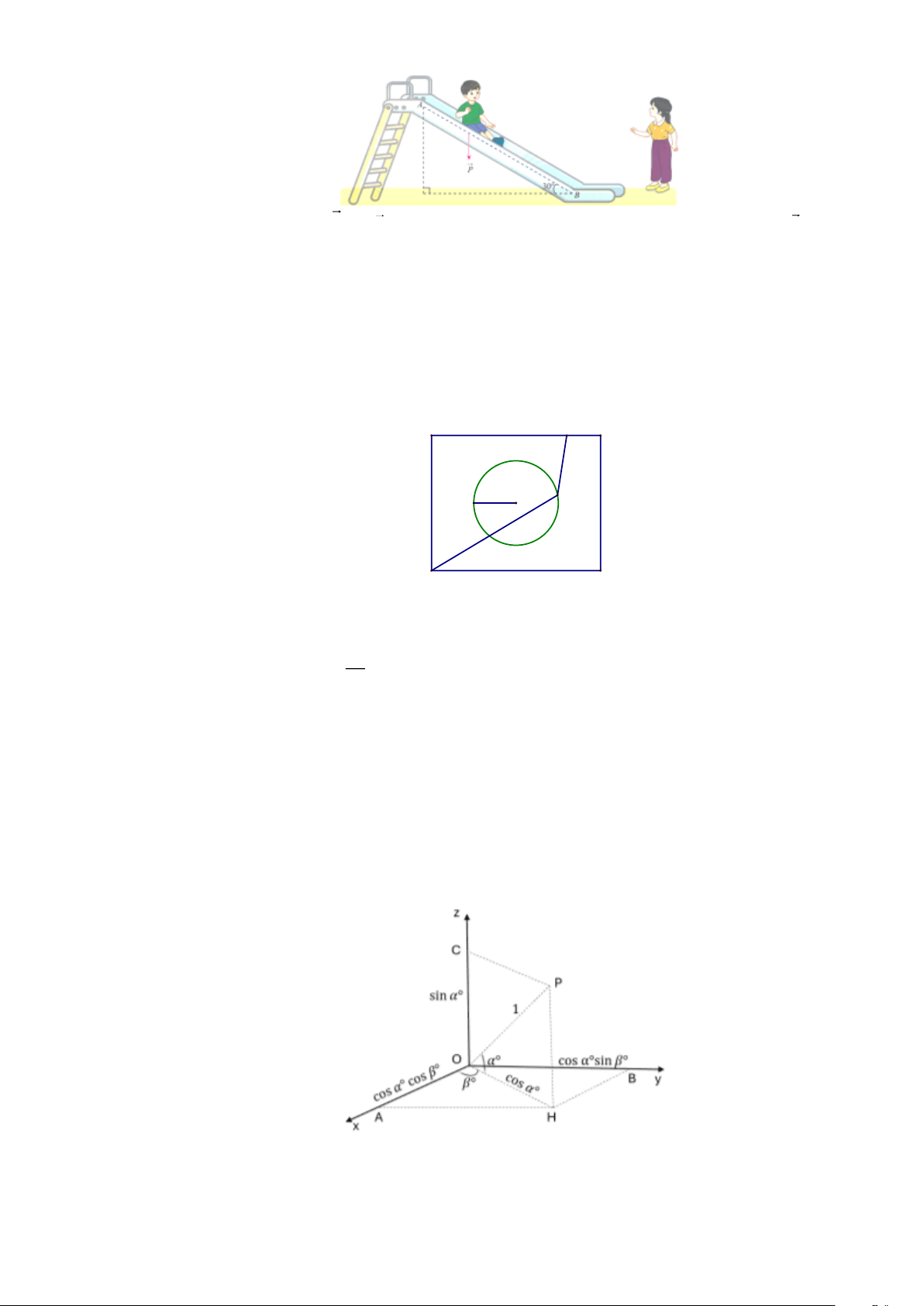
Câu 1. Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết rằng, cầu trượt có góc nghiêng
so với phương nằm ngang là 30 . Trang 8
Tính độ lớn của trọng lực P = mg tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do g có độ lớn là 2
g = 9,8 m/s . (làm tròn đến hàng đơn vị)
Câu 2. Trên sân vận động, người ta tổ chức một cuộc thi chạy thông minh. Sân vận động là hình chữ nhật
ABCD có kích thước AB =100m và CD = 80m. Ở chính giữa sân người ta vẽ một hình tròn có
tâm trùng với tâm của hình chữ nhật, bán kính bằng 25m như hình vẽ. Lấy E là một vị trí trên
cạnh AB sao cho EB = 20m. Mỗi vận động viên cần xuất phát từ một điểm M trên đường tròn và
chạy theo cung đường MDCBEM .
D Vận động viên thắng cuộc là người chạy với quãng đường
ngắn nhất. Tính độ dài quãng đường ngắn nhất vận động viên phải chạy. A E B 20m 80m 25m M O D 100m C
Câu 3. Giả sử tổng chi phí sản xuất x (0 x 50) đơn vị sản phẩm A mỗi ngày tại một nhà máy được 2 x
cho bởi công thức C ( x) =
+ 3x + 400 (nghìn đồng) và toàn bộ chúng được bán hết với giá 4
(900−6x) nghìn đồng một sản phẩm. Tìm mức sản lượng (đó là số lượng sản phẩm được sản xuất)
để chi phí trung bình tính trên mỗi đơn vị sản phẩm là đạt cực tiểu.
Câu 4. Giao điểm của đường khinh khí cầu bay với phạm vi kiểm soát Xét Trái Đất trong không gian
Oxyz, với O là tâm Trái Đất, tia Ox chứa giao điểm của kinh
tuyến gốc và xích đạo, tia Oz chứa điểm cực bắc N, tia Oy giao xích đạo tại điểm thuộc bán cầu
Đông, một đơn vị dài trong không gian Oxyz tương ứng với 6 371 km trong thực tế. Biết rằng nếu điểm M
có vĩ độ, kinh độ tương ứng là 0 0
N; E (0 90, 0 180) thì điểm M có tọa độ là M ( 0 0 0 0 0
cos cos ;cos sin ;sin ).
Tính khoảng cách giữa hai vị trí trên bề mặt Trái Đất là cầu Hiền Lương có vĩ
độ, kinh độ tương ứng là 0 0
17,0045 N; 107,0517 E và Dinh Độc Lập có vĩ độ, kinh độ tương ứng là 0 0
10,777 N; 106,695 E
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài. Trang 9
Câu 1. Ở một sân bay, một chiếc máy bay đã bay đến vị trí điểm M ( , a ,
b c) trong không gian Oxyz và
cách điểm xuất phát O là 50 km . Gọi H là hình chiếu vuông góc của điểm M lên mặt phẳng (
Oxy). Biết góc tạo bởi vectơ OH lần lượt với các véctơ i và OM lần lượt bằng 65 và 43.
Tính giá trị biểu thức P = a + b + c
Dựa vào hình vẽ ta có: a = O ;
A b = O ;
B c = OC = MH và OM = 50 km
Góc tạo bởi vectơ OH lần lượt với các véctơ i và OM lần lượt bằng 65 và 43. Suy ra HOM = 43 và HOA = 65 .
Trong tam giác vuông OHM . Ta có OH = OM.cos43 = 50.cos43.
Trong tam giác vuông OHA . Ta có a = OA = OH.cos65 = 50.cos43 . cos65
Trong tam giác vuông OHB . Ta có b = OB = OH.cos25 = 50.cos43 . cos25
Trong tam giác vuông OHM . Ta có c = HM = OM.sin43 = 50.sin43 .
Vậy P = a + b + c = 50(cos43 . cos65+ cos43 .
cos25+ sin43) 82,7.
Để theo dõi hành trình của một chiếc máy bay, người ta lập hệ toạ độ Oxyz có gốc toạ độ O trùng
với vị trí của trung tâm kiểm soát không lưu, mặt phẳng Oxy trùng với mặt đất với trục Ox hướng về phía
tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời. Sau khi cất cánh và đạt độ cao nhất
định, chiếc máy bay A duy trì hướng bay về phía nam với tốc độ 840 km/h. Sau thời điểm đó nửa giờ và ở độ
cao thấp hơn vị trí máy bay A 50km, máy bay B cũng duy trì hướng bay về phía nam với tốc độ 960km/h.
Tìm thời gian máy bay B bay trong khoảng thời gian 6h tính từ lúc máy bay B bay theo hướng nam để khoảng
cách giữa hai máy bay A và B ngắn nhất.
Câu 2. Ông Bình dự định sử dụng hết 2
5,5m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
dung tích lớn nhất bằng bao nhiêu (làm tròn đến hàng phần trăm)? Trang 10
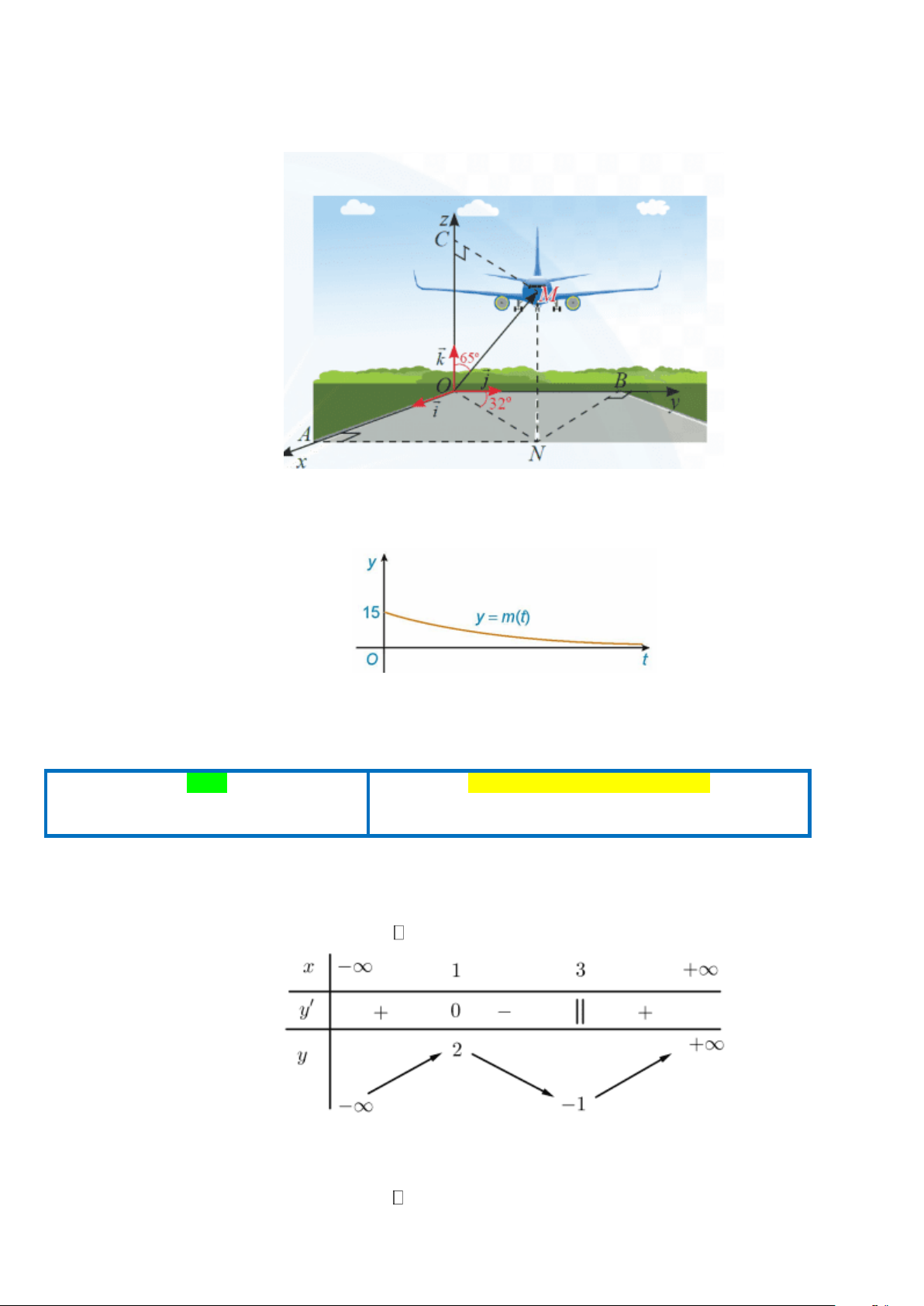
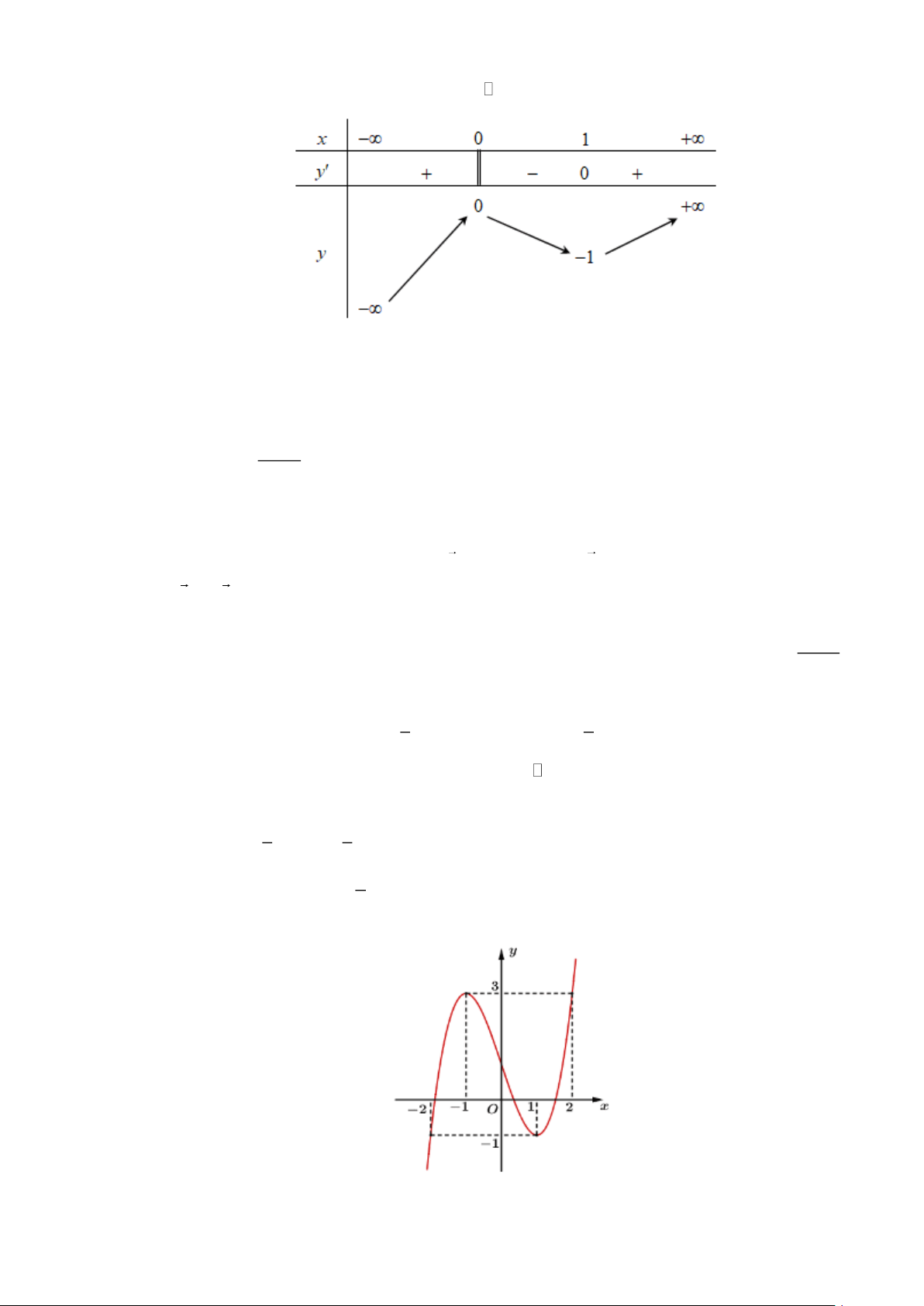
Câu 3. Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ Oxyz được thiết lập như hình bên dưới,
cho biết M là vị trí của máy bay,
OM =14, NOB = 32 ,
MOC = 65 . Tìm tọa độ điểm M .
Câu 4. Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số 0,012 ( ) 15 t m t e− = .
Khối lượng m(t) thay đổi ra sao khi t → + ?
Điều này thể hiện trên Hình như thế nào? ĐỀ 3
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f (x) liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại điểm x = 3.
B. Hàm số chỉ có một điểm cực trị.
C. Hàm số có giá trị nhỏ nhất trên bằng −1.
D. Hàm số có giá trị cực đại bằng 1. Trang 11
Câu 2. Số điểm cực tiểu của hàm số 4 2
y = x − 2x + 5 là A. 3 . B. 0 . C. 1. D. 2 .
Câu 3. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (1; + ) . B. ( 1 − ; ) 1 . C. (0 ; ) 1 . D. ( 1 − ;0) .
Câu 4. Trong không gian Oxyz , cho hai điểm A(1;1;− ) 1 , B(3;−3;− )
1 . Trung điểm M của AB có tọa độ là
A. M (2;−1;0).
B. M (2;−1;− ) 1 .
C. M (2;− 2;− ) 1 .
D. M (2;−1;− 2) .
Câu 5. Cho hàm số y = f (x) liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 0 .
B. Hàm số có đúng hai điểm cực trị.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 3 − .
D. Hàm số có giá trị cực tiểu bằng −1 và 1. x + 1
Câu 6. Tìm tiệm cận ngang của đồ thị hàm số y = . x - 1
A. y = 0 .
B. y = 1.
C. y = 2 . D. y = 1 − .
Câu 7. Cho hàm số y = f (x) có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = f (x) là A. 3. B. 0. C. 1. D. 2.
Câu 8. Hàm số nào sau đây nghịch biến trên các khoảng xác định của chúng? A. 4 2
y = x + 2x − 2018. B. 3
y = x − 3x + 2019 . x + 2019 x − 2 C. y = . D. y = . x − 2018 x + 2018 Trang 12
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(0;0; 6
− ) , B(8;0;0) . Độ dài đoạn thẳng AB bằng A. 2 . B. 100. C. 14 . D. 10.
Câu 10. Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = −x + 3x +1. B. 3 2
y = −x − 3x +1. C. 3 2
y = x + 3x +1. D. 3 2
y = x − 3x +1. 3
Câu 11. Giá trị lớn nhất của hàm số 3
y = x − 3x + 5 trên đoạn 0; là: 2 31 A. 5 . B. 3 . C. 7 . D. . 8
Câu 12. Cho hàm số f (x) xác định, liên tục trên và có đạo hàm cấp một xác định bởi công thức f (x) 2 '
= −x −1. Mệnh đề nào sau đây đúng? A. f ( ) 3 f (2). B. f ( ) 1 f (2). C. f ( ) 1 f (0).
D. f (0) f (− ) 1 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Trong không với hệ toạ độ Oxyz cho tam giác ABC có các đỉnh A(1; 2 − ;0),B(2;1; 2
− ),C(0;3;4) . 3 1
a) Toạ độ điểm M thuộc mặt phẳng xOz sao cho T = MC + MB nhỏ nhất là M ;0;− 2 2
b) Toạ độ của véc-tơ AB là (1;3; 2 − ) .
c) Toạ độ hình chiếu của điểm B trên mặt phẳng Oxy là H (0;0; 2 − )
d) Gọi điểm E ( ; a ;
b c) là hình chiếu của C lên AB , khi đó 7a +3b+c = 8 .
Câu 2. Một cơ sở đóng giày sản xuất mỗi ngày được x đôi giầy, 1 x 20. Tổng chi phí sản xuất x đôi
giày (đơn vị nghìn đồng) là 3 2
C(x) = x − 6x −88x + 592 . Giả sử cơ sở này bán hết sản phẩm mỗi
ngày với giá 200 nghìn đồng một đôi. Gọi T (x) là số tiền thu được sau khi bán hết x đôi giày và
L(x) là lợi nhuận thu được sau khi bán hết x đôi giày.
a) Doanh thu mỗi ngày của cơ sở sản xuất trên là T (x) = 200x (nghìn đồng).
b) Lợi nhuận mà cơ sở sản xuất thu được sau khi bán hết x đôi giày là 3 2
L(x) = x − 6x − 288x + 592 (nghìn đồng).
c) Giả sử trong một ngày nào đó cơ sở sản xuất được 10 đôi giày thì lợi nhuận thu được là 1888 (nghìn đồng). đồng).
d) Lợi nhuận tối đa mà cơ sở sản xuất trên thu được trong một ngày là 1980 nghìn đồng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Trong một nghiên cứu tại Viện Sức khỏe Tâm thần Quốc gia, các nhà khoa học theo dõi độ dày vỏ
não (cortex) của 307 trẻ em có IQ cao (121-149) qua tuổi t (tính bằng năm), với mô hình 3 2
S(t) = 0,000989t − 0,0486t + 0,7116t +1, 46, 5 t 19 Trang 13
Hỏi vỏ não của trẻ có IQ siêu trí tuệ đạt độ dày cực đại vào khoảng bao nhiêu tuổi (làm tròn kết
quản đến hàng đơn vị)
Câu 2. Trong không gian với một hệ trục toạ độ cho trước, ra đa phát hiện một chiếc máy bay di chuyển
với tốc độ và hướng không đổi từ điểm A(800;500;7) đến điểm B(940;550;9) trong 10 phút.
Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo
là điểm C (x; y; z) . Tính x+ y + z
Câu 3. Người ta treo một chiếc đèn trang trí có trọng lượng 200N lên trần nhà bằng ba sợi dây không giãn,
bằng nhau tại ba điểm A,B,C tạo thành tam giác đều. Mỗi sợi dây tạo với mặt phẳng trần nhà một
góc 30 đến được giữ ở trạng thái cân bằng. Hãy tính lực căng trong mỗi sợi dây.
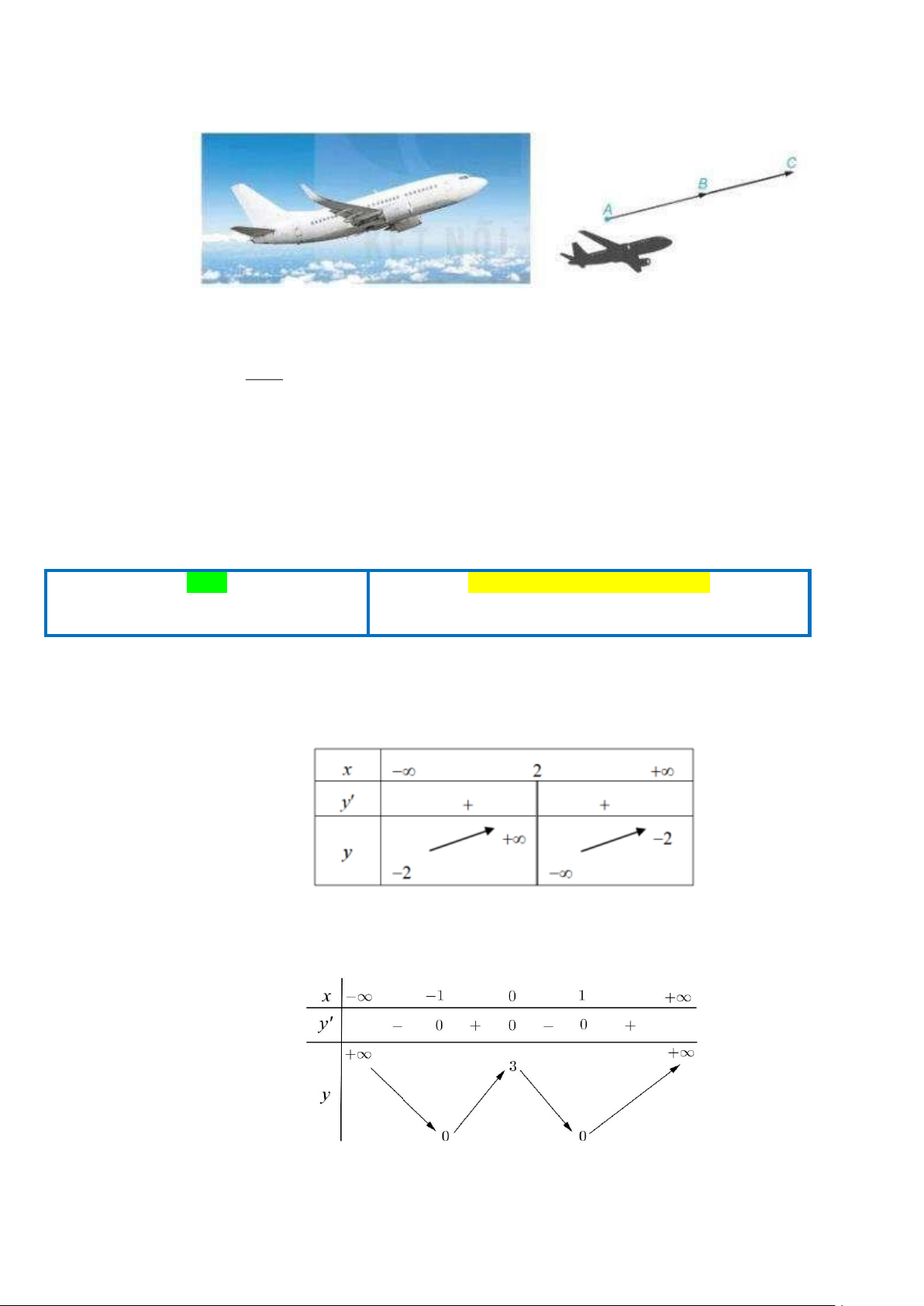
Câu 4. Một hồ nước hình bán nguyệt có đường kính AB = 150 .
m Một người chèo thuyền theo một đường
thẳng với vận tốc 1,5 km/h từ vị trí A đến vị trí C bất kỳ trên cung
AC . Tại vị trí C người đó
nghỉ 2 phút rồi tiếp tục đi bộ dọc theo cung nhỏ
CB đến B, sau đó đi bộ theo đường thẳng BA để
quay về A với vận tốc 3 km/h . Hỏi thời gian chậm nhất mà người đó về đến A là bao nhiêu phút?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Một người cưỡi ngựa xuất phát từ A đi đến C . Điểm A nằm trong vùng đất ướt nên vận tốc của
ngựa khi đi trong vùng này là 15km/h, Điểm C nằm trong vùng đất khô hơn nên vận tốc của ngựa
khi đi trong vùng này là là 30 km/h . Hai phần đất này giáp nhau bởi một đường thẳng d đi qua
trung điểm của AC và khoảng cách từ A và C đến đường này đều bằng 10 km . Biết AC = 5 41km
, thời gian ít nhất để đi từ A đến C là mấy giờ (làm tròn 2 chữ số sau dấy phẩy)?
Câu 2. Trong không gian với một hệ trục tọa độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một
chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800 ; 500 ; 7) đến điểm Trang 14
B(940 ; 550 ; 8) trong vòng 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì
tọa độ của máy bay sau 10 phút tiếp theo là gì?
Câu 3. Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là
C(x) = 2x + 50 (triệu đồng) C(x) Khi đó f (x) =
là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f (x) x
giảm và lim f (x) = 2 . Tính chất này nói lên điều gì? x→+
Câu 4. Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng 3 10 m , thùng tôn
hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là 2
90000 / m và giá tôn làm thành xung quanh thùng là 2
40000 / m . Hỏi người bán gạo đó cần đóng
thùng đựng gạo với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất? ĐỀ 4
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. x = 2, y = 2 − .
B. x = 2, y = 2 . C. x = 2 − , y = 2 − . D. x = 2 − , y = 2 . Câu 2.
Cho hàm số y = f (x) có bảng biến thiên như sau.
Mệnh đề nào dưới đây sai?
A. Hàm số có giá trị cực đại bằng 0 .
B. Hàm số có ba điểm cực trị.
C. Hàm số có giá trị cực đại bằng 3 .
D. Hàm số có hai điểm cực tiểu. Trang 15 Câu 3.
Cho hàm số y = f (x) xác định, liên trục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x =1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng −1.
D. Hàm số có giá trị cực tiểu bằng 1. x +1
Câu 4. Cho hàm số y =
.Mệnh đề nào dưới đây là đúng? 2x −1
A. Hàm số đồng biến trên khoảng (1;4).
B. Hàm số nghịch biến trên khoảng (1;4).
C. Hàm số đồng biến trên khoảng ( 1 − ;4).
D. Hàm số nghịch biến trên khoảng ( 4 − ; ) 1 . Câu 5.
Trong không gian Oxyz , cho hai vectơ a = (2; 4; − 2) và b = (1; − 2; 3). Tích vô hướng của hai
vectơ a và b bằng A. 22 − . B. 30. C. 6 . D. 12 − . 3x −1
Câu 6. (Sở GD ĐT Quảng Trị, năm học 2018-2019) Tìm giá trị lớn nhất M của hàm số y = trên x − 3 đoạn 0;2. 1 1 A. M = 5 −
B. M = − . C. M = .
D. M = 5. 3 3
Câu 7. Cho hàm số f (x) có đạo hàm f (x) = x(x − ) 3 1 , x
đồng biến trên khoảng nào? A. (0; ) 1 .
B. (−;0) . C. ( 1 − ; ) 1 . D. (1;+ ) . 1 1 Câu 8. Cho hàm số 3 2
y = x − x + . Giá trị cực tiểu của hàm số bằng 3 3 1 A. −1. B. . C. 0 . D. 2 . 3
Câu 9. Cho hàm số y = f (x) có đồ thị như hình vẽ sau
Hàm số đồng biến trên khoảng A. ( 2 − ;0) . B. ( 1 − ;0) . C. ( 2 − ;− ) 1 . D. (0;2) . Trang 16
Câu 10. Đồ thị hàm số nào sau đây không có tiệm cận ngang? 2 x x + 2 A. y = . B. . x +1 2 x +1 x + 2 C. 2
y = x + x −1 . D. y = . x −1
Câu 11. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 2 O x A. 3 2
y = −x + 3x + 2 . B. 3 2
y = x − 3x + 2. x + 2 C. y = . D. 4 3
y = x − 2x + 2 . x +1
Câu 12. Trong không gian Oxyz , cho hai điểm M (2; 5 − ; ) 1 , N (0;7; )
1 . Tọa độ trung điểm I của đoạn thẳng MN là
A. D(2;2;2). B. B(3; 4 − ;2) . C. C (6; 8 − ;4) . D. A(1;1; ) 1 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hình hộp ABCD A B C D
, biết điểm A(5; 2 − ;0), B(4;5; 2
− ),C(0;3;2), A(9;0;5). Gọi M là
trung điểm AA .
a) Điểm K di chuyển trên trục Ox . Đặt Q = 2 KA + KB + KC 3
+ KB + KC . Giá trị nhỏ nhất của Q bằng 6 37 .
b) Tọa độ D(1; 4 − ;4) . c) Giá trị (MB MD) 3 609 cos ; = . 609
d) AA + C D
− BC − AC = 3 29 .
Câu 2. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được
giám sát bởi bác sĩ. Biết nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t t
giờ được cho bởi công thức c (t) =
(mg / l) . 2 t +1
a) Sau khi tiêm thuốc 1 giờ thì nồng độ thuốc trong máu của bện nhân cao nhất.
b) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân có thể vượt quá 0,5 (mg / l) .
c) Sau khi tiêm thuốc 2 giờ thì nồng độ thuốc trong máu của bện nhân bằng 0, 4 (mg / l) .
d) Sau khi tiêm thuốc thì nồng độ thuốc trong máu của bệnh nhân cao nhất bằng 0,5 (mg / l) .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Một người muốn tạo một hộp đựng quà khối lăng trụ tam giác đều, không có nắp bằng cách cắt ba a
góc của một tam giác đều cạnh bằng a các đoạn bằng x, 0 x
như hình vẽ, rồi gấp lại tạo 2 a
thành khối lăng trụ tam giác đều. Thể tích khối lăng trụ lớn nhất khi x = . Tìm b . b Trang 17
Câu 2. Một cái hồ rộng có hình chữ nhật. Tại một góc hồ người ta đóng một cái cọc ở vị trí K cách bờ
AB là 2m và cách bờ AC là 8m , rồi dùng một cây sào thẳng PQ ngăn một góc của hồ để thả
bèo (như hình vẽ). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào hai bờ
AB, AC và cây cọc (kết quả làm tròn đến hàng đơn vị của mét).
Câu 3. Trong không gian với hệ trục tọa độ Oxyz . Một
khinh khí cầu từ vị trí điểm A( 1 − 6; 1
− 0;10) bay thẳng đến vị trí điểm B (24;20;0) hết 10 giờ.
Biết trạm kiểm soát không lưu đặt ở vị trí gốc toạ độ O kiểm soát được các vật thể cách trạm một khoảng tối
đa bằng 12 km. Thời gian kể từ khi trạm kiểm soát không lưu phát hiện ra khinh khí cầu đến khi khinh khí
cầu ra khỏi vùng kiểm soát là bao nhiêu phút?
Câu 4. Theo định luật II: Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ
lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật:
F = ma trong đó F là vectơ lực ( N ) , a là vectơ gia tốc ( 2
m / s ) , m(kg) là khối lượng của vật.
Muốn truyền cho quả bóng có khối lượng 0,5(kg) một gia tốc ( 2
50 m / s ) thì cần một lực đá có độ lớn là bao nhiêu?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Ở một sân bay, vị trí của máy bay được xác định bởi điểm M trong không gian Oxyz như hình vẽ. Gọi
H là hình chiếu vuông góc của
M xuống mặt phẳng (Oxy). Biết
OM = 79;(i,OH ) = 68 ;(OH,OM ) = 50 . Gọi toạ độ điểm M ( ; a ;
b c) . Giá trị của a +b + c là bao
nhiêu? (làm tròn đến hàng phần mười). Trang 18
Câu 2. Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa và các
suối nước đổ về hồ. Tính từ thời điểm 8 giờ sáng, độ sâu của mực nước trong hồ tính theo mét và 1
lên xuống theo thời gian t (giờ) trong ngày cho bởi công thức: h(t) 3 2
= − t + 5t + 24t (t 0) . 3
Biết rằng phải thông báo cho các hộ dân phải di dời trước khi xả nước theo quy định trước 5giờ.
Hỏi cần thông báo cho hộ dân di dời trước khi xả nước mấy giờ. Biết rằng mực nước trong hồ phải
lên cao nhất mới xả nước.
Câu 3. Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng
không đổi và có độ lớn bằng nhau. Hai tàu luôn giữ được lái sao cho chúng tạo với bờ cùng một
góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận
tốc dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi
tàu nào sang bờ bên kia trước?(Học sinh ghi số 1 hoặc số 2 vào ô đáp án)
Câu 4. Một người vay ngân hàng 200.000.000 đồng theo hình thức trả góp hàng tháng trong 48 tháng. Lãi
suất ngân hàng cố định 0,8% /tháng. Mỗi tháng người đó phải trả (lần đầu tiên phải trả là sau 1
tháng kể từ khi vay) số tiền gốc là số tiền vay ban đầu chia cho 48 và số tiền lãi sinh ra từ số tiền
còn nợ ngân hàng. Tính tổng số tiền lãi người đó đã trả trong toàn bộ quá trình nợ. ĐỀ 5
ĐỀ ÔN TẬP GIỮA HỌC KÌ I Trang 19
MÔN: TOÁN – LỚP 12
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Trong không gian Oxyz , tìm tọa độ của véc tơ u = 6
− i + 8 j + 4k . A. u = ( 3 − ;4;2) .
B. u = (6;8;4) .
C. u = (3;4;2) . D. u = ( 6 − ;8;4) .
Câu 2. Cho hàm số y = f (x) có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng A. 0 . B. 5 . C. 1. D. 2 . 2x −1
Câu 3. Đồ thị hàm số y =
có một đường tiện cận đứng là x + 3
A. x = 3.
B. y = 2. C. x = 3 − . D. y = −2.
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho hai véctơ u = (3;2;− ) 1 , v = (1; 4 − ;2) . Tích vô hướng
của chúng có giá trị bằng A. 13 − . B. 7 − . C. 7 . D. 13 .
Câu 5. Cho hàm số y = f (x) có bảng biến thiên như sau. Tìm đường tiệm cận ngang của đồ thị hàm số đó
A. y = 3.
B. x = 2.
C. y = 2.
D. x = 3.
Câu 6. Hàm số y = f (x) có đạo hàm 2
y = x . Mệnh đề nào sau đây đúng ?
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên (−;0) và nghịch biến trên (0;+ ) .
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên (−;0) và đồng biến trên (0;+ ) .
Câu 7. Cho hàm số y = f (x) có bảng biến thiên như sau Trang 20




