




























































Preview text:
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
BỘ ĐỀ THI CUỐI KỲ MÔN GIẢI TÍCH 1
Dành cho sinh viên trường Đại học Bách khoa Hà Nội
Biên soạn: Tài liệu HUST
ĐỀ CK GIẢI TÍCH 1 DANH SÁCH ĐỀ THI
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1) ............................................................................2
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1) ............................................................4
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 2 (Nhóm ngành 1) ............................................................................8
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1) ............................................................................9
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1) ......................................................... 10
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 4 (Nhóm ngành 1) ......................................................................... 15
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2) ......................................................................... 16
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2) ......................................................... 17
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 6 (Nhóm ngành 2) ......................................................................... 22
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 7 (Nhóm ngành 3) ......................................................................... 23
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 7 (Nhóm ngành 3) ......................................................... 24
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 8 (Nhóm ngành 3) ......................................................................... 29
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20192 – ĐỀ 1 (Nhóm ngành 1) ......................................................................... 30
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20192 – ĐỀ 1 (Nhóm ngành 1) ......................................................... 31
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 1 (Nhóm ngành 1) ......................................................................... 35
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 1 (Nhóm ngành 1) ......................................................... 36
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 2 (Nhóm ngành 1) ......................................................................... 40
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 1 (Nhóm ngành 1) ......................................................................... 41
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 1 (Nhóm ngành 1) ......................................................... 42
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 2 (Nhóm ngành 1) ......................................................................... 46
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 2 (Nhóm ngành 1) ......................................................... 47
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 3 (Nhóm ngành 1) ......................................................................... 48
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 3 (Nhóm ngành 1) ......................................................... 49
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 4 (Nhóm ngành 1) ......................................................................... 53
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 1
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 4 (Nhóm ngành 1) ......................................................... 54
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 5 (Nhóm ngành 2) ......................................................................... 55
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 5 (Nhóm ngành 2) ......................................................... 56
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 6 (Nhóm ngành 2) ......................................................................... 60
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 7 (Nhóm ngành 3) ......................................................................... 61
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 7 (Nhóm ngành 3) ......................................................... 62
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 8 (Nhóm ngành 3) ......................................................................... 65 (TaiLieuHust, 2022)
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 2
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: 1 ln(1 + x) x a) lim . x 0 → x 3 b) x y lim . 6 2 ( , x ) y ( → 0,0) 2x + 3y
Câu 2 (1 điểm). Tính gần đúng nhờ vi phân 2 2 A = 2,02 + 3,04 + 3 . 2 x
Câu 3 (1 điểm). Ch ng minh r ứ ằng cos x 1− , x 0 . 2
Câu 4 (1 điểm). Tính thể tích khối tròn xoay khi quay hình giới hạn bởi các đường 2
y = x − 3x
và y = 0 quanh trục Oy một vòng. −1 Câu 5 (1 điểm). Tính 2 2
2x−3 + 1− x dx.
Câu 6 (1 điểm). Hàm số 3
f (x) = x + x c là có hàm ngượ
y = g (x) . Tính g (2) . 2 2
z z 3 z Câu 7 (1 điể 1 m). Tính P = + + với z = . 2 2 x y y y (x + y )3 2 2
Câu 8 (1 điểm). Không khí được bơm vào một quả bóng bay hình c u vói t ầ ốc độ 3 100 cm / s . Tính tốc độ a bán kính qu tăng lên củ
ả bóng khi bán kính quả bóng bằng 50 cm.
Câu 9 (1 điểm). Tính 2 cot x dx . 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 3
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1) ln(1+ x ) 1 ln x + Câu 1: ln(1 x) x L = lim =lim x e . x 0 → x 0 x → ln(1+ x) ln(1+ x) ln ln 1+ − 1 Xét giới hạn x x K = lim = lim x 0 → x 0 x → x ln(1 + x) x→0 + x + ) Vì lim −1 = 1−1 = 0 ln(1 ) ln(1 x , nên ln 1+ − 1 ~ − 1 . x→ 0 x x x ln(1 + ) x −1 1 − 2 x + o( 2 x ) ln(1 + x) − x = lim x K (VC ) B = lim = 2 lim (Khai triển Maclaurin) 2 x→ 0 x→ 0 x x 2 x→ 0 x −1 2 x −1 2 = lim = 2 x 0 → x 2
Giới hạn đã cho bằng K 1/2 L e e− = = . 3 b) x y f ( , x y) = , ( , x y) 0. 6 2 2x + 3y +) Chọn M ( 3 , a a
. Khi a → 0 thì M ( 3 a, a → (0,0) . 1 ) 1 ) a a 1
Ta có: f (M )= f (a,a ) 3 3 3 = = 1 6 6 2a + 3a 5 f ( 1 M → khi M → (0,0) (1) 1 ) 1 5 +) Chọn M ( 3 − ,
b b . Khi b → 0 thì M ( 3 − , b b → (0,0). 2 ) 2 ) (− ) b b 1 −
Ta có: f (M )= f (−b,b ) 3 3 3 = = 2 6 6 2(−b ) + 3b 5 − f ( 1 M → khi M → (0,0) (2) 2 ) 2 5 3 x y
Từ (1) và (2) f (x, y) không cùng tiến tới một giá trị khi (x, y) → (0,0) lim 6 2
(x,y )→(0,0) 2x + 3y không tồn tại.
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 4
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST Câu 2. Xét hàm số 2 2 f ( , x ) y =
x + y + 3 . Ta có: x y x = 2, x = 0,02 f ( , x ) y , f = ( , x ) y = . Chọn 0 . x y 2 2 2 2 x + y +3 x + y +3 y = 3, y = 0,04 0
Áp dụng công thức tính g ần đúng: 2 2 A =
2,02 + 3,04 + 3 = f ( x + ,
x y + y f x , y + f
x , y x + f
x , y y 0 0 ) ( 0 0) x ( 0 0) y ( 0 0 ) 1 3 = f (2,3) + f + f = + + = x (2, 3) 0, 02 y (2, 3) 0, 04 4 0,02 0, 04 4,04 2 4 Vậy A 4,04 . 2 2 x x
Câu 3. Chứng minh: cosx 1− , x 0 cosx + − 1 0, x 0. 2 2 2 x Xét
f (x) = cos x +
−1 trên [0;+). Ta có: f (x) = −sin x + ,
x f (x) = − cos x +1 0, x 0 2 f ( x) ng bi đồ ến trên [0; ) f (x) f + (0) = 0, x 0 f ( x) ng bi đồ ến trên [0;+ )
f (x) f (0) = 0, x 0
Từ đó ta có được điều phải chứng minh. Dấu bằng xảy ra khi x = 0
Câu 4. Quay miền D là hình ph ng gi ẳ ới hạn bởi các đường 2 y = x − 3 ,
x y = 0, x = 0, x = 3 quay quanh trục
Oy thì thu được vật thể có thể tích là: 3 V = 2 x
( 2x −3x)dx =2 x ( 2
3x − x )dx (vì 0 2
x − 3x 0, x [0,3]) 3 4 3 x 27 = 2 ( 2 3 3x − x ) 3 dx = 2 x − = (đvtt) 0 4 2 0
Câu 5. Điều kiện: 3 2 2 2
2x − 3 0 x
1− x 0 1− x = x −1 , do đó: 2 −1 − 2 2
I = 2x − 3 + 1− x d
x = 2x − 3 + ( 2 x − 1) 12 d x 1 1 3 = 2x − 3 dx + dx = (2x − 3) + ln ( 2
x + x − 1 + C 2 ) − 3 x 1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 5
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST Câu 6. Ta có: 2 f (x) =3x 1 + . Với 3
y = 2 x + x = 2 x =1. 0 0 0 0 1 1 1
Vì y = g(x) c c là hàm ngượ ủa 3
f (x) = x + x nên: g ( y ) = = = . 0 f ( x f (1) 4 0 ) Vậy 1 g (2) = . 4
Câu 7. Điều kiện xác định P là y 0 . 2 2 2 z 12x − 3y
Do sự đối xứng của $x, y$ trong hàm z(x, y) nên: = . 2 x (x + y )7 2 2 2 2 2 2 2 2 z z 3 z
12x − 3y + 12 y − 3x 3 −3y P = + + = + 2 2 x y y y ( + )7 y x y ( x + y )5 2 2 2 2 9 9 = − = 0,y 0. (x + y )5 (x +y )5 2 2 2 2
Câu 8. Gọi thể tích của quả bóng tại thời điểm t( s) là V t ( 3 ( ) cm ) .
Theo bài ra, tốc độ bơm không khí vào quả bóng là 3 V t = ( 3 100 cm / s ( ) 100 cm / s) .
Tại thời điểm t nào đó, R (t = 50( cm) . 0 ) 0 4 Ta có: 3 = V (t) = ( ( R t)) . Lấy ạ
đ o hàm hai vế theo t , ta có: 2
V (t) 4 (R(t)) R (t) 3
Tại t =t , ta có: V (t ) = 4 R (t ) 2 R (t ) 2
100 = 4 (50) R t 0 0 0 0 ( 0 ) R ( 100 1 t = = (cm / s). 0 ) 2 4 (50) 100
Khi bán kính quà bóng bằng 50 cm, tốc độ a bán kính qu tăng lên củ ả bóng khi bán kính là 1 (cm / s) . 100 /2 Câu 9. I = cot x dx . 0 /2 /2 /2 sin x cos x sin x +cos x Xét L =
( tan x + cot x)dx = + d x = dx . 0 0 0 cos x sin x sin x cos x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 6
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
Đặt t = sin x − cos x dt = (cos x + sin x)dx . 2 − t 2 2 1
t = (sin x −cos ) x 1
= −2sin xcos x sin xcos x = . 2 Đổi cận: - Khi x 0+ → thì t → 1
− ; Khi x → thì t →1 2 1 dt 0 2 1 2 L = = dt + dt −1 2 −1 2 0 2 1− t 1− t 1 − t 2 0 2 B 2 = lim dt + lim dt + A ( → −1) A 2 B 1− 0 2 1− t → 1− t 0 B
= lim ( 2 arcsin )t + lim( 2 arcsin )t + − A→(−1) B 1 → A 0 − = lim (− 2 arcsin ) A + lim ( 2 arcsin ) B = − 2 + 2 = 2 A ( 1)+ B 1− → − → 2 2 /2 Giờ xét cot x dx , với f ( )
x = cot x 0 liên tục trên 0, . 0 2 + + x 0 → x 0 cos x 1 → 1 1 cot x = ~ ~ = , 1/2 sinx sinx x x /2 1 mà /2 1 dx hội tụ (vì = (0,1) cot x dx hội tụ. 1/ 2 0 x 0 2 Đổi biến t = − x x = − t , ta có: 2 2 /2 0 /2 /2 cot x dx = cot − t (−dt) = tan t dt = tan x d . x 0 /2 0 0 2 /2 /2 1 1 cot x dx =
( tan x + cot x )dx = L = . 0 0 2 2 2
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 7
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 2 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: 1 x x − a) e 1 lim . x→ 0 x 4 b) xy lim 2 8
( x, y)→(0,0) 4x + 3y
Câu 2 (1 điểm). Tính gần đúng nhờ vi phân 2 2 A = 4,03 + 2, 02 + 5 . 2 x
Câu 3 (1 điểm). Ch ng minh r ứ ằng x e 1+ x + , x 0. 2
Câu 4 (1 điểm). Tính thể tích khối tròn xoay khi quay hình giới hạn b ng ởi các đườ 2
y = x − 4x
và y = 0 quanh trục Oy một vòng. 1 −
Câu 5 (1 điểm). Tính 2 2 4
− −3x + 1− x dx .
Câu 6 (1 điểm). Hàm số 5
f (x) = x + x c là có hàm ngượ
y = g (x) . Tính g (2) . 2 2
z z 5 z Câu 7 1
(1 điểm). Tính P = + + với z = . 2 2 x y y y (x +y )5 2 2
Câu 8 (1 điểm). Không khí được bơm vào một quả bóng bay hình c u v ầ ới tốe độ 3 200 cm / s . Tính tốc độ a bán kính qu tăng lên củ
ả bóng khi bán kính quả bóng bằng 60 cm.
Câu 9 (1 diểm). Tính 2 tan x dx . 0
Cách giải tham kh s ảo đề ố 1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 8
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: a) x − lim . x → sin x 2 2y ln b) x lim . 2 2
(x,y )→ (1,0) ( x− 1) + y
Câu 2 (1 điểm). Phương trình 3 2 5
x + 3x y + y − 5 = 0 xác định hàm ẩn y = y(x) . Tính y (1) . 2x
Câu 3 (1 điểm). Tính đạo hàm của hàm số y = arctan , x 1 . 2 1− x
Câu 4 (1 điểm). Tìm khai triển Maclaurin của y = ln(1+ 2x) đến 3 x . Câu 5 x
(1 điểm). Tìm các tiệm cận c ủa đồ th hàm s ị ố y = . x e +1
Câu 6 (2 điểm). Tính các tích phân sau: a) tan(2 ) x dx . b) + dx . x + ( 2 0 ( 3) x − x+1)
Câu 7 (1 điểm). Quay đường 3 2 3 2 x +
y = 4 quanh trục Ox một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8 (1 điểm). Tìm cực tr c ị ủa hàm số 3 3 2
z = x + y − (x + y) .
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 9
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1) Câu 1. x − 1 1 lim = lim = = 1
− . (dạng vô định nên ta dùng L’Hospital) x → sin x x → cos x cos Vậy x − lim = −1 . x → sin x 2 2y ln x b) Đặt f ( , x y) = 2 2 (x 1 − ) + y 2 2 y ln1
+) Nếu x =1 và y → 0 thì f ( , x ) y =
= 0 → 0 khi y → 0 . (1) 2 2 0 + y
+) Nếu x 1 và (x, y) → (1,0) thì: 2 2 2y ln x ln x 2y (x −1) lim = lim lim 2 2 2 2 (x, y) ( → 1,0) ( x, y) ( → 1,0) (x, y) ( → 1,0) (x 1 − ) + y x 1 − (x 1 − ) + y x 1 x 1 x 1 Ta có: VCB lnx lnx x − 1 lim = lim = lim = 1 (x ,y )→(1,0) x 1 → x 1 x 1 − x 1 → − x 1 − 2 2 2 2y (x 1 − ) 2 | (x 1 − )y | (x 1 − ) + y 0 = | y | | y | |
= y | , mà lim | y |= 0 2 2 2 2 2 2 (x −1) + y ( x −1) + y (x − 1) + y ( x, y)→(1,0) 2 2 y ( x 1 − ) 2 − lim = 0 theo nguyên lý kẹp 2 y ( x 1) = 2 2 lim 0
(x,y )→(1,0) (x −1) + y 2 2
(x ,y )→(1,0) ( x 1) + y x 1 x 1 2 2y ln x lim = 1.0 = 0 (2) 2 2 ( x , y) (
→ 1,0) (x −1) + y x 2 Tù y x (1) và (2) 2 ln lim = 0 2 2 ( , x ) y (
→ 1,0) (x −1) + y Câu 2. +) Với x =1 thì 5 5
1+ 3y + y − 5 = 0 y + 3y = 4 y =1 y(1) =1. Theo bài ra: 3 2 5 x + 3x y( )
x +[ y(x)] −5 = 0
+) Lấy đạo hàm hai vế theo x , ta có: 2 2 4
3x + 6xy(x) + 3x y (x) + 5y (x)[ y(x)] = 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 10
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST Thay x =1 , ta có: 4
3 6y(1) 3y (1) 5y (1)[y(1)] 0
3 6 3y (1) 5y + + + = + + + (1) = 0 ( do ( y 1) = 1) − 9 y (1) = 8 Vậy 9 − y(1) = 8
Cách giải khác: Đặt 3 2 5
F(x, y) = x + 3x y + y − 5. − − + ( , ) x xy F x y x ( 2 3 6 ) Ta có: y ( ) x = = . (*) 2 4 F ( , x ) y 3x + 5 y y Với x =1 thì 5 5
1+ 3y + y −5 = 0 y + 3y = 4 y =1 y(1) = 1. Thay ( − 3 +6) 9 −
x = 1, y = 1 vào (*), ta có: y(1) = = . 3 + 5 8 2( 2 1− x ) 2
− 2x (−2x) 2x + 2 − − + (1 x )2 (1 x )2 2 2 2( 2 x )1 2 Câu 3. y = = = = , x 1. 2 4 2 2x x + 2x + 1 ( + x + + )2 2 2 x 1 1 1 1− x (1− x )2 2 2 Vậy 2 y = ,x 1 . 2 x +1 2 3 x x
Câu 4. Ta có khai triển Maclaurin: + x = x − + + o(x )3 ln(1 ) . 2 3
Khi x → 0 thì 2x → 0 , thay x bởi 2
x , ta có khai triển Maclaurin của y đến cấp 3 là: 2 3 (2 ) x (2 ) x y = ln(1 + 2 ) x = 2 x − + + o( 3 (2 ) x ) 2 8 3
= 2x −2x + x + o( 3x ) 2 3 3
Vậy khai triển cần tìm là 8 2 3
y = 2 x − 2x + x + o ( 3 x ). 3 Câu 5.
+) Tập xác định D =
Đồ thị hàm số không có tiệm c ng. ận đứ +) Khi L Hospital x →+ : x 1 lim y = lim = lim = 0 (Dạng vô định) x →+ →+ e +1 x x x x →+ e
y = 0 là tiệm cận ngang bên phải c ủa đồ thị hàm số.
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 11
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST +) Khi x → − : x x y 1 e 1 + x a = lim = lim = lim
= 1 0 ( vì lim e = 0 Khi x → − không có tiệm cận x →− ) x →− x →− x x x →− 0+ 1 ngang. x x xe x
b = lim ( y − a ) x = lim − x = lim = lim dạng x x x ( x x e +1 x e + 1 x 1+ e− →− →− →− →− L'Hospital 1 = lim = 0 ( do lim x e− = + x →− ) x x −e− →−
y = x là tiệm cận xiên bên trái của đồ thị hàm số.
Vậy đồ thị hàm số không có tiệm c ng, và có ận đứ
y = 0 là tiệm cận ngang bên phải, y là
tiệm cận xiên bên trái. Câu 6. sin(2 ) x 1 − 2 − sin(2 ) x d x 1 − ( d cos(2 ) x ) 1 − ) a tan(2 ) x dx = dx = = = ln | cos 2x | +C cos(2x) 2 cos(2x) 2 cos(2x) 2 Vậy 1 − tan(2 ) x dx = ln | cos 2 x | + . C 2 b) + dx A dx = lim 0 ( x +3)( 2 x − x + ) A→+ 0 1 ( x +3)( 2 x − x + ) 1 A 1 1 1 2x 1 − 7 1 lim d = − + x 2 2 A →+ 0 13 x + 3 26 x −x +1 26 1 3 x − + 2 4 A 1 2 + ln x − x +1 x − ln | x 3 | 7 2 2 = lim − + arctan A →+ 13 26 26 3 3 2 0 2 ln A − A + 1 ln | A+ 3 | 7 2 A−1 ln 3 7 = lim − + arctan − + A →+ 13 26 13 3 3 13 78 3
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 12
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 2 1 | A 1| 7 2 A 1 ln 3 7 + − = lim ln + arctan − + 2 A →+ 26 A − A 1 + 13 3 3 13 78 3 1 7 ln 3 7 14 ln 3 = ln1+ − + = − 26 13 3 2 13 78 3 39 3 13 14 ln 3
Vậy tích phân suy rộng cần tính bằng − . 39 3 13 2 2 3 3 Câu 7. x y 3 2 3 2 x + y =4 + 1 = 2 2 3 =
Tham số hoá đường cong: ( x t) 8cos t (0 t 2 ) 3 y (t) = 8sin t
Do tính đối xứng qua trục Ox và trục Oy , diện tích vật thể cần tính bằng 2 lần diện tích vật thể c, khi quay ph thu đượ ần ứng với 0 t quanh trục Ox. 2 Diện tí ch c c ần tính là: /2 = y t ( ' 2 2 | ( ) |
x (t) )2 + ( y (t) )2 /2 dt = 4 8sin t ( 2
− 4sin t cos t )2 + (24cost sin t )2 3 2 2 dt 0 0 /2 = 768
sin t sin t cos t (cos t + sin t ) /2 3 2 2 2 2 4 dt = 768
sin t cost dt 0 0 /2 /2 768 768 4 5 = 768
sin t d(cost ) = sin t = (dvdt) 0 5 5 0
Vậy diện tích cần tính là 768 (dvdt). 5 Câu 8. Tập xác định: D = Tìm điểm dừng: x = − y { = = 2 x y 0 2 2 2
z = 3x − 2(x + y) = 0 y = x 3x = 0 x 2 2 4
z = 3y − 2(x + y ) = 0
x − x − y = x = y x = y = y 3 2 2 0 { 2 3 3x − 4x = 0 4 4
hàm số có 2 điểm dừng là M , và M (0,0) . 1 3 3 2
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 13
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST +) Ta có:
A = z = 6 x− 2, B = z = 2
− , C = z = 6 y− 2 xx xy yy 2
= B − AC = 4− (6x −2)(6y − 2). 4 4 - Tại điểm M , , ta có = − và 1 32 0 A = 6 0 3 3 − 64 z(x, y) t c
đạ ực tiểu tại M (1,1), z = = . 1 z M CT ( 1 ) 27
- Tại điểm M (0,0) . 2 Xét 3 3 2 z
= z(0 + ,x0 + y
) − f (0,0) = ( ) x + ( y
) −(x + y) Khi x = − y
→ 0 ta có: z = 0, điều này chứng tỏ z (M = z M , với 2 ) ( 3) M ( x
,−y) thuộc lân cận của M hàm số không đạt cực tr t ị ại M 3 2 2 4 4 Vậy hàm số t c
đạ ực trị duy nhất tại m m là ột điể M ,
(cực tiểu), giá trị cực tiểu là 1 3 3 −64 z = = . CT z (M1 ) 27
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 14
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 4 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: a) 2 x − lim . x → cosx 2 3 2x ln y b) lim . 2 2
(x,y )→(0,1) x + ( y− 1)
Câu 2 (1điểm). Phương trình 4 3 5
x + 4xy + 3 y − 8 = 0 xác định hàm ẩn y = y(x) . Tính y (1) . 2x
Câu 3 (1điểm). Tính đạo hàm của hàm số y = arcsin , x 1. 2 1+ x
Câu 4 (1 điểm). Tìm khai triển Maclaurin của y = ln(1−3x) đến 3 x .
Câu 5 (1 điểm). Tìm các tiệm cận c ủa đồ th hàm s ị ố x y = . 2 x e + 1
Câu 6 (2 điểm). Tính các tích phân sau: a) cot(3x)dx . b) + dx 0 ( x + 4) ( 2 x + x +1)
Câu 7 (1 điểm). Quay đường 3 2 2 3 x +
y = 9 quanh trục Ox một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8 (1 điểm). Tìm cực tr c ị ủa hàm số 3 3 2
z = x + y + (x + y) .
Cách giải tham kh s ảo đề ố 3
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 15
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2) 2 1
Câu 1 (1 điểm). Tìm giới hạn lim − . 2 0 x x→ e −1 x 3 = +
Câu 2 (1 điểm). Cho hàm số x t t
y = f (x) xác định bởi . Tính
f (x), f (x) . 2 4 y = 2t + 3t
Câu 3 (1 điểm). Tìm cực tr c ị ủa hàm số 2 3 y = x(x − 3) . 2 2
Câu 4 (1 điểm). Ch ng minh r ứ
ằng vói mọi x 0 , ta có ln 1+ . x 2 + x 6 6 6 + ++ Câu 5 1 2
(1 điểm). Tìm giới hạn n lim . 7 n→ n
Câu 6 (2 điểm). Tính các tích phân sau: 3 sin xdx a) . sin x + cosx
b) 3arccot 3 − x dx . 2 Câu 7 + (1 điể d
m). Tính tích phân suy rộng x . x ( 4 1 3x − 2)
Câu 8 (1 điểm). Tính diện tích mặt tròn xoay tạo bởi đường tròn 2 2
x + ( y − 2) = 1 quanh trục Ox .
Câu 9 (1 điểm). Cho hàm số:
x arctan 3x, x 0 f (x) = 3 x
ae + bsin , x x 0
Tìm a và b để hàm số f (x) khả vi tại x = 0 .
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 16
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2) 2 2 1 2 x x −e 1 + Câu 1. L = lim − = lim 2 x → e 1 − x → ( 2 0 0 x x x e 1 − )x Dùng VCB: ( → x e − )x 0 2 1
~ 2x cho mẫu số, ta có: 2 VCB 2 x x − e + 1 L = lim (dạng 0 ) x→ 0 2x x 0 L H ospital 2 2 −2 x e L Hospital 2 x 0 − − = 4e 4e lim 0 (dạng ) = lim = = −1. x 0 → 4x 0 x 0 → 4 4
Vậy giới hạn cần tính bằng −1.
Cách giải 2: Dùng khai triển Maclaurin: 2 (2x) 2x − 2x + + o ( 2x) 2x −( 2 x e − )1 2! L = lim = lim (Khai triển Maclaurin) → ( 2 0 x x e −1)x x→ 0 2x x 2 2 − x − o( 2 x ) 2 2 − x = lim = lim = −1. 2 2 x 0 → x 0 2x → 2x Câu 2. x = x(t) Ta có công thức: Với
Xác định hàm y = f (x) y = y(t) y (t)
y (t )x (t) − y (t)x (t) f ( ) x = và f ( ) x = . 3 x (t) x (t)
Áp dụng công thức trên ta có: 3 + dy y (t) 4t 12t f ( ) x = = = = 4 .t 2 dx x (t) 1+ 3t 2 d y d dy d 1 d 1 4 f ( ) x = = = (4 ) t = (4 )t = 4 = . 2 2 2 dx dx dx x ( ) t dt x ( ) t dt 1 +3t 1 +3t Câu 3.
+) Tập xác định: D =
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 17
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST +) Sự biến thiên: − ( 2 x(x 3) ) 2
(x − 3) + 2(x − 3)x x − 3+ 2x y = = =
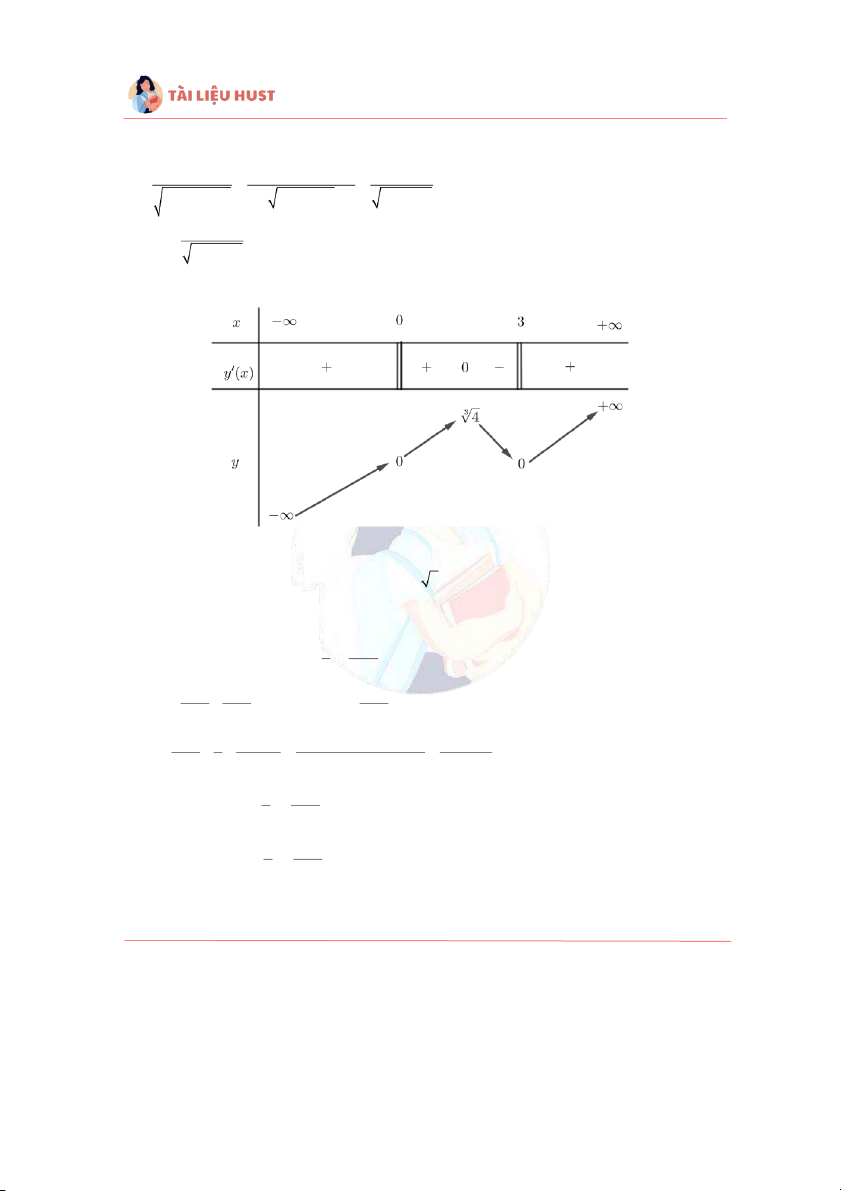
, x 0, x 3. ( 2 3 x x )2 3 2 4 3 2 x ( x −3) x ( x − − 3) ( 3) $ − + x 3 2 x y = 0 = 0 x= 1. 3 2 x (x − 3) Lập bảng biến thiên:
Dựa vào bàng biến thiên, ta kết luận hàm số có 2 điểm cực trị: - Hàm số t c
đạ ực đại tại điểm 3 x = 1, y = y(1) = 4 . CD - Hàm số t c
đạ ực tiểu tại điểm x = 3, y = y(3) = 0 . CT Câu 4. Xét hàm số 2 2 f ( ) x = ln(1 + ) − trên(0, + ) x 2 + x x + 2 2 2 f ( ) x =ln −
=ln( x +2) −ln x − ( do x 0) x 2+ x 2+ x 2 1 1 2
(x + 2)x − (x + 2) + 2x −4 f ( ) x = − + = = 0,x 0. 2 2 2 x + 2 x (x + 2) x(x + 2) x(2 + x ) 2 2 lim f ( ) x = lim ln 1+ − = + + + x 0 → x 0 → x 2 + x 2 2 lim f ( ) x = lim ln 1+ − = ln(1+ 0) − 0 = 0 x →+ x →+ x 2+ x Ta có bảng biến thiên:
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 18
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
Từ bảng biến thiên, suy ra: f (x) 0,x 0 2 2 ln 1+ − 0,x 0 x 2+ x 2 2 ln 1+ , x 0 (đpcm) x 2 + x Câu 5. 6 6 6 6 6 6 6 6 6 1 + 2 ++ n 1 1 + 2 ++ n 1 1 2 n L = lim = lim = lim + ++ 7 6 n → n → n n n n → n n n n 6 1 n k =lim n→ n n k =1 1 = f (x)d , x trong đó 6
f (x) = x hàm liên tục, khả tích trên [0,1]. 0 1 7 1 x 1 6 = x dx = = . 0 7 7 0
Vậy giới hạn cần tính bằng 1 . 7 Câu 6.
Giải: sin x + cos x = 2 sin x +
. Đặt t = x + x = t −
dx = dt . Tích phân cần tính trở 4 4 4 thành: 3 3 1 1 sin t − sint − cost 4 2 2 I = dt = dt 2 sin t 2 sin t 3 2 2 3 3
1 sin t −3sin t cos t +3sin t cos t −cos t 1 2 2 cos t = dt =
sin t − 3sin t cost + 3cos t − dt 4 sin t 4 sin t 1 1 1 3 3 3 cost =
− cos 2t − sin 2t + + cos 2t − ( 2 1 −sin t ) dt 4 2 2 2 2 2 sin t 1 3 cost =
2 + cos 2t − sin 2t −
+cos tsin t dt 4 2 sint
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 19
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 1 cos t 1 1 1 =
2 + cos 2t −sin 2t − d t =
2t + sin 2t + cos 2t −ln | sin t | + C 4 sin t 2 2 2 2 Thay t = x + 4 3 sin xdx 1 1 1 = 2x+ + sin 2x+ + cos 2x+ − ln sin x + + C sin x + cos x 4 2 2 2 2 2 4 x
cos(2x) −sin(2x) 1 = + − ln sin x + + C 1 2 8 4 4 b) Xét nguyên hàm
arccot 3 − x dx = arccot 3− x d(x − 4)
= (x − 4)arccot 3− x − (x − 4)d(arccot 3− x) −1 −1
= (x− 4)arccot 3− x − (x− 4) dx 2 1 +( 3 − x) 2 3 − x −1
= (x− 4)arccot 3− x −
dx = (x− 4) arccot 3− x − 3− x + C. 2 3 − x 3 3 − −
arccot 3 − x dx =[(x − 4)arccot 3 − x − 3 − x] = − −1 =1 2 2 2 2 Câu 7. 1 f ( ) x =
là hàm dương và liên tục trên [1, +) . x( 4 3 x −2) + dx
là tích phần suy rộng loại 1 với điểm bất thường + x ( 4 1 3x − ) 2 1 x →+ 1 1 = , mà + 1 dx hội tụ (do = 5 1) x( ~ 4 3 x − 2) 4 5 x 3x 3x 5 1 3 x + dx
hội tụ theo tiêu chuẩn so sánh. 1 x ( 4 3x − ) 2
Câu 8. Tham số hoá đường tròn 2 2
x + ( y − 2) = 1: x = cost (0 t 2 ). y = 2 + sin t
Diện tích mặt tròn xoay tạo bởi đường tròn 2 2
x + ( y − 2) = 1 quanh trục Ox là: 2 2 | = y(t) |
(x (t))2 +(y (t))2 2 2 2 dt = 2
|2 + sin t | (−sin t) + (cost) dt 0 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 20
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 2 2 2 = 2
(2+ sin t)dt ( vì 2 + sin t 0) = 2 (2t + cos t) = 8 ( dvdt ) 0 0 Câu 9.
Để hàm số f (x) khả vi tại x = 0 thì điều kiện cần là f (x) liên tục tại x = 0 , tức là: lim f ( ) x = lim f ( )
x = f (0) lim (
x arctan 3 x) = lim ( 3 x
ae + bsin x = + − + − ) 0 x →0 x →0 x →0 x →0 0
0 = ae + b sin 0 = 0 a = 0.
x arctan 3x , x 0,
Với a = 0 thì f ( ) x = s b in , x x 0 f ( ) x − f (0)
x arctan 3 x −0 x arctan 3 x x 3 x lim = lim = lim = lim = lim 3 = 3. + + + + + x →0 − x x 0 → x x →0 x x 0 → x x 0 0 → f ( ) x − f (0) bsin x −0 sin x lim = lim = b lim = b.1= b − − − x →0 − x →0 x →0 x 0 x x a = 0 a = 0
f (x) khả vi tại x = 0 f ( ) x − f (0) f ( )
x − f (0) lim = lim 3 = b + − x 0 → − x 0 x 0 → x − 0
Vạy (a,b) = (0, 3).
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 21
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 6 (Nhóm ngành 2) 1 3
Câu 1 (1 điểm). Tìm giới hạn lim − . 3 0 x x→ x e − 1 3 = + Câu 2 x 3
(1 điểm) Cho hàm số t t
y = f (x) xác định bởi . Tính
f (x), f (x) . 5 y = 5t −t
Câu 3 (1 điểm). Tìm cực tr c ị ủa hàm số 2 3 y = x (x − 3) . x + 1 2
Câu 4 (1 điểm). Chứng minh rằng với mọi x 1 , ta có ln .
x − 1 x − 1 5 5 5 + ++ Câu 5 1 2
(1 điểm). Tìm giới hạn n lim . 6 n→ n
Câu 6 (2 điểm). Tính các tích phân sau: 3 cos x dx a) . sin x + cosx b) 2 arctan 3− xdx . 1 Câu 7 + (1 điể d
m). Tính tích phân suy rộng x . x ( 4 1 2 x −1)
Câu 8 (1 điểm). Tính diện tích mặt tròn xoay tạo bởi đường tròn 2 2
x + ( y + 2) = 1 quanh trục Ox .
Câu 9 (1 điểm). Cho hàm số: x sin 3x, x 0 f ( x) =
a2x +barctan , x x 0
Tìm a và b để hàm số f (x) khả vi tại x = 0 .
Lời giải tham kh s ảo đề ố 5
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 22
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 7 (Nhóm ngành 3) Câu 1 (1 điể x − x m). Tính cos lim .
x →+ x − sin x −1
Câu 2 (1 điểm). Dùng vi phân tính gần đúng 3 7,988 .
Câu 3 (1 điểm). Tính hoặc xét sự phân kỳ + −x e x dx . 1
Câu 4 (1 điểm). Tính 3 x e sin(2x)dx . 0
Câu 5 (1 điểm). Cho 2 ( , ) xy z x y = e . Tính 2 d z .
Câu 6 (1 điểm). Tìm giá tr l
ị ớn nhất, giá tr bé nh ị ất của hàm số 2 2
z = 3x − 4 y trong miền đóng: 2 2 x y + 1. 4 3
Câu 7 (1 điểm). Tính 2 2
1− x − y dx dy , trong đó: 2 2
D : x + y 1, x 0, y 0 . D 1 x = 3 Câu 8 −
(1 điểm). Tìm các tiệm cận c ủa đồ th hàm s ị ố t 8 2t y = 3 t −8 Câu 9
(1 điểm). Tính arcsin x 18 2 + . − 1 sin x dx | | + 2 1 x e y Câu 10 x
(1 điểm) Tính z (x;y ) biết arccot , 0 = x z( ; x y) x 0 , x = 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 23
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 7 (Nhóm ngành 3) x →+
Câu 1. Vì cos x b ịchặn bởi 1 (cos x − ) x ~ (− ) x x →+
Tương tự, vì (−sin x −1) bị chặn bởi 2 (x − sin x −1) ~ x VCL cos x − x − x lim = lim = −1.
x→+ x − sin x −1 x→+ x
Vậy giới hạn cần tính bằng 1 − . Câu 2. 3 3
A = 7,988 = 8 − 0,012 Chọn x = 8, x
= −0,012 . Xét hàm số 3 f ( )
x = x trên (0, +) . 0 1 f x x f = ( 1 1 ( ) , 0 x = = . 0 ) 3 2 3 2 x 12 3 3 8
Áp dụng công thức tính gần đúng nhờ vi phân: 1 3
A = 7,988 = f ( x + x f x + f x x = 8 + ( 0 − ,012) = 1,999 0 ) ( 0) ( 0) 3 12 Vậy 3 A = 7,988 1,999 . − − Câu 3. − − − − − − x x e x x = x ( x e − ) x = e − x − ( x −e ) x x 1 d d
dx = −xe − e + C = + C . x e A + − − − − Ta có: A − x − x 1 x 1 A 2 e x dx = lim e x dx = lim = lim + . 1 →+ 1 x A A A→+ A e →+ e e 1 − − +) Xét giới hạn: 1 A lim A A →+ e 1 − lim = 0 (do lim A e = + ) A A→+ e A →+ + − 2 x 2 2 e x dx = 0 + =
tích phân đã cho hội tụ và bằng . 1 e e e Câu 4. 3x 3x 3x e e e 3x I =
e sin(2x )dx = sin(2x)d = sin(2x) − d(sin(2x)) 0 0 0 3 3 3 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 24
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 2 − 3x 2 = 0− cos(2 )d = cos(2 )d ( 3x e x x x e ) 0 0 3 9 3 −2 − 3 e x 2 3x 2 2 4 3 = cos(2x)e + e d(cos(2x)) x = −
e sin(2x)dx 0 0 9 9 9 9 0 3 3 2 2e 4 2 2e − − I = − I I = . 9 9 13 3
Vậy tích phân cần tính bằng 2 2e − . 13 Câu 5. 2 2 2 xy z y e , z = = 2 xy xye x y 2 2 2 2 2 4 xy xy 3 xy xy 2 2 z
= y e , z = z = 2ye
+ 2y xe , z = 2xe + 4 xy xx xy yx yy x y e 2 2 2 d z = z x + z x y + z y x d x 2 x d y d y d y 2 xy = + ( 2 2 xy xy + ) ( 2 2 4 2 3 xy 2 2 xy y e x ye y xe y + xe + x y e ) 2 d 2 2 2 dxd 2 4 dy Rút gọn lại, ta có: = + ( + ) + ( + ) 2 2 4 2 3 2 2 2 d d 4 4 d d 2 4 d xy z y x y y x x y x x y y e . 2 2 y x 4 1− 2 2 2 x y 3
Câu 6. Với điều kiện x 4 + 1 2 2 4 3 x y 3 2 y 3 1− 4 2 + x ) Ta có: 2 2 2 2
z = 3x − 4y 3x − 4 3 1−
6x −12 0 −12 = 1 − 2 4 2 2 x y + =1 x = 0 Đẳng thức xảy ra 4 3 = 2 y 3 x = 0 2 +) Ta có: 2 2 y 2 2
z = 3x − 4 y 3 4 1−
− 4y = 12 − 8y 12 − 0 = 12 3 2 2 x y + =1 x = 2
Đẳng thức xảy ra 4 3 y = 0 2 y = 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 25
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
Kết luận: Trên miền đã cho thì:
- Giá tr ịnhỏ nhất của z là −12 , đạt được tại (x, y) = (0, 3). - Giá tr l
ị ớn nhất của z c t
là 12, đạt đượ ại (x, y) = ( 2 ,0) .
Câu 7. D là miền được g ạch chéo như hình bên. x = r cos Đổi biến | J |= r . y = r sin − Miền 0
D trở thành E : 2 0 r 1 0 1 2 2 2 2 I =
1− x − y dx dy =
1− r |J | d dr = d 1− r r dr D E − 0 r 1 = 0 1 1 − − 2 = − r ( 2 − r ) 0 1 2 = − = = − ( 2r )3 0 1 d 1 d 1 1 d d − 0 − 6 2 2 2 2 3 2 r 0 =
Vậy tích phân cần tính bằng . 6 Câu 8.
+) Khi t → t (với t 2 ) thì limx và limy hữu hạn 0 0 t→ t → 0 t t 0 ng h trườ
ợp này không có tiệm cận. +) Khi 1
t → 2 thì limx = lim = 3 t 2 → t 2 → t − 8 2t 3 y Ta có: t − 8 a = lim = lim = lim(2t) = 4 0 t 2 → t 2 x → 1 t 2 → 3 t − 8 2t 4 2(t − 2)
b = lim( y − ax) = lim − = lim 3 3 t →
t → t − 8 t − 8 t → (t − 2) ( 2 2 2 2 t + 2t + 4 ) 2 2 1 = lim = = 2
t→2 t + 2t + 4 12 6 ng h trườ
ợp này đồ thị hàm số có tiệm cận xiên hai phía 1 y = 4 x + . 6
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 26
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST +) Khi 1 2t
t → thì limx = lim
= 0 (hữu hạn) và lim y = lim = 0 (hữu hạn) ng nên trườ 3 3 t→ t→ t − 8 t→ t→ t −8
hợp này không có tiệm cận.
Vậy đồ thị hàm số chỉ có duy nhất một tiệm cận, đó là tiệm cận xiên hai phía 1 y = 4x + . 6 Câu 9. /2 /2 /2 arcsin x 18 18 arcsin x 18 I = 1+ sin x dx = sin x dx + sin x dx − /2 | | /2 | | 1 x x + e + I 1 I 2 +) Xét 18
f (x) = sin x , ta có: f (−x) = f (x), x ) là hàm chẵn /2 18 17!! 17!! I = 2 sin x dx = 2 = 2 (tích phân Wallis). 0 18!! 2 18!! arcsin x +) Xét 18 g(x) =
sin x . Đề cho hơi dở, vì cận arcsin x không xác định trên toàn | | 1 x +e − bộ , , nên chỗ b này đề sai. ị 2 2 Sửa lại một chút: x x arcsin arcsin /2 /2 /2 18 18 18 I = − 1 + sin x dx = sin x dx + sin x dx | | − /2 − /2 | | 2 1 x x + e + 2 I x arcsin Lúc này, đặt 18 g(x) = sin x . | | 1 x + e −
Ta có g(−x) = −g(x) nên g(x) là hàm lẻ trên , 2 2 /2 I =
g(x)dx = 0 ẻ ận đố ứ 2 (tích phân hàm l , c i x ng). − /2 Vậy 17!!
I = I + I = . 1 2 18!! Câu 10. − − +) 1 y y
z (x, y ) = = , x 0 . x 2 2 2 2 y x x + y 1+ x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 27
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
+) Với mỗi điểm (0, y , xét giới hạn: 0 ) y y −
f (x y ) − f ( y ) 0 0 arccot 0 arccot , 0, 0 0 lim = lim x = lim x x→ 0 x→ 0 x→ 0 x −0 x −0 x - Nếu y y 0 0 y = 0 thì arccot = arccot 0 = lim
x . Giới hạn này không tồn tại h u h ữ ạn 0 →0 x 2 x x
không tồn tại z (0,0) . x y0 arccot - Nếu y y y 0 , ta xét: 0 0 lim = − lim arccot = lim
x = − không tồn tại 0 x 0 − x x 0 − x 2 x 0 − → → → x z (0,y (với y 0 ) . x 0 ) 0 y0 arccot - Nếu y y y 0 , ta xét: 0 0 lim = − lim arccot = lim
x = + không tồn tại 0 x 0 + x 0 + x 0 x x 2 + → → → x
z (0,y (với y 0 ) . x 0 ) 0 − − Tóm lại, 1 y y
z (x, y) = =
,x 0 . Còn z y không tồn tại. x (0, ) x 2 2 2 2 y x x + y 1 + x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 28
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 8 (Nhóm ngành 3) Câu 1 (1 điể x −x m). Tính cos lim .
x →+ x − sin x +1
Câu 2 (1 điểm). Dùng vi phân tính gần đúng 3 8,012 .
Câu 3 (1 điểm) Tính hoặc xét sự phân kỳ + x e x d . x 1
Câu 4 (1 điểm). Tính 3x e cos(2 ) x dx . 0
Câu 5 (1 điểm). Cho 2 ( , ) x y z x y = e . Tính 2 d z .
Câu 6 (1 điểm). Tìm giá tr l
ị ớn nhất, giá tr bé nh ị ất của hàm số 2 2
z = 4x − 3y trong miền đóng: 2 2 x y + 1. 3 4
Câu 7 (1 điểm). Tính 2 2
1+ x + y dx dy , trong đó: 2 2
D : x + y 1, x 0, y 0 . D 1 x = 3 Câu 8 −
(1 điểm). Tìm các tiệm cận c ủa đồ th hàm s ị ố 8 t 2t y = 3 8 − t
Câu 9 (1 điểm). Tính arcsin x 2 18 . − 1+ sin xdx | | 2 1 x + e y Câu 10 x
(1 điểm). Tính z ( ; x y) biết arccot , 0 = x z (x; y ) x 0 , x = 0
Lời giải tham kh 7 ảo đề
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 29
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20192 – ĐỀ 1 (Nhóm ngành 1)
Câu 1 (1 điểm). Xét tính chẵn, lẻ của hàm số 2
y = x + arcsin x . − Câu 2 2x 1
(1 điểm). Tìm các tiệm cận c ủa đồ th hàm s ị ố y = . 2 x +1 e cos( ln x)
Câu 3 (1 điểm). Tính tích phân dx . 1 x 2
Câu 4 (1 điểm). Tính giới hạn y sin x lim . ( x , y ) ( → 0,0) 2 4 2x +3y
Câu 5 (1 điểm). Tìm cực tr c
ị ủa hàm số z = x + y + ( x − )2 2 2 ( ) 1 −1.
Câu 6 (1 điểm). Ch ng minh r ứ ằng 2
x arctan x ln 1+ x với mọi x . + 1− cos Câu 7 x
(1 điểm). Xét sự hội tụ của tích phân suy rộng: I = dx . 0 5 x
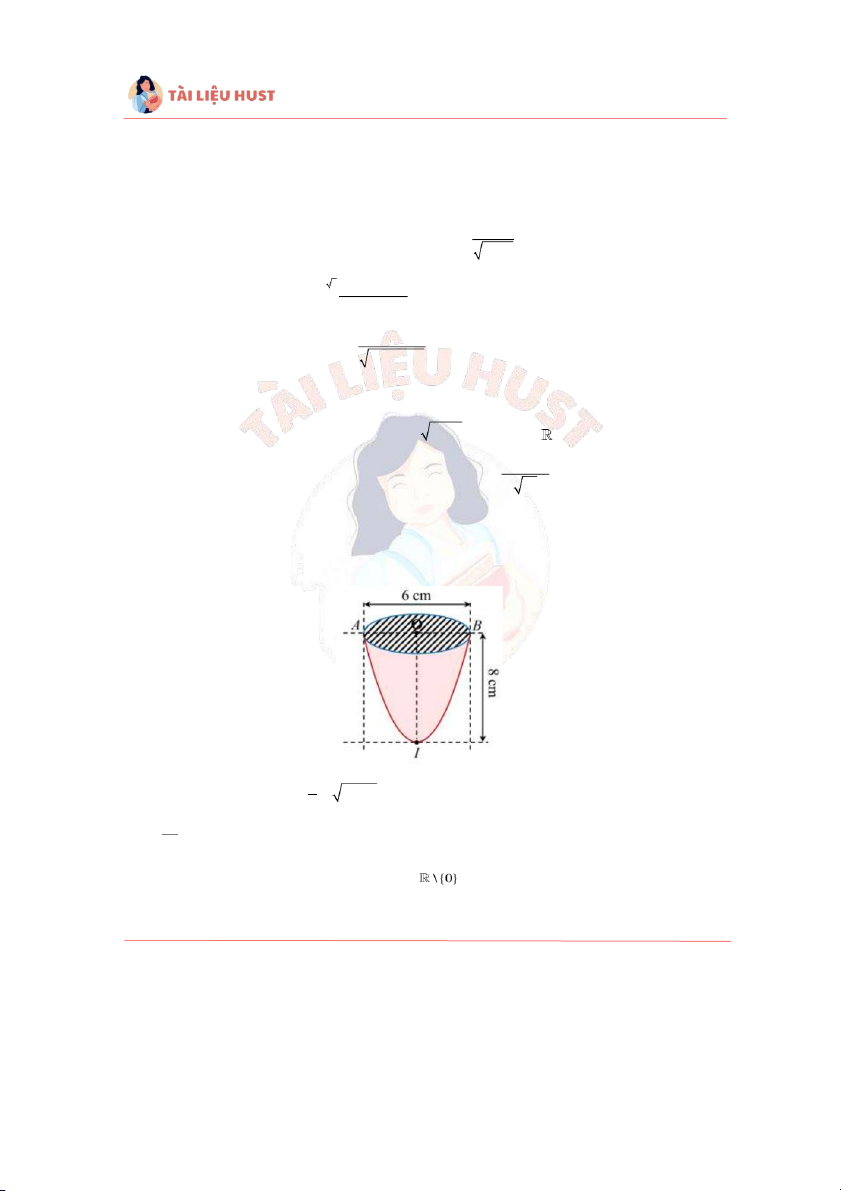
Câu 8 (1 điểm). Có một vật thể tròn xoay có dạng gi t cái ly nh ống như mộ ư hình vẽ. Người ta
đo được đường kính của miệng ly là 6 cm và chiều cao là 8 cm. Biết rằng mặt phẳng qua trục
OI cắt vật thể theo thiết diện là một parabol. Tính thể tích V ( 3
cm ) của vật thể đã cho.
Câu 9 (1 điểm). Biểu thức 1 2 z +
= y − z xác định hàm ẩn z = z( ,
x y) . Chứng minh rằng: x z 2 y x z + − = . x 1 0 2y
Câu 10 (1 điểm). Cho hàm số f (x) khả vi trên thoả mãn: 2 2 x f ( x)
(2 x 1) f (x) xf + − =
(x) − 1 với mọi x 0 và f (1) = 2 . Tính 2 f (x)dx . 1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 30
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20192 – ĐỀ 1 (Nhóm ngành 1) Câu 1. 2
y = x + arcsin x . Ta có: y(1) = 1+ arcsin1= 1+ 2
y(−1) y(1)
y(− x) = 1+ arcsin(− 1) = 1− 2
y(−x) = y(x), x không thể có:
y(−x) = − y(x), x 2
y = x + arcsin x không là hàm chãn, cũng không là hàm lẻ.
Câu 2. Tập xác định: D = , đồ thị hàm số không có tiệm cận đứng. − - Xét khi 2x 1 2x
x → +, ta có: lim y = lim = lim = 2 x →+ x →+ 2 +1 x→+ x x đồ th hàm s ị
ố có tiệm cận ngang y = 2 khi x → + . 2x −1 2x
- Xét khi x → − , ta có: lim y = lim = lim = −2 x →− x →−
2 +1 x→− −x x đồ th hàm s ị
ố có tiệm cận ngang y = −2 khi x → − .
Đồ thị hàm số không có tiệm cận xiên. Vậy
đồ thị có 2 tiệm cận ngang là y = 2 (về bên phải) và y = −2 (về bên trái). cos( ln ) 1 e e e x 1 Câu 3. dx =
cos( ln x)d(ln x) = sin( ln x) = . 1 1 x 1
Vậy tích phân cần tính bằng 1 . 2 y 1
Câu 4. Ta chứng minh , (
x, y) (0,0) . (*) 2 4 2x + 3 y 3 4 Thật vậy, (*) y 1 4 2 4
3y 2x +3y , luôn đúng. Vậy (*) đúng. 2 4 2x + 3y 3
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 31
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 2 2 y sin x y 1 1 0 = | sin x | sin x, mà lim sin x = 0 2 4 2 4 2 x + 3 y 2 x +3 y 3 (x ,y ) ( → 0,0) 3 2 2 y sin x y sin x lim = 0 lim = 0. (x ,y )→ (0,0) 2 4 (x, y )→ (0,0) 2 4 2x + 3 y 2x + 3y
Vậy giới hạn cần tính bằng 0. Câu 5. Tập xác định D =
z = 2(x + y)+ 2 x − x = y = −x x ( 2 )1 2 0 Tìm điểm dừng: z = 2(x + y) = 0 4x x − = y ( 2 1) 0
x= 0 x= 1 x= −1 y = 0 y = 1 − y = 1
hàm số có 3 điểm dừng là M (0,0), M (1,−1) và M ( 1 − ,1). 1 2 3 Ta có 2 A z x B z C z = = − = = = = xx 12 2, xy 2, yy 2.
Tại điểm M (0,0) , ta có 2 −
= , nên hàm số không đạt cực trị tại M . 1 B AC 8 0 1 2
B − AC = −16 0
Tại các điểm M (1, 1 − ) và M ( 1 − ,1) ta có
hàm số đạt cực tiểu tại các 2 3 A = 10 0 điểm M (1, 1 − ), M ( 1 − ,1). Giá tr c ị ực ti u b ểu đề ằng z = z(1, 1 − ) = z( 1 − ,1) = 1 − . 2 3 CT Câu 6. Xét hàm số 2 1 f ( )
x = xarctan x −ln 1 + x = xarctan x − ln ( 2 1 + x ) trên . 2 Ta có: 1 1 2x
f (x ) = arctan x + x − = arctan x . 2 2 1+ x 2 1+ x
f (x) = 0 arctan x = 0 x = 0. Bảng biến thiên có dạng:
Dựa vào bảng biến thiên ta thấy
f (x) 0,x R 2
x arctan x − ln 1+ x 0, x 2
x arctan x ln 1+ x , x (đpcm)
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 32
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST + − − + − Câu 7. 1 cos x 1 cos x 1 cos x I =
dx = I + I , trong đó 1 I = dx I = dx 1 2 1 và 2 . 0 5 x 0 5 x 1 5 x − + 1 cos x
) Xét I , ta có f x = x . Điể ất thườ m b ng . 1 ( ) 0, (0,1] x = 0 5 x 2 x x 0 1 cos x → − 1 2 1 1 1 ~ = , mà dx
hội tụ (vì = (0,1)) 1/2 5 5 1/2 x x 2x 0 2x 2 1 1− cos x I = dx
hội tụ theo tiêu chuẩn so sánh. 1 0 5 x 1− cos x
+) Xét I , ta có f ( ) x =
0 liên tục trên [1,+) . Điể ất thườ m b ng + . 2 5 x − + Ta có: 1 cos x 2 2 5 0 , mà dx hội tụ (vì = 1 ) 5/2 5 5/2 x x 1 x 2 + 1− cosx I = dx
hội tụ theo tiêu chuẩn so sánh. 2 1 5 x
Vì I và I hội tụ nên I hội tụ 1 2
Câu 8. Chiều dương như hình vẽ.
Phương trình parabol đi qua 3 điểm A, B, O có dạng: 2 x = ay + . b
Parabol qua hai điểm B(0,3) và I(8,0) 8 − 0 = 9a + b a = 8 − 2 9 x = y + 8. 8 = b 9 b = 8
Vật thể thu được là vật thể khi miền giới hạn bởi các 8 − 2 3 x = y + 8 y = 16 − 2x đường 9 4 quanh trục
x 0, y 0 0 x 8
Ox thể tích vật thể là: 8 2 2 8 8 8 2 3 9x 9x V =
y (x)dx = 16 − 2x dx = 9− dx = 9x − = 36( 3 cm ) 0 0 0 4 8 16 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 33
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST Câu 9. Đặt 1 2
F (x, y, z) = z + − y −z . x −1 y − 2 2 − − − F F y z x z = = , y x z = = . x F 1 y F 1 z 1 z + 1+ 2 2 2 y − z 2 y − z Ta có: y 1 1 z 2 2 − 2 − 2 y z 1 2 y z y 2 1 x z + + 1= x x + − 1 = + −1 = 1−1 = 0 x 2 2 y x 2 y 1 1 1 1 + 1 + 1+ 1+ 2 2 2 2 2 y − z 2 y − z 2 y − z 2 y − z Câu 10. 2 2
x f (x) (2x 1) f (x) xf + − =
(x) −1,x 0 2 2 2 x f ( ) x
2xf (x) 1 xf (x) f (x) (xf (x) 1) xf + + = + + = ( )
x + f (x) xf ( ) x + f ( ) x xf ( ) x + f ( ) x = 1, x 0 dx = dx 2 2 ( xf( ) x 1 + ) ( xf( ) x 1 + ) d(xf (x ) +1) 1 − = dx = x +C. 2 (xf ( ) x +1) xf (x) +1 Theo bài ra: −1 −1 −1 1 f (1) = 2 −
=1 + C C = 0. = x f ( ) x = − , 2 2 − +1 xf ( ) x +1 x x (TM) 2 2 2 1 − 1 1 1 − f (x)dx = −
dx = −ln | x | + = −ln 2 2 1 1 x x x 2 1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 34
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 1 (Nhóm ngành 1)
Câu 1 (1 điểm). Tìm chu kỳ của hàm số y = 3cos(5x) + 4sin(5x) .
Câu 2 (2 diểm). Tính: 3 cos x −1 a) lim 2 x 0 → sin x b) ( 2
ln x + x + 2)dx . 1 Câu 3 x x
(1 điểm). Xét sự hội tụ, phân kỷ của tích phân dx . 0 x 1− cos 2 4 Câu 4 x
(1 diểm). Tính lim . 2 4
(x ,y )→(0,0) x + y
Câu 5 (1 điểm). Tim cực tr c ị ủa hàm số 4 4 2 2
z = x + y + 2x − 2 y . − 1 + Câu 6 x 1
(1 điểm). Tim vả phân lọai điểm gián đọan y = arctan . x Câu 7 xyz
(1 điểm). Phương trình (x + y)z +e
= 0 xác định hàm ẩn z = z( ,x y). Tính dz(0,1) .
Câu 8 (1 điểm). Cho hàm số f (x) khả tích trên [0,1], | f ( ) x |1, x [ 0,1] . Chứng minh rằng
1− f (x)dx = 1− ( f(x)dx )2 1 1 2 . 0 0
Câu 9 (1 điểm). Cho hàm số f (x) liên tục trên [−1;1] và thoả mãn điều kiện: 2 f x = x + + x f ( 3 ( ) 2 x ) . Tinh 1 I = f (x)dx . −1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 35
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 1 (Nhóm ngành 1)
Câu 1. Chọn sao cho 3 4 sin = , cos = , ta có: 5 5 3 4 f ( ) x =3cos(5 ) x +4sin(5 ) x =5 cos(5 ) x + sin(5 ) x =5[sin cos(5 ) x +cos sin(5 )
x ] =5sin(5 x + ) 5 5
là hàm tuần hoàn với chu kỳ 2 2 T = = . | 5 | 5 2
Chú ý: Vớik 0 thì các hàm số sin(kx+ ),cos(kx+ ) là các hàm tuần hoàn với chu kỳ T = . | k | Câu 2.
a) Ta có: sin x ~ x khi x →0 và: 2 2 x→ 0 x→ 0 1 1 − − 3 x x 3
cos x − 1= 1+ (cos x− 1) − 1 ~ (cos x− 1) ~ = 3 3 2 6 2 − x 3 VCB − − Áp dụng: cos x 1 1 6 lim = lim = . 2 2 x→ 0 x→ 0 sin x x 6 −
Vậy giới hạn cần tính bằng 1 . 6 b) ( 2
x + x + ) x = ( 2x + x+ ) 1 ln 2 d ln 2 d x + 2 1 = x+ ( 2x + x+ ) 1 ln 2 − x + d (ln( 2x + x+ )2) 2 2 1 + = x+ ( 2 x + x+ ) 1 2x 1 ln 2 − x + dx 2 2 2 x + x+ 2 2 1 x + 1 = x+ ( 2x + x+ ) 2 ln 2 − 2 dx 2 2 1 7 x + + 2 4
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 36
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 1 x ( 2 x x ) 7 1 ln 2 2 1 = + + + − − dx 2 2 4 1 7 x + + 2 4 1 x + 1 = x+ ( 7 2 2 x + x+ ) 2 ln 2 − 2 x− arctan + C 2 4 7 7 2 1 + = x+ ( 2 x + x+ ) 2 x 1 ln 2 − 2 x+ 7 arctan + C. 2 7 x x Câu 3. f ( ) x = 0, x ( 0,1]. Điể ất thườ m b ng x = 0 . x 1 −cos 2 Ta có: x x x x 8 8 1 ~ = , mà 1 hội tụ (vì = (0,1) 2 1/2 x 1 1/2 0 1 cos x x − x 2 2 2 2 1 x x dx
là tích phân hội tụ theo tiêu chuẩn so sánh. 0 x 1− cos 2 4
Câu 4. Ta đi chứng minh x 2 x , ( , x )
y (0, 0) (*) 2 4 x + y 4 Thật vậy, (*) x 2 4 4 2 4
x x x + x y , luôn đúng (
x, y) (0,0). 2 4 x + y 4 x (*) y ta có: là đúng. Vậ 2 0
x ,(x, y) (0,0) 2 4 x + y 4 Mà 2 x lim x = 0 lim = 0 (theo nguyên lý kẹp). 2 4 (x, y) ( → 0,0) (x,y ) ( → 0,0) x + y
Câu 5. Tập xác định: D = . 3
z = 4x + 4x = 0 x = +) Tìm điểm dừng: 0 x 3 z = 4 y − 4 y = 0 y = 0 y = 1 y
hàm số có 3 điểm dừng là M (0,0), M (0,1) và M (0,−1) . 1 2 3 +) Ta có: A = 2 2 z
=12x + 4, B = z = 0,C = z =12y − 4. xx xy yy
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 37
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 2 B − AC = ( 2 x + )( 2 12 4 4 −12y ) .
- Tại điểm M (0,0) ta có: 2
B − AC = 16 0 hàm số không đạt cực tr t ị ại M (0,0) . 1 1 2
B − AC = −32 0
- Tại các điểm M (0,1) và M (0,−1) , ta có: 2 3 A = 4 0 hàm số t c
đạ ực tiểu tại các điểm M (0,1) và M (0,−1) . Giá tr c ị ực tiểu cùng bằng 2 3 z
= z(0,1) = z(0,−1) = 1 − . CT x+ 1 x 0
Câu 6. Hàm số xác định arctan 0 x x 1 −
x = 0 và x = 1
− là các điểm gián đoạn của hàm số. - Tại điểm x = 1 − , xét giới hạn: x →( 1 − ) 1 x +1 + lim + y = lim = + vì arctan ~ 0 x →( 1 − )+ x →(−1) + x +1 r a ctan x x x = 1
− là điểm gián đoạn loại 2 của hàm số.
- Tại điểm x = 0 , xét các giới hạn: + x→0 1 1 x +1 lim y = lim = do ~ + x →0+ x →0+ x + 1 c ar tan x x 2 x →0 1 1 x +1 − lim y = lim = do ~ − − − → → + x 0 x 0 x 1 − x arctan x 2
x = 0 là điểm gián đoạn loại 2 của hàm số (điểm gián đoạn bỏ được).
Câu 7. Đặt ( , , ) = ( + ) xyz F x y z x y z + e .
Ứng với x = 0, y = 1, thay vào phương trình đã cho ta có: 0
(0 +1)z + e = 0 z = 1 − .
Gọi điểm M (0,1, −1) . Ta có: xyz
F = z + zye , xyz
F = z + zxe , xyz
F = x + y + xye . x y z − − − ( ) F (M F M ) 2 − y 1 z (0,1) x = = = −2, z = (0,1) = = = −1.n x F (M ) 1 y F (M ) 1 z z
dz(0,1) = z (0,1)dx + z (0,1)dy = 2 − dx −d . y x y
Câu 8. Áp dụng bất đẳng thức tích phân:
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 38
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST ∫ 1 2 1
0 √1 − 𝑓 (𝑥)d𝑥 = ∫0 √1 − 𝑓(𝑥) ⋅ √1 + 𝑓(𝑥)d𝑥 ≤ √∫ 1 1 1 1
0 (1 − 𝑓(𝑥))d𝑥 ⋅ ∫0 [1 + 𝑓(𝑥)]d𝑥 = √(1 − ∫0 𝑓(𝑥)d𝑥) ⋅ (1 + ∫0 𝑓(𝑥)d𝑥) 2
= √1 − (∫ 10 𝑓(𝑥)d𝑥)
Đẳng thức xảy ra, chẳng hạn khi 𝑓(𝑥) = 1
Từ đó suy ra điều phải chứng minh. Câu 9. 2 f x = x + + x f ( 3 ( ) 2 x ), x [ 1 − ,1] 1 1 1 2 f (x)dx = x + 2 dx + x f ( 3x )dx −1 −1 −1
x = −1 u = −1 Đặt 3 2
u = x du = 3x dx . Đổi cận x = 1 u = 1 1 x f (x ) 1 du 1 1 2 3 dx = f (u) = f (x)dx . Do đó: −1 −1 −1 3 3 1 3 f (x)dx = x + 2 dx +
f (x)dx f (x)dx = x + 2 dx = + =13 13 −1. − − − − − ( (x 2) )1 1 1 1 1 1 3 1 1 1 1 1 3 2 −1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 39
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 2 (Nhóm ngành 1)
Câu 1 (1 điểm). Tìm chu kỳ của hàm số y = 4cos(5x) + 3sin(5x) .
Câu 2 (2 diểm). Tính: 3 cos x −1 a) lim 2 x 0 → tan x b) ( 2
ln x − x + 2)dx , 1 Câu 3 x x
(1 điểm). Xét sự hội tụ, phân kỳ của tích phân dx . 0 x 1− cos 3 4 Câu 4 y (1 điểm). Tính lim . 4 2
(x ,y )→(0,0) x + y
Câu 5 (1 điểm). Tìm cực tr c ị ủa hàm số 4 4 2 2
z = x + y − 2x + 2 y . − 1 Câu 6 (1 điể x
m). Tim và phân loại điểm gián đoạn y = arctan . x + 1 Câu 7 xyz
(1 điểm). Phương trình (x + y)z −e
= 0 xác định hàm ẩn z = z( ,x y). Tính dz(0,1) .
Câu 8 (1 điểm). Cho hàm số f (x) khả tích trền [0,1], | f (x) |1, x [0,1] . Chứng minh rằng
1− f (x)dx = 1− ( f(x)dx )2 1 1 2 . 0 0
Câu 9 (1 điểm). Cho hàm số f (x) liên tục trên [−1;1] và thoả mãn điều kiện: 2 2 f x = − x + x f ( 3 ( ) 4 x ) . Tính 1 I = f (x)dx . −1
Lời giải tham kh s ảo đề ố 1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 40
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 1 (Nhóm ngành 1) Câu 1 (1 điể x − x m). Tính giới hạn sin lim .
x →+ x − arctan x
Câu 2 (1 điểm). Cho 1 f (x) =
. Tính đạo hàm cấp cao (50) f (x) 2 x − 2x +1 5
Câu 3 (1 điểm). Tính tích phân 2 x − 9 dx . 0
3sin x + 4cosx
Câu 4 (1 điểm). Tính tích phân 2 dx . 0 4sin x + 3cosx 3 sin x
Câu 5 (1 điểm). Tính giới hạn lim . 2 2
(x, y)→(0,0) sin x + sin y
Câu 6 (1 điểm). Ch s ỉ ố ng m Shannon đo lườ
ức độ đa dạng của một hệ sinh thái, trong trường
hợp có hai loài, được xác định theo công thức: H = −xln x − y ln y , ở đó x, y là tỷ lệ các loài,
x 0, y 0 thoả mãn
. Tìm giá trị lớn nhất của H . x + y = 1 2 4 x x
Câu 7 (1 điểm). Ch ng minh r ứ ằng cosx 1− + , x 0, . 2 24 2 z
Câu 8 (1 điểm) Cho y
z = f (x, y) là hàm số ẩn xác định bởi phương trình z − xe = 0. Ứng
dụng vi phân, tính gần đúng f (0,02;0,99) . 1 (2n 1 − )!
Câu 9 (1 điểm). Tính lim n . n→+ n (n 1 − )! + ln(1+ 2x)
Câu 10 (1 điểm). Xét sự hội tụ, phân kỳ của tích phân suy rộng: dx . 0 x x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 41
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 1 (Nhóm ngành 1) sin x 1− x − sin x x 1 − 0 Câu 1. L = lim = lim = = 1
x →+ x −arctan x x →+ arctan x 1 −0 1 − x Giải thích: 1 − sin x 1 x x x sin x + lim = 0 (theo nguyên lý kẹp) 1 −1 x→+ x lim = lim = 0 x→+ x x →+ x arctan x +) lim arctan x = lim = 0. x →+ 2 x →+ x Vậy L = 1 . Câu 2. 1 1 2 − f ( ) x = = =( x 1 − ) . Do đó: 2 2 x − 2 x+ 1 ( x−1) − 1 51! (50) 52 50 f (x) = ( 2 − )( 3 − )( 4 − ) ( 5 − 0)( 5 − 1)(x 1 − ) = ( 1 − ) 51! = , x 1 52 52 (x −1) (x −1) Vậy (50) 51! f ( ) x =
, x 1. − Q + 52 (x −1) Câu 3. 5 3 5 2 2 2 2 2 I = x − 9 dx = 3 − x dx + x − 3 dx 0 0 3 3 5 2 2 x 9 x 9 x x x 9 9 − − 2 = + arcsin +
− ln x + x − 9 2 2 3 2 2 0 3 9 9 = +10 − ln 3 4 2 24 7 (4 sin x + 3cos ) x + (4 cos x −3sin ) x 3sin x + 4cos x Câu 4. 2 2 25 25 I = dx = dx 0 0 4sin x +3cos x 4sin x +3cos x 2 24
7 4 cos x −3sin x 24x 7 2 = + dx = +
ln | 4sin x + 3cos x | 12 7 4 = + ln 0 25
25 4sin x + 3cos x 25 25 25 25 3 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 42
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 2
Câu 5. Ta chứng minh: sin x
1 với (x, y) → (0,0) .(*) 2 2 sin x + sin y Thật vậy, (*) 2 2 2
sin x sin x + sin y , luôn đúng với (x, y) → (0,0). 3 2 Áp dụng: sin x sin x 0 =
| sin x || sin x | , khi (x, y) → (0, 0) . 2 2 2 2 sin x +sin y sin x + sin y 3 Mà sin x lim | sin x|= 0 lim = 0 theo nguyên lý kẹp 2 2 (x, y ) ( → 0,0) (x ,y ) (
→ 0,0) sin x+ sin y 3 sin x lim = 0. 2 2
(x,y )→ (0,0) sin x+ sin y Câu 6. x + y = 1 y = 1− x Ta có:
H = − x lnx− (1− x)ln(1− x)= f (x). x 0, y 0 0 x 1 Xét
f (x) trên (0,1) . Ta có: f (x) = − ln x− 1+ ln(1− x)+ 1= ln(1− ) x − ln x 1
f (x) = 0 ln x = ln(1− x) x = (0,1) 2 Xét dấu: 1 1
f (x ) 0 0 x ; f (x ) 0 x 1 2 2
Suy ra f (x) t giá tr đạ ị lớn nhất tại 1 x = . 2 1 1 1 max H = f = ln 2
, đạt tại (x, y) = , . 2 2 2 2 4 Câu 7. Xét hàm số x x f ( ) x = cos x 1 − + − liên tục trên 0, 2 24 2
Dùng khai triển Maclaurin với phần dư Lagrange, ta có: 5 5 cos c + cos c + 2 4 2 4 x x 2 5 x x 2 5 f ( ) x = 1 − + + x 1 − + − = x , ( c ( 0, ) x ), x 0, 2 24 5! 2 24 5! 2 Đánh giá: 5 5 5 c 3 + cos c + 0 2 2 2
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 43
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 2 4 x x
f (x) 0, x 0, cos x 1− + , x 0, 2 2 24 2
điều phải chứng minh (đẳng thức không xảy ra). z Câu 8. ( , , ) y
F x y z = z − xe , hàm ẩn z = f ( ,
x y) xác định bởi F (x, y, z) = 0 z z z xz x y F = e − ; y F = e ; F = 1 y − e x y 2 z y y
x = 0,x = 0,02 z Chọn 0
. Ứng với x = 0, y = 1 thì 1
z = 0.e z = 0 f (0;1) = 0 . = = − 0 y 1, y 0,01 − − F (0;1;0) F (0;1;0) f (0;1) = = 1; f (0;1) y x = = 0 x F (0;1;0) y F (0;1;0) z z Suy ra: f (0,02;0,99) f ( x ; x y ) y f (0;1) f (0;1) x f = + + +
+ (0;1) y =0 1 + .0,02 +0.( 0 − ,01) = 0,02 0 0 x y
Vậy f (0,02;0,99) 0,02 .
Câu 9. Xét giới hạn:
1 (2n −1)!
n (n +1)(2n − 2)(2n −1) L = lim ln = lim ln n n →+ n (n −1)! n n n →+ n n 1 1 0 1 2 n 1 − 1 − k = lim ln 1+ + ln 1+ + ln 1+ ++ ln 1+ = lim ln 1+ n→+ n n n n n n →+ n n k= 0 1 = f (x)dx
trong đó 𝑓(𝑥) = ln (1 + 𝑥) liên tục, khả tích trên [0,1] 0 1 1 1 x = ln(1 + )
x dx = xln(1 + ) x − dx 0 0 0 1+ x 1 1 1 = ln 2− 1−
dx = ln 2− (x − ln(1+ x)) = 2 ln 2− 1 0 0 1+ x 1 (2n−1)! L 2ln 2 1 − 4 lim n = e = e = . n→+ n (n −1)! e + ln(1+ 2x) 1 ln(1+ 2x) + ln(1+ 2x) Câu 10. I = dx = dx + dx 0 x x 1 I 2 I
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 44
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST ln(1+ 2x) f ( ) x =
0 liên tục trên (0;+). x x +) I m b có điể ất thường x = 0 . 1 1 Khi 2x 2 2 1 x 0+ → thì f (x) ~ ~ , mà dx
hội tụ (do = (0;1) ) 1/2 1/ 2 x x x 0 x 2
I hội tụ theo tiêu chuẩn so sánh. 1 + +) Vi ln(1 x) lim
=0 , với 0 nhỏ tuỳ ý . x x →+ Chọn 1 1/3 = ln(1 +2 ) x (2 ) x khi x → + 3 1/3 3 3 + Khi (2x) 2 2 7
x → + thì 0 f (x) = , mà dx hội tụ (do = 1 ) 7/6 7/6 x x x 1 x 6
I hội tụ theo tính chất so sánh. Tóm lại, I , I hội tụ hội tụ. 2 1 2 I 1
Cách 2: Để xét I , ta có thể chọn hàm g(x) = , ta có trinh bày sau: 2 7/6 x Xét 1 g(x) = 0, x 1. Ta có: 7 /6 x ln(1 +2x) f ( ) x x x ln(1+ 2 ) x lim = lim = lim (dạng ) 1/3 x →+ ( g ) x x →+ 1 x →+ x 7/6 x 2 x 6 1 2 = + lim = lim = 0 −2/3 1/3 x→+ 1 →+ 2 − /3 x x + 2 x x 3 + + 1 7 g(x)dx = dx hội tụ (do = ) 7 /6 1 1 x 6 + I = f (x)dx ộ ụ ệ quả ẩ 2 h i t theo h tiêu chu n so sánh. 1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 45
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 2 (Nhóm ngành 1) Câu 1 (1 điể − m). Tính giới hạn x cos x lim .
x →+ x − arccot x
Câu 2 (1 điểm). Cho 1 f (x ) =
. Tính đạo hàm cấp cao (50) f (x) 2 x + 2x +1 5
Câu 3 (1 điểm). Tính tích phân 2 x −16 dx . 0
5sinx + 6cosx
Câu 4 (1 điểm). Tính tích phân 2 dx . 0 6sin x + 5cosx 3 Câu 5 sin y
(1 điểm). Tính giới hạn lim . 2 2
(x, y)→(0,0) sin x + sin y
Câu 6 (1 điểm). Ch s ỉ ố ng m Shannon đo lườ
ức độ đa dạng của một hệ ng sinh thái, trong trườ
hợp có hai loài, được xác định theo công thức: H = −x ln x − y ln y , ở đó x, y là tỷ lệ các loài,
x 0, y 0 thoả mãn
. Tìm giá trị lớn nhất của H . x + y = 1 3 5 Câu 7 x x
(1 điểm). Ch ng minh r ứ
ằng sin x x − + , x 0, . 6 120 2 z
Câu 8 (1 điểm). Cho x
z = f (x, y) là hàm số ẩn xác định bởi phương trình z − ye = 0. Úng
dụng vi phân, tính gần đúng f (0,99;0,02) . 1 (2 ) n !
Câu 9 (1 điểm). Tính lim n . n→+ n n! + ln(1+ 3x)
Câu 10 (1 điểm). Xét sự hội tụ, phân kỳ của tích phân suy rộng: dx . 0 x x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 46
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 2 (Nhóm ngành 1)
Lời giải chi ti
ết tham khảo đề số 1 − Câu 1. x cos x lim =1.
x →+ x − arccot x Câu 2. (50) 51! f (x) = . 52 (x +1) 5 Câu 3. 2 15 x − 16 = 4 + − 8ln 2 . 0 2 + Câu 5. 5sin x 6 cos x 30 11 6 2 dx = + ln . 0 6sin x + 5cos x 61 61 5
Câu 6. max H = ln 2 c khi đạt đượ 1 x = y = . 2
Câu 7. Tương tự đề 1 (dấ ằng cũng không xả u b y ra).
Câu 8. f (0,99;0,02) 0,02 . 1 (2n)! 4 Câu 9. lim n = . n→+ n n! e + + Câu 10. ln(1 3x) dx hội tụ. 0 x x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 47
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 3 (Nhóm ngành 1)
Câu 1 (1 điểm). Tính giới hạn lim(cos x+ sin )x x . x→0
Câu 2 (1 điểm). Tìm tiệm cân xiên c ủa đồ th hàm s ị
ố y = xarccot x.
Câu 3 (1 điểm). Tính tích phân 3 4 tan x dx . 0 1
Câu 4 (1 diểm). Tính tích phân ln ( 2 x + x + )1dx . 0
Câu 5 (1 điểm). Tìm cực tr c ị ủa hàm số 2 2
z = 4(x − y) − x − y . 2 x Câu 6
yarctan , y 0, (1 điể Cho hàm s m). ố f ( , x y) = y . 0, y = 0
a) Xét tính liên tục của f (x, y) tại điểm A(1,0). b) Tính f (1,0). y Câu 7 + + (1 điểm). Cho x y tan x tan y 0 x, y . Chứng minh tan . 2 2 2 Câu 8 x sin x
(1 điểm). Tính tích phân 2 dx . − 1+ 3x 2 + arctan x dx
Câu 9 (1 điểm). Xét sự hội tụ, phân kỳ của tích phân suy rộng: . 0 x x +1 −cos x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 48
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 3 (Nhóm ngành 1) 1 ln(cosx+ sinx )
Câu 1. = lim(cos + sin ) x = lim x L x x e . x →0 x →0 + Xét ln(cos x sin x) K = lim (dạng 0 ) x → 0 x 0 -sin x+cos x 1 cos x+sin x K x = lim
=1 L= lim(cos x+sin x) =e =e x→0 1 Vậy L= . e Câu 2. ( y ) x lim
= lim arccot x = 0 đồ thị hàm số không có tiệm cận xiên bên phải. x →+ x x →+ ( y ) x lim
= lim arccot x = = a x →− x x →− −1 2 L Hospital 2 arccot x − 1+ x x
b = lim ( y − ) x = lim ( x arccot x − ) = lim = lim = lim =1 2 x →− x →− x →− 1 x→− 1 − x →− 1+ x 2 x x
y = x +1 là tiệm cận xiên (bên trái) duy nhất c ủa đồ thị hàm số. Câu 3. / 4 / 4 I = tan x dx = tanx (.1+ tan x) / 4 3 2 dx− tanx dx 0 0 0 /4 2 /4 /4 −sin x tan x 1 −ln 2 = tan xd(tan ) x + dx = + ln | cos x| = 0 0 cos x 2 2 0 − Vậy 1 ln 2 I = . 2 Câu 4. 1
I = (x + x + ) 1 2 x = ( 2 x + x + ) 1 ln 1 d ln 1 d x + 0 0 2 1 1 + = x+ ( x + x+ ) 1 2 1 2 x 1 ln 1 − x+ dx 2 0 2 2 x + x + 1 0
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 49
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 1 1 x + 1 3 3 1 3 3 2 ln 3 2 d = − − x 2 = ln 3− 2x − arctan 2 0 2 2 1 3 2 2 3 3 x + + 2 4 2 0 3 = ln 3− 2+ 2 2 3 Vậy 3 I = ln 3− 2+ . 2 2 3 Câu 5. 2 2
z(x, y) = 4(x − y) − x − y
+) Tập xác định: D = . +)
z = 4− 2x; z = −4− 2y x y z = 0 x = 2 Giải hệ x M (2,−2) m d là điể ừng z = 0 y = −2 y +) Ta có: A = z = 2
− ; B = z = 0; C = z = 2 − xx xy yy 2 B −AC = 4 − 0
hàm số đã cho đạt cực tr ịtại duy nhất 1 điểm là M (2, 2 − ), đây A = 2 − 0
là điểm cực đại, z = z(2,−2) = 8 . CÐ Câu 6. 2 2 a) Ta có x x y 0 : 0 |
f (x, y) |= y arctan | = y | arctan |
y | y = 0, (1) y y 2 f ( , x ) y =0 | f ( , x ) y | | = 0 | . (2) 2 Từ
(1) và (2) ta có: 0 |
f (x, y) | |
y | ,(x, y)
, mà lim | y | =0 , nên theo nguyên lý 2 (x ,y ) ( → 1,0) 2
kẹp ta có lim | f ( , x y) | =0 (x ,y ) ( → 1,0) lim
f (x, y) = 0 = f (1, 0) f ( ,
x y) liên tục tại B(1, 0) . (x, y )→ (1,0)
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 50
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 1 y arctan −0 2 − b) Xét giới hạn: f (1, y) f (1, 0) y 1 lim = lim = lim arctan = 2 y →0 y →0 y →0 y − 0 y y 2 −
f (1,y ) f (1, 0) f (1,0) = lim = y y 0 → y − 0 2 Câu 7. Xét hàm số
f (x) = tan x trên 0, . 2 1 2sin x f (x) = ; f (x) = 0,x 0, 2 3 cos x cos x 2
f (x) là hàm lồi trên 0,
. Do x, y 0; , áp dụng bất đẳng thức hàm lồi: 2 2 x + y x + y f ( ) x + f ( ) y 2 f
tan x + tan y 2 tan , , x y 0, 2 2 2 tan x + tan y x + y tan , x , y 0, 2 2 2
đpcm. Dấu bằng xảy ra khi x = , y x 0, 2 Câu 8. / 2 xsin x 0 xsin x / 2 x sin x I = dx = dx + dx −/2 x −/2 x 0 1+ 3 1+ 3 1+ 3x − = = Xét 0 xsin x x t I = dx
t = −x x = − t . Đổi cận . 1 . Đặt d d 2 2 − /2 1+ 3x
x = 0 t = 0 0 − − /2 /2 t sin( t) t sin t xsin x I = (−dt) = dt = dx 1 /2 −t 0 −t 0 1+ 3 1+ 3 1+ 3−x x /2 /2 /2 x sin x x sin x x sin x 3 x sin x I = + dx = + dx =
x sin x dx 0 x x − 0 x x 0 1+ 3 1+ 3 1+ 3 1+ 3 /2 /2 /2 =
x d(− cos x) = (− x cos x) −
(− cos x)dx = 1 0 0 0 Vậy I = 1 . arctan x dx arctan x dx + arctan x d Câu 9. 1 x I = = + 0 0 x x + 1− cos x x x + 1− cos x + − I2
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 51
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST arctan x arctan x f ( ) x = =
0 là hàm liên tục trên (0, +) . + 1− cos 2 x x x x x x + 2 sin 2 +) I m b có điể ất thường x = 0 . 1 2 Khi x x 0+ → ta có: (1− cos x) ~
, là VCB bậc cao hơn x x khi x → 0 2 1 1 Khi x 1 x 0+ → thì f (x) ~ ~ , mà 1 dx hội tụ (do = 1 ) 1/2 1/ 2 x x x 0 x 2
I hội tụ theo tiêu chuẩn so sánh. 1
x x + (1− cos x) x x 0
+) Xét I . Với x 1, ta có: 2 0 arctan x 2 + 2 2 3 0 f (x) = , x 1 , mà 2 dx hội tụ (do = 1 ) 3/2 3/2 x x x 1 x 2
I hội tụ theo tiêu chuẩn so sánh. Vậy I , I hội tụ 2 1 2 I hội tụ.
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 52
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 4 (Nhóm ngành 1) 1
Câu 1 (1 điểm). Tính giới hạn lim(cos x− sin ) x x . x→0
Câu 2 (1 điểm). Tìm tiệm cân xiên c ủa đồ th hàm s ị
ố y = x arctan x.
Câu 3 (1 điểm). Tính tích phân 4 4 tan x dx . 0 1
Câu 4 (1 điểm). Tính tích phân ln ( 2 x − x + )1dx . 0
Câu 5 (1 điểm). Tìm cực trị của hàm số 2 2
z = 4( y − x) − y − x . 2 y
xarctan , x 0,
Câu 6 (2 điểm). Cho hàm số f (x, y) = x 0, x = 0.
a) Xét tính liên tục của f (x, y) tại điểm B(0,1) . b) Tính f . x (0,1) Câu 7 + +
(1 điểm). Cho x y cot x cot y 0 , x y . Chứng minh cot . 2 2 2 Câu 8 x sin x
(1 điểm). Tính tích phân 2 − dx . 1 +2 x 2 + arctan x dx
Câu 9 (1 điểm). Xét sự hội tụ, phân kỳ của tích phân suy rộng: . 0
x x + x − sin x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 53
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 4 (Nhóm ngành 1)
Lời giải chi ti ết tham kh s ảo đề ố 3 1 Câu 1. 1
lim(cos x− sin ) x x = . x→ 0 e Câu 2. ( y ) x lim = lim arctan x = = a x →+ x x →+ 2 1 arctan x − 2 2 b = lim y −
x = lim x arctan x − = lim 1+ = lim x = −1 x →+ 2 x →+ 2 x →+ 1 x→+ 1 − x 2 x y =
x −1 là tiệm cận xiên bên phải . 2 −
Tương tự ta tìm được y = x 1
− là tiệm cận xiên bên trái. 2 Câu 3. /4 /4 4 2 tan x dx = t an x ( 2 1+ tan x) −( 2 1+ tan x) +1 d x 0 0 /4 3 tan x 2 = − tan x+ x = − . 3 4 3 0 Câu 4. 1ln
( 2x − x+1)dx = − 2 0 3 Câu 5. Hàm số t c
đạ ực trị tại duy nhất điểm M ( 2
− , 2) (cực đại), z = z( 2 − ,2) = 8. max
Câu 6. a) f (x, y) liên tục tại B(0,1) . b) f = x (0,1) 2
Câu 7. Tương tự đề trên. Câu 8. I = 1 + Câu 9. arctan x dx hội tụ. 0
x x + x −sin x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 54
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 5 (Nhóm ngành 2)
Câu 1 (1 điểm). Tìm a để hàm số sau liên tục tại điểm x =1 : 3
a −x, khi x 1 f (x) = a
rccos ,x khi 0 x 1
Câu 2 (1 điểm). Tìm hàm c c ngượ ủa hàm số 2x 2 x y − = −
Câu 3 (1 điểm). Cho hai hàm f(x)= 3 x , g(x)= 2 x , 1
− x 3 . Tìm số c (−1,3) − − sao cho f (c) f (3) f ( 1) =
. Điều này có mâu thuẫn với định lý Cauchy hay không? g (c) g(3) − g( 1 − ) Giải thích?
Câu 4 (1 điểm). Cho hai hàm số f (x), g(x) :
thoả mãn f (x) g(x) với mọi x . Chứng
minh rằng nếu f (x) là hàm đơn điệu tăng thì f ( f ( )
x ) g (g( x)) . Câu 5 (1 điể + + m). Tính tích phân 3x 1 dx . 0 ( x +1) ( 2 x + ) 1 1 1+ 2sin x
Câu 6 (1 điểm). Tính giới hạn lim ln . 3 x→0 x 1+ sin 2x Câu 7
(1 điểm). Tính độ dài cung y = ln(cos ) x , 0 x . 3 3 t x = 3 Câu 8 (1 điể
m). Tìm tiệm cận xiên của đường cong 1 −t . 2 t y = 1 − t
Câu 9 (1 điểm). Tính giới hạn: 1 1 2 n 1 − lim + ++ n→ 2 2 2 2 2 n+ 1 4 n + 1 4n + 2 4n + (n− 1)
Câu 10 (1 điểm). Cho hàm f(x) lồi, khả tích trên đoạn [a, b]. Ch ng minh r ứ ằng: 1 b
f (a) + f ( ) b
f (x )dx a b − a 2
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 55
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 5 (Nhóm ngành 2)
Câu 1. Ta có: f (1) = arccos1 = 0 . 3 3 lim f ( ) x = lim a − x = a 1 − , lim f ( )
x = lim arccos x = arccos1 = 0 x 1+ x 1+ x 1− x 1− → → → →
+) f (x) liên tục tại 3
x = 1 lim f (x) = lim f (x) = f (1)
a − 1 = 0 a = 1 + − x →1 x →1
Vậy a =1 là giá tr c ị ần tìm.
Câu 2. Với x , xét phương trình x − x x = − = ( x y y )2 2 2 2 2 −1 2 y − y + − x 4 y | y | 2 = = 0 (L) ( x )2 x 2 2 2
− y 2 −1 = 0 2 y + y + + x 4 y | y | 2 = = 0 (TM ) 2 2 2 y + y + 4 −1 x = log = 0 = f ( y) 2 2 2 + + − x x 4 c c Hàm ngượ ủa hàm số đã cho là 1 f ( ) x = log , x . 2 2 Câu 3. Ta có: 2 f ( ) x 3x , g = (x) = 2 ,
x x (−3,1) 2 3 3 − − − − − Do đó: f ( ) c f ( 3) f (1) 3c ( 3) 1 7 = = c = ( 3 − ,1) . 2 g (c) g( 3 − ) −g(1) 2c ( 3 − ) 1 − 3 − −
Như vậy tồn tại hằng số f c f f
c để thoả mãn đẳng thức ( ) ( 3) (1) = , điều này không mâu g (c )
g (−3)− g (1) thuẫn v nh lý Cauchy. ới đị
Thật vậy, định lý Cauchy áp dụng cho g (x) 0,x (a, )
b . Bài này ta có g(0) = 0, với 0 ( 3
− ,1) thế nên bài này không thoả u ki mãn điề
ện định lý Cauchy → bài này không nằm
trong vùng áp dụng định lý Cauchy, không mâu thuẫn.
Câu 4. Vì f là hàm đơn điệu tăng, mà theo bài ra f (x) g( ) x
f ( f (x)) f (g(x)). Lại có f (g(x)) g(g(x)) (vì f (y) g( y) ) đpcm.
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 56
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST + + + Câu 5. 3x 1 x 2 1 x = + − x (x + 1)( d d 2 0 x + ) 2 2 0 1
x + 1 x + 1 x + 1 A A x 2 1 1 = lim + − dx = lim ln
( 2x+1 + 2arctan x−ln | x+1| 2 2 ) A →+
0 x + 1 x +1 x +1 A→+ 2 0 1 = ( + A + ) 2 2 A 1 lim ln
1 + 2arctan A − ln | A +1| = lim ln + 2arctan A A→+ 2 A→+ A = ln1+ 2 = 2 Câu 6. VCB 1 1+ 2sin x 1 1+ 2sin x 1+ 2sin x L = lim ln = lim −1 do lim = 1 3 3 x →0 x → + 0 x → + 0 x 1 sin 2x x 1 sin 2x 1+ sin 2x 3 x x − + o (x ) 3 3 (2x ) 2 − 2x − + o ( 3x)
1 2sin x −sin 2x 1 3! 3! = lim = lim 3 3 x →0 x → + 0 x 1 sin 2 x x 1 +sin 2 x 3 1 x + o( 3 x ) 3 1 x 1 1 = lim = lim = lim = = 1. 3 3 x →0 x 0 → x 0 x 1+ sin 2x x 1+ sin 2x → 1+ sin 2x 1+ 0 Vậy L=1. − Câu 7. Ta có: sin x y ( ) x = , x 0,
. Độ dài cung cần tính là: cos x 3 2 + ( − x y ( ) x )2 sin 1 1 3 3 3 dx = 1+ dx = dx =
dx do cos x 0,x 0, 2 0 0 0 cosx cos x cosx 3 cos x dx d(sin x) d − (sin x) 3 3 2 = d(sin ) x = = 2 2 0 0 0 cos x 1 −sin x
(sin x −1)(sin x +1) 3 1 − sin x −1 = ln = ln(2+ 3) (đvđd). 2 sin x +1 0
Vậy độ dài cung cần tính là ln(2 + 3) (đvđd). Câu 8.
− Khi 𝑡 → ±∞ thì lim𝑡→±∞ 𝑥 = lim𝑡→±∞ 𝑡3 = −1 ⇒ ng h trườ
ợp này không có tiệm cận xiên. 1−𝑡3
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 57
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 3 - Khi t
t → t , với t 1 thì 0 lim x = hữu hạn ng h trườ
ợp này không có tiệm cận Xiên. 0 0 3 t→ t0 1− t0
- Khi t →1 thì x → . Ta có: 2 3 2 y t 1−t 1+ t + t lim = lim = lim = 3 = a 3 t 1 → t 1 → t→1 x 1 −t t t 2 t ( 2 t + t + ) 3 2 3 1 − 3 3 t t t
b = lim( y − ax) = lim( y − 3x) = lim − = lim 3 t → t →
t → 1− t 1 t − t → (1− t)( 2 1 1 1 1 1+ t + t ) 2 2 2 t (1− t) t (1− t) = lim = = t→ (1− t)( lim 0 2 1 1+ t + t ) 2 t 1 → 1+t +t
y = 3x là tiệm cận xiên của đường cong đã cho.
Câu 9. Giới hạn đã cho được viết lại là: 𝑛−1 𝑛−1 𝐿 = lim 1 𝑘 𝑛 1 𝑘 = lim 𝑛→+∞ 𝑛 + 1 ∑ 2 2
𝑛→+∞ 𝑛 + 1 ⋅ 𝑛 ∑ √4𝑛2 + 𝑘2 𝑘=1 √4𝑛 + 𝑘 𝑘=1 𝑛 1 𝑛−1 𝑘 𝑘 = lim ( vì với 𝑘 = 0 thì = 0)
𝑛→+∞ 𝑛 + 1 ⋅ 𝑛 ∑ √4𝑛2 + 𝑘2 √4𝑛2 + 𝑘2 𝑘=0 Xét giới hạn: 𝑛−1 𝑛−1 𝑘 𝐾 = lim 1 𝑘 1 = lim 𝑛
𝑛→+∞ 𝑛 ∑ √4𝑛2 + 𝑘2 𝑛→+∞ 𝑛 ∑ 2 𝑘=0 𝑘=0 √4 + (𝑘𝑛) 1 𝑥
= ∫ 𝑓(𝑥)d𝑥 (với 𝑓(𝑥) =
liên tục, khả tích trên [0,1] ) 0 √4 + 𝑥2 x = dx = 4+ x = 5 − 2 0 ( )1 1 2 2 0 4 + x n 1 n 1 − k L = lim lim = 1 ( 5 − 2) = 5 − 2. n→+ n →+ 2 2 n + 1
n k =0 4n + k
Câu 10. Với mỗi x [a,b] , luôn tồn tại duy nhất t [0,1] sao cho: x = ta + (1− t)b .
Do đó có thể đổi biến x = ta + (1− t)b dx = (a − b)dt . Đổi cận:
- Khi x = a thì t =1.
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 58
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
- Khi x = b thì t = 0 . b Lúc này: 1 1 0 1 f (x)dx =
f (ta +(1 −t) ) b (a − ) b dt =
f (ta +(1 −t) ) b d . t a 1 0 b − a b − a
Áp dụng tính chất hàm lồi: f (ta + (1− t)b) tf (a) + (1− t) f (b), t [0,1] . ⇒ ∫ 1 1
0 𝑓(𝑡𝑎 + (1 − 𝑡)𝑏)d𝑡 ≤ ∫0 [𝑡𝑓(𝑎) + (1 − 𝑡)𝑓(𝑏)]d𝑡 𝑡2 1 𝑡2 1 1 1
= 2| 𝑓(𝑎) + (𝑡 − 2)| 𝑓(𝑏) = 2𝑓(𝑎)+2𝑓(𝑏). 0 0
Suy ra điều phải chứng minh.
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 59
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 6 (Nhóm ngành 2)
Câu 1 (1 điểm). Tìm a để hàm số sau liên tục tại điểm x =1 : 3
a +x, khi x 1 f (x) = a
rccos ,x khi 0 x 1
Câu 2 (1 điểm). c c Tìm hàm ngượ ủa hàm số 3 x 3 . x y − = −
Câu 3 (1 điểm). Cho hàm số 3 2
f (x) = x , g(x) = x , −3 x 1 . Tìm số c ( 3 − ,1) sao cho f ( ) c f ( 3 − ) − f(1) =
. Điều này có mâu thuẫn với định lý Cauchy hay không? Giải thích? g( ) c ( g −3) − ( g 1)
Câu 4 (1 điểm). Cho hai hàm số f (x), g(x) :
thoả mãn f (x) g(x) với mọi x . Chứng
minh rằng nếu g(x) là hàm đơn điệu tăng thì f ( f (x)) g(g(x)) . Câu 5 + x + 3
(1 điểm). Tính tích phân dx . 0 ( x +1) ( 2 x + ) 1 1 1− 2sin Câu 6 x
(1 điểm). Tính giới hạn lim ln . 3 x→0 x 1− sin 2x Câu 7
(1 điểm). Tính độ dài cung y = ln(sin ) x , x . 6 2 2 t x = Câu 4
(1 điểm). Tìm tiệm cận xiên của đường cong 1− t . 3 3t y = 3 1 − t
Câu 9 (1 điểm). Tính giới hạn: 1 1 2 n 1 − lim + ++ n→ 2 2 2 2 2 n+ 1 4n − 1 4n − 2
4n − (n− 1)
Câu 4 (1 điểm). Cho hàm f(x) lõm, khả tích trên đoạn [a, b]. Ch ng minh r ứ ằng: 1 b
f (a) + f (b)
f (x )dx a b − a 2
Lời giải tham kh s ảo đề ố 5
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 60
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 7 (Nhóm ngành 3) Câu 1 x
(1 điểm). Tính dx . 2 x + 3x + 2 dx
Câu 2 (1 điểm). Xét sự hội tụ, phân kỳ của tích phân suy rộng: . 1 3 x − x+ 1 + x+ 1 2 2 x y
Câu 3 (1 điểm). Tính thể tích vật tròn xoay tạo bởi elip: +
=1 quay quanh trục Ox . 4 9 Câu 4 (1 điể − m). Tính cos x cos 4x lim . 2 x→ 0 x Câu 5 (1 điể x
m). Tìm và phân loại điểm gián đoạn của hàm số y = . 3 2
x − 2x + x − 2
Câu 6 (1 điểm). Cho hàm số 3 2 2 2
z = x y + x y − 3xy + 2 . Tính dz(1,1) .
Câu 7 (1 điểm). Tìm cực tr c
ị ủa hàm số z= xy+ ( − x− y)(2x+ 3y); là tham số thực . 2 2 1
x + y 4
Câu 8 (1 điểm). Tính tích phân kép
(x + y)dx dy , với D : D x y 3x
Câu 9 (1 điểm). Tồn tại hay không hàm f sao cho:
f (1) = − f (1), f (0) = 0 và f (x) 0, x ( 2 − , 2) Câu 10 (1 điể 2018 2019 m). Cho hàm số: z = x ( 2 2 x − y ) + ( 2 2 x − y ) + ( 2 2 sin 100 x − y ) . Chứng minh 2 z z x + xy = zy . y x
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 61
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 7 (Nhóm ngành 3) x x 2 1 Câu 1. dx = dx = − dx
= 2ln | x + 2 | −ln | x +1| +C 2 x +3x +2 (x 1 + )(x +2) x +2 x 1 + Câu 2. 1 f ( ) x = 0, x 1 . 3
x − x + 1+ x + 1
Điểm bất thường của tích phân suy rộng là + . Ta có: 1 x→+ 1 1 + dx 3 ~ = , mà hội tụ (do = 1 ) 3/2 3 3 − + 3/ 2 1+ + 1 x x x x x 1 x 2 dx
hội tụ theo tiêu chuẩn so sánh. 1 3
x − x +1 + x+1 Câu 3.
Chỉ cần quay nửa trên của elip (ứng với 𝑦 ≥ 0 ) thì sẽ thu được vật
thể đã cho. Nửa trên của elip là miền giới hạn bởi: 3 𝑦 = √
2 4 − 𝑥2, 𝑦 = 0, 𝑥 = −2, 𝑥 = 2.
Quay miền này quanh trục O𝑥 ta thu được vật thể có thể tích là: 2 3 2 9 2 9 𝑥3 2
𝑉 = 𝜋 ∫ ( √4 − 𝑥2) d𝑥 = (4 − 𝑥2)d𝑥 = −2 2 4 ∫ −2 4 (4𝑥 − 3 )| −2 = 24𝜋(dvtt) Câu 4. cos x− cos 4 x
− sin x+ 4sin 4 x L = lim = lim
(dạng 0 − 𝐿′𝐻𝑜𝑠𝑝𝑖𝑡𝑎𝑙) 2 x →0 x →0 x 2x 0
− cos x +16cos 4x − cos0 +16cos 0 15 = lim = = . x →0 2 2 2
Vậy giới hạn cần tính bằng 15 2
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 62
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST Câu 5. x x y = = . 3 2
x − x + x− x− ( 2 2 2 ( 2) x + 1) Tập xác định: D =
x = 2 là điểm gián đoạn của hàm số. 1 x 1 x 2 lim y = lim = + do lim = + , lim = 0 + + 2 + + 2 x →2 x →2 − + x →2 − x 2 x 2 x 1 x 2 → x + 1 5
x = 2 là điểm gián đoạn loại 2 của hàm số. Câu 6. 2 2 2
z = 3x y + 2xy − 3y z (1,1) = 2 x x 3 2
z = 2x y + 2x y − 3x z (1,1) = 1 y y
dz (1,1) = z (1,1)dx + z (1,1)dy = 2 dx + dy x y Câu 7. x = 0
z = −4 y − 4x + 2 = 0 Tìm điểm dừng: x
z = −4 x − 6 y + 3 = 0 y = y 2 M 0, m d là điể
ừng duy nhất của hàm số. 2 2 B −AC = − 8 0 A = z = 4 − , B = z = 4 − , C = z = 6 − xx xy yy A = 4 − 0 hàm số t c đạ ực đại tại 3 M 0, , giá tr c ị ực đại 2 z = . 2 CÐ 4 Câu 8. x = r cos Đổi biến | J |= r . y = r sin 1 r 2
Miền D trở thành 4 3 Tích phân cần tính là: /3 2 /3 2 2 I =
(x + y)dx dy = d
(r cos + r sin) r dr = d
(cos + sin)r dr D /4 1 /4 1
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 63
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST r 2 = 3 = /3 /3 /3 r 7 7 = (cos + sin) d =
(cos + sin )d = (sin − cos) /4 /4 3 3 3 r 1 = = /4 7 = ( 3 −1) . 6
Câu 9. Giả sử tồn tại hàm f (x) thoả mãn đề bài.
Vì f khả vi tới cấp 2 trên (-2,2) f khả vi trên (-2,2), liên tục trên [-2,2].
Áp dụng định lý Lagrange cho f (x) trên [0,1]: − Tồn tại f f (0,1) sao cho (1) (0) f ( ) =
= f (1) (vì f (0) = 0 ) 1− 0
Tương tự, áp dụng định lý Lagrange cho hàm f (x) liên tục trên [−1,0] , khả vi trên (−1,0) ta − − có: Tồn tại f f (−1, 0) sao cho (0) ( 1) f ( ) =
= − f (−1) = f (1) 0− (−1)
Như vậy, tồn tại , (−2,2), sao cho f ( ) f =
( ) , điều này mâu thuẫn với giả thiết
f (x) 0,x (−2, 2) không t n t ồ
ại hàm f thoả mãn đề bài. Câu 10.
Đặt 𝑢 = 𝑥2 − 𝑦2 và 𝑓(𝑢) = sin 𝑢 + 𝑢2018 + 100𝑢2019.
Ta có: 𝑧 = 𝑥𝑓(𝑢 . ) ∂𝑧 ∂𝑢
∂𝑥 = 𝑓(𝑢) + 𝑥𝑓′(𝑢) ⋅∂𝑥 = 𝑓(𝑢) + 𝑥𝑓′(𝑢) ⋅ 2𝑥 = 𝑓(𝑢) + 2𝑥2𝑓′(𝑢) ∂𝑧 ∂𝑢
∂𝑦 = 𝑥𝑓′(𝑢) ⋅∂𝑦 = 𝑥𝑓′(𝑢) ⋅ (−2𝑦) = −2𝑥𝑦𝑓′(𝑢) ∂𝑧 ⇒ 𝑥2 ∂𝑧
∂𝑦 + 𝑥𝑦 ∂𝑥 = −2𝑥3𝑦𝑓′(𝑢) + 𝑥𝑦𝑓(𝑢) + 2𝑥3𝑦𝑓′(𝑢) = 𝑥𝑓(𝑢) ⋅ 𝑦 = 𝑧𝑦. ⇒ đpcm.
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 64
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 8 (Nhóm ngành 3) Câu 1 x
(1 điểm). Tính dx . 2 x + 5x + 6 dx
Câu 2 (1 điểm). Xét sự hội tụ, phân kỳ của tích phân suy rộng: . 1 3
x + x +1 + x+1 2 2 x y
Câu 3 (1 điểm). Tính thể tích vật tròn xoay tạo bởi elip: +
= 1 quay quanh trục Ox . 9 4 Câu 4 (1 điể − m). Tính cos 4x cos x lim . 2 x→ 0 x Câu 5 (1 điể x
m). Tìm và phân loại điểm gián đoạn của hàm số y = . 3 2
x + 2 x + x + 2
Câu 6 (1 điểm). Cho hàm số 2 3 2 2
z = x y + x y − 3xy + 2 . Tính dz(1,1) .
Câu 7 (1 điểm). Tìm cực tr c
ị ủa hàm số z= xy+ ( − x− y)(2x+ 3y); là tham số thực . 2 2 1
x + y 4
Câu 8 (1 điểm). Tính tích phân kép
(x + y)dx dy , vói D : x D y x 3
Câu 9 (1 điểm). Tồn tại hay không hàm f sao cho: f (1) f (1), f (0) 0 và f = − = ( ) x 0, x (−2, 2) Câu 10 (1 điể 2018 2019
m). Cho hàm số z x ( 2 2 x y ) ( 2 2 x y ) ( 2 2 sin 100 x y ) = − + − + − . Chứng minh 2 z z x + xy = zy . y x
Lời giải tham kh s ảo đề ố 7
Tài liệu được chia sẻ miễn phí tại website Tailieuhust.com 65




