












Preview text:
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 12
VECTƠ VÀ HỆ TRỤC TOẠ ĐỘ TRONG KHÔNG GIAN BỘ ĐỀ ÔN TẬP CHƯƠNG
LUYỆN THI THPT QUỐC GIA
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Page: CLB GIÁO VIÊN TRẺ TP HUẾ TR¾C NGHIÖM CHUY£N §Ò M«n: To¸n 12 – KNTT ÔN TẬP CHƯƠNG 2
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 01_TrNg 2025 Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung tâm Km10- Hương Trà – Huế NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi, thí sinh chỉ chọn một phương án. Câu 1:
Trong không gian Oxyz ,cho hai điểm A(1;1; − )
1 , B(2;3;2) . Véctơ AB có tọa độ là A. (1; 2;3) . B. ( 1 − ;− 2;3) . C. (3;5; ) 1 . D. (3; 4; ) 1 . Câu 2:
Trong không gian Oxyz , cho véctơ OA = j − 2k . Tọa độ điểm A là A. (0;1; − 2) . B. (1; − 2;0) . C. (1;0; − 2) . D. (0; −1; 2) . Câu 3:
Trong không gian Oxyz , cho hình hộp ABC . D AB C D có A(1;0 )
;1 , B(2;1;2) , D(1; 1 − ) ;1 , C (4;5; 5
− ) . Tìm tọa độ đỉnh B của hình hộp ABC . D
A BCD . A. (4;6; −5) . B. (4;6;5) . C. (2;0; 2) . D. ( 4 − ; 6 − ;5) . Câu 4:
Trong không gian Oxyz, cho hai vectơ u = (1; 0 ;1), v = (0 ;1; − 2) . Tích vô hướng của u và v là
A. u.v = −2 .
B. u.v = 2 .
C. u.v = (0 ; 0 ; − 2) .
D. u.v = 0 . Câu 5:
Trong không gian Oxyz , cho hai điểm A( 1
− ;1;2) và B(3;−5;0) . Trung điểm của đoạn thẳng AB là
A. M (1;0; − 3) .
B. M (0; 2; − 3) .
C. M (1;− 2; ) 1 .
D. M (1; 2;3) . Câu 6:
Trong không gian Oxyz, cho hai vectơ a = (1; 2
− ;0) và b = 2a . Tìm tọa độ của vectơ b. A. (2; 4; 2). B. (2; 4 − ;0). C. (3;0; 2). D. (2; 4;0). Câu 7:
Trong không gian Oxyz, cho vectơ u = (1; 2 ; 0) . Mệnh đề nào sau đây đúng?
A. u = 2i + j .
B. u = i + 2 j .
C. u = j + 2k .
D. u = i + 2k . Câu 8:
Trong không gian Oxyz , cho hai điểm A(1; 2;0), B (2; 1 − )
;1 . Tìm điểm C có hoành độ dương
trên trục Ox sao cho ABC vuông tại C . A. C (3;0;0). B. C (5;0;0). C. C ( 5 − ;0;0). D. C (2;0;0). Câu 9:
Trong không gian Oxyz, cho hai điểm (
A 1;1;0) và B(0;1;2). Tìm điểm M thoả mãn điều kiện AM = −2 . AB A. M ( 1 − ;1; 4 − ). B. M (1;1; 4 − ). C. M (3;1; 4 − ). D. M ( 1 − ;1;4).
Câu 10: Trong không gian Oxyz , cho ba vectơ a = (1; 2 ; 3), b = ( 2 − ; 0 ;1), c = ( 1
− ; 0 ;1) . Tọa độ của
vectơ n = a + b + 2c − 3i là A. ( 6 − ; 2 ; 6) . B. (0 ; 2 ; 6) . C. (6 ; 2 ; − 6) . D. (6 ; 2 ; 6) .
Câu 11: Trong không gian Oxyz , cho hai vectơ a = (2 ;1; −1), b = (1; 3 ; m) . Tìm giá trị của tham số m
để (a ; b) = 90 .
A. m = −5 . B. m = 5 . C. m = 1. D. m = −2 .
Câu 12: Trong không gian Oxyz , cho hai vectơ a = (3; 2 ) ;1 ;b = ( 2
− ;0;1 ) . Tính cos(a,b) . A. (a b) 70 cos , = . B. (a b) 5 cos , = − . 14 14 + 5 C. (a b) 70 cos , = − . D. (a b) 5 cos , = − . 14 14
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn) Câu 1:
Trong không gian Oxyz , cho ba vectơ a = (1;0;0),b = (0; 2;0), c = (0;0; − ) 1 .
a) a + b = (1; 2;0) .
b) a + b − c = (1; 2 ) ;1 . c) a + b = 3
d) (a + b )(a + b − c ) = 5 . Câu 2:
Trong không gian Oxyz , cho ba vectơ a = (1;0;0),b = (0; 2;0), c = (0;0; − ) 1 .
a) 2a − b = (2; 2 − ;0) . 1
b) a − b = (1; 1 − ;0) . 2
c) (a,b ) = 0 .
d) (2a − b )c = 0 . Câu 3:
Trong không gian Oxyz , cho tam giác ABC có ba đỉnh A(1;1; ) 1 , B ( 1 − ;2 ) ;1 , C (1;2;− ) 1 . 1
a) Tọa độ trung điểm của AB là 1 − ; ;0 . 2 1 5 1
b) Tọa độ trọng tâm tam giác ABC là ; ; . 3 3 3 1 c) cos BAC = . 2 d) 2 2
AB + AC − 2AB AC cos A = 2 . Câu 4:
Trong không gian Oxyz , biết c = ( ;
x y; z) vuông góc với cả hai vectơ a =(1;3;4),b =( 1 − ;2;3) .
a) c a = 0 .
b) c (a + b ) = 0 .
c) x + 3y + 4z = 0 .
d) 5y + 7z = 0 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1:
Trong không gian Oxyz , cho hình lăng trụ tam giác đều ABC.AB C có A( 3; 1 − ) ;1 , hai
đỉnh B, C thuộc trục Oz và AA = 1 (C không trùng với O). Biết vectơ u = (a; ; b )
2 (với a,b )
cùng phương với AC . Tính 2 2
T = a + b . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 2:
Trong không gian Oxyz , cho hình thang ABCD với các đỉnh A(1; 2; ) 1 , B (2;0;− ) 1 , C (6;1;0) 7 7 4 và D ; ;
. Tính diện tích hình thang ABCD (làm tròn đến hàng phần trăm). 3 3 3 Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 3:
Trong không gian Oxyz , cho hình thang cân ABCD có các đáy lần lượt là AB,CD . Biết A(3;1; 2 − ) , B( 1 − ;3;2) , C ( 6
− ;3;6) . Tính tổng bình phương các tọa độ của điểm D . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 4:
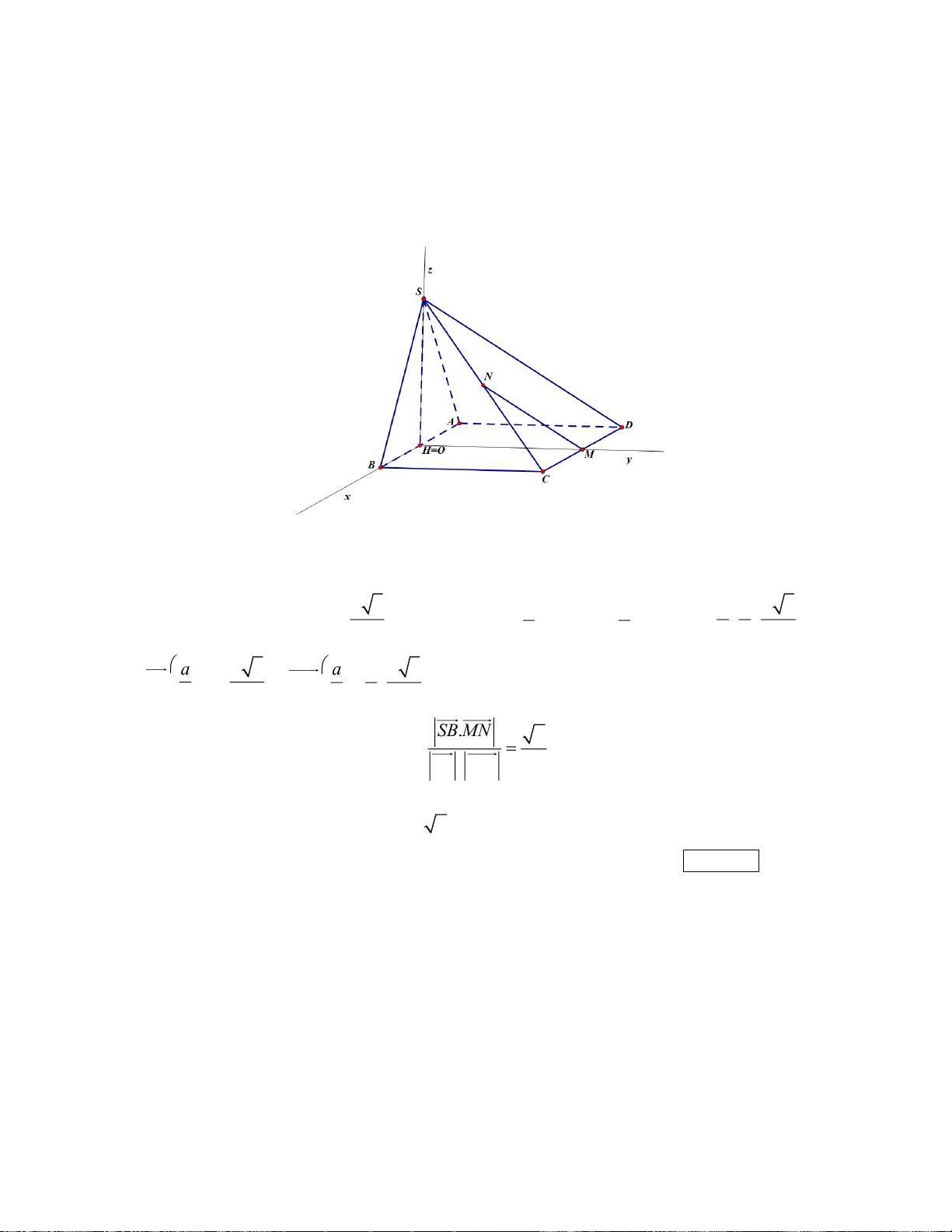
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi M , N lần lượt là trung điểm của CD, SC. Tính cô-
sin góc tạo bởi SB và MN (làm tròn đến hàng phần trăm) . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 5:
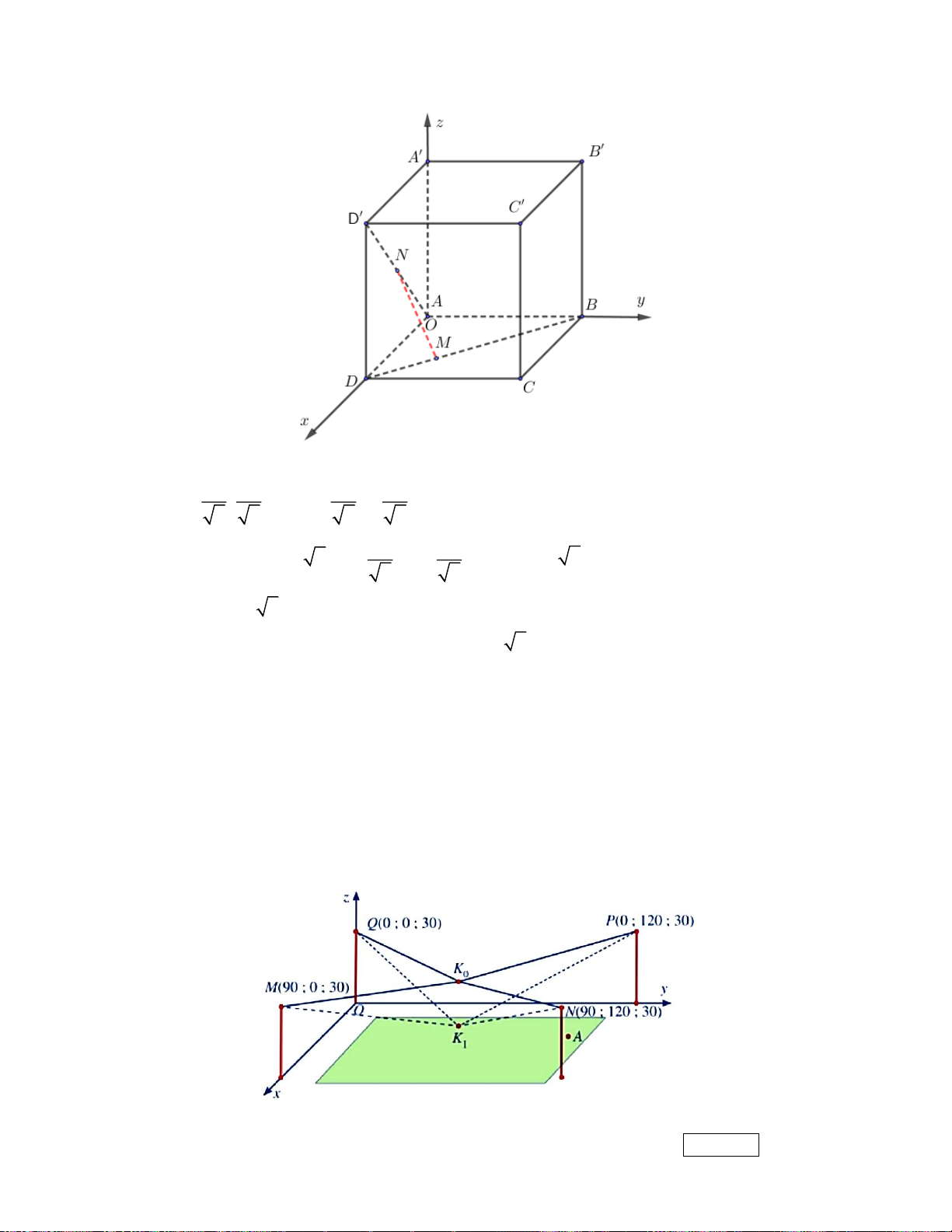
Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh bằng 9. Trên BD, A ’
D lần lượt lấy các điểm M ,
N sao cho MD = AN = x , (0 x 9 2). Xác định x để độ dài đoạn MN nhỏ nhất. Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 6:
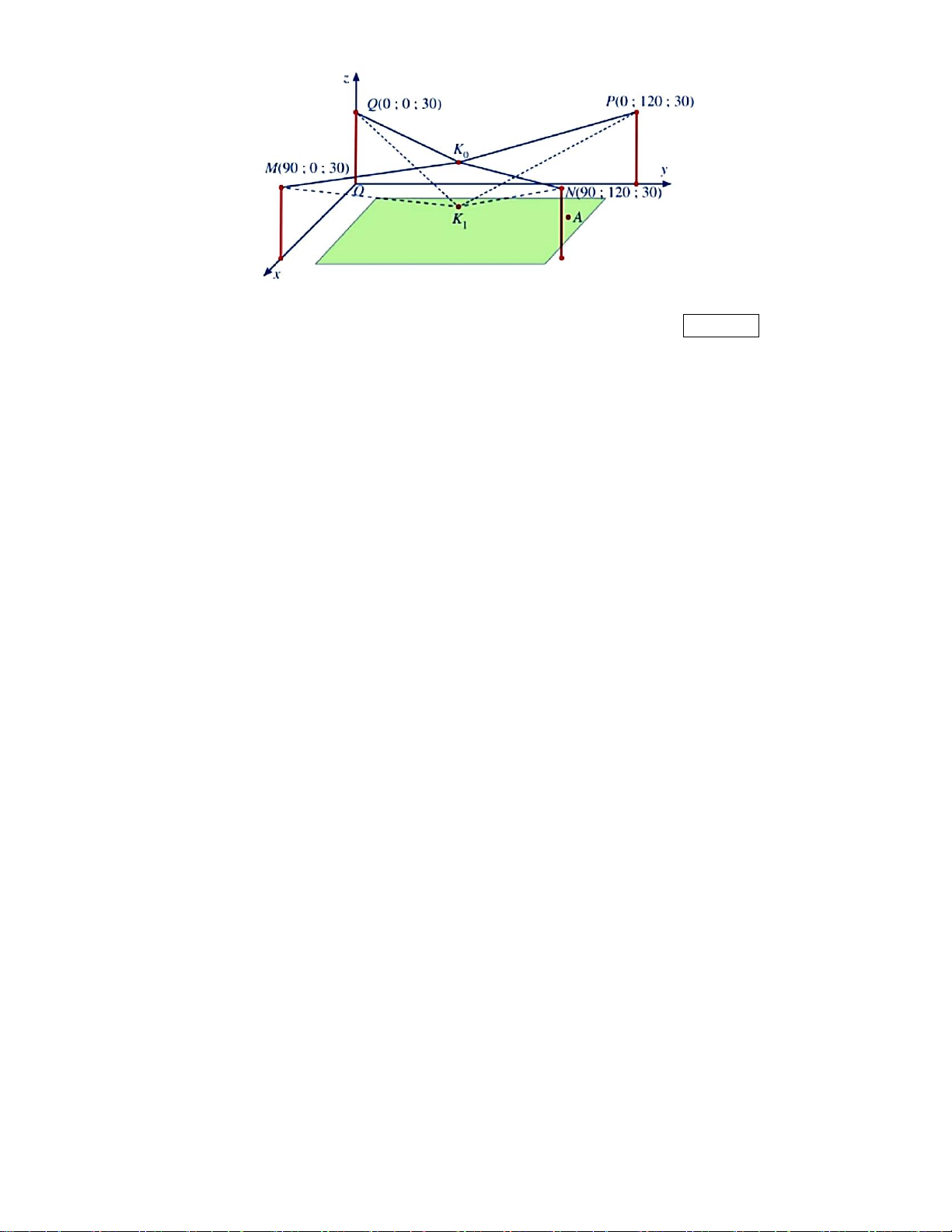
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá,
camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự
định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ
camera ở vị trí mong muốn. Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ
Oxyz (đơn vị độ dài trên mỗi trục là 1m), các đỉnh của bốn chiếc cột lần lượt là các điểm M (90;0;30), N
(90;120;30), P(0;120;30) và Q(0;0;30) (xem hình minh họa). Giả sử K
K M = K N = K P = K Q
0 là vị trí ban đầu của camera có cao độ bằng 25 và 0 0 0 0 . Để
theo dõi quả bóng đến vị trí A, camera được hạ thấp theo phương thẳng đứng xuống điểm K1 có cao độ bằng 19.
Tính tổng các tọa độ của K1 . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
____________________HẾT____________________
Huế, 17h20’ Ngày 25 tháng 7 năm 2024
Page: CLB GIÁO VIÊN TRẺ TP HUẾ TR¾C NGHIÖM CHUY£N §Ò M«n: To¸n 12 – KNTT ÔN TẬP CHƯƠNG 2
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 01_TrNg 2025
LỜI GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi, thí sinh chỉ chọn một phương án. Câu 1:
Trong không gian Oxyz ,cho hai điểm A(1;1; − )
1 , B(2;3;2) . Véctơ AB có tọa độ là A. (1; 2;3) . B. ( 1 − ;− 2;3) . C. (3;5; ) 1 . D. (3; 4; ) 1 . Lời giải:
AB = (2 −1;3−1;2 + ) 1 = (1;2;3) Câu 2:
Trong không gian Oxyz , cho véctơ OA = j − 2k . Tọa độ điểm A là A. (0;1; − 2) . B. (1; − 2;0) . C. (1;0; − 2) . D. (0; −1; 2) . Lời giải:
Ta có OA = j − 2k A(0;1; − 2) Câu 3:
Trong không gian Oxyz , cho hình hộp ABC . D AB C D có A(1;0 )
;1 , B(2;1;2) , D(1; 1 − ) ;1 , C (4;5; 5
− ) . Tìm tọa độ đỉnh B của hình hộp ABC . D
A BCD . A. (4;6; −5) . B. (4;6;5) . C. (2;0; 2) . D. ( 4 − ; 6 − ;5) . Lời giải: C' D' B' A' D C A B Gọi C( ;
x y; z) . Ta có A B = (1;1 ) ;1 ,C D
= (x −1; y +1; z − ) 1 x −1 =1 x = 2
Vì ABCD là hình bình hành nên A B = C D
y +1=1 y = 0 C(2;0;2) z 1 1 − = z = 2 Gọi B ( ; a ; b c) B B
= (a − 2;b −1;c − 2),C C = (2;5; 7 − ) . a = 4 Vì ABC . D AB C D
là hình hộp, ta có: B B = C C b
= 6 B (4;6;−5) . c = 5 − Câu 4:
Trong không gian Oxyz, cho hai vectơ u = (1; 0 ;1), v = (0 ;1; − 2) . Tích vô hướng của u và v là
A. u.v = −2 .
B. u.v = 2 .
C. u.v = (0 ; 0 ; − 2) .
D. u.v = 0 . Lời giải:
Ta có u.v = 1 0 + 0 1+1 (−2) = −2 . Câu 5:
Trong không gian Oxyz , cho hai điểm A( 1
− ;1;2) và B(3;−5;0) . Trung điểm của đoạn thẳng AB là
A. M (1;0; − 3) .
B. M (0; 2; − 3) .
C. M (1;− 2; ) 1 .
D. M (1; 2;3) . Lời giải:
Gọi M là trung điểm của đoạn thẳng . AB x + x A B x = = 1 M 2 y + y
Khi đó tọa độ của M được tính bởi: A B y = = −2 M 2 z + z A B z = = 1 M 2 Câu 6:
Trong không gian Oxyz, cho hai vectơ a = (1; 2
− ;0) và b = 2a . Tìm tọa độ của vectơ b. A. (2; 4; 2). B. (2; 4 − ;0). C. (3;0; 2). D. (2; 4;0). Lời giải: b = 2a = (2; 4 − ;0) Câu 7:
Trong không gian Oxyz, cho vectơ u = (1; 2 ; 0) . Mệnh đề nào sau đây đúng?
A. u = 2i + j .
B. u = i + 2 j .
C. u = j + 2k .
D. u = i + 2k . Lời giải:
Ta có: u = xi + yj + zk u = (x ; y ; z) .
Suy ra u = (1; 2 ; 0) u = i + 2 j . Câu 8:
Trong không gian Oxyz , cho hai điểm A(1; 2;0), B (2; 1 − )
;1 . Tìm điểm C có hoành độ dương
trên trục Ox sao cho ABC vuông tại C . A. C (3;0;0). B. C (5;0;0). C. C ( 5 − ;0;0). D. C (2;0;0). Lời giải: A B C ⎯⎯ → ⎯⎯ → Gọi C ( ;
x 0;0), x 0 . AC = ( x −1; 2
− ;0), BC = (x − 2;1;− ) 1 . ⎯⎯ → ⎯⎯ → x = 0
Vì ABC vuông tại C nên AC . BC = 0 ( x − ) 1 ( x − 2) − 2 = 0 2
x − 3x = 0 x = 3 (TM )
Vậy C (3;0;0) . Câu 9:
Trong không gian Oxyz, cho hai điểm (
A 1;1;0) và B(0;1;2). Tìm điểm M thoả mãn điều kiện AM = −2 . AB A. M ( 1 − ;1; 4 − ). B. M (1;1; 4 − ). C. M (3;1; 4 − ). D. M ( 1 − ;1;4). Lời giải: Gọi M ( ;
x y; z) . Ta có AB = ( 1
− ;0;2), AM = (x −1; y −1; z) x −1 = 2 x = 3 Do đó AM = 2
− AB y −1= 0 y =1 M (3;1; 4 − ). z 4 = − z = 4 −
Câu 10: Trong không gian Oxyz , cho ba vectơ a = (1; 2 ; 3), b = ( 2 − ; 0 ;1), c = ( 1
− ; 0 ;1) . Tọa độ của
vectơ n = a + b + 2c − 3i là A. ( 6 − ; 2 ; 6) . B. (0 ; 2 ; 6) . C. (6 ; 2 ; − 6) . D. (6 ; 2 ; 6) . Lời giải:
Ta có: n = a + b + 2c − 3i = (1; 2;3) + ( 2 − ;0;1) + 2( 1
− ;0;1) − 3(1;0;0) = ( 6 − ;2;6) .
Câu 11: Trong không gian Oxyz , cho hai vectơ a = (2 ;1; −1), b = (1; 3 ; m) . Tìm giá trị của tham số m
để (a ; b) = 90 .
A. m = −5 . B. m = 5 . C. m = 1. D. m = −2 . Lời giải:
Ta có (a;b) = 90 a b = 0 5 − m = 0 m = 5 .
Câu 12: Trong không gian Oxyz , cho hai vectơ a = (3; 2 ) ;1 ;b = ( 2
− ;0;1 ) . Tính cos(a,b) . A. (a b) 70 cos , = . B. (a b) 5 cos , = − . 14 14 + 5 C. (a b) 70 cos , = − . D. (a b) 5 cos , = − . 14 14 Lời giải: a b − + + Ta có (a b) . 6 0 1 70 cos , = = = − . a . b 14. 5 14
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn) Câu 1:
Trong không gian Oxyz , cho ba vectơ a = (1;0;0),b = (0; 2;0), c = (0;0; − ) 1 .
a) a + b = (1; 2;0) .
b) a + b − c = (1; 2 ) ;1 . c) a + b = 3
d) (a + b )(a + b − c ) = 5 . Lời giải: a) Đúng b) Đúng c) Sai d) Đúng
a) a + b = (1; 2;0) Đúng.
b) a + b − c = (1; 2 ) ;1 Đúng.
c) a + b = 3 Sai vì 2 2
a + b = 1 + 2 = 5 .
d) (a + b )(a + b − c ) = 5 Đúng vì 11+ 2 2 + 01 = 5 . Câu 2:
Trong không gian Oxyz , cho ba vectơ a = (1;0;0),b = (0; 2;0), c = (0;0; − ) 1 .
a) 2a − b = (2; 2 − ;0) . 1
b) a − b = (1; 1 − ;0) . 2
c) (a,b ) = 0 .
d) (2a − b )c = 0 . Lời giải: a) Đúng b) Đúng c) Sai d) Đúng
a) 2a − b = (2; 2 − ;0) Đúng. 1
b) a − b = (1; 1 − ;0) Đúng. 2
c) (a,b ) = 0 Sai vì a b = 0 , dẫn đến (a,b ) = 90 .
d) (2a − b )c = 0 Đúng. Câu 3:
Trong không gian Oxyz , cho tam giác ABC có ba đỉnh A(1;1; ) 1 , B ( 1 − ;2 ) ;1 , C (1;2;− ) 1 . 1
a) Tọa độ trung điểm của AB là 1 − ; ;0 . 2 1 5 1
b) Tọa độ trọng tâm tam giác ABC là ; ; . 3 3 3 1 c) cos BAC = . 2 d) 2 2
AB + AC − 2AB AC cos A = 2 . Lời giải: a) Sai b) Đúng c) Sai d) Sai 3
a) Sai, trung điểm AB là 0; ;1 . 2 b) Đúng. AB AC 1 1 c) Sai vì AB = ( 2 − ;1;0), AC = (0;1; 2
− ) , dẫn đếncos BAC = = = AB AC 5 5 5 d) Sai vì 2 2 2 2 2 2
AB + AC − 2AB AC cos A = BC = 2 + 0 + 2 = 8 . Câu 4:
Trong không gian Oxyz , biết c = ( ;
x y; z) vuông góc với cả hai vectơ a =(1;3;4),b =( 1 − ;2;3) .
a) c a = 0 .
b) c (a + b ) = 0 .
c) x + 3y + 4z = 0 .
d) 5y + 7z = 0 . Lời giải: a) Đúng b)Đúng c) Đúng d) Đúng
Theo giả thiết ta có c = ( ;
x y; z) vuông góc với cả hai vectơ a =(1;3;4),b =( 1 − ;2;3) nên c .a =0 1
x + 3 y + 4 z =0
x + 3 y + 4 z =0 .
c .b =0 1
− x + 2 y + 3 z =0 5 y + 7 z = 0
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1:
Trong không gian Oxyz , cho hình lăng trụ tam giác đều ABC.AB C có A( 3; 1 − ) ;1 , hai
đỉnh B, C thuộc trục Oz và AA = 1 (C không trùng với O). Biết vectơ u = (a; ; b )
2 (với a,b )
cùng phương với AC . Tính 2 2
T = a + b . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Lấy M là trung điểm BC. AM ⊥ BC Khi đó ta có
nên BC ⊥ AM tại M. AA ⊥ BC
Suy ra M là hình chiếu của A trên trục Oz M (0;0 ) ;1 v à A M = 2. Mặt khác 2 2 AM = A M − AA = 3. 3
Lại có ABC đều nên AM =
BC = 3 BC = 2 MC = 1. 2
Gọi C (0;0;c),c 0 suy ra MC = c −1 . c = 0
MC = 1 c −1 = 1
( loại c = 0 ) C (0;0; 2). c = 2 Suy ra A C = (− 3;1 ) ;1 nên u = ( 2 − 3;2;2) .
Vậy a = −2 3;b = 2. Suy ra 2 2
T = a + b = 16. Câu 2:
Trong không gian Oxyz , cho hình thang ABCD với các đỉnh A(1; 2; ) 1 , B (2;0;− ) 1 , C (6;1;0) 7 7 4 và D ; ;
. Tính diện tích hình thang ABCD (làm tròn đến hàng phần trăm). 3 3 3 Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: 4 1 1 Ta có AB = (1; 2 − ; 2 − ) , BC = (4;1 ) ;1 , AD = ; ;
AB = 3 , BC = 3 2 , AD = 2 . 3 3 3 4 1 1 A . B BC = 1.4 + ( 2) − .1+ ( 2)
− .1 = 0 AB ⊥ BC ; A . B AD = 1. + ( 2 − ). + ( 2
− ). = 0 AB ⊥ AD 3 3 3
Lúc đó hình thang ABCD vuông tại A và B .
AB ( AD + BC) 3( 2 + 3 2)
Vậy diện tích cần tìm là S = = = 6 2 8,49 ABCD . 2 2 Câu 3:
Trong không gian Oxyz , cho hình thang cân ABCD có các đáy lần lượt là AB,CD . Biết A(3;1; 2 − ) , B( 1 − ;3;2) , C ( 6
− ;3;6) . Tính tổng bình phương các tọa độ của điểm D . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Gọi D ( x; y ; z) . Ta có: AB = ( 4
− ;2;4);CD = (x + 6; y −3; z − 6)
Do ABCD là hình thang cân nên CD = k AB (k ) hay x = 6 − − 4t x + 6 y − 3 z − 6 = =
= k y = 3+ 2t ⎯⎯
→ D (−6 − 4t;3+ 2t;6 + 4t). 2 − 1 2 z = 6+ 4 t Lại có 2 2
AC = BD AC = BD (− )2 + + = (− − t)2 + ( t)2 + ( + t)2 2 2 9 2 8 5 4 2 4 4 t =1 . t = 0
+) Với t = 1 D ( 10
− ;5;10). Kiểm tra thấy: AD BC (Không thỏa mãn ABCD là hình thang cân).
+) Với t = 0 D (6; 3 − ; 6 − ). Kiểm tra thấy: ( 3
− ).AB = CD ( thỏa mãn). 2 2 Vậy 2 6 + ( 3 − ) + ( 6 − ) = 81. Cách khác: B A C D C' H
Định hướng giải: Tìm độ dài CH ⎯⎯
→CD và thiết lập mỗi liên lạc CD = kAB và chuyển vectơ để
tìm ra duy nhất 1 điểm . D
Hướng 1: Dùng công thức Hê-rông, tính được: 1 2SABC 2 2 S ⎯⎯ →S = H . B AB HB = ⎯⎯
→HC = BC − BH = 6. ABC ABC 2 AB CC CB
Hướng 2: Ta gọi C thỏa mãn: CC = BA = ( − − ) . 6 41 4; 2; 4 ⎯⎯ →cosBCC = = . CC . CB 41 HC 6 41 HC
Mặt khác: cos BCC = = HC = 6. BC 41 41
Vậy CD = 18 = 3AB ⎯⎯
→CD = 3BA D(6; 3 − ; 6 − ). Câu 4:
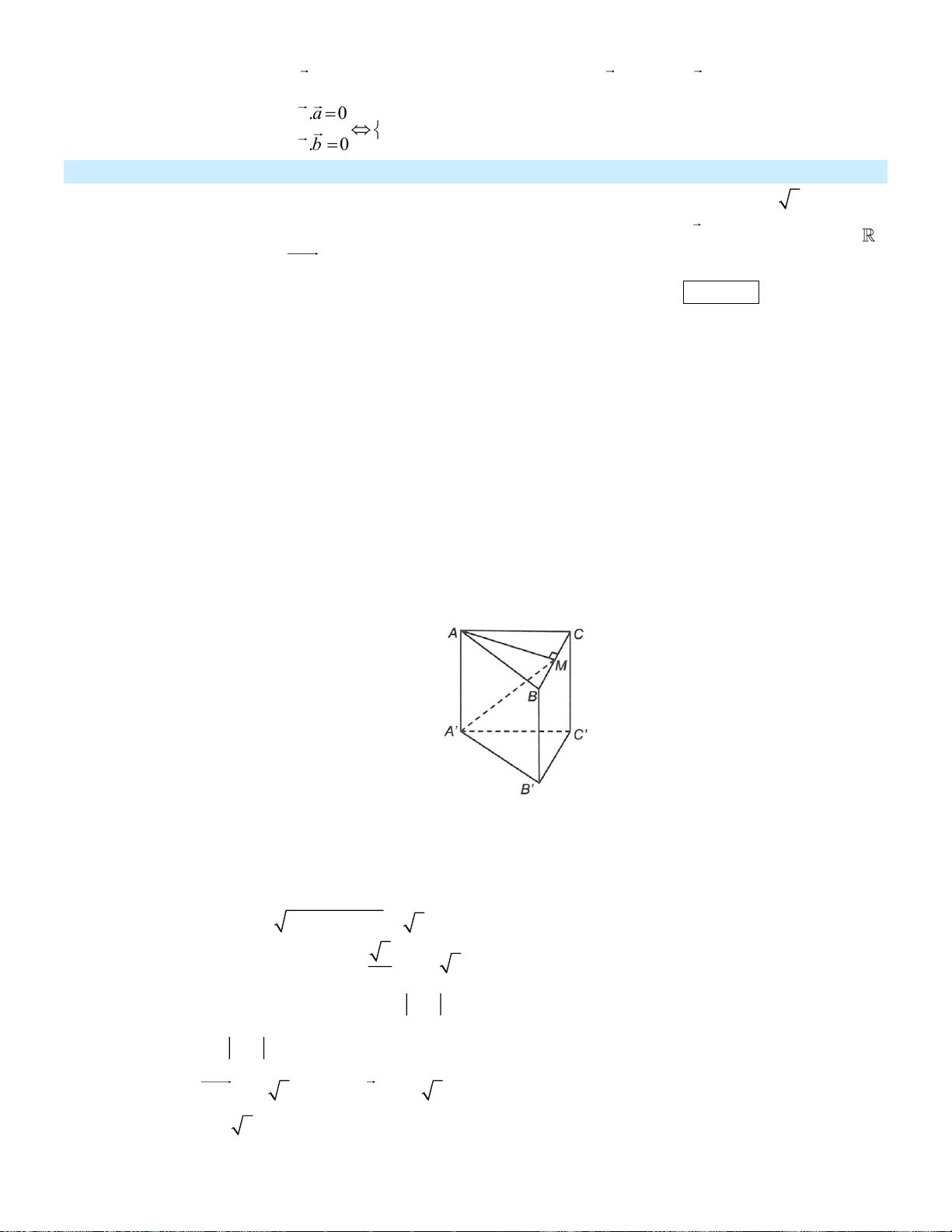
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi M , N lần lượt là trung điểm của CD, SC. Tính cô-
sin góc tạo bởi SB và MN (làm tròn đến hàng phần trăm) . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Chọn hệ trục tọa độ Oxyz như hình vẽ. a 3 a a a a a 3
Khi đó: H (0;0;0) , S 0;0; , M (0; ; a 0) , B ;0;0 , C ; ; a 0 , N ; ; , 2 2 2 4 2 4 a a 3 a a a 3 SB ;0;− , MN ; − ; . 2 2 4 2 4 . SB MN 2 Áp dụng công thức: cos ( ; SB MN ) = = 0,35. SB . MN 4 Câu 5:
Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh bằng 9. Trên BD, A ’
D lần lượt lấy các điểm M ,
N sao cho MD = AN = x , (0 x 9 2). Xác định x để độ dài đoạn MN nhỏ nhất. Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Chọn hệ tọa độ như hình vẽ, ta có A(0;0;0) , B (0;9;0) , D (9;0;0) , A(0;0;9) , D(9;0;9) , x x x x M 9 − ; ;0 , N ;0; . 2 2 2 2 x x
Khi đó MN = ( − x ) 2 2 2 2 9 2 + + 2
= 3x −18 2x + 81 2 2 = (x − )2 3 3 2 + 27 27 . Vậy MN nhỏ nhất 2
MN nhỏ nhất x = 3 2 4,24 . Câu 6:
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá,
camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự
định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ
camera ở vị trí mong muốn. Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ
Oxyz (đơn vị độ dài trên mỗi trục là 1m), các đỉnh của bốn chiếc cột lần lượt là các điểm M (90;0;30), N
(90;120;30), P(0;120;30) và Q(0;0;30) (xem hình minh họa). Giả sử K
K M = K N = K P = K Q
0 là vị trí ban đầu của camera có cao độ bằng 25 và 0 0 0 0 . Để
theo dõi quả bóng đến vị trí A, camera được hạ thấp theo phương thẳng đứng xuống điểm K1 có cao độ bằng 19.
Tính tổng các tọa độ của K1 . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
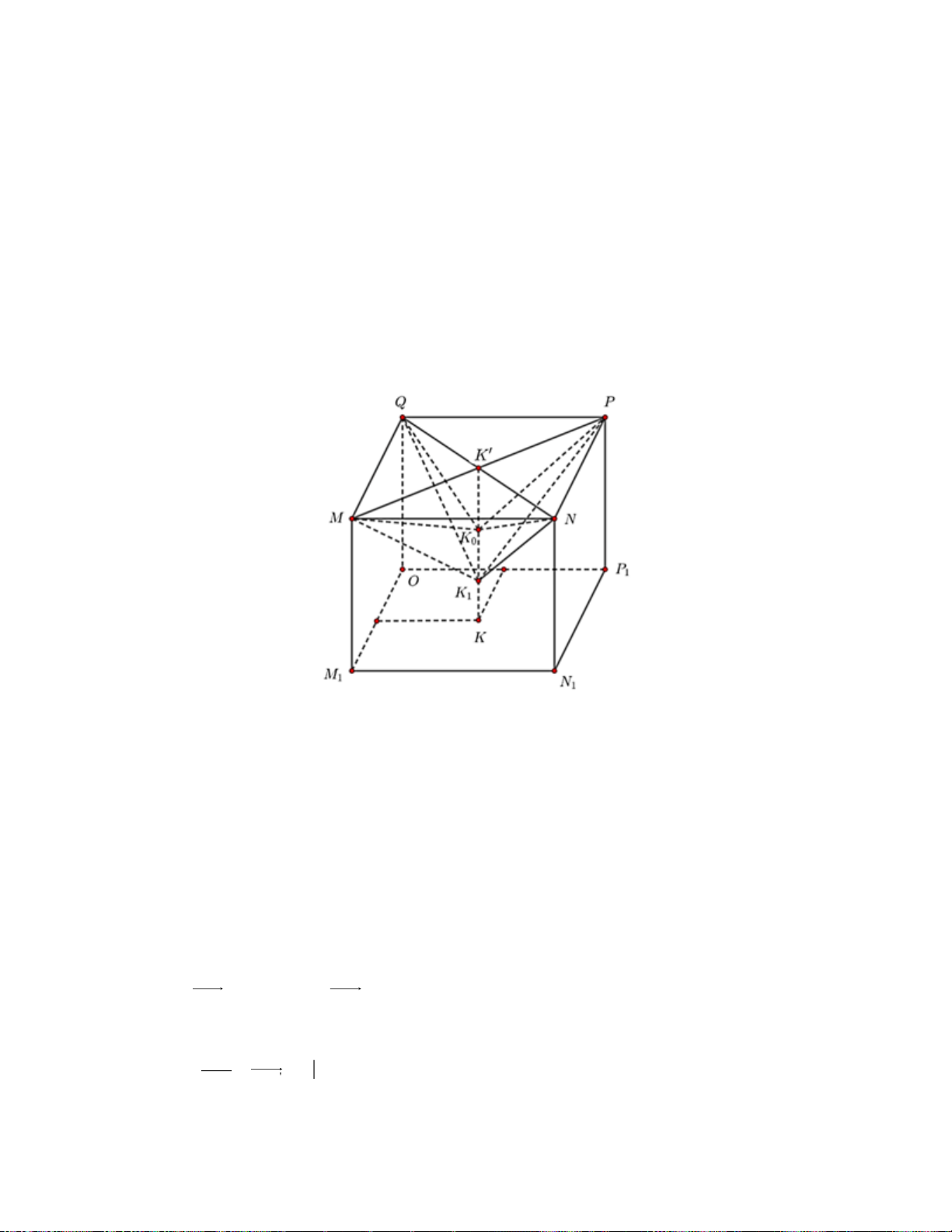
………………………………………………………………………………….…………………………. Lời giải: Gọi M , N , P
M , N, P, K 1 1
1 , K lần lượt là hình chiếu của
0 lên mặt phẳng (Oxy). Ta thấy M . NPQ M N PO 1 1 1
là hình hộp chữ nhật.
Gọi K' là giao hai đường chéo MP và NQ .
Khi đó KQ = KP = KN = KM ; V K M = K N = K P = K Q 1 0 0 0 0
và camera được hạ thấp theo
phương thẳng đứng từ điếm K K K , K , K 0 xuống điểm
1 nên các điểm K , 0 1 thẳng hàng.
Khi đó, các điểm K , K , K , K 0 1
có hoành độ và tung độ bằng nhau.
Theo bài ra, cao độ của K K 0 và
1 lần lượt là 25 và 19. Giả sử K ; x y;25 K ; x y;19 0 ( ) và 1 ( ). Ta có M . NPQ M N PO KK OQ 1 1 1
là hình hộp chữ nhật nên ' =
, suy ra cao độ của K bằng 30 . Do đó, K ( ; x y;30) . Ta có K Q = (− ;
x − y;0), NK = ( x − 90; y −120;0) .
Vì K là giao hai đường chéo của hình chữ nhật MNPQ nên K là trung điểm của NQ.
−x = x − 90 x = 45 Suy ra ' K Q
= NK −y = y −120 . y = 60 0 = 0 Do vậy, K 45;60;19 + + = 1 ( ) . Vậy 45 60 19 124 .
____________________HẾT____________________
Huế, 17h20’ Ngày 25 tháng 7 năm 2024
Page: CLB GIÁO VIÊN TRẺ TP HUẾ TR¾C NGHIÖM CHUY£N §Ò M«n: To¸n 12 – KNTT ÔN TẬP CHƯƠNG 2
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 02_TrNg 2025 Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung tâm Km10- Hương Trà – Huế NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi, thí sinh chỉ chọn một phương án. Câu 1:
Trong không gian Oxyz , cho a = −i + 2 j − 3k . Toạ độ của vectơ a là A. (2; 1 − ; 3 − ) . B. ( 3 − ;2; 1 − ) . C. ( 1 − ;2; 3 − ) . D. (2; 3 − ;− ) 1 . Câu 2:
Trong không gian Oxyz , cho điểm A( 2 − ; 1
− ;3). Gọi A , A , A 1 2
3 lần lượt là hình chiếu của điểm
A trên các mặt phẳng toạ độ (Oxy),(Oyz),(Ozx) . Tìm tọa độ các điểm A , A , A 1 2 3 A. A 2 − ; 1 − ;0 , A 0; 1 − ;3 , A 2 − ;0;3 A 2 − ;0;3 , A 0; 1 − ;3 , A 2 − ; 1 − ;0 1 ( ) 2 ( ) 3 ( ) . B. 1 ( ) 2 ( ) 3 ( ) . C. A 2 − ; 1 − ;0 , A 2 − ;0;3 , A 0; 1 − ;3 A 2 − ;0;3 , A 0; 1 − ;3 , A 2 − ;1;0 1 ( ) 2 ( ) 3 ( ) . D. 1 ( ) 2 ( ) 3 ( ) . Câu 3:
Trong không gian Oxyz , cho hai véctơ a = (2; 2 − ; 4 − ) và b = (1; 1 − )
;1 . Mệnh đề nào dưới đây sai?
A. a + b = (3; 3 − ; 3 − ).
B. a ⊥ b . C. | b |= 3.
D. a và b cùng phương. Câu 4:
Trong không gian Oxyz, cho véctơ u = (1;1; − )
1 và điểm B(2;3;2). Tìm toạ độ điểm C sao cho BC = u. A. (3; 4; ) 1 . B. ( 3 − ; 2 − ;− ) 1 . C. (3; 2; ) 1 . D. (2;3; ) 1 . Câu 5:
Trong không gian Oxyz , cho hai vectơ a = (1; 2;3),b = (4;5;6). Tọa độ a + b là A. (3;3;3) . B. (2;5;9) . C. (5; 7;9) . D. (4;10;18) . Câu 6:
Trong không gian Oxyz , cho vectơ u = 3i + 4 j − 5k và điểm A . Biết OA = u . Tìm tọa độ điểm . A
A. (3 ; 4 ; − 5) . B. (3 ; 4 ; 5) . C. ( 3 − ;− 4 ; 5). D. ( 3 − ; 4 ; 5) . Câu 7:
Trong không gian Oxyz , cho A(2;5; 2
− ) , B(1;1;3) , C(3;3;− )
1 . Tìm toạ độ điểm E sao cho C là
trọng tâm của tam giác ABE. A. (6;3;4) . B. (6;3;−4) . C. (6;− 3; 4 − ) . D. ( 6 − ;− 3; 4 − ) . Câu 8:
Trong không gian Oxyz , cho các vectơ a = (2; m −1;3),b = (1;3; 2
− n). Tìm m, n để các vectơ
a,b cùng hướng. 3 4
A. m = 7, n = − .
B. m = 1, n = 0 .
C. m = 7, n = − .
D. m = 4, n = −3. 4 3 Câu 9:
Cho hai vectơ a,b thỏa mãn: a = 3, b = 4, a + b = 6 . Tính a − b . A. 14 . B. 11 . C. 2 3 . D. 3 .
Câu 10: Trong không gian Oxyz , cho (
A 1; 2 ; 3), B( 2 − ; 0 ;1), C( 1
− ; 0 ;1) . Tính cos ABC. 3 3 − 7 3 A. . B. . C. . D. . 17 17 17 17
Câu 11: Trong không gian Oxyz , cho các vectơ a = (1;0; 2 − );b = ( 1
− ;1;4) , u = ( 5 − ;3;16). Tìm cặp số
( ;x y) để u = xa + y .b A. ( ; x y) = (2; 3 − ). B. ( ; x y) = ( 2 − ;3) . C. ( ; x y) = (2;3) . D. ( ; x y) = (2;− ) 1 .
Câu 12: Trong không gian Oxyz , cho hai điểm A(1;1; − )
1 , B (2;1;2) . Độ dài đoạn thẳng AB bằng A. 10 . B. 14 . C. 9 . D. 10 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn) Câu 1:
Cho hình lăng trụ tam giác đều ABC.AB C
có AB = a và AA' = a 2 .
a) AC = AB + BC.
b) Gọi M là trung điểm BC và A' M = A' A + A' B ' − CM . 2 3 c) ' . = a A M AC . 4
d) Góc giữa vectơ AB ' và BC ' bằng 60 . Câu 2:
Trong không gian Oxyz , cho ba điểm A(1;1; ) 1 , B ( 1 − ;2 ) ;1 , C (1;2;− ) 1 . a) AB = (2; 1 − ;0) .
b) AB + BC = (0;1; 2 − ) . c) AB = 5 .
d) BC + CA + BA = 2 5 . Câu 3:
Trong không gian Oxyz , cho hai điểm A(0;1; 2 − ) và B(3; 1 − ) ;1 và điểm M ( ;
x y; z) thỏa mãn AM = 3AB . a) AB = (3; 2 − ;3) . b) AM = ( ;
x y −1; z + 2) . c) AB = 22 . d) x = 9 . Câu 4:
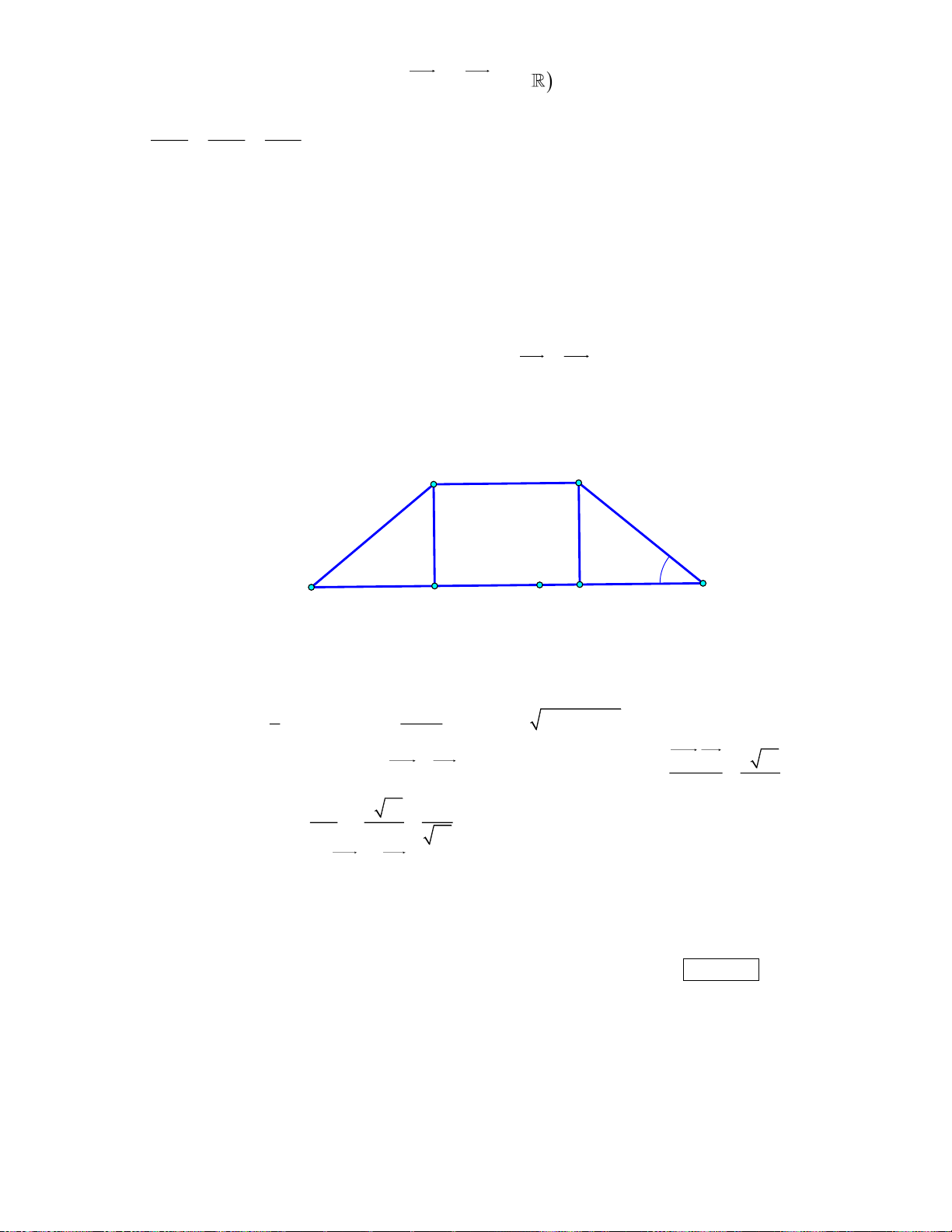
Hình minh họa sơ đồ một ngôi nhà trong không gian Oxyz , trong đó nền nhà, bốn bức tường
và hai mái nhà đều là hình chữ nhật.
a) Toạ độ điểm F (4;0;3) .
b) Toạ độ vectơ AH = (4;5;3) . c) AH.AF = 3.
d) Góc dốc của mái nhà, tức là số đo của góc nhị diện có cạnh là đường thẳng FG , hai mặt
lần lượt là ( FGQP) và ( FGHE ) gần bằng 26, 6 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Câu 1:
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a , BC = a 2 . Biết góc giữa hai véc tơ
AB và SC là k, tính k. Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 2:
Trong không gian Oxyz, cho hình hộp ABC . D AB C D
. Biết A(2;4;0) , B(4;0;0) , C ( 1
− ;4;− 7) và D(6;8;10) . Biết đỉnh B( ; a ;
b c), tính a + b + c. Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 3:
Trong không gian Oxyz , cho vectơ a = (1; 2
− ;4), b cùng phương. Biết vectơ b tạo với tia Oy
một góc nhọn và b = 21. Tính tổng bình phương các tọa độ của b . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….




