Bộ đề ôn thi HK1 Toán 12 năm học 2017 – 2018 trường THPT Đặng Huy Trứ – TT. Huế

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi học kỳ 1 môn Giới Toán 12 năm học 2017 – 2018 .Mời bạn đọc đón xem.

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

38 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TRƯỜNG THPT ĐẶNG HUY TRỨ
TỔ TOÁN
ĐỀ TỔNG ÔN TẬP SỐ 01
BỘ ĐỀ ÔN TẬP THI HỌC KÌ 1
Môn: TOÁN 12 - Năm học 2017 - 2018
Thời gian làm bài: 90 phút, không kể thời gian phát đề
I. PHẦN TRẮC NGHIỆM (8,0 điểm).
Câu 1. Gọi
M
,
N
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
31y x x
trên
0; 2 ,

tính
.MN
A.
B.
C.
D.
Câu 2. Tìm khoảng đồng biến của hàm số
3
3 2.y x x
A.
1;1 .
B.
; 1 1; .
C.
;. 
D.
;1
và
1; .
Câu 3. Tìm tất cả các giá trị thực của tham số
a
để phương trình
3
3 4 0x x a
có ba nghiệm
thực phân biệt.
A.
2 6.a
B.
2 6.a
C.
1 3.a
D.
1 3.a
Câu 4. Hàm số
y f x
liên tục trên
và có bảng biến thiên dưới đây. Khẳng định nào sau đây
đúng?
x

2
1

y
0
y

1
3

A. Hàm số đạt giá trị nhỏ nhất bằng
3
trên
.
B. Hàm số đồng biến trên
0; .
C. Đồ thị hàm số có tiệm cận đứng
2.x 
D. Hàm số có hai điểm cực trị.
Câu 5. Cho hàm số
y f x
xác định, liên tục trên
và có đồ thị
hàm số đạo hàm
y f x
như hình bên. Tìm số điểm cực đại của
hàm số
.y f x
A.
B.
C.
D.
x
y
O
Câu 6. Tìm các đường tiệm cận của đồ thị hàm số
2
.
2
x
y
x
A.
2; 1.xx
B.
1; 1.yx
C.
2; 1.xy
D.
2; 2.xx
Câu 7. Hàm số nào sao đây có hai điểm cực trị?
A.
3
.y x x
B.
32
3.y x x
C.
42
.y x x
D.
21
.
1
x
y
x
Câu 8. Tìm số đường tiệm cận của đồ thị hàm số
2
2
.
x
y
x
A. 2. B. 4. C. 3. D. 1.
Câu 9. Có bao nhiêu giá trị nguyên dương của tham số
k
để hàm số
3
2
2
2
3
kx
y kx x
đồng biến trên
;? 
A.
B.
C.
D.
Câu 10. Tìm giá trị cực đại của hàm số
42
2 2.y x x
A.
B.
1.
C.
D.
Câu 11. Cho hàm số
y f x
xác định và có đạo hàm trên
.
Khẳng định nào sau đây sai?
A. Nếu
0, ;f x x a b
thì hàm số
fx
đồng biến trên
;ab
.
B. Nếu
0, ;f x x a b
thì hàm số
fx
không đồng biến và không nghịch biến trên
;ab
.
C. Nếu
0, ;f x x a b
thì hàm số
fx
nghịch biến trên
;ab
.
D. Nếu
0, ;f x x a b
thì hàm số
fx
nghịch biến trên
;ab
.
Câu 12. Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm
số đó là hàm số nào?
A.
42
2.y x x
B.
42
2.y x x
C.
32
3 2.y x x
D.
32
3 2.y x x
x
y
1
O
1
Câu 13. Viết tất cả các phương trình tiếp tuyến của đồ thị
32
: 2 1,C y x x
biết tiếp tuyến
vuông góc với đường thẳng
7 0.xy
A.
365
7 5; 7 .
27
y x y x
B.
14
7 5; 7 .
27
y x y x
C.
365
7 5; 7 .
27
y x y x
D.
365
7 5; 7 .
27
y x y x
Câu 14. Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, hàm số nào có bảng
biến thiên sau?
x

1
3

y
0
0
y

1
29
3

A.
32
3 9 2y x x x
. B.
32
12
3
33
y x x x
.
C.
32
3 9 2y x x x
. D.
32
12
3
33
y x x x
.
Câu 15. Người ta cần làm một hộp giấy hình hộp chữ nhật có
đáy là hình vuông và không có nắp đậy. Nếu cần
2
64 cm
giấy
bìa cứng như hình vẽ để làm hộp giấy này, thì thể tích lớn nhất
của hộp này là bao nhiêu?
A.
3
512 2
.
27
cm
B.
3
256
.
7
cm
C.
3
256 3
.
9
cm
D.
3
144 2 .cm
Câu 16. Cho
a
là số thực dương khác 1. Đẳng thức nào dưới đây đúng với mọi số thực dương
,?xy
A.
log log log .
a a a
y
yx
x

B.
log log log .
a a a
x y x y
C.
log log .
aa
y
yx
x

D.
log
log .
log
a
a
a
y
y
xx
Câu 17. Tìm tập xác định của hàm số
1
2
7
9.yx
A.
; 3 3; .D 
B.
\ 3;3 .D 
C.
.D
D.
3;3 .D 
Câu 18. Với các số thực dương a và b bất kì. Đẳng thức nào dưới đây đúng?
A.
3
2 2 2
4
log 1 3log log .
a
ab
b



B.
3
2 2 2
41
log 2 log log .
3
a
ab
b



C.
3
2 2 2
4
log 2 3log log .
a
ab
b



D.
3
2 2 2
4
log 2 3log log .
a
ab
b



Câu 19. Cho
a
là số thực dương,
1,a a b
thỏa mãn
log 3.
a
b
Tính
log .
a
a
b
P
a
A.
1 3 3.P
B.
1 3.P 
C.
1 3.P
D.
1 3.P
Câu 20. Cho ba số thực dương
,,a b c
khác 1. Đồ thị các hàm số
log , log , log
a b c
y x y x y x
được cho như hình vẽ bên. Khẳng
định nào sau đây đúng?
x
y
log
c
x
log
b
x
x
log
a
O
1
A.
0 1 .c b a
B.
1.a b c
C.
0 1 .c b a
D.
0 1 .c a b
Câu 21. Ông A đi gửi ngân hàng
150
triệu đồng theo thể thức lãi kép với lãi suất
0,45% /
tháng.
Sau ít nhất bao nhiêu tháng thì ông A mới nhận được
200
triệu đồng?
A.
65
tháng. B.
64
tháng. C.
63
tháng. D.
67
tháng.
Câu 22. Tính đạo hàm của hàm số
2sin 3 .
e
yx
A.
1
2sin 3 cos .
e
y e x x

B.
1
2sin 3 .
e
y e x

C.
1
2 2sin 3 cos .
e
y e x x

D.
1
2 2sin 3 cos .
e
y e x x
Câu 23. Cho phương trình
2
2
2
log 3log 1 0.xx
Bằng cách đặt
2
log ,tx
ta được phương trình
nào sau đây?
A.
2
3 1 0.tt
B.
2
3
10
2
tt
C.
2
10t 
D.
2
6 1 0.tt
Câu 24. Biết tập nghiệm
T
của bất phương trình
3
log 2 1 1
x

có dạng
; , ; ,a b a b
tính
2 3 .S a b
A.
2.S
B.
10.S
C.
6.S
D.
8.S
Câu 25. Tìm tập hợp tất cả các giá trị thực của tham số
k
để hàm số
2
2018
2
x
x
e
y e kx
đồng
biến trên
0;ln 2 .

A.
; 2 .
B.
1
;.
4



C.
1
;.
4



D.
2; . 
Câu 26. Tìm nghiệm của bất phương trình
1
2
log 12 1.x 
A.
12 0x
. B.
12x 
. C.
1
0
2
x
. D.
23
12
2
x
.
Câu 27. Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
22
3
log 4 8 2x x m
có hai nghiệm thực phân biệt trái dấu.
A.
1;1 .
B.
; 1 1; . 
C.
; 1 1; . 

D.
1;1 .

Câu 28. Mỗi hình sau gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), tìm hình
không phải là đa diện.
(a)
(b)
(c)
(d)
A. hình (b). B. hình (d). C. hình (c). D. hình (a).
Câu 29. Tính tổng diện tích
S
tất cả các mặt của khối đa diện đều loại
3; 4
có cạnh bằng
.m
A.
2
5 3 .Sm
B.
2
2 3 .Sm
C.
2
3.Sm
D.
2
6.Sm
Câu 30. Cho lăng trụ đều
.ABC A B C
có cạnh đáy bằng
2.a
Biết góc giữa mặt phẳng
AB C

và
mặt đáy bằng
0
60 ,
tính thể tích
V
của khối lăng trụ
..ABC A B C
A.
3
3 3 .Va
B.
3
33
.
8
a
V
C.
3
3.Va
D.
3
3
.
8
a
V
Câu 31. Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
cạnh bên
SA
vuông góc với đáy và
2.SC a
Tính thể tích
V
của khối chóp
..S ABC
A.
3
.
4
a
V
B.
3
3
.
6
a
V
C.
3
3
.
12
a
V
D.
3
3
.
4
a
V
Câu 32. Cho tứ diện
ABCD
. Gọi
M
và
N
lần lượt là trung điểm của
AC
và
.AD
Tính tỉ số thể
tích của khối tứ diện
ABMN
và khối
.BMNDC
A.
1
.
2
B.
1
.
4
C.
1
.
3
D.
1
.
8
Câu 33. Một tấm kẽm hình vuông
ABCD
có cạnh bằng
30 .cm
Người ta gập tấm kẽm theo hai cạnh
EF
và
GH
cho đến khi
AD
và
BC
trùng nhau như hình vẽ dưới đây
để được một hình lăng trụ khuyết hai đáy. Tìm giá trị của
x
để thể tích khối lăng trụ lớn nhất.
A.
5.x cm
B.
9.x cm
C.
8.x cm
D.
10 .x cm
Câu 34. Một hình nón
N
sinh bởi một tam giác đều cạnh
a
khi quay quanh một đường cao. Tính
diện tích xung quanh
xq
S
của hình nón đó.
A.
2
.
4
xq
a
S
B.
2
.
2
xq
a
S
C.
2
3
.
4
xq
a
S
D.
2
.
xq
Sa
Câu 35. Khẳng định nào sau đây sai?
A. Hình trụ luôn chứa một đường tròn. B. Hình nón luôn chứa một đường tròn.
C. Hình nón luôn chứa một đường thẳng. D. Mặt trụ luôn chứa một đường thẳng.
Câu 36. Thiết diện qua trục của một hình trụ là hình vuông cạnh
2a
. Gọi
1
V
và
2
V
lần lượt là
diện tích xung quanh, diện tích toàn phần của hình trụ. Chọn kết luận đúng, trong các kết luận
sau:
A.
12
.VV
B.
12
3 2 .VV
C.
12
2.VV
D.
12
2 3 .VV
Câu 37. Một hình trụ có đáy là hai hình tròn
;6 , ';6OO
và
' 10.OO
Một hình nón có đỉnh
'O
và có đáy là hình tròn
;6 .O
Mặt xung quanh của hình nón chia khối trụ thành hai phần. Tính thể
tích
V
của phần khối trụ còn lại (không chứa khối nón).
A.
60 .V
B.
90 .V
C.
120 .V
D.
240 .V
Câu 38. Cho mặt cầu
S
tâm O, có bán kính bằng
3ra
. Mặt phẳng
cắt mặt cầu
S
theo
thiết diện là một đường tròn có diện tích
2
4 a
. Tính khoảng cách
d
từ O đến mặt phẳng
.
A.
3.da
B.
2.da
C.
5.da
D.
2 3 .da
Câu 39. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
1
, mặt bên
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích
V
của khối cầu ngoại tiếp hình
chóp đã cho.
A.
5 15
18
V
. B.
5 15
54
V
. C.
43
27
V
. D.
5
3
V
.
Câu 40. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích
V
của khối chóp có thể tích lớn nhất.
A.
144V
. B.
576V
. C.
576 2V
. D.
144 6V
.
II. TỰ LUẬN (2,0 điểm).
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số
42
2 1.y x x
Câu 2 (1,0 điểm). Giải phương trình:
24
log 2 log 3.
x
x
HẾT
ĐỀ TỔNG ÔN TẬP SỐ 02
I. PHẦN TRẮC NGHIỆM (8,0 điểm).
Câu 41. Cho hàm số
1
.
1
x
y
x
Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên
2; .
B. Hàm số nghịch biến trên
;0 .
C. Hàm số nghịch biến trên
\ 1 .
D. Hàm số nghịch biến trên
;1
và
1; .
Câu 42. Hàm số nào sau đây đồng biến trên
?
A.
1
.
1
x
y
x
B.
42
2.y x x
C.
sin2 3.yx
D.
3
3.y x x
Câu 43. Hàm số
y f x
liên tục trên
và có bảng biến thiên dưới đây. Khẳng định nào sau
đây đúng?
x

1
1

y
0
0
y

3
2

A. Hàm số đạt giá trị nhỏ nhất bằng
2
trên
.
B. Hàm số đồng biến trên
0; 2 .
C. Hàm số có điểm cực đại là
2.x 
D. Hàm số có cực tiểu bằng
2.
Câu 44. Cho hàm số
y f x
xác định, liên tục trên
và có đồ thị
hàm số đạo hàm
y f x
như hình bên. Tìm số điểm cực trị của
hàm số
.y f x
A.
B.
C.
D.
x
y
O
Câu 45. Tìm các đường tiệm cận của đồ thị hàm số
2
.
1
x
y
x
A.
1; 1.xy
B.
1; 2.xy
C.
2; 1.xy
D.
2; 1.xy
Câu 46. Viết phương trình tiếp tuyến của đồ thị
32
: 2 1C y x x
tại điểm
1;0 .A
A.
1.yx
B.
1.yx
C.
.yx
D.
2 2.yx
Câu 47. Hàm số nào sau đây không có giá trị lớn nhất và giá trị nhỏ nhất trên
0; 2 ?

A.
3
.y x x
B.
4
3 1.y x x
C.
21
.
1
x
y
x
D.
1
.
1
x
y
x
Câu 48. Gọi
12
,xx
lần lượt là điểm cực đại và điểm cực tiểu của hàm số
3
3 2.y x x
Tính
12
3.S x x
A.
2.S
B.
2.S 
C.
4.S
D.
3.S
Câu 49. Cho đồ thị hàm số
y f x
có đồ thị như hình vẽ dưới đây. Khẳng định nào sau đây
đúng?
x
2
y
-1
O
A. Đồ thị hàm số có tiệm cận đứng
2x
và tiệm cận ngang
1.y 
B. Đồ thị hàm số có tiệm cận đứng
1x 
và không có tiệm cận ngang.
C. Đồ thị hàm số có tiệm cận ngang
2y
và không có tiệm cận đứng.
D. Đồ thị hàm số có tiệm cận đứng
1x 
và tiệm cận ngang
2.y
Câu 50. Biết rằng đường thẳng
22yx
cắt đồ thị hàm số
3
2y x x
tại một điểm duy nhất,
ký hiệu
00
;xy
là tọa độ điểm đó. Tìm
0
y
.
A.
0
4y
. B.
0
0y
. C.
0
2y
. D.
0
1y
.
Câu 51. Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
2
3
14
x
y
mx

có hai đường tiệm cận ngang.
A.
.
B.
;1 .
C.
1; .
D.
1.
Câu 52. Đồ thị của hàm số
42
42y x x
và đồ thị của hàm số
2
6yx
có tất cả bao nhiêu
điểm chung?
A.
0
. B.
4
. C.
1
. D.
2
.
Câu 53. Tìm tập hợp tất cả giá trị thực của tham số
m
để hàm số
3 2 2
22
2 3 1
33
y x mx m x
có hai điểm cực trị
1
x
và
2
x
sao cho
1 2 1 2
2 1.x x x x
A.
2
0, .
3



B.
0.
C.
2
.
3



D.
.
Câu 54. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
tan 2
tan
x
y
xm
đồng biến trên
khoảng
0;
4



.
A.
0
.
12
m
m


B.
0.m
C.
1 2.m
D.
2.m
Câu 55. Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không có nắp và chứa đủ
được 10 lít nước. Hỏi bán kính đáy (đơn vị
cm
, làm tròn đến hàng phần chục) của chiếc xô bằng
bao nhiêu để cửa hàng tốn ít nguyên vật liệu nhất?
A.
14,7 .cm
B.
15,4 .cm
C.
15,2 .cm
D.
14,4 .cm
Câu 56. Tìm tập xác định của hàm số
5
1.yx
A.
.D
B.
1; .D 
C.
\ 1 .D
D.
1; .D 
Câu 57. Cho
a
là số thực khác
0,
đẳng thức nào sau đây đúng?
A.
2 2 2
22
log 2log .aa
B.
2 2 2
22
log 2log .aa
C.
2 2 2
22
log 4log .aa
D.
2 2 2
22
log 4log .aa
Câu 58. Tìm tập xác định của hàm số
2
2 log .yx
A.
0; 4 .D
B.
0; 4 .D

C.
0; .D
D.
0; 4 .D 
Câu 59. Đặt
33
log 2 ; log 5ab
;
3 3 3
1 2 99
log log ... log .
2 3 100
X
Biểu diễn
X
theo
,.ab
A.
2 2 .X a b
B.
2 2 .X a b
C.
2 2 .X a b
D.
2 2 .X a b
Câu 60. Tính giá trị của đạo hàm hàm số
2
ln 1x
y
x
tại
1x
.
A.
2 2ln2.
B.
2 2ln2.
C.
1 ln2.
D.
1 ln 2.
Câu 61. Tính đạo hàm của hàm số
xx
xx
ee
y
ee
.
A.
2
4
xx
ee
. B.
2
2
xx
xx
ee
ee
. C.
2
2
xx
ee
. D.
2
xx
xx
ee
ee
.
Câu 62. Biết rằng năm
2003
dân số Việt Nam là
80902000
người và tỉ lệ tăng dân số là
1,47%.
Hỏi nếu giữ nguyên tỉ lệ tăng dân số hằng năm đó thì năm
2020
dân số Việt Nam sẽ là bao nhiêu?
(Làm tròn kết quả đến hàng nghìn).
A.
101119000
người. B.
103681000
người.
C.
103870000
người. D.
106969000
người.
Câu 63. Cho ba số thực dương
, , .a b c
Đồ thị các hàm số
,,
a b c
y x y x y x
được cho như hình vẽ bên. Khẳng định nào sau
đây đúng?
A.
1.a b c
B.
1; 1 0.b a c
C.
1; 1 0.b c c
D.
1; 1 .b a c
x
y
O
x
a
x
b
x
c
1
1
Câu 64. Biết tập nghiệm của bất phương trình
53
log 2 log 2xx
có dạng
; , ; ,a b a b
tính
.S a b
A.
3.S 
B.
0.S
C.
3.S
D.
2.S
Câu 65. Tính giá trị của biểu thức sau
.
2
1
22
2
1
log log ; 0 1
a
a
a a a
A.
15
.
4
B.
13
.
4
C.
13
.
4
D.
17
.
4
Câu 66. Tìm tập hợp tất cả các giá trị của tham số
a
để hàm số
2
21
log
aa
yx

nghịch biến trên
khoảng
0; .
A.
0; 2 \ 1 .
B.
1; .
C.
;1 .
D.
1
; \ 1 .
2




Câu 67. Tìm nghiệm của phương trình
2 5.
x
A.
5
.
2
x
B.
5
log 2.x
C.
2
log 5.x
D.
ln5.x
Câu 68. Cho biểu thức
4
3
23
..P a a a
, với
0,a
khẳng định nào dưới đây đúng?
A.
1
2
Pa
. B.
13
24
Pa
. C.
1
4
Pa
. D.
2
3
Pa
.
Câu 69. Tìm số mặt phẳng đối xứng của hình lập phương.
A.
3
. B.
6
. C.
9
. D.
12
.
Câu 70. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, mặt bên
''BCC B
là hình vuông cạnh
2a
. Tính thể tích
V
của khối lăng trụ
. ' ' 'ABC A B C
.
A.
3
Va
. B.
3
2Va
. C.
3
2
3
a
V
. D.
3
2Va
.
Câu 71. Tính số cạnh
của đa diện đều loại
3;5 .
A.
30.C
B.
20.C
C.
12.C
D.
6.C
Câu 72. Nếu tăng gấp đôi độ dài của đường chéo của một mặt (không là mặt chéo) khối lập
phương thì thể tích khối lập phương thay đổi như thế nào?
A. Tăng gấp 2 lần. B. Tăng gấp 4 lần.
C. Tăng gấp 6 lần. D. Tăng gấp 8 lần.
Câu 73. Cho hình lăng trụ
. ' ' '.ABC A B C
Gọi
1 . ' ' 'A A B C
VV
và
2 . ' ' 'ABC A B C
VV
. Khẳng định nào sau
đây đúng?
A.
12
3
4
.VV
B.
12
1
2
.VV
C.
12
1
3
.VV
D.
12
2
3
.VV
Câu 74. Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
0
60ABC
,
SA
vuông góc với đáy,
SD
tạo với mặt phẳng
SAC
một góc bằng
0
45 .
Tính thể tích
V
của khối chóp
..S ABCD
A.
3
6
.
18
a
V
B.
3
3.Va
C.
3
6
.
3
a
V
D.
3
6
.
12
a
V
Câu 75. Cho mặt cầu
S
có tâm
I
và bán kính
3.R
Mặt phẳng
P
cắt mặt cầu theo giao
tuyến là đường tròn
C
và có chu vi
2.
Tính khoảng cách
d
từ tâm
I
đến mặt phẳng
.P
A.
2.d
B.
2 2.d
C.
7
.
2
d
D.
7.d
Câu 76. Mặt cầu
S
có thể tích
3
36 cm
. Tính diện tích của mặt cầu
.S
A.
2
24 .cm
B.
2
36 .cm
C.
2
18 .cm
D.
2
20 .cm
Câu 77. Cho mặt cầu bán kính
r
và một hình trụ có bán kính đáy
r
và chiều cao
2.r
Tính tỉ số
thể tích giữa khối cầu và khối trụ đã cho.
A.
B.
3
.
2
C.
2
.
3
D.
1
.
2
Câu 78. Một hình nón có đường sinh bằng
8 ,cm
diện tích xung quanh bằng
2
240 .cm
Tính
đường kính của đường tròn đáy hình nón.
A.
70 .cm
B.
30 .cm
C.
60 .cm
D.
35 .cm
Câu 79. Một hình thang vuông ABCD có đường cao
AD a
, đáy nhỏ
AB a
, đáy lớn
2CD a
.
Cho hình thang đó quay quanh CD, ta được khối tròn xoay có thể tích bằng
A.
3
4
3
Va
. B.
3
2Va
. C.
3
1
3
Va
. D.
3
3Va
.
Câu 80. Một một chiếc cốc nước hình trụ có chiều cao bằng đường kính quả bóng bàn. Người ta
đặt quả bóng lên chiếc cốc thấy phần ở ngoài của quả bóng có chiều cao bằng
chiều cao của nó.
Gọi
12
,VV
lần lượt là thể tích của quả bóng và chiếc cốc, khẳng định nào sau đây đúng?
A.
12
9 8 .VV
B.
12
3 2 .VV
C.
12
16 9 .VV
D.
12
27 8 .VV
II. TỰ LUẬN (2,0 điểm).
Câu 1 (1,0 điểm). Tìm
m
để phương trình
32
2 1 2 0x x m
có ba nghiệm thực phân biệt.
Câu 2 (1,0 điểm). Giải phương trình:
22
2 2 1
9 7.3 2.
x x x x x x

HẾT
ĐỀ TỔNG ÔN TẬP SỐ 03
I. PHẦN TRẮC NGHIỆM (8,0 điểm).
Câu 1. Số giao điểm của hai đồ thị hàm số
4
1yx
và
2
2yx
là
A.
0
. B.
1
. C.
2
. D.
4
.
Câu 2. Cho hàm số
42
23y x x
. Khẳng định nào sau đây là đúng?
A. Hàm số có một điểm cực tiểu và hai điểm cực đại.
B. Hàm số có một điểm cực đại và hai điểm cực tiểu
C. Hàm số có một điểm cực tiểu và không có điểm cực đại.
D. Hàm số có một điểm cực đại và không có điểm cực tiểu.
Câu 3. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
1
y
x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 4. Hàm số nào sau đây đồng biến trên
?
A.
3
31y x x
. B.
3
21y x x
. C.
32
2y x x
. D.
2
1
x
y
x
.
Câu 5. Cho hàm số
y f x
xác định trên
và có đạo hàm
23
11f x x x x
. Số điểm cực
trị của hàm số
y f x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 6. Cho hàm số
fx
có tính chất:
0fx
,
1,2x
và
0fx
khi
0x
hoặc
1x
.
Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng
1; 2
. B. Hàm số đồng biến trên khoảng
1;0
.
C. Hàm số nghịch biến trên khoảng
0;1
. D. Hàm số đồng biến trên khoảng
1; 2
.
Câu 7. Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
1
1 3 5 2 1
3
y x m x m x m
đồng biến trên
.
A.
3m
. B.
23m
. C.
2m
. D.
2m
hoặc
3m
.
Câu 8. Gọi
00
;M x y
là điểm cực tiểu của đồ thị của hàm số
4 3 2
3 7 1y x x x x
. Khi đó giá trị
của tổng
00
xy
bằng
A.
2
. B.
3
. C.
5
. D.
2
.
Câu 9. Gọi trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2
21
x
y
x
trên đoạn
1; 4

lần lượt là
M
và
m
? Giá trị của
Mm
là
A.
5
. B.
32
7
. C.
39
7
. D.
2
.
Câu 10. Cho hàm số
inx
3
sin cos2 s 2.y x x
Giá trị nhỏ nhất của hàm số trên
;
22




bằng
A. 0 . B.
23
27
. C.
1
3
. D.
23
27
.
Câu 11. Cho hàm số
fx
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Khẳng định nào sao đây là sai?
A. Đồ thị hàm số đã cho có hai điểm cực trị.
B. Đồ thị hàm số đã cho có một tiệm cận đứng.
C. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho luôn cắt trục hoành.
Câu 12. Tập hợp các giá trị của
m
để đồ thị hàm số
2
2
2
x mx
y
xm

có đúng một đường tiệm cận
đứng là
A.
. B.
\0
. C.
\ 1;1
. D.
\ 2; 2
.
Câu 13. Hàm số
32
y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0a b c d
B.
0, 0, 0, 0a b c d
C.
0, 0, 0, 0a b c d
D.
0, 0, 0, 0.a b c d
Câu 14. Đồ thị hàm số
32
3 2 1y x x x
cắt đồ thị hàm số
2
31y x x
tại hai điểm phân biệt
A
và
B
. Độ dài đoạn thẳng
AB
.
A.
3.AB
B.
2 2.AB
C.
2.AB
D.
1.AB
Câu 15. Tìm tất cả các giá trị thực của
m
để hàm số
32
5y x x x m
có giá trị lớn nhất trên
2; 2

bằng
1
.
A.
7
. B.
3
. C.
0
. D.
2
.
Câu 16. Cho các số dương
a
,
b
,
c
. Rút gọn biểu thức
333
log log log
a b c
P
b c a
ta được
A.
1
. B.
2
. C.
0
. D.
3
log abc
.
Câu 17. Cho các số thực dương
x
,
y
,
z
thỏa mãn
2
a
xy
,
4
b
yz
,
8
c
zx
với
a
,
b
,
c
. Tính
biểu thức
2 2 2
log log logP x y z
.
A.
23
2
a b c
P

. B.
23P a b c
. C.
2
a b c
P

. D.
3
2
abc
P
.
x

3
1
1

fx
0
0
fx

1


1

x
y
O
Câu 18. Tập xác định của hàm số
2
2
log 1yx
là
A.
\1
. B.
. C.
1; 
. D.
;1
.
Câu 19. Đạo hàm của hàm số
x
ye
là
A.
.
x
y x e
. B.
1
.
x
y x e
. C.
2
x
e
y
x
. D.
x
e
y
x
.
Câu 20. Khẳng định nào sau đây là sai?
A. Hàm số
log
a
yx
có tập xác định là
0;D
.
B. Hàm số
log
a
yx
có tập giá trị là
T
.
C. Đồ thị hàm số
log
a
yx
và
x
ya
đối xứng nhau qua đường thẳng
yx
.
D. Đồ thị hàm số
log
a
yx
có một đường tiệm cận ngang.
Câu 21. Hình vẽ nào sau đây là đồ thị của hàm số
21
x
y 
?
A. B.
C. D.
Câu 22. Cho hàm số
3
log 1yx
. Khẳng định nào say đây là đúng?
A. Hàm số đồng biến trên
. B. Hàm số đồng biến trên
1; 
C. Hàm số nghịch biến trên
. D. Hàm số nghịch biến trên
1; 
.
Câu 23. Biết phương trình
2
42
1
3
3
xx
có hai nghiệm
1
x
,
2
x
. Khi đó
22
12
xx
bằng
A.
10
. B.
9
. C.
8
. D.
7
.
Câu 24. Tập nghiệm của bất phương trình
2
22
log 4log 3 0xx
là
A.
1; 3
. B.
0; 2 8; 
. C.
2; 8
. D.
8; 
.
Câu 25. Chị Hoa muốn mua một chiếc tủ lạnh với giá
20
triệu đồng theo hình thức trả góp với số
tiền trả trước là
6
triệu đồng. Số tiền còn lại được trả góp trong
6
tháng với lãi suất
0,5%
/tháng
theo cách: sau đúng một tháng kể từ ngày mua, chị Hoa bắt đầu trả góp lần đầu tiên, hai lần trả
góp cách nhau đúng một tháng, số tiền trả góp mỗi tháng là như nhau. Hỏi, theo cách đó số tiền
O
y
x
1
3
y
x
3
1
O
O
y
x
1
2
y
x
O
2
1
mà chị Hoa phải trả trong mỗi lần là bao nhiều? (biết rằng lãi suất không thay đổi trong suốt quá
trình trả góp)
A.
2.375.000
đồng. B.
2.405.000
đồng. C.
2.760.000
đồng. D.
2.815.000
đồng.
Câu 26. Biết phương trình
1
5 .8 500
x
x
x
có hai nghiệm
1
x
,
2
x
. Giá trị của
12
xx
là
A.
2
3log 5
. B.
2
3log 5
. C.
5
3log 2
. D.
5
3log 2
.
Câu 27. Cho hai số dương
x
,
y
sao cho
2
2
2
41
2.4 ln 4
2
xy
x
x
xy




. Giá trị lớn nhất của biểu thức
2 2 2 2P x y x x y x
là:
A.
max
13P 
. B.
max
23P 
. C.
max
13P 
. D.
max
23P 
.
Câu 28. Số đỉnh của hình hai mươi mặt đều là
A.
12
. B.
20
. C.
24
. D.
30
.
Câu 29. Trong các khẳng định về khối đa diện, khẳng định nào sau đây là khẳng định sai?
A. Mỗi mặt của khối đa diện có ít nhất ba cạnh.
B. Hai mặt bất kì của khối đa diện luôn có ít nhất một điểm chung.
C. Mỗi cạnh của khối đa diện là cạnh chung của đúng 2 mặt của khối đa diện.
D. Mỗi đỉnh của khối đa diện là đỉnh chung của ít nhất 3 mặt.
Câu 30. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3AD a
. Tam giác
SAB
đều nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp
.S ABCD
là
A.
3
2
a
. B.
3
3
2
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 31. Cho hình chóp tam giác
.S ABC
có đáy
ABC
có diện tích bằng
2
3a
, hình chiếu của
S
lên
mặt phẳng đáy trùng với trọng tâm
của tam giác
ABC
và
3
2
a
SG
. Gọi
A
là trung điểm
cạnh
SA
,
B
nằm trên cạnh
SB
sao cho
2SB BB

. Tính thể tích khối chóp
.S A B C

.
A.
3
3
3
a
. B.
3
3
a
. C.
3
3
6
a
. D.
3
6
a
.
Câu 32. Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
2a
, diện tích tam giác
A BC
bằng
2
3a
. Thể tích của khối lăng trụ là
A.
3
2
3
a
. B.
3
2a
. C.
3
22a
. D.
3
32a
.
Câu 33. Cho khối cầu có thể tích là
3
cm36
. Bán kính
của khối cầu là
A.
cm6R
. B.
cm3R
. C.
cm32R
. D.
cm6R
.
Câu 34. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
AB a
. Cạnh bên
3SA a
và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
là ?
A.
5
2
a
. B.
5a
. C.
6a
. D.
6
2
a
.
Câu 35. Một mặt phẳng chứa trục cua một hinh tru cắt hình trụ theo thiết diện là hình chữ nhật có
độ dài đường chéo bằng
cm10
. Biết chu vi đáy của hình trụ bằng
2
cm6
. Thể tích khối trụ tương
ứng đó là
A.
3
cm48
. B.
3
cm9 91
. C.
3
cm72
. D.
3
cm18 34
.
Câu 36. Một khối trụ có bán kính đáy bằng
3a
, chiều cao bằng
23a
. Thể tích
V
của khối cầu
ngoại tiếp khối trụ là
A.
3
86Va
. B.
3
66Va
. C.
3
4
6
3
a
. D.
3
43Va
.
Câu 37. Cho lăng trụ
.ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
AB AC a
, biết rằng
A A A B A C a
. Tính theo
a
thể tích khối lăng trụ
.ABC A B C
A.
3
2
a
V
. B.
3
3
4
a
V
. C.
3
2
4
a
V
. D.
3
2
12
a
.
Câu 38. Quay tam giác đều
ABC
quanh trục
AM
với
M
là trung điểm
BC
ta được một hình nón
có diện tích đáy bằng
4
. Chiều cao của hình nón là
A.
2
. B.
3
. C.
22
. D.
23
.
Câu 39. Cho hình chóp đều
.S ABC
có cạnh đáy bằng
a
, chiều cao bằng
2.a
Hình nón ngoại tiếp
hình chóp
.S ABC
có diện tích xung quanh là
A.
2
13
.
3
a
B.
2
15
.
3
a
C.
2
11
.
3
a
D.
2
17
.
3
a
Câu 40. Cho mặt cầu tâm
O
, đường kính
2AB a
. Trên đoạn
AB
lấy điểm
I
sao cho
I
không
trùng với
A
,
B
,
O
. Gọi
J
là điểm đối xứng của
I
qua
O
. Mặt phẳng
qua
J
và vuông góc với
AB
cắt mặt cầu theo giao tuyến là một đường tròn
C
. Tính khoảng cách
IJ
sao cho thể tích khối
nón có đỉnh
I
và đáy là đường tròn
C
đạt giá trị lớn nhất.
A.
3
3
a
. B.
23
3
a
. C.
2
3
a
. D.
22
3
a
.
II. TỰ LUẬN (2,0 điểm).
Câu 1 (1,0 điểm). Biện luận theo tham số
m
số nghiệm của phương trình
42
20x x m
.
Câu 2 (1,0 điểm). Giải phương trình:
3 1 2
2 7.2 72 2 0
x x x
.
HẾT
ĐỀ TỔNG ÔN TẬP SỐ 04
Câu 1. Khẳng định nào sau đây là khẳng định đúng?
A.Đồ thị của hàm số
2
x
y
và
2
x
y
đối xứng qua trục tung.
B.Đồ thị hàm số
2
x
y
nằm bên phải trục tung.
C.Đồ thị hàm số
2
x
y
đi qua điểm (1; 0).
D.Đồ thị của hàm số
3
x
y
và
3
logyx
đối xứng qua trục hoành.
Câu 2. Viết phương trình tiếp tuyến của đồ thị hàm số
3
32y x x
tại điểm có hoành độ bằng
0.
A.
32yx
. B.
32yx
. C.
32yx
. D.
32yx
.
Câu 3. Tìm giá trị cực đại của hàm số
32
32y x x
.
A.1. B.0 C.-2 D.2.
Câu 4. Cho khối lăng trụ đều
..ABC A B C
có tất cả các cạnh bằng
a
. Tính thể tích V của khối
lăng trụ
..ABC A B C
A.
3
.Va
B.
3
.
3
a
V
C.
3
3
.
4
Va
D.
3
3
.
12
Va
Câu 5. Tìm tất cả các giá trị của
m
để đường thẳng
2ym
cắt đồ thị hàm số
42
23y x x
tại 4
điểm phân biệt.
A.
23m
. B.
3
1
2
m
. C.
23m
. D.
3
1
2
m
.
Câu 6. Cho hình chóp tam giác
.S ABC
có đáy
ABC
vuông tại
,B SA
vuông góc với mặt phẳng
ABC
,,SA AB a
0
30SCA
. Mặt phẳng
P
đi qua
A
vuông góc với
,SC
cắt
,SB SC
lần lượt tại
,.HK
Tính bán kính
của mặt cầu ngoại tiếp hình chóp
..A BCKH
A.
.
2
a
R
B.
.Ra
C.
2
.
2
a
R
D.
3
.
2
a
R
Câu 7. Một ngọn hải đăng đặt ở vị trí A cách
bờ 5km, trên bờ biển có một kho hàng
ở vị trí C cách B một khoảng 7km.
Người canh hải đăng có thể chèo
thuyền từ A đến M trên bờ biển với
vận tốc
4/km h
rồi đi bộ từ M đến C
với vận tốc
6 / .km h
Xác định độ dài
đoạn BM để người đó đi từ A đến C
nhanh nhất.
A.
7
.
2
km
B.
3 2 .km
C.
7
.
3
km
D.
2 5 .km
Câu 8. Đồ thị hàm số
12
1
x
y
x
có tiệm cận đứng là đường thẳng
A.
2x 
. B.
2y 
. C.
1y
. D.
1x
.
Câu 9. Cho
22
log 3, log 7ab
. Hãy biểu diễn
18
log 42
theo
,.ab
A.
18
1
log 42 .
2
ab
a

B.
18
1
log 42 .
1
ab
a
C.
18
log 42 .
12
ab
a
D.
18
1
log 42 .
12
ab
a

Câu 10. Giải phương trình
2 3 4
48
xx
.
A.
6
7
x
. B.
2
3
x
. C.
2x
. D.
4
5
x
.
B
M
C
5km
A
Câu 11. Cho
01ab
. Khẳng định nào sau đây là khẳng định sai?
A.
log 3 log 3.
ab
B.
lg lg .ab
C.
0 ln ln .ab
D.
11
.
22
ab
Câu 12. Số nghiệm của phương trình
4 3.2 4 0
xx
là
A.0. B.1. C.2. D.3.
Câu 13. Hàm số nào sau đây đồng biến trên
?
A.
42
25y x x
. B.
1yx
. C.
1
1
x
y
x
. D.
3
31y x x
.
Câu 14. Cho hình lập phương có cạnh bằng
a
. Tính diện tích
S
của mặt cầu ngoại tiếp hình lập
phương.
A.
2
.Sa
B.
2
2.Sa
C.
2
3.Sa
D.
2
4.Sa
Câu 15. Số giao điểm của đồ thị hàm số
2
( 2)( 1)y x x x
và trục hoành là
A.1. B.0. C.2. D.3.
Câu 16. Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
A.
32
31y x x
. B.
32
3 2.y x x
C.
32
31y x x
. D.
3
32y x x
.
Câu 17. Cho hàm số
1
ln
1
y
x
. Khẳng định nào sau đây là khẳng định đúng?
A.
1.
y
xy e
B.
1.
y
xy e
C.
1.
y
xy e

D.
1.
y
xy e

Câu 18. Tính khoảng cách
d
giữa hai điểm cực tiểu của đồ thị hàm số
42
4 1.y x x
A.
22d
. B.
3d
. C.
2d
. D.
1d
.
Câu 19. Hàm số
32
1
1
3
y x x
nghịch biến trên khoảng nào?
A.
( ;0)
. B.
.
C.
(2; )
. D.
(0; 2)
.
Câu 20. Tính
1 2 8 9
log log ... log log .
2 3 9 10
P
A.
2.P
B.
0.P
C.
1.P
D.
1.P 
Câu 21. Cho hình chóp
.S ABC
gọi
,,A B C
lần lượt là ảnh của
,,A B C
qua phép vị tự tâm
S
tỉ số
2.k
Gọi
,VV
lần lượt là thể tích khối chóp
.S ABC
và
.S A B C
. Tính tỉ số
'V
V
.
A.
'1
.
27
V
V
B.
'
8.
V
V
C.
'1
.
8
V
V
D.
'
2.
V
V
Câu 22. Tìm giá trị nhỏ nhất của hàm số
.e
x
yx
trên đoạn
[1; 2].
A.
[
2
1;2]
min 2 .
x
ye
B.
[
2
1;2]
min .
x
ye
C.
[1;2]
min .
2
x
e
y
D.
[1;2]
min .
x
ye
Câu 23. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật có
, 2 ,AB a BC a
cạnh bên
SA
vuông góc với đáy và
3SA a
. Tính thể tích
V
của khối chóp
..S ABCD
A.
3
3
3
Va
. B.
3
23
.
3
Va
C.
3
3.Va
D.
3
23Va
.
Câu 24. Tìm tập giá trị của hàm số
2
y x x
.
A.
[0;1]
. B.
1
0;
4



. C.
[0; 2]
. D.
1
0;
2



.
Câu 25. Tính đạo hàm của hàm số
3
2
1yx
.
A.
2
3
1
( 1)
3
yx

. B.
22
3
2
3 ( 1)
x
y
x
. C.
2
2
3
2
( 1)
3
x
yx

. D.
3
2
2
31
x
y
x
.
Câu 26. Tìm tất cả các giá trị của
m
để hàm số
42
( 1) 2( 2) 1y m x m x
có ba cực trị.
A.
1.m 
B.
1 2.m
C.
1 2.m
D.
2.m
Câu 27. Tìm tất cả các giá trị của
m
để hàm số
2
2
mx
y
xm
đồng biến trên mỗi khoảng xác định.
A.
2
2
m
m
. B.
22m
. C.
2
2
m
m
. D.
22m
.
Câu 28. Cho hàm số
2
2
( ) log ( 1)f x x
, tính
(1).f
A.
1
(1)
2
f
. B.
1
(1) ln 2
2
f
. C.
1
(1)
ln 2
f
. D.
2
(1) 2log 2f
.
Câu 29. Tìm tất cả các giá trị của
m
để đồ thị hàm số
2
2
32
xm
y
xx

có đúng hai đường tiệm cận?
A.
1m
và
4m
. B.
1m
. C.
4m
. D.
0m
.
Câu 30. Hàm số
()y f x
có đồ thị như hình vẽ. Khẳng định nào sau đây là khẳng định đúng?
A.Đồ thị hàm số có tiệm cận đứng là
1x
và tiệm cận ngang là
2y 
.
B.Hàm số đồng biến trên các khoảng
( ; 2),( 2, )
.
C.Đồ thị hàm số cắt trục hoành tại điểm
(0; 1)M
.
D.Hàm số nghịch biến trên các khoảng
( ; 2), ( 2; ) 
.
Câu 31. Trong các hàm số sau đây hàm số nào nghịch biến trên tập xác định?
A.
2
x
y
. B.
1
2
x
y



. C.
x
ye
. D.
12
x
y 
.
Câu 32. Tìm tập xác định
D
của hàm số
22
( 2 3)y x x
.
A.
D
. B.
( ; 3) (1; ).D
C.
{\ 3;1}D 
. D.
( 3;1).D 
Câu 33. Có bao nhiêu giá trị nguyên dương của
m
để phương trình
2
3 6.3 5 0
xx
m
có
nghiệm?
A.4. B.5. C.10. D.14
Câu 34. Khối lăng trụ đều
.ABCD A B C D
có thể tích
3
24 .cm
Tính thể tích
V
của khối tứ diện
.ACB D

A.
3
8.V cm
B.
3
6.V cm
C.
3
12 .V cm
D.
3
4.V cm
Câu 35. Tìm giá trị lớn nhất của hàm số
3
3y x x
trên đoạn
[0; 2]
.
A.
[]0;2
max 1
x
y
. B.
[0;2]
max 2
x
y

. C.
[0;2]
max 0
x
y
. D.
[0;2]
max 2
x
y
.
Câu 36. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a SA
vuông góc với đáy. Góc
giữa
SB
và mặt đáy bằng
0
60 .
Tính khoảng cách
h
từ
A
đến mặt phẳng
.SBC
A.
2
.
2
a
h
B.
3
.
2
a
h
C.
.
2
a
h
D.
.ha
Câu 37. Cho tứ diện
ABCD
có thể tích là
.V
Gọi
, , ,A B C D
lần lượt là trọng tâm của các tam
giác
, , ,BCD ACD ABD ABC
. Tính thể tích khối tứ diện
A B C D
theo
V
.
A.
.
8
V
B.
8
.
27
V
C.
.
27
V
D.
27
.
64
V
Câu 38. Khối lập phương thuộc loại khối đa diện đều nào?
A.
3; 3 .
B.
4; 3 .
C.
3; 4 .
D.
5; 3 .
Câu 39. Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
biết góc giữa cạnh bên và mặt đáy bằng
0
45 .
Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
2
.
6
Va
B.
3
3
.
3
Va
C.
3
2
.
3
Va
D.
3
2.Va
Câu 40. Cho khối tứ diện đều cạnh bằng
a
. Tính thể tích khối tám mặt đều mà các đỉnh là trung
điểm của các cạnh của khối tứ diện đã cho.
A.
3
2
.
24
a
B.
3
3
.
12
a
C.
3
2
.
6
a
D.
3
3
.
24
a
Câu 41. Đồ thị hàm số
3
33y x x
có bao nhiêu tiếp tuyến song song với trục hoành?
A.0. B.3. C.1. D.2.
Câu 42. Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh
tam giác
SAB
vuông
cân tại
,S
tam giác
SCD
đều. Tính khoảng cách
h
giữa hai đường thẳng
SA
và
.BD
A.
.ha
B.
.
2
a
h
C.
5
.
5
ha
D.
35
.
20
ha
Câu 43. Tính đạo hàm của hàm số
ln(2 1)yx
.
A.
1
21
y
x
. B.
2
21
y
x
. C.
1
y
x
. D.
2y
.
Câu 44. Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu của nước X
sẽ hết sau 100 năm nữa. Nhưng do nhu cầu thực tế mức tiêu thụ tăng lên
4%
mỗi năm.
Hỏi sau bao lâu số dầu dự trữ của nước X sẽ hết (kết quả gần đúng lấy đến 2 chữ số thập
phân sau dấu phẩy).
A.
45
năm. B.
43,11
năm. C.
41,04
năm. D.
39,25
năm.
Câu 45. Cho hình trụ có bán kính đáy
2cm
và chiều cao
3.cm
Tính diện tích toàn phần
tp
S
của
hình trụ.
A.
2
20 .
tp
S cm
B.
2
8.
tp
S cm
C.
2
16 .
tp
S cm
D.
2
12 .
tp
S cm
Câu 46. Cho hình chữ nhật
ABCD
có
,2AB a AD a
. Tính thể tích
V
của khối trụ tạo thành khi
quay hình chữ nhật
ABCD
quanh cạnh
AD
.
A.
3
.Va
B.
3
2Va
. C.
3
2.Va
D.
3
.Va
Câu 47. Nhà sản xuất muốn thiết kế một chiếc hộp sữa hình trụ có thể tích
V
. Để tiết kiệm
nguyên liệu thì diện tích toàn phần của hình trụ phải nhỏ nhất. Tính bán kính
của đáy
hình trụ để tiết kiệm được nhiều nguyên liệu nhất.
A.
3
.RV
B.
3
.
2
V
R
C.
3
.
4
V
R
D.
3
1
.
2
RV
Câu 48. Cho
log 3, log 2
aa
bc
. Tính
log
a
b
c
.
A.
log 1
a
b
c
. B.
log 3
a
b
c
. C.
3
log .
2
a
b
c

D.
log 5
a
b
c
.
Câu 49. Tìm
m
để giá trị nhỏ nhất của hàm số
32
36y x mx
trên đoạn
0;3

bằng
2
.
A.
2m
. B.
31
27
m
. C.
3
2
m
. D.
1m
.
Câu 50. Tìm tập nghiệm của phương trình
2
lg( 6 7) lg( 3)x x x
.
A.
4; 5 .
B.
3;4 .
C.
5.
D.
.
HẾT
ĐỀ TỔNG ÔN TẬP SỐ 05
Câu 1. Đồ thị hàm số
2
23
1
xx
y
x

có tiệm cận đứng là đường thẳng
A.
1y
.
B.
1x
.
C.
2x
.
D.
1x 
.
Câu 2. Tính đạo hàm của hàm số
2
sin
.
x
x
y
e
A.
2
2 sin cos
x
x x x
y
e
. B.
2
cos 2 sin
x
x x x
y
e
C.
2
cos 2 sin
x
x x x
y
e
. D.
2
cos 2 sin
x
x x x
y
e

Câu 3. Nêu
12
log 6 a
và
12
log 7 b
thì:
A.
2
log 7
1
a
b
. B.
2
log 7
1
a
b
. C.
2
log 7
1
b
a
. D.
2
log 7 .
1
b
a
Câu 4.
Tìm tập xác định của hàm số
2
9
log 1 ln 3 2.y x x
A.
;3D 
. B.
; 1 1; 3 .D 
C.
1;3D 
. D.
3;D 
Câu 5.
Môt hinh thang vuông
ABCD
có đường cao
2AD
, đay nho
2AB
, đay lơn
4CD
.
Cho hinh thang đo quanh quay AB ta đươc khôi tròn xoay có thể tích bằng:
A.
40
3
V
.
B.
16
3
V
.
C.
8
3
V
.
D.
16V
.
Câu 6.
Môt lăng tru đưng
.ABC A B C
có đáy là tam giác cân ,
AB AC a
,
120BAC
. Măt
phăng
AB C

tạo với đáy một góc
60
. Thê tich khôi lăng tru băng:
A.
3
a
.
B.
3
3
3
a
.
C.
3
3
8
a
.
D.
3
3
2
a
.
Câu 7.
Tính đạo hàm của hàm số
2
2016
log 5yx
.
A.
2
1
5
y
x
B.
2
2
5 ln 2016
x
y
x
C.
2
2016
x
y
D.
2
1
5 ln 2016
y
x
.
Câu 8.
Tìm
m
để phương trình
3
4 2 3
xx
m
có đúng hai nghiệm phân biệt
1;3 .x
A.
3
13
4
m
.
B.
13 3m
.
C.
93m
.
D.
3
3
4
m
.
Câu 9.
Cho hinh chop
.S ABCD
có đáy
ABCD
là hình chữ nhật . Hình chiếu vuông góc của
S
lên
măt phăng
ABCD
làtrung điêm
H
của
,AB
tam giac
SAB
vuông cân tai
Biêt
3,SH a
3CH a
. Khoảng cách giữa hai đường thẳng
SD
và
CH
là:
A.
2 66
11
a
.
B.
4 66
11
a
.
C.
66
11
a
.
D.
66
22
a
.
Câu 10.
Tìm giá trị nhỏ nhất của hàm số
2
33
log 4log 1y x x
trên đoan
1; 27 .

A.
1
. B.
3
.
C.
0
.
D.
2
.
Câu 11.
Cho hinh chop
.S ABC
có
4,SA
SA
vuông goc vơi đay . Tam giac
ABC
vuông tai
A
,
5BC
. Diên tích măt câu ngoai tiêp hinh chop la
A.
50S
.
B.
25S
.
C.
41S
.
D.
45S
.
Câu 12. Tông gia tri lơn nhât va giá trị nhỏ nhất của hàm số
42
23y x x
trên đoan
1;1

là:
A.
7
. B.
2
. C.
5
. D.
3
.
Câu 13. Giá trị lớn nhất của hàm số
1
2
x
y
x
trên đoan
1;0

là:
A.
2
. B.
2
3
. C.
0
. D.
1
2
.
Câu 14. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy
băng
60
. Khoảng cách từ điểm
S
đến mặt đáy
ABC
băng
A.
2a
. B.
3
2
a
. C.
3a
. D.
a
.
Câu 15. Chọn khẳng định sai trong cac khăng đinh sau:
A.
ln 0 1xx
. B.
2
log 0 0 1xx
.
C.
11
33
log log 0a b a b
. D.
11
22
log log 0a b a b
.
Câu 16. Cho hinh chop
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
13
2
a
SD
. Hình chiếu
vuông goc cua
S
lên măt phăng
ABCD
là trung điểm
H
của đoạn
.AB
Thê tich khôi
chóp
.S ABCD
là
A.
3
2
3
a
V
. B.
3
2Va
. C.
3
3Va
. D.
3
3
3
a
V
.
Câu 17. Hàm số
32
31y x x
có mấy điểm cực trị?
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 18. Hàm số
42
21y x x
nghịch biến trên khoang
A.
1;0
. B.
;1
. C.
1; 
. D.
;1
và
0;1 .
Câu 19. Cho
2
log 14 a
. Tính
49
log 32
theo
a
A.
49
5
log 32
21a
. B.
49
5
log 32 .
22a
C.
49
10
log 32
1a
. D.
49
2
log 32 .
51a
Câu 20. Nếu
3
2
3
2
aa
và
34
log log
45
bb
thì
A.
1, 0 1ab
. B.
b1, 1a 
.
C.
0 1, 1ab
. D.
0 1, 0 1ab
.
Câu 21. Tam giac
ABC
có
3, 4, 5AB AC BC
. Cho tam giac
ABC
quay quanh canh
AB
và
AC
ta đươc hai hinh non tron xoay co diên tich xung quanh la
1
S
và
2
S
. Hãy chọn kết
quả đung trong cac kêt qua sau
A.
1
2
3
5
S
S
. B.
1
2
4
3
S
S
. C.
1
2
3
4
S
S
. D.
1
2
4
5
S
S
.
Câu 22. Phương trinh
1
9 3 2 0
xx
có hai nghiệm là
1 2 1 2
,x x x x
. Giá trị của biểu thức
12
23A x x
là
A.
3
3log 2
. B.
3
4log 2
. C.
1
. D.
2
3log 3
.
Câu 23. Hàm số
2mx m
y
xm

nghịch biến trên các khoảng xác định thì tham số
m
thỏa mãn
A.
10m
. B.
01m
C.
21m
D.
21m
Câu 24. Cho hinh chop
.S ABC
có đáy là tam giác
ABC
vuông cân tai
,A AB AC a
. Tam giac
SAB
là tam giác đều và năm trong măt phăng vuông goc vơi
ABC
. Thê tich khôi chop
.S ABC
là
A.
3
3
6
a
V
. B.
3
3
8
a
V
. C.
3
3
27
a
V
. D.
3
3
12
a
V
.
Câu 25.
Đồ thị hàm số
2
3x
y
xx
có tiệm cận ngang la đương thăng
A.
0y
. B.
0x
C.
1y
D.
1y 
Câu 26. Hàm số
32
34y x x
đông biên trên khoang
A.
2;0
. B.
0; 
. C.
;3
. D.
10; 2
.
Câu 27. Cho hinh chop
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
. Tam giac
SAD
là tam giác
đều và
SAD
năm trong măt phăng vuông goc vơi măt phăng đay. Khoảng cách giữa hai
đương thăng
AD
và
SB
là
A.
14
7
a
. B.
2 14
7
a
. C.
14
3
a
. D.
2 21
7
a
.
Câu 28. Cho ham sô
y f x
xác định, liên tuc trên R va co bang biên thiên:
Khăng đinh nao sau đây sai?
A.Đường thẳng
2y 
căt đô thi ham sô
y f x
tại ba điêm phân biêt.
B.Hàm số đạt cực tiểu tại
2x 
.
C.
32
34f x x x
.
D.Hàm số nghịch biến trên
2;0
.
Câu 29. Hàm số
42
23y x x
có điểm cực tiểu là
A.
0; 4
. B.
0; 3
. C.
1; 4
. D.
1; 4
.
Câu 30. Cho ham sô
3
31y x x
có đồ thị
C
. Phương trinh tiêp tuyên cua đô thi
C
tại giao
điêm cua
C
vơi truc tung la đương thăng
A.
31yx
. B.
31yx
. C.
31yx
. D.
31yx
.
Câu 31. Hàm số
42
2 2 1y mx m x
có ba cưc tri khi
A.
0m
. B.
02m
. C.
02m
. D.
2m
.
Câu 32. Cho biêt đô thi ơ Hnh 2 là đồ thị của một trong bốn hàm
sô nêu dươi đây. Hỏi đó là đồ thị của hàm số nào?
A.
32
22y x x x
.
B.
3
31y x x
.
C.
32
3 3 1y x x x
.
D.
32
3 3 1y x x x
.
Hnh 2
Câu 33. Đồ thị hàm số
42
2y x mx
có ba điêm cưc tri tao thành một tam giác đều khi
A.
0m
hoăc
27m
. B.
0m
hoăc
3
3m
.
C.
3
3m
. D.
0m
.
Câu 34. Sôđường tiêm cân cua đô thi ham sô
2
31
4
x
y
x
là
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 35. Tìm
m
để hàm số
32
3 4 4y x mx mx
luôn đông biên trên R.
A.
3
0
4
m
. B.
4
0
3
m
. C.
3
0
4
m
. D.
4
0
3
m
.
Câu 36. Giải bất phương trình
3
log 2 1 2x 
ta đươc nghiêm la
A.
1
5
2
x
. B.
1
5
x
. C.
5x
. D.
5x
.
Câu 37. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tai
A
và
D
. Biêt
cạnh
2 , , 3AB a AD DC a SA a
và
SA
vuông goc vơi măt phăng đay . Thê tich khôi
chóp
.S BCD
là
A.
3
3
2
a
V
. B.
3
2
a
V
. C.
3
6
a
V
. D.
3
Va
.
Câu 38. Môt chât điêm chuyên đông theo quy luât
23
12 2s t t
. Thơi điêm
t
(giây) tại đó vận tốc
/v m s
của chuyển động đạt giá trị lớn nhất là:
A.
4t
. B.
5t
. C.
3t
. D.
2t
.
Câu 39. Tìm
m
để hàm số
3 2 2
1
1 3 2 5
3
y x m x m m x
đat cưc đai tai
0x
.
A.
6m
. B.
2m
.
C.
1m
. D.
1m
hoăc
2m
.
Câu 40. Môt hinh tru ngoai tiêp hinh lâp phương va co hai đay ngoai tiêp hai đay cua môt hinh
lâp phương. Biêt thê tich khôi tru đo la
2
thì thể tích khối lập phương bằng
A.
2
. B.
C.
. D.
1
.
Câu 41. Cho hình chóp
.S ABC
có đáy
ABC
là tam giac vuông tại
B
,
, 3.AB a BC a
Hình
chiêu vuông goc cua
S
trên măt đay la trung điêm
H
của
AC
. Biêt
2SB a
. Tính theo
a
khoảng cách từ
H
đến mặt phẳng
SAB
.
A.
3 21
7
a
. B.
21
3
a
. C.
21
7
a
. D.
7 21
3
a
.
Câu 42. Đồ thị hàm số
32
31y x x
căt đương thăng
ym
tại ba điêm phân biêt khi
A.
3m 
. B.
31m
. C.
1m
. D.
31m
.
Câu 43. Tính đạo hàm của hàm số
23
2 .8
x
yx

A.
2 3 2 3
8 2 8 ln8
xx
yx

. B.
23
2 2 8 ln8
x
yx

.
C.
2 3 2 3
8 2 2 8
xx
yx

. D.
2 3 2 3
8 2 2 8 ln8
xx
yx

.
Câu 44. Môt ngươi gưi 20 triêu đông vao ngân hang theo thê thưc lai kep , lãi suất
8,4%
năm va
lãi hàng năm được nhập vào vốn . Hỏi sau 3 năm ngươi đo thu đươc ca vôn lân lai la bao
nhiêu?
A.
3
20. 1,084
triêu đông. B.
4
20. 1,084
triêu đông.
C.
6
20. 1,084
triêu đông. D.
2
20. 1,084
triêu đông.
Câu 45. Trong cac phương trinh sau đây phương trinh nao co nghiêm?
A.
2
3
2
1 2 0xx
. B.
2
5
50x 
.
C.
1
2
2 3 0x 
. D.
4 8 2 0x
.
Câu 46. Rút gọn
3 2log
0, 1, 0
a
b
a a a b
băng
A.
3
ab
. B.
23
ab
. C.
32
ab
. D.
2
ab
.
Câu 47. Cho hinh chop tư giac đêu
.S ABCD
có cạnh bên tạo với đáy một góc
60
và cạnh đáy
băng
a
. Khoảng cách giữa
AD
và
SC
là
A.
42
7
a
. B.
2 42
7
a
. C.
3 42
7
a
. D.
42
14
a
.
Câu 48. Hàm số
3 2 2
2 3 6 1y x x m x m
nghịch biến trên khoảng
2;0
khi
m
thỏa mãn
A.
1m 
. B.
3
4
m 
. C.
3
4
m 
. D.
3m 
.
Câu 49. Cho hinh chop
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA
vuông goc vơi măt đay
ABC
. Góc giữa
SB
và mặt phẳng
ABC
băng
60
. Thê tich khôi chop
.S ABC
là
A.
3
3
6
a
V
. B.
3
4
a
V
. C.
3
3
12
a
V
. D.
3
2
a
V
.
Câu 50. Cho hình trụ có bán kính đường tròn đáy bằng
và độ dài đường cao là
h
. Diên tich
toàn phần của hình trụ là
A..
2 Rh
. B.
2 R h R
. C.
2
4 R
. D.
2R h R
.
HẾT
ĐỀ TỔNG ÔN TẬP SỐ 06
Câu 1. Tìm
m
để phương trình
32
3 2 1x x m
có
3
nghiệm phân biệt
A.
31m
. B.
03m
. C.
20m
. D.
24m
.
Câu 2. Khẳng định nào sau đây đúng về tính đơn điệu của hàm số
32
32y x x
A. Hàm số nghịch biến trên khoảng
0; 
.
B. Hàm số đồng biến trên khoảng
0; 2
.
C. Hàm số đồng biến trên khoảng
;0
và
2; 
.
D. Hàm số đồng biến trên
.
Câu 3. Đồ thị hàm số
21
1
x
y
x
có
A. Có hai đường tiệm cận đứng
2, 1xx
.
B. Đường tiệm cận đứng
1x
và không có tiệm cận ngang.
C. Đường tiệm cận ngang
2y
và không có tiệm cận đứng.
D. Đường tiệm cận đứng
1x
và tiệm cận ngang
2y
.
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành với
0
, 2 , 60AB a AD a BAD
.
SA
vuông góc với đáy, góc giữa
SC
và đáy là
0
60
. Thể tích khối chóp
.S ABCD
là
V
. Tỷ số
3
V
a
là :
A.
3
. B.
7
. C.
23
. D.
27
.
Câu 5. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1
32
x
y
x
trên đoạn
3; 2

là
A.
1
và
. B.
và
. C.
và
1
2
. D.
1
2
và
.
Câu 6. Khối
12
mặt đều thuộc loại
A.
3,5
. B.
3,6
. C.
5,3
. D.
4,4
.
Câu 7. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
42
84y x x
trên đoạn
1; 3

là
A.
1;3
1;3
max 13,min 12yy




. B.
1;3
1;3
max 13,min 3yy




.
C.
1;3
1;3
max 4,min 12yy




. D.
1;3
1;3
max 4,min 3yy




.
Câu 8. Hàm số
32
3 1 3 1y mx m x m x m
có cực trị khi và chỉ khi
A.
1
; \ 0
3
m




. B.
1
;
3
m




. C.
1
3
m
. D.
1m
.
Câu 9. Hàm số nào sau đây có bảng biến thiên như hình dưới đây
x

2

'y
y
2


2
A.
25
2
x
y
x
. B.
23
2
x
y
x
. C.
3
2
x
y
x
. D.
23
2
x
y
x
.
Câu 10. Cho các số thực
,ab
dương
1a
. Khẳng định nào sau đây đúng?
A.
4
log 4 4log
a
a
ab b
. B.
4
1
log log
4
a
a
ab b
.
C.
4
11
log log
44
a
a
ab b
. D.
4
log 2log
a
a
ab b
.
Câu 11. Đạo hàm của hàm số
6
3 .sin2
xx
y x e
A.
6
' 3 .2cos2 3 .ln 3.sin2 6.
x x x
y x x e
. B.
6
' 3 .2cos2 3 .ln3.sin2 6.
x x x
y x x e
.
C.
6
' 3 .ln3.sin2 6.
xx
y x e
. D.
6
' 3 .2cos2 6.
xx
y x e
.
Câu 12. Cho hàm số
( ) .coty f x x x
. Khi đó
'( )fx
là:
A.
cot x
. B.
2
cot
sin
x
x
x
. C.
2
sin
x
x
. D.
2
cot
sin
x
x
x
.
Câu 13. Cho hàm số
42
21y x x
. Khẳng định nào sau đây đúng:
A. Đồ thị hàm số có hai điểm cực tiểu. B. Hàm số đạt cực đại tại
1x
.
C. Hàm số đạt cực tiểu tại
1x 
. D. Giá trị cực tiểu bằng 0.
Câu 14. Cho lăng trụ
. ' ' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh
2a
, hình chiếu của
'A
lên
ABC
trùng với trọng tâm tam giác
ABC
. Biết góc giữa cạnh bên và mặt phẳng đáy bằng
0
60
. Khi
đó thể tích khối lăng trụ bằng:
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
23a
. D.
3
43a
.
Câu 15. Hàm số
4 2 2
11y x m x m m x
đạt cực đại tại
0x
khi
A.
1m
. B.
0m
. C.
0, 1mm
. D. Không tồn tại
m
.
Câu 16. Cho hàm số
42
,0y ax bx c a
có đồ thị là
C
. Khẳng định nào sau đây là sai:
A. Đồ thị
C
luôn có 3 điểm cực trị tạo thành một tam giác cân có đỉnh nằm trên
.Oy
B. Hàm số luôn có khoảng đồng biến và khoảng nghịch biến.
C. Trên
C
tồn tại vô số cặp điểm đối xứng nhau qua
Oy
.
D. Tồn tại
,,a b c
để đồ thị
C
chỉ cắt
Ox
tại một điểm.
Câu 17. Tập xác định của hàm số
32
( ) 3 2f x x x
là
A.
1; 2
. B.
; 
. C.
1; 2

. D.
1; 2
.
Câu 18. Đồ thị hàm số
2
1
2 3 1
x
y
xx

có
A. Hai đường tiệm cận đứng
1
1,
2
xx
và đường tiệm cận ngang
0y
.
B. Hai đường tiệm cận đứng
1
1,
2
xx
và đường tiệm cận ngang
1
2
y
.
C.Hai đường tiệm cận đứng
1
1,
2
xx
và không có tiệm cận ngang.
D. Một đường tiệm cận đứng
1x
và đường tiệm cận ngang
1
2
y
.
Câu 19. Tập xác định của hàm số
2
1
x
y
x
là:
A.
\2
. B.
;1
. C.
1; 
. D.
\1
Câu 20. Tìm
m
để hàm số
42
21y x m x m
có
3
cực trị.
A.
1m 
. B.
1m 
. C.
1m 
. D.
1m 
.
Câu 21. Đáy của hình chóp
.S ABCD
là hình vuông cạnh
a
. Cạnh bên
SA
vuông góc với đáy có độ
dài bằng
a
. Thể tích khối tứ diện
.BCDS
là :
A.
3
8
a
. B.
3
3
a
. C.
3
4
a
. D.
3
6
a
.
Câu 22. Tìm tất cả các giá trị của
m
để hàm số
32
1
2016
3
y x mx mx
nghịch biến trên
A.
1;0

. B.
; 1 0; 
C.
1;0
. D.
; 1 0;

.
Câu 23. Cho hình lập phương cạnh
a
. Thể tích của khối lập phương đã cho là:
A.
3
3a
. B.
3
a
. C.
2
a
. D.
3
3
a
.
Câu 24. Hàm số
32
1 3 1 3 2 5y m x m x m x m
nghịch biến trên
khi
A.
1m
. B.
1m
. C.
1m
. D.
41m
.
Câu 25. Tập xác định của hàm số
2
log
1
x
y
x
là :
A.
;1 2;
. B.
\ 1; 2
. C.
1; 2
. D.
\1
.
Câu 26. Hàm số
3
22
1 2 1
3
x
y m x m x m
đạt cực đại tại
1x
khi và chỉ khi:
A.
1m
. B.
0, 1mm
. C.
0m
. D. Không tồn tại
m
.
Câu 27. Cho hàm số
32
31y x x
. Khẳng định nào sau đây đúng:
A. Điểm cực tiểu của đồ thị hàm số là
(2; 5)
. B. Giá trị cực tiểu bằng
0
.
C. Giá trị cực đại của hàm số là
d
2
c
y 
. D. Hàm số đạt cực đại tại
2x
.
Câu 28. Đạo hàm của hàm số
2
8
log 3 8y x x
là :
A.
2
8
' 2 3 .log 3 8y x x x
. B.
2
23
'
38
x
y
xx

.
C.
2
23
'
( 3 8)ln 8
x
y
xx

. D.
2
23
' ln 8
38
x
y
xx

.
Câu 29. Gọi
,aA
lần lượt là giá trị nhỏ nhất , giá trị lớn nhất của hàm số
2
4y x x
. Khẳng
định nào sau đây là sai?
A.
2
8A
. B.
2
24Aa
. C.
20aA
. D.
2
aA
.
Câu 30. Hàm số
1
1
x
y
x
A. Đồng biến trên
. B. Đồng biến trên
\1
.
C. Nghịch biến trên
. D. Đồng biến trên
;1
và
1; 
.
Câu 31. Cho số dương
a
và
,1ba
. Tìm phát biểu sai.
A.
log 1 0
a
. B.
log 1
a
a
. C.
log
n
a
an
. D.
log
a
b
ab
.
Câu 32. Tìm
m
để đồ thị hàm số
42
22y x mx m
cắt trục
Ox
tại
4
điểm phân biệt
A.
2;m 
. B.
;1m 
.
C.
; 1 2;m  
. D.
0;m 
.
Câu 33. Cho
log 3
a
b
. Khi đó giá trị biểu thức
log
b
a
b
a
là
A.
31
32
. B.
31
. C.
31
. D.
31
32
.
Câu 34. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.
B. Tồn tại một hình đa diện có số đỉnh và số mặt bằng nhau.
C. Số đỉnh và số mặt của một hình đa diện luôn bằng nhau.
D. Tồn tại một hình đa diện có số cạnh và số mặt bằng nhau.
Câu 35. Tìm
m
để hàm số
3
2
1 3 2
3
x
y m x m x m
đồng biến trên
3; .
A.
0m
. B.
0m
. C.
0m
. D.
1m
.
Câu 36. Cho hình chóp tam giác có đường cao bằng
100 cm
và các cạnh đáy bằng
20 ,21 ,29cm cm cm
. Thể tích khối chóp đó là :
A.
3
7000cm
. B.
3
6213cm
. C.
3
6000cm
. D.
3
7000 2cm
.
Câu 37. Thể tích của khối đa diện tạo bởi hình sau là:
15 cm
14 cm
6 cm
7 cm
4 cm
A.
3
328cm
. B.
3
456cm
. C.
3
584cm
. D.
3
712cm
.
Câu 38. Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
, góc giữa
SC
và đáy
ABC
là
0
45
.
Hình chiếu vuông góc của
S
lên mặt phẳng
ABC
là điểm
H
thuộc
AB
sao cho
2HA HB
. Biết
7
3
a
CH
. Khoảng cách giữa
2
đường thẳng
,SA BC
là:
A.
210
15
a
. B.
210
45
a
. C.
210
30
a
. D.
210
20
a
.
Câu 39. Cho hình chóp
.S ABC
có
', 'AB
lần lượt là trung điểm của
,SA SB
. Khi đó, tỉ số
.
. ' '
S ABC
S A B C
V
V
là:
A.
. B.
2
. C.
. D.
4
.
Câu 40. Cho hình chóp đều
.S ABC
. Người ta tăng cạnh đáy lên
2
lần. Để thể tích khối chóp
.S ABC
giữ nguyên thì
tan
góc giữa cạnh bên và mặt phẳng đáy tăng lên bao nhiêu lần?
A.
8
. B.
2
. C.
3
. D.
4
.
Câu 41. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
31y x x
trên đoạn
1; 4

là
A.
1;4
1;4
max 51,min 3yy




. B.
1;4
1;4
max 1,min 1yy




.
C.
1;4
1;4
max 51,min 1yy




. D.
1;4
1;4
max 51,min 1yy





.
Câu 42. Khẳng định nào sau đây sai?
A. Hàm số
21
1
x
y
x
luôn đồng biến trên từng khoảng xác định.
B. Hàm số
2 cos2y x x
luôn đồng biến trên
.
C. Hàm số
3
31y x x
luôn nghịch biến trên
.
D. Hàm số
42
23y x x
nghịch biến trên khoảng
;0
Câu 43. Đạo hàm của hàm số
2
54
2
xx
y

là
A.
2
54
2 5 2 .ln2
xx
x

. B.
2
2 5 4
5 4 2
xx
xx


.
C.
2
2 5 4
5 4 2 .ln 2
xx
xx


. D.
2
54
2 5 2
xx
x

.
Câu 44. Đồ thị hình bên là đồ thị của hàm số nào dưới đây?
A.
42
23y x x
. B.
42
2y x x
. C.
42
23y x x
. D.
42
2y x x
.
Câu 45. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất.
A. Ba mặt. B. Năm mặt. C. Bốn mặt. D. Hai mặt.
Câu 46. Cho hình chóp tam giác
.S ABC
, có
,,SA SB SC
đôi một vuông góc,
SA SB SC a
. Khi
đó thể tích của khối chóp đã cho là:
A.
3
6
a
. B.
3
3
a
. C.
3
9
a
. D.
3
2
3
a
.
Câu 47. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
,
AC a
,
H
là trung điểm
của
AB
,
SH
vuông góc với
ABCD
, tam giác
SAB
vuông tại
S
. Khoảng cách giữa hai đường
thẳng
,BD SC
theo
a
là:
A.
3
13
a
. B.
2
13
a
. C.
13
a
. D.
2 13
a
.
Câu 48. Tọa độ giao điểm của đồ thị
C
:
2
23
x
y
x
và đường thẳng
21yx
là
A.
11
1;1 , ;
42
MN



. B.
13
1; 3 , ;
42
MN



.
C.
13
1;1 , ;
42
MN




. D.
11
1; 3 , ;
42
MN



.
Câu 49. Gọi
,mM
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
2
2
xx
y
x

trên
3;6

. Khi đó
A.
3
6mM
. B.
2Mm
. C.
3
2 Mm
. D.
22
113Mm
.
Câu 50. Một cô giáo gửi
200
triệu đồng loại kỳ hạn
6
tháng vào ngân hàng với lãi suất
6,9%
một
năm. Sau
6
năm
9
tháng cô giáo này rút được bao nhiêu tiền cả vốn lẫn lãi và lãi cô giáo không rút
ở tât cả các kỳ hạn, nếu rút trước ngân hàng sẽ trả lãi suất theo loại lãi suất không kỳ hạn là
0,002%
một ngày (1 tháng tính 30 ngày).
A. 471688328,8. B. 302088933,9. C. 311392005,1. D. 321556228.
HẾT
TRƯỜNG THPT ĐẶNG HUY TRỨ
TỔ TOÁN
ĐỀ TỔNG ÔN TẬP SỐ 01
ĐÁP ÁN BỘ ĐỀ ÔN TẬP THI HK 1
Môn: TOÁN 12 - Năm học 2017 - 2018
Thời gian làm bài: 90 phút, không kể thời gian phát đề
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 01
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
B
D
B
D
D
C
B
C
A
D
Câu
11
12
13
14
15
16
17
18
19
20
Đáp án
D
B
C
B
C
A
A
C
B
D
Câu
21
22
23
24
25
26
27
28
29
30
Đáp án
A
C
D
C
C
D
A
B
D
A
Câu
31
32
33
34
35
36
37
38
39
40
Đáp án
C
C
D
B
C
B
D
C
B
B
Huớng dẫn:
Câu 15.
Gọi
, ; 0x y x y
lần lượt là các chiều dài như hình vẽ bên. Diện
tích của tờ giấy
2
4S xy x
2
64
64 .
x
y
x
Thể tích của hình hộp chữ nhật:
2
2 2 3
64
. 64 .
x
V x y x x x
x
Xét
2
83
64 3 0
3
V x x
(loại nghiệm
83
3
x 
vì
0x
)
Lập bảng biến thiên suy ra hàm số
V
đạt giá trị lớn nhất tại
83
.
3
x
Khi đó,
43
3
y
. Giá trị lớn nhất của
V
là
2
8 3 4 3
.
33
V
256 3
.
9
Câu 25. Ta có:
2
2
2018 .
2
x
x x x
e
y e kx y e e k
Yêu cầu bài toán
22
0, 0;ln2 , 0;ln 2 .
x x x x
y e e k x k e e x
Đặt
, 0;ln 2 1; 2 ,
x
t e x t
ta xét hàm
2
1
, 1; 2 1 2 0 .
2
g t t t t g t t t

Ta có:
2
0;ln 2
1 1 1
1 0; 2 2; max .
2 4 4
xx
x
g g g e e




Vậy
1
4
k
hay
1
;
4
k



là các giá trị
k
cần tìm.
Câu 27. Phương trình
2 2 2 2
4 8 9 4 1 0x x m x x m
Để phương trình có hai nghiệm trái dấu thì
22
1. 1 0 1 0 1;1 .m m m
Câu 37.
+ Hình trụ có chiều cao
' 10h OO cm
và bán kính
đáy
6r cm
nên khối trụ có thể tích là
22
1
360V h r cm


.
+ Hình nón có đỉnh O', chiều cao
' 10h OO cm
và
bán kính đáy
6r cm
nên khối nón có thể tích là
22
2
1
120
3
V h r cm


.
Vậy
2
12
240V V V cm
.
6
h
O'
O
A
B
10
Câu 40.
Gọi độ dài cạnh đáy, chiều cao của hình chóp tứ giác đều lần
lượt là
; ( , 0)x h x h
. Ta có đáy là hình vuông với độ dài nửa
đường chéo bằng
2
x
suy ra độ dài cạnh bên
2
2
2
x
lh
. Ta
có bán kính mặt cầu ngoại tiếp hình chóp
2
2
2
22
2
9 36 2
22
x
h
l
R x h h
hh
.
Diện tích đáy của hình chóp
2
Sx
nên
22
11
. (36 2 )
33
V h x h h h
3
1 36 2
.( ) 576 576
33
h h h
V
Ta có:
2
11
.(36 2 ) . . (36 2 )
33
h h h h h h
.
Dấu bằng xảy ra khi
36 2 12, 12h h h h x
. Vậy
576
max
V
.
Cách khác: Gọi
h
là chiều cao hình chóp. Ta có: khoảng cách từ
O
đến mặt đáy là :
9h
cạnh đa giác đáy là:
2
22
2 9 9 36 2h h h
Thể tích hình chóp
2
1
36 2
3
V h h h
1
. 36 2
3
h h h
3
1 36 2
576
33
h h h



.
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 02
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
C
C
D
A
B
B
D
A
D
C
Câu
11
12
13
14
15
16
17
18
19
20
Đáp án
C
D
C
A
A
D
C
D
A
C
Câu
21
22
23
24
25
26
27
28
29
30
Đáp án
A
C
B
A
D
A
C
B
C
D
Câu
31
32
33
34
35
36
37
38
39
40
Đáp án
A
D
C
D
B
B
C
C
A
A
Huớng dẫn:
Câu 11. Đồ thị hàm số có hai đường tiệm cận ngang khi và chỉ khi hai giới hạn
lim , lim
xx
yy
 
tồn tại
hữu hạn và khác nhau. Vậy hàm số này phải xác định trên khoảng
;
, hay
2
1 4 0mx
với mọi
x
. Vậy các phương án B sai.
+) Nếu
3
1.
2
my
Hàm số này có duy nhất một tiệm cận ngang.
+) Với
1m
, ta có:
2
2
2
2
3
1
31
lim lim
41
14
1
3
1
31
lim lim
41
14
1
xx
xx
x
x
m
mx
m
x
x
x
m
mx
m
x
 
 




Đồ thị hàm số có hai
đường tiệm cận ngang là
1
y
m
và
1
y
m

. Vậy
1m
thỏa mãn yêu cầu của bài toán.
Câu 13. TXĐ:
.D
Ta có:
22
2 2 2 3 1 .y x mx m
Đồ thị hàm số có hai điểm cực trị khi và chỉ phương trình
0y
có hai nghiệm phân
biệt
2
2 13 2 13
13 4 0 *
13 13
m m m
. Ta có:
12
x x m
và
2
12
. 1 3x x m
.
Theo giả thiết:
2
1 2 1 2
0
2 1 1 3 2 1
2
3
m
x x x x m m
m

Kiểm tra điều kiện
*
, ta có
2
3
m
là yêu cầu bài toán.
Câu 14. Đặt
tan 0; 1t x t
. Khi đó, hàm số ban đầu trở thành
1t
gt
tm
với
01t
.
Lưu ý: Do hàm số
tan x
đồng biến nên yêu cầu bài toán tương đương
1t
gt
tm
đồng biến với
0 1.t
Ta có
22
2 . . 2
2
t t m t m t
m
gt
t m t m



.
Hàm số đồng biến trên
0; 1
khi
0
2
12
0;1
0
0;1
gt
m
m
m
m
m




.
Câu 15. Gọi
x
(
0x
) là bán kính của chiếc xô. Khi đó
2
2
V
V x h h
x
. Để tiết kiệm nguyên
vật liệu thì diện tích toàn phần của chiếc xô phải bé nhất.
Ta có:
33
10 10 10000l dm cm
.
Diện tích toàn phần của chiếc xô là:
2 2 2 2
2
10000 20000
( ) 2 2 2
V
S x x xh x x x x
xx
x
Ta có:
3
22
20000 2 20000
'( ) 2
x
S x x
xx
.
33
3
10000 10
'( ) 0 2 20000 0 10.S x x x x

Bảng biến thiên:
x
0
3
10
10.

'Sx
0
Sx
2039,4

Ta thấy diện tích toàn phần chiếc xô nhỏ nhất khi bán kính đáy xô là
3
10
10. 14,7 .x cm

Câu 22. Công thức tính dân số theo dữ kiện đã cho là
0,0147
80902000 ,
t
N t e
t
tính bằng năm và
0t
ứng với đầu năm
2003.
Ta có:
2020 2003 17
đầu năm
2020
ứng với
17.t
Vậy dân số Việt Nam đầu năm
2020
là
0,0147.17
17 80902000 103870000Ne
người.
Câu 24. Điều kiện:
2.x 
Ta có:
5
5 3 5 5
55
log 2
1
log 2 log 2 log 2 log 2 1 0 *
log 3 log 3
x
x x x x



Do
5
1
10
log 3

nên
5
* log 2 0 2 1 1.x x x
Kết hợp điều kiện suy ra tập nghiệm bất phương trình là
2; 1 2; 1 3.a b S a b
Câu 34. Do
ABCD
là hình thoi cạnh
a
và
0
60ABC
nên tam giác
ABC
đều. Vậy
22
33
2 2. .
42
ABCD ABC
aa
SS
Ta có:
BD AC
BD SAC
BD SA


0
; 45 .SD SAC DSO
Vậy tam giác
O
A
B
C
D
S
45
0
a
SOD
vuông cân tại
3
.
2
a
O SO DO
Xét tam giác
SAO
vuông tại
:A
22
2
2
a
SA SO AO
3
.
16
..
3 12
S ABCD ABCD
a
V SA S
Câu 39. Gọi
1
V
là thể tích khối nón đỉnh C,
đường cao
CH a
, bán kính đáy
BH a
nên:
3
2
1
1
.
33
a
V CH BH
.
Gọi
2
V
là thể tích khối trụ có đường cao
HD a
, bán kính đáy
AD a
nên:

23
2
.V HD AD a
.
Vậy thể tích khối tròn xoay cần tìm là:
3
12
4
3
a
V V V
.
H
a
a
a
D
C
a
B
A
Câu 40.
Gọi
h
là đường cao của hình trụ,
r
là bán kính của quả bóng,
là
bán kính của chiếc cốc nước.
=
2
2
h
h r r OA OB
Theo giả thiết:
44
hh
IB OI
( vì phần bên ngoài =
3
4
h
)
bán kính đáy của chiếc cốc là
22
3
.
4
h
R OA OI
Tỉ số thể tích là:
3
3
1
12
22
2
4
4
32
8
3
9 8 .
9
3
4
h
r
V
VV
V
Rh
h
h







ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 03
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
A
B
C
B
C
C
B
C
A
D
Câu
11
12
13
14
15
16
17
18
19
20
Đáp án
D
C
B
D
D
C
A
A
C
D
Câu
21
22
23
24
25
26
27
28
29
30
Đáp án
B
B
A
B
A
D
C
D
B
A
Câu
31
32
33
34
35
36
37
38
39
40
Đáp án
D
D
B
A
C
A
C
D
A
B
Huớng dẫn:
Câu 25.
Cách 1: Công thức: vay số tiền
A
lãi suất
%r
/tháng. Hỏi số tiền
a
hàng tháng phải trả là bao
nhiêu để
n
tháng hết nợ:

6
6
6
. . 1 14.10 .0,005. 1 0,005
2.375.000
1 1 1 0,005 1
n
n
A r r
a
r
đồng.
Cách 2: Gọi
a
là số tiền phải trả hàng tháng.
Sau lần trả thứ nhất, số tiền còn nợ là:
6 6 6
14.10 14.10 .0,005 14.10 .1,005aa
đồng.
Sau lần trả thứ hai, số tiền còn nợ là:
6 6 2
14.10 .1,005 .1,005 14.10 .1,005 1,005 1a a a
.
…
Sau lần trả thứ sáu, số tiền còn nợ là:
6 6 5 4
14.10 .1,005 1,005 1,005 ... 1a
.
Khi đó
6 6 5 4
14.10 .1,005 1,005 1,005 ... 1 0a
66
54
14.10 .1,005
2.375.000
1,005 1,005 ... 1
a
đồng.
Câu 27. Với
x
,
0y
ta có
22
2
2
2 4 1 2
41
2.4 ln 4 2 ln 4 1 2 ln 2
2
xy xy
xx
x
x xy
xy



Xét hàm số
2 ln
t
f t t
. Ta có
1
2 ln 2 0
t
fx
t
,
0t
. Suy ra hàm số
ft
đồng biến trên
0; 
Khi đó
22
4 1 2 4 1 2f x f xy x xy
.
Ta có
22
2 2 2 2 2 4 2 2 2 2 1 2 4 1P x y x x y x xy x xy x x x
.
Xét hàm số
2
2 1 2 4 1f x x x
với
0x
.
Ta có
2
8 3 3 3
20
63
41
x
f x x f x
x
.
Bảng biến thiên
Dựa vào BBT suy ra
fx
đạt giá trị lớn nhất bằng
33
3
khi
3
6
x
. Do đó
max
33
3
P
.
Câu 41.
x
0
3
6

fx
0
fx
13
Đặt
2IJ x
0 xa
. Ta có bán kính đường tròn
C
là
22
r a x
.
Khi đó
22
1
.2
3
nón
V x a x

. Xét hàm số
22
f x x a x
. Ta có
22
3
30
3
a
f x a x x
.
Lập bảng biến thiên ta suy ra được
fx
đạt giá trị lớn nhất khi
3
3
a
x
.
Khi đó thể tích khối chóp là lớn nhất và
23
.
3
IJ
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 04
1
2
3
4
5
6
7
8
9
10
A
A
C
C
D
D
D
D
D
A
11
12
13
14
15
16
17
18
19
20
C
B
D
C
A
B
C
A
D
D
21
22
23
24
25
26
27
28
29
30
B
D
B
D
B
C
B
C
A
B
31
32
33
34
35
36
37
38
39
40
B
C
A
A
D
B
C
B
A
A
41
42
43
44
45
46
47
48
49
50
D
C
B
C
A
C
B
D
D
C
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 05
1
2
3
4
5
6
7
8
9
10
B
C
D
B
A
C
B
A
A
B
11
12
13
14
15
16
17
18
19
20
C
C
C
D
C
A
D
D
B
C
21
22
23
24
25
26
27
28
29
30
B
A
D
D
A
A
D
B
B
C
31
32
33
34
35
36
37
38
39
40
C
B
C
A
B
A
B
D
B
D
41
42
43
44
45
46
47
48
49
50
C
D
D
A
C
C
A
D
B
B
A
B
I
J
O
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

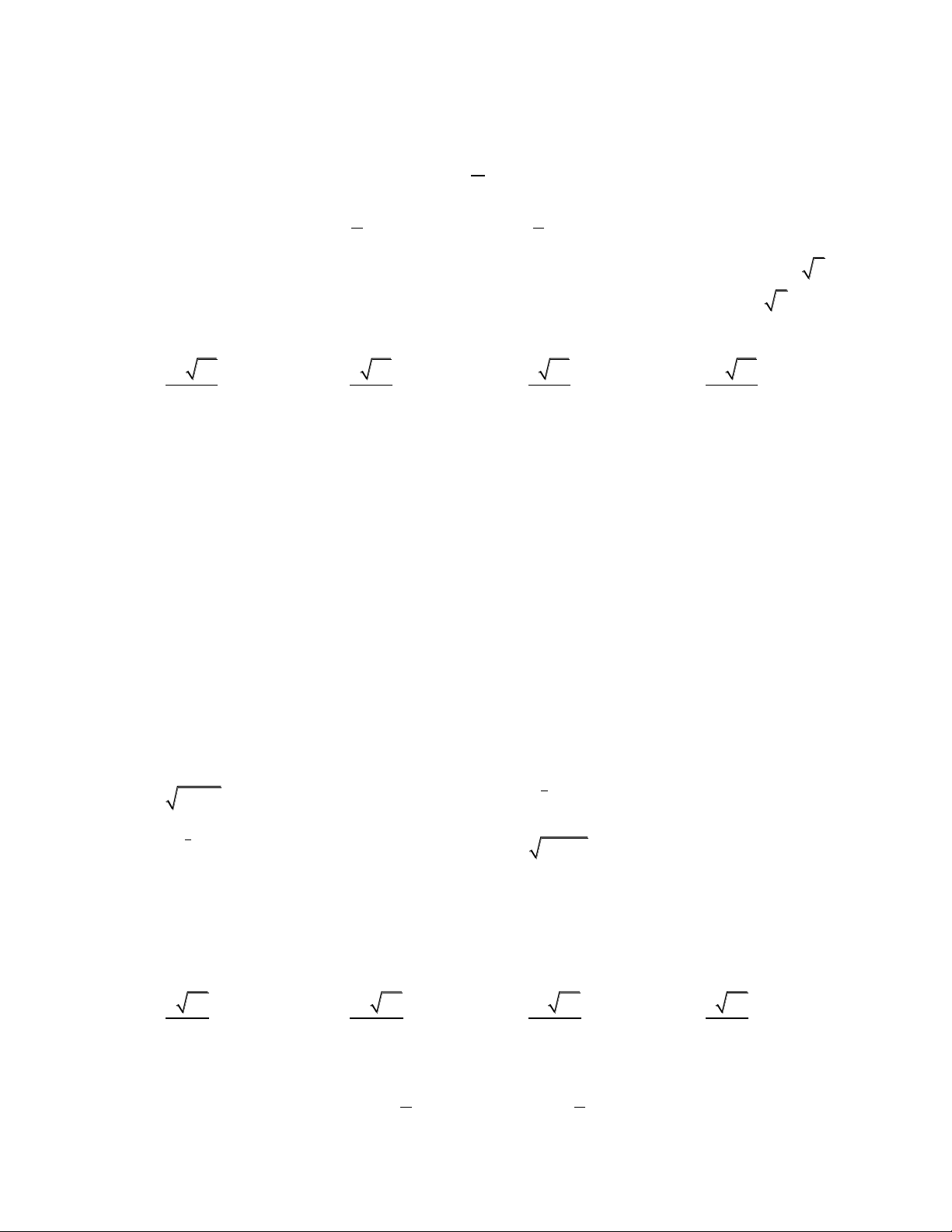
Preview text:

TRƯỜNG THPT ĐẶNG HUY TRỨ
BỘ ĐỀ ÔN TẬP THI HỌC KÌ 1 TỔ TOÁN
Môn: TOÁN 12 - Năm học 2017 - 2018
Thời gian làm bài: 90 phút, không kể thời gian phát đề
ĐỀ TỔNG ÔN TẬP SỐ 01
I. PHẦN TRẮC NGHIỆM (8,0 điểm).
Câu 1. Gọi M , N là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y x  3x  1 trên 0; 2 ,   tính M N. A. 6. B. 2. C. 3. D. 4.
Câu 2. Tìm khoảng đồng biến của hàm số 3
y x  3x  2. A.  1  ;  1 . B.  ;   
1 1; .C. ; . D. ;   1 và 1; .
Câu 3. Tìm tất cả các giá trị thực của tham số a để phương trình 3
x  3x  4  a  0 có ba nghiệm thực phân biệt. A. 2  a  6. B. 2  a  6. C. 1  a  3. D. 1  a  3.
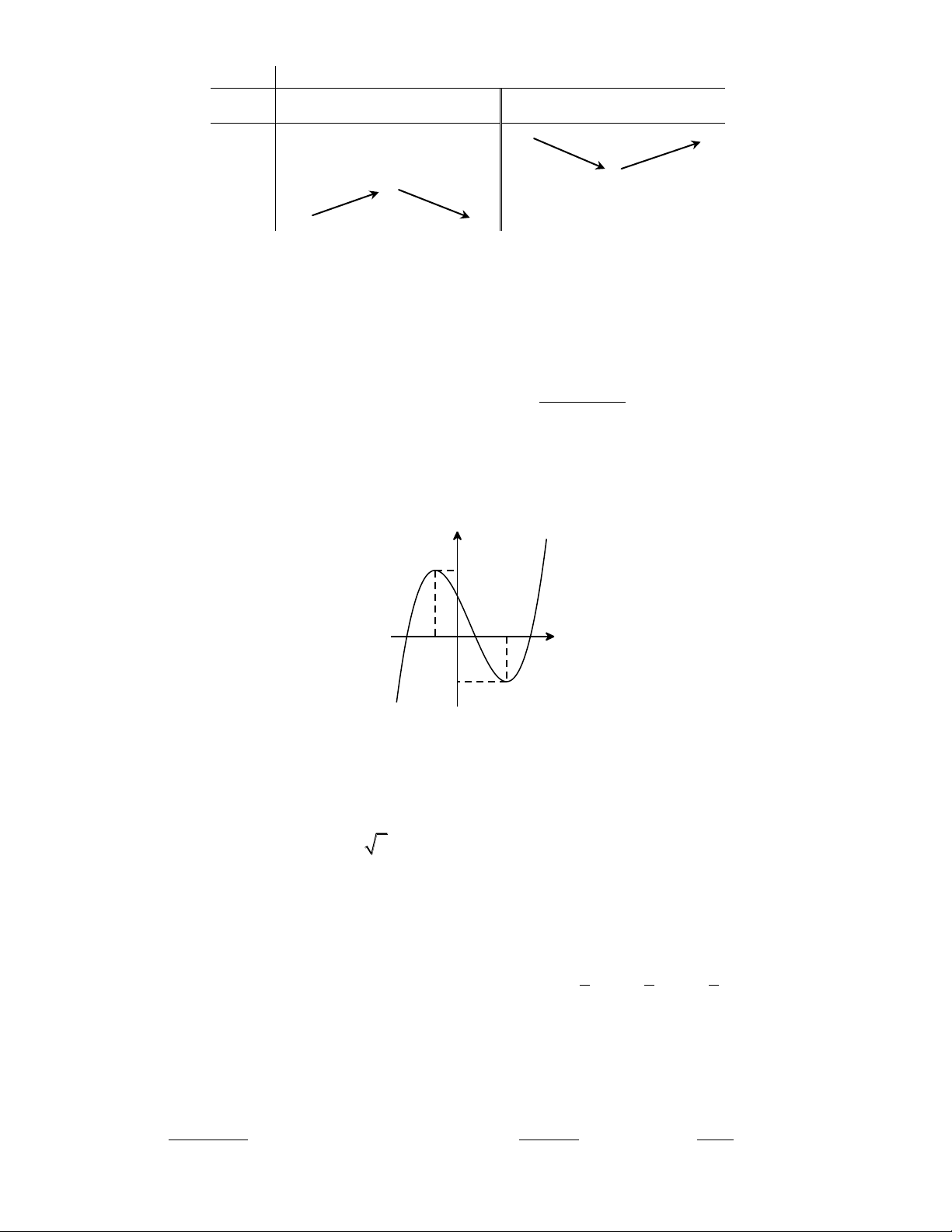
Câu 4. Hàm số y f x liên tục trên  và có bảng biến thiên dưới đây. Khẳng định nào sau đây đúng? x  2  1  y   0  1  y  3 
A. Hàm số đạt giá trị nhỏ nhất bằng 3  trên . 
B. Hàm số đồng biến trên 0; .
C. Đồ thị hàm số có tiệm cận đứng x  2. 
D. Hàm số có hai điểm cực trị.
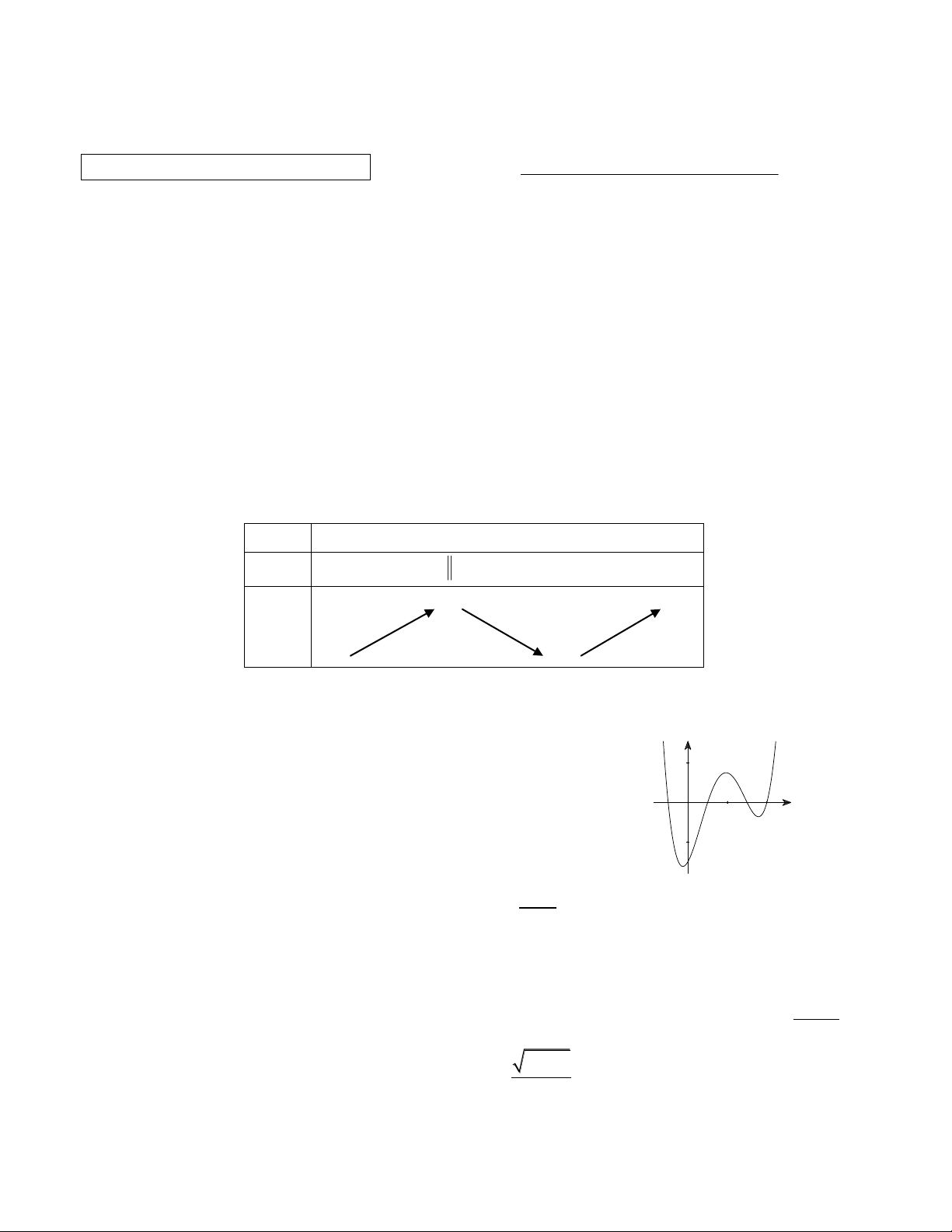
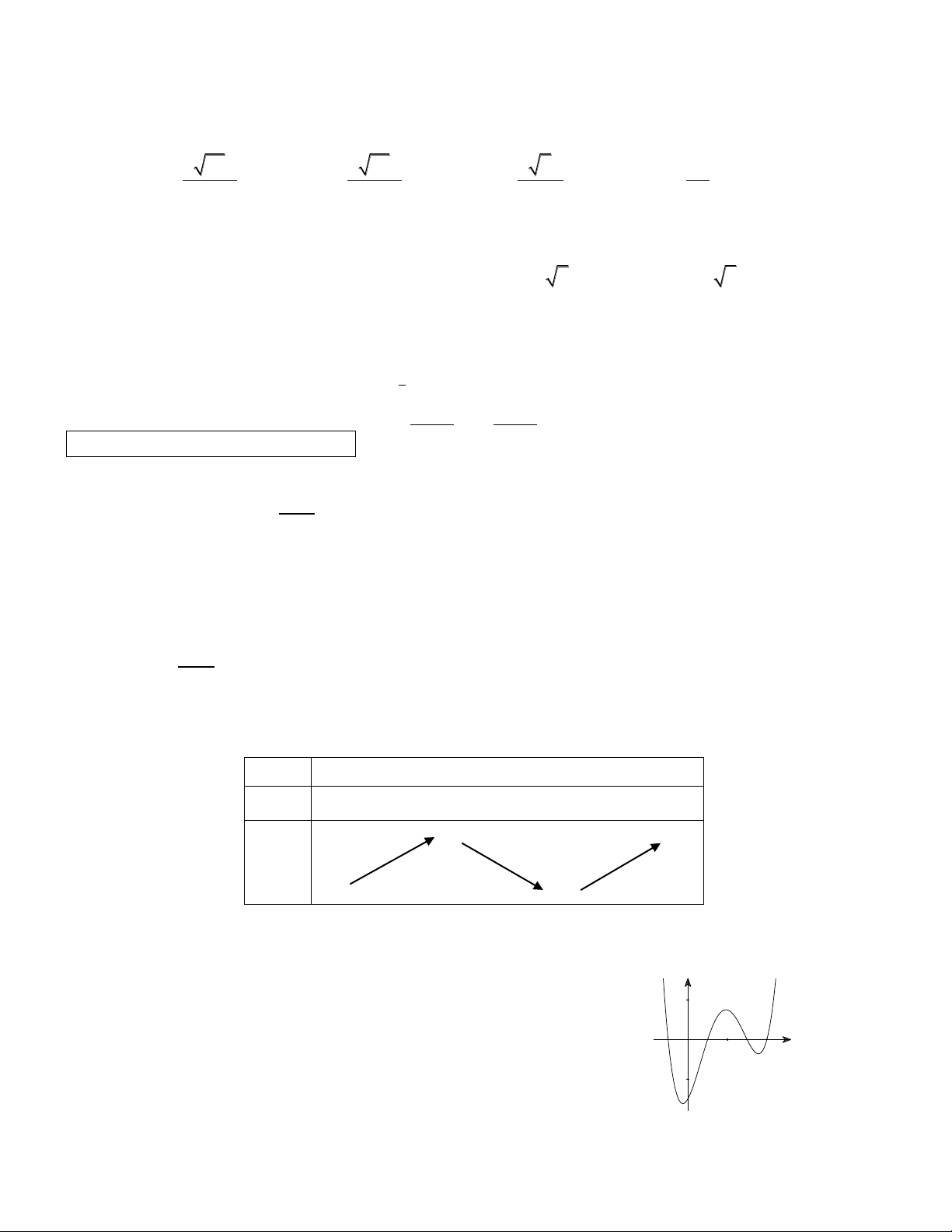
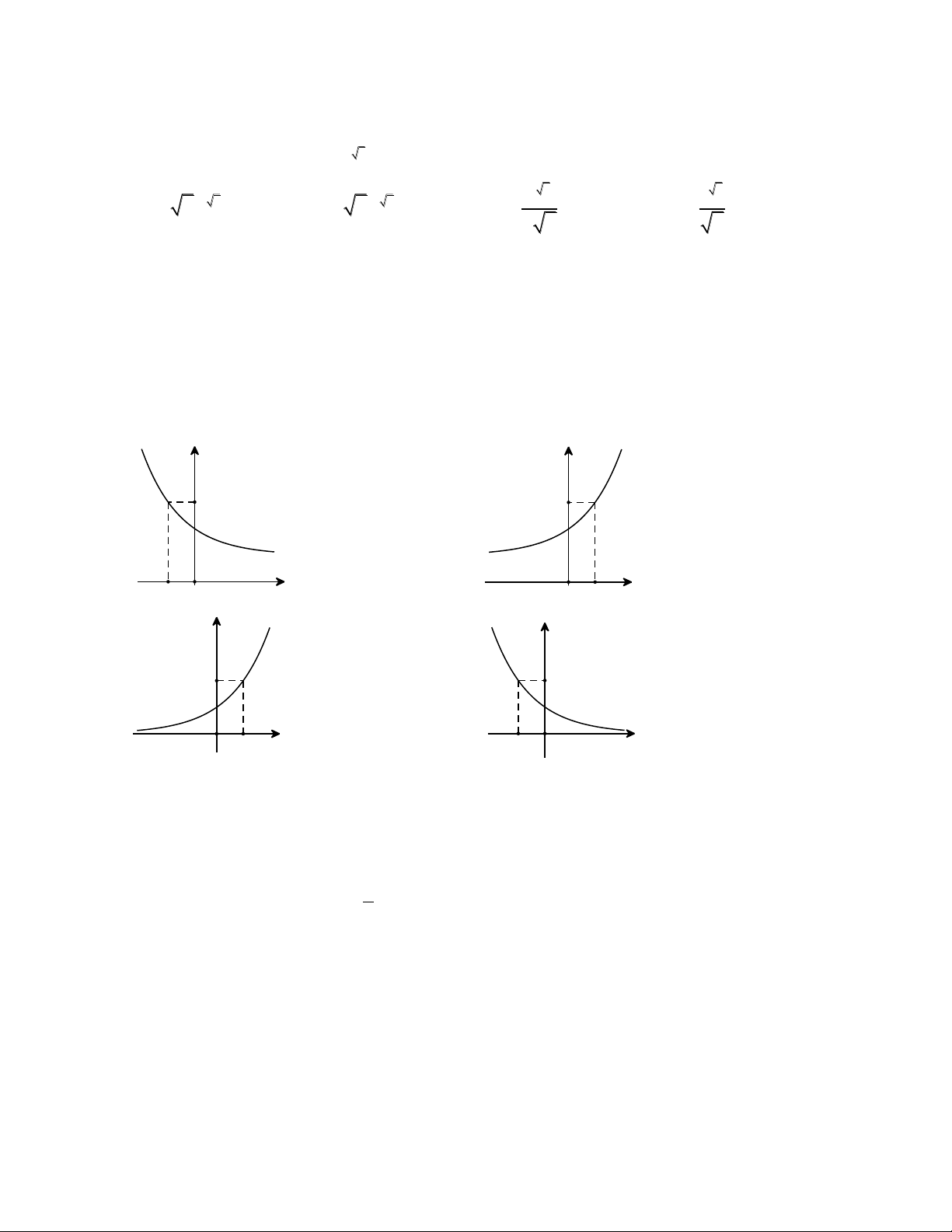
Câu 5. Cho hàm số y f x xác định, liên tục trên  và có đồ thị y
hàm số đạo hàm y f x như hình bên. Tìm số điểm cực đại của O
hàm số y f x. x A. 4. B. 3. C. 5. D. 2. x  2
Câu 6. Tìm các đường tiệm cận của đồ thị hàm số y  . x  2
A. x  2; x  1.
B. y  1; x  1.
C. x  2; y  1.
D. x  2; x  2  .
Câu 7. Hàm số nào sao đây có hai điểm cực trị? 2x  1 A. 3 y x  . x B. 3 2
y x  3x . C. 4 2
y x x . D. y  . x  1 2 x  2
Câu 8. Tìm số đường tiệm cận của đồ thị hàm số y  . x A. 2. B. 4. C. 3. D. 1. k 2 3x
Câu 9. Có bao nhiêu giá trị nguyên dương của tham số k để hàm số 2 y
kx x  2 3
đồng biến trên ; ? A. 2. B. 4. C. 5. D. 3.
Câu 10. Tìm giá trị cực đại của hàm số 4 2
y x  2x  2. A. 1. B. 1.  C. 0. D. 2.
Câu 11. Cho hàm số y f x xác định và có đạo hàm trên .
 Khẳng định nào sau đây sai?
A. Nếu f x  0, x   ;
a b thì hàm số f x đồng biến trên a; b .
B. Nếu f x  0, x   ;
a b thì hàm số f x không đồng biến và không nghịch biến trên a;b.
C. Nếu f x  0, x   ;
a b thì hàm số f x nghịch biến trên a; b .
D. Nếu f x  0, x   ;
a b thì hàm số f x nghịch biến trên a; b .
Câu 12. Đường cong trong hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm 1 số đó là hàm số nào? A. 4 2
y x  2x . B. 4 2
y  x  2x . O 1 x C. 3 2
y x  3x  2. D. 3 2
y  x  3x  2.
Câu 13. Viết tất cả các phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1, biết tiếp tuyến
vuông góc với đường thẳng x  7y  0. 365 14
A. y  7x  5; y  7x  .
B. y  7x  5; y  7x  . 27 27 365 365
C. y  7x  5; y  7x  .
D. y  7x  5; y  7x  . 27 27
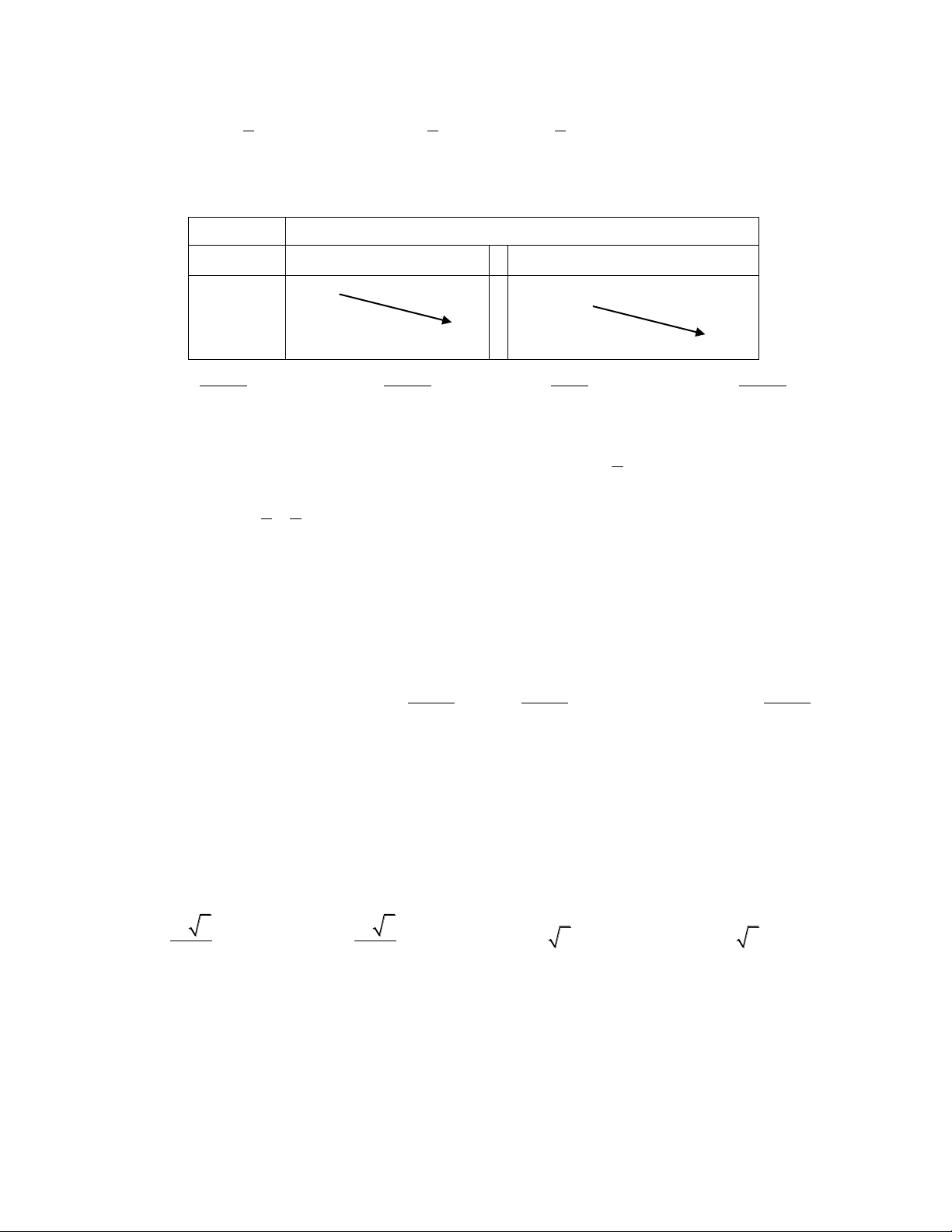
Câu 14. Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây, hàm số nào có bảng biến thiên sau? x  1  3  y  0  0  1  y 29   3 1 2 A. 3 2
y  x  3x  9x  2 . B. 3 2 y
x x  3x  . 3 3 1 2 C. 3 2
y x  3x  9x  2 . D. 3 2
y   x x  3x  . 3 3
Câu 15. Người ta cần làm một hộp giấy hình hộp chữ nhật có
đáy là hình vuông và không có nắp đậy. Nếu cần  2 64 cm  giấy
bìa cứng như hình vẽ để làm hộp giấy này, thì thể tích lớn nhất
của hộp này là bao nhiêu? 512 2 256 A.  3 cm . 3 B. cm . 27 7 256 3 3 3 C. cm . D. 144 2 cm . 9
Câu 16. Cho a là số thực dương khác 1. Đẳng thức nào dưới đây đúng với mọi số thực dương x, y ? y A. log  log y  log . x
B. log x y x y a   log log . a a a x a a y y log y C. log
 log y x. D. log a  . a a x a x log x a
Câu 17. Tìm tập xác định của hàm số y  x  1 2 7 9 . A. D   ;  3  3;. B. D    \ 3  ;  3 . C. D  .  D. D   3  ; 3.
Câu 18. Với các số thực dương a và b bất kì. Đẳng thức nào dưới đây đúng? 3  4a  3  4a  1 A. log 
  1 3log a  log . b B. log 
  2  log a  log . b 2 2 2  b  2 2 2  b  3 3  4a  3  4a  C. log 
  2  3log a  log . b D. log 
  2  3log a  log . b 2 2 2  b  2 2 2  b b
Câu 19. Cho a là số thực dương, a  1, a b thỏa mãn log b  3. Tính P  log . a a a a A. P  1
  3 3. B. P  1 3. C. P  1   3. D. P  1   3.
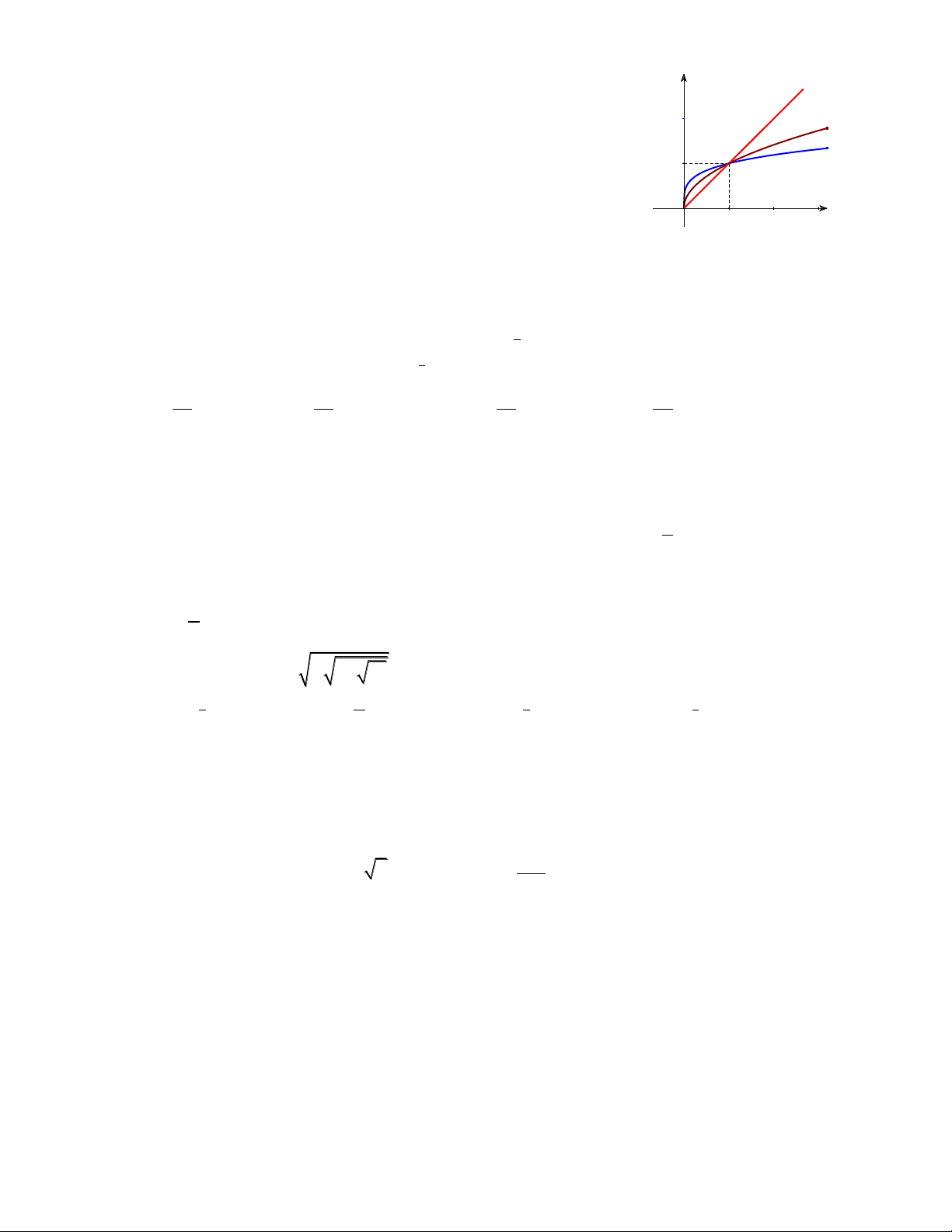
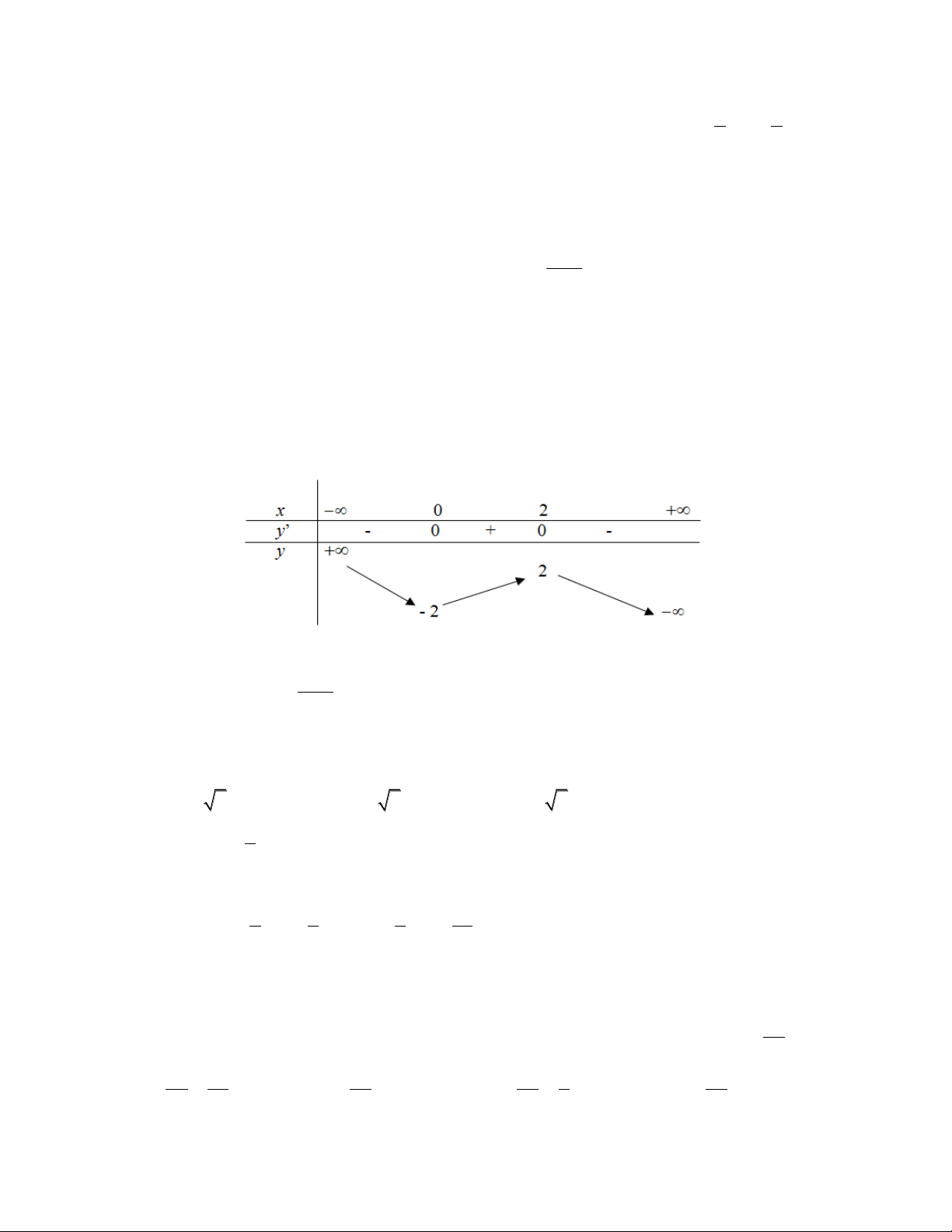
Câu 20. Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số y logax
y  log x, y  log x, y  log x được cho như hình vẽ bên. Khẳng a b c logbx
định nào sau đây đúng? O 1 x logcx
A. 0  c  1  b  .
a B. 1  a b  . c
C. 0  c b  1  .
a D. 0  c  1  a  . b
Câu 21. Ông A đi gửi ngân hàng 150 triệu đồng theo thể thức lãi kép với lãi suất 0,45% / tháng.
Sau ít nhất bao nhiêu tháng thì ông A mới nhận được 200 triệu đồng? A. 65 tháng. B. 64 tháng. C. 63 tháng. D. 67 tháng. e
Câu 22. Tính đạo hàm của hàm số y  2sin x  3 . ee
A. y  e x   1 2 sin 3 cos . x
B. y  e x   1 2 sin 3 . ee
C. y  e x   1 2 2 sin 3 cos . x
D. y   e x   1 2 2 sin 3 cos . x
Câu 23. Cho phương trình 2 log x  3log
x  1  0. Bằng cách đặt t  log x, ta được phương trình 2 2 2 nào sau đây? A. 2
t  3t  1  0. B. 2 3
t t  1  0 C. 2 t  1  0 D. 2
t  6t  1  0. 2
Câu 24. Biết tập nghiệm T của bất phương trình log 2x  1  1 có dạng  ; a b , ; a b   , tính 3   S  2a  3 . b A. S  2. B. S  10. C. S  6. D. S  8. 2x e
Câu 25. Tìm tập hợp tất cả các giá trị thực của tham số k để hàm số x y
e kx  2018 đồng 2 biến trên 0; ln 2 .    1   1  A. ; 2  .  B.   ; .  C. ;   . D.  2;    .  4  4 
Câu 26. Tìm nghiệm của bất phương trình log x  12  1. 1   2 1 23 A. 1  2  x  0. B. x  12  . C. 0  x  . D. 12   x   . 2 2
Câu 27. Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình log  2 2
x  4x m  8  2 có hai nghiệm thực phân biệt trái dấu. 3  A.  1  ;  1 . B.  ;    1 1; . C.  ;  1    1  ;    . D.  1  ;1.  
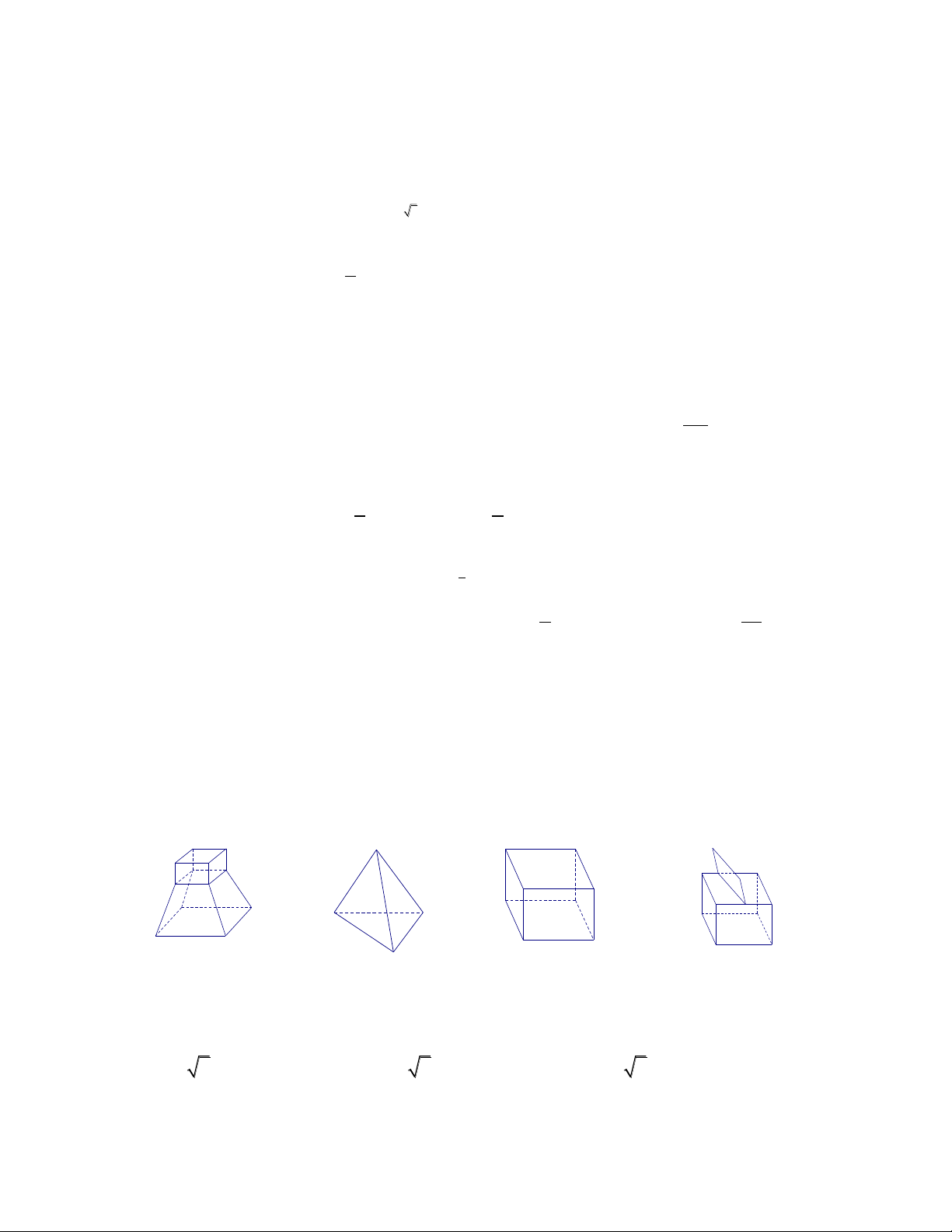
Câu 28. Mỗi hình sau gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), tìm hình
không phải là đa diện. (a) (b) (c) (d) A. hình (b). B. hình (d). C. hình (c). D. hình (a).
Câu 29. Tính tổng diện tích S tất cả các mặt của khối đa diện đều loại 3;  4 có cạnh bằng . m A. 2 S  5 3m . B. 2 S  2 3m . C. 2 S  3m . D. 2 S  6m .
Câu 30. Cho lăng trụ đều AB . C A BC
  có cạnh đáy bằng 2 .
a Biết góc giữa mặt phẳng  AB C   và mặt đáy bằng 0
60 , tính thể tích V của khối lăng trụ AB . C A BC  . 3 3 3a 3 3a A. 3 V  3 3a . B. V  . C. 3 V  3a . D. V  . 8 8
Câu 31. Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và SC  2 .
a Tính thể tích V của khối chóp . S AB . C 3 a 3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 4 6 12 4
Câu 32. Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AC và .
AD Tính tỉ số thể
tích của khối tứ diện ABMN và khối BMNDC. 1 1 1 1 A. . B. . C. . D. . 2 4 3 8
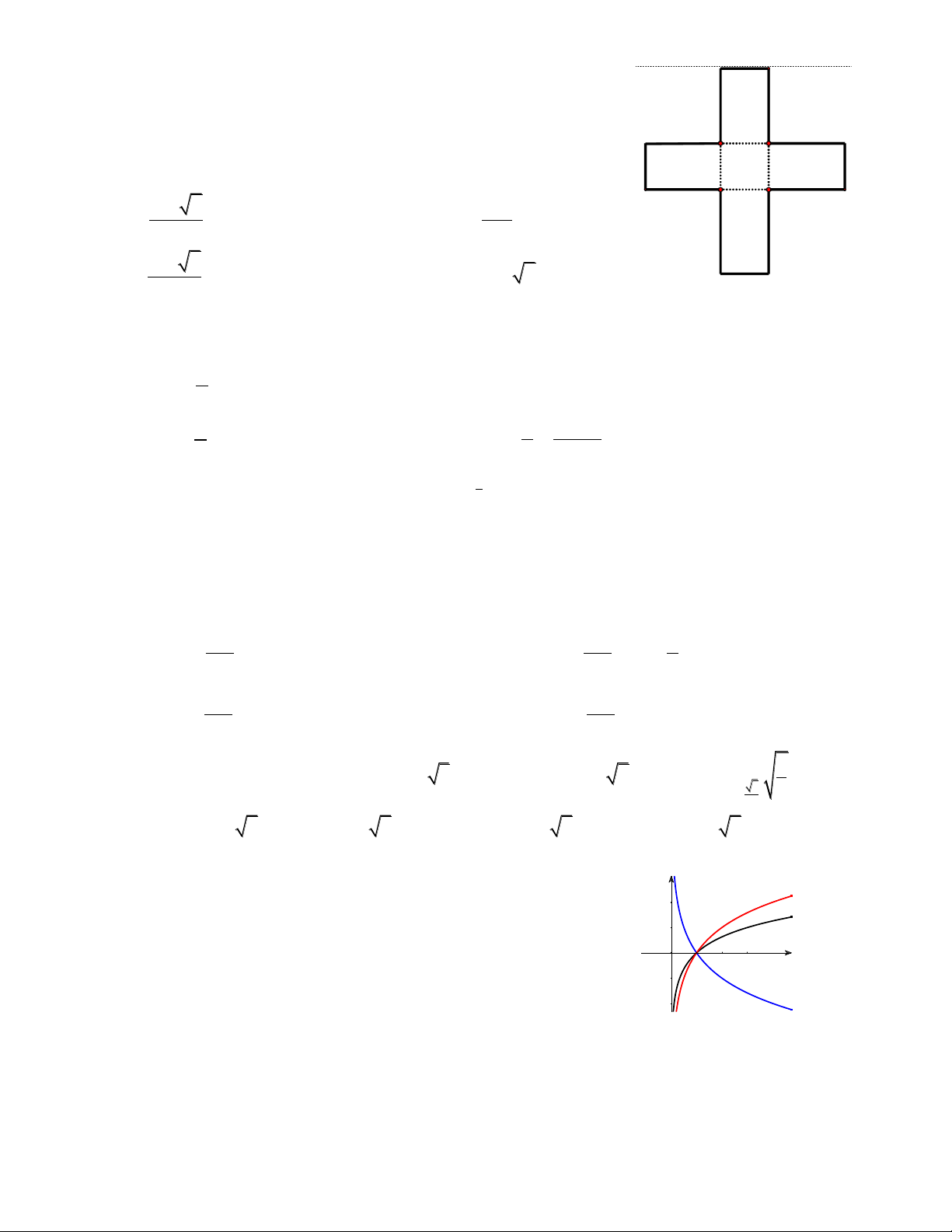
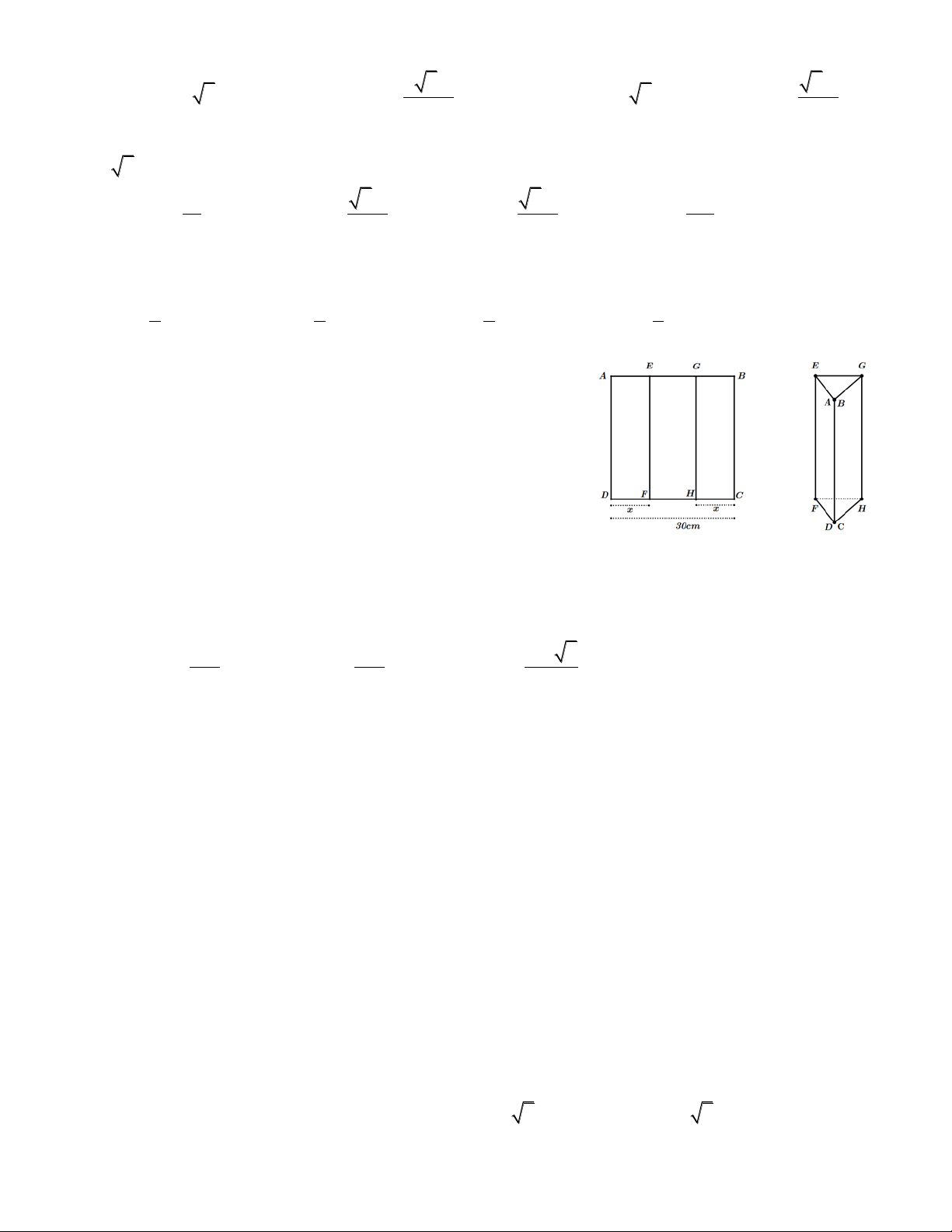
Câu 33. Một tấm kẽm hình vuông ABCD có cạnh bằng
30 cm. Người ta gập tấm kẽm theo hai cạnh EF và GH
cho đến khi AD và BC trùng nhau như hình vẽ dưới đây
để được một hình lăng trụ khuyết hai đáy. Tìm giá trị của
x để thể tích khối lăng trụ lớn nhất.
A. x  5 cm.
B. x  9 cm.
C. x  8 cm.
D. x  10 cm.
Câu 34. Một hình nón N sinh bởi một tam giác đều cạnh a khi quay quanh một đường cao. Tính
diện tích xung quanh S của hình nón đó. xq 2  a 2  a 2  a 3 A. S  . B. S  . C. S  . D. 2 S   a . xq 4 xq 2 xq 4 xq
Câu 35. Khẳng định nào sau đây sai?
A. Hình trụ luôn chứa một đường tròn.
B. Hình nón luôn chứa một đường tròn.
C. Hình nón luôn chứa một đường thẳng.
D. Mặt trụ luôn chứa một đường thẳng.
Câu 36. Thiết diện qua trục của một hình trụ là hình vuông cạnh 2a . Gọi V và V lần lượt là 1 2
diện tích xung quanh, diện tích toàn phần của hình trụ. Chọn kết luận đúng, trong các kết luận sau: A. V V . B. 3V  2V . C. 2V V . D. 2V  3V . 1 2 1 2 1 2 1 2
Câu 37. Một hình trụ có đáy là hai hình tròn  ;
O 6 ,O';6 và OO'  10. Một hình nón có đỉnh O'
và có đáy là hình tròn O; 6. Mặt xung quanh của hình nón chia khối trụ thành hai phần. Tính thể
tích V của phần khối trụ còn lại (không chứa khối nón). A. V  60. B. V  90. C. V  120. D. V  240.
Câu 38. Cho mặt cầu S tâm O, có bán kính bằng r  3a. Mặt phẳng   cắt mặt cầu S theo
thiết diện là một đường tròn có diện tích 2
4 a . Tính khoảng cách d từ O đến mặt phẳng  . A. d  3 . a B. d  2 . a C. d  5 . a D. d  2 3 . a
Câu 39. Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh bằng 1 , mặt bên SAB là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. 5 15 5 15 4 3 5 A. V  . B. V  . C. V  . D. V  . 18 54 27 3
Câu 40. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích
V của khối chóp có thể tích lớn nhất. A. V  144 . B. V  576 . C. V  576 2 . D. V  144 6 .
II. TỰ LUẬN (2,0 điểm).
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số 4 2
y x  2x 1.
Câu 2 (1,0 điểm). Giải phương trình: log 2  log x  3. 2 4 x HẾT
ĐỀ TỔNG ÔN TẬP SỐ 02
I. PHẦN TRẮC NGHIỆM (8,0 điểm). x  1
Câu 41. Cho hàm số y
. Khẳng định nào sau đây sai? x  1
A. Hàm số nghịch biến trên 2; . B. Hàm số nghịch biến trên ; 0.
C. Hàm số nghịch biến trên   \  1 .
D. Hàm số nghịch biến trên   ;1 và 1; .
Câu 42. Hàm số nào sau đây đồng biến trên  ? x  1 A. y  . B. 4 2
y x  2x .
C. y  sin 2x  3. D. 3 y x  3 . x x  1
Câu 43. Hàm số y f x liên tục trên  và có bảng biến thiên dưới đây. Khẳng định nào sau đây đúng? x  1  1  y  0  0  3  y  2 
A. Hàm số đạt giá trị nhỏ nhất bằng 2  trên .
 B. Hàm số đồng biến trên 0; 2.
C. Hàm số có điểm cực đại là x  2. 
D. Hàm số có cực tiểu bằng 2. 
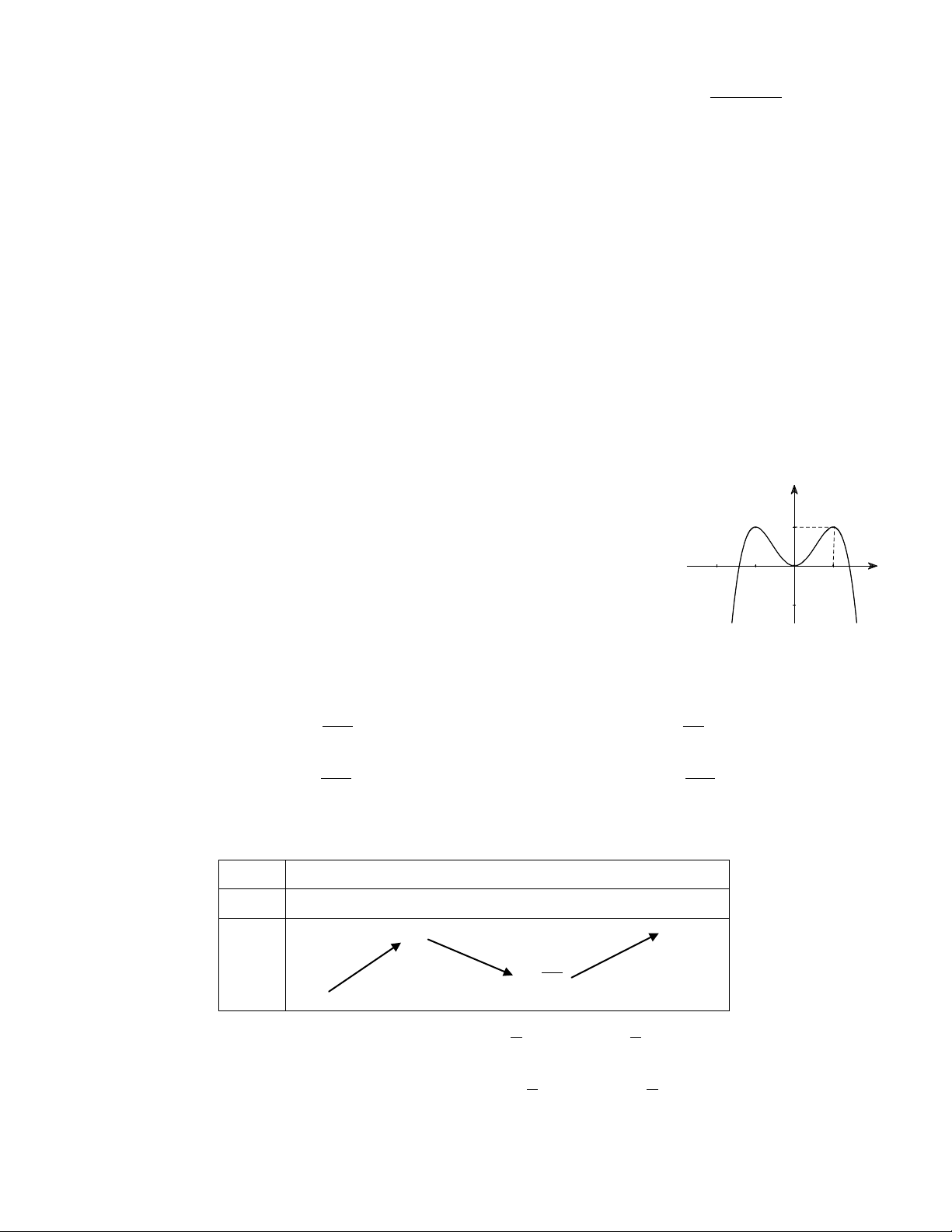
Câu 44. Cho hàm số y f x xác định, liên tục trên  và có đồ thị y
hàm số đạo hàm y f x như hình bên. Tìm số điểm cực trị của O
hàm số y f x. x A. 4. B. 5. C. 3. D. 2. 2x
Câu 45. Tìm các đường tiệm cận của đồ thị hàm số y  . x  1
A. x  1; y  1.
B. x  1; y  2.
C. x  2; y  1.
D. x  2; y  1.
Câu 46. Viết phương trình tiếp tuyến của đồ thị C 3 2
: y x  2x  1 tại điểm A1;0.
A. y x 1.
B. y  x  1. C. y   . x
D. y  2x  2.
Câu 47. Hàm số nào sau đây không có giá trị lớn nhất và giá trị nhỏ nhất trên 0; 2 ?   2x  1 x  1 A. 3 y x  . x B. 4
y x  3x  1. C. y  . D. y  . x  1 x  1
Câu 48. Gọi x , x lần lượt là điểm cực đại và điểm cực tiểu của hàm số 3
y x  3x  2. Tính 1 2
S x  3x . 1 2 A. S  2. B. S  2.  C. S  4. D. S  3.
Câu 49. Cho đồ thị hàm số y f x có đồ thị như hình vẽ dưới đây. Khẳng định nào sau đây đúng? y 2 O -1 x
A. Đồ thị hàm số có tiệm cận đứng x  2 và tiệm cận ngang y  1. 
B. Đồ thị hàm số có tiệm cận đứng x  1
 và không có tiệm cận ngang.
C. Đồ thị hàm số có tiệm cận ngang y  2 và không có tiệm cận đứng.
D. Đồ thị hàm số có tiệm cận đứng x  1
 và tiệm cận ngang y  2.
Câu 50. Biết rằng đường thẳng y  2
x  2 cắt đồ thị hàm số 3
y x x  2 tại một điểm duy nhất,
ký hiệu x ; y là tọa độ điểm đó. Tìm y . 0 0  0 A. y  4 . B. y  0 . C. y  2 . D. y  1. 0 0 0 0
Câu 51. Tìm tập hợp tất cả các giá trị thực của tham số m sao cho đồ thị hàm số x  3 y  
có hai đường tiệm cận ngang. m   2 1 x  4 A. .  B. ;  1 . C. 1; . D.   1 .
Câu 52. Đồ thị của hàm số 4 2
y x  4x  2 và đồ thị của hàm số 2
y  x  6 có tất cả bao nhiêu điểm chung? A. 0 . B. 4 . C. 1 . D. 2 . 2 2
Câu 53. Tìm tập hợp tất cả giá trị thực của tham số m để hàm số 3 2 y
x mx  2 2 3m   1 x  3 3
có hai điểm cực trị x và x sao cho x x  2 x x  1. 1 2  1 2 1 2  2  2  A. 0, . B.   0 . C.  . D. .   3  3  tan x  2
Câu 54. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  đồng biến trên tan x m    khoảng 0;  .  4  m  0 A.  . B. m  0. C. 1  m  2. D. m  2. 1  m   2
Câu 55. Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không có nắp và chứa đủ
được 10 lít nước. Hỏi bán kính đáy (đơn vị cm , làm tròn đến hàng phần chục) của chiếc xô bằng
bao nhiêu để cửa hàng tốn ít nguyên vật liệu nhất? A. 14,7 cm. B. 15,4cm. C. 15, 2cm. D. 14,4cm.
Câu 56. Tìm tập xác định của hàm số y  x   5 1 . A. D  .  B. D  1  ;   . C. D    \  1 .
D. D  1; .
Câu 57. Cho a là số thực khác 0, đẳng thức nào sau đây đúng? A. 2 2 2 log a  2 log . a B. 2 2 2
log a  2 log a . 2 2 2 2 C. 2 2 2
log a  4 log a . D. 2 2 2 log a  4 log . a 2 2 2 2
Câu 58. Tìm tập xác định của hàm số y  2  log x. 2 A. D  0; 4. B. D  0; 4 .  
C. D  0; . D. D  0; 4.  1 2 99
Câu 59. Đặt log 2  ;
a log 5  b ; X  log  log  ... log
. Biểu diễn X theo a, . b 3 3 3 3 3 2 3 100 A. X  2  a  2 . b B. X  2  a  2 . b
C. X  2a  2 . b
D. X  2a  2 . b  2 ln x   1
Câu 60. Tính giá trị của đạo hàm hàm số y  tại x  1. x A. 2  2ln 2. B. 2  2ln 2. C. 1 ln 2. D. 1 ln 2. xx e e
Câu 61. Tính đạo hàm của hàm số y  . xx e e 2  xx e e  4 2 x x e e A.  . B. . C. . D. . x x e e  2  x x e e 2  x x e e  2  x x e e 2
Câu 62. Biết rằng năm 2003 dân số Việt Nam là 80 902 000 người và tỉ lệ tăng dân số là 1,47%.
Hỏi nếu giữ nguyên tỉ lệ tăng dân số hằng năm đó thì năm 2020 dân số Việt Nam sẽ là bao nhiêu?
(Làm tròn kết quả đến hàng nghìn). A. 101119 000 người. B. 103681000 người. C. 103870 000 người. D. 106 969 000 người.
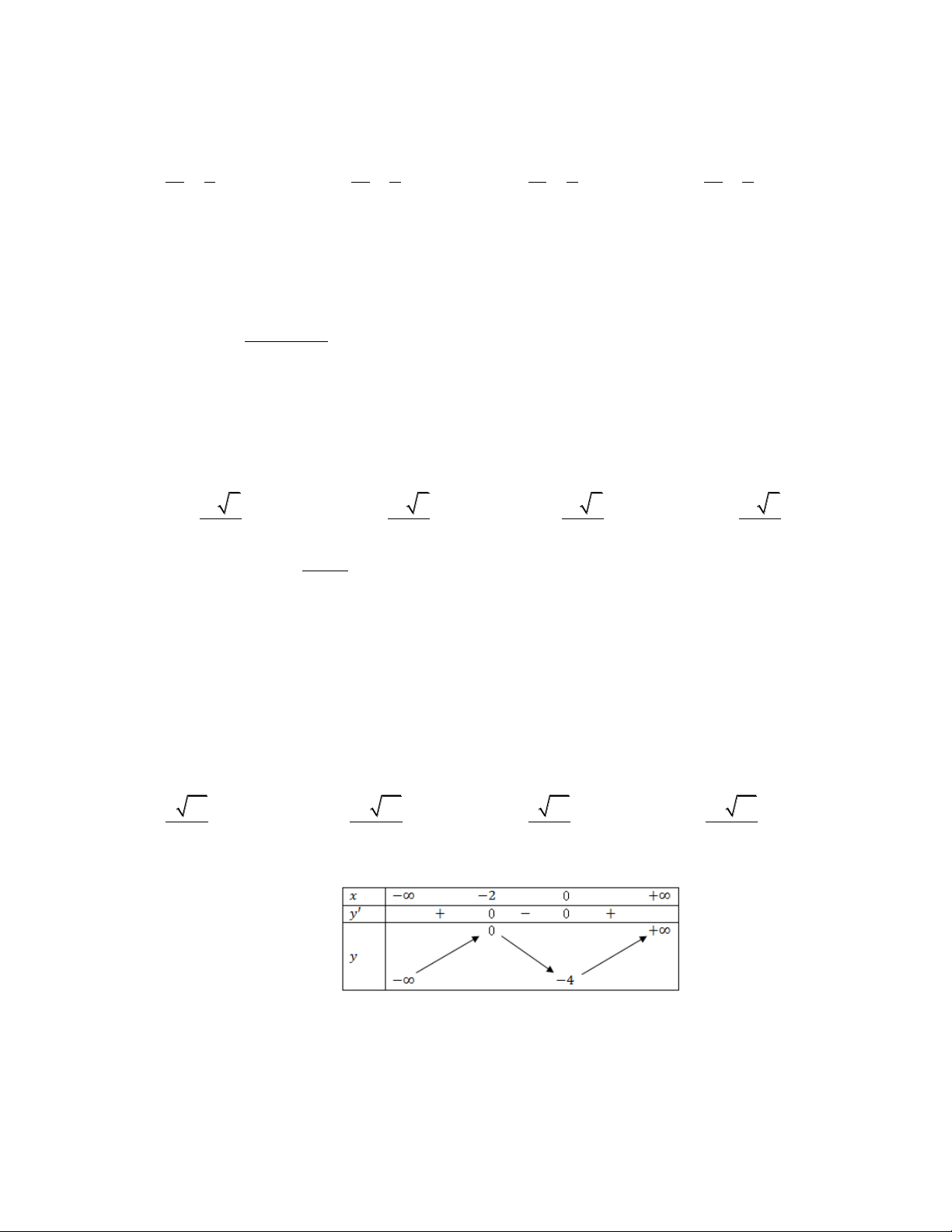
Câu 63. Cho ba số thực dương a, b, .
c Đồ thị các hàm số y xa a  , b  , c y x y x
y x được cho như hình vẽ bên. Khẳng định nào sau xb đây đúng? xc
A. 1  a b  . c 1
B. b  1; a  1  c  0.
C. b  1; c  1  c  0. D. b  1; a  1  . c O 1 x
Câu 64. Biết tập nghiệm của bất phương trình log x  2  log x  2 có dạng  ; a b , ; a b   , 5   3  
tính S a  . b A. S  3.  B. S  0. C. S  3. D. S  2. 1
Câu 65. Tính giá trị của biểu thức sau 2 2 2
log a  log a ; 0  a  1 2 1  . a a 15 13 13 17 A.  . B. . C.  . D. . 4 4 4 4
Câu 66. Tìm tập hợp tất cả các giá trị của tham số a để hàm số y  log
x nghịch biến trên 2 a 2a1 khoảng 0; .  1  A. 0; 2  \  1 . B. 1; . C. ;  1 . D. ;     \  1 .  2 
Câu 67. Tìm nghiệm của phương trình 2x  5. 5 A. x  . B. x  log 2. C. x  log 5. D. x  ln 5. 2 5 2
Câu 68. Cho biểu thức 4 3 2 3 P  .
a a . a , với a  0, khẳng định nào dưới đây đúng? 1 13 1 2 A. 2 P a . B. 24 P a . C. 4 P a . D. 3 P a .
Câu 69. Tìm số mặt phẳng đối xứng của hình lập phương. A. 3 . B. 6 . C. 9 . D. 12 .
Câu 70. Cho hình lăng trụ đứng AB .
C A' B'C' có đáy ABC là tam giác vuông cân tại A , mặt bên
BCC' B' là hình vuông cạnh 2a . Tính thể tích V của khối lăng trụ AB .
C A' B'C' . 3 2a A. 3 V a . B. 3 V a 2 . C. V  . D. 3 V  2a . 3
Câu 71. Tính số cạnh C của đa diện đều loại 3;  5 . A. C  30. B. C  20. C. C  12. D. C  6.
Câu 72. Nếu tăng gấp đôi độ dài của đường chéo của một mặt (không là mặt chéo) khối lập
phương thì thể tích khối lập phương thay đổi như thế nào? A. Tăng gấp 2 lần. B. Tăng gấp 4 lần. C. Tăng gấp 6 lần. D. Tăng gấp 8 lần.
Câu 73. Cho hình lăng trụ AB .
C A' B'C'. Gọi V V và V V . Khẳng định nào sau 1
A.A'B'C' 2
ABC.A'B'C' đây đúng? 3 1 1 2 A. V V . B. V V . C. V V . D. V V . 1 2 4 1 2 2 1 2 3 1 2 3 
Câu 74. Cho hình chóp .
S ABCD có đáy là hình thoi cạnh a, 0
ABC  60 , SA vuông góc với đáy,
SD tạo với mặt phẳng SAC một góc bằng 0
45 . Tính thể tích V của khối chóp . S ABC . D 3 6a 3 6a 3 6a A. V  . B. 3 V  3a . C. V  . D. V  . 18 3 12
Câu 75. Cho mặt cầu S có tâm I và bán kính R  3. Mặt phẳng P cắt mặt cầu theo giao
tuyến là đường tròn C và có chu vi 2. Tính khoảng cách d từ tâm I đến mặt phẳng P. 7 A. d  2. B. d  2 2. C. d  . D. d  7. 2
Câu 76. Mặt cầu S có thể tích   3 36
cm  . Tính diện tích của mặt cầu S. A.   2 24 cm . B.   2 36 cm . C.   2 18 cm . D.   2 20 cm .
Câu 77. Cho mặt cầu bán kính r và một hình trụ có bán kính đáy r và chiều cao 2r. Tính tỉ số
thể tích giữa khối cầu và khối trụ đã cho. 3 2 1 A. 2. B. . C. . D. . 2 3 2
Câu 78. Một hình nón có đường sinh bằng 8 cm, diện tích xung quanh bằng  2 240 cm . Tính
đường kính của đường tròn đáy hình nón. A. 70cm. B. 30cm. C. 60cm. D. 35cm.
Câu 79. Một hình thang vuông ABCD có đường cao AD a , đáy nhỏ AB a , đáy lớn CD  2a .
Cho hình thang đó quay quanh CD, ta được khối tròn xoay có thể tích bằng 4 1 A. 3 V   a . B. 3 V  2 a . C. 3 V   a . D. 3 V  3 a . 3 3
Câu 80. Một một chiếc cốc nước hình trụ có chiều cao bằng đường kính quả bóng bàn. Người ta 3
đặt quả bóng lên chiếc cốc thấy phần ở ngoài của quả bóng có chiều cao bằng chiều cao của nó. 4
Gọi V ,V lần lượt là thể tích của quả bóng và chiếc cốc, khẳng định nào sau đây đúng? 1 2 A. 9V  8V . B. 3V  2V . C. 16V  9V . D. 27V  8V . 1 2 1 2 1 2 1 2
II. TỰ LUẬN (2,0 điểm).
Câu 1 (1,0 điểm). Tìm m để phương trình 3 2
x  2x  1 2m  0 có ba nghiệm thực phân biệt. 2 2
Câu 2 (1,0 điểm). Giải phương trình:
x 2x x
x 2x x 1 9 7.3    2. HẾT
ĐỀ TỔNG ÔN TẬP SỐ 03
I. PHẦN TRẮC NGHIỆM (8,0 điểm).
Câu 1. Số giao điểm của hai đồ thị hàm số 4
y x  1 và 2
y x  2 là A. 0 . B. 1 . C. 2 . D. 4 . Câu 2. Cho hàm số 4 2
y x  2x  3 . Khẳng định nào sau đây là đúng?
A. Hàm số có một điểm cực tiểu và hai điểm cực đại.
B. Hàm số có một điểm cực đại và hai điểm cực tiểu
C. Hàm số có một điểm cực tiểu và không có điểm cực đại.
D. Hàm số có một điểm cực đại và không có điểm cực tiểu. 2
Câu 3. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y   là x  12 A. 0 . B. 1 . C. 2 . D. 3 .
Câu 4. Hàm số nào sau đây đồng biến trên  ? x  2 A. 3
y x  3x  1 . B. 3
y x  2x  1 . C. 3 2
y x x  2 . D. y  . x  1
Câu 5. Cho hàm số y f x xác định trên  và có đạo hàm f x  x 2 x   3 1 x   1 . Số điểm cực
trị của hàm số y f x là A. 0 . B. 1 . C. 2 . D. 3 .
Câu 6. Cho hàm số f x có tính chất: f x  0 , x   1
 ,2 và f x  0 khi x  0 hoặc x  1 .
Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng  1
 ; 2 . B. Hàm số đồng biến trên khoảng  1  ;0 .
C. Hàm số nghịch biến trên khoảng 0;1 . D. Hàm số đồng biến trên khoảng 1; 2 . 1
Câu 7. Tìm tất cả các giá trị thực của tham số m để hàm số 3
y x  m   2
1 x  3m  5 x  2m 1 3 đồng biến trên  . A. m  3 . B. 2  m  3 . C. m  2 .
D. m  2 hoặc m  3 .
Câu 8. Gọi M x ; y là điểm cực tiểu của đồ thị của hàm số 4 3 2
y x x  3x  7x 1 . Khi đó giá trị 0 0 
của tổng x y bằng 0 0 A. 2 . B. 3 . C. 5 . D. 2  . 2 x  2
Câu 9. Gọi trị lớn nhất và giá trị nhỏ nhất của hàm số y    
 lần lượt là M và
2x  trên đoạn 1; 4 1
m ? Giá trị của M m là 32 39 A. 5 . B. . C. . D. 2 . 7 7     Câu 10. Cho hàm số 3
y  sin x  cos 2x  s inx  2. Giá trị nhỏ nhất của hàm số trên  ;   bằng  2 2  23 1 23 A. 0 . B.  . C. . D. . 27 3 27
Câu 11. Cho hàm số f x liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: x  3  1  1  f x  0   0    f x 1 1    Khẳng định nào sao đâ y là sai?
A. Đồ thị hàm số đã cho có hai điểm cực trị.
B. Đồ thị hàm số đã cho có một tiệm cận đứng.
C. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho luôn cắt trục hoành. 2 x mx  2
Câu 12. Tập hợp các giá trị của m để đồ thị hàm số y
có đúng một đường tiệm cận x  2m đứng là A.  . B.   \  0 . C.   \ 1  ;  1 . D.   \ 2;   2 . Câu 13. Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng? y x O
A. a  0, b  0, c  0, d  0
B. a  0, b  0, c  0, d  0
C. a  0, b  0, c  0, d  0
D. a  0, b  0, c  0, d  0.
Câu 14. Đồ thị hàm số 3 2
y x  3x  2x 1 cắt đồ thị hàm số 2
y x  3x  1 tại hai điểm phân biệt
A và B . Độ dài đoạn thẳng AB . A. AB  3. B. AB  2 2. C. AB  2. D. AB  1.
Câu 15. Tìm tất cả các giá trị thực của m để hàm số 3 2
y x x  5x m có giá trị lớn nhất trên  2  ; 2   bằng 1 . A. 7 . B. 3 . C. 0 . D. 2  . a b c
Câu 16. Cho các số dương a , b , c . Rút gọn biểu thức P  log  log  log ta được 3 3 3 b c a A. 1 . B. 2 . C. 0 . D. log abc . 3  
Câu 17. Cho các số thực dương x , y , z thỏa mãn 2a xy  , 4b yz  , 8c zx
với a , b , c . Tính
biểu thức P  log x  log y  log z . 2 2 2
a  2b  3c
a b c 3abc A. P  .
B. P a  2b  3c . C. P  . D. P  . 2 2 2
Câu 18. Tập xác định của hàm số y  log x  2 1 là 2 A.   \  1 . B.  . C. 1;  . D.   ;1 .
Câu 19. Đạo hàm của hàm số x y e là x e x e A.   . x y x e . B. 1 . x y x e    . C. y  . D. y  . 2 x x
Câu 20. Khẳng định nào sau đây là sai?
A. Hàm số y  log x có tập xác định là D  0;  . a
B. Hàm số y  log x có tập giá trị là T   . a
C. Đồ thị hàm số y  log x và x
y a đối xứng nhau qua đường thẳng y x . a
D. Đồ thị hàm số y  log x có một đường tiệm cận ngang. a
Câu 21. Hình vẽ nào sau đây là đồ thị của hàm số 2x y   1 ? y y 3 3 x x A. 1  O B. O 1 y y 2 2 x x C. O 1 D. 1  O
Câu 22. Cho hàm số y  log x  1 . Khẳng định nào say đây là đúng? 3  
A. Hàm số đồng biến trên  .
B. Hàm số đồng biến trên 1; 
C. Hàm số nghịch biến trên  .
D. Hàm số nghịch biến trên 1;  . 2
Câu 23. Biết phương trình x 4x2 1 3
 có hai nghiệm x , x . Khi đó 2 2 x x bằng 3 1 2 1 2 A. 10 . B. 9 . C. 8 . D. 7 .
Câu 24. Tập nghiệm của bất phương trình 2
log x  4 log x  3  0 là 2 2 A. 1; 3.
B. 0; 2 8;  . C. 2; 8 . D. 8;  .
Câu 25. Chị Hoa muốn mua một chiếc tủ lạnh với giá 20 triệu đồng theo hình thức trả góp với số
tiền trả trước là 6 triệu đồng. Số tiền còn lại được trả góp trong 6 tháng với lãi suất 0, 5% /tháng
theo cách: sau đúng một tháng kể từ ngày mua, chị Hoa bắt đầu trả góp lần đầu tiên, hai lần trả
góp cách nhau đúng một tháng, số tiền trả góp mỗi tháng là như nhau. Hỏi, theo cách đó số tiền
mà chị Hoa phải trả trong mỗi lần là bao nhiều? (biết rằng lãi suất không thay đổi trong suốt quá trình trả góp)
A. 2.375.000 đồng. B. 2.405.000 đồng. C. 2.760.000 đồng. D. 2.815.000 đồng. x1
Câu 26. Biết phương trình 5x.8 x  500 có hai nghiệm x , x . Giá trị của x x là 1 2 1 2 A. 3log 5 . B. 3  log 5 . C. 3log 2 . D. 3  log 2 . 2 2 5 5 2    2 x
Câu 27. Cho hai số dương x , y sao cho 2x 4 1 2.4  ln
  4xy . Giá trị lớn nhất của biểu thức  2xy
P  2xy  2x  2 x y  2x là: A. P  1 3 . B. P  2  3 . C. P  1 3 . D. P  2  3 . max max max max
Câu 28. Số đỉnh của hình hai mươi mặt đều là A. 12 . B. 20 . C. 24 . D. 30 .
Câu 29. Trong các khẳng định về khối đa diện, khẳng định nào sau đây là khẳng định sai?
A. Mỗi mặt của khối đa diện có ít nhất ba cạnh.
B. Hai mặt bất kì của khối đa diện luôn có ít nhất một điểm chung.
C. Mỗi cạnh của khối đa diện là cạnh chung của đúng 2 mặt của khối đa diện.
D. Mỗi đỉnh của khối đa diện là đỉnh chung của ít nhất 3 mặt.
Câu 30. Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật, AB a , AD a 3 . Tam giác
SAB đều nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp . S ABCD là 3 a 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 2 3 6
Câu 31. Cho hình chóp tam giác .
S ABC có đáy ABC có diện tích bằng 2 a
3 , hình chiếu của S lên a 3
mặt phẳng đáy trùng với trọng tâm G của tam giác ABC và SG
. Gọi A là trung điểm 2
cạnh SA , B nằm trên cạnh SB sao cho SB  2BB . Tính thể tích khối chóp . S A BC  . 3 a 3 3 a 3 a 3 3 a A. . B. . C. . D. . 3 3 6 6
Câu 32. Cho hình lăng trụ tam giác đều AB . C A BC
  có cạnh đáy bằng 2a , diện tích tam giác A BC bằng 2
3a . Thể tích của khối lăng trụ là 3 a 2 A. . B. 3 a 2 . C. 3 2a 2 . D. 3 3a 2 . 3
Câu 33. Cho khối cầu có thể tích là 3
36 cm . Bán kính R của khối cầu là A. R  6 cm . B. R  3cm . C. R  3 2 cm . D. R  6 cm .
Câu 34. Cho hình chóp .
S ABC có đáy ABC là tam giác vuông cân tại B , AB a . Cạnh bên
SA a 3 và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp . S ABC là ? a 5 a 6 A. . B. a 5 . C. a 6 . D. . 2 2
Câu 35. Một mặt phẳng chứa trục cũa một hình trụ cắt hình trụ theo thiết diện là hình chữ nhật có
độ dài đường chéo bằng 10 cm . Biết chu vi đáy của hình trụ bằng 2
6 cm . Thể tích khối trụ tương ứng đó là A. 3 48 cm . B. 3 9 91 cm . C. 3 72 cm . D. 3 18 34 cm .
Câu 36. Một khối trụ có bán kính đáy bằng a 3 , chiều cao bằng 2a 3 . Thể tích V của khối cầu
ngoại tiếp khối trụ là 4 A. 3
V  8 6 a . B. 3
V  6 6 a . C. 3 6 a . D. 3
V  4 3 a . 3
Câu 37. Cho lăng trụ AB . C A BC
  có đáy ABC là tam giác vuông tại A , AB AC a, biết rằng A A   A B   A C
  a. Tính theo a thể tích khối lăng trụ AB . C A BC   3 a 3 a 3 3 a 2 3 a 2 A. V  . B. V  . C. V  . D. . 2 4 4 12
Câu 38. Quay tam giác đều ABC quanh trục AM với M là trung điểm BC ta được một hình nón
có diện tích đáy bằng 4 . Chiều cao của hình nón là A. 2 . B. 3 . C. 2 2 . D. 2 3 .
Câu 39. Cho hình chóp đều .
S ABC có cạnh đáy bằng a , chiều cao bằng 2 .
a Hình nón ngoại tiếp hình chóp .
S ABC có diện tích xung quanh là 2  a 13 2  a 15 2  a 11 2  a 17 A. . B. . C. . D. . 3 3 3 3
Câu 40. Cho mặt cầu tâm O , đường kính AB  2a . Trên đoạn AB lấy điểm I sao cho I không
trùng với A , B , O . Gọi J là điểm đối xứng của I qua O . Mặt phẳng   qua J và vuông góc với
AB cắt mặt cầu theo giao tuyến là một đường tròn C . Tính khoảng cách IJ sao cho thể tích khối
nón có đỉnh I và đáy là đường tròn C đạt giá trị lớn nhất. a 3 2a 3 a 2 2a 2 A. . B. . C. . D. . 3 3 3 3
II. TỰ LUẬN (2,0 điểm).
Câu 1 (1,0 điểm). Biện luận theo tham số m số nghiệm của phương trình 4 2
x  2x m  0 .
Câu 2 (1,0 điểm). Giải phương trình: 3x 1  2 2
7.2 x 72x  2  0 . HẾT
ĐỀ TỔNG ÔN TẬP SỐ 04 Câu 1.
Khẳng định nào sau đây là khẳng định đúng? A.Đồ thị của hàm số 2x y  và 2 x y  
đối xứng qua trục tung. B.Đồ thị hàm số 2x y
nằm bên phải trục tung. C.Đồ thị hàm số 2x y  đi qua điểm (1; 0). D.Đồ thị của hàm số 3x y
và y  log x đối xứng qua trục hoành. 3 Câu 2.
Viết phương trình tiếp tuyến của đồ thị hàm số 3
y x  3x  2 tại điểm có hoành độ bằng 0. A. y  3  x  2.
B. y  3x  2 .
C. y  3x  2 . D. y  3  x  2. Câu 3.
Tìm giá trị cực đại của hàm số 3 2
y x  3x  2 . A.1. B.0 C.-2 D.2. Câu 4.
Cho khối lăng trụ đều AB . C A BC
 . có tất cả các cạnh bằng a . Tính thể tích V của khối lăng trụ AB . C A BC  . 3 a 3 3 A. 3 V a . B. V  . C. 3 V a . D. 3 V a . 3 4 12 Câu 5.
Tìm tất cả các giá trị của m để đường thẳng y  2m cắt đồ thị hàm số 4 2
y x  2x  3 tại 4 điểm phân biệt. 3 3 A. 2  m  3 . B. 1  m  . C. 2  m  3 . D. 1  m  . 2 2 Câu 6. Cho hình chóp tam giác .
S ABC có đáy ABC vuông tại B,SA vuông góc với mặt phẳng
ABC ,SA AB   a, 0
SCA  30 . Mặt phẳng P đi qua A vuông góc với SC, cắt
SB,SC lần lượt tại H, K. Tính bán kính R của mặt cầu ngoại tiếp hình chóp . A BCK . H a a 2 a 3 A. R  . B. R  . a C. R  . D. R  . 2 2 2 Câu 7.
Một ngọn hải đăng đặt ở vị trí A cách A
bờ 5km, trên bờ biển có một kho hàng
ở vị trí C cách B một khoảng 7km. 5km
Người canh hải đăng có thể chèo
thuyền từ A đến M trên bờ biển với
vận tốc 4km / h rồi đi bộ từ M đến C B M C
với vận tốc 6km / .
h Xác định độ dài
đoạn BM để người đó đi từ A đến C nhanh nhất. 7 7 A. . km B. 3 2 . km C. . km D. 2 5 . km 2 3 1  2x Câu 8.
Đồ thị hàm số y
có tiệm cận đứng là đường thẳng x  1 A. x  2  . B. y  2  . C. y  1. D. x  1. Câu 9.
Cho a  log 3, b  log 7 . Hãy biểu diễn log 42 theo a, . b 2 2 18 1 a b 1 ab a b 1 a b A. log 42  . B. log 42  . log 42  . log 42  . 18 2a 18 1 C. a 18 1 D. 2a 18 1 2a
Câu 10. Giải phương trình 2x3 4 4  8 x . 6 2 4 A. x  . B. x  . C. x  2 . D. x  . 7 3 5
Câu 11. Cho 0  a  1  b . Khẳng định nào sau đây là khẳng định sai? a b  1   1  A. log 3  log 3. B. lg a  lg . b C. 0  ln a  ln . b D.      . a b  2   2 
Câu 12. Số nghiệm của phương trình 4x 3.2x   4  0 là A.0. B.1. C.2. D.3.
Câu 13. Hàm số nào sau đây đồng biến trên  ? x  1 A. 4 2
y x  2x  5 .
B. y  x  1. C. y  . D. 3
y x  3x  1 . x  1
Câu 14. Cho hình lập phương có cạnh bằng a . Tính diện tích S của mặt cầu ngoại tiếp hình lập phương. A. 2 S   a . B. 2 S  2 a . C. 2 S  3 a . D. 2 S  4 a .
Câu 15. Số giao điểm của đồ thị hàm số 2
y  (x  2)(x x  1) và trục hoành là A.1. B.0. C.2. D.3.
Câu 16. Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây? A. 3 2
y x  3x  1 . B. 3 2
y  x  3x  2. C. 3 2
y  x  3x  1 . D. 3
y  x  3x  2 . 1
Câu 17. Cho hàm số y  ln
. Khẳng định nào sau đây là khẳng định đúng? x  1 A.  1 y xy  e . B.  1 y xy  e . C.  1 y xye . D.  1 y xye .
Câu 18. Tính khoảng cách d giữa hai điểm cực tiểu của đồ thị hàm số 4 2
y x  4x  1. A. d  2 2 . B. d  3 . C. d  2 . D. d  1 . 1 Câu 19. Hàm số 3 2 y
x x  1 nghịch biến trên khoảng nào? 3 A. ( ;  0) . B. .  C. (2; )  . D. (0; 2) . 1 2 8 9
Câu 20. Tính P  log  log  ...  log  log . 2 3 9 10 A. P  2. B. P  0. C. P  1. D. P  1. 
Câu 21. Cho hình chóp .
S ABC gọi A, B,C lần lượt là ảnh của A, B,C qua phép vị tự tâm S tỉ số V '
k  2.Gọi V , V lần lượt là thể tích khối chóp . S ABC và . S A B
 C. Tính tỉ số . V V ' 1 V ' V ' 1 V ' A.  . B.  8. C.  . D.  2. V 27 V V 8 V
Câu 22. Tìm giá trị nhỏ nhất của hàm số  .ex y x trên đoạn [1; 2]. e A. 2 min y  2e . B. 2 min y e . C. min y  . D. min y  . e x [  1;2] x [  1;2] x [  1;2] 2 x [  1;2]
Câu 23. Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật có AB a, BC  2a,cạnh bên SA
vuông góc với đáy và SA a 3 . Tính thể tích V của khối chóp . S ABC . D 3 2 3 A. 3 V a . B. 3 V a . C. 3 V  3a . D. 3 V  2 3a . 3 3
Câu 24. Tìm tập giá trị của hàm số 2
y x x .  1  1 A.[0;1]. B. 0;   . C.[0; 2]. D. 0;   .  4   2 
Câu 25. Tính đạo hàm của hàm số 3 2 y x  1 . 2 1  2x 2 2x  2x A. 3
y  (x  1) . B. y  . C. 2 3 y  (x  1) . D. y  . 3 3 2 2 3 (x  1) 3 3 2 3 x  1
Câu 26. Tìm tất cả các giá trị của m để hàm số 4 2
y  (m  1)x  2(m  2)x  1 có ba cực trị. A. m  1.  B. 1   m  2. C. 1   m  2. D. m  2. mx  2
Câu 27. Tìm tất cả các giá trị của m để hàm số y
đồng biến trên mỗi khoảng xác định. 2x mm  2  m  2  A.  . B. 2   m  2 . C.  . D. 2   m  2 . m   2 m   2 Câu 28. Cho hàm số 2 f ( )
x  log (x  1) , tính f (  1). 2 1 1 1 A. f (  1)  . B. f (  1)  ln 2 . C. f (  1)  . D. f (  1)  2log 2. 2 2 ln 2 2 2 x m
Câu 29. Tìm tất cả các giá trị của m để đồ thị hàm số y
có đúng hai đường tiệm cận? 2 x  3x  2
A. m  1và m  4 . B. m  1. C. m  4 . D. m  0 .
Câu 30. Hàm số y f ( )
x có đồ thị như hình vẽ. Khẳng định nào sau đây là khẳng định đúng?
A.Đồ thị hàm số có tiệm cận đứng là x  1 và tiệm cận ngang là y  2  .
B.Hàm số đồng biến trên các khoảng ( ;  2  ),( 2  , )  .
C.Đồ thị hàm số cắt trục hoành tại điểm ( M 0; 1  ) .
D.Hàm số nghịch biến trên các khoảng ( ;  2  ), ( 2  ; )  .
Câu 31. Trong các hàm số sau đây hàm số nào nghịch biến trên tập xác định? x  1  x A. 2x y  . B. y    . C. x y e .
D. y  1 2 .  2 
Câu 32. Tìm tập xác định D của hàm số 2 2 y (x 2x 3)    . A. D   . B. D  ( ;  3  )(1;  )  . C. D   { \  3;1} . D. D  ( 3  ;1).
Câu 33. Có bao nhiêu giá trị nguyên dương của m để phương trình 2
3 x  6.3x m  5  0 có nghiệm? A.4. B.5. C.10. D.14
Câu 34. Khối lăng trụ đều ABC . D A BCD   có thể tích 3
24cm . Tính thể tích V của khối tứ diện ACB D  . A. 3 V  8cm . B. 3 V  6cm . C. 3 V  12cm . D. 3 V  4cm .
Câu 35. Tìm giá trị lớn nhất của hàm số 3
y  x  3x trên đoạn [0; 2]. A. max y  1 . B. max y  2  . C. max y  0 . D. max y  2 . x [  0;2] x [  0;2] x [  0;2] x [  0;2]
Câu 36. Cho hình chóp .
S ABCDcó đáy ABCD là hình vuông cạnh a,SA vuông góc với đáy. Góc
giữa SB và mặt đáy bằng 0
60 . Tính khoảng cách h từ A đến mặt phẳng SBC. a 2 a 3 a A. h  . B. h  . C. h  . D. h  . a 2 2 2
Câu 37. Cho tứ diện ABCD có thể tích là V . Gọi A,B,C,D lần lượt là trọng tâm của các tam
giác BCD, ACD, ABD, ABC . Tính thể tích khối tứ diện A BCD  theo V . V 8V V 27V A. . B. . C. . D. . 8 27 27 64
Câu 38. Khối lập phương thuộc loại khối đa diện đều nào? A.3;  3 . B.4;  3 . C.3;  4 . D.5;  3 .
Câu 39. Cho hình chóp đều .
S ABCDcó cạnh đáy bằng a, biết góc giữa cạnh bên và mặt đáy bằng 0
45 . Tính thể tích V của khối chóp . S ABCD. 2 3 2 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V  2a . 6 3 3
Câu 40. Cho khối tứ diện đều cạnh bằng a . Tính thể tích khối tám mặt đều mà các đỉnh là trung
điểm của các cạnh của khối tứ diện đã cho. 2 3 2 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 24 12 6 24
Câu 41. Đồ thị hàm số 3
y x  3x  3 có bao nhiêu tiếp tuyến song song với trục hoành? A.0. B.3. C.1. D.2.
Câu 42. Cho hình chóp tứ giác .
S ABCDcó đáy ABCD là hình vuông cạnh a, tam giác SAB vuông
cân tại S, tam giác SCD đều. Tính khoảng cách h giữa hai đường thẳng SA và . BD a 5 3 5 A. h  . a B. h  . C. h  . a D. h  . a 2 5 20
Câu 43. Tính đạo hàm của hàm số y  ln(2x  1) . 1 2 1 A. y  . B. y  . C. y  . D. y  2 . 2x  1 2x  1 x
Câu 44. Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu của nước X
sẽ hết sau 100 năm nữa. Nhưng do nhu cầu thực tế mức tiêu thụ tăng lên 4% mỗi năm.
Hỏi sau bao lâu số dầu dự trữ của nước X sẽ hết (kết quả gần đúng lấy đến 2 chữ số thập phân sau dấu phẩy). A. 45 năm. B. 43,11năm. C. 41,04 năm. D. 39,25 năm.
Câu 45. Cho hình trụ có bán kính đáy 2cm và chiều cao 3 .
cm Tính diện tích toàn phần S của tp hình trụ. A. 2 S  20 cm . B. 2 S  8 cm . C. 2 S  16 cm . D. 2
S  12 cm . tp tp tp tp
Câu 46. Cho hình chữ nhật ABCD có AB a, AD  2a . Tính thể tích V của khối trụ tạo thành khi
quay hình chữ nhật ABCD quanh cạnh AD . A. 3 V   a . B. 3 V  2a . C. 3 V  2 a . D. 3 V a .
Câu 47. Nhà sản xuất muốn thiết kế một chiếc hộp sữa hình trụ có thể tích V . Để tiết kiệm
nguyên liệu thì diện tích toàn phần của hình trụ phải nhỏ nhất. Tính bán kính R của đáy
hình trụ để tiết kiệm được nhiều nguyên liệu nhất. V V 1 A. 3 R V . B. 3 R  . C. 3 R  . D. 3 R V . 2 4 2 b
Câu 48. Cho log b  3, log c  2  . Tính log . a a a c b b b 3 b A. log  1. B. log  3. C. log   . D. log  5 . a c a c a c 2 a c
Câu 49. Tìm m để giá trị nhỏ nhất của hàm số 3 2
y x  3mx  6 trên đoạn 0; 3   bằng 2 . 31 3 A. m  2 . B. m  . C. m  . D. m  1. 27 2
Câu 50. Tìm tập nghiệm của phương trình 2
lg(x  6x  7)  lg(x  3) . A.4;  5 . B.3;  4 . C.  5 . D.  . HẾT
ĐỀ TỔNG ÔN TẬP SỐ 05 2 x  2x  3 Câu 1.
Đồ thị hàm số y x
có tiệm cận đứng là đường thẳng 1 A. y  1. B. x  1. C. x  2 . D. x  1  . sin x Câu 2.
Tính đạo hàm của hàm số y  . 2 x e
2x sin x  cos x
cos x  2x sin x A. y  . B. y  2 x 2 e x e
cos x  2x sin x
cos x  2xsin x C. y  . D. y  2 x 2 e x e Câu 3.
Nếu log 6  a và log 7  b thì: 12 12 a a b b A. log 7  . B. log 7  . C. log 7  . D. log 7  . 2 b  1 2 b  1 2 a  1 2 1  a 2
Câu 4. Tìm tập xác định của hàm số y  log x  1  ln 3  x  2. 9    
A. D  ; 3 . B. D   ;    1   1  ; 3. C. D   1  ; 3.
D. D  3; 
Câu 5. Một hình thang vuông ABCD có đường cao AD  2 , đáy nhõ AB  2 , đáy lớn CD  4 .
Cho hình thang đó quanh quay AB ta được khối tròn xoay có thể tích bằng: 40 16 8 A. V   . B. V   . C. V   . D. V  16 . 3 3 3
Câu 6. Một lăng trụ đứng AB . C A BC
 có đáy là tam giác cân , AB AC a, B
AC  120. Mặt phẵng  AB C
  tạo với đáy một góc 60. Thễ tích khối lăng trụ bằng: 3 a 3 3 3a 3 a 3 A. 3 a . B. . C. . D. . 3 8 2
Câu 7. Tính đạo hàm của hàm số y  log  2x 5 . 2016  1 2x A. y  B. y  2 x  5  2x 5ln2016 2x 1 C. y  D. y  . 2016  2x 5ln2016
Câu 8. Tìm m để phương trình x x3 4  2
 3  m có đúng hai nghiệm phân biệt x 1  ; 3. 3 A. 13   m   . B. 1  3  m  3. 4 3 C. 9   m  3. D.   m  3 . 4
Câu 9. Cho hình chóp .
S ABCDcó đáy ABCD là hình chữ nhật . Hình chiếu vuông góc của S lên
mặt phẵng  ABCD làtrung điễm H của AB, tam giác SAB vuông cân tại . S Biết
SH a 3, CH  3a . Khoảng cách giữa hai đường thẳng SD và CH là: 2a 66 4a 66 a 66 a 66 A. . B. . C. . D. . 11 11 11 22
Câu 10. Tìm giá trị nhỏ nhất của hàm số 2
y  log x  4 log x  1 trên đoạn 1  ; 27. 3 3   A. 1 . B. 3  . C. 0 . D. 2  .
Câu 11. Cho hình chóp .
S ABC có SA  4, SA vuông góc với đáy . Tam giác ABC vuông tại A ,
BC  5 . Diện tích mặt cầu ngoại tiếp hình chóp là A. S  50 . B. S  25 . C. S  41 . D.S  45 .
Câu 12. Tỗng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2
y x  2x  3 trên đoạn  1  ;1   là: A. 7 . B. 2 . C. 5 . D. 3 . x  1
Câu 13. Giá trị lớn nhất của hàm số y  trên đoạn  1  ;0   là: x  2 2 1 A. 2 . B.  . C. 0 . D.  . 3 2
Câu 14. Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy
bằng 60 . Khoảng cách từ điểm S đến mặt đáy  ABC bằng a 3 A. 2a . B. . C. a 3 . D. a . 2
Câu 15. Chọn khẳng định sai trong các khẵng định sau:
A. ln x  0  x  1.
B. log x  0  0  x  1 . 2
C. log a  log b a b  0 .
D. log a  log b a b  0 . 1 1 1 1 3 3 2 2 a 13
Câu 16. Cho hình chóp .
S ABCDcó đáy ABCD là hình vuông cạnh a , SD  . Hình chiếu 2
vuông góc cũa S lên mặt phẵng  ABCD là trung điểm H của đoạn .
AB Thễ tích khối chóp . S ABCDlà 3 a 2 3 a 3 A. V  . B. 3 V a 2 . C. 3 V a 3 . D. V  . 3 3 Câu 17. Hàm số 3 2
y x  3x  1 có mấy điểm cực trị? A. 1 . B. 3 . C. 0 . D. 2 . Câu 18. Hàm số 4 2
y x  2x  1nghịch biến trên khoãng A.  1  ;0 . B.   ;1 . C. 1;  . D. ;   1 và 0;  1 .
Câu 19. Cho log 14  a . Tính log 32 theo a 2 49 5 5 A. log 32  . B. log 32  . 49 2a  1 49 2a  2 10 2 C. log 32  . D. log 32  . 49 a  1 49 5a   1 3 2 3 4 Câu 20. Nếu 3 2 aa và log  log thì b 4 b 5
A. a  1, 0  b  1 . B. a  1, b  1.
C. 0  a  1, b  1.
D. 0  a  1, 0  b  1.
Câu 21. Tam giác ABC có AB  3, AC  4, BC  5 . Cho tam giác ABC quay quanh cạnh AB và
AC ta được hai hình nón tròn xoay có diện tích xung quanh là
S và S . Hãy chọn kết 1 2
quả đúng trong các kết quã sau S 3 S 4 S 3 S 4 A. 1  . B. 1  . C. 1  . D. 1  . S 5 S 3 S 4 S 5 2 2 2 2
Câu 22. Phương trình x x1 9  3
 2  0 có hai nghiệm là x , x x x . Giá trị của biểu thức 1 2  1 2 
A  2x  3x là 1 2 A. 3log 2 . B. 4 log 2 . C. 1 . D. 3log 3 . 3 3 2 mx m  2
Câu 23. Hàm số y
nghịch biến trên các khoảng xác định thì tham số m thỏa mãn x m A. 1   m  0 . B. 0  m  1 C. 2   m  1 D. 2   m  1
Câu 24. Cho hình chóp .
S ABC có đáy là tam giác ABC vuông cân tại A, AB AC a . Tam giác
SAB là tam giác đều và nằm trong mặt phẵng vuông góc với  ABC . Thễ tích khối chóp . S ABC là 3 a 3 3 a 3 3 a 3 3 a 3 A. V  . B. V  . C. V  . D. V  . 6 8 27 12 x  3
Câu 25. Đồ thị hàm số y
có tiệm cận ngang là đường thẵng 2 x x A. y  0 . B. x  0 C. y  1 D. y  1  Câu 26. Hàm số 3 2
y  x  3x  4 đồng biến trên khoãng A.  2  ;0. B. 0;  . C. ; 3 . D.  1  0; 2   .
Câu 27. Cho hình chóp .
S ABCDcó đáy ABCD là hình vuông cạnh 2a . Tam giác SAD là tam giác
đều và SAD nằm trong mặt phẵng vuông góc với mặt phẵng đáy . Khoảng cách giữa hai
đường thẵng AD và SB là a 14 2a 14 a 14 2a 21 A. . B. . C. . D. . 7 7 3 7
Câu 28. Cho hàm số y f x xác định, liên tục trên R và có bãng biến thiên:
Khẵng định nào sau đây sai?
A.Đường thẳng y  2
 cắt đồ thị hàm số y f x tại ba điễm phân biệt.
B.Hàm số đạt cực tiểu tại x  2  . C. f x 3 2
x  3x  4 .
D.Hàm số nghịch biến trên  2  ;0. Câu 29. Hàm số 4 2
y  x  2x  3 có điểm cực tiểu là A. 0; 4 . B. 0; 3 . C. 1; 4 . D.  1  ; 4 .
Câu 30. Cho hàm số 3
y x  3x  1 có đồ thị C . Phương trình tiếp tuyến cũa đồ thị C tại giao
điễm cũa C với trục tung là đường thẵng A. y  3  x 1.
B. y  3x  1 . C. y  3  x 1.
D. y  3x  1. Câu 31. Hàm số 4
y mx  m   2 2
2 x  1 có ba cực trị khi A. m  0 . B. 0  m  2 . C. 0  m  2 . D. m  2 .
Câu 32. Cho biết đồ thị ỡ Hình 2 là đồ thị của một trong bốn hàm
số nêu dưới đây. Hỏi đó là đồ thị của hàm số nào? A. 3 2
y  x  2x x  2 . B. 3
y  x  3x  1 . C. 3 2
y x  3x  3x  1 . D. 3 2
y x  3x  3x  1. Hình 2
Câu 33. Đồ thị hàm số 4 2
y  x  2mx có ba điễm cực trị tạo thành một tam giác đều khi
A. m  0 hoặc m  27 . B. m  0 hoặc 3 m  3 . C. 3 m  3 . D. m  0 . 3x  1
Câu 34. Số đường tiệm cận cũa đồ thị hàm số y  là 2 x  4 A. 3 . B. 2 . C. 1 . D. 4 .
Câu 35. Tìm m để hàm số 3 2
y x  3mx  4mx  4 luôn đồng biến trên R. 3 4 3 4 A. 0  m  . B.   m  0 . C.   m  0 . D. 0  m  . 4 3 4 3
Câu 36. Giải bất phương trình log 2x 1  2 ta được nghiệm là 3   1 1 A.  x  5 . B. x  . C. x  5 . D. x  5 . 2 5
Câu 37. Cho hình chóp .
S ABCDcó đáy ABCD là hình thang vuông tại
A và D . Biết
cạnh AB  2a, AD DC a, SA  3a vàSA vuông góc với mặt phẵng đáy . Thễ tích khối chóp . S BCDlà 3 3a 3 a 3 a A. V  . B. V  . C. V  . D. 3 V a . 2 2 6
Câu 38. Một chất điễm chuyễn động theo quy luật 2 3
s  12t  2t . Thời điễm t (giây) tại đó vận tốc
vm / s của chuyển động đạt giá trị lớn nhất là: A. t  4 . B. t  5 . C. t  3 . D. t  2 . 1
Câu 39. Tìm m để hàm số 3
y x  m   2 1 x   2
m  3m  2x  5 đạt cực đại tại x  0 . 3 A. m  6 . B. m  2 . C. m  1.
D. m  1 hoặc m  2 .
Câu 40. Một hình trụ ngoại tiếp hình lập phương và có hai đáy ngoại tiếp hai đáy cũa một hình 
lập phương. Biết thễ tích khối trụ đó là
thì thể tích khối lập phương bằng 2 1 3 A. 2 . B. C. . D. 1 . 4 4
Câu 41. Cho hình chóp .
S ABC có đáy ABC là tam giác vuông tại B , AB a, BC a 3. Hình
chiếu vuông góc cũa S trên mặt đáy là trung điễm H của AC . Biết SB a 2 . Tính theo
a khoảng cách từ H đến mặt phẳng SAB . 3a 21 a 21 a 21 7a 21 A. . B. . C. . D. . 7 3 7 3
Câu 42. Đồ thị hàm số 3 2
y x  3x  1 cắt đường thằng y m tại ba điễm phân biệt khi A. m  3  . B. 3   m  1. C. m  1. D. 3   m  1.
Câu 43. Tính đạo hàm của hàm số   2 3 2 .8 x y x    A. 2x3 y 
 x   2x3 8 2 8 ln 8 .
B. y  x   2x3 2 2 8 ln 8 . C. 2x3 y 
 x   2x3 8 2 2 8 . D. 2x3 y 
 x   2x3 8 2 2 8 ln 8 .
Câu 44. Một người gữi 20 triệu đồng vào ngân hàng theo thễ thức lâi kép , lãi suất 8,4% năm và
lãi hàng năm được nhập vào vốn . Hỏi sau 3 năm người đó thu được cã vốn lâ̂n lâi là bao nhiêu? A.  3 20. 1,084 triệu đồng. B.  4 20. 1,084 triệu đồng. C.  6 20. 1,084 triệu đồng. D.  2 20. 1,084 triệu đồng.
Câu 45. Trong các phương trình sau đây phương trình nào có nghiệm? 2
A. x   x  2 3 2 1 2  0 . B. 5 x  5  0 . 1 C. 2 2x  3  0 .
D. 4x  8  2  0 .
Câu 46. Rút gọn 32log b a a
a  0,a  1,b  0 bằng A. 3 a b . B. 2 3 a b . C. 3 2 a b . D. 2 ab .
Câu 47. Cho hình chóp tứ giác đều .
S ABCDcó cạnh bên tạo với đáy một góc 60 và cạnh đáy
bằng a . Khoảng cách giữa AD và SC là a 42 2a 42 3a 42 a 42 A. . B. . C. . D. . 7 7 7 14 Câu 48. Hàm số 3 2
y x x  m   2 2 3 6
1 x m nghịch biến trên khoảng  2
 ;0 khi m thỏa mãn 3 3 A. m  1  . B. m   . C. m   . D. m  3  . 4 4
Câu 49. Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt đáy
ABC. Góc giữa SBvà mặt phẳng ABC bằng 60. Thễ tích khối chóp .SABC là 3 a 3 3 a 3 a 3 3 a A. V  . B. V  . C. V  . D. V  . 6 4 12 2
Câu 50. Cho hình trụ có bán kính đường tròn đáy bằng
R và độ dài đường cao là h . Diện tích
toàn phần của hình trụ là A.. 2 Rh .
B. 2 Rh R . C. 2 4 R .
D. R2h R . HẾT
ĐỀ TỔNG ÔN TẬP SỐ 06
Câu 1. Tìm m để phương trình 3 2
x  3x  2  m  1 có 3 nghiệm phân biệt A. 3   m  1. B. 0  m  3 . C. 2   m  0. D. 2  m  4 . Câu 2.
Khẳng định nào sau đây đúng về tính đơn điệu của hàm số 3 2
y x  3x  2
A. Hàm số nghịch biến trên khoảng 0;  .
B. Hàm số đồng biến trên khoảng 0; 2 .
C. Hàm số đồng biến trên khoảng ; 0 và 2;  .
D. Hàm số đồng biến trên  . 2x  1 Câu 3.
Đồ thị hàm số y  có x  1
A. Có hai đường tiệm cận đứng x  2, x  1.
B. Đường tiệm cận đứng x  1 và không có tiệm cận ngang.
C. Đường tiệm cận ngang y  2 và không có tiệm cận đứng.
D. Đường tiệm cận đứng x  1 và tiệm cận ngang y  2 .  Câu 4. Cho hình chóp .
S ABCDcó đáy ABCD là hình bình hành với 0
AB a, AD  2a,BAD  60 . V
SA vuông góc với đáy, góc giữa SC và đáy là 0
60 . Thể tích khối chóp .
S ABCDlà V . Tỷ số là : 3 a A. 3 . B. 7 . C. 2 3 . D. 2 7 . x  1 Câu 5.
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  trên đoạn  3  ; 2     là 3x  2 3 3 4 3 1 1 4 A. 1 và . B. và . C. và  . D.  và . 4 4 7 4 2 2 7 Câu 6.
Khối 12 mặt đều thuộc loại A. 3,  5 . B. 3,  6 . C. 5,  3 . D. 4,  4 . Câu 7.
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 2
y x  8x  4 trên đoạn  1  ; 3   là
A. max y  13,min y  1  2 .
B. max y  13,min y  3  .  1  ;3  1  ;3      1  ;3  1  ;3    
C. max y  4,min y  1  2.
D. max y  4,min y  3  .  1  ;3  1  ;3      1  ;3  1  ;3     Câu 8. Hàm số 3
y mx  m   2 3
1 x  3m  
1 x m có cực trị khi và chỉ khi  1   1  1 A. m   ;   \  0 . B. m    ;  . C. m  . D. m  1 .  3   3  3 Câu 9.
Hàm số nào sau đây có bảng biến thiên như hình dưới đây x  2  y '   y 2   2 2x  5 2x  3 x  3 2x  3 A. y  . B. y  . C. y  . D. y  . x  2 x  2 x  2 x  2
Câu 10. Cho các số thực a,b dương a  1 . Khẳng định nào sau đây đúng? 1 A. log
ab  4  4 log b . B. log ab  log b . 4   4   a a 4 a a 1 1 C. log ab   log b . D. log
ab  2 log b . 4   4   4 4 a a a a
Câu 11. Đạo hàm của hàm số x 6  3 .sin2 x y x e A. x x 6 '  3
 .2cos2  3 .ln3.sin2  6. x y x x e . B. x x 6
'  3 .2cos 2  3 .ln 3.sin 2  6. x y x x e . C. x 6
'  3 .ln 3.sin 2  6. x y x e . D. x 6
'  3 .2 cos 2  6. x y x e .
Câu 12. Cho hàm số y f ( ) x  .
x cot x . Khi đó f '(x) là: xx x A. cot x . B. cot x  . C. . D. cot x  . 2 sin x 2 sin x 2 sin x Câu 13. Cho hàm số 4 2
y  x  2x  1 . Khẳng định nào sau đây đúng:
A. Đồ thị hàm số có hai điểm cực tiểu.
B. Hàm số đạt cực đại tại x  1.
C. Hàm số đạt cực tiểu tại x  1  .
D. Giá trị cực tiểu bằng 0.
Câu 14. Cho lăng trụ AB . C ' A ' B '
Ccó đáy ABC là tam giác đều cạnh 2a , hình chiếu của A' lên
ABCtrùng với trọng tâm tam giác ABC . Biết góc giữa cạnh bên và mặt phẳng đáy bằng 0 60 . Khi
đó thể tích khối lăng trụ bằng: 3 a 3 3 a 3 A. . B. . C. 3 2a 3 . D. 3 4a 3 . 4 2 Câu 15. Hàm số 4
y x  m   2 x   2 1
m mx 1 đạt cực đại tại x  0 khi A. m  1. B. m  0 .
C. m  0,m  1.
D. Không tồn tại m . Câu 16. Cho hàm số 4 2
y ax bx c,a  0 có đồ thị là C . Khẳng định nào sau đây là sai:
A. Đồ thị C luôn có 3 điểm cực trị tạo thành một tam giác cân có đỉnh nằm trên . Oy
B. Hàm số luôn có khoảng đồng biến và khoảng nghịch biến.
C. Trên C tồn tại vô số cặp điểm đối xứng nhau qua Oy .
D. Tồn tại a,b,c để đồ thị C chỉ cắt Ox tại một điểm.
Câu 17. Tập xác định của hàm số 3 2 f ( )
x  x  3x  2 là A. 1; 2 . B. ;  . C. 1  ; 2   . D. 1  ; 2  . x  1
Câu 18. Đồ thị hàm số y  có 2 2x  3x  1 1
A. Hai đường tiệm cận đứng x  1, x
và đường tiệm cận ngang y  0 . 2 1 1
B. Hai đường tiệm cận đứng x  1, x
và đường tiệm cận ngang y  . 2 2 1
C.Hai đường tiệm cận đứng x  1, x
và không có tiệm cận ngang. 2 1
D. Một đường tiệm cận đứng x  1 và đường tiệm cận ngang y  . 2 x  2
Câu 19. Tập xác định của hàm số y  là: x  1 A.   \  2 . B.   ;1 . C. 1;  . D.   \  1
Câu 20. Tìm m để hàm số 4
y x  m   2 2
1 x m có 3 cực trị. A. m  1  . B. m  1  . C. m  1  . D. m  1  .
Câu 21. Đáy của hình chóp .
S ABCDlà hình vuông cạnh a . Cạnh bên SA vuông góc với đáy có độ
dài bằng a . Thể tích khối tứ diện . S BCD là : 3 a 3 a 3 a 3 a A. . B. . C. . D. . 8 3 4 6 1
Câu 22. Tìm tất cả các giá trị của m để hàm số 3 2
y   x mx mx  2016 nghịch biến trên  3 A.  1  ;0   . B.  ;    1 0;  C.  1  ;0 . D.  ;  1    0;    .
Câu 23. Cho hình lập phương cạnh a . Thể tích của khối lập phương đã cho là: 3 a A. 3 3a . B. 3 a . C. 2 a . D. . 3
Câu 24. Hàm số y  m   3
x  m   2 1 3
1 x  32m  5 x m nghịch biến trên  khi A. m  1 . B. m  1 . C. m  1. D. 4   m  1. x  2
Câu 25. Tập xác định của hàm số y  log 1 là : x A.  ;  
1 2;  . B.   \ 1;  2 . C. 1; 2 . D.   \  1 . 3 x
Câu 26. Hàm số y   m  2 x   2 1 2m  
1 x m đạt cực đại tại x  1 khi và chỉ khi: 3 A. m  1.
B. m  0,m  1. C. m  0 .
D. Không tồn tại m . Câu 27. Cho hàm số 3 2
y x  3x  1 . Khẳng định nào sau đây đúng:
A. Điểm cực tiểu của đồ thị hàm số là (2; 5  ) .
B. Giá trị cực tiểu bằng 0 .
C. Giá trị cực đại của hàm số là y  2
 . D. Hàm số đạt cực đại tại x  2 . d c
Câu 28. Đạo hàm của hàm số y  log  2
x  3x  8 là : 8  2x  3
A. y'  2x  3.log  2
x  3x  8 . B. y'  . 8  2 x  3x  8 2x  3 2x  3 C. y'  . D. y'  ln 8 . 2
(x  3x  8)ln 8 2 x  3x  8
Câu 29. Gọi a, A lần lượt là giá trị nhỏ nhất , giá trị lớn nhất của hàm số 2
y x  4  x . Khẳng
định nào sau đây là sai? A. 2 A  8 . B. 2
A  2a  4 .
C. 2a A  0 . D. 2 a A . x  1
Câu 30. Hàm số y x  1 A. Đồng biến trên  .
B. Đồng biến trên   \ 1  .
C. Nghịch biến trên  .
D. Đồng biến trên ;   1 và  1;   .
Câu 31. Cho số dương a và b,a  1 . Tìm phát biểu sai. A. log 1  0 . B. log a  1.
C. log a n . D. log b a ab . a a n a
Câu 32. Tìm m để đồ thị hàm số 4 2
y x  2mx m  2 cắt trục Ox tại 4 điểm phân biệt
A. m2;  . B. m  ;1 . C. m ;    1 2;  .
D. m0;  . b
Câu 33. Cho log b  3 . Khi đó giá trị biểu thức log là a b a a 3  1 3  1 A. . B. 3  1. C. 3  1. D. . 3  2 3  2
Câu 34. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.
B. Tồn tại một hình đa diện có số đỉnh và số mặt bằng nhau.
C. Số đỉnh và số mặt của một hình đa diện luôn bằng nhau.
D. Tồn tại một hình đa diện có số cạnh và số mặt bằng nhau. 3 x
Câu 35. Tìm m để hàm số y   m  2
1 x  3m  2 x m đồng biến trên 3; . 3 A. m  0 . B. m  0 . C. m  0 . D. m  1 .
Câu 36. Cho hình chóp tam giác có đường cao bằng 100cm và các cạnh đáy bằng 20c , m 21c ,
m 29 cm . Thể tích khối chóp đó là : A. 3 7000cm . B. 3 6213cm . C. 3 6000cm . D. 3 7000 2cm .
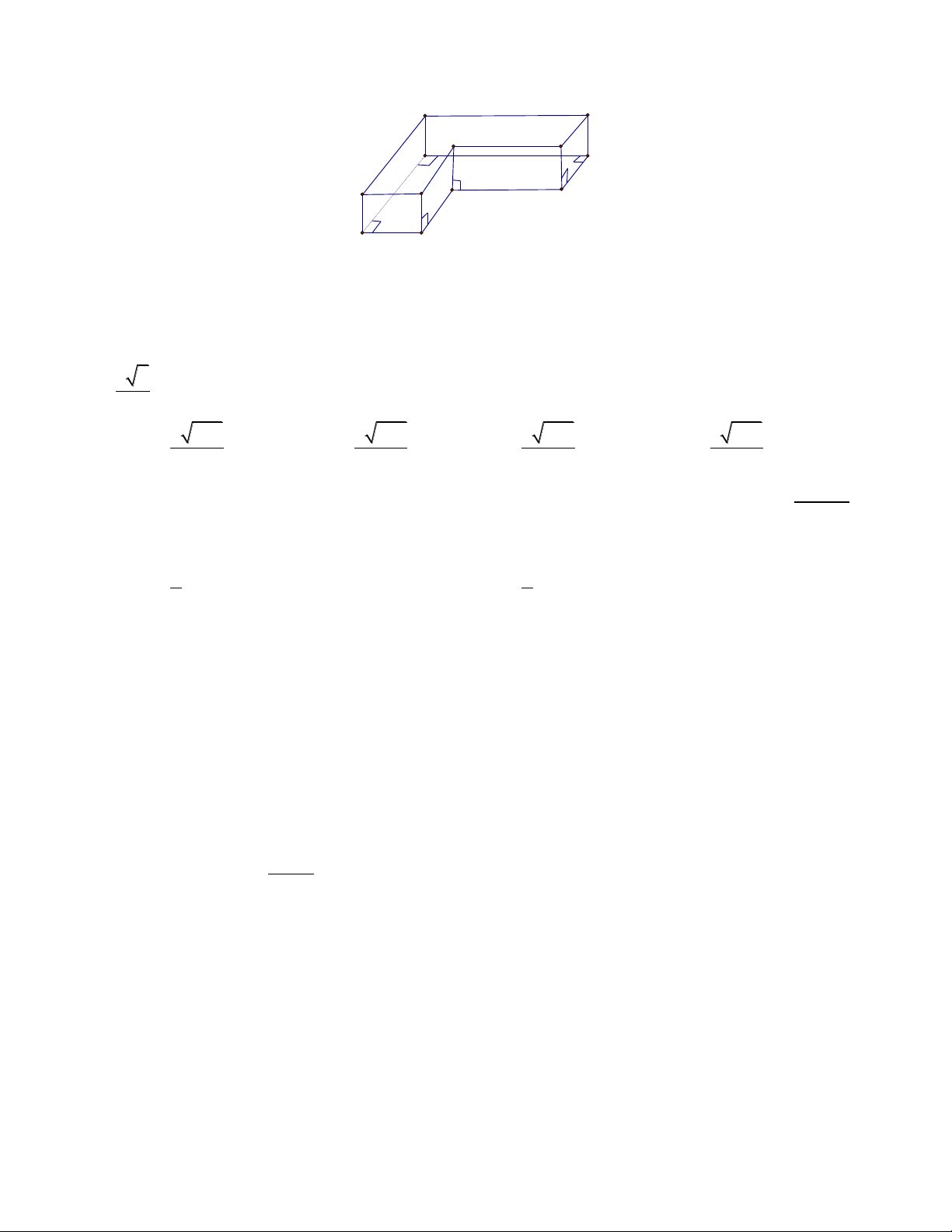
Câu 37. Thể tích của khối đa diện tạo bởi hình sau là: 14 cm 4 cm 15 cm 7 cm 6 cm A. 3 328cm . B. 3 456cm . C. 3 584cm . D. 3 712cm .
Câu 38. Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a , góc giữa SC và đáy  ABC là 0 45 .
Hình chiếu vuông góc của S lên mặt phẳng  ABC là điểm H thuộc AB sao cho HA  2HB. Biết a 7 CH
. Khoảng cách giữa 2 đường thẳng SA, BC là: 3 a 210 a 210 a 210 a 210 A. . B. . C. . D. . 15 45 30 20 V
Câu 39. Cho hình chóp .
S ABC có A', B' lần lượt là trung điểm của SA,SB . Khi đó, tỉ số S.ABC
VS.A'B'C là: 1 1 A. . B. 2 . C. . D. 4 . 2 4
Câu 40. Cho hình chóp đều .
S ABC . Người ta tăng cạnh đáy lên 2 lần. Để thể tích khối chóp .
S ABC giữ nguyên thì tan góc giữa cạnh bên và mặt phẳng đáy tăng lên bao nhiêu lần? A. 8 . B. 2 . C. 3 . D. 4 .
Câu 41. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y x  3x  1 trên đoạn  1  ; 4   là
A. max y  51,min y  3  .
B. max y  1,min y  1  .  1  ;4  1  ;4      1  ;4  1  ;4    
C. max y  51,min y  1  .
D. max y  51,min y  1 .  1  ;4  1  ;4      1  ;4  1  ;4    
Câu 42. Khẳng định nào sau đây sai? 2x  1 A. Hàm số y
luôn đồng biến trên từng khoảng xác định. x  1
B. Hàm số y  2x  cos 2x luôn đồng biến trên  . C. Hàm số 3
y  x  3x  1 luôn nghịch biến trên  . D. Hàm số 4 2
y  2x x  3 nghịch biến trên khoảng ; 0 2
Câu 43. Đạo hàm của hàm số 5 4 2x x y    là
A.  x   2x5x4 2 5 2 .ln 2 . B.   2 2 5 4 5 4 2x x x x     .
C. x x   2 2 x 5x4 5 4 2 .ln 2 . D.   2 5 4 2 5 2x x x    .
Câu 44. Đồ thị hình bên là đồ thị của hàm số nào dưới đây? A. 4 2
y x  2x  3 . B. 4 2
y x  2x . C. 4 2
y  x  2x  3 . D. 4 2
y  x  2x .
Câu 45. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất. A. Ba mặt. B. Năm mặt. C. Bốn mặt. D. Hai mặt.
Câu 46. Cho hình chóp tam giác .
S ABC , có SA,SB,SC đôi một vuông góc, SA SB SC a . Khi
đó thể tích của khối chóp đã cho là: 3 a 3 a 3 a 3 2a A. . B. . C. . D. . 6 3 9 3
Câu 47. Cho hình chóp .
S ABCDcó đáy ABCD là hình thoi cạnh a , AC a , H là trung điểm
của AB , SH vuông góc với  ABCD , tam giác SAB vuông tại S . Khoảng cách giữa hai đường
thẳng BD,SC theo a là: 3a 2a a a A. . B. . C. . D. . 13 13 13 2 13 x  2
Câu 48. Tọa độ giao điểm của đồ thị C : y
và đường thẳng y  2x 1 là 2x  3     A. M   1 1 1;1 , N ;    . B. M    1 3 1; 3 , N  ;    .  4 2   4 2      C. M   1 3 1;1 , N  ;    . D. M    1 1 1; 3 , N ;    .  4 2   4 2  2 x x  2
Câu 49. Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số y x  trên 2 3;6   . Khi đó A. 3 m M  6 . B. M  2m . C. 3 2 M m . D. 2 2
M m  113 .
Câu 50. Một cô giáo gửi 200 triệu đồng loại kỳ hạn 6 tháng vào ngân hàng với lãi suất 6,9%một
năm. Sau 6 năm 9 tháng cô giáo này rút được bao nhiêu tiền cả vốn lẫn lãi và lãi cô giáo không rút
ở tât cả các kỳ hạn, nếu rút trước ngân hàng sẽ trả lãi suất theo loại lãi suất không kỳ hạn là
0,002%một ngày (1 tháng tính 30 ngày). A. 471688328,8. B. 302088933,9. C. 311392005,1. D. 321556228. HẾT
TRƯỜNG THPT ĐẶNG HUY TRỨ
ĐÁP ÁN BỘ ĐỀ ÔN TẬP THI HK 1 TỔ TOÁN
Môn: TOÁN 12 - Năm học 2017 - 2018
Thời gian làm bài: 90 phút, không kể thời gian phát đề
ĐỀ TỔNG ÔN TẬP SỐ 01
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 01 Câu 1 2 3 4 5 6 7 8 9 10 Đáp án B D B D D C B C A D Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D B C B C A A C B D Câu 21 22 23 24 25 26 27 28 29 30 Đáp án A C D C C D A B D A Câu 31 32 33 34 35 36 37 38 39 40 Đáp án C C D B C B D C B B Huớng dẫn: Câu 15.
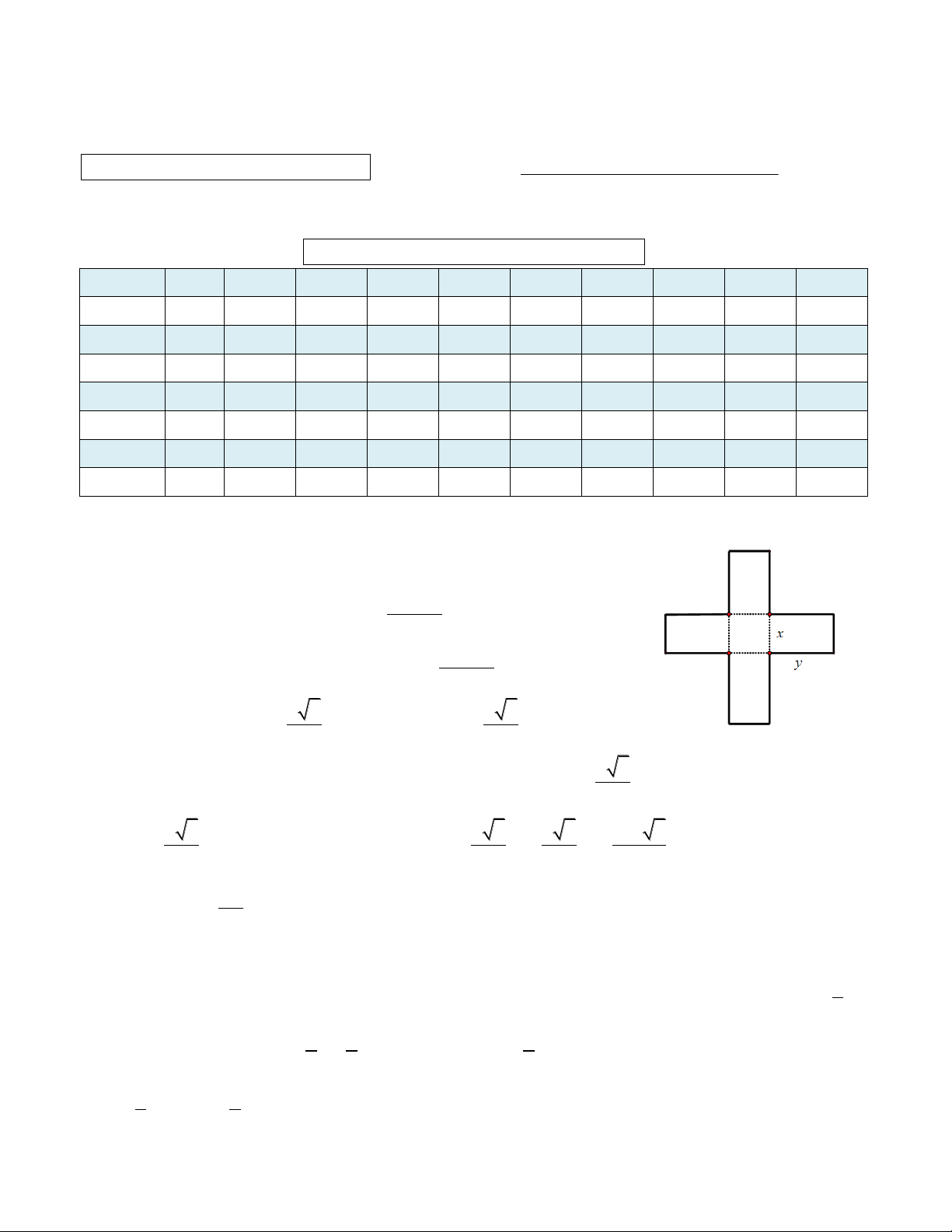
Gọi x, y x; y  0 lần lượt là các chiều dài như hình vẽ bên. Diện 2 64  x tích của tờ giấy 2
S  4xy x  64  y  . x 2 64  x
Thể tích của hình hộp chữ nhật: 2 2 3
V x y x .  64x x . x 8 3 Xét 2 8 3
V   64  3x  0  x
(loại nghiệm x   vì x  0 ) 3 3 8 3
Lập bảng biến thiên suy ra hàm số V đạt giá trị lớn nhất tại x  . 3 2 4 3  8 3   4 3  256 3 Khi đó, y
. Giá trị lớn nhất của V là V    .   . 3  3   3      9 2x e Câu 25. Ta có: x 2 y
e kx  2018 x x
y  e e k. 2 Yêu cầu bài toán 2x x       x 2 0,   0; ln 2 x y e e k x
  k e e , x  0;ln2.     Đặt x
t e , x
 0;ln 2  t  1  ; 2 ,   
 ta xét hàm gt 2 1
t t , t  1  ; 2  g  
t 12t  0  t  . 2  1  1 x x 1 Ta có: g  
1  0; g 2  2  ; g   max  2 e e     . x0;ln 2  2  4    4 1  1  Vậy k  hay k  ;  
 là các giá trị k cần tìm. 4 4 
Câu 27. Phương trình 2 2 2 2
x  4x m  8  9  x  4x m 1  0
Để phương trình có hai nghiệm trái dấu thì  2 m   2 1.
1  0  m  1  0  m 1  ;  1 . Câu 37.
+ Hình trụ có chiều cao h OO'  10 cm và bán kính O'
đáy r  6 cm nên khối trụ có thể tích là 2
V hr  360  2 cm . 1 
+ Hình nón có đỉnh O', chiều cao h OO'  10 cm và 10 h
bán kính đáy r  6 cm nên khối nón có thể tích là 1 2
V hr  120 6  2 cm . 2  3 A O B
Vậy V V V  240  2 cm . 1 2  Câu 40.
Gọi độ dài cạnh đáy, chiều cao của hình chóp tứ giác đều lần lượt là ;
x h(x,h  0) . Ta có đáy là hình vuông với độ dài nửa x 2 x đường chéo bằng
suy ra độ dài cạnh bên 2 l h  . Ta 2 2
có bán kính mặt cầu ngoại tiếp hình chóp 2 2 x  2 h l 2 2 2 R  
 9  x  36h  2h . 2h 2h
Diện tích đáy của hình chóp 2 S x nên 1    2 1 2 1 h h 36 2h V  . h x  (
h 36h  2h ) 3  .(
)  576  V  576 3 3 3 3 1 1 Ta có: 2 .
h (36h  2h )  . . h ( h 36  2h) . 3 3
Dấu bằng xảy ra khi h h  36  2h h  12, x  12 . Vậy V  576 . max
Cách khác: Gọi h là chiều cao hình chóp. Ta có: khoảng cách từ O đến mặt đáy là : h  9
 cạnh đa giác đáy là: h  2 2 2 2 9 9  36h  2h 3 1 1
1  h h  36  2h
Thể tích hình chóp V h  2
36h  2h   .
h h36  2h     576 . 3 3 3  3 
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 02 Câu 1 2 3 4 5 6 7 8 9 10 Đáp án C C D A B B D A D C Câu 11 12 13 14 15 16 17 18 19 20 Đáp án C D C A A D C D A C Câu 21 22 23 24 25 26 27 28 29 30 Đáp án A C B A D A C B C D Câu 31 32 33 34 35 36 37 38 39 40 Đáp án A D C D B B C C A A Huớng dẫn:
Câu 11. Đồ thị hàm số có hai đường tiệm cận ngang khi và chỉ khi hai giới hạn lim y, lim y tồn tại x x
hữu hạn và khác nhau. Vậy hàm số này phải xác định trên khoảng ;   , hay m   2 1 x  4  0
với mọi x   . Vậy các phương án B sai. 3
+) Nếu m  1  y  . Hàm số này có duy nhất một tiệm cận ngang. 2 3  1  x  3 1  lim x    x m1 lim 2 x  4 x 4 m  1  m  1  2 x
+) Với m  1, ta có:
  Đồ thị hàm số có hai 3 1   x  3 1  lim x     x m1 lim 2 x  4 x 4 m  1  m 1  2 x  1 1
đường tiệm cận ngang là y  và y  
. Vậy m  1 thỏa mãn yêu cầu của bài toán. m m
Câu 13. TXĐ: D  .  Ta có: 2
y  x mx   2 2 2 2 3m   1 .
Đồ thị hàm số có hai điểm cực trị khi và chỉ phương trình y  0 có hai nghiệm phân biệt 2 2 13 2 13
 13m  4  0  m    m
* . Ta có: x x m và 2
x .x  1 3m . 13 13 1 2 1 2 m  0 Theo giả thiết: x x 2x x  2 1 1 3m 2m 1          1 2 1 2 2 m   3 2
Kiểm tra điều kiện * , ta có m  là yêu cầu bài toán. 3 t
Câu 14. Đặt t  tan x t 0; 
1 . Khi đó, hàm số ban đầu trở thành g t 1  với 0  t  1. t m t
Lưu ý: Do hàm số tan x đồng biến nên yêu cầu bài toán tương đương g t 1  đồng biến với t m  
t  2 . t m t m . t  2 2  m
0  t  1. Ta có gt            . t m2 t m2
gt  0 m  2 1   m  2
Hàm số đồng biến trên 0; 1 khi      . m  0; 1 m  0;1 m  0 V
Câu 15. Gọi x ( x  0 ) là bán kính của chiếc xô. Khi đó 2
V   x h h  . Để tiết kiệm nguyên 2  x
vật liệu thì diện tích toàn phần của chiếc xô phải bé nhất. Ta có: l   3 dm    3 10 10 10 000 cm  . V 10000 20000
Diện tích toàn phần của chiếc xô là: 2 2 2 2 (
S x)   x  2 xh   x  2 x   x  2   x  2  x x x 3 20000 2 x 20000 10000 10
Ta có: S'(x) 2   x   . 3 3 3
S'(x)  0  2 x  20000  0  x   x  10. 2 2 x x   Bảng biến thiên: x 0 10  3 10.  S'x  0   Sx 2 039,4 10
Ta thấy diện tích toàn phần chiếc xô nhỏ nhất khi bán kính đáy xô là 3 x  10.  14,7 cm. 
Câu 22. Công thức tính dân số theo dữ kiện đã cho là   0,0147  80902000 t N t e
, t tính bằng năm và
t  0 ứng với đầu năm 2003.
Ta có: 2020  2003  17  đầu năm 2020 ứng với t  17.
Vậy dân số Việt Nam đầu năm 2020 là N   0,0147.17 17  80 902 000e  103870000 người.
Câu 24. Điều kiện: x  2.  log x  2  1 
Ta có: log x  2  log x  2  log x  2   log x  2 1   0 * 5   3   5   5   5     log 3 log 3 5  5  1 Do 1 
 0 nên *  log x  2  0  x  2  1  x  1  . 5   log 3 5
Kết hợp điều kiện suy ra tập nghiệm bất phương trình là  2  ;   1  a  2  ;b  1
  S a b  3  .
Câu 34. Do ABCD là hình thoi cạnh a và S  0
ABC  60 nên tam giác ABC đều. Vậy 450 2 2 3a 3a S  2S  2.  . ABCD ABC 4 2 BD AC Ta có: 
BD  SACA D BD   SA a   O
SD SAC  0 ;
DSO  45 . Vậy tam giác B C a 3 SOD vuông cân tại
O SO DO  . Xét tam giác SAO vuông tại A : 2 3 2 2 a 2 1 6a
SA SO AO   VS . A S  . 2 S.ABCD 3 ABCD 12
Câu 39. Gọi V là thể tích khối nón đỉnh C, 1 C
đường cao CH a , bán kính đáy BH a nên: 1 3  2 a V CH. BH  . 1 3 3 a
Gọi V là thể tích khối trụ có đường cao 2 a H B
HD a , bán kính đáy AD a nên: V HD  2 . AD 3 a . 2 a
Vậy thể tích khối tròn xoay cần tìm là: 43 a
V V V  . 1 2 3 A a D Câu 40.
Gọi h là đường cao của hình trụ, r là bán kính của quả bóng, R là
bán kính của chiếc cốc nước. h
=  h  2r r OA OB  2 h h 3
Theo giả thiết: IB
OI  ( vì phần bên ngoài = h ) 4 4 4 h
bán kính đáy của chiếc cốc là 2 2 3
R OA OI  . 4 3 4 4  h  3 r    V 3  2  8 Tỉ số thể tích là: 1 3  
  9V  8V . 2 2 1 2 VR h   9 2 h 3    h  4   
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 03 Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A B C B C C B C A D Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D C B D D C A A C D Câu 21 22 23 24 25 26 27 28 29 30 Đáp án B B A B A D C D B A Câu 31 32 33 34 35 36 37 38 39 40 Đáp án D D B A C A C D A B Huớng dẫn: Câu 25.
Cách 1: Công thức: vay số tiền A lãi suất r% /tháng. Hỏi số tiền a hàng tháng phải trả là bao n . A r.1 r 14.10 .0,005.1 0,0056 6
nhiêu để n tháng hết nợ: a     2.375.000 đồng. n 1 r 1 10,0056 1
Cách 2: Gọi a là số tiền phải trả hàng tháng.
Sau lần trả thứ nhất, số tiền còn nợ là: 6  6  a  6 14.10 14.10 .0,005
14.10 .1,005  a đồng.
Sau lần trả thứ hai, số tiền còn nợ là:  6  a  a  6 2 14.10 .1,005 .1,005
14.10 .1,005  a1,005 1 . …
Sau lần trả thứ sáu, số tiền còn nợ là: 6 6  a 5  4 14.10 .1,005 1,005 1,005  ...   1 . Khi đó 6 6  a 5  4 14.10 .1,005 1,005 1,005 ...  1  0 6 6  a  14.10 .1,005  2.375.000 đồng. 5 1,005  4 1,005  ...  1 2    2 2 x 4x 1
Câu 27. Với x , y  0 ta có 2 xy 4x 1 2.4  ln   4  2  ln 2 4x   2
1  2 xy  ln 2xy  2xy
Xét hàm số    2t f t
 lnt . Ta có f xt 1
 2 ln 2   0 , t
  0. Suy ra hàm số f t đồng biến trên t
0; Khi đó f  2x    f xy 2 4 1 2
 4x 1  2xy .
Ta có P xy x  xy 2 2 2 2 2
 2x  2xy  4x  2 2xy  2x  2x 1 2 4x 1 .
Xét hàm số f x 2
 2x 1 2 4x 1 với x  0 . 8x 3 3  3
Ta có f x  2   0  x
f x  . 2  6 3 4x 1 Bảng biến thiên x 3 0  6 f x  0   f x 1 3 3  3 3 3  3
Dựa vào BBT suy ra f x đạt giá trị lớn nhất bằng khi x  . Do đó P  . 3 6 max 3 Câu 41. A I O J B
Đặt IJ  2x 0  x a . Ta có bán kính đường tròn C  là 2 2
r a x . 1 a 3 Khi đó V
 .2xa x . Xét hàm số     2 2 f x
x a x  . Ta có f  x 2 2
a  3x  0  x  . nón  2 2 3 3 a 3
Lập bảng biến thiên ta suy ra được f x đạt giá trị lớn nhất khi x  . 3 2 3
Khi đó thể tích khối chóp là lớn nhất và IJ  . 3
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 04 1 2 3 4 5 6 7 8 9 10 A A C C D D D D D A 11 12 13 14 15 16 17 18 19 20 C B D C A B C A D D 21 22 23 24 25 26 27 28 29 30 B D B D B C B C A B 31 32 33 34 35 36 37 38 39 40 B C A A D B C B A A 41 42 43 44 45 46 47 48 49 50 D C B C A C B D D C
ĐÁP ÁN ĐỀ TỔNG ÔN TẬP SỐ 05 1 2 3 4 5 6 7 8 9 10 B C D B A C B A A B 11 12 13 14 15 16 17 18 19 20 C C C D C A D D B C 21 22 23 24 25 26 27 28 29 30 B A D D A A D B B C 31 32 33 34 35 36 37 38 39 40 C B C A B A B D B D 41 42 43 44 45 46 47 48 49 50 C D D A C C A D B B