Bộ đề ôn thi học kỳ 1 Toán 12 năm học 2019 – 2020 có đáp án

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi học kỳ 1 môn Giới Toán 12 năm học 2019 – 2021 .Mời bạn đọc đón xem.

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

115 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Biªn so¹n: Ths. Lª V¨n §oµn
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 1 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 01
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Cho hàm số
3 2
3 4.
y x x
Mệnh đề nào dưới đây đúng ?
A. Đồng biến trên khoảng
(0;2).
B. Nghịch biến trên khoảng
( ;2).

C. Đồng biến trên khoảng

D. Nghịch biến trên khoảng
(0;2).
Câu 2. Cho hàm số
2
1
x
y
x
Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên
( ;1) (1; ).
 
B. Hàm số nghịch biến trên
\ {1}.
C. Hàm số nghịch biến trên
( ;1)

và
(1; ).

D. Hàm số nghịch biến trên với
1.
x
Câu 3. Có bao nhiêu giá trị nguyên của
m
để hàm số
4
mx
y
x m
nghịch biến các khoảng xác định ?
A.
2.
B.
3.
C.
5.
D. Vô số.
Câu 4. Cho hàm số
( )
xác định, liên tục trên
\ {1}
và có bảng biến thiên:
x

1
0
1

y
0
y


1
1


Hỏi khẳng định nào sau đây là đúng ?
A. Hàm số có
3
cực trị.
B. Hàm số đạt cực đại tại
1,
x
cực tiểu tại
0.
x
C. Hàm số đạt cực đại tại
1,
x
cực tiểu tại
0.
x
D. Hàm số có giá trị lớn nhất bằng
1
và giá trị nhỏ nhất bằng
1.
Câu 5. Cho hàm số
3
3 4.
y x x
Khẳng định nào đúng ?
A. Hàm số đạt cực đại tại
1
x
và đạt cực tiểu tại
1.
x
B. Hàm số nghịch biến trên
( ; 1).

C. Hàm số có hai điểm cực trị nằm về hai phía của trục hoành.
D. Hàm số có giá trị cực đại là
6.
Câu 6. Có mấy giá trị nguyên của
m
để hàm số
3 2 2
2 (2 1) ( 1) 2
y x m x m x
có hai điểm cực trị.
A.
4.
B.
5.
C.
3.
D.
6.
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 2 -
Câu 7. Tìm giá trị thực của tham số m để hàm số
3 2 2
1
( 1) 1
3
y x mx m m x
đạt cực trị tại hai
điểm
1
x và
2
x thỏa mãn
1 2
4.x x
A. 1.m B. 2.m
C. 2.m D. 2.m
Câu 8. Giá trị lớn nhất của hàm số
3 1
3
x
y
x
trên đoạn [0;2] bằng
A. 5. B. 5.
C.
1
3
D.
1
3
Câu 9. Cho hàm số ( )y f x liên tục trên đoạn [ 1; 3] và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số
2
(3 cos 1)y f x bằng
A. 0.
B. 1.
C. 3.
D. 2.
Câu 10. Cho hàm số
3 2
( 1) 1.y x m x m Tìm tham số m để giá trị nhỏ nhất trên [0;1] bằng 5.
A. 1.m B. 2.m
C. 4.m D. 3.m
Câu 11. Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
3
1
x
y
x
A. 1, 1.x y B. 1, 1.x y
C. 1, 1.x y D. 1, 1.x y
Câu 12. Cho hàm số ( )y f x xác định trên \ {1} D và có bảng biến thiên:
x

0
1

( )f x
0
( )f x
2
0

5
3
Hỏi mệnh đề nào dưới đây đúng ?
A. Giá trị cực tiểu của hàm số là bằng 3.
B. Giá trị cực đại của hàm số bằng 5.
C. Đồ thị hàm số có hai tiệm cận ngang là 0, 5y y và tiệm cận đứng là 1.x
D. Hàm số có giá trị lớn nhất bằng 5.
Câu 13. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ?
A.
4 2
2 1.y x x
B.
4 2
2 1.y x x
C.
3 2
1.y x x
D.
3 2
1.y x x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 3 -
Câu 14. Cho đồ thị hàm số
ax b
y
cx d
như hình vẽ. Tìm khẳng định đúng ?
A.
0, 2.
y x
B.
0, 1.
y x
C.
0, 2.
y x
D.
0, 1.
y x
Câu 15. Cho đồ thị hàm số
3 2
y ax bx cx d
như hình. Tìm mệnh đề đúng ?
A.
0, 0, 0, 0.
a b c d
B.
0, 0, 0, 0.
a b c d
C.
0, 0, 0, 0.
a b c d
D.
0, 0, 0, 0.
a b c d
Câu 16. Cho đồ thị hàm số
4 2
2
y x x
như hình vẽ. Tìm tham số
m
để phương trình
4 2
2
x x m
có
đúng
4
nghiệm phân biệt ?
A.
0.
m
B.
0 1.
m
C.
0 1.
m
D.
1.
m
Câu 17. Cho biểu thức
4
3
2 3
. . ,
P x x x
với
0.
x
Mệnh đề nào đúng ?
A.
1
2
.
P x
B.
13
24
.
P x
C.
1
4
.
P x
D.
2
3
.
P x
Câu 18. Cho
3
log 2
a
và
2
1
log .
2
b Giá trị của
2
3 3 1
4
2 log log (3 ) log
I a b
bằng
A.
0.
B.
4.
C.
5
4
D.
3
2
Câu 19. Tìm tập xác định
D
của hàm số
1
2 2
3
2
(2 ) log ( 1) .
y x x x
A.
(0;2).
D
B.
(0;1).
D
C.
\ {0;2}.
D
D.
(0;2) \ {1}.
D
Câu 20. Giá trị của tham số
m
để
(e) 2 1
y m
với
ln(2 1)
y x
bằng
A.
1 2e
4e 2
B.
1 2e
4e 2
C.
1 2e
4e 2
D.
1 2e
4e 2
Câu 21. Chọn khẳng định sai ?
A. Hàm số
2
x
y
đồng biến trên
( ; ).
 
B. Hàm số
0,5
log
y x
nghịch biến trên

C. Hàm số
2
y x
có tập xác định là

D. Hàm số
2
log
y x
đồng biến
( ; ).
 
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 4 -
Câu 22. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
m
của hàm số
2
2 ln
y x x
trên
1
[e ;e].
Tổng
M m
bằng
A.
2 2
e e .
B.
2
e 3.
C.
2
e 2.
D.
2
e 1.
Câu 23. Gọi
1 2 1 2
, ( )
x x x x
là hai nghiệm của phương trình
2
1 2
9 3 .
x x
Giá trị của
1 2
2 3
x x
bằng
A.
5.
B.
10.
C.
11.
D.
28.
Câu 24. Tổng các nghiệm của phương trình
2
3
log ( 3 5 17) 2
x x
bằng
A.
5/3.
B.
5/3.
C.
8/3.
D.
8/3.
Câu 25. Tổng các nghiệm của phương trình
1
4 3.2 7 0
x x
bằng
A.
2
log 7.
B.
12.
C.
28.
D.
2
log 28.
Câu 26. Gọi
1
,
x
2
x
là nghiệm của
2
2 2 5
log 3 log 5.log 2 0.
x x
Giá trị của
2 2
1 2
x x
bằng
A.
20.
B.
5.
C.
36.
D.
25.
Câu 27. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
9 3 3
log log (3 1) log
x x m
có nghiệm ?
A.
2.
B.
3.
C.
4.
D. Vô số.
Câu 28. Có bao nhiêu giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 45 0
x x
m m
có
hai nghiệm phân biệt ?
A.
13.
B.
3.
C.
6.
D.
4.
Câu 29. Bất phương trình
2
4 12
1
1
3
x x
có tất cả bao nghiêu nghiệm nguyên ?
A.
3.
B.
5.
C.
7.
D. Vô số.
Câu 30. Tập nghiệm của bất phương trình
3 0,5
log (log ) 0
x
là
A.
1
0;
2
S
B.
1
0;
2
S
C.
1 1
;
4 2
S
D.
1
0;
4
S
Câu 31. Các nguyên hàm của hàm số
2
2
2
( )f x x
x
là
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 5 -
A
C
B
S
S
A
B
C
D
O
B'
C'
A'
D'
A
B
C
D
A
B
C
S
H
C'
B'
A
C
B
A'
A.
3
2
.
3
x
C
x
B.
3
1
.
3
x
C
x
C.
3
2
.
3
x
C
x
D.
3
1
.
3
x
C
x
Câu 32. Họ nguyên hàm của hàm số
2
1 1
( ) 2
2 1
cos
f x x
x
x
là
A.
2
ln 2 1 tan .x x x C B.
2
1
ln 2 1 tan .
2
x x x C
C.
2
1
ln 2 1 tan .
2 2
x
x x C D.
2
1
ln 2 1 tan .
2
x x x C
Câu 33. Tìm nguyên hàm ( )F x của hàm số ( ) sin cosf x x x thỏa mãn
2.
2
F
A.
cos sin 3.x x
B.
cos sin 3.x x
C. sin cos 1.x x D.
cos sin 1.x x
Câu 34. Cho hình chóp .S ABC có đáy là tam giác vuông tại ,B cạnh SA vuông góc với đáy và
,
AB a
2 .SA AC a Thể tích của khối chóp .S ABC bằng
A.
3
2 3
3
a
B.
3
2
3
a
C.
3
3
3
a
D.
3
3 .a
Câu 35. Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2 .a Thể tích khối chóp bằng
A.
3
4 2
3
a
B.
3
8
3
a
C.
3
8 2
3
a
D.
3
2 2
3
a
Câu 36. Cho hình chóp .S ABC có ,SA a đáy ABC là tam giác đều. Tam giác SAB vuông cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp đã cho bằng
A.
3
6
4
a
B.
3
6
24
a
C.
3
6
12
a
D.
3
6
8
a
Câu 37. Cho khối lập phương .ABCD A B C D
có .AC a
Thể tích khối lập phương bằng
A.
3
27
a
B.
3
3 .a
C.
3
3 3 .a
D.
3
3
9
a
Câu 38. Cho lăng trụ đứng .ABC A B C
có đáy ABC là tam giác vuông cân tại , 2 ,A BC a
3 .
A B a
Thể tích của khối lăng trụ .ABC A B C
bằng
A.
3
2 /3.
a
B.
3
2 .a
C.
3
10
3
a
D.
3
7 .a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 6 -
P
N
M
S
B
C
A
C
A
B
A
C
B
D
Câu 39. Cho lăng trụ tam giác đều .ABC A B C
có cạnh đáy là bằng 4, diện tích tam giác A BC
bằng 8.
Thể tích khối lăng trụ .ABC A B C
bằng
A.
2 3.
B.
10 3.
C.
4 3.
D.
8 3.
Câu 40. Hình chóp .S ABC có , , M N P lần lượt trung điểm của , , .SA SB SC Gọi
1
V là thể tích khối
.MNP ABC và
2
V là thể tích khối . .S ABC Tỉ số
1
2
V
V
bằng
A.
1
8
B. 8.
C.
7
8
D.
8
7
Câu 41. Cho khối nón có bán kính đáy bằng 3 và diện tích xung quanh bằng 15 . Thể tích hình nón bằng
A. 12 . B. 20 .
C. 36 . D. 60 .
Câu 42. Trong không gian cho tam giác ABC vuông tại , A AB a và
30 .ACB Thể tích của khối nón
nhận được khi quay tam giác ABC quanh cạnh AC bằng
A.
3
.a B.
3
3 .a
C.
3
3
9
a
D.
3
3
3
a
Câu 43. Cho tứ diện đều ABCD cạnh 3 .a Diện tích xung quanh của hình nón đỉnh A và đường tròn đáy là
đường tròn ngoại tiếp tam giác BCD bằng
A.
2
6 .a
B.
2
3 3 .a
C.
2
12 .a
D.
2
6 3 .a
Câu 44. Cho khối trụ có bán kính đáy bằng 4 và diện tích xung quanh bằng 16 . Thể tích khối trụ bằng
A. 32 .
B. 64 .
C. 16 .
D. 48 .
Câu 45. Cho hình chữ nhật ABCD có , 5.AB a AC a Diện tích xung quanh của hình trụ khi quay hình
chữ nhật xung quanh trục AB bằng
A.
2
2 .a
B.
2
4 .a
C.
2
2 .a
D.
2
4 .a
Câu 46. Cho hình lăng trụ tam giác đều .ABC A B C
có độ dài cạnh đáy bằng ,a chiều cao là .h Tính thể
tích V của khối trụ ngoại tiếp hình lăng trụ.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 7 -
O
I
R
x
r
R
A.
2
9
a h
V
B.
2
3 .V a h
C.
2
.V a h D.
2
3
a h
V
Câu 47. Cho khối cầu có thể tích bằng 36
3
cm . Diện tích mặt cầu đã cho bằng
A.
2
64 cm . B.
2
18 cm .
C.
2
36 cm . D.
2
27 cm .
Câu 48. Một khối đồ chơi gồm một khối hình trụ ( ),T một khối hình nón ( )N và một nửa khối cầu ( )S gắn
vào với nhau như hình vẽ. Biết rằng khối đồ chơi có chiều cao 17cm,h chõm cầu, khối trụ và khối
nón có bán kính đáy bằng nhau, khối trụ có chiều cao
1
7cm,h khối nón có đường sinh hợp với đáy
một góc 30 . Diện tích toàn phần của khối đồ chơi bằng
A.
2
677,17cm .
B.
2
883,13cm .
C.
2
726,15cm .
D.
2
566,27cm .
Câu 49. Cho hình lăng trụ tam giác đều .ABC A B C
có 9 cạnh bằng nhau và bằng 2 .a Diện tích của mặt
cầu ngoại tiếp hình lăng trụ đã cho bằng
A.
2
28
9
a
B.
2
7
9
a
C.
2
28
3
a
D.
2
7
3
a
Câu 50. Cho khối cầu tâm O bán kính
R
(cho trước). Mặt phẳng ( )P cách O một khoảng x cắt khối cầu theo
một hình tròn ( ).C Một khối nón ( ) có đỉnh thuộc mặt cầu, đáy là hình tròn ( ).C Biết khối nón
( )
có thể tích lớn nhất, khi đó giá trị của x bằng
A.
3
R
x
B.
2
R
x
C.
2
2
R
x
D.
3
4
R
x
ĐÁP ÁN ĐỀ SỐ 01
1.A 2.C 3.B 4.B 5.D 6.B 7.C 8.D 9.D 10.C
11.C 12.C 13.A 14.A 15.A 16.C 17.B 18.D 19.D 20.C
21.D 22.D 23.B 24.B 25.D 26.A 27.A 28.B 29.C 30.B
31.A 32.D 33.D 34.C 35.A 36.C 37.D 38.D 39.D 40.C
41.A 42.D 43.B 44.A 45.B 46.D 47.C 48.A 49.C 50.A
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 8 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 02
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Cho hàm số
4 2
2 4.
y x x
Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên các khoảng
( ; 1)
và

B. Hàm số nghịch biến trên các khoảng
( 1;0)
và
(1; ).

C. Hàm số đồng biến trên các khoảng
( ; 1)
và
(0;1).
D. Hàm số đồng biến trên các khoảng
( 1;0)
và
(1; ).

Câu 2. Cho hàm số
( )
f x
xác định, liên tục trên
và có đồ thị của hàm số
( )
f x
là đường cong như hình vẽ
bên dưới. Hỏi khẳng định nào đúng ?
A. Hàm số
( )
f x
đồng biến trên khoảng
(0;2).
B. Hàm số
( )
f x
nghịch biến trên khoảng
( 2;2).
C. Hàm số
( )
f x
đồng biến trên khoảng
( ; 1).

D. Hàm số
( )
f x
nghịch biến trên khoảng
( ;0).

Câu 3. Tìm tham số
m
để hàm số
3 2
2 3
y x mx m
đồng biến trên
( ; ).
 
A.
0.
m
B.
0.
m
C.
0.
m
D.
0.
m
Câu 4. Cho hàm số
( )
f x
có bảng biến thiên như sau:
x

2
2

y
0
0
y
3


0
Tìm giá trị cực đại
y
C
Đ
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
3, 2.
y y
CĐ CT
B.
2, 2.
y y
CĐ CT
C.
2, 0.
y y
CĐ CT
D.
3, 0.
y y
CĐ CT
Câu 5. Gọi
, ,
A B C
là ba điểm cực trị của đồ thị hàm số
4 2
2 4 1.
y x x
Diện tích tam giác
ABC
bằng
A.
4.
B.
2.
C.
1.
D.
3.
Câu 6. Tìm tham số
m
để hàm số
4 2
( 2) 5
y x m x
có ba cực trị.
A.
2.
m
B.
3.
m
C.
3 2.
m
D.
1.
m
Câu 7. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
6 2 1
y x x mx
có hai điểm cực trị
1 2
,
x x
thỏa mãn
2 2
1 2
12.
x x
A.
1.
m
B.
3.
m
C.
1.
m
D.
3.
m
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 9 -
O
x
y
1
1
3
O
x
y
Câu 8. Cho hàm số ( )y f x xác định và liên tục trên khoảng ( 3;2),
3
lim ( ) 5,
x
f x

2
lim ( ) 3
x
f x
và có
bảng biến thiên như sau:
x

3
1
1
2

y
0
0
y
0
3
5
2
Mệnh đề nào dưới đây sai ?
A. Hàm số không có giá trị nhỏ nhất trên khoảng ( 3;2).
B. Giá trị cực đại của hàm số bằng 0.
C. Giá trị lớn nhất của hàm số trên khoảng ( 3;2) bằng 0.
D. Giá trị cực tiểu của hàm số bằng 2.
Câu 9. Giá trị lớn nhất của hàm số
3 2
cos 2 sin cosy x x x bằng
A.
58
27
B.
2147
999
C.
7159
3333
D.
43
20
Câu 10. Cho hàm số ( )y f x liên tục trên có đồ thị ( )y f x
như hình vẽ. Đặt
2
( ) 2 ( ) ( 1) .
g x f x x
Mệnh đề nào dưới đây đúng ?
A.
[ 3;3]
min ( ) (1).g x g
B.
[ 3;3]
max ( ) (1).g x g
C.
[ 3;3]
max ( ) (3).g x g
D. Không tồn tại
[ 3;3]
max ( ).g x
Câu 11. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ?
A.
4 2
2 .y x x
B.
4 2
2 1.y x x
C.
4 2
2 .y x x
D.
4 2
2 .y x x
Câu 12. Đồ thị sau là của hàm số nào ?
A.
2
1
x
y
x
B.
2
1
x
y
x
C.
2
1
x
y
x
D.
2
1
x
y
x
Câu 13. Cho đồ thị hàm số
3 2
y ax bx cx d như hình vẽ. Tìm mệnh đề đúng ?
A. 0, 0, 0, 0.a b c d
B. 0, 0, 0, 0.a b c d
C. 0, 0, 0, 0.a b c d
D. 0, 0, 0, 0.a b c d
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 10 -
y
x
O
1
3
1
1
1
Câu 14. Cho đồ thị hàm số
3
3 1.
y x x
Tìm tham số
m
để phương trình
3
3 0
x x m
có đúng
3
nghiệm phân biệt ?
A.
2 3.
m
B.
2 2.
m
C.
2 2.
m
D.
1 3.
m
Câu 15. Phương trình tiếp của đồ thị
3 2
( ) :
1
x
C y
x
tại giao điểm của
( )
C
và đường thẳng
3
y x
là
A.
3
y x
và
1.
y x
B.
3
y x
và
1.
y x
C.
3
y x
và
1.
y x
D.
3
y x
và
1.
y x
Câu 16. Tìm tọa độ giao điểm của đường thẳng
1
y x
với đồ thị hàm số
1
2
x
y
x
A.
(4; 3), (0; 1).
A B
B.
( 1;3).
C
C.
(3; 1).
D
D.
( 1;0), (3; 4).
E F
Câu 17. Cho biểu thức
7 1 2 7
5 2 2 2 2
.
( 0).
2 ( )
a a
P a
a a
Mệnh đề nào dưới đây đúng ?
A.
5
.
P a
B.
5
.
P a
C.
0,5.
P
D.
2.
P
Câu 18. Cho
log 2
a
b
và
log 3.
a
c
Tính
2 3
log ( ).
a
P b c
A.
31.
P
B.
13.
P
C.
30.
P
D.
108.
P
Câu 19. Cho
,
a x
là các số thực dương, biết
3 1
3
3
log 2 log log .
x a a
Tính
x
theo
.
a
A.
4
.
x a
B.
3
.
x a
C.
3 .
x a
D.
3.
x a
Câu 20. Tìm tập xác định
D
của hàm số
2
2 3 2
2
2
5 log ( 6).
x x
y x x
A.
(3; ).

D
B.
( 3;2).
D
C.
( ;2).

D
D.
( ; 3) (2; ).
 
D
Câu 21. Tìm tập xác định
D
của hàm số
log100 2 2020
( 2) ( ) .
y x x x
A.
( ;0) (1; ) \ {2}.
 
D
B.
(2; ).

D
C.
( ;0) (1; ).
 
D
D.
( ;0] [1; ).
 
D
Câu 22. Cho hàm số
.
y x
Giá trị của
(1)
y
bằng
A.
2
ln .
B.
ln .
C.
0.
D.
( 1).
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 11 -
Câu 23. Cho hàm số
( ) ln(2e )
x
f x m
thỏa mãn
3
( ln 2)
2
f
Mệnh đề nào đúng ?
A.
(1;3).
m
B.
( 5; 2).
m
C.
(1; ).
m

D.
( ;3).
m

Câu 24. Với giá trị nào của
a
thì hàm số
2
(1 3 )
x
y a a
đồng biến trên
( ; )
 
?
A.
0.
a
B.
0 2.
a
C.
3.
a
D.
0 3.
a
Câu 25. Gọi
1 2
,
x x
là hai nghiệm của phương trình
2
3 10
2 1.
x x
Giá trị của
1 2 1 2
5( )
x x x x
bằng
A.
8.
B.
3.
C.
8.
D.
3.
Câu 26. Tìm tập nghiệm
S
của phương trình
2
2 2
log ( 4 3) log (4 4).
x x x
A.
{1;7}.
S
B.
{7}.
S
C.
{1}.
S
D.
{3;7}.
S
Câu 27. Tổng các nghiệm của phương trình
2
4 3.2 log 3 0
x x
bằng
A.
3.
B.
2 2
log (log 3).
C.
2
log 3.
D.
3
log 2.
Câu 28. Tích tất cả các nghiệm của phương trình
3 3
log (3 ).log 2
x x
bằng
A.
1
9
B.
28
9
C.
26
3
D.
1
3
Câu 29. Tìm tất cả giá trị thực của
m
để phương trình
4 2 .2 2 0
x x
m m
có
2
nghiệm phân biệt
1 2
,
x x
sao cho
1 2
3.
x x
A.
1.
m
B.
3.
m
C.
4.
m
D.
2.
m
Câu 30. Giải bất phương trình
2 1 3 2
1 1
2 2
x x
A.
( ;3).
S

B.
(3; ).
S

C.
( ; 3).
S

D.
1
;3
2
S
Câu 31. Giải bất phương trình
2
log(3 1) log(4 ).
x x
A.
1
3
x
hoặc
1.
x
B.
1
0
3
x
hoặc
1.
x
C.
0 1.
x
D.
1/3 1.
x
Câu 32. Tập nghiệm của của bất phương trình
0,5
1 2
log 0
x
x
là
A.
1
;
3
S

B.
1
0;
3
S
C.
1 1
;
3 2
S
D.
1
;
3
S

Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 12 -
C
A
D
B
S
Câu 33. Tập nghiệm của bất phương trình 16 5.4 4 0
x x
là
A. ( ;1) (4; ).S  
B. ( ;1] [4; ).S  
C. ( ;0) (1; ).S  
D. ( ;0] [1; ).S  
Câu 34. Một nguyên hàm ( )F x của hàm số
2
( ) 2e 3
x
f x x thỏa
9
(0)
2
F là
A.
3
3
2e
2
x
x B.
3
5
2e
2
x
x
C.
3
7
e
2
x
x D.
3
9
2e
2
x
x
Câu 35. Tìm hàm số ( )f x thỏa mãn ( ) 2 3
x
f x x
và
16
(4)
ln2
f Mệnh đề nào đúng ?
A.
3
16
2 2 32.
ln2
x
x B.
3
2
8.
ln2
x
x
C.
3
16
2 24.
ln 2
x
x D.
3
2
2 16.
ln2
x
x
Câu 36. Một nguyên hàm ( )F x của hàm số ( ) sin cos2f x x x thỏa
2
4 2
F
là
A.
1 1
cos sin 2
2 2
x x B.
1 1
cos sin 2
2 2
x x
C.
1 2
cos sin 2
2 2
x x D.
1 2
cos sin 2
2 2
x x
Câu 37. Cho hình chóp .S ABCD
có đáy là hình vuông cạnh 3cm, các mặt bên ( )SAB và ( )SAD vuông góc
với mặt phẳng đáy, góc giữa SC
và mặt đáy là 60 . Thể tích của khối chóp .S ABCD bằng
A.
3
6 6 cm .
B.
3
9 6 cm .
C.
3
9 3
cm .
2
D.
3
3 6 cm .
Câu 38. Cho hình chóp tam giác đều có cạnh đáy bằng
3a
và cạnh bên tạo với đáy một góc 60 . Thể tích
của khối chóp đó bằng
A.
3
3
12
a
B.
3
3
4
a
C.
3
12
a
D.
3
4
a
Câu 39. Cho hình chóp .S ABCD có đáy là hình chữ nhật, mặt bên ( )SAB là tam giác đều cạnh 2a và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy (tham khảo hình vẽ). Biết mặt phẳng ( )SCD tạo với
mặt phẳng đáy một góc 30 . Thể tích khối chóp .S ABCD bằng
A.
3
3
2
a
B.
3
2 3 .a
C.
3
2 3
3
a
D.
3
4 3
3
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 13 -
A
B C
Câu 40. Thể tích của vật thể với các kích thước được cho trong hình vẽ bên bằng
A.
3
6600cm .
B.
3
5700cm .
C.
3
6400cm .
D.
3
7800cm .
Câu 41. Lăng trụ tam giác .ABC A B C
có đáy tam giác đều diện tích bằng 3, góc giữa cạnh bên và đáy
bằng 30 . Hình chiếu của A
lên mặt phẳng ( )ABC là trung điểm H của .BC Thể tích của khối
lăng trụ đã cho bằng
A.
9
8
B.
3
3
C.
3 3.
D.
2 3.
Câu 42. Cho khối nón có đường sinh bằng 5 và diện tích đáy bằng 9 . Thể tích của khối nón đã cho bằng
A. 12 .
B. 24 .
C. 36 .
D. 45 .
Câu 43. Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay tam giác ABC quanh trục BC thì
được khối tròn xoay có thể tích là
A.
2 .
B. 2 .
C.
2
.
3
D. 2 .
Câu 44. Cho hình chóp tam giác đều .S ABC có cạnh đáy bằng ,a cạnh bên 2 .SA a Thể tích của khối nón
có đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC bằng
A.
3
2
a
B.
3
33
27
a
C.
3
6
a
D.
3
2
2
a
Câu 45. Cho hình trụ có diện tích xung quang bằng 50 và độ dài đường sinh bằng đường kính của đường
tròn đáy. Tính bán kính r của đường tròn đáy ?
A.
5 2
2
r
B.
5 2
2
r
C.
5 .r
D. 5.r
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 14 -
18
36
G
M
C
A
B
S
B
A
D C
Câu 46. Cho hình bình hành ABCD có 2 ,AD a 3 ,AB a
45BAD (hình vẽ). Thể tích của khối tròn
xoay nhận được khi quay hình bình hành ABCD quanh trục AB bằng
A.
3
5
2
a
B.
3
5 .a
C.
3
6 .a D.
3
9
2
a
Câu 47. Cho hình hộp chữ nhật .ABCD A B C D
có 8,AD 6,CD 12.AC
Diện tích toàn phần của
hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A B C D
bằng
A.
576 .
B. 10(2 11 5) .
C. 26 .
D. 5(4 11 4) .
Câu 48. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ như hình vẽ bên. Các kích thước được
ghi (cùng đơn vị dm). Thể tích của bồn chứa bằng
A.
3
3
4
3
B.
2
5
4
3
C.
2 5
4 .3 . D.
5 2
4 .3 .
Câu 49. Cho hình chóp . ,S ABC có đáy là tam giác đều cạnh 3cm, 2cmSC và SC vuông góc với đáy. Thể
tích của khối cầu ngoại tiếp hình chóp .S ABC bằng
A.
3
8 cm .
B.
3
256
cm .
3
C.
3
36 cm .
D.
3
32
cm .
3
Câu 50. Cho hình nón có bán kính đáy 5 ,R a độ dài đường sinh 13 .a Thể tích khối cầu nội tiếp hình
nón bằng
A.
3
40
9
a
B.
3
400
27
a
C.
3
4000
27
a
D.
3
4000
81
a
ĐÁP ÁN ĐỀ SỐ 02
1.D 2.C 3.B 4.D 5.B 6.A 7.B 8.C 9.A 10.B
11.A 12.C 13.C 14.B 15.B 16.D 17.C 18.B 19.B 20.B
21.C 22.D 23.D 24.D 25.B 26.B 27.B 28.D 29.C 30.A
31.B 32.C 33.D 34.B 35.D 36.B 37.B 38.B 39.B 40.A
41.C 42.A 43.C 44.B 45.B 46.C 47.B 48.C 49.D 50.D
Mặt cắt qua trục của nón
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 15 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 03
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Cho hàm số
( )
có bảng xét dấu đạo hàm như sau:
x

1
0
2

y
0
0
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng
( 2;0).
B. Hàm số đồng biến trên khoảng
( ;0).

C. Hàm số nghịch biến trên khoảng
(0;2).
D. Hàm số đồng biến trên khoảng
( ;2).

Câu 2. Cho hàm số
( )
f x
xác định, liên tục trên
và có đồ thị của hàm số
( )
f x
là đường cong như hình vẽ
bên dưới. Hỏi khẳng định nào sau đây là đúng ?
A. Hàm số
( )
f x
đồng biến trên khoảng
(0;2).
B. Hàm số
( )
f x
nghịch biến trên khoảng
( 2;2).
C. Hàm số
( )
f x
đồng biến trên khoảng
( ; 1).

D. Hàm số
( )
f x
nghịch biến trên khoảng
( ;0).

Câu 3. Tìm tham số
m
sao cho hàm số
6 5
mx m
y
x m
đồng biến trên

A.
1 3.
m
B.
1 5.
m
C.
1 5.
m
D.
1 3.
m
Câu 4. Cho hàm số
( )
có đồ thị như hình vẽ. Hàm số
( )
f x
đạt cực tiểu tại điểm nào dưới đây ?
A.
1.
x
B.
1.
x
C.
2.
x
D.
0.
x
Câu 5. Khẳng định nào sau đây đúng ?
A. Hàm số
1
2
x
y
x
có một điểm cực trị.
B. Hàm số
4 2
2 3
y x x
có ba điểm cực trị.
C. Hàm số
4 2
2 3
y x x
có ba điểm cực trị.
D. Hàm số
3
3 4
y x x
có hai điểm cực trị.
Câu 6. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
3 2
( 2) 3 5
y m x x mx
có điểm cực
đại nằm bên trái điểm cực tiểu.
A.
2.
B.
3.
C. Vô số. D.
1.
Câu 7. Cho hàm số
3 2 2
( 3) ( 2 ) 2.
y x m x m m x
Tìm tất cả các giá trị thực của tham số
m
sao
cho hàm số có hai điểm cực trị
1 2
,
x x
thỏa
1 2 1 2
6( ) 4 0.
x x x x
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 16 -
O
x
y
1
1
1
1
A. 2m hoặc 12.m
B. 2.m
C.
3 2 3 2
2 2
m
D.
3 2
2
2
m
Câu 8. Gọi , M m là giá trị lớn nhất và giá trị nhỏ nhất của
2
3
2
x
y
x
trên
3
1; .
2
Giá trị
M m
bằng
A.
8
3
B.
7
2
C.
13
6
D.
4
3
Câu 9. Tìm giá trị của x để hàm số
2
4y x x đạt giá trị lớn nhất.
A.
2.x
B.
2 2.x
C. 2.x D. 1.x
Câu 10. Đồ thị hàm số
2
2
4
3 4
x
y
x x
có tất cả bao nhiêu đường tiệm cận ?
A. 0. B. 3.
C. 1. D. 2.
Câu 11. Đồ thị sau là của hàm số nào ?
A.
2 1
1
x
y
x
B.
2 1
1
x
y
x
C.
1
1
x
y
x
D.
1
1
x
y
x
Câu 12. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ?
A.
4 2
2 1.y x x
B.
4 2
2 1.y x x
C.
4 2
3 1.y x x
D.
4 2
2 1.y x x
Câu 13. Cho đồ thị hàm số
3 2
y ax bx cx d như hình vẽ. Tìm mệnh đề đúng ?
A. 0, 0, 0, 0.a b c d
B. 0, 0, 0, 0.a b c d
C. 0, 0, 0, 0.a b c d
D. 0, 0, 0, 0.a b c d
Câu 14. Cho hàm số ( )y f x có đồ thị như hình. Phương trình ( )f x x có bao nhiêu nghiệm ?
A. 0 nghiệm.
B. 1 nghiệm.
C. 2 nghiệm.
D. 3 nghiệm.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 17 -
Câu 15. Viết phương trình tiếp tuyến của đồ thị
1
,
1
x
y
x
biết tiếp tuyến có hệ số góc là
1
2
A.
1 1
2 2
y x
và
1 7
2 2
y x
B.
1 1
2 2
y x
và
1 7
2 2
y x
C.
1 1
2 2
y x
và
1 7
2 2
y x
D.
1 1
2 2
y x
và
1 7
2 2
y x
Câu 16. Biết đồ thị hàm số
4 2
3 5
y x x
và đường thẳng
9
y
cắt nhau tại hai điểm phân biệt
1 1 2 2
( ; ), ( ; ).
A x y B x y
Giá trị của
1 2
x x
bằng
A.
3.
B.
0.
C.
18.
D.
5.
Câu 17. Cho
9 9 23.
x x
Giá trị của biểu thức
5 3 3
1 3 3
x x
x x
K
bằng
A.
5
2
B.
1
2
C.
5
2
D.
3
2
Câu 18. Với
0 ; 1,
a b
giá trị của biểu thức
2
3 6
log log
a
a
T b b
bằng
A.
9 log .
a
b
B.
27 log .
a
b
C.
a
b
D.
6 log .
a
b
Câu 19. Biết rằng
, , 1
a b c
thỏa
log ( ) 2.
ab
bc
Giá trị của biểu thức
4
log log ( )
c c
b a
P a ab
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 20. Tìm tập xác định
D
của hàm số
0
2018
1
(3 ) log
2
x
y x
x
A.
[1; ).

D
B.
( 2;1).
D
C.
( ; 2) (1; ).
 
D
D.
( ; 2) (1; ) \ {3}.
 
D
Câu 21. Tìm tập xác định
D
của hàm số
lg100
2 1 log( 2) .
x
y x
A.
(2; ).

D
B.
[0; ).

D
C.
[0; ) \ {2}.

D
D.
(0; ) \ {2}.

D
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 18 -
Câu 22. Cho hàm số
2
( )e .
x
y x mx
Biết
(0) 1
y
thì
(1)
y
bằng
A.
6e.
B.
3e.
C.
5e.
D.
4e.
Câu 23. Phương trình
1
3 .5 7
x x
có nghiệm dạng
log
a
x b
với
0 , 1.
a b
Giá trị của
b a
bằng
A.
20.
B.
16.
C.
20.
D.
16.
Câu 24. Cho phương trình
1 1
9 13.6 4 0.
x x x
Phát biểu nào sao đây đúng ?
A. Phương trình có
2
nghiệm nguyên.
B. Phương trình có
2
nghiệm dương.
C. Phương trình có
1
nghiệm dương.
D. Phương trình có
2
nghiệm vô tỉ.
Câu 25. Tổng các nghiệm của phương trình
2
3 3
log log (9 ) 2 0
x x
bằng
A.
10.
B.
3.
C.
0.
D.
4.
Câu 26. Tìm giá trị thực của tham số
m
để phương trình
2
3 3
log log 2 7 0
x m x m
có hai nghiệm thực
1 2
,
x x
thỏa mãn
1 2
81.
x x
A.
4.
m
B.
4.
m
C.
81.
m
D.
44.
m
Câu 27. Tập nghiệm của bất phương trình
2 6
2 2
x x
là
A.
(0;6).
B.
( ;6).

C.
(0;64).
D.
(6; ).

Câu 28. Tập nghiệm
S
của bất phương trình
/6 3
log log ( 2) 0
x
là
( ; ).
a b
Giá trị của
b a
bằng
A.
2.
B.
4.
C.
3.
D.
5.
Câu 29. Tập nghiệm của bất phương trình
2 2
log ( 3) log 2
x x
là
A.

B.
[4; ).

C.
(3;4].
D.
( ;1] [4; ).
 
Câu 30. Biết
[ ; ]
S a b
là tập nghiệm của bất phương trình
3.9 10.3 3 0.
x x
Giá trị của
b a
bằng
A.
8
3
B.
10
3
C.
1.
D.
2.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 19 -
C
A
B
D
S
A
C
B
S
Câu 31. Họ nguyên hàm của hàm số
1
( ) sin
2 2
x
f x x
là
A.
2
1
cos .
4 2
x
x C
B.
2
1
cos .
2 2
x
x C
C.
2
1 1
cos .
4 2 2
x
x C
D.
2
1 1
cos .
4 4 2
x
x C
Câu 32. Họ nguyên hàm của hàm số
6
2
1 1
( ) 7 2
f x x
x
x
là
A.
7
1
ln 2 .
x x x C
x
B.
7
1
ln 2 .
x x x
x
C.
7
1
ln 2 .
x x x C
x
D.
7
1
ln 2 .
x x x C
x
Câu 33. Họ nguyên hàm của hàm số
2
( ) 2 3
4
x x
x
x
f x
là
A.
12 2
.
ln12 3
x
x x
C
B.
12 .
x
x x C
C.
2
2 3 ln 4
ln2 ln 3
4
x x
x
x x
D.
2
2 3
ln2 ln 3
4
x x
x
x x
Câu 34. Cho khối chóp
.
S ABCD
có đáy là hình chữ nhật,
( ),
SA ABCD
3 ,
AB a
2 ,
AD a
5 .
SB a
Thể tích của khối chóp
.
S ABCD
bằng
A.
2
8 .
a
B.
3
24 .
a
C.
3
10 .
a
D.
3
8 .
a
Câu 35. Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2 .
a
Thể tích của khối
chóp
.
S ABC
bằng
A.
3
13
12
a
B.
3
11
12
a
C.
3
11
6
a
D.
3
11
4
a
Câu 36. Cho hình chóp
.
S ABC
có thể tích bằng
.
V
Gọi
G
là trọng tâm tam giác
.
SBC
Mặt phẳng
( )
đi qua
hai điểm
,
A G
và song song với
.
BC
Mặt phẳng
( )
cắt các cạnh
,
SB SC
lần lượt tại các điểm
M
và
.
N
Thể tích khối chóp
.
S AMN
bằng
A.
9
V
B.
2
V
C.
4
9
V
D.
4
V
Câu 37. Cho lăng trụ đứng
. .
ABC A B C
Gọi
M
là trung điểm
.
AA
Tỉ số
.
.
M ABC
ABC A B C
V
V
bằng
A.
1
6
B.
1
3
C.
1
12
D.
1
2
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 20 -
l
r
h
O
C
A
B
D
A'
D'
D
B
C'
C
A
B'
A'
B'
C
A
B
C'
Câu 38. Cho hình hộp chữ nhật
.
ABCD A B C D
có
2cm,
AB
3cm,
AD
7cm.
AC
Thể tích của khối
hộp
.
ABCD A B C D
bằng
A.
3
42cm .
B.
3
36cm .
C.
3
24cm .
D.
3
12cm .
Câu 39. Thể tích của khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
,
C
2 ,
AB a
,
AC a
2
BC a
bằng
A.
3
4 .
a
B.
3
3.
a
C.
3
3
6
a
D.
3
3
2
a
Câu 40. Cho lăng trụ tam giác đều
.
ABC A B C
có diện tích đáy bằng
2
3
4
a
Mặt phẳng
(
)
A BC
hợp với
mặt phẳng đáy một góc
60 .
Thể tích khối lăng trụ
.
ABC A B C
bằng
A.
3
3 3
8
a
B.
3
3
8
a
C.
3
5 3
12
a
D.
3
3 2
8
a
Câu 41. Một hình nón có đường sinh bằng đường kính đáy. Diện tích toàn phần của hình nón bằng
9 .
Chiều
cao của hình nón đã cho bằng
A.
3.
B.
3.
C.
3
2
D.
3
3
Câu 42. Khi quay một tam giác đều cạnh bằng
a
quanh một cạnh của nó ta được một khối tròn xoay. Thể tích
của khối tròn xoay đó bằng
A.
3
4
a
B.
3
3
8
a
C.
3
3
4
a
D.
3
3
24
a
Câu 43. Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh bằng
3.
Tính diện tích xung quanh của hình
nón có đáy là đường tròn ngoại tiếp tứ giác
ABCD
và chiều cao bằng chiều cao của hình chóp.
A.
9
2
B.
9 2
4
C.
9 .
D.
9 2
2
Câu 44.
Cho khối trụ
( )
T
có bán kính đáy
R
và diện tích toàn phần
2
8 .
R
Thể tích của khối trụ
( )
T
bằng
A.
3
3 .
R
B.
3
6 .
R
C.
3
4 .
R
D.
3
8 .
R
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 21 -
A
B
C
D
H
I
B
A
P
R
A
I
H
A
B
D
C
D
O
N
A
C
B
S
Câu 45. Cho hình thang ABCD vuông tại A và ,D có độ dài các cạnh là ,AD a 5 ,AB a 2 .CD a Thể
tích của vật thể tròn xoay khi quay hình thang trên quanh trục AB bằng
A.
3
5 .a
B.
3
6 .a
C.
3
3 .a
D.
3
11 .a
Câu 46. Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh
xq
S
của hình trụ có một đường
tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện .ABCD
A.
xq
16 2
3
S
B.
xq
8 2 .S
C.
xq
16 3
3
S
D.
xq
8 3 .S
Câu 47. Cho hình tròn đường kính 4cmAB quay xung quanh .AB Thể tích khối tròn xoay tạo thành bằng
A.
3
32 cm . B.
3
16 cm .
C.
3
16
cm .
3
D.
3
32
cm .
3
Câu 48. Cho hình cầu đường kính
2 3.a
Mặt phẳng ( )P cắt hình cầu theo thiết diện là hình tròn có bán kính
bằng
2.a
Khoảng cách từ tâm hình cầu đến mặt phẳng ( ).P
A. .a B.
10.a
C.
2
a
D.
10
2
a
Câu 49. Cho hình chóp tam giác đều có cạnh đáy bằng
,a
góc giữa cạnh bên và mặt đáy bằng 45 . Mặt cầu
ngoại tiếp hình chóp có bán kính bằng
A.
3
2
a
B.
3
3
a
C.
3.a
D.
3
5
a
Câu 50. Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước,
có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là .V Biết rằng
khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa khối cầu chìm trong nước
như hình vẽ. Thể tích nước còn lại trong ly bằng
A. .V B.
1
.
V
C.
1
.
3
V D.
1
.
6
V
ĐÁP ÁN ĐỀ SỐ 03
1.C 2.C 3.A 4.D 5.B 6.A 7.B 8.A 9.A 10.D
11.C 12.B 13.A 14.D 15.A 16.B 17.A 18.D 19.C 20.D
21.C 22.C 23.A 24.A 25.D 26.B 27.B 28.A 29.B 30.D
31.D 32.C 33.A 34.D 35.B 36.D 37.A 38.B 39.D 40.A
41.A 42.A 43.D 44.A 45.C 46.A 47.D 48.A 49.B 50.C
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 22 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 04
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Cho hàm số
3 2
1
2.
3
y x x x Khẳng định nào sau đây là đúng ?
A. Hàm số luôn đồng biến trên ( ; ). 
B. Hàm số đồng biến trên khoảng ( ;1), nghịch biến trên khoảng (1; ).
C. Hàm số nghịch biến trên khoảng ( ;1), đồng biến trên khoảng (1; ).
D. Hàm số luôn nghịch biến trên ( ; ). 
Câu 2. Cho bản biến thiên của hàm số
4
y ax bx c
sau:
x

0

y
0
y


2
Bảng biến thiên trên là của hàm số
A.
4 2
2 2.y x x B.
4 2
2 2.y x x
C.
4 2
2 2.y x x D.
4 2
2 1.y x x
Câu 3. Tìm các giá trị của tham số m sao cho hàm số
3 2
6 1y x x mx đồng biến trên (0; ).
A. 12.m
B.
0.m
C.
0 12.m
D.
0.m
Câu 4. Điểm cực tiểu của hàm số
2
2 5 4
2
x x
y
x
là
A. 1.x B. ( 1;1).M
C. 3.x D. ( 3; 7).N
Câu 5. Cho hàm số ( )y f x có đạo hàm trên và đồ thị hàm số ( )y f x
trên như hình bên dưới. Tìm
khẳng định đúng ?
A. Hàm số ( )y f x có 1 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số ( )y f x có 2 điểm cực đại và 2 điểm cực tiểu.
C. Hàm số ( )y f x có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số ( )y f x có 2 điểm cực đại và 1 điểm cực tiểu.
Câu 6. Có bao nhiêu giá trị nguyên của m để hàm số
3
( 2) 2y m x mx không có điểm cực trị ?
A. 1. B. Vô số.
C. 3. D. 5.
Câu 7. Cho hàm số
3 2 2
1 1
(2 1) ( 2) 1.
3 2
y x m x m x Tìm tất cả các giá trị thực của tham số m sao
cho hàm số có hai điểm cực trị
1 2
, x x thỏa
1 2 1 2
3 5( ) 7 0.x x x x
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 23 -
A.
1
4
m B. 2.m
C. 4.m D. 8.m
Câu 8. Gọi , M m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 cos 2
.
cos 2
x
y
x
Khi đó giá trị
của biểu thức 3M m bằng
A. 4. B.
4
.
3
C. 1. D. 3.
Câu 9. Các đường tiệm cận của đồ thị hàm số
5 4
2 3
x
y
x
tạo với hai trục toạ độ một hình chữ nhật có diện
tích bằng
A. 1. B. 2.
C. 3. D.
3
2
Câu 10. Đồ thị hàm số
2
1
2
x
y
x
có tất cả bao nhiêu đường tiệm cận ?
A. 1. B. 3.
C. 2. D. 0.
Câu 11. Cho bảng biến thiên của hàm số bậc ba. Tìm hàm số thỏa mãn bảng biến thiên đã cho.
A.
3 2
3 1.y x x
B.
3 2
2 6 1.y x x
C.
3 2
3 1.y x x
D.
3 2
3 1.y x x
Câu 12. Cho đồ thị hàm số
4 2
y ax bx c như hình vẽ. Tìm mệnh đề đúng ?
A. 0, 0, 0.a b c
B. 0, 0, 0.a b c
C. 0, 0, 0.a b c
D. 0, 0, 0.a b c
Câu 13. Cho đồ thị của hàm số nhất biến như hình vẽ. Hỏi đó là hàm số nào ?
A.
2 1
1
x
y
x
B.
2 1
1
x
y
x
C.
2 1
1
x
y
x
D.
2 1
1
x
y
x
Câu 14. Cho bảng biến thiên của hàm số
4 2
2 4 1.y x x Tìm m để phương trình
4 2
2 4 1x x m
có
8 nghiệm ?
A.
0 1.m
B. 0 1.m
C. 0 1.m
D. 0 1.m
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 24 -
Câu 15. Đồ thị hàm số
2
y x x
và
3
5y
x
cắt nhau tại hai điểm
A
và
.
B
Độ dài
AB
bằng
A.
8 5.
B.
25.
C.
4 2.
D.
10 2.
Câu 16. Giá trị của biểu thức
2016 2016
(1 3) (3 3)
P
bằng
A.
1008
12 .
B.
1008
4 .
C.
1008
(1 3) .
D.
1008
(3 3) .
Câu 17. Cho
0 1
a
và
,
x y
thỏa mãn
log 3
a
x
và
log 2 .
a
y
Khi đó
6
( )log
x y a
bằng
A.
2
( ) .
x y
B.
2( ).
x y
C.
.
x y
D.
1.
Câu 18. Cho
log 3,
a
x
log 4
b
x
với
, 1.
a b
Giá trị của biểu thức
log
ab
P x
bằng
A.
7
12
B.
1
12
C.
12.
D.
12/7.
Câu 19. Tìm tập xác định
D
của hàm số
2
cos
2
6 9
(2 ) ln
1
x x
y x
x
A.
(3; ).

D
B.
(1; ) \ {2; 3}.

D
C.
(1;2).
D
D.
(1; ) \ {3}.

D
Câu 20. Tìm tập xác định
D
của hàm số
e 2
( 1) .
y x x
A.
( 1;1).
D
B.
\ { 1;1}.
D
C.
(1; ).

D
D.
.
D
Câu 21. Hãy tính đạo hàm của hàm số
3
2 3
.
y x x
trên khoảng

A.
6
7
. .
6
x
B.
7
6
7
x
C.
3
4 .
x
D.
9
.
x
Câu 22. Hàm số
2
0,5
log ( 2 )
y x x
đồng biến trên khoảng
A.
(
)
.
;1

B.
(0;1).
C.
(1; ).

D.
(1;2).
Câu 23. Giá trị nhỏ nhất của hàm số
2 2
( 2)e
x
y x
trên đoạn
[ 1;2]
bằng
A.
2
e .
B.
2e.
C.
4
2e .
D.
2
2e .
Câu 24. Giải phương trình
5
3 3 121
x x
được dạng
3
log
x a
với
0.
a
Khẳng định nào đúng ?
A.
0 2.
a
B.
1 3.
a
C.
2 5.
a
D.
4.
a
Câu 25. Số nghiệm của phương trình
2
2
log ( 3) 1 log
x x
là bao nhiêu ?
A.
1.
B.
3.
C.
0.
D.
2.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 25 -
Câu 26. Tích tất cả các nghiệm của phương trình
( 2 1) ( 2 1) 2 2 0
x x
bằng
A.
2.
B.
1.
C.
1
2
D.
1.
Câu 27. Tổng tất cả các nghiệm của phương trình
1
2 4
log (2 1).log (2 2) 1
x x
bằng
A.
2
log 15.
B.
1.
C.
2
15
log
4
D.
3.
Câu 28. Bất phương trình
2 2
log (3 2) log (6 5 )
x x
có tập nghiệm là
( ; ).
a b
Giá trị của
a b
bằng
A.
11
5
B.
31
6
C.
28
15
D.
8
3
Câu 29. Cho hàm số
2
( ) e .
x
f x x
Bất phương trình
( ) 0
f x
có tập nghiệm là
A.
[ 2;2].
B.
( ; 2] [0; ).
 
C.
( ;0] [2; ).
 
D.
[0;2].
Câu 30. Giải bất phương trình
2
3 3
log 2 log (3 ) 1 0
x x
được tập nghiệm
( ; ),
S a b
với
,
a b
là hai số thực
và
.
a b
Giá trị của biểu thức
3
T a b
bằng
A.
3.
B.
3.
C.
11.
D.
28.
Câu 31. Cho
( )
F x
là một nguyên hàm của hàm số
( ) e 2
x
f x x
thỏa mãn
3
(0)
2
F
Tìm
( ).
F x
A.
2
3
e
2
x
x
B.
2
1
2e
2
x
x
C.
2
5
e
2
x
x
D.
2
1
e
2
x
x
Câu 32. Tìm nguyên hàm của hàm số
( ) 2 1.
f x x
A.
1
2 1 .
2
x C
B.
1
(2 1) 2 1 .
3
x x C
C.
1
2 1 .
3
x C
D.
2
(2 1) 2 1 .
3
x x C
Câu 33. Cho hàm số
( )
y f x
xác định trên
\ {0}
thỏa mãn
2
2 ( ) ( ) 1
xf x x f x
và
(1) 0.
f
Phương trình
tiếp tuyến của đồ thị hàm số
( )
y f x
tại giao điểm với trục hoành là
A.
1.
y x
B.
2 2.
y x
C.
.
y x
D.
.
y x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 26 -
A
C
B
S
A
C
B
S
B'
C'
A'
D'
A
B
C
D
A'
B'
C
A
B
C'
D'
C'
B'
A
D
B
C
S
A'
Câu 34. Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
và
3.
SC a
Hai mặt bên
( )
SAB
và
( )
SAC
cùng vuông góc với đáy. Thể tích khối chóp
.
S ABC
bằng
A.
3
2 6
9
a
B.
3
6
12
a
C.
3
3
2
a
D.
3
3
4
a
Câu 35. Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
tam giác
SAB
cân tại
S
và nằm trong
mặt phẳng vuông góc với đáy,
2 .
SA a
Thể tích khối chóp
.
S ABCD
bằng
A.
3
15
6
a
B.
3
15
12
a
C.
3
2
3
a
D.
3
2 .
a
Câu 36. Cho hình chóp đều
.
S ABC
có cạnh bằng
,
a
mặt bên hợp với đáy một góc
60
.
Thể tích của khối
chóp
.
S ABC
bằng
A.
3
3
12
a
B.
3
3
72
a
C.
3
3
24
a
D.
3
3
6
a
Câu 37. Cho hình lập phương
.
ABCD A B C D
có diện tích tam giác
ACD
bằng
2
3 .
a
Thể tích của hình
lập phương đã cho bằng
A.
3
3 3 .
a
B.
3
2 2 .
a
C.
3
.
a
D.
3
8 .
a
Câu 38. Tính thể tích của khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
,
C
2 ,
AB a
,
AC a
2 .
BC a
A.
3
4 .
a
B.
3
4 /3.
a
C.
3
3
2
a
D.
3
3
6
a
Câu 39. Cho hình lăng trụ tam giác
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
,
A
,
AB a
3.
AC a
Hình chiếu vuông góc của
A
lên
( )
ABC
là trung điểm của
.
BC
Góc giữa
AA
và
( )
ABC
bằng
60 .
Thể tích của khối lăng trụ đã cho bằng
A.
3
2
a
B.
3
3
2
a
C.
3
3
2
a
D.
3
3 3
2
a
Câu 40. Cho hình chóp tứ giác
.
S ABCD
có thể tích bằng
.
V
Lấy điểm
A
trên cạnh
SA
sao cho
3 .
SA SA
Mặt phẳng qua
A
và song song với đáy của hình chóp cắt các cạnh
,
SB
,
SC
SD
lần lượt tại
, , .
B C D
Thể tích khối chóp
.
S A B C D
bằng
A.
3
V
B.
81
V
C.
9
V
D.
27
V
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 27 -
A
B
S
A
C
B
A
B
D
C
Câu 41. Hình nón có thiết diện qua trục là một tam giác cân có góc ở đỉnh bằng 120 và có cạnh bên bằng
.
a
Diện tích xung quanh của hình nón đó bằng
A.
2
3
2
a
B.
2
3.a
C.
2
.a D.
2
2 3.a
Câu 42. Cho tam giác ABC vuông tại , ,A AB a
3.AC a
Quay tam giác đó quanh đường thẳng BC
ta được khối tròn xoay. Tính thể tích V của khối tròn xoay này ?
A.
3
2
a
B.
3
4
a
C.
3
2
3
a
D.
3
3
a
Câu 43. Cho hình chóp tứ giác đều .S ABCD có các cạnh đều bằng
2.a
Thể tích khối nón có đỉnh S và
đường tròn đáy là đường tròn nội tiếp tứ giác ABCD bằng
A.
2
2
6
a
B.
3
2
2
a
C.
3
.a D.
3
6
a
Câu 44. Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có
4 ,
AB a
3 .BC a Thể tích của khối trụ đã cho bằng
A.
3
12 .a
B.
3
16 .a
C.
3
4 .a
D.
3
8 .a
Câu 45. Cho hình thang ABCD vuông tại A và ,D ,AD CD a 2 .AB a Quay hình thang ABCD
quanh đường thẳng .CD Thể tích khối tròn xoay thu được bằng
A.
3
7
3
a
B.
3
.a
C.
3
4
3
a
D.
3
5
3
a
Câu 46. Cho hình chóp tứ giác đều .S ABCD có tất cả các cạnh đều bằng 4. Tính diện tích xung quanh của
hình trụ có một đường tròn đáy là đường tròn nội tiếp tứ giác ABCD và chiều cao bằng chiều cao
hình chóp .S ABCD đỉnh .S
A.
xq
16 2 .S
B.
xq
8 2 .S
C.
xq
16 3 .S
D.
xq
8 3 .S
Câu 47. Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi , I J lần lượt là
trung điểm của , .AB CD Biết 4AB và 6.AD Thể tích của vật thể tròn xoay khi quay mô hình
trên quanh trục IJ bằng
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 28 -
A.
56
3
B.
104
3
C.
40
3
D.
88
3
Câu 48. Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng
1 m
và
1, 4 m.
Chủ cơ sở dự định làm một bể nước mới, hình trụ, có cùng chiều cao và có thể tích bằng
tổng thể tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kể quả nào
dưới đây ?
A.
1,7 m.
B.
1,5 m.
C.
1,9 m.
D.
2, 4 m
Câu 49. Cho mặt cầu
( )
S
tâm
,
O
bán kính
3.
R
Mặt phẳng
( )
P
cách
O
một khoảng bằng
1
và cắt
( )
S
theo
giao tuyến là đường tròn
( )
C
có tâm
.
H
Gọi
T
là giao điểm của tia
HO
với
( ).
S
Thể tích của khối
nón có đỉnh
T
và đáy là hình tròn
( )
C
bằng
A.
32
3
B.
16
3
C.
32 .
D.
16 .
Câu 50. Cho chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
C
với
,
CA CB a
3,
SA a
5
SB a
và
2.
SC a
Bán kính
R
của mặt cầu ngoại tiếp chóp
.
S ABC
bằng
A.
11
6
a
B.
11
2
a
C.
11
3
a
D.
11
4
a
ĐÁP ÁN ĐỀ SỐ 04
1.D 2.C 3.A 4.A 5.A 6.C 7.B 8.A 9.C 10.B
11.D 12.B 13.C 14.A 15.C 16.A 17.D 18.D 19.B 20.C
21.A 22.D 23.A 24.B 25.A 26.B 27.C 28.A 29.D 30.D
31.D 32.B 33.A 34.B 35.A 36.C 37.B 38.C 39.C 40.D
41.A 42.A 43.D 44.A 45.D 46.B 47.D 48.A 49.A 50.B
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 29 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 05
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Hàm số
2
1
1
mx m
y
x
với
m
là tham số. Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên
\ { 1}.
B. Hàm số đồng biến trên
.
C. Hàm số nghịch biến trên các khoảng xác định.
D. Hàm số đồng biến trên các khoảng xác định.
Câu 2. Hàm số nào sau đây có bảng biến thiên như hình bên dưới ?
x

1

y
y

2
2

A.
2 3
1
x
y
x
B.
2 3
1
x
y
x
C.
2 3
1
x
y
x
D.
1
2
x
y
x
Câu 3. Tìm tham số
m
sao cho hàm số
cos 2
cos
x
y
x m
đồng biến trên khoảng
0;
2
A.
0
m
hoặc
1 2.
m
B.
0.
m
C.
1 2.
m
D.
2.
m
Câu 4. Một hàm số
( )
f x
có đạo hàm là
2 3 5
( ) ( 1) ( 2) ( 3) .
f x x x x x
Hỏi hàm số
( )
f x
có tất cả bao nhiêu
điểm cực trị ?
A.
4.
B.
3.
C.
2.
D.
1.
Câu 5. Hàm số
3 2
1
3
2
y x x x
đạt cực trị tại
2
điểm
1 2
, .
x x
Tính tổng
2 2
1 2
.
S x x
A.
11
3
S
B.
13
3
S
C.
1
2
S
D.
3
2
S
Câu 6. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
4 2 2
( 2) 2
y mx m x
có hai cực tiểu
và một cực đại.
A.
2.
m
B.
2 0.
m
C.
2.
m
D.
0 2.
m
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 30 -
Câu 7. Cho hàm số
3 2
1
( 1) ( 2) ( 3) 1.
3
y m x m x m x
Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số có
2
điểm cực trị
1 2
,
x x
thỏa
1 2
(4 1)(4 1) 18.
x x
A.
1.
m
B.
4.
m
C.
7.
m
D.
8.
m
Câu 8. Giá trị nhỏ nhất của hàm số
tan 1
tan 2
x
y
x
trên
0;
4
bằng
A.
0;
4
1
min
2
y
B.
0;
4
1
min
2
y
C.
0;
4
1
min
3
y
D.
0;
4
1
min
3
y
Câu 9. Giá trị lớn nhất của hàm số
3
2
cos
cos 3 cos 1
3
x
y x x
trên
4
;
3 3
bằng
A.
4
;
3 3
65
max
24
y
B.
4
;
3 3
5
max
24
y
C.
4
;
3 3
2
max
3
y
D.
4
;
3 3
2
max
3
y
Câu 10. Tìm tọa độ giao điểm
I
của hai đường tiệm cận của đồ thị hàm số
2 1
2
x
y
x
A.
( 2;2).
I
B.
(2;2).
I
C.
(2; 2).
I
D.
( 2; 2).
I
Câu 11. Số đường tiệm cận đứng của đồ thị hàm số
2
3 2
1
x
y
x
là bao nhiêu ?
A.
0.
B.
1.
C.
3.
D.
2.
Câu 12. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ?
A.
4 2
3 1.
y x x
B.
3 2
3 1.
y x x
C.
3 2
3 1.
y x x
D.
4 2
3 1.
y x x
Câu 13. Cho đồ thị hàm số
3 2
.
y ax bx cx d
Tìm mệnh đề đúng ?
A.
0, .
y x
B.
0, .
y x
C.
0, 1.
y x
D.
0, 1.
y x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 31 -
1
x
y
1
O
Câu 14. Cho đồ thị hàm số
1
ax b
y
x
như hình vẽ. Tìm khẳng định đúng ?
A.
0 .b a
B.
0 .a b
C.
0.a b
D.
0 .b a
Câu 15. Cho bảng biến thiên của hàm số
3 2
( ) .y f x ax bx cx d Tìm tham số m để phương trình
( )f x m có 4 nghiệm phân biệt thỏa mãn
1 2 3 4
1
.
2
x x x x
A.
0 1.m
B.
1
1.
2
m
C. 0 1.m
D.
1
1.
2
m
Câu 16. Viết phương trình tiếp tuyến của đường cong
4 2
3
( ) : 1,
2
C y x x biết tiếp tuyến vuông góc với
đường thẳng : 8 16 0.d x y
A.
13
8
2
y x B.
13
8
2
y x
C.
13
8
2
y x D.
13
8
2
y x
Câu 17. Đồ thị của hàm số
4 2
2y x x cắt trục hoành tại bao nhiêu điểm ?
A. 0. B. 2.
C. 4. D. 3.
Câu 18. Với
0 a b
thì giá trị của biểu thức
1
2
( ) (4 )T a b ab
bằng
A.
.a b
B. .b a
C. .b a
D. .a b
Câu 19. Cho , 0a b thỏa mãn
2
8 4
log log 5a b và
2
4 8
log log 7.a b Giá trị .a b bằng
A.
9
2 . B. 8.
C.
18
2 . D. 2.
Câu 20. Cho , 1x y thỏa
2 2
9 6 .x y xy Tính giá trị của
12 12
12
1 log log
2 log ( 3 )
x y
I
x y
A.
1
4
I B. 1.I
C.
1
2
I D.
1
3
I
Câu 21. Tìm tập xác định D của hàm số
2
2018 2
(2 3) 2018 .
x
y x x
A. ( 2; 2]. D B. ( 2; 2). D
C. [ 2; 2]. D D. ( ; 2].  D
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 32 -
Câu 22. Tìm tập xác định
D
của hàm số
1
2
1
log
x
y
x
A.
(1; ).

D
B.
( ;0) (1; ).
 
D
C.
(0;1).
D
D.
\ {0}.
D
Câu 23. Hãy tính đạo hàm của hàm số
4
1
y
x x
trên khoảng

A.
4
9
5
4
x
B.
4
2
1
x x
C.
4
5
.
4
x
D.
4
5
1
4
x
Câu 24. Cho hàm số
2
ln( 1)
( )
x
f x
x
Biết rằng
(1) ln 2
f a b
với
, .
a b
Tìm
.
a b
A.
1.
a b
B.
1.
a b
C.
2.
a b
D.
2.
a b
Câu 25. Hỏi hàm số
2
4 4
e
x x
y
đồng biến trên những khoảng nào sau đây ?
A.
( ; ).
 
B.
( ;2) (2; ).
 
C.
(2; ).

D.
( ;2)

và
(2; ).

Câu 26. Cho hàm số
3 2
2 2 2
( ) 8 log 6 log 12 log 3.
f x x x x
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
trên đoạn
1
;4
4
lần lượt là
A.
19
và
61.
B.
19
và
60.
C.
23
và
64.
D.
23
và
60.
Câu 27. Cho
2
3
( ) .
x x
f x e
Biết phương trình
( ) 0
f x
có hai nghiệm
1 2
, .
x x
Tính
1 2
.
x x
A.
1 2
9
4
x x
B.
1 2
7
4
x x
C.
1 2
3
2
x x
D.
1 2
3.
x x
Câu 28. Tìm nghiệm của phương trình
3 1
2
log (3 1) 3.
x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 33 -
A.
2.
x
B.
1.
x
C.
3.
x
D.
8.
x
Câu 29. Gọi
1 2
,
x x
1 2
( )
x x
là hai nghiệm của
1
2 1
1
3
( 17 4) ( 17 4) .
x
x
x
x
Giá trị của
1
2
x
x
là
A.
7 2 6
5
B.
7 2 6
5
C.
1 6
5
D.
1 6
5
Câu 30. Biết phương trình
(7 4 3) (2 3) 6
x x
có nghiệm dạng
2
log
a
x b
với
,
a b
là số dương.
Tổng
2 2
a b
bằng
A.
13.
B.
8.
C.
7.
D.
11.
Câu 31. Cho phương trình
2
0,5 2
log ( 6 ) log (3 2 ) 0.
m x x x
Có mấy giá trị nguyên dương của tham số
m
để phương trình đã cho có nghiệm ?
A.
17.
B.
18.
C.
23.
D.
15.
Câu 32. Tìm tập nghiệm
S
của bất phương trình
2
3 2 .
x x
A.
(0; ).
x

B.
2
(0; log 3).
x
C.
3
(0; log 2).
x
D.
(0;1).
x
Câu 33. Gọi
S
là tập nghiệm của bất phương trình
2 2
log (2 5) log ( 1).
x x
Hỏi trong tập
S
có bao nhiêu
phần tử là số nguyên dương bé hơn
10.
A.
9.
B.
15.
C.
8.
D.
10.
Câu 34. Tìm tập nghiệm của bất phương trình
2 2
log (2 3) log (3 )
m m
x x x x
với
m
là tham số thực
dương khác
1,
biết
1
x
là một nghiệm của bất phương trình đã cho.
A.
1
( 2;0) ;3
3
B.
1
[ 1;0] ; 3
3
C.
( 1;0) (1;3].
D.
1
[ 1;0) ; 3
3
Câu 35. Giải bất phương trình
1
2 1
2
log (2 1).log (2 2) 2
x x
ta được tập nghiệm có dạng
( ; ),
S a b
với
,
a b
là các số thực và
.
a b
Tính giá trị của biểu thức
.
T a b
A.
1.
T
B.
2
15
log
2
T
C.
2
3
log
2
T
D.
2
log 5.
T
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 34 -
Câu 36. Cho hình chóp tứ giác
.
S ABCD
có đáy
ABCD
là hình vuông, cạnh bên
SA
vuông góc với mặt đáy
và
3.
SA AC a
Tính thể tích
V
của khối chóp
. ?
S ABCD
A.
3
2 .
V a
B.
3
3
2
a
V
C.
3
6
2
a
V
D.
3
6
3
a
V
Câu 37. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
,
B
,
AB a
( ).
SA ABC
Cạnh bên
SB
hợp với đáy một góc
45 .
Tính thể tích
V
của khối chóp
. .
S ABC
A.
3
3
3
a
V
B.
3
3
a
V
C.
3
2
6
a
V
D.
3
6
a
V
Câu 38. Cho hình chóp tứ giác đều
. ,
S ABCD
cạnh đáy
2 3,
AB a
mặt bên tạo với đáy góc
60 .
Tính thể
tích
V
của khối chóp
. .
S ABCD
A.
3
8 .
V a
B.
3
12 .
V a
C.
3
9 .
V a
D.
3
12 3 .
V a
Câu 39. Cho hình hộp chữ nhật
.
ABCD A B C D
có đáy là hình vuông, cạnh bên
3
AA a
và đường chéo
5 .
AC a
Tính thể tích
V
của khối hộp
. .
ABCD A B C D
A.
3
.
V a
B.
3
24 .
V a
C.
3
8 .
V a
D.
3
4 .
V a
Câu 40. Cho hình lăng trụ đứng tam giác
.
ABC A B C
có đáy là
ABC
đều cạnh
4
a
và biết diện tích
tam giác
A BC
bằng
8.
Tính thể tích
V
của khối lăng trụ
. .
ABC A B C
A.
2 3.
V
B.
4 3.
V
C.
6 3.
V
D.
8 3.
V
Câu 41. Cho lăng trụ
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật tâm
O
và
,
AB a
3,
AD a
A O
vuông góc với đáy
( ).
ABCD
Cạnh bên
AA
hợp với mặt đáy
( )
ABCD
một góc
45 .
Tính theo
a
thể
tích
V
của khối lăng trụ đã cho.
A.
3
3
6
a
V
B.
3
6
2
a
V
C.
3
3
3
a
V
D.
3
3 .
V a
Câu 42. Hình nón có chiều cao
10 3cm,
góc giữa một đường sinh và mặt đáy bằng
60 .
Diện tích xung quanh
của hình nón đó bằng
A.
2
100 cm .
B.
2
200 cm .
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 35 -
l
r
h
O
C
A
B
D
A
B
M
O
O’
h
r
h
A
B
C
D
E
F
O
O
C.
2
50 3 cm .
D.
2
100 3 cm .
Câu 43. Cho hình thoi ABCD cạnh bằng ,a có góc
60 .ABC Quay hình thoi này quanh đường chéo
,
BD
ta thu được khối tròn xoay có thể tích bằng
A.
3
2.a
B.
3
3
12
a
C.
3
3
6
a
D.
3
2 3.a
Câu 44. Cho hình chóp tứ giác đều .S ABCD có cạnh bên
2SA a
và .AB a Thể tích của khối nón có
đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tứ giác ABCD bằng
A.
3
6
12
a
B.
3
2
6
a
C.
3
.a
D.
3
2
2
a
Câu 45. Cho hình trụ có trục ,OO
thiết diện qua trục là một hình vuông cạnh 2 .a Mặt phẳng ( )P song song
với trục và cách trục một khoảng
2
a
Tính diện tích thiết diện
td
S của trụ cắt bởi mặt phẳng ( ).P
A.
2
5 5cm .S
B.
2
6 5cm .S
C.
2
3 5cm .S
D.
2
10 5cm .S
Câu 46. Cho lục giác đều ABCDEF có cạnh bằng 4. Quay lục giác đều đó quanh đường thẳng .AD Thể tích
V của khối tròn xoay được sinh ra bằng
A. 32 .V
B.
128
3
V
C.
111
2
V
D. 64 .V
Câu 47. Cho hình lăng trụ tứ giác đều . .ABCD EFGH Tính tỉ số k giữa thể tích khối trụ ngoại tiếp và thể tích
khối trụ nội tiếp hình lăng trụ trên.
A.
2.k
B. 2.k
C.
2 2.k
D. 4.k
Câu 48. Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm ,O AD là đường kính của đường
tròn tâm .O Thể tích V của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên dưới) quay
quanh đường thẳng AD bằng bao nhiêu ?
M
ặ
t c
ắ
t song song đáy
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 36 -
A
B
C
D
H
O
M N
I
A.
3
23 3
126
a
B.
3
3
24
a
C.
3
20 3
217
a
D.
3
4 3
27
a
Câu 49. Cho mặt cầu ( )S có tâm ,I bán kính
5.R
Một đường thằng cắt ( )S tại hai điểm , M N nhưng
không đi qua .I Đặt 2 .MN m Để diện tích tam giác IMN lớn nhất thì m bằng
A.
3 2.m
B.
10.m
C.
5.m
D.
5 2
2
m
Câu 50. Cho hình chóp .S ABC có ( ),SA ABC 2 .SA a Tam giác ABC cân tại A có
2 2,
BC a
1
cos
3
ACB Tính diện tích của mặt cầu ngoại tiếp hình chóp . .S ABC
A.
2
65
4
a
S
B.
2
13 .S a
C.
2
97
4
a
S
D.
2
4 .S a
ĐÁP ÁN ĐỀ 05
1.D 2.B 3.D 4.B 5.B 6.D 7.C 8.A 9.C 10.A
11.B 12.D 13.D 14.B 15.B 16.D 17.D 18.C 19.A 20.B
21.C 22.B 23.A 24.C 25.C 26.A 27.B 28.B 29.B 30.B
31.A 32.C 33.C 34.D 35.B 36.B 37.D 38.B 39.B 40.D
41.D 42.B 43.B 44.A 45.D 46.D 47.B 48.A 49.D 50.C
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 37 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 06
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Tìm tham số
m
để hàm số
1
x m
y
x
đồng biến trên từng khoảng xác định của nó.
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 2. Tìm
m
để hàm số
1
x
y
x m
nghịch biến trên khoảng
( ;2).
A.
(1, ).
B.
[1, ).

C.
(2, ).
D.
[2, ).
Câu 3. Tìm tham số
m
sao cho hàm số
4 cos 1
cos
x
y
x m
đồng biến trên khoảng
0;
3
A.
0
m
hoặc
1 1
4 2
m
B.
1 1
4 2
m
hoặc
1.
m
C.
1
4
m
D.
0
m
hoặc
1
1.
4
m
Câu 4. Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
3 2
1
4
3
y x mx x m
đồng biến
trên khoảng
( ; ).

A.
4.
B.
3.
C.
2.
D.
5.
Câu 5. Tìm tham số
m
sao cho hàm số
3 2 2
3 3( 1)
y x x m x
đồng biến trên khoảng
(1;2).
A.
2 2.
m
B.
2
m
hoặc
2.
m
C.
2 2.
m
D.
2
m
hoặc
2.
m
Câu 6. Có bao nhiêu giá trị nguyên
( 20;20)
m
để hàm số
3
3
5 45
9
3
2
y x mx
x
đồng biến
(0; ).
A.
20.
B.
21.
C.
22.
D.
23.
Câu 7. Tìm
m
sao cho hàm số
sin
y x mx
luôn đồng biến trên
( ; ).

A.
1.
m
B.
1.
m
C.
1 1.
m
D.
1.
m
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 38 -
O
x
y
Câu 8. Tìm tham số m để hàm số
3 2
3 ( 1) 2y x x m x có hai điểm cực trị.
A. 2.m B.
2.m
C.
2.m
D.
4.m
Câu 9. Tìm tất cả các giá trị thực của m để đồ thị hàm số
4 2
2 3y x mx m có ba điểm cực trị tạo
thành một tam giác cân.
A. 0.m B.
1.m
C. 0.m D.
3.m
Câu 10. Tìm tham số m để đồ thị hàm số
3 2
2 3( 1) 6( 2) 1y x m x m x có cực đại, cực tiểu thỏa
mãn
CT
2.x x
CĐ
A.
1.m
B.
2.m
C.
1.m
D.
2.m
Câu 11. Cho hàm số ( )y f x xác định trên \ { 1}, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình sau
x
 1 3

y
0
y
2



4
Tìm tham số thực m sao cho phương trình ( )f x m có đúng ba nghiệm thực phân biệt
A. ( 4;2).m B. [ 4;2).m
C. ( 4;2].m D. ( ;2].m 
Câu 12. Cho đồ thị hàm số ( )y f x như hình vẽ. Tìm tất cả các giá trị thực m để phương trình
( ) 1f x m có ba nghiệm phân biệt.
A. 0 5.m
B.
1 5.m
C.
1 4.m
D.
0 4.m
Câu 13. Đường cong hình bên là đồ thị hàm số
4 2
y ax bx c với , , a b c là các số thực. Mệnh đề nào
dưới đây đúng ?
A. 0,a 0,b 0.c
B. 0,a 0,b 0.c
C. 0,a 0,b 0.c
D. 0,a 0,b 0.c
Câu 14. Cho hàm số
3 2
y ax bx cx d có đồ thị như hình. Mệnh đề nào đúng ?
A. 0, 0, 0, 0.a b c d
B. 0, 0, 0, 0.a b c d
C. 0, 0, 0, 0.a b c d
D. 0, 0, 0, 0.a b c d
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 39 -
O
x
y
2
1
Câu 15. Cho hàm số
1
ax
y
bx c
có đồ thị như hình vẽ bên dưới. Giá trị của
a b c
bằng
A.
2.
B.
4.
C.
3.
D.
1.
Câu 16. Cho hàm số
2
( ) 3
x m
f x
thỏa mãn
(1) 18 ln 3.
f
Khẳng định nào đúng ?
A.
2.
m
B.
3 0.
m
C.
0 2.
m
D.
3.
m
Câu 17. Cho hàm số
2
ln
x
y
x
với
0.
x
Mệnh đề nào sau đây đúng ?
A.
2
1
ln .
2
xy x y x
B.
2
2 ln .
xy x y x
C.
2
1
ln .
2
xy x y x
D.
2
2 ln .
xy x y x
Câu 18. Cho hàm số
2018
( ) ln
1
x
f x
x
Tính
(1) (2) (2017) (2018).
S f f f f
A.
2018
2019
S
B.
1.
S
C.
ln 2018.
S
D.
2018.
S
Câu 19. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 45 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử ?
A.
13.
B.
3.
C.
6.
D.
4.
Câu 20. Tìm
m
để
4 2 .2 2 0
x x
m m
có
2
nghiệm phân biệt
1 2
,
x x
thỏa
1 2
3.
x x
A.
1.
m
B.
3.
m
C.
4.
m
D.
2.
m
Câu 21. Tìm giá trị thực của tham số
m
để phương trình
2
3 3
log log 2 7 0
x m x m
có hai nghiệm thực
1 2
,
x x
thỏa mãn
1 2
81.
x x
A.
4.
m
B.
4.
m
C.
81.
m
D.
44.
m
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 40 -
l
O
A
B
C
D
Câu 22. Tìm
m
để phương trình
2
25 2.10 .4 0
x x x
m
có
2
nghiệm trái dấu.
A.
( 1;0) (0;1).
B.
( ;1].

C.
( ; 1) (1; ).
 
D.
( 1; ).
Câu 23. Cho phương trình
2
0,5 2
log ( 6 ) log (3 2 ) 0.
m x x x
Có bao nhiêu giá trị nguyên dương của
tham số
m
để phương trình đã cho có nghiệm ?
A.
17.
B.
18.
C.
23.
D.
15.
Câu 24. Có bao nhiêu giá trị nguyên của
m
để phương trình
1
9 3 0
x x
m
có nghiệm thuộc
(0;1).
A.
11.
B.
12.
C.
13.
D.
14.
Câu 25. Cho phương trình
2 2 2
2 3 2 2
3 9 3 3 .
x x m x x x x m
Có mấy giá trị nguyên của tham số
[ 2018;2018]
m
để phương trình đã cho có
4
nghiệm phân biệt ?
A.
2018.
B.
2019.
C.
2020.
D.
2021.
Câu 26. Có bao nhiêu giá trị nguyên của
m
để phương trình
2 2 sin sin
m m x x
có nghiệm thực ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 27. Cho tứ diện đều
ABCD
cạnh
.
a
Diện tích xung quanh của hình nón đỉnh
A
và đường tròn đáy là
đường tròn ngoại tiếp tam giác
BCD
là
A.
2
3
.
3
a
B.
2
.
a
C.
2
3 .
a
D.
2
2 3 .
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 41 -
A
B
C
D
A
B
C
D
O
O
Câu 28. Cho hình chóp tam giác đều
.S ABC
có các cạnh đều bằng .a Tính thể tích
V
của khối nón có đỉnh
S
và đường tròn đáy là đường tròn nội tiếp tam giác
.ABC
A.
3
2
a
V
B.
3
6
108
a
V
C.
3
.V a
D.
3
2
2
a
V
Câu 29. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
,a
cạnh bên hợp với đáy một góc
60 .
Hình
nón có đỉnh là
,S
đáy là đường tròn nội tiếp tứ giác
ABCD
có diện tích xung quanh bằng
A.
2
1,5 .a
B.
2
6
.
4
a
C.
2
( 7 1)
4
a
D.
2
7
4
a
Câu 30. Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
3.
Tính diện tích xung quanh của hình
nón có đáy là đường tròn ngoại tiếp tứ giác
ABCD
và chiều cao bằng chiều cao của hình chóp.
A.
xq
4 .
S
B.
xq
9 2 .S
C.
xq
9 .S
D.
xq
9 2
2
S
Câu 31. Cho hình lập phương .ABCD A B C D
có cạnh bằng .a Gọi
S
là diện tích xung quanh hình trụ có
hai đường tròn đáy ngoại tiếp hai hình vuông
ABCD
và .A B C D
Diện tích
S
bằng
A.
2
.a
B.
2
2 .a
C.
2
3 .a
D.
2
2
2
a
Câu 32. Cho hình lăng trụ tam giác đều .ABC A B C
có độ dài cạnh đáy bằng
,a
chiều cao là
.h
Tính thể
tích
V
của khối trụ ngoại tiếp hình lăng trụ.
A.
2
9
a h
V
B.
2
3 .V a h
C.
2
.V a h
D.
2
3
a h
V
Câu 33. Cho hình lăng trụ đều .ABC A B C
có cạnh đáy bằng
3,
a
cạnh bên bằng 4 .a Thể tích của hình
trụ có hai đáy nội tiếp hình lăng trụ bằng
A.
3
18
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 42 -
R
r
h
B.
3
6
a
C.
3
.a
D.
3
12
a
Câu 34. Khi quay một tam giác đều cạnh bằng a quanh một cạnh của nó ta được một khối tròn xoay. Thể
tích của khối tròn xoay đó bằng
A.
3
4
a
B.
3
3 .a
C.
3
3
4
a
D.
3
3
24
a
Câu 35. Cho tam giác ABC có 3,AB 5,BC 7.CA Tính thể tích V của khối tròn xoay sinh ra do
hình tam giác ABC quay quanh đường thẳng .AB
A. 50 .V
B.
75
4
V
C.
275
8
V
D.
125
8
V
Câu 36. Trong không gian, cho hình thang
ABCD
vuông tại
A
và ,D có độ dài các cạnh là ,AD a
5 ,AB a
2 .CD a
Tính thể tích
V
của vật thể tròn xoay khi quay hình thang trên quanh trục
.AB
A.
3
5 .V a
B.
3
6 .V a
C.
3
3 .V a
D.
3
11 .V a
Câu 37. Cho hình cầu bán kính bằng 5cm, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo thành
là một đường tròn đường kính 4cm. Tính thể tích khối nón có đáy là thiết diện vừa tạo và đỉnh là
tâm của hình cầu đã cho.
A.
3
19,18cm .
B.
3
19,20cm .
C.
3
19,21cm .
D.
3
19,19cm .
Câu 38. Cho khối cầu tâm O bán kính 6. Mặt phẳng ( )P cách O một khoảng x cắt khối cầu theo một hình
tròn ( ).C Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn ( ).C Biết khối nón có thể tích lớn
nhất, khi đó giá trị của x bằng
A. 2.x
B. 1.x
C.
3 2.x
D.
6 2.x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 43 -
O
O’
I
A
R
h
r
Câu 39. Cho hình trụ có chiều cao bằng
4
nội tiếp trong hình cầu bán kính bằng
3.
Tính thể tích
V
của khối
trụ này.
A.
40 .
V
B.
20 .
V
C.
36 .
V
D.
20
3
V
Câu 40. Cho mặt cầu
( )
S
bán kính
R
không đổi (cho trước). Một hình trụ có chiều cao
h
và bán kính đáy
r
thay đổi nội tiếp mặt cầu. Tính chiều cao
h
theo
R
sao cho diện tích xung quanh của hình trụ lớn
nhất.
A.
2.
h R
B.
3
2
R
h
C.
3
2
R
h
D.
2
2
R
h
Câu 41. Hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
,
A
SA
vuông góc với mặt phẳng
( ),
ABC
,
SA a
,
AB b
.
AC c
Tính bán kính
R
của mặt cầu ngoại tiếp
. .
S ABC
A.
2 2 2
.
R a b c
B.
2 2 2
.
2
R a b c
C.
2 2 2
.
2
a b c
R
D.
2( )
3
a b c
R
Câu 42. Cho hình chóp
.
S ABC
có đáy là tam giác
ABC
đều cạnh
3 ,
a
cạnh bên
2
SA a
và
SA
vuông góc
với mặt phẳng đáy. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
. .
S ABC
A.
2 3
3
a
R
B.
3 .
R a
C.
2 .
R a
D.
13
2
a
R
Câu 43. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật với
3 ,
AB a
4 ,
BC a
12
SA a
và
SA
vuông
góc với đáy. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
. .
S ABCD
A.
5
2
a
R
B.
17
2
a
R
C.
6 .
R a
D.
13
2
a
R
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng
,
a
góc giữa cạnh bên và mặt đáy bằng
60 .
Tính bán
kính mặt cầu ngoại tiếp hình chóp đã cho.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 44 -
D
O
N
A
C
B
S
O
H
D
B
A
C
S
R
2
R
1
O
D
B
C
A
S
A.
2
3
a
B. 2 .a
C.
2 3
3
a
D.
4 3
3
a
Câu 45. Cho hình chóp tứ giác đều .S ABCD có cạnh đáy bằng
3 2 ,a
cạnh bên bằng 5 .a Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp . .S ABCD
A.
3.R a
B.
2.R a
C.
25
8
a
R
D.
2 .R a
Câu 46. Cho hình chóp .S ABCD đáy là hình vuông cạnh ,a tam giác SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt đáy. Bán kính
R
của mặt cầu ngoại tiếp hình chóp .S ABCD bằng
A.
30
3
a
B.
30
6
a
C.
5
2
a
D.
21
6
a
Câu 47. Cho hình chóp .S ABC có SA vuông góc với mặt phẳng ( ),ABC ,SA a ,AB a 2 ,AC a
60 .BAC Diện tích của hình cầu ngoại tiếp hình chóp .S ABC bằng
A.
2
5
3
a
B.
2
20 .a
C.
2
5 .a
D.
2
20
3
a
Câu 48. Cho hình chóp .S ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB nằm trong mặt phẳng
vuông góc với đáy và có
, 3, 60 .AB a BC a ASB Diện tích của mặt cầu ngoại tiếp hình
chóp .S ABCD bằng
A.
2
13
2
a
B.
2
13
3
a
C.
2
11
2
a
D.
2
11
3
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 45 -
A
B
C
A
B
C
I
Câu 49. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
và
.
BC a
Cạnh bên
SA
vuông
góc với đáy
( ).
ABC
Gọi
,
H K
lần lượt là hình chiếu vuông góc của
A
lên cạnh bên
SB
và
.
SC
Thể tích của khối cầu ngoại tiếp hình chóp
.
A HKB
bằng
A.
3
2
a
B.
3
2
3
a
C.
3
2 .
a
D.
3
6
a
Câu 50. Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông cân tại
,
A
,
AB AC a
2 .
AA a
Thể tích khối cầu ngoại tiếp hình tứ diện
AB A C
là
A.
3
.
a
B.
3
4
3
a
C.
3
3
a
D.
3
4 .
a
ĐÁP ÁN ĐỀ 06
1.B 2.D 3.B 4.C 5.C 6.C 7.D 8.B 9.C 10.C
11.A 12.B 13.C 14.A 15.A 16.D 17.B 18.A 19.B 20.C
21.B 22.A 23.A 24.C 25.C 26.C 27.A 28.B 29.D 30.D
31.B 32.D 33.C 34.A 35.B 36.C 37.B 38.A 39.B 40.A
41.C 42.C 43.D 44.A 45.C 46.D 47.C 48.B 49.B 50.B
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 46 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 07
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
4
x m
y
mx
đồng biến trên từng khoảng xác
định ?
A.
2.
B.
4.
C.
3.
D.
5.
Câu 2. Tìm tham số
m
để hàm số
9
mx
y
x m
đồng biến trên khoảng

(2; ).
A.
3 2.
m
B.
3 2.
m
C.
2.
m
D.
2 3.
m
Câu 3. Tìm tham số
m
để hàm số
2 cos 3
2 cos
x
y
x m
nghịch biến trên khoảng
0;
3
A.
( 3;1] [2; ).
m

B.
( ; 3] [2; ).
m
C.
( ; 3).
m
D.
( 3; ).
m

Câu 4. Có bao nhiêu giá trị nguyên của
m
để hàm số
3 2
1
(3 2) 1
3
y x mx m x
nghịch biến trên
( ; ).

A.
2.
B.
4.
C.
7.
D. Vô số.
Câu 5. Tìm
m
sao cho hàm số
3 2
3 3 201
y x x mx
nghịch biến trên
(0; ).

A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 6. Tìm
m
sao cho hàm số
sin ( 4)
y x m x
luôn đồng biến trên
( ; ).

A.
2.
m
B.
2.
m
C.
2 2.
m
D.
2.
m
Câu 7. Có bao nhiêu giá trị nguyên dương của
m
để hàm số
4 2
4
3 1
( 1)
4
4
y x m x
x
đồng biến trên
khoảng

A.
1.
B.
2.
C.
3.
D.
4.
Câu 8. Có bao nhiêu số nguyên của tham số
m
để hàm số
4 2 2
2( 5) 4
y mx m x
có ba điểm cực trị,
trong đó có đúng
2
điểm cực tiểu và
1
điểm cực đại ?
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 47 -
A.
2.
B.
4.
C. 5. D.
3.
Câu 9. Cho
3 2 2
( 3) 2( 1) ( 4) 1.y m x m m x m x Gọi
S
là tập tất cả các giá trị nguyên của m
để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục .Oy Hỏi
S
có bao nhiêu phần
tử ?
A.
4.
B.
5.
C.
6.
D.
7.
Câu 10. Cho hàm số
3 2
3 3
( ) ( 1) 3
2 2
m
f x x m x mx
Có tất cả bao nhiêu giá trị nguyên của
( 20;18)m sao cho đồ thị của hàm số đã cho có hai điểm cực trị nằm cùng một phía đối với trục
hoành ?
A.
1.
B.
19.
C.
20.
D.
18.
Câu 11. Có tất cả bao nhiêu giá trị nguyên của m để phương trình
3 2
6 0x x m
có ba nghiệm phân
biệt.
A.
31.
B.
32.
C.
21.
D.
34.
Câu 12. Cho hàm số ( )y f x có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên dương của tham số m
để phương trình
2
( ) logf x m
có đúng ba nghiệm thực phân biệt ?
A.
5.
B.
8.
C.
6.
D.
7.
Câu 13. Cho hàm số
3 2
y ax bx cx d có đồ thị như hình bên. Khẳng định nào đúng ?
A. 0, 0, 0, 0.a b c d
B. 0, 0, 0, 0.a b c d
C. 0, 0, 0, 0.a b c d
D. 0, 0, 0, 0.a b c d
Câu 14. Cho hàm số
4 2
y ax bx c có đồ thị như hình vẽ. Mệnh đề nào đúng ?
A. 0, 0, 0.a b c
B. 0, 0, 0.a b c
C. 0, 0, 0.a b c
D. 0, 0, 0.a b c
O
x
y
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 48 -
O
x
y
2
1
2
1
Câu 15. Hàm số
2
ax
y
cx b
có đồ thị như hình. Tính
.
a b c
A.
1.
a b c
B.
3.
a b c
C.
4.
a b c
D.
0.
a b c
Câu 16. Cho hàm số
2
ln( ).
x
y e m
Với giá trị nào của
m
thì
(1) 0, 5.
y
A.
.
m e
B.
.
m e
C.
1
m
e
D.
.
m e
Câu 17. Cho hàm số
3
log (3 ),
x
y x
biết
1
(1)
4 ln 3
a
y
b
với
, .
a b
Tính
.
a b
A.
7.
B.
2.
C.
4.
D.
1.
a b
Câu 18. Cho hàm số
4
x
x m
y
thỏa mãn
(1) 1.
y
Mệnh đề nào đúng ?
A.
( 5; 2).
m
B.
( ; 5).
m

C.
( 2;3).
m
D.
(3; ).
m

Câu 19. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
25 .5 7 7 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử ?
A.
7.
B.
1.
C.
2.
D.
3.
Câu 20. Tìm giá trị thực của tham số
m
để phương trình
1
9 2.3 0
x x
m
có hai nghiệm thực
1 2
,
x x
thỏa mãn điều kiện
1 2
1.
x x
A.
6.
m
B.
3.
m
C.
3.
m
D.
1.
m
Câu 21. Tìm tất cả giá trị của tham số
m
để phương trình
2
3 3
log ( 2)log 3 1 0
x m x m
có
2
nghiệm
1 2
,
x x
sao cho
1 2
. 27.
x x
A.
1.
m
B.
4
3
m
C.
25.
m
D.
28
3
m
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 49 -
Câu 22. Tìm tập hợp tham số
m
để phương trình
4 .2 2 5 0
x x
m m
có hai nghiệm trái dấu.
A.
5
;
2

B.
5
0;
2
C.

D.
5
; 4
2
Câu 23. Số giá trị nguyên âm của
m
để phương trình
5
5
log ( 1) log ( 4 )
x mx x
có nghiệm.
A.
4.
B.
3.
C.
2.
D. Vô số.
Câu 24. Có mấy giá trị nguyên của
m
sao cho phương trình
.2 ( 1) (2 1)
x x
x x x m m
có hai nghiệm
?
A.
1.
B.
2.
C.
3.
D. Vô số.
Câu 25. Cho phương trình
5
5 log ( )
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
( 20;20)
m
để phương trình đã cho có nghiệm ?
A.
20.
B.
19.
C.
9.
D.
21.
Câu 26. Tìm các giá trị của
m
để phương trình ln ln( )
m m x x
có nhiều nghiệm nhất.
A.
0.
m
B.
1.
m
C.
.
m e
D.
1.
m
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 50 -
l
O
A
B
C
D
Câu 27. Cho tứ diện đều
ABCD
cạnh
3 .a
Diện tích xung quanh của hình nón đỉnh
A
và đường tròn đáy
là đường tròn ngoại tiếp tam giác
BCD
là
A.
2
xq
6 .S a
B.
2
xq
3 3 .S a
C.
2
xq
12 .S a
D.
2
xq
6 3 .S a
Câu 28. Diện tích xung quanh của hình nón tròn xoay nội tiếp trong tứ diện đều có cạnh a bằng
A.
2
4
a
B.
2
2
6
a
C.
2
2
a
D.
2
3
6
a
Câu 29. Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
,a
diện tích mỗi mặt bên bằng
2
.a
Thể tích khối nón
có đỉnh
S
và đường tròn đáy nội tiếp hình vuông
ABCD
bằng
A.
3
15
24
a
B.
3
15
8
a
C.
3
15
12
a
D.
3
21.a
Câu 30. Diện tích xung quanh của hình nón ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a và cạnh
bên bằng
4a
bằng
A.
2
2 2 .a
B.
2
4 .a
C.
2
3 .a
D.
2
2 .a
Câu 31. Tính thể tích
V
của khối trụ ngoại tiếp hình lập phương có cạnh bằng
.a
A.
3
4
a
V
B.
3
.V a
C.
3
6
a
V
D.
3
2
a
V
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 51 -
Câu 32. Tính diện tích xung quanh của hình trụ tròn xoay ngoại tiếp một hình lăng trụ tam giác đều có tất
cả các cạnh bằng
1.
A.
xq
2 3
3
S
B.
xq
2 3
3
S
C.
xq
3.
S
D.
xq
3
S
Câu 33. Cho hình lăng trụ đứng
.
ABC A B C
có cạnh đáy
ABC
là tam giác vuông tại
A
với
3 , 4
AB a AC a
và
8 .
AA a
Thể tích của hình trụ có hai đáy nội tiếp hình lăng trụ đã cho
bằng
A.
3
8
3
a
B.
3
8 .
a
C.
3
12
a
D.
3
6
a
Câu 34. Tam giác
ABC
vuông cân đỉnh
A
có cạnh huyền là
2.
Quay tam giác
ABC
quanh trục
BC
thì
được khối tròn xoay có thể tích là
A.
2 .
B.
2 .
C.
2
.
3
D.
4
.
3
Câu 35. Cho tam giác
ABC
có
45 ,
ABC
30 ,
ACB
2
2
AB
Quay tam giác
ABC
xung quanh
cạnh
BC
ta được khối tròn xoay có thể tích
V
bằng
A.
(3 3).
B.
(1 3)
24
C.
(1 3)
8
D.
(1 3)
3
Câu 36. Trong không gian, cho hình thang vuông
ABCD
vuông tại
A
và
D
có
3
AB
và
1.
DC AD
Tính thể tích
V
của khối tròn xoay nhận được khi quay hình thang
ABCD
xung quanh trục
.
DC
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 52 -
A.
2 .
V
B.
7
3
V
C.
3 .
V
D.
4
3
V
Câu 37. Cho hình cầu bán kính bằng
10cm,
cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo
thành là một đường tròn có chu
16 .
Tính thể tích khối nón có đáy là thiết diện vừa tạo và đỉnh là
tâm của hình cầu đã cho.
A.
3
128 cm .
B.
3
126 cm .
C.
3
136 cm .
D.
3
132 cm .
Câu 38. Cho mặt cầu tâm
,
O
bán kính
.
R
Xét mặt phẳng
( )
P
thay đổi cắt mặt cầu theo giao tuyến là đường
tròn
( ).
C
Hình nón
( )
N
có đỉnh
S
nằm trên mặt cầu, có đáy là đường tròn
( )
C
và có chiều cao là
h
với
.
h R
Tính
h
để thể tích khối nón được tạo nên bởi
( )
N
có giá trị lớn nhất.
A.
3.
h R
B.
2.
h R
C.
4
3
R
h
D.
3
2
R
h
Câu 39. Một hình trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính
.
R
Diện tích
xung quanh của hình trụ bằng
A.
2
4 .
R
B.
2
2 .
R
C.
2
2 2 .
R
D.
2
2 .
R
Câu 40. Cho mặt cầu
( )
S
bán kính
5.
R
Một hình trụ có chiều cao
h
và bán kính đáy
r
thay đổi nội tiếp
mặt cầu. Tính chiều cao
h
để diện tích xung quanh của hình trụ lớn nhất.
A.
2 2.
h
B.
4 2.
h
C.
5 2.
h
D.
3 2.
h
Câu 41. Cho tứ diện
OABC
có
,
OA
,
OB
OC
đôi một vuông góc nhau và
,
OA a
2 ,
OB a
3 .
OC a
Tính diện tích
S
của mặt cầu ngoại tiếp tứ diện
.
OABC
A.
2
8 .
S a
B.
2
14 .
S a
C.
2
12 .
S a
D.
2
10 .
S a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 53 -
G
M
C
A
B
S
O
D
B
C
A
S
D
O
N
A
C
B
S
H
D
B
A
C
S
Câu 42. Cho hình chóp
. ,
S ABC
có đáy là tam giác đều cạnh
3cm,
2cm
SC
và
SC
vuông góc với đáy.
Tính thể tích của khối cầu ngoại tiếp hình chóp
. .
S ABC
A.
3
4
cm .
3
V
B.
3
256
cm .
3
V
C.
3
36 cm .
V
D.
3
32
cm .
3
V
Câu 43. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng
,
a
SA
vuông góc với đáy và
2.
SA a
Tính thể tích
V
của khối cầu ngoại tiếp hình chóp
. .
S ABCD
A.
3
32
3
a
V
B.
3
4
3
a
V
C.
3
4 .
V a
D.
3
4 2
3
a
V
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng
,
a
góc giữa cạnh bên và mặt đáy bằng
45 .
Mặt cầu
ngoại tiếp hình chóp có bán kính bằng
A.
3
2
a
B.
3
3
a
C.
3.
a
D.
3
5
a
Câu 45. Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
2 .
a
Biết góc tạo bởi cạnh bên và mặt đáy của hình
chóp bằng
60 .
Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp.
A.
6
3
a
R
B.
3.
R a
C.
2 3.
R a
D.
2 6
3
a
R
Câu 46. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
, 2 .
AB a AD a
Mặt bên
SAB
là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Bán kính
R
của mặt cầu ngoại
tiếp hình chiếu hình chóp
.
S ABCD
bằng
A.
2 2
3
a
B.
3 2
2
a
C.
3 3
2
a
D.
2 3
3
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 54 -
I
O
A
B
C
D
E
F
A
B
C
D
E
F
Câu 47. Cho tứ diện
ABCD
có
AB
vuông góc với
( )
BCD
và
2.
AB a
Biết tam giác
BCD
có
,
BC a
3
BD a
và
30 .
CBD
Thể tích khối cầu ngoại tiếp tứ diện bằng
A.
3
6
3
a
B.
3
6 .
a
C.
3
3 6
4
a
D.
3
6
2
a
Câu 48. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
6,
mặt bên
SAB
là tam giác cân
tại
S
nằm trong mặt phẳng vuông góc với đáy và có góc
120 .
ASB
Tính diện tích
mc
S
của mặt
cầu ngoại tiếp hình chóp
. .
S ABCD
A.
mc
84 .
S
B.
mc
28 .
S
C.
mc
14 .
S
D.
mc
42 .
S
Câu 49. Cho hình chóp
.
S ABC
có
( ),
SA ABC
,
AB a
2,
AC a
45 .
BAC
Gọi
1
,
B
1
C
lần lượt là
hình chiếu vuông góc của
A
lên
,
SB
.
SC
Thể tích khối cầu ngoại tiếp hình chóp
1 1
.
A BCC B
bằng
A.
3
2
3
a
B.
3
2.
a
C.
3
4
.
3
a
D.
3
2
2
a
Câu 50. Cho hình lăng trụ lục giác đều có cạnh đáy bằng
2,
a
cạnh bên bằng
2 2.
a
Tính diện tích mặt cầu
ngoại tiếp hình lăng trụ đã cho.
A.
2
16 .
a
B.
2
8 .
a
C.
2
4 .
a
D.
2
2 .
a
BẢNG ĐÁP ÁN ĐỀ SỐ 07
1.C 2.A 3.C 4.A 5.A 6.D 7.C 8.A 9.C 10.D
11.A 12.D 13.A 14.B 15.D 16.D 17.A 18.C 19.C 20.C
21.A 22.D 23.B 24.B 25.B 26.B 27.B 28.A 29.A 30.A
31.D 32.A 33.B 34.C 35.B 36.B 37.A 38.C 39.B 40.C
41.B 42.D 43.B 44.B 45.D 46.D 47.B 48.A 49.A 50.A
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 55 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 08
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Có tất cả bao nhiêu số nguyên
m
để hàm số
( 1) 2
m x
y
x m
đồng biến trên từng khoảng xác định
của nó ?
A.
1.
B.
0.
C.
2.
D.
3.
Câu 2. Tìm
m
sao cho hàm số
9
( )
mx
f x
x m
luôn nghịch biến trên khoảng
( ;1).
A.
3 1.
m
B.
3 1.
m
C.
3 3.
m
D.
3 3.
m
Câu 3. Tìm tham số
m
sao cho hàm số
tan 2
tan 2
x
y
m x
đồng biến trên khoảng
0;
4
A.
1.
m
B.
1 2.
m
C.
1 2.
m
D.
1 2.
m
Câu 4. Có mấy giá trị nguyên của tham số
m
để hàm số
3 2
1 1
2018
3 2
y x mx x đồng biến trên
( ; ).

A.
5.
B.
3.
C.
4.
D.
2.
Câu 5. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
3 2
6 (3 6)
y x x m x
đồng
biến trên khoảng
(0; ).
A.
2.
m
B.
2.
m
C.
.
m
D.
2.
m
Câu 6. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
cos
y x mx
luôn nghịch biến trên
( ; ).
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 7. Giá trị nguyên lớn nhất của tham số
m
để hàm số
2019
2017
1
2018
2019
2017
x
y mx
x
luôn đồng
biến trên mỗi khoảng xác định của nó là
A.
2018.
B.
0.
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 56 -
C.
2.
D.
1.
Câu 8. Biết rằng đồ thị hàm số
3 2
1 1
( ) 2
3 2
f x x mx x
có giá trị tuyệt đối của hoành độ hai điểm cực
trị là độ dài hai cạnh của tam giác vuông có cạnh huyền là 7. Hỏi có mấy giá trị của m ?
A.
3.
B.
1.
C. Không có .m
D.
2.
Câu 9. Gọi ,A
B
là hai điểm cực trị của đồ thị hàm số
3 2
( ) 3f x x x m với m là tham số thực khác
0.
Tìm tất cả các giá trị thực của tham số m
để trọng tâm tam giác
OAB
thuộc đường thẳng
3 3 8 0.x y
A.
5.m
B.
2.m
C.
6.m
D.
4.m
Câu 10. Tìm tham số m để đồ thị hàm số
4 2 2
2 2y x m x m có ba điểm cực trị , , A B C sao cho
, , , O A B C là ba đỉnh của một hình thoi (với
O
là gốc tọa độ).
A.
1.m
B.
1.m
C.
2.m
D.
3.m
Câu 11. Có bao nhiêu giá trị nguyên của tham số m để phương trình
4 2
8 3 4 0x x m
có bốn nghiệm
phân biệt ?
A.
6.
B.
5.
C.
4.
D.
3.
Câu 12. Cho hàm số ( )y f x xác định, liên tục trên
và có bảng biến thiên sau:
Tìm tham số m để phương trình ( ) 1f x m có đúng hai nghiệm.
A. 2,m 1.m B. 0,m
1.m
C. 2,m
1.m
D.
2 1.m
Câu 13. Cho hàm số bậc ba
3 2
y ax bx cx d có đồ thị như hình vẽ.
Dấu của , , , a b c d là
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0, 0, 0, 0.a b c d
D.
0, 0, 0, 0.a b c d
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 57 -
O
x
y
Câu 14. Cho hàm số
ax b
y
x c
có đồ thị như hình vẽ. Tìm câu đúng ?
A. 0, 0, 0.a b c
B. 0, 0, 0.a b c
C. 0, 0, 0.a b c
D. 0, 0, 0.a b c
Câu 15. Hàm số
4 2
,y ax bx c ( 0)a có đồ thị như hình vẽ bên. Mệnh đề nào đúng ?
A. 0,a 0,b 0.c
B. 0,a 0,b 0.c
C. 0,a 0,b 0.c
D. 0,a 0,b 0.c
Câu 16. Cho hàm số ( ) ln(2 )
x
f x e m thỏa mãn
3
( ln 2)
2
f
Mệnh đề nào đúng ?
A. (1;3).m
B. ( 5; 2).m
C. (1; ).m
D. ( ;3).m 
Câu 17. Với 1 0,m cho hàm số log (2 5)
m
y x thỏa
4
(3)
ln 3
y
Tìm câu đúng ?
A.
0 1.m
B.
1 4.m
C. 4 8.m
D. 8.m
Câu 18. Cho hàm số
1
( ) ln 2018 ln
x
f x
x
Tính (1) (2) (2017).S f f f
A.
4035
2018
S
B. 2018.S
C.
2018
2019
S
D.
2017
2018
S
Câu 19. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình
1 2
9 .3 3 75 0
x x
m m
có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử ?
A. 8.
B. 4.
C. 19.
D. 5.
Câu 20. Tìm tất cả các giá trị của tham số m để phương trình
9 2 .3 2 0
x x
m m
có hai nghiệm phân biệt
1 2
, x x
sao cho
1 2
3.x x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 58 -
A.
9.
m
B.
27
2
m
C.
3 3
2
m
D.
3
2
m
Câu 21. Giả sử
m
là số thực sao cho phương trình
2
3 3
log ( 2)log 3 2 0
x m x m
có hai nghiệm
1 2
,
x x
thỏa mãn
1 2
. 9.
x x
Khi đó
m
thỏa mãn tính chất nào sau đây ?
A.
(4;6).
m
B.
( 1;1).
m
C.
(3; 4).
m
D.
(1; 3).
m
Câu 22. Tìm tham số
m
để phương trình
1
4 .2 3 3 0
x x
m m
có hai nghiệm trái dấu.
A.
( ;2).
m

B.
(1; ).
m
C.
(1;2).
m
D.
(0;2).
m
Câu 23. Số các giá trị nguyên của tham số
m
để phương trình
2
2
log ( 1) log ( 8)
x mx
có hai nghiệm
phân biệt là
A.
3.
B.
4.
C.
5.
D. Vô số.
Câu 24. Phương trình
2 2
sin 1 cos
2 2
x x
m
có nghiệm khi và chỉ khi
A.
4 3 2.
m
B.
3 2 5.
m
C.
0 5.
m
D.
4 5.
m
Câu 25. Tìm
m
để
2 2 2
2 6 2 2 2 4 2
5 5 5 25 0
x x m x x x x m
có
4
nghiệm phân biệt.
A.
0 1.
m
B.
2 3.
m
C.
4 3.
m
D.
1 3.
m
Câu 26. Có bao nhiêu giá trị nguyên của tham số thực
m
nhỏ hơn
10
sao cho phương trình
x x
m m e e
có nghiệm thực ?
A.
9.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 59 -
B. 8.
C. 10.
D.
7.
Câu 27. Có mấy số nguyên m để phương trình
2
2
2
2
3 3 1
log 5 2
2 1
x x m
x x m
x x
có hai nghiệm
phân biệt lớn hơn 1.
A. 3.
B. Vô số.
C.
2.
D.
4.
Câu 28. Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
,a
cạnh bên
2 .SA a
Thể tích của khối nón
có đỉnh
S
và đường tròn đáy là đường tròn ngoại tiếp
ABC
bằng
A.
3
2
a
B.
3
33
27
a
C.
3
6
a
D.
3
2
2
a
Câu 29. Cho hình chóp tam giác đều có cạnh đáy bằng a và đường cao bằng
6 .a
Thể tích khối nón
V
nội
tiếp hình chóp đó.
A.
3
9
a
V
B.
3
6
a
V
C.
3
3
a
V
D.
3
4
a
V
Câu 30. Cho hình chóp tứ giác đều
.S ABCD
có cạnh bên
2SA a
và
.AB a
Thể tích của khối nón có
đỉnh
S
và đường tròn đáy là đường tròn ngoại tiếp tứ giác
ABCD
bằng
A.
3
6
12
a
B.
3
2
6
a
C.
3
6
a
D.
3
2
2
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 60 -
D'
B'
C'
A'
B
A
O
O'
D
C
Câu 31. Cho hình hộp chữ nhật
.
ABCD A B C D
có
2 ,
AB a
3
AD a
và
4 .
AA a
Tính thể tích
V
của khối trụ ngoại tiếp hình hộp chữ nhật
. .
ABCD A B C D
A.
3
144
13
a
V
B.
3
13 .
V a
C.
3
24 .
V a
D.
3
13 .
V a
Câu 32. Lăng trụ tam giác đều
.
ABC A B C
có cạnh đáy bằng
,
a
cạnh bên bằng
3
a
và có hai đáy là hai tam
giác nội tiếp hai đường tròn đáy của hình trụ
( ).
T
Tính thể tích
V
của khối trụ
( ).
T
A.
3
.
V a
B.
3
3 .
V a
C.
3
6 .
V a
D.
3
3 3 .
V a
Câu 33. Cho hình lăng trụ đứng
.
ABC A B C
có cạnh đáy
ABC
là tam giác vuông tại
A
với
6 , 8
AB a AC a
và
12 .
AA a
Thể tích của hình trụ có hai đáy nội tiếp hình lăng trụ đã cho
bằng
A.
3
12
a
B.
3
6
a
C.
3
48 .
a
D.
3
48
5
a
Câu 34. Cho tam giác
ABC
vuông tại
, ,
A AB a
3.
AC a
Quay tam giác đó quanh đường thẳng
BC
ta được khối tròn xoay. Tính thể tích
V
của khối tròn xoay này ?
A.
3
2
a
V
B.
3
4
a
V
C.
3
2
3
a
V
D.
3
3
a
V
Câu 35. Cho hình vuông
ABCD
có cạnh bằng
.
a
Quay hình vuông này xung quanh đường chéo
,
AC
ta
thu được khối tròn xoay có thể tích bằng
A.
3
2
6
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 61 -
B.
3
3 2.a
C.
3
2 2.a
D.
3
2
3
a
Câu 36. Cho hình thang
ABCD
vuông tại
A
và ,D ,AD CD a
2 .AB a
Quay hình thang
ABCD
quanh đường thẳng
.CD
Thể tích khối tròn xoay thu được bằng
A.
3
7
3
a
B.
3
.a
C.
3
4
3
a
D.
3
5
3
a
Câu 37. Cho mặt cầu ( )S tâm ,O bán kính
R
(không đổi). Mặt phẳng ( )P cách O một khoảng bằng
, ( )x x R
và cắt ( )S theo giao tuyến là đường tròn ( )C có tâm .H Gọi T là giao điểm của tia HO
với ( ).S Thể tích của khối nón có đỉnh T và đáy là hình tròn ( )C bằng
A.
2 2
( )( )
6
R x R x
B.
2 2
2 ( )( ).R x R x
C.
2 2
( )( ).R x R x
D.
2 2
( )( )
3
R x R x
Câu 38. Trong các hình nón nội tiếp hình cầu có bán kính bằng 9, tính bán kính đường tròn đáy r của hình
nón có thể tích lớn nhất ?
A. 4 2.r
B. 5 2.r
C. 6 2.r
D. 3 2.x
Câu 39. Hình trụ
( )T
bán kính đáy bằng
3 ,R
chiều cao bằng 8R có hai đáy nằm trên mặt cầu
( ).S
Thể tích
của khối cầu bằng
A.
3
125 .R
B.
3
25 .R
C.
3
500
3
R
D.
3
375
4
R
Câu 40. Cho mặt cầu ( )S bán kính 4.R Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp
mặt cầu. Diện tích xung quanh lớn nhất của khối trụ bằng
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 62 -
A.
8 .
B.
64 .
C.
32 .
D.
16 .
Câu 41. Cho tứ diện
ABCD
có đáy
BCD
là tam giác vuông tại
C
và
AB
( ).
BCD
Biết
5 , 3 ,
AB a BC a
4 .
CD a
Tính bán kính
R
của mặt cầu ngoại tiếp tứ diện.
A.
5 2
3
a
R
B.
5 3.
R a
C.
5 2
2
a
R
D.
5 3
2
a
R
Câu 42. Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh bằng
1,
SA
vuông góc với đáy, góc giữa mặt bên
( )
SBC
và đáy bằng
60 .
Tính diện tích mặt cầu ngoại tiếp hình chóp.
A.
43
48
S
B.
43
36
S
C.
43
4
S
D.
43
12
S
Câu 43. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
,
a
SA
vuông góc với đáy. Biết
SC
tạo với mặt phẳng
(
)
ABCD
một góc
45 .
Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp.
A.
2
4 .
S a
B.
2
6 .
S a
C.
2
8 .
S a
D.
2
12 .
S a
Câu 44. Tính diện tích
S
của mặt cầu ngoại tiếp hình tứ diện đều cạnh
.
a
A.
2
3
4
a
S
B.
2
3
2
a
S
C.
2
6 .
S a
D.
2
3 .
S a
Câu 45. Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh đều bằng
2 .
a
Hãy tính theo
a
thể tích của
khối cầu ngoại tiếp hình chóp
. .
S ABCD
A.
3
8 2 .
a
B.
3
8 2
3
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 63 -
C.
3
4 2 .
a
D.
3
2
3
a
Câu 46. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
3 ,
AB a
,
SAB
là tam giác
đều và nằm trong mặt phẳng vuông góc với đáy. Diện tích của mặt cầu ngoại tiếp hình chóp
.
S ABCD
bằng
A.
2
10 .
S a
B.
2
5 .
S a
C.
2
4 .
S a
D.
2
2 .
S a
Câu 47. Cho hình chóp
.
S ABC
có
( ),
SA ABC
2 .
SA a
Tam giác
ABC
cân tại đỉnh
A
có
2 2
BC a
và
1
cos
3
ACB
Diện tích của mặt cầu ngoại tiếp hình chóp bằng
A.
2
65
4
a
`
B.
2
13 .
a
C.
2
4 .
a
D.
2
97
4
a
Câu 48. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh bằng
1,
mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết
120 .
ASB
Thể tích của khối cầu
ngoại tiếp hình chóp đã cho bằng
A.
5 15
54
B.
4 3
27
C.
5
3
D.
13 78
27
Câu 49. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
SA
vuông góc với đáy,
,
SA a
5 ,
AD a
2 .
AB a
Điểm
E
thuộc cạnh
BC
sao cho
.
CE a
Bán kính mặt cầu ngoại tiếp tứ diện
SAED
bằng
A.
26
4
a
B.
26
3
a
C.
26
2
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 64 -
A
B
C
A
B
C
I
O
O
D.
2 26
3
a
Câu 50. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
9
cạnh bằng nhau và bằng
2 .
a
Tính diện tích
S
của mặt cầu ngoại tiếp hình lăng trụ đã cho.
A.
2
28
9
a
S
B.
2
7
9
a
S
C.
2
28
3
a
S
D.
2
7
3
a
S
BẢNG ĐÁP ÁN ĐỀ SỐ 08
1.C 2.B 3.D 4.B 5.B 6.B 7.C 8.D 9.A 10.B
11.C 12.C 13.B 14.D 15.C 16.D 17.B 18.D 19.B 20.B
21.B 22.C 23.A 24.D 25.D 26.C 27.C 28.B 29.B 30.A
31.B 32.A 33.C 34.A 35.A 36.D 37.D 38.C 39.C 40.C
41.C 42.D 43.A 44.B 45.B 46.B 47.D 48.A 49.C 50.C
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 65 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 09
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Gọi
S
là tập hợp tất cả các giá trị nguyên chẵn của tham số
( 10;22)
m
để hàm số
3
1
mx
y
x
đồng biến trên từng khoảng xác định của nó. Tổng các phần tử của
S
là
A.
96.
B.
52.
C.
104.
D.
108.
Câu 2. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
7 8
mx m
y
x m
đồng biến trên khoảng
(0; ).
A.
3.
B.
6.
C.
8.
D.
7.
Câu 3. Tìm tham số
m
sao cho hàm số
cos 2
cos
x
y
x m
đồng biến trên khoảng
0;
2
A.
0
m
hoặc
1 2.
m
B.
0.
m
C.
1 2.
m
D.
2.
m
Câu 4. Có bao nhiêu giá trị nguyên của
m
để hàm số
3 2
1
(3 2) 1
3
y x mx m x
nghịch biến trên
( ; ).
A.
2.
B.
4.
C.
7.
D. Vô số.
Câu 5. Tìm
m
sao cho hàm số
3 2
1
3
y x x mx
đồng biến trên khoảng
(1; ).
A.
1.
m
B.
1 3.
m
C.
3.
m
D.
3.
m
Câu 6. Tìm
m
sao cho hàm số
(2 ) cos
y m x x
luôn nghịch biến trên
( ; ).
 
A.
3.
m
B.
3.
m
C.
3 3.
m
D.
3.
m
Câu 7. Gọi
S
là tập các giá trị của tham số thực m để hàm số
2
ln( 2)
y x x m
đồng biến trên tập
xác định của nó. Biết
( ; ].
S a b

Tổng
K a b
là
A.
5.
K
B.
5.
K
C.
0.
K
D.
2.
K
Câu 8. Cho hàm số
3 2
( ) 3 1,
f x x x mx
tìm giá trị của tham số
m
để hàm số có hai cực trị
1
,
x
2
x
thỏa
2 2
1 2
3.
x x
A.
3
2
m
B.
1.
m
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 66 -
O
y
x
C.
2.m
D.
1
2
m
Câu 9. Cho hàm số
4 2
2( 4) 5y x m x m
có đồ thị
( ).
m
C
Tìm m để
( )
m
C
có ba điểm cực trị tạo
thành một tam giác nhận gốc tọa độ
O
làm trọng tâm.
A. 1,m
17
2
m
B.
1.m
C.
4.m
D.
17
2
m
Câu 10. Gọi
1
,m
2
m
là các giá trị của tham số m để đồ thị hàm số
3 2
2 3 1y x x m
có hai điểm cực
trị là ,B
C
sao cho tam giác
OBC
có diện tích bằng 2, với
O
là gốc tọa độ. Giá trị của tích số
1 2
m m
bằng
A.
15.
B.
12.
C.
6.
D.
20.
Câu 11. Cho hàm số
4 2
2y x x
có đồ thị như hình vẽ. Tìm tất cả các giá trị thực của tham số
m
để
phương trình
4 2
2 0x x m có bốn nghiệm thực phân biệt.
A. 0.m
B. 0 1.m
C. 0 1.m
D. 1.m
Câu 12. Cho hàm số ( )y f x xác định trên tập \ { 1}, D liên tục trên mỗi khoảng xác định và có bảng
biến thiên như sau:
Tìm
m
sao cho phương trình ( ) 1f x m có hai nghiệm thực phân biệt.
A. 1m hoặc 5.m
B. 1 5.m
C. 1.m
D. 5.m
Câu 13. Cho hàm số
bx c
y
x a
có đồ thị như hình bên. Khẳng định nào đúng ?
A. 0,a 0,b 0.c ab
B. 0,a 0,b 0.c ab
C. 0,a 0,b 0.c ab
D. 0,a 0,b 0.c ab
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 67 -
Câu 14. Cho hàm số
3 2
( )
f x ax bx cx d
có đồ thị như hình. Mệnh đề nào đúng ?
A.
0,
a
0,
b
0,
c
0.
d
B.
0,
a
0,
b
0,
c
0.
d
C.
0,
a
0,
b
0,
c
0.
d
D.
0,
a
0,
b
0,
c
0.
d
Câu 15. Cho hàm số
4 2
y ax bx c
có đồ thị là hình vẽ bên. Mệnh đề nào đúng ?
A.
2
0, 0, 0, 4 0.
a b c b ac
B.
2
0, 0, 0, 8 0.
a b c b ac
C.
2
0, 0, 0, 4 0.
a b c b ac
D.
2
0, 0, 0, 8 0.
a b c b ac
Câu 16. Cho hàm số
2
( ) .
x
y x mx e
Biết
(0) 1
y
thì
(1)
y
bằng
A.
6 .
e
B.
3 .
e
C.
5 .
e
D.
4 .
e
Câu 17. Cho hàm số
ln( 1)
y m x
thỏa mãn
1
(8)
24
y
Tìm khẳng định đúng ?
A.
2.
m
B.
2 2.
m
C.
2 5.
m
D.
5.
m
Câu 18. Cho hàm số
2
2
x
e
y
x
Mệnh đề nào sau đây đúng ?
A.
2
1
.
2
x
y xy e
B.
2
1
.
2
x
y xy e
C.
2
1
.
2
x
y xy e
D.
2
1
.
2
x
y xy e
Câu 19. Có mấy giá trị nguyên dương của
m
để
16 ( 2)9 2.12
x x x
m
có nghiệm dương.
A.
1.
B.
2.
C.
4.
D.
3.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 68 -
Câu 20. Tìm tất cả các giá trị của tham số
m
để phương trình
9 2 .3 2 0
x x
m m
có hai nghiệm phân biệt
1 2
,
x x
sao cho
1 2
3.
x x
A.
3
2
m
B.
27
2
m
C.
3 3.
m
D.
9
2
m
Câu 21. Giá trị thực của tham số
m
để phương trình
2
3 3
log 3 log 2 7 0
x x m
có hai nghiệm thực
1 2
,
x x
thỏa mãn
1 2
( 3)( 3) 72
x x
thuộc khoảng nào sau đây ?
A.
(0;3).
B.
( 6; 3).
C.
(3;6).
D.
( 3;0).
Câu 22. Tìm
m
để
( 3).16 (2 1).4 1 0
x x
m m m
có hai nghiệm trái dấu.
A.
3
1
4
m
B.
3
3.
4
m
C.
3
3.
4
m
D.
3
0.
4
m
Câu 23. Phương trình
(2 3) (2 3)
x x
m
có nghiệm khi
A.
( ;5).
m
B.
(2; ).
m
C.
( ;5].
m

D.
[2; ).
m

Câu 24. Tìm tham số thực
m
để phương trình
2
2 2
log 4 log 0
x x m
có nghiệm thuộc khoảng
(0;1).
A.
( 4; ).
B.
[ 4; ).
C.
[ 4;0).
D.
[ 2; 0].
Câu 25. Tìm tập hợp các giá trị thực của
m
để phương trình
2
log( 1) log( 2 )
x x x m
có nghiệm duy
nhất ?
A.
5
( ;1)
4
B.
5
1;
4
C.
]
5
( ;1
4
D.
5
4
Câu 26. Cho phương trình
2
2 log ( )
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
( 18;18)
m
để phương trình đã cho có nghiệm ?
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 69 -
A.
9.
B.
19.
C. 17.
D.
18.
Câu 27. Cho phương trình
2
2
3
2
2
log 4 .
1
x x m
x x m
x
Có bao nhiêu giá trị nguyên của tham số
[ 2018;2018]m để phương trình có hai nghiệm trái dấu ?
A. 2022.
B. 2021.
C. 2016.
D. 2015.
Câu 28. Cho hình chóp tam giác đều
.S ABC
có cạnh ,AB a góc tạo bởi ( )SAB và ( )ABC bằng
60 .
Diện
tích xung quanh của hình nón đỉnh
S
và có đường tròn đáy ngoại tiếp tam giác
ABC
bằng
A.
2
7
3
a
B.
2
7
6
a
C.
2
3
2
a
D.
2
3
6
a
Câu 29. Cho hình chóp tứ giác đều
.S ABCD
có các cạnh đều bằng 2.a Thể tích khối nón có đỉnh
S
và
đường tròn đáy là đường tròn nội tiếp tứ giác
ABCD
bằng
A.
2
2
6
a
B.
3
2
2
a
C.
3
.a
D.
3
6
a
Câu 30. Cho hình chóp tứ giác đều
.S ABCD
có cạnh bên 2SA a và
.AB a
Thể tích của khối nón có
đỉnh
S
và đường tròn đáy là đường tròn ngoại tiếp tứ giác
ABCD
bằng
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 70 -
D'
B'
C'
A'
B
A
O
O'
D
C
A.
3
6
12
a
B.
3
2
6
a
C.
3
6
a
D.
3
2
2
a
Câu 31. Cho hình lập phương .ABCD A B C D
có đường chéo
3.BD x
Tính
xq
S
của hình trụ có hai đường
tròn đáy ngoại tiếp hai hình vuông
ABCD
và .A B C D
A.
2
xq
.S x
B.
2
xq
2
2
x
S
C.
2
xq
3.S x
D.
2
xq
2.S x
Câu 32. Cho hình lăng trụ đứng .ABC A B C
có tam giác
ABC
vuông cân tại ,B
2AB a
và cạnh bên
6.AA a
Tính diện tích xung quanh
xq
S
của hình trụ ngoại tiếp hình lăng trụ đã cho bằng bao
nhiêu ?
A.
2
xq
4 6.S a
B.
2
xq
4 .S a
C.
2
xq
2 6.S a
D.
2
xq
6.S a
Câu 33. Cho lăng trụ đứng .ABC A B C
có cạnh bên 2 .AA a
Tam giác
ABC
vuông tại
A
có
2 3.BC a
Tính thể tích
V
của khối trụ ngoại tiếp khối lăng trụ này.
A.
3
2 .V a
B.
3
4 .V a
C.
3
8 .V a
D.
3
6 .V a
Câu 34. Cho tam giác ABC vuông tại A có 3 , 4 .AB a AC a Khi tam giác ABC quay quanh đường
thẳng BC ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
A.
3
.V a
B.
3
96
5
a
V
C.
3
3 .V a
D.
3
48
5
a
V
Câu 35. Cho hình vuông ABCD có cạnh bằng
2.a
Quay hình vuông này xung quanh đường chéo ,BD ta
thu được khối tròn xoay có thể tích bằng
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 71 -
A.
3
2 2
3
a
B.
3
3 2
2
a
V
C.
3
2 2.
V a
D.
3
2
2
a
V
Câu 36. Cho hình thang vuông
ABCD
có độ dài hai đáy
2 , 4 ,
AB a DC a
đường cao
2 .
AD a
Quay
hình thang
ABCD
quanh đường thẳng
AB
thu được khối tròn xoay
( ).
H
Tính thể tích
V
của khối
( ).
H
A.
3
8 .
V a
B.
3
20
3
a
V
C.
3
16 .
V a
D.
3
40
3
a
V
Câu 37. Cho mặt cầu
( )
S
tâm
,
O
bán kính
3.
R
Mặt phẳng
( )
P
cách
O
một khoảng bằng
1
và cắt
( )
S
theo giao tuyến là đường tròn
( )
C
có tâm
.
H
Gọi
T
là giao điểm của tia
HO
với
( ).
S
Tính thể tích
V
của khối nón có đỉnh
T
và đáy là hình tròn
( ).
C
A.
32
3
V
B.
16 .
V
C.
32 .
V
D.
16
3
V
Câu 38. Cho hình nón có bán kính đáy
5 ,
R a
độ dài đường sinh
13 .
a
Thể tích khối cầu nội tiếp hình
nón bằng
A.
3
40
9
a
B.
3
400
27
a
C.
3
4000
27
a
D.
3
4000
81
a
Câu 39. Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính
R
và có đường cao bằng bán
kính mặt cầu. Diện tích toàn phần của hình trụ đó bằng
A.
2
(3 2 3)
3
R
B.
2
(3 2 3)
2
R
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 72 -
C.
2
(3 2 2)
2
R
D.
2
(3 2 2)
3
R
Câu 40. Cho mặt cầu
( )
S
có bán kính bằng
4,
hình trụ
( )
H
có chiều cao bằng
4
và hai đường tròn đáy nằm
trên
( ).
S
Gọi
1
V
là thể tích khối trụ
( )
H
và
2
V
là thể tích khối cầu
( ).
S
Tính tỉ số
1
2
V
V
A.
1
2
9
16
V
V
B.
1
2
1
3
V
V
C.
1
2
3
16
V
V
D.
1
2
2
3
V
V
Câu 41. Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
,
B
hai mặt bên
SAB
và
SAC
cùng vuông góc
với đáy,
2 ,
SB a
.
AB BC a
Tính thể tích của khối cầu ngoại tiếp hình chóp
. .
S ABC
A.
3
3 6
2
a
V
B.
3
3 5.
V a
C.
3
5 5
6
a
V
D.
3
5
6
a
V
Câu 42. Cho hình chóp
. ,
S ABC
có đáy là tam giác đều cạnh
3 ,
a
2
SB a
và
SB
vuông góc với đáy. Tính
bán kính
R
của mặt cầu ngoại tiếp hình chóp
. .
S ABC
A.
4 .
R a
B.
3
2
a
R
C.
2
a
R
D.
2 .
R a
Câu 43. Cho hình chóp
.
S ABCD
có
( ),
SA ABCD
đáy
ABCD
là hình chữ nhật,
,
2 ,
AD a
góc
giữa đường thẳng
SC
và đáy bằng
45 .
Tính thể tích
V
khối cầu ngoại tiếp hình chóp
. .
S ABCD
A.
3
10
3
a
V
B.
3
6 .
V a
C.
3
5
6
a
V
D.
3
5 10
3
a
V
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 73 -
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng
6
và chiều cao
1.
h
Diện tích của mặt cầu ngoại
tiếp của hình chóp đó bằng
A.
9 .
S
B.
6 .
S
C.
5 .
S
D.
27 .
S
Câu 45. Cho hình chóp đều
.
S ABCD
có cạnh đáy bằng
2,
a
góc giữa cạnh bên và mặt đáy bằng
o
45 .
Diện
tích mặt cầu ngoại tiếp hình chóp
.
S ABCD
bằng
A.
2
4
3
a
B.
2
4 .
a
C.
2
6 .
a
D.
2
16
3
a
Câu 46. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
.
a
Tam giác
SAB
vuông tại
S
nằm
trong mặt phẳng vuông góc với đáy,
SH AB
và đường cao
5.
SH a
Góc giữa
AB
và
( )
SAD
là
60 .
Diện tích mặt cầu ngoại tiếp hình chóp
. .
S ABCD
A.
2
160
7
a
B.
2
20 .
a
C.
2
30 .
a
D.
2
160
3
a
Câu 47. Cho hình chóp
.
S ABC
có
3.
AB
Hình chiếu của
S
lên mặt phẳng
( )
ABC
là điểm
H
thuộc miền
trong tam giác
ABC
sao cho
120 .
AHB
Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
. ,
S HAB
biết
4 3.
SH
A.
5.
R
B.
3 5.
R
C.
15.
R
D.
2 3.
R
Câu 48. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
3 , ,
AB a AD a
tam giác
SAB
nằm
trong mặt phẳng vuông góc với mặt phẳng đáy và
60 .
ASB
Diện tích của mặt cầu ngoại tiếp
hình chóp
.
S ABCD
bằng
A.
2
5
.
4
a
B.
2
5 .
a
C.
2
5
.
2
a
D.
2
9
.
4
a
Câu 49. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
,
a
góc
120 .
BAD
Cạnh bên
SA
vuông
góc với đáy
(
)
ABCD
và
3 .
SA a
Bán kính
R
của mặt cầu ngoại tiếp khối chóp
.
S BCD
bằng
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 74 -
A.
3
3
a
B.
5
3
a
C.
5
3
a
D.
4
3
a
Câu 50. Cho hình lăng trụ tam giác đều .ABC A B C
có độ dài cạnh đáy bằng a và chiều cao bằng 2 .a Tính
thể tích V của khối cầu ngoại tiếp hình lăng trụ . .ABC A B C
A.
3
32 3
27
a
V
B.
3
32 3
9
a
V
C.
3
8 3
27
a
V
D.
3
32 3
81
a
V
BẢNG ĐÁP ÁN ĐỀ SỐ 09
1.D 2.C 3.D 4.A 5.C 6.B 7.C 8.A 9.B 10.A
11.B 12.A 13.B 14.C 15.A 16.C 17.B 18.D 19.B 20.B
21.C 22.A 23.D 24.B 25.C 26.C 27.D 28.B 29.D 30.A
31.D 32.C 33.D 34.A 35.A 36.D 37.A 38.D 39.B 40.A
41.C 42.D 43.D 44.A 45.B 46.D 47.C 48.B 49.C 50.A
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 75 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020
TRUNG TÂM HOÀNG GIA Môn thi: TOÁN – ĐỀ SỐ 10
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú (Thời gian làm bài 60 phút)
Câu 1. Hỏi có bao nhiêu giá trị nguyên của tham số
m
sao cho hàm số
7 8
mx m
y
x m
đồng biến trên
từng khoảng xác định của nó.
A.
8.
B. Không có.
C.
3.
D. Vô số.
Câu 2. Có bao nhiêu giá trị nguyên của tham số
( 20;20)
m
để hàm số
1
x
y
x m
nghịch biến trên
khoảng
( ;2).
A.
16.
B.
19.
C.
17.
D.
18.
Câu 3. Giá trị
m
để hàm số
cot 2
cot
x
y
x m
nghịch biến trên
;
4 2
là
A.
0.
m
B.
0
m
hoặc
1 2.
m
C.
1 2.
m
D.
2.
m
Câu 4. Có bao nhiêu giá trị nguyên của
m
để hàm số
3 2
1
(2 3) 2
3
y x mx m x
đồng biến trên
( ; ).
 
A. Vô số.
B.
5.
C.
3.
D.
7.
Câu 5. Tìm
m
sao cho hàm số
3 2
3 4
y x x mx
nghịch biến trên khoảng
(0; ).

A.
0.
m
B.
0.
m
C.
0.
m
D.
0.
m
Câu 6. Tìm
m
sao cho hàm số
cos
y x mx
luôn đồng biến trên
( ; ).
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 7. Có bao nhiêu giá trị nguyên dương của
( 10;20)
m
để hàm
4
11
1
11
y x mx
x
đồng biến trên
khoảng
(0; ).
A.
8.
B.
9.
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 76 -
C.
16.
D.
15.
Câu 8. Có bao nhiêu số nguyên
m
để hàm số
3 2
3 4
y x x mx
có hai điểm cực trị thuộc khoảng
( 3; 3).
A.
12.
B.
11.
C.
13.
D.
10.
Câu 9. Cho hàm số
4 2
( 3) 2 1.
y mx m x m
Tìm tham số
m
để hàm số đã cho chỉ đạt cực đại mà
không có cực tiểu.
A.
3.
m
B.
3.
m
C.
3 0.
m
D.
0
m
hoặc
3.
m
Câu 10. Cho hàm số
3 2 2
( 3 ) 4.
y x mx m m x
Tìm tham số
m
để hàm số đạt cực trị tại hai điểm
1
,
x
2
x
sao cho
1 2
. 0.
x x
A.
( ; 0] [3; ).
m
 
B.
( ; 0) (3; ).
m
C.
[0;3].
m
D.
(0; 3).
m
Câu 11. Cho hàm số
( )
y f x
liên tục trên các khoảng
( ; 0)

và
(0; ),
có bảng biến thiên:
x
1
x
0
2
x

y
0
0
y
2
3

3
4
Tìm tham số
m
để phương trình
( ) 0
f x m
có
4
nghiệm phân biệt.
A.
4 3.
m
B.
3 3.
m
C.
4 2.
m
D.
3 2.
m
Câu 12. Cho hàm số
3 2
3 2
y x x
có đồ thị như hình vẽ. Tìm tập hợp
S
tất cả các giá của tham số thực
m
sao cho phương trình
3 2
3 2 0
x x m
có ba nghiệm thực phân biệt.
A.
.
S
B.
[ 2;2].
S
C.
( 2;1).
S
D.
( 2;2).
S
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 77 -
O
x
y
1
1
2
2
x
y
O
O
x
y
Câu 13. Cho hàm số
1
ax b
y
x
có đồ thị như hình dưới.
Khẳng định nào dưới đây là đúng ?
A. 0 .b a
B. 0 .b a
C. 0.b a
D. 0 .a b
Câu 14. Cho hàm số
3 2
y ax bx cx d
có đồ thị là đường cong trong hình dưới đây. Mệnh đề nào sau
đây đúng ?
A. 0,a 0,c 0.d
B. 0,a 0,c 0.d
C. 0,a 0,c 0.d
D. 0,a 0,c 0.d
Câu 15. Hàm số
4 2
y ax bx c
có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng ?
A. 0,a 0,b 0.c
B. 0,a 0,b 0.c
C. 0,a 0,b 0.c
D. 0,a 0,b 0.c
Câu 16. Cho hàm số ( ) ln .f x x x Tính ( ).f e
A. ( ) 2.f e
B.
1
( )f e
e
C. ) 3.(f e
D. ) .(f e e
Câu 17. Cho hàm số
lnx
y
x
Mệnh đề nào sau đây đúng ?
A.
2
1
y xy
x
B.
2
1
2y xy
x
C.
2
1
y xy
x
D.
2
1
2y xy
x
Câu 18. Cho hàm số
2
( ) 2
x a
f x
và có (1) 2 ln 2.f
Hỏi mệnh đề nào sau đây đúng ?
A. 1.a
B. 2 0.a
C. 0 1.a
D. 2.a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 78 -
Câu 19. Cho phương trình
1
4 ( 1)2 8 0.
x x
m
Biết phương trình có hai nghiệm
1
,
x
2
x
thỏa mãn
1 2
( 1)( 1) 6.
x x
Khẳng định nào sau đây đúng ?
A. Không có
.
m
B.
1 3.
m
C.
3.
m
D.
2.
m
Câu 20. Giá trị thực của tham số
m
để phương trình
2
3 3
log 3 log 2 7 0
x x m
có hai nghiệm thực
1 2
,
x x
thỏa mãn
1 2
( 3)( 3) 72
x x
thuộc khoảng nào sau đây ?
A.
(0;3).
B.
( 6; 3).
C.
(3;6).
D.
( 3;0).
Câu 21. Tìm tập hợp
m
để phương trình
25 .5 2 5 0
x x
m m
có hai nghiệm trái dấu.
A.
5
;
2

B.
5
0;
2
C.
(0; ).
D.
5
; 4
2
Câu 22. Tìm tham số
m
để phương trình
2
4 (1 3 )2 2 0
x x
m m m
có nghiệm.
A.
( ; ).
B.
( ;1) (1; ).
C.
(0; ).
D.
(1; ).
Câu 23. Có mấy giá trị nguyên của
m
để
2 2
2 2
log log 3
x x m
có nghiệm
[1;8].
x
A.
5.
B.
2.
C.
4.
D. Vô số.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 79 -
Câu 24. Tập hợp các giá trị thực của
m
để phương trình
2
3 1
3
log (1 ) log ( 4) 0
x x m
có hai nghiệm
thực phân biệt là
( ; ),
T a b
trong đó
,
a b
là các số nguyên hoặc phân số tối giản. Giá trị của
M a b
bằng
A.
33
6
B.
17
3
C.
9
2
D.
41
4
Câu 25. Có bao nhiêu giá trị nguyên của
m
để
3
3
3 3 sin sin
m m x x
có nghiệm ?
A.
7.
B.
3.
C.
5.
D.
2.
Câu 26. Cho dãy số
( )
n
u
thỏa mãn
1
6,
n n
u u
2
n
và
2 5 9
2
log log 8 11.
u u Đặt
1 2
.
n n
S u u u
Tìm số tự nhiên
n
nhỏ nhất thỏa mãn
20172018.
n
S
A.
2587.
B.
2590.
C.
2593.
D.
2584.
Câu 27. Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
,
a
cạnh bên
2 .
SA a
Thể tích của khối nón
có đỉnh
S
và đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
bằng
A.
3
2
a
B.
3
33
27
a
C.
3
6
a
D.
3
2
2
a
Câu 28. Cho hình chóp tứ giác đều
.
S ABCD
có cạnh bên
SA
bằng
2
a
và
SA
tạo đáy góc
45 .
Thể tích
khối nón có đỉnh
S
và đường tròn đáy nội tiếp tứ giác
ABCD
bằng
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 80 -
A.
3
3
a
B.
3
2
6
a
C.
3
6
a
D.
3
2
2
a
Câu 29. Cho hình chóp tứ giác đều
.S ABCD
có cạnh bên
2SA a
và
.AB a
Thể tích của khối nón có
đỉnh
S
và đường tròn đáy là đường tròn ngoại tiếp tứ giác
ABCD
bằng
A.
3
6
12
a
B.
3
2
6
a
C.
3
6
a
D.
3
2
2
a
Câu 30. Cho hình hộp chữ nhật .ABCD A B C D
có 8,AD 6,CD 12.AC
Diện tích toàn phần của
hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật
ABCD
và A B C D
bằng
A.
576 .
B. 10(2 11 5) .
C.
26 .
D. 5(4 11 4) .
Câu 31. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh bằng
1.
Tính thể tích của khối trụ đó.
A.
2
B.
4
C. .
D.
3
Câu 32. Cho hình lăng trụ đều .ABC A B C
có cạnh đáy bằng ,a cạnh bên bằng 2 .a Thể tích của hình trụ
có hai đáy nội tiếp hình lăng trụ bằng
A.
3
18
a
B.
3
6
a
C.
3
.a
D.
3
12
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 81 -
O
I
R
x
r
R
Câu 33. Cho một khối lăng trụ tam giác đều có thể tích là
3
3
2
a
Tính thể tích
V
của khối trụ ngoại tiếp lăng
trụ đã cho.
A.
3
3
a
V
B.
3
2
3
a
V
C.
3
. 3.
V a
D.
3
2 . 3
3
a
V
Câu 34. Cho tam giác
ABC
có
13cm, 5cm
AB BC
và
2cm.
AC
Thể tích
V
của khối tròn xoay
được tạo thành khi quay tam giác
ABC
quanh trục
.
AC
A.
3
10
cm .
3
V
B.
3
8 cm .
V
C.
3
16
cm .
3
V
D.
3
8
cm .
3
V
Câu 35. Cho hình thoi
ABCD
cạnh bằng
,
a
có góc
60 .
ABC
Quay hình thoi này quanh đường chéo
,
BD
ta thu được khối tròn xoay có thể tích bằng
A.
3
2 3.
a
B.
3
3
12
a
C.
3
2.
a
D.
3
3
6
a
Câu 36. Cho hình thang cân
ABCD
có đáy nhỏ
1,
AB
đáy lớn
3,
CD
cạnh bên
2.
AD
Quay hình
thang quanh đường thẳng
.
AB
Tính thể tích
V
của khối tròn xoay tạo thành.
A.
3 .
V
B.
4
3
V
C.
7
3
V
D.
5 .
V
Câu 37. Cho khối cầu tâm
O
bán kính
R
(cho trước). Mặt phẳng
( )
P
cách
O
một khoảng
x
cắt khối cầu
theo một hình tròn
( ).
C
Một khối nón
( )
có đỉnh thuộc mặt cầu, đáy là hình tròn
( ).
C
Biết khối
nón
( )
có thể tích lớn nhất, khi đó giá trị của
x
bằng
A.
3
R
x
B.
2
R
x
C.
2
2
R
x
D.
3
4
R
x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 82 -
O
O’
I
A
R
h
r
Câu 38. Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối
cầu có đường kính bằng một nửa chiều cao của bình nước và đo được thể tích tràn ra là
3
32
(dm ).
3
Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và toàn bộ khối cầu chìm trong
nước, trong đó mặt nước là tiết diện của khối cầu (hình vẽ). Thể tích nước còn lại trong bình bằng
A.
3
16
(dm ).
3
B.
3
32
(dm ).
3
C.
3
40
(dm ).
3
D.
3
64
(dm ).
3
Câu 39. Cho hình trụ có bán kính đáy
,R
trục 2OO R
và mặt cầu có đường kính
.OO
Kí hiệu
1 2
, V V
lần lượt là thể tích của các khối trụ và khối cầu. Tính tỉ số
1
2
V
V
A.
1
2
3
2
V
V
B.
1
2
2
3
V
V
C.
1
2
3
4
V
V
D.
1
2
4
3
V
V
Câu 40. Cho khối cầu ( )S tâm ,I bán kính
R
không đổi (cho trước). Một khối trụ thay đổi có chiều cao h
và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo
R
sao cho thể tích của khối trụ lớn nhất.
A.
2 3
3
R
h
B.
2
2
R
h
C.
3
2
R
h
D.
2.h R
Câu 41. Một hình trụ gọi là nội tiếp nửa mặt cầu
( ; )S O R
nếu một đáy của hình trụ nằm trong đáy của nửa
mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết
1R
và khối trụ
có thể tích lớn nhất thì giá trị của bán kính r và chiều cao h lần lượt là
A.
6
3
và
3
3
B.
3
2
và
6
2
C.
6
2
và
3
2
D.
3
3
và
6
3
Câu 42. Cho hình chóp .S ABC có cạnh bên SA vuông góc với đáy, 2,AB a
,BC a
2SC a và
30 .SCA Tính bán kính
R
của mặt cầu ngoại tiếp tứ diện . .S ABC
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 83 -
A.
3.R a
B.
3
2
a
R
C.
.R a
D.
2
.
3
a
R
Câu 43. Cho hình chóp .S ABC có đáy là tam giác ABC đều cạnh
3 ,a
cạnh bên 2SA a và SA vuông góc
với mặt phẳng đáy. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp . .S ABC
A.
2 3
3
a
R
B.
3 .R a
C.
2 .R a
D.
13
2
a
R
Câu 44. Cho hình chóp .S ABCD có đáy là hình chữ nhật với
3 ,AB a
4 ,BC a
12SA a và SA vuông
góc với đáy. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp . .S ABCD
A.
5
2
a
R
B.
17
2
a
R
C.
6 .R a
D.
13
2
a
R
Câu 45. Cho tứ diện đều ABCD cạnh bằng .a Gọi H là hình chiếu vuông góc của A trên mặt phẳng
( )
BCD
và I là trung điểm của .AH Bán kính
R
của mặt cầu ngoại tiếp tứ diện IBCD bằng
A.
6
4
a
R
B.
3
4
a
R
C.
6
2
a
R
D.
3
2
a
R
Câu 46. Cho hình chóp tứ giác đều .S ABCD có đáy hợp với mặt bên một góc 45 . Bán kính mặt cầu ngoại
tiếp hình chóp .S ABCD bằng
2.
Tính thể tích V của khối chóp . .S ABCD
A.
64 2
81
V
B.
64 2
27
V
C.
28 2
81
V
D.
32 2
9
V
Câu 47. Cho hình chóp .S ABC có đáy ABC là tam giác vuông tại .C Tam giác SAB vuông tại S và nằm
trong mặt phẳng vuông góc với đáy. Góc giữa SB và mặt phẳng đáy là 60 ,
3.SA a
Tìm bán
kính
R
của mặt cầu ngoại tiếp hình chóp . .S ABC
A.
3.R a
B.
5.R a
C.
3 .R a
D.
5 .R a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 84 -
Câu 48. Hình chóp .S ABC có đáy tam giác vuông,
3,
BA BC a
SA vuông với đáy và .SA a Gọi
D là điểm đối xứng của S qua .A Diện tích mặt cầu ngoại tiếp .S BCD bằng
A.
2
52
.
3
a
B.
2
25
.
3
a
C.
2
20 .a
D.
2
160
.
3
a
Câu 49. Cho hình chóp .S ABCD có đáy ABCD là hình vuông cạnh .a Cạnh bên SA vuông góc với mặt
đáy ( )ABCD và .SA a Gọi E là trung điểm của cạnh .CD Mặt cầu đi qua bốn điểm , , , S A B E
có bán kính là
A.
41
8
a
B.
41
24
a
C.
41
16
a
D.
2
16
a
Câu 50. Cho hình lăng trụ đứng .ABC A B C
có đáy ABC là tam giác vuông tại ,A
3,
AB a
2 ,BC a
đường thẳng AC
tạo với mặt phẳng ( )BCC B
một góc 30 (tham khảo hình vẽ bên). Diện tích
của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
A.
2
24 .a
B.
2
6 .a
C.
2
4 .a
D.
2
3 .a
BẢNG ĐÁP ÁN ĐỀ SỐ 10
1.A 2.D 3.B 4.B 5.A 6.C 7.D 8.B 9.C 10.D
11.D 12.D 13.C 14.B 15.A 16.B 17.D 18.B 19.B 20.C
21.D 22.C 23.A 24.D 25.C 26.C 27.B 28.C 29.A 30.B
31.B 32.B 33.B 34.D 35.B 36.C 37.A 38.B 39.A 40.A
41.A 42.C 43.C 44.D 45.A 46.A 47.A 48.B 49.A 50.B
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 85 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
TRƯỜNG THPT TRẦN PHÚ Môn thi: TOÁN – ĐỀ SỐ 11
(Thời gian làm bài 60 phút)
PHẦN 1. TRẮC NGHIỆM (6,0 điểm)
Câu 1. Cho hàm số
2 1
1
x
y
x
Tìm khẳng định đúng ?
A.
y
nghịch biến trên
( ; ) \ {1}.
 
B.
y
nghịch biến trên
( ;1),

đồng biến trên
(1; ).

C.
y
nghịch biến trên
( ;1)

và
(1; ).

D.
y
đồng biến trên
( ;1),

nghịch biến trên
(1; ).

Câu 2. Gọi
,
M m
là giá trị lớn nhất, nhỏ nhất của hàm số
4
2
2
4
x
y x
trên
[ 1;2].
Tính
.
M m
A.
13
4
M m
B.
4.
M m
C.
3.
M m
D.
9
4
M m
Câu 3. Cho hàm số
3 6
2 4
x
y
x
có đồ thị là
( ).
C
Tìm khẳng định đúng ?
A.
( )
C
có hai tiệm cận
2, 3.
x y
B.
( )
C
có hai tiệm cận
3, 2.
x y
C.
( )
C
có hai tiệm cận
3
2,
2
x y
D.
( )
C
có hai tiệm cận
3
3,
4
x y
Câu 4. Đồ thị được cho như hình dưới đây là đồ thị của hàm số nào ?
A.
3 2
– 3 1.
y x x
B.
3 2
3 1.
y x x
C.
3 2
– 6 1.
y x x
D.
3 2
– 3 1.
y x x
Câu 5. Cho hàm số
1
x
y
x
có đồ thị là
( )
C
và đường thẳng
: .
d y x m
Tìm tất cả các giá trị thực
của tham số m để
d
cắt
( )
C
tại hai điểm phân biệt.
A.
1
1
m
m
B.
0 4.
m
C.
0
4
m
m
D.
–1 4.
m
Câu 6. Cho
3 2
( ) : 2 3 3,
C y x x x
gọi
M
là giao điểm của
( )
C
và trục tung. Viết phương trình tiếp
tuyến của
( )
C
tại
.
M
A.
2 3.
y x
B.
3.
y x
C.
3 3.
y x
D.
2 3.
y x
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 86 -
Câu 7. Cho
2
( ) :
6
x
C
x
y
và đường thẳng
: 2 1.
d y x
Viết phương trình tất cả các tiếp tuyến của
( ),
C
biết các tiếp tuyến này song song với
.
d
A.
2 13.
y x
B.
2 – 3.
y x
C.
2 – 3, 2 13.
y x y x
D.
2 .
y x
Câu 8. Cho hàm số
( )
liên tục trên tập số thực và có đồ thị như hình vẽ. Tìm tham số
m
để phương
trình
( )
f x m
có
4
nghiệm phân biệt.
A.
0 4.
m
B.
–1 4.
m
C.
1 4.
m
D.
–1 1.
m
Câu 9. Tìm
m
để hàm số
4 2 2 2
3
(
) 3
y x m m x m m
có ba cực trị.
A.
–3 0.
m
B.
3
m
hoặc
0.
m
C.
0.
m
D.
–3.
m
Câu 10. Giải phương trình:
6
2 ( 2) 16 0.
x x
A.
8.
x
B.
6.
x
C.
4.
x
D.
2.
x
Câu 11. Tìm tập nghiệm của bất phương trình:
2
1
1
9
3
x
x
A.
( ;0).

B.
( ; 1).

C.

D.
(1; ).

Câu 12. Cho hình chóp
.
S ABC
có
( ),
SA ABC
tam giác
ABC
vuông tại
, ,
B AB a
2 ,
BC a
góc giữa
SB
và
(
)
ABC
bằng
60 .
Thể tích của khối chóp
.
S ABC
bằng
A.
3
3
a
B.
3
3
2
a
C.
3
3
9
a
D.
3
3
3
a
Câu 13. Cho hình lăng trụ đều
.
ABC A B C
có
,
AB a
diện tích của mỗi mặt bên bằng diện tích đáy. Thể
tích của khối lăng trụ đều
.
ABC A B C
bằng
A.
3
3
4
a
B.
3
3
8
a
C.
3
3
16
a
D.
3
3 3
16
a
Câu 14. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
)
, (
a SA ABC
D
và
.
AB SA a
Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
. .
S ABCD
A.
2
a
R
B.
2
2
a
R
C.
3
2
a
R
D.
.
R a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 87 -
Câu 15. Thiết diện qua trục của hình trụ là hình vuông cạnh
.
a
Tính diện tích xung quanh
xq
S
của hình hình
trụ này.
A.
2
xq
2
S
a
B.
2
xq
2 .
S
a
C.
2
xq
2
3
S
a
D.
2
xq
.
S
a
Câu 16. Hình chữ nhật
ABCD
có
2 , .
AB a BC a
Tính thể tích
V
của khối trụ được tạo thành khi cho
hình chữ nhật
ABCD
quay quanh
.
AB
A.
3
2 .
V a
B.
3
4 3.
V a
C.
3
3.
V a
D.
3
3 .
V a
Câu 17. Một hình nón có góc ở đỉnh bằng
60 ,
đường sinh có độ dài bằng
.
a
Tính thể tích
V
của hình nón
này.
A.
3
3
6
a
V
B.
3
24
a
V
C.
3
3
24
a
V
D.
3
3
a
V
Câu 18. Một hình nón có bán kính đáy bằng
,
a
góc giữa đường sinh và mặt đáy bằng
45 .
Diện tích toàn
phần của hình nón này bằng
A.
2
(2 2).
a
B.
2
(1 2).
a
C.
2
2
2
a
D.
2
2
3
a
Câu 19. Tìm
m
để hàm số
3
2 2
( 1) ( 1)
3
x
y m x m x
đồng biến trên
( ; ).
 
A.
1
2
m
B.
1
2
m
C.
1
2
m
D.
1
2
m
Câu 20. Tìm tập xác định
D
của hàm số
1 log .
y x
A.
.
(0;
]
10
D
B.
(0; ).

D
C.
.
1;
[ ]
10
D
D.
[1; ).

D
Câu 21. Gọi
( )
C
là đồ thị hàm số
4 2
2 .
y x x m
Tìm tất cả các giá trị thực của tham số
m
để
( )
C
và
trục hoành có
4
giao điểm phân biệt.
A.
0
1
m
m
B.
0 1.
m
C.
–1 0.
m
D.
–1 1.
m
Câu 22. Đặt
2 3
log 7, log 4.
a b
Biểu thị
7
log 6
theo
a
và
.
b
A.
7
log 6
2
a
ab
B.
7
log 6
2
b
ab
C.
7
log 6
2
ab
a
D.
7
log 6
2
ab
b
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 88 -
Câu 23. Cho hàm số
)
ln(1
x
y e
có đồ thị là
( ),
C
đường thẳng
ln2
x
cắt
( )
C
tại
.
M
Tiếp tuyến của
( )
C
tại
M
có hệ số góc là
.
k
Tìm khẳng định đúng ?
A.
2 3.
k
B.
1 2.
k
C.
0 1.
k
D.
0.
k
Câu 24. Cho hình chóp đều
.
S ABCD
có
,
AB a
tam giác
SBD
vuông. Thể tích của khối chóp đều
.
S ABCD
bằng
A.
3
2
6
a
B.
3
2
2
a
C.
3
2
3
a
D.
3
6
a
Câu 25. Cho hình lăng trụ đứng
. .
ABC A B C
Tam giác
ABC
vuông tại
, 5,
A BC
10,
A B
13.
A C
Thể tích của khối lăng trụ
.
ABC A B C
bằng
A.
1.
B.
2.
C.
3.
D.
4.
Câu 26. Đồ thị hàm số
2
2
3 2
( 4 4)
x x
y
x x x
có tất cả bao nhiêu đường tiệm cận ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 27. Đồ thị hàm số
3 2
3 1
y x x
có hai điểm cực trị là
M
và
.
N
Tính diện tích
S
của tam giác
OMN
(
O
là gốc tọa độ).
A.
1.
S
B.
2.
S
C.
2.
S
D.
3
2
S
Câu 28. Tìm
m
để phương trình
2
log – ( – 1) – 1
[
log
]
x m x x
có duy nhất một nghiệm.
A.
(1;10).
m
B.
(0;1).
m
C.
( ; ).
m
 
D.
(0; ).
m

Câu 29. Cho hình chóp
.
S ABCD
có
ABCD
là hình bình hành tâm
.
O
Trên các đoạn thẳng
, ,
SA SB SO
lần lượt lấy các điểm
, ,
M N K
sao cho
M
là trung điểm của
,
SA N
là trung điểm của
2 .
, 3
SB SK
SO
Mặt phẳng
(
)
MNK
chia khối chóp
.
S ABCD
thành hai khối đa diện có thể tích là
1
V
và
2
V
1 2
( ).
V V
Tính tỷ số
1
2
V
k
V
A.
3
4
k
B.
3
5
k
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 89 -
C.
1
6
k
D.
2
3
k
Câu 30. Cho hình lăng trụ
.
ABCD A B C D
có đáy
ABC
D
là hình vuông cạnh
,
a
tâm
O
và
),
(
A O ABC
D
góc giữa
AB
và mặt phẳng
(
)
ABC
D
bằng
60 .
Tính thể
V
của khối lăng trụ
. .
ABCD A B C D
A.
3
10
2
a
B.
3
30
2
a
C.
3
30
4
a
D.
3
10
4
a
PHẦN 2. TỰ LUẬN (4,0 điểm)
Câu 1. (1.0 đ). Tìm
m
để hàm số
2
( 2) 6
2
m x m
y
x
đồng biến trên từng khoảng xác định.
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Câu 2. (1.0 đ). Cho
3 2
( ) : .
C y x mx mx
Tìm
m
để
( )
C
cắt trục hoành tại 3 điểm phân biệt.
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Câu 3. (1.0 đ). Giải phương trình:
1
9 10.3 1 0.
x x
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Câu 4. (1.0 đ). Giải phương trình:
2 2
2 2
log ( 2 1) 4.log ( 1) 0.
x x x
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
ĐÁP ÁN ĐỀ 11
1C 2C 3A 4A 5C 6C 7C 8C 9B 10C
11B 12D 13C 14C 15D 16A 17C 18B 19A 20A
21B 22B 23C 24A 25C 26D 27A 28C 29B 30B
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 90 -
ĐÁP ÁN & THANG ĐIỂM PHẦN TỰ LUẬN
Câu 1. (1.0 điểm)
2
2
2 4 6
( 2)
m m
y
x
0.25đ
2
2 4 – 6 0
m m
0.25đ
2
1
3
m
0.5đ
Câu 2. (1.0 điểm)
PTHĐGD của
( )
C
và trục hoành:
3 2
0
x mx mx
0.25đ
0
x
hay
2
0
x mx m
0.25đ
0
m
hay
4
m
0.5đ
Câu 3. (1.0 điểm)
9.9 – 10.3 1 0.
x x
0.25đ
3 1
1
3
9
x
x
0.25đ
0
2
x
x
0.5đ
Câu 4. (1.0 điểm)
2
2 2
4 log ( 1) 4.log ( 1) 0
x x
(Điều kiện:
1).
x
0.25đ
2
2
log ( 1) 0
log ( 1) 1
x
x
0.25đ
2
3
x
x
0.5đ
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 91 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
TRƯỜNG THPT TÂN BÌNH Môn thi: TOÁN – ĐỀ SỐ 12
(Thời gian làm bài 60 phút)
PHẦN 1. TRẮC NGHIỆM (8,0 điểm)
Câu 1. Tập nghiệm của bất phương trình
2
log 2
x
là
A.

B.
(0;2).
C.
(0;4).
D.
.
Câu 2. Cho hàm số
x
e
y
Khẳng định nào đúng ?
A. Đồng biến trên
.
B. Nghịch biến trên khoảng
( ;0)

và đồng biến trên khoảng

C. Nghịch biến trên
.
D. Đồng biến trên khoảng
( ;0)

và nghịch biến trên khoảng

Câu 3. Cho hàm số
2
3 1
1 2
x
y
x
Khẳng định nào sau đây đúng ?
A. Đồ thị hàm số có ba tiệm cận.
B. Đồ thị hàm số có một tiệm cận ngang là
3.
y
C. Đồ thị hàm số có một tiệm cận.
D. Đồ thị hàm số không có tiệm cận.
Câu 4. Đồ thị hàm số nào sau đây có
3
điểm cực trị ?
A.
4 2
2 4 1.
y x x
B.
4 2
2 1.
y x x
C.
4 2
2 1.
y x x
D.
4 2
2 1.
y x x
Câu 5. Số nghiệm của phương trình
6.4 7
x
là
A.
1.
B.
0.
C.
2.
D.
3.
Câu 6. Cho hình lập phương có cạnh là
2 .
a
Thể tích hình lập phương đó là bao nhiêu ?
A.
3
4 .
a
B.
3
2 .
a
C.
3
8 .
a
D.
3
.
a
Câu 7. Cho mặt cầu có diện tích bằng
2
8
3
a
Tính bán kính
R
của mặt cầu đã cho.
A.
3
3
a
R
B.
6
2
a
R
C.
6
3
a
R
D.
2
3
a
R
Câu 8. Rút gọn biểu thức
1
6
3
.
P x x
với
0.
x
A.
.
P x
B.
2
.
P x
C.
1
6
.
P x
D.
1
18
.
P x
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 92 -
6
4
2
2
5 5
1
3
y
x
5
-2
-1
4
2
1
O
Câu 9. Đường cong ở hình bên là đồ thị của hàm nào ?
A.
2 1
1
x
y
x
B.
2 1
1
x
y
x
C.
2 1
1
x
y
x
D.
2 1
1
x
y
x
Câu 10. Hàm số
2 1
3
x
y
x
có số điểm cực trị là
A.
0.
B.
3.
C.
2.
D.
1.
Câu 11. Cho hình chóp
.
S ABCD
đáy là hình vuông cạnh
,
a SA
vuông góc đáy và
3.
SA a
Thể tích khối
chóp
.
S ABCD
bằng
A.
3
6
6
a
B.
3
6
9
a
C.
3
3
3
a
D.
3
6
3
a
Câu 12. Đồ thị hàm số
4 2
2
y x x
cắt trục
Ox
tại bao nhiêu điểm ?
A.
2.
B.
3.
C.
1.
D.
4.
Câu 13. Tiệm cận đứng của đồ thị hàm số
2 1
3
x
y
x
là
A.
2.
x
B.
3.
x
C.
2.
x
D.
3.
x
Câu 14. Cho hàm số
3 2
3 1
y x x
( ).
C
Tìm hệ số góc
k
của tiếp tuyến của đồ thị
( )
C
tại điểm có hoành
độ bằng
1.
A.
1.
k
B.
1.
k
C.
3.
k
D.
3.
k
Câu 15. Cho các số thực dương
,
a b
với
a
khác
1.
Khẳng định nào đúng ?
A.
4
1
log ( ) log .
4
a
a
ab b
B.
4
log ( ) 4 4 log .
a
a
ab b
C.
4
log ( ) 4 log .
a
a
ab b
D.
4
1 1
log ( ) log .
4 4
a
a
ab b
Câu 16. Tìm khoảng nghịch biến của hàm số
3 2
1
3 .
3
y x x x
.
A.

B.
(
–1;3).
C.
( ; 1).

D.
( ; 1) (3; ).

Câu 17. Hàm số
3 2
2 9 12 5
y x x x
có mấy điểm cực trị ?
A.
3.
B.
1.
C.
4.
D.
2.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 93 -
x
y
1
2
O
Câu 18. Giá trị lớn nhất của hàm số
x
y e
trên đoạn
[0;2]
bằng
A.
1.
B.
2.
C.
2
.
e
D.
0.
Câu 19. Tìm giá trị nhỏ nhất của hàm số
2 4
1
x
y
x
trên đoạn
[0;3].
A.
4.
B.
1.
C.
1
2
D.
0.
Câu 20. Đồ thị hàm số
4
2017
y x
cắt trục hoành tại mấy điểm ?
A.
3.
B.
1.
C.
2.
D.
0.
Câu 21. Tập giá trị của hàm số
log
y x
là
A.

B.
.
C.
[0; ).

D.
(1; ).

Câu 22. Tập giá trị của hàm số
1
2
x
y
là
A.
(1; ).

B.

C.
.
D.
[0; ).

Câu 23. Cho hình nón có bán kính đáy là
3 ,
a
chiều cao là
4 .
a
Tính thể tích
V
của khối nón giới hạn bởi hình
nón đã cho.
A.
3
.
15
V
a
B.
3
36 .
V
a
C.
3
.
12
V
a
D.
3
.
24
V
a
Câu 24. Tìm tập xác định
D
của hàm số
2 4
( 1) .
y x
A.
[ 1;1].
D
B.
\ { 1;1}.
D
C.
( 1;1).
D
D.
( ; 1) (1; ).
 
D
Câu 25. Cho
,
a b
là các số thực dương thỏa mãn
1
a
và
log 4.
a
b
Tính
2
3
log .
a
P b
A.
6.
P
B.
2.
P
C.
1,5.
P
D.
3.
P
Câu 26. Cho đồ thị hàm số
ax b
y
cx d
Tìm khẳng định đúng ?
A.
0, 2.
y x
B.
0, 1.
y x
C.
0, 2.
y x
D.
0, 1.
y x
Câu 27. Cho hàm số
( )
liên tục trên
[ 2;2],
có đồ thị như trong hình vẽ bên. Hỏi phương trình
( ) 1 1
f x
có bao nhiêu nghiệm phân biệt trên đoạn
[ 2;2].
A.
4.
B.
6.
C.
3.
D.
5.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 94 -
Câu 28. Tìm tọa dộ tâm đối xứng của đồ thị hàm số
3
2
2 3 1.
3
x
y x x
A.
1
1;
3
B.
1
2;
3
C.
(3; –1).
D.
(0; –1).
Câu 29. Hình trụ có diện tích xung quanh bằng
100
2
cm
và có đường sinh bằng
10cm
thì có bán kính đáy
là bao nhiêu ?
A.
20cm.
B.
25cm.
C.
5cm.
D.
10cm.
Câu 30. Cho
log 2
a
b
và
log 5
a
c
( , , 0; 1).
a b c a
Tính
3
log
a
a b
P
c
A.
5
3
P
B.
2
3
P
C.
4
3
P
D.
5
3
P
Câu 31. Cho
1.
a
Mệnh đề nào dưới đây sai ?
A.
log 0
a
x
khi
0 1.
x
B. Đồ thị hàm số
log
a
y x
có tiệm cận ngang là trục hoành.
C. Nếu
1 2
x x
thì
1 2
log log .
a a
x x
D.
log 0
a
x
khi
1.
x
Câu 32. Hình nón ngoại tiếp hình chóp tam giác đều có tất cả các cạnh bằng
a
có diện tích xung quanh bằng
bao nhiêu ?
A.
2
2
3
a
B.
2
3
a
C.
2
3 .
a
D.
2
3
a
Câu 33. Hàm số
2
1
y x
nghịch biến trên khoảng nào ?
A.
(
; 1).

B.
(0;1).
C.
( 1;1).
D.

Câu 34. Cho lăng trụ đứng
.
ABC A B C
có tất cả các cạnh đều bằng
3.
a
Tính thể tích của khối lăng trụ
. .
ABC A B C
A.
3
3
4
a
B.
3
9
4
a
C.
3
3 3
4
a
D.
3
9 3
4
a
Câu 35. Ông An gửi vào ngân hàng 100 triệu đồng lúc con ông ta vừa tròn 1 tuổi. Biết lãi xuất ngân hàng 10
năm đầu ổn định là 8%, các năm tiếp theo lãi xuất ổn định là 12%. Khi con ông An lớn lên ông An
đến ngân hàng rút hết tiền để hổ trợ cho việc tiếp tục việc học của con ông ta, thì ông An nhận được
số tiền là 477,2695351 triệu đồng (chưa làm tròn). Hỏi lúc đó con ông An được bao nhiêu tuổi ?
A.
19.
B.
17.
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 95 -
C.
16.
D.
18.
Câu 36. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
SA
vuông góc
( ),
và
.
SA a
Thể tích khối chóp
.
S BCD
tính theo
a
bằng bao nhiêu ?
A.
3
3
a
B.
3
8
a
C.
3
6
a
D.
3
12
a
Câu 37. Gọi
M
là giao điểm của
1
( ) :
1
x
C y
x
với trục tung. Tìm hệ số góc
k
của tiếp tuyến với
( )
C
tại
điểm
.
M
A.
2.
k
B.
1.
k
C.
1.
k
D.
2.
k
Câu 38. Một người thợ định làm một thùng để đựng
3
2m
nước dạng hình trụ (không nắp). Để tiết kiệm vật
liệu nhất cần làm đáy của thùng có bán kính là bao nhiêu ?
A.
1
(m).
B.
2
(m).
C.
3
2
(m).
D.
3
1
(m).
Câu 39. Tính
1 2
5 5 ,
x x
S
biết
1
x
và
2
x
là hai nghiệm của phương trình
25 6.5 5 0.
x x
A.
1.
S
B.
6.
S
C.
2.
S
D.
3.
S
Câu 40. Cho hàm số
4 2
2 1
y x x
có đồ thị
( ),
C
phương trình tiếp tuyến với
( )
C
tại điểm cực đại của
đồ thị hàm số là
A.
1.
y
B.
0.
y
C.
1.
x
D.
0.
x
PHẦN 2. TỰ LUẬN (2,0 điểm)
ĐỀ LẺ: DÀNH CHO HỌC SINH CÓ SỐ BÁO DANH LẺ
Bài 1. Giải phương trình:
2 2
2 2 2
log ( 2) log ( 10) 4 log 3.
x x
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 96 -
..................................................................................................................................................................................
Bài 2. Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và mặt bên tạo với đáy một góc
60 .
Hãy xác
định tâm và tính bán kính mặt cầu ngọai tiếp khối chóp
. .
S ABC
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
ĐỀ CHẴN: DÀNH CHO HỌC SINH CÓ SỐ BÁO DANH CHẴN
Bài 1. Giải phương trình:
5.36 3.16 2.81 .
x x x
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
Bài 2. Cho
ABC
vuông tại
A
có
AB a
và
3.
AC a
Gọi
H
là trung điểm
,
BC
trên đường thẳng
Hx
vuông góc
( )
ABC
lấy điểm
S
sao cho
.
3
SB
a
Xác định tâm và tính bán kính mặt cầu ngoại tiếp
hình chóp
.
SABC
.................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 97 -
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
THPT BÌNH HƯNG HÒA Môn thi: TOÁN – ĐỀ SỐ 13
(Thời gian làm bài 60 phút)
PHẦN 1. TRẮC NGHIỆM (8,0 điểm)
Câu 1. Đặt
7
log 12a và
12
log 24.b Tính giá trị của
54
log 168P theo a và
.b
A.
1
.
8 5
ab
P
a b
B.
1
(8 5 )
ab
P
a b
C.
8 5
ab
P
a b
D.
(8 5 )
ab
P
a b
Câu 2. Tìm tập xác định
D
của hàm số
1
2
log (3 2 ).y x
A.
3
;
2

D
B.
3
;
2
D
C.
2
;
3

D
D.
2
;
3
D
Câu 3. Tìm nghiệm của phương trình
3
log (2 3) 2.x
A.
3.x
B.
5
2
x
C.
3
2
x
D.
2
3
x
Câu 4. Đồ thị hình bên dưới là của hàm số nào ?
A.
3 2
2 1.y x x
B.
4 2
2 1.y x x
C.
4 2
3 1.y x x
D.
4 2
2 1.
y x x
Câu 5. Rút gọn biểu thức
3
4
2
P x x với 0.x
A.
.P x
B.
3
4
.P x
C.
1
3
.P x D.
2
.P x
Câu 6. Tìm giá trị lớn nhất
M
của hàm số
4 2
2y x x
trên đoạn [0;2].
A.
2.M
B.
1.M
C.
0.M
D.
8.M
Câu 7. Cho hình chóp tứ giác đều
.S ABCD
có có độ dài cạnh đáy bằng a và cạnh bên bằng
2 .a
Tính bán
kính
R
của mặt cầu ngoại tiếp hình chóp đã cho.
A.
6
2
a
R B.
2 14
7
a
R
C.
14
7
a
R D.
2 6
3
a
R
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 98 -
2
1
1
+
+
y
y'
x
Câu 8. Cho khối trụ có bán kính đáy
4
r
và chiều cao
4 2.
h
Thể tích của khối trụ bằng
A.
64 2
.
3
V
B.
64 2 .
V
C.
32 .
V
D.
32 2 .
V
Câu 9. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
cạnh bên
SA
vuông góc với mặt
phẳng đáy và
2 .
SA a
Tính thể tích
V
của khối chóp
. .
S ABCD
A.
3
2
3
a
V
B.
3
2 .
V a
C.
3
4
3
a
V
D.
3
.
V a
Câu 10. Tính đạo hàm của hàm số
ln 3 .
y x
A.
1
ln 3
y
x
B.
3
y
x
C.
1
y
x
D.
1
3
y
x
Câu 11. Hàm số nào dưới đây đồng biến trên khoảng
( ; ).
 
A.
1
.
2
x
y
x
B.
3 2
.
y x x x
C.
3 2
.
y x x x
D.
4 2
3 1.
y x x
Câu 12. Tính thể tích V của khối lập phương
. ,
ABCD A B C D
biết
6.
AC a
A.
3
2 2 .
V a
B.
3
3 3 .
V a
C.
3
.
V a
D.
3
2 2
3
a
V
Câu 13. Viết phương trình tiếp tuyến của đồ thị hàm số
4 2
4 1
y x x
tại điểm có hoành độ
1.
x
A.
4 6.
y x
B.
4 2.
y x
C.
4 6.
y x
D.
4 2.
y x
Câu 14. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số
2 1
3
x
y
x
A.
2.
y
B.
2.
x
C.
3.
x
D.
3.
y
Câu 15. Trong không gian, cho tam giác
ABC
vuông tại
,
A
, 3.
AB a AC a
Tính độ dài đường sinh
của hình nón, nhận được khi quay tam giác
ABC
xung quanh trục
.
AC
A.
.
a
B.
2 .
a
C.
3 .
a
D.
2 .
a
Câu 16. Cho
a
là số thực dương khác 1. Tính
2
log .
a
I a
A.
2.
I
B.
1.
I
C.
1
2
I
D.
1
4
I
Câu 17. Bảng biến thiên sau đây là của hàm số nào ?
A.
1
2
x
y
x
B.
3
2
x
y
x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 99 -
C.
2 1
2
x
y
x
D.
3
2
x
y
x
Câu 18. Với mọi
, ,
a b x
là các số thực dương thỏa mãn
3 3 3
log 4 log 7 log .
x a b
Mệnh đề nào dưới đây
đúng ?
A.
4 7 .
x a b
B.
4 7
.
x a b
C.
4 7
.
x a b
D.
28 .
x ab
Câu 19. Biết rằng đường thẳng
1
y x
cắt đồ thị hàm số
3 2
2 2 1
y x x x
tại điểm duy nhất; kí hiệu
( ; )
x y
là tọa độ điểm đó. Tìm
.
y
A.
0.
y
B.
1.
y
C.
1.
y
D.
2.
y
Câu 20. Tìm tập nghiệm
S
của phương trình
2 2
log ( 3) log ( 1) 3.
x x
A.
{ 1}.
S
B.
{ 5;1}.
S
C.
{5}.
S
D.
{ 1;5}.
S
Câu 21. Tìm tập nghiệm
S
của bất phương trình
2
log ( 1) 3.
x
A.
( ;9).
S

B.
(7; ).
S

C.
( ;6).
S

D.
(9; ).
S

Câu 22. Hàm số
11
2 1
x
y
x
có bao nhiêu điểm cực trị ?
A.
2.
B.
0.
C.
1.
D.
3.
Câu 23. Cho phương trình
1
9 3 3 0
x x
. Khi đặt
3 ,
x
t
ta được phương trình nào ?
A.
2
3 3 0.
t t
B.
2
2 3 0.
t
C.
2
3 0.
t t
D.
6 3 0.
t
Câu 24. Hàm số
3 2
3
y x x
nghịch biến trên khoảng nào dưới đây ?
A.
( ; ).
 
B.
( ; 2)

và

C.
(0;2).
D.
( 2; 0).
Câu 25. Cho khối lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
.
a
Hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
là trung điểm của cạnh
BC
và
AA
tạo với đáy một góc
30 .
Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
24
a
V
B.
3
3
6
a
V
C.
3
3
8
a
V
D.
3
3
2
a
V
Câu 26. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng
.
a
Tính thể tích
V
của khối trụ ngoại tiếp
hình lăng trụ đã cho.
A.
3
3
a
V
B.
3
9
a
V
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 100 -
C.
3
3
4
a
V
D.
3
2
a
V
Câu 27. Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
,
B
3,
AB a
cạnh bên
SA
vuông
góc với đáy và
SB
tạo với đáy một góc
30 .
Tính thể tích
V
của khối chóp đã cho.
A.
3
3
2
a
V
B.
3
.
V a
C.
3
3
4
a
V
D.
3
2
a
V
Câu 28. Cho hàm
2
( 2)( 3 4)
y x x x
có đồ thị
( ).
C
Tìm số giao điểm
( )
C
và trục hoành.
A.
0.
B.
1 .
C.
3.
D.
2.
Câu 29. Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo.
Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 260 triệu đồng bao gồm cả gốc
và lãi ? Giả định trong suốt thời gian gửi, lãi suốt không thay đổi và người đó không rút tiền ra.
A. 15 năm. B. 14 năm.
C. 16 năm. D. 13 năm.
Câu 30. Cho
log 5
a
x
và
log
.
4
b
x
với
,
a b
là các số thực lớn hơn 1. Tính
log .
ab
P x
A.
1
.
9
P
B.
9.
P
C.
20
.
9
P
D.
9
.
20
P
Câu 31. Tìm tham số
m
để hàm số
3 2
( 3) 1
y x m x m
đạt cực đại tại
1.
x
A.
3
.
2
m
B.
10.
m
C.
3
.
2
m
D.
9
.
2
m
Câu 32. Tìm các giá trị thực của
m
để phương trình
2
5 5
log ( 2)log 3 1 0
x m x m
có hai nghiệm
1 2
,
x x
thỏa mãn
1 2
. 125.
x x
A.
1.
m
B.
2.
m
C.
1.
m
D.
5.
m
Câu 33. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh bằng
3,
mặt bên
SAB
là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích
V
của khối cầu ngoại tiếp hình
chóp đã cho.
A.
5 15
27
V
B.
5 15
108
V
C.
5 15
54
V
D.
5 15
2
V
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 101 -
Câu 34. Một vật chuyển động theo quy luật
3 2
2
6 2
3
s t t
với
t
(giây) là khoảng thời gian tính từ lúc
bắt đầu chuyển động và
( 2) 22
y
(mét) là quãng đường vật đi được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được
bằng bao nhiêu ?
A.
.
m
8 (
/s)
3
B.
.
m
7 (
/s)
2
C.
.
7
(
4 m/s)
D.
.
m
8 (
/s)
1
Câu 35. Tìm tất cả các giá trị của tham số m để đường thẳng
2
y x m
cắt đồ thị hàm số
2 4
1
x
y
x
tại
hai điểm phân biệt.
A.
( ; 4 4 2) ( 4 4 2; ).
m
 
B.
( ; 4) (4; ).
m
 
C.
( 4 4 2; 4 4 2).
m
D.
( 4;4).
m
Câu 36. Cho hình nón tròn xoay có đường cao
3
h
và bán kính đáy
5.
r
Một thiết diện đi qua đỉnh của
hình nón cắt mặt đáy theo một dây cung có độ dài bằng
6 2.
Tính diện tích
S
của thiết diện đó.
A.
24 2.
S
B.
12 2.
S
C.
8 2.
S
D.
6 2.
S
Câu 37. Gọi
S
là tập hợp các giá trị
m
để đồ thị
3 2 2 3
3 3( 1) 4 1
y x mx m x m m
có hai điểm cực
trị
A
và
B
sao cho tam giác
OAB
vuông tại
O
(với
O
là gốc tọa độ). Tính tổng tất cả các phần tử
của
.
S
A.
2.
B.
2.
C.
1.
D.
1.
Câu 38. Xét các số thực dương a, b thỏa mãn
4 4
log ( ) log ( ) 1.
a b a b
Giá trị nhỏ nhất của biểu thức
2
P a b
bằng
A.
3 2.
B.
10 3
3
C.
2 21 2 3
3
D.
2 3.
Câu 39. Trong tất cả các hình chóp tam giác đều ngoại tiếp mặt cầu có bán kính bằng
6,
tính thể tích
V
của
khối chóp có thể tích nhỏ nhất.
A.
1728 3.
V
B.
576.
V
C.
576 3.
V
D.
1728 6.
V
Câu 40. Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
,
a
cạnh bên
SA
vuông góc với mặt phẳng đáy
và
2 .
SA a
Gọi
,
M N
lần lượt là trung điểm của
,
SA SB
và
P
là hình chiếu vuông góc của
A
lên
đường thẳng
.
SC
Tính thể tích
V
của khối chóp
. .
S MNP
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 102 -
A.
3
3
150
a
V
B.
3
3
30
a
V
C.
3
3
6
a
V
D.
3
3
48
a
V
PHẦN 2. TỰ LUẬN (2,0 điểm)
Câu 1. Giải phương trình
2
3
log ( 2 ) 2.
x x
................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Câu 2. Giải phương trình
1
4 5.2 1 0.
x x
.............................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Câu 3. Cho khối nón có đường kính đường tròn đáy bằng 8 và diện tích xung quanh bằng
64 .
Tính thể tích
của khối nón đã cho. ...........................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Câu 4. Trong không gian, cho hình chữ nhật ABCD có
2
AB
và
4.
AC
Gọi
,
E F
lần lượt là trung điểm
của
AD
và
.
BC
Quay hình chữ nhật đó xung quanh trục
,
EF
ta được một hình trụ. Tính diện tích
toàn phần của hình trụ đó.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Câu 5. Tìm tham số
m
để hàm số
2
ln( 2 4)
y x mx
có tập xác định là
.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
THPT NGUYỄN THƯỢNG HIỀN Môn thi: TOÁN – ĐỀ SỐ 14
(Thời gian làm bài 60 phút)
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 103 -
PHẦN 1. TRẮC NGHIỆM (6,0 điểm)
Câu 1. Cho tứ diện đều
.
A BCD
cạnh
.
a
Mặt cầu ngoại tiếp tứ diện này có diện tích bằng
A.
2
3
4
a
B.
2
3
2
a
C.
2
4
3
a
D.
2
5
2
a
Câu 2. Bất phương trình
3 1
3
log ( 2) 1 log
x x
có tập nghiệm là nửa khoảng
( ; ],
a b
khi đó tổng
a b
bằng
A.
1.
B.
2.
C.
3.
D.
2.
Câu 3. Cho hàm số
1
y
x
có đồ thị
( ).
H
Tích số các khoảng cách từ một điểm
M
tùy ý thuộc
( )
H
đến hai
đường tiệm cận của
( )
H
bằng
A.
2.
B.
1.
C.
3.
D.
4.
Câu 4. Gọi
1
V
là thể tích của khối trụ ngoại tiếp một hình lập phương, gọi
2
V
là thể tích của khối trụ nội tiếp
hình lập phương nói trên. Tỉ lệ
1
2
V
V
là
A.
2
3
B.
1
2
C.
1, 5.
D.
2.
Câu 5. Phương trình
2
log 3 log 2 4
x
x
có tổng các nghiệm là
A.
0.
B.
6.
C.
7.
D.
10.
Câu 6. Cho hàm số
( )
liên tục và có đạo hàm trên
,
biết
( )
y f x
có đồ thị như hình vẽ. Hàm số
( )
nghịch biến trên khoảng nào ?
A.
(1; ).

B.
(2; ).

C.
( ; ).
 
D.
( ;2).

Câu 7. Phương trình
2
5 7.5 32 0
x x
có 1 nghiệm nguyên là
1
x
và 1 nghiệm
2 5
log .
x b
Giá trị của biểu
thức
1
T x b
bằng
A.
32.
B.
9.
C.
5.
D.
10.
Câu 8. Cho hàm số
2 1
1
x
y
x
có đồ thị
( )
C
và điểm
( 1;6).
M
Đường thẳng
: 2
d y m x
cắt
( )
C
tại hai
điểm
A
và
B
phân biệt để diện tích
ABM
bằng
5
4
khi
m
thỏa
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 104 -
A.
1.
m
B.
9.
m
C.
.
m
D.
9
m
và
1.
m
Câu 9. Xác định
m
để đồ thị hàm số
2
2
2
2 3
x x m
y
x x
có một đường tiệm cận ngang và hai đường tiệm cận
đứng
A.
15
.
1
m
m
B.
15
.
1
m
m
C.
15.
m
D.
1.
m
Câu 10. Người ta cần làm một cái hộp có thể tích không đổi sao cho đáy là một hình vuông cạnh
,
a
cạnh bên
vuông góc với đáy có độ dài là
.
h
Để tốn ít nguyên liệu nhất thì mối liên hệ giữa h và
a
là
A.
.
h a
B.
2 .
h a
C.
2
a
h
D.
3 .
h a
Câu 11. Khối bát diện đều được gọi là khối đa diện đều loại
A.
{5;3}.
B.
{3;3}.
C.
{3;4}.
D.
{4; 3}.
Câu 12. Phương trình
2 2
2 1 2 2
2 9.2 2 0
x x x x
có hai nghiệm
1 2 1 2
, ( ).
x x x x
Khi đó giá trị biểu thức
1 2
2 3
K x x
bằng
A.
4.
B.
5.
C.
0.
D.
2.
Câu 13. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2
2 4
y x mx
có ba điểm cực trị nằm
trên các trục tọa độ.
A.
2
m
hoặc
2.
m
B.
2.
m
C. Không có giá trị m nào.
D.
2.
m
Câu 14. Cho hình nón đỉnh
S
có thiết diện qua trục là tam giác đều có chu vi là
12.
Khi đó diện tích toàn
phần của hình nón bằng
A. 8 B.
10 .
C. 12 D.
9 .
Câu 15. Đồ thị trong hình là của hàm số
3 2
( ) 3 4.
f x x x
Với giá trị nào của tham số
m
thì phương
trình
( ) 1
f x m
có 4 nghiệm thực phân biệt ?
A.
4
m
hay
0.
m
B.
4 0.
m
C.
0 4.
m
D.
1 3.
m
-2
-4
1
O
3
-1
2
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 105 -
Câu 16. Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ?
A.
6
mặt phẳng. B.
3
mặt phẳng.
C.
4
mặt phẳng. D.
9
mặt phẳng.
Câu 17. Cho lăng trụ tam giác đều
.
ABC A B C
có cạnh đáy
,
AB a
góc giữa hai mặt phẳng
( )
A BC
và
( )
ABC
là
45 .
Khi đó thể tích khối lăng trụ
.
ABC A B C
là
A.
3
3
a
B.
3
.
a
C.
3
3
8
a
D.
3
2
3
a
Câu 18. Giá trị lớn nhất của hàm số
1
1
x
y
x
trên
[ 10;0]
bằng
A.
0.
B.
10.
C.
1.
D.
9
11
Câu 19. Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
,
a
mặt phẳng
( )
SBC
vuông góc mặt phẳng
( ).
ABC
Gọi
, ,
M N P
lần lượt là trung điểm
, , .
AB SA AC
Khoảng cách giữa hai mặt phẳng
( )
MNP
và
( )
SBC
bằng
A.
3
3
a
B.
3
4
a
C.
3
2
a
D.
2
6
a
Câu 20. Tích hai nghiệm của phương trình
2 2
3 3
log 2 log 1 7 0
x x
là
A.
1.
B.
3.
C.
3.
D.
2 3.
Câu 21. Cho các số thực dương
,
a
b
với
1.
a
Khẳng định nào đúng ?
A.
2
1 1
log ( ) log .
2 2
a
a
ab b
B.
2
log ( ) 2 log .
a
a
ab b
C.
2
1
log ( ) log .
4
a
a
ab b
D.
2
1
log ( ) log .
2
a
a
ab b
Câu 22. Một hình nón có đường sinh bằng
và góc giữa đường sinh và đáy bằng
.
Diện tích xung quanh
của hình nón là
A.
2
cos .
B.
2
cos .
C.
2
sin .
D.
2
sin .
Câu 23. Hàm số
2 2017
( 4 3)
y x x
có tập xác định
D
là
A.
\ { 3; 1}.
D
B.
.
D
C.
( 3; 1).
D
D.
( ; 3) ( 1; ).
 
D
Câu 24. Bất phương trình
3 6
6 64
log ( ) log
x x x
có nghiệm là
A.
0.
x
B.
0 64.
x
C.
64.
x
D.
64.
x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 106 -
Câu 25. Một người gửi số tiền
M
triệu đồng vào một ngân hàng với lãi suất
0,7% /
tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban
đầu (người ta gọi đó là lãi kép). Sau ba năm, người đó muốn lãnh được số tiền là 5 triệu đồng, nếu
trong khoảng thời gian này không rút tiền ra và lãi suất không đổi, thì người đó cần gửi số tiền
M
là
A.
3, 8
triệu. B.
3,6
triệu.
C.
3,9
triệu. D.
3, 7
triệu.
Câu 26. Một khối cầu ngọai tiếp tứ diện đều có thể tích
3
27 6 .
a
Khi đó độ dài một cạnh của tứ diện đều là
A.
4 3.
a
B.
4 .
a
C.
6 .
a
D.
6 2.
a
Câu 27. Cho một khối trụ có bán kính đáy
2 2
R
và chiều cao
10.
h
Cắt khối trụ bởi hai mặt phẳng song
song với nhau và cùng vuông góc với mặt phẳng đáy. Biết khoảng cách từ tâm của đường tròn đáy
đến mỗi mặt phẳng đó là
2.
d
Khối trụ được chia làm ba phần. Thể tích của phần nằm giữa là
A.
80
3
B.
160.
C.
80 40 .
D.
40 .
Câu 28. Giá trị của
3 4 2047 2048
log 2.log 3......log 2046.log 2047
A
là
A.
1.
B.
11.
C.
11
2 .
D.
1
11
Câu 29. Xác định
m
để hàm số
3
3
y x mx m
đồng biến trên
.
A.
0.
m
B.
0.
m
C.
0.
m
D.
0.
m
Câu 30. Cho hàm số
3 2
2
x
y
x
có đồ thị
( ).
C
Tọa độ những điểm trên
( )
C
mà tại đó tiếp tuyến có hệ số góc
bằng
4
là
A.
(1;1)
và
(3;7).
B.
(1; 1)
và
(3; 7).
C.
( 1; 1)
và
( 3;7).
D.
( 1;1).
và
( 3; 7).
PHẦN 2. TỰ LUẬN (4,0 điểm)
Bài 1. (1 điểm) Giải phương trình
2
3 3
2 log 2) log 4) 0.
( (x x
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Bài 2. (1 điểm) Tìm tham số
m
để phương trình
(2 3) (2 3)
x x
m
có hai nghiệm phân biệt.
................................................................................................................................................................................
................................................................................................................................................................................
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 107 -
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Bài 3. (1 điểm) Cho hàm số
3 2
1
x
y
x
Tìm tham số
m
để đường thẳng
:
d y x m
cắt đồ thị
( )
C
tại
hai điểm phân biệt.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Bài 4. (1 điểm) Cho hình chóp
.
S ABCD
có đáy là hình thoi, tam giác
SAB
đều và nằm trong mặt phẳng
vuông góc với
( ).
Biết
2 , 4 .
AC a BD a
Tính theo
a
thể tích khối chóp
. .
S ABCD
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
BẢNG ĐÁP ÁN TRẮC NGHIỆM
1B 2A 3B 4D 5D 6D 7B 8D 9B 10A
11C 12A 13B 14C 15D 16B 17C 18D 19B 20A
21A 22A 23A 24B 25C 26C 27C 28D 29C 30C
ĐÁP ÁN TỰ LUẬN
Bài 1.
{3; 3 2}.
S
Bài 2.
2.
m
Bài 3.
6
m
hoặc
2.
m
Bài 4.
3
.
3
S ABCD
a
V
SỞ GD & ĐT TP. HỒ CHÍ MINH ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
THCS – THPT NGUYỄN KHUYẾN Môn thi: TOÁN – ĐỀ SỐ 15
(Thời gian làm bài 60 phút)
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 108 -
PHẦN 1. TRẮC NGHIỆM (8,0 điểm)
Câu 1. Đồ thị trong hình bên là đồ thị của hàm số nào dưới đây ?
A.
3 2
3 1.
y x x
B.
3 2
3 1.
y x x
C.
3
3 1.
y x x
D.
3 2
3 1.
y x x
Câu 2. Hàm số
4 2
4 7
y x x
luôn đồng biến trên khoảng nào dưới đây ?
A.
( ;0).

B.
(0; 2).
C.
( 2; 2).
D.
( 2; ).

Câu 3. Cho hàm số
2
(3 ).
y x x
Khẳng định nào sau đây đúng ?
A. Hàm số nghịch biến trên khoảng
(0;2).
B. Hàm số đồng biến trên khoảng
( ;0).

C. Hàm số nghịch biến trên khoảng
(2; ).

D. Hàm số đồng biến trên khoảng
( 1;2).
Câu 4. Cho hình hộp chữ nhật
.
ABCD A B C D
có các cạnh
1, 2, 21.
AB BC A C
Thể tích của
khối hộp đã cho bằng
A.
8.
B.
3 5.
C.
4 5.
D.
4.
Câu 5. Cho hàm số
( )
có
2
( ) ( 2)( 1) .
f x x x
Khẳng định nào sau đây là đúng ?
A. Hàm số
( )
đạt cực tiểu tại
1.
x
B. Hàm số
( )
đạt cực đại tại
2.
x
C. Hàm số
( )
đạt cực đại tại
1.
x
D. Hàm số
( )
đạt cực tiểu tại
2.
x
Câu 6. Cho hàm số
( )
có bảng biến thiên như hình vẽ dưới đây
x

1
x
2
x
3
x

y
0
y


Hỏi đồ thị của hàm số đã cho có bao nhiêu điểm cực trị ?
A. Một. B. Hai.
C. Ba. D. Không có.
Câu 7. Hàm số
2 3 4
(16 6 )
y x x x
có tập xác định là
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 109 -
A.
\ {0}.
D
B.
\ ( 8;2).
D
C.
\ { 8; 0;2}.
D
D.
( 8;2) \ {0}.
D
Câu 8. Mệnh đề nào sau đây là sai ?
A. Khối tứ diện là khối đa diện lồi.
B. Lắp ghép hai khối hộp luôn được một khối đa diện lồi.
C. Khối hộp là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Câu 9. Đồ thị hàm số
16
y x
x
đạt cực đại tại điểm
1 1
( ; )
x y
và đạt cực tiểu tại điểm
2 2
( ; )
x y
thì giá trị của
1 2
y y
bằng
A.
16.
B.
8.
C.
0.
D.
16.
Câu 10. Cho hai số thực dương
,
a b
với
1
a
. Khẳng định nào sau đây là đúng?
A.
3
1
log 3 1 log .
2
a
a
a
b
b
B.
3
1 1
log 1 log .
3 2
a
a
a
b
b
C.
3
1
log 1 2 log .
3
a
a
a
b
b
D.
3
1 1
log 1 log .
3 2
a
a
a
b
b
Câu 11. Hàm số
4 2 2
2( 1) 4
y x m x m
có ba điểm cực trị khi và chỉ khi
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 12. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
1 2
2
x
y
x
có phương trình lần lượt là
A.
2; 1.
x y
B.
1; 2.
x y
C.
2; 1.
x y
D.
2; 2.
x y
Câu 13. Khẳng định nào dưới đây là sai ?
A. Đồ thị hàm số
4 2
2
y x x
có 2 điểm uốn.
B. Đồ thị hàm số
4 2
y x x
không có điểm uốn.
C. Đồ thị hàm số
2 1
1
x
y
x
có 1 điểm uốn.
D. Đồ thị hàm số
3 2
y x x
có 1 điểm uốn.
Câu 14. Cho hàm số
( )
có bảng biến thiên như sau
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 110 -
Mệnh đề nào sau đây là sai ?
A. Hàm số có hai cực trị.
B. Hàm số có giá trị lớn nhất bằng 3.
C. Giá trị nhỏ nhất của hàm số là 0. D. Hàm số có ba điểm cực trị.
Câu 15. Hàm số nào sau đây đồng biến trên khoảng
( ; )
 
?
A.
4 2
2 .
y x x
B.
2
.
y x
x
C.
5
ln .
2
x
y
D.
10
.
3
x
y
Câu 16. Cho hàm số
3 2
1
3 2
3
y x x
có đồ thị (C). Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng
: 9 27 0
d x y
có phương trình là
A.
9 43
y x
. B.
9 7
y x
.
C.
9 11
y x
. D.
9 34
y x
.
Câu 17. Đồ thị (C) của hàm số
( 1) 2
1
a x
y
x b
nhận gốc tọa độ O làm tâm đối xứng thì tổng
a b
là
A.
1.
B.
0.
C.
1.
D.
2.
Câu 18. Cho khối chóp đều S.ABCD có cạnh đáy bằng
2
a
, đường cao bằng
a
. Góc giữa mặt bên và mặt đáy
của khối chóp bằng
A.
0
45
. B.
0
54
.
C.
0
60 .
D.
0
30
.
Câu 19. Hình chữ nhật ABCD có
2 8
AB BC
. Gọi M, N lần lượt là trung điểm của cạnh AB, CD. Khi
quay hình chữ nhật ABCD quanh trục MN ta được một hình trụ tròn xoay có diện tích toàn phần là
A.
96 .
B.
64 .
C.
48 .
D.
128 .
Câu 20. Cho hàm số
ax b
y
cx d
có đồ thị như hình bên. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường cận ngang là
2
x
.
B. Hàm số nghịch biến trên
\ 1
.
C. Đồ thị của hàm số có tâm đối xứng là
1;2
I
.
D. Hàm số đồng biến trên
\ 1
.
Câu 21. Tổng tất cả các nghiệm của phương trình
2
3
6 log
1
312
97344
x
bằng
A.
0.
B.
10
.
3
C.
10.
D.
82
.
9
Câu 22. Gọi
,
a A
là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2
2018
y x x
. Tính
S A a
.
A.
1010.
S
B.
1008.
S
C.
2018.
S
D.
2017.
S
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 111 -
Câu 23. Cho hàm số
y f x có đồ thị như hình bên. Tìm tất cả các giá trị của tham số m để phương trình
2f x m có bốn nghiệm phân biệt.
A.
4 3m
.
B.
2 1m
.
C.
3 2m .
D. 4 3m .
Câu 24. Khối lập phương có diện tích toàn phần bằng 96 cm
2
. Mặt cầu đi qua tất cả các đỉnh của hình lập
phương đó có thể tích V là
A.
28 3
cm
3
. B.
72
cm
3
.
C.
32 3
cm
3
. D.
36 2
cm
3
.
Câu 25. Cho hình chóp SABCD có đáy là hình chữ nhật với AB a ;
3AD a
. Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với mặt đáy, đồng thời cạnh SB tạo với mặt phẳng đáy một góc bằng 45
0
. Tính
thể tích khối chóp S.BCD bằng
A.
3
6
6
a
. B.
3
3
2
a
.
C.
3
2
3
a
. D.
3
3
6
a
.
Câu 26. Trong hình vẽ dưới đây có đồ thị của các hàm số
x
y a ,
x
y b , log
c
y x . Chọn mệnh đề đúng
trong các mệnh đề sau
A.
0 .a c b
B.
0 .c a b
C.
0 .b c a
D.
0 .a b c
Câu 27. Giả sử phương trình
2 3
ln ln 2 0x x có hai nghiệm
1 2
,x x đồng thời
1 2
x x . Khẳng định nào
sau đây là đúng?
A.
2 2
1 2
1x x e . B.
2 1
2 0x x
C.
2
1 2
0x x . D.
2
1 2
2 2x x e .
Câu 28. Một hình trụ có chiều cao bằng 6 nội tiếp trong hình cầu có bán kính bằng 5 như hình vẽ. Thể tích của
khối trụ này.
A. 36 .
B. 96 .
C. 48 .
D. 192 .
Câu 29. Số điểm thuộc đồ thị của hàm số
4 2
3 2y x x mà tiếp tuyến tại những điểm đó song song với
trục hoành là
A. 1. B. 2.
C. 3. D. 4.
O
1
1
2
3
1
2
3
x
y
x
y a
x
y b
log
c
y x
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 112 -
Câu 30. Số tất cả các giá trị nguyên
m
để hàm số
3
2 2
3 27 2
3
x
y m x m x m
nghịch biến
trên khoảng
;

là
A. 6 số. B. 10 số.
C. 12 số. D. 16 số.
Câu 31. Dân số thế giới năm 1950 là 2,56 tỉ người và năm 1960 là 3,04 tỉ người. Biết dân số thế giới tăng theo
hàm số
0
kt
P t P e
, trong đó k là tỉ lệ tăng dân số theo thời gian t (năm). Hỏi dân số thế giới vào
năm 2020 sẽ là bao nhiêu người?
A. 6,052 tỉ. B.
8,525 tỉ.
C. 9,152 tỉ. D. 7,179 tỉ.
Câu 32. Bất phương trình
2 2
3 3 82
x x
có tập nghiệm là
;
S a b
thì
2 2
2 3
b a
bằng
A.
4
. B. 8.
C. 12. D. 20.
Câu 33. Tứ diện SABC có cạnh AB, AC, AS đôi một vuông góc nhau và
, 3,
AB a AC a
6.
SA a
Gọi
M là trung điểm của cạnh SB, N là điểm trên cạnh SC sao cho
3
SN NC
. Tính thể tích của khối
chóp A.BCNM
theo a.
A.
3
7 2
.
16
a
B.
3
5 3
.
12
a
C.
3
2
.
16
a
D.
3
7 3
.
24
a
Câu 34. Cho lăng trụ ABCD.A’B’C’D’ có đáy là hình vuông cạnh bằng 10. Hình chiếu vuông góc của A’ lên
mặt đáy ABCD trùng với tâm O của hình vuông ABCD. Biết cạnh bên tạo với mặt đáy một góc 60
0
.
Tính thể tích V của lăng trụ đã cho.
A.
150 6.
B.
250 6.
C.
300 6.
D.
500 6.
Câu 35. Một cốc nước có dạng hình trụ có đường kính đáy
8
cm
, lượng nước trong cốc cao
5
cm
. Thả vào cốc
nước 6 viên bi sắt có cùng bán kính
2
cm
thì lượng nước trong cốc dâng cao cách mép cốc là 2cm. Hỏi
cốc nước đó có thể tích là bao nhiêu? (làm tròn đến hàng đơn vị, bỏ qua độ dày của cốc)
A.
503
ml
.
B.
553
ml
.
C.
584
ml
.
D.
603
ml
.
Câu 36. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên tạo với mặt đáy của hình chóp một
góc bằng 60
0
. Một hình nón ngoại tiếp hình chóp S.ABC có thể tích
Nón
V
bằng
A.
3
.
9
a
B.
3
3
.
3
a
C.
3
3
.
6
a
D.
3
.
3
a
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 113 -
Câu 37. Có tất cả bao nhiêu số nguyên dương của tham số k để đồ thị hàm số
2
( 3)( 4 2)
y x x x k
cắt trục hoành tại ba điểm phân biệt?
A. 3. B. 4.
C. 5. D. 6.
Câu 38. Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu EF bắt qua sông biết
rằng thành phố A cách con sông một khoảng là 5 km và thành phố B cách con sông một khoảng là 7
km (hình vẽ), biết tổng độ dài
24
HE KF km
. Hỏi xây cây cầu cách thành phố A là bao nhiêu
để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường AEFB)
A.
5 3
km
.
B.
10 2
km
.
C.
5 5
km
.
D.
7,5
km
.
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
2 , 5
AB a BC a
. Tam giác SAB
vuông tại S và nằm trong mặt phẳng vuông góc với mặt đáy ABCD. Mặt cầu ngoại tiếp hình chóp
S.ABCD có bán kính là
A.
.
R a
B.
3
.
2
R a
C.
2 .
R a
D.
3 .
R a
Câu 40. Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a với
0
120
ABC
. Nếu
2
SA SB SC a
thì
khoảng cách d giữa hai đường thẳng SB và AC theo a là
A.
2 93
.
31
a
d B.
93
.
31
a
d
C.
6
.
4
a
d D.
3
.
4
a
d
PHẦN 2. TỰ LUẬN (2,0 điểm)
Câu 1. (1 điểm) Khảo sát sự biến thiên và vẽ đồ thị
( )
C
của hàm số
2 1
1
x
y
x
.
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607 15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 114 -
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Câu 2. (1 điểm) Giải phương trình
4 2 2 4
log (log ) log (log ) 2.
x x
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
ĐÁP ÁN ĐỀ 15
1 C 11 C 21 D 31 B
2 B 12 D 22 C 32 A
3 C 13 C 23 B 33 A
4 A 14 B 24 C 34 D
5 D 15 D 25 D 35 B
6 B 16 C 26 A 36 A
7 D 17 B 27 C 37 B
8 B 18 A 28 B 38 C
9 A 19 B 29 C 39 B
10 D 20 C 30 C 40 D
| 1/115
| | Tải xuống

Có thể bạn quan tâm:

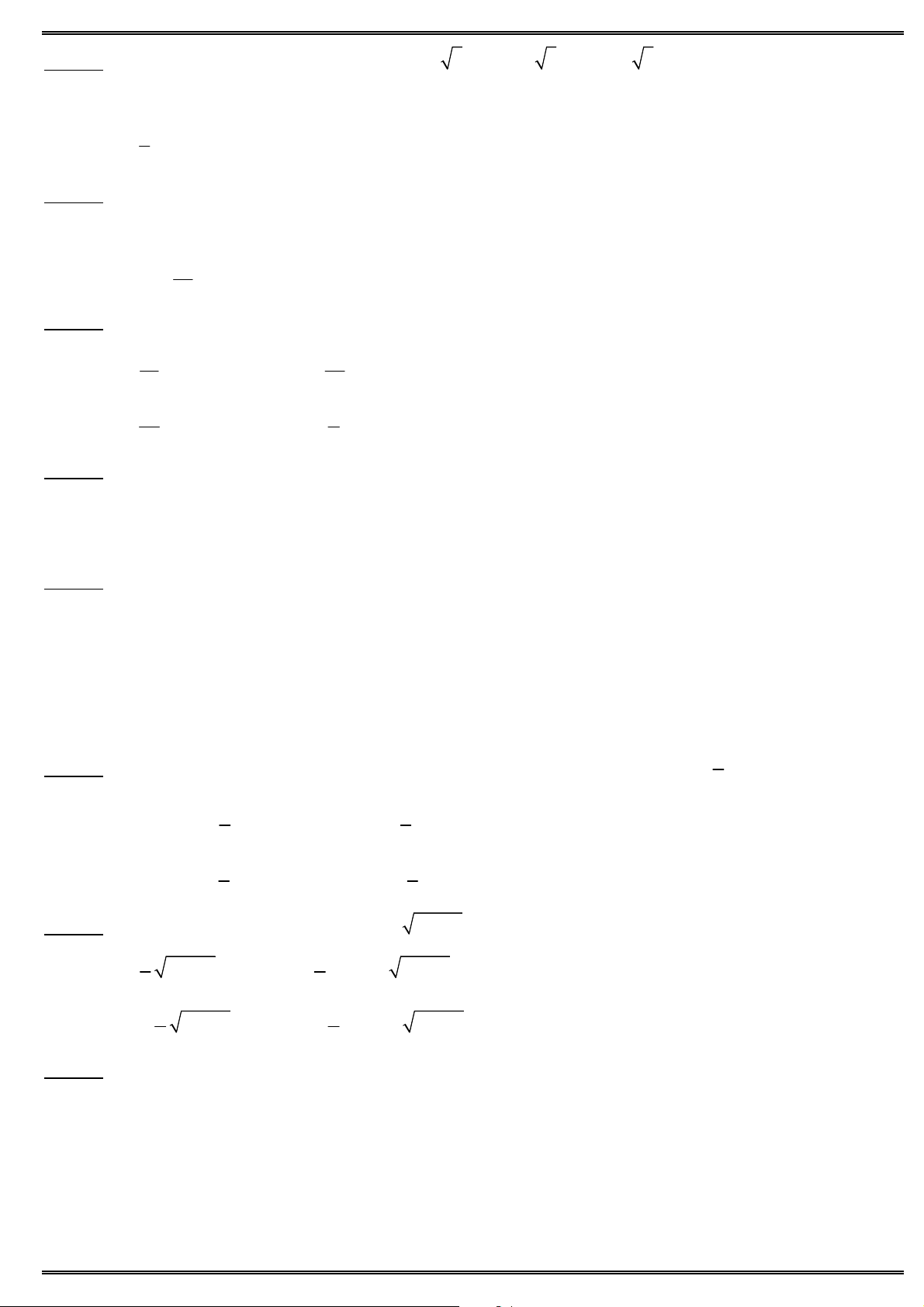
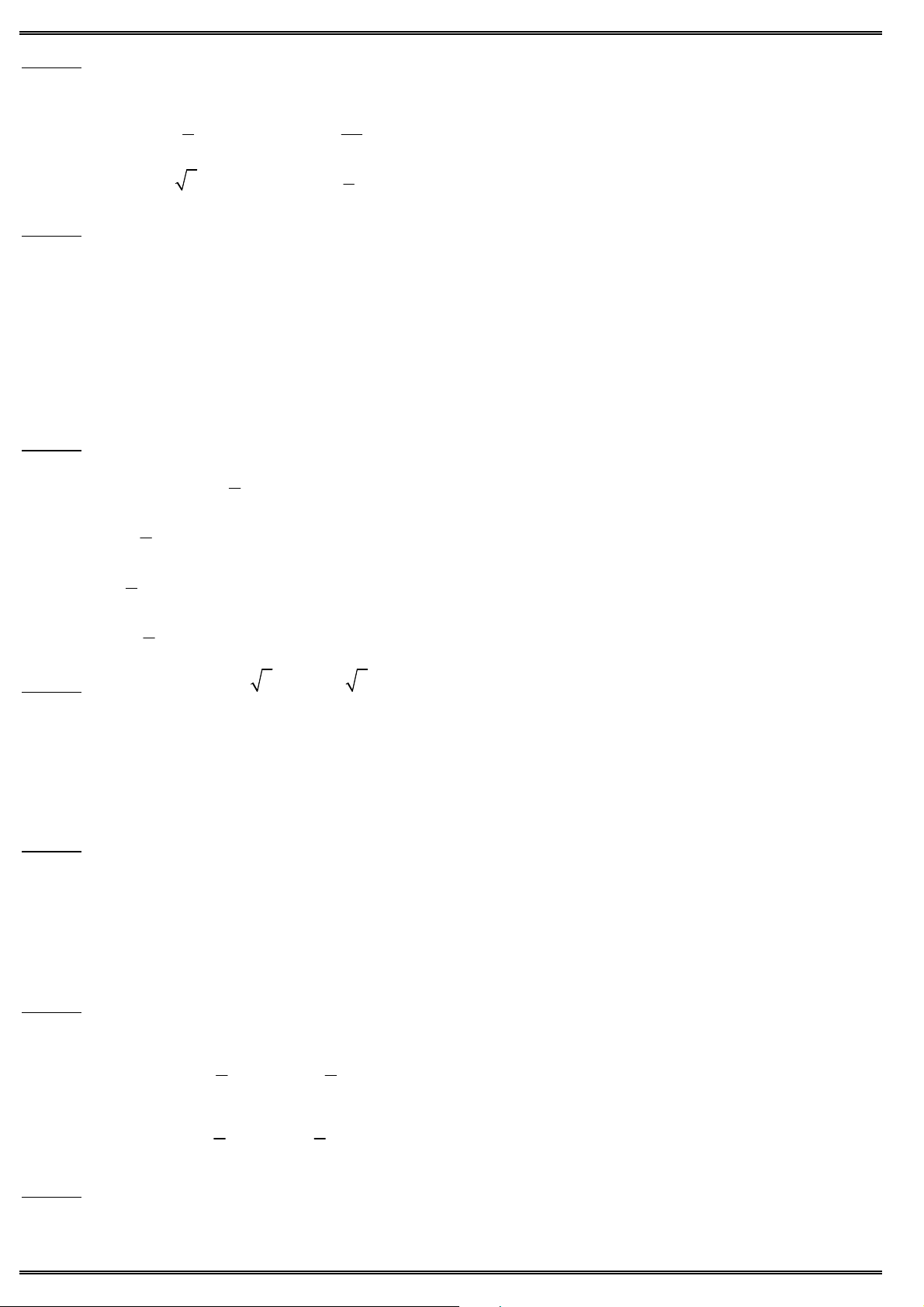
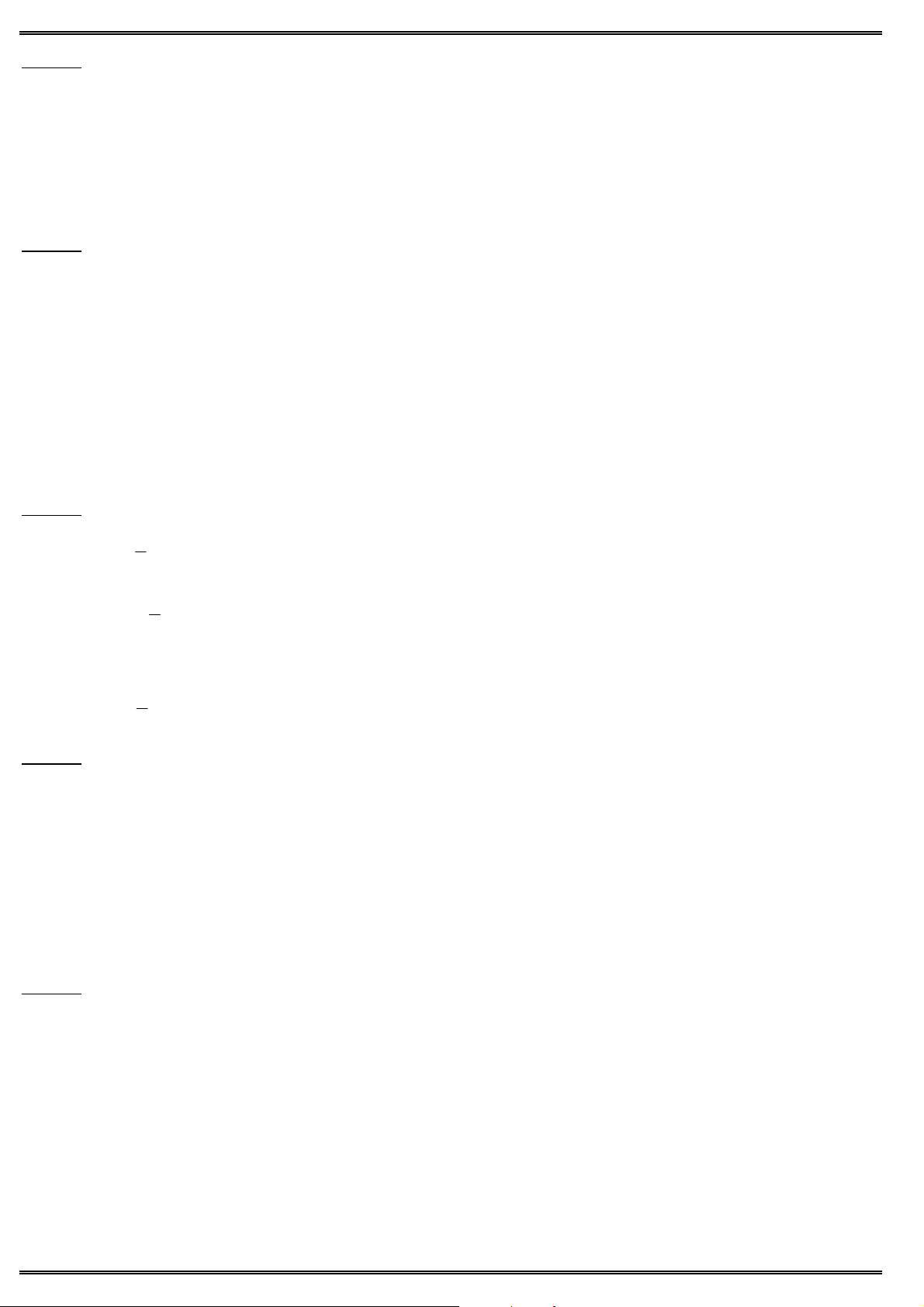
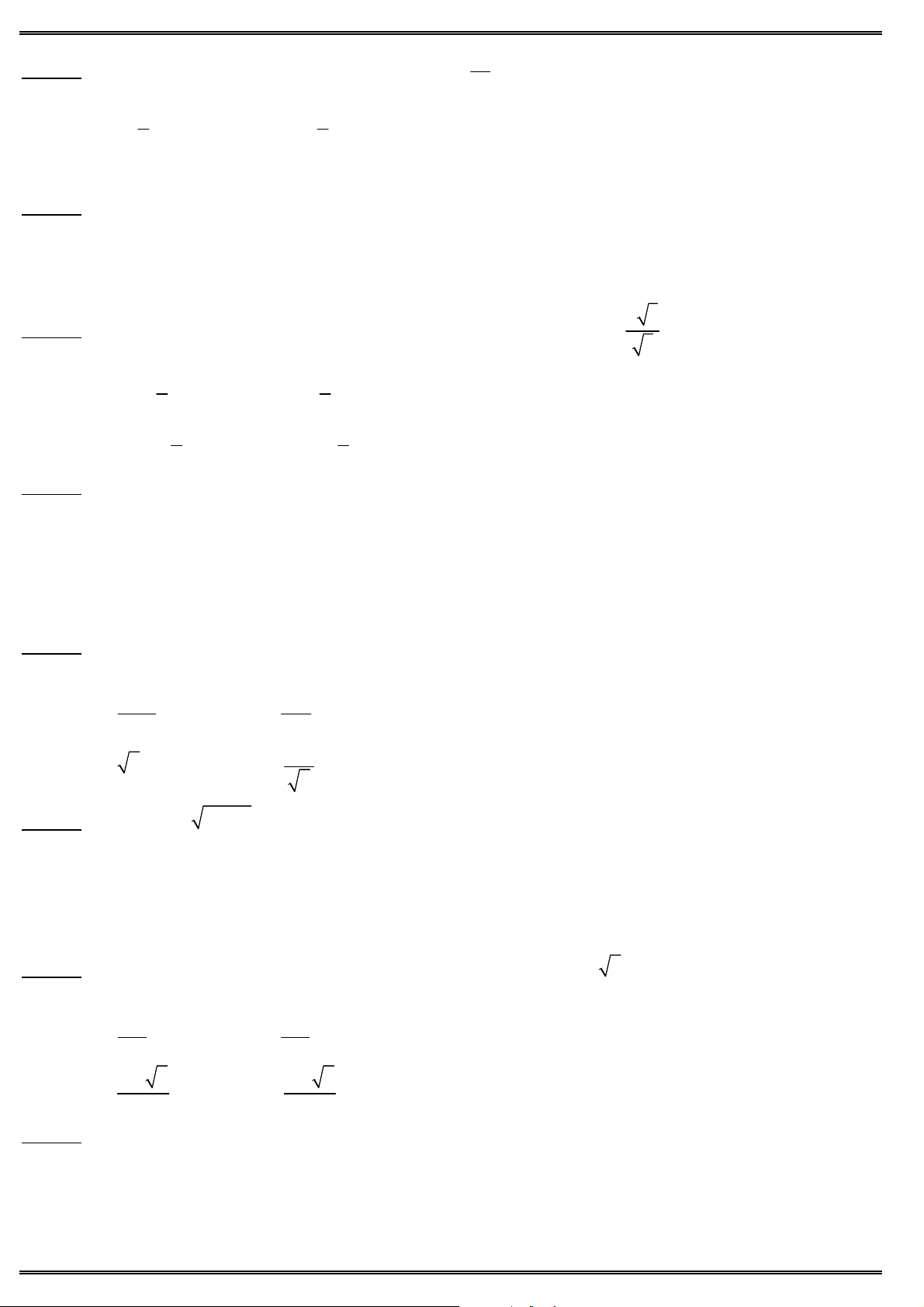
Preview text:

Biªn so¹n: Ths. Lª V¨n §oµn
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 01
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! Câu 1. Cho hàm số 3 2 y x
  3x  4. Mệnh đề nào dưới đây đúng ?
A. Đồng biến trên khoảng (0;2).
B. Nghịch biến trên khoảng ( ;  2).
C. Đồng biến trên khoảng (0;  )  .
D. Nghịch biến trên khoảng (0;2). x  2
Câu 2. Cho hàm số y
 Mệnh đề nào dưới đây đúng ? x  1
A. Hàm số nghịch biến trên ( ;  1)  (1; )  .
B. Hàm số nghịch biến trên  \ {1}.
C. Hàm số nghịch biến trên ( ;  1) và (1; )  .
D. Hàm số nghịch biến trên với x  1. mx  4
Câu 3. Có bao nhiêu giá trị nguyên của m để hàm số y
nghịch biến các khoảng xác định ? x m A. 2. B. 3. C. 5. D. Vô số.
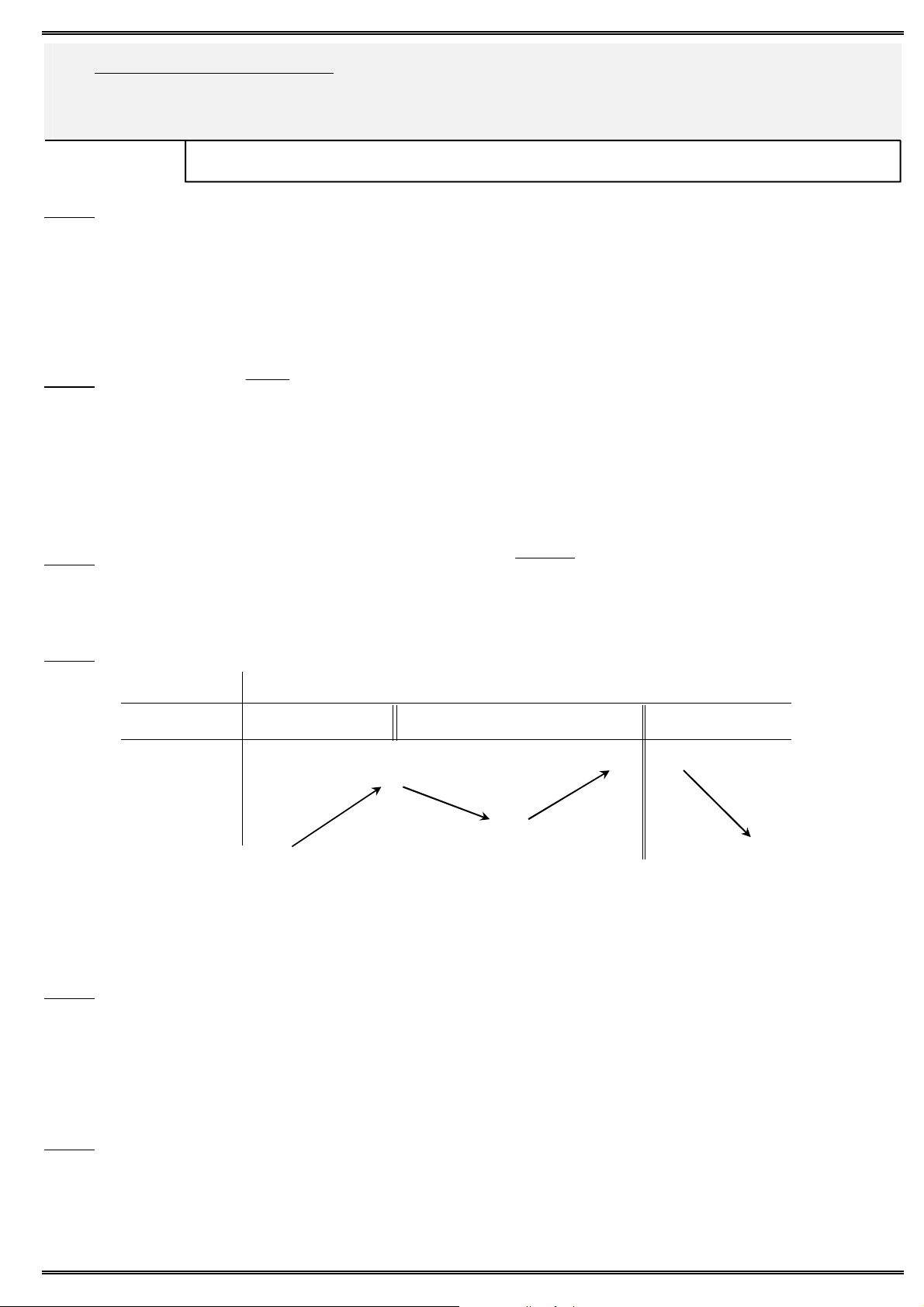
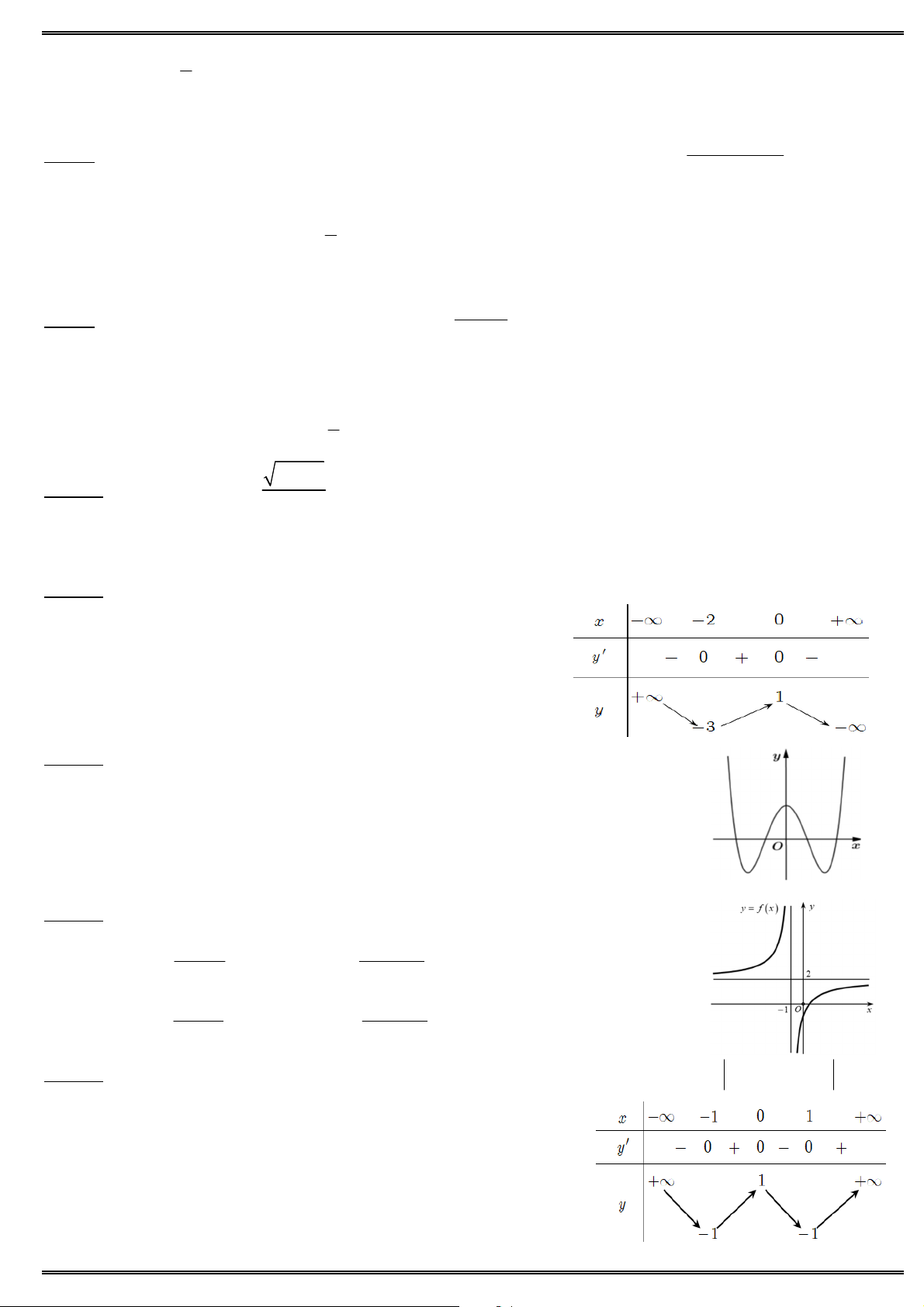
Câu 4. Cho hàm số y f (x) xác định, liên tục trên  \ {1} và có bảng biến thiên: x  1 0 1  y 0   y 1 1  
Hỏi khẳng định nào sau đây là đúng ?
A. Hàm số có 3 cực trị.
B. Hàm số đạt cực đại tại x  1
 , cực tiểu tại x  0.
C. Hàm số đạt cực đại tại x  1
 , cực tiểu tại x  0.
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 1. Câu 5. Cho hàm số 3
y x  3x  4. Khẳng định nào đúng ?
A. Hàm số đạt cực đại tại x  1 và đạt cực tiểu tại x  1.
B. Hàm số nghịch biến trên ( ;  1  ).
C. Hàm số có hai điểm cực trị nằm về hai phía của trục hoành.
D. Hàm số có giá trị cực đại là 6.
Câu 6. Có mấy giá trị nguyên của m để hàm số 3 2 2
y  2x  (2m  1)x  (m  1)x  2 có hai điểm cực trị. A. 4. B. 5. C. 3. D. 6.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 1 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 1
Câu 7. Tìm giá trị thực của tham số m để hàm số 3 2 2
y x mx  (m m  1)x  1 đạt cực trị tại hai 3
điểm x và x thỏa mãn x x  4. 1 2 1 2 A. m  1. B. m  2. C. m  2. D. m  2. 3x  1
Câu 8. Giá trị lớn nhất của hàm số y  trên đoạn [0;2] bằng x  3 A. 5. B. 5. 1 1 C.   D. 3 3
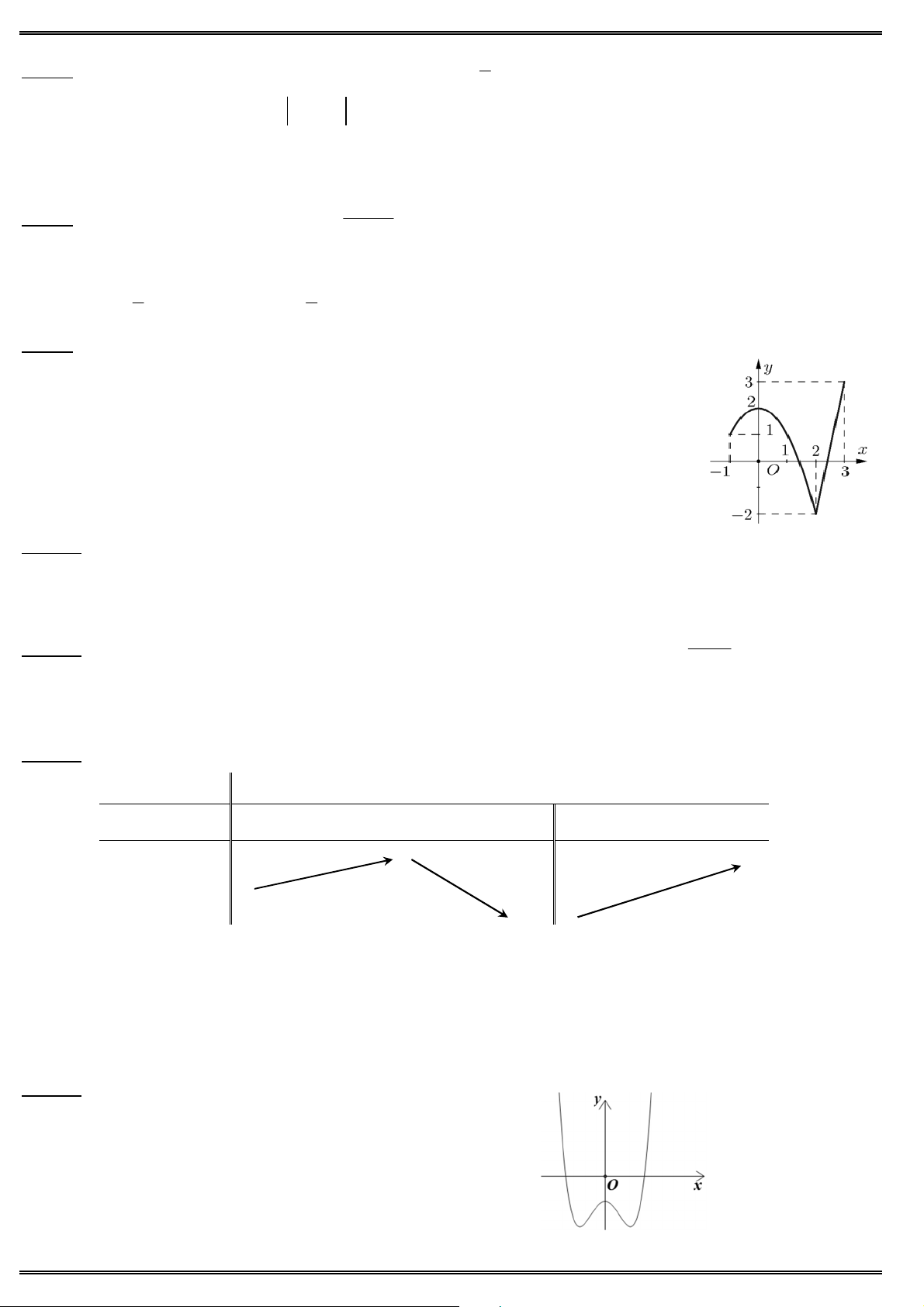
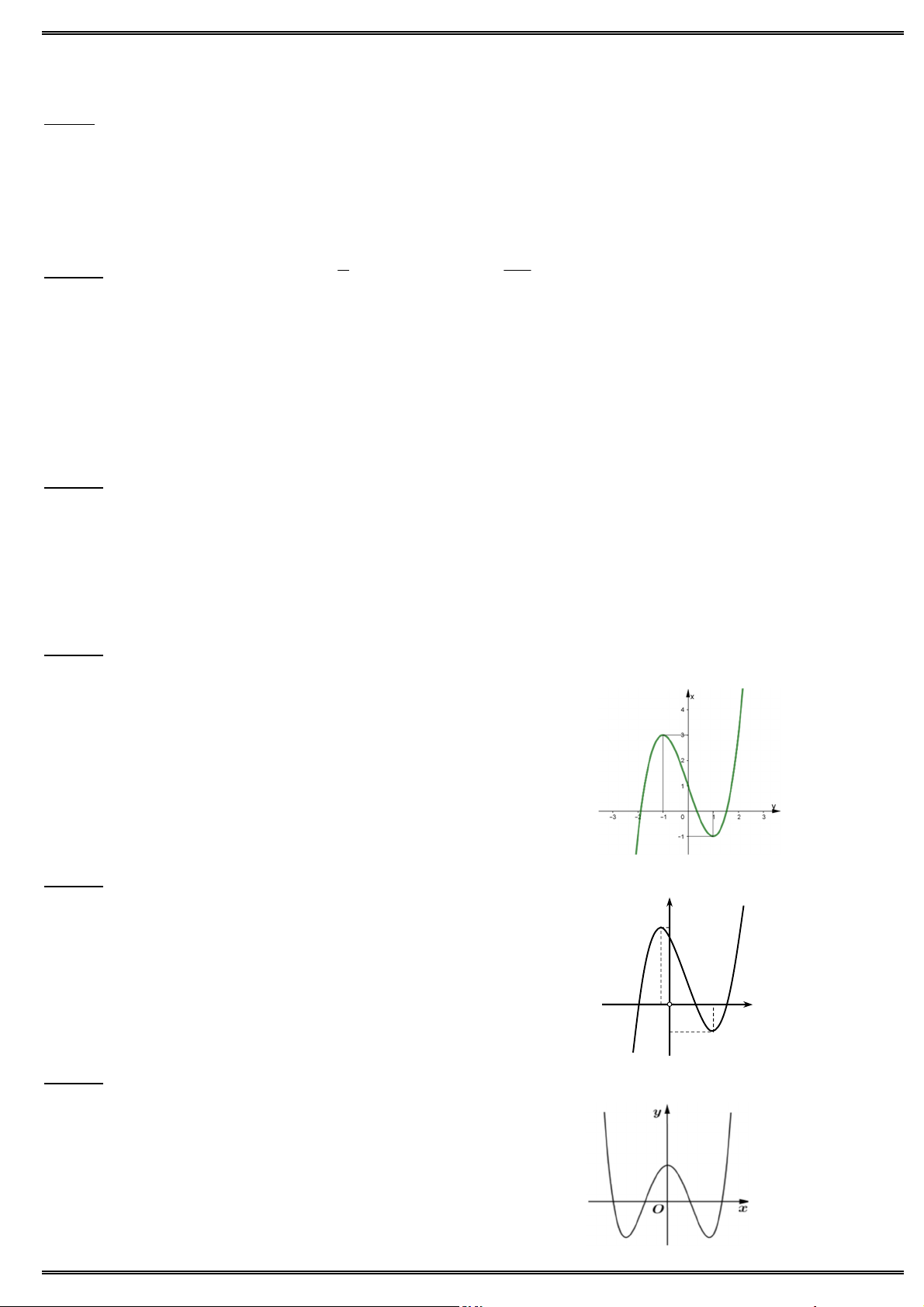
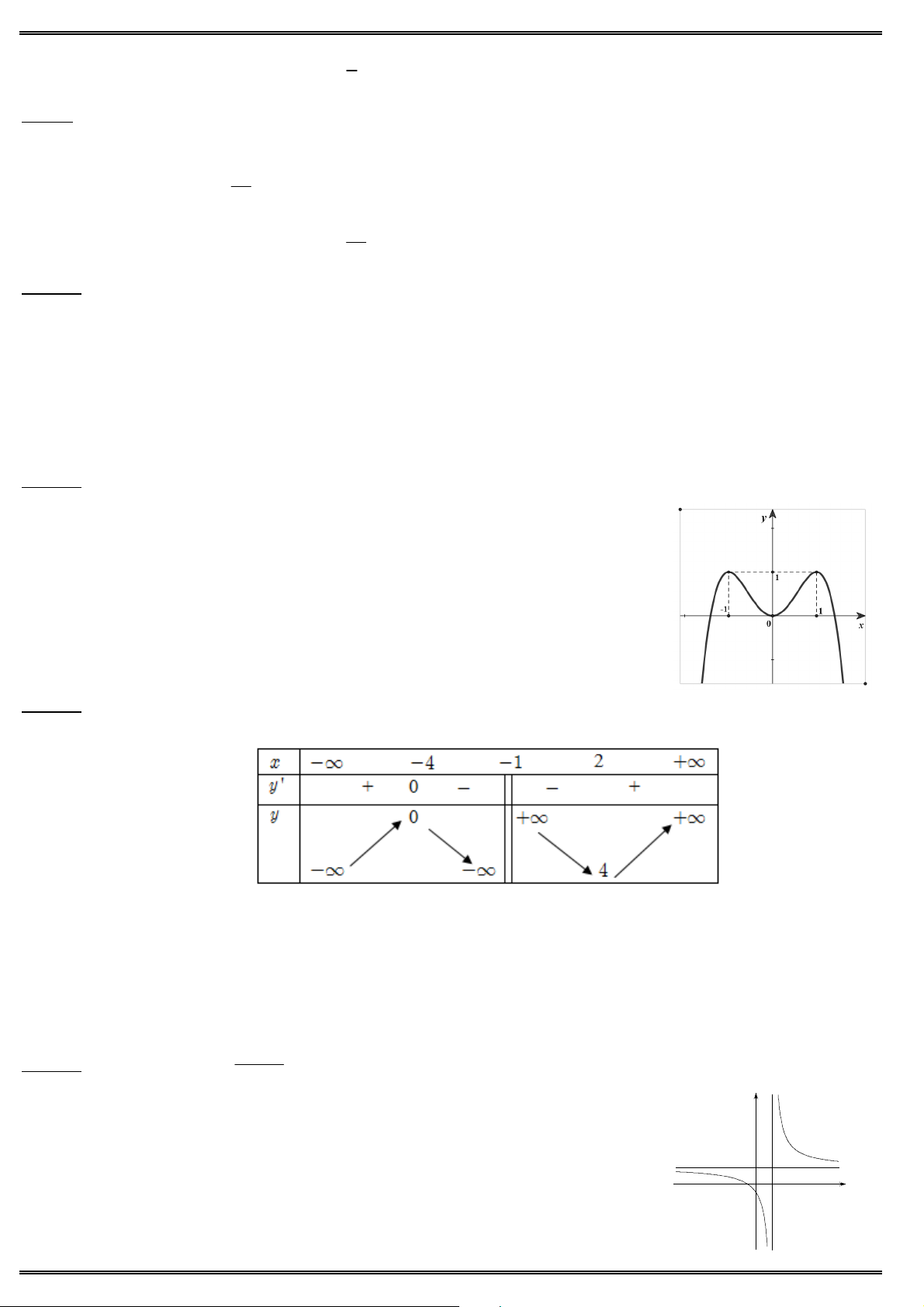
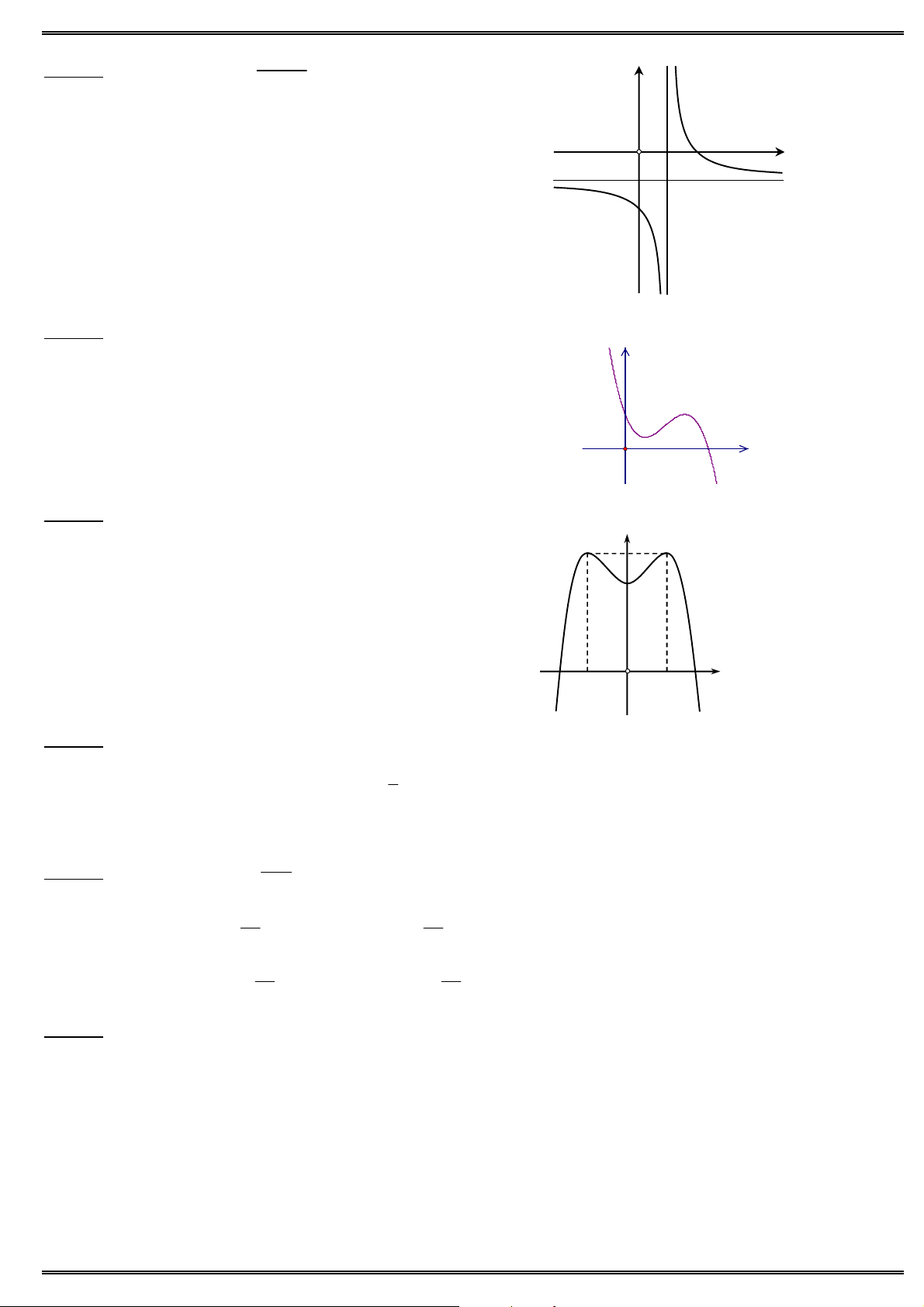
Câu 9. Cho hàm số y f (x) liên tục trên đoạn [1; 3] và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số 2
y f (3 cos x  1) bằng A. 0. B. 1. C. 3. D. 2. Câu 10. Cho hàm số 3 2
y x  (m  1)x m  1. Tìm tham số m để giá trị nhỏ nhất trên [0;1] bằng 5.
A. m  1.
B. m  2.
C. m  4.
D. m  3. x  3
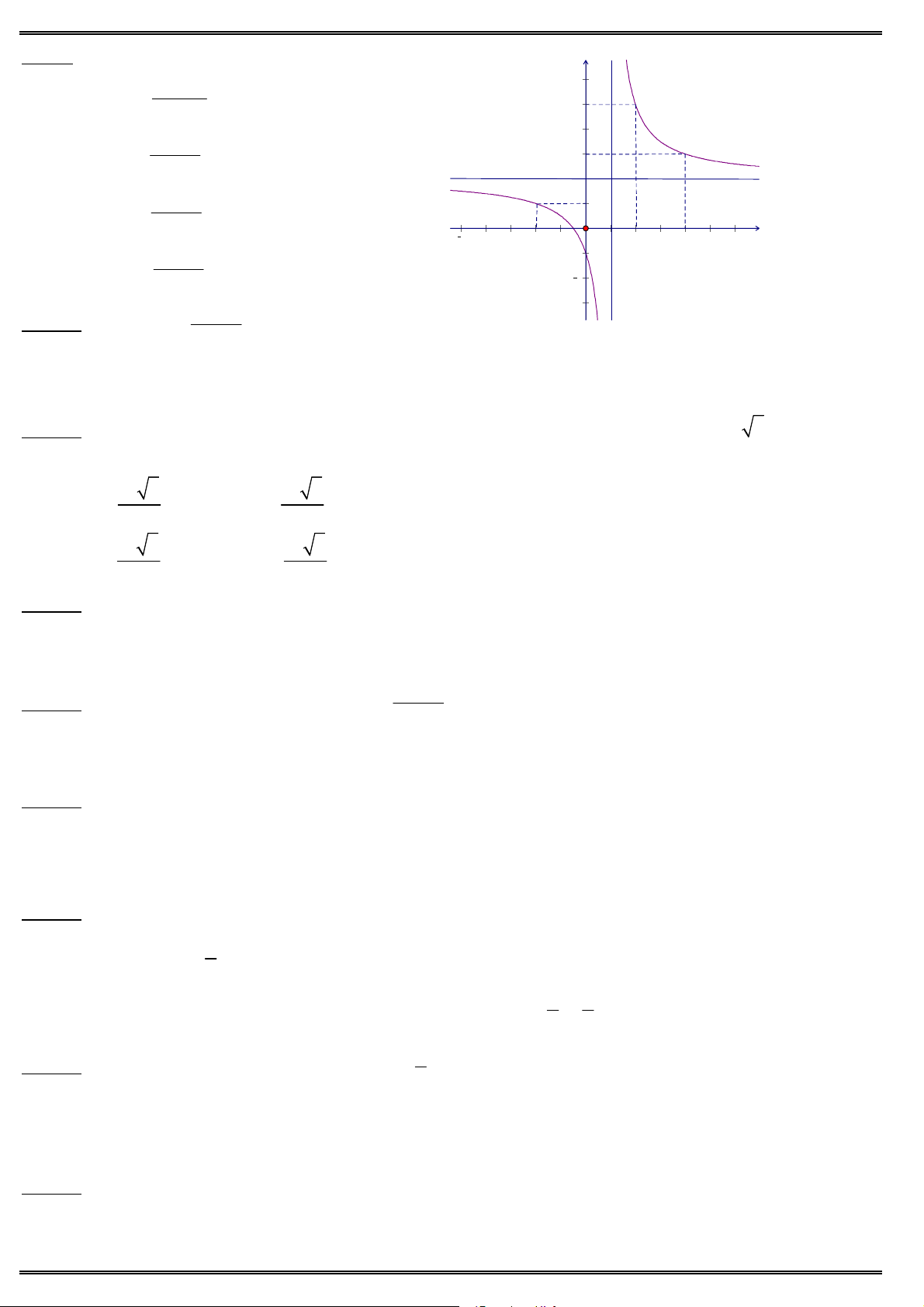
Câu 11. Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y   x  1
A. x  1, y  1  .
B. x  1, y  1. C. x  1  , y  1. D. x  1  , y  1  .
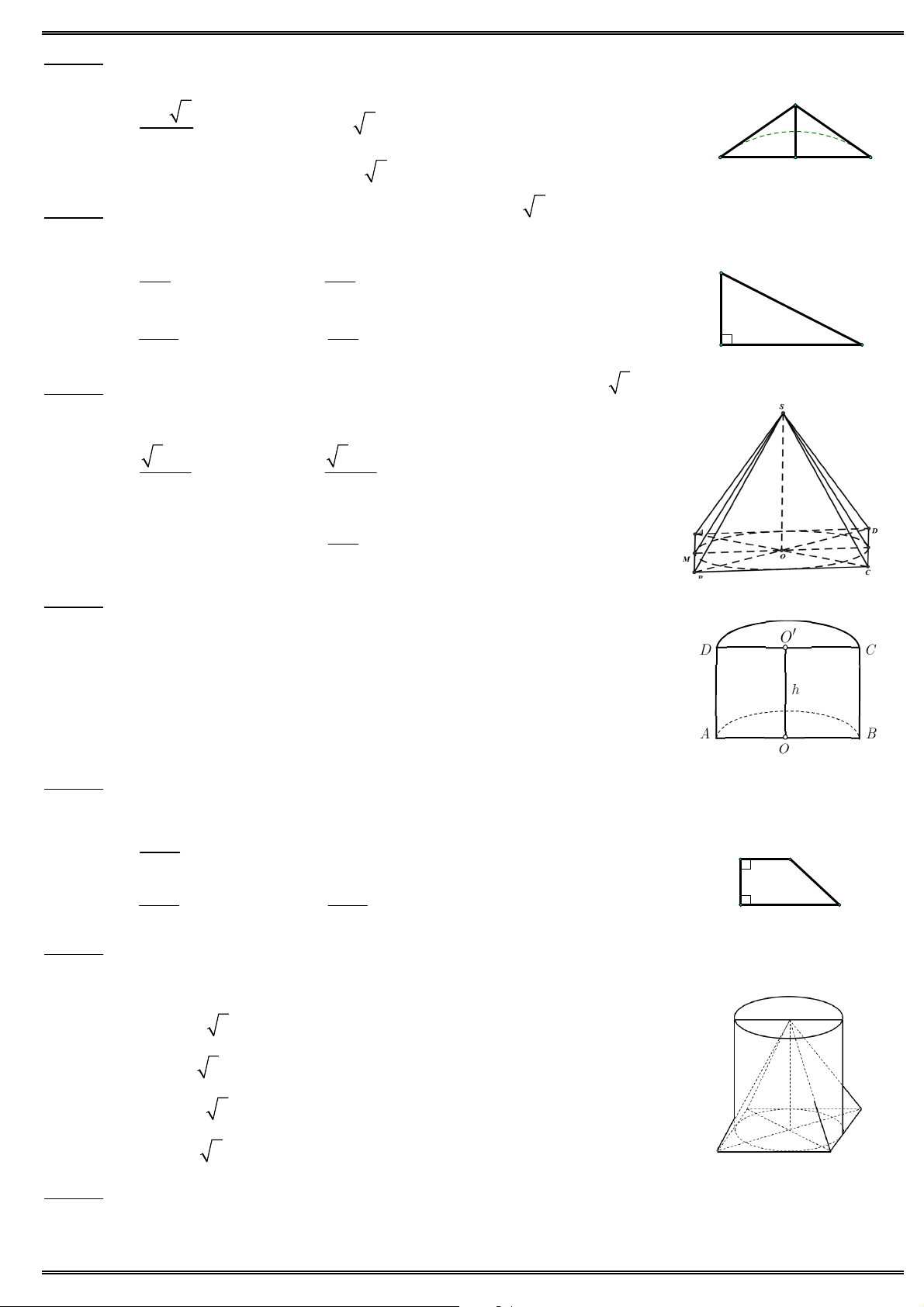
Câu 12. Cho hàm số y f (x) xác định trên D   \ {1} và có bảng biến thiên: x  0 1  f (  x)  0   2 5 f (x) 0  3
Hỏi mệnh đề nào dưới đây đúng ?
A. Giá trị cực tiểu của hàm số là bằng 3.
B. Giá trị cực đại của hàm số bằng 5.
C. Đồ thị hàm số có hai tiệm cận ngang là y  0, y  5 và tiệm cận đứng là x  1.
D. Hàm số có giá trị lớn nhất bằng 5.
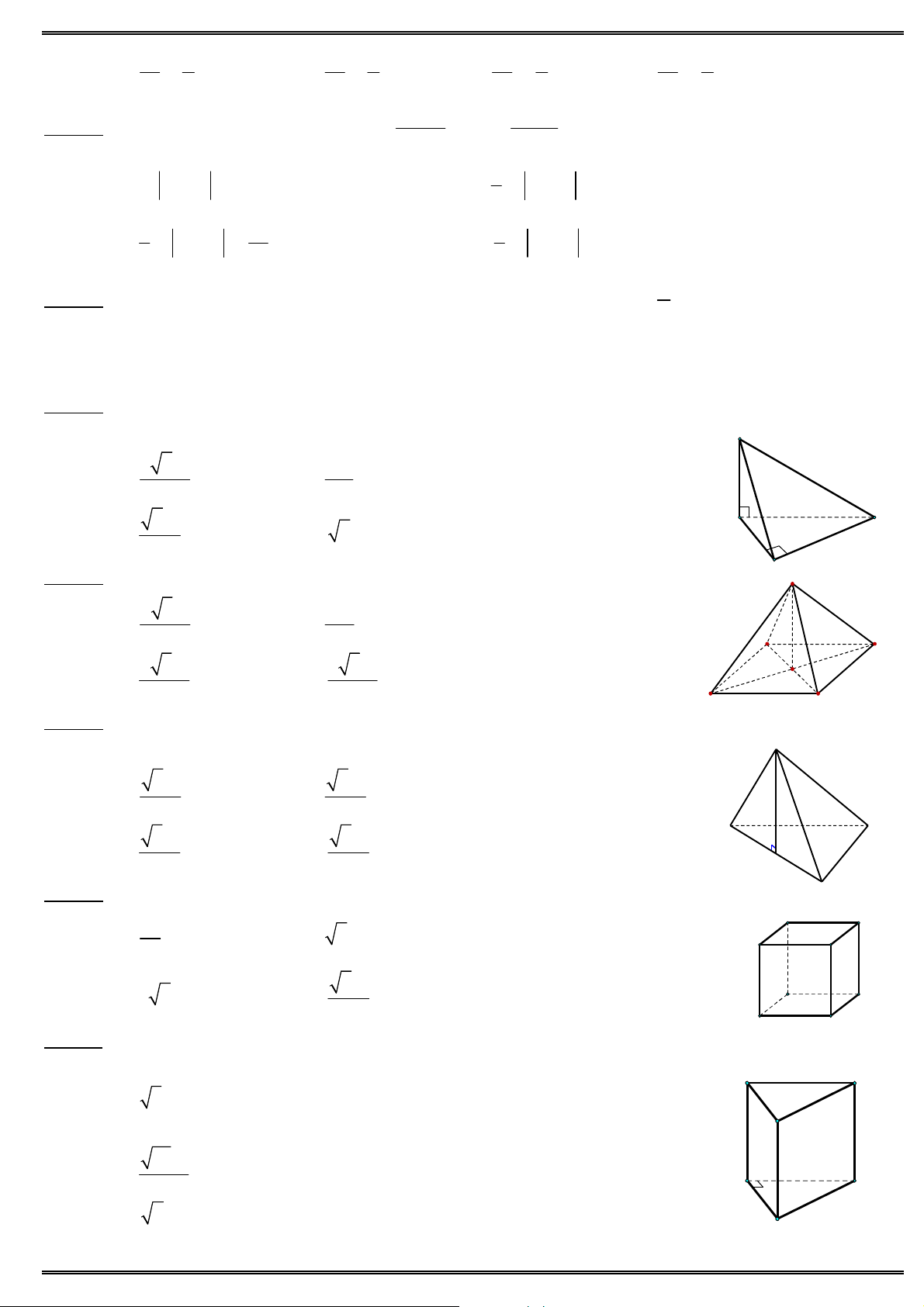
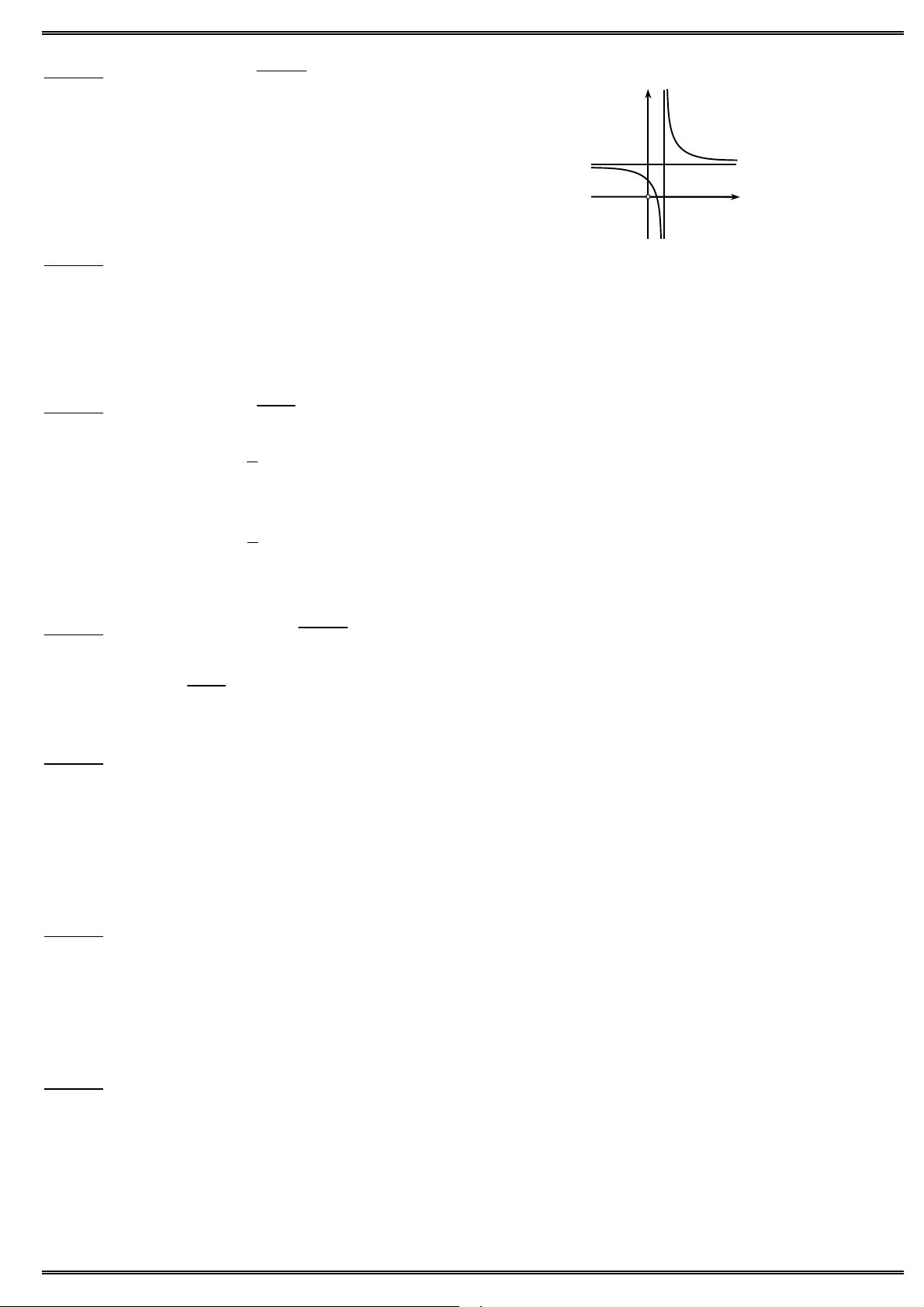
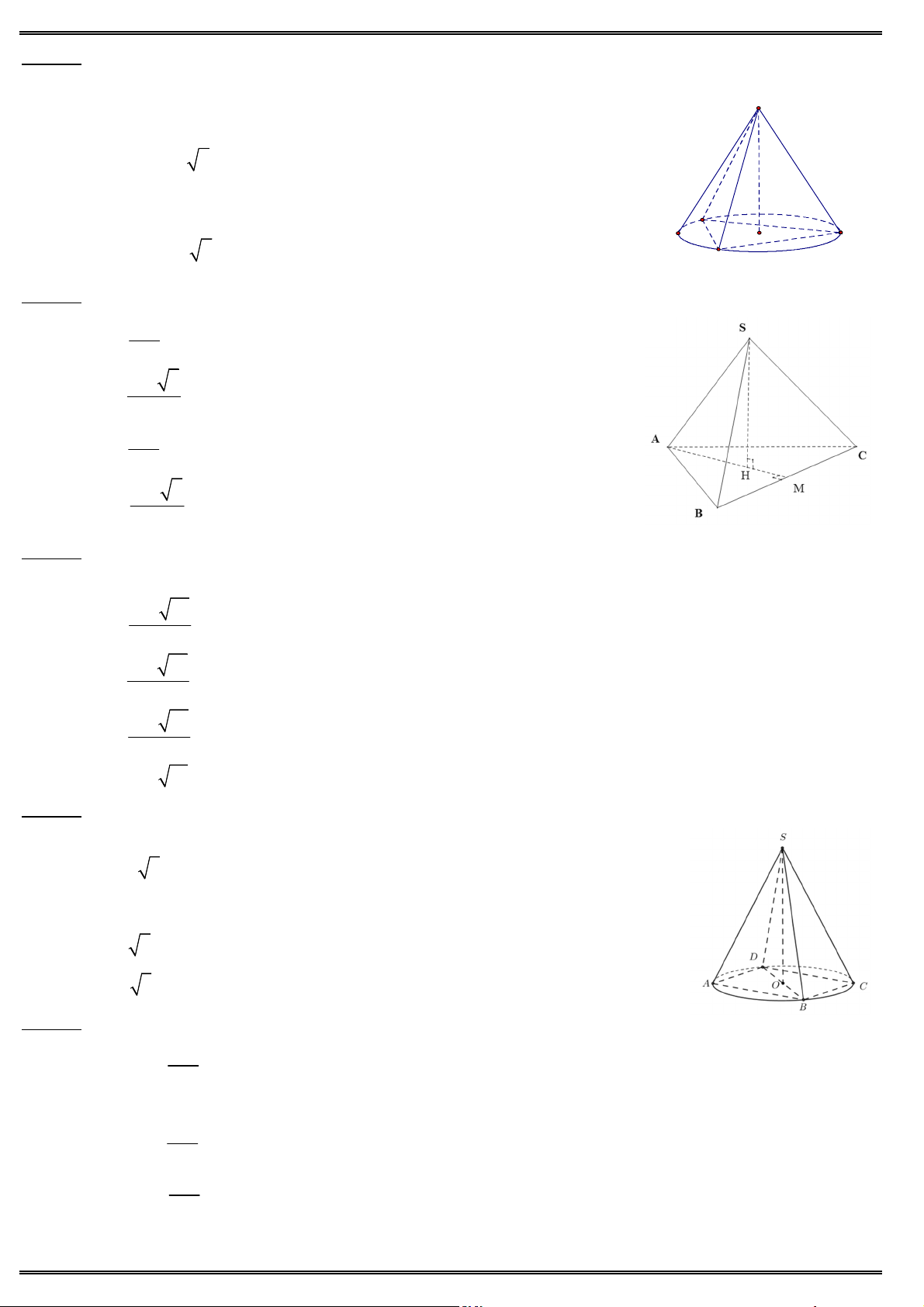
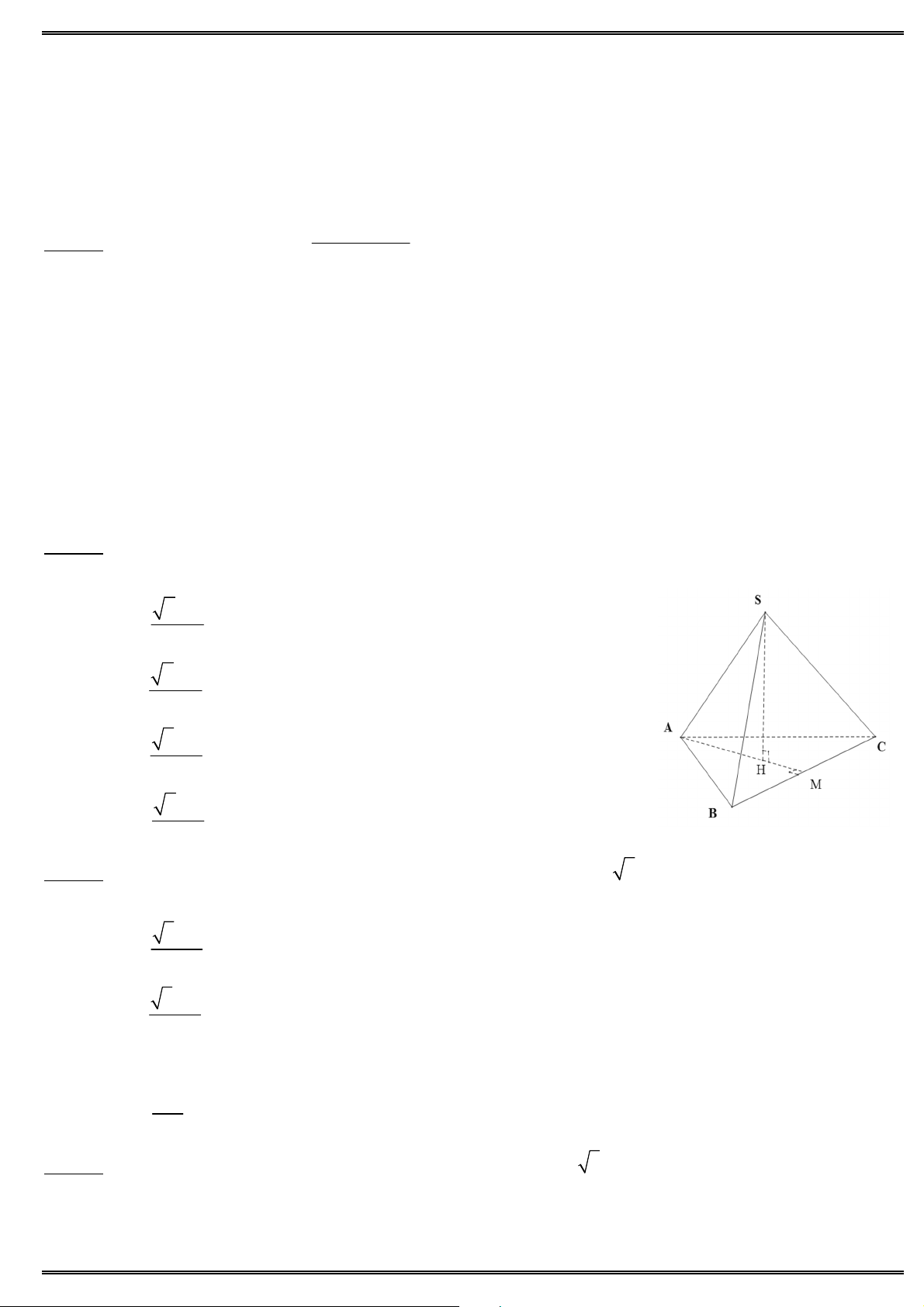
Câu 13. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ? A. 4 2
y x  2x  1. B. 4 2 y x
  2x  1. C. 3 2
y x x  1. D. 3 2 y x   x  1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 2 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 ax b
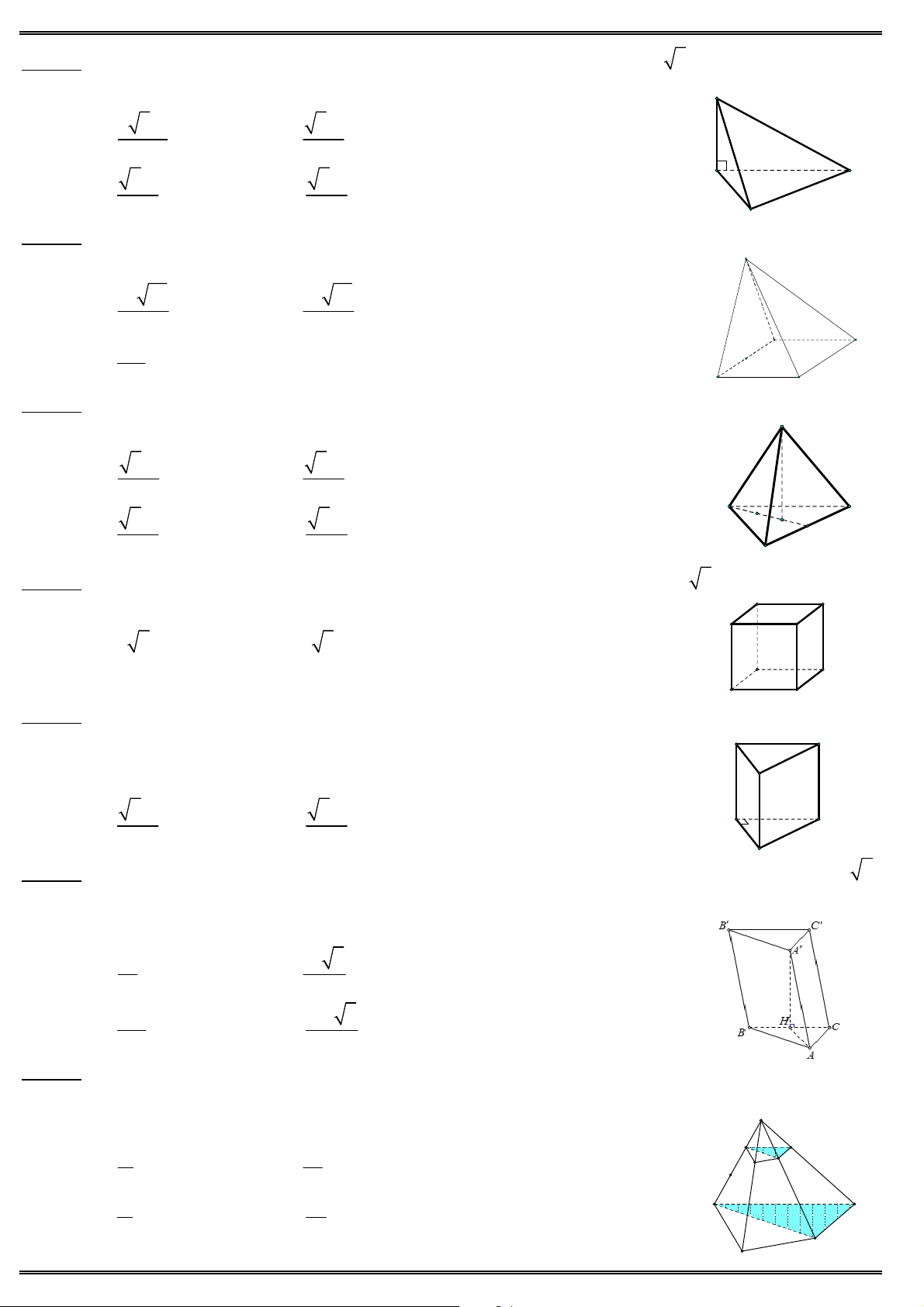
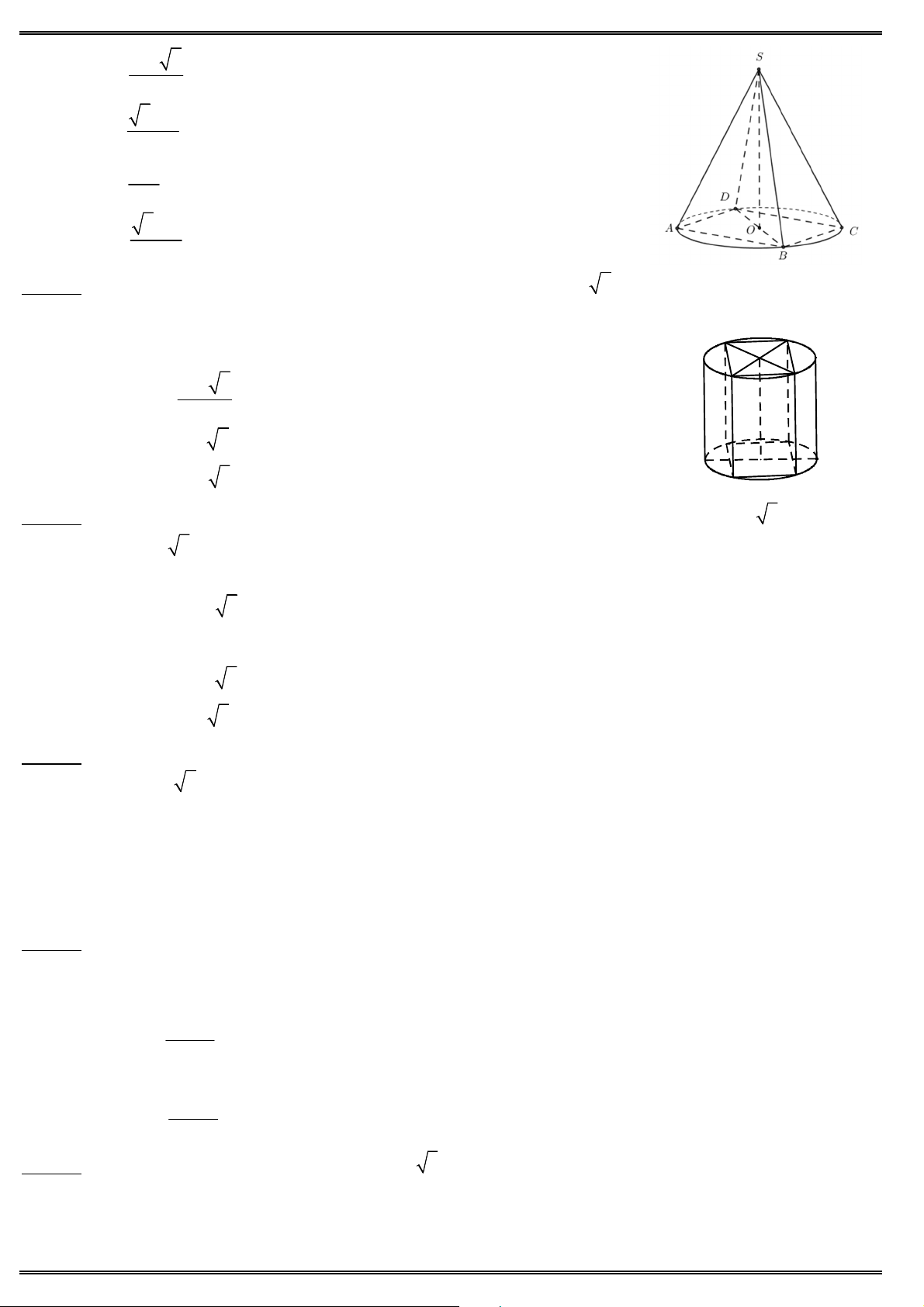
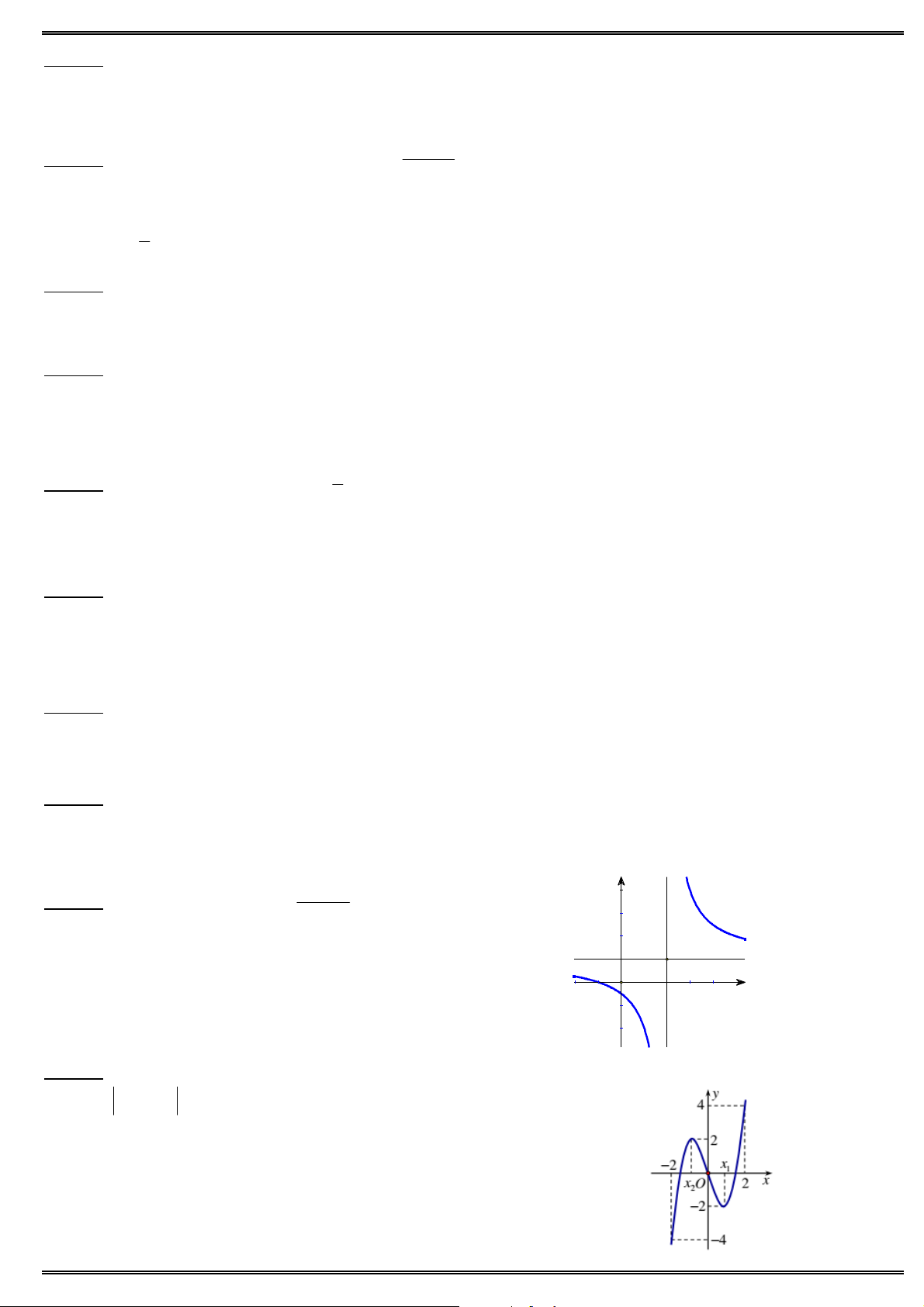
Câu 14. Cho đồ thị hàm số y
như hình vẽ. Tìm khẳng định đúng ? cx d
A. y  0, x  2.
B. y  0, x  1.
C. y  0, x  2.
D. y  0, x  1.
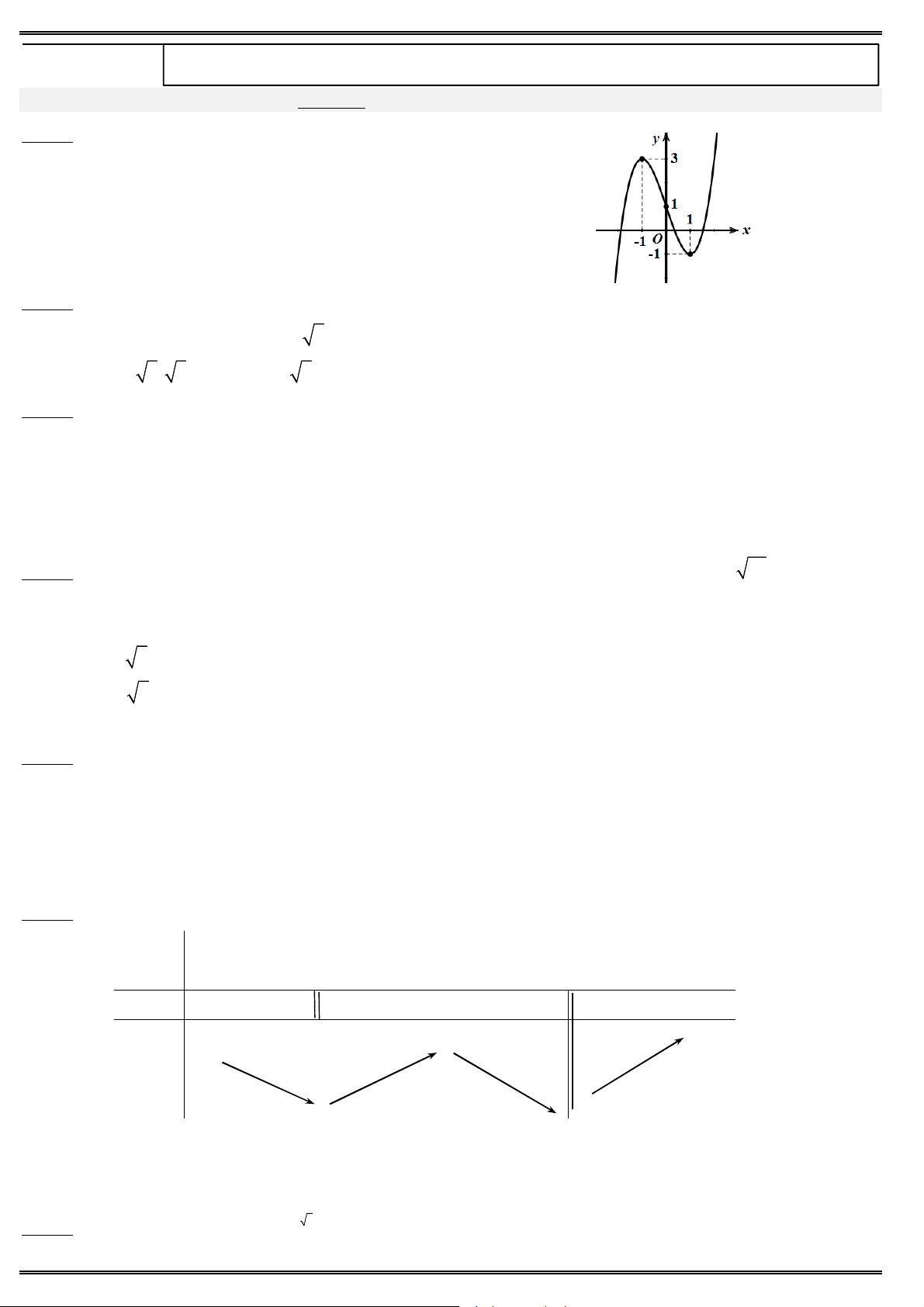
Câu 15. Cho đồ thị hàm số 3 2
y ax bx cx d như hình. Tìm mệnh đề đúng ?
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0.
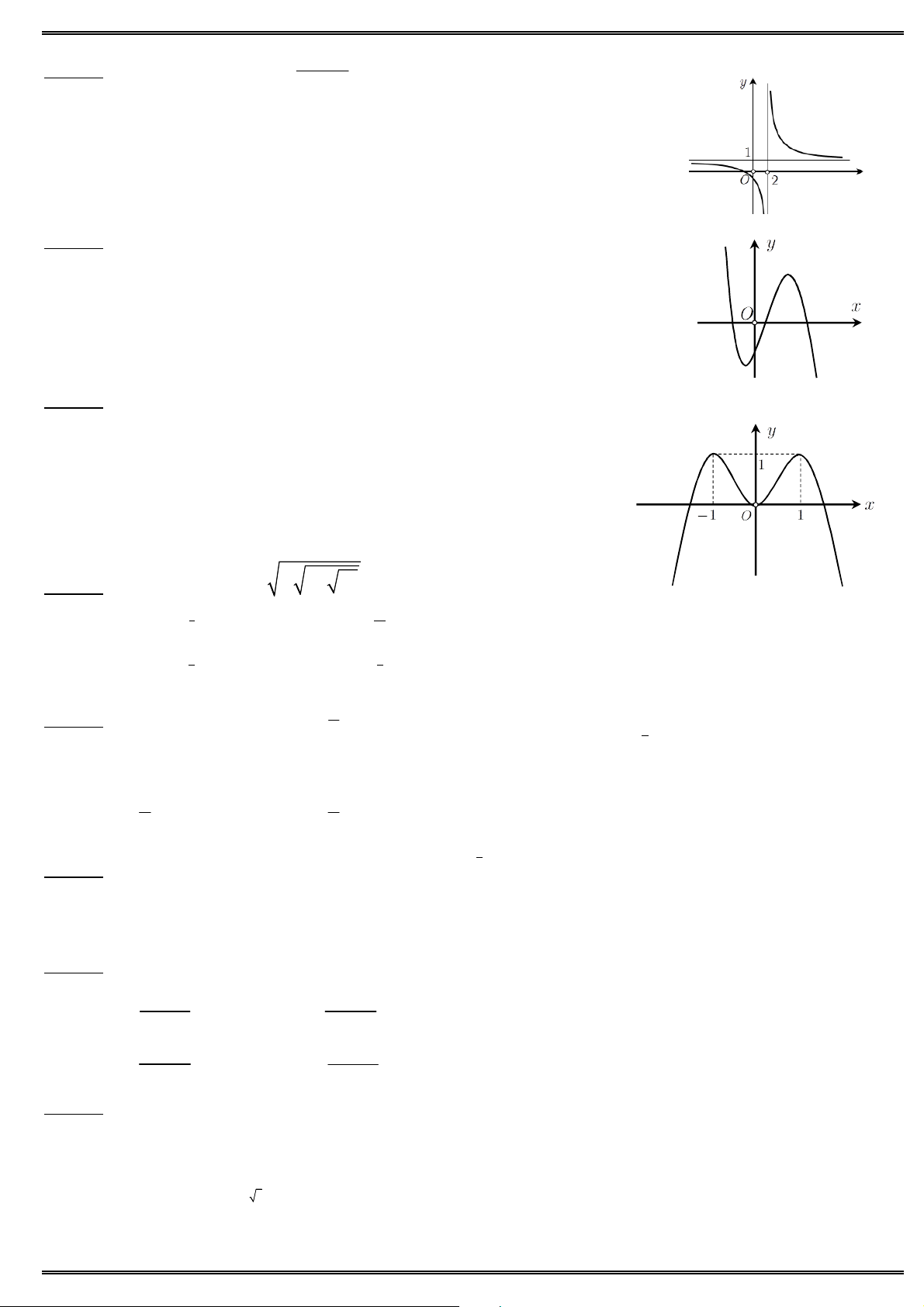
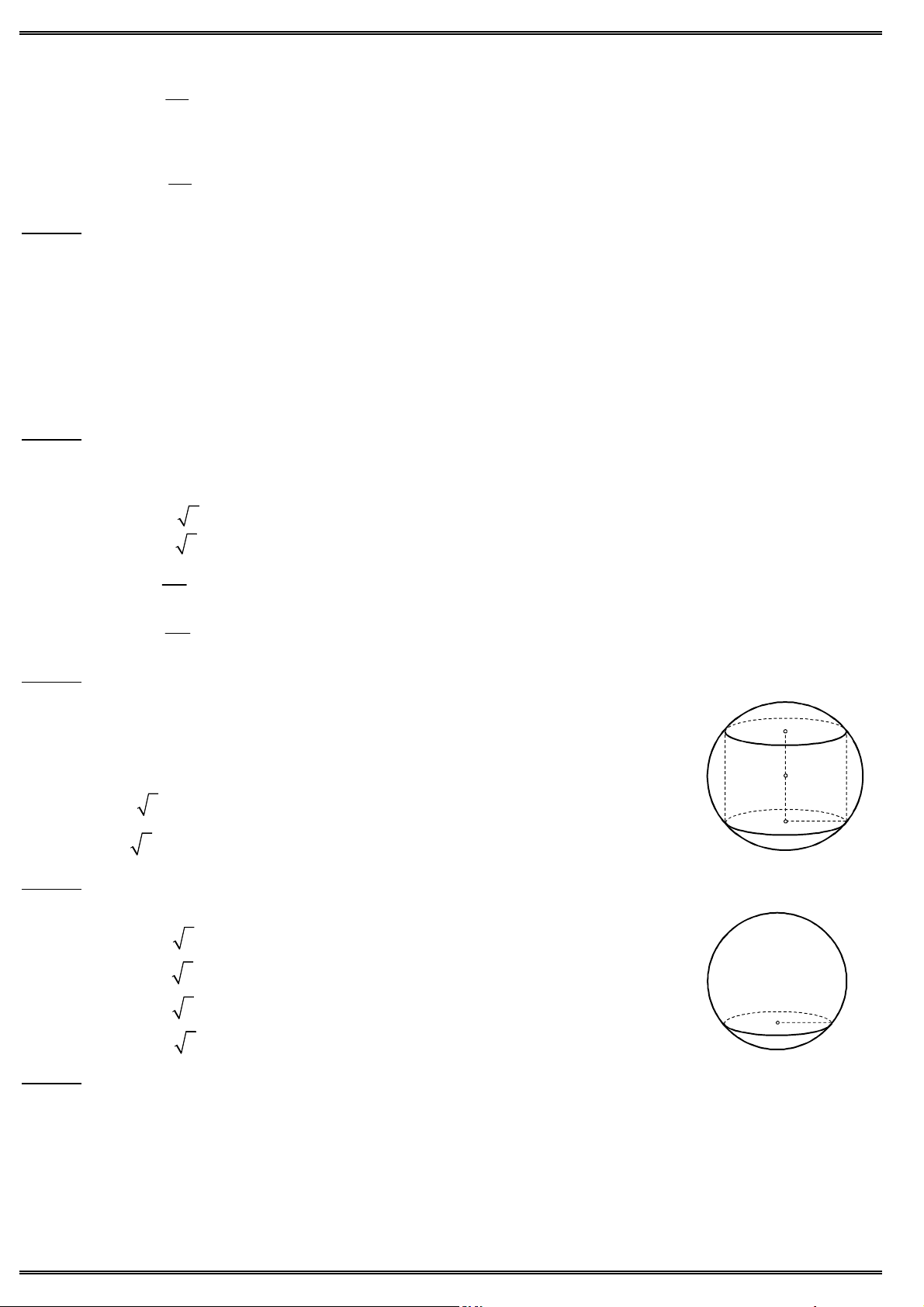
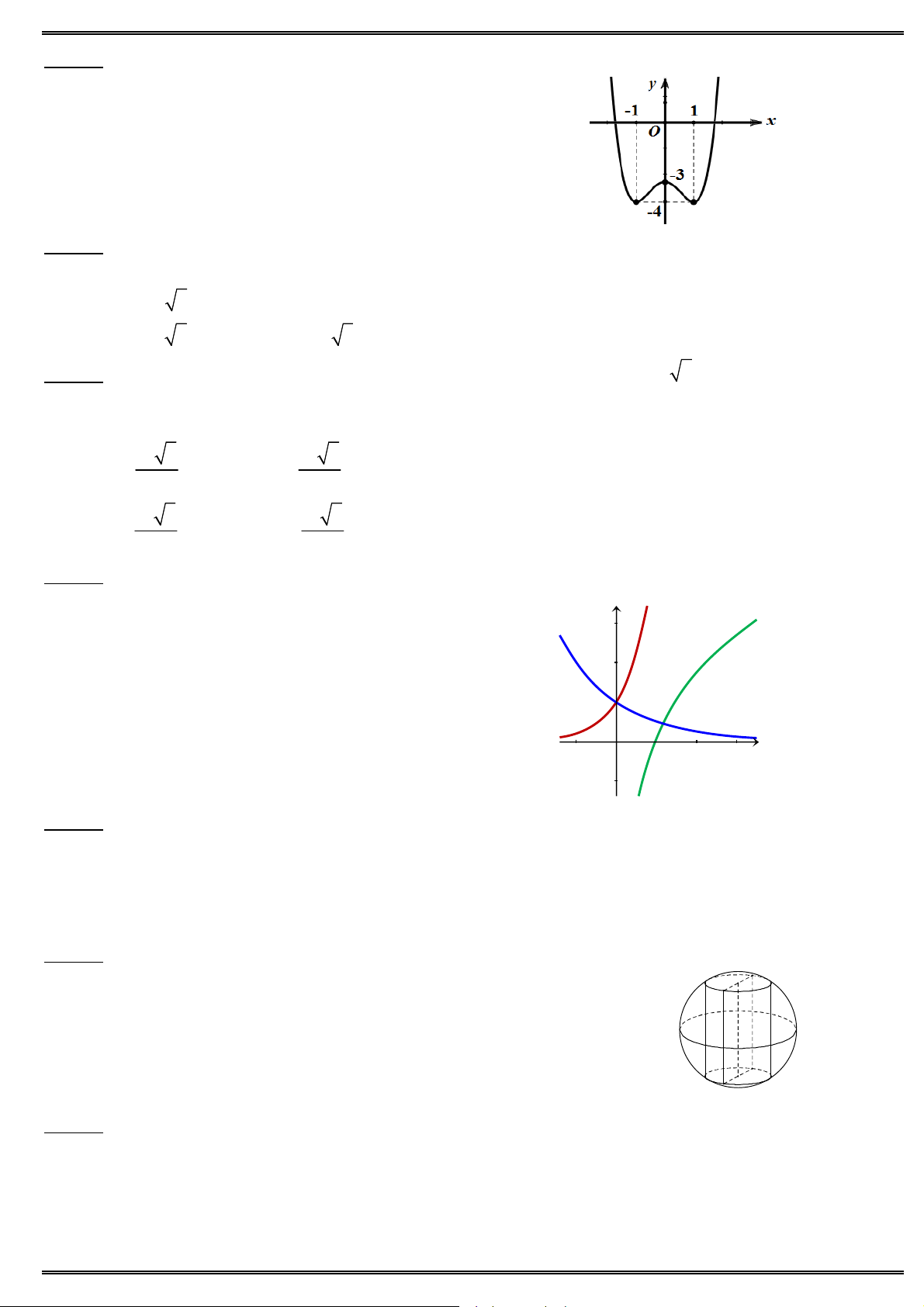
Câu 16. Cho đồ thị hàm số 4 2 y x
  2x như hình vẽ. Tìm tham số m để phương trình 4 2 x
 2x m có
đúng 4 nghiệm phân biệt ?
A. m  0.
B. 0  m  1.
C. 0  m  1.
D. m  1. 4 3
Câu 17. Cho biểu thức 2 3
P x. x . x , với x  0. Mệnh đề nào đúng ? 1 13 A. 2
P x . B. 24
P x . 1 2 C. 4
P x . D. 3
P x . 1
Câu 18. Cho log a  2 và log b  . Giá trị của 2 I 2 log log (3a)   log b 3 2 2 3  3  bằng 1 4 A. 0. B. 4. 5 3 C. D. 4 2 1
Câu 19. Tìm tập xác định D của hàm số 2 2 3
y  (2x x )  log (x  1) . 2
A. D  (0;2).
B. D  (0;1).
C. D   \ {0;2}.
D. D  (0;2) \ {1}.
Câu 20. Giá trị của tham số m để y (
 e)  2m  1 với y  ln(2x  1) bằng 1  2e 1  2e A. B. 4e  2 4e  2 1  2e 1  2e C. D.  4e  2 4e  2
Câu 21. Chọn khẳng định sai ? A. Hàm số 2x y  đồng biến trên ( ;   )  .
B. Hàm số y  log
x nghịch biến trên (0; )  . 0,5 C. Hàm số 2
y x có tập xác định là (0; )  .
D. Hàm số y  log x đồng biến ( ;   )  . 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 3 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 22. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất m của hàm số 2
y x  2 ln x trên 1 [e ;e].
Tổng M m bằng A. 2 2 e e  . B. 2 e  3. C. 2 e  2. D. 2 e  1. 2 Câu 23. x x
Gọi x , x (x x ) là hai nghiệm của phương trình x 1  x 2 9 3   . Giá trị của 1 2 2  3 bằng 1 2 1 2 A. 5. B. 10. C. 11. D. 28.
Câu 24. Tổng các nghiệm của phương trình 2 log ( 3
x  5x  17)  2 bằng 3 A. 5/3. B. 5/3. C. 8/3. D. 8/3.
Câu 25. Tổng các nghiệm của phương trình x 1
4   3.2x  7  0 bằng A. log 7. B. 12. 2 C. 28. D. log 28. 2
Câu 26. Gọi x , x là nghiệm của 2
log x  3 log 5.log x  2  0. Giá trị của 2 2 x x bằng 1 2 2 2 5 1 2 A. 20. B. 5. C. 36. D. 25.
Câu 27. Có bao nhiêu giá trị nguyên của m để phương trình 2
log x  log (3x  1)  log m có nghiệm ? 9 3 3 A. 2. B. 3. C. 4. D. Vô số.
Câu 28. Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình x x 1  2 16  m.4
 5m  45  0 có hai nghiệm phân biệt ? A. 13. B. 3. C. 6. D. 4. 2 x 4  x 1  2 1  
Câu 29. Bất phương trình    1 
có tất cả bao nghiêu nghiệm nguyên ? 3 A. 3. B. 5. C. 7. D. Vô số.
Câu 30. Tập nghiệm của bất phương trình log (log x)  0 là 3 0,5  1    1
A. S  0;       S 0;   B.  2  2  1 1  1
C. S   ;       D. S 0;  4 2      4 2
Câu 31. Các nguyên hàm của hàm số 2
f (x)  x  là 2 x
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 4 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 x 2 3 x 1 3 x 2 3 x 1 A.  C. B.  C. C.  C. D.  C. 3 x 3 x 3 x 3 x 1 1
Câu 32. Họ nguyên hàm của hàm số f (x)   2x  là 2 2x  1 cos x 1 A. 2
ln 2x  1  x  tan x C. B. 2
ln 2x  1  x  tan x C. 2 2 1 x 1
C. ln 2x  1 
 tan x C. D. 2
ln 2x  1  x  tan x C. 2 2 2   
Câu 33. Tìm nguyên hàm F(x) của hàm số f (x)  sin x  cos x thỏa mãn F    2.   2 
A. cos x  sin x  3.
B.  cos x  sin x  3.
C. sin x  cos x  1.
D.  cos x  sin x  1.
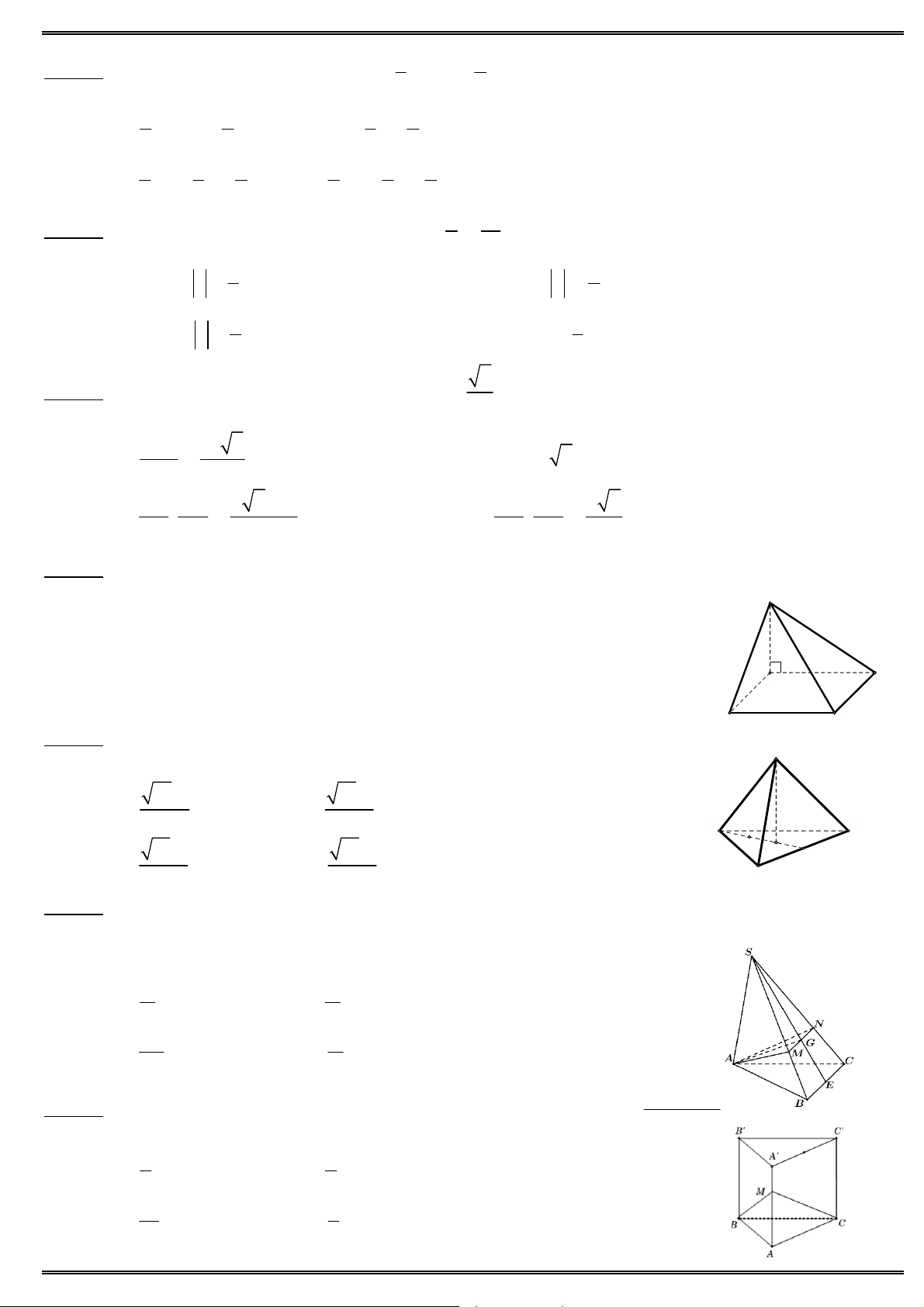
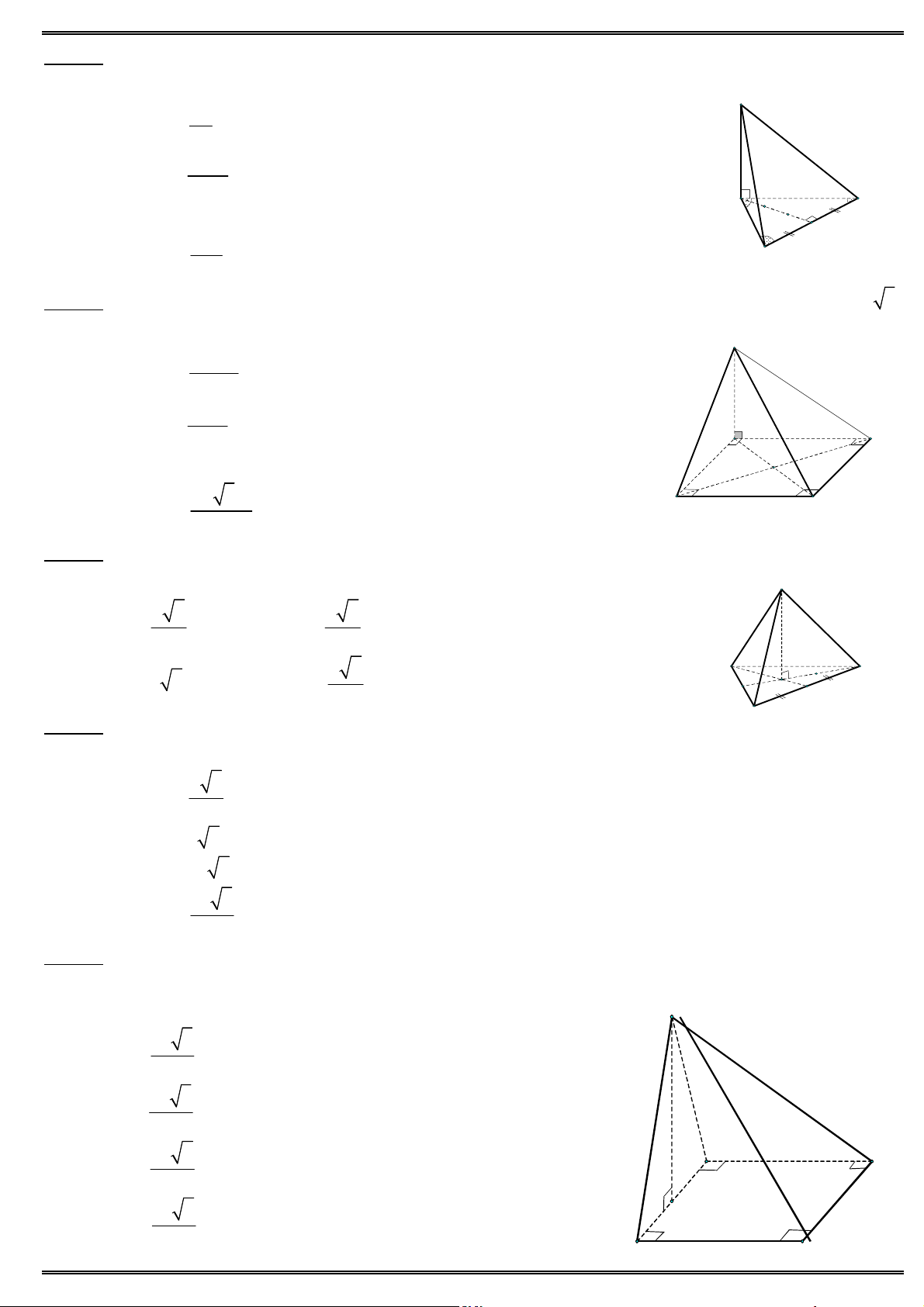
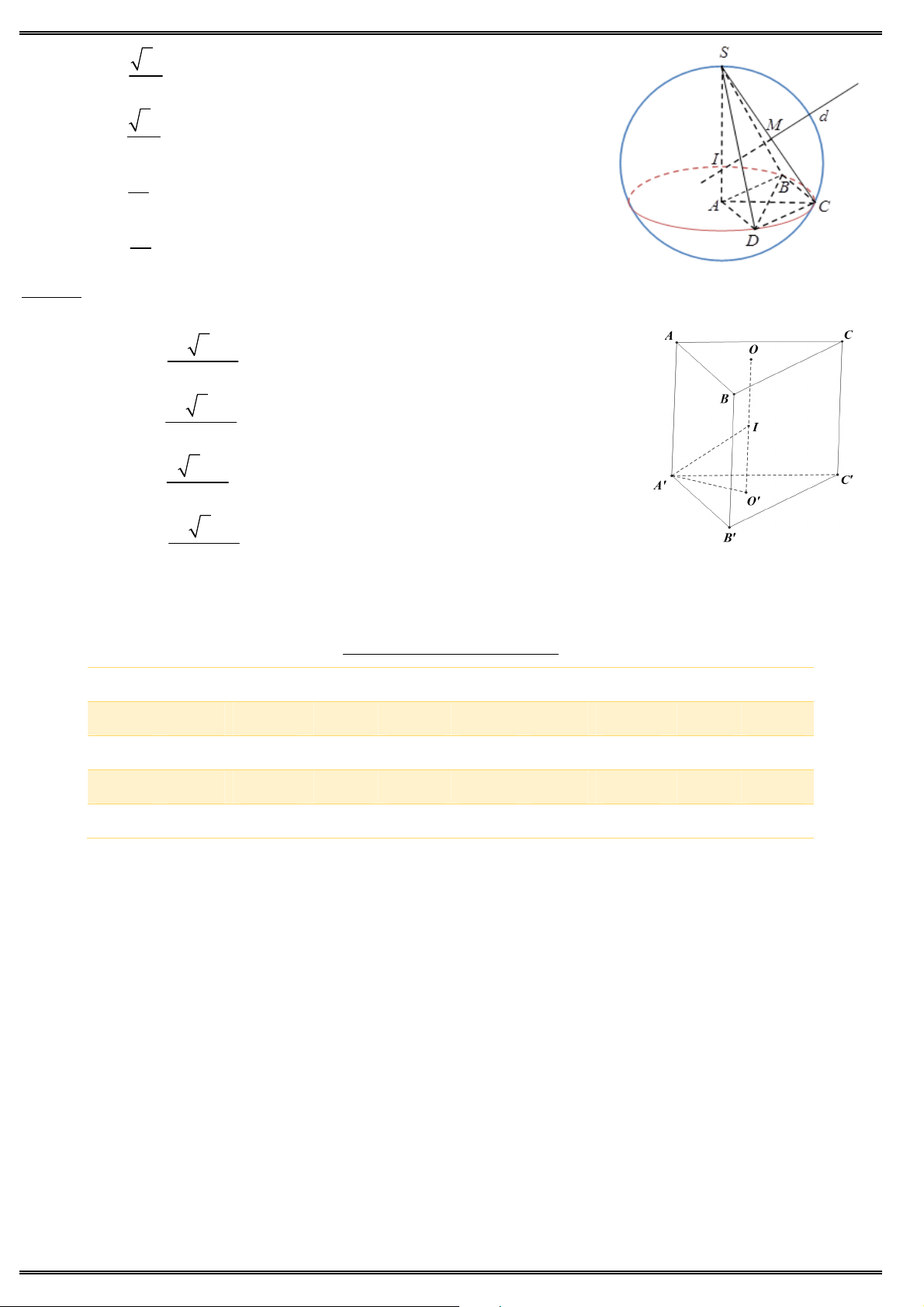
Câu 34. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh SA vuông góc với đáy và AB  , a
SA AC  2a. S ABC S
Thể tích của khối chóp . bằng 3 2 3a 3 2a A. B. 3 3 3 A C 3a C. D. 3 3a . 3 B S
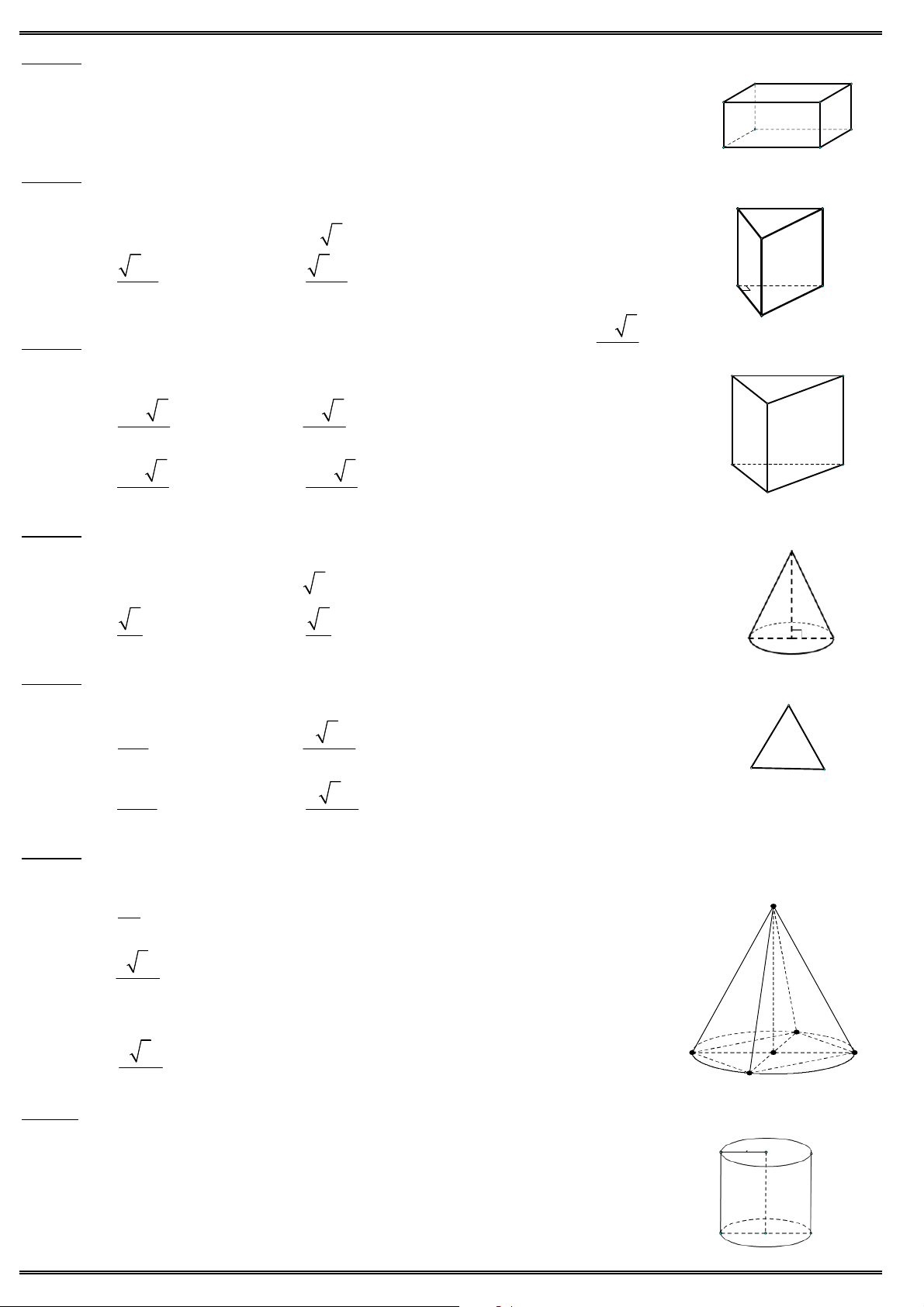
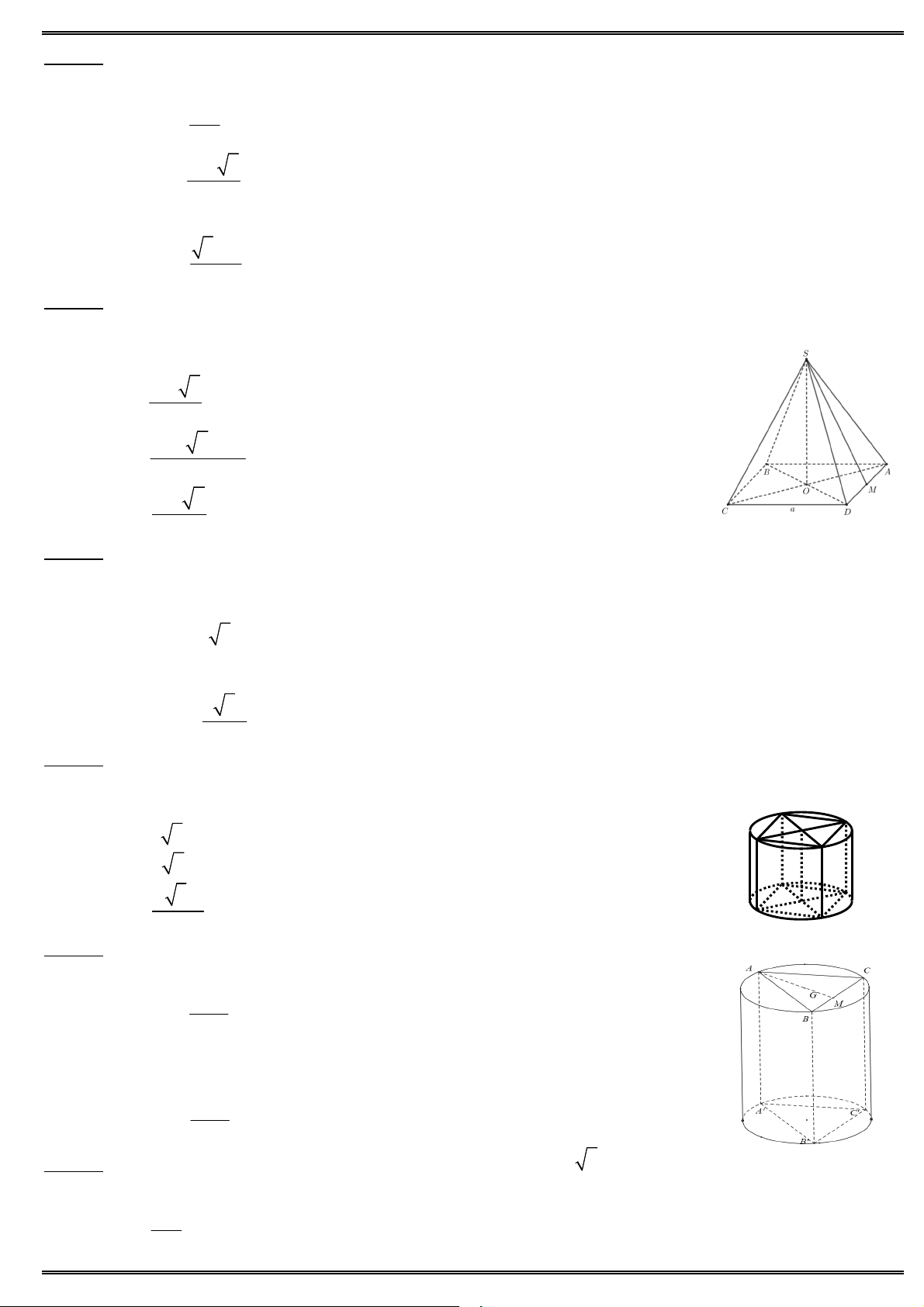
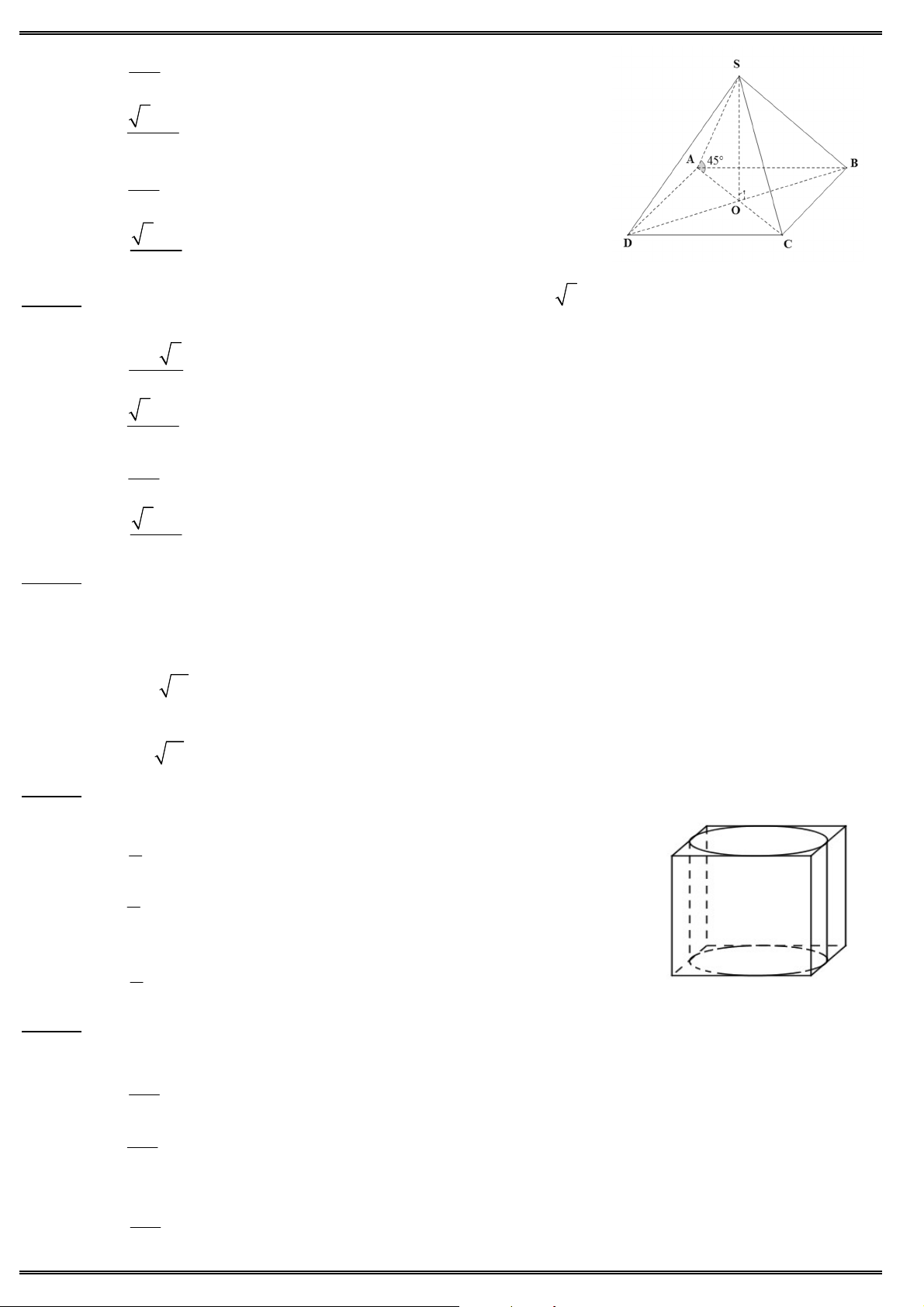
Câu 35. Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích khối chóp bằng 3 4 2a 3 8a A. B.  3 3 A D 3 8 2a 3 2 2a C. D. O 3 3 B C
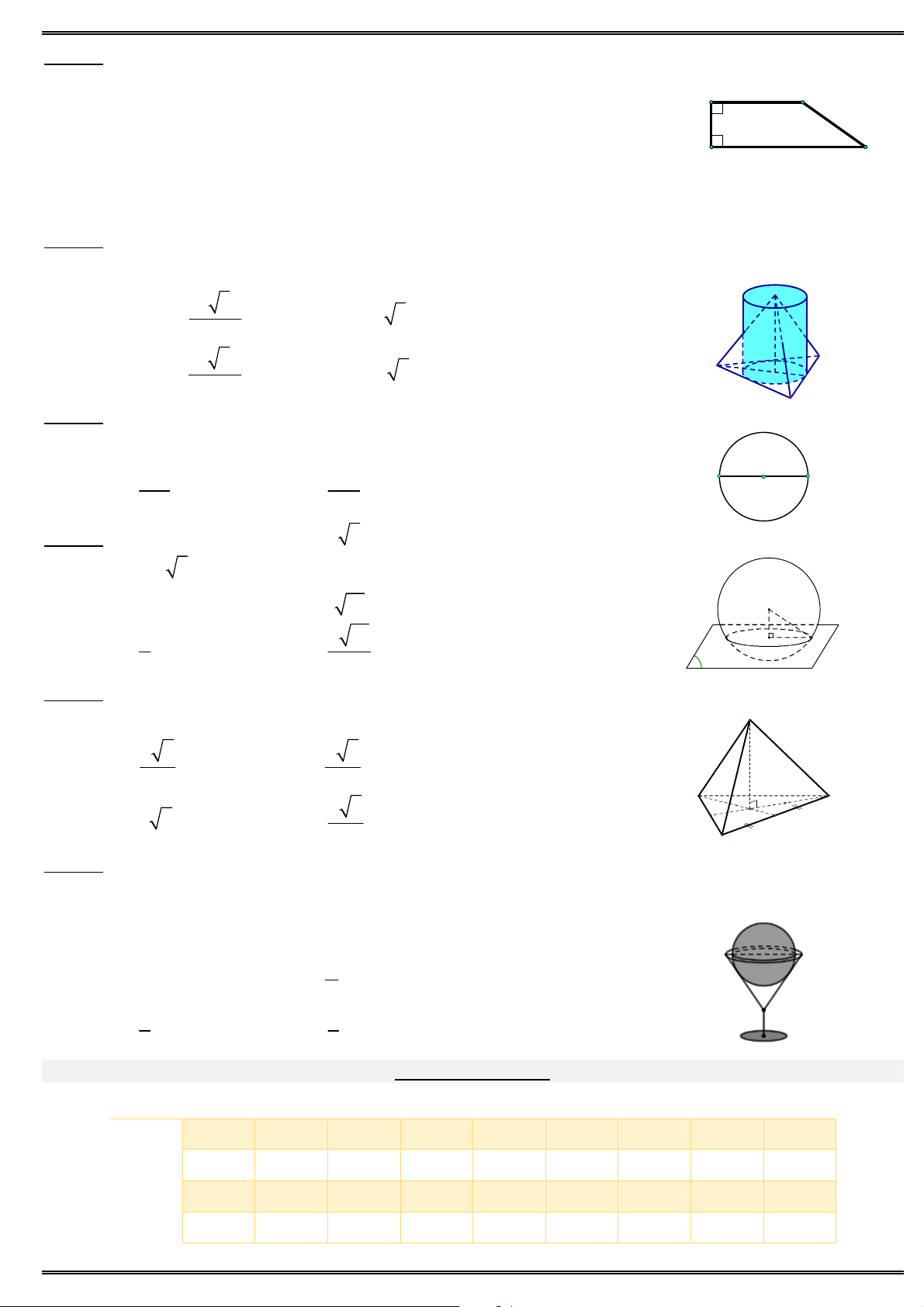
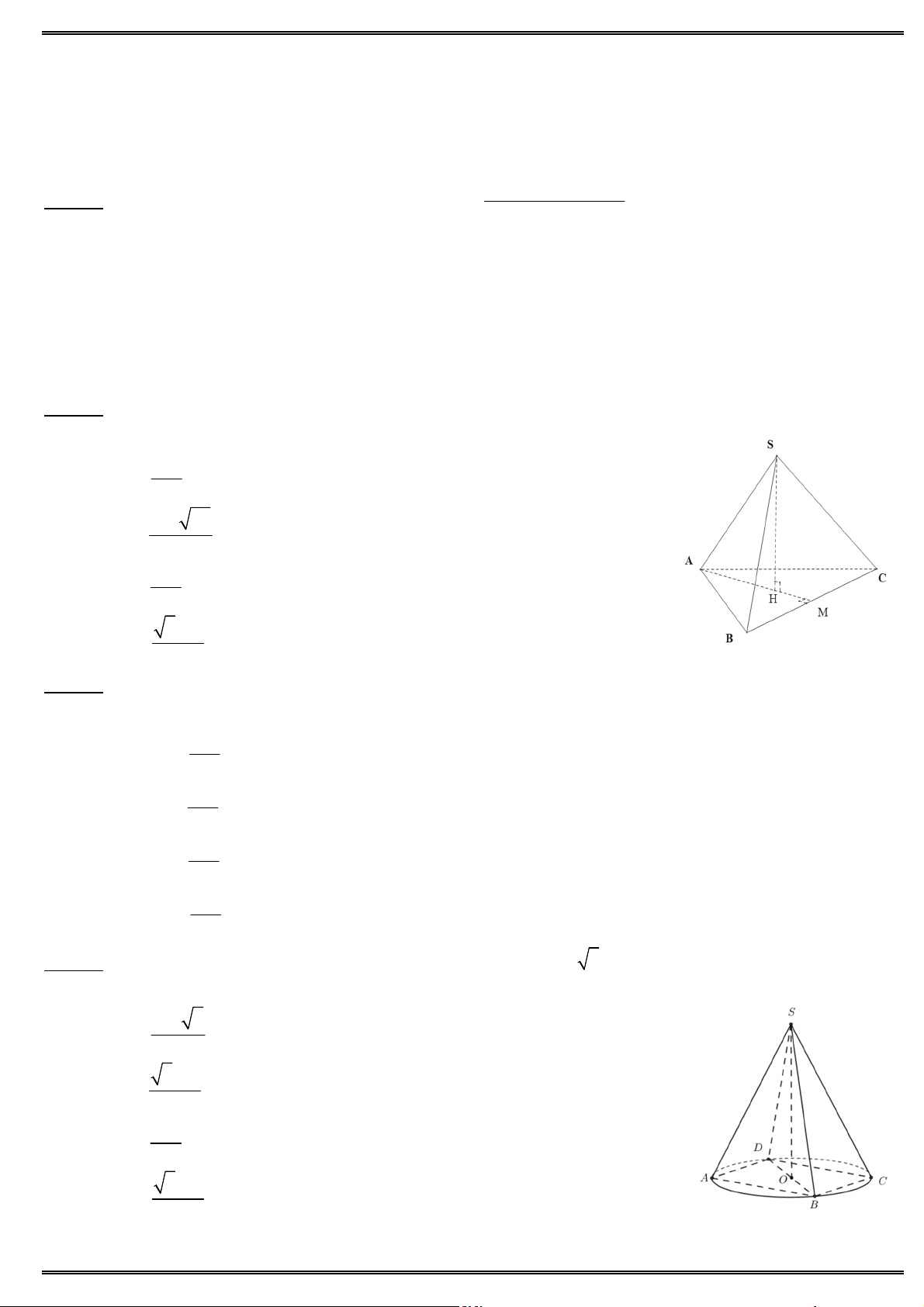
Câu 36. Cho hình chóp S.ABC có SA a, đáy ABC là tam giác đều. Tam giác SAB vuông cân tại S và S
nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp đã cho bằng 3 6a 3 6a A. B. 4 24 A C 3 6a 3 6a C. D. H 12 8 ABCD AB CD   AC   a B
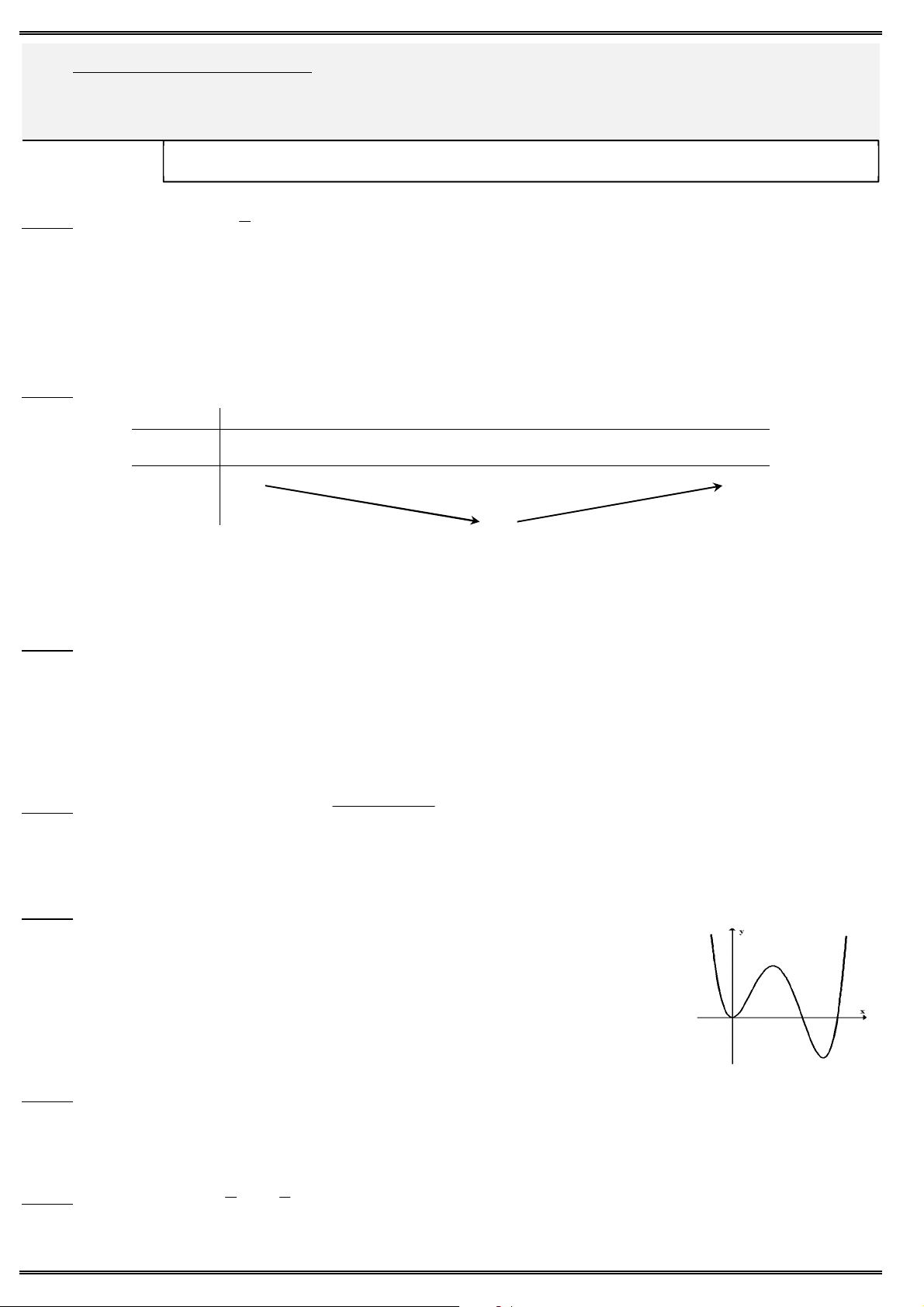
Câu 37. Cho khối lập phương . có
. Thể tích khối lập phương bằng 3 A' D' a A. B. 3 3a . B' C' 27 3 3a A D C. 3 3 3a . D. 9 B C
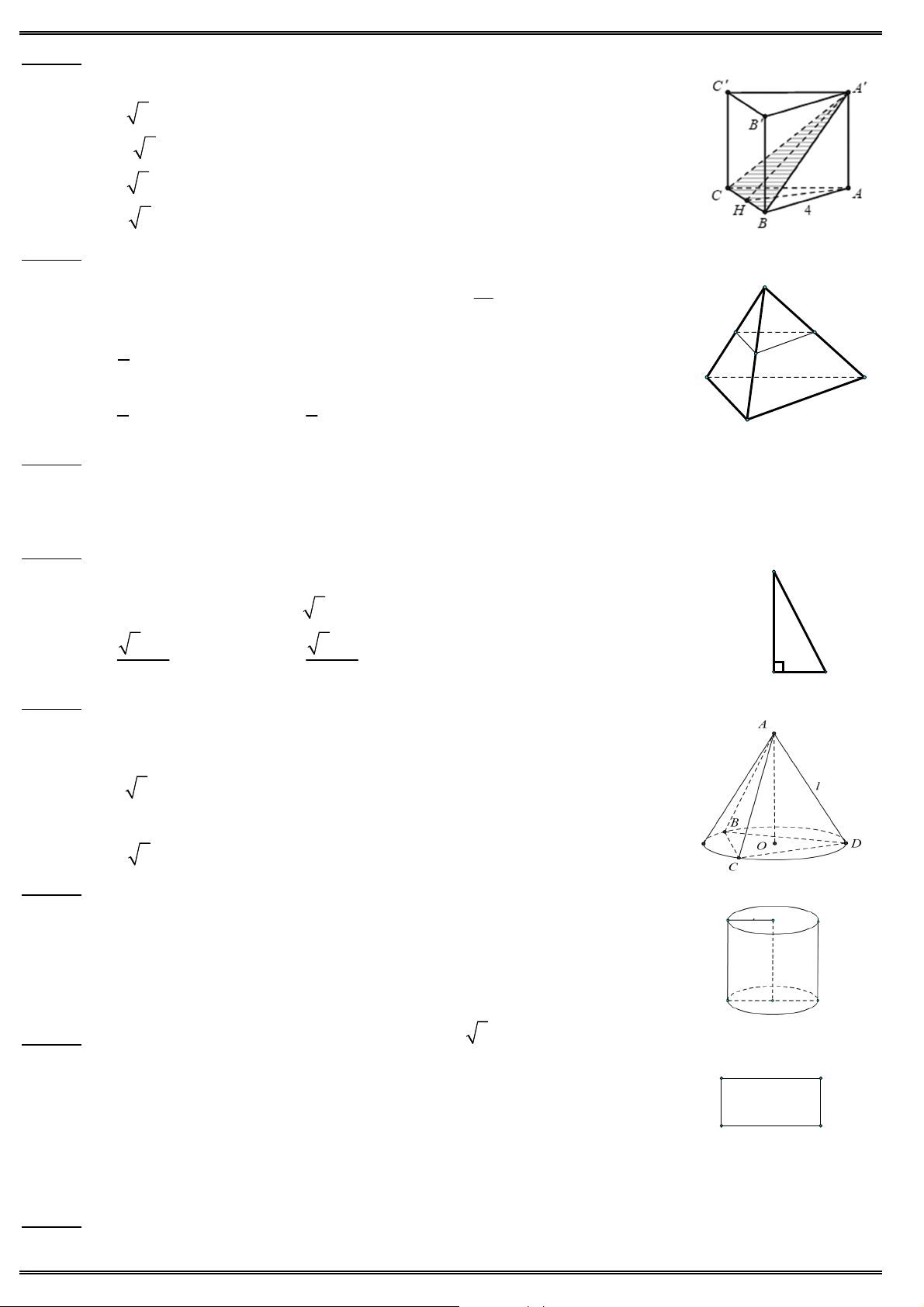
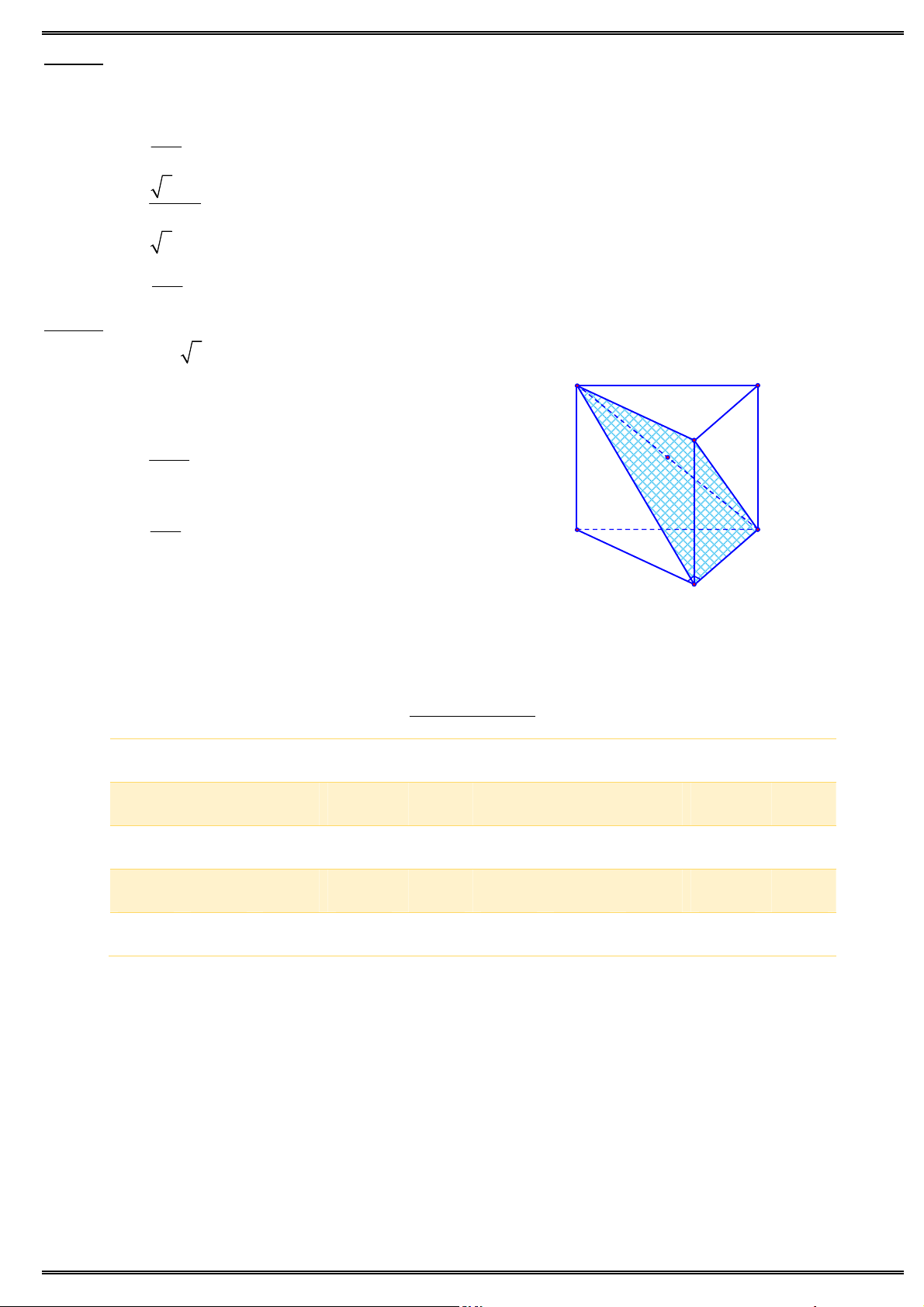
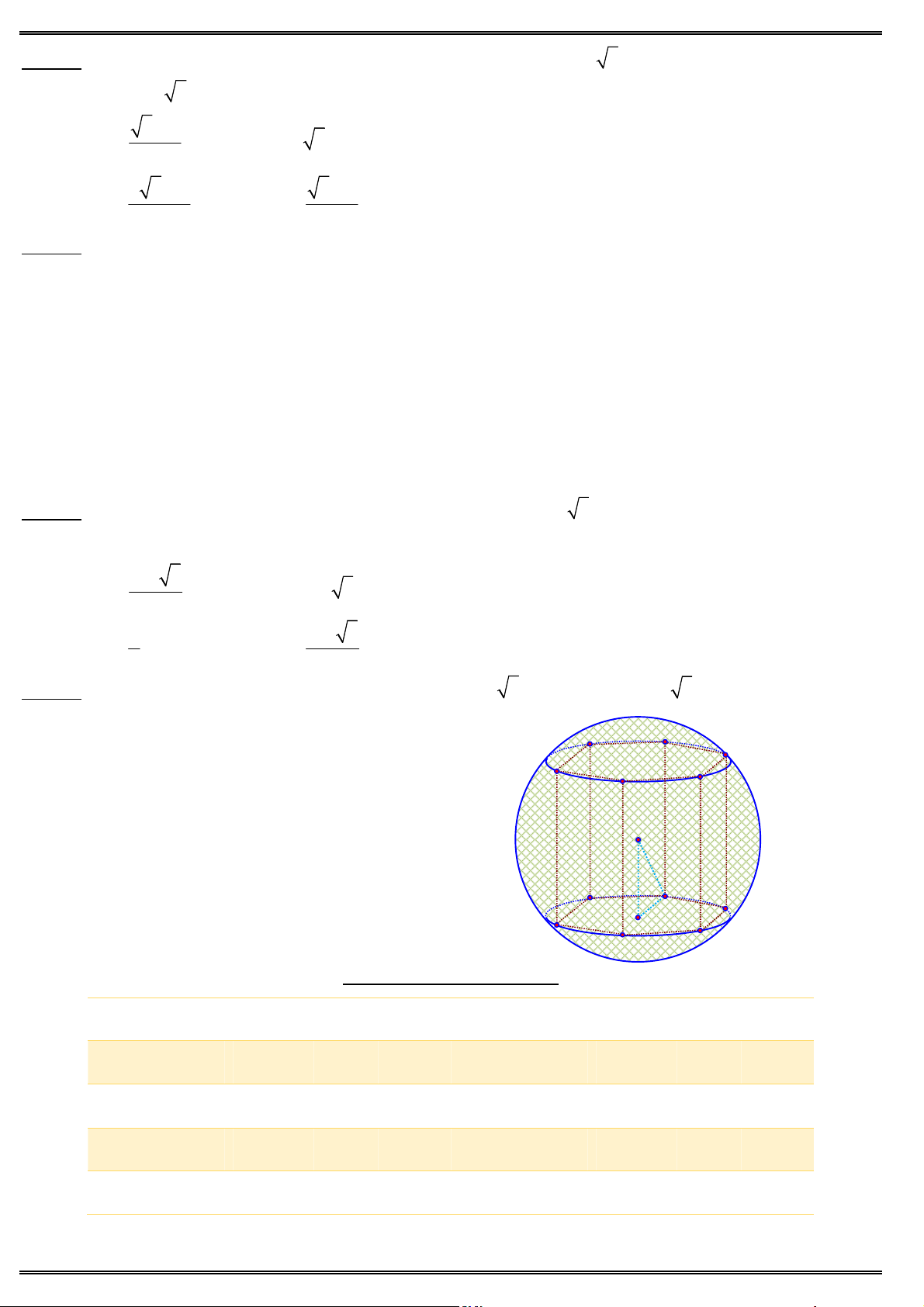
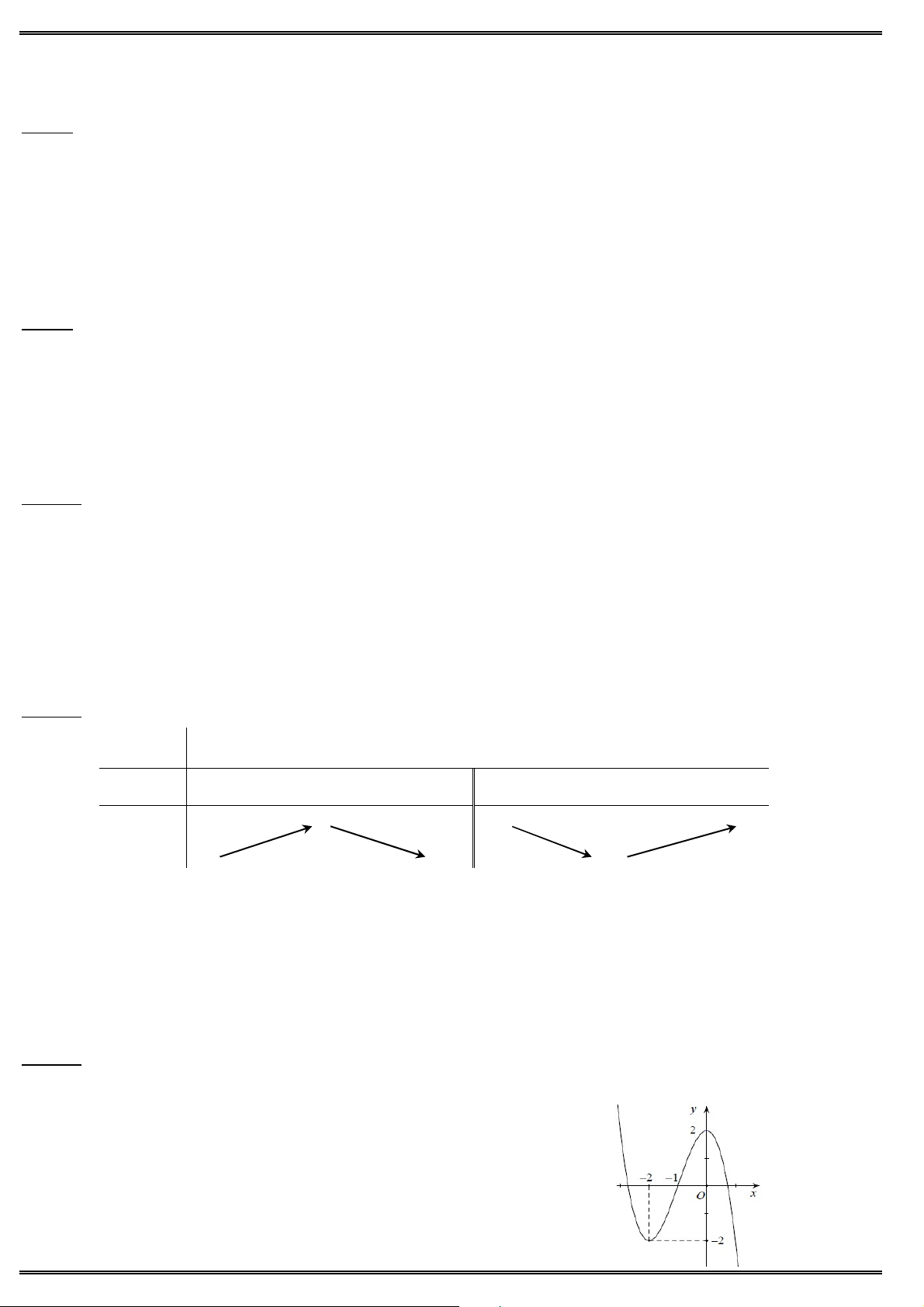
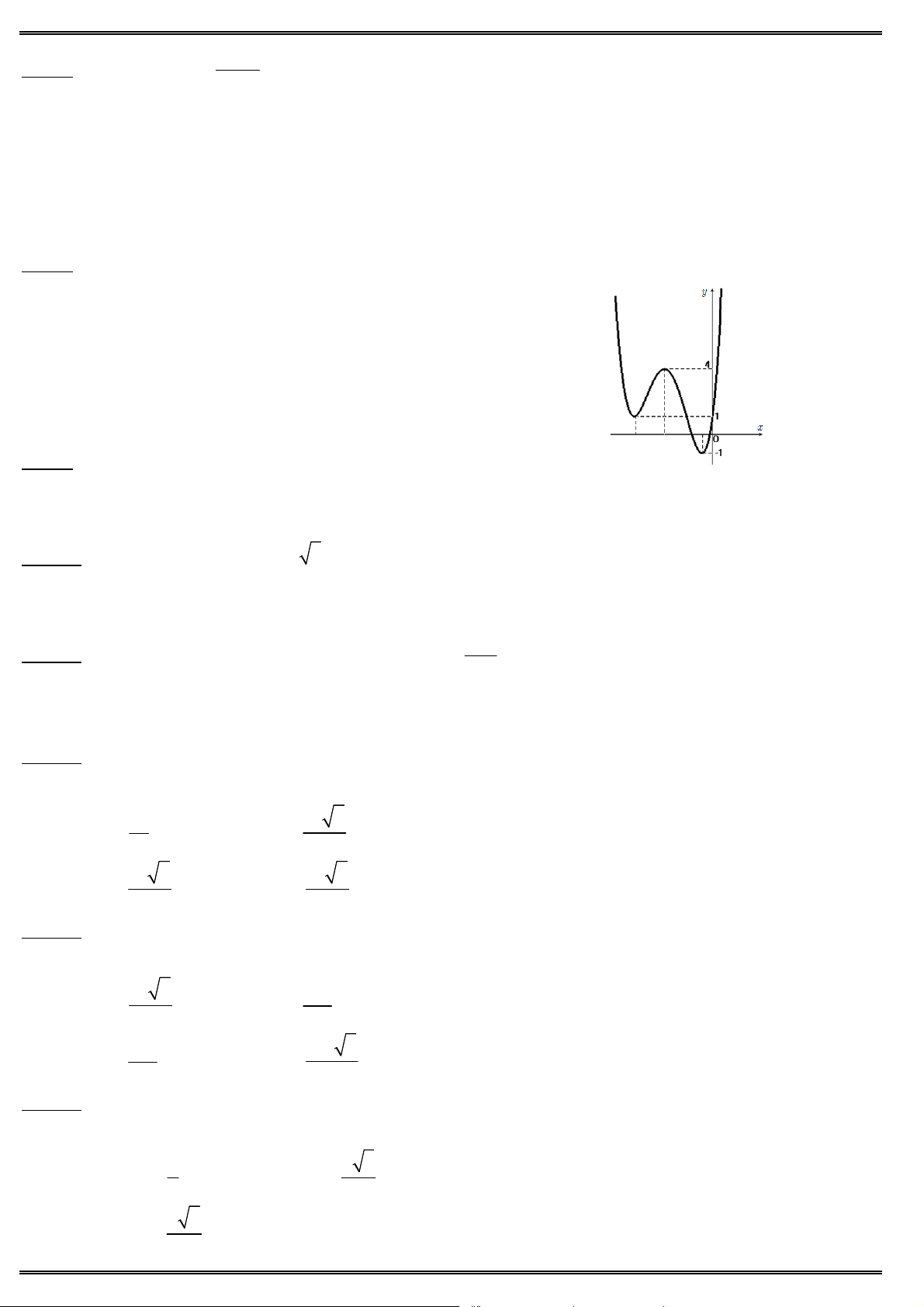
Câu 38. Cho lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông cân tại ,
A BC  2a, AB  3a.
Thể tích của khối lăng trụ ABC .AB C   bằng A' C' A. 3 2a /3. B' B. 3 2a . 3 10a C. A C 3 D. 3 7a . B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 5 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
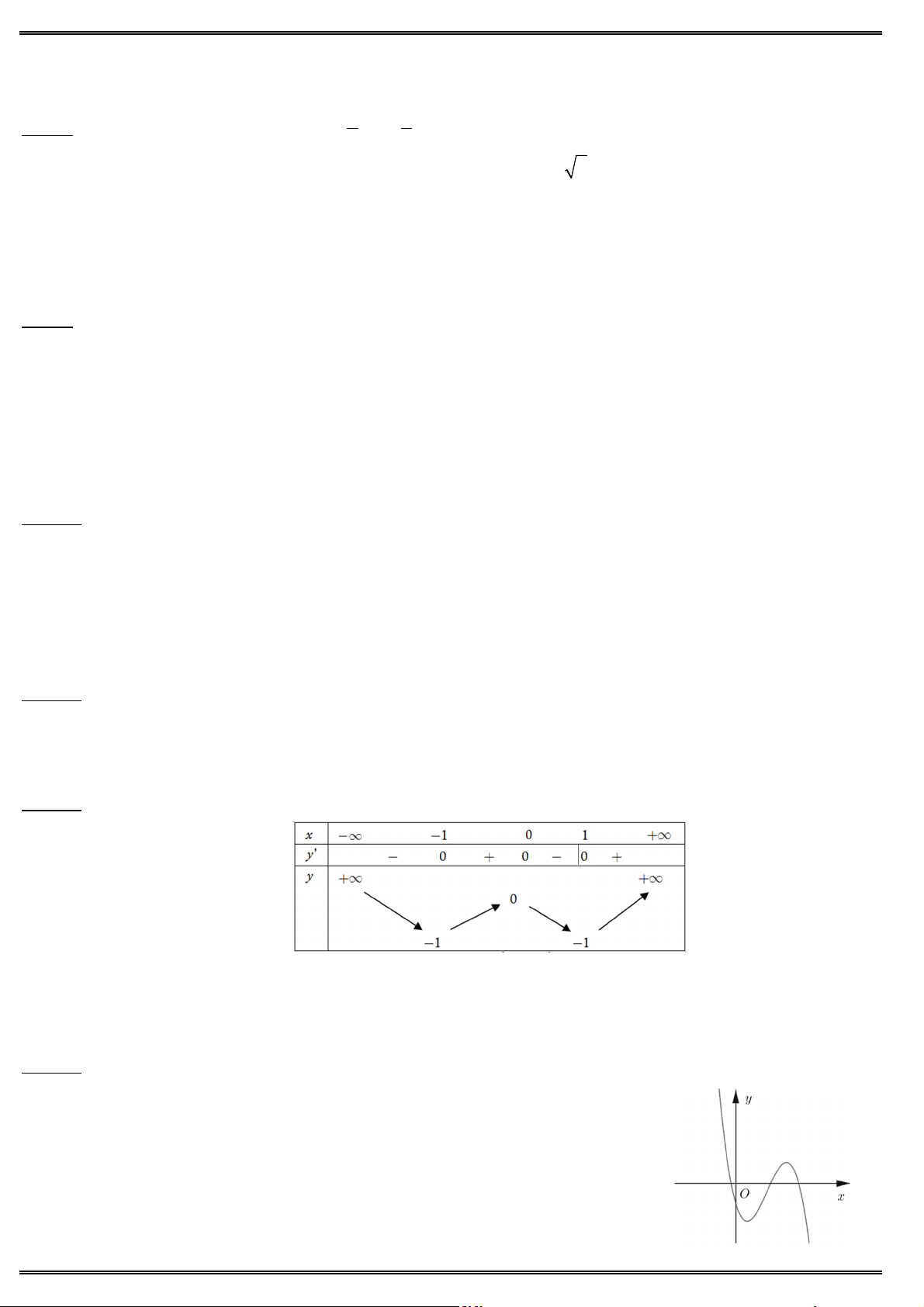
Câu 39. Cho lăng trụ tam giác đều ABC .AB C
  có cạnh đáy là bằng 4, diện tích tam giác ABC bằng 8.
Thể tích khối lăng trụ ABC .AB C   bằng A. 2 3. B. 10 3. C. 4 3. D. 8 3.
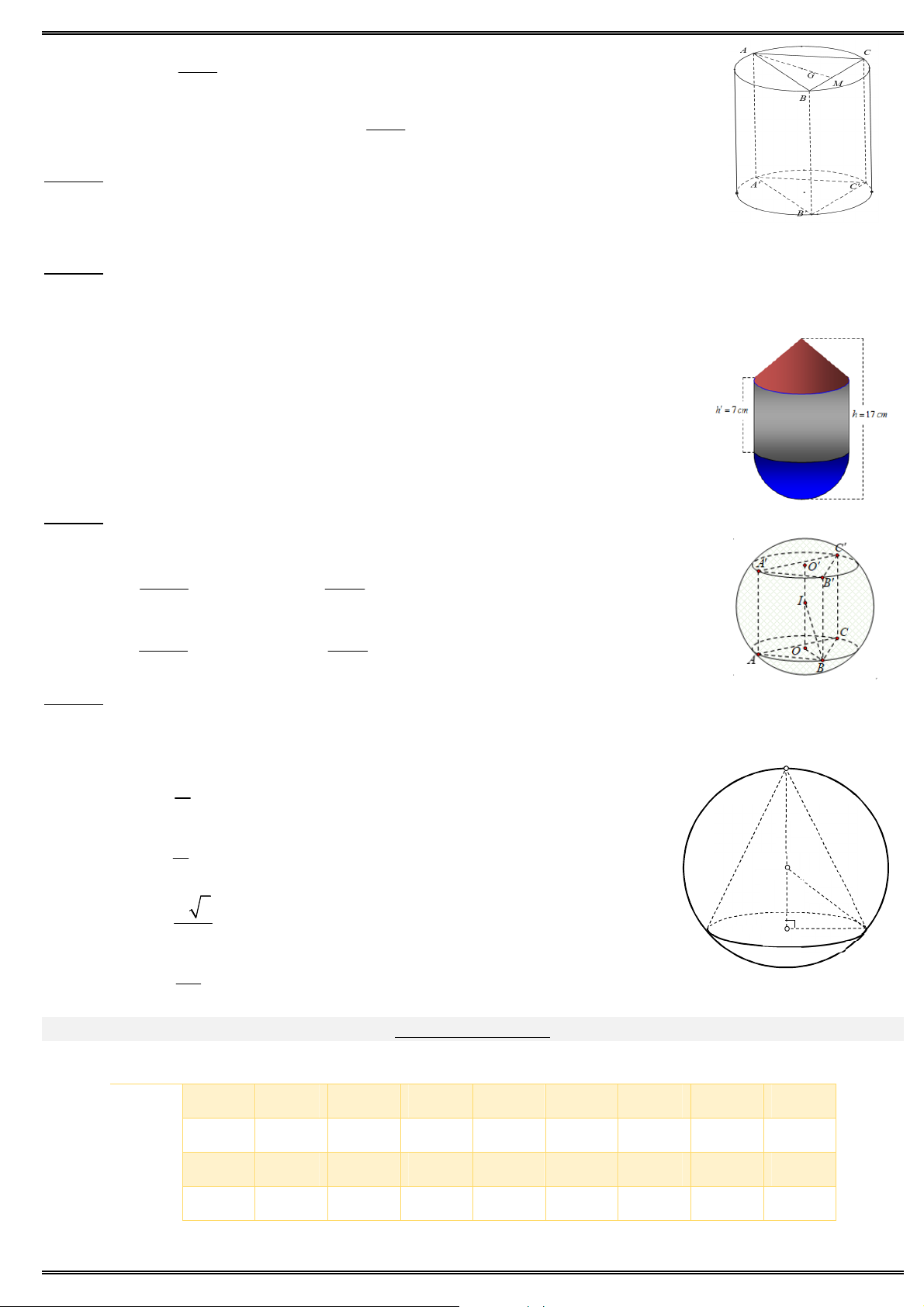
Câu 40. Hình chóp S.ABC có M, N, P lần lượt trung điểm của S , A S ,
B SC. Gọi V là thể tích khối 1 V S
MNP.ABC và V là thể tích khối S.ABC. Tỉ số 1 bằng 2 V2 M P 1 A. B. 8. N 8 A C 7 8 C. D. B 8 7
Câu 41. Cho khối nón có bán kính đáy bằng 3 và diện tích xung quanh bằng 15 .
Thể tích hình nón bằng A. 12 . B. 20 . C. 36 . D. 60 .
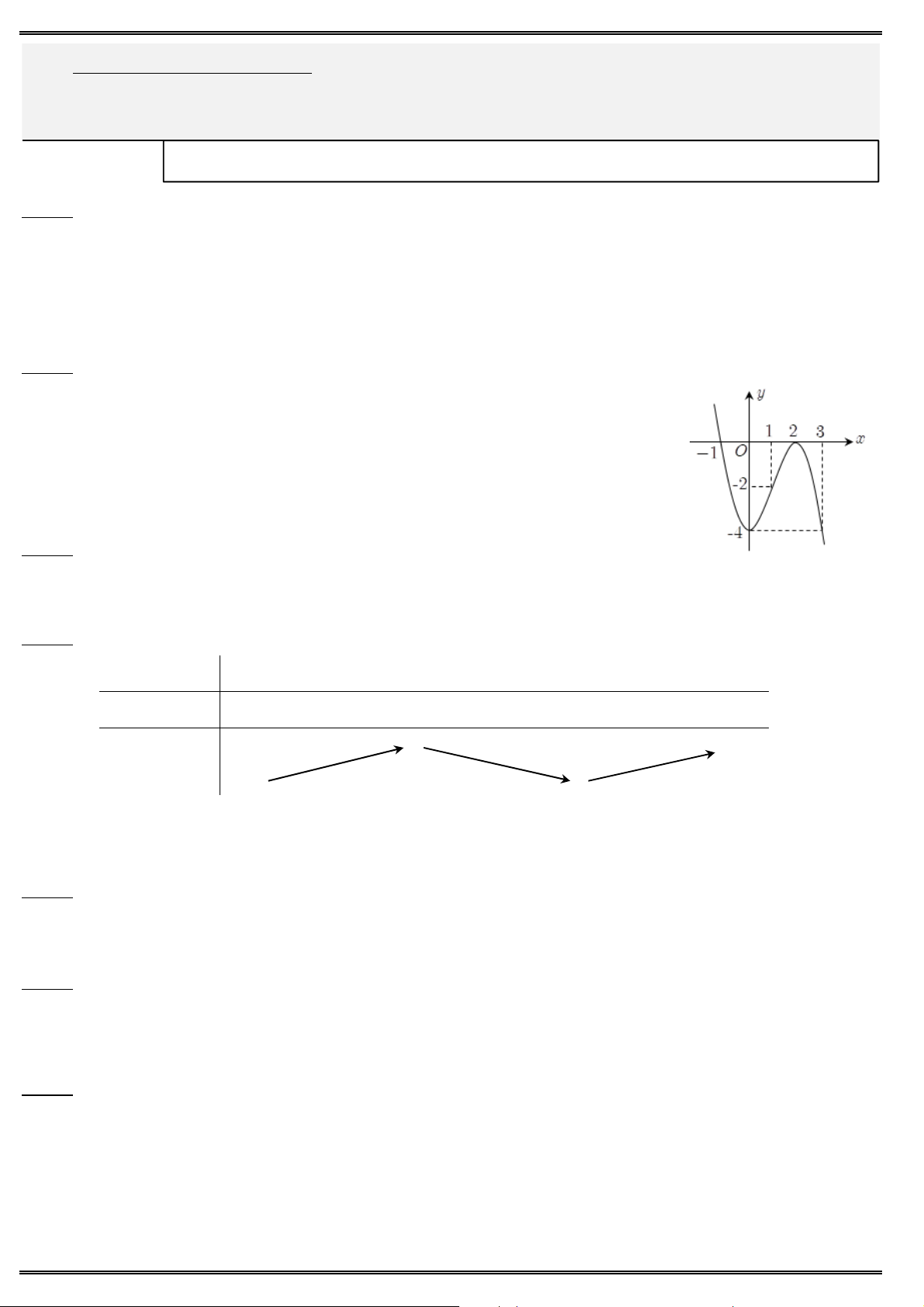
Câu 42. Trong không gian cho tam giác ABC vuông tại ,
A AB a và ACB  30. Thể tích của khối nón C
nhận được khi quay tam giác ABC quanh cạnh AC bằng A. 3 a . B. 3 3 a . 3 3 a 3 3 a C. D. A B 9 3
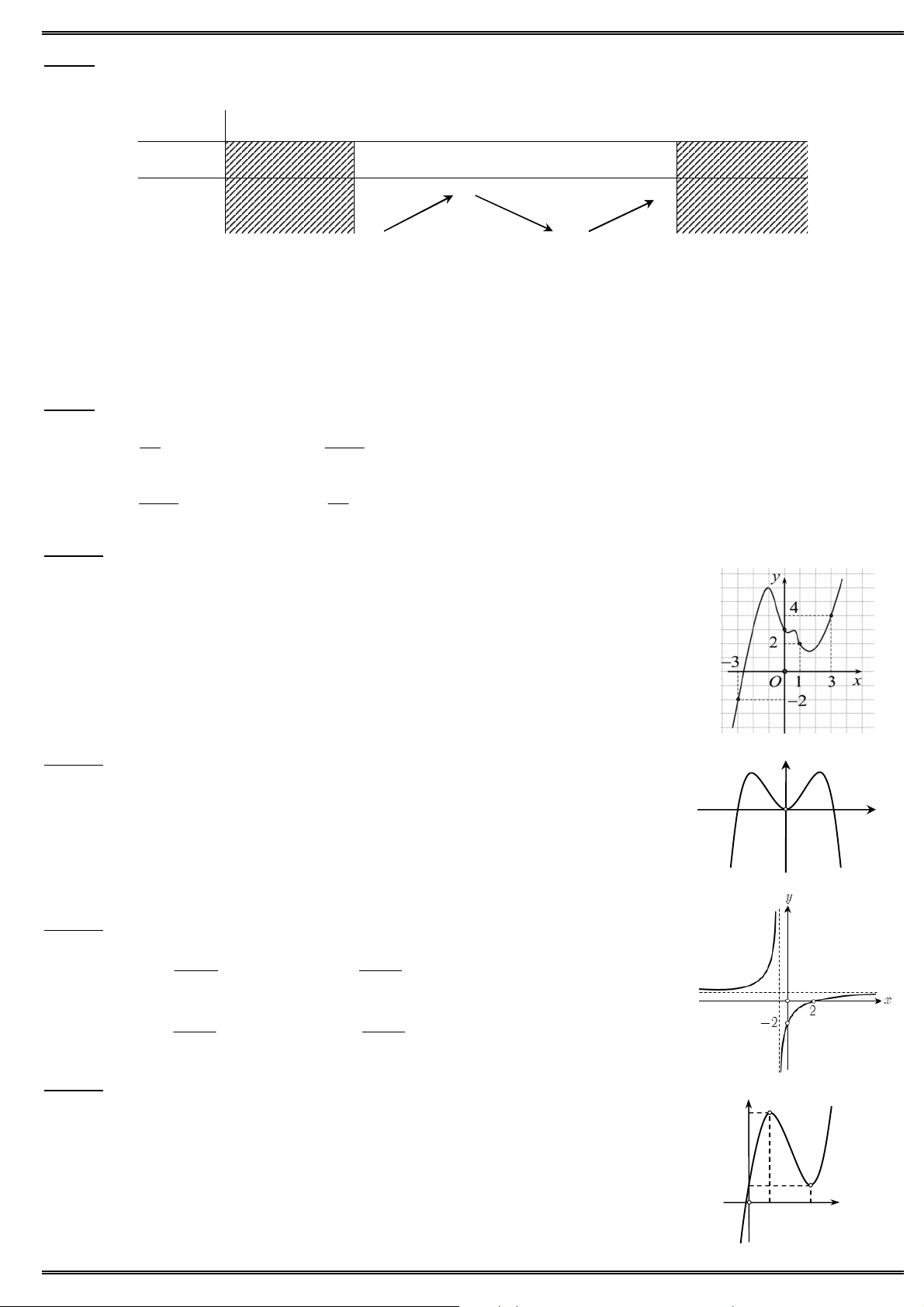
Câu 43. Cho tứ diện đều ABCD cạnh 3a. Diện tích xung quanh của hình nón đỉnh A và đường tròn đáy là
đường tròn ngoại tiếp tam giác BCD bằng A. 2 6 a . B. 2 3 3 a . C. 2 12 a . D. 2 6 3 a .
Câu 44. Cho khối trụ có bán kính đáy bằng 4 và diện tích xung quanh bằng 16 .
Thể tích khối trụ bằng A. 32 . B. 64 . C. 16 . D. 48 .
Câu 45. Cho hình chữ nhật ABCD có AB a, AC a 5. Diện tích xung quanh của hình trụ khi quay hình
chữ nhật xung quanh trục AB bằng D C A. 2 2 a . B. 2 4 a . A B C. 2 2a . D. 2 4a .
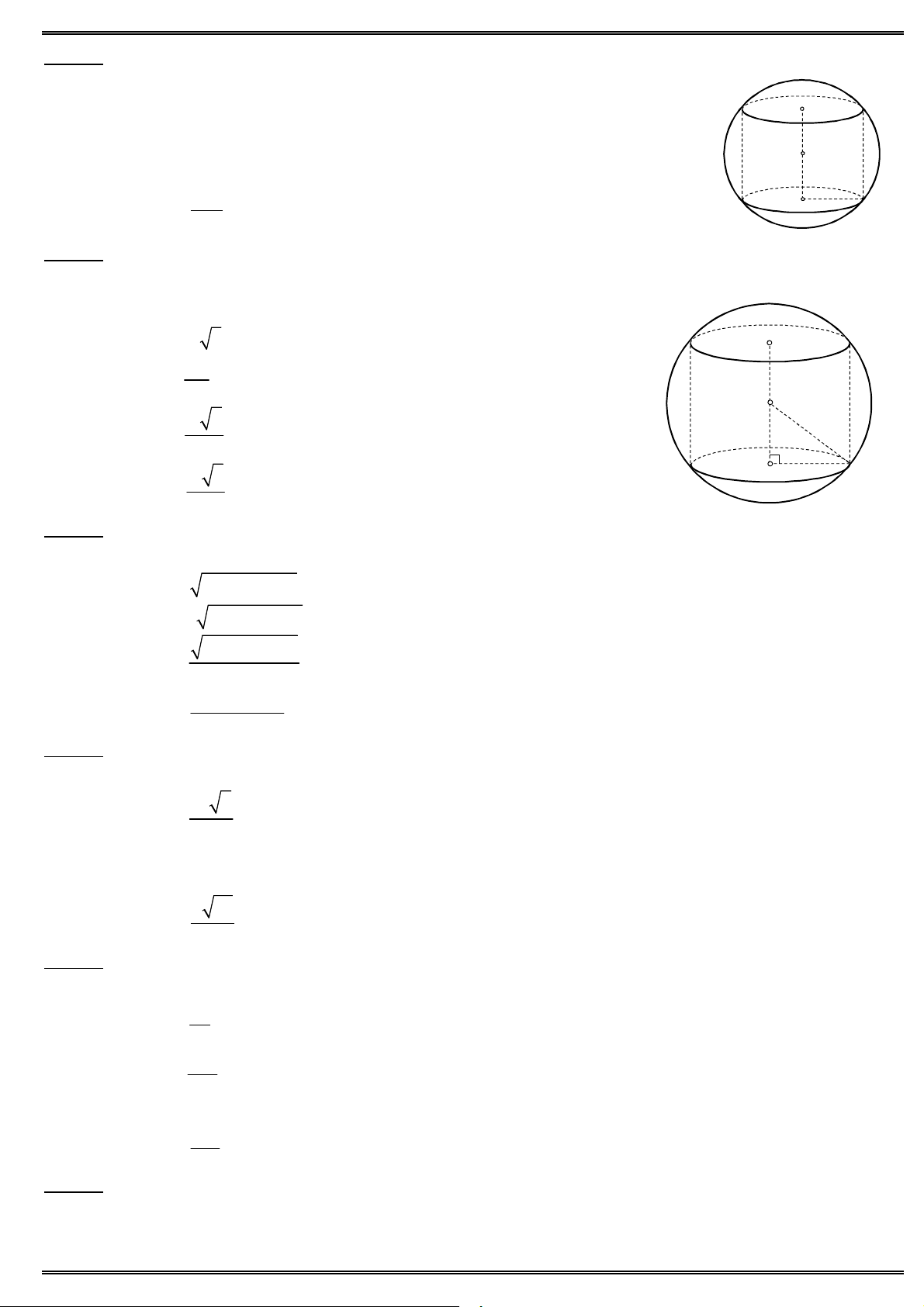
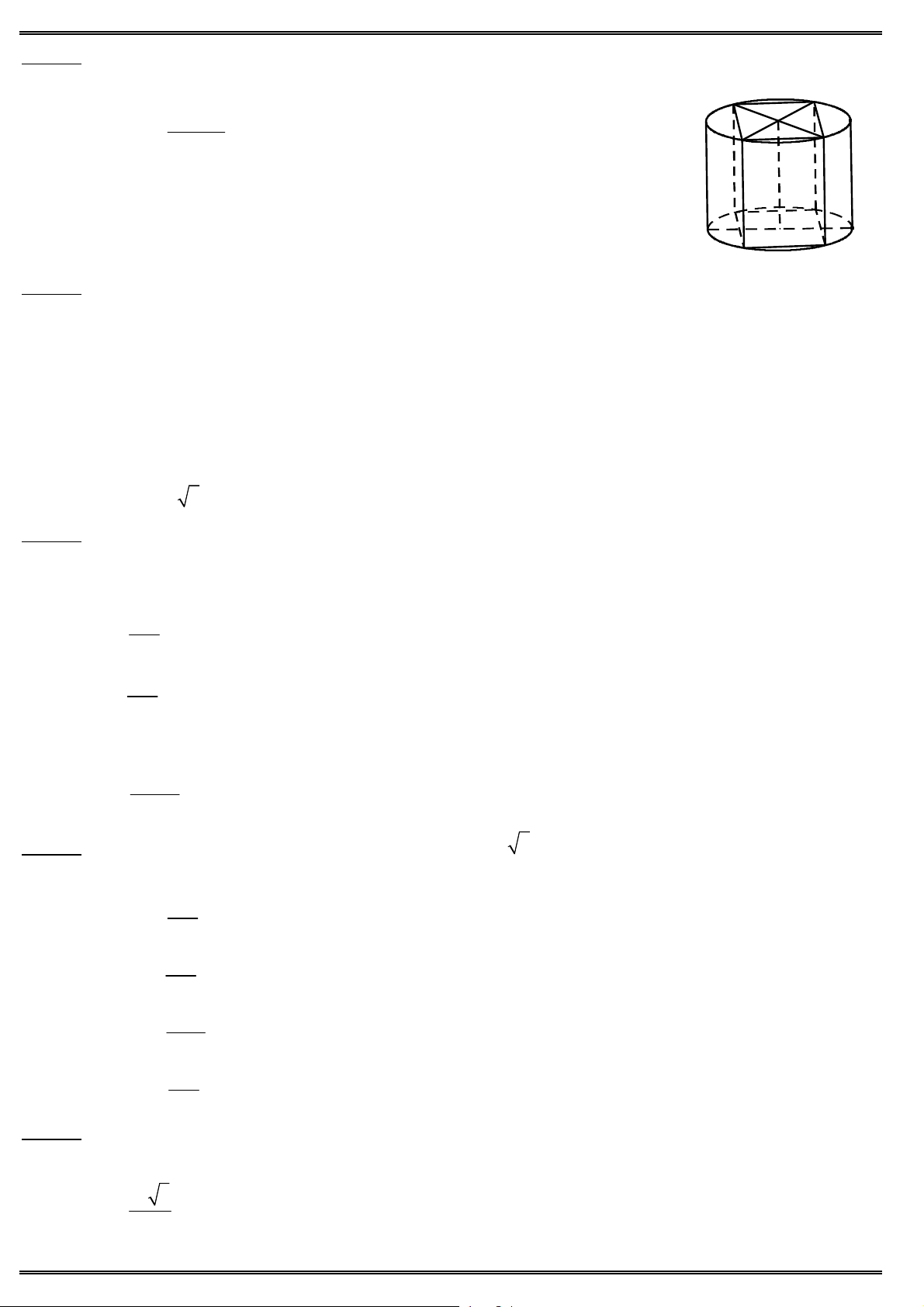
Câu 46. Cho hình lăng trụ tam giác đều ABC .AB C
  có độ dài cạnh đáy bằng a, chiều cao là h. Tính thể
tích V của khối trụ ngoại tiếp hình lăng trụ.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 6 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 2 a  h A. V   B. 2 V  3 a  h. 9 2 a  h C. 2 V a  h. D. V   3
Câu 47. Cho khối cầu có thể tích bằng 36 3
cm . Diện tích mặt cầu đã cho bằng A. 2 64 cm . B. 2 18 cm . C. 2 36 cm . D. 2 27 cm .
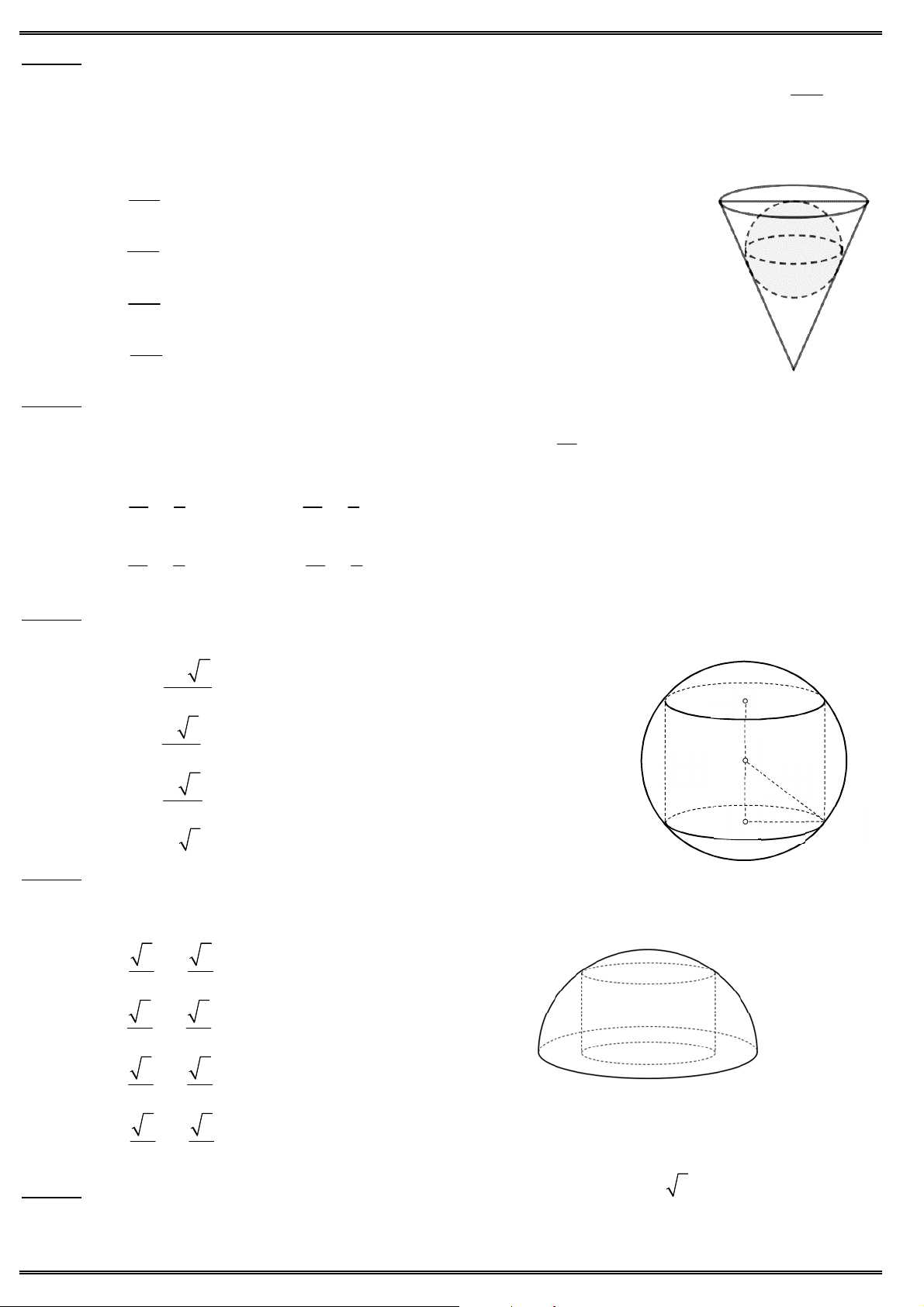
Câu 48. Một khối đồ chơi gồm một khối hình trụ (T ), một khối hình nón (N ) và một nửa khối cầu (S) gắn
vào với nhau như hình vẽ. Biết rằng khối đồ chơi có chiều cao h  17cm, chõm cầu, khối trụ và khối
nón có bán kính đáy bằng nhau, khối trụ có chiều cao h  7cm, khối nón có đường sinh hợp với đáy 1
một góc 30. Diện tích toàn phần của khối đồ chơi bằng A. 2 677,17cm . B. 2 883,13cm . C. 2 726,15cm . D. 2 566,27cm .
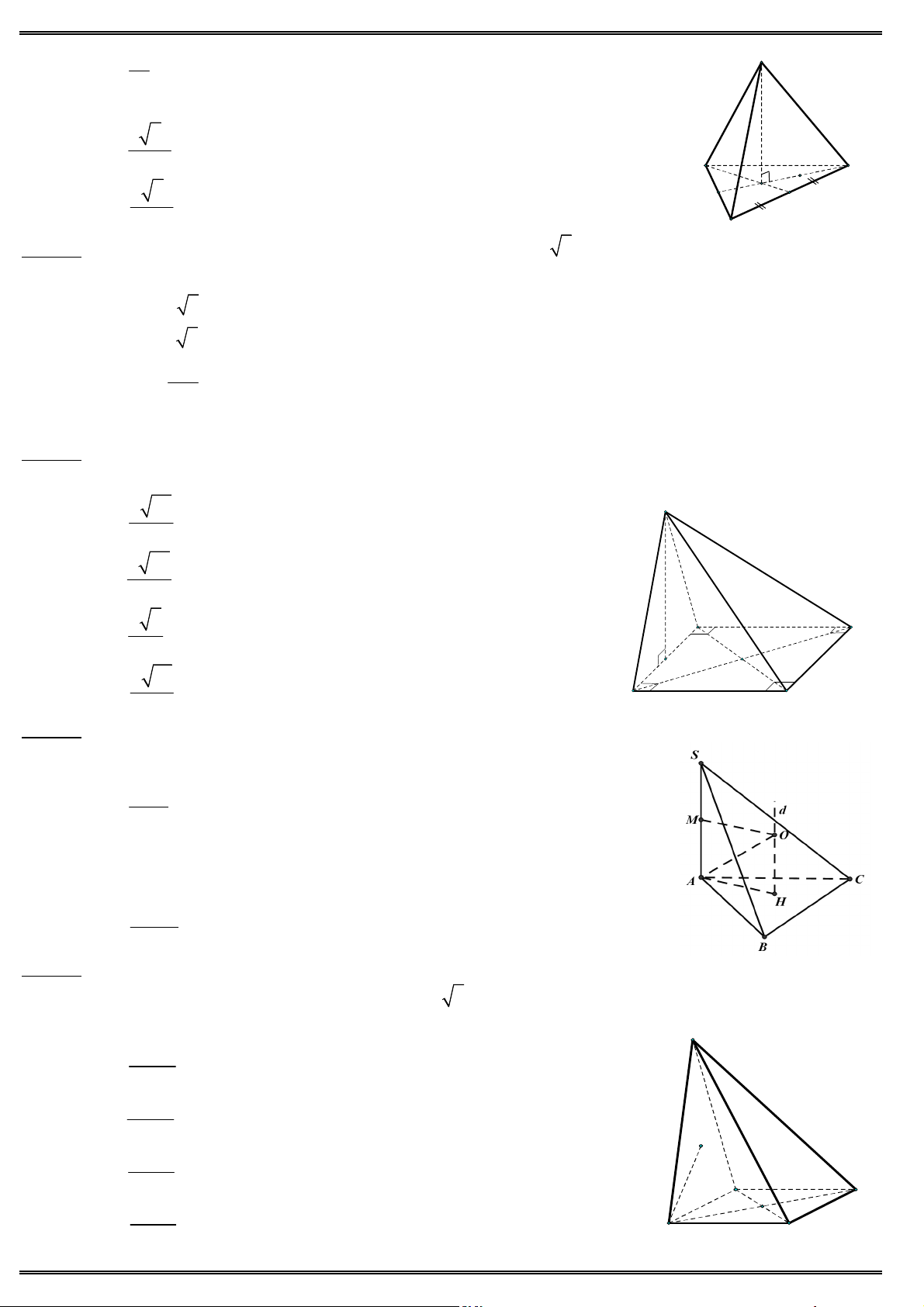
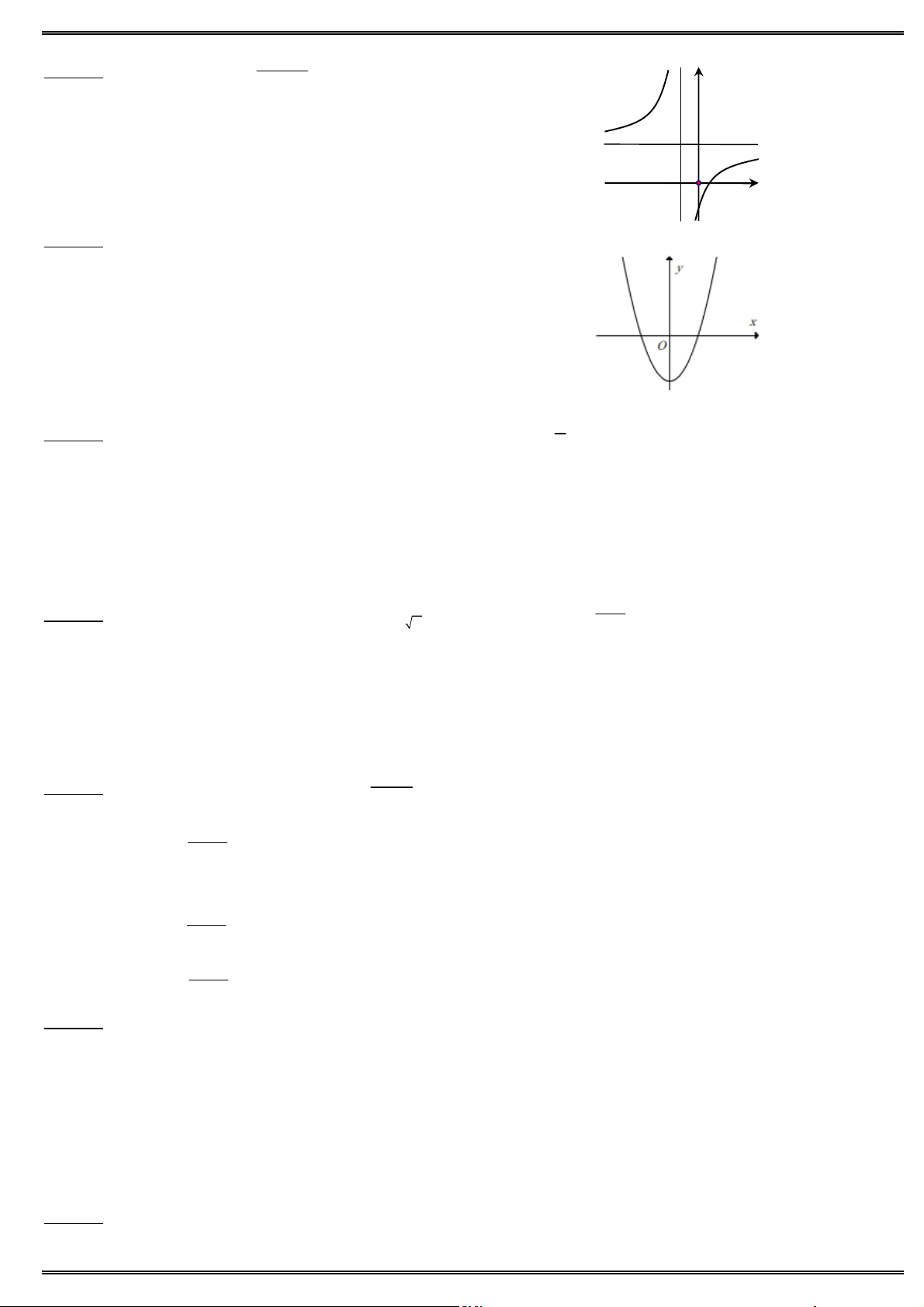
Câu 49. Cho hình lăng trụ tam giác đều ABC .AB C
  có 9 cạnh bằng nhau và bằng 2a. Diện tích của mặt
cầu ngoại tiếp hình lăng trụ đã cho bằng 2 28 a 2 7 a A. B. 9 9 2 28 a 2 7 a C. D. 3 3
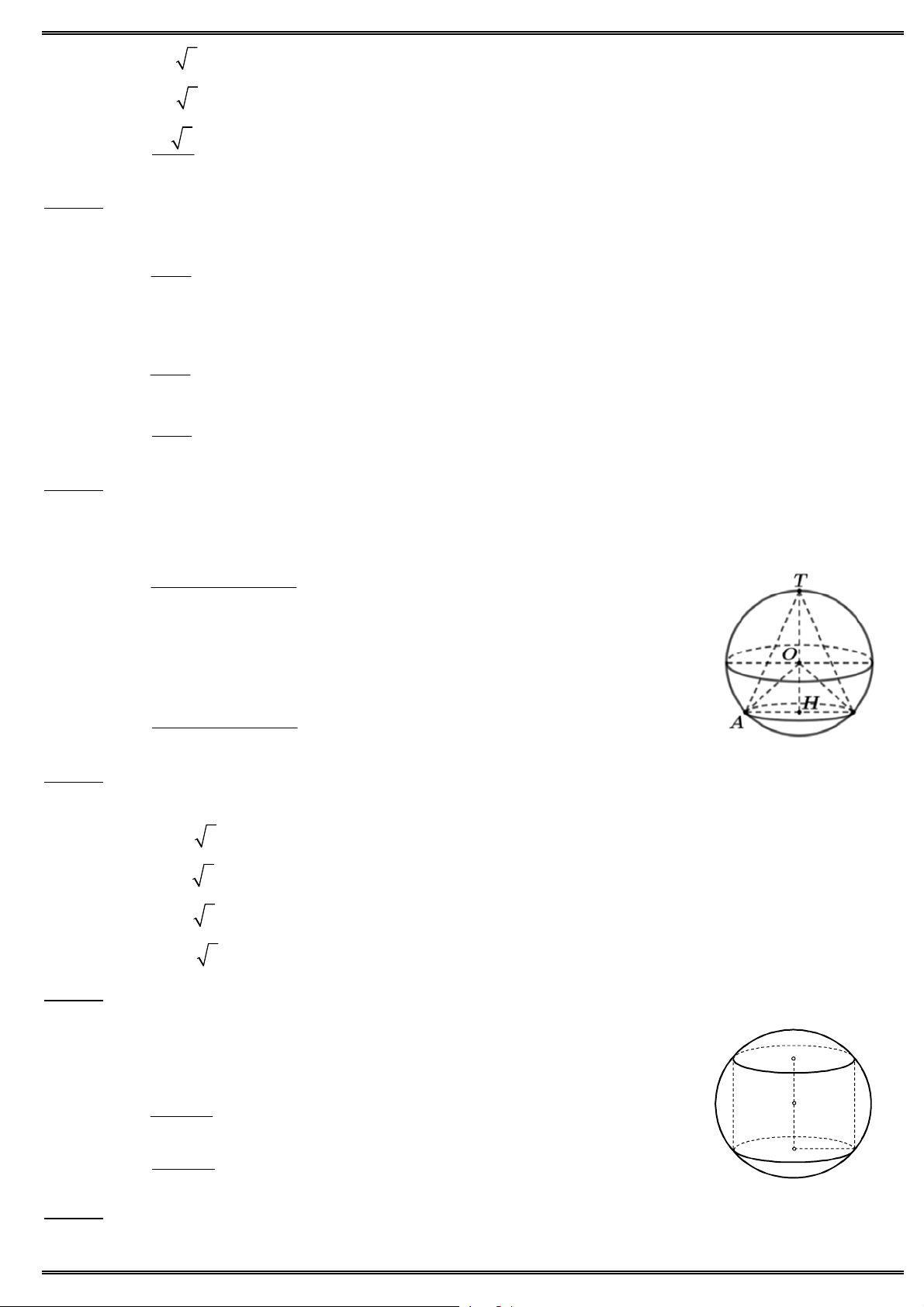
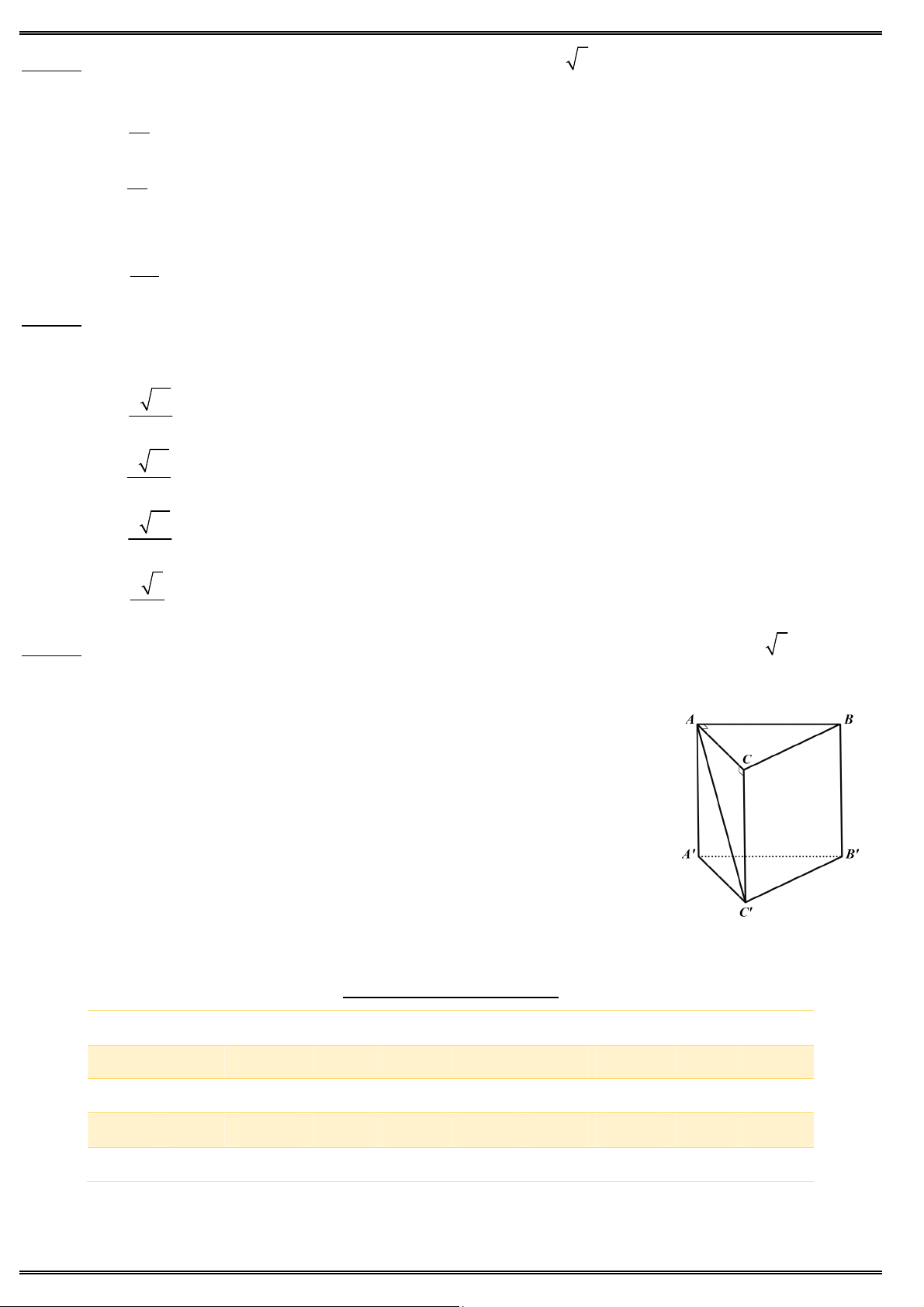
Câu 50. Cho khối cầu tâm O bán kính R (cho trước). Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo
một hình tròn (C ). Một khối nón ( )
 có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón ( ) 
có thể tích lớn nhất, khi đó giá trị của x bằng R A. x   3 R R B. x   O 2 R x R 2 C. x   I 2 r 3R D. x   4
ĐÁP ÁN ĐỀ SỐ 01 1.A 2.C 3.B 4.B 5.D 6.B 7.C 8.D 9.D 10.C 11.C 12.C 13.A 14.A 15.A 16.C 17.B 18.D 19.D 20.C 21.D 22.D 23.B 24.B 25.D 26.A 27.A 28.B 29.C 30.B 31.A 32.D 33.D 34.C 35.A 36.C 37.D 38.D 39.D 40.C 41.A 42.D 43.B 44.A 45.B 46.D 47.C 48.A 49.C 50.A
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 7 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 02
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! Câu 1. Cho hàm số 4 2
y x  2x  4. Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên các khoảng ( ;  1  ) và (0; )  .
B. Hàm số nghịch biến trên các khoảng ( 1  ;0) và (1; )  .
C. Hàm số đồng biến trên các khoảng ( ;  1  ) và (0;1).
D. Hàm số đồng biến trên các khoảng ( 1  ;0) và (1; )  .
Câu 2. Cho hàm số f (x) xác định, liên tục trên  và có đồ thị của hàm số f (
x) là đường cong như hình vẽ
bên dưới. Hỏi khẳng định nào đúng ?
A. Hàm số f (x) đồng biến trên khoảng (0;2).
B. Hàm số f (x) nghịch biến trên khoảng ( 2  ;2).
C. Hàm số f (x) đồng biến trên khoảng ( ;  1  ).
D. Hàm số f (x) nghịch biến trên khoảng ( ;  0).
Câu 3. Tìm tham số m để hàm số 3 2
y x  2mx  3m đồng biến trên ( ;   )  . A. m  0. B. m  0. C. m  0.
D. m  0.
Câu 4. Cho hàm số f (x) có bảng biến thiên như sau: x  2 2  y  0  0  y 3   0
Tìm giá trị cực đại y và giá trị cực tiểu y của hàm số đã cho. CĐ CT A. y
 3, y  2. B. y  2
 , y  2. C. y  2, y  0. D. y
 3, y  0. CĐ CT CĐ CT CĐ CT CĐ CT Câu 5. Gọi , A ,
B C là ba điểm cực trị của đồ thị hàm số 4 2
y  2x  4x  1. Diện tích tam giác ABC bằng A. 4. B. 2. C. 1. D. 3.
Câu 6. Tìm tham số m để hàm số 4 2 y x
  (m  2)x  5 có ba cực trị. A. m  2. B. m  3.
C. 3  m  2. D. m  1.
Câu 7. Tìm tất cả các giá trị của tham số m để hàm số 3 2
y x  6x  2mx  1 có hai điểm cực trị x , x 1 2 thỏa mãn 2 2 x x  12. 1 2 A. m  1. B. m  3. C. m  1. D. m  3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 8 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 8. Cho hàm số y f (x) xác định và liên tục trên khoảng ( 3
 ;2), lim f (x)  5, lim f (x)  3 và có x 3  x 2 
bảng biến thiên như sau: x  3 1 1 2  y  0  0  y 0 3 5 2
Mệnh đề nào dưới đây sai ?
A. Hàm số không có giá trị nhỏ nhất trên khoảng ( 3  ;2).
B. Giá trị cực đại của hàm số bằng 0.
C. Giá trị lớn nhất của hàm số trên khoảng ( 3  ;2) bằng 0.
D. Giá trị cực tiểu của hàm số bằng 2.
Câu 9. Giá trị lớn nhất của hàm số 3 2
y  cos x  2 sin x  cos x bằng 58 2147 A. B.  27 999 7159 43 C. D. 3333 20
Câu 10. Cho hàm số y f (x) liên tục trên  có đồ thị y f (
x) như hình vẽ. Đặt 2
g(x)  2f (x)  (x  1) .
Mệnh đề nào dưới đây đúng ?
A. min g(x)  g(1). [ 3  ;3]
B. max g(x)  g(1). [ 3  ;3]
C. max g(x)  g(3). [ 3  ;3]
D. Không tồn tại max g(x). [3;3] y
Câu 11. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ? A. 4 2 y x   2x . x O B. 4 2
y x  2x  1. C. 4 2 y x   2x . D. 4 2
y x  2x .
Câu 12. Đồ thị sau là của hàm số nào ? x  2 2  x A. y   B. y   x  1 x  1 x  2 x  2 C. y   D. y   x  1 x  1
Câu 13. Cho đồ thị hàm số 3 2
y ax bx cx d như hình vẽ. Tìm mệnh đề đúng ? y
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0. 1
C. a  0, b  0, c  0, d  0. O 1 3 x
D. a  0, b  0, c  0, d  0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 9 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 14. Cho đồ thị hàm số 3
y x  3x  1. Tìm tham số m để phương trình 3
x  3x m  0 có đúng 3 y
nghiệm phân biệt ? 3
A. 2  m  3.
B. 2  m  2. 1 1 x C. 2
  m  2. 1 O 1
D. 1  m  3. 3  2x
Câu 15. Phương trình tiếp của đồ thị (C ) : y
tại giao điểm của (C ) và đường thẳng y x  3 là x  1
A. y x
  3 và y x   1.
B. y x
  3 và y x   1.
C. y x  3 và y x  1.
D. y x
  3 và y x   1. x  1
Câu 16. Tìm tọa độ giao điểm của đường thẳng y x  1 với đồ thị hàm số y   x  2 A. ( A 4; 3), B(0; 1  ). B. C( 1  ; 3). C. D(3; 1  ). D. E( 1
 ;0), F(3; 4). 7 1  2 7 a .a
Câu 17. Cho biểu thức P
(a  0). Mệnh đề nào dưới đây đúng ? 5 2 2  2 2 2a (a )  A. 5
P a . B. 5 P a  .
C. P  0, 5.
D. P  2.
Câu 18. Cho log b  2 và log c  3. Tính 2 3
P  log (b c ). a a a
A. P  31.
B. P  13.
C. P  30.
D. P  108.
Câu 19. Cho a, x là các số thực dương, biết log x  2 log a  log a. Tính x theo a. 3 3 1 3 A. 4
x a . B. 3
x a .
C. x  3a.
D. x a  3. 2
Câu 20. Tìm tập xác định D của hàm số x  2  x 3 2 y  5  log ( x
  x  6). 2 2 A. D  (3; )  . B. D  ( 3  ;2). C. D  ( ;  2). D. D  ( ;  3  )  (2; )  .
Câu 21. Tìm tập xác định D của hàm số log100 2 2020 y  (x  2)  (x x) . A. D  ( ;  0)  (1; )  \ {2}. B. D  (2; )  . C. D  ( ;  0)  (1; )  . D. D  ( ;  0]  [1; )  .
Câu 22. Cho hàm số y x 
. Giá trị của y (  1) bằng A. 2 ln . B. ln . C. 0. D. (
   1).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 10 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3
Câu 23. Cho hàm số ( )  ln(2ex f x
m) thỏa mãn f (ln 2)   Mệnh đề nào đúng ? 2
A. m  (1; 3). B. m  ( 5  ; 2  ). C. m  (1;  )  . D. m  ( ;  3).
Câu 24. Với giá trị nào của a thì hàm số 2  (1  3  )x y a a đồng biến trên ( ;   )  ?
A. a  0.
B. 0  a  2.
C. a  3.
D. 0  a  3. 2
Câu 25. Gọi x , x là hai nghiệm của phương trình x 3x 1  0 2
 1. Giá trị của 5(x x )  x x bằng 1 2 1 2 1 2 A. 8. B. 3. C. 8. D. 3.
Câu 26. Tìm tập nghiệm S của phương trình 2
log (x  4x  3)  log (4x  4). 2 2 A. S  {1;7}. B. S  {7}. C. S  {1}. D. S  {3;7}.
Câu 27. Tổng các nghiệm của phương trình 4x 3.2x   log 3  0 bằng 2 A. 3. B. log (log 3). 2 2 C. log 3. D. log 2. 2 3
Câu 28. Tích tất cả các nghiệm của phương trình log (3x).log x  2 bằng 3 3 1 28 A. B.  9 9 26 1 C. D. 3 3
Câu 29. Tìm tất cả giá trị thực của m để phương trình 4x  2 .2x m
 2m  0 có 2 nghiệm phân biệt x , x 1 2
sao cho x x  3. 1 2
A. m  1.
B. m  3.
C. m  4.
D. m  2. 2x 1  3x 2  1 1    
Câu 30. Giải bất phương trình        2   2  1    A. S  ( ;  3).
B. S  (3;  )  . C. S  ( ;  3
 ). D. S    ;3    2 
Câu 31. Giải bất phương trình 2
log(3x  1)  log(4x). 1 1 A. x
hoặc x  1. B. 0  x  hoặc x  1. 3 3
C. 0  x  1.
D. 1/3  x  1. 1  2x
Câu 32. Tập nghiệm của của bất phương trình log  0 là 0,5 x 1     1  
A. S   ;      S  0;   B. 3   3 1 1    1  
C. S   ;    S    ;    D. 3 2  3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 11 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 33. Tập nghiệm của bất phương trình 16x 5.4x   4  0 là A. S  ( ;  1)  (4; )  . B. S  ( ;  1]  [4; )  . C. S  ( ;  0)  (1; )  . D. S  ( ;  0]  [1; )  . 9
Câu 34. Một nguyên hàm F(x) của hàm số x 2
f (x)  2e  3x thỏa F(0)  là 2 x 5 x 3 A. 3
2e  x   B. 3
2e  x   2 2 x 9 x 7 C. 3 e  x   D. 3 2e  x   2 2 16
Câu 35. Tìm hàm số f (x) thỏa mãn (  )  2x f x
 3 x và f (4) 
 Mệnh đề nào đúng ? ln 2 2x x 16 A. 3 2  2 x   32. B. 3  x  8. ln 2 ln 2 2x x 16 C. 3 2  x   24. D. 3  2 x  16. ln 2 ln 2     2
Câu 36. Một nguyên hàm F(x) của hàm số f (x)  sin x  cos 2x thỏa F       là  4  2 1 1 1 1
A.  cos x  sin 2x  
B.  cos x  sin 2x   2 2 2 2 1 2 1 2 C.  cos x  sin 2x   D.  cos x  sin 2x   2 2 2 2
Câu 37. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3cm, các mặt bên (SAB) và (SAD) vuông góc
với mặt phẳng đáy, góc giữa SC và mặt đáy là 60. Thể tích của khối chóp S.ABCD bằng S A. 3 6 6 cm . B. 3 9 6 cm . 9 3 A D C. 3 cm . D. 3 3 6 cm . 2 B C
Câu 38. Cho hình chóp tam giác đều có cạnh đáy bằng a 3 và cạnh bên tạo với đáy một góc 60. Thể tích
của khối chóp đó bằng 3 a 3 3 3a A. B. 12 4 3 a 3 a C. D. 12 4
Câu 39. Cho hình chóp S.ABCD có đáy là hình chữ nhật, mặt bên (SAB) là tam giác đều cạnh 2a và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy (tham khảo hình vẽ). Biết mặt phẳng (SCD) tạo với
mặt phẳng đáy một góc 30. Thể tích khối chóp S.ABCD bằng 3 3a A. B. 3 2 3a . 2 3 2 3a 3 4 3a C. D. 3 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 12 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 40. Thể tích của vật thể với các kích thước được cho trong hình vẽ bên bằng A. 3 6600cm . B. 3 5700cm . C. 3 6400cm . D. 3 7800cm .
Câu 41. Lăng trụ tam giác ABC .AB C
  có đáy tam giác đều diện tích bằng 3, góc giữa cạnh bên và đáy
bằng 30. Hình chiếu của A lên mặt phẳng (ABC ) là trung điểm H của BC . Thể tích của khối lăng trụ đã cho bằng 9 A. 8 3 B. 3 C. 3 3. D. 2 3.
Câu 42. Cho khối nón có đường sinh bằng 5 và diện tích đáy bằng 9 .
Thể tích của khối nón đã cho bằng A. 12 . B. 24 . C. 36 . D. 45 .
Câu 43. Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay tam giác ABC quanh trục BC thì
được khối tròn xoay có thể tích là A A. 2 . B. 2 . B C 2 C. . 3 D. 2 .
Câu 44. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên SA  2a. Thể tích của khối nón
có đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC bằng 3 a A. 2 3 a 33 B. 27 3 a C. 6 3 2 a D. 2
Câu 45. Cho hình trụ có diện tích xung quang bằng 50 và độ dài đường sinh bằng đường kính của đường
tròn đáy. Tính bán kính r của đường tròn đáy ? 5 2 5 2 A. r   B. r   2 2
C. r  5 .
D. r  5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 13 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 46. Cho hình bình hành ABCD có AD  2a, AB  3 ,
a BAD  45 (hình vẽ). Thể tích của khối tròn
xoay nhận được khi quay hình bình hành ABCD quanh trục AB bằng D C 3 5 a A. B. 3 5 a . 2 A B 3 9 a C. 3 6 a . D. 2
Câu 47. Cho hình hộp chữ nhật ABCD.AB CD
  có AD  8, CD  6, AC   12. Diện tích toàn phần của
hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và AB CD   bằng A. 576 . B. 10(2 11  5) . C. 26 . D. 5(4 11  4) .
Câu 48. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ như hình vẽ bên. Các kích thước được
ghi (cùng đơn vị dm). Thể tích của bồn chứa bằng 36 3 4 2 4 A. B. 3 5 18 3 3 C. 2 5 4 .3 . D. 5 2 4 .3 .
Câu 49. Cho hình chóp S.ABC, có đáy là tam giác đều cạnh 3cm, SC  2cm và SC vuông góc với đáy. Thể
tích của khối cầu ngoại tiếp hình chóp S.ABC bằng S A. 3 8cm . 256 B. 3 cm . 3 C A C. 3 36 cm . G 32 M D. 3 cm . 3 B
Câu 50. Cho hình nón có bán kính đáy R  5a, độ dài đường sinh   13a. Thể tích khối cầu nội tiếp hình nón bằng 3 40 a A.  9 3 400 a B. 27 3 4000 a C.  27
Mặt cắt qua trục của nón 3 4000 a D. 81
ĐÁP ÁN ĐỀ SỐ 02 1.D 2.C 3.B 4.D 5.B 6.A 7.B 8.C 9.A 10.B 11.A 12.C 13.C 14.B 15.B 16.D 17.C 18.B 19.B 20.B 21.C 22.D 23.D 24.D 25.B 26.B 27.B 28.D 29.C 30.A 31.B 32.C 33.D 34.B 35.D 36.B 37.B 38.B 39.B 40.A 41.C 42.A 43.C 44.B 45.B 46.C 47.B 48.C 49.D 50.D
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 14 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 03
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
Câu 1. Cho hàm số y f (x) có bảng xét dấu đạo hàm như sau: x  1 0 2 
y  0   0 
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng ( 2  ; 0).
B. Hàm số đồng biến trên khoảng ( ;  0).
C. Hàm số nghịch biến trên khoảng (0;2).
D. Hàm số đồng biến trên khoảng ( ;  2).
Câu 2. Cho hàm số f (x) xác định, liên tục trên  và có đồ thị của hàm số f (
x) là đường cong như hình vẽ
bên dưới. Hỏi khẳng định nào sau đây là đúng ?
A. Hàm số f (x) đồng biến trên khoảng (0;2).
B. Hàm số f (x) nghịch biến trên khoảng ( 2  ;2).
C. Hàm số f (x) đồng biến trên khoảng ( ;  1  ).
D. Hàm số f (x) nghịch biến trên khoảng ( ;  0). mx  6m  5
Câu 3. Tìm tham số m sao cho hàm số y  đồng biến trên (3;  )  . x m
A. 1  m  3.
B. 1  m  5.
C. 1  m  5.
D. 1  m  3.
Câu 4. Cho hàm số y f (x) có đồ thị như hình vẽ. Hàm số f (x) đạt cực tiểu tại điểm nào dưới đây ? A. x  1. B. x  1. C. x  2.
D. x  0.
Câu 5. Khẳng định nào sau đây đúng ? x  1
A. Hàm số y
có một điểm cực trị. x  2 B. Hàm số 4 2
y x  2x  3 có ba điểm cực trị. C. Hàm số 4 2 y x
  2x  3 có ba điểm cực trị. D. Hàm số 3
y x  3x  4 có hai điểm cực trị.
Câu 6. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2
y  (m  2)x  3x mx  5 có điểm cực
đại nằm bên trái điểm cực tiểu. A. 2. B. 3. C. Vô số. D. 1. Câu 7. Cho hàm số 3 2 2 y x
  (m  3)x  (m  2m)x  2. Tìm tất cả các giá trị thực của tham số m sao
cho hàm số có hai điểm cực trị x , x thỏa x x  6(x x )  4  0. 1 2 1 2 1 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 15 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
A. m  2 hoặc m  12.
B. m  2. 3 2 3 2 C.   m   2 2 3 2
D. 2  m   2 2 x  3  3
Câu 8. Gọi M, m là giá trị lớn nhất và giá trị nhỏ nhất của y
trên 1;  . Giá trị M m bằng x  2  2   8 7 A. B. 3 2 13 4 C. D. 6 3
Câu 9. Tìm giá trị của x để hàm số 2
y x  4  x đạt giá trị lớn nhất. A. x  2. B. x  2 2. C. x  2. D. x  1. 2 4  x
Câu 10. Đồ thị hàm số y
có tất cả bao nhiêu đường tiệm cận ? 2 x  3x  4 A. 0. B. 3. C. 1. D. 2. y
Câu 11. Đồ thị sau là của hàm số nào ? 2x  1 2x  1 A. y   B. y   1 x  1 x  1 1  O 1 x x  1 x  1 1  C. y   D. y   x  1 x  1
Câu 12. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ? A. 4 2 y x
  2x  1. B. 4 2 y x
  2x  1. C. 4 2
y x  3x  1. D. 4 2
y x  2x  1.
Câu 13. Cho đồ thị hàm số 3 2
y ax bx cx d như hình vẽ. Tìm mệnh đề đúng ?
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0.
Câu 14. Cho hàm số y f (x) có đồ thị như hình. Phương trình f (x)  x có bao nhiêu nghiệm ? A. 0 nghiệm.
B. 1 nghiệm.
C. 2 nghiệm. D. 3 nghiệm.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 16 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 x  1 1
Câu 15. Viết phương trình tiếp tuyến của đồ thị y
, biết tiếp tuyến có hệ số góc là  x  1 2 1 1 1 7 A. y
x  và y x   2 2 2 2 1 1 1 7 B. y
x  và y x   2 2 2 2 1 1 1 7 C. y
x  và y x   2 2 2 2 1 1 1 7 D. y
x  và y x   2 2 2 2
Câu 16. Biết đồ thị hàm số 4 2
y x  3x  5 và đường thẳng y  9 cắt nhau tại hai điểm phân biệt (
A x ;y ), B(x ;y ). Giá trị của x x bằng 1 1 2 2 1 2 A. 3. B. 0. C. 18. D. 5. 5  3x  3 xCâu 17. Cho 9x 9 x  
 23. Giá trị của biểu thức K  bằng 1  3x  3 x  5 1 A.   B. 2 2 5 3 C. D. 2 2
Câu 18. Với 0  a; b  1, giá trị của biểu thức 3 6
T  log b  log b bằng 2 a a A. 9 log . b
B. 27 log b. a a
C. 15 log b. D. 6 log . b a a
Câu 19. Biết rằng a, ,
b c  1 thỏa log (bc)  2. Giá trị của biểu thức 4
P  log a  log (ab) bằng ab c c b a A. 1. B. 2. C. 3. D. 4. x  1
Câu 20. Tìm tập xác định D của hàm số 0
y  (3  x)  log  2018 x  2 A. D  [1; )  . B. D  ( 2  ;1). C. D  ( ;  2  )  (1; )  . D. D  ( ;  2  )  (1; )  \ {3}.
Câu 21. Tìm tập xác định D của hàm số x lg100
y  2  1  log(x  2) . A. D  (2; )  . B. D  [0; )  . C. D  [0; )  \ {2}. D. D  (0; )  \ {2}.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 17 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 Câu 22. Cho hàm số 2  (  )ex y x mx . Biết y (
 0)  1 thì y (1) bằng A. 6e. B. 3e. C. 5e. D. 4e.
Câu 23. Phương trình x x 1
3 .5   7 có nghiệm dạng x  log b với 0  a, b  1. Giá trị của b a bằng a A. 20. B. 16. C. 20. D. 16.
Câu 24. Cho phương trình x 1  x x 1 9 13.6 4   
 0. Phát biểu nào sao đây đúng ?
A. Phương trình có 2 nghiệm nguyên.
B. Phương trình có 2 nghiệm dương.
C. Phương trình có 1 nghiệm dương.
D. Phương trình có 2 nghiệm vô tỉ.
Câu 25. Tổng các nghiệm của phương trình 2
log x  log (9x)  2  0 bằng 3 3 A. 10. B. 3. C. 0. D. 4.
Câu 26. Tìm giá trị thực của tham số m để phương trình 2
log x m log x  2m  7  0 có hai nghiệm thực 3 3
x , x thỏa mãn x x  81. 1 2 1 2
A. m  4.
B. m  4.
C. m  81.
D. m  44.
Câu 27. Tập nghiệm của bất phương trình 2x x 6 2  2 là A. (0; 6). B. ( ;  6). C. (0; 64). D. (6; )  .
Câu 28. Tập nghiệm S của bất phương trình log log (x 2)   0
a b Giá trị của b a bằng /6  3  là ( ; ). A. 2. B. 4. C. 3. D. 5.
Câu 29. Tập nghiệm của bất phương trình log (x  3)  log x  2 là 2 2 A. (3;  )  . B. [4; )  . C. (3; 4]. D. ( ;  1]  [4; )  .
Câu 30. Biết S  [a;b] là tập nghiệm của bất phương trình 3.9x 10.3x
 3  0. Giá trị của b a bằng 8 10 A. B.  3 3 C. 1. D. 2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 18 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 1  x   
Câu 31. Họ nguyên hàm của hàm số f (x)  x   sin  là 2  2  1 x 1 x A. 2
x  cos C. B. 2
x  cos C. 4 2 2 2 1 1 x 1 1 x C. 2
x  cos C. D. 2
x  cos C. 4 2 2 4 4 2 1 1
Câu 32. Họ nguyên hàm của hàm số 6
f (x)  7x    2 là 2 x x 1 1 A. 7
x ln x  2x C  . B. 7
x  ln x   2x. x x 1 1 C. 7
x  ln x  2x C. D. 7
x lnx  2x  . C x x  x 
Câu 33. Họ nguyên hàm của hàm số 2
f (x)  2 x 3x      là  4x    12x 2x x A.  C.
B. 12x x x C . ln12 3 2 2 x  3x x x ln 4 2 2 x  3x x x  C.      D.      ln 2 ln 3 4x      ln 2 ln 3 4x   
Câu 34. Cho khối chóp S.ABCD có đáy là hình chữ nhật, SA  (ABCD), AB  3 ,
a AD  2a, SB  5a.
Thể tích của khối chóp S.ABCD bằng S A. 2 8a . B. 3 24a . A B C. 3 10a . D. 3 8a . D C
Câu 35. Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Thể tích của khối S
chóp S.ABC bằng 3 13a 3 11a A. B. 12 12 A C 3 11a 3 11a C. D. B 6 4
Câu 36. Cho hình chóp S.ABC có thể tích bằng V. Gọi G là trọng tâm tam giác SBC . Mặt phẳng ( ) đi qua hai điểm ,
A G và song song với BC. Mặt phẳng ( )
cắt các cạnh S ,
B SC lần lượt tại các điểm M
và N . Thể tích khối chóp S.AMN bằng V V A. B. 9 2 4V V C. D. 9 4 V
Câu 37. Cho lăng trụ đứng ABC .AB C
 . Gọi M là trung điểm AA . Tỉ số M .ABC bằng
VABC.AB C 1 1 A. B. 6 3 1 1 C. D.  12 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 19 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 38. Cho hình hộp chữ nhật ABCD.AB CD
  có AB  2cm, AD  3cm, AC   7cm. Thể tích của khối A' D'
hộp ABCD.AB CD   bằng B' C' A. 3 42cm . B. 3 36cm . A D C. 3 24cm . D. 3 12cm . B C
Câu 39. Thể tích của khối lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông tại C, AB  2a,
AC a, BC   2a bằng C' A' B' A. 3 4a . B. 3 a 3. 3 3a 3 3a C. D. C A 6 2 2 B a 3
Câu 40. Cho lăng trụ tam giác đều ABC .AB C
  có diện tích đáy bằng
 Mặt phẳng (ABC) hợp với 4
mặt phẳng đáy một góc 60 .
 Thể tích khối lăng trụ ABC .AB C   bằng 3 3a 3 3 a 3 A. B. 8 8 3 5a 3 3 3a 2 C. D. 12 8
Câu 41. Một hình nón có đường sinh bằng đường kính đáy. Diện tích toàn phần của hình nón bằng 9 . Chiều
cao của hình nón đã cho bằng A. 3. B. 3. 3 3 C. D. 2 3
Câu 42. Khi quay một tam giác đều cạnh bằng a quanh một cạnh của nó ta được một khối tròn xoay. Thể tích
của khối tròn xoay đó bằng 3 a 3 3a A. B. 4 8 3 3 a 3 3a C. D. 4 24
Câu 43. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 3. Tính diện tích xung quanh của hình
nón có đáy là đường tròn ngoại tiếp tứ giác ABCD và chiều cao bằng chiều cao của hình chóp. 9 A. 2 9 2 B. h l 4 C. 9 . D r 9 2 C O A D. B 2
Câu 44. Cho khối trụ (T ) có bán kính đáy R và diện tích toàn phần 2 8 R
. Thể tích của khối trụ (T ) bằng A. 3 3 R . B. 3 6 R . C. 3 4 R . D. 3 8 R .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 20 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 45. Cho hình thang ABCD vuông tại A và D, có độ dài các cạnh là AD a, AB  5a, CD  2a. Thể
tích của vật thể tròn xoay khi quay hình thang trên quanh trục AB bằng D C A. 3 5 a . B. 3 6 a . A B C. 3 3 a . D. 3 11 a .
Câu 46. Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh S của hình trụ có một đường xq
tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. A 16 2 A. S   B. S  8 2 . xq 3 xq D 16 3 B C. S   D. S  8 3 . xq xq H I 3 C
Câu 47. Cho hình tròn đường kính AB  4cm quay xung quanh AB. Thể tích khối tròn xoay tạo thành bằng A. 3 32cm . B. 3 16cm . A B 16 32 C. 3 cm . D. 3 cm . 3 3
Câu 48. Cho hình cầu đường kính 2a 3. Mặt phẳng (P) cắt hình cầu theo thiết diện là hình tròn có bán kính
bằng a 2. Khoảng cách từ tâm hình cầu đến mặt phẳng (P). I A. a.
B. a 10. R a H a 10 A C. D. P 2 2
Câu 49. Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 45. Mặt cầu S
ngoại tiếp hình chóp có bán kính bằng a 3 a 3 A. B. 2 3 A C a 3 D O N C. a 3. D. 5 B
Câu 50. Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước,
có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V . Biết rằng
khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa khối cầu chìm trong nước
như hình vẽ. Thể tích nước còn lại trong ly bằng 1 A. V . B. V . 1 1 C. V . D. V . 3 6
ĐÁP ÁN ĐỀ SỐ 03 1.C 2.C 3.A 4.D 5.B 6.A 7.B 8.A 9.A 10.D 11.C 12.B 13.A 14.D 15.A 16.B 17.A 18.D 19.C 20.D 21.C 22.C 23.A 24.A 25.D 26.B 27.B 28.A 29.B 30.D 31.D 32.C 33.A 34.D 35.B 36.D 37.A 38.B 39.D 40.A 41.A 42.A 43.D 44.A 45.C 46.A 47.D 48.A 49.B 50.C
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 21 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 04
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! 1 Câu 1. Cho hàm số 3 2
y   x x x  2. Khẳng định nào sau đây là đúng ? 3
A. Hàm số luôn đồng biến trên ( ;   )  .
B. Hàm số đồng biến trên khoảng ( ;
 1), nghịch biến trên khoảng (1; )  .
C. Hàm số nghịch biến trên khoảng ( ;
 1), đồng biến trên khoảng (1; )  .
D. Hàm số luôn nghịch biến trên ( ;   )  .
Câu 2. Cho bản biến thiên của hàm số 4 y ax bx     c sau: x  0  y  0    y 2
Bảng biến thiên trên là của hàm số A. 4 2
y x  2x  2. B. 4 2 y x
  2x  2. C. 4 2
y x  2x  2. D. 4 2
y x  2x  1.
Câu 3. Tìm các giá trị của tham số m sao cho hàm số 3 2
y x  6x mx  1 đồng biến trên (0; )  .
A. m  12.
B. m  0.
C. 0  m  12.
D. m  0. 2 2x  5x  4
Câu 4. Điểm cực tiểu của hàm số y  là x  2
A. x  1. B. M( 1  ;1).
C. x  3. D. N( 3  ; 7  ).
Câu 5. Cho hàm số y f (x) có đạo hàm trên  và đồ thị hàm số y f (
x) trên  như hình bên dưới. Tìm
khẳng định đúng ?
A. Hàm số y f (x) có 1 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số y f (x) có 2 điểm cực đại và 2 điểm cực tiểu.
C. Hàm số y f (x) có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số y f (x) có 2 điểm cực đại và 1 điểm cực tiểu.
Câu 6. Có bao nhiêu giá trị nguyên của m để hàm số 3
y  (m  2)x mx  2 không có điểm cực trị ? A. 1. B. Vô số. C. 3. D. 5. 1 1 Câu 7. Cho hàm số 3 2 2
y x  (2m  1)x  (m  2)x  1. Tìm tất cả các giá trị thực của tham số m sao 3 2
cho hàm số có hai điểm cực trị x , x thỏa 3x x  5(x x )  7  0. 1 2 1 2 1 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 22 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 1 A. m  
B. m  2. 4
C. m  4.
D. m  8. 2  cos x  2
Câu 8. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  . Khi đó giá trị cosx  2
của biểu thức M  3m bằng 4 A. 4. B. . 3 C. 1. D. 3. 5  4x
Câu 9. Các đường tiệm cận của đồ thị hàm số y
tạo với hai trục toạ độ một hình chữ nhật có diện 2x  3 tích bằng A. 1. B. 2. 3 C. 3. D. 2 2 x  1
Câu 10. Đồ thị hàm số y
có tất cả bao nhiêu đường tiệm cận ? x  2 A. 1. B. 3. C. 2. D. 0.
Câu 11. Cho bảng biến thiên của hàm số bậc ba. Tìm hàm số thỏa mãn bảng biến thiên đã cho. A. 3 2 y x
  3x  1. B. 3 2
y  2x  6x  1. C. 3 2
y x  3x  1. D. 3 2 y x   3x  1.
Câu 12. Cho đồ thị hàm số 4 2
y ax bx c như hình vẽ. Tìm mệnh đề đúng ?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0.
D. a  0, b  0, c  0.
Câu 13. Cho đồ thị của hàm số nhất biến như hình vẽ. Hỏi đó là hàm số nào ? 2x  1 2x  1 A. y   B. y   x  1 x  1 2x  1 2x  1 C. y   D. y   x  1 x  1
Câu 14. Cho bảng biến thiên của hàm số 4 2
y  2x  4x  1. Tìm m để phương trình 4 2
2x  4x  1  m có 8 nghiệm ?
A. 0  m  1.
B. 0  m  1.
C. 0  m  1.
D. 0  m  1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 23 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3
Câu 15. Đồ thị hàm số 2
y x x và y  5  cắt nhau tại hai điểm A và B. Độ dài AB bằng x A. 8 5. B. 25. C. 4 2. D. 10 2.
Câu 16. Giá trị của biểu thức 2016 2016 P  (1  3) (3  3) bằng A. 1008 12 . B. 1008 4 . C. 1008 (1  3) . D. 1008 (3  3) .
Câu 17. Cho 0  a  1 và x, y   thỏa mãn log 3  x và log 2  y. Khi đó (x y)log a bằng a a 6 A. 2
(x y) .
B. 2(x y).
C. x y. D. 1.
Câu 18. Cho log x  3, log x  4 với a, b  1. Giá trị của biểu thức P  log x bằng a b ab 7 1 A. B. 12 12 C. 12. D. 12/7. 2 cos x  6x  9
Câu 19. Tìm tập xác định D của hàm số 2 y  (2  x)  ln  x  1 A. D  (3; )  . B. D  (1; )  \ {2; 3}. C. D  (1;2). D. D  (1; )  \ {3}.
Câu 20. Tìm tập xác định D của hàm số e 2 y x (x 1)    . A. D  ( 1  ;1). B. D   \ { 1  ;1}. C. D  (1; )  . D. D  .  3
Câu 21. Hãy tính đạo hàm của hàm số 2 3
y x . x trên khoảng (0; )  . 7 6 A. 6 . x . B. 6 7 7 x C. 3 4 x .
D. 9 x . Câu 22. Hàm số 2 y  log ( x
  2x) đồng biến trên khoảng 0,5 A. ( ;  ) 1 . B. (0;1). C. (1; )  . D. (1;2).
Câu 23. Giá trị nhỏ nhất của hàm số 2 2  (  2)e x y x
trên đoạn [1;2] bằng A. 2 e  . B. 2e. C. 4 2e . D. 2 2e .
Câu 24. Giải phương trình x 5
3   3x  121 được dạng x  log a với a  0. Khẳng định nào đúng ? 3
A. 0  a  2.
B. 1  a  3.
C. 2  a  5.
D. a  4.
Câu 25. Số nghiệm của phương trình log (x  3)  1  log x là bao nhiêu ? 2 2 A. 1. B. 3. C. 0. D. 2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 24 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 26. Tích tất cả các nghiệm của phương trình ( 2 1)x ( 2 1)x     2 2  0 bằng A. 2. B. 1. 1 C. D. 1. 2
Câu 27. Tổng tất cả các nghiệm của phương trình x x 1 log (2 1).log (2    2)  1 bằng 2 4 A. log 15. B. 1. 2 15 C. log  D. 3. 2 4
Câu 28. Bất phương trình log (3x  2)  log (6  5x) có tập nghiệm là (a;b). Giá trị của a b bằng 2 2 11 31 A. B.  5 6 28 8 C. D.  15 3 Câu 29. Cho hàm số 2 ( ) e x f x x  
. Bất phương trình f (
x)  0 có tập nghiệm là A. [ 2  ;2]. B. ( ;  2  ]  [0; )  . C. ( ;  0]  [2; )  . D. [0;2].
Câu 30. Giải bất phương trình 2
log x  2 log (3x)  1  0 được tập nghiệm S  (a;b), với a, b là hai số thực 3 3 và a  .
b Giá trị của biểu thức T  3a b bằng A. 3. B. 3. C. 11. D. 28. x 3
Câu 31. Cho F(x) là một nguyên hàm của hàm số f (x)  e  2x thỏa mãn F(0)   Tìm F(x). 2 x 1 x 3 A. 2 e  x   B. 2
2e  x   2 2 x 1 x 5 C. 2 e  x   D. 2 e  x   2 2
Câu 32. Tìm nguyên hàm của hàm số f (x)  2x  1. 1 1 A.
2x  1  C .
B. (2x  1) 2x  1  C . 2 3 1 2 C.
2x  1  C. D. (2x  1) 2x  1  C . 3 3
Câu 33. Cho hàm số y f (x) xác định trên  \ {0} thỏa mãn 2
2xf (x)  x f (
x)  1 và f(1)  0. Phương trình
tiếp tuyến của đồ thị hàm số y f (x) tại giao điểm với trục hoành là
A. y x 1.
B. y  2x  2.
C. y x. D. y x  .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 25 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 34. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và SC a 3. Hai mặt bên (SAB) và
(SAC ) cùng vuông góc với đáy. Thể tích khối chóp S.ABC bằng S 3 2 6a 3 6a A. B. 9 12 A C 3 3a 3 3a C. D. 2 4 B
Câu 35. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong
mặt phẳng vuông góc với đáy, SA  2a. Thể tích khối chóp S.ABCD bằng 3 a 15 3 a 15 A. B. 6 12 3 2a C. D. 3 2a . 3
Câu 36. Cho hình chóp đều S.ABC có cạnh bằng a, mặt bên hợp với đáy một góc 60. Thể tích của khối S
chóp S.ABC bằng 3 3a 3 3a A. B. 12 72 A C 3 3a 3 3a C. D. 24 6 B
Câu 37. Cho hình lập phương ABCD.AB CD
  có diện tích tam giác ACD bằng 2
3a . Thể tích của hình A' D'
lập phương đã cho bằng B' C' A. 3 3 3a . B. 3 2 2a . A D C. 3 a . D. 3 8a . B C
Câu 38. Tính thể tích của khối lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông tại C, AB  2a,
AC a, BC   2a. C' A' B' A. 3 4a . B. 3 4a /3. 3 3a 3 3a C A C. D. 2 6 B
Câu 39. Cho hình lăng trụ tam giác ABC .AB C
  có đáy ABC là tam giác vuông tại , A AB  ,
a AC a 3.
Hình chiếu vuông góc của A lên (ABC ) là trung điểm của BC . Góc giữa AA và (ABC ) bằng 60.
Thể tích của khối lăng trụ đã cho bằng 3 a 3 a 3 A. B. 2 2 3 3a 3 3a 3 C. D.  2 2
Câu 40. Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A trên cạnh SA sao cho SA  3SA .
Mặt phẳng qua A và song song với đáy của hình chóp cắt các cạnh S ,
B SC, SD lần lượt tại S
B , C , D . Thể tích khối chóp S.AB CD   bằng D' A' V V C'   B' A. B. 3 81 V V A D C. D. 9 27 C B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 26 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 41. Hình nón có thiết diện qua trục là một tam giác cân có góc ở đỉnh bằng 120 và có cạnh bên bằng a.
Diện tích xung quanh của hình nón đó bằng S 2 a 3 A. B. 2 a 3. 2 A B C. 2 a . D. 2 2 a 3.
Câu 42. Cho tam giác ABC vuông tại ,
A AB a, AC a 3. Quay tam giác đó quanh đường thẳng BC
ta được khối tròn xoay. Tính thể tích V của khối tròn xoay này ? 3 3 B a a A. B. 2 4 3 2 a 3 a C. D. 3 3 A C
Câu 43. Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng a 2. Thể tích khối nón có đỉnh S và
đường tròn đáy là đường tròn nội tiếp tứ giác ABCD bằng 2 2 a 3 2 a A. B. 6 2 3 a C. 3 a . D. 6
Câu 44. Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB  4a,
BC  3a. Thể tích của khối trụ đã cho bằng A. 3 12 a . B. 3 16 a . C. 3 4 a . D. 3 8 a .
Câu 45. Cho hình thang ABCD vuông tại A và D, AD CD a, AB  2a. Quay hình thang ABCD
quanh đường thẳng CD. Thể tích khối tròn xoay thu được bằng 3 7 a A. B. 3 a . D C 3 3 4 a 3 5 a C. D. 3 3 A B
Câu 46. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 4. Tính diện tích xung quanh của
hình trụ có một đường tròn đáy là đường tròn nội tiếp tứ giác ABCD và chiều cao bằng chiều cao
hình chóp S.ABCD đỉnh S. A. S  16 2 . xq B. S  8 2 . xq C. S  16 3 . xq D. S  8 3 . xq
Câu 47. Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi I, J lần lượt là trung điểm của A ,
B CD. Biết AB  4 và AD  6. Thể tích của vật thể tròn xoay khi quay mô hình
trên quanh trục IJ bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 27 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 56 104 A. B. 3 3 40 88 C. D.  3 3
Câu 48. Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng 1 m
và 1, 4 m. Chủ cơ sở dự định làm một bể nước mới, hình trụ, có cùng chiều cao và có thể tích bằng
tổng thể tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kể quả nào dưới đây ? A. 1, 7 m. B. 1, 5 m. C. 1, 9 m. D. 2, 4 m
Câu 49. Cho mặt cầu (S) tâm ,
O bán kính R  3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S) theo
giao tuyến là đường tròn (C ) có tâm H . Gọi T là giao điểm của tia HO với (S). Thể tích của khối
nón có đỉnh T và đáy là hình tròn (C ) bằng 32 16 A. B. 3 3 C. 32 . D. 16 .
Câu 50. Cho chóp S.ABC có đáy ABC là tam giác vuông cân tại C với CA CB a, SA a 3,
SB a 5 và SC a 2. Bán kính R của mặt cầu ngoại tiếp chóp S.ABC bằng a 11 A. 6 a 11 B. 2 a 11 C. 3 a 11 D. 4
ĐÁP ÁN ĐỀ SỐ 04 1.D 2.C 3.A 4.A 5.A 6.C 7.B 8.A 9.C 10.B 11.D 12.B 13.C 14.A 15.C 16.A 17.D 18.D 19.B 20.C 21.A 22.D 23.A 24.B 25.A 26.B 27.C 28.A 29.D 30.D 31.D 32.B 33.A 34.B 35.A 36.C 37.B 38.C 39.C 40.D 41.A 42.A 43.D 44.A 45.D 46.B 47.D 48.A 49.A 50.B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 28 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 05
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! 2 mx  1  m
Câu 1. Hàm số y
với m là tham số. Mệnh đề nào dưới đây là đúng ? x  1
A. Hàm số đồng biến trên  \ { 1  }.
B. Hàm số đồng biến trên .
C. Hàm số nghịch biến trên các khoảng xác định.
D. Hàm số đồng biến trên các khoảng xác định.
Câu 2. Hàm số nào sau đây có bảng biến thiên như hình bên dưới ? x  1  y    2 y 2  2x  3 2x  3 2x  3 1  x A. y   B. y   C. y   D. y   x  1 x  1 1  x x  2 cos x  2    
Câu 3. Tìm tham số m sao cho hàm số y
đồng biến trên khoảng 0  ;  cos x m  2
A. m  0 hoặc 1  m  2.
B. m  0.
C. 1  m  2.
D. m  2.
Câu 4. Một hàm số f (x) có đạo hàm là 2 3 5 f (
x)  x(x 1) (x  2) (x  3) . Hỏi hàm số f (x) có tất cả bao nhiêu điểm cực trị ? A. 4. B. 3. C. 2. D. 1. 1 Câu 5. Hàm số 3 2 y x
  3x x đạt cực trị tại 2 điểm x , x . Tính tổng 2 2
S x x . 2 1 2 1 2 11 13 A. S   B. S   3 3 1 3 C. S   D. S   2 2
Câu 6. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4 2 2
y mx  (m  2)x  2 có hai cực tiểu và một cực đại. A. m   2.
B.  2  m  0. C. m  2.
D. 0  m  2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 29 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 1 Câu 7. Cho hàm số 3 2
y  (m  1)x  (m  2)x  (m  3)x  1. Tìm tất cả các giá trị thực của tham số m 3
sao cho hàm số có 2 điểm cực trị x , x thỏa (4x  1)(4x  1)  18. 1 2 1 2
A. m  1.
B. m  4.
C. m  7.
D. m  8. tan x  1 
Câu 8. Giá trị nhỏ nhất của hàm số y  trên 0;  bằng tan x  2  4    1 1 A. min y  
B. min y     2   2 0;     0; 4      4   1 1 C. min y  
D. min y      3   3 0;     0; 4      4   3 cos x4
Câu 9. Giá trị lớn nhất của hàm số 2 y
 cos x  3 cos x  1 trên  ;  bằng 3  3 3    65 5 A. max y   B. max y   4 24    24  4 ;     ; 3 3      3 3   2 2 C. max y  
D. max y    4 3    3  4 ;     ; 3 3      3 3   2x  1
Câu 10. Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị hàm số y   x  2 A. I ( 2  ;2). B. I(2;2). C. I (2; 2  ). D. I( 2  ; 2  ). x  3  2
Câu 11. Số đường tiệm cận đứng của đồ thị hàm số y  là bao nhiêu ? 2 x  1 A. 0. B. 1. C. 3. D. 2.
Câu 12. Cho đồ thị như hình vẽ. Hỏi đồ thị là của hàm số nào ? A. 4 2
y x  3x  1. B. 3 2
y x  3x  1. C. 3 2 y x
  3x  1. D. 4 2 y x
  3x  1.
Câu 13. Cho đồ thị hàm số 3 2
y ax bx cx d. Tìm mệnh đề đúng ?
A. y  0, x  . 
B. y  0, x  . 
C. y  0, x  1.
D. y  0, x  1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 30 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 ax b y
Câu 14. Cho đồ thị hàm số y
như hình vẽ. Tìm khẳng định đúng ? x  1
A. b  0  a. 1
B. 0  a b. 1  x a b O C. 0.
D. 0  b a.
Câu 15. Cho bảng biến thiên của hàm số 3 2
y f (x)  ax bx cx d. Tìm tham số m để phương trình 1
f (x)  m có 4 nghiệm phân biệt thỏa mãn x x x   x . 1 2 3 4 2
A. 0  m  1. 1 B. m  1. 2
C. 0  m  1. 1 D. m  1. 2 3
Câu 16. Viết phương trình tiếp tuyến của đường cong 4 2
(C ) : y x x  1, biết tiếp tuyến vuông góc với 2
đường thẳng d : x  8y  16  0. 13 13 A. y  8  x  
B. y  8x   2 2 13 13 C. y  8  x  
D. y  8x   2 2
Câu 17. Đồ thị của hàm số 4 2
y x  2x cắt trục hoành tại bao nhiêu điểm ? A. 0. B. 2. C. 4. D. 3. 1
Câu 18. Với 0  a b thì giá trị của biểu thức 2 T (a b ) (4 ab)    bằng A. a b  .
B. b a. C. b a  . D. a b  .
Câu 19. Cho a, b  0 thỏa mãn 2
log a  log b  5 và 2
log a  log b  7. Giá trị a.b bằng 8 4 4 8 A. 9 2 . B. 8. C. 18 2 . D. 2.
1  log x  log y
Câu 20. Cho x, y  1 thỏa 2 2
x  9y  6xy. Tính giá trị của 12 12 I   2 log (x  3y) 12 1 A. I  
B. I  1. 4 1 1 C. I   D. I   2 3 2
Câu 21. Tìm tập xác định D của hàm số 2018 2 (2 3) 2018 x y x x      . A. D  ( 2; 2].
B. D  ( 2; 2). C. D  [ 2; 2]. D. D  ( ;   2].
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 31 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 x  1
Câu 22. Tìm tập xác định D của hàm số y  log  1 x 2 A. D  (1; )  . B. D  ( ;  0)  (1; )  .
C. D  (0;1).
D. D   \ {0}. 1
Câu 23. Hãy tính đạo hàm của hàm số y  trên khoảng (0;  )  . 4 x x 5 1 A.   B. 4 9 4 x 2 4 x x 5 1 C. 4 x. D.   4 4 5 4 x 2 ln(x  1)
Câu 24. Cho hàm số f (x) 
 Biết rằng f (1)  a ln 2 b với a, b  .  Tìm a  . b x
A. a b  1.
B. a b  1.
C. a b  2.
D. a b  2. 2
Câu 25. Hỏi hàm số 4 4 ex x y   
đồng biến trên những khoảng nào sau đây ? A. ( ;   )  . B. ( ;  2)  (2; )  . C. (2;  )  . D. ( ;  2) và (2; )  . Câu 26. Cho hàm số 3 2
f (x)  8 log x  6 log x  12 log x  3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2 2  1  trên đoạn  ; 4  lần lượt là 4   
A. 19 và 61.
B. 19 và 60.
C. 23 và 64. D. 23 và 60. 2 Câu 27. Cho 3 ( ) x x f x e  
. Biết phương trình f  (
x)  0 có hai nghiệm x , x . Tính x x . 1 2 1 2 9 A. x x   1 2 4 7 B. x x   1 2 4 3 C. x x   1 2 2
D. x x  3. 1 2
Câu 28. Tìm nghiệm của phương trình 3x 1
log (3   1)  3. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 32 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
A. x  2.
B. x  1.
C. x  3.
D. x  8. 2x 1  x 1  x
Câu 29. Gọi x , x (x x ) là hai nghiệm của 3x x 1 ( 17 4) ( 17 4)    
. Giá trị của 1 là 1 2 1 2 x2 7  2 6 7  2 6 A. B. 5 5 1  6 1  6 C. D. 5 5
Câu 30. Biết phương trình (7 4 3)x (2 3)x   
 6 có nghiệm dạng x  log
b với a, b là số dương. 2 a Tổng 2 2
a b bằng A. 13. B. 8. C. 7. D. 11.
Câu 31. Cho phương trình 2
log (m  6x)  log (3  2x x )  0. Có mấy giá trị nguyên dương của tham số 0,5 2
m để phương trình đã cho có nghiệm ? A. 17. B. 18. C. 23. D. 15. 2
Câu 32. Tìm tập nghiệm S của bất phương trình 3x 2x  .
A. x  (0;  )  .
B. x  (0; log 3). 2
C. x  (0; log 2).
D. x  (0;1). 3
Câu 33. Gọi S là tập nghiệm của bất phương trình log (2x  5)  log (x  1). Hỏi trong tập S có bao nhiêu 2 2
phần tử là số nguyên dương bé hơn 10. A. 9. B. 15. C. 8. D. 10.
Câu 34. Tìm tập nghiệm của bất phương trình 2 2
log (2x x  3)  log (3x x) với m là tham số thực m m
dương khác 1, biết x  1 là một nghiệm của bất phương trình đã cho. 1  1  A. (2; 0)    ;3       [ 1; 0]  ; 3   B. 3     3  1  C. ( 1  ;0)  (1; 3]. D. [1; 0)    ; 3   3 
Câu 35. Giải bất phương trình x x 1 log (2 1).log (2  
 2)  2 ta được tập nghiệm có dạng S  (a;b), với 2 1 2
a, b là các số thực và a  .
b Tính giá trị của biểu thức T a b. 15 A. T  1. B. T  log  2 2 3 C. T  log 
D. T  log 5. 2 2 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 33 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 36. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt đáy
và SA AC a 3. Tính thể tích V của khối chóp S.ABCD ? 3 3a A. 3
V  2a . B. V   2 3 6a 3 6a C. V   D. V   2 3
Câu 37. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB  ,
a SA  (ABC ). Cạnh bên SB
hợp với đáy một góc 45. Tính thể tích V của khối chóp S.ABC . 3 3a 3 a A. V   B. V   3 3 3 2a 3 a C. V   D. V   6 6
Câu 38. Cho hình chóp tứ giác đều S.ABC ,
D cạnh đáy AB  2a 3, mặt bên tạo với đáy góc 60. Tính thể
tích V của khối chóp S.ABCD. A. 3
V  8a . B. 3
V  12a . C. 3
V  9a . D. 3
V  12 3a .
Câu 39. Cho hình hộp chữ nhật ABCD.AB CD
  có đáy là hình vuông, cạnh bên AA  3a và đường chéo
AC   5a. Tính thể tích V của khối hộp ABCD.AB CD  . A. 3
V a . B. 3
V  24a . C. 3
V  8a . D. 3
V  4a .
Câu 40. Cho hình lăng trụ đứng tam giác ABC .AB C   có đáy là A
BC đều cạnh a  4 và biết diện tích
tam giác ABC bằng 8. Tính thể tích V của khối lăng trụ ABC.AB C  .
A. V  2 3.
B. V  4 3.
C. V  6 3.
D. V  8 3.
Câu 41. Cho lăng trụ ABCD.AB CD
  có đáy ABCD là hình chữ nhật tâm O và AB  ,
a AD a 3, AO
vuông góc với đáy (ABCD). Cạnh bên AA hợp với mặt đáy (ABCD) một góc 45. Tính theo a thể
tích V của khối lăng trụ đã cho. 3 3a 3 6a A. V   B. V   6 2 3 3a C. V   D. 3
V  3a . 3
Câu 42. Hình nón có chiều cao 10 3cm, góc giữa một đường sinh và mặt đáy bằng 60 .  Diện tích xung quanh
của hình nón đó bằng A. 2 100cm . B. 2 200cm .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 34 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 C. 2 50 3cm . D. 2 100 3cm .
Câu 43. Cho hình thoi ABCD cạnh bằng a, có góc ABC  60. Quay hình thoi này quanh đường chéo BD,
ta thu được khối tròn xoay có thể tích bằng 3 a 3 A. 3 a 2. B. 12 3 a 3 C. D. 3 2 a 3. 6
Câu 44. Cho hình chóp tứ giác đều S.ABCD có cạnh bên SA a 2 và AB a. Thể tích của khối nón có
đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tứ giác ABCD bằng 3 a 6 A. 12 3 2 a h l B. 6 D C. 3 a . r C O A 3 2 a B D. 2
Câu 45. Cho hình trụ có trục OO , thiết diện qua trục là một hình vuông cạnh 2a. Mặt phẳng (P) song song a
với trục và cách trục một khoảng  Tính diện tích thiết diện S của trụ cắt bởi mặt phẳng (P). 2 td A. 2 S  5 5cm . O’ B. 2 S  6 5cm . h h C. 2 S  3 5cm . M B A r O D. 2 S  10 5cm .
Câu 46. Cho lục giác đều ABCDEF có cạnh bằng 4. Quay lục giác đều đó quanh đường thẳng AD. Thể tích
V của khối tròn xoay được sinh ra bằng A A. V  32 . F B O 128 V   B. 3 O 111 E C. V   C 2 D D. V  64 .
Câu 47. Cho hình lăng trụ tứ giác đều ABCD.EFGH . Tính tỉ số k giữa thể tích khối trụ ngoại tiếp và thể tích
khối trụ nội tiếp hình lăng trụ trên.
A. k  2.
B. k  2.
C. k  2 2.
Mặt cắt song song đáy
D. k  4.
Câu 48. Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm ,
O AD là đường kính của đường tròn tâm .
O Thể tích V của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên dưới) quay
quanh đường thẳng AD bằng bao nhiêu ?
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 35 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 233a A A.  126 3 3a B. 24 O 3 203a H C. B C 217 3 43a D D. 27
Câu 49. Cho mặt cầu (S) có tâm I, bán kính R  5. Một đường thằng  cắt (S) tại hai điểm M, N nhưng
không đi qua I. Đặt MN  2m. Để diện tích tam giác IMN lớn nhất thì m bằng
A. m  3 2.
B. m  10. I
C. m  5. 5 2 M N D. m   2
Câu 50. Cho hình chóp S.ABC có SA  (ABC ), SA  2a. Tam giác ABC cân tại A có BC  2a 2,  1
cos ACB   Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABC. 3 2 65 a A. S   4 B. 2 S  13 a . 2 97 a C. S   4 D. 2 S  4 a . ĐÁP ÁN ĐỀ 05 1.D 2.B 3.D 4.B 5.B 6.D 7.C 8.A 9.C 10.A 11.B 12.D 13.D 14.B 15.B 16.D 17.D 18.C 19.A 20.B 21.C 22.B 23.A 24.C 25.C 26.A 27.B 28.B 29.B 30.B 31.A 32.C 33.C 34.D 35.B 36.B 37.D 38.B 39.B 40.D 41.D 42.B 43.B 44.A 45.D 46.D 47.B 48.A 49.D 50.C
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 36 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 06
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! x m Câu 1.
Tìm tham số m để hàm số y
đồng biến trên từng khoảng xác định của nó. x  1
A. m  1. B. m  1  .
C. m  1.
D. m  1. x  1 Câu 2.
Tìm m để hàm số y
nghịch biến trên khoảng ( ;  2). x m A. (1, )  . B. [1,  )  . C. (2,  )  . D. [2, )  . 4 cosx  1     Câu 3.
Tìm tham số m sao cho hàm số y
đồng biến trên khoảng 0;   cos x m  3 1 1
A. m  0 hoặc  m   4 2 1 1 B.
m  hoặc m  1. 4 2 1 C. m   4 1
D. m  0 hoặc  m  1. 4 1 Câu 4.
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 3 2
y x mx  4x m đồng biến 3 trên khoảng ( ;   )  . A. 4. B. 3. C. 2. D. 5. Câu 5.
Tìm tham số m sao cho hàm số 3 2 2
y x  3x  3(m  1)x đồng biến trên khoảng (1;2). A. 2
  m  2.
B. m  2 hoặc m  2. C. 2
  m  2.
D. m  2 hoặc m  2. 5 45 Câu 6.
Có bao nhiêu giá trị nguyên m  ( 2  0;20) để hàm số 3 y x
 9mx đồng biến (0; )  . 3 3 2x A. 20. B. 21. C. 22. D. 23. Câu 7.
Tìm m sao cho hàm số y  sin x mx luôn đồng biến trên ( ;   )  . A. m  1  .
B. m  1. C. 1
  m  1. D. m  1  .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 37 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 Câu 8.
Tìm tham số m để hàm số 3 2
y x  3x  (m  1)x  2 có hai điểm cực trị. A. m  2. B. m  2. C. m  2. D. m  4. Câu 9.
Tìm tất cả các giá trị thực của m để đồ thị hàm số 4 2
y x  2mx m  3 có ba điểm cực trị tạo
thành một tam giác cân. A. m  0.
B. m  1. C. m  0. D. m  3.
Câu 10. Tìm tham số m để đồ thị hàm số 3 2
y  2x  3(m  1)x  6(m  2)x  1 có cực đại, cực tiểu thỏa mãn xx  2. CĐ CT A. m  1. B. m  2. C. m  1  . D. m  2  .
Câu 11. Cho hàm số y f (x) xác định trên  \ { 1
 }, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau x  1 3  y   0   y 2   4 
Tìm tham số thực m sao cho phương trình f (x)  m có đúng ba nghiệm thực phân biệt A. m  ( 4  ;2). B. m  [ 4  ;2). C. m  ( 4  ;2]. D. m  ( ;  2].
Câu 12. Cho đồ thị hàm số y f (x) như hình vẽ. Tìm tất cả các giá trị thực m để phương trình
f (x)  1  m có ba nghiệm phân biệt.
A. 0  m  5.
B. 1  m  5.
C. 1  m  4.
D. 0  m  4.
Câu 13. Đường cong hình bên là đồ thị hàm số 4 2
y ax bx c với a, ,
b c là các số thực. Mệnh đề nào dưới đây đúng ?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0.
D. a  0, b  0, c  0. Câu 14. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình. Mệnh đề nào đúng ? a b c d y A. 0, 0, 0, 0.
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0. O x
D. a  0, b  0, c  0, d  0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 38 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 ax  1
Câu 15. Cho hàm số y
có đồ thị như hình vẽ bên dưới. Giá trị của a b c bằng bx c y A. 2. B. 4. 2 C. 3. O x 1 D. 1. 2
Câu 16. Cho hàm số ( ) 3x m f x   thỏa mãn f (
 1)  18 ln 3. Khẳng định nào đúng ? A. m  2.
B. 3  m  0.
C. 0  m  2. D. m  3. 2 ln x
Câu 17. Cho hàm số y
với x  0. Mệnh đề nào sau đây đúng ? x 1 A. 2
xy x y  ln x. 2 B. 2
xy x y  2 ln x. 1 C. 2
xy x y  ln x. 2 D. 2
xy x y  2 ln x. 2018x
Câu 18. Cho hàm số f (x)  ln
 Tính S f (
 1)  f (2)   f (2017)  f (2018). x  1 2018 A. S  
B. S  1. 2019
C. S  ln 2018.
D. S  2018.
Câu 19. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 16  m.4
 5m  45  0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử ? A. 13. B. 3. C. 6. D. 4.
Câu 20. Tìm m để 4x  2 .2x m
 2m  0 có 2 nghiệm phân biệt x , x thỏa x x  3. 1 2 1 2 A. m  1  .
B. m  3.
C. m  4. D. m  2  .
Câu 21. Tìm giá trị thực của tham số m để phương trình 2
log x m log x  2m  7  0 có hai nghiệm thực 3 3
x , x thỏa mãn x x  81. 1 2 1 2 A. m  4  .
B. m  4.
C. m  81.
D. m  44.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 39 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 22. Tìm m để phương trình x x 2 25  2.10  .4x m
 0 có 2 nghiệm trái dấu. A. ( 1  ;0)  (0;1). B. ( ;  1]. C. ( ;  1  )  (1; )  . D. (1;  )  .
Câu 23. Cho phương trình 2
log (m  6x)  log (3  2x x )  0. Có bao nhiêu giá trị nguyên dương của 0,5 2
tham số m để phương trình đã cho có nghiệm ? A. 17. B. 18. C. 23. D. 15.
Câu 24. Có bao nhiêu giá trị nguyên của m để phương trình x x 1 9 3  
m  0 có nghiệm thuộc (0;1). A. 11. B. 12. C. 13. D. 14. 2 2 2
Câu 25. Cho phương trình 2x 3x mx x  2  x 2 3 9 3 3  x m    
. Có mấy giá trị nguyên của tham số m  [ 2
 018;2018] để phương trình đã cho có 4 nghiệm phân biệt ? A. 2018. B. 2019. C. 2020. D. 2021.
Câu 26. Có bao nhiêu giá trị nguyên của m để phương trình m  2 m  2 sin x  sin x có nghiệm thực ? A. 0. B. 1. C. 2. D. 3.
Câu 27. Cho tứ diện đều ABCD cạnh a. Diện tích xung quanh của hình nón đỉnh A và đường tròn đáy là
đường tròn ngoại tiếp tam giác BCD là A 3 A. 2 a . 3 l B. 2 a . B C. 2 3 a . O D D. 2 2 3 a . C
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 40 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 28. Cho hình chóp tam giác đều S.ABC có các cạnh đều bằng a. Tính thể tích V của khối nón có đỉnh
S và đường tròn đáy là đường tròn nội tiếp tam giác ABC. 3 a A. V   2 3 a 6 B. V   108 C. 3 V a . 3 2 a D. V   2
Câu 29. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 .  Hình
nón có đỉnh là S, đáy là đường tròn nội tiếp tứ giác ABCD có diện tích xung quanh bằng A. 2 1, 5 a . 2 a 6 B. . 4 2 a ( 7  1) C. 4 2 a 7 D. 4
Câu 30. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 3. Tính diện tích xung quanh của hình
nón có đáy là đường tròn ngoại tiếp tứ giác ABCD và chiều cao bằng chiều cao của hình chóp. A. S  4 . xq B. S  9 2 . xq C. S  9 . xq 9 2 D. S   xq 2
Câu 31. Cho hình lập phương ABCD.AB CD   có cạnh bằng .
a Gọi S là diện tích xung quanh hình trụ có
hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và AB CD
 . Diện tích S bằng AA. 2 a . DOBB. 2
2a . CC. 2
3a . A D 2 2a O D. B 2 C
Câu 32. Cho hình lăng trụ tam giác đều ABC .AB C
  có độ dài cạnh đáy bằng , a chiều cao là . h Tính thể
tích V của khối trụ ngoại tiếp hình lăng trụ. 2 a  h A. V   9 B. 2 V  3 a  h. C. 2 V a  h. 2 a  h D. V   3
Câu 33. Cho hình lăng trụ đều ABC .AB C
  có cạnh đáy bằng a 3, cạnh bên bằng 4a. Thể tích của hình
trụ có hai đáy nội tiếp hình lăng trụ bằng 3 a A. 18
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 41 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 a B. 6 C. 3 a . 3 a D. 12
Câu 34. Khi quay một tam giác đều cạnh bằng a quanh một cạnh của nó ta được một khối tròn xoay. Thể
tích của khối tròn xoay đó bằng 3 a A. 4 B. 3 3a . 3 3 a C. 4 3 3a D. 24
Câu 35. Cho tam giác ABC có AB  3, BC  5, CA  7. Tính thể tích V của khối tròn xoay sinh ra do
hình tam giác ABC quay quanh đường thẳng AB. A. V  50 . 75 B. V   4 275 C. V   8 125 D. V   8
Câu 36. Trong không gian, cho hình thang ABCD vuông tại A và D, có độ dài các cạnh là AD a,
AB  5a, CD  2 .
a Tính thể tích V của vật thể tròn xoay khi quay hình thang trên quanh trục A . B A. 3 V  5 a . B. 3 V  6 a . C. 3 V  3 a . D. 3 V  11 a .
Câu 37. Cho hình cầu bán kính bằng 5cm, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo thành
là một đường tròn đường kính 4cm. Tính thể tích khối nón có đáy là thiết diện vừa tạo và đỉnh là
tâm của hình cầu đã cho. A. 3  19,18cm . B. 3  19,20cm . Rh C. 3 19,21cm . r D. 3 19,19cm .
Câu 38. Cho khối cầu tâm O bán kính 6. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình
tròn (C ). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C ). Biết khối nón có thể tích lớn
nhất, khi đó giá trị của x bằng
A. x  2.
B. x  1.
C. x  3 2.
D. x  6 2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 42 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 39. Cho hình trụ có chiều cao bằng 4 nội tiếp trong hình cầu bán kính bằng 3. Tính thể tích V của khối trụ này. A. V  40 .
B. V  20. C. V  36 . 20 D. V   3
Câu 40. Cho mặt cầu (S) bán kính R không đổi (cho trước). Một hình trụ có chiều cao h và bán kính đáy
r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A. h R 2. O’ 3R B. h   2 I h R 3 R C. h   2 O A r R 2 D. h   2
Câu 41. Hình chóp S.ABC có đáy ABC là tam giác vuông tại ,
A SA vuông góc với mặt phẳng (ABC), SA  , a AB  ,
b AC c. Tính bán kính R của mặt cầu ngoại tiếp S.ABC. A. 2 2 2
R a b c . B. 2 2 2
R  2 a b c . 2 2 2
a b c C. R  . 2
2(a b c) D. R   3
Câu 42. Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh 3 ,
a cạnh bên SA  2a và SA vuông góc
với mặt phẳng đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC . 2a 3 A. R   3
B. R  3a.
C. R  2a. a 13 D. R   2
Câu 43. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  3 , a BC  4 ,
a SA  12a và SA vuông
góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD. 5a A. R   2 17a B. R   2
C. R  6a. 13a D. R   2
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60. Tính bán
kính mặt cầu ngoại tiếp hình chóp đã cho.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 43 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 S 2a A. 3 B. 2a. 2 3a C. A 3 C 4 3a D O N D. 3 B
Câu 45. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2a, cạnh bên bằng 5a. Tính bán kính R
của mặt cầu ngoại tiếp hình chóp S.ABCD.
A. R a 3.
B. R a 2. 25a C. R   8
D. R  2a.
Câu 46. Cho hình chóp S.ABCD đáy là hình vuông cạnh a, tam giác SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt đáy. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD bằng S a 30 A. 3 a 30 B. 6 a 5 A D C. 2 H O a 21 D. B C 6
Câu 47. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC ), SA a, AB  ,
a AC  2a, 
BAC  60. Diện tích của hình cầu ngoại tiếp hình chóp S.ABC bằng 2 5 a A. 3 B. 2 20 a . C. 2 5 a . 2 20 a D. 3
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB nằm trong mặt phẳng 
vuông góc với đáy và có AB a, BC a 3, ASB  60 .
 Diện tích của mặt cầu ngoại tiếp hình
chóp S.ABCD bằng S 2 13 a A. 2 2 13 a B. 3 2 11 a C. R2 A 2 R1 D 2 11 a O D. B C 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 44 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 49. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC a. Cạnh bên SA vuông
góc với đáy (ABC ). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC.
Thể tích của khối cầu ngoại tiếp hình chóp . A HKB bằng 3 a A. 2 3 2 a B. 3 C. 3 2 a . 3 a D. 6
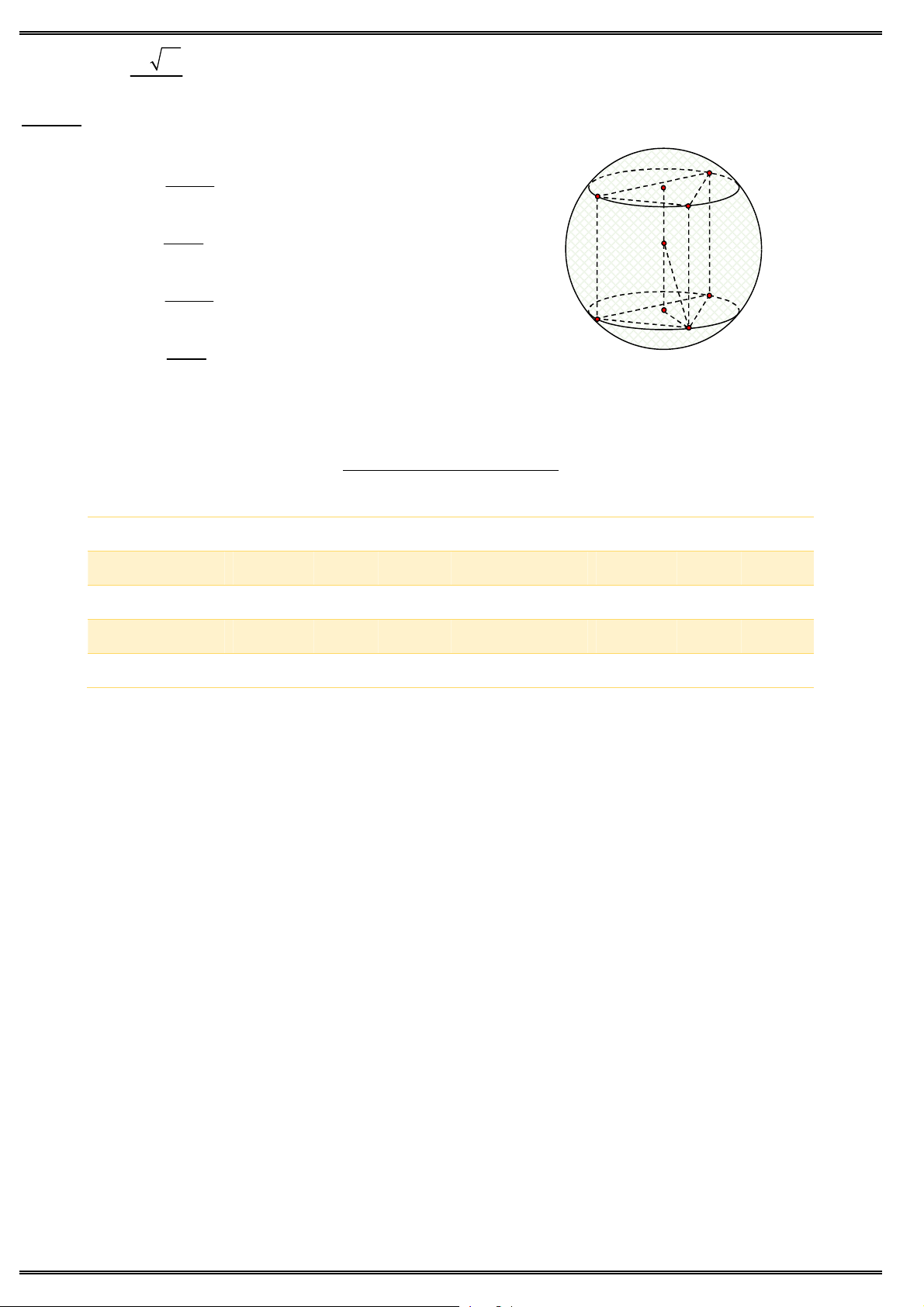
Câu 50. Cho hình lăng trụ đứng ABC .AB C
  có đáy là tam giác vuông cân tại ,
A AB AC a,
AA  2a. Thể tích khối cầu ngoại tiếp hình tứ diện AB A  C là BC A. 3 a . 3 A 4 a B. I 3 3 a C. B C 3 a A D. 3 4 . ĐÁP ÁN ĐỀ 06 1.B 2.D 3.B 4.C 5.C 6.C 7.D 8.B 9.C 10.C 11.A 12.B 13.C 14.A 15.A 16.D 17.B 18.A 19.B 20.C 21.B 22.A 23.A 24.C 25.C 26.C 27.A 28.B 29.D 30.D 31.B 32.D 33.C 34.A 35.B 36.C 37.B 38.A 39.B 40.A 41.C 42.C 43.D 44.A 45.C 46.D 47.C 48.B 49.B 50.B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 45 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 07
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! x m Câu 1.
Có tất cả bao nhiêu giá trị nguyên của m để hàm số y
đồng biến trên từng khoảng xác mx  4 định ? A. 2. B. 4. C. 3. D. 5. mx  9 Câu 2.
Tìm tham số m để hàm số y
đồng biến trên khoảng (2; ). x m
A. 3  m  2.
B. 3  m  2.
C. m  2.
D. 2  m  3. 2 cos x  3     Câu 3.
Tìm tham số m để hàm số y
nghịch biến trên khoảng 0;   2 cos x m  3 A. m  ( 3  ;1]  [2; )  . B. m  ( ;  3  ] [2; )  . C. m  ( ;  3  ). D. m  ( 3  ; )  . 1 Câu 4.
Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y   x mx  (3m  2)x  1 nghịch biến trên 3 ( ;   )  . A. 2. B. 4. C. 7. D. Vô số. Câu 5.
Tìm m sao cho hàm số 3 2 y x
  3x  3mx  201 nghịch biến trên (0; )  . A. m  1  .
B. m  1. C. m  1  .
D. m  1. Câu 6.
Tìm m sao cho hàm số y  sin x  (m  4)x luôn đồng biến trên ( ;   )  . A. m  2  .
B. m  2. C. 2
  m  2.
D. m  2. 3 1 Câu 7.
Có bao nhiêu giá trị nguyên dương của m để hàm số 4 2
y x  (m  1)x đồng biến trên 4 4 4x khoảng (0;  )  . A. 1. B. 2. C. 3. D. 4. Câu 8.
Có bao nhiêu số nguyên của tham số m để hàm số 4 2 2
y mx  2(m  5)x  4 có ba điểm cực trị,
trong đó có đúng 2 điểm cực tiểu và 1 điểm cực đại ?
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 46 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 A. 2. B. 4. C. 5. D. 3. Câu 9. Cho 3 2 2
y  (m  3)x  2(m m  1)x  (m  4)x  1. Gọi S là tập tất cả các giá trị nguyên của m
để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục Oy. Hỏi S có bao nhiêu phần tử ? A. 4. B. 5. C. 6. D. 7. 3 3m Câu 10. Cho hàm số 3 2
f (x)  x  (m  1)x  3mx
 Có tất cả bao nhiêu giá trị nguyên của 2 2 m  ( 2
 0;18) sao cho đồ thị của hàm số đã cho có hai điểm cực trị nằm cùng một phía đối với trục hoành ? A. 1. B. 19. C. 20. D. 18.
Câu 11. Có tất cả bao nhiêu giá trị nguyên của m để phương trình 3 2
x  6x m  0 có ba nghiệm phân biệt. A. 31. B. 32. C. 21. D. 34.
Câu 12. Cho hàm số y f (x) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên dương của tham số m
để phương trình f (x)  log m có đúng ba nghiệm thực phân biệt ? 2 A. 5. B. 8. C. 6. D. 7. Câu 13. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Khẳng định nào đúng ?
A. a  0, b  0, c  0, d  0. y
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0. O x
D. a  0, b  0, c  0, d  0. Câu 14. Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ. Mệnh đề nào đúng ?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0.
D. a  0, b  0, c  0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 47 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 ax  2
Câu 15. Hàm số y
có đồ thị như hình. Tính a b c. y cx b
A. a b c  1. 1
B. a b c  3. 2  O 2 x
C. a b c  4. 1 
D. a b c  0. Câu 16. Cho hàm số x 2
y  ln(e m ). Với giá trị nào của m thì y (1)  0,5. A. m  . e
B. m e  . 1 C. m  
D. m   e. e a 1
Câu 17. Cho hàm số  log (3x y
x), biết y (  1)   với , a b  .
 Tính a b. 3 4 b ln 3
A. a b  7.
B. a b  2.
C. a b  4.
D. a b  1. x m
Câu 18. Cho hàm số y  thỏa mãn y (
 1)  1. Mệnh đề nào đúng ? 4x A. m  ( 5  ; 2  ). B. m  ( ;  5  ). C. m  ( 2  ; 3). D. m  (3;  )  .
Câu 19. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 25  . m 5
 7m  7  0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử ? A. 7. B. 1. C. 2. D. 3.
Câu 20. Tìm giá trị thực của tham số m để phương trình x x 1 9  2.3
m  0 có hai nghiệm thực x , x 1 2
thỏa mãn điều kiện x x  1. 1 2 A. m  6. B. m  3  . C. m  3.
D. m  1.
Câu 21. Tìm tất cả giá trị của tham số m để phương trình 2
log x  (m  2)log x  3m  1  0 có 2 nghiệm 3 3
x , x sao cho x .x  27. 1 2 1 2 4
A. m  1. B. m   3 28
C. m  25. D. m   3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 48 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 22. Tìm tập hợp tham số m để phương trình 4x  .2x m
 2m  5  0 có hai nghiệm trái dấu. 5    A.  ;   2   5   B. 0;     2 C. (0;  )  . 5    D.  ; 4   2 
Câu 23. Số giá trị nguyên âm của m để phương trình log (x  1)  log (mx  4x) có nghiệm. 5 5 A. 4. B. 3. C. 2. D. Vô số.
Câu 24. Có mấy giá trị nguyên của m sao cho phương trình .2x  (   1)  (2x x x x m m  1) có hai nghiệm ? A. 1. B. 2. C. 3. D. Vô số.
Câu 25. Cho phương trình 5x m  log (x m) với m là tham số. Có bao nhiêu giá trị nguyên của 5 m  ( 2
 0;20) để phương trình đã cho có nghiệm ? A. 20. B. 19. C. 9. D. 21.
Câu 26. Tìm các giá trị của m để phương trình ln m  ln(m x)    x  
có nhiều nghiệm nhất.
A. m  0.
B. m  1. C. m  . e D. m  1  .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 49 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 27. Cho tứ diện đều ABCD cạnh 3a. Diện tích xung quanh của hình nón đỉnh A và đường tròn đáy
là đường tròn ngoại tiếp tam giác BCD là A A. 2 S  6 a . xq B. 2 S  3 3 a . l xq C. 2 S  12 a . B xq O D D. 2 S  6 3 a . xq C
Câu 28. Diện tích xung quanh của hình nón tròn xoay nội tiếp trong tứ diện đều có cạnh a bằng 2 a A. 4 2 a 2 B. 6 2 a C. 2 2 a 3 D. 6
Câu 29. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng 2
a . Thể tích khối nón
có đỉnh S và đường tròn đáy nội tiếp hình vuông ABCD bằng 3 a 15 A. 24 3 a 15 B. 8 3 a 15 C. 12 D. 3 a 21.
Câu 30. Diện tích xung quanh của hình nón ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng 4a bằng A. 2 2 2 a . B. 2 4 a . C. 2 3 a . D. 2 2 a .
Câu 31. Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng . a 3 a A. V   4 B. 3 V a . 3 a C. V   6 3 a D. V   2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 50 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 32. Tính diện tích xung quanh của hình trụ tròn xoay ngoại tiếp một hình lăng trụ tam giác đều có tất cả các cạnh bằng 1. 23 A. S   xq 3 2 3 B. S   xq 3 C. S3. xq D. S   xq 3
Câu 33. Cho hình lăng trụ đứng ABC .AB C
  có cạnh đáy ABC là tam giác vuông tại A với
AB  3a, AC  4a và AA  8a. Thể tích của hình trụ có hai đáy nội tiếp hình lăng trụ đã cho bằng 3 8 a A. 3 B. 3 8 a . 3 a C. 12 3 a D. 6
Câu 34. Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay tam giác ABC quanh trục BC thì
được khối tròn xoay có thể tích là A. 2 . B. 2 . 2 C. . 3 4 D. . 3   2
Câu 35. Cho tam giác ABC có ABC  45 ,
ACB  30 , AB
 Quay tam giác ABC xung quanh 2
cạnh BC ta được khối tròn xoay có thể tích V bằng A. ( 3  3). ( 1  3) B. 24 ( 1  3) C. 8 ( 1  3) D. 3
Câu 36. Trong không gian, cho hình thang vuông ABCD vuông tại A và D có AB  3 và DC AD  1.
Tính thể tích V của khối tròn xoay nhận được khi quay hình thang ABCD xung quanh trục DC.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 51 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 A. V  2 . 7 B. V   3 C. V  3 . 4 D. V   3
Câu 37. Cho hình cầu bán kính bằng 10cm, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo
thành là một đường tròn có chu 16 .
Tính thể tích khối nón có đáy là thiết diện vừa tạo và đỉnh là
tâm của hình cầu đã cho. A. 3 128 cm . B. 3 126cm . C. 3 136cm . D. 3 132cm .
Câu 38. Cho mặt cầu tâm , O bán kính .
R Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường
tròn (C ). Hình nón (N ) có đỉnh S nằm trên mặt cầu, có đáy là đường tròn (C ) và có chiều cao là h với h  .
R Tính h để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
A. h R 3.
B. h R 2. 4R C. h   3 3R D. h   2
Câu 39. Một hình trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính . R Diện tích
xung quanh của hình trụ bằng A. 2 4R . B. 2 2 R . C. 2 2 2 R . D. 2 2R .
Câu 40. Cho mặt cầu (S) bán kính R  5. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp
mặt cầu. Tính chiều cao h để diện tích xung quanh của hình trụ lớn nhất.
A. h  2 2.
B. h  4 2.
C. h  5 2.
D. h  3 2.
Câu 41. Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc nhau và OA  , a OB  2 ,
a OC  3a.
Tính diện tích S của mặt cầu ngoại tiếp tứ diện OABC. 2
A. S  8 a . 2
B. S  14 a . 2
C. S  12 a . 2
D. S  10 a .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 52 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 42. Cho hình chóp S.ABC, có đáy là tam giác đều cạnh 3cm, SC  2cm và SC vuông góc với đáy.
Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC . S 4 A. 3 V  cm . 3 256 B. 3 V  cm . 3 C A 3 C. V  36 c m . G M 32 D. 3 V  cm . B 3
Câu 43. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy và SA a 2.
Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD. S 3 32 a A. V   3 3 4 a B. V   A 3 D 3
C. V  4 a . O 3 42a B C D. V   3
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 45. Mặt cầu
ngoại tiếp hình chóp có bán kính bằng S a 3 a 3 A. B. 2 3 A C a 3 C. a 3. D. D O N 5 B
Câu 45. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Biết góc tạo bởi cạnh bên và mặt đáy của hình
chóp bằng 60. Tính bán kính R của mặt cầu ngoại tiếp hình chóp. a 6 A. R   3
B. R a 3.
C. R  2a 3. 2a 6 D. R   3
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD  2a. Mặt bên SAB là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Bán kính R của mặt cầu ngoại
tiếp hình chiếu hình chóp S.ABCD bằng S 2a 2 A. 3 3a 2 B. 2 3a 3 A D C. 2 2a 3 H D. 3 B C
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 53 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 47. Cho tứ diện ABCD có AB vuông góc với (BCD) và AB a 2. Biết tam giác BCD có BC a, BD a 3 
và CBD  30. Thể tích khối cầu ngoại tiếp tứ diện bằng 3 6 a A. B. 3 6 a . 3 3 3 6 a 3 6 a C. D. 4 2
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 6, mặt bên SAB là tam giác cân 
tại S nằm trong mặt phẳng vuông góc với đáy và có góc ASB  120. Tính diện tích S của mặt mc
cầu ngoại tiếp hình chóp S.ABCD. A. S  84 . mc B. S  28 . mc C. S  14 . mc D. S  42 . mc 
Câu 49. Cho hình chóp S.ABC có SA  (ABC), AB  ,
a AC a 2, BAC  45. Gọi B , C lần lượt là 1 1
hình chiếu vuông góc của A lên S ,
B SC. Thể tích khối cầu ngoại tiếp hình chóp . A BCC B bằng 1 1 3 a 2 A. B. 3 a 2. 3 4 3 a 2 C. 3 a . D. 3 2
Câu 50. Cho hình lăng trụ lục giác đều có cạnh đáy bằng a 2, cạnh bên bằng 2a 2. Tính diện tích mặt cầu
ngoại tiếp hình lăng trụ đã cho. FABA. 2 16 a . ECDB. 2 8 a . I C. 2 4 a . F A D. 2 2 a . B O E C D
BẢNG ĐÁP ÁN ĐỀ SỐ 07 1.C 2.A 3.C 4.A 5.A 6.D 7.C 8.A 9.C 10.D 11.A 12.D 13.A 14.B 15.D 16.D 17.A 18.C 19.C 20.C 21.A 22.D 23.B 24.B 25.B 26.B 27.B 28.A 29.A 30.A 31.D 32.A 33.B 34.C 35.B 36.B 37.A 38.C 39.B 40.C 41.B 42.D 43.B 44.B 45.D 46.D 47.B 48.A 49.A 50.A
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 54 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 08
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! (m  1)x  2 Câu 1.
Có tất cả bao nhiêu số nguyên m để hàm số y
đồng biến trên từng khoảng xác định x m của nó ? A. 1. B. 0. C. 2. D. 3. mx  9 Câu 2.
Tìm m sao cho hàm số f (x) 
luôn nghịch biến trên khoảng ( ;  1). x m
A. 3  m  1  .
B. 3  m  1  . C. 3
  m  3. D. 3
  m  3. tan x  2     Câu 3.
Tìm tham số m sao cho hàm số y
đồng biến trên khoảng 0;   m tan x  2  4  A. m  1  . B. 1
  m  2.
C. 1  m  2.
D. 1  m  2. 1 1 Câu 4.
Có mấy giá trị nguyên của tham số m để hàm số 3 2
y x mx x  2018 đồng biến trên 3 2 ( ;   )  . A. 5. B. 3. C. 4. D. 2. Câu 5.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y x  6x  (3m  6)x đồng biến trên khoảng (0; )  . A. m  2  .
B. m  2. C. m  . 
D. m  2. Câu 6.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  cos x mx luôn nghịch biến trên ( ;   )  . A. m  1  . B. m  1  .
C. m  1.
D. m  1. 2019 x 1 Câu 7.
Giá trị nguyên lớn nhất của tham số m để hàm số y  
mx  2018 luôn đồng 2017 2019 2017x
biến trên mỗi khoảng xác định của nó là A. 2018. B. 0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 55 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 C. 2. D. 1. 1 1 Câu 8.
Biết rằng đồ thị hàm số 3 2
f (x)  x mx x  2 có giá trị tuyệt đối của hoành độ hai điểm cực 3 2
trị là độ dài hai cạnh của tam giác vuông có cạnh huyền là 7. Hỏi có mấy giá trị của m ? A. 3. B. 1.
C. Không có m. D. 2. Câu 9. Gọi ,
A B là hai điểm cực trị của đồ thị hàm số 3 2
f (x)  x  3x m với m là tham số thực khác
0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng
3x  3y  8  0. A. m  5. B. m  2. C. m  6. D. m  4.
Câu 10. Tìm tham số m để đồ thị hàm số 4 2 2
y x  2m x  2m có ba điểm cực trị , A , B C sao cho , O ,
A B, C là ba đỉnh của một hình thoi (với O là gốc tọa độ). A. m  1  . B. m  1. C. m  2. D. m  3.
Câu 11. Có bao nhiêu giá trị nguyên của tham số m để phương trình 4 2
x  8x  3  4m  0 có bốn nghiệm phân biệt ? A. 6. B. 5. C. 4. D. 3.
Câu 12. Cho hàm số y f (x) xác định, liên tục trên  và có bảng biến thiên sau:
Tìm tham số m để phương trình f (x)  1  m có đúng hai nghiệm.
A. m  2, m  1  .
B. m  0, m  1  .
C. m  2, m  1.
D. 2  m  1.
Câu 13. Cho hàm số bậc ba 3 2
y ax bx cx d có đồ thị như hình vẽ. Dấu của a, , b , c d là
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 56 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 ax b
Câu 14. Cho hàm số y
có đồ thị như hình vẽ. Tìm câu đúng ? y x c
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0. O x
D. a  0, b  0, c  0. Câu 15. Hàm số 4 2
y ax bx  ,
c (a  0) có đồ thị như hình vẽ bên. Mệnh đề nào đúng ?
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0.
D. a  0, b  0, c  0. 3
Câu 16. Cho hàm số ( )  ln(2 x f x
e m) thỏa mãn f (
 ln 2)   Mệnh đề nào đúng ? 2
A. m  (1; 3). B. m  ( 5  ; 2  ).
C. m  (1;  )  . D. m  ( ;  3). 4
Câu 17. Với 1  m  0, cho hàm số y  log
(2x  5) thỏa y (  3) 
 Tìm câu đúng ? m ln 3
A. 0  m  1.
B. 1  m  4.
C. 4  m  8.
D. m  8. x  1
Câu 18. Cho hàm số f (x)  ln 2018  ln
 Tính S f (1)  f (2)   f (2017). x 4035 A. S   2018
B. S  2018. 2018 C. S   2019 2017 D. S   2018
Câu 19. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 9  . m 3
 3m  75  0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử ? A. 8. B. 4. C. 19. D. 5.
Câu 20. Tìm tất cả các giá trị của tham số m để phương trình 9x  2 .3x m
 2m  0 có hai nghiệm phân biệt
x , x sao cho x x  3. 1 2 1 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 57 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 27
A. m  9. B. m   2 3 3 3 C. m  
D. m    2 2
Câu 21. Giả sử m là số thực sao cho phương trình 2
log x  (m  2)log x  3m  2  0 có hai nghiệm x , x 3 3 1 2
thỏa mãn x .x  9. Khi đó m thỏa mãn tính chất nào sau đây ? 1 2
A. m  (4; 6). B. m  ( 1  ;1).
C. m  (3; 4).
D. m  (1; 3).
Câu 22. Tìm tham số m để phương trình x x 1 4 . m 2  
 3m  3  0 có hai nghiệm trái dấu. A. m  ( ;  2).
B. m  (1;  )  .
C. m  (1;2).
D. m  (0; 2).
Câu 23. Số các giá trị nguyên của tham số m để phương trình log (x  1)  log (mx  8) có hai nghiệm 2 2 phân biệt là A. 3. B. 4. C. 5. D. Vô số. 2 2
Câu 24. Phương trình sin x 1cos 2  2
x m có nghiệm khi và chỉ khi
A. 4  m  3 2.
B. 3 2  m  5.
C. 0  m  5.
D. 4  m  5. 2 2 2
Câu 25. Tìm m để 2x 6  x 2  m x 2  x 2  x 4  x 2 5  5  5
m  25  0 có 4 nghiệm phân biệt.
A. 0  m  1.
B. 2  m  3.
C. 4  m  3.
D. 1  m  3.
Câu 26. Có bao nhiêu giá trị nguyên của tham số thực m nhỏ hơn 10 sao cho phương trình x x
m m e e có nghiệm thực ? A. 9.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 58 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 B. 8. C. 10. D. 7. 2
3x  3x m  1
Câu 27. Có mấy số nguyên m để phương trình 2 log
x  5x  2  m có hai nghiệm 2 2 2x x  1
phân biệt lớn hơn 1. A. 3. B. Vô số. C. 2. D. 4.
Câu 28. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên SA  2a. Thể tích của khối nón
có đỉnh S và đường tròn đáy là đường tròn ngoại tiếp ABC bằng 3 a A. 2 3 a 33 B. 27 3 a C. 6 3 2 a D. 2
Câu 29. Cho hình chóp tam giác đều có cạnh đáy bằng a và đường cao bằng 6a. Thể tích khối nón V nội
tiếp hình chóp đó. 3 a A. V   9 3 a B. V   6 3 a C. V   3 3 a D. V   4
Câu 30. Cho hình chóp tứ giác đều S.ABCD có cạnh bên SA a 2 và AB  .
a Thể tích của khối nón có
đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tứ giác ABCD bằng 3 a 6 A. 12 3 2 a B. 6 3 a C. 6 3 2 a D. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 59 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 31. Cho hình hộp chữ nhật ABCD.AB CD
  có AB  2a, AD  3a và AA  4a. Tính thể tích V
của khối trụ ngoại tiếp hình hộp chữ nhật ABCD.AB CD  . A D 3 O 144 a V   B C A. 13 B. 3 V  13 a . D' A' C. 3 V  24 a . O' D. 3
V  13a . B' C'
Câu 32. Lăng trụ tam giác đều ABC .AB C
  có cạnh đáy bằng ,
a cạnh bên bằng 3a và có hai đáy là hai tam
giác nội tiếp hai đường tròn đáy của hình trụ (T ). Tính thể tích V của khối trụ (T ). A. 3 V a . B. 3 V  3 a . C. 3 V  6 a . D. 3 V  3 3 a .
Câu 33. Cho hình lăng trụ đứng ABC .AB C
  có cạnh đáy ABC là tam giác vuông tại A với AB  6 ,
a AC  8a và AA  12a. Thể tích của hình trụ có hai đáy nội tiếp hình lăng trụ đã cho bằng 3 a A. 12 3 a B. 6 C. 3 48 a . 3 48 a D. 5
Câu 34. Cho tam giác ABC vuông tại ,
A AB a, AC a 3. Quay tam giác đó quanh đường thẳng BC
ta được khối tròn xoay. Tính thể tích V của khối tròn xoay này ? 3 a A. V   2 3 a B. V   4 3 2 a C. V   3 3 a D. V   3
Câu 35. Cho hình vuông ABCD có cạnh bằng a. Quay hình vuông này xung quanh đường chéo AC, ta
thu được khối tròn xoay có thể tích bằng 3 a 2 A. 6
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 60 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 B. 3 3a 2. C. 3 2a 2. 3 a 2 D. 3
Câu 36. Cho hình thang ABCD vuông tại A và D, AD CD a, AB  2 .
a Quay hình thang ABCD
quanh đường thẳng C .
D Thể tích khối tròn xoay thu được bằng 3 7 a A. 3 B. 3 a . 3 4 a C. 3 3 5 a D. 3
Câu 37. Cho mặt cầu (S) tâm ,
O bán kính R (không đổi). Mặt phẳng (P) cách O một khoảng bằng
x, (x R) và cắt (S) theo giao tuyến là đường tròn (C ) có tâm H . Gọi T là giao điểm của tia HO
với (S). Thể tích của khối nón có đỉnh T và đáy là hình tròn (C ) bằng 2 2 (
 R x )(R x) A. 6 B. 2 2 2 (
 R x )(R x). C. 2 2 (
 R x )(R x). 2 2 (
 R x )(R x) D.  3
Câu 38. Trong các hình nón nội tiếp hình cầu có bán kính bằng 9, tính bán kính đường tròn đáy r của hình
nón có thể tích lớn nhất ?
A. r  4 2.
B. r  5 2.
C. r  6 2.
D. x  3 2.
Câu 39. Hình trụ (T ) bán kính đáy bằng 3 ,
R chiều cao bằng 8R có hai đáy nằm trên mặt cầu (S ). Thể tích của khối cầu bằng A. 3 125R . B. 3 25R . 3 500R C. 3 3 375 R D. 4
Câu 40. Cho mặt cầu (S) bán kính R  4. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp
mặt cầu. Diện tích xung quanh lớn nhất của khối trụ bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 61 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 A. 8 . B. 64 . C. 32 . D. 16 .
Câu 41. Cho tứ diện ABCD có đáy BCD là tam giác vuông tại C và AB  (BC ) D . Biết AB  5 , a BC  3 ,
a CD  4a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện. 5a 2 A. R   3
B. R  5a 3. 5a 2 C. R   2 5a 3 D. R   2
Câu 42. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 1, SA vuông góc với đáy, góc giữa mặt bên
(SBC) và đáy bằng 60 .
 Tính diện tích mặt cầu ngoại tiếp hình chóp. 43 A. S   48 43 B. S   36 43 C. S   4 43 D. S   12
Câu 43. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với đáy. Biết
SC tạo với mặt phẳng (ABCD) một góc 45 .
 Tính diện tích S của mặt cầu ngoại tiếp hình chóp. A. 2 S  4 a . B. 2 S  6 a . C. 2 S  8 a . D. 2 S  12 a .
Câu 44. Tính diện tích S của mặt cầu ngoại tiếp hình tứ diện đều cạnh a. 2 3 a A. S   4 2 3 a B. S   2 C. 2 S  6 a . D. 2 S  3 a .
Câu 45. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Hãy tính theo a thể tích của
khối cầu ngoại tiếp hình chóp S.ABC . D A. 3
82a . 3 82a B. 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 62 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 C. 3
42a . 3 2a D. 3
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  3a, AD  , a SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với đáy. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. 2 S  10 a . B. 2 S  5 a . C. 2 S  4 a . D. 2 S  2 a .
Câu 47. Cho hình chóp S.ABC có SA  (ABC ), SA  2a. Tam giác ABC cân tại đỉnh A có BC  2a 2  1 và cos ACB
 Diện tích của mặt cầu ngoại tiếp hình chóp bằng 3 2 65 a A. ` 4 B. 2 13 a . C. 2 4 a . 2 97 a D. 4
Câu 48. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết ASB  120 .
 Thể tích của khối cầu
ngoại tiếp hình chóp đã cho bằng 5 15 A. 54 4 3 B. 27 5 C. 3 13 78 D. 27
Câu 49. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy, SA a, AD  5 , a
AB  2a. Điểm E thuộc cạnh BC sao cho CE a. Bán kính mặt cầu ngoại tiếp tứ diện SAED bằng a 26 A. 4 a 26 B. 3 a 26 C. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 63 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 2a 26 D.  3
Câu 50. Cho hình lăng trụ tam giác đều ABC.AB C
  có 9 cạnh bằng nhau và bằng 2a. Tính diện tích S
của mặt cầu ngoại tiếp hình lăng trụ đã cho. 2 C 28 a A. S   AO 9 B 2 7 a B. S   I 9 2 28 a C C. S   3 O A 2 B 7 a D. S   3
BẢNG ĐÁP ÁN ĐỀ SỐ 08 1.C 2.B 3.D 4.B 5.B 6.B 7.C 8.D 9.A 10.B 11.C 12.C 13.B 14.D 15.C 16.D 17.B 18.D 19.B 20.B 21.B 22.C 23.A 24.D 25.D 26.C 27.C 28.B 29.B 30.A 31.B 32.A 33.C 34.A 35.A 36.D 37.D 38.C 39.C 40.C 41.C 42.D 43.A 44.B 45.B 46.B 47.D 48.A 49.C 50.C
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 64 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 09
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! mx  3 Câu 1.
Gọi S là tập hợp tất cả các giá trị nguyên chẵn của tham số m  (10;22) để hàm số y x  1
đồng biến trên từng khoảng xác định của nó. Tổng các phần tử của S là A. 96. B. 52. C. 104. D. 108. mx  7m  8 Câu 2.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y
đồng biến trên khoảng x m (0; )  . A. 3. B. 6. C. 8. D. 7. cos x  2     Câu 3.
Tìm tham số m sao cho hàm số y
đồng biến trên khoảng 0;   cos x m  2 
A. m  0 hoặc 1  m  2.
B. m  0.
C. 1  m  2.
D. m  2. 1 Câu 4.
Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y   x mx  (3m  2)x  1 nghịch biến trên 3 ( ;   )  . A. 2. B. 4. C. 7. D. Vô số. 1 Câu 5.
Tìm m sao cho hàm số 3 2 y
x x mx đồng biến trên khoảng (1;). 3 A. m  1  . B. 1   m  3  .
C. m  3.
D. m  3. Câu 6.
Tìm m sao cho hàm số y  (2  m)x  cos x luôn nghịch biến trên ( ;   )  .
A. m  3.
B. m  3.
C. 3  m  3.
D. m  3. Câu 7.
Gọi S là tập các giá trị của tham số thực m để hàm số 2
y x  ln(x m  2) đồng biến trên tập
xác định của nó. Biết S  ( ;
a b ]. Tổng K a b là A. K  5  . B. K  5. C. K  0. D. K  2. Câu 8. Cho hàm số 3 2
f (x)  x  3x mx  1, tìm giá trị của tham số m để hàm số có hai cực trị x , x 1 2 thỏa 2 2 x x  3. 1 2 3 A. m   B. m  1. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 65 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 1 C. m  2  . D. m   2 Câu 9. Cho hàm số 4 2
y x  2(m  4)x m  5 có đồ thị (C ). Tìm m để (C ) có ba điểm cực trị tạo m m
thành một tam giác nhận gốc tọa độ O làm trọng tâm. 17
A. m  1, m   B. m  1. 2 17 C. m  4. D. m   2
Câu 10. Gọi m , m là các giá trị của tham số m để đồ thị hàm số 3 2
y  2x  3x m  1 có hai điểm cực 1 2
trị là B, C sao cho tam giác OBC có diện tích bằng 2, với O là gốc tọa độ. Giá trị của tích số m m 1 2 bằng A. 1  5. B. 12. C. 6. D. 2  0. Câu 11. Cho hàm số 4 2 y x
 2x có đồ thị như hình vẽ. Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x  2x m  0 có bốn nghiệm thực phân biệt. A. m  0.
B. 0  m  1.
C. 0  m  1. D. m  1.
Câu 12. Cho hàm số y f (x ) xác định trên tập D   \ {1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tìm m sao cho phương trình f (x)  1  m có hai nghiệm thực phân biệt.
A. m  1 hoặc m  5.
B. 1  m  5. C. m  1. D. m  5. bx c
Câu 13. Cho hàm số y
có đồ thị như hình bên. Khẳng định nào đúng ? x a y
A. a  0, b  0, c ab  0.
B. a  0, b  0, c ab  0. O x
C. a  0, b  0, c ab  0.
D. a  0, b  0, c ab  0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 66 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 Câu 14. Cho hàm số 3 2
f (x)  ax bx cx d có đồ thị như hình. Mệnh đề nào đúng ?
A. a  0, b  0, c  0, d  0.
B. a  0, b  0, c  0, d  0.
C. a  0, b  0, c  0, d  0.
D. a  0, b  0, c  0, d  0. Câu 15. Cho hàm số 4 2
y ax bx c có đồ thị là hình vẽ bên. Mệnh đề nào đúng ? A. 2
a  0, b  0, c  0, b  4ac  0. B. 2
a  0, b  0, c  0, b  8ac  0. C. 2
a  0, b  0, c  0, b  4ac  0. D. 2
a  0, b  0, c  0, b  8ac  0. Câu 16. Cho hàm số 2  (  ) x y x
mx e . Biết y (
 0)  1 thì y (1) bằng A. 6 . e B. 3 . e C. 5 . e D. 4 . e 1
Câu 17. Cho hàm số y  ln(m x  1) thỏa mãn y (  8) 
 Tìm khẳng định đúng ? 24
A. m  2.
B. 2  m  2.
C. 2  m  5.
D. m  5. 2x e
Câu 18. Cho hàm số y
 Mệnh đề nào sau đây đúng ? 2x 1 A. 2x
y  xy  e . 2 1 B. 2x
y  xy  e . 2 1 C. 2x
y  xy  e . 2 1 D. 2x
y  xy  e . 2
Câu 19. Có mấy giá trị nguyên dương của m để 16x  (
 2)9x  2.12x m có nghiệm dương. A. 1. B. 2. C. 4. D. 3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 67 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 20. Tìm tất cả các giá trị của tham số m để phương trình 9x  2 .3x m
 2m  0 có hai nghiệm phân biệt
x , x sao cho x x  3. 1 2 1 2 3 27
A. m    B. m   2 2 9 C. m  3 3. D. m   2
Câu 21. Giá trị thực của tham số m để phương trình 2
log x  3 log x  2m  7  0 có hai nghiệm thực 3 3
x , x thỏa mãn (x  3)(x  3)  72 thuộc khoảng nào sau đây ? 1 2 1 2 A. (0; 3). B. ( 6  ; 3  ). C. (3;6). D. ( 3  ;0).
Câu 22. Tìm m để (
 3).16x  (2  1).4x m m
m  1  0 có hai nghiệm trái dấu. 3
A. 1  m    4 3 B.   m  3. 4 3 C. m  3. 4 3 D.   m  0. 4
Câu 23. Phương trình (2  3)x  (2  3)x m có nghiệm khi A. m  ( ;  5).
B. m  (2; )  . C. m  ( ;  5].
D. m  [2;  )  .
Câu 24. Tìm tham số thực m để phương trình 2
log x  4 log x m  0 có nghiệm thuộc khoảng (0;1). 2 2 A. (4;  )  . B. [4; )  . C. [4; 0). D. [2; 0].
Câu 25. Tìm tập hợp các giá trị thực của m để phương trình 2
log(x  1)  log(x  2x m) có nghiệm duy nhất ? 5    5   A. ( ;  1)     1  ;    B. 4    4   5   5   C. ( ;  ] 1         D. 4   4  
Câu 26. Cho phương trình 2x m  log (x m) với m là tham số. Có bao nhiêu giá trị nguyên của 2
m  (18;18) để phương trình đã cho có nghiệm ?
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 68 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 A. 9. B. 19. C. 17. D. 18. 2
2x x m
Câu 27. Cho phương trình 2 log
x x  4  .
m Có bao nhiêu giá trị nguyên của tham số 3 2 x  1
m  [2018;2018] để phương trình có hai nghiệm trái dấu ? A. 2022. B. 2021. C. 2016. D. 2015.
Câu 28. Cho hình chóp tam giác đều S.ABC có cạnh AB  ,
a góc tạo bởi (SAB) và (ABC) bằng 60 .  Diện
tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp tam giác ABC bằng 2 7 a A. 3 2 7 a B. 6 2 3 a C. 2 2 3 a D. 6
Câu 29. Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng a 2. Thể tích khối nón có đỉnh S và
đường tròn đáy là đường tròn nội tiếp tứ giác ABCD bằng 2 2 a A. 6 3 2 a B. 2 C. 3 a . 3 a D. 6
Câu 30. Cho hình chóp tứ giác đều S.ABCD có cạnh bên SA a 2 và AB  .
a Thể tích của khối nón có
đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tứ giác ABCD bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 69 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 a 6 A. 12 3 2 a B. 6 3 a C. 6 3 2 a D. 2
Câu 31. Cho hình lập phương ABCD.AB CD
  có đường chéo BD   x 3. Tính S của hình trụ có hai đường xq
tròn đáy ngoại tiếp hai hình vuông ABCD và AB CD  . A D S x . O A. 2 xq B C 2 x 2 B. S   xq 2 D' A' C. 2 S x 3. xq O' D. 2 S x 2. B' C' xq
Câu 32. Cho hình lăng trụ đứng ABC.AB C
  có tam giác ABC vuông cân tại ,
B AB a 2 và cạnh bên
AA  a 6. Tính diện tích xung quanh S của hình trụ ngoại tiếp hình lăng trụ đã cho bằng bao xq nhiêu ? A. 2 S  4 a 6. xq B. 2 S  4 a . xq C. 2 S  2 a 6. xq D. 2 S a 6. xq
Câu 33. Cho lăng trụ đứng ABC.AB C
  có cạnh bên AA  2a. Tam giác ABC vuông tại A có
BC  2a 3. Tính thể tích V của khối trụ ngoại tiếp khối lăng trụ này. A. 3 V  2 a . B. 3 V  4 a . C. 3 V  8 a . D. 3 V  6 a .
Câu 34. Cho tam giác ABC vuông tại A có AB  3a, AC  4a. Khi tam giác ABC quay quanh đường
thẳng BC ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó. A. 3 V a . 3 96 a B. V   5 C. 3 V  3 a . 3 48 a D. V   5
Câu 35. Cho hình vuông ABCD có cạnh bằng a 2. Quay hình vuông này xung quanh đường chéo BD, ta
thu được khối tròn xoay có thể tích bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 70 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 2 a 2 A. 3 3 3a 2 B. V   2 C. 3 V  2a 2. 3 a 2 D. V   2
Câu 36. Cho hình thang vuông ABCD có độ dài hai đáy AB  2 , a DC  4 ,
a đường cao AD  2 . a Quay
hình thang ABCD quanh đường thẳng AB thu được khối tròn xoay (H ). Tính thể tích V của khối (H). A. 3 V  8 a . 3 20 a B. V   3 C. 3 V  16 a . 3 40 a D. V   3
Câu 37. Cho mặt cầu (S ) tâm O, bán kính R  3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S )
theo giao tuyến là đường tròn (C ) có tâm H . Gọi T là giao điểm của tia HO với (S ). Tính thể tích
V của khối nón có đỉnh T và đáy là hình tròn (C ). 32 A. V   3
B. V  16.
C. V  32. 16 D. V   3
Câu 38. Cho hình nón có bán kính đáy R  5a, độ dài đường sinh   13a. Thể tích khối cầu nội tiếp hình nón bằng 3 40 a A. 9 3 400 a B. 27 3 4000 a C. 27 3 4000 a D. 81
Câu 39. Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán
kính mặt cầu. Diện tích toàn phần của hình trụ đó bằng 2 (3  2 3) R A. 3 2 (3  2 3) R B. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 71 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 2 (3  2 2)R C. 2 2 (3  2 2)R D. 3
Câu 40. Cho mặt cầu (S ) có bán kính bằng 4, hình trụ (H ) có chiều cao bằng 4 và hai đường tròn đáy nằm V
trên (S ). Gọi V là thể tích khối trụ (H ) và V là thể tích khối cầu (S ). Tính tỉ số 1  1 2 V2 V 9 A. 1   V 16 2 V 1 B. 1   V 3 2 V 3 C. 1   V 16 2 V 2 D. 1   V 3 2
Câu 41. Cho hình chóp S.ABC có đáy là tam giác vuông tại ,
B hai mặt bên SAB và SAC cùng vuông góc với đáy, SB  2 ,
a AB BC a. Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC. 3 3 a 6 A. V   2 B. 3 V  3 a 5. 3 5 a 5 C. V   6 3 a 5 D. V   6
Câu 42. Cho hình chóp S.ABC, có đáy là tam giác đều cạnh 3 ,
a SB  2a và SB vuông góc với đáy. Tính
bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC.
A. R  4a. 3a B. R   2 a C. R   2
D. R  2a.
Câu 43. Cho hình chóp S.ABCD có SA  (ABCD), đáy ABCD là hình chữ nhật, AB  , a AD  2 , a góc
giữa đường thẳng SC và đáy bằng 45 .
 Tính thể tích V khối cầu ngoại tiếp hình chóp S.ABC . D 3 10 a A. V   3 B. 3 V  6 a . 3 5 a C. V   6 3 5 10 a D. V   3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 72 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 44. Cho hình chóp tam giác đều có cạnh đáy bằng 6 và chiều cao h  1. Diện tích của mặt cầu ngoại
tiếp của hình chóp đó bằng A. S  9 . B. S  6 . C. S  5 . D. S  27 .
Câu 45. Cho hình chóp đều S.ABCD có cạnh đáy bằng a 2, góc giữa cạnh bên và mặt đáy bằng o 45 . Diện
tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng 2 4 a A. 3 B. 2 4 a . C. 2 6 a . 2 16 a D. 3
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S nằm
trong mặt phẳng vuông góc với đáy, SH AB và đường cao SH a 5. Góc giữa AB và (SAD) là 60 .
 Diện tích mặt cầu ngoại tiếp hình chóp S.ABC . D 2 160 a A. 7 B. 2 20a . C. 2 30a . 2 160 a D. 3
Câu 47. Cho hình chóp S.ABC có AB  3. Hình chiếu của S lên mặt phẳng (ABC ) là điểm H thuộc miền 
trong tam giác ABC sao cho AHB  120 .
 Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.HA ,
B biết SH  4 3.
A. R  5.
B. R  3 5.
C. R  15.
D. R  2 3.
Câu 48. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB
3a, AD a, tam giác SAB nằm 
trong mặt phẳng vuông góc với mặt phẳng đáy và ASB  60 .
 Diện tích của mặt cầu ngoại tiếp
hình chóp S.ABCD bằng 5 A. 2 a . 4 B. 2 5 a . 5 C. 2 a . 2 9 D. 2 a . 4 
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc BAD  120 .
 Cạnh bên SA vuông
góc với đáy (ABCD) và SA  3a. Bán kính R của mặt cầu ngoại tiếp khối chóp S.BCD bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 73 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3a A. 3 5a B. 3 5a C. 3 4a D. 3
Câu 50. Cho hình lăng trụ tam giác đều ABC.AB C
  có độ dài cạnh đáy bằng a và chiều cao bằng 2a. Tính
thể tích V của khối cầu ngoại tiếp hình lăng trụ ABC.AB C  . 3 32 3 a A. V   27 3 32 3 a B. V   9 3 8 3 a C. V   27 3 32 3 a D. V   81
BẢNG ĐÁP ÁN ĐỀ SỐ 09 1.D 2.C 3.D 4.A 5.C 6.B 7.C 8.A 9.B 10.A 11.B 12.A 13.B 14.C 15.A 16.C 17.B 18.D 19.B 20.B 21.C 22.A 23.D 24.B 25.C 26.C 27.D 28.B 29.D 30.A 31.D 32.C 33.D 34.A 35.A 36.D 37.A 38.D 39.B 40.A 41.C 42.D 43.D 44.A 45.B 46.D 47.C 48.B 49.C 50.A
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 74 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ ÔN TẬP HỌC KỲ 1 NĂM HỌC 2019 – 2020 TRUNG TÂM HOÀNG GIA
Môn thi: TOÁN – ĐỀ SỐ 10
56 – Phố Chợ – P. Tân Thành – Q. Tân Phú
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi ! mx  7m  8 Câu 1.
Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số y  đồng biến trên x m
từng khoảng xác định của nó. A. 8. B. Không có. C. 3. D. Vô số. x  1 Câu 2.
Có bao nhiêu giá trị nguyên của tham số m  (20;20) để hàm số y  nghịch biến trên x m khoảng ( ;  2). A. 16. B. 19. C. 17. D. 18. cotx  2     Câu 3.
Giá trị m để hàm số y
nghịch biến trên  ;  là cot x m 4 2 A. m  0.
B. m  0 hoặc 1  m  2.
C. 1  m  2. D. m  2. 1 Câu 4.
Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y x mx  (2m  3)x  2 đồng biến trên 3 ( ;   )  . A. Vô số. B. 5. C. 3. D. 7. Câu 5.
Tìm m sao cho hàm số 3 2 y x
  3x mx  4 nghịch biến trên khoảng (0; )  .
A. m  0.
B. m  0.
C. m  0.
D. m  0. Câu 6.
Tìm m sao cho hàm số y  cos x mx luôn đồng biến trên ( ;   )  .
A. m  1.
B. m  1.
C. m  1.
D. m  1. 1 Câu 7.
Có bao nhiêu giá trị nguyên dương của m  (10;20) để hàm 4
y x mx  đồng biến trên 11 11x khoảng (0; ). A. 8. B. 9.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 75 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 C. 16. D. 15. Câu 8.
Có bao nhiêu số nguyên m để hàm số 3 2
y x  3x mx  4 có hai điểm cực trị thuộc khoảng (3; 3). A. 12. B. 11. C. 13. D. 10. Câu 9. Cho hàm số 4 2
y mx  (m  3)x  2m  1. Tìm tham số m để hàm số đã cho chỉ đạt cực đại mà không có cực tiểu. A. m  3. B. m  3  . C. 3   m  0.
D. m  0 hoặc m  3. Câu 10. Cho hàm số 3 2 2
y x mx  (m  3m)x  4. Tìm tham số m để hàm số đạt cực trị tại hai điểm x , 1
x sao cho x .x  0. 2 1 2 A. m  ( ;  0]  [3; )  . B. m  ( ;  0)  (3; )  .
C. m  [0; 3].
D. m  (0; 3).
Câu 11. Cho hàm số y f (x ) liên tục trên các khoảng ( ;  0) và (0; )
 , có bảng biến thiên: x  x 0 x  1 2 y  0   0   y 2 3 3   4 
Tìm tham số m để phương trình f (x)  m  0 có 4 nghiệm phân biệt. A. 4   m  3. B. 3   m  3. C. 4   m  2. D. 3   m  2. Câu 12. Cho hàm số 3 2 y x
  3x  2 có đồ thị như hình vẽ. Tìm tập hợp S tất cả các giá của tham số thực
m sao cho phương trình 3 2
x  3x m  2  0 có ba nghiệm thực phân biệt. A. S  . 
B. S  [2;2].
C. S  (2;1).
D. S  (2;2).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 76 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 ax b
Câu 13. Cho hàm số y
có đồ thị như hình dưới. y x  1
Khẳng định nào dưới đây là đúng ? 1 2 x
A. b  0  a. O 1 
B. 0  b a. 2 
C. b a  0. D. 0  a  . b Câu 14. Cho hàm số 3 2
y ax bx cx d có đồ thị là đường cong trong hình dưới đây. Mệnh đề nào sau y đây đúng ?
A. a  0, c  0, d  0.
B. a  0, c  0, d  0.
C. a  0, c  0, d  0. O x
D. a  0, c  0, d  0. Câu 15. Hàm số 4 2
y ax bx c có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng ? y
A. a  0, b  0, c  0.
B. a  0, b  0, c  0.
C. a  0, b  0, c  0. O x
D. a  0, b  0, c  0.
Câu 16. Cho hàm số f (x )  x ln x. Tính f  (  e). 1 A. f  (  e)  2. B. f  (  e)   e C. f  (  e)  3. D. f  (  e)  . e ln x
Câu 17. Cho hàm số y
 Mệnh đề nào sau đây đúng ? x 1 1
A. y  xy 
B. 2y  xy   2 x 2 x 1 1
C. y  xy  
D. 2y  xy    2 x 2 x 2
Câu 18. Cho hàm số ( ) 2x a f x   và có f (
 1)  2 ln 2. Hỏi mệnh đề nào sau đây đúng ?
A. a  1.
B. 2  a  0.
C. 0  a  1. D. a  2  .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 77 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 19. Cho phương trình x x 1 4 (m 1)2   
 8  0. Biết phương trình có hai nghiệm x , x thỏa mãn 1 2
(x  1)(x  1)  6. Khẳng định nào sau đây đúng ? 1 2 A. Không có . m
B. 1  m  3.
C. m  3.
D. m  2.
Câu 20. Giá trị thực của tham số m để phương trình 2
log x  3 log x  2m  7  0 có hai nghiệm thực 3 3
x , x thỏa mãn (x  3)(x  3)  72 thuộc khoảng nào sau đây ? 1 2 1 2 A. (0; 3).
B. (6;3). C. (3; 6). D. (3; 0).
Câu 21. Tìm tập hợp m để phương trình 25x  .5x m
 2m  5  0 có hai nghiệm trái dấu. 5    A.  ;      2   5   B. 0;     2 C. (0; )  . 5    D.  ; 4   2 
Câu 22. Tìm tham số m để phương trình x x 2
4  (1  3m)2  2m m  0 có nghiệm. A. ( ;   )  . B. ( ;  1) (1; )  . C. (0; )  . D. (1; )  .
Câu 23. Có mấy giá trị nguyên của m để 2 log x  2
log x  3  m có nghiệm x  [1;8]. 2 2 A. 5. B. 2. C. 4. D. Vô số.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 78 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 24. Tập hợp các giá trị thực của m để phương trình 2
log (1  x )  log (x m  4)  0 có hai nghiệm 3 1 3
thực phân biệt là T  (a;b), trong đó ,
a b là các số nguyên hoặc phân số tối giản. Giá trị của
M a b bằng 33 A. 6 17 B. 3 9 C. 2 41 D. 4
Câu 25. Có bao nhiêu giá trị nguyên của m để 3 3
m  3 m  3 sin x  sin x có nghiệm ? A. 7. B. 3. C. 5. D. 2.
Câu 26. Cho dãy số (u ) thỏa mãn u u
 6, n  2 và log u  log u  8  11. Đặt n n n 1  2 5 2 9
S u u    u . Tìm số tự nhiên n nhỏ nhất thỏa mãn S  20172018. n 1 2 n n A. 2587. B. 2590. C. 2593. D. 2584.
Câu 27. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên SA  2a. Thể tích của khối nón
có đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC bằng 3 a A. 2 3 a 33 B. 27 3 a C. 6 3 2 a D. 2
Câu 28. Cho hình chóp tứ giác đều S.ABCD có cạnh bên SA bằng a 2 và SA tạo đáy góc 45 .  Thể tích
khối nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 79 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 a A. 3 3 2 a B. 6 3 a C. 6 3 2 a D. 2
Câu 29. Cho hình chóp tứ giác đều S.ABCD có cạnh bên SA a 2 và AB  .
a Thể tích của khối nón có
đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tứ giác ABCD bằng 3 a 6 A. 12 3 2 a B. 6 3 a C. 6 3 2 a D. 2
Câu 30. Cho hình hộp chữ nhật ABCD.AB CD
  có AD  8, CD  6, AC   12. Diện tích toàn phần của
hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và AB CD   bằng A. 576 . B. 10(2 11  5) . C. 26 . D. 5(4 11  4) .
Câu 31. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh bằng 1.
Tính thể tích của khối trụ đó. A. 2 B. 4 C. . D.  3
Câu 32. Cho hình lăng trụ đều ABC .AB C
  có cạnh đáy bằng a, cạnh bên bằng 2a. Thể tích của hình trụ
có hai đáy nội tiếp hình lăng trụ bằng 3 a A. 18 3 a B. 6 C. 3 a . 3 a D. 12
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 80 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 a 3
Câu 33. Cho một khối lăng trụ tam giác đều có thể tích là
 Tính thể tích V của khối trụ ngoại tiếp lăng 2 trụ đã cho. 3 a A. V   3 3 2 a B. V   3 C. 3 V a . 3. 3 2 a . 3 D. V   3
Câu 34. Cho tam giác ABC có AB  13cm, BC  5cm và AC  2cm. Thể tích V của khối tròn xoay
được tạo thành khi quay tam giác ABC quanh trục AC. 10 A. 3 V  cm . B. 3
V  8cm . 3 16 8 C. 3 V  cm . D. 3 V  cm . 3 3 
Câu 35. Cho hình thoi ABCD cạnh bằng a, có góc ABC  60. Quay hình thoi này quanh đường chéo
BD, ta thu được khối tròn xoay có thể tích bằng A. 3 2 a 3. 3 a 3 B. 12 C. 3 a 2. 3 a 3 D. 6
Câu 36. Cho hình thang cân ABCD có đáy nhỏ AB  1, đáy lớn CD  3, cạnh bên AD  2. Quay hình
thang quanh đường thẳng A .
B Tính thể tích V của khối tròn xoay tạo thành. A. V  3 . 4 B. V   3 7 C. V   3 D. V  5 .
Câu 37. Cho khối cầu tâm O bán kính R (cho trước). Mặt phẳng (P) cách O một khoảng x cắt khối cầu
theo một hình tròn (C ). Một khối nón ( )
 có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón ( )
 có thể tích lớn nhất, khi đó giá trị của x bằng R A. x   3 R R B. x   2 O R R 2 x C. x   2 I r 3R D. x   4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 81 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 38. Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối 32
cầu có đường kính bằng một nửa chiều cao của bình nước và đo được thể tích tràn ra là 3 (dm ). 3
Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và toàn bộ khối cầu chìm trong
nước, trong đó mặt nước là tiết diện của khối cầu (hình vẽ). Thể tích nước còn lại trong bình bằng 16 A. 3 (dm ). 3 32 B. 3 (dm ). 3 40 C. 3 (dm ). 3 64 D. 3 (dm ). 3
Câu 39. Cho hình trụ có bán kính đáy ,
R trục OO  2R và mặt cầu có đường kính OO . Kí hiệu V , V 1 2 V
lần lượt là thể tích của các khối trụ và khối cầu. Tính tỉ số 1  V2 V 3 V 2 A. 1   B. 1   V 2 V 3 2 2 V 3 V 4 C. 1   D. 1   V 4 V 3 2 2
Câu 40. Cho khối cầu (S) tâm I, bán kính R không đổi (cho trước). Một khối trụ thay đổi có chiều cao h
và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất. 2R 3 A. h   3 O’ R 2 B. h   2 I h R R 3 C. h   2 O A r
D. h R 2.
Câu 41. Một hình trụ gọi là nội tiếp nửa mặt cầu S(O;R) nếu một đáy của hình trụ nằm trong đáy của nửa
mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R  1 và khối trụ
có thể tích lớn nhất thì giá trị của bán kính r và chiều cao h lần lượt là 6 3 A. và 3 3 3 6 B. và 2 2 6 3 C. và 2 2 3 6 D. và 3 3
Câu 42. Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, AB a 2, BC  ,
a SC  2a và 
SCA  30. Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ABC.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 82 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 a 3
A. R a 3. B. R   2 2a
C. R a. D. R  . 3
Câu 43. Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh 3 ,
a cạnh bên SA  2a và SA vuông góc
với mặt phẳng đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC . 2a 3 A. R  
B. R  3a. 3 a 13
C. R  2a. D. R   2
Câu 44. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  3 , a BC  4 ,
a SA  12a và SA vuông
góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD. 5a 17a A. R   B. R   2 2 13a
C. R  6a. D. R   2
Câu 45. Cho tứ diện đều ABCD cạnh bằng a. Gọi H là hình chiếu vuông góc của A trên mặt phẳng (BCD)
và I là trung điểm của AH . Bán kính R của mặt cầu ngoại tiếp tứ diện IBCD bằng a 6 a 3 A. R   B. R   4 4 a 6 a 3 C. R   D. R   2 2
Câu 46. Cho hình chóp tứ giác đều S.ABCD có đáy hợp với mặt bên một góc 45. Bán kính mặt cầu ngoại
tiếp hình chóp S.ABCD bằng 2. Tính thể tích V của khối chóp S.ABCD. 64 2 A. V   81 64 2 B. V   27 28 2 C. V   81 32 2 D. V   9
Câu 47. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C . Tam giác SAB vuông tại S và nằm
trong mặt phẳng vuông góc với đáy. Góc giữa SB và mặt phẳng đáy là 60 ,
SA a 3. Tìm bán
kính R của mặt cầu ngoại tiếp hình chóp S.ABC .
A. R a 3.
B. R a 5.
C. R  3a.
D. R  5a.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 83 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 48. Hình chóp S.ABC có đáy tam giác vuông, BA BC a 3, SA vuông với đáy và SA a. Gọi
D là điểm đối xứng của S qua .
A Diện tích mặt cầu ngoại tiếp S.BCD bằng 52 A. 2 a . 3 25 B. 2 a . 3 C. 2 20 a . 160 D. 2 a . 3
Câu 49. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt
đáy (ABCD) và SA a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, , A , B E có bán kính là a 41 A. 8 a 41 B. 24 a 41 C. 16 a 2 D. 16
Câu 50. Cho hình lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông tại ,
A AB a 3, BC  2a,
đường thẳng AC  tạo với mặt phẳng (BCC B  )
 một góc 30 (tham khảo hình vẽ bên). Diện tích
của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng A. 2 24 a . B. 2 6 a . C. 2 4 a . D. 2 3 a .
BẢNG ĐÁP ÁN ĐỀ SỐ 10 1.A 2.D 3.B 4.B 5.A 6.C 7.D 8.B 9.C 10.D 11.D 12.D 13.C 14.B 15.A 16.B 17.D 18.B 19.B 20.C 21.D 22.C 23.A 24.D 25.C 26.C 27.B 28.C 29.A 30.B 31.B 32.B 33.B 34.D 35.B 36.C 37.A 38.B 39.A 40.A 41.A 42.C 43.C 44.D 45.A 46.A 47.A 48.B 49.A 50.B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 84 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
TRƯỜNG THPT TRẦN PHÚ
Môn thi: TOÁN – ĐỀ SỐ 11
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
PHẦN 1. TRẮC NGHIỆM (6,0 điểm) 2x  1 Câu 1. Cho hàm số y
 Tìm khẳng định đúng ? x  1
A. y nghịch biến trên ( ;   )  \ {1}.
B. y nghịch biến trên ( ;
 1), đồng biến trên (1; )  .
C. y nghịch biến trên ( ;  1) và (1; )  .
D. y đồng biến trên ( ;
 1), nghịch biến trên (1; )  . 4 x Câu 2.
Gọi M, m là giá trị lớn nhất, nhỏ nhất của hàm số 2 y
x  2 trên [1;2]. Tính M m. 4 13
A. M m  
B. M m  4. 4 9
C. M m  3.
D. M m   4 3  6x Câu 3. Cho hàm số y
có đồ thị là (C ). Tìm khẳng định đúng ? 2x  4
A. (C ) có hai tiệm cận x  2, y  3  .
B. (C ) có hai tiệm cận x  3  , y  2. 3 3
C. (C ) có hai tiệm cận x  2, y  
D. (C ) có hai tiệm cận x  3, y   2 4 Câu 4.
Đồ thị được cho như hình dưới đây là đồ thị của hàm số nào ? A. 3 2
y x – 3x  1. B. 3 2
y x  3x  1. C. 3 2
y x – 6x  1. D. 3 2
y  –x  3x  1. x Câu 5. Cho hàm số y
có đồ thị là (C ) và đường thẳng d : y x m. Tìm tất cả các giá trị thực x  1
của tham số m để d cắt (C ) tại hai điểm phân biệt. m   1  A.
B. 0  m  4. m   1  m   0  C.
D. –1  m  4. m   4  Câu 6. Cho 3 2
(C ) : y x  2x  3x  3, gọi M là giao điểm của (C ) và trục tung. Viết phương trình tiếp
tuyến của (C ) tại M . A. y  2  x  3.
B. y x  3.
C. y  3x  3. D. y  2  x  3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 85 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 x  6 Câu 7. Cho (C ) : y
và đường thẳng d : y  2x  1. Viết phương trình tất cả các tiếp tuyến của x  2
(C), biết các tiếp tuyến này song song với d.
A. y  2x  13.
B. y  2x – 3.
C. y  2x – 3, y  2x  13.
D. y  2x. Câu 8.
Cho hàm số y f (x) liên tục trên tập số thực và có đồ thị như hình vẽ. Tìm tham số m để phương
trình f (x)  m có 4 nghiệm phân biệt.
A. 0  m  4.
B. –1  m  4.
C. 1  m  4.
D. –1  m  1. Câu 9.
Tìm m để hàm số 4 2 2 2
y x  (m  3m)x m  3m có ba cực trị.
A. –3  m  0.
B. m  3 hoặc m  0. C. m  0. D. m  –3.
Câu 10. Giải phương trình: x x 6 2  ( 2)  16  0. A. x  8. B. x  6. C. x  4.
D. x  2. x  1
Câu 11. Tìm tập nghiệm của bất phương trình: 2 9   x 1 3  A. ( ;  0). B. ( ;  1). C. (0;  )  . D. (1; )  .
Câu 12. Cho hình chóp S.ABC có SA  (ABC ), tam giác ABC vuông tại , B AB  , a BC  2 , a góc giữa
SB và (ABC) bằng 60 .
 Thể tích của khối chóp S.ABC bằng 3 a 3 a 3 A.B.  3 2 3 a 3 3 a 3 C.D.  9 3
Câu 13. Cho hình lăng trụ đều ABC .AB C   có AB  ,
a diện tích của mỗi mặt bên bằng diện tích đáy. Thể
tích của khối lăng trụ đều ABC .AB C   bằng 3 a 3 3 3a A.B.  4 8 3 3a 3 3a 3 C.D.  16 16
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA  (ABCD) và AB SA  . a
Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC . D a a 2 A. R   B. R   2 2 a 3 C. R  
D. R a. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 86 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 15. Thiết diện qua trục của hình trụ là hình vuông cạnh a. Tính diện tích xung quanh S của hình hình xq trụ này. 2 a A. S   B. 2 S  2 a . xq 2 xq 2 2 a C. S   D. 2 S a . xq 3 xq
Câu 16. Hình chữ nhật ABCD có AB  2a, BC a. Tính thể tích V của khối trụ được tạo thành khi cho
hình chữ nhật ABCD quay quanh A . B A. 3 V  2 a . B. 3 V  4 a 3. C. 3 V a 3. D. 3 V  3 a .
Câu 17. Một hình nón có góc ở đỉnh bằng 60 ,
 đường sinh có độ dài bằng a. Tính thể tích V của hình nón này. 3 a 3 3 a A. V   B. V   6 24 3 a 3 3 a C. V   D. V   24 3
Câu 18. Một hình nón có bán kính đáy bằng ,
a góc giữa đường sinh và mặt đáy bằng 45 .  Diện tích toàn
phần của hình nón này bằng A. 2 a (2  2). B. 2 a (1  2). 2 a 2 2 a 2 C.D.  2 3 3 x
Câu 19. Tìm m để hàm số 2 2 y
 (m  1)x m (x  1)đồng biến trên ( ;   )  . 3 1 1 A. m   B. m   2 2 1 1 C. m   D. m   2 2
Câu 20. Tìm tập xác định D của hàm số y  1  log x . A. D  (0;10]. B. D  (0; )  . C. D  1 [ ;10]. D. D  [1; )  .
Câu 21. Gọi (C ) là đồ thị hàm số 4 2
y x  2x m. Tìm tất cả các giá trị thực của tham số m để (C ) và
trục hoành có 4 giao điểm phân biệt. m   0  A.
B. 0  m  1. m   1 
C. –1  m  0.
D. –1  m  1.
Câu 22. Đặt a  log 7, b  log 4. Biểu thị log 6 theo a và . b 2 3 7 a  2 b  2 A. log 6   B. log 6   7 ab 7 ab ab ab C. log 6   D. log 6   7 a  2 7 b  2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 87 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 23. Cho hàm số  ln(1 x y
e ) có đồ thị là (C), đường thẳng x  ln2 cắt (C ) tại M. Tiếp tuyến của
(C ) tại M có hệ số góc là k. Tìm khẳng định đúng ?
A. 2  k  3.
B. 1  k  2.
C. 0  k  1. D. k  0.
Câu 24. Cho hình chóp đều S.ABCD có AB  ,
a tam giác SBD vuông. Thể tích của khối chóp đều S.ABCD bằng 3 a 2 3 a 2 A.B.  6 2 3 a 2 3 a C.D. 3 6
Câu 25. Cho hình lăng trụ đứng ABC .AB C
 . Tam giác ABC vuông tại ,
A BC  5, AB  10,
AC  13. Thể tích của khối lăng trụ ABC.AB C   bằng A. 1. B. 2. C. 3. D. 4. 2 x  3x  2
Câu 26. Đồ thị hàm số y
có tất cả bao nhiêu đường tiệm cận ? 2
x(x  4x  4) A. 0. B. 1. C. 2. D. 3.
Câu 27. Đồ thị hàm số 3 2
y x  3x  1 có hai điểm cực trị là M và N. Tính diện tích S của tam giác OMN
(O là gốc tọa độ). A. S  1. B. S  2. 3 C. S  2. D. S   2
Câu 28. Tìm m để phương trình 2
log[x – (m – 1)x – 1]  log x có duy nhất một nghiệm.
A. m  (1;10). B. m  (0;1). C. m  ( ;   )  . D. m  (0;  )  .
Câu 29. Cho hình chóp S.ABCD có ABCD là hình bình hành tâm .
O Trên các đoạn thẳng S , A S , B SO
lần lượt lấy các điểm M, N, K sao cho M là trung điểm của S ,
A N là trung điểm của S ,
B 3SK  2SO. Mặt phẳng (MNK) chia khối chóp S.ABCD thành hai khối đa diện có thể tích là V
V và V (V V ).Tính tỷ số 1 k   1 2 1 2 V2 3 3 A. k   B. k   4 5
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 88 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 1 2 C. k   D. k   6 3
Câu 30. Cho hình lăng trụ ABCD.AB CD
  có đáy ABCD là hình vuông cạnh , a tâm O và
AO  (ABCD), góc giữa AB và mặt phẳng (ABCD) bằng 60 .
 Tính thể V của khối lăng trụ
ABCD.AB CD  . 3 a 10 3 a 30 A.B.  2 2 3 a 30 3 a 10 C.D.  4 4
PHẦN 2. TỰ LUẬN (4,0 điểm) 2
(m  2)x  6m
Câu 1. (1.0 đ). Tìm m để hàm số y
đồng biến trên từng khoảng xác định. x  2
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
............................................................................................................................................................................................... Câu 2. (1.0 đ). Cho 3 2
(C ) : y x mx mx. Tìm m để (C ) cắt trục hoành tại 3 điểm phân biệt.
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Câu 3. (1.0 đ). Giải phương trình: 1 9 x
  10.3x  1  0.
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Câu 4. (1.0 đ). Giải phương trình: 2 2
log (x  2x  1)  4.log (x 1)  0. 2 2
...............................................................................................................................................................................................
...............................................................................................................................................................................................
............................................................................................................................................................................................... ĐÁP ÁN ĐỀ 11 1C 2C 3A 4A 5C 6C 7C 8C 9B 10C 11B 12D 13C 14C 15D 16A 17C 18B 19A 20A 21B 22B 23C 24A 25C 26D 27A 28C 29B 30B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 89 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
ĐÁP ÁN & THANG ĐIỂM PHẦN TỰ LUẬN Câu 1. (1.0 điểm) 2 2m  4  6my  0.25đ 2 (x  2)  2
2m  4 – 6m  0 0.25đ 2
  m  1 0.5đ 3 Câu 2. (1.0 điểm)
PTHĐGD của (C ) và trục hoành: 3 2
x mx mx  0 0.25đ
x  0 hay 2
x mx m  0 0.25đ
m  0 hay m  4 0.5đ Câu 3. (1.0 điểm)
9.9x – 10.3x  1  0. 0.25đ 3x  1    0.25đ x 1 3   9 x  0   0.5đ x  2  Câu 4. (1.0 điểm)  2
4 log (x 1)  4.log (x  1)  0 (Điều kiện: x  1). 0.25đ 2 2 log (x 1)  0   2  0.25đ log (x  1)  1  2  x  2   0.5đ x  3 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 90 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
TRƯỜNG THPT TÂN BÌNH
Môn thi: TOÁN – ĐỀ SỐ 12
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
PHẦN 1. TRẮC NGHIỆM (8,0 điểm)
Câu 1. Tập nghiệm của bất phương trình log x  2 là 2 A. (4;  )  . B. (0;2). C. (0; 4). D. .  xe   
Câu 2. Cho hàm số y     
Khẳng định nào đúng ? 
A. Đồng biến trên . 
B. Nghịch biến trên khoảng ( ;
 0) và đồng biến trên khoảng (0; )  .
C. Nghịch biến trên . 
D. Đồng biến trên khoảng ( ;
 0) và nghịch biến trên khoảng (0; )  . 3x  1
Câu 3. Cho hàm số y
 Khẳng định nào sau đây đúng ? 2 1  2x
A. Đồ thị hàm số có ba tiệm cận.
B. Đồ thị hàm số có một tiệm cận ngang là y  3.
C. Đồ thị hàm số có một tiệm cận.
D. Đồ thị hàm số không có tiệm cận.
Câu 4. Đồ thị hàm số nào sau đây có 3 điểm cực trị ? A. 4 2
y  2x  4x  1. B. 4 2
y x  2x  1. C. 4 2 y x   2x  1. D. 4 2
y x  2x  1.
Câu 5. Số nghiệm của phương trình 6.4x  7 là A. 1. B. 0. C. 2. D. 3.
Câu 6. Cho hình lập phương có cạnh là 2 .
a Thể tích hình lập phương đó là bao nhiêu ? A. 3 4a . B. 3 2a . C. 3 8a . D. 3 a . 2 8 a
Câu 7. Cho mặt cầu có diện tích bằng
 Tính bán kính R của mặt cầu đã cho. 3 a 3 a 6 A. R   B. R   3 2 a 6 a 2 C. R   D. R   3 3 1
Câu 8. Rút gọn biểu thức 6 3
P x . x với x  0.
A. P x . B. 2 P x . 1 1 C. 6 P x . D. 18 P x .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 91 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 9. Đường cong ở hình bên là đồ thị của hàm nào ? y 6 2x  1 A. y   5 x   1 4 2x  1 y   3 B. x  1 2 2x  1 1 C. y   O x  1 2 1 4 x 5 -2 5 -1 2x  1 D. y   2 x  1 2x  1
Câu 10. Hàm số y
có số điểm cực trị là x  3 A. 0. B. 3. C. 2. D. 1.
Câu 11. Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA vuông góc đáy và SA a 3. Thể tích khối
chóp S.ABCD bằng 3 a 6 3 a 6 A. B.  6 9 3 a 3 3 a 6 C. D.  3 3
Câu 12. Đồ thị hàm số 4 2
y x x  2 cắt trục Ox tại bao nhiêu điểm ? A. 2. B. 3. C. 1. D. 4. 2x  1
Câu 13. Tiệm cận đứng của đồ thị hàm số y  là x  3 A. x  2. B. x  3. C. x  2  . D. x  3  . Câu 14. Cho hàm số 3 2
y x  3x  1 (C ). Tìm hệ số góc k của tiếp tuyến của đồ thị (C ) tại điểm có hoành độ bằng 1. A. k  1  . B. k  1. C. k  3. D. k  3  .
Câu 15. Cho các số thực dương ,
a b với a khác 1. Khẳng định nào đúng ? 1 A. log (ab)  log . b
B. log (ab)  4  4 log . b 4 a 4 a 4 a a 1 1
C. log (ab)  4 log . b D. log (ab)   log . b 4 a a 4 a 4 4 a 1
Câu 16. Tìm khoảng nghịch biến của hàm số 3 2
y x x  3x. . 3 A. (3;  )  . B. (–1; 3). C. ( ;  1). D. ( ;  1  )  (3; )  . Câu 17. Hàm số 3 2
y  2x  9x  12x  5 có mấy điểm cực trị ? A. 3. B. 1. C. 4. D. 2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 92 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 18. Giá trị lớn nhất của hàm số x
y e trên đoạn [0;2] bằng A. 1. B. 2. C. 2 e . D. 0. 2x  4
Câu 19. Tìm giá trị nhỏ nhất của hàm số y  trên đoạn [0; 3]. x  1 A. 4. B. 1. 1 C. D. 0. 2
Câu 20. Đồ thị hàm số 4
y x  2017 cắt trục hoành tại mấy điểm ? A. 3. B. 1. C. 2. D. 0.
Câu 21. Tập giá trị của hàm số y  log x là A. (0;  )  . B. .  C. [0;  )  . D. (1; )  . x 1  
Câu 22. Tập giá trị của hàm số y     là 2 A. (1; )  . B. (0;  )  . C. .  D. [0;  )  .
Câu 23. Cho hình nón có bán kính đáy là 3a, chiều cao là 4a. Tính thể tích V của khối nón giới hạn bởi hình nón đã cho. A. 3 V  15 a . B. 3 V  36 a . C. 3 V  12 a . D. 3 V  24 a .
Câu 24. Tìm tập xác định D của hàm số 2 4
y  (x  1) . A. D  [ 1  ;1]. B. D   \ { 1  ;1}. C. D  ( 1  ;1). D. D  ( ;  1  )  (1; )  . Câu 25. Cho ,
a b là các số thực dương thỏa mãn a  1 và log b  4. Tính 3 P  log b . a 2 a A. P  6. B. P  2. C. P  1, 5. D. P  3. y ax b
Câu 26. Cho đồ thị hàm số y
 Tìm khẳng định đúng ? cx d
A. y  0, x   2. 1 x
B. y   0, x  1. 2 O
C. y  0, x   2.
D. y   0, x  1.
Câu 27. Cho hàm số y f (x) liên tục trên [ 2
 ;2], có đồ thị như trong hình vẽ bên. Hỏi phương trình
f (x)  1  1 có bao nhiêu nghiệm phân biệt trên đoạn [ 2  ;2]. A. 4. B. 6. C. 3. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 93 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 x
Câu 28. Tìm tọa dộ tâm đối xứng của đồ thị hàm số 2 y
 2x  3x  1. 3  1    1   A. 1  ;   2  ;   B.  3  3 C. (3; –1). D. (0; –1).
Câu 29. Hình trụ có diện tích xung quanh bằng 100 2
cm và có đường sinh bằng 10cm thì có bán kính đáy là bao nhiêu ? A. 20cm. B. 25cm. C. 5cm. D. 10cm. a b
Câu 30. Cho log b  2  và log c  5 ( , a ,
b c  0; a  1). Tính P  log  a a a 3 c 5 2 A. P   B. P   3 3 4 5
C. P   
D. P    3 3
Câu 31. Cho a  1. Mệnh đề nào dưới đây sai ?
A. log x  0 khi 0  x  1. a
B. Đồ thị hàm số y  log x có tiệm cận ngang là trục hoành. a
C. Nếu x x thì log x  log x . 1 2 a 1 a 2
D. log x  0 khi x  1. a
Câu 32. Hình nón ngoại tiếp hình chóp tam giác đều có tất cả các cạnh bằng a có diện tích xung quanh bằng bao nhiêu ? 2 2 a 2 a A. B.  3 3 2 a C. 2 3 a . D.  3 Câu 33. Hàm số 2
y  1  x nghịch biến trên khoảng nào ? A. ( ;  1). B. (0;1). C. ( 1  ;1). D. (0;  )  .
Câu 34. Cho lăng trụ đứng ABC .AB C
  có tất cả các cạnh đều bằng a 3. Tính thể tích của khối lăng trụ
ABC .AB C  . 3 3a 3 9a A. B.  4 4 3 3a 3 3 9a 3 C. D.  4 4
Câu 35. Ông An gửi vào ngân hàng 100 triệu đồng lúc con ông ta vừa tròn 1 tuổi. Biết lãi xuất ngân hàng 10
năm đầu ổn định là 8%, các năm tiếp theo lãi xuất ổn định là 12%. Khi con ông An lớn lên ông An
đến ngân hàng rút hết tiền để hổ trợ cho việc tiếp tục việc học của con ông ta, thì ông An nhận được
số tiền là 477,2695351 triệu đồng (chưa làm tròn). Hỏi lúc đó con ông An được bao nhiêu tuổi ? A. 19. B. 17.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 94 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 C. 16. D. 18.
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA vuông góc (ABCD),và SA  . a
Thể tích khối chóp S.BCD tính theo a bằng bao nhiêu ? 3 a 3 a A. B.  3 8 3 a 3 a C. D.  6 12 x  1
Câu 37. Gọi M là giao điểm của (C ) : y
với trục tung. Tìm hệ số góc k của tiếp tuyến với (C ) tại x  1 điểm M. A. k  2  . B. k  1. C. k  1  . D. k  2.
Câu 38. Một người thợ định làm một thùng để đựng 3
2m nước dạng hình trụ (không nắp). Để tiết kiệm vật
liệu nhất cần làm đáy của thùng có bán kính là bao nhiêu ? 1 2 A. (m). B. (m). 2 1 C. 3 (m). D. 3 (m). x x Câu 39. Tính 1 2
S  5  5 , biết x và x là hai nghiệm của phương trình 25x 6.5x   5  0. 1 2 A. S  1. B. S  6. C. S  2. D. S  3. Câu 40. Cho hàm số 4 2
y x  2x  1 có đồ thị (C), phương trình tiếp tuyến với (C ) tại điểm cực đại của đồ thị hàm số là A. y  1. B. y  0. C. x  1. D. x  0.
PHẦN 2. TỰ LUẬN (2,0 điểm)
ĐỀ LẺ: DÀNH CHO HỌC SINH CÓ SỐ BÁO DANH LẺ
Bài 1. Giải phương trình: 2 2
log (x  2)  log (x  10)  4 log 3. 2 2 2
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 95 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
..................................................................................................................................................................................
Bài 2. Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên tạo với đáy một góc 60 .  Hãy xác
định tâm và tính bán kính mặt cầu ngọai tiếp khối chóp S.ABC.
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
ĐỀ CHẴN: DÀNH CHO HỌC SINH CÓ SỐ BÁO DANH CHẴN
Bài 1. Giải phương trình: 5.36x 3.16x 2.81x   .
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
.................................................................................................................................................................................. Bài 2. Cho A
BC vuông tại A có AB a và AC a 3. Gọi H là trung điểm BC, trên đường thẳng Hx
vuông góc (ABC ) lấy điểm S sao cho SB  3 .
a Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp SABC.
.................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
..................................................................................................................................................................................
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 96 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028 THPT BÌNH HƯNG HÒA
Môn thi: TOÁN – ĐỀ SỐ 13
(Thời gian làm bài 60 phút)
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
PHẦN 1. TRẮC NGHIỆM (8,0 điểm)
Câu 1. Đặt a  log 12 và b  log 24. Tính giá trị của P  log 168 theo a và . b 7 12 54 ab  1 ab  1 A. P  . B. P   8a  5b a(8  5b) ab ab C. P   D. P   8a  5b a(8  5b)
Câu 2. Tìm tập xác định D của hàm số y  log (3  2x). 1 2  3   3    A. D    ;    D   ;     B.  2 2   2   2    C. D    ;    D   ;     D.  3 3 
Câu 3. Tìm nghiệm của phương trình log (2x  3)  2. 3 5 A. x  3. B. x   2 3 2 C. x   D. x   2 3
Câu 4. Đồ thị hình bên dưới là của hàm số nào ? A. 3 2 y x   2x  1. B. 4 2
y x  2x  1. C. 4 2
y x  3x  1. D. 4 2 y x   2x  1. 3
Câu 5. Rút gọn biểu thức 2 4 P x
x với x  0. 3
A. P x. B. 4 P x . 1 C. 3 P x . D. 2 P x .
Câu 6. Tìm giá trị lớn nhất M của hàm số 4 2
y x  2x trên đoạn [0;2]. A. M  2. B. M  1  . C. M  0. D. M  8.
Câu 7. Cho hình chóp tứ giác đều S.ABCD có có độ dài cạnh đáy bằng a và cạnh bên bằng 2 . a Tính bán
kính R của mặt cầu ngoại tiếp hình chóp đã cho. 6a 2 14a A. R   B. R   2 7 14a 2 6a C. R   D. R   7 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 97 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 8. Cho khối trụ có bán kính đáy r  4 và chiều cao h  4 2. Thể tích của khối trụ bằng 64 2 A. V  .
B. V  64 2. 3 C. V  32 .
D. V  32 2.
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a cạnh bên SA vuông góc với mặt
phẳng đáy và SA  2 .
a Tính thể tích V của khối chóp S.ABC . D 3 2a A. V   B. 3 V  2a . 3 3 4a C. V   D. 3 V a . 3
Câu 10. Tính đạo hàm của hàm số y  ln 3x. 1 3 1 1 A. y   B. y   C. y   D. y   x ln 3 x x 3x
Câu 11. Hàm số nào dưới đây đồng biến trên khoảng ( ;   )  . x  1 A. y  . B. 3 2 y x   x x. x  2 C. 3 2
y x x x. D. 4 2
y x  3x  1.
Câu 12. Tính thể tích V của khối lập phương ABCD.AB CD
 , biết AC   a 6. A. 3 V  2 2a . B. 3 V  3 3a . 3 2 2a C. 3 V a . D. V   3
Câu 13. Viết phương trình tiếp tuyến của đồ thị hàm số 4 2
y x  4x  1 tại điểm có hoành độ x  1. A. y  4  x  6. B. y  4  x  2. C. y  4  x  6.
D. y  4x  2. 2x  1
Câu 14. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số y   x  3 A. y  2. B. x  2. C. x  3. D. y  3.
Câu 15. Trong không gian, cho tam giác ABC vuông tại ,
A AB a, AC a 3. Tính độ dài đường sinh 
của hình nón, nhận được khi quay tam giác ABC xung quanh trục AC. A.   . a B.   2a. C.   3a. D.   2 . a
Câu 16. Cho a là số thực dương khác 1. Tính I  log a. 2 a A. I  2. B. I  1. 1 1 C. I   D. I   2 4
Câu 17. Bảng biến thiên sau đây là của hàm số nào ? x  2 + x  1 x  3 A. y   B. y   y' x  2 x  2 1 + y  1
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 98 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 2x  1 x  3 C. y   D. y   x  2 x  2 Câu 18. Với mọi , a ,
b x là các số thực dương thỏa mãn log x  4 log a  7 log .
b Mệnh đề nào dưới đây 3 3 3 đúng ?
A. x  4a  7b. B. 4 7
x a b . C. 4 7 x a b .
D. x  28a . b
Câu 19. Biết rằng đường thẳng y x
  1 cắt đồ thị hàm số 3 2
y x  2x  2x  1 tại điểm duy nhất; kí hiệu
(x ;y ) là tọa độ điểm đó. Tìm y .    A. y  0. B. y  1.   C. y  1. D. y  2.  
Câu 20. Tìm tập nghiệm S của phương trình log (x  3)  log (x  1)  3. 2 2 A. S  { 1  }. B. S  { 5  ;1}. C. S  {5}. D. S  { 1  ;5}.
Câu 21. Tìm tập nghiệm S của bất phương trình log (x  1)  3. 2 A. S  ( ;  9).
B. S  (7;  )  . C. S  ( ;  6). D. S  (9;  )  . x  11
Câu 22. Hàm số y
có bao nhiêu điểm cực trị ? 2x  1 A. 2. B. 0. C. 1. D. 3.
Câu 23. Cho phương trình x x 1 9 3    3  0 . Khi đặt 3x t
, ta được phương trình nào ? A. 2
t  3t  3  0. B. 2 2t  3  0. 2
C. t t  3  0. D. 6t  3  0. Câu 24. Hàm số 3 2
y x  3x nghịch biến trên khoảng nào dưới đây ? A. ( ;   )  . B. ( ;  2  ) và (0; )  . C. (0;2). D. ( 2  ; 0).
Câu 25. Cho khối lăng trụ ABC .AB C
  có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A
lên mặt phẳng (ABC ) là trung điểm của cạnh BC và AA tạo với đáy một góc 30 .
 Tính thể tích V
của khối lăng trụ đã cho. 3 a 3 3 a 3 A. V   B. V   24 6 3 a 3 3 a 3 C. V   D. V   8 2
Câu 26. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a. Tính thể tích V của khối trụ ngoại tiếp hình lăng trụ đã cho. 3 a 3 a A. V   B. V   3 9
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 99 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 a 3 3 a C. V   D. V   4 2
Câu 27. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB a 3, cạnh bên SA vuông
góc với đáy và SB tạo với đáy một góc 30 .
 Tính thể tích V của khối chóp đã cho. 3 3a A. V   B. 3 V a . 2 3 a 3 3 a C. V   D. V   4 2 Câu 28. Cho hàm 2
y  (x  2)(x  3x  4) có đồ thị (C ). Tìm số giao điểm (C ) và trục hoành. A. 0. B. 1 . C. 3. D. 2.
Câu 29. Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo.
Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 260 triệu đồng bao gồm cả gốc
và lãi ? Giả định trong suốt thời gian gửi, lãi suốt không thay đổi và người đó không rút tiền ra. A. 15 năm. B. 14 năm. C. 16 năm. D. 13 năm.
Câu 30. Cho log x  5 và log x  4. với ,
a b là các số thực lớn hơn 1. Tính P  log x. a b ab 1 A. P  . B. P  9. 9 20 9 C. P  . D. P  . 9 20
Câu 31. Tìm tham số m để hàm số 3 2
y x  (m  3)x  1  m đạt cực đại tại x  1  . 3 A. m   . B. m  1  0. 2 3 9 C. m  . D. m   . 2 2
Câu 32. Tìm các giá trị thực của m để phương trình 2
log x (m  2)log x  3m 1  0 có hai nghiệm x ,x 5 5 1 2
thỏa mãn x .x  125. 1 2 A. m  1  . B. m  2. C. m  1. D. m  5.
Câu 33. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 3, mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. 5 15 5 15 A. V   B. V   27 108 5 15 5 15 C. V   D. V   54 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 100 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 2
Câu 34. Một vật chuyển động theo quy luật 3 2
s   t  6t  2 với t (giây) là khoảng thời gian tính từ lúc 3
bắt đầu chuyển động và y( 2
 )  22 (mét) là quãng đường vật đi được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ? A. 8 3 m ( /s). B. 7 2 m ( /s). C. 7 4 (m/s . ) D. 8 1 m ( /s . ) 2x  4
Câu 35. Tìm tất cả các giá trị của tham số m để đường thẳng y  2
x m cắt đồ thị hàm số y  tại x  1 hai điểm phân biệt. A. m  ( ;  4   4 2)  ( 4   4 2; )  . B. m  ( ;  4  )  (4; )  . C. m  ( 4   4 2; 4   4 2). D. m  ( 4  ;4).
Câu 36. Cho hình nón tròn xoay có đường cao h  3 và bán kính đáy r  5. Một thiết diện đi qua đỉnh của
hình nón cắt mặt đáy theo một dây cung có độ dài bằng 6 2. Tính diện tích S của thiết diện đó. A. S  24 2. B. S  12 2. C. S  8 2. D. S  6 2.
Câu 37. Gọi S là tập hợp các giá trị m để đồ thị 3 2 2 3
y x  3mx  3(m  1)x m  4m  1 có hai điểm cực
trị A và B sao cho tam giác OAB vuông tại O (với O là gốc tọa độ). Tính tổng tất cả các phần tử của S. A. 2  . B. 2. C. 1. D. 1  .
Câu 38. Xét các số thực dương a, b thỏa mãn log (a b)  log (a b)  1. Giá trị nhỏ nhất của biểu thức 4 4
P  2a b bằng 10 3 A. 3 2. B.  3 2 21  2 3 C.D. 2 3. 3
Câu 39. Trong tất cả các hình chóp tam giác đều ngoại tiếp mặt cầu có bán kính bằng 6, tính thể tích V của
khối chóp có thể tích nhỏ nhất.
A. V  1728 3. B. V  576. C. V  576 3.
D. V  1728 6.
Câu 40. Cho hình chóp S.ABC có đáy là tam giác đều cạnh ,
a cạnh bên SA vuông góc với mặt phẳng đáy và SA  2 .
a Gọi M, N lần lượt là trung điểm của S ,
A SB và P là hình chiếu vuông góc của A lên
đường thẳng SC. Tính thể tích V của khối chóp S.MN . P
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 101 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 3a 3 3a A. V   B. V   150 30 3 3a 3 3a C. V   D. V   6 48
PHẦN 2. TỰ LUẬN (2,0 điểm)
Câu 1. Giải phương trình 2
log (x  2x)  2. ................................................................................................................ 3
................................................................................................................................................................................
................................................................................................................................................................................
Câu 2. Giải phương trình x 1
4   5.2x  1  0. .............................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Câu 3. Cho khối nón có đường kính đường tròn đáy bằng 8 và diện tích xung quanh bằng 64 . Tính thể tích
của khối nón đã cho. ...........................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Câu 4. Trong không gian, cho hình chữ nhật ABCD có AB  2 và AC  4. Gọi E, F lần lượt là trung điểm
của AD và BC. Quay hình chữ nhật đó xung quanh trục EF, ta được một hình trụ. Tính diện tích
toàn phần của hình trụ đó.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Câu 5. Tìm tham số m để hàm số 2
y  ln(x  2mx  4) có tập xác định là . 
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
THPT NGUYỄN THƯỢNG HIỀN
Môn thi: TOÁN – ĐỀ SỐ 14
(Thời gian làm bài 60 phút)
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 102 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
PHẦN 1. TRẮC NGHIỆM (6,0 điểm)
Câu 1. Cho tứ diện đều . A BCD cạnh .
a Mặt cầu ngoại tiếp tứ diện này có diện tích bằng 2 3 a 2 3 a A. B.  4 2 2 4 a 2 5 a C. D.  3 2
Câu 2. Bất phương trình log (x  2)  1  log x có tập nghiệm là nửa khoảng (a;b], khi đó tổng a b bằng 3 1 3 A. 1. B. 2. C. 3. D. 2. 1
Câu 3. Cho hàm số y
có đồ thị (H ). Tích số các khoảng cách từ một điểm M tùy ý thuộc (H ) đến hai x
đường tiệm cận của (H ) bằng A. 2. B. 1. C. 3. D. 4.
Câu 4. Gọi V là thể tích của khối trụ ngoại tiếp một hình lập phương, gọi V là thể tích của khối trụ nội tiếp 1 2 V
hình lập phương nói trên. Tỉ lệ 1 là V2 2 1 A. B.  3 2 C. 1, 5. D. 2.
Câu 5. Phương trình log x  3 log 2  4 có tổng các nghiệm là 2 x A. 0. B. 6. C. 7. D. 10.
Câu 6. Cho hàm số y f (x) liên tục và có đạo hàm trên ,
 biết y f (x) có đồ thị như hình vẽ. Hàm số
y f (x) nghịch biến trên khoảng nào ? A. (1;  )  . B. (2; )  . C. ( ;   )  . D. ( ;  2).
Câu 7. Phương trình x 2 5 7.5 x  
 32  0 có 1 nghiệm nguyên là x và 1 nghiệm x  log .
b Giá trị của biểu 1 2 5
thức T x b bằng 1 A. 32. B. 9. C. 5. D. 10. 2x  1
Câu 8. Cho hàm số y
có đồ thị (C ) và điểm M( 1
 ;6). Đường thẳng d : y m  2x cắt (C ) tại hai x  1 5
điểm A và B phân biệt để diện tích A
BM bằng khi m thỏa 4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 103 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 A. m  1  . B. m  9. C. m  . 
D. m  9 và m  1  . 2
x  2x m
Câu 9. Xác định m để đồ thị hàm số y
có một đường tiệm cận ngang và hai đường tiệm cận 2 x  2x  3 đứng m   15   m   15  A. . B.  . m   1     m 1  C. m  15. D. m  1.
Câu 10. Người ta cần làm một cái hộp có thể tích không đổi sao cho đáy là một hình vuông cạnh a, cạnh bên
vuông góc với đáy có độ dài là h. Để tốn ít nguyên liệu nhất thì mối liên hệ giữa h và a là
A. h a.
B. h  2a. a C. h  
D. h  3a. 2
Câu 11. Khối bát diện đều được gọi là khối đa diện đều loại A. {5; 3}. B. {3; 3}. C. {3; 4}. D. {4; 3}. 2 2
Câu 12. Phương trình 2x 1 x x 2x 2 2  9.2  2
 0 có hai nghiệm x , x (x x ). Khi đó giá trị biểu thức 1 2 1 2
K  2x  3x bằng 1 2 A. 4. B. 5. C. 0. D. 2.
Câu 13. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4 2
y x  2mx  4 có ba điểm cực trị nằm
trên các trục tọa độ.
A. m  2 hoặc m  2. B. m  2.
C. Không có giá trị m nào. D. m  2.
Câu 14. Cho hình nón đỉnh S có thiết diện qua trục là tam giác đều có chu vi là 12. Khi đó diện tích toàn
phần của hình nón bằng A. 8 B. 10 . C. 12 D. 9 .
Câu 15. Đồ thị trong hình là của hàm số 3 2
f (x )  x
 3x  4. Với giá trị nào của tham số m thì phương
trình f (x )  m  1 có 4 nghiệm thực phân biệt ? A. m  4  hay m  0. 1 O 3 -1 2 B. 4   m  0. -2
C. 0  m  4.
D. 1  m  3. -4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 104 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 16. Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ?
A. 6 mặt phẳng.
B. 3 mặt phẳng. C. 4 mặt phẳng.
D. 9 mặt phẳng.
Câu 17. Cho lăng trụ tam giác đều ABC .AB C
  có cạnh đáy AB  ,
a góc giữa hai mặt phẳng (ABC ) và (ABC) là 45 .
 Khi đó thể tích khối lăng trụ ABC.AB C   là 3 a A. B. 3 a . 3 3 3a 3 2a C. D.  8 3 x  1
Câu 18. Giá trị lớn nhất của hàm số y  trên [ 1  0; 0] bằng x  1 A. 0. B. 10. 9 C. 1. D.  11
Câu 19. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SBC ) vuông góc mặt phẳng
(ABC ). Gọi M, N, P lần lượt là trung điểm A , B S ,
A AC. Khoảng cách giữa hai mặt phẳng
(MNP) và (SBC ) bằng a 3 a 3 A. B.  3 4 a 3 a 2 C. D.  2 6
Câu 20. Tích hai nghiệm của phương trình 2 2
log x  2 log x  1  7  0 là 3 3 A. 1. B. 3. C. 3. D. 2 3.
Câu 21. Cho các số thực dương a, b với a  1. Khẳng định nào đúng ? 1 1 A. log (ab)   log . b
B. log (ab)  2  log . b 2 a 2 2 a 2 a a 1 1 C. log (ab)  log . b D. log (ab)  log . b 2 a 4 a 2 a 2 a
Câu 22. Một hình nón có đường sinh bằng  và góc giữa đường sinh và đáy bằng .
Diện tích xung quanh của hình nón là A. 2  cos . B. 2  cos . C. 2  sin . D. 2  sin . Câu 23. Hàm số 2 2017
y  (x  4x  3) có tập xác định D là A. D   \ { 3  ; 1  }. B. D  .  C. D  ( 3  ; 1  ). D. D  ( ;  3  )  ( 1  ; )  .
Câu 24. Bất phương trình 3 6
log ( x x )  log x có nghiệm là 6 64 A. x  0.
B. 0  x  64. C. x  64. D. x  64.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 105 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 25. Một người gửi số tiền M triệu đồng vào một ngân hàng với lãi suất 0, 7% / tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban
đầu (người ta gọi đó là lãi kép). Sau ba năm, người đó muốn lãnh được số tiền là 5 triệu đồng, nếu
trong khoảng thời gian này không rút tiền ra và lãi suất không đổi, thì người đó cần gửi số tiền M là A. 3, 8 triệu. B. 3, 6 triệu. C. 3, 9 triệu. D. 3, 7 triệu.
Câu 26. Một khối cầu ngọai tiếp tứ diện đều có thể tích 3 27 6 a
. Khi đó độ dài một cạnh của tứ diện đều là A. 4a 3. B. 4a. C. 6a. D. 6a 2.
Câu 27. Cho một khối trụ có bán kính đáy R  2 2 và chiều cao h  10. Cắt khối trụ bởi hai mặt phẳng song
song với nhau và cùng vuông góc với mặt phẳng đáy. Biết khoảng cách từ tâm của đường tròn đáy
đến mỗi mặt phẳng đó là d  2. Khối trụ được chia làm ba phần. Thể tích của phần nằm giữa là 80 A.  3 B. 160. C. 80  40 . D. 40.
Câu 28. Giá trị của A  log 2. log 3...... log 2046.log 2047 là 3 4 2047 2048 1 A. 1. B. 11. C. 11 2 . D.  11
Câu 29. Xác định m để hàm số 3
y x  3mx m đồng biến trên .  A. m  0. B. m  0. C. m  0. D. m  0. 3x  2
Câu 30. Cho hàm số y
có đồ thị (C ). Tọa độ những điểm trên (C ) mà tại đó tiếp tuyến có hệ số góc x  2 bằng 4 là A. (1;1) và (3;7). B. (1; 1  ) và (3; 7  ). C. ( 1  ;1) và ( 3  ;7). D. ( 1  ;1). và ( 3  ; 7  ).
PHẦN 2. TỰ LUẬN (4,0 điểm)
Bài 1. (1 điểm) Giải phương trình 2
2 log (x  2)  log (x  4)  0. 3 3
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Bài 2. (1 điểm) Tìm tham số m để phương trình (2  3)x  (2  3)x m có hai nghiệm phân biệt.
................................................................................................................................................................................
................................................................................................................................................................................
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 106 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................ 3x  2
Bài 3. (1 điểm) Cho hàm số y
 Tìm tham số m để đường thẳng d : y x
  m cắt đồ thị (C) tại x  1 hai điểm phân biệt.
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
Bài 4. (1 điểm) Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng
vuông góc với (ABCD). Biết AC  2a, BD  4a. Tính theo a thể tích khối chóp S.ABC . D
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
................................................................................................................................................................................
BẢNG ĐÁP ÁN TRẮC NGHIỆM 1B 2A 3B 4D 5D 6D 7B 8D 9B 10A 11C 12A 13B 14C 15D 16B 17C 18D 19B 20A 21A 22A 23A 24B 25C 26C 27C 28D 29C 30C ĐÁP ÁN TỰ LUẬN
Bài 1. S  {3; 3  2}.
Bài 2. m  2. 3 2a 15
Bài 3. m  6 hoặc m  2. Bài 4. V   S .ABCD 3
SỞ GD & ĐT TP. HỒ CHÍ MINH
ĐỀ THI HỌC KỲ 1 NĂM HỌC 2017 – 2028
THCS – THPT NGUYỄN KHUYẾN
Môn thi: TOÁN – ĐỀ SỐ 15
(Thời gian làm bài 60 phút)
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 107 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Thaø ñeå nhöõng gioït moà hoâi rôi treân trang vôû, ñöøng ñeå gioït nöôùc maét rôi treân baøi thi !
PHẦN 1. TRẮC NGHIỆM (8,0 điểm)
Câu 1. Đồ thị trong hình bên là đồ thị của hàm số nào dưới đây ? A. 3 2 y x
  3x  1. B. 3 2
y x  3x  1. C. 3
y x  3x  1. D. 3 2 y x
  3x  1. Câu 2. Hàm số 4 2 y x
  4x  7 luôn đồng biến trên khoảng nào dưới đây ? A. ( ;  0). B. (0; 2). C. ( 2; 2). D. ( 2;  )  . Câu 3. Cho hàm số 2
y x (3  x). Khẳng định nào sau đây đúng ?
A. Hàm số nghịch biến trên khoảng (0;2).
B. Hàm số đồng biến trên khoảng ( ;  0).
C. Hàm số nghịch biến trên khoảng (2; )  .
D. Hàm số đồng biến trên khoảng ( 1  ;2).
Câu 4. Cho hình hộp chữ nhật ABCD.AB CD
  có các cạnhAB  1, BC  2, AC  21. Thể tích của khối hộp đã cho bằng A. 8. B. 3 5. C. 4 5. D. 4.
Câu 5. Cho hàm số y f (x) có 2 f (
x)  (x  2)(x  1) . Khẳng định nào sau đây là đúng ?
A. Hàm số y f (x) đạt cực tiểu tại x  1.
B. Hàm số y f (x) đạt cực đại tại x  2  .
C. Hàm số y f (x) đạt cực đại tại x  1.
D. Hàm số y f (x) đạt cực tiểu tại x  2  .
Câu 6. Cho hàm số y f (x) có bảng biến thiên như hình vẽ dưới đây
 x x x 1 2 3 x  y   0     y
Hỏi đồ thị của hàm số đã cho có bao nhiêu điểm cực trị ? A. Một. B. Hai. C. Ba. D. Không có. Câu 7. Hàm số 2 3 4 y (16 6x x ) x     có tập xác định là
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 108 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 A. D   \ {0}. B. D   \ ( 8  ;2). C. D   \ { 8  ; 0;2}. D. D  ( 8  ;2) \ {0}.
Câu 8. Mệnh đề nào sau đây là sai ?
A. Khối tứ diện là khối đa diện lồi.
B. Lắp ghép hai khối hộp luôn được một khối đa diện lồi.
C. Khối hộp là khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi. 16
Câu 9. Đồ thị hàm số y x
đạt cực đại tại điểm (x ;y ) và đạt cực tiểu tại điểm (x ;y ) thì giá trị của x 1 1 2 2 y y bằng 1 2 A. 16. B. 8  . C. 0. D. 16.
Câu 10. Cho hai số thực dương a,b với a  1 . Khẳng định nào sau đây là đúng?  a   1      A. log    3 1  
  log b. 3 a       2 a  ba  1  1      B. log    1  
  log b. 3 a     3  2 ab   a    1 C. log    1  2 log b . 3     a     3 a ba  1  1      D. log    1  
  log b. 3 a     3  2 ab  Câu 11. Hàm số 4 2 2
y x  2(m  1)x m  4 có ba điểm cực trị khi và chỉ khi A. m  1. B. m  1. C. m  1. D. m  1. 1  2x
Câu 12. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y
có phương trình lần lượt là x  2
A. x  2; y  1.
B. x  1; y  2  .
C. x  2; y  1. D. x  2; y  2  .
Câu 13. Khẳng định nào dưới đây là sai ?
A. Đồ thị hàm số 4 2
y x  2x có 2 điểm uốn.
B. Đồ thị hàm số 4 2
y x x không có điểm uốn. 2x  1
C. Đồ thị hàm số y  có 1 điểm uốn. x  1
D. Đồ thị hàm số 3 2
y x x có 1 điểm uốn.
Câu 14. Cho hàm số y f (x) có bảng biến thiên như sau
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 109 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Mệnh đề nào sau đây là sai ?
A. Hàm số có hai cực trị.
B. Hàm số có giá trị lớn nhất bằng 3.
C. Giá trị nhỏ nhất của hàm số là 0.
D. Hàm số có ba điểm cực trị.
Câu 15. Hàm số nào sau đây đồng biến trên khoảng ( ;   )  ? 2 A. 4 2
y x  2x .
B. y x  . x x x  5      10 
C. y  ln  .     y   .  D.  2  3    1 Câu 16. Cho hàm số 3 2
y x  3x  2 có đồ thị (C). Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng 3
d : x  9y  27  0 có phương trình là A. y  9
x  43 . B. y  9x  7 . C. y  9
x  11 . D. y  9x  34 . (a  1)x  2
Câu 17. Đồ thị (C) của hàm số y
nhận gốc tọa độ O làm tâm đối xứng thì tổng a b là x b  1 A. 1  . B. 0. C. 1. D. 2.
Câu 18. Cho khối chóp đều S.ABCD có cạnh đáy bằng 2a , đường cao bằng a . Góc giữa mặt bên và mặt đáy của khối chóp bằng A. 0 45 . B. 0 54 . C. 0 60 . D. 0 30 .
Câu 19. Hình chữ nhật ABCD có AB  2BC  8 . Gọi M, N lần lượt là trung điểm của cạnh AB, CD. Khi
quay hình chữ nhật ABCD quanh trục MN ta được một hình trụ tròn xoay có diện tích toàn phần là A. 96 . B. 64 . C. 48 . D. 128 . ax b
Câu 20. Cho hàm số y
có đồ thị như hình bên. Phát biểu nào sau đây là đúng? cx d
A. Đồ thị hàm số có đường cận ngang là x  2 .
B. Hàm số nghịch biến trên  \   1 .
C. Đồ thị của hàm số có tâm đối xứng là I 1;2.
D. Hàm số đồng biến trên  \   1 . 2 6log x 1
Câu 21. Tổng tất cả các nghiệm của phương trình 3 312  bằng 97344 10 A. 0. B. . 3 82 C. 10. D. . 9 Câu 22. Gọi ,
a A là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2
y x 2018  x . Tính S A a .
A. S  1010.
B. S  1008.
C. S  2018.
D. S  2017.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 110 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 23. Cho hàm số y f x  có đồ thị như hình bên. Tìm tất cả các giá trị của tham số m để phương trình
f x  m  2 có bốn nghiệm phân biệt.
A. 4  m  3 .
B. 2  m  1. C. 3   m  2  . D. 4   m  3  .
Câu 24. Khối lập phương có diện tích toàn phần bằng 96 cm2. Mặt cầu đi qua tất cả các đỉnh của hình lập
phương đó có thể tích V là
A. 283 cm3.
B. 72cm3.
C. 323 cm3. D. 362 cm3.
Câu 25. Cho hình chóp SABCD có đáy là hình chữ nhật với AB a ; AD a 3 . Hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với mặt đáy, đồng thời cạnh SB tạo với mặt phẳng đáy một góc bằng 450. Tính
thể tích khối chóp S.BCD bằng 3 a 6 3 a 3 A. . B. . 6 2 3 a 2 3 a 3 C. . D. . 3 6
Câu 26. Trong hình vẽ dưới đây có đồ thị của các hàm số x y ay x , x y b , log . Chọn mệnh đề đúng c trong các mệnh đề sau y x y b x y a 3
A. 0  a c  . b 2 y  log x c
B. 0  c a  . b 1
C. 0  b c a. 1  O 1 2 3 x
D. 0  a b  . c
Câu 27. Giả sử phương trình 2 3
ln x  ln x  2  0 có hai nghiệm x ,x đồng thời x x . Khẳng định nào 1 2 1 2 sau đây là đúng? A. 2 2
x x  1  e . B. x  2x  0 1 2 2 1 C. 2 x x  0 . D. 2
x  2x  2e . 1 2 1 2
Câu 28. Một hình trụ có chiều cao bằng 6 nội tiếp trong hình cầu có bán kính bằng 5 như hình vẽ. Thể tích của khối trụ này.
A. 36.
B. 96.
C. 48.
D. 192.
Câu 29. Số điểm thuộc đồ thị của hàm số 4 2
y x  3x  2 mà tiếp tuyến tại những điểm đó song song với trục hoành là A. 1. B. 2. C. 3. D. 4.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 111 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020 3 x
Câu 30. Số tất cả các giá trị nguyên m để hàm số y    m   2
x  m   2 3
27 x m  2 nghịch biến 3 trên khoảng  ;   là A. 6 số. B. 10 số. C. 12 số. D. 16 số.
Câu 31. Dân số thế giới năm 1950 là 2,56 tỉ người và năm 1960 là 3,04 tỉ người. Biết dân số thế giới tăng theo hàm số    0 kt P t P
e , trong đó k là tỉ lệ tăng dân số theo thời gian t (năm). Hỏi dân số thế giới vào
năm 2020 sẽ là bao nhiêu người? A. 6,052 tỉ. B. 8,525 tỉ. C. 9,152 tỉ. D. 7,179 tỉ.
Câu 32. Bất phương trình 2 x  2 3 3 x  
 82 có tập nghiệm là S a;b thì 2 2
2b  3a bằng A. 4  . B. 8. C. 12. D. 20.
Câu 33. Tứ diện SABC có cạnh AB, AC, AS đôi một vuông góc nhau và AB a, AC a 3, SA a 6. Gọi
M là trung điểm của cạnh SB, N là điểm trên cạnh SC sao cho 3SN NC . Tính thể tích của khối chóp A.BCNM theo a. 3 7a 2 3 5a 3 A. . B. . 16 12 3 a 2 3 7a 3 C. . D. . 16 24
Câu 34. Cho lăng trụ ABCD.A’B’C’D’ có đáy là hình vuông cạnh bằng 10. Hình chiếu vuông góc của A’ lên
mặt đáy ABCD trùng với tâm O của hình vuông ABCD. Biết cạnh bên tạo với mặt đáy một góc 600.
Tính thể tích V của lăng trụ đã cho. A. 150 6. B. 250 6. C. 300 6. D. 500 6.
Câu 35. Một cốc nước có dạng hình trụ có đường kính đáy 8cm , lượng nước trong cốc cao 5cm . Thả vào cốc
nước 6 viên bi sắt có cùng bán kính 2cm thì lượng nước trong cốc dâng cao cách mép cốc là 2cm. Hỏi
cốc nước đó có thể tích là bao nhiêu? (làm tròn đến hàng đơn vị, bỏ qua độ dày của cốc) A. 503 ml . B. 553 ml . C. 584 ml . D. 603 ml .
Câu 36. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên tạo với mặt đáy của hình chóp một
góc bằng 600. Một hình nón ngoại tiếp hình chóp S.ABC có thể tích V bằng Nón 3 a 3 3 a A. . B. . 9 3 3 3 a 3 a C. . D. . 6 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 112 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
Câu 37. Có tất cả bao nhiêu số nguyên dương của tham số k để đồ thị hàm số 2
y  (x  3)(x  4x k  2)
cắt trục hoành tại ba điểm phân biệt? A. 3. B. 4. C. 5. D. 6.
Câu 38. Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu EF bắt qua sông biết
rằng thành phố A cách con sông một khoảng là 5 km và thành phố B cách con sông một khoảng là 7
km (hình vẽ), biết tổng độ dài HE KF  24 km . Hỏi xây cây cầu cách thành phố A là bao nhiêu
để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường AEFB) A. 5 3 km . B. 10 2 km . C. 5 5 km . D. 7, 5 km .
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  2a, BC a 5 . Tam giác SAB
vuông tại S và nằm trong mặt phẳng vuông góc với mặt đáy ABCD. Mặt cầu ngoại tiếp hình chóp S.ABCD có bán kính là 3
A. R a. B. R a. 2
C. R  2a.
D. R  3a. 
Câu 40. Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a với 0
ABC  120 . Nếu SA SB SC  2a thì
khoảng cách d giữa hai đường thẳng SB và AC theo a là 2a 93 a 93 A. d  . B. d  . 31 31 a 6 a 3 C. d  . D. d  . 4 4
PHẦN 2. TỰ LUẬN (2,0 điểm) 2x  1
Câu 1. (1 điểm) Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số y  . x  1
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 113 -
Bieân soaïn & giaûng daïy: Ths. Leâ Vaên Ñoaøn – 0933.755.607
15 ®Ò «n tËp häc k× 1 líp 12 n¨m häc 2019 – 2020
...............................................................................................................................................................................................
...............................................................................................................................................................................................
Câu 2. (1 điểm) Giải phương trình log (log x)  log (log x)  2. 4 2 2 4
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
...............................................................................................................................................................................................
............................................................................................................................................................................................... ĐÁP ÁN ĐỀ 15 1 C 11 C 21 D 31 B 2 B 12 D 22 C 32 A 3 C 13 C 23 B 33 A 4 A 14 B 24 C 34 D 5 D 15 D 25 D 35 B 6 B 16 C 26 A 36 A 7 D 17 B 27 C 37 B 8 B 18 A 28 B 38 C 9 A 19 B 29 C 39 B 10 D 20 C 30 C 40 D
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng” Trang - 114 -