21 trang 12 lượt tải

Bộ đề ôn thi THPT Quốc gia 2023 môn Toán - Đề ôn tập số 2

24

Bộ đề ôn thi THPT Quốc gia 2023 môn Toán - Đề ôn tập số 2. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.

Chủ đề: Tài liệu ôn thi THPTQG môn Toán 335 tài liệu

Môn: Toán 2.3 K tài liệu

Tác giả:

Profile

Toàn Võ

2 tuần trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/21
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
Bé §Ò VÒ §ÝCH
¤N THI THPT QuèC GIA 2023
Thời gian làm bài: 90 phút
Theo Ma trận Đề tham khảo 2023
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
NỘI DUNG ĐỀ BÀI
Câu 1: Cho số phức
23zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z
là điểm có
tọa độ là
A.
2;3
. B.
3; 2
. C.
. D.
2; 3
.
Câu 2: Đạo hàm của hàm số
10
x
y
là
A.
10
ln10
x
y
. B.
10 .ln10
x
y
. C.
10
x
y
. D.
10
10 log
x
ye
.
Câu 3: Tập xác định
D
của hàm số
1
3
2yx
là
A.
;2D
. B.
;D  
. C.
;2D
. D.
2;D 
.
Câu 4: Bất phương trình
3 81 0
x

có tất cả bao nhiêu nghiệm nguyên dương?
A.
3
. B.
4
. C. vô số. D.
5
.
Câu 5: Cho cấp số nhân
()
n
u
với
1
1u
và
4
8u
. Công bội của cấp số nhân đã cho bằng
A.
2.
B.
7.
C.
8.
D.
4.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:. P x y z4 3 2 0
. Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng
P
?
A.
;;n
2
1 4 3
. B.
;; n
3
1 4 3
. C.
4
1; 4;3n
. D.
;;n
1
1 4 3
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Cho hàm số
fx
có đạo hàm trên ,
12 f
và
3 2.f
Tính
3
1
d
I f x x
.
A.
4.I
B.
0.I
C.
3.I
D.
4.I
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới?
A.
42
23y x x
. B.
3
33y x x
. C.
42
23y x x
. D.
42
23y x x
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
:S
2 2 2
2 6 4 2 0. x y z x y z
Xác định tọa độ
tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 3;2 , 16IR
. B.
1; 3;2 , 4IR
. C.
1;3; 2 , 16IR
.D.
1;3; 2 , 4IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oyz
và
Oxz
bằng
A.
30 .
B.
90 .
C.
60 .
D.
45 .
Câu 12: Các điểm
, , , M N P Q
trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
1 2 3 4
, , ,z z z z
. Khi đó
1 2 3 4
3w z z z z
bằng
Q
P
N
M
-1
3
1
-2
2
x
y
O
1
-1
2
-2
-3
A.
64wi
. B.
64wi
. C.
43wi
. D.
34wi
.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
1
2
V Bh
. B.
1
3
V Bh
. C.
1
6
V Bh
. D.
V Bh
.
Câu 14: Cho khối hộp chữ nhật
.ABCD A B C D
có
2, 3, 4
AB AD AA
(tham khảo hình vẽ).
D
C
B
A
D'
C'
B'
A'
Thể tích khối hộp đã cho bằng
A.
24
. B.
20
. C.
9
. D.
8
.
Câu 15: Một khối cầu có bán kính bằng
2
, một mặt phẳng
cắt khối cầu đó theo một hình tròn có
diện tích là
2
. Khoảng cách từ tâm khối cầu đến mặt phẳng
bằng
A.
2
. B.
1
. C.
2
2
. D.
2
4
.
Câu 16: Môđun của số phức
34zi
bằng
A.
5
. B.
3
. C.
7
. D.
7
.
Câu 17: Tính chiều cao
h
của hình trụ biết chiều cao
h
bằng bán kính đáy và thể tích khối trụ đó là
8
.
A.
3
32h
. B.
3
4h
. C.
22h
. D.
2h
.
Câu 18: Trong không gian
Oxyz
, điểm nào dưới đây không thuộc đường thẳng
12
:
2 1 1
x y z
d


?
A.
1; 2;0Q
. B.
1;2;0M
. C.
1; 3;1N 
. D.
3; 1; 1P 
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2x
. C.
0x
. D.
1x
.
Câu 20: Đường tiệm cận đứng của đồ thị hàm số
32
1
x
y
x
có phương trình là
A.
2x 
. B.
1x 
. C.
3x
. D.
1x
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
(0;1]
. B.
( ;2]
. C.
0;2
. D.
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là
A.
12
P
. B. 36. C.
3
12
C
. D.
3
12
A
.
Câu 23: Cho hàm số
y f x
thỏa mãn
2 7cosf x x

,
03f
. Mệnh đề nào dưới đây đúng?
A.
2 7sin 3f x x x
. B.
2 7sin 3f x x
.
C.
2 sin 9f x x x
. D.
2 7sin 3f x x x
.
Câu 24: Nếu
4
0
d5f x x
và
4
2
d1f x x 
thì
2
0
df x x
bằng
A.
6
. B.
4
. C.
4
. D.
6
.
Câu 25: Họ tất cả các nguyên hàm của hàm số
24
x
f x x
là
A.
2
2 ln2 2
x
xC
. B.
2
2
2
ln2
x
xC
. C.
2 ln2
x
C
. D.
2
ln2
x
C
.
Câu 26: Cho hàm số
fx
có bảng biến biên dưới đây:
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng
;1
.
B. Hàm số đã cho nghịch biến trên khoảng
0;1
.
C. Hàm số đã cho đồng biến trên khoảng
1; 
.
D. Hàm số đã cho nghịch biến trên khoảng
3; 2
.
Câu 27: Cho hàm số
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là
A.
3y 
. B.
1y
. C.
4y 
. D.
4y
.
Câu 28: Biết
5
2
logyx
. Khi đó
A.
5logyx
. B.
2
5logyx
. C.
2
5 logyx
. D.
2
1
log
5
yx
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
là
A.
9
2
V
. B.
81
10
V
. C.
81
10
V
. D.
9
2
V
.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với
mặt phẳng đáy và
32
2
a
SA
(minh họa như hình bên dưới).
Góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 31: Cho hàm số
23
2
x
y
x
có đồ thị
(C)
và đường thẳng
:d y x m
. Với tất cả giá trị nào của
m
thì
d
cắt
(C)
tại hai điểm phân biệt?
A.
. B.
2m
. C.
6m
. D.
2
6
m
m
.
Câu 32: Cho hàm số
y f x
liên tục trên , có đạo hàm
23
2 2 5 ,
f x x x x x
.
Hàm số
y f x
nghịch biến trên khoảng nào sau đây?
A.
;2
. B.
5;
. C.
2;5
. D.
2; 
.
Câu 33: Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10,
lấy ngẫu nhiên
5
quả cầu.
Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho 3 bằng
A.
11
12
. B.
5
12
. C.
7
12
. D.
1
12
.
Câu 34: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Tính
12
xx
.
A.
12
4xx
. B.
12
1
8
xx
. C.
12
1
2
xx
. D.
12
3xx 
.
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức
,z x yi x y
thỏa mãn
23z i z i
là đường thẳng có phương trình là
A.
1yx
. B.
1yx
. C.
1yx
. D.
1yx
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
qua
3;5;6M
và vuông góc với mặt phẳng
:2 3 4 2 0P x y z
thì đường thẳng
d
có phương trình là
A.
3 5 6
2 3 4
xyz

. B.
3 5 6
234
x y z

.
C.
3 5 6
2 3 4
x y z


. D.
1 2 10
2 3 4

x y z
.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxz
có
tọa độ là
A.
1;2;3
. B.
1;2; 3
. C.
1;0; 3
. D.
1; 2;3
.
Câu 38: Cho hình lập phương
.ABCD A B C D
có cạnh
a
.
A'
B'
C'
D'
D
C
B
A
Khoảng cách từ
A
đến
BDD B

bằng
A.
2a
. B.
2
2
a
. C.
2
a
. D.
a
.
Câu 39: Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
22
3 9 2 0
x x x
m
có 5
nghiệm nguyên?
A. 65021. B. 65024. C. 65022. D. 65023.
Câu 40: Biết
()Fx
và
()Gx
là hai nguyên hàm của hàm số
()fx
trên và
3
0
( ) (3) (0) , ( 0)
f x dx F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( ), ( ), 0y F x y G x x
và
3x
. Khi
15S
thì
a
bằng
A.
15
. B.
12
. C.
18
. D.
5
.
Câu 41: Hàm số
2
2y x mx x m
đồng biến trên tập xác định khi và chỉ khi
A.
(1; )m 
. B.
5
;
2
m




. C.
[1; )m 
. D.
5
;
2
m



.
Câu 42: Cho số phức
z
thỏa mãn
_
2 3 1z i i z
. Giá trị lớn nhất của
1z
bằng
A.
38 13
. B.
26 13
. C.
3 2 38
. D.
3 2 26
.
Câu 43: Cho hình chóp tứ giác
.S ABCD
có đáy là hình vuông cạnh
a
. Tam giác
SAD
cân tại
S
và
mặt bên
SAD
vuông góc với mặt phẳng đáy. Biết thể tích khối chóp
.S ABCD
bằng
3
a
.
Tính khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
6
37
a
. B.
37
a
. C.
3a
. D.
3
37
a
.
Câu 44: Cho đường cong
3
:C y x
. Xét điểm
A
có hoành độ dương thuộc đồ thị
C
. Tiếp tuyến
của
C
tại
A
tạo với
C
một hình phẳng có diện tích bằng
27
. Hoành độ của điểm
A
thuộc khoảng nào dưới đây?
A.
1
0;
2



. B.
1
;1
2



. C.
3
1;
2



D.
3
;2
2



.
Câu 45: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
2 6 5 0z mz m
có hai
nghiệm phức phân biệt
12
,zz
thỏa mãn
12
?zz
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 46: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1; 2;1 , 3; 4;1AB
. Đường thẳng
AB
cắt mặt phẳng
zOx
tại
M
. Tỉ số
MB
MA
bằng
A.
2
. B.
1
2
. C.
1
. D.
3
.
Câu 47: Cho hàm số
1
2
x
y
và
22
x
y 
có đồ thị như hình vẽ bên. Diện tích tam giác
ABC
bằng
A.
3
. B.
3
2
. C.
3
4
. D.
6
.
Câu 48: Cho một hình trụ có chiều cao bằng
6
và bán kính bằng
5.
Lấy hai điểm
A
và
'A
thuộc hai
đường tròn đáy khác nhau của hình trụ và
' 10AA
. Khoảng cách giữa đường thẳng
'AA
và
trục của hình trụ đã cho bằng
A.
3
. B.
2 21
. C.
5
. D.
.
Câu 49: Trong không gian
,Oxyz
cho điểm
1;1;1A
, mặt phẳng
: 3 0P x y z
và đường thẳng
2
:
1 2 1
x y z
d

. Xét đường thẳng
qua
A
, nằm trong mặt phẳng
P
và cách đường
thẳng
d
một khoảng lớn nhất. Đường thẳng
đi qua điểm nào dưới đây?
A.
2 ;1;0M
. B.
1; 1;3N
. C.
3;3;3P
D.
1;2;4Q
.
Câu 50: Cho hàm số
y f x
có đạo hàm
22
' 2 5 ,f x x x x mx x
. Số giá trị nguyên
âm của
m
để hàm số
2
2g x f x x
đồng biến trên khoảng
1; 
là
A.
3
. B.
4
. C.
5
. D.
7
.
________________________HẾT________________________
Huế, 13h30’ Ngày 02 tháng 3 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
Bé §Ò VÒ §ÝCH
¤N THI THPT QuèC GIA 2023
Thời gian làm bài: 90 phút
Theo Ma trận Đề tham khảo 2023
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức
23zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z
là điểm có
tọa độ là
A.
2;3
. B.
3; 2
. C.
. D.
2; 3
.
Lời giải:
Câu 2: Đạo hàm của hàm số
10
x
y
là
A.
10
ln10
x
y
. B.
10 .ln10
x
y
. C.
10
x
y
. D.
10
10 log
x
ye
.
Lời giải:
10 10 .ln10
xx
yy
.
Câu 3: Tập xác định
D
của hàm số
1
3
2yx
là
A.
;2D 
. B.
;D  
. C.
;2D
. D.
2;D 
.
Lời giải:
Tập xác định:
2 0 2xx
Vậy tập xác định của hàm số là
;2D
.
Câu 4: Bất phương trình
3 81 0
x

có tất cả bao nhiêu nghiệm nguyên dương?
A.
3
. B.
4
. C. vô số. D.
5
.
Lời giải:
Ta có:
*
3 81 0 3 81 4 1;2;3; 4 .
x
xx
xx
Câu 5: Cho cấp số nhân
()
n
u
với
1
1u
và
4
8u
. Công bội của cấp số nhân đã cho bằng
A.
2.
B.
7.
C.
8.
D.
4.
Lời giải:
Ta có:
33
41
. 8 2.u u q q q
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:. P x y z4 3 2 0
Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng
P
?
A.
;;n
2
1 4 3
. B.
;; n
3
1 4 3
. C.
4
1; 4;3n
. D.
;;n
1
1 4 3
.
Lời giải:
Mặt phẳng
: P x y z4 3 2 0
có một vectơ pháp tuyến là
;;n
2
1 4 3
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Cho hàm số
fx
có đạo hàm trên ,
12 f
và
3 2.f
Tính
3
1
d
I f x x
.
A.
4.I
B.
0.I
C.
3.I
D.
4.I
Lời giải:
Ta có
3
1
dI f x x
3
3 1 2 2 4
1
f x f f
.
Vậy
4I
.
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới?
A.
42
23y x x
. B.
3
33y x x
. C.
42
23y x x
. D.
42
23y x x
.
Lời giải:
Nhìn hình vẽ ta thấy là đồ thị hàm bậc 4 trùng phương
42
0f x ax bx c a
có hệ số
a
dương. Do vậy chọn đáp án D.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
:S
2 2 2
2 6 4 2 0. x y z x y z
Xác định tọa độ
tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 3;2 , 16IR
. B.
1; 3;2 , 4IR
. C.
1;3; 2 , 16IR
.D.
1;3; 2 , 4IR
.
Lời giải:
Ta có mặt cầu
S
:
2 2 2
2 6 4 2 0. x y z x y z
có tâm
1; 3;2I
và bán kính
2
22
1 3 2 2 4R
.
Vậy mặt cầu
S
có tâm
1; 3;2I
và bán kính
4R
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oyz
và
Oxz
bằng
A.
30 .
B.
90 .
C.
60 .
D.
45 .
Câu 12: Các điểm
, , , M N P Q
trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
1 2 3 4
, , ,z z z z
. Khi đó
1 2 3 4
3w z z z z
bằng
Q
P
N
M
-1
3
1
-2
2
x
y
O
1
-1
2
-2
-3
A.
64wi
. B.
64wi
. C.
43wi
. D.
34wi
.
Lời giải:
Ta có
1 2 3 4
3 2 ; 2 ; 3 ; 2 2z i z i z i z i
.
Suy ra
1 2 3 4
3 3 3 2 2 3 2 2 6 4w z z z z i i i i i
.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
1
2
V Bh
. B.
1
3
V Bh
. C.
1
6
V Bh
. D.
V Bh
.
Câu 14: Cho khối hộp chữ nhật
.ABCD A B C D
có
2, 3, 4
AB AD AA
(tham khảo hình vẽ).
D
C
B
A
D'
C'
B'
A'
Thể tích khối hộp đã cho bằng
A.
24
. B.
20
. C.
9
. D.
8
.
Lời giải:
Thể tích khối hộp chữ nhật đã cho bằng:
2.3.4 24V 
.
Câu 15: Một khối cầu có bán kính bằng
2
, một mặt phẳng
cắt khối cầu đó theo một hình tròn có
diện tích là
2
. Khoảng cách từ tâm khối cầu đến mặt phẳng
bằng
A.
2
. B.
1
. C.
2
2
. D.
2
4
.
Lời giải:
Gọi
,OH
lần lượt là tâm khối cầu và tâm hình tròn.
,Rr
lần lượt là bán kính mặt cầu và bán
kính hình tròn.
Diện tích hình tròn
2
2
2
S
s r r

.
Gọi
h
là khoảng cách từ tâm khối cầu đến mặt phẳng
suy ra
22
2.h R r
Câu 16: Môđun của số phức
34zi
bằng
A.
5
. B.
3
. C.
7
. D.
7
.
Lời giải:
Ta có:
32
3 4 5z
.
Câu 17: Tính chiều cao
h
của hình trụ biết chiều cao
h
bằng bán kính đáy và thể tích khối trụ đó là
8
.
A.
3
32h
. B.
3
4h
. C.
22h
. D.
2h
.
Lời giải:
Gọi
R
là bán kính của hình trụ khi đó
Rh
.
Ta có thể tích khối trụ là
23
V R h h


3
8
82
V
hh

.
Vậy chiều cao của khối trụ là
2h
.
Câu 18: Trong không gian
Oxyz
, điểm nào dưới đây không thuộc đường thẳng
12
:
2 1 1
x y z
d


?
A.
1; 2;0Q
. B.
1;2;0M
. C.
1; 3;1N 
. D.
3; 1; 1P 
.
Lời giải:
Điểm
12
;;
2 1 1
a b c
I a b c d

đúng.
Kiểm tra các điểm
; ; ;Q M N P
trong các phương án A, B, C, D ta thay điểm
1;2;0M
vào
phương trình
d
ta có:
1 1 2 2 0
2 1 1

(vô lý) . Vậy điểm
M
không thuộc đường thẳng
d
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2x
. C.
0x
. D.
1x
.
Lời giải:
Vì
y
đổi dấu từ âm sang dương duy nhất tại
2x
nên hàm số đã cho đạt cực tiểu tại
2x
Câu 20: Đường tiệm cận đứng của đồ thị hàm số
32
1
x
y
x
có phương trình là
A.
2x 
. B.
1x 
. C.
3x
. D.
1x
.
Lời giải:
Ta có:
( 1) ( 1)
32
lim lim
1
xx
x
y
x


.
Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng
1x 
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
(0;1]
. B.
( ;2]
. C.
0;2
. D.
Lời giải:
Điều kiện:
0.x
Bất phương trình đã cho tương đương
0
02
2
x
x
x
Vậy tập nghiệm của bất phương trình là
(0;2].S
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là
A.
12
P
. B. 36. C.
3
12
C
. D.
3
12
A
.
Lời giải:
Cách chọn 3 học sinh trong 12 học sinh không xếp thứ tự là tổ hợp chập 3 của 12:
3
12
C
Câu 23: Cho hàm số
y f x
thỏa mãn
2 7cosf x x

,
03f
. Mệnh đề nào dưới đây đúng?
A.
2 7sin 3f x x x
. B.
2 7sin 3f x x
.
C.
2 sin 9f x x x
. D.
2 7sin 3f x x x
.
Lời giải:
Ta có:
2 7cos 2 7sinf x x dx x x C
.
Mặt khác:
0 3 3fC
2 7sin 3f x x x
.
Câu 24: Nếu
4
0
d5f x x
và
4
2
d1f x x 
thì
2
0
df x x
bằng
A.
6
. B.
4
. C.
4
. D.
6
.
Lời giải:
Ta có
4 2 4 2 4 4
0 0 2 0 0 2
d d d d d d 5 1 6f x x f x x f x x f x x f x x f x x
.
Câu 25: Họ tất cả các nguyên hàm của hàm số
24
x
f x x
là
A.
2
2 ln2 2
x
xC
. B.
2
2
2
ln2
x
xC
. C.
2 ln2
x
C
. D.
2
ln2
x
C
.
Lời giải:
Ta có
2
2
d 2 4 d 2
ln2
x
x
f x x x x x C

.
Câu 26: Cho hàm số
fx
có bảng biến biên dưới đây:
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng
;1
.
B. Hàm số đã cho nghịch biến trên khoảng
0;1
.
C. Hàm số đã cho đồng biến trên khoảng
1; 
.
D. Hàm số đã cho nghịch biến trên khoảng
3; 2
.
Lời giải:
Câu A: Sai vì hàm số không liên tục từ
;1
.
Câu B: Đúng vì hàm số nghịch biến trên khoảng
2;1
và khoảng
2;1
chứa khoảng
0;1
Câu C: Đúng quá rõ ràng.
Câu D: Đúng vì hàm số nghịch biến trên khoảng
;2
và khoảng
;2
chứa khoảng
3; 2
Câu 27: Cho hàm số
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là
A.
3y 
. B.
1y
. C.
4y 
. D.
4y
.
Lời giải:
Từ bảng biến thiên của hàm số
y f x
, suy ra giá trị cực tiểu của hàm số là
4y 
(đạt tại
3)x 
.
Câu 28: Biết
5
2
logyx
. Khi đó
A.
5logyx
. B.
2
5logyx
. C.
2
5 logyx
. D.
2
1
log
5
yx
.
Lời giải:
Ta có
5
22
log 5logy x x
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
là
A.
9
2
V
. B.
81
10
V
. C.
81
10
V
. D.
9
2
V
.
Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số
2
54y x x
và trục
Ox
ta có:
2
1
5 4 0
4
x
xx
x
Thể tích của khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
44
2
22
11
81
54
10
V f x dx x x dx


.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với
mặt phẳng đáy và
32
2
a
SA
(minh họa như hình bên dưới).
Góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Lời giải:
Do
SA ABCD
nên hình chiếu vuông góc của
SO
lên mặt phẳng
ABC D
là
AO
. Khi đó
góc giữa đường thẳng
SO
và mặt phẳng
ABC D
là
SOA
.
ABD
đều cạnh
2a
nên
36
22
a
AO AB
.
SOA
vuông tại
A
có
32
2
a
SA
,
6
2
a
AO
nên
3 2 6
tan : 3
22
SA a a
SOA
AO
60SOA
.
Vậy góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
60
.
Câu 31: Cho hàm số
23
2
x
y
x
có đồ thị
(C)
và đường thẳng
:d y x m
. Với tất cả giá trị nào của
m
thì
d
cắt
(C)
tại hai điểm phân biệt?
A.
. B.
2m
. C.
6m
. D.
2
6
m
m
.
Lời giải:
Phương trình hoành độ giao điểm là
2
23
( 2) 2 3 ( 2)( ) 2 3 0 (1)
2
x
x m x x x x m x mx m
x
Để
d
cắt
(C)
tại hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt khác
2
2
0
2
.
6
( 2) 2 2 3 0
m
m
mm


Câu 32: Cho hàm số
y f x
liên tục trên , có đạo hàm
23
2 2 5 ,
f x x x x x
.
Hàm số
y f x
nghịch biến trên khoảng nào sau đây?
A.
;2
. B.
5;
. C.
2;5
. D.
2; 
.
Lời giải:
Xét phương trình
0fx
23
2
2 2 5 0 2.
5
x
x x x x
x
Bảng xét dấu:
Suy ra hàm số
()y f x
nghịch biến trên khoảng
2;5
.
Câu 33: Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10,
lấy ngẫu nhiên
5
quả cầu.
Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho 3 bằng
A.
11
12
. B.
5
12
. C.
7
12
. D.
1
12
.
Lời giải:
Số phần tử của không gian mẫu
5
10
nC
.
Gọi
A
là biến cố: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó chia hết cho 3”
Biến cố
A
: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó không chia hết cho 3”
Tính
nA
:
Để tích các số trên 5 quả cầu được chọn không chia hết cho 3 thì trong 5 quả cầu đó không có
các quả cầu mang số 3, 6, 9. Vậy
5
7
n A C
.
5
7
5
10
1
12
nA
C
PA
nC
.
11
1
12
P A P A
.
Câu 34: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Tính
12
xx
.
A.
12
4xx
. B.
12
1
8
xx
. C.
12
1
2
xx
. D.
12
3xx 
.
Lời giải:
ĐKXĐ:
0x
.
Ta có
22
2 2 2 2
2
2
log 2log 2 1 0 log 2log 3 0
1
log 1
2
log 3
8


x x x x
x
x
x
x
Vậy
12
4xx
.
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức
,z x yi x y
thỏa mãn
23z i z i
là đường thẳng có phương trình là
A.
1yx
. B.
1yx
. C.
1yx
. D.
1yx
.
Lời giải:
2 3 2 1 3z i z i x y i x y i
2 2 2
2 2 2 2 2
2 1 3 4 4 2 1 6 9x y x y x x y y x y y
4 4 4 1y x y x
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
qua
3;5;6M
và vuông góc với mặt phẳng
:2 3 4 2 0P x y z
thì đường thẳng
d
có phương trình là
A.
3 5 6
2 3 4
xyz

. B.
3 5 6
234
x y z

.
C.
3 5 6
2 3 4
x y z


. D.
1 2 10
2 3 4

x y z
.
Lời giải:
Ta có
:2 3 4 2 0P x y z
có vectơ pháp tuyến
2; 3;4n 
.
dP
d
nhận vectơ pháp tuyến của
P
làm vectơ chỉ phương.
Do đó đường thẳng
d
qua
3;5;6M
và có vectơ chỉ phương
2; 3;4u 
.
Kiểm tra phương án D thỏa mãn.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxz
có
tọa độ là
A.
1;2;3
. B.
1;2; 3
. C.
1;0; 3
. D.
1; 2;3
.
Câu 38: Cho hình lập phương
.ABCD A B C D
có cạnh
a
.
A'
B'
C'
D'
D
C
B
A
Khoảng cách từ
A
đến
BDD B

bằng
A.
2a
. B.
2
2
a
. C.
2
a
. D.
a
.
Lời giải:
Trong
ABCD
, gọi
O AC BD
.
Hình lập phương
.ABCD A B C D
có
DD ABCD
. Suy ra
DD AC
.
Mà
ABCD
là hình vuông nên
AC BD
.
Do đó,
AC BDD B

. Lại có,
AC BDD B O


.
Xét hình vuông
ABCD
có
2
22
AC a
AO 
.
Nên khoảng cách từ A đến
BDD B

là
2
,
2
a
d A BDD B AO


.
Câu 39: Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
22
3 9 2 0
x x x
m
có 5
nghiệm nguyên?
A. 65021. B. 65024. C. 65022. D. 65023.
Lời giải:
TH1:
2
2
3 9 0 2 1 2
xx
x x x
Bất phương trình đã cho không thể có 5 nghiệm nguyên.
TH2:
2
2
3 9 0
20
xx
x
m


: không thoả mãn bất phương trình có 5 nghiệm nguyên.’
TH3:
2
2
2
2
1
3 9 0
2
20
log
xx
x
x
x
m
xm



Để bất phương trình đã cho có 5 nghiệm nguyên thì
2
3 log 4 512;65536mm
Vậy có
65024
giá trị nguyên của
m
để bất phương trình đã cho có 5 nghiệm nguyên.
Câu 40: Biết
()Fx
và
()Gx
là hai nguyên hàm của hàm số
()fx
trên và
3
0
( ) (3) (0) , ( 0)
f x dx F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
( ), ( ), 0y F x y G x x
và
3x
. Khi
15S
thì
a
bằng
A.
15
. B.
12
. C.
18
. D.
5
.
Lời giải:
Ta có:
( ), ( )F x G x
là nguyên hàm của
( ) ( ) ( )f x F x G x C
3 3 3
0 0 0
( ) ( ) 3 15 5 5S F x G x dx C dx Cdx C C C
3
0
( ) (3) (0) (3) ( (0) ) (3) (0) (3) (0)f x dx F F F G C F G C F G a
5aC
(do
0a
)
Câu 41: Hàm số
2
2y x mx x m
đồng biến trên tập xác định khi và chỉ khi
A.
(1; )m 
. B.
5
;
2
m



. C.
[1; )m 
. D.
5
;
2
m



.
Lời giải:
Điều kiện:
2 0 2x m x m
Ta có:
1
2 0, 2
22
x m x m
xm
y

1
2 2 4 4 0, 2
22
y x m m x m
xm

Đặt
2, 0t x m t
Ta có:
2
1
2 4 0, 0
2
y t m t
t

2
1
24
2
m t t
Đặt
2
1
24
2
g t t
t
2
1
40
2
g t t
t
1
2
t
Bảng biến thiên:
5
max
2
gt
khi
1
.
2
t
Vậy
5
2
m
.
Câu 42: Cho số phức
z
thỏa mãn
_
2 3 1z i i z
. Giá trị lớn nhất của
1z
bằng
A.
38 13
. B.
26 13
. C.
3 2 38
. D.
3 2 26
.
Lời giải:
Gọi
,z x yi x y
có điểm biểu diễn là
;M x y
.
Ta có
_
22
2 2 2 2
2 3 1 2 3 2 4 6 13 0 1z i i z x y x y x y x y
.
Nhận thấy
1
là phương trình của đường tròn
C
có tâm
2;3I
và bán kính
26R
.
Mặt khác
2
2
11z x y MA
với
MC
còn
1;0A
nằm trong đường tròn
C
.
Do đó
1 26 3 2
max
z R IA
.
Câu 43: Cho hình chóp tứ giác
.S ABCD
có đáy là hình vuông cạnh
a
. Tam giác
SAD
cân tại
S
và
mặt bên
SAD
vuông góc với mặt phẳng đáy. Biết thể tích khối chóp
.S ABCD
bằng
3
a
.
Tính khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
6
37
a
. B.
37
a
. C.
3a
. D.
3
37
a
.
Lời giải:
Gọi
M
là trung điểm
AD
.
Vì tam giác
SAD
cân tại
S
và mặt bên
SAD
vuông góc với mặt phẳng đáy nên
SM ABCD
.
Ta có:
3
2
3
13
.3
3
ABCD
ABCD ABCD
ABCD
V
a
V S SM SM a
Sa
.
Ta có:
//AB CD
// , ,AB SCD d B SCD d A SCD
Mà
, 2 ,d A SCD d M SCD
(do
M
là trung điểm
AD
)
Nên
, 2 ,d B SCD d M SCD
1
.
Ta có:
CD AD
(gt),
CD SM
(vì
SM ABCD
)
CD SAD
.
Trong tam giác
SMD
, gọi
H
là hình chiếu vuông góc của
M
lên cạnh
SD
.
Khi đó ta có:
HM SD
và
HM CD
(vì
CD SAD
mà
HM SAD
)
HM SCD
,d M SCD MH
2
.
Trong
SMD
vuông tại
M
, đường cao
MH
có:
22
2 2 2 2
1 1 1 1 1 37
9
3
1
2
MH SM MD a
a
a



3
37
a
MH
.
Từ
1
và
2
suy ra
6
,
37
a
d B SCD
.
Câu 44: Cho đường cong
3
:C y x
. Xét điểm
A
có hoành độ dương thuộc đồ thị
C
. Tiếp tuyến
của
C
tại
A
tạo với
C
một hình phẳng có diện tích bằng
27
. Hoành độ của điểm
A
thuộc khoảng nào dưới đây?
A.
1
0;
2



. B.
1
;1
2



. C.
3
1;
2



D.
3
;2
2



.
Lời giải:
Xét
3
; , 0 A a a C a
tiếp tuyến tại
2 3 2 3
: 3 3 2A y a x a a a x a
Phương trình hoành độ giao điểm:
2
3 2 3 3 2 3
3 2 3 2 0 2 0
2
xa
x a x a x a x a x a x a
xa

3 2 3 3 2 3 4
22
27
3 2 3 2 27 2 0
4
aa
aa
S x a x a dx x a x a dx a a a
.
Câu 45: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
2 6 5 0z mz m
có hai
nghiệm phức phân biệt
12
,zz
thỏa mãn
12
?zz
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải:
2
2 6 5 0 *z mz m
+ TH1 : Ycbt
Phương trình
*
có hai nghiệm thực phân biệt
12
,zz
thỏa mãn
12
zz
1 2 1 2
00z z z z m
.
+ TH2 : Ycbt
2
6 5 0 1 5m m m
.
Vì
2;3;4mm
.
Vậy có tất cả
4
giá trị
m
cần tìm.
Câu 46: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1; 2;1 , 3; 4;1AB
. Đường thẳng
AB
cắt mặt phẳng
zOx
tại
M
. Tỉ số
MB
MA
bằng
A.
2
. B.
1
2
. C.
1
. D.
3
.
Lời giải:
Ta có
2; 2;0AB 
là vtcp của đường thẳng
AB
nên
AB
có phương trình:
1
2
1
xt
yt
z

.
Thay phương trình
AB
vào phương trình
x : 0Oz y
ta được:
2 0 2tt
.
Suy ra
x 1;0;1AB Oz M
nên ta có:
22
22
4 4 0
2
22
MB
MA


.
Câu 47: Cho hàm số
1
2
x
y
và
22
x
y 
có đồ thị như hình vẽ bên. Diện tích tam giác
ABC
bằng
A.
3
. B.
3
2
. C.
3
4
. D.
6
.
Lời giải:
Ta có
1
1
:2
x
Cy
giao với trục
Oy
tại điểm
1
0;
2
B



và
2
: 2 2
x
Cy
giao với trục
Oy
tại
điểm
0; 1C
.
Giao điểm của hai đường
1
C
;
2
C
có hoành độ là nghiệm của phương trình
1
1
2 2 2 .2 2 2 2 4 2 2;2
2
x x x x x
xA
.
Vậy
1 1 3 3
. , . .2
2 2 2 2
ABC
S BC d A Oy
.
Câu 48: Cho một hình trụ có chiều cao bằng
6
và bán kính bằng
5.
Lấy hai điểm
A
và
'A
thuộc hai
đường tròn đáy khác nhau của hình trụ và
' 10AA
. Khoảng cách giữa đường thẳng
'AA
và
trục của hình trụ đã cho bằng
A.
3
. B.
2 21
. C.
5
. D.
.
Lời giải:
Kẻ đường sinh AB, ta có:
'/ /( ' ) ( '; ') ( ';( ' )) ( ;( ' ))OO AA B d OO AA d OO AA B d O AA B OH
(
H
là trung điểm
A’B
)
Ta có
22
1
' ' 8 ' 4
2
A B AA AB BH A B
.
Khi đó
22
3OH OB HB
Câu 49: Trong không gian
,Oxyz
cho điểm
1;1;1A
, mặt phẳng
: 3 0P x y z
và đường thẳng
2
:
1 2 1
x y z
d

. Xét đường thẳng
qua
A
, nằm trong mặt phẳng
P
và cách đường
thẳng
d
một khoảng lớn nhất. Đường thẳng
đi qua điểm nào dưới đây?
A.
2 ;1;0M
. B.
1; 1;3N
. C.
3;3;3P
D.
1;2;4Q
.
Lời giải:
Gọi
( ; ; )H x y z
là hình chiếu của
A
trên
d
ta có
AH. 0
d
Hd
u
nên
2
1 2 1
1 1 2 1 1 1 0
x y z
x y z

2
0 2;0;0
0
x
yH
z
.
Khi đó:
,3d A d AH
.
Dấu
""
xảy ra khi và chỉ khi
AH
AH
n
, 0; 2;2
P
P
u
AH u n
u


.
1
: 1 2 ,
12
x
y t t
zt

đi qua điểm
1; 1;3N
.
Câu 50: Cho hàm số
y f x
có đạo hàm
22
' 2 5 ,f x x x x mx x
. Số giá trị nguyên
âm của
m
để hàm số
2
2g x f x x
đồng biến trên khoảng
1; 
là
A.
3
. B.
4
. C.
5
. D.
7
.

Tài liệu khác của Toán

Preview text:

Page: CLB GIÁO VIÊN TRẺ TP HUẾ Bé §Ò VÒ §ÝCH ¤N THI THPT QuèC GIA 2023
Thời gian làm bài: 90 phút
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
Theo Ma trận Đề tham khảo 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ. NỘI DUNG ĐỀ BÀI
Câu 1: Cho số phức z  2  3i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z là điểm có tọa độ là A. 2;3 .
B. 3;  2 . C. 3; 2 . D. 2;  3 .
Câu 2: Đạo hàm của hàm số 10x y  là 10x A. y  . B. 10x y  .ln10 . C. 10x y  . D.   10x y log e . ln10 10
Câu 3: Tập xác định D của hàm số y    x13 2 là
A. D   ;  2. B. D   ;  .
C. D   ;  2 .
D. D  2;  .
Câu 4: Bất phương trình 3x  81  0 có tất cả bao nhiêu nghiệm nguyên dương? A. 3 . B. 4 . C. vô số. D. 5 .
Câu 5: Cho cấp số nhân (u ) với u  1 và u  8 . Công bội của cấp số nhân đã cho bằng n 1 4 A. 2. B. 7. C. 8. D. 4.
Câu 6: Trong không gian Oxyz , cho mặt phẳng  P : x  4 y  3z  2  0. . Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng  P ? A. n  1 4 3 n  1 4 3 n   n  1 4 3 2  ; ;  . B. 3  ; ; . C. 1; 4;3 . D. 1  ; ;  . 4   ax b
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d y O 2 x -2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là A. 0; 2 . B. 2;0 . C. 2;0 . D. 0; 2 . 3
Câu 8: Cho hàm số f x có đạo hàm trên , f   1  2
 và f 3  2. Tính I f   xdx. 1  A. I  4. B. I  0. C. I  3. D. I  4.
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới? A. 4 2
y  x  2x  3 . B. 3
y x  3x  3 . C. 4 2
y  x  2x  3 . D. 4 2
y x  2x  3 .
Câu 10: Trong không gian Oxyz , cho mặt cầu S  : 2 2 2
x y z  2x  6 y  4z  2  0. Xác định tọa độ
tâm I và bán kính R của mặt cầu S  . A. I 1; 3
 ;2, R 16 . B. I 1; 3
 ;2, R  4 . C. I  1  ;3; 2
 , R 16 .D. I  1  ;3; 2
 , R  4 .
Câu 11: Trong không gian Oxyz , góc giữa hai mặt phẳng Oyz và Oxz bằng A. 30 .  B. 90 .  C. 60 .  D. 45 . 
Câu 12: Các điểm M , N , P, Q trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
z , z , z , z . Khi đó w  3z z z z bằng 1 2 3 4 1 2 3 4 y M 2 1 P -3 -1 O 1 2 3 x -2 -1 N Q -2
A. w  6  4i .
B. w  6  4i .
C. w  4  3i .
D. w  3  4i .
Câu 13: Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 1 1 1 A. V Bh . B. V Bh . C. V Bh .
D. V Bh . 2 3 6
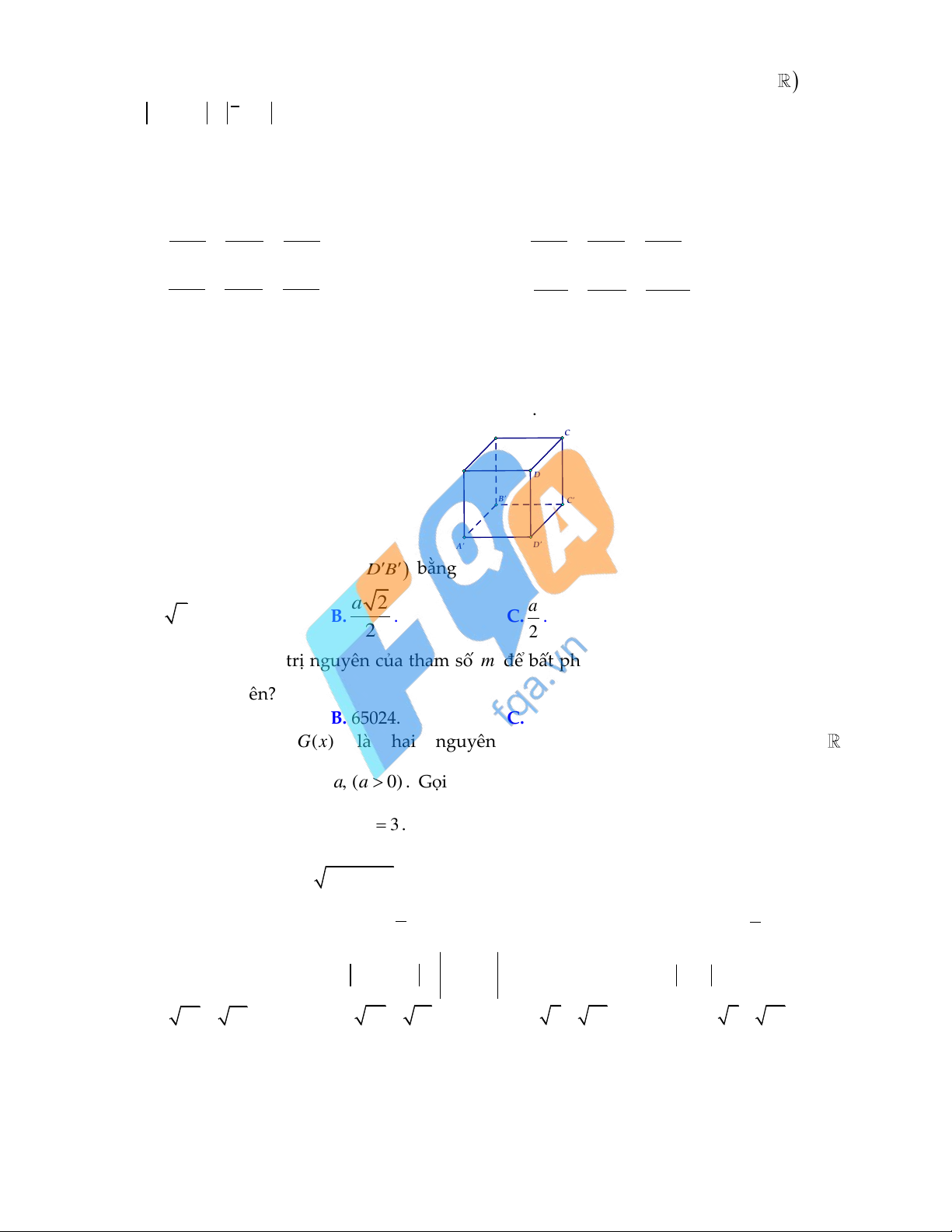
Câu 14: Cho khối hộp chữ nhật ABC . D AB CD
  có AB  2, AD  3, 
AA  4 (tham khảo hình vẽ). A' D' C' B' A D B C
Thể tích khối hộp đã cho bằng A. 24 . B. 20 . C. 9 . D. 8 .
Câu 15: Một khối cầu có bán kính bằng 2 , một mặt phẳng   cắt khối cầu đó theo một hình tròn có
diện tích là 2 . Khoảng cách từ tâm khối cầu đến mặt phẳng   bằng 2 2 A. 2 . B. 1 . C. . D. . 2 4
Câu 16: Môđun của số phức z  3  4i bằng A. 5 . B. 3 . C. 7 . D. 7 .
Câu 17: Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích khối trụ đó là 8 . A. 3 h  32 . B. 3 h  4 . C. h  2 2 . D. h  2 . x 1 y  2 z
Câu 18: Trong không gian Oxyz , điểm nào dưới đây không thuộc đường thẳng d :   2 1 1  ? A. Q 1; 2  ;0 . B. M  1  ;2;0 . C. N  1  ; 3  ;  1 . D. P 3; 1  ;  1 .
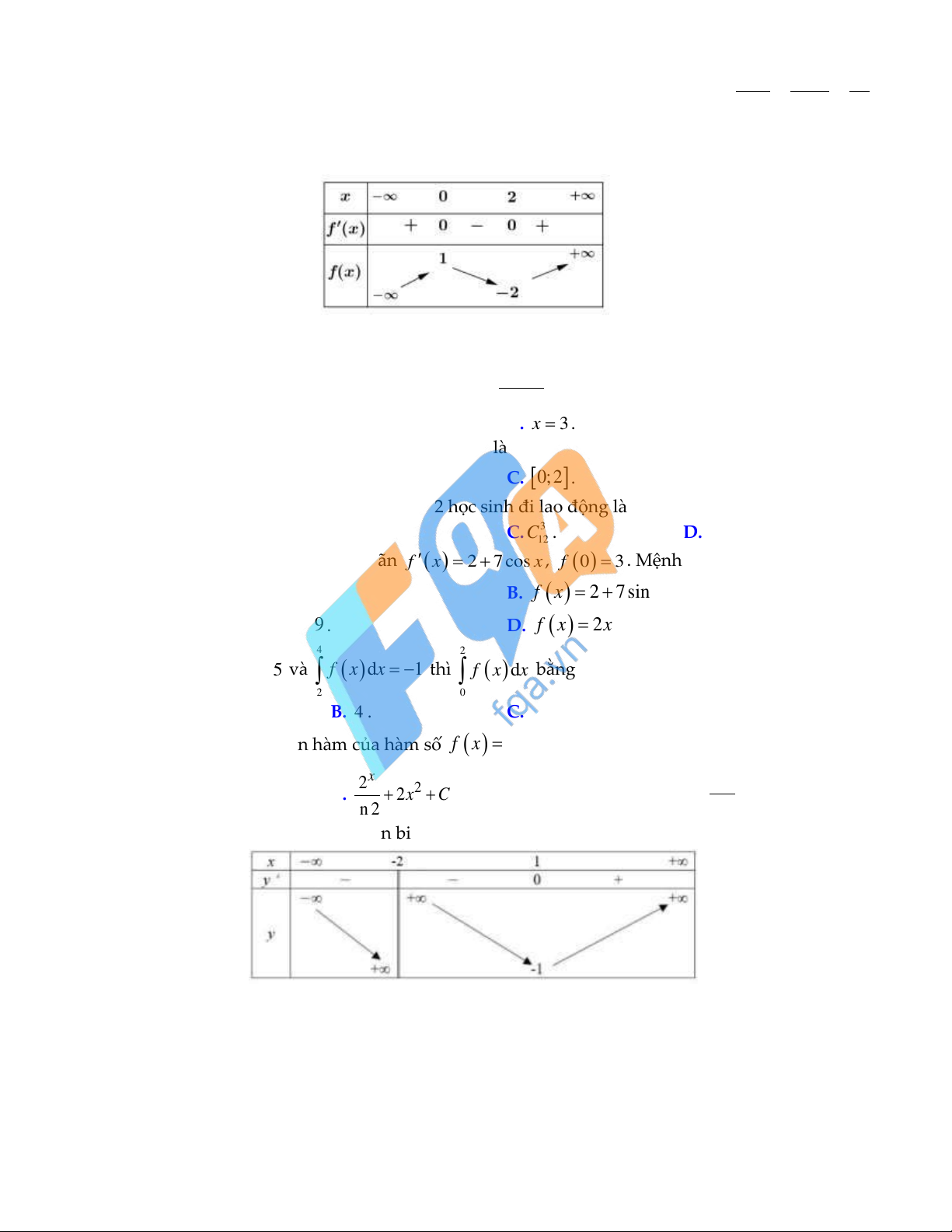
Câu 19: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A. x  2 . B. x  2 . C. x  0 .
D. x  1 . 3x  2
Câu 20: Đường tiệm cận đứng của đồ thị hàm số y  có phương trình là x 1 A. x  2 . B. x  1 . C. x  3 . D. x  1 .
Câu 21: Tập nghiệm của bất phương trình log x  1 là 2 A. (0;1] . B. (; 2] . C. 0; 2. D. (0; 2].
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là A. P . B. 36. C. 3 C . D. 3 A . 12 12 12
Câu 23: Cho hàm số y f x thỏa mãn f  x  2  7 cos x , f 0  3 . Mệnh đề nào dưới đây đúng?
A. f x  2x  7 sin x  3.
B. f x  2  7 sin x  3 .
C. f x  2x  sin x  9 .
D. f x  2x  7 sin x  3. 4 4 2 Câu 24: Nếu f
 xdx  5 và f xdx  1  
thì f xdx  bằng 0 2 0 A. 6 . B. 4 . C. 4  . D. 6  . x
Câu 25: Họ tất cả các nguyên hàm của hàm số f x  2  4x là x 2x 2 A. x 2
2 ln 2  2x C . B. 2  x 2x C .
C. 2 ln 2  C . D. C . ln 2 ln 2
Câu 26: Cho hàm số f x có bảng biến biên dưới đây:
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng  ;    1 .
B. Hàm số đã cho nghịch biến trên khoảng 0;  1 .
C. Hàm số đã cho đồng biến trên khoảng 1;  .
D. Hàm số đã cho nghịch biến trên khoảng 3; 2 .
Câu 27: Cho hàm số f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là A. y  3 . B. y  1. C. y  4 . D. y  4 . Câu 28: Biết 5
y  log x . Khi đó 2 1
A. y  5log x .
B. y  5log x .
C. y  5  log x .
D. y  log x . 2 2 2 5
Câu 29: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  5x  4 và trục Ox . Thể tích của
khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox là 9 81 81 9 A. V  . B. V  . C. V  . D. V  . 2 10 10 2
Câu 30: Cho hình chóp S.ABCD có đáy là hình thoi tâm O , ABD đều cạnh a 2 , SA vuông góc với 3a 2
mặt phẳng đáy và SA
(minh họa như hình bên dưới). 2
Góc giữa đường thẳng SO và mặt phẳng  ABCD bằng A. 45 . B. 30 . C. 60 . D. 90 . 2x  3
Câu 31: Cho hàm số y
có đồ thị (C) và đường thẳng d : y x m . Với tất cả giá trị nào của x  2
m thì d cắt (C) tại hai điểm phân biệt? m  2
A. m  2 .
B. m  2 . C. m  6 . D.  . m  6 2 3
Câu 32: Cho hàm số y f x liên tục trên
, có đạo hàm f  x  2  x  x  2  x  5,x  .
Hàm số y f x nghịch biến trên khoảng nào sau đây? A.  ;  2. B. 5;  . C. 2;5 .
D. 2;  .
Câu 33: Một hộp chứa 10 quả cầu được đánh số theo thứ tự từ 1 đến 10, lấy ngẫu nhiên 5 quả cầu.
Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 bằng 11 5 7 1 A. . B. . C. . D. . 12 12 12 12
Câu 34: Biết phương trình 2 log x  2 log
2x 1  0 có hai nghiệm x , x . Tính x x . 2 2   1 2 1 2 1 1 A. x x  4 . B. x x  . C. x x  .
D. x x  3 . 1 2 1 2 8 1 2 2 1 2
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z x yi  , x y   thỏa mãn
z  2  i z  3i là đường thẳng có phương trình là
A. y x 1.
B. y  x 1.
C. y x 1.
D. y  x 1 .
Câu 36: Trong không gian Oxyz , đường thẳng d qua M  3
 ;5;6 và vuông góc với mặt phẳng
P:2x 3y  4z  2  0 thì đường thẳng d có phương trình là x  3 y  5 z  6 x  3 y  5 z  6 A.     . 2 3  . B. 4 2 3 4 x  3 y  5 z  6 x 1 y  2 z 10 C.     . 2 3  4  . D. 2 3  4
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua mặt phẳng Oxz có tọa độ là A. 1; 2;3 . B. 1; 2; 3  . C.  1  ;0; 3   . D. 1; 2;3 .
Câu 38: Cho hình lập phương ABC . D AB CD   có cạnh a . B C A D B' C' A' D'
Khoảng cách từ A đến  BDD B   bằng a 2 a A. 2a . B. . C. . D. a . 2 2 2 2 
Câu 39: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình 3x x 92x m  0 có 5 nghiệm nguyên? A. 65021. B. 65024. C. 65022. D. 65023. Câu 40: Biết
F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên và 3 ( )  (3)  (0)  , (  0)  f x dx F G a a
. Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y F (x), y G(x), x  0 và x  3 . Khi S  15 thì a bằng A. 15 . B. 12 . C. 18 . D. 5 . Câu 41: Hàm số 2
y x mx x m  2 đồng biến trên tập xác định khi và chỉ khi  5  5 
A. m  (1; ) . B. m  ;  m   m  ; 2  . C. [1; ) . D.   .   2 
Câu 42: Cho số phức z thỏa mãn z   i    i _ 2 3 1
z . Giá trị lớn nhất của z 1 bằng A. 38  13 . B. 26  13 . C. 3 2  38 . D. 3 2  26 .
Câu 43: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a . Tam giác SAD cân tại S và
mặt bên  SAD vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 3 a .
Tính khoảng cách từ điểm B đến mặt phẳng  SCD . 6a a 3a A. . B. . C. 3a . D. . 37 37 37
Câu 44: Cho đường cong C  3
: y x . Xét điểm A có hoành độ dương thuộc đồ thị C  . Tiếp tuyến
của C  tại A tạo với C  một hình phẳng có diện tích bằng 27 . Hoành độ của điểm A
thuộc khoảng nào dưới đây?  1   1   3   3  A. 0;   . B. ;1   . C. 1;   D. ; 2   .  2   2   2   2 
Câu 45: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
z  2mz  6m  5  0 có hai
nghiệm phức phân biệt z , z thỏa mãn z z ? 1 2 1 2 A. 5 . B. 4 . C. 6 . D. 3 .
Câu 46: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2;  1 , B 3;4; 
1 . Đường thẳng AB MB cắt mặt phẳng  z
Ox  tại M . Tỉ số bằng MA 1 A. 2 . B. . C. 1. D. 3 . 2 Câu 47: Cho hàm số 1 2x y   và 2x y
 2 có đồ thị như hình vẽ bên. Diện tích tam giác ABC bằng 3 3 A. 3 . B. . C. . D. 6 . 2 4
Câu 48: Cho một hình trụ có chiều cao bằng 6 và bán kính bằng 5. Lấy hai điểm A và A' thuộc hai
đường tròn đáy khác nhau của hình trụ và AA '  10 . Khoảng cách giữa đường thẳng AA' và
trục của hình trụ đã cho bằng A. 3 . B. 2 21 . C. 5 . D. 4 21 .
Câu 49: Trong không gian Oxyz, cho điểm A 
1;1;1 , mặt phẳng  P : x y z  3  0 và đường thẳng x  2 y z d :  
. Xét đường thẳng  qua A , nằm trong mặt phẳng  P và cách đường 1 2 1 
thẳng d một khoảng lớn nhất. Đường thẳng  đi qua điểm nào dưới đây?
A. M 2 ;1;0 .
B. N 1; 1;3 . C. P  3  ;3;3
D. Q 1; 2; 4 .
Câu 50: Cho hàm số y f x có đạo hàm f x 2
x x   2 ' 2
x mx  5, x
  . Số giá trị nguyên
âm của m để hàm số g x  f  2
x x  2 đồng biến trên khoảng 1;   là A. 3 . B. 4 . C. 5 . D. 7 .
________________________HẾT________________________
Huế, 13h30’ Ngày 02 tháng 3 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ Bé §Ò VÒ §ÝCH ¤N THI THPT QuèC GIA 2023
Thời gian làm bài: 90 phút
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
Theo Ma trận Đề tham khảo 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ.
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức z  2  3i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z là điểm có tọa độ là A. 2;3 .
B. 3;  2 . C. 3; 2 . D. 2;  3 . Lời giải:
Câu 2: Đạo hàm của hàm số 10x y  là 10x A. y  . B. 10x y  .ln10 . C. 10x y  . D.   10x y log e . ln10 10 Lời giải: 10x  10 .x y y ln10 .
Câu 3: Tập xác định D của hàm số y    x13 2 là
A. D   ;  2. B. D   ;  .
C. D   ;  2 .
D. D  2;  . Lời giải:
Tập xác định: 2  x  0  x  2
Vậy tập xác định của hàm số là D   ;  2 .
Câu 4: Bất phương trình 3x  81  0 có tất cả bao nhiêu nghiệm nguyên dương? A. 3 . B. 4 . C. vô số. D. 5 . Lời giải: * Ta có: 3x 81 0 3x 81 x 4 x        x1;2;3;  4 .
Câu 5: Cho cấp số nhân (u ) với u  1 và u  8 . Công bội của cấp số nhân đã cho bằng n 1 4 A. 2. B. 7. C. 8. D. 4. Lời giải: Ta có: 3 3
u u .q q  8  q  2. 4 1
Câu 6: Trong không gian Oxyz , cho mặt phẳng  P : x  4 y  3z  2  0. Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng  P ? A. n  1 4 3 n  1 4 3 n   n  1 4 3 2  ; ;  . B. 3  ; ; . C. 1; 4;3 . D. 1  ; ;  . 4   Lời giải:
Mặt phẳng  P : x  4 y  3z  2  0 có một vectơ pháp tuyến là n  1 4 3 2  ; ;  . ax b
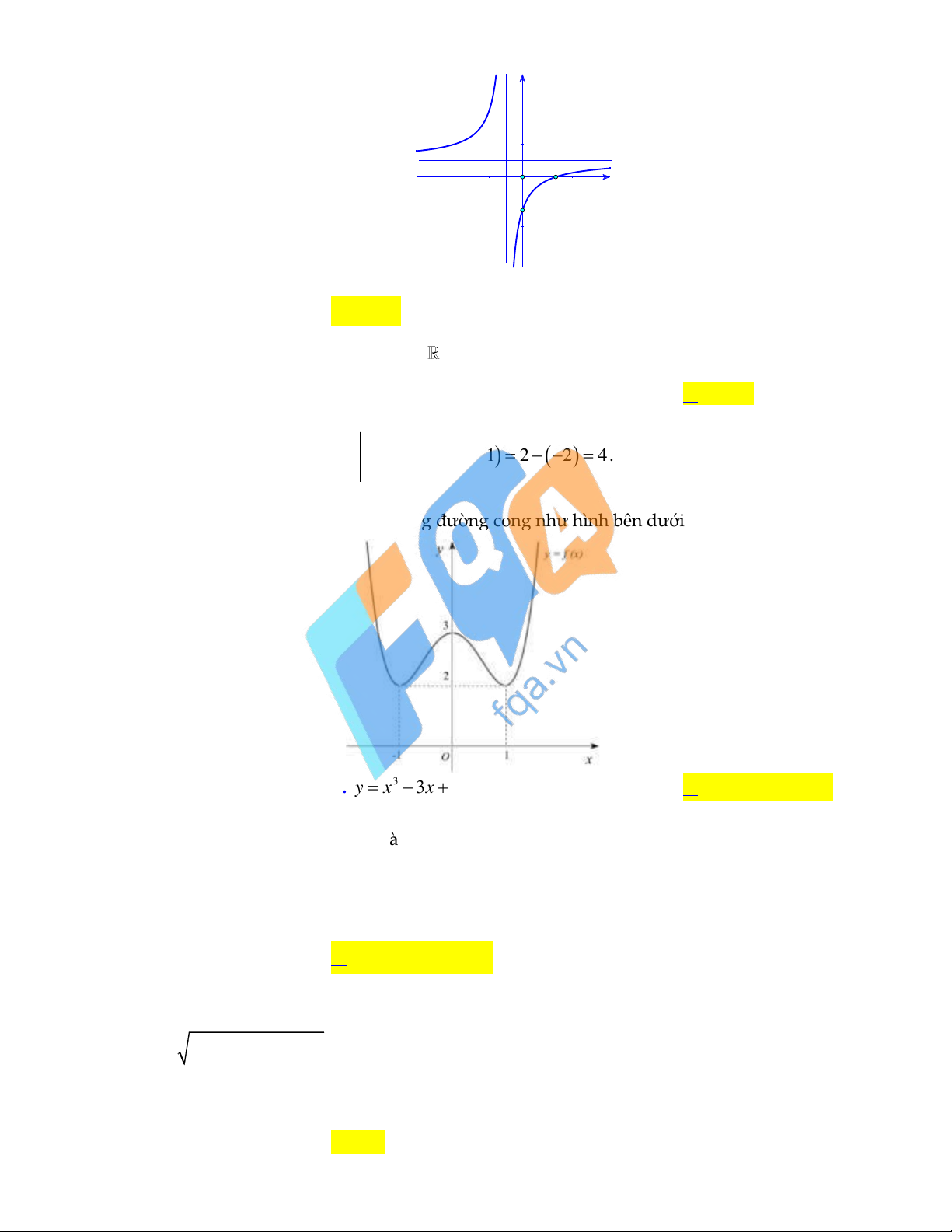
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d y O 2 x -2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là A. 0; 2 . B. 2;0 . C. 2;0 . D. 0; 2 . 3
Câu 8: Cho hàm số f x có đạo hàm trên , f   1  2
 và f 3  2. Tính I f   xdx. 1  A. I  4. B. I  0. C. I  3. D. I  4. Lời giải: 3 3 Ta có I f
 xdx f x  f 3 f  1  2 2    4 1  . 1  Vậy I  4 .
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới? A. 4 2
y  x  2x  3 . B. 3
y x  3x  3 . C. 4 2
y  x  2x  3 . D. 4 2
y x  2x  3 . Lời giải:
Nhìn hình vẽ ta thấy là đồ thị hàm bậc 4 trùng phương f x  4 2
ax bx c a  0 có hệ số a
dương. Do vậy chọn đáp án D.
Câu 10: Trong không gian Oxyz , cho mặt cầu S  : 2 2 2
x y z  2x  6 y  4z  2  0. Xác định tọa độ
tâm I và bán kính R của mặt cầu S  . A. I 1; 3
 ;2, R 16 . B. I 1; 3
 ;2, R  4 . C. I  1  ;3; 2
 , R 16 .D. I  1  ;3; 2
 , R  4 . Lời giải:
Ta có mặt cầu  S  : 2 2 2
x y z  2x  6 y  4z  2  0. có tâm I 1; 3  ;2 và bán kính R    2 2 2 1 3  2  2  4 .
Vậy mặt cầu S  có tâm I 1; 3
 ;2 và bán kính R  4 .
Câu 11: Trong không gian Oxyz , góc giữa hai mặt phẳng Oyz và Oxz bằng A. 30 .  B. 90 .  C. 60 .  D. 45 . 
Câu 12: Các điểm M , N , P, Q trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
z , z , z , z . Khi đó w  3z z z z bằng 1 2 3 4 1 2 3 4 y M 2 1 P -3 -1 O 1 2 3 x -2 -1 N Q -2
A. w  6  4i .
B. w  6  4i .
C. w  4  3i .
D. w  3  4i . Lời giải:
Ta có z  3  2i; z  2
  i; z  3 ;i z  2  2i . 1 2 3 4
Suy ra w  3z z z z  3 3   2i  2
  i  3 i  2  2i  6   4i . 1 2 3 4        
Câu 13: Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 1 1 1 A. V Bh . B. V Bh . C. V Bh .
D. V Bh . 2 3 6
Câu 14: Cho khối hộp chữ nhật ABC . D AB CD
  có AB  2, AD  3, 
AA  4 (tham khảo hình vẽ). A' D' C' B' A D B C
Thể tích khối hộp đã cho bằng A. 24 . B. 20 . C. 9 . D. 8 . Lời giải:
Thể tích khối hộp chữ nhật đã cho bằng: V  2.3.4  24 .
Câu 15: Một khối cầu có bán kính bằng 2 , một mặt phẳng   cắt khối cầu đó theo một hình tròn có
diện tích là 2 . Khoảng cách từ tâm khối cầu đến mặt phẳng   bằng 2 2 A. 2 . B. 1 . C. . D. . 2 4 Lời giải:
Gọi O, H lần lượt là tâm khối cầu và tâm hình tròn. R ,r lần lượt là bán kính mặt cầu và bán kính hình tròn. S  Diện tích hình tròn 2 2
s   r r    2   .
Gọi h là khoảng cách từ tâm khối cầu đến mặt phẳng   suy ra 2 2
h R r  2.
Câu 16: Môđun của số phức z  3  4i bằng A. 5 . B. 3 . C. 7 . D. 7 . Lời giải: Ta có: 3 2 z  3  4  5 .
Câu 17: Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích khối trụ đó là 8 . A. 3 h  32 . B. 3 h  4 . C. h  2 2 . D. h  2 . Lời giải:
Gọi R là bán kính của hình trụ khi đó R h . V 8
Ta có thể tích khối trụ là 2 3
V   R h   h 3  h    8  h  2   .
Vậy chiều cao của khối trụ là h  2 . x 1 y  2 z
Câu 18: Trong không gian Oxyz , điểm nào dưới đây không thuộc đường thẳng d :   2 1 1  ? A. Q 1; 2  ;0 . B. M  1  ;2;0 . C. N  1  ; 3  ;  1 . D. P 3; 1  ;  1 . Lời giải: a b c
Điểm I a b c 1 2 ; ; d    2 1 1  đúng. Kiểm tra các điểm ;
Q M ; N; P trong các phương án A, B, C, D ta thay điểm M  1  ;2;0 vào 1  1 2  2 0
phương trình d ta có:   2 1 1
 (vô lý) . Vậy điểm M không thuộc đường thẳng d .
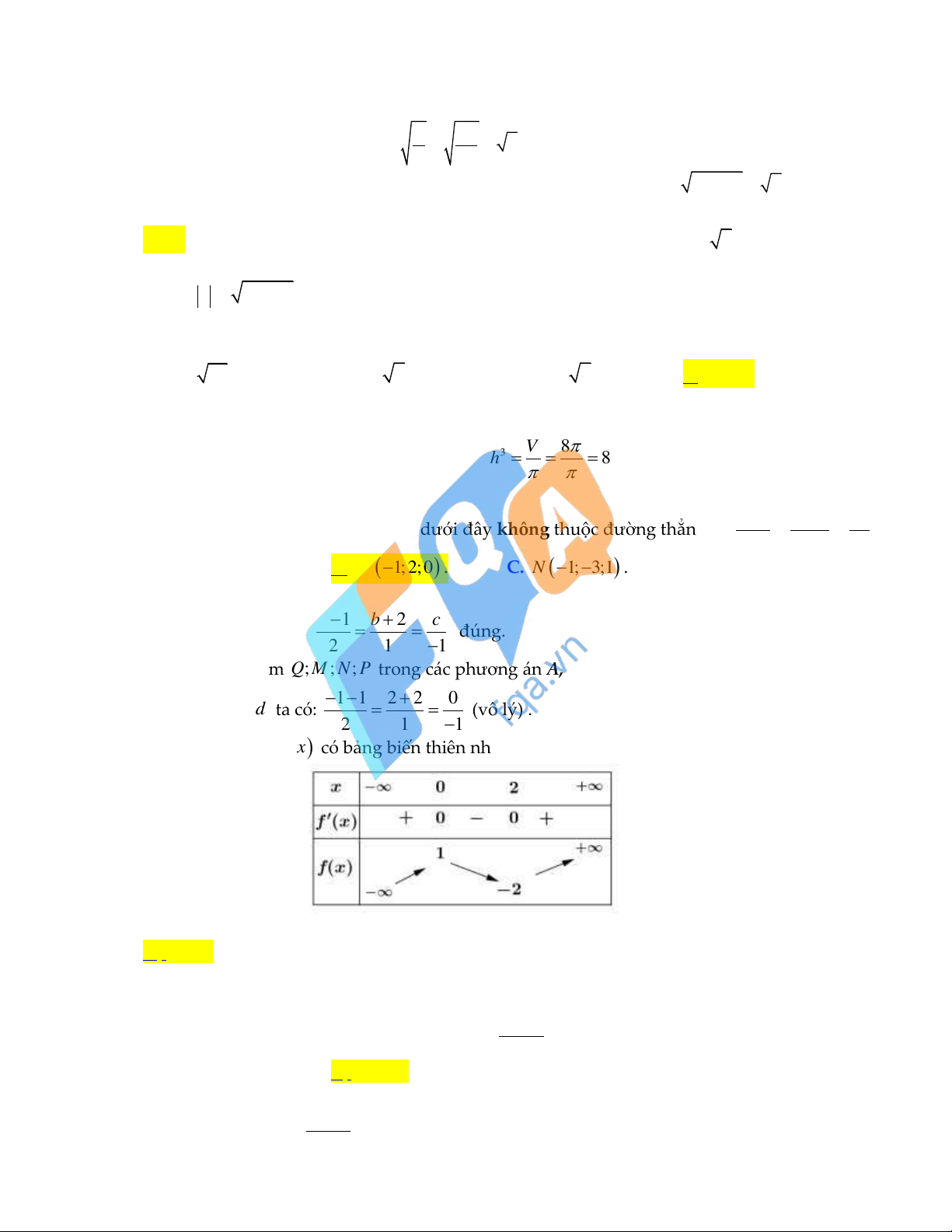
Câu 19: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A. x  2 . B. x  2 . C. x  0 .
D. x  1 . Lời giải:
Vì y đổi dấu từ âm sang dương duy nhất tại x  2 nên hàm số đã cho đạt cực tiểu tại x  2 3x  2
Câu 20: Đường tiệm cận đứng của đồ thị hàm số y  có phương trình là x 1 A. x  2 . B. x  1 . C. x  3 . D. x  1 . Lời giải: 3x  2 Ta có: lim y  lim   .   x (  1  ) x (  1  ) x  1
Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng x  1 .
Câu 21: Tập nghiệm của bất phương trình log x  1 là 2 A. (0;1] . B. (; 2] . C. 0; 2. D. (0; 2]. Lời giải:
Điều kiện: x  0. x  0
Bất phương trình đã cho tương đương   0  x  2 x  2
Vậy tập nghiệm của bất phương trình là S  (0; 2].
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là A. P . B. 36. C. 3 C . D. 3 A . 12 12 12 Lời giải:
Cách chọn 3 học sinh trong 12 học sinh không xếp thứ tự là tổ hợp chập 3 của 12: 3 C 12
Câu 23: Cho hàm số y f x thỏa mãn f  x  2  7 cos x , f 0  3 . Mệnh đề nào dưới đây đúng?
A. f x  2x  7 sin x  3.
B. f x  2  7 sin x  3 .
C. f x  2x  sin x  9 .
D. f x  2x  7 sin x  3. Lời giải:
Ta có: f x  2  7cos xdx  2x  7sin x C .
Mặt khác: f 0  3  C  3  f x  2x  7 sin x  3 . 4 4 2 Câu 24: Nếu f
 xdx  5 và f xdx  1  
thì f xdx  bằng 0 2 0 A. 6 . B. 4 . C. 4  . D. 6  . Lời giải: 4 2 4 2 4 4 Ta có f
 xdx f
 xdxf
 xdx f
 xdx f
 xdx f  xdx 5     1  6 . 0 0 2 0 0 2 x
Câu 25: Họ tất cả các nguyên hàm của hàm số f x  2  4x là x 2x 2 A. x 2
2 ln 2  2x C . B. 2  x 2x C .
C. 2 ln 2  C . D. C . ln 2 ln 2 Lời giải: 2x x Ta có f
 xdx  2 4x 2 dx   2x C . ln 2
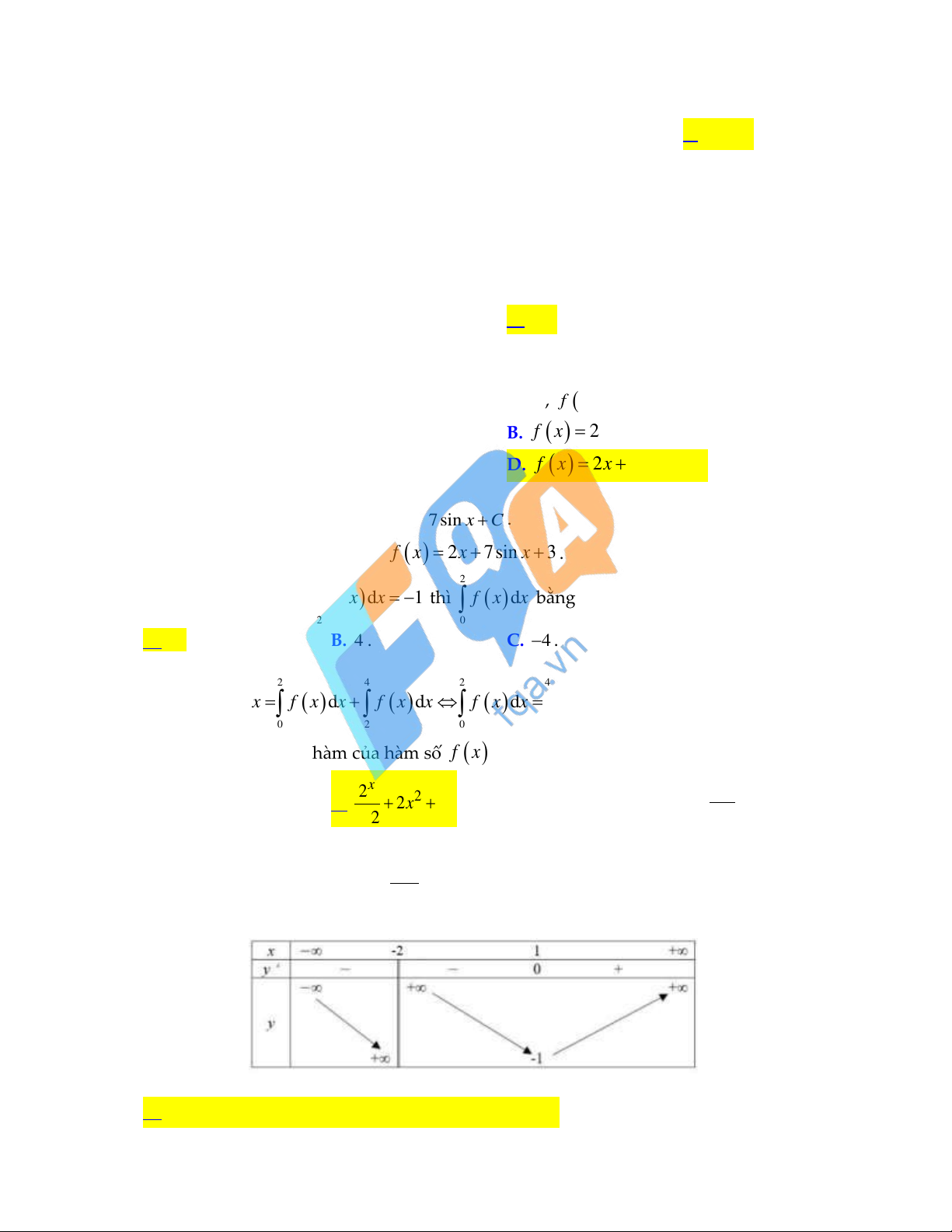
Câu 26: Cho hàm số f x có bảng biến biên dưới đây:
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng  ;    1 .
B. Hàm số đã cho nghịch biến trên khoảng 0;  1 .
C. Hàm số đã cho đồng biến trên khoảng 1;  .
D. Hàm số đã cho nghịch biến trên khoảng 3; 2 . Lời giải:
Câu A: Sai vì hàm số không liên tục từ  ;    1 .
Câu B: Đúng vì hàm số nghịch biến trên khoảng 2;  1 và khoảng 2;  1 chứa khoảng
0; 1 Câu C: Đúng quá rõ ràng.
Câu D: Đúng vì hàm số nghịch biến trên khoảng  ;
 2và khoảng  ;  2chứa khoảng 3;2
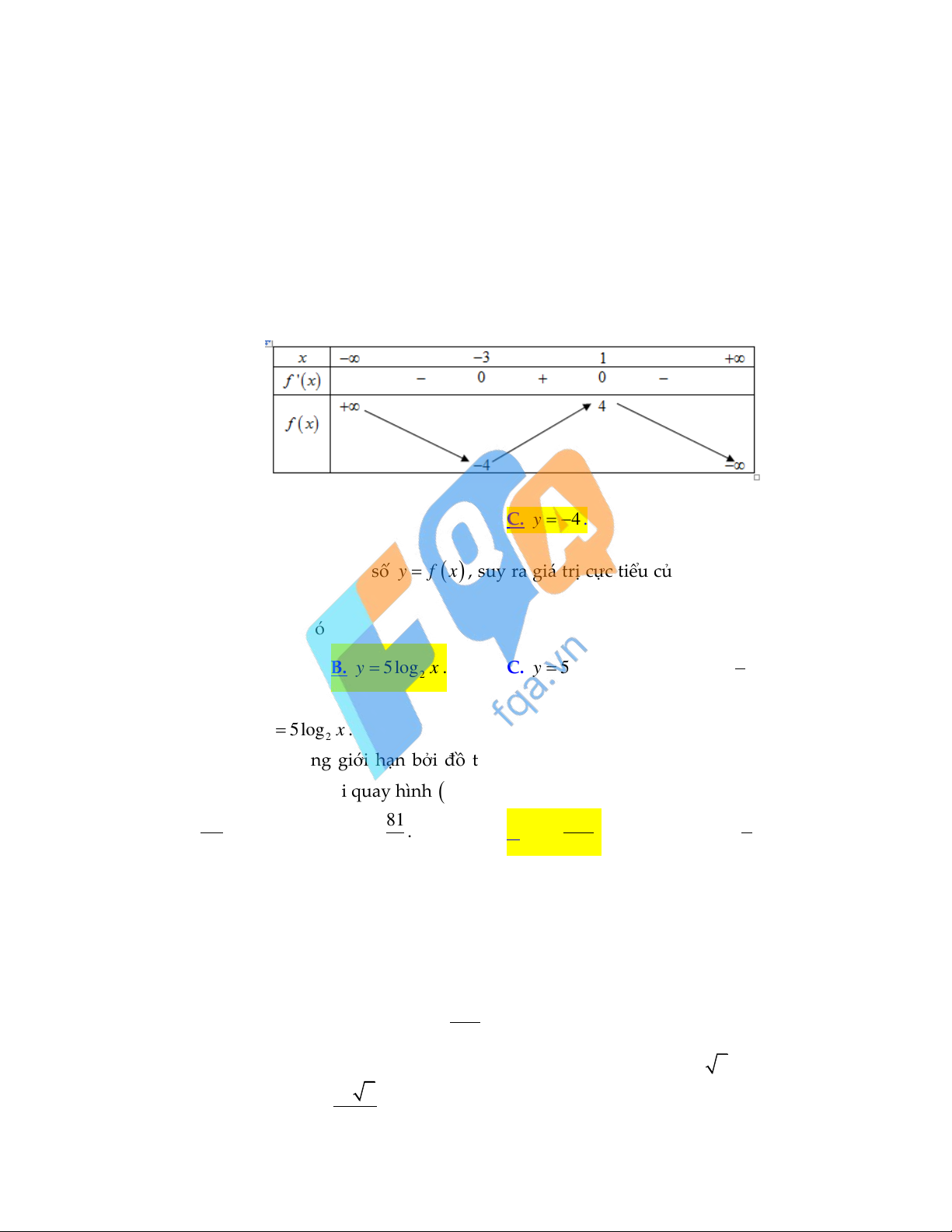
Câu 27: Cho hàm số f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là A. y  3 . B. y  1. C. y  4 . D. y  4 . Lời giải:
Từ bảng biến thiên của hàm số y f x , suy ra giá trị cực tiểu của hàm số là y  4 (đạt tại x  3) . Câu 28: Biết 5
y  log x . Khi đó 2 1
A. y  5log x .
B. y  5log x .
C. y  5  log x .
D. y  log x . 2 2 2 5 Lời giải: Ta có 5
y  log x  5 log x . 2 2
Câu 29: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  5x  4 và trục Ox . Thể tích của
khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox là 9 81 81 9 A. V  . B. V  . C. V  . D. V  . 2 10 10 2 Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số 2
y x  5x  4 và trục Ox ta có: x 1 2
x  5x  4  0   x  4
Thể tích của khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox 4 4  V  
f xdx    x  5x  42 81 2 2 dx    . 10 1 1
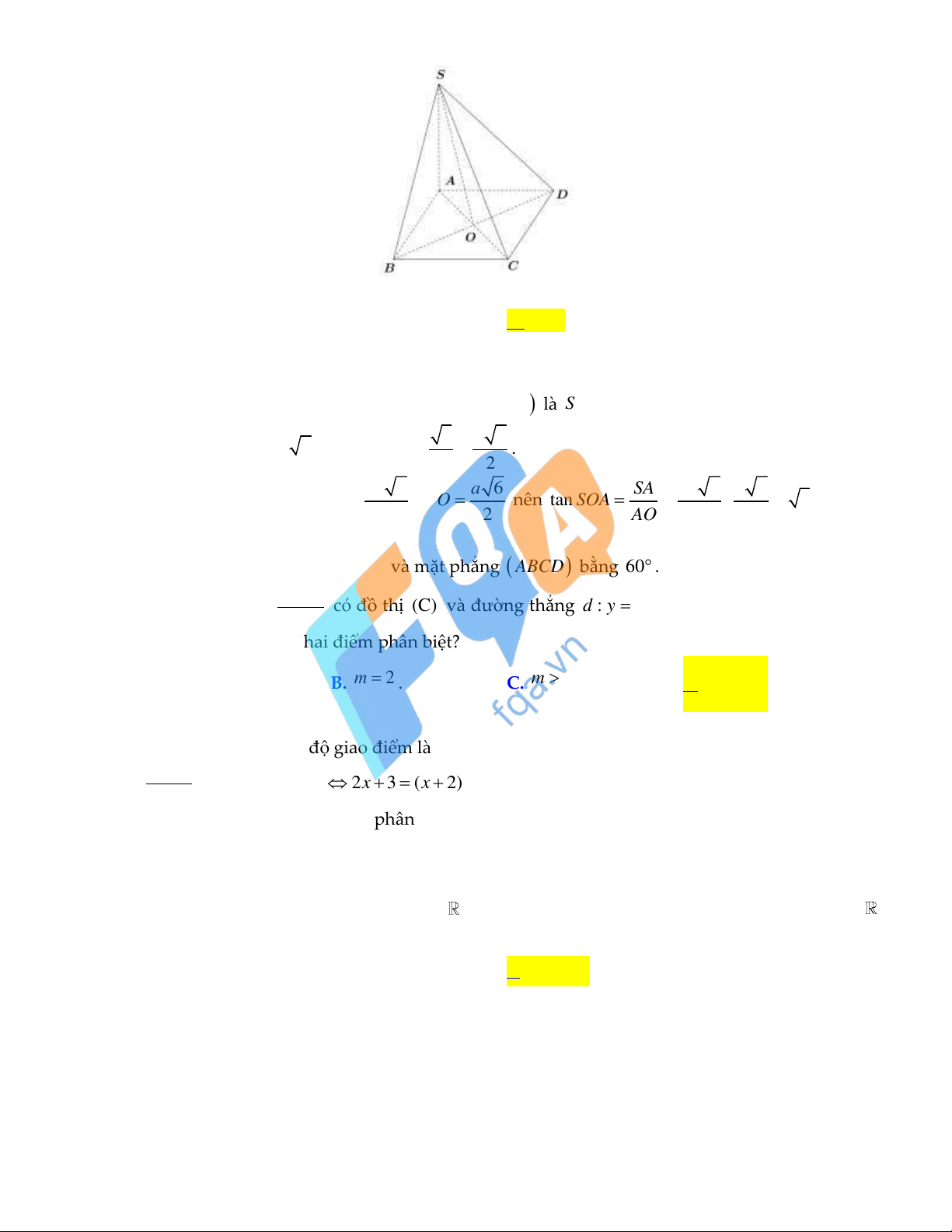
Câu 30: Cho hình chóp S.ABCD có đáy là hình thoi tâm O , ABD đều cạnh a 2 , SA vuông góc với 3a 2
mặt phẳng đáy và SA
(minh họa như hình bên dưới). 2
Góc giữa đường thẳng SO và mặt phẳng  ABCD bằng A. 45 . B. 30 . C. 60 . D. 90 . Lời giải:
Do SA   ABCD nên hình chiếu vuông góc của SO lên mặt phẳng  ABCD là AO . Khi đó
góc giữa đường thẳng SO và mặt phẳng  ABCD là SOA .  3 a 6
ABD đều cạnh a 2 nên AO AB  . 2 2  3a 2 a 6 SA 3a 2 a 6
SOA vuông tại A có SA  , AO  nên tan SOA   :  3 2 2 AO 2 2  SOA  60.
Vậy góc giữa đường thẳng SO và mặt phẳng  ABCD bằng 60 . 2x  3
Câu 31: Cho hàm số y
có đồ thị (C) và đường thẳng d : y x m . Với tất cả giá trị nào của x  2
m thì d cắt (C) tại hai điểm phân biệt? m  2
A. m  2 .
B. m  2 . C. m  6 . D.  . m  6 Lời giải:
Phương trình hoành độ giao điểm là 2x  3 2
x m (x  2
 )  2x  3  (x  2)(x  )
m x mx  2m  3  0 (1) x  2
Để d cắt (C) tại hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân   0 m  2 biệt khác 2     .  2 ( 2
 )  2m  2m  3  0 m  6 2 3
Câu 32: Cho hàm số y f x liên tục trên
, có đạo hàm f  x  2  x  x  2  x  5,x  .
Hàm số y f x nghịch biến trên khoảng nào sau đây? A.  ;  2. B. 5;  . C. 2;5 .
D. 2;  . Lời giải: x  2 2 3 
Xét phương trình f  x  0  2  x  x  2  x  5  0  x  2  .  x  5  Bảng xét dấu:
Suy ra hàm số y f (x) nghịch biến trên khoảng 2;5 .
Câu 33: Một hộp chứa 10 quả cầu được đánh số theo thứ tự từ 1 đến 10, lấy ngẫu nhiên 5 quả cầu.
Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 bằng 11 5 7 1 A. . B. . C. . D. . 12 12 12 12 Lời giải:
Số phần tử của không gian mẫu n  5  C . 10
Gọi A là biến cố: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó chia hết cho 3”
 Biến cố A : “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó không chia hết cho 3”
Tính n A :
Để tích các số trên 5 quả cầu được chọn không chia hết cho 3 thì trong 5 quả cầu đó không có
các quả cầu mang số 3, 6, 9. Vậy n A 5  C . 7
P AnA 5 C 1 7    . n  5 C 12 10
PA   PA 11 1  . 12
Câu 34: Biết phương trình 2 log x  2 log
2x 1  0 có hai nghiệm x , x . Tính x x . 2 2   1 2 1 2 1 1 A. x x  4 . B. x x  . C. x x  .
D. x x  3 . 1 2 1 2 8 1 2 2 1 2 Lời giải:
ĐKXĐ: x  0 . Ta có 2
log x  2 log 2x 2
1  0  log x  2log x  3  0 2 2 2 2  1 log x  1  x  2     2 log x  3   2 x  8
Vậy x x  4 . 1 2
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z x yi  , x y   thỏa mãn
z  2  i z  3i là đường thẳng có phương trình là
A. y x 1.
B. y  x 1.
C. y x 1.
D. y  x 1 . Lời giải:
z  2  i z  3i   x  2   y  
1 i x   y  3i
 x  2   y  2  x   y  2 2 2 2 2 2 2 1 3
x  4x  4  y  2y 1 x y  6y  9
4 y  4x  4  y x 1.
Câu 36: Trong không gian Oxyz , đường thẳng d qua M  3
 ;5;6 và vuông góc với mặt phẳng
P:2x 3y  4z  2  0 thì đường thẳng d có phương trình là x  3 y  5 z  6 x  3 y  5 z  6 A.     . 2 3  . B. 4 2 3 4 x  3 y  5 z  6 x 1 y  2 z 10 C.     . 2 3  4  . D. 2 3  4 Lời giải:
Ta có  P : 2x  3y  4z  2  0 có vectơ pháp tuyến n  2; 3  ;4.
d   P  d nhận vectơ pháp tuyến của  P làm vectơ chỉ phương.
Do đó đường thẳng d qua M  3
 ;5;6 và có vectơ chỉ phương u  2; 3  ;4.
Kiểm tra phương án D thỏa mãn.
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua mặt phẳng Oxz có tọa độ là A. 1; 2;3 . B. 1; 2; 3  . C.  1  ;0; 3   . D. 1; 2;3 .
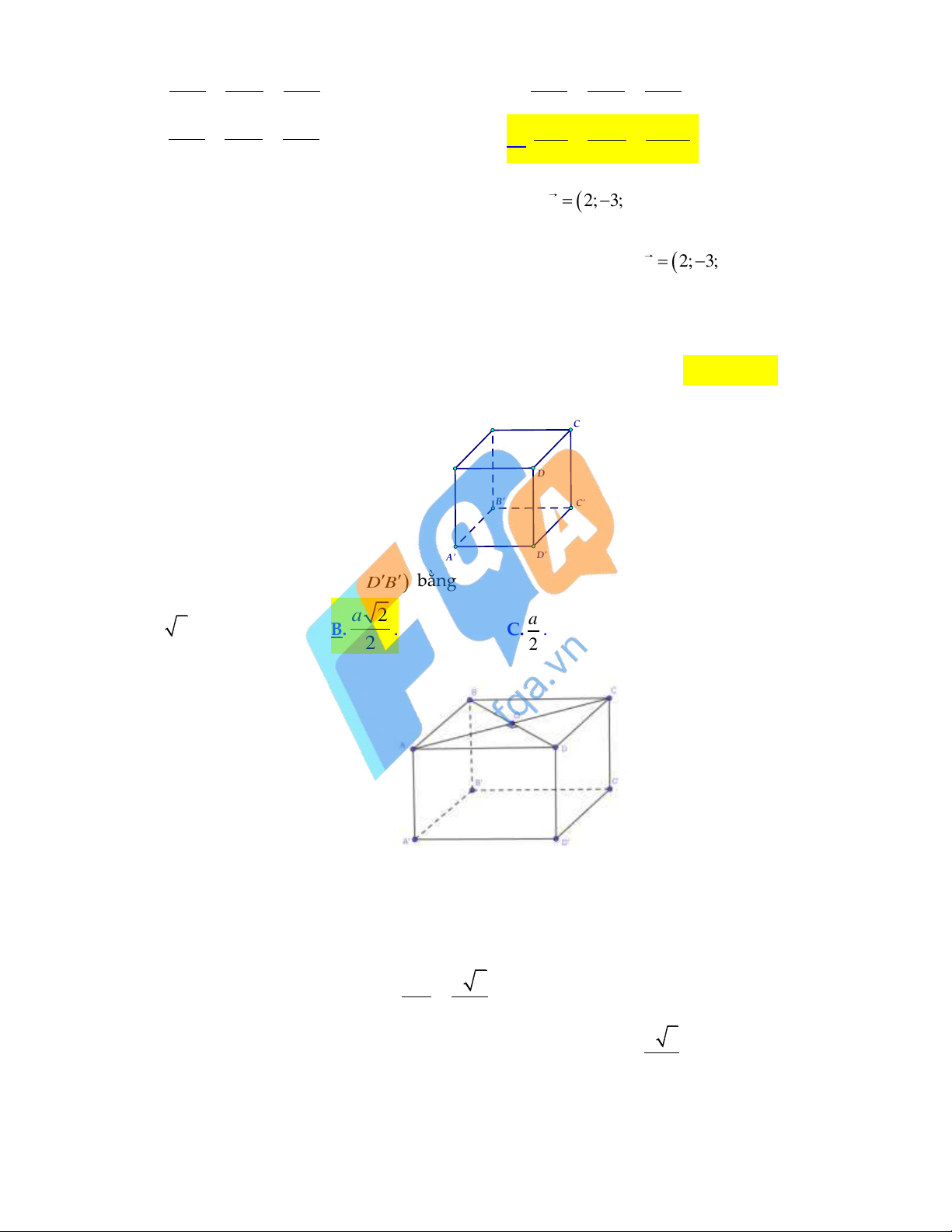
Câu 38: Cho hình lập phương ABC . D AB CD   có cạnh a . B C A D B' C' A' D'
Khoảng cách từ A đến  BDD B   bằng a 2 a A. 2a . B. . C. . D. a . 2 2 Lời giải:
Trong  ABCD , gọi O AC BD .
Hình lập phương ABC . D AB CD
  có DD   ABCD . Suy ra DD  AC .
Mà ABCD là hình vuông nên AC BD .
Do đó, AC   BDD B
  . Lại có, AC BDD B    O . AC a 2
Xét hình vuông ABCD có AO   . 2 2 a
Nên khoảng cách từ A đến  d  , A BDD B    2 BDD B   là    AO  . 2 2 2 
Câu 39: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình 3x x 92x m  0 có 5 nghiệm nguyên? A. 65021. B. 65024. C. 65022. D. 65023. Lời giải: 2
TH1: x x 2 3
 9  0  x x  2  1
  x  2
Bất phương trình đã cho không thể có 5 nghiệm nguyên. 2 3x x   9  0 TH2:
: không thoả mãn bất phương trình có 5 nghiệm nguyên.’ 2
2x m  0 x  1 2 3x x   9  0  TH3:   x  2 2
2x m  0  2 x  log m  2
Để bất phương trình đã cho có 5 nghiệm nguyên thì 3  log m  4  m  512;65536 2  
Vậy có 65024 giá trị nguyên của m để bất phương trình đã cho có 5 nghiệm nguyên. Câu 40: Biết
F (x) và G(x) là hai nguyên hàm của hàm số f (x) trên và 3 ( )  (3)  (0)  , (  0)  f x dx F G a a
. Gọi S là diện tích hình phẳng giới hạn bởi các đường 0
y F (x), y G(x), x  0 và x  3 . Khi S  15 thì a bằng A. 15 . B. 12 . C. 18 . D. 5 . Lời giải:
Ta có: F (x),G(x) là nguyên hàm của f (x)  F (x)  G(x)  C 3 3 3
S F(x)  G(x) dx C dx Cdx  3C 15  C  5  C  5     0 0 0 3
f (x)dx F (3)  F (0)  F (3)  (G(0)  C)  F (3)  G(0)  C F (3)  G(0)  a  0
a  C  5 (do a  0 ) Câu 41: Hàm số 2
y x mx x m  2 đồng biến trên tập xác định khi và chỉ khi  5  5 
A. m  (1; ) . B. m  ;  m   m  ; 2  . C. [1; ) . D.   .   2  Lời giải:
Điều kiện: x m  2  0  x m  2 1
Ta có: y  2x m   0, x   m  2 2 x m  2 1
y  2x  2m  4 
m  4  0, x   m  2 2 x m  2
Đặt t x m  2,t  0 Ta có: 2 1 y  2t
m  4  0, t   0 2 1  m  2
t t  4 2t 2 1 1 Đặt g t 2 1  2  t
 4  gt  4  t   0  t  2t 2 2t 2 Bảng biến thiên: 1  gt 5 max  t . 2 khi  2 5 Vậy m  2 .
Câu 42: Cho số phức z thỏa mãn z   i    i _ 2 3 1
z . Giá trị lớn nhất của z 1 bằng A. 38  13 . B. 26  13 . C. 3 2  38 . D. 3 2  26 . Lời giải:
Gọi z x yi x, y   có điểm biểu diễn là M x ; y . _ 2 2
Ta có z   i    iz   x     y     2 2 x y  2 2 2 3 1 2 3 2
x y  4x  6y 13  0   1 . Nhận thấy  
1 là phương trình của đường tròn C  có tâm I 2;3 và bán kính R  26 .
Mặt khác z    x  2 2 1
1  y MA với M  C  còn A1;0 nằm trong đường tròn C  . Do đó z 1
R IA  26  3 2 . max
Câu 43: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a . Tam giác SAD cân tại S và
mặt bên  SAD vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 3 a .
Tính khoảng cách từ điểm B đến mặt phẳng  SCD . 6a a 3a A. . B. . C. 3a . D. . 37 37 37 Lời giải:
Gọi M là trung điểm AD .
Vì tam giác SAD cân tại S và mặt bên  SAD vuông góc với mặt phẳng đáy nên
SM   ABCD . 3 1 3V 3a Ta có: VS . ABCD SM SM    3a . ABCD ABCD 2 3 S a ABCD
Ta có: AB//CD AB// SCD  d B ,SCD  d A,SCD
Mà d A,SCD  2d M ,SCD (do M là trung điểm AD )
Nên d B ,SCD  2d M ,SCD   1 .
Ta có: CD AD (gt), CD SM (vì SM   ABCD )  CD  SAD .
Trong tam giác SMD , gọi H là hình chiếu vuông góc của M lên cạnh SD .
Khi đó ta có: HM SD và HM CD (vì CD  SAD mà HM  SAD )
HM  SCD  d M ,SCD  MH 2 .
Trong SMD vuông tại M , đường cao MH có: 1 1 1 1 1 37      3aMH  . 2 2 2 MH SM MD 3a2 2 2  1  9a 37 a    2  a Từ  
1 và 2 suy ra d B SCD 6 ,  . 37
Câu 44: Cho đường cong C  3
: y x . Xét điểm A có hoành độ dương thuộc đồ thị C  . Tiếp tuyến
của C  tại A tạo với C  một hình phẳng có diện tích bằng 27 . Hoành độ của điểm A
thuộc khoảng nào dưới đây?  1   1   3   3  A. 0;   . B. ;1   . C. 1;   D. ; 2   .  2   2   2   2  Lời giải: Xét A 3
a ; a C ,a  0  tiếp tuyến tại 2 A
y a x a 3 2 3 : 3
a  3a x  2a
Phương trình hoành độ giao điểm:  
x a x a x a x a
 x a2 x a 3 2 3 3 2 3 3 2 3 2 0
x  2a  0   x  2  a a a 27 3 2 3  S
x  3a x  2a dx     3 2 3
x  3a x  2a  4 dx
a  27  a  2 a  0 . 4 2  a 2  a
Câu 45: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
z  2mz  6m  5  0 có hai
nghiệm phức phân biệt z , z thỏa mãn z z ? 1 2 1 2 A. 5 . B. 4 . C. 6 . D. 3 . Lời giải: 2
z  2mz  6m  5  0 *
+ TH1 : Ycbt  Phương trình * có hai nghiệm thực phân biệt z , z thỏa mãn z z 1 2 1 2
z  z z z  0  m  0 . 1 2 1 2 + TH2 : Ycbt  2
  m  6m  5  0  1  m  5 . Vì m   m2;3;  4 .
Vậy có tất cả 4 giá trị m cần tìm.
Câu 46: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2;  1 , B 3;4; 
1 . Đường thẳng AB MB cắt mặt phẳng  z
Ox  tại M . Tỉ số bằng MA 1 A. 2 . B. . C. 1. D. 3 . 2 Lời giải: x 1 t  Ta có AB  2; 2
 ;0 là vtcp của đường thẳng AB nên AB có phương trình: y  2   t . z 1 
Thay phương trình AB vào phương trình Ozx : y  0 ta được: 2  t  0  t  2 . 2 2 MB 4  4  0
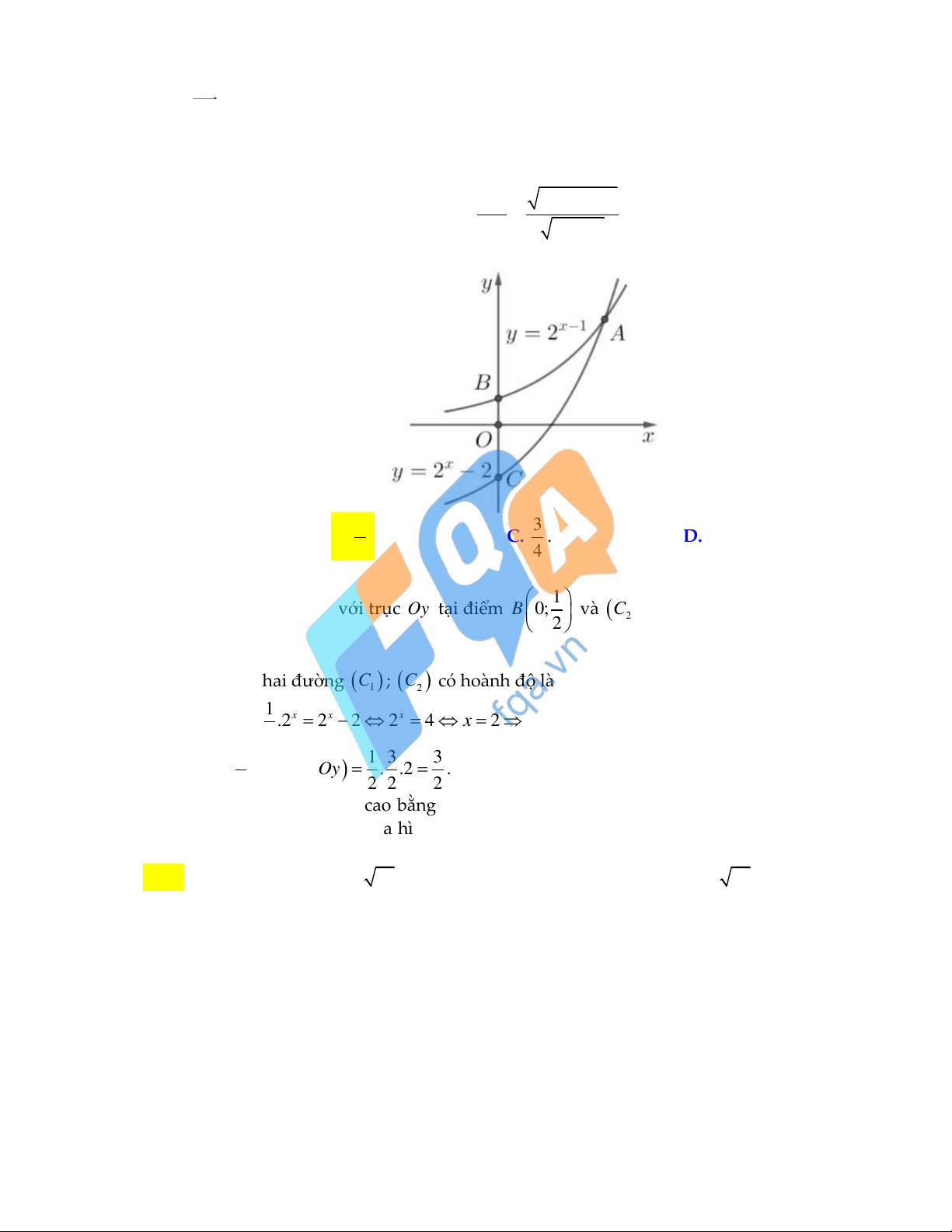
Suy ra AB  Ozx  M  1  ;0  ;1 nên ta có:   2 . 2 2 MA 2  2 Câu 47: Cho hàm số 1 2x y   và 2x y
 2 có đồ thị như hình vẽ bên. Diện tích tam giác ABC bằng 3 3 A. 3 . B. . C. . D. 6 . 2 4 Lời giải:  1  Ta có   1 : 2x C y  
giao với trục Oy tại điểm B 0; và  : 2x C y
 2 giao với trục Oy tại 2  1    2  điểm C 0;   1 .
Giao điểm của hai đường C ; C có hoành độ là nghiệm của phương trình 2  1  xx 1 1 2
 2  2  .2x  2x  2  2x  4  x  2  A2;2 . 2 1 1 3 3 Vậy S
BC.d A Oy   . ABC  ,  . .2 2 2 2 2
Câu 48: Cho một hình trụ có chiều cao bằng 6 và bán kính bằng 5. Lấy hai điểm A và A' thuộc hai
đường tròn đáy khác nhau của hình trụ và AA '  10 . Khoảng cách giữa đường thẳng AA' và
trục của hình trụ đã cho bằng A. 3 . B. 2 21 . C. 5 . D. 4 21 . Lời giải:
Kẻ đường sinh AB, ta có:
OO '/ /( AA ' B)  d (OO '; AA ')  d (OO '; ( AA ' B))  d ( ;
O ( AA ' B))  OH
( H là trung điểm A’B ) 1 Ta có 2 2 A' B
AA'  AB  8  BH A ' B  4 . 2 Khi đó 2 2
OH OB HB  3
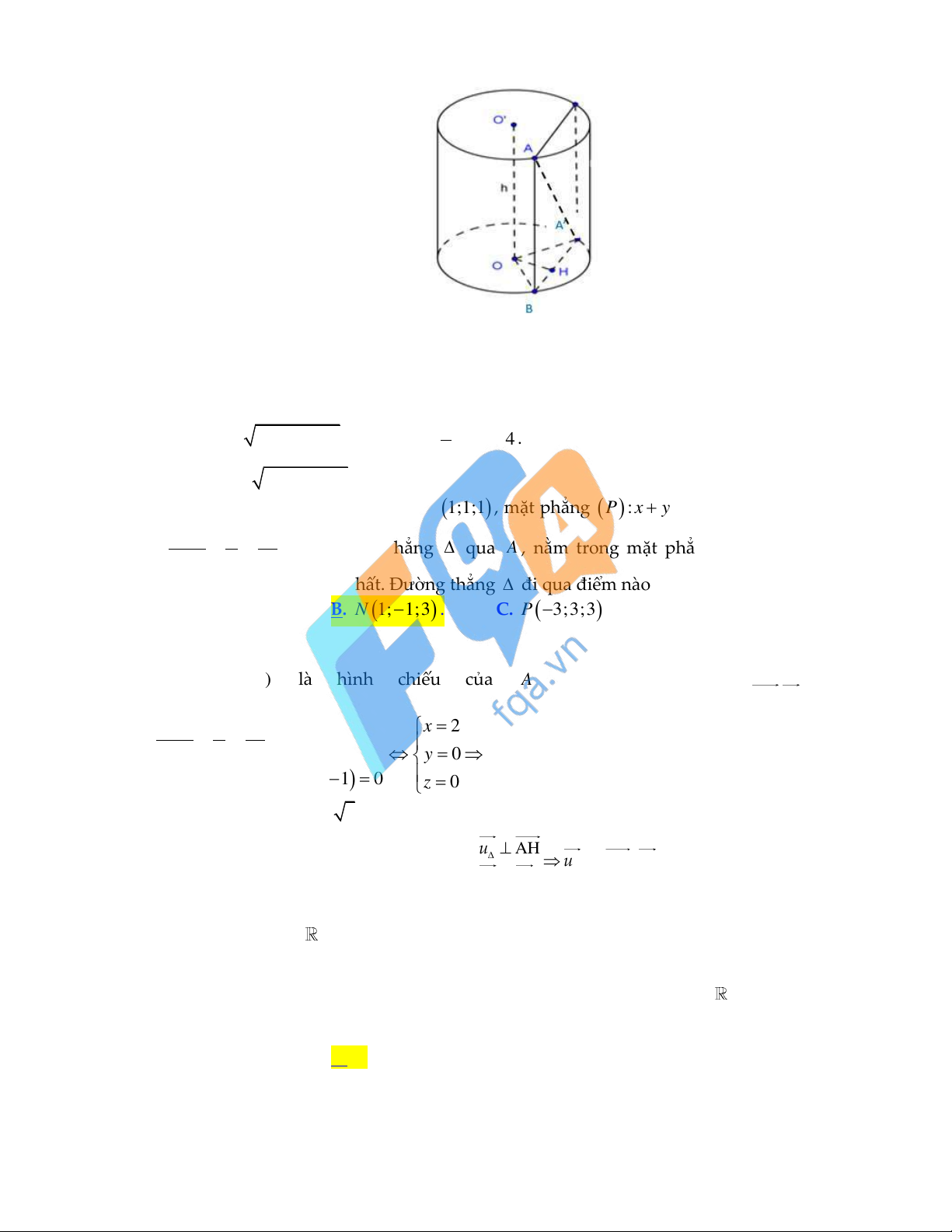
Câu 49: Trong không gian Oxyz, cho điểm A 
1;1;1 , mặt phẳng  P : x y z  3  0 và đường thẳng x  2 y z d :  
. Xét đường thẳng  qua A , nằm trong mặt phẳng  P và cách đường 1 2 1 
thẳng d một khoảng lớn nhất. Đường thẳng  đi qua điểm nào dưới đây?
A. M 2 ;1;0 .
B. N 1; 1;3 . C. P  3  ;3;3
D. Q 1; 2; 4 . Lời giải: H d  Gọi H ( ; x y; z) là hình chiếu của A trên d ta có  nên AH.u  0  dx  2 y zx  2      1 2 1 
 y  0  H 2;0;0 . 1
 x  1 2y  11z  1  0 z  0  Khi đó: d  ,
A d   AH  3 . u   AH
Dấu "  " xảy ra khi và chỉ khi   AH   
u  AH ,n     0; 2;2 . P    u   n   Px 1 
  : y 1 2t , t  đi qua điểm N 1;1;3 . z 1 2t
Câu 50: Cho hàm số y f x có đạo hàm f x 2
x x   2 ' 2
x mx  5, x
  . Số giá trị nguyên
âm của m để hàm số g x  f  2
x x  2 đồng biến trên khoảng 1;   là A. 3 . B. 4 . C. 5 . D. 7 .

Tài liệu liên quan: