Bộ Đề Thi Giữa Học Kỳ 2 Toán 8 Năm 2025-2026 Có Đáp Án

ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8
A. TNKQ (3đ) Khoanh tròn chọn một chữ cái đứng trước mỗi câu trả lời đúng.
Câu 1: Phương trình nào sau đây là phương trình bậc nhất một ẩn? 2x 2 A/ 0x + 2 = 2 B/ 5x + 2y = 0 C/ +1 = 0 = 0 D/ + 4 = 0 3 3x
Câu 2: Phương trình x = 1 tương đương với phương trình nào sau đây? A/ x2 = 1
B/ x(x – 1) = 0 C/ x2 + x – 2 = 0 D/ 2x – 1= x
Câu 3: Tập nghiệm phương trình x – 3 = 0 được viết như thế nào?
A. S = {0} B. S ={3} C. S = {3; 0} D. S = {–3} x x −1
Câu 4. Điều kiện xác định của phương trình: −
=1 là kết luận nào sau đây? x − 3 x
A. x  0 B. x  3 C. x  0; x  3 D. x  0; x  –3
Câu 5. Tập nghiệm S = { 1,2} là của phương trình nào sau đây? A. 5x – 6 = 0
B. 6x – 5 = 0 C. (x – 1)(x – 2) = 0 D. 1x = 2
Câu 6: Số nào sau đây nghiệm đúng phương trình 1= 2x + 3 ? A/ x = 1 B/ x = –1 C/ x = –2 D/ x = 0
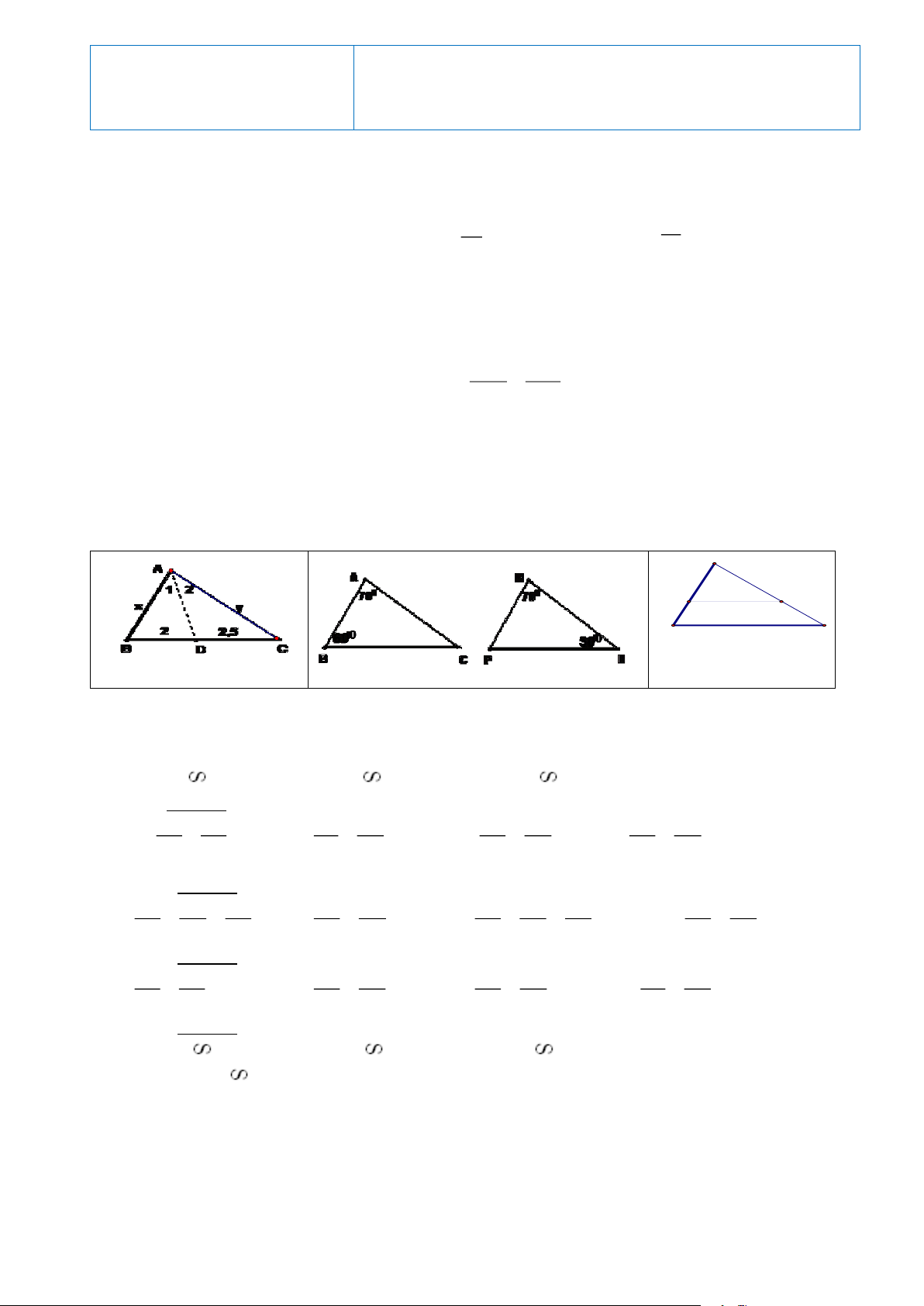
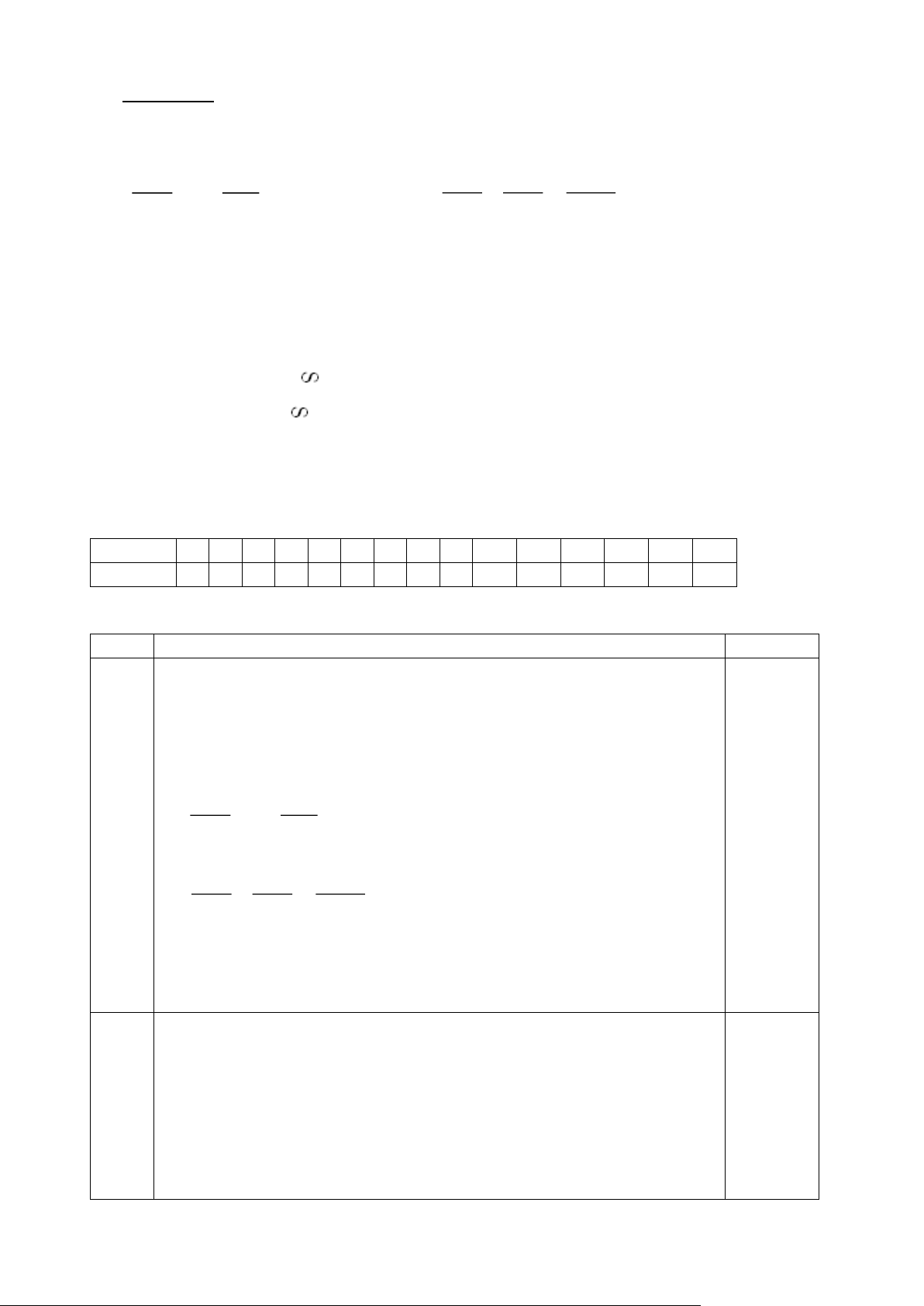
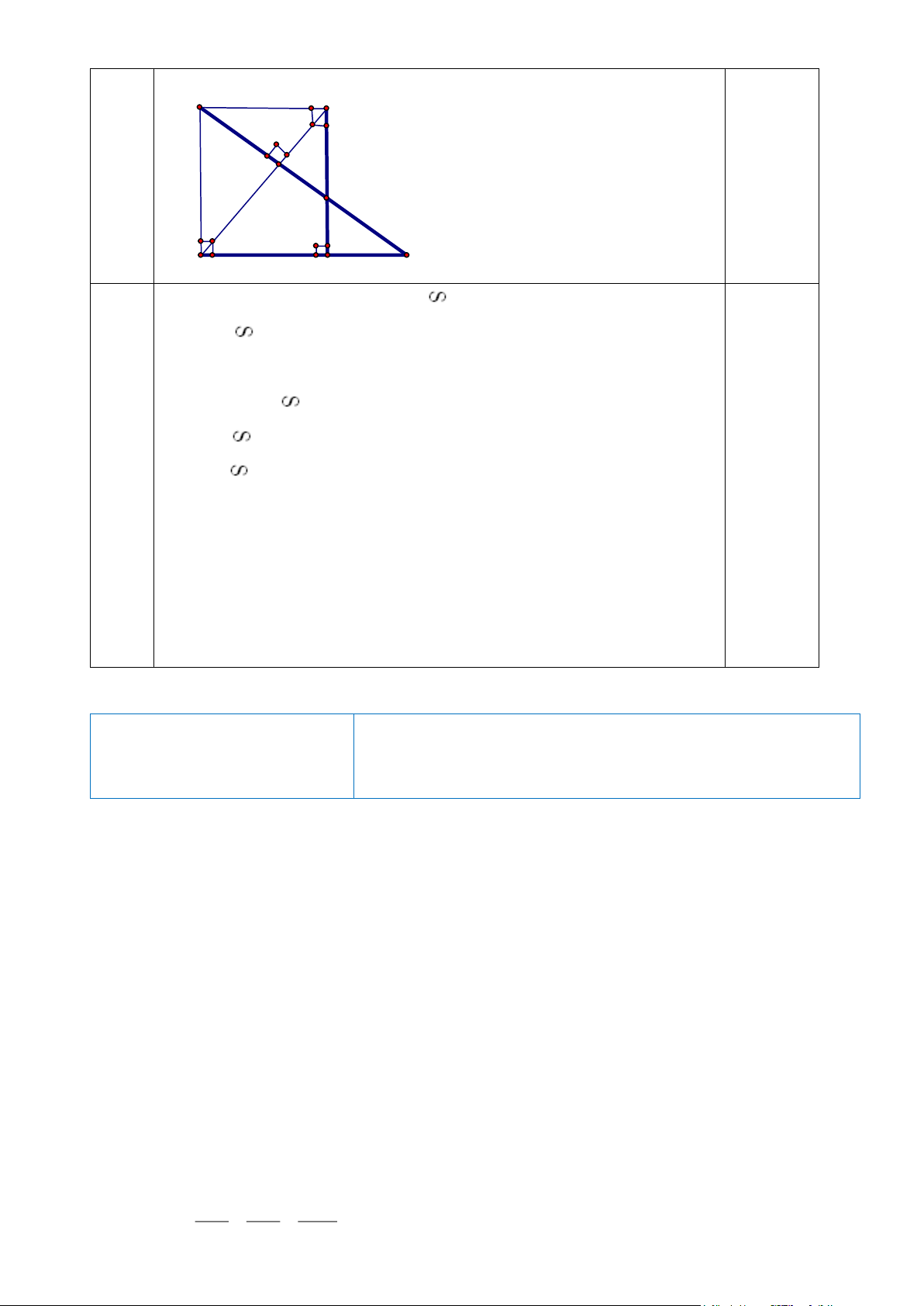
Cho ba hình vẽ có các số liệu minh họa kèm theo sau đây: A E F B C Hình 1 Hình 2 Hình 3
Câu 7. Hình 1, biết AD là tia phân giác của A . Tỷ số x: y bằng tỉ số nào sau đây? A. 5 : 2 B. 5 : 4 C. 2 : 5 D. 4 : 5
Câu 8. Hình 2, ký hiệu cặp tam giác nào sau đây đồng dạng với nhau là đúng? a. ∆ABC ∆ACB b. ∆ABC ∆MPN c. ∆ABC
∆MNP d. Cả a, b, c đều đúng.
Câu 9: Hình 3, nếu EF // BC, tỉ lệ thức nào đúng theo định lí Ta - lét? A/ AE CF = B/ EA AF = C/ AE AF = D/ AE AC = EB CA EB FC EB AC AB AF
Câu 10: Hình 3, nếu EF // BC, theo hệ quả của định lí Ta-lét ta có tỉ lệ thức nào? A/ AE AF EF = = B/ AE AF = C/ AE AF EF = = D/ AE AF = BA AC BC AB AC AB FC BC EB FC
Câu 11: Hình 3, tỉ lệ thức nào sau đây đúng sẽ cho ta kết luận EF// BC? A/ AE EF = B/ AE AF = C/ AE AF = D/ FE AF = AB BC BE FC EB AC CB FC
Câu 12: Hình 3, nếu EF // BC, ta có cặp tam giác nào đồng dạng sau đây là đúng? a. ∆ABC ∆AFE b. ∆ABC
∆EAF c. ∆BAC ∆EAF d. Cả a, b, c đều đúng. Câu 13. ABC
DEF biết ˆA = 500, ˆE = 700, AB = 4cm, ta kết luận được gì sau đây?
A. góc B = 700 B. góc B = 500 C. BC = 4cm D. BC = 4cm
Câu 14. Diện tích một hình chữ nhật thay đổi thế nào nếu tăng chiều rộng lên gấp đôi và
giảm chiều dài đi ba lần?
A. Tăng 2 lần B. Giảm 1,5 lần C. Tăng 1,5 lần D. Giảm 1,5 lần
Câu 15. Cạnh hình thoi dài 5cm, một đường chéo dài 6cm thì có diện tích bao nhiêu?
A. S = 36cm2 B. S = 30cm2 C. S = 25cm2 D. S = 24cm2 Trang 1
B. TỰ LUẬN (7 điểm)
Câu 16. (2,5 đ) Giải các phương trình sau:
a) 4x + 2 = 0 b/ x(x – 2) + 5(x – 2) = 0 x − + x 2 x x +1 x +1 c/ 2 1 = x + d/ + = 3 2 2 x +1 x −1 x −1
Câu 17. (2,0 đ) Giải bài toán bằng cách lập phương trình
Một ca– no xuôi dòng từ bến A đến bến B trên một đoạn sông Văn Úc hết 4 giờ, còn một
khóm bèo trôi tự nhiên thẳng giữa dòng sông cùng lúc được 5km/h. Khi ca-no đi ngược
dòng từ bến B trở về A mất 6 giờ Tính khoảng cách hai bến A và B trên dòng sông nà
Câu 18: (2,5đ) Cho hình chữ nhật ABCD ( AB < BC). Kẻ đường cao AH của ∆ABC.
Kéo dài AH cắt BC tại E và cắt CD tại F.
a/ Chứng tỏ rằng ∆HBA ∆BAE và AB2 = AH. AE. b/ Chứng minh: ∆HBE
∆HAB từ đó suy ra hệ thức HB2 = HA. HE.
C/ Chứng minh rằng: AH2 = HE. HF.
ĐÁP ÁN, HƯỚNG DẪN CHẤM TOÁN 8 GIỮA HỌC KỲ II
Phần I: Trắc nghiệm khách quan(3 điểm) Mỗi đáp án đúng cho 0,2 điểm Câu
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Đáp án C D B C A B D C B A B C A C D
Phần II: Tự luận(7 điểm) Câu
Lời giải sơ lược Điểm 16
a. 4x + 2 = 0  4x = – 2  x = – 2/4 = – 0,5 0,25
Tập nghiệm của PT là S = {– 1/2 } 0,25
b/ x(x – 2) + 5(x – 2) = 0  (x – 2)(x + 5) = 0
x − 2 = 0 = x = 2 0,25  
Tập nghiệm PT là S = {– 5; 2 } 0,25
x + 5 = 0 = x = 5 − x − 2 1+ x c/ = x +
 2(x – 2) = 6x +3( 1+ x) 0,25 3 2 0,25
 x = – 1 Tập nghiệm của PT là S = {– 1} 0,25 2 x x +1 x +1 d/ + = 2 x +1 x −1 x −1
- ĐKXĐ: x ≠ –1; x ≠ 1 ( ĐKXĐ: x ≠ ±1) 0,25
=> x(x – 1)+ (x + 1)(x +1) = x2 +1 0,25
 x2 + x = 0  x(x +1) = 0  x = 0; x = –1 ( loại) 0,25
Tập nghiệm của PT là S = {0} 0,25 17
- Gọi vận tốc của ca-no khi nước yên lặng là x ( km/h), x > 5 0,25
- Vận tốc của ca –no khi xuôi dòng là: x + 5 0,25
- Vận tốc của ca – no khi ngược dòng là: x – 5 0,25
- Quãng đường AB khi xuôi dòng là 4( x + 5) 0,25
- Quãng đường ngược dòng B về A là 6( x – 5) 0,25
- Theo bài ta có PT: 6( x – 5) = 4( x + 5)  x = 25 ( t/m ĐK) 0,25
=> Vận tốc riêng của ca-no là 25km/h, 0,25
Và khoảng cách AB dài 4( 25+5) = 120 (km) 0,25 Trang 2 18
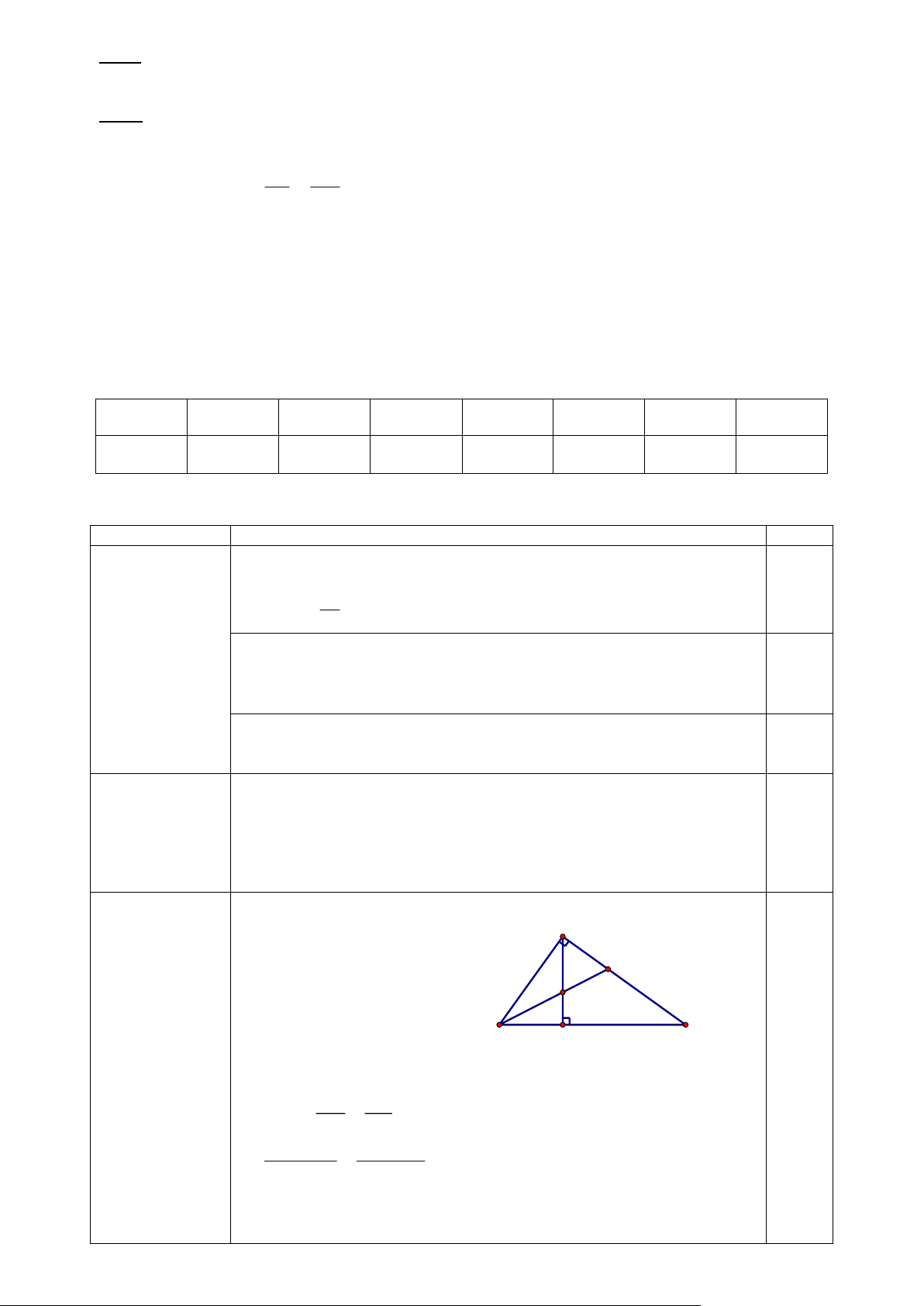
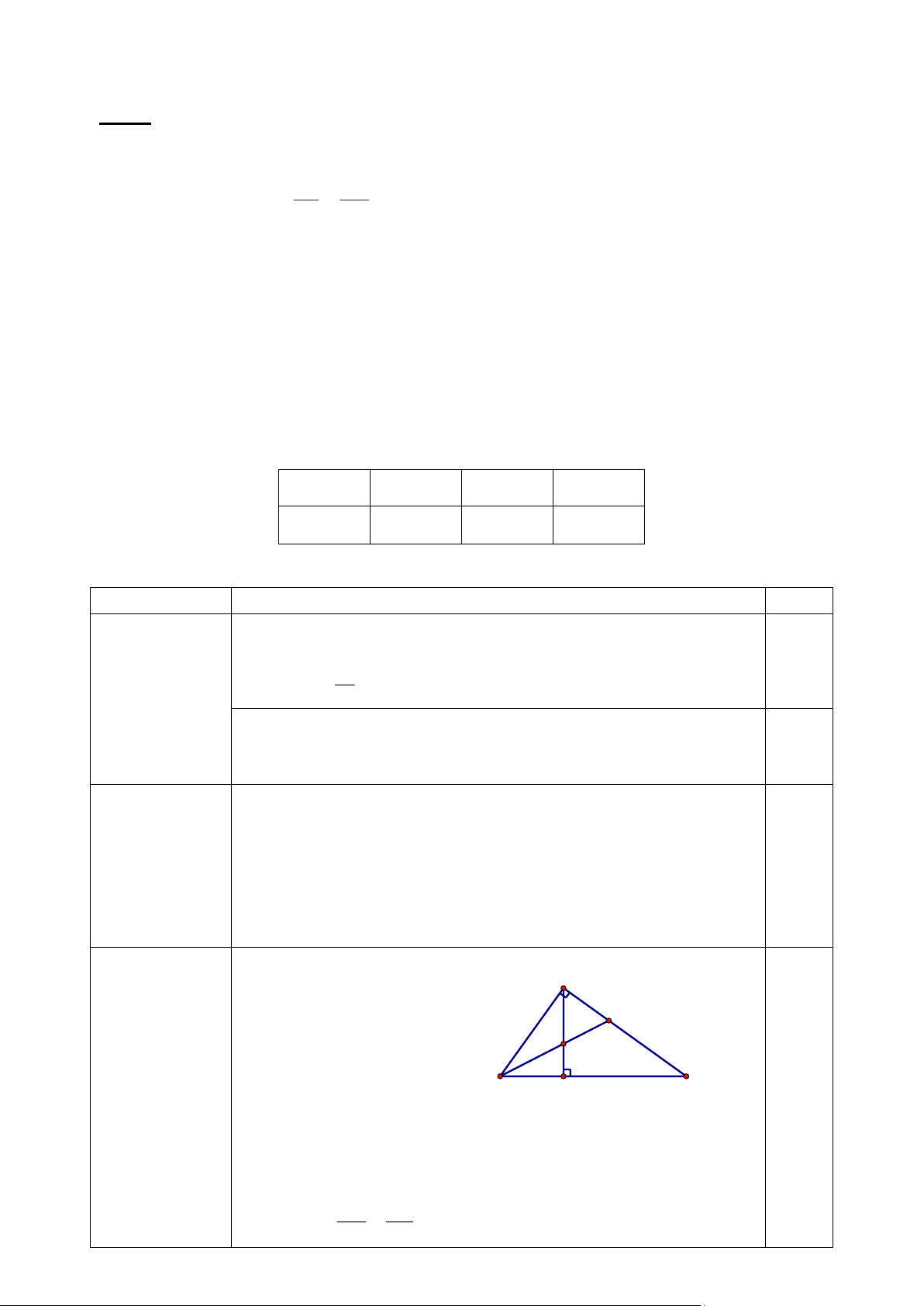
- vẽ đúng hình chữ nhật ABCD có đường cao AH của ∆ABD 1 A 1 2 B 0,25 2 1 E H 0,25 2 D C F
a. C/m: a/ Chứng tỏ rằng ∆HBA ∆BAE và AB2 = AH. AE. 0,25 -∆HBA
∆ABC ( g.g) góc H = góc B và chung góc A1
=> HB : AB = AB : BC => AB2 = AH. AE. 0,25 b/ C/m ∆HBE
∆HAB từ đó suy ra HB2 = HA. HE. - HBA
∆ABE ( g.g) góc H = góc B = 900,chung góc A1 0,25 0,25 -∆HBA
∆HEB ( g.g) góc H = góc B = 900, và chung góc E1
=> HB : HA = HE: HB => HB2 = HA. AE.
C/ Chứng minh rằng: AH2 = HE. HF.
- Theo định lý Ta-let, từ AB // DC => AH : HF = BH : HD 0,25 0,25
- Lại có BC // AD => BH : HD = HE : HA 0,5
=> AH : HF = HE : HA => AH2 = HE. HF.
Cách giải khác, đúng cho đủ điểm thành phần theo cơ cấu của mỗi phần của đề bài. ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8
Câu 1: Phát biểu định nghĩa phương trình bậc nhất một ẩn?
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một
ẩn. Xác định các hệ số a,b.
a) 2x – 4 = 0 b) x - 9y = 0
Câu 2:Viết một phương trình chứa ẩn ở mẫu và cho biết ĐKXĐ của phương trình đó?
Câu 3: Hãy nêu định lý Talet (thuận) trong tam giác và viết giả thiết kết
luận cho định lý?
Câu 4: Giải phương trình:
a, Giải phương trình : 3x – 9 = 0 b) x(x - 3) + 2(x - 3) = 0
c) x −1 x −1 x −1 + + = 0 2 3 2016 Trang 3
Câu 5: Một học sinh đi xe đạp từ nhà đến trường với vận tốc 15km/h. Lúc
về nhà đi với vận tốc 12km/h nên thời gian về nhiều hơn thời gian đi là 10 phút.
Tính quãng đường từ nhà đến trường.
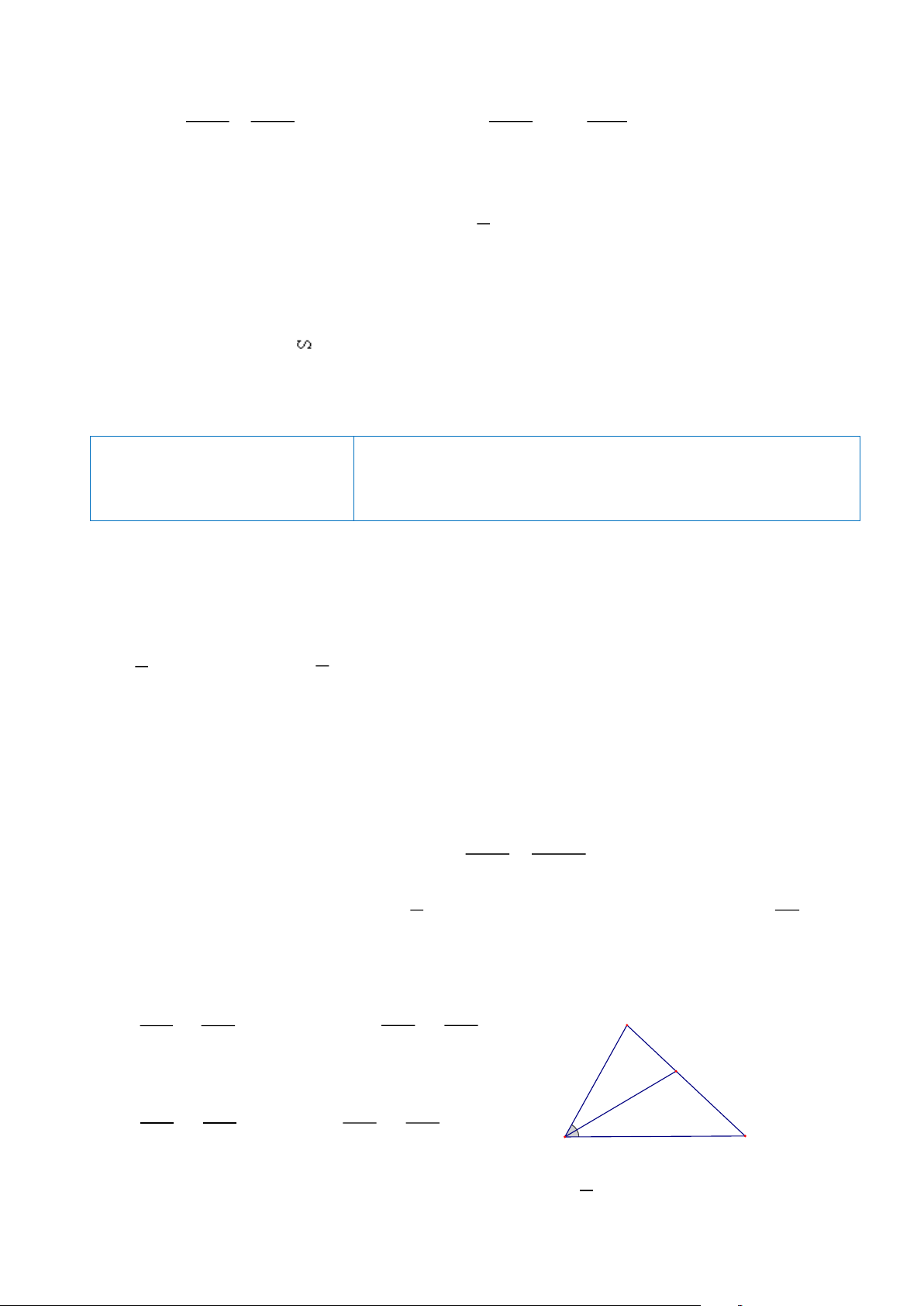
Câu 6: Cho ΔABC có AB = 8cm, AC = 12cm. Trên cạnh AB lấy điểm D
sao cho BD = 2cm, trên cạnh AC lấy điểm E sao cho AE = 9cm. a) Tính các tỉ số AE AD ; . AD AC
b) Chứng minh: ΔADE đồng dạng ΔABC.
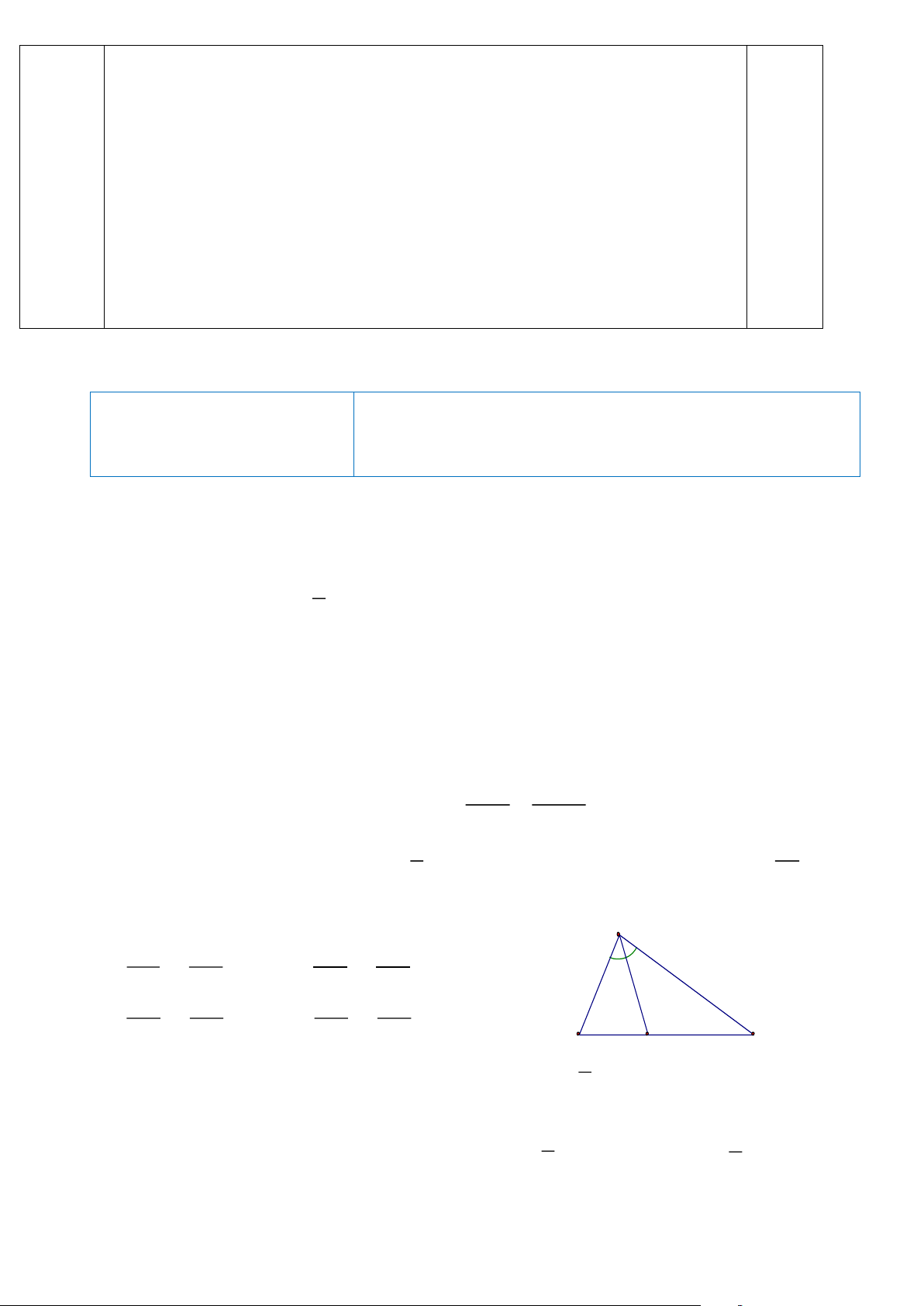
c) Đường phân giác của C Aˆ B
cắt BC tại I. Chứng minh: IB.AE = IC.AD.
HƯỚN DẪN CHẤM KIỂM TRA GIỮA HỌC KÌ 2- MÔN TOÁN LỚP 8 Câu Đáp án Điểm
- Nêu đúng định nghĩa pt bậc nhất một ẩn 0,5
Câu 1 a) 2x – 4 = 0 ( a = 2; b = -4) 0,5
- Nêu được đúng nội dung định lý Talet. 0,5
Câu 2 - Viết được đúng giả thiết, kết luận nội dung định lý Talet. 0,5
- Viết đúng phương trình chứa ẩn ở mẫu. 0,5
Câu 3 Tìm đúng ĐKXĐ cho phương trình vừa viết 0,5 Trang 4 a, Giải phương trình 3x – 9 = 0  3x = 9 0,25  x = 3 0,25
Vậy tập nghiệm của pt là S = {3}
b, Giải các phương trình x(x - 3) + 2(x - 3) = 0 0,25  (x - 3)(x + 2) = 0 Câu 4 x − 3 = 0 x = 3    x 2 0  + = x = 2 − 0,25
Vậy tập nghiệm của phương trình là S =3;−  2 C, Giải phương trình x −1 x −1 x −1 + + = 0 2 3 2016 0,25 (    x − ) 1 1 1 1 + + = 0    2 3 2016 
 x −1 = 0  x = 1 0,25
Vậy tập nghiệm của phương trình là S =  1
Đổi 10 phút = 1 (h) 6 0,25
Gọi x là quãng đường từ nhà đến trường (x > 0) 0,25
Thời gian đi: x (h) 15 0,25 0,25
Câu 5 Thời gian về: x (h) 12 0,5 x x 1
Theo đề bài ta có phương trình: − = 12 15 6 0,25
Giải phương trình ta được: x = 10 0,25
Vậy quãng đường từ nhà đến trường là 10 km. a) Ta có AD = 6 cm, nên 0,75 AE 9 3 = = AD 6 2 Câu 6 AD 6 1 = = 0,75 AC 12 2
b) Xét tam giác ADE và tam giác ABC có: 0,25 Trang 5
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KHẢO SÁT CHẤT LƯỢNG GIỮA KÌ II QUẬN HÀ ĐÔNG Môn: TOÁN 8 A góc c ĐỀ hu C ng HÍ NH THỨC AD AE 3 = = 0,5 AB AC 4 0,25 Nên A
 DE đồng dạng ABC  (c.g.c)
c) Vì I là chân đường phân giác của C Aˆ B 0,25 IB AB 0,25 Nên = IC AC 0,25 Mà AB AD = AC AE 0,25 Do đó IB AD = Vậy IB.AE = IC.AD IC AE ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8
Bài 1.(3 điểm) Giải các phương trình : a) (x - 5)2 + 3(x – 5) = 0 2x −1 5x + 2 b) − = x +13 3 7 x-1 x 7x − 6 c) − = 2 x + 2 x − 2 4 − x
Bài 2. (3,0 điểm) Giải bài toán bằng cách lập phương trình:
Một xe máy đi từ A đến B với vận tốc và thời gian dự định trước. Sau khi đi
được nửa quãng đường, xe tăng vận tốc thêm 10km/h vì vậy xe máy đi đến B sớm
hơn 30 phút so với dự định. Tính vận tốc dự định của xe máy, biết quãng đường AB dài 120 km. Bài 3. (3,5 điểm)
Cho ∆ABC vuông tại A, đường cao AH. Đường phân giác của góc ABC cắt
AC tại D và cắt AH tại E.
a) Chứng minh: ΔABC đồng dạng ΔHBA và AB2 = BC.BH Trang 6
b) Biết AB = 9cm, BC = 15cm. Tính DC và AD
c) Gọi I là trung điểm của ED. Chứng minh: góc BIH = góc ACB.
Bài 4. (0,5điểm) 3 3 3
Giải phương trình (2017 - x) + (2019 - x) + (2x - 4036) = 0
-----------------Hết------------------
(Giám thị coi thi không giải thích gì thêm) HƯỚNG DẪN Bài Nội dung điểm Bài 1 a ( x − )2 ) 5 + 3( x – 5) = 0 0,5đ (3,0
 (x – 5)(x – 2)= 0 điểm) x − 2 = 0 x = 2    0,5đ x 5 0  − = x = 5 2x −1 5x + 2 b) − = x +13 3 7 0,25đ  7 (2x − )
1 − 3(5x + 2) = 21( x +13)  21
− x +14x −15x = 273 + 6 + 7 0,25đ 0,25đ  22 − x = 286 0,25đ  x = −13
c) Điều kiện: x  2; x  2 − 0,25đ x-1 x 7x − 6 − = 2 x + 2 x − 2 4 − x  (x- )
1 ( x − 2) − x( x + 2) = 6 − 7x 0,25đ 2 2
 x − 3x + 2 − x − 2x = 6 − 7x 0,25đ
 2x = 4  x = 2(ktmdk)
Vậy phương trình vô nghiệm 0,25đ
Bài 2 Gọi x km/h là vận tốc dự định của xe máy (x > 0) 0,25đ Lập luận để lập PT 0,25 đ (3,0
điểm) +) Thời gian dự định đi từ A đến B là: 120 (h) x 0,25đ
+) Thời gian xe máy đi nửa quãng đường đầu: 60 ( h) x 0,5đ
+) Thời gian đi nửa quãng đường còn lại: 60 ( h) x +10 1
+) Vì xe máy đi đến B sớm hơn 30 phút = h so với dự định, nên ta 0,5đ 2 1,0đ Trang 7 120 1 60 60 có phương trình: − = + x 2 x x +10 0,25đ
Giải ra ta được: x = 30 (tmđk); x = - 40 (ktmđk)
Vậy vận tốc dự định của xe máy là 30km/h Bài 3 (3,5
Vẽ hình viết GT – KL đúng điểm) 0,5đ A D E I C B H
a) Chứng minh được: ΔABC đồng dạng ΔHBA (g-g) 0,5 đ Từ đó suy ra AB2 = BC.BH 0,5 đ
b) Áp dụng định lý Py ta go tính được AC = 12cm 0,5 đ
Vì BD là tia phân của góc ABC (gt) CD AD  = 0,5đ (t / c) CB AB
Áp dụng tính chất của dãy tỉ số bằng nhau có 0,25đ CD AD AC 12 1  = = = = CB AB AB + CB 9 +15 2  CD = 7,5c , m AD = 4,5cm 0,25đ
c) +) Chứng minh AED cân tại A ( góc AED = góc ADE)
Suy ra AI vuông góc với DE tại I
+) Chứng minh EHB và EIA đồng dạng (g-g) 0,25đ Từ đó suy ra EI EA = EH EB
+) Chứng minh được AEB và IEH đồng dạng (c-g-c) suy ra góc EAB = góc EIH 0,25đ
Mà góc EAB = góc ACB (cùng phụ với góc ABC) Do đó góc BIH = góc ACB Bài 4
Đặt a = 2017 – x; b = 2019 – x; c = 2x – 4036 (0,5
+) Ta có: a + b + c = 2017 – x + 2019 – x + 2x – 4036 = 0 Trang 8 điểm) và 3 3 3 a + b + c = 0 (* ) 0.25 đ +) Vì a + b + c = 0 3 3 3
 a + b = - c  a + b + c = 3abc
Kết hợp với (*) suy ra abc = 0
Do đó (2017 – x) (2019 – x) (2x – 4036) = 0 2017 − x = 0 x = 2017 0,25 đ  2019 x 0   − =  x = 2019   2x − 4036 = 0 x = 2018  
Vậy x = 2017, x = 2018, x = 2019
(HS giải theo cách khác nếu đúng vẫn cho điểm tối đa) ĐỀ 4
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8
I/ TRẮC NGHIỆM (3 ĐIỂM):
Chọn chữ cái đứng trước câu trả lời đúng nhất.
Câu 1: Phương trình nào sau đây là phương trình bậc nhất một ẩn? 1 A. 3x2 + 2x = 0 B. − 3 = 0 C. x + 1 = 0 D. x2 = 0 x
Câu 2: x = 1 là nghiệm của phương trình nào trong các phương trình dưới đây?
A. 2x − 3 = x + 2
B. x − 4 = 2x + 2
C. 3x + 2 = 4 − x
D. 5x − 2 = 2x +1
Câu 3: Phương trình vô nghiệm có tập nghiệm là: A. S =  B. S = {} C. S = {0} D. S = 0 2 x
Câu 4: Điều kiện xác định của phương trình = là: x + 2 2x − 3 3 3 −
A. x  2; x  3 B. x  2; − x 
C. x  −2; x  3
D. x  2; x  2 2
Câu 5: Trong hình vẽ có · ·
BA D = DA C , theo tính chất đường phân giác của tam giác thì A
tỉ lệ thức nào sau đây là đúng? A B DB A B BD A. = B. = A D DC DC A C DB A B A D DB C. = D. = DC A C A C DC B D C 2
Câu 6: Nếu ABC  ∽ DEF 
theo tỉ số đồng dạng là k = thì DEF  ∽ ABC  theo tỉ 1 5 số đồng dạng là: 2 5
A. k = 2 B. k = 5 C. k = k = 2 2 D. 2 5 2 2
II. TỰ LUẬN (7 điểm)
Câu 7 (2,5 điểm) Giải các phương trình sau: Trang 9 a/ 3x + 12 = 0 b/ 2x(x - 2) + 5(x - 2) = 0 x − 5 x + 5 x − 2 1+ x c) + = 2 d/ = x + x −1 x +1 3 2
Câu 8 (1,5 điểm): Giải bài toán bằng cách lập phương trình
Một phân số có tử số nhỏ hơn mẫu số 12 đơn vị, nếu tăng tử số lên 3 đơn vị và giảm 2
mẫu số đi 4 đơn vị thì được một phân số bằng . Tìm phân số đó? 3 Câu 9 (3 điểm):
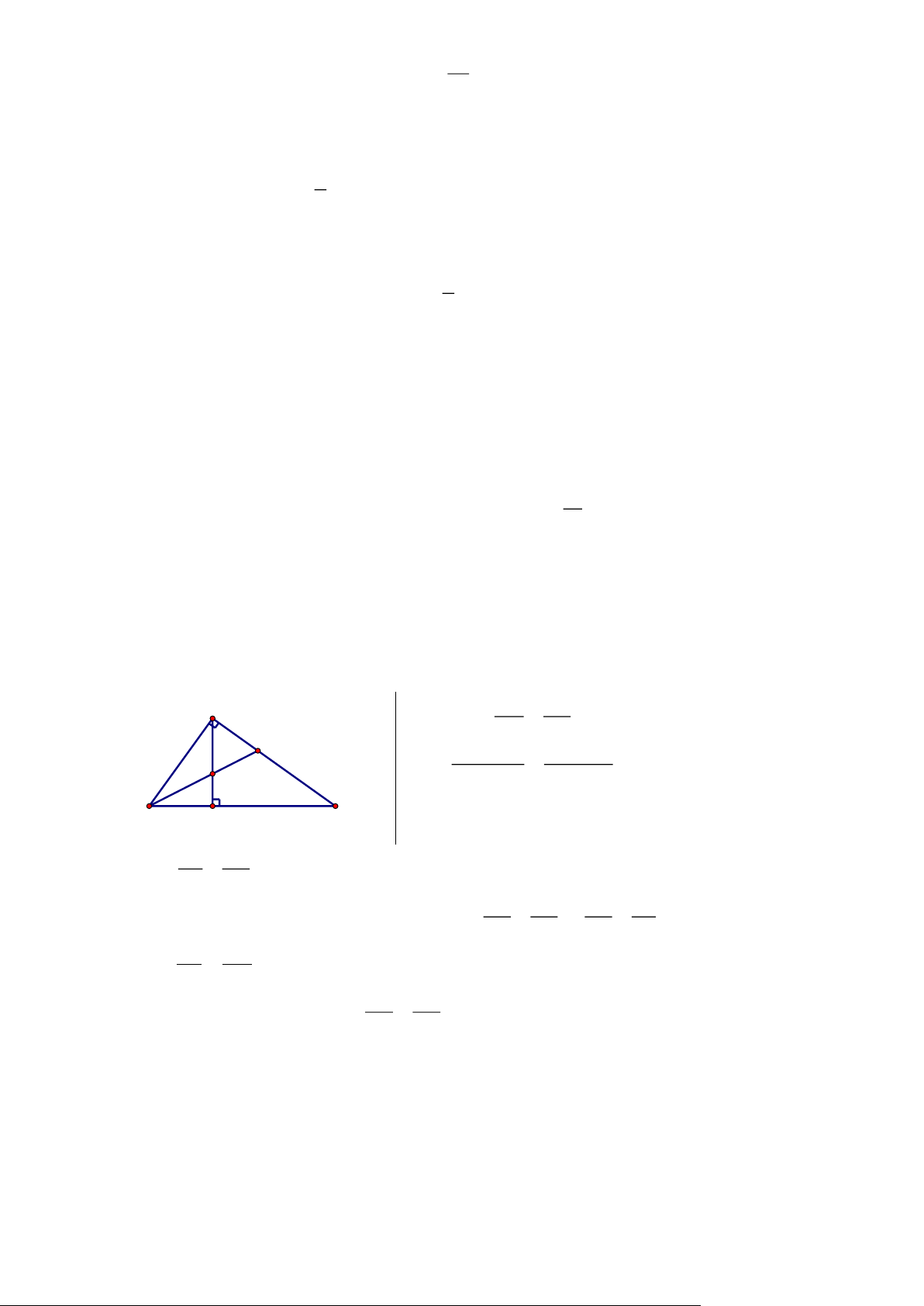
Cho hình chữ nhật ABCD có AB = 8cm; BC = 6cm. Vẽ đường cao AH của tam giác ABD.
a) Chứng minh: AHB BCD. b) Tính độ dài BD, AH. c) Chứng minh AD2 = DH.DB ĐỀ 5
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8
I/ TRẮC NGHIỆM (3 ĐIỂM):
Chọn chữ cái đứng trước câu trả lời đúng nhất.
Câu 1: Phương trình nào sau đây không là phương trình bậc nhất một ẩn? 1 1 A. − 5x = 0 B. − 3 = 0 C. 2x + 1 = 0 D. x = 0 2 x
Câu 2: x = 3 là nghiệm của phương trình nào trong các phương trình dưới đây?
A. 2x − 3 = x + 2
B. 3x + 2 = 4 − x
C. x + 4 = 2x + 1
D. 5x − 2 = 2x +1
Câu 3: Phương trình vô số nghiệm có tập nghiệm là: A. S = N B. S = Z C. S = Q D. S = R 2 x
Câu 4: Điều kiện xác định của phương trình = là: x − 2 2x + 3 3 3 −
A. x  2; x  3 B. x  2; − x 
C. x  −2; x  3
D. x  2; x  2 2
Câu 5: Trong hình vẽ có · ·
A BD = DBC , theo tính chất đường phân giác của tam giác thì
tỉ lệ thức nào sau đây là đúng? A B A D A B BD A A. = B. = BC DC DC A C D DB A B A D DB C. = D. = DC A C A C DC B C 4
Câu 6: Nếu ABC  ∽ DEF 
theo tỉ số đồng dạng là k = thì tỉ số chu vi của hai tam 3 giác đó bằng Trang 10 4 16 A. 4 B. 3 C. D. 3 9
II. TỰ LUẬN (7 điểm)
Câu 7 (2,5 điểm) Giải các phương trình sau: a/ 4x - 24 = 0
b/ 2x(x + 2) - 5(x + 2) = 0 x − 3 x + 3 x + 2 1− x c) + = 2 d/ = x + x − 2 x + 2 4 3
Câu 8 (1,5 điểm): Giải bài toán bằng cách lập phương trình
Một phân số có mẫu số nhỏ hơn tử số 12 đơn vị, nếu tăng mẫu số lên 3 đơn vị và giảm 3
tử số đi 4 đơn vị thì được một phân số bằng . Tìm phân số đó? 2
Câu 9 (3 điểm): Cho hình chữ nhật ABCD có AB = 12cm; BC = 9cm. Vẽ đường cao AH của tam giác ABD.
a) Chứng minh: AHB BCD. b) Tính độ dài BD, AH. c) Chứng minh AD2 = DH.DB. ĐỀ 6
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8 A.TRẮC NGHIỆM
Câu 1. Điều kiện xác định của phương trình x x 2x + = là: 3(x − ) 1 2x + 4 (x+2)(x−1)
A. x  1 B. x  1 và x  −2 C. x  −2 D. x  1 và x  2
Câu 2. x = −2 là nghiệm của phương trình 2 x + 4x + 4 A. ( 1
x2 + 1)(x + 2) = 0 B. = 0 C. 2 2
x + 7x + 6 = 0 D. = x + 2 2 x − 4 x + 2
Câu 3. Phương trình x3 −1 = 0 tương đương với phương trình ( 2 x − ) 1 A. 1 1 x + = 1+ B. 3 2
x − x + x −1 = 0 C. = 0 D. 2
x − 3x + 2 = 0 x −1 x −1 x − 1
Câu 4. Cho : x(2x + 5) = 0( )
1 ; 2y + 3 = 2y − 3(2); u2 + 2 = 0(3) ; (3t + ) 1 (t − ) 1 = 0(4)
A. Phương trình (1) có tập nghiệm là  − 5 S =  ; 0   2 
B. Phương trình (3) có tập nghiệm là S =
C. Phương trình (2) tương đương với phương trình (3)
D. Phương trình (4) có tập nghiệm là  1 S = − ; 1   3
Câu 5.Cho ΔMNP,EF / /MP,E MN,F  NP ta có Trang 11 A. ME PF = B. NE FP = C. EM FP = D. EF EN = EN PN EM FN MN PN MP EM
Câu 6. Cho ABC , AD là phân giác của BAC ,(D  BC) . Biết AB = 6c ;
m AC = 15cm , khi đó BD bằng. BC A. 2 B. 5 C. 2 D. 7 5 2 7 3 2
Câu 7. Cho ABC đồng dạng với HIK theo tỷ số đồng dạng k = , chu vi ABC bằng 3
60cm , chu vi HIK bằng: A. 30cm B. 90cm
C. 9dm D. 40cm
Câu 8. Cho ABC đồng dạng với HIK theo tỷ số đồng dạng k, HIK đồng dạng với
DEF theo tỷ số đồng dạng m. DEF đồng dạng với ABC theo tỷ số đồng dạng
A. k.m B. k C. 1 D. m m k m . k B. TỰ LUẬN
Bài 1: Giải các phương trình sau: − + 2 1 3x −11 a. x 3 1 2x + = 6 b. ( x − )( 2 2 3 x + ) 1 = 0 c. − = 5 3 x +1 x − 2 (x + ) 1 (x − 2)
Bài 2: Giải bài toán bằng cách lập phương trình.
Một số tự nhiên lẻ có hai chữ số và chia hết cho 5. Hiệu của số đó và chữ số hàng chục
của nó bằng 86 . Tìm số đó.
Bài 3: Cho ABC vuông ở ,
A AB = 6, AC = 8 ; đường cao AH , phân giác BD . Gọi I là
giao điểm của AH và BD . a. Tính: AD, DC. b. CMR: IH AD =
c. CMR: AB.BI = BD.HB và AID cân. IA DC Bài 4: Tìm ;
x y thỏa mãn phương trình sau: 2 2
x − 4x + y − 6y +15 = 2 *** HƯỚNG DẪN GIẢI A. TRẮC NGHIỆM Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 B A B A C C B C B. TỰ LUẬN 94
Bài 1: a. Biến đổi: 13x − 94 = 0  13x = 94  x = . 13 Trang 12 94
Vậy tâp nghiệm của phương trình là: S =   13  b. ( x − )( 2 2 3 x + )
1 = 0  2x – 3 = 0 hoặc 2 x +1 = 0 3
+ Ta có: 2x – 3 = 0  x = . 2 + 2 x +1  0 nên 2 x +1 = 0 (VN) 3
Vậy tập nghiệm của phương trình là S =   2 x  −1 c. ĐKXĐ:  . MTC: ( x + ) 1 ( x − 2) . x  2
Quy đồng và khử mẫu ta được: 2( x − 2) − ( x + )
1 = 3x −11  x = 3(n)
Vậy tập nghiệm của phương trình là S =   3
Bài 2: Gọi x là chữ số hàng chục của số phải tìm (ĐK: x là chữ số, x  0 ).
Do số đó là số tự nhiên lẽ và chia hết cho 5 nên có dạng: x5.
Số cần tìm có độ lớn là: 10x + 5 .
- Biểu diễn các đại lượng qua ẩn ta có: (10x + 5) − x = 86  x = 9(n)
Vậy số cần tìm là: 95 .
Bài 3: a. Ta tính được: BC = 10cm A - Lập tỉ số AD AB = DC BC D 6 8 Nên: AD AB = I DC + AD BC + AB
Thay số vào: AD = 3c , m DC = 5cm B H C b. Ta có: IH HB = IA AB
Dễ chứng minh đươc: HBA ∽ ABC . Do đó HB AB AB HI =  = AB BC BC IA - Suy ra: IH AD = . IA DC
c. Ta có: ABD ∽ HBI . Nên: AB BD = . HB BI Do đó: . AB BI = . BD HB
Mặt khác: ABD ∽ HBI . Suy ra: BIH = ADI
Mà: BIH = AID . Nên: AID = ADI . Vậy: AID cân Bài 4: 2 2
x − 4x + y − 6y +15 = 2
Biến đổi ta được: ( x − )2 + ( y − )2 2 3 = 0 . Trang 13 (  x − 2  )2  0 x − 2 = 0 x = 2 Nhận xét: 
 (x − 2)2 + ( y − 3)2 = 0     . (  y −  )2  y − 3 = 0 y = 3 3 0  x = 2 Vậy:  là giá trị cần tìm.  y = 3 ĐỀ 7
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8
A.Trắc nghiệm khách quan(2 điểm):
Khoanh tròn vào chữ cái đứng trước phương án trả lời đúng trong mỗi câu sau. x x 2x
Câu 1. Điều kiện xác định của phương trình + = là ( 3 x − ) 1 2x + 4 (x + )( 2 x − ) 1
A. x  1 B. x  1 và x  −2 C. x  −2 D. x  1 và x  2
Câu 2. x= -2 là nghiệm của phương trình 2 x + 4x + 4 1 A. ( 2 x + )( 1 x + ) 2 = 0 B. = 0 C. 2 2
x + 7x + 6 = 0 D. = x + 2 2 x − 4 x + 2
Câu 3. Phương trình 3
x −1 = 0 tương đương với phương trình 1 1 (x − ) 1 2 A. x + = 1+ B. 3 2
x − x + x −1 = 0 C. = 0 D. 2
x − 3x + 2 = 0 x −1 x −1 x −1
Câu 4. Cho các phương trình: x(2x+5)=0 (1); 2y+3=2y-3 (2); 2
u + 2 = 0 (3); (3t+1)(t-1)=0 (4)  − 5
A. Phương trình (1) có tập nghiệm là S =  ; 0   2 
B. Phương trình (3) có tập nghiệm là S = R
C. Phương trình (2) tương đương với phương trình (3)  1
D. Phương trình (4) có tập nghiệm là S = − ; 1   3
Câu 5.Cho MNP, F
E //MP, E  MN, F  NP ta có ME PF NE FP EM FP EF EN A. = B. = C. = D. = EN PN EM FN MN PN MP EM BD
Câu 6. Cho ABC , AD là phân giác của góc BAC, DBC. Biết AB=6cm; AC=15cm, khi đó bằng BC 2 5 2 7 A. B. C. D. 5 2 7 3 2
Câu 7. Cho ABC đồng dạng với HIK theo tỷ số đồng dạng k = , chu vi ABC bằng 60cm, chu vi 3 HIK bằng: A. 30cm B.90cm C.9dm D.40cm
Câu 8. Cho ABC đồng dạng với HIK theo tỷ số đồng dạng k, HIK đồng dạng với DEF theo tỷ
số đồng dạng m. DEF đồng dạng với ABC theo tỷ số đồng dạng k 1 m A. k.m B. C. D. m k m . k B. TỰ LUẬN (8 ĐIỂM)
Bài 1 (2 điểm): Giải các phương trình sau: x − 3 1+ 2x a) + = 6 5 3 b) (2x - 3)(x2 +1) = 0 2 1 3x −11 c) − = x +1 x − 2 (x + )( 1 x − ) 2 Trang 14
Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.
Một số tự nhiên lẻ có hai chữ số và chia hết cho 5. Hiệu của số đó và chữ số hàng chục của nó bằng 86. Tìm số đó.
Bài 3 (3 điểm): Cho tam giác ABC vuông ở A, AB = 6, AC = 8; đường cao AH, phân giác BD. Gọi I là giao điểm của AH và BD. a. Tính AD, DC. IH AD b. Chứng minh = IA DC
c. Chứng minh AB.BI = BD.HB và tam giác AID cân.
Bài 4 (1 điểm): Tìm x; y thỏa mãn phương trình sau: x2 - 4x + y2 - 6y + 15 = 2
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN: TOÁN - LỚP 8
A. TRẮC NGHIỆM (2 ĐIỂM)
Mỗi câu đúng cho 0,25 điểm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 B A,C A,B, D A, C C C B,C C
B. TỰ LUẬN (8 ĐIỂM) Hướng dẫn chấm Điểm Bài 1 a. Biến đổi về dạng: ( 2 điểm) 13x - 94 = 0 hay 13x = 94 0,25 94 0,25 Giải ra x =
và kết luận tập nghiệm PT 13 b. (2x - 3)(x2 +1) = 0
 2x – 3 = 0 hoặc x2 +1= 0 0,25
- Giải PT: 2x – 3 = 0 đúng 0,25
- Giải thích PT: x2 +1= 0 vô nghiệm, kết luận tập nghiệm PT 0,25
c. - Tìm ĐKXĐ: x ≠ -1 và x ≠ 2 0,25
- Quy đồng khử mẫu đúng: 2(x-2) - (x+1) = 3x-11 0,25
- Giải ra x = 3 va kết luận tập nghiệm PT 0,25 Bài 2
- Chọn ẩn và ĐK đúng: 0,25 (2 điểm)
Gọi x là chữ số hàng chục của số phải tìm (ĐK: x là chữ số, x>0)
- Biểu diễn các ĐL qua ẩn, lập PT đúng: 0,5 (10x + 5) - x = 86 - Giải PT đúng: x = 9 0,5 - Trả lời 0,25 Bài 3 (3 điểm) A D 6 8 I B a.Tính AD, DC H C - Tính BC = 10 cm 0,25 AD AB - Lập tỉ số = DC BC 0,25 AD AB 0,25  = DC + AD BC + AB 0,25 Thay số, tính: AD = 3cm, DC = 5cm Trang 15 b. 0,25 IH HB - Lập tỉ số: = IA AB 0,25
- Chứng minh  HBA   ABC 0,25 HB AB AB HI  =  = AB BC BC IA 0,25 IH AD - Suy ra: = IA DC
c - Chứng minh  ABD  HBI 0,25 AB BD  =  A . B BI = B . D HB HB BI 0,25
-  ABD  HBI  BIH = ADI
Mà: BIH = AID  AID = ADI 0,25 Vậy  AID cân 0,25 Bài 4 x2 - 4x + y2 - 6y + 15 = 2 (1 điểm)
Biến đổi về dạng: (x-2)2 + (y-3)2 = 0 0,5
Lập luận dẫn tới x – 2 = 0 và y – 3 = 0 0,25 Tìm được x = 2; y = 3 0,25
Ghi chú: - Bài 3: không vẽ hình hoặc hình vẽ sai không chấm.
- Các cách làm khác đúng cho điểm tối đa tương ứng từng phần. ĐỀ 8
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2025 –2026 MÔN TOÁN 8
A.Trắc nghiệm khách quan(2 điểm):
Khoanh tròn vào chữ cái đứng trước phương án trả lời đúng trong mỗi câu sau.
Câu 1. Điều kiện xác định của phương trình x x 2 + = x là ( 3 x − ) 1 2x + 4 (x + )( 2 x − ) 1
A. x  1 B. x  1 và x  −2 C. x  −2 D. x  1 và x  2
Câu 2. x= -2 là nghiệm của phương trình 2 x + 4x + 4 A. 1 ( 2 x + )( 1 x + ) 2 = 0 B.
= 0 C. 2𝑥2 + 7𝑥 + 5 = 0 D. = x + 2 2 x − 4 x + 2
Câu 3. Phương trình 3
x −1 = 0 không tương đương với phương trình (x − ) 1 2 A. 1 1 x + = 1+ B. 3 2
x − x + x −1 = 0 C. = 0 D. 2
x − 3x + 2 = 0 x −1 x −1 x −1
Câu 4. Cho ABC , AD là phân giác của góc BAC, DBC. Biết AB=6cm; AC=15cm,
khi đó tỉ số của BD và DC bằng A. 2 B. 5 C. 2 D. 7 5 2 7 3 B. TỰ LUẬN (8 ĐIỂM)
Bài 1 (2 điểm): Giải các phương trình sau: − + d) x 3 1 2x + = 6 5 3 x − e) 2 1 3 11 − = x +1 x − 2 (x + )( 1 x − ) 2
Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình. Trang 16
Một số tự nhiên lẻ có hai chữ số và chia hết cho 5. Hiệu của số đó và chữ số hàng
chục của nó bằng 86. Tìm số đó.
Bài 3 (3 điểm): Cho tam giác ABC vuông ở A, AB = 6, AC = 8; đường cao AH,
phân giác BD. Gọi I là giao điểm của AH và BD. a. Tính AD, DC. b. Chứng minh IH AD = IA DC
c. Chứng minh AB.BI = BD.HB và tam giác AID cân.
Bài 4 (1 điểm): Tìm x; y thỏa mãn phương trình sau: x2 - 4x + y2 - 6y + 15 = 2 - Hết –
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN: TOÁN - LỚP 8
A. TRẮC NGHIỆM (2 ĐIỂM)
Mỗi câu đúng cho 0,5 điểm Câu 1 Câu 2 Câu 3 Câu 4 B A C A
B. TỰ LUẬN (8 ĐIỂM) Hướng dẫn chấm Điểm Bài 1 a. Biến đổi về dạng: ( 2 điểm) 13x - 94 = 0 hay 13x = 94 0,5
Giải ra x = 94 và kết luận tập nghiệm PT 0,5 13
b. - Tìm ĐKXĐ: x ≠ -1 và x ≠ 2 0,25
- Quy đồng khử mẫu đúng: 2(x-2) - (x+1) = 3x-11 0,25
- Giải ra x = 3 va kết luận tập nghiệm PT 0,5 Bài 2
- Chọn ẩn và ĐK đúng: 0,25 (2 điểm)
Gọi x là chữ số hàng chục của số phải tìm (ĐK: x là chữ số, x>0) 0,5
- Biểu diễn các ĐL qua ẩn, lập PT đúng: (10x + 5) - x = 86 0,5 - Giải PT đúng: x = 9 0,25 - Trả lời Bài 3 (3 điểm) A D 6 8 I B H C a.Tính AD, DC - Tính BC = 10 cm 0,25 - Lập tỉ số AD AB = DC BC 0,25 Trang 17 AD AB  = 0,25 DC + AD BC + AB Thay số, tính: AD = 3cm, 0,25 DC = 5cm b. 0,25 - Lập tỉ số: IH HB = IA AB 0,25
- Chứng minh  HBA   ABC 0,25  HB AB AB HI =  = AB BC BC IA 0,25 - Suy ra: IH AD = IA DC
c - Chứng minh  ABD  HBI 0,25 AB BD  =  A . B BI = B . D HB HB BI 0,25
-  ABD  HBI  BIH = ADI
Mà: BIH = AID  AID = ADI 0,25 Vậy  AID cân 0,25 Bài 4 x2 - 4x + y2 - 6y + 15 = 2 (1 điểm)
Biến đổi về dạng: (x-2)2 + (y-3)2 = 0 0,5
Lập luận dẫn tới x – 2 = 0 và y – 3 = 0 0,25 Tìm được x = 2; y = 3 0,25
Ghi chú: - Bài 3: không vẽ hình hoặc hình vẽ sai không chấm.
- Các cách làm khác đúng cho điểm tối đa tương ứng từng phần. Trang 18