













Preview text:
Tailieumontoan.com
Trịnh Bình sưu tầm tổng hợp BỘ ĐỀ THI TOÁN
VÀO LỚP 10 TỈNH THANH HÓA
Thanh Hóa, ngày 16 tháng 4 năm 2020 1
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2019 – 2020 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 1
Bài 1. (2 điểm) Cho biểu thức: x + 2 5 1 A = − −
với x ≥ 0; x ≠ 4. x + 3 x + x − 6 x − 2 1. Rút gọn A
2. Tìm giá trị của cảu A khi x = 6 + 4 2 Bài 2. (2 điểm)
1. Cho đường thẳng (d ): y = ax+b . Tìm a, b để đường thẳng (d) song song
với đường thẳng (d ') : y = 5x+6 và đi qua điểm A(2;3) + =
2. Giải hệ phương trình 3x 2y 11 x + 2y = 5 Bài 3: ( 2 điểm) 1. Giải phương trình 2
x − 4x + 3 = 0 2. Cho phương trình: 2
x − 2(m −1) x + 2m − 5 = 0 với m là tham số.Chứng minh
rằng phương trình luôn có hai nghiệm phân biệt x1, x2 với mọi m. Tìm m để các
nghiệm đó thỏa mãn hệ thức ( 2
x − 2mx − x + 2m − 3 x 2mx x 2m 3 19 . 1 1 2 )( 2 − − + − 2 2 1 ) =
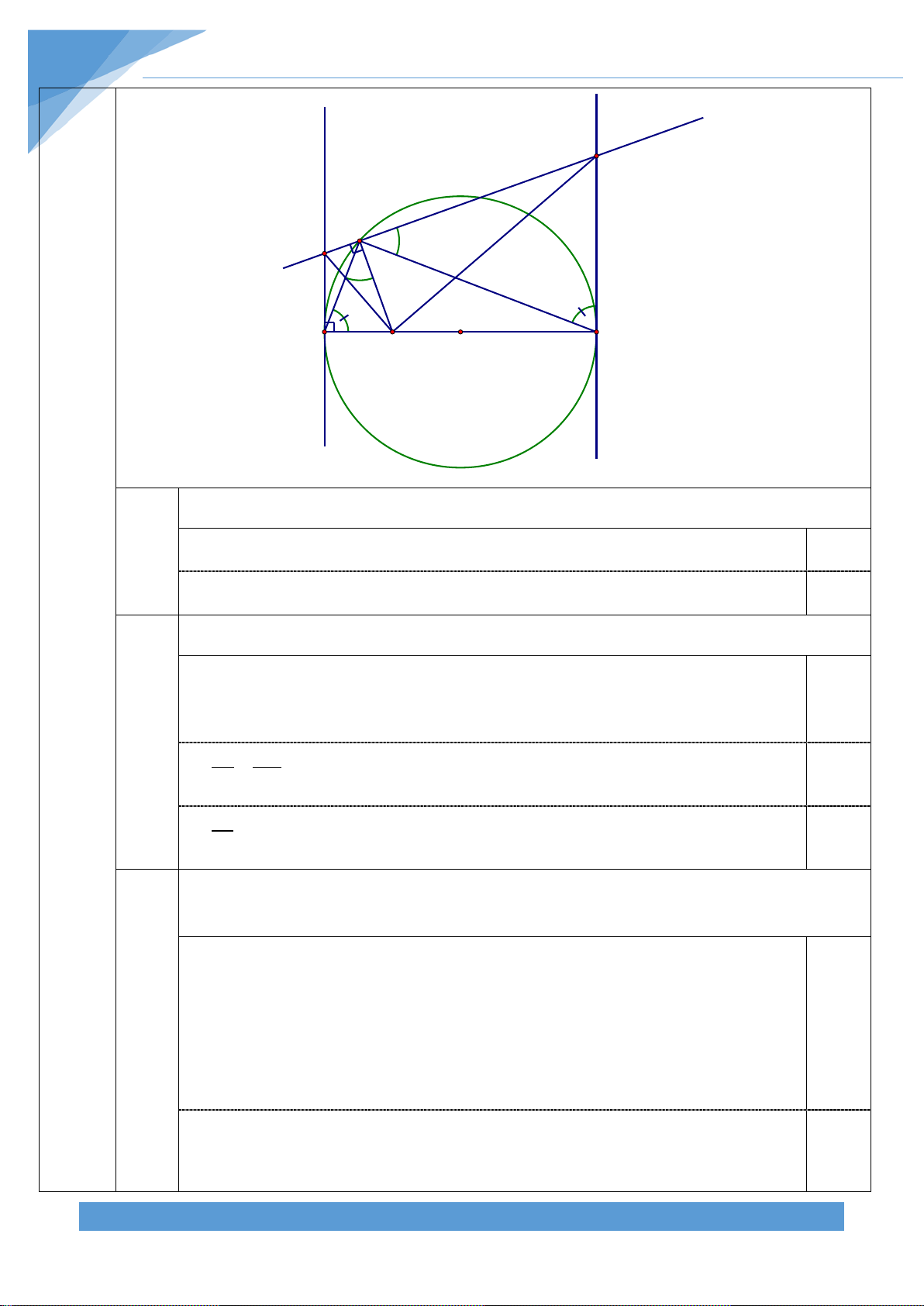
Bài 4. (3,0 điểm) Từ một điểm A nằm ngoài đường tròn tâm O bán kính R, kẻ các tiếp
tuyến AB, AC với đường tròn ( B, C là các tiếp điểm). Trê cung nhỏ BC lấy một điểm M
bất kỳ khác B và C. Gọi I,K,P lần lượt là hình chiếu vuông góc của M trên các đường thẳng AB, AC, BC
1) Chứng minh AIMK là tứ giác nội tiếp; 2) Chứng minh MPK = MBC
3) Xác định vị trí điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị nhỏ nhât.
Bài 5. (1,0 điểm) Cho các số thực a, b, c thỏa mãn abc = 1, Chứng minh rằng: ab + bc + ca ≤ 1 4 a + 4 b + 4 ab b + 4 c + 4 bc c + 4 a + ca
----------Hết----------
Họ và tên ....................................................................Số báo danh ........................................
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 2
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2018 – 2019 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 2
Câu I: (2,0 điểm) 1. Giải phương trình: 2
x + 8x + 7 = 0 . − = −
2. Giải hệ phương trình: 2x y 6 . 5 x + y = 20 +
Câu II: (2,0 điểm) Cho biểu thức x 1 x x A = : + , với x > 0 .
x + 4 x + 4 x + 2 x x + 2
1. Rút gọn biểu thức A.
2. Tìm tất cả các giá trị của x để 1 A ≥ . 3 x
Câu III: (2,0 điểm)
1. Cho đường thẳng (d ) : y = ax + b . Tìm a, b để đường thẳng (d ) song song với
đường thẳng (d ') : y = 2x + 3 và đi qua điểm A(1;− ) 1 . 2. Cho phương trình 2
x − (m − 2)x − 3 = 0 ( m là tham số). Chứng minh phương
trình luôn có hai nghiệm phân biệt x ; x với mọi m . Tìm m để các nghiệm đó thỏa mãn 1 2 hệ thức 2 2 x + 2018 − x = x + 2018 + x . 1 1 2 2
Câu IV: (3,0 điểm) Cho đường tròn tâm O, đường kính AB = 2R . Gọi d và d lần lượt là 1 2
các tiếp tuyến của đường tròn (O) tại A và B , I là trung điểm của đoạn thẳng OA, E là
điểm thay đổi trên đường tròn (O) sao cho E không trùng với A và B . Đường thẳng d
đi qua E và vuông góc với đường thẳng EI cắt d , d lần lượt tại M , N . 1 2
1. Chứng minh AMEI là tứ giác nội tiếp. 2. Chứng minh .
IB NE = 3.IE.NB .
3. Khi điểm E thay đổi, chứng minh tích AM.BN có giá trị không đổi và tìm giá trị
nhỏ nhất của diện tích tam giác MNI theo R .
Câu V: (1,0 điểm) Cho a,b,c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh 1 1 + ≥ 30. 2 2 2 a + b + c abc
------------ Hết ------------
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 3
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2017 – 2018 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 3
Câu 1. (2,0 điểm) 1. Cho phương trình: 2
mx + x − 2 = 0 (1), với m là tham số.
a. Giải phương trình (1) khi m = 0 .
b. Giải phương trình (1) khi m = 1. x − y =
2. Giải hệ phương trình: 3 2 6 x + 2y = 10 4 y 8y y 1 2 −
Câu 2. (2,0 điểm) Cho biểu thức: A = + : − y y , với > 0 , ≠ 4 ,
2 + y 4 − y y − 2 y y y ≠ 9 .
1. Rút gọn biểu thức A .
2. Tìm y để A = 2 − .
Câu 3. (2,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = 2x − m + 3 và parabol (P) 2 : y = x .
1. Tìm m để đường thẳng (d) đi qua điểm A(2;0) .
2. Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành
độ lần lượt là x , x thỏa mãn 2
x − 2x + x x = 16. 1 2 1 2 1 2
Câu 4. (3,0 điểm) Cho nửa đường tròn (O) đường kính MN = 2R . Gọi (d) là tiếp tuyến
của (O) tại N . Trên cung MN lấy điểm E tùy ý. ( E không trùng với M và N ),
tia ME cắt đường thẳng (d) tại F . Gọi P là trung điểm của ME , tia OP cắt (d) tại Q .
1. Chứng minh ONFP là tứ giác nội tiếp.
2. Chứng minh OF ⊥ MQ và PM.PF = P . O PQ .
3. Xác định vị trí điểm E trên cung MN để tổng MF + 2ME đạt giá trị nhỏ nhất.
Câu 5. (1,0 điểm) Cho a , b , c là các số dương thay đổi thỏa mãn: 1 1 1 + +
= 2017 . Tìm giá trị lớn nhất của biểu thức:
a + b b + c c + a 1 1 1 P = + + .
2a + 3b + 3c 3a + 2b + 3c 3a + 3b + 2c
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 4
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2016 – 2017 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 4 Câu I: (2,0 điểm)
1. Giải các phương trình: a. x – 6 = 0 b. x2 – 5x + 4 = 0 2.
Giải hệ phương trình: 2x - y = 3 3x + y = 2 2 -1 +1 (y−2 y y y y y + ) 1
Câu II: (2,0 điểm) Cho biểu thức: A = − :
với y > 0; y ≠ 1 y - y y + y y −1
1. Rút gọn biểu thức B.
2. Tìm các số nguyên y để biểu thức B khi có giá trị nguyên.
Câu III: (2,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = nx +1 và Parabol (P): 2 y = 2x .
1. Tìm n để đường thẳng (d) đi qua điểm B(1; 2).
2. Chứng minh rằng đường thẳng (d) luôn cắt Parabol (P) tại hai điểm phân biệt có
hoàng độ lần lượt M(x1; y1), N(x2; y2). Hãy tính giá trị của biểu thức S = x x + y y 1 2 1 2
Câu IV: (3,0 điểm) Cho tứ giác MNPQ nội tiếp đường tròn đường kính MQ. Hai đường
chéo MP và NQ cắt nhau tại E. Gọi F là điểm thuộc đường thẳng MQ sao cho EF vuông
góc với MQ. Đường thẳng PF cắt đường tròn đường kính MQ tại điểm thứ 2 là K. Gọi L là
giao điểm của NQ và PF. Chứng minh rằng:
1. Tứ giác PEFQ nội tiếp đường tròn.
2. FM là đường phân giác của góc NFK 3. NQ.LE= NE.LQ
Câu V: (1,0 điểm)
Cho các số dương m, n, p thỏa mãn: 2 2 2
m + 2n ≤ 3p . Chứng minh rằng 1 2 3 + ≥ m n p
-----------------------------------Hết----------------------------------
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 5
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2015 – 2016 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 5 Câu 1 (2 điểm) :
1. Giải phương trình mx2 + x – 2 = 0 a) Khi m = 0 b) Khi m = 1 + = 2. x y Giải hệ phương trình: 5 x − y =1
Câu 2 (2 điểm): Cho biểu thức Q = 4 3 6 b + 2 + − (Với b ≥ 0 và b ≠ 1) b −1 b +1 b −1 1. Rút gọn Q
2. Tính giá trị của biểu thức Q khi b = 6 + 2 5
Câu 3 (2 điểm): Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = x + n – 1 và parabol (P) : y = x2
1. Tìm n để (d) đi qua điểm B(0;2)
2. Tìm n để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là x 1 1 1, x2 thỏa mãn: 4 + − x x + 3 = 0 1 2 x x 1 2
Câu 4 (3 điểm): Cho đường tròn tâm O bán kính R và đường thẳng (d) không đi qua O, cắt
đường tròn (O) tại 2 điểm E, F. Lấy điểm M bất kì trên tia đối FE, qua M kẻ hai tiếp tuyến
MC, MD với đường tròn (C, D là các tiếp điểm).
1. Chứng minh tứ giác MCOD nội tiếp trong một đường tròn.
2. Gọi K là trung điểm của đoạn thẳng EF. Chứng minh KM là phân giác của góc CKD.
3. Đường thẳng đi qua O và vuông góc với MO cắt các tia MC, MD theo thứ tự tại R,
T. Tìm vị trí của điểm M trên (d) sao cho diện tích tam giác MRT nhỏ nhất.
Câu 5 (1 điểm): Cho x, y, z là các số dương thay đổi thỏa mãn điều kiện: 5x2 + 2xyz + 4y2 + 3z2 = 60
Tìm giá trị nhỏ nhất của biểu thức B = x + y + z.
------------ Hết ------------
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 6
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2014 – 2015 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 6 Câu 1. (2.0 đ)
1. Giải các phương trình sau: a. y - 3 = 0 b. y2 – 3y + 2 = 0 x + 2y = 4
b. Giải hệ phương trình: 3 x −2y =4 −
Câu 2. (2.0 đ) Cho biểu thức y 1 1 1 B = : −
, với y > 0 và y ≠ 1. 2 y y − y y +1
a. Rút gọn biểu thức B.
b. Tính giá trị của B khi x = 3 + 2 2 .
Câu 3 (2.0 đ) Trong mặt phẳng toạ độ Oxy cho đường thẳng (d): y = nx – 3 và parabol (p) y = x2.
1. Tìm n để đường thẳng (d) đi qua điểm B(1; 0)
2. Tìm n để (d) cắt (p) tại hai điểm phân biệt có hoành độ lần lượt là x1, x2 thoả mãn x − x = 2 1 2
Câu 4 (3.0 đ) Cho đường tròn tâm O đường kính EF = 2R. Gọi C là trung điểm của OE; qua
C kẻ đường vuông góc với OE cắt đường tròn đó tại hai điểm phân biệt M và N. Trên
cung nhỏ FM lấy điểm K ( K ≠ F và K ≠ M), trên tia KN lấy điểm I sao cho KI = KM. gọi D
là giao điểm của EK và MN. Chứng minh rằng:
a. Tứ giác FCDKlà tứ giác nội tiếp. b. EK . ED = R2 c. NI = FK.
Câu 5 (1 đ) Cho các số thực dương a, b, c thoả mãn abc = 1.
Tìm giá trị lớn nhất của biểu thức P 1 + 1 + 1 a + b +1 b + c +1 c + a +1
------------ Hết ------------
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 7
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2013 – 2014 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 7
Câu 1 (2.0 điểm):
1. Cho phương trình bậc hai: x2 +2x – 3 = 0, với các hệ số a = 1, b = 2, c = -3 a.Tính tổng: S = a + b + c
b.Giải phương trình trên x − 3y = 2
2. Giải hệ phương trình: 2x + 3y = 4 1 1 y +1
Câu 2 (2.0 điểm): Cho biểu thức: Q = + : ( Với y > 0; y − y y −1 y − 2 y +1 y ≠1) a. Rút gọn biểu thức Q
b. Tính giá trị biểu thức Q khi y = 3 − 2 2
Câu 3 (2.0 điểm): Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = 2bx + 1 và Parabol (P): y = - 2x2.
a. Tìm b để đường thẳng (d) đi qua điểm B(1;5)
b. Tìm b để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có hoành độ thỏa
mãn điều kiện: x12 + x22 + 4(x1 + x2) = 0.
Câu 4 (3.0 điểm): Cho (O; R) đường kính EF. Bán kính OI vuông góc với EF, gọi J là điểm
bất kỳ trên Cung nhỏ EI (J khác E và I), FJ cắt EI tại L; Kẻ LS vuông góc với EF (S thuộc EF).
a. Chứng minh tứ giác IFSL nội tiếp.
b. Trên đoạn thẳng FJ lấy điểm N sao cho FN = EJ. Chứng minh rằng, tam giác IJN vuông cân.
c. Gọi (d) là tiếp tuyến tại điểm E. Lấy D là điểm nằm trên (d) sao cho hai điểm D và
I cùng nằm trên cùng một nữa mặt phẳng bờ là đường thẳng FE và ED.JF = JE.OF. Chứng
minh rằng đường thẳng FD đi qua trung điểm của đoạn thẳng LS.
Câu 5 ( 1.0 điểm): Cho a, b, c là các số thực dương thỏa mãn: ab + bc + ca ≥ 3. 4 4 4 a b c 3 Chứng minh rằng: + + ≥ b + 3c c + 3a a + 3b 4
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 8
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2012 – 2013 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 8
Bài 1: (2.0 điểm) 1- Giải các phương trình sau : a) x - 1 = 0 b) x2 - 3x + 2 = 0 2x − y =
2- Giải hệ phương trình : 7 x + y = 2 2
Bài 2: (2.0 điểm) Cho biẻu thức : A = 1 + 1 - a +1 2 + 2 a 2 − 2 a 2 1 − a
1- Tìm điều kiện xác định và rút gọn biểu thức A
2- Tìm giá trị của a ; biết A < 1 3
Bài 3: (2.0 điểm)
1- Cho đường thẳng (d) : y = ax + b .Tìm a; b để đường thẳng (d) đi qua điểm A( -1 ; 3)
và song song với đường thẳng (d’) : y = 5x + 3
2- Cho phương trình ax2 + 3(a + 1)x + 2a + 4 = 0 ( x là ẩn số ) .Tìm a để phươmg trình đã
cho có hai nghiệm phân biệt x1 ; x2 thoả mãn 2 x + 2 x = 4 1 2
Bài 4: (3.0 điểm) Cho tam tam giác đều ABC có đường cao AH . Trên cạnh BC lấy điểm M
bất kỳ ( M không trùng B ; C; H ) Từ M kẻ MP ; MQ lần lượt vuông góc với các cạnh AB ;
AC ( P thuộc AB ; Q thuộc AC)
1- Chứng minh :Tứ giác APMQ nội tiếp đường tròn
2- Gọi O là tâm đường tròn ngoại tiếp tứ giác APMQ .Chứng minh OH ⊥ PQ
3- Chứng minh rằng : MP +MQ = AH
Bài 5: (1.0 điểm) Cho hai số thực a; b thay đổi , thoả mãn điều kiện a + b ≥ 1 và a > 0 2
Tìm giá trị nhỏ nhất của biểu thức A = 8a + b 2 + b 4a
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 9
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2011 – 2012 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 9 Bài 1(1.5đ):
1. Cho hai số a1 = 1+ 2 ; a2 = 1- 2 . Tính a1+a2. x + 2 y = 2. 1
Giải hệ phương trình:
2x − y = −3 a a a −
Bài 2(2đ): Cho biểu thức A = 4 1 1 − + : (Với a ≥ 0;a ≠ 4 ) a + 2 a − 2 a − 4 a + 2
1. Rút gọn biểu thức A.
2. Tính giá trị của A tại a = 6+4 2
Bài 3(2,5đ): Cho phương trình: x2 – (2m-1)x + m(m-1) = 0 (1). (Với m là tham số)
a. Giải phương trình (1) với m = 2.
b. Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt với mọi m.
c. Gọi x1 và x2 là hai nghiệm của phương trình (1). (Với x1 < x2).
Chứng minh rằng x12 – 2x2 + 3 ≥ 0.
Bài 4(3đ): Cho tam giác ABC có ba góc nhọn. Đường cao BD và CK cắt nhau tại H.
1. Chứng minh tứ giác AKHD nội tiếp được trong một đường tròn
2. Chứng minh tam giác AKD và tam giác ACB đồng dạng.
3. kẻ tiếp tuyến Dx tại D của đường tròn tâm O đường kính BC cắt AH tại M. Chứng
minh M là trung điểm của AH
Bài 5(1đ): Cho ba số dương a, b, c. Chứng minh bất đẳng thức: a + b + c ≥ 2 b + c a + c a + b
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 10
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2011 – 2012 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 10
Bài I (2,0 điểm)
Cho phương trình : x2 + nx – 4 = 0 (1) (với n là tham số)
1. Giải phương trình (1) khi n = 3
2. Giả sử x1,x2 là nghiệm của phương trình (1),tìm n để :
x1(x22 +1 ) + x2( x12 + 1 ) > 6 + −
Bài II (2,0 điểm) Cho biểu thức a 3 a 3 1 1 A = − −
với a > 0; a ≠ 9 a − 3 a + 3 3 a 1.Rút gọn A
2.Tìm a để biểu thức A nhận giá trị nguyên.
Bài III (2,0 điểm) Trong mặt phẳng toạ độ Oxy
Cho parabol (P): y = x2 và các điểm A,B thuộc parabol (P) v ới xA = -1,xB = 2
1.T ìm toạ độ c ác điểm A,B và viết phương trình đường th ẳng AB.
2. Tìm m để đường thẳng (d) : y = (2m2 – m)x + m + 1 (với m là tham số ) song song với đường thẳng AB.
Bài IV (3,0 điểm) Cho tam giác PQR có ba góc nhọn nội tiếp đường tròn tâm O, các đường
cao QM, RN của tam giác cắt nhau tại H.
1.Chứng minh tứ gi ác QRMN là tứ giác nội tiếp trong một đường tròn.
2. Kéo dài PO cắt đường tròn O tại K.Chứng minh tứ giác QHRK là hình bình hành.
3. Cho cạnh QR cố định,P thay đổi trên cung lớn QR sao cho tam giác PQR luôn
nhọn.Xác định vị trí điểm P đ ể diện tích tam giác QRH lớn nhất.
Bài V ( 1,0 điểm) Cho x,y là các số dương thoả mãn : x + y = 4
Tìm giá trị nhỏ nhất của : 33 2 2
P = x + y + xy
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 11
Website:tailieumontoan.com
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT THANH HÓA THANH HÓA
NĂM HỌC 2011 – 2012 MÔN THI: TOÁN
Đề chí nh thức
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề số 11
Bài 1 (1,5 điểm) Cho phương trình: x2 – 4x + n = 0 (1) với n là tham số.
1.Giải phương trình (1) khi n = 3.
2. Tìm n để phương trình (1) có nghiệm. + =
Bài 2 (1,5 điểm) Giải hệ phương trình: x 2y 5 2x + y = 7
Bài 3 (2,5 điểm) Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x2 và điểm B(0;1)
1. Viết phương trình đường thẳng (d) đi qua điểm B(0;1) và có hệ số k.
2. Chứng minh rằng đường thẳng (d) luôn cắt Parabol (P) tại hai điểm phân biệt E và F với mọi k.
3. Gọi hoành độ của E và F lần lượt là x1 và x2. Chứng minh rằng x1 .x2 = - 1, từ đó suy
ra tam giác EOF là tam giác vuông.
Bài 4 (3,5 điểm) Cho nửa đường tròn tâm O đường kính AB = 2R. Trên tia đối của tia BA
lấy điểm G (khác với điểm B) . Từ các điểm G; A; B kẻ các tiếp tuyến với đường tròn (O) .
Tiếp tuyến kẻ từ G cắt hai tiếp tuyến kẻ từ A và B lần lượt tại C và D.
1. Gọi N là tiếp điểm của tiếp tuyến kẻ từ G tới nửa đường tròn (O). Chứng minh tứ
giác BDNO nội tiếp được.
2. Chứng minh tam giác BGD đồng dạng với tam giác AGC, từ đó suy ra CN DN = . CG DG 3. Đặt
BOD = α Tính độ dài các đoạn thẳng AC và BD theo R và α. Chứng tỏ rằng
tích AC.BD chỉ phụ thuộc R, không phụ thuộc α. 2
Bài 5 (1,0 điểm) Cho số thực m, n, p thỏa mãn : 3m 2 2
n + np + p = 1 − . 2
Tìm giá trị lớn nhất và nhỏ nhất của biểu thức : B = m + n + p.
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 12
Website:tailieumontoan.com HƯỚNG DẪN GIẢI Đề số 1 Câu I.
1. Rút gọn biểu thức A với với x ≥ 0; x ≠ 4.
x − 4 − 5 − ( x + 3) x + 2 5 1 x − x −12 x − 4 A = − − = = = x + 3
( x +3)( x −2) x −2 ( x +3)( x −2) ( x +3)( x −2) x −2
2. Tìm giá trị của cảu A khi x = 6 + 4 2 x = + = ( + )2 6 4 2 2 2 tmđk (2+ 2)−4 2− 2
x = 2 + 2 thay vào A ta đc: A = ( = = − 2 + 2 ) 1 2 − 2 2
Vậy với x = 6 + 4 2 thì A =1− 2 Bài 2. (2 điểm) 1.
Cho đường thẳng (d ) : y = ax+b . Tìm a, b để đường thẳng (d) song song với
đường thẳng (d ') : y = 5x+6 và đi qua điểm A(2;3) = Vì ( a
d ) / / (d ') nên 5 b ≠ 6
Vì (d) đi qua A(2;3) nên ta có: 3 = 5.2+b ⇒ b = 7 −
Vậy a = 5;b = 7
− ta có (d ) : y = 5x − 7 2. x + y = Giải hệ phương trình 3 2 11 x + 2y = 5 3 x + 2y =11 x = 3 ⇔ ⇔ 2x = 6 y =1 Bài 3: ( 2 điểm) 1. Giải phương trình 2
x − 4x + 3 = 0
PT có : a + b + c =1− 4 + 3 = 0 nên PT có hai nghiệm: x =1; x = 3 1 2 2. 2 2
Ta có: ∆ = (m − ) − m + = 2 ' 1 2
5 m − 4m + 6 = (m − 2) + 2 > 0 ∀m nên phương
trình luôn có hai nghiệm phân biệt x1, x2 với mọi m Có : 2
x − 2(m −1) x + 2m − 5 = 0 ⇔ 2
x − 2mx + 2m − 3 = 2 − 2x
Vì x1, x2 là các nghiệm của PT (1) nên ta có: 2
x − 2mx + 2m − 3 = 2 − 2x ; 2
x − 2mx + 2m − 3 = 2 − 2x thay vào (*) ta đc: 1 1 1 2 2 2
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 13
Website:tailieumontoan.com ( 2
x − 2mx − x + 2m − 3 x 2mx x 2m 3 19 1 1 2 )( 2 − − + − 2 2 1 ) =
⇔ (2 − 2x − x )(2 − 2x − x ) = 19 1 2 2 1 ⇔ 2(x + x 6 x x x x 15 1 2 )2 − ( + 1 2 ) + = 1 2
x + x = 2 m 1 1 2 ( − ) Theo Vi-et có thay vào ta đc: x x = 2m − 5 1 2 m = 0 ⇔ (m − )2 8
1 − 12(m −1) + 2m − 5 = 15 2
⇔ 8m − 26m = 0 ⇔ m = 13 4 m = 0 Vây: m = 13 4 Bài 4. (3,0 điểm)
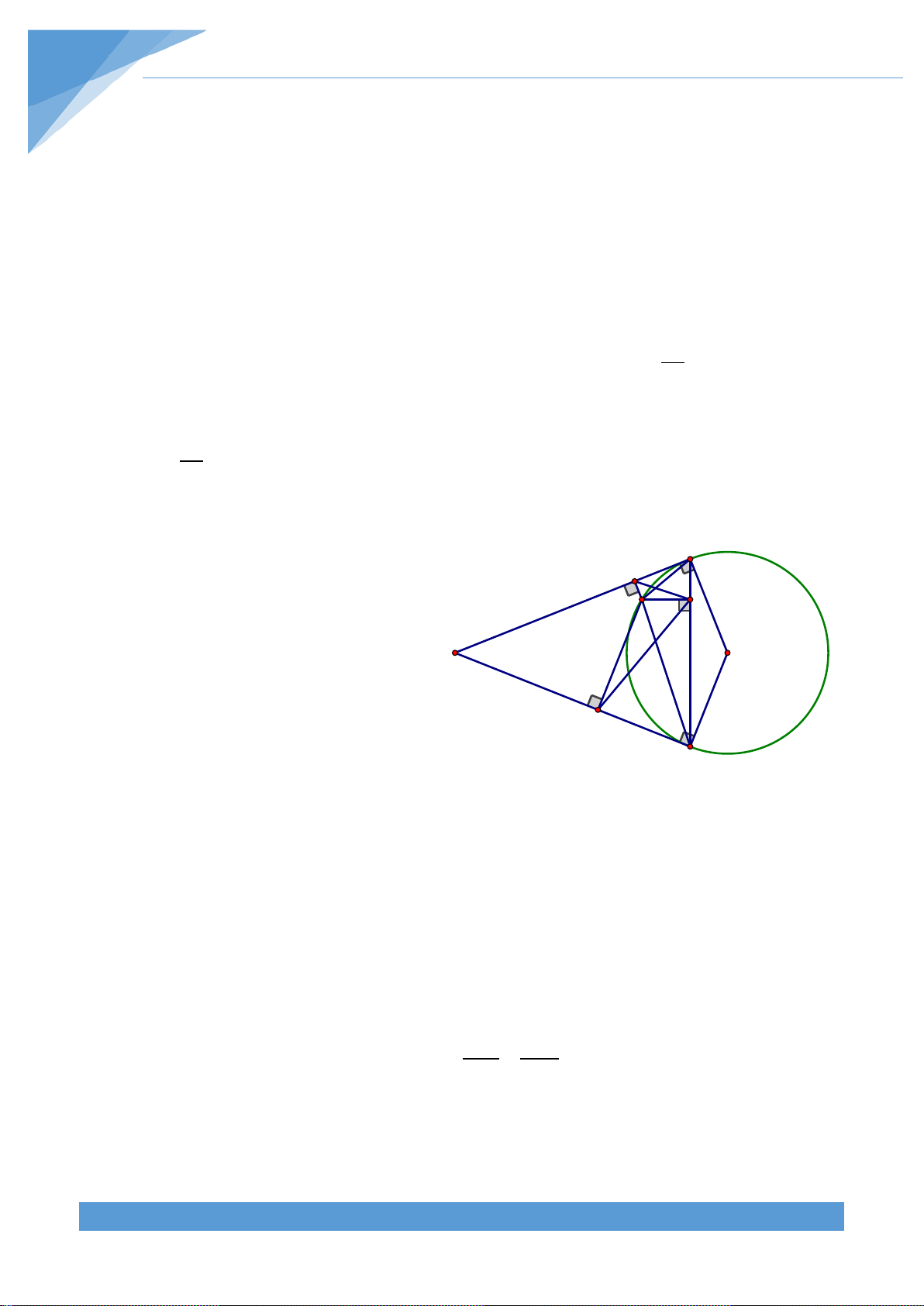
1. Chứng minh AIMK là tứ giác B nội tiếp; I Có: = = 90o AIM AKM nên tứ giác M P AIMK nội tiếp. A O 2. Chứng minh MPK = MBC .
TT câu a ta cm đc tứ giác KCPM nội K tiếp. C Suy ra: MCK = MPK ( hai góc nt cùng chắn cung MK) (1) Mà MCK =
PBM ( góc tạo bởi tia tiếp tuyến và dây và góc nt cùng chắn cung MC của (O)) (2) Từ (1) và (2) suy ra MPK = MBP hay MPK = MBC
1) Xác định vị trí điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị nhỏ nhât. IM MP
Chứng minh được ∆IMP ∽ ∆PMK nên: = MP MK ⇒ MI MK = 2
MP ⇒ MI MK MP = 3 . . . MP
Để MI.MK.MP lớn nhất khi chỉ khi MP lớn nhất, nên M là điểm chính giữa cung nhỏ BC
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 14
Website:tailieumontoan.com
Bài 5. (1,0 điểm) Cho các số thực a, b, c thỏa mãn abc = 1, Chứng minh rằng: ab + bc + ca ≤ 1 4 a + 4 b + 4 ab b + 4 c + 4 bc c + 4 a + ca Ta có: ab ab 1 4 + 4 ≥ ( 2 + 2 a b ab a b ) ⇒ ≤ 4 4 a b ab ab( 2 a + 2 b ) = + + + 2 ab a + 2 b +1 Tương tự có: bc ≤ 1 ; ca ≤ 1 4 b + 4 c + 2 bc b + 2 c +1 4 c + 4 a + 2 ca c + 2 a +1 Suy ra VT ≤ 1 + 1 + 1 2 a + 2 b + 2 1 b + 2 c + 2 1 c + 2 a +1 Đặt 2 a = 3 2 x b = 3 2 y c = 3 ; '
z ta có: xyz = 1 ( do abc = 1) Suy ra: VT ≤ 1 + 1 + 1 3 x + 3 y + 3 1 y + 3 z + 3 1 z + 3 x +1 Dễ cm đc 3 + 3 x
y ≥ xy ( x + y) VT ≤ 1 1 1 xy ( x y) + 1 yz(y z) + + +
+ +1 zx (z + x) +1 ≤ z x y VT xyz( x y) + z xyz(y z) + + +
+ + x zxy (z + x) + y ≤ z + x + y VT = 1 x + y + z
x + y + z zx + y + z
Vậy VT ≤ 1 Dấu “_” xảy ra khi a = b = c Đề số 2 Điể Câu Ý NỘI DUNG m
Giải phương trình: 2
x + 8x + 7 = 0 . 1
Ta thấy phương trình có các hệ số thỏa mãn a − b + c =1−8 + 7 = 0 . 0,5
(1,0đ) Do đó phương trình có hai nghiệm x= 1−; x= 7− 0,5 I − = −
Giải hệ phương trình: 2x y 6 5 x + y = 20 (2,0đ) 2 = =
Hệ tương đương với 7x 14 x 2 ⇔ 0,5 (1,0đ) 5 x + y = 20 5 x + y = 20 x = 2 = ⇔ x 2 ⇔ . 0,5 10 + y = 20 y =10
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 15
Website:tailieumontoan.com
Rút gọn biểu thức x +1 x x A = : +
, với x > 0 .
x + 4 x + 4 x + 2 x x + 2 Ta có: x +1 x x A = : +
x + 4 x + 4 x + 2 x x + 2 0,25 x +1 x x = : + 1 2 ( x + 2) x( x + 2) x + 2 (1,0đ) x +1 x x = : + 0,25 2 ( x + 2) x + 2 x + 2 x +1 x ( x +1) = 0,25 II : 2 ( x + 2) x + 2 (2,0đ) 1 = 0,25 x ( x + 2)
Tìm tất cả các giá trị của x để 1 A ≥ . 3 x Với x > 0 ta có 1 A =
và x > 0 ; x + 2 > 0. + 2 x ( x 2) 0,5 (1,0đ) Khi đó 1 1 1 A ≥ ⇔ ≥ ⇔ x + 2 ≤ 3 3 x
x ( x + 2) 3 x
⇔ x ≤ 1 ⇔ x ≤ 1 0,25
Kết hợp với điều kiện ta được: 0 < x ≤1. 0,25
Cho đường thẳng (d ) : y = ax + b . Tìm a, b để đường thẳng (d ) song song với
đường thẳng (d ') : y = 2x + 3 và đi qua điểm A(1;− ) 1 .
Đường thẳng (d ) = + song song với đường thẳng (d ') = + 1 : y ax b : y 2x 3 a = 0,5 III (1,0đ) nên ta có 2 . b ≠ 3 (2,0đ)
Khi đó (d ) : y = 2x + b đi qua điểm A(1;− ) 1 nên: 0,5 1
− = 2.1+ b ⇔ b = 3
− (thỏa mãn điều kiện b ≠ 3) . Vậy a = 2 , b = 3 − . 2 Cho phương trình 2
x − (m − 2)x − 3 = 0 ( m là tham số). Chứng minh phương
(1,0đ) trình luôn có hai nghiệm phân biệt x ; x với mọi m . Tìm m để các nghiệm đó 1 2
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 16
Website:tailieumontoan.com
thỏa mãn hệ thức: 2 2 x + 2018 − x =
x + 2018 + x . 1 1 2 2 Ta có 2
∆ = (m − 2) +12 > 0, m
∀ nên phương trình luôn có hai nghiệm phân
biệt x , x với mọi m. 1 2 0,25
(Lưu ý: Học sinh có thể nhận xét ac = 3
− < 0 để suy ra phương trình luôn
có hai nghiệm phân biệt, trái dấu với mọi m ) Ta có: 2 2 x + 2018 − x = x + 2018 + x 1 1 2 2 2 2
⇔ x + 2018 − x + 2018 = x + x 1 2 2 1 0,25 2 2 x − x 1 2 ⇔ = x + x 2 1 2 2 x + 2018 + x + 2018 1 2 x + x = 0 (1) ⇔ 1 2 2 2
x + 2018 + x + 2018 = x − x (2) 1 2 1 2 0,25
Theo định lí Viet ta có: x + x = m − 2 . Khi đó: 1 2
(1) ⇔ m − 2 = 0 ⇔ m = 2 .
(2) không xảy ra. Thật vậy: Do 2
x + 2018 > x ; 2
x + 2018 > x suy ra 0,25 1 1 2 2 2 2 x + 2018 +
x + 2018 > x + x ≥ x − x . Vậy m = 2 . 1 2 1 2 1 2
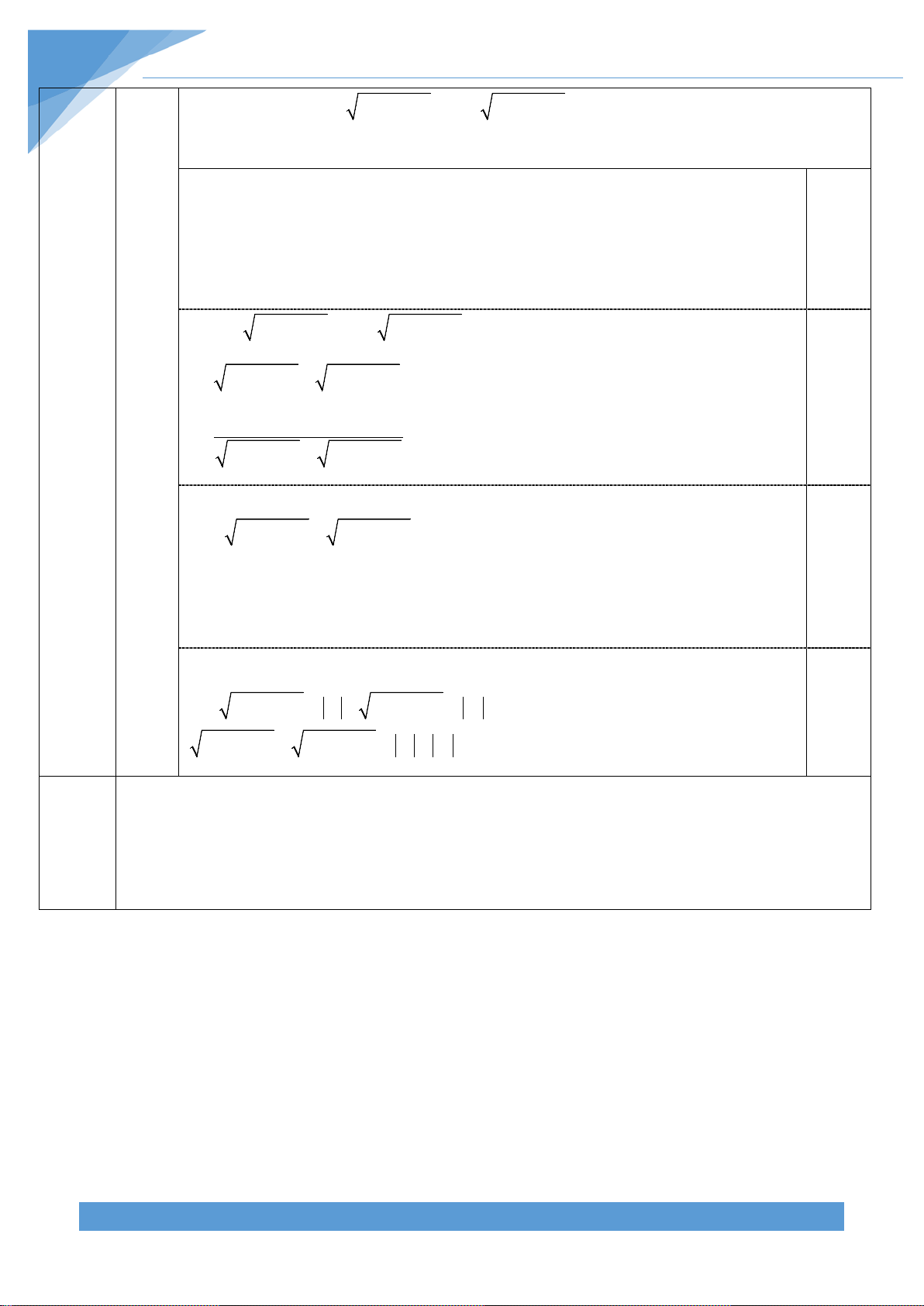
Cho đường tròn tâm O , đường kính AB = 2R . Gọi d và d lần lượt là các tiếp tuyến 1 2 IV
của đường tròn (O) tại A và B , I là trung điểm của đoạn thẳng OA, E là điểm thay
(3,0đ) đổi trên đường tròn (O) sao cho E không trùng với A và B . Đường thẳng d đi qua E
và vuông góc với đường thẳng EI cắt d , d lần lượt tại M , N . 1 2
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 17
Website:tailieumontoan.com d N E M A B I O d1 d2
Chứng minh AMEI là tứ giác nội tiếp. 1 = 0 MAI MEI = 90 0,5
(1,0đ) Suy ra + 0 MAI
MEI = 180 . Vậy AMEI nội tiếp. 0,5 Chứng minh .
IB NE = 3.IE.NB . +) = EAI
EBN (cùng phụ với EBA ) 0,5 2 +) = AEI
BEN (cùng phụ với IEB ). Suy ra I ∆ AE N ∆ BE . (1,0đ) IA NB ⇒ = ⇒ .
IA NE = IE.NB 0,25 IE NE IB ⇒
.NE = IE.NB ⇒ .
IB NE = 3IE.NB (đpcm). 0,25 3
Khi điểm E thay đổi, chứng minh tích AM.BN có giá trị không đổi và tìm giá
trị nhỏ nhất của diện tích tam giác MNI theo R .
Do tứ giác AMEI nội tiếp nên = AMI AEI (1). 3
Tương tự ta có tứ giác BNEI nên = BIN BEN (2). 0,25
(1,0đ) Theo trên ta có = AEI BEN (3).
Từ (1), (2), (3) suy ra = AMI BIN (4).
Do tam giác AMI và BIN vuông tại A và B , suy ra A ∆ MI B ∆ IN . 0,25
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 18
Website:tailieumontoan.com Suy ra: AM AI =
⇒ AM.BN = AI.BI không đổi. BI BN
Từ (4) ta có: + = + 0 BIN AIM AMI AIM = 90 ⇒ 0 MIN = 90 hay MN ∆ I vuông tại 1 1 I . Khi đó: 2 2 2 2 S = IM.IN =
AM + AI . BN + BI MN ∆ I 2 2 0,25 2 1 R 3R 3R ≥
2 AM .AI . 2BN.BI =
AM .BN.AI.BI = AI.BI = . = 2 2 2 4 2 Dấu “=” xảy ra khi 3R
AM = AI , BN = BI . Vậy S đạt GTNN bằng 0,25 MN ∆ I 4 Cho a, ,
b c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh 1 1 + ≥ 30. 2 2 2 a + b + c abc
Áp dụng BĐT Cauchy ta có: 3 1
= a + b + c ≥ 3 abc > 0 0,25 1 9
⇒ ab + bc + ca ≥ 9abc > 0 ⇒ ≥
ab + bc + ca ≥ 3 (abc)2 3 > 0 + + abc ab bc ca Khi đó: 1 1 1 9 + ≥ + = 2 2 2 2 2 2 a + b + c abc a + b + c
ab + bc + ca 1 1 1 7 = + + + 1 2 2 2 ( ) V a + b + c
ab + bc + ca
ab + bc + ca
ab + bc + ca
Áp dụng bất đẳng thức 1 1 1 9 + + ≥
với mọi x, y, z > 0 ta được 0,25 (1,0đ) x y z x + y + z (1,0đ) 1 1 1 9 + + ≥ 2 2 2 2 2 2 a + b + c
ab + bc + ca
ab + bc + ca
a + b + c + 2 (ab + bc + ca) 9 = = 9 2 2 ( )
(a +b + c)
Lại có = (a + b + c)2 2 2 2 1
= a + b + c + 2(ab + bc + ca) ≥ 3(ab + bc + ca) (3) 0,25 Thay ( 1 1 2),(3) vào ( ) 1 ta được + ≥ 9 + 7.3 = 30 . 2 2 2 a + b + c abc 0,25
Dấu “=” xảy ra khi và chỉ khi 1
a = b = c = . 3
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC 19
Website:tailieumontoan.com Đề số 3 Câu 1: 1. Cho phương trình: 2
mx + x − 2 = 0 (1), với m là tham số
a. Giải phương trình (1) khi m = 0 .
Khi m = 0 , ta có phương trình: x − 2 = 0 ⇔ x = 2
Vậy phương trình có một nghiệm duy nhất là x = 2 .
b. Giải phương trình (1) khi m = 1.
Khi m = 1, ta có phương trình: 2 x + x − 2 = 0
Ta thấy: a + b + c = 0 nên phương trình có hai nghiệm phân biệt là: x = 1; x = 2 − . 1 2
2. Giải hệ phương trình: x − y = x = x = x = 3 2 6 ⇔ 4 16 4 4 ⇔ ⇔ x + 2y = 10 x + 2y = 10 4 + 2y = 10 y = 3
Vậy nghiệm của hệ phương trình là: (x;y) = (4;3) 4 y 8y y 1 2 −
Câu 2: Cho biểu thức: A = + : − y y y
, với > 0 , ≠ 4 , ≠ 9 .
2 + y 4 − y y − 2 y y
1. Rút gọn biểu thức A .
4 y ( y 2) 8y − − y −1 2 A = ( − y )( y ) : 2
2 y ( y 2) y − + − y −1− 2 − y − y ( y −2 4 8 ) = ( y − )( y + ) : 2 2 y ( y −2) 4 − y ( y +2) − y + 3 = ( y − )( y + ) : 2 2 y ( y −2) y − y ( y −2 4 ) = ( y − 2) . − y +3 4 y =
(với y > 0 , y ≠ 4 , y ≠ 9 ). y − 3
2. Tìm y để A = 2 − .
Liên hệ tài liệu word môn toán zalo: 039.373.2038 TÀI LIỆU TOÁN HỌC



