BT4 Chương 4 - Phân Tích FIRST và FOLLOW trong Ngữ Pháp. Môn Chương trình dịch (Phenika) | Đại học Trường Đại học Phenika.

lOMoAR cPSD| 59285474 lOMoAR cPSD| 59285474 lOMoAR cPSD| 59285474 Tính FIRST •
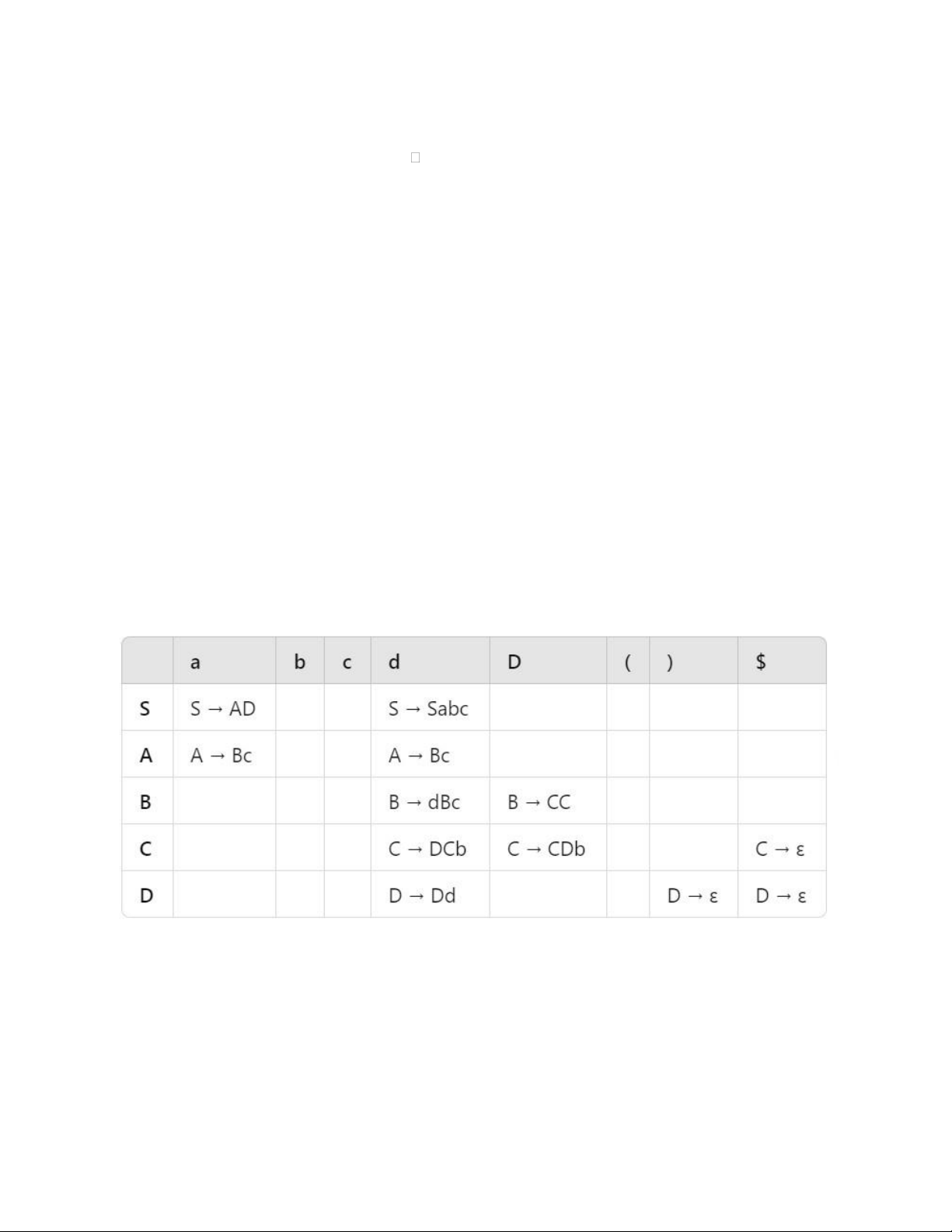
FIRST(A) = FIRST(Bc) = FIRST(B) = {d, ε} • FIRST(B) = {d, C} • FIRST(C) = {D, C, ε} • FIRST(D) = {d, ε} • FIRST(S) = {a, d} Tính FOLLOW • FOLLOW(S) = {$} • FOLLOW(A) = {c} • FOLLOW(B) = {c} • FOLLOW(C) = {b} • FOLLOW(D) = {c}
Luật sinh S → AD | Sabc •
Tính FIRST(AD) = FIRST(A) = {a} •
Tính FIRST(Sabc) = FIRST(S) = {a, d}
⇒ M[S, a] chứa S → AD
⇒ M[S, d] chứa S → Sabc Luật sinh B → dBc | CC • Tính FIRST(dBc) = {d} •
Tính FIRST(CC) = FIRST(C) = {D, ε}
⇒ M[B, d] chứa B → dBc
⇒ M[B, D] chứa B → CC lOMoAR cPSD| 59285474
Luật sinh C → DCb | CDb | ε •
Tính FIRST(DCb) = FIRST(D) = {d, ε} Tính FIRST(CDb) = FIRST(C) = {D, ε} • FIRST(ε) = {ε}
⇒ M[C, d] chứa C → DCb
⇒ M[C, D] chứa C → CDb
⇒ Nếu ε ∈ FIRST(C), thêm FOLLOW(C) vào M[C, b] Luật sinh A → Bc •
Tính FIRST(Bc) = FIRST(B) = {d, D, ε}
⇒ M[A, d] chứa A → Bc
⇒ M[A, D] chứa A → Bc Luật sinh D → Dd | ε • Tính FIRST(Dd) = {D} • FIRST(ε) = {ε}
⇒ M[D, D] chứa D → Dd
⇒ Nếu ε ∈ FIRST(D), thêm FOLLOW(D) vào M[D, c] lOMoAR cPSD| 59285474 Tính FIRST • FIRST(F) = {a} • FIRST(S) = {a, (} Tính FOLLOW • FOLLOW(S) = {+, )} •
FOLLOW(F) = {+, ), $} Luật sinh S → F • Tính FIRST(F) = {a}
⇒ M[S, a] chứa S → F lOMoAR cPSD| 59285474
Luật sinh S → (S + F) •
Tính FIRST((S + F)) = {(}
⇒ M[S, (] chứa S → (S + F) Luật sinh F → a •
Tính FIRST(a) = {a} ⇒ M[F, a] chứa F → a
Phân tích w = (a + a) 1. S → (S + F) 2. S → (F + F) 3. F → a 4. F → a Tính FIRST •
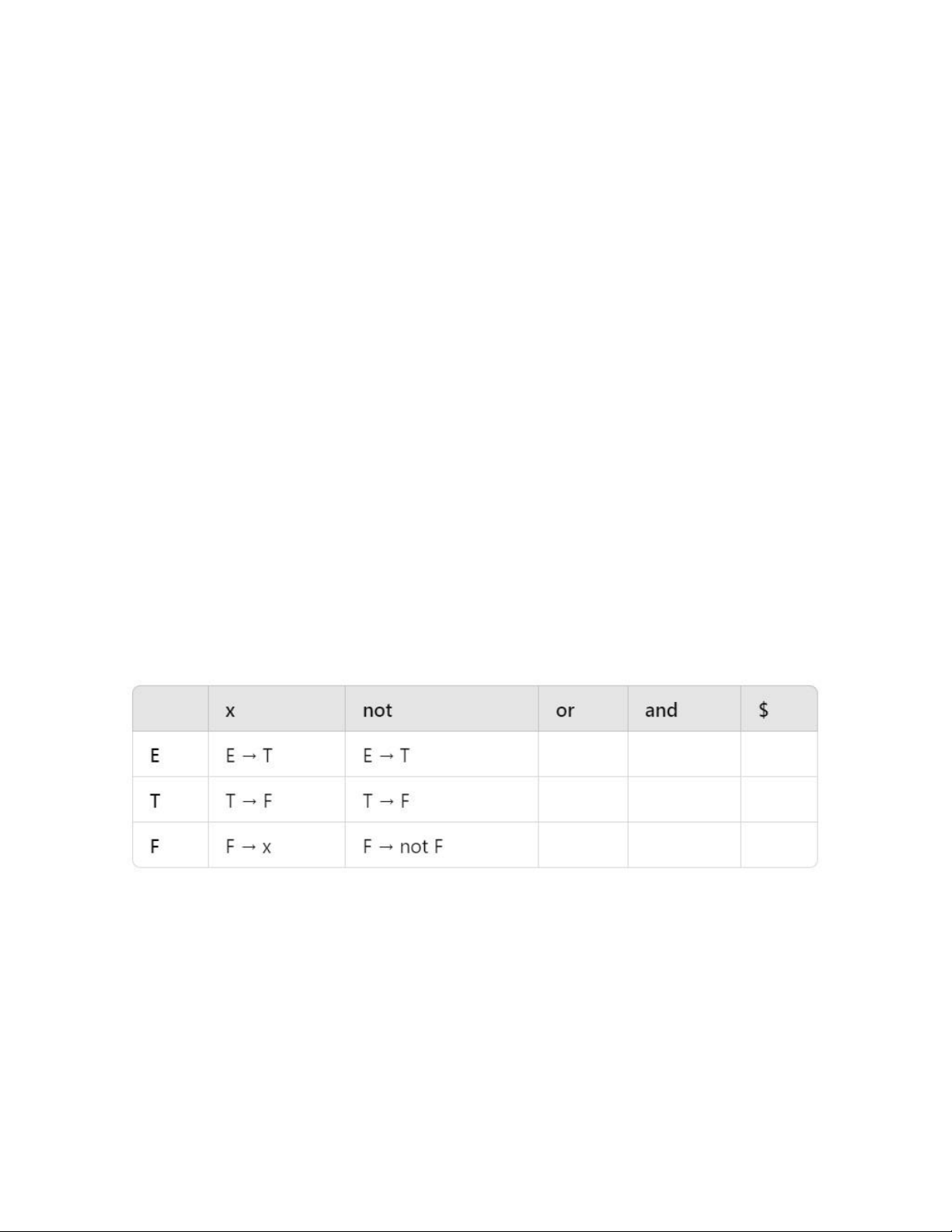
FIRST(E) = FIRST(T) = {x, not} FIRST(T) = FIRST(F) = {x, not} • FIRST(F) = {x, not} Tính FOLLOW • FOLLOW(E) = {$} • FOLLOW(T) = {or, $} lOMoAR cPSD| 59285474 • FOLLOW(F) = {and, or, $}
Luật sinh E → E or T | T •
Tính FIRST(E or T) = FIRST(E) = {x, (} •
Tính FIRST(T) = {x, (}
⇒ M[E, x] chứa E → T
⇒ M[E, (] chứa E → T
Luật sinh T → T and F | F •
Tính FIRST(T and F) = FIRST(T) = {x, (} •
Tính FIRST(F) = {x, (}
⇒ M[T, x] chứa T → F
⇒ M[T, (] chứa T → F
Luật sinh F → not F | (E) | x •
Tính FIRST(not F) = {not} • Tính FIRST((E)) = {(} • Tính FIRST(x) = {x}
⇒ M[F, not] chứa F → not F
⇒ M[F, (] chứa F → (E)
⇒ M[F, x] chứa F → x
Phân tích w = (x and not x) or x 1. E → E or T 2. E → T and F 3. T → F 4. F → x 5. F → not F lOMoAR cPSD| 59285474 6. F → x
Chuỗi w = (x and not x) or x có thể phân tích. Tính FIRST • FIRST(S) = {a} FIRST(B) = {c} • FIRST(C) = {b, ε} FIRST(D) = {g, ε} • FIRST(E) = {g, ε} • FIRST(F) = {f, ε} Tính FOLLOW • FOLLOW(S) = {$} • FOLLOW(B) = {D} • FOLLOW(C) = {h} FOLLOW(D) = {h} • FOLLOW(E) = {F} • FOLLOW(F) = {h} Luật sinh S → aBDh •
Tính FIRST(aBDh) = {a}
⇒ M[S, a] chứa S → aBDh Luật sinh B → cC • Tính FIRST(cC) = {c}
⇒ M[B, c] chứa B → cC
Luật sinh C → bC | ε • Tính FIRST(bC) = {b} lOMoAR cPSD| 59285474 • FIRST(ε) = {ε}
⇒ M[C, b] chứa C → bC
⇒ Nếu ε ∈ FIRST(C), thêm FOLLOW(C) vào M[C, …] Luật sinh D → EF •
Tính FIRST(EF) = FIRST(E) = {g, ε}
⇒ M[D, g] chứa D → EF
⇒ Nếu ε ∈ FIRST(D), thêm FOLLOW(D) vào M[D, …]
Luật sinh E → g | ε • Tính FIRST(g) = {g} • FIRST(ε) = {ε}
⇒ M[E, g] chứa E → g
⇒ Nếu ε ∈ FIRST(E), thêm FOLLOW(E) vào M[E, …]
Luật sinh F → f | ε • Tính FIRST(f) = {f} • FIRST(ε) = {ε}
⇒ M[F, f] chứa F → f
⇒ Nếu ε ∈ FIRST(F), thêm FOLLOW(F) vào M[F, …]
Phân tích w = accgfhl lOMoAR cPSD| 59285474 1. S → aBDh 2. B → cC 3. C → c 4. D → EF 5. E → g 6. F → f 7. h
Chuỗi w = accgfhl có thể phân tích.