
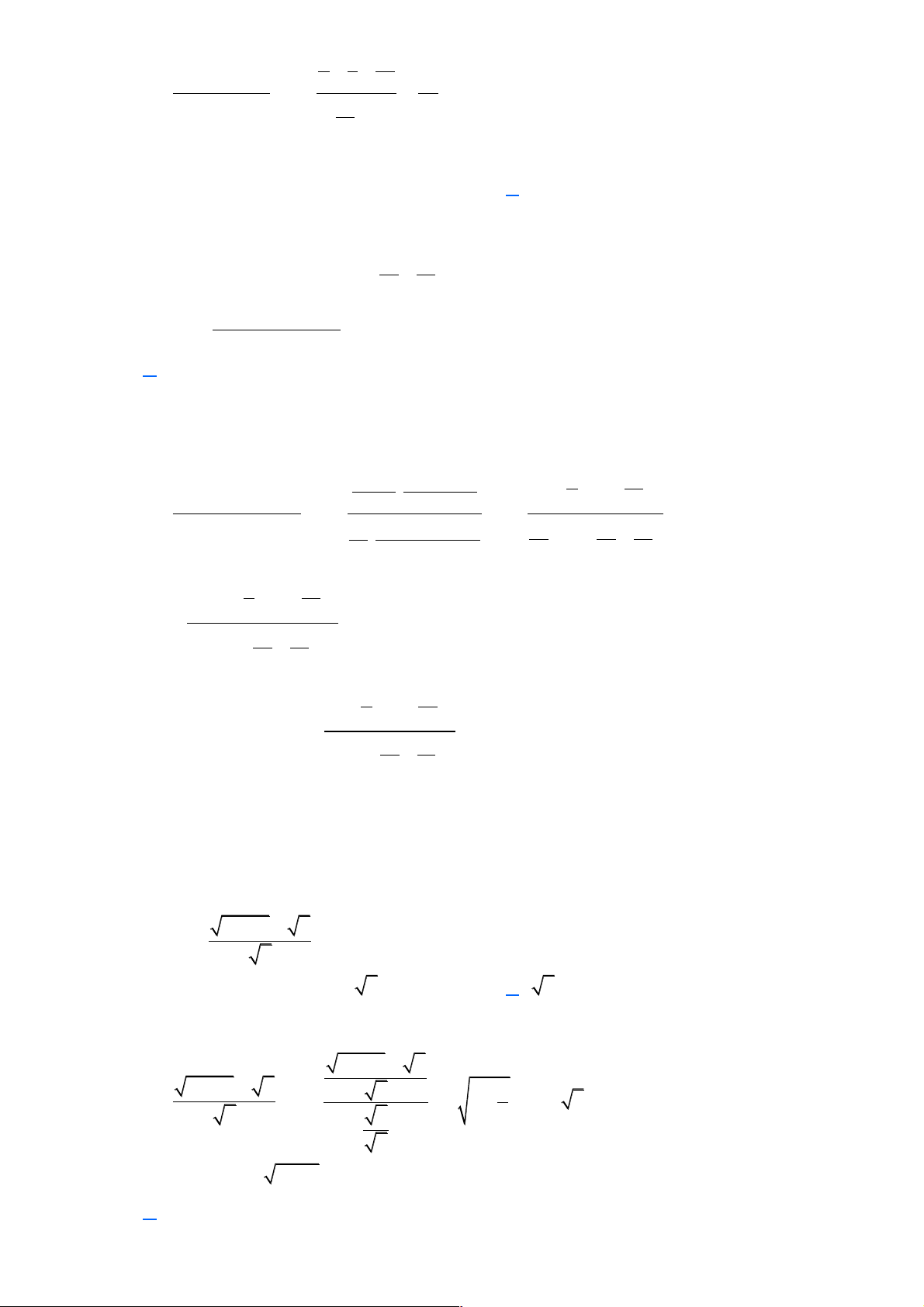
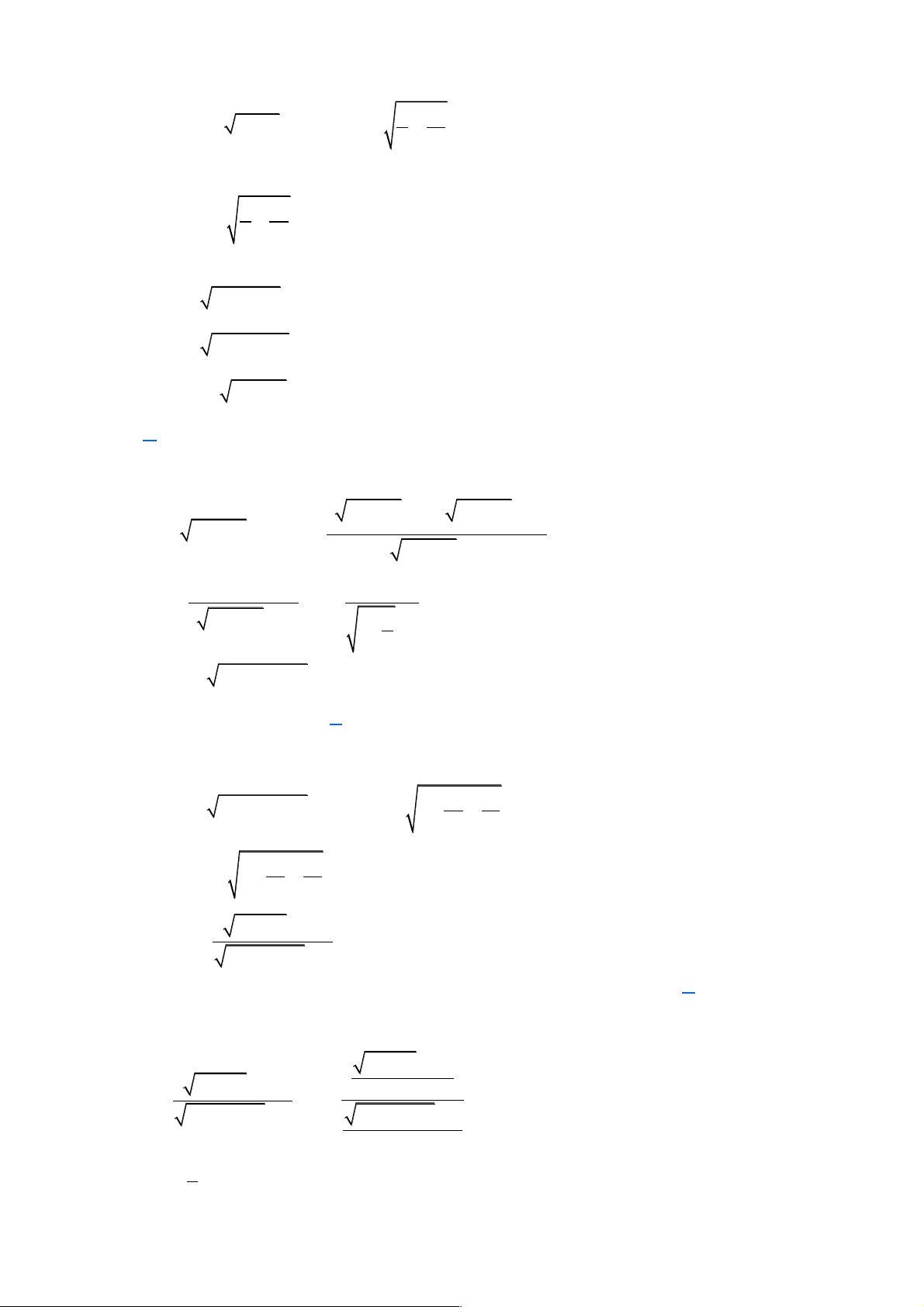







Preview text:
CÁC DẠNG BÀI TẬP TRẮC NGHIỆM GIỚI HẠN DÃY SỐ
I. LÝ THUYẾT CẦN NHỚ
1. Các giới hạn đặc biệt 1 a. lim
= 0 với k nguyên dương. k n
b. limqn = 0 nếu q <1.
c. Nếu u = c ( c là hằng số) thì limu = limc = c. n n d. lim k
n = +¥ với k nguyên dương. e. lim n
q = +¥ nếu q > 1.
2. Tổng của cấp số nhận lùi vô hạn u
Cấp số nhân vô hạn (u ) có công bội q với q < 1: 1
S = u + u + ...+ u + ... = . n n 1 2 n 1- q
Các định lí về giới hạn. a) Nếu limu = ;
a limv = b. Khi đó: n n
lim(u + v ) = limu + limv = a + b . n n n n
lim(u - v ) = limu - limv = a - b n n n n u a
lim n = (b ¹ 0) . v b n
b) Nếu u ³ 0, n
" và limu = a thì a ³ 0 và lim u = a n n n
c) lim u = a và 3 3
lim u = a lim u = a và 3 3 lim u = a . n n n n Định lí 2 u a) Nếu limu = ;
a limv = ±¥ thì lim n = 0. n n vn u
b) Nếu limu = a > 0; limv = 0 và v > 0 với mọi n thì lim n = +¥. n n n vn c) Nếu limu = + ;
¥ limv = b > 0 limu = +¥ thì limu .v = +¥. n n n n n
II. CÁC DẠNG BÀI TẬP
Dạng 1: Tính giới hạn dãy số đa thức hoặc phân thức hữu tỉ P(n) Khi u =
(trong đó P(n) và Q(n) là các là các đa thức của n ) n Q(n)
Phương pháp giải: Chia tử và mẫu cho k n với k
n là lũy thừa có số mũ cao nhất của P(n) và
Q(n), sau đó áp dụng các định lí về giới hạn hữu hạn (u ) là đa thức bậc k , ta đặt n k
n làm nhân tử chung, sau đó sử dụng định lí 2 về giới hạn. 3 2 2n - 3n + 2 Câu 1: Tính lim 4 2 - n A. 0 . B. +¥ . C. không tồn tại. D. -¥ . Lời giải Chọn A Trang 1 2 3 2 3 2 - + 4 2n - 3n + 2 0 lim = lim n n = = 0. 4 2 - n 2 -1 -1 4 n Câu 2: Tính 3 lim( 2
- n + 3n -1) A. +¥ . B. 2 - . C. -¥ . D. không tồn tại. Lời giải Chọn C 3 1 3 3 lim( 2 - n + 3n-1) = limn ( 2 - + - ) = -¥. 2 3 n n 2 3 (2n -1)(3n + 2) Câu 3: Tính lim 5 3 2 - n + 4n -1 A. -¥ . B. +¥ . C. 27 - . D. -3. Lời giải Chọn A Chia cả tử và mẫu cho 7 n ta có: 3 2 3 2n -1 (3n + 2) æ 1 öæ 2 ö . 2 - 3 + 2 3 ç ÷ç 2 ÷ 6 (2n -1)(3n + 2) n n è n øè n lim lim lim ø = = 5 3 5 3 2 - n + 4n -1 1 2 - n + 4n -1 1 æ 4 1 ö . 2 - + - 2 5 2 ç 2 5 ÷ n n n è n n ø 3 2 æ 1 öæ 2 ö n 2 - 3 + ç ÷ç 2 ÷ è n øè n lim ø = = -¥ . æ 4 1 ö 2 - + - ç 2 5 ÷ è n n ø 3 æ 1 öæ 2 ö 2 - 3 + ç ÷ç 2 ÷ Vì 2 limn = +¥ nên è n øè n lim ø = 27 - . 4 1 2 - + - 2 5 n n
Dạng 2: Tính giới hạn dãy số có chứa căn.
Hướng 1: Đánh giá bậc của tử và mẫu. Sau đó, chia cả tử và mẫu cho k
n với k là số mũ lớn nhất của
P(n) và Q(n) (hoặc rút k
n là lũy thừa lớn nhất của P(n) và Q(n) ra làm nhân tử). Áp dụng
các định lí về giới hạn để tìm giới hạn.
Hướng 2: Nhân với biểu thức liên hợp. 2n + 2 - n Câu 4: Tìm lim n A. 0. B. 2 . C. 2 - . 1 D. 2 Lời giải Chọn C 2n + 2 - n 2n + 2 - n æ 2 ö lim = lim n = ç 2 + -1÷ = 2 - . 1 n n ç n ÷ è ø n Câu 5: Tính ( 2
lim n - n 4n +1) A. +¥ . B. -¥ . C. 1. D. 0. Trang 2 Lời giải Chọn A ( æ 4 1 ö 2
lim n - n 4n +1)= 2 limn ç1- + ÷ 2 ç n n ÷ è ø Vì 2 limn = +¥ æ 4 1 ö và limç1- + ÷ =1> 0 2 ç n n ÷ è ø
Chú ý: Có thể kết luận kết quả của các giới hạn sau: 1) 2 lim
n + n +1 + n = +¥ ( ) 2) 4 lim
n + 3n +1 - n = +¥ . ( ) Câu 6: Tính 2 lim
n - 4n - n ( ) A. 2 - . B. -¥ . C. 0. D. +¥ Lời giải Chọn A 2 2
n - 4n - n
n - 4n + n 2 lim
n - 4n - n = lim ( ) ( )( )
( 2n -4n +n) 4 - n 4 - = lim = lim = - 2.
( 2n -4n +n) 4 1- +1 n Câu 7: 3 3
lim n - 8n + 3n + 2 bằng bao nhiêu? ( ) A. +¥ . B. -¥ . C. 1 - . D. 0 . Lời giải Chọn B æ 3 2 ö 3 3
lim n - 8n + 3n + 2 = 3 limnç1- 8 + + ÷ = -¥ ( ) 2 3 ç n n ÷ è ø æ 3 2 ö Vì 3 limç1- 8 + + ÷ = 1
- < 0 và limn = +¥ . 2 3 ç n n ÷ è ø 2 4n +1 - 2n Câu 8: Tính lim . 2
n + 4n +1 - n A. +¥ . B. -¥ . C. 2 . D. 0 . Lời giải Chọn D 2 4n +1 - 2n 2 4n +1 - 2n lim = lim n
không xác định được vì rơi vào giới hạn vô định 2
n + 4n +1 - n 2
n + 4n +1 - n n 0 dạng 0 Trang 3 2 4n +1 - 2n 2 2 2 ( 4n +1 - 2 ) n ( 4n +1 + 2 )
n ( n + 4n +1 + ) n lim = lim 2
n + 4n +1 - n 2 2 2 ( n + 4n +1 - ) n ( 4n +1 + 2 )
n ( n + 4n +1 + ) n
( 2n +4n+1+n) = lim (4n + )1( 2 4n +1 + 2n) 1 æ 4 1 ö ç 1+ + +1÷ 2 n n n = lim è ø = 0 æ 1 öæ 1 ö 4 + ç ÷ç 4 + + 2÷ 2 è n ø n è ø
Dạng 3: Tính giới hạn dãy số chứa lũy thừa. ( P n u = P(n) Q(n) n , n, n a b c ... n ) ( ) (trong đó và
là các biểu thức chứa hàm mũ Q (n)
Phương pháp giải: Chia cả tử và mẫu cho n
a trong đó a là cơ số lớn nhất. n 1 1 3 + - Câu 9: Tìm lim 1+ 3n 2 A. . B. 1 - . C. 1. D. 3 - . 3 Lời giải Chọn D æ 1 n ö -3 n 1 1 3 + - 1- 3.3n ç ÷ lim = lim = è 3 lim ø = 3 - . 1+ 3n 1+ 3n æ 1 n ö +1 ç ÷ è 3 ø 9n - 3.4n Câu 10: Tìm: lim 6.7n + 8n A. 1. B. +¥ 1 . C. - . D. -¥ . 2 Lời giải Chọn B é 4 n ù æ ö 1 ê - 3.ç ÷ ú 9n - 3.4n ê è 9 ø ë ú lim = lim û = +¥ 6.7n + 8n é 7 n 8 n ù æ ö æ ö ê6. + ç ÷ ç ÷ ú ê è 9 ø è 9 ø ë úû 4 n é ù æ ö 7 n 8 n é ù æ ö æ ö 7 n 8 n æ ö æ ö Vì lim 1
ê - 3.ç ÷ ú= 1 > 0; limê6. + ç ÷ ç ÷ ú= 0; lim6. + > 0. ç ÷ ç ÷ ê è 9 ø ë úû ê è 9 ø è 9 ø ë úû è 9 ø è 9 ø
Câu 11: lim(5n 2n - ) bằng A. -¥ . B. 3. C. +¥ 5 . D. 2 Lời giải Chọn C Trang 4 æ ö n n n æ 2 n ö
Ta có 5 - 2 = 5 ç1- ç ÷ ÷ ç 5 ÷ è ø è ø n æ ö æ ö Vì lim5n = +¥ 2
và limç1- ç ÷ ÷ =1> 0. ç 5 ÷ è ø è ø 1+ 2 + 3 + ... + n Câu 12: lim bằng 2 n A. -¥ . B. +¥ 1 . C. . D. 1. 2 Lời giải Chọn C n(n + ) 1
Ta có 1+ 2 + 3 + ...+ n = 2 TIẾT 51 1+ 2 + 3 + ...+ n n(n + ) 1 1 Nên lim = = . 2 2 n 2n 2 1
Câu 13: Tính tổng của dãy số u = . n 4n 3 1 A. . B. +¥ 1 . C. . D. 4 3 4 Lời giải Chọn C 1 1
Ta có: u là cấp số nhân lùi vô hạn với u = ;q = n 1 1 4 4 1 1 1 1 1 u 1
Nên tổng các số hạng của dãy số là 1 4 S = + + + ...+ = = = . n 2 3 4 4 4 4n 1- q 1 3 1- 4
CHÚ Ý: MỘT SỐ KỸ THUẬT GIẢI NHANH
Quy ước: Trong máy tính không có biến n nên ta ghi x thay cho n.
Ghi nhớ cách nhập giá trị của x.
x ® +¥ thì ta nhập x = 9999999999 (10 số 9)
x ® -¥ thì ta nhập x = 9999999999 - (10 số 9)
Đề bài yêu cầu tính lim(u n ® -¥
n ) thì ta hiểu rằng, biến .
Ghi nhớ cách hiển thị kết quả
Gặp hằng số .10n c
(trong đó a là số nguyên âm, thông thường a = 10 - ,a = 12 - ,...)
MỘT SỐ VÍ DỤ MINH HỌA Ví dụ 1: 12
15.10- là số rất nhỏ và gần bằng 0. Gặp hằng số 10 20 .1 c 0 , .1
c 0 ,... đọc là (dấu của c) nhân vô cực với c là hằng số (chú ý có thể lớn hơn 10). Ví dụ 2: 10 5.10 - là âm vô cực, ghi là 10 ;5
-¥ .10 là dương vô cực, ghi là +¥ . 1
Ví dụ 3. Tính giới hạn sau: lim . n +1 Lời giải Cách bấm máy:
Nhập vào máy tính biểu thức sau: Trang 5
Sau đó bấm CALC, màn hình sẽ xuất hiện như hình bên. Ta hiểu rằng “Bạn muốn gán x bằng bao nhiêu?”
Nhập: x = 9999999999 , sau đó bấm “=”, ta được kết quả: Kết quả: 10 1.10- 1
là một giá trị rất rất nhỏ gần bằng 0. Vậy lim = 0. n +1 (- )1n
Ví dụ 4. Tính giới hạn sau: lim . n + 5 Lời giải Cách bấm máy:
Nhập vào máy tính biểu thức sau: Sau đó bấm CALC.
Nhập x = 9999999999 , sau đó bấm “=”, ta được kết quả: Kết quả: 11 9,999999996.10- -
là một giá trị rất nhỏ gần bằng 0. (- )1n Vậy lim = 0. n + 5 (- )1n .cosn
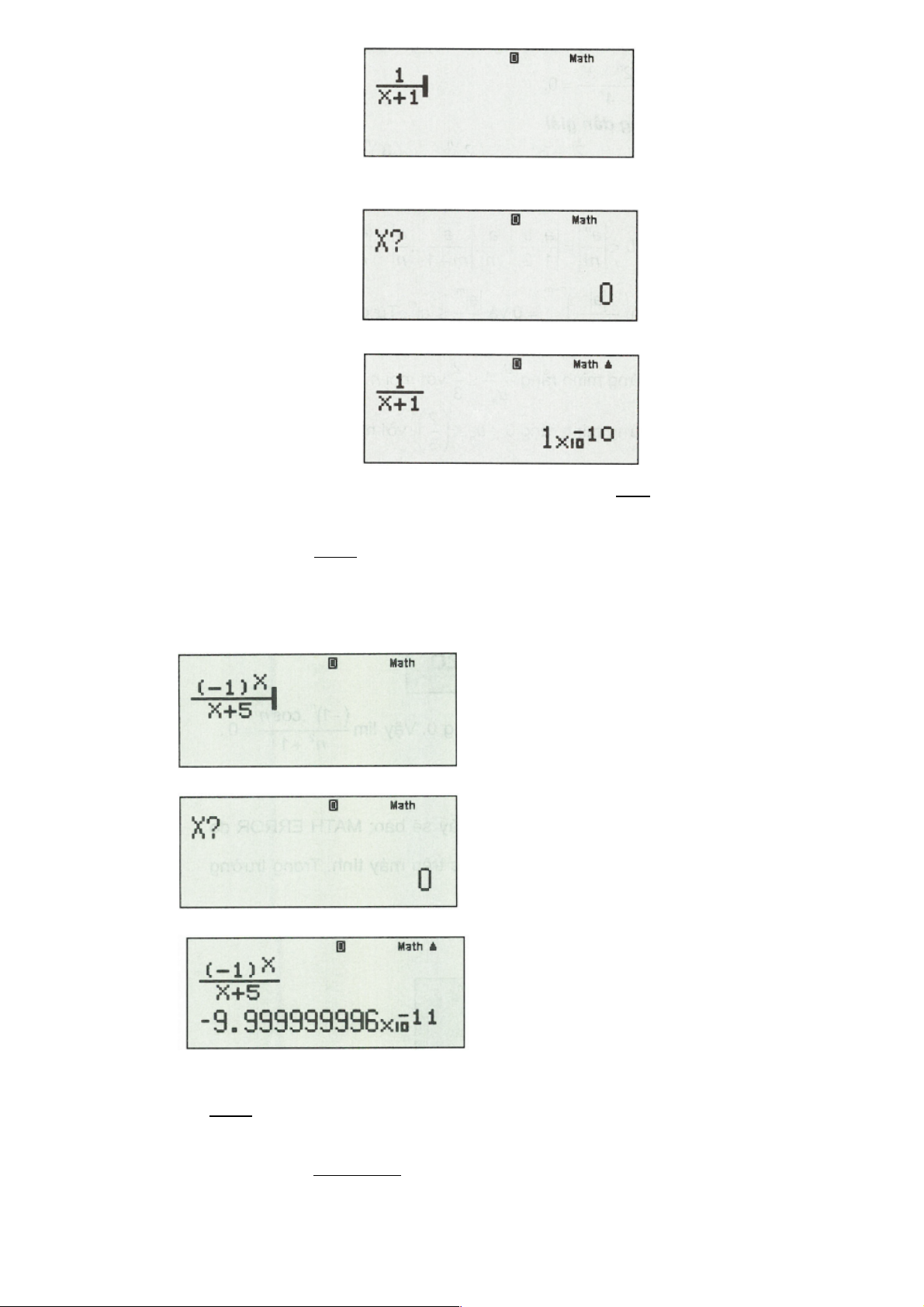
Ví dụ 5. Tính giới hạn sau: lim . 2 n +1 Trang 6 (- )1n .cosn Nếu ta nhập
, sau đó CALC như trên máy sẽ báo: MATH ERROR. 2 n +1 Lời giải
Vận dụng định lí 1 nếu u £ v với mọi n và limv = 0 thì limu = 0. n n n n
(- )1n .cosn cosn 1 1 Ta có đánh giá sau: < < , ta chỉ cần ghi
vào máy tính là sẽ tính 2 2 2 n +1 n +1 n +1 2 n +1 được. Cách bấm máy:
Nhập vào máy tính biểu thức sau: Sau đó bấm CALC.
Nhập: x = 9999999999 , sau đó bấm “=”, ta được kết quả: (- )1n .cosn Kết quả: 20
1.10- là một giá trị rất rất nhỏ gần bằng 0. Vậy lim = 0. 2 n +1 (- )1n
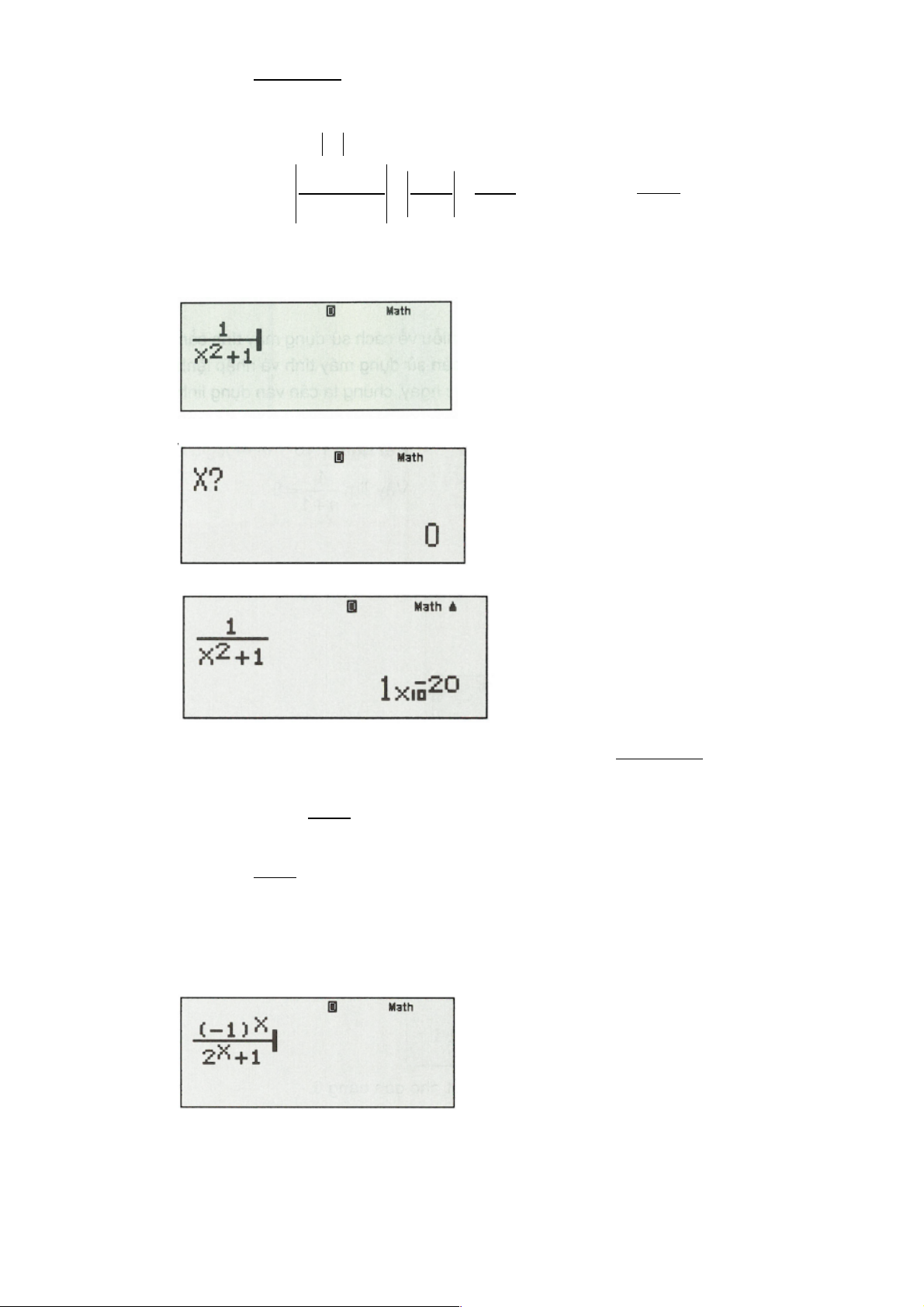
Ví dụ 6. Tính giới hạn sau lim . 2n +1 (- )1n Nếu ta nhập
, sau đó CALC như trên máy sẽ báo: MATH ERROR do hàm số mũ tăng 2n +1
rất nhanh nên sẽ không tính được trên máy tính. Trong trường hợp này ta sẽ xử lý như sau: Lời giải Cách bấm máy:
Nhập vào máy tính biểu thức sau: Bấm CALC. Trang 7
Nhâp: x = 100 , sau đó bấm “=”, ta được kết quả: Kết quả: 31
7,888609052.10- là một giá trị rất rất nhỏ gần bằng 0. (- )1n Vậy lim = 0. 2n +1
NHẬN XÉT: Qua 4 ví dụ trên, phần nfao bạn đọc đã hiểu về cách sử dụng máy tính cầm tay
(MTCT) để giải các bài toán về dãy số có giới hạn là 0. Có những bài toán sử dụng máy tính và
nhập lệnh CALC x = 9999999999 sẽ ra luôn kết quả, có những bài toán không ra được ngay,
chúng ta cần vận dụng linh hoạt các cách đánh giá cũng như đổi cách bấm máy để ra được kết
quả bài toán. Qua đây, đòi hỏi chúng ta cần có kiến thức khá chắc chắn về định nghĩa giới hạn
dãy số để có thể vận dụng làm các bài tập cho tốt hơn. BÀI TẬP TỰ LUYỆN Câu 1. ( 3 lim n - 2n + ) 1 bằng A. 0 . B. 1. C. -¥ . D. +¥ . Lời giải Chọn D æ 2 1 ö Ta có: 3 3
n - 2n +1 = n 1- + . ç 2 3 ÷ è n n ø æ 2 1 ö Vì 3 lim n = +¥ và lim 1- +
= 1 > 0 nên theo quy tắc 2, ( 3 lim n - 2n + ) 1 = +¥ ç 2 3 ÷ è n n ø Câu 2. ( 2 lim 5n - n + ) 1 bằng A. + . ¥ B. . -¥ C. 5 . D. 1. - Lời giải Chọn B æ 5 1 ö Ta có 2 2
5n - n +1 = n 1 - + + . ç 2 ÷ è n n ø æ 5 1 ö Vì 2 lim n = +¥ và lim 1 - + + = 1 - < 0 nên ( 2 lim 5n - n + ) 1 = -¥(theo quy tắc 2). ç 2 ÷ è n n ø
Tổng quát: Cho k là một số nguyên dương. a) lim( k k 1
a n + a n - +...+ a n + a = +¥ a > 0. k k 1 - 1 0 ) nếu k b) lim( k k 1
a n + a n - +...+ a n + a = -¥ a < 0. k k 1 - 1 0 ) nếu k Chẳng hạn: ( 3 lim n - 2n + )
1 = +¥ vì a = 1 > 0; ( 2 lim 5n - n + ) 1 = -¥ vì a = 1 - < 0. 3 2 2 5n + 3n - 7 Câu 3. limu , với u = bằng: n n 2 n A. 0. B. 5. C. 3. D. 7. - Trang 8 Lời giải Chọn B 2 æ 5n 3n 7 ö æ 3 7 ö Ta có: limu = limç + - ÷ = lim 5+ - = 5. n 2 2 2 ç 2 ÷ è n n n ø è n n ø 3 2
2n - 3n + n + 5 Câu 4.
lim u , với u = bằng n n 3 2 n - n + 7 A. 3. - B. 1. C. 2. D. 0. Lời giải Chọn C
Chia cả tử và mẫu của phân thức cho 3 n ( 3
n là lũy thừa bậc cao nhất của n trong phân thức), 3 1 5 2 - + + 2 3 æ 3 1 5 ö æ 1 7 ö ta được: n n n u = . Vì lim 2 - + + = 2 và lim 1- + =1¹ 0 nên n 1 7 ç 2 3 ÷ ç ÷ 1- + è n n n ø 3 è n n ø 3 n n 3 2
2n - 3n + n + 5 2 lim = = 2. 3 2 n - n + 7 1 3 n + 2n +1
Câu 5. Giới hạn của dãy số (u u = n ) , với bằng n 4 3 2
n + 3n + 5n + 6 A. 1. B. 0. C. + . ¥ 1 D. . 3 Lời giải Chọn B
Chia cả tử và mẫu của phân thức cho 4 n ( 4
n là bậc cao nhất của n trong phân thức), ta được 1 2 1 3 + + 3 4 n + 2n +1 0 lim = lim = lim n n n u = = 0. n 4 3 2
n + 3n + 5n + 6 3 5 6 1 1+ + + 2 3 n n n 3 3n + 2n -1
Câu 6. Giới hạn của dãy số (u u = n ) với , bằng n 2 2n - n 3 A. . B. 0. C. + . ¥ D. 1. 2 Lời giải Chọn C
Chia cả tử và mẫu cho 2 n ( 2
n là lũy thừa bậc cao nhất của n trong mẫu thức), ta được 2 1 3 3n + - 2 3n + 2n -1 n n æ 3n ö u = = . Vậy limu = lim = +¥ n 2 2n - n 1 n ç ÷ 2 - è 2 ø n (- )1n Câu 7. lim bằng n(n + ) 1 A. 1. - B. 1. C. + . ¥ D. 0. Lời giải Chọn D (- )1n n 1 1 1 1 (- )1 Ta có = < = mà lim = 0 nên suy ra lim = 0 n(n + ) 1 n(n + ) 2 1 . n n n 2 n n(n + ) 1 Trang 9 1 æ 2 ö
Câu 8. Cho dãy số (u u =1, u = çu + n ³ 1
n ) được xác định bởi ÷ với mọi . Tìm giới hạn của 1 n 1 + 2 n u è n ø (un ).
A. limu = 1. B. limu = 1 - .
C. limu = 2 . D. limu = - 2 . n n n n Lời giải Chọn C
Bằng phương pháp quy nạp, dễ dàng chứng minh được u > 0 n n với mọi
Đề bài không cho biết dãy số (un ) có giới hạn hữu hạn hay không, tuy nhiên các đáp án đề bài
cho đều là các giới hạn hữu hạn. Do đó có thể khẳng định được dãy số (un ) có giới hạn hữu
hạn. Đặt limu = L ³ 0 n 1 æ 2 ö limu = lim çu + n 1 + ÷ 2 n u è n ø 1 æ 2 ö 2 Hay 2 L = L +
Þ L = Þ L = 2 Þ L = 2 ç ÷ 2 è L ø L Vậy limu = 2 n
(loại trường hợp L = - 2 ). Vậy limu = 2 . n 1 1 1
Câu 9. Tổng S =1+ + + + ... bằng: 2 4 8 3 A.1. B. 2 2 . C. . D. . 3 2 Chọn B Lời giải
S là tổng của cấp số nhân lùi vô hạn có u = 1 1 và q = . 1 2 1 Do đó S = = 2 . 1 1- 2 é 1 1 1 ù Câu 10. Tính limê + +…+ ú bằng: 1.3 3.5 (2n- )1(2n+ ë )1û 1 1 A. 0. B. 1. C. . D. . 2 3 Chọn C Lời giải 1 1 1 1 æ 1 1 1 1 1 ö 1 æ 1 ö Ta có: + +…+ = 1- + - +…+ - = 1- ç ÷ ç ÷ 1.3 3.5
(2n - )1(2n + )1 2è 3 3 5
2n -1 2n +1ø 2 è 2n +1ø é 1 1 1 ù 1 æ 1 ö 1 Vậy limê + +…+ ú = lim 1- = . ç ÷ 1.3 3.5 ë (2n - )1(2n + )1 2 û è 2n +1ø 2
Câu 11. Biết limu = +¥ . Chọn mệnh đề đúng trong các mệnh đề sau. n u +1 1 u +1 u +1 1 u +1 A. lim n = . B. lim n = 0. C. lim n = . D. lim n = +¥ . 2 3u + 5 3 2 3u + 5 2 3u + 5 5 2 3u + 5 n n n n Trang 10 Lời giải Chọn B 1 1 + 2 u +1 u u 1 Ta có: n n n = . Vì limu = +¥ 1 nên lim = 0, lim = 0 . 2 3u + 5 5 n u 2 u n 3 + n n 2 un u +1 0 + 0 0 Vậy lim n = = = 0. 2 3u + 5 3 + 0 3 n (2n - )2 1 (n - ) 1 Câu 12. lim bằng bao nhiêu? ( 2n + )1(2n+ )1 A. 1. B. 2 . C. 0 . D. +¥ . Lời giải Chọn B
Bậc của tử và mẫu thức đều bằng 3 nên dãy có giới hạn hữu hạn. Hệ số của 3 n trên tử bằng 4 2 2 .1 = 4, hệ số của 3
n dưới mẫu bằng 1.2 = 2 nên giới hạn là = 2. 2
Câu 13. Trong bốn giới hạn sau đây, giới hạn nào là +¥ ? 2 3 n + 3n + 2 2 2n - 3n 3 n + 2n -1 2 n - n +1 A. lim . C. lim . B. lim . D. lim . 2 n + n 3 n + 3n 3 n - 2n 1- 2n Lời giải Chọn A 2 3 n + 3n + 2 Phân thức
có bậc của tử thức cao hơn bậc của mẫu thức, đồng thời hệ số của lũy 2 n + n
thừa bậc cao nhất của tử thức và hệ số của lũy thừa bậc cao nhất của mẫu thức đều dương nên
suy ra giới hạn của dãy số tương ứng bằng +¥ . 3 n + 2n -1 1 (Phân thức
có bậc tử bằng bậc mẫu nên giới hạn dãy số tương ứng bằng - . Phân 3 n - 2n 2 2 2n - 3n thức
có bậc của tử thấp hơn bậc của mẫu nên giới hạn dãy số tương ứng bằng 0 . 3 n + 3n 2 n - n +1 Phân thức
có bậc tử lớn hơn bậc mẫu nhưng hệ số của lũy thừa bậc cao nhất trên tử 1- 2n
và hệ số của lũy thừa bậc cao nhất dưới mẫu trái dấu nhau nên giới hạn dãy số tương ứng bằng -¥ ). Câu 14. 2 3 3 lim
n + n +1 - n + 3n + 2 bằng: ( ) 1 A. . B. 0 . C. +¥ . D. -¥ . 2 Lời giải Chọn A 1 2 3 3 é 2 3 3 lim n n 1 n 3n 2 lim n n 1 n n n 3n 2 ù + + - + + = + + - + - + + = ( ) êë( ) ( )úû 2 Trang 11 Câu 15. ( n 1
lim 3.2 + - 5.3n + 7n) bằng: A. -¥ . B. +¥ . C. 3. D. 5 - . Lời giải Chọn A n æ ö + æ ö n lim( n n n 2 1
3.2 - 5.3 + 7n) = 3 ç 5 - + 6 + 7 ç ÷ ÷ = -¥. ç 3 3n ÷ è ø è ø Trang 12




