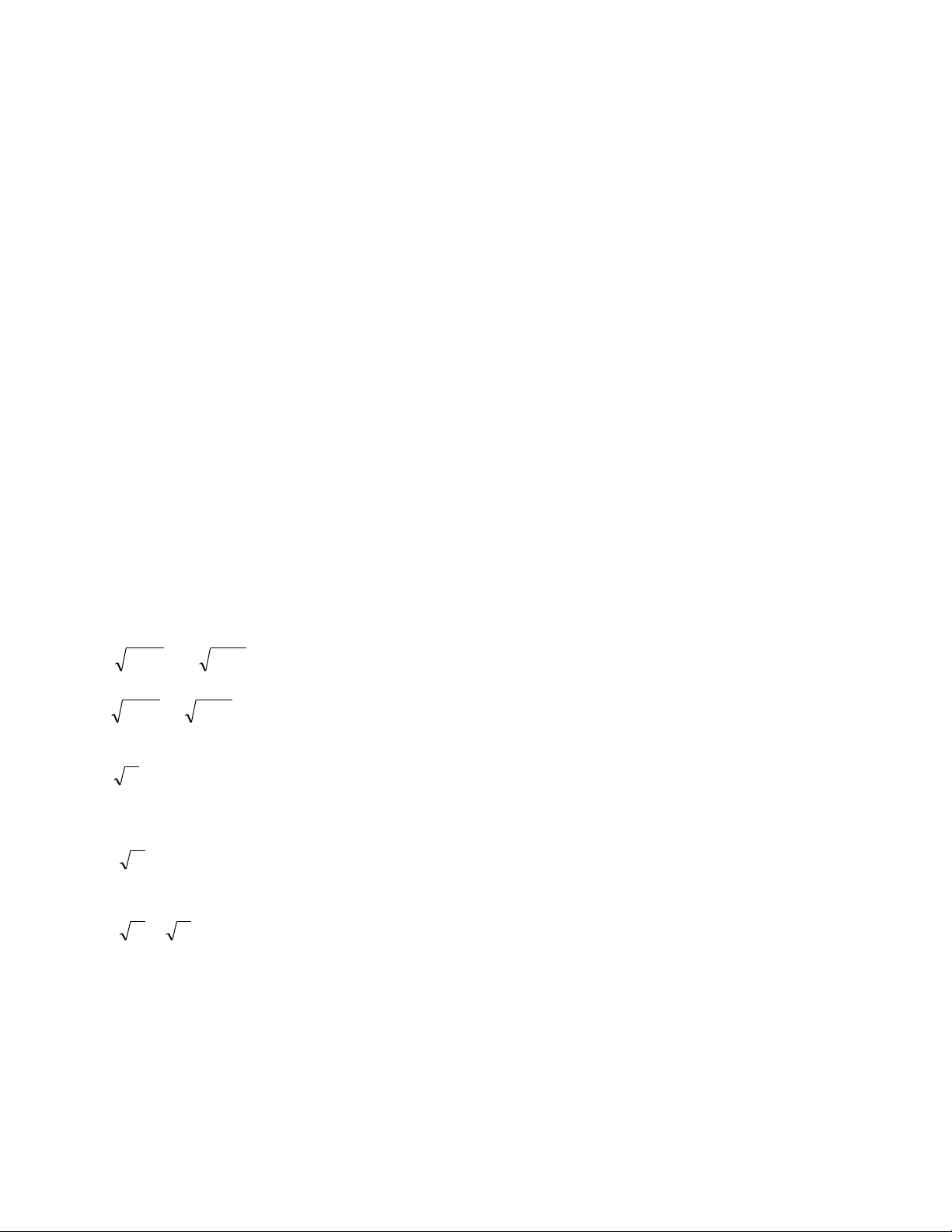




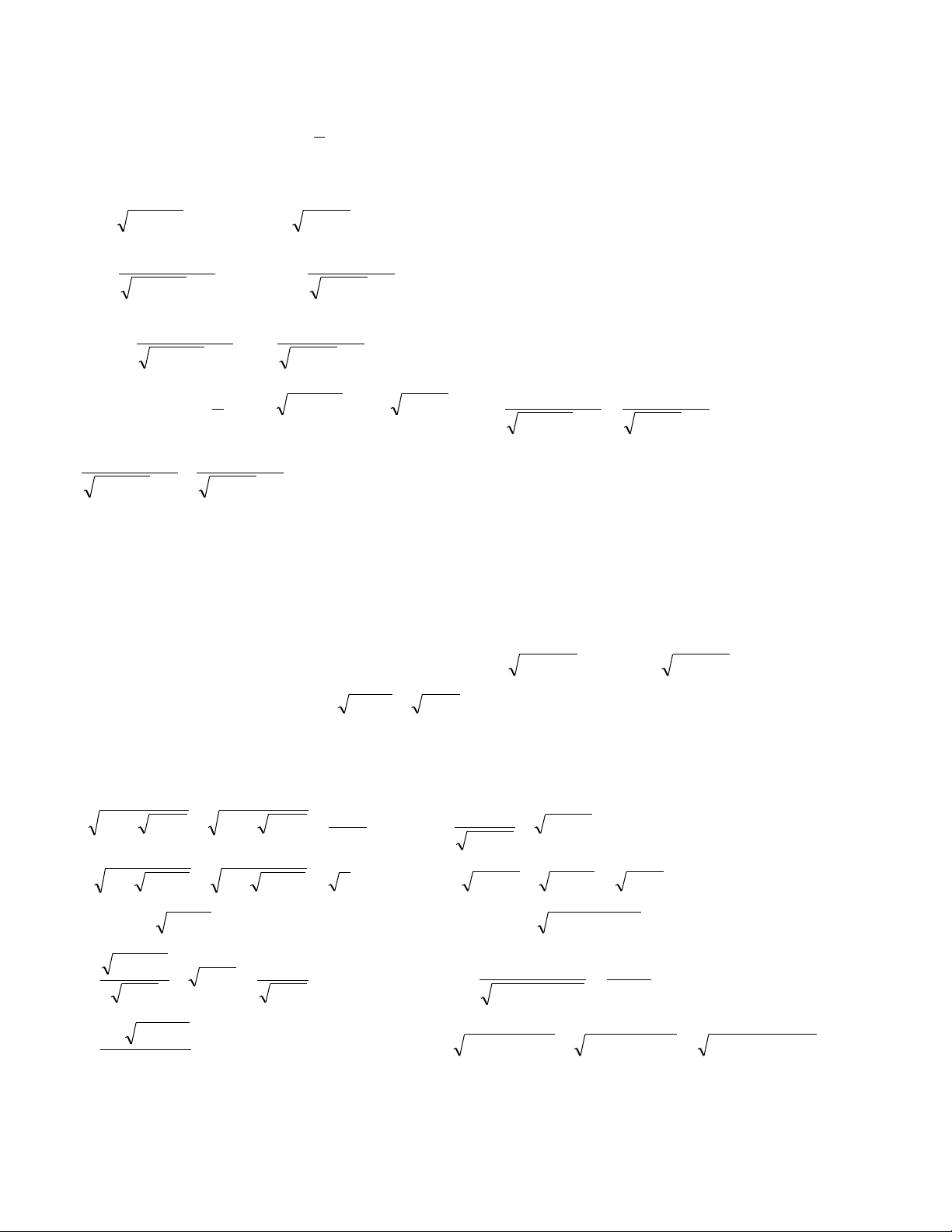








Preview text:
CÁC DẠNG BẤT PHƢƠNG TRÌNH VÔ TỈ VÀ CÁCH GIẢI
A. PHƢƠNG PHÁP BIẾN ĐỔI TƢƠNG ĐƢƠNG.
* Hai bất phƣơng trình đƣợc gọi tƣơng đƣơng khi chúng có cùng tập nghiệm.
* Một số phép biến đổi tƣơng đƣơng:
+) Cộng (trừ) hai vế của bất phương trình với cùng một biểu thức mà không làm thay đổi
điều kiện của bất phương trình.
+) Nhân (chia) hai vế của bất phương trình với cùng một biểu thức ( luôn dương hoặc
âm) mà không làm thay đổi điều kiện của bất phương trình.
+) Lũy thừa bậc lẻ hai vế, khai căn bậc lẻ hai vế của một bất phương trình.
+) Lũy thừa bậc chẵn hai vế, khai căn bậc chẵn hai vế khi hai vế của bất phương trình cùng dương.
+) Nghịch đảo hai vế của bất phương trình khi hai vế cùng dương ta phải đổi chiều.
I. Kỹ thuật lũy thừa hai vế.
1. Phép lũy thừa hai vế: a) 2k 1 f (x) 2k 1
g(x) f (x) g(x) . g(x) 0
b) 2k f (x) 2k g(x) .
f (x) g(x) B 0 B 0
*) A B hoặc . A 2 B A 0 B 0
*) A B A 0 . A 2 B
*) A B 0 A B .
( Đối với các trường hợp còn lại với dấu , ,
< các bạn có thể tự suy luận ). 2. Lƣu ý:
Đặc biệt chú ý tới điều kiện của Bài toán. Nếu điều kiện đơn giản có thể kết hợp vào
bất phương trình, còn điều kiện phức tạp nên để riêng. 3. Ví dụ:
Bài 1: Giải các BPT sau:
a) x 3 2x 1 ; b) 2
x x 1 x 3
c) 3x 2 4x 3 ; d) 3 2
x x 4 x 1 Giải: 1 x 2x 1 0 2
a) x 3 2x 1 x 3 0 x 3 x 3 .
x 3 2x 1 2 4 2
x 5x 4 0
Vậy bất phương trình có tập nghiệm là: ; 3 . 2
x x 1 0 2 8
b) x x 1 x 3 x 3 0 x . 2
x x 1 x 7 3 2
Vậy tập nghiệm của bất phương trình là: 8 ; . 7
Hai Bài tập còn lại các bạn tự giải.
Bài 2: Giải BPT: x 4 1 x 1 2x (1). Giải: 1 x 0 1 1 2x 0 4 x
* (1) x 4 1 x 1 2x 2 x 4 0 2 2x 1 2x 3x 1 2
x 4 1 x 1 2x 1 4 x 2 1 4 x 1 2 x 2 2x 1 0 4 x 0 . 1 2x 1 0 x 2 2
x 3x 1 2x 2 1 2 7
x 0 2
* Vậy tập nghiệm: [-4;0].
Bài tập tƣơng tự : Giải BPT: 5x 1 x 1 2x 4 (TS (A)_ 2005).
Đáp số: Tập nghiệm T=[2;10).
II. Kỹ thuật chia điều kiện. 1. Kỹ thuật:
Nếu Bài toán có điều kiện là x D mà D D D ... D ta có thể chia Bài toán theo 1 2 n
n trường hợp của điều kiện:
+) Trường hợp 1: x D , giải bất phương trình ta tìm được tập nghiệm T . 1 1
+) Trường hợp 2: x D , giải bất phương trình tìm được tập nghiệm T 2 2.
………………………………….
+) Trường hợp n: x D , giải bất phương trình tìm được tập nghiệm T n n.
Tập nghiệm của bất phương trình là T T T ... T . 1 2 n 2. Yêu cầu:
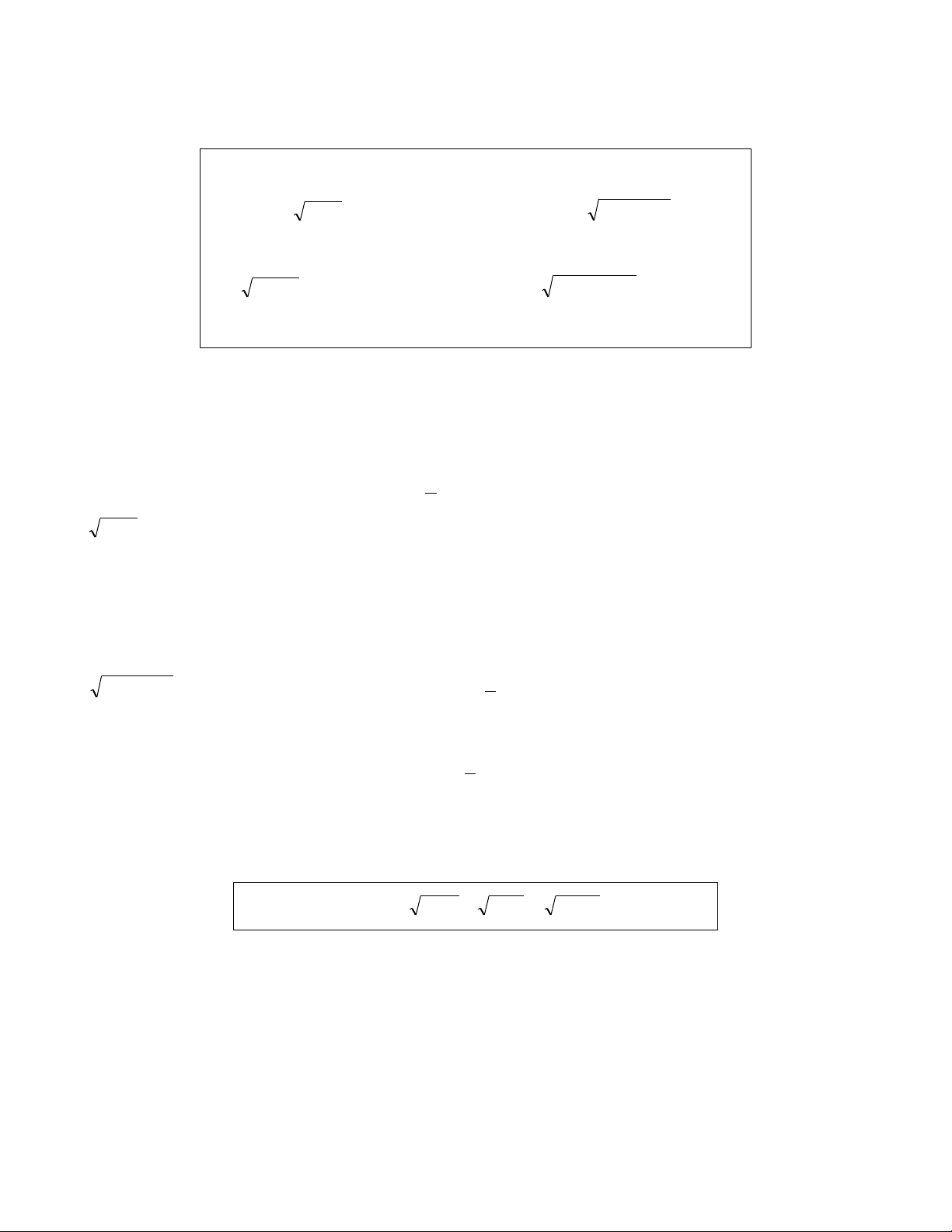
Cần phải xác định giao, hợp trên các tập con của R thành thạo. 3. Ví dụ: 3 2
x x 4 2 Bài 1: Giải BPT: 2 x (1) Giải: x 0 * Điều kiện: 4 . 1 x 3 2x 2 * Với 0 4 0 x (i) ta có (1) 2
3x x 4 2x 2 3 2
3x x 4 2x 22 x 1 9 x (ii) 7 2
x 9x 0 7
Kết hợp (i) và (ii) ta có tập nghiệm là 9 4 T . 1 ; 7 3
* Với 1 x 0 thì (1) luôn đúng. Tập nghiệm trong trường hợp này là T2 = [-1 ;0).
Vậy tập nghiệm của (1) là 9 4
T T T ; . 1 2 0; 1 7 3 Bài tập : Giải BPT : 2 x 3x 2 2
x 4x 3 2 2
x 5x 4 .
Đáp số : x 4 hoặc x = 1.
III. Kỹ thuật khai căn.
1) Đƣa biểu thức ra ngoài căn thức : ( A A ) 0 * 2 A A . ( A A ) 0 2 A y A y * (E, x ) 0 . 2 E x E x
* 2n A2n A * 2n1 A2n1 A 2) Lƣu ý :
Biến đổi các biểu thức trong căn thức thành hằng đẳng thức. 3) Ví dụ : Giải BPT 3
: x 2 x 1 x 2 x 1 2 (1) Giải : 3 2 2 3
(1) x 1 2 x 1 1 x 1 2 x 1 1 x 1 1 x 1 1 2 2 x 1 3
x 1 1 x 1 1 ( ) 2 2
* Với x 1 1 0 x 11 x 2 luôn thỏa mãn bpt (2).
Vậy trong trường hợp này tập ngiệm là T 1=[2 ;+ ) . x * Với 1
x 1 1 0
1 x 2 bpt (2) trở thành : x 1 1 3 3
x 1 11 x 1 2 (luôn đúng). 2 2
Vậy tập nghiệm của (1) trong trường hợp này là T2=[1 ;2).
KL : Tập nghiệm của (1) là T=T T . 1 ;1 2
* Chú ý : Bài này ta có thể giải bằng phương pháp bình phương hai vế..
IV. Kỹ thuật phân tích thành nhân tử đƣa về bất phƣơng trình tích.
1. Bất phƣơng trình tích : Trên điều kiện của bpt ta có :
f (x) 0 f (x) 0
g(x) 0
f (x) 0 *
f (x)g(x) 0
f (x)g(x) 0 * f (x) g(x) 0 0
g(x) 0
f (x) 0 g(x) 0
Các trường hợp còn lại, các bạn tự suy luận. 2. Lƣu ý :
Đây là kỹ thuật giải đòi hỏi có tư duy cao, kỹ năng phân tích thành nhân tử thành thạo,
cần phải nhìn ra nhân tử chung nhanh. 3. Ví dụ : Giải BPT : x 1 3 2 x x 1 3 3 x 1 0 (1) Giải :
Điều kiện : x ( 1 *) (1) x 1 3 2 x x 1
x 1 x x 1 3 3 x x 0 x 1 x 1 3 2 x
1 x x 1 3 2 x 1 0
x 1 x x 1 3 2 x 1 0
x 1 x 0 (do x 1 3 2
x 1 0 khi x 1).
x 1 x x 1 2 2
x x x 1 0 (vô nghiệm).
Vậy BPT đã cho vô nghiệm.
V. Kỹ thuật nhân chia liên hợp :
1. Biểu thức nhân chia liên hợp: A B * A B ( A B) . A B 1 A B * ( A B) . A B A B 2. Lƣu ý:
+) Nên nhẩm với một số nghiệm nguyên đơn giản.
+) Chú ý tới các biểu thức nhân chia liên hợp. 3. Ví dụ: Giải BPT : 2
x 15 3x 2 2 x 8 (1) Giải: * Ta có (1) 2 x 15 2
x 8 3x 2 2 x 15 2 x 8 7 3x 2 3x 2 (2). 2 x 15 2 x 8 2 x 15 2 x 8 Từ (2) ta có 2
3x 2 0 x . 3 * Mặt khác: (1) 2
x 15 4 3x 3 2 x 8 3 2 x 1 2 x 1 ( 3 x ) 1 2 x 15 4 2 x 8 3 x x 1 x 1 1 3 0 (3) 2 x 15 4 2 x 8 3 * Lại có 2 x x 2 2 1 1
: Vì x nên x 15 4 x 8 3 3 2 x 15 4 2 x 8 3 x 1 x 1 3 0 . 2 x 15 4 2 x 8 3
Vậy (3) x 1 0 x 1.
KL : BPT (1) có tập nghiệm là T= ; 1 .
* Chú ý : Trong Bài toán này, việc thêm bớt, nhóm các số hạng với nhau để xuất hiện
nhân tử chung xuất phát từ việc nhẩm được khi x=1 thì hai vể của BPT bằng nhau.
Thường dùng cách giải tương tự cho Bài toán : 2 2 2 2
x a cx d x b .
Bài tập tương tự : Giải BPT : 3x 1 6 x 3 2
x 14x 8 0 (Dựa vào ĐH_B_2010).
VI. Một số Bài tập tự luyện : Giải các BPT sau : 3 x2 1, x x 4 x 4
x 4 x 4 . 2,
3x 2 1 x . 2 3x 2
3, x 2x 1 x 2x 1 2 . 4, 3x 4 2x 1 3 x . 5, (4x ) 1 2 x 1 2 2
x 2x 1. 6, 2 x 3x 2 2
x 3x 2 0 (ĐH_D_2002 ) 2 x 16 5 1 1 7, x 3 . 8, . x 3 x 3 2 x x 2x 1 2 3 5 1 1 4 2 x 9, 3. 10, 2 x 8x 15 2
x 2x 15 4 2
x 18x 18 . x 2 2 x 11, x . 12, 4 x 1
2x 101 3 x2 2 2 . 2 3 9 x 21 2 3 1 1 2 1 4 2 2 x2 13, x x
14, x x 1 xx x 1 . x2 x2 x x
B. PHƢƠNG PHÁP ĐẶT ẨN PHỤ .
I. Một số yêu cầu :
- Dạng này học sinh cần nhớ cách đặt ẩn. Từ đó mở rộng cho Bài toán tương tự.
- Chú ý tới các điều kiện của ẩn.
II. Một số dạng toán và các Bài toán làm mẫu.
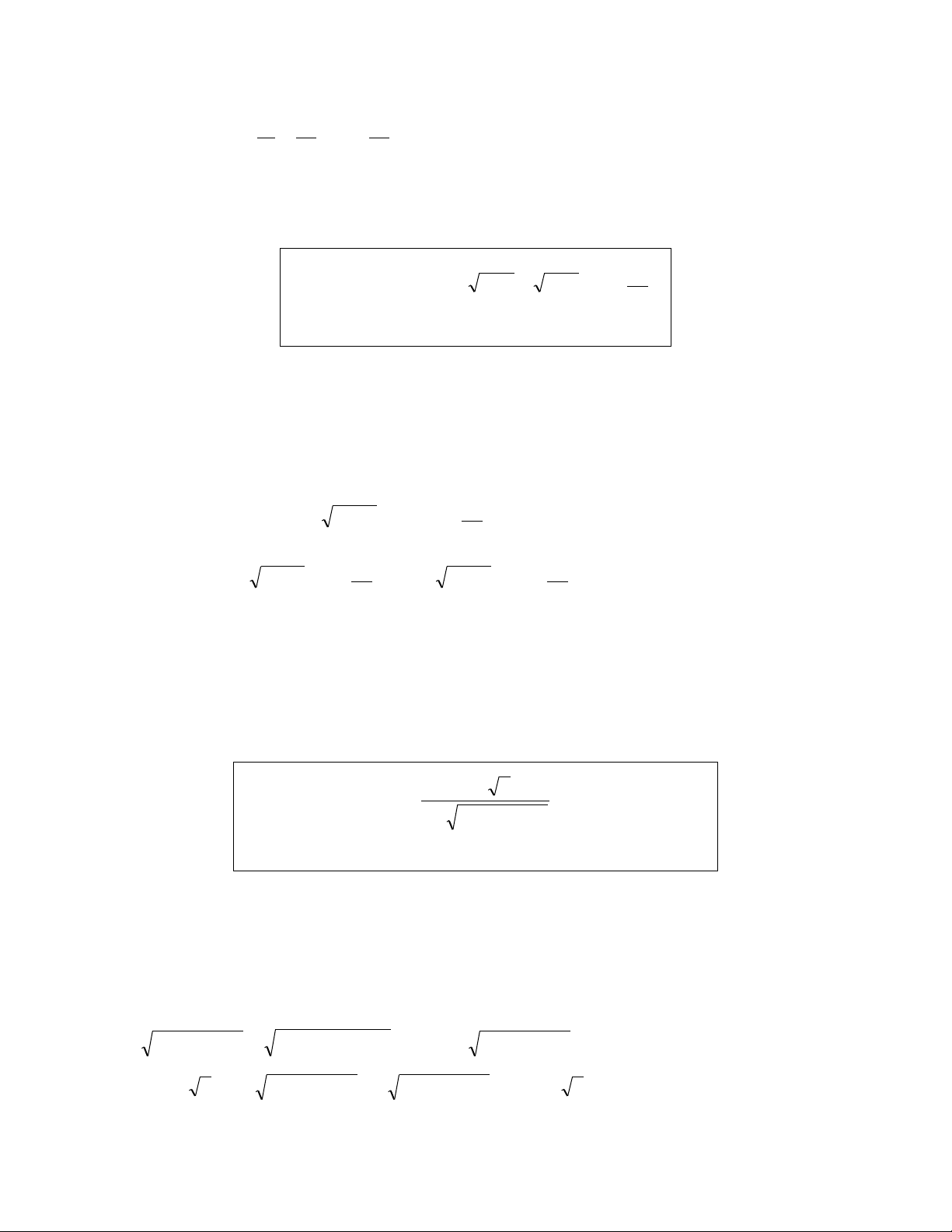
1. Đặt ẩn phụ đƣa về bpt đơn giản hơn : x x 1 Bài 1 :Giải BPT : 2 3 x 1 x (1) Giải : x 0 * Điều kiện : (*) x 1 * Đặt x 1 1 t (t ). 0 BPT (1) trở thành : 2t 3 2 3 t 3 2 t 1 ( 0 t ) 0 x 2 t t 1 2 2 t t 1 1 0 0 t . 2 Vậy x 1 1 4 0 x 1 . x 2 3 1 1 Bài 2 : Giải BPT : 5 x 2x 4 2 x 2x (2) Giải : * Điều kiện : x>0. * Đặt 1 t x
t 2 (theo bất đẳng thức Côsi) 2 x 2 1 1 t x 1 2x 2 2 t 2 . 4x 2x t 2 * BPT (2) trở thành : 2
5t 2t 2 4 t t kết hợp với 2 ta được 2 . t 1 2 2 2 3 x x 2
* Khi đó x 1 2 2 2 . 2 x 2 2 3 0 x 0 x 2 2 2 KL :
* Chú ý : Bài toán có thể mở rộng cho dạng : a f (x) 1 f (x) 2 b f (x) 2 f
(x) c 0.
2. Đặt ẩn phụ đƣa về bất phƣơng trình lƣợng giác : Giải BPT : 5 1 2 x 5 x 1 (1). Giải :
* Điều kiện : x 1 ; 0 . * Đặt
x cos t với t ; 0
. BPT (1) trở thành : sin5 t cos5 t 1. 2 Do 5 sin t 2
sin t và nên sin5 t cos5 t sin2 t cos2 t 1 với t ;0 . 2
* Do đó BPT đã cho có nghiệm là x 1 ; 0 .
3. Bài tập tự luyện: Giải các BPT: 1) 2 x 3x 3 2
x 3x 6 .
3 2) 7x 7 7x 6 2 49x2 7x 42 18114x . 3) 2 1 1 x x 2
1 2 1 x . 4) 2x 3 x 1 3x 2 2 2
x 5x 3 16 . 1 1
5) xx 4 2
x 4x x 22 2. 6) 1 x x . x x 7) 2 x x 1 2
x x 1 2 . 8) 2 2
x 1 x x 1 x 2 1
9) x 2x x 3x 1 10) 3 x 35 3 x 3 x 35 3 x 30 x x 2 3 3 2 1 2 11) 2 2
1 1 x 2x 12) 1 1 x
1 x 1 x 3 3
13) x 3 x 2x 9 x 18 168x 14) 4 3 x 1 4 2 x 7x 1 1 3x 1 2x 1 2x 15) 1
16) 1 2x 1 2x 2 2 1 x 1 x 1 2x 1 2x 1 12x 8 17) 4 2 1 x x
18) 2x 4 2 2 x 4 2 9 2 x 16
C. PHƢƠNG PHÁP ĐÁNH GIÁ.
* Nhớ được cách xét tính đơn điệu của một hàm số, lập bảng biến thiên…
* Nhớ các bất đẳng thức.
* Thường áp dụng cho các Bài toán đặc thù, phức tạp không có thuật toán cụ thể nhưng
hay có trong các kì thi đại học các năm gần đây.
I. Kỹ thuật sử dụng BĐT để đánh giá hai vế:
1) Bất đẳng thức thông dụng:
* Bất đẳng thức Côsi:
a a a ... Với a , 0 a ,..., 0 a 0 ta có 1 2 n n a a a ... . 1 2 n 1 2 n n
Dấu “=” xảy ra khi a a ... a . 1 2 n
* Bất đẳng thức Bunhiacopski :
Với mọi a , a ,..., a ,b ,b ,...,b ta luôn có : 1 2 n 1 2 n
a b a b ... a b
a a ... a b b ... b . 1 1 2 n n 2 2 2 2 2 1 2 n 2 2 2 1 2 n Dấu « a a a = » xảy ra khi 1 2 n ... . b b b 1 2 n 2) Ví dụ : 2 x
Bài 1 : Giải BPT : 1 x 1 x 2 4 (1) Giải : x * Điều kiện 1 0 : 1 x 1 (*) 1 x 0 4 * Khi đó ( x
1) 1 x 1 x 2 1 2 x 4 2 x 16 4 4 2 x x 1 2 x 2 1 2 x 1 0 1 2 x 1 0 16 16
Điều này luôn đúng với mọi x thỏa mãn điều kiện (*).
Vậy nghiệm của BPT là x 1 ; 1 . x x Bài 2 : Giải BPT : (2) 1
2 2x x 1 1 (ĐH_A_2010) Giải:
* Điều kiện: x 0 (*). * Ta có:
2 2x x 1 2
x x 1 2 1 1 1
2 2x x 1 0.
Vậy (2) x x 1
2 x2 x 1
2x2 x 1 1 x x (3).
Mặt khác: Theo BĐT bunhiacopski ta có: 2 2 2
2 x x 1
1 1 1 x x 1 x x (4) 1
x x 1 x2 * Dấu bằng xảy ra khi x 3 5 x . 1
x x 0 1 x 0 2 KL:
III. Kỹ thuật sử dụng tích vô hƣớng của hai vectơ. 1. Định nghĩa: .
u v u .v cos(u, v) .
a) Biểu thức tọa độ của tích vô hướng:
+) Trong hệ tọa độ Oxy, nếu u ( ;
x y), v (x'; y') thì . u v . x x' . y y' .
+) Trong hệ tọa độ Oxyz, nếu u ( ; x ;
y z), v (x'; y'; z') thì . u v . x x' . y y' . z z'. b) u v
. u .v . Dấu bằng xảy ra khi và chỉ khi u, v cùng phương.
c) u v u v . Dấu bằng xảy ra khi và chỉ khi u,v cùng hướng.
2) Ví dụ: Ta quay lại Bài thi ĐH_A_2010: Giải BPT x x : (1) 1
2 2x x 1 1 (ĐH_A_2010) Giải:
* Điều kiện: x . 0 * Do ( 2 2 x x ) 1 = (2 2
x 2x 1 >1 nên bất phương trình (1) tương đương với x x 1 ( 2 x2 x ) 1 (
2 x2 x 1 1 ( x) x (2)
Trong mặt phẳng tọa độ lấy a 1 ( ; x x) , b ) 1 ; 1 ( . Khi đó: .
a b 1 x
x; a .b
2 2x x 1.
Vậy (2) trở thành a b a b
. . Điều này xảy ra khi a,b cùng hướng tức là tồn tại k>0 sao cho 1 x k 3 5 a kb x . x k 2
Nhận xét: Ta có thể xây dựng được một lớp các Bài toán tương tự trên bằng cách lấy các vectơ thích hợp.
IV. Kỹ thuật sử dụng khảo sát hàm số để đánh giá. 1. Thuật toán:
Để giải bất phương trình f ( ) x g( ); x f ( ) x g( ); x f ( ) x g( ); x f ( ) x g( )
x ta khảo sát hoặc
căn cứ vào tính chất của các hàm số y = f(x) và y = g(x), đưa ra bảng biến thiên và từ
bảng biến thiên đưa ra kết luận.
2. Lƣu ý: Nếu m là tham số thì y = h(m) là đường thẳng song song hoặc trùng với trục hoành. 3. Ví dụ:
Bài 1: Tìm a để BPT sau có nghiệm: 3 x 3 2
x 1 a x x 1 (1) Giải:
* Điều kiện: x . 1 Khi đó:
(1) x x 1x3 3x2 1 a (1’).
* Đặt f (x) 3 x 3 2 x
1 x x 1. Ta có: 2 3 2 1 1
f '(x) 3x 6x x x 1 x 3x 1 0x 1
2 x 2 x 1
Do đó f(x) là hàm đồng biến trên ; 1 . * Bảng biến thiên: x 1 f(x) 3
Nhìn vào bảng biến thiên ta thấy bpt (1) có nghiệm khi a 3.
Bài 2: Tìm m để BPT 2x2 mx 2
1 3 2x3 x (1) nghiệm đúng với mọi x 0. Giải: 2 3 1 1
Ta có (1) 2mx 2x 1 3 2x x 2m 2x 3 2x (x ) 0 (1’) x x * Đặt 1 1 t 2x
. Do x 0 nên theo BĐT Côsi ta có t 2 2 . x 2 2 . x x
(Có thể sử dụng bảng biến thiên để tìm điều kiện của t)
Khi đó (1’) trở thành : 1
m t 3 t (t 2 2) (2). 2 (1)
nghiệm đúng với mọi x 0 khi và chỉ khi (2) nghiệm đúng với mọi t 2 2 . * Xét hàm số t 3 t 1 3 2 t 3 g(t) có g' t ( ) . 2 2 2 4 t 4 t 9
g'(t) 0 2 t 3 0 t . 4
* Ta có bảng biến thiên : 9 t 2 2 4 g’(t) + g(t) 3 2 2 2 2
Nhìn vào bảng biến thiên ta 3 2 2
thấy (2) nghiệm đúng với mọi t 2 2 khi m 2 . 2
V. Kỹ thuật sử dụng tính đơn điệu của hàm số trên miền xác định. 1. Thuật toán :
Giả sử hàm số y = f(x) đơn điệu trên D, u(x) và v(x) có miền giá trị là tập con của D.
Khi đó ta có : f (u( )) x f ( ( v )) x u( ) x ( v ). x f (u( )) x f ( ( v )) x u( ) x ( v )
x hoặc u(x) v(x)
(Tương tự cho các dấu ,, ) 2. Ví dụ :
Giải BPT : x 3
x 1 x
3 1 x 2x 0 (1) Giải : x * Điều kiện 1 0 : 1 x 1 (*) 1 x 0 * Khi đó 1 x 1
x 1 x
1 2 x 1 1 x 1 x 1 x 2 1 x 3 2 3 2
x 1 x 1 2 x 1 1 x 1 x 2 1 x (2)
* Xét hàm số f t() t3 t2 t 2 với t 0 :
Có f '(t) 3 2
t 2t 2 0t 0 nên f (t) là hàm đồng biến trên ; 0 .
* Mặt khác : (2) f ( x )
1 f ( 1 x)
x 1 1 x
x 1 1 x x 0 kết hợp với điều kiện (*) ta được : 1 x 0 . KL :
VI. Kỹ thuật sử dụng tính đối xứng của hai nghiệm.
Tìm m để BPT sau có nghiệm duy nhất :
x 1 x 2m x1 x 2 x x 2 4 1
m m (1) Giải :
* Điều kiện : 0 x 1 (*)
* Nhận xét : Nếu x là nghiệm của (1) thì (1- x ) cũng là nghiệm của (1). Do đó phương 0 0
trình có nghiệm duy nhất thì 1
x 1 x x . 0 0 0 2 1 1 1 1 1 1 1
Thay x vào (1) ta được 2m . 24 . 2 2
m m m 0 m 0. 0 2 2 2 2 2 2 2
* Với m=0 thì (1) trở thành : 2
x 1 x 24 x1 x 0 4 4
x 1 x 0 1 4 4
x 1 x 0 x 1 x x (thỏa mãn (*)). 2
Vậy bất phương trình (1) có nghiệm duy nhất khi m=0.
VII. Một số Bài tập tự luyện :
Bài 1 : Giải các BPT : x 9 x 2 1 1 1, 2 x 2
4 x . 2, 1 x2 x 2 100 2 x 40x 40
3, x 1 2x 3 50 3x 12 4, 2
x 2x 2x 1 3 2 x 4x 1
5, x x 1 3 x 2 2 x 1 6, 2 x 4x 5 2
x 10x 50 5 7, x 2 4 2
x x 6x 11 8, 3 x 2 3
x 1 5 2x
40 34x 10x x
Bài 2 : Tìm m để BPT sau vô nghiệm : 2 2
m 1 x 1 x 2 4 2 2
1 x 1 x 1 x . (ĐH_B_2004)
Bài 3: Tìm a để BPT sau có nghiệm : 4x2 2x 1 4x2 2x 1 a 2 .
Bài 4 : Tìm các giá trị của m để bất phương trình sau có nghiệm :
4 2x 2x 24 6 x 2 6 x m
Bài 5: Tìm m để bất phương trình sau có nghiệm: 4 2
3 x 1 m x 1 2 x 1 . 2
Bài 6: Tìm m để BPT sau nghiệm đúng với mọi x 1 ; 0 : m x x2 x 1 x 3




