











Preview text:
BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
A. TRỌNG TÂM KIẾN THỨC
1. Khái niệm bất phương trình bậc nhất một ẩn
1.1 Bất phương trình bậc nhất một ẩn
Bất phương trình dạng ax + b 0 (hoặc ax + b 0;ax + b 0;ax + b 0 ) trong đó a,b là hai số đã
cho, a 0 được gọi là bất phương trình bậc nhất một ẩn x
1.2 Nghiệm của bất phương trình
✓ Số x là một nghiệm của bất phương trình (
A x) B(x) nếu (
A x ) B(x ) là khẳng định đúng 0 0 0
✓ Giải một bất phương trình là tìm tất cả các nghiệm của bất phương trình đó
2. Cách giải bất phương trình bậc nhất một ẩn
✓ Bất phương trình bậc nhất một ẩn ax + b 0 được giải như sau: ax + b 0 ax −b
+ Nếu a 0 thì − b x a
+ Nếu a 0 thì − b x a
! – Các bất phương trình ax + b 0, ax + b 0,ax + b 0 được giải tương tự-
- Ta cũng có thể giải được các bất phương trình một ẩn đưa được về dạng ax + b 0 ,
ax + b 0, ax + b 0, ax + b 0 B. CÁC DẠNG BÀI TẬP
Dạng 1: Nhận biết bất phương trình bậc nhất, nghiệm của bất phương trình
*Ví dụ 1: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? a) 0x 0 b) 3x 0 c) 3 x +1 0 d) −x +1 0 e) a + 2023 0 f) 0x − 5 0 g) 5x − 7 0 h) 2 x +1 0 Lời giải:
✓ Hai bất phương trình 0x 0 và 3
x +1 0 không phải là bất phương trình bậc nhất một ẩn
✓ Bất phương trình 3x 0 có dạng ax + b 0 với a = 3 0 và b = 0 nên nó là bất phương trình bậc nhất một ẩn
✓ Bất phương trình −x +1 0 có dạng ax + b 0 với a = −1 0 và b = 1 nên nó là bất phương
trình bậc nhất một ẩn
✓ Bất phương trình a + 2023 0 có dạng ax + b 0 với a = 1 0 và b = 2023, nên nó là bất
phương trình bậc nhất một ẩn
✓ Bất phương trình 5x − 7 0 có dạng ax + b 0 với a = 5 và b = −7 , nên nó là bất phương trình bậc nhất một ẩn
✓ Hai bất phương trình 0x − 5 0 và 2
x +1 0 không phải là bất phương trình bậc nhất một ẩn
* Ví dụ 2: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? a) 3x +16 0 b) −5x + 5 0 c) 2 x − 4 0 d) −3x 0 e) −3x + 7 0 f) 3 4x − 0 g) 3 x 0 h) 2 2x −19 0 2 Lời giải:
✓ a), b), d), e), f) là bất phương trình bậc nhất một ẩn x
✓ c), h) không là bất phương trình bậc nhất một ẩn x vì 2 2
x − 4, 2x −19 là các đa thức bậc hai.
✓ g) không là là bất phương trình bậc nhất một ẩn x vì 3
x là một đa thức bậc ba.
*Ví dụ 3: Kiểm tra xem giá trị x = 5 có phải là nghiệm của mỗi bất phương trình bậc nhất sau đây không? Trang 1 a) 6x − 29 0 b) 11x − 52 0 c) x − 2 0 Lời giải:
a) Thay x = 5 , ta có 6.5 − 29 0 là khẳng định đúng .
Vậy x = 5 là nghiệm của bất phương trình 6x − 29 0
b) Thay x = 5 ,ta có 11.5 − 52 0 là khẳng định đúng .
Vậy x = 5 là nghiệm của bất phương trình 11x − 52 0
c) Thay x = 5 , ta có 5 − 2 0 là khẳng định không đúng
Vậy x = 5 là nghiệm của bất phương trình x − 2 0
*Ví dụ 4: Trong hai giá trị x = 1 và x = 2 , giá trị nào là nghiệm của bất phương trình 3x − 4 0 Lời giải:
a) Thay x = 1 vào bất phương trình, ta được 3.1− 4 0 là khẳng định đúng.
Vậy x = 1là một nghiệm của bất phương trình đã cho
b) Thay x = 2 vào bất phương trình, ta được 3.2 − 4 0 là khẳng định sai.
Vậy x = 2 không là nghiệm của bất phương trình đã cho
*Ví dụ 5: Tìm một số là nghiệm và một số không phải là nghiệm của bất phương trình 4x + 5 0 Lời giải:
a) Lâý x = 0 thay vào bất phương trình đã cho, ta thấy 0.4 + 5 0 là khẳng định đúng.
Vậy x = 0 là một nghiệm của bất phương trình đã cho
b) Lấy x = −2 thay vào bất phương trình đã cho, ta thấy 4.( 2
− ) + 5 0 là khẳng định sai.
Vậy x = −2 không phải là một nghiệm của bất phương trình đã cho
* Ví dụ 6: Nêu hai ví dụ về bất phương trình một ẩn x Lời giải:
Hai bất phương trình một ẩn x là a) 2x + 4 0 b) −x − 3 0
*Ví dụ 7: Trong các số −2;0;5 , những số nào là nghiệm của bất phương trình 2x −10 0 Lời giải:
Chỉ có −2 và 0 là nghiệm của phương trình đã cho
*Ví dụ 8: Kiểm tra xem x = −5 có phải là nghiệm của bất phương trình 2x + 7 1− 3x không? Lời giải:
Thay x = −5 vào hai vế của bất phương trình đã cho, ta được: 2. − ( 5 − ) + 7 1− 3.( 5 − )
Hay −3 16 (bất đẳng thức đúng)
Vậy x = −5 là một nghiệm của bất phương trình đã cho
Dạng 2: Giải bất phương trình bậc nhất một ẩn
*Ví dụ 9: Giải các bất phuương trình sau\ a) −2x − 4 0 b) 2x +1 0 c) 0,5x − 6 0 d) −2x + 3 0 e) 5x − 3 0 d) −6x − 2 0 Lời giải:
a) Ta có: −2x − 4 0
−2x 0 + 4 (Công cả hai vế của bất phương trình với 4 ) 1 x 4. −
(Nhân cả hai vế với số âm 1
− và đổi chiều bất đẳng thức) 2 2 x −2
Vậy nghiệm của bất phương trình là x −2 b) Ta có: 2x +1 0
2x −1 (Cộng hai vế với 1 − ) Trang 2 1 1 2 . x ( 1 − ). (Nhân hai vế 1 ) 2 2 2 1 x − 2
Vậy nghiệm của bất phương trình là 1 x − 2
c) Ta có: 0,5x − 6 0
0,5x 6 (Cộng hai vế với 6 )
(0,5x).2 6.2 (Nhân hai vế với 2 ) x 12
Vậy nghiệm của bất phương trình là x 12
d) Ta có: −2x + 3 0 2 − x 3 − (Cộng hai vế với 3 − ) 1 1 ( 2 − x). − ( 3 − ). − (Nhân hai vế với 1 − ) 2 2 2 3 x 2
Vậy nghiệm của bất phương trình là 3 x 2
e) Ta có: 5x − 3 0
5x 3 (Cộng hai vế với 3 ) 1 1 5 . x
3. (Nhân hai vế với 1 ) 5 5 5 3 x 5
Vậy nghiệm của bất phương trình là 3 x 5
f) Ta có : −6x − 2 0
−6x 2 (Cộng hai vế với 2 ) 1 1 ( 6 − x). − 2. − (Nhân hai vế với 1 − ) 6 6 6 1 x 3
Vậy nghiệm của bất phương trình là 1 x 3
*Ví dụ 10: Giải các bất phương trình : a) 6x + 5 0 b) −2x − 7 0
c) 2x + 5 3x − 4 d) 3 − x + 5 4 − x + 3
e) 5x + 7 8x − 5
f) −4x + 3 3x −1 g) −0,3x +12 0 h) 3 x − 6 0 4 Lời giải:
a) Ta có: 6x + 5 0
b) Ta có: −2x − 7 0 6x −5 −2x 7 − 5 x 7 x − 6 2 −
Vậy nghiệm của bất phương trình là 5 x
Vậy nghiệm của bất phương trình là 7 x − 6 2
c) Ta có 2x + 5 3x − 4 d) ta có: 3 − x + 5 4 − x + 3 Trang 3 2x − 3x 4 − − 5 3
− x + 4x 3 − 5 −x −9 x −2 x 9
Vậy nghiệm của bất phương trình là x −2
Vậy nghiệm của bất phương trình là x 9
f) Ta có: −4x + 3 3x −1
e) T a có: 5x + 7 8x − 5 3
− x + 4x 3x −1 5x − 8x 5 − − 7 7 − x 4 − −3x −12 4 x x 4 7
Vậy nghiệm của bất phương trình là x 4
Vậy nghiệm của bất phương trình là 4 x
g) Ta có: −0,3x +12 0 7 0 − ,3x 12 −
h) Ta có: 3 x − 6 0 − 12 4 x 0 − ,3 3 x 6 x 40 4
Vậy nghiệm của bất phương trình là x 40 4 x 6. 5 x 8
Vậy nghiệm của bất phương trình là x 8
*Ví dụ 11: Giải các bất phương trình: a) −8x − 27 0 b) 5 x + 20 0 4
c) 2x − 5 4x + 3
d) 5 + 7x 4x − 7
e) 3x − (6 + 2x) 3.(x + 4)
f) 2(x − 0,5) −1, 4 1,5 − (x +1, 2) Lời giải:
a) Ta có: −8x − 27 0
b) Ta có: 5 x + 20 0 8 − x 27 4 − 27 x 5 x 20 − 8 4 −
Vậy nghiệm của bất phương trình là 27 x 4 x 20. − 8 5
c)Ta có: 2x − 5 4x + 3 x −16 5
− − 3 4x − 2x
Vậy nghiệm của bất phương trình là x −16 −8 2x
d) ta có: 5 + 7x 4x − 7 −4 x 7x − 4x 7 − − 5
Vậy nghiệm của bất phương trình là −4 x 3x 12 −
e) Ta có: 3x − (6 + 2x) 3.(x + 4) x −4
3x − 6 − 2x 3x +12
Vậy nghiệm của bất phương trình là x −4
x − 6 3x +12
f) Ta có: 2(x − 0,5) −1, 4 1,5 − (x +1, 2) 6
− −12 3x − x
2x −1−1, 4 1,5 − x −1, 2 18 − 2x
2x −1,5 0,3 − x x −9 3x 1,8
Vậy nghiệm của bất phương trình là x −9 x 0,6
Vậy nghiệm của bất phương trình là x 0,6
*Ví dụ 12: Giải các bất phương trình: x − x + x − − a) 2 5 4 3 b) 4 1 5 3 x 18 10 9 6 Trang 4 Lời giải: x − x + x − − a) Ta có: 2 5 4 3 b) Ta có: 4 1 5 3 x 18 10 9 6 5(2x − 5) 9(4x + 3) x − − 2(4 1) 3(5 3x) 90 10 18 18
10x − 25 36x + 27
8x − 2 15 − 9x
10x − 36x 27 + 25
8x + 9x 15 + 2 − 26x 52 17x 17 x 52 1 x 26 −
Vậy nghiệm của bất phương trình là x 1 x −2
Vậy nghiệm của bất phương trình là x −2
*Ví dụ 13 Giải các bất phương trình: x + x − x + x + a) 5 2 4 3 b) 3(2 1) 3 13 +1 5 4 20 10 Lời giải: x + x − x + x + a) Ta có: 5 2 4 3 b) Ta có: 3(2 1) 3 13 +1 5 4 20 10 4(5x + 2) 5(4x − 3) x + x + 3(2 1) 20 2(3 13) + 20 20 20 30 20
20x + 8 20x −15
6x + 3 + 20 6x + 26
20x − 20x 8 − −15
6x − 6x 26 − 3 − 20 0x 23 − 0x 3
Bất phương trình này vô nghiệm
Bất phương trình này có nghiệm bất kì
*Ví dụ 14: Tìm nghiệm chung của hai bất phương trình: x + x + x − x − 3 17 5 22 (1) và 4 2 7 −1 (2) 10 15 30 24 Lời giải: x + x + x − x − Ta có 3 17 5 22 Ta có : 4 2 7 −1 10 15 30 24 3(3x +17) 2(5x + 22) x − x − 4( 4) 120 5(2 7) − 30 30 120 120 120
9x + 51 10x + 44
4x −16 −120 10x − 35
9x −10x 44 − 51
4x −10x 16 +120 − 35 − x 7 − − 6x 101 x 7 (*) 101 x − (**) 6
Từ (*) và (**) suy ra nghiệm chung của hai bất phương trình là 101 x − 6
*Ví dụ 15: Tìm nghiệm nguyên âm của bất phương trình x + x − x − x − 2 4 4 7 2 5 2 1 − − 3 18 9 15 Lời giải: Trang 5 x + x − x − x − Ta có: 2 4 4 7 2 5 2 1 − − 3 18 9 15 2x + 4 4x − 7 2x − 5 2x −1 − − 3 18 9 15
30(2x + 4) 5(4x −17) 10(2x − 5) 6(2x −1) − − 90 90 90 90
60x +120 − 20x + 35 20x − 50 −12x + 6
60x − 20x − 20x +12x 120 − − 35 − 50 + 6 32x 199 − 199 − x 32
Vì x là số nguyên âm nên x 6 − , 5 − , 4 − , 3 − , 2 − , − 1
Dạng 3: Giải bài toán bằng cách lập bất phương trình
*Ví dụ 16: Bạn Thanh có 100 nghìn đồng. Bạn muốn mua một cái bút giá 18 nghìn đồng và một
số quyển vở, mỗi quyển vở giá 17 nghìn đồng. Hỏi bạn Thanh mua được nhiều nhất bao nhiêu quyển vở? Lời giải:
Gọi x (quyển) là số vở mà Thanh có thể mua. Theo bài ta ta có bất phương trình 7x +18 100 7x 100 −18 x 82 82 x 7
Vì số vở là số tự nhiên nên Thanh có thể mua nhiều nhất 11 quyển vở
*Ví dụ 17: Để hưởng ứng phong trào “Trồng cây gây rừng” lớp 9A có kế hoạch trồng ít nhất
1000 cây xanh. Lớp 9a đã trồng được 540 cây. Để đạt được kế hoạch đề ra, lớp 9A cần trồng
thêm bao nhiêu cây xanh nữa? Lời giải:
Gọi x là số cây xanh cần trồng thêm của lớp 9A
Theo đề bài, để lớp 9A đạt được kế hoạch đề ra, ta phải có: x + 540 1000 x 1000 − 540 x 460
Vậy để đạt được kế hoạch đề ra, lớp 9A phải trồng thêm ít nhất 460 cây xanh nữa
*Ví dụ 18: Trong một kì thi gồm ba môn Toán, Ngữ Văn và Tiếng Anh, điểm số môm Toán và
Ngữ văn tính theo hệ số 2 , điểm môn Tiếng Anh tính theo hệ số 1. Để trúng tuyến, điểm số trung
bình của ba môn ít nhất bằng 8 . Bạn Na đã đạt 9,1 điểm môn Toán, và 6,9 môn Ngữ Văn. Hãy
lập và giải phương trình để tìm điểm số môn Tiếng Anh tối thiểu mà bạn Na phải đạt để trúng tuyển. Lời giải:
Gọi x là điểm số môn Tiếng Anh của bạn Na
Theo đề bài, để bạn Na trùng tuyển, ta phải có: Trang 6 2.9,1+ 2.6,9 + x 8 5
2.9,1+ 2.6,9 + x 40 18, 2 +13,8 + x 40 x 8
Vậy để trúng tuyển, bạn Na phải đạt được ít nhất 8 điểm môn Tiếng Anh
*Ví dụ 19: Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 12 tháng là 7, 4% . Bà Mai
dự kiến gửi một khoản tiền vài ngân hàng này và cần số tiền lãi hàng năm ít nhất là 60 triệu để
chi tiêu. Hỏi số tiền bà Mai cần gửi tiết kiệm ít nhất là bao nhiêu (làm tròn đến triệu đồng) Lời giải:
Gọi x (triệu đồng) là số tiền bà Mai cần gửi tiết kiệm
Ta có số tiền lãi gửi gửi tiết kiệm x (triệu đồng) trong một năm là 0,074.x (triệu đồng)
Để có số tiền lãi ít nhất là 60 triệu đồng/năm thì ta phải có: 0, 074x 60 x 60 : 0, 074 x 810,81
Vậy bà Mai cần gửi ngân hàng ít nhất 811 triệu đồng
*Ví dụ 20: Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển
phải trả lời 25 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn đáp án, trong đó có một đáp
án đúng. Người ứng tuyển chọn đáp đúng sẽ được cộng thêm 2 điểm, chọn đáp án sai bị trừ đi 1
điểm. Ở vòng sơ tuyển, ban tổ chức tặng mỗi người dự thi 5 điểm và theo quy định người ứng
tuyển phải trả lời hết 25 câu hỏi: người nào có số điểm từ 25 trở lên mới được thi vòng tiếp theo.
Hỏi người ứng tuyển phải trả lời chính xác ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển thì mới
được vào vòng tiếp theo? Lời giải:
Gọi x, 25 − x (x N, x 5) lần lượt là số câu trả lời đúng và sai của người ứng tuyển
Số điểm của người ứng tuyển sau 25 câu hỏi là 5 + 2x − (25 − x) = 3x − 20 điểm
Để vượt qua vòng sơ tuyển cần ít nhất 25 điểm nên ta có bất phương trình: 3x − 20 25 3x 45 x 15
Vậy người ứng tuyển phải trả lời chính xác ít nhất 15 câu hỏi
*Ví dụ 21: Bác Ngọc gửi tiền tiết kiệm kì hạn 12 tháng ở một ngân hàng với lãi suất 7, 2% /
năm. Bác Ngọc dự định tổng số tiền nhận được sau khi gửi 12 tháng ít nhất là 21440000 .Hỏi bác
Ngọc phải gửi số tiền tiết kiệm ít nhất là bao nhiêu để đạt được dự định đó? Lời giải:
Gỉa sử bác Ngọc gửi x (đồng) tiền tiết kiệm kì hạn 12 tháng ( x 0 ). Khi đó, tổng số tiền bác
Ngọc nhận được sau 12 tháng là 7, 2 1072 134 x + 7, 2%.x = 1+ x = x = x (đồng) 100 1000 125
Theo giả thiết, ta có 134 x 21440000 125
Giải bất phương trình trên, ta có: Trang 7 134 x 21440000 125 125 x 21440000. 134 x 20000000
Vậy bác Ngọc phải gửi số tiền tiết kiệm ít nhất là 20 triệu đồng để đạt được dự định
*Ví dụ 22: Tổng chi phí của một doanh nghiệp sản xuất áo sơ mi là 410 triệu đồng/ tháng. Gía
bán của mỗi chiếc áo sơ mi là 350 nghìn đồng. Hỏi trung bình mỗi tháng doanh nghiệp phải bán
được ít nhất bao nhiêu chiếc áo sơ mi để thu được lợi nhuận ít nhất là 1,38 tỉ đồng sau 1 năm? Lời giải:
Giả sử trung bình mỗi tháng doang nghiệp bán được x chiếc áo sơ mi ( * x )
Lợi nhuận của doanh nghiệp sau 12 tháng là:
12(350 000x − 410 000 000) (đồng)
Do đó để doanh nghiệp thu được lợi nhuận ý nhât là 1,38 tỉ đồng thì
12(350 000x − 410 000 000) 1380 000 000
Giải bất phương trình trên, ta có:
12(350 000x − 410 000 000) 1380 000 000
350000x − 410000000 115000000
350000x 115000000 + 410000000 350000x 525000000 525000000 x 350000 x 1500
Vậy trung bình mỗi thnangs doang nghiệp phải bán được ít nhất 1500 chiếc áo sơ mi để doanh
nghiệp thu được lợi nhuận ít nhất là 1,38 tỉ đồng sau 1 năm C. BÀI TẬP VẬN DỤNG
Bài 1: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? a) 2x − 5 0 b) 3y +1 0 c) 0x − 3 0 d) 2 x 0 Lời giải:
a) 2x − 5 0 là bất phương trình bậc nhất ẩn x
b) 3y +1 0 là bất phương trình bậc nhất ẩn y
c) 0x − 3 0 , vì a = 0 nên không phải là bất phương trình bậc nhất một ẩn d) 2
x 0 vì có chứa 2
x nên không phải là bất phương trình bậc nhất một ẩn
Bài 2: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? a) 3x − 6 0 b) −13x + 20 0 c) 7 y 0 Lời giải:
Bất phương trình ở các câu a,b,c là bất phương trình bậc nhất một ẩn
Bài 3: Kiểm tra xem số nào là nghiệm của mỗi bát phương trình tương ứng sau đây. a) 2
x − 3x + 2 0 với x = −3; x = 1,5
b) 2 − 2x 3x +1 với 2 1 x = ; x = 5 5 Lời giải
a) Thay x = −3 , ta có 2 ( 3 − ) − 3.( 3
− ) + 2 0 là khẳng định đúng
Vậy x = −3 là nghiệm của bất phương trình
Thay x = −1,5, ta có : 2 ( 1 − ,5) − 3.( 1
− ,5) + 2 0 là khẳng định không đúng
Vậy x = −1,5 không là nghiệm của bất phương trình Trang 8 b) Thay 2 x = , ta có 2 2
2 − 2. 3. +1 là khẳng định đúng 5 5 5 Vậy 2
x = là nghiệm của bất phương trình 5 Thay 1 x = , ta có 1 1
2 − 2. 3. +1 là khẳng định không đúng 5 5 5 Vậy 1
x = không là nghiệm của bất phương trình 5
Bài 4: Tìm x sao cho:
a) Gía trị biểu thức 2x +1 là số dương
b) Gía trị biểu thức 3x − 5 là số âm Lời giải
a) Giá trị biểu thức 2x +1 là số dương nên 2x +1 0 2x −1 (Cộng 1 − vào cả hai vế) − 1 x (nhân 1 vào cả hai vế) 2 2 − Vậy 1 x 2
b) Giá trị biểu thức 3x − 5 là số âm nên 3x − 5 0
3x 5 (Cộng 5 vào cả hai vế) 5
x ( nhân 5 vào cả hai vế) 3 3 Vậy 5 x 3
Bài 5: Giải các bất phương trình sau: a) x − 5 0 b) x + 5 0 c) −2x − 6 0 d) 4x −12 0 Lời giải a) x − 5 0 b) x + 5 0 c) −2x − 6 0 d) 4x −12 0 x 5 x −5 −2x 6 4x 12 x −3 x 3
Bài 6: Giải các bất phương trình sau: a) 6 x − 3 b) 1 .x 5 c) −8x +1 5 d) 7 2x +1 2 Lời giải
a) Giải bất phương trình 6 x − 3
6 + 3 x (cộng 3 vào cả hai vế) 9 x
Vậy nghiệm của bất phương trình là 9 x
b) Giải bất phương trình 1 .x 5 2
x 10 ( nhân 2 vào cả hai vế)
Vậy nghiệm của bất phương trình là x 10
c) Giải bất phương trình −8x +1 5 −8x 4 (cộng 1 − vào cả hai vế) − 4 x
( nhân 1 vào cả hai vế) 8 − 8 Trang 9 − 1 x
(nhân số âm đảo chiều) 2 −
Vậy nghiệm của bất phương trình là 1 x 2
d) Giải bất phương trình 7 2x +1 6 2x (cộng 1 − vào cả hai vế)
6 x ( nhân 1 vào cả hai vế) 2 2 3 x
Vậy nghiệm của bất phương trình là 3 x
Bài 7: Giải các bất phương trình sau:
a) x − 7 2 − x
b) x + 2 2 + 3x
c) 4 + x 5 − 3x
d) −x + 7 x − 3 Lời giải
a) Giải bất phương trình x − 7 2 − x
x 9 − x (cộng 7 vào cả hai vế)
2x 9 (cộng x vào cả hai vế) 9
x ( nhân 1 vào cả hai vế) 2 2
Vậy nghiệm của bất phương trình là 9 x 2
b) Giải bất phương trình x + 2 2 + 3x
x 3x (cộng −2 vào cả hai vế)
0 2x (cộng −x vào cả hai vế)
0 x ( nhân 1 vào cả hai vế) 2
Nghiệm của bất phương trình là 0 x
c) Giải bất phương trình 4 + x 5 − 3x
4x 1 ( cộng 3x và −4 từ cả hai bên) 1
x (Nhân hai vế cho 1 ) 4 4
Nghiệm của bất phương trình là 1 x 4
d) Giải bất phương trình −x + 7 x − 3
7 2x − 3 (Cộng x vào cả hai vế)
10 2x (Cộng 3 vào cả hai vế)
5 x ( nhân 1 vào cả hai vế) 2
Nghiệm của bất phương trình là 5 x
Bài 8: Giải các bất phương trình sau:
a) 3x + 2 2x + 3 b) 5x + 4 3 − x − 2
c) 2 (2x + 3) 7 − 4x
d) 1 (x − 3) 3− 2x 3 4 Lời giải
a) Giải bất phương trình 3x + 2 2x + 3
3x − 2x 3 − 2 (Cộng −2x vào cả hai vế) x 1
Vậy nghiệm của bất phương trình là x 1
b) Giải bất phương trình 5x + 4 3 − x − 2 Trang 10 5x + 3x 2
− − 4 (Cộng 3x vào cả hai vế) 8x −6 3
x − ( nhân 1 vào cả hai vế) 4 8
Vậy nghiệm của bất phương trình là 3 x − 4
c) Giải bất phương trình 2 (2x + 3) 7 − 4x 3 21 2x + 3
− 6x ( nhân 3 vào cả hai vế) 2 2 21 8x + 3
(Cộng 6x vào cả hai vế) 2 15 8x − 3 (Cộng 3 − vào cả hai vế) 2 15 8x
(Cộng 3 vào cả hai vế) 2 15 x
( nhân 1 vào cả hai vế) 16 8
Vậy nghiệm của bất phương trình là 15 x 16
d) Giải bất phương trình 1 (x − 3) 3− 2x 4
(x − 3) 4.(3 − 2x) ( nhân 4 vào cả hai vế)
x − 3 12 − 8x (nhân phân phối 4 và mở ngoặc)
9x − 3 12 (Cộng 8x vào cả hai vế)
9x 15 (Cộng 3 vào cả hai vế) 5
x ( nhân 1 vào cả hai vế) 3 9
Vậy nghiệm của bất phương trình là 5 x 3
Bài 9: Giải bất phương trình a) 2x + 6 1
b) 0,6x + 2 6x + 9
c) 1,7x + 4 2 +1,5x − + x − d) 8 3x − x x x 5 e) 6 4 3 − 2x − 0 f) 2 4 0,7x + − 1 2 3 3 6 Lời giải a) 2x + 6 1
b) 0,6x + 2 6x + 9 2x 1− 6
0,6x − 6x 9 − 2 2x 5 − 5 − , 4x 7 5 x − x − 7 : ( 5, 4) 2 35 x −
Vậy nghiệm của bất phương trình là 5 x − 27 2
c) 1,7x + 4 2 +1,5x
Vậy nghiệm của bất phương trình là 35 x − 27 1
− ,7x −1,5x 2 − 4 − x 0, 2x 2 − d) 8 3 − x 5 2 x 2 − : 0, 2 x 10 − Trang 11
Vậy nghiệm của bất phương trình là x −10
8 − 3x − 2x 10 + e) 6 4x 3 − 2x − 0 − 5x 10 − 8 3 x 2 : (−5)
9 − 6x − (6 + 4x) 0 x −0, 4
9 − 6x − 6 − 4x 0
Vậy nghiệm của bất phương trình là x 0 − , 4 10 − x 3 − x − x x ( 3 − ) : ( 10) − f) 2 4 0,7x + − 1 3 6 x 0 − ,3
4, 2x + 2(2x − 4) − x 6
Vậy nghiệm của bất phương trình là x −0,3
4, 2x + 4x − 8 − x 6
4, 2x + 4x − x 6 + 8 7, 2x 14 x 14 : 7, 2 35 x 18
Vậy nghiệm của bất phương trình là 35 x 18
Bài 10: Tìm số nguyên lớn nhất thỏa mãn bất phương trình sau: x − x + a) 9 − 5x 1,5 b) 3 17 5 1 20 15 Lời giải
a) Ta có: 9 − 5x 1,5 5 − x −7,5 7,5 x 5
Do đó số nguyên lớn nhất thỏa mãn bất phương trình trên là x = 1 x − x + b) Ta có: 3 17 5 1 20 15 x − x + 15(3 17) 20(5 1) 300 300
45x − 255 100x + 20 −55x 275 275 x − 55 x −5
Do đó số nguyên lớn nhất thỏa mãn bất phương trình trên là x −5
Bài 11: Tìm nghiệm chung của hai bất phương trình x −
a) 15x − 4 8 và 7 − 6x −20 b) 2 x + 5 9 và 18 1 3 7 Lời giải
a) Ta có 15x − 4 8 hay 15x 12 suy ra 12 x 5
Ta có 7 − 6x −20 hay −6x −27 , suy ra 27 x 6
Vậy nghiệm chung của hai bất phương trình trên là x 1;2;3; 4 Trang 12
b) Ta có: 2 x + 5 9 hay 2 x 4 , suy ra x 6 3 3 x − Ta có
18 1 hay x −18 7 , suy ra x 25 7
Vậy nghiệm chung của hai bất phương trình trên là x 25 − x −
Bài 12: Tìm tập hợp các giá trị của x
x để biểu thức 3 2 lớn hơn giá trị của biểu thức 14 5 10 Lời giải
Giải bất phương trình 3 − 2x x −14 5 10 2(3 − 2x) x −14 10 10
6 − 4x x −14 20 5x 20 x 5 x 4
Vậy x 4 là giá trị cần tìm
Bài 13: Cho phương trình 5x − 4 = 3m + 2(1) trong đó x là ẩn số, m là một số cho trước. Tìm giá
trị của m để phương trình (1) có nghiệm dương Lời giải + m +
Giải phương trình (1) theo m , ta được 3 6 = m x . Ta có x 0 khi 3
6 0, hay 3m −6 , suy ra 5 5 m −2
Vậy m −2 là giá trị cần tìm
Bài 14: Giải bất phương trình sau: x + x + x − x − x − a) 3(2 1) 3 52 +1 b) 4 1 6 19 9 11 + 20 10 2 6 3 Lời giải x + x + x − x − x − a) 3(2 1) 3 52 +1 b) 4 1 6 19 9 11 + 20 10 2 6 3 3(2x +1) 20 2(3x + 52) x − x − x − + 3(4 1) 6 19 2(9 11) + 20 20 20 6 6 6
6x + 3 + 20 6x +104
12x − 3 + 6x −19 18x − 22 0x 81 0x 0
Vậy bất phương trình vô nghiệm
Bất phương trình có nghiệm bất kì
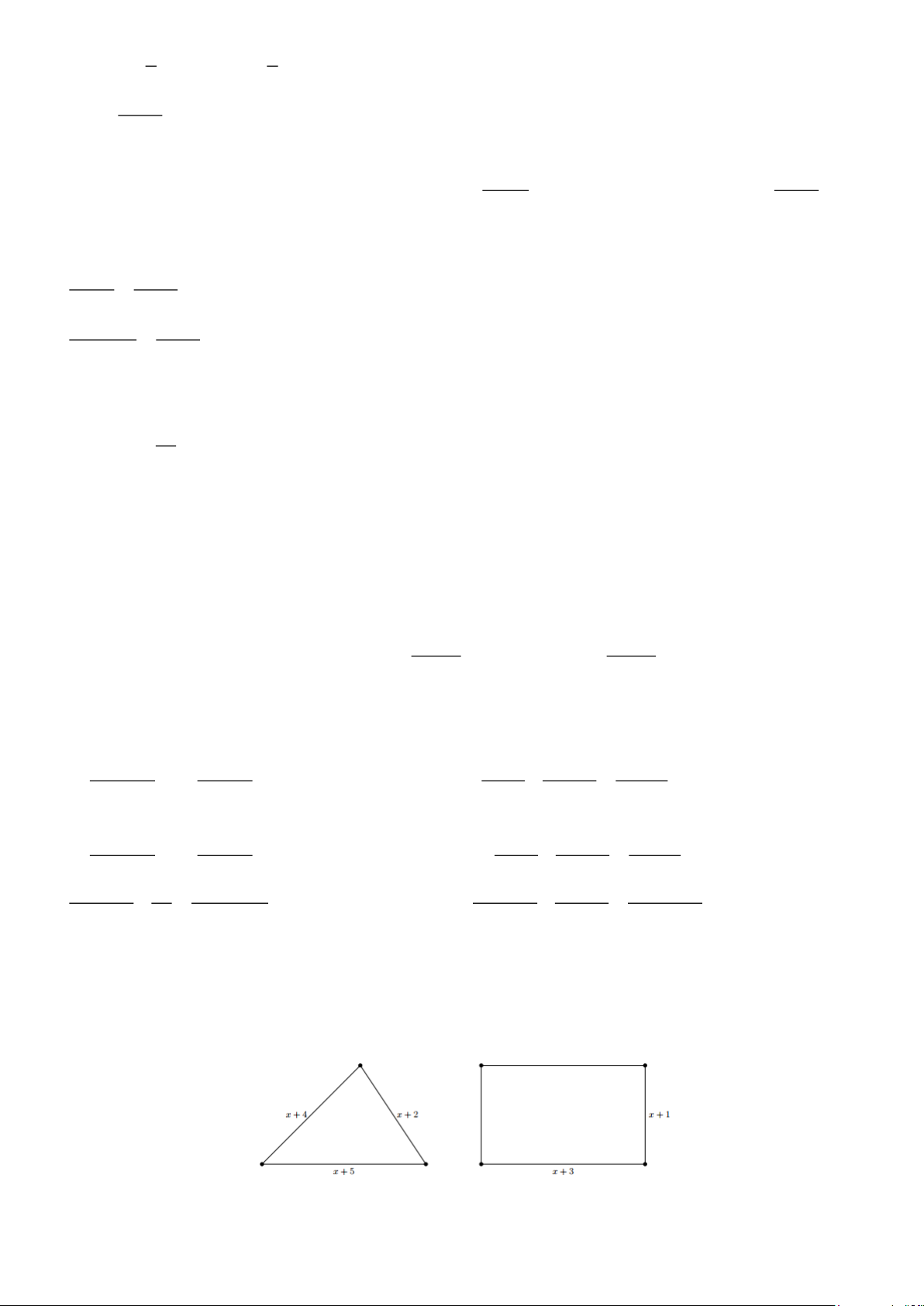
Bài 15: Tìm x 0 sao cho ở hình vẽ bên dưới chu vi của hình tam giác luôn lớn hơn chu vi hình chữ nhật Lời giải Trang 13
Chu vi tam giác là : x + 2 + x + 4 + x + 5 = 3x +11
Chu vi hình chữ nhật là 2(x + 3 + x +1) = 4x + 8 Theo bài ra ta có:
3x +11 4x + 8
3x − 4x 8 −11 − x −3 x 3 Vậy 0 x 3
Bài 16: Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 1 tháng là 0, 4% . Hỏi nếu muốn
có một số tiền lãi hãng tháng ít nhất là 3 triệu đồng thì số tiền gửi tiết kiệm ít nhất là bao nhiêu
(làm tròn đến triệu đồng)? Lời giải
Gọi x (triệu đồng) là số tiền cần gửi. Theo bài ra ta có bất phương trình 0, 4%x 3 0, 4 .x 3 100 3.1000 x 4 x 750
Vậy để có lãi ít nhất 3 triệu đồng thì số tiền gửi tiết kiệm ít nhất là 750 triệu
Bài 17:Một hãng taxi có giá mở cửa là 15 nghìn đồng và giá 12 nghìn đồng cho mỗi ki lô mét
tiếp theo. Hỏi với 200 nghìn đồng thì hành khách có thể di chuyển được tối đa là bao nhiêu ki lô
mét (làm tròn đến hàng đơn vị) Lời giải
Gọi x km ( x 0 ) là số km mà hành khách có thể đi, ta có bất phương trình: 15 +12x −12 200 12x 200 − 3 197 x =16,416..... 12
Vậy số km tối đa khách hàng có thể đi là 16 km
Bài 18: Người ta dùng một loại xe tải để chở bia cho một nhà máy. Mỗi thùng bia 24 lon nặng
trung bình 6,7 kg. Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà
xe có thể chở) là 5, 25 tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng bia, biết bác lái xe nặng 65 kg? Lời giải Gọi x thùng ( * x
) là thùng bia mà xe có thể chở, ta có bất phương trình:
65 + 6,7x 5, 25.1000 6,7x 5185 5185 x = 773,880.... 6,7
Vậy số thùng bi tối đa mà xe có thể chở là 773 thùng
Bài 19: Một kho chứa 100 tấn xi măng, mỗi ngày đều xuất đi 20 tấn xi măng. Gọi x là số ngày
xuất xi măng của kho đó. Tìm x sao cho khối lượng xi măng còn lại trong kho ít nhất là 10 tấn
sau x ngày xuất hàng Lời giải Trang 14
Sau x ngày khối lượng xi măng được xuất đi là 20x
Khối lượng xi măng còn lại trong kho sau x ngày là 100 − 20x
Theo bài ra ta có: 100 − 20x x
100 − 20x x 20
− x − x 100 − − 21x 100 − x ( 100) − : ( 21 − ) 100 x 21
Vậy x 1;2;3; 4
Bài 20: Một kì thi Tiếng Anh gồm bốn kĩ năng: nghe, nói, đọc, viết. Kết quả của bài thi là điểm
trung bình của bốn kỹ năng này. Bạn Hà đã đạt được điểm số của ba kĩ năng nghe, nói, viết lần lượt là 6,5;6,5;5,5
Hỏi bạn Hà cần đạt bao nhiêu điểm trong kĩ năng nói để kết quả được của bài thi ít nhất là 6, 25 ? Lời giải
✓Để tính điểm trung bình cần đạt, chúng ta có thể sử dụng công thức sau:
Điểm trung bình = 𝑇ổ𝑛𝑔 đ𝑖ể𝑚 𝑐á𝑐 𝑘ĩ 𝑛ă𝑛𝑔
𝑆ố 𝑙ượ𝑛𝑔 𝑘ĩ 𝑛ă𝑛𝑔
✓Trong trường hợp này, chúng ta muốn biết điểm số cần đạt trong kĩ năng “nói” để đạt được
điểm trung bình ít nhất là 6, 25 . Điểm số trung bình mong muốn là trung bình của 6,5;6,5;5,5 và
một số x (điểm số trong kĩ năng “nói”). Ta có bất phương trình
6,5 + 6,5 + 5,5 + x 6,25 4 18,5 + x 25 x 25 −18,5 x 6,5
✓Vậy để đạt được điểm trung bình ít nhất là 6, 25 , bạn Hà cần đạt ít nhất 6,5 điểm trong kĩ năng “nói” Trang 15



