






















































































Preview text:
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 11 GIỚI HẠN DÃY SỐ 1D4-1
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 0. CÂU HỎI LÝ THUYẾT .................................................................................................................................. 1
DẠNG 1. DÃY SỐ DẠNG PHÂN THỨC ...................................................................................................................... 2
Dạng 1.1 Phân thức bậc tử bé hơn bậc mẫu ................................................................................................................. 2
Dạng 1.2 Phân thức bậc tử bằng bậc mẫu .................................................................................................................... 4
Dạng 1.3 Phân thức bậc tử lớn hơn bậc mẫu ................................................................................................................ 8
Dạng 1.4 Phân thức chứa căn ....................................................................................................................................... 9
DẠNG 2. DÃY SỐ CHỨA CĂN THỨC ......................................................................................................................... 9
DẠNG 3. DÃY SỐ CHỨA LŨY THỪA ....................................................................................................................... 11
DẠNG 4. TỔNG CẤP SỐ NHÂN LÙI VÔ HẠNG ...................................................................................................... 13
DẠNG 5. MỘT SỐ BÀI TOÁN KHÁC ........................................................................................................................ 13
PHẦN B. LỜI GIẢI THAM KHẢO .............................................................................................................................. 16
DẠNG 0. CÂU HỎI LÝ THUYẾT ................................................................................................................................ 16
DẠNG 1. DÃY SỐ DẠNG PHÂN THỨC .................................................................................................................... 17
Dạng 1.1 Phân thức bậc tử bé hơn bậc mẫu ............................................................................................................... 17
Dạng 1.2 Phân thức bậc tử bằng bậc mẫu .................................................................................................................. 20
Dạng 1.3 Phân thức bậc tử lớn hơn bậc mẫu .............................................................................................................. 25
Dạng 1.4 Phân thức chứa căn ..................................................................................................................................... 26
DẠNG 2. DÃY SỐ CHỨA CĂN THỨC ....................................................................................................................... 26
DẠNG 3. DÃY SỐ CHỨA LŨY THỪA ....................................................................................................................... 31
DẠNG 4. TỔNG CẤP SỐ NHÂN LÙI VÔ HẠNG ...................................................................................................... 33
DẠNG 5. MỘT SỐ BÀI TOÁN KHÁC ........................................................................................................................ 34 PHẦN A. CÂU HỎI
DẠNG 0. CÂU HỎI LÝ THUYẾT Câu 1.
Trong các mệnh đề dưới đây, mệnh đề nào sai?.
A. Nếu lim u và limv a 0 thì lim u v . n n n n u
B. Nếu lim u a 0 và limv thì lim n 0 . n n v n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 u
C. Nếu lim u a 0 và limv 0 thì lim n . n n v n u
D. Nếu lim u a 0 và limv 0 và v 0 với mọi n thì lim n . n n n v n Câu 2.
Tìm dạng hữu tỷ của số thập phân vô hạn tuần hoàn P 2,13131313... , 212 213 211 211 A. P B. P . C. P . D. P . 99 100 100 99 Câu 3.
Khẳng định nào sau đây là đúng?
A. Ta nói dãy số u có giới hạn là số a (hay u dần tới a ) khi n , nếu lim u a . n 0 n n n
B. Ta nói dãy số u có giới hạn là 0 khi n dần tới vô cực, nếu u có thể lớn hơn một số dương n n
tùy ý, kể từ một số hạng nào đó trở đi.
C. Ta nói dãy số u có giới hạn khi n nếu u có thể nhỏ hơn một số dương bất kì, kể n n
từ một số hạng nào đó trở đi.
D. Ta nói dãy số u có giới hạn khi n nếu u có thể lớn hơn một số dương bất kì, kể n n
từ một số hạng nào đó trở đi. u Câu 4.
Cho các dãy số u , v và lim u a, lim v thì lim n bằng n n n n vn A. 1. B. 0 . C. . D. . Câu 5.
Trong các khẳng định dưới đây có bao nhiêu khẳng định đúng? (I) lim k
n với k nguyên dương. (II) lim n
q nếu q 1 . (III) lim n
q nếu q 1 A. 0 . B. 1. C. 3 . D. 2 . 1 Câu 6.
Cho dãy số u thỏa u 2
với mọi n * . Khi đó n n 3 n
A. lim u không tồn tại. B. lim u 1 .
C. lim u 0 .
D. lim u 2 . n n n n Câu 7.
(THPT CHUYÊN HÙNG VƯƠNG - PHÚ THỌ - LẦN 1 - 2018) Phát biểu nào sau đây là sai?
A. lim u c ( u c là hằng số ). B. lim n
q 0 q 1 . n n 1 1 C. lim 0 . D. lim 0 k 1 . n k n
DẠNG 1. DÃY SỐ DẠNG PHÂN THỨC
Dạng 1.1 Phân thức bậc tử bé hơn bậc mẫu
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n 1 Câu 8.
(THPT Chuyên Thái Bình - lần 3 - 2019) Tính L lim . 3 n 3 A. L 1. B. L 0. C. L 3. D. L 2. 1 Câu 9.
(Mã đề 101 BGD&ĐT NĂM 2018) lim bằng 5n 3 1 1 A. 0 . B. . C. . D. . 3 5 1
Câu 10. (Mã đề 103 BGD&ĐT NĂM 2018) lim bằng 2n 7 1 1 A. . B. . C. . D. 0 . 7 2 1
Câu 11. (Mã đề 104 BGD&ĐT NĂM 2018) lim bằng 2n 5 1 1 A. . B. 0 . C. . D. . 2 5 1
Câu 12. (THPT QUỐC GIA 2018 - MÃ ĐỀ 102) lim bằng 5n 2 1 1 A. . B. 0 . C. . D. . 5 2 2 3 7n 2n 1
Câu 13. (THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018) Tìm I lim . 3 2 3n 2n 1 7 2 A. . B. . C. 0 . D. 1. 3 3 2 2n 3
Câu 14. (HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018) lim bằng: 6 5 n 5n 3 A. 2 . B. 0 . C. . D. 3 . 5 2018 lim Câu 15. n bằng A. . B. 0 . C. 1. D. . 2n 1
Câu 16. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Tính giới hạn L lim ? 2 2 n n
A. L . B. L 2 . C. L 1 . D. L 0 .
Câu 17. (TRƯỜNG THPT THANH THỦY 2018 -2019) Dãy số nào sau đây có giới hạn bằng 0 ? 2 n 2 2 n 2n 1 2n 2 1 2n A. u . B. u . C. u . D. u . n 2 5n 3n n 2 5n 3n n 2 5n 3n n 2 5n 3n 2n 3
Câu 18. (THPT PHAN CHU TRINH - ĐẮC LẮC - 2018) Tính I lim 2 2n 3n 1
A. I . B. I 0 .
C. I . D. I 1.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1 1
Câu 19. Tìm lim u biết u ... . n n 2 2 2 2 1 3 1 n 1 3 3 2 4 A. . B. . C. D. . 4 5 3 3 1 1 1 1
Câu 20. (THPT XUÂN HÒA - VP - LẦN 1 - 2018) Tính giới hạn lim ... . 1.2 2.3 3.4 n n 1 3 A. 0 . B. 2 . C. 1. D. . 2 Câu 21. (THPT CHUYÊN LƯƠNG VĂN CHÁNH - PHÚ YÊN - 2018) Tìm 1 1 1 L lim ... 1 1 2
1 2 ... n 5 3 A. L .
B. L .
C. L 2 . D. L . 2 2 1 1 1
Câu 22. Với n là số nguyên dương, đặt S ... . Khi đó n 1 2 2 1 2 3 3 2
n n 1 n 1 n lim S bằng n 1 1 1 A. B. . C. 1. D. . 2 1 2 1 2 2 cos n sin n
Câu 23. (THPT NGUYỄN TẤT THÀNH - YÊN BÁI - 2018) Tính giá trị của lim . 2 n 1 A. 1. B. 0. C. . D. .
Dạng 1.2 Phân thức bậc tử bằng bậc mẫu 2 n
Câu 24. (THPT CHUYÊN HOÀNG VĂN THỤ - HÒA BÌNH - 2018) Giá trị của lim bằng n 1 A. 1. B. 2 . C. 1 . D. 0 . n 2
Câu 25. (THPT THUẬN THÀNH - BẮC NINH - 2018) Kết quả của lim bằng: 3n 1 1 1 A. . B. . C. 2 . D. 1. 3 3 3n 2
Câu 26. (THPT YÊN LẠC - LẦN 4 - 2018) Tìm giới hạn I lim . n 3 2 A. I . B. I 1. C. I 3 . D. k . 3 1 2n
Câu 27. (THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN - LẦN 2 - 2018) Giới hạn lim bằng? 3n 1 2 1 2 A. . B. . C. 1. D. . 3 3 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2n 2017
Câu 28. (SGD&ĐT BẮC NINH - 2018) Tính giới hạn I lim . 3n 2018 2 3 2017 A. I . B. I . C. I . D. I 1. 3 2 2018 119n lim
Câu 29. (THPT Quỳnh Lưu- Nghệ An- 2019) 18n 19 bằng 19 1 1 A. . B. . C. . D. . 18 18 19
Câu 30. (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Dãy số nào sau đây có giới hạn khác 0 ? 1 1 n 1 sin n A. . B. . C. . D. . n n n n 2 1 n
Câu 31. (CHUYÊN HÀ TĨNH - LẦN 1 - 2018) lim bằng 2 2n 1 1 1 1 A. 0 . B. . C. . D. . 2 3 2 4n 2018
Câu 32. (SGD THANH HÓA - LẦN 1 - 2018) Tính giới hạn lim . 2n 1 1 A. . B. 4 . C. 2 . D. 2018 . 2 5 3 8n 2n 1
Câu 33. (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Tìm lim . 5 2 4n 2n 1 A. 2 . B. 8 . C. 1. D. 4 . 2n 1
Câu 34. (CHUYÊN VĨNH PHÚC - LẦN 1 - 2018) Tính lim được kết quả là 1 n 1 A. 2 . B. 0 . C. . D. 1. 2 4 2n 2n 2
Câu 35. (THPT LÊ XOAY - LẦN 3 - 2018) lim bằng 4 4n 2n 5 2 1 A. . B. . C. . D. 0 . 11 2 2 2n 3
Câu 36. (Thi thử SGD Cần Thơ mã 121 – 2019) Giá trị của lim bằng 2 1 2n A. 3 . B. 2 . C. 1 . D. 0 . 2 n n A lim 2 Câu 37. Giá trị 12n 1 bằng 1 1 1 A. . B. 0 . C. . D. . 12 6 24 5n 3 lim Câu 38. Tính 2n 1 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 5 A. 1. B. . C. 2. D. . 2 3 n 4n 5 lim 3 2 Câu 39.
3n n 7 bằng 1 1 1 A. 1. B. . C. . D. . 3 4 2 2 3 n 3n
Câu 40. Tính giới hạn lim . 3 2n 5n 2 1 3 1 A. . B. 0 . C. . D. . 5 2 2 2n 1
Câu 41. Giới hạn của dãy số u với * u , n là: n n 3 n 2 1 A. 2 . B. . C. 1. D. . 3 3 10n 3
Câu 42. Tính giới hạn I lim ta được kết quả: 3n 15 10 10 3 2 A. I . B. I . C. I . D. I . 3 3 10 5 2n 1 lim Câu 43. n 1 bằng A. 1. B. 2 . C. 2 . D. . 2 3n 1 lim 2 Câu 44. n 2 bằng: 1 1 A. 3 . B. 0 . C. . D. . 2 2 2 8n 3n 1 lim 2 Câu 45. Tính
4 5n 2n . 1 1 A. 2 . B. . C. 4 . D. . 2 4 1 3 u
Câu 46. Cho hai dãy số u và v có u ; v . Tính lim n . n n n n 1 n n 3 vn 1 A. 0 . B. 3 . C. . D. . 3 5 3 8n 2n 1 lim 2 5 Câu 47. Giới hạn
2n 4n 2019 bằng A. 2 . B. 4 . C. . D. 0 . 2 4n 3n 1
Câu 48. Giá trị của B lim bằng: 3n 2 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 4 4 A. . B. . C. 0 . D. 4 9 3 3 2 n n 1
Câu 49. (THPT CHUYÊN THĂNG LONG - ĐÀ LẠT - 2018) Tính L lim 3 2018 3n 1 1 A. . B. 3 . C. . D. . 2018 3
Câu 50. (Thi thử chuyên Hùng Vương Gia Lai lần -2019) Gọi S là tập hợp các tham số nguyên a thỏa 3n 2 mãn 2 lim
a 4a 0
. Tổng các phần tử của S bằng n 2 A. 4 . B. 3 . C. 5 . D. 2 . 2 2 an a n 1
Câu 51. (Chuyên Lào Cai Lần 3 2017-2018) Cho a sao cho giới hạn 2 lim a a 1 n 2 1
.Khi đó khẳng định nào sau đây là đúng? 1
A. 0 a 2 . B. 0 a . C. 1 a 0 .
D. 1 a 3 . 2 3n 1 3 n2 a
Câu 52. Dãy số u với u
có giới hạn bằng phân số tối giản . Tính . a b n n 4n 53 b A. 192 B. 68 C. 32 D. 128 3 2 2n n 4 1 Câu 53. Biết lim
với a là tham số. Khi đó 2 a a bằng 3 an 2 2 A. 12 . B. 2 . C. 0 . D. 6 .
1 2 3 ... n
Câu 54. Cho dãy số u với u
. Mệnh đề nào sau đây đúng? n n 2 n 1 A. limu 0 . n 1 B. lim u . n 2
C. Dãy số u không có giới hạn khi n . n D. limu 1 . n 2 2 2 2 2
1 2 3 4 ... n
Câu 55. (THPT Ninh Giang-Hải Dương năm 2017-2018) Giới hạn lim có giá 3 n 2n 7 trị bằng? 2 1 1 A. . B. . C. 0 . D. . 3 6 3
1 3 5 ... 2n 1 lim 2 Câu 56. 3n 4 bằng 2 1 A. . B. 0 . C. . D. . 3 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 2 3 n Lim ... 2 2 2 2 Câu 57. n n n n bằng 1 1 A. 1. B. 0 . C. . D. . 3 2 1 3 2n 1
Câu 58. Cho dãy số u xác định bởi: u với *
n Giá trị của limu bằng: n n 2 2 2 n n n n A. 0`. B. . C. . D. 1 1 2 n
Câu 59. (THPT HAI BÀ TRƯNG - HUẾ - 2018) Tìm lim ... . 2 2 2 n n n 1 1 A. . B. . C. . D. 0 . 2 n Câu 60. (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Tính giới hạn: 1 1 1 lim 1 1 ... 1 . 2 2 2 2 3 n 1 1 3 A. 1. B. . C. . D. . 2 4 2
Câu 61. (CHUYÊN TRẦN PHÚ - HẢI PHÒNG - LẦN 1 - 2018) Cho dãy số u với n 1 1 1 u ... Tính lim u . n
n n . 1.3 3.5 2 1 . 2 1 n 1 1 A. . B. 0. C. 1. D. . 2 4 2019 2018
Câu 62. Tính lim(2n 3n 4) ? A. . B. . C. 2 . D. 2019 .
Dạng 1.3 Phân thức bậc tử lớn hơn bậc mẫu
n4 n 3 lim 2 3 1 Câu 63. là: A. B. C. 81 D. 2 3 n 2n L lim 2
Câu 64. Tính giới hạn 3n n 2 1 A. L . B. L 0 . C. L . D. L . 3 3
2 3n 2n
Câu 65. Tính giới hạn của dãy số u n 3n 2 2 A. . B. . C. 1. D. . 3
1 5 ... 4n 3 lim Câu 66. Giới hạn 2n 1 bằng
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 A. 1. B. . C. . D. 0 . 2
Dạng 1.4 Phân thức chứa căn 2
4n 1 n 2
Câu 67. (THPT HÀ HUY TẬP - LẦN 2 - 2018) lim bằng 2n 3 3 A. . B. 2. C. 1. D. . 2 2 4n 5 n
Câu 68. (THPT LÝ THÁI TỔ - BẮC NINH - 2018) Cho I lim
. Khi đó giá trị của I là: 2 4n n 1 5 3
A. I 1. B. I . C. I 1 . D. I . 3 4
Câu 69. (CỤM 5 TRƯỜNG CHUYÊN - ĐBSH - LẦN 1 - 2018) Tính giới hạn 2 2
4x x 1 x x 3 lim x 3x 2 1 2 1 2 A. . B. . C. . D. . 3 3 3 3
n 1 3 5 ... 2n 1
Câu 70. Tìm lim u biết u n n 2 2n 1 1 A. . B. . C. 1. D. . 2 2 2 3 2
1 2 3 ... n
Câu 71. (HỒNG QUANG - HẢI DƯƠNG - LẦN 1 - 2018) Tính lim
2n n 76n 5 1 1 1 A. . B. . C. . D. . 6 2 6 2
DẠNG 2. DÃY SỐ CHỨA CĂN THỨC 2 lim
n 3n 1 n Câu 72. bằng 3 A. 3 . B. . C. 0 . D. . 2
Câu 73. Trong các giới hạn sau đây, giới hạn nào có giá trị bằng 1? n 1 3 2n 2 3n n A. lim . B. lim . 5 3n 2 4n 5 3 2n 3 C. 2 2 lim
n 2n n 1 . D. lim . 2 1 2n
lim n n 4 n 3 Câu 74. Giới hạn bằng
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 7 1 A. 0 . B. . C. . D. . 2 2
Câu 75. Tính giới hạn 2
lim n n 4n . A. 3 . B. 1. C. 2 . D. 4 . 2
Câu 76. Có bao nhiêu giá trị nguyên của a để lim n 4n 7 a n 0 ? A. 3 . B. 1. C. 2. D. 0 .
Câu 77. (LÊ QUÝ ĐÔN - HẢI PHÒNG - LẦN 1 - 2018) Tính I n 2 2 lim n 2 n 1 . 3
A. I . B. I .
C. I 1, 499 . D. I 0 . 2
Câu 78. (LÊ QUÝ ĐÔN - QUẢNG TRỊ - LẦN 1 - 2018) Tính n 2 3 3 lim
4n 3 8n n . 2 A. . B. 1. C. . D. . 3 L 2 2 lim
9n 2n 1 4n 1
Câu 79. Tính giới hạn . 9 A. . B. 1. C. . D. . 4 L 2 lim
4n n 1 9n
Câu 80. Tính giới hạn . 9 A. . B. 7 . C. . D. . 4 1
Câu 81. Tính giới hạn L 2 2 lim 4n n
4n 2 . ĐS: . 4 1 A. . B. 7 . C. . D. . 4 L 2 lim
n 3n 5 n 25
Câu 82. Tính giới hạn . 53 9 A. . B. 7 . C. . D. . 2 4
2n 1 n 3 L lim
Câu 83. Tính giới hạn 4n 5 . 53 2 1 A. . B. 7 . C. . D. . 2 2
Câu 84. Tính giới hạn sau L 3 3 lim
n 4 n 1 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 53 A. . B. 7 . C. . D. 0 . 2
Câu 85. Tính giới hạn L 3 3 2 3 2 3 lim
8n 3n 2 5n 8n . 53 2 A. . B. 7 . C. . D. . 2 3
Câu 86. Tính giới hạn L 3 3 2 lim
8n 3n 4 2n 6 . 25 53 1 A. . B. . C. . D. . 4 2 2
Câu 87. Tính giới hạn L 3 3 lim
2n n n 1 . 53 1 A. . B. 1. C. . D. . 2 2
Câu 88. Tính giới hạn L 3 3 lim
n n n 2 . 1 A. . B. 2 . C. 1. D. . 2
Câu 89. Tính giới hạn L 3 3 2 lim
n 2n n 1 . 5 53 5 A. . B. . C. . D. . 4 2 3
Câu 90. Tính giới hạn L 4 2 3 6 lim
n n n 1 . 5 1 5 A. . B. . C. . D. . 4 2 3
Câu 91. Tính giới hạn L lim 2 3 3 2
n n 1 n n . 5 53 1 A. . B. . C. . D. . 4 2 6
DẠNG 3. DÃY SỐ CHỨA LŨY THỪA
Câu 92. (THPT HÀ HUY TẬP - HÀ TĨNH - LẦN 1 - 2018) Dãy số nào sau đây có giới hạn bằng 0 ? n n n n 4 1 5 5 A. . B. . C. . D. . e 3 3 3
Câu 93. (THPT THÁI PHIÊN - HẢI PHÒNG - LẦN 1 - 2018) lim 2n bằng. n A. 2 . B. . C. . D. 0 .
Câu 94. Trong các giới hạn sau giới hạn nào bằng 0
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n n n 2 5 4 n A. lim . B. lim . C. lim . D. lim 2 . 3 3 3 n 2018 lim Câu 95. 2019 bằng. 1 A. 0 . B. . C. . D. 2 . 2
Câu 96. Dãy số nào sau đây có giới hạn bằng 0 ? n n n n A. 0,999 . B. 1 . C. 1 , 0001 . D. 1, 2345 . n 1 100 3.99n lim 2n n 1 Câu 97. 10 2.98 là 1 A. . B. 100 . C. . D. 0 . 100 lim 3n 4n Câu 98. là 4 A. . B. . C. . D. 1. 3 n 1 n 1 3.2 2.3
Câu 99. Tính giới hạn lim . 4 3n 3 6 A. . B. 0 . C. . D. 6 . 2 5
Câu 100. Trong bốn giới hạn sau đây, giới hạn nào bằng 0 ? 1 2.2017n 1 2.2018n A. lim . B. lim . 2016n 2018n n n 1 2016 2017 1 2.2018n n 1 2.2018 2018 C. lim . D. lim . 2017n 2018n 2016n 2018n 2n 1 lim n Câu 101. Tính 2.2 3 . 1 A. 2. B. 0. C. 1. D. . 2
Câu 102. (Chuyên - Vĩnh Phúc - lần 3 - 2019) Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc n n 1 9 3 1
khoảng 0; 2019 để lim ?
5n 9na 2187 A. 2018 . B. 2012 . C. 2019 . D. 2011.
Câu 103. (THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018) Tính giới hạn n 1 n n 1 lim 16 4 16 3n T . 1 1 1 A. T 0 . B. T . C. T . D. T . 4 8 16
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
DẠNG 4. TỔNG CẤP SỐ NHÂN LÙI VÔ HẠNG
Câu 104. (THPT YÊN LẠC - LẦN 4 - 2018) Tính tổng S của cấp số nhân lùi vô hạn có số hạng đầu u 1 1 1
và công bội q . 2 3 2 A. S 2 . B. S . C. S 1 . D. S . 2 3 2 2 2
Câu 105. Tổng vô hạn sau đây S 2 ...
... có giá trị bằng 2 3 3 3n 8 A. . B. 3 . C. 4 . D. 2 . 3
Câu 106. Số thập phân vô hạn tuần hoàn 3,15555... 3,15 viết dưới dạng hữu tỉ là 63 142 1 7 A. . B. . C. . D. . 20 45 18 2 1 1 1 1 ... Câu 107. Tổng 2 4 2n bằng 1 A. . B. 2. C. 1. D. . 2 u 3 1
Câu 108. (Chu Văn An - Hà Nội - lần 2 - 2019) Cho dãy số *
(u ), n , thỏa mãn điều kiện . n un u n 1 5
Gọi S u u u ... u là tổng n số hạng đầu tiên của dãy số đã cho. Khi đó lim S bằng 1 2 3 n n 1 3 5 A. . B. . C. 0 . D. . 2 5 2 u 1 1
Câu 109. Cho dãy số u thoả mãn . Tìm limu . n 2 * n u u 4, n n 1 3 n A. limu 1 .
B. lim u 4 .
C. lim u 12 . D. limu 3. n n n n n
Câu 110. Cho cấp số cộng u có số hạng đầu u 2 và công sai d 3 . Tìm lim . n 1 un 1 1 A. L . B. L . C. L 3 . D. L 2 3 2
DẠNG 5. MỘT SỐ BÀI TOÁN KHÁC
Câu 111. (THTT số 5-488 tháng 2 năm 2018) Cho dãy số u thỏa mãn n * u
n 2018 n 2017, n
. Khẳng định nào sau đây sai? n
A. Dãy số u là dãy tăng. B. lim u 0 . n n n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 u C. * 0 u , n . D. n 1 lim 1 . n 2 2018 n un
Câu 112. (THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018) Đặt f n n n 2 2
1 1, xét dãy số u sao n f
1 . f 3. f 5... f 2n 1 cho u . Tìm lim n u . n
f 2. f 4.f 6... f 2n n 1 1 A. lim n u .
B. lim n u 3 . C. lim n u . D. lim n u 2 . n n n n 3 2
Câu 113. (THTT số 6-489 tháng 3 năm 2018) Cho dãy số u xác định bởi u 0 và u
u 4n 3 , n 1 n 1 n n 1 . Biết 2019 u u u ... u 2 2018 n 4n a b 4 n 4 lim n u u u ... u c 2 2018 n 2n 2 n 2 n
với a , b , c là các số nguyên dương và b 2019 . Tính giá trị S a b c . A. S 1 . B. S 0 . C. S 2017 . D. S 2018 .
Câu 114. (THTT Số 2-485 tháng 11-năm học 2017-2018) Dãy số u nào sau đây có giới hạn khác số 1 n
khi n dần đến vô cùng? 2017 n2018 A. u
. B. u n 2 2
n 2018 n 2016 . n n
n 2018 n2017 u 2017 1 1 1 1 1 C. 1 . D. u ... . n u
u 1 , n 1, 2, 3... 1.2 2.3 3.4 n n 1 n 1 n 2
Câu 115. (THPT CHU VĂN AN -THÁI NGUYÊN - 2018) Cho dãy số u được xác định như sau n 2 u 2016;u n u u , với mọi *
n , n 2 , tìm giới hạn của dãy số u . n 1 n 1 n 1 n A. 1011. B. 1010 . C. 1008 . D. 1009 . n
Câu 116. Cho dãy số u như sau: u , n
1 , 2 ,... Tính giới hạn lim u u ... u . 1 2 n n n 2 4 1 n n x 1 1 1 A. . B. 1. C. . D. . 4 2 3
Câu 117. (THPT NGUYỄN HUỆ - TT HUẾ - 2018) Cho dãy số u thỏa mãn n u 2 1 . Tính lim u . 3 4u 1
4u 1 4, n n n n * 1 1 3 1 2 A. . B. . C. . D. . 3 4 2 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 u 2
Câu 118. (THPT GANG THÉP - LẦN 3 - 2018) Cho dãy số u biết 1 , khi đó n
u 3u 1, n 2 n n 1 u L lim n 3n 5 A. Không xác định.
B. L . C. L . D. L 0 . 6
Câu 119. (THPT HẬU LỘC 2 - TH - 2018) Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam
giác ABC được gọi là tam giác trung bình của tam giác ABC .
Ta xây dựng dãy các tam giác A B C , A B C , A B C ,... sao cho A B C là một tam giác đều 1 1 1 2 2 2 3 3 3 1 1 1
cạnh bằng 3 và với mỗi số nguyên dương n 2 , tam giác A B C là tam giác trung bình của tam n n n giác A B C
. Với mỗi số nguyên dương n , kí hiệu S tương ứng là diện tích hình tròn ngoại n 1 n 1 n 1 n
tiếp tam giác A B C . Tính tổng S S S ... S ... ? n n n 1 2 n 15 9 A. S . B. S 4 . C. S . D. S 5. 4 2
Câu 120. (CTN - LẦN 1 - 2018) Trong các dãy số u cho dưới đây, dãy số nào có giới hạn khác 1? n
n n 20182017 A. u
. B. u n 2 2
n 2020 4n 2017 . n n n 20172018 u 2018 2 2 2 1 C. u . D. . n 1 1.3 3.5 2n 1 2n 3 u u 1 , n 1 n 1 n 2 2
Câu 121. (SGD&ĐT BRVT - 2018) Cho dãy số (u ) thỏa mãn: u 1 ; 2 * u
u a , n . Biết rằng n 1 n 1 3 n lim 2 2 2
u u ... u 2n b . Giá trị của biểu thức là 1 2 n T ab A. 2 . B. 1 . C. 1. D. 2 .
Câu 122. (THPT TRẦN PHÚ - ĐÀ NẴNG - 2018) Với n là số tự nhiên lớn hơn 2 , đặt 1 1 1 1 S ... . Tính lim S n 3 3 4 3 C C C C n 3 4 5 n 3 1 A. 1. B. . C. 3 . D. . 2 3
Câu 123. (THPT CHUYÊN NGUYỄN QUANG DIÊU - ĐỒNG THÁP - 2018) Có bao nhiêu giá trị n n 1 9 3 1
nguyên của tham số a thuộc khoảng 0; 2018 để có lim ?
5n 9na 2187 A. 2011 . B. 2016 . C. 2019 . D. 2009 .
Câu 124. Từ độ cao 55, 8m của tháp nghiêng Pisa nước Italia người ta thả một quả bóng cao su chạm xuống 1
đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
độ cao mà quả bóng đạt trước 10
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
đó. Tổng độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt
đất thuộc khoảng nào trong các khoảng sau đây? A. 67m ; 69m . B. 60m ; 63m . C. 64m ; 66m . D. 69m ; 72m .
Câu 125. (THPT THUẬN THÀNH 1) Cho hai dãy số u , v đều tồn tại giới hạn hữu hạn. Biết rằng n n
hai dãy số đồng thời thỏa mãn các hệ thức u 4v 2, v
u 1 với mọi n . Giá trị n 1 n n 1 n
của giới hạn lim u 2v bằng n n n 3 1 A. 0. B. . C. 1 . D. . 2 2
Câu 126. Một mô hình gồm các khối cầu xếp chồng lên nhau tạo thành một cột thẳng đứng. Biết rằng mỗi
khối cầu có bán kính gấp đôi khối cầu nằm ngay trên nó và bán kính khối cầu dưới cùng là 50 cm.
Hỏi mệnh đề nào sau đây là đúng?
A. Chiều cao mô hình không quá 1, 5 mét
B. Chiều cao mô hình tối đa là 2 mét
C. Chiều cao mô hình dưới 2 mét.
D. Mô hình có thể đạt được chiều cao tùy ý.
Câu 127. Trong một lần Đoàn trường Lê Văn Hưu tổ chức chơi bóng chuyền hơi, bạn Nam thả một quả bóng
chuyền hơi từ tầng ba, độ cao 8m so với mặt đất và thấy rằng mỗi lần chạm đất thì quả bóng lại
nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết quả bóng chuyển động vuông góc với
mặt đất. Khi đó tổng quảng đường quả bóng đã bay từ lúc thả bóng đến khi quả bóng không máy
nữa gần bằng số nào dưới đây nhất? A. 57m . B. 54m . C. 56m . D. 58m .
Câu 128. Với mỗi số nguyên dương n , gọi s là số cặp số nguyên x; y thỏa mãn 2 2 2
x y n . (nếu a b n
thì hai cặp số a;b và ;
b a khác nhau). Khẳng định nào sau đây là đúng? s s s s A. lim n 2 . B. lim n 2 . C. lim n . D. lim n 4 . n n n n n n n n
PHẦN B. LỜI GIẢI THAM KHẢO
DẠNG 0. CÂU HỎI LÝ THUYẾT Câu 1. Chọn C u
Nếu lim u a 0 và limv 0 thì lim n
là mệnh đề sai vì chưa rõ dấu của v là dương n n v n n hay âm. Câu 2. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Lấy máy tính bấm từng phương án thì phần D ra kết quả đề bài Câu 3. Chọn A Câu 4. Chọn B
Dùng tính chất giới hạn: cho dãy số u , v và lim u a, lim v trong đó a hữu hạn thì n n n n u lim n 0 . vn Câu 5. Chọn D (I) lim k
n với k nguyên dương I là khẳng định đúng. (II) lim n
q nếu q 1 II là khẳng định sai vì lim n
q 0 nếu q 1 . (III) lim n
q nếu q 1 III là khẳng định đúng.
Vậy số khẳng định đúng là 2 . Câu 6. Chọn D 1 1 Ta có: u 2 lim u 2 im l
u 2 0 lim u 2 . n lim 0 n 3 n 3 n n n Câu 7.
Theo định nghĩa giới hạn hữu hạn của dãy số (SGK ĐS11-Chương 4) thì lim n
q 0 q 1 .
DẠNG 1. DÃY SỐ DẠNG PHÂN THỨC
Dạng 1.1 Phân thức bậc tử bé hơn bậc mẫu Câu 8. Chọn B 1 1 2 3 n 1 0 Ta có lim lim n n 0 . 3 n 3 3 1 1 3 n Câu 9. Chọn A 1 1 Ta có lim lim n 0 . 5n 3 3 5 n
Câu 10. Chọn D 1 1 Ta có: lim lim n 0 . 2n 7 7 2 n
Câu 11. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1 1 Ta có: lim lim . 0 . 2n 5 n 5 2 n
Câu 12. Chọn B 1 1 1 1 lim lim 0. 0 . 5n 2 n 2 5 5 n Câu 13.
Hướng dẫn giải Chọn B 7 1 2 3 2 3 7n 2n 1 2 Ta có lim lim n n I . 3 2 3n 2n 1 2 1 3 3 3 n n 2 3 2 2n 3 4 6 Câu 14. Ta có lim lim n n 0 . 6 5 n 5n 5 1 n
Câu 15. Chọn B
Câu 16. Chọn D 2 1 2 2n 1 Ta có: lim lim n n L 0 . 2 2 n n 2 1 1 2 n n
Câu 17. Chọn C 2 2 1 2 n 2 1 Xét đáp án A. lim lim n . 2 5n 3n 5 3 3 n 2 2 1 n 2n 1 Xét đáp án B. lim lim n 2 5n 3n 5 3 3 n 1 2 2 1 2n Xét đáp án C. lim lim n n 0 . 2 5n 3n 5 3 n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 2 2 2 1 2n 2 Xét đáp án D. lim lim n . 2 5n 3n 5 3 3 n 2 3 2 n 2 3 2n 3 2 n n 2 Câu 18. I lim lim lim n n 0 . 2 2n 3n 1 3 1 2 3 1 n 2 2 2 2 n n n n
Câu 19. Chọn A 1 1 1 1 1 1 1 Ta có: u ... ... n 2 2 2 2 1 3 1 n 1 1.3 2.4 3.5 n 1 n 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 ... . 2 1 3 2 4 3 5 n 1 n 1 2 1 2 n 1 4 2n 1 3 1 3
Suy ra: lim u lim . n 4 2 n 1 4 1 1 1 1 1 1 1 1 1 1 1 1 Câu 20. Ta có: ... 1 1 . 1.2 2.3 3.4 n n 1 1 2 2 3 n 1 n n n 1 n 1 1 1 1 1 1 Vậy lim ... lim 1 1 . 1.2 2.3 3.4 n n 1 n 1 1 k k
Câu 21. Ta có 1 2 3 ... k là tổng của cấp số cộng có u 1 , d 1 nên 1 2 3 ... k 1 2 1 2 2 2 , * k . 1 2 ... k k k 1 k k 1 2 2 2 2 2 2 2 2 2 2 L lim ... lim 2 . 1 2 2 3 3 4 n n 1 1 n 1 Câu 22.
Hướng dẫn giải Chọn C 1 1 n 1 n 1 1 Ta có .
n n 1 n 1 n
n n 1 n 1 n n n 1 n n 1 Suy ra 1 1 1 S ... . n 1 2 2 1 2 3 3 2
n n 1 n 1 n 1 1 1 1 1 1 1 .... 1 . 1 2 2 3 n n 1 n 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Suy ra lim S 1 n cos n sin n cos n sin n 2 2 Câu 23. Ta có 0 và lim 0 . 2 2 2 n 1 n 1 n 1 2 n 1 cos n sin n Suy ra lim 0. 2 n 1
Dạng 1.2 Phân thức bậc tử bằng bậc mẫu 2 1 2 n 0 1 Câu 24. Ta có: lim lim n 1 . n 1 1 1 0 1 n 2 2 n 1 1 n 2 n 1 Câu 25. Ta có lim lim lim n . 3n 1 1 1 3 n 3 3 n n 2 3 3n 2
Câu 26. Ta có lim lim n I 3 . n 3 3 1 n 1 2 1 2n 2 Câu 27. Ta có lim lim n . 3n 1 1 3 3 n 2017 2 2n 2017 2
Câu 28. Ta có I lim lim n . 3n 2018 2018 3 3 n
Câu 29. Chọn A 1 19 119n 19 Ta có lim lim n . 18n 19 19 18 18 n
Câu 30. Chọn C n 1 1 Có lim lim1 lim 1 . n n 1 2 1 1 n 2 1 Câu 31. Ta có lim lim n . 2 2n 1 1 2 2 2 n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2018 4 4n 2018 Câu 32. Ta có lim lim n 2 . 2n 1 1 2 n
Câu 33. Chọn A 2 1 5 n 8 2 1 5 3 8 8n 2n 1 2 5 n n 2 5 8 Ta có lim lim = lim n n 2 . 5 2 4n 2n 1 2 1 2 1 5 4 n 4 4 3 5 3 5 n n n n 1 1 n 2 2 2n 1 n 2 0 Câu 34. Ta có lim lim lim n 2 . 1 n 1 1 0 1 n 1 1 n n 2 2 4 2 3 4 2n 2n 2 1 Câu 35. Ta có lim lim n n . 4 4n 2n 5 2 5 2 4 3 4 n n
Câu 36. Chọn C 3 2 2 2 2n 3 lim lim n 1. 2 1 2n 1 2 2 n
Câu 37. Chọn A 1 2 1 n n 1 lim lim n A . 2 12n 1 1 12 12 2 n 1 Vậy A . 12
Câu 38. Chọn D 3 5 5n 3 5 Ta có lim lim n . 2n 1 1 2 2 n
Câu 39. Chọn B 4 5 3 1 n 4n 5 2 3 1 Ta có: lim lim n n . 3 2 3n n 7 1 7 3 3 3 n n
Câu 40. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 3 n 3 1 2 3 3 n 3n n 3 Ta có: lim lim lim n . 3 2n 5n 2 5 2 5 2 3 2 n 2 2 2 3 2 3 n n n n
Câu 41. Chọn D 1 2 2n 1 1 Ta có lim lim lim n u . n 3 n 3 3 1 n
Câu 42. Chọn B 3 10 10n 3 10 Ta có lim lim n I . 3n 15 15 3 3 n
Câu 43. Chọn B 1 2 2n 1 Ta có lim lim n 2 . n 1 1 1 n
Câu 44. Chọn A 1 2 3 2 3n 1 lim lim n 3 2 n 2 2 1 2 n
Câu 45. Chọn C 3 1 2 8 2 8n 3n 1 Ta có lim lim n n 4 . 2 4 5n 2n 4 5 2 2 n n
Câu 46. Chọn C 1 3 1 u n 3 1
Ta có I lim n n 1 lim lim lim n . v 3 3n 1 1 3 n 3 1 n 3 n
Câu 47. Chọn A 2 1 5 3 8 8n 2n 1 2 5 Ta có: lim lim n n 2 . 2 5
2n 4n 2019 2 2019 4 3 5 n n
Câu 48. Chọn A.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3 1 3 1 2 n 4 4 2 2 2 4n 3n 1 n n n n 4 0 0 4 Ta có: B lim lim lim 3n 2 2 2 1 1 1 3 02 9 2 n 3 3 n n 1 1 3 2 1 3 n n 1 1 Câu 49. lim lim n n L 3 2018 3n 2018 3 3 3 n
Câu 50. Chọn A 3n 2 Ta có: 2 lim a 4a n 2 2
2 2a 8a 2 2 a a 2 4
3 n 2 2a 8a
a 4a 3 lim n 2 lim
a 4a 3 . n 2 2 1 n 3n 2 Theo giả thiết: 2 2 lim
a 4a 0 a 4a 3 0 a 3 a 1 . n 2 Vậy S 1; 3 1 3 4 .
Câu 51. Chọn A 2 a 1 2 2 2 2 a 2 an a n 1 an a n 1 Ta có lim lim lim n n a . n 2 2 1 n 2n 1 2 1 1 2 n n 2
a a 1 a 2
a 2a 1 0 a 1.
Câu 52. Chọn A 2 1 3 3 1 3n 1 3 n2 n n 3 a Ta có: lim lim . Do đó: . a b 192 4n 53 3 5 64 b 4 n
Câu 53. Chọn A 1 4 3 3 2 n 2 3 2n n 4 n n 2 1 Ta có lim lim . 3 an 2 2 3 a 2
n a 3 n
Suy ra a 4 . Khi đó 2 2
a a 4 4 12 .
Câu 54. Chọn B
1 2 3 ... n n n 1 1 Ta có: lim u lim lim . n 2 n 1 2 2 n 1 2
Câu 55. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n n 1 2n 1
Ta có kết quả quen thuộc 2 2 2 2
1 2 3 ... n . 6 1 1 1 2 2 2 2 2 2
1 2 3 4 ... n n n 1 2n 1 n n 1.2 1 Do đó lim lim lim . 3 n 2n 7 6 3
n 2n 7 2 7 6 3 6 1 2 3 n n Câu 56. Chọn C. 1 2n 1 n 1
Ta có 1 3 5 ... 2n 1 n 2 1 . 2 2 1
1 3 5 ... 2n 1 n 2 1 2 1 1 lim lim lim n n . 2 2 3n 4 3n 4 4 3 3 2 n
Câu 57. Chọn D 1 2 3 n
1 2 3 ... n ( n n 1) 1 1 1 Lim ... lim lim lim 2 2 2 2 2 2 n n n n n 2n 2 2n 2
Câu 58. Chọn D 1 3 2n 1
1 3 ... 2n 1 n 2 2
Ta có 1 3 ... 2n 1 n ... 1 2 2 2 2 2 n n n n n Suy ra limu 1. n 1 1 1 2 n
1 2 ... n
n n 1 1 Câu 59. lim ... n lim lim lim . 2 2 2 2 n n n n 2 2n 2 2
Câu 60. Chọn B 1 1 1
Xét dãy số u , với u 1 1 ... 1
, n 2, n . n n 2 2 2 2 3 n Ta có: 1 3 2 1 u 1 ; 2 2 2 4 2.2 1 1 3 8 4 3 1 u 1 . 1 . ; 3 2 2 2 3 4 9 6 2.3 1 1 1 3 8 15 5 4 1 u 1 . 1 1 . . 4 2 2 2 2 3 4 4 9 16 8 2.4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n 1 u . n 2n n 1
Dễ dàng chứng minh bằng phương pháp qui nạp để khẳng định u , n 2 n 2n 1 1 1 n 1 1 Khi đó lim 1 1 ... 1 lim . 2 2 2 2 3 n 2n 2 1 1 1 1 1 1 1 1 1 1
Câu 61. Ta có : u ... n
n n ... 1.3 3.5 2 1 . 2 1 2 1 3 3 5 2n 1 2n 1 1 1 1 n 2 1 2n 1 2n 1 n 1 Suy ra : lim u lim . n 2n 1 2
Dạng 1.3 Phân thức bậc tử lớn hơn bậc mẫu
Câu 62. Chọn A 3 4 Ta có lim 2019 2018 2 n 3n 4 2019 lim n . 2 . 2019 n n
Câu 63. Chọn B 4 3 2 1
lim 2 3n4 n 3 7 1 lim n 3 1 n n Ta có 7 lim n 4 2 lim 3 3 4 4 3 n 3 1 lim 1 1 n
n4 n 3 lim 2 3 1
Câu 64. Chọn A 2 3 1 2 n 2n Ta có: lim lim n L . 2 3n n 2 3 1 2 2 3 n n n
Câu 65. Chọn B 2 2 3 n 2n
2 3n 2n 2 1 2 lim lim n do 2 2 lim n 2n lim n 2 3n 2 2 3 n n n 3 n 2 và lim 3 3 0 . n Câu 66.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Lời giải Chọn B 1 4n 1.
1 5 ... 4n 3 n 1 4 4 1 Ta có: lim lim lim . 2n 1 2n 1 3 2n 1
Dạng 1.4 Phân thức chứa căn 1 1 2 2 4
4n 1 n 2 2 2 n n n 2 0 Câu 67. Ta có: lim lim 1. 2n 3 3 2 2 n 5 4 1 2 4n 5 n 2 n
Câu 68. Ta có I lim lim 1 2 4n n 1 1 4 1 2 n . 1 1 1 3 x x 2 2 4 1
4x x 1 x x 3 2 2 x x x x Câu 69. lim lim x 3x 2 x 3x 2 1 1 1 3 4 1 2 2 x x x x 1 lim . x 2 3 3 x
Câu 70. Chọn A
n 1 3 5 ... 2n 2 2 1 n n n 1 1 lim u lim lim lim lim . n 2 2 2 2n 1 2n 1 2n 1 1 2 2 2 n n n 1 2n 1 2 2 2 2
Câu 71. Ta có: 1 2 3 ... n . 6 1 1 1 2 2 2 3 2
1 2 3 ... n n n 1 2n 1 n n 1 Khi đó: lim lim lim .
2n n 76n 5
12n n 76n 5 7 5 6 12 1 6 n n
DẠNG 2. DÃY SỐ CHỨA CĂN THỨC
Câu 72. Chọn D 1 3 3 n 1 Ta có 2 3 1 n n n n 2
n 3n 1 n 3 1 1 1 2 n n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3 Nên lim 2
n 3n 1 n 2
Câu 73. Chọn C 2 2
n 2n n 1 2 2
n 2n n 1 Ta có: 2 2 lim
n 2n n 1 lim 2 2
n 2n n 1 1 1 2 2n 1 2 = lim lim n = lim n 1. 2 2
n 2n n 1 2 2 n 2n n 1 2 1 1 1 2 2 n n n n
Câu 74. Chọn D
n n n 1 1 1 lim 4 3 lim n lim .
n 4 n 3 4 3 2 1 1 n n
Câu 75. Chọn C 2
n n 4n 2
n n 4n 2
Ta có lim n n 4n lim 2
n n 4n 4n 4 lim lim 2 . 2
n n 4n 4 1 1 n
Câu 76. Chọn C 2 7 a 2 2a 4
n an a lim 4 7 2
2 4 7 lim lim n n n a n a 2 2
n 4n 7 a n 4 7 a 1 1 2 n n n Để 2 lim
n 4n 7 a n 0 thì a 2 0 a 2 . 3n 3 3
Câu 77. Ta có: I n 2 2 lim n 2 n 1 lim lim 2 2
n 2 n 1 2 1 2 1 1 2 2 n n Câu 78. Ta có: n 2 3 3 lim
4n 3 8n n n 2 n n 3 3 lim 4 3 2 2n 8n n n 2 n n n 3 3 lim 4 3 2 2n 8n n . 3n 3 3 Ta có: n 2 lim
4n 3 2n lim lim . 2
4n 3 2n 3 4 4 2 2 n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 n Ta có: n 3 3 lim
2n 8n n lim 2 3
4n 2n 8n n 3 3 8n n2 3 1 1 lim . 2 12 1 1 3 3 4 2 8 8 2 2 n n 3 1 2 Vậy lim n 2 3 3
4n 3 8n n . 4 12 3 2
9n 2n 1 2 4n 1 Câu 79. L 2 2 lim
9n 2n 1 4n 1 lim 2 2
9n 2n 1 4n 1 2 2 2 n 5 2 2 2 5 5n 2n 2 2 n n 2 lim lim lim n n n 2 2
9n 2n 1 4n 1 2 1 1 2 1 1 n 9 4 9 4 2 2 n n n 2 2 n n n . Câu 80. 1 1 2 n 77 2 2
4n n 1 81n 2 7
7n n 1 2 2 n n
L lim 4n n 1 9n lim lim lim 2
4n n 1 9n 2
4n n 1 9n 1 1 n 4 9 2 n n 1 1 77 2 lim n n n 1 1 4 9 2 n n 1 1 77 2
Vì : lim n và lim n n 7 0 . 1 1 4 9 2 n n Câu 81.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 n 1
4n n 2 4n 2 n 2 n L lim lim lim 2 2
4n n 4n 2 2 2
4n n 4n 2 1 2 n 4 4 2 n n 2 1 1 0 1 lim n . 1 2 4 0 4 0 4 4 4 2 n n Câu 82. 2
n 3n 5 2 n 3n 5 2
L lim 25 lim n 3n 5 n 25 lim 25 lim 2
n 3n 5 n 2
n 3n 5 n 5 n 3 5 3 n 3 0 53 25 lim 25 lim n 25 . 3 5 3 5 1 0 0 1 2 n 1 1 1 1 2 n n 2 n n
2n 1 n 3 n 2 Câu 83. L lim lim
4n 5 2n 1 n 3
4n 5 2n 1 n 3 2 n 1 2 1 n lim lim n 5 1 3 5 1 3 n 4 2 1 4 2 1 n n n n n n 1 0 2 1 .
4 0 2 0 1 0 2 Câu 84. 3 L 3 3 lim
n 4 n 1 lim n 42 3
n 4.n 1 n 2 3 3 1 3 lim 2 2 4 4 1 1 2 2 2 3 3 3 n . 1 n . 1 . 1 n . 1 n n n n 3 lim 0 . 2 2 4 4 1 1 3 2 3 3 3 n 1 1 . 1 1 n n n n Câu 85.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 L 3 3 2 3 2 3 lim
8n 3n 2 5n 8n 2 8n 2 lim
8n 3n 22 3
8n 3n 2.5n 8n 5n 8n 2 3 2 3 2 2 3 2 3 3 3 2 8 2 8 2 lim n . 2 2 3 2 3 2 5 5 3 3 3 3 8 8 . 8 8 3 3 n n n n n n Câu 86. L 3 3 2 lim
8n 3n 4 2n 6 3 3 2 6 lim
8n 3n 4 2n 4 2 3 3n 4 2 6 lim 6 lim n 2 3 2
8n 3n 42 3 3 2 2 3 2 .
n 8n 3n 4 4n 3 4 3 4 3 3 8 2. 8 4 3 3 n n n n 1 25 6 . 4 4 Câu 87. 3 2n 3 L 3 3 lim
2n n n 1 1
lim 2n n n 1 lim 3 2n n 2 3 3 2 3
n 2n 2n n 2 1 lim n 1 0 1 . 2 2 2 3 3 1 1 1 2 2 n n Câu 88. n L 3 3 lim
n n n 2 3 3 2 lim
n n n 2 lim 3 n n 2 3 3 2 3 .
n n n n 1 2 lim n 2 0 2 . 2 1 1 3 3 1 1 1 2 2 n n Câu 89. 2 2n L 3 3 2 lim
n 2n n 1 3 3 2 1 lim
n 2n n 1 lim 3 2 n 2n 2 3 3 2 2 3 .
n 2n 2n n 2 2 5 1 lim 1 . 2 2 2 3 3 3 3 1 1 1 n n Câu 90.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 L 4 2 3 6 lim
n n n 1 4 2 2 n n n 3 6 2 lim n 1 n 4 2 4
n n n 6 n 6 1 n 4 2 2
n n n 3 6 2 lim lim
n 1 n lim lim 4 2 2
n n n 6 n 2 2 3 6 4 3 1 n n 1 n 2 n 1 1 1 lim lim lim 0 4 2 2
n n n 6 1 2 n 2 2 3 6 4 3 1 n n 1 n 1 1 2 n Câu 91. L 2 3 3 2 n n n n 2n n n 3 3 2 lim 1 lim 1 n n n 3 1 n 3 2 2 2 n n n n n lim 2 3 2
n n 1 n
n n n n 3 2 n n 2 2 3 3 2 n 1 n lim 2 3 2
n n 1 n
n n n n 3 2 n n 2 2 3 3 1 n 1 2 n n lim 2 1 1 1 1 2 n 1 1 3 3 2 n 1 1 1 n n n n 1 1 1 1 1 1 lim n 2 1 1 1 1 2 3 6 1 1 3 3 2 1 1 1 n n n n
DẠNG 3. DÃY SỐ CHỨA LŨY THỪA
Câu 92. Ta có lim n
q 0 nếu q 1 . n 4 5 5 1 1 Mặt khác 1; 1 ; 1. Vậy lim 0 . e 3 3 3 3 Câu 93. ChỌn B.
Câu 94. Chọn A lim n
q 0 ( q 1) .
Câu 95. Chọn A Áp dụng lim n
q 0 , q 1
Câu 96. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n
Do 0,999 1 nên lim 0,999 0 .
Câu 97. Chọn B n 99 100 3. n 1 100 3.99n 100 lim lim 100 2n n 1 10 2.98 n 98 1 2. 100
Câu 98. Chọn B n n 3
Ta có: lim 3n 4n lim4 1 . 4
Câu 99. Chọn D n 2 6. 6 n 1 n 1 3.2 2.3 3 Ta có lim lim 6 . 4 3n n 1 4. 1 3
Câu 100. Chọn A n n 1 2017 2. 1 2.2017n 2018 2018 Ta có lim lim 0 . 2016n 2018n n 2016 1 2018
Câu 101. Chọn D n 1 1 2n 1 2 1 0 1 Ta có: lim lim 2.2n 3 n 1 2 0 2 2 3. 2
Câu 102. Chọn B n 1 1 3 n n 1 9 3 3 1 1 1 1 Ta có lim lim a 7. n na n a a 7 5 9 5 3 2187 3 3 9a 9
Do a nguyên thuộc khoảng 0; 2019 nên a 7;8;...; 201 8 .
Câu 103. Chọn C 4n 3n Ta có T n 1 n n 1 lim 16 4 16 3 lim n 1 n n 1 16 4 16 3n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n 3 1 4n 3n 4 1 1 lim lim .
16.16n 4n 16.16n 3n n n 1 3 4 4 8 16 16 4 4
DẠNG 4. TỔNG CẤP SỐ NHÂN LÙI VÔ HẠNG u 1 2 Câu 104. 1 S . 1 q 1 3 1 2
Câu 105. Chọn B 2 2 2 1 Ta có 2; ; ;...;
;... là một cấp số nhân lùi vô hạn với công bội q 1. 2 3 3 3n 3 2 2 2 1 S 2 ... ... 2. 3. 2 3 3 3n 1 1 3
Câu 106. Chọn B 1 2 1 1 142 10 3,15555... 3,1 5 3,1 5 ... 3,1 5. 2 3 10 10 1 45 1 10
Câu 107. Chọn B 1 1 1 1 Ta có 1
... là tổng của một cấp số nhân lùi vô hạn với u 1, q . 2 4 2n 1 2 u 1 1 1
Áp dụng công thức được 1 S kết quả 1 ... 2 . 1 q 2 4 2n
Câu 108. Chọn D un u 1 1 Ta có n 1 5 do đó dãy *
(u ), n là một cấp số nhân lùi vô hạn có u 3 , d . u u 5 n 1 5 n n u 3 5 Suy ra 1 lim S . n 1 q 1 2 1 5
Câu 109. Chọn C Đặt *
v u 12, n . n n 2 2 2 Khi đó * v u 12 u 4 12 (u 12) v , n . n 1 n 1 3 n 3 n 3 n 2
Suy ra dãy số v là cấp số nhân với công bội q
và số hạng đầu v 1 1. n 3 1 n 1 n 1 2 2 Suy ra * v 11
, n . Từ đó * u 11 12,n . n n 3 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Vậy lim u 12 . n
DẠNG 5. MỘT SỐ BÀI TOÁN KHÁC
Câu 110. Chọn A
Ta có u u n 1 d 2 n 1 3 3n 1. n 1 n n 1 1 lim lim lim . u 3n 1 1 3 n 3 n
Câu 111. Chọn A 1 Ta có: u
n 2018 n 2017 . n
n 2018 n 2017 u
n 2018 n 2017 Suy ra: n 1 1 với mọi * n . u n n n 2019 2018
Do đó, dãy số u giảm. n Vậy Chọn A Chú ý: 1 + lim u lim 0 . n n n
n 2018 n 2017 u
n 2018 n 2017 + n 1 lim lim 1 . n n u n n n 2019 2018 1 1 1 + 0 u . n
n 2018 n 2017 2 n 2017 2 2018
Câu 112. Chọn C 2 2
Ta có f n 2 n n 2 1 1 n 1 n 1 1 . 1 1 2 1 3 1 4 1 ... 2n 2 2 2 2 2 2 1 1 4n 1 Do đó u n 2 1 3 1 4 1 5
1 ... 4n 1 2n 2 2 2 2 2 2 1 1 2 2 2n u
n u n . n 2 2n 2 1 1 2n 1 1 2 2n 2 1
lim n u n lim lim . 2 2n 2 1 1 1 1 2 2 2 n n
Câu 113. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Ta có
u u 4.1 3 2 1
u u 4.2 3 3 2 ... u u 4. n 1 3 n n 1
Cộng vế theo vế và rút gọn ta được n n 1
u u 4. 1 2 ... n 1 3 n 1 4 3n 1 2
2n n 3 , với mọi n 1. n 1 2 Suy ra u 2 n n n 2 2 2 3 2 2 2 2 u 2 2 n 2 n 3 2 2 n ... 2 2018 2018 u 2 2 n 2 n 3 2018 2 n Và u 2 n n n 4 2 4 3 4 2 2 2 u 2 4 n 4 n 3 2 4 n ... 2 2018 2018 u 2 4 n 4 n 3 2018 4 n u u u ... u 2 2018 n 4 n Do đó 4 n 4 lim n u u u ... u 2 2018 n 2 n 2 n 2 n 2018 1 3 4 3 2 2.4 ... 24 2 4 3 2 2018 2 2 2 n n n n n n lim 2018 1 3 2 3 2 2.2 ... 22 2 2 3 2 2018 2 2 2 n n n n n n 2019 1 4 2 2 2018 1 4 4 ... 4 1 2019 1 4 1 2019 2 1 1 4 . 2 2 2018 1 2 2 ... 2 2019 1 2 2019 3 2 1 3 1 2 a 2 Vì 2019 2
2019 cho nên sự xác định ở trên là duy nhất nên b 1 c 3
Vậy S a b c 0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 114. Chọn A
Ta tính giới hạn của các dãy số trong từng đáp án: 2017 n2018 2017
2017 n 2017 n
+) Đáp án A: lim u lim lim . n
n 2018 n2017 n 2018 n 2017 2017 1 2017 lim 1 n 1 . n 2018 1 n 2 2
n n 2018 n 2016
+) Đáp án B: lim u lim n n n n 2 2 2018 2016 lim 2 2
n 2018 n 2016 2n 2 lim lim 1. 2 2
n 2018 n 2016 2018 2016 1 1 2 2 n n
+) Đáp án C: 1 1 1 Cách 1: Ta có u 1
u 1 u 1 u u n 1 ... 1 n 1 n 1 1 n 1 n 2 2 2 n 2016 1 u 1 u 4032. 1 lim u 1 . n n 1 2 n n 2 Cách 2:
Bước 1: Ta chứng minh u giảm và bị chặn dưới bởi 1. n
Thật vậy bằng quy nạp ta có u 2017 1. 1 1 1
Giả sử u 1 u u 1 11 1 n n 1 n 2 2 Vậy *
u 1n . n 1 Hơn nữa u u 1 u
0 nên u là dãy giảm n n 1 n n 2
Suy ra u có giới hạn lim u a n n 1 1 1 1 1
Bước 2: Ta có a lim u lim u lim u 1 lim u a n n 1 n 2 2 n 2 2 2 a 1.
+) Đáp án D:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1 1 1 1 1 1 1 1 1 n Ta có u ... 1 ... 1 n 1.2 2.3 3.4 n n 1 2 2 3 n n 1 n 1 n 1 n lim u lim 1 . n n 1 n 1 n 1 Câu 115. Ta có 2 u n u u u
n 1 n u u . .u . Khi đó ta có: n 1 2 2 n 1 n 1 n n n n 1 n n 1 3 u . .u 2 1 2 2 2 4 u . .u 3 2 3 3 … n 1 n 1 u . .u n n 1 n n n 1 n 1
Nhân theo vế các đẳng thức trên ta có u .u
.1008 . Vậy lim u 1008 . n 1 2n n n n n 1 1 1
Câu 116. Ta có u n 1 2 2 n n 1 2 2 2 n n n n 2 2 1
2 n n 1 n n 1 1 1 1 1 1 1 1 1 1 1
Ta có u u ... u 1 ... 1 2 n 2 2 2 3 3 7 7 13 13 21 n n 1 n n 1 2 1 1 1 n n 1 2 2 2 n n 1 2 n n 1 1 1 1 1 Suy ra lim ... lim n u u u . 1 2 n 2 1 1 2 1 2 n n
Câu 117. Chứng minh u là dãy giảm, tức là chứng minh: * u u , n . n n 1 n 10
- Với n 1 , ta có: 3 4u 1 4u 1 4 u u . 2 1 2 1 9
- Giả sử mệnh đề đúng với n k , tức là: * u u , n . k 1 k
- Ta cần chứng minh mệnh đề đúng với n k 1 , tức là chứng minh: u u . Ta có: k 2 k 1 3 4u 1 4u 1 4
4u 1 4 33 4u 1 u u . k 2 k 1 k k 1 k 2 k 1
- Vậy theo nguyên lý quy nạp suy ra * u u , n
, tức u là dãy giảm. n n 1 n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3
Tương tự, dùng quy nạp ta dễ dàng chứng minh được
u 2 , tức dãy u bị chặn. Từ đó n 4 n
suy ra dãy số có giới hạn.
Đặt x lim u . Khi n thì u x và n n 1 3
3 4x 1 4x 1 4 36x 9 4x 116 8 4x 1
4x 1 4x 1 x . 4 3 Vậy lim u . n 4
Câu 118. Chọn C 1 1 1
Đặt u v
, thay vào biểu thức truy hồi ta có v 3 v
1 v 3v , n 2 . n n 2 n n 1 n n 1 2 2 1 1 5 5
Dễ thấy v là cấp số nhân với v u 2
, công bội q 3 , suy ra n 1 v .3 . n 1 1 2 2 2 n 2 1 5 n 1 Do đó 1 u v .3 n . n n 1 2 2 2 u 5 1 5
Vậy L lim n lim . 3n 6 2.3n 6
Câu 119. Vì dãy các tam giác A B C , A B C , A B C ,... là các tam giác đều nên bán kính đường tròn 1 1 1 2 2 2 3 3 3 3
ngoại tiếp các tam giác bằng cạnh . 3
Với n 1 thì tam giác đều A B C có cạnh bằng 3 nên đường tròn ngoại tiếp tam giác A B C có 1 1 1 1 1 1 2 3 3 bán kính R 3. S 3. . 1 3 1 3 3
Với n 2 thì tam giác đều A B C có cạnh bằng
nên đường tròn ngoại tiếp tam giác A B C 2 2 2 2 2 2 2 2 1 3 1 3
có bán kính R 3. . S 3. . . 2 2 3 2 2 3 3
Với n 3 thì tam giác đều A B C có cạnh bằng
nên đường tròn ngoại tiếp tam giác A B C 3 3 3 4 2 2 2 2 1 3 1 3
có bán kính R 3. . S 3. . . 3 4 3 3 4 3 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n 1 1
Như vậy tam giác đều A B C có cạnh bằng 3.
nên đường tròn ngoại tiếp tam giác A B C n n n n n n 2 2 n 1 n 1 1 3 1 3 có bán kính R 3. . S 3. . . n n 2 3 2 3
Khi đó ta được dãy S , S , ...S ... là một cấp số nhân lùi vô hạn với số hạng đầu u S 3 và 1 2 n 1 1 1 công bội q . 4 u
Do đó tổng S S S ... S ... 1 4 . 1 2 n 1 q
Câu 120. + Với phương án A:
n n 20182017 2017 . n n u 1 . n n 20172018 2018 n + Với phương án B: u n 2 2 n n n 2 2 2020 4 2017
n 4n .
n n . n + Với phương án C: 1 1 1 1 1 1 1 u 1 1 . n 3 3 5 2n 1 2n 3 2n 3 2 + Với phương án D: 1 1 u u 1 u 1 u 1 . n 1 n n 1 n 2 2 v 2017 1
Đặt v u 1 , ta có . n n 1 v .v , n 1 n 1 2 n 1
Suy ra dãy v là một cấp số nhân có số hạng đầu bằng 2017 , công bội bằng nên n 2 n 1 1 v 2017. n 1 . n 2 n 1 1 Suy ra u 2017. 1 n
1 , do đó lim u 1 . n n 2 Chú ý:
Ở phương án D, ta có thể chứng minh u 1 với mọi n 1 và u là dãy giảm nên u sẽ có n n n
giới hạn. Gọi lim u a . n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1 Khi đó từ u
u 1 , n 1 suy ra a a
1 a 1 , do đó lim u 1 . n 1 n 2 2 n Câu 121. Ta có * n , 2 2 2 2 u
u a u 3a u a . n n n 2 3 1 1 n 3 3 2 Đặt 2
v u 3a thì v là cấp số nhân với v 1 3a và công bội q . n n n 1 3 n 1 n 1 2 2 Do đó v
a u v a
a a . n 1 3 2 3 n n 1 3 3 3 3 n 2 1 n Suy ra 3 2 2 2 2
u u ... u 2n 1 3a
2n 3na 3 1 3a 1 n 3a 2 . 1 2 n 2 3 1 3 Vì lim 2 2 2
u u ... u 2n b nên 1 2 n n 2 3 a 2 0 2 a
lim 31 3a1 n3a 2 b 3 , 3 b 3 1 3a b 3
suy ra T ab 2 . n!
n 3 ! n 2 n 1 n n n 1 n 2 1 6 3
Câu 122. Ta có C n 3 ! n 3! n 3! 6 6 3 C n n 1 n 2 n 6 6 6 6 Vậy ta có S ... n 1.2.3 2.3.4 3.4.5 n n 1 n 2 2 1 1 2 1 1 2 1 1 Nhận xét ; ;…; 1.2.3 1.2 2.3 2.3.4 2.3 3.4
n 2n 1 n
n 2n 1 n 1 n 1 1 1 1 1 1 1 1 1 1 n 2 3n 6 S 3 ... 3 3 n 1.2 2.3 2.3 3.4 n 2 n 1 n 1 n 2 n 2n 2n 6 3 3n 6 3 Vậy lim lim lim n S . n 2n 2 2 n 1 1 3. n n 1 9 3 n n 1 n n 1 9 3 9 3 3 1 1 Câu 123. Do 0 với n nên lim lim lim .
5n 9na
5n 9na
5n 9na n 5 9a 3a 9a 9
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n n 1 9 3 1 1 1 Theo đề bài ta có lim
a 7 . Do a là số nguyên thuộc khoảng
5n 9na 2187 3a 2187
0;2018 nên có a 7;8;9;...;20
17 có 2011 giá trị của a .
Câu 124. Chọn A 1
Theo đề, mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
độ cao mà quả bóng đạt trước đó 10
và sau đó lại rơi xuống từ độ cao thứ hai. Do đó độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến:
Thời điểm chạm đất lần thứ nhất là d 55,8m . 1 55,8
Thời điểm chạm đất lần thứ 2 là d 55,8 2. . 2 10 55,8 55,8
Thời điểm chạm đất lần thứ 3 là d 55,8 2. 2. . 3 2 10 10 55,8 55,8 55,8
Thời điểm chạm đất lần thứ 4 là d 55,8 2. 2. 2. . 4 2 3 10 10 10
……………………………………. 55,8 55,8 55,8
Thời điểm chạm đất lần thứ n, n 1 là d 55,8 2. 2. ... 2. . n 2 n1 10 10 10
Do đó độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm yên trên mặt đất là 55,8 55,8 55,8 d 55,8 2. 2. ... 2. ... (mét). 2 1 10 10 10n 55,8 55,8 55,8 55,8 1 Vì 2. , 2. , 2. , …, 2.
,…, là một cấp số nhân lùi vô hạn, công bội q , nên 10 2 10 3 10 1 10n 10 55,8 2. 55,8 55,8 55,8 ta có 10 2. 2. ... 2. ... 12,4 . 2 n1 10 10 10 1 1 10 55,8 55,8 55,8 Vậy d 55,8 2. 2. ... 2.
... 55,8 12,4 68,2 . 2 1 10 10 10n
Câu 125. Chọn A 2 a lim u a lim u lim 4v 2 n 1 n a 4b 2 3 Giả sử n , ta có . lim v b lim v lim u 1 b a 1 1 n 1 n n b 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 1
Vậy lim u 2v a 2b 2. 0 . n n n 3 3
Câu 126. Chọn C
Gọi bán kính khối cầu dưới cùng là R 50 cm. 1
Gọi R , R ,…, R lần lượt là bán kính của các khối cầu R , R ,..., R nằm nằm ngay trên khối cầu 2 3 n 2 3 n dưới cùng. R R R R R Ta có 1 R , 2 1 R ,…., n 1 1 R 2 2 3 2 4 n n 1 2 2
Gọi h là chiều cao của mô hình gồm có n khối cầu chồng lên nhau. n Ta có 1 1 1 1 1 1
h 2R 2R 2R ... 2R 2 R R R ... R 2R 1 ... n 1 2 3 n 1 1 1 n 1 1 1 n 1 2 4 2 2 4 2 1 1 1
Suy ra chiều cao mô hình là h lim h lim 2R 1 ... n 1 n 1 n n 2 4 2 1 1 1 1 1 Xét dãy số 1; ; ;...; ;
;... là một cấp số nhân có u 1 và công bội q nên là dãy cấp n 1 2 4 2 2n 1 2 1 1 1 1 1
số nhân lùi vô hạn. Do đó 1 ... ... 2 n 1 2 4 2 2n 1 1 2
Suy ra h 2R .2 200 cm. Vậy chiều cao mô hình nhỏ hơn 200 cm. 1
Câu 127. Chọn C
Lần đầu rơi xuống, quảng đường quả bóng đã bay đến lúc chạm đất là 8m .
Sau đó quả bóng nảy lên và rơi xuống chạm đất lần thứ 2 thì quảng đường quả bóng đã bay là 3 8 2.8. . 4
Tương tự, khi quả bóng nảy lên và rơi xuống chạm đất lần thứ n thì quảng đường quả bóng đã bay 3 1 ( )n 3 3 n 3 là 1 4 n 1
8 2.8. ....... 2.8.( ) 8 8 48(1 ( ) ) . 4 4 3 4 1 4
Quảng đường quả bóng đã bay từ lúc thả đến lúc không máy nữa bằng: 3 n 1 lim[8 48(1 ( ) )] 8 48 56 . 4
Câu 128. Chọn C Cách 1:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Xét điểm M x; y bất kì nằm trong (tính cả biên) của hình tròn C : 2 2 2
x y n . n
Mỗi điểm M tương ứng với một và chỉ một hình vuông đơn vị S M nhận M là đỉnh ở góc trái,
phía dưới, có các cạnh lần lượt song song hoặc nằm trên các trục tọa độ.
Ta được s bằng số các hình vuông S M và bằng tổng diện tích của S M , với M C . n n
Nhận xét: các hình vuông S M , S M đều nằm trong hình tròn C
: x y n 2 2 2 2 . n 2
Do đó s n 2 2 . 1 n
Mặt khác, các hình vuông S M phủ kín hình tròn C
: x y n 2 2 2 2 . n 2
Vì thế s n 2 2 . 2 n Từ
1 và 2 , suy ra n 2 s n 2 , * n , n 2 . n 2 s n 2 1 1 n n n 2 2 s Mà lim 1 lim 1
, theo nguyên lí kẹp, ta được . lim n n n n
Cách 2: Gọi D là số cặp số nguyên x; y thỏa mãn 2 2 2
x y n với x y và E là số cặp số n n
nguyên x; x thỏa mãn 2 2 2
x y n . Ta có E là số các số nguyên k sao cho 2 2 2k n , từ n 2 n 2 n 2 n 2 k
n , ta có n và k . Cho nên E 2 1 . 2 2 2 n 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tiếp theo, ta đánh giá D . n
Tổng số cặp số nguyên ; x y thỏa mãn 2 2 2
x y n với x y là 4N với N là số các cặp số tự n n
nhiên x; y thỏa mãn 2 2 2
x y n và x y . Giả sử x y 2 ; thỏa mãn 2 2 2
x y n , khi đó 0 x n , 2 2 0 y n x .
Nên ta có đánh giá với D là 2 2 2 2 4 n n x
4N D 4 n x n n n . 0 xn 0 xn Vì thế cho nên từ
s E D , có
4n 1 T s 1 T , trong đó n n n n n n n 2 2 2 T 2 4 n x n . 2 1 xn s 1 n 2 Suy ra n 2 2 lim lim 2 4 n x
. Do đánh giá về phần nguyên 2 2 n n n n 2 1 xn n 2 n 2 2 2 2 2 2 4 n x 2 4 n x , 2 xn 2 1 1xn n 2 n 2 2 2 2 4 n x 2 4 2 2 n x 1 2 xn 2 1 1xn 2 s 4 4 x Nên ta được n 2 2 lim lim n x lim 1 2 2 n n n n n n n 1 x n 1 x n 1
Về bản chất, kết quả giới hạn này là giá trị của tích phân xác định 2
I 4 1 x dx . 0 s Vậy lim n . n n
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 11 1D4-2 GIỚI HẠN HÀM SỐ
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. GIỚI HẠN HỮU HẠN .................................................................................................................................... 1
DẠNG 2. GIỚI HẠN MỘT BÊN .................................................................................................................................... 3
DẠNG 3. GIỚI HẠN TẠI VÔ CỰC ............................................................................................................................... 6
DẠNG 4. GIỚI HẠN VÔ ĐỊNH .................................................................................................................................... 13
DẠNG 4.1 DẠNG 00 ................................................................................................................................................ 13
Dạng 4.1.1 Không chứa căn ................................................................................................................................... 13
Dạng 4.1.2 Chứa căn .............................................................................................................................................. 15
DẠNG 4.2 DẠNG ∞ − ∞ ......................................................................................................................................... 19
PHẦN B. LỜI GIẢI THAM KHẢO .............................................................................................................................. 21
DẠNG 1. GIỚI HẠN HỮU HẠN .................................................................................................................................. 21
DẠNG 2. GIỚI HẠN MỘT BÊN .................................................................................................................................. 23
DẠNG 3. GIỚI HẠN TẠI VÔ CỰC ............................................................................................................................. 26
DẠNG 4. GIỚI HẠN VÔ ĐỊNH .................................................................................................................................... 35
DẠNG 4.1 DẠNG 00 ................................................................................................................................................ 35
Dạng 4.1.1 Không chứa căn ................................................................................................................................... 35
Dạng 4.1.2 Chứa căn .............................................................................................................................................. 38
DẠNG 4.2 DẠNG ∞ − ∞ ......................................................................................................................................... 45 PHẦN A. CÂU HỎI
DẠNG 1. GIỚI HẠN HỮU HẠN Câu 1.
(THPT THANH MIỆN I - HẢI DƯƠNG - LẦN 1 - 2018) Cho các giới hạn: lim f x 2 ; x 0 x
lim g x 3 , hỏi lim 3 f x 4g x bằng x 0 x x 0 x A. 5 . B. 2 . C. 6 . D. 3 . Câu 2.
(THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018) Giá trị của lim 2
2x 3x 1 bằng x 1 A. 2 . B. 1. C. . D. 0 . x 3 Câu 3.
(THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Tính giới hạn L lim x3 x 3
A. L . B. L 0 .
C. L . D. L 1 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 4.
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Giá trị của lim 2
3x 2x 1 bằng: x 1 A. . B. 2 . C. 1. D. 3 . Câu 5.
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Giới hạn lim 2
x x 7 bằng? x 1 A. 5 . B. 9 . C. 0 . D. 7 . 2 x 2x 3 Câu 6.
(THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Giới hạn lim bằng? x 1 x 1 A. 1. B. 0 . C. 3 . D. 2 . x 2 Câu 7. Tính giới hạn lim ta được kết quả x2 x 1 A. 4 . B. 1. C. 2 . D. 3 . Câu 8. 2 lim x 4 bằng x 3 A. 5 . B. 1. C. 5 . D. 1 . x 1 Câu 9. lim bằng x 1 x 2 1 2 A. . B. . C. . D. . 2 3 3 2
x 2x 2020 Câu 10. Tính lim . x 1 2x 1 A. 0 . B. . C. D. 2019 . 2
2 x 1 5 x 3 Câu 11. lim bằng. x2 2x 3 1 1 A. . B. . C. 7 . D. 3 . 3 7 x 1
Câu 12. (THPT Đoàn Thượng-Hải Dương-HKI 18-19) Tìm giới hạn A lim . 2 x 2 x x 4 1 A. . B. . C. . D. 1. 6
Câu 13. Giới hạn nào sau đây có kết quả bằng ? x 3 x 2 x 1 x 1 A. lim B. lim C. lim D. lim
x x 2 1 1
x x 2 1 1
x x 2 1 1
x x 2 1 1
Câu 14. Cho lim f x 2
. Tính lim f x 4x 1 . x3 x3 A. 5 . B. 6 . C. 11. D. 9 . sin x
Câu 15. Biểu thức lim bằng x x 2 2 A. 0 . B. . C. . D. 1. 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 3x 1 1 2 x x 2
Câu 16. (THPT CHUYÊN BẮC NINH - LẦN 1 - 2018) Cho I lim và J lim x0 x x 1 x 1
. Tính I J . A. 6. B. 3. C. 6 . D. 0.
Câu 17. (THCS&THPT NGUYỄN KHUYẾN - BÌNH DƯƠNG - 2018) Gọi A là giới hạn của hàm số 2 3 50
x x x ... x 50 f x
khi x tiến đến 1. Tính giá trị của . A x 1
A. A không tồn tại. B. A 1725 .
C. A 1527 . D. A 1275 .
DẠNG 2. GIỚI HẠN MỘT BÊN
Câu 18. (THPT CHUYÊN HÙNG VƯƠNG - PHÚ THỌ - LẦN 1 - 2018) Cho hàm số y f x liên
tục trên khoảng a; b . Điều kiện cần và đủ để hàm số liên tục trên đoạn a; b là?
A. lim f x f a và lim f x f b .
B. lim f x f a và lim f x f b . x a x b x a x b
C. lim f x f a và lim f x f b .
D. lim f x f a và lim f x f b . x a x b x a x b
Câu 19. (THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018) Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim . B. lim . C. lim . D. lim . 5 x 0 x x 0 x x0 x x 0 x
Câu 20. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Trong bốn giới hạn sau đây,
giới hạn nào bằng ? 3x 4 3x 4 3 x 4 3x 4 A. lim . B. lim . C. lim . D. lim . x x 2 x 2 x 2 x 2 x 2 x x 2
Câu 21. Trong các giới hạn dưới đây, giới hạn nào là ? 2x 2 1 x x 1 2x 1 A. lim . B. x x . C. lim . D. lim . x 3 lim 2 3 x 4 4 x x x 1 x4 4 x 2 x 1
Câu 22. (THPT Đông Sơn 1 - Thanh Hóa - Lần 2 - Năm học 2018 - 2019) Giới hạn lim bằng x 1 x 1 2 1 A. . B. . C. . D. . 3 3 x 2 Câu 23. lim bằng: x 1 x 1 1 1 A. . B. . C. D. . 2 2 2 3x 1 x Câu 24. lim bằng? x 1 x 1 1 1 3 3 A. . B. . C. D. . 2 2 2 2 1 Câu 25. Tính lim . x 3 x 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 A. . B. . C. 0 . D. . 6 x 1 Câu 26. Tính lim . x 1 x 1 A. 0 . B. . C. 1. D. . 1
Câu 27. Giới hạn lim bằng: x a x a 1 A. . B. 0 . C. . D. . 2a x
Câu 28. Giới hạn lim x 2 bằng: 2 x2 x 4 1 A. . B. 0 . C. . D. Kết quả khác. 2 2x 1 Câu 29. Tính lim bằng x 1 x 1 2 1 A. . B. . C. . D. . 3 3 x
Câu 30. Cho lim (x 2) . Tính giới hạn đó. 2 x2 x 4 A. . B. 1 C. 0. D. x 1 Câu 31. lim bằng x 1 x 1 A. . B. . C. 1. D. 0 1 2x Câu 32. Tìm lim . x 1 x 1 A. . B. 2 . C. 0 . D. . 2 x 1
Câu 33. (Chuyên Lê Quý Đôn – Điện Biên lần 3 - 2019) Tính giới hạn lim . x 1 x 1 A. 0. B. . C. . D. 1.
Câu 34. (LIÊN TRƯỜNG - NGHỆ AN - LẦN 2 - 2018) Trong các mệnh đề sau mệnh đề nào sai 3 3x 2 A. lim
x x x . B. lim . x 2 1 2 2 x 1 x 1 3x 2 C. . D. lim . 2 lim x x 1 x 2 x x 1 x 1 4x 3
Câu 35. (THPT NGUYỄN TRÃI - ĐÀ NẴNG - 2018) Tìm giới hạn lim x 1 x 1 A. . B. 2 . C. . D. 2 . 3 2x
Câu 36. (THPT CHUYÊN BIÊN HÒA - HÀ NAM - 2018) Tính giới hạn lim . x 2 x 2 3 A. . B. 2 . C. . D. . 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
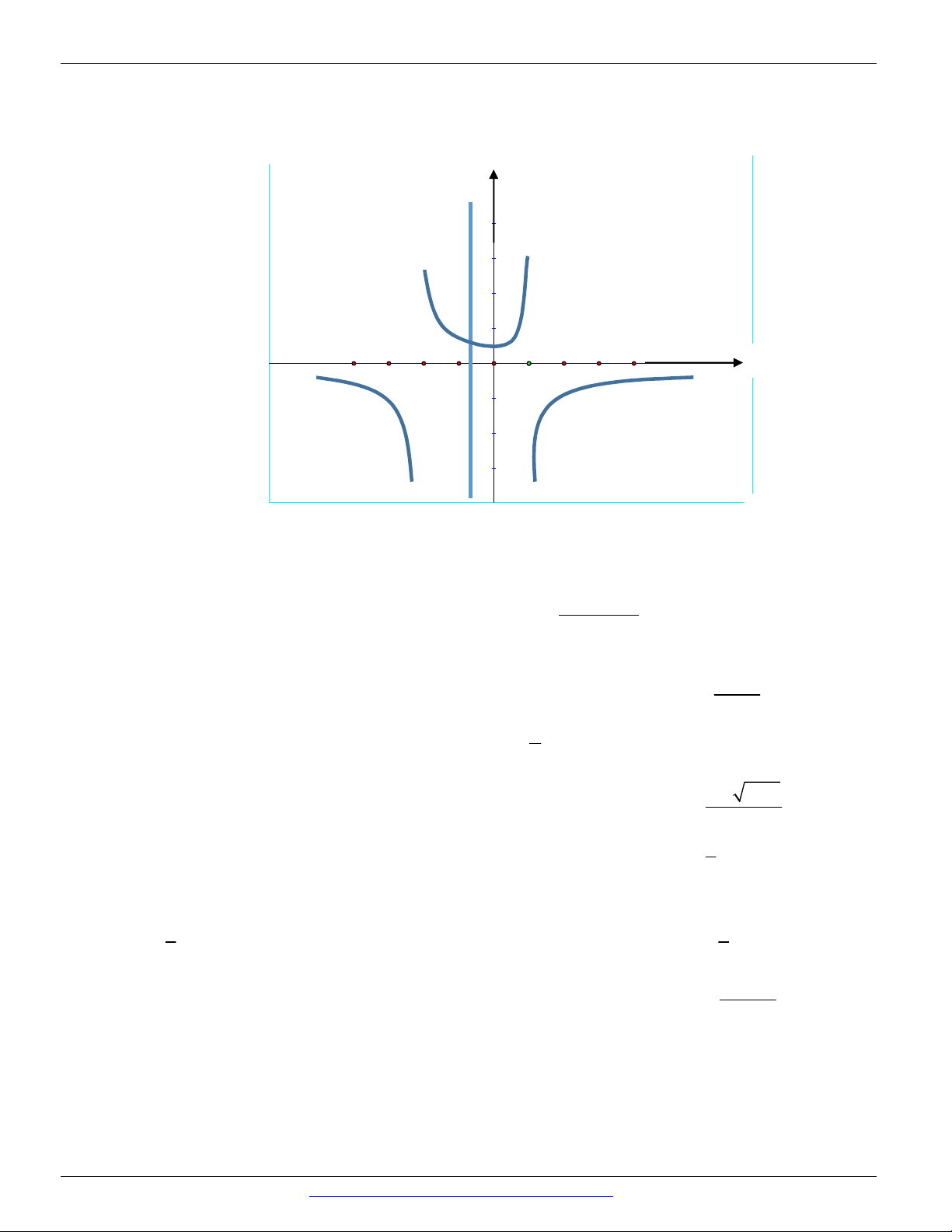
Câu 37. (THPT BÌNH GIANG - HẢI DƯƠNG - 2018) Cho hàm số f x liên tục trên ; 2 , 2 ;1
, 1; , f x không xác định tại x 2
và x 1, f x có đồ thị như hình vẽ. Chọn khẳng định đúng. -4 -3 -2 -1 O 1 2 3 4
A. lim f x , lim f x .
B. lim f x , lim f x . x 1 x 2 x 1 x 2
C. lim f x , lim f x .
D. lim f x , lim f x . x 1 x 2 x 1 x 2 2 x 2x 3
Câu 38. (THPT THANH CHƯƠNG - NGHỆ AN - 2018) lim bằng x 1 x 1 A. 0 . B. 4 . C. 3 . D. 1. 3x 7
Câu 39. (SỞ GD&ĐT YÊN BÁI - 2018) Tính giới hạn bên phải của hàm số f x khi x 2 . x 2 7 A. . B. 3 . C. . D. . 2
2 x 3 khi x 1 2
Câu 40. (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Cho hàm số y f x x 1 1 khi x 1 8
. Tính lim f x . x 1 1 1 A. . B. . C. 0 . D. . 8 8 f (x)
Câu 41. (THPT Tứ Kỳ-Hải Dương năm 2017-2018) Biết lim f (x) 4 . Khi đó lim bằng: x 1
x x 4 1 1 A. . B. 4 . C. . D. 0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1 khi x 2 3 x 2 x 8
Câu 42. Cho hàm số f x
. Với giá trị nào của tham số m thì hàm số có giới 2 m x 2m khi x 2 2 hạn tại x 2 .
A. m 3 hoặc m 2 . B. m 1 hoặc m 3 .
C. m 0 hoặc m 1 .
D. m 2 hoặc m 1 . 2
x ax b , x 2
Câu 43. Gọi a, b là các giá trị để hàm số f x 2 x 4
có giới hạn hữu hạn khi x dần tới
x 1, x 2 2
. Tính 3a b ? A. 8. B. 4. C. 24. D. 12.
Câu 44. (THPT Đông Sơn 1 - Thanh Hóa - Lần 2 - Năm học 2018 - 2019) Tìm a để hàm số 2
x ax 1 khi x 2
f x
có giới hạn tại x 2. 2
2x x 1 khi x 2 A. 1 . B. 2 . C. 2 . D. 1. x 4 2 khi x 0
Câu 45. (SỞ GD&ĐT BÌNH PHƯỚC - LẦN 1 - 2018) Cho hàm số x f x , m 1 mx m khi x 0 4
là tham số. Tìm giá trị của m để hàm số có giới hạn tại x 0 . 1 1 A. m . B. m 1. C. m 0 . D. m . 2 2
DẠNG 3. GIỚI HẠN TẠI VÔ CỰC
Câu 46. (THPT LÊ HOÀN - THANH HÓA - LẦN 1 - 2018) Giả sử ta có lim f x a và lim g x b x x
. Trong các mệnh đề sau, mệnh đề nào sai?
A. lim f x.g x . a b .
B. lim f x g x a b . x x f x a C. lim .
D. lim f x g x a b .
x g x b x
Câu 47. (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Chọn kết quả đúng của 5 3 lim 4
x 3x x 1 . x A. 0. B. . C. . D. 4 .
Câu 48. (THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018) Tính giới hạn 3 2
lim 2x x 1 x A. . B. . C. 2 . D. 0 .
Câu 49. (LÊ QUÝ ĐÔN - HẢI PHÒNG - LẦN 1 - 2018) Giới hạn 3 2
lim 3x 5x 9 2x 2017 bằng x A. . B. 3 . C. 3 . D. .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2x 1
Câu 50. (THPT HÀM RỒNG - THANH HÓA - 2018) Tính giới hạn lim .
x 4x 2 1 1 1 A. . B. 1. C. . D. 2 4 2 3 x
Câu 51. (THPT Yên Mỹ Hưng Yên lần 1 - 2019) Cho bảng biến thiên hàm số: y , phát biểu nào x 2 sau đây là đúng:
A. a là lim y .
B. b là lim y .
C. b là lim y .
D. a là lim y . x x x 1 x 1
Câu 52. (SGD&ĐT BẮC GIANG - LẦN 1 - 2018) lim bằng:
x 2x 5 1 A. 0 . B. . C. . D. . 2 1 x
Câu 53. (THPT CHUYÊN AN GIANG - 2018) lim bằng:
x 3x 2 1 1 1 1 A. . B. . C. . D. . 3 2 3 2 3x 1
Câu 54. (THPT CHUYÊN NGỮ - HÀ NỘI - 2018) lim bằng:
x x 5 1 A. 3 . B. 3 . C. . D. 5 . 5 3 4x
Câu 55. (HỒNG BÀNG - HẢI PHÒNG - LẦN 1 - 2018) lim bằng
x 5x 2 5 5 4 4 A. . B. . C. . D. . 4 4 5 5 2x 8
Câu 56. (SGD - HÀ TĨNH - HK 2 - 2018) lim bằng
x x 2 A. 2 . B. 4 . C. 4 . D. 2 . 2x 1
Câu 57. (SỞ GD&ĐT PHÚ THỌ - 2018) Tính L lim . x x 1 1 A. L 2 . B. L 1 . C. L . D. L 2 . 2 2x 1
Câu 58. (SỞ GD&ĐT QUẢNG NAM - 2018) lim bằng.
x 3 x 2 A. 2 . B. . C. 1. D. 2 . 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2
x 2018x 3
Câu 59. (Gia Bình I Bắc Ninh - L3 - 2018) Tính giới hạn lim được. 2 x 2x 2018x 1 1 A. 2018. B. . C. 2. D. . 2 2018 2 x 3x 2
Câu 60. (Bình Minh - Ninh Bình - Lần 4 - 2018) Giới hạn lim có kết quả là 2 x 2x 1 1 A. B. C. 2 D. 2 5 3 2x 3x 1
Câu 61. (THPT QUẢNG YÊN - QUẢNG NINH - 2018) Giới hạn lim bằng 3 4 5
x 4x 2x x 3 1 3 A. 2 . B. . C. 3 . D. . 2 2 x 1 x 2
Câu 62. (THPT NGUYỄN HUỆ - TT HUẾ - 2018) lim bằng 2 x x 9 2 1 A. . B. 1. C. 1 . D. . 9 9 x s inx Câu 63. Tính lim ? x x 1 A. . B. . C. 1. D. 0 . 2
Câu 64. (Bỉm Sơn - Thanh Hóa - 2019) Tính ? 2 lim 2x x x x A. . B. 1 . C. . D. 0 . 2 x 3x 5
Câu 65. (HỒNG QUANG - HẢI DƯƠNG - LẦN 1 - 2018) Tìm lim . x 4x 1 1 1 A. . B. 1. C. 0 . D. . 4 4 2x 1
Câu 66. (THPT CHUYÊN ĐH VINH - LẦN 3 - 2018) Giá trị của lim bằng x 2 x 1 1 A. 0 . B. 2 . C. . D. 2 . x 2
Câu 67. (Đề tham khảo BGD năm 2017-2018) lim bằng
x x 3 2 A. . B. 1. C. 2 . D. 3 . 3 3x 2
Câu 68. (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Tính giới hạn I lim .
x 2x 1 3 3 A. I 2 . B. I . C. I 2 . D. I . 2 2 x
Câu 69. (Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018) lim bằng. 2
x x 1 A. . B. 1. C. . D. 0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 3x
Câu 70. (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Chọn kết quả đúng của lim . x 2 2x 3 3 2 2 3 2 2 A. . B. . C. . D. . 2 2 2 2 1 x
Câu 71. (THPT Chuyên Thoại Ngọc Hầu – An Giang - Lần 3 năm 2017 – 2018) lim bằng
x 3x 2 1 1 1 1 A. . B. . C. . D. . 3 2 3 2 3x 1
Câu 72. (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) lim bằng
x x 5 1 A. 3 . B. 3 . C. . D. 5 . 5 2 cx a
(THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Giới hạn lim bằng? 2 Câu 73.
x x b a b A. a . B. b . C. c . D. . c 4x 1
Câu 74. (THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018) lim bằng
x x 1 A. 2 . B. 4 . C. 1 . D. 4 . x 1
Câu 75. (SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018) lim bằng
x 6x 2 1 1 1 A. . B. . C. . D. 1. 2 6 3 x 1
Câu 76. (SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018) lim bằng
x 4x 3 1 1 A. . B. . C. 3 . D. 1. 3 4 2 x 2 2
Câu 77. Giới hạn lim bằng x x 2 A. . B. 1. C. . D. -1 2 x 3
Câu 78. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Giá trị của lim bằng x x 3 A. . B. 1 . C. . D. 1. 2 x 3
Câu 79. (ĐỘI CẤN VĨNH PHÚC LẦN 1 2018-2019) Giá trị của lim là. x x 3 A. . B. 1. C. . D. 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 4 2 x x 2
Câu 80. Giới hạn lim có kết quả là x 3 x 1 3x 1 3 3 A. 3 B. C. 3 D. 3 3 4x 3 1 2x 4 1
Câu 81. Cho hàm số f x
. Tính lim f x . 3 2x7 x A. 2 . B. 8 . C. 4 . D. 0 . 2 m x 7x 5
Câu 82. Tìm tất cả các giá trị thực của tham số m thỏa mãn lim 4. 2
x 2x 8x 1 A. m 4 . B. m 8 .
C. m 2 . D. m 3 . 2
4x 3x 1
Câu 83. Cho hai số thực a và b thỏa mãn lim
ax b 0
. Khi đó a b bằng x x 2 A. 4 . B. 4 . C. 7 . D. 7 . 2 x 2018 Câu 84. lim bằng x x 1 A. 1. B. 1. C. . D. 2018. 2 x 1
Câu 85. Giới hạn lim bằng
x x 1 A. 0 . B. . C. . D. 1. 2
ax x 3x 5 Câu 86. Biết lim 2 . Khi đó x 2x 7
A. 1 a 2 .
B. a 1 .
C. a 5 .
D. 2 a 5 . x 3 lim 2
Câu 87. (ĐỀ KT NĂNG LỰC GV THUẬN THÀNH 1 BẮC NINH 2018-2019) x x 2 bằng 3 A. 2 . B. . C. 1. D. 0 . 2 sin x
Câu 88. Tính giới hạn lim ?
x x A. 0 .
B. Giới hạn không tồn tại.
C. 1. D. . x 3 Câu 89. lim bằng x x 2 3 A. . B. 3 . C. 1 . D. 1. 2 2018 2 x 4x 1
Câu 90. Tìm giới hạn: lim 2x 2019 x 1 1 1 1 A. 0. B. . C. . D. . 2018 2 2019 2 2017 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2
x 3x 1 Câu 91. Cho lim +ax b 1
.Khi đó giá trị của biểu thức T a b bằng x x 1 A. 2 . B. 0 . C. 1. D. 2 . 2 x 1
Câu 92. Biết rằng lim
ax b 5
. Tính tổng a b . x x 2 A. 6 . B. 7 . C. 8 . D. 5 . 2 x 3x 5
Câu 93. (Chuyên Lê Quý Đôn Điện Biên Lần 2 năm 2018-2019) Tính giới hạn lim . 2 x 2 3x 1 1 2 A. . B. . C. . D. . 2 3 3 5x 3 Câu 94.
(Trường THPT Chuyên Lam Sơn_2018-2019) Giới hạn lim bằng số nào sau đây?
x 1 2x 5 2 3 A. . B. . C. 5. D. . 2 3 2 x 2
Câu 95. (Tham khảo 2018) lim bằng.
x x 3 2 A. . B. 1 . C. 2 . D. 3 . 3 2x 5 Câu 96. lim bằng
x x 3 5 A. . B. 1. C. 3. D. 2. 3 3x 1
Câu 97. Tìm giới hạn L lim
x 1 2x 1 3 3 A. L 3 . B. L . C. L . D. L . 2 2 2 2 x 3
Câu 98. Giá trị của lim bằng: x x 3 A. . B. 1 . C. . D. 1. 2x 3
Câu 99. (THPT Đoàn Thượng – Hải Dương) Tính lim ? x 2 x 1 x A. 0. B. . C. 1. D. 1. 2 5x 2x 3
Câu 100. (SGD&ĐT ĐỒNG THÁP - 2018) Tính giới hạn lim . 2 x x 1 A. 5 . B. 4 . C. 3 . D. 2 .
Câu 101. (THPT XUÂN HÒA - VP - LẦN 1 - 2018) Trong các mệnh đề sau, mệnh đề nào đúng? 4 x x 4 x x 4 x x 4 x x A. lim . B. lim 1. C. lim . D. lim 0 . x 1 2x x 1 2x x 1 2x x 1 2x 2x 3
Câu 102. (THPT CHUYÊN LAM SƠN - THANH HÓA - 2018) Tìm giới hạn lim :
x 1 3x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 3 A. . B. . C. . D. 2 . 3 3 2
Câu 103. (THPT CHUYÊN NGUYỄN QUANG DIÊU - ĐỒNG THÁP - 2018) Tính giới hạn 2 4x 1 K lim . x x 1 A. K 0 . B. K 1. C. K 2 . D. K 4 . x 1
Câu 104. (THPT CHUYÊN THÁI BÌNH - LẦN 4 - 2018) Tính lim . 2018 x x 1 A. 1. B. 1. C. 2 . D. 0 . 2 1 x x
Câu 105. (CỤM CHUYÊN MÔN 4 - HẢI PHÒNG - LẦN 1 - 2018) Tính giới hạn lim x x A. 0 . B. . C. 1. D. . 2
x x x
Câu 106. (THPT QUỲNH LƯU - NGHỆ AN - 2018) lim bằng x x 1 A. 2 . B. 2 . C. 0 . D. . 2 2x x
Câu 107. (THPT HOÀNG MAI - NGHỆ AN - 2018) lim bằng 2 x x 1 A. 2 . B. 1. C. 2 . D. 1 . sin x 1
Câu 108. (THPT CHU VĂN AN - HÀ NỘI - 2018) Giới hạn lim bằng x x A. . B. 1. C. . D. 0 . 2 x x 1
Câu 109. (THPT PHÚ LƯƠNG - THÁI NGUYÊN - 2018) Tính giới hạn lim . x 2 x 1 1 A. . B. . C. . D. . 2 2
Câu 110. (THPT NGUYỄN HUỆ - NINH BÌNH - 2018) Cho a , b , c là các số thực khác 0 . Để giới hạn 2
x 3x ax lim 3 thì x bx 1 a 1 a 1 a 1 a 1 A. 3. B. 3 . C. 3. D. 3. b b b b
Câu 111. (XUÂN TRƯỜNG - NAM ĐỊNH - LẦN 1 - 2018) Cho số thực a thỏa mãn 2
a 2x 3 2017 1 lim
. Khi đó giá trị của a là x 2x 2018 2 2 2 1 1 A. a . B. a . C. a . D. a . 2 2 2 2 2
4x x 1 4 1
Câu 112. (THPT HOÀNG MAI - NGHỆ AN - 2018) Để lim
. Giá trị của m thuộc x mx 2 2
tập hợp nào sau đây? A. 3;6 . B. 3; 0 . C. 6 ; 3 . D. 1; 3 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
2 a x 3
Câu 113. (THPT BÌNH GIANG - HẢI DƯƠNG - 2018) Biết lim
(với a là tham số). x 2 x x 1 Giá trị nhỏ nhất của 2
P a 2a 4 là. A. 4 . B. 3 . C. 5 . D. 1. 2 2
4x x 1 x x 3
Câu 114. (Chuyên ĐB Sông Hồng –Lần 1 năm 2017 – 2018) Tính giới hạn lim x 3x 2 . 1 2 1 2 A. . B. . C. . D. . 3 3 3 3 x 3
Câu 115. (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Tính lim x 2 4x 1 2 1 1 3 A. . B. . C. . D. 0 . 4 2 2
DẠNG 4. GIỚI HẠN VÔ ĐỊNH DẠNG 4.1 DẠNG
Dạng 4.1.1 Không chứa căn x 1
Câu 116. (THPT Chuyên ĐH Vinh – Lần 2 – năm 2017 – 2018) Giới hạn lim bằng
x x 22 2 3 A. . B. . C. 0 . D. . 16 3 x 1
Câu 117. (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Tính giới hạn A lim . x 1 x 1 A. A . B. A 0. C. A 3. D. A . 2 x 12x 35
Câu 118. (THPT Chuyên Trần Phú-Hải Phòng lần 1 năm 2017-2018) Tính lim . x 5 25 5x 2 2 A. . B. . C. . D. . 5 5 2 x 4
Câu 119. (THPT Kinh Môn 2-Hải Dương năm 2017-2018) Kết quả của giới hạn lim bằng x2 x 2 A. 0 . B. 4 . C. 4 . D. 2 . 2 x 9
Câu 120. (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Tính lim bằng: x3 x 3 A. 3 . B. 6 . C. . D. 3 . 2 x 5x 6
Câu 121. (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Tính giới hạn I lim . x2 x 2 A. I 1 . B. I 0 . C. I 1. D. I 5 . 2 x 3x 2
Câu 122. (NGÔ GIA TỰ LẦN 1_2018-2019) Tính giới hạn lim x 1 x 1 A. 1. B. 1. C. 2 . D. 2 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 x 3x 2 a a
Câu 123. Cho giới hạn lim trong đó
là phân số tối giản. Tính 2 2
S a b . 2 x2 x 4 b b A. S 20 .
B. S 17 .
C. S 10 . D. S 25 . 2 2018 x 4 Câu 124. Tính lim . 2018 2018 x2 x 2 A. 2019 2 . B. 2018 2 . C. 2. D. . 2018 x x 2 a a
Câu 125. Giá trị của lim bằng , với
là phân số tối giản. Tính giá trị của 2 2
a b . 2017 x 1 x x 2 b b A. 4037 . B. 4035 . C. 4 035 . D. 4033. 10 2x Câu 126. lim là 2 x5 x 6x 5 1 1 A. . B. 0 . C. . D. . 2 2 3 x 2
1 a x a Câu 127. Tìm lim . 3 3 xa x a 2 2a 2 2a 1 2 2 2a 1 A. . B. . C. . D. . 2 a 3 2 3a 3 3 4 2 x 3x 2 Câu 128. Tìm lim . 3 x 1 x 2x 3 5 2 1 A. . B. . C. . D. . 2 5 5 3 x 1 a a Câu 129. Cho lim
với a, b là các số nguyên dương và
là phân số tối giản. Tính tổng S a b 2 x 1 x 1 b b . A. 5 . B. 10 . C. 3 . D. 4 . 2
x bx c Câu 130. Biết lim 8. ( ,
b c ). Tính P b . c x3 x 3 A. P 13. B. P 11. C. P 5. D. P 12. 2
x x 2 1
Câu 131. (Chuyên Quốc Học Huế lần 2 - 2018-2019) Tính giới hạn L lim . 2 x 1 3x 8x 5 3 1 A. L . B. L .
C. L . D. L 0 . 2 2 2
x ax b
Câu 132. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Cặp a,b thỏa mãn lim 3 là x3 x 3
A. a 3 , b 0 .
B. a 3 , b 0 .
C. a 0 , b 9 .
D. không tồn tại cặp a,b thỏa mãn như vậy.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 2
Câu 133. (THPT TRẦN PHÚ - ĐÀ NẴNG - 2018) Giới hạn lim bằng 2 x2 x 4 1 A. 2 . B. 4 . C. . D. 0 . 4 2 x 3x 4
Câu 134. [KIM LIÊN - HÀ NỘI - LẦN 1 - 2018] Tính L lim . x 1 x 1 A. L 5 . B. L 0 . C. L 3 . D. L 5 . 2 ax bx 5
Câu 135. (THPT BÌNH GIANG - HẢI DƯƠNG - 2018) Cho a, b là số nguyên và lim 7 . x 1 x 1 Tính 2 2
a b a b . A. 18 . B. 1. C. 15 . D. 5 .
Câu 136. (THPT LƯƠNG ĐẮC BẰNG - THANH HÓA - LẦN 1 - 2018) Hãy xác định xem kết quả nào sai x 1 x 2 A. lim 2 . B. lim 1 . x 1 x
x x 4 2 x 3x 2 2 x 16 9 C. lim 1 . D. lim . x 1 x 1 2
x4 x x 20 8
1 cos 3x cos 5x cos 7x
Câu 137. (THPT CHUYÊN VĨNH PHÚC - LẦN 3 - 2018) Cho hàm số y f x 2 sin 7x
. Tính lim f x . x0 83 105 15 83 A. . B. . C. . D. . 49 49 49 98 3
x ax a 1
Câu 138. (THPT YÊN KHÁNH A - LẦN 2 - 2018) Biết lim 2 . Tính 2
M a 2a . x 1 x 1 A. M 3 . B. M 1 . C. M 1 . D. M 8 . cos x
Câu 139. (THPT Đô Lương 4-Nghệ An năm 2017-2018) Tìm giới hạn L lim . x 2 x 2 A. L 1 . B. L 1 . C. L 0 . D. L . 2 2
x ax b 1
Câu 140. (THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018) Cho lim a,b . 2 x 1 x 1 2 Tổng 2 2
S a b bằng A. S 13. B. S 9. C. S 4. D. S 1. Dạng 4.1.2 Chứa căn
Câu 141. (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Số nào trong các số sau là bằng 2 x x 2 3 lim ? x3 x 3 3 3 7 3 7 3 A. . B. . C. . D. . 12 12 12 12
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3
2 1 x 8 x
Câu 142. (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Cho hàm số y f x . x
Tính lim f x . x0 1 13 10 A. . B. . C. . D. . 12 12 11 2 5 5 x a
Câu 143. (Chuyên Lam Sơn-KSCL-lần 2-2018-2019) Biết lim
, trong đó a là số x0 2 x 16 4 b
nguyên, b là số nguyên tố. Ta có tổng a 2b bằng : A. 13 . B. 3 . C. 14. D. 8 . 2
x 3x 4 2
Câu 144. (THPT THUẬN THÀNH 1) Giới hạn lim bằng x0 x 1 1 3 2 A. . B. . C. . D. . 2 2 4 3 2 x 3x 2 Câu 145. Tính lim . x 1
6 x 8 x 17 1 A. . B. 0 . C. . D. . 6 3 2 8 x 2 Câu 146. Tính lim . 2 x0 x 1 1 1 1 A. . B. . C. . D. . 12 4 3 6 3 2
x x 1 1
Câu 147. Giá trị của lim bằng 2 x0 x 1 A. 1. B. . C. 1. D. 0 . 2
Câu 148. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Giới hạn
x 1 5x 1 a a lim
, với a, b Z , b 0 và
là phân số tối giản. Giá trị của a b là x3 x 4x 3 b b 8 1 A. 1. B. 1. C. . D. . 9 9 2 x 5x 6 Câu 149. Tìm lim là x2 4x 1 3 3 2 3 1 A. . B. . C. . D. . 2 3 2 2 x 2x 1 Câu 150. Tìm lim . 2 x 1 x x 2 A. 5 . B. . C. 0 . D. 1. x 1 2 a a Câu 151. Biết lim (
là phân số tối giản). Tình a b 2018 . 2 x3 x 3 b b
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 2021 . B. 2023 . C. 2024 . D. 2022 .
3 ax 1 1 bx
Câu 152. Cho a, b là hai số nguyên thỏa mãn 2a 5b 8 và lim
4 . Mệnh đề nào dưới x0 x đây sai? A. a 5.
B. a b 1. C. 2 2 a b 50.
D. a b 9.
f x 2018
1009 f x 2018 Câu 153. Cho lim 2019. Tính lim . x4 x 4
x4 x 2 2019 f x 2019 2019 A. 2019 B. 2020 C. 2021 D. 2018
x 1 5x 1 a
Câu 154. Giới hạn lim bằng
(phân số tối giản). Giá trị của a b là x 3 x 4x 3 b 1 9 A. . B. . C. 1. D. 1 . 9 8 2
ax 1bx 2
Câu 155. Cho biết lim
a,b có kết quả là một số thực. Giá trị của biểu thức 3 x 1 x 3x 2 2 2
a b bằng? 45 9 A. 6 5 3 . B. . D. 87 48 3 16 C. 4
x 1 5x 1 a
Câu 156. Cho giới hạn lim
(phân số tối giản). Giá trị của T 2a b là x3 x 4x 3 b 1 9 A. . B. 1. C. 10 . D. . 9 8 2 x 2x 8
Câu 157. (Trường THPT Hoàng Hoa Thám - Hưng Yên, năm 2019) Tính lim . x 2 2x 5 1 1 A. 3 . B. . C. 6 . D. 8. 2 f (x) 16
Câu 158. Cho hàm số
f (x) xác định trên thỏa mãn lim 12 . Tính giới hạn x2 x 2
3 5 f (x) 16 4 lim 2 x2 x 2x 8 5 1 5 1 A. . B. . C. . D. . 24 5 12 4 x 3 2
Câu 159. (SGD&ĐT HÀ NỘI - 2018) lim bằng x 1 x 1 1 1 A. . B. . C. . D. 1. 4 2 4x 1 1
Câu 160. (THPT HẬU LỘC 2 - TH - 2018) Tính giới hạn K lim . 2 x0 x 3x 2 2 4 A. K . B. K . C. K . D. K 0 . 3 3 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 2 2
Câu 161. (CHUYÊN KHTN - LẦN 1 - 2018) Giới hạn lim x2 x 2 bằng 1 1 A. . B. . C. 0 . D. 1. 2 4 1 x
Câu 162. (PHAN ĐĂNG LƯU - HUẾ - LẦN 1 - 2018) Tính gới hạn L lim . x 1 2 x 1 A. L 6 . B. L 4 . C. L 2 . D. L 2 . 2 2x 6
Câu 163. (THPT HÀ HUY TẬP - HÀ TĨNH - LẦN 1 - 2018) Tính lim
a b ( a , b nguyên). x 3 x 3
Khi đó giá trị của P a b bằng A. 7 . B. 10 . C. 5 . D. 6 . 3x 1 1 a
Câu 164. (THPT CHUYÊN HẠ LONG - LẦN 1 - 2018) Biết lim
, trong đó a , b là các số x0 x b a
nguyên dương và phân số
tối giản. Tính giá trị biểu thức 2 2
P a b . b A. P 13 . B. P 0 . C. P 5 . D. P 40 . 2
4x 2x 1 1 2x
Câu 165. (THPT HẢI AN - HẢI PHÒNG - LẦN 1 - 2018) Tính giới hạn lim . x0 x A. 2 . B. 1 . C. 2 . D. 0 . 2 3
x x 2 7x 1 a 2
Câu 166. (THPT TRIỆU THỊ TRINH - LẦN 1 - 2018) Biết lim
c với a , b x 1 2 x 1 b a , c và
là phân số tối giản. Giá trị của a b c bằng: b A. 5 . B. 37 . C. 13 . D. 51. x 2
Câu 167. (THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018) Giá trị của I lim bằng 2
x 2 x 2 1 A. 2 . B. . C. 1. D. 2 . 2 2 2x x 3
Câu 168. (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Tính I lim ? 2 x 1 x 1 7 3 3 3 A. I . B. I . C. I . D. I . 8 2 8 4 2 2
x x 4x 1
Câu 169. (THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018) Giá trị giới hạn lim bằng: x 2x 3 1 1 A. . B. . C. . D. . 2 2
Câu 170. (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Cho f x là đa thức thỏa mãn
f x 20
3 6 f x 5 5 lim
10 . Tính T lim x2 x 2 2 x2 x x 6
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 12 4 4 6 A. T . B. T . C. T . D. T . 25 25 15 25 3x 1 4
Câu 171. (THPT Ninh Giang-Hải Dương năm 2017-2018) Giới hạn: lim có giá trị bằng: x 5 3 x 4 9 3 A. . B. 3 . C. 18 . D. . 4 8
Câu 172. (THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018) Cho f x là một đa thức thỏa mãn f x 16 f x 16 lim
24 . Tính I lim x 1 x 1 x 1 x
1 2 f x 4 6 A. 24.
B. I . C. I 2 . D. I 0 . x a a
Câu 173. (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Cho lim ( là phân 7
x0 x 1. x 4 2 b b
số tối giản). Tính tổng L a b . A. L 43 . B. L 23 . C. L 13 . D. L 53 . 3
x 1 x 5
Câu 174. (THPT CHUYÊN KHTN - LẦN 3 - 2018) Giới hạn lim . x3 x 3 1 1 1 A. 0 . B. . C. . D. . 2 3 6 DẠNG 4.2 DẠNG ∞ − ∞
Câu 175. Trong các giới hạn sau, giới hạn nào có kết quả là 0 ? x 1 2x 5 2 x 1 A. lim . B. lim . C. lim . D. . 2 lim x 1 x x 3 x 1 x 1 x 2 x 10 2 x 1 x 3x 2 Câu 176. Cho 2 lim
9x ax 3x . Tính giá trị của a . 2 x A. 6 . B. 12 . C. 6 . D. 12
Câu 177. Tìm giới hạn 2 2 M lim x 4x x x Ta được M bằng . x 3 1 3 1 A. . B. . C. . D. . 2 2 2 2 Câu 178. Biết
với a, b . Tính S 5a b . 2 lim 5x 2x
x 5 a 5 b x A. S 5 . B. S 1 . C. S 1 . D. S 5 . Câu 179. Tìm 2 lim
x x 2x x A. 2 . B. . C. 1. D. . Câu 180. Tìm . 2 lim x x 2 x 2 x 3 A. . B. 0 . C. . D. 2 . 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 181. Giới hạn bằng: 2 lim 3x 9x 1 x A. . B. 0 . C. . D. 1 . Câu 182. Biết 2 lim
4x ax 1 bx . Tính giá của biểu thức 2 3
P a 2b . 1 x A. P 32 . B. P 0 . C. P 16 . D. P 8 . Câu 183. bằng 2 lim 4x 8x 1 2x x A. . B. 0 . C. 2 . D. Câu 184. Tìm . 3 3 lim x 1 x 2 x A. 1 . B. . C. . D. 1 . a a
Câu 185. Biết rằng
, ( a ; b ,
tối giản). Tổng a b có giá trị là 2 lim 2x 3x 1 x 2 2 x b b A. 1. B. 5. C. 4 . D. 7 . 20
Câu 186. Cho giới hạn lim
x ax x b
và đường thẳng : y ax 6b đi qua điểm x 2 36 5 1 6 3
M 3; 42 với a,b . Giá trị của biểu thức 2 2
T a b là: A. 104 . B. 100 . C. 41 . D. 169 . Câu 187. Cho 2 lim
x ax 5 x . Khi đó giá trị a là 5 x A. 10 . B. 6 . C. 6 . D. 1 0 .
Câu 188. (THPT YÊN LẠC - LẦN 4 - 2018) Tìm giới hạn I . 2 lim x 4x 1 x x A. I 2 . B. I 4 . C. I 1. D. I 1 .
Câu 189. (THTP LÊ QUÝ ĐÔN - HÀ NỘI - LẦN 1 - 2018) Tính . 2 lim x 4x 2 x x A. 4 . B. 2 . C. 4 . D. 2 .
Câu 190. (QUẢNG XƯƠNG - THANH HÓA - LẦN 1 - 2018) lim x 1 x 3 bằng x A. 0 . B. 2 . C. . D. .
Câu 191. (THPT LƯƠNG ĐẮC BẰNG - THANH HÓA - LẦN 1 - 2018) bằng: 2 lim x 5x 6 x x 5 5 A. 3 . B. . C. . D. 3 . 2 2
Câu 192. (CHUYÊN VĨNH PHÚC - LẦN 1 - 2018)Cho 2 lim
x ax 5 x thì giá trị của a là một 5 x
nghiệm của phương trình nào trong các phương trình sau? A. 2
x 11x 10 0 . B. 2
x 5x 6 0 . C. 2
x 8x 15 0 . D. 2
x 9x 10 0 .
Câu 193. (THPT NGHEN - HÀ TĨNH - LẦN 1 - 2018) Biết . Tính 2 lim 4x
3x 1 ax b 0 x
a 4b ta được A. 3 . B. 5 . C. 1 . D. 2 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 194. (THPT CHUYÊN NGUYỄN ĐÌNH TRIỂU - ĐỒNG THÁP - LẦN 1 - 2018) lim x bằng 2 2 x 5x 4 x 5x 2 x A. 3 . B. 1. C. 0 . D. .
Câu 195. (THPT Đoàn Thượng-Hải Dương-lần 2 năm 2017-2018) Giới hạn nào dưới đây có kết quả là 1 ? 2 x A.
x x . B. x . 2 lim x 1 x x x 2 lim 1 2 x C.
x x . D. x . 2 lim x 1 x x x 2 lim 1 2 2 a x 1 2017 1
Câu 196. (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Cho lim ; x x 2018 2 2 lim
x bx 1 x . Tính P 4a b . 2 x A. P 3 . B. P 1 . C. P 2 . D. P 1 .
Câu 197. (THPT Lê Quý Đôn-Hà Nội năm 2017-2018) Tính 2 lim x 4x 2 x x A. 4 . B. 2 . C. 4 . D. 2 .
Câu 198. (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Tìm giới hạn I . 2 lim x 1 x x 2 x
A. I 1 2 .
B. I 46 31 . C. I 17 11. D. I 3 2 .
PHẦN B. LỜI GIẢI THAM KHẢO
DẠNG 1. GIỚI HẠN HỮU HẠN Câu 1.
Ta có lim 3 f x 4g x
lim 3 f x lim 4g x 3 lim f x 4 lim g x 6 . x xx xx xx xx 0 x 0 0 0 0 Câu 2. Chọn D Ta có: lim 2
2x 3x 1 0 . x 1 Câu 3. Chọn B x 3 3 3 Ta có L lim 0 . x3 x 3 3 3 Câu 4. Chọn B lim 2
3x 2x 2 1 3.1 2.11 2. x 1 Câu 5. Chọn B 2 Ta có lim 2
x x 7 1 1 7 9 . x 1 Câu 6. Chọn A 2 2 x 2x 3 1 2.1 3 Ta có: lim 1 . x 1 x 1 11 Câu 7. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 2 2 2 Dễ thấy lim 4 x2 x 1 2 1 Câu 8. Chọn B 2
lim x 4 3 4 1 x 3 Câu 9. Chọn C x 1 2 lim x 1 x 2 3
Câu 10. Chọn D 3 2
x 2x 2020 3 2 1 2.1 2020 lim 2019 . x 1 2x 1 2.11
Câu 11. Chọn D 2
2 x 1 5 x 3 2 5 Ta có lim 3 . x 2 2x 3 1
Câu 12. Chọn A Ta có: Với x 2 ; 2
x x 4 0 x 1 2 1 1 Nên A lim . 2
x2 x x 4 22 2 4 6
Câu 13. Chọn D Ta có x 2 1 0, x 1
Do đó để giới hạn bằng thì giới hạn của tử phải dương x 1 Vậy lim .
x x 2 1 1
Câu 14. Chọn D
Ta có lim f x 4x 1 9 . x3
Câu 15. Chọn B sin x 2 Vì sin 1 nên lim . 2 x x 2 Câu 16. Ta có 2 3x 1 1 6x 6 I lim lim lim 3 . x0 x0 x
x 3x 1 x0 1 3x 1 1 2 x x 2 x 1 x 2 J lim lim
lim x 2 3 . x1 x 1 x 1 x 1 x 1
Khi đó I J 6 . 2 3 50
x x x ... x 50
Câu 17. Có: lim f x lim x 1 x 1 x 1 lim 1 x 1 2 x x 1 .... 49 48 x x ... 1 x 1
1 2 3 ..... 50 251 50 1275.
Vậy lim f x 1275 . x 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
DẠNG 2. GIỚI HẠN MỘT BÊN
Câu 18. Hàm số f xác định trên đoạn a; b được gọi là liên tục trên đoạn a; b nếu nó liên tục trên
khoảng a; b, đồng thời lim f x f a và lim f x f b . x a x b
Câu 19. Chọn B 1 Ta có: lim
do lim x 0 và x 0 . Vậy đáp án A đúng. x 0 x x 0 Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A.
Câu 20. Chọn C 3x 4 3x 4 Dễ thấy lim 3 ; lim 3 (loại). x x 2 x x 2 3x 4 Vì lim 3 x 4 2
; lim x 2 0; x 2 0, x 2 nên lim x 2 x 2 x 2 x 2
Câu 21. Chọn A 2x 1 Xét lim x 4 4 x
Ta có lim 2x , lim
và 4 x 0 với mọi x 4 4 x 0 1 7 0 x 4 x 4 2x 1 Do đó lim . x 4 4 x
Câu 22. Chọn B Ta có lim 2 x 1 1
0 , lim x
1 0 , x 1 0 khi x 1 . x 1 x 1 2 x 1 Suy ra lim . x 1 x 1
Câu 23. Chọn C
lim x 2 3 0 x 1 x 2 lim
vì lim x 1 0 . x 1 x 1 x 1
x 1 0, x 1
Câu 24. Chọn D 2 3x 1 x 4 1 3 Ta có: lim . x 1 x 1 1 1 2
Câu 25. Chọn B
Ta có lim x 3 0, x 3 0, x 3 . x 3
Câu 26. Chọn D x 1 lim
do lim x
1 2 0 , lim x
1 0 và x 1 0 với x 1. x 1 x 1 x 1 x 1
Câu 27. Chọn D lim 1 1 0 xa
Ta có: lim 1 a 0 xa
x a 0 khi x a
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 Vậy lim . x a x a
Câu 28. Chọn B x x x 2
Ta có lim x 2 lim 0 . 2 x 2 x 2 x 4 x 2 Câu 29. Lời giải Chọn B lim 2x 1 1 x 1 2x 1 lim x 1 0 lim x 1 x 1 x 1
x 1 x 1 0
Câu 30. Chọn C x 2 x(x 2) (x 2)x lim (x 2) = lim lim 0 2 2 x2 x 4 x 2 x 2 x 4 x 2
Câu 31. Chọn A
Đặt f x x 1; g x x 1. Ta có lim f x 2; lim g x 0; g x 0khi x 1 x 1 x 1 x 1 Vậy lim . x 1 x 1
Câu 32. Chọn A
Ta có lim 1 2x 1 ; lim x
1 0 và x 1 0, x 1 x 1 x 1 1 2x lim . x 1 x 1
Câu 33. Chọn C Ta có: lim
và x 1 0, x 1 (do x 1 ) 2 x 1 2 0; lim x 1 0 x 1 x 1 2 x 1 lim . x 1 x 1
x x 1 x 22 2 3x 3 Câu 34. Ta có: lim lim 2 lim x x 1 x 2 x
x 2x x1x2 x 2x x1x2 3 3 3 lim x
đáp án A đúng. x 1 1 2 2 1 1 2 x x x lim
x x x x . x 1 1 2 2 1 2 lim 1 1 2 x x x x 1 1 2 1 1 2
Do lim x và lim 1 1
2 0 nên lim x 1 1 x 2 x x x x 2 x x x x đáp án C đúng. 3x 2
Do lim 3x 2 1
0 và x 1 0 với x 1 nên lim
đáp án B sai. x 1 x 1 x 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3x 2
Do lim 3x 2 1 0 và x 1 0 với x 1 nên lim
đáp án D đúng. x 1 x 1 x 1 4x 3 Câu 35. Ta có lim
vì lim 4x 3 1 , lim x
1 0 , x 1 0 khi x 1 . x 1 x 1 x 1 x 1 3 2x Câu 36. Xét lim
thấy: lim 3 2x 1 , lim x 2 0 và x 2 0 với mọi x 2 nên x 2 x 2 x 2 x 2 3 2x lim . x 2 x 2
Câu 37. Ta thấy lim f x và lim f x . x 1 x 2 2 x 2x 3 x 1 x 3 Câu 38. Ta có lim lim
lim x 3 4 . x 1 x 1 x 1 x 1 x 1
lim 3x 7 1 0 x2 3x 7
Câu 39. lim x 2 0 lim . x2 x2 x 2
x 2 x 2 0
Câu 40. Chọn B 2 x 3 4 x 3 1
Ta có lim f x lim lim lim . 2 x 1 x 1 x 1 x 1 x 1 x
1 2 x 3 x 1 x 1 2 x 3 Câu 41.
Hướng dẫn giải Chọn C
Ta có: + lim f (x) 4 0 . x 1 + lim x 4 1 0 và với x 1 thì x 4 1 0 . x 1 f (x) Suy ra lim .
x x 4 1 1
Câu 42. Chọn B 1 12 2 x 2x 8
x 2 x 4
Ta có : lim f x lim lim lim 3 x2
x2 x 2 x 8 x
x 2 2
x 2x 4 x x 2 2 2 2
x 2x 4 x 4 1 lim 2 x2 x 2x 4 2 2 2 m m
lim f x lim x 2m 2m 2 x 2 x 2 2 2 2 m 1
Hàm só có giới hạn tại x 2 khi chỉ khi lim f x lim f x 2m 2 x 2 x 2 2 2 2 m 3 m 3 2m 0 . 2 2 m 1
Câu 43. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Do hàm số f x có giới hạn hữu hạn khi x dần tới 2 nên x 2
là nghiệm của phương trình 2
x ax b 0 , do đó ta 4 2a b 0 .
x 2 a , x 2
Ta viết lại hàm số f x x 2
x 1, x 2
Mặt khác hàm số tồn tại giới hạn 2 2 a
lim f x lim f 2 1
a 8 b 12 x 2 x 2 2 2
Do đó 3a b 12 .
Câu 44. Chọn D D .
Xét: lim f x lim 2 x ax
1 2a 5; lim f x lim 2 2x x 1 7. x2 x2 x2 x2
Hàm số y f x có giới hạn tại x 2 khi và chỉ khi
lim f x lim f x 2x 5 7 a 1. . x 2 x 2 Câu 45. Ta có: x 4 2 x 4 2 2 x 1 1
lim f x lim lim lim lim . x 0 x 0 x x 0
x x 4 2 x 0
x x 4 2 x 0 x 4 2 4 1 1
lim f x lim mx m m x 0 x 0 4 4
Hàm số đã cho có giới hạn tại x 0 khi và chỉ khi lim f x lim f x x 0 x 0 1 1 m m 0 . 4 4
DẠNG 3. GIỚI HẠN TẠI VÔ CỰC
Câu 46. Vì có thể b 0 .
Câu 47. Chọn B 3 1 1 Ta có 5 3 lim 4
x 3x x 1 5 lim x 4 . x 2 4 5 x x x x 3 1 1 lim 4 4 0 2 4 5 Vì x x x x . 5 lim x x
Câu 48. Chọn B 1 1 Ta có lim 3 2 2x x 3 1 lim x 2 . 2 3 x x x x 1 1 1 Câu 49. 3 2
lim 3x 5x 9 2x 2017 3 lim x 3 5 9 2 2017 . x 2 3 x x x x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 2 2x 1 1 Câu 50. lim lim x .
x 4x 2 x 2 2 4 x
Câu 51. Chọn D
Ta có a lim y . x 1 1
Câu 52. Áp dụng quy tắc tìm giới hạn, ta có: lim lim 0 . x 2 5 x x 5 x 2 x 1 1 1 x 1 Câu 53. Ta có lim lim x .
x 3x 2 x 2 3 3 x 1 3 3x 1 Câu 54. Ta có lim lim x 3 .
x x 5 x 5 1 x 3 3 x 4 4 3 4x x x 4 Câu 55. lim lim lim .
x 5x 2 x 2 x 2 5 x 5 5 x x 8 x 2 8 2 2x 8 x Câu 56. lim lim lim x 2 .
x x 2 x 2 x 2 x 1 1 x x 1 x 2 1 2 2x 1 x 2 0 x
Câu 57. Ta có L lim lim lim 2 .
x x 1 x 1 x 1 1 0 x 1 1 x x 1 2 2x 1 Câu 58. Ta có: lim lim x 2 .
x 3 x x 3 1 x
Câu 59. Chọn B 2018 3 2 1
x 2018x 3 2 1 lim lim x x 2 x 2x 2018x x 2018 2 2 x
Câu 60. Chọn D 3 2 2 1 2 x 3x 2 1 Ta có lim lim x x 2 x 2x 1 x 1 2 2 2 x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3 1 5 3 2 2x 3x 1 2 5 Câu 61. lim lim x x 2 . 3 4 5
x 4x 2x x 3 x 4 2 3 1 2 5 x x x 1 2 1 1 x 1 x 2 x x Câu 62. lim lim 1. 2 x x 9 x 9 1 2 x
Câu 63. ChọnC x s inx x sin x sin x Ta có lim lim lim 1 lim 1 0 1. x x x x x x x x sin x 1 1 sin x ( Do
khi x , mà lim 0 lim 0 ). x x x x x x
Câu 64. Chọn A 1 Ta có 2 lim x 2 x 2 lim 2x x x x x x 1 1 lim x 2
x lim x 2 1. x x x x 1
Vì lim x và lim 2 2
1 1 2 0 nên lim
x x x 2x . x x x 3 5 2 1 x 3x 5 2 x x 1 Câu 65. Ta có lim lim . x 4x 1 x 1 4 4 x 1 2 2x 1 2x 1 Câu 66. Ta có: lim lim lim x 2 . x 2 x 1 1 x 1 x 1 1 x 1 1 1 2 x 2 x x
Câu 67. Chọn B 2 1 x 2 1
Chia cả tử và mẫu cho x , ta có lim lim x 1.
x x 3 x 3 1 1 x
Câu 68. Chọn D 2 3 3x 2 3 Ta có lim lim x I .
x 2x 1 x 1 2 2 x Câu 69.
Hướng dẫn giải Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 x Ta có: lim lim x 0 . 2
x x 1 x 1 1 2 x
Câu 70. Chọn C 1 1 x 3 3 1 3x x 3 3 2 Ta có: lim lim lim x . x 2 2x 3 x 3 x 3 2 2 x 2 2 2 2 x x
Câu 71. Chọn C 1 1 1 x 1 Ta có lim lim x .
x 3x 2 x 2 3 3 x
Câu 72. Chọn A 1 3 3x 1 Ta có lim lim x 3 .
x x 5 x 5 1 x Chọn C Câu 73. a 2 c 2 cx a c 0 Ta có lim lim x c . 2 x x x b b 1 0 1 2 x
Câu 74. Chọn D 1 4 4x 1 lim lim x 4 .
x x 1 x 1 1 x
Câu 75. Chọn B 1 1 x 1 1 Ta có lim lim x .
x 6x 2 x 2 6 6 x
Câu 76. Chọn B 1 1 x 1 1 Ta có lim lim x .
x 4x 3 x 3 4 4 x
Câu 77. Chọn D 2 2 2 x 1 2 1 2 2 2 x 2 2 x x x lim lim lim 1 x x 2 x x 2 x 2 1 x Câu 78. Lời giải
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Chọn B 3 2 3 3 x 1 x 1 1 2 2 2 2 x 3 x x x lim lim lim lim 1 . x x 3 x x 3 x x 3 x 3 1 x Câu 79. Lờigiải Chọn B 3 3 2 x 1 1 x 3 x x Ta có: lim lim lim 1 x x 3 x 3 x 3 x(1 ) (1 ) x x .
Câu 80. Chọn B 1 2 1 2 4 x 1 1 4 2 2 4 2 4 x x 2 x x x x 3 Ta có: lim lim lim . x 3 x 1 3x 1 x x 4 1 1 1 1 3 x 1 3 1 3 3 3 x x x x
Trắc nghiệm: Sử dụng máy tính Casio
+ Bước 1: Nhập biểu thức vào màn hình máy tính: + Bước 2: Nhấn phím
+ Bước 3: Nhập giá trị của X: và nhấn phím + Bước 4: Kết quả . Vậy chọn đáp án B
Câu 81. Chọn B 3 4 1 1 4 2 4x 3 1 2x 4 1 x x lim f x 3 lim lim 2 8 . x x 3 2x7 7 x 3 2 x
Câu 82. Chọn B 7 5 2 m 2 m x 7x 5 m 4 lim lim x x m 8 2
x 2x 8x 1 x 8 1 2 2 2 x x
Câu 83. Chọn D 2
4x 3x 1 23 4 a 0 a 4 lim
ax b 0
lim 4 a x b 11 0 x x 2 x x 2 11 b 0 b 11
a b 7 .
Câu 84. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2018 2018 2 x 1 1 2 2 x 2018 x x Ta có lim lim lim 1. x x 1 x 1 x 1 x 1 1 x x
Câu 85. Chọn C 1 2 1 x 1 2 lim lim x x .
x x 1 x 1 1 x Câu 86. Lờigiải Chọn D 3 5 2 a 1
ax x 3x 5 2 a 1 a 1 Ta có lim 2 x x lim 2 2 3 . x 2x 7 x 7 2 2 2 x
a 1 6 a 5
Câu 87. Chọn D 1 3 x 3 2 0 Ta có lim lim x x 0 . 2
x x 2 x 2 1 1 2 x
Câu 88. Chọn B 1
Xét mọi dãy số x sao cho lim x lim 0 n n xn sin x sin x Ta có lim lim n
x x x n sin x 1 1 sin x Ta có n mà lim 0 n nên
nhỏ hơn một số dương bé tùy ý kể từ số hạng x x x x n n n n nào đó trở đi sin x
Theo định nghĩa dãy số có giới hạn 0 ta có lim n 0 x n sin x Vậy lim 0
x x
Câu 89. Chọn C. 3 1 x 3 lim lim x 1 .
x x 2 x 2 1 x
Câu 90. Chọn B Ta có:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 2018 x .x. 4 2018 2 2018 2 x 4x 1 x 4x 2 1 x lim lim lim 2019 2019 2019 x 2x x x 1 1 1 2019 x 2 x 2 x x 1 4 2 x 4 0 2 1 lim 2019 2019 2019 2018 x 2 2 1 2 0 2 x
Câu 91. Chọn A 2 2 x 3x 1 a
1 x a b 3 x b 1 lim +ax b 1 lim 1 x x 1 x x 1 b 1 a
1 x a b 3 lim x 1 x 1 1 x a 1 0 a 1
a b 3 1
T a b 2 . b 1 b 1 0
Câu 92. Chọn A 2 x 1 a 2
1 x 2a b x 2b 1 lim
ax b lim 5 x x 2 x x 2 a 1 0 a 1 2a b 5 b 7
Vậy a b 6
Câu 93. Chọn C 3 5 2 1 2 x 3x 5 1 lim lim x x . 2 x 2 3 x x 2 3 3 2 x
Câu 94. Chọn A 3 5 5x 3 5 Ta có: lim lim x . x 1 2 x x 1 2 2 x Câu 95. Lời giải Chọn B 2 1 x 2 lim lim x 1.
x x 3 x 3 1 x
Câu 96. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 5 2 2x 5 2 lim lim x 2.
x x 3 x 3 1 1 x
Câu 97. Chọn C 1 3 3x 1 3 0 3 Ta có: lim lim x L . x 1 2 x x 1 0 2 2 2 x Câu 98. Lời giải Chọn B 3 2 3 3 x 1 x 1 1 2 2 2 2 x 3 x x x lim lim lim lim 1 . x x 3 x x 3 x x 3 x 3 1 x
Câu 99. Chọn C 2x 3 2x 3 2x 3 Ta có: lim lim lim x 2 x 1 x x 1 x 1 2 x (1 ) x x 1 x 2 2 x x 3 2 lim x 1 . x 1 1 1 2 x 2 3 2 5 5x 2x 3 2 Câu 100. Ta có: lim lim x x 5 . 2 x x 1 x 1 1 2 x 1 1 2 2 4 . x x x x x x x Câu 101. Vì lim lim lim . Vậy A đúng. x 1 2 x x 1 x 1 x 2x 2x x x 3 2 2x 3 2 Câu 102. Ta có: lim lim x .
x 1 3x x 1 3 3 x 1 1 2 x 4 4 2 2 4x 1 Câu 103. Ta có: x x K lim lim lim 2 . x x 1 x x 1 x 1 1 x 1 1 2 x 1 1 x x Câu 104. lim lim . 0 . 2018 2017 x x 1 x x 1 1 2017 x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 1 1 2 x ( 1) 2 1 x x 1 1 Câu 105. lim lim x x lim x( 1) 2 x x x x x x x 1 1 2 x x 1 1 1
x x x x x Câu 106. Ta có: lim lim lim 2 . x x 1 x x 1 x 1 1 x 2 2x x Câu 107. lim 2 . 2 x x 1 sin x 1 sin x 1 Câu 108. lim lim lim 0 0 0 . x x x x x x 1 1 1 1 2 x 1 1 2 2 x x 1 x x x x 1 Câu 109. lim lim lim x 2 x x 2 x x 2 2 1 1 1 1 2 x 1 1 2 2 x x 1 x x x x 1 lim lim lim Sửa x 2 x x 2 x x 2 2 2 2 2
x 3x ax 2
x 3x ax
x 1 a x 3 Câu 110. Ta có lim lim lim x bx 1
x bx 1 2
x 3x ax x bx 1 2
x 3x ax 2 a 3 1 2 1 a a 1 lim x 3 . x 1 3 b 1 a b b 1 a x x 3 2017 a 2 2
a 2x 3 2017 1 2 x x 1 a 2 1 2 Câu 111. Ta có: lim lim a . x 2x 2018 2 x 2018 2 2 2 2 2 x 1 1 4 4 2
4x x 1 4 2 x x x 2 Câu 112. Ta có lim lim . x mx 2 x 2 m m x 2 1 Theo bài ra ta có:
m 4 6; 3 . m 2
2 a x 3 Câu 113. Ta có lim
lim 2 a x 3 x x
2 a 0 a 2. x x 2 1 2 x x 1
Với a 2 a a 2 0 suy ra P a a 2 4 4 .
Câu 114. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1 1 3 2 2 x 4 x 1
4x x 1 x x 3 2 2 x x x x lim lim x 3x 2 x 3x 2 1 1 1 3 4 1 2 2 x x x x 1 lim . x 2 3 3 x
Câu 115. Chọn B 3 1 x 3 x 3 1 Ta có: lim lim lim x . x 2 4x 1 2 x 1 x 1 2 2 x 4 2 4 2 x 2 x x
DẠNG 4. GIỚI HẠN VÔ ĐỊNH DẠNG 4.1 DẠNG
Dạng 4.1.1 Không chứa căn
Câu 116. Chọn A x 1 1 Ta có: lim lim . x 1 . 2 2 x 2 x 2
x2 x 2 1 Do lim
và lim x 1 1 0 .
x x 22 2 x 2
Câu 117. Chọn C 3 2 x 1 x
1 x x 1 A lim lim lim 2 x x 1 3 . x 1 x 1 x 1 x 1 x 1
Câu 118. Chọn C 2 x 12x 35
x 7 x 5 x 7 2 Ta có lim lim lim . x 5 x5 25 5x 5 x 5 x5 5 5
Câu 119. Chọn B 2 x 4
x 2 x 2 Ta có: lim lim
lim x 2 4 . x2 x2 x2 x 2 x 2
Câu 120. Chọn B 2 x 9 Ta có: lim
lim x 3 6 . x3 x 3 x3
Câu 121. Chọn A 2 x 5x 6
x 2 x 3 I lim lim
lim x 3 1. x2 x 2 x2 x 2 x2
Câu 122. Chọn B 2 x 3x 2
(x 1)(x 2) Ta có: lim lim
lim(x 2) 1 x 1 x 1 x 1 x 1 x 1
Câu 123. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 x 3x 2
(x 1)(x 2) x 1 1 lim lim lim . 2 x2 x2 x2 x 4
(x 2)(x 2) x 2 4
Do đó a 1; b 4 suy ra 2 2 S 1 4 17.
Câu 124. Chọn A 2 2018 x 4 2018 2018 (x 2 )(x 2 ) lim = 2018 2019 lim lim (x 2 ) 2 . 2018 2018 2018 x2 x 2 2018 2018 x2 x2 (x 2 )
Câu 125. Chọn A 2018 x x 2 2018 x 1 x 1 Ta có lim lim 2017 x 1 x x 2 2017 x 1 x 1 x 1 x 1 2017 2016 x x ... x 1 x 1 2017 2016 x x ... x 2 lim lim
x x 1 2016 2015 1 x x ... x 1 x 1 2016 2015 x 1 x x ... x 2 11 .... 1 2 2019 11 ... 1 2 2018 Vậy 2 2
a b 4037 .
Câu 126. Chọn D 10 2x 2x 10 2 1 lim lim lim 2 2 x 5 x 5 x 5 x 6x 5 x 6x 5 x 1 2
Câu 127. Chọn B 3 x 2 1 a 3 2 x a
x a x x a
x x a 2 1 2a 1 lim lim lim . 3 3 xa xa x a
x a 2 2
x ax a 2 2 2
xa x ax a 3a
Câu 128. Chọn B 4 2 2 2 x 3x 2 x 1 x 1 x 2 x 1 x 2 2 lim lim lim . 3 x 1 x 2x 3 x x 1 2 1 x x 3 2 x 1 x x 3 5
Câu 129. Chọn A 3 2 x 1 x x 1 3 a 3 Ta có: lim lim S 5 . 2 x 1 x 1 x 1 x 1 2 b 2
Câu 130. Chọn A 2
x bx c Vì lim
8 là hữu hạn nên tam thức 2
x bx c có nghiệm x 3 x3 x 3
3b c 9 0 c 93b Khi đó 2 2
x bx c
x bx 9 3b x
3 x 3 b lim lim lim x3 x3 x3 x 3 x 3 x 3
limx 3b 8 6 b 8 b 2 c 15 x3
Vậy P b c 13 .
Câu 131. Chọn A 2 x x 2 x 1 x 2 x 2 3 L lim lim lim . 2 x 1 x 1 3x 8x 5 x 1 3x 5 x 1 3x 5 2
Câu 132. Cách 1: 2
x ax b Để lim 3 thì ta phải có 2
x ax b x 3 x m . x3 x 3
Khi đó 3 m 3 m 0 . Vậy 2
x ax b x 3 x 2 x 3x .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Suy ra a 3 và b 0 . Cách 2: 2
x ax b 3a b 9 Ta có
x a 3 . x 3 x 3 2
x ax b 3
a b 9 0 a 3 Vậy để có lim 3 thì ta phải có . x3 x 3 a 6 3 b 0 x 2 x 2 1 1 Câu 133. lim lim lim . 2 x2 x2 x 4
x 2 x 2 x2 x 2 4 2 x 3x 4 x 1 x 4
Câu 134. Ta có: L lim lim
lim x 4 5 . x 1 x 1 x 1 x 1 x 1 2 ax bx 5 Câu 135. Vì lim
7 hữu hạn nên x 1 phải là nghiệm của phương trình 2
ax bx 5 0 suy ra x 1 x 1
a b 5 0 b 5 a . 2
ax 5 a x 5 x 1 ax 5 Khi đó lim lim
a 5 7 a 2 nên b 3 x 1 x 1 x 1 x 1 Suy ra: 2 2
a b a b 18 . 2 x 16
x 4 x 4 x 4 8 Câu 136. lim lim lim . 2 x4 x4 x x 20
x 4 x 5 x4 x 5 9
1 cos 3x cos 5x cos 7x
Câu 137. Ta có lim f x lim 2 x0 x0 sin 7x
1 cos 3x cos 3x cos 3x cos 5x cos 3x cos 5x cos 3x cos 5x cos 7x lim 2 x0 sin 7x 1 cos 3x
cos 3x 1 cos 5x
cos 3x cos 5x 1 cos 7x lim lim lim 2 2 2 x0 x0 x0 sin 7x sin 7x sin 7x 3x 5x 7x 2 2 2 2 sin 2sin 2 sin 2 2 2 lim lim lim 2 2 2 x0 x0 x0 sin 7x sin 7x sin 7x 9 25 49 2 4 4 4 83 . 49 98 x 1 2 3 x x 1 a x x ax a 1 1 Câu 138. lim lim lim 2
x x 1 a 3 a a 1. x 1 x 1 x 1 x 1 x 1 Vậy 2
M a 2a 3 .
Câu 139. Chọn B
Đặt: t x . 2 cos t 2 sin t Khi x
thì t 0 . Vậy L lim lim 1. 2 t0 t0 t t
Câu 140. Chọn D
Vì hàm số có giới hạn hữu hạn tại x 1 nên biểu thức tử nhận x 1 làm nghiệm, hay 1 a b 0 . 2
x ax 1 a 1 x
1 x 1 a 1
Áp dụng vào giả thiết, được lim lim . 2 x 1 x 1 x 1 2 x 1 x 1 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 1 a 1 2 a 1 lim a 3 . Suy ra b 2 . x 1 x 1 2 2 2 Vậy 2 2
a b 13 . Dạng 4.1.2 Chứa căn
Câu 141. Chọn C 2 x x 2 3 2 x x 12 Ta có lim lim x3 x 3
x3 x 3 2x x 2 3
x 3 x 4 x 4 3 4 7 7 3 lim lim .
x3 x 3 2x x 2 3 x3 2x x 2 3 2 3 3 2 3 4 3 12
Câu 142. Chọn B 3 3
2 1 x 8 x
2 1 x 22 8 x 2 1 x 1 3 2 8 x Ta có: x x x x 2 1 . Do vậy: 1 x 1
4 2 8 x 8 x2 3 3 2 1
lim f x lim x0 x0 3 1 x 1 3
4 2 8 x 8 x2 2 1 lim lim x0 x0 3 1 x 1 3
4 2 8 x 8 x2 1 13 1 . 12 12
Câu 143. Chọn C Ta có x 2 5 5 x 2 2 x 16 4 5 5 2 2 16 4 x x 2 5 5 x 2 5 5 x 2 x 2 x 16 4 2x 16 4 2 x 2 5 5 x 2 x 2 5 5 x 2 5 5 x Khi đó ta có x 2 2 x 16 4 5 5 4 lim lim
a 2b 14 x0 2 x0 x 16 4 2 5 5 x 5
Câu 144. Chọn C 2
x 3x 4 2 2
x 3x 4 4 x 3 3 lim lim lim . x0 x x0 x 2
x 3x 4 2 x 0 2
x 3x 4 2 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 145. Chọn C 2 x x x
1 x 26 x 8 x 17
x 26 x 8 x 17 3 2 lim lim lim x
6 x 8 x 17 x x 2 1 1 x 1 1 x 1
Ta có lim x 2
6 x 8 x 17 36 x 1 lim x
1 0 và x 1 0 x 1 2 x 3x 2 lim . x 1
6 x 8 x 17
Câu 146. Chọn A 3 2 8 x 2 2 8 x 8 Ta có: lim lim . 2 x0 x x 0 2 x 2 8 x 2 3 2 3 2 8 x 4 1 1 lim . x 0 2 x 2 3 2 3 12 8 2 8 x 4
Câu 147. Chọn B 3 2
x x 1 1 3 2 x x 11 x 1 1 lim lim lim . 2 x0 x x0 2 x 3 2
x x 1 1 x0 3 2
x x 2 1 1
Câu 148. Chọn A 2
x 1 5x 1
x 4x 3 x 1 5x 1 2
x 4x 3 x 3x lim lim . lim . x3 x 4x 3 2 x3 2
x 1 5x 1 x 4x 3 x3
x 1 5x 1 x 4x 3
x 4x 3 x 6 3 9 lim . .
a 9 , b 8 a b 1. x3
x 1 5x 1 x 1 8 2 8
Câu 149. Chọn C 2 x x
x 2 x 3 4x 1 3
x 3 4x 1 3 5 6 3 lim lim lim . x2 x2 4x 1 3 4 x 2 x2 4 2
Câu 150. Chọn C 2 x 2x 1 x 2x 1 x 1 Ta có lim lim lim 0 . 2 x 1 x 1 x x 2 x
1 x 2 x 2x 1 x 1
x 2x 2x 1
Câu 151. Chọn D x 1 2 x 3 1 1 lim lim lim . x3 x 3 x3 2
x 3 x 1 2 x3 x 1 2 2
Suy ra a 1;b 2 .
a b 2018 1 2 2018 2021.
Câu 152. Chọn A 3 3 3
ax 1 1 bx
ax 1 11 1 bx
ax 1 1 1 1 bx + lim lim lim x0 x0 x0 x x x x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 ax 11 1 1 bx lim x 2 0 3 3 x 1 1 1 1 1 bx x ax ax a b a b lim x ax 12 0 3 3 1 1 bx 3 2 ax 1 1
3 ax 1 1 bx a b Theo giả thiết lim 4
4 2a 3b 24 x0 x 3 2
2a 5b 8 a 6 + Ta có hệ nên a 5 là sai. 2a 3b 24 b 4
Câu 153. Chọn D
Theo giả thiết ta có f 4 2018
1009 f x 2018 Ta có lim
x4 x 2 2019 f x 2019 2019
1009 f x 2018 x 2 1009.4.2019 lim 2018
x4 x 4 2019 f x 2019 2019 2019.2018 2019 2019
Câu 154. Chọn C 2
x 3xx 4x 3
xx 4x 3
x 1 5x 1 Ta có: lim lim lim x 3 x 4x 3 x 3 2 x 4x
3 x 1 5x 1 x 3 x
1 x 1 5x 1 3.6 9 a 9 . Vậy
a b 1. 2.8 8 b 8
Câu 155. Chọn B 2 2
ax 1bx 2
ax 1bx 2 Ta có lim lim ,
L với L (*) 3 x 1 x 1 x 3x 2 x 2 1 x 2 b 2 b 2
Khi đó a 1 b 2 0 a 1 b 2 2 2 a
1 b 4b 4 a
b 4b 3 Thay 2
a b 4b 3 vào (*): ax bx
2b 4b 2 2
3 x 1bx 2 1 2 lim lim 3 x 1 x 3x 2 x 2 1 x 2 x 1
b 4b
3 x 1bx 22 2 2 lim x 1 x 2
1 x 2 2
b 4b 2
3 x 1 bx 2 4b 2 3 x 4bx 3 lim x 1 x 2
1 x 2 2
b 4b 2
3 x 1 bx 2 4b 3 x 3 lim
L, L . x 1 x
1 x 2 2
b 4b 2
3 x 1 bx 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Khi đó: b 3 4
3 3 0 b 3 a . 2 4 45 Vậy 2 2 a b 16
Câu 156. Chọn C x x 2
x 3x x 4x 3 1 5 1 lim lim x3 x 3 x 4x 3 2
x 4x 3 x 1 5x 1
x x 4x 3 3.3 3 9 lim .
x3 x
1 x 1 5x 1 2.4 4 8
Vậy T 2a b 10 .
Câu 157. Chọn C 2 x 2x 8
(x 2)(x 4)( 2x 5 1)
(x 2)(x 4)( 2x 5 1) Ta có: lim lim lim x 2 x 2 x 2 2x 5 1
( 2x 5 1)( 2x 5 1) 2(x 2)
(x 4)( 2x 5 1) lim 6 x2 2
Câu 158. Chọn A f (x) 16 Do lim
12 nên ta có f (2) 16 0 hay f (2) 16 . x2 x 2
3 5 f (x) 16 4 5( f (x) 16) lim lim 2 x2 x2 2 3 x 2x 8 3
(x 2)(x 4)( (5 f (x) 16) 4 5 f (x) 16 16) f (x) 16 5 lim . x2 2 3 x 2 3
(x 4)( (5 f (x) 16) 4 5 f (x) 16 16) 5 5 12. . 6.48 24 x 3 2 x 3 4 1 1 Câu 159. Ta có: lim lim lim . x 1 x 1 x 1 x
1 x 3 2 x 1 x 3 2 4
Câu 160. Chọn A 4x 1 1 4x 4 2 Ta có K lim lim lim . 2 x0 x 3x
x0 x x 3 4x 1 1
x0 x 3 4x 1 1 3 x 2 2 x 2 1 1 Câu 161. lim lim lim . x2 x 2
x2 x 2 x 2 2 x2 x 2 2 4
1 x 2 x x 1 1
Câu 162. L lim lim
lim 2 x 1 2 . x 1 x 1 x 1 2 x 1 x 1 2 x 2 2 x 3 2 6 Câu 163. Ta có lim lim
lim 2 x 3 4 3 . x 3 x 3 x 3 x 3 x 3
Suy ra a 4 , b 3 . Vậy P a b 7 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3x 1 1 3x 11 3 3 Câu 164. Ta có: lim lim lim . x0 x0 x
x 3x 1 x0 1 3x 1 1 2 Câu 165. Ta có: 2
4x 2x 1 1 2x 2 4x lim lim x0 x x0 x 2
4x 2x 1 1 2x 4x lim 0 . x0 2
4x 2x 1 1 2x 2 3 2 3
x x 2 7x 1
x x 2 2 2 7x 1 Câu 166. Ta có lim lim x 1 2 x x 1 1 2 x 1 2 3
x x 2 2 2 7x 1 lim lim I J . x 1 2 x x 1 1 2 x 1 2 2
x x 2 2
x x 2 4 Tính I lim lim x 1 2 x x 1 1 2 x 1 2
x x 2 2 x 1 x 2 x 2 3 lim lim . x 1 x 2 x x x 1
2x x 4 2 2 1 2 2 2 2 2 3 2 7x 1 8 7x 1 và J lim lim x 2 x 2 1 x 1 1 2 x 3 1 4 2 7x 1 3 7x 1 7 7 lim . x x x 2 1 3 3 12 2 2 4 2 7 1 7 1 2 3
x x 2 7x 1 2 Do đó lim I J x 1 2 x 1 12
Suy ra a 1 , b 12 , c 0 . Vậy a b c 13 .
Câu 167. Chọn B x 2 x 2 1 1 I lim lim lim . 2 x 2 x 2 x 2
x 2x 2 x 2 x 2 2 2
Câu 168. Chọn A x x
2x x 32x x 3 2 3 2 4x x 3 I lim lim lim 2 x 1 x 1 x 1 x 1 x
1 2x x 3 x 1 x 1 x
1 2x x 3 x 1 4x 3 4x 3 7 lim lim x 1 x 1 x
1 2x x 3 x 1 x
1 2x x 3 8
Câu 169. Chọn D Ta có
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 1 1 1 2 2 x 1 x 4 x 1 x 4 2 2
x x 4x 1 x x x x lim lim lim x 2x 3 x 3 x 3 x 2 x 2 x x 1 1 1 4 2 x x 1 0 4 0 1 lim x 3 2 0 2 2 x
Câu 170. Chọn B Cách 1:
f x 20 10x 20 10 x 2
Chọn f x 10x , ta có lim lim lim 10 . x2 x2 x2 x 2 x 2 x 2 3 6 f x 3 3 5 5 60x 5 5 60x 5 5 Lúc đó T lim lim lim 2 2 x2 x2 x2 x x 6 x x 6
x 2 x 3 3 60x 5 5 lim 2
x2 x 2 x 33 3
60x 5 5 60x 5 25 60 x 2 lim 2
x2 x 2 x 33 3
60x 5 5 60x 5 25 60 4 lim 2
x2 x 3 3 x x 25 3 60 5 5 60 5 25 Cách 2:
Theo giả thiết có lim f x 20 0 hay lim f x 20 * x2 x2
3 6 f x 5 5
6 f x 5 125 Khi đó T lim lim 2 2 x2 x2 x x 6 2
x x 6 3 6 f x 5 5 3 6 f x 5 25
6 f x 20 T lim 2 x2
x 2 x 3 3 6 f x 5 5 3 6 f x 5 25 10.6 4 T . 5.75 25
Câu 171. Chọn A x 3x 1 16 3 x 4 3 1 4
33 x 4 18 9 Ta có lim lim lim . x5 x5 3 x 4
9 x 4 x5 8 4
3x 1 4 3x 1 4 Câu 172.
Hướng dẫn giải Chọn C f x 16 f x 16 Vì lim 24 f
1 16 vì nếu f 1 16 thì lim . x 1 x 1 x 1 x 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 f x 16 1 f x 16 Ta có I lim lim 2 . x 1 x
1 2 f x 4 6 x 1 12 x 1
Câu 173. Chọn C x x lim lim 7
x0 x 1. x 4 2 7
x0 x 1. x 4 x 4 x 4 2 x lim
x0 x 4.7 x 1 1 x 4 2
x x 4 2 6 5 4 3 2 x x x x x x 1 lim x0 x 4. x 1 1 x 4 2 6 5 4 3 2 x x x x x x 1 2 x 4 2
x 4 2 6 5 4 3 2 x x x x x x 1 4 lim . x0 x 4 x 4 2 6 5 4 3 2 x x x x x x 1 9
Suy ra a 4 , b 9 , L a b 13 . Trình bày lại: Chọn A x a 7 1
x 1. x 4 2 b Đặt L lim thì lim . 7 x0
x 1. x 4 2 b L x a Ta có 7 7 b
x 1. x 4 x 4 x 4 2
x 1. x 4 x 4 x 4 2 lim lim lim x0 x0 x0 a x x x
. x 4 7 x 1 1 7 x t 1 Xét L lim .Đặt 7 t x 1 .Khi đó: 1 x0 x
x 0 t 1 7
t 3 t 7 1 t 3 2 L lim lim 1 7 t t 1 t 6 5 4 3 2 1 1
t t t t t t 1 7 x
x 4 2 x 4 2 4 2 1 1 Xét L lim lim lim 2 x0 x0 x
x x 4 2 x0 x 4 2 4 b 2 1 15 Vậy
a 28,b 15 a b 43 a b 43 . a 7 4 28 Câu 174. Ta có 3 3
x 1 x 5 x 1 2 x 5 2 lim lim . x3 x3 x 3 x 3 x 3 x 1 4 x 5 8 lim
x3 x 3 x 1 2 x 3 3 x 5 2 3
2 x 5 4 1 1 1 1 1 lim x3 x 1 2 3 x 52 3 4 12 6 2 x 5 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 DẠNG 4.2 DẠNG ∞ − ∞
Câu 175. Chọn D 2 2 x 1 x 1 Xét lim lim 0 . 2 lim x 1 x x x 2 x 2 x 1 x x 1 x
Câu 176. Chọn B ax a a lim
x ax x x 2 9 3 lim lim x 2 x
x ax x a 6 9 3 9 3 x a 2 a 12 6
Câu 177. Chọn C 3 x Ta có: M lim
x x x x x 2 2 4 lim x 2 2 x 4x x x 3 x 3 3 lim lim . x 4 1 x 4 1 2 x . 1 1 1 1 x x x x
Câu 178. Chọn C x 1 lim
x x x 5 . x 2 2 2 5 2 5 lim lim x 2
5x 2x x 5 x 2 5 5 5 x 1 Suy ra: a
, b 0 . Vậy S 1 . 5
Câu 179. Chọn B 1 1 Ta có: 2 lim
x x 2x lim x 1
2x lim x 1 2x x x x x x 1 1
lim x 2 1 vì lim x và lim 2 1 1. x x x x x
Câu 180. Chọn A
x x 2 x 22 2 3 x 2 lim lim . 2 lim x x 2 x 2 x
x 2x x2 x2 x 2x x2x2 2 3 3 lim x . x 1 2 2 2 1 1 2 x x x
Câu 181. Chọn C lim x x x x x x 1 1 2 3 9 1 lim 3 9 lim 3 9 2 2 x x x x
Câu 182. Chọn D 1 a ax 1 a TH1: b 2 lim x
x ax x x 2 4 1 2 lim lim . x 2
4x ax 1 2 x x a 1 4 4 2 2 x x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 a
x ax bx a . x 2 lim 4 1 1 1 4 4 a 1 neáu b > 2 TH2: b 2 lim
x ax bx x b x 2 4 1 lim 4 2 x x x neáu b < 2 Vậy 2 3
a 4,b 2 P a 2b 0 .
Câu 183. Chọn C 1 8 8x 1 - 2 lim ( 4 8 1 2 ) lim lim x x x x 2 ------------------------ x x 2
4x 8x 1 2 x x 8 1 4 2 2 x x ----------------------.
Câu 184. Chọn D 2 Ta có: lim x x x 3 3 1 2 lim 1 x 3
x x x 2 3 x 22 2 3 3 2 2 2 = lim 1 lim 1 x 1 2 2 x x 2 2 2 2 2 3 3 3 3 x 1 1 1 1 1 1 3 3 3 3 x x x x Vậy lim 3 3 x 1 x 2 1 x
Câu 185. Chọn D 2 2
x x x lim
x x x x 2 3 1 2 2 2 3 1 2 lim x 2
2x 3x 1 x 2 1 1 x 3 3 x 3 2 lim lim x x 3 1 x 3 1 4 x 2 2 2 2 2 2 x x x x
Vậy a 3 ; b 4 a b 7 .
Câu 186. Chọn C
Đường thẳng : y ax 6b đi qua điểm M 3; 42 nên 3a 6b 42 a 2b 14 . ax lim
x ax x b b x 5 1 2 36 5 1 6 lim x 2
36x 5ax 1 6 1 5a 5a lim x b b . x 5a 1 12 36 6 2 x x 5a 20 5
a 12b 80 a 4 Do đó b
5a 12b 80 . Ta có hệ: . 12 3 a 2b 14 b 5 Vậy 2 2
T a b 41.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 187. Chọn D
2x ax5 x 2x ax5 x 2 Ta có: lim
x ax x x 5 lim x 2
x ax 5 x 5 a ax 5 a lim lim x . x 2 x ax 5 x x a 5 2 1 1 2 x x a Do đó:
x ax x a . x 2 lim 5 5 5 10 2
Câu 188. Cách 1: Sử dụng máy tính cầm tay tính giá trị biểu thức 2
x 4x 1 x tại 10 x 1 0 : Vậy I 2 . Chọn đáp án A. 2 lim x 4x 1 x x 1 4 4x 1
Cách 2: Ta có I lim lim x 2 lim x 4x 1 x x
x 2x 4x1x x 4 1 1 1 2 x x 4 2 . 2 2 2 2 4
x 4x 2 x 4 x 2 Câu 189. lim lim lim x 2 lim x 4x 2 x x
x 2x 4x2x x 2x 4x2x x 4 2 1 1 2 x x 2 .
x 1 x 3 4
Câu 190. lim x 1 x 3 lim lim 0 . x x x 1 x 3 x x 1 x 3 6 5 5x 6 5 Câu 191. Ta có lim x
x x x . x 2 5 6 lim lim x 2 x 5x 6 x x 5 6 2 1 1 2 x x 2 2
x ax 5 x ax 5 Câu 192. Ta có: 2 lim
x ax 5 x lim 5 lim 5 5 x x 2
x ax 5 x x 2
x ax 5 x 5 a a lim x 5 5 a 10 . x a 5 2 1 1 2 x x
Vì vậy giá trị của a là một nghiệm của phương trình 2
x 9x 10 0 . Câu 193. Ta có
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
x x ax b x 2 lim 4 3 1 0 2 lim 4x
3x 1 ax b 0 x 2 2 2 2 2
4x 3x 1 a x
4 a x 3x 1 lim b 0 lim b 0 x 2
4x 3x 1 ax x 2 4x 3x 1 ax 2 4 a 0 a 2 a 0 3 . b 3 4 b 0 2 a
Vậy a 4b 5 . 6x Câu 194. lim x x x x x x 2 2 5 4 5 2 lim x 2 2
x 5x 4 x 5x 2 6x lim 3 . x 5 4 5 2 x 1 1 2 2 x x x x
Câu 195. Chọn D x x x Xét: lim x x x . x 2 1 lim lim lim x 2 x 1 x x 1 x 1 x 1 x x 1 x 2 2 x x 1 1 lim . x 1 2 1 1 2 x
Câu 196. Chọn C 1 2017 x 1 2017 a 1 a 2 2 1 a x 1 2017 x x 2 x x Ta có: lim lim lim a . x x 2018 x 2018 x 2018 x 1 1 x x 1 1 Nên a a . 2 2
2x bx 1 x 2x bx1 x Ta có: lim 2 lim x bx 1 x x x 2
x bx 1 x 1 x b 1 b bx 1 x b lim lim lim x . x b 1 x b 1 x b 1 2 x 1 1 x 1 1 1 1 2 x x 2 2 x x x x b Nên 2 b 4 . 2 1 Vậy P 4 4 2 . 2
Câu 197. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 2 4
x 4x 2 x 4 x 2 lim lim lim x 2 2 lim x 4x 2 x x
x 2x 4x2x x 2x 4x2x x 4 2 1 1 2 x x .
Câu 198. Chọn D 2 2
x x x 2 x 2 Ta có: I I lim
1 I lim 1 2 lim x 1 x x 2 x x 2 x 2
x x x 2
x x x 2 2 1 3 lim x I 1 I . x 1 2 2 1 1 2 x x
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 11 1D4-3 HÀM SỐ LIÊN TỤC
DẠNG 1. CÂU HỎI LÝ THUYẾT .................................................................................................................................. 1
DẠNG 2. LIÊN TỤC TẠI MỘT ĐIỂM ........................................................................................................................... 3
Dạng 2.1 Xét tính liên tục tại điểm của hàm số............................................................................................................ 3
Dạng 2.1 Điểm gián đoạn của hàm số .......................................................................................................................... 4
Dạng 2.3 Bài toán chứa tham số ................................................................................................................................... 4
DẠNG 3. LIÊN TỤC TRÊN KHOẢNG ........................................................................................................................ 11
Dạng 3.1 Xét tính liên tục trên khoảng của hàm số .................................................................................................... 11
Dạng 3.2 Bài toán chứa tham số ................................................................................................................................. 12
DẠNG 4. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM ....................................................................................... 14
DẠNG 1. CÂU HỎI LÝ THUYẾT ................................................................................................................................ 15
DẠNG 2. LIÊN TỤC TẠI MỘT ĐIỂM ......................................................................................................................... 15
Dạng 2.1 Xét tính liên tục tại điểm của hàm số.......................................................................................................... 15
Dạng 2.1 Điểm gián đoạn của hàm số ........................................................................................................................ 16
Dạng 2.3 Bài toán chứa tham số ................................................................................................................................. 17
DẠNG 3. LIÊN TỤC TRÊN KHOẢNG ........................................................................................................................ 24
Dạng 3.1 Xét tính liên tục trên khoảng của hàm số .................................................................................................... 24
Dạng 3.2 Bài toán chứa tham số ................................................................................................................................. 26
DẠNG 4. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM ....................................................................................... 29
DẠNG 1. CÂU HỎI LÝ THUYẾT Câu 1.
(THPT THẠCH THANH 2 - THANH HÓA - LẦN 1 - 2018) Cho hàm số y f x liên tục trên
a;b . Điều kiện cần và đủ để hàm số liên tục trên a;b là
A. lim f x f a và lim f x f b .
B. lim f x f a và lim f x f b . x a x b x a x b
C. lim f x f a và lim f x f b .
D. lim f x f a và lim f x f b . x a x b x a x b Câu 2.
(THPT LÊ HOÀN - THANH HÓA - LẦN 1 - 2018) Cho hàm số f x xác định trên a;b . Tìm mệnh đề đúng.
A. Nếu hàm số f x liên tục trên a;b và f a f b 0 thì phương trình f x 0 không có
nghiệm trong khoảng a;b .
B. Nếu f a f b 0 thì phương trình f x 0 có ít nhất một nghiệm trong khoảng a;b .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
C. Nếu hàm số f x liên tục, tăng trên a;b và f a f b 0 thì phương trình f x 0 không
có nghiệm trong khoảng a;b .
D. Nếu phương trình f x 0 có nghiệm trong khoảng a;b thì hàm số f x phải liên tục trên a;b . Câu 3.
Cho hàm số y f (x) liên tục trên đoạn ;
a b . Mệnh đề nào dưới đây đúng?
A. Nếu f (a). f (b) 0 thì phương trình f (x) 0 không có nghiệm nằm trong a;b .
B. Nếu f (a). f (b) 0 thì phương trình f (x) 0 có ít nhất một nghiệm nằm trong ; a b .
C. Nếu f (a). f (b) 0 thì phương trình f (x) 0 có ít nhất một nghiệm nằm trong ; a b .
D. Nếu phương trình f (x) 0 có ít nhất một nghiệm nằm trong ;
a b thì f (a). f (b) 0 . Câu 4.
Cho đồ thị của hàm số y f x như hình vẽ sau: y 7 6 5 4 3 2 1 x -4 -3 -2 -1 1 2 3 4 5 -1 -2
Chọn mệnh đề đúng.
A. Hàm số y f x có đạo hàm tại điểm x 0 nhưng không liên tục tại điểm x 0 .
B. Hàm số y f x liên tục tại điểm x 0 nhưng không có đạo hàm tại điểm x 0 .
C. Hàm số y f x liên tục và có đạo hàm tại điểm x 0 .
D. Hàm số y f x không liên tục và không có đạo hàm tại điểm x 0 . Câu 5.
Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x 1 ? A. . B. .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 C. . D. . Câu 6.
(Thi thử SGD Hưng Yên) Cho các mệnh đề:
1. Nếu hàm số y f x liên tục trên a;b và f a. f b 0 thì tồn tại x ; a b sao cho 0 f x 0 . 0
2. Nếu hàm số y f x liên tục trên a;b và f a. f b 0 thì phương trình f x 0 có nghiệm.
3. Nếu hàm số y f x liên tục, đơn điệu trên a;b và f a. f b 0 thì phương trình
f x 0 có nghiệm duy nhất.
A. Có đúng hai mệnh đề sai.
B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai.
D. Có đúng một mệnh đề sai.
DẠNG 2. LIÊN TỤC TẠI MỘT ĐIỂM
Dạng 2.1 Xét tính liên tục tại điểm của hàm số 3 1 x , khi x 1 Câu 7.
Cho hàm số y 1 x
. Hãy chọn kết luận đúng 1 , khi x 1
A. y liên tục phải tại x 1 .
B. y liên tục tại x 1 .
C. y liên tục trái tại x 1 .
D. y liên tục trên . 2
x 7x 12 khi x 3 Câu 8.
Cho hàm số y x 3
. Mệnh đề nào sau đây đúng? 1 khi x 3
A. Hàm số liên tục nhưng không có đạo hàm tại x 3. 0
B. Hàm số gián đoạn và không có đạo hàm tại x 3. 0
C. Hàm số có đạo hàm nhưng không liên tục tại x 3. 0
D. Hàm số liên tục và có đạo hàm tại x 3. 0 x 2 khi x 2 Câu 9.
Cho hàm số f x x 2 2 . Chọn mệnh đề đúng? 4 khi x 2
A. Hàm số liên tục tại x 2 .
B. Hàm số gián đoạn tại x 2 .
C. f 4 2 .
D. lim f x 2 . x2 2x 1
Câu 10. Cho hàm số f x
. Kết luận nào sau đây đúng? 3 x x
A. Hàm số liên tục tại x 1 .
B. Hàm số liên tục tại x 0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1
C. Hàm số liên tục tại x 1 .
D. Hàm số liên tục tại x . 2
Câu 11. (THPT NAM TRỰC - NAM ĐỊNH - 2018) Hàm số nào sau đây liên tục tại x 1 : 2 x x 1 2 x x 2 2 x x 1 x
A. f x
. B. f x
. C. f x
. D. f x 1 . x 1 2 x 1 x x 1
Dạng 2.1 Điểm gián đoạn của hàm số
Câu 12. (THPT THUẬN THÀNH - BẮC NINH - 2018) Hàm số nào dưới đây gián đoạn tại điểm x 1 0 . 2x 1 x x 1
A. y x 2
1 x 2 . B. y . C. y . D. y . x 1 x 1 2 x 1
Câu 13. Hàm số nào sau đây gián đoạn tại x 2 ? 3x 4 A. y .
B. y sin x . C. 4 2
y x 2x 1
D. y tan x . x 2 x
Câu 14. Hàm số y
gián đoạn tại điểm x bằng? x 1 0 A. x 2018 . B. x 1. C. x 0 D. x 1 . 0 0 0 0 x 3
Câu 15. Cho hàm số y
. Mệnh đề nào sau đây đúng? 2 x 1
A. Hàm số không liên tục tại các điểm x 1
. B. Hàm số liên tục tại mọi x .
C. Hàm số liên tục tại các điểm x 1 .
D. Hàm số liên tục tại các điểm x 1 . 1 cos x khi x 0
Câu 16. (THPT CHUYÊN BẮC NINH - LẦN 1 - 2018) Cho hàm số f x 2 x . 1 khi x 0
Khẳng định nào đúng trong các khẳng định sau?
A. f x có đạo hàm tại x 0 .
B. f 2 0 .
C. f x liên tục tại x 0 .
D. f x gián đoạn tại x 0 .
x cos x, x 0 2 x
Câu 17. (THPT HAI BÀ TRƯNG - HUẾ - 2018) Cho hàm số f x
, 0 x 1 . Khẳng định nào 1 x 3 x , x 1 sau đây đúng?
A. Hàm số f x liên tục tại mọi điểm x thuộc .
B. Hàm số f x bị gián đoạn tại điểm x 0 .
C. Hàm số f x bị gián đoạn tại điểm x 1 .
D. Hàm số f x bị gián đoạn tại điểm x 0 và x 1 .
Dạng 2.3 Bài toán chứa tham số
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 x 4 khi x 2
Câu 18. Tìm m để hàm số f (x) x 2
liên tục tại x 2 m khi x 2 A. m 4 . B. m 2 . C. m 4 . D. m 0 . 3 x 1 khi x 1
Câu 19. Cho hàm số y f (x) x 1
. Giá trị của tham số m để hàm số liên tục tại điểm x 1 0
2m 1 khi x 1 là: 1 A. m . B. m 2 . C. m 1. D. m 0 . 2 2
x 3x 2 khi x 1
Câu 20. Để hàm số y
liên tục tại điểm x 1
thì giá trị của a là 4x a khi x 1 A. 4 . B. 4. C. 1. D. 1. 3 2
x x 2x 2 khi x 1
Câu 21. Tìm giá trị thực của tham số m để hàm số f x x 1
liên tục tại x 1. 3 x m khi x 1 A. m 0. B. m 6. C. m 4 . D. m 2 . 2016 x x 2 khi x 1
Câu 22. Cho hàm số f x 2018x 1 x 2018
. Tìm k để hàm số f x liên tục tại x 1 k khi x 1 . 2017. 2018 20016
A. k 2 2019 . B. k . C. k 1. D. k 2019 . 2 2017 x 1 khi x 1
Câu 23. Cho hàm số f x x 1
. Tìm a để hàm số liên tục tại x 1. 0 a khi x 1 1 1 A. a 0 . B. a . C. a . D. a 1 . 2 2
x b khi x
Câu 24. Biết hàm số f x 3 1
liên tục tại x 1. Mệnh đề nào dưới đây đúng? x
a khi x 1
A. a b 2 . B. a 2 b .
C. a 2 b .
D. a b 2 . 3 x khi x 3
Câu 25. Cho hàm số f x x 1 2
. Hàm số đã cho liên tục tại x 3 khi m ? m khi x=3 A. 1 . B. 1. C. 4 . D. 4 . 2
ax bx 5 khi x 1
Câu 26. Biết hàm số f x
liên tục tại x 1 Tính giá trị của biểu thức 2ax 3b khi x 1
P a 4b . A. P 4 . B. P 5 . C. P 5 . D. P 4 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 x x khi x 1
Câu 27. Tìm m để hàm số f (x) x 1
liên tục tại x 1
m 1 khi x 1 A. m 0 . B. m 1 . C. m 1 D. m 2 . 2
x 3x 2 khi x 1
Câu 28. Có bao nhiêu số tự nhiên m để hàm số f x x 1
liên tục tại điểm x 1? 2 m m 1 khi x 1 A. 0. B. 3 . C. 2 . D. 1. x 2 2 khi x 2
Câu 29. Tìm a để hàm số f x x 2
liên tục tại x 2 ? 2x a khi x 2 15 15 1 A. . B. . C. . D. 1 . 4 4 4 2
x 3x2 khi x 2
Câu 30. Cho hàm số f x x 2 2
, m là tham số. Có bao nhiêu giá trị của m để hàm 2 m
x4m6 khi x 2
số đã cho liên tục tại x 2 ? A. 3 . B. 0 . C. 2 . D. 1 2
3x 2x 1 2 , x 1
Câu 31. Cho hàm số f x 2 x 1
. Hàm số f x liên tục tại x 1 khi 0 4 m x 1 A. m 3 . B. m 3 . C. m 7 . D. m 7 .
Câu 32. (Chuyên Lê Thánh Tông-Quảng Nam-2018-2019) Tìm giá trị của tham số m để hàm số 2
x 3x 2 khi x 1 f x 2 x 1
liên tục tại x 1 . mx 2 khi x 1 3 5 3 5 A. m . B. m .
C. m . D. m . 2 2 2 2 2 x 4 2 khi x 0 2
Câu 33. Cho hàm số ( ) x f x
. Tìm giá trị thực của tham số a để hàm số f ( x) 5 2a khi x 0 4
liên tục tại x 0 . 3 4 4 3 A. a . B. a . C. a . D. a . 4 3 3 4 2
x 2x 3 khi x 1
Câu 34. Cho hàm số f x
. Tìm m để hàm số liên tục tại x 1. 0
3x m 1 khi x 1 A. m 1. B. m 3 . C. m 0 . D. m 2 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2
x 3x 2 khi x 2
Câu 35. Cho hàm số f (x) x 2
. Hàm số liên tục tại x 2 khi a bằng a khi x 2 A. 1. B. 0 . C. 2 . D. 1 . 3 x khi x 3
Câu 36. Cho hàm số f x x 1 2
. Hàm số liên tục tại điểm x 3 khi m bằng: mx 2 khi x 3 A. 2 . B. 4 . C. 4 . D. 2 . 2 x 16 khi x 4
Câu 37. Tìm m để hàm số f x x 4
liên tục tại điểm x 4 .
mx 1 khi x 4 7 7 A. m . B. m 8 . C. m . D. m 8 . 4 4
Câu 38. (THPT Yên Mỹ Hưng Yên lần 1 - 2019) Tìm tất cả các giá trị của tham số m để hàm số
liên tục tại x 2 . A. m 3 . B. m 2 . C. m 2 .
D. Không tồn tại m .
x 3 m khi x 1
Câu 39. (THPT THUẬN THÀNH 1) Cho hàm số f x . x 1 Để hàm số liên tục n khi x 1
tại x 1 thì giá trị của biểu thức m n tương ứng bằng: 0 3 1 9 A. . B. 1. C. . D. . 4 2 4 3 2
x 6x 11x 6 khi x 3
Câu 40. Cho hàm số f x x 3
. Tìm giá trị của m để hàm số liên tục tại x 3 m khi x 3 ? A. m 1. B. m 2 . C. m 3 . D. m 0 .
cos 3x cos 7x
Câu 41. Giới hạn lim
. Tìm giá trị của m để hàm số liên tục tại x 3 ? 2 x0 x A. 40 . B. 0 . C. 4 . D. 20 . 2
x x 2 khi x 1
Câu 42. Tìm m để hàm số f (x) x 1
liên tục tại x 1. 2
mx 2m khi x 1 3 3 3 A. m 1 ; . B. m 1 .
C. m . D. m 1 ; .. 2 2 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2
x 3x 2 khi x 2
Câu 43. Tìm các giá trị của tham số m để hàm số f x 2 x 2x
liên tục tại điểm x 2
mx m 1 khi x 2 . 1 1 1 1 A. m . B. m . C. m . D. m . 6 6 2 2 2 x 4 2 khi x 0 2
Câu 44. Cho hàm số x f x
. Tìm các giá trị thực của tham số a để hàm số f x 5
2a khi x 0 4
liên tục tại x 0 . 3 4 4 3 A. a . B. a . C. a . D. a . 4 3 3 4 2
ax 1 bx 2 1 khi x 3 1
Câu 45. Cho hàm số f x 4x 3x 1 2
, a,b, c . Biết hàm số liên tục tại x . c 1 2 khi x 2 2
Tính S abc . A. S 3 6 . B. S 18 . C. S 36 . D. S 18 . 2 x 1 khi x 1
Câu 46. (Chuyên - Vĩnh Phúc - lần 3 - 2019) Tìm a để hàm số f x x 1 liên tục tại a khi x 1
điểm x 1. 0 A. a 1. B. a 0 . C. a 2 . D. a 1 .
Câu 47. (THPT Chuyên Thái Bình - lần 3 - 2019) Tìm giá trị thực của tham số m để hàm số 2
x x 2 khi x 2
f (x) x 2
liên tục tại x=2. m khi x=2 A. m 3. B. m 1. C. m 2. D. m 0. 2
2x 3x 1 khi x 1
Câu 48. Để hàm số f x 2 x 1
liên tục tại x 1 thì giá trị m bằng m khi x 1 A. 0, 5 . B. 1,5. C. 1. D. 2 . 2
x x 2 khi x 1
Câu 49. (THPT CHUYÊN BẮC NINH - LẦN 1 - 2018) Cho hàm số f x x 1 . Tìm 3 m khi x 1
tất cả các giá trị thực của tham số m để hàm số gián đoạn tại x 1. A. m 2. B. m 1. C. m 2. D. m 3.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 50. (THPT CHUYÊN HÙNG VƯƠNG - PHÚ THỌ - LẦN 1 - 2018) Tìm tất cả các giá trị của m
1 x 1 x khi x 0 để hàm số x f x
liên tục tại x 0 . 1 x m khi x 0 1 x A. m 1. B. m 2 . C. m 1 . D. m 0 . ax e 1 khi x 0 x
Câu 51. (TOÁN HỌC VÀ TUỔI TRẺ SỐ 1 - 2018) Cho hàm số f x . Tìm giá trị 1 khi x 0 2
của a để hàm số liên tục tại x 0 . 0 1 1 A. a 1 . B. a . C. a 1 . D. a . 2 2 2
ax (a 2)x 2 khi x 1
Câu 52. (THPT HẬU LỘC 2 - TH - 2018) Cho hàm số f (x) x 3 2 . Có tất cả 2 8 a khi x 1
bao nhiêu giá trị của a để hàm số liên tục tại x 1 ? A. 1. B. 0 . C. 3 . D. 2 .
Câu 53. (THPT CHUYÊN HOÀNG VĂN THỤ - HÒA BÌNH - 2018) Giá trị của tham số a để hàm số x 2 2
y f x khi x 2 x 2
liên tục tại x 2 . a 2x khi x 2 1 15 A. . B. 1. C. . D. 4 . 4 4 2
x 1 khi x 1
Câu 54. (PHAN ĐĂNG LƯU - HUẾ - LẦN 1 - 2018) Hàm số f x liên tục tại điểm
x m khi x 1
x 1 khi m nhận giá trị 0 A. m 2 . B. m 2 . C. m 1 . D. m 1.
Câu 55. (CHUYÊN TRẦN PHÚ - HẢI PHÒNG - LẦN 1 - 2018) Cho hàm số
2x 1 x 5 f x khi x 4 x 4
. Tìm tất cả các giá trị thực của tham số a để hàm số liên a 2 khi x 4 tục tại x 4 . 0 5 11 A. a . B. a .
C. a 3.
D. a 2 . 2 6
Câu 56. (THPT CHUYÊN THÁI BÌNH - LẦN 5 - 2018) Tìm tham số thực m để hàm số y f x 2
x x 12 khi x 4 x 4
liên tục tại điểm x 4 . 0 mx 1 khi x 4 A. m 4 . B. m 3 . C. m 2 . D. m 5 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 57. (THPT TRẦN PHÚ - ĐÀ NẴNG - 2018) Tìm giá trị của tham số m để hàm số 3x 1 2 f x khi x 1 x 1
liên tục tại điểm x 1. 0 m khi x 1 3 1 A. m 3 . B. m 1 . C. m . D. m . 4 2 Câu 58. (THPT HÀ HUY TẬP - HÀ TĨNH - LẦN 1 - 2018) Cho hàm số x 3 2 khi x 1 f x x 1
. Tìm tất cả các giá trị của tham số thực m để hàm số f x 1 2 m m khi x 1 4
liên tục tại x 1 . A. m 0 ;1 .
B. m 0; 1 . C. m 1 . D. m 0 .
Câu 59. (THPT KINH MÔN - HẢI DƯƠNG - LẦN 1 - 2018) Tìm a để hàm số liên tục trên : 2x a khi x 1 f x 3 2
x x 2x 2 khi x 1. x 1 A. a 2 . B. a 1. C. a 2 . D. a 1 .
Câu 60. (THPT CHUYÊN HẠ LONG - LẦN 1 - 2018) Tìm tất cả các giá trị thực của m để hàm số 2
x x 2 khi x 2
f x x 2
liên tục tại x 2 . 2 m khi x 2 A. m 3 .
B. m 1.
C. m 3 . D. m 1 . 2
x 4x 3 khi x 1
Câu 61. (THPT LÝ THÁI TỔ - BẮC NINH - 2018) Tìm m để hàm số f (x) x 1 mx 2 khi x 1
liên tục tại điểm x 1 . A. m 2 . B. m 0 . C. m 4 . D. m 4 . 3 x 8 khi x 2
Câu 62. (THPT HẢI AN - HẢI PHÒNG - LẦN 1 - 2018) Cho hàm số f x x 2 . Tìm
2m 1 khi x 2
m để hàm số liên tục tại điểm x 2 . 0 3 13 11 1 A. m . B. m . C. m . D. m . 2 2 2 2 Câu 63. (THPT CHUYÊN THĂNG LONG - ĐÀ LẠT - 2018) Cho hàm số 2
x 2x 8 khi x 2 f (x) x 2
m . Biết hàm số f x liên tục tại x 2 . Số giá trị 0 2 2 m x 5mx khi x 2
nguyên của m thỏa mãn yêu cầu bài toán là A. 3 . B. 2 . C. 1. D. 0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
DẠNG 3. LIÊN TỤC TRÊN KHOẢNG
Dạng 3.1 Xét tính liên tục trên khoảng của hàm số
Câu 64. Trong các hàm số sau, hàm số nào liên tục trên ? 2x 1 A. 3
y x x .
B. y cot x . C. y . D. 2 y x 1 . x 1
Câu 65. (PHAN ĐĂNG LƯU - HUẾ - LẦN 1 - 2018) Cho bốn hàm số f x 3
2x 3x 1 , 1 3x 1 f x , f
x cos x 3 và f
x log x . Hỏi có bao nhiêu hàm số liên tục trên tập ? 4 3 2 x 2 3 A. 1. B. 3 . C. 4 . D. 2 .
Câu 66. Trong các hàm số sau, hàm số nào liên tục trên ? 2 x 3 x 5
A. f x tan x 5 .
B. f x .
C. f x x 6 .
D. f x . 5 x 2 x 4 2
x x 3 khi x 2
Câu 67. Cho hàm số y
. Chọn mệnh đề sai trong các mệnh đề sau: 5x 2 khi x 2
A. Hàm số liên tục tại x 1. 0
B. Hàm số liên tục trên .
C. Hàm số liên tục trên các khoảng ; 2 , 2; .
D. Hàm số gián đoạn tại x 2 . 0
Câu 68. Hàm số nào sau đây liên tục trên ? 4 2 x 4x 4 2 x 4x
A. f x x .
B. f x 4 2 x 4x .
C. f x
. D. f x . x 1 x 1 2 x
khi x 1, x 0 x
Câu 69. (THPT XUÂN HÒA - VP - LẦN 1 - 2018) Cho hàm số f x 0 khi x 0 . Khẳng x khi x 1 định nào đúng
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn 0; 1 .
B. Hàm số liên tục tại mọi điểm trừ điểm x 0 .
C. Hàm số liên tục tại mọi điểm thuộc .
D. Hàm số liên tục tại mọi điểm trừ điểm x 1 . si n x khi x 1
Câu 70. (THPT NGUYỄN HUỆ - NINH BÌNH - 2018) Cho hàm số f x . Mệnh x 1 khi x 1
đề nào sau đây là đúng?
A. Hàm số liên tục trên .
B. Hàm số liên tục trên các khoảng ; 1 và 1; .
C. Hàm số liên tục trên các khoảng ; 1 và 1; .
D. Hàm số gián đoạn tại x 1 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 71. (CHUYÊN VINH - LẦN 1 - 2018) Hàm số nào trong các hàm số dưới đây không liên tục trên ? x x
A. y x . B. y .
C. y sin x . D. y . x 1 x 1
sin x neu cos x 0
Câu 72. (THPT CHUYÊN KHTN - LẦN 3 - 2018) Cho hàm số f x . Hỏi hàm
1 cos x neu cos x 0
số f có tất cả bao nhiêu điểm gián đoạn trên khoảng 0; 2018 ? A. 2018 . B. 1009 . C. 642 . D. 321.
Dạng 3.2 Bài toán chứa tham số 3
2 x x 1 , x 1
Câu 73. Tìm m để hàm số y x 1 liên tục trên .
mx 1 ,x 1 4 1 4 2 A. m . B. m . C. m . D. m . 3 3 3 3
Câu 74. (KSCL LẦN 1 CHUYÊN LAM SƠN - THANH HÓA_2018-2019) Cho hàm số 3 4x 2 , x 2
f (x) x 2
. Xác định a để hàm số liên tục trên . ax 3 , x 2 1 4 4 A. a 1 . B. a . C. a . D. a . 6 3 3 2 x 1 khi x 1
Câu 75. Cho hàm số f x x 1
. Tìm m để hàm số f x liên tục trên .
m 2 khi x 1 A. m 1. B. m 2 . C. m 4 . D. m 4 .
Câu 76. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Tìm m để hàm số 2
x 2 x 2 khi x 2
y f x liên tục trên ? 2 5
x 5m m khi x 2
A. m 2; m 3 . B. m 2 ; m 3 .
C. m 1; m 6 . D. m 1 ; m 6 .
3x a 1 khi x 0
Câu 77. Cho hàm số f x 1 2x 1
. Tìm tất cả giá trị thực của a để hàm số đã cho liên khi x 0 x tục trên . A. a 1. B. a 3. C. a 4 . D. a 2 . 3 2
x 3x 2x khi x x 2 0 x x 2
Câu 78. Cho biết hàm số f x a khi x 0
liên tục trên . Tính 2 2
T a b . b khi x 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
A. T 2 .
B. T 122 .
C. T 101.
D. T 145 .
Câu 79. (TOÁN HỌC TUỔI TRẺ SỐ 5) Tìm tất cả các giá trị của tham số m để hàm số sau liên tục trên x 1 khi x 1
f x ln x x 1 2 . m e 1 2mx khi x 1 1 A. m 1. B. m 1 . C. m . D. m 0 . 2
Câu 80. (THPT CHUYÊN THÁI BÌNH - LẦN 4 - 2018) Có bao nhiêu giá trị thực của tham số m để hàm 2 2 m x khi x 2
số f x liên tục trên ?
1 m x khi x 2 A. 0 . B. 2 . C. 3 . D. 4 .
x m khi x 0
Câu 81. (THPT CHUYÊN VĨNH PHÚC - LẦN 4 - 2018) Cho hàm số f x . Tìm
mx 1 khi x 0
tất cả các giá trị của m để f x liên tục trên .
A. m 1.
B. m 0 . C. m 1 .
D. m 2 . 2
x 4x 3 khi x 1
Câu 82. (THPT YÊN LẠC - LẦN 4 - 2018) Tìm P để hàm số y x 1 liên tục trên 6Px 3 khi x 1 . 5 1 1 1 A. P . B. P . C. P . D. P . 6 2 6 3
ax b 1, khi x 0
Câu 83. (THPT TỨ KỲ - HẢI DƯƠNG - LẦN 2 - 2018) Hàm số f (x) liên
a cos x b sin x, khi x 0
tục trên khi và chỉ khi
A. a b 1.
B. a b 1 .
C. a b 1
D. a b 1 3
x 1 khi x 1
Câu 84. (THPT YÊN LẠC - LẦN 3 - 2018) Cho hàm số y
, m là tham số. Tìm m x m khi x 1
để hàm số liên tục trên . A. m 5 . B. m 1 . C. m 3 . D. m 3 .
Câu 85. (THPT CHUYÊN BIÊN HÒA - HÀ NAM - 2018) Tìm tất cả các giá trị thực của m để hàm số x 1 1
khi x 0 f (x) x liên tục trên . 2
x 1 m khi x 0 3 1 1 A. m . B. m . C. m 2 . D. m . 2 2 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 x 16 5 khi x 3
Câu 86. (THPT GANG THÉP - LẦN 3 - 2018) Cho hàm số y f x x 3 . Tập a khi x 3
các giá trị của a để hàm số đã cho liên tục trên là: 2 1 3 A. . B. . C. 0 . D. . 5 5 5
Câu 87. (SỞ GD&ĐT BÌNH THUẬN - 2018) Tìm tất cả các giá trị thực của tham số m để hàm số 2 x 16 khi x 4
f x x 4 liên tục trên . mx 1 khi x 4 7 7
A. m 8 hoặc m . B. m . 4 4 7 7 C. m . D. m 8 hoặc m . 4 4 2
x ax b khi x 5
Câu 88. (PTNK CƠ SỞ 2 - TPHCM - LẦN 1 - 2018) Nếu hàm số f x x 17 khi 5 x 10
ax b 10 khi x 10
liên tục trên thì a b bằng A. 1 . B. 0 . C. 1. D. 2 .
DẠNG 4. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM
Câu 89. Cho phương trình 4 2
2x 5x x 1 0 (1) . Chọn khẳng định đúng trong các khẳng định sau
A. Phương trình
1 có đúng một nghiệm trên khoảng 2 ;1 .
B. Phương trình 1 vô nghiệm.
C. Phương trình
1 có ít nhất hai nghiệm trên khoảng 0; 2 .
D. Phương trình
1 vô nghiệm trên khoảng 1 ; 1 .
Câu 90. (THPT HẢI AN - HẢI PHÒNG - LẦN 1 - 2018) Phương trình nào dưới đây có nghiệm trong khoảng 0; 1 A. 2
2x 3x 4 0 .
B. x 5 7 1 x 2 0 . C. 4 2
3x 4x 5 0 . D. 2017 3x 8x 4 0 .
Câu 91. (THPT CHUYÊN HÙNG VƯƠNG - GIA LAI - LẦN 2 - 2018) Cho phương trình 4 2
4x 2x x 3 0
1 . Mệnh đề nào dưới đây đúng?
A. Phương trình
1 vô nghiệm trên khoảng 1 ;1 .
B. Phương trình
1 có đúng một nghiệm trên khoảng 1 ;1 .
C. Phương trình
1 có đúng hai nghiệm trên khoảng 1 ;1 .
D. Phương trình
1 có ít nhất hai nghiệm trên khoảng 1 ;1 .
Câu 92. Phương trình 5 3
3x 5x 10 0 có nghiệm thuộc khoảng nào sau đây? A. 2; 1 . B. 1 0; 2 . C. 0 ;1 . D. 1 ; 0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 93. Cho phương trình 3
2x 8x 1 0
1 . Khẳng định nào sai?
A. Phương trình không có nghiệm lớn hơn 3 .
B. Phương trình có đúng 3 nghiệm phân biệt.
C. Phương trình có 2 nghiệm lớn hơn 2 .
D. Phương trình có nghiệm trong khoảng 5; 1 .
Câu 94. Cho hàm số y f x liên tục trên đoạn a;b và thỏa mãn f a b , f b a với a,b 0 ,
a b . Khi đó phương trình nào sau đây có nghiệm trên khoảng a;b .
A. f x 0 .
B. f x x .
C. f x x .
D. f x a .
8 4a 2b c 0
Câu 95. Cho số thực a , b , c thỏa mãn
. Số giao điểm của đồ thị hàm số
8 4a 2b c 0 3 2
y x ax bx c và trục Ox là A. 2 . B. 0 . C. 3 . D. 1.
Câu 96. (LÊ QUÝ ĐÔN - QUẢNG TRỊ - LẦN 1 - 2018) Cho các số thực a , b , c thỏa mãn
a c b 1
. Tìm số giao điểm của đồ thị hàm số 3 2
y x ax bx c và trục Ox .
a b c 1 0 A. 0 . B. 1. C. 2 . D. 3 .
DẠNG 1. CÂU HỎI LÝ THUYẾT Câu 1.
Theo định nghĩa hàm số liên tục trên đoạn a;b . Chọn: lim f x f a và lim f x f b . x a x b Câu 2.
Vì f a f b 0 nên f a và f b cùng dương hoặc cùng âm. Mà f x liên tục, tăng trên
a;b nên đồ thị hàm f x nằm trên hoặc nằm dưới trục hoành trên a;b hay phương trình
f x 0 không có nghiệm trong khoảng a;b . Câu 3. Chọn B
Vì theo định lý 3 trang 139/sgk. Câu 4. Chọn B
Đồ thị là một đường liền nét, nhưng bị “gãy” tại điểm x 0 nên nó liên tục tại điểm x 0 nhưng
không có đạo hàm tại điểm x 0 . Câu 5. Chọn D
Vì lim y lim y nên hàm số không liên tục tại x 1 . x 1 x 1 Câu 6. Chọn D
Khẳng định thứ nhất sai vì thiếu tính liên tục trên đoạn a;b .
DẠNG 2. LIÊN TỤC TẠI MỘT ĐIỂM
Dạng 2.1 Xét tính liên tục tại điểm của hàm số Câu 7. Chọn A Ta có: y 1 1 . 1 x 2 3 1 1 x x x
Ta có: lim y 1; lim y lim lim lim 2 1 x x 4 x 1 x 1 x 1 1 x x 1 1 x x 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nhận thấy: lim y y
1 . Suy ra y liên tục phải tại x 1 . x 1 Câu 8. Chọn D 2 x 7x 12 lim
lim x 4 1
y 3 nên hàm số liên tục tại x 3. 0 x3 x3 x 3 2
x 7x 12 2 3 7.3 12 2
x 7x 12 lim lim
lim x 4 1 y '3 1. x3 x3 x3 x 3 x 3 Câu 9. Chọn A
Tập xác định: D x 2
x 2 x 2 2
lim f x lim lim
lim x 2 2 4 x2 x2 x 2 2 x2 x 2 x2 f 2 4
lim f x f 2 x2
Vậy hàm số liên tục tại x 2 .
Câu 10. Chọn D 1 2x 1 1 Tại x
, ta có: lim f x lim
0 f . Vậy hàm số liên tục tại x 2 . 2 3 1 1 x x x 1 2 2 2 2 x x 1
Câu 11. A) f x x 1
lim f x suy ra f x không liên tục tại x 1. x 1 2 x x 2
B) f x 2 x 1 f x x 2 lim lim
suy ra f x không liên tục tại x 1. x 1 x 1 x 1 2 x x 1
C) f x x 2 x f x x 1 lim lim 3 f
1 suy ra f x liên tục tại x 1. x 1 x 1 x x
D) f x 1 x 1 f x x 1 lim lim
suy ra f x không liên tục tại x 1. x 1 x 1 x 1
Dạng 2.1 Điểm gián đoạn của hàm số 2x 1
Câu 12. Ta có y
không xác định tại x 1
nên gián đoạn tại x 1 . x 1 0 0
Câu 13. Chọn A 3x 4 Ta có: y
có tập xác định: D \
2 , do đó gián đoạn tại x 2 . x 2
Câu 14. Chọn D x Vì hàm số y
có TXĐ: D \
1 nên hàm số gián đoạn tại điểm x 1 . x 1 0
Câu 15. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 3 Hàm số y
có tập xác định \
1 . Do đó hàm số không liên tục tại các điểm x 1 . 2 x 1
Câu 16. Hàm số xác định trên x 2 2sin 1 cos x 1
Ta có f 0 1 và f x 2 lim lim lim 2 2 x0 x0 x0 x x 2 4. 2
Vì f 0 lim f x nên f x gián đoạn tại x 0 . Do đó f x không có đạo hàm tại x 0 . x0 1 cos x x
0 f x
0 nên f 2 0.VậyA, B,C sai. 2 x
Câu 17. * f x liên tục tại x 0 và x 1. * Tại x 0 2 x
lim f x lim x cos x 0 , lim f x lim
0 , f 0 0 . x 0 x 0 x 0 x 0 1 x
Suy ra lim f x lim f x f 0 . Hàm số liên tục tại x 0 . x 0 x 0 * Tại x 1 2 x 1
lim f x lim , lim f x 3 lim x 1. x 1 x 1 1 x 2 x 1 x 1
Suy ra lim f x lim f x . Hàm số gián đoạn tại x 1 . x 1 x 1
Dạng 2.3 Bài toán chứa tham số
Câu 18. Chọn A 2 x 4
Hàm số liên tục tại x 2 khi và chỉ khi lim
lim m m m 4 x 2 x 2 x 2
Câu 19. Chọn C
Ta có f (1) 2m 1 3 x 1 2 lim y lim
lim(x x 1) 3 x 1 x 1 x 1 x 1
Để hàm số liên tục tại điểm x 1thì f (1) lim y 2m 1 3 m 1 . 0 x 1
Câu 20. Chọn B
Hàm số liên tục tại x 1
khi và chỉ khi lim y lim y y 1 x 1 x 1
lim 4x a lim
a 4 0 a 4 . 2 x
3x 2 y 1 x1 x1
Câu 21. Chọn A Ta có: f 1 m 3.
x x x x 1 2 3 2 x 2 2 2
lim f x lim lim lim 2 x 2 3. x 1 x 1 x 1 x 1 x 1 x 1
Để hàm số f x liên tục tại x 1 thì lim f x f 1 3 m 3 m 0 . x 1
Câu 22. Chọn A x x 2016 2016 x 1 x
1 2018x 1 x 2018 2 Ta có: lim lim x 1 x 1
2018x 1 x 2018 2017x 2017
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 1 2015 2014 x x
... x 1
1 2018x 1 x 2018 lim 2 2019 x 1 2017 x 1
Để hàm số liên tục tại x 1 lim f x f 1 k 2 2019 . x 1
Câu 23. Chọn C x 1 x 1 1 1
Ta có lim f x lim lim lim . x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 2 1
Để hàm số liên tục tại x 1 khi lim f x f 1 a . 0 x 1 2
Câu 24. Chọn A
lim f x f
1 b 3 ; lim f x a 1. Để liên tục tại x=-1 ta có b 3 a 1 a b 2 x 1 x 1
Câu 25. Chọn D f 3 m 3 x
3 x x 1 2
lim f x lim lim
lim x 1 2 4 x3 x3 x 1 2 x3 x 3 x3
Để hàm số liên tục tại x 3 thì lim f x f 3 x3 Suy ra, m 4 .
Câu 26. Chọn B
Ta có: lim f x lim . 2 ax bx 5 a b 5 f 1 x 1 x 1
lim f x lim 2ax 3b 2a 3b . x 1 x 1
Do hàm số liên tục tại x 1 nên a b 5 2a 3b a 4b 5 .
Câu 27. Chọn D TXĐ: D R 2 x x
Ta có lim f (x) lim lim x 1 x 1 x 1 x 1 x 1
Và f (1) m 1.
Hàm số liên tục tại x 1 m 1 1 m 2
Câu 28. Chọn D 2 x 3x 2 x 1 x 2 lim lim
lim x 2 1 . x 1 x 1 x 1 x 1 x 1
Để hàm số f x liên tục tại điểm x 1 cần: lim f x f 1 x 1 2
m m 1 1 m 0 (TM) 2
m m 0 . m 1 (L)
Câu 29. Chọn B
Ta có f 2 4 a . x 2 4 1 1
Ta tính được lim f x lim lim . x2
x2 x 2 x 2 2 x2 x 2 2 4 1 15
Hàm số đã cho liên tục tại x 2 khi và chỉ khi f 2 lim f x 4 a a . x2 4 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 15
Vậy hàm số liên tục tại x 2 khi a . 4
Câu 30. Chọn D Ta có 2 x x
x 2 x 1 x 2 2 3 2
lim f (x) lim lim lim x 1 x 2 2 4 x2 x2 x2 x2 x 2 2 x 2
lim f (x) lim 2 m x 4m 6 2 2m 4m 6 x2 x2 2
f (2) 2m 4m 6
Để hàm số liên tục tại x 2 thì 2 2
lim f (x) lim f (x) f (2) 2m 4m 6 4 2m 4m 2 0 m 1 x 2 x 2
Vậy có một giá trị của m thỏa mãn hàm số đã cho liên tục tại x 2 .
Câu 31. Chọn A
Tập xác định D , x 1 . 0 Ta có f 1 4 m . 2
3x 2x 1 2 x 1 3x 5
lim f x lim lim x 1 x 1 x 1 x 1 x 1 x 1 x 1 2
3x 2x 1 2 3x 5 lim 1 x 1 x 1 2
3x 2x 1 2
Hàm số f x liên tục tại x 1 khi và chỉ khi lim x f
1 4 m 1 m 3 . 0 x 1
Câu 32. Chọn D - Ta có: + f 1 m 2 .
+ lim f x m 2. x 1 2 x 3x 2
x 1 x 2 x 2 1
+ lim f x lim lim lim . 2 x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 2 1 5
- Hàm số liên tục tại x 1 f
1 lim f x lim f x m 2 m . x 1 x 1 2 2 Câu 33. . Chọn D
Tập xác định: D . x
2x 4 2 2 2 x 4 2 4 2
lim f (x) lim lim 2 x0 x0 x0 2 x x 2 x 4 2 2 x 4 4 1 1 lim lim . x0 2 2 x0 2 4
x ( x 4 2) x 4 2 5 f (0) 2a . 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 5 1 3
Hàm số f ( x) liên tục tại x 0 lim f (x) f (0) 2a a . x 0 4 4 4 3 Vậy a . 4
Câu 34. Chọn C TXĐ D Ta có f 1 2 m .
lim f x lim 2
x 2x 3 2 . x 1 x 1
Hàm số liên tục tại x 1 lim f x f
1 2 m 2 m 0 . 0 x 1
Câu 35. Chọn A
Hàm số liên tục tại x 2 lim f (x) f (2) . x2 2 x 3x 2
Ta có f (2) a, lim f (x) lim
lim(x 1) 1 . Do đó a 1 x2 x2 x2 x 2
Câu 36. Chọn A
Tập xác định D . 3 x
Ta có f 3 3m 2 và lim f x lim lim x 1 2 4 . x 3 x 3 x 1 2 x3
Hàm số đã cho liên tục tại điểm x 3 lim f x f 3 3m 2 4 m 2 . x 3
Câu 37. Chọn A 2 x 16
Ta có lim f x f 4 4m 1; lim f x lim
lim x 4 8. x 4 x 4 x 4 x 4 x 4 7
Hàm số liên tục tại điểm x 4 lim f x lim f x f 4 4m 1 8 m . x 4 x 4 4
Câu 38. Chọn A 2 x 2x x x 2
Ta có lim f x lim lim lim x 2 . x 2 x 2 x 2 x 2 x 2 x 2
lim f x lim mx 4 2m 4 x 2 x 2
Hàm số liên tục tại x 2 khi lim f x lim f x 2m 4 2 m 3. x 2 x 2
Câu 39. Chọn D Ta có: f 1 n. x m lim f x 3 2 lim . x1
x1 x
1 x 3 m 2 x 3 m
Hàm số liên tục tại x 1 lim f x f 1 n lim (1). x 1 x 1 x
1 x 3 m m 2 lim f x
tồn tại khi 1 là nghiệm của phương trình: 2 1 3 m 0 . x1 m 2 x 1 1 1
+ Khi m 2 thì 1 n lim n lim n . x 1 x 1 x 3 x 1 4 2 x 3 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1
+ Khi m 2 thì 1 n lim
suy ra không tồn tại n. x1 x 3 2 1 9
Vậy m n 2 . 4 4
Câu 40. Chọn B
Ta có: f 3 m . 3 2
x 6x 11x 6
lim f x lim lim 2
x 3x 2 2 . x 3 x 3 x 3 x3
Câu 41. Chọn B
cos 3x cos 7x 2 sin 5x sin 2x Ta có: lim lim 2.5.2 20 . 2 x0 x 2 x0 x
Câu 42. Chọn A
Tập xác định D R . * 2
f (1) m 2m * 2 2
lim f (x) lim (mx 2m ) m 2m . x 1 x 1 2 x x 2
(x 1)(x 2)
* lim f (x) lim lim
lim (x 2) 3. x 1 x 1 x 1 x 1 x 1 x 1
Hàm số liên tục tại x 1 khi và chỉ khi lim f (x) lim f (x) f ( 1 ) x 1 x 1 m 1 2 2
m 2m 3
2m m 3 0 3 . m 2 3
Vậy các giá trị của m là m 1 ; . 2
Câu 43. Chọn B 2 x 3x 2
x 2 x 1 x 1 1 Ta có: lim lim lim . 2 x2 x2 x 2x x x 2 x2 x 2
f 2 3m 1 . 1 1
Để hàm số liên tục tại điểm x 2 3m 1 m . 2 6
Câu 44. Chọn D 5
+ Ta có f 0 2a . 4 2 2 x 4 2 x 1 1
+ lim f x lim lim lim . 2 x0 x 0 x0 2 x x 2
x 4 2 x0 2 4 x 4 2 5 1 3
Hàm số f x liên tục tại x 0
lim f x f 0 2a a . khi x0 4 4 4
Câu 45. Chọn A
ax bx
ax 12 bx22 2 2 a b 2 2 x 4bx 3 1 2 Ta có . 3 4x 3x 1 2x 2 1 x
1 ax 1 bx 2 2x 2 2 1 x 1 2
ax 1 bx 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
a b x 4bx 3 m2x 2 2 2 1 m 3 1
Để hàm số liên tục tại x b 3 . 2 a b 1 2 0 a 3 4 2 2 2
ax 1 bx 2 1
2x 12x 3 Khi đó lim lim 3 1 1 x 4x 3x 1 x 2x 2 1 x 1 2 3
x 1 3x 2 2 2 3 3 c lim 2 c 4 . 1 x x 2 3 2 1 3
x 1 3x 2 2 2
Vậy S abc 3 3 4 3 6 . Câu 46. Lời giải Chọn C
Tập xác định D R . f 1 a . 2 x 1
lim f x lim lim x 1 2 . x 1 x 1 x 1 x 1
f x liên tục tại x 1 khi và chỉ khi lim f x f 1 a 2 . 0 x 1
Câu 47. Chọn A 2 x x 2
(x 2)(x 1) Ta có: lim lim lim(x 1) 3. x2 x2 x2 x 2 x 2
Hàm số liên tục tại x=2 lim f (x) f (2) m 3. x2
Câu 48. Chọn A f 1 m . 2 2x 3x 1 x 1 2x 1 2x 1 1
lim f x lim lim lim . x 1 x 1 2 x x 1 1 2 x x 1 1 2 2 1
Để hàm số f x liên tục tại x 1 thì lim f x f 1 m . x 1 2
Câu 49. Tập xác định của hàm số là . 2 x x 2
Hàm số gián đoạn tại x 1 khi lim f x f 1 lim 3m x 1 x 1 x 1 x 1 x 2 lim
3m lim x 2 3m 3 3m m 1. x 1 x 1 x 1 Câu 50. Ta có 1 x
lim f x lim m m 1 . x 0 x 0 1 x
1 x 1 x 2 x 2
lim f x lim lim lim 1 . x 0 x 0 x x0
x 1 x 1 x x0 1 x 1 x
f 0 m 1
Để hàm liên tục tại x 0 thì lim f x lim f x f 0 m 1 1 m 2 . x 0 x 0
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 51. Tập xác định: D . ax e 1 ax e 1
lim f x lim lim .a a . x0 x0 x0 x ax 1 1 f 0
; hàm số liên tục tại x 0 khi và chỉ khi: lim f x f 0 a . 2 0 x0 2
Câu 52. Tập xác định: D 3; . 2
ax a 2 x 2
lim f x lim . x 1 x 1 x 3 2 x
1 ax 2 x 3 2 lim . x 1 x 1
lim ax 2 x 3 2 4a 2 . x 1 f 2 1 8 a . a 0
Hàm số đã cho liên tục tại x 1 khi lim f x f 1 a 2 4 2 8 a . x 1 a 4
Vậy có 2 giá trị của a để hàm số đã cho liên tục tại x 1 . x 2 2 x 2 1 1
Câu 53. Ta có: lim f x lim lim lim . x2 x2 x2 x 2
x 2 x 2 2 x2 x 2 2 4 1 15
Hàm số liên tục tại x 2 lim f x f 2 a 4 a . x2 4 4
Câu 54. Ta có lim f x lim 2 x
; lim f x lim x m 1 m . Để hàm số liên tục tại x 1 1 2 0 x 1 x 1 x 1 x 1
thì lim f x lim f x 2 m 1 m 1. x 1 x 1 Câu 55. Lời giải
2x 1 x 5 x 4 1 1
lim f x lim lim lim x4 x4 x4 x 4
x 4 2x 1 x 5 x4 2x 1 x 5 6
f 4 a 2 . 1 11
Hàm số liên tục tại x 4 khi: lim f x f 4
a 2 a . 0 x4 6 6
Câu 56. Tập xác định: D . Ta có: 2 x x 12
x 3 x 4
+ lim f x lim lim
lim x 3 7 . x 4 x4 x 4 x4 x 4 x4 + f 4
4m 1.
Hàm số f x liên tục tại điểm x 4
khi và chỉ khi lim f x f 4
4m 1 7 0 x 4 m 2 . 3x 1 2 2 3x 1 2 3 3 Câu 57. Ta có lim lim lim . x 1 x 1 x 1 x 1 3x 1 2 x 1 3x 1 2 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3 Với f
1 m ta suy ra hàm số liện tục tại x 1 khi m . 4 x 3 2 1 1 1
Câu 58. Ta có lim f x lim lim ; f
1 lim f x 2 m m . x 1 x 1 x 1 x 1 x 3 2 4 x 1 4 1 1 m 1
Để hàm số f x liên tục tại x 1 thì 2 m m . 4 4 m 0
Câu 59. Khi x 1 thì f x 2x a là hàm đa thức nên liên tục trên khoảng ;1 . 3 2
x x 2x 2
Khi x 1 thì f x
là hàm phân thức hữu tỉ xác định trên khoảng 1; nên x 1
liên tục trên khoảng 1; .
Xét tính liên tục của hàm số tại điểm x 1 , ta có: + f 1 2 a .
+ lim f x lim 2x a 2 a . x 1 x 1
x x x x 1 2 3 2 x 2 2 2
+ lim f x lim lim lim . 2 x 2 3 x 1 x 1 x 1 x 1 x 1 x 1
Hàm số f x liên tục trên hàm số f x liên tục tại x 1
lim f x lim f x f
1 2a 1 3 a 1. x 1 x 1 2 x x 2
Câu 60. Hàm số f x liên tục tại lim f x f 2 2 lim m 2
3 m m 3 . x2 x2 x 2 2 x 4x 3 x 1 x 3
Câu 61. Ta có: lim f x lim lim
lim x 3 2 . x 1 x 1 x 1 x 1 x 1 x 1
lim f x lim mx 2 m 2 . x 1 x 1 f 1 m 2 .
Để hàm số đã cho liên tục tại điểm x 1 thì lim f x lim f x f 1 2 m 2 x 1 x 1 m 0 .
Câu 62. f 2 2m 1. x x 2 2 3 x 2x 4 8
lim f x lim lim lim 2
x 2x 4 12 . x2 x2 x2 x2 x 2 x 2 11
Hàm số liên tục tại x 2 f 2 lim f x 2m 1 12 m . 0 x2 2 2
x 2x 8
Câu 63. TXĐ: D ; có: lim f (x) lim 6, f 2 2 4m 10m . x 2 x 2 x 2 m 3
Hàm số liên tục tại x 2 khi và chỉ khi 2 2 4m 10m 6 4m 10m 6 0 0 1 m 2
Mà m là số nguyên nên m 3 .
DẠNG 3. LIÊN TỤC TRÊN KHOẢNG
Dạng 3.1 Xét tính liên tục trên khoảng của hàm số
Câu 64. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Vì 3
y x x là đa thức nên nó liên tục trên . 3x 1
Câu 65. * Ta có hai hàm số f x và f
x log x có tập xác định không phải là tập nên 4 2 x 2 3 không thỏa yêu cầu.
* Cả hai hàm số f x 3
2x 3x 1 và f
x cos x 3 đều có tập xác định là đồng thời liên 3 1 tục trên .
Câu 66. Chọn D x 5 x 5
Hàm số f x
là hàm phân thức hữu tỉ và có TXĐ là D do đó hàm số f x 2 x 4 2 x 4 liên tục trên .
Câu 67. Chọn B
+ Với x 2 , ta có f x 2
x x 3 là hàm đa thức
hàm số f x liên tục trên khoảng 2; .
+ Với x 2 , ta có f x 5x 2 là hàm đa thức
hàm số f x liên tục trên khoảng ; 2 . + Tại x 2
lim f x lim 2 x x 3 1 x2 x2
lim f x lim 5x 2 12 x2 x2
lim f x lim f x không tồn tại lim f x hàm số gián đoạn tại x 2 . 0 x 2 x 2 x2
Hàm số không liên tục trên .
Câu 68. Chọn B
Vì hàm số f x 4 2
x 4x có dạng đa thức với TXĐ: D nên hàm số này liên tục trên
Câu 69. Tập xác định D .
Nếu x 0 , x 1 thì hàm số y f x liên tục trên mỗi khoảng ; 0,0 ;1 và 1; . 2 2 x x
Nếu x 0 thì f 0 0 và lim f x lim
lim x 0; lim f x lim lim x 0 . x 0 x 0 x 0 x 0 x 0 x 0 x x
Suy ra: lim f x 0 f 0 . x0
Do đó, hàm số y f x liên tục tại x 0 . 2 x lim f x lim lim x 1
Nếu x 1 thì f 1 1 và x 1 x 1 x 1 x
lim f x 1 f 1 . x 1
lim f x lim x 1 x 1 x 1
Do đó, hàm số y f x liên tục tại x 1 .
Vậy hàm số y f x liên tục trên .
Câu 70. Ta có: lim x
1 2 và lim sin x 0 lim f x lim f x do đó hàm số gián đoạn tại x 1 x 1 x 1 x 1 x 1 .
Tương tự: lim x
1 0 và lim sin x 0 x 1 x 1
lim f x lim f x lim f x f
1 do đó hàm số liên tục tại x 1 . x 1 x 1 x 1
Với x 1 thì hàm số liên tục trên tập xác định.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Vậy hàm số đã cho liên tục trên các khoảng ; 1 và 1; . x
Câu 71. Tập xác định của hàm số y là \ 1 . x 1
Hàm số liên tục trên từng khoảng ;
1 và 1; nên hàm số không liên tục trên .
Câu 72. Vì f là hàm lượng giác nên hàm số f gián đoạn khi và chỉ khi hàm số f gián đoạn tại x làm 1 2018
cho cos x 0 x
k k 0; 2018 0
k 2018 0 k 2 2 2 1 2018 1 k 0 k 641 . 2 2
Dạng 3.2 Bài toán chứa tham số
Câu 73. Chọn A 3 2 x x 1
+) Xét x 1 , hàm số y
liên tục trên khoảng ; 1 và 1; . x 1
+) Xét x 1 , ta có y 1 m 1 và 2 3 3 x 1 x x x 1 2 1 2 2 1 lim y lim lim lim 1 1 . x 1 x 1 x 1 x 1 3 2 3 x 1 x 1 3 3 x x 1 1 4
Đề hàm số liên tục tại x 1 thì lim y y 1 m 1 m . x 1 3 3 4 Vậy với m
thì hàm số liên tục trên . 3
Câu 74. Chọn D
Tập xác định của hàm số là D . 3 4x 2 3 4x 2
Nếu x 2 , ta có f x
. Hàm số f x
xác định và liên tục trên mỗi khoảng x 2 x 2 ;
2 và 2; .
Tại x 2 , ta có:
f 2 2a 3. 3 4x 2
lim f x lim x2 x2 x 2
4x 2 4x2 3 3 3 2 4x 4 lim 2 x2
x 2 3 4x 3 2 4x 4 4 x 2 lim 2
x2 x 2 3 4x 3 2 4x 4 4 lim x 4x2 2 3 3 2 4x 4 1 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 4
Hàm số liên tục tại x 2 khi và chỉ khi lim f x f 2 2a 3 a . x2 3 3 4
Vậy hàm số liên tục trên khi và chỉ khi a . 3
Câu 75. Chọn C 2 x 1
Do lim f x lim lim x
1 2 nên hàm số liên tục tại x 1 khi x 1 x 1 x 1 x 1
lim f x f
1 m 2 2 m 4 . Khi đó hàm số liên tục trên . x 1
Câu 76. Chọn A TXĐ: .
+ Xét trên 2; khi đó f x 2
x 2 x 2 . x
2; : lim 2
x 2 x 2 2
x 2 x 2 f x hàm số liên tục trên 2; . 0 0 0 0 0 0 x 0 x + Xét trên ;
2 khi đó f x 2
5x 5m m là hàm đa thức liên tục trên hàm số liên tục trên ; 2 .
+ Xét tại x 2 , ta có: f 2 4 . 0
lim f x lim . 2 x 2 x
2 4; lim f x lim 2 5x 5m m 2 m 5m 10 x 2 x 2 x2 x 2
Để hàm số đã cho liên tục trên thì nó phải liên tục tại x 2 . 0 m 2
lim f x lim f x f 2 2 2
m 5m 10 4 m 5m 6 0 . x 2 x 2 m 3
Câu 77. Chọn D
Hàm số liên tục tại mọi điểm x 0 với bất kỳ a.
Với x 0 Ta có f 0 a 1;
lim f x lim 3x a 1 a 1; x 0 x 0 1 2x 1 2x 2
lim f x lim lim lim 1; x 0 x 0 x 0 x
x 1 2x x 0 1 1 2x 1
Hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x 0 a 11 a 2 .
Câu 78. Chọn A
Vì hàm số f x liên tục trên suy ra hàm số cũng liên tục tại x 0 và x 2 . Do đó 3 2
x 3x 2x x x 1 x 2 x 1 x 2
lim f x lim lim f 0 lim
a a 1 . x 0 x 0 x x 2 x 0 x x 2 x0 x 2 3 2
x 3x 2x x x 1 x 2 x x 1
lim f x lim lim f 2 lim
b b 1. x2 x2 x x 2 x2 x x 2 x2 x Vậy 2 2
T a b 1 1 2 .
Câu 79. Tập xác định D , f 1 1 m .
Ta thấy hàm số f x liên tục trên các khoảng ; 1 và 1; . x 1 lim f x lim
1, lim f x lim . x 1 2 . m e 1 2mx 1 m x 1 x 1 ln x x 1 x 1
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Hàm số f x liên tục trên khi và chỉ khi hàm số f x liên tục tại x 1
lim f x lim f x f 1 . x 1 x 1
1 m 1 m 0 .
Câu 80. Ta có hàm số luôn liên tục x 2 .
Tại x 2 , ta có lim f x lim 1 m x 1 m 2 ; x 2 x 2
lim f x lim ; f 2 2 4m . 2 2 m x 2 4m x2 x2
Hàm số liên tục tại x 2 khi và chỉ khi
lim f x lim f x f 2 2
4m 1 m 2
2 4m 2m 2 0 1 x 2 x 2
Phương trình (1) luôn có hai nghiệm thực phân biệt. Vậy có hai giá trị của m .
Câu 81. Hàm số f x liên tục trên f x liên tục tại x 0 .
lim f x lim
; lim f x lim mx
1 1; f 0 m . x m m x0 x0 x 0 x 0
f x liên tục tại x 0 lim f x lim f x f 0 m 1 m 1 . x 0 x 0
Câu 82. Hàm số y f x liên tục trên y f x liên tục tại x 1
lim f x lim f x f 1 x 1 x 1 2 x 4x 3
lim f x lim
lim x 3 2 x 1 x 1 x 1 x 1
lim f x lim 6Px 3 6P 3 x 1 x 1 f 1 6P 3 1
Do đó lim f x lim f x f 1 6P 3 2 P . x 1 x 1 6
Câu 83. Khi x 0 thì f x a cos x b sin x liên tục với x 0 .
Khi x 0 thì f x ax b 1 liên tục với mọi x 0 .
Tại x 0 ta có f 0 a .
lim f x lim ax b 1 b 1. x 0 x 0
lim f x lim a cos x bsin x a . x 0 x 0
Để hàm số liên tục tại x 0 thì lim f x lim f x f 0 a b 1 a b 1 . x 0 x 0
Câu 84. Ta có hàm số liên tục trên các khoảng ; 1 và 1; .
Xét tính liên tục của hàm số tại x 1 . Có y 1 2
lim y và lim y 1 m . x 1 x 1
Để hàm số liên tục trên thì y
1 lim y lim y 2 1
m m 1 . x 1 x 1 x 1 1
Câu 85. Khi x 0 ta có: f (x)
liên tục trên khoảng 0; . x Khi x 0 ta có: 2 f (x)
x 1 m liên tục trên khoảng ; 0 .
Hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x 0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 1 1 1 1
Ta có: lim f (x) lim lim . x 0 x 0 x 0 x x 1 1 2
lim f (x) lim
x m m f . x 2 1 1 0 x 0 0 1 1
Do đó hàm số liên tục tại x 0 khi và chỉ khi
1 m m . 2 2
Câu 86. Tập xác định D . 2 x 16 5
Khi x 3 thì f x
xác định và liên tục trên các khoảng ;
3 và 3; . x 3 2 x 16 5 x 3 3
Khi x 3 thì f 3 a và lim f x lim lim . x3 x3 x 3 x3 2 x 16 5 5 3
Hàm số đã cho liên tục trên khi và chỉ khi nó liên tục tại điểm x 3 a . 5 2 x 16
Câu 87. *) Với x 4 thì f x
là hàm phân thức nên liên tục trên TXĐ của nó f x liên tục x 4 trên 4; .
*) Với x 4 thì f x mx 1 là hàm đa thức nên liên tục trên f x liên tục trên ; 4 .
Do vậy hàm số f x đã liên tục trên các khoảng 4; , ; 4 .
Suy ra: Hàm số f x liên tục trên f x liên tục tại x 4 . 2 x 16
lim f x lim f x f 4 lim lim mx
1 4m 1 lim x 4 4m 1 x 4 x 4 x 4 x 4 x 4 x 4 7
4m 1 8 m . 4
Câu 88. Với x 5 ta có 2
f x x ax b , là hàm đa thức nên liên tục trên ; 5 .
Với 5 x 10 ta có f x x 7 , là hàm đa thức nên liên tục trên 5;10 .
Với x 10 ta có f x ax b 10 , là hàm đa thức nên liên tục trên 10; .
Để hàm số liên tục trên thì hàm số phải liên tục tại x 5 và x 10 . Ta có:
f 5 12 ; f 10 17 .
lim f x lim 2
x ax b 5
a b 25 . x 5 x 5
lim f x lim x 17 12 . x 5 x 5
lim f x lim x 17 27 . x 10 x 10
lim f x lim ax b 10 10a b 10 . x 10 x 10
Hàm số liên tục tại x 5 và x 10 khi 5
a b 25 12
5a b 13 a 2
a b 1
10a b 10 27 10a b 17 b 3
DẠNG 4. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM
Câu 89. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 f (0) 1
Vì ta có: f (1) 1 . f (2) 15
Câu 90. Xét hàm số f x 2017 3x 8x 4 .
Hàm số liên tục trên đoạn 0
;1 và f 0. f 1 4. 1 4
f 0. f 1 0 . Vậy phương trình 2017 3x
8x 4 0 có nghiệm trong khoảng 0; 1 .
Câu 91. Xét f x 4 2
4x 2x x 3 0 trên khoảng 1 ;1 .
Ta có f x liên tục trên đoạn 1 ;1 . f
1 4 , f 0 3 , f
1 2 f
1 . f 0 0 , f 1 . f 0 0 .
Như vậy phương trình f x 0 có hai nghiệm trong khoảng 1 ;1 .
Mặt khác f x 3
6x 4x 1 . Ta có f
1 11 , f
1 9 f 1 . f 1 0 . Do đó phương
trình f x 0 có nghiệm trong khoảng 1 ;1 . f x 2
18x 4 0 với x 1
;1 nên f x là hàm số đồng biến trên khoảng 1 ;1
phương trình f x 0 có duy nhất nghiệm trên khoảng 1
;1 . Do đó f x 0 có tối đa hai
nghiệm trên khoảng 1 ;1 . Vậy phương trình
1 có đúng hai nghiệm trên khoảng 1 ;1 .
Câu 92. Chọn A
Đặt f x 5 3
3x 5x 10
f x liên tục trên nên f x liên tục trên 2; 1 1 f 2 12 6 Ta có: f 1 2
Suy ra f 2. f 1 126.2 2 52 0 2 Từ
1 và 2 suy ra f x 0 có nghiệm thuộc khoảng 2; 1 .
Câu 93. Chọn C
Hàm số f x 3
2x 8x 1 liên tục trên . Do f 5 2 11, f
1 5 0, f 2 1
0, f 3 29 0 nên phương trình có ít nhất 3
nghiệm trên 5; 1 , 1
; 2,2;3 . Mà phương trình bậc ba có tối đa 3 nghiệm nên phương trình
có đúng 3 nghiệm trên . Do đó C sai.
Câu 94. Chọn B
Hàm số y f x x liên tục trên đoạn a;b .
f a a f b b
b a a b a b2 0 .
Suy ra: phương trình f x x có nghiệm trên khoảng a;b .
Câu 95. Chọn C f
2 8 4a 2b c 0 Đặt 3 2
f x x ax bx c . Khi đó f
2 8 4a 2b c 0
f x là hàm đa thức liên tục trên .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 f 2 0
f 2. f 2 0 đồ thị hàm số y f x cắt trục Ox tại ít nhất một điểm f 2 0 trong khoảng 2 ; 2 . f 2 0
đồ thị hàm số y f x cắt trục Ox tại ít nhất một điểm trong khoảng
lim f x x 2; . f 2 0
đồ thị hàm số y f x cắt trục Ox tại ít nhất một điểm trong khoảng
lim f x x ; 2 .
Mà hàm số f x là hàm bậc ba nên đồ thị của nó cắt trục Ox tối đa tại 3 điểm.
Vậy đồ thị hàm số y f x cắt trục Ox tại đúng 3 điểm.
Câu 96. Vì hàm số đã cho là hàm đa thức bậc ba nên đồ thị hàm số liên tục trên và số giao điểm của
đồ thị hàm số với trục Ox nhiều nhất là 3 .
Theo đề bài ta có lim y , lim y x x y
1 a c b 1 0 , y
1 a b c 1 0 ,
Do đó hàm số đã cho có ít nhất một nghiệm trên mỗi khoảng ; 1 , 1 ;1 , 1; .
Từ đó suy ra số giao điểm cần tìm là 3 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
Document Outline
- 1576144576_1D4-1 GIỚI HẠN DÃY SỐ
- 1576144645_1D4-2 GIỚI HẠN HÀM SỐ
- 1576144726_1D4-3 HÀM SỐ LIÊN TỤC




