Các dạng toán và bài tập giới hạn và liên tục – Nguyễn Trọng

Tài liệu gồm 154 trang, được biên soạn bởi thầy giáo Nguyễn Trọng, tóm tắt lý thuyết, hướng dẫn giải các dạng toán và tuyển chọn các bài tập chuyên đề giới hạn và liên tục

95 48 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT)

Môn: Toán 11

Thông tin:

154 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
1
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
CHƯƠNG 4 GIỚI HẠN
Mc lc
BÀI 1. GIỚI HẠN CỦA DÃY SỐ ................................................................................................. 1
A. TÓM TẮT LÝ THUYẾT .................................................................................................... 2
B. DẠNG TOÁN VÀ BÀI TẬP ............................................................................................... 3
C. BÀI TẬP RÈN LUYỆN ..................................................................................................... 22
BÀI 2. GIỚI HẠN CỦA HÀM SỐ .............................................................................................. 25
A. TÓM TẮT LÝ THUYẾT .................................................................................................. 25
B. DẠNG TON V BÀI TẬP ............................................................................................. 26
C. BÀI TẬP RÈN LUYỆN ..................................................................................................... 70
BÀI 3. HÀM SỐ LIÊN TỤC ...................................................................................................... 113
A. TÓM TẮT LÝ THUYẾT ................................................................................................ 113
B. DẠNG TOÁN VÀ BÀI TẬP ........................................................................................... 114
C. BÀI TẬP RÈN LUYỆN ................................................................................................... 138
BÀI 4. ÔN TẬP CHƯƠNG IV .................................................................................................. 139
A. BÀI TẬP .......................................................................................................................... 139
B. LỜI GIẢI.......................................................................................................................... 145
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
2
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
BÀI 1. GIỚI HẠN CỦA DÃY SỐ
A. TÓM TẮT LÝ THUYẾT
Định nghĩa 1 (Giới hạn bằng
0
). Ta nói dãy số
( )
n
u
có giới hạn là 0 nếu với mỗi số dương nhỏ tùy ý
cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều có giá trị tuyệt đối nhỏ hơn số
dương đó. Khi đó ta viết
lim 0
n
n
u
→+
=
hay
lim 0
n
u =
hay
0
n
u →
khi
n → +
.
Định nghĩa 2 (Giới hạn bằng
). Ta nói dãy số
( )
n
u
có giới hạn là số thực
nếu
( )
lim 0
n
ua−=
. Khi
đó ta viết
lim
n
n
ua
→+
=
hay
lim
n
ua=
hay
n
ua→
khi
n → +
. Dãy số có giới hạn là số
a
hữu hạn gọi là
dãy số có giới hạn hữu hạn.
Định nghĩa 3 (Giới hạn vô cực).
1. Ta nói dãy số
( )
n
u
có giới hạn là
+
khi
n → +
nếu
n
u
có thể lớn hơn một số dương bất kỳ,
kể từ một số hạng nào đó trở đi.
Ký hiệu:
lim
n
u = +
hay
n
u → +
khi
n → +
.
2. Dãy số
( )
n
u
có giới hạn là
−
khi
n → +
nếu
( )
lim
n
u− = +
.
Ký hiệu:
lim
n
u = −
hay
n
u → −
khi
n → +
.
GIỚI HẠN HỮU HẠN
GIỚI HẠN VÔ CỰC
Các giới hạn đặc biệt
•
( )
*
1
lim 0,
k
k
n
=
.
•
( )
lim 0, 1
n
qq=
.
•
( )
lim ,C C C=
Các giới hạn đặc biệt
•
( )
*
lim ,
k
nk= +
.
•
( )
lim 0, 1
n
qq=
.
Định lí 1. Nếu
lim
n
ua=
và
lim
n
vb=
thì
•
( )
lim
nn
u v a b =
.
•
( )
lim
nn
u v a b =
.
•
( )
lim 0
n
n
u
a
b
vb
=
.
• Nếu
0,
n
un
và
lim
n
ua=
thì
0a
và
lim
n
ua=
.
Định lí 2.
• Nếu
lim
n
ua=
và
lim
n
v = 
thì
lim 0
n
n
u
v
=
.
• Nếu
lim 0
n
ua=
và
lim 0
n
v =
và
0,
n
vn
thì
lim
n
n
u
v
= +
.
• Nếu
lim
n
u = +
và
lim 0
n
va=
thì
( )
lim
nn
uv = +
.
Định lí 3 (Nguyên lý kẹp). Cho ba dãy số
( ) ( ) ( )
,,
n n n
u v w
. Lúc đó, nếu
,
n n n
u v w n
và
( )
lim lim ,
nn
u w a a= =
thì
lim
n
va=
.
Định nghĩa 4. Cấp số nhân
( )
n
u
có công bội
q
được gọi kà cấp số nhân lùi vô hạn nếu
1q
.
Nhận xét. Cho cấp số nhân lùi vô hạn
( )
n
u
có công bội
. Với mỗi
*
n
, đặt
12
...
n
S u u u= + + +
. Lúc
đó:
( )
1
lim 4.1
1
n
u
S
q
=
−
Định nghĩa 5. Giới hạn
( )
4.1
được gọi là tổng của cấp số nhân lùi vô hạn
( )
n
u
và được ký hiệu là
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
3
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
12
...
n
S u u u= + + +
Như vậy:
( )
1
S lim , 1
1
n
u
Sq
q
= =
−
B. DẠNG TOÁN VÀ BÀI TẬP
Dạng 1. Tính giới hạn
( )
( )
lim
Pn
L
Qn
=
với
( ) ( )
,P n Q n
là các đa thức.
Phương pháp giải:
Rút lũy thừa bậc cao nhất của tử và mẫu, rồi sử dụng các công thức:
•
( )
*
lim 0, ,
k
c
kc
n
=
.
•
( )
lim
lim
lim 0
n
nn
n
u
uv
va
= +
= +
=
.
•
( )
lim
lim
lim 0
n
nn
n
u
uv
va
= +
= −
=
.
•
( )
*
lim
k
nk= +
.
•
( )
lim
lim
lim 0
n
nn
n
u
uv
va
= −
= −
=
.
•
( )
lim
lim
lim 0
n
nn
n
u
uv
va
= −
= +
=
.
VÍ DỤ
Ví dụ 1. Tính giới hạn
2
2
41
lim
32
nn
L
n
. ĐS:
2L =
Lời giải
Ta có
2
2
2
2
2
2
11
11
4
4
400
lim lim 2
3
3
02
2
2
n
nn
nn
L
n
n
n

−−
−−

−−

= = = =
+

+
+


.
Nhận xét: Nếu bậc tử
( )
Pn
bằng bậc mẫu
( )
Qn
thì
( )
( )
lim
Pn
Qn
=
(Hệ số bậc cao nhất của tử)
(Hệ số bậc cao nhất của mẫu).
Ví dụ 2. Tính giới hạn
5
4
2
4
62
2 4 1
lim
20 2 1
n n n
L
n n n
.
ĐS:
128
5
L =
Lời giải
Ta có
54
2
4
62
2
12
24
lim
31
20 2
nn
nn
L
nn
nn
−−
=


−+




ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
4
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( ) ( )
( )
5 4 5 4
10 4
54
4 4 4
68
22
1 2 1 2
2 4 2 4
2 0 4 0
128
lim lim lim
5
20 2 0 0
3 1 3 1
20 2 20 2
nn
n n n n
nn
n n n n
− − − −
−−
= = = =
−+
− + − +
Nhận xét: Với bài toán có lũy thừa bậc cao, ta thường rút bậc cao trong từng dấu ngoặc, sau
đó áp dụng công thức
( )
..
n
nn
a b a b=
và tính toán như các bài trước.
Ví dụ 3. Tính giới hạn
2
3
3
lim
2
nn
L
nn
−+
=
+
.
ĐS:
0L =
Lời giải
Ta có
2
2
2
3
2
2
13
13
1
1
1 1 0 0
lim lim . 0. 0
2
2
10
1
1
n
nn
nn
L
n
n
n
n


−+
−+


−+

= = = =

+


+
+



Nhận xét: Nếu bậc tử
( )
Pn
nhỏ hơn bậc mẫu
( )
Qn
thì
(n)
lim 0
(n)
P
L
Q
==
Ví dụ 4. Tính giới hạn
3
2
2 11 1
lim
2
nn
L
n
−+
=
−
. ĐS:
L = +
Lời giải
3
3
3
2
2
2
11 1
11 1
2
2
lim lim .
2
2
1
1
n
nn
nn
Ln
n
n
n


−+
−+



= = = +



−
−



(vì
limn = +
và
3
2
11 1
2
lim 2 0
2
1
nn
n

−+

=


−

).
Nhận xét: - Nếu bậc tử
( )
Pn
lớn hơn bậc mẫu
( )
Qn
thì
(n)
lim
(n)
P
L
Q
= = 
.
- Để biết là
+
hay
−
ta dựa vào dấu của giới hạn trong tích theo quy tắc “cùng
dấu thì tích dương, trái dấu thì tích âm”. Thông thường, sẽ để dấu
=
và xét dấu
sẽ điền vào sau.
- Về trắc nghiệm, đó chính là tích của hệ số bậc cao nhất của tử và mẫu.
Ví dụ 5. Tính giới hạn
2
1 3 5 7 (2 1)
lim
34
n
L
n
+ + + + +
=
+
.
ĐS:
1
3
L =
Lời giải
Xét cấp số cộng
1,3,5,7,9,...,2 1n+
có số hạng đầu tiên
1
1u =
công sai
2d =
và số hạng cuối
cùng là
21
m
un=+
ta có:
1
( 1) 2 1 1 2( 1) 2 1 1.u m d n m n m n+ − = + + − = + = +
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
5
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Vậy cấp số cộng có
1n+
số hạng. Suy ra tổng
2
1
1
1 3 5 7 2 1 ( ) (1 2 1) 2 1
22
m
mn
S n u u n n n
+
= + + + + + + = + = + + = + +
Vì thế
2
2
2
2
2
2
2
2
21
21
1
1
2 1 1 0 0 1
lim lim lim
4
4
3 4 3 0 3
3
3
n
nn
nn
nn
L
n
n
n
n
.
Nhận xét: Cần nhớ công thức cấp số cộng:
1kk
u u d
+
−=
, với
d
là công sai.
( )
1
1
n
u u n d= + −
, với
d
là công sai.
11
2 , 2
k k k
u u u k
.
1 2 1
2
n n n
n
S u u u u u
.
Ví dụ 6. Tính giới hạn
( )
1 1 1 1 1
lim .
1.2 2.3 3.4 4.5 1
L
nn

= + + + + +

+

ĐS:
1L =
Lời giải
Số hạng tổng quát
( )
1 1 1
; 1,2,...,
(k 1) 1
kn
k k k
= − =
++
do đó
1 1 1 1 1 1 1 1
lim 1
2 2 3 3 4 4 1
L
nn

= − + − + − + − + −

+

1 1 1
lim 1 lim lim 1
1
1 1 1 0
1
n
nn
n
= − = = = =
+ + +
+
Nhận xét: Phân tích
( )
1
11
ab
k k k k
=+
++
với
01
11
1; 1
1
kk
ab
kk
= =−
= = = = −
+
.
BÀI TẬP ÁP DỤNG
Bài 1. Tính giới hạn sau:
a)
2
2
35
lim
21
nn
L
n
; b)
3
33
3
lim
2 3 1
nn
L
nn
;
c)
3
32
6 2 1
lim
51
nn
L
n n n n
; d)
2
9
4
17
2 1 2
lim
1
nn
L
n
;
e)
2
3
32
2 1 3 4
lim
4 2 2
nn
L
nn
; f)
3
2
2
4
32
3 1 2 5 9 4
lim
2 4 2 1 2 7
n n n
L
n n n
;
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
6
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
g)
3
2
2
2
21
lim
1 2 3
nn
L
nn
.
Bài 2. Tính giới hạn sau:
a)
32
43
7 2 1
lim
5
nn
L
n n n
++
=
++
; b)
23
73
lim
2 3 4
n
L
nn
+
=
++
;
c)
2
32
45
lim
37
nn
L
nn
+−
=
++
; d)
32
43
2 3 4
lim
4
nn
L
n n n
− + +
=
++
;
e)
2
4
22
lim
35
nn
L
n
− + +
=
+
.
Bài 3. Tính giới hạn sau:
a)
3
2
53
lim
31
nn
L
nn
−+
=
+−
; b)
4 3 2
23
5 5 3
lim
31
n n n
L
nn
− + +
=
−−
;
c)
42
3
3 2 1
lim
29
nn
L
nn
+−
=
++
; d)
54
4 3 2
3 2 2 7
lim
6 2 1
n n n
L
n n n
− + +
=
− + + −
;
Bài 4. Tính giới hạn sau:
a)
2
1 2 3 ...
lim
31
n
L
n
+ + + +
=
+
; b)
( )
2
1 3 5 7 ... 2 1
lim
31
n
L
nn
+ + + + + −
=
++
;
c)
2
1 2 3 ...
lim
29
n
L
nn
+ + + +
=
−+
; d)
( )
2
5 9 13 ... 4 3
lim
3 5 1
n
L
nn
+ + + + −
=
+−
;
e)
( )
1 2 3 4 ... 2 1 2
lim
21
nn
L
n
− + − + + − −
=
+
; f)
( )
1 1 1 1
lim ...
1.3 2.4 3.5 2
[]L
nn
= + + + +
+
;
g)
( )( )
1 1 1 1
lim ...
1.3 3.5 5.7 2 1 2 1
[]L
nn
= + + + +
−+
;
h)
( )( )
1 1 1 1
lim ...
1.3 3.5 5.7 2 1 2 1
[]L
nn
= + + + +
−+
.
LỜI GIẢI
Bài 1. a)
2
2
2
2
2
2
2
2
15
15
3
3
3 5 3 0 0 3
lim lim lim
1
1
2 1 2 0 2
2
2
n
nn
nn
nn
L
n
n
n
n
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
7
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
b)
3
3
23
23
3
3
13
1
3
lim lim
21
2 3 1
3
n
nn
nn
L
nn
n
nn
23
3
13
1
1
lim
21
3
3
nn
nn
.
c)
3
33
23
23
32
32
3
2
2
21
21
6
6
6 2 1 6 2 1 3
lim lim lim lim
11
11
42
51
4
4
n
n n n n
nn
nn
L
n n n
n n n n
n
nn
nn
.
d)
2 9 2 9
89
2
9
4
44
17
17
17 17
1 2 1 2
2 1 2 1
2 1 2
lim lim lim
11
1
11
nn
nn
n n n n
L
n
n
nn
29
(2 0) .(1 0)
lim 4
10
++
==
+
.
e)
( )
( )
( ) ( )
22
23
2
3
33
3 2 3 2 3 2
32
1 3 1 3
2 4 2 4
2 1 3 4
lim lim lim
4 2 2
2 1 2 1
4 2 4 2
nn
nn
n n n n
L
nn
nn
n n n n
− − − −
−−
= = =
+−
+ − + −
2
32
2 0 0 4
1
lim
4
4 0 2 0
.
f)
( )
( ) ( )
( )
( )( )
3
2
2
4
32
3 1 2 5 9 4
lim
2 4 2 1 2 7
n n n
L
n n n
− + +
=
− + −
32
2
2
4
4 3 2
32
1 5 4
3 2 9
lim
4 1 7
2 2 2
n n n
n n n
L
n n n
n n n
− + +
=
− + −
32
2
4
32
1 5 4
3 2 9
lim
4 1 7
2 2 2
n n n
n n n
− + +
=
− + −
32
4
3 0 2 0 9 0
243
lim
16
2 0 2 0 2 0
.
g)
( )
( )
( )
( )
33
23
3
2
22
2 2 2
2
4
22
2 1 2 1
1 1 1 1
21
lim lim lim
1 3 1 3
1 2 3
1 2 1 2
nn
nn
n n n n
L
nn
nn
n n n n
+ − + −
+−
= = =
++
+ + + +
3
2
1 0 1 0
1
lim
4
1 0 2 0
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
8
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 2. a)
3
32
3
43
4
3
21
7
7 2 1
lim lim
51
5
1
n
nn
nn
L
n n n
n
nn

++

++

==
++

++


3
3
21
7
1
lim . 0
51
1
nn
n
nn

++

==


++

(Vì
1
lim 0;
n
và
3
3
21
7
lim 7
51
1
nn
nn
).
b)
23
73
lim
2 3 4
n
L
nn
2
3
3
3
3
3
7
7
1
lim lim . 0
24
24
3
3
n
n
n
n
n
nn
nn
(Vì
2
1
lim 0
n
và
3
3
7
7
lim
24
3
3
n
nn
).
c)
2
2
2
32
3
3
45
1
45
lim lim
17
37
3
n
nn
nn
L
nn
n
nn

+−

+−

==
++

++


2
3
45
1
1
lim . 0
17
3
nn
n
nn

+−

==


++

(Vì
1
lim 0
n
=
và
2
3
45
1
1
lim
17
3
3
nn
nn
+−
=
++
).
d)
32
43
2 3 4
lim
4
nn
L
n n n
− + +
=
++
3
3
4
3
34
2
lim
41
1
n
nn
n
nn

− + +


=

++


3
3
34
2
1
lim . 0
41
1
nn
n
nn
(Vì
1
lim 0
n
và
3
3
34
2
2
41
1
nn
lim
nn
).
e)
2
4
22
lim
35
nn
L
n
− + +
=
+
2
2
2
2
4
4
4
12
12
2
2
1
lim lim . 0
5
5
3
3
n
nn
nn
n
n
n
n


− + +
− + +



= = =



+
+



.
(Vì
2
1
lim 0
n
và
2
4
12
2
2
lim
5
3
3
nn
n
).
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
9
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 3. a)
3
3
23
23
2
2
2
2
53
53
1
1
53
lim lim lim .
11
11
31
3
3
n
nn
nn
nn
Ln
nn
n
nn
nn


−+
−+


−+

= = = = +

+−


+−
+−



(Vì
limn = +
và
23
2
53
1
1
lim
11
3
3
nn
nn
−+
=
+−
).
b)
4
4 3 2
24
24
23
3
3
3
1 5 3
1 5 3
5
5
5 5 3
lim lim lim .
11
11
31
3
3
n
n n n
n n n
n n n
Ln
nn
n
nn
nn


− + +
− + +


− + +

= = = = −

−−


−−
−−



.
(Vì
limn = +
và
24
3
1 5 3
5
5
lim
11
3
3
n n n
nn
− + +
=−
−−
).
c)
4
42
24
24
3
3
23
23
21
21
3
3
3 2 1
lim lim lim .
29
29
29
1
1
n
nn
nn
nn
Ln
nn
n
nn
nn


+−
+−


+−

= = = = +

++


++
++



.
(Vì
limn = +
và
24
23
21
3
lim 3
29
1
nn
nn
+−
=
++
).
d)
5
54
45
45
4 3 2
4
24
24
2 2 7
2 2 7
3
3
3 2 2 7
lim lim lim .
2 1 1
2 1 1
6 2 1
6
6
n
n n n
n n n
n n n
Ln
n n n
n
n n n
n n n


− + +
− + +


− + +

= = = = −

− + + −


− + + −
− + + −



.
(Vì
limn = +
và
45
24
2 2 7
3
1
lim
2 1 1
2
6
n n n
n n n
+ + +
=−
− + + −
).
Bài 4. a) Theo tính chất của cấp số cộng, ta có
( )
2
1
1 2 3 ...
22
nn
nn
n
+
+
+ + + + = =
Do đó
2
2
22
2
2
1
1 2 3 ... 2 1
lim lim lim
2
3 1 6 2 6
6
nn
n
L
nn
n
+
+ + + + +
= = = =
++
+
.
b) Theo tính chất của cấp số cộng, ta có
( )
( )
( )
2
1 2 1
1 3 5 7 ... 2 1
2
nn
nn
+−
+ + + + + − = =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
10
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Do đó
( )
2
22
2
1 3 5 7 ... 2 1
1
lim lim lim 1
31
3 1 3 1
1
n
n
L
n n n n
nn
+ + + + + −
= = = =
+ + + +
++
.
c) Theo tính chất của cấp số cộng, ta có
( )
2
1
1 2 3 ...
22
nn
nn
n
+
+
+ + + + = =
Do đó
2
22
2
1
1
1 2 3 ... 1
lim lim lim
2 18
2 9 4 2 18 4
4
n n n
n
L
n n n n
nn
+
+ + + + +
= = = =
− + − +
−+
.
d) Xét cấp số cộng với
1
5; 4ud==
( ) ( )
( )( )
2
1
5 4 3 1
5 2 4 4 3 5 9 13 ... 4 3 2 1
2
n
nn
u n n n n n
−
+ − −
= + − = − + + + + − = = − −
Do đó
( )
2
2
22
2
11
2
5 9 13 ... 4 3
2 1 2
lim lim lim
51
3 5 1 3 5 1 3
3
n
nn
nn
L
n n n n
nn
−−
+ + + + −
−−
= = = =
+ − + −
+−
.
e) Ta có
( ) ( ) ( ) ( )
( )
( ) ( ) ( )
1 2 3 4 ... 2 1 2 1 2 3 4 ... 2 1 2 1 1 ... 1n n n n n− + − + + − − = − + − + + − − = − + − + + − = −
Do đó
( )
1 2 3 4 ... 2 1 2
11
lim lim lim
1
2 1 2 1 2
2
nn
n
L
nn
n
− + − + + − −
−−
= = = = −
++
+
.
f) Ta có
( )
1 1 1 1 1 1 1 1 1 1 1
... ...
1.3 2.4 3.5 2 2 1 3 2 4 2n n n n

+ + + + = − + − + + −

++

1 1 1 1 3 1 1
1
2 2 1 2 4 2 2 2 4n n n n

= + − − = − −

+ + + +

Do đó
( )
1 1 1 1 3 1 1 3
lim ...
1.3 2.4 3.5 2 4 2 2 2 4 4
[ ]=limL
n n n n

= + + + + − − =

+ + +

.
g) Ta có
( )( )
1 1 1 1 1 1 1 1 1 1 1 1 1
... ... 1
1.3 3.5 5.7 2 1 2 1 2 1 3 3 5 2 1 2 1 2 2 1n n n n n
+ + + + = − + − + + − = −
− + − + +
Do đó
( )( )
1 1 1 1 1 1 1
lim ... lim 1
1.3 3.5 5.7 2 1 2 1 2 2 1 2
[ ]= [ ]L
n n n

= + + + + − =

− + +

.
h) Ta có
( )( )
1 1 1 1
...
1.4 4.7 7.10 3 2 3 1nn
+ + + +
−+
1 1 1 1 1 1 1 1
1 ...
3 4 4 7 7 10 3 2 3 1nn

= − + − + − + + +

−+

11
1
3 3 1n

=−

+

.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
11
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Dạng 2. Tính giới hạn dạng
( )
( )
lim
Pn
L
Qn
=
với
( ) ( )
,P n Q n
là các hàm mũ
n
a
.
Phương pháp giải:
Áp dụng
lim 0
n
q =
với
1q
.
Sử dụng công thức mũ, rồi chia cả và mẫu cho
n
a
với
a
là cơ số lớn nhất.
Công thức mũ cần nhớ
.
m n m n
a a a
+
=
và
m
mn
n
a
a
a
−
=
.
VÍ DỤ
Ví dụ 1. Tính giới hạn
2
1 2 1
1 3 4.5
lim
2 3 5
nn
n n n
L
+
+ + +
−+
=
++
. ĐS:
20L =
Lời giải
Chia cả tử và mẫu cho
5
n
, ta có
13
13
100
100
0 0 100
55
55
lim lim 20.
23
0 0 5
23
2. 9. 5
2. 9. 5
55
55
nn
n
nn
n n n n
nn
L
−+
−+
−+
= = = =
++
++
++
Nhận xét: Ta chia cho
n
a
với
a
là cơ số lớn nhất vì sau khi chia luôn tạo ra cơ số có trị tuyệt
đối nhỏ hơn
1
để áp dụng công thức
lim 0
n
q =
với
1q
.
Ví dụ 2. Tính giới hạn
23
1 2 2 2 ... 2
lim
5.2 1
n
n
L
+ + + + +
=
+
. ĐS:
2
5
L =
Lời giải
Xét cấp số nhân
23
1,2,2 ,2 ,...,2
n
có số hạng đầu tiên
1
1u =
, công bội
2q =
và có số hạng tổng
quát
1
1
2 2 1 1
n m n
m
u u q m n m n
−
= = − = = +
.
Suy ra tổng các số hạng của cấp số nhân trên là:
1
1
1
1 2 1
21
1 2 1
mn
n
m
q
Su
q
+
+
−−
= = = −
−−
.
Suy ra
1
1
2
2 1 2 0 2
2
lim lim .
5.2 1 5 0 5
1
5
2
n
n
n
n
L
+

−

−−

= = = =
++

+


Nhận xét: Các công thức cần nhớ về cấp số nhân
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
12
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
1
1.
k
k
u
q
u
+
=
(
q
là công bội).
1 2 1
1
2. ... .
1
n
nn
q
S u u u u
q
−
= + + + =
−
.
1
1
3.
n
n
u u q
−
=
.
2
11
4. .
k k k
u u u
+−
=
với
2k
.
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau:
a)
1
4.3 5
lim .
3.2 5
nn
nn
L
+
+
=
+
ĐS:
5.L =
b)
21
13
46
lim .
5 2.6
nn
nn
L
++
−+
+
=
+
ĐS:
1
72
L =
.
c)
22
1 2 1
2 3 3.5
lim .
2 3 5
n n n
n n n
L
−+
− + +
−+
=
++
ĐS:
15L =
. d)
2
1 2 1
2 3 5
lim .
2 3 5
n n n
n n n
L
+
+ + +
−+
=
++
ĐS:
5L =
.
e)
( )
1
3 4.5
lim .
2.4 3.5
n
n
nn
L
+
−−
=
+
ĐS:
20
3
L =−
. f)
( )
( )
25
lim .
2.3 3. 5
n
n
n
n
L
+−
=
+−
ĐS:
1
3
L =
.
g)
( )
51
52
1 .2
lim .
3
n
n
n
L
+
+
−
=
ĐS:
0L =
.
Bài 2. Tính các giới hạn sau:
a)
23
23
1 2 2 2 ... 2
lim .
1 3 3 3 ... 3
n
n
L
+ + + + +
=
+ + + + +
ĐS:
0L =
.
b)
1 1 1
1 ...
2 4 2
lim .
1 1 1
1 ...
3 9 3
n
n
L
+ + + +
=
+ + + +
ĐS:
4
3
L =
.
LỜI GIẢI
Bài 1. a)
1
4.3 5
lim
3.2 5
nn
nn
L
+
+
=
+
3
4. 5
05
5
lim 5.
01
2
3. 1
5
n
n

+

+

= = =
+

+


b)
21
13
2
16. 6
4 6 0 6 1
3
lim lim
5 2.6 0 432 72
15
. 432
56
n
nn
n
nn
L
++
−+

+

++

= = = =
++

+


.
c)
22
1 2 1
2 1 3
. 75
2 3 3.5 0 0 75
5 9 5
lim lim 15
2 3 5 0 0 5
1 2 3
. 9. 5
2 5 5
nn
n n n
nn
n n n
L
−+
− + +
−+
− + − +
= = = =
+ + + +
++
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
13
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
d)
2
1 2 1
23
25
2 3 5 0 0 25
55
lim lim 5
2 3 5 0 0 5
23
2. 9. 5
55
nn
n n n
nn
n n n
L
+
+ + +
−+
− + − +
= = = =
+ + + +
++
.
e)
( )
1
3
20
3 4.5
0 20 20
5
lim lim
2.4 3.5 0 3 3
4
2. 3
5
n
n
n
n
nn
L
+

−−

−−
−

= = = = −
++

+


.
f)
2
1
25
0 1 1
5
lim lim
0 3 3
2.3 3. 5 3
2. 3
5
n
n
n
nn
n
L
.
g)
( )
51
52
1 32
.2.
1 .2
0
243 243
lim lim 0
3 9 9
nn
n
n
n
L
+
+
−
−
= = = =
.
Bài 2. a) Áp dụng công thức tính tổng của một cấp số nhân, ta lần lượt có
1
2 3 1
21
1 2 2 2 ... 2 2 1
21
n
nn
+
+
−
+ + + + + = = −
−
11
23
3 1 3 1
1 3 3 3 ... 3
3 1 2
nn
n
++
−−
+ + + + + = =
−
Do đó
1
1
21
2.
2 1 2.2 1 0 0
33
lim 2.lim 2.lim 2. 0.
31
3.3 1 3 0
1
3
2
3
nn
nn
nn
n
L
+
+
−
− − −
= = = = =
−
−−

−


b) Áp dụng công thức tính tổng của một cấp số nhân, ta lần lượt có
( )
1
1
1
1 1 1 1 1
2
1 ... 2 . 1
1
2 4 2 2 2
1
2
n
n
n
+

−




+ + + + = = − −





−
1
1
1
1 1 1 3 1 1
3
1 ... . 1
1
3 9 3 2 3 3
1
3
n
n
n
+

−



+ + + + = = − −



−
Do đó
( )
11
1
2 . 1
.0 1
22
44
2
lim . .
1
33
3 1 1
.0 1
.1
3
2 3 3
n
n
L


−−


−



= = =

−
−−



ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
14
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Dạng 3. Tính giới hạn của dãy số chứa căn thức.
Phương pháp giải: Rút lũy thừa bậc cao hoặc liên hợp và sử dụng
lim
k
n =
.
Lưu ý: Dấu hiệu nhận dạng liên hợp (dạng
.0+
) là sau khi rút
có mũ cao trong căn và nhóm thừa
số, xuất hiện số
0
. Chẳng hạn:
- Tính giới hạn dãy
2
35
n
u n n n= + + −
: biểu thức trong căn có
2
n
là lũy thừa cao nhất và
ta quan tâm đến nó, những hạng tử sau bỏ hết, có nghĩa ta xem
2
0
n
u n n n n= − = − =
nên cần liên hợp.
- Tính giới hạn dãy
2
2 3 5
n
u n n n= + + −
: biểu thức trong căn có
2
2n
là lũy thừa cao nhất
nên nháp
( )
2
2 2 2 1n n n n n− = − = −
, có
2 1 0−
nên ta không cần liên hợp mà rút ra
giải trực tiếp.
VÍ DỤ
Ví dụ 1. Tính giới hạn
(
)
2
lim 2 3 5 .L n n n= + + −
ĐS:
L = +
.
Lời giải
Ta có:
2
2
2
2 3 5
lim
nn
L n n
n


++

=−




2
35
lim 2nn
nn

= + + −



2
35
lim 2 1n
nn

= + + −



Vì
limn = +
và
2
35
lim 2 1 2 1 0
nn

+ + − = −



nên
L
.
Ví dụ 2. Tính giới hạn
(
)
2
lim 9 3 4 3 20 .L n n n= + − − +
ĐS:
41
2
L =
.
Lời giải
Ta có:
2
lim20 lim 9 3 4 3L n n n
2
34
20 lim
9 3 4 3
n
n n n
2
4
3
20 lim
34
93
n
n
nn
nn
2
4
3
20 lim
34
93
n
nn
30
20
9 0 0 3
41
2
.
Cần nhớ : Liên hợp là hình thức trục căn dựa vào HĐT
( )( )
( )
( )
22
2 2 3 3
a b a b a b
a b a ab b a b
− + = −
+ =
.
➢
ab
ab
ab
−
−=
+
.
33
3 2 3 2
3
ab
ab
a ab b
+
+=
−+
.
➢
2
ab
ab
ab
−
−=
+
.
3
3
3 2 2
3
ab
ab
a ab b
−
−=
++
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
15
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
➢
33
3 2 3 2
3
ab
ab
a ab b
−
−=
++
.
3
3
3 2 2
3
ab
ab
a ab b
+
+=
−+
.
Ví dụ 3. Tính giới hạn
( )
33
lim 2L n n= + −
ĐS:
0L =
.
Lời giải
Ta có:
22
33
33
2
lim
22
nn
L
n n n n
2
2
33
33
2
lim
22
11n n n n
nn
3
2
2
2
3
2
33
33
2
20
lim lim 0
3
22
22
1 1 1
1 1 1
n
n
nn
nn
.
Cần nhớ:
33
3 2 3 2
3
ab
ab
a ab b
−
−=
++
.
Ví dụ 4. Tính giới hạn
(
)
3 3 2
8im 2l 3 5 2n n nL + − + −=
. ĐS:
21
4
L =
.
Lời giải
Ta có:
32
3
8 3 2lm 5i 2n n nL
32
3
lim5 lim 8 3 2 2n n n
32
3
5 lim 8 3 2 2n n n
3 2 3
2
3 2 3 2 2
33
8 3 2 8
5 lim
8 3 2 8 3 2 2 4
n n n
n n n n n n
2
2
3 3 2
3
33
32
5 lim
3 2 3 2
8 8 .2 4
n
n n n n
n n n n
2
2
33
23
2
3
5 lim
3 2 3 2
8 8 2 4
n
n n n n
3 21
5
4 4 4 4
.
Cần nhớ:
3
3
22
3
3
ab
ab
a a b b
−
−=
+ +
. Trong lời giải trên, đã sử dụng hai tính chất:
➢
( )
lim lim lim
n n n n
u v u v+ = +
.
➢
limCC=
với
C
là hằng số
C
.
Ví dụ 5. Tính giới hạn
(
)
2 3 3 2
im 1l n n n nL + + − +=
. ĐS:
1
6
L =
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
16
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Lời giải
Ta có:
(
)
2 3 3 2
im 1l n n n nL + + − +=
(
)
(
)
2 3 3 2
lim 1n n n n n n

= + + − + − +


(
)
(
)
2 3 3 2
lim 1 limn n n n n n= + + − + − +
( )
(
)
3 3 2
22
2
2
2 3 3 2 3 3 2
1
lim lim
1
n n n
n n n
n n n
n n n n n n
−+
+ + −
=+
+ + +
+ + + +
(
)
2
2
2
2 3 3 2 3 3 2
1
lim lim
1
nn
n n n
n n n n n n
+−
=+
+ + +
+ + + +
2
2
3
3
1
1
1
lim
11
11
11
1 1 1
n
nn
nn
+
−
=+

+ + +
+ + + +


1 1 1
2 3 6
= − =
.
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau:
a)
2
91
lim
42
nn
L
n
. ĐS:
3
4
b)
2
2
41
lim
93
n n n
L
nn
. ĐS:
1
3
c)
4
2
2 3 2
lim
23
nn
L
nn
. ĐS:
2
2
d)
2 1 3
lim
45
nn
L
n
. ĐS:
21
2
e)
2 3 2
3
24
4
4 1 8 2 3
lim
16 4 1
n n n
L
n n n
. ĐS:
4
3
L
f)
63
3
7 5 8
lim
2
n n n
L
n
. ĐS:
L
g)
( )
24
1 4 7 3 1
2 2 1
lim
n
L
n n n
+ + ++ +
=
+ + +
. ĐS:
0L =
Bài 2. Tính các giới hạn sau:
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
17
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
a)
2
lim 4 1 9L n n n
. ĐS:
b)
22
lim 9 2 1 4 1L n n n
. ĐS:
c)
22
lim 4 4 2L n n n
. ĐS:
1
4
d)
2
lim 1 10L n n n
ĐS:
21
2
e)
2
lim 3 5 25L n n n
. ĐS:
53
2
f)
24
lim 2019 3 1L n n n
. ĐS:
2019L
g)
2
lim 3 5 9 1L n n
. ĐS:
5L
h)
22
lim 1 2L n n n
. ĐS:
1
2
L
Bài 3. Tính các giới hạn sau:
a)
33
lim 4 1 L n n
. ĐS:
0L
b)
32
3
lim 8 3 4 2 6L n n n
. ĐS:
25
4
L
c)
3
3
lim 2 1L n n n
. ĐS:
1L
d)
3
3
lim 2L n n n
. ĐS:
2L
e)
3
32
lim 2 1L n n n
. ĐS:
5
3
L
f)
4 2 6
3
lim 1L n n n
. ĐS:
1
2
L
g)
2 3 2
3
lim 1L n n n n
. ĐS:
1
6
L
Bài 4. Tính các giới hạn sau:
f)
4 2 6
3
lim 1L n n n
. ĐS:
1
2
L
g)
2 3 2
3
lim 1L n n n n
. ĐS:
1
6
L
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
18
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
LỜI GIẢI
Bài 1. a)
2
2
2
2
11
11
9
9
91
lim lim lim
22
42
44
n
n
nn
nn
nn
L
n
nn
nn

−+
−+

−+

= = =
−
−−
2
11
9
lim
2
4
nn
n
9 0 0
40
3
4
.
b)
2
2
41
lim
93
n n n
L
nn
− + −
=
+
2
11
41
lim
3
9
nn
n
− + −
=
+
4 0 0 1
90
− + −
=
+
1
3
=
.
c)
4
2
2 3 2
lim
23
nn
L
nn
+−
=
−+
2
34
2
2
32
2
lim
13
2
n
nn
n
nn
+−
=

−+


34
2
32
2
lim
13
2
nn
nn
+−
=
−+
2 0 0 2
2 0 0 2
+−
==
−+
.
d)
13
13
21
21
2 1 3 2 1
lim lim lim
2
4 5 5 5
. 4 4
n
nn
nn
nn
L
n
n
nn

+ − +

+ − +
+ − + −

= = = =
−
−−
.
e)
23
3
23
3
2 3 2
24
4
24
4
4
1 2 3
4 8
4 1 8 2 3
lim lim
41
16 4 1
16 1
nn
n n n
n n n
L
n n n
nn
nn
− + + −
− + + −
==
+ − +
+ − +
33
2 3 2 3
44
44
1 2 3 1 2 3
4 8 4 8
lim lim
4 1 4 1
16 1 16 1
nn
n n n n n n
nn
n n n n
− + + − − + + −
==
+ − + + − +
2 2 4
4 1 3
+
==
−
.
f)
3 56
6
3
3
63
7 5 8
1
7 5 8
lim lim
22
n
n n n
n n n
L
nn
=

−
−+
− − +
=
+
+
2
3
3 5 6
7 5 8
. 1
lim
2
.1
n
n n n
n
n
− − +
=

+


3
3 5 6
7 5 8
1
.
2
1
n n n
n
n
− − +
=
+
lim
=+
(Vì
limn = +
và
3
3 5 6
7 5 8
1
1
2
1
n n n
n
− − +
=
+
lim
).
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
19
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
g)
( ) ( )( )
(
)
24
24
1 4 7 3 1 1 3 2
2 2 1
2 2 2 1
n n n
L
n n n
n n n
+ + ++ + + +
==
+ + +
+ + +
lim lim
2
24
3 5 2
2 2 2 2 1
lim
nn
n n n
++
=
+ + +
4
23
2
3
4
4
4
3 5 2
21
2 2 2 1
n
n n n
nn
nn

++


=
+



++
lim
4
2
2 3 2 3
2
3 4 3
2
4
4
3 5 2 3 5 2
0
lim lim 0
2 1 2 1 3 2
2 2 2 1 2 2 2 1
n
n n n n n n
nn
n n n n
.
Bài 2. a)
(
)
22
22
1 1 1 1
lim 4 1 9 lim 4 9 lim 4 9L n n n n n n n
n n n n



= + + − = + + − = + + −








2
11
lim . 4 9n
nn

+ + −



(Vì
lim n = +
và
2
11
lim 4 9 7 0
nn

+ + − = −



).
b)
(
)
22
22
2 1 1
lim 9 2 1 4 1 lim 9 4L n n n n
n n n

= + − − + = + − − + = +



(Vì
lim n = +
và
22
2 1 1
lim 9 4 1 0
n n n

+ − − + =



).
c)
(
)
22
lim 4 4 2L n n n= + − +
( ) ( )
22
22
4 4 2
lim
4 4 2
n n n
n n n
+ − +
=
+ + +
22
2
lim
4 4 2
n
n n n
−
=
+ + +
2
2
1
lim
12
44
n
nn
−
=
+ + +
1 0 1
4
4 0 4 0
−
==
+ + +
.
d)
2
lim 1 10L n n n
2
lim10 lim 1n n n
2
1
10 lim
1
n
n n n
2
1
1
10 lim
11
11
n
nn
1 0 1
10 10
2
1 0 0 1
21
2
.
e)
2
lim 3 5 25L n n n
2
lim25 lim 3 5n n n
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
20
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
22
2
35
25 lim
35
n n n
n n n
2
25 lim
5
35
3n n n
n
2
3
25 lim
35
5
11
n
nn
3 0 53
25
2
1 0 0 1
.
f)
24
lim 2019 3 1L n n n
24
lim2019 lim 3 1n n n
44
24
31
2019 lim
3 1
n n n
n n n
24
31
2019 lim
3 1
n
n n n
2
34
31
2019 lim
31
11
nn
nn
0 0
2019
1 1 0 0
2019 0 2019
.
g)
2
lim 3 5 9 1L n n
2
lim 3 9 1 lim5nn
22
2
9 9 1
lim lim5
3 9 1
nn
nn
2
1
lim lim5
3 9 1nn
0 5 5
.
h)
22
lim 1 2L n n n
22
22
1 2
lim
1 2
n n n
nn
22
lim
1 2
n
nn
22
1 1
lim
2
12
1 1
nn
.
Bài 3. a)
( )
33
lim 4 1 L n n= + − +
( ) ( ) ( ) ( )
22
33
3
3
4 4 . 1 1
lim
n n n n
=
+ + + + + +
22
2 2 2
33
3
3
4 4 1 1
. 1 . 1 . 1 . 1
lim
n n n
n n n n
=
+ + + + − +
22
3
2
33
3
3
0
4 4 1 1
1 1 . 1 1
lim
n
n n n n
==


+ + + + + +


.
b)
32
3
lim 8 3 4 2 6L n n n
32
3
lim 8 3 4 2 6n n n
32
3
6 lim 8 3 4 2n n n
2
2
3 2 3 2 2
3
3
3 4
6 lim
8 3 4 2 . 8 3 4 4
n
n n n n n n
2
2
3
3
33
4
3
6 lim
3 4 3 4
8 2. 8 4
n
n n n n
1 25
6
44
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
21
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
c)
(
)
3
3
lim 2 1L n n n= − + −
(
)
3
3
lim 2 1n n n= − + −
(
)
3
3
1 2 lim n n n= − + − +
( )
2
3
3 3 2
3
2
1 lim
2 2 2
n
n n n n n n
=− +
− − − +
2
3
3
22
2
1
22
1 1 1
n
nn
= − +

− − − +


lim
1 0 1= − + =−
.
d)
3
3
lim 2L n n n
3
3
lim 2n n n
3
3
2 lim n n n
2
3
3 3 2
3
2 lim
.
n
n n n n n n
2
3
3
22
1
2 lim
11
1 1 1
n
nn
2 0 2
.
e)
3
32
lim 2 1L n n n
3
32
lim 2 1n n n
3
32
1 lim 2 n n n
2
2
3
3 2 3 2 2
3
2
1 lim
2 . 2 2
n
n n n n n n
2
3
3
2
1 lim
22
1 1 1
nn
25
1
33
.
Bài 4. a)
4 2 6
3
lim 1L n n n
4 2 2 6 2
3
lim 1n n n n n
4 2 2 6 2
3
lim lim 1n n n n n
4 2 4 6 6
4 2 2 2
6 2 6 4
3
3
1
lim lim
11
n n n n n
n n n
n n n n
2
4 2 2 2
6 2 6 4
3
3
1
lim lim
11
n
n n n
n n n n
2
11
lim 0
2
1
11
n
.
b)
2 3 2
3
lim 1L n n n n
2 3 2
3
lim 1n n n n n n
3 3 2
22
2
2
2 3 2 3 2
33
1
lim
1
n n n
n n n
n n n
n n n n n n
2
2
2
2 3 2 3 2
33
1
lim
1
nn
n n n
n n n n n n
2
33
2
1
1
1
lim
11
11
11
1 1 1
n
nn
nn
1 1 1
2 3 6
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
22
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
C. BÀI TẬP RÈN LUYỆN
Bài 1. Tính các giới hạn sau:
1)
2
2
2 3 1
lim
53
nn
n
−+
+
. ĐS:
2
5
. 2)
2
2
53
lim
2 3 1
nn
nn
−+
+−
. ĐS:
5
2
.
3)
3
23
3
lim
2 3 1
nn
nn
−+
+−
. ĐS:
1
3
. 4)
32
23
8 2 1
lim
1 3 2
nn
nn
−+
−+
. ĐS:
4
.
5)
( )
3
32
6 2 1
lim
21
nn
n n n n
−+
− + −
. ĐS:
6
. 6)
( )
( )
( )
( )
23
2
2 3 2
lim
3 2 5
n n n
nn
+ − +
+−
. ĐS:
1
3
−
.
7)
( )
( )
( ) ( )
2
3
32
2 1 3 4
lim
4 2 2
nn
nn
−−
+−
. ĐS:
1
4
−
. 8)
( )
( )
2
9
4
17
2 1 2
lim
1
nn
n
++
+
. ĐS:
4
.
9)
( )
( )
( )( )
2
2
3
21
lim
1 2 3
nn
nn
+−
++
. ĐS:
1
8
. 10)
( )( )
( )
42
2
41
lim
2 1 3 2
nn
n n n
−+
+ − +
. ĐS:
2−
.
11)
( ) ( )
( )
( )
3
2
2
23
lim
3 2 5
nn
nn
+−
+−
. ĐS:
1
3
−
. 12)
( ) ( )
( )
( )
35
3
2
2
23
lim
3 2 1 5
nn
n n n
+−
+ + −
. ĐS:
1
27
−
.
13)
22
11
lim
2 2 3n n n

−

++

. ĐS:
0
. 14)
32
2
lim
2 1 2 1
nn
nn

−

−+

.
ĐS:
1
4
.
Bài 2. Tính các giới hạn sau
1)
24
lim
43
nn
nn
+
−
. ĐS:
1
. 2)
3.2 5
lim
5.4 6.5
nn
nn
−
+
. ĐS:
1
6
−
.
3)
4 2.3
lim
53
nn
n
+
+
. ĐS:
+
. 4)
1 2.3
lim
53
n
n
+
+
. ĐS:
.
5)
1
4.3 5
lim
3.2 5
nn
nn
+
+
+
. ĐS:
5
. 6)
21
13
46
lim
5 2.6
nn
nn
++
−+
+
+
. ĐS:
1
72
.
7)
( )
1
3 4.5
lim
2.4 3.5
n
n
nn
+
−−
+
. ĐS:
20
3
−
. 8)
2
1 2 1
2 3 4.5
lim
2 3 5
n n n
n n n
+
+ + +
−+
++
. ĐS:
20
.
9)
2
1 2 1
2 3 5
lim
2 3 5
n n n
n n n
+
+ + +
−+
++
. ĐS:
5
. 10)
( )
( )
25
lim
2.3 3. 5
n
n
n
n
+−
+−
. ĐS:
1
3
.
11)
91
lim
31
n
n
+
−
. ĐS:
1
. 12)
2
1
lim
.3
n
nn
n
++
. ĐS:
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
23
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
13)
( )
51
52
1 .2
lim
3
n
n
n
+
+
−
. ĐS:
. 14)
( )
( )
1
1
54
lim
74
n
n
n
n
+
+
−+
−+
. ĐS:
.
15)
( )
21
21
4 2.2
lim
5.2 3
nn
n
n
+
+
+
+
. ĐS:
1
4
−
. 16)
3 2 5
lim
3 2.5
nn
nn
−+
−
. ĐS:
1
2
−
.
17)
11
2 3 4
lim
2 3 4
n n n
n n n++
+−
++
. ĐS:
1
4
. 18)
12
11
4 2.3 4
lim
2 3 4
nn
n n n
−−
++
+−
++
.ĐS:
1
64
−
.
19)
( )
( )
2
1
35
lim
3 5 2
n
n
n
n
−
+
−−
− + +
. ĐS:
1
5
−
. 20)
12
21
3 .2 3
lim
36
n n n
nn
−+
++
+
+
. ĐS:
1
12
.
Bài 3. Tính các giới hạn sau:
1)
2
2
41
lim
93
n n n
nn
. ĐS:
1
3
. 2)
2 1 3
lim
45
nn
n
. ĐS:
21
2
.
3)
2 3 2
3
24
4
4 1 8 2 3
lim
16 4 1
n n n
n n n
. ĐS:
4
3
. 4)
23
3
4
4
3
lim
16 1
n n n n
n
. ĐS:
1
.
5)
2
lim 3 5n n n
. ĐS: . 6)
32
3
lim 8 2n n n n
. ĐS: .
Bài 4. Tính các giới hạn sau:
1)
(
)
2
lim 1n n n+ + −
. ĐS:
1
2
. 2)
(
)
22
lim 4 4 2n n n+ − +
. ĐS:
1
4
.
3)
(
)
2
lim 3 5n n n+ + −
. ĐS:
3
2
. 4)
(
)
2
lim 4 3 2n n n+−
. ĐS:
3
4
.
5)
( )
lim 1n n n

+−

. ĐS:
+
. 6)
(
)
22
lim 1 2n n n

+ − +


. ĐS:
1
2
−
.
7)
(
)
2
lim 2 3n n n+ − +
. ĐS:
4
. 8)
(
)
2
lim 4 3 1 2 1n n n+ + − +
. ĐS:
7
4
.
9)
(
)
2
lim 9 3 4 3 2n n n+ − − +
. ĐS:
5
2
. 10)
(
)
24
lim 1 3 1n n n+ − + +
. ĐS:
1
.
11)
( )
33
lim 2nn+−
. ĐS:
0
. 12)
(
)
3
32
lim 3n n n+−
. ĐS:
1
.
13)
(
)
3
3
lim 2n n n− + +
. ĐS:
2
. 14)
(
)
3
3
lim 2 1n n n− + −
. ĐS:
1−
.
15)
(
)
3
32
lim 2 1n n n− − −
. ĐS:
5
3
−
. 16)
(
)
3
32
lim 8 4 2 2 3n n n+ + − +
. ĐS:
10
3
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
24
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 5. Tính các giới hạn sau:
1)
2
2 5 8 3 1
lim
41
n
n
. ĐS:
3
8
.
2)
24
1 4 7 3 1
lim
2 2 1
n
n n n
. ĐS:
0
.
3)
2 4 2
lim
3.2 1
n
n
. ĐS:
2
3
.
4)
1 1 1
lim
1 2 2 1 2 3 3 2 1 1n n n n
. ĐS: 1.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
25
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
BÀI 2. GIỚI HẠN CỦA HÀM SỐ
A. TÓM TẮT LÝ THUYẾT
Định nghĩa 1 (Giới hạn của hàm số tại một điểm).
Giả sử là một khoảng chứa điểm và là một hàm số xác định trên tập hợp
. Ta nói rằng hàm số có giới hạn là số thực khi dần đến (hoặc tại điểm ) nếu
với mọi dãy số trong tập hợp mà ta đều có .
Khi đó ta viết hoặc khi .
Định nghĩa 2 (Giới hạn của hàm số tại vô cực).
Giả sử hàm số xác định trên khoảng . Ta nói rằng hàm số có giới hạn là số thực
khi dần tới nếu với mọi dãy số trong khoảng mà ta đều có
.
Khi đó ta viết hoặc khi .
GIỚI HẠN HỮA HẠN
GIỚI HẠN VÔ CỰC
Giới hạn đặc biệt
1) .
2) .
Giới hạn đặc biệt
1) . 2) .
3) . 4) .
5)
Định lí
Nếu và thì
1) .
2) .
3) với .
Nếu và thì
và .
Định lí 1
Nếu và thì
.
Nếu thì
.
Giới hạn một bên
.
( )
;ab
0
x
f
( )
0
;\a b x
f
L
x
0
x
0
x
( )
n
x
( )
0
;\a b x
0
lim
n
xx=
( )
lim
n
f x L=
( )
0
lim
xx
f x L
→
=
( )
fx L→
0
xx→
f
( )
;a +
f
L
x
+
( )
n
x
( )
;a +
lim
n
x =+
( )
lim
n
f x L=
( )
lim
x
f x L
→+
=
( )
fx L→
x → +
0
0
lim
xx
xx
→
=
0
lim
xx
cc
→
=
( )
c
lim
k
x
x
→+
=+
lim 0
x
k
c
x
→
=
0
1
lim
x
x
−
→
=−
0
1
lim
x
x
+
→
=+
( )
khi 2 0
li
khi 2
m
x
k
kk
k
x
→−
+
=
−
( )
0
lim
xx
f x L
→
=
( )
0
lim
xx
g x M
→
=
( ) ( )
0
lim
xx
f x g x L M
→
=


( ) ( )
0
lim . .
xx
f x g x L M
→
=


( )
( )
0
lim
xx
fx
L
g x M
→
=
0M
( )
0fx
( )
0
lim
xx
f x L
→
=
( )
0
lim
xx
f x L
→
=
( )
0
lim
xx
f x L
→
=
( )
0
lim 0
xx
f x L
→
=
( )
0
lim
xx
fx
→
=
( ) ( )
( )
( )
0
0
0
khi .lim 0
lim .
khi .lim 0
xx
xx
xx
L g x
f x g x
L g x
→
→
→
+
=


−
( )
0
lim 0
xx
gx
→
=
( )
( )
( )
( )
0
khi . 0
lim
khi . 0
xx
L g x
fx
gx
L g x
→
+
=
−
( ) ( ) ( )
0
00
lim li ilm m
xx
xx
xx
f x f x Lf x L
+−
→
→→
= ==
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
26
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
B. DẠNG TON V BÀI TẬP
Dạng 1. Tính giới hạn vô định dạng , trong đ t thức và mu thức là các đa thức.
Phương pháp giải:
Khử dạng vô định bằng cách phân tích thành tích bằng cách chia Hooc – nơ (đầu rơi, nhân tới, cộng
cho), rồi sau đó đơn giản biểu thức để khử dạng vô định.
VÍ DỤ
Ví dụ 1. Tính giới hạn . Đs: .
Lời giải
Ta có
! Cần nhớ: với là 2 nghiệm của phương trnh
. Hc sinh thường quên nhân thêm .
Ví dụ 2. Tính giới hạn . Đs: .
Lời giải
Nhận xt: Bng chia Hooc – nơ (đầu rơi, nhân tới cộng cho) như sau:
Phân tích thành tích số:
Phân tích thành tích số:
.
Ví dụ 3. Tính giới hạn . Đs: .
Lời giải
0
0
2
2
2
2 3 14
lim
4
x
xx
A
x
→
+−
=
−
11
4
A =
2
2
2 2 2
7
2(x 2)(x )
2 3 14 2 7 11
2
lim lim lim
4 (x 2)(x 2) 2 4
x x x
x x x
A
xx
→ → →
−+
+ − +
= = = =
− − + +
( )( )
2
12
( ) af x x bx c a x x x x= + + = − −
12
,xx
( )
0fx=
a
32
32
2
2 5 2 3
lim
4 13 4 3
x
x x x
A
x x x
→
− − −
=
− + −
11
17
A =
( )
( )
( )
( )
2
3 2 2
3 2 2
2
3 3 3
3 2 1
2 5 2 3 2 1 11
lim lim lim
4 13 4 3 4 1 17
3 4 1
x x x
x x x
x x x x x
A
x x x x x
x x x
→ → →
− + +
− − − + +
= = = =
− + − − +
− − +
32
2 5 2 3x x x− − −
( )
( )
3 2 2
2 5 2 3 3 2 1x x x x x x − − − = − + +
32
4 13 4 3x x x− + −
( )
( )
3 2 2
4 13 4 3 3 4 1x x x x x x − + − = − − +
100
50
1
21
lim
21
x
xx
A
xx
→
−+
=
−+
49
24
A =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
27
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta có
!Cần nhớ: Hằng đng thức
Chứng minh: Xt cấp số nhân có
số hạng và
Khi đó
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau:
1) . ĐS: . 2) . ĐS: .
3) . ĐS: . 4) . ĐS: .
5) . ĐS: . 6) . ĐS: .
7) . ĐS: . 8) .ĐS: .
9) . ĐS: . 10) . ĐS: .
Bài 2. Tính các giới hạn sau:
1) . ĐS: . 2) . ĐS: .
3) . ĐS: . 4) . ĐS: .
( )
( )
( )
( )
99
100 100
50 50
49
1 1 1
11
2 1 ( ) ( 1)
lim lim lim
2 1 ( ) ( 1)
11
x x x
x x x
x x x x x
A
x x x x x
x x x
→ → →
− − −
− + − − −
= = =
− + − − −
− − −
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
98 97 96
48 47 46
1
99 98 97 2
49 48 47 2
1
1 .... 1 1
lim
1 .... 1 1
1 .... 1
lim
1 .... 1
x
x
x x x x x x x
x x x x x x x
x x x x x x
x x x x x x
→
→
− + + + + + − −
=
− + + + + + − −
− + + + + + −
=
− + + + + + −
( )
( )
99 98 97 2
49 48 47 2
1
.... 1
98 49
lim
48 24
.... 1
x
x x x x x
x x x x x
→
+ + + + + −
= = =
+ + + + + −
( )
( )
1 2 2
1 1 .... 1 .
n n n
x x x x x x
−−
− = − + + + + +
2 3 1
1, , , ,....,
n
x x x x
−
n
1
1, .u q x==
( )
( )
2 1 2 1
1
11
1 ... 1. 1 1 1 ... .
11
nn
n n n
n
qx
S x x x u x x x x x
qx
−−
−−
= + + + + = = − = − + + + +
−−
2
2
2
32
lim
4
x
xx
A
x
→
−+
=
−
1
4
A =
2
2
1
1
lim
34
x
x
A
xx
→
−
=
+−
2
5
A =
2
2
3
7 12
lim
9
x
xx
A
x
→
−+
=
−
1
6
A =−
2
2
5
9 20
lim
5
x
xx
A
xx
→
−+
=
−
1
5
A =
2
2
3
3 10 3
lim
56
x
xx
A
xx
→
−+
=
−+
8A =
2
2
1
23
lim
21
x
xx
A
xx
→
+−
=
−−
4
3
A =
4
2
2
16
lim
68
x
x
A
xx
→−
−
=
++
16A =−
1
23
lim
54
x
xx
A
xx
→
−−
=
−+
4
3
A =−
3
2
2
8
lim
32
x
x
A
xx
→
−
=
−+
12A =
3
2
2
8
lim
11 18
x
x
A
xx
→−
+
=
++
12
7
A =
32
2
1
2 5 2 1
lim
1
x
x x x
A
x
→
− + +
=
−
1A =−
3
4
1
32
lim
43
x
xx
A
xx
→
−+
=
−+
1
2
A =
32
32
1
2 5 4 1
lim
1
x
x x x
A
x x x
→−
+ + +
=
+ − −
1
2
A =
43
32
1
1
lim
5 7 3
x
x x x
A
x x x
→
− − +
=
− + −
3
2
A =−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
28
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
5) . ĐS: .
6) . ĐS: .
7) . ĐS: . 8) . ĐS: .
9) . ĐS: .
10) . ĐS: .
Bài 3. Tính các giới hạn sau:
1) . ĐS: . 2) . ĐS: .
3) (Với là số nguyên). ĐS: .
4) . ĐS: .
5) ( là số nguyên) . ĐS: .
6) . ĐS: .
LỜI GIẢI
Bài 1. 1) Ta có .
2) Ta có .
3) Ta có .
4) Ta có .
5) Ta có .
32
2
3
2 3 9 7 3
lim
3
x
x x x
A
x
→−
− + + +
=
−
18 19 3
6
A
+
=
32
42
3
5 3 9
lim
89
x
x x x
A
xx
→
− + +
=
−−
0A =
3
42
1
1
lim
43
x
x
A
xx
→
−
=
−+
3
4
A =
3
2
1 12
lim
28
x
A
xx
→

=−

−−

1
2
A =
22
2
11
lim
3 2 5 6
x
A
x x x x
→

=+

− − − −

2A =−
23
1
11
lim
21
x
A
x x x
→

=−

+ − −

1
9
A =
20
30
1
21
lim
21
x
xx
A
xx
→
−+
=
−+
8
14
A =
50
2
1
1
lim
32
x
x
A
xx
→
−
=
−+
50A =−
( )
2
1
1
lim
1
n
x
x nx n
A
x
→
− + −
=
−
n
2
2
nn
A
−
=
( )
( )
1
2
1
1
lim
1
n
x
x n x n
A
x
+
→
− + +
=
−
( )
1
2
nn
A
+
=
23
23
1
...
lim
...
n
m
x
x x x x n
A
x x x x m
→
+ + + + −
=
+ + + + −
,mn
( )
( )
1
1
nn
A
mm
+
=
+
1
lim
11
mn
x
mn
A
xx
→

=−

−−

2
mn
A
−
=
( )( )
( )( )
2
2
2 2 2
12
3 2 1 1
lim lim lim
4 2 2 2 4
x x x
xx
x x x
A
x x x x
→ → →
−−
− + −
= = = =
− − + +
( )( )
( )( )
2
2
1 1 1
11
1 1 2
lim lim lim
3 4 1 4 4 5
x x x
xx
xx
A
x x x x x
→ → →
−+
−+
= = = =
+ − − + +
( )( )
( )( )
2
2
3 3 3
34
7 12 4 1
lim lim lim
9 3 3 3 6
x x x
xx
x x x
A
x x x x
→ → →
−−
− + −
= = = = −
− − + +
( )( )
( )
2
2
5 5 5
45
9 20 4 1
lim lim lim
5 5 5
x x x
xx
x x x
A
x x x x x
→ → →
−−
− + −
= = = =
−−
( )( )
( )( )
2
2
3 3 3
3 1 3
3 10 3 3 1
lim lim lim 8
5 6 2 3 2
x x x
xx
x x x
A
x x x x x
→ → →
−−
− + −
= = = =
− + − − −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
29
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
6) Ta có .
7) Ta có .
8) Ta có .
9) Ta có .
! Cn nh: Hằng đng thức và .
10) Ta có .
Bài 2. 1) .
2) .
3) .
4) .
5) Ta có
.
6) Ta có .
7) Ta có .
( )( )
( )( )
2
2
1 1 1
13
2 3 3 4
lim lim lim
2 1 1 2 1 2 1 3
x x x
xx
x x x
A
x x x x x
→ → →
−+
+ − +
= = = =
− − − + +
( )( )
( )
( )( )
( )
( )
( )
22
4
2
2 2 2
2 2 4 2 4
16
lim lim lim 16
6 8 2 4 4
x x x
x x x x x
x
A
x x x x x
→− →− →−
− + + − +
−
= = = = −
+ + + + +
( )( )
( )( )
( )
( )
1 1 1
1 3 3
2 3 4
lim lim lim
3
54
1 4 4
x x x
x x x
xx
A
xx
x x x
→ → →
− + +
−−
= = = = −
−+
− − −
( )
( )
( )( )
( )
( )
22
3
2
2 2 2
2 2 4 2 4
8
lim lim lim 12
3 2 2 1 1
x x x
x x x x x
x
A
x x x x x
→ → →
− + + + +
−
= = = =
− + − − −
( )
( )
3 3 2 2
a b a b a ab b+ = + − +
( )
( )
3 3 2 2
a b a b a ab b− = − + +
( )
( )
( )( )
( )
( )
22
3
2
2 2 2
2 2 4 2 4
8 12
lim lim lim
11 18 2 9 9 7
x x x
x x x x x
x
A
x x x x x
→− →− →−
+ − + − +
+
= = = =
+ + + + +
( )
( )
( )( )
2
3 2 2
2
1 1 1
1 2 3 1
2 5 2 1 2 3 1
lim lim lim 1
1 1 1 1
x x x
x x x
x x x x x
A
x x x x
→ → →
− − −
− + + − −
= = = = −
− − + +
( ) ( )
( )
( )
2
3
2
42
2
1 1 1
12
3 2 2 1
lim lim lim
4 3 2 3 2
1 2 3
x x x
xx
x x x
A
x x x x
x x x
→ → →
−+
− + +
= = = =
− + + +
− + +
( ) ( )
( ) ( )
2
32
2
32
1 1 1
1 2 1
2 5 4 1 2 1 1
lim lim lim
1 1 2
11
x x x
xx
x x x x
A
x x x x
xx
→− →− →−
++
+ + + +
= = = =
+ − − −
+−
( )
( )
( ) ( )
2
2
4 3 2
2
32
1 1 1
11
1 1 3
lim lim lim
5 7 3 3 2
13
x x x
x x x
x x x x x
A
x x x x
xx
→ → →
− + +
− − + + +
= = = = −
− + − −
−−
( ) ( )
( )
( )( )
2
32
2
33
3 2 3 2 3 7 3 3
2 3 9 7 3
lim lim
3
33
xx
x x x
x x x
A
x
xx
→− →−

+ − + + +
− + + +

= = −

−
+−


( )
2
3
2 3 2 3 7 3 3
18 19 3
lim
6
3
x
xx
x
→−

− + + +
+

= − =

−

( )( )
( )( )
( )
( )( )
( )
( )
2
32
42
22
3 3 3
1 3 1 3
5 3 9
lim lim lim 0
89
3 3 1 3 1
x x x
x x x x
x x x
A
xx
x x x x x
→ → →
− − − −
− + +
= = = =
−−
− + + + +
( )
( )
( )
( )
( )
( )
22
3
42
3 2 3 2
1 1 1
1 1 1
13
lim lim lim
4 3 4
1 3 3 3 3
x x x
x x x x x
x
A
xx
x x x x x x x
→ → →
− − − − − − −
−
= = = =
−+
− + − − + − −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
30
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
8) Ta có
.
9) Ta có
.
10) Ta có
.
Bài 3. 1) Ta có
.
2) Ta có
3) Ta có
.
( )
( )
3
3
3
22
1 12 12 16
lim lim
28
28
xx
xx
A
xx
xx
→→
−+

= − =

−−
−−

( )( )
( )
( )
2
2
2
2
22
42
41
lim lim
2 4 2
2 2 4
xx
xx
x
xx
x x x
→→
+−
+
= = =
++
− + +
( )( )
22
22
22
22
1 1 5 6 3 2
lim lim
3 2 5 6
3 2 5 6
xx
x x x x
A
x x x x
x x x x
→→
− − + − −

= + =

− − − −
− − − −

( )
( ) ( )( )
( )( )
2
2
22
22
2
lim lim 2
31
2 3 1
xx
x
xx
x x x
→→
−
= = = −
−−
− − −
( )( ) ( )( )
3 2 3 2
23
2 3 2 3
1 1 1
1 1 1 2 1
lim lim lim
21
2 1 2 1
x x x
x x x x x x
A
x x x
x x x x x x
→ → →
− − − + − − +

= − = =

+ − −
+ − − + − −

( ) ( )
( ) ( )
( )
( )
( )
2
2
2
2
11
11
11
lim lim
9
21
1 2 1
xx
xx
x
x x x
x x x x
→→
−+
+
= = =
+ + +
− + + +
( )
( )
( )
( )
( )
( )
19
20
20
30 30
29
1 1 1
11
1
21
lim lim lim
2 1 1
11
x x x
x x x
x x x
xx
A
x x x x x
x x x
→ → →
− − −
− − −
−+
= = =
− + − − −
− − −
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
18 17 19 18
28 27 29 28
11
1 ... 1 1 1 ... 1
lim lim
1 ... 1 1 1 ... 1
xx
x x x x x x x x x x
x x x x x x x x x x
→→
− + + + + − − − + + + −
==
− + + + + − − − + + + −
( )
( )
19 18
29 28
1
... 1
18 9
lim
28 24
... 1
x
x x x
x x x
→
+ + + −
= = =
+ + + −
( )
( )
( )( )
49 48
50 49 48
2
1 1 1
1 ... x 1
1 ... x 1
lim lim lim 50
3 2 1 2 2
x x x
x x x
x x x
A
x x x x x
→ → →
− + + + +
− + + + +
= = = = −
− + − − −
( )
( )
( )
( )
22
11
11
1
lim lim
11
n
n
xx
x n x
x nx n
A
xx
→→
− − −
− + −
==
−−
( )
( )
( )
( )
12
2
1
1 ... x 1 1
lim
1
nn
x
x x x n x
x
−−
→
− + + + + − −
=
−
( )
( )
( )
12
12
2
11
1 ... x 1
... x 1
lim lim
1
1
nn
nn
xx
x x x n
x x n
x
x
−−
−−
→→
− + + + + −
+ + + + −
==
−
−
1 2 2
1
1 1 ... x 1 1
lim
1
nn
x
x x x
x
−−
→
− + − + + − + −
=
−
( )
( )
( )
( )
( )
2 3 3 4
1
1 ... x 1 1 ... x 1 ... 1
lim
1
n n n n
x
x x x x x x x
x
− − − −
→
− + + + + + − + + + + + + −
=
−
( ) ( )
2 3 3 4
1
lim ... x 1 ... x 1 ... 1
n n n n
x
x x x x
− − − −
→

= + + + + + + + + + + +

( ) ( )
2
1 2 ... 1
2
nn
nn
−
= − + − + + =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
31
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
4) Ta có
.
5) Ta có
.
6) Ta có
Và
Tương tự ta có
Vậy .
( )
( )
( )
( )
( )
( )
( )
( )
1
1
2 2 2
1 1 1
1 1 1
1
lim lim lim
1 1 1
nn
n
x x x
x x n x x x n x
x n x n
A
x x x
+
+
→ → →
− − − − − −
− + +
= = =
− − −
( )
( )
( )
( )
( )
( )
( )
1 2 1
22
11
1 ... x 1 1 1 ... x
lim lim
11
n n n n
xx
x x x x n x x x x n
xx
− − −
→→
− + + + + − − − + + + −
==
−−
1 2 1 2
11
... x 1 1 ... x 1 1
lim lim
11
n n n n
xx
x x x n x x x
xx
−−
→→
+ + + + − − + − + + − + −
==
−−
( )
( )
( )
( )
( )
1 2 2 3
1
1 ... x 1 1 ... x 1 ... 1
lim
1
n n n n
x
x x x x x x x
x
− − − −
→
− + + + + + − + + + + + + −
=
−
( ) ( )
1 2 2 3
1
lim ... x 1 ... x 1 ... 1
n n n n
x
x x x x
− − − −
→

= + + + + + + + + + + +

( ) ( )
( )
1
1 2 ... 1
2
nn
n n n
+
= + − + − + + =
2 3 1 2
2 3 1 2
11
... 1 1 ... 1 1
lim lim
... 1 1 ... 1 1
n n n
m m m
xx
x x x x n x x x x
A
x x x x m x x x x
−
−
→→
+ + + + − − + − + + − + −
==
+ + + + − − + − + + − + −
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1 2 2 3
1 2 2 3
1
1 ... x 1 1 ... x 1 ... 1
lim
1 ... x 1 1 ... x 1 ... 1
n n n n
m m m m
x
x x x x x x x
x x x x x x x
− − − −
− − − −
→
− + + + + + − + + + + + + −
=
− + + + + + − + + + + + + −
( ) ( )
( ) ( )
1 2 2 3
1 2 2 3
1
... x 1 ... x 1 ... 1
lim
... x 1 ... x 1 ... 1
n n n n
m m m m
x
x x x x
x x x x
− − − −
− − − −
→
+ + + + + + + + + + +
=
+ + + + + + + + + + +
( ) ( )
( ) ( )
( )
( )
1
1 2 ... 1 1
lim
1 2 ... 1 1
x
n n n n n
m m m m m
→
+ − + − + + +
==
+ − + − + + +
11
11
lim lim
1 1 1 1 1 1
m n m n
xx
m n m n
A
x x x x x x
→→

= − = − − −

− − − − − −

11
11
lim lim
1 1 1 1
mn
xx
mn
x x x x
→→
= − − −
− − − −
( )
( )
( ) ( )
2 1 2 1
1 1 1
1 ... x 1 1 ... 1 x
1
lim lim lim
1 1 1 1 x
mm
m m m
x x x
m x x x x
m
x x x
−−
→ → →
− + + + + − + − + + −

− = =

− − − −

( ) ( )
( )
( )
( )
22
21
1
1 1 1 .... 1 ...
lim
1 1 ...
m
m
x
x x x x x
x x x x
−
−
→

− + + + + + + + +

=
− + + + +
( )
( )
22
21
1
1 1 .... 1 ...
1 2 3 ... 1 1
lim
1 ... 2
m
m
x
x x x x
mm
x x x m
−
−
→
+ + + + + + + +
+ + + + − −
= = =
+ + + +
1
11
lim
1 1 2
n
x
nn
xx
→
−

−=

−−

1
11
lim
1 1 2 2 2
mn
x
m n m n m n
xx
→
− − −

− = − =

−−

ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
32
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Dạng 2. Tính giới hạn vô định dạng , trong đ t thức và mu thức có chứa căn thức.
Phương pháp giải:
Nhân lượng liên hợp để khử dạng vô định.
VÍ DỤ
Ví dụ 1. Tính giới hạn . Đs: .
Lời giải
Ta có:
Ví dụ 2. Tính giới hạn . Đs: .
Lời giải
Ta có
Suy ra .
Ví dụ 3. Tính giới hạn . Đs: .
Lời giải
0
0
6
33
lim
6
x
x
B
x
→
−+
=
−
1
6
B =−
( )( )
( )
( )
66
3 3 3 3
33
lim lim
6
6 3 3
xx
xx
x
B
x
xx
→→
− + + +
−+
==
−
− + +
( )
( )
( )
( )
( )
666
93
6 1 1 1
lim lim lim
6
3 3 3 6 3
6 3 3 6 3 3
xxx
x
x
x
x x x x
→→→
−+
− − −
= = = = = −
+ + + +
− + + − + +
3
2
3 2 5 6
lim
2
x
xx
E
x
→
+ − −
=
−
1E =−
3
3
2 2 2
3 2 2 2 5 6
3 2 2 2 5 6
lim lim lim
2 2 2
x x x
AB
xx
xx
E
x x x
3
22
2
3
3
3 2 8
3 2 2
lim lim
2
2 3 2 2. 3 2 4
xx
x
x
A
x
x x x
2
22
2
3
3
3
3
32
31
lim lim
4
3 2 2. 3 2 4
2 3 2 2. 3 2 4
xx
x
xx
x x x
2 2 2
4 5 6 5 2
2 5 6
lim lim lim
2
2 2 5 6 2 2 5 6
x x x
xx
x
B
x
x x x x
2
55
lim
4
2 2 5 6
x
xx
15
1
44
E A B
3
1
5 3 2
lim
1
x
x
L
x
→−
−+
=
+
5
12
L =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
33
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta có:
.
Ví dụ 4. Tính giới hạn . Đs: .
Lời giải
Ta có
.
Ví dụ 5. Tính giới hạn . Đs:
.
Lời giải
.
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau:
3
11
2
3
3
5 3 8
5 3 2
lim lim
1
1 5 3 2. 5 3 4
xx
x
x
L
x
x x x
2
11
2
3
3
3
3
51
55
lim lim
12
5 3 2. 5 3 4
1 5 3 2. 5 3 4
xx
x
xx
x x x
3
2
3 2 3 2
lim
2
x
xx
E
x
→
+ − −
=
−
1
2
E
−
=
3
3
2 2 2
3 2 2 3 2 2
3 2 2 3 2 2
lim lim lim
2 2 2
x x x
xx
xx
E
x x x
22
2
3
3
3 2 8 3 2 4
lim lim
2 3 2 2
2 3 2 2. 3 2 4
xx
xx
xx
x x x
22
2
3
3
3 2 3 2
lim lim
2 3 2 2
2 3 2 2. 3 2 4
xx
xx
xx
x x x
2
22
3
3
3 3 1 3 1
lim lim
4 4 2
3 2 2
3 2 2. 3 2 4
xx
x
xx
3
0
1 2 . 1 4 1
lim
x
xx
F
x
→
+ + −
=
7
F
3
=
3
3
00
1 2 . 1 4 1 1 2 1
1 2 . 1 4 1
lim lim
xx
x x x
xx
F
xx
3
00
1 2 . 1 4 1
1 2 1
lim lim
xx
xx
x
xx
00
2
3
3
1 2 . 1 4 1
1 2 1
lim lim
1 2 1
1 4 1 4 1
xx
xx
x
xx
x x x
2
00
3
3
4. 1 2 2 4 7
lim lim 1
33
1 2 1
1 4 1 4 1
xx
x
x
xx
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
34
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
1) . Đs: 2) . Đs:
3) . Đs: 4) . Đs:
5) . Đs: 6) . Đs:
7) . Đs: 8) . Đs:
9) . Đs:
Bài 2. Tính các giới hạn sau:
1) . Đs: 2) . Đs:
3) . Đs: 4) . Đs:
5) . Đs: 6) . Đs:
7) . Đs:
Bài 3. Tính các giới hạn sau:
1) . Đs:
2) . Đs:
3) . Đs:
4) . Đs:
5) . Đs:
8
8
lim
31
x
x
B
x
6B
2
1
42
lim
1
x
xx
B
x
1
4
B
2
3
23
lim
26
x
x x x
B
x
1
4
B
2
2
22
lim
4
x
x
B
x
1
16
B
2
2
2 3 2
lim
4
x
x
B
x
3
16
B
2
9
3
lim
9
x
x
B
xx
1
54
B
2
2
22
lim
2 10
x
x
B
xx
1
36
B
2
1
7 2 2
lim
1
x
xx
B
x
1
3
B
2
2
1
2 5 2 8
lim
32
x
x x x
B
xx
5
2
B
1
3 1 3
lim
83
x
xx
B
x
3B
1
32
lim
4 5 3 6
x
x
B
xx
3
2
B
2
22
lim
13
x
xx
B
xx
1
4
B
3
1 3 5
lim
2 3 6
x
xx
B
xx
3B
2
4
1
21
lim
x
x x x
B
xx
0B
4
1
4 3 1
lim
1
x
x
B
x
1B
2
2
2
2 1 2 5
lim
13
x
xx
B
xx
25
3
B
0
9 16 7
lim
x
xx
L
x
7
24
B
1
2 2 5 4 5
lim
1
x
xx
L
x
4
3
B
3
2 6 2 2 8
lim
3
x
xx
L
x
5
6
L
2
2
2 1 8
lim
2
x
x x x
L
x
8L
6
5 4 2 3 84
lim
6
x
x x x
L
x
74
3
L
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
35
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
6) . Đs:
7) . Đs:
8) . Đs:
9) . Đs:
10) . Đs:
Bài 4. Tính các giới hạn sau:
1) . Đs: 2) . Đs:
3) . Đs: 4) . Đs:
5) . Đs: 6) . Đs:
7) . Đs: 8) . Đs:
9) . Đs:
10) Đs:
11) Đs:
12) Đs:
Bài 5. Tính các giới hạn sau:
1) Đs:
0
1 4 1 6 1
lim
x
xx
L
x
5L
2
0
4 3 2 1 3 1
lim
21
x
x x x
L
xx
5
2
L
2
1
3 7 4 3 2 2 1
lim
21
x
x x x
L
xx
17
16
L
2
0
4 4 9 6 5
lim
x
xx
L
x
5
12
L
2
2
1
6 3 2 5
lim
1
x
x x x
L
x
11
6
L
3
2
42
lim
2
x
x
L
x
1
3
L
3
0
11
lim
x
x
L
x
1
3
L
3
2
3
12
lim
3
x
x
L
x
1
2
L
3
1
72
lim
1
x
x
L
x
1
6
L
3
8
2
lim
2 9 5
x
x
L
x
5
12
L
3
3
1
1
lim
21
x
x
L
x
1L
3
3
2
1
10 2 1
lim
32
x
xx
L
xx
3
2
L
3
2
2
8 11 7
lim
32
x
xx
L
xx
7
54
L
32
3
1
73
lim
1
x
xx
L
x
1
4
L
3
0
2 1 8
lim .
x
xx
L
x
11
12
L
2
3
2
2
2 4 11 7
lim .
4
x
x x x
L
x
5
72
L
3
2
0
4 . 8 3 4
lim .
x
xx
L
xx
1L
0
11
lim .
n
x
ax
F
x
a
n
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
36
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
2) Đs:
3) Đs:
4) Đs:
LỜI GIẢI
Bài 1. 1)
.
2)
.
3)
.
4)
.
5)
.
0
11
lim .
nm
x
ax bx
F
x
ab
nm
0
11
lim ( 0).
11
n
m
x
ax
F ab
bx
am
bn
0
11
lim .
11
nm
x
ax bx
F
x
2
ab
nm
8 8 8
8 3 1 8 3 1
8
lim lim lim
91
31
3 1 3 1
x x x
x x x x
x
B
x
x
xx
88
8 3 1
lim lim 3 1 6
8
xx
xx
x
x
22
2
11
2
4 2 4 2
42
lim lim
1
1 4 2
xx
x x x x
xx
B
x
x x x
2
2
111
22
1
4 4 1
lim lim lim
4
42
1 4 2 1 4 2
xxx
xx
x x x
xx
x x x x x x
22
2
33
2
2 3 2 3
23
lim lim
26
2 6 2 3
xx
x x x x x x
x x x
B
x
x x x x
33
22
3
1
lim lim
4
2 3 2 3 2 2 3
xx
xx
x
x x x x x x x
2
2
22
2 2 2 2
22
lim lim
4
4 2 2
xx
xx
x
B
x
xx
2
2
lim
2 2 2 2
x
x
x x x
2
11
lim
16
2 2 2
x
xx
2
22
2 2 2
2 3 2 2 3 2
4 3 2
2 3 2
lim lim lim
4
4 2 3 2 4 2 3 2
x x x
xx
x
x
B
x
x x x x
22
32
33
lim lim
16
2 2 2 3 2 2 2 3 2
xx
x
x x x x x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
37
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
6) .
7) .
8)
.
9)
.
Bài 2. 1)
2)
.
3) .
4)
.
5)
2
2
9 9 9
33
39
lim lim lim
9
9 3 9 3
x x x
xx
xx
B
xx
x x x x x x
9
11
lim
54
3
x
xx
2
22
2 2 2
lim lim
2 10
2 2 5 2 2
xx
xx
B
xx
x x x
2
11
lim
36
2 5 2 2
x
xx
2
2
2
11
7 2 2
7 2 2
lim lim
1
1 7 2 2
xx
xx
xx
B
x
x x x
2
2
1
23
lim
1 7 2 2
x
xx
x x x
1
13
lim
1 1 7 2 2
x
xx
x x x x
1
31
lim
3
1 7 2 2
x
x
x x x
2
2
2
2
11
22
2 5 2 8
2 5 2 8
lim lim
32
3 2 2 5 2 8
xx
x x x
x x x
B
xx
x x x x x
2
11
2 2 2
1 2 17
2 19 17
lim lim
3 2 2 5 2 8 1 2 2 5 2 8
xx
xx
xx
x x x x x x x x x x
1
2
2 17
5
lim
2
2 2 5 2 8
x
x
x x x x
1 1 1
2 1 8 3 2 8 3
3 1 3
lim lim lim 3
8 3 3 1 3
1 3 1 3
x x x
x x x
xx
B
x x x
x x x
1
32
lim
4 5 3 6
x
x
B
xx
1
1 4 5 3 6
lim
1 3 2
x
x x x
xx
1
4 5 3 6
lim
32
x
xx
x
3
2
2
22
lim
13
x
xx
B
xx
2
2 1 3
lim
2 2 2 2
x
x x x
x x x
2
13
lim
2 2 2
x
xx
xx
1
4
3
1 3 5
lim
2 3 6
x
xx
B
xx
3
2 3 2 3 6
lim
3 1 3 5
x
x x x
x x x
3
2 2 3 6
lim
1 3 5
x
xx
xx
3
2
4
1
21
lim
x
x x x
B
xx
2
1
22
21
lim
1 2 2 1
x
x x x
x x x x x x x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
38
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
.
6)
.
7)
.
Bài 3. 1)
.
2)
.
3)
.
2
1
22
1
lim
1 2 2 1
x
x
x x x x x x x
1
22
1
lim
2 2 1
x
x
x x x x x x
0
4
1
4 3 1
lim
1
x
x
B
x
1
32
4
44
41
lim
1 4 3 4 3 4 3 1
x
x
x x x x
32
1
4
44
4
lim
4 3 4 3 4 3 1
x
x x x
1
2
2
2
2 1 2 5
lim
13
x
xx
B
xx
22
2
22
2 2 4 1 3
lim
2 2 1 2 5
x
x x x x
x x x x
2
2
2
2 1 3
lim
2 1 2 5
x
xx
xx
25
3
0
9 16 7
lim
x
xx
L
x
0
9 3 9 4
lim
x
xx
x
0
9 3 16 4
lim
x
xx
xx
x
0
11
lim
9 3 16 4
x
xx
7
24
1
2 2 5 4 5
lim
1
x
xx
L
x
1
2 2 2 5 4 3
lim
x
xx
x
1
2 1 5 1
2 2 2 5 4 3
lim
1
x
xx
xx
x
1
25
lim
2 2 2 5 4 3
x
xx
4
3
3
2 6 2 2 8
lim
3
x
xx
L
x
3
2 6 6 2 2 2
lim
3
x
xx
x
3
6 9 2 2 4
2
6 3 2 2 2
lim
3
x
xx
xx
x
3
33
22
6 3 2 2 2
lim
3
x
xx
xx
x
3
22
lim
6 3 2 2 2
x
xx
5
6
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
39
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
4)
.
5)
.
6)
.
7)
.
8)
.
2
2
2 1 8
lim
2
x
x x x
L
x
22
2
2 1 2 4
lim
2
x
x x x x
x
2
2
44
2 2 2
21
lim
2
x
xx
x x x
xx
x
2
2
2
2 2 2
21
lim
2
x
x
x x x
xx
x
2
2
lim 2 2
21
x
x
xx
xx
8
6
5 4 2 3 84
lim
6
x
x x x
L
x
6
5 4 2 3 3 5 4 16 96
lim
6
x
x x x x
x
6
5 4 2 3 3 16 6
lim
6
x
x x x
x
6
26
5 4 16 6
2 3 3
lim
6
x
x
xx
x
x
6
10 8
lim 16
2 3 3
x
x
x
74
3
0
1 4 1 6 1
lim
x
xx
L
x
2
0
24 10 1 1
lim
x
xx
x
2
0
2
24 10 1 1
lim
24 10 1 1
x
xx
x x x
0
2
24 10
lim
24 10 1 1
x
xx
x x x
2
0
24 10
lim
24 10 1 1
x
x
xx
5
2
1
4 3 2 1 3 1
lim
21
x
x x x
L
xx
22
1
4 3 2 1
21
lim
11
x
xx
xx
xx
2
2
22
1
4 3 2 1
21
lim
1 2 1 1 4 3 2 1
x
xx
xx
x x x x x x
1
14
lim
2 1 4 3 2 1
x
x x x x
5
2
2
1
3 7 4 3 2 2 1
lim
21
x
x x x
L
xx
2
1
4 3 7 2 2 1 2
lim
1
x
x x x x
x
2
2
2
1
4 2 1 4
16 48 14 49
2 2 2 1
7 4 3
lim
1
x
xx
x x x
xx
xx
x
22
2
1
1 4 1
2 2 2 1
7 4 3
lim
1
x
xx
xx
xx
x
1
14
lim
7 4 3 2 2 2 1
x
x x x x
17
16
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
40
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
9)
.
10)
.
Bài 4. 1) .
2) .
3)
.
4)
.
5) .
2
0
4 4 9 6 5
lim
x
xx
L
x
2
0
4 4 2 9 6 3
lim
x
x x x x
x
22
2
0
4 4 4 4 9 6 6 9
4 4 2 9 6 3
lim
x
x x x x x x
x x x x
x
22
2
0
2 4 3 9 6 3
lim
x
xx
x x x x
x
0
11
lim
2 4 4 9 6 3
x
x x x x
5
12
2
2
1
6 3 2 5
lim
1
x
x x x
L
x
2
2
1
2 2 1 6 3
lim
1
x
x x x
x
2
2
2
1
6 3 4 4
21
6 3 2
lim
1
x
x x x
x
xx
x
2
2
2
1
1
21
6 3 2
lim
1
x
x
x
xx
x
1
1
lim 2
6 3 2
x
xx
11
6
3
2
42
lim
2
x
x
L
x
2
3
2
3
48
lim
2 16 2 4 4
x
x
x x x
3
2
2
3
4
lim
16 2 4 4
x
xx
1
3
3
0
11
lim
x
x
L
x
0
2
3
3
11
lim
1 1 1
x
x
x x x
2
0
3
3
1
lim
1 1 1
x
xx
1
3
3
2
3
12
lim
3
x
x
L
x
2
3
2
3
22
3
9
lim
3 1 2 1 4
x
x
x x x
2
3
3
22
3
3
lim
1 2 1 4
x
x
xx
1
2
3
1
72
lim
1
x
x
L
x
1
2
3
3
1
lim
1
. 7 2 7 4
1
x
x
x
xx
x
2
1
3
3
1
lim
7 2 7 4
x
x
xx
1
6
3
8
2
lim
2 9 5
x
x
L
x
3
2
3
8
8
24
lim
2 16
2 9 5
x
x
xx
x
x
8
2
3
3
2 9 5
lim
2 2 4
x
x
xx
5
12
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
41
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
6) .
7)
.
8)
.
9)
.
3
3
1
1
lim
21
x
x
L
x
3
2
3
1
2
3
3
1
1
lim
1
2 2 1
x
x
xx
x
xx
2
3
3
3
2
1
3
2 2 1
lim
1
x
xx
xx
1
3
3
2
1
10 2 1
lim
32
x
xx
L
xx
3
3
1
10 2 2 1
lim
12
x
xx
xx
3
2
33
3
3
1
22
1
10 2 2 10 2 4
lim
12
x
x
x
xx
xx
2
2
33
3
3
1
2 1 1
1
10 2 2 10 2 4
lim
12
x
x x x
x
xx
xx
2
2
33
3
3
1
21
1
10 2 2 10 2 4
lim
2
x
xx
xx
x
3
2
3
2
2
8 11 7
lim
32
x
xx
L
xx
3
2
2
8 11 3
lim
32
x
x
xx
2
2
73
lim
32
x
x
xx
2
2
3
3
8 11 27
lim
1 2 8 11 3 8 11 9
x
x
x x x x
2
79
lim
1 2 7 3
x
x
x x x
2
2
3
3
8
lim
1 8 11 3 8 11 9
x
x x x
2
1
lim
1 7 3
x
xx
8 1 7
27 7 54
3 2 3 2
33
1 1 1
7 3 7 2 3 2
lim lim lim
1 1 1
x x x
x x x x
L
x x x
32
11
22
33
3
3
7 8 3 4
lim lim
1 3 2
1 7 2 7 4
xx
xx
xx
x x x
32
11
22
33
3
3
11
lim lim
1 3 2
1 7 2 7 4
xx
xx
xx
x x x
2
22
11
33
3
3
1 1 1 1 1
lim lim
4 2 4
32
7 2 7 4
xx
x x x
x
xx
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
42
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
10)
.
11)
12)
Bài 5. 1)
2)
33
0 0 0
2 1 8 2 1 2 8 2
lim lim lim
x x x
x x x x
L
x x x
00
2
3
3
4 1 4
88
lim lim
2 1 2
8 2 8 4
xx
x
x
xx
x x x
2
00
3
3
4 1 1 11
lim lim 1
12 12
2 1 2
8 2 8 4
xx
x
xx
22
33
2 2 2
2 2 2
2 4 11 7 2 4 11 3 7 3
lim lim lim
4 4 4
x x x
x x x x x x
L
x x x
2
3
2
22
2
2 2 2
3
3
2 4 11 27 7 9
lim lim
4 7 3
4 2 4 11 3 2 4 11 9
xx
x x x
xx
x x x x x
2
22
2
2 2 2
3
3
2 2 4
2
lim lim
4 7 3
4 2 4 11 3 2 4 11 9
xx
xx
x
xx
x x x x x
22
2
22
3
3
24
1
lim lim
2 7 3
2 2 4 11 3 2 4 11 9
xx
x
xx
x x x x x
1 1 5
9 24 72
3
3
22
00
4 . 8 3 2 2 4 4
4 . 8 3 4
lim lim
xx
x x x
xx
L
x x x x
3
22
00
00
2
3
3
00
2
3
3
4 . 8 3 2
2 4 4
lim lim
4 . 8 3 8 2 4 4
lim lim
1 4 2
1 8 3 2 8 3 4)
4 .3 2
lim lim
1 4 2
1 8 3 2 8 3 4
11
1.
22
xx
xx
xx
xx
x
x x x x
x x x
x x x
x x x x
x
xx
x x x
00
12
1 1 1 1
lim lim
1 1 ... 1 1
n
xx
nn
n
nn
ax ax
F
x
x ax ax ax
12
0
lim .
1 1 ... 1 1
nn
x
n
nn
aa
n
ax ax ax
00
1 1 1 1
11
lim lim
nm
nm
xx
ax bx
ax bx
F
xx
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
43
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3)
Xét
4)
Ta có
.
Dạng 3. Giới hạn của hàm số khi .
Phương pháp giải:
- Đối với dạng đa thức không căn, ta rút bậc cao và áp dụng công thức khi
1.
2.
3. (c hằng số)
- Đối với dạng phân số không căn, ta làm tương tự như giới hạn dãy số, tức rút bậc cao nhất của tử
và mẫu, sau đó áp dụng công thức trên.
- Ngoài việc đưa ra khỏi căn bậc chẵn cần có trị tuyệt đối, học sinh cần phân biệt khi nào đưa ra ngoài
căn, khi nào liên hợp. Phương pháp suy luận cũng tương tự như giới hạn của dãy số, nhưng cần phân
biệt khi hoặc
00
1 1 1 1
lim lim .
nm
xx
ax bx a b
x x n m
00
1 1 1 1 1
lim lim .
1 1 1 1
nn
mm
xx
ax ax
F
x
bx bx
x
0
11
lim ;
n
x
ax a
A
xn
0
11
lim
m
x
bx b
B
xm
1
..
a am
F
b
n bn
m
00
1 1 1 1
11
lim lim
1 1 1 1
nm
nm
xx
ax bx
ax bx
F
xx
00
1 1 1 1
lim lim
1 1 1 1
nm
xx
ax bx
xx
00
1 1 1 1
lim . lim .
1 1 1 1
nm
xx
ax x bx x
xx
xx
0
11
lim
n
x
ax a
A
xn
0
11
lim
m
x
bx b
B
xm
0 0 0
11
lim lim lim 1 1 2
11
11
x x x
xx
x
Cx
x
x
.2 .2 2
a b a b
F
n m n m
x →
x → +
lim
k
x
x
→+
= +
2
lim
21
k
x
khik l
x
khik l
→−
+ =
=
− = +
lim 0
k
x
c
x
→+
=
x → +
x → −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
44
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
VÍ DỤ
Ví dụ 1. Tính giới hạn
Đs: .
Lời giải
(vì và ).
Ví dụ 2. Tính giới hạn . Đs: .
Lời giải
.
Ví dụ 2. Tính giới hạn . Đs: .
Lời giải
(Vì và ).
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau:
1) . Đs: . 2) . Đs: .
3) . Đs: . 4) . Đs: .
5) . Đs: .
Bài 2. Tính các giới hạn sau:
1) . Đs: .
2) . Đs: .
( )
32
lim 6 9 1 .
x
A x x x
→+
= − − + +
3
23
6 9 1
lim 1
x
Ax
x x x
3
lim
x
x
23
6 9 1
lim 1 1
x
x x x
3
23
31
lim
2 6 6
x
xx
B
xx
1
6
3
23
23
3
3
3
31
31
1
1
1 0 0 1
lim lim
26
26
0 0 6 6
6
6
xx
x
xx
xx
B
x
xx
xx
2
lim 1 2
x
C x x x
2
22
1 1 1 1
lim 1 2 lim 1 2
xx
C x x x x
x x x x
→− →−
= + + + = + + +
22
1 1 1 1
lim 1 2 lim 2 1
xx
x x x
x x x x
→− →−


= − + + + = − + + = −





lim
x
x
2
11
lim 2 1 2 1 1 0
x
xx
32
lim 3 2
x
A x x
32
lim 3 1
x
A x x
42
lim 2 1
x
A x x
42
lim 2 3
x
A x x
42
lim 6
x
A x x
18
lim
21
x
x
B
x
4B
2
lim
1
x
x
B
x
1B
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
45
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3) . Đs: .
4) . Đs: .
5) . Đs: .
6) . Đs: .
7) . Đs: .
8) . Đs: .
9) . Đs: .
10) . Đs: .
Bài 3. Tính các giới hạn sau:
1) . Đs: .
2) . Đs: .
3) . Đs: 14.
4) . Đs: .
5) . Đs: .
6) . Đs: .
7) . Đs: .
8) . Đs: -2.
43
4
2 7 15
lim
1
x
xx
B
x
2B
3
32
2 3 4
lim
1
x
xx
B
xx
2B
2
3
37
lim
21
x
xx
B
x
0B
32
2
lim
3 4 3 2
x
xx
B
xx
2
9
B
34
7
4 3 2 1
lim
22
x
xx
B
x
8B
20 30
50
2 3 3 2
lim
12
x
xx
B
x
30
3
2
B
2
33
lim
4
x
xx
B
x
B
3
2 2 3
lim
5
x
xx
B
x
B
2
lim 3 2 10
x
C x x x
17
2
42
21
lim
12
x
xx
C
x
2
lim 4 4 1 2 13
x
C x x x
2
lim 5
x
C x x x
9
2
2
lim 2 1
x
C x x
2
lim 4 2021
x
C x x x
2019
22
lim 1
x
C x x x
1
2
2
23
lim
5
x
x
C
xx
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
46
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
9) . Đs: .
10) . Đs: .
11) . Đs: .
12) . Đs: .
13) . Đs:
14) . Đs: 1.
15) Đs: 4
16) Đs: -1
17) Đs:
18) Đs:
19) . Đs:
Bài 4. Tính các giới hạn sau:
1) . Đs: .
2) . Đs: 2.
3) . Đs: 4.
4) Đs: .
4 2 2
lim 4 3 1 2
x
C x x x
3
4
2
2
lim
23
x
x x x
C
x
1
2
2
lim 1 1
x
C x x x
3
2
2
lim
10
x
x x x
C
x
2
22
lim 4 9 21 4 7 13
x
C x x x x
1
2
22
2
2
4 3 7 1
lim
2 1 . 3
x
x x x x
C
x x x
2
lim 4 4 1 2 3 .
x
C x x x
3
3
lim 1 .
53
x
x
Cx
xx
2
lim 16 3 4 5 .
x
C x x x
43
8
3
52
2
lim .
3
x
xx
Cx
xx
2
2
lim 3 1
x
C x x x
5
2
3
52
2
lim .
3
x
xx
x
xx
2
2
23
lim
5
x
x
xx
2
2
2 3 1
lim
4 1 1
x
x x x
xx
4 2 2
23
lim
52
x
x x x x
xx
21
2
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
47
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
5) . Đs: .
6) . Đs: .
7) . Đs: .
8) . Đs:
9) . Đs: 1.
10) . Đs: 2.
11) . Đs: .
12) . Đs: .
Bài 5. Tính các giới hạn sau:
. Đs: .
. Đs: .
. Đs: 0.
. Đs: .
. Đs: 0.
. Đs: .
. Đs: .
. Đs: .
2
2
2 1 3 4 5
lim
1 3 2 9 10
x
x x x
x x x
8
3
3
23
3 1 1 8
lim
69
x
xx
x
1
6
2
2
2 1 3
lim
5
x
xx
xx
2
5
2
2
4 3 1
lim
9 3 5 3
x
x x x
x x x
1
4
22
21
lim
x
x
x x x x
2
83
lim
6 4 3
x
x
x x x
2
2
1 7 2
lim
3 2 5 3
x
xx
x x x
1
2 1 2
lim
1
x
xx
x
1
2
1) lim
x
x x x
2
2) lim 4
x
x x x
2
3) lim 2 2
x
xx
22
4) lim 1
x
x x x
1
2
2
5) lim 4 1 2
x
x x x
2
6) lim 3 5 1
x
x x x
5
2
3
32
7) lim 27 3
x
x x x
1
27
2
8) lim 2 4 2 1
x
x x x
1
2
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
48
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
. Đs: .
. Đs: .
. Đs: .
. Đs: .
. Đs: .
. Đs: .
LỜI GIẢI
Bài 1. 1) , (vì và ).
2) .
3) .
4) .
5) .
Bài 2. 1) .
2) .
3) .
2
9) lim 2 3 4 4 3
x
x x x
4
4 2 2
10) lim 4 3 1 2
x
x x x
3
4
2
11) lim 4 3 1 2 4
x
x x x
19
4
2
12) lim 4 4 1 2 3
x
x x x
4
3
23
2
4
13) lim
2 4 3
x
x x x
x x x
16
9
3
3
14) lim 8 1 2 1
x
xx
1
3
3
32
lim 1
x
Ax
xx
3
lim
x
x
3
32
lim 1 1 0
x
xx
33
33
3 1 3 1
lim 1 , ì lim à lim 1 1 0
x x x
A x v x v
x x x x
44
2 4 2 4
2 1 2 1
lim 1 , ì lim à lim 1 1 0
x x x
A x v x v
x x x x
44
2 4 2 4
2 3 2 3
lim 1 , ì lim à lim 1 1 0
x x x
A x v x v
x x x x
44
2 4 2 4
1 6 1 6
lim 1 , ì lim à lim 1 1 0
x x x
A x v x v
x x x x
1
1
8
8
1 8 0 8
lim lim lim 4
1
1
2 1 2 0
2
2
x x x
x
x
x
x
B
x
x
x
x
2
2
1
1
2 1 0
lim lim lim 1
1
1
1 1 0
1
1
x x x
x
x
x
x
B
x
x
x
x
4
43
4
4
4
4
4
4
7 15
7 15
2
2
2 7 15 2 0 0
lim lim lim 2
1
1
1 1 0
1
1
x x x
x
xx
xx
xx
B
x
x
x
x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
49
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
4) .
5) .
6)
7) .
8) .
9)
.
10)
.
3
3
2 3 2 3
32
3
33
3 4 3 4
22
2 3 4 2 0 0
lim lim lim 2
1 1 1 1
1 1 0 0
11
x x x
x
xx
x x x x
B
xx
x
x x x x
2
3
37
lim
21
x
xx
B
x
3
2 3 2 3
3
33
3 1 7 3 1 7
0 0 0
lim lim 0
11
20
22
xx
x
x x x x x x
x
xx
32
2
lim
3 4 3 2
x
xx
B
xx
2
2
24
lim
3 4 3 2
x
xx
xx
3
3
22
44
22
lim lim
4 2 4 2
3 3 3 3
xx
x
xx
x
x x x x
2 0 2
3 0 3 0 9
34
7
4 3 2 1
lim
22
x
xx
B
x
34
34
77
31
42
4 0 2 0
lim 8
3 2 0
2
x
xx
x
20 30
50
2 3 3 2
lim
12
x
xx
B
x
20 30
20 30
30
50 50
32
23
2 0 3 0
3
lim
2
1 2 0
2
x
xx
x
2
33
lim
4
x
xx
B
x
2
2
2
13
13
3
3
lim lim . ,
4
4
1
1
xx
x
xx
xx
x
x
x
x
2
13
3
ì lim à lim 3
4
1
xx
xx
v x v
x
3
2 2 3
lim
5
x
xx
B
x
3
23
23
2
23
23
2
2
lim lim . ,
5
5
1
1
xx
x
xx
xx
x
x
x
x
23
2
23
2
ì lim à lim 2
5
1
xx
xx
v x v
x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
50
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 3. 1)
.
2) ,
3)
4)
.
2
lim 3 2 10
x
C x x x
2
10 lim 3 2
x
x x x
2
32
10 lim
32
x
x
x x x
2
32
10 lim
32
x
x
x x x
2
2
3
10 lim
32
11
x
x
xx
3 17
10
22
42
21
lim
12
x
xx
C
x
2
2 4 2 4
1 1 1 1
22
lim lim
1
1
2
2
xx
x
x x x x
x
x
x
x
24
11
2
2
ì lim à lim 0
1
2
2
xx
xx
v x v
x
2
lim 4 4 1 2 13
x
C x x x
2
13 lim 4 4 1 2
x
x x x
22
2
4 4 1 4
13 lim
4 4 1 2
x
x x x
x x x
2
2
41
13 lim
41
42
x
x
xx
xx
2
1
4
13 lim
41
42
x
x
x
xx
xx
2
1
4
13 lim
41
42
x
x
x
xx
xx
2
1
4
13 lim 14
41
42
x
x
xx
2
lim 5
x
C x x x
11
5 lim 1 5 lim 1 1
xx
x x x
xx
1
11
19
5 lim 5 lim
2
11
1 1 1 1
xx
x
x
xx
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
51
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
5) ,
.
6)
.
7)
8) .
9)
.
10)
.
2
lim 2 1
x
C x x
22
11
lim 2 lim 1 2
xx
x x x
xx
2
1
ì lim 1 2 1 2 0 à lim
xx
v v x
x
2
lim 4 2021
x
C x x x
44
2021 lim 1 2021 lim 1 1
xx
x x x
xx
4
11
44
2021 lim 2021 lim 2021 2019
2
44
1 1 1 1
xx
x
x
xx
22
22
1
lim 1 lim
1
xx
x
C x x x
x x x
22
2
11
lim lim
1 1 1 1
1 1 1 1
1
1
1
lim
2
11
11
xx
x
xx
x x x x
x x x x
x
xx
2
23
lim
5
x
x
C
xx
22
2
3
23
20
lim lim 2
1 5 1 5 1 0 0
11
xx
x
x
xx
x
x x x x
4 2 2
lim 4 3 1 2
x
C x x x
22
24
31
lim 4 2
x
xx
xx
2 4 2
2
2 4 2 4
3 1 1
4 4 3
3
lim lim
4
3 1 3 1
4 2 4 2
xx
x x x
x
x x x x
2
2
lim
23
x
x x x
C
x
1
12
lim
23
x
xx
x
x
1
1
12
12
1 2 1
lim lim
3
3
22
2
2
xx
x
x
x
x
x
x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
52
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
11)
.
12) .
13)
.
14)
15)
.
16)
2
lim 1 1
x
C x x x
2
11
1 lim 1
x
xx
xx
2
11
1 lim 1 1
x
x
xx
2
2
11
11
1 lim
11
11
x
xx
x
xx
2
1
1
13
1 lim 1
22
11
11
x
x
xx
2
lim
10
x
x x x
C
x
11
11
11
lim lim 2
10
10 1
1
xx
x
xx
x x x
x
x
22
lim 4 9 21 4 7 13
x
C x x x x
22
9 21 7 13
lim 4 4
x
xx
x x x x
22
22
9 21 7 13
44
lim
9 21 7 13
44
x
x x x x
x
x x x x
22
34
2
21
lim
2 2 2
9 21 7 13
44
x
x
x x x x
22
2
2
4 3 7 1
lim
2 1 . 3
x
x x x x
C
x x x
3
2 3 2 3
22
2
2
44
3 7 1 3 7 1
4
lim lim 1
2 .1
1 3 1 3
2 . 1 2 . 1
xx
xx
x
x x x x x x x x
xx
x x x x
2
lim 4 4 1 2 3
x
C x x x
2
41
3 lim 4 2
x
xx
xx
2
2
41
44
3 lim
41
42
x
xx
x
xx
2
1
4
4
3 lim 3 4
4
41
42
x
x
xx
3
3
lim 1
53
x
x
Cx
xx
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
53
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
.
17)
18)
19)
.
Bài 4.
.
.
2
3 2 2
33
11
1 1 0 1
lim 1 lim 1 1. 1
5 3 5 3
0 0 1
11
xx
xx
x
xx
x
x x x x
2
lim 16 3 4 5
x
C x x x
33
5 lim 16 4 5 lim 16 4
3
16 16
3 3 3 43
5 lim 5 lim 5 5 .
4 4 8 8
33
16 4 16 4
xx
xx
x x x
xx
x
x
xx
3
52
2
lim
3
x
xx
Cx
xx
3
2
2
5
35
35
1
1
2
2
lim lim 2.
13
13
1
1
xx
x
x
x
x
x
xx
xx
2
lim 3 1
x
C x x x
2
11
3 lim 1
x
xx
xx
2
11
3 lim 1 1
x
x
xx
2
2
11
11
3 lim
11
11
x
xx
x
xx
2
1
1
15
3 lim 3
22
11
11
x
x
xx
1)
33
5 2 2 5 2
24
1
2
22
lim . lim . . lim 1 . 2
13
33
x x x
x
x
x x x x
x
xx
x x x x x
x
xx
2)
2
22
3
2
23
23
lim lim lim 2
1 5 1 5
5
11
x x x
x
x
x
xx
x
x x x x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
54
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
.
.
.
.
.
.
.
.
.
.
3)
2
22
2
22
1 2 1 2 1
1 3 1 1 3
2 3 1 1 3
lim lim lim 4
21
1 1 1
4 1 1
4 1 4 1
x x x
xx
x x x
x x x x x
xx
xx
x x x
4)
22
4 2 2
22
2
1 3 1 3
2 1 2 1
2 3 2 1
lim lim lim
55
5 2 2
22
x x x
xx
x x x x
x x x x
xx
x
xx
5)
2
22
2
22
1 5 1 1 5
2 1 3 4 2 3 4
2 1 3 4 5 8
lim lim lim
3
1 10 1 1 10
1 3 2 9 10
1 3 2 9 3 2 9
x x x
xx
x x x
x x x x x
x x x
xx
x x x x x
6)
3
23
2 3 2 3
1 1 1 1
3 1 8 3 1 8
3 1 1 8 1
lim lim lim
9
6 9 6 9 6
6
x x x
xx
xx
x x x x
xx
x
7)
2
22
13
3
2 1 1
2 1 1
2 1 3
2
lim lim lim
1
5 5 5
5
x x x
xx
xx
xx
x
x x x x
x
8)
2
22
2
22
3 1 3 1
4 1 4
4 3 1 1
lim lim lim
4
1 3 1 3 3
9 3 5 3
9 5 3 9 5
x x x
xx
x x x
x x x x
x x x
xx
x x x x x
9)
22
1
2
2 1 2 1 2
lim lim lim 1
2
1 1 1 1
1 1 1 1
x x x
xx
x
x x x x
xx
x x x x
10)
2
22
3
8
8 3 8 3
lim lim lim 2
1 3 1 3
6 4 3
6 4 6 4
x x x
xx
x
x x x
xx
x x x x
11)
2
22
2
22
1 1 2
1 7 2 1 7
1 7 2
lim lim lim 1
3 2 3 2 3
3 2 5 3
1 5 3 1 5
x x x
xx
xx
x x x
x x x
x x x
x x x x x
12)
22
1 2 1 2
2 1 2
2 1 2
lim lim lim 1
1
11
1
x x x
xx
xx
x x x x
xx
x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
55
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 5.
.
.
.
.
.
.
.
.
2
11
1) lim lim 1 lim 1 1
x x x
x x x x x x
xx
1
ì lim à lim 1 1 2
xx
V x v
x
22
2
2
44
2) lim 4 lim lim 2
4
4
11
x x x
x x x x
x x x
x x x
x
x
22
4
3) lim 2 2 lim lim 0
22
22
11
x x x
xx
xx
xx
x
xx
4 1 1
ì lim 0 à lim
2
22
11
xx
Vv
x
xx
22
22
22
2
1
1
4) lim 1 lim lim
11
1
11
x x x
x x x
x
x x x
x x x
xx
xx
2
1
1
1
lim
2
11
11
x
x
xx
2
2
2
2
2
4 1 2
3
5) lim 4 1 2 lim lim
41
4 1 2
12
x x x
x x x
x x x
x x x
xx
xx
2
3
lim 0
4 1 2
11
x
x
x x x
2
2
2
2
2
3 5 1
54
6) lim 3 5 1 lim lim
35
3 5 1
11
x x x
x x x
x
x x x
x x x
xx
xx
2
4
5
5
lim
2
3 5 1
11
x
x
x x x
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
56
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
.
.
.
.
3 2 3
3
32
2
33
3 2 3 2 2
27 27
7) lim 27 3 lim
27 3 27 9
xx
x x x
x x x
x x x x x x
2
22
2 2 2
3 3 3 3
11
lim lim
27
1 1 1 1
27 3 27 9 27 3 27 9
xx
x
x x x
x x x x
22
2
2
2
4 4 2 1 2 1
8) lim 2 4 2 1 lim lim
21
2 4 2 1
24
x x x
x x x x
x x x
x x x
xx
xx
2
1
2
1
lim
2
21
24
x
x
xx
2
2
2
22
2 3 4 4 3
16 6
9) lim 2 3 4 4 3 lim lim
2 3 4 4 3 2 3 4 4 3
x x x
x x x
x
x x x
x x x x x x
22
6
16
16 6
lim lim 4
4 3 3 4 3
2 3 4 2 4
xx
x
x
xx
x x x x x
4 2 4 2
4 2 2
4 2 2
22
24
4 3 1 4 3 1
10) lim 4 3 1 2 lim lim
31
4 3 1 2
42
x x x
x x x x
x x x
x x x
xx
xx
2
24
1
3
3
lim
4
31
42
x
x
xx
2
2
2
2
2
4 3 1 2 4
19 15
11) lim 4 3 1 2 4 lim lim
31
4 3 1 2 4
4 2 4
x x x
x x x
x
x x x
x x x
xx
xx
2
15
19
19
lim
4
3 1 4
42
x
x
x x x
2
2
2
2
2
4 4 1 2 3
16 8
12) lim 4 4 1 2 3 lim lim
41
4 4 1 2 3
4 2 3
x x x
x x x
x
x x x
x x x
xx
xx
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
57
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
.
13)
14)
Dạng 4. Giới hạn một bên hoặc .
Phương pháp giải:
- Sử dụng các định lý về giới hạn hàm số
Chú ý:
VÍ DỤ
Ví dụ 1. Tính giới hạn Đs:
Lời giải
Vì .
Ví dụ 2. Tính giới hạn Đs:
Lời giải
2
8
16
lim 4
4 1 3
42
x
x
x x x
3
2 3 3 2 3 2
2
22
2
33
2 2 3 2 3
4 4 2 4 3
lim lim .
4 4 3
2 4 3
44
xx
x x x x x x x x x
xxx
x x x
x x x x x x
2
33
3
24
4 16
lim . .
39
44
1 1 1
x
x
xx
3
3
3
3
2
2
33
33
8 1 2 1
lim 8 1 2 1 lim
8 1 2 1 8 1 2 1
xx
xx
xx
x x x x
2
2
2
33
33
12 6 2
lim
8 1 2 1 8 1 2 1
x
xx
x x x x
2
2
2
33
33
62
12
lim 1.
1 1 1 1
8 2 8 2
x
xx
x x x x
0
xx
+
→
0
xx
−
→
0 0 0
0x x x xxx
+
−→
0 0 0
0x x x xxx
−
−→
1
23
lim .
1
x
x
A
x
+
→
−
=
−
.−
1
11
lim 2 3 1 0
23
lim 1 0 lim
1
1 1 1 0
x
xx
x
x
xA
x
x x x
2
15
lim .
2
x
x
A
x
+
→
−
=
−
.−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
58
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Vì .
Ví dụ 3. Tính giới hạn Đs:
Lời giải
Vì .
Ví dụ 4. Tính giới hạn Đs:
Lời giải
Vì .
Ví dụ 5. Tính giới hạn Đs:
Lời giải
Vì .
Ví dụ 6. Tính giới hạn Đs:
Lời giải
Vì .
Ví dụ 7. Tính giới hạn Đs:
Lời giải
2
22
lim 15 13 0
15
lim 2 0 lim
2
2 2 2 0
x
xx
x
x
xA
x
x x x
3
2
lim .
3
x
x
A
x
−
→
−
=
−
.−
( )
( )
3
33
lim 2 1 0
2
lim 3 0 lim
3
3 3 3 0
x
xx
x
x
xA
x
x x x
−
−−
→
→→
−
− = −
−
− = = = −
−
→ −
2
1
lim .
24
x
x
A
x
+
→
+
=
−
.+
( )
( )
2
22
lim 1 3 0
1
lim 2 4 0 lim
24
2 2 2 4 0
x
xx
x
x
xA
x
x x x
+
++
→
→→
+
+ =
+
− = = = +
−
→ −
( )
2
4
5
lim .
4
x
x
A
x
−
→
−
=
−
.−
( )
( )
( )
( )
4
2
2
44
2
lim 5 1 0
5
lim 4 0 lim
4
4 4 0
x
xx
x
x
xA
x
xx
−
−−
→
→→
−
− = −
−
− = = = −
−
→ −
( )
2
3
38
lim .
3
x
x
A
x
−
→
−
=
−
.+
( )
( )
( )
( )
3
2
2
33
2
lim 3 8 1 0
38
lim 3 0 lim
3
3 3 0
x
xx
x
x
xA
x
xx
−
−−
→
→→
−
− =
−
− = = = +
−
→ −
( )
( )
2
2
3
2 5 3
lim .
3
x
xx
A
x
+
→−
+−
=
+
.−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
59
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta có
Vì .
Ví dụ 8. Tính giới hạn Đs:
Lời giải
Ta có:
Vì .
Ví dụ 9. Tính giới hạn Đs:
Lời giải
Vì
Do đó .
Ví dụ 10. Tính giới hạn Đs:
Lời giải
Vì
Do đó .
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau:
1) Đs:
2) Đs: Không tồn tại.
( )
( )
( )
( )( )
( )
( )
2
22
3 3 3
2 1 3
2 5 3 2 1
lim lim lim
3
33
x x x
xx
x x x
x
xx
+ + +
→ − → − → −
−+
+ − −
==
+
++
( )
( )
( )
( )
( )
( )
( )
3
2
2
33
lim 2 1 7 0
2 5 3
lim 3 0 lim
3
3 3 3 0
x
xx
x
xx
xA
x
x x x
+
++
→−
→ − → −
+
− = −
+−
+ = = = −
+
→ − − +
2
2
11
lim .
24
x
A
xx
−
→

=−

−−

.−
( )( )
2
22
1 1 1
lim lim
2 4 2 2
xx
x
A
x x x x
−−
→→
+

= − =

− − − +

( )
( )( )
( )( )
2
2
22
lim 1 3 0
11
lim 2 2 0 lim
24
2 2 2 2 0
x
xx
x
x x A
xx
x x x x
−
−−
→
→→
−
+ =

− + = = − = −



−−

→ − +
2
2
2
lim .
2 5 2
x
x
B
xx
−
→
−
=
−+
1
.
3
−
2 2 2 2x x x x
−
→ − = −
( )( )
22
2 1 1
lim lim
2 2 1 2 1 3
xx
x
B
x x x
−−
→→
−−
= = = −
− − −
3
3
lim .
5 15
x
x
B
x
+
→
−
=
−
1
.
5
3 3 3 3x x x x
+
→ − = −
( )
33
3 1 1
lim lim
5 3 5 5
xx
x
B
x
−−
→→
−
= = =
−
3
1
1
lim .
23
x
x
A
xx
−
→
−
=
+−
1
.
7
−
2
2
lim .
2
x
x
B
x
→
−
=
−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
60
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3) Đs: Không tồn tại.
Bài 2. Tính các giới hạn sau:
1) Đs:
2) Đs:
3) Đs:
4) Đs:
5) Đs:
6) Đs:
7) Đs:
Bài 3. 1) Tính giới hạn với Đs:
2) Tính giới hạn với Đs: .
3) Tính giới hạn với Đs: .
Bài 4. Tìm để hàm số có giới hạn tại
Đs: hoặc .
2
3
9
lim .
3
x
x
C
x
→
−
=
−
2
2
1
2 2 1 3
lim .
21
x
x x x x
C
xx
−
→
− + − +
=
−+
7
.
4
2
2
lim .
11
x
x
C
x
−
→
−
=
−−
2.−
2
2
3
7 12
lim .
9
x
xx
D
x
−
→
−+
=
−
1
.
6
2
2
2
56
lim .
4
x
xx
D
x
−
→
−+
=
−
1
.
2
23
1
11
lim .
x
xx
D
xx
−
→
− + −
=
−
1.
( )
32
1
5
lim 1 .
23
x
x
Dx
xx
+
→
+
=−
+−
0.
3
2
1
32
lim .
54
x
xx
D
xx
−
→
−+
=
−+
3
.
3
( )
1
lim
x
C f x
→
=
( )
42
3
5 6 1
.
31
x x x khi x
fx
x x khi x
− −
=
−
2−
( )
1
lim
x
C f x
→
=
( )
2
31
.
1 7 2 1
x khi x
fx
x khi x
−
=
− +
2−
( )
2
lim
x
C f x
→−
=
( )
32
2
.
1
10 2
x
khi x
fx
x
x khi x
−
−
=
+
+ −
8
m
( )
3
22
1
1
1
1
x
khi x
fx
x
mx x m khi x
+
−
=
+
− + −
1.x =−
1m =
2m =−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
61
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
LỜI GIẢI
Bài 1. 1)
Vì
Do đó
2)
+) Vì nên .
+) Vì nên .
Suy ra nên không tồn tại giới hạn của
3)
Ta có Do đó:
+)
+)
Suy ra giới hạn của không tồn tại.
Bài 2. 1)
Vì . Do đó
2)
3
1
1
lim .
23
x
x
A
xx
−
→
−
=
+−
( )
1 1 1 1 .x x x x
−
→ − = − −
( )
( )
( )
2
2
11
1
11
lim lim .
2 2 3 7
1 2 2 3
xx
x
A
xx
x x x
−−
→→
−−
−
= = = −
++
− + +
2
2
lim .
2
x
x
B
x
→
−
=
−
( )
2 2 2 2x x x x
−
→ − = − −
( )
( )
22
2
lim lim 1 1
2
xx
x
x
−−
→→
−−
= − = −
−
2 2 2 2x x x x
+
→ − = −
22
2
lim lim1 1
2
xx
x
x
−−
→→
−
==
−
22
22
lim lim
22
xx
xx
xx
−+
→→
−−
−−
2
2
lim .
2
x
x
B
x
→
−
=
−
2
3
9
lim .
3
x
x
C
x
→
−
=
−
3
3 . 3
lim .
3
x
xx
C
x
→
−+
=
−
( )
2
3 3 3
9
3 . 3
lim lim lim 3 6.
33
x x x
x
xx
x
xx
+ + +
→ → →
−
−+
= = + =
−−
( )
( )
2
3 3 3
9
3 . 3
lim lim lim 3 6.
33
x x x
x
xx
x
xx
− − −
→ → →
−
− − +
= = − + = −
−−
2
3
9
lim
3
x
x
C
x
→
−
=
−
2
2
1
2 2 1 3
lim .
21
x
x x x x
C
xx
−
→
− + − +
=
−+
( )
1 1 0 1 1x x x x
−
→ − − = − −
( ) ( )
( )
( )
( )
2
2
1 1 1
2 1 1 3
2 3 4 3
lim lim lim
1
1
1 2 3
x x x
x x x x
x x x x
C
x
x
x x x
− − −
→ → →
− − − +
− + − −
= = =
−
−
− + +
( )( )
( )
( )
11
1 4 3
4 3 7
lim lim .
4
23
1 2 3
xx
xx
x
xx
x x x
−−
→→
−+
+
= = =
++
− + +
2
2
lim .
11
x
x
C
x
−
→
−
=
−−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
62
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Vì . Do đó:
.
3)
Ta có
4)
Ta có
5)
Ta có
6)
Ta có
7)
Ta có
Bài 3. 1) Ta có:
+)
+)
+) Vì nên hàm số có giới hạn tại và
( )
2 2 0 2 2x x x x
−
→ − − = − −
( )
( )
( )
( )
22
2 1 1
lim lim 1 1 2
11
xx
xx
Cx
x
−−
→→
− − − +

= = − − + = −

−−
2
2
3
7 12
lim .
9
x
xx
D
x
−
→
−+
=
−
( )( )
( )( )
3 3 3
34
3 . 4 4 1
lim lim lim .
3 . 3 3 6
33
x x x
xx
x x x
D
x x x
xx
− − −
→ → →
−−
− − −
= = = =
− + +
−+
2
2
2
56
lim .
4
x
xx
D
x
−
→
−+
=
−
( )( )
( )( )
2 2 2
23
2 . 3 3 1
lim lim lim .
2
2 . 2 2
22
x x x
xx
x x x
D
x x x
xx
− − −
→ → →
−−
− − −
= = = =
− + +
−+
23
1
11
lim .
x
xx
D
xx
−
→
− + −
=
−
( )
( )
( )
2
2
1 1 1
11
11
11
lim lim lim 1.
1
1
x x x
xx
xx
x
D
x
xx
xx
− − −
→ → →
− − −
− − −
−−
= = = =
−
−
( )
32
1
5
lim 1 .
23
x
x
Dx
xx
+
→
+
=−
+−
( ) ( )
( )
( )
( )( )
2
2
2
11
1 5 1 5
lim lim 0.
33
1 3 3
xx
x x x x
D
xx
x x x
++
→→


− + − +

= − = − =

++

− + +



3
2
1
32
lim .
54
x
xx
D
xx
−
→
−+
=
−+
( ) ( )
( )( )
( )
( )( )
2
1 1 1
12
12
23
lim lim lim .
1 4 1 4 4 3
x x x
xx
xx
x
D
x x x x x
− − −
→ → →
−+
−+
+
= = = =
− − − − −
( )
( )
3
11
lim lim 3 2.
xx
f x x x
−−
→→
= − = −
( )
( )
42
11
lim lim 5 6 5 6 1 2.
xx
f x x x x
++
→→
= − − = − − = −
( ) ( )
11
lim lim 2
xx
f x f x
−+
→→
= = −
( )
fx
1x =
( )
1
lim 2.
x
fx
→
=−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
63
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
2) Ta có:
+)
+)
+) Vì nên
3) Ta có:
+)
+)
+)Vì nên
Bài 4. Ta có:
+)
+)
+) Để hàm số có giới hạn tại thì
Dạng 5. Giới hạn của hàm số lượng giác
Phương pháp giải:
- Sử dụng các định lý về giới hạn hàm số
- Sử dụng các công thức biến đổi lượng giác
- Lưu ý:
VÍ DỤ
Ví dụ 1. Tính giới hạn Đs:
Lời giải
Ta có:
Ví dụ 2. Tính giới hạn Đs:
( ) ( )
11
lim lim 3 2.
xx
f x x
−−
→→
= − = −
( )
(
)
2
11
lim lim 1 7 2 2.
xx
f x x
++
→→
= − + = −
( ) ( )
11
lim lim 2
xx
f x f x
−+
→→
= = −
( )
1
lim 2.
x
C f x
→
= = −
( )
( )
( )
22
32
lim lim 8.
1
xx
x
fx
x
−−
→ − → −
−
==
+
( )
( )
( )
( )
22
lim lim 10 8.
xx
f x x
++
→ − → −
= + =
( )
( )
( )
( )
22
lim lim 8
xx
f x f x
−+
→ − → −
==
( )
2
lim 8.
x
C f x
→−
==
( )
( )
( ) ( )
( )
3
2
1 1 1
1
lim lim lim 1 3.
1
x x x
x
f x x x
x
− − −
→ − → − → −
+
= = − + =
+
( )
( )
( )
( )
2 2 2
11
lim lim 1.
xx
f x mx x m m m
++
→ − → −
= − + = + +
1x =−
22
1
3 1 2 0 .
2
m
m m m m
m
=
= + + + − =
=−
0
sin
lim 1
x
x
x
2
6
2sin 1
lim .
4cos 3
x
x
A
x
→
−
=
−
1
.
2
A =−
( )
22
2
6 6 6 6
2sin 1 2sin 1 2sin 1 1 1
lim lim lim lim .
4cos 3 1 4sin 1 2sin 2
4 1 sin 3
x x x x
x x x
A
x x x
x
→ → → →
− − − −
= = = = = −
− − +
−−
2
4
2sin 1
lim .
2cos 1
x
x
A
x
→
−
=
−
1
.
2
A =−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
64
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Lời giải
Ta có:
Ví dụ 3. Tính giới hạn Đs:
Lời giải
Ta có:
Ví dụ 4. Tính giới hạn Đs:
Lời giải
Ta có:
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau:
1)
0
1 sin2 cos2
lim .
1 sin2 cos2
x
xx
A
xx
→
+−
=
−−
Đs:
1.A =−
2)
0
sin2
lim .
1 sin2 cos2
x
x
A
xx
→
=
−−
Đs:
1.A =−
3)
0
sin7 sin5
lim .
sin
x
xx
A
x
→
−
=
Đs:
2.A =
4)
0
sin5 sin3
lim .
sin
x
xx
A
x
→
−
=
Đs:
2.A =
5)
0
1 cos
lim .
sin
x
x
A
x
→
−
=
Đs:
0.A =
6)
3
cos3 2cos2 2
lim .
sin3
x
xx
A
x
→
++
=
Đs:
23
.
3
A =
7)
2
1 sin 2 cos2
lim .
cos
x
xx
A
x
→
++
=
Đs:
2.A =
Bài 2. Tính các giới hạn sau:
1)
0
1 cos
lim .
1 cos
x
ax
B
bx
→
−
=
−
Đs:
2
.
a
B
b

=


2)
0
sin5
lim .
x
x
B
x
→
=
Đs:
5.B =
( )
22
2
4 4 4 4
2sin 1 2sin 1 2sin 1 1 1
lim lim lim lim .
2cos 1 1 2sin 2
2 1 sin 1
1 2sin
x x x x
x x x
A
xx
x
x
→ → → →
− − − −
= = = = = −
−−
−−
+
0
cos4 1
lim .
sin4
x
x
A
x
→
−
=
0.A =
2 2 2 2
00
cos4 1 cos 2 sin 2 cos 2 sin 2
lim lim
sin4 2sin2 cos2
xx
x x x x x
A
x x x
→→
− − − −
==
2
00
2sin 2 sin2
lim lim 0.
2sin2 cos2 cos2
xx
xx
x x x
→→
−−
= = =
0
1 sin2 cos2
lim .
1 sin2 cos2
x
xx
A
xx
→
−−
=
+−
1.A =−
( )
( )
22
22
00
1 2sin cos cos sin
1 sin2 cos2
lim lim .
1 sin2 cos2
1 2sin cos cos sin
xx
x x x x
xx
A
xx
x x x x
→→
− − −
−−
==
+−
+ − −
( )
( )
2
2
0 0 0
2sin sin cos
2sin 2sin cos sin cos
lim lim lim 1.
2sin 2sin cos 2sin sin cos sin cos
x x x
x x x
x x x x x
x x x x x x x x
→ → →
−
−−
= = = = −
+ + +
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
65
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3)
3
0
sin5 .sin3 .sin
lim
45
x
x x x
B
x
→
=
. Đs:
1
.
3
B =
4)
2
0
1 cos
lim
x
x
B
x
→
−
=
. Đs:
1
.
2
B =
5)
0
1 cos5
lim
1 cos3
x
x
B
x
→
−
=
−
. Đs:
25
9
B =
. 6)
2
0
1 cosa
lim
x
x
B
x
→
−
=
. Đs:
2
2
a
B =
.
7)
2
0
1 cos 2
lim
sin
x
x
B
xx
→
−
=
. Đs:
4B =
. 8)
3
0
sin tan
lim
x
xx
B
x
→
−
=
. Đs:
1
.
2
B =−
9)
3
0
tan sin
lim
sin
x
xx
B
x
→
−
=
. Đs:
1
2
B =
. 10)
3
0
1 cos
lim
sin
x
x
B
xx
→
−
=
. Đs:
3
2
B =
.
Bài 3. Tính các giới hạn sau:
1)
( )
2
4
0
cos8 1 sin 3
lim
3.
x
xx
B
x
→
−
=
. Đs:
48B =−
. 2)
0
1 2 1
lim
sin2
x
x
B
x
→
−+
=
. Đs:
1
2
B
−
=
.
3)
2
0
1 cos cos2
lim
x
x
B
x
→
−
=
. Đs:
3
2
B =
. 4)
3
2
0
1 cos
lim
tan
x
x
B
x
→
−
=
. Đs:
1
6
B =
.
5)
3
2
4
tanx 1
lim
2sin 1
x
B
x
→
−
=
−
. Đs:
1
.
3
B =
6)
3
0
1 tan 1 sin
lim
x
xx
B
x
→
+ − +
=
. Đs:
1
4
B =
. 7)
( )
2
0
1 cos
lim .
11
x
x
B
x
→
−
=
−−
Đs:
2B =
.
8)
2
2
0
1 cos
lim
x
xx
B
x
→
+−
=
. Đs:
1B =
. 9)
0
1 2 1 sin
lim
3 4 2
x
xx
B
xx
→
− + +
=
+ − −
. Đs:
0B =
.
10)
3
2
0
2 1 1
lim
sin
x
xx
B
x
→
+ − +
=
. Đs:
1.
Bài 4. Tính các giới hạn sau:
1)
4
lim tan2 tan .
4
x
C x x
→


=−




Đs:
1
2
C =
2)
( )
2
1 cos
lim .
x
x
C
x
→
+
=
−
Đs:
1
2
C =
3)
( )
2
sin 1
lim .
43
x
x
C
xx
→
−
=
−+
Đs:
1
.
2
C
−
=
4)
sin sin
lim .
xa
xa
C
xa
→
−
=
−
Đs:
cos .Ca=
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
66
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
LỜI GIẢI
Bài 1. 1)
( )
( )
22
22
00
1 2sin cos cos sin
1 sin2 cos2
lim lim .
1 sin2 cos2
1 2sin cos cos sin
xx
x x x x
xx
A
xx
x x x x
→→
+ − −
+−
==
−−
− − −
( )
( )
2
2
0 0 0
2sin sin cos
2sin 2sin cos sin cos
lim lim lim 1.
2sin 2sin cos 2sin sin cos sin cos
x x x
x x x
x x x x x
x x x x x x x x
→ → →
+
++
= = = = −
− − −
2)
( )
22
00
sin2 2sin cos
lim lim .
1 sin2 cos2
1 2sin cos cos sin
xx
x x x
A
xx
x x x x
→→
==
−−
− − −
( )
2
0 0 0
2sin cos 2sin cos cos
lim lim lim 1.
2sin 2sin cos 2sin sin cos sin cos
x x x
x x x x x
x x x x x x x x
→ → →
= = = = −
− − −
3)
0 0 0
sin7 sin5 2cos6 .sin
lim lim lim2cos6 2
sin sin
x x x
x x x x
Ax
xx
→ → →
−
= = = =
.
4)
0 0 0
sin5 sin3 2cos4 .sin
lim lim lim2cos4 2
sin sin
x x x
x x x x
Ax
xx
→ → →
−
= = = =
.
5)
2
0 0 0
2sin sin
1 cos
22
lim lim lim 0
sin
2sin .cos cos
2 2 2
x x x
xx
x
A
x x x
x
→ → →
−
= = = =
.
6)
( )
3 2 2
3
33
4cos 3cos 2 cos sin 2
cos3 2cos2 2
lim lim
sin3 3sin 4sin
xx
x x x x
xx
A
x x x

→→
− + − +
++
==
−
( )
( )
( )
2
32
2
2
33
cos 4cos 3 4cos
4cos 3cos 4cos
lim lim
sin 3 4sin
sin 3 4 1 cos
xx
x x x
x x x
xx
xx

→→
−+
−+
==

−
−−

( )
( )( )
( )( )
( )
( )
2
2
3 3 3
cos 2cos 1 4
cos 2cos 3 2cos 1 cos 2cos 3
23
lim lim lim .
sin 2cos 1 2cos 1 sin 2cos 1 3
sin 4cos 1
x x x
xx
x x x x x
x x x x x
xx
→ → →

+−
+ − +

= = = =
− + +

−

7)
2
22
1 sin2 cos2 2cos 2sin cos
lim lim
cos cos
xx
x x x x x
A
xx

→→
+ + +
==
( )
( )
22
2cos cos sin
lim lim2 cos sin 2.
cos
xx
x x x
xx
x

→→
+
= = + =
Bài 2. 1)
2
2
2
0 0 0
2
2sin sin
1 cos
2 2 2
lim lim lim . . .
1 cos
2sin sin
2 2 2
x x x
ax ax bx
ax a a
A
bx ax bx
bx b b
→ → →


−

= = = =


−



ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
67
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
(Vì
0
sin
2
lim 1
2
x
ax
ax
→
=
và
0
2
lim 1
sin
2
x
bx
bx
→
=
).
2)
00
sin5 sin5
lim lim 5. 5
5
xx
xx
B
xx
→→

= = =


. (Vì
0
sin5
lim 1
5
x
x
x
→
=
).
3)
3
00
sin5 .sin3 .sin sin5 sin3 sin 1 1
lim lim . . .
45 5 3 3 3
xx
x x x x x x
B
x x x x
→→

= = =


(Vì
0
sin5
lim 1
5
x
x
x
→
=
,
0
sin3
lim 1
3
x
x
x
→
=
,
0
sin
lim 1
x
x
x
→
=
).
4)
2
2
2
00
2sin
1 cos 1
2
lim lim
2
.4
2
xx
x
x
B
x
x
→→
−
= = =



, (vì
2
2
0
sin
2
lim 1
2
x
x
x
→
=



.
5)
2
2
2
2
0 0 0
2
2
53
5
sin .
2sin
1 cos5 25 25
22
2
lim lim lim .
3
1 cos3 9 9
53
2sin
.sin
2
22
x x x
xx
x
x
B
x
x
xx
→ → →




−


= = = =

−





(Vì
2
2
0
5
sin
2
lim 1
5
2
x
x
x
→
=



và
2
0
2
3
2
lim 1
3
sin
2
x
x
x
→



=
).
6)
2
22
2
2
00
2sin
1 cosa
2
lim lim .
42
2
xx
ax
x a a
B
x
ax
→→


−

= = =






, (vì
2
2
0
sin
2
lim 1
2
x
ax
ax
→
=



).
7)
2 2 2
2
0 0 0
sin 2 4sin .cos sin
lim lim lim .4cos 4
.sin .sin
x x x
x x x x
Bx
x x x x x
→ → →

= = = =


, (vì
0
sinx
lim 1
x
x
→
=
).
8)
3 3 3
0 0 0
sin
sin
sin tan sin .cos sin
cos
lim lim lim
cos
x x x
x
x
x x x x x
x
B
x x x x
→ → →
−
−−
= = =
( )
2
2
3
00
sin
sin 1 cos
2sin 2 1
2
lim lim . .
cos 4cos 2
2
xx
x
xx
x
x x x x
x
→→


−−
− − −

= = =






.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
68
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
(vì
0
sinx
lim 1
x
x
→
=
và
2
2
0
sin
2
lim 1
2
x
x
x
→



=



).
9)
3 3 3
0 0 0
sin
sin
tan sin sin sin .cos
cos
lim lim lim
sin sin sin xcos
x x x
x
x
x x x x x
x
B
x x x
→ → →
−
−−
= = =
2
2
0 0 0
2 2 2
2sin
1 cos 1 1
2
lim lim lim
sin x.cos 2
4.sin .cos .cos cos .cos
2 2 2
x x x
x
x
x x x
x
xx
→ → →
−
= = = =
10)
( )
( )
( )
22
2
00
2sin 1 cos cos
1 cos 1 cos cos
2
lim lim
sin
2 .sin .cos
22
xx
x
xx
x x x
B
xx
xx
x
→→
++
− + +
==
2
0
sin
1 cos cos 3
2
lim .
2
2cos
22
x
x
xx
xx
→


++
==



, (vì
0
sin
2
lim 1
2
x
x
x
→
=
).
Bài 3. 1)
( )
( )
( ) ( )
2
2
22
4
44
0 0 0
cos8 1 sin 3
cos8 1 sin 3
2sin 4 sin 3
lim lim lim
3
3 cos8 1 3 cos8 1
x x x
xx
xx
xx
B
x
x x x x
→ → →
−
−
−
= = =
++
=
22
0
sin4 sin3 96
lim . . 48
43
cos8 1
x
xx
xx
x
→

−
=−

+


2)
00
1 2 1 2 1 1
lim lim .
sin2 sin2 2
1 2 1
xx
xx
B
xx
x
→→
− + −

= = = −

++

3)
( )
( )
( )
22
2
2
22
0 0 0
1 cos 1 2sin
1 cos cos2 1 cos cos2
lim lim lim
1 cos cos2 1 cos cos2
x x x
x
x x x x
B
x
x x x x x x
→ → →
−−
−−
= = =
++
( )
( ) ( )
2 2 2 2
2 2 2
22
00
2
2
0
sin cos cos 1 2sin
sin 2sin cos
lim lim
1 cos cos2 1 cos cos2
sinx 1 2cos 3
lim . .
2
1 cos cos2
xx
x
x x x x
x x x
x x x x x x
x
x
xx
→→
→
+ − −
+
==
++

+

==


+



4)
(
)
3
2
2
00
3
2
3
2
1 cos 1 cos
lim lim
sin
tan
1 cos cos
cos
xx
xx
B
x
x
xx
x
→→
−−
==
++
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
69
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
(
)
(
)
22
2
00
33
2 2 2 2 2
33
4sin cos
cos 1
2
lim lim
6
2sin cos 1 cos cos 2cos 1 cos cos
22
xx
x
x
x
x x x
x x x x
x
→→
= = =
+ + + +
.
5)
( )
(
)
3
2
3
2 2 2
3
44
tanx 1 tan 1
lim lim
2sin 1
sin cos tan tan 1
xx
x
B
x
x x x x

→→
−−
==
−
− + +
( )
(
)
( )
(
)
33
2 2 2 2
33
44
sin cos
11
cos
lim lim .
3
sin cos tan tan 1 cos sin cos tan tan 1
xx
xx
x
x x x x x x x x x

→→
−
= = =
− + + + + +
6)
( )
3
3
00
1 tan 1 sin tan sin
lim lim
1 tan 1 sin
xx
x x x x
B
x
x x x
→→
+ − + −
==
+ + +
( ) ( )
( )
2
33
00
2
0
2sin sin
sin sin cos
2
lim lim
cos 1 tan 1 sin cos 1 tan 1 sin
sin
sin 2 1
2
lim . .
4
4 1 tan 1 sin
2
xx
x
x
x
x x x
x x x x x x x x
x
x
x
x
xx
→→
→
−
==
+ + + + + +





==


+ + +




7)
( )
( )
( )
2
2
2
2
2
2
0 0 0
2sin 1 1 sin
2 1 1
1 cos
22
lim lim lim . 2
4
11
2
x x x
xx
x
x
x
B
x
x
x
→ → →


+−

+−

−

= = = =


−−




.
8)
(
)
(
)
2 2 2 2 2
2
0 0 0
2 2 2 2
1 cos 1 cos sin
lim lim lim
1 cos 1 cos
x x x
x x x x x x
B
x
x x x x x x
→ → →
+ − + − +
= = =
+ + + +
2
2
22
0
sin 1 1 1 1
=lim . 1
22
1 cos 1 cos
x
x
x
x x x x
→

+ = + =

+ + + +

.
9)
0 0 0
1 2 1 sin 1 2 1 sin
lim =lim lim
3 4 2 3 4 2 3 4 2
x x x
x x x x
B
x x x x x x
→ → →
− + + − +
=+
+ − − + − − + − −
( )
( )
( )
( )
( )
( )
( )
( )
2
00
00
2 3 4 2 sin 3 4 2
lim lim
1
1 2 1
2 3 4 2
sin 3 4 2
lim lim .
1
1 1 2 1
4 4 0.
xx
xx
x x x x x x
xx
x x x
xx
x x x
xx
xx
→→
→→
− + + + + + +
=+
−+
− − + +
− + + +

+ + +
=+


−−
− − + +

=−=
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
70
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
10)
3 3 3
2 2 2
0 0 0 0
2 1 1 2 1 1 1 1 2 1 1 1 1
lim lim lim lim
sin sin sin sin
x x x x
x x x x x x
B
x x x x
→ → → →
+ − + + − + − + + − − +
= = = +
( )
( )
2
00
2
3
22
3
2
lim lim 1
sin 2 1 1
sin 1 1 1
xx
xx
xx
x x x
→→
−
= + =

++
+ + + +


.
Bài 4. 1)
4
lim tan2 tan
4
x
C x x
→


=−




Đặt
4
tx
=−
, vì
0.
4
xt
→ →
Khi đó:
( )
2
0 0 0
cos2 1
lim tan 2 ( 1)tan lim cot 2 tan lim
2 2cos 2
t t t
t
C t t t t
t
→ → →


= + − = = =




.
2)
( )
2
1 cos
lim
x
x
C
x
→
+
=
−
Đặt
tx
=−
, vì
0.xt
→ →
Khi đó:
2
22
00
2sin
1 cos 1
2
lim lim .
2
tt
t
t
C
tt
→→
−
= = =
3)
( )
2
sin 1
lim
43
x
x
C
xx
→
−
=
−+
Đặt
tx
=−
, vì
1 0.xt→ →
Khi đó:
( ) ( )
( )( ) ( )
2
0
sin 1 sin 1
sint 1
lim lim lim
4 3 1 3 2 2
x x t
xx
C
x x x x t t

→ → →
−−
= = = = −
− + − − −
.
4)
sin sin
lim
xa
xa
C
xa
→
−
=
−
Đặt
t x a=−
. vì
0.x a t→ →
Khi đó:
( )
00
2
2cos .sin
sin sin
22
lim lim cos
2.
2
tt
t a t
t a a
Ca
t
t
→→
+
+−
= = =
.
C. BÀI TẬP RÈN LUYỆN
Bài 1. Tính các giới hạn sau:
1.
2
3
3
lim .
6
x
x
xx
→
−
−−
ĐS:
1
5
2.
2
3
2 15
lim .
3
x
xx
x
→
+−
−
ĐS : 8
3.
2
3
3
lim
23
x
x
xx
→−
+
+−
ĐS:
1
4
4.
2
2
2
32
lim .
4
x
xx
x
→
−+
−
ĐS:
1
.
4
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
71
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
5.
2
2
2
32
lim .
4
x
xx
x
→−
++
−
ĐS:
1
4
−
6.
2
2
3
7 12
lim .
9
x
xx
x
→
−+
−
ĐS:
1
6
−
.
7.
2
2
1
1
lim .
34
x
x
xx
→
−
+−
ĐS:
2
5
8.
2
2
2
6
lim .
4
x
xx
x
→
+−
−
ĐS:
5
.
4
9.
2
2
2
2 3 14
lim .
4
x
xx
x
→
+−
−
ĐS:
11
.
4
10.
2
2
3
9
lim .
43
x
x
xx
→
−
−+
ĐS:
3
11.
2
2
2
3 10
lim .
4 18
x
xx
xx
→
−−
+−
ĐS:
11
7
. 12.
2
2
5
5
lim .
25
x
xx
x
→
−
−
ĐS:
1
.
2
13.
2
2
2
4
lim .
2 10 12
x
x
xx
→
−
−+
ĐS: 2 14.
2
2
2
4
lim .
26
x
x
xx
→
−
−−
ĐS:
4
.
7
−
15.
2
2
3
56
lim .
3
x
xx
xx
→
−+
−
ĐS:
1
.
3
16.
2
2
5
9 20
lim .
5
x
xx
xx
→
−+
−
ĐS:
1
.
5
17.
2
2
3
3 10 3
lim .
56
x
xx
xx
→
−+
−+
ĐS: 8 18.
2
2
3
23
lim .
21
x
xx
xx
→
+−
−−
ĐS: 4
19.
32
2
3
56
lim .
9
x
x x x
x
→
−+
−
ĐS:
1
.
2
−
20.
4
2
2
16
lim .
68
x
x
xx
→−
−
++
ĐS:
16.−
21.
3
2
2
8
lim .
56
x
x
xx
→
−
−+
ĐS: 12 22.
3
2
2
8
lim .
11 18
x
x
xx
→−
+
++
ĐS:
12
.
7
23.
2
3
2
22
lim .
22
x
xx
x
→
− − +
−
ĐS:
2 2 1
.
6
−
24.
3
2
2
8
lim .
32
x
x
xx
→
−
−+
ĐS:
12.
25.
3
2
2
22
lim .
2
x
x
x
→−
+
−
ĐS:
32
.
2
−
26.
( )
3
0
11
lim .
x
x
x
→
+−
ĐS:
3.
27.
( )
3
0
1 27
lim .
x
x
x
→
+−
ĐS:
27.
28.
4
2
3
27
lim .
2 3 9
x
xx
xx
→
−
−−
ĐS:
9.
29.
32
2
5 10 8
lim .
2
x
x x x
x
→
− + −
−
ĐS:
2.
30.
32
2
1
2 5 2 1
lim .
1
x
x x x
x
→
− + +
−
ĐS:
1.−
31.
3
2
2
24
lim .
4
x
xx
x
→
−−
−
ĐS:
5
.
2
32.
32
2
2
32
lim .
6
x
x x x
xx
→−
++
−−
ĐS:
2
.
5
−
33.
2
3
2
2 10
lim .
6
x
xx
xx
→−
−−
−+
ĐS:
9
.
11
−
34.
32
2
1
1
lim .
21
x
x x x
xx
→
− − +
−+
ĐS:
2.
35.
2
3
2
4
lim .
32
x
x
xx
→
−
−−
ĐS:
4
.
9
36.
32
2
2
22
lim .
4
x
x x x
x
→
− − +
−
ĐS:
3
.
4
37.
2
32
1
34
23
lim
x
xx
xx
→
+−
+−
. ĐS:
5
8
38.
32
2
1
3 4 2 3
lim
3 2 1
x
x x x
xx
→
− − +
−−
. ĐS:
1
4
−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
72
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
39.
32
2
2
52
lim
32
x
x x x
xx
→
+ − −
−+
ĐS: 11 40.
3
2
1
2 5 3
lim
32
x
xx
xx
→
−+
−+
ĐS: -1
41.
2
32
2
28
lim
3 4 6
x
xx
x x x
→−
−−
+ − +
ĐS:
6
19
−
. 42.
3
42
1
1
lim
43
x
x
xx
→
−
−+
ĐS:
3
4
.
43.
32
42
3
5 3 9
lim
89
x
x x x
xx
→
− + +
−−
ĐS:
. 44.
32
42
1
3
6 5 4 1
lim
9 8 1
x
x x x
xx
→
− + −
+−
ĐS:
2
5
.
45.
1
23
lim
54
x
xx
xx
→
+−
−+
ĐS:
4
3
−
. 46.
3
4
1
32
lim
43
x
xx
xx
→
−+
−+
ĐS:
1
2
.
47.
54
2
2
22
lim
4
x
x x x
x
→
− + −
−
ĐS:
17
4
. 48.
43
32
1
1
lim
5 7 3
x
x x x
x x x
→
− − +
− + −
ĐS:
3
2
−
.
49.
32
32
3
2 5 2 3
lim
4 13 4 3
x
x x x
x x x
→
− − −
− + −
ĐS:
11
17
. 50.
32
32
1
2 5 4 1
lim
1
x
x x x
x x x
→−
+ + +
+ − −
ĐS:
1
2
.
51.
32
32
3
2 5 2 3
lim
4 12 4 12
x
x x x
x x x
→
− − −
− + −
ĐS:
11
20
. 52.
3
2
3
2
1
21
lim
( 1)
x
xx
x
→
−+
−
ĐS:
1
9
.
53.
4 3 2
32
2
2 8 7 4 4
lim
3 14 20 8
x
x x x x
x x x
→−
+ + − −
+ + +
ĐS:
7
4
−
. 54.
32
2
3
2 3 9 7 3
lim
3
x
x x x
x
→−
− + + +
−
ĐS:
73
6
55.
4 3 2
4 3 2
1
5 9 7 2
lim
3 3 2
x
x x x x
x x x x
→
− + − +
− + + −
ĐS:
0
. 56.
5 4 3 2
2
1
5
lim
1
x
x x x x x
x
→
+ + + + −
−
ĐS:
15
2
.
57.
2
1
12
lim
11
x
xx
→

−

−−

ĐS:
1
2
. 58.
3
2
1 12
lim
28
x
xx
→

−

−−

ĐS:
1
2
.
59.
22
2
11
lim
3 2 5 6
x
x x x x
→

+

− + − +

ĐS:
2−
. 60.
2
2
2 3 26
lim
24
x
xx
xx
→−
−−

−

+−

ĐS:
7
2
.
61.
23
1
11
lim
21
x
x x x
→

−

+ − −

ĐS:
2
9
. 62.
0
(1 )(1 2 )(1 3 ) 1
lim
x
x x x
x
→
+ + + −
ĐS:
6
.
63.
1
1
lim
1
n
m
x
x
x
→
−
−
ĐS:
n
m
. 64.
2
1
1
lim
( 1)
n
x
x nx n
x
→
− + −
−
ĐS:
( 2)( 1)
2
nn−−
.
65.
100
50
1
21
lim
21
x
xx
xx
→
−+
−+
ĐS:
2
. 66.
2
1
...
lim
1
n
x
x x x n
x
→
+ + + −
−
ĐS:
( 1)
2
nn+
.
Lời giải
1.
( )( )
2
3 3 3
3 3 1 1
lim lim =lim .
6 2 3 2 5
x x x
xx
x x x x x
→ → →
−−
==
− − + − +
2.
( )( )
( )
2
3 3 3
35
2 15
lim lim =lim 5 8
33
x x x
xx
xx
x
xx
→ → →
−+
+−
= + =
−−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
73
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3.
2
3
3
lim
23
x
x
xx
→−
+
+−
( )( )
3
3
lim
31
x
x
xx
→−
+
=
+−
4.
2
2
2
32
lim
4
x
xx
x
→
−+
−
( )( )
( )( )
2
12
lim
22
x
xx
xx
→
−−
=
−+
3
11
lim .
14
x
x
→−
==
−
2
11
lim .
24
x
x
x
→
−
==
+
5.
( )( )
( )( )
2
2
2 2 2
12
3 2 1 1
lim lim = lim .
4 2 2 2 4
x x x
xx
x x x
x x x x
→− →− →−
++
+ + +
= = −
− − + −
6.
( )( )
( )( )
2
2
3 3 3
34
7 12 4 1
lim lim =lim .
9 3 3 3 6
x x x
xx
x x x
x x x x
→ → →
−−
− + −
= = −
− − + +
7.
( )( )
( )( )
2
2
1 1 1
11
1 1 2
lim lim =lim
3 4 1 4 4 5
x x x
xx
xx
x x x x x
→ → →
−+
−+
==
+ − − + +
8.
( )( )
( )( )
2
2
2 2 2
23
6 3 5
lim lim =lim .
4 2 2 2 4
x x x
xx
x x x
x x x x
→ → →
−+
+ − +
==
− − + +
9.
( )( )
( )( )
2
2
2 2 2
2 2 7
2 3 14 2 7 11
lim lim =lim .
4 2 2 2 4
x x x
xx
x x x
x x x x
→ → →
−+
+ − +
==
− − + +
10.
( )( )
( )( )
2
2
3 3 3
33
93
lim lim =lim 3.
4 3 3 1 1
x x x
xx
xx
x x x x x
→ → →
−+
−+
==
− + − − −
11.
( )( )
( )( )
2
2
2 2 2
2 3 5
3 10 3 5 11
lim lim =lim .
4 18 2 4 9 4 9 17
x x x
xx
x x x
x x x x x
→ → →
−+
− − +
==
+ − − + +
12.
( )
( )( )
2
2
5 5 5
5
51
lim lim =lim .
25 5 5 5 2
x x x
xx
x x x
x x x x
→ → →
−
−
==
− − + +
13.
( )( )
( )( ) ( )
2
2
2 2 2
22
42
lim lim lim 2.
2 10 12 2 2 3 2 3
x x x
xx
xx
x x x x x
→ → →
−+
− − −
= = =
− + − − −
14.
( )( )
( )( )
2
2
2 2 2
22
4 2 4
lim lim lim .
2 6 2 2 3 2 3 7
x x x
xx
xx
x x x x x
→ → →
−+
− − − −
= = =
− − − + +
15.
( )( )
( )
2
2
3 3 3
23
5 6 2 1
lim lim =lim .
3 2 2 3
x x x
xx
x x x
x x x x
→ → →
−−
− + −
==
−−
16.
( )( )
( )
2
2
5 5 5
45
9 20 4 1
lim lim =lim .
5 5 5
x x x
xx
x x x
x x x x x
→ → →
−−
− + −
==
−−
17.
( )( )
( )( )
2
2
3 3 3
3 3 1
5 6 3 1
lim lim =lim 8.
3 2 3 2
x x x
xx
x x x
x x x x x
→ → →
−−
− + −
==
− − − −
18.
( )( )
( )( )
2
2
3 3 3
13
2 3 3
lim lim =lim 4.
2 1 1 2 1 2 1
x x x
xx
x x x
x x x x x
→ → →
−+
+ − +
==
− − − − −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
74
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
19.
( )( )
( )( )
( )
32
2
3 3 3
2 3 2
5 6 1
lim lim =lim
9 3 3 3 2
x x x
x x x x x
x x x
x x x x
→ → →
− − −
−+
= = −
− − + − −
20.
( )
( )( )
( )( )
( )
( )
22
4
2
2 2 2
4 2 2 4 2
16
lim lim = lim 16
6 8 2 4 4
x x x
x x x x x
x
x x x x x
→− →− →−
+ − + + −
−
= = −
+ + + + +
21.
3
2
2
8
lim
56
x
x
xx
→
−
−+
=
( )
( )
( )( )
2
2
2 4 2
lim
23
x
x x x
xx
→
− + +
−−
22.
( )
( )
( )( )
2
3
2
22
2 2 4
8
lim lim
11 18 2 9
xx
x x x
x
x x x x
→− →−
+ − +
+
=
+ + + +
( )
2
2
24
lim 12.
3
x
xx
x
→
− + +
==
−
2
2
2 4 12
lim .
97
x
xx
x
→−
−+
==
+
23.
( )( )
( )( )
2
32
2
2 2 2
2 1 2
2 2 1 2 2 2 1
lim lim = lim .
6
2 2 2 2
2 2 2
x x x
xx
x x x
x x x
x x x
→ → →
− − +
− − + − + −
==
− + +
− + +
24.
( )
( )
( )( )
2
32
2
2 2 2
2 2 4
8 2 4
lim lim =lim 12.
3 2 1 2 1
x x x
x x x
x x x
x x x x x
→ → →
− + +
− + +
==
− + − − −
25.
( )( )
( )( )
2
32
2
2 2 2
2 2 2
2 2 2 2 3 2
lim lim = lim .
22
2
22
x x x
x x x
x x x
x
x
xx
→− →− →−
− − +
+ − +
= = −
−
−
−+
26.
( )
( )
3
32
2
0 0 0
11
33
lim lim lim 3 3 3.
x x x
x
x x x
xx
xx
→ → →
+−
++
= = + + =
27.
( )
( ) ( )
( ) ( )
2
3
2
0 0 0
3 3 3 9
1 27
lim lim =lim 3 3 3 9 27.
x x x
x x x
x
xx
xx
→ → →

+ + + +
+−


= + + + + =

28.
( )
( )
( )( )
( )
22
4
2
3 3 3
3 3 9 3 9
27
lim lim =lim 9.
2 3 9 3 2 3 2 3
x x x
x x x x x x x
xx
x x x x x
→ → →
− + + + +
−
==
− − − + +
29.
( )
( )
( )
2
32
2
2 2 2
2 3 4
5 10 8
lim lim =lim 3 4 2.
22
x x x
x x x
x x x
xx
xx
→ → →
− − +
− + −
= − + =
−−
30
( )
( )
( )( )
2
3 2 2
2
1 1 1
1 2 3 1
2 5 2 1 2 3 1
lim lim =lim 1.
1 1 1 1
x x x
x x x
x x x x x
x x x x
→ → →
− − −
− + + − −
= = −
− − + +
31.
( )
( )
( )( )
2
32
2
2 2 2
2 2 2
2 4 2 2 5
lim lim =lim .
4 2 2 2 2
x x x
x x x
x x x x
x x x x
→ → →
− + +
− − + +
==
− − + +
32.
( )( )
( )( )
( )
32
2
2 2 2
1 2 1
3 2 2
lim lim = lim .
6 2 3 3 5
x x x
x x x x x
x x x
x x x x x
→− →− →−
+ + +
++
= = −
− − + − −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
75
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
33.
( )( )
( )
( )
2
32
2
2 2 2
2 2 5
2 10 2 5 9
lim lim lim .
6 2 3 11
2 2 3
x x x
xx
x x x
x x x x
x x x
→− →− →−
+−
− − +
= = = −
− + − +
+ − +
34.
( ) ( )
( )
( )
2
32
2
2
1 1 1
11
1
lim . lim =lim 1 2.
21
1
x x x
xx
x x x
x
xx
x
→ → →
−+
− − +
= + =
−+
−
35.
( )( )
( )( ) ( )
2
22
3
2 2 2
22
4 2 4
lim lim =lim .
3 2 9
2 1 1
x x x
xx
xx
xx
x x x
→ → →
−+
−+
==
−−
− + +
36.
( )
( )
( )( )
2
3 2 2
2
2 2 2
21
2 2 1 3
lim lim =lim .
4 2 2 2 4
x x x
xx
x x x x
x x x x
→ → →
−−
− − + −
==
− − + +
37.
2
3 2 2 2
1 1 1
3 4 ( 1)( 4) 4 5
lim lim lim
2 3 ( 1)(2 3 3) 2 3 3 8
x x x
x x x x x
x x x x x x x
→ → →
+ − − + +
= = =
+ − − + + + +
38
3 2 2 2
2
1 1 1
3 4 2 3 ( 1)(3 3) 3 3 1
lim lim lim
3 2 1 ( 1)(3 1) 3 1 4
x x x
x x x x x x x x
x x x x x
→ → →
− − + − − − − −
= = = −
− − − + +
39.
3 2 2 2
2
2 2 2
5 2 ( 2)( 3 1) 3 1
lim lim lim 11
3 2 ( 2)( 1) 1
x x x
x x x x x x x x
x x x x x
→ → →
+ − − − + + + +
= = =
− + − − −
.
40.
3 2 2
2
1 1 1
2 5 3 ( 1)(2 2 3) 2 2 3
lim lim lim 1
3 2 ( 2)( 1) 2
x x x
x x x x x x x
x x x x x
→ → →
− + − + − + −
= = = −
− + − − −
.
41.
2
3 2 2 2
2 2 2
2 8 ( 2)( 4) 4 6
lim lim lim
3 4 6 ( 2)(3 2 3) 3 2 3 19
x x x
x x x x x
x x x x x x x x
→− →− →−
− − + − −
= = = −
+ − + + − + − +
.
42.
3 2 2
4 2 3 2 3 2
1 1 1
1 ( 1)( 1) 1 3
lim lim lim
4 3 ( 1)( 3 3) 3 3 4
x x x
x x x x x x
x x x x x x x x x
→ → →
− − − − − − − −
= = =
− + − + − − + − −
.
43.
3 2 2 2
4 2 3 2 3 2
3 3 3
5 3 9 ( 3)( 2 3) 2 3
lim lim lim 0
8 9 ( 3)( 3 3) 3 3
x x x
x x x x x x x x
x x x x x x x x x
→ → →
− + + − − − − −
= = =
− − − + + + + + +
.
44.
3 2 2 2
4 2 3 2 3 2
1 1 1
3 3 3
6 5 4 1 (3 1)(2 1) 2 1 2
lim lim lim
9 8 1 (3 1)(3 3 1) 3 3 1 5
x x x
x x x x x x x x
x x x x x x x x x
→ → →
− + − − − + − +
= = =
+ − − + + + + + +
.
45.
1 1 1
2 3 ( 1)( 3) 3 4
lim lim lim
3
5 4 ( 1)( 4) 4
x x x
x x x x x
x x x x x
→ → →
+ − − + +
= = = −
− + − − −
.
46.
32
4 2 2 2
1 1 1
3 2 ( 2)( 2 1) 2 1
lim lim lim
4 3 ( 2 1)( 2 3) 2 3 2
x x x
x x x x x x
x x x x x x x x
→ → →
− + + − + +
= = =
− + − + + + + +
.
47.
5 4 4 4
2
2 2 2
2 2 ( 2)( 1) 1 17
lim lim lim
4 ( 2)( 2) 2 4
x x x
x x x x x x
x x x x
→ → →
− + − − + +
= = =
− − + +
.
48.
4 3 2 2 2
3 2 2
1 1 1
1 ( 2 1)( 1) 1 3
lim lim lim
5 7 3 ( 2 1)( 3) 3 2
x x x
x x x x x x x x x
x x x x x x x
→ → →
− − + − + + + + +
= = = −
− + − − + − −
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
76
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
49.
3 2 2 2
3 2 2 2
3 3 3
2 5 2 3 ( 3)(2 1) 2 1 11
lim lim lim
4 13 4 3 ( 3)(4 1) 4 1 17
x x x
x x x x x x x x
x x x x x x x x
→ → →
− − − − + + + +
= = =
− + − − − + − +
.
50.
3 2 2
3 2 2
1 1 1
2 5 4 1 (2 1)( 2 1) 2 1 1
lim lim lim
1 ( 1)( 2 1) 1 2
x x x
x x x x x x x
x x x x x x x
→− →− →−
+ + + + + + +
= = =
+ − − − + + −
.
51.
3 2 2 2
3 2 2 2
3 3 3
2 5 2 3 ( 3)(2 1) 2 1 11
lim lim lim
4 12 4 12 4( 3)( 1) 4( 1) 20
x x x
x x x x x x x x
x x x x x x
→ → →
− − − − + + + +
= = =
− + − − + +
.
52.
3
22
33
2
33
2 2 2 2 2
1 1 1
3 3 3
2 1 ( 1) 1 1
lim lim lim
( 1) 9
( 1) ( 1) ( 1)
x x x
x x x
x
x x x x x
→ → →
− + −
= = =
−
− + + + +
.
53.
4 3 2 2 2 2
3 2 2
2 2 2
2 8 7 4 4 (2 1)( 4 4) 2 1 7
lim lim lim
3 14 20 8 (3 2)( 4 4) 3 2 4
x x x
x x x x x x x x
x x x x x x x
→− →− →−
+ + − − − + + −
= = = −
+ + + + + + +
.
54.
3 2 2
2
33
2 3 9 7 3 ( 3)(2 (3 2 3) 7 3 3)
lim lim
3
( 3 )( 3 )
xx
x x x x x x
x
xx
→− →−
− + + + + − − + −
=
−
−+
2
3
2 (3 2 3) 7 3 3 7 3
lim
6
3
x
xx
x
→−
− − + −
==
−
55.
4 3 2 3
4 3 2 2
1 1 1
5 9 7 2 ( 1) ( 2) 1
lim lim lim 0
3 3 2 ( 1) ( 2)( 1) 1
x x x
x x x x x x x
x x x x x x x x
→ → →
− + − + − − −
= = =
− + + − − − + +
.
56.
5 4 3 2 4 3 2
2
11
5 ( 1)( 2 3 4 5)
lim lim
1 ( 1)( 1)
xx
x x x x x x x x x x
x x x
→→
+ + + + − − + + + +
=
− − +
4 3 2
1
2 3 4 5 15
lim
12
x
x x x x
x
→
+ + + +
==
+
.
57.
2
1 1 1
1 2 1 1 1
lim lim lim
1 1 ( 1)( 1) 1 2
x x x
x
x x x x x
→ → →
−

− = = =

− − − + +

.
58.
3 2 2
2 2 2
1 12 ( 2)( 4) 4 1
lim lim lim
2 8 ( 2)( 2 4) 2 4 2
x x x
x x x
x x x x x x x
→ → →
− + +

− = = =

− − − + + + +

.
59.
22
2 2 2
1 1 2( 2) 2
lim lim lim 2
3 2 5 6 ( 2)( 3)( 1) ( 3)( 1)
x x x
x
x x x x x x x x x
→ → →
−

+ = = = −

− + − + − − − − −

.
60.
2
2 2 2
2 3 26 2( 5)( 2) 2( 5) 7
lim lim lim
2 4 ( 2)( 2) 2 2
x x x
x x x x x
x x x x x
→− →− →−
− − − + −

− = = =

+ − − + −

.
61.
2 3 2 2
1 1 1
1 1 ( 1)( 1) 1 2
lim lim lim
2 1 ( 1)( 2)( 1) ( 2)( 1) 9
x x x
x x x
x x x x x x x x x x
→ → →
− + +

− = = =

+ − − − + + + + + +

.
62.
( )
2
2
0 0 0
(1 )(1 2 )(1 3 ) 1 (6 11 6)
lim lim lim 6 11 6 6
x x x
x x x x x x
xx
xx
→ → →
+ + + − + +
= = + + =
.
63.
1 2 1 2
1 2 1 2
1 1 1
1 ( 1)( ... 1) ... 1
lim lim lim
1 ( 1)( ... 1) ... 1
n n n n n
m m m m m
x x x
x x x x x x x x n
x x x x x x x x m
− − − −
− − − −
→ → →
− − + + + + + + + +
= = =
− − + + + + + + + +
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
77
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
64.
12
22
11
1 ( 1)( ... 1) n( 1)
lim lim
( 1) ( 1)
n n n
xx
x nx n x x x x x
xx
−−
→→
− + − − + + + + − −
=
−−
1 2 2
1
( 1) ( 1) ... ( 1) ( 1)
lim
1
nn
x
x x x x
x
−−
→
− + − + + − + −
=
−
( )
2 3 3 4
1
lim ( ... 1) ( ... 1) ... 1
n n n n
x
x x x x x x
− − − −
→
= + + + + + + + + + + +
( 2)( 1)
( 2) ( 3) ... 2 1
2
nn
nn
−−
= − + − + + + =
65.
100
50
1
21
lim
21
x
xx
xx
→
−+
−+
.
99 98
49 48
1
( 1)( ... 1) ( 1)
lim
( 1)( ... 1) ( 1)
x
x x x x x
x x x x x
→
− + + + + − −
=
− + + + + − −
99 98
49 48
1
... 49
lim
... 24
x
x x x
x x x
→
+ + +
==
+ + +
66.
22
11
... ( 1) ( 1) ... ( 1)
lim lim
11
nn
xx
x x x n x x x
xx
→→
+ + + − − + − + + −
=
−−
12
1
( 1) ( 1)( 1) ... ( 1)( ... 1)
lim
1
nn
x
x x x x x x x
x
−−
→
− + − + + + − + + + +
=
−
12
1
lim(1 ( 1) ... ( ... 1))
nn
x
x x x x
−−
→
= + + + + + + + +
( 1)
1 2 3 ... n
2
nn+
= + + + + =
Bài 2. Tính các giới hạn sau:
1.
1
32
lim
1
x
x
x
→
+−
−
ĐS:
1
4
. 2.
2
2
lim
31
x
x
x
→−
+
+−
ĐS:
2
3.
6
33
lim
6
x
x
x
→
−+
−
ĐS:
1
6
−
. 4.
8
8
lim
31
x
x
x
→
−
−+
ĐS:
6−
.
5.
2
1
42
lim
1
x
xx
x
→−
+ + −
+
ĐS:
1
4
−
. 6.
2
3
3
lim
26
x
x x x
x
→
−−
−
ĐS:
1
4
.
7.
2
2
22
lim
4
x
x
x
→
+−
−
ĐS:
1
16
. 8.
2
2
2 3 2
lim
4
x
x
x
→
−−
−
ĐS:
3
16
−
.
9.
2
3
9
lim
12
x
x
x
→
−
+−
ĐS: 24. 10.
2
9
3
lim
9
x
x
xx
→
−
−
ĐS:
1
54
−
.
11.
2
7
49
lim
23
x
x
x
→
−
−−
ĐS:
56−
. 12.
2
1
23
lim
1
x
xx
x
→
−+
−
ĐS:
7
8
.
13.
2
3
32
lim
3
x
xx
xx
→
−+
−
ĐS:
2
9
. 14.
2
2
1
lim
21
x
xx
xx
→
−
−−
ĐS:
.
15.
2
2
4 1 3
lim
2
x
x
xx
→
+−
−
ĐS:
1
3
. 16.
2
4
3 3 3
lim
4
x
x
xx
→
−−
−
ĐS:
1
8
.
17.
2
2
22
lim
2 10
x
x
xx
→
+−
+−
ĐS:
1
4
. 18.
2
2
32
lim
11
x
xx
x
→
−+
−−
ĐS:
2
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
78
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
19.
2
4
34
lim
53
x
xx
x
→
−−
+−
ĐS:
30
. 20.
2
1
3 1 2
lim
2
x
x
xx
→
+−
+−
ĐS:
1
4
.
21.
2
1
1
lim
1
x
x
x
→
−
−
ĐS:
1
4
. 22.
2
2
3 3( 1)
lim
3 4 1
x
xx
x
→
−+
−+
ĐS:
12−
.
23.
3
2
0
11
lim
x
x
xx
→
+−
+
ĐS:
. 24.
3
2
2
lim
13
x
x
x
→−
+
−−
ĐS:
1
2
−
.
25.
2
2
1
21
lim
x
xx
xx
→
−−
−
ĐS:
. 26.
2
2
2 5 5
lim
2
x
xx
xx
→
+ + −
−
ĐS:
2
3
.
27.
2
1
lim
2 7 4
x
xx
xx
→
−
+ + −
ĐS:
3
4
. 28.
2
1
2 7 2
lim
1
x
xx
x
→−
− + −
−
ĐS:
1
6
.
29.
2
2
1
2 5 2 8
lim
32
x
x x x
xx
→−
+ − + +
++
ĐS:
5
2
. 30.
2
5 6 2
lim
2
x
xx
x
→
− − +
−
ĐS:
1
.
31.
1
33
lim
3 2 2
x
x
xx
→−
+
+ − +
ĐS:
. 32.
22
2
3
2 6 2 6
lim
43
x
x x x x
xx
→
− + − + −
−+
ĐS:
1
3
−
.
33.
2
4
1
21
lim
4
x
x x x
x
→−
+ + − −
+
ĐS:
. 34.
2
22
lim
73
x
x
x
→
−+
+−
ĐS:
3
2
−
.
35.
9
3
lim
52
x
x
x
→
−
−−
ĐS:
2
3
−
. 36.
1
3 1 3
lim
83
x
xx
x
→
+ − +
+−
ĐS:
3
.
37.
2
22
lim
13
x
xx
xx
→
+−
− − −
ĐS:
1
4
−
. 38.
1
32
lim
4 5 3 6
x
x
xx
→
+−
+ − +
ĐS:
3
2
.
39.
3
1 3 5
lim
2 3 6
x
xx
xx
→
+ − −
+ − +
ĐS:
3−
. 40.
2
2
2
2 1 2 5
lim
13
x
xx
xx
→
+ − +
+ − +
ĐS:
25
3
.
41.
2
1
1
lim
33
x
x
x x x
→
−
+ + −
ĐS:
4
3
−
. 42.
4
1
4 3 1
lim
1
x
x
x
→
+−
−
ĐS:
1
.
43.
4 3 2
2
1 3 3
lim
22
x
x x x x
x
→
− + − + +
−
ĐS:
1
.
Lời giải
1. Ta có
1 1 1
3 2 ( 3 2)( 3 2) 1 1
lim lim lim
14
( 1)( 3 2) 3 2
x x x
x x x
x
x x x
→ → →
+ − + − + +
= = =
−
− + + + +
.
2. Ta có
2 2 2
2 ( 2)( 3 1)
lim lim lim( 3 1) 2
3 1 ( 3 1)( 3 1)
x x x
x x x
x
x x x
→− →− →−
+ + + +
= = + + =
+ − + − + +
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
79
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3. Ta có
6 6 6
3 3 (3 3)(3 3) 1 1
lim lim lim
66
( 6)(3 3) 3 3
x x x
x x x
x
x x x
→ → →
− + − + + + −
= = = −
−
− + + + +
4. Ta có
8 8 8
8 ( 8)(3 1) 3 1
lim lim lim 6
1
3 1 (3 1)(3 1)
x x x
x x x x
x x x
→ → →
− − + + + +
= = = −
−
− + − + + +
.
5. Ta có
2
22
1 1 1
4 2 ( 1) 1
lim lim lim
14
( 1)( 4 2) 4 2
x x x
x x x x x
x
x x x x x
→− →− →−
+ + − +
= = = −
+
+ + + − + + −
.
6. Ta có
2 2 2
2
33
2 3 ( 2 3 )( 2 3 )
lim lim
26
(2 6)( 2 3 )
xx
x x x x x x x x x
x
x x x x
→→
− − − − − +
=
−
− − +
22
33
( 3) 1
lim lim
4
2( 3)( 2 3 ) 2( 2 3 )
xx
x x x
x x x x x x x
→→
−
= = =
− − + − +
.
7. Ta có
2
2 2 2
2 2 2 1 1
lim lim lim
4 16
( 2)( 2)( 2 2) ( 2)( 2 2)
x x x
xx
x
x x x x x
→ → →
+ − −
= = =
−
− + + − + + −
.
8. Ta có
2
2 2 2
2 3 2 3(2 ) 3 3
lim lim lim
4 16
( 2)( 2)(2 3 2) ( 2)(2 3 2)
x x x
xx
x
x x x x x
→ → →
− − −
= = = −
−
− + + − + + −
.
9. Ta có
2
3 3 3
9 ( 3)( 3)( 1 2)
lim lim lim ( 3)( 1 2) 24
1 2 ( 1 2)( 1 2)
x x x
x x x x
xx
x x x
→ → →
− + − + +

= = + + + =

+ − + − + +
.
10. Ta có
2
9 9 9
3 9 1 1
lim lim lim
9 54
(9 )( 3) ( 3)
x x x
xx
xx
x x x x x
→ → →
− − −
= = = −
−
− + +
.
11. Ta có
2
77
49 ( 7)( 7)(2 3)
lim lim
2 3 (2 3)(2 3)
xx
x x x x
x x x
→→
− − + + −
=
− − − − + −
77
( 7)( 7)(2 3)
lim lim( 7)(2 3) 56
7
xx
x x x
xx
x
→→
− + + −
= = − + + − = −
−
12. Ta có
2
2
1 1 1
2 3 4 3 4 3 7
lim lim lim
18
( 1)( 1)(2 3) ( 1)(2 3)
x x x
x x x x x
x
x x x x x x x
→ → →
− + − − +
= = =
−
− + + + + + +
.
13. Ta có
2
2
3 3 3
3 2 2 3 1 2
lim lim lim
39
( 3)( 3 2 ) ( 3 2 )
x x x
x x x x x
xx
x x x x x x x
→ → →
− + − − +
= = =
−
− + + + +
.
14. Ta có
2 2 2
2
2
1 1 1
( 1)( 2 1) ( 2 1)
lim lim lim
2 1 ( 1)
21
x x x
x x x x x x x x x
x x x
xx
→ → →
− − − + − +
= = =
− + − − −
−−
.
15. Ta có
2
2 2 2
4 1 3 4( 2) 4 1
lim lim lim
23
( 2)( 4 1 3) ( 4 1 3)
x x x
xx
xx
x x x x x
→ → →
+ − −
= = =
−
− + + + +
.
16. Ta có
2
4 4 4
3 3 3 3( 4) 3 1
lim lim lim
48
( 4)( 3 3 3) ( 3 3 3)
x x x
xx
xx
x x x x x
→ → →
− − −
= = =
−
− − + − +
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
80
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
17. Ta có
2
2 2 2
2 2 ( 2 2)( 2 2) 2
lim lim lim
2 10
( 2)(2 5)( 2 2) (2 5)( 2)( 2 2)
x x x
x x x x
xx
x x x x x x
→ → →
+ − + − + + −
==
+−
− − + + − − + +
2
11
lim
4
(2 5)( 2 2)
x
xx
→
= = −
− + +
18. Ta có
2
2 2 2
3 2 ( 1)( 2)( 1 1)
lim lim lim( 1)( 1 1) 2
1 1 ( 1 1)( 1 1)
x x x
x x x x x
xx
x x x
→ → →
− + − − − +
= = − − + =
− − − − − +
.
19. Ta có
2
4 4 4
3 4 ( 1)( 4)( 5 3)
lim lim lim( 1)( 5 3) 30
4
53
x x x
x x x x x
xx
x
x
→ → →
− − + − + +
= = + + + =
−
+−
.
20. Ta có
2
1 1 1
3 1 2 3( 1) 3 1
lim lim lim
24
( 1)( 2)( 3 1 2) ( 2)( 3 1 2)
x x x
xx
xx
x x x x x
→ → →
+ − −
= = =
+−
− + + + + + +
.
21. Ta có
2
1 1 1
1 1 1 1
lim lim lim
14
( 1)( 1)( 1) ( 1)( 1)
x x x
xx
x
x x x x x
→ → →
−−
= = =
−
+ − + + +
.
22. Ta có
2
22
3 4( 1) ( 2)(3 2)(3 4 1)
lim lim
3 4 1 (3 4 1)(3 4 1)
xx
x x x x x
x x x
→→
− + − + + +
=
− + − + + +
2
( 2)(3 2)(3 4 1)
lim
4(2 )
x
x x x
x
→
− + + +
=
−
2
(3 2)(3 4 1)
lim 12
4
x
xx
→
+ + +
= = −
.
23. Ta có
3 3 2
2
33
0 0 0
11
lim lim lim 0
( 1)( 1 1) ( 1)( 1 1)
x x x
x x x
xx
x x x x x
→ → →
+−
= = =
+
+ + + + + +
.
24. Ta có
33
22
3
2 2 2
2 ( 2)( 1 3) 1 3 1
lim lim lim
( 2)( 2 4) ( 2 4) 2
13
x x x
x x x x
x x x x x
x
→− →− →−
+ + − + − +
= = =
− + − + − − +
−−
.
25. Ta có
22
2
22
1 1 1
2 1 ( 1) ( 1)
lim lim lim 0
( 1)( 2 1) ( 2 1)
x x x
x x x x
xx
x x x x x x x
→ → →
− − − − − −
= = =
−
− − + − +
26. Ta có
2
2
22
2 5 5 12 20
lim lim
2
( 2)( 2 5 ( 5))
xx
x x x x
xx
x x x x
→→
+ + − − + −
=
−
− + − +
22
( 2)( 10) ( 10) 2
lim lim
3
( 2)( 2 5 ( 5)) ( 2 5 ( 5))
xx
x x x
x x x x x x x
→→
− − − − −
= = =
− + − + + − +
27. Ta có
2
2
1 1 1
( 1)( 2 7 ( 4) ( 2 7 ( 4) 3
lim lim lim
10 9 ( 9) 4
2 7 4
x x x
x x x x x x x x x
x x x
xx
→ → →
− − + − − + − −
= = =
− + − − −
+ + −
28. Ta có
2
2
11
2 7 2 2 3
lim lim
1
( 1)( 1)(( 2) 7 2 )
xx
x x x x
x
x x x x
→− →−
− + − − −
=
−
− + − − −
1
31
lim
6
( 1)(( 2) 7 2 )
x
x
x x x
→−
+
==
− − − −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
81
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
29. Ta có
2
2
2
11
2 5 2 8 2 17 5
lim lim
3 2 2
( 2)((2 5) 2 8)
xx
x x x x
xx
x x x x
→− →−
+ − + + +
==
++
+ + + + +
30. Ta có
2 2 2
5 6 2 4( 2) 4
lim lim lim 1
2
( 2)( 5 6 2) ( 5 6 2)
x x x
x x x
x
x x x x x
→ → →
− − + −
= = =
−
− − + + − + +
.
31. Ta có
11
3 3 3( 1)( 3 2 2)
lim lim
1
3 2 2
xx
x x x x
x
xx
→− →−
+ + + + +
=
+
+ − +
1
lim3( 3 2 2) 6
x
xx
→−
= + + + =
.
32. Ta có
22
2
22
33
2 6 2 6 4 1
lim lim
4 3 3
( 1)( 2 6 2 6)
xx
x x x x
xx
x x x x x
→→
− + − + − −
==
−+
− − + + + −
.
33. Ta có
2
4
22
11
2 1 1
lim lim 0
( 1)( 2 1 )
xx
x x x x
xx
x x x x x x
→− →−
+ + − − +
==
+
− + + + + −
.
34. Ta có
22
2 2 7 3 3
lim lim
2
7 3 2 2
xx
xx
xx
→→
− + + +
= − = −
+ − + +
.
35. Ta có
99
3 5 2 2
lim lim
3
5 2 3
xx
xx
xx
→→
− − +
= − = −
− − +
.
36. Ta có
11
3 1 3 2( 8 3)
lim lim 3
8 3 3 1 3
xx
x x x
x x x
→→
+ − + + +
==
+ − + + +
.
37. Ta có
22
2 2 1 3 1
lim lim
4
1 3 2 2
xx
x x x x
x x x x
→→
+ − − + −
= = −
− − − + +
.
38. Ta có
11
3 2 4 5 3 6 3
lim lim
2
4 5 3 6 3 2
xx
x x x
x x x
→→
+ − + + +
==
+ − + + +
.
39. Ta có
33
1 3 5 2 3 6
lim 2lim 3
2 3 6 1 3 5
xx
x x x x
x x x x
→→
+ − + + + +
= − = −
+ − + + + +
.
40. Ta có
22
22
22
2 1 2 5 1 3 2 5
lim lim2
3
1 3 2 1 2 5
xx
x x x x
x x x x
→→
+ − + + + +
==
+ − + + + +
.
41. Ta có
2
32
2
11
1 3 ( 3 ) 4
lim lim
5 4 3 3
33
xx
x x x x
x x x
x x x
→→
− + − −
= = −
− + − −
+ + −
.
42. Ta có
4
32
11
4
44
4 3 1 4
lim lim 1
1
(4 3) (4 3) 4 3 1
xx
x
x
x x x
→→
−−
==
−
− + − + − +
.
43. Ta có
4 3 2
2
1 3 3
lim 1
22
x
x x x x
x
→
− + − + +
=
−
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
82
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 3. Tính các giới hạn sau:
1.
3
2
42
lim
2
x
x
x
→
−
−
. ĐS:
1
3
. 2.
3
1
5 3 2
lim
1
x
x
x
→−
−+
+
ĐS:
5
12
.
3.
3
2
0
11
lim
x
x
xx
→
−−
+
ĐS:
1
3
. 4.
3
1
2 5 3
lim
1
x
x
x
→
−+
−
ĐS:
5
12
−
.
5.
3
2
3
3
lim
12
x
x
x
→
−
−−
ĐS:
. 6.
3
1
1
lim
12
x
x
x
→
−
+−
ĐS:
3
.
7.
3
2
1
54
lim
21
x
xx
xx
→
−−
−−
ĐS:
2
9
. 8.
3
1
1
lim
1
x
x
x
→
−
−
ĐS:
3
.
9.
3
3
2
3
27
lim
1 4 28
x
x
xx
→
−
+ − +
ĐS:
54
. 10.
3
3
3
52
lim
30
x
x
xx
→
+−
+−
ĐS:
1
336
.
11.
3
3
2
1
10 2 1
lim
32
x
xx
xx
→−
+ + −
++
. ĐS:
3
2
. 12.
3
2
1
1
lim
32
x
x
x
→
−
+ + −
ĐS:
2
3
.
13.
3
1
1
lim
72
x
x
x
→
−
+−
. ĐS:
. 14.
2
3
1
32
lim
1
x
x
x
→−
+−
+
ĐS:
3
2
−
.
15.
33
1
21
lim
1
x
xx
x
→
−−
−
. ĐS:
2
3
. 16.
3
2
1
1
lim
21
x
x
x
→
−
−+
ĐS:
1
.
17.
3
3
1
1
lim
4 4 2
x
x
x
→
−
+−
. ĐS:
1
. 18.
33
2
1
2
lim
1
x
xx
x
→−
++
−
ĐS:
1
3
−
.
19.
33
3
1
9 2 6
lim
1
x
xx
x
→
+ + −
+
. ĐS:
1
12
. 20.
3
3
3
19 2
lim
4 3 3
x
x
x
→
−+
−−
ĐS:
27
8
−
.
21.
33
2
0
11
lim
4
x
xx
xx
→
+ − −
−
. ĐS:
1
6
−
. 22.
3
3
1
2 1 1
lim
1
x
x
x
→
−−
−
ĐS:
2
9
.
23.
3
2
32
lim
3 2 2
x
xx
x
→
+−
−−
. ĐS:
1−
. 24.
3
4
0
11
lim
2 1 1
x
x
x
→
+−
+−
ĐS:
2
3
.
Lời giải
1) Ta có
3
3
2
22
3
4 2 4 1
lim lim .
23
16 2 4 4
xx
x
x
xx
→→
−
==
−
++
2) Ta có
( )
3
2
11
3
3
5 3 2 5 5
lim lim .
1 12
5 3 2 5 3 4
xx
x
x
xx
→− →−
−+
==
+
− − − +
3) Ta có
( ) ( )
( )
3
2
00
2
3
3
1 1 1 1
lim lim .
3
1 1 1 1
xx
x
xx
x x x
→→
−−
==
+
+ + − + −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
83
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
4) Ta có
( )
3
2
11
3
3
2 5 3 5 5
lim lim .
1 12
4 2 5 3 5 3
xx
x
x
xx
→→
− + −
= = −
−
+ + + +
5) Ta có
( )
2
3
22
3
3
2
33
1 2 1 4
3
lim lim 2.
3
12
xx
xx
x
x
x
→→
− + − +
−
==
+
−−
6) Ta có
( )
( )
2
3
3
3
11
1
lim lim 1 2 2 3.
12
xx
x
xx
x
→→
−
= − − + − =
+−
7) Ta có
( ) ( )
( )
2
3
2
11
2
3
3
5 4 4 2
lim lim .
2 1 9
2 1 5 4 5 4 4
xx
x x x x
xx
x x x
→→
− − − − +
==
−−
+ − + − +
8) Ta có
(
)
3
2
3
3
11
1
lim lim 1 3.
1
xx
x
xx
x
→→
−
= + + =
−
9) Ta có
3
3
2
3
27
lim
1 4 28
x
x
xx
→
−
+ − +
( )
( )
( ) ( )
( )
( )
( )
2
2
3
2 2 2
3
2
3
3 3 9 1 1 4 28 4 28
lim
3 2 9
x
x x x x x x x
x x x
→

− + + + + + + + +


=
− + +
( )
( ) ( )
( )
2
2
3
2 2 2
3
2
3
3 9 1 1 4 28 4 28
lim 72.
29
x
x x x x x x
xx
→

+ + + + + + + +


==
++
10) Ta có
( )
( )
3
3
33
2
2
3
3
5 2 1 1
lim lim .
30 336
3 10 5 5 4
xx
x
xx
x x x x
→→
+−
==
+−

+ + + + + +


11) Ta có
3
3
2
1
10 2 1
lim
32
x
xx
xx
→−
+ + −
++
( )( )
( )
( ) ( )
32
1
2
2
3
33
3
3 3 3 9
lim
1 2 10 2 1 10 2 1
x
x x x
x x x x x x
→−
− + +
=

+ + + + − + + −


( )
( )
( ) ( )
2
1
2
2
3
33
3
3 6 9 3
lim .
2
2 10 2 1 10 2 1
x
xx
x x x x x
→−
−+
==

+ + + − + + −


12) Ta có
( )
(
)
2
3
2
11
3
2
3
1 3 2 2
lim lim .
3
32
11
xx
xx
x
x x x
→→
− + +
==
+−
+ + +
13) Ta có
( )
2
3
3
3
11
7 2 7 4
1
lim lim 6.
7 2 1
xx
xx
x
xx
→→
+ + + +
−
==
+ − +
14) Ta có
( )
(
)
3
2
3
2
3
2
11
11
3 2 3
lim lim .
2
1
32
xx
x x x
x
x
x
→− →−
− − +
+−
= = −
+
++
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
84
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
15) Ta có
( ) ( )
33
2
11
3
2
3
3
2 1 1 2
lim lim .
3
1
2 1 2 1
xx
x x x
x
x x x x
→→
− − +
==
−
− + − +
16) Ta có
( )
2
3
3
3
3
3
2
11
3
2 2 1
1
lim lim 1.
21
1
xx
xx
x
x
xx
→→
− − − +
−
==
−+
++
17) Ta có
( )
(
)
2
3
3
3
3
11
3
2
3
4 4 2 4 4 4
1
lim lim 1.
4 4 2
41
xx
xx
x
x
xx
→→
+ + + +
−
==
+−
++
18) Ta có
( ) ( ) ( )
33
2
11
2
3
2
3
3
2 2 1
lim lim .
13
1 2 2
xx
xx
x
x x x x x
→− →−
++
= = −
−

− + − + +


19) Ta có
33
3
1
9 2 6
lim
1
x
xx
x
→−
+ + −
+
( )
( ) ( )( ) ( )
1
22
2
33
3
31
lim .
2
1 9 9 2 6 2 6
x
x x x x x x
→−
==

− + + − + − + +


20) Ta có
( )
( )
( )
2
3
3
33
2
3
33
3
9 3 4 3 3
19 2 27
lim lim .
8
4 3 3
4 19 2 19 4
xx
x x x
x
x
xx
→→
− + − +
−+
= = −

−−
− − − − +


21) Ta có
( ) ( ) ( )
33
2
00
22
3
2
33
1 1 2 1
lim lim .
46
4 1 1 1
xx
xx
xx
x x x x
→→
+ − −
= = −
−

− + + − + −


22) Ta có
( )
( )
3
3
11
2
2
3
3
2 1 1 2 2
lim lim .
19
1 2 1 2 1 1
xx
x
x
x x x x
→→
−−
==
−

+ + − + − +


23) Ta có
( )
( )
( )
2
3
22
2
2
3
3
1 3 2 2
32
lim lim 1.
3 2 2
3 3 2 3 2
xx
xx
xx
x
x x x x
→→
− + − +
+−
= = −

−−
+ + + +


24) Ta có
( )( )
( )
4
3
4
00
2
3
3
2 1 1 2 1 1
1 1 2
lim lim .
3
2 1 1
2 1 1 1
xx
xx
x
x
xx
→→
+ + + +
+−
==

+−
+ + + +


Bài 4. Tính các giới hạn sau:
1)
0
9 16 7
lim .
x
xx
x
→
+ + + −
ĐS:
7
24
2)
1
2 2 5 4 5
lim .
1
x
xx
x
→
+ + + −
−
ĐS:
4
3
3)
3
2 6 2 2 8
lim .
3
x
xx
x
→
+ + − −
−
ĐS:
5
6
4)
0
2 1 4 4
lim .
x
xx
x
→
+ + + −
ĐS:
5
4
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
85
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
5)
2
2 7 7
lim .
2
x
x x x
x
→
+ + + −
−
ĐS:
8
3
6)
2
2
2 1 8
lim .
2
x
x x x
x
→
− + −
−
ĐS:
8
7)
( )
6
5 4 2 3 84
lim .
6
x
x x x
x
→
− − + −
−
ĐS:
74
3
8)
3
0
1 2 1 3
lim .
x
xx
x
→
+ − +
ĐS:
9)
3
32
1
73
lim .
1
x
xx
x
→
+ − +
−
ĐS:
1
4
−
10)
3
2
2
8 11 7
lim .
32
x
xx
xx
→
+ − +
−+
ĐS:
7
54
11)
3
0
2 1 8
lim .
x
xx
x
→
+ − −
ĐS:
13
12
12)
3
2
1
3 5 3
lim .
1
x
xx
x
→
+ − +
−
ĐS:
1
4
13)
2
3
1
75
lim .
1
x
xx
x
→
+ − −
−
ĐS:
7
12
14)
3
2
3 2 3 2
lim .
2
x
xx
x
→
+ − −
−
ĐS:
1
2
−
15)
3
2
3 2 5 6
lim .
2
x
xx
x
→
+ − −
−
ĐS:
1−
16)
3
2
2
2
2 4 11 7
lim .
4
x
x x x
x
→
+ + − +
−
ĐS:
5
.
72
17)
3
32
2
1
57
lim .
1
x
xx
x
→
− − +
−
ĐS:
11
24
−
18)
3
3
2
2
3 4 24 2 8 2 3
lim .
4
x
x x x
x
→
− + + − −
−
ĐS:
17
16
−
19)
3
2
2
1
3 2 4 2
lim .
32
x
x x x
xx
→
− − − −
−+
ĐS:
5
6
20)
3
2
1
2 1 3 2 2
lim .
1
x
x x x
x
→
− + − −
−
ĐS:
3
2
21)
3
2
4
2
0
1 1 2
lim .
x
xx
xx
→
+ − −
+
ĐS:
1
2
22)
3
4
2
6 7 2
lim .
2
x
xx
x
→
+ − +
−
ĐS:
13
96
−
23)
0
1 4 . 1 6 1
lim .
x
xx
x
→
+ + −
ĐS:
5
24)
3
0
1 2 . 1 4 1
lim .
x
xx
x
→
+ + −
ĐS:
7
3
25)
3
1
3 1. 2 2
lim .
1
x
xx
x
→
+ − −
−
ĐS:
1
12
26)
3
2
0
4 . 8 3 4
lim .
x
xx
xx
→
+ + −
+
ĐS:
1
27)
2
0
4 4 9 6 5
lim .
x
xx
x
→
+ + − −
ĐS:
5
12
−
28)
3
2
0
1 2 1 3
lim .
x
xx
x
→
+ − +
ĐS:
1
2
29)
( )
2
2
1
6 3 2 5
lim .
1
x
x x x
x
→
+ + −
−
ĐS:
11
6
30)
2
1
4 3 2 1 3 1
lim .
21
x
x x x
xx
→
− + − − +
−+
ĐS:
5
.
2
−
31)
2
1
3 7 4 3 2 2 1
lim .
21
x
x x x
xx
→
− − + + + −
−+
ĐS:
17
16
−
32)
2
2
2
44
lim .
2 8 2 2 3 4
x
xx
x x x
→
−+
+ − − + −
ĐS:
8
9
33)
3
2
32
1
6 2 2
lim .
1
x
xx
x x x
→
+−
− − +
ĐS:
1
8
34)
( )
3
22
2
2
2 6 5 3 9 7
lim
2
x
x x x x
x
→
− + − − +
−
ĐS:
1
2
35)
3
2
0
1 2 1 3
lim .
x
xx
x
→
+ − +
ĐS:
1
2
36)
3
2
0
1 4 1 6
lim .
x
xx
x
→
+ − +
ĐS:
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
86
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Lời giải
1)
0
9 16 7
lim .
x
xx
I
x
→
+ + + −
=
Ta có
0
9 3 16 4
lim
x
xx
I
xx
→

+ − + −
=+



( )( )
( )
( )( )
( )
0
9 3 9 3 16 4 16 4
lim
9 3 16 4
x
x x x x
x x x x
→

+ − + + + − + +

=+

+ + + +

( ) ( ) ( ) ( )
00
9 9 16 16
lim lim
9 3 16 4 9 3 16 4
xx
x x x x
x x x x x x x x
→→
+ − + −
= + = +
+ + + + + + + +
0
1 1 1 1 7
lim .
6 8 24
9 3 16 4
x
xx
→

= + = + =

+ + + +

2)
1
2 2 5 4 5
lim .
1
x
xx
I
x
→
+ + + −
=
−
Ta có
1
2 2 2 5 4 3
lim
11
x
xx
I
xx
→

+ − + −
=+


−−

( )( )
( )
( )
( )( )
( )
( )
1
2 2 2 2 2 2 5 4 3 5 4 3
lim
1 2 2 2 1 5 4 3
x
x x x x
x x x x
→

+ − + + + − + +

=+

− + + − + +

( )
( )
( )
( )
1
2 2 4 5 4 9
lim
1 2 2 2 1 5 4 3
x
xx
x x x x
→

+ − + −

=+

− + + − + +

( )
( )
( )
( )
( )
( )
1
2 1 5 1
lim
1 2 2 2 1 5 4 3
x
xx
x x x x
→

−−

=+

− + + − + +

1
2 5 2 5 4
lim .
4 6 3
2 2 2 5 4 3
x
xx
→

= + = + =

+ + + +

3)
3
2 6 2 2 8
lim .
3
x
xx
I
x
→
+ + − −
=
−
Ta có
3
2 6 6 2 2 2
lim
33
x
xx
I
xx
→

+ − − −
=+


−−

( )( )
( )
( )
( )( )
( )
( )
3
2 6 3 6 3 2 2 2 2 2 2
lim
3 6 3 3 2 2 2
x
x x x x
x x x x
→

+ − + + − − − +

=+

− + + − − +

( )
( )
( )
( )
( )
3
2 6 9
2 2 4
lim
3 6 3 3 2 2 2
x
x
x
x x x x
→

+−
−−

=+

− + + − − +

ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
87
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
( )
( )
( )
( )
( )
3
2 3 2 3
lim
3 6 3 3 2 2 2
x
xx
x x x x
→

−−

=+

− + + − − +

3
2 2 2 2 5
lim .
6 4 6
6 3 2 2 2
x
xx
→

= + = + =

+ + − +

4)
0
2 1 4 4
lim .
x
xx
I
x
→
+ + + −
=
Ta có
0
2 1 2 4 2
lim
x
xx
I
xx
→

+ − + −
=+



( )( )
( )
( )( )
( )
0
2 1 1 1 1 4 2 4 2
lim
1 1 4 2
x
x x x x
x x x x
→

+ − + + + − + +

=+

+ + + +

( )
( ) ( )
0
2 1 1
44
lim
1 1 4 2
x
x
x
x x x x
→

+−
+−

=+

+ + + +

0
2 1 2 1 5
lim
2 4 4
1 1 4 2
x
xx
→

= + = + =

+ + + +

5)
2
2 7 7
lim .
2
x
x x x
I
x
→
+ + + −
=
−
Ta có
( )
2
2 2 2 2 4 7 3
lim
2
x
x x x x
I
x
→
− + + + − + + −
=
−
2
2 2 4 7 3
lim 2
22
x
xx
x
xx
→

+ − + −
= + + +


−−

( )( )
( )
( )
( )( )
( )
( )
2
2 2 2 2 2 7 3 7 3
2 lim
2 2 2 2 7 3
x
x x x x
x x x x
→

+ − + + + − + +

= + +

− + + − + +

2
2 1 2 1 8
2 lim 2 .
4 6 3
2 2 7 3
x
xx
→

= + + = + + =

+ + + +

6)
2
2
2 1 8
lim .
2
x
x x x
I
x
→
− + −
=
−
Ta có
( )
2
2
2 2 1 4 1 4 4
lim
2
x
x x x x
I
x
→
− − + − − + −
=
−
2
2
4 1 4 4
lim 2 1
22
x
xx
x
xx
→

− − −
= − + +


−−

( )( )
( )
( )
( )( ) ( )
( )
( )
22
4 1 1 1 1
2 2 4 1 1
2 lim 2 lim 2
2
2 1 1 2 1 1
xx
xx
x x x
x
x
x x x x
→→
− − − +
− + − −
= + + = + + +
−
− + + − + +
2
44
2 lim 2 2 4 8.
2
11
x
x
x
→

= + + + = + + =

−+

7)
( )
6
5 4 2 3 84
lim .
6
x
x x x
I
x
→
− − + −
=
−
Ta có
( )
6
5 30 2 3 26 2 3 78 6
lim
6
x
x x x x
I
x
→
− − + − − + −
=
−
( )
( )
6
26 2 3 3
5 6 2 3
6
lim
6 6 6
x
x
xx
x
x x x
→

−−
−−
−

= + +

− − −

ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
88
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )( )
( )
( )
6
26 2 3 3 2 3 3
lim 5 2 3 1
6 2 3 3
x
xx
x
xx
→

− − − +

= − + +

− − +

( )
( )
( )
( )
( )
( )
66
26 2 3 9 26.2 6
15 lim 1 15 lim 1
6 2 3 3 6 2 3 3
xx
xx
x x x x
→→
− − −
= + + = + +
− − + − − +
6
52 52 74
15 lim 1 15 1 .
63
2 3 3
x
x
→
= + + = + + =
−+
8)
3
0
1 2 1 3
lim .
x
xx
I
x
→
+ − +
=
Ta có
33
00
1 2 1 1 1 3 1 2 1 1 1 3
lim lim
xx
x x x x
I
x x x
→→

+ − + − + + − − +
= = +



( )( )
( )
( )
( )
( )
( )
( )
2
33
3
0
2
3
3
1 1 3 1 1 3 1 3
1 2 1 1 2 1
lim
1 2 1
1 1 3 1 3
x
x x x
xx
xx
x x x
→

− + + + + +
+ − + +

=+

++
+ + + +


( )
( )
( )
( )
( )
2
00
2
3
3
3
3
1 1 3
1 2 1 2 3
lim lim
1 2 1
1 2 1
1 1 3 1 3
1 1 3 1 3
xx
x
x
x
xx
xx
x x x
→→


−+

+ − −

= + = +


++
++
+ + + +
+ + + +



23
0.
23
−
= + =
9)
3
32
1
73
lim .
1
x
xx
I
x
→
+ − +
=
−
Ta có
3
32
1
7 2 2 3
lim
1
x
xx
I
x
→
+ − + − +
=
−
3
32
1
7 2 2 3
lim
11
x
xx
xx
→

+ − − +
=+


−−

(
)
( )
( )
( )
(
)
(
)
( )
(
)
2
33
3 3 3
3
22
1
2
2
3
33
3
7 2 7 2 7 4
2 3 2 3
lim
1 2 3
1 7 2 7 4
x
x x x
xx
xx
x x x
→


+ − + + + +

− + + +



=+


− + +
− + + + +




( )
( )
( )
( )
(
)
2
3
1
2
2
3
33
3
43
78
lim
1 2 3
1 7 2 7 4
x
x
x
xx
x x x
→


−+
+−

=+


− + +
− + + + +




( )
( )
( )
(
)
32
1
2
2
3
33
3
11
lim
1 2 3
1 7 2 7 4
x
xx
xx
x x x
→


−−

=+


− + +
− + + + +




( )
2
22
1
3
33
3
1 1 3 2 1
lim .
12 4 4
23
7 2 7 4
x
x x x
x
xx
→

+ + +

= − = − = −

++
+ + + +


ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
89
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
10)
3
2
2
8 11 7
lim .
32
x
xx
I
xx
→
+ − +
=
−+
Ta có
33
2 2 2
22
8 11 3 3 7 8 11 3 3 7
lim lim
3 2 3 2 3 2
xx
x x x x
I
x x x x x x
→→

+ − + − + + − − +
= = +


− + − + − +

( )
( )
( )
( )
( )
( )
( )( )
( )
( )
2
33
3
2
2
2
2
3
3
8 11 3 8 11 3 8 11 9
3 7 3 7
lim
3 2 3 7
3 2 8 11 3 8 11 9
x
x x x
xx
x x x
x x x x
→

+ − + + + +
− + + +

=+

− + + +
− + + + + +


( )
( )
( )
( )
( )
( )
2
2
2
2
3
3
97
8 11 27
lim
3 2 3 7
3 2 8 11 3 8 11 9
x
x
x
x x x
x x x x
→

−+

+−
=+

− + + +
− + + + + +


( )
( )( ) ( )
( )
( )( )
( )
2
2
3
3
82
2
lim
1 2 3 7
1 2 8 11 3 8 11 9
x
x
x
x x x
x x x x
→

−

−
=+

− − + +
− − + + + +


( ) ( )
( )
( )
( )
2
2
3
3
8 1 8 1 7
lim .
27 6 54
1 3 7
1 8 11 3 8 11 9
x
xx
x x x
→


= − = − =

− + +
− + + + +


11)
3
0
2 1 8
lim .
x
xx
I
x
→
+ − −
=
Ta có
33
00
2 1 2 2 8 2 1 2 2 8
lim lim
xx
x x x x
I
x x x
→→

+ − + − − + − − −
= = +



( )( )
( )
( )
( )
( )
( )
( )
2
33
3
0
2
3
3
2 8 4 2 8 8
2 1 1 1 1
lim
11
4 2 8 8
x
x x x
xx
xx
x x x
→

− − + − + −
+ − + +

=+

++
+ − + −


( )
( )
( )
( )
( )
0
2
3
3
2 1 1 8 8
lim
11
4 2 8 8
x
xx
xx
x x x
→

+ − − −

=+

++
+ − + −


( )
2
0
3
3
2 1 2 1 13
lim .
2 12 12
11
4 2 8 8
x
x
xx
→


= + = + =

++
+ − + −

12)
3
2
1
3 5 3
lim .
1
x
xx
I
x
→
+ − +
=
−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
90
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta có
33
22
11
3 5 2 2 3 3 5 2 2 3
lim lim
1 1 1
xx
x x x x
I
x x x
→→

+ − + − + + − − +
= = +


− − −

(
)
( )
( )
( )
( )( )
( )
( )
2
33
2 2 2
3
1
2
3
22
3
3 5 2 3 5 2 3 5 4
2 3 2 3
lim
1 2 3
1 3 5 2 3 5 4
x
x x x
xx
xx
x x x
→


+ − + + + +


− + + +


=+


− + +
− + + + +




( )
( )
( )
( )
( )
2
1
2
3
22
3
43
3 5 8
lim
1 2 3
1 3 5 2 3 5 4
x
x
x
xx
x x x
→


−+
+−

=+


− + +
− + + + +




( )
( )
( )
( )
( )
2
1
2
3
22
3
31
1
lim
1 2 3
1 3 5 2 3 5 4
x
x
x
xx
x x x
→


−
−

=+


− + +
− + + + +




( )
( )
2
1
3
22
3
31
1 6 1 1
lim .
12 4 4
23
3 5 2 3 5 4
x
x
x
xx
→

+

= − = − =

++
+ + + +


13)
2
3
1
75
lim .
1
x
xx
I
x
→
+ − −
=
−
Ta có
22
33
11
7 2 2 5 7 2 2 5
lim lim
1 1 1
xx
x x x x
I
x x x
→→

+ − + − − + − − −
= = +


− − −

( )
( )
( )
( ) ( )
( )
(
)
(
)
( )
(
)
2
33
22
3
1
2
2
3
3
7 2 7 2 7 4
2 5 2 5
lim
1 2 5
1 7 2 7 4
x
x x x
xx
xx
x x x
→

+ − + + + +
− − + −

=+

− + −
− + + + +


( ) ( )
( )
( )
( )
(
)
2
1
2
2
3
3
45
78
lim
1 2 5
1 7 2 7 4
x
x
x
xx
x x x
→

−−

+−
=+

− + −
− + + + +


( ) ( )
( )
( )
(
)
2
1
2
2
3
3
11
lim
1 2 5
1 7 2 7 4
x
xx
xx
x x x
→


−−
=+

− + −
− + + + +


( )
22
1
3
3
1 1 1 2 7
lim .
12 4 12
25
7 2 7 4
x
x
x
xx
→

+

= + = + =

+−
+ + + +

14)
3
2
3 2 3 2
lim .
2
x
xx
I
x
→
+ − −
=
−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
91
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta có
33
22
3 2 2 2 3 2 3 2 2 2 3 2
lim lim
2 2 2
xx
x x x x
I
x x x
→→

+ − + − − + − − −
= = +


− − −

( )
( )
( )
( ) ( )
( )
( )( )
( )
( )
2
33
3
2
2
3
3
3 2 2 3 2 2 3 2 4
2 3 2 2 3 2
lim
2 2 3 2
2 3 2 2 3 2 4
x
x x x
xx
xx
x x x
→

+ − + + + +
− − + −

=+

− + −
− + + + +


( ) ( )
( )
( )
( )
( )
2
2
3
3
4 3 2
3 2 8
lim
2 2 3 2
2 3 2 2 3 2 4
x
x
x
xx
x x x
→

−−

+−
=+

− + −
− + + + +


( )
( ) ( )
( )
( )
( )
2
2
3
3
32
63
lim
2 2 3 2
2 3 2 2 3 2 4
x
x
x
xx
x x x
→

−

−
=+

− + −
− + + + +


( )
2
2
3
3
3 3 3 3 1
lim .
12 4 2
2 3 2
3 2 2 3 2 4
x
x
xx
→

−

= − = + = −

+−
+ + + +

15)
3
2
3 2 5 6
lim .
2
x
xx
I
x
→
+ − −
=
−
Ta có
33
22
3 2 2 2 5 6 3 2 2 2 5 6
lim lim
2 2 2
xx
x x x x
I
x x x
→→

+ − + − − + − − −
= = +


− − −

( )
( )
( )
( ) ( )
( )
( )( )
( )
( )
2
33
3
2
2
3
3
3 2 2 3 2 2 3 2 4
2 5 6 2 5 6
lim
2 2 5 6
2 3 2 2 3 2 4
x
x x x
xx
xx
x x x
→

+ − + + + +
− − + −

=+

− + −
− + + + +


( ) ( )
( )
( )
( )
( )
2
2
3
3
4 5 6
3 2 8
lim
2 2 5 6
2 3 2 2 3 2 4
x
x
x
xx
x x x
→

−−

+−
=+

− + −
− + + + +


( )
( ) ( )
( )
( )
( )
2
2
3
3
32
10 5
lim
2 2 5 6
2 3 2 2 3 2 4
x
x
x
xx
x x x
→

−

−
=+

− + −
− + + + +


( )
2
2
3
3
3 5 3 5
lim 1.
12 4
2 5 6
3 2 2 3 2 4
x
x
xx
→

−

= − = + = −

+−
+ + + +

16)
3
2
2
2
2 4 11 7
lim .
4
x
x x x
I
x
→
+ + − +
=
−
Ta có
33
22
2 2 2
22
2 4 11 3 3 7 2 4 11 3 3 7
lim lim
4 4 4
xx
x x x x x x
I
x x x
→→

+ + − + − + + + − − +
= = +


− − −

ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
92
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
(
)
( )
( ) ( )
( )( )
( )
( )
2
33
2 2 2
3
2
2
2
3
2 2 2
3
2 4 11 3 2 4 11 3 2 4 11 9
3 7 3 7
lim
4 3 7
4 2 4 11 3 2 4 11 9
x
x x x x x x
xx
xx
x x x x x
→


+ + − + + + + + +


− + + +


=+


− + +
− + + + + + +




( ) ( )
( )
( )
( )
2
2
2
2
3
2 2 2
3
97
2 4 11 27
lim
4 3 7
4 2 4 11 3 2 4 11 9
x
x
xx
xx
x x x x x
→


−+
+ + −

=+


− + +
− + + + + + +




( ) ( )
( )
( )
2
2
2
2
3
2 2 2
3
2 4 16 2
lim
4 3 7
4 2 4 11 3 2 4 11 9
x
x x x
xx
x x x x x
→


+ − −

=+


− + +
− + + + + + +




( )( )
( ) ( )
( )
( )
2
2
2
3
2 2 2
3
2 2 4
2
lim
4 3 7
4 2 4 11 3 2 4 11 9
x
xx
x
xx
x x x x x
→


−+
−

=+


− + +
− + + + + + +




( )
( )
( )
( )
( )
2
2
3
22
3
24
1 12 1 5
lim .
108 24 72
2 3 7
2 2 4 11 3 2 4 11 9
x
x
xx
x x x x x
→


+
−

= − = + =


+ + +
+ + + + + + +




17)
3
32
2
1
57
lim .
1
x
xx
I
x
→
− − +
=
−
Ta có
33
3 2 3 2
2 2 2
11
5 2 2 7 5 2 2 7
lim lim
1 1 1
xx
x x x x
I
x x x
→→

− − + − + − − − +
= = +


− − −

(
)
(
)
( )
(
)
(
)
( )
( ) ( )
2
33
2 2 2
3
33
1
2
23
3
2 2 2
3
2 7 4 2 7 7
5 2 5 2
lim
1 5 2
1 4 2 7 7
x
x x x
xx
xx
x x x
→


− + + + + +

− − − +



=+


− − +
− + + + +




( )
(
)
( )
( ) ( )
2
3
1
2
23
3
2 2 2
3
87
54
lim
1 5 2
1 4 2 7 7
x
x
x
xx
x x x
→


−+
−−

=+


− − +
− + + + +




ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
93
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
(
)
( ) ( )
32
1
2
23
3
2 2 2
3
11
lim
1 5 2
1 4 2 7 7
x
xx
xx
x x x
→


−−

=+


− − +
− + + + +




( )
( )
(
)
( )
2
2
1
3
3
22
3
1
1 3 1 11
lim .
8 12 24
1 5 2
4 2 7 7
x
xx
xx
xx
→

− + +
−−

= + = − + = −

+ − +
+ + + +


18)
3
3
2
2
3 4 24 2 8 2 3
lim .
4
x
x x x
I
x
→
− + + − −
=
−
Ta có
3
3
2
2
3 4 24 6 2 2 8 8 2 3
lim
4
x
x x x
I
x
→
− − + + − + − −
=
−
1 2 3
3
3
2 2 2
2 2 2
3 4 24 6 2 2 8 8 2 3
lim lim lim
4 4 4
x x x
I I I
x x x
x x x
→ → →
− − + − − −
= + +
− − −
1
I
3
3
2
2
3 4 24 6
lim
4
x
x
x
→
−−
=
−
(
)
( )
2
3 3 3
3 3 3 2
2
2
33
2 3 3 2
3 4 24 2 4 24 4 24.2 2
lim
4 4 24 4 24.2 2
x
x x x
x x x
→

− − − + − +


=

− − + − +


( )
( )
(
)
3
2
2
33
2 3 3 2
3 4 24 8
lim
4 4 24 4 24.2 2
x
x
x x x
→
−−
=

− − + − +


( )
( )
(
)
3
2
2
33
2 3 3 2
3.4 8
lim
4 4 24 4 24.2 2
x
x
x x x
→
−
=

− − + − +


( )
( )
( )( )
(
)
2
2
2
33
3 3 2
12 2 2 4
lim
2 2 4 24 4 24.2 2
x
x x x
x x x x
→
− + +
=

− + − + − +


( )
( )
(
)
2
2
2
33
3 3 2
12 2 4
lim
2 4 24 4 24.2 2
x
xx
x x x
→
− + +
=

+ − + − +


144
3
48
= − = −
.
2
I
2
2
22
lim
4
x
x
x
→
+−
=
−
( )( )
( )
( )
2
2
2 2 2 2
lim
4 2 2
x
xx
xx
→
+ − + +
=
− + +
( )
( )( )
( )
2
24
lim
2 2 2 2
x
x
x x x
→
+−
=
− + + +
( )
( )
11
lim
16
2 2 2
x
xx
→
−
= = −
+ + +
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
94
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3
I
2
2
8 8 2 3
lim
4
x
x
x
→
−−
=
−
( )( )
( )
( )
2
2
8 1 2 3 1 2 3
lim
4 1 2 3
x
xx
xx
→
− − + −
=
− + −
( )
( )
( )( )
2
8 1 2 3
lim
22
x
x
xx
→
−−
=
+−
( )
( )( )
( )
2
8.2 2
lim
2 2 1 2 3
x
x
x x x
→
−
=
− + + +
( )
( )
2
16
lim
2 1 1 2 3
x
xx
→
=
+ + + −
16
2
8
==
1
32
16
I = − − +
17
16
=−
.
Bài 5. Tính các giới hạn sau:
1
( )
3
lim 2 3
x
xx
→+
−
ĐS:
+
2.
( )
32
lim 3 2
x
xx
→−
−+
ĐS:
−
3.
( )
32
lim 6 9 1
x
x x x
→+
− − + +
ĐS:
−
4.
( )
3
lim 3 1
x
xx
→−
− + −
ĐS:
+
5.
( )
42
lim 2 1
x
xx
→+
−+
ĐS:
+
6.
( )
42
lim 8 10
x
xx
→−
−+
ĐS:
+
7.
( )
42
lim 2 3
x
xx
→+
− + +
ĐS:
−
8.
( )
42
lim 6
x
xx
→−
− − +
ĐS:
−
9.
2
lim 3 4
x
xx
→
−+
ĐS:
+
10.
(
)
2
lim 2 1
x
xx
→−
++
ĐS:
+
11.
(
)
2
lim 1 2
x
x x x
→−
+ + +
ĐS:
−
12.
(
)
2
lim 4 1
x
x x x
→+
+ + −
ĐS:
+
13.
( )
lim 1 9 1
x
xx
→+
+ − +
ĐS:
−
14.
( )
lim 16 7 9 3
x
xx
→−
+ + +
ĐS: không tồn tại giới hạn
Lời giải
1.
( )
3
lim 2 3
x
I x x
→+
=−
Ta có
( )
3
lim 2 3
x
I x x
→+
=−
3
2
3
lim 2
x
x
x
→+

= − = +


. (vì
3
lim
x
x
→+
= +
và
2
3
lim 2 2 0
x
x
→+

− =


)
2.
( )
32
lim 3 2
x
I x x
→−
= − +
.
Ta có
( )
32
lim 3 2
x
I x x
→−
= − +
3
3
32
lim 1
x
x
xx
→−

= − + = −


. (vì
3
lim
x
x
→−
= −
và
3
32
lim 1 1
x
xx
→−

− + =


).
3.
( )
32
lim 6 9 1
x
I x x x
→+
= − − + +
.
Ta có
3
23
6 9 1
lim 1
x
Ix
x x x
→+

= − − + + = −


.
(vì
3
lim
x
x
→+
= +
và
23
6 9 1
lim 1 1 0
x
x x x
→+

− − + + = −


).
4.
( )
3
lim 3 1
x
I x x
→−
= − + −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
95
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta có
3
23
31
lim 1
x
Ix
xx
→−

= − + − = +


. (vì
3
lim
x
x
→−
= −
và
23
31
lim 1 1 0
x
xx
→−

− + − = −


).
5.
( )
42
lim 2 1
x
I x x
→+
= − +
Ta có
4
24
21
lim 1
x
Ix
xx
→+

= − + = +


. (vì
4
lim
x
x
→+
= +
và
24
21
lim 1 1 0
x
xx
→+

− + =


).
6.
( )
42
lim 8 10
x
I x x
→−
= − +
Ta có
4
24
8 10
lim 1 1 0
x
Ix
xx
→−

= − + =


(vì
4
lim
x
x
→−
= +
và
24
8 10
lim 1 1 0
x
xx
→−

− + =


)
7.
( )
42
lim 2 3
x
I x x
→+
= − + +
Ta có
4
24
23
lim 1
x
Ix
xx
→+

= − + + = −


. ( vì
4
lim
x
x
→+
= +
và
24
23
lim 1 1 0
x
xx
→+

− + + = −


).
8.
( )
42
lim 6
x
I x x
→−
= − − +
Ta có
4
24
16
lim 1
x
Ix
xx
→−

= − − + = −


. (vì
4
lim
x
x
→−
= +
và
24
16
lim 1 1
x
xx
→−

− − + = −


)
9.
2
lim 3 4
x
I x x
→
= − +
.
Ta có
2
2
34
lim 1
x
Ix
xx
→

= − +


2
34
lim 1
x
x
xx
→

= − + = +


.
(vì
lim
x
x
→
= +
và
2
34
lim 1 1 0
x
xx
→

− + =


).
10.
(
)
2
lim 2 1
x
I x x
→−
= + +
Ta có
(
)
2
lim 2 1
x
I x x
→−
= + +
2
1
lim 2 1
x
x
x
→−

= − + + = +



.
(vì
lim
x
x
→−
= −
và
2
1
lim 2 1 2 1 0
x
x
→−

− + + = − +



).
11.
(
)
2
lim 1 2
x
I x x x
→−
= + + +
2
11
lim 1 2
x
x
xx
→−

= − + + + = −



.
(vì
lim
x
x
→−
= −
,
2
11
lim 1 2 1 0
x
xx
→−

− + + + =



).
12.
(
)
2
lim 4 1
x
I x x x
→+
= + + −
2
11
lim 4 1
x
x
xx
→+

= + + − = +



(vì
lim
x
x
→+
= +
,
2
11
lim 4 1 1 0
x
xx
→+

= + + − =



).
13.
( )
lim 1 9 1
x
I x x
→+
= + − +
11
lim 1 9
x
x
xx
→+

= + − + = −



.
(vì
lim
x
x
→+
= +
,
11
lim 1 9
x
x
xx
→+

= + − + = −



).
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
96
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
14.
( )
lim 16 7 9 3
x
I x x
→−
= + + +
Tập xác định của hàm số
( )
16 7 9 3f x x x= + + +
là
1
;
3
D

= − +

.
Ta có khi
x → −
hàm số
( )
16 7 9 3f x x x= + + +
không xác định. Do đó
( )
lim 16 7 9 3
x
xx
→−
+ + +
không tồn tại.
Bài 6. Tính các giới hạn sau:
1.
2
lim
1
x
x
x
→+
+
−
. ĐS:
1
2.
2
lim
1
x
x
x
→−
+
. ĐS:
2
3.
1
lim
21
x
x
x
→+
−
−
.ĐS:
1
2
−
4.
32
lim
1
x
x
x
→−
−
+
. ĐS:
3
5.
3
32
2 3 4
lim
1
x
xx
xx
→+
+−
− − +
. ĐS:
2−
6.
( )
( )
( )
2
2
3 2 1
lim
5 1 2
x
xx
x x x
→+
−
−+
. ĐS:
6
5
7.
43
4
2 7 15
lim
1
x
xx
x
→−
+−
+
. ĐS:
2
8.
( )
( )
( )
( )
2
3
4 1 7 1
lim
2 1 3
x
xx
xx
→+
+−
−+
. ĐS:
0
9.
( ) ( )
( )
22
4
1 5 2
lim
31
x
xx
x
→−
−+
+
. ĐS:
25
81
10.
( ) ( )
( )
( )
43
5
2
1 1 2
lim
2 2 3
x
xx
xx
→−
+−
++
.ĐS:
1
4
−
11.
( )
( )
( )
( )
2
2
2
2
22
lim
2 1 1
x
xx
xx
→−
++
+−
. ĐS:
−
12.
( ) ( )
( )
34
5
2
21
lim
12
x
xx
xx
→−
+−
−
. ĐS:
1
32
−
13.
32
2
lim
3 4 3 2
x
xx
xx
→−

−

−+

. ĐS:
2
9
14.
2
3
37
lim
21
x
xx
x
→−
−+
−
.ĐS:
15.
3
4
22
lim
23
x
xx
xx
→+
++
++
ĐS:
0
16.
( )
( )
( )
( )
2
3
4 1 7 1
lim
2 1 3
x
xx
xx
→+
+−
−+
ĐS:
17.
( )
( )
2
2
4 1 2 3
lim
61
x
xx
xx
→−
++
−+
ĐS:
−
18.
3
2
22
lim
23
x
xx
xx
→+
++
++
ĐS:
+
19.
43
3
22
lim
23
x
x x x
xx
→−
+ + +
++
ĐS:
−
20.
43
23
22
lim
2
x
x x x
xx
→+
+ + +
−
ĐS:
−
21.
43
11
lim
27
x
xx
x
→+
−+
−
ĐS:
+
22.
42
21
lim
12
x
xx
x
→+
+−
−
ĐS:
+
23.
4
lim
12
x
xx
x
→+
−
−
ĐS:
+
24.
( )( )
53
3
23
21
lim
21
x
xx
x x x
→+
+−
−+
ĐS:
1
25.
3
3
1
lim
21
x
xx
x
→+
++
+
ĐS:
1
26.
42
21
lim
12
x
xx
x
→+
+−
−
ĐS:
−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
97
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Lời giải
1.
2
lim
1
x
x
I
x
→+
+
=
−
2
1
lim
1
1
x
x
x
x
x
→+

+


=

−


2
1
lim
1
1
x
x
x
→+

+


=

−


1=
.
2.
2
lim
1
x
x
I
x
→−
=
+
2
lim
1
1
x
x
x
x
→−

+


2
lim
1
1
x
x
→−
=
+
2=
.
3.
1
lim
21
x
x
I
x
→+
−
=
−
1
1
lim
1
2
x
x
x
x
x
→+

−


=

−


1
1
1
lim
1
2
2
x
x
x
→+
−
= = −
−
.
4.
32
lim
1
x
x
I
x
→−
−
=
+
2
3
lim
1
1
x
x
x
x
x
→−

−


=

+


2
3
lim
1
1
x
x
x
→−

−


=

+


3=
.
5.
3
32
2 3 4
lim
1
x
xx
I
xx
→+
+−
=
− − +
3
23
3
3
34
2
lim
11
1
x
x
xx
x
xx
→+

+−


=

− − +


23
3
34
2
lim 2
11
1
x
xx
xx
→+

+−


=−

− − +


.
6.
2
2
2
1
3 . 2
lim
12
51
x
xx
x
I
xx
xx
→+

−


=
−+
2
1
32
6
lim
12
5
51
x
x
xx
→+

−


==
−+
.
7.
43
4
2 7 15
lim
1
x
xx
I
x
→−
+−
=
+
4
4
4
4
7 15
2
lim
1
1
x
x
xx
x
x
→−

+−


=

+


4
4
7 15
2
lim 2
1
1
x
xx
x
→−

+−


==

+


.
8.
( )
( )
( )
( )
2
3
4 1 7 1
lim
2 1 3
x
xx
I
xx
→+
+−
=
−+
2
2
3
3
11
47
lim
13
21
x
xx
xx
xx
xx
→+
+−
=
−+
2
3
11
47
lim 0
13
21
x
x
xx
x
xx
→+
+−
==
−+
.
9.
( ) ( )
( )
22
4
1 5 2
lim
31
x
xx
I
x
→−
−+
=
+
22
22
4
4
12
15
lim
1
3
x
xx
xx
x
x
→−
−+
=

+


22
4
12
15
25
lim
81
1
3
x
xx
x
→−
−+
==

+


.
10.
( ) ( )
( )
( )
43
5
2
1 1 2
lim
2 2 3
x
xx
I
xx
→−
+−
=
++
43
43
5
52
2
11
12
lim
23
21
x
xx
xx
xx
xx
→−
+−
=
++
43
5
2
11
12
1
lim
4
23
21
x
xx
xx
→−
+−
= = −
++
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
98
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
11.
( )
( )
( )
( )
2
2
2
2
22
lim
2 1 1
x
xx
I
xx
→−
++
=
+−
2
4
2
2
22
2
22
11
lim
11
21
x
xx
xx
xx
xx
→−
++
=
+−
2
2
2
2
22
. 1 1
lim
11
21
x
x
xx
xx
→−
++
= = −
+−
(vì
lim
x
x
→−
= −
,
2
2
2
2
22
11
1
lim 0
2
11
21
x
xx
xx
→−
++
=
+−
).
12.
( ) ( )
( )
34
5
2
21
lim
12
x
xx
I
xx
→−
+−
=
−
34
34
5
52
21
11
lim
1
2.
x
xx
xx
xx
x
→−
+−
=

−


34
5
21
11
1
lim
32
1
2
x
xx
x
→−
+−
= = −

−


.
13.
32
2
lim
3 4 3 2
x
xx
I
xx
→−

=−

−+

.
Ta có
32
2
lim
3 4 3 2
x
xx
I
xx
→−

=−

−+

( )
( )
( )
( )
3 2 2
2
3 2 3 4
lim
3 4 3 2
x
x x x x
xx
→−
+ − −
=
−+
( )
( )
32
2
24
lim
3 4 3 2
x
xx
xx
→−
+
=
−+
3
2
4
2
lim
42
33
x
x
x
xx
xx
→−

+


=
−+
4
2
2
lim
42
9
33
x
x
xx
→−

+


==
−+
.
14.
2
3
37
lim
21
x
xx
I
x
→−
−+
=
−
2
2
3
3
3 1 7
lim
1
2
x
x
x x x
x
x
→−

−+


=

−


2
3
3 1 7
lim 0
1
2
x
x x x
x
→−

−+


=

−


.
Bài 7. Tính các giới hạn sau:
1.
1
23
lim
1
x
x
x
+
→
−
−
. ĐS:
−
2.
2
15
lim
2
x
x
x
+
→
−
−
. ĐS:
−
3.
3
2
lim
3
x
x
x
−
→
−
−
. ĐS:
+
4.
( )
2
4
5
lim
4
x
x
x
−
→
−
−
. ĐS:
−
5.
2
31
lim
2
x
x
x
−
→
−+
−
. ĐS:
+
6.
1
31
lim
1
x
x
x
−
→
−
−
. ĐS:
−
7.
2
65
lim
48
x
x
x
+
→
−
−
. ĐS:
−
8.
2
1
lim
24
x
x
x
+
→
+
−
. ĐS:
+
9.
3
3
lim
5 15
x
x
x
+
→
−
−
. ĐS:
1
5
10.
( )
3
71
lim
3
x
x
x
−
→−
−
+
.ĐS:
−
11.
2
2
2
lim
2 5 2
x
x
xx
−
→
−
−+
. ĐS:
1
3
12.
3
1
1
lim
23
x
x
xx
+
→
−
+−
. ĐS:
1
7
13.
3
1
1
lim
23
x
x
xx
−
→
−
+−
. ĐS:
1
7
−
14.
2
2
32
lim
2
x
xx
x
+
→
−+
−
.ĐS:
1
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
99
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
15.
2
3
9
lim
3
x
x
x
→
−
−
ĐS: không tồn tại 16.
2
4
4
lim
20
x
x
xx
→
−
+−
ĐS: không tồn tại
17.
2
2
lim
11
x
x
x
−
→
−
−−
ĐS:
18.
3
3
lim
5 11 2
x
x
x
−
→
−
−−
ĐS:
4
5
−
19.
3
2
2
lim
11
x
x
x
−
→
−
−−
ĐS:
3−
20.
2
3
5
25
lim
41
x
x
x
−
→
−
−−
ĐS:
30−
21.
( )
2
3
38
lim
3
x
x
x
+
→
−
−
ĐS:
+
22.
3
2
2
25 3
lim
2
x
x
xx
→
+−
−−
ĐS:
1
81
23.
2
2
32
lim
4 16
x
x
x
+
→
+
−
ĐS:
+
24.
0
lim
x
xx
xx
+
→
+
−
ĐS:
1−
25.
2
2
4
lim
2
x
x
x
+
→
−
−
ĐS:
26.
0
2
lim
x
xx
xx
+
→
+
−
ĐS:
2−
27.
( )
( )( )
1
21
lim
11
x
xx
xx
+
→−
++
+ − −
ĐS:
1
28.
2
2
3
69
lim
9
x
xx
x
−
→
−+
−
ĐS:
1
6
−
29.
2
2
1
43
lim
65
x
xx
xx
−
→
−+
− + −
ĐS:
−
30.
( )
2
54
1
32
lim
x
xx
xx
+
→−
++
+
ĐS:
0
31.
( )
2
2
lim 2
4
x
x
x
x
+
→
−
−
ĐS:
32.
( )
( )
3
2
1
lim 1
1
x
x
x
x
+
→−
+
−
ĐS:
0
33.
( )
2
1
5
lim 1
23
x
x
x
xx
+
→
+
−
+−
ĐS:
0
34.
1
1
lim
2 1 1
x
xx
xx
−
→
−
− + −
ĐS:
1
2
35.
0
1
lim 2
x
x
x
x
+
→

−



ĐS:
0
36.
( )
( )
2
2
3
2 5 3
lim
3
x
xx
x
+
→−
+−
+
ĐS:
−
37.
2
2
11
lim
24
x
xx
−
→

−

−−

ĐS:
−
38.
3
2
1
32
lim
54
x
xx
xx
−
→
−+
−+
ĐS:
3
5
−
Lời giải
1
1
23
lim
1
x
x
x
+
→
−
= −
−
vì
( )
( )
1
1
lim 2 3 1
lim 1 0
1 0, 1
x
x
x
x
xx
+
+
→
→
+
− = −
−=
− →
.
2.
2
15
lim
2
x
x
x
+
→
−
= −
−
vì
( )
( )
2
2
lim 15 13
lim 2 0
2 0, 2
x
x
x
x
xx
+
+
→
→
+
− = −
−=
− →
.
3.
3
2
lim
3
x
x
x
−
→
−
= +
−
vì
( )
( )
3
3
lim 2 1
lim 3 0
3 0, 3
x
x
x
x
xx
−
−
→
→
−
− = −
−=
− →
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
100
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
4.
( )
2
4
5
lim
4
x
x
x
−
→
−
= −
−
vì
( )
( )
( )
4
2
4
2
lim 5 1
lim 4 0
4 0, 4
x
x
x
x
xx
−
−
→
→
−
− = −
−=
− →
.
5.
2
31
lim
2
x
x
x
−
→
−+
= +
−
vì
( )
( )
2
2
lim 3 1 5
lim 2 0
2 0, 2
x
x
x
x
xx
−
−
→
→
−
− + = −
−=
− →
.
6.
1
31
lim
1
x
x
x
−
→
−
= −
−
vì
( )
( )
1
1
lim 3 1 2
lim 1 0
1 0, 1
x
x
x
x
xx
−
−
→
→
−
−=
−=
− →
.
7.
2
65
lim
48
x
x
x
+
→
−
= −
−
vì
( )
( )
2
2
lim 6 5 4
lim 4 8 0
4 8 0, 2
x
x
x
x
xx
+
+
→
→
+
− = −
−=
− →
.
8.
2
1
lim
24
x
x
x
+
→
+
= +
−
vì
( )
( )
2
2
lim 1 3
lim 2 4 0
2 4 0, 2
x
x
x
x
xx
+
+
→
→
+
+=
−=
− →
.
9. Do
3x
+
→
nên
33xx− = −
suy ra
33
3
3
lim lim
5 15 5 15
xx
x
x
xx
++
→→
−
−
==
−−
3
11
lim
55
x
+
→
=
.
10.
( )
3
71
lim
3
x
x
x
−
→−
−
= −
+
vì
( )
( )
( )
( )
3
3
lim 7 1 22
lim 3 0
3 0, 3
x
x
x
x
xx
−
−
→−
→−
−
− = −
+=
+ → −
.
11. Do
2x
−
→
nên
22xx− = −
suy ra
( )( )
2
22
2
2
lim lim
2 5 2 2 1 2
xx
x
x
x x x x
−−
→→
−
−
=
− + − −
2
11
lim
2 1 3
x
x
−
→
==
−
.
12. Do
1x
+
→
nên
11xx− = −
suy ra
( )
( )
3
2
11
1
1
lim lim
23
1 2 2 3
xx
x
x
xx
x x x
++
→→
−
−
=
+−
− + +
2
1
11
lim
2 2 3 7
x
xx
+
→
=
++
.
13. Do
1x
−
→
nên
11xx− = −
suy ra
( )
( )
3
2
11
1
1
lim lim
23
1 2 2 3
xx
x
x
xx
x x x
−−
→→
−
−
=
+−
− + +
2
1
11
lim
2 2 3 7
x
xx
−
→
−
=−
++
.
14. Ta có
( )( )
2
3 2 1 2x x x x− + = − −
, do
2x
+
→
nên
2
3 2 0xx− +
, suy ra
( )( )
( )
2
2 2 2
32
12
lim lim lim 1 1
22
x x x
xx
xx
x
xx
+ + +
→ → →
−+
−−
= = − =
−−
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
101
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
15. Ta có
( )( )
2
33
9
33
lim lim
33
xx
x
xx
xx
→→
−
+−
=
−−
TH1:
3x
ta có
( )( )
( )
2
3 3 3
9
33
lim lim lim 3 6
33
x x x
x
xx
x
xx
+ + +
→ → →
−
+−
= = + =
−−
.
TH2:
3x
ta có
( )( )
( )
2
3 3 3
9
33
lim lim lim 3 6
33
x x x
x
xx
x
xx
− − −
→ → →
−
− + −
= = − − = −
−−
.
Do
22
33
99
lim lim
33
xx
xx
xx
+−
→→
−−
−−
nên không tồn tại
2
3
9
lim
3
x
x
x
→
−
−
.
16. Ta có
( )( )
2
44
44
lim lim
45
20
xx
xx
xx
xx
→→
−−
=
−+
+−
TH1:
4x
, ta có
( )( )
2
4 4 4
4 4 1 1
lim lim lim
4 5 5 9
20
x x x
xx
x x x
xx
+ + +
→ → →
−−
= = =
− + +
+−
TH2:
4x
, ta có
( )( )
2
4 4 4
4 4 1 1
lim lim lim
4 5 5 9
20
x x x
xx
x x x
xx
+ − −
→ → →
− − − −
= = =
− + +
+−
Do
2
4
4
lim
20
x
x
xx
+
→
−
+−
2
4
4
lim
20
x
x
xx
−
→
−
+−
nên không tồn tại
2
4
4
lim
20
x
x
xx
→
−
+−
.
17. Do
2x
−
→
nên
22xx− = −
suy ra
2
2
lim
11
x
x
x
−
→
−
−−
( )
( )
2
2 1 1
lim
11
x
xx
x
−
→
− − +
=
−−
( )
2
lim 1 1 2
x
x
−
→
− + =
.
18. Do
3x
−
→
nên
23xx− = −
suy ra
3
3
lim
5 11 2
x
x
x
−
→
−
−−
( )
( )
3
3 5 11 2
lim
5 11 4
x
xx
x
−
→
− − +
=
−−
( )
3
5 11 2
4
lim
55
x
x
−
→
− − +
= = −
.
19. Do
2x
−
→
nên
22xx− = −
suy ra
3
2
2
lim
11
x
x
x
−
→
−
−−
( )
(
)
2
33
2
2 1 1 1
lim
11
x
x x x
x
−
→
− − + − +
=
−−
(
)
( )
2
33
2
lim 1 1 1 3
x
xx
−
→
= − − + − + = −
.
20. Ta có
( )( )
2
25 5 5x x x− = − +
, do
5x
−
→
nên
2
25 0x −
, suy ra
2
3
5
25
lim
41
x
x
x
−
→
−
−−
( )
(
)
2
2
33
5
25 4 4 1
lim
41
x
x x x
x
−
→
− − + − +
=
−−
( )
( )
(
)
2
33
5
lim 5 4 4 1 30
x
x x x
−
→
= − + − + − + = −
.
21.
( )
2
3
38
lim
3
x
x
x
+
→
−
= +
−
, vì
( )
( )
( )
3
2
3
2
lim 3 8 1
lim 3 0
3 0, 3
x
x
x
x
xx
+
+
→
→
+
−=
−=
− →
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
102
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
22. Ta có
3
2
2
25 3
lim
2
x
x
xx
→
+−
−−
( )( )
(
)
2
2
33
25 27
lim
2 1 25 3 25 9
x
x
x x x x
→
+−
=
− + + + + +
( )
(
)
2
2
33
11
lim
81
1 25 3 25 9
x
x x x
→
==
+ + + + +
.
23.
2
2
32
lim
4 16
x
x
x
+
→
+
= +
−
, vì
( )
2
2
2
2
lim 3 2 8
lim 4 16 0
4 16 0, 2
x
x
x
x
xx
+
+
→
→
+
+=
−=
− →
.
24.
0
lim
x
xx
xx
+
→
+
−
( )
( )
00
1
1
lim lim 1
1
1
xx
xx
x
x
xx
++
→→
+
+
= = = −
−
−
.
25.
2
2
4
lim
2
x
x
x
+
→
−
−
( )( )
( )
22
22
lim lim 2 2 0
2
xx
xx
xx
x
++
→→
−+
= = − + =
−
.
26.
0
2
lim
x
xx
xx
+
→
+
−
=
( )
( )
00
2
2
lim lim 2
1
1
xx
xx
x
x
xx
++
→→
+
+
= = −
−
−
.
27. Ta có
( )
( )( )
1
21
lim
11
x
xx
xx
+
→−
++
+ − −
( )
( )
( )
11
2 1 2
lim lim 1
11
1 1 1
xx
x x x
x
xx
++
→ − → −
+ + +
= = =
−+
+ − +
.
28. Ta có
( )
2
2
6 9 3 3x x x x− + = − = −
, do
3x
−
→
nên
2
6 9 3x x x− + = −
, suy ra
2
2
3
69
lim
9
x
xx
x
−
→
−+
−
( )( )
2
2
3 3 3
6 9 3 1 1
lim lim lim
9 3 3 3 6
x x x
x x x
x x x x
− − −
→ → →
− + − −
= = = = −
− − + +
.
29. Do
1x
−
→
nên
10x−
, từ đó ta có
2
2
1
43
lim
65
x
xx
xx
−
→
−+
− + −
( )( )
( )( )
1
13
lim
15
x
xx
xx
−
→
−−
=
− − −
( )( )
1
13
lim
15
x
xx
xx
−
→
−−
=
− − −
( )
1
3
lim
15
x
x
xx
−
→
−
=
−−
1
13
lim .
5
1
x
x
x
x
−
→

−
= = −


−
−

.
vì
1
32
lim
54
x
x
x
−
→
−
=−
−
và
1
1
lim
1
x
x
−
→

= +

−

.
30.
( )
2
54
1
32
lim
x
xx
xx
+
→−
++
+
( )
( )( )
2
1
12
lim
1
x
xx
xx
+
→−
++
=
+
( )
( )
2
1
12
lim 0
x
xx
x
+
→−
++
==
.
31.
( )
2
2
lim 2
4
x
x
x
x
+
→
−
−
( )
( )( )
( )
22
2
lim 2 lim 0
2 2 2
xx
xx
x
x
x x x
++
→→
−
= − = =
− + +
.
32. Ta có
( )
( )
3
2
1
lim 1
1
x
x
x
x
+
→−
+
−
( )
( )
( )
( )( )
2
1
lim 1 1
11
x
x
x x x
xx
+
→−
= + − +
−+
( )
( )
( )
2
1
1
lim 1 0
1
x
xx
xx
x
+
→−
+
= − + =
−
.
33. Do
1x
+
→
nên
10x−
, vì thế ta có
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
103
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
2
1
5
lim 1
23
x
x
x
xx
+
→
+
−
+−
( )( )
( )( )
2
1
51
lim
13
x
xx
xx
+
→

+−

=

−+

( )( )
1
51
lim 0
3
x
xx
x
+
→

+−

==

+

.
34.
( )
11
11
lim lim
2 1 1
1 2 1
xx
x x x x
xx
xx
−−
→→
−−
=
− + −
− + −
1
1
lim
2
21
x
x
x
−
→
==
+−
.
35.
0
1
lim 2
x
x
x
x
+
→

−



( )
2
0
1
lim 2
x
xx
x
+
→

−

=


( )
0
lim 2 1 0
x
xx
+
→
= − =
.
36.
( )
( )
2
2
3
2 5 3
lim
3
x
xx
x
+
→−
+−
+
( )
( )( )
( )
( )
2
33
2 1 3
21
lim lim
3
3
xx
xx
x
x
x
++
→ − → −
−+
−
= = = −
+
+
.
37.
2
2
11
lim
24
x
xx
−
→

−

−−

( )( )
2
21
lim
22
x
x
xx
−
→

+−
=


−+

2
11
lim .
22
x
x
xx
−
→
+

= = −

+−

.
38. Do
1x
−
→
nên
10x−
, suy ra
( )
2
1 1 1x x x− = − = −
nên ta có
3
2
1
32
lim
54
x
xx
xx
−
→
−+
−+
( )( )
( )( )
2
1
21
lim
14
x
xx
xx
−
→
+−
=
−+
( )
( )( )
1
12
lim
14
x
xx
xx
−
→
−+
=
−+
1
23
lim
45
x
x
x
−
→
−+
= = −
+
.
Bài 8. Tính các giới hạn sau:
1)
0
sin5
lim
x
x
x
→
. ĐS:
5
2)
0
tan2
lim
3
x
x
x
→
. ĐS:
2
3
3)
2
0
1 cos
lim
x
x
x
→
−
. ĐS:
1
2
4)
3
0
sin5 .sin3 .sin
lim
45
x
x x x
x
→
. ĐS:
1
3
5)
0
1 cos5
lim
1 cos3
x
x
x
→
−
−
6)
2
0
1 cos 2
lim
.sin
x
x
xx
→
−
. ĐS:
7)
( )
0
sin
lim 0
1 cos
x
x ax
a
ax
→
−
. ĐS:
2
a
8)
0
1 cos
lim
1 cos
x
ax
bx
→
−
−
. ĐS:
2
2
a
b
9)
( )
2
0
1 cos
lim ; 0
x
x
a
x
→
−
ĐS:
2
2
a
10)
3
0
sin tan
lim
x
xx
x
→
−
ĐS:
1
2
−
11)
3
0
tan sin
lim .
sin
x
xx
x
→
−
ĐS:
1
2
12)
sin sin
lim .
xa
xa
xa
→
−
−
ĐS:
cosa
13)
cos cos
lim
xb
xb
xb
→
−
−
ĐS:
sinb−
14)
0
1 2 1
lim
sin 2
x
x
x
→
−+
ĐS:
1
2
−
15)
( ) ( )
0
cos cos
lim
x
a x a x
x
→
+ − −
ĐS:
2sina−
16)
tan tan
lim
xc
xc
xc
→
−
−
ĐS:
2
1
cos c
17)
3
0
1 cos
lim
sin
x
x
xx
→
−
ĐS:
3
2
18)
22
22
sin sin
lim
xa
xa
xa
→
−
−
ĐS:
sin2
2
a
a
19)
2
0
cos cos
lim
x
xx
x

→
−
ĐS:
22
2

−
20)
( )
3
2
8
lim
tan 2
x
x
x
→−
+
+
ĐS:12
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
104
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
21)
0
1 cos cos2 cos3
lim .
1 cos
x
x x x
x
→
−
−
ĐS:1422)
( ) ( )
2
0
sin 2 2sin sin
lim .
x
a x a x a
x
→
+ − + +
ĐS:
( )
sin
−
23)
0
sin tan
lim ;( 0)
()
x
ax bx
ab
a b x
→
+
+
+
ĐS: 1 24)
2
0
cos3 cos5 cos7
lim
x
x x x
x
→
−
ĐS:
33
2
−
25)
0
cos cos cos
lim .
1 cos
x
ax bx cx
x
→
−
−
ĐS:
2 2 2
2
bac−−
26)
( ) ( )
0
sin sin
lim
tan( ) tan( )
x
a x a x
a x a x
→
+ − −
+ − −
ĐS:
3
cos a
27)
3
2
0
2 1 1
lim .
sin
x
xx
x
→
+ − +
ĐS: 1 28)
2
4
0
sin 2 sin sin4
lim
x
x x x
x
→
−
ĐS: 6
29)
2
cos
lim .
2
x
x
x
→−
+
ĐS: 1 30)
0
2
sin sin2
lim
1 sin
2
x
xx
x
x
→
−

−


ĐS: -1
31)
2
2
0
1 cos
lim .
x
xx
x
→
+−
ĐS: 1 32)
3
0
1 tan 1 sin
lim
x
xx
x
→
+ − +
ĐS:
1
4
33)
2
0
1 cos5 cos7
lim .
sin 11
x
xx
x
→
−
ĐS:
37
121
34)
1
32
lim
tan( 1)
x
x
x
→
+−
−
ĐS:
1
4
35)
( )
2
1 cos
lim .
x
x
x
→
+
−
ĐS:
1
2
36)
2
1
sin( 1)
lim
43
x
x
xx
→
−
−+
ĐS:
1
2
−
37)
2
2
0
1 cos2
lim .
x
xx
x
→
+−
ĐS:
5
2
38)
2
0
1 cos cos2
lim
x
xx
x
→
−
ĐS:
3
2
Lời giải.
1)
00
sin5 sin5
lim lim 5 5
5
xx
xx
xx
→→

= =


.
2)
00
tan2 2 tan2 2
lim lim .
3 3 2 3
xx
xx
xx
→→

= =


3)
2
2
22
0 0 0
2sin
sin
1 cos 1 1
2
2
lim lim lim 2
42
2
x x x
x
x
x
x
xx
→ → →








−



= = =









.
4)
3
00
sin5 sin3 sin 1 sin5 sin3 sin 1
lim lim
45 3 5 3 3
xx
x x x x x x
x x x x
→→

= =


.
5)
22
2
0 0 0
2
5 5 3
2sin sin
1 cos5 25 4 25
2 2 2
lim lim lim
3 5 3
1 cos3 4 9 9
2sin sin
2 2 2
x x x
x x x
x
x x x
x
→ → →


−

= = =
−



.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
105
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
6)
2 2 2
2
0 0 0 0
1 cos 2 sin 2 4sin cos sin
lim lim lim lim 4cos 4
sin sin
x x x x
x x x x x
x
x x x x x x
→ → → →
−

= = = =


.
7)
2
2
0 0 0
2
sin sin 1 sin 4 2
2
lim lim lim
1 cos 2
2sin sin
22
x x x
ax
x ax x ax ax
a
ax ax
ax ax a a
→ → →





= = =

−





.
8)
22
2
22
22
0 0 0
2
2sin sin
1 cos 4
2 2 2
lim lim lim
1 cos 4
2sin sin
2 2 2
x x x
ax ax bx
ax a a
bx ax bx
bx b b
→ → →


−

= = =
−



.
9)
2
2
22
22
0 0 0
2sin sin
1 cos
22
lim lim lim 2
42
2
x x x
ax ax
ax a a
ax
xx
→ → →




−

= = =






.
10) Ta có
( )
33
00
sin cos 1
sin tan
lim lim
cos
xx
xx
xx
x x x
→→
−
−
=
2
2
3
00
2sin sin sin
2 sin 1 1
22
lim lim .
cos cos 4 2
2
xx
xx
x
x
x
x x x x
→→


−



= = − = −






11)
( )
( )
( )
3
2
0 0 0
sin 1 cos
tan sin 1 1
lim lim lim .
sin cos 1 cos 2
cos sin 1 cos
x x x
xx
xx
x x x
x x x
→ → →

−
−
= = =


+
−

12) Ta có
2cos sin
sin sin
22
lim lim
xa
xa
x a x a
xa
x a x a
→
→
+−
−
=
−−
sin
2
lim cos cos .
2
2
xa
xa
xa
a
xa
→
−


+
= =

−


13) Ta có
2sin sin
cos cos
22
lim lim
x b x b
x b x b
xb
x b x b
→→
+−
−
−
=
−−
sin
2
lim sin sin .
2
2
xb
xb
xb
b
xb
→
−


+
= − = −

−


14) Ta có
( )
00
1 2 1 1 2 1
lim lim
sin 2
sin 2 1 2 1
xx
xx
x
xx
→→
− + − −
=
++
0
1 2 1
lim .
sin 2 2
1 2 1
x
x
x
x
→

= − = −

++

15) Ta có
00
2sin sin
cos( ) cos( )
22
lim lim
xx
a x a x a x a x
a x a x
xx
→→
+ + − + − +
−
+ − −
=
0
sin
lim 2sin 2sin .
x
x
aa
x
→

= − = −


ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
106
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
16)
( )
( )
( )
2
sin sin
tan tan 1 1
lim lim lim
cos cos cos cos cos .
x c x c x c
x c x c
xc
x c x c x c x c x c c
→ → →
−−

−
= = =

− − −

17) Ta có
( )
( )
2
3
00
1 cos 1 cos cos
1 cos
lim lim
sin sin
xx
x x x
x
x x x x
→→
− + +
−
=
( )
22
2
00
2sin 1 cos cos sin
1 cos cos 1 3
22
lim lim .
22
2 sin cos cos
2 2 2 2
xx
xx
xx
xx
x x x x
x
→→

++

++
= = =



18) Ta có
( )( )
22
22
1 cos2 1 cos2
sin sin
22
lim lim
x a x a
xa
xa
x a x a x a
→→
−−
−
−
=
− − +
( ) ( )
2sin sin
cos2 cos2
lim lim
2( )( ) 2( )( )
x a x a
a x a x
ax
x a x a x a x a
→→
− + −
−
==
− + − +
sin( ) sin( ) sin2
lim .
2
xa
a x a x a
x a a x a
→
+−

= =

+−

19) Ta có
( ) ( )
22
00
2sin sin
cos cos
22
lim lim
xx
xx
xx
xx

→→
+−
−
−
=
( )
( )
( )
( )
22
0
sin sin
22
lim 2 .
2 2 2
22
x
xx
xx
→
+−


+ − −
= − =

+−



20) Ta có
( )
( )
( )
( )
( )
2
3
2
2 2 2
2 2 4
2
8
lim lim lim 2 4 12.
tan 2 tan( 2) tan( 2)
x x x
x x x
x
x
xx
x x x
→− →− →−
+ − +
+

+
= = − + =

+ + +

21) Ta có
00
1 cos cos2 cos3 1 cos cos (1 cos2 ) cos cos2 (1 cos3 )
lim lim
1 cos 1 cos
xx
x x x x x x x x x
xx
→→
− − + − + −
=
−−
2
2
0
22
3
2sin
2sin
2
lim 1 cos cos cos2
2sin 2sin
22
x
x
x
x x x
xx
→


= + +



2 2 2
2
0
3
sin
sin
2 2 2
lim 1 4cos 9cos cos2 1 4 9 14.
3
sin sin sin
2 2 2
x
x x x
x
x x x
x x x
x
→




= + + = + + =





22) Ta có
( ) ( ) ( )
22
00
sin 2 2sin( ) sin 2sin cos 2sin
lim lim
xx
a x a x a a x x a x
xx
→→
+ − + + + − +
=
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
107
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
2
22
00
4sin sin
2sin( )(cos 1)
2
lim lim
xx
x
ax
a x x
xx
→→
−+
+−
==
( )
2
0
sin
1
2
lim 4sin sin .
4
2
x
x
a x a
x
→





= − + = −






23) Ta có
0 0 0
sin tan sin tan
sin tan
lim lim lim 1.
( ) ( )
x x x
ax bx ax bx
ax bx a b
ax bx a b
ax bx ax bx
a b x a b x a b a b
→ → →
+
++
= = = =
+ + + +
24) Ta có
22
00
cos3 cos5 cos7 cos3 cos5 cos5 cos5 cos7
lim lim
xx
x x x x x x x x
xx
→→
− − + −
=
2
22
00
7
2sin 4 sin 2cos5 sin
2sin 4 sin cos5 (1 cos7 )
2
lim lim
xx
x
x x x
x x x x
xx
→→
−
+−
==
2
0
7
sin
sin 4 sin 49 49 33
2
lim 8 2 cos5 8 .
7
4 4 2 2
2
x
x
xx
x
x
xx
→





= − = − = −






25) Ta có
22
00
cos cos cos cos cos cos cos cos
lim lim
xx
ax bx cx ax bx bx bx cx
xx
→→
− − + −
=
( ) ( )
2
22
00
( ) ( )
2sin sin cos (1 cos ) 2sin sin 2cos sin
2 2 2 2 2
lim lim
xx
b a x b a x
a b x a b x cx
bx cx bx
xx
→→
−−
++
+ − −
==
( )
( )
2
2 2 2 2 2 2 2 2 2
0
()
sin sin sin
2 2 2
lim 2 2 cos .
()
4 4 2 2 2
22
2
x
b a x
a b x cx
b a c b a c b a c
bx
a b x cx
b a x
→

−
+



− − − −

= − = − =

+
−





26) Ta có
( ) ( )
( ) ( )
00
sin( ) sin( ) 2cos sin
lim lim
sin 2
tan tan
cos cos
xx
a x a x a x
x
a x a x
a x a x
→→
+ − −
=
+ − −
+−
( ) ( )
3
0
cos cos cos
lim cos
cos
x
a a x a x
a
x
→
+−
==
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
108
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
27) Ta có
33
22
00
2 1 1 2 1 1 1 1
lim lim
cos sin
xx
x x x x
xx
→→
+ − + + − + − +
=
(
)
2
2
33
22
0
2
2 1 1
1 1 1
lim
sin
x
xx
x
xx
x
→
−
+
++
+ + + +
=
(
)
2
33
22
0
2
2 1 1
1 1 1
lim 1.
sin
x
xx
x
xx
x
x
→
−
++
+ + + +
==
28) Ta có
( )
2
44
00
sin2 sin2 2sin cos2
sin 2 sin sin4
lim lim
xx
x x x x
x x x
xx
→→
−
−
=
( )
44
00
3
4sin 2 sin sin sin
2sin 2 sin cos cos2
22
lim lim
xx
xx
xx
x x x x
xx
→→
−
==
0
3
sin sin
3 sin 2 sin
22
lim 4 6.
3
22
22
x
xx
xx
xx
xx
→


= =



29)
22
sin
cos
2
lim lim 1
22
xx
x
x
xx


→− →−

+


==
++
.
30)
( )
0 0 0
2
sin 1 2cos
sin sin2 sin 1 2cos
lim lim lim 1
cos cos
1 2sin
2
x x x
xx
x x x x
x
x x x x
x
→ → →
−
−−

= = = −



−


.
31) Ta có
22
22
00
1 cos 1 1 1 cos
lim lim
xx
x x x x
xx
→→
+ − + − + −
=
2
22
0
1 1 1 cos
lim
x
xx
xx
→

+ − −
=+



(
)
2
2
2
0
22
2sin
11
2
lim
11
x
x
x
x
xx
→


+−
=+

++


2
2
0
sin
1 1 1 1
2
lim 1
22
1
2
2
1
x
x
x
x
→





= + = + =


++




.
32)
( )
3
3
00
1 tan 1 sin 1 tan 1 sin
lim lim
1 tan 1 sin
xx
x x x x
x
x x x
→→
+ − + + − −
=
+ + +
( )
( )
3
0
sin 1 cos
lim
cos 1 tan 1 sin
x
xx
x x x x
→
−
=
+ + +
( )
2
3
0
2sin sin
2
lim
cos 1 tan 1 sin
x
x
x
x x x x
→
=
+ + +
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
109
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
2
0
sin
2 sin 1 1
2
lim
44
cos 1 tan 1 sin
2
x
x
x
x
x
x x x
→





= =


+ + +




.
33)
( )
22
00
1 cos5 cos5 1 cos7
1 cos5 cos7
lim lim
sin 11 sin 11
xx
x x x
xx
xx
→→
− + −
−
=
22
22
0
57
2sin 2cos5 sin
22
lim
sin 11 sin 11
x
xx
x
xx
→


=+



22
22
0
57
sin sin
25 11 49 11
22
lim cos5
57
242 sin11 242 sin11
22
x
xx
xx
x
xx
xx
→



= +



25 49 37
242 242 121
= + =
.
34)
( )
( )
( )
11
3 2 3 4
lim lim
tan 1
tan 1 3 2
xx
xx
x
xx
→→
+ − + −
=
−
− + +
( )
1
1 1 1
lim
tan 1 4
32
x
x
x
x
→

−
= =


−
++

.
35)
( ) ( )
2
22
2cos
1 cos
2
lim lim
xx
x
x
xx


→→
+
=
−−
( )
2
2
2
2sin sin
11
22
lim lim
22
2
xx
xx
x
x


→→

− −




= = =

−

−





.
36)
( ) ( )
( )( )
( )
2
1 1 1
sin 1 sin 1 sin 1
11
lim lim lim .
4 3 1 3 1 3 2
x x x
x x x
x x x x x x
→ → →
− − −

= = = −

− + − − − −

.
37)
22
22
00
1 cos2 1 1 1 cos2
lim lim
xx
x x x x
xx
→→
+ − + − + −
=
(
)
2 2 2
2 2 2
00
22
1 1 1 cos2 1 1 2sin
lim lim
11
xx
x x x x
x x x
xx
→→


+ − − + −

= + = +



++



2
2
0
1 sin 1 5
lim 2 2
22
11
x
x
x
x
→


= + = + =




++

.
38)
( )
22
00
1 cos cos 1 cos2
1 cos cos2
lim lim
xx
x x x
xx
xx
→→
− + −
−
=
( )
( )
( )
2
2 2 2
2
00
2sin
cos 1 cos2
cos 1 cos2
1 cos
2
lim lim
1 cos2
xx
x
xx
xx
x
x x x
xx
→→


−

−
−

= + = +


+



ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
110
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
2
2
2
00
sin sin
1 1 sin 1 3
22
lim lim 1
2 2 2 2
1 cos2
1 cos2
xx
xx
x
x
x
xx
→→




= = = + =

+


+


Bài 9. Tính các giới hạn sau:
1)
0
cos3 cos
lim
cos5 cos
x
xx
xx
→
−
−
ĐS:
1
3
2)
2
6
1 2sin
lim
4cos 3
x
x
x
→
−
−
ĐS:
1
2
3)
2
1 sin 2 cos2
lim
cos
x
xx
x
→
++
ĐS: 24)
0
sin7 sin5
lim
sin
x
xx
x
→
−
ĐS: 2
5)
4
2 2cos
lim
sin
4
x
x
x
→
−

−


ĐS:
2
6)
3
0
1 cos
lim
sin
x
x
x
→
−
ĐS:
1
6
7)
3
3
sin cos
lim
sin3
x
xx
x
→
−
ĐS:
2
3
−
8)
4
lim tan2 .tan
4
x
xx
→


−




ĐS: 1
9)
3
cos3 2cos2 2
lim
sin3
x
xx
x
→
++
ĐS:
23
3
10)
3
2
3
tan 1
lim
2sin 1
x
x
x
→
−
−
ĐS:
1
12
−
Lời giải
1)
0 0 0 0
sin
cos3 cos 2sin 2 sin sin 1
lim lim lim lim
sin3
cos5 cos 2sin3 sin2 sin3 3
3
3
x x x x
x
x x x x x
x
x
x x x x x
x
→ → → →
−−
= = = =
−−
.
2)
22
6 6 6
1 2sin 1 2sin 1 1
lim lim lim
4cos 3 1 4sin 1 2sin 2
x x x
xx
x x x
→ → →
−−
= = =
− − +
.
3)
( )
2
2 2 2
1 sin2 cos2 2cos sin2
lim lim lim 2cos 2sin 2
cos cos
x x x
x x x x
xx
xx
→ → →
+ + +
= = + =
.
4)
0 0 0
sin7 sin5 2cos6 sin
lim lim lim2cos6 2
sin sin
x x x
x x x x
x
xx
→ → →
−
= = =
.
5)
4 4 4
2
2 cos
2 cos cos
2
2 2cos
4
lim lim lim
sin sin sin
4 4 4
x x x
x
x
x
x x x
→ → →


−

−

−
==
− − −
4
4sin sin
8 2 8 2
lim
2sin cos
2 8 2 8
x
xx
xx


→
− + −
=
−−
4
2sin
82
lim 2
cos
28
x
x
x
→

+


==

−


ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
111
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
6)
( )
2
3
2
00
3
3
22
1 cos cos
1 cos
lim lim
tan
sin 1 cos cos
xx
xx
x
x
x x x
→→
−
−
=

+ +


( )
2
0
3
3
2
cos 1
lim
6
1 cos 1 cos cos
x
x
x x x
→
==

+ + +


7)
( )
sin 3
3 3 3
3 3 3
2sin 3
3
sin 3
2sin
3
sin 3cos 2
3
lim lim lim lim
sin3 sin 3 3
sin 3
3
3
3
3
x x x
xx
x
x
x
xx
xx
x
x



→ → →
→ − − −






−







−
−



−

= = = = −
−+


−




−

−


.
8)
( )
2
2
4 4 4
2tan 1 tan 2tan
lim tan2 tan lim lim 1
4 1 tan 1 tan
1 tan
x x x
x x x
xx
xx
x
→ → →
−
− = = =



−+
+

.
9)
32
3
33
cos3 2cos2 2 4cos 3cos 4cos
lim lim
sin3 3sin 4sin
xx
x x x x x
x x x

→→
+ + − +
=
−
( )( )
( )( )
3
2cos 1 2cos 3 cos
lim
2sin 3 2sin 3 sin
x
x x x
x x x
→
−+
=
+−
( )
3
cos cos 2cos 3 cos
3
lim
3
x
x x x
→

−+


=
( )
( )
3
sin 2cos 3 cos
23
26
lim
3
cos 2sin 3 sin
26
x
x
xx
x
xx
→

− + +


==

++


10)
( )
( )
( )
2
3
2
2
2
33
44
tan 1 cos
tan 1
lim lim
2sin 1
1 tan . tan tan 1
xx
xx
x
x
x x x

→→
−
−
=
−

− + +


( )
( )
2
2
33
4
cos
lim
1 tan tan tan 1
x
x
x x x
→
−
=

+ + +


1
12
=−
.
Bài 10. Tính các giới hạn sau:
1)
0
cos4 1
lim
sin4
x
x
x
→
−
ĐS: 0 2)
0
1 sin2 cos2
lim
1 sin2 cos2
x
xx
xx
→
+−
−−
ĐS:
1−
3)
0
sin2
lim
1 sin2 cos2
x
x
xx
→
−−
ĐS:
1−
4)
0
1 cos
lim
sin
x
x
x
→
−
ĐS: 0
5)
0
sin5 sin3
lim
sin
x
xx
x
→
−
ĐS: 2 6)
0
11
lim
sin tan
x
xx
→

−


ĐS: 0
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
112
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
7)
2
4
2sin 1
lim
2cos 1
x
x
x
→
−
−
ĐS:
2
4
−
8)
6
sin
6
lim
1 2sin
x
x
x
→

−


−
ĐS:
23
3
9)
4
sin
4
lim
1 2 sin
x
x
x
→

−


−
ĐS:
2
10)
0
2
lim cot
sin 2
x
x
x
→

−


ĐS: 0
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
113
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
BÀI 3. HÀM SỐ LIÊN TỤC
A. TÓM TẮT LÝ THUYẾT
1. Hàm số liên tục tại 1 điểm
– Giả sử hàm số
( )
fx
xác định trên khoảng
( )
;ab
và
( )
0
;x a b
. Hàm số
( )
y f x=
gọi là liên
tục tại điểm
0
x
nếu
( ) ( )
0
0
lim
xx
f x f x
→
=
.
– Hàm số không liên tục tại điểm
0
x
gọi là gián đoạn tại
0
x
.
2. Hàm số liên tục trên một khoảng, đoạn
– Giả sử hàm số
( )
fx
liên tục trên khoảng
( )
;ab
. Ta nói rằng hàm số
( )
y f x=
liên tục trên
khoảng
( )
;ab
nếu nó liên tục tại mọi điểm của khoảng đó.
– Hàm số
( )
y f x=
gọi là liên tục trên đoạn
;ab
nếu nó liên tục trên khoảng
( )
;ab
và
( ) ( ) ( ) ( )
lim , lim
x a x b
f x f a f x f b
+−
→→
==
.
Nhận xét:
– Nếu hai hàm
( )
fx
và
( )
gx
liên tục tại điểm
0
x
thì các hàm số
( ) ( )
f x g x
,
( ) ( )
.f x g x
,
( )
.c f x
(với
c
là hằng số) đều liên tục tại điểm
0
x
.
– Hàm số đa thức liên tục trên . Hàm số phân thức và lượng giác liên tục trên từng khoảng
xác định của chúng.
3. Tính chất của hàm số liên tục
– Định lý về giá trị trung gian: Giả sử hàm số
f
liên tục trên đoạn
;ab
. Nếu
( ) ( )
f a f b
thì với
mỗi số thực
M
nằm giữa
( ) ( )
,f a f b
tồn tại ít nhất một điểm
( )
;c a b
thoả mãn
( )
f c M=
.
– Ý nghĩa hình học: Nếu hàm số
f
liên tục trên đoạn
;ab
và
M
là một số thực nằm giữa
( ) ( )
,f a f b
th đường thẳng
yM=
cắt đồ thị hàm số
( )
y f x=
tại ít nhất một điểm có hoành độ
( )
;c a b
.
– Hệ quả: Nếu hàm số
f
liên tục trên đoạn
;ab
và
( ) ( )
.0f a f b
thì tồn tại ít nhất một điểm
( )
;c a b
sao cho
( )
0fc=
. Ta thường vận dụng theo hai hướng sai:
+ Vận dụng chứng minh phương trình c nghiệm: “Nếu hàm số
( )
y f x=
liên tục trên đoạn
;ab
và
( ) ( )
.0f a f b
th phương trnh
( )
0fx=
có ít nhất một nghiệm trong khoảng
( )
;ab
”.
+ Vận dụng trong tương giao đồ thị: “Nếu hàm số
( )
y f x=
liên tục trên đoạn
;ab
và
( ) ( )
.0f a f b
th đồ thị của hàm số
( )
y f x=
cắt trục hoành ít nhất tại một điểm có hoành độ
( )
;c a b
”.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
114
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
B. DẠNG TOÁN VÀ BÀI TẬP
_DẠNG 1. XÉT TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM
Phương pháp giải:
Hàm số liên tục tại điểm
0
xx=
khi
( ) ( )
0
0
lim
xx
f x f x
→
=
hoặc
( ) ( ) ( )
00
0
lim lim
x x x x
f x f x f x
−+
→→
==
VÍ DỤ
Ví dụ 1. Xét tính liên tục của hàm số
2
32
2
()
2
4 7 2
xx
khi x
fx
x
x khi x
−+
=
−
−=
tại điểm
0
2x =
.
ĐS: Liên tục
Lời giải
Ta có
0
( ) (2) 4.2 7 1f x f= = − =
2
2 2 2
3 2 ( 2)( 1)
lim ( ) lim lim 1
22
x x x
x x x x
fx
xx
→ → →
− + − −
= = =
−−
Suy ra
2
(2) lim ( )
x
f f x
→
=
nên hàm số
()fx
liên tục tại điểm
0
2.x =
Ví dụ 2. Xét tính liên tục của hàm số
32
1
1
()
1
1
3
x
khi x
x
fx
khi x
+−
−
=
=
tại điểm
0
1x =
.
ĐS: Không liên tục
Lời giải
Ta có
0
1
( ) (1) .
3
f x f==
1 1 1 1
3 2 1 1 1
lim ( ) lim lim lim
14
( 1)( 3 2) 3 2
x x x x
xx
fx
x
x x x
→ → → →
+ − −
= = = =
−
− + + + +
Suy ra
1
(1) lim ( )
x
f f x
→
nên hàm số
()fx
không liên tục tại điểm
0
1x =
(hay gián đoạn tại
điểm
0
1x =
).
Ví dụ 3. Xét tính liên tục của hàm số
2
3 3 2
()
1 2 3
2
2
x x khi x
fx
x
khi x
x
− +
=
−−
−
tại điểm
0
2x =
ĐS: Liên tục
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
115
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Lời giải
Ta có
2
0
( ) (2) 2 3.2 3 1f x f= = − + =
2
22
2 2 2 2
lim ( ) lim( 3 3) 1
1 2 3 1 2 3 2
lim ( ) lim lim lim 1
2
(2 )(1 2 3) 1 2 3
xx
x x x x
f x x x
xx
fx
x
x x x
−−
+ + + +
→→
→ → → →
= − + =
− − − +
= = = =
−
− + − + −
Suy ra
22
(2) lim ( ) lim ( )
xx
f f x f x
−+
→→
==
nên hàm số
()fx
liên tục tại điểm
0
2x =
.
Ví dụ 4. Xét tính liên tục của hàm số
2
9
3
()
12
2 12 3
x
khi x
fx
x
x khi x
−
=
+−
+
tại điểm
0
3x =
.
ĐS: Không liên tục
Lời giải
Ta có
0
( ) (3) 18f x f==
33
lim ( ) lim(2 12) 18
xx
f x x
−−
→→
= + =
2
3 3 3
9 ( 3)( 3)( 1 2)
lim ( ) lim lim
3
12
x x x
x x x x
fx
x
x
+ + +
→ → →
− − + + +
==
−
+−
3
lim( 3)( 1 2) 24
x
xx
+
→
= + + + =
Suy ra
33
(3) lim ( ) lim ( )
xx
f f x f x
−+
→→
=
nên hàm số
()fx
không liên tục tại điểm
0
3x =
.
Ví dụ 5. Xét tính liên tục của hàm số
32
2
13
1
1
3
( ) 1
4
3 6 3 6
1
3 14 11
xx
khi x
x
f x khi x
x x x
khi x
xx
+ − +
−
==
− − +
−+
tại điểm
0
1x =
.
ĐS: Liên tục
Lời giải
Ta có
0
3
( ) (1)
4
f x f==
3 2 2 2
2
1 1 1 1
3 6 3 6 ( 1)(3 3 6) 3 3 6 3
lim ( ) lim lim lim
3 14 11 ( 1)(3 11) 3 11 4
x x x x
x x x x x x x x
fx
x x x x x
− − − −
→ → → →
− − + − − − − −
= = = =
− + − − −
2
1 1 1 1
1 3 ( 1) ( 3) 2 3
lim ( ) lim lim lim
14
( 1)( 1 3) 1 3
x x x x
x x x x x
fx
x
x x x x x
+ + + +
→ → → →
+ − + − − + +
= = = =
−
− + + + + + +
Suy ra
11
(1) lim ( ) lim ( )
xx
f f x f x
−+
→→
==
nên hàm số
()fx
liên tục tại điểm
0
1.x =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
116
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ví dụ 6. Xét tính liên tục của hàm số
42
2cos5 .cos3 cos8 1
0
()
20
x x x
khi x
fx
xx
khi x
−−
=
+
=
tại điểm
0
0x =
.
ĐS: Không liên tục
Lời giải
Ta có
0
( ) (0) 2f x f==
4 2 4 2
0 0 0
2cos5 .cos3 cos8 1 cos8 cos2 cos8 1
lim ( ) lim lim
x x x
x x x x x x
fx
x x x x
→ → →
− − + − −
==
++
2
2
4 2 2 2 2
0 0 0
cos2 1 2sin 2
lim lim lim . 2
( 1) 1
x x x
x x sinx
x x x x x x
→ → →

− − −

= = = = −


+ + +



Suy ra
0
(0) lim ( )
x
f f x
→
nên hàm số
()fx
không liên tục tại điểm
0
0x =
(hay gián đoạn tại
điểm
0
0x =
).
Ví dụ 7. Tìm
a
để hàm số
32
3
2 5 6
2
4
()
1
( ) 2
8
x x x
khi x
xx
fx
a x khi x
+ − −
−
=
+=
liên tục tại điểm
0
2.x =
ĐS:
13a =
Lời giải
Ta có
1
(2) ( 2)
8
fa=+
3 2 2 2
3
2 2 2 2
2 5 6 ( 2)( 4 3) 4 3 15
lim ( ) lim lim lim
4 ( 2)( 2) ( 2) 8
x x x x
x x x x x x x x
fx
x x x x x x x
→ → → →
+ − − − + + + +
= = = =
− − + +
Hàm số liên tục tại điểm
0
2
1 15
2 (2) lim ( ) (a 2) 13.
88
x
x f f x a
→
= = + = =
Ví dụ 8. Tìm
m
để hàm số
2
2( 4)
2
()
2
2 10 2
x
khi x
fx
xx
m m x khi x
−
=
+−
+ + −
liên tục tại điểm
0
2x =
.
ĐS:
2m =
Lời giải
Ta có
(2) 2 20f m m= + + −
2
2
2 2 2
3( 4) 3( 2)( 2)( 2 )
lim lim lim
2
2
x x x
x x x x x
xx
xx
+ + +
→ → →
− − + + +
==
+−
+−
22
3( 2)( 2)( 2 ) 3( 2)( 2 )
lim lim 16
( 1)( 2) ( 1)
xx
x x x x x x x
x x x
++
→→
− + + + + + +
= = = −
− + − − +
22
lim lim( 2 10 ) 2 20
xx
m m x m m
−−
→→
= + + − = + + −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
117
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Hàm số
()fx
liên tục tại điểm
0
22
2 lim ( ) lim ( ) (2) 2 20 16
xx
x f x f x f m m
+−
→→
= = = + + − = −
2
4
4
2 4 2
27
9 14 0
m
m
m m m
mm
mm
+ = − =

= =
− + =
BÀI TẬP ÁP DỤNG
Bài 1. Xét tính liên tục của các hàm số sau tại các điểm được chỉ ra:
1.
2
31
2
()
2
2 2 2
x
khi x
fx
x
x khi x
−−
=
−
−=
tại điểm
0
2x =
. Đs: Liên tục
2.
23
2
2 7 5
2
()
32
12
x x x
khi x
fx
xx
khi x
− + −
=
−+
=
tại điểm
0
2x =
. Đs: Liên tục
3.
2
2
32
1
()
1
21
xx
khi x
fx
x
x x khi x
++
−
=
−−
+ = −
tại điểm
0
1x =−
. Đs: Liên tục
Bài 2. Xét tính liên tục của các hàm số sau tại các điểm được chỉ ra:
1.
2
3 2 1
1
()
1
2 2 1
xx
khi x
fx
x
x khi x
−−
=
−
+
tại điểm
0
1x =
. Đs: Liên tục
2.
2
2
23
1
2
()
17
1
3
xx
khi x
xx
y f x
x
khi x
+−
+−
==
++
tại điểm
0
1x =
. Đs: Không liên tục
3.
3
34
4
()
53
4 46 4
xx
khi x
fx
x
x khi x
−−
=
+−
− +
tại điểm
0
4x =
. Đs: Liên tục
Bài 3. Tìm các giá trị thực của tham số
m
để hàm các hàm số sau liên tục tại các điểm được chỉ ra:
1.
32
2
5 7 3
1
()
1
2 1 1
x x x
khi x
fx
x
m khi x
− + −
=
−
+=
tại điểm
0
1x =
. Đs:
1
2
m =−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
118
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
2.
( )
11
0
4
5 0
2
xx
khi x
x
fx
x
m khi x
x
+ − −
=
−
− + =
+
liên tục tại điểm
0
0x =
. Đs:
1
5
m =
3.
( )
3
62
2
2
2 2
x
khi x
fx
x
x m khi x
+−
=
−
−=
liên tục tại điểm
0
2x =
. Đs:
47
12
m =
4.
( )
3
22
12 4 2
1
1
8 2 1
x
khi x
fx
x
m x mx khi x
−−
=
−
+ + =
liên tục tại điểm
0
1x =
. Đs:
1m =−
Bài 4. Tìm các giá trị thực của tham số
m
để hàm các hàm số sau liên tục tại các điểm được chỉ ra:
1.
3
2
8
2
()
26
10 2
x
khi x
fx
xx
mx khi x
−
=
−−
+
tại điểm
0
2x =
. Đs:
29
7
m =−
2.
( )
2
2 1 1
1
23
1
x
khi x
fx
xx
x m khi x
−−
=
+−
+
liên tục tại điểm
0
1x =
. Đs:
3
4
m =−
3.
m
để
( )
2
2 7 6
2
2
1
2
2
xx
khi x
x
fx
x
m khi x
x
−+
−
=
−
+
+
liên tục tại điểm
0
2x =
. Đs:
3
4
m =−
4.
( )
2
2
2
3 3 1 5 4
1
21
1
3 1
3
x x x
khi x
xx
fx
m x m khi x
− + − +
−+
=
+ −
liên tục tại điểm
0
1x =
. Đs:
1m =
hoặc
2m =
5.
( )
2
7 3 4
3
21
3
2 3
2
x
khi x
x
fx
m mx khi x
−−
−
−−
=
− − −
liên tục tại điểm
0
3x =−
. Đs:
0m =
hoặc
6m =
6.
( )
( )
2
3
3
5 16
1 3
3
x
khi x
x
fx
m
x m khi x
−
−+
=
+ +
liên tục tại điểm
0
3x =
. Đs:
5m =−
hoặc
1m =
7.
( )
( )
2
34
2
2
2 10 2
x
khi x
fx
xx
m m x khi x
−
=
+−
+ + −
liên tục tại điểm
0
2x =
. Đs:
2m =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
119
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
LỜI GIẢI
Bài 1. 1. Xét tính liên tục của hàm số
2
31
2
()
2
2 2 2
x
khi x
fx
x
x khi x
−−
=
−
−=
tại điểm
0
2x =
.
Ta có
0
( ) (2) 2f x f==
22
22
2 2 2 2
3 1 4 2
lim ( ) lim lim lim 2
2
( 2)( 3 1) 3 1
x x x x
x x x
fx
x
x x x
→ → → →
− − − +
= = = =
−
− − + − +
Suy ra
2
(2) lim ( )
x
f f x
→
=
nên hàm số
()fx
liên tục tại điểm
0
2.x =
2. Xét tinh liên tục của hàm số
23
2
2 7 5
2
()
32
12
x x x
khi x
fx
xx
khi x
− + −
=
−+
=
tại điểm
0
2x =
.
Ta có
0
( ) (2) 1f x f==
2 3 2 2
2
2 2 2 2
2 7 5 ( 2)( 3 1) 3 1
lim ( ) lim lim lim 1
3 2 ( 2)( 1) 1
x x x x
x x x x x x x x
fx
x x x x x
→ → → →
− + − − − + − − + −
= = = =
− + − − −
Suy ra
2
(2) lim ( )
x
f f x
→
=
nên hàm số
()fx
liên tục tại điểm
0
2x =
.
3. Xét tinh liên tục của hàm số
2
2
32
1
()
1
21
xx
khi x
fx
x
x x khi x
++
−
=
−−
+ = −
tại điểm
0
1x =−
.
Ta có
0
( ) ( 1) 1f x f= − = −
2
1 1 1 1
3 2 ( 1)( 2) 2
lim ( ) lim lim lim 1
1 ( 1) 1
x x x x
x x x x x
fx
xx
→− →− →− →−
+ + + + +
= = = = −
− − − + −
Suy ra
1
( 1) lim ( )
x
f f x
→−
−=
nên hàm số
()fx
liên tục tại điểm
0
1x =−
.
Bài 2. 1. Xét tính liên tục của hàm số
3
34
4
()
53
4 46 4
xx
khi x
fx
x
x khi x
−−
=
+−
− +
tại điểm
0
4x =
.
Ta có
0
( ) (4) 30f x f==
44
2
4 4 4 4
lim ( ) lim( 4 46) 30
3 4 ( 4)( 1)( 5 3)
lim ( ) lim lim lim( 1)( 5 3) 30
4
53
xx
x x x x
f x x
x x x x x
f x x x
x
x
−−
+ + + +
→→
→ → → →
= − + =
− − − + + +
= = = + + + =
−
+−
Suy ra
44
(4) lim ( ) lim ( )
xx
f f x f x
−+
→→
==
nên hàm số
()fx
liên tục tại điểm
0
4x =
.
2. Xét tính liên tục của hàm số
2
3 2 1
1
()
1
2 2 1
xx
khi x
fx
x
x khi x
−−
=
−
+
tại điểm
0
1x =
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
120
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta có
0
( ) (1) 4f x f==
11
lim ( ) lim(2 2) 4
xx
f x x
++
→→
= + =
2
1 1 1 1
3 2 1 ( 1)(3 1)
lim ( ) lim lim lim(3 1) 4
11
x x x x
x x x x
f x x
xx
− − − −
→ → → →
− − − +
= = = + =
−−
Suy ra
11
(1) lim ( ) lim ( )
xx
f f x f x
+−
→→
==
nên hàm số
()fx
liên tục tại điểm
0
1x =
.
3. Xét tính liên tục của hàm số
2
2
23
1
2
()
17
1
3
xx
khi x
xx
y f x
x
khi x
+−
+−
==
++
tại điểm
0
1x =
.
Ta có
0
27
( ) (1)
3
f x f
+
==
11
2
2
1 1 1 1
1 7 2 7
lim ( ) lim
33
2 3 ( 1)( 3) 3 4
lim ( ) lim lim lim
2 ( 1)( 2) 2 3
xx
x x x x
x
fx
x x x x x
fx
x x x x x
−−
+ + + +
→→
→ → → →
+ + +
==
+ − − + +
= = = =
+ − − + +
Suy ra
11
(1) lim ( ) lim ( )
xx
f f x f x
−+
→→
=
nên hàm số
()fx
không liên tục tại điểm
0
1x =
.
4. Xét tính liên tục của hàm số
3
34
4
()
53
4 46 4
xx
khi x
fx
x
x khi x
−−
=
+−
− +
tại điểm
0
4x =
.
Ta có
0
( ) (4) 30f x f==
44
2
4 4 4 4
lim ( ) lim( 4 46) 30
3 4 ( 4)( 1)( 5 3)
lim ( ) lim lim lim( 1)( 5 3) 30
4
53
xx
x x x x
f x x
x x x x x
f x x x
x
x
−−
+ + + +
→→
→ → → →
= − + =
− − − + + +
= = = + + + =
−
+−
Suy ra
44
(4) lim ( ) lim ( )
xx
f f x f x
−+
→→
==
nên hàm số
()fx
liên tục tại điểm
0
4x =
.
Bài 3. 1. Tìm
m
để hàm số
32
2
5 7 3
1
()
1
2 1 1
x x x
khi x
fx
x
m khi x
− + −
=
−
+=
tại điểm
0
1x =
.
Ta có
0
( ) (1) 2 1f x f m= = +
3 2 2
2
1 1 1 1
5 7 3 ( 1) (x 3) ( 1)( 3)
lim ( ) lim lim lim 0
1 ( 1)(x 1) 1
x x x x
x x x x x x
fx
x x x
→ → → →
− + − − − − +
= = = =
− − + +
Hàm số
()fx
liên tục tại điểm
0
1
1
1 lim ( ) (1) 2 1 0
2
x
x f x f m m
→
= = + = = −
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
121
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
2. Tìm
m
để hàm số
( )
11
khi 0
4
5 khi 0
2
xx
x
x
fx
x
mx
x
+ − −
=
−
− + =
+
liên tục tại điểm
0
0x =
.
Ta có:
( )
0 5 2fm= − +
( )
( )
0 0 0 0
1 1 2 2
lim lim lim lim 1
11
11
x x x x
x x x
fx
x
xx
x x x
→ → → →
+ − −
= = = =
+ + −
+ + −
Hàm số liên tục tại điểm
0
0x =
khi và chỉ khi
( ) ( )
0
1
lim 0 5 2 1
5
x
f x f m m
→
= − + = =
Vậy
1
5
m =
.
3. Tìm
m
để hàm số
( )
3
62
khi 2
2
2 khi 2
x
x
fx
x
x m x
+−
=
−
−=
liên tục tại điểm
0
2x =
.
Ta có
( )
24fm=−
( )
( ) ( )
( )
( )
3
2
2 2 2 2
2
3
3
3
3
6 2 2 1 1
lim lim lim lim
2 12
6 2 6 4
2 6 2 6 4
x x x x
xx
fx
x
xx
x x x
→ → → →
+ − −
= = = =
−
+ + + +
− + + + +
Hàm số liên tục tại điểm
0
2x =
khi và chỉ khi
( ) ( )
2
1 47
lim 2 4
12 12
x
f x f m m
→
= − = =
Vậy
47
12
m =
.
4. Tìm
m
để
( )
3
22
12 4 2
khi 1
1
8 2 khi 1
x
x
fx
x
m x mx x
−−
=
−
+ + =
liên tục tại điểm
0
1x =
.
Ta có
( )
2
1 8 2f m m= + +
( )
( )
( ) ( )
( )
3
1 1 1
2
3
3
12 1
12 4 2
lim lim lim
1
1 12 4 2 12 4 4
x x x
x
x
fx
x
x x x
→ → →
−
−−
==
−
− − + − +
( )
2
1
3
3
12
lim 1
12 4 2 12 4 4
x
xx
→
==
− + − +
Hàm số liên tục tại điểm
0
1x =
khi và chỉ khi
( ) ( )
2
1
lim 1 8 2 1
x
f x f m m
→
= + + =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
122
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
2
2
2
1
1
2
1 2 0
1
1
2
8 1 2
3 4 7 0
7
3
m
m
m
m
m
mm
mm
m
−


= −
=−
+ = −

− + + =
=
Vậy
1m =−
.
Bài 4. 1. Tìm
m
để hàm số
3
2
8
2
()
26
10 2
x
khi x
fx
xx
mx khi x
−
=
−−
+
tại điểm
0
2x =
.
Ta có
0
( ) (2) 2 10f x f m= = +
22
3 2 2
2
2 2 2 2
lim ( ) lim(m 10) 2 10
8 ( 2)(x 2 4) 2 4 12
lim ( ) lim lim lim
2 6 ( 2)(2x 3) 2 3 7
xx
x x x x
f x x m
x x x x x
fx
x x x x
−−
+ + + +
→→
→ → → →
= + = +
− − + + + +
= = = =
− − − + +
Hàm số
()fx
liên tục tại điểm
0
22
12 29
2 lim ( ) lim ( ) (2) 2 10
77
xx
x f x f x f m m
+−
→→
= = = + = = −
2. Tìm
m
để
( )
2
2 1 1
khi 1
23
khi 1
x
x
fx
xx
x m x
−−
=
+−
+
liên tục tại điểm
0
1x =
.
Ta có
( )
11fm=+
( )
( )
( )( )
( )
( )
( )
2
1 1 1 1
21
2 1 1 2 1
lim lim lim lim
2 3 4
1 3 2 1 1 3 2 1 1
x x x x
x
x
fx
xx
x x x x x
+ + + +
→ → → →
−
−−
= = = =
+−
− + − + + − +
( ) ( )
11
lim lim 1
xx
f x x m m
−−
→→
= + = +
Hàm số liên tục tại điểm
0
1x =
khi và chỉ khi
( ) ( ) ( )
11
13
lim lim 1 1
44
xx
f x f x f m m
+−
→→
= = + = = −
Vậy
3
4
m =−
.
3. Tìm
m
để
( )
2
2 7 6
khi 2
2
1
khi 2
2
xx
x
x
fx
x
mx
x
−+
−
=
−
+
+
liên tục tại điểm
0
2x =
.
Ta có
( )
1
2
4
fm=−
( )
22
11
lim lim
24
xx
x
f x m m
x
++
→→
−

= + = −

+

ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
123
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
( )( )
( )( )
( )
2
2 2 2 2
2
2 7 6
2 2 3
2 2 3
lim lim lim lim
2 2 2
lim 2 3 1
x x x x
x
xx
xx
xx
fx
x x x
x
− − − −
−
→ → → →
→
−+
−−
− − −
= = =
− − −
= − + = −
Hàm số liên tục tại điểm
0
3x =−
khi và chỉ khi
( ) ( ) ( )
22
13
lim lim 2 1
44
xx
f x f x f m m
+−
→→
= = − = − = −
Vậy
3
4
m =−
.
4. Tìm
m
để
( )
2
2
2
3 3 1 5 4
1
21
1
3 1
3
x x x
khi x
xx
fx
m x m khi x
− + − +
−+
=
+ −
liên tục tại điểm
0
1x =
.
Ta có
( )
2
1
13
3
f m m= + −
( )
22
11
11
lim lim 3 3
33
xx
f x m x m m m
++
→→

= + − = + −


( )
( )
(
)
( )
2
2
2
2
1 1 1
1 3 5 4
3 3 1 5 4
lim lim lim
21
1
x x x
xx
x x x
fx
xx
x
− − −
→ → →
− − +
− + − +
==
−+
−
( )
(
)
( )
2
2
2
11
1 3 5 4
3 5 4
lim lim
1
1
xx
xx
x
x
x
−−
→→
− − +
−+
==
−
−
( )( )
( )
(
)
( )
2
2
11
5 1 1 5 1
5
lim lim
3
3 5 4
1 3 5 4
xx
x x x
x
xx
−−
→→
− − + − +
= = = −
++
− + +
Hàm số liên tục tại điểm
0
1x =
khi và chỉ khi
( ) ( ) ( )
22
11
1
15
lim lim 1 3 3 2 0
2
33
xx
m
f x f x f m m m m
m
+−
→→
=
= = + − = − − + =
=
Vậy
1m =
hoặc
2m =
.
5. Tìm
m
để
( )
2
7 3 4
3
21
3
2 3
2
x
khi x
x
fx
m mx khi x
−−
−
−−
=
− − −
liên tục tại điểm
0
3x =−
.
Ta có
( )
2
3
36
2
f m m− = + −
( )
22
33
33
lim lim 2 6
22
xx
f x m mx m m
−−
→− →−

= − − = + −


ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
124
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
( )
( )
( )
( )
( )
3 3 3 3
3 3 2 1 3 2 1
7 3 4 3
lim lim lim lim
2
2 1 7 3 4
3 7 3 4
x x x x
x x x
x
fx
xx
xx
+ + + +
→− →− →− →−
− + + − − + −
−−
= = = = −
− − − +
+ − +
Hàm số liên tục tại điểm
0
3x =−
khi và chỉ khi
( ) ( ) ( )
22
33
0
33
lim lim 3 6 6 0
6
22
xx
m
f x f x f m m m m
m
+−
→− →−
=
= = − + − = − + =
=−
Vậy
0m =
hoặc
6m =−
.
6. Tìm
m
để
( )
( )
2
3
3
5 16
1 3
3
x
khi x
x
fx
m
x m khi x
−
−+
=
+ +
liên tục tại điểm
0
3x =
.
Ta có
( ) ( )
34
3
m
fm=+
.
( ) ( ) ( )
33
lim lim 1 4
33
xx
mm
f x x m m
−−
→→
= + + = +
.
( )
( )
(
)
( )( )
2
2
2
3 3 3 3
3 5 16
3 5 16 5
lim lim lim lim
3 3 3 3
5 16
x x x x
xx
xx
fx
x x x
x
+ + + +
→ → → →
− + +
− + +
= = = =
− + +
−+
.
Hàm số liên tục tại điểm
0
3x =
khi và chỉ khi
( ) ( ) ( )
33
lim lim 3
xx
f x f x f
+−
→→
==
( )
2
1
5
4 4 5 0
5
33
m
m
m m m
m
=
+ = + − =
=−
Vậy
5m =−
hoặc
1m =
.
7. Tìm
m
để
( )
( )
2
34
2
2
2 10 2
x
khi x
fx
xx
m m x khi x
−
=
+−
+ + −
liên tục tại điểm
0
2x =
.
Ta có
( )
2 2 20f m m= + + −
.
( )
( )
22
lim lim 2 10 2 20
xx
f x m m x m m
−−
→→
= + + − = + + −
.
( )
( )
( )( )
( )
( )( )
2
2 2 2
3 2 2 2
34
lim lim lim
21
2
x x x
x x x x
x
fx
xx
xx
+ + +
→ → →
− + + +
−
==
− − +
+−
( )
( )
( )
2
3 2 2
lim 16
1
x
x x x
x
+
→
+ + +
= = −
−+
.
Hàm số liên tục tại điểm
0
2x =
khi và chỉ khi
( ) ( ) ( )
( )
2
22
40
lim lim 2 2 4
24
xx
m
f x f x f m m
mm
−+
→→
−
= = + = −
+ = −
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
125
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
2
4
4
2
2
9 14 0
7
m
m
m
m
mm
m
=
=

− + =
=
.
Vậy
2m =
.
BÀI TẬP RÈN LUYỆN
Bài 1. Xét tính liên tục của hàm số
( )
3
2
27
3
2 5 3
4
3
5
x
khi x
xx
fx
x
khi x
+
−
+−
=
+
=−
tại điểm
0
3x =−
. ĐS: K liên tục.
Bài 2. Xét tính liên tục của hàm số
( )
2
28
2
1 4 3
5 2 2
x
khi x
fx
x
x khi x
−+
−
=
−−
− −
tại điểm
0
2x =−
. ĐS: Liên tục.
Bài 3. Xét tính liên tục của hàm số
( )
2
9
3
12
2 12 3
x
khi x
fx
x
x khi x
−
=
+−
+
tại điểm
0
3x =
. ĐS: Không liên tục.
Bài 4. Xét tính liên tục của hàm số
( )
2
4
2
7 10
8
2
3
x
khi x
xx
fx
x
hi x
−
−−
=
−=
tại điểm
0
2x =
. ĐS: Liên tục.
Bài 5. Xét tính liên tục của hàm số
( )
( )
2
5 3 5
5
5
2 1 3
x khi x
fx
x
khi x
x
− +
=
−
−−
tại điểm
0
5x =
. ĐS: Liên tục.
Bài 6. Xét tính liên tục của hàm số
( )
2
2
12
3
3
5
3
1
xx
khi x
x
fx
x
khi x
x
+−
−
=
+
=
−
tại điểm
0
3x =
. ĐS: Liên tục.
Bài 7. Xét tính liên tục của hàm số
( )
4 5 5
5
5
2
5
25
x
khi x
x
fx
x
khi x
+−
−
=
tại điểm
0
5x =
. ĐS: Liên tục.
Bài 8. Xét tính liên tục của hàm số
( )
32
3 1 5
1
23
2 1 1
xx
khi x
fx
x x x
x khi x
+ − −
=
− + −
− +
tại điểm
0
1x =
. ĐS: Liên tục.
Bài 9. Xét tính liên tục của hàm số
( )
2
2 4 2
56
2
22
42
x x khi x
xx
f x khi x
x
khi x
− −
−+
=
+−
−=
tại điểm
0
2x =
. ĐS: Liên tục.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
126
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 10. Xét tính liên tục của hàm số
( )
2
32
1
83
1 6 1
xx
khi x
fx
x
x x khi x
−+
=
+−
− −
tại điểm
0
1x =
. ĐS: Liên tục.
Bài 11. Tìm
m
để hàm số
( )
( )
3
3
22
23
1
1
14
1
2
xx
khi x
x
fx
mx
khi x
x
+−
−
=
−+
+
liên tục tại điểm
0
1x =
. ĐS:
2m =
.
Bài 12. Tìm
m
để hàm số
( )
42
32
6 27
3
33
33
xx
khi x
fx
x x x
mx khi x
−−
−
=
+ + +
+ = −
liên tục tại điểm
0
3x =−
. ĐS:
10
3
m =
.
Bài 13. Tìm
m
để hàm số
( )
3
2
27
3
2 4 6
83
x
khi x
fx
xx
mx khi x
−
=
−−
+
liên tục tại điểm
0
3x =
. ĐS:
37
24
m =−
.
Bài 14. Tìm
m
để hàm số
( )
2
2
22
22
x
khi x
fx
x
x m khi x
−
=
+−
+=
liên tục tại điểm
0
2x =
. ĐS:
2m =
.
Bài 15. Tìm
m
để hàm số
( )
( )
2
2
2
2
25
5
45
55
x
khi x
xx
fx
x m khi x
−
−−
=
− +
liên tục tại điểm
0
5x =
. ĐS:
15
3
m =
.
_DẠNG 2. XÉT TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TXĐ
Phương pháp giải:
Hàm số liên tục tại điểm
0
xx=
khi
( ) ( )
0
0
lim
xx
f x f x
→
=
hoặc
( ) ( ) ( )
00
0
lim lim
x x x x
f x f x f x
−+
→→
==
VÍ DỤ
Ví dụ 1. Xét tính liên tục của hàm số
( )
3
3
23
1
1
7
1
3
xx
khi x
x
fx
khi x
++
−
+
=
=−
trên .
ĐS: Liên tục trên .
Lời giải
+ Tập xác định của hàm số là
D =
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
127
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
+ Xét
1x −
thì
( )
3
3
23
1
xx
fx
x
++
=
+
là hàm phân thức hữu tỉ nên liên tục trên các khoảng
( )
;1− −
và
( )
1;− +
mà nó xác định.
+ Xét tính liên tục của hàm số
( )
fx
tại
1x =−
Ta có
( )
( )
( )
( )
( )
2
32
32
2
1 1 1 1
1 2 2 3
2 3 2 2 3 7
lim lim lim lim
1 1 3
11
x x x x
x x x
x x x x
fx
x x x
x x x
→− →− →− →−
+ − +
+ + − +
= = = =
+ − +
+ − +
.
( )
7
1
3
f −=
.
Suy ra
( ) ( )
1
lim 1
x
f x f
→−
=−
nên hàm số đã cho liên tục tại
0
1x =−
.
+ Vậy hàm số đã cho liên tục trên .
Ví dụ 2. Xét tính liên tục của hàm số
( )
2
43
1
1
51
xx
khi x
fx
x
x khi x
−+
=
−
− −
trên .
ĐS: Liên tục trên .
Lời giải
+ Tập xác định của hàm số là
D =
.
+ Với mọi
( )
0
1;x +
,
( ) ( )
00
2
0
43
lim lim
1
x x x x
xx
f x f x
x
→→
−+
==
−
.
Suy ra hàm số đã cho liên tục trên
khoảng
( )
1;+
.
+ Với mọi
( )
0
;1x −
, ta có
( )
( )
( )
00
00
lim lim 5 5
x x x x
f x x x f x
→→
= − − = − − =
.
Suy ra hàm số đã
cho liên tục trên khoảng
( )
;1−
.
+ Xét tính liên tục của hàm số tại
1x =
( )
1 5 1 2f = − − =
.
-
( )
( )
11
lim lim 5 2
xx
f x x
−−
→→
= − − − = −
.
-
( )
( )( )
( )
1 1 1
13
lim lim lim 3 2
1
x x x
xx
f x x
x
+ + +
→ → →
−−
= = − = −
−
.
Suy ra
( ) ( ) ( )
11
lim lim 1
xx
f x f x f
−+
→→
==
nên hàm số đã cho liên tục tại
1x =
.
Vậy hàm số đã cho liên tục trên .
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
128
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ví dụ 3. Tìm
a
để hàm số
( )
( )
2
2
6
2
2 3 2
2 3 2
xx
khi x
xx
fx
x a khi x
+−
+ − −
=
− +
liên tục trên . ĐS:
11a =−
.
Lời giải
Với
( )
;2x −
ta có:
-
( )
2
00
0
00
6
2 3 2
xx
fx
xx
+−
=
+ − −
.
-
( ) ( ) ( )
00
22
0
lim lim 2 3 2 3
x x x x
f x x a x a
→→

= − + = − +

.
Suy ra
( ) ( )
0
0
lim
xx
f x f x
→
=
nên hàm số liên tục trên khoảng
( )
;2−
.
Với
( )
2;x +
ta có
-
( ) ( )
2
00
23f x x a= − +
.
-
( ) ( ) ( )
00
22
0
lim lim 2 3 2 3
x x x x
f x x a x a
→→

= − + = − +

.
Suy ra
( ) ( )
0
0
lim
xx
f x f x
→
=
nên hàm số liên tục trên khoảng
( )
2;+
.
Lại có:
-
( )
21fa=+
.
-
( )
2
22
6
lim lim 10
2 3 2
xx
xx
fx
xx
++
→→
+−
= = −
+ − −
.
-
( ) ( )
2
22
lim lim 2 3 1
xx
f x x a a
−−
→→

= − + = +

.
Khi đó hàm số liên tục trên thì sẽ liên tục tại
2x =
khi và chỉ khi
( ) ( ) ( )
22
lim lim 2 10 1
xx
f x f x f a
+−
→→
= = − = +
.
Suy ra
11a =−
là giá trị cần tìm.
BÀI TẬP ÁP DỤNG
Bài 1. Xét tính liên tục của hàm số
( )
32
2 6 3
3
3
19 3
x x x
khi x
fx
x
khi x
+ + +
−
=
+
=−
trên .
Lời giải
Tập xác định của hàm số là
D =
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
129
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
- Xét
3x −
thì
( )
32
2 6 3
3
x x x
fx
x
+ + +
=
+
là hàm phân thức hữu tỉ nên liên tục trên các khoảng
( )
;3− −
và
( )
3;− +
mà nó xác định.
- Xét tính liên tục của hàm số
( )
fx
tại
3x =−
( )
( )
( ) ( )
( )
( )
( )
( )
2
32
2
3 3 3 3
3 2 1
2 6 3
lim lim lim lim 2 1 19
33
x x x x
xx
x x x
f x x
xx
→ − → − → − → −
++
+ + +
= = = + =
−+
.
Suy ra
( )
( ) ( )
3
lim 3
x
f x f
→−
=−
nên hàm số đã cho liên tục tại
3x =−
.
Vậy hàm số đã cho liên tục trên .
Bài 2. Xét tính liên tục của hàm số
( )
2
3
56
2
2 16
22
xx
khi x
fx
x
x khi x
−+
=
−
−
trên .
Lời giải
Tập xác định
D =
.
- Với mọi
( ) ( ) ( )
00
2
00
3
56
;2 , lim lim
2 16
x x x x
xx
x f x f x
x
→→
−+
− = =
−
.
Suy ra hàm số đã cho liên tục trên khoảng
( )
;2−
.
- Với mọi
( ) ( ) ( ) ( )
00
0 0 0
2; ,lim lim 2 2
x x x x
x f x x x f x
→→
+ = − = − =
.
Suy ra hàm số đã cho liên tục trên khoảng
( )
2;+
.
- Xét tính liên tục của hàm số tại
2x =
( )
20f =
.
( )
( )( )
( )
( ) ( )
2
3
22
2 2 2 2
23
5 6 3 1
lim lim lim lim
2 16 24
2 2 2 4 2 2 4
x x x x
xx
x x x
fx
x
x x x x x
− − − −
→ → → →
−−
− + −
= = = = −
−
− + + + +
( ) ( )
22
lim lim 2 0
xx
f x x
++
→→
= − =
.
Suy ra hàm số không liên tục tại
2x =
.
Bài 3. Tìm
a
để
( )
2
32
3
23
1
1
1
xx
khi x
fx
x x x
a khi x
−−
−
=
+ + +
=−
liên tục trên .
Lời giải
Ta có với
1x
thif
( )
2
32
23
1
xx
fx
x x x
−−
=
+ + +
là hàm phân thức hữu tỉ nên nó liên tục trên từng
khoảng mà nó xác định. Lại có
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
130
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
-
( )
3
1fa−=
.
-
( )
( )( )
( )
( )
2
3 2 2
2
1 1 1 1
1 2 3
2 3 2 3 5
lim lim lim lim
1 1 2
11
x x x x
xx
x x x
fx
x x x x
xx
→− →− →− →−
+−
− − −
= = = = −
+ + + + +
++
.
Khi đó hàm số liên tục trên thì sẽ liên tục tại
1x =−
khi và chỉ khi
( ) ( )
3
1
5
lim 1
2
x
f x f a
→−
= − == −
.
Suy ra
3
5
2
a =−
là giá trị cần tìm.
BÀI TẬP RÈN LUYỆN
Bài 1. Xét tính liên tục của hàm số
( )
3
1
1
1
12
1
2
x
khi x
x
fx
x
khi x
x
−
−
=
−+
+
liên tục trên .
Bài 2. Tìm
m
để
( )
2
5
0
11
20
xx
khi x
fx
x
m khi x
+
=
−−
+
liên tục trên .
Bài 3. Tìm
m
để
( )
2
32
1
1
1
cos 1
x
khi x
fx
x x x
m khi x
−
−
=
+ + +
=−
liên tục trên .
Bài 4. Tìm
m
để
( )
3
2 2 1
1
1
3 2 1
xx
khi x
fx
x
m khi x
− + −
=
−
−=
liên tục trên .
Bài 5. Tìm
m
để
( )
2
11
0
2 3 1 0
x
khi x
fx
x
x m khi x
+−
=
+ +
liên tục trên .
_DẠNG 3. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM
Phương pháp giải:
- Để chứng minh phương trnh
( )
0fx=
có ít nhất một nghiệm trên
D
, ta chứng minh hàm số
( )
fx
liên tục trên
D
và có hai số
,a b D
sao cho
( ) ( )
.0f a f b
.
- Để chứng minh phương trnh
( )
0fx=
có
k
nghiệm trên
D
, ta chứng minh hàm số
( )
fx
liên tục
trên
D
và tồn tại
khoảng rời nhau
( )
1
;
ii
aa
+
với
1;2;...;ik=
nằm trong
D
sao cho
( ) ( )
1
.0
ii
f a f a
+
.
Chú ý: Hàm số đã thức liên tục trên . Hàm số phân thức và lượng giác liên tục trên
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
131
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
từng khong xác định của chúng.
Khi hàm số đã liên tục trên rồi, sẽ lieent ục trên mỗi khong
( )
1
;
ii
aa
+
mà ta cần tìm.
VÍ DỤ
Ví dụ 1. Chứng minh phương trnh
32
4 8 1 0xx− + =
có nghiệm trong khoảng
( )
1;2−
.
Lời giải
- Đặt
( )
32
4 8 1f x x x= − +
và
( )
fx
là hàm đa thức nên liên tục trên , suy ra liên tục trên
1;2−
.
- Ta có
( )
( )
( ) ( ) ( ) ( )
00
1 11
1 . 2 11 0 1;2 : 0
21
f
f f x f x
f
− = −
− = − − =
=
,
Nghĩa là phương trnhf
( )
32
4 8 1 0f x x x= − + =
có ít nhất một nghiệm trong khoảng
( )
1;2−
.
Ví dụ 2. Chứng minh phương trnh
3
31xx−+
có đúng ba nghiệm phân biệt.
Lời giải
Đặt
( )
3
31f x x x= − +
và
( )
fx
là hàm đa thức nên liên tục trên , suy ra hàm số liên tục trên
các đoạn
2;0 ; 0;1 ; 1;2−
.
- Ta có
( )
( )
( ) ( )
11
2 . 0 1 0
01
f
ff
f
− = −
− = −
=
phương trnh
( )
3
3 1 0f x x x= − + =
có ít nhất
một nghiệm thuộc khoảng
( )
2;0−
. (1)
- Ta có
( )
( )
( ) ( )
01
0 . 1 1 0
11
f
ff
f
=
= −
=−
phương trnh
( )
3
3 1 0f x x x= − + =
có ít nhất một
nghiệm thuộc khoảng
( )
0;1
. (2)
- Ta có
( )
( )
( ) ( )
11
1 . 2 3 0
23
f
ff
f
=−
= −
=
phương trnh
( )
3
3 1 0f x x x= − + =
có ít nhất
một nghiệm thuộc khoảng
( )
1;2
. (3)
Từ
( ) ( ) ( )
1 , 2 , 3
suy ra phương trnh có ít nhất ba nghiệm phân biệt thuộc các khoảng
( )
2;0−
,
( )
0;1
,
( )
1;2
. Mà
( )
fx
là đa thức bậc ba nên phương trnh
( )
0fx=
có tối đa ba nghiệm. Suy
ra phương trnh đã cho có đúng ba nghiệm phân biệt.
Chú ý: Với sự hỗ trợ của chức năng mode
7
trong casio, ta dễ dàng tìm được các khong
( )
2;0−
,
( )
0;1
,
( )
1;2
như trên. Công việc còn lại là trình bày sao cho đúng ngôn ngữ.
Ví dụ 3. Chứng minh rằng phương trnh
3
10xx+ + =
có ít nhất một nghiệm âm lớn hơn
1−
.
Lời giải
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
132
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Đặt
( )
3
1f x x x= + +
, vì
( )
fx
là hàm đa thức nên liên tục trên , suy ra hàm số liên tục trên
đoạn
1;0−
.
Ta có
( )
( )
( ) ( )
11
1 . 0 1 0
01
f
ff
f
− = −
− = −
=
phương trnh
( )
0fx=
có ít nhất một nghiệm
thuộc khoảng
( )
1;0−
.
Suy ra phương trnh
( )
0fx=
có ít nhất một nghiệm âm lớn hơn
1−
.
Ví dụ 4. Chứng minh rằng phương trnh
32
5 2 0xx+ − =
có ít nhất hai nghiệm.
Lời giải
Đặt
( )
32
52f x x x= + −
,
( )
fx
là hàm đa thức trên , suy ra hàm số liên tục trên đoạn
1;0−
;
0;1
- Ta có
( )
( )
( ) ( )
12
1 . 0 4 0
02
f
ff
f
−=
− = −
=−
phương trnh
( )
0fx=
có ít nhất một nghiệm
thuộc khoảng
( )
1;0−
. (1)
- Tương tự
( )
( )
( ) ( )
02
1 . 0 8 0
14
f
ff
f
=−
− = −
=
phương trnh
( )
0fx=
có ít nhất một
nghiệm thuộc khoảng
( )
0;1
. (2)
Từ
( )
1
và
( )
2
ta suy ra phương trnh
( )
0fx=
có ít nhất hai nghiệm.
Ví dụ 5. Chứng minh rằng phương trnh
43
4 2 3 0x x x+ − − =
có ít nhất hai nghiệm.
Lời giải
Đặt
( )
43
4 2 3f x x x x= + − −
,
( )
fx
là hàm đa thức trên , suy ra hàm số liên tục trên đoạn
1;0−
,
0;1
.
- Ta có
( )
( )
( ) ( )
14
1 . 0 12 0
03
f
ff
f
−=
− = −
=−
phương trnh
( )
0fx=
có ít nhất một nghiệm
thuộc khoảng
( )
1;0−
. (1)
- Tương tự
( )
( )
( ) ( )
03
1 . 0 6 0
12
f
ff
f
=−
− = −
=
phương trnh
( )
0fx=
có ít nhất một
nghiệm thuộc khoảng
( )
0;1
. (2)
Từ
( )
1
và
( )
2
ta suy ra phương trnh
( )
0fx=
có ít nhất hai nghiệm.
Ví dụ 6. Chứng minh rằng phương trnh
( )
25
1 3 1 0m x x− − − =
luôn có nghiệm với mọi
m
.
Lời giải
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
133
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Đặt
( )
( )
25
1 3 1f x m x x= − − −
và
( )
fx
là hàm đa thức liên tục trên
( )
fx
liên tục trên
đoạn
1;0−
.
Ta có
( )
( )
( ) ( ) ( ) ( )
2
00
11
1 . 0 0 1;0 : 0
01
fm
f f x f x
f
− = +
− − =
=−
.
Do đó phương trnh
( )
0fx=
luôn có nghiệm với mọi
m
(đpcm).
Chú ý: Đối với bài toán chứa tham số
m
, ta chn khong
( )
;ab
sao cho tại vị trí
và
b
triệt
tiêu đi
m
hoặc là biểu thức luôn dương hoặc luôn âm dựa vào kinh nghiệm người gii toán.
Một số trường hợp sử dụng dấu tam thức bậc hai để đánh giá, tức
2
0
0,
0
a
ax bx c x
+ +

.
2
0
0,
0
a
ax bx c x
+ +

.
Ví dụ 7. Chứng minh rằng phương trnh
42
2 1 0x mx mx+ − − =
có nghiệm với mọi
m
.
Lời giải
Đặt
( )
42
21f x x mx mx= + − −
và
( )
fx
là hàm đa thức liên tục trên
( )
fx
liên tục trên
đoạn
0;2
.
Ta có
( )
( )
( ) ( )
01
1 . 2 15
2 15
f
ff
f
=−
− = −
=
phương trnh
( )
0fx=
luôn có nghiệm với mọi
m
.
Ví dụ 8. Chứng minh rằng phương trnh
( )( )
2 3 2 5 0m x x m− − + − =
có nghiệm với mọi
m
.
Lời giải
Đặt
( ) ( )( )
2 3 2 5f x m x x x= − − −
và
( )
fx
là hàm đa thức liên tục trên
( )
fx
liên tục
trên đoạn
2;3
.
Ta có
( )
( )
( ) ( )
21
2 . 3 1
31
f
ff
f
=−
= −
=
phương trnh
( )
0fx=
luôn có nghiệm với mọi
m
.
Ví dụ 9. Chứng minh phương trnh
( )( ) ( )( ) ( )( )
0x a x b x b x c x c x a− − + − − + − − =
có ít nhất một
nghiệm với mọi số thực
a
,
b
,
c
.
Lời giải
Đặt
( ) ( )( ) ( )( ) ( )( )
f x x a x b x b x c x c x a= − − + − − + − −
. Vì
( )
fx
là hàm đa thức nên sẽ liên
tục trên . Không mất tính tổng quát, có thể giả sử
abc
.
- Nếu
ab=
hoặc
bc=
thì
( ) ( )( )
f b b a b c= − −
, suy ra phương trnh có nghiệm
.xb=
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
134
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
- Nếu
abc
thì
( ) ( )( )
( ) ( )( )
0
0
f a a b a c
f b b a b c
= − −
= − −
( ) ( )
.0f a f b
. Do đó phương trnh có ít
nhất một nghiệm trong khoảng
( )
;ab
.
Suy ra phương trnh có ít nhất một nghiệm (đpcm).
Ví dụ 10. Cho ba số
a
,
,
c
thỏa mãn hệ thức
2 3 6 0a b c+ + =
. Chứng minh rằng phương trnh
2
0ax bx c+ + =
có ít nhất một nghiệm thuộc khoảng
( )
0;1
.
Lời giải
Đặt
( )
2
f x ax bx c= + +
và
( )
fx
là hàm đa thức nên liên tục trên .
- Ta có
( )
0fc=
và có
( )
2 3 6 0
2 4 2 2
2 3 6
3 9 3 3 3 3
a b c
cc
f a b c a b c
+ + =

= + + = + + − = −


.
- Nếu
0c =
thì
2
0
3
f

=


, suy ra phương trnh có nghiệm
( )
2
0;1
3
x =
.
- Nếu
0c
thì ta có
( )
2
2
0 . 0
33
c
ff

= −


( )
0fx=
có nghiệm
( )
2
0; 0;1
3
xa

=


.
Vậy phương trnh có ít nhất một nghiệm thuộc khoảng
( )
0;1
.
Ví dụ 11. Cho hàm số
( )
32
31f x x x= − −
. Chứng minh rằng phương trnh có nghiệm
( )
0
3;4x
. Không
tính
( )
5
36f
và
( )
5
1 36f +
, chứng minh rằng
5
0
1 36x +
.
Lời giải
Ta có:
( )
( )
( ) ( )
32
32
3 3 3.3 1 1
3 . 4 15 0
4 4 3.4 1 15
f
ff
f
= − − = −
= −
= − − =
.
Suy ra phương trnh có nghiệm
( )
0
3;4x
.
Ta có
( ) ( ) ( )
3
32
3 1 1 3 1 3f x x x x x= − − = − − − −
.
Vì
0
x
là nghiệm của phương trnh
( )
0fx=
nên ta có
( )
0
0fx =
( ) ( )
3
00
1 3 1 3 0xx − − − − =
.
Đặt
0
1x
=−
và
( ) ( )
0
3;4 2;3x
. Khi đó, ta có
33
3 3 0 3 3 2. 9 6
− − = = + =
65
5
36 36 36
.
Dấu “
” xảy ra khi và chỉ khi
( )
3 3 1 2;3

= =
.
Do đó, dấu “
” không xảy ra, tức là ta luôn có
5 5 5
00
36 1 36 1 36.xx
− +
Suy ra điều phải chứng minh.
BÀI TẬP ÁP DỤNG
Bài 1. Chứng minh phương trnh
( )
2 3 2 2 2
1 2 4 1 0m x m x x m+ − − + + =
có ba nghiệm phân biệt.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
135
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 2. Chứng minh phương trnh
( )
52
1 9 16 0m x mx x m− + − − =
có ít nhất hai nghiệm phân biệt.
Bài 3. Chứng minh phương trnh
( )
22
3 2 4 0
n
m m x x− + − − =
có ít nhất một nghiệm âm với mọi
m
.
Bài 4. Chứng minh phương trnh
( ) ( )
3
4 1 1 0m x m x m+ − + + =
có nghiệm với mọi
m
.
Bài 5. Chứng minh phương trnh
( )( )
( )
2002
3 2001
1 1 2 2 3 0m x x x− − + + + =
có nghiệm với mọi
m
.
Bài 6. Chứng minh phương trnh
( )
2 3 2 2 2
1 2 4 1 0m x m x x m+ − − + + =
có ba nghiệm phân biệt.
Bài 7. Chứng minh rằng phương trnh
( )
( )
33
1 4 3 1 0m x x x x x− − + − + =
có ít nhất ba nghiệm.
Bài 8. Cho
và
thỏa mãn
0


. Chứng minh rằng phương trnh sau có nghiệm
2 10 2 2
10
sin sin
sin xx

+ − −
−=
+
.
Bài 9. Chứng minh rằng nếu
0
a b c
k n m
+ + =
,
( )
0k n m
và
2
km n
thì phương trnh
2
0ax bx c+ + =
có nghiệm thuộc khoảng
( )
0;1
.
LỜI GIẢI
Bài 1. Đặt
( )
( )
2 3 2 2 2
1 2 4 1f x m x m x x m= + − − + +
,
( )
fx
liên tục với mọi
x
.
Có:
( )
( )
( ) ( ) ( )
32
2 2 2 2
3 1 . 3 2 . 3 4. 3 1 44 14 0f m m m m− = + − − − − − + + = − −
;
( )
( )
2 3 2 2 2 2
0 1 .0 2 .0 4.0 1 1 0f m m m m= + − − + + = +
;
( )
( )
2 3 2 2 2
1 1 .1 2 .1 4.1 1 2 0f m m m= + − − + + = −
;
( )
( )
2 3 2 2 2 2
2 1 .2 2 .2 4.2 1 1 0f m m m m= + − − + + = +
.
Ta thấy
( ) ( )
3 . 0 0ff−
;
( ) ( )
0 . 1 0ff
;
( ) ( )
1 . 2 0ff
nên phương trnh
( )
2 3 2 2 2
1 2 4 1 0m x m x x m+ − − + + =
có ít nhất 1 nghiệm trong khoảng
( )
3;0−
, ít nhất 1 nghiệm
trong khoảng
( )
0;1
, ít nhất 1 nghiệm trong khoảng
( )
1;2
.
Vậy phương trnh
( )
2 3 2 2 2
1 2 4 1 0m x m x x m+ − − + + =
có ít nhất 3 nghiệm phân biệt.
Bài 2. Đặt
( ) ( )
52
1 9 16f x m x mx x m= − + − −
,
( )
fx
liên tục trên .
Trường hợp 1:
0m =
, ta có phương trnh
5
16 0xx−=
có nghiệm
0; 2x
.
Vậy với
0m =
thì phương trnh
( )
52
1 9 16 0m x mx x m− + − − =
có ít nhất hai nghiệm phân biệt.
Trường hợp 2:
0m
, ta có:
( ) ( )( ) ( ) ( )
52
2 1 2 9 2 16. 2 67f m m m m− = − − + − − − − =
;
( ) ( )
52
0 1 .0 9 .0 16.0f m m m m= − + − − = −
;
( ) ( )
52
2 1 .2 9 .2 16.2 3f m m m m= − + − − = −
.
Ta thấy
( ) ( )
2
2 . 0 67 0f f m− = −
,
( ) ( )
2
0 . 2 3 0f f m= −
với mọi
0m
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
136
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Suy ra phương trnh
( )
52
1 9 16 0m x mx x m− + − − =
có ít nhất 1 nghiệm trong khoảng
( )
2;0−
,
ít nhất 1 nghiệm trong khoảng
( )
0;2
.
Vậy phương trnh
( )
52
1 9 16 0m x mx x m− + − − =
có ít nhất hai nghiệm phân biệt.
Bài 3. Đặt
( )
( )
22
3 2 4
n
f x m m x x= − + − −
,
( )
fx
liên tục trên .
Xét
( )
( )
( ) ( )
( )
2
22
2 3 2 2. 2 4 3 .4 0
n
n
f m m m m− = − + − − − − = − +
.
Xét
( )
( )
22
0 3 .0 2.0 4 4 0
n
f m m= − + − − = −
.
Ta thấy
( ) ( )
2 . 0 0ff−
với mọi
0m
.
Suy ra phương trnh
( )
22
3 2 4 0
n
m m x x− + − − =
có ít nhất 1 nghiệm trong khoảng
( )
2;0−
.
Vậy phương trnh
( )
22
3 2 4 0
n
m m x x− + − − =
có ít nhất một nghiệm âm.
Bài 4. Trường hợp 1:
0m =
, ta có phương trnh
3
0xx−=
luôn có nghiệm
0x =
;
1x =
.
Trường hợp 2:
0m
.
Đặt
( ) ( ) ( )
3
4 1 1f x m x m x m= + − + +
,
( )
fx
liên tục với mọi
x
.
Có:
( ) ( )( ) ( )( )
3
1 4 1 1 1 1 2f m m m m− = + − − + − + = −
;
( ) ( ) ( )
3
0 4 1 .0 1 .0f m m m m= + − + + =
.
Ta thấy
( ) ( )
2
1 . 0 2 0f f m− = −
nên phương trnh
( ) ( )
3
4 1 1 0m x m x m+ − + + =
có ít nhất 1
nghiệm trong khoảng
( )
1;0−
.
Vậy phương trnh
( ) ( )
3
4 1 1 0m x m x m+ − + + =
có nghiệm với mọi
m
.
Bài 5. Đặt
( )
( )( )
( )
2002
3 2001
1 1 2 2 3f x m x x x= − − + + +
,
( )
fx
liên tục với mọi
x
.
Xét
( )
( )
( ) ( ) ( )
2002
2001
3
2 1 2 1 2 2 2. 2 3 1fm

− = − − − − + + − + = −



.
Xét
( )
( )( )
( )
2002
3 2001
1 1 1 1 1 2 2.1 3 5fm= − − + + + =
.
Ta thấy
( ) ( )
2 . 1 1.5 5 0ff− = − = −
với mọi
m
.
Suy ra phương trnh
( )( )
( )
2002
3 2001
1 1 2 2 3 0m x x x− − + + + =
có ít nhất 1 nghiệm trong khoảng
( )
2;1−
.
Vậy phương trnh
( )( )
( )
2002
3 2001
1 1 2 2 3 0m x x x− − + + + =
có nghiệm với mọi
m
.
Bài 6. Đặt
( )
( )
2 3 2 2 2
1 2 4 1f x m x m x x m= + − − + +
,
( )
fx
liên tục với mọi
x
.
Có:
( )
( )
( ) ( ) ( )
32
2 2 2 2
3 1 . 3 2 . 3 4. 3 1 44 14 0f m m m m− = + − − − − − + + = − −
;
( )
( )
2 3 2 2 2 2
0 1 .0 2 .0 4.0 1 1 0f m m m m= + − − + + = +
;
( )
( )
2 3 2 2 2
1 1 .1 2 .1 4.1 1 2 0f m m m= + − − + + = −
;
( )
( )
2 3 2 2 2 2
2 1 .2 2 .2 4.2 1 1 0f m m m m= + − − + + = +
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
137
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Ta thấy
( ) ( )
3 . 0 0ff−
,
( ) ( )
0 . 1 0ff
,
( ) ( )
1 . 2 0ff
. Suy ra phương trnh
( )
2 3 2 2 2
1 2 4 1 0m x m x x m+ − − + + =
có ít nhất 1 nghiệm trong khoảng
( )
3;0−
, ít nhất 1 nghiệm
trong khoảng
( )
0;1
, ít nhất 1 nghiệm trong khoảng
( )
1;2
.
Vậy phương trnh
( )
2 3 2 2 2
1 2 4 1 0m x m x x m+ − − + + =
có ba nghiệm phân biệt.
Bài 7. Đặt
( ) ( )
( )
33
1 4 3 1f x m x x x x x= − − + − +
,
( )
fx
liên tục với mọi
x
.
Có:
( ) ( ) ( ) ( ) ( ) ( )
33
2 2 1 2 4. 2 2 3. 2 1 1fm

− = − − − − − + − − − + = −

;
( ) ( )
( )
33
0 0 1 0 4.0 0 3.0 1 1fm= − − + − + =
;
( ) ( )
( )
33
1 1 1 1 4.1 1 3.1 1 1fm= − − + − + = −
;
( ) ( )
( )
33
2 2 1 2 4.2 2 3.2 1 1fm= − − + − + =
.
Ta thấy
( ) ( )
2 . 0 0ff−
,
( ) ( )
0 . 1 0ff
,
( ) ( )
1 . 2 0ff
nên phương trnh
( )
( )
33
1 4 3 1 0m x x x x x− − + − + =
có ít nhất 1 nghiệm trong khoảng
( )
2;0−
, ít nhất 1 nghiệm
trong khoảng
( )
0;1
, ít nhất 1 nghiệm trong khoảng
( )
1;2
.
Vậy phương trnh
( )
( )
33
1 4 3 1 0m x x x x x− − + − + =
có ít nhất ba nghiệm.
Bài 8. Đặt
( )
2 10 2 2
10
sin sin
sinf x x x

+ − −
= − −
+
, hàm số
( )
fx
liên tục trên .
Ta có
( )
lim
x
fx
→−
= +
nên tồn tại
0m
sao cho
( )
0fm
.
Mà
( )
lim
x
fx
→+
= −
nên tồn tại
0M
sao cho
( )
0fM
.
Do đó, hàm số
( )
fx
liên tục trên
;mM
và
( ) ( )
.0f m f M
nên phương trnh
( )
0fx=
có
nghiệm.
Bài 9. Xét phương trnh
2
0ax bx c+ + =
( )
1
.
Đặt
( )
2
f x ax bx c= + +
thì
( )
fx
liên tục trên .
Ta có
( )
0fc=
;
2
2
..
n n n
f a b c
k k k

= + +


.
Suy ra
( )
2 2 2
2
0 . 1 1
n n a b c n n
f f c c c
k k k n m km km

= + + + − = −


(do
0
a b c
k n m
+ + =
).
Vì
2
0c
;
2
0n km
2
1
n
km

, do đó
( )
2
2
0 . 1 0
nn
f f c
k km


= −




.
- Với
0c =
phương trnh đã cho trở thành
2
0ax bx+=
. Suy ra
0x =
hoặc
0ax b+=
( )
2
.
+ Nếu
0a =
thì từ
0ca==
và điều kiện
0
a b c
k n m
+ + =
suy ra
0b =
. Khi đó phương trnh
( )
2
có nghiệm là
x
, suy ra phương trnh
( )
1
có nghiệm
( )
0;1x
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
138
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
+ Nếu
0a
thì
0b
(vì nếu
0b =
,
0c =
thì từ điều kiện
0
a b c
k n m
+ + =
suy ra
0a =
), suy ra
phương trnh
( )
2
có nghiệm
b
x
a
=−
. Khi đó từ điều kiện
0
a b c
k n m
+ + =
;
0k n m
và
0c =
suy ra
( )
0;1
bn
x
ak
= − =
. Do đó phương trnh
( )
1
có nghiệm
( )
0;1x
.
- Với
2
10
n
km
−=
0
nn
f
kk

=


là nghiệm thuộc
( )
0;1
.
- Với
0c
và
( )
2
1 0 0 . 0
nn
ff
km k

−


thì
( )
fx
có ít nhất 1 nghiệm thuộc
0;
n
k



. Mà
( )
0; 0;1
n
k



(vì
01
n
k

) nên phương trnh
( )
1
có nghiệm
( )
0;1x
.
Vậy phương trnh
( )
1
luôn có nghiệm
( )
0;1x
.
C. BÀI TẬP RÈN LUYỆN
Bài 1. Chứng minh rằng phương trnh
4 3 2
2 15 25 0x x x x− − − − =
có ít nhất một nghiệm âm và ít nhất
một nghiệm dương.
ĐS:
( )
1;0−
;
( )
3;4
.
Bài 2. Chứng minh rằng phương trnh
32
4 2 0xx+ − =
có ba nghiệm trong khoảng
( )
4;1−
.
ĐS:
7
4;
2

−−


;
1
1;
2

−−


;
1
;1
2



.
Bài 3. Chứng minh rằng phương trnh
53
5 4 1 0x x x− + − =
có đúng năm nghiệm.
ĐS:
3
2;
2

−−


;
3
;1
2

−−


;
1
1;
2

−


;
1
;1
2



;
( )
1;3
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
139
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
BÀI 4. ÔN TẬP CHƯƠNG IV
A. BÀI TẬP
Bài 1. (HKII - THPT Lương Văn Can)
1) Tính các giới hạn sau
a)
2
2
22
lim
4
x
x
x
→
+−
−
. b)
2
4 3 1
lim
1
x
xx
x
→+
++
−
.
2) Xét tính liên tục của hàm số
( )
2
3 2 1
khi 1
1
2 2 khi 1
xx
x
fx
x
xx
−−
=
−
+
tại
0
1x =
.
Bài 2. (HKII - THPT Sương Nguyệt Anh)
1) Tính các giới hạn sau
a)
2
3
2
2 10
lim
6
x
xx
xx
→−
−−
−+
. b)
(
)
2
lim 3 2 3
x
x x x
→−
+ − +
.
2) Xét tính liên tục của hàm số
( )
2
31
khi 2
2
2 2 khi 2
x
x
fx
x
xx
−−
=
−
−=
tại
0
2x =
.
Bài 3. (HKII – THPT Bùi Thị Xuân)
1. Tính các giới hạn sau
a)
32
42
1
3
6 5 4 1
lim
9 8 1
x
x x x
xx
→
− + −
+−
. ĐS:
2
5
. b)
(
)
2
lim 9 3 1 3 1
x
x x x
→−
+ + + +
ĐS:
1
2
.
2. Tìm
,ab
để hàm số
( )
2
2
khi 1
2 5 7
khi 1
1
2 3 khi 1
a b x=
xx
f x x
x
x bx a x
+
+−
=
−
+ +
liên tục tại
0
1x =
. ĐS:
10, 19ab= − =
3. Chứng minh rằng phương trnh
( )( )
( )( )
22
3 2 3 2 3 2 3 2 0m m x x x m− + − + + − − =
có nghiệm
với mọi
m
.
Bài 4. (HKII – THPT Nguyễn Hữu Huân)
1. Tính các giới hạn sau
a)
2
1
1
lim
1
x
x
x
→
−
−
. ĐS:
1
4
. b)
32
2
2
32
lim
6
x
x x x
xx
→−
++
−−
ĐS:
2
5
−
.
2. Xét tính liên tục của hàm số
( )
2
32
khi 1
1
1 khi 1
xx
x
fx
x
x
−+
=
−
−=
tại
0
1x =
. ĐS: liên tục
Bài 5. (HKII – THPT Hermann Gmeiner)
1. Tính các giới hạn sau
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
140
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
a)
32
2
1
1
lim
21
x
x x x
xx
→
− − +
−+
. ĐS:
2
. b)
3
2
13
lim
2
x
x
x
→−
−−
+
ĐS:
2−
.
c)
( )
2
4
5
lim
4
x
x
x
−
→
−
−
. ĐS:
−
. d)
(
)
2
lim 1
x
x x x
→−
+ + +
ĐS:
1
2
−
.
2. Tìm
a
để hàm số
( )
khi 0
11
4
5 khi 0
1
x
x
x
fx
x
ax
x
−−
=
−
− +
+
liên tục tại
0
0x =
. ĐS:
3a =
.
Bài 6. (HKII – THPT Hoàng Hoa Thám)
1. Tính giới hạn sau
2
2
23
lim
4 1 2
x
x x x
xx
→−
++
+ − +
. ĐS:
2
3
−
.
2. Tìm
a
để hàm số
( )
2
2 khi 1
4
5 khi 1
1
ax x x
fx
x
ax
x
+
=
−
− +
+
liên tục tại
0
1x =
. ĐS:
1a =−
.
3. Chứng minh rằng phương trnh
4 3 2
2 15 25 0x x x x− − − − =
có ít nhất một nghiệm dương và
một nghiệm âm.
Bài 7. (HKII – THPT Hàn Thuyên)
1. Tính các giới hạn sau
a)
2
3
3
lim
2 15
x
x
xx
→
−
+−
. ĐS:
1
8
. b)
( )
2
2
3 1 2 3
lim
3
x
xx
xx
→−
+−
−+
ĐS:
2
.
2. Tìm
m
để hàm số
( )
1
khi 1
77
khi 1
2
x
x
x
fx
x
mx
−
−
=
−
liên tục tại
0
1x =
. ĐS:
3
7
m =
.
Bài 8. (HKII – THPT Hùng Vương)
1. Tính giới hạn sau
32
2
1
4 7 19 16
lim
5 8 3
x
x x x
xx
→
− + −
−+
. ĐS:
17
2
.
2. Tìm
m
để hàm số
( )
2
4
khi 2
21
2 khi 2
x
x
fx
x
x m x
−
=
+−
−
liên tục tại
0
2x =
. ĐS:
4m =
.
3. Chứng minh rằng phương trnh
( )
2 2015
4 2 1 0m m x x− + − + =
có ít nhất một nghiệm âm với
mọi giá trị của tham số
m
.
Bài 9. (HKII – THPT Hưng Đạo)
1. Tính các giới hạn sau
a).
56
lim
32
x
x
x
→+
−
+
. ĐS:
3−
. b).
2
3
lim
2
x
x
x
+
→
−
−
. ĐS:
−
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
141
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
c).
( )
3
lim 3 2
x
xx
→−
−
ĐS:
+
.
2. Tìm
m
để hàm số
( )
2
3
34
khi 1
1
khi 1
xx
x
fx
x
mx
+−
=
−
=
liên tục tại
0
1x =
. ĐS:
5
3
m =
.
Bài 10. (HKII – THPT Bà Điểm)
1) Tính các giới hạn sau
a)
2
2
2
32
lim
4
x
xx
x
→
−+
−
. ĐS:
1
4
b)
(
)
22
lim
x
x x x x
→+
+ − −
. ĐS: 1
2) Xét tính liên tục của hàm số
( )
( )
2
5 3 khi 5
5
khi 5
2 1 3
xx
fx
x
x
x
− +
=
−
−−
tại điểm
0
5x =
ĐS: liên tục.
3) Tìm
m
để hàm số
( )
2
56
khi 3
3
2 1 khi 3
xx
x
fx
x
mx x
−+
=
−
+=
liên tục tại điểm
0
3x =
.
Bài 11. (HKII-THPT Bình Tân)
1) Tìm
m
để hàm số
( )
22
khi 2
2
1
khi 2
4
x
x
x
fx
mx x
+−
−
=
+
.
2) Chứng minh rằng phương trnh
( )
25
1 3 1 0m x x− − − =
có ít nhất một nghiệm với mọi giá trị
của tham số
m
.
Bài 12. (HKII-THPT Củ Chi)
1) Tính các giới hạn sau
a)
2
2
39
lim
12
nn
n
−+
−
. ĐS:
3
2
−
b)
( )
( )
2
3
2
7
1 3 1
lim
32
nn
n
−+
−
. ĐS:
9−
c)
(
)
2
lim 3 1
x
x x x
→−
− + − +
. ĐS:
5
2
−
2) Xét tính liên tục của hàm số
( )
2
4
khi 2
7 10
8
khi 2
3
x
x
xx
fx
x
x
−
−−
=
−
=
tại điểm
0
2x =
. ĐS: liên tục
3) Chứng minh rằng phương trnh
42
4 2 3 0x x x+ − − =
có ít nhất hai nghiệm.
Bài 13. (HKII-THPT Đinh Thiện Lý)
1) Tính các giới hạn sau
a)
43
32
lim
2 5 2
n
A
n n n
+
=
+ − +
. ĐS: 0 b)
36
lim
43
nn
n
B
−
=
+
. ĐS:
−
c)
32
2
3
2 5 2 3
lim
9
x
x x x
C
x
→
− − −
=
−
ĐS:
11
3
d)
(
)
2
lim 4 1 2
x
D x x x
→+
= + + −
ĐS:
1
4
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
142
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
2) Cho hàm số
( )
2
khi 2
73
2 3 khi 2
x
x
fx
x
ax x
−
=
+−
+
.
a) Khi
1a =
, xét tính liên tục của hàm số tại
2x =
. ĐS: Không liên tục
b) Tìm giá trị của
để hàm số liên tục tại
2x =
. ĐS:
9
4
a =−
3) Chứng minh rằng phương trnh
54
3 5 2 0x x x− + − =
có ít nhất ba nghiệm phân biệt.
Bài 14. (HKII- THPT Lý Tự Trọng)
1) Tính các giới hạn sau
a)
5
5
lim
5
x
x
x
→
−
−
. ĐS: 0 b)
2
2
53
lim
2
x
x
x
→−
+−
+
. ĐS:
2
3
−
2) Tìm
a
để hàm số
( )
2
43
khi 3
3
4 5 khi 3
xx
x
fx
x
ax x
−+
=
−
+=
liên tục tại điểm
0
3x =
. ĐS:
7
12
a =−
3) Chứng minh rằng phương trnh
5 4 3
5 3 4 5 0x x x− + − =
có ít nhất một nghiệm.
Bài 15. (HKII-THPT Lê Quý Đôn)
1) Tìm giá trị của
a
để hàm số
( )
2
32
khi 1
2 3 1
2 7 khi 1
x
x
fx
xx
ax
+−
=
−+
− +
liên tục tại
0
1x =
. ĐS:
27
8
a =
2) Chứng minh phương trnh
( )
23
3 3 2 3 0m m x x− + + − =
có nghiệm với mọi
m
.
Bài 16. (HKII – THPT Chuyên Nguyễn Thượng Hiền)
1) Tính giới hạn sau
a)
(
)
22
lim 1
x
x x x
→−
+ − +
. ĐS:
1
2
−
b)
3
0
tan sin
lim
4
x
xx
x
→
−
. ĐS:
1
8
2) Tìm tham số
m
để hàm số
( )
22
1
khi 1
83
7 khi 1
x
x
fx
x
m x m m
−
=
+−
+
liên tục tại
0
1x =
. ĐS:
1m =−
và
6m =−
3) Chứng minh phương trnh
( )
14 2 15
3 7 5 0mx m x− + − =
luôn có ít nhất một nghiệm với mọi
m
.
Bài 17. (HKII – THPT An Lạc)
Tính các giới hạn sau
a)
2
2
2
4 5 26
lim
2
x
xx
x x x
→
+−
− + −
. ĐS:
84−
b)
(
)
2
lim 4 2 1
x
x x x
→−
− + −
. ĐS:
3
4
−
Tìm
m
để hàm số
( )
32
3
2
22
khi 1
1
4 6 1 khi 1
x x x
x
fx
x
mx x x
− + −
=
−
+ + =
liên tục tại điểm
0
1x =
. ĐS:
2m =−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
143
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 18. (HKII – THPT Nam Kỳ Khỏi Nghĩa)
Tính các giới hạn sau
a)
32
42
3
5 3 9
lim
89
x
x x x
xx
→
− + +
−−
. ĐS: 0 b)
22
1 4 1
lim
3
x
xx
x
→−
+ − +
−
. ĐS:
1−
Tìm
m
để hàm số
( )
3
2
43
khi 1
43
1
khi 1
4
xx
x
xx
fx
mx x
−+
−+
=
=
liên tục tại điểm
0
1x =
ĐS:
2m =
Bài 19. (HKII – THPT Nguyễn Chí Thanh).
Tính các giới hạn sau
a)
32
3
2
3 9 2
lim
76
x
x x x
xx
→−
− − +
−−
. ĐS: 3
b)
(
)
2
lim 2 1 4 4 3
x
x x x
→+
− − − −
. ĐS: 0
Tìm
để hàm số
( )
2
56
khi 3
63
3 khi 3
xx
x
fx
x
ax x
−+
=
+−
+
liên tục tại điểm
0
3x =
. ĐS:
1a =
Bài 20. (HKII – THPT Nguyễn An Ninh).
Tính các giới hạn sau
a)
32
2
2
2 3 8 12
lim
6
x
x x x
xx
→−
+ − −
−−
. ĐS:
4
5
−
b)
(
)
2
lim 2 4 5
x
x x x
→−
+ + +
. ĐS:
1
4
−
Tìm
m
để hàm số
( )
2
74
khi 3
3
2 khi 3
x
x
fx
x
x m x
+−
=
−
−=
liên tục tại điểm
0
3x =
. ĐS:
9
8
m =
Bài 21. (HKII – THPT Nguyễn Du).
Tính các giới hạn sau
a)
2
32
2
56
lim
3 7 10
x
xx
x x x
→
−+
− + −
. ĐS:
1
7
−
b)
(
)
2
lim 1
x
x x x
→−

++


. ĐS:
1
2
−
Tìm
m
để hàm số
( )
2
2
32
khi 1
1
1
khi 1
2
x
x
x
fx
m x x
+−
−
=
−=
liên tục tại điểm
0
1x =
. ĐS:
1m =
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
144
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Bài 22. (HKII – THPT Mạc ĐĨnh Chi).
Tính các giới hạn sau
a)
2.3 3.7 4
lim
3.2 4
nn
n

−+

+

. ĐS:
−
b)
2
2
0
42
lim
x
xx
xx
→

− + −


+

. ĐS:
1
4
−
c)
(
)
2
lim 3 1 9 3 4
x
x x x
→−
+ + + +
. ĐS:
1
2
Xét tính liên tục của hàm số
( )
4 5 5
khi 5
5
2
khi 5
25
x
x
x
fx
x
x
+−
−
=
tại
0
5x =
. ĐS: liên tục
Bài 23. (HKII – THPT Gia Định).
Tính các giới hạn sau
a)
43
2
3
2 6 3
lim
4 11 3
x
x x x
xx
→
− + −
−−
. ĐS:
55
13
b)
3
32
4
7 8. 9 28 12
lim
4 2 8
x
xx
x x x
→

+ − −


− + −

. ĐS:
17
54
c)
3
32
0
12 4 36 8
lim
2 12
x
xx
xx
→
+ − +
−
. ĐS:
3
16
−
d)
(
)
3
32
lim 64 4 4 1
x
x x x
→+
− − +
. ĐS:
11
12
Xét tính liên tục của hàm số
( )
32
2
13
khi 1
1
3
khi 1
4
3 6 3 6
khi 1
3 14 11
xx
x
x
f x x
x x x
x
xx
+ − +
−
==
− − +
−+
tại
0
1x =
. ĐS: liên tục
Bài 24. (HKII – Nguyễn Hiền).
Tính các giới hạn sau
a)
42
3
3
9 82 9
lim
2 54
x
xx
x
→
−+
−
. ĐS:
80
9
b)
( )
( )
2
2
2 3 4
lim
25
x
xx
x
→−
++
+
. ĐS:
1
2
−
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
145
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Xét tính liên tục của hàm số
( )
32
3 1 5
khi 1
23
2 1 khi 1
xx
x
fx
x x x
xx
+ − −
=
− + −
− +
tại điểm
0
1x =
. ĐS: liên
tục
Bài 25. (HKII – THPT Nguyễn Hữu Cảnh).
Tính các giới hạn sau
a)
2
2
1
2 3 1
lim
43
x
xx
xx
→
−+
−−
. ĐS:
1
5
−
b)
2
2
6
lim
32
x
xx
xx
→
−−
− + −
. ĐS:
5
4
−
Xét tính liên tục của hàm số
( )
12
khi 3
3
2
khi 3
4
x
x
x
fx
x
x
+−
−
=
−
tại điểm
0
3x =
. ĐS: liên tục
Bài 26. (HKII – THPT Nguyễn Thái Bình).
Xét tính liên tục của hàm số
( )
2
2
12
khi 3
3
5
khi 3
1
xx
x
x
fx
x
x
x
+−
−
=
+
=
−
tại điểm
3x =
. ĐS: liên tục
Chứng minh phương trnh
( )
( )
22
3 2 2 4 0m m x x x+ + − + + − =
có nghiệm
m
.
Bài 27. (HKII – THPT Tây Hạnh).
Tính các giới hạn sau
a)
32
2
3
56
lim
9
x
x x x
x
→
−+
−
. ĐS:
1
2
−
b)
(
)
2
lim 4 2
x
x x x
→−
−+
. ĐS:
1
4
Tìm
m
để hàm số
( )
( )
2
3 khi 2
2
khi 2
5 2 3
m m x
fx
x
x
xx
−=
=
−
− − −
liên tục tại
0
2x =
.ĐS:
1m =
và
2m =−
Chứng minh phương trnh
4 3 2
5 3 6 1 0x x x x+ − − + =
có ít nhất hai nghiệm trong khoảng
( )
1;1−
.
B. LỜI GIẢI
Bài 1. 1)
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
146
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
a) Ta có
( )
( )
2
22
2 2 1 1
lim lim
4 16
2 2 2
xx
x
x
xx
→→
+−
==
−
+ + +
.
b) Ta có
2
2
31
4
4 3 1
lim lim 2
1
1
1
xx
x
xx
xx
x
x
x
→+ →+
++
++
==
−

−


.
2) Ta có:
+)
( )
14f =
.
+)
( ) ( )
11
lim lim 2 2 4
xx
f x x
++
→→
= + =
.
+)
( ) ( )
2
1 1 1
3 2 1
lim lim lim 3 1 4
1
x x x
xx
f x x
x
− − −
→ → →
−−
= = + =
−
.
Suy ra
( ) ( ) ( )
11
lim lim 1
xx
f x f x f
−+
→→
==
, nên hàm số đã cho liên tục tại
0
1x =
.
Bài 2. 1) Tính:
a)
( )( )
( )
( )
2
32
2
2 2 2
2 2 5
2 10 2 5 9
lim lim lim
6 2 3 11
2 2 3
x x x
xx
x x x
x x x x
x x x
→− →− →−
+−
− − −
= = = −
− + − +
+ − +
.
b)
(
)
2
2
2
8 2 3
lim 3 2 3 lim
3 2 3
xx
xx
x x x
x x x
→− →−
+−
+ − + =
− − +
2
2
2
23
8
lim
23
31
x
x
xx
x
xx
→−

+−


= = −

+ − +


.
2. Ta có
-
( )
22f =
.
-
( )
2
2
2 2 2
3 1 2
lim lim lim 2
2
31
x x x
xx
fx
x
x
→ → →
− − +
= = =
−
−+
.
Bài 3. 1.
a ) Ta có
( )
( )
( )
( )
2
3 2 2
4 2 3 2
32
1 1 1
3 3 3
3 1 2 1
6 5 4 1 2 1 2
lim lim lim
9 8 1 3 3 1 5
3 1 3 3 1
x x x
x x x
x x x x x
x x x x x
x x x x
→ → →
− − +
− + − − +
= = =
+ − + + +
− + + +
b) Ta có
(
)
2
2
3
lim 9 3 1 3 1 lim
3 1 1
93
xx
x
x x x
x
x x x
→− →−
−
+ + + + =

− + + − −


2
31
lim
2
3 1 1
93
x
x x x
→−
−
= =
− + + − −
2. Ta có
( )
1f a b=+
.
-
( )
( )
2
11
lim lim 2 3 3 2 1
xx
f x x bx a a b
−−
→→
= + + = + +
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
147
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
-
( ) ( )
2
1 1 1
2 5 7
lim lim lim 2 7 9
1
x x x
xx
f x x
x
+ + +
→ → →
+−
= = + =
−
.
Hàm số
( )
fx
liên tục tại
0
1x =
khi và chỉ khi
( ) ( ) ( )
11
3 2 1 9 10
lim lim 1
9 19
xx
a b a
f x f x f
a b b
−+
→→
+ + = = −

= =

+ = =

3. Ta có hàm số
( )
( )( )
( )( )
22
3 2 3 2 3 2 3 2f x m m x x x m= − + − + + − −
liên tục trên .
Mặt khác
( ) ( ) ( )( ) ( )
2
1 2 3 2 2 3 2 3f f m m m = − − = − −
.
- Nếu
3
2
m =
thì
( ) ( )
1 2 0ff=
nên phương trnh có nghiệm
1; 2xx==
.
- Nếu
3
2
m
thì
( ) ( )
1 2 0ff
nên phương trnh đã cho có ít nhất một nghiệm
thuộc khoảng
( )
1;2
.
Vây phương trnh
( )( )
( )( )
22
3 2 3 2 3 2 3 2 0m m x x x m− + − + + − − =
luôn có nghiệm
với mọi
m
.
Bài 4. 1. a) Ta có
( )
( )
2
11
1 1 1
lim lim
14
11
xx
x
x
xx
→→
−
==
−
++
.
b) Ta có
( )( )
( )( )
( )
32
2
2 2 2
1 2 1
3 2 2
lim lim lim
6 2 3 3 5
x x x
x x x x x
x x x
x x x x x
→− →− →−
+ + +
++
= = = −
− − + − −
.
2. Ta có
-
( )
11f =−
.
-
( ) ( )
2
1 1 1
32
lim lim lim 2 1
1
x x x
xx
f x x
x
→ → →
−+
= = − = −
−
.
Suy ra
( ) ( )
1
lim 1
x
f x f
→
=
nên hàm số đã cho liên tục tại
0
1x =
.
Bài 5. 1. a) Ta có
( ) ( )
( )
( )
2
32
2
2
1 1 1
11
1
lim lim lim 1 2
21
1
x x x
xx
x x x
x
xx
x
→ → →
−+
− − +
= = + =
−+
−
.
b) Ta có
( )
( )
(
)
( )
32
3
3
2 2 2
3
8 2 4
13
lim lim lim 2
2
13
2 1 3
x x x
x x x
x
x
x
xx
→− →− →−
− + − − +
−−
= = = −
+
−+
+ − +
.
c) Ta có
( )
( )
( )
( )
4
2
2
44
2
lim 5 1 0
5
lim 4 0 lim
4
4 0 khi 4
x
xx
x
x
x
x
xx
−
−−
→
→→
− = −
−
− = = −
−
−
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
148
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
d) Ta có
(
)
2
2
1
lim 1 lim
1
xx
x
x x x
x x x
→− →−
+
+ + + =
+ + −
1
1
1
lim
2
1
11
x
x
x
xx
x
→−

+


= = −

− + + −


2) Ta có
-
( )
01fa=−
.
-
( )
( )
0 0 0
11
lim lim lim 2
11
x x x
xx
x
fx
x
x
− − −
→ → →
+−
= = =
−−
.
-
( )
00
4
lim lim 5 1
1
xx
x
f x a a
x
++
→→
−

= − + = −

+

.
Hàm số
( )
fx
liên tục tại
0
0x =
khi và chỉ khi.
( ) ( ) ( )
00
lim lim 0 1 2 3
xx
f x f x f a a
−+
→→
= = − = =
.
Bài 6. 1. Ta có
2
2
2
2
13
2 3 2
lim lim
3
12
4 1 2
41
xx
x
x
x x x
xx
x
xx
→− →−

− + +

++

= = −

+ − +
− + − +


.
2. Ta có
-
( )
11f =
.
-
( )
( )
2
11
lim lim 2 2
xx
f x ax x a
−−
→→
= + = +
.
-
( ) ( )
11
lim lim cos 1 1
xx
f x x
++
→→
= − =
.
Hàm số
( )
fx
liên tục tại
0
1x =
khi và chỉ khi.
( ) ( ) ( )
11
lim lim 1 2 1 1
xx
f x f x f a a
−+
→→
= = + = = −
.
3. Ta có hàm số
( )
4 3 2
2 15 25f x x x x x= − − − −
liên tục trên .
Mặt khác
( )
0 25 0f = −
.
( )
4 3 2
lim 2 15 25
x
x x x x
→−
− − − − = +
.
( )
4 3 2
lim 2 15 25
x
x x x x
→+
− − − − = +
.
Vậy phương trnh
4 3 2
2 15 25 0x x x x− − − − =
có ít nhất một nghiệm trên khoảng
( )
;0−
và có ít nhất một nghiệm trên khoảng
( )
0;+
.
Do đó phương trnh
4 3 2
2 15 25 0x x x x− − − − =
có ít nhất một nghiệm dương và một
nghiệm âm.
Bài 7. 1) a) Ta có
( )( )
2
3 3 3
3 3 1 1
lim lim lim
2 15 3 5 5 8
x x x
xx
x x x x x
→ → →
−−
= = =
+ − − + +
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
149
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
b) Ta có
( )
22
2
2
2
1 3 1 3
3 2 3 2
3 1 2 3
lim lim lim 2
11
3
33
x x x
xx
x x x x
xx
xx
x
xx
→− →− →−
+ − − + − −
+−
= = =
−+
− + − +
.
2) Ta có
-
( )
1
1
2
fm=−
.
-
( )
( )
11
11
lim lim
14
71
xx
fx
x
→→
−
= = −
+
Hàm số
( )
fx
liên tục tại
0
1x =
khi và chỉ khi.
( ) ( )
1
1 1 3
lim 1
2 14 7
x
f x f m m
→
−
= − = − =
.
Bài 8. 1. Ta có
( )
( )
( )( )
2
3 2 2
2
1
1 4 3 16
4 7 19 16 4 3 16 17
lim lim lim
5 8 3 1 5 3 5 3 2
x x x
x x x
x x x x x
x x x x x
→ →− →−
− − +
− + − − +
= = =
− + − − −
.
2. Ta có
-
( )
24fm=−
.
-
( ) ( )
22
lim lim 2 4
xx
f x x m m
−−
→→
= − = −
.
-
( )
2
22
4
lim lim 0
21
xx
x
fx
x
++
→→
−
==
+−
.
Hàm số
( )
fx
liên tục tại
0
2x =
khi và chỉ khi.
( ) ( ) ( )
22
lim lim 2 4 0 4
xx
f x f x f m m
−+
→→
= = − = =
.
3. Ta có hàm số
( )
4 3 2
2 15 25f x x x x x= − − − −
liên tục trên .
Mặt khác
( )
0 1 0f =
.
( )
2015 2
2014 2015
21
lim lim 4
xx
f x x m m x
xx
→− →−

= − + − + = −


. (Vì
2
40mm− +
với mọi
m
)
( )
4 3 2
lim 2 15 25
x
x x x x
→+
− − − − = +
.
Vậy phương trnh
( )
2 2015
4 2 1 0m m x x− + − + =
có ít nhất một nghiệm trên khoảng
( )
;0−
(nghiệm âm) với mọi giá trị của tham số
m
.
Bài 9. 1) a. Ta có
5
6
56
lim lim 3
3
32
2
xx
x
x
x
x
x
x
→+ →+

−

−

= = −
+

+


.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
150
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
b. Ta có
2
3
lim
2
x
x
x
+
→
−
= −
−
vì
( )
( )
2
2
lim 3 1 0
lim 2 0
2 0 khi 2
x
x
x
x
xx
+
+
→
→
− = −
−=
−
.
c. Ta có
( )
33
2
3
lim 3 2 lim 2
xx
x x x
x
→− →−

− = − = +


.
2) Ta có:
( )
1fm=
( )
( )( )
( )
( )
2
32
2
1 1 1 1
14
3 4 4 5
lim lim lim lim
1 1 3
11
x x x x
xx
x x x
fx
x x x
x x x
→ → → →
−+
+ − +
= = = =
− + +
− + +
.
Hàm số
( )
fx
liên tục tại
0
1x =
khi và chỉ khi
( ) ( )
1
5
lim 1
3
x
f x f m
→
= =
.
Bài 10. 1) a. Ta có
( )( )
( )( )
2
2
2 2 2
21
3 2 1 1
lim lim lim
4 2 2 2 4
x x x
xx
x x x
x x x x
→ → →
−−
− + −
= = =
− − + +
.
b. Ta có
(
)
22
22
22
lim \ lim lim 1
11
11
x x x
xx
x x x x
x x x x
x
xx
→+ →+ →+
+ − − = = =

+ + −
+ + −


.
2) Ta có
( )
53f =
,
( ) ( )
( )
2
55
lim lim 5 3 3
xx
f x x
−−
→→
= − + =
,
( )
( )
( )
( )
5 5 5
5 2 1 3
5
lim lim lim 3
25
2 1 3
x x x
xx
x
fx
x
x
+ + +
→ → →
− − +
−
= = =
−
−−
.
Suy ra
( ) ( ) ( )
55
lim lim 5
xx
f x f x f
−+
→→
==
nên hàm số đã cho liên tục tại
0
5x =
.
3) Ta có:
( )
3 6 1fm=+
,
( )
( )( )
2
3 3 3
32
56
lim lim lim 1
33
x x x
xx
xx
fx
xx
→ → →
−−
−+
= = =
−−
.
Hàm số đã cho liên tục tại
0
3x =
khi và chỉ khi
( ) ( )
3
lim 3 6 1 1 0
x
f x f m m
→
= + = =
.
Bài 11. 1) Ta có
( )
1
22
4
fm=+
;
( )
( )
( )
22
22
lim lim
2 2 2
xx
x
fx
xx
++
→→
+−
==
− + +
( )
( )
( )
2 2 2
2 2 1 1
lim lim lim
4
22
2 2 2
x x x
x
fx
x
xx
+ + +
→ → →
+−
= = =
++
− + +
.
Hàm số đã cho liên tục tại điểm
0
2x =
khi
11
20
44
mm+ = =
.
2) Đặt
( )
( )
25
1 3 1f x m x x= − − −
. Ta có,
( ) ( )
2
0 1, 1 1f f m= − − = +
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
151
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
Suy ra,
( ) ( )
2
0 . 1 1 0,f f m m− = − −
. Mặt khác, v
( )
fx
là hàm số đa thức liên tục trên
nên
( )
fx
liên tục trên
1;0−
. Do đó, phương trnh đã cho có ít nhất một nghiệm trong khoảng
( )
1;0−
với mọi giá trị của
m
. Vậy ta có đpcm.
Bài 12. 1) Tính các giới hạn
a)
2
2
2
2
19
3
3 9 3 0 0 3
lim lim
1
1 2 0 2 2
2
nn
nn
n
n
−+
− + − +
= = = −
−−
−
.
b)
( )
( )
( ) ( )
32
2
3
32
2
2
7
7
11
31
1 3 1
0 3 1 0
lim lim 9
2
3 2 3 0
3
nn
nn
n
n
−+
−+
−+
= = = −
−−
−
.
c)
(
)
( )
( )
2
2
2
2
31
lim 3 1 lim
31
xx
x x x
x x x
x x x
→− →−
− − − +
− + − + =
− − − +
2
58
lim
11
31
x
x
xx
xx
→−
−+
=
− − − +
2
8
5
5
lim
2
3 1 1
11
x
x
x x x
→−
−+
= = −
− + − +
.
2) Ta có
( )
16
2
3
f =−
.
( )
( )
( )
( )
2
2
2
2 2 2
4 7 10 2 7 10
4 16
lim lim lim
7 10 5 3
7 10
x x x
x x x x x x
x
x x x
xx
→ → →
− + − + + −
−
= = = −
− + −
−−
.
Ta thấy
( ) ( )
2
2 lim
x
f f x
→
=
. Vậy hàm số đã cho liên tục tại
0
2x =
.
3) Đặt
( )
42
4 2 3f x x x x= + − −
. Ta có,
( ) ( ) ( )
1 4, 0 3, 1 2f f f− = = − =
.
Suy ra,
( ) ( ) ( ) ( )
1 . 0 12 0, 0 . 1 6 0f f f f− = − = −
.
Vì
( )
fx
là hàm số đa thức liên tục trên nên
( )
fx
liên tục trên các đoạn
1;0−
và
0;1
.
Do đó, phương trnh
( )
0fx=
có ít nhất một nghiệm trên mỗi khoảng
( )
1;0−
và
( )
1;0
.
Vậy phương trnh đã cho có ít nhất hai nghiệm.
Bài 13. 1) Tính các giới hạn
a)
34
43
34
32
32
lim lim 0
2 5 2
2 5 2
1
n
nn
A
n n n
n n n
+
+
= = =
+ − +
+ − +
.
b)
1
1
36
2
lim lim
43
23
36
n
nn
n
n
n
B

−

−

= = = −
+

+


.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
152
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
c)
( )
( )
( )( )
2
3 2 2
2
3 3 3
3 2 1
2 5 2 3 2 1 11
lim lim lim
9 3 3 3 3
x x x
x x x
x x x x x
C
x x x x
→ → →
− + +
− − − + +
= = = =
− − + +
.
d)
(
)
22
2
2
2
1
1
4 1 4 1
lim 4 1 2 lim lim
4
11
4 1 2
42
x x x
x x x
x
D x x x
x x x
xx
→+ →+ →+
+
+ + −
= + + − = = =
+ + +
+ + +
.
2)
( )
2
khi 2
73
2 3 khi 2
x
x
y f x
x
ax x
−
==
+−
+
.
a) Khi
1a =
, ta được
( )
2
khi 2
73
2 3 khi 2
x
x
y f x
x
xx
−
==
+−
+
.
Ta thấy
( )
27f =
.
( ) ( )
22
lim lim 2 3 7
xx
f x x
−−
→→
= + =
.
( )
( )
( )
( )
2 2 2 2
2 7 3
2
lim lim lim lim 7 3 6
79
73
x x x x
xx
x
f x x
x
x
+ + + +
→ → → →
− + +
−
= = = − + − = −
+−
+−
.
Vì
( ) ( )
22
lim lim
xx
f x f x
−+
→→
nên hàm số đã cho không liên tục tại
2x =
.
b) Ta có
( ) ( )
2
2 lim 4 3
x
f f x a
−
→
= = +
.
( )
2
lim 6
x
fx
+
→
=−
.
Do đó hàm số đã cho liên tục tại
2x =
khi
9
4 3 6
4
aa+ = − = −
.
3) Đặt
( )
54
3 5 2f x x x x= − + −
. Ta có,
( ) ( ) ( ) ( )
0 2, 1 1, 2 8, 3 13f f f f= − = = − =
.
Suy ra,
( ) ( ) ( ) ( ) ( ) ( )
0 . 1 2 0, 1 . 2 8 0, 2 . 3 104 0f f f f f f= − = − = −
.
Mặt khác, v
( )
fx
là hàm đa thức liên tục trên nên
( )
fx
liên tục trên các đoạn
0;1 , 1;2 , 2,3
.Do đó, phương trnh
( )
0fx=
có ít nhất một nghiệm trên các khoảng
( ) ( ) ( )
0;1 , 1;2 , 2;3
.
Vậy phương trnh đã cho có ít nhất 3 nghiệm.
Bài 14. 1) Tìm các giới hạn
a)
5
5
lim
5
x
x
x
→
−
−
=0.
b)
( )
(
)
22
2
2 2 2
2
5 3 5 9 2 2
lim lim lim
23
53
2 5 3
x x x
x x x
x
x
xx
→− →− →−
+ − + − −
= = = −
+
++
+ + +
.
2) Ta có
( )
3 12 5fa=+
.
( )
( )( )
( )
2
3 3 3 3
31
43
lim lim lim lim 1 2
33
x x x x
xx
xx
f x x
xx
→ → → →
−−
−+
= = = − + = −
−−
.
Hàm số đã cho liên tục tại điểm
0
3x =
khi
7
12 5 2
12
aa+ = − = −
.
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
153
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
3) Đặt
( )
5 4 3
3 4 5f x x x x= − + −
. Ta có,
( ) ( )
0 5, 1 1ff= − =
.
Suy ra,
( ) ( )
0 . 1 5 0ff= −
.
Mặt khác, v
( )
fx
là hàm đa thức liên tục trên nên
( )
fx
liên tục trên các đoạn
0;1
.Do
đó, phương trnh
( )
0fx=
có ít nhất một nghiệm trên các khoảng
( )
0;1
.
Vậy phương trnh đã cho có ít nhất một nghiệm trong khoảng
( )
0;1
. Vậy ta có dpcm.
Bài 15. Ta có
( )
1 2 7fa= − +
( ) ( )
11
lim lim 2 7 2 7
xx
f x a a
++
→→
= − + = − +
( )
( )( )
( )
( )
( )
2
1 1 1 1
3 2 3 4 1 1
lim lim lim lim
2 3 1 4
2 2 1 3 2 2 1 3 2
x x x x
xx
fx
xx
x x x x x
− − − −
→ → → →
+ − + −
= − = =
−+
− − + + − + +
.
Hàm số đã cho liên tục tại
0
1x =
khi
1 27
27
48
aa− + = =
. Vậy
27
8
a =
là giá trị cần tìm.
Đặt
( )
( )
23
3 3 2 3 0f x m m x x= − + + − =
.
Ta có
( )
03f =−
,
( )
2
2
3
2 8 24 25 8 7 0
2
f m m m m

= − + = − +


. Suy ra
( ) ( )
0 2 0f f m
.
Mặt khác, vì
( )
fx
là hàm đa thức liên tục trên nên
( )
fx
liên tục trên đoạn
0;2
.
Do đó phương trnh
( )
0fx=
luôn có ít nhất một nghiệm trong khoảng
( )
0;2
với mọi
m
.
Vậy ta có đpcm.
Bài 16. Tính các giới hạn
a)
(
)
22
22
22
1
lim 1 lim
1
xx
x x x
x x x
x x x
→− →−
+ − −
+ − + =
+ + +
2
1
lim
11
11
x
x
xx
xx
→−
−
=
+ + +
2
1
1
1
lim
2
11
11
x
x
xx
→−
−
= = −
− + − +
.
b)
( )
3 3 3
0 0 0
sin
sin
sin 1 cos
tan sin
cos
lim lim lim
4 4 cos .4
x x x
x
x
xx
xx
x
x x x x
→ → →
−
−
−
==
2
3
0
sin .2sin
2
lim
cos .4
x
x
x
xx
→
=
2
2
0
sin
1 sin 1
2
lim . .
8cos 8
2
x
x
x
xx
x
→



==






Ta có
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
154
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
( )
2
17f m m=+
( )
( )
2 2 2
11
lim lim 7 7
xx
f x m x mx m m
−−
→→
= + = +
( )
( )
( )
( )
1 1 1 1
1 8 3
1
lim lim lim lim 8 3 6
89
83
x x x x
xx
x
f x x
x
x
+ + + +
→ → → →
− + +
−
= = = − + − = −
+−
+−
Do đó, hàm số đã cho liên tục tại
0
1x =
khi
22
1
7 6 7 6 0
6
m
m m m m
m
=−
+ = − + + =
=−
.
Vậy
1, 6mm= − = −
là các giá trị cần tìm.
Đặt
( )
( )
14 2 15
3 7 5f x mx m x= − + −
.
Ta có
( ) ( )
2
22
17
0 5, 1 3 2 2 0
24
f f m m m m m

= − − = + + = + + +


. Suy ra
( ) ( )
1 0 0f f m−
.
Mặt khác, vì
( )
fx
là hàm số đa thức liên tục trên nên liên tục trên đoạn
1;0−
.
Do đó phương trnh
( )
0fx=
có ít nhất một nghiệm trong khoảng
( )
1;0−
.
Vậy phương trnh đã cho luôn có ít nhất một nghiệm với mọi
m
.
| 1/154
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
CHƯƠNG 4 GIỚI HẠN Mục lục
BÀI 1. GIỚI HẠN CỦA DÃY SỐ ................................................................................................. 1
A. TÓM TẮT LÝ THUYẾT .................................................................................................... 2
B. DẠNG TOÁN VÀ BÀI TẬP ............................................................................................... 3
C. BÀI TẬP RÈN LUYỆN ..................................................................................................... 22
BÀI 2. GIỚI HẠN CỦA HÀM SỐ .............................................................................................. 25
A. TÓM TẮT LÝ THUYẾT .................................................................................................. 25
B. DẠNG TOÁN VÀ BÀI TẬP ............................................................................................. 26
C. BÀI TẬP RÈN LUYỆN ..................................................................................................... 70
BÀI 3. HÀM SỐ LIÊN TỤC ...................................................................................................... 113
A. TÓM TẮT LÝ THUYẾT ................................................................................................ 113
B. DẠNG TOÁN VÀ BÀI TẬP ........................................................................................... 114
C. BÀI TẬP RÈN LUYỆN ................................................................................................... 138
BÀI 4. ÔN TẬP CHƯƠNG IV .................................................................................................. 139
A. BÀI TẬP .......................................................................................................................... 139
B. LỜI GIẢI.......................................................................................................................... 145 1
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
BÀI 1. GIỚI HẠN CỦA DÃY SỐ
A. TÓM TẮT LÝ THUYẾT
Định nghĩa 1 (Giới hạn bằng 0 ). Ta nói dãy số (u có giới hạn là 0 nếu với mỗi số dương nhỏ tùy ý n )
cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều có giá trị tuyệt đối nhỏ hơn số
dương đó. Khi đó ta viết lim u = 0 hay limu = 0 hay u → 0 khi n → + . n n n n→+
Định nghĩa 2 (Giới hạn bằng a ). Ta nói dãy số (u có giới hạn là số thực a nếu lim(u − a = . Khi n ) 0 n )
đó ta viết lim u = a hay limu = a hay u → a khi n → + . Dãy số có giới hạn là số a hữu hạn gọi là n n n n→+
dãy số có giới hạn hữu hạn.
Định nghĩa 3 (Giới hạn vô cực).
1. Ta nói dãy số (u có giới hạn là + khi n → + nếu u có thể lớn hơn một số dương bất kỳ, n ) n
kể từ một số hạng nào đó trở đi.
Ký hiệu: limu = + hay u → + khi n → + . n n
2. Dãy số (u có giới hạn là − khi n → + nếu lim( u − = + . n ) n )
Ký hiệu: limu = − hay u → − khi n → + . n n
GIỚI HẠN HỮU HẠN GIỚI HẠN VÔ CỰC
Các giới hạn đặc biệt
Các giới hạn đặc biệt • 1 • k * = +  lim n , (k ). lim = 0, k  . k ( * ) n • n =  • lim q 0, (q )1. lim n q = 0, ( q  ) 1 .
• limC = C , (C  )
Định lí 1. Nếu limu = a và limv = b thì Định lí 2. n n
• lim(u v = a b .
• Nếu limu = a và limv =  thì n n ) n n • u
lim(u v = a b . n = . n n ) lim 0 vn • u a lim n = (b  0).
• Nếu limu = a  0 và limv = 0 và v b n n n • u
Nếu u  0, n
 và limu = a thì a  0 v  0, n
 thì lim n = + . n n n vn và lim u = a . n
• Nếu limu = + và limv = a  0 thì n n
lim(u v = + . n n )
Định lí 3 (Nguyên lý kẹp). Cho ba dãy số (u ),(v ), w . Lúc đó, nếu u v w , n  và n n ( n ) n n n
limu = lim w = a , a
thì limv = a . n n ( ) n
Định nghĩa 4. Cấp số nhân (u có công bội q được gọi kà cấp số nhân lùi vô hạn nếu q 1. n )
Nhận xét. Cho cấp số nhân lùi vô hạn (u có công bội q . Với mỗi * n
, đặt S = u + u + ...+ u . Lúc n ) 1 2 n đó: u1 lim S = n (4 ) .1 1 − q
Định nghĩa 5. Giới hạn ( )
4.1 được gọi là tổng của cấp số nhân lùi vô hạn (u và được ký hiệu là n ) 2
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
S = u + u + ... + u 1 2 n Như vậy: u1 S = lim S = , q n ( )1 1 − q
B. DẠNG TOÁN VÀ BÀI TẬP P (n)
Dạng 1. Tính giới hạn L = lim
với P(n),Q(n) là các đa thức. Q (n) Phương pháp giải:
Rút lũy thừa bậc cao nhất của tử và mẫu, rồi sử dụng các công thức: • * = +  • c lim k n (k ). = ( * lim 0, k  , c  . k ) n limu = −  = + • n
 lim(u v = − . n n ) • limu n
 lim(u v = + . lim v = a  0  n n ) n lim v = a  0  n limu = −  = + • n
 lim(u v = + . n n ) • limu n
 lim(u v = − . lim v = a  0  n n ) n limv = a  0  n VÍ DỤ 2 4n n 1
Ví dụ 1. Tính giới hạn L lim . ĐS: L = 2 2 3 2n Lời giải  1 1  2 1 1 n 4 − −   − − 2 4 2  n n  4 − 0 − 0 Ta có = lim = lim n n L = = 2 .  3  3 + 2 0 2 n + 2 + 2   2 2  nn P (n)
Nhận xét: Nếu bậc tử P (n) bằng bậc mẫu Q(n) thì lim
= (Hệ số bậc cao nhất của tử) Q (n)
(Hệ số bậc cao nhất của mẫu). 5 4 2 2n n 4n 1
Ví dụ 2. Tính giới hạn L lim . ĐS: 128 L = 4 6 2 20n 2n n 1 5 Lời giải 5 4   1    2  2 n 2 − n 4 −         n    n  Ta có L = lim 4   3 1  6 2 20n n 2 − +    2    n n  3
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 5 4 5 4  1   2   1   2  10 4 n 2 − n 4 − 2 − 4 −          n   n   n   n  (2−0)5 (4−0)4 128 = lim = lim = lim = 4 4  3 1   3 1  20(2 − 0 + 0)4 5 6 8 20n n 2 − + 20 2 − +     2 2  n n   n n
Nhận xét: Với bài toán có lũy thừa bậc cao, ta thường rút bậc cao trong từng dấu ngoặc, sau đó áp dụ n ng công thức ( . ) n = . n a b
a b và tính toán như các bài trước. 2 n − n + 3
Ví dụ 3. Tính giới hạn L = lim . ĐS: L = 0 3 n + 2n Lời giải  1 3  2  1 3  n 1− +   − + 2 1  2  n n  1  1− 0 + 0 Ta có = lim = lim . n n L  = 0. = 0  2  n 2 + 3 1 0 n 1+  1+    2 2  n   nP(n)
Nhận xét: Nếu bậc tử P (n) nhỏ hơn bậc mẫu Q (n) thì L = lim = 0 Q(n) 3 2n −11n +1
Ví dụ 4. Tính giới hạn L = lim . ĐS: L = + 2 n − 2 Lời giải  11 1  3  11 1  n 2 − +   − + 3 2  3 n n    = lim = lim . n n L n  = +  2  2 2 n 1−  1−    2 2  n   n   11 1  2 − +  3 
(vì lim n = + và lim n n   = 2  0 ). 2  1−  2  nP(n)
Nhận xét: - Nếu bậc tử P (n) lớn hơn bậc mẫu Q (n) thì L = lim =  . Q(n)
- Để biết là + hay − ta dựa vào dấu của giới hạn trong tích theo quy tắc “cùng
dấu thì tích dương, trái dấu thì tích âm”. Thông thường, sẽ để dấu =  và xét dấu
sẽ điền vào sau.
- Về trắc nghiệm, đó chính là tích của hệ số bậc cao nhất của tử và mẫu. 1+ 3 + 5 + 7 + (2n +1)
Ví dụ 5. Tính giới hạn L = lim . ĐS: 1 L = 2 3n + 4 3 Lời giải
Xét cấp số cộng 1,3,5, 7,9,..., 2n +1 có số hạng đầu tiên u = 1 công sai d = 2 và số hạng cuối 1
cùng là u = 2n +1ta có: m
u + (m −1)d = 2n +1  1+ 2(m −1) = 2n +1  m = n +1. 1 4
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
Vậy cấp số cộng có n +1 số hạng. Suy ra tổng m n +1 2 S = 1+ 3 + 5 + 7 +
+ 2n +1= (u + u ) =
(1+ 2n +1) = n + 2n +1 1 2 m 2 2 1 2 2 1 n 1 2 2 1 2 n 2n 1 n n 1 0 0 1 Vì thế lim lim lim n n L . 2 3n 4 4 4 2 3 0 3 n 3 3 2 2 n n
Nhận xét: Cần nhớ công thức cấp số cộng: u
− u = d , với d là công sai. k 1 + k
u = u + n −1 d , với d là công sai. n 1 ( ) u u 2u , k 2 . k 1 k 1 k n S u u u u u . n 1 2 n 1 2 n  1 1 1 1 1 
Ví dụ 6. Tính giới hạn L = lim  + + + + +  ĐS: L = 1 n (n +  ) . 1.2 2.3 3.4 4.5 1  Lời giải 1 1 1 Số hạng tổng quát = − ;( k
 =1,2,..., n) do đó k(k+1) k k +1  1 1 1 1 1 1 1 1  L = lim 1− + − + − + − + −    2 2 3 3 4 4 n n +1   1   n  1 1 = lim 1− = lim = lim = =1     n +1  n +1 1  1+ 0 1+ n 1 a b 1 1
Nhận xét: Phân tích = + a = =1;b = = 1 − k (k + ) 1 k k + với 1 k + . 1 k k =0 k = 1 −
BÀI TẬP ÁP DỤNG
Bài 1. Tính giới hạn sau: 2 3n n 5 3 n n 3 a) L lim ; b) L lim ; 2 2n 1 3 3 2n 3n 1 2 9 3 4 6n 2n 1 2n 1 n 2 c) L lim ; d) L lim ; 3 2 5n n n n 1 17 n 1 2 3 3 2 2n 1 3 4n 2 3n 1 2n 5 9n 4 e) L lim ; f) L lim ; 3 2 4 4n 2 2 n 3 2 2n 4 2n 1 2n 7 5
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2 n 2 n 1 g) L lim . 2 2 n 1 2n 3
Bài 2. Tính giới hạn sau: 3 2 7n + 2n +1 7n + 3 a) L = lim ; b) L = lim ; 4 3
n + 5n + n 2 3 2n + 3n + 4 2 n + 4n − 5 3 2 2 − n + 3n + 4 c) L = lim ; d) L = lim ; 3 2 3n + n + 7 4 3
n + 4n + n 2 2 − n + n + 2 e) L = lim . 4 3n + 5
Bài 3. Tính giới hạn sau: 3 n − 5n + 3 4 3 2
5n − n + 5n + 3 a) L = lim ; b) L = lim ; 2 3n + n −1 2 3 n − 3n −1 4 2 3n + 2n −1 5 4
3n − 2n + 2n + 7 c) L = lim ; d) L = lim ; 3 n + 2n + 9 4 3 2 6
− n + 2n + n −1
Bài 4. Tính giới hạn sau: 1+ 2 + 3 + ... + n
1+ 3 + 5 + 7 + ... + (2n − ) 1 a) L = lim ; b) L = lim ; 2 3n +1 2 n + 3n +1 1+ 2 + 3 + ... + n
5 + 9 +13 + ... + (4n − 3) c) L = lim ; d) L = lim ; 2 2n − n + 9 2 3n + 5n −1
1− 2 + 3 − 4 + ... + (2n − ) 1 − 2n 1 1 1 1 e) L = lim ; f) L = lim[ + + +...+ ]; 2n +1 1.3 2.4 3.5 n (n + 2) 1 1 1 1 g) L = lim[ + + +...+ ] ; 1.3 3.5 5.7 (2n− ) 1 (2n + ) 1 1 1 1 1 h) L = lim[ + + +...+ ] . 1.3 3.5 5.7 (2n− ) 1 (2n + ) 1  LỜI GIẢI 1 5 2 1 5 n 3 2 2 3 2 3n n 5 n n 3 0 0 3 Bài 1. a) lim lim lim n n L . 2 2n 1 1 1 2 2 0 2 n 2 2 2 2 n n 6
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 1 3 3 n 1 1 3 3 2 3 1 n n 3 n n 2 3 1 b) L lim lim lim n n . 2 3 2n 3n 1 2 1 2 1 3 3 n 3 3 3 n n 3 n n 2 1 3 2 1 n 6 3 3 2 3 6 2 3 6n 2n 1 6n 2n 1 n n 3 c) lim lim lim lim n n L . 3 2 3 2 5n n n n 1 4n n n 1 1 1 1 3 2 n 4 4 2 2 n n n n 2 9 2 9 1 2 1 2 8 9 2 9 4 n 2 n 1 2 1 4 4 2n 1 n 2 n n n n d) L lim lim lim 17 n 1 1 1 17 n 1 1 17 17 n n 2 9 (2 + 0) .(1+ 0) = lim = 4 . 1+ 0 2 2  1   3   1   3  ( n − n − − − 2n − ) 1 (3− 4n ) 2 3 2 3 2 4 2 4         3 3  n   n   n   n  e) L = lim = = ( 4n + 2) lim lim 3 (2 − n)2 3 2 3 2  2   1   2   1  3 2 n 4 + n 2 − 4 + 2 −          n   n   n   n  2 2 0 0 4 1 lim . 3 2 4 0 2 0 4 (3n − )3 1 (2n + 5)2 2 (9n+ 4) f) L = lim ( 2n − 4)4 ( 3 2n + ) 1 ( 2 2n − 7) 3 2   3 2 1    5   4        2 1 5 4 n 3 − n 2 + n 9 +         3 − 2 + 9 +       2   n    n   n  2  n   n   n L = lim = lim 4  4 4   1   7   4   1  7  4 3 2 n 2 − n 2 + n 2 −       2 − 2 + 2 −      3 2  n   n   n  3 2  n   n  n  3 2 3 0 2 0 9 0 243 lim . 4 2 0 2 0 2 0 16 3 3 (        n + n − + − n + 2) 2 1 2 1 (n− ) 2 3 3 2 1 1 1 1        2 2 1  n   n   n  n  g) L = lim = lim = lim ( n + ) 1 (2n + 3)2 2 2 2  1   3   1  3  4 n 1+ n 2 + 1+ 2 +        2 2  n   n   n  n  3 1 0 1 0 1 lim . 2 1 0 2 0 4 7
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  2 1  3  2 1  n 7 + +   + + 3 2 3 7 7n + 2n +1  n n   3 1  Bài 2. a) L = lim = lim = lim . n n = 0 4 3
n + 5n + n  5 1  n 5 1 4 n 1+ +    1+ +  3  n n  3  n n  2 1 7 1 3 (Vì lim 0; và lim n n 7 ). n 5 1 1 3 n n 3 3 n 7 7 7n 3 n 1 b) L lim lim lim . n 0 2 3 2n 3n 4 2 2 4 n 2 4 3 n 3 3 3 3 n n n n 3 7 1 7 (Vì lim 0 và lim n ). 2 n 2 4 3 3 3 n n  4 5  2   n 1+ −   4 5 + − 2 2 1 n + 4n − 5  n n   2 1  c) L = lim = lim = lim . n n  = 0 3 2 3n + n + 7  1 7  n 1 7 3 n 3 + +    3 + +  3  n n  3  n n  4 5 1+ − 1 2 1 (Vì n n lim = 0 và lim = ). n 1 7 3 3 + + 3 n n  3 4  3 n 2 − + +   3 2 2 − n + 3n + 4 3  n n  d) L = lim = lim 4 3 n + 4n + n  4 1  4 n 1+ +   3  n n  3 4 3 4 2 2 3 1 1 3 lim . n n 0 (Vì lim 0 và n n lim 2 ). n 4 1 4 1 1 n 1 3 n n 3 n n  1 2  2  1 2  n 2 − + +   − + + 2 2 2 − n + n + 2 2  2 n n 1    e) L = lim = lim = lim . n n  = 0. 4 3n + 5 2  5  n 5 4 n 3 +  3 +    4 4  n   n  1 2 2 1 2 2 (Vì lim 0 và lim n n ). 2 n 5 3 3 4 n 8
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  5 3  3  5 3  n 1− +   − + 3 2 3 1 − +  2 3 n 5n 3  n n   Bài 3. a) = lim = lim = lim . n n L n  = + 2 3n + n −1  1 1  1 1 2 n 3 + −  3+ −    2 2  n n   n n  5 3 1− + 2 3 1
(Vì lim n = + và lim n n = ). 1 1 3 3 + − 2 n n  1 5 3  4  1 5 3  n 5 − + +   − + + 4 3 2 2 4 5 − + +  2 4 5n n 5n 3  n n n   b) = lim = lim = lim . n n n L n  = − . 2 3 n − 3n −1  1 1  1 1 3 n − 3 −  − 3−    3 3  n n   n n  1 5 3 5 − + + 2 4 5
(Vì lim n = + và lim n n
n = − ). 1 1 3 − 3− 3 n n  2 1  4  2 1  n 3 + −   + − 4 2 2 4 3 + −  2 4 3n 2n 1  n n   c) = lim = lim = lim . n n L n  = + . 3 n + 2n + 9  2 9  2 9 3 n 1+ +  1+ +    2 3 2 3  n n   n n  2 1 3 + − 2 4
(Vì lim n = + và lim n n = 3). 2 9 1+ + 2 3 n n  2 2 7  5  2 2 7  n 3 − + +   − + + 5 4 4 5 3 − + +  4 5 3n 2n 2n 7  n n n   d) = lim = lim = lim . n n n L n  = − . 4 3 2 6
− n + 2n + n −1  2 1 1  2 1 1 4 n 6 − + + −  6 − + + −    2 4 2 4  n n n   n n n  2 2 7 3 + + + 4 5 1
(Vì lim n = + và lim n n n = − ). 2 1 1 2 6 − + + − 2 4 n n n n (n + ) 2 1 n + n Bài 4.
a) Theo tính chất của cấp số cộng, ta có 1+ 2 + 3 + ... + n = = 2 2 2 + 2 1 2 1+ 2 + 3 + ... + n n + 2 1 Do đó = lim = lim = lim n L = . 2 2 3n +1 6n + 2 2 6 6 + 2 n (1+ 2n−1 )n
b) Theo tính chất của cấp số cộng, ta có 1+ 3 + 5 + 7 + ... + (2n − ) ( ) 2 1 = = n 2 9
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
1+ 3 + 5 + 7 + ... + (2n − ) 2 1 Do đó n 1 L = lim = lim = lim =1. 2 2 n + 3n +1 n + 3n +1 3 1 1+ + 2 n n n (n + ) 2 1 n + n
c) Theo tính chất của cấp số cộng, ta có 1+ 2 + 3 + ... + n = = 2 2 1 + 2 1 1+ 2 + 3 + ... + n n + n 1 Do đó = lim = lim = lim n L = . 2 2 2n − n + 9 4n − 2n +18 2 18 4 4 − + 2 n n
d) Xét cấp số cộng với u = 5; d = 4 1 + n − n −  u = 5+ n −
= n −  + + + + n − = = n − n − n−
( 2)4 4 3 5 9 13 ... (4 3) (5 4 3)( ) 1 2 2 1 1 2 1 1 − −
5 + 9 +13 + ... + (4n − 3) 2 2 2 2n − n −1 2 Do đó = lim = lim = lim n n L = . 2 2 3n + 5n −1 3n + 5n −1 5 1 3 3 + − 2 n n e) Ta có
1− 2 + 3 − 4 + ... + (2n − )
1 − 2n = (1− 2) + (3 − 4) + ... + ((2n − ) 1 − 2n) = (− ) 1 + (− ) 1 + ... + (− ) 1 = −n
1− 2 + 3 − 4 + ... + (2n − ) 1 − 2n − − Do đó n 1 1 L = lim = lim = lim = − . 2n +1 2n +1 1 2 2 + n 1 1 1 1 1 1 1 1 1 1 1  f) Ta có + + +...+ = − + − + + −   n (n + ) ... 1.3 2.4 3.5 2 2 1 3 2 4 n n + 2  1  1 1 1  3 1 1 = 1+ − − = − −   2  2 n +1 n + 2  4 2n + 2 2n + 4 1 1 1 1  3 1 1  3 Do đó L = lim[ + + +...+ ]=lim − − =   . 1.3 2.4 3.5 n (n + 2)
 4 2n + 2 2n + 4  4 g) Ta có 1 1 1 1 1 1 1 1 1 1 1  1  1  + + +...+ ( = − + − + + − = −     n − )( n + ) ... 1 1.3 3.5 5.7 2 1 2 1 2 1 3 3 5 2n −1 2n +1  2  2n +1  1 1 1 1 1  1  1 Do đó L = lim[ + + +...+ ( − =   .
n − )( n + ) ]= lim[ 1 ] 1.3 3.5 5.7 2 1 2 1 2  2n +1  2 1 1 1 1 h) Ta có + + +...+ 1.4 4.7 7.10 (3n−2)(3n+ ) 1 1  1 1 1 1 1 1 1  = 1  1  1− + − + − +...+ +   = 1−   . 3  4 4 7 7 10 3n − 2 3n +1  3  3n +1  10
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC P (n)
Dạng 2. Tính giới hạn dạng L = lim
với P (n),Q (n) là các hàm mũ n a . Q (n) Phương pháp giải: Áp dụng lim n
q = 0 với q  1 .
Sử dụng công thức mũ, rồi chia cả và mẫu cho n
a với a là cơ số lớn nhất.
Công thức mũ cần nhớ m − a m+n m = . n a
a a và m n a = . n a VÍ DỤ n n+2 − + Ví dụ 1. 1 3 4.5
Tính giới hạn L = lim . ĐS: L = 20 n 1 + n+2 n 1 2 + 3 + 5 + Lời giải
Chia cả tử và mẫu cho 5n , ta có n n 1 3n  1   3  − +100 − +100     5n 5n  5   5  0 − 0 +100 L = lim = lim = = 20. 2n 3n n n  2   3  0 + 0 + 5 2. + 9. + 5 + + n n 2. 9. 5     5 5  5   5 
Nhận xét: Ta chia cho n
a với a là cơ số lớn nhất vì sau khi chia luôn tạo ra cơ số có trị tuyệt
đối nhỏ hơn 1 để áp dụng công thức lim n
q = 0 với q  1 . 2 3 n + + + + + Ví dụ 2. 1 2 2 2 ... 2
Tính giới hạn L = lim . ĐS: 2 L = 5.2n +1 5 Lời giải Xét cấp số nhân 2 3
1, 2, 2 , 2 ,..., 2n có số hạng đầu tiên u = 1 , công bội q = 2 và có số hạng tổng 1 quát n m 1 u 2 u q − = 
= 2n m −1= n m = n +1. m 1
Suy ra tổng các số hạng của cấp số nhân trên là: m n 1 q −1 2 + −1 + n 1 S = u = = 2 −1. m 1 q −1 2 −1 Suy ra n  1  2 −   n 1 2 + −1  2  2 − 0 2 L = lim = lim = = . 5.2n +1 n  1  5 + 0 5 5 +    2 
Nhận xét: Các công thức cần nhớ về cấp số nhân 11
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC u n q −1 1
1. k+ = q ( q là công bội).
2. S = u + u + ... + u = u . . u n 1 2 n 1 q −1 k 1 3. n u u q − = . 2 4. u .u
= u với k  2 . n 1 k 1 + k 1 − k
BÀI TẬP ÁP DỤNG Bài 1.
Tính các giới hạn sau: n n 1 4.3 5 + + n+2 n 1 4 + 6 + a) L = lim . ĐS: L = 5. b) L = lim . L = . 3.2n + 5n n 1 − n+3 5 + ĐS: 1 2.6 72 n n−2 n+2 2 − 3 + 3.5 n n n+2 2 − 3 + 5 c) L = lim . ĐS: L =15 . d) L = lim . L = . n 1 − n+2 n 1 2 + 3 + 5 + n 1 + n+2 n 1 + 2 + 3 + ĐS: 5 5 ( )n n 1 n 3 4.5 + − − 2n + ( 5 − ) e) L = lim . L = − . f) L = lim . ĐS: 1 L = . 2.4n + ĐS: 20 3.5n 3 n 2.3n + 3.( 5 − ) 3 (− )n 5n 1 1 .2 + g) L = lim . ĐS: L = 0 . 5n+2 3 Bài 2. Tính các giới hạn sau: 2 3 1+ 2 + 2 + 2 + ... + 2n a) L = lim . L = . 2 3 1+ 3 + 3 + 3 + ... + ĐS: 0 3n 1 1 1 1+ + +...+ n b) 2 4 2 L = lim . ĐS: 4 L = . 1 1 1 1+ + +...+ 3 3 9 3n LỜI GIẢI n  3  4. + 5 n n 1   4.3 5 + +  5  0 + 5 Bài 1. a) L = lim = lim = = 5. 3.2n + 5n n  2  0 +1 3. +1    5  n  2  16. + 6   n+2 n 1 4 + 6 +  3  0 + 6 1 b) L = lim = lim = = . n 1 − n+3 5 + 2.6 n 1  5  0 + 432 72 . + 432   5  6  n n  2  1  3  − . + 75     n n−2 n+2 2 − 3 + 3.5  5  9  5  0 − 0 + 75 c) L = lim = lim = =15 . n 1 − n+2 n 1 2 + 3 + 5 + n n 1  2   3  0 + 0 + 5 . + 9. + 5     2  5   5  12
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC n n  2   3  − + 25     n n n+2 2 − 3 + 5  5   5  0 − 0 + 25 d) L = lim = lim = = 5. n 1 + n+2 n 1 2 + 3 + 5 + n n  2   3  0 + 0 + 5 2. + 9. + 5      5   5  n  3  ( − − n   3 − ) n+ 20 1 − 4.5  5  0 − 20 20 e) L = lim = lim = = − . 2.4n + 3.5n n  4  0 + 3 3 2. + 3    5  n 2 n n 1 2 5 5 0 1 1 f) L lim lim . n n 2.3n 3. 5 3 0 3 3 2. 3 5 n n  1   32  (− ) − n n+ .2. 5 1     1 .2  243   243  0 g) L = lim = lim = = 0 . 5n+2 3 9 9 Bài 2.
a) Áp dụng công thức tính tổng của một cấp số nhân, ta lần lượt có n 1 + − n 2 1 2 3 n 1 1+ 2 + 2 + 2 + ... + 2 = = 2 + −1 2 −1 n 1 + n 1 + − − n 3 1 3 1 2 3 1+ 3 + 3 + 3 + ... + 3 = = 3 −1 2 n n  2   1  2. −     n 1 2 + −1 2.2n −1  3   3  0 − 0 Do đó L = lim = 2.lim = 2.lim = 2. = 0. n 1 3 + −1 3.3n −1 n  1  3 − 0 3 −   2  3 
b) Áp dụng công thức tính tổng của một cấp số nhân, ta lần lượt có n 1 +  1  −1   n 1 1 1  2      1+ + +...+ = = −  −    n ( 2) 1 1 . 1 2 4 2 1 2  2  −1   2 n 1 +  1  −1   n 1 1 1  3  3 1 1      1+ + +...+ = = −    . −1    3 9 3n 1  2  3  3  −1   3 n (     2 − ) 1 1  . −1 1    .0 −1 2  2    4 4 Do đó 2 L = lim = . = . n   3 1 3  3  1  1  .0 −1 −    . −1    3  2  3  3    13
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
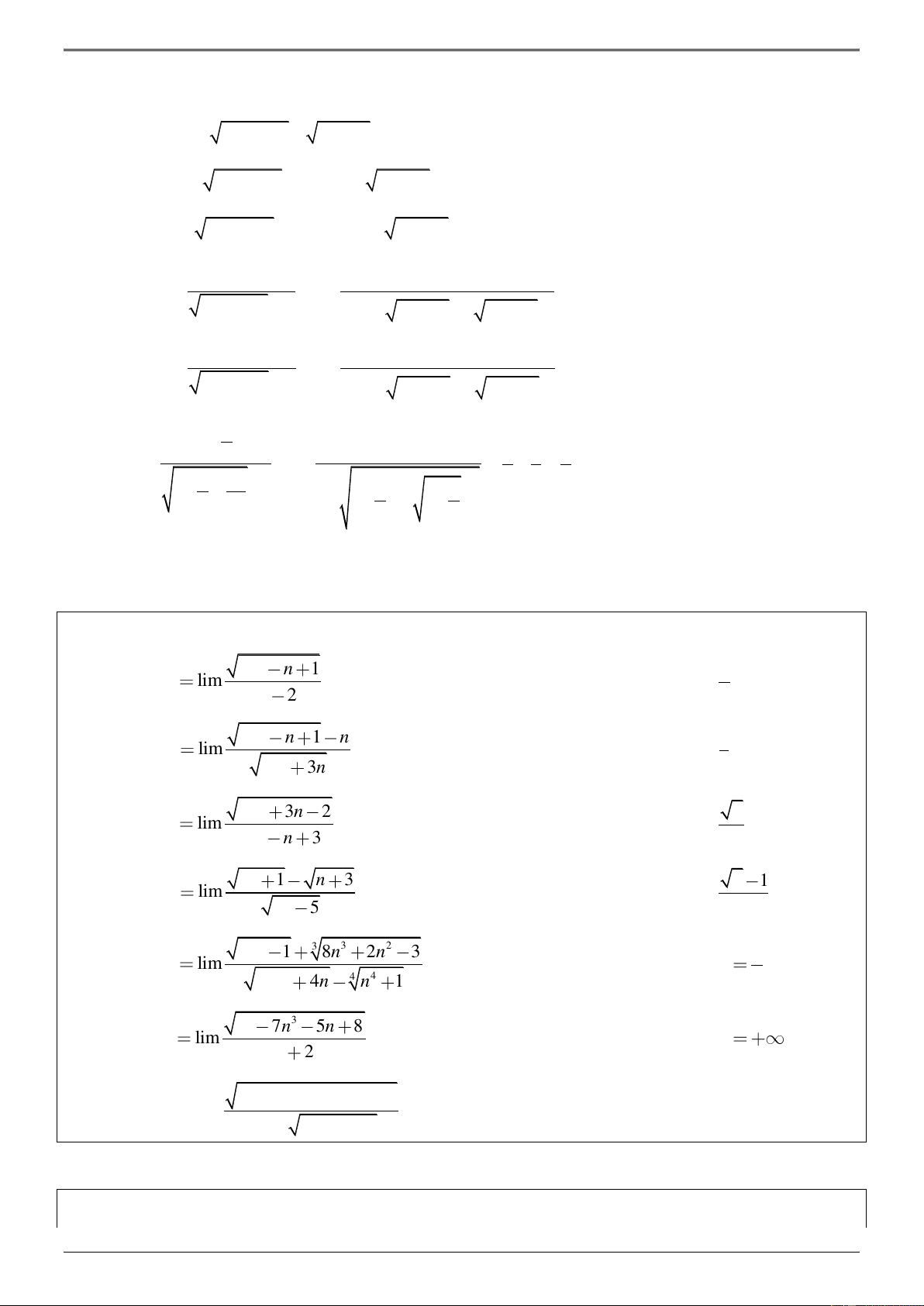
Dạng 3. Tính giới hạn của dãy số chứa căn thức.
Phương pháp giải: Rút lũy thừa bậc cao hoặc liên hợp và sử dụng lim k n =  .
Lưu ý: Dấu hiệu nhận dạng liên hợp (dạng .0
+ ) là sau khi rút n có mũ cao trong căn và nhóm thừa
số, xuất hiện số 0 . Chẳng hạn:
- Tính giới hạn dãy 2 u =
n + 3n + 5 − n : biểu thức trong căn có 2
n là lũy thừa cao nhất và n
ta quan tâm đến nó, những hạng tử sau bỏ hết, có nghĩa ta xem 2 u =
n − n = n − n = 0 n
nên cần liên hợp.
- Tính giới hạn dãy 2 u =
2n + 3n + 5 − n : biểu thức trong căn có 2
2n là lũy thừa cao nhất n nên nháp 2
2n − n = n 2 − n = n ( 2 − )
1 , có 2 −1  0 nên ta không cần liên hợp mà rút ra giải trực tiếp. VÍ DỤ
Ví dụ 1. Tính giới hạn L = ( 2 lim
2n + 3n + 5 − n). ĐS: L = + . Lời giải  2 
 2n + 3n + 5   3 5   3 5  Ta có: 2
L = lim  n
 − n = lim n 2 + +
− n = limn 2 + + −1 2   n    2   2    n n   n n    3 5 
Vì lim n = + và lim  2 + + −1 = 2 −1 0  nên L . 2  n n  
Ví dụ 2. Tính giới hạn L = ( 2 lim
9n + 3n − 4 − 3n + 20). ĐS: 41 L = . 2 Lời giải 3n 4 Ta có: 2 L lim 20 lim 9n 3n 4 3n 20 lim 2 9n 3n 4 3n 4 n 3 4 3 n 20 lim 20 lim n 3 4 3 4 n 9 3n 9 3 2 n n 2 n n 3 0 41 20 . 9 0 0 3 2 (a −b  )(a +b) 2 2 = a − b
Cần nhớ : Liên hợp là hình thức trục căn dựa vào HĐT ( . a b  )  ( 2 2 a ab + b ) 3 3 = a b − + ➢ a b a b a − b = . 3 3 a + b = . a + b 3 2 3 3 2
a − ab + b 2 − 3 a − b ➢ a b a − b =
. 3 a − b = . a + b 3 2 3 2
a + ab + b 14
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC − 3 + ➢ a b a b 3 3 a − b =
. 3 a + b = . 3 2 3 3 2
a + ab + b 3 2 3 2
a − ab + b
Ví dụ 3. Tính giới hạn L = (3 3 lim
n + 2 − n ) ĐS: L = 0 . Lời giải n 2 n 2 Ta có: L lim lim 2 2 2 3 3 3 3 n 2 n 2 n n 2 2 2 3 3 3 3 n 1 n 1 n n n n 2 3 2 2 n 0 lim lim 0 . 2 2 3 2 2 2 2 3 2 3 3 3 3 n 1 1 1 1 1 1 n n n n − Cần nhớ: a b 3 3 a − b = . 3 2 3 3 2
a + ab + b
Ví dụ 4. Tính giới hạn L = im l (3 3 2
8n + 3n − 2 + 5 − 2n) . ĐS: 21 L = . 4 Lời giải Ta có: 3 3 2 L l m i 8n 3n 2 5 2n 3 3 2 lim5 lim 8n 3n 2 2n 3 2 3 8n 3n 2 8n 3 3 2 5 lim 8n 3n 2 2n 5 lim 2 3 3 2 3 3 2 2 8n 3n 2 8n 3n 2 2n 4n 2 3n 2 5 lim 2 3 2 3 2 3 3 2 3 n 8 n 8 .2n 4n 3 3 n n n n 2 3 2 3 21 5 lim n 5 . 2 3 2 3 2 4 4 4 4 3 3 8 8 2 4 2 3 n n n n 3 − Cần nhớ: a b 3 a − b =
. Trong lời giải trên, đã sử dụng hai tính chất: 3 2 3 2
a + a b + b
➢ lim(u + v ) = limu + lim v . n n n n
➢ limC = C với C là hằng số C  .
Ví dụ 5. Tính giới hạn L = l ( 2 3 3 2 im
n + n +1 − n + n ) . ĐS: 1 L = . 6 15
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Lời giải Ta có: L = l ( 2 3 3 2 im
n + n +1 − n + n )  ( 2  =
n + n + − n) + ( 3 3 2 lim 1
n − n + n ) =
( 2n +n+ −n)+ ( 3 3 2 lim 1
lim n − n + n ) 3 + +1− n − ( 3 2 2 2 n + n n n n ) = lim + lim
n + n +1 + n
n + n n + n + ( n + n )2 2 2 3 3 2 3 3 2 2 n +1 −n = lim + lim
n + n +1 + n
n + n n + n + ( n + n )2 2 2 3 3 2 3 3 2 1 1+ 1 n − = + 1 1 1 lim = − = . 2 1 1 2 3 6 1 1 1  1  + + + 2 + 3 3 1 1+ +  1 n n +  n n  
BÀI TẬP ÁP DỤNG Bài 1.
Tính các giới hạn sau: 2 9n n 1 3 a) L lim . ĐS: 4n 2 4 2 4n n 1 n 1 b) L lim . ĐS: 2 9n 3n 3 4 2n 3n 2 2 c) L lim . ĐS: 2 2n n 3 2 2n 1 n 3 2 1 d) L lim . ĐS: 4n 5 2 2 3 3 2 4n 1 8n 2n 3 4 e) L lim . ĐS: L 2 4 4 16n 4n n 1 3 3 6 3 n 7n 5n 8 f) L lim . ĐS: L n 2 1 + 4 + 7 ++ (3 +1) g) = lim n L . ĐS: L = 0 2 4
2n + n + 2n +1 Bài 2.
Tính các giới hạn sau: 16
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC a) 2 L lim 4n n 1 9n . ĐS: b) 2 2 L lim 9n 2n 1 4n 1 . ĐS: 1 c) 2 2 L lim 4n n 4n 2 . ĐS: 4 21 d) 2 L lim n n 1 n 10 ĐS: 2 53 e) 2 L lim n 3n 5 n 25 . ĐS: 2 f) 2 4 L lim n 2019 n 3n 1 . ĐS: L 2019 g) 2 L lim 3n 5 9n 1 . ĐS: L 5 1 h) 2 2 L lim n n 1 n 2 . ĐS: L 2 Bài 3. Tính các giới hạn sau: a) 3 3 L lim n 4 n 1 . ĐS: L 0 25 b) 3 3 2 L lim 8n 3n 4 2n 6 . ĐS: L 4 c) 3 3 L lim 2n n n 1 . ĐS: L 1 d) 3 3 L lim n n n 2 . ĐS: L 2 5 e) 3 3 2 L lim n 2n n 1 . ĐS: L 3 1 f) 4 2 3 6 L lim n n n 1 . ĐS: L 2 1 g) 2 3 3 2 L lim n n 1 n n . ĐS: L 6 Bài 4. Tính các giới hạn sau: 1 f) 4 2 3 6 L lim n n n 1 . ĐS: L 2 1 g) 2 3 3 2 L lim n n 1 n n . ĐS: L 6 17
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC LỜI GIẢI  1 1  2 1 1 n 9 − +   − + 2 2 n 9 2 9n − n +1  n n Bài 1. a) n n L = lim = lim = lim 4n − 2  2   2  n 4 − n 4 −      n   n  1 1 9 2 n n 9 0 0 3 lim . 2 4 0 4 4 n 1 1 − + − 2 4 1
4n − n +1 − n 2 4 − 0 + 0 −1 1 b) L = lim n n = lim = = . 2 9n + 3n 3 9 + 0 3 9 + n 3 2 3 2 2 + − + − 4 n 2 2 2n + 3n − 2 3 4 3 4 n n 2 + 0 − 0 2 c) L = lim n n = lim = = = lim 2 2n − n + 3  1 3  1 3 − + . 2 2 0 0 2 n 2 − +   2 − + 2  n n  2 n n  1 3  1 3 n  2 + − 1+  2 + − 1+ 2n +1 − n + 3 n n   n n 2 −1 d) L = lim = lim = lim = . 4n − 5 5 5 2 n. 4 − 4 − n n  1   2 3  2 3 − + 3 n 4 n 8 + −     2 3 3 2 2 3
4n −1 + 8n + 2n − 3  n   n n  e) L = lim = lim 2 4 4
16n + 4n − n +1  4   1  2 4 + − 4 n 16 n 1+     4  n   n  1 2 3 1 2 3 3 3 n 4 − + n 8 + − 4 − + 8 + − 2 3 2 3 n n n n n n = 2 + 2 4 lim = lim = = . 4 1 4 1 4 −1 3 4 4 n 16 + − n 1+ 16 + − 1+ 4 4 n n n n  7 5 8  6 7 5 8 3 n 1− +  −  2 3 n . 1− − + 3 6 3 3 5 6
n − 7n − 5n + 8  n n n  3 5 6 n n n f) L = lim = lim = lim n + 2 n + 2  2  . n 1+    n  7 5 8 7 5 8 3 1− − + 3 1− − + 3 5 6 n n n 3 5 6 = lim n n n . n = + lim =1). 2
(Vì lim n = + và 2 1+ 1+ n n 18
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
1 + 4 + 7 ++ (3n +1) (n +1) (3n + 2) g) L = lim = lim 2 4
2n + n + 2n +1 2 ( 2 4
2n + n + 2n +1 )  3 5 2  4 n + +   2 3 + 5 + 2 2 3 4 = lim n nn n n  = lim 2 4
2 2n + 2 n + 2n +1  2 1  2 4 2 2n + 2 n 1+ +   3 4  n n  3 5 2 3 5 2 2 n 2 3 4 2 3 4 n n n n n n 0 lim lim 0 . 2 1 2 1 3 2 2 2 2 2n 2n 1 2 2 2 1 3 4 3 4 n n n n   1 1    1 1  Bài 2. a) L = lim ( 2
4n + n +1 − 9n) 2 = lim n 4 + + − 9n    = limn 4 + + − 9n 2    2   n n n n      1 1   1 1  lim . n  4 + + − 9 
(Vì lim n = + và lim 4 + + −9 = 7 −  0 ). 2    n n   2 n n    2 1 1  b) L = lim ( 2 2
9n + 2n −1 − 4n +1) = limn 9 + − − 4 +  = +  2 2  n n n    2 1 1 
(Vì lim n = + và lim 9 + − − 4 +  =1 0  ). 2 2  n n n   ( 2 4n + n) − ( 2 4n + 2) n − 2 c) L = ( 2 2 lim
4n + n − 4n + 2 ) = lim = lim 2 2
4n + n + 4n + 2 2 2
4n + n + 4n + 2 2 1− − = 1 0 1 lim n = = . 1 2 4 + 0 + 4 + 0 4 4 + + 4 + 2 n n d) 2 L lim n n 1 n 10 2 lim10 lim n n 1 n 1 1 n 1 1 0 1 21 10 lim 10 lim n 10 10 . 2 n n 1 n 1 1 1 0 0 1 2 2 1 1 2 n n e) 2 L lim n 3n 5 n 25 2 lim 25 lim n 3n 5 n 19
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 5 2 2 n 3n 5 n 3 3n 5 25 lim 25 lim 25 lim n 2 n 3n 5 n 2 n 3n 5 n 3 5 1 1 2 n n 3 0 53 25 . 1 0 0 1 2 f) 2 4 L lim n 2019 n 3n 1 2 4 lim2019 lim n n 3n 1 4 4 n n 3n 1 3n 1 2019 lim 2019 lim 2 4 n n 3n 1 2 4 n n 3n 1 3 1 2 0 0 2019 lim n n 2019 2019 0 2019 . 3 1 1 1 0 0 1 1 3 4 n n g) 2 L lim 3n 5 9n 1 2 lim 3n 9n 1 lim5 2 2 9n 9n 1 1 lim lim5 lim lim5 0 5 5. 2 3n 9n 1 2 3n 9n 1 h) 2 2 L lim n n 1 n 2 2 2 n n 1 n 2 n 1 1 lim lim lim . 2 2 n 1 n 2 2 2 n 1 n 2 1 2 2 1 1 2 2 n n 3 Bài 3. a) L = (3 3 lim
n + 4 − n +1 ) = lim (n + 4)2 3 + (n + 4).(n + ) 1 + (n + )2 3 3 1 3 = lim 2 2  4   4   1   1  2 2 2 3 + + 3 3 n . 1 n . 1+ . 1+ − n . 1+          n   n   n   n  3 = lim = 0. 2 2    4   4   1   1  3 2  3 + + 3 3 n 1 1+ . 1+ + 1+            n   n   n   n     b) 3 3 2 L lim 8n 3n 4 2n 6 3 3 2 lim 8n 3n 4 2n 6 2 3n 4 3 3 2 6 lim 8n 3n 4 2n 6 lim 2 3 2 3 3 2 2 3 8n 3n 4 2 . n 8n 3n 4 4n 4 3 2 1 25 6 lim n 6 . 2 3 4 3 4 4 4 3 3 8 2. 8 4 3 3 n n n n 20
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC c) L = (3 3 lim
2n − n + n − ) 1 = (3 3 lim
2n − n + n − ) 1 = − + lim ( 3 3 1
2n − n + n) 2 2n = 1 − + lim = − 1 n + lim = 1 − + 0 = 1 − . ( 3 2n − n )2 3 3 2 3
− n 2n − 2n + 2 n  2  2 3 3 −1 − −1 +1   2 2  nn d) 3 3 L lim n n n 2 3 3 lim n n n 2 3 3 2 lim n n n 1 n 2 lim 2 lim n 2 0 2 . 2 2 3 3 3 2 3 n n . n n n n 1 1 3 3 1 1 1 2 2 n n e) 3 3 2 L lim n 2n n 1 3 3 2 lim n 2n n 1 3 3 2 1 lim n 2n n 2 2n 2 1 lim 1 lim 2 3 2 3 3 2 2 2 3 n 2n . n 2n 2n n 2 2 3 3 1 1 1 n n 2 5 1 . 3 3 Bài 4. a) 4 2 3 6 L lim n n n 1 4 2 2 3 6 2 lim n n n n 1 n 4 2 2 3 6 2 lim n n n lim n 1 n 4 2 4 6 6 n n n n 1 n lim lim 4 2 2 2 6 2 3 6 4 n n n 3 n 1 n n 1 n 2 n 1 1 1 lim lim lim 0 . 4 2 2 2 6 2 3 6 4 n n n 3 n 1 n n 1 n 1 2 1 1 2 n b) 2 3 3 2 L lim n n 1 n n 2 3 3 2 lim n n 1 n n n n 3 3 2 2 2 1 n n n n n n lim 2 2 2 3 3 2 3 3 2 n n 1 n n n n n n n 2 n 1 n lim 2 2 2 3 3 2 3 3 2 n n 1 n n n n n n n 1 1 1 1 1 1 lim n . 2 1 1 1 1 2 3 6 1 1 3 3 2 1 1 1 n n n n 21
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
C. BÀI TẬP RÈN LUYỆN Bài 1. Tính các giới hạn sau: 2 2n − 3n +1 2 5n − n + 3 1) lim . ĐS: 2 . 2) lim . ĐS: 5 . 2 5n + 3 5 2 2n + 3n −1 2 3 n − n + 3 3 2 8n − 2n +1 3) lim . ĐS: 1 . 4) lim . ĐS: 4 . 2 3 2n + 3n −1 3 2 3 1− 3n + 2n 3 ( 2n +2) 3 6n − 2n +1 (3−n)+ 2n 5) lim . ĐS: 6 . 6) lim . ĐS: 1 − . 3 2n − n ( 2 n + n − ) 1 ( 2 3n + 2)(5 − n) 3 ( 2 9 2n − )2 1 ( 3 3 − 4n ) ( 4 2n + ) 1 (n + 2) 7) lim − ( . ĐS: 1 . 8) lim . ĐS: 4 . 17
4n + 2)3 (2 − n)2 4 n +1 (n +2)(n− )2 2 1 4 2 4n − n +1 9) lim − ( . ĐS: 1 . 10) lim . ĐS: 2 . n + ) 1 (2n + 3)3 8 (2n + ) 1 (3 − n)( 2 n + 2) ( 3 5
n + 2)3 (3 − n) (n + 2) (3− n) 11) lim ( . ĐS: 1 − . 12) lim . ĐS: 1 − . 3
3n + 2)(5 − n)2 2 3
(3n +2n+ )1 (5−n)2 2 27  1 1  3 2  n n  13) lim −   . ĐS: 0 . 14) lim  −  . ĐS: 1 . 2 2  n + 2n 2n + 3  2
 2n −1 2n +1 4 Bài 2. Tính các giới hạn sau 2n + 4n 3.2n − 5n 1) lim . ĐS: 1. 2) lim . ĐS: 1 − . 4n − 3n 5.4n + 6.5n 6 4n + 2.3n 1+ 2.3n 3) lim . ĐS: + . 4) lim . ĐS: 2 . 5 + 3n 5 + 3n n n 1 4.3 5 + + n+2 n 1 4 + 6 + 5) lim . ĐS: 5 . 6) lim . ĐS: 1 . 3.2n + 5n n 1 − n+3 5 + 2.6 72 ( )n n 1 3 4.5 + − − − + 20 n n n 2 2 − 3 + 4.5 7) lim . 8) lim . ĐS: 20 . 2.4n + . ĐS: 3.5n 3 n 1 + n+2 n 1 2 + 3 + 5 + n n n+2 n 2 − 3 + 5 2n + ( 5 − ) 1 9) lim . ĐS: 5 . 10) lim . ĐS: . n 1 + n+2 n 1 2 + 3 + 5 + n 2.3n + 3.( 5 − ) 3 9n +1 2 n + n +1 11) lim . ĐS: 1. 12) lim . ĐS: 0 . 3n −1 .3n n 22
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC (− )n 5n 1 1 .2 + ( n 5 − ) + 4n 13) lim . ĐS: 0 . 14) lim . ĐS: 0 . 5n+2 3 ( n+ 7 − ) 1 n 1 + 4 + n 2n 1 4 + 2.2 + 1 − 3 − 2n + 5n 1 − 15) lim . ĐS: . 16) lim . ĐS: . 2(n+ ) 1 5.2 + 3n 4 3n − 2.5n 2
2n + 3n − 4n − − 1 n 1 n 2 4 + 2.3 − 4 1 17) lim . ĐS: . 18) lim .ĐS: − . n n 1 + n 1 2 + 3 + 4 + + + 4 n n 1 n 1 2 + 3 + 4 64 ( n 3 − ) −5n − + 1 − n n 1 n 2 3 .2 + 3 1 19) lim ( . ĐS: . 20) lim . ĐS: . n− n+2 n 1 + 3 − ) 2 n 1 + 5 + + 2 5 3 + 6 12 Bài 3. Tính các giới hạn sau: 2 4n n 1 n 1 2n 1 n 3 2 1 1) lim . ĐS: . 2) lim . ĐS: . 2 9n 3n 3 4n 5 2 2 3 3 2 4n 1 8n 2n 3 4 2 3 3 n n n 3n 3) lim . ĐS: . 4) lim . ĐS: 1. 2 4 4 16n 4n n 1 3 4 4 16n 1 5) 2 lim 3n n 5 n . ĐS: . 6) 3 3 2 lim 8n n n 2 n . ĐS: . Bài 4.
Tính các giới hạn sau: 1 1 1) ( 2 lim
n + n +1 − n) . ĐS: . 2) ( 2 2 lim
4n + n − 4n + 2 ). ĐS: . 2 4 3 3 3) ( 2 lim
n + 3n + 5 − n) . ĐS: . 4) ( 2 lim
4n + 3n − 2n) . ĐS: . 2 4   1 − 5) lim n 2 2 + − +
 ( n +1 − n ) . ĐS: + . 6) lim n  ( n 1 n 2 ) . ĐS: . 2 7 7) ( 2 lim
n + 2n − n + 3). ĐS: 4 . 8) ( 2 lim
4n + 3n +1 − 2n + ) 1 . ĐS: . 4 5 9) ( 2 lim
9n + 3n − 4 − 3n + 2) . ĐS: . 10) ( 2 4
lim 1+ n − n + 3n +1) . ĐS: 1. 2 11) (3 3 lim
n + 2 − n ) . ĐS: 0 . 12) (3 3 2 lim
n + 3n − n). ĐS: 1. 13) (3 3 lim
n − n + n + 2). ĐS: 2 . 14) (3 3 lim
2n − n + n − ) 1 . ĐS: 1 − . 5 − 10 15) (3 3 2 lim
n − 2n − n − ) 1 . ĐS: . 16) (3 3 2 lim
8n + 4n + 2 − 2n + 3). ĐS: . 3 3 23
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Bài 5. Tính các giới hạn sau: 2 5 8 3n 1 3 1) lim . ĐS: . 2 4n 1 8 1 4 7 3n 1 2) lim . ĐS: 0 . 2 4 2n n 2n 1 2 4 2n 2 3) lim . ĐS: . 3.2n 1 3 1 1 1 4) lim . ĐS: 1. 1 2 2 1 2 3 3 2 n n 1 n 1 n 24
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
BÀI 2. GIỚI HẠN CỦA HÀM SỐ
A. TÓM TẮT LÝ THUYẾT
Định nghĩa 1 (Giới hạn của hàm số tại một điểm).
Giả sử (a;b) là một khoảng chứa điểm x f 0 và
là một hàm số xác định trên tập hợp
(a;b) \x f L x x x
0  . Ta nói rằng hàm số
có giới hạn là số thực khi
dần đến 0 (hoặc tại điểm 0 ) nếu
với mọi dãy số ( x
(a;b) \x lim x = x
lim f ( x = L n ) 0  n ) trong tập hợp mà n 0 ta đều có .
Khi đó ta viết lim f (x) = L hoặc f ( x) → L khi x → x0 . x→x0
Định nghĩa 2 (Giới hạn của hàm số tại vô cực).
Giả sử hàm số f xác định trên khoảng (a; +) . Ta nói rằng hàm số f có giới hạn là số thực
L khi x dần tới + nếu với mọi dãy số ( x (a;+) lim x = + n ) trong khoảng mà n ta đều có
lim f ( x = L n ) .
Khi đó ta viết lim f ( x) = L hoặc f ( x) → L khi x → + . x→+
GIỚI HẠN HỮA HẠN GIỚI HẠN VÔ CỰC
Giới hạn đặc biệt
Giới hạn đặc biệt 1) lim x = x c 0 . = + = x→ lim k x lim 0 0 x 1) . 2) . x→+ x k → x
2) lim c = c (c  ) . x→ 1 1 0 x 3) lim = − . 4) lim = + . − + x 0 → x x 0 → x
+ khi k 2 k k ( 0) 5) lim x =  x→−
− khi k  2 Định lí Định lí 1
Nếu lim f ( x) = L và lim g ( x) = M thì
Nếu lim f ( x) = L  0 và lim f ( x) =  thì x→x x→x x→x x→x 0 0 0 0 1) lim  f
 ( x)  g ( x) = L M .  + khi .
L lim g ( x)  0 x→  x→x 0 x lim  f
 ( x).g ( x) 0  =   . x→x0 − khi . L lim g  (x)  2) lim  f
 ( x).g ( x) = . L M .  0 x→xx→ 0 0 x f ( x)
Nếu lim g ( x) = 0 thì L 3) lim = với M  0 . x→x0 x→ 0 x g ( x) M f ( x) + khi . L g  (x)  0 =
Nếu f ( x)  0 và lim f ( x) = L thì lim  .
x→x0 g ( x) − khi . L g  (x)  x→x 0 0
lim f ( x) = L và lim
f ( x) = L . x→ → 0 x x 0 x
Giới hạn một bên i
l m f ( x) = L  lim f ( x) = lim f ( x) = L . x + − → → → 0 x x 0 x x 0 x 25
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
B. DẠNG TOÁN VÀ BÀI TẬP 0
Dạng 1. Tính giới hạn vô định dạng
, trong đó tử thức và mẫu thức là các đa thức. 0 Phương pháp giải:
Khử dạng vô định bằng cách phân tích thành tích bằng cách chia Hooc – nơ (đầu rơi, nhân tới, cộng
chéo), rồi sau đó đơn giản biểu thức để khử dạng vô định.  VÍ DỤ 2 2x + 3x −14 11
Ví dụ 1. Tính giới hạn A = lim . Đs: A = . 2 x→2 x − 4 4 Lời giải 7 − + 2 2(x 2)(x ) 2x + 3x −14 2x + 7 11 Ta có 2 A = lim = lim = lim = 2 x→2 x→2 x→2 x − 4 (x− 2)(x+ 2) x + 2 4 ! Cần nhớ: 2
f (x) = ax + bx + c = a ( x − x x − x x , x 1 ) ( 2 ) với 1
2 là 2 nghiệm của phương trình
f ( x) = 0 . Học sinh thường quên nhân thêm a . 3 2
2x − 5x − 2x − 3 11
Ví dụ 2. Tính giới hạn A = lim . Đs: A = . 3 2
x→2 4x −13x + 4x − 3 17 Lời giải − − − (x −3)( 2 3 2 2x + x x x x + ) 2 1 2 5 2 3 2x + x +1 11 A = lim = lim = lim = 3 2 x→
4x −13x + 4x − 3 x→ (x −3)( 2 3 3 4x − x + ) 2 x 3 1
→ 4x − x +1 17
Nhận xét: Bảng chia Hooc – nơ (đầu rơi, nhân tới cộng chéo) như sau: Phân tích 3 2
2x − 5x − 2x − 3 thành tích số: 3 2
x − x − x − = (x − )( 2 2 5 2 3 3 2x + x + ) 1 Phân tích 3 2
4x −13x + 4x − 3 thành tích số: 3 2
x − x + x − = (x − )( 2 4 13 4 3 3 4x − x + ) 1 . 100 x − 2x +1 49
Ví dụ 3. Tính giới hạn A = lim . Đs: A = . 50 x 1 → x − 2x +1 24 Lời giải 26
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC − + − − − x ( 99 100 100 x − ) 1 − ( x x x x x x − ) 1 2 1 ( ) ( 1) Ta có A = lim = lim = lim 50 50 x→ x − 2x +1 x→
(x − x) − (x −1) x→ x ( 49 1 1 1 x − ) 1 − ( x − ) 1 x ( x − ) 1 ( 98 97 96
x + x + x + .... + x + ) 1 − ( x − ) 1 = lim x→ x ( x − ) 1 ( 48 47 46 1 x + x + x +....+ x + ) 1 − ( x − ) 1 (x − ) 1 ( 99 98 97 2
x + x + x + .... + x + x − ) 1 = lim x→ ( x − ) 1 ( 49 48 47 2 1
x + x + x + .... + x + x − ) 1 ( 99 98 97 2
x + x + x + .... + x + x − ) 1 98 49 = lim = = x→ ( 49 48 47 2 1
x + x + x + .... + x + x − ) 1 48 24 − −
!Cần nhớ: Hằng đẳng thức n
x − = ( x − )( n 1 n 2 2 1 1 x + x
+ ....+ x + x + ) 1 .
Chứng minh: Xét cấp số nhân 2 3 1 1, , , ,...., n x x x x − có n = = số hạng và u 1, q . x 1 Khi đó n − q −1 n x − n 1 2 1
S = 1+ x + x + ... + x = u =1. n
x −1= x −
+ x + x + + x − n ( ) 1 ( 2 n 1 1 ... . 1 ) q −1 x −1
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau: 2 x − 3x + 2 1 2 x −1 2 1) A = lim . ĐS: A = . 2) A = lim . ĐS: A = . 2 x→2 x − 4 4 2 x 1 → x + 3x − 4 5 2 x − 7x +12 1 2 x − 9x + 20 1 3) A = lim . ĐS: A = − . 4) A = lim . ĐS: A = . 2 x 3 → x − 9 6 2 x 5 → x − 5x 5 2 3x −10x + 3 2 x + 2x − 3 4 5) A = lim . ĐS: A = 8 . 6) A = lim . ĐS: A = . 2 x 3 → x − 5x + 6 2 x 1
→ 2x − x −1 3 4 x −16 x − 2 x − 3 4 7) A = lim . ĐS: A = 16 − . 8) A = lim .ĐS: A = − . 2 x 2
→− x + 6x + 8 x 1
→ x − 5 x + 4 3 3 x − 8 3 x + 8 12 9) A = lim . ĐS: A = 12 . 10) A = lim . ĐS: A = . 2
x→2 x − 3x + 2 2 x 2
→− x +11x +18 7 Bài 2. Tính các giới hạn sau: 3 2
2x − 5x + 2x +1 3 x − 3x + 2 1 1) A = lim . ĐS: A = −1 . 2) A = lim . ĐS: A = . 2 x 1 → x −1 4 x 1 → x − 4x + 3 2 3 2
2x + 5x + 4x +1 1 4 3
x − x − x +1 3 3) A = lim . ĐS: A = . 4) A = lim . ĐS: A = − . 3 2 x 1 →−
x + x − x −1 2 3 2 x 1
→ x − 5x + 7x − 3 2 27
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2
2x − 3x + x + 9 + 7 3 18 +19 3 5) A = lim . ĐS: A = . 2 x→− 3 3 − x 6 3 2
x − 5x + 3x + 9 6) A = lim . ĐS: A = 0 . 4 2 x 3 → x − 8x − 9 3 1− x 3  1 12  1 7) A = lim . ĐS: A = . 8) A = lim −   . ĐS: A = . 4 2 3 x 1 → x − 4x + 3 4
x→2  x − 2 x − 8  2  1 1  9) A = lim +   . ĐS: A = 2 − . 2 2
x→2  x − 3x − 2
x − 5x − 6   1 1  1 10) A = lim −   . ĐS: A = . 2 3 x 1
→  x + x − 2 x −1 9 Bài 3. Tính các giới hạn sau: 20 x − 2x +1 8 50 x −1 1) A = lim . ĐS: A = . 2) A = lim . ĐS: A = 50 − . 30 x 1 → x − 2x +1 14 2 x 1 → x − 3x + 2 n
x − nx + n −1 2 n − n 3) A = lim
(Với n là số nguyên). ĐS: A = . x→ (x − )2 1 1 2 n 1 x + − (n + ) 1 x + n n (n + ) 1 4) A = lim . ĐS: A = . x→ (x − )2 1 1 2 2 3
x + x + x + ... n + x − n n (n + ) 1 5) A = lim
( m, n là số nguyên) . ĐS: A = . 2 3 1
→ x + x + x + ... m x + x − m m (m + ) 1  m nm − n 6) A = lim −   . ĐS: A = . 1 → 1 m − x 1 n x − x  2  LỜI GIẢI 2 x − 3x + 2 (x − ) 1 ( x − 2) x −1 1 Bài 1. 1) Ta có A = lim = lim = lim = . 2 x→2 x→2 x − 4
(x −2)(x + 2) x→2 x + 2 4 2 x −1 (x − ) 1 ( x + ) 1 x +1 2 2) Ta có A = lim = lim = lim = . 2 x 1 → x 1 x + 3x − 4 → ( x − ) 1 ( x + 4) x 1 → x + 4 5 2 x − 7x +12 (x −3)(x −4) x − 4 1 3) Ta có A = lim = lim = lim = − . 2 x 3 → x 3 x − 9
→ ( x − 3)( x + 3) x 3 → x + 3 6 2 x − 9x + 20 (x −4)(x −5) x − 4 1 4) Ta có A = lim = lim = lim = . 2 x 5 → x 5 x − 5x → x ( x − 5) x 5 → x 5 2 3x −10x + 3 (3x − ) 1 ( x − 3) 3x −1 5) Ta có A = lim = lim = lim = 8 . 2 x 3 → x 3 x − 5x + 6
→ ( x − 2)( x − 3) x 3 → x − 2 28
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x + 2x − 3 (x − ) 1 ( x + 3) x + 3 4 6) Ta có A = lim = lim = lim = . 2 x 1 → x 1 2x − x −1 → ( x − ) 1 (2x + ) x 1 1 → 2x +1 3 x −
(x −2)(x + 2)( 2x + 4) (x −2)( 2 4 x + 4 16 ) 7) Ta có A = lim = lim = lim = 1 − 6 . 2 x→ 2 − x→ 2 x + 6x + 8 − (x + 2)(x + 4) x→ 2 − (x + 4) − + + x − x − ( x )1( x 3) ( x 3 2 3 ) 4 8) Ta có A = lim = lim = lim = − . x 1 → x 1 x − 5 x + 4 → ( x − ) 1 ( x − 4) x 1 → ( x − 4) 3 x −
(x −2)( 2x +2x +4) ( 2 3 x + 2x + 4 8 ) 9) Ta có A = lim = lim = lim =12 . 2 x→2 x→2 x − 3x + 2 (x −2)(x − ) x→2 1 (x − ) 1
! Cần nhớ: Hằng đẳng thức 3 3 + = ( + )( 2 2 a b a b
a − ab + b ) và 3 3 − = ( − )( 2 2 a b a b
a + ab + b ) . x +
(x + 2)( 2x −2x+ 4) ( 2 3 x − 2x + 4 8 ) 12 10) Ta có A = lim = lim = lim = . 2 x→ 2 − x→ 2 x +11x +18 − (x + 2)(x +9) x→ 2 − (x +9) 7 − + + (x − ) 1 ( 2 3 2 2x − 3x x x x − ) 2 1 2 5 2 1 2x − 3x −1 Bài 2. 1) A = lim = lim = lim = 1 − . 2 x 1 → x 1 x −1 → (x − ) 1 ( x + ) x 1 1 → x +1 x − 3x + 2 (x − )2 3 1 ( x + 2) x + 2 1 2) A = lim = lim = lim = . 4 x→ x − 4x + 3 x→ ( x − )2 1 ( x + 2x + 3) 2 2 1 1 x 1 → x + 2x + 3 2
2x + 5x + 4x +1 (x + )2 3 2 1 (2x + ) 1 2x +1 1 3) A = lim = lim = lim = . 3 2 x→ 1 − x→ 1
x + x − x −1 − (x + )2 1 ( x − ) x→ 1 1 − x −1 2 − − + (x − )2 1 ( 2 4 3 x + x x x x + ) 2 1 1 x + x +1 3 4) A = lim = lim = lim = − . 3 2 x 1 → x 1
x − 5x + 7x − 3 → (x − )2 1 ( x − 3) x 1 → x − 3 2   + − + + +
x − x + x + + (x 3)  ( 2 3 2 2x (3 2 3)x 7 3 3 2 3 9 7 3 ) 5) Ta có A = lim = lim − 2 −   x→− 3 x→− 3 3 x  (x+ 3)( 3−x)    2
 2x −(3+2 3)x+7+3 3  18+19 3 lim   = − = . x→− 3  3 − x  6  
x − 5x + 3x + 9 (x − ) 1 ( x − 3)2 3 2 (x − ) 1 ( x − 3) 6) Ta có A = lim = lim = lim = 0 . 4 2 x→ x − 8x − 9 x→
(x −3)(x +3)( 2x + )1 x→ (x+3)( 2 3 3 3 x + ) 1 − (x − ) 1 ( 2 −x − x − ) 1 ( 2 3 −x − x x − ) 1 1 3 7) Ta có A = lim = lim = lim = . 4 2 x→ x − 4x + 3 x→ ( x − ) 1 ( 3 2
x + x − 3x − 3) x→ ( 3 2 1 1 1
x + x − 3x − 3) 4 29
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3  1 12  x −12x +16 8) Ta có A = lim − = lim   3 x→  x − 2 x − 8 x→  (x −2)( 3 2 2 x − 8)
(x + 4)(x − 2)2 x + 4 1 = lim = lim = . x→
(x − 2)2 (x + 2x + 4) 2 2 2
x→2 x + 2x + 4 2 2 2  1 1 
x − 5x − 6 + x − 3x − 2 9) Ta có A = lim + = lim   2 2
x→  x − 3x − 2 x − 5x − 6 x→ 
( 2x −3x−2)( 2 2 2 x − 5x − 6) 2( x − 2)2 2 = lim = lim = 2 − . x→ (x −2)2 2
(x −3)(x − ) x→2 1 (x −3)(x − ) 1 3 2 3 2  1 1 
x −1− x − x + 2
x − x − x +1 10) Ta có A = lim − = lim = lim   2 3
x→  x + x − 2 x −1 x→ 
( 2x + x−2)( 3x − )1 x→ ( 2x + x−2)( 3 1 1 1 x − ) 1 (x − )2 1 ( x + ) 1 x +1 1 = lim = lim = . x→ ( x − )2 1 ( x + 2)( 2 1 x + x + ) x 1 1 → ( x + 2)( 2 x + x + ) 1 9 20 x − 2x +1
x − x − ( x − ) 1 x ( 19 20 x − ) 1 − ( x − ) 1 Bài 3. 1) Ta có A = lim = lim = lim 30 30 x→ x − 2x +1 x→
x − x − ( x − ) 1 x→ x ( 29 1 1 1 x − ) 1 − ( x − ) 1 x ( x − ) 1 ( 18 17
x + x + ... + x + ) 1 − ( x − ) 1 (x − ) 1 ( 19 18
x + x + ... + x − ) 1 = lim = x→ x ( x − ) 1 ( lim 28 27
x + x + ... + x + ) 1 − ( x − ) 1 x→ ( x − ) 1 ( 29 28 1 1
x + x + ... + x − ) 1 ( 19 18
x + x + ... + x − ) 1 18 9 = lim = = . x→ ( 29 28 1
x + x + ... + x − ) 1 28 24 x − (x − ) 1 ( 49 48 50
x + x + ... + x+ ) 49 48 1 1
x + x + ... + x+1 2) Ta có A = lim = lim = lim = 5 − 0 2 x 1 → x 1 x − 3x + 2 → (x − ) 1 ( x − 2) x 1 → x − 2 − + − ( n n x − ) 1 − n ( x x nx n − ) 1 1 3) Ta có A = lim = x→ (x − ) lim 2 1 x→ (x − )2 1 1 1 (x − ) 1 ( n 1 − n−2 x + x +...+ x+ )
1 − n ( x − ) 1 = lim x→ (x − )2 1 1 (x − ) 1 ( n 1 − n−2 x + x +...+ x+1− n) n 1 − n−2 x + x +...+ x+1− n = lim = lim x→ (x − )2 1 x 1 1 → x −1 n 1 − n−2 2 x −1+ x
−1+...+ x −1+ x −1 = lim x 1 → x −1 (x − ) 1 ( n−2 n−3 x + x +...+ x+ ) 1 + ( x − ) 1 ( n−3 n−4 x + x + ...+ x+ ) 1 + ... + ( x − ) 1 = lim x 1 → x −1 = n − n lim ( n−2 n−3 x + x +...+ x+ ) 1 + ( n−3 n−4 x + x +...+ x+ )
1 + ... +1 = (n − ) + (n − ) 2 1 2 + ... +1 = x 1 → 2 . 30
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC + + x − (n + ) n n n 1 x + n ( 1 1 x
− x) − n(x − ) 1 x (x − )
1 − n ( x − ) 1 4) Ta có A = lim = = x→ (x − ) lim lim 2 1 x→ (x − )2 1 x→ (x − )2 1 1 1 1 x ( x − ) 1 ( n 1 − n−2 x + x +...+ x+ )
1 − n ( x − ) 1 (x − ) 1 ( n n 1
x + x − + ... + x− n) = lim = x→ (x − ) lim 2 1 x→ (x − )2 1 1 1 n n 1 − 2 n n 1 − 2 x + x
+...+ x + x − n x −1+ x
−1+...+ x −1+ x −1 = lim = lim x 1 → x 1 x −1 → x −1 (x − ) 1 ( n 1 − n−2 x + x +...+ x+ ) 1 + ( x − ) 1 ( n−2 n−3 x + x + ...+ x+ ) 1 + ... + ( x − ) 1 = lim x 1 → x −1
= lim ( n 1− n−2 x + x +...+ x+ ) 1 + ( n−2 n−3 x + x +...+ x+ ) 1 + ... +1 x 1 → +
= n + (n − ) + (n − ) n (n ) 1 1 2 + ... +1 = . 2 2 3 n n n 1 − 2
x + x + x + ... + x − n x −1+ x
−1+...+ x −1+ x −1 5) Ta có A = lim = lim 2 3 m m m 1 − 2 x 1 → x 1
x + x + x + ... + x − m → x −1+ x
−1+...+ x −1+ x −1 (x − ) 1 ( n 1 − n−2 x + x +...+ x+ ) 1 + ( x − ) 1 ( n−2 n−3 x + x +...+ x+ ) 1 + ... + ( x − ) 1 = lim − − − − x→ ( x − ) 1 ( m 1 m 2 x + x +...+ x+ ) 1 + ( x − ) 1 ( m 2 m 3 1 x + x +...+ x+ ) 1 + ... + ( x − ) 1 ( n 1− n−2 x + x +...+ x+ ) 1 + ( n−2 n−3 x + x +...+ x+ ) 1 + ... +1 = lim − − − − x→ ( m 1 m 2 x + x +...+ x+ ) 1 + ( m 2 m 3 1 x + x +...+ x+ ) 1 + ... +1 n + (n − ) 1 + (n − 2) + ...+1 n (n + ) 1 = lim = . x 1 → m + (m − ) 1 + (m − 2) + ...+1 m (m + ) 1  m n   m 1   n 1  6) Ta có A = lim − = lim − − −       1 m n → 1 1− x 1− x →  1 m − x 1− x   1 n x x − x 1− x   m 1   n 1  = lim − − lim −     1 m → 1 1− x 1− x →  1 n x x − x 1− x m −   ( 2 m 1
1+ x + x + ... + x − ) (1− x)+( 2 1− x − m )+...+( m 1 1− x 1 ) Và lim − = lim = lim   1 m → 1 m → 1 1− x 1− x  1− x → 1− xm x x x (1− x) 1  + (1+ x) +....+  ( 2 m−2
1+ x + x + ... + x ) = lim − x→ (1− x)( 2 m 1 1
1+ x + x + ... + x ) 1+ (1+ x) + .... + ( 2 m−2
1+ x + x + ... + x
) 1+2+3+...+m−1 m−1 = lim = = 2 m 1 − x 1 →
1+ x + x + ... + x m 2  n 1  n −1 Tương tự ta có lim − =   1 → 1 n x − x 1− x  2  m n
m −1 n −1 m − n Vậy lim − = − =   . 1 → 1 m − x 1 n x − x  2 2 2 31
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 0
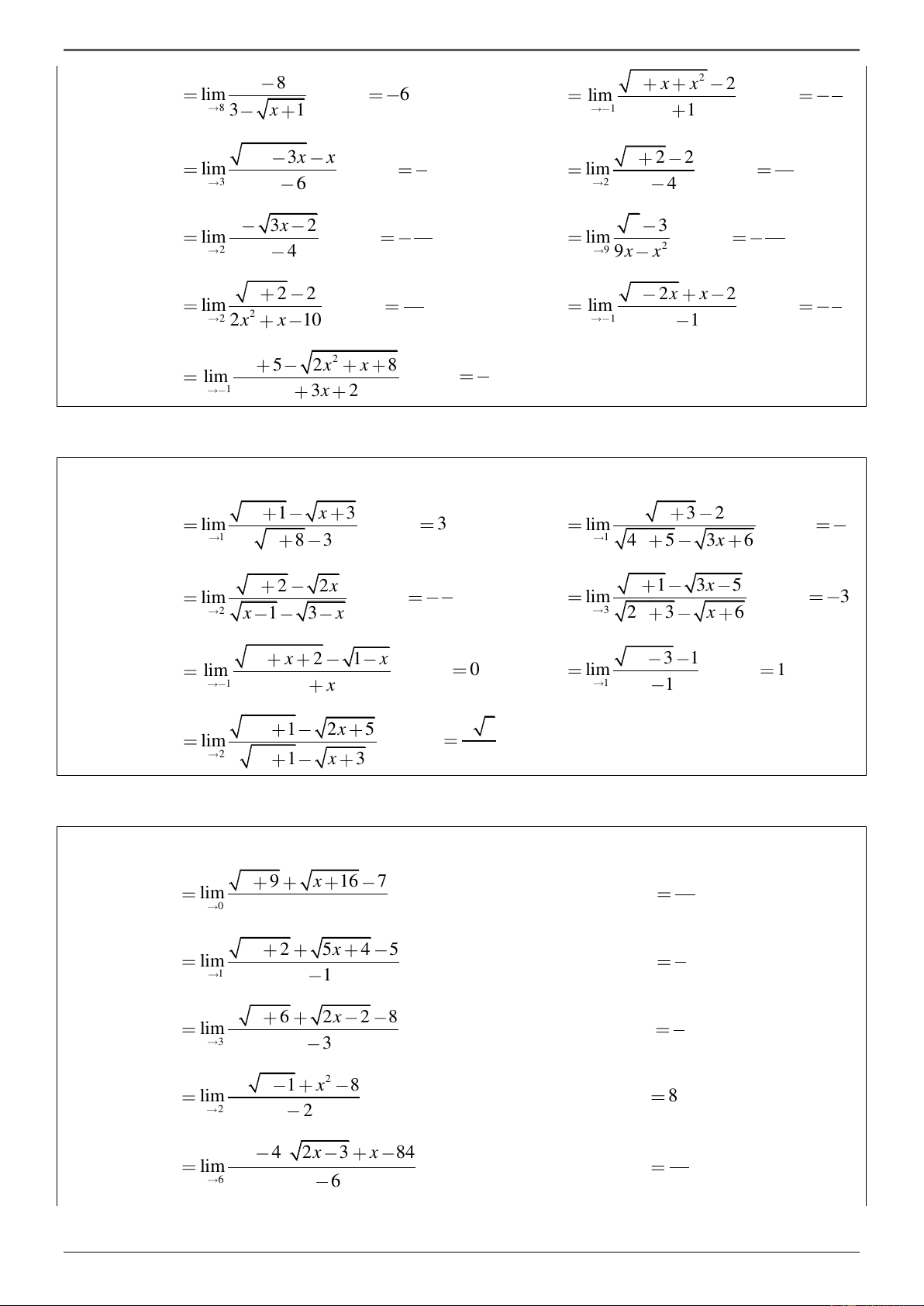
Dạng 2. Tính giới hạn vô định dạng , trong đó tử thức và mẫu thức có chứa căn thức. 0 Phương pháp giải:
Nhân lượng liên hợp để khử dạng vô định. VÍ DỤ 3 − x + 3 1
Ví dụ 1. Tính giới hạn B = lim . Đs: B = − . x→6 x − 6 6 Lời giải − + + + − x + (3 x 3)(3 x 3 3 3 ) Ta có: B = lim = lim x→6 x→6 x − 6 (x −6)(3+ x+3) 9 − ( x + 3) 6 − x 1 − 1 − 1 = lim = lim = lim = = −
x→6 ( x − 6)(3+ x + 3) x→6 (x − 6)(3+ x + 3) x→6 3+ x + 3 3+ 6 + 3 6
3 3x + 2 − 5x − 6
Ví dụ 2. Tính giới hạn E = lim . Đs: E = 1 − . x→2 x − 2 Lời giải 3 3x 2 2 2 5x 6 3 3x 2 2 2 5x 6 Ta có E lim lim lim x 2 x 2 x 2 x 2 x 2 x 2 A B 3 3x 2 2 3x 2 8 A lim lim x 2 x 2 2 x 2 3 3 x 2 3x 2 2. 3x 2 4 3 x 2 3 1 lim lim x 2 2 x 2 2 3 3 3 3 4 x 2 3x 2 2. 3x 2 4 3x 2 2. 3x 2 4 2 5x 6 4 5x 6 5 2 x B lim lim lim x 2 x 2 x 2 x 2 x 2 2 5x 6 x 2 2 5x 6 5 5 lim x 2 x 2 2 5x 6 4 1 5 Suy ra E A B 1 . 4 4 3 5x − 3 + 2 5
Ví dụ 3. Tính giới hạn L = lim . Đs: L = . x 1 →− x +1 12 Lời giải 32
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 5x 3 2 5x 3 8 Ta có: L lim lim x 1 x 1 2 x 1 3 3 x 1 5x 3 2. 5x 3 4 5 x 1 5 5 lim lim . x 1 2 x 1 2 3 3 3 3 12 x 1 5x 3 2. 5x 3 4 5x 3 2. 5x 3 4
3 3x + 2 − 3x − 2 1 −
Ví dụ 4. Tính giới hạn E = lim . Đs: E = . x→2 x − 2 2 Lời giải 3 3x 2 2 3x 2 2 3 3x 2 2 3x 2 2 Ta có E lim lim lim x 2 x 2 x 2 x 2 x 2 x 2 3x 2 8 3x 2 4 lim lim x 2 2 x 2 3 3 x 2 3x 2 2 x 2 3x 2 2. 3x 2 4 3 x 2 3 x 2 lim lim x 2 2 x 2 3 3 x 2 3x 2 2 x 2 3x 2 2. 3x 2 4 3 3 1 3 1 lim lim . x 2 2 x 2 3 3 3x 2 2 4 4 2 3x 2 2. 3x 2 4 3
1+ 2x. 1+ 4x −1
Ví dụ 5. Tính giới hạn F = 7 lim . Đs: F = . x→0 x 3 Lời giải 3 3 1 2x. 1 4x 1 1 2x 1 1 2x. 1 4x 1 F lim lim x 0 x 0 x x 3 1 2x. 1 4x 1 1 2x 1 lim lim x 0 x 0 x x 1 2x. 1 4x 1 1 2x 1 lim lim x 0 2 x 0 3 3 x 1 2x 1 x 1 4x 1 4x 1 4. 1 2x 2 4 7 lim lim 1 . x 0 2 x 0 3 3 1 2x 1 3 3 1 4x 1 4x 1
BÀI TẬP ÁP DỤNG Bài 1.
Tính các giới hạn sau: 33
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x 8 2 4 x x 2 1 1) B lim . Đs: B 6 2) B lim . Đs: B x 8 3 x 1 x 1 x 1 4 2 2x 3x x 1 x 2 2 1 3) B lim . Đs: B 4) B lim . Đs: B x 3 2x 6 4 2 x 2 x 4 16 2 3x 2 3 x 3 1 5) B lim . Đs: B 6) B lim . Đs: B 2 x 2 x 4 16 2 x 9 9x x 54 x 2 2 1 7 2x x 2 1 7) B lim . Đs: B 8) B lim . Đs: B 2 x 2 2x x 10 36 2 x 1 x 1 3 2 2x 5 2x x 8 5 9) B lim . Đs: B 2 x 1 x 3x 2 2 Bài 2.
Tính các giới hạn sau: 3x 1 x 3 x 3 2 3 1) B lim . Đs: B 3 2) B lim . Đs: B x 1 x 8 3 x 1 4x 5 3x 6 2 x 2 2x 1 x 1 3x 5 3) B lim . Đs: B 4) B lim . Đs: B 3 x 2 x 1 3 x 4 x 3 2x 3 x 6 2 x x 2 1 x 4 4x 3 1 5) B lim . Đs: B 0 6) B lim . Đs: B 1 4 x 1 x x x 1 x 1 2 2x 1 2x 5 2 5 7) B lim . Đs: B x 2 2 x 1 x 3 3 Bài 3.
Tính các giới hạn sau: x 9 x 16 7 7 1) L lim . Đs: B x 0 x 24 2x 2 5x 4 5 4 2) L lim . Đs: B x 1 x 1 3 2 x 6 2x 2 8 5 3) L lim . Đs: L x 3 x 3 6 2 2x x 1 x 8 4) L lim . Đs: L 8 x 2 x 2 5x 4 2x 3 x 84 74 5) L lim . Đs: L x 6 x 6 3 34
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 1 4x 1 6x 1 6) L lim . Đs: L 5 x 0 x 4x 3 2x 1 3x 1 5 7) L lim . Đs: L 2 x 0 x 2x 1 2 3x 7 4 x 3 2 2x 1 17 8) L lim . Đs: L 2 x 1 x 2x 1 16 4x 4 9 6x 5 5 9) L lim . Đs: L 2 x 0 x 12 2 6x 3 2x 5x 11 10) L lim . Đs: L 2 x 1 x 1 6 Bài 4.
Tính các giới hạn sau: 3 4x 2 1 3 1 1 x 1 1) L lim . Đs: L 2) L lim . Đs: L x 2 x 2 3 x 0 x 3 3 2 x 1 2 1 3 x 7 2 1 3) L lim . Đs: L 4) L lim . Đs: L x 3 x 3 2 x 1 x 1 6 3 x 2 5 3 x 1 5) L lim . Đs: L 6) L lim . Đs: L 1 x 8 2x 9 5 12 3 x 1 x 2 1 3 3 10 2x x 1 3 3 8x 11 x 7 7 7) L lim . Đs: L 8) L lim . Đs: L 2 2 x 1 x 3x 2 2 x 2 x 3x 2 54 3 3 2 x 7 x 3 1 9) L lim . Đs: L x 1 x 1 4 3 2 1 x 8 x 11 10) L lim . Đs: L x 0 x 12 3 2 2x 4x 11 x 7 5 11) L lim . Đs: L 2 x 2 x 4 72 3 4 x. 8 3x 4 12) L lim . Đs: L 1 2 x 0 x x Bài 5.
Tính các giới hạn sau: n 1 ax 1 a 1) F lim . Đs: x 0 x n 35
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC n 1 m ax 1 bx a b 2) F lim . Đs: x 0 x n m n 1 ax 1 am 3) F lim (ab 0). Đs: x 0 m 1 bx 1 bn n 1 m ax 1 bx a b 4) F lim . Đs: 2 x 0 1 x 1 n m LỜI GIẢI x 8 3 x 1 x 8 3 x 1 x 8 Bài 1. 1) B lim lim lim x 8 x 8 x 8 3 x 1 3 x 1 3 x 1 9 x 1 x 8 3 x 1 lim lim 3 x 1 6 . x 8 x 8 8 x 2 2 2 4 x x 2 4 x x 2 4 x x 2 2) B lim lim x 1 x 1 2 x 1 x 1 4 x x 2 2 4 x x 4 x x 1 x 1 lim lim lim . x 1 2 x 1 2 x 1 2 4 x 1 4 x x 2 x 1 4 x x 2 4 x x 2 2 2 2 2x 3x x 2x 3 2 3 x x x x x 3) B lim lim x 3 x 3 2 2x 6 2x 6 2x 3x x x x 3 x 1 lim lim . x 3 2 x 3 2 4 2 x 3 2x 3x x 2 2x 3x x x 2 2 x 2 2 x 2 2 4) B lim lim 2 x 2 x 2 2 x 4 x 4 x 2 2 x 2 1 1 lim lim . x 2 x 2 x 2 x 2 2 x 2 x 2 x 2 2 16 2 3x 2 2 3x 2 2 3x 2 4 3x 2 5) B lim lim lim 2 x 2 x 2 2 x 2 2 x 4 x 4 2 3x 2 x 4 2 3x 2 3 2 x 3 3 lim lim . x 2 x 2 x 2 x 2 2 3x 2 x 2 2 3x 2 16 36
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x 3 x 3 x 3 x 9 1 1 6) B lim lim lim lim . 2 x 9 x 9 2 x 9 9x x 9x x x 3 x 9 x x 3 x 9 x x 3 54 x 2 2 x 2 1 1 7) B lim lim lim . 2 x 2 x 2 2x x 10 x 2 2x 5 x 2 2 x 2 2x 5 x 2 2 36 2 7 2x x 2 7 2x x 2 2 x 2x 3 8) B lim lim lim 2 x 1 x 1 2 x 1 x 1 7 2x 2 x x 1 2 x 1 7 2x 2 x x 1 3 x 3 x 1 lim lim . x 1 x 1 x 1 7 2x 2 x x 1 x 1 7 2x 2 x 3 2 2 2 2x 5 2x x 8 2x 5 2x x 8 9) B lim lim 2 x 1 x 1 2 2 x 3x 2 x 3x 2 2x 5 2x x 8 2 2x 19x 17 x 1 2x 17 lim lim x 1 2 2 x 1 2 x 3x 2 2x 5 2x x 8 x 1 x 2 2x 5 2x x 8 2x 17 5 lim . x 1 2 2 x 2 2x 5 2x x 8 2 x 1 x 8 3 2 x 8 3 3x 1 x 3 Bài 2. 1) B lim lim lim 3 x 1 x 1 x 1 x 8 3 x 1 3x 1 x 3 3x 1 x 3 x 3 2 x 1 4x 5 3x 6 2) B lim lim x 1 4x 5 3x 6 x 1 x 1 x 3 2 4x 5 3x 6 3 lim . x 1 x 3 2 2 x 2 2x 2 x x 1 3 x x 1 3 x 1 3) B lim lim lim . x 2 x 1 3 x x 2 2 x 2 x 2 2x x 2 2 x 2 2x 4 x 1 3x 5 2 3 x 2x 3 x 6 4) B lim lim x 3 2x 3 x 6 x 3 x 3 x 1 3x 5 2 2x 3 x 6 lim 3 . x 3 x 1 3x 5 2 2 x x 2 1 x x x 2 1 x 5) B lim lim 4 x 1 x x x 1 2 2 x x 1 x x 2 x x 2 1 x 37
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x 1 x 1 lim lim x 1 2 2 x x 1 x x 2 x x 2 1 x x 1 2 2 x x x 2 x x 2 1 x 0 . 4 4x 3 1 4 x 1 6) B lim lim x 1 x 1 x 1 3 2 4 4 4 x 1 4x 3 4x 3 4x 3 1 4 lim 1 . x 1 3 2 4 4 4 4x 3 4x 3 4x 3 1 2 2 2 2x 2x 4 x 1 x 3 2x 1 2x 5 7) B lim lim x 2 2 x 1 x 3 x 2 2 2 x x 2 2x 1 2x 5 2 2 x 1 x 3 2 5 lim . x 2 2 2x 1 2x 5 3 x 9 x 16 7 x 9 3 x 9 4 Bài 3. 1) L lim lim x 0 x x 0 x x x x 9 3 x 16 4 1 1 7 lim lim . x 0 x x 0 x 9 3 x 16 4 24 2x 2 5x 4 5 2x 2 2 5x 4 3 2) L lim lim x 1 x 1 x 1 x 2 x 1 5 x 1 2x 2 2 5x 4 3 2 5 4 lim lim . x 1 x 1 x 1 2x 2 2 5x 4 3 3 2 x 6 2x 2 8 2 x 6 6 2x 2 2 3) L lim lim x 3 x 3 x 3 x 3 x 6 9 2x 2 4 x 3 x 3 2 2 2 x 6 3 2x 2 2 x 6 3 2x 2 2 lim lim x 3 x 3 x 3 x 3 2 2 5 lim . x 3 x 6 3 2x 2 2 6 38
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 2 2 2x x 1 x 8 2x x 1 x 2 x 4 4) L lim lim x 2 x 2 x 2 x 2 2 2 4x 4 x x 2 x 2 x 2 x 2 x 2 x 2 x 2 2 x 1 x 2 x 1 x lim lim x 2 x 2 x 2 x 2 x 2 lim x 2 x 2 8 . x 2 2 x 1 x 5x 4 2x 3 x 84 5x 4 2x 3 3 5x 4 16x 96 5) L lim lim x 6 x 6 x 6 x 6 2 x 6 5x 4 2x 3 3 16 x 6 5x 4 16 x 6 lim 2x 3 3 lim x 6 x 6 x 6 x 6 10x 8 74 lim 16 . x 6 2x 3 3 3 1 4x 1 6x 1 2 24x 10x 1 1 2 24x 10x 1 1 6) L lim lim lim x 0 x x 0 x x 0 2 x 24x 10x 1 1 x 24x 10 24x 10 lim lim 5 . x 0 2 x 24x 10x 1 1 x 0 2 24x 10x 1 1 4x 3 2x 1 3x 1 2x 1 x 4x 3 2x 1 7) L lim lim 2 2 2 x 1 x 2x 1 x 1 x 1 x 1 2 2 2x 1 x 4x 3 2x 1 lim 2 2 x 1 x 1 2x 1 x x 1 4x 3 2x 1 1 4 5 lim . x 1 2x 1 x 4x 3 2x 1 2 3x 7 4 x 3 2 2x 1 4 x 3 x 7 2 2x 1 2x 8) L lim lim 2 2 x 1 x 2x 1 x 1 x 1 2 2 2 2 16x 48 x 14x 49 4 2x 1 4x x 1 4 x 1 x 7 4 x 3 2x 2 2x 1 x 7 4 x 3 2x 2 2x 1 lim lim 2 x 1 2 x 1 x 1 x 1 1 4 17 lim . x 1 x 7 4 x 3 2x 2 2x 1 16 39
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 4x 4 9 6x 5 4x 4 x 2 9 6x x 3 9) L lim lim 2 x 0 x 2 x 0 x 2 2 4x 4 x 4x 4 9 6x x 6x 9 2 2 x x 4x 4 x 2 9 6x x 3 x 2 4x 3 9 6x x 3 lim lim 2 x 0 x 2 x 0 x 1 1 5 lim . x 0 x 2 4x 4 9 6x x 3 12 2 2 6x 3 2x 5x 2 x 2x 1 6x 3 10) L lim lim 2 x 1 2 x 1 x 1 x 1 2 2 2 6x 3 x 4x 4 2 x 1 2 x 1 2 x 1 6x 3 x 2 6x 3 x 2 lim lim 2 x 1 2 x 1 x 1 x 1 1 11 lim 2 . x 1 6x 3 x 2 6 3 4x 2 4x 8 4 1 Bài 4. 1) L lim lim lim . x 2 x 2 x 2 3 2 3 x 2 3 2 3 x 2 16x 2 4x 4 16x 2 4x 4 3 3 1 1 x 1 1 x 1 1 2) L lim lim lim . x 0 x x 0 2 x 0 2 3 3 3 x 1 1 x 1 x 3 3 1 1 x 1 x 3 2 x 1 2 2 x 9 3) L lim lim x 3 x 3 x 3 2 2 3 2 3 x 3 x 1 2 x 1 4 x 3 1 lim . x 3 2 2 3 2 2 3 x 1 2 x 1 4 3 x 7 2 x 1 4) L lim lim x 1 x 1 x 1 x 1 2 3 3 . x 7 2 x 7 4 x 1 x 1 1 lim . x 1 2 3 3 x 7 2 x 7 4 6 x 8 3 x 2 3 2 3 2x 9 5 5 5) L lim x 2 x 4 lim lim . x 8 2x 9 5 x 8 2x 16 x 8 3 2 3 2 x 2 x 4 12 2x 9 5 40
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x 1 2 3 3 3 x 1 3 2 3 x 2 x 2 1 6) x x 1 L lim lim lim 1 . 3 x 1 x 2 1 x 1 x 1 x 1 3 2 3 x x 1 2 3 3 x 2 x 2 1 3 3 3 3 10 2x x 1 10 2x 2 x 1 7) L lim lim 2 x 1 x 3x 2 x 1 x 1 x 2 3 2x 2 x 1 2 3 3 3 3 10 2x 2 10 2x 4 lim x 1 x 1 x 2 2 2 x 1 x x 1 x 1 2 3 3 3 3 10 2x 2 10 2x 4 lim x 1 x 1 x 2 2 2 x x 1 1 2 3 3 3 3 10 2x 2 10 2x 4 3 lim . x 1 x 2 2 3 8x 11 x 7 3 8x 11 3 x 7 3 8) L lim lim lim 2 x 2 x 3x 2 2 x 2 x 3x 2 2 x 2 x 3x 2 8x 11 27 x 7 9 lim lim x 2 2 x 2 3 3 x 1 x 2 8x 11 3 8x 11 9 x 1 x 2 x 7 3 8 1 8 1 7 lim lim . x 2 2 x 2 3 3 x 1 8x 11 3 8x 11 9 x 1 x 7 3 27 7 54 3 3 2 3 3 2 x 7 x 3 x 7 2 x 3 2 9) L lim lim lim x 1 x 1 x 1 x 1 x 1 x 1 3 2 x 7 8 x 3 4 lim lim x 1 2 x 1 2 3 3 3 3 x 1 x 3 2 x 1 x 7 2 x 7 4 3 2 x 1 x 1 lim lim x 1 2 x 1 2 3 3 3 3 x 1 x 3 2 x 1 x 7 2 x 7 4 2 x x 1 x 1 1 1 1 lim lim . x 1 2 x 1 2 3 3 3 4 2 4 3 x 3 2 x 7 2 x 7 4 41
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 3 2 1 x 8 x 2 1 x 2 8 x 2 10) L lim lim lim x 0 x 0 x 0 x x x 4 1 x 4 8 x 8 lim lim x 0 x 0 2 x 2 1 x 2 3 3 x 8 x 2 8 x 4 4 1 1 11 lim lim 1 . x 0 x 0 2 2 1 x 2 3 3 12 12 8 x 2 8 x 4 3 2 3 2 2x 4x 11 x 7 2x 4x 11 3 x 7 3 11) L lim lim lim 2 2 2 x 2 x 2 x 2 x 4 x 4 x 4 3 2 2x 4x 11 27 x 7 9 lim lim x 2 2 x 2 2 2 2 3 2 3 x 4 x 7 3 x 4 2x 4x 11 3 2x 4x 11 9 2 x 2 x 4 x 2 lim lim x 2 2 x 2 2 2 2 3 2 3 x 4 x 7 3 x 4 2x 4x 11 3 2x 4x 11 9 2 x 4 1 lim lim x 2 2 x 2 2 3 2 3 x 2 x 7 3 x 2 2x 4x 11 3 2x 4x 11 9 1 1 5 9 24 72 3 3 4 x. 8 3x 2 2 4 x 4 4 x. 8 3x 4 12) L lim lim 2 2 x 0 x 0 x x x x 3 4 x. 8 3x 2 2 4 x 4 lim lim 2 2 x 0 x 0 x x x x 4 x. 8 3x 8 2 4 x 4 lim lim x 0 2 x 0 3 3 x x 1 4 x 2 x x 1 8 3x 2 8 3x 4) 4 x.3 2 lim lim x 0 2 x 0 3 3 x 1 4 x 2 x 1 8 3x 2 8 3x 4 1 1 1. 2 2 n 1 ax 1 1 ax 1 Bài 5. 1) F lim lim x 0 x 0 n 1 n 2 x n x 1 n ax 1 ax ... n 1 ax 1 a a lim . x 0 n 1 n 2 n 1 n 1 ... n 1 1 n ax ax ax n 1 ax 1 m n m 1 bx 1 1 ax 1 bx 2) F lim lim x 0 x 0 x x 42
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC n 1 ax 1 m 1 bx 1 a b lim lim . x 0 x 0 x x n m n 1 ax 1 n 1 ax 1 1 3) F lim lim . x 0 m x 0 1 bx 1 m x 1 bx 1 x n 1 ax 1 a m 1 bx 1 b Xét A lim ; B lim x 0 x n x 0 x m a 1 am F . . n b bn m n 1 ax 1 m n m 1 bx 1 1 ax 1 bx 4) F lim lim x 0 x 0 1 x 1 1 x 1 n 1 ax 1 m 1 bx 1 lim lim x 0 x 0 1 x 1 1 x 1 n 1 ax 1 m x 1 bx 1 x lim . lim . x 0 x 0 x 1 x 1 x 1 x 1 n 1 ax 1 a Ta có A lim x 0 x n m 1 bx 1 b x 1 x 1 x B lim C lim lim lim 1 x 1 2 x 0 x m x 0 x 0 x 0 1 x 1 1 x 1 a b a b F .2 .2 2 . n m n m
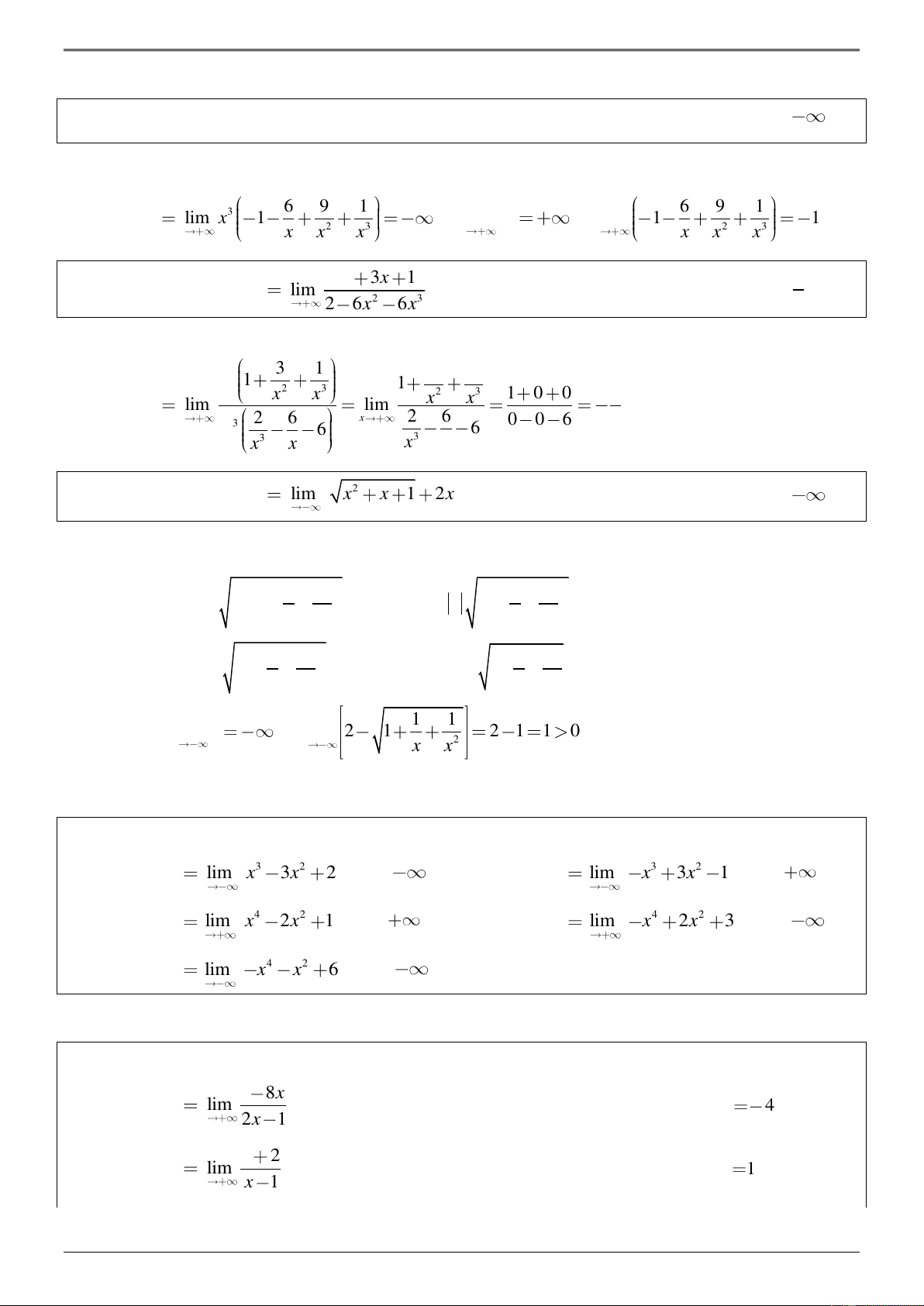
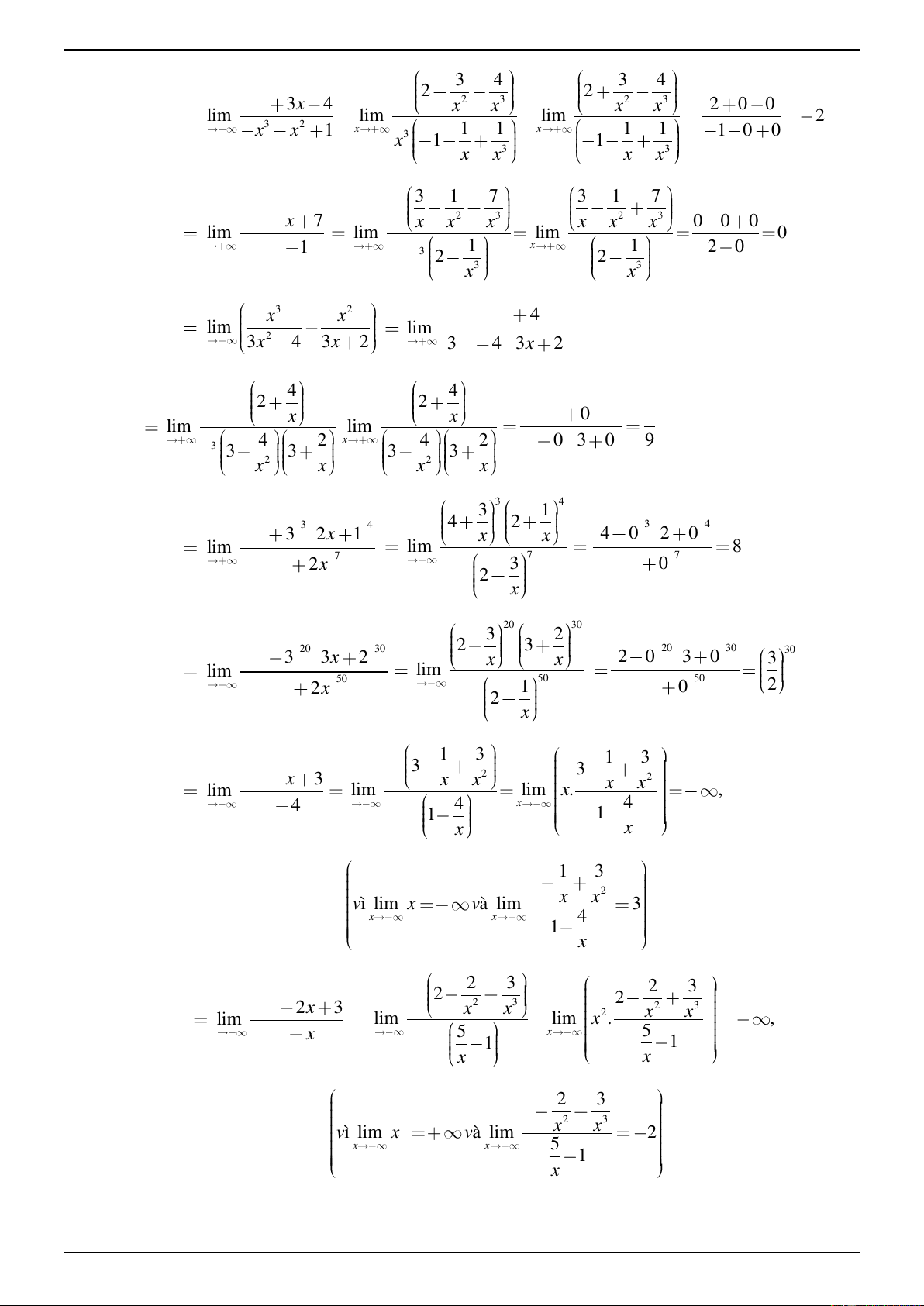
Dạng 3. Giới hạn của hàm số khi x →  . Phương pháp giải:
- Đối với dạng đa thức không căn, ta rút bậc cao và áp dụng công thức khi x → + 1. lim k x = + x→+
 + khi k = 2l 2. lim k x =  x→−
− khi k = 2l +1 c 3. lim = 0 (c hằng số) k x→+ x
- Đối với dạng phân số không căn, ta làm tương tự như giới hạn dãy số, tức rút bậc cao nhất của tử
và mẫu, sau đó áp dụng công thức trên.
- Ngoài việc đưa ra khỏi căn bậc chẵn cần có trị tuyệt đối, học sinh cần phân biệt khi nào đưa ra ngoài
căn, khi nào liên hợp. Phương pháp suy luận cũng tương tự như giới hạn của dãy số, nhưng cần phân
biệt khi x → + hoặc x → − 43
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC VÍ DỤ
Ví dụ 1. Tính giới hạn A = ( 3 2
lim −x − 6x + 9x + ) 1 . Đs: . x→+ Lời giải 6 9 1 6 9 1 3 A lim x 1 (vì 3 lim x và lim 1 1 ). 2 3 x x x x x 2 3 x x x x 3 x 3x 1 1
Ví dụ 2. Tính giới hạn B lim . Đs: . 2 3 x 2 6x 6x 6 Lời giải 3 1 3 3 1 x 1 2 3 1 2 3 x x 1 0 0 1 lim lim x x B . x 2 6 x 2 6 3 0 0 6 6 x 6 6 3 3 x x x x
Ví dụ 2. Tính giới hạn 2 C lim x x 1 2x . Đs: . x Lời giải  1 1   1 1      2
C = lim  x 1+ + + 2x    = lim  x 1+ + + 2x    2 2 x→− x   x x →−      x x      1 1     1 1  = lim −x 1+ + + 2x  
 = lim x2 − 1+ +  = − 2  2  x→− x   x x →−     x x    1 1 (Vì lim x và lim 2 1 2 1 1 0 ). x 2 x x x
BÀI TẬP ÁP DỤNG Bài 1. Tính các giới hạn sau: 1) 3 2 A lim x 3x 2 . Đs: . 2) 3 2 A lim x 3x 1 . Đs: . x x 3) 4 2 A lim x 2x 1 . Đs: . 4) 4 2 A lim x 2x 3 . Đs: . x x 5) 4 2 A lim x x 6 . Đs: . x Bài 2. Tính các giới hạn sau: 1 8x 1) B lim . Đs: B 4 . x 2x 1 x 2 2) B lim . Đs: B 1. x x 1 44
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 4 3 2x 7x 15 3) B lim . Đs: B 2 . 4 x x 1 3 2x 3x 4 4) B lim . Đs: B 2 . 3 2 x x x 1 2 3x x 7 5) B lim . Đs: B 0 . 3 x 2x 1 3 2 x x 2 6) B lim . Đs: B . 2 x 3x 4 3x 2 9 3 4 4x 3 2x 1 7) B lim . Đs: B 8 . 7 x 2 2x 20 30 30 2x 3 3x 2 3 8) B lim . Đs: B . 50 x 1 2x 2 2 3x x 3 9) B lim . Đs: B . x x 4 3 2x 2x 3 10) B lim . Đs: B . x 5 x Bài 3. Tính các giới hạn sau: 17 1) 2 C lim x 3x 2 x 10 . Đs: . x 2 4 2 2x x 1 2) C lim . Đs: . x 1 2x 3) 2 C lim 4x 4x 1 2x 13 . Đs: 14. x 9 4) 2 C lim x x x 5 . Đs: . x 2 5) 2 C lim 2x 1 x . Đs: . x 6) 2 C lim x 4x x 2021 . Đs: 2019 . x 1 7) 2 2 C lim x x x 1 . Đs: . x 2 2 x 3 8) C lim . Đs: -2. x 2 x x 5 45
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 9) 4 2 2 C lim 4x 3x 1 2x . Đs: . x 4 2 x x 2x 1 10) C lim . Đs: . x 2x 3 2 3 11) 2 C lim x x 1 x 1 . Đs: . x 2 2 x x x 12) C lim . Đs: 2 . x x 10 1 13) 2 2 C lim 4x 9x 21 4x 7x 13 . Đs: x 2 2 2 4x x 3x 7x 1 14) C lim . Đs: 1. 2 x 2 2x 1 . x 3x 15) 2 C lim 4x 4x 1 2x 3 . Đs: 4 x 3 x 16) C lim x 1 . Đs: -1 3 x 5 3x x 43 17) 2 C lim 16x 3x 4x 5 . Đs: x 8 3 2x x 18) C lim x . Đs: 2 5 2 x x x 3 5 19) 2 C lim x 3 x x 1 . Đs: x 2 Bài 4. Tính các giới hạn sau: 3 2x x 1) lim . x . Đs: 2 . 5 2 x x x 3 2 x 3 2) lim . Đs: 2. x 2 x x 5 2 x x 2 3x 1 3) lim . Đs: 4. x 2 4x 1 1 x 4 2 2 2x x x x 3 2 1 4) lim Đs: . x x 5 2x 2 46
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 2x 1 3 4x x 5 8 5) lim . Đs: . x 2 1 3x 2 9x x 10 3 2 3 3 3 x 1 1 8x 1 6) lim . Đs: . x 6x 9 6 2 2x 1 x 3 2 7) lim . Đs: . 2 x x 5x 5 2 x 4x 3x 1 1 8) lim . Đs: x 2 9x x 3 5x 3 4 2x 1 9) lim . Đs: 1. x 2 2 x x x x 8x 3 10) lim . Đs: 2. x 2 6x 4x x 3 2 x 1 7x 2 11) lim . Đs: 1 . x 2 x 3x 2 5x 3 x 2 1 2x 12) lim . Đs: 1 . x 1 x Bài 5. Tính các giới hạn sau: 2 1) lim x x x . Đs: . x 2 2) lim x 4x x . Đs: 2 . x 3) lim x 2 x 2 . Đs: 0. x 1 2 2 4) lim x x x 1 . Đs: . x 2 2 5) lim x 4x 1 x 2 . Đs: 0. x 5 2 6) lim x 3x 5 x 1 . Đs: . x 2 1 3 3 2 7) lim 27x x 3x . Đs: . x 27 1 2 8) lim 2x 4x 2x 1 . Đs: . x 2 47
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 9) lim 2x 3 4x 4x 3 . Đs: 4 . x 3 4 2 2 10) lim 4x 3x 1 2x . Đs: . x 4 19 2 11) lim 4x 3x 1 2x 4 . Đs: . x 4 2 12) lim 4x 4x 1 2x 3 . Đs: 4 . x 3 2 3 x 4x x 16 13) lim . Đs: . x 2 2x 4x 3x 9 3 3 14) lim 8x 1 2x 1 . Đs: 1 . x LỜI GIẢI 3 2 3 2 Bài 1. 1) 3 A lim x 1 , (vì 3 lim x và lim 1 1 0 ). 3 x x x x 3 x x x 3 1 3 1 2) 3 3 A lim x 1 , ì v lim x à v lim 1 1 0 . 3 3 x x x x x x x 2 1 2 1 3) 4 4 A lim x 1 , ì v lim x à v lim 1 1 0 . 2 4 2 4 x x x x x x x 2 3 2 3 4) 4 4 A lim x 1 , ì v lim x à v lim 1 1 0 . 2 4 2 4 x x x x x x x 1 6 1 6 5) 4 4 A lim x 1 , ì v lim x à v lim 1 1 0 . 2 4 2 4 x x x x x x x 1 1 x 8 8 1 8x x 0 8 Bài 2. 1) lim lim lim x B 4 . x 2x 1 x 1 x 1 2 0 x 2 2 x x 2 2 x 1 1 x 2 x 1 0 2) lim lim lim x B 1. x x 1 x 1 x 1 1 0 x 1 1 x x 7 15 4 7 15 x 2 4 3 4 2 4 2x 7x 15 x x 2 0 0 3) lim lim lim x x B 2 . 4 x x 1 x 1 x 1 4 1 0 x 1 1 4 4 x x 48
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 4 3 4 3 x 2 2 3 2 3 2 3 2x 3x 4 x x x x 2 0 0 4) B lim lim lim 2 . 3 2 x x x 1 x 1 1 x 1 1 3 1 0 0 x 1 1 3 3 x x x x 3 1 7 3 1 7 3 x 2 3x x 7 2 3 2 3 x x x x x x 0 0 0 5) B lim lim lim 0 . 3 x 2x 1 x 1 x 1 3 2 0 x 2 2 3 3 x x 3 2 x x 2 x 2x 4 6) B lim lim 2 x 3x 4 3x 2 2 x 3x 4 3x 2 4 4 3 x 2 2 x x 2 0 2 lim lim x 4 2 x 4 2 3 3 0 3 0 9 x 3 3 3 3 2 2 x x x x 3 4 3 1 3 4 4 2 3 4 4x 3 2x 1 x x 4 0 2 0 7) B lim lim 8 . 7 7 7 x 2 2x x 3 2 0 2 x 20 30 3 2 20 30 2 3 20 30 30 2x 3 3x 2 x x 2 0 3 0 3 8) B lim lim . 50 50 50 x 1 2x x 1 2 0 2 2 x 1 3 2 1 3 x 3 2 3 3x x 3 2 2 x x 9) B lim lim lim . x x x , x x 4 x 4 x 4 x 1 1 x x 1 3 3 2 ì lim à lim x x v x v 3 . x x 4 1 x 2 3 3 2 3 x 2 3 2 2x 2x 3 2 3 2 3 x x 10) B lim 2 lim lim . x x x , x 5 x x 5 x 5 x 1 1 x x 2 3 2 2 3 2 ì lim à lim x x v x v 2 . x x 5 1 x 49
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Bài 3. 1) 2 C lim x 3x 2 x 10 2 10 lim x 3x 2 x x x 3x 2 3x 2 10 lim 10 lim x 2 x 3x 2 x x 2 x 3x 2 x 2 3 3 17 10 lim x 10 . x 3 2 2 2 1 1 2 x x 1 1 1 1 2 4 2 x 2 2 2x x 1 2 4 2 4 2) C lim x x x x lim lim x , x 1 2x x 1 x 1 x 2 2 x x 1 1 2 2 4 x x 2 ì v lim x à v lim 0 x x 1 2 2 x 3) 2 C lim 4x 4x 1 2x 13 2 13 lim 4x 4x 1 2x x x 2 2 4x 4x 1 4x 4x 1 13 lim 13 lim x 2 4x 4x 1 2x x 4 1 2 x 4 2x 2 x x 1 1 x 4 x 4 x x 13 lim 13 lim x 4 1 x 4 1 x 4 2x x 4 2x 2 x x 2 x x 1 4 13 lim x 14 x 4 1 4 2 2 x x 1 1 4) 2 C lim x x x 5 5 lim x 1 x 5 lim x 1 1 x x x x x 1 1 1 1 9 5 lim x x 5 lim . x 1 x 1 2 1 1 1 1 x x 50
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 1 1 5) 2 C lim 2x 1 x lim x 2 x lim x 1 2 , x 2 2 x x x x 1 ì v lim 1 2 1 2 0 à v lim x . 2 x x x 4 4 6) 2 C lim x 4x x 2021 2021 lim x 1 x 2021 lim x 1 1 x x x x x 4 1 1 4 4 2021 lim x x 2021 lim 2021 2019 . x 4 x 4 2 1 1 1 1 x x x 1 7) 2 2 C lim x x x 1 lim x x 2 2 x x x 1 x 1 x 1 lim lim x 1 1 x 1 1 x 1 x 1 x 1 x 1 2 2 x x x x 1 1 1 lim x x 1 1 2 1 1 2 x x 2 x 3 2 x 3 2 x 3 2 0 8) C lim lim lim x x 2 . x 2 x x 5 x 1 5 x 1 5 1 0 0 x 1 1 2 2 x x x x 3 1 9) 4 2 2 C lim 4x 3x 1 2x 2 2 lim x 4 2x x 2 4 x x x 3 1 1 4 4 3 2 4 2 3 2 lim x x lim x x . x 3 1 x 3 1 4 4 2 4 2 2 4 2 4 x x x x 1 x 1 2x 2 x x 2x x 10) C lim lim x 2x 3 x 2x 3 1 1 x 1 2 1 2 x x 1 2 1 lim lim . x 3 x 3 2 2 x 2 2 x x 51
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 1 1 11) 2 C lim x x 1 x 1 1 lim x 1 x x 2 x x x 1 1 1 1 1 1 2 1 lim x 1 1 1 lim x x x 2 x x x x 1 1 1 1 2 x x 1 1 1 3 1 lim x 1 . x 1 1 2 2 1 1 2 x x 1 x 1 2 x x 1 1 x x x x x x 1 1 12) C lim lim lim 2 . x x 10 x x 10 x 10 1 1 x 9 21 7 13 13) 2 2 C lim 4x 9x 21 4x 7x 13 lim x 4 x 4 x 2 2 x x x x x 9 21 7 13 34 4 4 2 2 2 2 1 lim x x x x x lim x . x 9 21 7 13 x 9 21 7 13 2 2 2 4 4 4 4 2 2 x x x x 2 2 x x x x 2 2 4x x 3x 7x 1 14) C lim 2 x 2 2x 1 . x 3x 4 x 3 7 1 4 x 3 7 1 3 x 2 3 2 3 x x x x x x x x 4 lim lim 1 2 2 2 x 1 3 x 1 3 2 .1 2 x 2 . x 1 2 . 1 x x x x 4 1 15) 2 C lim 4x 4x 1 2x 3 3 lim x 4 2x x 2 x x x 4 1 1 4 4 4 2 4 3 lim x x x 3 lim x 3 4 . x 4 1 x 4 1 4 4 2 4 2 2 x x 2 x x 3 x 16) C lim x 1 3 x 5 3x x 52
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 3 1 1 1 1 0 1 lim 1 x lim 1 x x 1. 1 . x x 5 3 x x 5 3 2 0 0 1 x 1 1 3 2 2 x x x x 17) 2 C lim 16x 3x 4x 5 x 3 3 5 lim x 16 4x 5 lim x 16 4 x x x x 3 16 16 3 3 3 43 5 lim x x 5 lim 5 5 . x 3 x 3 4 4 8 8 16 4 16 4 x x 1 3 1 x 2 3 2 2x x 2 2 x 18) x C lim x lim x lim 2. 5 2 x x x 3 x 1 3 x 1 3 5 x 1 1 3 5 3 5 x x x x 1 1 19) 2 C lim x 3 x x 1 3 lim x x 1 x 2 x x x 1 1 1 1 1 1 2 3 lim x 1 1 3 lim x x x 2 x x x x 1 1 1 1 2 x x 1 1 1 5 3 lim x 3 . x 1 1 2 2 1 1 2 x x Bài 4. 1 3 3 2x 2x x x 2x x 1) lim . lim . . lim 1 . x x x 2 . 5 2 2 5 2 x x x 3 x x x x 3 x 1 3 x 2 4 x x 3 2 2 x 3 2x 3 2) lim lim lim x 2 . x 2 x x 5 x 1 5 x 1 5 x 1 1 2 2 x x x x 53
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 1 2 1 2 1 2 x 1 3x 1 1 3 2 2 x x 2 3x 1 x x x x x 1 3 3) lim lim lim 4 . x 2 4x 1 1 x x 1 x 1 1 2 1 x 4 1 x 4 1 2 2 x x x 1 3 1 3 2 2 4 2 2 x 2 x 1 2 1 2 2 2x x x x 3 x x x x 2 1 4) lim lim lim . x x 5 2 x x 5 x 5 2 2 x 2 2 x x 1 5 1 1 5 2 2x 1 3x 4 2 3 4 2 2 2x 1 3 4x x 5 x x x x x 8 5) lim lim lim . x 2 1 3x 2 9x x 10 x 1 10 x 1 1 10 3 1 3x 2x 9 3 2 9 2 2 x x x x x 1 1 1 1 2 3 3 3x 1 x 8 3 1 8 2 3 2 3 3 x 1 1 8x x x x x 1 6) lim lim lim . x 6x 9 x 6x 9 x 9 6 6 x 3 1 3 2x 1 x 1 2 1 1 2 2x 1 x 3 x x x 2 7) lim lim lim . 2 2 x x 5 x x x 5 x x 1 5 5 x 3 1 3 1 2 x x 4 1 4 2 2 x 4x 3x 1 x x x x 1 8) lim lim lim . x 2 9x x 3 5x 3 x 1 3 x 1 3 3 4 x 9 5x 3 9 5 2 2 x x x x x 1 2 2x 1 2x 1 2 9) lim lim lim x 1 . x 2 2 x x x x x 1 1 x 1 1 2 x 1 x 1 1 1 x x x x 3 8 8x 3 8x 3 10) lim lim lim x 2 . x 2 6x 4x x 3 x 1 3 x 1 3 6x x 4 6 4 2 2 x x x x 1 1 2 2 x 1 7x 2 1 7 2 2 x 1 7x 2 11) x x x lim lim lim 1 . x 2 x 3x 2 5x 3 x 3 2 x 3 2 3 x 1 5x 3 x 1 5 2 2 x x x x x 1 2 1 2 x 2x 1 2 2 2 x 2 1 2x 12) x x x x lim lim lim 1 . x 1 x x 1 x x 1 1 x 54
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Bài 5. 1 1 2 1) lim x x x lim x 1 x lim x 1 1 . x x x x x 1 ì V lim x à v lim 1 1 2 . x x x 2 2 x 4x x 4x 2 2) lim x 4x x lim lim 2 . x x 2 x 4 x x x 4 x 1 1 x x 2 x 2 4 3) lim x 2 x 2 lim lim 0 . x x x 2 x 2 x 2 2 x 1 1 x x 4 1 1 ì V lim 0 à v lim . x x x 2 2 2 1 1 x x 2 2 x x x 1 x 1 2 2 4) lim x x x 1 lim lim x x 2 2 x x x 1 x 1 1 x 1 x 1 2 x x 1 1 1 lim x . x 1 1 2 1 1 2 x x 2 2 x 4x 1 x 2 3 2 5) lim x 4x 1 x 2 lim lim x x 2 x 4x 1 x 2 x 4 1 x 1 x 2 2 x x 3 lim 0 . x 4 1 2 x 1 1 2 x x x 2 2 x 3x 5 x 1 5x 4 2 6) lim x 3x 5 x 1 lim lim x x 2 x 3x 5 x 1 x 3 5 x 1 x 1 2 x x 4 5 5 lim x . x 3 5 1 2 1 1 2 x x x 55
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2 3 27x x 27x 3 3 2 7) lim 27x x 3x lim 2 x x 3 3 2 3 3 2 2 27x x 3x 27x x 9x 2 x 1 1 lim lim . 2 2 x x 27 1 1 1 1 2 2 2 3 3 3 3 x 27 3x 27 9x 27 3 27 9 x x x x 2 2 4x 4x 2x 1 2x 1 2 8) lim 2x 4x 2x 1 lim lim x x 2 2x 4x 2x 1 x 2 1 2x x 4 2 x x 1 2 1 lim x . x 2 1 2 2 4 2 x x 2 2 2x 3 4x 4x 3 16x 6 2 9) lim 2x 3 4x 4x 3 lim lim x x 2 x 2 2x 3 4x 4x 3 2x 3 4x 4x 3 6 16 16x 6 lim lim x 4 x 4 3 x 3 4 3 2x 3 x 4 2 4 2 2 x x x x x 4 2 4 2 4x 3x 1 4x 3x 1 4 2 2 10) lim 4x 3x 1 2x lim lim x x 4 2 2 4x 3x 1 2 x x 3 1 2 2 x 4 2x 2 4 x x 1 3 2 3 lim x . x 3 1 4 4 2 2 4 x x 2 2 4x 3x 1 2x 4 19x 15 2 11) lim 4x 3x 1 2x 4 lim lim x x 2 4x 3x 1 2x 4 x 3 1 x 4 2x 4 2 x x 15 19 19 lim x . x 3 1 4 4 4 2 2 x x x 2 2 4x 4x 1 2x 3 16x 8 2 12) lim 4x 4x 1 2x 3 lim lim x x 2 4x 4x 1 2x 3 x 4 1 x 4 2x 3 2 x x 56
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 8 16 lim x 4 . x 4 1 3 4 2 2 x x x 3 2 3 3 2 3 2 x 4x x x 4x x 2x 4x 3x 13) lim lim . 2 2 2 x 2 x 4x 4x 3x 2 3 2 3 3 2 3 2x 4x 3x x x 4x x 4x x 3 2 4 4 x 16 lim . . 2 x 3 9 4 4 3 3 1 1 1 x x 3 3 8x 1 2x 1 14) 3 3 lim 8x 1 2x 1 lim 2 x x 2 3 3 3 3 8x 1 2x 1 8x 1 2x 1 6 2 2 12 12x 6x 2 2 lim lim x x 1. 2 2 x 2 x 2 3 3 3 3 8x 1 2x 1 8x 1 2x 1 1 1 1 1 3 3 8 2 8 2 3 3 x x x x
Dạng 4. Giới hạn một bên x x+ → hoặc x x− → . 0 0 Phương pháp giải:
- Sử dụng các định lý về giới hạn hàm số
Chú ý: x → x+  x x x − x  0 0 0 0
x → x−  x x x − x  0 0 0 0  VÍ DỤ 2x − 3
Ví dụ 1. Tính giới hạn A = lim . Đs: . − + x 1 → x −1 Lời giải lim 2x 3 1 0 x 1 2x 3 Vì lim x 1 0 A lim . x 1 x 1 x 1 x 1 x 1 x 1 0 x −15
Ví dụ 2. Tính giới hạn A = lim . Đs: . − + x→2 x − 2 Lời giải 57
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC lim x 15 13 0 x 2 x 15 Vì lim x 2 0 A lim . x 2 x 2 x 2 x 2 x 2 x 2 0 2 − x
Ví dụ 3. Tính giới hạn A = lim . Đs: . − − x 3 → 3 − x Lời giải
lim (2 − x) = −1 0 − x→3  2 − x
Vì lim (3 − x) = 0  A = lim = − . − − x→3 x→3 3 − x
x → 3−  x  3  3 − x  0  x +1
Ví dụ 4. Tính giới hạn A = lim . Đs: + x→2 2x − . + 4 Lời giải lim (x + ) 1 = 3  0 + x→2  x +1
Vì  lim (2x − 4) = 0  A = lim = + . + + x→2 x→2 2x − 4 
x → 2+  x  2  2x − 4  0  x − 5
Ví dụ 5. Tính giới hạn A = lim . Đs: . − − x→ (x −4)2 4 Lời giải lim (x −5) = 1 −  0 − x→4   − 2 x 5
Vì  lim ( x − 4) = 0  A = lim = − . − − x→ x→  (x − 4)2 4 4 x → 4−   (x − 4)2  0 3x − 8
Ví dụ 6. Tính giới hạn A = lim . Đs: . + − x→ (3− x)2 3 Lời giải
lim (3x −8) =1 0 − x→3   − 2 3x 8
Vì lim (3 − x) = 0  A = lim = + . − − x→ x→  (3− x)2 3 3 x → 3−   (3− x)2  0 2 + − Ví dụ 7. 2x 5x 3
Tính giới hạn A = lim . Đs: . − + x ( → − ) (x +3)2 3 Lời giải 58
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 2x + 5x − 3 (2x − ) 1 ( x + 3) 2x −1 Ta có lim = lim = lim + + + x ( → − ) (x +3)2 x→(− ) (x +3)2 3 3 x→( 3 − ) x + 3  lim (2x − ) 1 = 7 −  0 + x→( 3−) 2  2x + 5x − 3
Vì  lim ( x + 3) = 0  A = lim = − . + + x→(− ) x→(− )  (x +3)2 3 3 + x →  ( 3 − )  x  3 −  x + 3  0  1 1 
Ví dụ 8. Tính giới hạn A = lim − .   Đs: . − − 2
x→2  x − 2 x − 4  Lời giải  1 1  x +1 Ta có: A = lim − = lim   − 2 − x→2  − − x→2 x 2 x 4  (x − 2)(x + 2) lim (x + ) 1 = 3  0 − x→2   1 1 
Vì  lim ( x − 2)( x + 2) = 0  A = lim − = −    . − − 2 x→2 x→2 
x − 2 x − 4 
x → 2−  x  2  
(x − 2)(x + 2)  0 2 − x 1
Ví dụ 9. Tính giới hạn B = lim . Đs: − . − 2 x→2 2x − 5x + 2 3 Lời giải −
Vì x → 2  x  2  2 − x = 2 − x − − Do đó 2 x 1 1 B = lim = lim = − . − −
x→2 ( x − 2)(2x − ) x→2 1 2x −1 3 x − 3 1
Ví dụ 10. Tính giới hạn B = lim . Đs: . + x 3 → 5x −15 5 Lời giải Vì x 3+ →
x  3  x − 3 = x − 3 − Do đó x 3 1 1 B = lim = lim = . − − x 3 → 5( x − 3) x 3 → 5 5
BÀI TẬP ÁP DỤNG
Bài 1. Tính các giới hạn sau: x −1 1 1) A = lim . Đs: − . − 3 x 1 → 2x + x − 3 7 x − 2 2) B = lim .
Đs: Không tồn tại. x→2 x − 2 59
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x − 9 3) C = lim .
Đs: Không tồn tại. x→3 x − 3 Bài 2. Tính các giới hạn sau: 2
2x − 2x + x −1 x + 3 7 1) C = lim . Đs: . − 2 x 1 → x − 2x +1 4 x − 2 2) C = lim . Đs: 2. − − x→2 x −1 −1 2 x − 7x +12 1 3) D = lim . Đs: . − → 2 x 3 9 − x 6 2 x − 5x + 6 1 4) D = lim . Đs: . − → 2 x 2 4 − x 2 1− x + x −1 5) D = lim . Đs: 1. − → 2 3 x 1 x − x x + 5
6) D = lim (1− x) . Đs: 0. + 3 2 x 1 → x + 2x − 3 3 x − 3x + 2 3 7) D = lim . Đs: . − 2 x 1 → x − 5x + 4 3 4 2 5
 x −6x − x khi x 1 Bài 3.
1) Tính giới hạn C = lim f ( x) với f ( x) =  . Đs: −2 x 1 → 3 x −3x khi x  1 x − 3 khi x  1 
2) Tính giới hạn C = lim f ( x) với f ( x) =  . Đs: −2 . x 1 → 2 1
 − 7x + 2 khi x 1 3x − 2  khi x  2 −
3) Tính giới hạn C = lim f ( x) với f ( x) =  x +1 . Đs:8 . x 2 →−
x +10 khi x  2 − 3  x +1  khi x  1 − Bài 4.
Tìm m để hàm số f ( x) =  x +1
có giới hạn tại x = 1. −  2 2
mx − x + m khi x  1 −
Đs: m =1 hoặc m = 2 − . 60
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC LỜI GIẢI x −1 Bài 1. 1) A = lim . − 3 x 1 → 2x + x − 3 −
Vì x →1  x  1  x −1 = − ( x − ) 1 . −(x − ) − Do đó 1 1 1 A = lim = lim = − . − − x→ (x − ) 1 ( 2 1 2x + 2x + 3) 2 x 1 → 2x + 2x + 3 7 x − 2 2) B = lim . x→2 x − 2 −(x − 2) −
+) Vì x → 2  x  2  x − 2 = − ( x − 2) nên lim = lim (− ) 1 = 1 − . − − x→2 − x→2 x 2 + x − 2
+) Vì x → 2  x  2  x − 2 = x − 2 nên lim = lim1=1 . − − x→2 − x→2 x 2 x − 2 x − 2 x − 2 Suy ra lim  lim
nên không tồn tại giới hạn của B = lim . − + x→2 − x→2 x 2 x − 2 x→2 x − 2 2 x − 9 3) C = lim . x→3 x − 3 x − 3 . x + 3 Ta có C = lim . Do đó: x 3 → x − 3 2 x − 9 (x −3). x +3 +) lim = lim = lim x + 3 = 6. + + + x→3 − x→3 − x→3 x 3 x 3 2 x − 9
−(x −3). x + 3 +) lim = lim = lim − + = − − − − ( x 3 ) 6. x→3 − x→3 − x→3 x 3 x 3 2 x − 9
Suy ra giới hạn của C = lim không tồn tại. x→3 x − 3 2
2x − 2x + x −1 x + 3 Bài 2. 1) C = lim . − 2 x 1 → x − 2x +1 −
Vì x → 1  x −1  0  x −1 = − ( x − ) 1 . Do đó 2x ( x − ) 1 − ( x − ) 2 1 x + 3 2x − x + 3 4x − x − 3 C = lim = lim = lim − − − x→ (x − )2 1 x 1 → − x 1 1 x 1 → (x − ) 1 (2x + x + 3) (x − ) 1 (4x + 3) 4x + 3 7 = lim = lim = . − − x 1 → (x − )
1 (2x + x + 3) x 1 → 2x + x + 3 4 x − 2 2) C = lim . − x→2 x −1 −1 61
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC −
Vì x → 2  x − 2  0  x − 2 = − ( x − 2) . Do đó:
−(x − 2)( x −1+ ) 1 C = lim = lim − − +  = − − − − −  ( x 1 )1 2.  x→2 (x ) x→2 1 1 2 x − 7x +12 3) D = lim . − → 2 x 3 9 − x (x −3)(x −4) 3 − x. 4 − x 4 − x 1 Ta có D = lim = lim = lim = . − − − x 3 →
(3− x)(3+ x) x 3 → x 3 3 − x. 3 + x → 3 + x 6 2 x − 5x + 6 4) D = lim . − → 2 x 2 4 − x (x −2)(x −3) 2 − x. 3 − x 3 − x 1 Ta có D = lim = lim = lim = . − − − x→2
(2− x)(2+ x) x→2 x→2 2 − x. 2 + x 2 + x 2 1− x + x −1 5) D = lim . − → 2 3 x 1 x − x
1− x − (1− x)
1− x − (1− x)2 1− 1− x Ta có D = lim = lim = lim =1. − → 2 − − x 1 x (1− x) x 1 → x 1 x 1− x → x x + 5
6) D = lim (1− x) . + 3 2 x 1 → x + 2x − 3  (  x − )2 1 ( x + 5)  (x − ) 1 ( x + 5)  Ta có D = lim −  = lim −  = 0. + + x→  (x − ) 1 ( 2 1 x + 3x + 3) 2  x 1 →  x + 3x + 3      3 x − 3x + 2 7) D = lim . − 2 x 1 → x − 5x + 4 (x − )2 1 ( x + 2) (1− x) x + 2 x + 2 3 Ta có D = lim = lim = lim = . − − − x 1 → (x − ) 1 ( x − 4) x 1 → (x − ) 1 ( x − 4) x 1 → 4 − x 3 Bài 3. 1) Ta có:
+) lim f ( x) = lim ( 3 x − 3x = − − − ) 2. x 1 → x 1 →
+) lim f ( x) = lim ( 4 2
5x − 6x − x = − − = − + + ) 5 6 1 2. x 1 → x 1 →
+) Vì lim f ( x) = lim f ( x) = 2
− nên hàm số f (x) có giới hạn tại x =1 và − + x 1 → x 1 → lim f ( x) = 2 − . x 1 → 62
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2) Ta có:
+) lim f ( x) = lim ( x − 3) = 2 − . − − x 1 → x 1 →
+) lim f ( x) = lim − x + = − + + → x→ ( 2 1 7 2 2. x 1 1 )
+) Vì lim f ( x) = lim f ( x) = 2
− nên C = lim f (x) = 2 − . − + x 1 → x 1 → x 1 → 3) Ta có: 3x − 2
+) lim f ( x) = lim = 8. − − x ( → 2 − ) x ( → 2 − ) x +1
+) lim f ( x) = lim ( x +10) = 8. + + x ( → 2 − ) x ( → 2 − )
+)Vì lim f ( x) = lim f ( x) = 8 nên C = lim f ( x) = 8. − + x ( → 2 − ) x ( → 2 − ) x 2 →− Bài 4. Ta có: 3 x +1
+) lim f ( x) = lim = lim − + = − − − ( 2 x x )1 3. x→(− ) 1 x→(− ) 1 x +1 x→(− ) 1
+) lim f ( x) = lim − + = + + + + ( 2 2 mx x m ) 2 m m 1. x ( → − ) 1 x→(− ) 1
+) Để hàm số có giới hạn tại x = 1 − thì m =1 2 2
3 = m + m +1  m + m − 2 = 0  .  m = 2 −
Dạng 5. Giới hạn của hàm số lượng giác Phương pháp giải:
- Sử dụng các định lý về giới hạn hàm số
- Sử dụng các công thức biến đổi lượng giác sin x - Lưu ý: lim 1 x 0 x VÍ DỤ 2sin x −1 1
Ví dụ 1. Tính giới hạn A = lim . Đs: A = − . 2  − x→ 4 cos x 3 2 6 Lời giải 2sin x −1 2sin x −1 2sin x −1 1 − 1 Ta có: A = lim = lim = lim = lim = − . 2     − − − − + x→ 4 cos x 3 x→ 4( 2 1 sin x) 2 3 x→ 1 4sin x x→ 1 2sin x 2 6 6 6 6 2 sin x −1 1
Ví dụ 2. Tính giới hạn A = lim . Đs: A = − . 2  − x→ 2 cos x 1 2 4 63
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Lời giải 2 sin x −1 2 sin x −1 2 sin x −1 1 − 1 Ta có: A = lim = lim = lim = lim = − . 2     − − − − + x→ 2 cos x 1 x→ 2( 2 1 sin x) 2 1 x→ 1 2sin x x→ 1 2 sin x 2 4 4 4 4 cos 4x −1
Ví dụ 3. Tính giới hạn A = lim . Đs: A = 0. x 0 → sin 4x Lời giải 2 2 2 2 cos 4x −1
cos 2x − sin 2x − cos 2x − sin 2x Ta có: A = lim = lim x 0 → x 0 sin 4x → 2sin 2x cos 2x 2 2 − sin 2x −sin 2x = lim = lim = 0. x 0 → x 0 2sin 2x cos 2x → cos 2x
1− sin 2x − cos 2x
Ví dụ 4. Tính giới hạn A = lim . Đs: A = − x 0 → 1+ sin 2x − 1. cos 2x Lời giải − −
1− 2sin x cos x − ( 2 2 cos x − sin 1 sin 2 cos 2 x x x ) Ta có: A = lim = lim .
x→ 1+ sin 2x − cos 2 x x
→ 1+ 2sin x cos x − ( 2 2 0 0 cos x − sin x) 2
2sin x − 2sin x cos x
2sin x (sin x − cos x) sin x − cos x = lim = lim = lim = 1 − . 2 x→0 x→0
2sin x + 2sin x cos x
2sin x (sin x + cos x)
x→0 sin x + cos x
BÀI TẬP ÁP DỤNG Bài 1. Tính các giới hạn sau:
1+ sin 2x − cos 2x sin 2x 1) A = lim . Đs: A = 1. − 2) A = lim . Đs: A = 1. − x 0
→ 1− sin 2x − cos 2x x 0
→ 1− sin 2x − cos 2x
sin 7x − sin 5x
sin 5x − sin 3x 3) A = lim . Đs: A = 2. 4) A = lim . Đs: A = 2. x 0 → sin x x 0 → sin x 1− cos x 5) A = lim . Đs: A = 0. x 0 → sin x
cos 3x + 2 cos 2x + 2 2 3 6) A = lim . Đs: A = .  x→ sin 3x 3 3
1+ sin 2x + cos 2x 7) A = lim . Đs: A = 2.  x→ cos x 2 Bài 2. Tính các giới hạn sau: 2 1− cos axa  sin 5x 1) B = lim . Đs: B = .   2) B = lim . Đs: B = 5. x 0 → 1− cosbxb x 0 → x 64
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC sin 5 . x sin 3 . x sin x 1 1− cos x 1 3) B = lim . Đs: B = . 4) B = lim . Đs: B = . 3 x 0 → 45x 3 2 x 0 → x 2 1− cos 5x 25 1− cosa x 2 a 5) B = lim . Đs: B = . 6) B = lim . Đs: B = . x 0 → 1− cos3x 9 2 x 0 → x 2 2 1− cos 2x sin x − tan x 1 7) B = lim . Đs: B = 4 . 8) B = lim
. Đs: B = − . x 0 → x sin x 3 x 0 → x 2 tan x − sin x 1 3 1− cos x 3 9) B = lim . Đs: B = . 10) B = lim . Đs: B = . 3 x 0 → sin x 2 x→0 x sin x 2 Bài 3. Tính các giới hạn sau: ( cos8x − ) 2 1 sin 3x 1− 2x +1 1 − 1) B = lim . Đs: B = 48 − . 2) B = lim . Đs: B = . 4 x→0 3.x x→0 sin 2x 2 1− cos cos 2x 3 3 1− cos x 1 3) B = lim . Đs: B = . 4) B = lim . Đs: B = . 2 x→0 x 2 2 x→0 tan x 6 3 tanx −1 1 5) B = lim . Đs: B = . 2  − x→ 2sin x 1 3 4
1+ tan x − 1+ sin x 1 1− cos x 6) B = lim . Đs: B = . 7) B = lim . Đs: B = 2 . 3 x→0 x 4 x→ (1− 1−x)2 0 2 1+ x − cos x
1− 2x +1 + sin x 8) B = lim . Đs: B = 1. 9) B = lim . Đs: B = 0 . 2 x→0 x x→0
3x + 4 − 2 − x 3 2 2x +1 − x +1 10) B = lim . Đs: 1. x→0 sin x
Bài 4. Tính các giới hạn sau:     1
1) C = lim tan 2x tan − x .    Đs: C =   x→   4  2 4 1+ cos x 1 2) C = lim Đs: C = x  → ( x − ) . 2 2 sin ( x − ) 1 1 − 3) C = lim . Đs: C = . 2 x  → x − 4x + 3 2 sin x − sin a 4) C = lim . Đs: C = cos . a x→a x − a 65
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC LỜI GIẢI + −
1+ 2sin x cos x − ( 2 2 cos x − sin 1 sin 2 cos 2 x x x ) Bài 1. 1) A = lim = lim
x→ 1− sin 2x − cos 2 x x
→ 1− 2sin x cos x − ( . 2 2 0 0 cos x − sin x) 2
2sin x + 2sin x cos x
2sin x (sin x + cos x) sin x + cos x = lim = lim = lim = 1 − . 2 x→0 x→0
2sin x − 2sin x cos x
2sin x (sin x − cos x)
x→0 sin x − cos x sin 2x 2sin x cos x 2) A = lim = lim
x→ 1− sin 2x − cos 2 x x
→ 1− 2sin x cos x − ( . 2 2 0 0 cos x − sin x) 2sin x cos x 2sin x cos x cos x = lim = lim = lim = 1 − . 2 x→0 x→0
2sin x − 2sin x cos x
2sin x (sin x − cos x)
x→0 sin x − cos x
sin 7x − sin 5x 2cos 6 . x sin x 3) A = lim = lim = lim2cos6x = 2 . x 0 → x 0 → x 0 sin x sin x →
sin 5x − sin 3x 2cos 4 . x sin x 4) A = lim = lim = lim2cos 4x = 2. x 0 → x 0 → x 0 sin x sin x → x x 2 2sin sin 1− cos x 5) 2 2 A = lim = lim = lim = 0. x→0 x→0 x x x x→0 sin x 2sin .cos cos 2 2 2 3 + +
4 cos x − 3cos x + 2( 2 2 cos x − sin x x x )+2 cos 3 2 cos 2 2 6) A = lim = lim 3   − x→ sin 3x x→ 3sin x 4sin x 3 3 − + cos x ( 2 3 2 4 cos x − 3 + 4 cos 4 cos 3cos 4 cos x x x x ) = lim =   −  − −  x→ sin x ( lim 2 3 4sin x) x→ sin x 3 4  ( 2 1 cos x 3 3 )
cos x (2cos x + )2 1 − 4 cos x  
(2cos x +3)(2cos x − ) 1
cos x (2cos x + 3) 2 3 = lim = lim = lim = .  2    −  − + + x→ sin x 4 cos x 1 x→ sin x (2cos x ) 1 (2cos x ) 1 x→ sin x (2cos x ) 1 3   3 3 3 2
1+ sin 2x + cos 2x
2 cos x + 2sin x cos x 7) A = lim = lim   x→ cos x x→ cos x 2 2
2 cos x (cos x + sin x) = lim
= lim 2(cos x + sin x) = 2.   x→ cos x x→ 2 2 2 axax bx  2 2 2sin sin 1− cos axa   a Bài 2. 1) 2 2 2 A = lim = lim = lim . .  = .   x→0 x→0 − bx bx x→0 1 cos b ax bx 2  b  2sin  sin  2  2 2  66
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC ax bx sin (Vì 2 lim =1 và 2 lim =1). x→0 ax x→0 bx sin 2 2 sin 5x  sin 5x  sin 5x 2) B = lim = lim 5. = 5   . (Vì lim =1). x→0 x→0 x  5x x 0 → 5x sin 5 . x sin 3 . x sin x
 sin 5x sin 3x sin x 1  1 3) B = lim = lim . . . =   3 x→0 x→0 45x  5x 3x x 3  3 sin 5x sin 3x sin x (Vì lim =1, lim =1, lim =1). x 0 → 5x x 0 → 3x x 0 → x x x 2 2sin 2 sin 1− cos x 1 4) 2 B = lim = lim = , (vì 2 lim =1. 2 2 2 x→0 x→0 xx  2 x→0  x  .4      2   2  2  5x  3  5 x x  2 2 sin . 2sin    1− cos 5x 2 = = =   2  25 25 5) 2 B lim lim lim .  = 2 x→0 x→0 1− cos 3x 3x x→0   2  5x  3x 9 9 2 2sin  .sin    2  2  2  2 5x  3x  2 sin    2  (Vì 2 lim =1 và lim =1). 2 x→0  5x x→0 3x 2   sin  2  2   ax ax 2 2sin  2 2 2 sin 1− cosa x a a 6) = =  2 B lim lim .  = , (vì 2 lim =1). 2 2 2 x→0 x→0 xax 4    2 x→0  ax          2    2  2 2 2 sin 2x 4sin . x cos x  sin x  sinx 7) 2 B = lim = lim = lim .4 cos x = 4   , (vì lim =1). x→0 x→0 x→0 . x sin x . x sin xxx 0 → x sin x sin x − sin x − tan x sin .
x cos x − sin x 8) cos = lim = lim x B = lim 3 3 3 x→0 x→0 x→0 x x x cos x   x   − x ( − x) 2 sin sin 1 cos 2 − sin x 2 − 1 = =  2 − lim lim . .  = . 3 2 x→0 x→0 x cos xx x 4 cos x    2       2   67
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x  2 sin   sinx  2  (vì lim =1và lim =1). 2 x 0 → x x→0  x     2  sin x −sin x tan x − sin x sin x − sin . x cos x 9) cos = lim = lim x B = lim 3 3 3 x→0 x→0 x→0 sin x sin x sin x cos x x 2 2sin 1− cos x 1 1 2 = lim = lim = lim = 2 x→0 x→0 x x x x→0 sin x .cos x 2 2 2 2 4.sin .cos .cos x cos .cos x 2 2 2 ( − )( + + ) x 2 2sin ( 2 2 1+ cos x + cos 1 cos 1 cos cos x x x x ) 10) 2 B = lim = lim x→0 x→0 x sin x x x 2 . x sin .cos 2 2  xx sin 2  sin
1+ cos x + cos x  3 2 = lim .  = , (vì 2 lim =1). x→0 x x 2  x→0 x 2 cos   2 2  2 ( cos8x − ) 2 1 sin 3x (cos8x − ) 2 2 2 1 sin 3x 2 − sin 4xsin 3x Bài 3. 1) B = lim = lim = lim 4 x→0 x→0 4 3x 3x ( cos8x + ) x→0 4 1 3x ( cos8x + ) 1 2 2
 sin 4x   sin3x  9 − 6  = lim  . .      = 4 − 8
x→0  4x   3x  cos8x +1   1− 2x +1  2x 1 −  1 2) B = lim = lim . = −   x→0 x→0 sin 2x
sin 2x 1+ 2x +1 2 2 − − 1− cos ( 2 2 1− 2 sin 1 cos cos 2 1 cos cos 2 x x x x x ) 3) B = lim = lim = lim 2 x→0 x→0 2 x
x (1+ cos x cos 2x ) x→0 2
x (1+ cos x cos 2x ) 2 2 2
sin x + cos x − cos x ( 2 1− 2sin x) 2 2 2
sin x + 2sin x cos x = lim = lim x→0 2
x (1+ cos x cos 2x ) x→0 2
x (1+ cos x cos 2x ) 2 2  sinx  1+ 2 cos x  3 = lim  .    = .
x→0  x  1+ cos x cos 2x   2  3 1− cos x 1− cos x 4) B = lim = lim 2 2 x→0 x→0 tan x
sin x 1+ cos x + cos x 2 ( 3 3 2 ) cos x 68
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x 2 2 4sin cos x 2 cos x 1 2 = lim = lim = . x→0 x x → x 2 2 ( x 3 2 + x + x ) 0 3 2 ( 3 3 2 + x + x ) 6 2sin cos 1 cos cos 2 cos 1 cos cos x 2 2 3 tanx −1 tan x −1 5) B = lim = lim 2   − x→ 2 sin x 1 x→ ( 2 2
sin x − cos x)( 3 2 3 tan x + tan x +1 4 4 ) sin x − cos x 1 1 cos = lim x = =   x→ ( lim . 2 2 x − x)( 3 2 3 x + x + ) x→ x ( x + x)( 3 2 3 3 sin cos tan tan 1 cos sin cos tan x + tan x +1 4 4 )
1+ tan x − 1+ sin x tan x − sin x 6) B = lim = lim 3 x→0 x→0 3 x
x ( 1+ tan x + 1+ sin x ) x 2 2 sin x sin
sin x − sin x cos x 2 = lim = lim x→0 3
x cos x ( 1+ tan x + 1+ sin x ) x→0 3
x cos x ( 1+ tan x + 1+ sin x ) 2  x     sin    sin x 2 1 2 = lim  .  .  = x→0  x x
 4( 1+ tan x + 1+ sin x ) 4   2     xx    2 sin − (1+ 1−x) 2 2  sin   2(1+ 1−  1 cos x x )2 2 7) 2 2 B = lim = =    = . x→ ( → → − − x ) lim lim . 2 2 2 0 x 0 x 0 x x  4 1 1     2     2 2 2 2 2 1+ x − cos x 1+ x − cos x x + sin x 8) B = lim = lim = lim 2 x→0 x→0 2 x → x ( 2
1+ x + cos x) x 0 2 x ( 2 1+ x + cos x) 2  sin x 1 1  1 1 = lim  . +  = + =1. 2 x→0 2 2 x  + + + + 2 2 1 x cos x 1 x cos x
1− 2x +1 + sin x 1− 2x +1 sin x 9) B = lim = lim + lim x→0 x→0 x→0
3x + 4 − 2 − x
3x + 4 − 2 − x
3x + 4 − 2 − x 2
− x( 3x + 4 + 2+ x)
sin x ( 3x + 4 + 2 + x) = lim + lim x→0 ( 2
−x − x)(1+ 2x +1) x→0 −x(x + ) 1 2
− ( 3x + 4 + 2+ x)
 sin x 3x + 4 + 2 + x  = lim + lim .   
x→0 (−x − )
1 (1+ 2x +1) x→0 x −x −1   = 4 − 4 = 0. 69
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2 3 2 3 2 2x +1 − x +1
2x +1 −1+1− x +1 2x +1 −1 1− x +1 10) B = lim = lim = lim + lim x→0 x→0 x→0 x→0 sin x sin x sin x sin x 2 2x −x = lim + lim =1.
x→0 sin x ( 2x +1 + ) x→0 1  
sin x 1+ x +1 + ( x +  )2 3 2 2 3 1        Bài 4.
1) C = lim tan 2x tan − x      x→   4  4  
Đặt t = x − , vì x →  t → 0. Khi đó: 4 4      C = t + − t =   ( t t ) cos 2t 1 lim tan 2 ( 1) tan lim cot 2 tan = lim =   . 2 t →0 t →0 t →0   2   2 cos t 2 1+ cos x 2) C = lim x  → ( x − )2
Đặt t = x − , vì x →  t → 0. Khi đó: t 2 2 sin 1− cos t 1 2 C = lim = lim = . 2 2 t →0 t →0 t t 2 sin ( x − ) 1 3) C = lim 2 x  → x − 4x + 3
Đặt t = x − , vì x →1 t → 0. Khi đó: sin ( x − ) 1 sin ( x − ) 1 sint 1 C = lim = lim = lim = − . 2 x  → x − 4x + 3 x  → ( x − ) 1 ( x − 3)
t→0 t (t − 2) 2 sin x − sin a 4) C = lim x→a x − a
Đặt t = x − a . vì x → a t → 0. Khi đó: t + 2a t (t + a) 2 cos .sin sin − sin a 2 2 C = lim = lim = cos a . t→0 t→0 t t 2. 2
C. BÀI TẬP RÈN LUYỆN Bài 1. Tính các giới hạn sau: x − 3 2 x + 2x −15 1. lim . ĐS: 1 2. lim . ĐS : 8 2 x 3
→ x − x − 6 5 x 3 → x − 3 x + 3 2 x − 3x + 2 3. lim ĐS: 1 4. lim . ĐS: 1 . 2 x 3
→− x + 2x − 3 4 2 x→2 x − 4 4 70
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x + 3x + 2 − 2 x − 7x +12 5. lim . ĐS: 1 6. lim . ĐS: 1 − . 2 x 2 →− 4 − x 4 2 x 3 → x − 9 6 2 x −1 2 x + x − 6 7. lim . ĐS: 2 8. lim . ĐS: 5 . 2 x 1 → x + 3x − 4 5 2 x→2 x − 4 4 2 2x + 3x −14 2 x − 9 9. lim . ĐS: 11. 10. l im . ĐS: 3 2 x→2 x − 4 4 2 x 3 → x − 4x + 3 2 3x − x −10 2 x − 5x 11. lim . ĐS: 11 . 12. lim . ĐS: 1 . 2
x→2 4x + x −18 7 2 x 5 → x − 25 2 2 4 − x 2 4 − x − 13. lim . ĐS: 2 14. lim . ĐS: 4 . 2
x→2 2x −10x +12 2
x→2 2x − x − 6 7 2 x − 5x + 6 2 x − 9x + 20 15. lim . ĐS: 1 . 16. lim . ĐS: 1 . 2 x 3 → x − 3x 3 2 x 5 → x − 5x 5 2 3x −10x + 3 2 x + 2x − 3 17. lim . ĐS: 8 18. lim . ĐS: 4 2 x 3 → x − 5x + 6 2 x 3
→ 2x − x −1 3 2
x − 5x + 6x 4 x −16 19. lim . ĐS: 1 − . 20. lim . ĐS: 16. − 2 x 3 → 9 − x 2 2 x 2
→− x + 6x + 8 3 8 − x 3 8 + x 21. lim . ĐS: 12 22. lim . ĐS: 12 . 2
x→2 x − 5x + 6 2 x 2
→− x +11x +18 7 2
x − x − 2 + 2 − 3 x − 8 23. lim . ĐS: 2 2 1. 24. lim . ĐS: 12. 3 2 x→ 2 x − 2 2 6
x→2 x − 3x + 2 3 x + 2 2 (x + )3 1 −1 25. lim . ĐS: 3 2 − . 26. lim . ĐS: 3. 2 x→− 2 x − 2 2 x→0 x (x + )3 1 − 27 4 x − 27x 27. lim . ĐS: 27. 28. lim . ĐS: 9. x→0 x 2 x 3
→ 2x − 3x − 9 3 2
x − 5x +10x − 8 3 2
2x − 5x + 2x +1 29. lim . ĐS: 2. 30. lim . ĐS: 1. − x→2 x − 2 2 x 1 → x −1 3 x − 2x − 4 3 2
x + 3x + 2x 31. lim . ĐS: 5 . 32. lim . ĐS: 2 − . 2 x→2 x − 4 2 2 x 2 →− x − x − 6 5 2 2x − x −10 3 2
x − x − x +1 33. lim . ĐS: 9 − . 34. lim . ĐS: 2. 3 x 2 →− x − x + 6 11 2 x 1 → x − 2x +1 2 x − 4 3 2
x − 2x − x + 2 3 35. lim . ĐS: 4 . 36. lim . ĐS: . 3
x→2 x − 3x − 2 9 2 x→2 x − 4 4 2 x + 3x − 4 3 2
3x − 4x − 2x + 3 37. lim . ĐS: 5 38. lim . ĐS: 1 − 3 2 x 1 → 2x + x − 3 8 2 x 1 → 3x − 2x −1 4 71
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2
x + x − 5x − 2 3 2x − 5x + 3 39. lim ĐS: 11 40. lim ĐS: -1 2 x→2 x − 3x + 2 2 x 1 → x − 3x + 2 2 x − 2x − 8 3 1− x 41. lim ĐS: 6 − . 42. lim ĐS: 3 . 3 2 x 2
→− 3x + 4x − x + 6 19 4 2 x 1 → x − 4x + 3 4 3 2
x − 5x + 3x + 9 3 2
6x − 5x + 4x −1 43. lim ĐS: 0 . 44. lim ĐS: 2 . 4 2 x 3 → x − 8x − 9 4 2 1 + − x→ 9x 8x 1 5 3 x + 2 x − 3 3 x − 3x + 2 45. lim ĐS: 4 − . 46. lim ĐS: 1 . x 1
→ x − 5 x + 4 3 4 x 1 → x − 4x + 3 2 5 4
x − 2x + x − 2 4 3
x − x − x +1 47. lim ĐS: 17 . 48. lim ĐS: 3 − . 2 x→2 x − 4 4 3 2 x 1
→ x − 5x + 7x − 3 2 3 2
2x − 5x − 2x − 3 3 2
2x + 5x + 4x +1 49. lim ĐS: 11 . 50. lim ĐS: 1 . 3 2 x 3
→ 4x −13x + 4x − 3 17 3 2 x 1 →−
x + x − x −1 2 3 2
2x − 5x − 2x − 3 3 2 3 x − 2 x +1 51. lim ĐS: 11 . 52. lim ĐS: 1 . 3 2 x 3
→ 4x −12x + 4x −12 20 2 x 1 → (x −1) 9 4 3 2
2x + 8x + 7x − 4x − 4 3 2
2x − 3x + x + 9 + 7 3 53. lim ĐS: 7 − . 54. lim ĐS: 7 3 3 2 x 2 →−
3x +14x + 20x + 8 4 2 x→− 3 3 − x 6 4 3 2
x − 5x + 9x − 7x + 2 5 4 3 2
x + x + x + x + x − 5 55. lim ĐS: 0 . 56. lim ĐS: 15 . 4 3 2 x 1 →
x − 3x + x + 3x − 2 2 x 1 → x −1 2  1 2   1 12  57. lim −   ĐS: 1 . 58. lim −   ĐS: 1 . 2 x 1
→  x −1 x −1 2 3
x→2  x − 2 x − 8  2  1 1 
 2x − 3 x − 26  59. lim +   ĐS: −2 . 60. lim −   ĐS: 7 . 2 2
x→2  x − 3x + 2 x − 5x + 6  2 x 2 →−  x + 2 4 − x  2  1 1 
(1+ x)(1+ 2x)(1+ 3x) −1 61. lim −   ĐS: 2 . 62. lim ĐS: 6 . 2 3 x 1
→  x + x − 2 x −1 9 x 0 → x n x −1 n
x − nx + n −1 n − n − 63. lim ĐS: n . 64. lim ĐS: ( 2)( 1) . 1 m x→ x −1 m 2 x 1 → (x −1) 2 100 x − 2x +1 2 x + x + ... n + x − n n n + 65. lim ĐS: 2 . 66. lim ĐS: ( 1) . 50 x 1 → x − 2x +1 x 1 → x −1 2 Lời giải x − 3 x − 3 1 1 1. lim = lim = lim = . 2 x 3 → x 3 x − x − 6
→ ( x + 2)( x − 3) x 3 → x + 2 5 2 x + 2x −15 (x −3)(x +5) 2. lim = lim = lim( x + 5) = 8 x 3 → x 3 → x 3 x − 3 x − 3 → 72
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x + 3 x + 3 3. lim = lim 2 x 3
→− x + 2x − 3 x 3
→− ( x + 3)( x − ) 1 2 x − 3x + 2 (x − ) 1 ( x − 2) 1 1 x −1 1 4. lim = lim = lim = . = lim = . 2 x→2 x − 4
x→2 ( x − 2)( x + 2) x 3 →− x −1 4 x→2 x + 2 4 2 x + 3x + 2 (x + ) 1 ( x + 2) x +1 1 5. lim = lim = lim = − . 2 x→ 2 − x→ 2 4 − x
− (2 − x)(2 + x) x→ 2 − 2 − x 4 2 x − 7x +12 (x −3)(x −4) x − 4 1 6. lim = lim = lim = − . 2 x 3 → x 3 x − 9
→ ( x − 3)( x + 3) x 3 → x + 3 6 2 x −1 (x − ) 1 ( x + ) 1 x +1 2 7. lim = lim = lim = 2 x 1 → x 1 x + 3x − 4 → ( x − ) 1 ( x + 4) x 1 → x + 4 5 2 x + x − 6 (x −2)(x +3) x + 3 5 8. lim = lim = lim = . 2 x→2 x→2 x − 4
(x −2)(x + 2) x→2 x + 2 4 2 2x + 3x −14 (x −2)(2x +7) 2x + 7 11 9. lim = lim = lim = . 2 x→2 x→2 x − 4
(x −2)(x + 2) x→2 x + 2 4 2 x − 9 (x −3)(x +3) x + 3 10. l im = lim = lim = 3. 2 x 3 → x 3 x − 4x + 3
→ ( x − 3)( x − ) x 3 1 → x −1 2 3x − x −10 (x −2)(3x +5) 3x + 5 11 11. lim = lim = lim = . 2 x→2 x→2 4x + x −18
(x −2)(4x +9) x→2 4x +9 17 2 x − 5x x ( x − 5) x 1 12. lim = lim = lim = . 2 x 5 → x 5 x − 25
→ ( x − 5)( x + 5) x 5 → x + 5 2 2 4 − x (2− x)(2+ x) −x − 2 13. lim = lim = lim = 2. 2 x→2 x→2 2x −10x +12
2( x − 2)( x − 3) x→2 2 ( x − 3) 2 4 − x (2− x)(2+ x) −x − 2 4 − 14. lim = lim = lim = . 2 x→2 x→2 2x − x − 6
(x − 2)(2x +3) x→2 2x +3 7 2 x − 5x + 6 (x −2)(x −3) x − 2 1 15. lim = lim = lim = . 2 x 3 → x 3 x − 3x → x ( x − 2) x 3 → 2 3 2 x − 9x + 20 (x −4)(x −5) x − 4 1 16. lim = lim = lim = . 2 x 5 → x 5 x − 5x → x ( x − 5) x 5 → x 5 2 x − 5x + 6
(x −3)(3x − ) 1 3x −1 17. lim = lim = lim = 8. 2 x 3 → x 3 x − 3x
→ ( x − 2)( x − 3) x 3 → x − 2 2 x + 2x − 3 (x − ) 1 ( x + 3) x + 3 18. lim = lim = lim = 4. 2 x 3 → x 3 2x − x −1 → ( x − ) 1 (2x − ) x 3 1 → 2x −1 73
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2
x − 5x + 6x
x ( x − 2)( x − 3) x ( x − 2) 1 19. lim = lim = lim = − 2 x 3 → x 3 9 − x →
(3− x)(3+ x) x 3 → −x − 3 2 x −
( 2x +4)(x−2)(x+2) ( 2 4 x + 4)( x − 2 16 ) 20. lim = lim = lim = 1 − 6 2 x→ 2 − x→ 2 x + 6x + 8 − (x + 2)(4+ x) x→ 2 − x + 4 3 2 8 − x
(2− x)(4+2x+ x ) 21. lim = lim 2
x→2 x − 5x + 6 x→2 (x −2)(x −3) + −( 2 x + 2x + 4) x (x + 2)( 2 3 x − 2x + 4 8 ) 22. lim = lim = lim = 12. 2 x→ 2 − x→ 2 x +11x +18 − (x + 2)(x +9) x→2 x − 3 2 x − 2x + 4 12 = lim = . x 2 →− x + 9 7 2 − − + x − x − + (x 2)(x 1 2 2 2 ) x −1+ 2 2 2 −1 23. lim = lim = lim = . 3 x→ x − 2 2 x→ (x− 2)( 2 2 2 x + 2x + 2) 2 x→ 2 x + 2x + 2 6 x − (x −2)( 2 3 x + 2x + 4 8 ) 2 x + 2x + 4 24. lim = lim = lim =12. 2 x→2 x→2 x − 3x + 2 (x − ) 1 ( x − 2) x→2 x −1 − − + x + (x 2)( 2 3 x 2x 2 2 2 ) 2 x − 2x + 2 3 2 25. lim = lim = lim = − . 2 x→− 2 x→− 2 x − 2
(x− 2)(x+ 2) x→− 2 x− 2 2 (x + )3 3 2 1 −1
x + 3x + 3x 26. lim = lim = lim( 2
x + 3x + 3) = 3. x→0 x→0 x→0 x x (  + + + +  x + ) x − (x 3)2 3 3( x 3) 9 1 27   2 27. lim = lim
= lim ( x + 3) + 3( x + 3) + 9 = 27.   x→0 x→0 x→0 x x − x x x
(x −3)( 2x +3x+9) x ( 2 4 x + 3x + 9 27 ) 28. lim = lim = lim = 9. 2 x 3 → x 3 2x − 3x − 9 → (x −3)(2x +3) x 3 → 2x + 3 x − x + x − (x − 2)( 2 3 2 x − 3x + 4 5 10 8 ) 29. lim = lim = lim ( 2
x − 3x + 4) = 2. x→2 x→2 x→2 x − 2 x − 2 − + + (x − ) 1 ( 2 3 2 2x − 3x x x x − ) 2 1 2 5 2 1 2x − 3x −1 30 lim = lim = lim = 1 − . 2 x 1 → x 1 x −1 → (x − ) 1 ( x + ) x 1 1 → x +1 x − x − (x −2)( 2 3 x + 2x + 2 2 4 ) 2 x + 2x + 2 5 31. lim = lim = lim = . 2 x→2 x→2 x − 4 (x −2)(x + 2) x→2 x + 2 2 3 2
x + 3x + 2x x ( x + ) 1 ( x + 2) x ( x + ) 1 2 32. lim = lim = lim = − . 2 x→ 2 − x→ 2 x − x − 6 −
(x + 2)(x −3) x→ 2− x −3 5 74
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 2x − x −10 (x + 2)(2x −5) 2x + 5 9 33. lim = lim = lim = − . 3 x→− x − x + 6
x→− ( x + 2)( 2 2 2 x − 2x + 3) 2 x→ 2 − x − 2x + 3 11
x − x − x +1 (x − )2 3 2 1 ( x + ) 1 34. lim . = lim = lim x +1 = 2. 2 2 ( ) x 1 → x 1 x − 2x +1 → (x − ) x 1 1 → 2 x − 4 (x −2)(x + 2) x + 2 4 35. lim = lim = lim = . 3 x→2 x→2 x − 3x − 2
(x −2)(x + )2 x→2 1 (x + )2 1 9 − − + (x −2)( 2 3 2 x x x x − ) 2 1 2 2 x −1 3 36. lim = lim = lim = . 2 x→2 x→2 x − 4
(x −2)(x + 2) x→2 x + 2 4 2 x + 3x − 4 (x −1)(x + 4) x + 4 5 37. lim = lim = lim = 3 2 2 2 x 1 → x 1 → x 1 2x + x − 3
(x −1)(2x + 3x + 3) → 2x + 3x + 3 8 3 2 2 2
3x − 4x − 2x + 3
(x −1)(3x − x − 3) 3x − x − 3 1 38 lim = lim = lim = − 2 x 1 → x 1 → x 1 3x − 2x −1 (x −1)(3x +1) → 3x +1 4 3 2 2 2
x + x − 5x − 2
(x − 2)(x + 3x +1) x + 3x +1 39. lim = lim = lim =11. 2 x→2 x→2 x→2 x − 3x + 2
(x − 2)(x −1) x −1 3 2 2 2x − 5x + 3
(x −1)(2x + 2x − 3) 2x + 2x − 3 40. lim = lim = lim = 1 − . 2 x 1 → x 1 → x 1 x − 3x + 2
(x − 2)(x −1) → x − 2 2 x − 2x − 8 (x + 2)(x − 4) x − 4 6 41. lim = lim = lim = − . 3 2 2 2 x→ 2 − x→ 2 − x→ 2
3x + 4x − x + 6
(x + 2)(3x − 2x + 3)
− 3x − 2x + 3 19 3 2 2 1− x
(x −1)(−x − x −1) −x − x −1 3 42. lim = lim = lim = . 4 2 3 2 3 2 x 1 → x 1 → x 1 x − 4x + 3
(x −1)(x + x − 3x − 3)
→ x + x − 3x − 3 4 3 2 2 2
x − 5x + 3x + 9
(x − 3)(x − 2x − 3) x − 2x − 3 43. lim = lim = lim = 0 . 4 2 3 2 3 2 x 3 → x 3 → x 3 x − 8x − 9
(x − 3)(x + 3x + x + 3)
→ x + 3x + x + 3 3 2 2 2
6x − 5x + 4x −1
(3x −1)(2x − x +1) 2x − x +1 2 44. lim = lim = lim = . 4 2 3 2 3 2 1 1 1 + − − + + + + + + x→ 9x 8x 1 x→ (3x 1)(3x x 3x 1) x→ 3x x 3x 1 5 3 3 3 x + 2 x − 3
( x −1)( x + 3) x + 3 4 45. lim = lim = lim = − . x 1 → x 1 → x 1 x − 5 x + 4
( x −1)( x − 4) → x − 4 3 3 2 x − 3x + 2
(x + 2)(x − 2x +1) x + 2 1 46. lim = lim = lim = . 4 2 2 2 x 1 → x 1 → x 1 x − 4x + 3
(x − 2x +1)(x + 2x + 3) → x + 2x + 3 2 5 4 4 4
x − 2x + x − 2 (x − 2)(x +1) x +1 17 47. lim = lim = lim = . 2 x→2 x→2 x→2 x − 4 (x − 2)(x + 2) x + 2 4 4 3 2 2 2
x − x − x +1
(x − 2x +1)(x + x +1) x + x +1 3 48. lim = lim = lim = − . 3 2 2 x 1 → x 1 → x 1
x − 5x + 7x − 3
(x − 2x +1)(x − 3) → x − 3 2 75
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2 2 2
2x − 5x − 2x − 3
(x − 3)(2x + x +1) 2x + x +1 11 49. lim = lim = lim = . 3 2 2 2 x 3 → x 3 → x 3
4x −13x + 4x − 3
(x − 3)(4x − x +1)
→ 4x − x +1 17 3 2 2
2x + 5x + 4x +1
(2x +1)(x + 2x +1) 2x +1 1 50. lim = lim = lim = . 3 2 2 x→ 1 − x→ 1 − x→ 1
x + x − x −1
(x −1)(x + 2x +1) − x −1 2 3 2 2 2
2x − 5x − 2x − 3
(x − 3)(2x + x +1) 2x + x +1 11 51. lim = lim = lim = . 3 2 2 2 x 3 → x 3 → x 3
4x −12x + 4x −12 4(x − 3)(x +1) → 4(x +1) 20 3 2 3 3 2 x − 2 x +1 ( x −1) 1 1 52. lim = lim = lim = . 2 x 1 → x 1 → 3 2 3 2 3 2 x 1 → 3 2 3 2 (x −1) − + + + + 9 ( x 1) ( x x 1) ( x x 1) 4 3 2 2 2 2
2x + 8x + 7x − 4x − 4
(2x −1)(x + 4x + 4) 2x −1 7 53. lim = lim = lim = − . 3 2 2 x→ 2 − x→ 2 − x→ 2
3x +14x + 20x + 8
(3x + 2)(x + 4x + 4) − 3x + 2 4 3 2 2
2x − 3x + x + 9 + 7 3
(x + 3)(2x − (3 − 2 3)x + 7 − 3 3) 54. lim = lim 2 x→− 3 x→− 3 3 − x
( 3 − x)( 3 + x) 2
2x − (3 − 2 3)x + 7 − 3 3 7 3 = lim = x→− 3 3 − x 6 4 3 2 3
x − 5x + 9x − 7x + 2
(x −1) (x − 2) x −1 55. lim = lim = lim = 0. 4 3 2 2 x 1 → x 1 → x 1
x − 3x + x + 3x − 2
(x −1) (x − 2)(x +1) → x +1 5 4 3 2 4 3 2
x + x + x + x + x − 5
(x −1)(x + 2x + 3x + 4x + 5) 56. lim = lim 2 x 1 → x 1 x −1 → (x −1)(x +1) 4 3 2
x + 2x + 3x + 4x + 5 15 = lim = . x 1 → x +1 2  1 2  x −1 1 1 57. lim − = lim = lim =   . 2 x 1 → x 1 → x 1
x −1 x −1 (x −1)(x +1) → x +1 2  1 12  (x − 2)(x + 4) x + 4 1 58. lim − = lim = lim =   . 3 2 2 x→2 x→2 x→2
x − 2 x −8 
(x − 2)(x + 2x + 4) x + 2x + 4 2  1 1  2(x − 2) 2 59. lim + = lim = lim = 2 −   . 2 2 x→2 x→2 x→2
x − 3x + 2 x − 5x + 6 
(x − 2)(x − 3)(x −1)
(x − 3)(x −1)
 2x − 3 x − 26 
2(x − 5)(x + 2) 2(x − 5) 7 60. lim − = lim = lim =   . 2 x→ 2 − x→ 2 − x→ 2  x + 2 4 − x  (x − 2)(x + 2) − x − 2 2  1 1  (x −1)(x +1) x +1 2 61. lim − = lim = lim =   . 2 3 2 2 x 1 → x 1 → x 1
x + x − 2 x −1
(x −1)(x + 2)(x + x +1)
→ (x + 2)(x + x +1) 9 2
(1+ x)(1+ 2x)(1+ 3x) −1
x(6x +11x + 6) 62. lim = lim = lim( 2
6x +11x + 6) = 6 . x 0 → x 0 → x 0 x x → n n 1 − n−2 n 1 − n−2 x −1 (x −1)(x + x +...+ x +1) x + x +...+ x +1 n 63. lim = lim = lim = . m m 1 − m−2 m 1 − m−2 x 1 → x 1 → x 1 x −1 (x −1)(x + x +...+ x +1) → x + x +...+ x +1 m 76
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC n n 1 − n−2
x − nx + n −1 (x −1)(x + x
+...+ x +1) − n(x −1) 64. lim = lim 2 2 x 1 → x 1 (x −1) → (x −1) n 1 − n−2 2 (x −1) + (x
−1) +...+ (x −1) + (x −1) = lim x 1 → x −1 = lim( n−2 n−3 n−3 n−4 (x
+ x +...+ x +1) + (x + x +...+ x +1) +...+ ) 1 x 1 →
(n − 2)(n −1)
= (n − 2) + (n −3) +...+ 2 +1= 2 100 x − 2x +1 99 98
(x −1)(x + x + ... + x +1) − (x −1) 99 98
x + x + ... + x 49 65. lim . = lim = lim = 50 x 1 → x − 2x +1 49 48 x 1
→ (x −1)(x + x + ... + x +1) − (x −1) 49 48 x 1
→ x + x + ...+ x 24 2 n 2
x + x + ... + x − n
(x −1) + (x −1) + ...+ ( n x −1) 66. lim = lim x 1 → x 1 x −1 → x −1 n 1 − n−2
(x −1) + (x −1)(x +1) + ... + (x −1)(x + x +...+ x +1) = lim x 1 → x −1 n n + n 1 − n−2
= lim(1+ (x +1) +...+ (x + x +...+ x + ( 1) 1)) = 1+ 2 + 3 + ... + n = x 1 → 2 Bài 2.
Tính các giới hạn sau: x + 3 − 2 x + 2 1. lim . 2. lim ĐS: 2 x 1 → x − ĐS: 1 1 4 x 2 →− x + 3 −1 3 − x + 3 x − 8 3. lim − . 4. lim ĐS: 6 − . x→6 x − ĐS: 1 6 6 x 8 → 3 − x +1 2 4 + x + x − 2 2
x − 3x − x 5. lim ĐS: 1 − . 6. lim ĐS: 1 . x 1 →− x +1 4 x 3 → 2x − 6 4 x + 2 − 2 2 − 3x − 2 7. lim . 8. lim − . 2 x→2 x − ĐS: 1 4 16 2 x→2 x − ĐS: 3 4 16 2 x − 9 x − 3 9. lim ĐS: 24. 10. lim − . 2 x 3 → x +1 − 2 x→9 9x − ĐS: 1 x 54 2 x − 49 2x − x + 3 11. lim ĐS: 56 − . 12. lim . 2
x→7 2 − x − 3 x 1 → x − ĐS: 7 1 8 x − 3 + 2x 2 x − x 13. lim . 14. lim ĐS:  . 2 x→3 x − ĐS: 2 3x 9 x 1 → 2 2x − x −1 4x +1 − 3 3x − 3 − 3 15. lim . 16. lim . 2 x→2 x − ĐS: 1 2x 3 2 x→4 x − ĐS: 1 4x 8 x + 2 − 2 2 x − 3x + 2 17. lim . 18. lim ĐS: 2 . 2
x→2 2x + x − ĐS: 1 10 4 x→2 x −1 −1 77
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x − 3x − 4 3x +1 − 2 19. lim ĐS: 30 . 20. lim . 2 x→4 x + 5 − 3 x 1 → x + x − ĐS: 1 2 4 x −1 2 3x − 3(x +1) 21. lim . 22. lim ĐS: 12 − . 2 x 1 → x − ĐS: 1 1 4 x→2 3 − 4x +1 3 x +1 −1 x + 2 23. lim ĐS: 0 . 24. lim ĐS: 1 − . 2 x→0 x + x x 2 →− 3 1− x − 3 2 2 2x − x −1 2x + 5 + x − 5 25. lim ĐS: 0 . 26. lim . 2 2 x 1 → x − x x→2 x − ĐS: 2 2x 3 2 x − x
x − 2 + 7 − 2x 27. lim ĐS: 3 . 28. lim . 2 x 1 → 2x + 7 + x − 4 4 x 1 →− x − ĐS: 1 1 6 2
2x + 5 − 2x + x + 8
5x − 6 − x + 2 29. lim ĐS: 5 . 30. lim 2 x 1 →− x + 3x + 2 → − ĐS: 1. 2 x 2 x 2 3x + 3 2 2
x − 2x + 6 − x + 2x − 6 31. lim ĐS: 6 . 32. lim ĐS: 1 − . x 1 →− 3 + 2x − x + 2 2 x 3 → x − 4x + 3 3 2
x + x + 2 − 1− x 2 − x + 2 33. lim ĐS: 0 . 34. lim ĐS: 3 − . 4 x 1 →− x + 4 x→2 x + 7 − 3 2 3 − x 3x +1 − x + 3 35. lim ĐS: 2 − . 36. lim ĐS: 3 . x→9 x − 5 − 2 3 x 1 → x + 8 − 3 x + 2 − 2x x + 3 − 2 37. lim ĐS: 1 − . 38. lim ĐS: 3 . x→2
x −1 − 3 − x 4 x 1 →
4x + 5 − 3x + 6 2
x +1 − 3x − 5 2 2x +1 − 2x + 5 39. lim ĐS: 3 − . 40. lim ĐS: 2 5 . x→3 2x + 3 − x + 6 x→2 2 x +1 − x + 3 3 x −1 4 4x + 3 −1 41. lim ĐS: 4 − . 42. lim 2 x 1 →
x + 3 + x − 3x 3 x 1 → x − ĐS: 1. 1 4 3 2
x −1 + x − 3x + x + 3 43. lim ĐS: 1. x→2 2x − 2 Lời giải x + 3 − 2
( x + 3 − 2)( x + 3 + 2) 1 1 1. Ta có lim = lim = lim = . x 1 → x 1 → x 1 x −1
(x −1)( x + 3 + 2) → x + 3 + 2 4 x + 2
(x + 2)( x + 3 +1) 2. Ta có lim = lim = lim( x + 3 +1) = 2 . x→ 2 − x→ 2 − x→ 2 x + 3 −1
( x + 3 −1)( x + 3 +1) − 78
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 − x + 3 (3 − x + 3)(3 + x + 3) 1 − 1 3. Ta có lim = lim = lim = − x→6 x→6 x→6 x − 6 (x − 6)(3 + x + 3) 3 + x + 3 6 x − 8
(x − 8)(3 + x +1) 3 + x +1 4. Ta có lim = lim = lim = 6 − . x 8 → x 8 → x 8 3 − x +1 (3 − x +1)(3 + x +1) → 1 − 2 4 + x + x − 2 x(x +1) x 1 5. Ta có lim = lim = lim = − . x→ 1 − x→ 1 − 2 x→ 1 − 2 x +1 + + + − + + − 4 (x 1)( 4 x x 2) 4 x x 2 2 2 2
2x − 3x − x
( 2x − 3x − x)( 2x − 3x + x) 6. Ta có lim = lim x 3 → x 3 → 2 2x − 6
(2x − 6)( 2x − 3x + x) x(x − 3) x 1 = lim = lim = . x→3 2 x→3 2 − − + − + 4 2(x 3)( 2x 3x x) 2( 2x 3x x) 2 + x − 2 x − 2 1 1 7. Ta có lim = lim = lim = . 2 x→2 x→2 x→2 x − 4
(x − 2)(x + 2)( 2 + x − 2)
(x + 2)( 2 + x − 2) 16 2 − 3x − 2 3(2 − x) 3 3 8. Ta có lim = lim = lim = − . 2 x→2 x→2 x→2 x − 4
(x − 2)(x + 2)(2 + 3x − 2)
(x + 2)(2 + 3x − 2) 16 2 x − 9
(x + 3)(x − 3)( x +1 + 2) 9. Ta có lim = lim
= lim (x + 3)( x +1 + 2) = 24   . x 3 → x 3 → x 3 x +1 − 2
( x +1 − 2)( x +1 + 2) → x − 3 x − 9 1 − 1 10. Ta có lim = lim = lim = − . 2 x 9 → x 9 → x 9 9x − x
x(9 − x)( x + 3) → x( x + 3) 54 2 x − 49
(x − 7)(x + 7)(2 + x − 3) 11. Ta có lim = lim x→7 x→7 2 − x − 3 (2 − x − 3)(2 + x − 3)
(x − 7)(x + 7)(2 + x − 3) = lim
= −lim(x + 7)(2 + x − 3) = 5 − 6 x→7 x→7 7 − x 2 2x − x + 3 4x − x − 3 4x + 3 7 12. Ta có lim = lim = lim = . 2 x 1 → x 1 → x 1 x −1
(x −1)(x +1)(2x + x + 3)
→ (x +1)(2x + x + 3) 8 2 x − 3 + 2x x − 2x − 3 x +1 2 13. Ta có lim = lim = lim = . 2 x 3 → x 3 → x 3 x − 3x
x(x − 3)(x + 3 + 2x )
→ x(x + 3 + 2x) 9 2 2 2 x − x
x(x −1)( 2x − x +1)
x( 2x − x +1) 14. Ta có lim = lim = lim =  . 2 x 1 → 2 x 1 → x 1 − − −x + 2x −1 → −(x −1) 2x x 1 4x +1 − 3 4(x − 2) 4 1 15. Ta có lim = lim = lim = . 2 x→2 x→2 x→2 x − 2x
x(x − 2)( 4x +1 + 3) x( 4x +1 + 3) 3 3x − 3 − 3 3(x − 4) 3 1 16. Ta có lim = lim = lim = . 2 x→4 x→4 x→4 x − 4x
x(x − 4)( 3x − 3 + 3) x( 3x − 3 + 3) 8 79
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x + 2 − 2
( x + 2 − 2)( x + 2 + 2) x − 2 17. Ta có lim = lim = lim 2 x→2 x→2 x→2 2x + x −10
(x − 2)(2x − 5)( x + 2 + 2)
(2x − 5)(x − 2)( x + 2 + 2) 1 1 = lim = −
x→2 (2x − 5)( x + 2 + 2) 4 2 x − 3x + 2
(x −1)(x − 2)( x −1 +1) 18. Ta có lim = lim
= lim(x −1)( x −1 +1) = 2 . x→2 x→2 x→2 x −1 −1
( x −1 −1)( x −1 +1) 2 x − 3x − 4
(x +1)(x − 4)( x + 5 + 3) 19. Ta có lim = lim
= lim(x +1)( x + 5 + 3) = 30 . x→4 x→4 x→4 x + 5 − 3 x − 4 3x +1 − 2 3(x −1) 3 1 20. Ta có lim = lim = lim = . 2 x 1 → x 1 → x 1 x + x − 2
(x −1)(x + 2)( 3x +1 + 2)
→ (x + 2)( 3x +1 + 2) 4 x −1 x −1 1 1 21. Ta có lim = lim = lim = . 2 x 1 → x 1 → x 1 x −1
(x +1)(x −1)( x +1)
→ (x +1)( x +1) 4 2 3x − 4(x +1)
(x − 2)(3x + 2)(3 + 4x +1)
(x − 2)(3x + 2)(3 + 4x +1) 22. Ta có lim = lim = lim x→2 x→2 3 − 4x +1
(3 − 4x +1)(3 + 4x +1) x→2 4(2 − x)
(3x + 2)(3 + 4x +1) = lim = 1 − 2 . x→2 4 3 3 2 x +1 −1 x x 23. Ta có lim = lim = lim = 0 2 x→0 x→0 3 x→0 3 x + x
x(x +1)( x +1 +1) (x +1)( x +1 +1) . 3 3 x + 2
(x + 2)( 1− x + 3) 1− x + 3 1 24. Ta có lim = lim = lim = . 2 2 x→ 2 − 3 x→ 2 − x→−2 − −
−(x + 2)(x − 2x + 4)
−(x − 2x + 4) 2 1 x 3 2 2 2x − x −1 ( − x −1) −(x −1) 25. Ta có lim = lim = lim = 0 2 x 1 → x 1 → 2 x 1 → 2 x − x
x(x −1)( 2x − x +1)
x( 2x − x +1) 2 2x + 5 + x − 5 −x +12x − 20 26. Ta có lim = lim 2 x→2 x→2 x − 2x
x(x − 2)( 2x + 5 − (x + 5))
−(x − 2)(x −10) −(x −10) 2 = lim = lim = x→2 x→2
x(x − 2)( 2x + 5 − (x + 5))
x( 2x + 5 − (x + 5)) 3 2 x − x
x(x −1)( 2x + 7 − (x − 4)
x( 2x + 7 − (x − 4) 3 27. Ta có lim = lim = lim = 2 x 1 → x 1 → x 1 2x + 7 + x − 4 −x +10x − 9 → −(x − 9) 4 2
x − 2 + 7 − 2x x − 2x − 3 28. Ta có lim = lim 2 x→ 1 − x→ 1 x −1
− (x −1)(x +1)((x − 2) − 7 − 2x) x + 3 1 = lim = x 1
→− (x −1)((x − 2) − 7 − 2x) 6 80
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2
2x + 5 − 2x + x + 8 2x +17 5 29. Ta có lim = lim = 2 x→ 1 − x→ 1 − 2 x + 3x + 2 + + + + + 2 (x 2)((2x 5) 2x x 8)
5x − 6 − x + 2 4(x − 2) 4 30. Ta có lim = lim = lim =1. x→2 x→2 x→2 x − 2
(x − 2)( 5x − 6 + x + 2) ( 5x − 6 + x + 2) 3x + 3
3(x +1)( 3 + 2x + x + 2) 31. Ta có lim = lim
= lim 3( 3+ 2x + x + 2) = 6. x→ 1 − x→ 1 3 + 2x − x + 2 − x +1 x 1 →− 2 2
x − 2x + 6 − x + 2x − 6 4 − 1 32. Ta có lim = lim = . 2 x 3 → x 3 → 2 2 x − 4x + 3 − − + + + − 3 (x 1)( x 2x 6 x 2x 6) 2
x + x + 2 − 1− x x +1 33. Ta có lim = lim = 0. 4 x→ 1 − x→ 1 − 2 2 x + x
x(x − x +1)( x + x + 2 + 1− x ) 2 − x + 2 x + 7 + 3 3 34. Ta có lim = −lim = − . x→2 x→2 x + 7 − 3 2 + x + 2 2 3 − x x − 5 + 2 2 35. Ta có lim = −lim = − . x→9 x→9 x − 5 − 2 3 + x 3 3x +1 − x + 3 2( x + 8 + 3) 36. Ta có lim = lim = 3. x 1 → x 1 x + 8 − 3 → 3x +1 + x + 3 x + 2 − 2x x −1 + 3 − x 1 37. Ta có lim = lim = − . x→2 x→2
x −1 − 3 − x x + 2 + 2x 4 x + 3 − 2 4x + 5 + 3x + 6 3 38. Ta có lim = lim = . x 1 → x 1
4x + 5 − 3x + 6 → x + 3 + 2 2 x +1 − 3x + 5 2x + 3 + x + 6 39. Ta có lim = 2 − lim = 3 − . x→3 x→3 2x + 3 − x + 6 x +1 + 3x + 5 2 2 2x +1 − 2x + 5 x +1 + x + 3 2 5 40. Ta có lim = lim 2 = . x→2 2 x→2 2 + − + + + + 3 x 1 x 3 2x 1 2x 5 2 x −1
x + 3 − (x − 3x) 4 41. Ta có lim = lim = − . 2 3 2 x 1 → x 1
x + 3 + x − 3x
→ −x + 5x − 4x − 3 3 4 4x − 3 −1 4 42. Ta có lim = lim =1. x 1 → x 1 → 3 2 − 4 4 4 x 1
(4x − 3) + (4x − 3) + 4x − 3 +1 4 3 2
x −1 + x − 3x + x + 3 43. Ta có lim =1. x→2 2x − 2 81
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Bài 3.
Tính các giới hạn sau: 3 4x − 2 3 5x − 3 + 2 1. lim . 2. lim . x→2 x − . ĐS: 1 2 3 x 1 →− x + ĐS: 5 1 12 3 1− 1− x 3 2 − 5x + 3 3. lim . 4. lim − . 2 x→0 x + ĐS: 1 x 3 x 1 → x − ĐS: 5 1 12 x − 3 x −1 5. lim ĐS: 2 . 6. lim ĐS: 3 . x→3 3 2 x −1 − 2 → 3 x 1 1+ x − 2 3 5x − 4 − x x −1 7. lim . 8. lim ĐS: 3 . 2 x 1 → 2x − x − ĐS: 2 1 9 → 3 x 1 x −1 3 x − 27 3 x + 5 − 2 9. lim ĐS: 54 . 10. lim . x→3 3 2 3 x +1− 4x + 28
x→3 x + x − ĐS: 1 30 336 3 3 10 + 2x + x −1 3 x −1 2 11. lim . ĐS: 3 . 12. lim ĐS: . 2 x 1 →− x + 3x + 2 2 x 1 → 2 x + 3 + − 2 3 x −1 2 x + 3 − 2 13. lim . ĐS: 6 . 14. lim ĐS: 3 − . → 3 x 1 x + 7 − 2 →− 3 x 1 x +1 2 3 3 2x −1 − x 3 x −1 15. lim . ĐS: 2 . 16. lim ĐS: 1. x 1 → x −1 3 x 1 → 2 x − 2 +1 3 x −1 3 3 x + 2 + x 17. lim . ĐS: 1. 18. lim − . → 3 x 1 4x + 4 − 2 2 x 1 →− x − ĐS: 1 1 3 3 3 x + 9 + 2x − 6 3 3 19 − x + 2 19. lim . 20. lim ĐS: 27 − . 3 x 1 → x + . ĐS: 1 1 12 x 3 → 4x − 3 − 3 8 3 3 1+ x − 1− x 3 2x −1 −1 21. lim − . 22. lim . 2 x→0 x − . ĐS: 1 4x 6 3 x 1 → x − ĐS: 2 1 9 3 3x + 2 − x 3 x +1 −1 23. lim . ĐS: 1 − . 24. lim ĐS: 2 . x→2 3x − 2 − 2 → 4 x 0 2x +1 −1 3 Lời giải 3 4x − 2 4 1 1) Ta có lim = lim = . x→2 x→2 3 2 3 x − 2 + + 3 16x 2 4x 4 3 5x − 3 + 2 5 5 2) Ta có lim = lim = . x→ 1 − x→ 1 x +1 − 3 ( x − )2 3 12 5 3 − 2 5x − 3 + 4 3 1− 1− x 1 1 3) Ta có lim = lim = . 2 x→0 x→0 x + x
(x + )( + −x + ( −x)2 3 3 ) 3 1 1 1 1 82
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2 − 5x + 3 5 − 5 4) Ta có lim = lim = − . x 1 → x 1 x −1 → 3 3 + x + + ( x + )2 12 4 2 5 3 5 3 − + − + x − ( 2x )2 3 2 3 1 2 x 1 4 3 5) Ta có lim = lim = 2. x→3 3 2 x→3 − − x + 3 x 1 2 x −1 2 6) Ta có lim = lim 1− x − 2 + x − 2 = 3. → 3 x 1 x 1 → + − ( 3 3 ( ) ) 1 x 2 3 2 5x − 4 − x −x − x + 4 2 7) Ta có lim = lim = . 2 x 1 → x 1 2x − x −1
→ ( x + )(3 ( x− )2 3 + x − + ) 9 2 1 5 4 5 4 4 x −1 8) Ta có lim = lim x + x + = x→ x→ ( 3 2 3 1 3. 3 1 1 ) x −1 3 x − 27 9) Ta có lim x→3 3 2 x +1− 4x + 28 (   x − 3)( 2
x + 3x + 9) ( x + ) 1 + ( x + ) 2 1 4x + 28 +  ( 2 3 4x + 28)2 2 3    = lim x→ (x −3)( 2 3 x + 2x + 9) (   2
x + 3x + 9) ( x + ) 1 + ( x + ) 2 1 4x + 28 +  ( 2 3 4x + 28)2 2 3    = lim = 72. 2 x→3 x + 2x + 9 3 x + 5 − 2 1 1 10) Ta có lim = lim = . 3 x 3 → x 3 x + x − 30 → (   x + x + ) 3 (x+ )2 2 3 336 3 10 5 + x + 5 + 4   3 3 10 + 2x + x −1 3 2
3x − 3x + 3x + 9 11) Ta có lim = lim 2 x 1 →− x + 3x + 2 x 1 →− (   x + ) 1 ( x + 2)  ( 3
10 + 2x )2 + ( x − ) 3 3 1
10 + 2x + ( x − )2 3 1    2 3x − 6x + 9 3 = lim = . x 1 →− (   x + 2)  ( 3
10 + 2x )2 + ( x − ) 3 2 3 1
10 + 2x + ( x − )2 3 1    3 2 x −1 x + 3 + 2 2 12) Ta có lim = lim = . x 1 → 2 x 1 x → + − (x + )(3 2 3 x + x + ) 3 3 2 1 1 3 x −1 (x + 7)2 3 + 2 x + 7 + 4 13) Ta có lim = lim = 6. → 3 x 1 x 1 x + 7 − 2 → x +1 (x − ) 1 + − (3 2 3 2 x − x + x )1 3 2 3 14) Ta có lim = lim = − . →− 3 x 1 x→ 1 − 2 x +1 + + 2 x 3 2 83
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 3 2x −1 − x x +1 2 15) Ta có lim = lim = . x 1 → x 1 x −1 → (2x − )2 1 + x(2x − ) 3 2 3 3 3 1 + x 3 3 x −1 (x −2)2 3 − x − 2 +1 16) Ta có lim = lim =1. → 3 x 1 x 1 → 3 2 3 x − 2 +1 x + x +1 3 3 x −1 (4x + 4)2 3 + 2 4x + 4 + 4 17) Ta có lim = lim =1. → 3 x 1 x 1 4x + 4 − 2 → 4 ( 3 2 3 x + x + ) 1 3 3 x + 2 + x 2 1 18) Ta có lim = lim = − . 2 x→ 1 − x→ 1 x −1 − (   x − ) 1
(x + 2)2 − x(x + 2) 3 2 3 3 3 + x   3 3 x + 9 + 2x − 6 19) Ta có lim 3 x 1 →− x +1 3 1 = lim = . x 1 →− (   x − x + ) 1 (x +9)2 2 3
− (x + 9)(2x − 6) + (2x + 6)2 2 3 3   − + − + − x + ( 2 3 3 9 3x x )( 4x 3 3 19 2 ) 27 20) Ta có lim = lim = − . x→3 x→3 4x − 3 − 3   4 −  ( 3 19 − x )2 3 3 8 3 − 2 19 − x + 4   3 3 1+ x − 1− x 2 1 21) Ta có lim = lim = − . 2 x→0 x→0 x − 4x (   x − )
( + x)2 + − x + ( − x)2 3 2 3 3 6 4 1 1 1   3 2x −1 −1 2 2 22) Ta có lim = lim = . 3 x 1 → x 1 x −1 → (  
x + x + ) 3 ( x − )2 2 3 9 1 2 1 + 2x −1 +1   − + − + x + − x (x )2 3 1 ( 3x 2 2 3 2 ) 23) Ta có lim = lim = 1 − . x→2 x→2 3x − 2 − 2   3 3 (3x + 2)2 3 2
+ x 3x + 2 + x   + + + + x + − (4 3 2x 1 )1( 2x 1 )1 1 1 2 24) Ta có lim = lim = . → 4 x 0 x→0 2x +1 −1   3 2 (x + )2 3 3 1 + x +1 +1   Bài 4.
Tính các giới hạn sau: x + 9 + x +16 − 7
2x + 2 + 5x + 4 − 5 1) lim . ĐS: 7 2) lim . ĐS: 4 x→0 x 24 x 1 → x −1 3
2 x + 6 + 2x − 2 − 8 2 x +1 + x + 4 − 4 3) lim . ĐS: 5 4) lim . ĐS: 5 x→3 x − 3 6 x→0 x 4 84
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x x + 2 + x + 7 − 7 2
2x x −1 + x − 8 5) lim . ĐS: 8 6) lim . ĐS: 8 x→2 x − 2 3 x→2 x − 2
(5x −4) 2x −3 + x −84 3 1+ 2x − 1+ 3x 7) lim . ĐS: 74 8) lim . ĐS: 0 x→6 x − 6 3 x→0 x 3 3 2 x + 7 − x + 3
3 8x +11 − x + 7 9) lim . ĐS: 1 − 10) lim . ĐS: 7 x 1 → x −1 4 2 x→2 x − 3x + 2 54 3
2 1+ x − 8 − x 3 2 3x + 5 − x + 3 11) lim . ĐS: 13 12) lim . ĐS: 1 x→0 x 12 x 1 → x −1 4 3 2
x + 7 − 5 − x
3 3x + 2 − 3x − 2 13) lim . ĐS: 7 14) lim . ĐS: 1 − x 1 → x −1 12 x→2 x − 2 2
3 3x + 2 − 5x − 6 3 2
2x + 4x +11 − x + 7 15) lim . ĐS: 1 − 16) lim . ĐS: 5 . x→2 x − 2 2 x→2 x − 4 72 3 3 2
5 − x − x + 7 3 3
3 4x − 24 + x + 2 − 8 2x − 3 17) lim . ĐS: 11 − 18) lim . ĐS: 17 − 2 x 1 → x −1 24 2 x→2 4 − x 16 3 2
3x − 2 − 4x − x − 2 3
x 2x −1 + 3x − 2 − 2 19) lim . ĐS: 5 20) lim . ĐS: 3 2 x 1 → x − 3x + 2 6 2 x 1 → x −1 2 3 2 4 1+ x − 1− 2x 3 4 x + 6 − 7x + 2 21) lim . ĐS: 1 22) lim . ĐS: 13 − 2 x→0 x + x 2 x→2 x − 2 96
1+ 4x. 1+ 6x −1 3
1+ 2x. 1+ 4x −1 23) lim . ĐS: 5 24) lim . ĐS: 7 x→0 x x→0 x 3 3
3x +1. 2 − x − 2 3
4 + x. 8 + 3x − 4 25) lim . ĐS: 1 26) lim . ĐS:1 x 1 → x −1 12 2 x→0 x + x
4x + 4 + 9 − 6x − 5 3 1+ 2x − 1+ 3x 27) lim . ĐS: 5 − 28) lim . ĐS: 1 2 x→0 x 12 2 x→0 x 2 2
6x + 3 + 2x − 5x
4x − 3 + 2x −1 − 3x +1 29) lim ĐS: 11 30) lim . ĐS: 5 − . 2 x→ (x − ) . 2 1 1 6 x 1 → x − 2x +1 2 3
− x − 7 + 4 x + 3 + 2 2x −1 2 x − 4x + 4 31) lim . ĐS: 17 − 32) lim . ĐS: 8 2 x 1 → x − 2x +1 16 x→2 2
2x + 8 − 2 2x − 3 + x − 4 9 3 2 6x + 2 − 2 x 2 3 2
2x − 6x + 5 − 3x − 9x + 7 33) lim . 34) lim ĐS: 1 3 2 2 x 1 →
x − x − x + ĐS: 1 1 8 x→2 (x − 2) 2 3 1+ 2x − 1+ 3x 3 1+ 4x − 1+ 6x 35) lim . ĐS: 1 36) lim . ĐS: 2 2 x→0 x 2 2 x→0 x 85
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Lời giải x + 9 + x +16 − 7 1) I = lim . x→0 xx + 9 −3 x +16 − 4  Ta có I = lim +    x→0 x x  
( x+9 −3)( x+9 +3) ( x+16 −4)( x+16 + 4) = lim  +  x→0  x  ( x+9 +3) x ( x +16 + 4)       x + 9 − 9 x +16 −16 x x = lim  +  = lim  +  x→0  x
 ( x + 9 + 3) x( x +16 + 4) x→0   x
 ( x + 9 + 3) x ( x +16 + 4)  1 1  1 1 7 = lim + = + = .  
x→0  x + 9 + 3 x +16 + 4  6 8 24
2x + 2 + 5x + 4 − 5 2) I = lim . x 1 → x −1  2x + 2 − 2 5x + 4 − 3  Ta có I = lim +    x 1 → x −1 x −1  
( 2x+ 2 −2)( 2x+2 +2) ( 5x+4 −3)( 5x+4 +3) = lim  +  x 1 →  (x − )1  ( 2x+2 +2) (x − ) 1 ( 5x + 4 + 3)     2x + 2 − 4 5x + 4 − 9 = lim  +  x 1 → (x − ) 1 
( 2x+2 +2) (x− )1( 5x+4 +3)   2 ( x − ) 1 5( x − ) 1 = lim  +  x 1 → (x − ) 1 
( 2x+2 +2) (x− )1( 5x+4 +3)  2 5  2 5 4 = lim + = + = .   x 1 →  2x + 2 + 2 5x + 4 + 3  4 6 3
2 x + 6 + 2x − 2 − 8 3) I = lim . x→3 x − 3  2 x + 6 −6 2x − 2 − 2  Ta có I = lim +    x 3 → x − 3 x − 3  
2( x+6 −3)( x+6 +3) ( 2x−2 −2)( 2x−2 +2) = lim  +  x→3  (x −3)  ( x+6 +3)
(x −3)( 2x−2 +2)    2( x + 6 − 9) 2x − 2 − 4 = lim  + 
x→3  ( x − 3) 
( x+6 +3) (x−3)( 2x−2 +2) 86
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC   2( x − 3) 2 ( x − 3) = lim  + 
x→3  ( x − 3) 
( x+6 +3) (x−3)( 2x−2 +2)  2 2  2 2 5 = lim + = + = .  
x→3  x + 6 + 3 2x − 2 + 2  6 4 6 2 x +1 + x + 4 − 4 4) I = lim . x→0 x  2 x +1 − 2 x + 4 − 2  Ta có I = lim +    x→0 x x  
2( x+1− )1( x+1+ )1 ( x+ 4 −2)( x+4 +2) = lim  +  x→0  x  ( x+1+ )1 x ( x + 4 + 2)     2 ( x +1− ) 1 x + 4 − 4 =  2 1  2 1 5 lim  +  = lim + = + =   x→0  x x→0  + + + +  ( x +1 + ) 1
x ( x + 4 + 2) x 1 1 x 4 2  2 4 4 x x + 2 + x + 7 − 7 5) I = lim . x→2 x − 2
(x −2) x + 2 + 2 x + 2 −4+ x +7 −3  2 x + 2 − 4 x + 7 − 3  Ta có I = lim = lim x + 2 + +    x→2 x − 2 x→2 x − 2 x − 2  
2( x+ 2 −2)( x+2 +2) ( x+7 −3)( x+7 +3) = 2 + lim  +  x→2  (x − 2)  ( x+2 +2)
(x − 2)( x+7 +3)   2 1  2 1 8 = 2 + lim + = 2 + + = .  
x→2  x + 2 + 2 x + 7 + 3  4 6 3 2
2x x −1 + x − 8 6) I = lim . x→2 x − 2 2( x − 2) 2
x −1 + 4 x −1 − 4 + x − 4 2  4 x −1 − 4 x − 4  Ta có I = lim = lim 2 x −1 + +    x→2 x − 2 x→2 x − 2 x − 2  
4( x−1− )1( x−1+ )1 (    x − 2)( x + 2) 4 ( x −1− ) 1 = 2 + lim  +  = 2 + lim  + x + 2 x→2 
(x − 2)( x+1+ ) x→2 1 x − 2 
(x − 2)( x+1+    )1    4  4 = 2 + lim + x + 2 = 2 + + 4 = 8.  
x→2  x −1 +1  2
(5x −4) 2x −3 + x −84 7) I = lim . x→6 x − 6
(5x −30) 2x −3 + 26 2x −3 −78+ x −6 Ta có I = lim x→6 x − 6  ( − − − −  x ) 26 x ( 2x 3 3 5 6 2 3 ) x−6 = lim  + +  x→6  x − 6 x − 6 x − 6    87
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
26 ( 2x − 3 − 3)( 2x − 3 + 3)  = lim 5 2x − 3 + +1 x→6  (x −6)  ( 2x−3+3)   26(2x − 3 − 9) 26.2( x − 6) =15 + lim +1=15 + lim +1
x→6 ( x − 6)( 2x −3 + 3)
x→6 ( x − 6)( 2x −3 + 3) 52 52 74 =15+ lim +1=15+ +1= . x 6 → 2x − 3 + 3 6 3 3 1+ 2x − 1+ 3x 8) I = lim . x→0 x 3 3
1+ 2x −1+1− 1+ 3x
 1+ 2x −1 1− 1+ 3x  Ta có I = lim = lim +    x→0 x→0 x x x   ( + − )( + +  ) ( 
1− 1+ 3x )(1+ 1+3x + (1+3 1 2 1 1 2 1 x x x )2 3 3 3 ) = lim +   x→0 x  ( 1+2x + )1
x (1+ 1+3x + (1+3x)2 3 3 )         1+ 2x −1 1− (1+ 3x)  2 3 −   = lim + = lim +   x→0 x  ( 1+ 2x + ) 1 →  + +  x ( 3 x 3
1+ 1+ 3x + (1+ 3x)2 ) 0 3 1 2x 1 3 
1+ 1+ 3x + (1+ 3x)2     2 3 − = + = 0. 2 3 3 3 2 x + 7 − x + 3 9) I = lim . x 1 → x −1 3 3 2
x + 7 − 2 + 2 − x + 3 3 3 2  x 7 2 2 x 3  + − − + Ta có I = lim = lim +  x 1 → x −1 x 1 →  x −1 x −1     (    3 x + 7 − 2) ( 3 x + 7)2 3 3 3 3 + 2 x + 7 + 4 ( 2 2 − x + 3 )( 2 2 + x + 3 )   = lim  +  x 1 →  (   − + +  x − ) ( 3 x + )2 3 3 + x + + (x )1  ( 2 3 2 x 3 1 7 2 7 4 )          + − 4 − +  x ( 2 3 x 3 7 8 ) = lim  +  x 1 → (   − + +  x − ) ( 3 x + )2 3 3 + x + + (x )1  ( 2 3 2 x 3 1 7 2 7 4 )          3 2  x −1 1− x = lim  +  x 1 → (   − + +  x − ) ( 3 x + )2 3 3 + x + + (x )1  ( 2 3 2 x 3 1 7 2 7 4 )         2  x + x +1 x +1  3 2 1 = lim − = − = − .   x 1 →  ( 3x + )2 2 3 3 + + 12 4 4 3 2 x 3 7 + 2 x + 7 + 4    88
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
3 8x +11 − x + 7 10) I = lim . 2 x→2 x − 3x + 2 3 3
8x +11 − 3 + 3 − x + 7
 8x +11 −3 3− x + 7  Ta có I = lim = lim +  2  2 2  x→2 x→2 x − 3x + 2 x − 3x + 2 x − 3x + 2    ( 
8x +11 − 3)( 3 (8x +1 )2 3 3 1
+ 3 8x +11 + 9) (3− x+7)(3+ x+7)  = lim +  
x→2  (x − x + )(3 ( x+ )2 2 3 + x +
+ ) ( 2x −3x+2)(3+ x+7 3 2 8 11 3 8 11 9 )      8x +11− 27 9 − ( x + 7)  = lim +  
x→2 (x − x + )(3 ( x+ )2 2 3 + x +
+ ) ( 2x −3x+2)(3+ x+7 3 2 8 11 3 8 11 9 )      8( x − 2) 2 − x  = lim +  
x→2 (x − )(x − )(3 ( x+ )2 3 + x +
+ ) (x− )1(x−2)(3+ x+7 1 2 8 11 3 8 11 9 )      8 1  8 1 7 = lim − = − = .  
x→2 (x − )(3 ( x+ )2 3 + x +
+ ) (x− )1(3+ x+7 1 8 11 3 8 11 9 ) 27 6 54    3
2 1+ x − 8 − x 11) I = lim . x→0 x 3 3
2 1+ x − 2 + 2 − 8 − x
 2 1+ x − 2 2 − 8− x  Ta có I = lim = lim +    x→0 x→0 x x x    ( + − )( + +  ) ( 
2 − 8 − x )(4+ 2 8− x + (8 2 1 1 1 1 − x x x )2 3 3 3 ) = lim +   x→0 x  ( 1+ x + )1
x (4+ 2 8− x + (8− x)2 3 3 )       2(1+ x − ) 1 8 − (8 − x)  = lim +   x→0 x  ( 1+ x + ) 1
x (4+ 2 8− x + (8− x)2 3 3 )     2 1 2 1 13 lim   = + = + = . x→0  + +  3 1 x 1 3
4 + 2 8 − x + (8 − x)2 2 12 12   3 2 3x + 5 − x + 3 12) I = lim . x 1 → x − 1 89
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2 3 2 3x 5 2 2 x 3  3x 5 2 2 x 3  + − + − + + − − + Ta có I = lim = lim +  x 1 → x 1 x −1 →  x −1 x −1     (    2 3x + 5 − 2) ( 2 3x + 5)2 3 3 2 3 + 2 3x + 5 + 4 
 (2 − x + 3)(2 + x + 3) = lim  +  x 1 →  (   − + +  x − ) ( 2 x + )2 3 2 3 (x ) 1 + x + + (2 x 3 1 3 5 2 3 5 4 )           2  3x + 5 − 8 4 − ( x + 3) = lim  +  x 1 → (   − + +  x − ) ( 2 x + )2 3 2 3 (x )1 + x + + (2 x 3 1 3 5 2 3 5 4 )           3( 2 x − ) 1  1− x = lim  +  x 1 → (   − + +  x − ) ( 2 x + )2 3 2 3 (x )1 + x + + (2 x 3 1 3 5 2 3 5 4 )           3( x + ) 1 1  6 1 1 = lim − = − = .   x 1 →  ( 2 + + 3x + 5)2 3 2 2 x 3 12 4 4 3 + 2 3x + 5 + 4    3 2
x + 7 − 5 − x 13) I = lim . x 1 → x −1 3 2  3 2 x 7 2 2 5 x x 7 2 2 5 x  + − + − − + − − − Ta có I = lim = lim +  x 1 → x 1 x −1 →  x −1 x −1     ( 
x + 7 − 2)( 3 (x + 7)2 3 3 + 2 x + 7 + 4) ( 2 2 − 5 − x )( 2 2 + 5 − x ) = lim +   x 1 →  (x − )
1 ( 3 (x + 7)2 + 2 x + 7 + 4) (x − ) 1 ( 2 3 2 + 5 − x )       + − 4 − ( 2 5 7 8 − x x )  = lim +   x 1 → (x − )
1 ( 3 (x + 7)2 + 2 x + 7 + 4) (x − ) 1 ( 2 3 2 + 5 − x )     2  x −1 x −1  = lim +   x 1 → (x − )
1 ( 3 (x + 7)2 + 2 x + 7 + 4) (x − ) 1 ( 2 3 2 + 5 − x )     1 x +1 1 2 7 lim   = + = + = . x 1 →   3 ( x + 7)2 2 3 + + + + − 12 4 12 2 x 7 4 2 5 x  
3 3x + 2 − 3x − 2 14) I = lim . x→2 x − 2 90
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 3
3x + 2 − 2 + 2 − 3x − 2
 3x + 2 − 2 2 − 3x − 2  Ta có I = lim = lim +    x→2 x→2 x − 2 x − 2 x − 2    ( 
3x + 2 − 2)( 3 (3x + 2)2 3 3
+ 2 3x + 2 + 4) (2− 3x−2)(2+ 3x−2) = lim +   x→2 
(x − )(3 ( x+ )2 3 + x + + )
(x − 2)(2+ 3x−2 2 3 2 2 3 2 4 )       3x + 2 − 8 4 − (3x − 2)  = lim +  
x→2 (x − )(3 ( x+ )2 3 + x +
+ ) (x−2)(2+ 3x−2 2 3 2 2 3 2 4 )      3( x − 2) 6 − 3x  = lim +  
x→2 (x − )(3 ( x+ )2 3 + x +
+ ) (x−2)(2+ 3x−2 2 3 2 2 3 2 4 )     3 3 3 3 − 1 lim   = − = + = − . x→2  + −  3 (3x + 2)2 3 2 3x 2 12 4 2 + 2 3x + 2 + 4  
3 3x + 2 − 5x − 6 15) I = lim . x→2 x − 2 3 3
3x + 2 − 2 + 2 − 5x − 6
 3x + 2 − 2 2 − 5x −6  Ta có I = lim = lim +    x→2 x→2 x − 2 x − 2 x − 2    ( 
3x + 2 − 2)( 3 (3x + 2)2 3 3
+ 2 3x + 2 + 4) (2− 5x−6)(2+ 5x−6) = lim +   x→2 
(x − )(3 ( x+ )2 3 + x + + )
(x − 2)(2+ 5x−6 2 3 2 2 3 2 4 )       3x + 2 − 8 4 − (5x − 6)  = lim +  
x→2 (x − )(3 ( x+ )2 3 + x +
+ ) (x−2)(2+ 5x−6 2 3 2 2 3 2 4 )      3( x − 2) 10 − 5x  = lim +  
x→2 (x − )(3 ( x+ )2 3 + x +
+ ) (x−2)(2+ 5x−6 2 3 2 2 3 2 4 )     3 5 3 5 − lim   = − = + = −1. x→2  + −  3 (3x + 2)2 3 2 5x 6 12 4 + 2 3x + 2 + 4   3 2
2x + 4x +11 − x + 7 16) I = lim . 2 x→2 x − 4 3 2 3 2 2x 4x 11 3 3 x 7  2x 4x 11 3 3 x 7  + + − + − + + + − − + Ta có I = lim = lim +  2 2 2 x→2 x→2 x − 4  x − 4 x − 4    91
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  (    2
2x + 4x +11 − 3) ( 2 2x + 4x + )2 3 3 2 3 11
+ 3 2x + 4x +11 + 9 
 (3− x + 7 )(3+ x + 7 ) = lim  +  x→2  (   2 − + +  x − ) ( 2 x + x + )2 3 2 3 + x + x + + ( 2x 4)(3 x 7 4 2 4 11 3 2 4 11 9 )           2 
2x + 4x +11− 27 9 − ( x + 7) = lim  +  x→2 (   2 − + +  x − ) ( 2 x + x + )2 3 2 3 + x + x + + ( 2x 4)(3 x 7 4 2 4 11 3 2 4 11 9 )           2  2x + 4x −16 2 − x = lim  +  x→2 (   2 − + +  x − ) ( 2 x + x + )2 3 2 3 + x + x + + ( 2x 4)(3 x 7 4 2 4 11 3 2 4 11 9 )           2 ( x 2)( x 4)  − + 2 − x = lim  +  x→2 (   2 − + +  x − ) ( 2 x + x + )2 3 2 3 + x + x + + ( 2x 4)(3 x 7 4 2 4 11 3 2 4 11 9 )           2 ( x 4)  + 1 12 1 − 5 = lim  −  = + = . x→2 (   + + +  x + 2) ( 2 2x + 4x + )2 3 2 x 2 3 x 7 108 24 72 3 ( ) 11
+ 3 2x + 4x +11 + 9 ( )        3 3 2
5 − x − x + 7 17) I = lim . 2 x 1 → x −1 3 3 2 3 3 2 5 x 2 2 x 7  5 x 2 2 x 7  − − + − + − − − + Ta có I = lim = lim +  2 2 2 x 1 → x 1 x −1 →  x −1 x −1     (  
− x − )( − x + ) ( 2 2 − x + 7 ) 2 4 + 2 x + 7 +  ( 2 3 3 3 x + 7 5 2 5 2 )2 3 3    = lim  +  x 1 →  ( 2x − )1( 3 5 − x + 2) (   2  x − ) 3 2 1 4 + 2 x + 7 +  ( 2 3 x + 7)2           − − 8 − +  x ( 2 3 x 7 5 4 ) = lim  +  x 1 → ( 2 x − ) 1 ( 3 5 − x + 2) (   2  x − ) 3 2 1 4 + 2 x + 7 +  ( 2 3 x + 7)2        92
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC    3 2  1− x 1− x = lim  +  x 1 → ( 2 x − ) 1 ( 3 5 − x + 2) (   2  x − ) 3 2 1 4 + 2 x + 7 +  ( 2 3 x + 7)2         −  (  2 x + x + ) 1 1 −  3 1 − 11 = lim + = − + = − .   x 1 → (x + )( 3 − x + ) 3 2 4 + 2 x + 7 + ( 2 8 12 24 1 5 2 3 x + 7)2    3 3
3 4x − 24 + x + 2 − 8 2x − 3 18) I = lim . 2 x→2 4 − x 3 3
3 4x − 24 − 6 + x + 2 − 2 + 8 − 8 2x − 3 Ta có I = lim 2 x→2 4 − x 3 3 3 4x − 24 − 6 x + 2 − 2 8 − 8 2x − 3 = lim + lim + lim 2 2 2 x→2 x→2 x→2 4 − x 4 − x 4 − x 1 I I2 I3   3( 3 4x − 24 − 2) 2 3 3 3 3 3 2
 4x − 24 + 4x − 24.2 + 2  3 3 3 4x − 24 − 6   I = lim = lim 1 2 x→2 4 − x x→ (   2 4 − x ) 2 2 3 3 3 3 2
 4x − 24 + 4x − 24.2 + 2    3( 3 4x − 24 − 8) = lim x→ (   2 4 − x )( 3 4x − 24 )2 2 3 3 3 2 + 4x − 24.2 + 2    3.4( 3 x − 8) = lim x→ (   2 4 − x )( 3 4x − 24 )2 2 3 3 3 2 + 4x − 24.2 + 2    12( x − 2)( 2 x + 2x + 4) = lim x→ (  
2 − x)(2 + x)( 3 4x − 24 )2 2 3 3 3 2 + 4x − 24.2 + 2    1 − 2( 2 x + 2x + 4) = 144 lim = − = 3 − . x→ (   48 2 + x)( 3 4x − 24 )2 2 3 3 3 2 + 4x − 24.2 + 2   
( x+2 −2)( x+2 +2) x + 2 − 2 (x + 2−4) I = lim = lim = lim 2 2 x→2 4 − x x→2 ( 2
4 − x )( x + 2 + 2)
x→2 (2 − x)(2 + x)( x + 2 + 2) 1 − 1 = lim = − x→
(2+ x)( x+2 +2) 16 93
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
8(1− 2x − 3)(1+ 2x − 3) 8 − 8 2x − 3 8(1− (2x − 3)) I = lim = lim = lim 3 2 x→2 4 − x x→2 ( 2
4 − x )(1+ 2x − 3)
x→2 (2 + x)(2 − x) 8.2(2 − x) = 16 16 lim = lim = = 2
x→2 (2 − x)(2 + x)(1+ 2x + 3)
x→2 (2 + x)(1+ 1+ 2x −3) 8 1 17 I = 3 − − + 2 = − . 16 16 Bài 5.
Tính các giới hạn sau: 1 ( 3
lim 2x − 3x) ĐS: + 2. ( 3 2
lim x − 3x + 2) ĐS: − x→+ x→− 3. ( 3 2
lim −x − 6x + 9x + ) 1 ĐS: − 4. ( 3
lim −x + 3x − ) 1 ĐS: + x→+ x→− 5. ( 4 2 lim x − 2x + ) 1 ĐS: + 6. ( 4 2
lim x − 8x +10) ĐS: + x→+ x→− 7. ( 4 2
lim −x + 2x + ) 3 ĐS: − 8. ( 4 2
lim −x − x + 6) ĐS: − x→+ x→− 9. 2 lim
x − 3x + 4 ĐS: + 10. + + ĐS: + →− ( 2 lim 2x 1 x x ) x→ 11. + + + ĐS: − 12. + + − ĐS: + →+ ( 2 lim 4x x 1 x x ) →− ( 2 lim x x 1 2x x ) 13. lim + − + ĐS: − →+ ( x 1 9x 1) x 14. lim + + +
ĐS: không tồn tại giới hạn →− ( 16x 7 9x 3 ) x Lời giải 1. I = ( 3 lim 2x − 3x) x→+  3   3  Ta có I = ( 3 lim 2x − 3x) 3 = lim x 2 − = +   . (vì 3
lim x = + và lim 2 − = 2  0   ) x→+ 2 x→+  x x→+ 2 x→+  x  2. I = ( 3 2
lim x − 3x + 2) . x→−  3 2  Ta có I = ( 3 2
lim x − 3x + 2) 3 = lim x 1− + = −   . (vì 3 lim x = − và x→− 3 x→−  x x x→−  3 2  lim 1− + =1   ). 3 x→−  x x  3. I = ( 3 2
lim −x − 6x + 9x + ) 1 . x→+  6 9 1  Ta có 3 I = lim x 1 − − + + = −   . 2 3 x→+  x x x   6 9 1  (vì 3 lim x = + và lim 1 − − + + = 1 −  0   ). x→+ 2 3 x→+  x x x  4. I = ( 3
lim −x + 3x − ) 1 x→− 94
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  3 1   3 1  Ta có 3 I = lim x 1 − + − = +   . (vì 3 lim x = − và lim 1 − + − = 1 −  0   ). 2 3 x→−  x x x→− 2 3 x→−  x x  5. I = ( 4 2 lim x − 2x + ) 1 x→+  2 1   2 1  Ta có 4 I = lim x 1− + = +   . (vì 4
lim x = + và lim 1− + =1  0   ). 2 4 x→+  x x x→+ 2 4 x→+  x x  6. I = ( 4 2
lim x − 8x +10) x→−  8 10   8 10  Ta có 4 I = lim x 1− + =1  0   (vì 4
lim x = + và lim 1− + =1  0   ) 2 4 x→−  x x x→− 2 4 x→−  x x  7. I = ( 4 2
lim −x + 2x + ) 3 x→+  2 3   2 3  Ta có 4 I = lim x 1 − + + = −   . ( vì 4 lim x = + và lim 1 − + + = 1 −  0   ). 2 4 x→+  x x x→+ 2 4 x→+  x x  8. I = ( 4 2
lim −x − x + 6) x→−  1 6   1 6  Ta có 4 I = lim x 1 − − + = −   . (vì 4 lim x = + và lim 1 − − + = 1 −   ) 2 4 x→−  x x x→− 2 4 x→−  x x  9. 2 I = lim x − 3x + 4 . x→  3 4   3 4  Ta có 2 I = lim x 1− +   = lim x 1− + = +   . 2 x→  x x  2 x→  x x   3 4 
(vì lim x = + và lim 1− + = 1  0   ). x→ 2 x→  x x  10. I = + + →− ( 2 lim 2x 1 x x )  1  Ta có I = + + = lim x− 2 + +1 = + . →− ( 2 lim 2x 1 x   x ) 2 x→− x    1 
(vì lim x = − và lim  − 2 + +1 = − 2 +1 0   ). x→− 2 x→− x    1 1  11. I = + + + = lim x− 1+ + + 2 = − . →− ( 2 lim x x 1 2x   x ) 2 x→− x x    1 1 
(vì lim x = − , lim  − 1+ + + 2 =1 0   ). x→− 2 x→− x x    1 1  12. I = + + − = lim x 4 + + −1 = + →+ ( 2 lim 4x x 1 x   x ) 2 x→+ x x    1 1 
(vì lim x = + , = lim  4 + + −1 =1 0   ). x→+ 2 x→+ x x     13. I = lim + − + 1 1
= lim x  1+ − 9 +  = − . →+ ( x 1 9x 1)   x x→+ x x    1 1  (vì lim x = + , = lim x  1+ − 9 +  = −   ). x→+ x→+ x x   95
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 14. I = lim + + + →− ( 16x 7 9x 3 ) x  1 
Tập xác định của hàm số f ( x) = 16x + 7 + 9x + 3 là D = − ; +   .  3 
Ta có khi x → − hàm số f ( x) = 16x + 7 + 9x + 3 không xác định. Do đó lim + + + không tồn tại. →− ( 16x 7 9x 3 ) x Bài 6.
Tính các giới hạn sau: x + 2 2x 1. lim . ĐS: 1 2. lim . ĐS: 2 x→+ x −1 x→− x +1 1− x 3x − 2 3. lim .ĐS: 1 − 4. lim . ĐS: 3 x→+ 2x −1 2 x→− x +1 3 3x ( 2 2x − ) 2x + 3x − 4 1 5. lim . ĐS: −2 6. lim . ĐS: 6 3 2
x→+ −x − x +1
x→+ (5x − ) 1 ( 2 x + 2x) 5 4 3 ( 2 4x + ) 2x + 7x −15 1 (7x − ) 1 7. lim . ĐS: 2 8. lim . ĐS: 0 4 x→− x +1 x→+ ( 3 2x − ) 1 ( x + 3) ( 4 3 x − )2 1 (5x + 2)2 (x + ) 1 (1− 2x) 9. lim . ĐS: 25 10. lim .ĐS: 1 − 5 x→− (3x + )4 1 81
x→− (2x + 2) ( 2 x + 3) 4 (x +2)2 2 (x + 2)
(x + 2)3 (1− x)4 11. lim . ĐS: − 12. lim . ĐS: 1 − x→− ( 5 2x + ) 1 (1− x)2 2 x→− (1−2x) 2x 32 3 2  x x  2 3x − x + 7 13. lim  −  . ĐS: 2 14. lim .ĐS: 0 2
x→−  3x − 4 3x + 2  9 3 x→− 2x −1 3 ( 2 4x + ) x + 2x + 2 1 (7x − ) 1 15. lim ĐS: 0 16. lim ĐS: 0 4
x→+ 2x + x + 3 x→+ ( 3 2x − ) 1 ( x + 3) ( 2 4x + ) 1 (2x + 3) 3 x + 2x + 2 17. lim ĐS: − 18. lim ĐS: + 2 x→− x − 6x +1 2
x→+ 2x + x + 3 4 3
x + 2x + x + 2 4 3
x + 2x + x + 2 19. lim ĐS: − 20. lim ĐS: − 3 x→− 2x + x + 3 2 3 x→+ 2x − x 4 3 x − x +11 4 2 2x + x −1 21. lim ĐS: + 22. lim ĐS: + x→+ 2x − 7 x→+ 1− 2x 4 x − x 5 3 2x + x −1 23. lim ĐS: + 24. lim 3 ĐS: 1 x→+ 1− 2x x→+ ( 2 2x − ) 1 ( 3 x + x) 3 3 x + x +1 4 2 2x + x −1 25. lim ĐS: 1 26. lim ĐS: − x→+ 2x +1 x→+ 1− 2x 96
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Lời giải  2   2  x 1+   1+   x + 2  x   x  1. I = lim = lim = lim =1. x→+ x −1 x→+  1  x→+  1  x 1−   1−    x   x  2x 2x 2 2. I = lim lim = lim = 2 .
x→− x +1 x→−  1  x→− 1 x 1+   1+  x x  1  x −1   1 −1 1− xx  1 3. I = lim = lim = lim x = − . x→+ 2x −1 x→+  1  x→+ 1 2 x 2 −   2 −  x x  2   2  x 3 −   3 −   3x − 2  x   x  4. I = lim = lim = lim = 3. x→− x +1 x→−  1  x→−  1  x 1+   1+    x   x   3 4   3 4  3 x 2 + −   2 + −   3 2x + 3x − 4 2 3  x x  2 3  x x  5. I = lim = lim lim = 2 − . 3 2
x→+ −x − x +1 x→+  1 1  x→+  1 1  3 x 1 − − +   1 − − +   3  x x  3  x x   1   1  2 3 . x x 2 −   3 2 −   2  x  2  x  6 6. I = lim = lim = . x→+  1   2  x→+  1   2  2 5 x 5 − x 1+     5 − 1+     x   x   x  x   7 15   7 15  4 x 2 + −   2 + −   4 3 2x + 7x −15 4  x x  4  x x  7. I = lim = lim = lim = 2 . 4 x→− x +1 x→−  1  x→−  1  4 x 1+   1+   4  x  4  x  (  1   1   1   1  2 + − + − 2 x 4 x 7 4 x 7 4x + ) 1 (7x − ) 1         2  x   x  2  x   x  8. I = lim = lim = lim = 0. x→+ ( 3 2x − ) 1 ( x + 3) x→+  1   3  x→+  1   3  3 x 2 − x 1+     2 − x 1+     3  x   x  3  x   x  2 2  2 2 1   2   1   2  ( 2 2 x 1− x 5 +     1− 5 +     x − )2 1 (5x + 2)2  x   x   x   x  25 9. I = lim = lim = lim = . x→− ( 4 4 3x + )4 1 x→−  1  x→−  1  81 4 x 3 +   3 +    x   x  4 3  4 3 1   1   1   1  ( 4 3 x 1+ x − 2     1+ − 2     x + )4 1 (1− 2x)3  x   x   x   x  1 10. I = lim = lim = lim = − . x→− ( 5 5 2x + 2)5 ( 2 x + 3) x→−  2   3  x→−  2   3  4 5 2 x 2 + x 1+     2 + 1+     2  x   x  2  x   x  97
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 2 (  2   2   2   2  4 + + + + x + 2)2 2 (x + 2) x 1 x 1     . x 1 1     2  x   x  2  x   x  11. I = lim = lim = lim = − x→− ( 2 2 2x + ) 1 (1− x)2 2 x→−  1   1  x→−  1  1  2 2 x 2 + x −1     2 + −1    2  x   x  2  x  x  2  2   2  1+ 1+     2  x   x  1
(vì lim x = − , lim =  0 ). x→− 2 x→−  1  1  2 2 + −1    2  x  x  3 4  3 4 2   1   2   1  ( 3 4 x 1+ x −1     1+ −1    
x + 2)3 (1− x)4  x   x   x   x  1 12. I = lim = lim = lim = − . x→− ( 5 5 1− 2x)5 2 x x→−  1  x→−  1  32 5 2 x − 2 .x   − 2    x   x  3 2  x x  13. I = lim  −  . 2
x→−  3x − 4 3x + 2  3 2  3 2 2 x x
x (3x + 2) − x (3x − 4) 3 2 2x + 4x Ta có I = lim  −  = lim = lim 2
x→−  3x − 4 3x + 2  x→− ( 2
3x − 4)(3x + 2) x→− ( 2
3x − 4)(3x + 2)  4   4  3 x 2 +   2 +    x  =  x  2 lim = lim = . x→−  4   2  x→−  4  2  2 9 x 3 − x 3 +     3 − 3 +     x   x   x  x   3 1 7   3 1 7  2 x − +   − +   2 3x − x + 7 2  x x x  2  x x x  14. I = lim = lim lim = 0 . 3 x→− 2x −1 x→−  1  x→−  1  3 x 2 −   2 −   3  x  3  x Bài 7.
Tính các giới hạn sau: 2x − 3 x −15 1. lim . ĐS: − 2. lim . ĐS: − + + x 1 → x −1 x→2 x − 2 2 − x x − 5 3. lim . ĐS: + 4. lim . ĐS: − − − x 3 → 3 − x x→ (x − 4)2 4 3 − x +1 3x −1 5. lim . ĐS: + 6. lim . ĐS: − − − x→2 x − 2 x 1 → x −1 6 − 5x x +1 7. lim . ĐS: − 8. lim . ĐS: + + + x→2 4x − 8 x→2 2x − 4 x − 3 7x −1 9. lim . ĐS: 1 10. lim .ĐS: − + − x 3 → 5x −15 5 x ( → − ) 3 x + 3 2 − x x −1 11. lim . ĐS: 1 12. lim . ĐS: 1 − 2 + 3 x→2 2x − 5x + 2 3 x 1 → 2x + x − 3 7 2 x −1 x − 3x + 2 13. lim . ĐS: 1 − 14. lim .ĐS: 1 − 3 + x 1 → 2x + x − 3 7 x→2 x − 2 98
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x − 9 x − 4 15. lim lim ĐS: không tồn tại x→3 x − ĐS: không tồn tại 16. 3 2
x→4 x + x − 20 x − 2 x − 3 17. lim ĐS: 2 18. lim ĐS: 4 − − − x→2 x −1 −1 x 3 → 5x −11 − 2 5 2 x − 2 x − 25 19. lim ĐS: 3 − 20. lim ĐS: 30 − − 3 − x→2 x −1 −1 3 x→5 x − 4 −1 3x − 8 3 x + 25 − 3 21. lim ĐS: + 22. lim ĐS: 1 + 2 x→ (3− x)2 3 x→2 x − x − 2 81 3x + 2 x + x 23. lim ĐS: + 24. lim ĐS: 1 − + → 2 + x 2 4x −16 x→0 x − x 2 4 − x x + 2 x 25. lim ĐS: 0 26. lim ĐS: −2 + + x→2 2 − x x→0 x − x (x + 2)(x + ) 1 2 x − 6x + 9 27. lim ĐS: 1 28. lim ĐS: 1 − + − 2 x→(− ) 1 x +1 − x −1 x 3 → x − 9 6 2 x − 4x + 3 2 x + 3x + 2 29. lim ĐS: − 30. lim ĐS: 0 − 2 + x 1 → −x + 6x − 5 x→(− ) 5 4 1 x + x x x 31. lim ( x − 2) lim + + ( 3 x )1 + 2 2 x→2 x − ĐS: 0 32. 4 x ( → − ) 1 x − ĐS: 0 1 x + 5 x 1− x 33. lim (1− x) lim ĐS: 1 + 2 − x 1 → x + 2x − ĐS: 0 34. 3 x 1 → 2 1− x +1− x 2  1− x  2 2x + 5x − 3 35. lim  2x  ĐS: 0 36. lim ĐS: − +   + 2 x→0 x   x ( → 3 − ) (x +3)  1 1  3 x − 3x + 2 37. lim −   ĐS: − 38. lim ĐS: 3 − − 2 − 2
x→2  x − 2 x − 4  x 1 → x − 5x + 4 5 Lời giải lim (2x −3) = 1 − + x 1 →  2x − 3  1 lim
= − vì lim (x − ) 1 = 0 . + + x 1 → x −1 x 1 → 
x −1  0, x  →1+  lim (x −15) = 13 − + x→2  x −15  2. lim
= − vì lim (x − 2) = 0 . + + x→2 x − 2 x→2 
x − 2  0, x  → 2+  lim (2 − x) = −1 − x→3  2 − x  3. lim
= + vì lim (3− x) = 0 . − − x 3 → 3 − x x→3  3
 − x  0, x  → 3−  99
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC lim (x −5) = 1 − − x→4  x − 5  2 4. lim
= − vì lim (x − 4) = 0 . − − x→ (x −4)2 4 x→4 (x−4  )2  0, x  → 4− lim ( 3 − x + ) 1 = 5 − − x→2  3 − x +1  5. lim
= + vì lim (x − 2) = 0 . − − x→2 x − 2 x→2 
x − 2  0, x  → 2−  lim (3x − ) 1 = 2 − x 1 →  3x −1  6. lim
= − vì lim (x − ) 1 = 0 . − − x 1 → x −1 x 1 → 
x −1 0, x  →1−  lim (6 − 5x) = 4 − + x→2  6 − 5x  7. lim
= − vì lim (4x −8) = 0 . + + x→2 4x − 8 x→2 
4x − 8  0, x  → 2+   lim (x + ) 1 = 3 + x→2  x +1  8. lim
= + vì lim (2x − 4) = 0 . + + x→2 2x − 4 x→2 
2x − 4  0, x  → 2+  x − 3 x − 3 1 1 9. Do x 3+
→ nên x − 3 = x − 3 suy ra lim = lim = lim = . + + + x 3 → − x 3 5x 15 → 5x −15 x 3 → 5 5  lim (7x − ) 1 = 22 − − x→( 3−) 7x −1  10. lim = −  lim x + 3 = 0 . − − x ( → − ) 3 x + vì 3 x→( 3 − )  −
x +3  0, x  →  (−3) 2 − x 2 − x 11. Do x 2−
→ nên 2 − x = 2 − x suy ra lim = lim − 2 − x→2 − + x→2 2x 5x 2 (2x − ) 1 ( x − 2) 1 1 = lim = . − x→2 2x −1 3 x −1 x −1 12. Do x 1+
→ nên x −1 = x −1 suy ra lim = lim + 3 + x→ 2x + x − 3 x→ (x − ) 1 ( 2 1 1 2x + 2x + 3) 1 1 lim = . + 2 x 1 → 2x + 2x + 3 7 x −1 1− x 13. Do x 1−
→ nên x −1 =1− x suy ra lim = lim − 3 − x→ 2x + x − 3 x→ (x − ) 1 ( 2 1 1 2x + 2x + 3) 1 − 1 lim = − . − 2 x 1 → 2x + 2x + 3 7 14. Ta có 2
x − 3x + 2 = ( x − )
1 ( x − 2) , do x 2+ → nên 2
x − 3x + 2  0 , suy ra 2 x − 3x + 2 (x − ) 1 ( x − 2) lim = lim = lim (x − ) 1 = 1 + + + x→2 − x→2 − . x→2 x 2 x 2 100
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x − 9 (x +3)(x −3) 15. Ta có lim = lim x→3 x→3 x − 3 x − 3 2 x − 9 (x +3)(x −3) TH1: x  3 ta có lim = lim = lim (x + 3) = 6 + + + x→3 − x→3 − . x→3 x 3 x 3 2 x − 9
−(x + 3)(x − 3) TH2: x  3 ta có lim = lim = lim (−x −3) = 6 − − − − x→3 − x→3 − . x→3 x 3 x 3 2 2 x − 9 x − 9 2 x − 9 Do lim  lim lim + − x→3 − x→3 x 3 x − nên không tồn tại 3 x→3 x − . 3 x − 4 x − 4 16. Ta có lim = lim 2 x→4 x→4 x + x − 20 (x − 4)(x +5) x − 4 x − 4 1 1
TH1: x  4 , ta có lim = lim = lim = + 2 + + x→4 x→4 x + x − 20
(x −4)(x +5) x→4 x +5 9 x − 4 x − 4 1 − 1 −
TH2: x  4 , ta có lim = lim = lim = + 2 − − x→4 x→4 x + x − 20
(4− x)(x +5) x→4 x +5 9 x − 4 x − 4 x − 4 Do lim  lim nên không tồn tại lim . + 2 − x→4 x + x − 20 2 x→4 x + x − 20 2
x→4 x + x − 20 x − 2
(x − 2)( x−1+ )1 17. Do x 2−
→ nên x − 2 = 2 − x suy ra lim = lim − − x→2 x −1 −1 x→2 x −1−1 lim − + = . − ( x 1 )1 2 x→2 x − 3
(3− x)( 5x−11+2) 18. Do x 3−
→ nên x − 2 = 3 − x suy ra lim = lim − − x 3 → 5x −11 − 2 x 3 → 5x −11− 4 −( 5x −11+ 2) 4 = lim = − . − x 3 → 5 5 (2− x)( 2 3 3 x −1 + x −1 + ) x − 2 1 19. Do x 2−
→ nên x − 2 = 2 − x suy ra lim = lim − 3 − x→2 x −1 −1 x→2 x −1−1 = lim − − + − + = − . − → ( ( 2 3 3 x 1 x 1 1 3 x 2 ) 2 x − 25 20. Ta có 2
x − 25 = ( x − 5)( x + 5) , do x 5− → nên 2
x − 25  0 , suy ra lim− 3 x→5 x − 4 −1 (25− x )( 2 2 3 3 x − 4 + x − 4 + ) 1 = 2 lim = lim − + − + − + = − . − ( (5 x)) → (3 3 x 4 x 4 1 30 x 5 ) − x→5 x − 4 −1 lim (3x −8) =1 + x→3  3x − 8  2 21. lim
= + , vì lim (3− x) = 0 . + + x→ (3− x)2 3 x→3 (3−x  )2  0, x  → 3+ 101
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 x + 25 − 3 x + 25 − 27 22. Ta có lim = lim 2 x→2 x − x − 2 x→ (x −2)(x + ) 1 ( 2 2 3 3
x + 25 + 3 x + 25 + 9) 1 1 = lim = . x→ (x + )( 2 2 3 3 x + + x + + ) 81 1 25 3 25 9 lim (3x + 2) = 8 + x→2  3x + 2  23. lim = + , vì 2 lim 4x −16 = 0 . + → 2 + x 2 4x −16 x→2  2
 4x −16  0, x  → 2+  x ( x + ) x + x 1 x +1 24. lim = lim = lim = 1 − . + + + x→0 x − x x→0
x ( x − ) x→0 1 x −1 2 4 − x (2− x)(2+ x) 25. lim = lim
= lim 2 − x (2 + x) = 0 . + + + x→2 2 − x x→2 x→2 2 − x x ( x + 2) x + 2 x x + 2 26. lim = lim = lim = 2 − . + + + x→0 x − x x→0
x ( x − ) x→0 1 x −1 (x + 2)(x + ) 1 x + 2 x +1 x + 2 27. Ta có lim = lim = lim =1. + + + x→(− ) 1 x +1 − x −1 x→(− ) 1
x +1 (1− x +1) x→(− )1 1− x +1 28. Ta có − x − x + = (x − )2 2 6 9 3
= x −3 , do x → 3 nên 2
x − 6x + 9 = 3 − x , suy ra 2 x − 6x + 9 2 x − 6x + 9 3 − x 1 − 1 lim = lim = lim = lim = − − 2 − 2 − − x 3 → x − 9 x 3 → − x 3 x 9 →
(x −3)(x +3) x 3 → x + . 3 6 29. Do x 1−
→ nên x −1 0 , từ đó ta có 2 x − 4x + 3
(x − )1(x −3) 1− x 3 − x 3 − x lim = lim = lim = lim − 2 − − − x 1 → −x + 6x − 5 x 1 → −(x − ) 1 ( x − 5) x 1 → −(x − ) 1 ( x − 5) x 1 →
1− x ( x − 5)  1 3 − x  = lim  .  = − . −   x 1 → 1− x x − 5   3 − x 2  1  vì lim = − và lim = +   . − − x 1 → x − 5 4 x 1 →  1− x  2 x + 3x + 2 (x + )1(x + 2) x +1 ( x + 2) 30. lim = lim = lim = 0 . + + 2 + 2 x→(− ) 5 4 1 x + x x ( → − ) 1 x x +1 x→(− ) 1 x x x x ( x − 2) 31. lim ( x − 2) = lim (x − 2) = lim = 0 + 2 + + x→2 x − 4 x→2
(x − 2)(x + 2) x→2 x + . 2 x x 32. Ta có lim + = lim (x + ) 1 − + + ( 2x x )1 + ( 3 x )1 x ( → − ) 2 1 x −1 x ( → − ) 1 (x − ) 1 ( x + ) 1 x x + = lim − + = . + ( 1 2 x x ) ( ) 1 0 x ( → − ) 1 x −1 33. Do x 1+
→ nên 1− x  0 , vì thế ta có 102
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2    + −  ( + (x +5)(x − ) (x 5)(x ) − 1 1 x) x 5 lim 1 = lim   = lim   = 0 . + 2 + + x 1 → x + 2x − 3 x 1 →  (x − ) 1 ( x + 3)  →  +    x 1 x 3   x 1− x x 1− x x 1 34. lim = lim = lim = . − − − x 1 → x 1 2 1− x +1− x →
1− x (2 + 1− x ) x 1 → 2 + 1− x 2  2   1− x x (1− x) 35. lim  2x  = lim  2
 = lim 2 x(1− x) = 0. +   + + x→0 x   x→0  x    x→0 2 2x + 5x − 3 (2x − ) 1 ( x + 3) 2x −1 36. lim = lim = lim = − . + + 2 + x ( → − ) (x +3)2 3 x ( → 3 − ) (x +3) x ( → 3 − ) x + 3  1 1   x + 2 −1   x +1 1  37. lim −   = lim   = lim . = −   . − 2 −   −
x→2  x − 2 x − 4 
x→2  ( x − 2)( x + 2) 
x→2  x + 2 x − 2  38. Do x 1−
→ nên x −1 0 , suy ra (x − )2 1
= x −1 =1− x nên ta có 2 3 x − 3x + 2 (x + 2)(x − ) 1 (1− x) x + 2 − x + 2 3 lim = lim = lim = lim = − . − 2 − − − x 1 → x − 5x + 4 x 1 → (x − ) 1 ( x + 4) x 1 → ( x − ) 1 ( x + 4) x 1 → x + 4 5 Bài 8.
Tính các giới hạn sau: sin 5x tan 2x 1) lim . ĐS: 5 2) lim . ĐS: 2 x 0 → x x 0 → 3x 3 1− cos x sin 5 . x sin 3 . x sin x 3) lim . ĐS: 1 4) lim . ĐS: 1 2 x 0 → x 2 3 x 0 → 45x 3 1− cos 5x 2 1− cos 2x 5) lim 6) lim . ĐS: 4 x 0 → 1− cos3x x 0 → . x sin x x sin ax 1− cos ax 2 a 7) lim (a  0). ĐS: 2 8) lim . ĐS: x 0 → 1− cos ax a x 0 → 1− cosbx 2 b 1− cos x 2 a sin x − tan x 9) lim ; a  0 ĐS: 10) lim ĐS: 1 − 2 ( ) x 0 → x 2 3 x 0 → x 2 tan x − sin x sin x − sin a 11) lim . ĐS: 1 12) lim . ĐS: cos a 3 x 0 → sin x 2 x→a x − a cos x − cos b 1− 2x +1 − 13) lim ĐS: −sin b 14) lim ĐS: 1 x b → x − b x→0 sin 2x 2
cos (a + x) − cos(a − x) tan x − tan c 1 15) lim ĐS: 2 − sin a 16) lim ĐS: x 0 → x x c → x − c 2 cos c 3 1− cos x 2 2 sin x − sin a a 17) lim ĐS: 3 18) lim ĐS: sin 2 x→0 x sin x 2 2 2 x→a x − a 2a
cos x − cos  x 2 2  − 3 x + 8 19) lim ĐS: 20) lim ĐS:12 2 x 0 → x 2 x 2 →− tan ( x + 2) 103
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
1− cos x cos 2x cos 3x
sin (a + 2x) − 2sin (a + x) + sin a 21) lim . ĐS:1422) lim . ĐS: − sin ( ) x 0 → 1− cos x 2 x 0 → x sin ax + tan bx
cos 3x − cos 5x cos 7x 23) lim
;(a + b  0) ĐS: 1 24) lim ĐS: 33 − x→0 (a + b)x 2 x 0 → x 2
cos ax − cos bx cos cx 2 2 2
b − a − c
sin (a + x) − sin (a − x) 25) lim . ĐS: 26) lim ĐS: 3 cos a x 0 → 1− cos x 2
x→0 tan(a + x) − tan(a − x) 3 2 2x +1 − x +1 2
sin 2x − sin x sin 4x 27) lim . ĐS: 1 28) lim ĐS: 6 x→0 sin x 4 x 0 → x cos x sin x − sin 2x 29) lim . ĐS: 1 30) lim ĐS: -1  →−  →   x + x 0 x 2 2 x x 1− sin   2  2  2 1+ x − cos x
1+ tan x − 1+ sin x 31) lim . ĐS: 1 32) lim ĐS: 1 2 x→0 x 3 x→0 x 4
1− cos 5x cos 7x x + 3 − 2 33) lim . ĐS: 37 34) lim 2 x 0 → sin 11x 121 x 1 → tan(x − ĐS: 1 1) 4 1+ cos x sin(x −1) 35) lim ĐS: 1 36) lim ĐS: 1 − x  → ( 2 x −  ) . 2 2 x 1 → x − 4x + 3 2 2 x +1 − cos 2x
1− cos x cos 2x 37) lim . ĐS: 5 38) lim ĐS: 3 2 x→0 x 2 2 x→0 x 2 Lời giải. sin 5x  sin 5x  1) lim = lim 5 = 5   . x→0 x→0 x  5x  tan 2x  2 tan 2x  2 2) lim = lim  = .   x→0 x→0 3x  3 2x  3 2   x     2   2 sin x      sin  1− cos x  2  1   1 3) 2 lim = lim  = lim 2    = . 2 2 x→0 x→0 x→0 xx   4 x  2        2     
sin 5x sin 3x sin x
 1 sin 5x sin 3x sin x  1 4) lim = lim    =   . 3 x→0 x→0 45x  3 5x 3x x  3 2 2 5x  5x 3x      2 2sin  sin  1− cos 5x 25   4   25 5) 2 2 2 lim = lim = lim        = . x→0 x→0 1− cos 3x 3x x→0  4 5x 9 3x 2  9 2sin    sin    2  2   2    104
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 2 2 1− cos 2x sin 2x 4sin x cos x  sin x  6) 2 lim = lim = lim = lim 4cos x = 4   . x→0 x→0 x→0 x→0 x sin x x sin x xx  2  ax      x sin ax x sin ax 1 sin ax 4   2 7) 2 lim = lim = lim  a       = . 2 x→0 x→0 − ax ax x→0 1 cos  ax a ax 2 2  a 2sin  sin    2  2    2 2 axax bx      2 2sin  2 sin  2 1− cos ax a   4   a 8) 2 2 2 lim = lim = lim        = . 2 2 x→0 x→0 − bx bx x→0 1 cos  ax b bx 2 4  b 2sin    sin    2  2   2    2 axax    2 2sin  2 sin  2 1− cos ax a   a 9) 2 2 lim = lim = lim 2     = . 2 2 x→0 x→0 x→0 x x  4 ax  2      2    sin x − tan x
sin x (cos x − ) 1 10) Ta có lim = lim 3 3 x 0 → x 0 x → x cos x 2 xx    2 2 − sin xsin  sin  2 sin x 1   1 2 2 = lim = lim −       = − . 3 x→0 x→0 x cos x  cos x x 4 x  2      2    tan x − sin x
sin x (1− cos x)  1  1 11) lim = lim = lim  = . 3   x→ sin x x
→ cos x sin x ( 2 0 0 1− cos x) x→0 cos x  (1+ cos x) 2  x + a x − ax − a  2 cos sin sin sin x − sin ax + a  12) Ta có 2 2 lim = lim 2 = limcos   = cos . a x→a − − → x − a x→a x a x a x a 2    2  x + b x − bx − b  2 − sin sin sin cos x − cos bx + b  13) Ta có 2 2 lim = lim 2 = lim−sin   = −sin . b x→b x→b x − b x − b x→b 2 x − b    2  1− 2x +1 1− 2x −1  1 2x  1 14) Ta có lim = lim = lim −  = − .   x→0 x→0 sin 2x
sin 2x (1+ 2x +1)
x→0  1+ 2x +1 sin 2x  2
a + x + a − x
a + x − a + x 2 − sin sin
cos(a + x) − cos(a − x) 15) Ta có 2 2 lim = lim x→0 x→0 x x  sin x  = lim 2 − sin a  = 2 − sin . a   x→0  x  105
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC tan x − tan c sin ( x − c)
 sin (x − c) 1  1 16) lim = lim =    = x→c x→c x − c (x −c) lim 2 cos x cos x→c c x − c cos x cos c cos . c   − (1−cos x)( 2 3 1+ cos x + cos 1 cos x x ) 17) Ta có lim = lim x→0 x→0 x sin x x sin x xx  2 2sin ( 2
1+ cos x + cos x) 2 sin
1+ cos x + cos x 1  3 2 2 = lim = lim    = . x→0 x x x→0 x 2 x 2 2x sin cos  cos  2 2  2 2  1− cos 2x 1− cos 2a − 2 2 sin x − sin a 18) Ta có 2 2 lim = lim 2 2 x→a x→a x − a
(x −a)(x + a)
cos 2a − cos 2x 2
− sin (a + x)sin(a − x) = lim = lim
x→a 2(x − a)(x + a) x→a
2(x − a)(x + a)
 sin(a + x) sin(a − x)  sin 2a = lim  = .   x→a x + a a − x  2a
( +  ) x ( −  ) x 2 − sin sin
cos x − cos  x 19) Ta có 2 2 lim = lim 2 2 x→0 x→0 x x  ( +  ) x ( −  ) x   sin sin 2 2    + 2  −  2  − = lim 2 −      = . x→0  2 ( +  ) x 2 ( −  ) x  2    2 2  x + 8 (x + 2)( 2 3 x − 2x + 4)  x + 2  20) Ta có lim = lim = lim ( 2 x − 2x + 4) ( )   =12. x→ 2
− tan ( x + 2) x→ 2 − x→ 2 tan(x + 2) − tan(x + 2)  
1− cos x cos 2x cos 3x
1− cos x + cos x(1− cos 2 )
x + cos x cos 2 ( x 1− cos 3 ) x 21) Ta có lim = lim x 0 → x 0 1− cos x → 1− cos x  3x  2 2 2sin  2sin x  2 = lim1+ cos x + cos x cos 2xx→0 x x 2 2  2sin 2sin   2 2  2 2 2  x 3x x        2  sin   sin x        2 2 2 = lim1+ 4cos x  
 + 9cos x cos 2x      =1+ 4 + 9 =14. x→0   x x 3x x    sin   sin   sin     2   2   2   
sin (a + 2x) − 2sin(a + x) + sin a
2sin (a + x)cos x − 2sin (a + x) 22) Ta có lim = lim 2 2 x 0 → x 0 x → x 106
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x 4
− sin (a + x) 2 sin
2 sin(a + x)(cos x −1) 2 = lim = lim 2 2 x→0 x→0 x x 2  x     sin  = − (    a + x) 1 2 lim 4 sin      = −sin . a x→0  4 x       2    sin ax tan bx sin ax tan bx ax  + bxa  b sin ax + tan bx a + b 23) Ta có lim = lim ax bx = lim ax bx = =1. x→0 x→0 x→0 (a + b)x (a + b)x a + b a + b
cos 3x − cos 5x cos 7x
cos 3x − cos 5x + cos 5x − cos 5x cos 7x 24) Ta có lim = lim 2 2 x 0 → x 0 x → x 7x 2
2 sin 4x sin x − 2 cos 5x sin
2 sin 4x sin x + cos 5x(1− cos 7x) 2 = lim = lim 2 2 x→0 x→0 x x 2  7x     sin  sin 4x sin x 49   49 33 2 = lim8  − 2 cos5x     = 8 − = − . x→0  4x x 4 7x  2 2      2   
cos ax − cos bx cos cx
cos ax − cos bx + cos bx − cos bx cos cx 25) Ta có lim = lim 2 2 x 0 → x 0 x → x (a + b)x (b−a)x (a + b)x (b−a)x cx 2 2sin sin
+ cosbx(1− coscx) 2sin sin − 2cosbxsin 2 2 2 2 2 = lim = lim 2 2 x→0 x→0 x x  (a + b)x (b − a) 2 xcx    2 2 sin sin 2 sin  2 2 2 2 2 2 b − a   2 2 c 2 b − a c
b − a − c = lim 2   − 2 cosbx     = − = . x→0  4 (a + b)x
(b − a) x 4 cx  2 2 2     2 2  2   
sin(a + x) − sin(a − x) 2 cos a sin x 26) Ta có lim = lim
x→0 tan (a + x) − tan (a − x) x→0 sin 2x
cos (a + x) cos (a − x)
cos a cos (a + x)cos(a − x) 3 = lim = cos a x 0 → cos x 107
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2 3 2 2x +1 − x +1
2x +1 −1+1− x +1 27) Ta có lim = lim x→0 x→0 cos x sin x 2 2x −x + 2x +1 +1 2 1+ x +1 + ( 2 x +1)2 3 3 = lim x→0 sin x 2x x − 2x +1 +1 2 1+ x +1 + ( 2 x +1)2 3 3 = lim =1. x→0 sin x x 2
sin 2x − sin x sin 4x
sin 2x (sin 2x − 2sin x cos 2x) 28) Ta có lim = lim 4 4 x 0 → x 0 x → x 3x x x x ( x − x)
4 sin 2x sin x sin sin 2 sin 2 sin cos cos 2 2 2 = lim = lim 4 4 x→0 x→0 x x  3x x  sin sin
 3 sin 2x sin x  2 2 = lim4      = 6. x→0 2 2x x 3x x    2 2     sin x +   cos x  2  29) lim = lim =1.  →−   →−  x x + + 2 x 2 x 2 2 sin x − sin 2x
sin x (1− 2cos x)
 sin x 1− 2cos x  30) lim = lim = lim  = 1 −   . x→0 x→0 x→0  x  2 x cos xx cos xx 1− 2sin    2  2 2 1+ x − cos x
1+ x −1+1− cos x 2
 1 x 1 1 cos x  + − − 31) Ta có lim = lim = lim +  2 2 x→0 x→0 x x 2 2 x→0  x x     2 x   x    2 2 2sin   sin  1+ x −1    = 1 1 1 1  +  2 = lim +     = + = 1 . x→  ( → 1+ + ) 2 lim 2 0 2 2 1 x x xx 0 2  + + 2 x  2 x 1 2 1        2   
1+ tan x − 1+ sin x
1+ tan x −1− sin x 32) lim = lim 3 x→0 x→0 3 x
x ( 1+ tan x + 1+ sin x ) x 2
sin x (1− cos x) 2sin x sin = lim 2 = lim x→0 3
x cos x ( 1+ tan x + 1+ sin x ) x→0 3
x cos x ( 1+ tan x + 1+ sin x ) 108
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2  x     sin  2 sin x 1   1 2 = lim       = .
x→0  cos x ( 1+ tan x + 1+ sin x ) x 4 x  4      2     5x 7x  2 2 2sin 2 cos 5x sin
1− cos 5x cos 7x
1− cos 5x + cos 5x (1− cos 7x)   33) lim = lim 2 2 = lim +  2 2 2 2 x 0 → x 0 sin 11x → sin 11x x→0 sin 11x sin 11x     2 2  5x 7x      2 2  sin sin  25    11x  49    11 2 2 x  = 25 49 37 lim    + cos 5x         = + = . x→0  242 5x  sin11x  242 7x  sin11x       242 242 121    2   2    x + 3 − 2 x + 3 − 4  1 x −1  1 34) lim = lim = lim   =   . x 1 → tan ( x − ) x 1 1 → tan ( x − ) 1 ( x + 3 + 2) x 1 → x + 3 + 2 tan  (x − ) 1 4  2   x   − x     − x   2 2 2 cos 2sin    sin      1+ cos x  2  1   2  1  35) 2 lim = = lim = lim   = . 2 x  → ( → →  −   −  x − ) lim 2 x   → (x − )2 x  (  ) x  2 x x  2      2      sin ( x − ) 1 sin ( x − ) 1  sin (x − ) 1 1  1 36) lim = lim = lim .  = − . 2 x 1 → x 1 x − 4x + 3 → ( x − ) 1 ( x − 3) x 1 → x −1 x − 3 2   2 2 x +1 − cos 2x
x +1 −1+1− cos 2x 37) lim = lim 2 2 x→0 x→0 x x   2 2 2
x 1 1 1 cos2x  + − −  x +1−1 2sin x  = lim +  = lim + 2 2     x→ x x x →     ( +1+ ) 2 0 0 2 2 1 x x x   2  1 sin x    1 5 = lim + 2   = + 2 =   . x→0 2  + +  x  2 2 x 1 1 
1− cos x + cos x − (1− cos2 1 cos cos 2 x x x ) 38) lim = lim 2 2 x→0 x→0 x xx   −  1− cos x x ( x ) 2 2sin cos 1 cos 2 
cos x (1− cos 2x)    2 = lim + = lim +  2 2 2 x→0   x→0 2 x x x
x (1+ cos 2x )      109
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2   x    x   2 sin   sin  1   1   sin x   1 3 2 2 = lim   = lim       = +1 = x→0 2 2 
x (1+ cos 2x ) x→0  2
1+ cos 2x x   2 2              Bài 9.
Tính các giới hạn sau: cos 3x − cos x 1− 2sin x 1) lim ĐS: 1 2) lim ĐS: 1 x 0
→ cos5x − cos x 3 2  − x→ 4 cos x 3 2 6
1+ sin 2x + cos 2x
sin 7x − sin 5x 3) lim ĐS: 24) lim ĐS: 2  x 0 → x→ cos x sin x 2 2 − 2 cos x 3 1− cos x 5) lim ĐS: 2 lim ĐS: 1  6) →    → x x 0 sin x 6 4 sin x −    4  3 sin x − cos x     7) lim ĐS: 2 − 8) lim tan 2 . x tan − x    ĐS: 1    x→ sin 3x 3 x→   4  3 4
cos 3x + 2 cos 2x + 2 3 tan x −1 9) lim ĐS: 2 3 10) lim ĐS: 1 −  2  − x→ sin 3x 3 x→ 2sin x 1 12 3 3 Lời giải sin x cos 3x − cos x 2 − sin 2xsin x sin x 1 1) lim = lim = lim = lim x = . x→0 x→0 x→0 x→0 cos 5x − cos x 2 − sin 3xsin 2x sin 3x sin 3x 3 3 3x 1− 2sin x 1− 2sin x 1 1 2) lim = lim = lim = . 2 2    − − + x→ 4 cos x 3 x→ 1 4sin x x→ 1 2sin x 2 6 6 6 2
1+ sin 2x + cos 2x 2 cos x + sin 2x 3) lim = lim
= lim (2cos x + 2sin x) = 2 .    x→ cos x x→ cos x x→ 2 2 2
sin 7x − sin 5x 2cos 6x sin x 4) lim = lim = lim2cos6x = 2 . x 0 → x 0 → x 0 sin x sin x →  2     2 − cos x 2 cos − cos x   2 − 2 cos x 2    4  5) lim = lim = lim    →    →    →    x x x 4 sin x − 4 sin x − 4 sin x −        4   4   4    x    x    x  4 − sin + sin −     2sin +    8 2   8 2  =  8 2  lim = lim = 2   →       →    x x x x x 4 2 sin − cos −     4 cos −    2 8   2 8   2 8  110
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 1− cos x (1−cos x) 2 3 cos x 6) lim = lim 2 x→0 x→0 tan x   2 3 3 2
sin x  1+ cos x + cos x    2 cos x 1 = lim = x→0 (   + x) 3 3 2 6 1 cos
1+ cos x + cos x        2sin 3 x −      3         2sin x − sin 3 x −     
sin x − 3 cos x  3    3  2 7) lim = lim = = = − .      − +     → →   → − − − →     x x x ( x ) lim lim sin 3 sin 3 x x x 3 sin 3    3 3 3 3   3 3  sin 3 x −      3  3 −     3 x −    3     
 2 tan x 1− tan x  2 tan x 8) lim tan 2x  tan − x = lim  = lim =1     . 2         − + x→ 4 x→
1 tan x 1 tan x x→ (1+ tan x)2 4 4 4 3 2
cos 3x + 2 cos 2x + 2
4 cos x − 3cos x + 4 cos x 9) lim = lim 3   − x→ sin 3x x→ 3sin x 4sin x 3 3    ( cos x − cos 
(2cos x + 3)cos x 2 cos x − )
1 (2cos x + 3)cos x =  3  lim = lim   x→ 2sin x + 3
2sin x − 3 sin x x→ 3 3 ( )( ) 3  x   −sin + 
(2cos x + 3)cos x  2 6  2 3 = lim =  →    x x 3 3 cos + 
(2sin x + 3)sin x  2 6  tan x −1 (tan x − ) 2 3 1 cos x 10) lim = lim 2   −   x→ 2sin x 1 x→
(1−tan x).( tanx)2 2 3 3 + + 4 4 tan x 1   2 −cos x = 1 lim = − .    x→ (1+ tan x) 12 ( tan x )2 3 3 + + 4 tan x 1   Bài 10.
Tính các giới hạn sau: cos 4x −1
1+ sin 2x − cos 2x 1) lim ĐS: 0 2) lim ĐS: 1 − x 0 → sin 4x x 0
→ 1− sin 2x − cos 2x sin 2x 1− cos x 3) lim ĐS: 1 − 4) lim ĐS: 0 x 0
→ 1− sin 2x − cos 2x x 0 → sin x
sin 5x − sin 3x  1 1  5) lim ĐS: 2 6) lim −   ĐS: 0 x 0 → sin x x→0  sin x tan x  111
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC    sin − x   2 sin x −1 2  6  2 3 7) lim ĐS: − 8) lim ĐS: 2  −  − x→ 2 cos x 1 4 x→ 1 2sin x 3 4 6    sin − x    4   2  9) lim ĐS: 2 lim − cot x   ĐS: 0  − 10) x→0 x→ 1 2 sin x  sin 2x  4 112
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
BÀI 3. HÀM SỐ LIÊN TỤC
A. TÓM TẮT LÝ THUYẾT
1. Hàm số liên tục tại 1 điểm
– Giả sử hàm số f ( x) xác định trên khoảng (a;b) và x  ;
a b . Hàm số y = f ( x) gọi là liên 0 ( )
tục tại điểm x nếu lim f ( x) = f ( x . 0 ) 0 x→x0
– Hàm số không liên tục tại điểm x gọi là gián đoạn tại x . 0 0
2. Hàm số liên tục trên một khoảng, đoạn
– Giả sử hàm số f ( x) liên tục trên khoảng (a;b) . Ta nói rằng hàm số y = f ( x) liên tục trên
khoảng (a;b) nếu nó liên tục tại mọi điểm của khoảng đó.
– Hàm số y = f ( x) gọi là liên tục trên đoạn a;b nếu nó liên tục trên khoảng (a;b) và
lim f ( x) = f (a), lim f ( x) = f (b) . + − x→a x b → Nhận xét:
– Nếu hai hàm f ( x) và g ( x) liên tục tại điểm x thì các hàm số f ( x)  g ( x) , f ( x).g ( x) , 0 .
c f ( x) (với c là hằng số) đều liên tục tại điểm x . 0
– Hàm số đa thức liên tục trên
. Hàm số phân thức và lượng giác liên tục trên từng khoảng xác định của chúng.
3. Tính chất của hàm số liên tục
– Định lý về giá trị trung gian: Giả sử hàm số f liên tục trên đoạn a;b. Nếu f (a)  f (b) thì với
mỗi số thực M nằm giữa f (a), f (b) tồn tại ít nhất một điểm c  (a;b) thoả mãn f (c) = M .
– Ý nghĩa hình học: Nếu hàm số f liên tục trên đoạn a;bvà M là một số thực nằm giữa f (a), f (b)
thì đường thẳng y = M cắt đồ thị hàm số y = f ( x) tại ít nhất một điểm có hoành độ c (a;b) .
– Hệ quả: Nếu hàm số f liên tục trên đoạn a;b và f (a). f (b)  0 thì tồn tại ít nhất một điểm
c  (a;b) sao cho f (c) = 0 . Ta thường vận dụng theo hai hướng sai:
+ Vận dụng chứng minh phương trình có nghiệm: “Nếu hàm số y = f ( x) liên tục trên đoạn a;b và
f (a). f (b)  0 thì phương trình f ( x) = 0 có ít nhất một nghiệm trong khoảng (a;b) ”.
+ Vận dụng trong tương giao đồ thị: “Nếu hàm số y = f ( x) liên tục trên đoạn a;b và
f (a). f (b)  0 thì đồ thị của hàm số y = f ( x) cắt trục hoành ít nhất tại một điểm có hoành độ c  (a;b) ”. 113
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
B. DẠNG TOÁN VÀ BÀI TẬP
_DẠNG 1. XÉT TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM Phương pháp giải:
Hàm số liên tục tại điểm x = x khi f ( x = lim f x hoặc f ( x = lim f x = lim f x 0 ) ( ) ( ) 0 ) ( ) 0 x→x − + → → 0 x 0 x x 0 x VÍ DỤ 2  x − 3x + 2  khi x  2
Ví dụ 1. Xét tính liên tục của hàm số f (x) =  x − 2 tại điểm x = 2 .  0 4x − 7 khi x = 2
ĐS: Liên tục Lời giải
Ta có f (x ) = f (2) = 4.2 − 7 = 1 0 2 x − 3x + 2
(x − 2)(x −1) lim f (x) = lim = lim =1 x→2 x→2 x→2 x − 2 x − 2
Suy ra f (2) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 2. 0 x→2  x + 3 − 2  khi x  1  −
Ví dụ 2. Xét tính liên tục của hàm số x 1 f (x) =  tại điểm x = 1. 0 1  khi x = 1 3
ĐS: Không liên tục Lời giải 1
Ta có f (x ) = f (1) = . 0 3 x + 3 − 2 x −1 1 1 lim f (x) = lim = lim = lim = x 1 → x 1 → x 1 → x 1 x −1
(x −1)( x + 3 + 2) → x + 3 + 2 4
Suy ra f (1)  lim f (x) nên hàm số f (x) không liên tục tại điểm x = 1 (hay gián đoạn tại 0 x 1 → điểm x = 1 ). 0 2
x −3x + 3 khi x  2 
Ví dụ 3. Xét tính liên tục của hàm số f (x) = 1  − 2x −3 tại điểm x = 2 0  khi x  2  2 − x ĐS: Liên tục 114
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Lời giải Ta có 2
f (x ) = f (2) = 2 − 3.2 + 3 = 1 0 2
lim f (x) = lim (x − 3x + 3) = 1 − − x→2 x→2 1− 2x − 3 1− 2x + 3 2 lim f (x) = lim = lim = lim =1 + + + + x→2 x→2 − x→2 x→2 2 x
(2 − x)(1+ 2x − 3) 1+ 2x − 3
Suy ra f (2) = lim f (x) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 2 . − + 0 x→2 x→2 2  x −9  khi x  3
Ví dụ 4. Xét tính liên tục của hàm số f (x) =  x +1 − 2 tại điểm x = 3 . 0 2x+12 khi x  3
ĐS: Không liên tục Lời giải
Ta có f (x ) = f (3) = 18 0 2 x − 9
(x − 3)(x + 3)( x +1 + 2)
lim f (x) = lim (2x +12) = 18 lim f (x) = lim = lim − − + + + x→3 x→3 x→3 x→3 x→3 x +1 − 2 x − 3
= lim(x +3)( x +1 + 2) = 24 + x 3 →
Suy ra f (3) = lim f (x)  lim f (x) nên hàm số f (x) không liên tục tại điểm x = 3 . − + 0 x→3 x→3
x +1− x + 3  khi x  1 x −1  3
Ví dụ 5. Xét tính liên tục của hàm số f (x) = 
khi x = 1 tại điểm x = 1. 4  0 3 2
3x − 6x −3x + 6 khi x 1  2
 3x −14x +11 ĐS: Liên tục Lời giải 3
Ta có f (x ) = f (1) = 0 4 3 2 2 2
3x − 6x − 3x + 6
(x −1)(3x − 3x − 6) 3x − 3x − 6 3 lim f (x) = lim = lim = lim = − − 2 − − x 1 → x 1 → − + x 1 → − − x 1 3x 14x 11 (x 1)(3x 11) → 3x −11 4 2 x +1− x + 3
(x −1) − (x + 3) x + 2 3 lim f (x) = lim = lim = lim = + + + + x 1 → x 1 → − x 1 → x 1 x 1
(x −1)(x +1+ x + 3) → x +1+ x + 3 4
Suy ra f (1) = lim f (x) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 1. − + 0 x 1 → x 1 → 115
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2cos5 .
x cos 3x − cos 8x −1  khi x  0
Ví dụ 6. Xét tính liên tục của hàm số 4 2 f (x) =  x + x tại điểm x = 0 .  0 2 khi x = 0
ĐS: Không liên tục Lời giải
Ta có f (x ) = f (0) = 2 0 2cos 5 .
x cos 3x − cos8x −1
cos8x + cos 2x − cos8x −1 lim f (x) = lim = lim 4 2 4 2 x 0 → x 0 → x 0 x + x → x + x 2 2 cos 2x −1 2 − sin x  sinx  2 −  = lim = lim = lim  .    = 2 − 4 2 2 2 2 x→0 x→0 x→0 x + x x (x +1)
 x x +1  
Suy ra f (0)  lim f (x) nên hàm số f (x) không liên tục tại điểm x = 0 (hay gián đoạn tại 0 x→0 điểm x = 0 ). 0 3 2
x + 2x − 5x − 6 khi x  2  3  x − 4x
Ví dụ 7. Tìm a để hàm số f (x) = 
liên tục tại điểm x = 2. 0 1  (a + x) khi x = 2 8 ĐS: a =13 Lời giải 1
Ta có f (2) = (a + 2) 8 3 2 2 2
x + 2x − 5x − 6
(x − 2)(x + 4x + 3) x + 4x + 3 15 lim f (x) = lim = lim = lim = 3 x→2 x→2 x→2 x→2 x − 4x
x(x − 2)(x + 2) x(x + 2) 8 1 15
Hàm số liên tục tại điểm x = 2  f (2) = lim f (x)  (a+ 2) =  a =13. 0 x 2 → 8 8 2  2(x − 4) khi x  2 
Ví dụ 8. Tìm m để hàm số f (x) =  x + 2 − x
liên tục tại điểm x = 2 .  0
m + 2 + m −10x khi x  2 ĐS: m = 2 Lời giải
Ta có f (2) = m + 2 + m − 20 2 3(x − 4)
3(x − 2)(x + 2)( x + 2 + x) lim = lim = lim + + + 2 x→2 x→2 x→2 x + 2 − x x + 2 − x
3(x − 2)(x + 2)( x + 2 + x)
3(x + 2)( x + 2 + x) = lim = lim = 1 − 6 + + x→2 − + − x→2 (x 1)(x 2) −(x +1)
lim = lim( m + 2 + m −10 )
x = m + 2 + m − 20 − − x 2 → x 2 → 116
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
Hàm số f (x) liên tục tại điểm
x = 2  lim f ( ) x = lim f ( )
x = f (2)  m + 2 + m − 20 = 1 − 6 0 + − x 2 → x 2 → m  4 m  4
m + 2 = 4 − m      m = 2 2
m − 9m +14 = 0
m = 2  m = 7
BÀI TẬP ÁP DỤNG Bài 1.
Xét tính liên tục của các hàm số sau tại các điểm được chỉ ra: 2  x −3 −1  khi x  2 1. f (x) =  x − 2 tại điểm x = 2 . Đs: Liên tục  0 2x − 2 khi x = 2 2 3
2 − 7x + 5x − xkhi x  2 2. 2 f (x) =  x − 3x + 2
tại điểm x = 2 . Đs: Liên tục  0 1  khi x = 2 2  x + 3x + 2  khi x  1 −
3. f (x) =  −x −1 tại điểm x = 1 − . Đs: Liên tục 0  2 x + 2x khi x = 1 − Bài 2.
Xét tính liên tục của các hàm số sau tại các điểm được chỉ ra: 2
3x − 2x −1  khi x  1 1. f (x) =  x −1 tại điểm x = 1. Đs: Liên tục  0 2x + 2 khi x  1 2
x + 2x − 3 khi x 1  2  x + x − 2
2. y = f (x) =  tại điểm x = 1.
Đs: Không liên tục 0  x +1 + 7 khi x  1  3 3
x − 3x − 4  khi x  4
3. f (x) =  x + 5 − 3 tại điểm x = 4 . Đs: Liên tục 0  4 − x + 46 khi x  4 Bài 3.
Tìm các giá trị thực của tham số m để hàm các hàm số sau liên tục tại các điểm được chỉ ra: 3 2
x − 5x + 7x − 3  khi x  1 1. 2 f (x) =  x −1 tại điểm x = 1. Đs: 1 m = −  0 2 2m +1 khi x = 1 117
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
 1+ x − 1− xkhi x  0  2. ( ) x f x = 
liên tục tại điểm x = 0 . Đs: 1 m = 0 4 − x  5 5 − m + khi x = 0  x + 2 3  6 + x − 2  khi x  2
3. f ( x) =  x − 2
liên tục tại điểm x = 2 . Đs: 47 m = 0  12
2x − m khi x = 2 3  12x − 4 − 2  khi x  1
4. f ( x) =  x −1
liên tục tại điểm x = 1. Đs: m = 1 −  0 2 2
m x + 8 + 2mx khi x =1 Bài 4.
Tìm các giá trị thực của tham số m để hàm các hàm số sau liên tục tại các điểm được chỉ ra: 3  x −8  khi x  2 29 1. 2
f (x) = 2x − x − 6 tại điểm x = 2 . Đs: m = −  0 7 mx +10 khi x  2  2x −1 −1  khi x  1 3 2. f ( x) 2
=  x + 2x −3
liên tục tại điểm x = 1. Đs: m = − 0  4
x + m khi x 1 2
 2x − 7x + 6  khi x  2  3 3. m để − f ( x) x 2 = 
liên tục tại điểm x = 2 . Đs: m = − 0  1− x 4 m + khi x  2  x + 2 2
3x −3+ x −1 5x + 4  khi x  1 2  4. − + f ( x) x 2x 1 = 
liên tục tại điểm x = 1.
Đs: m = 1 hoặc m = 2 0  1 2 m +
x − 3m khi x  1  3  7 −3x − 4  khi x  3 −  − − 5. ( ) 2 1 x f x = 
liên tục tại điểm x = 3 − .
Đs: m = 0 hoặc m = 6 0  3 2 m − 2mx − khi x  3 −  2  3 − x khi x  3  2 5 − x +16
6. f ( x) = 
liên tục tại điểm x = 3 . Đs: m = 5 − hoặc m =1  0
m (x + m + )1 khi x  3  3  ( 2 3 x − 4)  khi x  2
7. f ( x) =  x + 2 − x
liên tục tại điểm x = 2 . Đs: m = 2 0 
m + 2 + m −10x khi x  2 118
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC LỜI GIẢI 2  x −3 −1  khi x  2 Bài 1.
1. Xét tính liên tục của hàm số f (x) =  x − 2 tại điểm x = 2 .  0 2x − 2 khi x = 2
Ta có f (x ) = f (2) = 2 0 2 2 x − 3 −1 x − 4 x + 2 lim f (x) = lim = lim = lim = 2 x→2 x→2 x→2 2 x→2 2 x − 2
(x − 2)( x − 3 +1) x − 3 +1
Suy ra f (2) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 2. 0 x→2 2 3
2 − 7x + 5x − xkhi x  2
2. Xét tinh liên tục của hàm số 2 f (x) =  x − 3x + 2 tại điểm x = 2 .  0 1  khi x = 2
Ta có f (x ) = f (2) = 1 0 2 3 2 2
2 − 7x + 5x − x
(x − 2)(−x + 3x −1) −x + 3x −1 lim f (x) = lim = lim = lim =1 2 x→2 x→2 x→2 x→2 x − 3x + 2
(x − 2)(x −1) x −1
Suy ra f (2) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 2 . 0 x→2 2  x + 3x + 2  khi x  1 −
3. Xét tinh liên tục của hàm số f (x) =  −x −1 tại điểm x = 1 − . 0  2 x + 2x khi x = 1 −
Ta có f (x ) = f ( 1 − ) = 1 − 0 2 x + 3x + 2 (x +1)(x + 2) x + 2 lim f (x) = lim = lim = lim = 1 − x→ 1 − x→ 1 − x→ 1 − x→ 1 −x −1 −(x +1) − 1 − Suy ra f ( 1
− ) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 1 − . 0 x 1 →− 3
x − 3x − 4  khi x  4 Bài 2.
1. Xét tính liên tục của hàm số f (x) =  x + 5 − 3 tại điểm x = 4 . 0  4 − x + 46 khi x  4
Ta có f (x ) = f (4) = 30 0
lim f (x) = lim ( 4 − x + 46) = 30 − − x→4 x→4 2 x − 3x − 4
(x − 4)(x +1)( x + 5 + 3) lim f (x) = lim = lim
= lim(x +1)( x + 5 + 3) = 30 + + + + x→4 x→4 x→4 + − − x→4 x 5 3 x 4
Suy ra f (4) = lim f (x) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 4 . − + 0 x→4 x→4 2
3x − 2x −1  khi x  1
2. Xét tính liên tục của hàm số f (x) =  x −1 tại điểm x = 1.  0 2x + 2 khi x  1 119
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
Ta có f (x ) = f (1) = 4 0 2 3x − 2x −1 (x −1)(3x +1)
lim f (x) = lim(2x + 2) = 4 lim f (x) = lim = lim = lim(3x +1) = 4 + + − − − − x 1 → x 1 → x 1 → x 1 → − x 1 → − x 1 x 1 x 1 →
Suy ra f (1) = lim f (x) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 1. + − 0 x 1 → x 1 → 2
x + 2x − 3 khi x 1  2  x + x − 2
3. Xét tính liên tục của hàm số y = f (x) =  tại điểm x = 1. 0  x +1 + 7 khi x  1  3 2 + 7
Ta có f (x ) = f (1) = 0 3 x +1 + 7 2 + 7 lim f (x) = lim = − − x 1 → x 1 → 3 3 2 x + 2x − 3 (x −1)(x + 3) x + 3 4 lim f (x) = lim = lim = lim = + + 2 + + x 1 → x 1 → + − x 1 → − + x 1 x x 2 (x 1)(x 2) → x + 2 3
Suy ra f (1) = lim f (x)  lim f (x) nên hàm số f (x) x = 1. − +
không liên tục tại điểm 0 x 1 → x 1 → 3
x − 3x − 4  khi x  4
4. Xét tính liên tục của hàm số f (x) =  x + 5 − 3 tại điểm x = 4 . 0  4 − x + 46 khi x  4
Ta có f (x ) = f (4) = 30 0
lim f (x) = lim ( 4 − x + 46) = 30 − − x→4 x→4 2 x − 3x − 4
(x − 4)(x +1)( x + 5 + 3) lim f (x) = lim = lim
= lim(x +1)( x + 5 + 3) = 30 + + + + x→4 x→4 x→4 + − − x→4 x 5 3 x 4
Suy ra f (4) = lim f (x) = lim f (x) nên hàm số f (x) liên tục tại điểm x = 4 . − + 0 x→4 x→4 3 2
x − 5x + 7x − 3  khi x  1 Bài 3.
1. Tìm m để hàm số 2 f (x) =  x −1
tại điểm x = 1.  0 2m +1 khi x = 1
Ta có f (x ) = f (1) = 2m +1 0 3 2 2
x − 5x + 7x − 3 (x −1) (x− 3) (x −1)(x + 3) lim f (x) = lim = lim = lim = 0 2 x 1 → x 1 → x 1 → x 1 x −1 (x −1)(x+1) → x +1 1
Hàm số f (x) liên tục tại điểm x = 1  lim f (x) = f (1)  2m +1 = 0  m = − . 0 x 1 → 2 120
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
 1+ x − 1− x  khi x  0 
2. Tìm m để hàm số ( ) x f x = 
liên tục tại điểm x = 0 . 0 4 − x  5 − m + khi x = 0  x + 2 Ta có: f (0) = 5 − m + 2 + − − f ( x) 1 x 1 x 2x 2 lim = lim = lim = lim =1 x→0 x→0 x→0 x
x ( 1+ x + 1− x ) x→0 1+ x + 1− x 1
Hàm số liên tục tại điểm x = 0 khi và chỉ khi lim f ( x) = f (0)  5
− m + 2 =1 m = 0 x 0 → 5 1 Vậy m = . 5 3  6 + x − 2  khi x  2
3. Tìm m để hàm số f ( x) =  x − 2
liên tục tại điểm x = 2 . 0
2x−m khi x = 2
Ta có f (2) = 4 − m + − − f ( x) 3 6 x 2 x 2 1 1 lim = lim = lim = lim = x→2 x→2 x→2 x − 2 ( x→
x − 2)( 3 (6+ x)2 3 + 2 6 + x + 4) 2 3 ( + x)2 3 12 6 + 2 6 + x + 4 1 47
Hàm số liên tục tại điểm x = 2 khi và chỉ khi lim f ( x) = f (2)  4 − m =  m = 0 x→2 12 12 47 Vậy m = . 12 3  12x − 4 − 2  khi x  1
4. Tìm m để f ( x) =  x −1
liên tục tại điểm x = 1.  0 2 2
m x + 8 + 2mx khi x =1 Ta có f ( ) 2 1 = m + 8 + 2m x − − x − lim f ( x) 3 12 4 2 12( ) 1 = lim = lim x 1 → x 1 → x 1 x −1 → (x − ) 1 ( 3 (12x −4)2 3 + 2 12x − 4 + 4) 12 = lim =1 x 1 → 3 (12x − 4)2 3 + 2 12x − 4 + 4
Hàm số liên tục tại điểm x = 1 khi và chỉ khi lim f ( x) = f ( ) 2
1  m + 8 + 2m = 1 0 x 1 → 121
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  1 m    1 2 1  − 2m  0  m      
 m = −  m = − m + 8 =  (1−2m) 2 1 1 2 2 2    3
− m + 4m + 7 = 0 7 m =  3 Vậy m = 1 − . 3  x −8  khi x  2 Bài 4.
1. Tìm m để hàm số 2
f (x) = 2x − x − 6 tại điểm x = 2 .  0 mx +10 khi x  2
Ta có f (x ) = f (2) = 2m +10 0
lim f (x) = lim (m x +10) = 2m +10 − − x→2 x→2 3 2 2 x − 8
(x − 2)(x + 2x + 4) x + 2x + 4 12 lim f (x) = lim = lim = lim = + + 2 + + x→2 x→2 − − x→2 − + x→2 2x x 6 (x 2)(2 x 3) 2x + 3 7
Hàm số f (x) liên tục tại điểm 12 29
x = 2  lim f (x) = lim f (x) = f (2)  2m +10 =  m = − 0 + − x→2 x→2 7 7  2x −1 −1  khi x  1
2. Tìm m để f ( x) 2
=  x + 2x −3
liên tục tại điểm x = 1. 0
x+m khi x 1 Ta có f ( ) 1 = 1+ m − − − f ( x) 2x 1 1 2 ( x ) 1 2 1 lim = lim = lim = lim = + + 2 + + x 1 → x 1 → + − x 1 x 2x 3 → (x − )
1 ( x + 3)( 2x −1 + ) x 1 1 →
(x +3)( 2x−1+ )1 4
lim f ( x) = lim ( x + m) =1+ m − − x 1 → x 1 →
Hàm số liên tục tại điểm x = 1 khi và chỉ khi 0 f ( x) =
f ( x) = f ( ) 1 3 lim lim 1  1+ m =  m = − + − x 1 → x 1 → 4 4 3 Vậy m = − . 4 2
 2x − 7x + 6  khi x  2  −
3. Tìm m để f ( x) x 2 = 
liên tục tại điểm x = 2 . 0  1− x m + khi x  2  x + 2 Ta có f ( ) 1 2 = m − 4  −  f ( x) 1 x 1 lim = lim m + = m −   + + x→2 x→2  x + 2  4 122
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 x − x + x − x − − x − x − lim f ( x) 2 7 6 ( 2)(2 3) ( 2)(2 3) = lim = lim = lim − − − − x→2 x→2 − x→2 − x→2 x 2 x 2 x − 2 = lim ( 2 − x + 3) = 1 − − x→2
Hàm số liên tục tại điểm x = 3 − khi và chỉ khi 0 f ( x) =
f ( x) = f ( ) 1 3 lim lim 2  m − = 1 −  m = − + − x→2 x→2 4 4 3 Vậy m = − . 4 2
3x −3+ x −1 5x + 4  khi x  1 2 
4. Tìm m để − + f ( x) x 2x 1 = 
liên tục tại điểm x = 1. 0  1 2 m +
x − 3m khi x  1  3 1 Ta có f ( ) 2 1 = m + −3m 3   lim f ( x) 1 1 2 2
= lim m + x − 3m = m + − 3m   + + x 1 → x 1 →  3  3 − + − + (x − )1 − + x x x ( 2 2 3 5x 4 3 3 1 5 4 ) lim f ( x) = lim = lim − − 2 − x 1 → x 1 → − + x 1 x 2x 1 → (x − )2 1 (x − ) 1 ( 2 3 − 5x + 4 ) 2 3 − 5x + 4 = lim = − − x→ (x − ) lim 2 1 x 1 1 → x −1 5 − (x − ) 1 ( x + ) 1 5 − (x + ) 1 5 = lim = lim = − − − x 1 → (x − ) 1 ( 2 3 + 5x + 4 ) → 2 x 1 + + 3 3 5x 4
Hàm số liên tục tại điểm x = 1 khi và chỉ khi 0 m =
lim f ( x) = lim f ( x) = f ( ) 1 5 1 2 2 1  m +
− 3m = −  m − 3m + 2 = 0   + − x 1 → x 1 → 3 3 m = 2
Vậy m = 1 hoặc m = 2 .  7 −3x − 4  khi x  3 −  − −
5. Tìm m để ( ) 2 1 x f x = 
liên tục tại điểm x = 3 − . 0  3 2 m − 2mx − khi x  3 −  2 3 Ta có f ( 3 − ) 2 = m + 6m − 2   lim f ( x) 3 3 2 2
= lim m − 2mx − = m + 6m −   − − x→ 3 − x→ 3 −  2  2 123
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 − − −
(x +3)(2+ 1− x) 3 − (2+ 1− 7 3 4 x x ) f ( x) 3 lim = lim = lim = lim = − + + + + x→ 3 − x→ 3 − x→ 3 2 − 1− x −
(x +3)( 7−3x +4) x→ 3− 7−3x +4 2
Hàm số liên tục tại điểm x = 3 − khi và chỉ khi 0 m =
lim f ( x) = lim f ( x) = f ( 3 − ) 3 3 0 2 2
m + 6m − = −  m + 6m = 0   + − x→ 3 − x→ 3 − 2 2 m = 6 −
Vậy m = 0 hoặc m = 6 − .  3 − x khi x  3  2 5 − x +16
6. Tìm m để f ( x) = 
liên tục tại điểm x = 3 .  0
m (x + m + )1 khi x  3  3 m Ta có f (3) = (4+ m). 3 m m lim f ( x) = lim (x +m+ ) 1 = (4+ m) . − − x 3 → x 3 → 3 3 (3− x) + + − x ( 2 5 x 16 3 ) + + f ( x) 2 5 x 16 5 lim = lim = lim = lim = . + + → → 2 + + x 3 x 3 x→3 − x + (3− x)(3+ x) x→3 3 + x 3 5 16
Hàm số liên tục tại điểm x = 3 khi và chỉ khi 0 m 5 m =1
lim f ( x) = lim f ( x) = f (3)  (4+ m) 2
=  m + 4m − 5 = 0   + − x 3 → x 3 → 3 3 m = 5 − Vậy m = 5 − hoặc m =1.  ( 2 3 x − 4)  khi x  2
7. Tìm m để f ( x) =  x + 2 − x
liên tục tại điểm x = 2 . 0 
m + 2 + m −10x khi x  2
Ta có f (2) = m + 2 + m − 20 .
lim f ( x) = lim + + − = + + − . − − ( m 2 m 10x) m 2 m 20 x→2 x→2 3( 2 x − 4)
3( x − 2)( x + 2)( x + 2 + x) lim f ( x) = lim = lim + + + x→2 x→2 x→2 x + 2 − x
−(x − 2)(x + ) 1
3( x + 2)( x + 2 + x) = lim = 1 − 6 . + x→2 −(x + ) 1
Hàm số liên tục tại điểm x = 2 khi và chỉ khi 0  −   f ( x) =
f ( x) = f ( ) 4 m 0 lim lim
2  m + 2 = 4 − m   − + x→ x→ m + 2 =  (4−m)2 2 2 124
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC m  4 m  4   
 m = 2  m = 2. 2
m − 9m +14 = 0  m = 7 Vậy m = 2 .
BÀI TẬP RÈN LUYỆN 3  x + 27 khi x  3 −  2 2x + 5x −3 Bài 1.
Xét tính liên tục của hàm số f ( x) =  tại điểm x = 3
− . ĐS: K liên tục. 0 4 + xkhi x = 3 −  5 2  2 − x + 8  khi x  2 − Bài 2.
Xét tính liên tục của hàm số f ( x) =  1− 4x − 3 tại điểm x = 2
− . ĐS: Liên tục. 0 5  x − 2 khi x  2 − 2  x − 9  khi x  3 Bài 3.
Xét tính liên tục của hàm số f ( x) =  x +1 − 2
tại điểm x = 3 . ĐS: Không liên tục. 0
2x+12 khi x  3 2  x − 4 khi x  2
x − 7x −10 Bài 4.
Xét tính liên tục của hàm số f ( x) = 
tại điểm x = 2 . ĐS: Liên tục.  0 8x − hi x = 2  3 (  x − )2 5 + 3 khi x  5  Bài 5.
Xét tính liên tục của hàm số f ( x) =  x − 5
tại điểm x = 5 . ĐS: Liên tục.  0 khi x  5  2x −1 − 3 2  x + x −12 khi x  3  x −3 Bài 6.
Xét tính liên tục của hàm số f ( x) = 
tại điểm x = 3 . ĐS: Liên tục. 2  0 x + 5 khi x = 3  x −1  4x + 5 −5  khi x  5  − Bài 7.
Xét tính liên tục của hàm số f ( x) x 5 = 
tại điểm x = 5 . ĐS: Liên tục. 0 2xkhi x  5 25
 3x +1 − 5− xkhi x  1 Bài 8.
Xét tính liên tục của hàm số f ( x) 3 2 =  2
− x + 3x − x
tại điểm x = 1. ĐS: Liên tục. 0  2 − x +1 khi x  1
x 2 − x − 4 khi x  2   x − 5x + 6 Bài 9.
Xét tính liên tục của hàm số f ( x) 2 = 
khi x  2 tại điểm x = 2 . ĐS: Liên tục. 0 x + 2 − 2   4 − khi x = 2  125
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2  x − 3x + 2 khi x  1 
Bài 10. Xét tính liên tục của hàm số f ( x) =  x + 8 − 3
tại điểm x = 1. ĐS: Liên tục.  0
x 1− x − 6 khi x  1 3 2x + x − 3 khi x  1  3  x −1
Bài 11. Tìm m để hàm số f ( x) = 
liên tục tại điểm x = 1. ĐS: m = 2  . 0 ( 2 m − ) 2 1 x + 4 khi x  1  x + 2 4 2
x − 6x − 27  khi x  3 −
Bài 12. Tìm m để hàm số f ( x) 3 2
=  x + 3x + x + 3
liên tục tại điểm x = 3 − . ĐS: 10 m = .  0 3 mx + 3 khi x = −3 3  x − 27  khi x  3
Bài 13. Tìm m để hàm số f ( x) 2
= 2x − 4x − 6
liên tục tại điểm x = 3 . ĐS: 37 m = − .  0 24 mx + 8 khi x  3  x − 2  khi x  2
Bài 14. Tìm m để hàm số f ( x) =  x + 2 − 2
liên tục tại điểm x = 2 . ĐS: m = 2 . 0 x+2m khi x = 2 2  x − 25 khi x  5 
Bài 15. Tìm m để hàm số f ( x) 2
=  x − 4x −5
liên tục tại điểm x = 5 . ĐS: 15 m = . 0 (  3 x − 5  )2 2 + m khi x  5
_DẠNG 2. XÉT TÍNH LIÊN TỤC CỦA HÀM SỐ TRÊN TXĐ Phương pháp giải:
Hàm số liên tục tại điểm x = x khi f ( x = lim f x hoặc f ( x = lim f x = lim f x 0 ) ( ) ( ) 0 ) ( ) 0 x→x − + → → 0 x 0 x x 0 x VÍ DỤ 3
2x + x + 3 khi x  1 −  3  x +1
Ví dụ 1. Xét tính liên tục của hàm số f ( x) =  trên . 7  khi x = 1 − 3 ĐS: Liên tục trên . Lời giải
+ Tập xác định của hàm số là D = . 126
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2x + x + 3 + Xét x  1 − thì f (x) 3 =
là hàm phân thức hữu tỉ nên liên tục trên các khoảng 3 x +1 (−;− ) 1 và ( 1;
− +  ) mà nó xác định.
+ Xét tính liên tục của hàm số f ( x) tại x = 1 − x + x + (x + ) 1 ( 2 3 2x − 2x + 3 2 3 ) 2 2x − 2x + 3 7
Ta có lim f ( x) = lim = lim = lim = . 3 x→− x→− x +1 x→− (x + ) 1 ( 2 1 1 1 x − x + ) 2 x→ 1 1 − x − x +1 3 f (− ) 7 1 = . 3
Suy ra lim f ( x) = f (− )
1 nên hàm số đã cho liên tục tại x = 1 − . 0 x 1 →−
+ Vậy hàm số đã cho liên tục trên . 2  x − 4x + 3  khi x  1
Ví dụ 2. Xét tính liên tục của hàm số f ( x) =  x −1 trên .  − 5 − x khi x  1 ĐS: Liên tục trên . Lời giải
+ Tập xác định của hàm số là D = . 2 x − 4x + 3
+ Với mọi x  1; +  , lim f ( x) = lim
= f (x Suy ra hàm số đã cho liên tục trên 0 ) 0 ( ) x→ → − 0 x x 0 x x 1 . khoảng (1; + ) .
+ Với mọi x  −;1 , ta có lim f ( x) = lim − − = − − = Suy ra hàm số đã → → ( 5 x ) 5 x f x 0 ( 0) 0 ( ) x 0 x x 0 x .
cho liên tục trên khoảng (− ) ;1 .
+ Xét tính liên tục của hàm số tại x =1 f ( ) 1 = − 5 −1 = 2 .
- lim f ( x) = lim (− 5 − − x = − . − − ) 2 x 1 → x 1 → x −1 x − 3 - lim f ( x) ( )( ) = lim = lim (x −3) = 2 − . + + + x 1 → x 1 → − x 1 x 1 →
Suy ra lim f ( x) = lim f ( x) = f ( )
1 nên hàm số đã cho liên tục tại x =1 . − + x 1 → x 1 →
Vậy hàm số đã cho liên tục trên . 127
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2  x + x − 6 khi x  2 
Ví dụ 3. Tìm a để hàm số f ( x) =  x + 2 − 3x − 2 liên tục trên . ĐS: a = 11 − . (  2x −3  )2 + a khi x  2 Lời giải Với x  (−;2) ta có: x + x − 6 - f ( x ) 2 0 0 = . 0
x + 2 − 3x − 2 0 0 2 2
- lim f ( x) = lim (2x − 3) + a = (2x − 3 + a 0 )   . x→ → 0 x x 0 x
Suy ra lim f ( x) = f ( x nên hàm số liên tục trên khoảng (−; 2) . 0 ) x→x0 Với x  (2;+ ) ta có
- f ( x ) = (2x − 3)2 + a . 0 0 2 2
- lim f ( x) = lim (2x − 3) + a = (2x − 3 + a 0 )   . x→ → 0 x x 0 x
Suy ra lim f ( x) = f ( x nên hàm số liên tục trên khoảng (2; + ) . 0 ) x→x0 Lại có:
- f (2) = 1+ a . x + x − 6 - lim f ( x) 2 = lim = 1 − 0 . + + x→2 x→2
x + 2 − 3x − 2
- lim f ( x) = lim (
 2x −3)2 + a =1+ a − −   . x→2 x→2
Khi đó hàm số liên tục trên
thì sẽ liên tục tại x = 2 khi và chỉ khi
lim f ( x) = lim f ( x) = f (2)  1 − 0 =1+ a . + − x→2 x→2 Suy ra a = 11
− là giá trị cần tìm.
BÀI TẬP ÁP DỤNG 3 2
2x + 6x + x + 3  khi x  3 − Bài 1.
Xét tính liên tục của hàm số f ( x) =  x + 3 trên . 1  9 khi x = 3 − Lời giải
Tập xác định của hàm số là D = . 128
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
x + x + x + - Xét x  3 − thì f (x) 3 2 2 6 3 =
là hàm phân thức hữu tỉ nên liên tục trên các khoảng x + 3 (−;−3) và ( 3;
− + ) mà nó xác định.
- Xét tính liên tục của hàm số f ( x) tại x = 3 − + + + (x +3)( 2 3 2 2x x x x + ) f ( x) 1 2 6 3 lim = lim = lim = lim ( 2 2x + ) 1 = 19 x→( 3 − ) x→( 3 − ) x→ − (−3) x→ + . (−3) x 3 x 3
Suy ra lim f ( x) = f ( 3
− ) nên hàm số đã cho liên tục tại x = 3 − . x ( → 3 − )
Vậy hàm số đã cho liên tục trên . 2  x − 5x + 6  khi x  2 Bài 2.
Xét tính liên tục của hàm số f ( x) 3 =  2x −16 trên . 2− x khi x  2 Lời giải Tập xác định D = . 2 x − 5x + 6
- Với mọi x  − ;  2 , lim f x = lim = f x . 0 ( ) ( ) 3 ( 0) x→ → − 0 x x 0 x 2x 16
Suy ra hàm số đã cho liên tục trên khoảng (−; 2) .
- Với mọi x  2; +  , lim f x = lim 2 − x = 2 − x = f x . 0 ( ) ( ) ( ) 0 ( 0) x→x x→x 0 0
Suy ra hàm số đã cho liên tục trên khoảng (2; + ) .
- Xét tính liên tục của hàm số tại x = 2 f (2) = 0 . 2 x − 5x + 6 x − 2 x − 3 x − 3 1 lim f ( x) ( )( ) = lim = lim = lim = − − − 3 − − x→ x→ 2x −16 x→ 2( x − 2)( 2
x + 2x + 4) x→ 2( 2 2 2 2 2 x + 2x + 4) 24
lim f ( x) = lim (2 − x) = 0 . + + x→2 x→2
Suy ra hàm số không liên tục tại x = 2 . 2
 2x − x −3  khi x  1 − Bài 3.
Tìm a để f ( x) 3 2
= x + x + x +1 liên tục trên .  3 a khi x = 1 − Lời giải 2x − x − 3
Ta có với x  1 thif f ( x) 2 =
là hàm phân thức hữu tỉ nên nó liên tục trên từng 3 2
x + x + x +1
khoảng mà nó xác định. Lại có 129
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC - f (− ) 3 1 = a . 2 2x − x − 3 x +1 2x − 3 2x − 3 5 - lim f ( x) ( )( ) = lim = lim = lim = − . 3 2 x→−
x→− x + x + x +1 x→− (x + ) 1 ( 2 1 1 1 x + ) 2 x→ 1 1 − x + 1 + 2
Khi đó hàm số liên tục trên
thì sẽ liên tục tại x = 1 − khi và chỉ khi
lim f ( x) = f (− ) 5 3 1  a == − . x 1 →− 2 5 Suy ra 3 a = − là giá trị cần tìm. 2
BÀI TẬP RÈN LUYỆN 3  x −1  khi x  1  x −1 Bài 1.
Xét tính liên tục của hàm số f ( x) =  liên tục trên .
 1− x + 2 khi x 1  x + 2 2  x + 5xkhi x  0 Bài 2.
Tìm m để f ( x) =  x −1 −1 liên tục trên . m+2 khi x  0 2  x −1  khi x  1 − Bài 3.
Tìm m để f ( x) 3 2
=  x + x + x +1 liên tục trên . cosm khi x = 1 − 3
x − 2 + 2x −1  khi x  1 Bài 4.
Tìm m để f ( x) =  x −1 liên tục trên . 3  m − 2 khi x = 1  x +1 −1  khi x  0 Bài 5.
Tìm m để f ( x) =  x liên tục trên .  2
2x + 3m +1 khi x  0
_DẠNG 3. CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM Phương pháp giải:
- Để chứng minh phương trình f ( x) = 0 có ít nhất một nghiệm trên D , ta chứng minh hàm số
f ( x) liên tục trên D và có hai số a ,b D sao cho f (a). f (b)  0 .
- Để chứng minh phương trình f ( x) = 0 có k nghiệm trên D , ta chứng minh hàm số f ( x) liên tục
trên D và tồn tại k khoảng rời nhau (a ; a
với i =1; 2;...; k nằm trong D sao cho i i 1 + )
f (a ). f (a  0 . i i 1 + )
Chú ý: Hàm số đã thức liên tục trên
. Hàm số phân thức và lượng giác liên tục trên 130
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
từng khoảng xác định của chúng.
Khi hàm số đã liên tục trên
rồi, sẽ lieent ục trên mỗi khoảng (a ; a mà ta cần tìm. i i 1 + )  VÍ DỤ
Ví dụ 1. Chứng minh phương trình 3 2
4x − 8x +1 = 0 có nghiệm trong khoảng ( 1; − 2) . Lời giải - Đặt f ( x) 3 2
= 4x − 8x +1 và f ( x) là hàm đa thức nên liên tục trên , suy ra liên tục trên −1;2.  f  (− ) 1 = 1 − 1 - Ta có   f (− ) 1 . f (2) = 1 − 1 0  x   1 − ;2 : f x = 0 , 0 ( ) ( 0)  f  (2) =1
Nghĩa là phương trnhf f ( x) 3 2
= 4x − 8x +1 = 0 có ít nhất một nghiệm trong khoảng ( 1; − 2) .
Ví dụ 2. Chứng minh phương trình 3
x − 3x +1 có đúng ba nghiệm phân biệt. Lời giải Đặt f ( x) 3
= x − 3x +1 và f ( x) là hàm đa thức nên liên tục trên , suy ra hàm số liên tục trên các đoạn  2 − ;0;0  ;1 ;1; 2 .  f  (− ) 1 = 1 − - Ta có   f ( 2
− ). f (0) = −   phương trình f (x) 3
= x − 3x +1 = 0 có ít nhất  f  ( ) 1 0 0 = 1
một nghiệm thuộc khoảng ( 2 − ;0) . (1)  f  (0) =1 - Ta có 
f (0). f ( ) = −   phương trình f (x) 3
= x − 3x +1 = 0 có ít nhất một  f  ( ) 1 1 0 1 = 1 −
nghiệm thuộc khoảng (0; ) 1 . (2)  f  ( ) 1 = 1 − - Ta có   f ( )
1 . f (2) = −   phương trình f ( x) 3
= x − 3x +1 = 0 có ít nhất  f  ( ) 3 0 2 = 3
một nghiệm thuộc khoảng (1; 2) . (3) Từ ( )
1 , (2),(3) suy ra phương trình có ít nhất ba nghiệm phân biệt thuộc các khoảng (−2;0) , (0; )
1 , (1; 2) . Mà f ( x) là đa thức bậc ba nên phương trình f ( x) = 0 có tối đa ba nghiệm. Suy
ra phương trình đã cho có đúng ba nghiệm phân biệt.
Chú ý: Với sự hỗ trợ của chức năng mode 7 trong casio, ta dễ dàng tìm được các khoảng (−2;0), (0; )
1 , (1; 2) như trên. Công việc còn lại là trình bày sao cho đúng ngôn ngữ.
Ví dụ 3. Chứng minh rằng phương trình 3
x + x +1 = 0 có ít nhất một nghiệm âm lớn hơn 1 − . Lời giải 131
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Đặt f ( x) 3
= x + x +1, vì f ( x) là hàm đa thức nên liên tục trên , suy ra hàm số liên tục trên đoạn  1; − 0.  f  (− ) 1 = 1 − Ta có   f (− )
1 . f (0) = −   phương trình f ( x) = 0 có ít nhất một nghiệm  f  ( ) 1 0 0 = 1 thuộc khoảng ( 1; − 0) .
Suy ra phương trình f ( x) = 0 có ít nhất một nghiệm âm lớn hơn 1 − .
Ví dụ 4. Chứng minh rằng phương trình 3 2
x + 5x − 2 = 0 có ít nhất hai nghiệm. Lời giải Đặt f ( x) 3 2
= x + 5x − 2 , f ( x) là hàm đa thức trên , suy ra hàm số liên tục trên đoạn  1; − 0 ; 0;  1  f  (− ) 1 = 2 - Ta có   f (− )
1 . f (0) = −   phương trình f ( x) = 0 có ít nhất một nghiệm  f  ( ) 4 0 0 = 2 − thuộc khoảng ( 1; − 0) . (1)  f  (0) = 2 − - Tương tự   f (− )
1 . f (0) = −   phương trình f ( x) = 0 có ít nhất một  f  ( ) 8 0 1 = 4
nghiệm thuộc khoảng (0; ) 1 . (2) Từ ( )
1 và ( 2) ta suy ra phương trình f ( x) = 0 có ít nhất hai nghiệm.
Ví dụ 5. Chứng minh rằng phương trình 4 3
4x + 2x − x − 3 = 0 có ít nhất hai nghiệm. Lời giải Đặt f ( x) 4 3
= 4x + 2x − x − 3 , f ( x) là hàm đa thức trên , suy ra hàm số liên tục trên đoạn  1; − 0, 0;  1 .  f  (− ) 1 = 4 - Ta có   f (− ) 1 . f (0) = −
  phương trình f (x) = 0 có ít nhất một nghiệm  f  ( ) 12 0 0 = 3 − thuộc khoảng ( 1; − 0) . (1)  f  (0) = 3 − - Tương tự   f (− )
1 . f (0) = −   phương trình f ( x) = 0 có ít nhất một  f  ( ) 6 0 1 = 2
nghiệm thuộc khoảng (0; ) 1 . (2) Từ ( )
1 và ( 2) ta suy ra phương trình f ( x) = 0 có ít nhất hai nghiệm.
Ví dụ 6. Chứng minh rằng phương trình ( 2 − m ) 5 1
x − 3x −1 = 0 luôn có nghiệm với mọi m . Lời giải 132
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
Đặt f ( x) = ( 2 − m ) 5 1
x − 3x −1 và f ( x) là hàm đa thức liên tục trên
f ( x) liên tục trên đoạn  1; − 0.  f (− ) 2 1 = m +1 Ta có   f (− )
1 . f (0)  0  x   1 − ;0 : f x = 0 . 0 ( ) ( 0)  f  (0) = 1 −
Do đó phương trình f ( x) = 0 luôn có nghiệm với mọi m (đpcm).
Chú ý: Đối với bài toán chứa tham số m , ta chọn khoảng (a;b) sao cho tại vị trí a và b triệt
tiêu đi m hoặc là biểu thức luôn dương hoặc luôn âm dựa vào kinh nghiệm người giải toán.
Một số trường hợp sử dụng dấu tam thức bậc hai để đánh giá, tức a  0 2
ax + bx + c  0, x     .   0 a  0 2
ax + bx + c  0, x     .   0
Ví dụ 7. Chứng minh rằng phương trình 4 2
x + mx − 2mx −1 = 0 có nghiệm với mọi m . Lời giải Đặt f ( x) 4 2
= x + mx − 2mx −1 và f ( x) là hàm đa thức liên tục trên  f ( x) liên tục trên đoạn 0;2 .  f  (0) = 1 − Ta có   f (− ) 1 . f (2) = −
 phương trình f (x) = 0 luôn có nghiệm với mọi m .  f  ( ) 15 2 = 15
Ví dụ 8. Chứng minh rằng phương trình m ( x − 2)( x − 3) + 2m − 5 = 0 có nghiệm với mọi m . Lời giải
Đặt f ( x) = m( x − 2)( x − 3) 2x − 5 và f ( x) là hàm đa thức liên tục trên  f ( x) liên tục trên đoạn 2;3.  f  (2) = 1 − Ta có 
f (2). f (3) = −  phương trình f (x) = 0 luôn có nghiệm với mọi m .  f  ( ) 1 3 = 1
Ví dụ 9. Chứng minh phương trình ( x − a)( x − b) + ( x − b)( x − c) + ( x − c)( x − a) = 0 có ít nhất một
nghiệm với mọi số thực a , b , c . Lời giải
Đặt f ( x) = ( x − a)( x − b) + (x − b)(x − c) + (x − c)(x − a). Vì f ( x) là hàm đa thức nên sẽ liên tục trên
. Không mất tính tổng quát, có thể giả sử a b c .
- Nếu a = b hoặc b = c thì f (b) = (b − a)(b − c) , suy ra phương trình có nghiệm x = . b 133
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC f
 (a) = (a − b)(a − c)  0
- Nếu a b c thì 
f (a). f (b)  0. Do đó phương trình có ít  f
 (b) = (b − a)(b − c)  0
nhất một nghiệm trong khoảng (a;b) .
Suy ra phương trình có ít nhất một nghiệm (đpcm).
Ví dụ 10. Cho ba số a , b , c thỏa mãn hệ thức 2a + 3b + 6c = 0 . Chứng minh rằng phương trình 2
ax + bx + c = 0 có ít nhất một nghiệm thuộc khoảng (0; ) 1 . Lời giải Đặt ( ) 2
f x = ax + bx + c và f ( x) là hàm đa thức nên liên tục trên .
2a + 3b + 6c = 0 
- Ta có f (0) = c và có   2  4 2 2 = + + = .  ( c c f a b c
2a + 3b + 6c) − = −     3  9 3 3 3 3  2  2
- Nếu c = 0 thì f = 0  
, suy ra phương trình có nghiệm x = (0; ) 1 .  3  3   c
- Nếu c  0 thì ta có f ( ) 2 2 0 . f = −  0    3  3   2 
f ( x) = 0 có nghiệm x = a  0;    (0 ) ;1 .  3 
Vậy phương trình có ít nhất một nghiệm thuộc khoảng (0; ) 1 .
Ví dụ 11. Cho hàm số f ( x) 3 2
= x − 3x −1. Chứng minh rằng phương trình có nghiệm x  3;4 . Không 0 ( )
tính f ( 5 36) và f ( 5 1+ 36 ) , chứng minh rằng 5 x  1+ 36 . 0 Lời giải Ta có: f (3) 3 2 = 3 −3.3 −1 = 1
−  f (3).f (4)=−  . f (4) 15 0 3 2 = 4 −3.4 −1 =15
Suy ra phương trình có nghiệm x  3; 4 . 0 ( ) 3 Ta có f ( x) 3 2
= x − 3x −1 = (x − ) 1 − 3( x − ) 1 − 3 .
Vì x là nghiệm của phương trình f ( x) = 0 nên ta có f ( x = 0 0 ) 0  ( x − )3
1 − 3 x −1 − 3 = 0 . 0 ( 0 )
Đặt  = x −1 và x  3;4    2;3 . Khi đó, ta có 0 ( ) ( ) 0 3 3
 −3 −3 = 0   = 3 + 3  2. 9 = 6  6 5 5
   36    36    36 .
Dấu “ = ” xảy ra khi và chỉ khi 3 = 3   = 1 (2;3) .
Do đó, dấu “ = ” không xảy ra, tức là ta luôn có 5 5 5
  36  x −1  36  x 1+ 36. 0 0
Suy ra điều phải chứng minh.
BÀI TẬP ÁP DỤNG Bài 1.
Chứng minh phương trình ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1 = 0 có ba nghiệm phân biệt. 134
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Bài 2.
Chứng minh phương trình ( − m) 5 2 1
x + 9mx −16x − m = 0 có ít nhất hai nghiệm phân biệt. Bài 3.
Chứng minh phương trình ( 2 − + ) 2 3 n m m x
− 2x − 4 = 0 có ít nhất một nghiệm âm với mọi m . Bài 4.
Chứng minh phương trình ( m + ) 3 4 1 x − (m + )
1 x + m = 0 có nghiệm với mọi m . Bài 5.
Chứng minh phương trình (m − )( x − )(x + )2002 3 2001 1 1 2
+ 2x + 3 = 0 có nghiệm với mọi m . Bài 6.
Chứng minh phương trình ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1 = 0 có ba nghiệm phân biệt. Bài 7.
Chứng minh rằng phương trình m ( x − )( 3 x − x) 3 1 4
+ x − 3x +1 = 0 có ít nhất ba nghiệm. Bài 8.
Cho  và  thỏa mãn 0     . Chứng minh rằng phương trình sau có nghiệm 2 10 2 2
 sin  +  sin  − −  10 sin x − x =  . +  a b c Bài 9. Chứng minh rằng nếu + +
= 0 , (k n m  0) và 2
km n thì phương trình k n m 2
ax + bx + c = 0 có nghiệm thuộc khoảng (0; ) 1 . LỜI GIẢI Bài 1.
Đặt f ( x) = ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1, f ( x) liên tục với mọi x  . Có:
f (− ) = (m + ) (− )3 − m (− )2 2 2 − (− ) 2 2 3 1 . 3 2 . 3 4. 3 + m +1 = 4 − 4m −14  0 ; f ( ) = ( 2 m + ) 3 2 2 2 2 0
1 .0 − 2m .0 − 4.0 + m +1 = m +1  0 ; f ( ) = ( 2 m + ) 3 2 2 2 1
1 .1 − 2m .1 − 4.1+ m +1 = 2 −  0 ; f ( ) = ( 2 m + ) 3 2 2 2 2 2
1 .2 − 2m .2 − 4.2 + m +1 = m +1  0 . Ta thấy f ( 3 − ). f (0)  0 ; f (0). f ( ) 1  0 ; f ( ) 1 . f (2)  0 nên phương trình ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1 = 0 có ít nhất 1 nghiệm trong khoảng (−3;0) , ít nhất 1 nghiệm trong khoảng (0; )
1 , ít nhất 1 nghiệm trong khoảng (1; 2) . Vậy phương trình ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1 = 0 có ít nhất 3 nghiệm phân biệt. Bài 2.
Đặt f ( x) = ( − m) 5 2 1
x + 9mx −16x − m , f ( x) liên tục trên .
Trường hợp 1: m = 0, ta có phương trình 5
x −16x = 0 có nghiệm x 0;   2 .
Vậy với m = 0 thì phương trình ( − m) 5 2 1
x + 9mx −16x − m = 0 có ít nhất hai nghiệm phân biệt.
Trường hợp 2: m  0 , ta có:
f (− ) = ( − m)(− )5 + m (− )2 2 1 2 9 2 −16.( 2
− ) − m = 67m ;
f ( ) = ( − m) 5 2 0 1 .0 + 9 .
m 0 −16.0 − m = −m ;
f ( ) = ( − m) 5 2 2 1 .2 + 9 .
m 2 −16.2 − m = 3 − m .
Ta thấy f (− ) f ( ) 2 2 . 0 = 67
− m  0, f ( ) f ( ) 2 0 . 2 = 3
− m  0 với mọi m  0 . 135
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
Suy ra phương trình ( − m) 5 2 1
x + 9mx −16x − m = 0 có ít nhất 1 nghiệm trong khoảng (−2;0) ,
ít nhất 1 nghiệm trong khoảng (0; 2) .
Vậy phương trình ( − m) 5 2 1
x + 9mx −16x − m = 0 có ít nhất hai nghiệm phân biệt. Bài 3. Đặt ( ) = ( 2 − + ) 2 3 n f x m m x
− 2x − 4 , f ( x) liên tục trên . 2n Xét
(− ) = ( 2 − + )(− ) − (− )− = ( 2 2 3 2 2. 2 4 − + 3).4n f m m m m  0 . Xét ( ) = ( 2 − + ) 2 0 3 .0 n f m m − 2.0 − 4 = 4 −  0 . Ta thấy f ( 2
− ). f (0)  0 với mọi m  0 .
Suy ra phương trình ( 2 − + ) 2 3 n m m x
− 2x − 4 = 0 có ít nhất 1 nghiệm trong khoảng (−2;0) .
Vậy phương trình ( 2 − + ) 2 3 n m m x
− 2x − 4 = 0 có ít nhất một nghiệm âm. Bài 4.
Trường hợp 1: m = 0, ta có phương trình 3
x − x = 0 luôn có nghiệm x = 0 ; x = 1  .
Trường hợp 2: m  0 .
Đặt f ( x) = ( m + ) 3 4 1 x − (m + )
1 x + m , f ( x) liên tục với mọi x  . Có:
f (− ) = ( m + )(− )3 1 4 1 1 − (m + ) 1 (− ) 1 + m = 2 − m ;
f ( ) = ( m + ) 3 0 4 1 .0 − (m + ) 1 .0 + m = m .
Ta thấy f (− ) f ( ) 2 1 . 0 = 2
− m  0 nên phương trình ( m + ) 3 4 1 x − (m + )
1 x + m = 0 có ít nhất 1 nghiệm trong khoảng ( 1; − 0) .
Vậy phương trình ( m + ) 3 4 1 x − (m + )
1 x + m = 0 có nghiệm với mọi m . Bài 5.
Đặt f ( x) = (m − )(x − )(x + )2002 3 2001 1 1 2
+ 2x + 3, f (x) liên tục với mọi x . 2001 2002 Xét f (− ) = ( 3 2 m − ) 1 (  2 − ) −1 (  2 −    )+ 2 + 2.  ( 2 − ) +3 = 1 − .
Xét f ( ) = (m − )( − )( + )2002 3 2001 1 1 1 1 1 2 + 2.1+ 3 = 5 . Ta thấy f ( 2 − ). f ( ) 1 = 1 − .5 = 5
−  0 với mọi m .
Suy ra phương trình (m − )( x − )(x + )2002 3 2001 1 1 2
+ 2x + 3 = 0 có ít nhất 1 nghiệm trong khoảng (−2; ) 1 .
Vậy phương trình (m − )( x − )(x + )2002 3 2001 1 1 2
+ 2x + 3 = 0 có nghiệm với mọi m . Bài 6.
Đặt f ( x) = ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1, f ( x) liên tục với mọi x  . Có:
f (− ) = (m + ) (− )3 − m (− )2 2 2 − (− ) 2 2 3 1 . 3 2 . 3 4. 3 + m +1 = 4 − 4m −14  0 ; f ( ) = ( 2 m + ) 3 2 2 2 2 0
1 .0 − 2m .0 − 4.0 + m +1 = m +1  0 ; f ( ) = ( 2 m + ) 3 2 2 2 1
1 .1 − 2m .1 − 4.1+ m +1 = 2 −  0 ; f ( ) = ( 2 m + ) 3 2 2 2 2 2
1 .2 − 2m .2 − 4.2 + m +1 = m +1  0 . 136
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Ta thấy f ( 3
− ). f (0)  0 , f (0). f ( ) 1  0 , f ( )
1 . f (2)  0 . Suy ra phương trình ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1 = 0 có ít nhất 1 nghiệm trong khoảng (−3;0) , ít nhất 1 nghiệm trong khoảng (0; )
1 , ít nhất 1 nghiệm trong khoảng (1; 2) . Vậy phương trình ( 2 m + ) 3 2 2 2
1 x − 2m x − 4x + m +1 = 0 có ba nghiệm phân biệt. Bài 7.
Đặt f ( x) = m( x − )( 3 x − x) 3 1 4
+ x − 3x +1, f ( x) liên tục với mọi x . Có:
f (− ) = m(− − ) (
 − )3 − (− ) +(− )3 2 2 1 2 4. 2 2 −3.( 2 − )+1= 1 −   ;
f ( ) = m ( − )( 3 − ) 3 0 0 1 0 4.0 + 0 − 3.0 +1 = 1;
f ( ) = m( − )( 3 − ) 3 1 1 1 1 4.1 +1 − 3.1+1 = 1 − ;
f ( ) = m ( − )( 3 − ) 3 2 2 1 2 4.2 + 2 − 3.2 +1 = 1. Ta thấy f ( 2 − ). f (0)  0 , f (0). f ( ) 1  0 , f ( ) 1 . f (2)  0 nên phương trình m ( x − )( 3 x − x) 3 1 4
+ x − 3x +1 = 0 có ít nhất 1 nghiệm trong khoảng (−2;0) , ít nhất 1 nghiệm trong khoảng (0; )
1 , ít nhất 1 nghiệm trong khoảng (1; 2) .
Vậy phương trình m ( x − )( 3 x − x) 3 1 4
+ x − 3x +1 = 0 có ít nhất ba nghiệm.
 sin  +  sin  − −  Bài 8. Đặt f (x) 2 10 2 2 10
= sin x − x − 
, hàm số f ( x) liên tục trên . + 
Ta có lim f ( x) = + nên tồn tại m  0 sao cho f (m)  0 . x→−
Mà lim f ( x) = − nên tồn tại M  0 sao cho f (M )  0 . x→+
Do đó, hàm số f ( x) liên tục trên m; M  và f (m). f (M )  0 nên phương trình f ( x) = 0 có nghiệm. Bài 9. Xét phương trình 2
ax + bx + c = 0 ( ) 1 . Đặt ( ) 2
f x = ax + bx + c thì f ( x) liên tục trên . 2  n n n
Ta có f (0) = c ; f = . a + . b + c   . 2  k k kn
n a b c   n   n a b c Suy ra f ( ) 2 2 2 2 0 . f = c    + + + c   1−  = c 1−  (do + + = 0 ).  k k   k n m   km   km k n m 2 nn   n  Vì 2 c  0 ; 2
n km  0  1, do đó f ( ) 2 2 0 . f = c   1−   0 . kmk   km
- Với c = 0 phương trình đã cho trở thành 2
ax + bx = 0 . Suy ra x = 0 hoặc ax + b = 0 ( 2) . a b c
+ Nếu a = 0 thì từ c = a = 0 và điều kiện + +
= 0 suy ra b = 0. Khi đó phương trình (2) k n m có nghiệm là x
  , suy ra phương trình ( )
1 có nghiệm x  (0; ) 1 . 137
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC a b c
+ Nếu a  0 thì b  0 (vì nếu b = 0 , c = 0 thì từ điều kiện + +
= 0 suy ra a = 0 ), suy ra k n m phương trình ( b a b c
2) có nghiệm x = − . Khi đó từ điều kiện + +
= 0 ; k n m  0 và a k n m b n
c = 0 suy ra x = − = (0; )
1 . Do đó phương trình ( )
1 có nghiệm x  (0; ) 1 . a k 2 nn n - Với 1− = 0  f = 0    là nghiệm thuộc (0; ) 1 . kmk k 2 nn   n
- Với c  0 và 1−
 0  f (0). f  0  
thì f ( x) có ít nhất 1 nghiệm thuộc 0;   . Mà kmk   k   n n 0;    (0 ) ;1 (vì 0 
1) nên phương trình ( )
1 có nghiệm x  (0; ) 1 .  k k Vậy phương trình ( )
1 luôn có nghiệm x  (0; ) 1 .
C. BÀI TẬP RÈN LUYỆN Bài 1.
Chứng minh rằng phương trình 4 3 2
x − x − 2x −15x − 25 = 0 có ít nhất một nghiệm âm và ít nhất một nghiệm dương. ĐS: ( 1; − 0) ; (3;4) . Bài 2.
Chứng minh rằng phương trình 3 2
x + 4x − 2 = 0 có ba nghiệm trong khoảng (−4; ) 1 .       ĐS: 7 1 1 4; − −   ; 1; − −   ; ;1   .  2   2   2  Bài 3.
Chứng minh rằng phương trình 5 3
x − 5x + 4x −1 = 0 có đúng năm nghiệm.         ĐS: 3 3 1 1 2; − −   ; − ; 1 −   ; 1; −   ; ;1   ; (1;3) .  2   2   2   2  138
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
BÀI 4. ÔN TẬP CHƯƠNG IV A. BÀI TẬP Bài 1.
(HKII - THPT Lương Văn Can)
1) Tính các giới hạn sau x + 2 − 2 2 4x + 3x +1 a) lim . b) lim . 2 x→2 x − 4 x→+ x −1 2
3x − 2x −1  khi x  1
2) Xét tính liên tục của hàm số f ( x) =  x −1 tại x = 1.  0 2x + 2 khi x  1 Bài 2.
(HKII - THPT Sương Nguyệt Anh)
1) Tính các giới hạn sau 2 2x − x −10 a) lim . b) + − + . →− ( 2 lim 3x x 2x 3 x ) 3 x 2 →− x − x + 6 2  x −3 −1  khi x  2
2) Xét tính liên tục của hàm số f ( x) =  x − 2 tại x = 2 .  0 2x − 2 khi x = 2 Bài 3.
(HKII – THPT Bùi Thị Xuân)
1. Tính các giới hạn sau 3 2
6x − 5x + 4x −1 a) lim . ĐS: 2 . b)
x + x + + x + ĐS: 1 . x→− ( 2 lim 9 3 1 3 )1 4 2 1 + − x→ 9x 8x 1 5 2 3 a + b khi x = 1 
 2x + 5x − 7
2. Tìm a,b để hàm số f ( x) 2 = 
khi x  1 liên tục tại x = 1. ĐS: a = 1 − 0,b =19 x −1 0  2
x + 2bx + 3a khi x 1 
3. Chứng minh rằng phương trình ( 2 m − m + )( 2 3 2
x − 3x + 2) + (3 − 2x)(3 − 2m) = 0 có nghiệm với mọi m . Bài 4.
(HKII – THPT Nguyễn Hữu Huân)
1. Tính các giới hạn sau x −1 3 2
x + 3x + 2x − a) lim . ĐS: 1 . b) lim ĐS: 2 . 2 x 1 → x −1 4 2 x 2 →− x − x − 6 5 2  x − 3x + 2  khi x  1
2. Xét tính liên tục của hàm số f ( x) =  x −1
tại x = 1. ĐS: liên tục  0  1 − khi x = 1 Bài 5.
(HKII – THPT Hermann Gmeiner)
1. Tính các giới hạn sau 139
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3 2
x − x − x +1 3 1− x − 3 a) lim . ĐS: 2 . b) lim ĐS: −2 . 2 x 1 → x − 2x +1 x 2 →− x + 2 x − 5 c) lim . ĐS: − . d) + + + ĐS: 1 − . →− ( 2 lim x x 1 x x ) − x→ (x − 4)2 4 2  x khi x  0 1  − 1− x
2. Tìm a để hàm số f ( x) = 
liên tục tại x = 0 . ĐS: a = 3. 0 4 − xa −5+ khi x  0  x +1 Bài 6.
(HKII – THPT Hoàng Hoa Thám) 2
x + 2x + 3x − 1. Tính giới hạn sau lim . ĐS: 2 . x→− 2 4x +1 − x + 2 3 2
ax + 2x khi x 1 
2. Tìm a để hàm số f ( x) =  4 − x
liên tục tại x = 1. ĐS: a = 1 − . 0 a − 5 + khi x  1  x +1
3. Chứng minh rằng phương trình 4 3 2
x − x − 2x −15x − 25 = 0 có ít nhất một nghiệm dương và một nghiệm âm. Bài 7.
(HKII – THPT Hàn Thuyên)
1. Tính các giới hạn sau x − 3 (3x + ) 2 1 2x − 3 a) lim . ĐS: 1 . b) lim 2 2 x 3 → x + 2x −15 8 x→− 3 − x + ĐS: 2 . xx −1  khi x  1  −
2. Tìm m để hàm số ( ) 7 7x f x = 
liên tục tại x = 1. ĐS: 3 m = . 0 x  7 m − khi x  1  2 Bài 8.
(HKII – THPT Hùng Vương) 3 2
4x − 7x +19x −16 1. Tính giới hạn sau lim . ĐS: 17 . 2 x 1 → 5x − 8x + 3 2 2  4 − x  khi x  2
2. Tìm m để hàm số f ( x) =  x + 2 −1
liên tục tại x = 2 . ĐS: m = 4 . 0 2x−m khi x  2
3. Chứng minh rằng phương trình ( 2 m − m + ) 2015 4 x
− 2x +1 = 0 có ít nhất một nghiệm âm với
mọi giá trị của tham số m . Bài 9.
(HKII – THPT Hưng Đạo)
1. Tính các giới hạn sau 5 − 6x x − 3 a). lim . ĐS: 3 − . b). lim . ĐS: − . x→+ 3 + 2x + x→2 x − 2 140
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC c). ( 3
lim 3x − 2x ) ĐS: + . x→− 2  x + 3x − 4  khi x  1
2. Tìm m để hàm số f ( x) 3 =  x −1
liên tục tại x = 1. ĐS: 5 m = .  0 3 m khi x = 1
Bài 10. (HKII – THPT Bà Điểm)
1) Tính các giới hạn sau 2 x − 3x + 2 a) lim . ĐS: 1 b) + − − . ĐS: 1 →+ ( 2 2 lim x x x x x ) 2 x→2 x − 4 4 (  x − )2 5 + 3 khi x  5 
2) Xét tính liên tục của hàm số f ( x) =  x − 5
tại điểm x = 5 ĐS: liên tục.  0 khi x  5  2x −1 − 3 2  x − 5x + 6  khi x  3
3) Tìm m để hàm số f ( x) =  x − 3
liên tục tại điểm x = 3 .  0
2mx +1 khi x = 3 Bài 11.
(HKII-THPT Bình Tân) x + 2 − 2  khi x  2  −
1) Tìm m để hàm số f ( x) x 2 =  . 1
mx + khi x  2  4
2) Chứng minh rằng phương trình ( 2 − m ) 5 1
x − 3x −1 = 0 có ít nhất một nghiệm với mọi giá trị của tham số m . Bài 12. (HKII-THPT Củ Chi)
1) Tính các giới hạn sau 2 3n − n + 9 (1−3n) (n + )2 3 2 1 a) lim . ĐS: 3 − b) lim . ĐS: 9 − 2 1− 2n 2 7 3n − 2 c) − + − + . ĐS: 5 − →− ( 2 lim x 3 x x 1 x ) 2 2  x − 4 khi x  2
x− 7x−10
2) Xét tính liên tục của hàm số f ( x) = 
tại điểm x = 2 . ĐS: liên tục  0 8
− x khi x = 2  3
3) Chứng minh rằng phương trình 4 2
4x + 2x − x − 3 = 0 có ít nhất hai nghiệm.
Bài 13. (HKII-THPT Đinh Thiện Lý)
1) Tính các giới hạn sau 3n + 2 3n − 6n a) A = lim . ĐS: 0 b) B = lim . ĐS: − 4 3
n + 2n − 5n + 2 4n + 3 3 2
2x − 5x − 2x − 3 c) C = lim ĐS: 11 d) D = + + − ĐS: 1 →+ ( 2 lim 4x x 1 2x x ) 2 x 3 → x − 9 3 4 141
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  2 − x  khi x  2
2) Cho hàm số f ( x) =  x + 7 − 3 .
2ax+3 khi x  2
a) Khi a =1, xét tính liên tục của hàm số tại x = 2 . ĐS: Không liên tục 9
b) Tìm giá trị của a để hàm số liên tục tại x = 2 . ĐS: a = − 4
3) Chứng minh rằng phương trình 5 4
x − 3x + 5x − 2 = 0 có ít nhất ba nghiệm phân biệt.
Bài 14. (HKII- THPT Lý Tự Trọng)
1) Tính các giới hạn sau x − 5 2 x + 5 − 3 a) lim . ĐS: 0 b) lim . ĐS: 2 − x 5 → x − 5 x 2 →− x + 2 3 2  x − 4x + 3  khi x  3
2) Tìm a để hàm số f ( x) =  3 − x
liên tục tại điểm x = 3 . ĐS: 7 a = −  0 12
4ax + 5 khi x = 3
3) Chứng minh rằng phương trình 5 4 3
5x − 3x + 4x − 5 = 0 có ít nhất một nghiệm.
Bài 15. (HKII-THPT Lê Quý Đôn) x + 3 − 2  khi x  1
1) Tìm giá trị của a để hàm số f ( x) 2 = 2x −3x +1
liên tục tại x = 1. ĐS: 27 a = 0  8  2
− a + 7 khi x 1
2) Chứng minh phương trình ( 2 m − m + ) 3 3
3 x + 2x − 3 = 0 có nghiệm với mọi m .
Bài 16. (HKII – THPT Chuyên Nguyễn Thượng Hiền) 1) Tính giới hạn sau 1 tan x − sin x 1 a) + − + . ĐS: − b) lim . ĐS: →− ( 2 2 lim x x x 1 x ) 2 3 x 0 → 4x 8  1− x khi x  1 
2) Tìm tham số m để hàm số f ( x) =  x + 8 − 3
liên tục tại x = 1. ĐS: m = 1 − và 0  2 2
m x + 7m khi m 1 m = 6 −
3) Chứng minh phương trình 14 mx − ( 2 m + ) 15 3
7 x − 5 = 0 luôn có ít nhất một nghiệm với mọi m . Bài 17. (HKII – THPT An Lạc)
 Tính các giới hạn sau 2 4x + 5x − 26 3 a) lim . ĐS: 84 − b)
x − x + x − . ĐS: − x→− ( 2 lim 4 2 )1 x→2 2
x − x + x − 2 4 3 2
x − x + 2x − 2  khi x  1
 Tìm m để hàm số f ( x) 3 =  1− x
liên tục tại điểm x = 1. ĐS: m = 2 − 0  2 4mx + 6x +1 khi x = 1 142
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC Bài 18.
(HKII – THPT Nam Kỳ Khỏi Nghĩa)
 Tính các giới hạn sau 3 2
x − 5x + 3x + 9 2 2 x +1 − 4x +1 a) lim . ĐS: 0 b) lim . ĐS: 1 − 4 2 x 3 → x − 8x − 9 x→− 3 − x 3
x − 4x + 3 khi x 1  2   x − 4x + 3
Tìm m để hàm số f ( x) = 
liên tục tại điểm x = 1 ĐS: m = 2 0 1  mx khi x = 1 4
Bài 19. (HKII – THPT Nguyễn Chí Thanh).
 Tính các giới hạn sau 3 2
x − 3x − 9x + 2 a) lim . ĐS: 3 3 x 2 →− x − 7x − 6 b) − − − − . ĐS: 0 →+ ( 2 lim 2x 1 4x 4x 3 x ) 2  x − 5x + 6  khi x  3
 Tìm a để hàm số f ( x) =  x + 6 − 3
liên tục tại điểm x = 3 . ĐS: a =1 0 ax+3 khi x  3 Bài 20.
(HKII – THPT Nguyễn An Ninh).
 Tính các giới hạn sau 3 2
2x + 3x − 8x −12 a) lim . ĐS: 4 − 2 x 2 →− x − x − 6 5 b) + + + . ĐS: 1 − →− ( 2 lim 2x 4x x 5 x ) 4 2  x + 7 − 4    khi x 3
Tìm m để hàm số f ( x) =  x − 3
liên tục tại điểm x = 3 . ĐS: 9 m = 0  8 x − 2m khi x = 3
Bài 21. (HKII – THPT Nguyễn Du).
 Tính các giới hạn sau 2 x − 5x + 6 a) lim . ĐS: 1 − 3 2
x→2 x − 3x + 7x −10 7   b) x + + − →−   ( 2 lim x 1 x x ). ĐS: 12 2  x +3 − 2  khi x  1   −
Tìm m để hàm số f ( x) x 1 = 
liên tục tại điểm x = 1. ĐS: m = 1  0  1 2 m x − khi x = 1  2 143
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
Bài 22. (HKII – THPT Mạc ĐĨnh Chi).
 Tính các giới hạn sau
 2.3n − 3.7n + 4  a) lim   . ĐS: −  3.2n + 4  2  x x 4 2  − + − b) lim   . ĐS: 1 − 2 x→0  x + x    4 c) + + + + . ĐS: 1 →− ( 2 lim 3x 1 9x 3x 4 x ) 2  4x + 5 − 5  khi x  5   −
Xét tính liên tục của hàm số f ( x) x 5 = 
tại x = 5 . ĐS: liên tục 0 2x  khi x  5 25 Bài 23.
(HKII – THPT Gia Định).
 Tính các giới hạn sau 4 3
2x − 6x + x − 3 a) lim . ĐS: 55 2 x 3 → 4x −11x − 3 13 3
 7x +8. 9x − 28 −12  b) lim    . ĐS: 17 3 2  x→4
x − 4x + 2x − 8   54 3
12x + 4 − 36x + 8 c) lim . ĐS: 3 − 3 2 x→0 2x −12x 16 d) (3 3 2 lim
64x − 4x − 4x + . ĐS: 11 →+ )1 x 12
x +1− x + 3  khi x  1 x −1    3
Xét tính liên tục của hàm số f ( x) = 
khi x = 1 tại x = 1. ĐS: liên tục 4  0 3 2
3x − 6x −3x + 6 khi x 1  2
 3x −14x +11 Bài 24.
(HKII – Nguyễn Hiền).
 Tính các giới hạn sau 4 2 9x − 82x + 9 a) lim . ĐS: 80 3 x 3 → 2x − 54 9 (2x +3) 2x + 4 b) lim . ĐS: 1 − x→− (2x +5)2 2 144
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
 3x +1 − 5− x    khi x 1
Xét tính liên tục của hàm số f ( x) 3 2 =  2
− x + 3x − x
tại điểm x = 1. ĐS: liên 0  2 − x +1 khi x  1 tục
Bài 25. (HKII – THPT Nguyễn Hữu Cảnh).
 Tính các giới hạn sau 2 2x − 3x +1 a) lim . ĐS: 1 − 2 x 1
→ 4 − 3x − x 5 x − 6 − x b) lim . ĐS: 5 − 2
x→2 −x + 3x − 2 4  x +1 − 2  khi x  3   x − 3
Xét tính liên tục của hàm số f ( x) = 
tại điểm x = 3 . ĐS: liên tục x − 2 0  khi x  3  4
Bài 26. (HKII – THPT Nguyễn Thái Bình). 2
x + x −12 khi x  3  −  x 3
Xét tính liên tục của hàm số f ( x) = 
tại điểm x = 3 . ĐS: liên tục 2  x + 5 khi x = 3  x −1
 Chứng minh phương trình ( 2
m + m + )( x − ) 2 3
2 + x + 2x − 4 = 0 có nghiệm m  .
Bài 27. (HKII – THPT Tây Hạnh).
 Tính các giới hạn sau 3 2
x − 5x + 6x a) lim . ĐS: 1 − 2 x 3 → 9 − x 2 b) − + . ĐS: 1 →− ( 2 lim 4x x 2x x ) 4 m( 2 m − 3) khi x = 2 
 Tìm m để hàm số f ( x) =  x − 2
liên tục tại x = 2 .ĐS: m = 1 và  0 khi x  2
 5 − 2x − 3− x m = 2 −
 Chứng minh phương trình 4 3 2
5x + 3x − 6x − x +1 = 0 có ít nhất hai nghiệm trong khoảng ( 1 − ) ;1 . B. LỜI GIẢI Bài 1. 1) 145
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC x + 2 − 2 1 1 a) Ta có lim = lim = . 2 x→2 x→2 x − 4
(x + 2)( x+ 2 + 2) 16 3 1 + + 2 x 4 2 4x + 3x +1 x x b) Ta có lim = lim = 2 . x→+ x −1 x→+  1  x 1−    x  2) Ta có: +) f ( ) 1 = 4 .
+) lim f ( x) = lim (2x + 2) = 4 . + + x 1 → x 1 → 2 3x − 2x −1
+) lim f ( x) = lim = lim (3x + ) 1 = 4 . − − − x 1 → x 1 → − x 1 x 1 →
Suy ra lim f ( x) = lim f ( x) = f ( )
1 , nên hàm số đã cho liên tục tại x = 1. − + 0 x 1 → x 1 → Bài 2. 1) Tính: 2 2x − x −10 (x + 2)(2x −5) 2x − 5 9 a) lim = lim = lim = − . 3 x→− x − x + 6
x→− ( x + 2)( 2 2 2 x − 2x + 3) 2 x→ 2 − x − 2x + 3 11 8x + 2x − 3 b) lim x + x − x + = x→− (3 2 3 ) 2 2 lim x→− 2
3x − x − 2x + 3  2 3  2 x 8 + −   2  x x  = lim = − . x→−  2 3  x 3 + 1− +  2 x x   2. Ta có - f (2) = 2 . x − 3 −1 x + 2 - lim f ( x) 2 = lim = lim = 2 . x→2 x→2 x→2 2 x − 2 x − 3 +1 Bài 3. 1. − + − (3x − ) 1 ( 2 3 2 2x − x x x x + ) 2 1 6 5 4 1 2x − x +1 2 a ) Ta có lim = lim = lim =  4 2 + − − + + + + + + x→ 9x 8x 1 x→ (3x ) 1 ( 3 2 1 1 3x x 3x ) 3 2 1 1 x→ 3x x 3x 1 5 3 3 3 3 − x b) Ta có lim
x + x + + x + = x→− ( 2 9 3 1 3 )1 lim x→−  3 1 1  x  − 9 + + − 3−  2 x x x   3 − 1 = lim =  x→− 3 1 1 2 − 9 + + − 3− 2 x x x 2. Ta có f ( ) 1 = a + b .
- lim f ( x) = lim + + = + + . − − ( 2 x
2bx 3a) 3a 2b 1 x 1 → x 1 → 146
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 2 2x + 5x − 7
- lim f ( x) = lim = lim (2x + 7) = 9 . + + + x 1 → x 1 → − x 1 x 1 →
Hàm số f ( x) liên tục tại x = 1 khi và chỉ khi 0  + + =  = − f ( x) =
f ( x) = f ( ) 3a 2b 1 9 a 10 lim lim 1     − + x 1 → x 1 → a + b = 9 b  =19
3. Ta có hàm số f ( x) = ( 2 m − m + )( 2 3 2
x − 3x + 2) + (3 − 2x)(3 − 2m) liên tục trên .
Mặt khác f ( ) f ( ) = ( − m)( m − ) = −( m − )2 1 2 3 2 2 3 2 3 . 3 - Nếu m = thì f ( )
1  f (2) = 0 nên phương trình có nghiệm x = 1; x = 2. 2 3 - Nếu m  thì f ( )
1  f (2)  0 nên phương trình đã cho có ít nhất một nghiệm 2 thuộc khoảng (1; 2) . Vây phương trình ( 2 m − m + )( 2 3 2
x − 3x + 2) + (3 − 2x)(3 − 2m) = 0 luôn có nghiệm với mọi m . x −1 1 1 Bài 4. 1. a) Ta có lim = lim = . 2 x 1 → x 1 x −1 → ( x + ) 1 ( x + ) 1 4 3 2
x + 3x + 2x x ( x + ) 1 ( x + 2) x ( x + ) 1 2 b) Ta có lim = lim = lim = − . 2 x→ 2 − x→ 2 x − x − 6 −
(x + 2)(x −3) x→ 2− x −3 5 2. Ta có - f ( ) 1 = 1 − . 2 x − 3x + 2
- lim f ( x) = lim = lim(x − 2) = 1 − . x 1 → x 1 → x 1 x −1 →
Suy ra lim f ( x) = f ( )
1 nên hàm số đã cho liên tục tại x = 1. 0 x 1 →
x − x − x +1 (x − )2 3 2 1 ( x + ) 1 Bài 5. 1. a) Ta có lim = lim = lim x +1 = 2. 2 2 ( ) x 1 → x 1 x − 2x +1 → (x − ) x 1 1 → − x − −( 3 x + 8) −( 2 3 x − 2x + 4 1 3 ) b) Ta có lim = lim = lim = 2 − . x→ 2 − x→ 2 x + 2 − ( →− x + 2)( 3 1− x + 3) x 2 3 1− x + 3 lim (x −5) = 1 −  0 − x→4   − 2 x 5
c) Ta có  lim ( x − 4) = 0  lim = − . − − x→ x→  (x − 4)2 4 4 (  x − 4  )2  0 khi x  4 147
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  1  x +1   x +1  x  1 d) Ta có lim
x + x + + x = = lim = −  x→− ( 2 1 ) lim x→− 2
x + x +1 − x x→−  1  2 x  − x +1+ −1 x   2) Ta có
- f (0) = a −1. x (1+ 1− x x )
- lim f ( x) = lim = lim = 2 . − − − x→0 x→0 x→0 1− 1− x x  4 − x
- lim f ( x) = lim a − 5 + = a −1   . + + x→0 x→0  x +1 
Hàm số f ( x) liên tục tại x = 0 khi và chỉ khi. 0
lim f ( x) = lim f ( x) = f (0)  a −1 = 2  a = 3 . − + x→0 x→0  2  x  − 1+ + 3 2
x + 2x + 3x x   2 Bài 6. 1. Ta có lim = lim = − . x→− 2 4x +1 − x + 2 x→−  1 2  3 x  − 4 + −1+  2 x x   2. Ta có - f ( ) 1 = 1.
- lim f ( x) = lim + = + . − − ( 2 ax 2x) a 2 x 1 → x 1 →
- lim f ( x) = lim cos( x − ) 1 = 1. + + x 1 → x 1 →
Hàm số f ( x) liên tục tại x = 1 khi và chỉ khi. 0
lim f ( x) = lim f ( x) = f ( )
1  a + 2 = 1  a = 1 − . − + x 1 → x 1 →
3. Ta có hàm số f ( x) 4 3 2
= x − x − 2x −15x − 25 liên tục trên . Mặt khác f (0) = 2 − 5  0 . ( 4 3 2
lim x − x − 2x −15x − 25) = + . x→− ( 4 3 2
lim x − x − 2x −15x − 25) = + . x→+ Vậy phương trình 4 3 2
x − x − 2x −15x − 25 = 0 có ít nhất một nghiệm trên khoảng ( ;
− 0) và có ít nhất một nghiệm trên khoảng (0;+) . Do đó phương trình 4 3 2
x − x − 2x −15x − 25 = 0 có ít nhất một nghiệm dương và một nghiệm âm. x − 3 x − 3 1 1 Bài 7. 1) a) Ta có lim = lim = lim = 2 x 3 → x 3 x + 2x −15
→ ( x − 3)( x + 5) x 3 → x + . 5 8 148
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC  1  3   1  3  ( x +   −x −  +   − −  3x + ) 3 2 3 2 2 2 2 1 2x − 3  x x    x x   b) Ta có lim = lim = lim = 2 . 2 x→− 3 x − x + x →−  1 x→−   1  2 x 3 − + 3 − +      x   x  2) Ta có - f ( ) 1 1 = m − . 2 1 − 1
- lim f ( x) = lim = − x 1 → x 1 → 7( x + ) 1 14
Hàm số f ( x) liên tục tại x = 1 khi và chỉ khi. 0 −
f ( x) = f ( ) 1 1 3 lim 1  m − = −  m = . x 1 → 2 14 7 x − x + x − (x − ) 1 ( 2 3 2 4x − 3x +16 4 7 19 16 ) 2 4x − 3x +16 17 Bài 8. 1. Ta có lim = lim = lim = . 2 x 1 → 5x − 8x + 3 x→− (x − ) 1 (5x − 3) x→− 5x − 3 2 2. Ta có
- f (2) = 4 − m .
- lim f ( x) = lim (2x − m) = 4 − m . − − x→2 x→2 4 − x - lim f ( x) 2 = lim = 0 . + + x→2 x→2 x + 2 −1
Hàm số f ( x) liên tục tại x = 2 khi và chỉ khi. 0
lim f ( x) = lim f ( x) = f (2)  4 − m = 0  m = 4 . − + x→2 x→2
3. Ta có hàm số f ( x) 4 3 2
= x − x − 2x −15x − 25 liên tục trên .
Mặt khác f (0) =1  0 .   lim f ( x) 2 1 2015 2 = lim x m − m + 4 − x + = −   . (Vì 2
m − m + 4  0 với mọi 2014 2015 x→− x→−  x xm ) ( 4 3 2
lim x − x − 2x −15x − 25) = + . x→+ Vậy phương trình ( 2 m − m + ) 2015 4 x
− 2x +1 = 0 có ít nhất một nghiệm trên khoảng ( ;
− 0) (nghiệm âm) với mọi giá trị của tham số m .  5  x − 6   5 − 6xxBài 9. 1) a. Ta có lim = lim = 3 − . x→+ 3 + 2 x x →+  3  x + 2    x  149
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
 lim (x − 3) = −1 0 + x→2  x − 3  b. Ta có lim
= − vì lim ( x − 2) = 0 . + + x→2 x − 2 x→2 
x − 2  0 khi x  2   3  c. Ta có lim ( 3 3x − 2x ) 3 = lim x − 2 = +   . 2 x→− x→−  x  2) Ta có: f ( ) 1 = m + − − + + f ( x) 2 x 3x 4 (x ) 1 ( x 4) x 4 5 lim = lim = lim = lim = . 3 x→ x→ x −1 x→ ( x − ) 1 ( 2 1 1 1 x + x + ) 2 x 1 1 → x + x +1 3 Hàm số 5
f ( x) liên tục tại x = 1 khi và chỉ khi lim f ( x) = f ( ) 1  m = . 0 x 1 → 3 2 x − 3x + 2 (x −2)(x − ) 1 x −1 1
Bài 10. 1) a. Ta có lim = lim = lim = . 2 x→2 x→2 x − 4
(x −2)(x + 2) x→2 x + 2 4 2x 2x b. Ta có lim \
x + x − x − x = = = . x→+ ( 2 2 ) lim lim 1 x→+ 2 2 x
x + x + x − x →+  1 1  x  1+ + 1−  x x   2) Ta có 2
f (5) = 3 , lim f ( x) = lim − + = , − − → → ( x 5) 3) 3 x 5 x 5 − − + x − (x 5)( 2x 1 3 5 ) lim f ( x) = lim = lim = 3. + + + x→5 x→5 x→5 2x −1 − 3 2 ( x − 5)
Suy ra lim f ( x) = lim f ( x) = f (5) nên hàm số đã cho liên tục tại x = 5 . − + 0 x 5 → x 5 → 2 x − 5x + 6 x − 3 x − 2
3) Ta có: f (3) = 6m +1, lim f ( x) ( )( ) = lim = lim =1. x 3 → x 3 → x 3 x − 3 → x − 3
Hàm số đã cho liên tục tại x = 3 khi và chỉ khi lim f ( x) = f (3)  6m +1 = 1  m = 0 . 0 x 3 → x + 2 − 2
Bài 11. 1) Ta có f ( ) 1 2 = 2m +
; lim f ( x) = lim = 4 + + x→2
x→2 ( x − 2)( x + 2 + 2) + − f ( x) x 2 2 1 1 lim = lim = lim = . + + + x→2
x→2 ( x − 2)( x + 2 + 2) x→2 x + 2 + 2 4 1 1
Hàm số đã cho liên tục tại điểm x = 2 khi 2m + =  m = 0 . 0 4 4
2) Đặt f ( x) = ( 2 − m ) 5 1
x − 3x −1. Ta có, f ( ) = − f (− ) 2 0 1, 1 = m +1 . 150
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC
Suy ra, f ( ) f (− ) 2 0 .
1 = −m −1  0, m
 . Mặt khác, vì f ( x) là hàm số đa thức liên tục trên
nên f ( x) liên tục trên  1
− ;0 . Do đó, phương trình đã cho có ít nhất một nghiệm trong khoảng
(−1;0) với mọi giá trị của m . Vậy ta có đpcm. Bài 12. 1) Tính các giới hạn 1 9 − + 2 3 2 3n − n + 9 3 − 0 + 0 3 a) lim = lim n n = = − . 2 1− 2n 1 0 − 2 2 2 n − 2 3 2  1   1  ( − + 1− 3n) ( 2 n + )2 3 3 1     2 1  n   n  (0−3)3 (1+ 0)2 b) lim = lim = = 9 − . 7 3n − 2 2 3 − 0 3 − 7 n 2 2 x − 3 − x − x +1
c) lim x − + x − x + = x→− ( 2 3 1) ( ) ( ) lim x→− 2
x − 3 − x − x +1 5 − x + 8 = lim x→− 1 1
x − 3 − x 1− + 2 x x 8 5 − + 5 = lim x = − . x→− 3 1 1 2 1− + 1− + 2 x x x 2) Ta có f ( ) 16 2 = − . 3 − + − + + − x − ( 2 2 x 4)(x 7x 10 )
(x 2)(x 7x 10 4 ) 16 lim = lim = lim = − . 2 x→2 x→2 x→2 x − 7x −10 x − 7x +10 x − 5 3
Ta thấy f (2) = lim f ( x) . Vậy hàm số đã cho liên tục tại x = 2 . 0 x→2 3) Đặt f ( x) 4 2
= 4x + 2x − x − 3. Ta có, f (− ) 1 = 4, f (0) = 3 − , f ( ) 1 = 2 . Suy ra, f (− ) 1 . f (0) = 1
− 2  0, f (0). f ( ) 1 = 6 −  0 .
Vì f ( x) là hàm số đa thức liên tục trên
nên f ( x) liên tục trên các đoạn  1 − ;0 và 0;  1 .
Do đó, phương trình f ( x) = 0 có ít nhất một nghiệm trên mỗi khoảng (−1;0) và (1;0) .
Vậy phương trình đã cho có ít nhất hai nghiệm. Bài 13. 1) Tính các giới hạn 3 2 + 3 4 3n + 2 a) = lim = lim n n A = 0 . 4 3
n + 2n − 5n + 2 2 5 2 1+ − + 3 4 n n n n  1  −1   3n − 6n  2  b) B = lim = lim = − . 4n + 3 n  2  3 +    3  6n 151
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC − − − (x −3)( 2 3 2 2x + x x x x + ) 2 1 2 5 2 3 2x + x +1 11 c) C = lim = lim = lim = . 2 x 3 → x 3 x − 9 → (x −3)(x +3) x 3 → x + 3 3 1 1+
4x + x +1− 4x 1 d) = lim x D
x + x + − x = = = . x→+ ( 4 1 2 ) 2 2 2 lim lim x→+ 2 4x + x +1 + 2 x x →+ 1 1 4 4 + + + 2 2 x x  2 − x  khi x  2
2) y = f ( x) =  x + 7 − 3 .
2ax+3 khi x  2  2 − x  khi x  2
a) Khi a =1, ta được y = f ( x) =  x + 7 − 3 .
2x+3 khi x  2 Ta thấy f (2) = 7 .
lim f ( x) = lim (2x + 3) = 7 . − − x→2 x→2 − + + − x (2 x)( x 7 3 2 ) lim f ( x) = lim = lim = lim − + − = − . + + + + ( x 7 3) 6 x→2 x→2 x→2 + − + − x→2 x 7 3 x 7 9
Vì lim f ( x)  lim f ( x) nên hàm số đã cho không liên tục tại x = 2 . − + x→2 x→2
b) Ta có f (2) = lim f ( x) = 4a + 3 . − x→2 lim f ( x) = 6 − . + x→2
Do đó hàm số đã cho liên tục tại 9
x = 2 khi 4a + 3 = 6 −  a = − . 4 3) Đặt f ( x) 5 4
= x − 3x + 5x − 2 . Ta có, f (0) = 2 − , f ( ) 1 = 1, f (2) = 8 − , f (3) =13 .
Suy ra, f (0). f ( ) 1 = 2 −  0, f ( ) 1 . f (2) = 8
−  0, f (2). f (3) = 1 − 04  0 .
Mặt khác, vì f ( x) là hàm đa thức liên tục trên nên f ( x) liên tục trên các đoạn 0  ;1 ,1; 2,2, 
3 .Do đó, phương trình f ( x) = 0 có ít nhất một nghiệm trên các khoảng (0 ) ;1 , (1; 2),(2;3) .
Vậy phương trình đã cho có ít nhất 3 nghiệm. Bài 14. 1) Tìm các giới hạn x − 5 a) lim =0. x 5 → x − 5 2 2 x + 5 − 3 x + 5 − 9 x − 2 2 b) lim = lim = lim = − . x→ 2 − x→ 2 x + 2 − ( →− x + 2)( 2 x + 5 + 3) x 2 2 + + 3 x 5 3
2) Ta có f (3) = 12a + 5. x − x + x − x − lim f ( x) 2 4 3 ( 3)( ) 1 = lim = lim = lim(−x + ) 1 = 2 − . x 3 → x 3 → x 3 → x 3 3 − x 3 − x →
Hàm số đã cho liên tục tại điểm 7
x = 3 khi 12a + 5 = 2 −  a = − . 0 12 152
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC 3) Đặt f ( x) 5 4 3
= x − 3x + 4x − 5 . Ta có, f (0) = 5 − , f ( ) 1 = 1.
Suy ra, f (0). f ( ) 1 = 5 −  0 .
Mặt khác, vì f ( x) là hàm đa thức liên tục trên nên f ( x) liên tục trên các đoạn 0;  1 .Do
đó, phương trình f ( x) = 0 có ít nhất một nghiệm trên các khoảng (0; ) 1 .
Vậy phương trình đã cho có ít nhất một nghiệm trong khoảng (0; ) 1 . Vậy ta có dpcm. Bài 15.  Ta có f ( ) 1 = 2 − a + 7
lim f ( x) = lim ( 2 − a + 7) = 2 − a + 7 + + x 1 → x 1 → + − + − f ( x) x 3 2 x 3 4 1 1 lim = lim − lim = lim = . − − 2 − − x 1 → x 1 → − + x 1 2x 3x 1 →
(x − 2)(2x − )
1 ( x + 3 + 2) x 1 → (2x − ) 1 ( x + 3 + 2) 4 1 27 27
Hàm số đã cho liên tục tại x = 1 khi 2
− a + 7 =  a = . Vậy a = là giá trị cần tìm. 0 4 8 8
 Đặt f ( x) = ( 2 m − m + ) 3 3
3 x + 2x − 3 = 0 . 2  3 
Ta có f (0) = −3 , f (2) 2
= 8m − 24m + 25 = 8 m − + 7  0 m   
. Suy ra f (0) f (2)  0 m  .  2 
Mặt khác, vì f ( x) là hàm đa thức liên tục trên
nên f ( x) liên tục trên đoạn 0; 2 .
Do đó phương trình f ( x) = 0 luôn có ít nhất một nghiệm trong khoảng (0;2) với mọi m . Vậy ta có đpcm. Bài 16.  Tính các giới hạn
x + x − x −1 x −1 a) lim
x + x − x + = = lim x→− ( 1) 2 2 2 2 lim x→− 2 2 x + x + x +1 x→− 1 1 x 1+ + x 1+ 2 x x 1 1− 1 = lim x = − . x→− 1 1 2 − 1+ − 1+ 2 x x sin x − x sin x 2 sin .2 x sin tan x − sin x
sin x (1− cos x) b) cos lim = lim x = lim 2 = lim 3 3 3 x→0 x→0 x→0 4x 4x cos .4 x x 3 x→0 cos .4 x x   x 2  sin  1 sin x 1  2 lim . .  = = 2
x→0  8 cos x x x    8       2    Ta có 153
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !
ĐS&GT_11_CHƯƠNG 4_GIỚI HẠN VÀ LIÊN TỤC f ( ) 2 1 = m + 7m
lim f ( x) = lim ( 2 2 m x + 7mx) 2 = m + 7m − − x 1 → x 1 → − + + − x (1 x)( x 8 3 1 ) lim f ( x) = lim = lim = lim − + − = − + + + + ( x 8 3) 6 x 1 → x 1 → x 1 → + − + − x 1 x 8 3 x 8 9 → m = 1 −
Do đó, hàm số đã cho liên tục tại x = 1 khi 2 2 m + 7m = 6
−  m + 7m + 6 = 0  . 0  m = 6 − Vậy m = 1 − ,m = 6
− là các giá trị cần tìm.
 Đặt f ( x) 14 = mx − ( 2 m + ) 15 3 7 x − 5 . 2  1  7 Ta có f (0) = 5 − , f (− ) 2 2
1 = 3m + m + 2 = 2m + m + +  0 m    . Suy ra  2  4 f (− ) 1 f (0)  0 m  .
Mặt khác, vì f ( x) là hàm số đa thức liên tục trên
nên liên tục trên đoạn  1 − ;0 .
Do đó phương trình f ( x) = 0 có ít nhất một nghiệm trong khoảng (−1;0) .
Vậy phương trình đã cho luôn có ít nhất một nghiệm với mọi m . 154
Fb: ThayTrongDGL Tài liệu biên soạn và sưu tầm Chúc các em học tốt !