Các dạng toán về giới hàm số lớp 11 (có lời giải)

CÁC DẠNG TOÁN VỀ GIỚI HẠN SỐ LỚP 11
¦Dạng ➊ Sử dụng định nghĩa giới hạn dãy số và những quy tắc cơ bản
1 Phương pháp giải
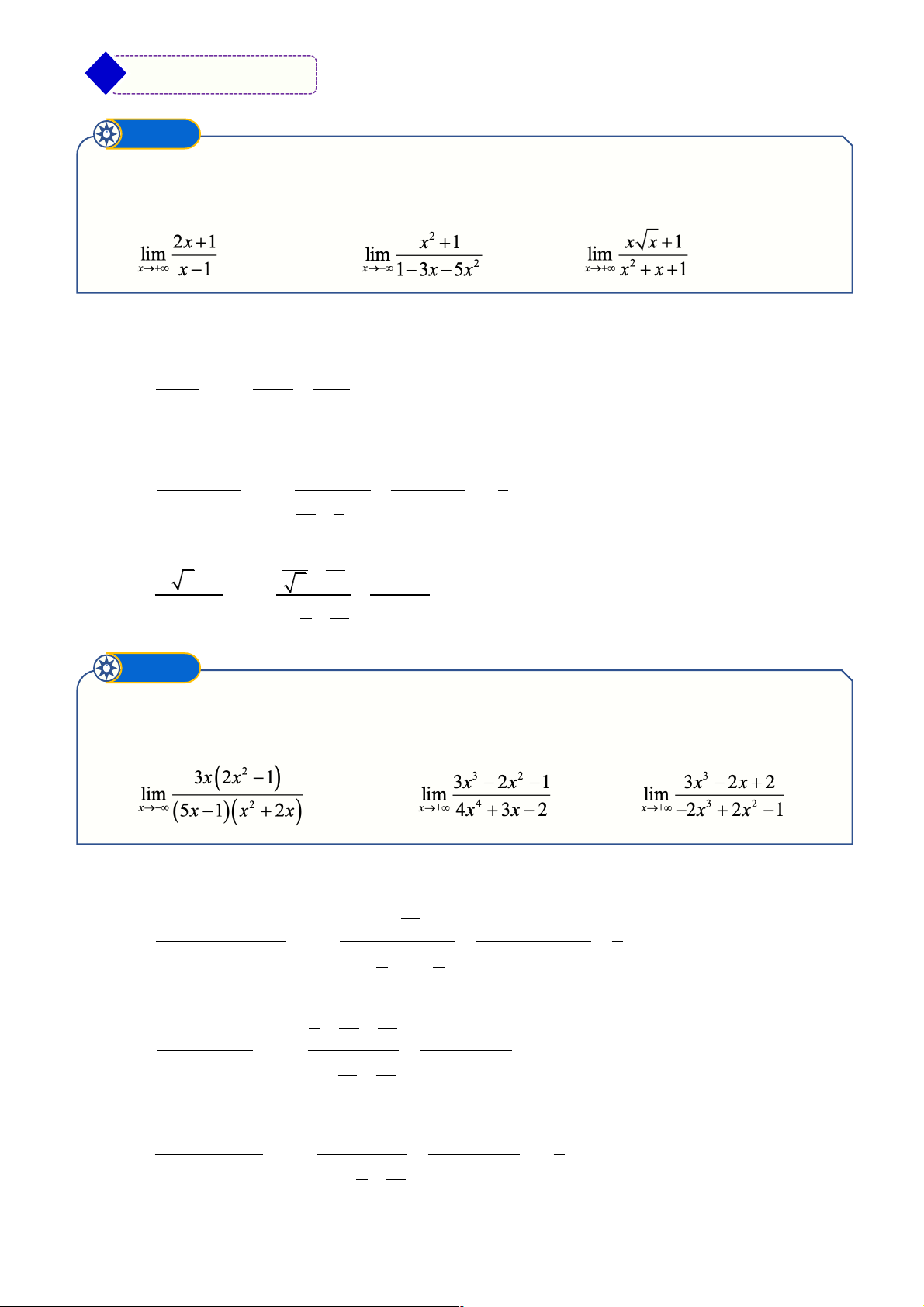
• Theo định nghĩa thì giới hạn hàm số
trên cơ sở giới hạn các dãy . Nếu có 2
dãy và cùng tiến đến mà thì không tồn tại
• Với mọi số nguyên dương k, ta có: • Xác định dấu hoặc
dựa trên dấu của tích số, thương số, & Ví dụ minh họa Ví dụ ➊
Tính giới hạn của các hàm số a) khi b) khi § Lời giải
a) Tập xác định của hàm số là [ 5;
- + ¥). Chọn dãy số (x x Î[ 5; - + ¥ lim x = 3 - n ) n ) với sao cho . n
Theo định nghĩa lim 2x +10 = lim 2x +10 3 n x®- n®¥
Theo định lí về giới hạn của dãy số, ta có 𝑙𝑖𝑚 $2𝑥! + 10 = +𝑙𝑖𝑚(2𝑥! + 10) !→# !→# = 2.lim x +10 = 2. - + = = n ( 3) 10 4 2. n®¥ F Vậy lim 2x +10 = 2 x 3 ®-
b) Tập xác định của hàm số là ℝ nên chọn dãy số (xn ) sao cho 𝑙𝑖𝑚𝑥! = 3 !→# lim(2x + 3) 2x + 3 2x + 3 Ta có n lim f (x) = lim = lim n n®¥ = 2 2 2 x 3 ® x 3 ® 3 + 6 n®¥ x + 6 lim(x + 6) n n n®¥ 2.lim x + 3 n + n®¥ 2.3 3 3 = = = . 2 2 lim x + 6 3 + 6 5 n n®¥ 2x + 3 3 FVậy lim = 2 x®3 x + 6 5 Trang 1
@ Chú ý: Nếu hàm số f (x) là một đa thức, là một phân thức đại số hoặc một hàm số lượng giác có tập xác
định là D thì với mỗi x Î D ta có lim f (x) = f (x0 ) 0 x® 0 x Ví dụ ➋
Tính giới hạn của các hàm số a) khi b) khi § Lời giải lim( 2 2 x x + + )1 1
a) Theo định lí 1, ta có lim f (x) x 3 = lim ® = x 3 ® x 3 ® 2 x lim 2 x x 3 ® 2
lim x + lim1 lim.lim+ lim1 3.3+1 5 x 3 ® x 3 ® x 3 ® x 3 ® x 3 ® = = = = . lim 2.lim x lim 2. limx 2 3 3 x 3 ® x 3 ® x 3 ® x 3 ® 2 x +1 5 F Vậy lim = x 3 ® 2 x 3 b) Vì ( 2
2x - x - 6) ® 0 khi x ® 2 nên chưa thể áp dụng ngay Định lí 1. 2 ìx + 3x -10 = ï (x - 2)(x + 5) x +
Nhưng với x ¹ 2 , ta có í suy ra f (x) 5 = . 2 ï2x - x - 6 = î (x - 2)(2x + 3) 2x + 3 lim x + (x +5) lim x + lim5 5 2 + 5 F Vậy x®2 x®2 x®2 lim f (x) = lim = = = =1 x®2 x®2 2x + 3
lim(2x + 3) 2.lim x + lim3 2.2 + 3 x®2 x®2 x®2 Ví dụ ➌ Tìm các giới hạn sau: a) b) c) § Lời giải æ x -1 æ ö ( 3 - )2 2 -1ö 8 a) lim ç ÷ = lim ç ÷ = - = 4 - x 3 ®- x 3 è x +1 ®- ç ø 3 - +1 ÷ 2 - è ø 2 æ 4 - x ö
æ (2 - x)(2 + x) ö b) lim ç ÷ = lim ç ÷ = lim (2 - x) = 4 x 2 ®- x 2 ®- x 2 è x + 2 ø x + 2 ®- è ø æ æ + - ö + - + + ö æ ö x ( x 3 3)( x 3 3 3 3 ) x - 6 1 1 c) lim ç ÷ limç ÷ limç ÷ = = = lim = x®6 ç ÷ x®6 - ç - ÷ x®6 x 6 x 6 ç è ø (x - 6)
x®6 ( x + 3 + 3) 6 è ø è ( x+3 +3)÷ø Trang 2
¦Dạng ➋ Khử dạng vô định về 0/0
1 Xét bài toàn: Tính khi , trong đó là các đa thức và căn thức.
1 Phương pháp
• Phân tích tử và mẫu thành các nhân tử và giản ước: • Nếu đều chứa nhân tử
ta sẽ tiếp tục phân tích thành các nhân tử. & Chú ý: • Với
là đa thức (thường là hàm số bậc hai, bậc ba, bậc bốn…) thì ta phân tích
nhân tử bằng việc giải phương trình • Với
là căn thức, ta sẽ sử dụng phương pháp nhân liên hợp (liên hợp số hoặc
liên hợp biến) để phân tích nhân tử.
• Sử dụng các hằng đẳng thức, nhóm số hạng, phân tích ra thừa số bậc 2, chia đa thức, sơ đồ Hoócne,…
• Chia tách thành các phân thức bằng cách thêm bớt đại lượng đơn giản nhất theo x hoặc
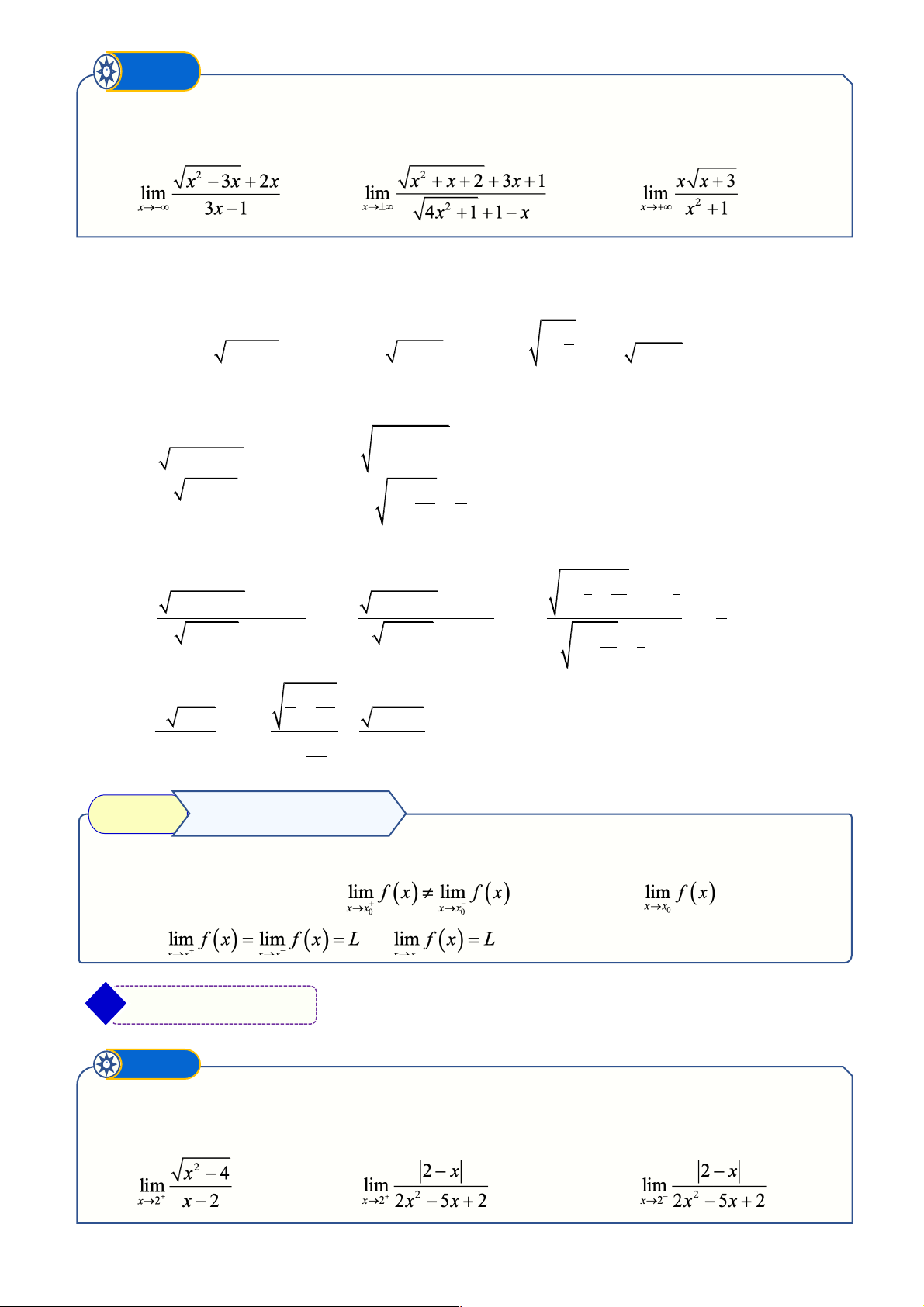
hằng số mà các giới hạn mới vẫn giữ nguyên dạng vô định . • Nếu thì & Ví dụ minh họa Ví dụ ➊ Tìm các giới hạn sau a) b) c) d) § Lời giải 2 x - 3x + 2 (x - )1(x - 2) a) lim = lim = lim(x - ) 1 = 1 x®2 x®2 x®2 x - 2 x - 2 2 x - 2x x ( x - 2) x ( x - 2) x b) lim = lim = lim = lim = 1 - 2 x® 2
- x + 6x - 4 x® 2 - ( 2 2 2
x - 3x + 2) x®2 2 - (x - ) 1 (x - 2) x®2 2 - (x - ) 1 Trang 3 x - 3x + 2 (x - )2 3 1 (x + 2) æ x + 2 ö 3 1 c) lim = lim = lim = = 4 ç ÷ x 1 ® x 1 x - 4x + 3 ® (x - )2 1 (x + 2x + 3) 2 2 x 1
® è x + 2x + 3 ø 6 2
x - x - x +1 (x - )2 3 2 1 (x + ) 1 (x - )1(x + )1 d) lim = lim = lim = 0 2 x 1 ® x 1 -x + 3x - 2 ® -( x - ) 1 (x + 2) x 1 ® x + 2 Ví dụ ➋
Tìm giới hạn các hàm số sau: a) b) c) d) § Lời giải x - x - (x -3)( 3 2 4 2
x + 3x + 8x + 24 72 ) 3 2
x + 3x + 8x + 24 51 a) lim = lim = lim = 2 x 3 ® x 3 x - 2x - 3 ® (x + )1(x -3) x 3 ® x +1 2
x - x + x + (x - 3)( 2 3 2 x - 2x - 3 5 3 9 ) 2 x - 2x - 3 b) lim = lim = lim = 0 4 2 x® x - 8x - 9 x® ( x - 3)( 3 2 3 3
x + 3x + x + 3) 3 2
x®3 x + 3x + x + 3 - + (x - )1( 5 4 3 2 2 6
4x + 4x + 4x + 4 5 4 x - x x x x ) 5 4 3 2
4x + 4x + 4x + 4x - x c) lim = lim = lim = ¥ x® (1- x)2 x® (1- x)2 1 1 x 1 ® (x - )1 - (x - a)( 3 2 2 3 4 4
x + ax + a x + a x a ) d) = = ( 3 2 2 3
x + ax + a x + a ) 3 lim lim lim = 4a x®a x®a x®a x - a x - a Ví dụ ➌ Tính các giới hạn sau a) b) c) § Lời giải 2 x -16 (x - 4)(x + 4) x + 4 8 a) lim = lim = lim = 2 x®4 x®4 x + x - 20
(x - 4)(x + 5) x®4 x + 5 9 2 4 - x (2 - x)(2 + x) 2 - x 1 b) lim = lim = lim = 3 x®- x + 8 x®- ( x + 2)( 2 2 2 x - 2x + 4) 2 x 2 ®- x - 2x + 4 3 2 x + 3x + 2 (x + )1(x + 2) x +1 1 c) lim = lim = lim = 2 x 2 ®- x 2 2x + x - 6
®- ( x + 2)(2x - 3) x 2 ®- 2x - 3 9 Trang 4
¦Dạng ➌ Khử dạng vô định ∞/∞, 0.∞ hoặc ∞ - ∞
➀ Bài toàn 1: Tính khi , trong đó là các đa thức và căn thức.
1 Phương pháp giải: Chia cả tử và mẫu cho
với n là số mũ bậc cao nhất của biến số x trong mẫu thức. Nếu
có chứa biến x trong dấu căn thức thì đưa ra ngoài dấu
căn (với k là số mũ bậc cao nhất của x trong dấu căn). & Chú ý: • Khi
thì ta xử lý giống như với giới hạn của dãy số. • Khi ta cần lưu ý khi đưa
ra ngoài dấu căn thức bậc chẵn.
& Dạng hay gặp chính là khi và khi @ Xét hàm số
có hệ số của hạng tử bậc cao nhất của
lần lượt là a,b. Và kí hiệu
lần lượt là bậc của thì: • Nếu thì • Nếu thì • Nếu thì
➋ Bài toán 2: Tính khi và
1 Phương pháp giải: Ta biến đổi để đưa về dạng Hoặc biến đổi để đưa về dạng .
➌ Bài toán 3: Tính khi và
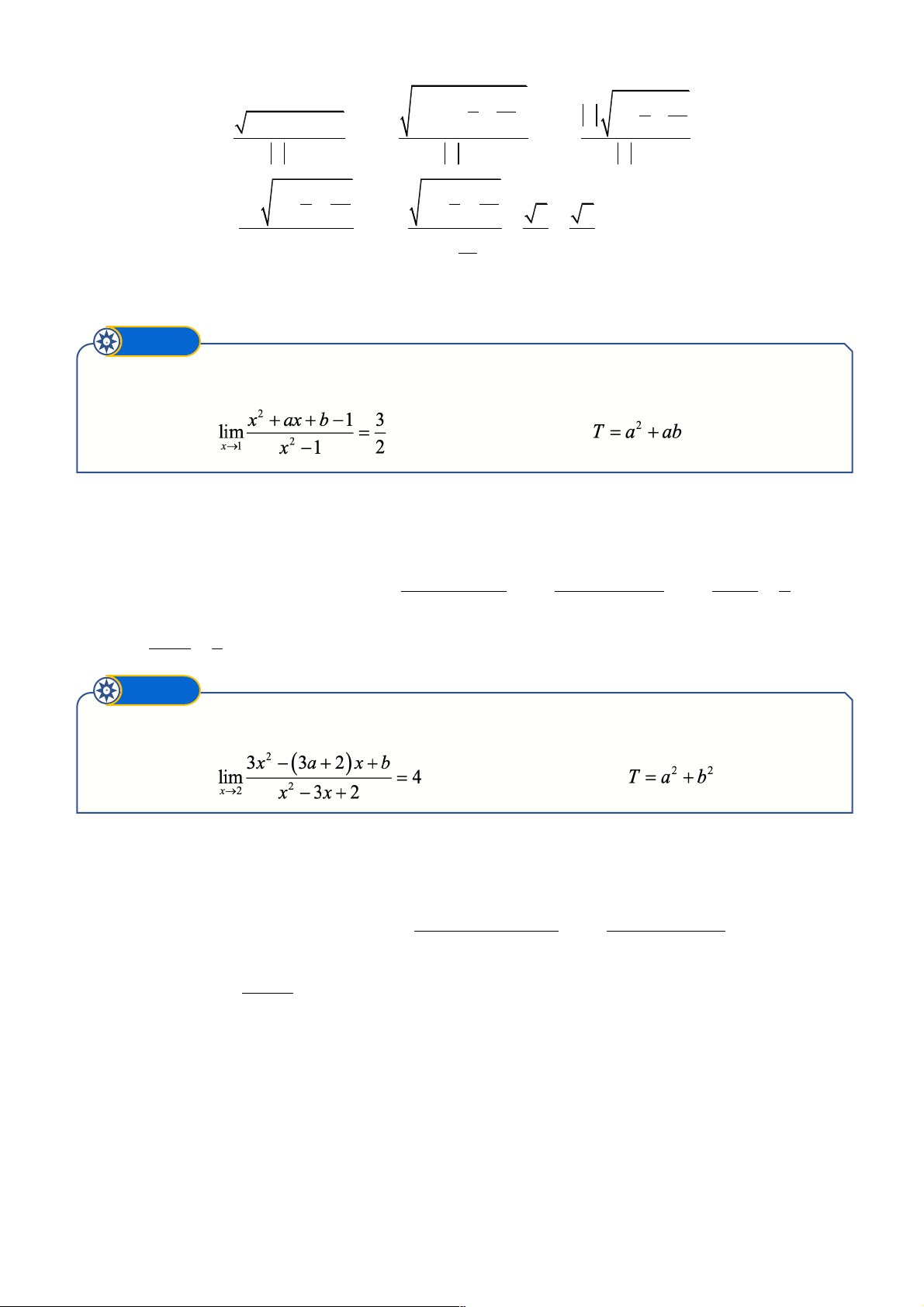
1 Phương pháp giải: Nhân hoặc chia với biểu thức liên hợp hoặc quy đồng để đưa về cùng một phân thức. Trang 5 & Ví dụ minh họa Ví dụ ➊ Tính các giới hạn sau a) b) c) § Lời giải 1 2 + 2x +1 2 + 0 a) lim = lim x = = 2 x®+¥ x -1 x®+¥ 1 1- 0 1- x 1 2 1+ 2 x +1 1+ 0 1 b) lim = lim x = = - 2 x®-¥ 1- 3x - 5 x x ®-¥ 1 3 0 - 3.0 - 5 5 - - 5 2 x x 1 1 + 2 x x +1 x x 0 + 0 c) lim = lim = = 0 2
x®+¥ x + x +1 x®+¥ 1 1 1+ 0 + 0 1+ + 2 x x Ví dụ ➋ Tính các giới hạn sau a) b) c) § Lời giải x ( 3 2 x ) 6 3 2 1 - - 2 x 6 - 3.0 6 a) lim = lim = = x®-¥ (5x - ) 1 ( 2
x + 2x) x®-¥ æ 1 öæ 2 ö (5 - 0)(1+ 2.0) 5 5 - 1+ ç ÷ç ÷ è x øè x ø 3 2 1 - - 3 2 2 4 3x - 2x -1 x x x 3.0 - 2.0 - 0 b) lim = lim = = 0 4
x®±¥ 4x + 3x - 2 x®±¥ 3 2 4 + 3.0 - 2.0 4 + - 3 4 x x 2 2 - + 3 3 2 3 3x - 2x + 2 x x 3 - 2.0 + 2.0 3 c) lim = lim = = - 3 2 x®±¥ 2
- x + 2x -1 x®±¥ 2 1 2 - + 2.0 - 0 2 2 - + - 3 x x Trang 6 Ví dụ ➌ Tính các giới hạn sau a) b) c) § Lời giải
a) Đặt x = t
- . Với x ® -¥ Þ t = +¥ 3 + - 2 2 1 2
x - 3x + 2x
t + 3t - 2t t 1+ 3.0 - 2 1 ­ Khi đó lim = lim = = lim = = x®-¥ 3x -1 t®-¥ 3 - t -1 t®-¥ 1 3 - - 0 3 3 - - t 1 2 1 1 + + + 3 + 2 2
x + x + 2 + 3x +1 b) lim = lim x x x = 4 x®+¥ 2 4x +1 +1 x - x ®+¥ 1 1 4 + + -1 2 x x ­ Đặt x = t
- . Với x ® -¥ Þ t = +¥ . Khi đó 1 2 1 1- + - 3 + 2 2 2
x + x + 2 + 3x +1
t - t + 2 - 3t +1 t t t 2 lim = lim = lim = - x®-¥ 2 t®+¥ 2 4x +1 +1- x 4t +1 +1 t + t ®+¥ 1 1 3 4 + + +1 2 t t 1 3 + 2 x x + 3 x x 0 + 3.0 c) lim = lim = = 0 2 x®+¥ x +1 x®+¥ 1 1+ 0 1+ 2 x
¦Dạng ➍ Giới hạn một bên
1 Phương pháp giải: * Nếu thì không tồn tại * Nếu thì & Ví dụ minh họa Ví dụ ➊ Tính các giới hạn sau a) b) c) Trang 7 § Lời giải 2 x - 4 x + 2 a) lim = lim = +¥ x 2+ - x 2 x 2 + ® ® x - 2 2 - x x - 2 1 1 b) lim = lim = lim = + 2 x 2 x 2 2x - 5x + 2
+ ( x - 2)(2x - ) x 2 1 + ® ® ® 2x -1 3 2 - x 2 - x 1 - 1 c) lim = lim = lim = - - 2 x 2 x 2 2x - 5x + 2
- ( x - 2)(2x - ) x 2 1 - ® ® ® 2x -1 3 Ví dụ ➋
Tìm các giới hạn của các hàm số tại các điểm chỉ ra: a) tại b) tại § Lời giải 2 x - 2x x x - 2 x 2 1
a) lim f ( x) ( ) = lim = lim = - lim = - = - + + 3 x® x® 8 - x x + ® (2- x)( 2 2 2 2 4 + 2x + x ) + 2 2
x®2 x + 2x + 4 2 + 2.2 + 4 6 x -
(x - 2)(x + 2)( 2 4 x + 4 16 ) lim f ( x) = lim = lim = lim (x + 2) + = = - - - - ( 2x 4) 4.8 32 x®2 x®2 - x®2 - x®2 x 2 x 2
Þ lim f (x) ¹ lim f (x).. Do đó, không tồn tại lim f (x) x 2+ x 2- ® ® x®2 2 x - 3x + 2 (x - )1(x - 2) x - 2 1- 2 1 b) lim = lim = lim = lim = = - + + 2 x 1 x 1 x 1 x -1 + ( x - ) 1 (x + ) x 1 1 + ® ® ® ® x +1 1+1 2 - f ( x) x 1 lim = lim = - x 1- x 1- ® ® 2 2 1 1
Nhận thấy lim f ( x) = lim f ( x) = - . Do đó lim f ( x) = - x 1- x 1+ ® ® 2 x 1 ® 2 Trang 8 Ví dụ ➌
Tìm các giới hạn của hàm số tại các điểm chỉ ra: a) tại b) tại § Lời giải
a) Ta có lim f (x) = lim (x + m) = m x 0- x 0- ® ® 2 x +100x + 3 3
và lim f (x) = lim = = 1 x 0- x 0- ® ® x + 3 0 + 3
• Để tồn tại lim f (x) thì lim f (x) = lim f (x) Þ m =1 x 1 ®- x 0- x 0+ ® ®
• Với m = 1 thì lim f (x) = 1 = lim f (x) x 0- x 0+ ® ®
• Vậy với m = 1 thì lim f (x) =1 x 1 ®
b) Ta có lim f (x) = lim (x + 3m) = 3m -1 x 1- x 1- ® ®-
và lim f (x) = lim + + + = - + + = + + + ( 2 x
x m 3) 1 1 m 3 m 3 x 1 ® x® 1 -
• Để tồn tại lim f (x) thì lim f (x) = lim f (x) Þ 3m -1= m +3 Þ 2m = 4 Þ m = 2 x 1 ®- x 1- x 1+ ®- ®-
lim f (x) = 3.2 -1 = 5üï • -
Với m = 2 thì x 1 ®-
ý Þ lim f ( x) = lim f (x) = 5 lim f (x) x 1- ®- x 1 = 2 + 3 = 5 + ®- ï x 1+ ®- þ
• Vậy với m = 2 thì lim f (x) = 5 x 1 ®-
¦Dạng ➎ Một số bài toán giới hạn ẩn tham số đặc sắc & Ví dụ minh họa Ví dụ ➊ Kết quả giới hạn
, với là phân số tối giản. Tính giá trị của biểu thức Trang 9 § Lời giải 2 æ 7 12 ö 7 12 x 2 - + ç ÷ - + 2 2 x 2 2 2x - 7x +12 è x x ­ Ta có ø = lim = lim = lim x x L x®-¥ 3 x -17 x®-¥ 3 x -17 x®-¥ 3 x -17 7 12 7 12 -x 2 - + 2 - + 2 2 x x x x 2 a ìa = 2 = lim = lim = = ® í . x®-¥ 3 - x -17 x®-¥ 17 3 b b î = 3 3 + x Vậy P = 13 Ví dụ ➋ Cho giới hạn
. Tính giá trị của biểu thức . § Lời giải ­ Đặt f (x) 2
= x + ax + b -1Þ f ( ) 1 = 0 2
x + ax + b -1
x -1 x - x x - x 3
­ Khi đó f ( x) = (x - ) 1 ( x - x Þ lim = lim = lim = 0 ) ( )( 0 ) 0 2 2 x 1 ® x 1 ® x 1 x -1 x -1 ® x +1 2 1- x 3 0 Û
= Þ x = -2 Þ f x = x -1 x + 2 = x + x - 2 Þ a = 1; b = -1 Þ T = 0 0 ( ) ( )( ) 2 . 2 2 Ví dụ ➌ Cho giới hạn
. Tính giá trị của biểu thức . § Lời giải ­ Đặt f (x) 2 = 3x + (2a + )
1 x + b Þ f (2) = 0 2
3x - 3a + 2 x + b
x - 2 3x - m
­ Khi đó: f (x) = (x - 2)(3x - m) ( ) ( )( ) Þ lim = lim = 4 2 x®2 x®2 x - 3x + 2 (x - 2)(x - )1 3x - m Û lim
= 4 Û 6 - m = 4 Û m = 2 x®2 x -1 ìa = 2
ð Suy ra f (x) = (x - 2)(3x - 2) 2
= 3x -8x + 4 Þ í Þ T = 20. b î = 4 Trang 10