Các dạng toán về giới hạn dãy số 11 (có lời giải)
Các dạng toán về giới hạn dãy số 11 có lời giải chi tiết được soạn dưới dạng file PDF gồm 17 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.
Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT)
Môn: Toán 11
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
CÁC DẠNG TOÁN VỀ GIỚI HẠN DÃY SỐ LỚP 11
⯎
Dạng ➀ | Chứng minh dãy số có giới hạn là 0 |
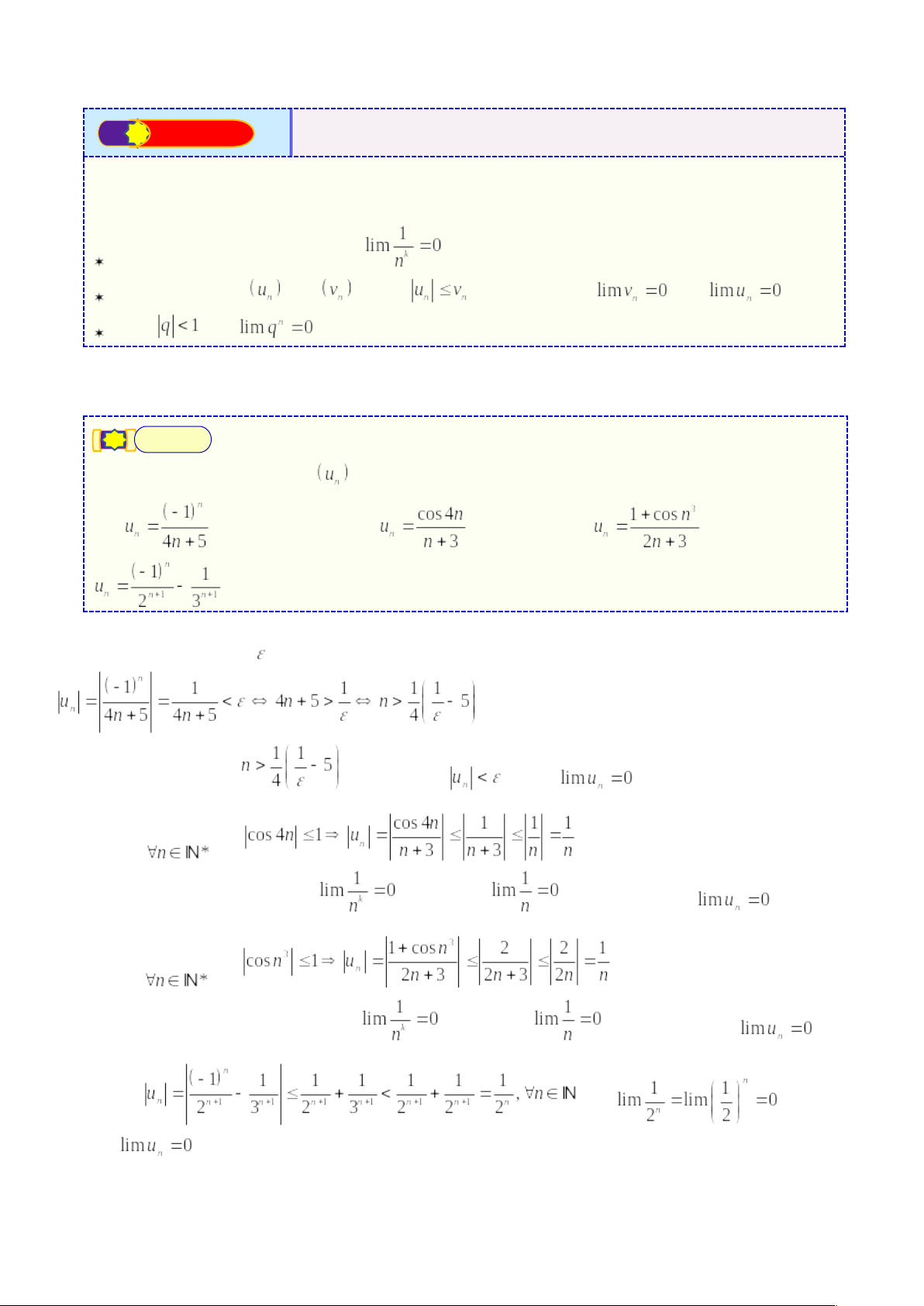
⯎ Phương pháp: 🔿Cách 1: Áp dụng định nghĩa. 🔿Cách 2: Sử dụng các định lí sau:
| |
Nếu k là số thực dương thì 
.
Với hai dãy số 
và 
, nếu 
với mọi n và 
thì 
.
Nếu 
thì 
.
🗵. Ví dụ minh họa:
🞜
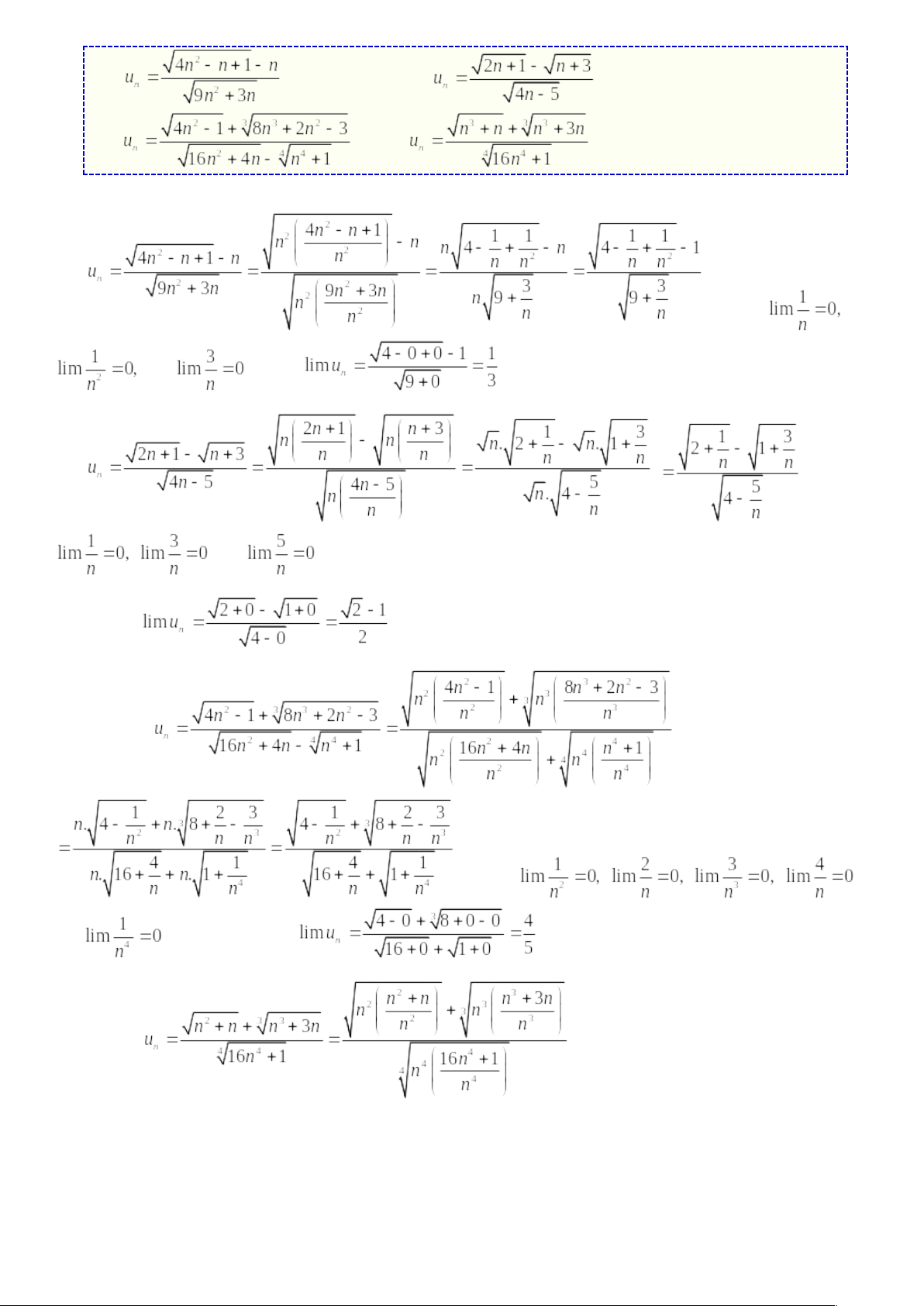
Ví dụ ➊ Chứng minh các dãy số a). |
sau đây có giới hạn là 0. 
b). 
c). 
d). 
🞔 Lời giải
a). Với mỗi số dương 
b). Ta có 
c). Ta có 
d). Ta có 
⯎
Dạng ➁ | Dùng định nghĩa chứng minh dãy số | |
⯎ Phương pháp: Chứng minh | ||
có giới hạn L.
.🗵. Ví dụ minh họa:
🞜
Ví dụ ➊ Chứng minh: |
b). 
c). 
.🞔 Lời giải
a). gọi 
Vì 
b). Gọi 
Vì 
c). Gọi 
⯎
Dạng ➂ | Tìm giới hạn của dãy | |
⯎ Phương pháp: 🔿DẠNG 1: Phương pháp: Chia cả tử và mẫu cho 🔿DẠNG 2: 🔿DẠNG 3: 🔿DẠNG 4 : Nhân lượng liên hợp: PHƯƠNG PHÁP : Sử dụng các công thức nhân lượng liên hợp sau:
🔿DẠNG 5 : TÍNH GIỚI HẠN DỰA VÀO ĐỊNH LÍ KẸP: PHƯƠNG PHÁP: Dựa vào định lí: Cho ba dãy số 🔿DẠNG 6: Phương pháp: Tìm công thức tổng quát của Chứng minh dãy số có giới hạn hữu hạn (có nghĩa chứng minh dãy số tăng và bị chặn trên hoặc dãy số giảm và bị chặn dưới) sau đó dựa vào hệ thức truy hồi để tìm giới hạn. 🔿DẠNG 7: DÃY SỐ CÓ GIỚI HẠN VÔ CỰC: | ||
có giới hạn hữu hạn:
là một phân thức hữu tỉ dạng 
( trong đó 
là hai đa thức của n).
với 
là lũy thừa có số mũ lớn nhất của 
và 
( hoặc rút 
là lũy thừa có số mũ lớn nhất của 
và 
ra làm nhân tử) sau đó áp dụng các định lý về giới hạn.
là một phân thức hữu tỉ dạng 
( trong đó 
là các biểu thức chứa căn của n).
là một phân thức hữu tỉ dạng 
( trong đó 
là các biểu thức chứa hàm mũ 
,…. Chia cả tử và mẫu cho 
với a là cơ số lớn nhất ).
.
.
.
và 
. Nếu 
và 
thì 
.
được xác định bởi một công thức truy hồi.
theo n, sau đó tìm 
.
🗵. Ví dụ minh họa:
🞜
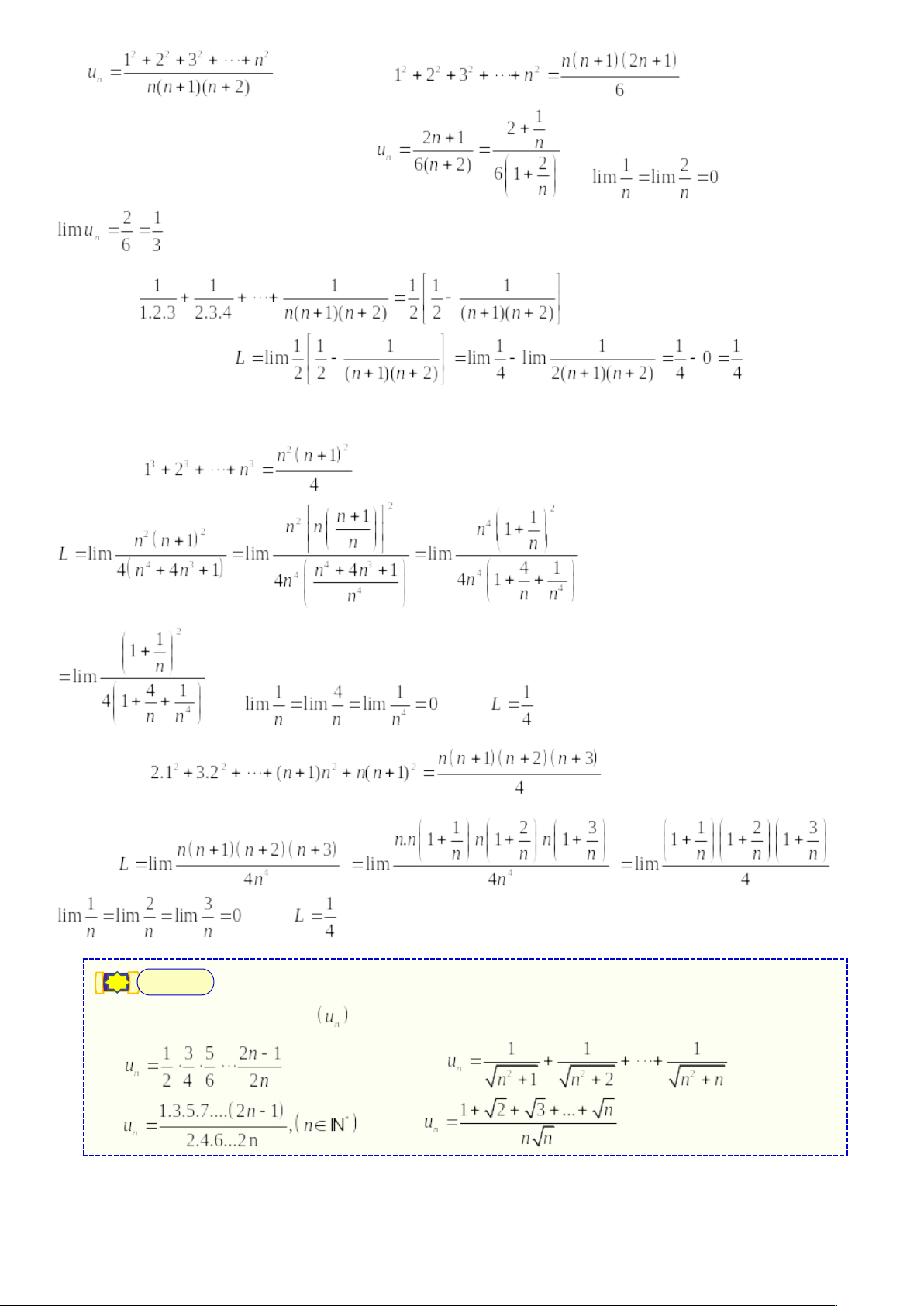
Ví dụ ➊ Tìm giới hạn của dãy a). d). |
biết:
b). 
c). 
e). 
f). 
🞔 Lời giải
a). Ta thấy 
b). Dễ dàng thấy 
c). Có 
d). Bước đầu tiên qui đồng mẫu 
Ta có 
e). 
Từ đó 
f). 
🞜
Ví dụ ➋ Tìm giới hạn của dãy a). c). |
biết:
b). 
d). 
🞔 Lời giải
a). 
b). 
Từ đó có 
c). Ta có 
d). Ta có 
🞜
Ví dụ ➌ Tìm giới hạn của dãy a). d). |
biết:
b). 
c). 
e). 
f). 
🞔 Lời giải
a).Ta có 
b). Ta có 
c). Ta có 
Do đó 
d). Ta có 
e). Ta có : 
f). Ta có 
🞜
Ví dụ ❹ Tìm giới hạn của dãy a). c). e). . |
biết:
b). 
d). 
. f).
🞔 Lời giải
a). Ta có 
Do đó 
b). 
c).
d). 
Ta có 
e).
Có 
Nên
Từ đó suy ra 
f).
Do đó 
🞜
Ví dụ ❺ Tìm các giới hạn sau: a). c). |
b). 
d). 
🞔 Lời giải
a). Ta có 
Do đó 
b).
Ta có
và 
Do đó 
c). 
Tính 
Và 
Do đó 
d).
Có
Do đó 
Từ đó suy ra 
🞜
Ví dụ ❻ Tìm giới hạn của dãy a). c). e). g). |
biết:
b). 
d). 
f). 
h). 
🞔 Lời giải
a). Ta có 
Nên 
b). Ta có 
c). 
Nên 
d). 
Ta có dãy số 
e). 
f). Ta có 
g). Ta có 
h). Ta có 
Do đó 
🞜
Ví dụ ❼ Tìm giới hạn của dãy a). c). |
biết:
b). 
d). 
.🞔 Lời giải
a). Ta có 
Do đó 
b). Ta có:
…………………
Cộng các bất đẳng thức trên, vế theo vế ta được 
Mà 
c). Rõ ràng 
Do đó ta có 
d). Dễ dàng chứng minh 
Từ (1) và (2) suy ra 
🞜
Ví dụ ❽ Cho dãy số Tìm công thức số hạng tổng quát và giới hạn dãy số |
xác định như sau: 
?🞔 Lời giải
Ta có 
Do đó: 
Suy ra:
Vậy
Mặt khác 
🞜
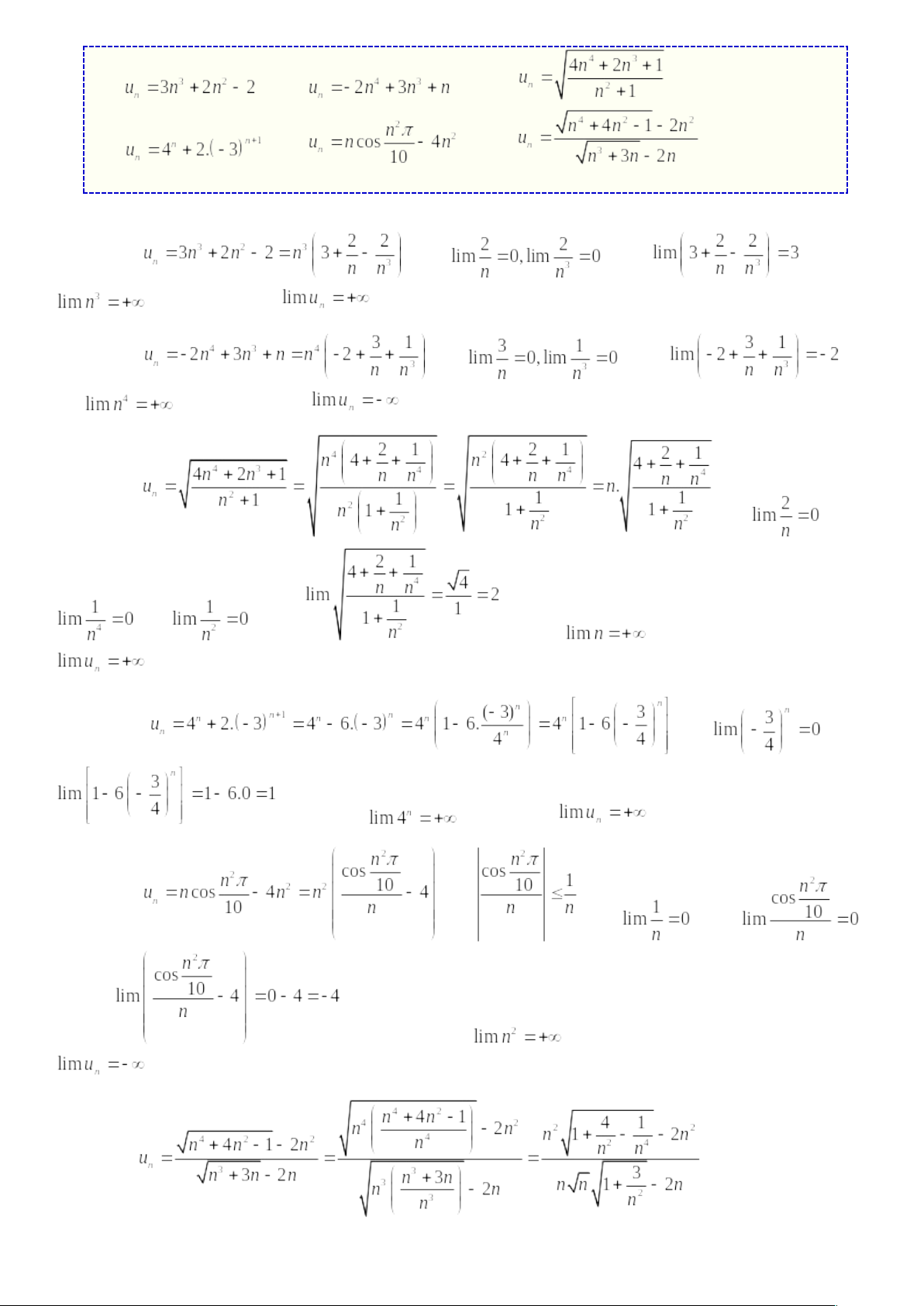
Ví dụ ❻ Tìm giới hạn của dãy a). d). |
biết:
b). 
c). 
e). 
f). 
. 🞔 Lời giải
a). Ta có 
b). Ta có 
c). Ta có 
d). Ta có 
e). Ta có 
f). Ta có 
Từ (1) và (2) suy ra 