Các dạng trắc nghiệm Đường thẳng song song với mặt phẳng (có đáp án )

Các dạng trắc nghiệm Đường thẳng song song với mặt phẳng có lời giải chi tiết và đáp án được soạn dưới dạng file PDF gồm 37 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

57 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Quan hệ song song trong không gian (KNTT)

Môn: Toán 11

Thông tin:

37 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
CÁC DẠNG TOÁN TRẮC NGHIỆM
BÀI ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
1. Vị trí tương đối của đường thẳng và mặt phẳng.
Cho đường thẳng và mặt phẳng , ta có ba vị trí tương đối giữa chúng là:
¨ và cắt nhau tại điểm , kí hiêu hoặc để đơn giản ta kí hiệu
(h1)
¨ song song với , kí hiệu hoặc ( h2)
¨ nằm trong , kí hiệu (h3)
2. Các định lí và tính chất.
¨ Nếu đường thẳng không nằm trong mặt phẳng và song song với đường thẳng nằm
trong thì song song với .
Vậy
¨ Cho đường thẳng song song với mặt phẳng . Nếu mặt phẳng đi qua và cắt theo
giao tuyến thì .
Vậy .
d
( )
a
d
( )
a
M
{ } ( )
=ÇMd
a
( )
=ÇMd
a
d
( )
a
( )
!d
a
( )
! d
a
d
( )
a
( )
Ìd
a
h1
α
M
d
h2
α
d
h3
α
d
( )
a
d
'd
( )
a
d
( )
a
( )
( )
( )
'
'
Ë
ì
ï
Þ
í
ï
Ì
î
!!
d
dd d
d
a
a
a
d
( )
a
( )
b
d
( )
a
'd
' !dd
( )
( )
( ) ( )
'
'
ì
ï
ÌÞ
í
ï
Ç=
î
!
!
d
ddd
d
a
b
ab
d'
d
h3
α
d'
d
β
α
Trang 2
¨ Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng ( nếu
có) cũng song song với đường thẳng đó.
Vậy .
¨Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song
với đường thẳng kia.
DẠNG 1
LÝ THUYẾT
( )
( )
( ) ( )
'
'
ì
ï
Þ
í
ï
Ç=
î
!
!!
d
ddd
d
a
b
ab
d'
d
β
α
d
l
m
α
Trang 3
Câu 1. Trong không gian có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng?
A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn C.
Vị trí tương đối của đường thẳng và mặt phẳng là
Đường thẳng nằm trong mặt phẳng.
Đường thẳng song song với mặt phẳng.
Đường thẳng cắt mặt phẳng.
Câu 2. Cho hai đường thẳng a và b chéo nhau.
Có bao nhiêu mặt phẳng chứa và song song với ?
A. 0. B. 1. C. 2. D. Vô số.
Lời giải
Chọn B.
Theo định lý 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và
song song với đường thẳng kia.
Câu 3. Cho hai đường thẳng song song và . Có bao nhiêu mặt phẳng chứa và song song với ?
A. B. C. D. vô số.
Lời giải
Chọn D.
Theo tính chất: Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Câu 4. Cho mặt phẳng và đường thẳng . Khẳng định nào sau đây sai?
A. Nếu thì trong tồn tại đường thẳng sao cho .
B. Nếu và đường thẳng thì .
C. Nếu thì .
D. Nếu và đường thẳng thì và hoặc cắt nhau hoặc chéo nhau.
Lời giải
Chọn B.
a
b
a
b
a
b
0.
1.
2.
( )
a
( )
Ëd
a
( )
//d
a
( )
a
( )
a
//ad
( )
//d
a
( )
Ìb
a
//bd
( )
// Ìdc
a
( )
//d
a
( )
Ç=dA
a
( )
¢
Ìd
a
d
¢
d
Trang 4
Khi và đường thẳng thì ngoài trường hợp còn có trường hợp và
chéo nhau.
Câu 5. Cho hai đường thẳng và cùng song song với . Khẳng định nào sau đây không sai?
A. .
B. và cắt nhau.
C. và chéo nhau.
D. Chưa đủ điều kiện để kết luận vị trí tương đối của và .
Lời giải
Chọn D.
Cho qua không thẳng hàng.
Giả sử phân biệt là các đường thẳng nằm ngoài thỏa
Trong trường hợp này
Nếu và đồng phẳng thì cắt
Nếu và không đồng phẳng thì và chéo nhau.
Câu 6. Khẳng định nào sau đây đúng?
A.Đường thẳng và đường thẳng
B. Tồn tại đường thẳng
C.Nếu đường thẳng song song với và cắt đường thẳng thì cắt đường thẳng
D. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì 2 đường thẳng đó song song
nhau.
Lời giải
Chọn D.
a
b
d
( ) ( )
//d
a
( ) ( )
Ìb
a
( ) ( )
//bd
( )
b
( )
d
a
b
( )
mp P
//ab
a
b
a
b
a
b
( )
mp P
,,ABC
,,abc
( )
mp P
// , // , // .aABbABcBC
// .ab
a
c
a
.c
a
c
a
c
( )
ÌampP
( )
//mp P
D
Þ
// .Da
( )
//DÞmp P
( )
':'//.DÌ D Dmp P
D
( )
mp P
( )
P
a
D
.a
Trang 5
Ta có
Câu 7. Cho và hai đường thẳng song song và
1. Nếu song song với thì
2. Nếu song song với thì chứa
3. Nếu song song với thì hoặc chứa
4. Nếu cắt thì cũng cắt
5. Nếu cắt thì có thể song song với
6. Nếu chứa thì có thể song song với
Có bao nhiêu nhận xét đúng?
A. 5. B. 2. C. 3. D. 4.
Lời giải
Chọn C.
1. sai
2. sai
3. đúng
4. đúng Chọn D.
cắt suy ra không song song mà cũng
không chứa , vậy cắt .
5. sai
6. đúng:
( )
( )
// '
// .
'
DD
ü
ï
ÞD
ý
DÌ
ï
þ
P
P
( )
mp P
a
.b
( )
mp P
a
( )
//Pb
( )
mp P
a
( )
P
b
( )
mp P
a
( )
//Pb
b
( )
mp P
a
b
( )
mp P
a
( )
P
b
( )
mp P
a
( )
P
b
( )
( ) ( )
//
// .
//
ü
ï
ÞÚÌ
ý
ï
þ
ab
bPbP
aP
a
( )
P
b
( )
P
( )
P
b
b
( )
P
( )
( )
( )
// // .
Ì
ü
ï
Þ
ý
ï
Ë
þ
aP
ab b P
bP
Trang 6
Câu 8. Cho đường thẳng nằm trong và đường thẳng . Mệnh đề nào sau đây đúng?
A. Nếu thì
B. Nếu cắt thì cắt
C. Nếu thì
D. Nếu cắt và chứa thì giao tuyến của và là đường thẳng cắt cả và .
Lời giải
Chọn C.
Câu 9. Cho hai đường thẳng và chéo nhau. Có bao nhiêu mặt phẳng chứa và song song với ?
A. B. C. D. Vô số.
Lời giải
Chọn B.
Gọi là chứa và song song
có vtpt
Đồng thời qua với
Do đó xác định duy nhất.
a
( )
mp
a
( )
Ëb
a
( )
//b
a
// .ba
b
( )
a
b
.a
//ba
( )
// .b
a
b
( )
a
( )
mp
b
b
( )
a
( )
b
a
b
( )
( ) ( )
// .
//
Ì
ü
ï
ËÞ
ý
ï
þ
a
bb
ab
a
aa
a
b
a
b
0.
1.
2.
( )
a
mp
a
.b
( )
a
;
éù
=
ëû
!!" ! !" ! !"
ab
nuu
a
( )
a
A
.ÎAa
( )
a
Trang 7
DẠNG 2
CHỨNG MINH ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
Phương pháp 1
Cơ sở của phương pháp là dùng điều kiện cần và đủ để chứng minh đường thẳng song song với mặt
phẳng .
¨ Bước 1: Quan sát và quản lí giả thiết tìm đường thẳng ưu việt và chứng minh .
¨ Bước 2: Kết luận .
Phương pháp 2
Cơ sở của phương pháp là dùng định lý phương giao tuyến song song.
¨ Bước 1: Chứng minh
mà
¨ Bước 2: Kết luận .
d
()
a
()DÌ
a
D!d
()!d
a
() ()=Çd
bg
() ()
() ( )
Ç=
ì
ï
Ç=
í
ï
î
!
a
b
ab
ba
ga
()!d
a
Trang 8
Câu 10. Cho hình chóp có đáy là hình bình hành. Gọi là giao tuyến của hai mặt
phẳng và . Khẳng định nào sau đây đúng?
A. qua và song song với . B. qua và song song với .
C. qua và song song với . D. qua và song song với .
Lời giải
Chọn A.
Ta có (Theo hệ quả của định lý 2 (Giao tuyến của ba mặt phẳng)).
Câu 11. Cho hình chóp có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng
và
A. là đường thẳng đi qua S song song với AB, CD
B. là đường thẳng đi qua S
C. là điểm S
.S ABCD
ABCD
d
( )
SAD
( )
SBC
d
S
BC
d
S
DC
d
S
AB
d
S
BD
C
S
B
A
D
d
( )
( )
( ) ( )
//
//
Ì
ì
ï
Ì
ï
Þ
í
=Ç
ï
ï
î
AD SAD
BC SAC
d BC
d SAD SAC
AD BC
.S ABCD
ABCD
( )
SAB
( )
SCD
Trang 9
D. là mặt phẳng (SAD)
Lời giải
Chọn A
Ta có
.
Câu 12. Cho hình bình hành và một điểm không nằm trong mặt phẳng . Giao tuyến
của hai mặt phẳng và là một đường thẳng song song với đường thẳng nào sau đây?
A. . B. . C. . D. .
Lời giải
Chọn A.
Xét và có là điềm chung
d
B
D
C
A
S
( )
( )
( ) ( )
Ì
ì
ï
Ì
ï
í
ï
ï
ÎÇ
î
!
AB SAB
CD SCD
AB CD
S SAB SCD
( ) ( )
,ÞÇ = Î!!SAB SCD d AB CD S d
ABCD
S
( )
ABCD
( )
SAB
( )
SCD
AB
AC
BC
SA
x
A
B
D
C
S
( )
SAB
( )
SCD
S
( )
( )
//
ì
ï
Ì
í
ï
Ì
î
AB CD
AB SAB
CD SCD
( ) ( )
// //ÞÇ =SAB SCD Sx AB CD
Trang 10
Các bạn muốn tải đầy đủ 38 chuyên đề ôn thi 12 file word (hơn 5500 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 12 file word thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Câu 13. Cho tứ diện . và theo thứ tự là trung điểm của và , là trọng tâm tam giác
. Giao tuyến của hai mặt phẳng và là đường thẳng :
A. qua và song song với B. qua và song song với
C. qua và song song với D. qua và song song với
Lời giải
Chọn C.
Gọi là giao tuyến của và .
Ta có , , , .
Suy ra đi qua và song song với .
Câu 14. Cho hình chóp có đáy là hình bình hành tâm , là trung điểm cạnh .
Khẳng định nào sau đây SAI?
A. .
B. .
C. cắt hình chóp theo thiết diện là một tứ giác.
D. .
Lời giải
Chọn C.
ABCD
I
J
AD
AC
G
BCD
( )
GIJ
( )
BCD
I
.AB
J
.BD
G
.CD
G
.BC
A
B
C
D
I
J
G
d
( )
GIJ
( )
BCD
( ) ( )
ÎÇGGIJ BCD
//IJ CD
( )
ÌIJ G IJ
( )
ÌCD BCD
d
G
CD
.S ABCD
ABCD
O
I
SC
( )
// mpIO SAB
( )
// mpIO SAD
( )
mp IBD
.S ABCD
( ) ( )
=!IBD SA C IO
Trang 11
Ta có: nên A đúng.
Ta có: nên B đúng.
Ta có: cắt hình chóp theo thiết diện là tam giác nên Chọn C.
Ta có: nên D đúng.
Câu 15. Cho tứ diện . Gọi và lần lượt là trọng tâm các tam giác và .
Chọn Câu sai :
A. . B. .
C. , và đồng qui D. .
Lời giải
Chọn D.
và lần lượt là trọng tâm các tam giác và nên , và đồng qui tại (là
trung điểm của ) .
Vì nên và .
I
O
D
C
B
A
S
( )
( )
//
//
ü
ï
Þ
ý
Ë
ï
þ
OI SA
OI SAB
OI SAB
( )
( )
//
//
ü
ï
Þ
ý
Ë
ï
þ
OI SA
OI SAD
OI SAD
( )
IBD
IBD
( ) ( )
=!IBD SA C IO
ABCD
1
G
2
G
BCD
ACD
( )
12
//GG ABD
( )
12
//GG ABC
1
BG
2
AG
CD
12
2
3
=GG AB
M
A
B
D
C
G2
G1
1
G
2
G
BCD
ACD
1
BG
2
AG
CD
M
CD
12
//GG AB
( )
12
//GG ABD
( )
12
//GG ABC
Trang 12
Lại có nên chọn đáp án D.
Câu 16. Cho hình chóp có đáy là hình bình hành. Mặt phẳng qua và song
song với , mặt phẳng cắt tại Khẳng định nào sau đây là khẳng định đúng ?
A. B. C. D.
Lời giải
Chọn C.
Gọi là giao điểm của và . Do mặt phẳng qua nên
Trong tam giác , kẻ song song
Do
Trong tam giác ta có là đường trung bình của
Vậy
Câu 17. Cho tứ diện với lần lượt là trọng tâm các tam giác ,
Xét các khẳng định sau:
(I) .
(II) .
(III) .
(IV)) .
Các mệnh đề nào đúng?
A. I, II. B. II, III. C. III, IV. D. I, IV.
Lời giải
Chọn A.
12
1
3
=GG AB
.S ABCD
ABCD
( )
a
BD
SA
( )
a
SC
.K
2.=SK KC
3.=SK KC
.=SK K C
1
.
2
=SK KC
O
AC
BD
( )
a
BD
( )
.ÎO
a
SAC
OK
SA
( )
.ÎKSC
( )
( )
( ) ( ) { }
.
ì
ï
ÞÌÞÇ=
í
ï
Î
î
!
!
SA
OK SA OK SC K
O
a
aa
a
SAC
ì
Þ
í
=
î
!OK SA
OK
OA OC
.DSAC
.=SK K C
ABCD
,MN
ABD
ACD
( )
//mpMN ABC
( )
//MN mp BCD
( )
//MN mp ACD
( )
//MN mp CDA
Trang 13
Gọi là trung điểm của .
Do là trọng tâm tam giác nên
Theo định lý Talet có .
Mà .
Vậy .
Câu 18. Cho tứ diện . Gọi lần lượt là trung điểm của các cạnh Gọi
lần lượt là trọng tâm của tam giác và tam giác . Gọi là giao tuyến của hai mặt phẳng
và . Khi đó khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Lời giải
Chọn C.
Ta có là đường trung bình của tam giác , suy ra
N
M
I
A
C
D
B
I
AD
,MN
,ABD ACD
1
3
==
IM IN
IB IC
//MN BC
( ) ( )
,ÌÌBC BCD BC ABC
( ) ( )
// , //MN BCD MN ABC
ABCD
,, ,IJKH
,,C,.BA AC B AD
,EF
ABD
ACD
d
()DIJ
()DBC
()dIHK!
()dJHK!
()d AEF!
()dDIJ!
IJ
ABC
.BC IJ!
Trang 14
Như vậy suy ra giao tuyến của 2 mặt phẳng và là đường thẳng
qua và song song với .
lần lượt là trọng tâm của tam giác và tam giác nên vì
Do đó .
Câu 19. Cho hình chóp . Gọi lần lượt là trọng tâm của và . Lấy lần
lượt là trung điểm của . Xét các mệnh đề sau:
(1) Đường thẳng song song với .
(2) Đường thẳng song song với .
(3) Đường thẳng song song với .
(4) Đường thẳng và đường thẳng trùng nhau.
(5) Đường thẳng và đường thẳng song song.
Số mệnh đề sai là:
A. . B. . C. . D. .
Lời giải
Chọn A.
Hai mệnh đề sai là (2) và (4).
(2) sai vì .
(4) sai vì .
()( )
(), ( )
DDIJ DBC
IJ BC
IJ DIJ BC DBC
ÎÇ
ì
ï
í
ï
ÌÌ
î
!
d
()DIJ
()DBC
D
,IJ BC
,EF
ABD
ACD
IJ EF!
2
3
DE DF
DI DJ
==
()
()
dEF
dAEF
EF AEF
ì
Þ
í
Ì
î
!
!
.DS ABC
,GE
DSAD
DSCD
,MN
,AB BC
MN
( )
GAC
MN
( )
DAC
GE
( )
AMN
GE
MN
GE
MN
2
0
3
1
( )
MN DACÌ
GE MN!
Trang 15
DẠNG 3
XÁC ĐỊNH THIẾT DIỆN SONG SONG VỚI ĐƯỜNG THẲNG.
Trong phần này ta sẽ xét thiết diện của mặt phẳng đi qua một điểm song song với hai đường thẳng
chéo nhau hoặc chứa một đường thẳng và song song với một đường thẳng; để xác định thiết diện
loại này ta sử dụng tính chất:
Câu 20. Cho hình chóp có đáy là hình thang với các cạnh đáy là và . Gọi
lần lượt là trung điểm của các cạnh và và là trọng tâm của tam giác .
a) Tìm giao tuyến của hai mặt phẳng và .
A. là đường thẳng song song với AB
( )
a
( )
a
( )
( )
( ) ( )
( ) ( )
', '
ì
ï
ÌÞÇ=Î
í
ï
ÎÇ
î
!
!
d
dddMd
M
a
bab
ab
.S ABCD
ABCD
AB
CD
,IJ
AD
BC
G
SAB
( )
SAB
( )
IJG
Trang 16
B. là đường thẳng song song vơi CD
C. là đường thẳng song song với đường trung bình của hình thang ABCD
D. Cả A, B, C đều đúng
b) Tìm điều kiện của và để thiết diện của và hình chóp là một hình bình hành.
A. B. C. D.
Lời giải
a) Chọn D.
Ta có là hình thang và là trung điểm của nên .
Vậy
với
.
b) Chọn D.
Dễ thấy thiết diện là tứ giác .
Do là trọng tâm tam giác và nên
( là trung điểm của ).
.
Lại có . Vì nên là hình thang, do đó là hình bình hành khi
AB
CD
( )
IJG
2
3
=AB CD
=AB C D
3
2
=AB CD
3=AB CD
N
M
E
J
I
D
C
A
S
B
G
ABCD
,IJ
,AD BC
//IJ AB
( ) ( )
( )
( )
ÎÇ
ì
ï
Ì
ï
í
Ì
ï
ï
î
!
GSAB IJG
AB SAB
IJ IJG
AB IJ
( ) ( )
ÞÇ=!!SAB IJG MN IJ AB
,ÎÎMSANSB
MNJI
G
SAB
!MN AB
2
3
==
MN SG
AB SE
E
AB
2
3
Þ=MN AB
( )
1
2
=+IJ AB CD
!MN IJ
MNIJ
MNIJ
=MN IJ
Trang 17
.
Vậy thết diện là hình bình hành khi .
Câu 21. Cho hình chóp có đáy là hình thang, , , là trung điểm
. Mặt phẳng cắt hình chóp theo thiết diện là
A. tam giác. B. hình bình hành. C. hình thang vuông. D. hình chữ nhật.
Lời giải
Chọn B.
Sử dụng định lý ba đường giao tuyến ta có giao tuyến của với là sao cho
Ta có: nên thiết diện là hình thang.
Lại có và là trung điểm
là đường trung bình,
Vậy thiết diện là hình bình hành.
Câu 22. Cho tứ diện và là điểm ở trên cạnh . Mặt phẳng qua và song song với
và . Thiết diện của tứ diện cắt bởi là
A. hình bình hành. B. hình chữ nhật. C. hình thang. D. hình thoi.
Lời giải
Chọn A.
( )
21
3
32
Û= +Û=AB AB CD AB CD
3=AB CD
.S ABCD
ABCD
//AD BC
2.=AD BC
M
SA
( )
MBC
S
A
B
C
D
M
N
( )
MBC
( )
SAD
MN
//MN BC
// //MN BC AD
AMND
//MN BC
M
SA
Þ MN
1
2
==MN AD BC
MNCB
ABCD
M
AC
( )
a
M
AB
CD
( )
a
A
B
C
D
M
N
P
Q
Trang 18
Trên kẻ
Trên kẻ
Ta có chính là mặt phẳng
Sử dụng đính lý ba giao tuyến ta có với
Ta có
thiết diện là hình bình hành.
Câu 23. Cho hình chóp với đáy là tứ giác lồi. Thiết diện của mặt phẳng tuỳ ý với
hình chóp không thể là:
A. Lục giác. B. Ngũ giác. C. Tứ giác. D. Tam giác.
Lời giải
Chọn A.
Thiết diện của mặt phẳng với hình chóp là đa giác được tạo bởi các giao tuyến của mặt phẳng đó với mỗi
mặt của hình chóp.
Hai mặt phẳng bất kì có nhiều nhất một giao tuyến.
Hình chóp tứ giác có 5 mặt nên thiết diện của với có không qua 5 cạnh, không
thể là hình lục giác 6 cạnh.
Sử dụng định lý ba đường giao tuyến ta có giao tuyến của với là sao cho
Ta có: nên thiết diện là hình thang.
Câu 24. Cho hình chóp có đáy là hình bình hành tâm . Lấy điểm trên đoạn
sao cho , cắt tại và cắt tại . là hình gì ?
A. Hình thang. B. Hình bình hành.
C. Hình chữ nhật. D. Tứ diện vì và chéo nhau.
Lời giải
Chọn A.
( )
ABC
// ; ÎMN AB N BC
( )
BCD
// ; ÎNP CD P BD
( )
a
( )
MNP
( ) { }
Ç=MNP AD Q
// //MQ CD NP
// //
// //
ü
Þ
ý
þ
MQ NP CD
MN PQ AB
MNPQ
.S ABCD
ABCD
( )
a
S
A
B
C
D
M
N
.S ABCD
( )
a
.S ABCD
( )
ADM
( )
SBC
MN
//MN BC
// //MN BC AD
AMND
.S ABCD
ABCD
O
I
SO
2
3
=
SI
SO
BI
SD
M
DI
SB
N
MNBD
MN
BD
Trang 19
trên đoạn và nên là trọng tâm tam giác . Suy ra là trung điểm là trung
điểm
Do đó và nên là hình thang.
Các bạn muốn tải đầy đủ bộ tài liệu lớp 11 file word ( 3042 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 9 file word ( 1062 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Câu 25. Cho tứ diện . là điểm nằm trong tam giác qua và song song với
và .Thiết diện của cắt bởi là:
A.Tam giác. B. Hình chữ nhật. C. Hình vuông. D. Hình bình hành.
Lời giải
Chọn D.
nên giao tuyến và là đường thẳng song song
Trong Qua vẽ Ta có
Tương tự trong qua vẽ suy ra
I
O
A
D
B
S
C
M
N
I
SO
2
3
=
SI
SO
I
SBD
M
;SD
N
.SB
//MN BD
1
2
=MN BD
MNBD
ABCD
M
( )
,ABC mp
a
M
AB
CD
ABCD
( )
mp
a
A
C
B
D
G
F
E
H
M
( )
//AB
a
( )
a
( )
ABC
.AB
( )
.ABC
M
( )
// 1EF AB
( )
,.ÎÎEBCF AC
( ) ( )
.Ç=ABC MN
a
( )
,mp BCD
E
( ) ( )
// 2 ÎEH DC H BD
( ) ( )
.Ç=BCD HE
a
Trang 20
Trong qua vẽ suy ra
Thiết diện của cắt bởi là tứ giác
Ta có
Từ là hình bình hành.
Câu 26. Cho hình chóp tứ giác . Gọi và lần lượt là trung điểm của và . Khẳng
định nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn A.
là đường trung bình của nên
Ta có
Câu 27. Cho hình chóp có đáy là hình chữ nhật tâm . là trung điểm của , Mặt
phẳng qua song song với và . Thiết diện của hình chóp vớimặt phẳng là:
A. Hình tam giác. B. Hình bình hành. C. Hình chữ nhật. D. Hình ngũ giác.
Lời giải
Chọn A.
( )
,mp ABD
H
( ) ( )
// 3 ,ÎHG AB G AD
( ) ( )
.Ç=ABD GH
a
ABCD
( )
a
.EFGH
( ) ( )
( )
( )
// 4
//
Ç=
ü
ï
Þ
ý
ï
þ
ADC FG
FG DC
DC
a
a
( ) ( ) ( ) ( )
//
1, 2,3, 4
//
ì
ÞÞ
í
î
EF GH
EFGH
EH GF
.S ABCD
M
N
SA
SC
( )
// .MN mp ABCD
( )
// .MN mp SAB
( )
// .MN mp SCD
( )
// .MN mp SBC
N
M
A
D
B
C
S
MN
DSAC
// .MN AC
( )
( )
( )
//
// .
ü
ï
ÌÞ
ý
ï
Ë
þ
MN AC
AC ABCD MN ABCD
MN ABCD
.S ABCD
ABCD
O
M
OC
( )
a
M
SA
BD
( )
a
Trang 21
Ta có:
.
Lại có: .
Vậy thiết diện cần tìm là tam giác .
Câu 28. Cho tứ diện có . Mặt phẳng qua trung điểm của và song song với ,
cắt theo thiết diện là
A.hình tam giác. B.hình vuông. C.hình thoi. D.hình chữ nhật.
Lời giải
Chọn C.
Gọi là trung điểm của .
( ) ( )
( ) ( )
( ) ( ) ( )
//
// , ,
ÎÇ
ì
ï
í
Ì
ï
î
ÞÇ = Î Î Î
M ABCD
BD ABCD
ABCD EF BD M EF E BC F CD
a
a
a
( ) ( )
( ) ( )
( ) ( ) ( )
//
//
ÎÇ
ì
ï
ÞÇ = Î
í
Ì
ï
î
M SAC
SAC MN SA N SC
SA SAC
a
a
a
NEF
ABCD
=AB C D
( )
a
AC
AB
CD
ABCD
M
AC
Trang 22
Ta có: , là trung điểm .
, là trung điểm .
, là trung điểm .
Khi đó thiết diện là hình bình hành .
Lại có: suy ra .
Vậy thiết diện cần tìm là hình thoi .
Câu 29. Cho hình chóp có đáy là hình bình hành. là một điểm lấy trên cạnh (
không trùng với và ). qua ba điểm cắt hình chóp theo thiết diện là:
A. Tam giác. B. Hình thang. C. Hình bình hành. D. Hình chữ nhật.
Lời giải
Chọn B.
Ta có :
Ta có nên và có giao tuyến song song
Trong , vẽ
Thiết diện của cắt bởi là tứ giác Do (cùng song song ) nên
là hình thang.
( ) ( )
( ) ( )
( ) ( ) ( )
//
//
ÎÇ
ì
ï
ÞÇ = Î
í
Ì
ï
î
MABC
ABC MN AB N BC
AB ABC
a
a
a
N
BC
( ) ( )
( ) ( )
( ) ( ) ( )
//
//
ÎÇ
ì
ï
ÞÇ = Î
í
Ì
ï
î
N BCD
BCD NP CD P BD
CD BCD
a
a
a
P
BD
( ) ( )
( ) ( )
( ) ( ) ( )
//
//
ÎÇ
ì
ï
ÞÇ = Î
í
Ì
ï
î
PBDA
BDA PQ AB Q AD
AB BDA
a
a
a
Q
AD
( ) ( )
( ) ( )
//
//
=Ç
ì
ï
Þ
í
Ì
ï
î
MQ ADC
QM CD
CD ADC
a
a
MNPQ
=AB C D
=MN NP
MNPQ
.S ABCD
ABCD
M
SA
M
S
A
( )
Mp
a
,,MBC
.S ABCD
A
D
B
C
S
M
N
( )
( )
( )
//
// .
Ì
ü
ï
Þ
ý
Ë
ï
þ
AD BC MBC
AD MBC
AD MBC
( )
//MBC AD
( )
MBC
( )
SAD
.AD
( )
SAD
( )
// ÎMN AD N SD
( ) ( )
.Þ= ÇMN MBC SAD
.S ABCD
( )
MBC
.BCNM
//MN BC
AD
BCNM
Trang 23
Câu 30. Cho hình chóp có đáy là hình thang, đáy lớn là là trung điểm
Mặt phẳng qua song song với và cắt lần lượt tại và Nói gì về thiết
diện của mặt phẳng với khối chóp ?
A. Là một hình bình hành. B. Là một hình thang có đáy lớn là
C. Là tam giác D. Là một hình thang có đáy lớn là
Lời giải
Chọn B.
Trong mặt phẳng , qua kẻ đường thẳng Khi đó,
Trong mặt phẳng , qua kẻ đường thẳng Khi đó,
Vậy
Xét hai mặt phẳng và có hai mặt phẳng cắt nhau theo một
giao tuyến đi qua điểm và song song với
Trong mặt phẳng kẻ Khi đó, là giao tuyến của mặt phẳng với mặt
phẳng . Vậy mặt phẳng cắt khối chóp theo thiết diện là tứ giác
Tứ giác có là hình bình hành. Từ đó suy ra
Trong tam giác có thuộc đoạn , thuộc đoạn và nên
Tứ giác có là hình thang có đáy lớn là
.S ABCD
ABCD
.AB
M
.CD
( )
a
M
BC
.SA
( )
a
,AB SB
N
.P
( )
a
.S ABCD
.MN
.MNP
.NP
( )
ABCD
M
( )
.Î!MN BC N BC
( )
.ÌMN
a
( )
SAB
N
( )
.Î!NP SA P SB
( )
.ÌNP
a
( ) ( )
.º MNP
a
( )
MNP
( )
SBC
( )
( )
( ) ( )
,
Ì
ì
ï
Ì
ï
Þ
í
ï
ï
ÎÎ
î
!
MN MNP
BC SBC
MN BC
P MNP P SBC
P
.BC
( )
SBC
( )
.Î!PQ BC Q SC
PQ
( )
a
( )
SBC
( )
a
.S ABCD
.MNPQ
MNBC
ì
Þ
í
î
!
!
MN BC
MNBC
MC NB
.=MN BC
SBC
P
SB
Q
SC
!PQ BC
.<PQ BC
MNPQ
ì
Þ
í
<
î
!MN PQ
MNPQ
PQ MN
.MN
Trang 24
Câu 31. Cho tứ diện . Gọi là điểm nằm trong tam giác , là mặt phẳng đi qua và
song song với các đường thẳng và . Thiết diện của tứ diện và mp là hình gì ?
A. Hình bình hành. B. Hình tứ diện. C. Hình vuông. D. Hình thang.
Lời giải
Chọn A.
Ta có:
Từ , , , , , ta được thiết diện cần tìm là hình bình hành .
Câu 32. Cho hình chóp có đáy là một hình bình hành tâm Gọi là ba
điểm trên các cạnh Thiết diện của hình chóp với mặt phẳng là hình gì?
A. Ngũ giác. B. Tứ giác. C. Hình thang. D. Hình bình hành.
Lời giải
Chọn A.
ABCD
M
ABC
( )
a
M
AB
CD
( )
a
( ) ( )
,PQ// . P AC,Q BCABC PQ AB
a
Ç= ÎÎ
( )
1
( ) ( )
,PS//CD. ADACD PS S
a
Ç= Î
( )
2
( ) ( )
,QR //CD. DBCD QR R B
a
Ç= Î
( )
3
( ) ( )
,//ABD RS RS AB
a
Ç=
( )
4
( )
//PQ //RS AB
( )
5
( )
PS//RQ //CD
( )
6
( )
1
( )
2
( )
3
( )
4
( )
5
( )
6
PQRS
.S ABCD
ABCD
.O
,M
,N
P
,AD
,CD
.SO
( )
MNP
Trang 25
Trong gọi lần lượt là giao điểm của với
Trong gọi
Trong gọi
Trong gọi
Ta có:
Lí luận tương tự ta có
Thiết diện là ngũ giác
Câu 33. Cho hình chóp có đáy là hình vuông cạnh , gọi là tâm của đáy. Tam giác
là tam giác đều. Gọi là điểm trên cạnh . Mặt phẳng đi qua và song song với
cắt hình chóp theo thiết diện là hình gì?
A. Hình vuông. B. Hình chữ nhật. C. Hình thang cân. D. Hình thang vuông.
Lời giải
Chọn C.
T
R
H
M
N
K
E
O
C
D
A
B
S
P
( )
mp ABCD
,E
,K
F
MN
,DA
,DB
.DC
( )
mp SDB
H KP SB=Ç
( )
mp SAB
T EH SA=Ç
( )
mp SBC
R FH SC=Ç
( )
EMN
EH MNP
HKP
Î
ì
ÞÌ
í
Î
î
( )
TSA
TSA MNP
TEH
Î
ì
Þ= Ç
í
Î
î
( )
RSC MNP=Ç
.MNRHT
.S ABCD
ABCD
a
O
SAB
M
BC
( )
P
M
,SA SB
Trang 26
Qua kẻ một đường thẳng song song với , cắt tại .
Qua kẻ một đường thẳng song song với , cắt tại .
Gọi Qua kẻ đường thẳng song song với , cắt tại .
Thiết diện tạo bởi và hình chóp là tứ giác .
Do nên
Đặt Có
Tương tự,
Từ (1) và (2) ta có thiết diện là hình thang cân.
Câu 34. Cho hình chóp có đáy là hình thang, đáy lớn là là trung điểm
Mặt phẳng qua song song với và cắt lần lượt tại và Nói gì về thiết
diện của mặt phẳng với khối chóp ?
A. Là một hình bình hành. B. Là một hình thang có đáy lớn là
C. Là tam giác D. Là một hình thang có đáy lớn là
Lời giải
Chọn B.
M
SB
SC
Q
Q
SA
AC
O
.M MO AD=Ç
N
SA
SD
P
( )
P
.S ABCD
MNPQ
// ; // ; //MQ SB QO SA NP SA
// (1)
CM CQ CO DP
MN PQ
CB CS CA DS
===Þ
.BM x=
//
MQ CM
MQ SB
SB CB
Þ=
.()aCM SB a x
MQ a x
CB a
-
== =-
(2)NP a x MQ NP=-Þ =
MNPQ
.S ABCD
ABCD
.AB
M
.CD
( )
a
M
BC
.SA
( )
a
,AB SB
N
.P
( )
a
.S ABCD
.MN
.MNP
.NP
Trang 27
Trong mặt phẳng , qua kẻ đường thẳng Khi đó,
Trong mặt phẳng , qua kẻ đường thẳng Khi đó,
Vậy
Xét hai mặt phẳng và có hai mặt phẳng cắt nhau theo một
giao tuyến đi qua điểm và song song với
Trong mặt phẳng kẻ Khi đó, là giao tuyến của mặt phẳng với mặt
phẳng . Vậy mặt phẳng cắt khối chóp theo thiết diện là tứ giác
Tứ giác có là hình bình hành. Từ đó suy ra
Trong tam giác có thuộc đoạn , thuộc đoạn và nên
Tứ giác có là hình thang có đáy lớn là
Câu 35. Cho hình chóp , là một điểm trên cạnh
,
là điểm trên cạnh . Mặt phẳng
chứa và song song với . Thiếtdiện củahình chópcắt bởi là hình thang thì điều kiện là:
A. . B. . C. . D. .
Lời giải
Chọn B.
( )
ABCD
M
( )
.MN BC N BCÎ!
( )
.MN
a
Ì
( )
SAB
N
( )
.NP SA P SBÎ!
( )
.NP
a
Ì
( ) ( )
.MNP
a
º
( )
MNP
( )
SBC
( )
( )
( ) ( )
,
MN MNP
BC SBC
MN BC
P MNP P SBC
Ì
ì
ï
Ì
ï
Þ
í
ï
ï
ÎÎ
î
!
P
.BC
( )
SBC
( )
.PQ BC Q SCÎ!
PQ
( )
a
( )
SBC
( )
a
.S ABCD
.MNPQ
MNBC
MN BC
MNBC
MC NB
ì
Þ
í
î
!
!
.MN BC=
SBC
P
SB
Q
SC
PQ BC!
.PQ BC<
MNPQ
MN PQ
MNPQ
PQ MN
ì
Þ
í
<
î
!
.MN
.S ABCD
M
AB
N
CD
( )
a
MN
SA
( )
a
2AD CD=
//MN BC
//BC AD
//MN AD
Trang 28
Do nên cắt và lần lượt theo các giao tuyến song song với
.
Trong kẻ .
Trong kẻ .
Trong kẻ .
Vậy thiết diện cần tìm là tứ giác
.
Ta có là hình thang thì
Xét (1)
vì .
: điều này vô lí.
Xét (2)
Có: .
Đảo lại nếu có thì vì
Câu 36. Cho hình chóp cóđáy là hình thoi cạnh
, ,
. là trung
điểm của đoạn . là một điểm trên cạnh . Đặt . Mặt phẳng chứa và
song song với . Thiết diện của hình chóp cắt bởi có diện tích tính theo là:
( )
//AB
a
( )
a
( )
SAB
( )
SAC
SA
( )
SAB
// ,MP SA P SBÎ
( )
ABCD
{ }
MN AC OÇ=
( )
SAC
// ,OQ SA Q SCÎ
MNQP
MNQP
( )
( )
//
//
1
2
MP QN
MN PQ
é
Þ
ê
ê
ë
( )
1//SA Q NÞ
//SA MP
( )
//SA SCDÞ
( ) ( )
( )
( )
//
//
BC ABCD SBC
MN ABCD
MN BC
PQ SBC
MN PQ
=Ç
ì
ï
Ì
ï
Þ
í
Ì
ï
ï
î
//MN BC
//MN PQ
( ) ( )
( )
( )
//
PQ SBC
BC SBC
MN
MN BC
a
a
=Ç
ì
ï
Ì
ï
í
Ì
ï
ï
î
.S ABCD
a
SA SB a==
3SC SD a==
E
SA
M
BC
( )
0BM x x a=££
( )
a
ME
AB
( )
a
,ax
Trang 29
A. . B. .
C. . D. .
Lời giải
Chọn A.
Do nên cắt và lần lượt theo các giao tuyến song song với
.
Trong kẻ (1).
Trong kẻ (2).
Từ (1) và (2),suy ra nên tứ giác là hình thang.
Hai tam giác và bằng nhau (c.c.c) nên .
Hai tam giác và bằng nhau (c.g.c) nên .
Vậy thiết diện là hình thang cân.
Áp dụng hệ quả của định lý hàm số cosin trong tam giác ta có:
.
Tam giác có
.
.
.
Ta có
22
3
16 8 3
16
a
xaxa++
22
16 8 3
16
a
xaxa++
22
3
16 4 3
16
a
xaxa-+
22
3
16 4 3
16
a
xaxa++
( )
//AB
a
( )
a
( )
ABCD
( )
SAB
AB
( )
ABCD
// ,MN AB N ADÎ
( )
SAB
// ,EF AB F SBÎ
//MN FE
MNEF
SAD
SBC
∑
∑
SAD SBC=
EAN
FBM
EN FM=
MNEF
SBC
∑
222222
2
31
cos
2. 2 2
SB BC SC a a a
SBC
SB BC a
+- +-
===-
FBM
∑
22
22 2 2 2
1
2. .cos 2..
42242
aa aax
FM BF BM BF BM SBC x x x
æö
=+ - =+- -=++
ç÷
èø
2
2
42
aax
FM xÞ=++
( )
1
.
2
MNEF
SMNEFFH=+
24
MN EF a
MH
-
==
Trang 30
.
Vậy .
Câu 37. Cho tứ diện đều có cạnh bằng . Điểm là trung điểm của . Tính diện tích thiết
diện của hình tứ diện cắt bởi đi qua và song song với và .
A. . B. . C. . D. .
Lời giải
Chọn D.
Qua kẻ 2 đường thẳng lần lượt song song với , cắt tại và cắt tại .
Thiết diện tạo bởi và tứ diện là tam giác đều .
Có
Diện tích thiết diện
.
Câu 38. Cho hình chóp ,đáy là hình vuông cạnh ,mặt bên là tam giác đều.Cho
.Gọi lần lượt là trung điểm của .Gọi là một điểm trên cạnh .Mặt
phẳng cắt tại .Cho biết là hình thang cân.Đặt .Tìm để diện
tích là nhỏ nhất.
22 2
222 2 2
3
4216216
aaxa axa
FH FM MH x x=-=++-=++
2
2
3
216
ax a
FH xÞ=++
( )
2
222
11 33
. 16 8 3
2 2 2 2 16 16
MNEF
a ax a a
S MN EF FH a x x ax a
æö
=+ =+++= ++
ç÷
èø
ABCD
a
M
AB
( )
mp P
M
AD
AC
2
3
8
a
2
2
8
a
2
93
16
a
2
3
16
a
M
AD
AC
BD
N
BC
P
( )
P
MNP
2
a
MN NP PM== =
22
1133
...
224216
MNP
aa
SMNMP===
.S ABCD
ABCD
a
( )
SAB
3SC SD a==
,HK
,SA SB
M
AD
( )
HKM
BC
N
( )
HKMN
( )
0AM x x a=££
x
HKMN
Trang 31
A. . B. . C. . D. .
Lời giải
Chọn C.
Ta có ngay và .Trong tam giác ,ta có
Trong tam giác ,ta có
.
Trong hình thang cân ,gọi là chân đường cao hạ từ ,ta có
.Suy ra
.
Ta có biến đổi: .
Vậy đạt được khi .
Câu 39. Cho hình chóp có đáy là hình bình hành. Gọi là điểm trên cạnh sao cho
, là điểm trên cạnh . Mặt phẳng qua và song song với . Xác định vị trí của
điểm để cắt hình chóp theo thiết diện là hình bình hành.
A. là trung điểm của . B. .
C. . D. .
5
a
x =
3
a
x =
4
a
x =
2
a
x =
MN a=
1
22
a
KH AB==
SAD
∑
222222
2
31
cos
2. . 2 2
SA AD SD a a a
SAD
SA A D a
+- +-
===-
HAM
∑
2
222 2
1
2. .cos 2...
422
aa
MH AH AM AH AM HAM x x
æö
=+ - =+- -
ç÷
èø
22
1
42
2
MH x ax aÞ= ++
MNKH
P
H
2
22 2 2 2
1
16 8 3
24
MN HK
HP MH MP MH x ax a
-
æö
=-=- = -+
ç÷
èø
( )
22 22
111 3
.16 8 3 16 8 3
2224 16
MNKH
aa
S MN KH HP a x ax a x ax a
æö
=+ =+ -+= -+
ç÷
èø
( )
2
2
22 2
3332
16 8 3 4 2
16 16 16
MNKH
aaa
Sxaxaxaa=-+=-+³
( )
2
min
32
16
MNKH
a
S =
4
a
x =
.S ABCD
ABCD
'C
SC
'1
'2
CS
CC
=
M
SA
( )
P
'CM
BC
M
( )
P
M
SA
2
MA
MS
=
1
2
MA
MS
=
2
3
MA
MS
=
Trang 32
Lời giải
Chọn B.
song song
Khi đó cắt hình chóp
theo thiết diện là tứ giác có nên thiết diện là hình thang.
Có
Tứ giác là hình bình hành khi
Câu 40. Cho tứ diện trong đó và là một điểm trên cạnh với
Mặt phẳng qua , song song với và . Tính diện tích thiết diện của
và tứ diện theo và .
A. . B. . C. . D. .
Lời giải
Chọn A.
( )
P
BC
( )
1
1
1
'
()
//
dquaC
PSBCd
dBC
ì
ÞÇ =
í
î
( )
1
;( )dSBNP SABMNÇ= Ç =
( )
2
2
2
()// ()// ()
//
dquaM
PBC PAD P SADd
dAD
ì
ÞÞÇ=
í
î
2
.dSDPÇ=
( )
P
.S ABCD
'MNC P
'//CN MP
'' 1 1
'// ' .
33
SC C N
CN BC CN BC
SC BC
Þ= =Þ =
'MNC P
11 1
'.
33 3
MP
MP NC BC AD
AD
== = Û=
1
// 2.
3
SM MA
MP AD
SA MS
Þ=Û=
ABCD
AB CD^
.AB AC CD a===
M
AC
( )
0.AM x x a=<<
( )
P
M
AB
CD
( )
P
ABCD
a
x
()xa x-
()
2
xa x-
()aa x-
()
2
aa x-
Trang 33
Qua kẻ các đường thẳng song song với và cắt và lần lượt tại và .
Qua kẻ đường thẳng song song với cắt tại .
Suy ra thiết diện là tứ giác có nên thiết diện là hình
chữ nhật.
Có
.
Câu 41. Cho tứ diện trong đó và là một điểm trên cạnh .
Mặt phẳng qua .
.
, song song với và . Diện tích thiết diện của và tứ diện đạt
giá trị lớn nhất bằng bao nhiêu?
A. . B. . C. . D. .
Lời giải
Chọn D.
M
AB
CD
BC
AD
Q
N
N
AB
BD
P
MNPQ
// ; // ;MN PQ MQ NP MP MQ^
MNPQ
.MN AM AM DC
MN x
DC AC AC
=Þ= =
MQ MC a x
MQ a x
AB AC a
-
== Þ=-
.()
MNPQ
SMNMQxaxÞ= =-
ABCD
AB CD^
.AB AC CD a===
M
AC
( )
P
AB
CD
mp
( )
P
ABCD
2
a
2
16
a
2
2
a
2
4
a
Trang 34
Qua kẻ các đường thẳng song song với và cắt và lần lượt tại và .
Qua kẻ đường thẳng song song với cắt tại .
Suy ra thiết diện là tứ giác có nên thiết diện là hình chữ
nhật.
Có
.
Theo bất đẳng thức Cô-si: khi .
Câu 42. Cho hình chóp , là một điểm nằm trong tam giác . Các đường thẳng qua
song song với cắt các mặt phẳng lần lượt tại .
có giá trị không đổi bằng bao nhiêu khi di động trong tam giác ?
A. . B. . C. . D. .
Lời giải
Chọn C.
M
AB
CD
BC
AD
Q
N
N
AB
BD
P
MNPQ
// ; // ;MN PQ MQ NP MP MQ^
MNPQ
.MN AM AM DC
MN x
DC AC AC
=Þ= =
MQ MC a x
MQ a x
AB AC a
-
== Þ=-
.()
MNPQ
SMNMQxaxÞ= =-
2
2
()
24
xax a
xa x
+-
æö
-£ =
ç÷
èø
2
a
x =
.S ABC
M
ABC
M
,,SA SB SC
( ) ( ) ( )
,,SBC SAC SAB
,,ABC
¢¢¢
MA MB MC
SA SB SC
¢¢ ¢
++
M
ABC
1
3
1
2
1
2
3
Trang 35
Do nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử là giao điểm của mặt phẳng này
với . Khi đó thẳng hàng và ta có: .
Tương tự ta có: . Vậy .
Câu 43. Cho hình chóp , là một điểm nằm trong tam giác . Các đường thẳng qua
song song với cắt các mặt phẳng lần lượt tại .
nhận giá trị lớn nhất. Khi đó vị trí của trong tam giác là:
A. Trực tâm . B. Trọng tâm .
C. Tâm ngoại tiếp . D. Tâm nội tiếp .
Lời giải
Chọn B.
Do nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử là giao điểm của mặt phẳng này
với . Khi đó thẳng hàng và ta có: .
Tương tự ta có: . Vậy .
Ap dụng bất đẳng thức Cauchy ta có :
MA SA
¢
∥
E
BC
,,AM E
MBC
ABC
S
MA ME
SA EA S
¢
==
,
MAC
MAB
ABC ABC
S
S
MB MC
SB S SC S
¢¢
==
1
MA MB MC
SA SB SC
¢¢ ¢
++ =
.S ABC
M
ABC
M
,,SA SB SC
( ) ( ) ( )
,,SBC SAC SAB
,,ABC
¢¢¢
..
MA MB MC
SA SB SC
¢¢ ¢
M
ABC
ABCD
ABCD
ABCD
ABCD
MA SA
¢
∥
E
BC
,,AM E
MBC
ABC
S
MA ME
SA EA S
¢
==
,
MAC
MAB
ABC ABC
S
S
MB MC
SB S SC S
¢¢
==
1
MA MB MC
SA SB SC
¢¢ ¢
++ =
Trang 36
.
Dầu bằng xảy ra khi và chỉ khi: .
Điều này chỉ xảy ra khi là trọng tâm tam giác . Vậy đáp án đúng là B.
Câu 44. Cho hình chóp với đáy là hình thang với đáy và .
Gọi lần lượt là trọng tâm các tam giác và . Mặt phẳng cắt lần lượt tại
. Mặt phẳng cắt lần lượt tại . Gọi là giao điểm của và , là giao
điểm của và . Trong các mệnh đề dưới đây, có bao nhiêu mệnh đề sai?
1) và song song với nhau.
2) và song song với nhau.
3) .
4)
A. . B. . C. . D. .
Lời giải
Chọn B.
Ta có , suy ra .
Do .
Ta có: , suy ra .
3
1
3.. ..
27
MA MB MC MA MB MC MA MB MC
SA SB SC SA SB SC SA SB SC
¢¢ ¢ ¢¢¢ ¢¢¢
++ ³ Þ £
MAC MAB MBC
MA MB MC
SSS
SA SB SC
¢¢ ¢
==Þ==
M
ABC
.S ABCD
ABCD
AD
BC
( )
AD a BC b=> =
,IJ
SAD
SBC
( )
ADJ
,SB SC
,MN
( )
BCI
,SA SD
,PQ
E
AM
PB
F
CQ
DN
MN
PQ
MN
EF
( )
2
5
EF a b=+
( )
1
4
EF a b=+
4
1
2
3
( )
ISADÎ
( ) ( )
ISAD BCIÎÇ
( ) ( )
( ) ( )
,
SAD BCI PQ
AD SAD BC BCI PQ AD BC
AD BC
Ç=
ì
ï
ÌÌÞ
í
ï
î
∥∥
∥
( )
JSBCÎ
( ) ( )
JSBC ADJÎÇ
Trang 37
Do .
Từ đó suy ra và song song với nhau.
Ta có: .
Suy ra . Gọi là giao điểm của với .
Do .
Theo định lý Thalet ta có: . Do song song với nên theo định lý Thalet ta có :
.
Tương tự ta cũng có: .
Từ đây suy ra .
( ) ( )
( ) ( )
,
SBC ADJ MN
BC SBC AD ADJ MN AD BC
AD BC
Ç=
ì
ï
ÌÌÞ
í
ï
î
∥∥
∥
MN
PQ
( ) ( )
( ) ( )
( ) ( )
EF ADNM BCQP
AD ADNM ABCD
EF AD
BC ABCD BCQP
AD BC
=Ç
ì
ï
=Ç
ï
Þ
í
=Ç
ï
ï
î
∥
∥
EF MN∥
K
CP
EF
EF EK KF=+
2
3
SP SM
PM AB
SA SB
== Þ ∥
22
35
PE PE
EB PB
=Þ =
EK
BC
22
55
PE EK
EK b
PB BC
==Þ=
2553322
.
3335535
QF QC PQ
FK PQ AD a
FC FC FK
=Þ =Þ =Þ = = =
( )
2
5
EF a b=+
| 1/37
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CÁC DẠNG TOÁN TRẮC NGHIỆM
BÀI ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
1. Vị trí tương đối của đường thẳng và mặt phẳng.
Cho đường thẳng d và mặt phẳng (a ), ta có ba vị trí tương đối giữa chúng là:
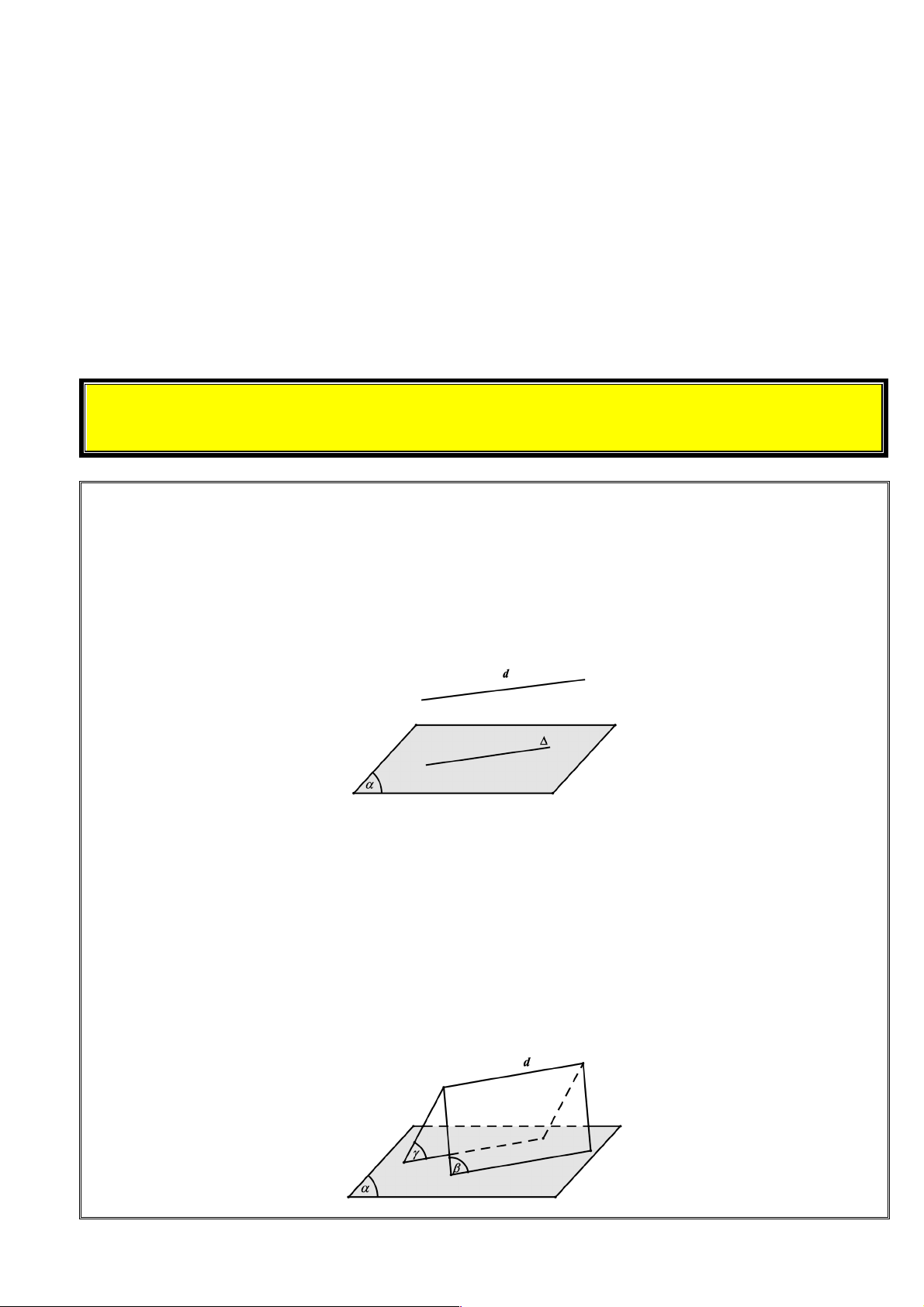
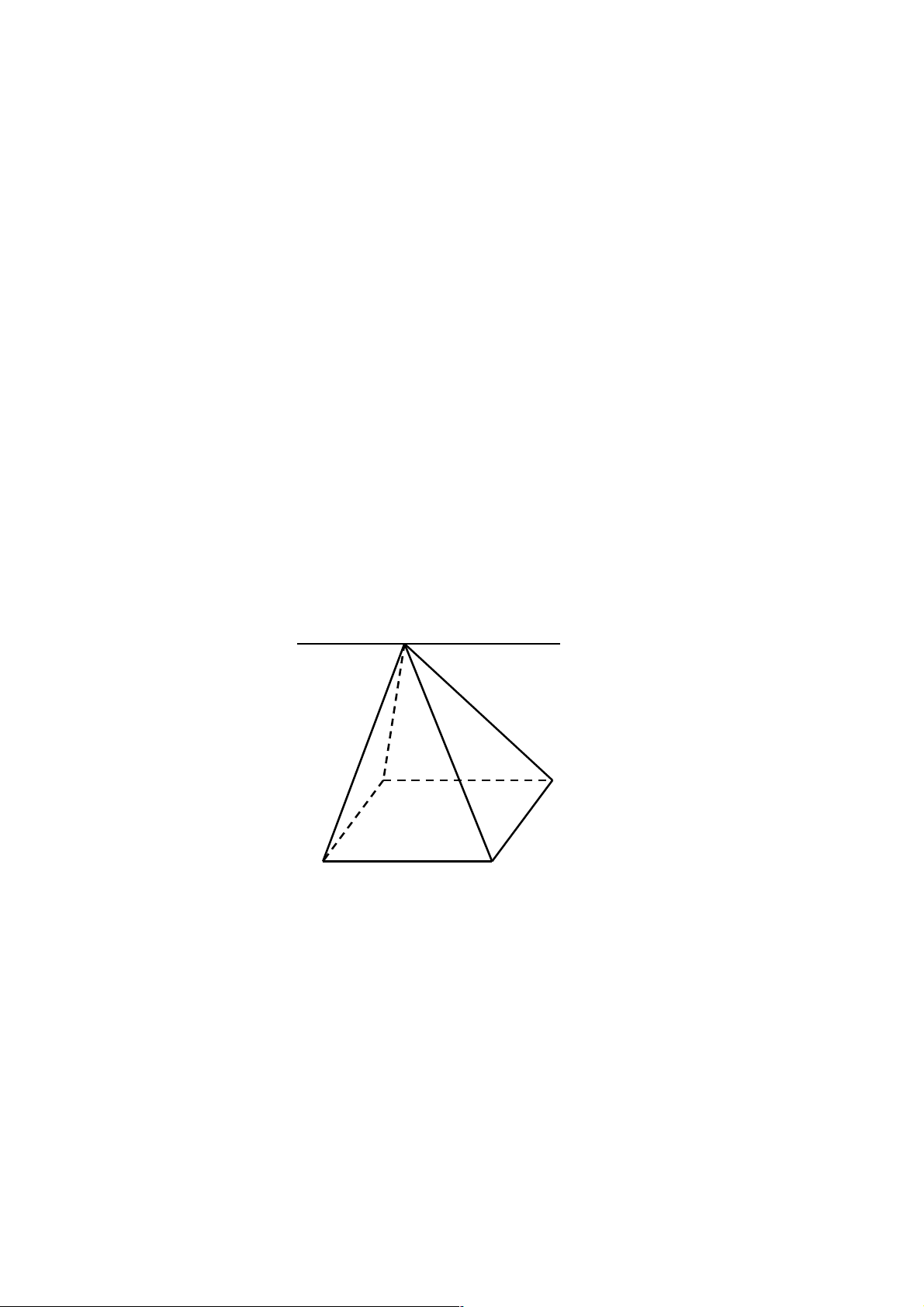
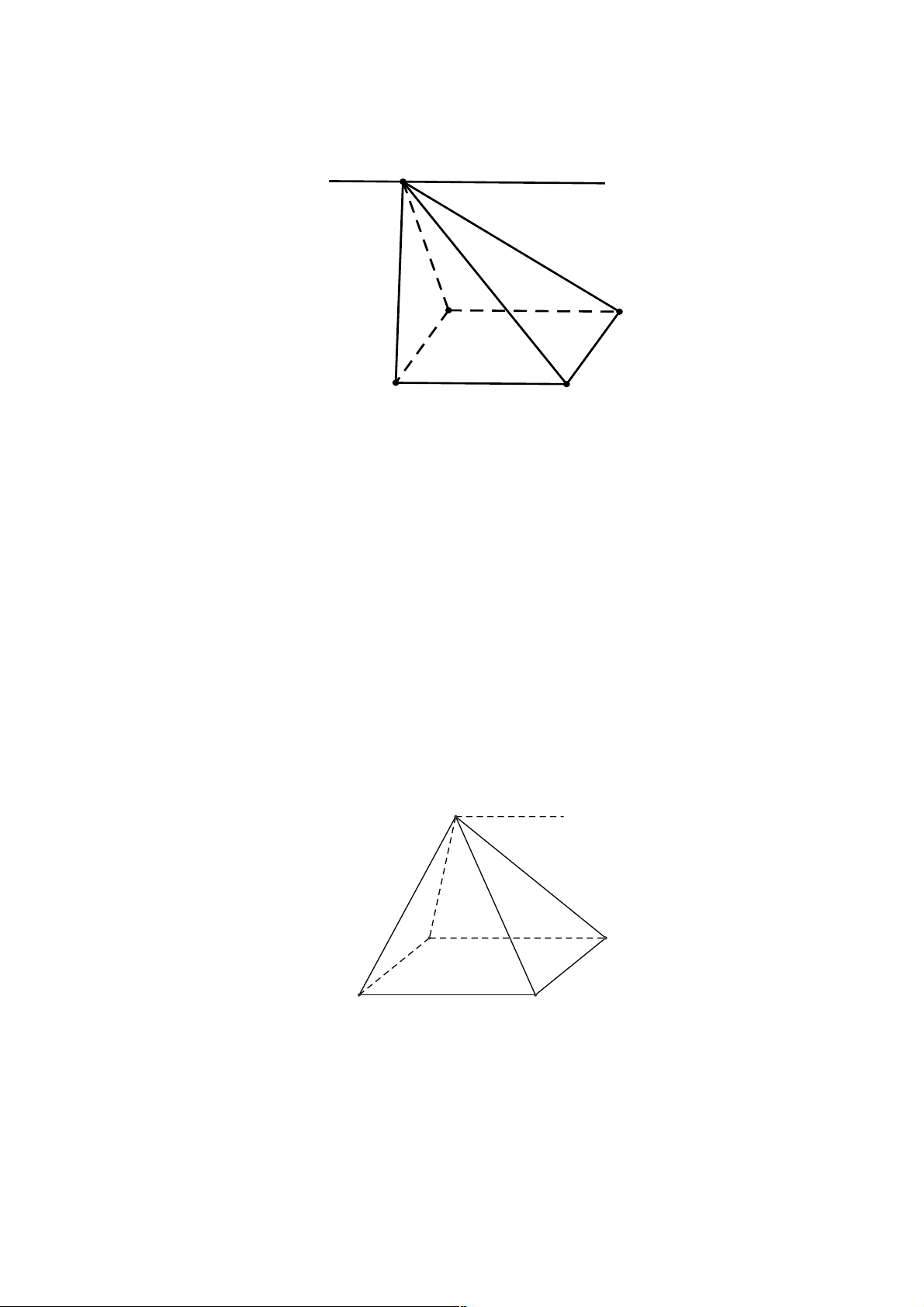
¨ d và (a ) cắt nhau tại điểm M , kí hiêu {M} = d Ç(a ) hoặc để đơn giản ta kí hiệu M = d Ç(a) (h1)
¨ d song song với (a ), kí hiệu d ! (a ) hoặc (a ) ! d ( h2)
¨ d nằm trong (a ), kí hiệu d Ì (a ) (h3) d d M d α α α h1 h2 h3
2. Các định lí và tính chất.
¨ Nếu đường thẳng d không nằm trong mặt phẳng (a ) và d song song với đường thẳng d ' nằm
trong (a )thì d song song với (a ). ìd Ë (a ) d ï Vậy íd ! d ' Þ d ! (a ) ïd ' Ì î (a ) d' α h3
¨ Cho đường thẳng d song song với mặt phẳng (a ). Nếu mặt phẳng (b ) đi qua d và cắt (a ) theo
giao tuyến d ' thì d ' ! d . ìd ! (a ) ï β d Vậy íd Ì (b ) Þ d ' ! d . ( ï î a ) Ç(b ) = d ' d' α Trang 1
¨ Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng ( nếu
có) cũng song song với đường thẳng đó. β ( ì a ) ! d d ï Vậy ( í b ) ! d Þ d ' ! d . α ( ï î a ) Ç(b ) = d ' d'
¨Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia. m l α d DẠNG 1 LÝ THUYẾT Trang 2
Câu 1. Trong không gian có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C.
Vị trí tương đối của đường thẳng và mặt phẳng là
Đường thẳng nằm trong mặt phẳng.
Đường thẳng song song với mặt phẳng.
Đường thẳng cắt mặt phẳng.
Câu 2. Cho hai đường thẳng a và b chéo nhau.
Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 0. B. 1. C. 2. D. Vô số. Lời giải Chọn B.
Theo định lý 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và
song song với đường thẳng kia.
Câu 3. Cho hai đường thẳng song song a và b . Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 0. B. 1. C. 2. D. vô số. Lời giải Chọn D.
Theo tính chất: Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Câu 4. Cho mặt phẳng (a ) và đường thẳng d Ë (a ). Khẳng định nào sau đây sai?
A. Nếu d / / (a ) thì trong (a ) tồn tại đường thẳng (a) sao cho a / /d .
B. Nếu d / / (a ) và đường thẳng b Ì (a ) thì b / /d .
C. Nếu d / /c Ì (a ) thì d / /(a ).
D. Nếu d Ç(a ) = A và đường thẳng d¢ Ì (a ) thì d và d¢ hoặc cắt nhau hoặc chéo nhau. Lời giải Chọn B. Trang 3 d b a
Khi (d ) / / (a ) và đường thẳng (b) Ì (a ) thì ngoài trường hợp (b) / / (d ) còn có trường hợp (b) và (d ) chéo nhau.
Câu 5. Cho hai đường thẳng a và b cùng song song với mp(P). Khẳng định nào sau đây không sai?
A. a / /b .
B. a và b cắt nhau.
C. a và b chéo nhau.
D. Chưa đủ điều kiện để kết luận vị trí tương đối của a và b . Lời giải Chọn D. Cho mp(P) qua ,
A B,C không thẳng hàng.
Giả sử a,b, c phân biệt là các đường thẳng nằm ngoài mp(P) thỏa a / / AB,b / / AB,c / /BC.
Trong trường hợp này a / / . b
Nếu a và c đồng phẳng thì a cắt . c
Nếu a và c không đồng phẳng thì a và c chéo nhau.
Câu 6. Khẳng định nào sau đây đúng?
A.Đường thẳng a Ì mp(P) và mp(P) / / đường thẳng D Þ a / / . D
B. D / /mp(P) Þ Tồn tại đường thẳng D' Ì mp(P): D'/ / . D
C.Nếu đường thẳng D song song với mp(P) và (P) cắt đường thẳng a thì D cắt đường thẳng . a
D. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì 2 đường thẳng đó song song nhau. Lời giải Chọn D. Trang 4 D / /D' üï Ta có ý Þ D / / P D Ì (P) ( ). ' ïþ
Câu 7. Cho mp(P) và hai đường thẳng song song a và . b
1. Nếu mp(P) song song với a thì (P) / /b
2. Nếu mp(P) song song với a thì (P) chứa b
3. Nếu mp(P) song song với a thì (P) / /b hoặc chứa b
4. Nếu mp(P) cắt a thì cũng cắt b
5. Nếu mp(P) cắt a thì (P) có thể song song với b
6. Nếu mp(P) chứa a thì (P) có thể song song với b
Có bao nhiêu nhận xét đúng? A. 5. B. 2. C. 3. D. 4. Lời giải Chọn C. 1. sai 2. sai 3. đúng
a / /b üïýÞb// P ÚbÌ P . a / / (P) ( ) ( ) ïþ 4. đúng Chọn D.
a cắt (P) suy ra b không song song (P) mà (P) cũng
không chứa b , vậy b cắt (P). 5. sai a Ì (P)üï
6. đúng: a / /b
ý Þ b / / (P). b (P)ï Ë þ Trang 5
Câu 8. Cho đường thẳng a nằm trong mp(a ) và đường thẳng b Ë (a ). Mệnh đề nào sau đây đúng?
A. Nếu b / / (a ) thì b / / . a
B. Nếu b cắt (a ) thì b cắt . a
C. Nếu b / /a thì b / / (a ) .
D. Nếu b cắt (a ) và mp(b ) chứa b thì giao tuyến của (a ) và (b ) là đường thẳng cắt cả a và b. Lời giải Chọn C. a Ì (a )ü b (a )ï Ë ý Þ b / / (a ). a / / ï b þ
Câu 9. Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 0. B.1. C. 2. D. Vô số. Lời giải Chọn B.
Gọi (a ) là mp chứa a và song song . b ( !!" !!" !!"
a ) có vtpt n = éu ;u ù a ë a b û
Đồng thời (a ) qua A với AÎ . a
Do đó (a ) xác định duy nhất. Trang 6 DẠNG 2
CHỨNG MINH ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG Phương pháp 1
Cơ sở của phương pháp là dùng điều kiện cần và đủ để chứng minh đường thẳng d song song với mặt phẳng (a ).
¨ Bước 1: Quan sát và quản lí giả thiết tìm đường thẳng ưu việt D Ì (a) và chứng minh d ! D.
¨ Bước 2: Kết luận d ! (a) . Phương pháp 2
Cơ sở của phương pháp là dùng định lý phương giao tuyến song song.
¨ Bước 1: Chứng minh d = (b ) Ç(g ) ì(b ) Ç (a) = a ï mà í(g ) Ç(a) = b ï îa ! b
¨ Bước 2: Kết luận d ! (a) . Trang 7
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt
phẳng (SAD) và (SBC). Khẳng định nào sau đây đúng?
A. d qua S và song song với BC .
B. d qua S và song song với DC .
C. d qua S và song song với AB .
D. d qua S và song song với BD. Lời giải Chọn A. S d B C A D ìAD Ì (SAD) ï ïBC Ì (SAC) Ta có í
Þ d //BC (Theo hệ quả của định lý 2 (Giao tuyến của ba mặt phẳng)).
ïd = (SAD) Ç(SAC ) ï îAD//BC
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
A. là đường thẳng đi qua S song song với AB, CD
B. là đường thẳng đi qua S C. là điểm S Trang 8
D. là mặt phẳng (SAD) Lời giải Chọn A S d A B D C ìAB Ì (SAB) ï ïCD Ì (SCD) Ta có í ïAB ! CD ïS Î(SAB)Ç î (SCD)
Þ (SAB)Ç(SCD) = d ! AB ! C , D S Îd .
Câu 12. Cho hình bình hành ABCD và một điểm S không nằm trong mặt phẳng ( ABCD). Giao tuyến
của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng nào sau đây? A. AB . B. AC . C. BC . D. SA . Lời giải Chọn A. S x A B D C ìAB//CD ï
Xét (SAB) và (SCD) có S là điềm chung íAB Ì (SAB) ïCD Ì î (SCD)
Þ (SAB)Ç(SCD) = Sx//AB//CD Trang 9
Các bạn muốn tải đầy đủ 38 chuyên đề ôn thi 12 file word (hơn 5500 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 12 file word thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Câu 13. Cho tứ diện ABCD . I và J theo thứ tự là trung điểm của AD và AC , G là trọng tâm tam giác
BCD . Giao tuyến của hai mặt phẳng (GIJ ) và (BCD) là đường thẳng :
A. qua I và song song với . AB
B. qua J và song song với . BD
C. qua G và song song với . CD
D. qua G và song song với BC. Lời giải Chọn C. A I J D B G C
Gọi d là giao tuyến của (GIJ ) và (BCD).
Ta có GÎ(GIJ )Ç(BCD), IJ //CD , IJ Ì (GIJ ), CD Ì (BCD).
Suy ra d đi qua G và song song với CD .
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , I là trung điểm cạnh SC .
Khẳng định nào sau đây SAI?
A. IO// mp(SAB) .
B. IO // mp(SAD).
C. mp(IBD)cắt hình chóp S.ABCD theo thiết diện là một tứ giác.
D. (IBD)!(SAC) = IO . Lời giải Chọn C. Trang 10 S I A D O B C OI //SA üï Ta có:
ý Þ OI // SAB nên A đúng. OI Ë (SAB) ( ) ïþ OI //SA üï Ta có:
ý Þ OI // SAD nên B đúng. OI Ë (SAD) ( ) ïþ
Ta có: (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên Chọn C.
Ta có: (IBD)!(SAC) = IOnên D đúng.
Câu 15. Cho tứ diện ABCD . Gọi G và G lần lượt là trọng tâm các tam giác BCD và ACD . 1 2 Chọn Câu sai :
A. G G // ABD G G // ABC 1 2 ( ) 1 2 ( ). B. . 2
C. BG , AG và CD đồng qui
D. G G = AB . 1 2 1 2 3 Lời giải Chọn D. A G2 B D G1 M C
G và G lần lượt là trọng tâm
các tam giác BCD và ACD nên BG , AG và CD đồng qui tại M (là 1 2 1 2
trung điểm của CD ) .
Vì G G / / AB nên G G / / ABD G G / / ABC 1 2 ( ) 1 2 ( )và . 1 2 Trang 11 1
Lại có G G = AB nên chọn đáp án D. 1 2 3
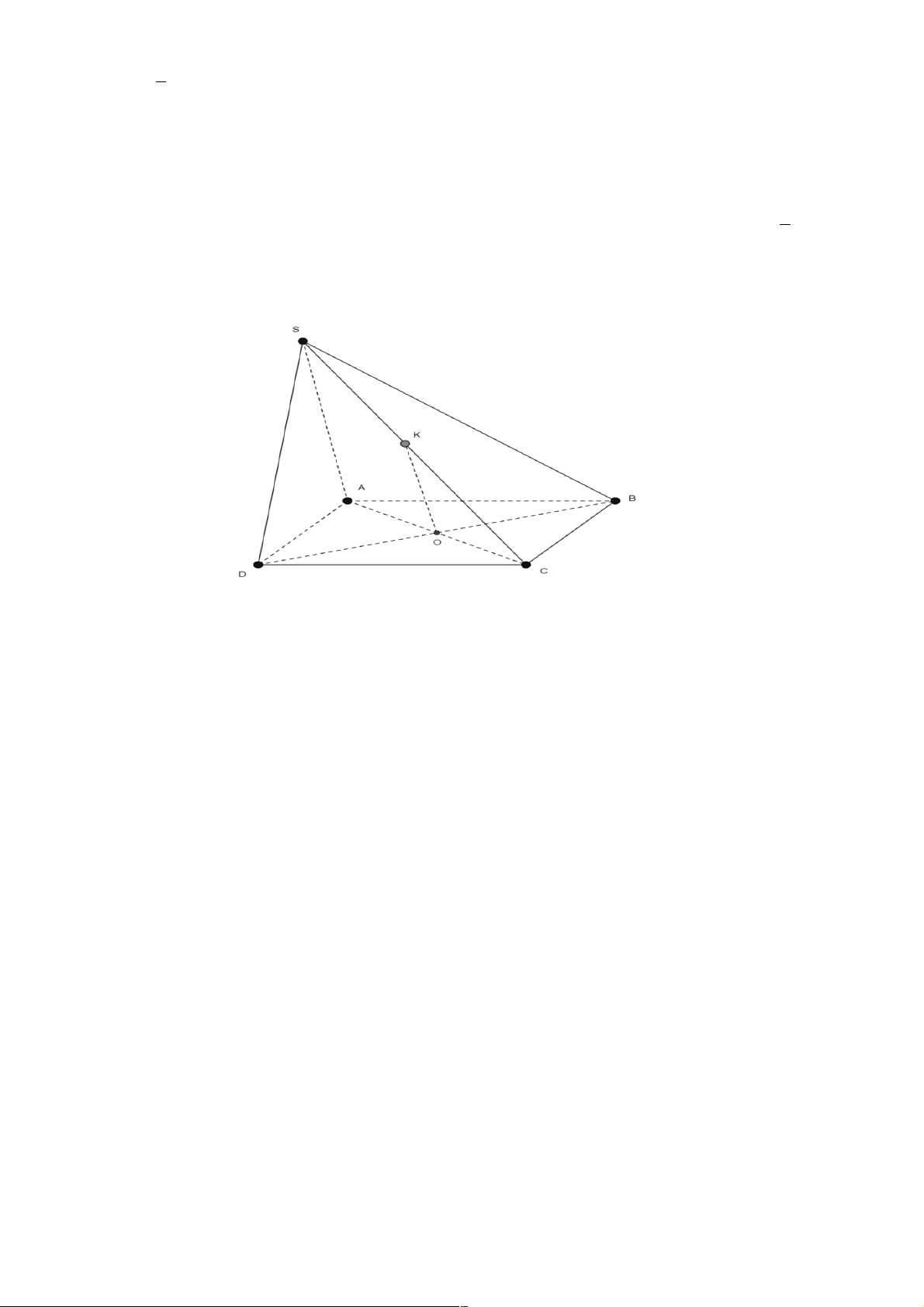
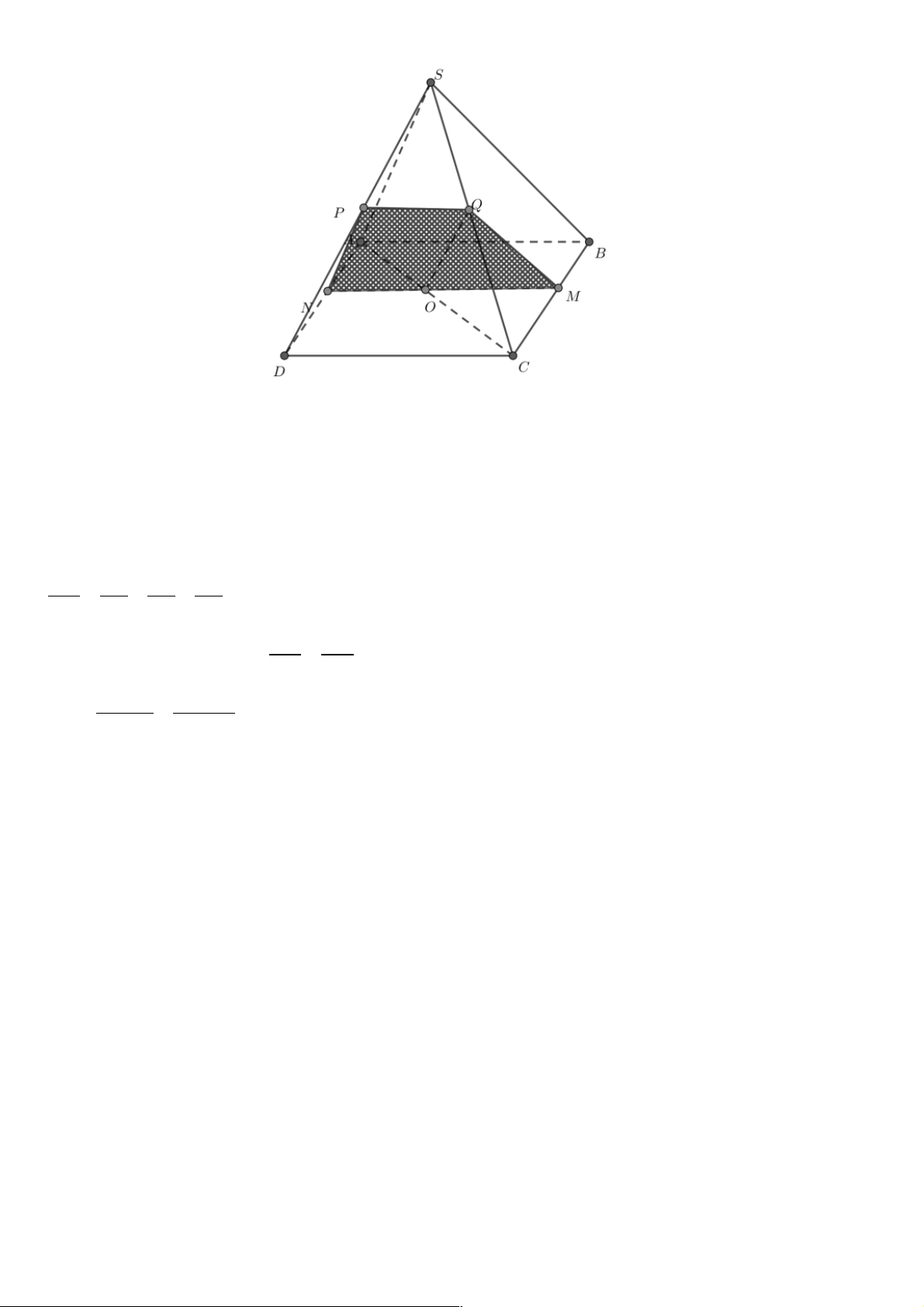
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (a ) qua BD và song
song với SA , mặt phẳng (a ) cắt SC tại K. Khẳng định nào sau đây là khẳng định đúng ? 1
A. SK = 2KC.
B. SK = 3KC.
C. SK = KC.
D. SK = KC. 2 Lời giải Chọn C.
Gọi O là giao điểm của AC và BD . Do mặt phẳng (a ) qua BD nên OÎ(a ) .
Trong tam giác SAC , kẻ OK song song SA (K ÎSC) . ( ì a ) ! SA ï
Do íOK ! SA Þ OK Ì (a ) Þ SC Ç(a ) = {K}. ïOÎ î (a ) ìOK ! SA
Trong tam giác SAC ta có í
Þ OK là đường trung bình của DSAC. îOA = OC
Vậy SK = KC.
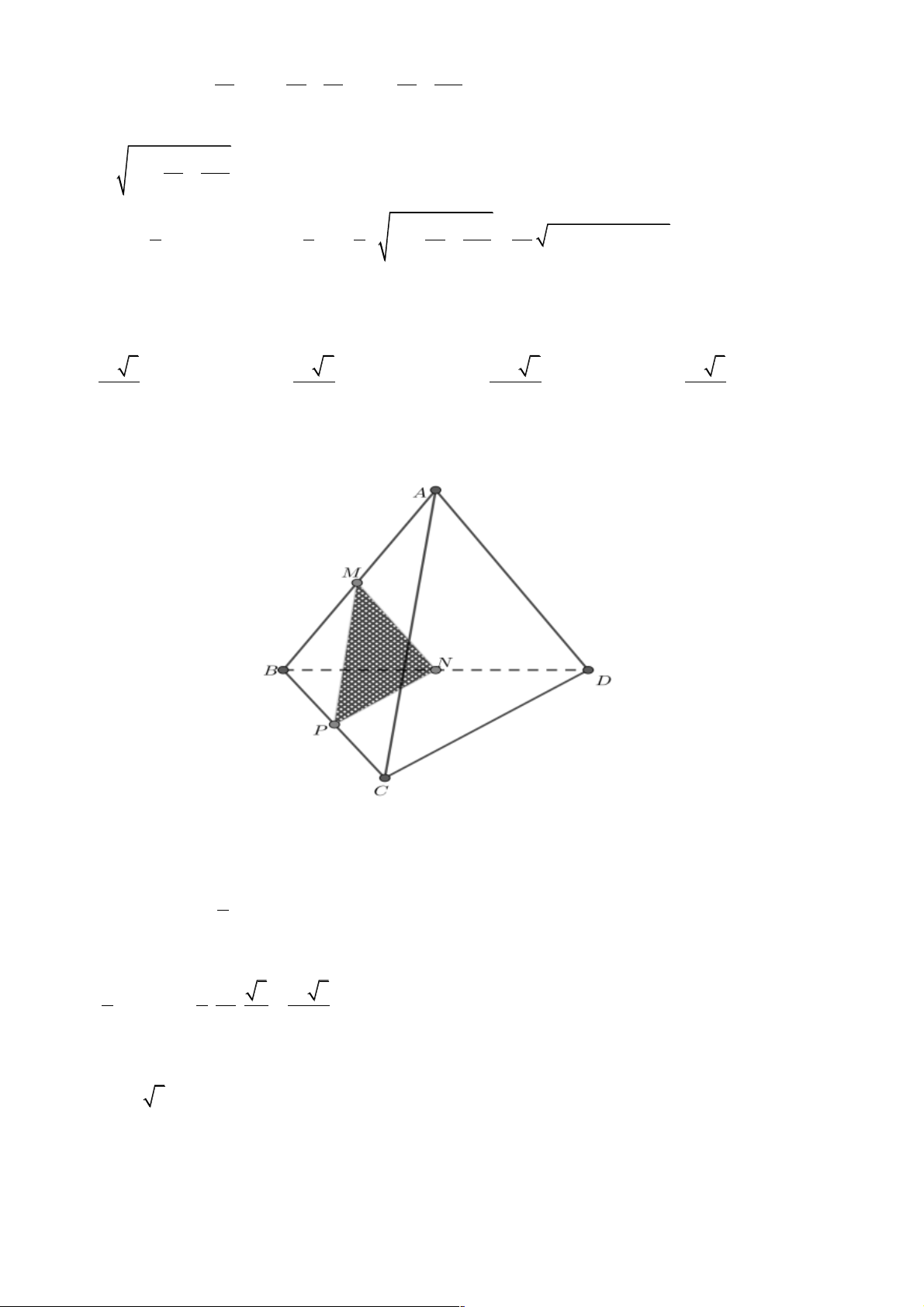
Câu 17. Cho tứ diện ABCD với M , N lần lượt là trọng tâm các tam giác ABD , ACD
Xét các khẳng định sau:
(I) MN / / mp( ABC).
(II) MN//mp(BCD).
(III) MN//mp( ACD).
(IV)) MN //mp(CDA).
Các mệnh đề nào đúng? A. I, II. B. II, III. C. III, IV. D. I, IV. Lời giải Chọn A. Trang 12 A I M N D B C
Gọi I là trung điểm của AD . IM IN 1
Do M , N là trọng tâm tam giác ABD, ACD nên = = IB IC 3
Theo định lý Talet có MN //BC .
Mà BC Ì (BCD), BC Ì ( ABC).
Vậy MN// (BCD),MN// ( ABC).
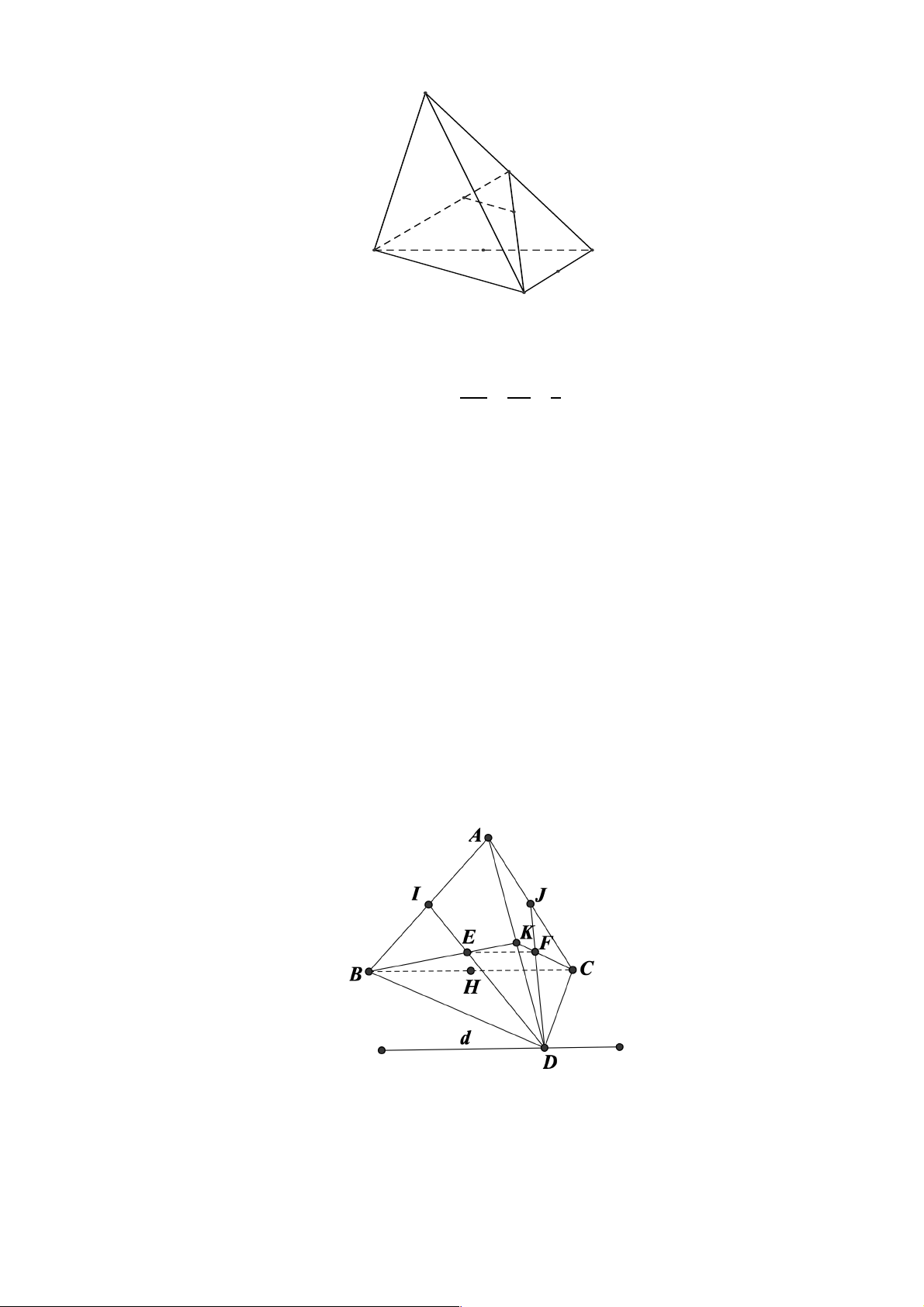
Câu 18. Cho tứ diện ABCD . Gọi I, J, K, H lần lượt là trung điểm của các cạnh , BA AC,C B, . AD Gọi
E, F lần lượt là trọng tâm của tam giác ABD và tam giác ACD . Gọi d là giao tuyến của hai mặt phẳng
(DIJ ) và (DBC). Khi đó khẳng định nào sau đây đúng?
A. d ! (IHK).
B. d ! (JHK).
C. d ! (AEF).
D. d ! (DIJ ) . Lời giải Chọn C.
Ta có IJ là đường trung bình của tam giác ABC , suy ra BC ! IJ. Trang 13
ìD Î(DIJ ) Ç (DBC) ï
Như vậy íIJ ! BC
suy ra giao tuyến d của 2 mặt phẳng (DIJ ) và (DBC)là đường thẳng
ïIJ Ì (DIJ),BC Ì (DBC) î
qua D và song song với IJ , BC . DE DF 2
E, F lần lượt là trọng tâm của tam giác ABD và tam giác ACD nên IJ ! EF vì = = DI DJ 3 ìd ! EF Do đó í Þ d ! (AEF) . îEF Ì (AEF)
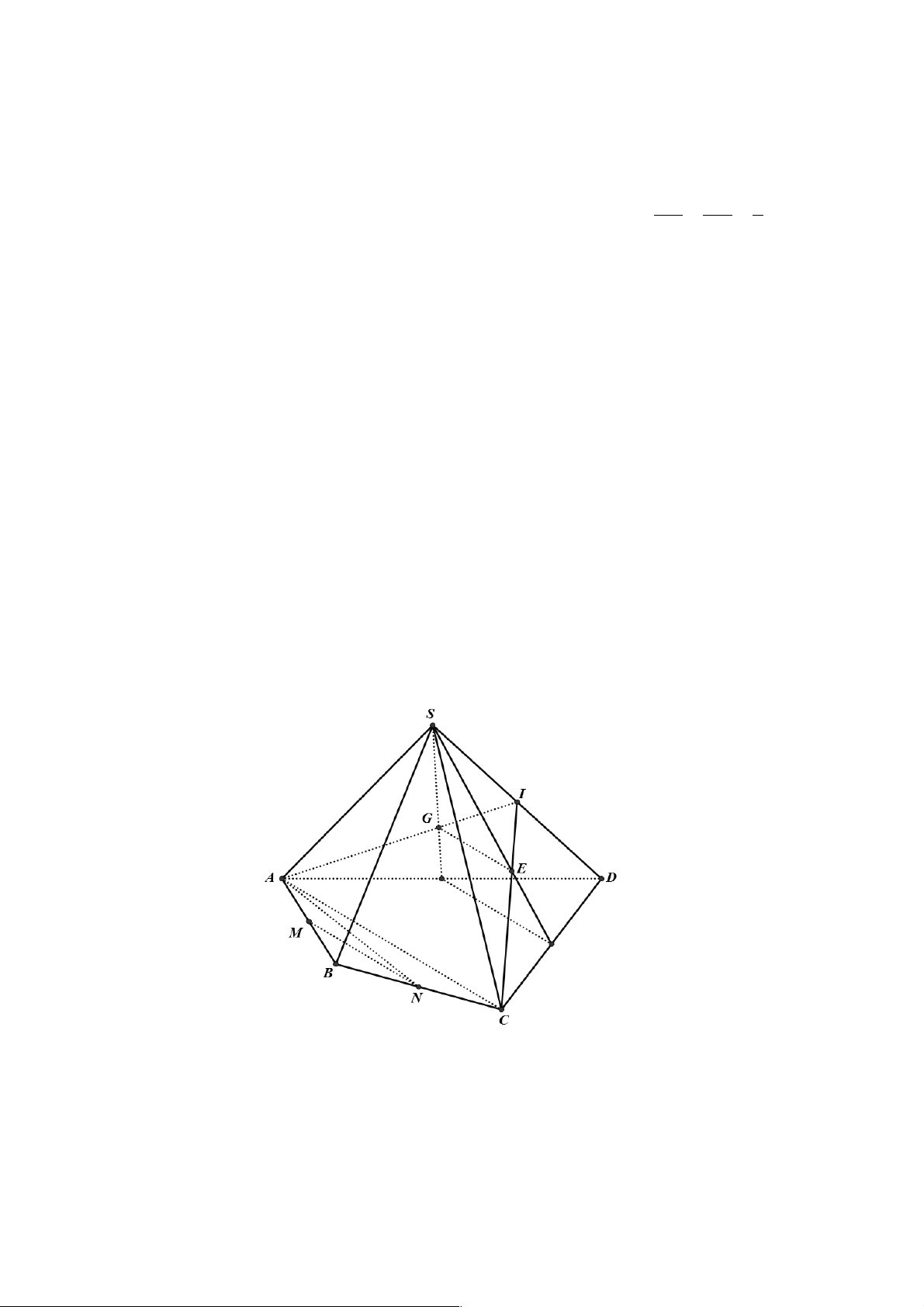
Câu 19. Cho hình chóp S.ABCD . Gọi G, E lần lượt là trọng tâm của D SA D và SC
D D . Lấy M , N lần
lượt là trung điểm của AB, BC. Xét các mệnh đề sau:
(1) Đường thẳng MN song song với (GAC).
(2) Đường thẳng MN song song với (DAC).
(3) Đường thẳng GE song song với ( AMN ).
(4) Đường thẳng GE và đường thẳng MN trùng nhau.
(5) Đường thẳng GE và đường thẳng MN song song.
Số mệnh đề sai là: A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn A.
Hai mệnh đề sai là (2) và (4).
(2) sai vì MN Ì (DAC).
(4) sai vì GE ! MN . Trang 14 DẠNG 3
XÁC ĐỊNH THIẾT DIỆN SONG SONG VỚI ĐƯỜNG THẲNG.
Trong phần này ta sẽ xét thiết diện của mặt phẳng (a ) đi qua một điểm song song với hai đường thẳng
chéo nhau hoặc (a ) chứa một đường thẳng và song song với một đường thẳng; để xác định thiết diện ( ì a ) ! d ï
loại này ta sử dụng tính chất: íd Ì (b )
Þ (a ) Ç(b ) = d ' ! d,M Îd ' ïM Î(a)Ç î (b )
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình thang với các cạnh đáy là AB và CD . Gọi I, J
lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm của tam giác SAB .
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (IJG).
A. là đường thẳng song song với AB Trang 15
B. là đường thẳng song song vơi CD
C. là đường thẳng song song với đường trung bình của hình thang ABCD
D. Cả A, B, C đều đúng
b) Tìm điều kiện của AB và CD để thiết diện của (IJG) và hình chóp là một hình bình hành. 2 3
A. AB = CD
B. AB = CD
C. AB = CD
D. AB = 3CD 3 2 Lời giải S G N M A B E I J D C a) Chọn D.
Ta có ABCD là hình thang và I, J là trung điểm của ,
AD BC nên IJ / / AB .
ìG Î(SAB) Ç(IJG) ï ïAB Ì (SAB) Vậy í ïIJ Ì (IJG) ï îAB ! IJ
Þ (SAB)Ç(IJG) = MN ! IJ ! AB với M Î S , A N Î SB. b) Chọn D.
Dễ thấy thiết diện là tứ giác MNJI . MN SG 2
Do G là trọng tâm tam giác SAB và MN ! AB nên = = AB SE 3
( E là trung điểm của AB ). 2 Þ MN = AB . 3 1
Lại có IJ = ( AB + CD). Vì MN ! IJ nên MNIJ là hình thang, do đó MNIJ là hình bình hành khi 2 MN = IJ Trang 16 2 1
Û AB = ( AB + CD) Û AB = 3CD. 3 2
Vậy thết diện là hình bình hành khi AB = 3CD .
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD//BC , AD = 2.BC , M là trung điểm
SA . Mặt phẳng (MBC) cắt hình chóp theo thiết diện là A. tam giác. B. hình bình hành. C. hình thang vuông. D. hình chữ nhật. Lời giải Chọn B. S M N A B C D
Sử dụng định lý ba đường giao tuyến ta có giao tuyến của (MBC) với (SAD) là MN sao cho MN //BC
Ta có: MN //BC//AD nên thiết diện AMND là hình thang.
Lại có MN //BC và M là trung điểm SA Þ 1
MN là đường trung bình, MN = AD = BC 2
Vậy thiết diện MNCB là hình bình hành.
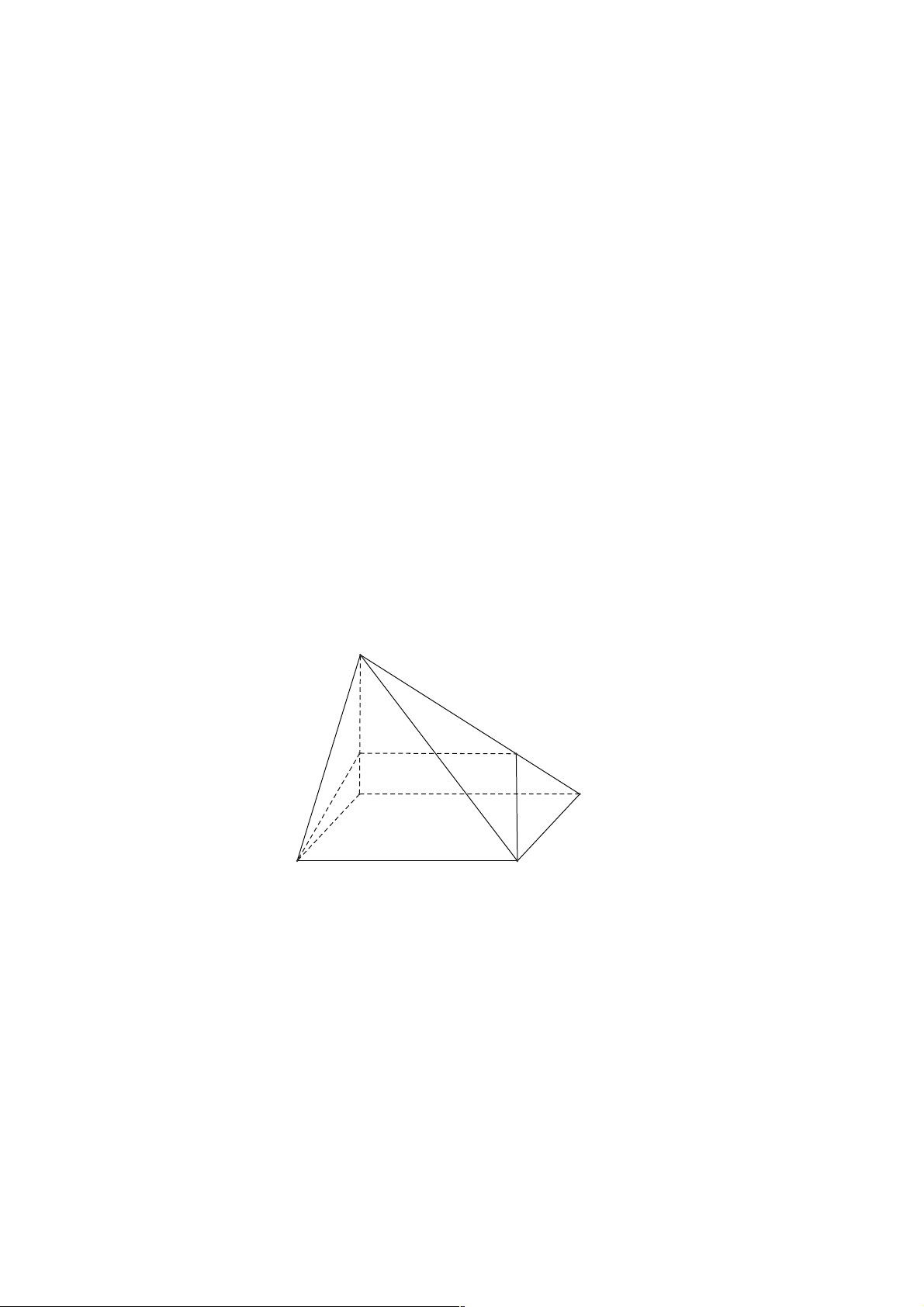
Câu 22. Cho tứ diện ABCD và M là điểm ở trên cạnh AC . Mặt phẳng (a ) qua và M song song với
AB và CD . Thiết diện của tứ diện cắt bởi (a ) là A. hình bình hành. B. hình chữ nhật. C. hình thang. D. hình thoi. Lời giải Chọn A. A Q M B P D N C Trang 17
Trên ( ABC) kẻ MN //A ; B N Î BC
Trên (BCD) kẻ NP// ; CD P Î BD
Ta có (a ) chính là mặt phẳng (MNP)
Sử dụng đính lý ba giao tuyến ta có (MNP)Ç AD ={ }
Q với MQ//CD//NP Ta có
MQ//NP//CDüýÞ thiết diện MNPQ là hình bình hành.
MN //PQ//AB þ
Câu 23. Cho hình chóp S.ABCD với đáy ABCD là tứ giác lồi. Thiết diện của mặt phẳng (a ) tuỳ ý với hình chóp không thể là: A. Lục giác. B. Ngũ giác. C. Tứ giác. D. Tam giác. Lời giải Chọn A. S M A B N D C
Thiết diện của mặt phẳng với hình chóp là đa giác được tạo bởi các giao tuyến của mặt phẳng đó với mỗi mặt của hình chóp.
Hai mặt phẳng bất kì có nhiều nhất một giao tuyến.
Hình chóp tứ giác S.ABCD có 5 mặt nên thiết diện của (a ) với S.ABCD có không qua 5 cạnh, không
thể là hình lục giác 6 cạnh.
Sử dụng định lý ba đường giao tuyến ta có giao tuyến của ( ADM ) với (SBC) là MN sao cho MN //BC
Ta có: MN //BC//AD nên thiết diện AMND là hình thang.
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Lấy điểm I trên đoạn SO SI 2 sao cho
= , BI cắt SD tại M và DI cắt SB tại N . MNBD là hình gì ? SO 3 A. Hình thang. B. Hình bình hành.
C. Hình chữ nhật.
D. Tứ diện vì MN và BD chéo nhau. Lời giải Chọn A. Trang 18 S M N I A D O B C SI 2
I trên đoạn SO và
= nên I là trọng tâm tam giác SBD . Suy ra M là trung điểm SD; N là trung SO 3 điểm . SB 1
Do đó MN //BD và MN = BD nên MNBD là hình thang. 2
Các bạn muốn tải đầy đủ bộ tài liệu lớp 11 file word ( 3042 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 9 file word ( 1062 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Câu 25. Cho tứ diện ABCD . M là điểm nằm trong tam giác ABC, mp(a ) qua M và song song với
AB và CD .Thiết diện của ABCD cắt bởi mp(a ) là: A.Tam giác. B. Hình chữ nhật. C. Hình vuông. D. Hình bình hành. Lời giải Chọn D. D G H F A C M E B
(a)/ /AB nên giao tuyến (a) và (ABC) là đường thẳng song song . AB
Trong ( ABC) .Qua M vẽ EF / /AB( )
1 (E Î BC, F Î AC) .Ta có (a )Ç( ABC) = MN.
Tương tự trong mp(BCD), qua E vẽ EH / /DC (2) (H ÎBD) suy ra (a )Ç(BCD) = H . E Trang 19
Trong mp( ABD), qua H vẽ HG / /AB ( )
3 (GÎ AD), suy ra (a )Ç( ABD) = GH.
Thiết diện của ABCD cắt bởi (a ) là tứ giác EFGH.
(a )Ç( ADC) = FGüï Ta có
ý Þ FG / /DC (4) (a ) / /DC ïþ ìEF GH Từ ( ) ( ) ( ) ( ) / / 1 , 2 , 3 , 4 Þ í
Þ EFGH là hình bình hành. îEH / /GF
Câu 26. Cho hình chóp tứ giác S.ABCD . Gọi M và N lần lượt là trung điểm của SA và SC . Khẳng
định nào sau đây đúng?
A. MN / /mp( ABCD).
B. MN / /mp(SAB).
C. MN / /mp(SCD).
D. MN / /mp(SBC). Lời giải Chọn A. S M N A D C B
là đường trung bình của MN
DSAC nên MN / / AC. Ta có MN / / AC ü ï
AC Ì ( ABCD) ý Þ MN / / ( ABCD). MN ( ABCD)ï Ë þ
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O . M là trung điểm của OC , Mặt
phẳng (a ) qua M song song với SA và BD. Thiết diện của hình chóp vớimặt phẳng (a )là: A. Hình tam giác. B. Hình bình hành. C. Hình chữ nhật. D. Hình ngũ giác. Lời giải Chọn A. Trang 20 Ta có: ìM Î ï (a )Ç(ABCD) ( í
ïî a ) //BD Ì ( ABCD) .
Þ (a ) Ç( ABCD) = EF//BD (M Î EF, E Î BC, F ÎCD) ìM Î ï (a )Ç(SAC) Lại có: í
Þ (a ) Ç(SAC) = MN //SA(N Î SC). (
ïî a ) //SA Ì (SAC)
Vậy thiết diện cần tìm là tam giác NEF .
Câu 28. Cho tứ diện ABCD có AB = CD . Mặt phẳng (a ) qua trung điểm của AC và song song với AB ,
CD cắt ABCD theo thiết diện là A.hình tam giác. B.hình vuông. C.hình thoi. D.hình chữ nhật. Lời giải Chọn C.
Gọi M là trung điểm của AC . Trang 21 ìM Î ï (a )Ç(ABC) Ta có: í
Þ (a ) Ç( ABC) = MN //AB(N Î BC), N là trung điểm BC . (
ïî a ) //AB Ì ( ABC) ìN Î ï (a )Ç(BCD) í
Þ (a ) Ç(BCD) = NP//CD(PÎ BD), P là trung điểm BD . (
ïî a ) //CD Ì (BCD) ìP Î ï (a )Ç(BDA) í
Þ (a ) Ç(BDA) = PQ//AB(Q Î AD), Q là trung điểm AD . (
ïî a ) //AB Ì (BDA) ìMQ = ï (a )Ç( ADC) í Þ QM CD (
ïî a ) CD Ì ( ADC) // //
Khi đó thiết diện là hình bình hành MNPQ.
Lại có: AB = CD suy ra MN = NP .
Vậy thiết diện cần tìm là hình thoi MNPQ.
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm lấy trên cạnh SA (
M không trùng với S và A ). Mp(a ) qua ba điểm M , B,C cắt hình chóp S.ABCD theo thiết diện là: A. Tam giác. B. Hình thang. C. Hình bình hành. D. Hình chữ nhật. Lời giải Chọn B. S M N A D B C Ta có :
AD / /BC Ì (MBC)üïýÞ AD/ /(MBC). AD Ë (MBC) ïþ
Ta có (MBC) / / AD nên (MBC) và (SAD) có giao tuyến song song . AD
Trong (SAD), vẽ MN / / AD(N ÎSD) Þ MN = (MBC)Ç(SAD).
Thiết diện của S.ABCD cắt bởi (MBC) là tứ giác BCNM. Do MN / /BC (cùng song song AD ) nên BCNM là hình thang. Trang 22
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là .
AB M là trung điểm . CD
Mặt phẳng (a ) qua M song song với BC và .
SA (a ) cắt AB, SB lần lượt tại N và .
P Nói gì về thiết
diện của mặt phẳng (a ) với khối chóp S.ABCD ?
A. Là một hình bình hành.
B. Là một hình thang có đáy lớn là MN.
C. Là tam giác MN . P
D. Là một hình thang có đáy lớn là . NP Lời giải Chọn B.
Trong mặt phẳng ( ABCD) , qua M kẻ đường thẳng MN ! BC(N ÎBC). Khi đó, MN Ì (a ).
Trong mặt phẳng (SAB) , qua N kẻ đường thẳng NP ! SA(PÎSB). Khi đó, NP Ì (a ) . Vậy (a ) º (MNP) . ìMN Ì (MNP) ï ïBC Ì (SBC )
Xét hai mặt phẳng (MNP) và (SBC) có í
Þ hai mặt phẳng cắt nhau theo một ïMN ! BC
ïPÎ(MNP),PÎ î (SBC)
giao tuyến đi qua điểm P và song song với BC.
Trong mặt phẳng (SBC) kẻ PQ ! BC (QÎSC) .Khi đó, PQ là giao tuyến của mặt phẳng (a ) với mặt
phẳng (SBC). Vậy mặt phẳng (a ) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ . ìMN ! BC
Tứ giác MNBC có í
Þ MNBC là hình bình hành. Từ đó suy ra MN = BC. îMC ! NB
Trong tam giác SBC có P thuộc đoạn SB , Q thuộc đoạn SC và PQ ! BC nên PQ < BC. ìMN ! PQ Tứ giác MNPQ có í
Þ MNPQ là hình thang có đáy lớn là MN. îPQ < MN Trang 23
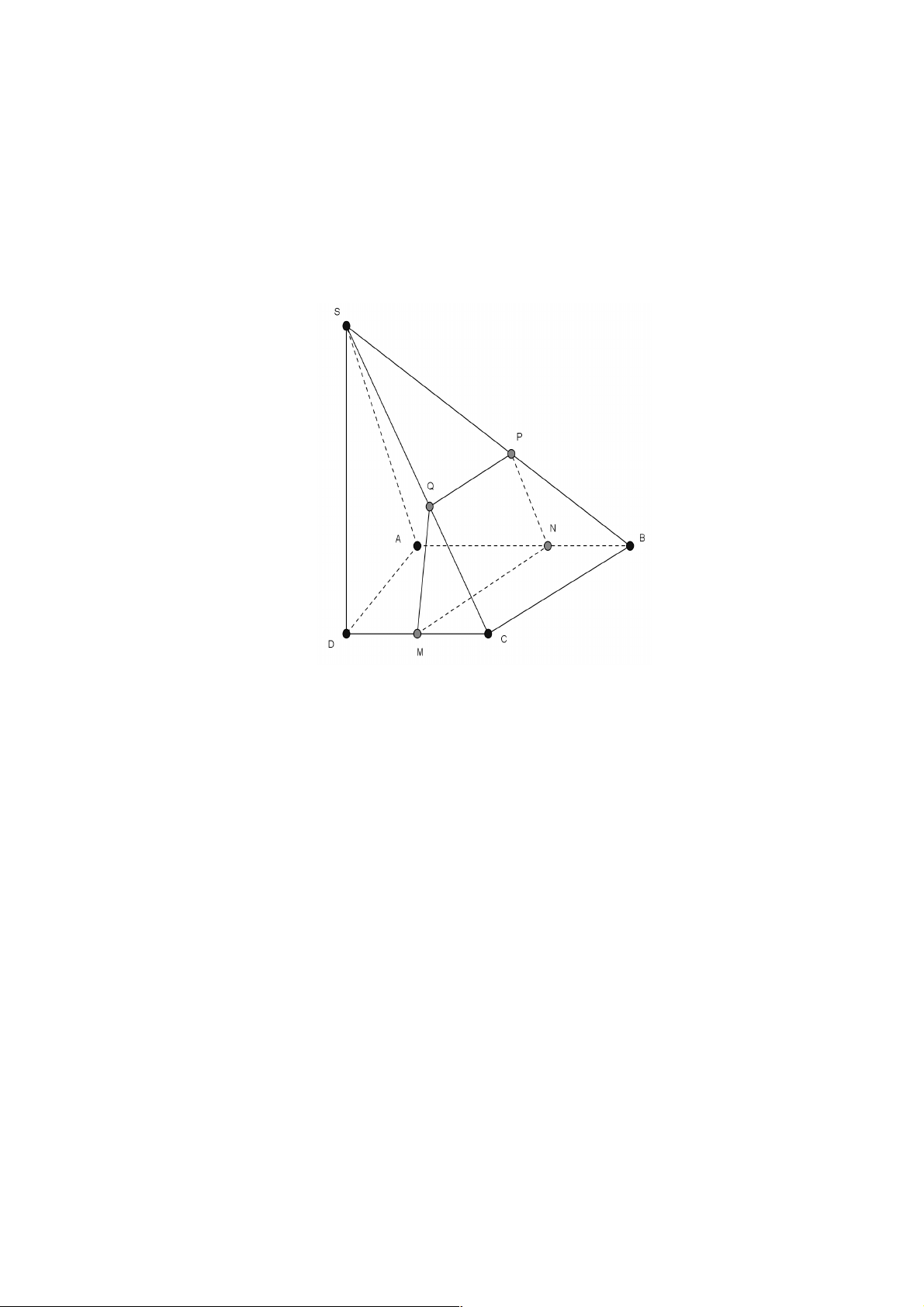
Câu 31. Cho tứ diện ABCD . Gọi M là điểm nằm trong tam giác ABC , (a ) là mặt phẳng đi qua M và
song song với các đường thẳng AB và CD . Thiết diện của tứ diện và mp (a ) là hình gì ? A. Hình bình hành. B. Hình tứ diện. C. Hình vuông. D. Hình thang. Lời giải Chọn A. Ta có: (a)Ç(ABC) = ,P PQ Q// . AB PÎAC,QÎBC ( ) 1
(a)Ç(ACD) = PS,PS//CD. S ÎAD (2)
(a)Ç(BCD) = Q ,Q
R R //CD. RÎ B D (3)
(a)Ç(ABD) = RS,RS//AB (4) RS//PQ (//AB) (5) PS//RQ (//CD) (6) Từ ( )
1 , (2) , (3), (4) , (5), (6) ta được thiết diện cần tìm là hình bình hành PQRS.
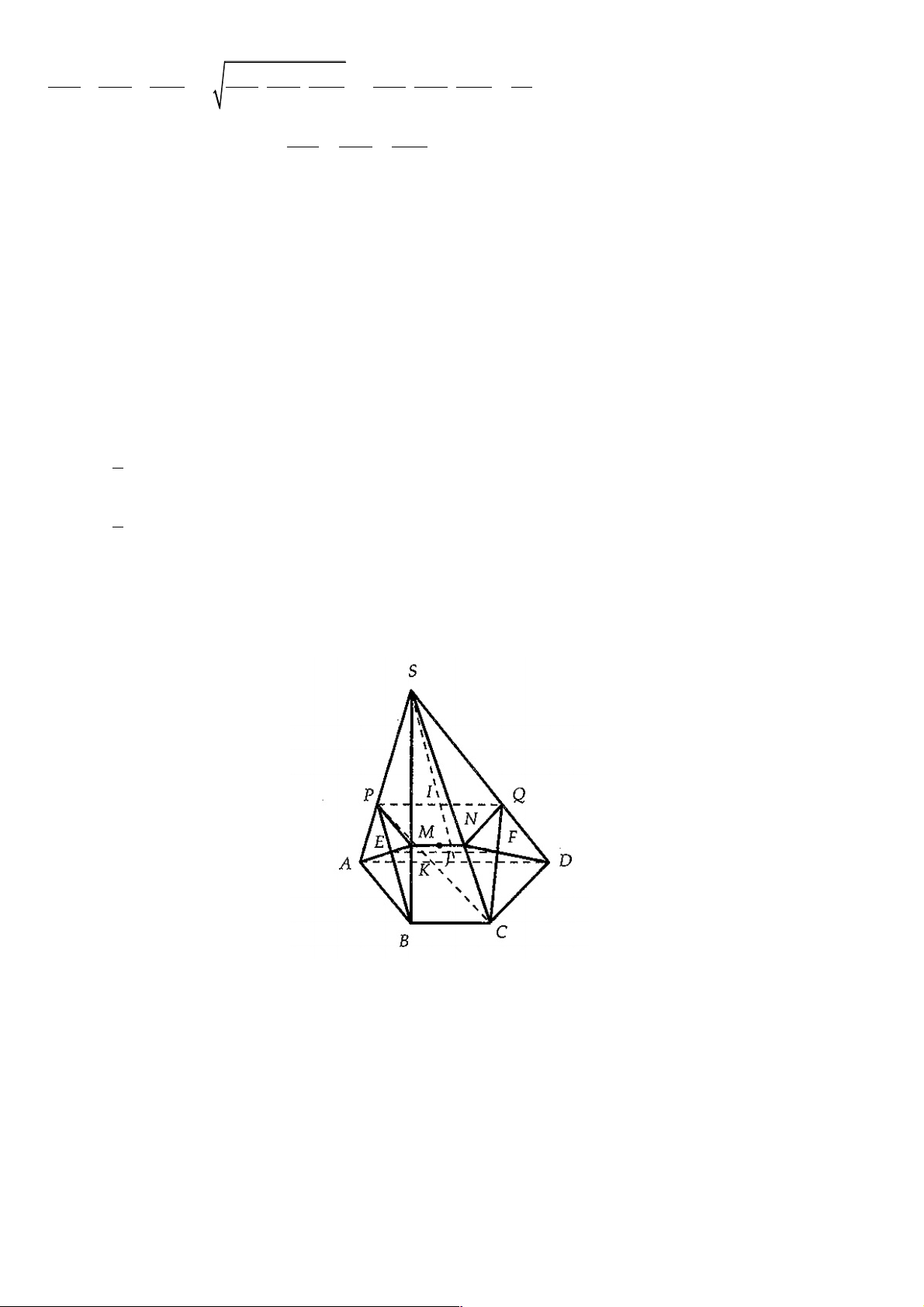
Câu 32. Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành tâm .
O Gọi M , N, P là ba điểm trên các cạnh , AD CD, .
SO Thiết diện của hình chóp với mặt phẳng (MNP) là hình gì? A. Ngũ giác. B. Tứ giác. C. Hình thang. D. Hình bình hành. Lời giải Chọn A. Trang 24 S H R P T D C N K M O E A B
Trong mp( ABCD) gọi E, K, F lần lượt là giao điểm của MN với , DA DB, DC .
Trong mp(SDB)gọi H = KP Ç SB
Trong mp(SAB)gọi T = EH Ç SA
Trong mp(SBC)gọi R = FH Ç SC ìE Î MN Ta có: í Þ EH Ì (MNP) îH Î KP T ì Î SA í
Þ T = SAÇ(MNP) T î Î EH
Lí luận tương tự ta có R = SC Ç(MNP)
Thiết diện là ngũ giác MNRHT.
Câu 33. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , gọi O là tâm của đáy. Tam giác
SAB là tam giác đều. Gọi M là điểm trên cạnh BC . Mặt phẳng (P) đi qua M và song song với , SA SB
cắt hình chóp theo thiết diện là hình gì? A. Hình vuông. B. Hình chữ nhật. C. Hình thang cân. D. Hình thang vuông. Lời giải Chọn C. Trang 25
Qua M kẻ một đường thẳng song song với SB , cắt SC tại Q .
Qua Q kẻ một đường thẳng song song với SA , cắt AC tại O . Gọi M = MO Ç .
AD Qua N kẻ đường thẳng song song với SA, cắt SD tại P .
Thiết diện tạo bởi (P) và hình chóp S.ABCD là tứ giác MNPQ. Do MQ / /S ; B QO / /S ; A NP / /SA nên CM CQ CO DP = = = Þ MN / /PQ(1) CB CS CA DS MQ CM Đặt BM = .
x Có MQ / /SB Þ = SB CB CM.SB (a - x)a MQ = = = a - x CB a
Tương tự, NP = a - x Þ MQ = NP(2)
Từ (1) và (2) ta có thiết diện MNPQlà hình thang cân.
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là .
AB M là trung điểm . CD
Mặt phẳng (a ) qua M song song với BC và .
SA (a ) cắt AB, SB lần lượt tại N và .
P Nói gì về thiết
diện của mặt phẳng (a ) với khối chóp S.ABCD ?
A. Là một hình bình hành.
B. Là một hình thang có đáy lớn là MN.
C. Là tam giác MN . P
D. Là một hình thang có đáy lớn là . NP Lời giải Chọn B. Trang 26
Trong mặt phẳng ( ABCD), qua M kẻ đường thẳng MN ! BC(N ÎBC). Khi đó, MN Ì (a ).
Trong mặt phẳng (SAB), qua N kẻ đường thẳng NP ! SA(PÎSB). Khi đó, NP Ì (a ) . Vậy (a ) º (MNP) . ìMN Ì (MNP) ï ïBC Ì (SBC )
Xét hai mặt phẳng (MNP) và (SBC) có í
Þhai mặt phẳng cắt nhau theo một MN ! BC ï
ïPÎ(MNP),PÎ î (SBC)
giao tuyến đi qua điểm P và song song với BC.
Trong mặt phẳng (SBC) kẻ PQ ! BC (QÎSC) .Khi đó, PQ là giao tuyến của mặt phẳng (a ) với mặt
phẳng (SBC). Vậy mặt phẳng (a ) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ . ìMN ! BC Tứ giác MNBC có í
Þ MNBC là hình bình hành. Từ đó suy ra MN = BC. îMC ! NB
Trong tam giác SBC có P thuộc đoạn SB , Q thuộc đoạn SC và PQ ! BC nên PQ < BC. ìMN ! PQ Tứ giác MNPQ có í
Þ MNPQ là hình thang có đáy lớn là MN. îPQ < MN
Câu 35. Cho hình chóp S.ABCD , M là một điểm trên cạnh AB , N là điểm trên cạnh CD . Mặt phẳng
(a) chứa MN và song song với SA. Thiếtdiện củahình chópcắt bởi (a) là hình thang thì điều kiện là:
A. AD = 2CD .
B. MN / /BC .
C. BC / / AD .
D. MN / / AD . Lời giải Chọn B. Trang 27
Do (a ) / / AB nên (a ) cắt (SAB) và (SAC) lần lượt theo các giao tuyến song song với SA.
Trong (SAB)kẻ MP / /S , A P Î SB .
Trong ( ABCD)kẻ MN Ç AC ={ } O .
Trong (SAC)kẻ OQ / /S , A Q Î SC .
Vậy thiết diện cần tìm là tứ giác MNQP. éMP / /QN ( ) 1
Ta có MNQPlà hình thang thì Þ ê êMN / /PQ ë ( 2) Xét (1)
( )1 Þ SA/ /QN vì SA/ /MP .
Þ SA / / (SCD) : điều này vô lí. Xét (2)
ìBC = ( ABCD) Ç(SBC) ï ïMN Ì ( ABCD) Có: í Þ MN / /BC . ïPQ Ì (SBC) ï îMN / /PQ
ìPQ = (a ) Ç(SBC) ï ïBC Ì (SBC)
Đảo lại nếu có MN / /BC thì MN / /PQ vì í ïMN Ì (a ) ï îMN / /BC
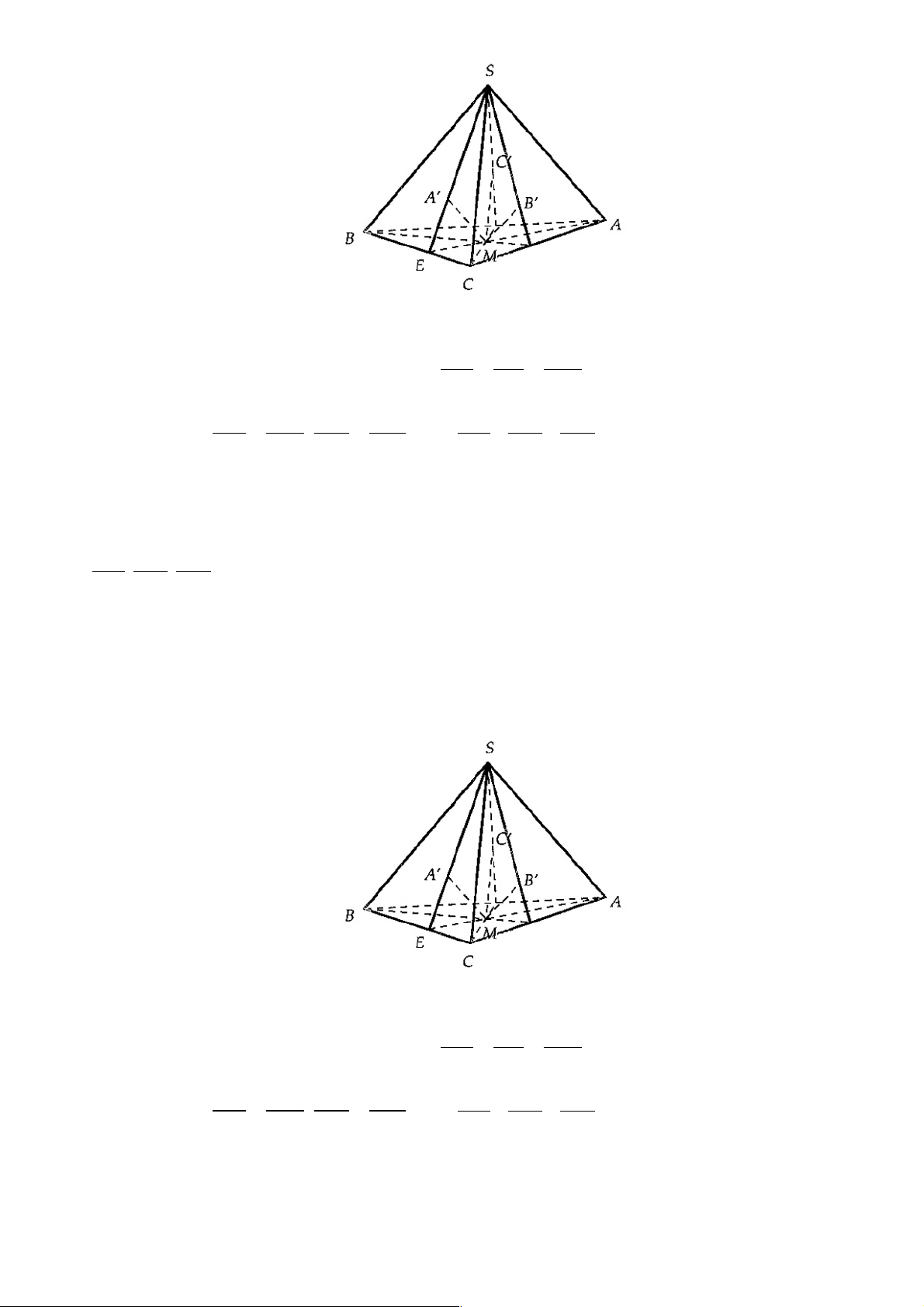
Câu 36. Cho hình chóp S.ABCD cóđáy là hình thoi cạnh a , SA = SB = a , SC = SD = 3a . E là trung
điểm của đoạn SA . M là một điểm trên cạnh BC . Đặt BM = x(0 £ x £ a). Mặt phẳng (a ) chứa ME và
song song với AB . Thiết diện của hình chóp cắt bởi (a ) có diện tích tính theo a, x là: Trang 28 3a a A. 2 2
16x + 8ax + 3a . B. 2 2
16x + 8ax + 3a . 16 16 3a 3a C. 2 2
16x - 4ax + 3a . D. 2 2
16x + 4ax + 3a . 16 16 Lời giải Chọn A.
Do (a ) / / AB nên (a ) cắt ( ABCD) và (SAB) lần lượt theo các giao tuyến song song với AB .
Trong ( ABCD)kẻ MN / / AB, N Î AD (1).
Trong (SAB)kẻ EF / / AB, F Î SB (2).
Từ (1) và (2),suy ra MN / /FE nên tứ giác MNEF là hình thang.
Hai tam giác SAD và SBC bằng nhau (c.c.c) nên ∑ ∑ SAD = SBC .
Hai tam giác EAN và FBM bằng nhau (c.g.c) nên EN = FM .
Vậy thiết diện MNEF là hình thang cân.
Áp dụng hệ quả của định lý hàm số cosin trong tam giác SBC ta có: ∑ 2 2 2 2 2 2
SB + BC - SC
a + a - 3a 1 cos SBC = = = - . 2 2 . SB BC 2a 2 Tam giác FBM có ∑ 2 2 a a æ 1 ö a ax 2 2 2 2 2
FM = BF + BM - 2BF.BM.cos SBC = + x - 2. .x - = + x + ç ÷ 4 2 è 2 ø 4 2 . 2 a ax 2 Þ FM = + x + . 4 2 1 S = MN + EF FH MNEF ( ). 2 . MN - EF a Ta có MH = = 2 4 Trang 29 2 2 2 a ax a ax 3a 2 2 2 2 2
FH = FM - MH = + x + - = x + + . 4 2 16 2 16 2 ax 3a 2 Þ FH = x + + 2 16 2 1 1 æ a ö ax 3a 3a Vậy S = MN + EF FH = a + x + + =
x + ax + a MNEF ( ) 2 2 2 . 16 8 3 . ç ÷ 2 2 è 2 ø 2 16 16
Câu 37. Cho tứ diện đều ABCD có cạnh bằng a . Điểm M là trung điểm của AB . Tính diện tích thiết
diện của hình tứ diện cắt bởi mp(P)đi qua M và song song với AD và AC . 2 a 3 2 a 2 2 9a 3 2 a 3 A. . B. . C. . D. . 8 8 16 16 Lời giải Chọn D.
Qua M kẻ 2 đường thẳng lần lượt song song với AD , AC cắt BD tại N và cắt BC tại P .
Thiết diện tạo bởi (P)và tứ diện là tam giác đều MNP . a
Có MN = NP = PM = 2 Diện tích thiết diện 2 2 1 1 a 3 a 3 S = MN.MP = . . = . MNP 2 2 4 2 16
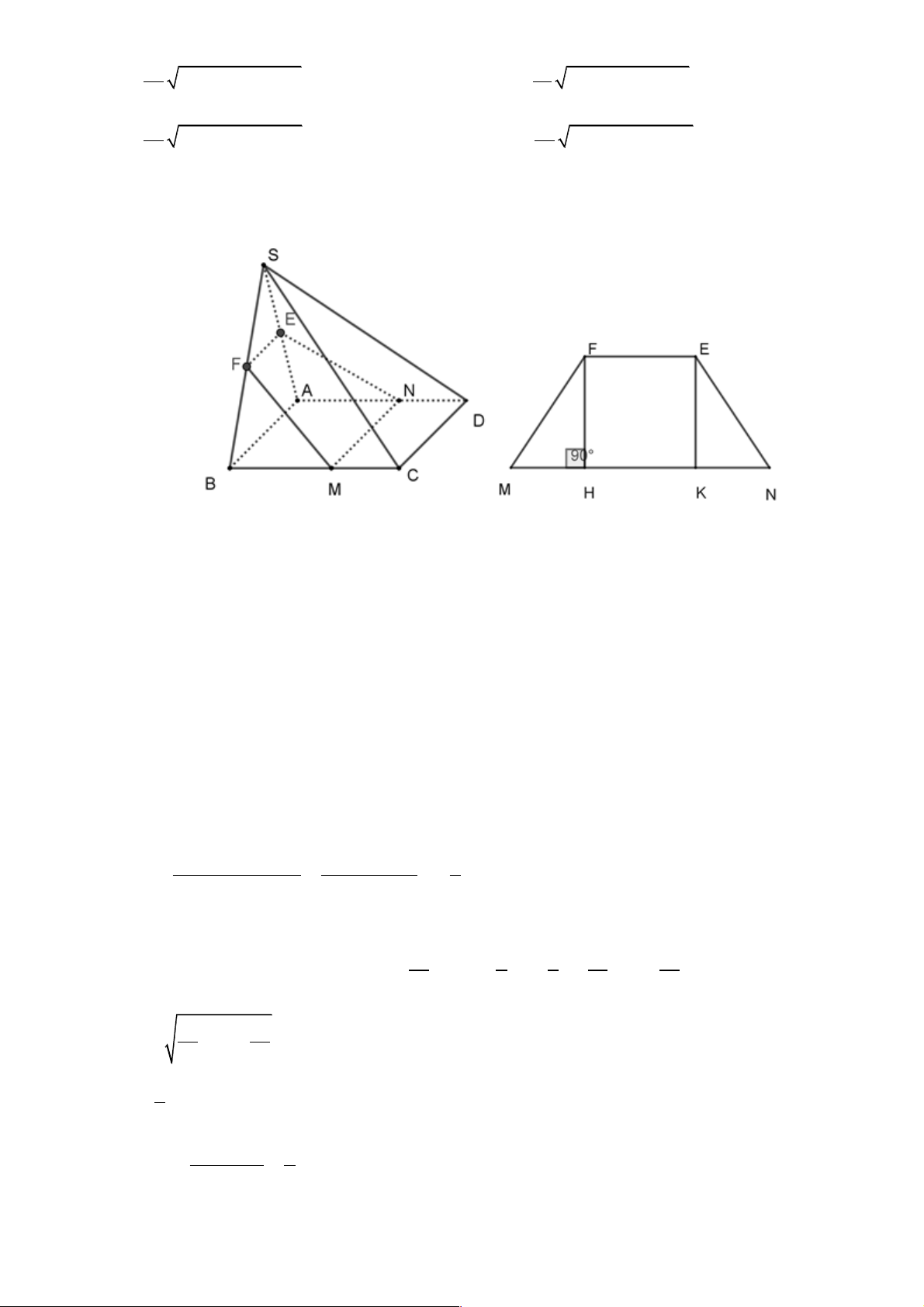
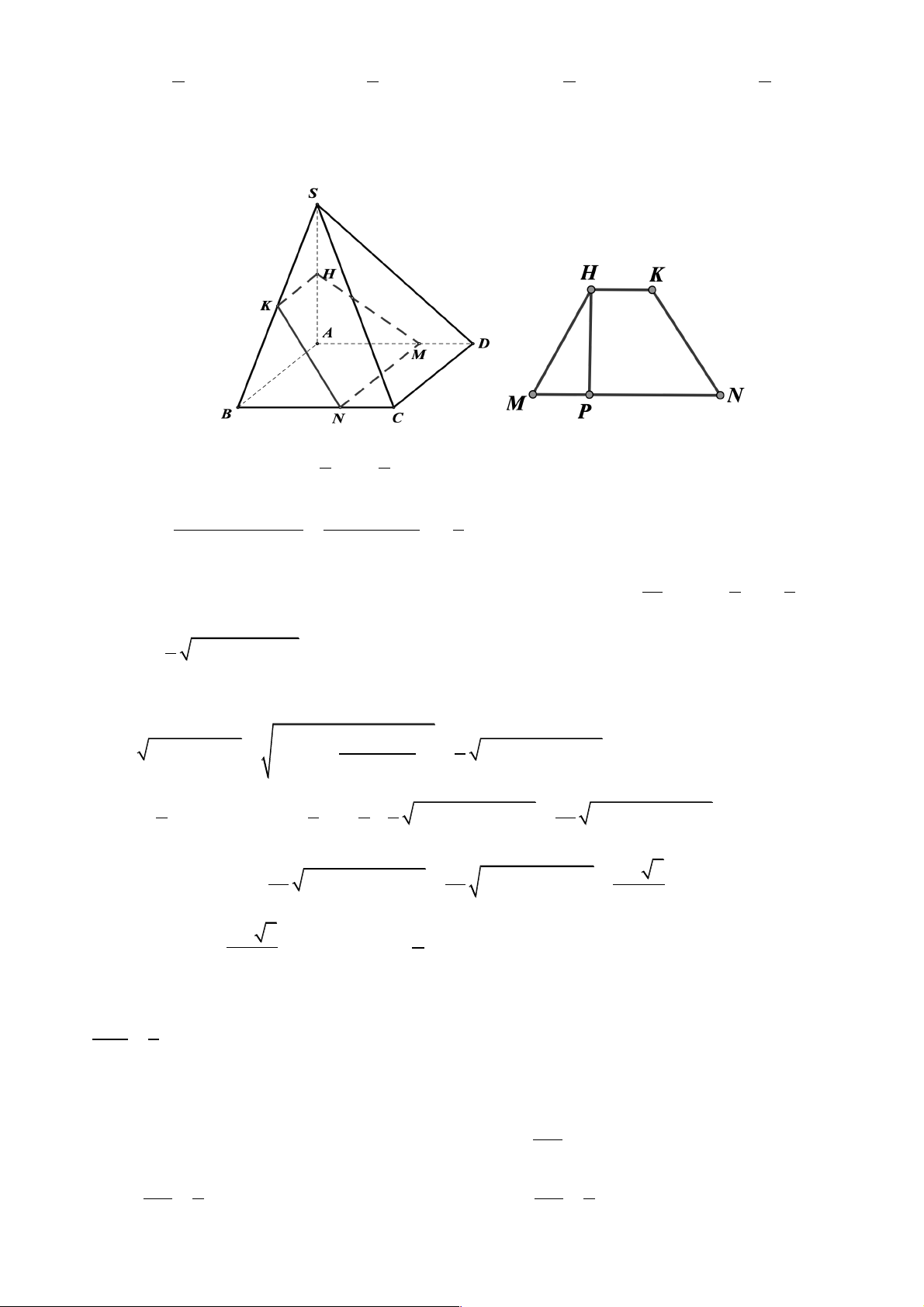
Câu 38. Cho hình chóp S.ABCD ,đáy ABCD là hình vuông cạnh a ,mặt bên (SAB)là tam giác đều.Cho
SC = SD = a 3 .Gọi H , K lần lượt là trung điểm của ,
SA SB.Gọi M là một điểm trên cạnh AD .Mặt
phẳng (HKM )cắt BC tại N .Cho biết (HKMN )là hình thang cân.Đặt AM = x(0 £ x £ a).Tìm x để diện
tích HKMN là nhỏ nhất. Trang 30 a a a a A. x = . B. x = . C. x = . D. x = . 5 3 4 2 Lời giải Chọn C. a Ta có ngay MN = 1
a và KH = AB = .Trong tam giác SAD ,ta có 2 2 ∑ 2 2 2 2 2 2
SA + AD - SD
a + a - 3a 1 cos SAD = = = - 2 2. . SA AD 2a 2 a a æ 1 ö
Trong tam giác HAM ,ta có ∑ 2 2 2 2 2
MH = AH + AM - 2AH.AM.cos HAM = + x - 2. . . x - ç ÷ 4 2 è 2 ø 1 2 2 Þ MH =
4x + 2ax + a . 2
Trong hình thang cân MNKH ,gọi P là chân đường cao hạ từ H ,ta có 2 æ MN - HK ö 1 2 2 2 2 2
HP = MH - MP = MH - =
16x -8ax + 3a .Suy ra ç ÷ è 2 ø 4 1 æ a ö a S = MN + KH HP = a +
x - ax + a =
x - ax + a MNKH ( ) 1 1 3 2 2 2 2 . 16 8 3 16 8 3 . ç ÷ 2 2 è 2 ø 4 16 2 3a 3a 3a 2 Ta có biến đổi: S =
16x - 8ax + 3a =
x - a + a ³ MNKH (4 )2 2 2 2 2 . 16 16 16 2 3a 2 a Vậy (S = x = MNKH ) đạt được khi . min 16 4
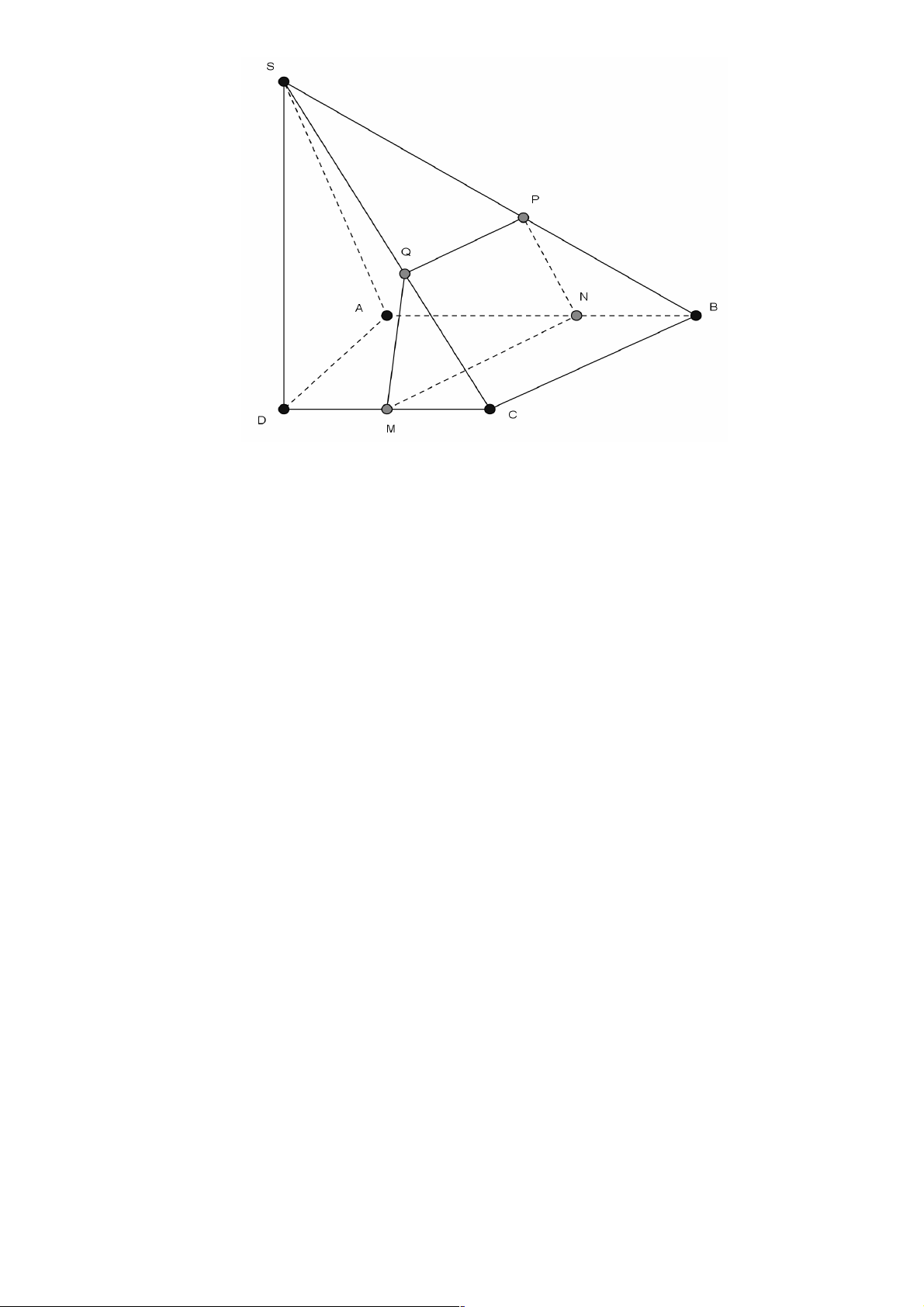
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi C ' là điểm trên cạnh SC sao cho C ' S 1
= , M là điểm trên cạnh SA. Mặt phẳng (P)qua C 'M và song song với BC . Xác định vị trí của C 'C 2
điểm M để (P)cắt hình chóp theo thiết diện là hình bình hành. MA
A. M là trung điểm của SA. B. = 2. MS MA 1 MA C. = 2 . D. = . MS 2 MS 3 Trang 31 Lời giải Chọn B. ( ìd qua C '
P) song song BC Þ (P) Ç(SBC) 1 = d í 1 d / /BC î 1
d Ç SB = N;( )
P Ç SAB = MN 1 ( ) ìd qua M
(P) / /BC Þ (P) / / AD Þ (P) Ç(SAD) 2 = d í d Ç SD = .
P Khi đó (P) cắt hình chóp 2 d / / AD î 2 2
S.ABCD theo thiết diện là tứ giác MNC ' P có C ' N / /MP nên thiết diện là hình thang.
SC ' C ' N 1 1
Có C ' N / /BC Þ =
= Þ C ' N = BC. SC BC 3 3 1 1 MP 1
Tứ giác MNC ' P là hình bình hành khi MP = NC ' = BC = AD Û = . 3 3 AD 3 SM 1 MA MP / / AD Þ = Û = 2. SA 3 MS
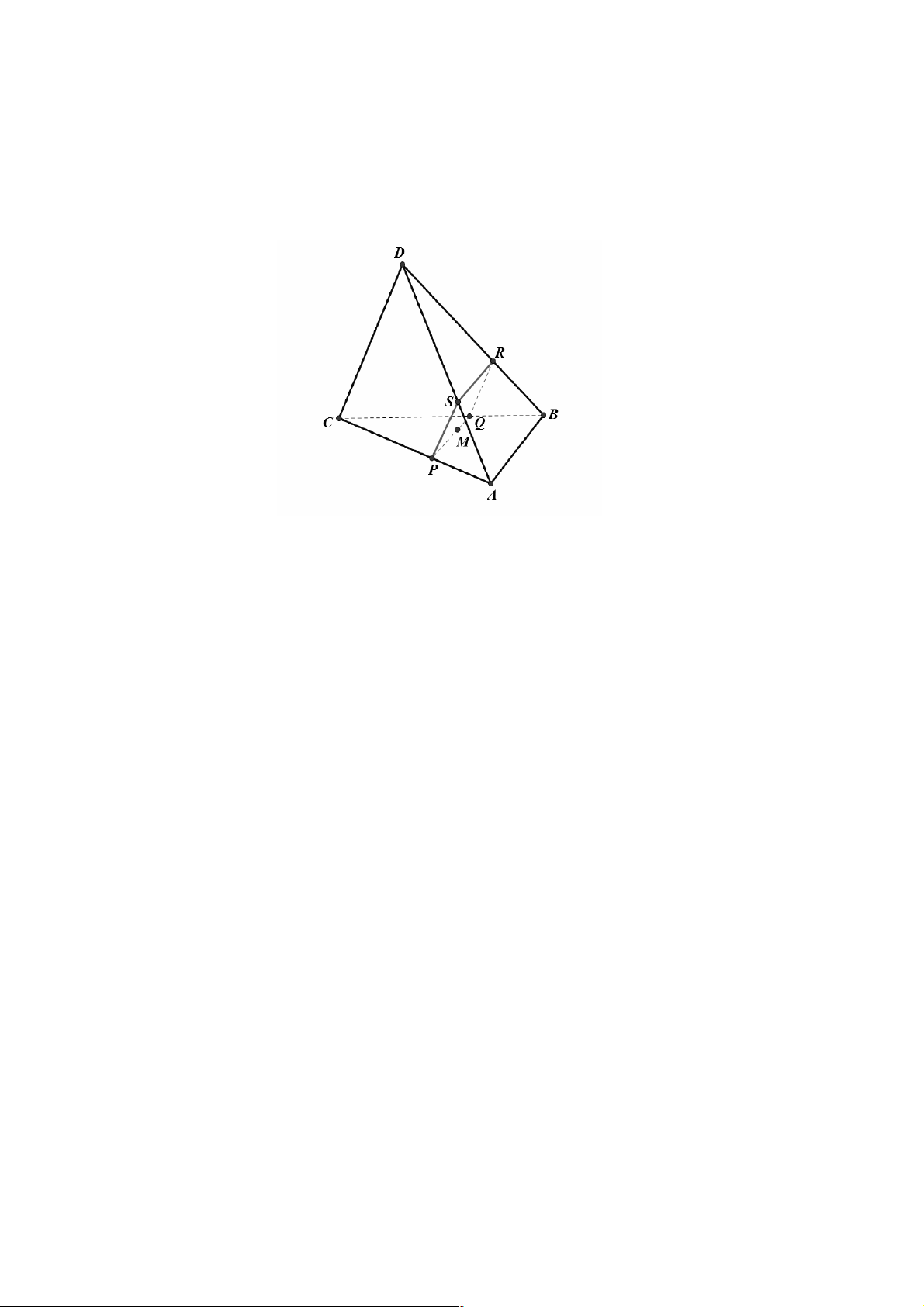
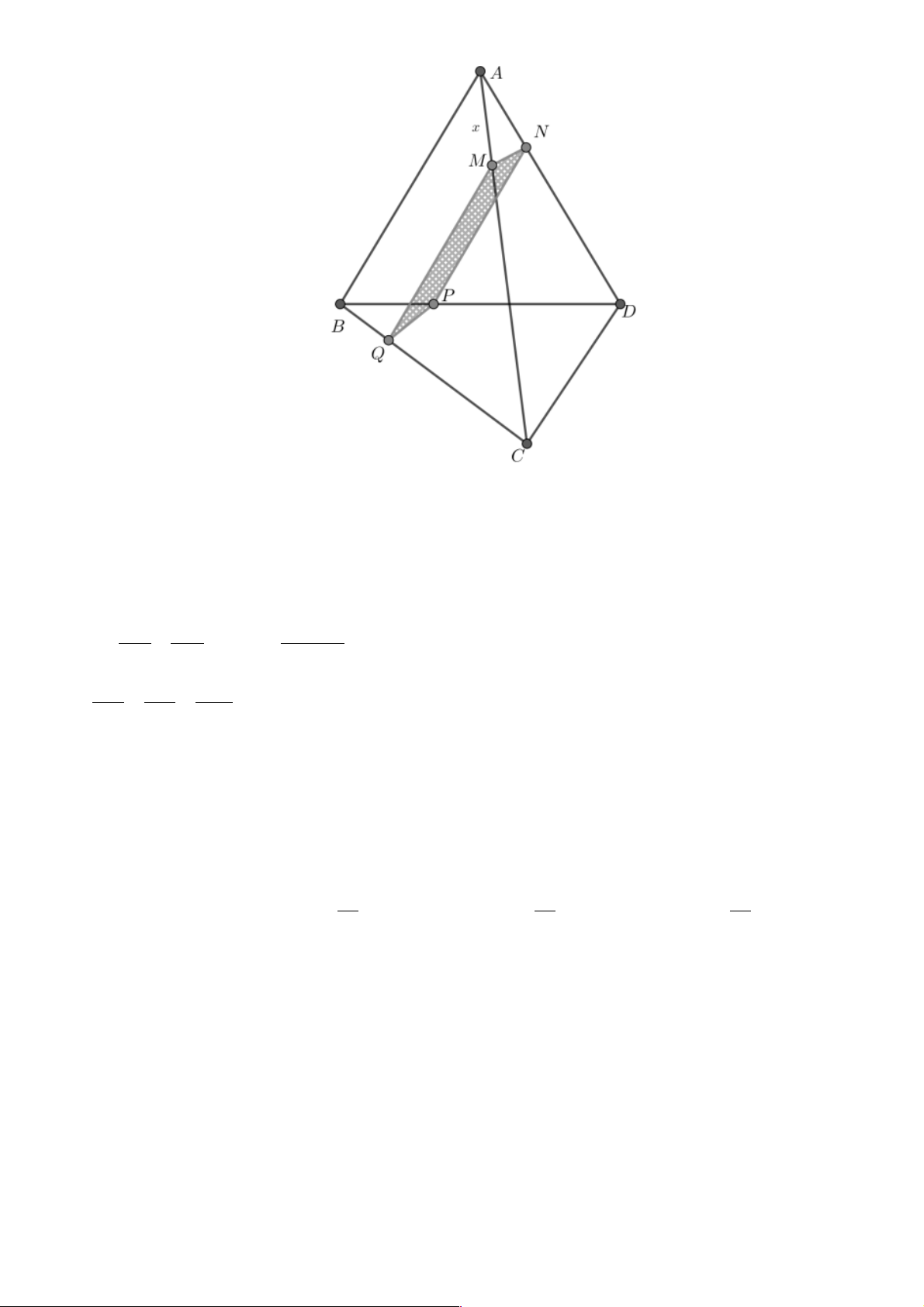
Câu 40. Cho tứ diện ABCD trong đó AB ^ CD và AB = AC = CD = .
a M là một điểm trên cạnh AC với
AM = x(0 < x < a).Mặt phẳng (P)qua M , song song với AB và CD . Tính diện tích thiết diện của (P)
và tứ diện ABCD theo a và x . x a - x a a - x A. x(a - ( ) x). B. . C. a(a - ( ) x) . D. . 2 2 Lời giải Chọn A. Trang 32
Qua M kẻ các đường thẳng song song với AB và CD cắt BC và AD lần lượt tại Q và N .
Qua N kẻ đường thẳng song song với AB cắt BD tại P .
Suy ra thiết diện là tứ giác MNPQ có MN / /P ; Q MQ / /N ;
P MP ^ MQ nên thiết diện MNPQ là hình chữ nhật. MN AM AM.DC Có = Þ MN = = x DC AC AC MQ MC a - x = =
Þ MQ = a - x AB AC a Þ S
= MN.MQ = x(a - x). MNPQ
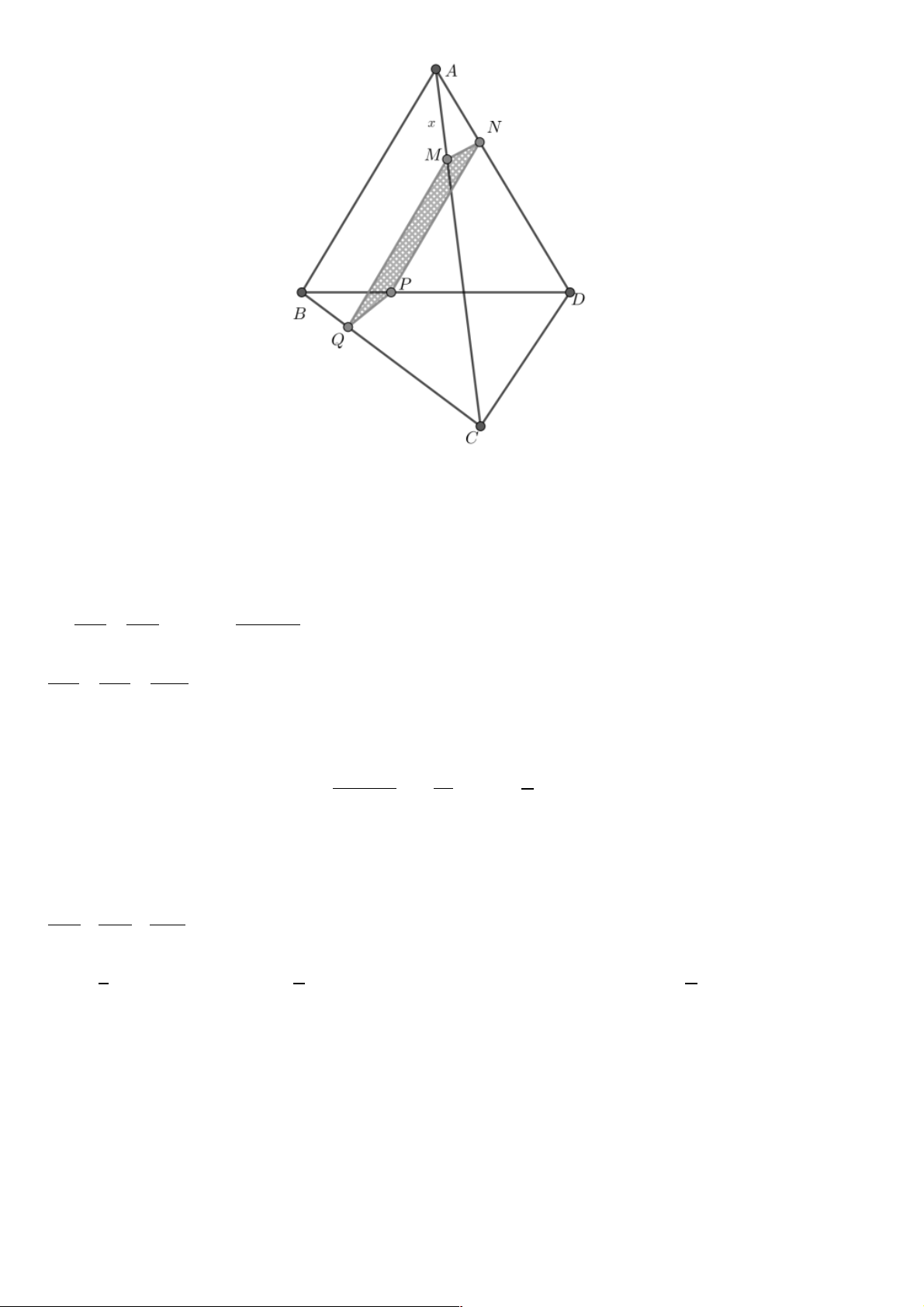
Câu 41. Cho tứ diện ABCD trong đó AB ^ CD và AB = AC = CD = .
a M là một điểm trên cạnh AC .
Mặt phẳng (P) qua .., song song với AB vàCD . Diện tích thiết diện của mp (P)và tứ diện ABCD đạt
giá trị lớn nhất bằng bao nhiêu? 2 a 2 a 2 a A. 2 a . B. . C. . D. . 16 2 4 Lời giải Chọn D. Trang 33 Qua
kẻ các đường thẳng song s M
ong với AB và CD cắt BC và AD lần lượt tại Q và N .
Qua N kẻ đường thẳng song song với AB cắt BD tại P .
Suy ra thiết diện là tứ giác MNPQ có MN / /P ; Q MQ / /N ;
P MP ^ MQ nên thiết diện MNPQ là hình chữ nhật. MN AM AM.DC Có = Þ MN = = x DC AC AC MQ MC a - x = =
Þ MQ = a - x AB AC a Þ S
= MN.MQ = x(a - x). MNPQ 2 2
æ x + a - x ö a a
Theo bất đẳng thức Cô-si: x(a - x) £ = khi x = . ç ÷ è 2 ø 4 2
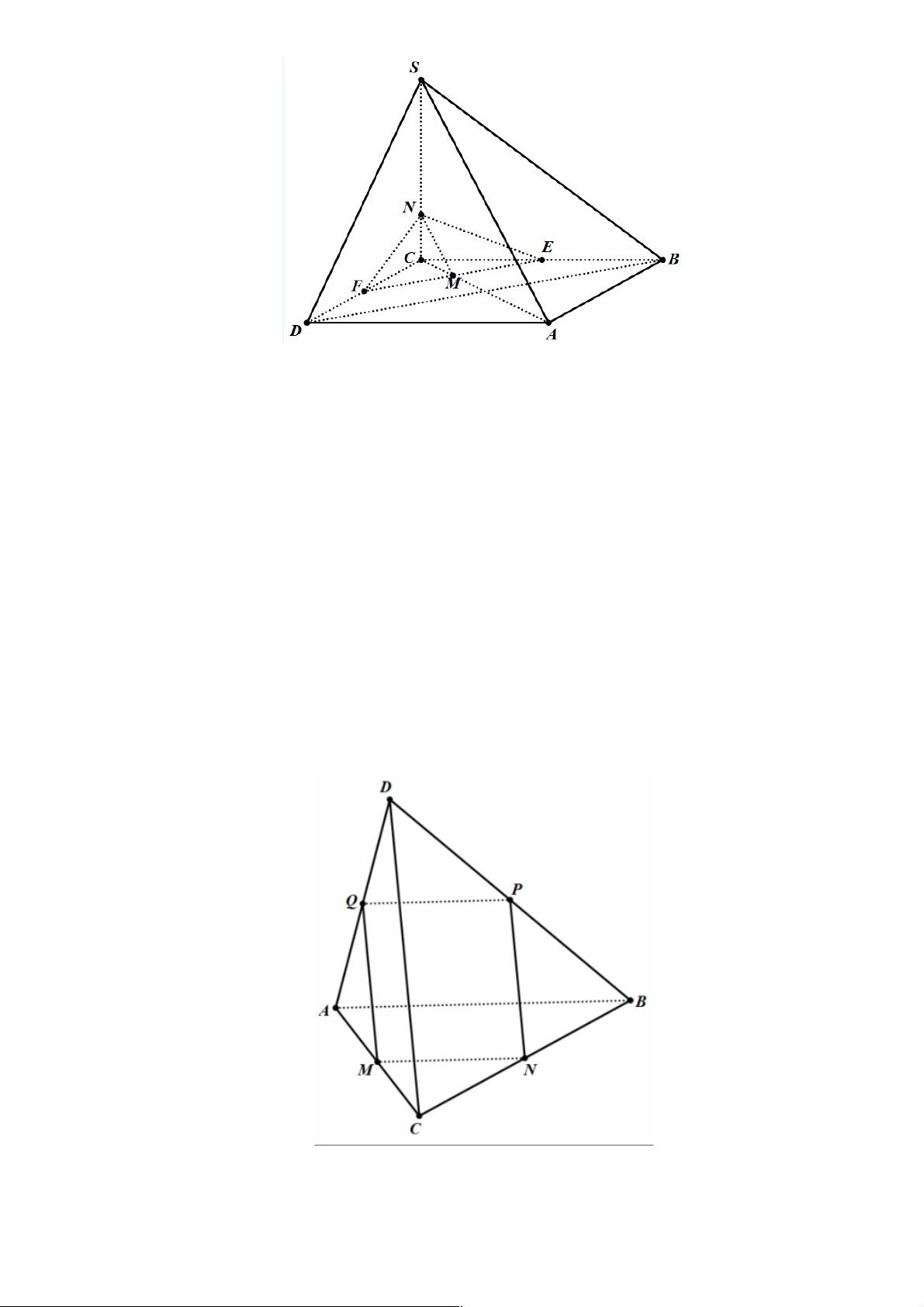
Câu 42. Cho hình chóp S.ABC , M là một điểm nằm trong tam giác ABC . Các đường thẳng qua M song song với ,
SA SB, SC cắt các mặt phẳng (SBC),(SAC),(SAB) lần lượt tại A ,¢ B ,¢C¢.
MA¢ MB¢ MC¢ + +
có giá trị không đổi bằng bao nhiêu khi M di động trong tam giác ABC ? SA SB SC 1 1 2 A. . B. . C. 1. D. . 3 2 3 Lời giải Chọn C. Trang 34 Do MA¢ SA ∥
nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử E là giao điểm của mặt phẳng này MA¢ ME S với BC . Khi đó ,
A M , E thẳng hàng và ta có: MBC = = . SA EA SABC MB¢ S MC¢ S
MA¢ MB¢ MC¢ Tương tự ta có: MAC = , MAB = . Vậy + + = . 1 SB S SC S SA SB SC ABC ABC
Câu 43. Cho hình chóp S.ABC , M là một điểm nằm trong tam giác ABC . Các đường thẳng qua M song song với ,
SA SB, SC cắt các mặt phẳng (SBC),(SAC),(SAB) lần lượt tại A ,¢ B ,¢C¢.
MA¢ MB¢ MC¢ . .
nhận giá trị lớn nhất. Khi đó vị trí của M trong tam giác ABC là: SA SB SC
A. Trực tâm ABC D .
B. Trọng tâm ABC D .
C. Tâm ngoại tiếp ABC D .
D. Tâm nội tiếp ABC D . Lời giải Chọn B. Do MA¢ SA ∥
nên bốn điểm này nằm trong cùng mặt phẳng. Giả sử E là giao điểm của mặt phẳng này MA¢ ME S với BC . Khi đó ,
A M , E thẳng hàng và ta có: MBC = = . SA EA SABC MB¢ S MC¢ S
MA¢ MB¢ MC¢ Tương tự ta có: MAC = , MAB = . Vậy + + = . 1 SB S SC S SA SB SC ABC ABC
Ap dụng bất đẳng thức Cauchy ta có : Trang 35
MA¢ MB¢ MC¢
MA¢ MB¢ MC¢
MA¢ MB¢ MC¢ 1 3 + + ³ 3 . . Þ . . £ . SA SB SC SA SB SC SA SB SC 27 MA¢ MB¢ MC¢
Dầu bằng xảy ra khi và chỉ khi: = = Þ S = S = S . MAC MAB MBC SA SB SC
Điều này chỉ xảy ra khi M là trọng tâm tam giác ABC . Vậy đáp án đúng là B.
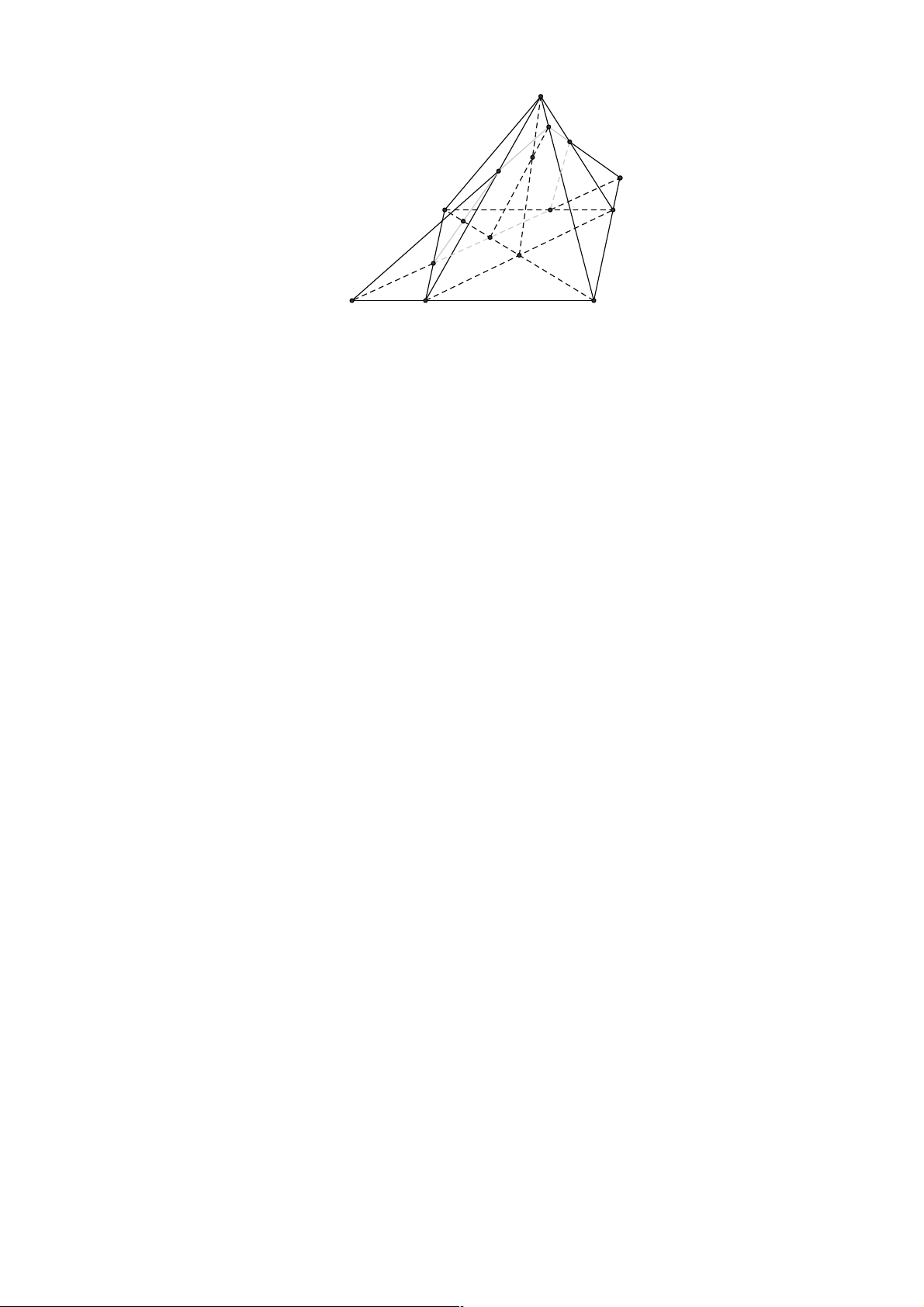
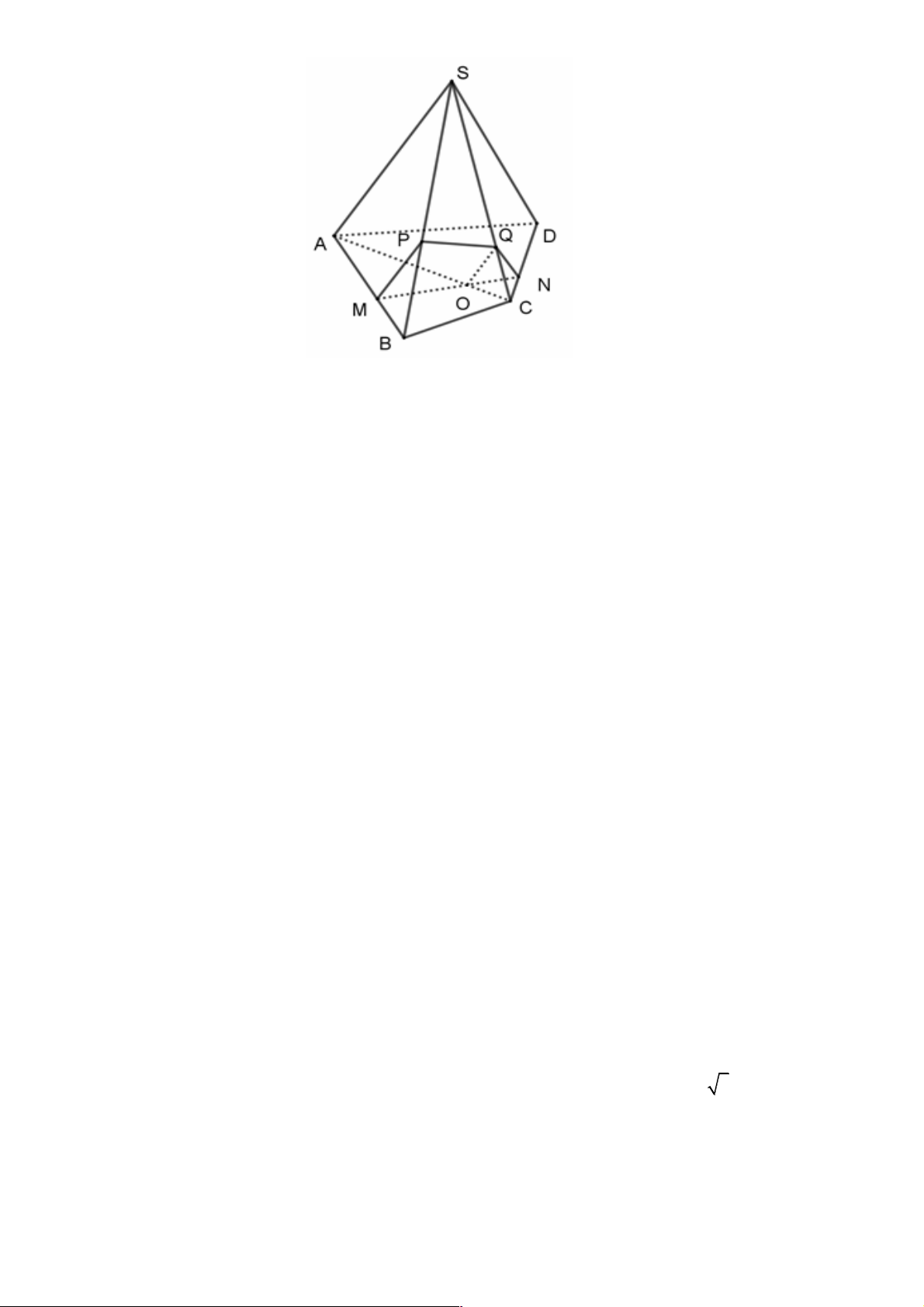
Câu 44. Cho hình chóp S.ABCD với đáy ABCD là hình thang với đáy AD và BC ( AD = a > BC = b).
Gọi I, J lần lượt là trọng tâm các tam giác SAD và SBC . Mặt phẳng ( ADJ ) cắt ,
SB SC lần lượt tại
M , N . Mặt phẳng (BCI ) cắt ,
SA SD lần lượt tại P,Q . Gọi E là giao điểm của AM và PB , F là giao
điểm của CQ và DN . Trong các mệnh đề dưới đây, có bao nhiêu mệnh đề sai?
1) MN và PQ song song với nhau.
2) MN và EF song song với nhau. 2
3) EF = (a + b). 5 1
4) EF = (a + b) 4 A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn B.
Ta có I Î(SAD), suy ra I Î(SAD)Ç(BCI ). (
ì SAD) Ç(BCI ) = PQ ï
Do íAD Ì (SAD), BC Ì (BCI ) Þ PQ∥AD B ∥ C . ïAD BC î ∥
Ta có: J Î(SBC), suy ra J Î(SBC)Ç( ADJ ). Trang 36 (
ì SBC) Ç( ADJ ) = MN ï
Do íBC Ì (SBC), AD Ì ( ADJ ) Þ MN∥AD BC ∥ . ïAD BC î ∥
Từ đó suy ra MN và PQ song song với nhau.
ìEF = ( ADNM ) Ç(BCQP) ï
ïAD = ( ADNM ) Ç( ABCD) Ta có: í Þ EF∥AD .
ïBC = ( ABCD) Ç(BCQP) ï îAD BC ∥ Suy ra EF M
∥ N . Gọi K là giao điểm của CP với EF EF = EK + KF . SP 2 SM Do = = Þ PM AB ∥ . SA 3 SB PE 2 PE 2
Theo định lý Thalet ta có: = Þ
= . Do EK song song với BC nên theo định lý Thalet ta có : EB 3 PB 5 PE EK 2 2 = = Þ EK = b. PB BC 5 5 QF 2 QC 5 PQ 5 3 3 2 2 Tương tự ta cũng có: = Þ = Þ
= Þ FK = PQ = . AD = a. FC 3 FC 3 FK 3 5 5 3 5 2
Từ đây suy ra EF = (a + b). 5 Trang 37