Các trường hợp bằng nhau của tam giác kèm ví dụ minh hoạ dễ hiểu
1. Định nghĩa tổng các góc trong của một tam giác
Đối với một tam giác bất kỳ, tổng các số đo góc bằng 180 độ.
Ví dụ: Cho tam giác ABC bất kì, hãy chứng minh rằng tổng ba góc của nó bằng 180⁰. Hướng dẫn giải:
Qua đỉnh A ta kẻ đường thẳng xy song song với BC.
Vì đường thẳng xy song song với BC nên góc CAy = ACB
Tương tự, vì đường thẳng xy song song với BC nên góc xAB = ABC
Ta có xAy = 180⁰, mà xAy = xAB + BAC + yAC = ABC + BAC + ACB = 180⁰
Mẹo ghi nhớ tổng ba góc của tam giác
Đối với một tam giác bất kỳ, tổng các số đo góc đều bằng 180 độ.
Định lý này đã được chấp nhận và ta hiểu rằng công thức tính tổng số đo các góc trong một đa giác như
sau: tổng số đo = (n – 2).180 (trong đó ẩn số n là số cạnh của đa giác).
Trong một tam giác vuông, tổng số đo của hai góc phụ bằng 90 độ.
Khi áp dụng định lý về tổng ba góc trong trong một tam giác vào tam giác vuông ta sẽ có: tam giác vuông có
một góc bằng 90 độ. Từ đó ta suy ra tổng hai góc còn lại bằng 90 độ. Vì vậy ta nói hai góc nhọn của tam giác vuông phụ nhau.
Góc ngoài của tam giác có tổng bằng hai góc trong không liền kề với nó.
Góc ngoài của tam giác và góc trong kề với nó sẽ có tổng số đo bằng 180 độ. Mà tổng ba góc bên trong của
tam giác bằng 180 độ. Từ đó ta suy ra được số đo góc bên ngoài của tam giác bằng tổng số đo hai góc
trong không liền kề với nó.
Góc ngoài của một tam giác lớn hơn từng góc bên trong không liền kề với nó.
Ta thấy góc ngoài của tam giác có tổng bằng hai góc trong không liền kề với nó. Do đó, ta suy ra được góc
ngoài luôn luôn lớn hơn mỗi góc bên trong.
2. Các trường hợp tam giác bằng nhau
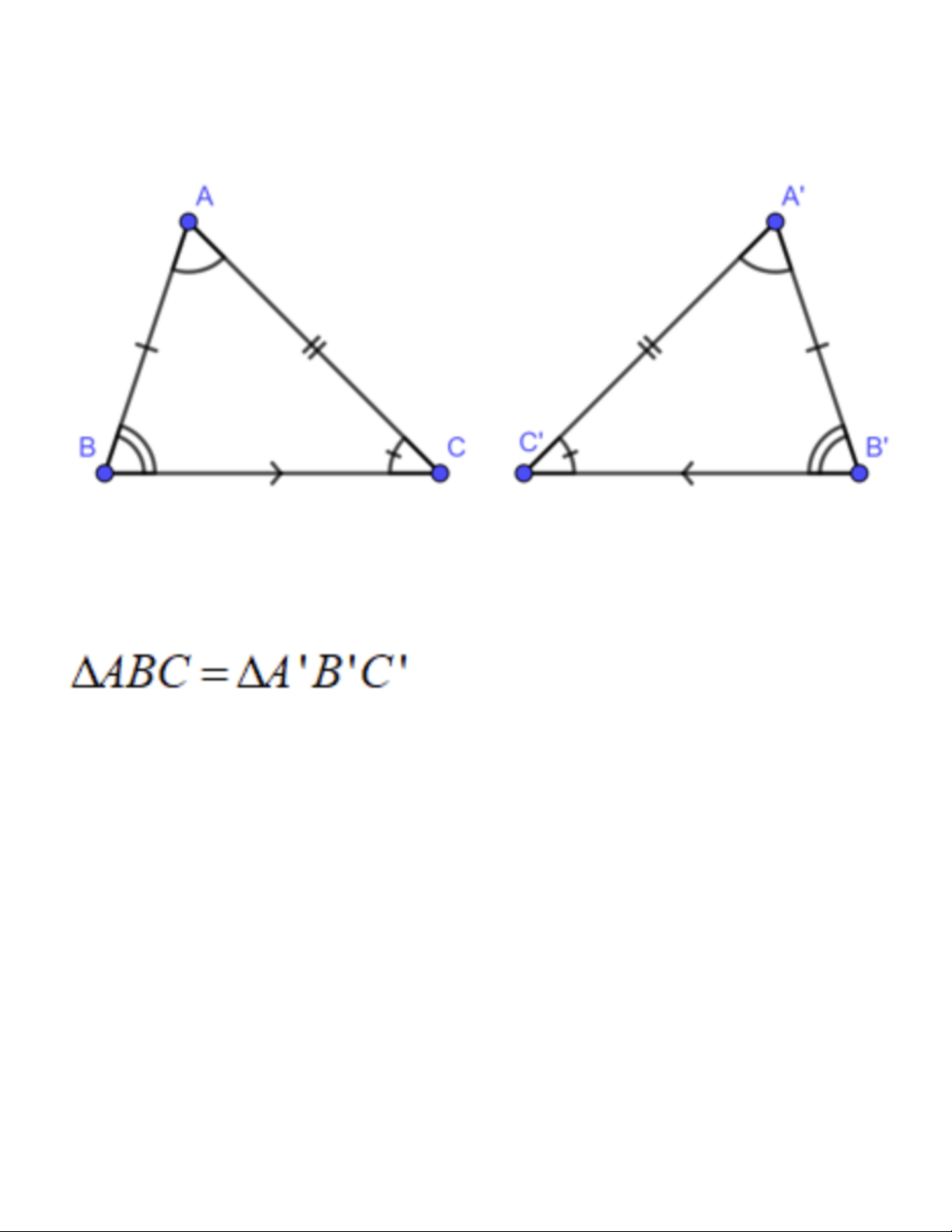
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2.1. Trường hợp bằng nhau thứ nhất của tam giác (cạnh – cạnh – cạnh)
Kiến thức cần nhớ
Chứng minh tam giác bằng nhau bằng cách nếu ba cạnh của một tam giác này bằng với ba cạnh của tam
giác khác thì hai tam giác đó bằng nhau theo trường hợp cạnh – cạnh – cạnh.
Dạng toán thường gặp
Dạng 1: Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh.
Sử dụng định nghĩa hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh: “nếu ba cạnh của một
tam giác này lần lượt bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau”.
Dạng 2: Sử dụng trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh để chứng minh các
cạnh góc bằng nhau và tính số đo góc. Phương pháp giải:
Xác định hai tam giác đó có các góc cần chứng minh bằng nhau và cần tính số đo.
Chứng minh hai tam giác bằng nhau theo trường hợp thứ nhất cạnh – cạnh – cạnh.
Suy ra hai góc tương ứng trong hai tam giác bằng nhau hoặc suy ra số đo góc cần tính.
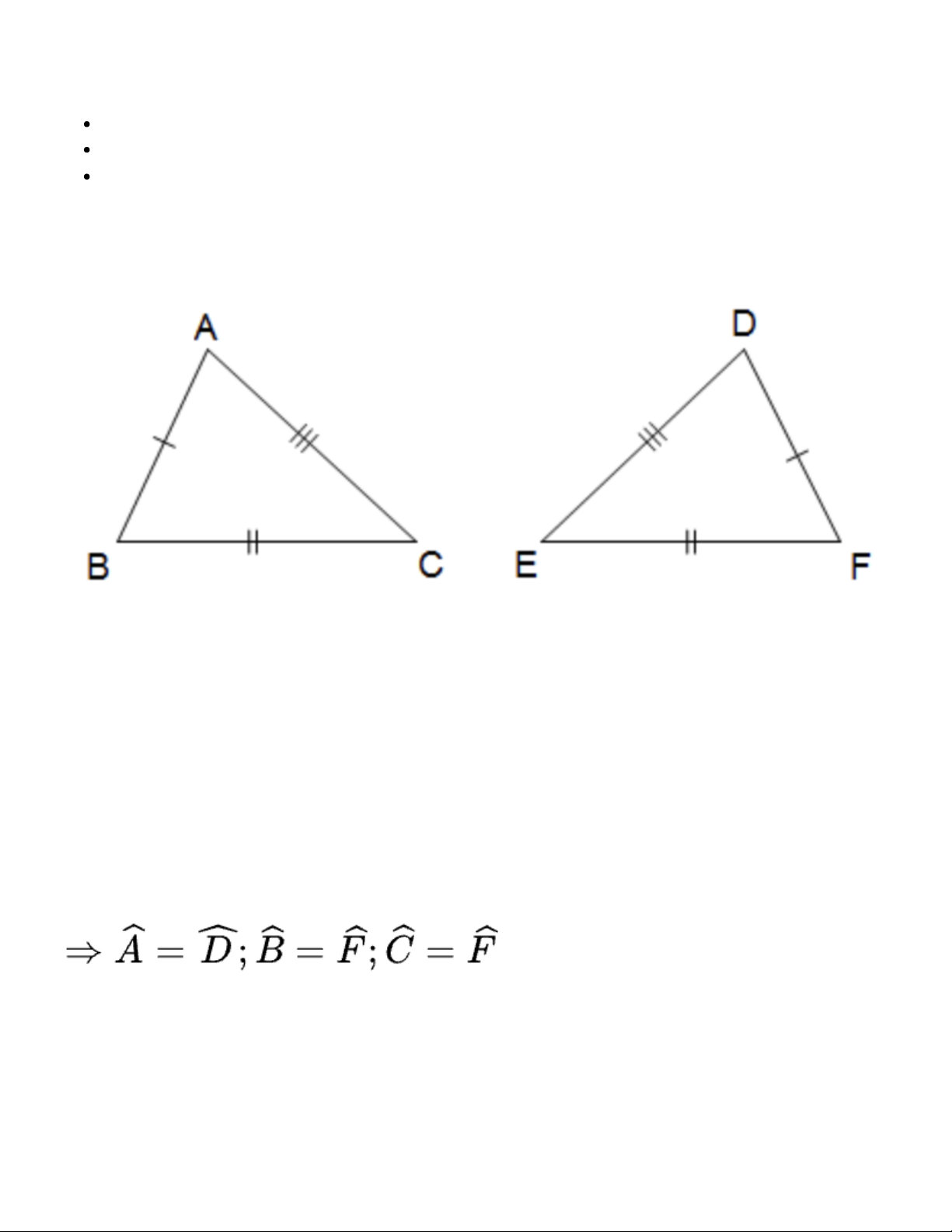
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. + Xét ∆ABC và ∆DFE có: AB = DF (gt) AC = DE (gt) BC = EF (gt)
Suy ra ∆ABC = ∆DFE (c - c - c)
(các cặp góc tương ứng)
2.2. Trường hợp bằng nhau thứ hai của tam giác (cạnh – góc – cạnh) Định lý
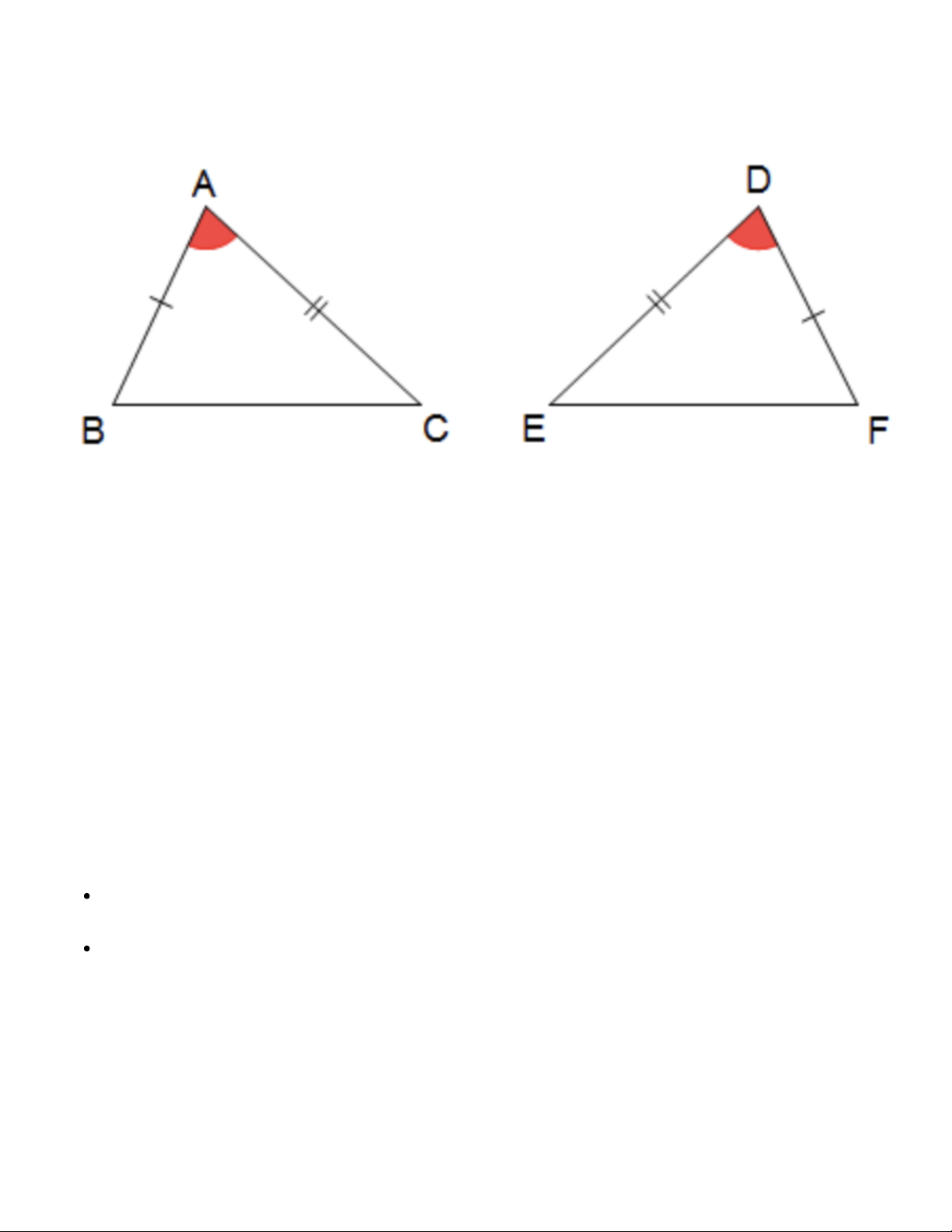
Nếu góc xen giữa và hai cạnh của tam giác này bằng góc xen giữa và hai cạnh của tam giác kia thì hai tam giác đó bằng nhau. + Xét ∆ABC và ∆DFE có: AB = DF (gt) Góc A = Góc D (gt) AC = DE (gt)
Suy ra ∆ABC = ∆DFE (c - g - c)
=> Góc B = Góc F; Góc C = Góc E (góc tương ứng) và BC = EF (cạnh tương ứng)
Lưu ý: Cặp góc bằng nhau phải xen giữa hai cặp cạnh bằng nhau thì mới kết luận được hai tam giác bằng nhau.
Áp dụng vào tam giác vuông
Nếu hai cạnh của một tam giác vuông này bằng với hai cạnh lần lượt của tam giác vuông kia thì hai
tam giác vuông đó bằng nhau.
Nếu cạnh góc vuông và cạnh huyền của một tam giác này lần lượt bằng cạnh góc vuông và cạnh
huyền của tam giác kia thì hai tam giác vuông đó nhau.
Dạng toán thường gặp
Dạng 1: Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ hai của tam giác cạnh – góc – cạnh. Phương pháp giải:
Sử dụng định nghĩa: “nếu góc xen giữa và hai cạnh của tam giác này bằng góc xen giữa và hai cạnh
của tam giác kia thì hai tam giác đó bằng nhau”.
Hoặc sử dụng hệ quả: “nếu hai cạnh của một tam giác vuông này bằng với hai cạnh lần lượt của tam
giác vuông kia thì hai tam giác vuông đó bằng nhau”.
Dạng 2: Chứng minh hai đoạn thẳng hoặc các góc bằng nhau. Tính độ dài của đoạn thẳng và số đo góc. Phương pháp giải:
Chọn hai tam giác có các yếu tố cần chứng minh hoặc cần tính.
Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ hai của tam giác cạnh – góc – cạnh.
Suy ra các yếu tố cần để giải được bài toán.
2.3. Trường hợp bằng nhau thứ ba của tam giác (góc – cạnh – góc) Định lý
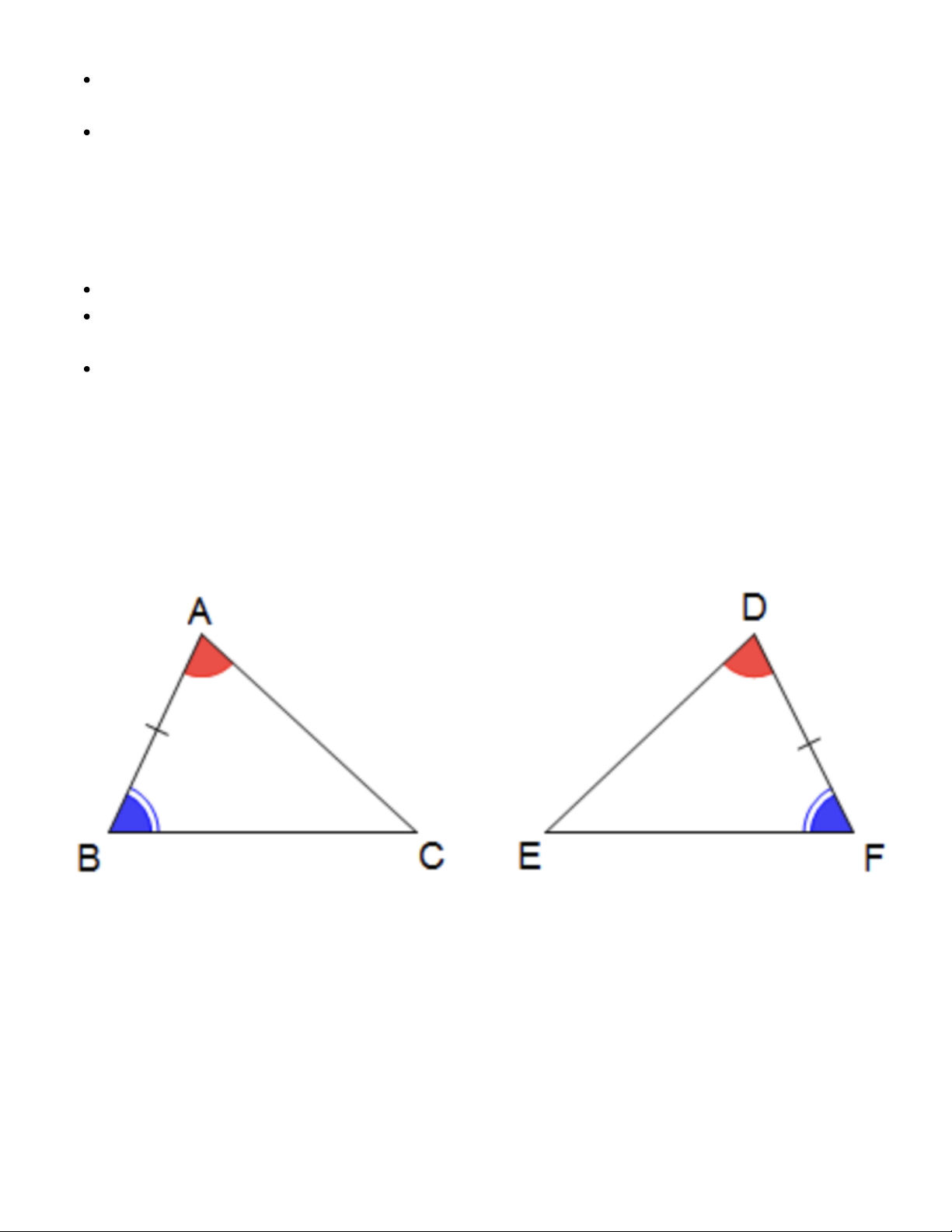
Nếu hai góc kề và một cạnh của một tam giác này bằng với hai góc kề và một cạnh của tam giác kia thì hai
tam giác đó là tam giác bằng nhau. + Xét ∆ABC và ∆DFE có: Góc A = Góc D (gt) AB = DF (gt) Góc B =. Góc F
Suy ra ∆ABC = ∆DFE (g - c - g)
=> Góc C = Góc E (góc tương ứng) và AC = DE, BC = EF (cạnh tương ứng) Lưu ý:
- Cặp cạnh bằng nhau phải là cạnh tạo nên hai cặp góc bằng nhau thì mới kết luận được hai tam giác bằng nhau.
- Khi hai tam giác đã chứng minh bằng nhau, ta có thể suy ra những yếu tố tương ứng còn lại bằng nhau.
Áp dụng vào tam giác vuông
Hệ quả 1: Nếu một góc nhọn của một tam giác vuông này bằng với một góc nhọn và một cạnh của
tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Hệ quả 2: Nếu góc nhọn và cạnh huyền của tam giác vuông này bằng với góc nhọn và cạnh huyền
của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Dạng toán thường gặp tam giác bằng nhau
Dạng 1: Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc. Phương pháp giải:
Sử dụng trường hợp bằng nhau cạnh huyền – góc nhọn của tam giác vuông và góc – cạnh – góc của tam
giác thường để chứng minh tam giác bằng nhau.
Dạng 2: Chứng minh 2 đoạn thẳng bằng nhau và tính độ dài của đoạn thẳng. Phương pháp giải:
Chọn 2 tam giác có chứa đoạn thẳng cần tính.
Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc.
Suy ra các yếu tố cần để giải được bài toán.
Dạng 3: Sử dụng những trường hợp tam giác bằng nhau. Phương pháp giải:
Sử dụng các trường hợp bằng nhau của tam giác như cạnh – góc – cạnh, cạnh – cạnh – cạnh, góc – cạnh
– góc và một số trường hợp bằng nhau của tam giác vuông.
3. Tam giác cân và đường trung trực của đoạn thẳng
Định nghĩa đường trung trực
Đường trung trực của đoạn thẳng: Một đường thẳng khi đi qua trung điểm và vuông góc với một đoạn
thẳng nào đó được gọi là đường trung điểm của đoạn thẳng đó.
Đường trung trực của tam giác: Trong một tam giác bất kì, đường trung trực của một cạnh là đường
trung trực của tam giác đó và mỗi tam giác sẽ có ba đường trung trực.
Tính chất đường trung trực
Tính chất trung trực trên đoạn thẳng:
Định lý 1: Một điểm nằm trên đường trung trực của một đoạn thẳng bất kì thì khoảng cách từ điểm đó
đến hai đầu mút của đoạn thẳng bằng nhau.
Định lý 2: Điểm cách đều hai đầu mút của đoạn thẳng nằm trên đường trung trực của đoạn thẳng.
Tính chất trung trực trong tam giác.
Định lý 1: Ba đường trung trực trong một tam giác đi qua cùng một điểm. Điểm này có khoảng cách từ
chính nó đến ba đỉnh của tam giác đều bằng nhau và được gọi là tâm đường tròn ngoại tiếp của tam giác đó.
Ta có: OA = OB = OC và O là tâm đường tròn ngoại tiếp tam giác ABC
Định lý 2: Trong một tam giác, đường trung trực ứng với cạnh đáy đồng thời cũng là đường trung
tuyến, đường phân giác và đường cao xuất phát từ đỉnh đối diện với cạnh đó.
Định lý 3: Trong một tam giác vuông, giao điểm của ba đường trung trực chính là trung điểm của cạnh huyền.