lOMoAR cPSD| 45619127
Các vấn đề và tác động của Imbalanced Dataset đến Machine Learning
Vấn đề chính của mất cân bằng dữ liệu là mô hình Machine Learning thường có xu
hướng tập trung vào các lớp chiếm đa số, dẫn đến việc bỏ qua hoặc không học được các
đặc điểm của lớp thiểu số. Điều này xuất phát từ việc hầu hết các thuật toán học máy
được thiết kế để tối ưu hóa độ chính xác tổng thể. Khi dữ liệu mất cân bằng, việc chỉ dự
đoán đúng các mẫu thuộc lớp chiếm đa số cũng đã mang lại một độ chính xác cao, khiến
mô hình không chú trọng đến các mẫu thuộc lớp thiểu số. Ví dụ, trong một tập dữ liệu
với 95% mẫu thuộc lớp "không gian lận" và 5% thuộc lớp "gian lận", một mô hình luôn
dự đoán "không gian lận" có thể đạt độ chính xác 95%. Tuy nhiên, mô hình này hoàn
toàn vô dụng trong việc phát hiện gian lận – mục tiêu chính của bài toán.
Tác động của mất cân bằng dữ liệu đối với mô hình Machine Learning là rất nghiêm
trọng. Đầu tiên phải nói đến hiệu suất của mô hình trên lớp thiểu số thường rất kém,
đặc biệt trong các ứng dụng nhạy cảm như y tế hoặc an ninh. Nguyên nhân chính là thuật
toán Machine Learning thường tối ưu hóa dựa trên tổng thể dữ liệu. Khi lớp chiếm đa
số (majority class) có nhiều mẫu hơn, mô hình sẽ ưu tiên học đặc trưng của lớp này,
trong khi bỏ qua hoặc học không đầy đủ các đặc điểm của lớp thiểu số (minority class).
Cụ thể trong ví dụ bài toán phát hiện gian lận thẻ tín dụng, giả sử có 100,000 giao dịch,
trong đó chỉ có 200 giao dịch là gian lận. Một mô hình học máy có thể đạt độ chính xác
lên tới 99.8% bằng cách dự đoán tất cả giao dịch là "không gian lận". Tuy nhiên, giá trị
thực tế của mô hình này là bằng không, vì tất cả các giao dịch gian lận đều bị bỏ qua.
Điều này đặc biệt nguy hiểm, bởi các giao dịch gian lận không được phát hiện sẽ gây
thiệt hại tài chính lớn cho ngân hàng và khách hàng.
Mất cân bằng dữ liệu cũng dẫn đến hiện tượng thiên vị trong dự đoán, khi mô hình có
xu hướng ưu tiên lớp chiếm đa số. Điều này không chỉ làm giảm hiệu quả của mô hình
mà còn có thể tạo ra sự bất công, đặc biệt trong các ứng dụng nhạy cảm như tuyển dụng
nhân sự hay cấp tín dụng. Ví dụ, trong một bài toán dự đoán khả năng trúng tuyển vào
một công ty, nếu tập dữ liệu bao gồm 90% mẫu từ nam giới và 10% mẫu từ nữ giới, mô
hình có thể học sai rằng giới tính nam là yếu tố quan trọng nhất. Khi áp dụng, mô hình
sẽ ưu tiên các ứng viên nam, dẫn đến sự bất công trong quá trình tuyển dụng.
Đánh giá sai hiệu quả của mô hình là một tác động khác do dữ liệu mất cân bằng. Các
chỉ số như Accuracy không phản ánh đúng hiệu quả thực sự của mô hình. Một mô hình lOMoAR cPSD| 45619127
có thể đạt độ chính xác rất cao mà không đưa ra bất kỳ dự đoán chính xác nào cho lớp
thiểu số, khiến nhà phát triển dễ bị đánh lừa bởi kết quả tốt đẹp nhưng không có giá trị
thực tế. Chẳng hạn, trong bài toán chẩn đoán bệnh ung thư, nếu 99% bệnh nhân không
mắc bệnh và chỉ 1% mắc bệnh, một mô hình dự đoán tất cả bệnh nhân là "không mắc
bệnh" sẽ đạt độ chính xác 99%. Tuy nhiên, điều này có thể dẫn đến hậu quả nghiêm
trọng, khi các bệnh nhân thật sự mắc ung thư không được phát hiện và điều trị kịp thời.
Một tác động khác là việc khó khăn trong việc tối ưu hóa mô hình. Khi dữ liệu mất
cân bằng, các thuật toán tối ưu hóa như Gradient Descent sẽ gặp khó khăn trong việc
cập nhật trọng số, vì gradient của các lớp chiếm đa số sẽ chi phối quá trình cập nhật này,
khiến mô hình không học được đầy đủ các đặc trưng của lớp thiểu số. Ví dụ trong bài
toán phân loại lỗi trong sản xuất, giả sử một nhà máy sản xuất 10,000 sản phẩm, trong
đó chỉ có 50 sản phẩm bị lỗi. Nếu gradient của các sản phẩm "không lỗi" chiếm ưu thế,
mô hình có thể gặp khó khăn trong việc nhận diện và dự đoán chính xác các sản phẩm
bị lỗi. Điều này có thể dẫn đến việc các sản phẩm không đạt tiêu chuẩn vẫn được phân phối ra thị trường.
Cuối cùng, dữ liệu mất cân bằng cũng có thể dẫn đến hiện tượng overfitting hoặc
underfitting. Overfitting xảy ra khi mô hình ghi nhớ quá kỹ các mẫu thuộc lớp thiểu số
mà không học được đặc điểm tổng quát, trong khi underfitting xảy ra khi mô hình không
đủ khả năng để học các đặc điểm của lớp thiểu số. Trong bài toán phát hiện lỗi phần
mềm, nếu chỉ có rất ít lỗi được ghi nhận trong tập dữ liệu, mô hình có thể ghi nhớ lỗi cụ
thể (overfitting) hoặc không học được cách phân biệt lỗi từ các mẫu thông thường
(underfitting), làm giảm giá trị ứng dụng trong thực tế.
Các phương pháp đánh giá mô hình với Imbalanced Dataset:
Như đã đề cập trong phần tác động, vì Accuracy chỉ đơn giản là tỷ lệ chính xác tổng thể,
nhưng trong trường hợp mất cân bằng dữ liệu, nếu lớp thiểu số là rất ít thì chỉ cần dự
đoán tất cả các mẫu là thuộc lớp chiếm đa số đã có thể đạt một độ chính xác cao mà thực
tế lại không có giá trị (vì mô hình không nhận diện được lớp thiểu số). Với hạn chế
không phản ánh đúng khả năng của mô hình trong việc dự đoán lớp thiểu số. Để đánh
giá chính xác hơn, cần sử dụng các phương pháp một cách toàn diện hơn như:
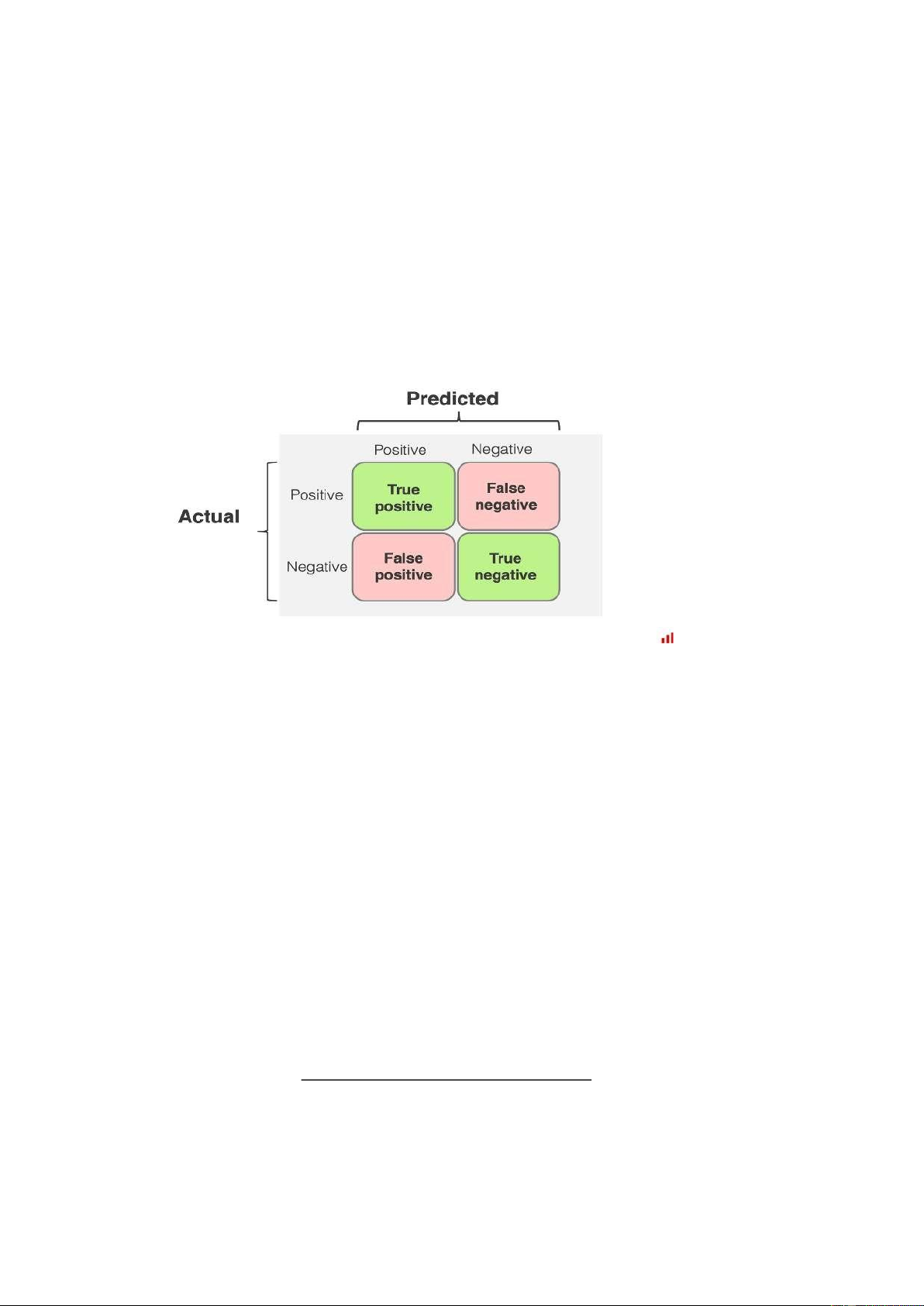
• Confusion Matrix đây là công cụ cơ bản nhất để phân tích hiệu suất của mô
hình. Nó chia các dự đoán thành bốn loại lần lượt là True Positive (TP) - số lượng lOMoAR cPSD| 45619127
mẫu thuộc lớp dương được dự đoán đúng, True Negative (TN) – số lượng mẫu
thuộc lớp âm được dự đoán đúng, False Positive (FP) - số lượng mẫu thuộc lớp
âm bị dự đoán nhầm thành lớp dương, và False Negative (FN) - số lượng mẫu
thuộc lớp dương bị dự đoán nhầm thành lớp âm. Ví dụ, trong một bài toán phát
hiện bệnh với 100 mẫu, nếu có 10 bệnh nhân thực sự bị bệnh và mô hình chỉ dự
đoán đúng 6 trong số đó (TP = 6), nhưng nhầm 4 người khỏe mạnh thành bị bệnh
(FP = 4), Confusion Matrix sẽ giúp phân tích chi tiết từng loại lỗi, từ đó cải thiện mô hình.
• Từ Confusion Matrix, các chỉ số như Precision và Recall được xây dựng để đánh
giá hiệu suất của mô hình theo từng khía cạnh, đặc biệt quan trọng trong trường
hợp dữ liệu không cân bằng. Những chỉ số này không chỉ cung cấp thông tin chi
tiết về chất lượng dự đoán mà còn giúp hiểu rõ hơn về loại lỗi mà mô hình thường
gặp phải. Đầu tiên, Precision (Độ chính xác dự đoán) đo lường mức độ chính
xác của các dự đoán thuộc lớp dương (positive class). Cụ thể, Precision được tính
bằng tỷ lệ giữa số lượng mẫu thuộc lớp dương được dự đoán đúng (True Positive)
so với tổng số mẫu mà mô hình dự đoán là lớp dương (True Positive + False Positive)
TruePositive(TP) Precision =
TruePositive(TP)+FalsePositive(FP)
Ví dụ, trong một bài toán chẩn đoán bệnh, nếu mô hình dự đoán có 10 bệnh nhân bị
bệnh, trong đó chỉ 6 người thực sự bị bệnh và 4 người còn lại không bị bệnh nhưng bị lOMoAR cPSD| 45619127
dự đoán nhầm, thì Precision của mô hình sẽ là 60%. Điều này có nghĩa là trong tất cả
các dự đoán "bị bệnh" của mô hình, chỉ có 60% là chính xác. Precision đặc biệt quan
trọng trong các ứng dụng mà việc đưa ra cảnh báo sai (False Positive) gây ra chi phí lớn,
chẳng hạn như hệ thống kiểm tra gian lận tài chính
• Tiếp đến là Recall (Độ bao phủ), đo lường khả năng của mô hình trong việc phát
hiện đúng các mẫu thực sự thuộc lớp dương. Recall được tính bằng tỷ lệ giữa số
lượng mẫu dương được dự đoán đúng (True Positive) so với tổng số mẫu thực sự
thuộc lớp dương (True Positive + False Negative).
True Positive(TP) Recall =
TruePositive(TP)+FalseNegative(FN)
Trong cùng ví dụ trên, giả sử có 10 bệnh nhân thực sự bị bệnh, nhưng mô hình chỉ phát
hiện đúng 6 người và bỏ sót 4 người, Recall của mô hình sẽ là 60%. Tức mô hình chỉ
phát hiện được 60% số bệnh nhân thực sự bị bệnh. Recall thường được ưu tiên trong các
ứng dụng mà việc bỏ sót (False Negative) gây ra hậu quả nghiêm trọng, chẳng hạn như
chẩn đoán ung thư. Nếu một bệnh nhân bị ung thư nhưng không được phát hiện, hậu
quả có thể rất nghiêm trọng.
• Trong nhiều trường hợp, Precision và Recall có thể mâu thuẫn với nhau. Ví dụ,
nếu mô hình cố gắng tối ưu Precision, nó có thể bỏ qua nhiều mẫu thuộc lớp
dương để giảm số lượng False Positive. Ngược lại, nếu tối ưu Recall, mô hình có
thể tăng số lượng dự đoán dương để không bỏ sót mẫu nào, dẫn đến nhiều dự
đoán sai (False Positive). Và chỉ số F1-Score (Điểm hài hòa) được sử dụng để
cân bằng giữa Precision và Recall, là trung bình điều hòa của hai chỉ số này. Precison× Recall
F1-Score = Precison+Recall
Với Precision = 0.6 và Recall = 0.6 trong ví dụ trên, dựa vào công thức của F1-Score có
được kết quả là 60%. F1-Score đặc biệt hữu ích trong các bài toán mà cả Precision và
Recall đều quan trọng, chẳng hạn như phát hiện gian lận hoặc cảnh báo nguy cơ.
• ROC Curve (Receiver Operating Characteristic) là một công cụ quan trọng
để đánh giá hiệu suất của mô hình phân loại, đặc biệt khi mô hình cần phân biệt lOMoAR cPSD| 45619127
giữa hai lớp: dương (positive) và âm (negative). Biểu đồ ROC biểu diễn mối quan
hệ giữa hai chỉ số chính:
True Positive Rate (TPR): Còn gọi là Recall, đo lường tỷ lệ các mẫu thuộc
lớp dương được dự đoán đúng. Công thức tính tương tự như Recall ở trên.
False Positive Rate (FPR): Đo lường tỷ lệ các mẫu thuộc lớp âm bị dự đoán nhầm là lớp dương
True Positive(TP) FPR =
TruePositive(TP)+FalseNegative(FN)
• AUC (Area Under Curve) là diện tích dưới đường cong ROC, biểu thị khả năng
phân biệt giữa hai lớp của mô hình. AUC càng gần 1.0 mô hình càng tốt.
Ví dụ, nếu một mô hình có AUC = 0.85, điều này có nghĩa là trong 85% các trường
hợp, mô hình có thể phân biệt đúng giữa một mẫu thuộc lớp dương và một mẫu thuộc lớp âm.
PR-AUC (Precision-Recall Curve - Area Under Curve)
PR Curve (Precision-Recall Curve) là một công cụ quan trọng để đánh giá hiệu quả
của mô hình trên dữ liệu mất cân bằng. Đây là biểu đồ thể hiện mối quan hệ giữa
Precision (độ chính xác của dự đoán lớp Positive) và Recall (khả năng phát hiện đầy
đủ các mẫu thuộc lớp Positive). Khác với ROC Curve, PR Curve tập trung vào hiệu
quả của mô hình trong việc dự đoán lớp thiểu số (Positive), đặc biệt quan trọng khi dữ
liệu có sự chênh lệch lớn giữa các lớp.
PR-AUC (Precision-Recall Area Under Curve) đo lường diện tích dưới đường PR
Curve. Giá trị PR-AUC càng cao, mô hình càng hiệu quả trong việc cân bằng giữa
Precision và Recall. Trong các bài toán có dữ liệu mất cân bằng, PR-AUC được coi là
một thước đo phù hợp hơn ROC-AUC, bởi vì nó không bị ảnh hưởng bởi số lượng
mẫu lớn từ lớp đa số (Negative).
Xét một bài toán phát hiện lỗi trong sản phẩm sản xuất, giả sử số lượng sản phẩm
không lỗi (Negative) chiếm 99% tổng số sản phẩm, trong khi số lượng sản phẩm lỗi
(Positive) chỉ chiếm 1%. Một mô hình dự đoán tất cả sản phẩm là không lỗi sẽ đạt lOMoAR cPSD| 45619127
được độ chính xác (Accuracy) rất cao, nhưng hoàn toàn không có giá trị trong việc
phát hiện lỗi. Trong trường hợp này, PR-AUC là thước đo quan trọng để đánh giá hiệu
quả thực sự của mô hình.
Nếu mô hình có PR-AUC = 0.85, điều này có nghĩa là mô hình đạt hiệu suất cao trong
việc cân bằng giữa Precision và Recall khi dự đoán sản phẩm lỗi. Một đường PR
Curve dốc lên và có diện tích lớn thể hiện rằng mô hình không chỉ phát hiện được
phần lớn các sản phẩm lỗi (Recall cao), mà còn đảm bảo rằng các dự đoán lỗi là chính
xác (Precision cao). Điều này rất hữu ích trong thực tế vì mỗi lần phát hiện sai một sản
phẩm không lỗi là lỗi (FP) có thể dẫn đến chi phí kiểm tra không cần thiết, trong khi
bỏ sót một sản phẩm lỗi (FN) có thể gây hậu quả nghiêm trọng cho khách hàng và doanh nghiệp.
Nhìn chung, các chỉ số đánh giá trên đều đóng vai trò quan trọng trong việc đánh giá
hiệu suất của mô hình khi xử lý dữ liệu không cân bằng. Sự lựa chọn phương pháp
đánh giá phụ thuộc vào mục tiêu cụ thể của bài toán, giúp đảm bảo mô hình không chỉ
hoạt động tốt trên lớp đa số mà còn đáp ứng yêu cầu của lớp thiểu số.
https://viblo.asia/p/imbalanced-multiclass-datasets-Do754dmQ5M6
https://phamdinhkhanh.github.io/2020/02/17/ImbalancedData.html
https://www.youtube.com/watch?v=yrQe6aFKMYg
https://www.analyticsvidhya.com/blog/2021/06/5-techniques-to-handle-
imbalanceddata-for-a-classification-problem/
https://www.youtube.com/watch?v=_fe7JOBGbuU&t=427s https://viblo.asia/p/8-
chien-thuat-chong-lai-van-de-mat-can-bang-du-lieu-trong-hocmay-gDVK2d7AlLj