Cách bấm máy tính tìm nguyên hàm F(x) của hàm số f(x) | Chuyên đề Toán 12
Bạn đang học giải tích và loay hoay không biết cách sử dụng máy tính cầm tay để tìm nguyên hàm một cách nhanh chóng, chính xác? Trong bài viết này, chúng tôi sẽ hướng dẫn cách bấm máy tính tìm nguyên hàm F(x) của hàm số f(x) bằng các dòng máy phổ biến như Casio fx-580VN X hoặc fx-570VN Plus. Đây là một kỹ năng cực kỳ hữu ích giúp bạn kiểm tra kết quả trong quá trình học và luyện thi môn Toán. Hãy cùng khám phá cách làm nhanh chóng chỉ trong vài bước đơn giản!
Chủ đề: Chuyên đề Toán 12 27 tài liệu
Môn: Toán 12 3.9 K tài liệu
Sách: Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Tác giả:
Preview text:
CÁCH BẤM MÁY TÍNH TÌM NGUYÊN HÀM F(X) CỦA HÀM SỐ f(x) CHO TRƯỚC
Thuật toán trên máy tính CASIO (A) d f (F x i ( )) x A dx
f : là hàm số cần xác định nguyên hàm
F x : là các đáp án nguyên hàm đã cho i ( )
A: hằng số tự chọn thuộc tập xác định và có giá trị nhỏ
Thay lần lượt các đáp án vào F x và chọn giá trị A thích hợp i ( )
Lựa chọn đáp án có kết quả xấp xỉ bằng 0: 4 2
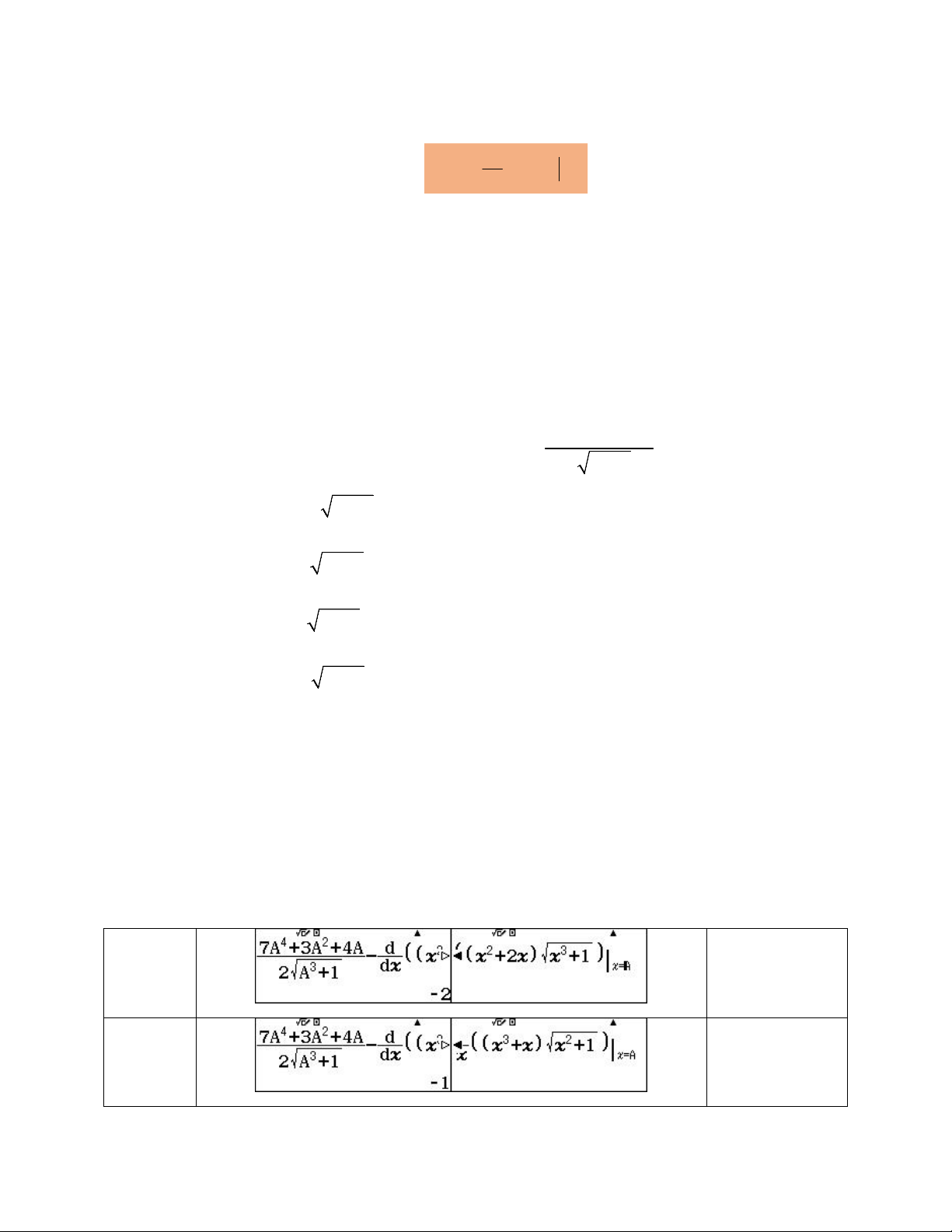
Bài toán 1.1 Tìm nguyên hàm của hàm số 7x 3x 4 ( ) x f x 3 2 x 1 2 3
A. f (x)dx (x 2x) x 1 C 3 2 B.
f (x)dx (x x) x 1 C 2 3
C. f (x)dx (x 1) x 1 C 3 3
D. f (x)dx (x x) x 1 C
Phân tích: Hàm số f (x) trên khá phức tạp do đó việc sử dụng máy tính CASIO
fx-580VN X để tìm nguyên hàm sẽ giúp các bạn chọn được đáp án đúng một
cách nhanh chóng và chính xác hơn. Hướng dẫn giải
Thay F x lần lượt bằng các đáp án và chọn A = 0 i ( ) Đáp án LOẠI A Đáp án LOẠI B Đáp án NHẬN C Đáp án LOẠI D
Khi làm bài thi các bạn không cần thử tất cả các đáp án trong đề mà chúng ta sẽ dừng
ngay việc thay đáp án khi chọn được biểu thức đúng
Bài toán 1.2 Tìm nguyên hàm của hàm số y 8sin 3xcos 2xsin 6x
2sin5x 2sin7x 2sin11 ( ) 2sin x f x dx x C A. 5 7 11
sin5x sin7x sin11 ( ) sin x f x dx x C B. 5 7 11
sin5x sin7x sin11 ( ) sin x f x dx x C C. 5 7 11
2sin5x 2sin7x 2sin11 ( ) 2sin x f x dx x C D. 5 7 11 Hướng dẫn giải
Để các phép toán lượng giác thực hiện chính xác hơn, chúng ta nên chuyển máy về chế độ Radian Chọn A Đáp án A NHẬN Đáp án B, C,
LOẠI vì A là đáp án đúng D
Bài toán 1.3 (Đề thi THPT Quốc gia 2017) Cho hàm số 1 F(x) là một nguyên 2 2x
hàm của hàm số f (x) . Tìm nguyên hàm của hàm số /f (x)ln x x / ln 1 ( )ln x f x xdx C A. 2 2 x x / ln x 1
f (x)ln xdx C B. 2 2 x 2x / ln x 1
f (x)ln xdx C C. 2 2 x 2x / ln 1 ( )ln x f x xdx C D. 2 2 x x Hướng dẫn giải Ta có / 1
f (x) F (x)x , suy ra / 2ln ( )ln x f x x 2 x 3 x
Nhập vào máy tính CASIO fx- 580VN X: 2ln A d G(x) , với G(x) lần lượt là 3 x A A dx
các hàm trong đáp án và A = 0.1
Document Outline
- CÁCH BẤM MÁY TÍNH TÌM NGUYÊN HÀM F(X) CỦA HÀM SỐ f