Câu hỏi ôn tập môn Sức bền vật liệu | Đại học Bách Khoa Hà Nội

L1: Phần lý thuyết (2 điểm)
Câu 1: Viết, giải thích công thức và trình bày trình tự giải bài toán kiểm tra bền của thanh chịu
kéo - nén đúng tâm làm bằng vật liệu dẻo?
Câu 2 Viết và giải thích công thức kiểm tra bền của thanh chịu kéo - nén đúng tâm làm bằng vật liệu giòn?
Câu 3: Viết, giải thích công thức và trình bày trình tự giải bài toán chọn kích thước mặt cắt
ngang của thanh chịu kéo - nén đúng tâm làm bằng vật liệu dẻo?
Câu 4:.Viết và giải thích công thức chọn kích thước mặt cắt ngang của thanh chịu kéo - nén
đúng tâm làm bằng vật liệu giòn?
Câu 5:a. Viết và giải thích công thức tính ứng suất tiếp tại một điểm bất kỳ của thanh tròn chịu xoắn thuần túy.
b.Vẽ biểu đồ phân bố ứng suất tiếp trên mặt cắt ngang của thanh tròn chịu xoắn thuần túy.
Câu 6: a.Viết biểu thức tính ứng suất tiếp tại một điểm bất kỳ trên mặt cắt ngang của thanh tròn
thẳng chịu xoắn thuần túy và giải thích các đại lượng trong biểu thức.
a) Viết biểu thức tính mô men quán tính và mô men chông uốn cho mặt cắt ngang hình chữ nhật có
chiều cao h và chiều rộng b đối với trục x.
Câu 7: Viết và giải thích công thức tính ứng suất tiếp trên mặt cắt ngang của thanh tròn đặc chịu xoắn thuần túy. Câu 8:
b) Viết biểu thức tính ứng suất tiếp tại một điểm bất kỳ trên mặt cắt ngang của thanh tròn thẳng chịu
xoắn thuần túy và giải thích các đại lượng trong biểu thức.
c) Viết biểu thức tính mô men quán tính và mô men chông uốn cho mặt cắt ngang hình chữ nhật có
chiều cao h và chiều rộng b đối với trục x.
Câu 9. Viết và giải thích công thức tính ứng suất tại một điểm bất kỳ trên mặt cắt ngang của thanh chịu uốn xiên.
L1: Phần bài tập uốn ngang phẳng (3 điểm) Câu 1.
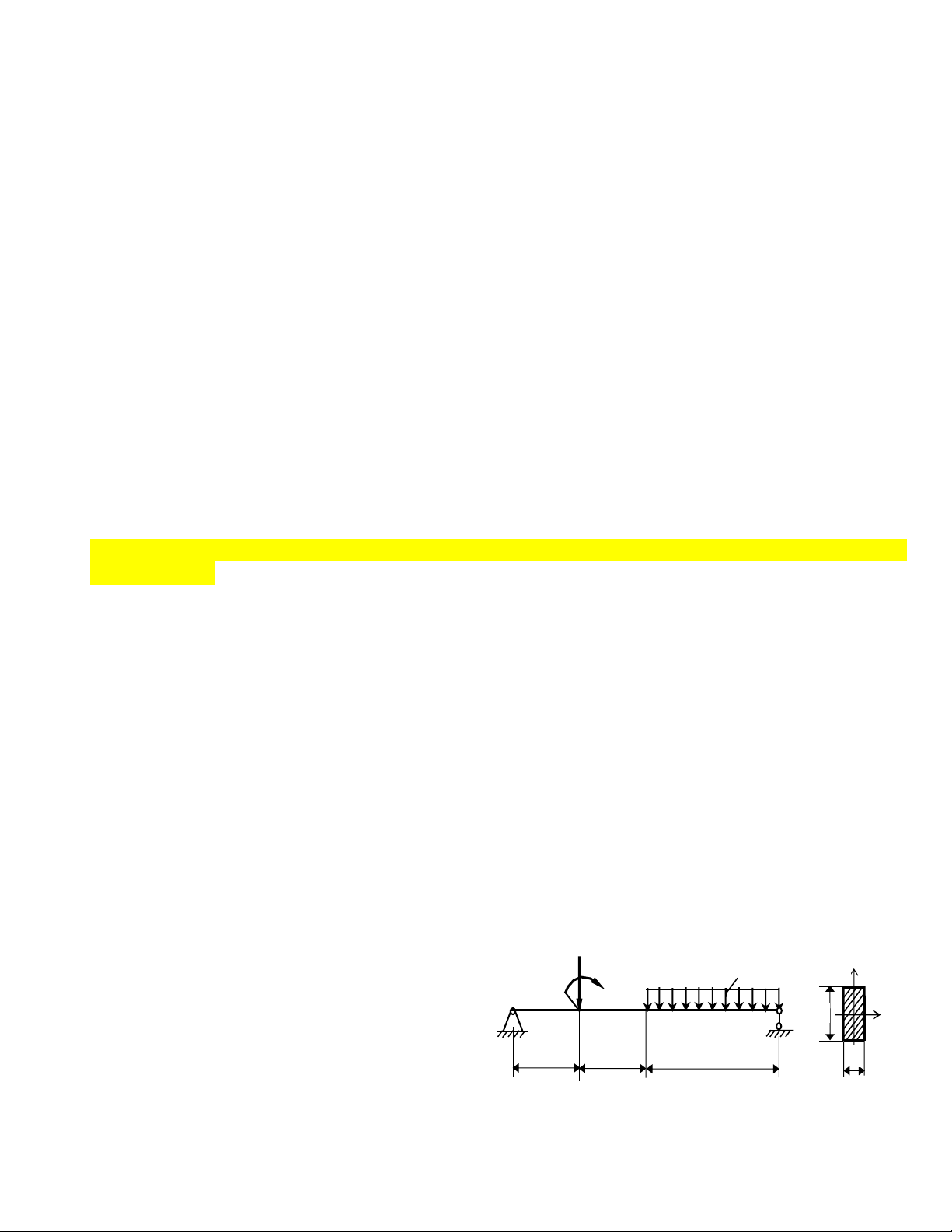
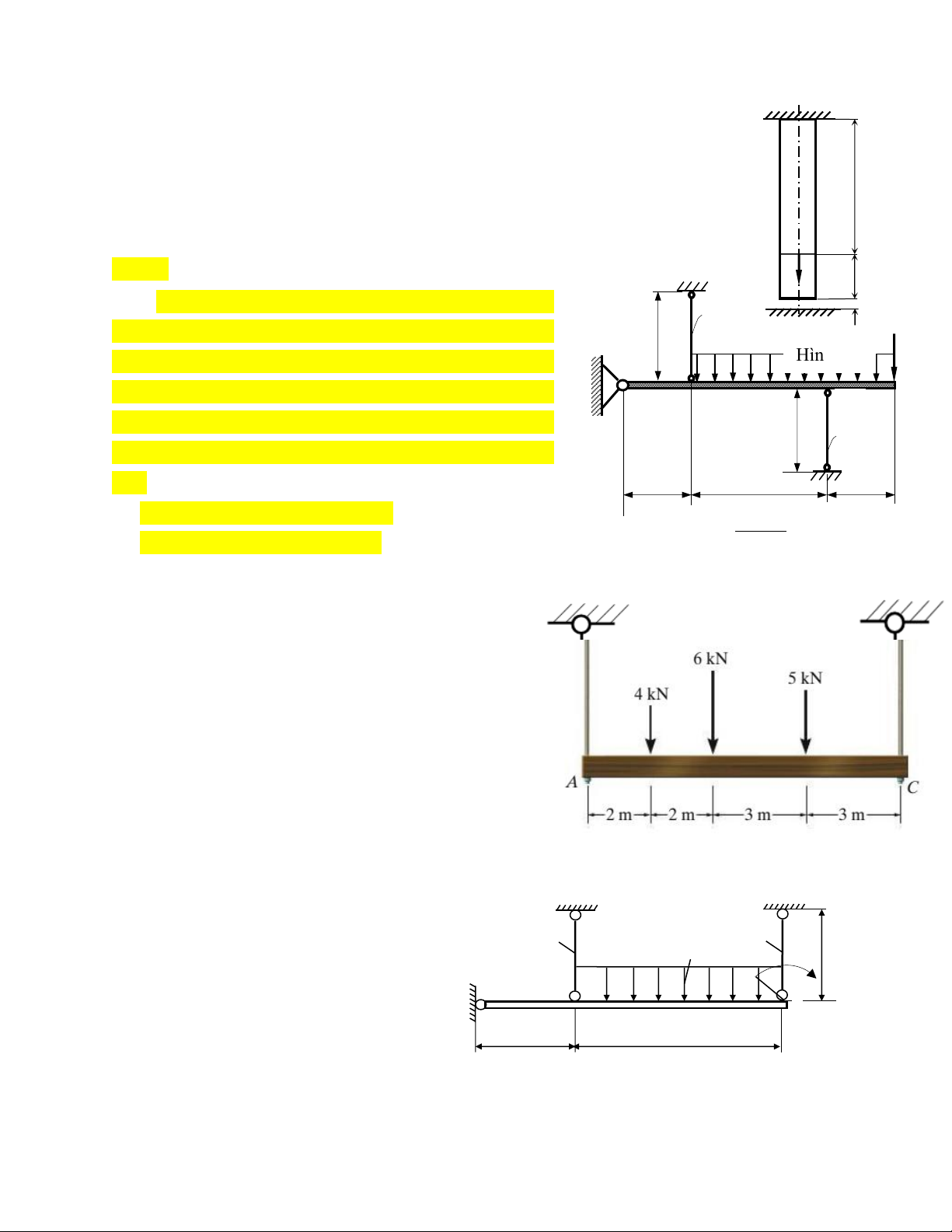
Dầm AB tiết diện không đổi có các kích thước P q
và chịu tác dụng của các lực như hình 84. Biết M y
dầm có mặt cắt ngang hình chữ nhật kích A C D B
thước b = 2a; P = 10 kN; q = 2 kN/m; M = 8 b x
kNm và [σ] = 160MN/m2. Hãy: 1m 1m 2m a
a. Vẽ biểu đồ Qy cho dầm.
b. Vẽ biểu đồ Mx cho dầm. Hình 84
c. Xác định vị trí nguy hiểm nhất của
dầm, vì sao (chỉ xét theo ảnh hưởng của ứng suất pháp)? Câu 2:
Cho dầm có tiết diện tròn với đường kính d, liên kết M M 2 P1 1 q
và chịu lực như hình 1. Biết P1 = 5qa; M1
= 5qa2; M2 = 2qa2. A B
a) Vẽ biểu đồ lực cắt Q C EJ D y và mômen uốn Mx theo q a x 2a a và a.
b) Tính giá trị ứng suất pháp lớn nhất trong dầm: Hình 1 max z, theo d,q,a.
Câu 3. Cho dầm AB có mặt cắt ngang hình chữ nhật chịu lực như hình 1. Biết M = qa2, P = 2qa,
a = 1m, q = 10kN/m, h = 2b = 0,2m.
a) Vẽ biểu đồ nội lực Qy của dầm
b) Vẽ biểu đồ nội lực Mx của dầm
c) Tính ứng suất pháp và ứng suất tiếp lớn nhất bên trong dầm. h b Hình 1 Câu 4: m
Cho dầm chịu lực như hình 1, với q = 6kN/m, q
a = 1m, m = 2qa2, P = 2qa dầm có mặt cắt ngang A B D
tròn đường kính d = 6cm. Hãy: P 2a a
a) Vẽ biểu đồ Qy cho dầm. Hình 1
b) Vẽ biểu đồ Mx cho dầm.
c) Tính ứng suất pháp lớn nhất phát sinh trong dầm.
Câu 5: Cho dầm AC có mặt cắt ngang hình tròn đường M
kính d = 5cm chịu lực như hình 1. Biết P = qa; M = qa2; q P
q = 1kN/m; a = 1m; [σ] = 10kN/cm2.
a) Vẽ biểu đồ lực cắt Q A C y B
b) Vẽ biểu đồ mômen uốn Mx.
c) Kiểm tra điều kiện bền cho dầm theo ứng suất pháp. 2a a Hình 1 Câu 6:
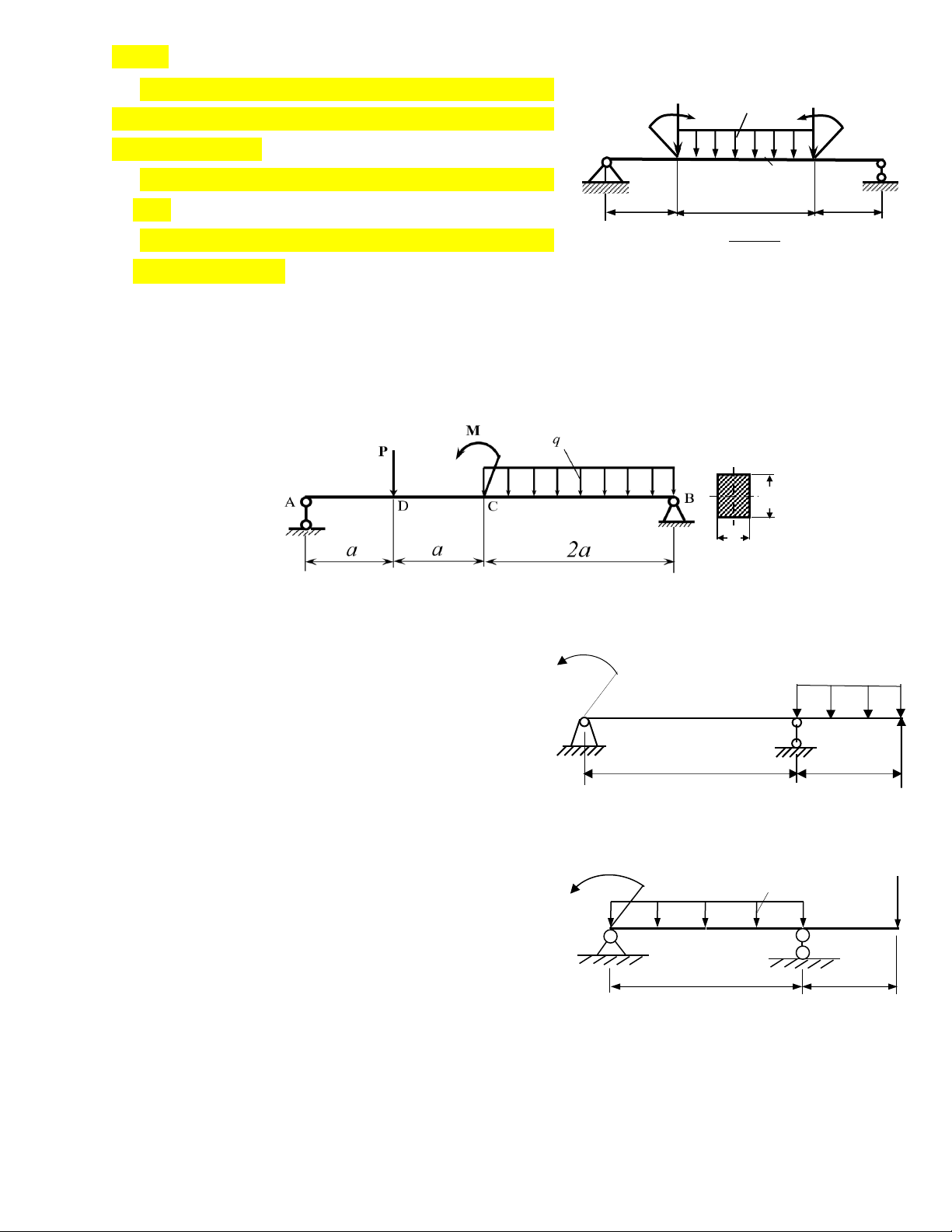
Dầm AB tiết diện không đổi có các kích thước
và chịu tác dụng của các lực như hình 86. Biết P M
dầm có mặt cắt ngang hình chữ nhật kích thước q y
b = 2a; P = 10 kN; q = 2 kN/m; M = 8 kNm và A C B [σ] = 160MN/m2. Hãy: D b x
a. Vẽ biểu đồ Qy cho dầm. 1m 1m 2 a
b. Vẽ biểu đồ Mx cho dầm. m
c. Xác định vị trí nguy hiểm nhất của dầm, Hình 86
vì sao (chỉ xét theo ảnh hưởng của ứng suất pháp)? Câu 7:
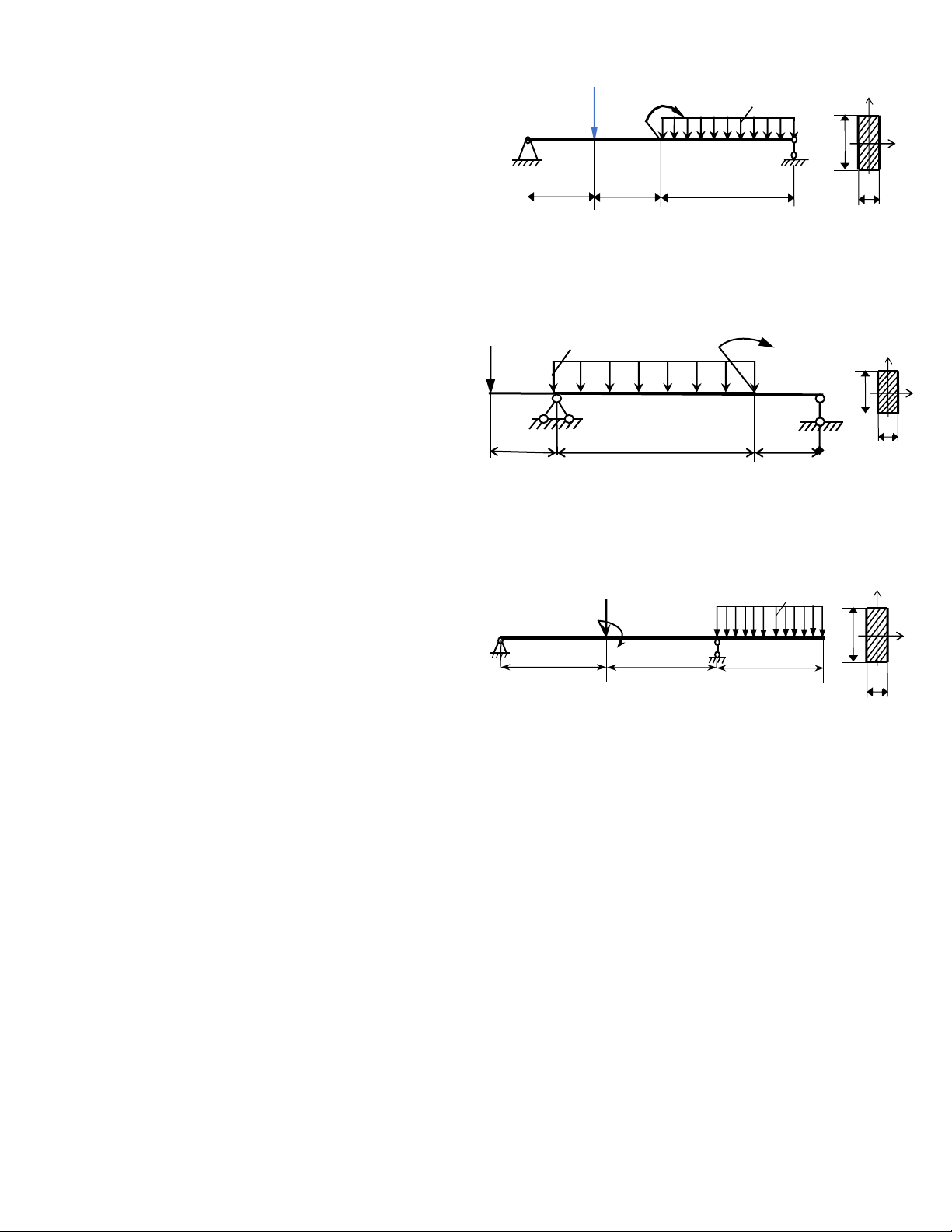
Dầm AB tiết diện không đổi có các P=qa q
kích thước và chịu tác dụng của các M=qa2 y
lực như hình 87. Biết dầm có mặt cắt
ngang hình chữ nhật kích thước b = 2a; a/ C b A D B x
P = 10 kN; M = 8kNm, q =2kN/m; a a
=1m và [σ] = 160MN/m2. Hãy: a 3a a
a. V ẽ biểu đồ Qy cho dầm. Hình 87
b. Vẽ biểu đồ Mx cho dầm.
c. Xác định vị trí nguy hiểm nhất của dầm, vì sao (chỉ xét theo ảnh hưởng của ứng suất pháp)? Câu 8
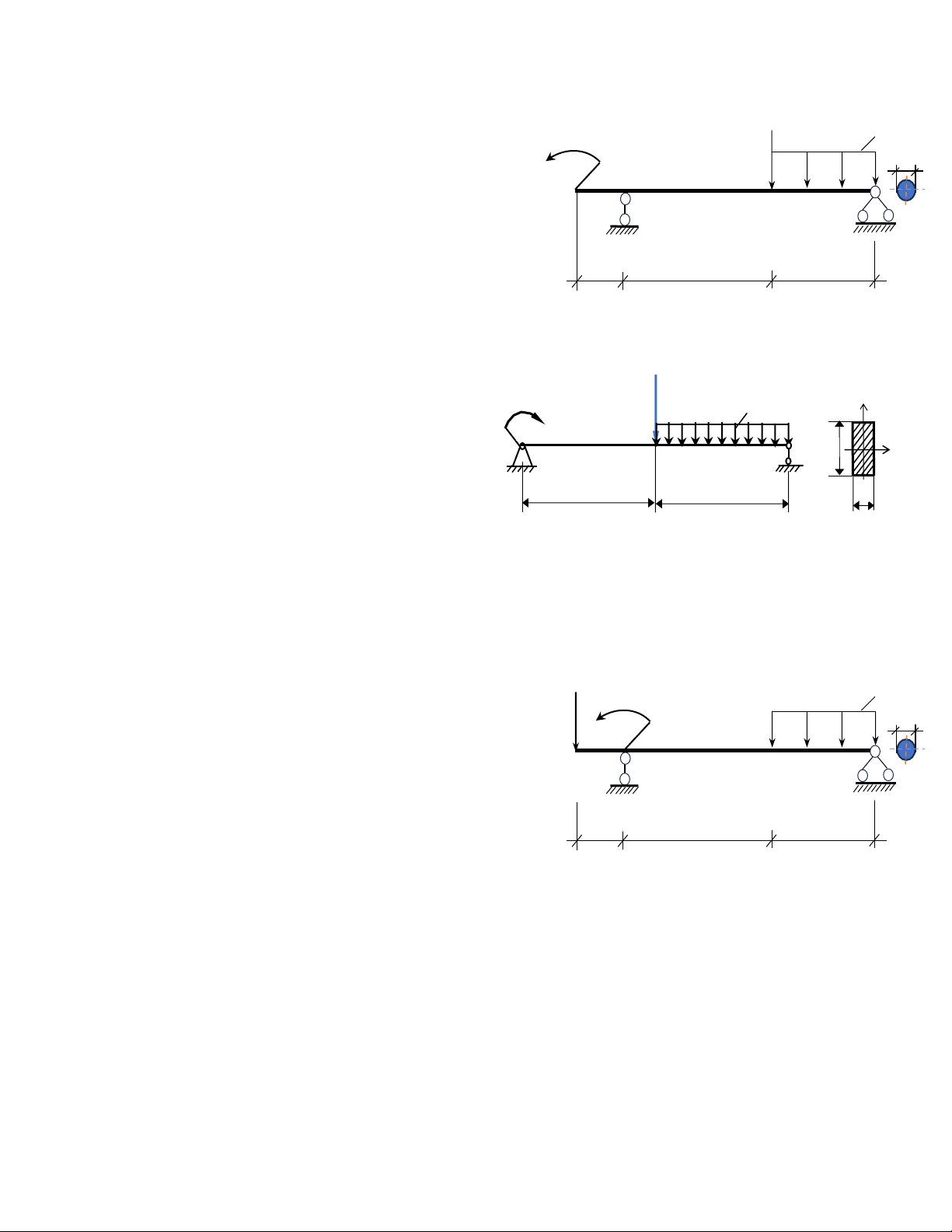
Dầm AB tiết diện không đổi có các kích P q y
thước và chịu tác dụng của các lực như hình M
88. Biết dầm có mặt cắt ngang hình chữ nhật A B b
kích thước b = 2a; P = 10 kN; M = 8kNm, q a C D a a x
=2kN/m; a =1m và [σ] = 160MN/m2. Hãy: Hình 88 a
a. Vẽ biểu đồ Qy cho dầm.
b. Vẽ biểu đồ Mx cho dầm.
c. Xác định vị trí nguy hiểm nhất của dầm, vì sao (chỉ xét theo ảnh hưởng của ứng suất pháp)? Câu 9:
Dầm AB tiết diện không đổi có các kích thước
và chịu tác dụng của các lực như hình 89. Biết P q
dầm có mặt cắt ngang hình tròn đặc đường kính M
d; P = 10 kN; q = 2 kN/m; M = 8 kNm và [σ] = d 160MN/m2. Hãy: a. Vẽ biểu đồ Q C D y cho dầm.
b. Vẽ biểu đồ Mx cho dầm. A B
c. Xác định vị trí nguy hiểm nhất của dầm, 1m 3m 2m
vì sao (chỉ xét theo ảnh hưởng của ứng Hình 89 suất pháp)? Câu 10:
Dầm AB tiết diện không đổi có các kích thước P M q y
và chịu tác dụng của các lực như hình 85. Biết
dầm có mặt cắt ngang hình chữ nhật kích thước A C B
b = 2a; P = 10 kN; q = 2 kN/m; M = 8 kNm và b x [σ] = 160MN/m2. Hãy: 2m 2m a
a. Vẽ biểu đồ Qy cho dầm.
b. Vẽ biểu đồ Mx cho dầm. Hình 85
c. Xác định vị trí nguy hiểm nhất của dầm,
vì sao (chỉ xét theo ảnh hưởng của ứng suất pháp)? Câu 11:
Dầm AB tiết diện không đổi có các kích thước và chịu
tác dụng của các lực như hình 90. Biết dầm có mặt cắt P M q
ngang hình tròn đặc đường kính d; P = 10 kN; q = 2
kN/m; M = 8 kNm và [σ] = 160MN/m2. Hãy: d
a. Vẽ biểu đồ Qy cho dầm. b. Vẽ biểu đồ M C D x cho dầm.
c. Xác định vị trí nguy hiểm nhất của dầm, vì sao A B
(chỉ xét theo ảnh hưởng của ứng suất pháp)? 1m 3m 2m Hình 90
L3: Phần bài tập kéo nén đúng tâm (2 điểm)
Câu 1. Cho thanh AB có liên kết và chịu lực như hình 2. Biết E = 2.104kN/cm2; A
FAB = 5cm2; a = 1m; δ=0,03cm.
a) Xác định giá trị lực P để B chạm vào D.
b) Khi cho lực P bằng 2 lần giá trị tìm được ở câu a, hãy tìm phản lực liên kết 3a tại B. C Câu 2: P a B
Cho hệ thanh có kích thước và chịu lực như hình 1 δ
2. Thanh AB tuyệt đối cứng và được giữ bởi các thanh D a q P ’’
treo 1 và 2. Các thanh treo làm cùng vật liệu với mô Hình 2
đun đàn hồi E = 2.104 kN/cm2 có diện tích mặt cắt B C D ngang F A
1 = 5cm2; F2 = 10cm2. Biết ứng suất a 2
cho phép [σ] = 16 kN/cm2; q = 1kN/cm; a =1m; P = 2qa. a 2a a
a) Tính lực dọc trên thanh 1, 2. Hình 2
b) Kiểm tra bền cho hệ thanh.
c) Tính ứng suất pháp lớn nhất phát sinh trong dầm. Câu 3: B D
Dầm AC được treo bởi 2 thanh thép AB và CD
cùng đường kính, cùng làm từ vật liệu có [] =
120MN/m2, E = 200.106kN/m2, chịu lực như hình 2. Hãy
a) Tính đường kính nhỏ nhất của 2 thanh AB, CD.
b) Tính biến dạng của thanh CD với chiều dài 5m. Hình 2
Câu 4: Cho hệ thanh chịu lực như hình 2,
thanh 1 và 2 có diện tích F, chiều dài L và 1 2
modun đàn hồi E = 2.104kN/cm2. Biết q L
q = 1kN/cm; a = 1m; L = 1m; [] = M A 16kN/cm2; M = qa2. C B a 2a
a) Tính nội lực trong các thanh 1 và 2.
b) Tính đường kính thanh treo 1 và 2 để đảm Hình 2
bảo điều kiện bền.
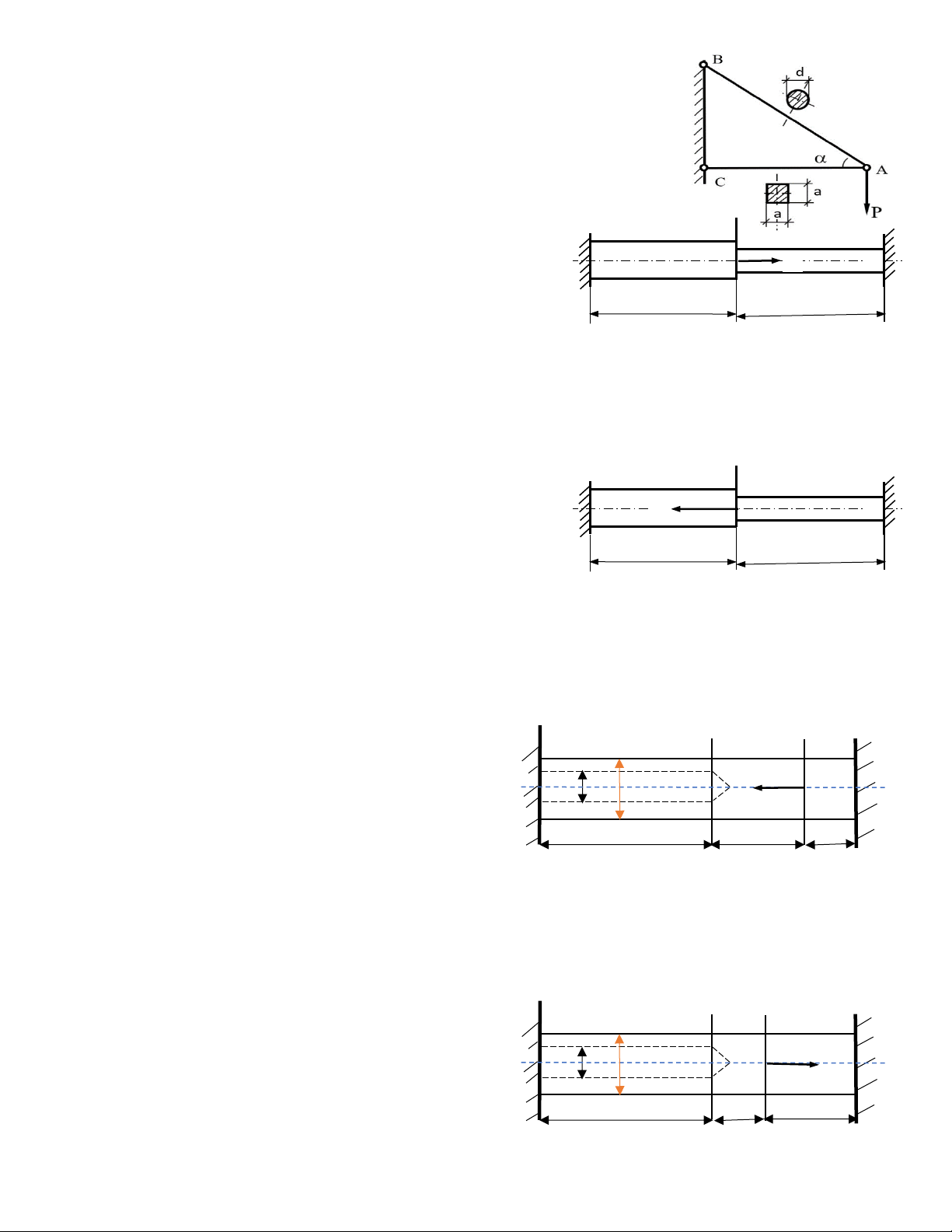
Câu 5: Cho kết cấu như hình 2, thanh AB có mặt cắt ngang tròn
đường kính d, thanh AC có mặt cắt ngang vuông cạnh a, cùng làm
bằng vật liệu có [σ] = 160kN/cm2 chịu tải P = 500kN;  = 300. Hình 129
a. Tính đường kính d của thanh AB để kết cấu làm việc an toàn.
b. Tính kích thước a của thanh AC để kết cấu làm việc an toàn.
Câu 6: Cho thanh AB có kích thước và chịu lực như hình 130. Biết A C P B
P = 100 KN; diện tích mặt cắt ngang các đoạn AC
là FAC = 20 cm2; CB là FCB = 10 cm2. Vật liệu làm l l
thanh AB là thép có [σ] = 160 MN/m2, E = 2.105 Hình 130 MN/m2
a. Xác định phản lực liên kết tại A hoặc B.
b. Kiểm tra điều kiện bền thanh AB.
Câu 7: Cho thanh AB có kích thước và chịu lực như hình 131. Biết A C P B
P = 100 KN; diện tích mặt cắt ngang các đoạn AC
là FAC = 20 cm2; CB là FCB = 10 cm2. Vật liệu làm l l
thanh AB là thép có [σ] = 160 MN/m2, E = 2.105 Hình 131 MN/m2
a. Xác định phản lực liên kết tại A hoặc B.
b. Kiểm tra điều kiện bền thanh AB.
Câu 8: Trục AB đường kính D có khoan
một lỗ dọc với đường kính d từ đầu bên trái
và chịu lực như hình 132. Biết P = 50 KN; P E B C
diện tích mặt cắt ngang các đoạn AC là F A d D AC
= 10 cm2; CB là FCB = 20 cm2, chiều dài l 4l 2l l
= 1m. Vật liệu làm thanh AB là thép có [σ]
= 160 MN/m2, E = 2.105 MN/m2 Hình 132
a. Xác định phản lực liên kết tại A hoặc B.
b. Kiểm tra điều kiện bền thanh AB.
Câu 9: Trục AB đường kính D có khoan
một lỗ dọc với đường kính d từ đầu bên trái
và chịu lực như hình 133. Biết P = 50 KN; P B
diện tích mặt cắt ngang các đoạn AC là F A d D C E AC
= 10 cm2; CB là FCB = 20 cm2; chiều dài l 4l l 2l
= 1m. Vật liệu làm thanh AB là thép có [σ]
= 160 MN/m2, E = 2.105 MN/m2 Hình 133
a. Xác định phản lực liên kết tại A hoặc B. A
b. Kiểm tra điều kiện bền thanh AB. d
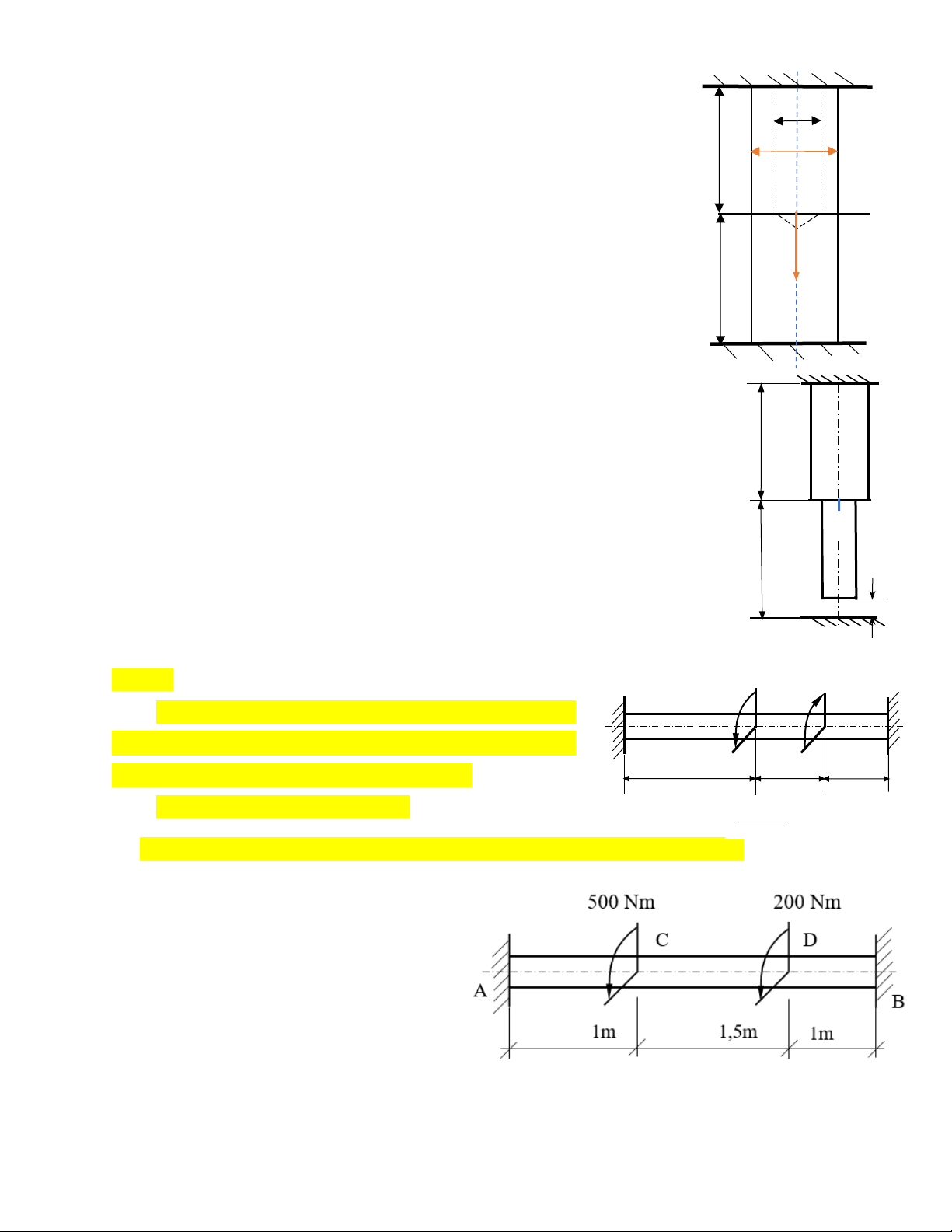
Câu 10: Trục AB đường kính D có khoan một lỗ dọc với đường l D
kính d từ đầu trên xuống và chịu lực như hình 134. Biết P = 100
KN; diện tích mặt cắt ngang các đoạn AC là FAC = 10 cm2; CB là F C Hình
CB = 20 cm2; chiều dài l = 1m. Vật liệu làm thanh AB là thép có 134
[σ] = 160 MN/m2, E = 2.105 MN/m2 P
a. Xác định phản lực liên kết tại A hoặc B. l
b. Kiểm tra điều kiện bền thanh AB.
Câu 11: Cho thanh AB có kích thước và chịu lực như hình 135. B A
Biết P đặt tại C; diện tích mặt cắt ngang các đoạn AC là FAC = 20 P
cm2; CB là FCB = 10 cm2; chiều dài l = 1m; t=0,02. Vật liệu làm thanh l
AB là thép có E = 2.105 MN/m2.
a. Xác định lực P để đầu thanh D chạm vào B. C Hình
b. Tính ứng suất lớn nhất với lực P vừa tìm được ở mục a 135 P l D t
L3: Phần bài tập xoắn thuần túy thanh tròn (3 điểm) B Câu 1: M1 M2 A
Cho trục AB có đường kính không đổi chịu ngẫu lực C D B
như hình 3. Biết M1 = 1200 Nm; M2 = 500Nm; [] = 1m
3000N/cm2; [] = 0,5 0/m; G = 8.106 N/cm2. 0,5m 0,5m
a) Vẽ biểu đồ mô men xoắn Mz. Hình 3
a) Tính đường kính của trục để đảm bảo điều kiện bền và điều kiện cứng. Câu 2:
Trục tròn AB có đường kính d = 60mm
chịu lực như hình 3. Biết [] = 80MN/m2, G = 2.105MN/m2. Hãy:
a) Tính nội lực cho thanh.
b) Kiểm tra bền cho trục.
c) Tính góc xoay tại C. Hình 3
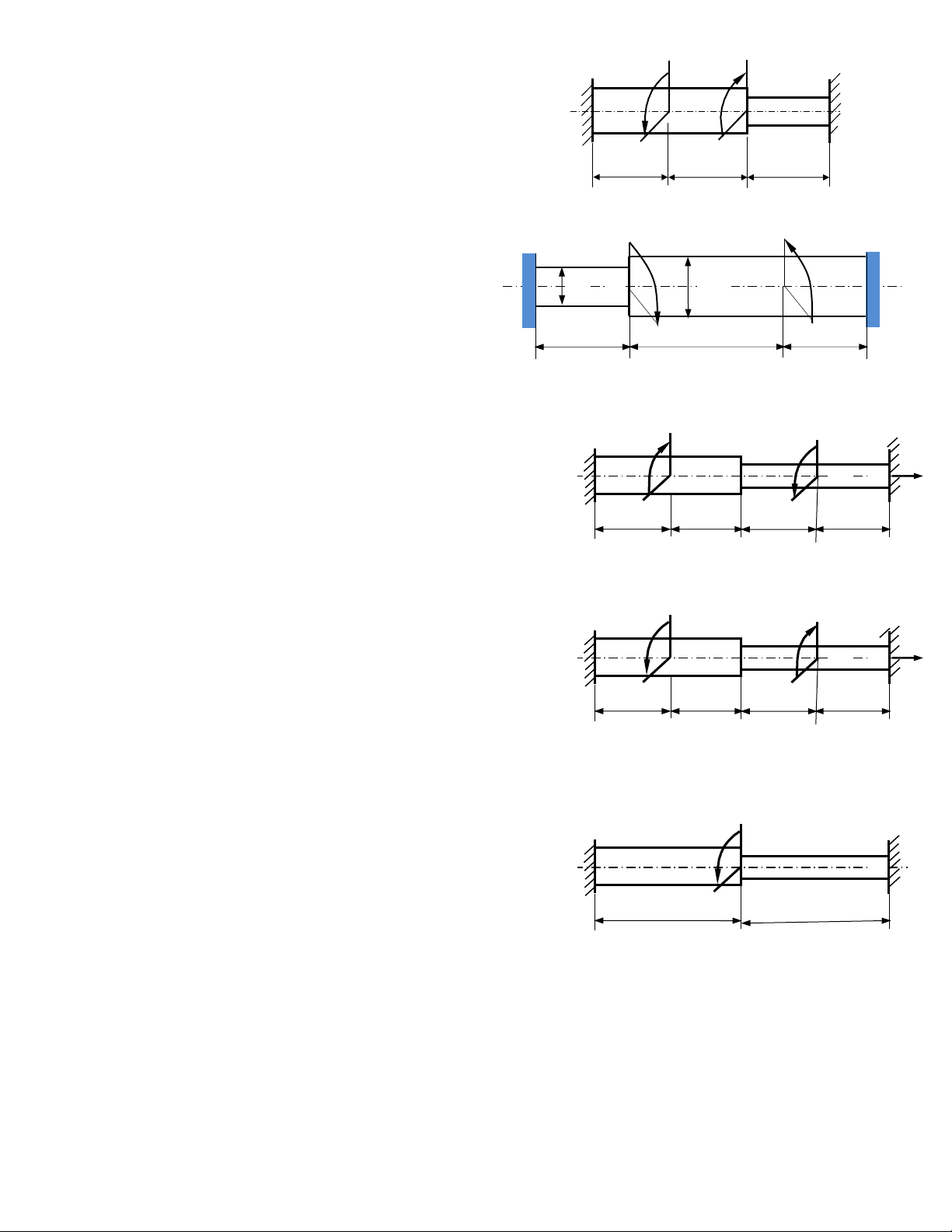
Câu 3. Trục tròn có đường kính thay đổi chịu các 3M M
mômen tác dụng như hình 3, đường kính các đoạn là dAD
= 10cm, dDB = 5cm. Biết rằng [] = 4000N/cm2, [] = 0,2O/m, G = 8.106N/cm2. B A
a) Tính các phản lực liên kết theo M. D C
b) Tìm giới hạn của M theo điều kiện bền. a a a
c) Tìm giới hạn của M theo điều kiện cứng. Hình 3
Câu 4: Cho trục có đường kính thay đổi chịu lực M
như hình 3. Biết a = 1m, d = 8cm, trục được làm 2M
bằng vật liệu có [] = 10kN/cm2; [] = 0,25.10-4 rad/cm; G = 8.105MN/m2. d A B 2d C D Hãy: a 2a a
a) Xác định phản lực liên kết tại A theo M.
b) Tính giá trị lớn nhất của M để trục đủ bền. Hình 3
c) Tính giá trị lớn nhất của M để trục đủ cứng.
`Câu 5: Một trục tròn đường kính thay đổi trong 2
đoạn, liên kết và chịu tải như hình 3. Biết đường kính 2M M
của các đoạn dAD = 10cm; dDB = 5 cm; l=1m; [] = 6 A E D z C B
kN/cm2; []=0,25.10-2 rad/m; G = 8.104MN/m2. Hãy:
a. Vẽ biểu đồ mô men xoắn Mz. l l l l
b. Tính giá trị lớn nhất của M để trục đủ bền. Hình 175
c. Tính giá trị lớn nhất của M để trục đủ cứng.
Câu 6: Một trục tròn đường kính thay đổi trong 2
đoạn, liên kết và chịu tải như hình 3. Biết đường kính 2M M
của các đoạn dAD = 10cm; dDB = 5 cm; l=1m; [] = 6 A E D z C B
kN/cm2; []=0,25.10-2 rad/m; G = 8.104MN/m2. Hãy:
a. Vẽ biểu đồ mô men xoắn Mz. l l l l
b. Tính giá trị lớn nhất của M để trục đủ bền. Hình 174
c. Tính giá trị lớn nhất của M để trục đủ cứng.
Câu 7: Một trục tròn đường kính thay đổi trong 2 M
đoạn, liên kết và chịu tải như hình 3. Biết đường kính
của các đoạn dAD = 10cm; dDB = 5 cm; l=1m; [] = 6 A C B
kN/cm2; []=0,25.10-2 rad/m; G = 8.104MN/m2. Hãy:
a. Vẽ biểu đồ mô men xoắn Mz. l l
b. Tính giá trị lớn nhất của M để trục đủ bền. Hình 176
c. Tính giá trị lớn nhất của M để trục đủ cứng.
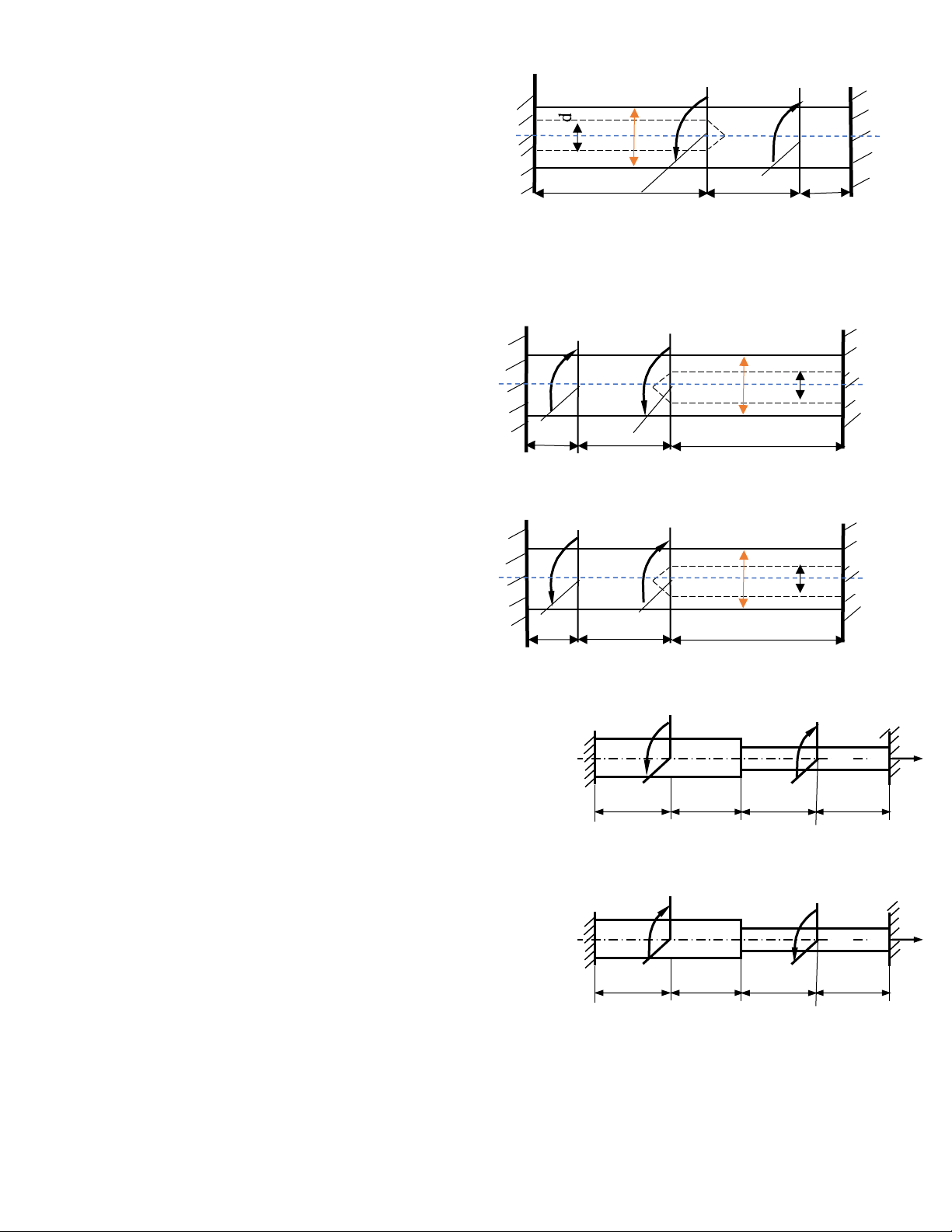
Câu 8: Trục AB đường kính D = 20cm có
khoan một lỗ dọc với đường kính d = 0,5D từ 3M M * *
đầu bên trái. Biết [𝜏] = 6 kN/cm2; A
[]=0,25.10-2 rad/m; G = 8.104MN/m2. B E
a) Vẽ biểu đồ mô men xoắn Mz. D C
b) Tính giá trị lớn nhất của M để trục 4a 2a a đủ bền.
c) Tính giá trị lớn nhất của M để trục Hình 177 đủ cứng.
Câu 9: Trục AB đường kính D = 20cm có khoan một lỗ dọc với đường kính d = 0,5D từ đầu bên phải.
Biết [𝜏] = 6 kN/cm2; []=0,25.10-2 rad/m; G 2M = 8.104MN/m2. M *
a) Vẽ biểu đồ mô men xoắn Mz. E
b) Tính giá trị lớn nhất của M để trục A C D d B đủ bền.
c) Tính giá trị lớn nhất của M để trục a 2a 4a đủ cứng. Hình 179
Câu 10: Trục AB đường kính D = 20cm có
khoan một lỗ dọc với đường kính d = 0,5D từ 2M M
đầu bên phải. Biết [𝜏] = 6 kN/cm2; G = 8.104MN/m2. E
a) Vẽ biểu đồ mô men xoắn Mz. A C D d B
b) Tính giá trị lớn nhất của M để trục đủ bền. a 2a 4a
c) Tính giá trị lớn nhất của M để trục Hình 180 đủ cứng.
Câu 11: Một trục tròn đường kính thay đổi trong 2
đoạn, liên kết và chịu tải như hình 3. Biết đường kính 2M M
của các đoạn dAD = 10cm; dDB = 5 cm; l=1m; [] = 6 A E D z C B
kN/cm2; []=0,25.10-2 rad/m; G = 8.104MN/m2. Hãy:
d. Vẽ biểu đồ mô men xoắn Mz. l l l l
e. Tính giá trị lớn nhất của M để trục đủ bền. Hình 174
f. Tính giá trị lớn nhất của M để trục đủ cứng.
`Câu 12: Một trục tròn đường kính thay đổi trong 2
đoạn, liên kết và chịu tải như hình 3. Biết đường kính 2M M
của các đoạn dAD = 10cm; dDB = 5 cm; l=1m; [] = 6 A E D z C B
kN/cm2; []=0,25.10-2 rad/m; G = 8.104MN/m2. Hãy:
d. Vẽ biểu đồ mô men xoắn Mz. l l l l
e. Tính giá trị lớn nhất của M để trục đủ bền. Hình 175
f. Tính giá trị lớn nhất của M để trục đủ cứng.
Câu 13: Một trục tròn đường kính thay đổi trong 2 M
đoạn, liên kết và chịu tải như hình 3. Biết đường kính
của các đoạn dAD = 10cm; dDB = 5 cm; l=1m; [] = 6 A C B
kN/cm2; []=0,25.10-2 rad/m; G = 8.104MN/m2. Hãy:
d. Vẽ biểu đồ mô men xoắn Mz. l l
e. Tính giá trị lớn nhất của M để trục đủ bền. Hình 176
f. Tính giá trị lớn nhất của M để trục đủ cứng.