













Preview text:
CÂU HỎI ÔN TẬP
Câu 1: Cho một không gian mẫu 𝛺 với 𝑛(𝛺) = 100, và một biến cố A có n(A)=10. Xác suất của A là A. 1/10 B. 1/9 C. 9/10 D. 1/5
Câu 2: Nếu hai biến cố A và B xung khắc thì
A. P(A+B) = P(A) - P(B) B. P(A.B) = 1 C. P(A.B) = 0 D. P(A + B) = 0
Câu 3: Xác suất của biến cố không thể bằng A. 1 B. 0,5 C. 0 D. Không xác định
Câu 4: Nếu trong phép thử có 𝑃(𝐴) = 0,6 thì xác suất biến cố đối của 𝐴 là 𝑃(𝐴̅) bằng A. 0,4 B. 0,6 C. 0,5 D. 1
Câu 5: Một hộp có 5 bi đỏ, 3 bi xanh, 2 bi vàng. Xác suất rút được bi xanh là? A. 0,2 B. 0,3 C. 0,4 D. 0,5
Câu 6: Có 2 hộp: Hộp 1: 2 đỏ, 3 vàng; Hộp 2: 4 đỏ, 1 vàng. Chọn ngẫu nhiên 1 hộp, và lấy ra 1 viên
bi tính xác suất rút được 1 bi vàng. A. 0,8 B. 0,6 C. 0,5 D. 0,4
Câu 7: Một sọt có 10 quả cam trong đó có 2 quả hỏng. Tính xác suất bạn Lan mua 3 quả cam có ít nhất 1 quả hỏng A. 7/15 B. 8/15 C. 1/15 D. 1/5
Câu 8: Tỉnh A có 40% dân số là nam, 60% là nữ. Xác suất mắc bệnh viêm phổi trong nam giới là
0,85 , với nữ giới là 0,7. Tính tỉ lệ người mắc bệnh viêm phổi của tỉnh A? A. 0,76 B. 0,79 C. 0,24 D. 0,21
Câu 9: Một phân xướng có 45% sản phẩm của máy I và 55% sản phẩm của máy II. Tỉ lệ phế phẩm
của 2 máy lần lượt là 0,2 và 0,1. Tính tỉ lệ phế phẩm của cả phân xưởng. A. 0,155 B. 0,145 C. 0,855 D. 0,845
Câu 10: Trường có 40% học sinh khối 10, 30% học sinh khối 11, còn lại là học sinh khối 12. Tỉ lệ
học sinh đạt học sinh giỏi của 3 khối 10,11,12 lần lượt là 0,4; 0,35 và 0,25. Tính tỉ lệ học sinh giỏi của toàn trường: A. 0,31 B. 0,675 C. 0,34 D. 0,69
Câu 11: Sinh viên của 1 lớp sau khi thực hành được 1 trong 2 giáo viên kiểm tra. Xác suất để sinh
viên do giáo viên thứ 1 kiểm tra là 0,55. Xác suất để sinh viên đạt yêu cầu được giáo viên thứ 1, thứ
2 công nhận lần lượt là 0,7 và 0,8. Tìm xác suất để sinh viên đó được công nhận. A. 0,7 B. 0,745 C. 0,255 D. 0,825
Câu 12: Sinh viên của 1 lớp sau khi thực hành được 1 trong 2 giáo viên kiểm tra. Xác suất để sinh
viên do giáo viên thứ 1 kiểm tra là 0,55. Xác suất để sinh viên đạt yêu cầu được giáo viên thứ 1, thứ
2 công nhận lần lượt là 0,7 và 0,8. Biết sinh viên đó được công nhận, tính xác suất sinh viên đó do giáo viên 1 hỏi thi. A. 77/149 B. 88/151 C. 63/151 D. 7/15
Câu 13: Công thức Bayes dùng để làm gì
A. Tính xác suất không có điều kiện.
B. Tính xác suất của biến cố ngẫu nhiên.
C. Tính xác suất của biến cố chắc chắn
D. Tính xác suất có điều kiện
Câu 14: Nếu 𝑃(𝐴) = 0,6; 𝑃(𝐵) = 0,3 và 𝑃(𝐴𝐵) = 0,18 thì hai biến cố 𝐴 và 𝐵 là hai biến cố A. Xung khắc B. Độc lập C. Đối lập
D. Chưa kết luận được
Câu 15: Trong một lớp học có 30% học sinh giỏi văn, 25% học sinh giỏi toán và có 10% học sinh
giỏi cả hai môn văn và toán. Tính xác suất học sinh giỏi ít nhất 1 trong 2 môn nói trên A. 0,55 B. 0,65 C. 0,35 D. 0,45
Câu 16: Một túi có 5 quả cầu đỏ và 3 quả cầu vàng. Lấy ra 2 quả cầu cùng lúc. Gọi X là số quả cầu
vàng lấy được. Tập giá trị của X là A. {1,2} B. {0,1,2,3} C. {0,1,2} D. {1,2,3}
Câu 17: Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như dưới. Hãy tính P(X=1) X 0 1 2 3 P 0,25 0,5 0,1 0,15 A. 0,5 B. 0,1 C. 0,25 D. 0,15
Câu 18: Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như dưới. Hãy tính P(X=1) X 2 3 4 5 P 0,25 0,3 0,3 0,15 A. 0,3 B. 0 C. 0,25 D. 0,15
Câu 19: Hãy tìm k nếu biết biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau: X 0 1 2 P 0,45 K 0,2 A. 0,35 B. 0,45 C. 0,2 D. 0,25
Câu 20: Nếu P(X=1)=0,3; P(X=2)=0,55; P(X=3)=0,15. Giá trị E(X) là: A. 1,6 B. 2,25 C. 3,85 D. 1,85
Câu 21: Nếu biến ngẫu nhiên rời rạc X có E(X)=1,3 và E(X2)=2,5 thì phương sai Var(X) bằng: A. 1,2 B. 1,3 C. 0,81 D. 3,8
Câu 22: Xác suất học sinh giải đúng một bài toán là 0,7. Giáo viên giao 5 bài cho học sinh làm. Tính
xác suất học sinh làm đúng 3 bài. A. 𝐶350,330,72 B. 0,730,32 C. 0,330,72 D. 𝐶350,730,32
Câu 23: Một lô hàng có 10 sản phẩm với tỉ lệ sản phẩm đạt chuẩn là 0,9. Lô hàng sẽ được nhập nếu
tất cả sản phẩm đạt chuẩn. Tính xác suất lô hàng được nhập. A. 𝐶0100,990,1⬚ B. 0,110 C. 0,910 D. 𝐶1100,910,19
Câu 24: Trong một bài thi có 10 câu trắc nghiệm, mỗi câu có 4 phương án trả lời trong đó chỉ có 1
câu trả lời đúng. Thí sinh trả lời đúng ít nhất 1 câu sẽ qua môn. Tính xác suất thí sinh bị trượt. 10 0 10 A. 1 − 𝐶0 0 10 (3) B. 𝐶 (1) (3) 4 10 4 4 9 C. 𝐶1 1 10 (3) D. 1 4 4
Câu 25: Một nhân viên bán hàng gọi điện cho 6 khách hàng, với xác suất chốt đơn mỗi cuộc gọi là
0,4. Tính xác suất có ít nhất 5 khách hàng chốt đơn. A. 𝐶5( 6 0,4)50,6 + (0,4)6 B. (0,4)6 C. 𝐶5( 1( 6 0,4)50,6 D. 𝐶6 0,6)50,4.
Câu 26: Cho dữ liệu về điểm môn Lý thuyết xác suất và thống kê toán của 10 sinh viên như sau : 9;
6; 7; 10; 6; 9; 4; 6; 8;7. Điểm trung bình của 10 học sinh trên là : A. 7,2 B. 6,2 C. 6,5 D. 7,9.
Câu 27: Để điều tra nhu cầu tiêu dùng hàng tháng của người tiêu dùng, công ty điều tra ngẫu nhiên
thu nhập của 100 người được bảng sau
Thu nhập (Triệu đồng/tháng) 10 15 20 25 Số người 22 18 37 23 A. 18,95 B. 18,25 C. 18,05 D. 18,75.
Câu 28: Khảo sát 1500 sinh viên tốt nghiệp ở trường Đại học Tài chính ngân hàng Hà Nội có 1135
sinh viên xếp loại xuất sắc. Tỉ lệ sinh viên tốt nghiệp xuất sắc của trường là A. 0,38 B. 0,24 C. 0,12 D. 0,76.
Câu 29: Cho một mẫu có kích thước mẫu là n = 100, ∑ 𝑛 2
𝑖 𝑥𝑖 = 150, ∑ 𝑛𝑖 𝑥𝑖 = 3700. Khi đó phương sai mẫu bằng A. 146 B. 35,12 C. 34,75 D. 35,5.
Câu 30: Cho một mẫu kích thước n = 25, phương sai mẫu là 6,25. Độ lệch tiêu chuẩn của mẫu là: A. 0,5 B. 2,5 C. 2,55 D. 2,39.
Câu 31: Cho một mẫu kích thước n = 25, phương sai mẫu là 12. Phương sai mẫu hiệu chỉnh là: A. 12,5 B. 3,54 C. 11,52 D. 150.
Câu 32: Một người thương lái bắt ngẫu nhiên 50 con cá trong hồ nuôi cân thử và được kết quả như sau:
Trọng lượng ( kg) 1- 1,5 1,5 - 2 2 – 2,5 2,5- 3 3 – 3,5 Số con 6 14 15 10 5
Với độ tin cậy 95%, hãy ước lượng cho trọng lượng trung bình của mỗi con cá trong hồ nuôi, biết
trọng lượng cá tuân theo quy luật phân phối chuẩn.
A. Đây là bài toán ước lượng cho tỉ lệ
B. Đây là bài toán ước lượng cho giá trị trung bình trong trường hợp phương sai chưa biết
C. Đây là bài toán ước lượng cho giá trị trung bình trong trường hợp phương sai đã biết
D. Đây là bài toán kiểm định cho giá trị trung bình trong trường hợp phương sai chưa biết.
Câu 33: Điều tra 64 sinh viên thấy số tiền tiêu vặt trung bình là 70 nghìn đồng trong 1 ngày với độ
lệch tiêu chuẩn hiệu chỉnh là 8 nghìn đồng. Với độ tin cậy 95% hãy ước lượng số tiền tiêu vặt trung
bình trong 1 ngày của sinh viên? A. [67;73] B. [65;75] C. [68,04;71,96] D. [67,5;72,5].
Câu 34: Để tìm hiểu nhu cầu của 3000 hộ dân cư trong vùng về nhu cầu tiêu dùng điện năng lượng
mặt trời. Điều tra 200 hộ dân cư thấy có 60 hộ có nhu cầu lắp đặt và sử dụng điện năng lượng mặt
trời. Với độ tin cậy 95% hãy ước lượng tỉ lệ hộ dân cư có nhu cầu trên trong vùng. A. [0,27;0,33] B. [0,29;0,31] C. [0,24;0,36] D. [0,22;0,38].
Câu 35: Hãy ước lượng số hộ dân cư trong vùng có nhu cầu lắp đặt và sử dụng điện năng lượng mặt trời. A. [810;990] B. [870;930] C. [720;1080] D. [660;1140].
Câu 36: Cân thử 36 gói mỳ thấy trọng lượng trung bình là 102g với độ lệch tiêu chuẩn mẫu là 5g.
Với độ tin cậy 95% hãy ước lượng cho trọng lượng trung bình của các gói mì. A. [100,4;103,6] B. [99;105] C. [101,2;102,8] D. [101;103].
Câu 37: Đo chiều cao của 25 sinh viên ta được 𝑥̅ = 168𝑐𝑚, 𝜎 = 6𝑐𝑚. Với độ tin cậy 95% hãy ước
lượng cho kì vọng của chiều cao của sinh viên. A. [165,648;170,352] B. [167,76;168,24] C. [166,8;169,2] D. [165;171].
Câu 38: Khảo sát 500 người dân thì có 320 người có nhu cầu mua xe điện. Với độ tin cậy 95% hãy
tìm khoảng ước lượng cho tỉ lệ người dân có nhu cầu mua xe điện. A. [0,61;0,69] B. [0,66;0,70] C. [0,60;0,70] D. [0,598;0,682].
Câu 39: Chọn ngẫu nhiên 49 bóng đèn của hãng Rạng Đông thì thấy tuổi thọ trung bình là 1200h với
độ lệch tiêu chuẩn mẫu hiệu chỉnh là 70h. Với độ tin cậy 95% hãy ước lượng cho kì vọng của tuổi thọ bóng đèn Rạng Đông. A. [1197,2;1202,8] B. [1175;1225] C. [1180,4;1219,6] D [1173;1227].
Câu 40: Thu thập số liệu giảm cân của 100 người theo phương pháp nhịn ăn giãn cách thấy trung
bình một người giảm được 5 kg với độ lệch tiêu chuẩn mẫu hiệu chỉnh là 2,1 kg. Với độ tin cậy 95%
xây dựng khoảng ước lượng về mức giảm cân trung bình của một người. A. [4,79;5,21] B. [4,59;5,41] C. [2,9;7,1] D [4,96;5,04].
Câu 41: Tỉnh A có tất cả 10.000 hộ gia đình, biết khoảng tin cậy cho tỉ lệ số hộ gia đình trong tỉnh A
có nhu cầu mua điện thoại Iphone là 0,54 < P < 0,76. Hãy ước lượng khoảng số hộ gia đình trong tỉnh A có nhu cầu mua Iphone. A. 5400 B. [5400;7600] C. 7600 D.[0,0054;0,0076].
Câu 42: Cân thử 100 quả trứng ta có kết quả sau Xi (g) 150 160 165 170 180 185 ni 4 16 25 30 15 10
Trứng có khối lượng nhỏ hơn 165 gam được coi là trứng loại 2. Tìm khoảng ước lượng cho tỷ lệ trứng
loại 2 với độ tin cậy 95%. A. [0,12;0,28] B. [0,18;0,22] C. [157,22;158,78] D [157,92;158,08].
Câu 43: Công ty bảo hiểm điều tra 400 người thấy có 40 có nhu cầu mua bảo hiểm. Với độ tin cậy
95% hãy ước lượng tỉ lệ người có nhu cầu mua bảo hiểm A. [0,01;0,19] B. [0,05;0,15] C. [0,09;0,12] D. [0,07;0,13].
Câu 44: Tại phòng vật tư, kiểm tra 40 kiện hàng, mỗi kiện hàng có 100 linh kiện thấy có 30 linh kiện
không đạt yêu cầu. Hãy chỉ ra kết luận đúng
A. Tỷ lệ linh kiện không đạt yêu cầu là ¾
B. Tỷ lệ linh kiện không đạt yêu cầu là 3/400
C. Tỷ lệ linh kiện không đạt yêu cầu là 2/5
D. Tỷ lệ linh kiện không đạt yêu cầu là 2/1500.
Câu 315: Hãng xe Honda điều tra nhu cầu mua xe điện của 8,5 triệu người dân thành phố Hà Nội.
Hãng phỏng vấn 1000 người thấy có 620 người có nhu cầu sử dụng xe điện. Hãy chỉ ra kết luận đúng
A. Tỷ số 620/1000 là tần suất mẫu
B. Tỷ số 620/8500000 là tần suất mẫu
C. Tỷ số 620/1000 là tỷ lệ người dân Hà Nội muốn mua xe điện
D. Tỷ số 620/8500000 là tỷ lệ người dân Hà Nội muốn mua xe điện
Câu 46: Điều tra năng suất giống lúa mới tại vùng A, người ta khảo sát 108 thửa ruộng và thu được kết quả trong bảng sau: Năng suất ( tạ/ha) 30-35 35-40 40-45 45-50 50-55 Số thửa ruộng 6 18 28 40 16
Với độ tin cậy 95% hãy nhận định ý kiến tỉ lệ các thửa ruộng có năng suất từ 50 tạ/ha là những thửa
ruộng đạt năng suất cao là 20%. Hãy chỉ ra kết luận đúng.
A. Đây là bài toán kiểm định cho kì vọng
B. Đây là bài toán kiểm định cho tỉ lệ
C. Đây là bài toán ước lượng cho kì vọng
D. Đây là bài toán ước lượng cho tỉ lệ.
Câu 47: Số liệu thống kê về doanh số (triệu đồng/ngày) bán của một siêu thị trong một số ngày như sau: Doanh số 24 30 36 42 48 54 60 65 Số ngày 5 12 25 35 24 15 12 10
Với độ tin cậy 95% hãy kiểm định ý kiến tỉ lệ những ngày bán hàng từ 60 triệu đồng trở lên là 30%?
Hãy chỉ ra kết luận đúng
A. Giả thiết H: p = 0,3; Đối thiết p > 0,3 và miền bác bỏ 𝑊𝛼 = [𝑈𝛼 2⁄, +∞)
B. Giả thiết H: p = 0,3; Đối thiết p < 0,3 và miền bác bỏ 𝑊𝛼 = (−∞; 𝑈𝛼 2⁄]
C. Giả thiết H: p = 0,3; Đối thiết p ≠0,3 và miền bác bỏ 𝑊𝛼 = (−∞; −𝑈𝛼 2⁄] ∪ [𝑈𝛼 2⁄, +∞)
D. Giả thiết H: 𝜇 = 60; Đối thiết 𝜇 > 60 và miền bác bỏ 𝑊𝛼 = [𝑈𝛼, +∞)
Câu 48: Nếu utn = 0 và miền bác bỏ 𝑊𝛼 = [1,96; +∞) thì khẳng định nào sau đây là đúng
A. utn∈ 𝑊 nên sẽ bác bỏ giả thiết H, chấp nhận đối thiết K
B. utn∈ 𝑊 nên sẽ chấp nhận giả thiết H, bác bỏ đối thiết K
C. utn∉ 𝑊 nên sẽ bác bỏ giả thiết H, chấp nhận đối thiết K
D. utn∉ 𝑊 nên sẽ chấp nhận giả thiết H, bác bỏ đối thiết K.
Câu 49: Điều tra năng suất giống lúa mới tại vùng A, người ta khảo sát 108 thửa ruộng và thu được kết quả trong bảng sau: Năng suất ( tạ/ha) 30-35 35-40 40-45 45-50 50-55 Số thửa ruộng 6 18 28 40 16
Giống lúa cũ tại vùng A có năng suất trung bình là 40 (tạ /ha). Với độ tin cậy 95%, hãy kiểm định lại
ý kiến cho rằng: Giống lúa mới cho năng suất cao hơn giống lúa cũ? Hãy chỉ ra cặp giả thiết, đối thiết phù hợp với bài toán 𝐻: 𝜇 ≥ 40 𝐻: 𝜇 = 40 A. { B. { 𝐾: 𝜇 ≠ 40 𝐾: 𝜇 > 40 𝐻: 𝜇 = 40 𝐻: 𝜇 ≠ 40 C. { D. { . 𝐾: 𝜇 < 40 𝐾: 𝜇 < 40
Câu 50: Điều tra doanh số (triệu đồng) hàng tháng của 100 hộ kinh doanh ta thu được số liệu sau: Doanh số
10,1 10,2 10,4 10,6 10,7 10,8 10,9 11,1 11,3 11,4 Số hộ 2 3 8 13 25 20 12 10 6 1
Hộ kinh doanh có doanh số từ 11 triệu đồng trở lên được gọi là doanh nhân thành đạt. Báo cáo của
tỉnh cho rằng tỉ lệ doanh nhân thành đạt là 20% trong tổng số các hộ kinh doanh của tỉnh. Với độ tin
cậy 95% hãy kiểm tra xem báo cáo có đúng không?
A. utn= -0,75 và báo cáo đưa ra là đúng
B. utn= -0,75 và báo cáo đưa ra là sai
C. utn= -14,46 và báo cáo đưa ra là đúng
D. utn= -14,46 và báo cáo đưa ra là sai.
Câu 51: Khảo sát 100 sinh viên ta được điểm trung bình môn Lý thuyết xác suất và thống kê toán ta
được điểm trung bình là 5,82 với độ lệch tiêu chuẩn mẫu là 1,82. Có ý kiến cho rằng, điểm trung bình
môn Toán của trường ĐH đã khảo sát lớn hơn 5. Hãy tính giá trị thực nghiệm của điểm trung bình với mẫu trên. A. ttn= 4,51 B. ttn= 0,02 C. ttn= 6,08 D. ttn= 0,45.
Câu 5232: Trọng lượng một loại sản phẩm của công ty kinh doanh đồ ăn khi sản xuất được quy định
là 35g, độ lệch tiêu chuẩn là 5g. Nghi ngờ việc sản xuất không đáp ứng được yêu cầu đề ra, lấy ngẫu
nhiên 100 sản phẩm kiểm tra và thu được trọng lượng bình quân là 34,5g. Hãy xét xem điều nghi ngờ
trên có đúng không? Hãy chọn phương án đúng dưới đây
A. Đây là bài toán ước lượng cho kì vọng trong trường hợp phương sai đã biết
B. Đây là bài toán ước lượng cho kì vọng trong trường hợp phương sai chưa biết
C. Đây là bài toán kiểm định cho kì vọng trong trường hợp phương sai chưa biết
D. Đây là bài toán kiểm định cho kì vọng trong trường hợp phương sai đã biết.
Câu 53: Nhịp mạch trung bình của một người là 72 lần/phút. Kiểm tra 64 người làm việc thường
xuyên với máy tính thấy nhịp mạch trung bình của họ là 78 lần/phút với độ lệch tiêu chuẩn điều chỉnh
của mẫu là 9 lần/phút. Với độ tin cậy 95% hãy xét xem làm việc thường xuyên với máy tính có làm
tăng nhịp mạch hay không?
A. Không làm tăng nhịp mạch
B. Có làm tăng nhịp mạch
C. Chưa kết luận được 𝐻: 𝜇 = 𝜇
Câu 54: Cho bài toán kiểm định {
0. Khi đó miền bác bỏ của bài toán là 𝐾: 𝜇 > 𝜇0
A. 𝑊𝛼 = {𝑢𝑡𝑛: 𝑢𝑡𝑛 < −𝑢𝛼}
B. 𝑊𝛼 = {𝑢𝑡𝑛: 𝑢𝑡𝑛 > 𝑢𝛼}
C. 𝑊𝛼 = {𝑢𝑡𝑛: |𝑢𝑡𝑛| > 𝑢𝛼}
D. 𝑊𝛼 = {𝑢𝑡𝑛: 𝑢𝑡𝑛 > −𝑢𝛼}.
Câu 55: Khảo sát 100 sinh viên thì có 40 sinh viên đi học muộn. Với độ tin cậy 95% hãy kiểm định 𝐻: 𝑝 = 0,5 bài toán { 𝐾: 𝑝 ≠ 0,5
A. utn = -2 ∈ 𝑊 nên bác bỏ H chấp nhận K 𝛼
B. utn = -2 ∉ 𝑊 nên bác bỏ H chấp nhận K 𝛼
C. utn = 1,5 ∉ 𝑊 nên chấp nhận H bác bỏ K 𝛼
D. utn = 2,5 ∈ 𝑊 nên bác bỏ H chấp nhận K. 𝛼
Câu 56: Hàm thống kê kiểm định cho tỉ lệ là: A. 𝑝̂−𝑝 𝑝̂−𝑝 𝑈 = 0 B. 𝑈 = 0 √𝑛 √𝑝0(1−𝑝0) √𝑝0(1−𝑝0) 𝑛 C. 𝑝̂−𝑝 𝑈 = 0 D. Cả A và B √𝑝0(1−𝑝0)
Câu 57: Một đại lý của hãng xe điện báo cáo trung bình có 500 xe điện bán trong 1 ngày. Công ty
kiểm tra trong 16 ngày thấy trung bình có 520 xe điện được bán trong 1 ngày với độ lệch chuẩn mẫu
hiệu chỉnh là 40 xe. Hãy tính giá trị thực nghiệm với giả thiết H:𝜇 = 500 và đối thiết K:𝜇 ≠ 500 A. 0,5 B. 3 C. 2 D. 1,5
Câu 58: Với giả thiết của câu 52 và cho 𝑡15 0,025 = 2,13, ta kết luận
A. Chấp nhận H vì ttn = 2 < 2,13
B. Bác bỏ H vì ttn = 3 > 2,13
C. Chấp nhận H vì ttn = 1,5 < 2,13
D. Chưa kết luận được.
Câu 59: Cân thử 25 gói mì thấy trọng lượng trung bình là 102g với độ lệch tiêu chuẩn mẫu là 5g. Xét
bài toán kiểm định với giả thiết H: 𝜇 = 100 và đối thiết K: 𝜇 ≠ 100. Hãy xác định giá trị thực nghiệm với mẫu trên. A. 0,4 B. -2 C. 2 D. 3.
Câu 60: Với độ tin cậy 95% và 𝑡0,025 24
= 2,06 hãy kết luận về bài toán kiểm định câu 54 A. Chấp nhận H B. Bác bỏ H C. Luôn bác bỏ H
D. Chưa kết luận.
Câu 61: Cho bảng phân bố tần số về sản lượng chè thu được trong 1 năm (kg/sào) của 20 hộ gia đình Sản lượng 111 112 113 114 115 116 117 Số hộ 1 3 4 5 4 2 1
Số trung bình của bảng số liệu trên là A. 113,9. B. 114. C. 113,5. D. 114,5.
Câu 62: Tuổi thọ của một loại sản phẩm là biến ngẫu nhiên phân phối chuẩn với tuổi thọ trung bình
là 18 năm, độ lệch chuẩn về tuổi thọ là 2 năm. Giả sử quy định thời gian bảo hành sản phẩm là 15
năm. Hãy tìm tỉ lệ sản phẩm phải bảo hành. A. 93,32% B. 43,32% C. 56,68% D. 6,68%
Câu 63: Bảng sau cho biết thời gian chạy cự li 100m của các bạn trong lớp Thời gian (giây) 12 13 14 15 16 Số bạn 5 7 10 8 6 Chỉ ra kết luận đúng:
A. Thời gian chạy trung bình của các bạn là 13 giây
B. Độ lệch chuẩn mẫu hiệu chỉnh là 1,3
C. Phương sai mẫu là 2
D. Độ lệch chuẩn mẫu là 1,34
Câu 64: Điều tra về chiều cao của 100 sinh viên ta có kết quả sau: Chiều cao (cm)
[150;152) [152;154) [154;156) [156;158) [158;160) [160;162) Số sinh viên 5 18 40 26 8 3 Chọn phát biểu đúng :
A. Phương sai mẫu là 5
B. Chiều cao trung bình của các bạn là 157cm
C. Phương sai mẫu hiệu chỉnh là 4,75
D. Độ lệch chuẩn mẫu là 2,2
Câu 65: Một bạn sinh viên đi từ nhà đến trường qua 3 chỗ có đèn giao thông. Giả sử xác suất gặp
đèn đỏ ở ba chỗ là như nhau và bằng 1/2 . Chỉ ra kết luận đúng:
A. Số đèn đỏ gặp trung bình trong một lần đến trường là 1,7 đèn.
B. Số đèn đỏ gặp trung bình trong một lần đến trường là 1,6 đèn.
C. Số đèn đỏ gặp trung bình trong một lần đến trường là 1,4 đèn.
D. Số đèn đỏ gặp trung bình trong một lần đến trường là 1,5 đèn.
Câu 66: Để đánh giá sức mua của người tiêu dùng, một công ty điều tra ngẫu nhiên thu nhập hàng
tháng của 100 hộ tại một địa bàn, thu được kết quả: Thu nhập bình quân 15 20 25 30 35 (triệu VND/người) Số người 8 15 38 22 17
Chỉ ra kết luận đúng: Với độ tin cậy 95%, thu nhập trung bình của các hộ trên địa bàn thỏa mãn:
A. 25,11<µ<27,37
B. 25,12<µ<27,38
C. 25,21<µ<27,39
D. 25,13<µ<27,49
Câu 67: Để đánh giá sức mua của người tiêu dùng, một công ty điều tra ngẫu nhiên thu nhập hàng
tháng của 100 hộ tại một địa bàn, thu được kết quả: Thu nhập bình quân 15 20 25 30 35 (triệu VND/người) Số người 8 15 38 22 17 Chỉ ra kết luận đúng
A. Trung bình mẫu là 26,35; trung bình bình phương mẫu là 721,50
B. Trung bình mẫu là 26,15; trung bình bình phương mẫu là 721,25
C. Trung bình mẫu là 26,20; trung bình bình phương mẫu là 721,15
D. Trung bình mẫu là 26,25; trung bình bình phương mẫu là 721,75
Câu 68: Để ước lượng khối lượng trung bình đàn cá thả trong hồ, người ta bắt ngẫu nhiên 200 con
lên cân và được bảng sau:
Khối lượng (kg) [1,2-1,4) [l,4-1,6) [1,6-1,8) [1,8-2,0) [2,0-2,2) Số con 20 20 60 80 20
Khối lượng trung bình mẫu là số nào sau đây: A. 1,76kg B. 1,77kg C. 1,74kg D. 1,78kg
Câu 69: Một người đi từ nhà đến cơ quan phải qua 3 chỗ có đèn giao thông. Ký hiệu A, B và C
tương ứng là biến cố gặp đèn đỏ ở chỗ thứ nhất, thứ hai và thứ ba. Chỉ ra kết luận đúng: A. 𝐴𝐵 ̅ 𝐶 ̅̅̅ + 𝐵𝐶̅𝐴 ̅̅̅ + 𝐶𝐴 ̅ 𝐵
̅̅̅ là biến cố gặp 1 đèn đỏ. B. 𝐴𝐵 ̅̅̅ 𝐶
̅̅̅ là biến cố không gặp đèn đỏ nào. C. 𝐴̅ + 𝐵
̅ + 𝐶̅ là biến cố không gặp đèn đỏ nào. D. 𝐴̅𝐵
̅𝐶 + 𝐴̅𝐵𝐶̅ + 𝐴𝐵̅𝐶̅ là biến cố gặp 1 đèn đỏ.
Câu 70: Một máy sản xuất tự động với tỉ lệ chính phẩm đạt 95%. Sau một thời gian hoạt động có ý
kiến cho rằng máy không còn hoạt động được như cũ. Để kiểm tra người ta tiến hành điều tra ngẫu
nhiên 200 sản phẩm thấy có 190 sản phẩm là chính phẩm. Với mức ý nghĩa 5%, cần kiểm định ý kiến trên.
Hãy chỉ ra cặp Giả thuyết – Đối thuyết phù hợp với bài toán:
A. Giả thuyết H: p=0,95. Đối thuyết K: p<0,95.
B. Giả thuyết H: p=0,95. Đối thuyết K: p>0,95.
C. Giả thuyết H: p≥0,95. Đối thuyết K: p>0,95.
D. Giả thuyết H: p>0,95. Đối thuyết K: p<0,95.
Câu 71: Đội tuyển sinh viên giỏi Toán của trường đại học gồm 8 sinh viên, trong đó có 5 sinh viên
nam. Chọn ngẫu nhiên 5 sinh viên đi thi sinh viên giỏi. Xác suất để 5 sinh viên được chọn đi thi có
cả nam và nữ và sinh viên nam nhiều hơn sinh viên nữ là A. 5 B. 45 C. 1 D. 11 6 56 30 56
Câu 72: Theo dõi thời gian hoàn thành một sản phẩm của 50 công nhân ta có bảng: Thời
[12-14) [14-16) [16-18) [18-20) [20-22) [22-24) [24-26) [26-28) gian(phút) Số người 4 10 1 12 14 2 6 1
Thời gian trung bình hoàn thành một sản phẩm của một công nhân là A. 20,23 B. 19,28 C. 21,05 D. 22,01
Câu 73: Khảo sát 100 000 trẻ sơ sinh ở một vùng dân cư người ta thấy có 50 300 bé trai. Có ý kiến
cho rằng tỉ lệ bé trai đã thực sự cao hơn bé gái. Cần kiểm tra nhận định trên. Hãy chỉ ra kết luận đúng:
A. Giả thuyết H: p=0,5. Đối thuyết K: p<0,5. Miền bác bỏ W=[Uα;+∞)
B. Giả thuyết H: p=0,5. Đối thuyết K: p>0,5. Miền bác bỏ W=[Uα/2;+∞)
C. Giả thuyết H: p=0,5. Đối thuyết K: p>0,5. Miền bác bỏ W=[Uα;+∞)
D. Giả thuyết H: p=0,5. Đối thuyết K: p>0,5. Miền bác bỏ W=[Uα/2;+∞)
Câu 74: Cho hai biến cố A và B, với P(B)=0,8,P(AB)=0,4. Tính P(A/B). A. 1 . B. 2. C. 1 . D. 1 . 4 8 2
Câu 75: Hai biến cố độc lập là:
A. Hai biến cố có thể cùng xảy ra trong một phép thử.
B. Hai biến cố mà sự xuất hiện hay không xuất hiện của một trong hai biến cố không làm ảnh
hưởng đến xác suất của biến cố còn lại.
C. Hai biến cố mà khả năng xảy ra hoặc không xảy ra của hai biến cố đó như nhau.
D. Hai biến cố không thể cùng xảy ra trong một phép thử.
Câu 76: Một công ty dự định mở siêu thị trong khu dân cư. Để đánh giá sức mua của người dân,
người ta điều tra thu nhập của 100 hộ gia đình và được bảng số liệu: Thu nhập bình quân 15 20 25 30 35 (triệu người/tháng) Số hộ 8 15 38 22 17
Theo kinh nghiệm thì siêu thị chỉ hoạt động được khi thu nhập bình quân mỗi tháng của các hộ lớn
hơn 25 triệu. Công ty có nên mở siêu thị? Hãy cho ý kiến với mức ý nghĩa 5%. Chỉ ra miền bác bỏ phù hợp: A. W=[1,96;+∞) B. W=(–∞;–1,96] C. W=[1,65;+∞) D. W=(–∞;1,645]
Câu 77: Một lô sản phẩm do hai máy sản xuất đã để chung với nhau. Biết số sản phẩm do máy I
sản xuất nhiều gấp 2 lần sản phẩm do máy II sản xuất. Lấy ra từ lô sản phẩm đó lần lượt 4 sản phẩm
(có hoàn lại). Tìm xác suất để trong 4 sản phẩm lấy ra có hai sản phẩm của máy I. A. 1/2 B. 4/9 C. 8/27 D. 2/3
Câu 78: Hai máy tự động sản xuất cùng một loại chi tiết, trong đó máy I sản xuất 35%, máy II sản
xuất 65% tổng sản lượng. Tỉ lệ phế phẩm của các máy lần lượt là 0,3% và 0,7%. Chọn ngẫu nhiên 1
sản phẩm từ kho. Tính xác suất để chọn được phế phẩm do máy I sản xuất? A. 0,0056 B. 0,1785 C. 0,1875 D. 0,015
Câu 79: Công thức tính xác suất có điều kiện P(A|B) là gì?
A. P(A|B) = P(A).P(B)
B. P(A|B) = P(A.B) / P(A)
C. P(A|B) = P(A.B) / P(B)
D. P(A|B) = P(A) + P(B)
Câu 80: Một hộp đựng 7 quả cầu màu trắng và 3 quả cầu màu đỏ. Lấy ngẫu nhiên từ hộp ra 4 quả
cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu màu đỏ. A. 62 . B. 20 . C. 21 . D. 3 . 211 71 71 10
Câu 81: Trong hộp có 4 bi xanh, 5 bi đỏ và 3 bi vàng có kích thước và khối lượng như nhau. Lấy
ngẫu nhiên từ trong hộp 5 viên bi. Tính xác suất để trong 5 bi lấy ra có nhiều nhất 3 viên bi đỏ. A. 1 . B. 41 . C. 21 . D. 245 . 132 132 22 264
Câu 82: Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau: X 0 1 2 3 P 0,1 0,2 P 0,4
Kỳ vọng E(X) là số nào sau đây: A. 3,5 B. 2 C. 3 D. 2,5
Câu 83: Ba biển cố A, B, C Thỏa mãn các điều kiện sau:
A + B + C = Ω; A.B = Ø; B.C = Ø; C.A= Ø
Biết P(A) = 0,1; P(B) = 0,6. Xác suất của C là: A. 0,7 B. 0,4 C. 0,3 D. 0,5
Câu 84: Người ta lấy ngẫu nhiên 1000 sản phẩm của lô hàng để kiểm tra và thấy có 945 sản phẩm
loại I. Nếu tỉ lệ hàng loại I đạt 95% thì lô hàng được xuất khẩu. Với mức ý nghĩa 5%, cần kiểm tra
xem lô hàng có xuất khẩu được không. Hãy chỉ ra cặp Đối thuyết – Miền bác bỏ phù hợp với bài toán:
A. Đối thuyết K: p<0,95. Miền bác bỏ W=(–∞;–1,96]
B. Đối thuyết K: p<0,95. Miền bác bỏ W=(–∞;–1,645]
C. Đối thuyết K: p<0,95. Miền bác bỏ W=[1,645;+∞)
D. Đối thuyết K: p>0,95. Miền bác bỏ W=(–∞;–1,645]
Câu 85: Theo dõi thời gian hoàn thành một sản phẩm của 50 công nhân ta có bảng sau: Thời gian
[12-14) [ 14-16) [16-18) [18-20) [20-22) [22-24) [24-26) [26-28) (phút) Số người 4 10 1 12 14 2 6 1 Kỳ vọng mẫu là A. 19,28 B. 22,01 C. 21,05 D. 20,23
Câu 86: Một túi có 5 bi đỏ và 3 bi xanh. Lấy 2 bi cùng lúc. Gọi X là biến ngẫu nhiên chỉ số bi đỏ
lấy được. Tập giá trị của X là A. {0,1,2} B. {1,2} C. {0,1,2,3} D. {1,2,3}
Câu 87: Hai biến cố đối lập là:
A. Hai biến cố có thể cùng xảy ra trong một phép thử.
B. Hai biến cố không thể đồng thời xảy ra và lập nên một hệ đầy đủ các biến cố.
C. Hai biến cố có xác suất xảy ra trong một phép thử là như nhau.
D. Hai biến cố mà khả năng xảy ra hoặc không xảy ra của hai biến cố đó như nhau.
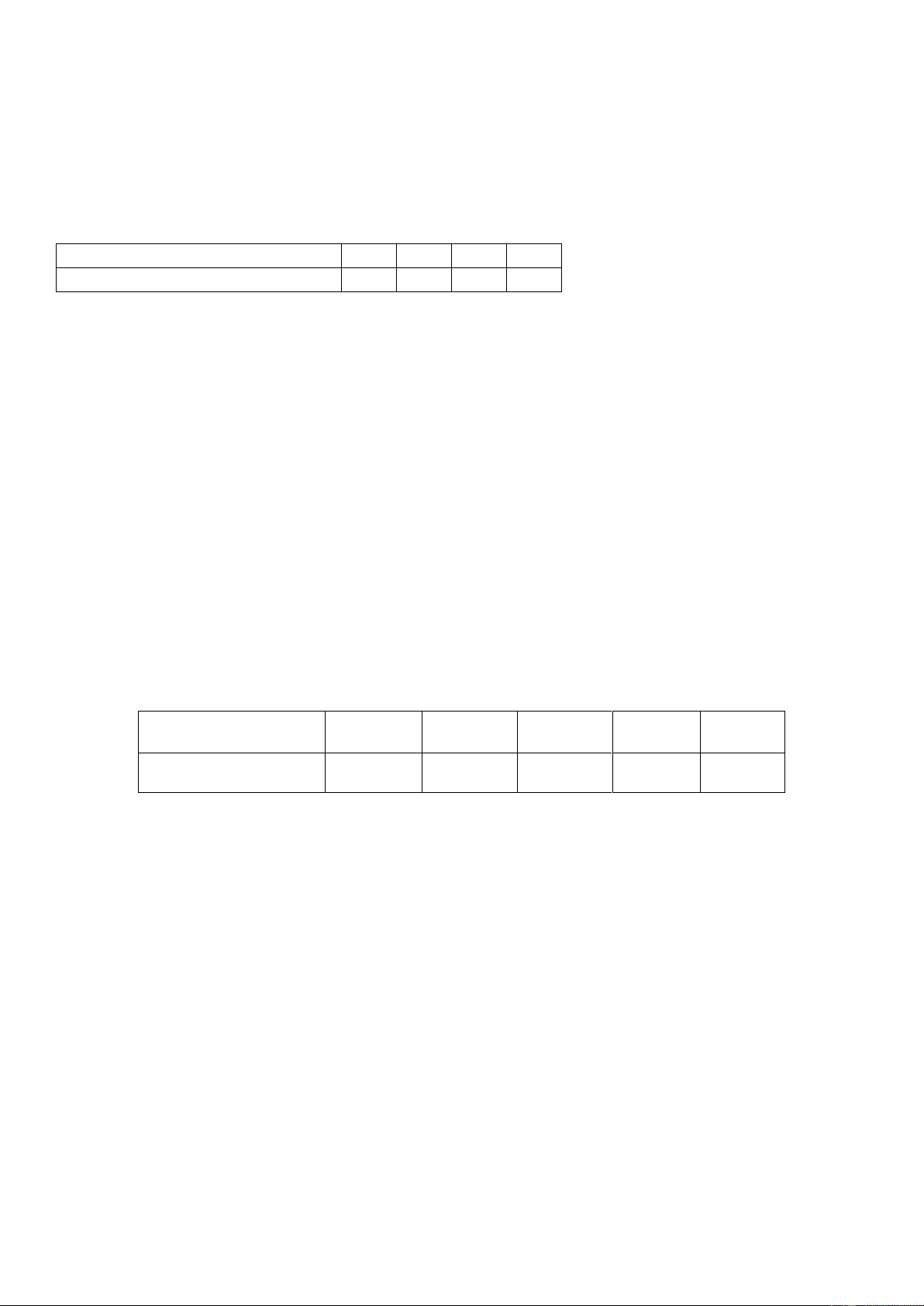
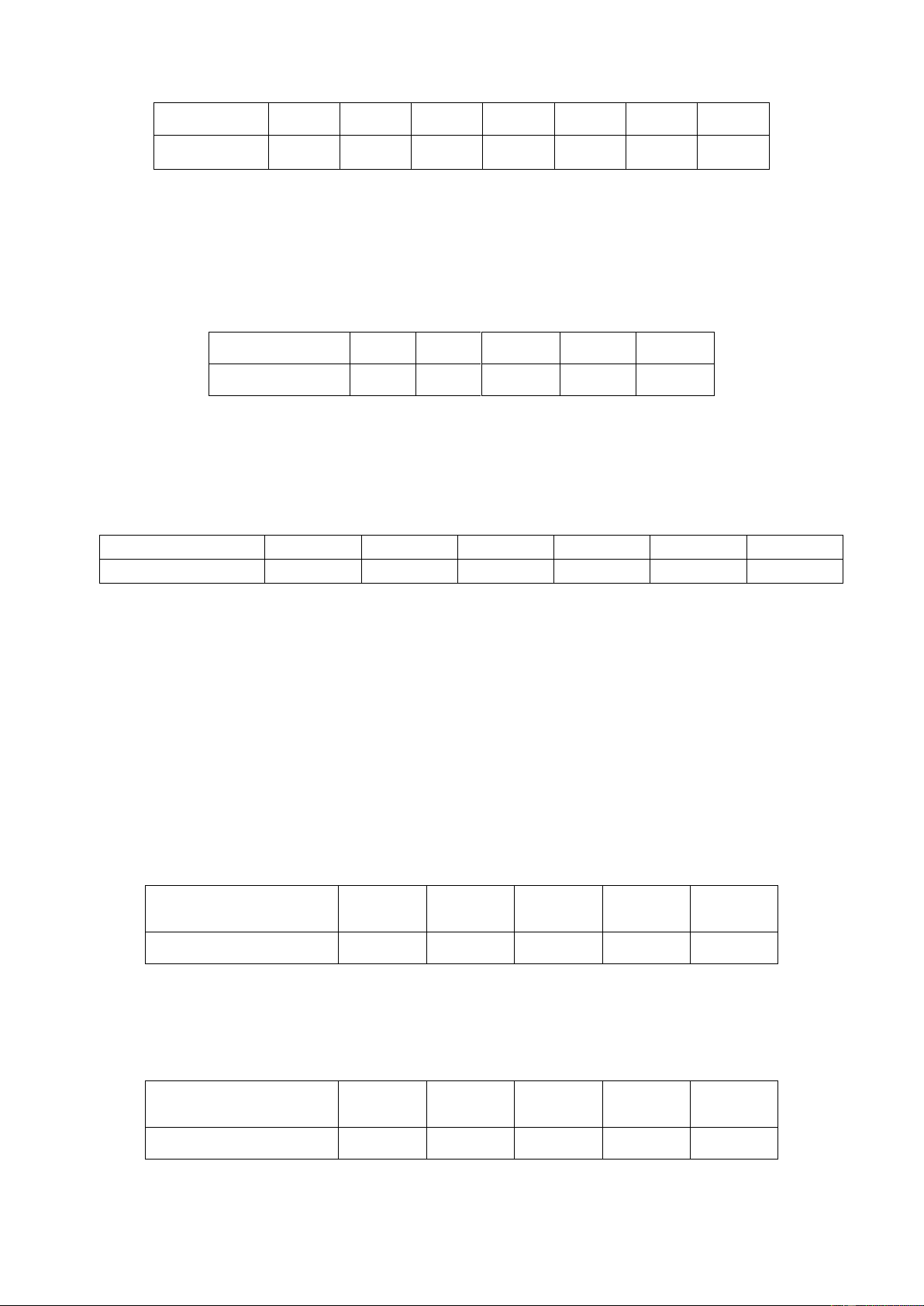
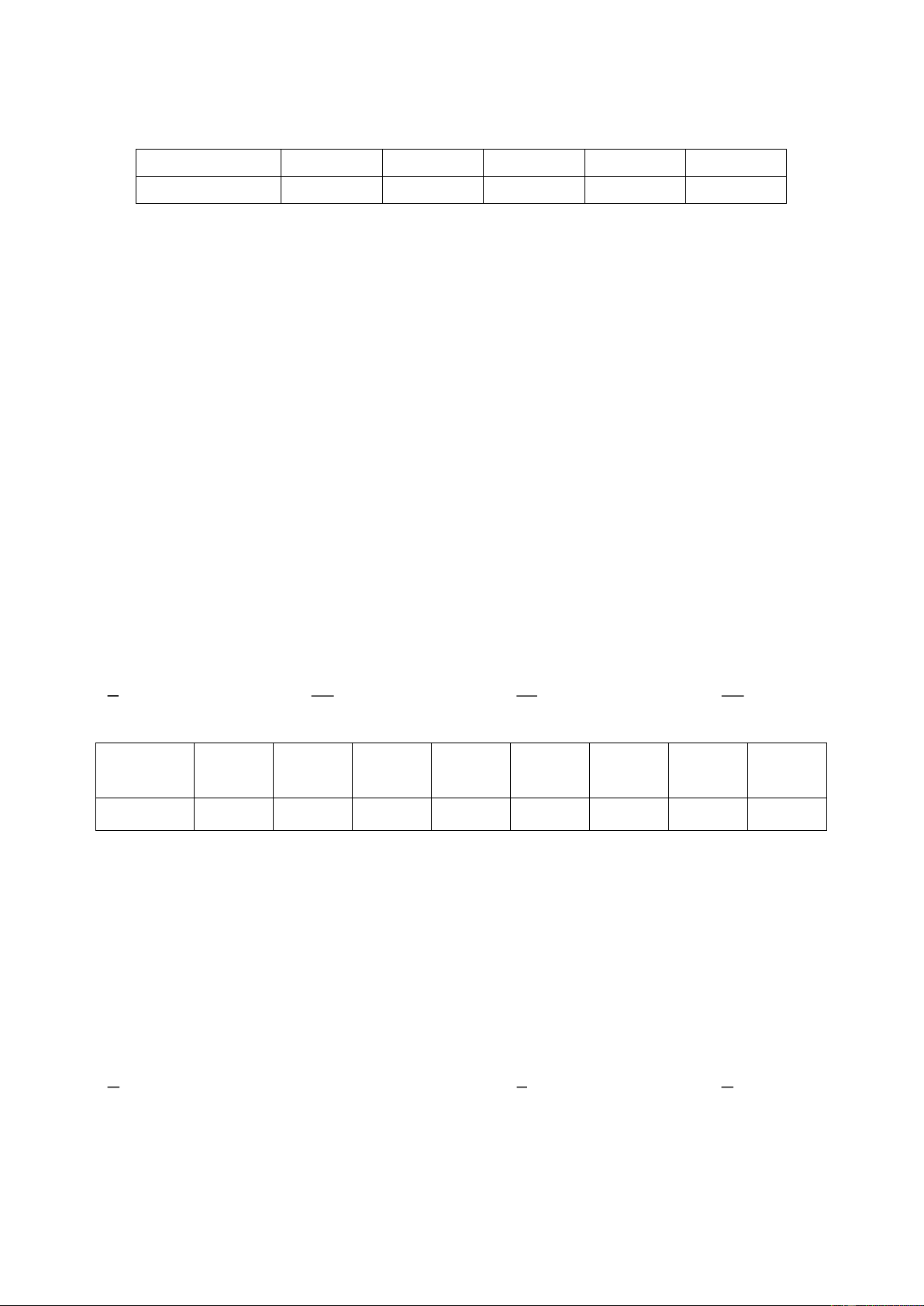
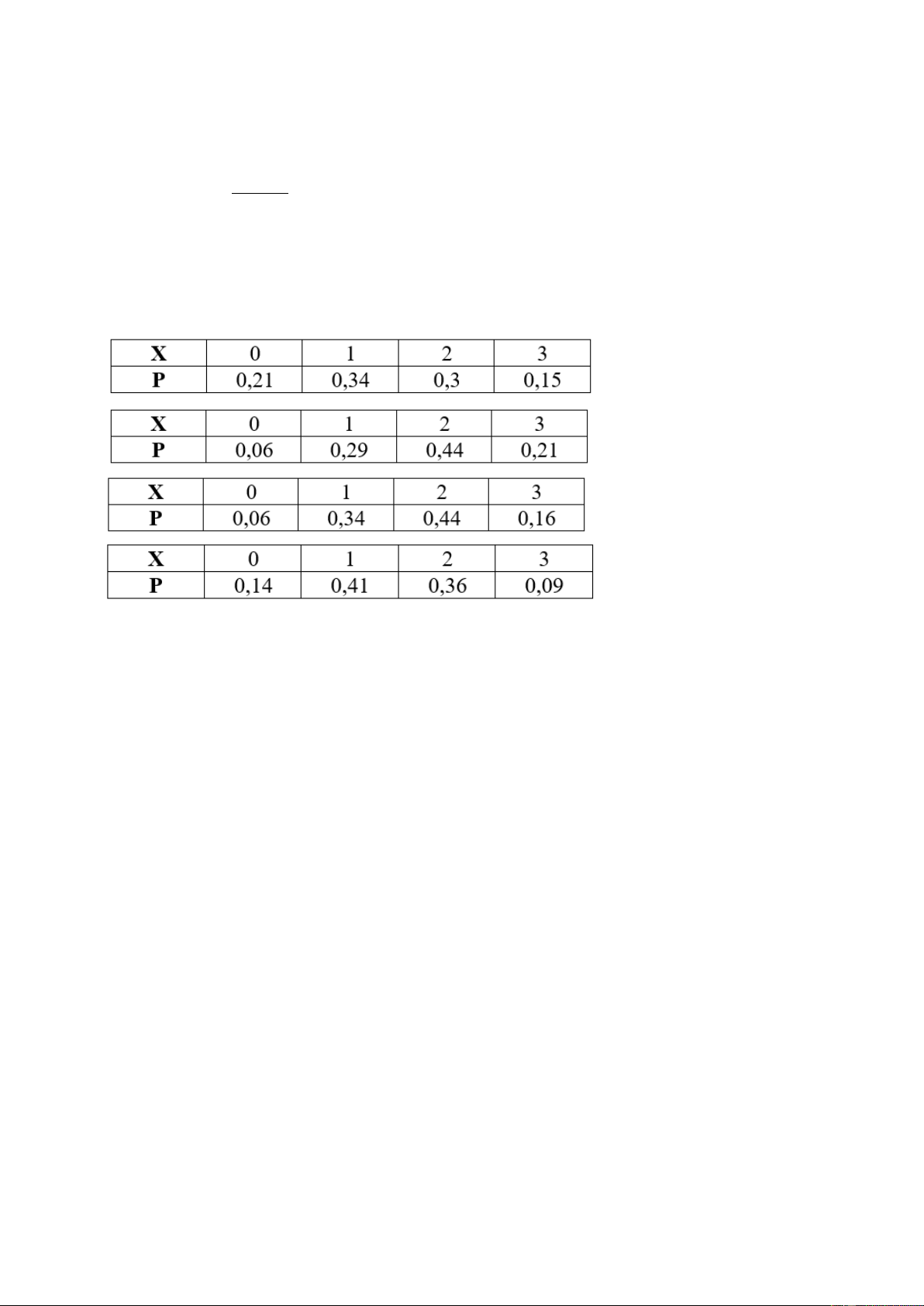
Câu 88: Có 3 người vào một cửa hàng với xác suất mua hàng lần lượt là 0,3; 0,5 và 0,6. Gọi X là
biến ngẫu nhiên chỉ số người mua hàng. Khi đó bảng phân phối xác suất của X là: A. B. C. D.
Câu 89: Khảo sát 100 000 trẻ sơ sinh ở một vùng dân cư người ta thấy có 50 300 bé trai. Có ý kiến
cho rằng tỉ lệ bé trai đã thực sự cao hơn bé gái. Cần kiểm tra nhận định trên. Hãy chỉ ra kết luận đúng:
A. Với mức ý nghĩa 5%, có thể kết luận tỉ lệ sinh bé trai cao hơn bé gái
B. Với mức ý nghĩa 2,5%, chưa thể kết luận tỉ lệ sinh bé trai cao hơn bé gái
C. Với mức ý nghĩa 5%, chưa thể kết luận tỉ lệ sinh bé trai cao hơn bé gái
D. Nếu khảo sát 1 000 000 trẻ sơ sinh trong vùng dân cư nói trên, chắc chắn có 503 000 bé trai
Câu 90: Gieo hai đồng tiền cân đối, đồng chất. Gọi X là biến ngẫu nhiên chỉ số đồng tiền xuất hiện mặt âm.
A. X nhận các giá trị {0; 1; 2}
B. X nhận các giá trị {1; 2; 3} C. P(X=0)=0,5 D. P(X=1)=0,25
Câu 91: Cho A, B, C là các biến cố bất kỳ. Biểu thức nào sau đây sai:
A. A.B = B.A
B. A + (B + C) = A + B + C C. A.A = A D. A ̅̅+ ̅̅̅B ̅̅ = A̅ + B̅
Câu 92: Người ta lấy ngẫu nhiên 1000 sản phẩm của lô hàng để kiểm tra và thấy có 945 sản phẩm
loại I. Nếu tỉ lệ hàng loại I đạt 95% thì lô hàng được xuất khẩu. Với mức ý nghĩa 5%, cần kiểm tra
xem lô hàng có xuất khẩu được không. Hãy chỉ ra khẳng định đúng:
A. Đây là bài toán ước lượng kỳ vọng
B. Đây là bài toán ước lượng tỉ lệ
C. Tỉ lệ hàng loại I của toàn bộ lô hàng là p = 94,5%
D. Tần suất mẫu f = 945/1000
Câu 93: Một máy sản xuất tự động với tỉ lệ chính phẩm đạt 95%. Sau một thời gian hoạt động có ý
kiến cho rằng máy không còn hoạt động được như cũ. Để kiểm tra người ta tiến hành điều tra ngẫu
nhiên 200 sản phẩm thấy có 190 sản phẩm là chính phẩm. Với mức ý nghĩa 5%, cần kiểm định ý kiến trên.
Hãy chỉ ra kết luận đúng:
A. Đã đủ cơ sở để kết luận máy hoạt động không tốt như trước
B. Sau một thời gian hoạt động, tỉ lệ phế phẩm giảm
C. 190/200 là tỉ lệ chính phẩm của mẫu
D. 190/200 là tỉ lệ chính phẩm của lô hàng
Câu 94: Để kiểm tra chất lượng của một lô hàng hóa, người ta lấy ngẫu nhiên từ lô ra 100 sản
phẩm và thấy có 20 sản phẩm loại II. Với độ tin cậy 95% hãy ước lượng tỉ lệ sản phẩm loại 2 của cả lô hàng. A. (0,130;0,270) B. (0,122;0,278) C. (0,150;0,250) D. (0,140;0,260)
Câu 95: Để kiểm tra mức độ mất cân bằng giới tính trong địa phương A, người ta thống kê ngẫu
nhiên 10650 trẻ sơ sinh ở một địa phương A thấy có 5510 bé trai. Hãy chỉ ra kết luận đúng:
A. Với mức ý nghĩa 1%, có thể cho rằng tỉ lệ sinh con trai thực sự cao hơn tỉ lệ sinh con gái.
B. Tỉ số 5510/10650 không phải là tần suất mẫu.
C. Tỉ số 5510/10650 là tỉ lệ sinh bé trai trong toàn bộ địa phương A.
D. Với mức ý nghĩa 5%, chưa thể cho rằng tỉ lệ sinh con trai thực sự cao hơn tỉ lệ sinh con gái.
Câu 96: Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau. Tìm kỳ vọng E(X). X 0 1 2 3 P 0,2 P 0,2 0,3 A. 2,3 B. 1,6 C. 2,5 D. 2
Câu 97: Khảo sát 100 000 trẻ sơ sinh ở một vùng dân cư người ta thấy có 50 300 bé trai. Có ý kiến
cho rằng tỉ lệ bé trai đã thực sự cao hơn bé gái. Cần kiểm tra nhận định trên. Hãy chỉ ra kết luận đúng:
A. Tỉ số 50300/100000 là tỉ lệ bé trai trong toàn bộ vùng dân cư.
B. Giả thuyết H: p<0,5. Đối thuyết K: p>0,5
C. Tỉ số 50300/100000 là tần suất sinh bé trai của mẫu khảo sát.
D. Giả thuyết H: p=0,5. Đối thuyết K: p<0,5
Câu 98: Chỉ ra khẳng định đúng:
A. Trời mưa hôm nay là một phép thử
B. Gieo một đồng xu là 1 biến cố
C. Số chấm xuất hiện trên xúc xắc là 1 phép thử
D. Rút một lá bài từ bộ bài 52 lá là 1 phép thử
Câu 99: Giả sử đường kính của một loại chi tiết máy là biến ngẫu nhiên phân phối chuẩn với độ
lệch tiêu chuẩn 𝜎=0,9cm. Lấy ngẫu nhiên một mẫu gồm 49 chi tiết và tính được đường kính trung
bình của một chi tiết là 20 cm. Với độ tin cậy 95%, hãy ước lượng đường kính trung bình của loại chi tiết máy đó.
A. (19,496; 20,504) B. (19,700; 20,300) C. (19,848; 20,152) D. (19,748; 20,252)
Câu 100: Đầu năm người ta thả 1 000 000 cá con xuống hồ. Cuối năm bắt lên 500 con cân kiểm
tra, thấy có 350 con cá đạt loại I. Người ta cần ước lượng tỉ lệ cá loại I bằng khoảng tin cậy đối
xứng, với độ tin cậy 95%. Hãy chỉ ra kết luận đúng:
A. Tỉ lệ cá loại I trong hồ thỏa mãn 0,66
B. Tỉ lệ cá loại I trong hồ thỏa mãn 0,68
C. Tỉ lệ cá loại I trong hồ thỏa mãn 0,68
D. Tỉ lệ cá loại I trong hồ thỏa mãn 0,66
Câu 101: Để đánh giá mức sống của người dân trong một địa bàn dân cư, người ta khảo sát ngẫu
nhiên thu nhập hàng tháng của 100 hộ trên địa bàn, thu được kết quả:
Thu nhập (triệu VND/tháng) 20 24 28 35 45 Số hộ 10 15 40 25 10 Chỉ ra kết luận đúng:
A. Với độ tin cậy 95%, thu nhập trung bình của toàn bộ dân cư trong địa bàn 28,72<µ<31,38
B. Với độ tin cậy 95%. thu nhập trung bình của toàn bộ dân cư trong địa bàn 29,72<µ<31,38
C. Với độ tin cậy 95%. thu nhập trung bình của toàn bộ dân cư trong địa bàn 28,72<µ<30,38
D. Chắc chắn 100%, thu nhập trung bình của toàn bộ dân cư trong địa bàn 28,72<µ<31,38
Câu 102: Người ta lấy ngẫu nhiên 1000 sản phẩm của lô hàng để kiểm tra và thấy có 945 sản phẩm
loại I. Nếu tỉ lệ hàng loại I đạt 95% thì lô hàng được xuất khẩu. Với mức ý nghĩa 5%, cần kiểm tra
xem lô hàng có xuất khẩu được không. Hãy chỉ ra công thức đúng: 𝑛
A. 𝑈𝑞𝑠 = (𝑓 − 𝑝0)√ B. 𝑈 √𝑓(1−𝑓) 𝑓(1−𝑓) 𝑞𝑠 = 𝑓 + 𝑈𝛼 2 𝑛 𝑛 𝑛
C. 𝑈𝑞𝑠 = (𝑓 − 𝑝0)√ D. 𝑈 𝑝 𝑞𝑠 = (𝑝0 − 𝑓)√ 0(1−𝑝0) 𝑝0(1−𝑝0)
Câu 103: Một xạ thủ dùng 4 viên đạn để thử súng, cứ 2 viên liên tiếp trúng đích thì dừng lại. Biết
xác suất trúng đích mỗi lần bắn của anh ta là 0,85. Gọi X là biến ngẫu nhiên chỉ số viên đạn đã bắn.
Tìm độ lệch chuẩn của X. A. 0,586 B. 0,451 C. 0,765 D. 0,468
Câu 104: Tung 1 con xúc xắc có 6 mặt 6 chấm. Gọi X là biến cố số chấm xuất hiện. Khi đó kỳ vọng E(X) là: A. 3,5 B. 5 C. 4 D. 3
Câu 105: Theo dõi thời gian hoàn thành một sản phẩm của 50 công nhân ta có bảng sau: Thời gian
[12-14) [ 14-16) [16-18) [18-20) [20-22) [22-24) [24-26) [26-28) (phút) Số người 4 10 1 12 14 2 6 1
Với độ tin cậy 95%, thời gian hoàn thành một sản phẩm của công nhân toàn nhà máy thuộc khoảng
A. 18,26 <µ<20,10
B. 18,00 <µ<20,00
C. 18,26 <µ<20,30
D. 18,00 <µ< 20,20
Câu 106: Xác suất bắn trúng đích của một xạ thủ là 0,85. Tìm xác suất để xạ thủ này bắn 8 viên
đạn thì có 5 viên trúng đích. A. 0,531 B. 0,207 C. 0,083 D. 0,425
Câu 107: Để đánh giá mức sống của người dân trong một địa bàn dân cư, người ta khảo sát ngẫu
nhiên thu nhập hàng tháng của 100 hộ trên địa bàn, thu được kết quả:
Thu nhập (triệu VND/tháng) 20 24 28 35 45 Số hộ 10 15 40 25 10 Chỉ ra kết luận đúng:
A. Độ lệch chuẩn mẫu là s=45,75 triệu VND/tháng.
B. Thu nhập trung bình cùa toàn bộ dân trong địa bàn là 30,05 triệu/tháng.
C. Thu nhập trung bình của 100 hộ khảo sát là 30,05 triệu/tháng.
D. Phương sai mẫu là s2=45.75.
Câu 108: Để ước lượng tỷ lệ chính phẩm trong một lô hàng, người ta lấy một mẫu gồm 100 sản
phẩm của lô hàng đó để kiểm tra và thấy có 8 phế phẩm. Với độ tin cậy 95%, chỉ ra khẳng định đúng:
A. Tần suất phế phẩm là 8/100.
B. Tần suất phế phẩm là 92/100.
C. Tỉ lệ chính phẩm của toàn lô hàng là 92/100.
D. Với độ tin cậy 95%, tỉ lệ chính phẩm của toàn lô hàng là 92/100.
Câu 109: Để ước lượng tỷ lệ chính phẩm trong một lô hàng, người ta lấy một mẫu gồm 100 sản
phẩm của lô hàng đó để kiểm tra và thấy có 8 phế phẩm. Với độ tin cậy 95%, ước lượng cho tỉ lệ chính phẩm là: A. 0,888
B. 0,867
C. 0,867
D. 0,888
Câu 110: Các biến cố A và B độc lập với nhau, và có P(A)=0,22; P(B)=0,55. Khi đó P(AB) là A. 0,025 B. 0,121 C. 0,4 D. 0,33
Câu 111: Đầu năm người ta thả 1 000 000 cá con xuống hồ. Cuối năm bắt lên 500 con cân kiểm
tra, thấy có 350 con cá đạt loại I. Hãy chỉ ra kết luận đúng:
A. Tỉ số 150/1000000 là tỉ lệ cá loại I trong hồ
B. Tỉ số 500/1000000 là tần suất mẫu
C. Tỉ số 350/500 là tần suất mẫu
D. Tỉ số 350/1000000 là tỉ lệ cá đạt loại I trong cả hồ cá
Câu 112: Trong một hội thao, thời gian chạy 200 m của một nhóm vận động viên được ghi lại ở bảng sau Thời gian [21;21,5) (giây)
[21,5;22) [22;22,5) [22,5;23) [23;23,5) Số VĐV 5 12 32 45 30
Độ lệch chuẩn mẫu là: A. 22,73 giây B. 22,58 giây C. 0,68 giây D. 22,64 giây
Câu 113: Công thức Bayes có thể được viết lại như thế nào?
A. P(A|B) = P(B|A) + P(A) / P(B)
B. P(A|B) = P(A) * P(B|A) + P(B)
C. P(A|B) = (P(B|A) * P(A)) / P(B)
D. P(A|B) = P(A) / P(B|A)
Câu 114: Gieo một con xúc xắc cho đến khi xuất hiện mặt 6 chấm thì dừng, không gieo nữa
(không hạn chế số lần gieo). Gọi X là biến ngẫu nhiên chỉ số lần gieo. Khẳng định nào sau đây đúng:
A. X nhận giá trị trong tập hợp số N+ = {1.2.3,...}
B. X nhận giá trị trong tập hợp số N = {0,1,2,3,...}
C. X nhận giá trị trong tập hợp số {0,1,2,3,4,5,6}
D. X nhận giá trị trong tập hợp số {1,2,3,4,5,6}
Câu 115: Một người cân nhắc giữa việc mua nhà và gửi tiết kiệm 1 năm với lãi suất 6%/năm và
chờ năm sau mua nhà. Biết rằng mức tăng giá nhà là biến ngẫu nhiên có phân phối chuẩn với mức
tăng trung bình là 9%/năm, độ lệch chuẩn là 10%/năm. Tìm khả năng rủi ro của người đó. A. 43,36% B. 50% C. 61,79% D. 34,46%
Câu 116: Một hộp có 4 quả cầu trắng, 3 quả cầu đen. Lấy ngẫu nhiên lần lượt từng quả cầu không
hoàn lại đến khi lấy được quả cầu trắng thì dừng. Hàm phân phối xác suất của số quả cầu trắng lấy ra là: 0 x 1; 0 x 1; 4 / 7 1 x 2; 0, 3 1 x 2;
A. f (x) = 6 / 7 2 x 3;
B. f (x) = 0,5 2 x 3; 34 / 35 3 x 4; 0,8 3 x 4; 1 x 4. 1 x 4. 0 x 1; 0 x 1; 0, 25 1 x 2; 1/ 8 1 x 2;
C. f (x) = 0,56 2 x 3;
D. f (x) = 3 / 8 2 x 3; 0,84 3 x 4; 5 / 8 3 x 4; 1 x 4. 1 x 4.
Câu 117: Một công ty có 7 máy tính hoạt động độc lập. Xác suất để mỗi máy bị hỏng trong một
ngày đều bằng 0,08. Tìm xác suất để trong một ngày có không quá hai máy bị hỏng. A. 98,6% B. 95,2% C. 62,1% D. 89,3%
Câu 118: Điều tra thu nhập cùa 100 hộ kinh doanh trong năm 2025 thu được kỳ vọng mẫu 24,8
(triệu VND/tháng) và độ lệch chuẩn mẫu s = 2,574. Với độ tin cậy 95%, khoảng tin cậy đối xứng
cho thu nhập trung bình của các hộ kinh doanh là:
A. 21,71<µ<24,61 B. 22<µ<24
C. 20,71<µ<23,71
D. 24,30<µ<25,30
Câu 119: Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi
trong hộp. Xác suất để 5 viên bi được chọn chỉ có một màu. A. 1 B. 1 C. 1 D. 1 8568 1428 306 408
Câu 120: Khảo sát về thu nhập (triệu đồng/tháng) của một số người trong công ty, ta thu được bảng số liệu: Thu nhập [6-10) (tr)
[10-12) [12-14) [14-16) [16-18) [18-20) [20-22) [22-30) Số người 15 17 35 36 39 30 20 8
Những người có thu nhập trên 16 triệu đồng/tháng là người có thu nhập cao. Hãy ước lượng tỉ lệ
những người có thu nhập cao ở công ty với độ tin cậy 98%, biết cả công ty có 2000 người. A. (0,400;0,610) B. (0,420;0,570) C. (0,403;0,567) D. (0,390;0,600)
Câu 121: Gieo 1 con xúc sắc, biến cố nào dưới đây là biến cố sơ cấp:
A. Được mặt chẵn.
B. Được mặt lẻ. C. Được mặt 4.
D. Được mặt lớn hơn 4.
Câu 122: Có 3 xe bus hoạt động độc lập. Kí hiệu 𝐴𝑖(𝑖 = 1,2,3) là biến cố: Xe thứ i về bến đúng giờ.
Phát biểu nào dưới đây là sai: A. 𝐴
là biến cố cả 3 xe về bên đúng giờ. 1𝐴2𝐴3 B. 𝐴
̅̅̅̅̅̅̅̅̅̅ là biến cố cả 3 xe về bến không đúng giờ. 1𝐴2𝐴3 C. 𝐴
là biến cố có xe về bến đúng giờ. 1 + 𝐴2 + 𝐴3 D. 𝐴𝐴 ̅̅̅
là biến cố chỉ xe thứ 2 về bến không đúng giờ. 2𝐴3
Câu 1233: Hộp bi gồm 5 bi trắng và 4 bi đen. Lấy ngẫu nhiên 3 lần, mỗi lần 1 viên và kí hiệu
𝑇𝑖 (𝑖 = 1, 2, 3) là biến cố lấy được bi trắng ở lần i. Đâu là biến cố: Chỉ được đúng 1 bi trắng sau 3 lần lấy: A. 𝑇 B. 1 + 𝑇2 + 𝑇3
𝑇1𝑇2 + 𝑇2𝑇3 + 𝑇3𝑇1 C. 𝑇 ̅̅̅̅̅̅ ̅ ̅ ̅̅̅̅̅̅ 1𝑇2𝑇3
D. 𝑇1𝑇2𝑇3 + 𝑇1𝑇2𝑇3 + 𝑇1𝑇2𝑇3
Câu 1234: 3 sinh viên vào ngẫu nhiên 3 quán trà sữa. Xác suất để không có 2 sinh viên vào cùng 1 quán là: A. 2
B. 3 C. 4 D. 1 9 9 9 9
Câu 1235: Hộp bi gồm 4 bi trắng và 3 bi đen. Nếu lấy ngẫu nhiên 2 viên thì xác suất được 2 viên khác màu là: A. 1
B. 2 C. 3 D. 4 7 7 7 7
Câu 1236: Cho 2 biến cố U và V của cùng một phép thử. Đâu là mệnh đề sai trong các mệnh đề dưới đây:
A. U, V độc lập nếu P(UV) = P(U).P(V)
B. U, V độc lập nếu biến cố này xảy ra không ảnh hưởng đến biến cố kia và ngược lại.
C. U, V độc lập nếu P(U|V) = P(U) và P(V|U) = P(V).
D. P(U + V) = P(U) + P(V)
Câu 127: Gieo 2 xúc sắc. Kí hiệu A là biến cố: xúc sắc 1 được mặt 3. Trong các biến cố dưới đây,
biến cố nào độc lập với A:
A. Tổng 2 mặt là số chẵn B. Tích 2 mặt là số lẻ
C. Xúc sắc thứ hai ra mặt chẵn C. Tích 2 mặt là số chẵn
Câu 1237: Cho A, B là 2 biến cố độc lập. Thế thì 𝑃(𝐴̅| 𝐵) =
A. P(A) B. P(𝐴̅) C. P(B) D. 𝑃(𝐵̅)
Câu 1238: 3 sinh viên An, Bình Chiến không quen nhau cùng đi thi xstk với xác suất dưới 5 điểm
tương ứng là 0,2; 0,3; và 0,4. Xác suất không ai dưới 5 điểm là:
A. 0,024 B. 0.976 C. 0.24 D. 0.336
Câu 130: 3 sinh viên An, Bình Chiến không quen nhau cùng đi thi xstk với xác suất dưới 5 điểm
tương ứng là 0,2; 0,3; và 0,4. Xác suất có ít nhất một bạn không dưới 5 điểm là:
A. 0,024 B. 0,976 C. 0,24 D. 0,336
Câu 39: Bạn Tùng ném bóng vào rổ 5 lần liên tiếp từ khoảng cách 3m. Nếu xác suất ném trúng là
một lần là 0,6 thì xác suất nếm trúng đúng 3 lần trong 5 lần ném của tùng là
A. 0,27 B. 0,36 C. 0,78 D. 0,65
Câu 40: Có hai hộp bi: Hộp 1 có 3 viên trắng và 5 viên đen, hộp 2 có 4 viên trắng và 5 viên đen. Lấy
ngẫu nhiên 1 viên từ hộp 1 sang hộp 2, rồi sau đó lấy ngẫu nhiên 1 viên từ hộp 2. Thế thì xác suất lấy
được bi trắng từ hộp 2 sẽ là A. 7
B. 1 C. 9 D. 3 16 2 16 8
Câu 41: Lớp có 3 tổ: Tổ 1 có 7 nam và 5 nữ; Tổ 2 có 6 nam và 8 nữ; tổ 3 có 5 nam và 9 nữ. Lấy ngẫu
nhiên 1 bạn thì được bạn nữ, thế thì xác suất bạn nữ đó thuộc tô 1 là bao nhiêu? A. 7
B. 9 C. 11 D. 5 22 22 22 22
Câu 42: Cho X là một đại lượng ngẫu nhiên rời rạc có hàm phân phối là F(x). Phát biểu nào dưới đây không đúng:
A. 𝐹(𝑥) ≥ 0 ∀𝑥
B. 𝐹(𝑥) ≤ 1 ∀𝑥
C. F(x) là hàm liên tục trên R.
D. F(x) là hàm đồng biến trên R.
Câu 43: Cho X, Y là hai đại lượng ngẫu nhiên rời rạc. phát biểu nào dưới đây không đúng
A. 𝐸(𝑋 + 𝑌) = 𝐸𝑋 + 𝐸𝑌
B. 𝐸(𝑘𝑋) = 𝑘. 𝐸𝑋 ∀𝑘 ∈ 𝑅
C. 𝐸(𝑘) = 𝑘 ∀𝑘 ∈ 𝑅 D. E(X.Y) = EX. EY
Câu 44: Một hộp bi có 4 viên trắng và 3 viên đen. Lấy ngẫu nhiên 3 viên và kí hiệu X là số bi trắng
trong 3 viên được lấy ra. Thế thì bảng phân phối xác suất của X sẽ là A. X 0 1 2 3 P 1/35 12/35 18/35 4/35 B. X 0 1 2 3 P 1/35 18/35 12/35 4/35 C. X 0 1 2 3 P 4/35 12/35 18/35 1/35 D. X 0 1 2 3 P 3/35 12/35 18/35 2/35
Câu 45: Một hộp bi có 4 viên trắng và 3 viên đen. Lấy ngẫu nhiên 3 viên và kí hiệu X là số bi trắng
trong 3 viên được lấy ra. Thế thì A. 10 11 12 13 𝐸𝑋 =
B. 𝐸𝑋 = C. 𝐸𝑋 = D. 𝐸𝑋 = 7 7 7 7
Câu 46: Một hộp bi có 4 viên trắng và 3 viên đen. Lấy ngẫu nhiên 3 viên và kí hiệu X là số bi trắng
trong 3 viên được lấy ra. Thế thì A. 24 25 26 27 𝑉𝑎𝑟𝑋 =
B. 𝑉𝑎𝑟𝑋 = C. 𝑉𝑎𝑟𝑋 = D. 𝑉𝑎𝑟𝑋 = 49 49 49 49
Câu 47: Một hộp bi có 4 viên trắng và 3 viên đen. Lấy ngẫu nhiên 3 viên và kí hiệu X là số bi trắng
trong 3 viên được lấy ra. Thế thì
A. ModX = 0 B. ModX = 1 C. ModX = 2 D. ModX = 3
Câu 48: Điều tra ngẫu nhiên chi tiêu hàng tháng của 100 sinh viên trường FBU (đơn vị: triệu đồng),
ta được bảng số liệu: Chi tiêu (X) 5 6 7 8 9 Số sinh viên 10 15 23 40 12 Trung bình mẫu sẽ là:
A. 𝑥̅ = 7 B. 𝑥̅ = 7,29 C. 𝑥̅ = 8 D. 𝑥̅ = 8,29
Câu 141: Vẫn với dữ liệu như câu trên, phương sai mẫu sẽ là
A. 𝑠2 = 1,06 B. 𝑠2 = 1,16 C. 𝑠2 = 1,26 D. 𝑠2 = 1,36
Câu 142: Vẫn với dữ liệu như câu trên, Mode mẫu sẽ là
A. Mode = 10 B. Mode = 5 C. Mode = 40 D. Mode = 8
Câu 143: Vẫn với dữ liệu như câu trên, Median mẫu sẽ là
A. Median =5 B. Median = 6 C. Median = 7 D. Median = 8
Câu 144: Để tìm hiểu mức độ chi tiêu hàng tháng của sinh viên FBU, người ta điều tra ngẫu nhiên
100 sinh viên FBU thì thấy trung bình mỗi tháng một sinh viên tiêu 7 triệu, và phương sai của mẫu là
1,44 triệu. Với độ tin cậy 95%, khoảng tin cậy cho trung bình chi tiêu hàng tháng của một sinh viên FBU sẽ là
A. (6,5; 7,5) B. (6,77; 7,23) C. (6, 95; 8,57) D. (6,06; 7,92)
Câu 145: Để tìm hiểu mức độ chi tiêu hàng tháng của sinh viên FBU, người ta điều tra ngẫu nhiên
100 sinh viên FBU thì thấy có 40 sinh viên tiêu trên 7 triệu mỗi tháng. Với độ tin cậy 95%, khoảng
tin cậy cho tỉ lệ sinh viên chi tiêu trên 7 triệu mỗi tháng của một sinh viên FBU sẽ là
A. (0,3; 0,5) B. (0,27; 0,53)
C. (0,35; 0.45) D. (0,25; 0,62)
Câu 146: Để tìm hiểu mức độ chi tiêu hàng tháng của sinh viên FBU, người ta điều tra ngẫu nhiên
100 sinh viên FBU thì thấy có 40 sinh viên tiêu trên 7 triệu mỗi tháng.. Kí hiệu M là số sinh viên tiêu
trên 7 triệu mỗi tháng. Cho biết FBU có 10.000 sinh viên, với độ tin cậy 95% hãy cho biết M nằm
trong khoảng nào dưới đây:
A. (3000, 6000) B. (3000, 5000) C. (3500, 6000) D. (4500, 7000)
Câu 147: Cho bài toán kiểm định giả thiết sau:
Có ý kiên cho rằng điểm trung bình môn XSTK của sinh viên là 6,75. Điều tra ngẫu nhiên điểm
XSTK của 64 sinh viên thì thấy điểm trung bình là 6,1 và độ lệch chuẩn mẫu là 1,75. Với mức ý nghĩa
0.05 có nên tin ý kiến này?
Miền bác bỏ trong bài toán này là:
A. (−∞, −2,58) B. (2,58; +∞)
C. (−∞, −2,58) ∪ (2,58; +∞) D. (−2,58; 2,58)
Câu 148: Cho bài toán kiểm định giả thiết sau:
Có ý kiên cho rằng điểm trung bình môn XSTK của sinh viên là 6,75. Điều tra ngẫu nhiên điểm
XSTK của 64 sinh viên thì thấy điểm trung bình là 6,1 và độ lệch chuẩn mẫu là 1,75. Với mức ý nghĩa
0.05 có nên cho rằng ý kiến này quá cường điệu?
Cặp Giả thiết – Đối giả thiết của bài toán này là:
A. 𝐻: 𝜇 = 6,75; 𝐾: 𝜇 ≠ 6,75
B. 𝐻: 𝜇 = 6,1; 𝐾: 𝜇 ≠ 6,1
C. 𝐻: 𝜇 = 6,75; 𝐾: 𝜇 > 6,75
D. 𝐻: 𝜇 = 6,75; 𝐾: 𝜇 < 6,75
Câu 149: Cho bài toán kiểm định giả thiết sau:
Có ý kiên cho rằng tỉ lệ sinh viên nam cao trên 1m70 là 50%. Điều tra ngẫu nhiên điểm chiều cao của
80 sinh viên nam thì thấy có 48 sinh viên cao trên 1m70. Với mức ý nghĩa 0.05 có nên cho rằng tỉ lệ 50% là quá thấp?
Cặp giả thiết – Đối giả thiết của bài toán này là:
A. 𝐻: 𝑝 = 0,5; 𝐾: 𝑝 > 0,5
B. 𝐻: 𝑝 > 0,5; 𝐾: 𝑝 = 0,5
C. 𝐻: 𝑝 = 0,5; 𝐾: 𝑝 < 0,5
D. 𝐻: 𝑝 < 0,5; 𝐾: 𝑝 = 0,5
Câu 150: Cho bài toán kiểm định giả thiết sau:
Có ý kiên cho rằng tỉ lệ sinh viên nam cao trên 1m70 là 50%. Điều tra ngẫu nhiên điểm chiều cao của
80 sinh viên nam thì thấy có 48 sinh viên cao trên 1m70. Với mức ý nghĩa 0.05 có nên cho rằng tỉ lệ 50% là quá thấp?
Test thống kê thực nghiệm của bài toán này là: A. 80 80 (0,6 − 0,5) √ B. (0,6 − 0,5) √ 0,6.0,6 0,5.0,5 C. 0,6.0,6
(0,6 − 0,5) √0,5.0,5 D. (0,6 − 0,5) √ 80 80
Câu 49: Điều tra ngẫu nhiên điểm XSTK của 64 sinh viên thì thấy điểm trung bình là 6,1 và độ lệch
chuẩn mẫu là 1,5. Với độ tin cậy 95%, độ chính xác của khoảng tin cậy cho điểm trung bình môn XSTK sẽ là A. 1,5 1,5 1,5 1,5 𝑢 B. C. D. 0.05 × 𝑢 𝑢 𝑢 64 0.025 × 64 0.05 × 8 0.025 × 8
Câu 50: Cho bài toán kiểm định giả thiết sau:
Một giáo viên toán cho rằng điểm trung bình môn XSTK của sinh viên là 6,75. Điều tra ngẫu nhiên
điểm XSTK của 64 sinh viên thì thấy điểm trung bình là 6,1 và độ lệch chuẩn mẫu là 1,75. Với mức
ý nghĩa 0.05 có nên cho rằng vị giáo viên này đã nói quá?
Miền bác bỏ trong bài toán này là:
𝐴. (−∞, −2,58) B. (2,58; +∞)
C. (−∞, −2,58) ∪ (2,58; +∞) D. (−2,58; 2,58)
Câu 51: Điều tra ngẫu nhiên chiều cao của 80 sinh viên nam thì thấy có 20 nam sinh viên cao trên
1m73. Khi đó, với dộ tin cậy 99%, độ chính xác của khoảng tin cậy cho tỉ lệ nam sinh viên cao trên 1m72 sẽ là A. 𝑢 B. 0,01√0,25.0,75 𝑢 80 0,005√0,25.0,75 80 C. 80 80 𝑢 D. 0,01√ 𝑢 0,25.0,75 0,005√0,25.0,75
Câu 52: Cho X là một đại lượng ngẫu nhiên, mệnh đề nào dưới đây là đúng:
A. X không nhận giá trị âm. B. EX không âm
C. VarX không âm D. ModX không âm
Câu 53: Một hộp gồm 5 bi trắng 1 bi đen. Lấy ngẫu nhiên từng viên không hoàn lại. Xác suất lần 3 được bi đen là
A. 1/3 B. 1/4 C. 2/9 D. 1/6
Câu 54: Một tổ học sinh có 6 nam và 4 nữ. Chọn ngẫu nhiên 2 bạn làm tổ trưởng và tổ phó và yêu
cầu đi họp ngay, sau đó lại chọn ngẫu nhiên một bạn làm bí thư. Xác suất để bí thư là nữ sẽ là
A. 1/8 B. 1/4 C. 3/10 D. 2/5
Câu 55: Một kho chứa giày do 2 nhà máy A và B gia công. Biết số giày do nhà máy A gia công gấp
4 lần số giày do nhà máy B gia công, và tỉ lệ giày lỗi của 2 nhà máy A, B lầ lượt là 5% và 3%. Lấy
ngâux nhiên một đôi thì được đôi giày lỗi, tính xác suất đôi này do B gia công.
A. 3/23 B. 4/23 C. 5/23 D. 6/23
Câu 56: Điều tra ngẫu nhiên cân nặng của 50 sinh viên nam thì thấy có 20 nam sinh viên nặng trên
65kg. Khi đó, với dộ tin cậy 95%, độ chính xác của khoảng tin cậy cho tỉ lệ nam sinh viên cao trên 1m72 sẽ là A. 50 50 𝑢 B. 0,05√ 𝑢 0,4.0.6 0,025√0,4.0.6 C. 0,4.0,6 0,4.0,6 𝑢 D. 0,025√ 𝑢 50 0,05√ 50
Câu 57: Cho bài toán kiểm định giả thiết sau:
Một cố vấn học tập cho biết trung bình một sinh viên đi làm thêm 9h mỗi tuần. Điều tra ngẫu nhiên
50 sinh viên thì thấy trung bình một sinh viên đi làm thêm 10 giờ mỗi tuần, với độ lệch chuẩn là 2
giờ. Với mức ý nghĩa 0.05 có nên cho rằng vị giáo viên này đã nói giảm số giờ đi làm thêm của sinh viên?
Cặp giả thiết – Đối giả thiết của bài toán này là:
A. 𝐻: 𝜇 = 9; 𝐾: 𝜇 ≠ 9
B . 𝐻: 𝜇 = 9; 𝐾: 𝜇 > 9
C. 𝐻: 𝜇 = 10; 𝐾: 𝜇 ≠ 10
D. 𝐻: 𝜇 = 10; 𝐾: 𝜇 < 10
Câu 58: Cho bài toán kiểm định giả thiết sau:
Một cố vấn học tập cho biết trung bình một sinh viên đi làm thêm 9h mỗi tuần. Điều tra ngẫu nhiên
81 sinh viên thì thấy trung bình một sinh viên đi làm thêm 10 giờ mỗi tuần, với độ lệch chuẩn là 2
giờ. Với mức ý nghĩa 0.05 có nên cho rằng vị giáo viên này đã nói giảm số giờ đi làm thêm của sinh viên?
Test thống kê thực nghiệm của bài toán này là:
A.2/9 B. 9/2 C. -2/9 D. -9/2
Câu 161: Điều tra ngẫu nhiên cân nặng của 100 nam sinh viên (đơn vị: kg) ta được bảng số liệu Cân nặng [50, 55) [55, 60) [60, 65) [65, 70) [70, 75) Số sinh viên 8 17 40 25 10
Trung bình mẫu và phương sai mẫu sẽ là:
A. 𝑥̅ = 63,1; 𝜎2 = 28,42 B. 𝑥̅ = 65,2; 𝜎2 = 38,85
C. 𝑥̅ = 60,5; 𝜎2 = 32,55 D. 𝑥̅ = 63,1; 𝜎2 = 38,42
Câu 162: Một chiếc hộp đựng 5 viên phấn trắng và 3 viên phấn xanh. Lấy ngẫu nhiên lần lượt ra 2
viên. Xác suất để lần 2 lấy được viên phấn trắng là bao nhiêu nếu lần 1 đã lấy được phấn trắng?
A. 2/7 B. 3/7 C. 4/7 D. 5/7
Câu 163: Trong một chiếc hộp có đựng 7 chính phẩm và 3 phế phẩm. Lấy ngẫu nhiên lần lượt ra 2
sản phẩm theo cách không hoàn lại. Xác suất để cả 2 sản phẩm đều là chính phẩm là:
A. 7/15 B. 8/15 C. 7/16 D. 1/2
Câu 164: Một bệnh viện Tai–Mũi–Họng có tỉ lệ bệnh nhân Tai, Mũi, Họng tương ứng là 25%, 40%,
35%; tỉ lệ phải phẫu thuật tương ứng là 1%, 2%, 3%. Chọn ngẫu nhiên một bệnh nhân từ thì được
người phải phẫu thuật. Xác suất để người được chọn bị bệnh Mũi là:
A. 0,08 B. 0,18 C. 0,28 D. 0,38
Câu 165: Cho bài toán kiểm định giả thiết:
Chiều cao trung bình của 81 trẻ em 2 tuổi là 81,1cm với độ lệch chuẩn là 3,11cm. Chiều cao chuẩn
của trẻ em 2 tuổi trong vùng là 86,5cm. Với mức ý nghĩa 0,01, test thống kê thực nghiệm sẽ là: A. 3,11 3,11 (81,1 − 86,5) × B. (81,1 − 86,5) × 9 81 C. 9 81 (81,1 − 86,5) × D. (81,1 − 86,5) × 3,11 3,11
Câu 166: Một lốc bia có 8 chai trong đó để lẫn 3 chai quá hạn sử dụng. Lấy ngẫu nhiên từ lốc bia
đó ra 3 chai. Xác suất lấy phải ít nhất 1 chai bia quá hạn sử dụng là:
A. 23/27 B. 23/28 C. 23/29 D. 23/30
Câu 167: Trong bài toán kiểm định giả thiết cho giá trị trung bình với cặp giả thuyết, đối thuyết:
H: 𝜇 = 𝜇0; K: 𝜇 ≠ 𝜇0
Nếu cỡ mẫu lớn hơn 30 thì, với mức ý nghĩa 𝛼, miền bác bỏ của bài toán sẽ là:
A. (−∞, −𝑢𝛼) B. (𝑢𝛼, +∞) 2 2
C. (−∞, −𝑢𝛼) ∪ (𝑢𝛼, +∞) D. (−𝑢𝛼, 𝑢𝛼) 2 2 2 2
Câu 168: Trong bài toán tìm khoảng tin cậy cho tỉ lệ phần tử có đặc tính A, nếu kí hiệu số phần tử
thỏa mãn A trong mẫu là k và cỡ mẫu là n thì n và k phải thỏa mãn yêu cầu nào dưới đây: A. 𝑘 ≥ 5 𝑛 + 𝑘 ≥ 25 𝑛/𝑘 ≥ 5 𝑘 ≥ 5 { B. { C. { D. { 𝑛 ≥ 5 𝑛 − 𝑘 ≥ 5 𝑛 + 𝑘 ≥ 25 𝑛 − 𝑘 ≥ 5
Câu 169: Điều tra ngẫu nhiên 80 sinh viên thì thấy 20 sinh viên đi làm 10 giờ mỗi tuần. Thế thì tần
suất sinh viên đi làm mỗi tuần 10 giờ trong mẫu này là:
A. 4 B. 1/4 C. 100 D. 60
Câu 170: Cho A, B là biến cố của 1 phép thử ngẫu nhiên. Đẳng thức nào dưới đây là sai:
A. 𝐴 ∩ 𝐴̅ = ∅ B. 𝐴 ∪ 𝐴̅ = Ω C. 𝐴 ̅̅ ∩ ̅̅̅𝐵
̅̅ = 𝐴̅ ∩ 𝐵̅ D. 𝐴 ̅̅ ∪ ̅̅̅𝐵 ̅̅ = 𝐴̅ ∩ 𝐵̅
Câu 171: Cho A, B là 2 biến cố của 1 phép thử ngẫu nhiên. Đẳng thức nào dưới đây là đúng:
A. P(A + B) = P(A) + P(B) B. P(A + B) = P(A) + P(B) + P(AB)
C. P(AB) = P(A).P(B) D. P(AB) = P(A).P(B| A)
Câu 172: Có 7 chìa khóa giống hệt nhau, trong đó có 1 chìa giả. Chìa thật mở được cửa, chìa giả thì
không. Thử mở cửa lần lượt từng chìa, thế thi xác suất gặp chìa giả ở lần thứ 3 là
A 1/7 B. 2/7 C. 3/7 D. 4/7
Câu 173: Điều tra ngẫu nhiên thu nhập hàng tháng của 140 hộ gia đình (đơn vị: triệu đồng) ta được bảng số liệu Thu nhập [15, 25) [25, 35) [35, 45) [45, 55) [55, 95) Số gia đình 10 22 56 38 14
Khi đó, trung bình mẫu và phương sai mẫu sẽ là
A. 𝑥̅ = 43,51; 𝑠2 = 13, 59 B. 𝑥̅ = 36,71; 𝑠2 = 13, 59
C. 𝑥̅ = 49,71; 𝑠2 = 183, 6 D. 𝑥̅ = 43,51; 𝑠2 = 183, 6
Câu 174: Với độ tin cậy (1 − 𝛼), khoảng tin cậy của biến lượng X khi có một mẫu cỡ n (n>30) sẽ là: A. 𝑢 𝑠 𝑢 𝑠 𝑠 𝑠 (𝑥̅ − 𝛼 ⋅ ; 𝑥̅ + 𝛼 ⋅
) B. (𝑥̅ − 𝑢𝛼 ⋅ ; 𝑥̅ + 𝑢𝛼 ⋅ ) 2 √𝑛 2 √𝑛 2 √𝑛 2 √𝑛 C. ( 𝑠 𝑠 𝑠 𝑥̅ 𝑠 𝑥̅ − 𝑢𝛼 ⋅ ; 𝑥̅ + 𝑢𝛼 ⋅
) D. (𝑥̅ − 𝑢𝛼 ⋅ ; + 𝑢𝛼 ⋅ ) √𝑛 √𝑛 2 √𝑛 2 √𝑛
Câu 175: X bài toán kiểm định giả thiết giá trị trung bình của biến lượng X:
𝐻: 𝜇 = 𝜇0; 𝐾: 𝜇 ≠ 𝜇0
Với mức ý nghĩa 𝛼, nếu có một mẫu cỡ n (n>30) thì Test thống kê thực nghiệm sẽ là
A. 𝑡 = (𝑥̅ − 𝜇 B. 0) √𝑛 𝑡 = (𝑥̅ − 𝜇 𝜎 0) 𝜎 √𝑛
C. 𝑡 = (𝑥̅ − 𝜇 D. 0) 𝑢𝛼
𝑡 = (𝑥̅ − 𝜇0) √𝑛 √𝑛 𝑢𝛼
Câu 176: Tỷ lệ sinh viên thi lại môn Triết học Mac-Lenin là 20%. Lấy ngẫu nhiên 20 sinh viên, xác
suất đúng 3 sinh viên thi lại môn Triết học Mac-Lenin là: A. 𝐶3 3 3
20. 0,23 B. 0,23. 0.817 C. 𝐶20. 0,23. 0.817 D. 𝐶20. 0,817
Câu 177: Tỷ lệ sinh viên thi lại môn Triết học Mac-Lenin là 20%. Lấy ngẫu nhiên 50 sinh viên và
kí hiệu X là số sinh thi lại môn Triết học Mac-Lenin trong 20 bạn đó. Thế thì:
A. EX = 10, VarX = 5 B. EX = 8, VarX = 10
C. EX = 5, VarX = 10 D. EX = 10, VarX = 8
Câu 178: Cho 2 biến cố A, B thỏa mãn:
𝑃(𝐵) = 0,6; 𝑃(𝐴| 𝐵) = 0,7; 𝑃(𝐴| 𝐵̅) = 0,4 Thế thì P(A) =
A. 0,7 B. 0,4 C. 0,58 D. 0,52
Câu 179: Cho 2 biến cố A, B thỏa mãn:
𝑃(𝐴) = 0,4; 𝑃(𝐵) = 0,3; 𝑃(𝐴| 𝐵) = 0,25 Thế thì P(B| A) =
A. 0,19 B. 0,29 C. 0,39 D. 0,49
Câu 180: Cho biết Bắc Ninh có 1 triệu công nhân và kí hiệu M là số công nhân thu nhập dưới 15
triệu mỗi tháng. Điều tra ngẫu nhiên 50 công nhân ở Bắc Ninh thì thấy có 30 công nhân thu nhập
dưới 15 triệu mỗi tháng. Với độ tin cậy 99%, M sẽ nằm trong khoảng
A (420000, 620000) B. (420000, 780000)
C. ( 320000, 680000) D. (500000, 800000)



