Bài giảng Cấu trúc dữ liệu môn Cơ Sở Dữ Liệu | Học viện Báo chí và Tuyên truyền

Cấu trúc dữ liệu Mở đầu
Bộ môn Công Nghệ Phần Mềm 1
Khoa CNTT&TT - Đại học Cần Thơ Nội dung
 Kiểu dữ liệu trừu tượng
 Độ phức tạp của giải thuật 2
Kiểu dữ liệu trừu tượng
(Abstract Data Types - ADT)
 Trừu tượng hóa trong tin học là đơn giản hóa:
che đi những chi tiết, làm nổi bật cái tổng thể.
- Trừu tượng hóa chương trình: phân chia
chương trình thành các chương trình con => che
dấu tất cả các lệnh cài đặt chi tiết trong các
chương trình con ở cấp độ chương trình chính.
- Trừu tượng hóa dữ liệu là định nghĩa các kiểu
dữ liệu trừu tượng. 3
Kiểu dữ liệu trừu tượng
(Abstract Data Types - ADT)
 Kiểu dữ liệu (Data type): là một tập hợp các
giá trị và một tập hợp các phép toán trên các giá trị đó.
 Có 2 loại kiểu dữ liệu:
- Kiểu dữ liệu sơ cấp
• Giá trị dữ liệu là đơn nhất. • Ví dụ: char, int, …
- Kiểu dữ liệu có cấu trúc (cấu trúc dữ liệu)
• Giá trị dữ liệu là sự kết hợp của các giá trị khác. • Ví dụ: mảng. 4
Kiểu dữ liệu trừu tượng
(Abstract Data Types - ADT)
Kiểu dữ liệu sơ cấp int
Kích thước lưu trữ Miền giá trị Các phép toán 2 bytes -32,768 to 32,767 +, -, *, /, % 4 bytes
-2,147,483,648 to 2,147,483,647
struct <tênkiểucấutrúc> { có uct Sự kết hợp
<kiểudữliệu>
<tênthànhphần1>; ệu của các giá trị … str
<kiểudữliệu>
<tênthànhphầnn>; dữ li úc };
<tênbiếnkiểucấutrúc>.<tênthànhphầni>; ểu = ; Ki cấu tr Các phép toán . = ; 5
Kiểu dữ liệu trừu tượng
(Abstract Data Types - ADT)
 Kiểu dữ liệu trừu tượng (ADT): một mô hình toán học
của cấu trúc dữ liệu mà nó xác định kiểu dữ liệu được
lưu trữ, các phép toán được hỗ trợ và các loại tham số trong phép toán.
 ADT xác định từng phép toán làm gì nhưng không xác
định cách thức nó thực hiện.
 Cài đặt kiểu dữ liệu trừu tượng:
– Tổ chức lưu trữ: cấu trúc dữ liệu (khai báo dữ liệu).
– Viết chương trình con thực hiện các phép toán (khai báo phép toán). 6
Kiểu dữ liệu trừu tượng
(Abstract Data Types - ADT)
 Ví dụ: kiểu dữ liệu trừu tượng danh sách đặc Tên phép toán Công dụng
makenullList(L) Khởi tạo một danh sách L rỗng
insertList(x,P,L) Xen phần tử có nội dung x
vào danh sách L tại vị trí P deleteList(P,L)
Xóa phần tử tại vị trí P trong danh sách L … … 7
Độ phức tạp của giải thuật (algorithm complexity)
Các bước tiếp cận một bài toán (từ bài toán đến chương trình): 1.
Mô hình hóa bài toán thực tế bằng một mô hình toán học. 2.
Tìm giải thuật (algorithms) trên mô hình này: chỉ nêu
phương hướng giải hoặc các bước giải một cách tổng quát. 3.
Hình thức hoá giải thuật bằng cách viết một thủ tục bằng
ngôn ngữ giả, rồi chi tiết hoá dần ("mịn hoá") các bước giải
tổng quát ở trên. Kết hợp việc dùng các kiểu dữ liệu trừu
tượng và các cấu trúc điều khiển trong ngôn ngữ lập trình
để mô tả giải thuật. 4.
Cài đặt giải thuật trong một ngôn ngữ lập trình (NNLT) cụ
thể. Các cấu trúc dữ liệu được cung cấp trong NNLT được
dùng để thể hiện các kiểu dữ liệu trừu tượng, các lệnh và
cấu trúc điều khiển trong NNLT được dùng để cài đặt các bước của giải thuật. 8
Độ phức tạp của giải thuật
• Giải thuật là chuỗi hữu hạn các thao tác để
giải một bài toán nào đó.
• Tính chất của giải thuật: – Hữu hạn – Xác định – Hiệu quả 9
Độ phức tạp của giải thuật
 Một bài toán có thể có nhiều cách giải khác nhau.
 Ta cần phải phân tích, đánh giá giải thuật để:
– Lựa chọn một giải thuật tốt nhất trong các giải
thuật để cài đặt chương trình giải quyết bài toán đặt ra.
– Cải tiến giải thuật hiện có để được một giải thuật tốt hơn.
 Khi phân tích giải thuật, ta thường quan tâm
nhiều nhất tới thời gian thực thi và không gian lưu trữ. 10
Độ phức tạp của giải thuật
Ví dụ: sắp xếp mảng có n phần tử theo thứ tự tăng dần.
 Giải thuật sắp xếp void Sort(int a[], int n){ Selectionsort
for (int i = 0; i < n-1; i++){
for (int j = i+1; j < n; j++){ if (a[i] > a[j]) { int tmp = a[i]; a[i] = a[j]; a[j] = tmp; } } } }
có độ phức tạp là O(n2)
 Giải thuật sắp xếp Quicksort có độ phức tạp O(n*log(n)). 11
Quy ước: log(n) được hiểu là log2n
Độ phức tạp của giải thuật
 Thời gian thực hiện một giải thuật là một hàm
của kích thước dữ liệu vào, ký hiệu T(n) trong
đó n là kích thước (độ lớn) của dữ liệu vào.
- Ví dụ : Chương trình tính tổng của n số có thời
gian thực hiện là T(n) = cn trong đó c là một hằng số.
 Thời gian thực hiện giải thuật là một hàm
không âm, tức là T(n)  0  n  0. 12
Độ phức tạp của giải thuật
 Thời gian thực hiện giải thuật không chỉ phụ
thuộc vào kích thước mà còn phụ thuộc vào
tính chất của dữ liệu vào.
 Ta thường coi T(n) là thời gian thực hiện giải
thuật trong trường hợp xấu nhất trên dữ liệu
vào có kích thước n, tức là: T(n) là thời gian
lớn nhất để thực hiện giải thuật đối với mọi dữ
liệu vào có cùng kích thước n. 13
Độ phức tạp của giải thuật
 Trong những ứng dụng thực tiễn, chúng ta không
cần biết chính xác hàm T(n) mà chỉ cần biết một
ước lượng đủ tốt của nó.
 Ước lượng thường dùng nhất là ước lượng cận
trên O-lớn. “big-Oh” O-lớn, “big-Omega“ Ω-lớn, “big-Theta” Θ-lớn
 Cho một hàm T(n), T(n) gọi là có độ phức tạp f(n)
nếu tồn tại các hằng C, N0 sao cho T(n) ≤ Cf(n)
với mọi n ≥ N0 (tức là T(n) có tỷ suất tăng là f(n)) và kí hiệu T(n)=O(f(n)).
 Chú ý: O(Cf(n))=O(f(n)) với C là hằng số. Ðặc biệt O(C)=O(1). 14
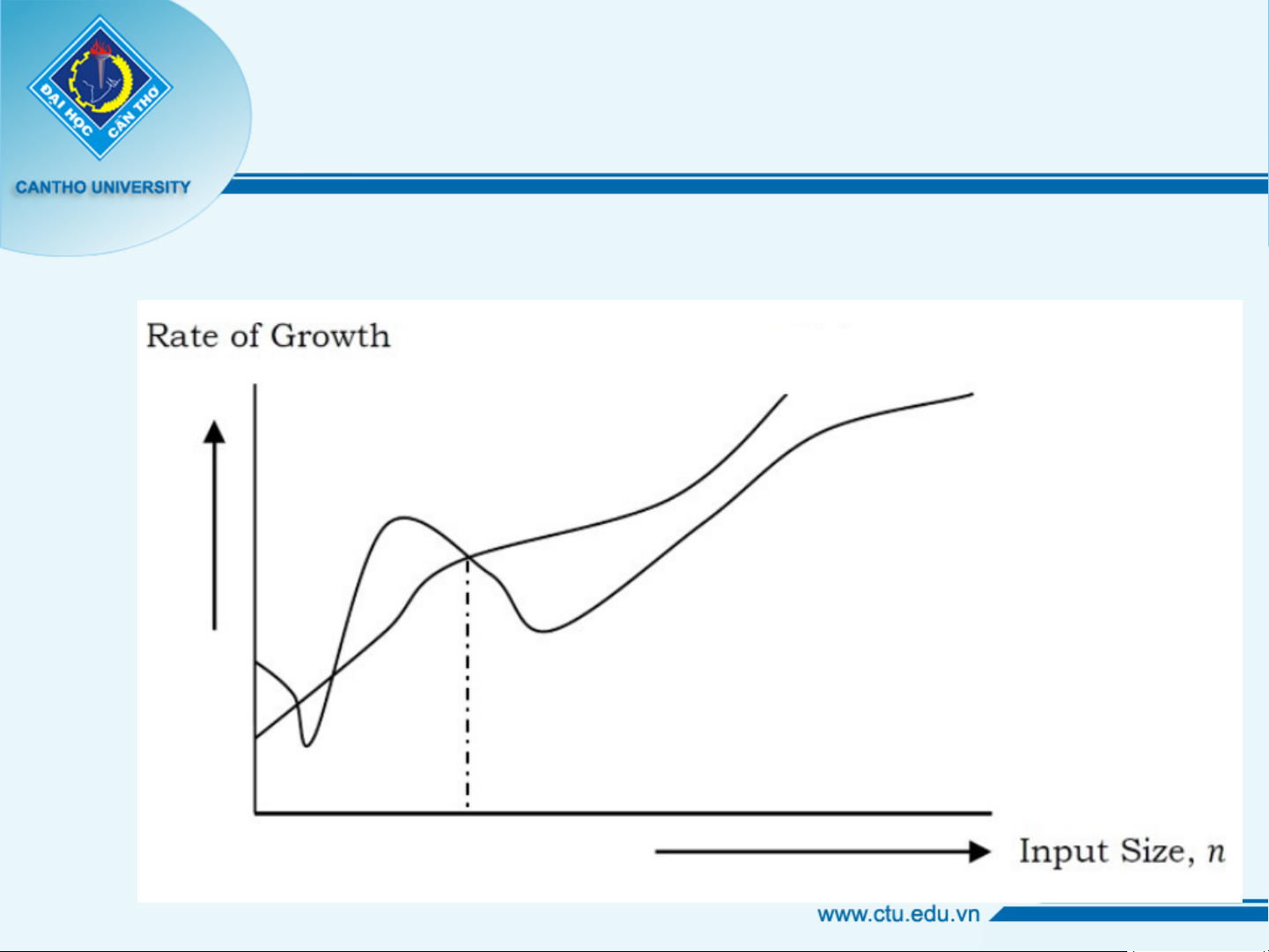
Độ phức tạp của giải thuật
 Ước lượng cận trên O-lớn Cf(n) T(n)
Cho một hàm T(n), T(n) gọi là có độ phức
tạp f(n) nếu tồn tại các hằng C, N0 sao
cho T(n) ≤ Cf(n) với mọi n ≥ N0 và kí hiệu T(n)=O(f(n)). N0 15
Data Structures And Algorithms Made Easy, Narasimha Karumanch,
CareerMonk Publications, 2017.
Độ phức tạp của giải thuật
Ví dụ: cho một hàm T(n) = n2 + 2n + 1. Hãy chứng
minh rằng T(n) = O(n2)? (Tìm độ phức tạp của T(n)?)
 Tìm C và N0 sao cho T(n) ≤ Cf(n) hay n2 + 2n + 1 ≤ C*n2 với mọi n ≥ N0.
 Đặt N0=1, thì 1 ≤ n ≤ n2 với mọi n ≥ 1(tức n ≥ N0).
Do đó, ta có: 1 + 2n + n2 ≤ n2 + 2n2 + n2 = 4n2 =Cf(n) Vậy, C=4. T(n)=O(n2) 16
Độ phức tạp của giải thuật
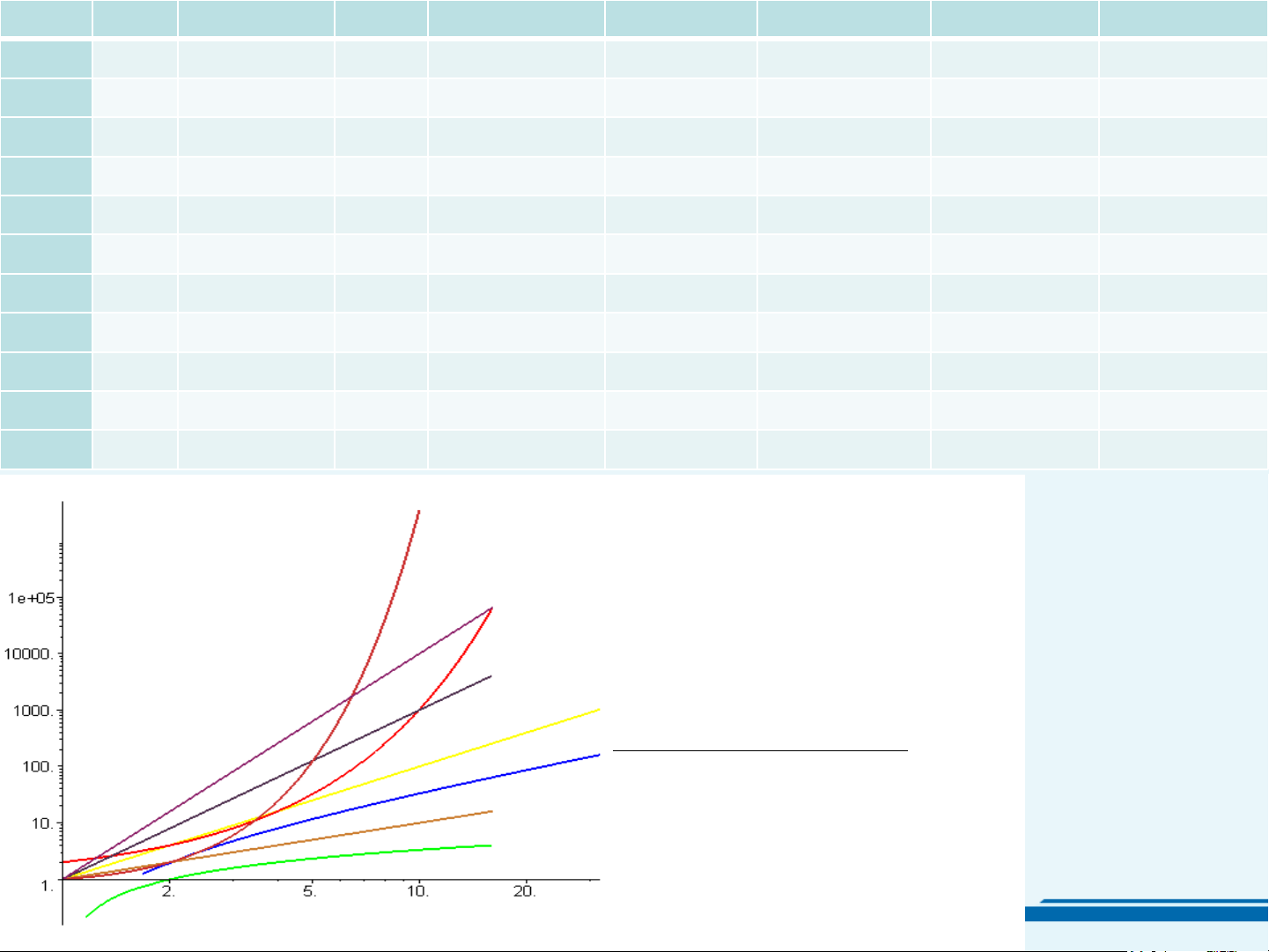
 Các dạng phức tạp thường gặp Hàm thể hiện Dạng phức tạp
Thời gian thực hiện độ phức tạp Hằng O(1) Lôgarit log(n) O(log(n)) Tuyến tính n O(n) Dạng n*log(n) O(n*log(n)) đa Bậc hai n2 thức O(n2) Khối n3 O(n3) Mũ 2n,n!,nk Dạng O(2n), O(n!), O(nk) mũ
 Một giải thuật có độ phức tạp hàm mũ thì phải tìm
cách cải tiến giải thuật. 17 n
O(1) O(log(n)) O(n) O(nlog(n)) O(n2) O(n3) O(2n) O(n!) 1 1 0 1 0 1 1 2 1 2 1 1 2 2 4 8 4 2 4 1 2 4 8 16 64 16 24 8 1 3 8 24 64 512 256 40320 16 1 4 16 64 256 4096 65536 2.092E+13 32 1 5 32 160 1024 32768 4.29E+09 2.631E+35 64 1 6 64 384 4096 262144 1.84E+19 1.269E+89 128 1 7 128 896 16384 2097152 3.4E+38 3.86E+215 256 1 8 256 2048 65536 16777216 1.16E+77 #NUM! 512 1 9 512 4608 262144 1.34E+08 1.3E+154 #NUM! 1024 1 10 1024 10240 1048576 1.07E+09 #NUM! #NUM! http:/ log(n) color=green /f n color=gold ac ul nlog(n) color=blue ty .juni nhí n2 color=yellow ata.edu/r t p n3 color=violet phé n4 color=purple hodes Số /c s2/c 2n color=red h12a.ht n! color=maroon m 18 Kích thước n
Ví dụ: nếu chúng ta lấy một máy tính loại trung bình của
năm 2008 với giả định rằng nó có thể thực hiện khoảng
50,000,000 phép toán cơ bản mỗi giây. Algorithm n=10 n=20 n=50 n=100 1,000 10,000 100,000 O(1) < 1 sec.
< 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. O(log(n)) < 1 sec.
< 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. O(n) < 1 sec.
< 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. O(n*log(n)) < 1 sec.
< 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. < 1 sec. O(n2) < 1 sec.
< 1 sec. < 1 sec. < 1 sec. < 1 sec. 2 sec. 3-4 min. 5.55 231.5 O(n3) < 1 sec.
< 1 sec. < 1 sec. < 1 sec. 20 sec. hours days 260 O(2n) < 1 sec. < 1 sec. treo treo treo treo days O(n!) < 1 sec. treo treo treo treo treo treo O(nn) 3-4 min. treo treo treo treo treo treo
https://introprogramming.info/english-intro-csharp-book/read- 10,0003/50,000,000/(60phut* 19
online/chapter-19-data-structures-and-algorithm-complexity/ 60giay) = 5.55 giờ
Tính độ phức tạp của giải thuật
Bài tập: giả sử máy tính có thể thực hiện 1 hoạt
động chính của giải thuật trong 1 micro giây (10-6 giây).
 Xác định thời gian (số năm) thực hiện giải thuật
có độ phức tạp O(2n), O(3n) và O(n!) khi n=10,
n=40 và n=100? (1 năm có 365.2425 ngày)
 Nếu tuổi thọ của một hành tinh khoảng 20 tỷ
năm thì hành tinh đó vẫn còn tồn tại khi giải
thuật có độ phức tạp O(2n) với n lần lượt có giá
trị là 40 và 100 thực hiện xong? 20