Chứng minh ma trận suy biến và ma trận khả nghịch | Toán Cao Cấp | Trường Đại học Thủy Lợi
Chứng minh ma trận suy biến và ma trận khả nghịch của Trường Đại học Thủy Lợi. Hi vọng tài liệu này sẽ giúp các bạn học tốt, ôn tập hiệu quả, đạt kết quả cao trong các bài thi, bài kiểm tra sắp tới. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.
Preview text:
*Biên soạn: Thầy Đặng Thành Nam
Thời gian làm bài: 180 phút (không kể thời gian giao ề)
Câu 1 [Q884749782] Cho A,B là các ma trận vuông cấp khả nghịch. Chứng minh rằng nếu n A + B khả nghịch thì −1 −1 cũng khả nghịch.
Câu 2 [Q775191769] Chứng minh rằng ma trận A vuông cấp n thoả mãn
akA + ak−1A +...+a1A + a0E = 0(a0 ≠ 0) thì ma trận khả nghịch và tìm ma trận nghịch ảo của nóA .
Câu 3 [Q463902904] Cho A,B là các ma trận thực vuông cấp khác nhau và thoả mãn iều kiện n A3 = B3 và 2 2 Chứng minh rằng ma trận 2 2 suy biến.
A B = BA . A + B Câu 4 [Q420078489] Cho là ma trận vuông. Điều kiện ể A A là ma trận ối xứng là A′ = A; iều kiện ể A là ma trận phản ối xứng là A′ = −A. Chứng minh rằng: a) Mọi ma trận phản ối xứng cấp lẻ ều suy biến.
- Mọi ma trận vuông cấp lẻ thì A A − A′ suy biến.
- Mọi ma trận vuông ều có thể phân tích thành tổng của một ma trận ối xứng và một ma trận phản ối xứng cùng cấp.
- Nếu là ma trận phản ối xứng cấp lẻ thì A E − A khả nghịch.
- Mọi giá trị riêng của ma trận thực ối xứng ều là các số thực; mọi giá trị riêng của ma trận thực phản ối xứng ều bằng 0 hoặc thuần ảo.
Câu 5 [Q274670397] Cho ma trận A vuông cấp thoả mãn n 2A3 − A = E. Chứng minh rằng ma trận E + 2A khả nghịch và tìm ma trận nghịch ảo của nó.
Câu 6 [Q577023277] Cho A,B là hai ma trận vuông cấp n ≥ 2 thoả mãn AB + A + B = O. Chứng minh rằng nếu A khả nghịch thì B khả nghịch.
Câu 7 [Q134708130] Cho A,B là hai ma trận vuông cùng cấp thoả mãn AB + 2019A + 2020B = O. Chứng minh
rằng các ma trận A + 2020E và B + 2019E khả nghịch.
Câu 8 [Q994907066] Cho A,B là hai ma trận vuông cùng cấp, có cấp là số lẻ thoả mãn AB = O. Chứng minh rằng ít nhất một trong hai ma trận A + A′ và B + B′ suy biến.
Câu 9 [Q520644347] Cho A = (aij)n×n với aij = −1,∀i = j;aij ∈ {0,2019},∀i ≠ j. Chứng minh rằng ma trận A khả nghịch.
Câu 10 [Q348005830] Cho A,B là hai ma trận vuông cấp thoả mãn n A2019 = O và B(A − E) = A + 3E. Chứng minh rằng ma trận B khả nghịch.
Câu 11 [Q366962072] Cho A,B là hai ma trận vuông cấp thoả mãn n A2019 = O và A + 2019B = AB. Chứng minh rằng ma trận B suy biến.
Câu 12 [Q273522021] Cho là ma trận vuông cấp A n. Chứng minh rằng nếu tồn tại số tự nhiên m sao cho Am = O thì các ma trận E − A và E + A khả nghịch.
Câu 13 [Q206185077] Cho A,B là hai ma trận vuông cấp thoả mãn n AB = BA và tồn tại các số nguyên dương m,p sao cho Am = O,Bp = O. Chứng minh rằng các ma trận E − A − B và E + A + B khả nghịch. Câu 14 [Q755163710] Cho A,B là hai ma trận vuông thực cấp 2019 thoả mãn:
det(A) = det(A + B) = det(A + 2B) =...= det(A + 2019B) = 0.
Chứng minh rằng với mọi x,y ∈ R ta có det(xA + yB) = 0.
BIÊN SOẠN: THẦY ĐẶNG THÀNH NAM – DUY NHẤT TẠI
Câu 15 [Q772233037] Cho ma trận A vuông cấp n. Chứng minh rằng nếu tồn tại số nguyên dương m thoả mãn m thì ma trận khả nghịch.
Câu 16 [Q035411977] Cho ma trận vuông cấp thoả mãn A n A2019 = 2019A. Chứng minh rằng ma trận A − E khả nghịch.
Câu 17 [Q657564177] Cho hai ma trận A,B vuông cùng cấp sao cho n E + AB khả nghịch. Chứng minh rằng
Câu 18 [Q144505346] Cho ma trận A = (aij)n×n với 0 ≤ aij < 1 và 0 < ∑ aij < 1,∀i,j = 1,2,...,n. Chứng i=1 minh rằng ma trận E − A khả nghịch.
Câu 19 [Q734345863] Cho A,B là hai ma trận vuông cùng cấp thoả mãn A2019 = 0,AB = A + B. Chứng minh rằng det(B) = 0.
Câu 20 [Q467231313] Cho A,B là hai ma trận vuông cùng cấp thoả mãn B2020 = 0,AB = 2A + 3B. Chứng minh rằng det(A) = 0.
Câu 21 [Q637018104] Cho A,B là hai ma trận vuông cùng cấp thoả mãn Bk = 0,AB = A + B,(k ∈ N∗). Chứng minh rằng det(A + B) = det(A).
Câu 22 [Q383488013] Cho A,B là hai ma trận vuông cùng cấp thoả mãn A2008 = E,B2009 = 0 và
AB + 4A + 2009B = 0. Chứng minh rằng (A + B) là ma trận không suy biến.
Câu 23 [Q386315904] Cho A,B là hai ma trận vuông cùng cấp thoả mãn A1999 = E,B2000 = E và AB = BA. Chứng minh rằng (A + B + E) là ma trận không suy biến.
Câu 24 [Q681868868] Cho ma trận A vuông cấp thoả mãn n A3 + 13A2 + 36A − 3E = 0. Chứng minh rằng ma
trận X = A + 9E khả nghịch và tìm ma trận nghịch ảo X−1 của nó theo A.
Câu 1 Có A(A−1 + B−1)B = AA−1B + AB−1B = EB + AE = B + A.
Do ó det(B + A) = det(A(A−1 + B−1)B) = det(A)det(A−1 + B−1)det(B).
Do det(A) ≠ 0;det(B) ≠ 0;det(A + B) ≠ 0 ⇒ det(A−1 + B−1) ≠ 0.Ta có iều phải chứng minh.
Câu 2 Có k k k−1 k−1 1 0 a k−1 ak−1 k−2 a1 a A + a A +...+a A = −a E ⇔ A(−A −...− E) = E. 0
Điều ó chứng tỏ ma trận khả nghịch và −1 ak k−1 a1
A A = − A − A −...− E. a0 a0 a0
Câu 3 Có (A2 + B2)(A + B) = A3 + A2B + B2A + B3 = 2A3 + 2B2A = 2(A2 + B2)A.
Giả sử det(A B2) ≠ 0 khi ó A + B = 2A ⇔ A = B (mâu thuẫn với giả thiết).
Câu 5 Có (E + 2A)(aA2 + bA + cE) = 2aA3 + (a + 2b)A2 + (b + 2c)A + cE.
Ta sẽ chọn sao cho 3 2 3 b = −
a,b,c 2aA + (a + 2b)A + (b + 2c)A = 2A − A ⇔ ⎨ ⇔ ⎨.
(E + 2A)(A − A − E) = 2A − A − E = E − E = E
Điều ó chứng tỏ ma trận khả nghịch và có ma trận nghịch ảo là −1 4 2 2 1
BIÊN SOẠN: THẦY ĐẶNG THÀNH NAM – DUY NHẤT TẠI
Câu 6 Có biến ổi từ giả thiết có A−1 như sau:
AB + A + B = O ⇒ A (AB + A + B) = O ⇔ A AB + A A + A B = O −1 −1 −1
⇔ B + E + A B = O ⇔ B(E + A ) = −E ⇒ det(B)det(E + A ) = det(−E).
Do ó det(B) ≠ 0;det(E + A−1) ≠ 0. Ta có iều phải chứng minh.
Câu 7 Có AB + 2019A + 2020B = O ⇔ (A + 2020E)(B + 2019E) = 2019.2020E.
Do ó det(A + 2020E).det(B + 2019E) = det(2019.2020E).
Suy ra det(A + 2020E) ≠ 0;det(B + 2019E) ≠ 0. Ta có iều phải chứng minh.
Câu 9 Theo ịnh nghĩa về ịnh thức có: det(A) − (−1)n chia hết cho 2019 do ó det(A) ≠ 0.
Câu 10 Có B(A − E) = A + 3E ⇒ det(B)det(A − E) = det(A + 3E).
Ta cần chứng minh det(A − E) ≠ 0;det(A + 3E) ≠ 0.
2019 2019 2019 2018 2017 2017 2018
−E = −E = A − E = (A − E)(A + EA +...+E A + E ).
Lấy ịnh thức hai vế có det(A − E) ≠ 0.
Tương tự có (3E)2019 = A2019 + (3E)2019 = (A + 3E)(A2018 − 3EA2017+...+(3E)2018).
Lấy ịnh thức hai vế có det(A + 3E) ≠ 0.
Câu 11 Có A2019 = O ⇒ (det(A))2019 = 0 ⇔ det(A) = 0.
Biến ổi 2019B = AB − A = A(B − E) ⇒ 2019n det(B) = det(A)det(B − E) = 0 ⇔ det(B) = 0.
Câu 12 Có E = Em = Em + Am = (E + A)(Em−1 − Em−2A+...+Am−1).
Lấy ịnh thức hai vế có det(E + A) ≠ 0.
Vì Am = 0 ⇒ A2m+1 = 0 ⇒ E = E2m+1 = E2m+1 − A2m+1 = (E − A)(E2m + E2m−1A+...+A2m).
Lấy ịnh thức hai vế có det(E − A) ≠ 0.
Câu 13 Có AB = BA nên (A + B)m+p = ∑ Cmk +pAm+p−kBk = O. k=1
Do ó theo câu 12 có ngay iều phải chứng minh.
Câu 14 Ta có P(t) = det(A + tB) là a thức bậc 2019 mà theo giả thiết có P(0) = P(1) =...= P(2019) = 0. Do
ó P(t) là a thức bậc 2019 có 2020 nghiệm vì vậy P(t) = 0,∀t.
Đặt Q(t) = det(tA + B) = t2019 det(A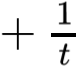 
B) = t2019P 
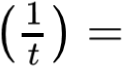t ≠ 0 ⇒ Q(t) = 0,∀t.
Nếu x = 0 ⇒ det(xA + yB) = det(yB) = y2019 det(B) = y2019Q(0) = 0.
Nếu x ≠ 0 ⇒ det(xA + yB) = x2019 det(A + xy B) = x2019P ( xy ) = 0.
Vậy với mọi x,y ∈ R ta có det(xA + yB) = 0.
A − 2019A = O ⇔ (A − E ) − 2019(A − E) = 2018E 2018 2017
⇔ (A − E)(A + A +...+A + E − 2019E) = 2018E 2018 2017
⇔ (A − E)(A + A +...+A − 2018E) = 2018E.
Lấy ịnh thức hai vế có det(A − E) ≠ 0.
BIÊN SOẠN: THẦY ĐẶNG THÀNH NAM – DUY NHẤT TẠI
Câu 17 Theo bất ẳng thức về hạng của ma trận ta có:
r((E − BA)(E + AB)) + n ⩾ r(E + AB) + r(E − BA) = n + r(E − BA)
r((E − BA)(E + AB)) ⩽ r(E − BA)
Vậy r((E − BA)(E + BA)) = r(E − BA). Điều ó chứng tỏ E − BA khả nghịch.
Câu 18 Giả sử ngược lại x2 sao cho
det(E − A) = 0 ⇒ ∃X = ≠ 0 (E − A)X = 0.
Giả sử |xk| = max{|xi|,i = 1,2,...,n} > 0. Xét phương trình thứ của hệ phương trình thuần nhất trên cók :
−ak1x1 − ak2x2−...+(1 − akk)xk−...−aknxn = 0 ⇒ xk = ak1x1 + ak2x2+...+aknxn. n n n Suy ra |xk| = |ak1x1 + ak2x2+...+aknxn| ≤ ∑ aki |xi| ≤ ∑ aki |xk| = (∑ aki)|xk| < |xk| (mâu thuẫn). | ||
Vậy det(E − A) ≠ 0, ta có iều phải chứng minh. Câu 19 Ta có A2019 = 0 ⇒ detA = 0 AB = A + B ⇔ (A − E)B = A ⇒ det(A − E)det(B) = det(A) = 0(∗). | ||
−E = 0 − E = A − E = (A − E)(A + EA +......+E A + E ) .
2018 2017 2017 2018 Kết hợp với
det(A − E)det(A + EA +......+E A + E ) = det(−E) ≠ 0 ⇒ det(A − E) ≠ 0.
Câu 20 Có B2020 = 0 ⇒ det(B) = 0.
2A = AB − 3B = (A − 3E)B ⇒ det(2A) = det(A − 3E)det(B) = 0 ⇒ 2 det(A) = 0 ⇒ det(A) = 0.
Câu 21 Có Bk = 0 ⇒ (detB)k = 0 ⇔ detB = 0.
Suy ra det(A + B) = det(AB) = detA.detB = 0.
Mặt khác AB = A + B ⇔ A(B − E) = B ⇒ det(A)det(B − E) = det(B) = 0(∗).
Mặt khác −E = 0 − Ek = Bk − Ek = (B − E)(Bk−1 + EBk−2+...+Ek−1).
Lấy ịnh thức hai vế có det(B − E)det(Bk−1 + EBk−2+...+Ek−1) = det(−E) ≠ 0 ⇒ det(B − E) ≠ 0. Kết
Câu 24 Xét phép nhân ma trận (A + 9E)(aA2 + bA + cE) = aA3 + (9a + b)A2 + (9b + c)A + 9cE
Ta tìm a,b,c sao cho aA3 + (9a + b)A2 + (9b + c)A = A3 + 13A2 + 36A ⇔ ⎨9a + b = 13 ⇔ ⎨ b = 4 (mục
9b + c = 36 c = 0 ích ể dùng ược giả thiết bài cho)
⇒ (A + 9E)(A + 4A) = A + 13A + 36A = 3E ⇔ (A + 9E)( A + A) = E ⇒ (A + 9E) = A + A.