











Preview text:
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ 1.1. SỐ THỰC 1.2. SỐ PHỨC 1.3. DÃY SỐ THỰC 9/19/2024 1
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ 1.1. SỐ THỰC
1.1.1. Các tính chất cơ bản của tập số thực
A. Sự cần thiết mở rộng tập số hữu tỉ - Tập các số tự nhiên 0, 1, 2, .. . - Tập các số nguyên
0, 1, 2, .. . p - Tập các số hữu tỉ q 0, , p q q
Tập số hữu tỉ với phép cộng và phép nhân và quan hệ có cấu trúc
trường sắp thứ tự toàn phần nhưng không đầy đủ, nghĩa là một tập
bị chặn trên chưa chắc tồn tại supremum, tương tự tập bị chặn dưới
chưa chắc tồn tại infimum. Chẳng hạn 2 {q
q 0;q 2} bị chặn nhưng không tồn tại supremum. 9/19/2024 2
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
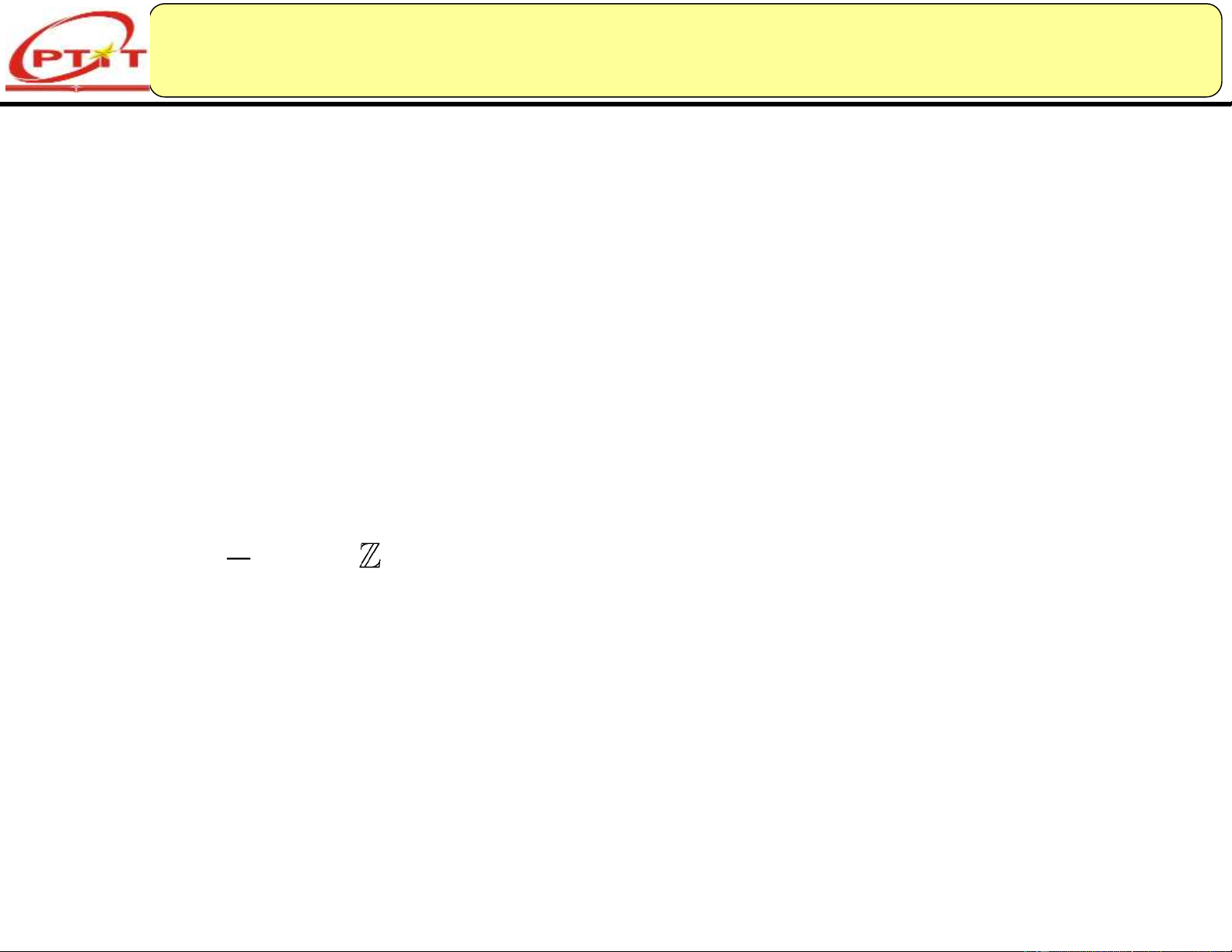
Do nhu cầu đòi hỏi của cuộc sống, tập các số tự nhiên , cơ sở của
phép đếm đã được mở rộng sang tập các số nguyên .
Sau đó, do trong không có các phần tử mà tích với 2 hoặc 3 bằng
1, nên nguời ta đã xây dựng tập các số hữu tỉ , đó là tập gồm các
số có thể được biểu diễn bởi tỉ số của hai số nguyên, tức là số thập
phân hữu hạn hoặc vô hạn tuần hoàn.
Nếu chỉ dừng lại trên tập số hữu tỉ thì trong toán học gặp phải
nhiều điều hạn chế, đặc biệt là gặp khó khăn trong việc giải thích
các hiện tượng của cuộc sống.
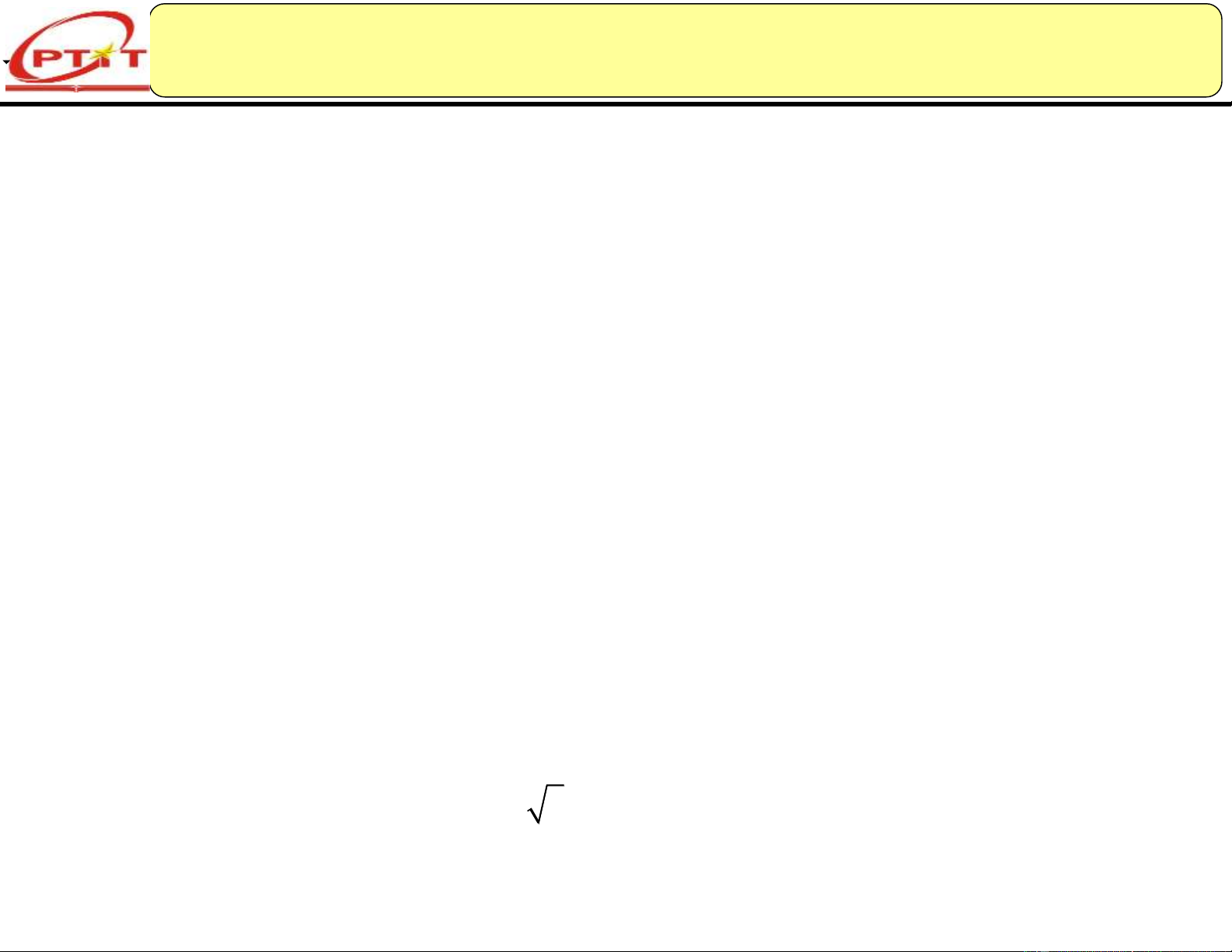
Chẳng hạn, việc tính đường chéo của hình vuông có kích thước
đơn vị. Đường chéo đó là 2 không thể mô tả bởi số hữu tỉ. 9/19/2024 3
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ B. Số vô tỉ p
Số hữu tỉ x có dạng x ; , p q ,q
0 . Thực hiện phép chia p cho q q
ta có thể đồng nhất dưới dạng sau và gọi là số thập phân
Có hai dạng số thập phân: số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn. tương ứng với k k 1 x x 10 x 10 x x 1 k 0 1 k x x 0 10 10k 10k
x x ,x x ...x x x ...x x x ...x ...x x ...x ... tương ứng với 0 1 2 k k k k k k k k k k 1 2 p 1 2 p 1 2 p p p p x x
x x 1 k 1 x x x . 0 k k k k 1 2 10 10
p 10k (10p 1) 9/19/2024 4
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
Ngược lại, mọi số thập phân hữu hạn hay vô hạn tuần hoàn đều
được biểu diễn dưới dạng một số hữu tỷ. Như vậy, ta có thể đồng
nhất tập các số hữu tỷ với tập các số thập phân hữu hạn hay vô hạn tuần hoàn.
Số thập phân vô hạn không tuần hoàn không biểu diễn được dưới p dạng ; , p q
. Ta gọi các số dạng này là số vô tỷ. q
Tập các số hữu tỷ và số vô tỷ gọi là số thực, ký hiệu . 9/19/2024 5
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
Tính chất 1: Tập (,,) là một trường.
1) Với mọi a,b : a +b , ab .
2) Với mọi a,b,c : (a+b)+c a+(b+c); (ab)c a(bc). (tính kết hợp)
3) Với mọi a,b : a+b b+a; ab ba. (tính giao hoán)
4) Phần tử trung hòa của phép cộng là 0 và phép nhân là 1
Với mọi a : a+0 0+a a; a.1 1.a a.
5) Phép nhân phân phối đối với phép cộng
Với mọi a,b,c : a(b+c) ab+ac; (b+c)a ba+ca.
6) Mọi số thực tồn tại phần tử đối của phép cộng:a , (a) : a (a) 0.
Mọi số thực khác 0 tồn tại phần tử nghịch đảo của phép nhân:
a *, a1* : aa 1 1; *\0. 9/19/2024 6
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
Tính chất 2: Tập là trường sắp thứ tự toàn phần. Đóng kín với tập các số thực dương.
1) Với mọi a : a a (tính phản xạ).
2) Với mọi a,b : a b và b a thì a = b (tính phản đối xứng)
3) Với mọi a,b, c : a b và b c thì a c (tính bắc cầu)
4) Với mọi a,b : a b hoặc b a (sắp thứ tự toàn phần)
5) Với mọi a,b,c : a b a c b c.
6) Với mọi a,b,c ; c 0: a b a c b c.
7) Với mọi a,b * : a b * và ab * . + + +
* là tập các số thực dương. + 9/19/2024 7
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
Tính chất 3: Tập , sắp thứ tự toàn phần, đầy đủ.
Cận trên đúng của X, ký hiệu supX: x X : x q x X : x q q sup X ( x X : x q ) q q 0, x X : q x 0 0
Cận dưới đúng của X, ký hiệu infX: x X : x q x X : x q q inf X ( x X : x q ) q q 0, x X : q x 0 0
Mọi tập con X khác rỗng của bị chặn trên trong đều có một cận
trên đúng thuộc và mọi tập con X khác rỗng của bị chặn dưới
trong đều có một cận dưới đúng thuộc . 9/19/2024 8
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
Nói chung supX, infX chưa chắc thuộc X.
Nếu M supXX thì M được gọi là phần tử lớn nhất của X, ký hiệu M maxX: x X : x M M x ma X M X
Nếu m infXX thì m được gọi là phần tử nhỏ nhất của X, ký hiệu m minX: x X : x m m n mi X m X 9/19/2024 9
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
1.1.2. Tập số thực mở rộng
Bổ sung vào tập số thực hai phần tử ký hiệu và nhận được
tập số thực mở rộng ký hiệu , { , .}
Các phép toán cộng (+), nhân (.) và quan hệ thứ tự của tập số thực mở rộng . 1. x :x ( ) ( ) x ;x ( ) ( ) x . 2. ( ) ( ) ;( ) ( ) . * 3. x : x( ) ( )x ;x( ) ( )x * x : x( ) ( )x ;x( ) ( )x . 4. ( )( ) ( )( ) ;( )( ) ( )( ) . 5. x : x ; ; . 0
Các trường hợp sau phép toán không thực hiện được:0. ; ; ; 0
Trong đó bao gồm cả hai trường hợp hoặc . 9/19/2024 10
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
1.1.3. Các khoảng, đoạn số thực
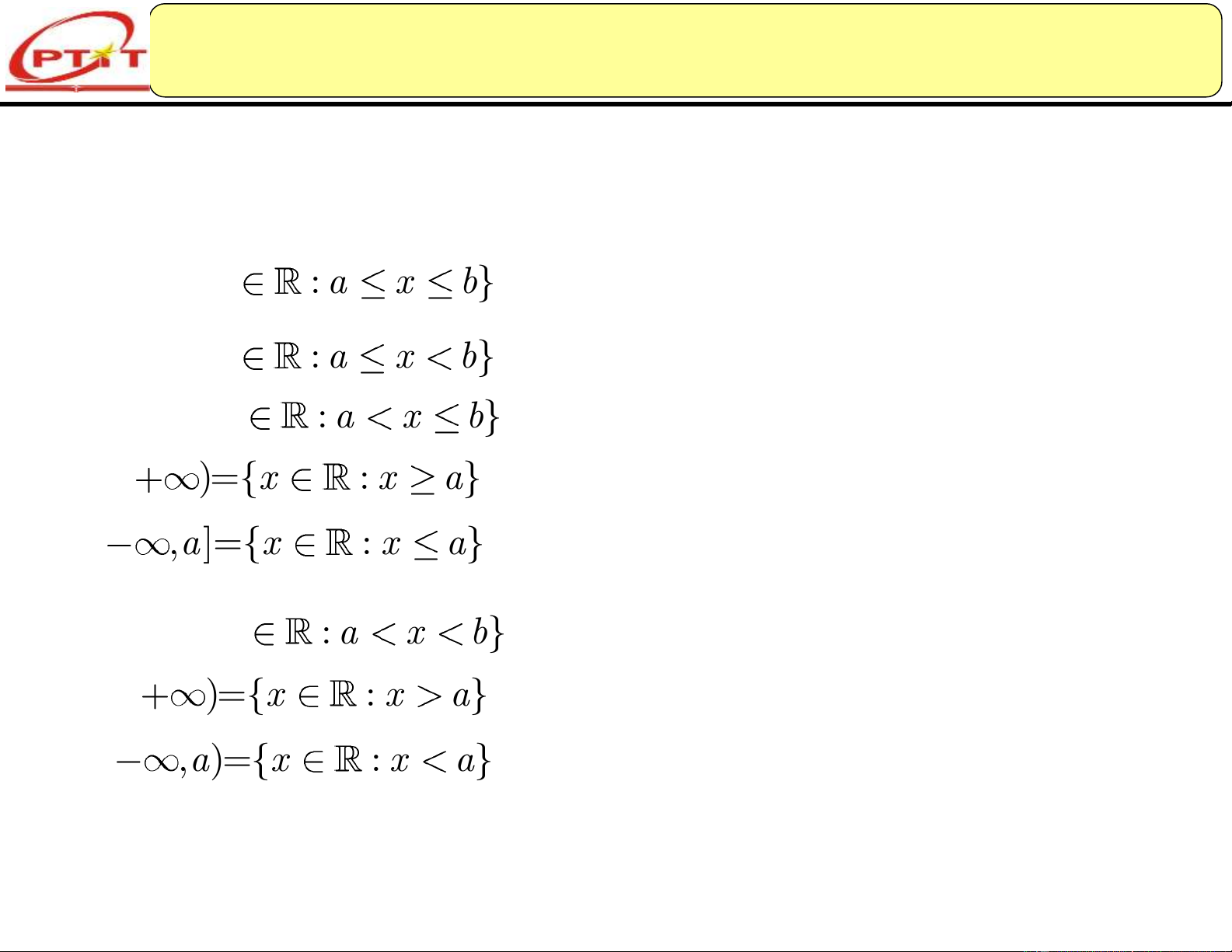
Cho a,b và a b, ta xét và ký hiệu các tập con sau đây của [ , a b]={x : a x }
b được gọi là đoạn hay khoảng đóng bị chặn [ , a b)={x : a x } b ( , a b]={x : a x } b [ , a )={x : x
a} được gọi là khoảng nửa đóng hoặc nửa mở ( ,a]={x : x a} ( , a b)={x : a x } b được gọi ( , a )={x : x a} là các khoảng mở (hữu hạn hoặc vô hạn) ( ,a)={x : x a}
Các số thực a, b gọi là các đầu mút của khoảng. 9/19/2024 11
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
1.1.4. Giá trị tuyệt đối của số thực
Định nghĩa: Giá trị tuyệt đối của số thực x ký hiệu |x| là số thực không âm xác định như sau: x khi x 0 x x khi x 0 Tính chất: 2 . 1 x
:| x | max{x, x }= x . 2 x :| x | 0 x 0 n n . 3 x,y : xy x y ; n *, x ,...,x : x x 1 n k k k 1 k 1 1 1 . 4 x * : . 5 x
,y : x y x y x x n n . 6 x,y : x y x y ; n *, x ,...,x : x x 1 n k k k 1 k 1
Dấu “=“ xảy ra khi và chỉ khi các số x ,..., x cùng dấu. 1 n 1 1 . 7 x,y : max(x,y) (x y | x
y |); min(x,y) (x y | x y |) 2 2 9/19/2024 12
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
1.1.5. Khoảng cách thông thường trong ℝ Tính chất: 9/19/2024 13
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ 1.2. TẬP SỐ PHỨC
1.2.1. Dạng đại số của số phức và các phép toán của số phức
1.2.1.1 Dạng đại số của số phức 2
z x iy;x,y , i 1
Re z x, Im z y là phần thực và phần ảo của z x iy
z x iy được gọi là số phức liên hợp với số phức z x iy x x 1 2 z x iy , z x iy ; z z 1 1 1 2 2 2 1 2 y y 1 2
Tập hợp tất cả các số phức ký hiệu . 9/19/2024 14
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
1.2.1.2 Các phép toán của số phức Phép cộng
(x iy ) (x iy ) (x x ) i(y y ) 1 1 2 2 1 2 1 2 Phép trừ
(x iy ) (x iy ) (x x ) i(y y ) 1 1 2 2 1 2 1 2 Phép nhân
(x iy )(x iy ) (x x y y ) i(x y y x ) 1 1 2 2 1 2 1 2 1 2 1 2 1 x y Phép chia i 2 2 2 2 x iy (số phức nghịch đảo) x y x y z x iy x x y y y x x y 1 1 1 1 1 2 1 2 1 2 1 2 z ; i 1 2 2 2 2 z z x iy 2 2 2 2 x y x y 2 2 2 2 9/19/2024 15
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ Tính chất 1.1
z z z z ;z z z z 1 2 2 1 1 2 2 1
z (z z ) (z z ) z ; z (z z ) (z z )z 1 2 3 1 2 3 1 2 3 1 2 3
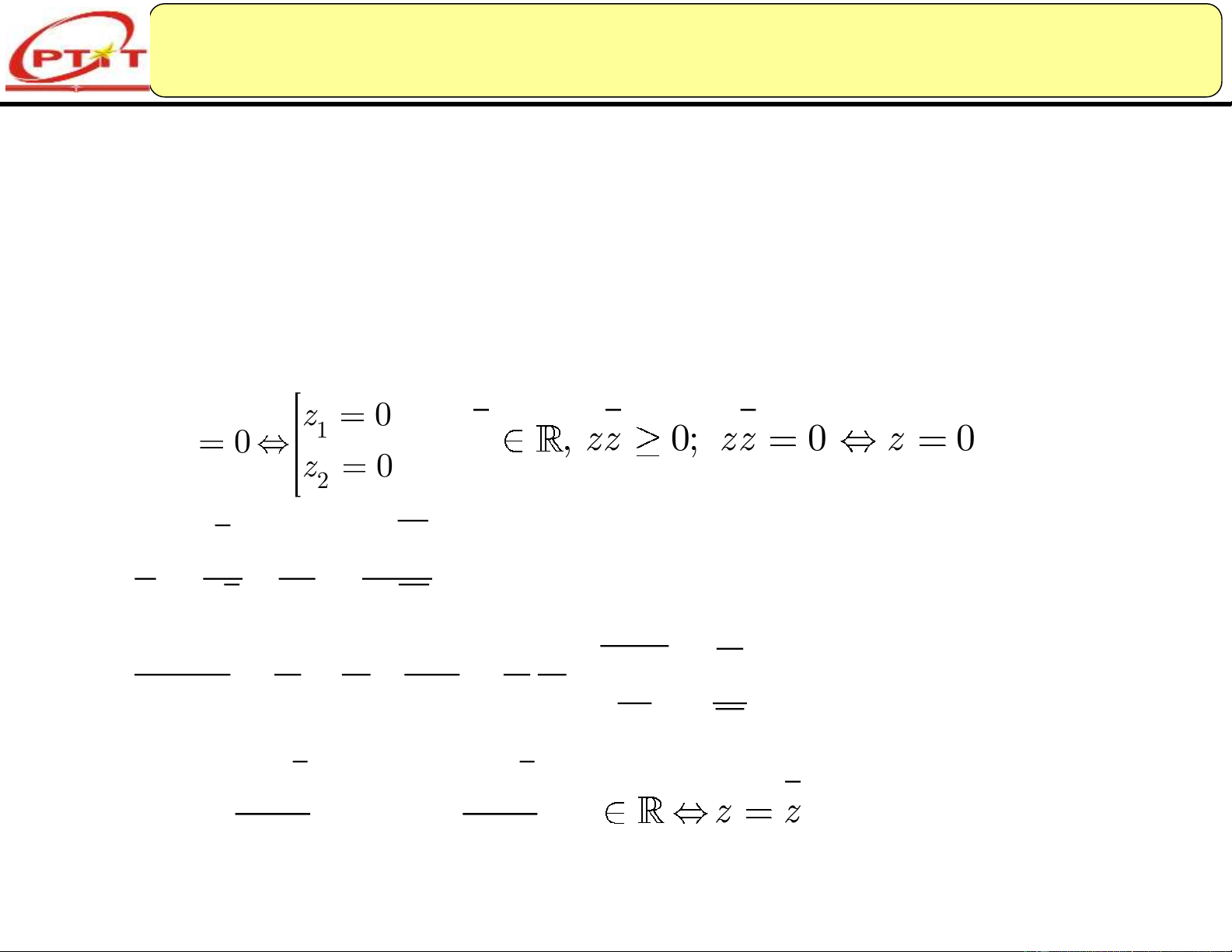
z (z z ) z z z z 1 2 3 1 2 1 3 z 0 1 z z 0 zz , zz 0; zz 0 z 0 1 2 z 0 2 1 z z z z 1 1 2 ; z zz z2 z z 2 2 z z 1 1
z z z z ; z z z z ; 1 2 1 2 1 2 1 2 z 2 z2 z z z z Re z ; Im z ; z z z 2 2i 9/19/2024 16
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ Ví dụ 1.1: 2 2 2 2 z x iy z (x iy) (x y ) i(2xy) 2 2
zz (x iy)(x iy) x y Ví dụ 1.2:
(3 2i)(1 3i) 3 6 ( i 2 9) 9 7i 5 5 5i i i
(4 3) i( 4 3) 5(1 )(4 3 ) 7 i 4 3i 16 9 25 5 5 2 3 4 5
i i i i i
i 1 i 1 i i i(1 i) i(1 i) 1 i 1 i 1 i 1 i
(1 i)(1 i) 2 2 2
Ví dụ 1.3: Tìm x, y thỏa mãn phương trình
5(x y)(1 i) (x 2i)(3 i) 3 11i 2x 5y 2 3 7 2x 5y 2 i(4x 5y 6) 3 11i x 3, y 4x 5y 6 11 5 9/19/2024 17
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ z iw 1 Ví dụ 1.4: Giải hệ phương trình
2z w 1 i
Nhân i vào phương trình thứ nhất, cộng vào phương trình thứ hai ta được 1 2i
(1 2i)(2 i) 4 3i
(2 i)z 1 2i z 2 i 5 5 1 z ( i 1 z) 1 3i 3 i w ( i z 1) i 2 i i 5 5 Cách 2: 2 i 4 3i 1 1 1 1 z i i 1 2i 5 D 1 2i;D 2 i;D 1 i 2 1 z 1 i 1 w 2 1 i 1 i 3 i w 1 2i 5
Ví dụ 1.5: Giải phương trình 2
z 2z 10 0 2 2 2 2 z 2z 10 (z 1) 9 (z 1) (3i) (z 1 3i)(z 1 3i) 0 z 1 3i,z 1 3i 1 2 9/19/2024 18
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
1.2.2. Công thức Euler i e cos i sin i i e e i cos e cos i sin 2 i e cos i sin i i e e sin 2i 9/19/2024 19
CHƯƠNG I: TẬP SỐ VÀ GIỚI HẠN CỦA DÃY SỐ
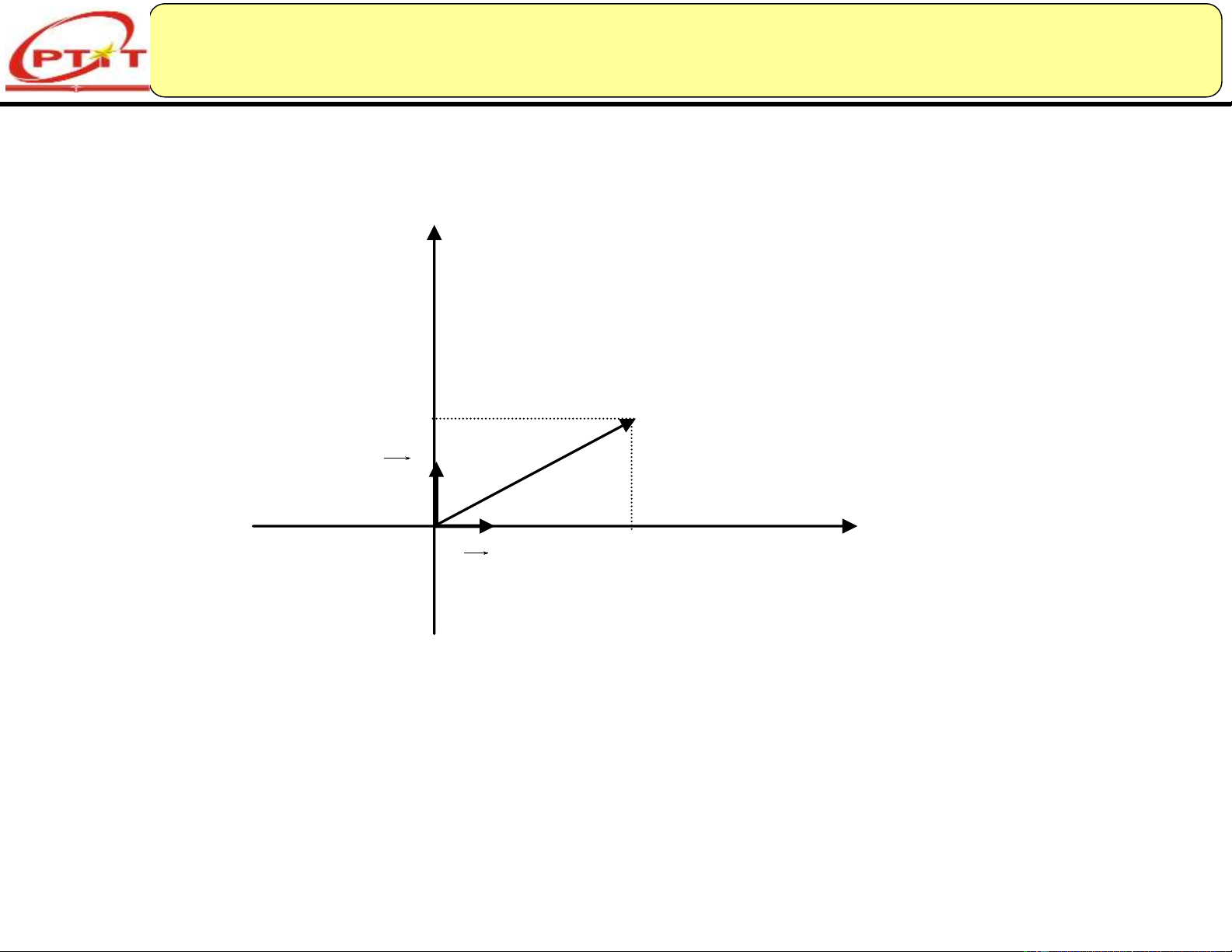
1.2.3. Biểu diễn hình học của số phức, mặt phẳng phức y y M j O x x i
Đồng nhất mỗi điểm có tọa độ (x,y) với số phức z x iy.
Lúc đó mặt phẳng này được gọi là mặt phẳng phức. 9/19/2024 20




