Chương 1-3 và Nguyên Lý Thứ Hai | Nhiệt động học và vật lý phân tử | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Nguyên lý số không của Nhiệt động lực học: - Nội dung: Nếu hai hệ (vật) có cân bằng nhiệt với cùng một hệ (vật) thứ ba thì chúng cũng cân bằng nhiệt với nhau. Ý nghĩa: Khi 2 vật cân bằng nhiệt với nhau thì chúng có cùng nhiệt độ có thể dùng các thiết bị, ví dụ nhiệt kế, … như hệ (vật) thứ ba và cho tiếp xúc với các vật cần đo nhiệt độ cho đến khi có cân bằng nhiệt để xác định được nhiệt độ của các vật. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Nhiệt động học và vật lý phân tử 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 0.9 K tài liệu
Tác giả:
Preview text:
Lý thuyết
(Chương 1. Nhiệt độ và nguyên lý số không nhiệt động lực học)
a. Các phương pháp đo nhiệt độ: thông qua trạng thái cân bằng nhiệt của vật cần đo nhiệt độ với
vật đo để chỉ thị nhiệt độ trực tiếp hoặc gián tiếp.
có thể đo nhiệt độ trên cơ sở nguyên lý số không của NĐLH, trong đó dựa vào sự cân bằng nhiệt giữa các vật.
b. Nguyên lý số không của Nhiệt động lực học:
- Nội dung: Nếu hai hệ (vật) có cân bằng nhiệt với cùng một hệ (vật) thứ ba thì chúng cũng cân bằng nhiệt với nhau.
Ý nghĩa: Khi 2 vật cân bằng nhiệt với nhau thì chúng có cùng nhiệt độ có thể dùng các thiết
bị, ví dụ nhiệt kế, … như hệ (vật) thứ ba và cho tiếp xúc với các vật cần đo nhiệt độ cho đến khi
có cân bằng nhiệt để xác định được nhiệt độ của các vật.
(Chương 2. Nội năng và nguyên lý thứ nhất của nhiệt động lực học)
a. Khái niệm chung về nội năng:
Nội năng U là năng lượng ứng với tổng các dạng năng lượng (các vận động) bên trong của hệ.
Nội năng chỉ phụ thuộc vào trạng thái của hệ và bao gồm:
- Động năng do chuyển động nhiệt của các phân tử (động năng tịnh tiến và quay), phụ thuộc
vào nhiệt độ T của hệ.
- Thế năng gây bởi lực tương tác giữa các phân tử, phụ thuộc vào khoảng cách r giữa chúng,
hay nói cách khác phụ thuộc vào thể tích V của hệ.
- Năng lượng tương tác bên trong phân tử (của các vỏ điện tử, các nguyên tử và ion, năng
lượng trong hạt nhân nguyên tử)
Như vậy nội năng U phụ thuộc vào nhiệt độ T và thể tích V của hệ.
b. Phân biệt U với nhiệt lượng và công: - Nhiệt lượng (nhiệt):
Nhiệt lượng Q là phần năng lượng trao đổi dưới dạng động năng của chuyển động hỗn loạn của
hệ. Nhiệt là năng lượng chuyển động nhiệt trao đổi trực tiếp giữa các phân tử của hệ với các phân tử ở
bên ngoài hệ khi có chênh lệch về nhiệt độ.
Theo quy ước, giá trị Q > 0 nếu hệ nhận nhiệt từ bên ngoài, Q < 0 nếu hệ tỏa nhiệt ra bên ngoài.
Khi Q > 0 thì U tăng, khi Q < 0 thì U giảm. - Công:
Công cơ học A là phần năng lượng trao đổi dưới dạng động năng của chuyển động có hướng của hệ.
Theo quy ước, giá trị A > 0 nếu hệ sinh (thực hiện) công, A < 0 nếu hệ nhận công từ bên ngoài.
Khi A < 0 thì U tăng, khi A > 0 thì U giảm.
Như vậy sự trao đổi năng lượng thông qua nhiệt và công đã làm biến đổi nội năng của hệ.
Công và nhiệt chỉ xuất hiện trong quá trình biến đổi trạng thái của hệ. Công và nhiệt là hàm của quá trình.
(Chương 2. Nội năng và nguyên lý thứ nhất của nhiệt động lực học)
a. Phát biểu nội dung nguyên lý thứ nhất của NĐLH:
+ Biểu thức: U = Q – A
b. Giải thích tại sao không thể chế tạo được động cơ nhiệt vĩnh cửu loại I (Ý nghĩa của nguyên lý thứ nhất):
Nguyên lý I là một trường hợp riêng của định luật bảo toàn và chuyển hóa năng lượng áp dụng
vào các hiện tượng, quá trình nhiệt động, nêu lên mối quan hệ định lượng giữa công, nhiệt và nội năng
của hệ. Không thể chế tạo được động cơ vĩnh cửu loại I vì động cơ này không thể hoạt động do trái với
định luật bảo toàn năng lượng.
Thật vậy, xét động cơ vĩnh cửu loại I là loại động cơ làm việc tuần hoàn, sinh công mà không
nhận nhiệt, hoặc sinh công nhiều hơn năng lượng nhận vào. Động cơ hoạt động được cần có cơ năng.
Cơ năng này không thể tự sinh ra mà phải được chuyển thành từ một dạng năng lượng ban đầu, ví dụ là
năng lượng của nước, hơi nước (do đốt củi, than, dầu, ...).
Nếu động cơ vĩnh cửu loại I làm việc tuần hoàn nhờ sinh công mà không trao đổi (nhận hoặc
tỏa) nhiệt thì A > 0 và Q = 0. Theo công thức NL thứ nhất của NĐLH: U = Q – A.= – A < 0 (1)
Mặt khác do hệ thay đổi trạng thái nhưng sau đó trở về trạng thái ban đầu (làm việc tuần hoàn) nên
năng lượng bên trong của hệ - nội năng là không thay đổi biến thiên nội năng: U = 0 (2)
So sánh (2) và (1) là mâu thuẫn, nên không thể chế tạo được động cơ vĩnh cửu loại I.
c. Áp dụng nguyên lý thứ nhất của nhiệt động lực học để giải thích hiện tượng nhiệt độ của hệ
khí giảm trong quá trình giãn nở đoạn nhiệt:
Quá trình đoạn nhiệt là quá trình xảy ra mà không có sự trao đổi nhiệt hay vật chất giữa hệ và
môi trường ngoài, Q = 0, và năng lượng được trao đổi chỉ là công A.
Theo công thức NL thứ nhất của NĐLH: U = Q – A.= – A. Khi hệ tăng thể tích (quá trình giãn
nở) sẽ cần thực hiện một công A > 0 U < 0. Có U = U2 – U1 với U1, U2 lần lượt là nội năng ban
đầu và sau khi giãn nở đoạn nhiệt của hệ U2 < U1 hay nội năng của hệ giảm.
Thực nghiệm chứng minh rằng nội năng U tỷ lệ thuận với nhiệt độ T của hệ khi nội năng
giảm chứng tỏ nhiệt độ của hệ giảm
(Chương 2. Nội năng và nguyên lý thứ nhất của nhiệt động lực học) Chú ý:
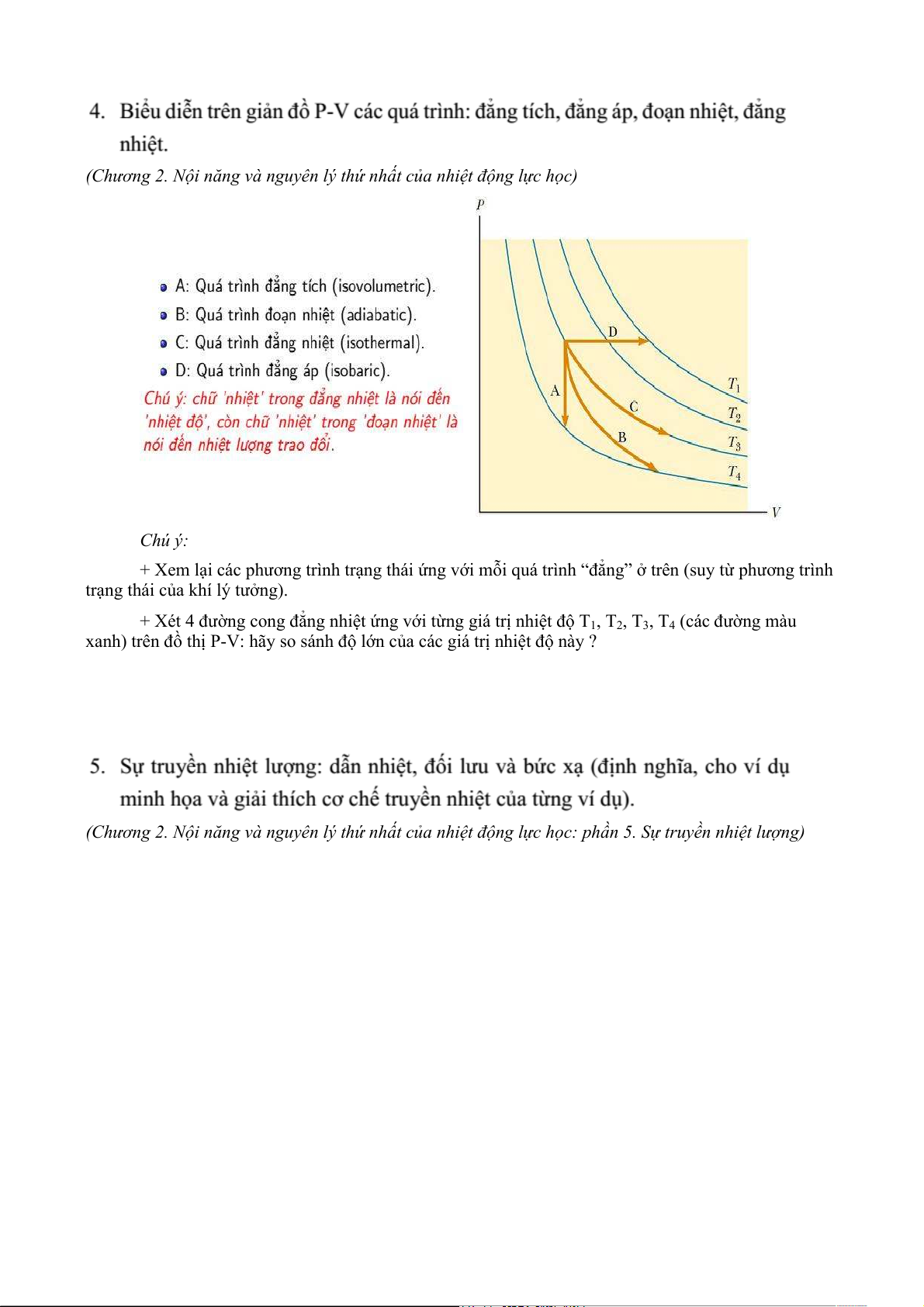
+ Xem lại các phương trình trạng thái ứng với mỗi quá trình “đẳng” ở trên (suy từ phương trình
trạng thái của khí lý tưởng).
+ Xét 4 đường cong đẳng nhiệt ứng với từng giá trị nhiệt độ T1, T2, T3, T4 (các đường màu
xanh) trên đồ thị P-V: hãy so sánh độ lớn của các giá trị nhiệt độ này ?
(Chương 2. Nội năng và nguyên lý thứ nhất của nhiệt động lực học: phần 5. Sự truyền nhiệt lượng)
(Chương 3. Động học chất khí)
(Chương 3. Động học chất khí)
a. Phương trình áp suất:
Liên hệ giữa áp suất và động năng trung bình của 1 phân tử chuyển động tịnh tiến:
Động năng trung bình của 1 phân tử chuyển động tịnh tiến
với m là khối lượng của 1 phân tử khí
Phương trình cơ bản của áp suất khí lý tưởng theo thuyết động học phân tử: (1)
b. Phương trình nhiệt độ:
Xét phương trình trạng thái của khí lý tưởng: p.V = n.R.T
với 1 mol khí lý tưởng thì số mol n = 1 nên: p.V = R.T (2)
Đồng thời với 1 mol khí lý tưởng, mật độ phân tử khí n0 là:
n0 = N / V = (m/).NA / V = n.NA / V = NA / V thay vào (1) sẽ có: (3) Từ (2) và (3) có: hay T = m.
/ (3.kB) là phương trình nhiệt độ của khí lý tưởng
theo thuyết động học phân tử với áp suất khí.
( Chương 3. Động học chất khí)
a. Thiết lập công thức:
với m là khối lượng của 1 phân tử khí (2.29) có:
mà số phân tử khí N = (m/).NA m/ = N / NA = 1 / NA (vì đang xét số phân tử khí N = 1), như vậy: (chú ý: R / NA = kB)
b. Định nghĩa về nhiệt độ:
(Chương 3. Động học chất khí) a. Định nghĩa:
Trọng Vật lý, bậc tự do của một hệ là số thông số xác định trạng thái của một hệ vật chất. Bậc
tự do của một vật là số tọa độ độc lập cần thiết để xác định vị trí của vật đó trong không gian. b. Giá trị bậc tự do:
Bậc tự do thường ký hiệu là chữ i (hoặc f) và có giá trị phụ thuộc vào mỗi loại khí:
c. Đinh luật phân bố đều năng lượng theo bậc tự do:
(Chương 3. Động học chất khí) a. Khái niệm:
+ Nhiệt dung: là một đại lượng Vật lý đo bằng nhiệt lượng cần cung cấp cho một hệ trong một
quá trình biến đổi nào đó để nhiệt độ của hệ tăng lên 1 độ.
+ Nhiệt dung riêng: là một đại lượng Vật lý đo bằng nhiệt lượng cần cung cấp cho 1 kg một
chất trong một quá trình biến đổi nào đó để nhiệt độ của nó tăng lên 1 độ.
b. Dẫn phương trình quan hệ giữa CV và CP:
Theo khái niệm về nội năng và xét một hệ khí lý tưởng thì nội năng U của hệ khí là tổng động
năng do chuyển động nhiệt của các phân tử (động năng tịnh tiến và quay). Nếu xét khí lý tưởng là đơn
nguyên tử thì có thể bỏ qua chuyển động quay và U chính bằng tổng động năng chuyển động tịnh tiến E của các phân tử khí. 3
Động năng trung bình chuyển động tịnh tiến của 1 phân tử khí là: E k . T d B . 2 . Xét khối
khí có n mol khí số phân tử khí là n.NA tổng động năng chuyển động tịnh tiến E của khối khí là: 3 3 3 E = n.N k . n.(N k . ) . n . .R. A. E d = n.NA. T B . 2 = T A B 2 = T 2
. Xét n = 1 mol khí thì nội năng của 3 3 khối khí: U = E = .R T . .R . T 2
biến thiên nội năng U = E = 2 .
Từ công thức của nguyên lý thứ nhất của NĐLH: U = Q – A E = Q – A. .
Theo định nghĩa thì nhiệt dung đẳng áp của 1 mol khí sẽ là:
(Chương 3. Động học chất khí)
a. Xem xét quá trình đẳng nhiệt: m V
Công hệ thực hiện trong quá trình đẳng nhiệt: A = - 2 RT ln 1 V trong đó: 1
- m là khối lượng khí lý tưởng, là khối lượng 1 mol khí, V1 và V2 là thể tích của khí trước và
sau quá trình đẳng nhiệt.
- R = … là hằng số khí lý tưởng.
Như vậy phương trình trên tương ứng với công A mà hệ khí lý tưởng thực hiện trong một
quá trình đăng nhiệt, với n = m/ là số mol khí.
b. Đồ thị P-V của quá trình đẳng nhiệt:
(Chương 3. Động học chất khí)
a. Quá trình đoạn nhiệt:
(với công mà hệ thực hiện A = - A’ công mà hệ nhận được) trong đó:
- m là khối lượng khí lý tưởng, là khối lượng 1 mol khí, P1, V1, T1 và P2, V2, T2 là áp suất, thể
tích, nhiệt độ của khí trước và sau quá trình đoạn nhiệt, T = T2 - T1.
- R = … là hằng số khí lý tưởng, i là số bậc tự do của khí b. Tính công A: ………
(với công mà hệ thực hiện A = - A’ công mà hệ nhận được)
(Chương 6. Nguyên lý thứ hai của nhiệt động lực học. Entropy)
a. Máy nhiệt: cấu tạo chung
b. Động cơ nhiệt: Cấu tạo, nguyên tắc hoạt động
c. Hiệu suất của động cơ nhiệt:
- Nhận xét: < 1. Ý nghĩa: nhiệt không thể chuyển hoá hoàn toàn thành công. Không thể
chế tạo được động cơ vĩnh cửu loại 2.
d. Phát biểu nguyên lý thứ hai của nhiệt động lực học theo cách của Thomson:
(Chương 6. Nguyên lý thứ hai của nhiệt động lực học. Entropy)
a. Máy nhiệt: gồm 2 loại là động cơ nhiệt và máy làm lạnh
b. Máy lạnh: Nguyên tắc hoạt động, hệ số máy làm lạnh
- Nhận xét: có thể > 1 nhưng không thể vô hạn (do A luôn khác 0).
c. Phát biểu nguyên lý thứ hai của nhiệt động lực học theo cách của Claudius:
(Chương 6. Nguyên lý thứ hai của nhiệt động lực học. Entropy)
a. Chu trình Carnot thuận nghịch: khái niệm, đồ thị P-V, các bước của chu trình
b. Hiệu suất chu trình Carnot:
c. Định lý Carnot và biểu thức:
- Định lý: Không một động cơ nhiệt nào hoạt động giữa 2 nguồn nhiệt lại có hiệu suất cao hơn
động cơ Carnot hoạt động với cùng 2 nguồn nhiệt đó.
- Biểu thức: hiệu suất của chu trình Carnot đối với khí lý tưởng chỉ phụ thuộc vào nhiệt độ
nguồn nóng T1 và nguồn lạnh T2
Với quá trình thuận nghịch: = 1 – T2 / T1
Với quá trình không thuận nghịch: < 1 – T2 / T1
(Chương 6. Nguyên lý thứ hai của nhiệt động lực học. Entropy) a. Khái niệm về entropy:
b. Tính chất của entropy: Entropy S là hàm trạng thái có các tính chất sau:
- Có giá trị xác định ở mỗi trạng thái của hệ, không phụ thuộc quá trình đưa hệ về trạng thái đó.
- Có tính chất cộng được, nghĩa là S của hệ bằng tổng các entropy của từng phần riêng biệt.
- Có giá trị sai khác nhau một hằng số S0, thông thường chọn S0 = 0 ở 0K. c. Ý nghĩa của entropy:
- Theo quan điểm nhiệt động lực học, entropy S là hàm trạng thái đặc trưng cho mức độ hỗn
loạn của các phân tử trong hệ: nếu nhiệt độ T của hệ tăng thì S tăng (hệ có thể chuyển trạng thái từ rắn
sang lòng, từ lỏng sang khí), nếu T giảm thì S giảm (hệ chuyển từ khí sang lỏng, từ lỏng sang rắn).
- Trong một hệ cô lập (không có nhiệt trao đổi: Q = 0), các quá trình nhiệt động luôn luôn xảy
ra theo chiều tăng của entropy, nghĩa là biến thiên entropy S 0 (dấu = ứng với quá trình thuận
nghịch. Dấu > ứng với quá trình không thuận nghịch)
d. Phát biểu, biểu thức nguyên lý thứ hai của NĐLH dựa trên khái niệm enttropy:
- Phát biểu, biểu thức Tồn tại một hàm trạng thái gọi là entropy ký hiệu là S, với dS là vi phân toàn phần của entropy S.
Giả sử có một biến đổi thuận nghịch vô cùng nhỏ trong đó hệ trao đổi với môi trường ở nhiệt độ
T một nhiệt lượng δQ, sự biến đổi entropy dS trong quá trình này là: - Biến thiên entropy: S >
Nếu hệ biến đối không thuận nghịch thì: