Thông tin
Hỏi đáp

Chương 1: Hàm số một biến số | Bài giảng môn Đại số các nhóm ngành chuẩn | Đại học Bách khoa hà nội

Phần Lôgic không dạy trực tiếp (phần này Đại số đã dạy) mà chỉ nhắc lại những phép suy luận cơ bản thông qua bài giảng các nội dung khác nếu thấy cần thiết. Tài liệu trắc nghiệm môn Đại số các nhóm ngành chuẩn giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Môn:

Đại số các nhóm ngành chuẩn (THH) (18)

Trường:

Đại học Bách Khoa Hà Nội (2.8 K)

Thông tin:

166 trang 2 tháng trước

Tác giả:

Lê Na

Đang cập nhật

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chương 1: Hàm số một biến số | Bài giảng môn Đại số các nhóm ngành chuẩn | Đại học Bách khoa hà nội

48 24 lượt tải Tải xuống

Chia sẻ

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI

VIỆN TOÁN ỨNG DỤNG & TIN HỌC

TS. BÙI XUÂN DIỆU

Bài Giảng

GIẢI TÍCH I

(lưu hành nội bộ)

HÀM SỐ MỘT BIẾN SỐ - TÍCH PHÂN - HÀM SỐ NHIỀU BIẾN SỐ

Tóm tắt lý thuyết, Các ví dụ, Bài tập và Lời giải

Hà Nội- 2019

(bản cập nhật Ngày 13 tháng 7 năm 2019)

Tập Bài giảng này vẫn đang trong quá trình hoàn thiện và có thể chứa những lỗi đánh

máy, những lỗi kí hiệu và những chỗ sai chưa được kiểm tra hết. Tác giả mong nhận được

sự đóng góp ý kiến để tập Bài giảng được hoàn thiện. Mọi ý kiến đóng góp xin vui lòng gửi

về địa chỉ “dieu.buixuan@hust.edu.vn”.

Warning: This lecture notes have not been reviewed and may contain errors or t ypos.

Use at your own risk!

Hà Nội, Ngày 13 tháng 7 năm 2019.

MỤC LỤC

Mục lục. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Chương 1 . Hàm số một biến số (13LT+13BT). . . . . . . . . . . . . . . . . 5

1 Sơ lược về các yếu tố Lôgic; các tập số: N, Z, Q, R . . . . . . . . . . . . . . . . 5

2 Trị tuyệt đối và tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

3 Hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

3.1 Định nghĩa hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

3.2 Hàm số đơn điệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

3.3 Hàm số bị chặn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

3.4 Hàm số chẵn, hàm số lẻ . . . . . . . . . . . . . . . . . . . . . . . . . . 7

3.5 Hàm số tuần hoàn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

3.6 Hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

3.7 Hàm ngược . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

3.8 Hàm số sơ cấp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

3.9 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

4 Dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

4.1 Dãy số và giới hạn của dãy số . . . . . . . . . . . . . . . . . . . . . . . 19

4.2 Các tiêu chuẩn tồn tại giới hạn . . . . . . . . . . . . . . . . . . . . . . 20

4.3 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

5 Giới hạn hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

5.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

5.2 Các phép toán trên giới hạn . . . . . . . . . . . . . . . . . . . . . . . . 27

5.3 Giới hạn của hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

5.4 Giới hạn vô cùng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

5.5 Các tiêu chuẩn tồn tại giới hạn . . . . . . . . . . . . . . . . . . . . . . 28

5.6 Mối liên hệ giữa giới hạn của dãy số và giới hạn của h àm số . . . . . 29

5.7 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

6 Vô cù ng lớn, vô cùng bé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

2 MỤC LỤC

6.1 Vô cùng bé (VCB) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

6.2 Vô cùng lớn (VCL) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

6.3 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

7 Hàm số liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

7.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

7.2 Các phép toán số học đối với hàm số liên tục . . . . . . . . . . . . . . 37

7.3 Sự liên tục của hàm ngược . . . . . . . . . . . . . . . . . . . . . . . . . 38

7.4 Sự liên tục của hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . 38

7.5 Các định lý về hàm liên tục . . . . . . . . . . . . . . . . . . . . . . . . 38

7.6 Điểm gián đoạn và phân loại điểm gián đoạn của hàm số . . . . . . . 39

7.7 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

8 Đạo hàm và vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

8.1 Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

8.2 Các phép toán trên đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . 43

8.3 Đạo hàm của hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

8.4 Đạo hàm của hàm ngược . . . . . . . . . . . . . . . . . . . . . . . . . . 44

8.5 Đạo hàm của các hàm số sơ cấp cơ bản . . . . . . . . . . . . . . . . . . 44

8.6 Vi phân của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

8.7 Đạo hàm cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

8.8 Vi phân cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

8.9 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

8.10 Đọc thêm: Về khái niệm vi phân . . . . . . . . . . . . . . . . . . . . . 54

9 Các định lý về hàm khả vi và ứng dụng . . . . . . . . . . . . . . . . . . . . . 56

9.1 Các định lý về hàm khả vi . . . . . . . . . . . . . . . . . . . . . . . . . 56

9.2 Các công thức khai triển Taylor, Maclaurin . . . . . . . . . . . . . . . 61

9.3 Quy tắc L’Hospital . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70

9.4 Về một số dạng vô định . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

9.5 Thay tương đương khi có hiệu hai VCB? . . . . . . . . . . . . . . . . . 73

9.6 Hiệu hai VCB tương đương . . . . . . . . . . . . . . . . . . . . . . . . 75

9.7 Ba phương pháp (mới) để tính giới hạn . . . . . . . . . . . . . . . . . . 76

9.8 Về các VCL tiêu biểu . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

9.9 Bài tập ôn tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

10 Các lược đồ khảo sát hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83

10.1 Khảo sát và vẽ đồ thị của hàm số y = f (x) . . . . . . . . . . . . . . . . 83

10.2 Khảo sát và vẽ đường cong cho dưới dạng tham số . . . . . . . . . . . 85

10.3 Khảo sát và vẽ đường cong trong hệ toạ độ cực . . . . . . . . . . . . . 86

10.4 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

MỤC LỤC 3

Chương 2 . Phép tính tích phân một biến số . . . . . . . . . . . . . . . . . 93

1 T ích phân bất định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

1.1 Nguyên hàm của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . 93

1.2 Các phương pháp tính tích phân bất định . . . . . . . . . . . . . . . . 95

1.3 T ích phân hàm phân thức hữu tỷ . . . . . . . . . . . . . . . . . . . . . 100

1.4 T ích phân hàm lượng giác . . . . . . . . . . . . . . . . . . . . . . . . . 102

1.5 T ích phân các biểu thức vô tỷ . . . . . . . . . . . . . . . . . . . . . . . 104

2 T ích phân xác định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

2.1 Định nghĩa tích phân xác định . . . . . . . . . . . . . . . . . . . . . . 109

2.2 Các tiêu chuẩn khả tích . . . . . . . . . . . . . . . . . . . . . . . . . . 109

2.3 Các tính chất của tích phân xác định . . . . . . . . . . . . . . . . . . . 110

2.4 T ích phân với cận trên thay đổi (hàm tích phân) . . . . . . . . . . . . 111

2.5 Các phương pháp tính tích phân xác định . . . . . . . . . . . . . . . . 112

2.6 Hệ thống bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

3 T ích phân suy rộng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124

3.1 T ích phân suy rộng với cận vô hạn . . . . . . . . . . . . . . . . . . . . 124

3.2 T ích phân suy rộng của hàm số không bị chặn . . . . . . . . . . . . . 126

3.3 Các tiêu chuẩn hội tụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 27

3.4 T ích phân suy rộng hội tụ tuyệt đối và bán hội tụ . . . . . . . . . . . 129

3.5 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130

4 Các ứng dụng của tích phân xác định . . . . . . . . . . . . . . . . . . . . . . . 136

4.1 T ính diện tích hình phằng . . . . . . . . . . . . . . . . . . . . . . . . . 136

4.2 T ính độ dài đường cong phẳng . . . . . . . . . . . . . . . . . . . . . . . 138

4.3 T ính thể tích vật thể . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139

4.4 T ính diện tích mặt tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . 141

Chương 3 . Hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . . . 145

1 Giới hạn của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . . . . . 145

1.1 Giới hạn của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . 145

1.2 T ính liên tục của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . 146

1.3 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146

2 Đạo hàm và vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148

2.1 Đạo hàm riêng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148

2.2 Vi phân toàn phần . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148

2.3 Đạo hàm của hàm số hợp . . . . . . . . . . . . . . . . . . . . . . . . . . 149

2.4 Đạo hàm và vi phân cấp cao . . . . . . . . . . . . . . . . . . . . . . . . 150

2.5 Đạo hàm theo hướng - Gradient . . . . . . . . . . . . . . . . . . . . . . 150

2.6 Hàm ẩn - Đạo hàm của hàm số ẩn . . . . . . . . . . . . . . . . . . . . 152

4 MỤC LỤC

2.7 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152

3 Cực trị của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . . . . . . 159

3.1 Cực trị tự do . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159

3.2 Cực trị có điều kiện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161

3.3 Giá trị lớn nhất - Giá trị nhỏ nhất . . . . . . . . . . . . . . . . . . . . 163

CHƯƠNG 1

HÀM SỐ MỘT BIẾN SỐ (13LT+13BT)

§1. SƠ LƯỢC VỀ CÁC YẾU TỐ LÔGIC; CÁC TẬP SỐ:

N, Z, Q, R

1. Phần Lôgic không dạy trự c tiếp (phần này Đại số đã dạy) mà chỉ nhắc lại những

phép suy luận cơ bản thông qua bài giảng các nội dung khác nếu thấy cần thiết.

2. Giới thiệu cá c tập số; cần nói rõ tập Q tuy đã rộng hơn Z nhưng vẫn chưa lấp đầy

trục số còn tập R đã lấp đầy trục số và chứa tất cả các giới hạn của các dãy số hội tụ,

ta có bao hàm thức

N ⊂ Z ⊂ Q ⊂ R.

§2. TRỊ TUYỆT ĐỐI VÀ TÍNH CHẤT

Nhắc lại định nghĩa và nêu các tính chất sau

•

≥ 0,

= 0 ⇐⇒ x = 0,

x + y

≤

;

•

x − y

≥

−

≥ A ⇐⇒ x ≥ A hoặc x ≤ −A

•

≤ B ⇐⇒ −B ≤ x ≤ B.

6 Chương 1. Hàm số một biến số (13LT+13BT)

§3. HÀM SỐ

3.1 Định nghĩa hàm số

Định nghĩa 1.1.

Một hàm số đi từ tập

vào tập

là một quy tắc cho tương ứng mỗi

phần tử

x ∈ X

với một và chỉ một phần tử

y ∈ Y

Một hàm số có thể được cho dưới dạng biểu thức giải tích y = f (x), chẳng hạn như hàm số

y = x

. Khi đó, cần phải xác định rõ miền xác định (hay tậ p xác định), tập hợp tất cả các

phần tử x ∈ X sao cho biểu thức f (x) được xác định, của hàm số.

Tập giá trị của hàm số: là tập tất cả các phần tử y ∈ Y sao cho tồn tại x ∈ X, f (x) = y.

Ví dụ 3.1 (Giữa kì, K61).

T ìm tập xác định và tập giá trị của hàm số

y = arcsin(cos 2x).

y = arcsin(2 cos x).

y = arccos(sin 2x).

y = arccos(2 sin x).

y = sin(π cos 3x).

y = cos(π sin 3x).

3.2 Hàm số đơn điệu

• Một hàm số f (x) được gọi là đơn điệu tăng trên khoảng (a, b) nếu:

∀x

, x

∈ (a, b), x

< x

⇒ f (x

) < f (x

• Một hàm số f (x) được gọi là đơn điệu giảm trên khoảng (a, b) nếu

∀x

, x

∈ (a, b), x

< x

⇒ f (x

) > f (x

Chú ý 1.1.

Trong Bài giảng này chúng ta chỉ quan tâm đến tính đơn điệu của hàm số

trên mỗi khoảng mà hàm số đó xác định. Chẳng hạn như, hàm số

f (x) =

có

′

(x) =

−

< 0 ∀x ∈

TXĐ

= R \{0}

nhưng nếu nói

f (x)

đơn điệu giảm trên

R \ {0}

thì sẽ dẫn

đến nghịch lý là

−1 < 1

nhưng

−1 = f (−1) < f (1) = 1

. Thay vì đó, ta nói hàm số

f (x)

đơn điệu giảm trên mỗi khoảng

(−∞, 0)

và

(0, +∞)

3.3 Hàm số bị chặn

• Một hàm số f (x) được gọi là bị chặn trên nếu tồn tại số M ∈ R sao cho f (x) ≤ M với

mọi x ∈ TXĐ.

3. Hàm số 7

• Một hàm số f (x) được gọi là bị chặn dưới nếu tồn tại số m ∈ R sao cho f (x) ≥ M với

mọi x ∈ TXĐ.

• Một hàm số f (x) được gọi là bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới.

3.4 Hàm số chẵn, hàm số lẻ

• Một hàm số f (x) được gọi là chẵn nếu







x ∈ TXĐ ⇒ −x ∈ TXĐ

f (−x) = f (x).

Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.

• Một hàm số f (x) được gọi là lẻ nếu







x ∈ TXĐ ⇒ −x ∈ TXĐ

f (−x) = −f (x).

Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

Ví dụ 3.2.

Chứng minh rằng bất kì hàm số

f (x)

nào xác định trong một khoảng đối xứng

(−a, a)

cũng đều biểu diễn được duy nhất dưới dạng tổng của một hàm số chẵn và một

hàm số lẻ.

[Gợi ý] Với mỗi f (x) bất kì ta luôn có

f (x) =

[ f (x) + f (−x)]

{z }

g(x)

[ f (x) − f (−x)]

{z }

h(x)

trong đó g(x) là một hàm số chẵn, c òn h(x) là một hàm số lẻ. Các bạn độc giả được khuyến

khích tự chứng minh tính duy nhất của phân tích này.

3.5 Hàm số tuần hoàn

Định nghĩa 1.2.

Một hàm số

f (x)

được gọi là tuần hoàn nếu n hư tồn tại số thực

T > 0

sao cho

f (x) = f (x + T) ∀x ∈

TXĐ

Ví dụ như các hàm số lượng giác y = sin x, y = cos x, y = tan x, y = cot x đã học ở phổ thông

là các hàm số tuần hoàn. Trong phạm vi Bài giảng này, chúng ta quan tâm chủ yếu là

xem có số T > 0 nào đó t hỏa mãn f

(

x + T

)

= f (x) mà không đi sâu vào việc tìm chu kỳ

(số T > 0 bé nhất).

Các câu hỏi sau đây tuy phát biểu đơn giản (và tưởng chừng như dễ trả lời) nhưng câu

trả lời sẽ rất thú vị:

8 Chương 1. Hàm số một biến số (13LT+13BT)

• Tổng (hiệu) của hai hàm số tuần hoàn có tuần hoàn không?

• Tích của hai hàm số tuần hoàn có tuần hoàn không?

• Thương của hai hàm số tuần hoàn có tuần hoàn không?

• Đạo hàm của hàm số tuần hoàn (nếu có) có tuần hoàn không?

• Nếu hàm số F(x) có đạo hàm trên R và F

′

(x) là một hàm số tuần hoàn thì F(x) có tuần

hoàn không? Nói cách khác, nếu f (x) là một hàm số tuần hoàn thì F(x) =

f (t)dt

có tuần hoàn không?

3.6 Hàm hợp

Cho hai hà m số f , g. Hàm hợp của f và g, kí hiệu là f ◦ g, là hàm số được định nghĩa

bởi

( f ◦ g)(x) = f [g(x)].

3.7 Hàm ngược

Định nghĩa 1.3.

Một h àm số

f : X → Y

được gọi là ánh xạ

1 −1

(hay còn gọi là đơn ánh)

nếu:

6= x

⇒ f (x

) 6= f (x

Định nghĩa 1.4.

Cho

là một đơn ánh với miền xác định

và miền giá trị

. Khi đó hàm

ngược

−1

, có miền xác định

và miền giá trị

, được định nghĩa bởi

−1

(y) = x ⇔ f (x) = y.

Miền xác định của f = Miền giá trị của f

−1

Miền giá trị của f = Miền xác định của f

−1

Chú ý 1.2.

Đồ thị của hàm ngược đối xứng với đồ thị của hàm

y = f (x)

qua đường phân

giác của góc phần tư thứ nhất .

Để tìm hàm số ngược của hàm số y = f (x) ta làm như sau:

• Viết y = f (x),

• Từ phương trình này giải x theo y, giả sử được x = g(y),

• Đổi vai trò của x và y để được hàm số ngược f

−1

(x) = g(x).

3. Hàm số 9

Ví dụ, tìm hàm ngược của hàm số y = 2x + 3, ta rút x theo y thì được x =

y−3

, sau đó

đổi vai trò của x và y để được hàm ngược là y =

x−3

. Tuy nhiên, cũng có nhiều khi hàm

số không phải là đơn ánh trên toàn trục số R, khi đó chúng ta phải xét hàm số trên các

khoảng mà hàm số đó là đơn ánh và tìm hàm ngược trên các khoảng tương ứng.

Định lý 1.1.

Nếu hàm số

f (x)

đơn điệu tăng (hoặc giảm) trên khoảng

(a, b)

thì tồn tại

hàm số ngược

−1

của

trên khoảng đó.

3.8 Hàm số sơ cấp

Năm loại hàm số sơ cấp cơ bản

1. Hàm lũy thừa y = x

. TXĐ của hàm số này phụ thuộc vào α.

• Nếu α nguyên dương, ví dụ hàm y = x

, hàm số xác định với mọi x ∈ R,

• Nếu α nguyên âm, ví dụ hàm y = x

−2

, hàm số y = y

−α

xác định với

mọi x ∈ R \{0},

• Nếu α =

, p nguyên dương chẵn, ví dụ y = x

1/2

√

x, thì hàm số xác định trên

≥0

• Nếu α =

, nguyên dương lẻ, ví dụ y = x

1/3

√

x, thì hàm số xác định trên R,

• Nếu α là số vô tỉ thì quy ước chỉ xét hàm số tại x > 0.

2. Hàm số mũ y = a

(0 < a 6= 1) có tập xác định là R và tập giá tr ị là R

. Hàm này

đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1.

3. Làm số logarit y = log

(x) (0 < a 6= 1), ngược với hàm số mũ, hàm số này có TXĐ

là R

và tập giá trị là R. Hàm số này đồng biến nếu a > 1 và nghịch biến nếu

0 < a < 1. Nó là hàm số ngược của hàm số mũ, do đó đồ thị của nó đối xứng với đồ

thị của hàm số y = a

qua đường phân giác của góc phần tư thứ nhất. Logarit cơ số

10 của x được kí hiệu là lg x. Logarit cơ số e của x được kí hiệu là ln x.

4. Các hàm lượng giác:

• Hàm số y = sin x xác định ∀x ∈ R, là hàm số lẻ, tuần hoàn chu kì 2π.

y = sin x

−

10 Chương 1. Hàm số một biến số (13LT+13BT)

• Hàm số y = cos x xác định ∀x ∈ R, là hàm số chẵn, tuần hoàn chu kì 2π.

y = cos x, 0 ≤ x ≤ π

• Hàm số y = tan x xác định ∀x ∈ R \{(2k + 1)

, k ∈ Z}, là hà m số lẻ, tuần hoàn

chu kì π.

−

• Hàm số y = cot x xác định ∀x ∈ R \{kπ, k ∈ Z}, là hàm số lẻ, tuần hoàn chu kì

π.

−

3. Hàm số 11

Ví dụ 3.3 (Ngụy biện toán học).

Chứng minh rằng

0 = 2

Chứng minh. Ta có

cos

x = 1 −sin

x ⇒ cos x =

1 −sin

x ⇒ 1 + cos x = 1 +

1 −sin

Thay x = π vào đẳng thức 1 + cos x = 1 +

1 −sin

x ta được 0 = 2.

5. Các hàm lượng giác ngược:

Muốn tìm hàm ngược của một hàm số, một yêu cầu đặt ra là hàm số đó phải là đơn

ánh. Tuy nhiên, các hàm lượng giác đều là cá c hàm số tuần hoàn (do đó, không phải

là đơn ánh). Chẳng hạn như, hàm số y = sin x không phải là đơn ánh trên R. Để

vượt qua khó khăn này, người ta hạn chế các hàm số lượng giác trên các khoảng mà

nó là đơn ánh. Chẳng hạn như, hàm số f (x) = sin x, −

≤ x ≤

là một đơn ánh.

−

y = sin x, −

≤ x ≤

• Hàm số ngược của hàm số y = sin x, kí hiệu là arcsin x, xác định như sau:

arcsin : [0, 1] →

−

x 7→ y = arcsin x ⇔ x = sin y

Hàm số y = arcsin x xác định trên [−1, 1], nhận giá trị trên



−



và là một

hàm số đơn điệu tăng.

sin x

arcsin x

−

12 Chương 1. Hàm số một biến số (13LT+13BT)

• Hàm số ngược của hàm số y = cos x, kí hiệu là y = arccos x, được xác định như

arccos : [0, 1] →

[

0, π

]

x 7→ y = arccos x ⇔ x = cos y

Hàm số y = arccos x xác định trên [−1, 1], nhận giá trị trên

[

0, π

]

và là một hàm

số đơn điệu giảm.

cos x

arccos x

−

• Hàm số ngược của hàm số y = tan x, kí hiệu là y = arctan x, được xác định như

arctan : (−∞, +∞) →



−



x 7→ y = arctan x ⇔ x = tan y

Hàm số y = arctan x xác định trên R, nhận giá trị trên



−



và là một hàm

số đơn điệu tăng.

tan x

arctan x

−

• Hàm số ngược của hàm số y = cot x, kí hiệu là y = arccot x, được xác định như

arccot : (−∞, +∞) →

(

0, π

)

x 7→ y = arccot x ⇔ x = cot y

3. Hàm số 13

Hàm số y = arccot x xác định trên R, nhận giá trị trên (0, π) và là một hàm số

đơn điệu giảm.

cot x

arccot x

−

Hàm số sơ cấp

Người ta gọi hàm số sơ cấp là hàm số được tạo thành bởi một số hữu hạn các phép toán

cộng, trừ, nhân, chia, phép lập hàm số đối với các hàm số sơ cấp cơ bả n. Các hàm số sơ cấp

được chia thành hai loại.

• Hàm số đại số: là những hàm số mà khi tính giá trị của nó ta chỉ phải làm một số

hữu hạn các phép toán cộng, trừ, nhân, chia và lũy thừa với số mũ hữu tỉ. Ví dụ: các

đa thức, phân thức hữu tỉ, .. .

• Hàm số siêu việt: là những hàm số sơ cấp nhưng không phải là hàm số đại số, như

y = ln x, y = sin x, . . .

3.9 Bài tập

Tìm TXĐ, MGT của hàm số

Bài tập 1.1. Tìm TXĐ của hàm số

a) y =

lg(tan x),

b) y = arcsin

1 + x

c) y =

√

sin πx

d) y = arccos(2 sin x).

[Đáp số]

a) {π/4 + kπ ≤ x < π/2 + kπ, k ∈ Z},

b) {−1/3 ≤ x ≤ 1},

c) {x ≥ 0, x 6∈ Z},

d) {−

+ kπ ≤ x ≤

+ kπ, k ∈ Z}.

Bài tập 1.2. Tìm miền giá trị của hàm số

14 Chương 1. Hàm số một biến số (13LT+13BT)

a) y = lg(1 −2 cos x)

b) y = arcsin





[Đáp số]

a) {−∞ < y ≤ lg 3} b) {−π/2 ≤ y ≤ π/2}

Tìm hàm ngược.

Bài tập 1.3. Tìm hàm ngược của hàm số (trên miền mà hàm số có hàm ngược)

a) y = 2x + 3,

b) y =

1 − x

1 + x

, c) y =

+ e

−x

[Đáp số]

a) y =

x −

b) y = y =

1 − x

1 + x

c) Ta có y

′

− e

−x

) không xác dịnh dấu, nên hàm số đã cho có thể không phải là

một đơn ánh. Trước hết,

y =

+ e

−x

) ⇔ e

= y ±

−1 ⇔ x = ln(y ±

−1).

Ta phải xét trên 2 miền:

• Trên miền x > 0, ta có song ánh:

(0, +∞) → (1, +∞)

x 7→ y =

+ e

−x

)

ln(y +

−1) ← y

Vậy hàm ngược trên miền x > 0 là y = ln(x +

√

−1), x > 1.

• Trên miền x < 0, tương tự ta có hàm ngược là y = ln(x −

√

−1), x > 1.

Ví dụ 3.4 (Giữa kì, K61).

T ìm hàm ngược của hàm số sau

y =

x+1

2x+1

. b)

y =

x−1

2x−1

Xét tính chẵn lẻ của hàm số

Bài tập 1.4. Xét tính chẵn lẻ của hàm số

3. Hàm số 15

a) f (x) = a

+ a

−x

(a > 0) b) f (x) = ln(x +

√

1 − x

) c) f (x) = sin x + cos x

[Đáp số]

a) Hàm số đã cho là hàm số chẵn.

b) Hàm số đã cho là hàm số lẻ.

c) Hàm số đã cho không chẵn, không lẻ.

Ví dụ 3.5 (Giữa kì, K61).

Xét tính chẵn lẻ của hàm số

y = tan(sin x)

. b)

y = sin(tan x)

Ví dụ 3.6.

Cho hàm số

f (x)

xác định và có đạo hàm trên

. Chứng minh rằng

a) nếu

f (x)

là một hàm số lẻ thì

′

(x)

là một hàm số chẵn.

b) nếu

f (x)

là một hàm số chẵn thì

′

(x)

là một hàm số lẻ.

Xét tính tuần hoàn của hàm số

Bài tập 1.5. Xét tính tuần hoàn và chu kì của hàm số sau (nếu có)

a) f (x) = A cos λx + B sin λx,

b) f (x) = sin x +

sin 2x +

sin 3x,

c) f (x) = sin

d) f (x) = sin(x

Chứng minh. a) Giả sử T > 0 là một chu kì của hàm số đã cho. Khi đó

f (x + T) = f (x)∀x ∈ R

⇔A cos λ(x + T) + B sin λ(x + T) = A cos λx + B sin λx ∀x ∈ R

⇔A[cos λx −cos λ(x + T)] + B[sin λx −sin λ(x + T)] = 0 ∀x ∈ R

⇔2 sin

−λT

[A sin(λx +

λT

) + B cos(λx +

λT

)] = 0 ∀x ∈ R

⇔sin

λT

= 0

⇔T =



2kπ



Vậy hàm số đã cho tu ần hoàn với chu kì T =

2π

|λ|

b) Theo câu a) thì hàm số sin x tuần hoàn với chu kì 2π, hàm số sin 2x tuần hoàn với

chu kì π, hàm số sin 3x tuần hoàn với chu kì

2π

. Vậy f (x) = sin x +

sin 2x +

sin 3x

tuần hoàn với chu kì T = 2π

16 Chương 1. Hàm số một biến số (13LT+13BT)

c) f (x) = sin

x =

1 −cos 2x

tuần hoàn với chu kì T = π

d) Giả sử hàm số đã cho tuần hoàn với chu kì T > 0.Khi đó

sin(x + T)

= sin(x

)∀x.

(a) Cho x = 0⇒T =

√

kπ, k ∈ Z, k > 0.

(b) Cho x =

√

π⇒k là số chính phương. Giả sử k = l

, l ∈ Z, l > 0.

ta suy ra điều mâu thuẫn.

Vậy hàm số đã cho kh ông tuần hoàn.

Nhận xét: Muốn chứng minh một hàm số không tuần hoàn, chúng ta có thể sử dụng

phương pháp phản chứng như đã trình bày ở trên. Giả sử hàm số đó tuần hoàn với chu kì

p > 0 sau đó cho một vài giá trị đặc biệt của x để suy ra điều mâu thuẫn. Ngoài phương

pháp phản chứng thì chúng ta cũng có thể sử dụng một số tính chất của hàm số tuần hoàn

để chứng minh. Chẳng hạn như:

• một hàm số tuần hoàn và liên tục thì bị chặn (tại sao?),

• một hàm số tuần hoàn và không phải là hàm hằng thì không tồn tại lim

x→∞

f (x) (tại

sao?),

• đạo hàm của một hàm số tuần hoàn (nếu có) thì cũng tuần hoàn (tại sao?).

Bài tập 1.6. Chứng minh các hàm số sau không tuần hoàn

(a) y = cos x + cos x

√

(b) y = sin x + sin x

√

(d) y = cos x

(e) y = sin

√

(f) y = cos

√

Chứng minh. a) Giả sử hàm số y = cos x + cos x

√

2 tuần hoàn với chu kì T > 0. Khi đó,

cos x + cos x

√

2 = cos(x + T) + cos(x + T)

√

2 ∀x ∈ R.

Cho x = 0 ta được 2 = cos T + cos T

√

2. Vì cos T ≤ 1, cos T

√

2 ≤ 1 nên

2 = cos T + cos T

√

2 ⇔







cos T = 1,

cos T

√

2 = 1.

⇒







T = k2π, 0 6= k ∈ N

√

2 = l2π, 0 6= l ∈ N.

Khi đó

√

2 =

∈ Q, điều này là vô lý vì

√

2 là một số vô tỉ. Như vậy, chúng ta đã trả lời

một câu hỏi trong Mục 3.5, rằng tổng của hai hàm số tuần hoàn có thể không phải là

3. Hàm số 17

một hàm số tuần hoàn. Hàm số f (x) = cos x + cos x

√

2 là một hàm số hầu tuần hoàn

(almost periodic). Tương tự như vậy, tích của hai hàm số tuần hoàn cũng không phải

là một hàm số tuần hoàn, vì

2 cos

1 +

√

x cos

1 −

√

x = cos x + cos x

√

Bài tập 1.7. [Giữa kì, K61] Cho f (x), g(x) là các hàm số xác định trên R và tuần hoàn

với chu kì lần lượt là T

> 0, T

> 0. Biết tỉ số

là một số hữu tỉ. Chứng minh rằng

f (x) + g(x) và f (x)g(x) cũng là các hàm số tuần hoàn.

Các dạng toán khác

Bài tập 1.8. Tìm f (x) biết

a) f



x +



= x

, b) f



1 + x



= x

[Đáp số]

a) f (x) = x

−2 với |x| ≥ 2.

b) f (x) =



1 − x



∀x 6= 1.

Bài tập 1.9. Cho f (x) = ax + b, f (0) = −2, f (3) = −5. Tìm f (x).

[Đáp số] f (x) =

x −2.

Bài tập 1.10. Cho f (x) = ax

+ bx + c, f (−2) = 0, f (0) = 1, f (1) = 5. Tìm f (x).

[Đáp số] f (x) =

x + 1.

Bài tập 1.11. Cho f (x) =

+ a

−x

), a > 0. Chứng minh rằng :

f (x + y) + f (x −y) = 2 f (x) f (y).

Bài tập 1.12. Giả sử f (x) + f (y) = f (z). Xác định z nếu:

a) f (x) = ax, a 6= 0,

b) f (x) = arctan x,

c) f (x) =

d) f (x) = lg

1 + x

1 − x

[Đáp số]

18 Chương 1. Hàm số một biến số (13LT+13BT)

a) z = x + y,

b) z =

x + y

1 − xy

c) z =

x + y

d) z =

x + y

1 + xy

4. Dãy số 19

§4. DÃY SỐ

4.1 Dãy số và giới hạn của dãy số

Định nghĩa 1.5.

Một dãy số là một hàm số

N → R, n 7→ a

. Kí hiệu

}

n∈N

Một dãy số được gọi là:

• đơn điệu tăng nếu a

< a

n+1

∀n, đơn điệu giảm nếu a

> a

n+1

∀n.

• bị chặn trên nếu tồn tại số M sao cho a

≤ M ∀n, bị chặn dưới nếu tồn tại số m sao

cho a

≥ m ∀n.

Định nghĩa 1.6.

Một dãy số

}

được gọi là có giới hạn là

và viết

lim

n→∞

= L

hay

→ L

khi

n → ∞,

nếu

•

(nói một cách nôm na) có thể làm cho các số hạng

gần

với một giá trị tùy ý bằng

cách chọn

đủ lớn.

•

(nói một cách chính xác) với mọi

ǫ > 0

, tồn tại số tự nhiên

sao cho

nếu

n > N

thì

− L| < ǫ.

Hình dung rằng lim

n→+∞

= L nghĩa là với mọi ǫ > 0 thì từ một lúc nào đó toàn bộ số hạng

của dãy

{

}

n≥N

sẽ chui vào trong khoảng (L − ǫ, L + ǫ).

L + ǫ

L −ǫ

, ∀n ≥ N

Hình 1.6

Một dãy số {a

} có lim

n→+∞

= L hữu hạn được gọi là hội tụ. Ngược lại, nó được gọi là phân

kì (nghĩa là lim

n→+∞

= ∞ hoặc là không tồn tại).

Định nghĩa 1.7 (Giới hạn vô cùng).

Ta nói

lim

n→∞

= +∞

nếu với mọi số thực dương

tồn tại số tự nhiên

sao cho

nếu

n > N

thì

> M.

Hãy phát biểu cho trường hợp

lim

n→∞

= −∞

20 Chương 1. Hàm số một biến số (13LT+13BT)

Định lý 1.2 (Các tính chất của giới hạn của dãy số).

•

Giới hạn của một dãy số, nếu tồn tại, là duy nhất.

•

Mọi dãy số hội tụ đều bị chặn.

Định lý 1.3 (Các phép toán trên giới hạn).

Giả sử

lim

n→+∞

= A, lim

n→+∞

= b

, ở đó

a, b

là các số thực hữu hạn. Khi đó:

•

Tổng:

lim

n→+∞

+ b

) = A + B

•

Hiệu:

lim

n→+∞

−b

) = A − B

•

T ích:

lim

n→+∞

) = AB

•

Thương:

lim

n→+∞

nếu

B 6= 0

Chú ý 1.3.

Các phép toán trên giới hạn sau không thực hiện được, chúng còn được gọi là

các dạng vô định:

∞ −∞, 0 ×∞,

∞

4.2 Các tiêu chuẩn tồn tại giới hạn

Định lý 1.4 (Tiêu chuẩn kẹp).

Giả sử

≤ b

≤ c

với mọi

n ∈ N

hoặc với mọi

n ≥ K

nào đó,

ii)

lim

n→+∞

= lim

n→+∞

= L

Khi đó,

lim

n→+∞

= L.

Định lý 1.5 (Tiêu chuẩn đơn điệu bị chặn).

Mọi dãy số đơn điệu tăng (đơn điệu giảm)

và bị chặn trên (tương ứng, bị chặn dưới) đều hội tụ.

Ví dụ 4.1.

Xét



1 +



Chứng minh rằng

}

là một dãy số tăng và bị chặn.

Chứng minh. Áp dụng bất đẳng thức Cauchy ta có :

1 +



1 +



+ . . . +



1 +



| {z }

n số hạng

≥ (n + 1)

n+1



1 +



4. Dãy số 21

⇒



1 +

n + 1



n+1

≥



1 +



Hơn nữa ta có



1 +



∑

k=0

k! = 1.2 . . . k ≥ 2

k−1

∀k ≥ 2

⇒C

n.(n −1) . . . (n −k + 1)

≤

k−1

⇒u

< 1 + 1 +

+ . . . +

k−1

< 3.

Chú ý 1.4.

Giới hạn

lim

n→+∞



1 +



là một số vô tỉ, được kí hiệu là

. Nó có giá tr ị xấp xỉ

2.71.

Ví dụ 4.2 (Giữa kì, 20173).

Xét sự hội tụ và tìm giới hạn (nếu có) của dãy số

} : x

> 0, x

n+1





, n ≥ 1.

[Lời giải] Từ x

> 0 ta có x

> 0 với mọi n.



n−1



≥ 1.

Do đó, x

n+1





≤ x

với mọi n. Như vậy, {x

} là một dãy số giảm và bị chặn

dưới nên tồn tại lim

n→+∞

= a.

n+1





⇒ a =



a +



⇒ a = 1.

Vậy lim

n→+∞

= 1.

Định nghĩa 1.8.

Dãy số

}

được gọi là dãy số Cauchy nếu với mọi

ǫ > 0

, tồn tại số tự

nhiên

sao cho

− a

| < ǫ

với mọi

m, n > N

Định lý 1.6 (Tiêu chuẩn Cauchy).

Dãy số

}

là hội tụ khi và chỉ khi nó là dãy số

Cauchy.

Ví dụ 4.3.

Chứng minh rằng dãy số

}

với

= 1 +

+ ··· +

là một dãy số phân kỳ.

22 Chương 1. Hàm số một biến số (13LT+13BT)

Ví dụ 4.4 (Ngụy biện toán học).

Cho

là một số thực và

L = lim

n→+∞

. Đổi biến số

n = m + 1

ta có

L = lim

m+1→+∞

m+1

= lim

m→+∞

x.x

= x. lim

m→+∞

= xL.

Vậy

L = xL ⇒ L(x −1) = 0

. Nếu

x 6= 1

thì

L = 0

. Nói cách khác,

lim

n→+∞

= 0 ∀x 6= 1.

Điều này dẫn đến, chẳng hạn,

lim

n→+∞

= 0

thật vô lý!

Giải thích tại sao lại dẫn đến mâu thuẫn trên?

4.3 Bài tập

Về bài tập tìm giới hạn của dãy số, về cơ bản cho đến thời điểm hiện tại chúng ta chưa

có nhiều công cụ để xử lý. Chủ yếu vẫn là các phương pháp nhân liên hợp để khử dạng

vô định ở phổ thông, sử dụng tiêu chuẩn đơn điệu bị chặn, tiêu chuẩn kẹp và tiêu chuẩn

Cauchy. Sau này, khi học đến giới hạn của hàm số, các công cụ sẽ phong phú hơn. Khi đó

các bài toán về giới hạn của dãy số có thể đưa về giới hạn của hàm số và tính toán dễ dàng.

Bài tập 1.13. Tìm giới hạn của các dãy số sau:

a) x

= n −

√

−n,

b) x

n(n + a) − n,

c) x

= n +

√

1 −n

d) x

sin

nπ

e) x

sin

n −cos

[Đáp số]

c) 0 d) phân kì e) 0

Bài tập 1.14. Xét dãy số x

= x

n−1

, x

= 1.

a) Chứng minh rằng dãy {x

} không có giới hạn hữu hạn.

b) Chứng minh rằng lim

n→∞

= +∞.

Bài tập 1.15. Cho s

= 1 +

+ . . . +

.Chứng minh rằng {s

} tăng và bị chặn.

Chú ý : lim

n→+∞

= e.

4. Dãy số 23

Bài tập 1.16. Tính lim

n→+∞

1 + a + . . . + a

1 + b + . . . + b

, |a| < 1, |b| < 1.

Chứng minh.

lim

n→+∞

1 + a + . . . + a

1 + b + . . . + b

= lim

n→+∞

1 − a

n+1

1 − a

1 −b

n+1

1 −b

1 − a

Bài tập 1.17. Tính lim

n→+∞

2 +

2 + . . . +

√

2 (n dấu căn).

Chứng minh. Đặt u

2 +

2 + . . . +

√

2 ta có u

n+1

= 2 + u

. Trước hết chứng minh

} là một dãy số tăng và bị chặn, 0 ≤ u

≤ 2. Theo tiêu chuẩn đơn điệu bị chặn, {u

}

là một dãy số hội tụ. Giả sử lim

n→∞

= a, 0 < a < 2 thì từ phương trình u

n+1

= 2 + u

, cho

n → ∞ ta có

= a + 2

Vậy a = 2 hay lim

n→+∞

2 +

2 + . . . +

√

2 = 2

Bài tập 1.18. Tính lim

n→+∞

(n −

√

−1) sin n.

[Gợi ý] lim

n→+∞

(n −

√

−1) sin n = lim

n→+∞

sin n

n +

√

−1

= 0 (theo tiêu chuẩn kẹp)

Bài tập 1.19. Tính lim

n→+∞

[cos(ln n) −cos(ln(n + 1))].

Chứng minh. Ta có

cos(ln n) − cos(ln(n + 1)) = −2 sin



ln n + ln(n + 1)



. sin



ln n −ln(n + 1)



= −2 sin

ln n(n + 1 )

sin

n+1

nên

0 ≤

cos(ln n) − cos(ln(n + 1))

≤ 2



sin

n+1



Mặt khác lim

n→∞

sin

n+1

= 0 nên theo nguyên lý giới hạn kẹp

lim

n→+∞

[cos(ln n) −cos(ln(n + 1))] = 0

Bài tập 1.20. Chứng minh rằng l im

n→+∞

= 0.

24 Chương 1. Hàm số một biến số (13LT+13BT)

[Gợi ý]

= (1 + 1)

n(n −1)

⇒0 <

n −1

Dùng nguyên lý kẹp ta có điều phải chứng minh.

Bài tập 1.21. Chứng minh rằng l im

n→+∞

= 0.

[Gợi ý] Ta có

0 <

. . .

< 2.

∀n ≥ 2.

Bài tập 1.22. Tính

a) lim

n→+∞



+ ··· +



b) lim

n→+∞



+ ··· +



[Gợi ý]

a. Tính S

−

⇒ lim

n→+∞

= 2. b. Tính S

−

⇒ lim

n→+∞

Bài tập 1.23. Chứng minh rằng l im

n→+∞

√

n = 1, lim

n→+∞

√

a = 1 với mọi a > 0.

[Gợi ý]

a) Đặt α

√

n −1⇒n = (1 + α

)

n(n −1)

⇒α

n −1

. Áp dụng nguyên lý giới

hạn kẹp ta có lim

n→∞

= 0. Vậy lim

n→∞

√

n = 1.

b) Xét lim

n→+∞

√

• Nếu a = 1, xong.

• Nếu a > 1, 1 ≤

√

a ≤

√

n ∀n > a⇒ lim

n→+∞

√

a = 1

• Nếu a < 1, đặt a

′

⇒lim

√

′

= 1⇒ lim

n→+∞

√

a = 1.

Bài tập 1.24. Tính lim

n→+∞

, ở đó x

2+···+

(n phép chia).

[Lời giải]

4. Dãy số 25

1) Trước hết ta chứng minh 0 < x

< −1 +

√

2 và x

2n+1

> −1 +

√

2. Thật vậy,

Nếu x

> −1 +

√

2 thì x

n+1

2 + x

2 + (−1 +

√

1 +

√

= −1 +

√

Nếu x

< −1 +

√

2 thì x

n+1

2 + x

2 + (−1 +

√

1 +

√

= −1 +

√

Như vậy, dãy {x

} này có quy luật là, cứ một số hạng nào đó nhỏ hơn −1 +

√

2 thì số

hạng đứng ngay sau nó lớn hơn −1 +

√

2, và ngược lại. Do đó,

> −1 +

√

2 ⇒ x

< −1 +

√

2 ⇒ x

> −1 +

√

2 ⇒ ···

dẫn đến việc







0 < x

< −1 +

√

2n+1

> −1 +

√

2) Tiếp theo, ta đi chứng minh dãy {x

} là một dãy số tăng, thật vậy,

2n+2

2 + x

2n+1

2 +

2+x

2 + x

5 + 2x

2n+2

> x

⇔

2 + x

5 + 2x

> x

⇔ 2x

+ 4x

−2 < 0 ⇔ −1 −

√

2 < x

< −1 +

√

Điều này luôn đúng, vì ta đã chứng minh ở trên, rằng dãy các số hạng chẵn thỏa

mãn x

< −1 +

√

Dãy số này tăng và bị chặn trên bởi −1 +

√

2 nên tồn tại lim

n→+∞

= a. Phương trình

2n+2

2+x

5+2x

dẫn đến a =

2+a

5+a

⇒ a = −1 +

√

3) Tương tự như vậy, dãy {x

2n+1

} sẽ là một dãy số giảm. Thật vậy,

2n+3

2 + x

2n+2

2 +

2+x

2n+1

2 + x

2n+1

5 + 2x

2n+1

2n+3

< x

2n+1

⇔ 2x

2n+1

+ 4x

2n+1

−2 > 0 ⇔ x

2n+1

> −1 +

√

2 hoặc x

2n+1

< −1 −

√

Điều này luôn đúng, vì ta đã chứng minh ở trên, rằng dãy các số hạng lẻ thỏa mãn

2n+1

> −1 +

√

Dãy số này giảm và bị chặn dưới, nên tồn tại giới hạn lim

n→+∞

2n+1

= b. Phương trình

2n+3

2+x

2n+1

5+2x

2n+1

dẫn đến b =

2+b

5+2b

⇒ b = −1 +

√

Kết luận: lim

n→+∞

= −1 +

√

26 Chương 1. Hàm số một biến số (13LT+13BT)

Bài tập 1.25. Dùng tiêu chuẩn Cauchy chứng minh rằ ng dãy số u

= 1 +

+ ··· +

phân kì.

Bài tập 1.26. Chứng minh rằng nếu lim

n→+∞

= a thì lim

n→+∞

+ a

+ ···+ a

= a.

Bài tập 1.27. Chứng minh rằng nếu lim

n→+∞

= a, a

> 0∀n thì lim

n→+∞

√

. . . a

= a.

5. Giới hạn hàm số 27

§5. GIỚI HẠN HÀM SỐ

5.1 Định nghĩa

Định nghĩa 1.9.

Giả sử rằng hàm số

f (x)

được xác định tại mọi điểm

x ∈ (a, b) \{x

}

. Ta

nói giới hạn của hàm số

f (x)

khi

tiến đến

bằng

và viết

lim

x→x

f (x) = L

•

(nói một cách nôm n a) nếu ta có thể làm cho giá trị của hàm số

f (x)

gần

với một

giá trị tùy ý bằng cách chọn

đủ gần

•

(nói một cách chính xác) nếu với mọi

ǫ > 0

, tồn tại số thực

δ > 0

sao cho

nếu

|x − x

| < δ

thì

|f (x) − L| < ǫ.

Hình dung rằng lim

x→x

f (x) = L nghĩa là với mọi ǫ > 0, tồn tại số δ > 0 sao cho đồ thị của

hàm số trong khoảng (x

−δ, x

+ δ) sẽ nằm hoàn toàn trong dải (L − ǫ, L + ǫ).

Hình 1.9

L + ǫ

L −ǫ

Các giới hạn một phía lim

x→x

= L, lim

x→x

−

= L và giới hạn lim

x→∞

f (x) = L được định nghĩa một

cách tư ơng tự.

Định lý 1.7 (Tính duy nhất của giới hạn).

Giới hạn của hàm số

lim

x→x

f (x)

, nếu tồn tại,

là duy nhất.

5.2 Các phép toán trên giới hạn

Định lý 1.8 (Các phép toán trên giới hạn).

Giả sử

lim

x→x

f (x) = a, lim

x→x

g(x) = b

, ở đó

a, b

là các số thực hữu hạn. Khi đó,

•

Tổng:

lim

x→x

[ f (x) + g(x)] = a + b

28 Chương 1. Hàm số một biến số (13LT+13BT)

•

Hiệu:

lim

x→x

[ f (x) − g(x)] = a − b

•

T ích:

lim

x→x

[ f (x)g(x)] = ab

•

Thương:

lim

x→x

f (x)

g(x)

, nếu

b 6= 0

Chú ý 1.5.

Các phép toán trên giới hạn sau không thực hiện được, chúng còn được gọi là

các dạng vô định:

∞ −∞, 0 ×∞,

∞

5.3 Giới hạn của hàm hợp

Nếu có lim

x→x

u(x) = u

, lim

u→u

f (u) = f (u

) và có hàm hợp f

(

u(x)

)

thì

lim

x→x

(

u(x)

)

= f (u

Áp dụng lim

x→x

A(x)

B(x)

= e

lim

x→x

B(x) ln A(x)

5.4 Giới hạn vô cùng

Định nghĩa 1.10.

Giả sử rằng hàm số

f (x)

được xác định tại mọi điểm

x ∈ (a, b) \ {x

}

Ta nói giới hạn của hàm số

f (x)

khi

tiến đến

bằng vô cùng và viết

lim

x→x

f (x) = ∞

nếu với mọi số

M > 0

, tồn tại số thực

δ > 0

sao cho

nếu

|x − x

| < δ

thì

|f (x)| > M.

Các giới hạn một phía lim

x→x

= ∞, lim

x→x

−

= ∞ và giới hạn lim

x→∞

f (x) = ∞ được định nghĩa một

cách tư ơng tự.

5.5 Các tiêu chuẩn tồn tại giới hạn

Định lý 1.9.

Nếu

f (x) ≤ g(x)

với mọi

trong một lân cận nào đó của

, và tồn tại các giới

hạn

lim

x→a

f (x), lim

x→a

g(x)

thì

lim

x→a

f (x) ≤ lim

x→a

g(x).

Hệ quả 1.1 (T iêu chuẩn kẹp).

Nếu

f (x) ≤ g(x) ≤ h(x)

trong một lân cận nào đó của

và tồn tại các giới hạn

lim

x→a

f (x) = lim

x→a

h(x)

. Khi đó tồn tại

lim

x→a

g(x)

, và

lim

x→a

f (x) = lim

x→a

g(x).

5. Giới hạn hàm số 29

5.6 Mối liên hệ giữa giới hạn của dãy số và giới hạn

của hàm số

Nhiều bài toán giới hạn của dãy số có thể được chuyển về giới hạn của hàm số và lợi

dụng các công cụ của giới hạn của hàm số để tính toán một cách dễ dàng. Chúng thể hiện

qua mối liên hệ sau.

Định lý 1.10. lim

x→x

f (x) = L

khi và chỉ khi với mọi dãy số

}

sao cho

lim

n→+∞

= x

thì

lim

n→+∞

f (x

) = L,

ở đó (chỉ riêng trong Định lý này)

và

có thể là một số thực hữu hạn

hoặc bằng vô cùng.

Chẳng hạn như, muốn chứng minh lim

n→+∞

ln n

= 0 ta có thể đưa về lim

x→∞

ln x

= 0.

5.7 Bài tập

Bài tập 1.28. Tính

a) lim

x→1

100

−2x + 1





b) lim

x→a

− a

) −na

n−1

(x − a)





Phương pháp phân tích đa thức thành nhân tử. Nếu P

) = Q

) = 0 thì

lim

x→x

(x)

= lim

x→x

(x − x

).P

n−1

(x)

(x − x

).Q

m−1

(x)

= lim

x→x

n−1

(x)

m−1

(x)

[Đáp số]

n(n −1)

n−2

Bài tập 1.29. Tìm giới hạn

a) lim

x→+∞

x +

√

x + 1



∞



b) lim

x→+∞

(

√

+ x

−1 − x)

(

∞ −∞

)

Chứng minh. a) Chia cả tử và mẫu cho

√

x ta được

lim

x→+∞

x +

√

x + 1

= lim

x→∞

1 +

1/x +

√

1/x

√

1 + 1/x

= 1.

b) Sử dụng phương pháp nhân liên hợp ta được

lim

x→+∞

(

+ x

−1 − x) = lim

x→∞

−1

+ x

−1)

+ x

√

+ x

−1 + x

30 Chương 1. Hàm số một biến số (13LT+13BT)

§6. VÔ CÙNG LỚN, VÔ CÙNG BÉ

6.1 Vô cùng bé (VCB)

Định nghĩa 1.11.

Hàm số

f (x)

được gọi là một

vô cùng bé

(viết tắt là VCB) khi

x → a

nếu

lim

x→a

f (x) = 0.

Mối liên hệ giữa giới hạn và VCB

lim

x→a

f (x) = ℓ ⇐⇒ f (x) = ℓ + α(x);

trong đó α(x) là một VCB trong quá trình x → a.

Một số tính chất của VCB

1. Tổng hai VCB (đối với một VCB người ta không quan tâm đến dấu của nó) là một

VCB.

2. Tích của VCB với một đại lượng bị chặn là một VCB.

3. Tích các VCB là một VCB.

Chú ý: Thương của hai VCB là một dạng vô định

So sánh các VCB

Định nghĩa 1.12 (VCB cùng bậc, tương đương).

Giả sử

α(x)

và

β(x)

là các VCB khi

x → a

i) Nếu

lim

x→a

α(x)

β(x)

= A 6= 0

, ta nói rằng

α(x), β(x)

là các VCB cùng bậc.

ii) Đặc biệt, nếu

lim

x→a

α(x)

β(x)

= 1

thì ta nói

α(x)

và

β(x)

là các VCB tương đương và viết

α(x) ∼ β(x).

Một số VCB tương đương hay dùng trong quá trình x → 0

• x ∼ sin x ∼ tan x ∼ arcsin x ∼ arctan x ∼ e

−1 ∼

−1

ln a

∼ ln(1 + x),

• (1 + x)

−1 ∼ ax. Đặc biệt,

√

1 + αx −1 ∼

αx

6. Vô cùng lớn, vô cùng bé 31

• 1 −cos x ∼

Định nghĩa 1.13 (VCB bậc cao).

Nếu

lim

x→a

α(x)

β(x)

= 0

, ta nói rằng

α(x)

là VCB bậc cao hơn

β(x)

và kí hiệu

α(x) = o(β(x))

Định lý 1.11.

a) Hiệu hai VCB tương đương là một VCB bậc cao hơn VCB đó.

b) Tích hai VCB là một VCB bậc cao hơn cả hai VCB đó.

Ứng dụng của VCB để tìm giới hạn

Định lý 1.12 (Quy tắc thay tương đương).

Nếu

(x) ∼ α

(x), β

(x) ∼ β

(x)

khi

x → a

thì

lim

x→a

(x)

= lim

x→a

(x)

, lim

x→a

(x)γ(x) = lim

x→a

(x)γ(x).

Định lý 1.13 (Quy tắc ngắt bỏ VCB bậc cao).

Nếu

(x) = o(α

(x)), β

(x) = o(β

(x))

khi

x → a

thì

(x) + α

(x) ∼ α

(x)

và

lim

x→a

(x) + α

(x)

(x) + β

(x)

= lim

x→a

(x)

Chú ý 1.6.

Sai lầm hay mắc: Thay tương đương khi có hiệu hai VCB. Chẳng hạn như, với

VCB

α(x) = sin x −tan x + x

khi

x → 0

ta có

i) Thay tương đương

α(x) ∼ x

ii) Thực tế,

α(x) ∼

Thật vậy,

lim

x→0

sin x −tan x + x

= 1 + lim

x→0

sin x



1 −

cos x



= 1 + lim

x→0

−sin x(1 − cos x)

cos x

Ví dụ 6.1 (Giữa kì, K61).

So sánh cặp vô cùng bé sau đây khi

x → 0

α(x) =

√

+ x

, β(x) = e

sin x

−1

α(x) =

√

+ x

, β(x) = e

tan x

−1

α(x) =

√

− x

, β(x) = l n(1 + tan x).

α(x) =

√

− x

, β(x) = l n(1 + sin x).

α(x) = e

√

−1, β(x) =

√

x + x

α(x) = e

−1, β(x) = x

+ x

32 Chương 1. Hàm số một biến số (13LT+13BT)

6.2 Vô cùng lớn (VCL)

Định nghĩa 1.14.

Hàm số

f (x)

được gọi là một

vô cùng lớn

(viết tắt là VCL) khi

x → a

nếu

lim

x→a

|f (x)| = ∞.

Nghịch đảo của một VCB là một VCL, và ngược lại.

So sánh các VCL

Định nghĩa 1.15 (VCL cùng bậc, tương đương).

Giả sử

α(x)

và

β(x)

là các VCL khi

x → a

i) Nếu

lim

x→a

α(x)

β(x)

= A 6= 0

, ta nói rằng

α(x), β(x)

là các VCL cùng bậc.

ii) Đặc biệt, nếu

lim

x→a

α(x)

β(x)

= 1

thì ta nói

α(x)

và

β(x)

là các VCL tương đương và viết

α(x) ∼ β(x).

Định nghĩa 1.16 (VCL bậc cao).

Nếu

lim

x→a

α(x)

β(x)

= ∞

, ta nói rằng

α(x)

là VCL bậc cao hơn

β(x)

Ứng dụng VCL khử dạ ng



∞



Định lý 1.14 (Quy tắc thay tương đương).

Nếu

(x) ∼ α

(x), β

(x) ∼ β

(x)

là các

VCL khi

x → a

thì

lim

x→a

(x)

= lim

x→a

(x)

, lim

x→a

(x)γ(x) = lim

x→a

(x)γ(x).

Định lý 1.15 (Quy tắc ngắt bỏ VCL bậc thấp).

Nếu

(x)

là VCL bậc cao hơn

(x)

và

(x)

là VCL bậc cao hơn

(x)

khi

x → a

thì

(x) + α

(x) ∼ α

(x)

và

lim

x→a

(x) + α

(x)

(x) + β

(x)

= lim

x→a

(x)

Chú ý 1.7.

Còn tồn đọng một số dạng vô định mà phương pháp sử dụng các VCB-VCL

chưa xử lý được, ví dụ

lim

x→0

x −sin x

, lim

x→0

sin x

, . . .

Các giới hạn này sẽ được xử lý khi chúng ta học đến công thức L’Hospital và khai triển

Maclaurin.

Ví dụ 6.2 (Giữa kì, K61).

T ính giới hạn

6. Vô cùng lớn, vô cùng bé 33

lim

x→0

−1

lim

x→0

√

−1

√

x+x

lim

x→0

1−cos x

ln(1+x

)

lim

x→0

−1

ln(1−3x)

6.3 Bài tập

Như vậy ngoài các phương pháp phân tích đa thức thành nhân tử và nhân liên

hợp đã trình bày ở trên, bài học hôm nay cung cấp cho chúng ta một công cụ mới để tìm

giới hạn, đó là các quy tắc thay tương đương và ngắt bỏ các VCB bậc cao. Đây có lẽ là một

trong những công cụ rất tốt của Giải tích để tính giới hạn.

Bài tập 1.30. Tìm giới hạn

a. lim

x→0

√

1 + αx −

1 + βx





b. lim

x→0

√

1 + αx.

1 + βx −1





Chứng minh. a.

√

1 + αx −

1 + βx

√

1 + αx −1

−

1 + βx −1

Vì

√

1 + αx −1 ∼

1 + βx −1 ∼

x, nên

lim

x→0

√

1 + αx −

1 + βx

−

lim

x→0

√

1 + αx.

1 + βx −1

= lim

x→0

√

1 + αx.

1 + βx −1

√

1 + αx −1

Chú ý 1.8.

i) Lưu ý kĩ thuật thêm bớt

ở trong các biểu thức có chứa

cos α(x), e

α(x)

và

ln(α(x)),

1 + α(x)

ii) Với nhiều bài toán nhìn qua tưởng rất phức tạp vì công thức rất cồng kềnh, thực chất

nếu dùng quy tắc thay tương đương và ngắt bỏ các VCB bậc cao thì sẽ thấy rất đơn

giản. Ví dụ, tính

lim

x→0

sin 2x + arcsin

x −arctan

Với tử số ta có

sin 2x ∼ 2x, arcsin

x ∼ x

, arctan

x ∼ x

. Như vậy giới hạn đã cho

bằng

Hoặc ví dụ như tính

lim

x→0

1 −cos x + 2 sin x −sin

x −x

+ 3x

tan

x −6 sin

x + x −5x

34 Chương 1. Hàm số một biến số (13LT+13BT)

Trông biểu thức này rất phức tạp nh ưng thực chất chúng ta có thể nhìn thấy ngay

giới hạn này bằng

lim

x→0

2 sin x

= 2

với nhận xét là

2 sin x ∼ 2x

là VCB bậc thấp nhất ở

tử số và

là VCB bậc thấp nhất ở mẫu số.

Bài tập 1.31. Tìm giới hạn

a) lim

x→a

sin x −sin a

x −a





b) lim

x→+∞

(sin

√

x + 1 −sin

√

c) lim

x→0

√

cos x −

√

cos x

sin





d) lim

x→0

1 −cos x cos 2x cos 3x

1 −cos x





[Đáp số]

a) cos a b) 0

−1

d) 14

Bài tập 1.32. Tìm giới hạn

a) lim

x→∞



−1

+ 1



x−1

x+1

b) lim

x→0

(cos

√

∞

)

c) lim

x→∞

[sin(ln(x + 1)) −sin(ln x)]

d) lim

n→∞

(

√

x −

n+1

√

x), x > 0.

Chứng minh. a) Đây không phải là dạng vô định, lim

x→∞



−1

+ 1



x−1

x+1

= 1.

b) Áp dụng công thức lim

x→x

A(x)

B(x)

= e

lim

x→x

B(x) ln A(x)

. Vì

lim

x→0



cos

√



= lim

x→0

ln cos

√

= lim

x→0

−sin

√

= −

nên

lim

x→0



cos

√



= e

−

c) Đáp số: 0.

6. Vô cùng lớn, vô cùng bé 35

lim

n→∞

(

√

x −

n+1

√

x), x > 0

= lim

n→∞

− x

n+1

)

= lim

n→∞

n+1

n(n+1)

−1)

= lim

n→∞

n+1

n(n+1)

−1

n(n + 1)

= lim

n→∞

n + 1

n+1

n(n+1)

−1

n(n + 1)

= ln x

So sánh các VCB-VCL.

Chú ý 1.9.

i) So sánh 2 VCB: Nếu

lim

x→a

α(x)

β(x)

= 0

thì ta nói

α(x)

là VCB bậc cao hơn

β(x)

, nhưng

ii) So sánh 2 VCL: Nếu

lim

x→a

α(x)

β(x)

= ∞

thì ta nói

α(x)

là VCL bậc cao hơn

β(x)

iii) Cùng một biểu thức

α(x) =

x +

√

chẳng hạn, thì nếu trong quá trình

x → 0

thì nó là VCB nên theo quy tắc ngắt bỏ VCB bậ c cao,

α(x) ∼

√

x = x

1/4

, còn nếu

xét trong quá trình

x → ∞

thì nó là VCL nên theo quy tắc ngắt bỏ VCL bậc thấp,

α(x) ∼

√

Bài tập 1.33. Khi x→0 cặp VCB sau có tương đương không ?

α(x) =

x +

√

x và β(x) = e

sin x

−cos x

[Đáp số] β(x) = o(α(x))

Bài tập 1.34. Tìm giới hạn

a) lim

x→0

(1 −2x)

∞

b) lim

x→

(sin x)

tan x

∞

c) lim

x→0



1 + tan x

1 + sin x



sin x

∞

d) lim

x→0



sin x



sin x

x−sin x

∞

36 Chương 1. Hàm số một biến số (13LT+13BT)

[Gợi ý] Áp dụng lim

x→x

A(x)

B(x)

= e

lim

x→x

B(x) ln A(x)

[Đáp số]

a) e

−2

b) 1 c) 1 d) e

Bài tập 1.35. Tìm giới hạn

a) lim

x→0

αx

−e

βx





, b) lim

x→0

αx

−e

βx

sin αx −sin βx





c) lim

x→a

− x

x −a





[Gợi ý] Sử dụng phương pháp thay tương đương.

[Đáp số]

a) α − β b) 1 c) a

(ln a −1)

7. Hàm số liên tục 37

§7. HÀM SỐ LIÊN TỤC

7.1 Định nghĩa

Định nghĩa 1.17.

Cho hàm số

f (x)

xác định trong một lân cận nào đó của

. Nó được

gọi là

i) liên tục phải tại

nếu

lim

x→x

= f (x

)

ii) liên tục trái tại

nếu

lim

x→x

−

= f (x

)

iii) liên tục tại

nếu

lim

x→x

= f (x

)

. Nói cách khác,

∀ε > 0, ∃δ(ε, x

) > 0 : ∀x,

x − x

< δ

ta có

f (x) − f (x

)

< ε.

Từ định nghĩa suy ra hàm số f (x) liên tục tại x

khi và chỉ khi nó liên tục phải và liên tục

trái tại x

Ví dụ 7.1.

Tất cả các hàm số sơ cấp đều liên tục trên tập xác định của chúng.

Ví dụ 7.2 (Giữa kì, K61).

T ìm

để hàm số sau liên tục tại

x = 1 :

f (x) =







(x −m)(x

+ x + 1),

nếu

x 6= 1,

1 + m,

nếu

x = 1.

f (x) =







(x + m)(x

+ x + 1),

nếu

x 6= 1,

1 −m,

nếu

x = 1.

Định nghĩa 1.18.

Hàm số

f (x)

được gọi là liên tục trên khoảng

(a, b)

nếu nó liên tục tại

mọi điểm

∈ (a, b)

. Nó được gọi là liên tục trên đoạn

[a, b]

nếu nó liên tục tại mọi điểm

∈ (a, b)

, đồng thời liên tục phải tại

và liên tục trái tại

7.2 Các phép toán số học đối với hàm số liên tục

Định lý 1.16.

Giả thiết các hàm số

f (x)

và

g(x)

liên tục tại

nào đó. Khi đó các hà m số

f (x) ± g(x), f (x)g(x)

cũng liên tục tại

. Hàm số

f (x)

g(x)

cũng liên tục tại

nếu

g(x

) 6= 0

Điều tương tự cũng đúng đối với các hàm số liên tục trái (phải) tại x

38 Chương 1. Hàm số một biến số (13LT+13BT)

7.3 Sự liên tục của hàm ngược

Định lý 1.17.

(Sự liên tục của hàm ngược)

Nếu

là một khoảng,

y = f (x)

đồng biến (nghịch biến) liên tục trên

. Khi đó có hàm

ngược

y = g(x)

cũng đồng biến (nghịch biến) và liên tục trên

(

)

Ví dụ: Các hàm số lượng giác ngược là liên tụ c trên tập xác định của chúng.

7.4 Sự liên tục của hàm hợp

Định lý 1.18.

Nếu hàm số

f (x)

liên tục tại

và

lim

x→a

g(x) = b

thì

lim

x→a

f (g(x)) = b

. Nói cách

khác,

lim

x→a

f (g(x)) = f (lim

x→a

g(x))

Hệ quả 1.2.

Nếu

g(x)

liên tục tại

và

f (x)

liên tục tại

g(a)

thì hàm số

f ◦ g

liên tục tại

7.5 Các định lý về hàm liên tục

Định lý 1.19.

Nếu

f (x)

liên tục trên khoảng

(a, b)

mà giá trị

f (x

), x

∈ (a, b)

dương (hay

âm) thì tồn tại một lân cận

U(x

)

sao cho

∀x ∈ U(x

)

f (x)

cũng dương hay âm. Hình ảnh

hình học.

Định lý 1.20.

Nếu

f (x)

liên tục trên đoạn

[

a, b

]

thì nó bị chặn trên đoạn đó. Hình ảnh

hình học.

Định lý 1.21.

Nếu

f (x)

liên tục trên đoạn

[

a, b

]

thì nó đạt được GTLN, NN trên đoạn này.

Hình ảnh hình học.

* Liên tục đều, hình ảnh hình học của liên tục đều.

Định lý 1.22.

(Định lý Cantor)

Nếu

f (x)

liên tục trên

[

a, b

]

thì nó liên tục đều trên đó (thay

[

a, b

]

bằng khoảng

(

a, b

)

thì

định lý không còn đúng). Mô tả hình học.

Định lý 1.23.

(Định lý Cauchy)

Nếu

f (x)

liên tục trên đoạn

[

a, b

]

và có

f (a). f (b) < 0

thì

∃α ∈

(

a, b

)

để

f (α) = 0

Ví dụ 7.3 (Giữa kì, 20173).

Cho hàm số

f : [1, 3] → [1, 3]

liên tục. Chứng minh rằng tồn

tại

∈ [1, 3]

sao cho

f (x

) = x

7. Hàm số liên tục 39

[Lời giải] Xét g(x) = f (x) − x ⇒ g(1) = f (1) −1 ≥ 0, g(3) = f (3) −3 ≤ 0. Theo Định lý

Cauchy, phương trình g(x) = 0 có nghiệm x

nào đó trong khoảng [1, 3] ⇒ f (x

) = x

Hệ quả 1.3.

Nếu

f (x)

liên tục trên đoạn

[

a, b

]

, A = f (a) 6= B = f (b)

thì nó nhận mọi giá

tr ị trung gian giữa

và

Hệ quả 1.4.

Cho

f (x)

liên tục trên

[

a, b

]

, m, M

lần lượt là các GTNN, LN của hàm số trên

đoạn này thì

[

m; M

]

là tập giá trị của hàm số.

7.6 Điểm gián đoạn và phân loại điểm gián đoạn của

hàm số

Định nghĩa 1.19.

Nếu hàm số không liên tục tại điểm

thì ta nói nó gián đoạn tại

Hình ảnh hình học: đồ thị không liền nét tại điểm gián đoạn.

Theo định nghĩa, hàm số f (x) liên tục tại x

nếu ba điều kiện sau được thỏa mãn:

• f (x) xác định tại x

• tồn tại lim

x→x

f (x),

• lim

x→x

f (x) = f (x

Như vậy nếu x

là điểm gián đoạn của f (x) thì

• hoặc x

6∈ TXĐ,

• hoặc x

∈ TXĐ và 6 ∃ lim

x→x

f (x),

• hoặc x

∈ TXĐ và ∃ lim

x→x

f (x) nhưng lim

x→x

f (x) 6= f (x

), ở đây x → x

theo nghĩa cả

hai phía hay một phía.

Nếu x

6∈ TXĐ của f (x) thì có thể có rất nhiều điểm gián đoạn, nên ta chỉ quan tâm

đến những điểm gián đoạn thuộc tập xác định h ay là những điểm đầu mút của khoảng

xác định.

Phân loại điểm gián đoạn

Giả sử x

là điểm gián đoạn của f (x).

40 Chương 1. Hàm số một biến số (13LT+13BT)

1. Điểm gián đoạn loại 1:

Nếu ∃ lim

x→x

f (x) = f





và lim

x→x

−

f (x) = f



−



thì x

được gọi là điểm gián đoạn

loại 1 của hàm số f (x). Khi đó, có thể xảy ra hai trường hợp:

• Nếu f





6= f



−



thì giá trị







− f



−





gọi là bước nhảy của hàm số.

• Đặc biệt

: nếu f





= f



−



thì x

được gọi là điểm gián đoạn bỏ được của

hàm số. Khi đó nếu hàm số chưa xác định tại x

thì ta có thể bổ sung thêm giá

trị của hàm số tại x

để hàm số liên tục tại điểm x

. Còn nếu hàm số xác định

tại điểm x

thì ta có thể thay đổi giá trị của hàm số tại điểm này để hàm số liên

tục tại x

2. Điểm gián đoạn loại 2:

Nếu x

không là điểm gián đoạn loại 1 thì ta nói nó là điểm gián đoạn loại 2.

Chú ý 1.10.

Với quan điểm xem điểm gián đoạn bỏ được là trường hợp đặc b iệt của điểm

gián đoạn loại 1, nếu

là điểm đầu mút của khoảng hay đoạn xác định của

f (x)

, mà có

lim

x→x

f (x)

hoặc

lim

x→x

−

f (x)

hữu hạn thì ta cũng xem

là điểm gián đoạn bỏ được của hàm

số.

Ví dụ 7.4 (Giữa kì, K61).

a) Điểm

x =

là điểm gián đoạn loại gì của hàm số

f (x) =

1−2

tan x

b) Điểm

x = −

là điểm gián đoạn loại gì của hàm số

f (x) =

1−2

tan x

Ví dụ 7.5 (Cuối kì, K61-Viện ĐTQT).

Điểm

x = 0

là điểm gián đoạn loại gì của hàm số

y = e

−arctan

y = e

−arccot

7.7 Bài tập

Xét tính liên tục của hàm số. Muốn kiểm tra xem f (x) có liên tục tại x

hay không

chúng ta đi kiểm tra lim

x→x

f (x) có bằng f (x

) hay không? Đôi khi phải xét lim

x→x

f (x) và

lim

x→x

−

f (x) nếu biểu thức củ a f (x) ở hai phía của x

được cho dưới các công thức khác nhau.

Thậm chí cũng có khi biểu thức của f (x) ở hai phía của x

được cho cùng một công thức

nhưng giới hạn trái và giới hạn phải của f (x) tại x

vẫn khác nhau. Ví dụ, xét sự liên tục

của hàm số f (x) =







1−2

cot x

, x 6= 0,

1, x = 0

. Hàm số này có lim

x→0

f (x) = 0 và lim

x→0

−

f (x) = 1 (tại

sao?). Do đó nó liên tục trái tại 0 và không liên tục phải tại 0.

Bài tập 1.36. Tìm a để hàm số liên tục tại x = 0

7. Hàm số liên tục 41

a) f (x) =







1−cos x

, nếu x 6= 0

a, nếu x = 0.

b) g(x) =







+ bx + 1, nếu x ≥ 0

a cos x + b sin x, nếu x < 0.

[Đáp số]

a) a =

b) a = 1

Bài tập 1.37. Điểm x = 0 là điểm gián đoạn loại gì của hàm số

a) y =

1 −2

cot x

b) y =

sin

−1

c) y =

−e

(a 6= b).

[Đáp số]

a) Loại I b) Loại II c) Bỏ được

Bài tập 1.38. Xét sự liên tục của các hàm số sau

a) f (x) =







x sin

, nếu x 6= 0

0, nếu x = 0

b) f (x) =







−

, nếu x 6= 0

0, nếu x = 0

c) f (x) =







sin πx, nếu x vô tỉ

0, nếu x hữu tỉ

[Đáp số]

a) liên tục b) liên tục c) gián đoạn

Bài tập 1.39. Chứng minh rằng nếu f , g là các hàm số liên tục t rên đoạn [a, b] và f (x) =

g(x) với mọi x là số hữu tỉ trong đoạn [a, b] thì f (x) = g(x)∀x ∈ [a, b].

Bài tập 1.40. Chứng minh rằng phương trình x

− 3x − 1 có ít nhất một nghiệm trong

khoảng (1, 2 ).

Bài tập 1.41. Cho f (x) = ax

+ bx + c, biết 2 a + 3b + 6c = 0. Chứng minh rằng f (x) có ít

nhất một nghiệm trong khoảng (0, 1).

Bài tập 1.42. Chứng minh rằng nếu f : [0, 1]→[0, 1] liên tục thì tồn tại x

∈ [0, 1] sao cho

f (x

) = x

Bài tập 1.43. Chứng minh rằng mọi đa thức bậc lẻ với hệ số thực đều có ít nhất một

nghiệm thực.

42 Chương 1. Hàm số một biến số (13LT+13BT)

§8. ĐẠO HÀM VÀ VI PHÂN

8.1 Định nghĩa

Định nghĩa 1.20.

Giới hạn, nếu có, của tỉ số

lim

∆x→0

f (x

+ ∆x) − f (x

)

∆x

được gọi là đạo hàm của hàm số

f (x)

tại

và được kí hiệu là

′

)

. Khi đó ta nói hàm số

f (x)

có đạo hàm tại

Nếu quá trình ∆x → 0 trong định nghĩa trên được thay bằng

• ∆x → 0

thì giới hạn đó được gọi là đạo hàm phải của hàm số f (x) tại x

, kí hiệu là

′

• ∆x → 0

−

thì giới hạn đó được gọi là đạo hàm trái của hàm số f (x) tại x

, kí hiệu là

′

−

Đương nhiên, một hàm số có đạo hàm tại x

khi và chỉ khi nó có đạo hàm trái và đạo hàm

phải tại x

Nếu tồn tại f

′

) thì f (x) liên tục tại x

. Tuy nhiên, điều ngược lại không đúng, chẳng

hạn như hàm số f (x) = |x| liên tục tại 0 nhưng không có đạo hàm tại đó.

Ví dụ 8.1 (Giữa kì, K61).

T ính

′

(0)

, biết

f (x) =







sin x,

nếu

x ≥ 0,

+ x,

nếu

x < 0.

f (x) =







tan x,

nếu

x ≥ 0,

−x

+ x,

nếu

x < 0.

Ví dụ 8.2 (Giữa kì, K61).

Hãy chỉ ra một hàm số

f (x)

xác định trên

, liên tục tại các

điểm

= 1, x

= 2

nhưng không có đạo hàm tại các điểm này.

Ví dụ 8.3 (Giữa kì, K59).

Cho hàm số

f (x)

khả vi tại

và biết rằng

lim

x→0

f (1 + 7x) − f (1 + 2x)

= 2.

T ính

′

(1)

[Lời giải] Ta có

lim

x→0

f (1 + 7x) − f (1 + 2x)

= lim

x→0



f (1 + 7x) − f (1)

−2.

f (1 + 2x) − f (1)



= 7 f

′

(1) −2 f

′

(1) ⇒ f

′

(1) =

8. Đạo hàm và vi phân 43

Ví dụ 8.4 (Giữa kì, 20173).

Cho hàm số

f (x) =







−

nếu

x > 0,

nếu

x = 0.

T ính

′

(0)

[Lời giải] Ta có

′

(0) = lim

x→0

f (x) − f (0)

x −0

= lim

x→0

−

Đặt t =

⇒ f

′

(0) = lim

t→+∞

= lim

t→+∞

= 0 (L’Hospital)

8.2 Các phép toán trên đạo hàm

Định lý 1.24.

Cho

u(x)

và

v(x)

là các hàm số có đạo hàm tại

. Khi đó,

(u ±v)

′

) = u

′

) ±v

′

)

ii)

(uv)

′

) = u

′

)v(x

) + u(x

′

)

iii)





) =

′

)v(x

)−u(x

′

)

nếu

v(x

) 6= 0

Ví dụ 8.5 (Giữa kì, K61-Viện ĐTQT).

T ính đạo hàm của hàm số

f (x) = x

sin x

, 0 < x <

f (x) = (sin x)

, 0 < x <

f (x) = x

cos x

, 0 < x <

f (x) = (cos x)

, 0 < x <

f (x) = (cos x)

sin x

, 0 < x <

f (x) = (sin x)

cos x

, 0 < x <

8.3 Đạo hàm của hàm hợp

Định lý 1.25.

Nếu

có đạo hàm tại

và

có đạo hàm tại

u(x)

thì hàm số hợp

F = f ◦ u

có đạo hàm tại

và

′

(x) = f

′

(u(x)).u

′

(x).

Ý tưởng chứng minh: ta có

(

+ ∆x

)

= u

(

)

+ u

′

(

)

∆x + o

(

∆x

)

[

(

+ ∆x

)]

− f

[

(

)]

= f







+ u

′

)∆x + o

(

∆x

)

{z }







− f

(

)

= f

′

(

)

.δ

+ o





=⇒ lim

∆x→0

[

(

+ ∆x

)]

− f

[

(

)]

∆x

44 Chương 1. Hàm số một biến số (13LT+13BT)

8.4 Đạo hàm của hàm ngược

Định lý 1.26.

Giả thiết

x = ϕ

(

)

có đạo hàm tại

và

′

(

)

6= 0

ii)

x = ϕ

(

)

có hàm ngược

y = f (x)

liên tục tại

= ϕ

(

)

Khi đó hàm ngược này có đạo hàm tại điểm

và

′

(

)

′

)

Định lý 1.27.

Giả thiết

x = ϕ(y)

có đạo hàm tại

và

′

(

)

6= 0

ii)

x = ϕ(y)

biến thiên đơn điệu trong lân cận điểm

Khi đó nó tồn tại hàm ngược

y = f (x)

, hàm ngược này cũng có đạo hàm tại điểm

và

′

) =

′

)

Từ đó xây dựng công thức đạo hàm của các hàm số lượng giác ngược.

8.5 Đạo hàm của các hàm số sơ cấp cơ bản

1. (x

)

′

= αx

α−1

2. (a

)

′

= a

ln a

3. (log

′

x ln a

4. (ln x)

′

5. (sin x)

′

= cos x

6. (cos x)

′

= −sin x

7. (tan x)

′

cos

8. (cot x)

′

= −

sin

9. (arcsin x)

′

√

1−x

10. (arccos x)

′

= −

√

1−x

11. (arctan x)

′

1+x

12. (arccot x)

′

= −

1+x

8.6 Vi phân của hàm số

Cho hàm số y = f (x) có đạo hàm tại x. Theo định nghĩa của đạo hàm,

′

(x) = lim

∆x→0

∆y

∆x

= li m

∆x→0

f (x + ∆x) − f (x)

∆x

8. Đạo hàm và vi phân 45

Do đó,

∆y

∆x

= f

′

(x) + α(∆x), trong đó α(∆x) là một VCB khi ∆x → 0. Vậy

∆y = f (x + ∆x) − f (x) = f

′

(x)∆x + α.∆x.

Số hạng α.∆x là một VCB bậc cao hơn ∆x. Do đó, ∆y và f

′

(x)∆x là hai VCB tương đương.

Định nghĩa 1.21.

Cho hàm số

f (x)

xác định trong một lân cận

)

. Nếu có

∆ f = A∆x + o(∆x),

ở đó

chỉ phụ thuộc vào

chứ không phụ thuộc vào

∆x

thì ta nói hàm số

f (x)

khả vi tại

và biểu thức

d f = A∆x

được gọi là vi phân của hàm số

f (x)

tại điểm

Mối liên hệ giữa đạo hàm và vi phân

Định lý 1.28.

Hàm số

f (x)

có đạo hàm tại

khi và chỉ khi nó khả vi tại

và

d f (x

) = f

′

)∆x.

Chú ý 1.11.

Khái niệm "có đạo hàm" và khái niệm "có vi phân" (hay khả vi) là hai khái

niệm khác nhau. Tuy nhiên, vì tính tương đương giữa hai khái niệm này đối với hàm số

một biến số mà nhiều người hiểu nhầm rằng chúng là một. Trong chương 3 của học phần

Giải tích I này, chúng ta sẽ thấy h ai khái niệm này là k hác nhau đối với hàm số nhiều

biến số.

Xét hàm số y = f (x) = x có d f (x) = dx = 1.∆x. Vì thế với biến số độc lập x ta quy ước viết

dx = ∆x và dy = d f (x) = f

′

(x)dx.

Tính bất biến của dạng thức vi phân (cấp 1)

Cho y = f (x) là một hàm số khả vi. Khi đó, ta đã biết nếu x là biến số độc lập thì

d f (x) = f

′

(x)dx.

Định lý 1.29.

Nếu

không phải là một biến số độc lập mà

x = x(t)

là một hàm số phụ

thuộc vào biến số

thì công thức

d f (x) = f

′

(x)dx

vẫn còn đúng.

46 Chương 1. Hàm số một biến số (13LT+13BT)

Chứng minh. Đặt F(t) = f (x(t)), khi đó F

′

(t) = f

′

(x(t))x

′

(t) và

d f (x(t)) = f

′

(x(t))x

′

(t)dt.

Mặt khác, dx = x

′

(t)dt nên d f (x) = f

′

(x)dx.

Chính vì vậy, tính chất này còn được gọi là tính bất biến của dạng thức vi phân cấp

một. Chú ý rằng tính chất này không còn đúng đối với các dạng thức vi phân cấp cao.

Ví dụ 8.6.

T ính

(

)



−2x

− x



Ý nghĩa hình học của vi phân

+ ∆y

+ ∆x

y = f (x)

d f (x

) =

∆y

Khi x thay đổi từ x

đến x

+ ∆x thì

i) d f (x

) =

MT thể hiện sự thay đổi của đường thẳng tiếp tuyến,

ii) ∆y = f (x

+ ∆x) − f (x

) thể hiện sự thay đổi của đường cong y = f (x).

Vi phân của tổng, hiệu, tích, thương

d(u ±v) = du ± dv, d(u.v) = udv + vdu, d





vdu −udv

Ví dụ 8.7 (Giữa kì, K61).

T ìm

′

(x)

nếu biết

[ f (2016x)] = x

. b)

[ f (2017x)] = x

8. Đạo hàm và vi phân 47

Ứng dụng vi phân tính gần đúng

Xuất phát từ công thức ∆y = f (x + ∆x) − f (x) = f

′

(x)∆x + o(∆x) ta ngắt bỏ phần VCB

bậc cao o(∆x) để được công thức tính gần đúng sau:

f (x

+ ∆x) ≈ f (x

) + f

′

)∆x.

Ví dụ 8.8 (Giữa kì, K61).

Sử dụng vi phân, tính gần đúng

√

7, 97.

√

8, 03.

8.7 Đạo hàm cấp cao

Định nghĩa 1.22.

Nếu hàm số

y = f (x)

có đạo hàm thì

′

= f

′

(x)

gọi là đạo hàm cấp một

của

f (x)

i) Đạo hàm, nếu có, của đạo hàm cấp một được gọi là đạo hàm cấp hai, kí hiệu là

′′

(x)

ii) Đạo hàm, nếu có, của đạo hàm cấp

n −1

được gọi là đạo hàm cấp

, kí hiệu là

(n)

(x)

Các phép toán trên đạo hàm cấp cao

Định lý 1.30.

Cho

u, v

là các hàm số khả vi đến cấp

. Khi đó,

(u ±v)

(n)

= u

(n)

±v

(n)

ii) (Công thức Leibniz)

(u.v)

(n)

∑

k=0

(n−k)

(k)

Ví dụ 8.9.

T ính đạo hàm cấp cao của các h àm số sau

y = x

, y =

x + a

, y = sin

(

ax + b

)

y = cos

(

ax + b

)

, y = e

, y =



+ 1



, y = e

sin x.

Đạo hàm cấp cao của một số hàm số cơ bản

1. (x

)

(n)

= α(α −1) . . . (α −n + 1)x

α−n

2. [(1 + x)

]

(n)

= α(α −1) . . . (α −n + 1).(1 + x)

α−n



1+x



(n)

= (−1)

(n)

(1+x)

n+1



1−x



(n)

(1−x)

n+1

48 Chương 1. Hàm số một biến số (13LT+13BT)

(

sin x

)

(n)

= sin



x +

nπ



(

cos x

)

(n)

= cos



x +

nπ



7. (a

)

(n)

= a

(

ln a

)

8. (ln x)

(n)

= (−1)

n−1

(n −1)!

Ví dụ 8.10 (Giữa kì, K61).

T ính đạo hàm cấp cao

(10)

(0)

với

y(x) = e

−x

y(x) = arctan x.

y(x) = arccot x.

[Lời giải]

a) Ta có y

′

(x) = 2xe

= 2xy. Lấy đạo hàm cấp n hai vế ta được

(n+1)

(x) = (2xy)

(n)

= 2xy

(n)

(x) + 2ny

(n−1)

(x). (Công thức Leibniz)

Thay x = 0 ta được có công thức truy hồi

(n+1)

(0) = 2ny

(n−1)

(0).

Do đó,

(10)

(0) = 2.9y

(8)

(0) = (2.9).(2.7)y

(6)

(0) = ··· = (2.9)(2.7)(2.5)(2.3)(2.1)y

(0)

(0) = 30240.

b) Tương tự câu a).

c) Ta có y

′

1+x

⇒ (1 + x

′

= 1. Lấy đạo hàm cấp n hai vế ta được

(1 + x

(n+1)

(x) + n.2x.y

(n)

(x) +

n(n −1)

.2.y

(n−1)

(x) = 0. (Công thức Leibniz)

Thay x = 0 vào ta được công thức truy hồi

(n+1)

(0) = −n(n −1)y

(n−1)

(0).

Do đó,

(10)

(0) = −9.8y

(8)

(0) = (−9.8)(−7.6)y

(6)

(0) = ··· = (−9.8)(−7.6)(−5.4)(−3.2)y

′′

(0) = 0

bởi vì, y

′

1+x

⇒ y

′′

(x) =

−2x

(1+x

)

⇒ y

′′

(0) = 0.

d) Tương tự câu c).

Ví dụ 8.11 (Giữa kì, K59).

T ính đạo hàm cấp cao

(19)

(0)

với

8. Đạo hàm và vi phân 49

y = arcsin x

, b)

y = arccos x

[Lời giải]

a) Ta có

′

√

1 − x

⇒ (1 −x

′

1 − x

⇒ (1 −x

′′

−2xy

′

−x

√

1 − x

⇒ (1 −x

′′

−xy

′

= 0.

Đạo hàm cấp n hai vế ta được

[(1 −x

′′

−xy

′

]

(n)

= 0 ⇒ (1 −x

(n+2)

−2nxy

(n+1)

−n(n −1)y

(n)

−xy

(n+1)

−ny

(n)

= 0.

Thay x = 0 vào ta được công thức truy hồi

(n+2)

(0) = n

(n)

(0) ⇒ y

(19)

(0) = 17

(17)

(0) = ··· = (17!!)

′

(0) = (17!!)

b) Tương tự câu a).

Ví dụ 8.12 (Cuối kì, K60).

T ính

(10)

(1)

với

f (x) = x

ln x

[Lời giải] Ta xét bài toán tổng quát hơn: tính g

(n+1)

(x) với g(x) = x

ln x. Nhận xét

i) g

′

(x) = nx

n−1

ln x + x

n−1

= nx

n−1



ln x +



ii) g

′′

(x) = n(n −1)x

n−1



ln x +

n−1



Do đó,

(n)

(x) = n!



ln x +

+ ···+



(n+1)

(x) =

⇒ f

(10)

(x) =

10!

⇒ f

(10)

(1) = 10!.

Ví dụ 8.13 (Cuối kì, 20152).

Cho hàm số

f (x) =

1+x

. Tính

f (0)

[Lời giải] Ta có (1 + x

) f (x) = x. Lấy đạo hàm cấp n hai vế ta được

(1 + x

) f

(n)

(x) + n.3x

. f

(n−1)

(x) +

n(n −1)

.6x. f

(n−2)

(x) +

n(n −1)(n −2)

.6. f

(n−3)

(x) = 0.

Cho x = 0 ta được công thức truy hồi

(n)

(0) = −n(n −1)(n −2) f

n−3

(0).

Do đó,

(10)

(0) = −10.9.8. f

(7)

(0) = (−10.9.8)(−7.6.5)(−4.3.2) f

(1)

(0) = −10! ⇒ d

f (0) = −10!dx

Ví dụ 8.14 (Giữa kì, K61).

T ính đạo hàm cấp cao

50 Chương 1. Hàm số một biến số (13LT+13BT)



−x



(60)





(50)

sin 2x)

(50)

cos 2x)

(60)

8.8 Vi phân cấp cao

Định nghĩa 1.23.

Nếu hàm số

y = f (x)

khả vi thì

dy = f

′

(x)dx

gọi là vi phân cấp một

của

f (x)

i) Vi phân, nếu có, của vi phân cấp một được gọi là vi phân cấp hai, kí hiệu là

f (x)

ii) Vi phân, nếu có, của vi phân cấp

n −1

được gọi là vi phân cấp

, kí hiệu là

f (x)

Biểu thức của vi phân cấp cao

Nếu x là biến số độc lập thì

f (x) = f

(n)

(x)dx

Vi phân cấp cao không có tính chất bất biến đối với hàm hợp

Ta có d f (x) = f

′

(x)dx nên

f (x) = d f

′

(x)dx + f

′

(x)d

x = f

′′

(x)dx

+ f

′

(x)d

Ví dụ 8.15.

Chứng minh rằng nếu

y = x

, x = t

thì

y 6= y

(2)

8.9 Bài tập

Bài tập 1.44. Tìm đạo hàm của hàm số

f (x) =











1 − x, khi x < 1

(1 − x)(2 − x), khi 1 ≤ x ≤ 2

x −2, khi x > 2.

Bài tập 1.45. Với điều kiện nào thì hàm số f (x) =







sin

, khi x 6= 0

0, khi x = 0

8. Đạo hàm và vi phân 51

a) liên tục tại x = 0, b) khả vi tại x = 0, c) có đạo hàm liên tục tại

x = 0.

[Đáp số]

a) n > 0, b) n > 1, c) n > 2.

Bài tập 1.46. Chứng minh rằng hàm số f (x) = |x − a|.ϕ(x), trong đó ϕ(x) là một hàm số

liên tục và ϕ(a) 6= 0, không khả vi tại điểm x = a.

[Gợi ý]

′

(a) = ϕ(a) 6= f

′

−

(a) = −ϕ(a)

Bài tập 1.47. Tìm vi phân của hàm số

a) y =

arctan

| (a 6= 0)

b) y = arcsin

(a 6= 0 )

c) y =



x −a

x + a



(a 6= 0 )

d) y = ln |x +

√

+ a|

[Đáp số]

a) dy =

+ x

b) dy =

√

− x

.(sign a)

c) dy =

− a

d) dy =

√

+ a

Bài tập 1.48. Tìm

a) I =

d(x

)

−2x

− x

b) J =

d(x

)

(

sin x

c) K =

d(sin x)

d(cos x)

[Đáp số]

a) I = −3x

−4x

+ 1, x 6= 0,

b) J =



cos x −

sin x



, x 6= 0,

c) K = −cot x, x 6= kπ, k ∈ Z.

Bài tập 1.49. Tính gần đúng giá trị của biểu thức

52 Chương 1. Hàm số một biến số (13LT+13BT)

a) lg 11

2 −0, 02

2 + 0, 02

[Gợi ý]

a) Xét f (x) = lg x, x

= 10, △x = 1, ta có lg 11 ≈ lg 10 +

10 ln 10

= 1, 043

b) Cách 1.

2 −0, 02

2 + 0, 02

−1. Xét f (x) =

−1, x

= 2, △x = 0, 02

Ta có

f (x + △x) =

−1 + 0, 02.

−1)

−6

−4

= 1 −0, 02.

Cách 2. Xét hàm số f (x) =

2−x

2+x

, với x

= 0, ∆x = 0, 02.

Bài tập 1.50. Tìm đạo hàm cấp cao của các hàm số

(a) y =

1 − x

, tính y

(8)

(b) y =

1 + x

√

1 − x

, tính y

(100)

, tính y

(10)

(d) y = x

sin x, tính y

(50)

[Đáp số]

(a) y

(8)

(1 − x)

, x 6= 1.

(b) y

(100)

197!

100

(1 − x)

100

√

1 − x

(399 − x), x < 1.

(10)

= 2



+ 10x +



(d) y

(50)

= −x

sin x + 100x cos x + 2450 si n x.

Bài tập 1.51. Tính đạo hàm cấp n của các hàm số

a) y =

−1

b) y =

−3x + 2

c) y =

√

1 + x

d) y = e

sin(bx + c).

[Đáp số]

a) y

(n)

(−1)



(x −1)

n+1

(x + 1)

n+1



b) y

(n)

= n!



(1 − x)

n+1

−

(2 − x)

n+1



8. Đạo hàm và vi phân 53

c) y

(n)

(−1)

n−1

(1.4 . . . (3n −5))

3n + 2x

(1 + x)

, n ≥ 2, x 6= 1.

d) Tính y

′

rồi dự đoán và chứng minh bằng quy nạp

(n)

= (a

+ b

)

sin(bx + c + nϕ), ở đó sin ϕ =

√

+ b

, cos ϕ =

√

+ b

Bài tập 1.52. Tính đạo hàm cấp n của các hàm số

a) y =

a + bx

b) y =

√

a + bx

c) y =

− a

d) y =

ax + b

cx + d

e) y = sin

f) y = sin

g) y = sin ax. sin bx,

h) y = sin

ax. cos bx,

i) y = sin

x + cos

j) y = x cos ax,

k) y = x

cos ax,

l) y = x

sin ax,

m) y = ln

a + bx

a −bx

[Đáp số]

a) y

(n)

(−1)

.n!b

(a + bx)

n+1

b) y

(n)

(−1)

.(2n −1)!!b

√

a + bx

c) y =

− a

(

x − a

−

x+a

) nên y

(n)

(−1)

.n!



x − a



n+1

−



x + a



n+1

d) y =

ax + b

cx + d



b −



x +

nên y

(n)



b −



(−1)

.n!



x +



n+1

e) y = sin

x =

−

cos 2x nên y

(n)

= −2

n−1

cos



2x +

nπ



f) y = sin

x =

sin x −

sin 3x nên y

(n)

sin



x +

nπ



−

sin



3x +

nπ



g) y = sin ax. sin bx =

[cos(a − b)x −cos(a + b)x] nên

(n)

(a − b)

cos

(a − b)x +

nπ

−

(a + b)

cos

(a + b)x +

nπ

h) y = sin

ax. cos bx =

cos bx

−

[cos(2a + b)x + cos(2a −b)x] nên

(n)

cos



bx +

nπ



−

(2a + b)

cos

(2a + b)x +

nπ

−

(2a −b)

cos

(2a − b)x +

nπ

54 Chương 1. Hàm số một biến số (13LT+13BT)

i) y = sin

x + cos

x =

cos 4x nên y

(n)

= 4

n−1

cos



4x +

nπ



j) y

(n)

= a

x cos



ax +

nπ



+ na

n−1

cos



ax +

(n−1)π



k) y

(n)

= a

sin



ax +

nπ



+ 2na

n−1

x sin



ax +

(n−1)π



+ n(n −1)a

n−2

sin



ax +

(n−2)π



l) y

(n)

= a

cos



ax +

nπ



+ 2na

n−1

x cos



ax +

(n−1)π



+ n(n −1)a

n−2

cos



ax +

(n−2)π



m) y

(n)

(n −1)!b

−b

)

[

(a + bx)

+ (−1)

(a − bx)

]

8.10 Đọc thêm: Về khái niệm vi phân

Vi phân có lẽ là một khái niệm trừu tượng và dễ gây hiểu nhầm nhất trong môn Giải

tích I. Theo sự hiểu biết của tác giả thì có nhiều cách tiếp cận khác nhau đối với phép tính

vi phân.

1) Người đầu tiên đưa ra khái niệm vi phân có lẽ là Leibniz, khi ông coi dy là một đại

lượng vô cùng bé thể hiện sự thay đổi của hàm số y = f (x) tương ứng với sự thay đổi

vô cùng bé dx của biến số x, nghĩa là ông định nghĩa

′

(x) :=

Kí hiệu

này là kí hiệu của Leibniz cho đạo hàm của hàm số f (x). Mặc dù có nh iều

chỉ trích cho kí hiệu này, nó vẫn được dùng cho đến ngày nay. Cũng chú ý thêm rằng,

kí hiệu f

′

(x) trên là kí hiệu của d’Alambert.

2) Cauchy là người đã cải tiến ý tưởng của Leibniz và những người đi trước như sau.

Trước hết, ông định nghĩa phép toá n đạo hàm

′

(x) := lim

∆x→0

f (x + ∆x) − f (x)

∆x

là giới hạn của tỉ số giữa số gia của hàm số và số gia của đối số khi số gia của đối số

tiến về 0. Sau đó ông định nghĩa vi phân

dy = f

′

(x)dx,

như một hàm số của hai biến số x và dx, ở đó dx là một biến số mới, có thể lấy giá trị

tùy ý, không nhất thiết phải là một đại lượng VCB như trong kí hiệu của Leibniz.

3) Ngày nay, vi phân được định nghĩa theo lối tiếp cận hiện đại như sau:

8. Đạo hàm và vi phân 55

Định nghĩa 1.24.

Cho hàm số

f (x)

có đạo hàm tại

. Ta gọi ánh xạ, kí hiệu là

xác định bởi

f : R → R,

h 7→ f

′

là vi phân của

tại

Vậy vi phân của f tại x

là một ánh xạ tuyến tính.

i) Như vậy, vi phân của hàm số một biến số f (x) là một hàm số d f của ha i biến số

và h cho bởi

f (h) = f

′

)h,

ở đó h là một biến số mới có thể nhận giá trị tùy ý.

ii) Kí hiệu Id là ánh xạ đồng nhất, khi đó, d

(Id)(h) = h, hay là d

(Id) = Id.

iii) Một cách lạm dụng kí hiệu, ta kí hiệu x là ánh xạ đồng nhất x := Id. Khi đó,

x = Id là ánh xạ đồng nhất và không phụ thuộc vào x

nên ta kí hiệu nó là

dx. Điều này dẫn đến d

f = f

′

)dx. Đôi khi, người ta bỏ x

trong d

f và, một

cách lạm dụng, thay x

bởi x trong f

′

) để có biểu thức cô đọng

d f = f

′

(x)dx.

56 Chương 1. Hàm số một biến số (13LT+13BT)

§9. CÁC ĐỊNH LÝ VỀ HÀM KHẢ VI VÀ ỨNG DỤNG

9.1 Các định lý về hàm khả vi

Định nghĩa 1.25 (Cực trị của hàm số).

Cho hàm số

f (x)

liên tục trên

(a, b)

, ta nói hàm

số đạt cực trị tại điểm

∈ (a, b)

nếu

∃U(x

) ⊂ (a, b)

sao cho

f (x) − f (x

)

không đổi dấu

∀x ∈ U(x

) \

{

}

• Nếu f (x) − f (x

) > 0 thì ta nói hàm số đạt cực t iểu tại x

• Nếu f (x) − f (x

) < 0 thì ta nói hàm số đạt cực đại tại x

Định lý 1.31 (Định lý Fermat).

Cho

f (x)

liên tục trên khoảng

(a, b)

, nếu hàm số đạt cực

tr ị tại điểm

∈ (a, b)

và có đạo hàm tại

thì

′

) = 0

Chứng minh. Nếu hàm số đạt cực đại tại x

thì th eo định nghĩa tồn tại một lân cận U(x

)

sao cho f (x) − f (x

) < 0∀x ∈ U(x

). Do đó, với h đủ nhỏ sao cho f (x

+ h) ∈ U(x

) thì

f (x

+ h) − f (x

) < 0.

• f

′

) = lim

h→0

f (x

+h)−f (x

)

≤ 0.

• f

′

−

) = lim

h→0

−

f (x

+h)−f (x

)

≥ 0.

Do giả thiết tồn tại f

′

) nên f

′

) = f

′

−

). Điều này chỉ xảy ra khi

′

) = f

′

−

) = 0.

Ví dụ 9.1 (Giữa kì, K61).

T ìm các cực trị của các hàm số

y =

cos x

2+sin x

trong khoảng

(0, 2π).

y =

sin x

2+cos x

trong khoảng

(0, 2π).

Ví dụ 9.2 (Cuối kì, K61-Viện ĐTQT).

Cho

f (x)

là một h àm số khả vi trên

và thỏa

mãn

′

(2) < λ < f

′

(3)

. Chứng minh rằng tồn tại

∈ (2, 3)

sao cho

′

) = λ.

[Lời giải] Xét hàm số g(x) = f (x) − λx. Khi đó,

i) g

′

(2) = f

′

(2) −λ < 0, do đó tồn tại x

∈ (2, 3) nào đó sao cho g(x

) < g(2), nếu không

thì

′

(2) = lim

x→2

g(x) − g(2)

x −2

≥ 0.

ii) g

′

(3) = f

′

(3) −λ > 0, do đó tồn tại x

∈ (2, 3) sao cho g(x

) < g(3), nếu không thì

′

−

(3) = lim

x→3

−

g(x) − g(2)

x −3

≤ 0.

9. Các định lý về hàm khả vi và ứng dụng 57

iii) Do đó, g(x) đạt cực tiểu tại điểm x

∈ (2, 3) ⇒ g

′

) = 0 ⇒ f

′

) = λ.

Định lý 1.32 (Định lý Rolle).

Nếu hàm số

f (x) :

i) Liên tục trong khoảng đóng

[a, b]

ii) Có đạo hàm trong khoảng mở

(a, b)

iii) thỏa mãn điều kiện

f (a) = f (b)

thì tồn tại ít nhất một điểm

c ∈ (a, b)

sao cho

′

Chứng minh. Do hàm số f (x) liên tục trên [a, b] nên nó đạt GTLN và GTNN trên [a, b]. Ta

chia làm các trường hợp sau:

• Nếu f (x) là hằng số trên [a, b] thì f

′

(x) = 0∀x ∈ (a, b).

• Nếu có số x ∈ (a, b) sao cho f (x) > f (a) = f (b) thì GTLN của f (x) sẽ phải đạt được

tại một điểm c nào đó thuộc (a, b) (do nó không đạt GTLN tại hai đầu mút). Khi đó,

theo Định lý Fermat, f

′

• Nếu có số x ∈ (a, b) sao cho f (x) < f (a) = f (b) thì GTNN của f (x) sẽ phải đạt được

tại một điểm c nào đó thuộc (a, b) (do nó không đạt GTNN tại hai đầu mút). Khi đó,

theo Định lý Fermat, f

′

Ví dụ 9.3 (Học kì 20163).

Cho hàm số

f (x) = (x − 1)(x

− 2)(x

− 3)

. Phương trình

′

(x) = 0

có bao nhiêu nghiệm thực? Giải thích.

[Lời giải] Phương trình f (x) = 0 có 5 nghiệm là x = −

√

3, x = −

√

2, x = 1, x =

√

2 và

x =

√

i) Vì f (−

√

3) = f (−

√

2) = 0 nên theo Định lý Rolle, tồn tại x

∈ (−

√

3, −

√

2) sao cho

′

) = 0.

ii) Vì f (−

√

2) = f (1) = 0 nên theo Định lý Rolle, tồn tại x

∈ (−

√

2, 1) sao cho f

′

) = 0.

iii) Vì f (1) = f (

√

2) = 0 nên theo Định lý Rolle, tồn tại x

∈ (1,

√

2) sao cho f

′

) = 0.

iv) Vì f (

√

2) = f (

√

3) = 0 nên theo Định lý Rolle, tồn tại x

∈ (

√

2) sao cho f

′

) = 0.

Vậy phương trình f

′

(x) = 0 có ít nhất 4 nghiệm. Mặt khác, f

′

(x) là một đa thức bậc bốn,

nên nó có nhiều nhất là bốn nghiệm. Kết luận: phương trình f

′

(x) = 0 có đúng 4 nghiệm

phân biệt.

Ví dụ 9.4 (Giữa kì, K62).

Cho ba số thực

a, b, c

thỏa mãn

a + b + c = 0

. Chứng minh rằng

58 Chương 1. Hàm số một biến số (13LT+13BT)

a) phương trình

3ax

+ 4bx + 5c = 0

có ít nhất một nghiệm thuộc khoảng

(1, +∞)

b) phương trình

2ax

+ 3bx + 4c = 0

có ít nhất một nghiệm thuộc khoảng

(1, +∞)

[Lời giải]

a) Xét hàm số f (x) = cx

+ bx

+ ax

thỏa mãn các điều kiện của Định lý Rolle trong

khoảng [0, 1]. Do đó,

∃x

∈ (0, 1)|f

′

) = 5cx

+ 4bx

+ 3ax

= 0 ⇒ 3a





+ 4b





+ 5c = 0.

Vậy phương trình 3ax

+ 4bx + 5c = 0 có nghiệm

∈ (1, +∞).

b) Xét hàm số f (x) = cx

+ bx

+ ax

thỏa mãn các điều kiện của Định lý Rolle trong

khoảng [0, 1]. Do đó,

∃x

∈ (0, 1)|f

′

) = 4cx

+ 3bx

+ 2ax

= 0 ⇒ 2a





+ 3b





+ 4c = 0.

Vậy phương trình 2ax

+ 3bc + 4c = 0 có nghiệm

∈ (1, +∞).

Ví dụ 9.5 (Cuối kì, K62).

Cho

liên tục trên

[a, b]

và thỏa mãn

f (x)dx = 0

. Chứng

minh rằng

∃c ∈ (a, b)

sao cho

2017

f (x)dx = f (c)

[Lời giải]

Xét hàm số g(x) =

f (t)dt, là một hàm số liên tục trên [a, b], khả vi trên (a, b) và

g(a) = g(b) = 0. Do đó, hàm số h(x) = e

−2017x

g(x) cũng là một hàm số liên tục trên [a, b],

khả vi trên (a, b) và h(a) = h(b) = 0. Áp dụng Định lý Rolle với hàm số h(x) trong khoảng

[a, b] ta có:

∃c ∈ (a, b) : h

′

(c)e

−2017c

−2017e

−2017c

g(c) = 0

⇔ g

′

⇔ f (c) = 2017

f (t)dt = 2017

f (x)dx.

Ví dụ 9.6 (Olympic Toán học sinh viên Toàn quốc 2018 - Bảng B).

Giả sử

f : [0, 1] →

là một hàm số khả vi sao cho

f (x)dx =

x f (x)dx

. Chứng minh rằng tồn tại số

c ∈ (0, 1)

sao cho

f (c) = 2018

f (x)dx.

9. Các định lý về hàm khả vi và ứng dụng 59

Chứng minh. i) Xét hàm số F(x) = x

f (t)dt −

t f (t)dt khả vi trên [0, 1] và F(0) =

F(1) = 0. Theo Định lý Rolle, tồn tại x

∈ (0, 1) sao cho F

′

) = 0 ⇔

f (t)dt = 0.

ii) Đặt G(x) = e

−2018x

f (t)dt thì G(x) là một hàm số khả vi trên [0, 1] với G(0) =

G(x

) = 0. Theo Định lý Rolle, tồn tại c ∈ (0, x

) sao cho

′

f (x)dx.

Ví dụ 9.7 (Olympic Toán học sinh viên Toàn quốc 2018 - Bảng A).

Giả sử

f : [0, 1] →

là một hàm số khả vi sao cho

f (x)dx =

x f (x)dx

. Chứng minh rằng tồn tại số

c ∈ (0, 1)

sao cho

f (c) = 2018 f

′

(c)

f (x)dx.

Chứng minh. i) Xét hàm số F(x) = x

f (t)dt −

t f (t)dt khả vi trên [0, 1] và F(0) =

F(1) = 0. Theo Định lý Rolle, tồn tại x

∈ (0, 1) sao cho F

′

) = 0 ⇔

f (t)dt = 0.

ii) Đặt G(x) = e

−2018 f (x)

f (t)dt thì G(x) là một hàm số khả vi trên [0, 1] với G(0) =

G(x

) = 0. Theo Định lý Rolle, tồn tại c ∈ (0, x

) sao cho

′

(c)

f (x)dx.

Định lý 1.33 (Định lý Lagrange).

Nếu hàm số

f (x) :

i) Liên tục trong khoảng đóng

[a, b]

ii) Có đạo hàm trong khoảng mở

(a, b)

60 Chương 1. Hàm số một biến số (13LT+13BT)

thì tồn tại ít nhất một điểm

c ∈ (a, b)

sao cho

′

f (b)−f (a)

b−a

Chứng minh. Xét hàm số

h(x) = f (x) − f (a) −

f (b) − f (a)

b − a

(x − a).

Có thể dễ dàng kiểm chứng h(x) thỏa mãn các điều kiện của Định lý Rolle, do đó tồn tại

c ∈ (a, b) sao cho h

′

f (b)−f (a)

b−a

= 0.

Ví dụ 9.8 (Giữa kì, K61).

Chứng minh các bất đẳng thức sau với

0 < a < b

a−b

1+a

< arccot b −arccot a <

a−b

1+b

b−a

1+b

< arctan b −arctan a <

b−a

1+a

[Lời giải]

a) Áp dụng Định lý Lagrange với hàm số f (x) = arccot x trong khoảng [a, b] ta có

arccot b −arccot a

b − a

= f

′

1 + c

với c ∈ (a, b) nào đó. Do đó,

−

1 + a

arccot b −arccot a

b − a

= −

1 + c

< −

1 + b

dẫn đến điều phải chứng minh.

b) Tương tự câu a).

Ví dụ 9.9 (Giữa kì, K59).

Cho hàm số

f : (0, +∞) → R

thỏa mãn

f (x) ≤ 1

và

′′

(x) ≥ 0

với mọi

x > 0

. Chứng minh rằng

′

(x) ≤ 0

với mọi

x > 0

[Lời giải]

Giả sử phản chứng, tồn tại x

> 0 sao cho f

′

) > 0.

i) Vì f

′′

(x) ≥ 0 nên f

′

(x) ≥ f

′

) với mọi x > x

ii) Áp dụng Định lý Lagrange cho h àm số f (x) trong khoảng [x

, x] ta có: tồn tại c ∈

, x) sao cho f (x) = f (x

) + f

′

(c)(x −x

) ≥ f (x

) + f

′

)(x −x

iii) Mặt khác, vì f

′

) > 0 nên lim

x→+∞

f (x

) + f

′

)(x − x

) = +∞ ⇒ lim

x→+∞

f (x) = +∞,

trái với giả thiết f (x) ≤ 1 với mọi x > 0.

Mâu thuẫn này chứng tỏ f

′

(x) ≤ 0 với mọi x > 0.

Định lý 1.34 (Định lý Cauchy).

Nếu các hàm số

f (x), g(x)

thỏa mãn các điều kiện:

9. Các định lý về hàm khả vi và ứng dụng 61

i) Liên tục trong khoảng đóng

[a, b]

ii) Có đạo hàm trong khoảng mở

(a, b)

iii)

′

(x)

không triệt tiêu trong khoảng mở

(a, b)

thì tồn tại ít nhất một điểm

c ∈ (a, b)

sao cho

f (b) − f (a)

g(b) − g(a)

′

(c)

′

(c)

Chú ý 1.12.

a) Định lý Rolle là trường hợp riêng của định lý Lagrange, định lý La-

grange là trường hợp riêng của định lý Cauchy. Các giả thiết trong các định lý này

là cần thiết.

b) Định lý Lagra nge còn có một dạng khác, đó là công thức số gia hữu hạn:

∆ f = f

′

(

+ θ∆x

)

, θ ∈ (0, 1).

9.2 Các công thức khai triển Taylor, Maclaurin

Định lý 1.35.

Nếu hàm số

f (x)

(i) Có đạo hàm đến cấp

trong khoảng đóng liên tục tại

(ii) Có đạo hàm đến cấp

n + 1

trong lân cận

)

thì

f (x)

có thể biểu diễn dưới dạng

f (x) = f (x

) +

′

)

(x − x

) + ···+

(n)

)

(x − x

)

(n+1)

(c)

(n + 1)!

(x − x

)

n+1

ở đó

là một số thực nằm giữa

và

nào đó.

Nếu x

= 0 thì công thức sau còn được gọi là công t hức Maclaurin:

f (x) = f (0) +

′

(0)

x + ···+

(n)

(0)

(n+1)

(c)

(n + 1)!

n+1

(1.1)

hay

f (x) = f (0) +

′

(0)

x + ···+

(n)

(0)

+ o(x

), (1.2)

ở đó o(x

) là một VCB bậc cao hơn x

62 Chương 1. Hàm số một biến số (13LT+13BT)

Một số khai triển Maclaurin quan trọng

(1) (1 + x)

= 1 + αx +

α(α−1)

+ ··· +

α(α−1)···(α−n+1)

+ o(x

)

(2)

1+x

= 1 − x + x

−···+ (−1)

+ o(x

)

(3)

1−x

= 1 + x + x

+ ···+ x

+ o(x

)

(4) e

= 1 + x +

+ ··· +

+ o(x

)

(5) sin x = x −

+ ··· + (−1)

2n+1

(2n+1)!

+ o(x

2n+1

)

(6) cos x = 1 −

+ ···+ (−1)

(2n)!

+ o(x

)

(7) ln(1 + x) = x −

+ ··· + (−1)

n−1

+ o(x

)

Các phép toán trên khai triển Maclaurin

Trên khai triển Maclaurin chúng ta có thể thực hiện các phép toán cơ b ản sau: cộng,

trừ, nhân, chia, hàm hợp, đạo hàm và tích phân. Các phép toán cộng, trừ, nhân, chia được

thực hiện hệt như cộng, trừ, nhân, chia các đa thức. Cho f (x) = a

+ a

x + a

+ a

··· + a

+ ··· và g(x) = b

+ b

x + b

+ b

+ ···+ b

+ ··· là các chuỗi Maclaurin

hình thức. Khi đó

1. Phép cộng (trừ)

f (x) ±g(x) = (a

±b

) + (a

±b

)x + (a

±b

+ (a

±b

+ ···+ (a

±b

+ ···

2. Phép nhân

f (x)g(x) = c

+ c

x + c

+ c

+ ··· + c

+ ··· ,

ở đó c

∑

i=0

n−i

. Chuỗi

+∞

∑

n=0

còn được gọi là tích chập của hai chuỗi

+∞

∑

n=0

và

+∞

∑

n=0

Ví dụ 9.10.

T ìm khai triển Maclaurin của hàm số

f (x) = e

sin x

[Lời giải] Xuất phát từ khai triển Maclaurin của hàm số g(x) = e

= 1 + x +

+ ··· +

+ o(x

)

và h(x) = sin x

sin x = x −

+ ···+ (−1)

2n+1

(2n + 1)!

+ o(x

2n+1

)

9. Các định lý về hàm khả vi và ứng dụng 63

ta có

sin x = x + x



−



+ ···

Ví dụ 9.11 (Giữa kì, 20173).

Cho

y = e

sin x

. Tính đạo hàm cấp cao

(6)

(0)

[Lời giải] Số hạng chứa x

trong khai triển Maclaurin của y = e

sin x là

x.(−1)

(−1)

x = −

Do đó,

(6)

(0)

= −

⇒ y

(6)

(0) = −8.

• Như vậy, nếu chỉ cần tìm một số số hạng đầu tiên trong khai triển Maclarin của

hàm số e

sin x thì có thể dùng phương pháp thực hiện phép nhân này.

• Tuy nhiên, để tìm được số hạng tổng quát thì phương pháp này lại không hiệu

quả. Thay vào đó, ta sẽ đi tính f

(n)

(x) bằng phương pháp quy nạp như trong Bài

tập 1.51d. Từ công thức

′

(x) = e

(sin x + cos x) =

√

sin



x +



và

′′

(x) =

√

sin



x +



+ cos



x +

i

= (

√

sin



x + 2.



suy ra

(n)

(x) = (

√

sin



x + n



Do đó,

sin x =

∞

∑

n=1

(

√

sin

nπ

3. Phép chia cũng thực hiện như phép chia đa thức một cách bình thường.

4. Phép lấy hàm hợp. Chúng ta bắt đầu bằng một ví dụ đơn giản sau. Tìm chuỗi Maclau-

rin của hàm số f (x) = sin x

. Muốn tìm chuỗi Maclaurin một cách trực tiếp, ta cần

tính các đạo hàm cấp cao của hàm số f (x) = sin x

rồi thay vào công thức

f (x) = f (0) +

′

(0)

x + ···+

(n)

(0)

+ o(x

Bằng cách tính các đạo hàm cấp một và cấp hai của f (x):

• f

′

(x) = 2x cos x

64 Chương 1. Hàm số một biến số (13LT+13BT)

• f

′′

(x) = −4x

sin x

+ 2 cos x

chúng ta thấy rằng quá trình này sẽ rất phức tạp. Chúng ta có một phương pháp

khác. Đó là thực hiện phép đổi biến số, thay x bằng x

trong khai triển Maclaurin

của hàm số

sin x = x −

+ ···+ (−1)

2n+1

(2n + 1)!

+ ···

để được

sin x

= x

−

+ ··· + (−1)

2(2n+1)

(2n + 1)!

+ ···

Bản chất của vấn đề ở đây là chúng ta cần đi tìm khai triển Maclaurin của hàm

số h ợp ( f ◦ g)(x) = f (g(x)). Để tìm hiểu sâu thêm về vấn đề này, công thức Faà di

Bruno sau đây giúp chúng ta tính đạo hàm cấp cao của hàm hợp.

Định lý 1.36 (Công thức Faà di Bruno).

f (g(x))

(n)

∑

! 1!

! 2!

··· m

! n!

· f

+···+m

)

(g(x)) ·

∏

j=1



(j)

(x)



ở đó tổng được lấy trên tất cả các bộ số không âm

, . . . , m

)

thỏa mãn

1 ·m

+ 2 · m

+ 3 · m

+ ···+ n ·m

= n.

Hệ quả 1.5.

Cho

f (x) =

∞

∑

n=0

và

g(x) =

∞

∑

n=0

là các chuỗi Maclaurin hình

thức và

= 0

. Khi đó, hàm số

( f ◦ g)(x)

có chuỗi Maclaurin hình thức là

∞

∑

n=0

ở đó

= a

và

∑

i∈C

···b

và

= {(i

, i

, . . . , i

) : 1 ≤ k ≤ n, i

+ i

+ ··· + i

= n}.

Trường hợp đơn giản nhất, g(x) = x

thì chỉ việc th ay x bằng x

trong khai triển

Maclaur in của f (x) để ra khai triển Maclaurin của f (x

) như trong ví dụ hàm số

f (x) = sin (x

) đã nêu ở trên.

5. Phép lấy đạo hàm. Giả sử hàm số f (x) có khai triển Maclaurin là

f (x) = a

+ a

x + a

+ a

+ ··· + a

+ ···

9. Các định lý về hàm khả vi và ứng dụng 65

Khi đó hàm số f

′

(x) có khai triển Maclaurin là

′

(x) = a

+ 2a

x + 3a

+ ···+ na

n−1

+ ···

được thực hiện bằng cá ch lấy đạo h àm của từng thành phần của chuỗi Maclaurin

của hàm f (x). Bạn đọc có thể tự kiểm tra bằng cách lấy đạo hàm chuỗi Maclaurin

của hàm sin x để ra chuỗi Maclaur in của hàm số cos x, hoặc lấy đạo hàm của chuỗi

Maclaur in của hàm số ln (1 + x) để ra chuỗi Maclaurin của hàm số

1+x

6. Phép lấy tích phân. Cũng tương tự như vậy, giả sử hàm số f (x) có khai triển Maclau-

rin là

f (x) = a

+ a

x + a

+ a

+ ···+ a

Khi đó hàm số

f (t)dt có khai triển Maclaurin là

f (t)dt = a

x + a

+ a

+ ··· + a

n+1

n + 1

+ ···

được thực hiện bằng cách lấy tích phân của từng thành phần của chuỗi Maclau-

rin của hàm f (x). Chẳng hạ n, muốn tìm khai triển Maclaurin của hàm số f (x) =

arctan x, đầu tiên ta tìm chuỗi Maclaurin của hàm số

1 + x

= 1 − x

+ x

−··· + (−1)

+ ··· ,

sau đó ta lấy tích phân hai vế thì được

arctan x =

1 + t

dt = x −

+ ··· + (−1)

2n+1

2n + 1

+ ···

Ứng dụng của khai triển Maclaurin

1. Tính gần đúng

Ví dụ 9.12.

T ính gần đúng số

với sai số nhỏ hơn

0, 0001.

Ta có e

= 1 + x +

+ ···+

n+1

(n+1)!

với c là một số thực nào đó nằm giữa 0 và x.

Do đó ta xấp xỉ số e bằng

e ≈ 1 + 1 +

+ ··· +

với sai số mong muốn

n+1

(n+1)!

< 0, 0001. Điều này xảy ra nếu (n + 1)! > 1000 ⇔

n > 6. Nói cách khác,

e ≈ 1 + 1 +

66 Chương 1. Hàm số một biến số (13LT+13BT)

2. Tính giới hạn

Ví dụ 9.13.

T ính

lim

x→0

x −sin x

Chứng minh. Dựa vào k hai triên Maclaurin của hàm f (x) = sin x ta có

sin x = x −

+ o(x

)

nên

x −sin x =

+ o(x

) ∼

+ o(x

)

(theo quy t ắc ngắt bỏ VCB bậc cao).

Do đó

lim

x→0

x −sin x

Chú ý 1.13.

Khi sử dụng khai triển Maclaurin để tính giới hạn, có thể khai triển

hàm số đến số hạng thích hợp. Chẳng hạn như ở Ví dụ bên trên, mẫu số là

nên ta

chỉ khai triển tử số đến số hạng

, còn phần VCB bậc cao ở phía sau sẽ được ngắt

bỏ.

Ví dụ 9.14 (Giữa kì, K61).

T ính giới hạn

lim

x→0

−

1−x

lim

x→0

−sin x−cos x

Ví dụ 9.15 (Giữa kì, K62).

T ìm

a, b ∈ R

sao cho

lim

x→0

+b ln(cos x)

= 1

lim

x→0

ax+b sin(sin x)

= 1

[Lời giải]

a) Ta có

ln(cos x) = ln



1 −

+ o(x

)





−



−



−

+ o(x

)



+ o(x

)

= −

−

+ o(x

Do đó,

1 = lim

x→0

+ b ln(cos x)

= lim

x→0



a −



−

+ o(x

)

⇒ a = −6, b = −12.

9. Các định lý về hàm khả vi và ứng dụng 67

sin(sin x) = sin



x −

+ o(x

)



= x −

−



x −

+ o(x

)



+ o(x

)

= x −

+ o(x

Do đó,

1 = lim

x→0

ax + b sin(sin x)

= lim

x→0

(a + b)x − b

+ o(x

)

⇒ a = 3, b = −3.

3. Tính đạo hàm cấp cao f

(n)

(0).

Ví dụ 9.16 (Giữa kì, K61).

T ính đạo hàm cấp cao

(10)

(0)

với

y(x) = e

−x

y(x) = arctan x

y(x) = arccot x.

[Lời giải] Ngoài phương pháp dựa vào công thức truy hồi nh ư ở Ví dụ 8.10, ta có thể

dựa vào khai triển Maclaurin.

a) Thay x bởi x

trong công thức khai triển Maclaurin của e

ta có

= 1 + x

)

+ ··· +

)

+ ··· =

+∞

∑

n=0

(n)

(0)

So sánh hệ số của x

ta được

(10)

(0)

10!

⇒ y

(10)

(0) =

10!

= 30240.

b) Tương tự câu a).

c) Thay x bằng x

trong khai triển Maclaurin của hàm số f (x) =

1+x

ta được khai

triển Maclaurin của hàm số f (x) =

1+x

như sau:

1 + x

= 1 − x

+ x

−··· + (−1)

+ ··· ,

Lấy tích phân hai vế ta được

arctan x =

1 + t

dt = x −

+ ··· + (−1)

2n+1

2n + 1

+ ··· =

+∞

∑

n=0

(n)

(0)

So sánh hệ số của x

hai vế ta được y

(10)

(0) = 0.

Ví dụ 9.17 (Cuối kì, K62).

T ính đạo hàm cấp cao

(10)

(0)

với

68 Chương 1. Hàm số một biến số (13LT+13BT)

y(x) = sin(x

)

. b)

y(x) = cos(x

)

[Lời giải]

a) Thay x bằn g x

trong khai triển Maclaurin của sin x

sin x =

+∞

∑

n=0

(−1)

2n+1

(2n + 1)!

ta được

sin(x

) =

+∞

∑

n=0

(−1)

2(2n+1)

(2n + 1)!

+∞

∑

n=0

(n)

(0)

So sánh hệ số của x

hai vế ta được

(10)

(0)

10!

= (−1)

⇒ y

(10)

(0) =

10!

= 30240.

b) Tương tự câu a).

Ví dụ 9.18 (Giữa kì, K62).

T ính đạo hàm cấp cao

(9)

(0)

với

f (x) = ln (1 − x + x

)

. b)

g(x) = ln(1 + x + x

)

[Lời giải]

a) Ta có

f (x) = ln (1 −x + x

) = ln(1 + x

) −ln(1 + x) = x

−

∑

n=1

(−1)

n−1

+ o(x

)

Hệ số của x

trong khai triển Maclaurin của f (x) bằng

(9)

(0)

−

Do đó,

(9)

(0) = 2.8! = 80640

b) Tương tự câu a).

Ví dụ 9.19.

a) Tìm khai triển Maclaurin của hàm số

f (x) = arcsin x

b) Tính đạo hàm cấp cao

arcsin

(n)

(0)

(Giữa kì, K59).

[Lời giải]

9. Các định lý về hàm khả vi và ứng dụng 69

a) Nhận xét (arcsin x)

′

√

1−x

. Trong trường hợp này có lẽ "không có" hoặc "rất

khó" để tìm ra công thức tính đạo hàm cấp cao của hàm số arcsin x. Vì vậy, ta

xuất phát từ công thức khai triển Maclaurin của hàm số (1 + x)

(1 + x)

∞

∑

n=0

α(α −1) . . . (α −n + 1)

Thay α = −

ta được

√

1 + x

∞

∑

n=0

−



−

−1



. . .



−

−(n −1)



∞

∑

n=0

(−1)

(2n −1)!!

Thay x bằng −x

ta được

(arcsin x)

′

√

1 − x

∞

∑

n=0

(−1)

(2n −1)!!

(−x

)

∞

∑

n=0

(2n −1)!!

(2n)!!

Do đó

arcsin x =

∞

∑

n=0

(2n −1)!!

(2n)!!

dt =

∞

∑

n=0

(2n −1)!!

(2n)!!

dt =

∞

∑

n=0

(2n −1)!!

(2n)!!

2n+1

2n + 1

b) Dựa vào công thức khai triển Maclaurin của hàm số arcsin x suy ra







arcsin

(2n)

(0) = 0,

arcsin

(2n+1)

(0) = [(2n −1)!! ]

Ví dụ 9.20 (Cuối kì, 20152).

Cho hàm số

f (x) =

1+x

. Tính

f (0)

[Lời giải] f (x) = x ·

1+x

, áp dụng công thức Leibniz ta có

(n)

(x) = x ·



1 + x



(n)

+ n.



1 + x



(n−1)

Thay x = 0, n = 10 vào ta có f

(10)

(0) = 10g

(9)

(0), với g(x) =

1+x

Ta có

1 + x

= 1 − x + x

−···+ (−1)

+ o(x

) ⇒

1 + x

= 1 − x

+ (x

)

−(x

)

+ ···

Từ đó suy ra hệ số của x

trong khai triển Maclaurin của g(x) =

1+x

bằng

−1 =

(9)

(0)

⇒ g

(9)

(0) = −9! ⇒ f

(10)

(0) = −10! ⇒ d

f (0) = −10!dx

Bài tập 1.53.

T ìm khai triển Maclaurin của hàm số

f (x) = arccos x

[Gợi ý] Có thể dựa vào đẳng thức arcsin x + arccos x =

để suy ra khai triển Maclau-

rin của hàm số f (x) = arccos x.

70 Chương 1. Hàm số một biến số (13LT+13BT)

9.3 Quy tắc L’Hospital

Định lý 1.37 (Quy tắc L’Hospital).

Giả thiết

i) Các hàm số

f (x), g(x)

khả vi trong một lân cận nào đó của điểm

(có thể trừ tại

điểm

) đồng thời

′

(x) 6= 0

trong lân cận ấy,

ii)

lim

x→x

f (x) = lim

x→x

g(x) = 0



khử dạng



Khi đó nếu tồn tại

lim

x→x

′

(x)

′

(x)

= A

(có thể hữu hạn hoặc vô hạn) thì

lim

x→x

f (x)

g(x)

= A.

Chú ý 1.14.

Quy tắc L’Hospital trên vẫn đúng nếu

•

thay quá trình

x → x

bởi một trong các quá trình

x → x

, x → x

−

, x → +∞

hoặc

x → −∞.

•

thay điều kiện

lim

x→x

f (x) = lim

x→x

g(x) = 0

bởi

lim

x→x

f (x) = ∞, lim

x→x

g(x) = ∞



khử dạng

∞



Ý tưởng chứng minh: Chúng ta chứng minh quy tắc L’Hospital cho trường hợp đơn giản,

′

) 6= 0.

1. Nếu f (x

) = g(x

) = 0 thì Với x 6= x

ta có

f (x)

g(x)

f (x) − f (x

)

g(x) − g(x

)

(Cauchy)

′

(c)

′

(c)

c nằm giữa x và x

Khi x → x

thì c → x

. Do lim

x→x

′

(x)

′

(x)

= A, suy ra

lim

x→x

f (x)

g(x)

= lim

c→x

′

(c)

′

(c)

= A.

2. Nếu chỉ có lim

x→x

f (x) = li m

x→x

g(x) = 0 mà các hàm số chưa chắc đã xác định tại x

. Ta

xây dựng

F(x) =







0, x = x

f (x), x 6= x

G(x) =







0, x = x

g(x), x 6= x

3. Nếu x → ∞, đặt y =

Ví dụ 9.21 (Giữa kì, K61).

T ính giới hạn

9. Các định lý về hàm khả vi và ứng dụng 71

lim

x→0

ln(1+x)−sin x

lim

x→0

−sin 2x

Ví dụ 9.22.

T ính các giới hạn sau:

lim

x→0

x −sin x

arcsin

lim

x→0

lim

x→0

ln x

lim

x→∞

Chú ý 1.15.

•

Hai qui tắc trên chỉ là điều kiện đủ để tìm

lim

f (x)

g(x)

Ví dụ như

lim

x→0

sin

sin x

= 0

theo nguyên lý giới hạn kẹp, nhưng nếu áp dụng quy tắc

L’H ospital thì sẽ dẫn đến kết quả sai.

•

Trong quá trình tìm giới hạn có dạng vô định, nên kết hợp cả thay tương đương với

dùng qui tắc L’Hospital để đạt được hiệu quả tốt nhất.

•

Có thể dùng qui tắc L’H ospital nhiều lần.

Chú ý 1.16.

Công thức L’Hospital được công bố lần đầu vào năm 1696 trong cuốn sách

Analyse des Infiniment Petits, pour intelligence des lignes courbes

của nhà toán học người

Pháp Marquis de l’Hospital (1661-1704), như ng nó lại được khám phá vào năm 1694 bởi

nhà toán học người Thụy Sỹ John (Johann) Bernoulli (1667-1748). Điều này được giải

thích vì h ai nhà toán học có một thỏa thuận lạ kì, rằng Marquis de l’Hospital mua quyền

sở hữu các phát minh của Bernoulli trong một khoảng thời gian nhất định. Bức thư sau

đây của l’Hopital vào ngày 17 tháng 3 năm 1694 đã đề xuất một trong những thỏa thuận

khác thường nhất trong lịch sử khoa học.

"I will be happy to give you a retainer of 300 poun ds, beginning with the first of Jan-

uary of this year ... I promise shortly to increase this retainer, which I know is very mod-

est, as soon as my affairs are somewhat straightened out ... I am not so unreasonable as

to demand in return all of your time, but I will ask you to give me at intervals some hours

of your time to work on what I request and also to communicate to me your discoveries, at

the same time asking you not to disclose any of them to others. I ask you even not to send

here to Mr. Varignon or to others any copies of the writings you have left with me; if they

are published, I will not be at all pleased. Answer me regarding all this ..."

9.4 Về một số dạng vô định

Quy tắc L’Hospital, ngoài việc được áp dụng để khử dạng vô định

∞

, còn có thể được

dùng để khử các dạng vô định sau:

72 Chương 1. Hàm số một biến số (13LT+13BT)

1. Dạng vô định 0 × ∞. Chẳng hạn như muốn tính giới hạn lim

x→x

f (x)g(x) ta có thể viết

nó dưới dạng

lim

x→x

f (x)

1/g(x)

để áp dụng công thức L’Hospital.

Ví dụ 9.23.

T ính

lim

x→0

x ln x.

2. Dạng vô định ∞ −∞. Để tính các giới hạn này chúng ta đưa phép trừ về dạng phép

thương, chẳng hạn như quy đồng mẫu số, đặt nhân tử chung.

Ví dụ 9.24.

T ính

lim

x→0



−

sin x



3. Tính các giới hạn có dạng lim

x→x

A(x)

B(x)

. Đặt f (x) = A(x)

B(x)

và đi tính

lim

x→x

ln f (x) = lim

x→x

B(x) ln A(x) = lim

x→x

ln A(x)

1/B(x)

bằng cách áp dụng công thức L’Hospital.

• Nếu lim

x→x

ln A(x)

1/B(x)

có dạng

, nghĩa là

lim

x→x

ln A(x) = 0, lim

x→x

1/B(x) = 0.

Khi đó, lim

x→x

A(x) = 1, lim

x→x

B(x) = ∞ ta có dạng vô định 1

∞

• Nếu lim

x→x

ln A(x)

1/B(x)

có dạng

∞

, nghĩa là

lim

x→x

ln A(x) = ∞, lim

x→x

1/B(x) = ∞.

Khi đó,

– hoặc lim

x→x

A(x) = 0, lim

x→x

B(x) = 0 ta có dạng vô định 0

– hoặc là lim

x→x

A(x) = ∞, lim

x→x

B(x) = 0 ta có dạng vô định ∞

Chú ý rằng chỉ có ba dạng vô định 0

, 1

∞

, ∞

cho các giới hạn có dạng lim

x→x

A(x)

B(x)

Các trường hợp khác hay bị nhầm lẫn sau đây đều không phải là dạng vô định

và có thể tính trực tiếp dựa vào các quy tắc tính giới hạn:

= 0, 0

+∞

= 0, 0

−∞

= +∞, 1

= 1, 1

= 1, ∞

= ∞, ∞

∞

= ∞.

9. Các định lý về hàm khả vi và ứng dụng 73

9.5 Thay tương đương khi có hiệu hai VCB?

Đây có lẽ là một câu hỏi thú vị và được rất nhiều bạn đọc quan tâm. Chúng ta bắt đầu

với một ví dụ sau đây.

Ví dụ 9.25 (Câu 6, Đề 4, Giữa kì K61).

T ính

lim

x→0

−sin x −cos x

[Lời giải]

Cách 1: Thay tương đương

lim

x→0

−sin x −cos x

= lim

x→0

−1) −sin x + (1 −cos x)

= lim

x→0

x −x +

Cách 2: Dùng quy tắc L’Hospital

lim

x→0

−sin x −cos x

= lim

x→0

−cos x + sin x

= lim

x→0

+ sin x + cos x

=1.

Trong hai cách giải trên chắc chắn có một cách giải sai, và sai lầm ở đâu? Đây là sai lầm

nhiều người hay mắc phải khi thay tương đương trong các biểu thức c ó chứa dấu ±.

Chú ý 1.17.

Nếu

(x), α

(x), β

(x)

là các VCB khi

x → x

và

(x) ∼ α

(x), β

(x) ∼

(x)

thì

• α

(x)β

(x) ∼ α

(x)β

(x)

• lim

x→x

(x)

= lim

x→x

(x)

nhưng chưa chắc

(x) ± β

(x) ∼ α

(x) ± β

(x)

. Chẳng hạn,

sin x ∼ x, tan x ∼ x

khi

x → 0

nhưng

tan x −sin x ∼

Vậy có thay tương đương được trong biểu thức có dấu ± hay không không? Đây là một

câu hỏi rất thú vị. Muốn biết biểu thức α

(x) − β

(x) có tương đương với α

(x) − β

(x) hay

không thì chúng ta quay về Định nghĩa, đi tính lim

x→a

(x)−β

(x)

(x)−β

(x)

. Ta chia làm 4 trường hợp

như sau:

1. Nếu α

(x) là VCB bậc cao hơn β

(x) thì lim

x→a

(x)

= lim

x→a

(x)

= 0 (theo định nghĩa của

VCB bậc cao). Khi đó lim

x→a

(x)−β

(x)

(x)−β

(x)

= lim

x→a

(x)

−1

(x)

−1

(x)

0−1

= 1. Vậy α

(x) − β

(x)

tương đương với α

(x) − β

(x).

74 Chương 1. Hàm số một biến số (13LT+13BT)

2. Nếu β

(x) là VCB bậc cao hơn α

(x) thì lim

x→a

(x)

= lim

x→a

(x)

= 0 (theo định nghĩa của

VCB bậc cao). Khi đó lim

x→a

(x)−β

(x)

(x)−β

(x)

= lim

x→a

(x)

−1

(x)

−1

(x)

0−1

= 1. Vậy α

(x) − β

(x)

tương đương với α

(x) − β

(x).

3. Nếu α

(x) và β

(x) là các VCB cùng bậc nhưng không tương đương thì lim

x→a

(x)

A 6= 1. Khi đó lim

x→a

(x)−β

(x)

(x)−β

(x)

= lim

x→a

(x)

−1

(x)

−1

(x)

A−1

= 1. Vậy α

(x) − β

(x) tương

đương với α

(x) − β

(x).

4. Nếu α

(x) và β

(x) là các VCB tương đương thì lim

x→a

(x)

= 1. Khi đó lim

x→a

(x)−β

(x)

(x)−β

(x)

lim

x→a

(x)

−1

(x)

−1

(x)

1−1

là dạng vô định

nên không xác định được giới hạn của nó.

5. Nếu α

(x) và β

(x) là các VCB không so sánh được với nhau, thì α

(x) − β

(x) và

(x) − β

(x) có thể không so sánh được với nhau.

Kết luận: Nếu α

(x), α

(x), β

(x) là các VCB khi x → x

và α

(x) ∼ α

(x), β

(x) ∼

(x) thì α

(x) − β

(x) ∼ α

(x) − β

(x) ngoại trừ trường hợp α

(x) và β

(x) là các

VCB tương đương hoặc không so sánh được với nhau. Ví dụ, không thay tương

đương được trong biểu thức tan x − sin x vì tan x ∼ sin x, nhưng vẫn thay tương đương

được trong biểu thức tan 2x −sin x ∼ 2x − x = x hoặc sin x −tan

x ∼ x −x

∼ x. Bạn đọc

cần nắm vững điều này, và trong trường hợp không chắc chắn thì tốt nhất nên

tránh thay tương đương trong các biểu thức có chứa dấu cộng và dấu trừ.

Trường hợp α

(x) + β

(x) có tương đương với α

(x) + β

(x) hay không chúng ta lập luận

tương tự. Vẫn thay tương đương được bình thường ngoại trừ trường hợp α

(x) và −β

(x)

là các VCB tương đương hoặc không so sánh được với nhau.

Quay trở lại Ví dụ 9.25 nêu trên thì sai lầm là ở chỗ chúng ta đã thay tương tương

−1) −sin x ∼ x − x = 0 để dẫn đến (e

−1) −sin x + (1 −cos x) ∼

. Chúng ta không

thực hiện được điều này bởi vì e

−1 ∼ sin x. Thực tế thì (e

−1) − sin x là một VCB khi

x → 0 và nếu nhìn vào khai triển Maclaurin của các hàm số e

và sin x thì ta thấy

• e

= 1 + x +

+ o(x

)

• sin x = x + o(x

) (số hạng tiếp theo trong khai triển này là −

= o(x

))

nên

−1) −sin x =

+ o(x

) ∼

Cho nên khi thay (e

− 1) − sin x ∼ x − x = 0 nghiễm nhiên chúng ta đã làm mất đi số

hạng

9. Các định lý về hàm khả vi và ứng dụng 75

Ví dụ 9.26 (Câu 5, Đề 1, Giữa kì K61).

T ính

lim

x→0

−cos x −ln(1 + x)

[Gợi ý] Một cách tương tự, hãy chỉ ra rằ ng với bài tập trên nếu

• thay tương đương ta được kết quả bằng

(SAI)

• dùng công thức L’Hospital hoặc khai triển Maclaurin ta được kết quả bằng

(ĐÚNG).

9.6 Hiệu hai VCB tương đương

Trong mục trước, chúng ta biết rằng không thay tương đương được trong biểu thức

α(x) − β(x) nếu α(x) và β(x) là các VCB tương đương. Vậy hiệu của hai VCB tương đương

là gì?

Bổ đề 1.1.

Hiệu của hai VCB tương đương là một VCB bậc cao hơn cả hai VCB đó.

Chứng minh. Giả sử α(x) ∼ β(x) khi x → x

. Khi đó,

lim

x→x

α(x) − β(x)

α(x)

= 1 − lim

x→x

β(x)

α(x)

= 1 −1 = 0.

Vậy theo định nghĩa, α(x) − β(x) là một VCB bậc cao hơn α(x).

Ví dụ 9.27 (Một số ví dụ về hiệu hai VCB tương đương).

x −sin x ∼

x −tan x ∼ −

x −arcsin x ∼ −

x −arctan x ∼

sin x −tan x ∼ −

sin x −arcsin x ∼ −

sin x −arctan x ∼

tan x −arcsin x ∼

tan x −arctan x ∼

arcsin x −arctan x ∼

x −(e

−1) ∼ −

x −ln(1 + x) ∼

(1 −cos x) −

∼ −

Hiệu hai VCB cùng bậc là một VCB bậc cao hơn cả hai VCB đó, vậy cụ thể, cao hơn là

bậc bằng bao nhiêu? Lấy, chẳng hạn, α(x) = x, ở ví dụ trên ta đã chỉ ra một số hiệu của

hai VCB tương đương "trong tự nhiên", như là x −sin x ∼

cùng bậc với VCB α(x) = x

còn x − (e

−1) ∼ −

cùng bậc với VCB β(x) = x

khi x → 0. Với các VCB tương đương

"nhân tạo" sau đây thì x − β(x) có thể cùng bậc với x

(a > 1) bất kì. Chẳng hạn như muốn

x − β(x) ∼ x

2017

thì chỉ cần chọn β(x) = x − x

2017

. Khi đó,

x ∼ x − x

2017

(ngắt bỏ VCB bậc cao), và x − (x − x

2017

) = x

2017

76 Chương 1. Hàm số một biến số (13LT+13BT)

9.7 Ba phương pháp (mới) để tính giới hạn

Như vậy đến thời điểm hiện tại chúng ta đã học được ba phương pháp mới để tính giới

hạn, đó là

• Phương pháp sử dụng VCB-VCL (thay tương đương, ngắt bỏ),

• Phương pháp dùng khai tr iển Maclaurin,

• Phương pháp dùng quy tắc L’Hospital.

Mỗi một phương pháp đều có các ưu, nhược điểm riêng và tương ứng với các bài toán đặc

thù. Để so sánh các phương pháp này với nhau, ta minh họa bằng vẽ và 6 Ví dụ sau đây.

L’Hospital

Maclaur in

VCB

VD 1VD 2 VD 3 VD 5 VD 6

VD 4

Ví dụ 1 (Cả ba phương pháp đều áp dụng được).

lim

x→0

1 −cos x

ln(1 + x

)

Ví dụ 2 (Sử dụng VCB hoặc khai triển Maclaurin. Không nên dùng L’Hospital).

lim

x→0

1 −cos x + x

−sin x

x + sin

x + arcsin

x + arctan

Ví dụ 3 (Sử dụng khai triển Maclaurin hoặc L’Hospital. Không thay tương đương).

lim

x→0

x −sin x + x

9. Các định lý về hàm khả vi và ứng dụng 77

Ví dụ 4 (Khai triển Maclau rin. Không thay tương đương (tử số) và L’Hospital).

lim

x→0

x −sin x − x

arcsin(arctan

Ví dụ 5 (Sử dụng L’Hospital. Không dùng VCB, Maclaurin).

lim

x→0

ln x

hoặc

lim

x→0

Ví dụ 6 (Không dùng cả ba phương pháp trên).

lim

x→+∞

x −sin x

x + cos x

[Lời giải]

lim

x→∞

x −sin x

x + cos x

= lim

x→∞

1 −

sin x

1 +

cos x

= 1.

Chú ý 1.18.

Trong quá trình tìm giới hạn của các dạng vô định, nên linh hoạt trong cách

xử lý, có thể kết hợp nhiều phương pháp với nhau để đạt hiệu quả tốt nhất. Chẳng hạn

như trong Ví dụ (4) nêu trên,

lim

x→0

x −sin x − x

arcsin(arctan

nên sử dụng khai triển Maclaurin ở tử số và thay tương đương ở mẫu số.

9.8 Về các VCL tiêu biểu

Chúng ta đã học về các VCB, VCL, các quy tắc thay tương đương, các quy tắc ngắt bỏ

VCB bậc cao, ngắt bỏ VCL bậc thấp. Tuy nhiên, các bài tập về VCL thường hay bị lãng

quên vì một lý do nào đó. Chúng ta đã học các VCB tương tương hay dùng, nhưng chưa có

nhiều ví dụ về các VCL. Chính vì vậy, mục này sẽ dành riêng để nói về ba VCL tiêu biểu

(khi x → +∞), đó là

• Các hàm số mũ với cơ số lớn hơn 1, ví dụ a

(a > 1),

• Các hàm số đa thức, các hàm số là lũy thừa của x, chẳng hạn x

, x

, (α > 0),

• Các hàm số logarit với cơ số lớn hơn 1, như ln x, log

x (a > 1).

Cả ba hàm số này đều tiến ra vô cùng khi x → +∞, tuy nhiên với tốc độ khác nhau. Trong

ba hàm số này thì hàm số mũ (với cơ số lớn hơn 1) là VCL có bậc cao nhất (tiến ra vô cùng

với tốc độ nhanh nhất), sau đó đến các hàm số đa thức, và cuối cùng là các h àm số logarit

(với cơ số lớn hơn 1).

78 Chương 1. Hàm số một biến số (13LT+13BT)

Hàm số mũ ≻ Hàm số đa thức ≻ Hàm số logarit

Cụ thể, bạn đọc có thể tự chứng minh dễ dàng hai giới hạn sau (bằng cách dùng quy

tắc L’Hospital):

lim

x→+∞

= ∞, lim

x→+∞

log

= ∞, ∀a > 1, α > 0.

Ví dụ 9.28.

T ính

lim

x→+∞

ln x + x

2016

+ e

log

x + x

2017

+ 2e

Áp dụng quy tắc ngắt bỏ VCL bậc thấp ta được,







ln x + x

2016

+ e

∼ e

log

x + x

2017

+ 2e

∼ 2e

khi

x → +∞

Do đó,

lim

x→+∞

ln x + x

2016

+ e

log

x + x

2017

+ 2e

Bạn đọc sẽ thường xuyên gặp lại các VCL này khi học về Tích phân suy rộng (tron g học

phần Giải tích I này) và Chuỗi số (trong học phần Giải tích III, học kì 2).

9.9 Bài tập ôn tập

Bài tập 1.54. Chứng minh rằng phương trình x

+ px + q với n nguyên dương không thể

có quá 2 nghiệm thực nếu n chẵn và không thể có quá 3 nghiệm thực nếu n lẻ.

Chứng minh. Xét n chẵn, giả sử phương trình có 3 nghiệm thực x

< x

, khi đó tồn

tại c

∈ (x

, x

), c

∈ (x

, x

) sao cho f

′

) = f

′

) = 0. Tức là phươn g trình x

n−1

= −

có

2 nghiệm thực, điều này mâu thuẫn do n chẵn.

Xét n lẻ, giả sử phương trình có 4 nghiệm thực x

< x

, khi đó theo định lý

Rolle, phương trình x

n−1

= 0 có 3 nghiệm thực, trong khi theo trên ta vừa chứng minh

thì nó không thể có quá 2 nghiệm thực do n −1 chẵn.

Bài tập 1.55. Giải thích tạ i sao công thức Cauchy dạng

f (b) − f (a)

g(b) − g(a)

′

(c)

′

(c)

không áp

dụng được với các hàm số f (x) = x

, g(x) = x

, −1 ≤ x ≤ 1

Bài tập 1.56. Chứng minh các bất đẳng thức

a) |sin x −sin y| ≤ |x −y|

a −b

< ln

a −b

, 0 ≤ b ≤ a.

9. Các định lý về hàm khả vi và ứng dụng 79

Chứng minh. a) Xét hàm số f (t) = sin t, thoả mãn điều kiện của định lý La grange

trong khoảng [x, y] bất kì. Khi đó ∃c ∈ [x, y] sao cho

sin x −sin y = f

′

(c).(x −y) = cos c.(x − y)⇒|sin x −sin y| ≤ |x −y|

b) Xét hàm số f (x) = ln x, thoả mãn điều kiện của định lý Lagrange trong khoảng [b, a]

nên

ln a −ln b = f

′

(c)(a − b)⇒ln

(b − a)⇒ln

a −b

Vậy

a −b

< ln

a −b

, do b < c < a.

Bài tập 1.57. Tìm giới hạn

(a) lim

x→+∞

x +

√

x − x (∞ − ∞),

(b) lim

x→1



x −1

−

ln x



(∞ −∞),

x→∞

−cos

1 −





(d) lim

x→0

sin x − x(1 + x)





(e) lim

x→1

tan

πx

ln(2 − x) (∞.0),

(f) lim

x→1

−

tan

πx

ln(1 − x)



∞



(g) lim

x→0

sin x

(h) lim

x→0

(1 − a tan

x sin x

∞

(i) lim

x→0

(1 −cos x)

tan x

(j) lim

x→

(sin x)

tan x

∞

[Gợi ý]

(a) Sử dụng phương pháp nhân liên hợp, đáp số:

(b) Quy đồng mẫu số rồi sử dụng công thức L’Hospital, đáp số:

, sau đó độc giả có thể dùng khai tr iển Maclaurin hoặc công thức L’Hospital,

đáp số: ∞.

(d) Sử dụng khai triển Maclaurin hoặc công thức L’Hospital, đáp số:

(e) Sử dụng trực tiếp công thức L’Hospital (đưa tan

πx

xuống mẫu số), hoặc đặt t = 1 − x

và dùng công thức thay tương đương. đáp số:

(f) Sử dụng công thức L’Hospital, đáp số: −∞.

(g) Sử dụng công thức lim A(x)

B(x)

= e

lim B(x) ln A(x)

, đáp số: 1.

80 Chương 1. Hàm số một biến số (13LT+13BT)

(h) Sử dụng công thức lim A(x)

B(x)

= e

lim B(x) ln A(x)

, đáp số: e

−a

(i) Sử dụng công thức lim A(x)

B(x)

= e

lim B(x) ln A(x)

, đáp số: 1.

(j) Sử dụng công thức lim A(x)

B(x)

= e

lim B(x) ln A(x)

, đáp số: 1.

Bài tập 1.58. Tính các giới hạn sau

(a) lim

x→∞

x − x



1 +

i

(b) lim

x→0



−cot x



sin x − x cos x

sin x

x→0

−5

[sin(sin x) − x.

√

1 − x

(d) lim

x→0

[ln(1 + x)

−

(e) lim

x→0

cos x −e

−

(f) lim

x→0

x −ln(1 + x)

(g) lim

x→0



−

sin x



sin x − x

x sin x

(h) lim

x→0



tan x − x

x −sin x



(i) lim

x→0



1 −cos

x sin 2x



(j) lim

x→0



−

−1



(k) lim

x→+∞

(

arctan x)

(l) lim

x→0

arctan x

sin x − x

(m) lim

x→0

ln x

1 + 2 ln(sin x)

(n) lim

x→0

sin x − x cos x

(o) lim

x→0

√

1 + x sin x −

√

cos x

(p) lim

x→0

ln(cos ax)

ln(cos bx)

, a 6= 0, b 6= 0.

[Gợi ý]

(a) Đáp số:

(b) Khai triển Taylor, đáp số:

(d) Khai triển Taylor, đáp số: −

(e) Khai triển Taylor, đáp số: −

(f) Khai triển Taylor hoặc L’Hospital, đáp

số:

(g) Khai triển Taylor hoặc L’Hospital, đáp

số: 0.

(h) L’Hospital, đáp số: 2.

(i) L’Hospital, đáp số:

(j) Quy đồng mẫu số và L’Hospital, đáp

số:

(k) ĐS: e

−

(l) L’Hospital, đáp số: ∞.

(m) L’Hospital, đáp số:

(n) L’Hospital, đáp số:

(o) Nhân liên hợp, đáp số:

9. Các định lý về hàm khả vi và ứng dụng 81

(p) L’Hospital, th ay tương đương, đáp số:

Bài tập 1.59. Chứng minh rằng lim

x→∞

x −sin x

x + cos x

tồn tại và bằng 1 nhưng không tính được

bằng quy tắc L’Hospital.

Chứng minh.

lim

x→∞

x −sin x

x + cos x

= lim

x→∞

1 −

sin x

1 +

cos x

= 1.

Nếu áp dụng quy tắc L’Hospital một cách hình thức thì ta có

lim

x→∞

x −sin x

x + cos x

= lim

x→∞

1 −cos x

1 −sin x

Tuy nhiên giới hạn ở vế phải không tồn tại, có thể kiểm tra bằng cách chọn 2 dãy x

2kπ và y

= 2kπ

Bài tập 1.60. Tính các giới hạn sau:

a) lim

x→∞



arctan x



b) lim

x→∞



1/x



, a, b > 0.

Bài tập 1.61. Dùng khai triển Maclaurin để tính các giới hạn sau:

a) lim

x→0

1−

√

1+x

cos x

x(tan x−sinh x)

(1)

b) lim

x→0

(cosh x−1) ln(1+x)−x

x(sin x−arcsin x)

(2)

Bài tập 1.62. Xác định a, b sao cho biểu thức sau đây có giới hạn hữu hạn khi x→0

f (x) =

sin

−

−sin

x(1 + ax + bx

)

sin

Chứng minh. Tại lân cận của x = 0, ta có thể viết

sin x = x −

+ o(x

)

do đó

Mẫu số = x

[x −

+ o(x

)]

= x

+ o(x

)

và

Tử số = x

−sin

x(1 + ax + bx

) = x

−[x

+ ax

+ (b −

+ cx

+ o(x

)]

⇒f (x) = −

+ (b −

+ cx

+ o(x

)

+ o(x

)

Do đó để tồn tại giới hạn hữu hạn của f (x) khi x→0, ta phải có a = 0, b =

(1)

sinh x =

−e

−x

(2)

cosh x =

−x

82 Chương 1. Hàm số một biến số (13LT+13BT)

Bài tập 1.63. Cho f là một hàm số thực, khả vi trên [a, b] và có đạo hàm f ” (x) trên (a, b),

chứng minh rằng ∀x ∈ (a, b) có thể tìm được ít nhất 1 điểm c ∈ (a, b) sao cho

f (x) − f (a) −

f (b) − f (a)

b − a

(x − a) =

(x − a)(x −b)

f ”(c)

Chứng minh. Lấy x

∈ (a, b) bất kì.

Đặt ϕ(x) := f (x) − f (a) −

f (b) − f (a)

b − a

(x − a) −

(x − a)(x −b)

.λ

Trong đó λ được xác định bởi điều kiện :

ϕ(x

) = f (x

) − f (a) −

f (b) − f (a)

b − a

− a) −

− a)(x

−b)

.λ = 0

Khi đó ta có ϕ(x

) = ϕ(a) = ϕ(b) = 0

Ta có hàm ϕ liên tục, khả vi trên [a, x

], đo đó ϕ thoả mãn các điều kiện trong định lý

Rolle, suy ra tồn tại c

∈ (a, x

) sao cho ϕ

′

) = 0. Tương tự như thế, tồn tại c

∈ (x

, b)

sao cho ϕ

′

) = 0. Mặt khác,

′

(x) = f

′

(x) −

f (b) − f (a)

b − a

−λ(x −

a + b

)

Theo giả thiết, f có đạo hàm cấp 2, do đó ϕ cũng có đạo hàm cấp 2, và ϕ”(c

) = ϕ”(c

) = 0,

nên theo định lý Rolle ta có tồn tại c ∈ (c

, c

) sao cho ϕ” (c) = f ”(c) − λ = 0⇒λ = f ”(c),

và ta có :

f (x) − f (a) −

f (b) − f (a)

b − a

(x − a) =

(x − a)(x −b)

f ”(c)

10. Các lược đồ khảo sát hàm số 83

§10. CÁC LƯỢC ĐỒ KHẢO SÁT HÀM SỐ

10.1 Khảo sát và vẽ đồ thị của hàm số y = f (x)

Mục này học sinh đã được nghiên cứu tương đối kĩ trong chương trình phổ thông nên

chỉ nhấn mạnh cho sinh viên những điểm cần chú ý trong quá trình khảo sát hàm số và

khảo sát một số hàm số khác với chương trình phổ thông như hàm số có chứa căn thức, ...

Sơ đồ khảo sát

1. Tìm TXĐ của hàm số, nhận xét tính chẵn, lẻ, tuần hoàn của hàm số (nếu có).

2. Xác định chiều biến thiên: tìm các khoảng tăng, giảm của hàm số.

3. Tìm cực trị (nếu có).

4. Xét tính lồi, lõm (nếu cần thiết), điểm uốn (nếu có).

5. Tìm các tiệm cận của hàm số (nếu có).

6. Lập bảng biến thiên.

7. Tìm một số điểm đặc biệt mà hàm số đi qua (ví dụ như giao điểm với các t rục toạ độ,

....) và vẽ đồ thị của hàm số.

Ví dụ 10.1 (Giữa kì, K61).

T ìm các cực trị của hàm số sau

y =

Ví dụ 10.2 (Giữa kì, K59).

T ìm các đường tiệm cận của đường cong

y = x

sin

[Lời giải] TXĐ = R \ {0}.

0 ≤



sin



≤ x

⇒ lim

x→0

sin

= 0 (giới hạn kẹp).

Đường cong không có tiệm cận đứng.

lim

x→∞

sin

= lim

x→∞

sin

= ∞

Đường cong không có tiệm cận ngang.

lim

x→∞

= lim

x→∞

sin

= 1.

lim

x→∞

(y − x) = lim

x→∞



x sin

−1



= lim

t→0



sin t

−1



= lim

t→0

sin t −t

= 0



đặt t =



Đường cong có một tiệm cận xiên là y = x.

84 Chương 1. Hàm số một biến số (13LT+13BT)

Ví dụ 10.3.

T ìm các tiệm cận xiên của đường cong

y = ln(1 + e

−2x

)

[Lời giải] Ta có

lim

x→+∞

= 0, a = lim

x→−∞

= lim

x→−∞

ln(1 + e

−2x

)

= lim

x→−∞

−2e

−2x

1 + e

−2x

= −2, (L’Hospital).

b = lim

x→−∞

(y + 2x) = lim

x→−∞

ln(1 + e

−2x

) + 2x = lim

x→−∞

ln[(1 + e

−2x

] = li m

x→−∞

ln(1 + e

) = 0.

Kết luận: y = −2x là tiệm cận xiên của đường cong.

Bài tập 1.64. Khảo sát và vẽ đường cong y =

2−x

1+x

Hình 1.64

Bài tập 1.65. Khảo sát và vẽ đường cong y =

√

− x

− x + 1.

Hình 1.65

Bài tập 1.66. Khảo sát và vẽ đường cong y =

x−2

√

10. Các lược đồ khảo sát hàm số 85

Hình 1.66

10.2 Khảo sát và vẽ đường cong cho dưới dạng tham số

Giả sử cần khảo sát và vẽ đường cong cho dưới dạng tham số







x = x(t)

y = y(t)

1. Tìm TXĐ, nhận xét tính chẵn, lẻ, tuần hoàn của các hàm số x(t), y(t) (nếu có).

2. Xác định chiều biến thiên của các hàm số x(t), y(t) theo biến t bằng cách xét dấu các

đạo hàm của nó.

3. Tìm các tiệm cận của đường cong

(a) Tiệm cận đứng: Nếu l im

t→t

(∞)

y(t) = ∞ và l im

t→t

(∞)

x(t) = x

thì x = x

là một tiệm

cận đứng của đường cong.

(b) Tiệm cận ngang: Nếu lim

t→t

(∞)

x(t) = ∞ và lim

t→t

(∞)

y(t) = y

thì y = y

là một tiệm

cận ngang của đường cong.

t→t

(∞)

y(t) = ∞ và lim

t→t

(∞)

x(t) = ∞ thì đường cong có thể có

tiệm cận xiên. Nếu

a = l im

t→t

(∞)

y(t)

x(t)

, b = lim

t→t

(∞)

[y(t) − ax(t)]

thì y = ax + b là một tiệm cận xiên của đồ thị h àm số.

4. Để vẽ đường cong được chính xác hơn, ta xác định tiếp tuyến của đường cong tại các

điểm đặc biệt. Hệ số góc của tiếp tuyến của đường cong tại mỗi điểm bằng

′

86 Chương 1. Hàm số một biến số (13LT+13BT)

Ngoài ra có thể khảo sát tính lồi lõm và điểm uốn (nếu cần thiết) bằng cách tính các

đạo hàm cấp hai



′



”x

′

−y

′

”

′3

5. Xác định một số điểm đặc biệt mà đồ thị hàm số đi qua và vẽ đồ thị hàm số.

Ví dụ 10.4 (Giữa kì, K61).

T ìm các tiệm cận của đường cong cho bởi phương trình tham

số







x =

2016t

1−t

y =

2016t

1−t







x =

2016t

1+t

y =

2016t

1+t

Bài tập 1.67. Khảo sát và vẽ đường cong







x = 2t −t

y = 3t −t

Hình 1.67

10.3 Khảo sát và vẽ đường cong trong hệ toạ độ cực

Bài tập 1.68. Khảo sát và vẽ đường cong r = a + b cos ϕ, (0 < a ≤ b).

10. Các lược đồ khảo sát hàm số 87

r = a + b cos ϕ

Hình 1.68

Bài tập 1.69. Khảo sát và vẽ đường cong r = a

(

1 + cos ϕ

) (

a > 0

)

, (đường Cardioid hay

đường hình tim, trường hợp đặc biệt của đường cong trong Bài tập 1.68 với a = b)

−a

Hình 1.69

Bài tập 1.70. Khảo sát và vẽ đường cong r =

√

cos 3ϕ

, (a > 0).

88 Chương 1. Hàm số một biến số (13LT+13BT)

r =

√

cos 3ϕ

Hình 1.70

Bài tập 1.71. Khảo sát và vẽ đường cong Lemniscate

+ y

)

= 2a

−y

) (a > 0 ).

Phương trình của đường Lemniscate trong tọa độ cực là r = a

2 cos 2ϕ.

r = a

2 cos 2ϕ

Hình 1.71

Bài tập 1.72. Khảo sát và vẽ đường cong



+ y



= 2a

(

a > 0

)

Tham số hoá đường cong đã cho, đặt

(

x = r cos ϕ

y = r sin ϕ

, phương trình đường cong tương đương

với r

= a

sin 2ϕ.

10. Các lược đồ khảo sát hàm số 89

r = a

sin 2ϕ

Hình 1.72

Bài tập 1.73. Khảo sát và vẽ đường cong x

+ y

= axy

(

a > 0

)

(Lá Descartes)

Tham số hoá đường cong đã cho, đặt

(

x = r cos ϕ

y = r sin ϕ

, phương trình đường cong tương đương

với

r =

a sin ϕ cos ϕ

sin

ϕ + cos

TCX: y = −x −

Hình 1.73

10.4 Bài tập

Bài tập 1.74. Khảo sát tính đơn điệu của hàm số

90 Chương 1. Hàm số một biến số (13LT+13BT)

a. y = x

+ x b. y = arctan x −x

[Đáp số]

a) hàm số tăng với mọi x b) hàm số giảm với mọi x

Bài tập 1.75. Chứng minh các bất đẳng thức

a. 2x arctan x ≥ ln(1 + x

) ∀x ∈ R

b. x −

≤ ln(1 + x) ≤ x ∀x ≥ 0

Chứng minh. a) Xét hàm số f (x) = 2x arctan x −ln(1 + x

)⇒f

′

(x) = 2 arctan x.

• Nếu x ≥ 0, f

′

(x) ≥ 0⇒f (x) ≥ f (0) = 0

• Nếu x ≤ 0, f

′

(x) ≤ 0⇒f (x) ≤ f (0) = 0

b) Tương tự, xét g(x) = x −

−ln(1 + x), h(x) = ln(1 + x) − x

′

(x) = −

1 + x

< 0, h

′

(x) = −

1 + x

< 0⇒g(x) ≤ g(0) = 0, h(x) ≤ h(0) = 0.

Bài tập 1.76. Tìm cực trị của hàm số

a) y =

+ 4x + 4

+ x + 1

b) y = x −ln(1 + x) c) y =

(1 − x)(x −2)

Chứng minh. a) y

′

−x(x+2)

+x+1)

, y

min

= y(−2) =

, y

max

= y(0) = 4.

b) y

′

1+x

, y

min

= y(0) = 0.

c) y

′

= −

√

(x−2)

√

(1−x)

√

1−x

√

x−2

−x

√

(1−x)

(x−2)

• Xét x

, ta có y

min

= y(

) = −

√

• Xét x

= 1, y

′

không đổi dấu, hàm số không đạt cực trị tại x

= 1

• Xét x

= 2, ta có y

max

= y(2) = 0

Bài tập 1.77. Chứng minh các bất đẳng thức sau

a) e

> 1 + x ∀x 6= 0

b) x −

< sin x < x ∀x > 0

c) tan x > x +

∀0 < x <

Bài tập 1.78. Chứng minh rằng với mọi x > 0 ta có



1 +



< e <



1 +



x+1

Bài tập 1.79. Tính các giới hạn sau

10. Các lược đồ khảo sát hàm số 91

(a) lim

x→∞

x − x

ln(1 +

)

(b) lim

x→0



−cot x



x→0

−5

sin(sin x) − x.

√

1 − x

(d) lim

x→0



ln(1 + x)

−



92 Chương 1. Hàm số một biến số (13LT+13BT)

CHƯƠNG 2

PHÉP TÍNH TÍCH PHÂN MỘT BIẾN SỐ

§1. TÍCH PHÂN BẤT ĐỊNH

1.1 Nguyên hàm của hàm số

Chương này trình bày về phép tính tích phân, đây là phép toán ngược của phép tính

đạo hàm (vi phân) của hàm số. Nếu ta cho trước một hàm số f (x) thì có tồn tại hay không

một hàm số F(x) có đạo hàm bằng f (x)? Nếu tồn tại, hãy tìm tất cả các hàm số F(x) như

vậy.

Định nghĩa 2.26.

Hàm số

F(x)

được gọi là một

nguyên hàm

của hàm số

f (x)

trên khoảng

nếu

′

(x) = f (x)

∀x ∈ D

hay

dF(x) = f (x)dx

Định lý sau đây nói rằng nguyên hàm của một hàm số cho trước không phải là duy nhất,

nếu biết một nguyên hà m thì ta có thể miêu tả được tất cả các nguyên hàm khác của hàm

số đó.

Định lý 2.38.

Nếu

F(x)

là một nguyên hàm của hàm số

f (x)

trên khoảng

, thì:

•

Hàm số

F(x) + C

cũng là một nguyên hàm của hàm số

f (x)

, với

là một hằng số bất

kỳ.

•

Ngược lại, mọi nguyên hàm của hàm số

f (x)

đều viết được dưới dạng

F(x) + C

, trong

đó

là một hằng số.

Như vậy biểu thức F(x) + C biểu diễn tất cả các nguyên hàm của hàm số f (x), mỗi hằng

số C tương ứng cho ta một nguyên hàm.

94 Chương 2. Phép tính tích phân một biến số

Định nghĩa 2.27.

T ích phân bất định của một hàm số

f (x)

là họ các nguyên hàm

F(x) +

, với

x ∈ D

, trong đó

là một nguyên hàm của hàm số

f (x)

và

là một hằng số bất

kỳ. Tích phân bất định của

f (x)dx

được ký hiệu là

f (x)dx

. Biểu thức

f (x)dx

được gọi là

biểu thức dưới dấu tích phân và hàm số

f (x)

được gọi là hàm số dưới dấu tích phân.

Vậy

f (x)dx = F(x) + C, với F(x) là nguyên hàm của f (x).

Các tính chất của tích phân bất định

•



f (x)dx



′

= f (x) hay d

f (x)dx = f (x)dx

•

′

(x)dx = F(x) + C hay

dF(x) = F(x) + C

•

a f (x)dx = a

f (x)dx (a là hằng số khác 0)

•

[

f (x) ± g(x)

]

dx =

f (x)dx ±

g(x)dx

Hai tính chất cuối cùng là tính chất tuyến tính của tích phân bất định, ta có thể viết

chung

[

α f (x) + βg(x)

]

dx = α

f (x)dx + β

g(x)dx

trong đó α, β là các hằng số không đồng thời bằng 0.

Các công thức tích phân dạng đơn giản

dx =

α+1

+ C, (α 6= −1 )

= ln

+ C

sin xdx = −cos x + C

cos xdx =

sin x + C

sin

= −cot x + C

cos

= tan x + C

dx =

ln a

+ C, (a > 0, a 6= 1)

dx = e

+ C

−x



a+x

a−x



+ C

arctan

+ C

10)

√

+α

= ln



x +

√

+ α



+ C

11)

√

−x

= arcsin

+ C

12)

√

− x

dx =

√

− x

arcsin

+ C

13)

√

+ adx =

√

+ a + a ln



x +

√

+ a



+ C

1. Tích phân bất định 95

1.2 Các phương pháp tính tích phân bất định

1. Phương pháp khai triển

Để tính một tích phân bất kỳ, ta cần sử dụng các phương pháp thích hợp để đưa về

các tích phân đã có trong bảng các công thức tích phân đơn giản ở trên. Một phương

pháp đơn giản là phương pháp khai triển. Phương pháp này dựa trên tính chất tuyến

tính của tích phân bất định:

[

α f (x) + βg(x)

]

dx = α

f (x)dx + β

g(x)dx

Ta phân tích hàm số dưới dấu tích phân thành tổng (hiệu) của các hàm số đơn giản

mà đã biết được nguyên hàm của chúng, các hằng số được đưa ra bên ngoài dấu tích

phân.

Ví dụ 1.1. •

(2x

√

x −3x

)dx = 2

dx −3

dx =

− x

+ C

•



2 sin x + x

−



dx = 2

sin xdx +

dx −

= −2 cos x +

−ln

+ C

•

(1 + x

)



−

1 + x



dx = −

+ arctan x + C

2. Phương pháp biến đổi biểu thức vi phân

Nhận xét: nếu

f (x)dx = F(x) + C thì

f (u)du = F(u) + C , trong đó u = u(x) là

một hàm số khả vi liên tục. Ta có thể kiểm tra lại bằng cách đạo hàm hai vế theo x.

Sử dụng tính chất này, ta biến đổi biểu thức dưới dấu tích phân g(x)dx về dạng

g(x)dx = f (u(x))u

′

(x)dx,

trong đó f (x) là một hàm số mà ta dễ dàng tìm được nguyên hàm F(x). Khi đó tích

phân cần tính trở thành

g(x)dx =

f (u(x))u

′

(x)dx =

f (u(x))du = F(u(x)) + C

Trong trường hợp đơn giản u(x) = ax + b thì du = adx, do đó nếu

f (x)dx = F(x) + C

ta suy ra

f (ax + b)dx =

F(ax + b) + C

Ví dụ 1.2.

(a)

sin axdx = −

cos ax + C

(b)

dx =

+ C

96 Chương 2. Phép tính tích phân một biến số

(c)

sin x

cos xdx =

sin x

d(sin x) = e

sin x

+ C

(d)

cos

(1 + tan

x)d(tan x) =

tan

+ tan x + C

(e)

√

1 + 3x

dx =

√

1 + 3x

d(1 + 3x

) =



√

1 + 3x



+ C

(f)

I =

arccos x arcsin x

√

1 − x

dx =



−arcsin x



arcsin xd(arcsin x)

nên

⇒ I =

arcsin

x −

arcsin

x + C

3. Phương pháp đổi biến

Xét tích phân I =

f (x)dx, trong đó f (x)là một hàm số liên tục. Để tính tích phân

này, ta tìm cách chuyển sang tính tích phân k hác của một hàm số khác bằng một

phép đổi biến x = ϕ(t), sao cho biểu thức dưới dấu tích phân đối với biến t có thể tìm

được nguyên hàm một cách đơn giản hơn.

Phép đổi biến thứ nhất:

Đặt x = ϕ(t), trong đó ϕ(t) là một hàm số đơn điệu, và có đạo hàm liên tục. Khi đó

ta có

I =

f (x)dx =

[

ϕ(t)

]

′

(t)dt

Giả sử hàm số g(t) = f

[

ϕ(t)

]

′

(t) có nguyên hà m là hàm G(t), và t = h(x) là hàm

số ngược của hàm số x = ϕ(t), ta có

g(t)dt = G(t) + C ⇒ I = G

[

h(x)

]

+ C

Phép đổi biến thứ hai:

Đặt t = ψ(x), trong đó ψ(x) là một hàm số có đạo hàm liên tục, và ta viết được hàm

f (x) = g

[

ψ(x)

]

′

(x). Khi đó ta có

I =

f (x)dx =

[

ψ(x)

]

′

(x)dx

Giả sử hàm số g(t) có nguyên hàm là hàm số G(t), ta có

I = G

[

ψ(x)

]

+ C

Chú ý: Khi tính tích phân bất định bằng phương pháp đổi biến số, sau khi tìm được

nguyên hàm theo biến số mới, phải đổi lại thành hàm số của biến số cũ.

1. Tích phân bất định 97

Ví dụ 1.3.

(a) Tính tích phân

2 − x

Đặt

x = 2 sin

t, t ∈





, ta tính được

dx = 4 sin t cos tdt,

2 − x

2 sin

2(1 − sin

= tan t

Suy ra

2 − x

dx = 4

sin

tdt = 2t −sin 2t + C

Đổi lại biến

, với

t = arcsin

, ta thu được

2 − x

dx = 2 arcsin

−

2x −x

+ C

(b) Tính tích phân

+ 1

Đặt

= t ⇒ e

dx = dt

, ta có

t + 1

dt =



1 −

t + 1



dt = t −ln

t + 1

+ C

Đổi lại biến

, ta được

= e

−ln(e

+ 1) + C

√

1 + 4

Đặt

t = 2

−x

⇒ dt = −2

−x

ln 2dx

, tích phân trở thành

−dt

t ln 2

√

1 + t

−2

= −

ln 2

√

+ 1

= −

ln 2

ln(t +

+ 1) + C

Đổi lại biến

, ta có:

= −

ln 2

ln(2

−x

√

−x

+ 1) + C

Ví dụ 1.4 (Giữa kì, K61).

T ính tích phân

x+1



1 +

+ ln x



. b)

x−1



1 −

+ ln x



4. Phương pháp tích phân từng phần

Giả sử u = u(x) và v = v(x) là các hàm số có đạo hàm liên t ục. Theo quy tắc lấy vi

phân

d(uv) = udv + vdu ⇒ uv =

d(uv) =

udv +

vdu

Suy ra

udv = uv −

vdu

98 Chương 2. Phép tính tích phân một biến số

Xét tích phân I =

f (x)dx. Ta cần biểu diễn

f (x)dx =

[

g(x)h(x)

]

dx = g(x)

[

h(x)dx

]

= udv

và áp dụng công thức tích phân từng phần với các hàm số u = g(x), v =

h(x)dx. Ta

thường sử dụng phương pháp này khi biểu th ức dưới dấu tích phân chứa một trong

các hàm số sau đây: ln x, a

, hàm số lượng giác, hàm số lượng giác ngược. Cụ thể:

• Trong các tích phân

dx;

sin kxdx;

cos kxdx , n nguyên dương, ta

thường chọn u = x

• Trong các tích phân

xdx, α 6= −1 và n nguyên dương, ta thường chọn

u = ln

• Trong tích phân

arctan kxdx;

arcsin kxdx, n nguyên dương, ta thường

chọn u = arctan kx hoặc u = arcsin kx; dv = x

dx.

Ví dụ 1.5.

T ính các tích phân bất định

(a)

ln xdx = x ln x −

dx = x ln x − x + C

(b)

sin xdx

Đặt

u = x

, dv = sin xdx ⇒ v = −cos x

, ta được

= −x

cos x + 2

x cos xdx

Đặt

u = x, dv = cos xdx ⇒ v = sin x

, ta được

= −x

cos x + 2



x sin x −

sin xdx



= −x

cos x + 2x sin x + 2 cos x + C

(c)

(x + 1)

Đặt

u = xe

; dv =

(x+1)

⇒ v = −

x+1

; du = (x + 1)e

, ta được

= −

x + 1

dx = −

x + 1

+ e

+ C =

x + 1

+ C

(d)

√

1 + e

Đặt

√

1 + e

= t ⇒

√

1+e

= 2dt

, ta có

= 2

[

ln(t −1) + ln(t + 1)

]

dt = 2(t −

1) ln(t −1 ) + 2(t + 1) ln(t + 1) −4t + C

Đổi lại biến

ta có

√

1 + e

= 2(x −2)

√

1 + e

+ 4 ln



1 +

√

1 + e



−2x + C

1. Tích phân bất định 99

(e)

x arcsin x

√

1 − x

Đặt

u = arcsin x; dv =

xdx

√

1−x

⇒ du =

√

1−x

; v = −

√

1 − x

, ta được

= −

1 − x

arcsin x +

dx = −

1 − x

arcsin x + x + C

(f)

cos 2xdx

Đặt

u = cos 2x; dv = e

dx ⇒ v = e

; du = −2 sin 2 xdx

, ta được

= e

cos 2x + 2

sin 2xdx

Đặt

u = sin 2x; dv = e

dx ⇒ v = e

; du = 2 cos 2xdx

, ta được

= e

cos 2x + 2



sin 2x −2

cos 2xdx



= e

cos 2x + 2e

sin 2x −4I

+ 5C

Vậy

(

cos 2x + 2 sin 2x

)

+ C

Ví dụ 1.6 (Giữa kì, K61).

T ính tích phân

arctan xdx

arccot xdx

sin 2xdx

cos 2xdx

Ví dụ 1.7 (Ngụy biện toán học).

Chứng minh rằng

0 = 1

Chứng minh. Xét tích phân

I =

x ln x

ln x

d ln x

ln x

. ln x −

ln xd



ln x



(tích phân từng phần)

= 1 −

ln x.

−1

= 1 −

x ln x

= 1 + I.

Phương trình I = 1 + I dẫn đến 0 = 1. Sai lầm ở đâu?

Trong các mục sau đây chúng ta sẽ xét tích phân bất định của một số dạng hàm cơ

bản: hàm phân thức hữu tỷ, hàm lượng giác, hàm chứa căn thức; và trình bày một

số phương pháp giải chung đối với tích phân các hàm này.

100 Chương 2. Phép tính tích phân một biến số

1.3 Tích phân hàm phân thức hữu tỷ

Định nghĩa 2.28. Một hàm phân thức hữu tỷ

là một hàm số có dạng

f (x) =

P(x)

Q(x)

, trong

đó

P(x), Q(x)

là các đa thức của

. Một phân thức hữu tỷ có bậc của đa thức ở tử số nhỏ

hơn bậc của đa thức ở mẫu số là một

phân thức hữu tỷ thực sự.

Bằng phép chia đa thức, chia P(x) cho Q(x) ta luôn đưa được một hàm phân thức hữu tỷ

về dạng

f (x) = H(x) +

r(x)

Q(x)

trong đó H(x) là đa thức thương, r(x) là phần dư trong phép chia. Khi đó

r(x)

Q(x)

là một phân

thức hữu tỷ thực sự. Nguyên hàm của đa thức được tìm bởi công thức tích phân cơ bản.

Ta sẽ xét việc tìm nguyên hàm của phân thức hữu tỷ còn lại

r(x)

Q(x)

trong hai trường hợp đặc

biệt: mẫu số của phân thức là đa thức bậc nhất hoặc đa thức bậc hai. Trong những trường

hợp mẫu số phức tạp hơn, chúng ta sử dụng phương pháp hệ số bất định để đưa về hai

trường hợp trên.

Phương pháp hệ số bất định

Giả sử chúng ta muốn phân tích một phân thức hữu tỷ thực sự

P(x)

Q(x)

thành tổng (hiệu)

của các phân thức hữu tỷ thực sự có mẫu số là đa thức bậc nhất hoặc bậc ha i. Trước hết

ta phân tích đa thức ở mẫu số Q(x) thành tích của các đa thức bậc nhất hoặc bậc hai vô

nghiệm

Q(x) = (x −α

)

...(x −α

)

+ p

x + q

)

...(x

+ p

x + q

)

trong đó α

, p

, q

là các hằng số, a

, b

là các số nguyên dương, 1 ≤ i ≤ m; 1 ≤ j ≤ n.

• Nếu trong phân tích của Q(x) xuất hiện đơn thức (x −α)

, a là số nguyên dương thì

trong phân tích của phân thức

P(x)

Q(x)

xuất hiện các hạng tử dạng

(x−α)

, trong đó A

là

hằng số và 1 ≤ i ≤ a.

• Nếu trong phân tích của Q(x) xuất hiện biểu thức (x

+ px + q)

, b là số nguyên

dương thì trong phân tích của phân thức

P(x)

Q(x)

xuất hiện các hạng tử dạng

x+C

+px+q)

trong đó B

, C

là các hằng số và 1 ≤ j ≤ b.

Sau khi viết được phân tích của

P(x)

Q(x)

, ta tìm các hằng số A

, B

, C

bằng cách quy đồng mẫu

số ở hai vế, rồi đồng nhất hệ số của x

, n ∈ R ở hai vế. Như vậy việc dùng phương pháp hệ

số bất định dẫn chúng ta tới việc tính bốn loại tích phân hữu tỷ cơ bản sau:

Adx

x − a

II.

Adx

(x − a)

(k ≥ 2)

III.

(Mx + N)dx

+ px + q

IV.

(Mx + N)dx

+ px + q)

(m ≥ 2)

trong đó

100

1. Tích phân bất định 101

Adx

x−a

= A ln |x −a|+ C

Adx

(x−a)

A(x −a)

−k

dx =

−A

(k−1)(x−a)

k−1

+ C

(Mx + N)dx

+ px + q

Mt + (N − Mp/2)

+ a

dt (a =

q − p

/4, đổi biến t = x + p/2)

Mtdt

+ a

(N − Mp/2)dt

+ a

ln(t

+ a

) +

(N − Mp/2) arctan

+ C

ln(x

+ px + q) +

2N − Mp

4q − p

arctan

2x + p

4q − p

+ C.

(Mx + N)dx

+ px + q)

Mt + (N − Mp/2)

+ a

)

dt (a =

q − p

/4, đổi biến t = x + p/2)

Mtdt

+ a

)

(N − Mp/2)dt

+ a

)

• Tích phân thứ nhất

Mtdt

)

= −

2(m−1)(t

)

m−1

+ C.

• Muốn xử lý tích phân thứ hai ta thực hiện phép đổi biến số lượng giác t = a tan z,

khi đó







+ a

cos

dt =

cos

dz.

Ta có

+ a

)

= a

2m−1

cos

2m−2

zdz.

T ích phân của hàm lượng giác này sẽ được nghiên cứu kĩ ở phần sau.

Ví dụ 1.8.

T ính các tích phân bất định

− x

+ 2x

−2x + 1

+ 2)(x −1)

Ta có

− x

+ 2x

−2x + 1

+ 2)(x −1)

= x +

+ 2)(x −1)

= x +

x −1

Bx + C

+ 2

Quy đồng mẫu số ở hai vế

3 = (A + B)x

+ (C − B + 2)x −C

101

102 Chương 2. Phép tính tích phân một biến số

Đồng nhất hệ số của

, x

và hệ số tự do, ta được











A + B = 0

C − B + 2 = 0

−C = 1

⇒











A = 1

B = −1

C = −1

Suy ra

− x

+ 2x

−2x + 3

+ 2)(x −1)

= x +

x −1

−

+ 2

−

+ 2

Vậy tích phân bằng

I =

+ ln

x −1

−

ln(x

+ 2)

−

√

arctan

√

+ C

+ 10x

+ 17x

+ 16x + 5

(x + 1)

+ 2x + 3)

Ta viết

+ 10x

+ 17x

+ 16x + 5

(x + 1)

+ 2x + 3)

= 2 +

x + 1

−

(x + 1)

−

+ 2x + 3

Suy ra

I = 2x + 2 ln

x + 1

−2

√

2 arctan

x + 1

√

+ C

Ví dụ 1.9 (Giữa kì, K61).

T ính các tích phân sau

+2016x

−2016x

xdx

+1)(x

+2)

xdx

+2)(x

+3)

Ví dụ 1.10 (Giữa kì, K61).

T ính tích phân

x ln(x

+ x + 1)dx

. b)

x ln(x

− x + 1)dx

1.4 Tích phân hàm lượng giác

1. Phương pháp chung

Xét tích phân

R(sin x, cos x)dx, trong đó hàm dưới dấu tích phân là một biểu thức

hữu tỷ đối với sin x, cos x. Ta có thể sử dụng phép đổi biến tổng quát t = tan

, khi đó

sin x =

1 + t

; cos x =

1 −t

1 + t

; tan x =

1 −t

; dx =

2dt

1 + t

tích phâ n đang xét được đưa về tích phân của phân thức hữu tỉ của biến t.

102

1. Tích phân bất định 103

Ví dụ 1.11.

T ính tích phân

sin x −cos x + 2

1 + sin x + cos x

Ta viết

sin x −cos x + 2

1 + sin x + cos x

dx = −

d(1 + sin x + cos x)

1 + sin x + cos x

+ 2

1 + sin x + cos x

Đặt

t = tan

, suy ra

1 + sin x + cos x

1 + t

= ln

1 + t

+ C

Thay lại biến cũ, ta được

sin x −cos x + 2

1 + sin x + cos x

dx = −ln

1 + sin x + cos x

+ ln



1 + tan



+ C

2. Tích phân dạng

sin

x cos

xdx, trong đó m, n là các số nguyên

• Nếu m là số nguyên dương lẻ, ta đặt t = cos x.

• Nếu n là số nguyên dương lẻ, ta đặt t = sin x.

• Nếu m, n là các số nguyên dương chẵn, ta sử dụng công thức hạ bậc:

sin

x =

1 −cos 2x

; cos

x =

1 + cos 2x

rồi đưa về tích phân dạng

sin

2x cos

2xdx.

Ví dụ 1.12.

T ính các tích phân bất định

• I

sin

x cos

xdx

Đặt

cos x = t ⇒ −sin xdx = dt

ta có

sin

x cos

xdx =

(1 −t

(−dt) =

−

+ C =

cos

−

cos

+ C

• I

sin

x cos

xdx

Sử dụng công thức hạ bậc ta có

(1 −cos 2x)

1 + cos 2x

dx =



1 −cos 2x −cos

2x + cos



⇒ I



x −

sin 2x

−

1+cos 4x

dx +

(1 −sin

2x)d(sin 2x)



Vậy

⇒ I

−

sin 2x

−

sin 4x

sin 2x

−

sin

+ C

103

104 Chương 2. Phép tính tích phân một biến số

Đối với tích phân

sau khi sử dụng công thức hạ bậc lần thứ nhất ta cũng có

thể tiếp tục hạ bậc của biểu thức lượng giác dưới dấu tích phân bởi công thức

sin

x =

3 sin x −sin 3x

; cos

x =

3 cos x + cos 3x

Áp dụng vào tích phân

, ta có:



1 −cos 2x −

1 + cos 4x

3 cos 2x + cos 6x





−

sin 2x

−

sin 4x

sin 6x



+ C

3. Tích phân

R(sin x, cos x)dx có dạng đặc biệt

• Đặt t = cos x nếu R(−sin x, cos x) = −R(sin x, cos x).

• Đặt t = sin x nếu R(sin x, −cos x) = −R(sin x, cos x).

• Đặt t = tan x nếu R(−sin x, −cos x) = R(sin x, cos x).

Ví dụ 1.13.

T ính tích phân

sin x cos

Đặt

t = cos x ⇒ dt = −sin xdx

, ta có

sin x cos

−dt

(1 −t



2(t −1)

−

2(t + 1)



= −

−



t −1

t + 1



+ C

nên

sin x cos

= −

3 cos x

−

cos x

1 −cos x

1 + cos x

+ C

1.5 Tích phân các biểu thức vô tỷ

Xét các tích phân có dạng

•

R(x,

√

+ α

)dx,

•

R(x,

√

−α

)dx,

•

R(x,

√

− x

)dx,

trong đó R(u, v) là các hàm số hữu tỷ.

Có hai phương pháp xử lý tích phân các biểu thức hữu tỉ là Phép thế lượng giác và

Phép thế Euler. Ý tưởng của cả hai phương pháp này đều là khử các biểu thức vô tỉ bằng

cách:

104

1. Tích phân bất định 105

1. đưa về tích phân của các hàm lượng giác bằng qua phép thế lượng giác,

2. đưa về tích phân của các hàm phân thức hữu tỉ bằng phép thế Euler.

Phép thế lượng giác

• Đặt x = α tan t đối với tích phân

R(x,

√

+ α

)dx.

• Đặt x =

cos t

hoặc x =

sin t

đối với tích phân

R(x,

√

−α

)dx.

• Đặt x = α sin t hoặc x = α cos t đối với tích phân

R(x,

√

− x

)dx.

Ví dụ 1.14.

T ính

√

−x

[Lời giải] Đặt x = α sin t, −

< t <

ta có











t = arcsin

dx = α cos tdt,

√

−x

α cos t

I =

dt = t + C = arcsin

+ C

Ví dụ 1.15.

T ính

√

− x

[Lời giải] Đặt x = α sin t, −

≤ t ≤

ta có











t = arcsin

dx = α cos tdt,

√

− x

= α cos t.

I = α

cos

tdt = α

1 + cos 2t

dt =

t +

sin 2t =

− x

arcsin

+ C.

Phép thế Euler

• Đặt t = x +

√

+ a đối với tích phân

R(x,

√

+ a)dx, ở đây a có thể âm hoặc dương,

nghĩa là a = ±α

đều áp dụng được. Khi đó,

dt = 1 +

√

+ a

x +

√

+ a

√

+ a

dx ⇒

√

+ a

và tích phân đã cho được đưa về tích phân của phân thức hữu tỉ.

105

106 Chương 2. Phép tính tích phân một biến số

• Đặt

√

− x

= xt + α đối với tích phân

R(x,

√

− x

)dx,. Khi đó,

− x

= (xt + α)

⇔ α

− x

= x

+ 2αxt + α

⇔ x = −

2αt

1 + t

và tích phân đã cho được đưa về tích phân của phân thức hữu tỉ.

Ví dụ 1.16.

T ính

√

[Lời giải] Đặt t = x +

√

+ a, khi đó

√

và

I =

= ln |t|+ C = ln



x +

+ a



+ C.

Ví dụ 1.17.

T ính

√

+ adx

[Lời giải] Sử dụng công thức tích phân từng phần ta có

I = x

+ a −

√

+ a

= x

+ a −

+ a) − a

√

+ a

= x

+ a + a

√

+ a

dx − I.

(2.1)

Do đó,

I =

+ a + a ln



x +

+ a



+ C.

Nói chung việc tính tích phân của các biểu thức vô tỷ thông thường được đưa về việc

tính bốn loại tích phân cơ bản sau

√

−x

= arcsin

+ C.

√

− x

dx =

√

− x

arcsin

+ C.

√

= ln



x +

√

+ a



+ C.

√

+ adx =

√

+ a + a ln



x +

√

+ a



+ C.

Ví dụ 1.18.

T ính các tích phân sau

(1 − x

)

−

Đặt

x = sin t, t ∈



−



⇒ dx = cos tdt,

√

1 − x

= cos t

, thì

(1 − x

)

−

dx =

cos

= tan t + C = tan(arcsin x) + C

106

1. Tích phân bất định 107

√

1+x

Đặt

x = tan t ⇒ dx =

cos

, ta có

√

1 + x

cos tdt

sin

= −

sin t

+ C = −

sin(arctan x)

+ C.

√

+x+1

Ta có

I =



x +





x +



= ln



x +

+ x + 1



+ C.

Tích phân có dạng

px+q

√

+bx+c

Viết

px + q

√

+ bx + c

dx =

d(ax

+ bx + c)

√

+ bx + c



q −



√

+ bx + c

để đưa về việc tính tích phân của hàm vô tỉ cơ bản.

Ví dụ 1.19.

T ính

4x−1

√

5−4x−x

Tích phân có dạng

(px+q)

√

+bx+c

Đặt u =

px+q

để đưa về việc tính tích phân của hàm vô tỉ cơ bản.

Ví dụ 1.20.

T ính

(1+x)

√

3+6x+x

Tính các tích phân có dạng





ax+b

cx+d



, ...,



ax+b

cx+d





Đặt

ax + b

cx + d

= t, với k là bội chung nhỏ nhất của n

, n

, . . . , n

, để đưa tích phân đã

cho về tích phân của phân thức hữu tỉ với biến t.

Ví dụ 1.21.

T ính

x+1

x+2

107

108 Chương 2. Phép tính tích phân một biến số

[Lời giải] Đặt t =

x+1

x+2

ta có x = −

−1

, dx =

−1)

dt và

I = 2

−1)



t −1

−

t + 1

(t −1)

(t + 1)



t −1

t + 1

−



t −1

−

t + 1



+ C

x+1

x+2

−1

x+1

x+2

+ 1

+ x + 2 + C.

(2.2)

Ví dụ 1.22.

T ính

√

[Gợi ý] Đặt

√

x = t, đáp số I = 2

√

x −3

√

x + 6

√

x −6 ln(1 +

√

x) + C.

Bài tập 2.1.

T ính các tích phân sau

√

x+9

√

x−1

√

x+1

√

x−1

√

x−

√

x−2

√

+ 1dx

√

3x+2

√

x−9

[Đáp số]

a) Đặt u =

√

x + 9, I = 2

√

x + 9 + 3 ln



√

x+9−3

√

x+9+3



+ C.

b) Đặt u =

√

x, I = x −4

√

x + 4 ln(

√

x + 1) + C.

c) Đặt u =

√

x, I =

ln(

√

+ 1) + C.

d) Đặt

√

x = u, I = 5



√

x + ln |

√

x −1|



+ C.

e) Đặt

√

x = u,

I =

√

+ 2

√

x +

√

+ 3

√

x + 4

√

x + 6

√

x + 12

√

x + 12 ln



√

x˘1



+ C.

f) Đặt

√

x −2 = u, I =



√

x˘2



+ 8

√

x˘2 + C.

g) Đặt

√

+ 1 = u, I = 2

√

+ 1 −ln



√

1˘

√



+ C.

h) Đặt

√

x = t, I = 2

√

x −3

√

x + 6

√

x −6 ln(1 +

√

x) + C.

i) Đặt

√

x −9 = u, I = 2(x −9)

3/2

+ 58

√

x −9 + C

108

§2. TÍCH PHÂN XÁC ĐỊNH

2.1 Định nghĩa tích phân xác định

Định nghĩa 2.29.

Giả sử hàm số

f (x)

xác định và bị chặn trên

[a, b]

. Chia

[a, b]

thành

khoảng nhỏ

, x

i+1

]

bởi phân hoạch

a = x

< x

< . . . < x

= b

. Trong mỗi đoạn

, x

i+1

]

ta chọn điểm

∈ [x

, x

i+1

]

và thành lập biểu thức

n−1

∑

i=0

f (ξ

) △ x

với

△ x

= x

i+1

− x

(2.3)

Biểu thức

được gọi là tổng tích phân. Gọi

λ = max

1≤i≤n

△x

. Nếu tồn tại giới hạn hữu

hạn

I = lim

λ→0

không phụ thuộc vào cách chia đoạn

[a, b]

và không phụ thuộc vào cách

chọn điểm

thì

được gọi là tích phân xác định của hàm số

f (x)

trên

[a, b]

và kí hiệu là

f (x)dx

. Trong trường hợp đó ta nói hàm số

f (x)

khả tích trên

[a, b]

Chú ý 2.19.

Trong định nghĩa trên ta đã xét hàm số

f (x)

trong khoảng đóng

[a, b]

tức là

đã giả thiết

a < b

. Bây giờ nếu

b < a

ta định nghĩa

f (x)dx := −

f (x)dx

và khi

a = b

ta định nghĩa

f (x)dx = 0

2.2 Các tiêu chuẩn khả tích

Định lý 2.39.

Điều kiện cần và đủ để hàm số bị chặn

f (x)

khả tích trên

[a, b]

là

lim

λ→0

(S −

s) = 0

, trong đó:

S =

n+1

∑

i=1

△ x

, s =

n+1

∑

i=1

△ x

= sup

x∈[x

i+1

]

f (x), m

= inf

x∈[x

i+1

]

f (x)

Áp dụng định lý 2.39 chúng ta có thể chứng minh được các định lý sau:

Định lý 2.40.

Nếu

f (x)

liên tục trên

[a, b]

thì

f (x)

khả tích trên

[a, b]

Định lý 2.41.

Nếu

f (x)

bị chặn trên

[a, b]

và có một số điểm gián đoạn trên

[a, b]

thì

f (x)

khả tích trên

[a, b]

Định lý 2.42.

Nếu

f (x)

bị chặn và đơn điệu trên

[a, b]

thì

f (x)

khả tích trên

[a, b]

109

110 Chương 2. Phép tính tích phân một biến số

2.3 Các tính chất của tích phân xác định

Trong các phần tiếp theo sau đây, nếu không có chú thích gì thì khi viết

f (x)dx ta

hiểu là f (x) được giả thiết là khả tích trên [a, b].

• Tính chất 1.

[α f (x) + βg(x)]dx = α

f (x)dx + β

g(x)dx

• Tính chất 2.

Cho 3 khoảng đóng [a, b], [a, c], [b, c], nếu f (x) khả tích trên khoảng có độ dài lớn nhất

thì cũng khả tích trên 2 đoạn còn lại, và

f (x)dx =

f (x)dx +

f (x)dx

• Tính chất 3. Giả thiết a < b. Khi đó:

(i) Nếu f (x) ≥ 0, ∀x ∈ [a, b] thì

f (x)dx ≥ 0

(ii) Nếu f (x) ≥ g(x)∀x ∈ [a, b] thì

f (x)dx ≥

g(x)dx

(iii) Nếu f (x) khả tích trên [a, b] thì |f (x)| khả tích trên [a, b] và:



f (x)dx



≤

|f (x)|dx

(iv) Nếu m ≤ f (x) ≤ M, ∀x ∈ [a, b] thì

m(b − a) ≤

f (x)dx ≤ M(b −a)

• Tính chất 4.(Định lý trung bình thứ nhất)

Giả sử f (x) khả tích trên [a, b] và m ≤ f (x) ≤ M, ∀x ∈ [a, b], khi đó tồn tại µ sao cho:

f (x)dx = µ(b − a), m ≤ µ ≤ M.

Đặc biệt, nếu f (x) liên tục trên [a, b] thì tồn tại c ∈ [a, b] sa o cho:

f (x)dx = f (c)(b − a).

110

2. Tích phân xác định 111

• Tính chất 5.(Định lý trung bình thứ hai)

Giả thiết

(i) f (x) và f (x)g(x) khả tích trên [a, b].

(ii) m ≤ f (x) ≤ M, ∀x ∈ [a, b].

(iii) g(x) không đổi dấu trên [a, b].

Khi đó

f (x)g(x)dx = µ

g(x)dx, m ≤ µ ≤ M.

Đặc biệt nếu f (x) liên tục trên [a, b] thì tồn tại c ∈ [a, b] sao cho:

f (x)g(x)dx = f (c)

g(x)dx.

Ví dụ 2.1 (Cuối kì, K61-Viện ĐTQT).

Chứng minh rằng nếu

f (x)

là một hàm số liên

tục trên

[3, 4]

sao cho

f (x) ≥ 0

với mọi

x ∈ [3, 4]

và

f (x)dx = 0

thì

f (x) = 0

với mọi

x ∈ [3, 4]

2.4 Tích phân với cận trên thay đ ổi (hàm tích phân)

Giả sử f (x) là một hàm khả tích trên [a, b], khi đó với mỗi x ∈ [a, b] th ì f cũng khả tích

trên [a, x]. Ta xác định hàm số F(x) =

f (t)dt.

Định lý 2.43. (1)

Nếu

f (t)

khả tích trên

[a, b]

thì

F(x)

liên tục trên

[a, b]

(2)

Nếu

liên tục tại

∈ [a, b]

thì

F(x)

có đạo hàm tại

và

′

) = f (x

)

Định lý 2.44 (Công thức Newton-Leibniz).

Nếu

f (x)

liên tục trong khoảng đóng

[a, b]

và

F(x)

là một nguyên hàm của

f (x)

thì

f (x)dx = F(b) − F(a).

111

112 Chương 2. Phép tính tích phân một biến số

2.5 Các phương pháp tính tích phân xác định

1. Sử dụng công thức tích phân từng phần.

Giả sử u(x), v(x) là các hàm số có đạo hàm liên tục trong [a, b]. Khi đó:

udv = uv|

−

vdu

2. Sử dụng các phép đổi biến số.

Định lý 2.45 (Đổi biến x := ϕ(t)).

Xét

I =

f (x)dx

với

f (x)

liên tục trong

[a, b]

. Thực hiện phép đổi biến

x = ϕ(t)

thoả

mãn 3 điều kiện sau:

(1) ϕ(t)

có đạo hàm liên tục trong

[a, b]

(2) ϕ(a) = α; ϕ(b) = β.

(3)

Khi

biến thiên trong

[α, β]

từ

đến

thì

x = ϕ(t)

biến thiên liên tục từ

đến

Khi đó ta có công thức:

f (x)dx =

f [ϕ(t)]ϕ

′

(t)dt.

Định lý 2.46 (Đổi biến t := ϕ(x)).

Giả sử tích phân cần tính có dạng

I =

f [ϕ(x)].ϕ

′

(x)dx

. Trong đó

ϕ(x)

biến thiên

đơn điệu ngặt và có đạo hàm liên tục trên

[a, b]

. Khi đó:

f [ϕ(x)].ϕ

′

(x)dx =

ϕ(b)

ϕ(a)

f (t)dt.

3. Sử dụng các phép truy hồi, quy nạp.

112

2. Tích phân xác định 113

2.6 Hệ thống bài tập

Dạng 1. Tính đạo hàm của hàm tích phân.

Chúng ta có các công thức sau:



f (t)dt



′

= f (x)

(2.4)



g(x)

f (t)dt



′

= f (g(x)).g

′

(x)

(2.5)

Công thức 2.4 chúng ta đã biết trong Định lý 2.43, còn công thức 2.5 được suy ra từ công

thức đạo hàm của hàm hợp.

Bài tập 2.1.

T ính các đạo hàm:

√

1+x

Chứng minh. a)

dt = −

dt = −e

( do y là hằng số)

dt = e

( do x là hằng số)

√

1 + x

= −

√

1 + x

√

1 + x

−2x

√

1 + x

√

1 + 12x

Dạng 2. Tính giới hạn của hàm số dựa vào công thức L’Hospital và đạo hàm của

hàm tích phân.

Bài tập 2.2.

T ìm giới hạn:

A = lim

x→0

sin x

√

tan tdt

tan x

√

sin tdt

B = lim

x→+∞

(arctan t)

√

113

114 Chương 2. Phép tính tích phân một biến số

Chứng minh. a) Nhận xét: lim

x→0

sin x

√

tan tdt = lim

x→0

tan x

√

sin tdt = 0 nên áp dụng quy

tắc L’Hospital ta có:

lim

x→0

sin x

√

tan tdt

′

tan x

√

sin tdt

′

= lim

x→0

tan(sin x). cos x

sin(tan x).

cos

= 1⇒A = 1

b) Nhận xét: lim

x→+∞

(arctan t)

dt = lim

x→+∞

√

+ 1 = ∞ nên áp dụng quy tắc L’Hospital

ta có:

lim

x→+∞

(arctan t)

′



√

+ 1



′

= lim

x→+∞

(arctan x)

√

⇒B =

Dạng 3. Sử dụng c ông thức tổng tích phân để tính giới hạn của một số dãy số

đặc biệt.

Xuất phát từ công thức tính tổng tích phân 2.3

n−1

∑

i=0

f (ξ

) △ x

với △ x

= x

i+1

− x

Nếu chúng ta chia đoạn [a, b] thành n khoảng có độ dài bằng nhau bởi phân hoạch a =

< x

< . . . < x

= b, trong đó x

= a + (b −a)

thì:

b − a

n−1

∑

i=0

f (ξ

) với ξ

∈ [x

, x

i+1

]

Khi đó nếu hàm f (x) khả tích trên [a, b], và chọn ξ

= x

ta được công thức:

lim

n→∞

b − a

n−1

∑

i=0

a +

b − a

f (x)dx

(2.6)

Còn nếu chọn ξ

= x

i+1

ta được công thức:

lim

n→∞

b − a

∑

i=1

a +

b − a

f (x)dx

(2.7)

114

2. Tích phân xác định 115

Bài tập 2.3.

Dùng định nghĩa và cách tính tích phân xác định, tìm các giới hạn:

A = lim

n→∞

nα

nα+β

nα+2β

+ ··· +

nα+(n−1)β

B = lim

n→∞



1 +

+ ··· +

1 +



Chứng minh. a) Viết

A = lim

n→∞

α +

2β

+ ··· +

α +

(n−1)β

Áp dụng công thức 2.6 với a = 0, b = 1, f (x) =

α+βx

ta được:

A =

α + βx

dx =

α + β

Nếu áp dụng công thức 2.7 với a = 0, b = 1, f (x) =

α+βx

ta được:

′

= lim

n→∞

nα + β

nα + 2β

+ ···+

nα + nβ

= A =

α + β

b) Áp dụng công thức 2.7 với a = 0, b = 1, f (x) =

√

1 + x ta được:

B =

√

1 + xdx =

√

2 −1)

Nếu áp dụng công thức 2.6 với a = 0, b = 1, f (x) =

√

1 + x ta được:

′

= lim

n→∞

1 +

+ ··· +

1 +

n −1

= B =

√

2 −1)

Bài tập 2.4.

T ính

lim

n→∞



(2n)!



[Gợi ý] Tính lim

n→∞



(2n)!



bằng cách viết biểu thức trong giới hạn dưới dạng tổng

tích phâ n.

Dạng 4. Tính tích phân xác định (xem mục 2.5)

Bài tập 2.5.

T ính các tích phân

115

116 Chương 2. Phép tính tích phân một biến số

| ln x | (x + 1 )dx

(x ln x)

−2x + 5)e

−

sin

x cos x

(1+tan

arcsin

1+x

cos

x cos nxdx

[Gợi ý]

a) I

b) I

−2

c) I

= 98 −

144

√

sin

x cos x

(1 + tan

sin

x. cos x. cos

xdx

sin

x.(1 −sin

x)d(sin x)

sin

(2)

−

2 sin

(2)

sin

(2)

116

2. Tích phân xác định 117

arcsin

1 + x

= x arcsin

1 + x



−

1 −

1+x

x+1

(x + 1)

= π −

√

x + 1

= π −

√

+ 1

.2tdt (đặt

√

x = t)

= π −

√



1 −

+ 1



= π −

(t −arctan t)



√

4π

−

√

cos

x cos nxdx

cos

xd sin nx

cos

x sin nx



sin nx.n. cos

n−1

x. sin xdx

sin nx. cos

n−1

x. sin xdx.

117

118 Chương 2. Phép tính tích phân một biến số

Suy ra

cos

x cos nxdx +

sin nx. cos

n−1

x. sin xdx

cos

n−1

x cos(n −1)xdx

= I

n−1

Vậy theo phép truy hồi ta có I





n+1

Bài tập 2.6.

T ính

sin

xdx

cos

xdx

Dạng 5. Chứng minh các đẳng thức tích phân

Bài tập 2.7.

Chứng minh rằng nếu

f (x)

liên tục trên

[0, 1]

thì:

f (sin x)dx =

f (sin x)dx

x f (sin x)dx =

f (cos x)dx.

[Gợi ý] Đây là bài tập dễ, câu a) đặt t =

− x, còn câu b) đặt t = π − x.

Bài tập 2.8.

Áp dụng kết quả của bài tập 2.7 hãy chứng minh

√

sin x

√

sin x +

√

cos x

dx =

√

cos x

√

sin x +

√

cos x

dx =

Bài tập 2.9.

Giả sử

f (x)

liên tục trên

[−a, a](a > 0)

, hãy chứng minh

I =

−a

f (x)dx =











nếu

f (x)

là hàm số lẻ trên

[−a, a]

f (x)dx

nếu

f (x)

là hàm số chẵn trên

[−a, a]

Bài tập 2.10.

Cho

f (x)

liên tục, chẵn trên

[−a, a]

, chứng minh

−a

f (x)dx

1 + b

f (x)dx

với

0 ≤ b 6= 1

Áp dụng tính

−1

+ 1)(e

+ 1)

dx, I

−

cos 2x

2002

+ 2

dx, I

−

| sin x |

1 + 2

118

2. Tích phân xác định 119

Bài tập 2.11.

Chứng minh

(a + b −x)

dx =

(a + b −x)

Áp dụng tính

(1 − x)

và chứng minh

∑

k=0

(−1)

k + 3

n + 1

−

n + 2

n + 3

Dạng 6. Chứng minh các bất đẳng thức tích phân

Bài tập 2.12.

Cho

f (x), g(x)

là hai hàm số khả tích trên

[a, b]

. Khi đó

(x), g

(x)

cũng

khả tích trên

[a, b]

. Chứng minh bất đẳng thức sau

(a < b)

f (x)g(x)dx

≤

(x)dx

(Bất đẳng thức Cauchy-Schwarzt)

Chứng minh. Xét 2 trườn g hợp:

TH1. Nếu

(x)dx =

(x)dx = 0 thì:

0 ≤



f (x)g(x)dx



≤

|f (x)g(x)|dx ≤

(x) + g

(x)

dx = 0

Khi đó ta có dấu ” = ” xảy ra.

TH2. Nếu ít nhất một trong hai tích phân

(x)dx,

(x)dx khác 0, không mất tính

tổng quát ta giả sử

(x)dx 6= 0

Khi đó [α f (x) + g(x)]

≥ 0⇒

[α f (x) + g(x)]

≥ 0. Suy ra



(x)dx



.α



f (x)g(x)dx



.α +

(x)dx ≥ 0∀α ∈ R (2.8)

119

120 Chương 2. Phép tính tích phân một biến số

Biểu thức ở vế trái là tam thức bậc 2 đối với α nên 2.8 đúng với mọi α ∈ R khi và chỉ

khi

△

′

f (x)g(x)dx

−

(x)dx

≤ 0.

Bài tập 2.13 (Cuối kì, K62).

Cho hàm số

f (x)

khả vi liên tục đến cấp hai trên

[a, b]

và

f (a) = f (b) = 0

. Chứng minh rằng





[ f

′

(x)]





≤

[ f (x)]

[ f

′′

(x)]

dx.

Chứng minh. Ta có

[ f

′

(x)]

dx =

′

(x)d f (x) = f (x) f

′

(x)



−

f (x) f

′′

(x)dx = −

f (x) f

′′

(x)dx.

Áp dụng bất đẳng thức Cauchy - Schwartz ta có





[ f

′

(x)]









−

f (x) f

′′

(x)dx





≤

[ f (x)]

[ f

′′

(x)]

dx.

Bài tập 2.14 (Cuối kì, K60).

Cho hàm số

f (x)

khả vi liên tục trên

[0, 1]

và

f (0) = 0

Chứng minh rằng

[ f (x)]

dx ≤

[ f

′

(x)]

Chứng minh. Ta có

f (x)

= [ f (x) − f (0)]





′

(t)dt





≤

[ f

′

(t)]

dt ·

= x

[ f

′

(t)]

dt ≤ x

[ f

′

(t)]

dt = x

[ f

′

(x)]

dx.

Do đó,

[ f (x)]

dx ≤

[ f

′

(x)]

dx ·

xdx =

[ f

′

(x)]

dx.

Bài tập 2.14 có thể được mở rộng như sau (với chứng minh hoàn toàn tương tự).

120

2. Tích phân xác định 121

Bài tập 2.15.

Cho

là một hàm số khả vi liên tục trên

[a, b]

. Chứng minh rằng

[ f (x) − f (a)]

dx ≤

b − a

[ f

′

(x)]

dx.

Cũng với ý tưởng viết f (x) − f (a) =

′

(t)dt, bạn đọc có thể chứng minh các kết quả sau.

Bài tập 2.16.

Cho

là một hàm số khả vi liên tục trên

[a, b]

và

f (a) = 0

. Chứng minh

rằng

b − a

|f (x)|dx ≤

′

(x)|dx.

[Lời giải] Thật vậy,

|f (x)| = |f (x) − f (a)| =



′

(t)dt



≤

′

(t)|dt ≤

|f (t)|dt.

Do đó,

|f (x)|dx ≤





|f (t)|dt





dx = (b − a)

|f (t)|dt = (b − a)

|f (x)|dx.

Bài tập 2.17.

Cho

là một hàm số khả vi liên tục trên

[a, b]

và

f (a) = 0

. Chứng minh

rằng

|f (x) f

′

(x)|dx ≤

b − a

[ f

′

(x)]

dx.

[Lời giải] Ta có f (x) = f (x) − f (a) =

f (t)dt nên

|f (x) f

′

(x)| ≤ |f

′

(x)|

′

(t)dt|.

Suy ra

|f (x) f

′

(x)|dx ≤





′

(x)|

′

(t)dt|





dx (2.9)

121

122 Chương 2. Phép tính tích phân một biến số

Vì





′

(t)|dt





′

= |f

′

(x)| nên











′

(t)|dt











′

= 2|f

′

(x)|

′

(t)dt|. Do đó,





′

(x)|

′

(t)dt|





dx =





′

(t)|dt







x=b

x=a





′

(x)|dx





≤

b − a

′

(x)|

dx.

(2.10)

Từ (2.9) và (2.10) ta có điều phải chứng minh.

Bài tập 2.18.

Cho

là một hàm số khả vi liên tục trên

[a, b], f (a) = 0

và

0 ≤ f

′

(x) ≤ 1

với

mọi

x ∈ [a, b]

. Chứng minh rằng

f (x)dx ≥



f (b)

− f (a)



[ f (x)]

dx ≤





f (x)dx





Chứng minh. a) Từ giả thiết ta có f (x) là một hàm số đơn điệu không giảm và f (x) ≥

f (a) = 0, ∀x ∈ [a, b]. Do đó,

f (x) ≥ f (x) f

′

(x), ∀x ∈ [a, b].

Suy ra

f (x)dx ≥

f (x) f

′

(x)dx =

[ f (x)]



f (b)

− f (a)

b) Xét hàm số

F(x) =





f (t)dt





−

[ f (t)]

dt, x ∈ [a, b].

Ta có

′

(x) = 2 f (x)

f (t)dt − f (x)

= f (x)





f (t)dt −[ f (x)]





Đặt G(x) = 2

f (t)dt −[ f (x)]

, ta có

′

(x) = 2 f (x) −2 f (x) f

′

(x) = 2 f (x)(1 − f

′

(x)) ≥ 0, ∀x ∈ [a, b]

⇒ G(x) ≥ G(a) = 0, ∀x ∈ [a, b].

Từ đó suy ra F

′

(x) ≥ 0, ∀x ∈ [a, b] ⇒ F(b) ≥ F(a) = 0 ⇒

[ f (x)]

dx ≤





f (x)dx





122

2. Tích phân xác định 123

Bài tập 2.19 (Olympic Toán học Sinh viên Toàn quốc 2018 -Bảng A).

Cho

f : [a, b] →

là một hàm số khả vi liên tục sao cho

f (x)dx = 0

. Chứng minh rằng

max

x∈[a,b]



f (t)dt



≤

(b − a)

max

x∈[a,b]

′

(x)|.

[Lời giải] Do f

′

(x) liên tục nên tồn tại M = max

x∈[a,b]

′

(x).

• Đặt

F(x) =

f (t)dt + M

(x − a)(x −b)

, x ∈ [a, b]. (2.11)

Ta có F(a) = F(b) = 0 và F

′′

(x) = f

′

(x) + M ≥ 0, ∀x ∈ [a, b].

• Vì F

′′

(x) ≥ 0 nên F(x) là hàm lồi trên [a, b], hơn nữa F(a) = F(b) = 0 nên F(x) ≤

0, ∀x ∈ [a, b]. Từ (2.11) ta có

f (t)dt ≤ M

(x − a)(b − x)

≤



(x − a) + (b − x)



(b − a)

M, ∀x ∈ [a, b].

• Một cách tương tự, đặt

G(x) =

f (t)dt − M

(x − a)(x −b)

, x ∈ [a, b] (2.12)

sẽ dẫn đến G là một hàm lõm trên [a, b] và bất đẳng thức

f (t)dt ≥ −

(b − a)

M, ∀x ∈ [a, b].

Kết luận:

max

x∈[a,b]



f (t)dt



≤

(b − a)

max

x∈[a,b]

′

(x)|.

123

124 Chương 2. Phép tính tích phân một biến số

§3. TÍCH PHÂN SUY RỘNG

Khi định nghĩa tích phân xác định, chúng ta đã xét các hàm số xác định trên một đoạn

hữu hạn

[

a, b

]

và bị chặn trên đoạn đó. Trong phần này chúng ta sẽ mở rộng khái niệm

tích phân, từ đó đưa vào khái niệm tích phân suy r ộng với cận vô hạn và tích phân của

hàm số không bị chặn.

3.1 Tích phân suy rộng với cận vô hạn

Giả sử f (x) là hàm số xác định trên khoảng [a, +∞)] và khả tích trên mọi đoạn hữu

hạn

[

a, A

]

, (a ≤ A < +∞).

Định nghĩa 2.30.

Giới hạn củ a tích phân

f (x)dx

khi

A → +∞

được gọi là tích phân

suy rộng của hàm số

f (x)

trên khoảng

[

a, +∞

)

và ký hiệu như sau

+∞

f (x)dx = lim

A→+∞

f (x)dx

Nếu giới hạn này tồn tại hữu hạn ta nói tích phân suy rộng

+∞

f (x)dx

hội tụ. Ngược lại,

nếu không tồn tại giới hạn này hoặc giới hạn bằng vô cùng ta nói tích phân đó phân kỳ.

Tương tự ta định nghĩa tích phân của một hàm số f (x) trên các khoảng

(

−∞, a

]

và

(

−∞, +∞

)

bởi các công thức sau

−∞

f (x)dx = lim

A→−∞

f (x)dx và

+∞

−∞

f (x)dx = lim

A→+∞,A

′

→−∞

′

f (x)dx

Ta có thể viết

+∞

−∞

f (x)dx =

+∞

f (x)dx +

−∞

f (x)dx

khi hai trong ba tích phân nói trên hội tụ.

Qua các định nghĩa trên ta thấy rằng tích phân suy rộng là giới hạn của tích phân xác

định (hiểu theo nghĩa thông thường) khi cho cận tích phân dần tới vô cùng. Do đó có thể

dùng công thức Leibniz để tính tích phân, sau đó cho cận tiến ra vô cùng.

f (x)dx = F(A) − F(a)

124

3. Tích phân suy rộng 125

kí hiệu

F(+∞) = lim

A→∞

F(A)

thì có thể viết

+∞

f (x)dx = F(+∞) − F(a) = F(x)

+∞

Ví dụ 3.1.

a) Tính tích phân

+∞

x ln x(ln ln x)

Ta có

x ln x(ln ln x)

= −

ln ln x



ln 2

−

ln ln A

nên

⇒ lim

A→+∞

x ln x(ln ln x)

ln 2

Vậy

+∞

x ln x(ln ln x)

ln 2

b) Tính tích phân

+∞

−∞

+ 1)

Trước hết ta tính

′

+1)

, đặt

x = tan t ⇒

(1+x

)

1+tan

= cos

tdt

′

+ 1)

arctan A

′

1 + cos 2t

dt =



sin 2t





arctan A

′

Khi

A → +∞, A

′

→ −∞

thì

arctan A →

; arctan A

′

→ −

, suy ra

+∞

−∞

+ 1)



sin 2t





−

−∞

x sin xdx = lim

A→−∞

x sin xdx = lim

A→−∞

(

−x cos x + sin x

)

= lim

A→−∞

(

A cos A −sin A

)

Giới hạn này không tồn tại, do đó tích phân phân kỳ.

d) Xét sự hội tụ của tích phân

I =

+∞

T ích phân suy rộng

hội tụ khi và chỉ khi

α > 1

, và phân kỳ khi và chỉ khi

α ≤ 1

125

126 Chương 2. Phép tính tích phân một biến số

3.2 Tích phân suy rộng của hàm số không bị chặn

Giả sử f (x) là hàm số xác định trên khoảng

[

a, b

)

và khả tích trên mọi đoạn

[

a, t

]

, (t < b

bất kỳ), và lim

x→b

f (x) = ∞. Điểm x = b được gọi là điểm bất thường (điểm kỳ dị) của hàm số

f (x).

Định nghĩa 2.31.

Giới hạn của tích phân

f (x)dx

khi

t → b

−

, được gọi là tích phân suy

rộng của hàm số

f (x)

trên khoảng

[

a, b

)

và được ký hiệu như sau:

f (x)dx = lim

t→b

−

f (x)dx

Nếu giới hạn ở vế phải tồn tại, ta nói tích phân suy rộng hội tụ. Ngược lại nếu không tồn

tại giới hạn này hoặc giới hạn bằng vô cùng, ta nói tích phân phân kỳ.

Tương tự ta định nghĩa tích phân suy rộng của hà m số f (x) không bị chặn trên khoảng

(

a, b

]

và

(

a, b

)

lần lượt nhận x = a và x = b làm điểm bất thường.

f (x)dx = lim

t→a

f (x)dx và

f (x)dx = lim

t→a

′

→b

−

′

f (x)dx

Đối với tích phân có hai điểm bất thường x = a, x = b, ta có thể viết

f (x)dx =

f (x)dx +

f (x)dx

khi hai trong ba tích phân nói trên hội tụ.

Ví dụ 3.2.

a) Xét sự hội tụ của tích phân

−1

√

1 − x

−1

√

1 − x

= lim

t→−1

√

1 − x

= lim

t→−1

arcsin x



= lim

t→−1

(

−arcsin t

)

√

1 − x

= lim

t→1

√

1 − x

= lim

t→1

arcsin x



= lim

t→1

arcsin t =

nên

−1

√

1 − x

−1

√

1 − x

√

1 − x

= π

126

3. Tích phân suy rộng 127

b) Xét sự hội tụ của tích phân

I =

T ích phân suy rộng

hội tụ khi và chỉ khi

α < 1

, phân kỳ khi và chỉ khi

α ≥ 1

3.3 Các tiêu chuẩn hội tụ

Định lý 2.47 (Tiêu chuẩn so sánh).

1. Cho hai hàm số

f (x)

và

g(x)

khả tích trên mọi khoảng hữu hạn

[a, A](a ≤ A)

và

0 ≤ f (x) ≤ g(x), x ≥ a.

Khi đó

i) Nếu

+∞

g(x)dx

hội tụ thì

+∞

f (x)dx

hội tụ

ii) Nếu

+∞

f (x)dx

phân kỳ thì

+∞

g(x)dx

phân kỳ.

2. Giả sử

f (x)

và

g(x)

là hai hàm số khả tích trên mọi đoạn hữu hạn

[a, A](a ≤ A)

và

lim

x→+∞

f (x)

g(x)

= k(0 < k < +∞)

. Khi đó các tích phân

+∞

f (x)dx

và

+∞

g(x)dx

hoặc cùng

hội tụ, hoặc cùng phân kỳ.

Hệ quả 2.6.

Cho

và

là hai hàm số dương khả tích trên

[a, +∞)

. Khi đó

1. Nếu

lim

x→+∞

f (x)

g(x)

= 0

và nếu

+∞

g(x)dx

hội tụ thì

+∞

f (x)dx

hội tụ.

2. Nếu

lim

x→+∞

f (x)

g(x)

= +∞

và nếu

+∞

g(x)dx

phân kì thì

+∞

f (x)dx

phân kì.

Tương tự chúng ta cũng có các t iêu chuẩn hội tụ cho trường hợp tích phân suy rộng của

hàm số không bị chặn.

Định lý 2.48 (Tiêu chuẩn so sánh).

1. Cho hai hàm số

f (x)

và

g(x)

khả tích trên

(a, b]

và có cùng điểm bất thường là

x = a

sao cho

0 ≤ f (x) ≤ g(x), ∀x ∈ (a, b]

Khi đó

127

128 Chương 2. Phép tính tích phân một biến số

i) Nếu

g(x)dx

hội tụ thì

f (x)dx

hội tụ

ii) Nếu

f (x)dx

phân kỳ thì

g(x)dx

phân kỳ

2. Giả sử

f (x)

và

g(x)

là hai hàm số dương khả tích trên

(a, b]

và có cùng điểm bất

thường

x = a

. Nếu tồn tại giới hạn

lim

x→a

f (x)

g(x)

= k(0 < k < +∞)

Khi đó các tích phân

f (x)dx

và

g(x)dx

hoặc cùng hội tụ, hoặc cùng phân kỳ.

Hệ quả 2.7.

Cho

và

là hai hàm số dương khả tích trên

(a, b]

và có cùng điểm bất

thường

x = a

. Khi đó

1. Nếu

lim

x→a

f (x)

g(x)

= 0

và nếu

g(x)dx

hội tụ thì

f (x)dx

hội tụ.

2. Nếu

lim

x→a

f (x)

g(x)

= +∞

và nếu

g(x)dx

phân kì thì

f (x)dx

phân kì.

Chú ý:

• Khi xét đến tính chất hội tụ hay phân kì của một t ích phân suy rộng, nói chung

chúng ta chỉ "quan tâm" tới dáng điệu của hàm số tại các điểm bất thường.

• Khi sử dụng tiêu chuẩn so sánh chúng ta thường hay so sánh các tích phân suy rộng

đã cho với hai loại tích phân suy rộng sau:

a) I

+∞







hội tụ nếu α > 1

phân kì nếu α ≤ 1

(x − a)







hội tụ nếu α < 1

phân kì nếu α ≥ 1

, I

′

(b − x)







hội tụ nếu α < 1

phân kì nếu α ≥ 1

Ví dụ 3.3 (Cuối kì, K61 Viện ĐTQT).

Xét sự hội tụ, phân kỳ của tích phân

128

3. Tích phân suy rộng 129

∞

(1−cos 2x)dx

ln(1+3

√

. b)

∞

(1−cos 3x)dx

ln(1+2

√

3.4 Tích phân suy rộng hội tụ tuyệt đối và bán hội tụ

Định lý 2.49.

1. Nếu

+∞

|f (x)|dx

hội tụ thì

+∞

f (x)dx

hội tụ

2. Nếu

|f (x)|dx

(có điểm bất thường là

hoặc

) hội tụ thì

+∞

f (x)dx

cũng hội tụ

Định nghĩa 2.32.

1. Nếu

+∞

|f (x)|dx

hội tụ thì ta nói

+∞

f (x)dx

hội tụ tuyệt đối, còn nếu

+∞

f (x)dx

hội tụ

nhưng

+∞

|f (x)|dx

phân kì thì ta nói

+∞

|f (x)|dx

bán hội tụ.

2. Nếu

|f (x)|dx

(có điểm bất thường là

hoặc

) hội tụ thì ta nói

f (x)dx

hội tụ

tuyệt đối, còn nếu

f (x)dx

hội tụ nhưng

|f (x)|dx

phân kì thì ta nói

|f (x)|dx

bán hội tụ.

Ví dụ 3.4.

Chứng minh rằng

+∞

cos x

hội tụ tuyệt đối.

Chứng minh. Ta có



cos x



≤

mà

+∞

hội tụ nên

+∞

cos x

hội tụ tuyệt đối.

Ví dụ 3.5 (Tích phân Dirichlet).

Chứng minh rằng

+∞

sin x

là bán hội tụ.

Chứng minh. Ta có

+∞

sin x

+∞

sin x

129

130 Chương 2. Phép tính tích phân một biến số

sin x

thực chất là tích phân xác định vì lim

x→0

sin x

= 1, do đó

sin x

∈ R. Vì vậy chỉ cần

chỉ ra rằng

+∞

sin x

là hội tụ. Theo công thức tích phân từng phần,

sin x

dx = −

cos x



cos x

= cos 1 −

cos M

cos x

dx.

Cho M → +∞ ta có

+∞

sin x

dx = cos 1 +

+∞

cos x

dx.

Mà

+∞

cos x

dx là h ội tụ nên

+∞

sin x

cũng hội tụ. Việc tiếp theo là chỉ ra

+∞



sin x



là phân kì. Thật vậy,

+∞



sin x



dx =

+∞

∑

n=0

(n+1)π

nπ



sin x



dx =

+∞

∑

n=0

sin v

v + nπ

dv.

Vì

v+nπ

≥

(n+1)π

với 0 ≤ v ≤ π nên

sin v

v + nπ

dv ≥

(n + 1)π

sin vdv =

(n + 1)π

Mà

+∞

∑

n=0

(n+1)π

là phân kì nên

+∞



sin x



dx là phân kì theo tiêu chuẩn so sánh.

3.5 Bài tập

Bài tập 2.1.

Xét sự hội tụ và tính (trong trường hợp hội tụ) cá c tích phân sau:

−∞

+∞

cos xdx

+∞

−∞

+ 1)

x(1 − x)

Chứng minh. a)

−∞

dx = e

(x −1)



−∞

= 1

+∞

cos xdx = sin x



+∞

. Do không tồn tại giới hạn lim

x→+∞

sin x nên tích phân đã cho

phân kì.

130

3. Tích phân suy rộng 131

+∞

−∞

+ 1)

= 2

+∞

+ 1)

. Đặt x = tan t thì I = 2

cos

tdt =

x(1 − x)

| {z }

x(1 − x)

{z }

• Xét tích phân I

có điểm b ất thường là x = 0. Khi x → 0,

x(1 − x)

∼

√

. Mặt

khác tích phân

√

hội tụ nên I

hội tụ.

• Xét tích phân I

có điểm bất thường là x = 1. Khi x → 1,

x(1 − x)

∼

√

1 − x

Mặt khác tích phân

√

1 − x

hội tụ nên I

hội tụ.

Vậy I = I

+ I

hội tụ.

Trong trường hợp tổng quát, muốn tính I =

(x − a)(b − x)

ta thực hiện phép đổi

biến

x = a cos

ϕ + b sin

sẽ chuyển I về tích phân xác định

I = 2

dϕ = π

Bài tập 2.2.

Xét sự hội tụ của cá c tích phân suy rộng sau

tan x−x

√

xdx

sin x

−1

√

xdx

√

1−x

+∞

ln(1+x)dx

+∞

−x

+∞

−x

Chứng minh. a) Tích phân đã cho có điểm bất thường là x = 0 và

lim

x→0

tan x − x

131

132 Chương 2. Phép tính tích phân một biến số

Mặc khác

phân kì nên

tan x − x

cũng phân kì.

b) Tích phân đã cho có điểm bất thường là x = 0 và khi x → 0, e

sin x

−1 ∼ sin x ∼ x nên

√

sin x

−1

∼

√

. Do

√

hội tụ nên

√

xdx

sin x

−1

cũng hội tụ.

c) Tích phân đã cho có điểm bất thường là x = và khi x → 1 thì

√

1 − x

√

(1 − x)(1 + x + x

+ x

)

∼

√

1 − x

√

1 − x

hội tụ nên

√

xdx

√

1 − x

cũng hội tụ.

d) Ta có

ln(1 + x)

với mọi x > e − 1. Mà

+∞

phân kì nên

+∞

ln(1 + x)dx

cũng

phân kì.

e) Ta có e

−x

< 1 với mọi x > 0 nên

−x

với mọi x > 0. Mặt khác

+∞

hội tụ nên

+∞

−x

dx cũng hội tụ.

f) Khi x → +∞ thì

− x

+ 1

∼

nên tích phân đã cho hội tụ.

Bài tập 2.3.

Nếu

+∞

f (x)dx

hội tụ thì có suy ra được

f (x) → 0

khi

x → +∞

không?

[Gợi ý]

+∞

f (x)dx hội tụ không suy ra được f (x) → 0 khi x → +∞.

Ví dụ như

+∞

sin(x

)dx hội tụ (xem bài tập 2.5) nhưng không tồn tại giới hạn lim

x→+∞

sin(x

Bài tập 2.4.

Cho hàm số

f (x)

liên tục trên

[a, +∞)

và

lim

x→+∞

f (x) = A 6= 0

. Hỏi

+∞

f (x)dx

có hội tụ không?

132

3. Tích phân suy rộng 133

[Gợi ý] Theo giả thiết lim

x→+∞

f (x)

= 1, mà

+∞

Adx phân kì nên

+∞

f (x)dx cũng phân

kì.

Bài tập 2.5.

Xét sự hội tụ của cá c tích phân suy rộng sau

+∞

sin(x

)dx

+∞

−x

+∞



1 −cos



(1 − x

)

(tan x)

p−1

(1 − x)

q−1

+∞

p−1

−x

f (x)dx

√

1 − x

, ( f

liên tục

)

Chứng minh. a) Thực hiện phép đổi biến x =

√

t, dx =

√

, đưa tích phân đã cho về

dạng

I =

+∞

sin tdt

√

Ta có thể viết

+∞

sin tdt

√

sin tdt

√

| {z }

+∞

sin tdt

√

| {z }

Vì lim

t→0

sin t

√

= 0 nên tích phân I

thực chất là tích phân xác định nên hội tụ, do đó chỉ

cần xét I

+∞

sin t

√

dt = −

+∞

d(cos t)

√

= −

cos t

√



+∞

−

+∞

cos t

3/2

dt = −

+∞

cos t

3/2

Vì



cos t

3/2



≤

3/2

nên

+∞

cos t

3/2

dt hội tụ. Vậy ta có I

cũng hội tụ và tích phân đã cho

hội tụ.

b) Ta có với x > 1 thì e

−x

< e

−x

mà

+∞

−x

dx = e

−1

hội tụ nên

+∞

−x

dx cũng hội tụ.

c) Khi x → +∞, 1 −cos

= 2 sin

∼

nên

+∞



1 −cos



dx hội tụ.

133

134 Chương 2. Phép tính tích phân một biến số

d) Khi x → 1,

(1 − x

)

[(1 − x)(1 + x)]

∼

√

32.

(1 − x)

nên

(1 − x

)

hội tụ.

e) Trước hết ta có nhận xét rằng I =

(tan x)

dx có điểm bất thường là x = 0 khi

p < 0 và x =

khi p > 0.

• Nếu p < 0 thì khi x → 0, (tan x)



cos x

sin x



−p

∼

−p

nên I hội tụ nếu −1 <

p < 0 và phân kì nếu p ≤ −1.

• Nếu p > 0 thì khi x →

, (tan x)



sin x

cos x









sin x

sin



− x









∼



− x



nên I hội tụ nếu 0 < p < 1 và phân kì nếu p ≥ 1.

Kết luận:

(tan x)

dx hội tụ khi |p| < 1 và phân kì k hi |p| ≥ 1.

f) Trước hết ta có nhận xét rằng nếu p < 1 thì x = 0 là điểm bất thường, còn nếu q < 1

thì x = 1 là điểm bất thường. Phân tích

I =

p−1

(1 − x)

q−1

dx =

p−1

(1 − x)

q−1

{z }

p−1

(1 − x)

q−1

| {z }

chỉ hội tụ khi 1 − p < 1, nghĩa là p > 0; còn I

chỉ hội tụ khi 1 − q < 1, nghĩa là

q > 0. Vậy I chỉ hội tụ khi p > 0, q > 0.

g) Nếu p ≥ 1 thì tích phân đã cho chỉ có điểm bất thường tại +∞ và

lim

x→+∞

p−1

−x

] :

= lim

x→+∞

p+1

= 0

nên

x→+∞

p−1

−x

dx hội tụ.

Nếu p < 1 thì x = 0 cũng là một điểm bất thường. Ta có

+∞

p−1

−x

dx =

p−1

−x

{z }

+∞

p−1

−x

{z }

134

3. Tích phân suy rộng 135

T ích phân I

hội tụ khi p > 0 và I

hội tụ với p bất kì.

Vậy

+∞

p−1

−x

dx hội tụ nếu p > 0.

h) Mặc dù tích phân đã cho là tích phân suy rộng có điểm bất thường là x = 1 nhưng ta

có thể đưa I về tích phân thường bằng cách đổi biến. Đặt x = sin θ, trên [0, c] ta có

f (x)dx

√

1 − x

= lim

c→1

−

f (x)dx

√

1 − x

= lim

c→1

−

arcsin c

f (sin θ)dθ =

f (sin θ)dθ

Vì f là một hàm số liên tục trên [0, 1] nên hàm hợp f (sin θ) là một hà m số liên tục và

bị chặn trên

và tích phân đã cho là tích phân xác định nên hội tụ.

Bài tập 2.6.

T ính các tích phân suy rộng sau

+∞

−ax

sin bxdx

+∞

−ax

cos bxdx

+∞

1 + x

Chứng minh. a)

+∞

−ax

sin bxdx = −

a sin bx + b cos bx

+ b

−ax



+∞

+ b

+∞

−ax

cos bxdx =

b sin bx −a cos bx

+ b

−ax



+∞

+ b

c) Thực hiện phép đổi biến x =

ta có

I =

+∞

1 + x

+∞

1 + t

+∞

1 + x

Do đó

2I =

+∞

1 + x

+∞

1 + x

+∞

(1 + x

)dx

1 + x

+∞



1 +



Lại đặt z = x −

ta được

I =

+∞

−∞

+ 2

√

arctan

√



+∞

−∞

√

135

136 Chương 2. Phép tính tích phân một biến số

§4. CÁC ỨNG DỤNG CỦA TÍCH PHÂN XÁC ĐỊNH

4.1 Tính diện tích hình phằng

1. Trường hợp biên của hình phẳng cho trong hệ toạ độ Descartes (tính diện tích "hình

thang cong")

Nếu S giới hạn bởi











a ≤ x ≤ b

y = f (x)

y = g(x)

f , g ∈ C[a, b]

thì S =

| f (x) − g(x) | dx

(2.13)

Nếu S giới hạn bởi











c ≤ y ≤ d

x = ϕ(y)

x = ψ(y)

ϕ, ψ ∈ [c, d]

thì S =

| ϕ(y) − ψ(y) | dy

(2.14)

Nếu S giới hạn bởi











a ≤ x ≤ b

y = 0







x = ϕ(t)

y = ψ(t)

thì S =

| ψ(t)ϕ

′

(t) | dt

(2.15)

Trong đó giả thiết rằng phương trình ϕ(t) = a, ψ(t) = b có nghiệm duy nhất là t

, t

và

ϕ, ψ, ϕ

′

∈ C[t

, t

Ví dụ 4.1 (Cuối kì, K61-Viện ĐTQT).

T ính diện tích của miền

D :







x + y ≥ 2

+ y

≤ 2x.

D :







x − y ≥ 2

+ y

≤ 2x.

Bài tập 2.1.

T ính diện tích hình phẳng giới hạn bởi:

a) Đường parabol

y = x

+ 4

và đường thẳng

x − y + 4 = 0

b) Parabol bậc ba

y = x

và các đường

y = x, y = 2x

c) Đường tròn

+ y

= 2x

và parabol

= x

d) Đường

= x

− x

136

4. Các ứng dụng của tích phân xác định 137

[Gợi ý]

Các câu a), b), c) có thể vẽ hình và tính toán dễ dàng như sau :

a) S =

[(x + 4) −(x

+ 4)]dx =

b) S =

(2x − x

)dx +

√

(2x − x

)dx =

c) S = 2

(

√

4x −x

) −

√

2x)dx = 2π −

d) Trước hết ta có điều kiện 0 ≤ x ≤ 1, và nhận xét rằng nếu M(x, y) ∈ C thì M

′

(±x, ±y) ∈

C . Do đó S = 4S(D), trong đó D là miền giới hạn bởi:







0 ≤ x ≤ 1

y =

√

− x

Do miền D nằm hoàn toàn trong hình vuông 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, hơn nữa hàm số

y =

√

− x

liên tục, y(0) = y(1) = 0 nên đồ thị của nó trong [0, 1] có hình dáng

như hình vẽ dưới đây:

Áp dụng công thức 2.13 ta có S(D) =

√

− x

dx =

⇒S =

2. Trường hợp biên của h ình phẳng cho trong hệ toạ độ cực (tính diện tích của miền có

dạng hình quạt)

Nếu S giới hạn bởi











ϕ = α

ϕ = β

r = r(ϕ)

r(ϕ) ∈ C[α, β]

thì S =

(ϕ)dϕ

(2.16)

137

138 Chương 2. Phép tính tích phân một biến số

Bài tập 2.2.

T ính diện tích hình phẳng giới hạn bởi đường hình tim

= a

cos 2ϕ

[Gợi ý]

r = a

cos 2ϕ

Hình 2.2

Khảo sát và vẽ đồ thị của đường cong trong toạ độ cực và nhận xét tính đối xứng của

hình vẽ ta có:

S = 4S(D) = 4.

(ϕ)dϕ = a

4.2 Tính độ dài đường cong phẳng

Trường hợp đường cong AB cho bởi phương trình y = f (x)











y = f (x)

a ≤ x ≤ b

f ∈ C

[a, b]

thì s =

1 + [ f

′

(x)]

(2.17)

Trường hợp đường cong AB cho bởi phương trình tham số:











x = x(t)

y = y(t)

α ≤ t ≤ β

x(t), y(t) ∈ C

[a, b]

′2

(t) + y

′2

(t) > 0∀t ∈ [α, β]

thì s =

′

(t)]

+ [y

′

(t)]

dt (2.18)

Trường hợp đường cong AB cho bởi phương trình trong toạ độ cực:











r = r(ϕ)

α ≤ ϕ ≤ β

r(ϕ) ∈ C

[α, β]

thì s =

(ϕ) + r

′2

(ϕ)dϕ (2.19)

138

4. Các ứng dụng của tích phân xác định 139

Bài tập 2.1.

T ính độ dài đường cong

y = ln

−1

khi

biến thiên từ

đến







x = a(cos t + ln tan

)

y = a sin t

khi

biến thiên từ

đến

Chứng minh. a) Ta có

1 + y

′2

(x) = 1 +

+ 1

−

−1

+ 1

−1

Nên áp dụng công thức 2.17 ta được:

s =

+ 1

−1

(t=e

)

t + 1

2t(t −1)

= ln

+ 1

b) Áp dụng công thức 2.18 ta có

′2

(t) + y

′2

(t) = a

cos

sin

⇒s = a

cos

sin

dt = a ln

√

4.3 Tính thể tích vật thể

Trường hợp vật thể được giới hạn bởi một mặt cong và hai mặt phẳng x = a, x = b. Giả

thiết ta biết rằng diện tích S của thiết diện của vật thể khi cắ t bởi mặt phẳn x = x

là

S(x

), và S(x) là hàm số xác định, khả tích trên [a, b]. Khi đó

V =

S(x)dx

(2.20)

Bài tập 2.1.

T ính thể tích của vật thể là phần chung của hai hình trụ

+ y

= a

và

+ z

= a

(a > 0).

Lời giải: Do tính đối xứng nên V = 8V

′

trong đó V

′

= V ∩ {x ≥ 0, y ≥ 0, z ≥ 0}. Một

điểm M(x, 0, 0) ∈ Ox, qua M ta dựng thiết diện của V

′

vuông góc với Ox thì được một hình

vuông có cạnh là

√

− x

, do đó S(x) = a

− x

. Áp dụng công thức 2.20 ta được

V = 8

− x

)dx =

139

140 Chương 2. Phép tính tích phân một biến số

Bài tập 2.2.

T ìm thể tích vật thể giới hạn bởi mặt paraboloit

z = 4 −y

, các mặt phẳng

toạ độ và mặt phẳng

x = a

Chứng minh. Sau khi vẽ hình và áp dụng công thức 2.20 ta có:

V =

S(x)dx mà S(x) =

(4 −y

)dy =

nên V =

Tính thể tích vật thể tròn xoay

Trường hợp vật thể là vật thể tròn xoay được tạo thành khi quay hình thang cong











a ≤ x ≤ b

y = 0

y = f (x)

quanh trục Ox, trong đó f ∈ C[a, b] thì

V = π

(x)dx

(2.21)

Tương tự, nêú vật thể là vật thể tròn xoay được tạo thành khi quay hình thang cong











c ≤ y ≤ d

x = 0

x = ϕ(y)

quanh trục Oy, trong đó ϕ ∈ C[c, d] thì

V = π

(y)dy

(2.22)

Bài tập 2.3.

T ính thể tích khối tròn xoay tạo nên khi quay hình giới hạn bởi các đường

y = 2x −x

và

y = 0

a) quanh trục Ox một vòng b) quanh trục Oy một vòng.

[Gợi ý]

a) Áp dụng công thức 2.21:

V = π

(2x − x

)dx =

b) Áp dụng công thức 2.22:

V = π



1 +

1 −y



dy −π



1 −

1 −y



140

4. Các ứng dụng của tích phân xác định 141

4.4 Tính diện tích mặt tròn xoay

Cho hình thang cong giới h ạn bởi











a ≤ x ≤ b

y = 0

y = f (x)

với f ∈ C

[a, b]. Quay hình thang cong

này quanh trục Ox thì ta được một vật thể tròn xoay. Khi đó diện tích xung quanh của vật

thể được tính theo công thức:

S = 2π

| f (x) |

1 + f

′2

(x)dx (2.23)

Tương tự nếu quay hình thang cong











c ≤ y ≤ d

x = 0

x = ϕ(y)

với ϕ ∈ C

[c, d], quanh trục Oy thì:

S = 2π

| ϕ(y) |

1 + ϕ

′2

(y)dy (2.24)

Bài tập 2.1.

T ính diện tích mặt tròn xoay tạo nên khi quay các đường sau

y = tan x, 0 < x ≤

quanh trục

= 1

quanh trục

Oy(a > b)

= x(3 − x)

, 0 ≤ x ≤ 3

quanh trục

141

142 Chương 2. Phép tính tích phân một biến số

Chứng minh. a) Áp dụng công thức 2.23 ta có:

S = 2π

tan x

1 + (1 + tan

x)dx

= 2π

1 + (1 + t

)

1 + t

(đặt t = tan x)

= π

1 + (1 + t

)

1 + t

.d(t

+ 1)

= π

√

1 + s

ds (đặt s = 1 + t

)

= π

√



1 +

−1



= π.

(

√

5 −

√

2 +

√

5 −1

√

2 −1

−ln

√

5 + 1

√

2 + 1

)

b) Nhận xét tính đối xứng của miền và áp dụng công thức 2.24 ta có:

S = 2.2π

−y

1 +



−y



= 4π

+ (a

−b

= 4π

−b

= 4π

−b

+ βdy( đặt β =

−b

)

= 4π

−b

+ β + β ln | y +

+ β |



+ βdy =

+ β + β ln | y +

+ β |

c) Trước hết

= x(3 − x)

⇒18yy

′

= 3(3 − x)(1 − x)⇒y

′

(3 − x)(1 − x)

⇒y

′2

(1 − x)

142

4. Các ứng dụng của tích phân xác định 143

Nên áp dụng công thức 2.23 ta có:

S = 2π

√

x(3 − x)

1 +

(1 − x)

dx = 2π.

(3 − x)(1 + x)dx = 3π.

"Nghịch lý sừng Gabriel"

Cho một vật thể tròn xoay tạo bởi khi xoay miền giới hạn bởi











1 ≤ x,

y = 0,

y =

quanh trục Ox.

T ính thể tích và diện tích mặt của nó.

[Lời giải] Ta có

V = π

+∞





dx = π

và

S = 2π

+∞

1 +



−



dx ≥ 2π

+∞

dx = +∞.

Như vậy, đây là một vật thể có diện tích mặt bằng +∞, trong khi đó lại có thể tích hữu

hạn. Giả sử bạn có một vật thể như vậy và cần sơn nó.

i) Một mặt, vì diện tích mặt là +∞, bạn cần một lượng vô hạn sơn để sơn nó.

ii) Mặt khác, vì miền giới hạn bởi vật đó có thể tích hữu hạn, bạn có thể đổ đầy nó bằng

một lượng hữu hạn sơn (ở đây là π đơn vị thể tích), và khi đó toàn bộ mặt trong của

nó sẽ được sơn.

Một nghịch lý phải không?

143

144 Chương 2. Phép tính tích phân một biến số

144

CHƯƠNG 3

HÀM SỐ NHIỀU BIẾN SỐ

§1. GIỚI HẠN CỦA HÀM SỐ NHIỀU BIẾN SỐ

1.1 Giới hạn của hàm số nhiều biến số

Ta nói rằng dãy điểm {M

, y

)} dần tới điểm M

, y

) trong R

và viết M

→ M

khi n → +∞ nếu lim

n→+∞

d(M

, M

) = 0 hay nếu x

→ x

, y

→ y

Định nghĩa 3.33.

Cho hàm số

z = f (M) = f (x, y)

xác định tron g một lân cận

nào đó

của điểm

, y

)

, có thể trừ tại điểm

. Ta nói rằng hàm số

f (x, y)

có giới hạn là

khi

dần đến

nếu

∀ǫ > 0, ∃δ > 0 :

nếu

d(M, M

) < δ

thì

|f (M) − L| < ǫ.

Một cách t ương đương, với mọi dãy điểm

, y

)

thuộc lân cận

dần đến

ta đều có

lim

n→+∞

f (x

, y

) = L.

Khi đó ta viết

lim

(x,y)→(x

)

f (x, y) = L

hay

lim

M→M

f (M) = L.

• Khái niệm giới hạn vô hạn cũng được định nghĩa tương tự như đối với hàm số một

biến số.

• Các định lý về giới hạn của tổng, hiệu, tích, thương đối với hàm số một biến số cũng

đúng cho hàm số nhiều biến số và được chứng minh tương tự.

Nhận xét:

145

146 Chương 3. Hàm số nhiều biến số

• Theo định nghĩa trên , muốn chứng minh sự tồn tại của giới hạn của hàm số nhiều

biến số là việc không dễ vì phải chỉ ra lim

n→+∞

f (x

, y

) = l với mọi dãy số {x

→

}, {y

→ y

}. Trong thực hành, muốn tìm giới hạn của hàm số nhiều biến số,

phương pháp chứng minh chủ yếu là đánh giá hàm số, dùng nguyên lý giới hạn kẹp

để đưa về giới hạn của hàm số một biến số.

• Với chiều ngược lại, muốn chứng minh sự không tồn tại giới hạn của hàm số nhiều

biến số, ta chỉ cần chỉ ra tồn tại hai dãy {x

→ x

, y

→ y

} và {x

′

→ x

, y

′

→ y

}

sao cho

lim

n→+∞

f (x

, y

) 6= lim

n→+∞

f (x

′

, y

′

)

hoặc chỉ ra tồn tại hai quá trình (x, y) → (x

, y

) khác nhau mà f (x, y) tiến tới hai

giới hạn khác nhau.

1.2 Tính liên tục của hàm số nhiều biến số

• Giả sử hàm số f (M) xác định trong miền D, M

là một điểm thuộc D. Ta nói rằng

hàm số f (M) liên tục tại điểm M

nếu

lim

M→M

f (M) = f (M

)

Nếu miền D đóng và M

là điểm biên của D thì lim

M→M

f (M) được hiểu là giới hạn

của f (M) khi M dần tới M

ở bên trong của D.

• Hàm số f (M) được gọi là liên tục trong miền D nếu nó liên tục tại mọi điểm thuộc

• Hàm số nhiều biến số liên tục cũng có những tính chất như hàm số một biến số liên

tục. Chẳng hạn, nếu hàm số nhiều biến số liên tục trong một miền đóng, bị chặn thì

nó liên tục đều, bị chặn trong miền ấy, đạt giá trị lớn nhất và giá trị nhỏ nhất trong

miền đó.

1.3 Bài tập

Bài tập 3.1. Tìm miền xác định của các hàm số sau

a) z =

+ y

−1

b) z =

+ y

−1)(4 − x

−y

)

c) z = arcsin

y −1

d) z =

x sin y

Bài tập 3.2. Tìm giới hạn (nếu có) của các hàm số sau

146

2. Đạo hàm và vi phân 147

a) f (x, y) =

−y

+ y

(x → 0, y → 0)

b) f (x, y) = sin

πx

2x + y

(x → ∞, y → ∞)

Chứng minh. a) Nếu cho (x, y) → (0, 0) theo phương của đường thẳng y = kx thì ta có

f (x, kx) =

−k

+ k

1 −k

1 + k

→

1 −k

1 + k

khi x → 0

Vậy khi (x, y) → (0, 0 theo những phương khác nhau thì f (x, y) dần tới những giới

hạn khác nhau. Do đó không tồn tại lim

(x,y)→(0,0)

f (x, y).

b) Nếu cho (x, y) → (∞, ∞) theo phương của đường thẳng y = kx thì ta có

f (x, kx) = sin

πx

2x + kx

= sin

2 + k

→ sin

2 + k

khi x → 0

Vậy khi (x, y) → (0, 0 theo những phương khác nhau thì f (x, y) dần tới những giới

hạn khác nhau. Do đó không tồn tại lim

(x,y)→(0,0)

f (x, y).

Bài tập 3.3. [Cuối kì, K62, GT2, Nhóm ngành 2] Tính các giới hạn

a) lim

(x,y)→(0,0)

+ y

+ 2y

. b) lim

(x,y)→(0,0)

+ 2y

+ y

[Lời giải] Ta có

lim

(x,y)→(0,0)

+ y

+ 2y

= lim

(x,y)→(0,0)

+ 2y

+ lim

(x,y)→(0,0)

+ 2y

= 0 + 0 = 0,

do 0 ≤

+ 2y

≤ 2x

, 0 ≤

+ 2y

≤

và nguyên lý giới hạ n kẹp.

lim

(x,y)→(0,0)

+ 2y

+ y

= lim

(x,y)→(0,0)

+ y

+ lim

(x,y)→(0,0)

+ y

= 0 + 0 = 0,

do 0 ≤

+ y

≤

, 0 ≤

+ y

≤ 2y

và nguyên lý giới hạ n kẹp.

Chú ý 3.20.

Không nhầm lẫn

lim

(x,y)→(x

)

f (x, y)

với các giới hạn lặp

lim

x→x

lim

y→y

f (x, y)

và

lim

y→y

lim

x→x

f (x, y)

. Chẳng hạn như, bạn đọc có thể kiểm tra với hàm số

f (x, y) =

ta có

lim

(x,y)→(0,0)

không tồn tại.

ii)

lim

x→0

lim

y→0

f (x, y)

= 1

iii)

lim

y→0

lim

x→0

= 0.

147

148 Chương 3. Hàm số nhiều biến số

§2. ĐẠO HÀM VÀ VI PHÂN

2.1 Đạo hàm riêng

• Cho hàm số f (x, y) xác định trong một miền D, điểm M(x

, y

) ∈ D. Nếu cho y = y

hàm số một biến số x 7→ f (x, y

) có đạo hàm tại điểm x = x

thì đạo hàm đó gọi là

đạo hàm riêng của f với biến x tại M

và được kí hiệu là

∂ f

∂x

hay

∂

∂x

f (x, y).

∂ f

∂x

= lim

△x→0

f (x

+ △x, y

) − f (x

, y

)

△x

• Cho hàm số f (x, y) xác định trong một miền D, điểm M(x

, y

) ∈ D. Nếu cho x = x

hàm số một biến số x 7→ f (x

, y) có đạo hàm tại điểm y = y

thì đạo hàm đó gọi là

đạo hàm riêng của f với biến x tại M

và được kí hiệu là

∂ f

∂y

hay

∂

∂y

f (x, y).

∂ f

∂y

= lim

△y→0

f (x

, y

+ △y) − f (x

, y

)

△y

Chú ý: Các đạo hàm riêng của các hàm số n biến số (với n ≥ 3) được định nghĩa tương tự.

Khi cần tính đạo hàm riêng của hàm số theo biến số nào, xem như hàm số chỉ phụ thuộc

vào biến đó, còn các biến còn lại là các hằng số và áp dụng các quy tắc tính đạo hàm như

hàm số một biến số.

2.2 Vi phân toàn phần

• Cho hàm số z = f (x, y) xác định trong miền D. Lấy các điểm M

, y

) ∈ D, M(x

△x

, y

+ △y

) ∈ D. Biểu thức △f = f (x

+ △x

, y

+ △y

) − f (x

, y

)(x

, y

) được

gọi là số gia toàn phần của f tại M

. Nếu như có thể biểu diễn số gia toàn phần dưới

dạng

△f = A. △ x + B △y + α △y + β △y

trong đó A, B là các hằng số chỉ phụ thuộc x

, y

còn α, β → 0 khi M → M

, thì ta nói

hàm số z khả vi tạ i M

, còn biểu thức A. △ x + B △y + α △y được gọi là vi phân toàn

phần của z = f (x, y) tại M

và được kí hiệu là dz.

Hàm số z = f (x, y) được gọi là khả vi trên miền D nếu nó khả vi tại mọi điểm của

miền ấy.

• Đối với hàm số một biến số, sự tồn tại đạo hàm tại điểm x

tưong đương với sự khả

vi của nó tại x

. Đối với hàm số nhiều biến số, sự tồn tại của các đạo hàm riêng tại

, y

) chưa đủ để nó khả vi tại M

(xem bài tập 3.4). Định lý sau đây cho ta điều

kiện đủ để hàm số z = f (x, y) khả vi tại M

148

2. Đạo hàm và vi phân 149

Định lý 3.50.

Nếu hàm số

f (x, y)

có các đạo hàm riêng trong lân cận của

và nếu các

đạo hàm riêng đó liên tục tại

thì

f (x, y)

khả vi tại

và

dz = f

′

△ x + f

′

△y

Ví dụ 2.1 (Cuối kì, K61 Viện ĐTQT).

Sử dụng vi phân, tính gần đúng

(8, 05)

+ (5, 96)

. b)

(6, 05)

+ (7, 96)

2.3 Đạo hàm của hàm số hợp

Cho D là một tập hợp trong R

và các hàm số

→ ϕ(D) ⊂ R

→ R

và F = f ◦ ϕ là hàm số hợp của hai h àm số f và ϕ:

F(x, y) = f (u(x, y), v(x, y))

Định lý 3.51.

Nếu

có các đạo hàm riêng

∂ f

∂x

∂ f

∂y

liên tục trong

ϕ(D)

và nếu

u, v

có các

đạo hàm riêng

∂u

∂x

∂u

∂y

∂v

∂x

∂v

∂y

trong

thì tồn tại các đạo hàm riêng

∂F

∂x

∂F

∂y

và











∂F

∂x

∂ f

∂u

∂x

∂ f

∂v

∂x

∂F

∂y

∂ f

∂u

∂y

∂ f

∂v

∂y

(3.1)

Công thức 3.1 có thể được viết dưới dạng ma trận như sau



∂F

∂x

∂F

∂y





∂ f

∂u

∂ f

∂v









∂u

∂x

∂u

∂y

∂v

∂x

∂v

∂y







trong đó ma trận







∂u

∂x

∂u

∂y

∂v

∂x

∂v

∂y







được gọi là ma trận Jacobi của ánh xạ ϕ, định thức của ma trận ấy được gọi là định thức

Jacobi của u, v với x, y và được kí hiệu là

D(u, v)

D(x, y)

149

150 Chương 3. Hàm số nhiều biến số

2.4 Đạo hàm và vi phân cấp cao

• Cho hàm số hai biến số z = f (x, y). Các đạo hàm riêng f

′

, f

′

là những đạo hàm riêng

cấp một. Các đạo hàm riêng của các đạo hàm riêng cấp một nếu tồn tại được gọi là

những đạo hàm riêng cấp hai. Có bốn đạo hàm riêng cấp hai được kí hiệu như sau:











( f

′

)

′

= f

”

∂

∂x



∂ f

∂x



∂

∂x

( f

′

)

′

= f

”

∂

∂y



∂ f

∂x



∂

∂y∂x

( f

′

)

′

= f

”

∂

∂x



∂ f

∂y



∂

∂x∂y

( f

′

)

′

= f

”

∂

∂y



∂ f

∂y



∂

∂y

Các đạo hàm riêng của các đạo hàm r iêng cấp hai, nếu tồn tại, được gọi là các đạo

hàm riêng cấp ba, ...

Định lý 3.52 (Schwarz).

Nếu trong một lân cận

nào đó của điểm

, y

)

hàm

số

z = f (x, y)

có các đạo hàm riêng

”

, f

”

và nếu các đạo hàm riêng ấy liên t ục tại

thì

”

= f

”

tại

• Xét hàm số z = f (x, y), vi phân toàn phần của nó dz = f

′

dx + f

′

dy, nếu tồn tại, cũng

là một hàm số với hai biến số x, y. Vi phân toàn phần của dz, nếu tồn tại, được gọi là

vi phân toàn phần cấp hai của z và được kí hiệu là d

z. Ta có công thức

z = f

”

+ 2 f

”

dxdy + f

”

Ví dụ 2.2 (Cuối kì, K62, GT2, Nhóm ngành 2).

Cho hàm số

z = z(x, y)

có các đạo hàm

r iêng cấp một liên tục, ở đó







x = r cos ϕ,

y = r sin ϕ.

Chứng minh rằng



∂z

∂x





∂z

∂y





∂z

∂r





∂z

∂ϕ



2.5 Đạo hàm theo hướng - Gradient

Định nghĩa 3.34.

Cho

f (x, y, z)

là một hàm số xác định trong một miền

D ∈ R

và

l =

, l

)

là một véctơ đơn vị bất kì trong

. Giới hạn, nếu có,

lim

t→0

f (M

+ t

l) − f (M)

(3.2)

150

2. Đạo hàm và vi phân 151

được gọi là đạo hàm của hàm số

theo hướng

tại

và được kí hiệu là

∂ f

∂

)

• Nếu

l không phải là véc tơ đơn vị thì giới hạn trong công thức 3.2 có thể được thay

bằng

lim

t→0

u(x

+ t cos α, y

+ t cos β, z

+ t cos γ) −u(x

, y

, z

)

trong đó cos α, cos β, cosγ là các cosin chỉ phương của

−→

l .

• Nếu

l trùng với véctơ đơn vị i của trục Ox thì đạo hàm theo hướng

l chính là đạo hàm

riêng theo biến x của hàm f

∂ f

∂

) =

∂ f

∂x

)

• Vậy đạo hàm riêng theo biến x chính là đạo hàm theo hướng của trục Ox, cũng như

vậy,

∂ f

∂y

∂ f

∂z

là các đạo hàm của f theo hướng của trục Oy và Oz. Định lý sau đây cho

ta mối liên hệ giữa đạo hàm theo hướng và đạo hàm riêng:

Định lý 3.53.

Nếu hàm số

f (x, y, z)

khả vi tại điểm

, y

, z

)

thì tại

có đạo hàm

theo mọi hướng

và ta có

∂ f

∂

) =

∂ f

∂x

) cos α +

∂ f

∂y

) cos β +

∂ f

∂z

) cos γ

trong đó

(cos α, cos β, cos γ)

là cosin chỉ phương của

Cho f (x, y, z) là hàm số có các đạo hàm riêng tại M

, y

, z

). Người ta gọi gradient của

f tại M

là véctơ



∂ f

∂x

∂ f

∂y

∂ f

∂z

)



và được kí hiệu là

−−→

grad f (M

Định lý 3.54.

Nếu

−→

là một véctơ đơn vị và hàm số

f (x, y, z)

khả vi tại

thì tại đó ta có

∂ f

∂

) =

−−→

grad f .

Chú ý:

∂ f

∂

) th ể hiện tốc độ biến thiên của hàm số f tại M

theo hướng

l. Từ công

thức

∂ f

∂

) =

−−→

grad f .

l =



−−→

grad f



. cos



−−→

grad f ,



ta có



∂ f

∂

)



đạt giá trị lớn nhất

bằng



−−→

grad f



nếu

l có cùng phương với

−−−→

grad f . Cụ thể

• Theo hướng

l, hàm số f tăng nhanh nhất tại M

nếu

l có cùng phương, cùng hướng

với

−−−→

grad f .

• Theo hướng

l, hàm số f giảm nhanh nhất tại M

nếu

l có cùng phương, ngược hướng

với

−−−→

grad f .

151

152 Chương 3. Hàm số nhiều biến số

2.6 Hàm ẩn - Đạo hàm của hàm số ẩn

• Cho phương trình F(x, y) = 0 trong đó F : U → R là một hàm số có các đạo hàm

riêng liên tục trên tập mở U ⊂ R

và F

′

, y

) 6= 0. Khi đó phương trình F(x, y) = 0

xác định một hàm số ẩn y = y(x) trong một lân cận nào đó của x

và có đạo hàm

′

(x) = −

′

• Tương tự, cho phương trình F(x, y, z) = 0 trong đó F : U → R là một hàm số có các

đạo hàm riêng liên tục trên tập mở U ⊂ R

và F

′

, y

, z

) 6= 0. Khi đó phương tr ình

F(x, y, z) = 0 xác định một hàm số ẩn z = z(x, y) trong một lân cận nào đó của (x

, y

)

và có đạo hàm

′

= −

′

, z

′

= −

′

2.7 Bài tập

Bài tập 3.4. Chứng minh rằng hàm số

f (x, y) =







+ y

nếu (x, y) 6= (0, 0)

0 nếu (x, y) = (0, 0)

có các đạo hàm riêng tại (0, 0) nhưng không liên tục tại (0, 0) và do đó không khả vi tại

(0, 0).

Bài tập 3.5. Tính các đạo hàm riêng của hàm số sau

a) z = ln



x +

+ y



b) z = y

sin

c) z = x

d) z = arctan

−y

e) u = x

(

x, y, z > 0

)

f) u = e

(

x, y, z > 0

)

Chứng minh. a)

′

1 +

√

x +

+ y

; z

′

√

x +

+ y

′

= y cos

; z

′

= 2y sin

− x cos

152

2. Đạo hàm và vi phân 153

′

= y

−1

; z

′

= 3y

ln x.x

′

−y

+ 1

∂

∂x

−y

+ y

−y

′

−y

+ 1

∂

∂y

−y

+ y

−y

′

= y

−1

; u

′

= x

z−1

. ln x; u

′

= x

ln y ln x

′

= e

−2x

(

+ y

+ z

)

; u

′

= e

−2y

(

+ y

+ z

)

; u

′

= e

−2z

(

+ y

+ z

)

Bài tập 3.6. Khảo sát sự liên tục và sự tồn tại, liên tục của các đạo hàm riêng của các

hàm số f

(

x, y

)

a) f

(

x, y

)







x arctan





nếu x 6= 0

0 nếu x = 0

b) f

(

x, y

)











x sin y − y sin x

+ y

nếu

(

x, y

)

(

0, 0

)

0 nếu

(

x, y

)

(

0, 0

)

Chứng minh. a) Dễ thấy hàm số liên tục với mọi

(

x, y

)

(

0, y

)

Xét x = 0, vì



x arctan







≤

nên lim

x→0

x. arctan





= 0 = f

(

0, y

)

. Vậy f

(

x, y

)

liên tục trên R

Với x 6= 0 các đạo hàm riêng tồn tại và liên tục:

′

= arctan





−

+ y

, z

′

+ y

Xét tại x = 0,











′

(

0, y

)

= lim

h→0

(

h, y

)

− f

(

0, y

)

= arctan









0, y = 0

, y 6= 0

′

(

0, y

)

= lim

k→0

(

0, y + k

)

− f

(

0, y

)

= lim

k→0

0 = 0

Vậy ta thấy f

′

(

x, y

)

liên tục trên R

(

0, 0

)

; f

′

(

x, y

)

liên tục trên R

153

154 Chương 3. Hàm số nhiều biến số

b) Hàm số liên tục trên R

(

0, 0

)

, còn tại (0, 0) thì

0 ≤



x sin y −ysinx

+ y



+ y



sin y

−

sin x





≤



sin y

−

sin x



nên

lim

x→0

y→0



x sin y −ysinx

+ y



= 0

Vậy f (x, y) liên tục trên R

Bài tập 3.7. Giả sử z = y f



−y



, ở đó f là hàm số khả vi. Chứng minh rằng đối với

hàm số z hệ thức sau luôn thoả mãn

′

Chứng minh. Ta có

′

= y f



−y



.2x, z

′

= f



−y



+ y. f



−y



(

−2y

)

nên

′



−y



Bài tập 3.8. Tìm đạo hàm của hàm số hợp sau đây

a) z = e

−2v

, u = cos x, v =

+ y

b) z = ln



+ v



, u = xy, v =

c) z = arcsin

(

x − y

)

, x = 3t, y = 4t

Chứng minh. a) Ta có

(

′

= −sin x

′

= 0

;







′

√

′

√

;

nên







′

= e

cos x

−2

(

)

[

−sin 2x −4x

]

′

= e

cos x

−2

(

)

[

−4y

]

b) Ta có

(

′

= y

′

= x

;

(

′

−x

nên

′

, z

′



−1



(

+ 1

)

154

2. Đạo hàm và vi phân 155

c) Ta có

(

′

= 3

′

= 12t

nên

′

1 −

(

x −y

)



3 −12t



Bài tập 3.9. Tìm vi phân toàn phần của các hàm số

a) z = sin



+ y



b) z = ln tan

c) z = arctan

x+y

x−y

d) u = x

Chứng minh. a)

dz = cos



+ y



(

2xdx + 2ydy

)

dz =

sin



xdy −ydx



dz =

(

x −y

)

dx +

(

x + y

)

(

x −y

)

(

x + y

)

du = x



dx + 2yz ln xdy + y

ln xdz



Bài tập 3.10. Tính gần đúng

a) A =

(

1, 02

)

(

0, 05

)

b) B = ln



√

1, 03 +

√

0, 98 −1



Chứng minh. a) Xét hàm f

(

x, y

)

+ y

, ∆x = 0, 02; ∆y = 0, 05; x = 1; y = 0. Ta có

′

(

+ y

)

2/3

2x; f

′

(

+ y

)

2/3

Khi đó

(

1 + ∆x, 0 + ∆y

)

≈ f

(

1, 0

)

+ f

′

(

1, 0

)

∆x + f

′

(

1, 0

)

∆y = 1 +

.0, 02 + 0.0, 05 = 1, 013.

155

156 Chương 3. Hàm số nhiều biến số

b) Xét hàm

(

x, y

)

= ln



√

x +

√

y −1



; x = 1; y = 1; ∆x = 0, 03; ∆y = 0, 02

Ta có

′

√

x +

√

y −1

; f

′

√

x +

√

y −1

Khi đó

(

1 + ∆x, 1 + ∆y

)

≈ f

(

1, 1

)

+ f

′

(

1, 1

)

∆x + f

′

(

1, 1

)

∆y

= 0 +

.0, 03 +

(

−0, 02

)

= 0, 005.

Bài tập 3.11. Tìm đạo hàm của các hàm số ẩn xác định bởi các phương trình sau

a) x

y −y

x = a

; tính y

′

b) arctan

x+y

; tính y

′

c) x + y + z = e

; tính z

′

, z

′

d) x

+ y

+ z

−3xyz = 0, tính z

′

, z

′

Chứng minh. a) Xét hàm số ẩn F

(

x, y

)

= x

y − y

x − a

= 0, có F

′

= 3x

y − y

; F

′

−3y

x. Vậy

′

−F

′

= −

y −y

−3y

b) Xét hàm số ẩn F

(

x, y

)

= arctan

x+y

−

có











′

(

x+y

)

(

x+y

)

′

(

x+y

)

−

−a

−

(

x+y

)

(

x+y

)

nên

′

(

x + y

)

c) Xét hàm số ẩn F

(

x, y, z

)

= x + y + z −e

có F

′

= 1; F

′

= 1; F

′

= 1 −e

nên

′

−1

1 −e

; z

′

−1

1 −e

d) Xét hàm số ẩn F

(

x, y

)

= x

+ y

+ z

−3xyz = 0 có F

′

= 3x

−3yz; F

′

= 3y

−3xz; F

′

−3xy nên

′

3yz −3x

−3xy

; z

′

3xz −3y

−3xy

Bài tập 3.12. Cho u =

x+z

y+z

, tính u

′

, u

′

biết rằng z là hàm số ẩn của x, y xác định bởi

phương trình z.e

= x.e

+ y.e

156

2. Đạo hàm và vi phân 157

Chứng minh. Xét hàm số F

(

x, y, z

)

= ze

− xe

−ye

= 0 có











′

= −

(

+ xe

)

′

= −

(

+ ye

)

′

= e

+ ze

nên











′

(

1 + z

′

)

(

y + z

)

−

(

x + z

) (

′

)

(

y + z

)



1 +

+xe

+ze



−

(

x + z

)

+xe

+ze

(

y + z

)

′

(

x + z

)



1 + z

′



−

(

y + z

)



′



(

y + z

)

(

x + z

)



1 +

+ye

+ze



−

(

y + z

)



+ye

+ze



(

y + z

)

Bài tập 3.13. Tìm đạo hàm của các hàm số ẩn y(x), z(x) xác định bởi hệ







x + y + z = 0

+ y

+ z

= 1

Chứng minh. Lấy đạo hàm hai vế của các phươn g trình của hệ ta có







1 + y

′

+ z

′

= 0

2x + 2yy

′

+ 2zz

′

= 0

nên











′

z − x

y −z

′

x − y

y −z

Bài tập 3.14. Phương trình z

−z

, xác định hàm ẩn z = z

(

x, y

)

. Chứng minh

rằng x

′

Chứng minh. Xét hàm số F

(

x, y, z

)

= z

−

−z

có











′

= −

′

−y

√

−z

′

= 2z +

√

−z

nên











′

2z +

√

−z

′

−y

√

−z

2z +

√

−z

Từ đó suy ra x

′

Bài tập 3.15. Tính các đạo hàm riêng cấp hai của các hàm số sau

157

158 Chương 3. Hàm số nhiều biến số

a) z =

(

+ y

)

b) z = x



+ y



c) z = arctan

Chứng minh. a) Ta có







′

= x

+ y

′

= y

+ y

⇒











′′

+ y

+ x

+ y

′′

+ y

+ 2y

+ y

′′

2xy

+ y

b) Ta có











′

= 2x ln

(

x + y

)

x + y

′

x + y

⇒











′′

= 2 ln

(

x + y

)

x + y

(

x + y

)

− x

(

x + y

)

′′

x + y

−x

(

x + y

)

′′

(

x + y

)

c) Ta có











′

1 +





−y

+ y

′

1 +





+ y

⇒











′′

2xy

(

+ y

)

′′

−



+ y



+ y.2y

(

+ y

)

− x

(

+ y

)

′′

−2xy

(

+ y

)

Bài tập 3.16. Tính vi phân cấp hai của các hàm số sau

a) z = xy

− x

y b) z =

(

)

Chứng minh. a) Ta có dz =



−2xy



dx +



2xy − x



dy nên

z = −2y

(

)

+ 4

(

y − x

)

dxdy+

(

) (

)

b) Ta có dz =

(

)

dx +

(

)

dy nên

z =

−3x

(

+ y

)

(

)

−

4xy

(

+ y

)

dxdy +

−3y

(

+ y

)

(

)

158

3. Cực trị của hàm số nhiều biến số 159

§3. CỰC TRỊ CỦA HÀM SỐ NHIỀU BIẾN SỐ

3.1 Cực trị tự do

Định nghĩa 3.35.

Cho hàm số

z = f (x, y)

xác định trong một miền

và

, y

) ∈ D

Ts nói rằng hàm số

f (x, y)

đạt

cực trị

tại

nếu với mọi điểm

trong lân cận nào đó của

nhưng khác

, hiệu số

f (M) − f (M

)

có dấu không đổi.

•

Nếu

f (M) − f (M

) > 0

trong một lân cận nào đó của

thì

được gọi là

cực tiểu

của hàm số

tại

•

Nếu

f (M) − f (M

) < 0

trong một lân cận nào đó của

thì

được gọi là

cực đại

của hàm số

tại

Trong phần tiếp theo chúng ta sử dụng các kí hiệu sau:

p = f

′

(M), q = f

(M), r = f

”(M), s = f

”(M), t = f

”(M)

Định lý 3.55.

Nếu hàm số

f (x, y)

đạt cực trị tạ i

và tại đó các đạo hàm riêng

p =

′

(M), q = f

(M)

tồn tại thì các đạo hàm riêng ấy bằng không.

Định lý 3.56.

Giả sử hàm số

z = f (x, y)

có các đạo hàm riêng đến cấp hai liên tục trong

một lân cận nào đó của

, y

)

. Giả sử tại

ta có

p = q = 0

, khi đó

1. Nếu

−rt < 0

thì

f (x, y)

đạt cực trị tại

. Đó là cực tiểu nếu

r > 0

, là cực đại nếu

r < 0

2. Nếu

−rt > 0

thì

f (x, y)

không đạt cực trị tại

Chú ý: Nếu s

− rt = 0 thì chưa kết luận được điều gì về điểm M

, nó có thể là cực trị,

cũng có thể không. Trong trường hợp đó ta sẽ dùng định nghĩa để xét xem M

có phải là

cực trị hay không b ằng cách xét hiệu f (M) − f (M

), nếu nó xác định dấu trong một lân

cận nào đó của M

thì nó là cực trị và ngược lại.

Ví dụ 3.1 (Cuối kì, K61 Viện ĐTQT).

T ìm các cực trị của hàm số

z = x

−2x + arctan(y

)

. b)

z = y

−2y + arctan(x

)

Bài tập 3.17. Tìm cực trị của các hàm số sau

159

160 Chương 3. Hàm số nhiều biến số

a) z = x

+ xy + y

+ x −y + 1

b) z = x + y − x.e

c) z = 2x

+ y

− x

−2y

d) z = x

+ y

−e

−

(

)

Chứng minh. a) Xét hệ phương trình







p = z

′

= 2x + y + 1 = 0

q = z

′

= x + 2y −1 = 0

⇔







x = −1

y = 1

. Vậy

ta có M

(

−1, 1

)

là điểm tới hạn duy nhất.

Ta có A = z

′′

(M) = 2; B = z

′′

(M) = 1; C = z

′′

(M) = 2 nên B

− AC = 1 −4 = −3 <

0. Vậy hàm số đạt cực trị tại M và do A > 0 nên M là điểm cực tiểu.

b) Xét hệ phương trình







p = 1 −e

= 0

q = 1 − xe

= 0

⇔







x = 1

y = 0

Vậy hàm số có điểm tới hạn duy nhất M

(

1, 0

)

. Ta có A = z

′′

(M) = 0; B = z

′′

(M) =

−1; C = z

′′

(M) = −1 nên B

− AC = 1 > 0. Hàm số đã cho không có cực trị.

c) Xét hệ phương t rình







′

= 8x

−2x

′

= 4y

−4y

⇔









−1



= 0



−1



= 0

⇔







x = 0 ∨ x =

∨ x = −

y = 0 ∨y = 1 ∨y = −1

Vậy các điểm tới hạn của hàm số là

(

0, 0

)

; M

(

0, 1

)

; M

(

0, −1

)

; M



, 0



; M



, 1





, −1



; M



−

, 0



; M



−

, 1



; M



−

, −1



Ta có z

′′

= 24x

−2; z

′′

= 0; z

′′

= 12y

−4.

• Tại M

(0, 0), A = −2; B = 0; C = −4; B

− AC = −8 < 0 nên M

là điểm cực đại

với z = 0.

• Tại M

(

0, 1

)

; M

(

0, −1

)

; A = −2; B = 0; C = 8; B

− AC = 16 > 0 nên M

, M

không phải là điểm cực đại với z = 0.

• Tại M



, 0



; M



−1

, 0



; A = 4; B = 0; C = −4; B

− AC = 16 > 0 nên M

, M

không phải là điểm cực đại với z = 0.

• Tại M



, 1



; M



, −1



; M



−

, 1



; M



−

, −1



; A = 4; B = 0; C = 8; B

−

AC = −32 < 0 nên M

, M

là các điểm cực tiểu với giá trị tại đó là

z = −

d) Xét hệ phương trình







p = z

′

= 2x + e

−

(

)

.2x = 0

q = z

′

= 2y + e

−

(

)

.2y = 0

⇔







x = 0

y = 0

160

3. Cực trị của hàm số nhiều biến số 161

Vậy M(0, 0) là điểm tới hạn duy nhất. Xét

′′

= 2 + 2.e

−

(

)

−4x

−

(

)

′′

= −4xy.e

−

(

)

′′

= 2 + 2.e

−

(

)

−4y

−

(

)

Tại M(0, 0) có A = 4; B = 0; C = 4; B

− AC = −16 < 0; A > 0 nên tại M hàm số đạt

cực tiểu.

3.2 Cực trị có điều kiện

Cho tập mở U ⊂ R

và hàm số f : U → R. Xét bài toán tìm cực trị của hàm số f (x, y)

khi các biến x, y thoả mãn phương trình

ϕ(x, y) = 0

Ta nói rằng tại điểm (x

, y

) ∈ U thoả mãn điều kiện ϕ(x

, y

) = 0 hàm f có cực đại tương

đối (tương ứng c ực tiểu tương đối) nếu tồn tại một lân cận V ⊂ U sao cho f (x, y) ≤ f (x

, y

)

(tương ứng f (x, y) ≥ f (x

, y

)) với mọi (x, y) ∈ V thoả mãn điều kiện ϕ(x, y) = 0. Điểm

, y

) được gọi là cực trị có điều kiện của hàm số f (x, y), còn điều kiện ϕ(x, y) = 0 được

gọi là điều kiện ràng buộc của bài toán. Nếu trong một lân cận của (x

, y

) từ hệ thức

ϕ(x, y) = 0 ta xác định được hàm số y = y(x) thì rõ ràng (x

, y(x

)) là cực trị địa phương

của hàm số một b iến số g(x) = f (x, y(x)). Như vậy, trong trường hợp này bài toán tìm cực

trị ràng buộc được đưa về bài toán tìm cực trị tự do của hàm số một biến số. Ta xét bài

toán sau đây

Bài tập 3.18. Tìm cực trị có điều kiện

a) z =

với điều kiện

b) z = x.y với điều kiện x + y = 1

Chứng minh. a) Đặt x =

sin t

; y =

cos t

, ta có

. Khi đó

z =

sin t

cos t

Ta có

′

cos t

−

sin t

√

sin



−t



= 0 ⇔ t =

∨t =

5π

Với t =

ta có x =

√

2a; y =

√

2a, hàm số đạt cực tiểu và z

−

√

Với t =

5π

ta có x = −

√

2a; y = −

√

2a, hàm số đạt cực đại và z

CĐ

√

161

162 Chương 3. Hàm số nhiều biến số

b) Từ điều kiện x + y = 1 ta suy ra y = 1 − x. Vậy z = xy = x(1 − x). Dễ dàng nhận

thấy hàm số x = x(1 − x) đạt cực đại tại x =

và z

CĐ

Tuy nhiên không phải lúc nào cũng tìm được hàm số y = y(x) từ điều kiện ϕ(x, y) = 0. Do

đó bài toán tìm cực trị điều kiện không phải lúc nào cũng đưa được về bài toán tìm cực trị

tự do. Trong trường hợp đó ta dùng phương pháp Lagrange được trình bày dưới đây.

Định lý 3.57 (Điều kiện cần để hàm số đạt cực trị điều kiện).

Giả sử

là một tập

mở tron g

f : U → R

và

, y

)

là điểm cực trị của hàm

với điều kiện

ϕ(x, y) = 0

Hơn nữa giả thiết rằng:

a. Các hàm

f (x, y), ϕ(x, y)

có các đạo hàm riêng liên tục trong một lân cận của

, y

)

∂ϕ

∂y

, y

) 6= 0

Khi đó tồn tại một số

cùng với

, y

tạo thành nghiệm của hệ phương trình sau (đối với

λ, x, y

)











∂φ

∂x

= 0

∂φ

∂y

= 0

∂φ

∂λ

= 0

⇔











∂ f

∂x

(x, y) + λ

∂ϕ

∂x

(x, y) = 0

∂ f

∂y

(x, y) + λ

∂ϕ

∂y

(x, y) = 0

ϕ(x, y) = 0

(3.3)

với

φ(x, y, λ) = f (x, y) + λϕ(x, y)

được gọi là hàm Lagrange.

Định lý trên chính là điều kiện cần của cực trị có ràng buộc. Giải hệ phương trình 3.3 ta

sẽ thu được các điểm tới hạn. Giả sử M(x

, y

) là một điểm tới hạn ứng với giá trị λ

. Ta

có

φ(x, y, λ

) −φ(x

, y

, λ

) = f (x, y) + λ

ϕ(x, y) − f (x

, y

) −λ

ϕ(x

, y

) = f (x, y) − f (x

, y

)

nên nếu M là một điểm cực trị của hàm số φ(x, y, λ

) thì M cũng là điểm cực trị của hàm

số f (x, y) với điều kiện ϕ(x, y) = 0. Muốn xét xem M có phải là điểm cực trị của hàm số

φ(x, y, λ

) hay không ta có thể quay lại sử dụng định lý 3.56 hoặc đi tính vi phân cấp hai

φ(x

, y

, λ

) =

∂

∂x

, y

, λ

)dx

+ 2

∂

∂x∂y

, y

, λ

)dxdy +

∂

∂y

, y

, λ

)dy

trong đó dx và dy liên hệ với nhau bởi hệ thức

∂ϕ

∂x

, y

)dx +

∂ϕ

∂y

, y

)dy = 0

hay

dy = −

∂ϕ

∂x

, y

)

∂ϕ

∂y

, y

)

162

3. Cực trị của hàm số nhiều biến số 163

Thay biểu thức này của dy vào d

φ(x

, y

, λ

) ta có

φ(x

, y

, λ

) = G(x

, y

, λ

)dx

Từ đó suy ra

• Nếu G(x

, y

, λ

) > 0 thì (x

, y

) là điểm cực tiểu có điều kiện.

• Nếu G(x

, y

, λ

) < 0 thì (x

, y

) là điểm cực đại có điều kiện.

Bài tập 3.19. Tìm cực trị có điều kiện của hàm số z =

với điều kiện

Chứng minh. Xét hàm số Lag ra nge φ(x, y, λ) =

+ λ(

−

). Từ hệ phương

trình











∂φ

∂x

= −

−

2λ

∂φ

∂y

= −

−

2λ

∂φ

∂λ

−

= 0

ta thu được các điểm tới hạn là M

√

2, a

√

2) ứng với λ

= −

√

, M

(−a

√

2, −a

√

2) ứng

với λ

√

. Ta có

φ =

∂

∂x

+ 2

∂

∂x∂y

dxdy +

∂

∂y



6λ





6λ



Từ điều kiện

−

= 0 suy ra −

dx −

dy = 0 nên dy = −

dx, thay vào biểu thức

φ ta có

• Tại M

, d

φ(M

) = −

√

(dx

+ dy

) = −

√

(dx

) < 0 nên M

là điểm cực đại có điều

kiện.

• Tại M

, d

φ(M

) =

√

(dx

+ dy

) =

√

(dx

) > 0 nên M

là điểm cực tiểu có điều

kiện.

3.3 Giá trị lớn nhất - Giá trị nhỏ nhất

Giả sử f : A → R là hàm số liên tục trên tập hợp đóng A của R

. Khi đó, f đạt giá trị

lớn nhất và giá trị nhỏ nhất trên A. Để tìm các giá trị này ta hãy tìm giá trị của hàm số

tại tất cả các điểm dừng trong miền A cũng như tại các điểm đạo hàm riêng không tồn tại,

sau đó so sánh các giá trị này với các giá trị của hàm trên biên ∂A của A (tức là ta phải

xét cực trị có điều kiện).

Bài tập 3.20. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

163

164 Chương 3. Hàm số nhiều biến số

a) z = x

y(4 − x −y) trong hình tam giác giới hạn bởi các đường x = 0, y = 0, x + y = 6.

b) z = sin x + sin y + sin(x + y) trong hình chữ nhật giới hạn bởi các đường x = 0, x =

, y = 0, y =

164

Bấm Tải xuống để xem toàn bộ.

| 1/166

| | Tải xuống

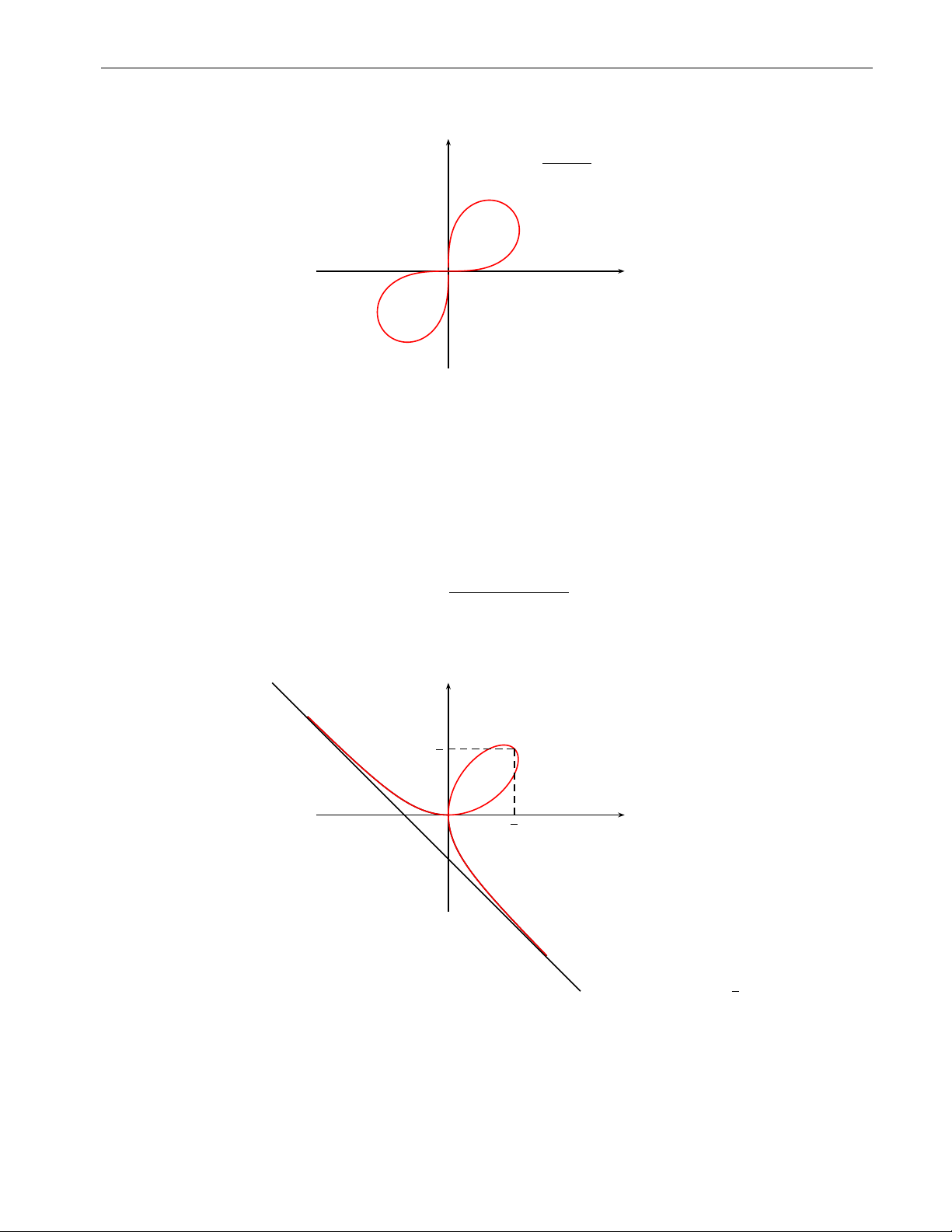
Preview text:

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN TOÁN ỨNG DỤNG & TIN HỌC TS. BÙI XUÂN DIỆU Bài Giảng GIẢI TÍCH I (lưu hành nội bộ)
HÀM SỐ MỘT BIẾN SỐ - TÍCH PHÂN - HÀM SỐ NHIỀU BIẾN SỐ
Tóm tắt lý thuyết, Các ví dụ, Bài tập và Lời giải Hà Nội- 2019
(bản cập nhật Ngày 13 tháng 7 năm 2019)
Tập Bài giảng này vẫn đang trong quá trình hoàn thiện và có thể chứa những lỗi đánh
máy, những lỗi kí hiệu và những chỗ sai chưa được kiểm tra hết. Tác giả mong nhận được
sự đóng góp ý kiến để tập Bài giảng được hoàn thiện. Mọi ý kiến đóng góp xin vui lòng gửi
về địa chỉ “dieu.buixuan@hust.edu.vn”.
Warning: This lecture notes have not been reviewed and may contain errors or typos. Use at your own risk!
Hà Nội, Ngày 13 tháng 7 năm 2019. MỤC LỤC
Mục lục. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Chương 1 . Hàm số một biến số (13LT+13BT). . . . . . . . . . . . . . . . . 5 1
Sơ lược về các yếu tố Lôgic; các tập số: N, Z, Q, R . . . . . . . . . . . . . . . . 5 2
Trị tuyệt đối và tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 3
Hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 3.1
Định nghĩa hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 3.2
Hàm số đơn điệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 3.3
Hàm số bị chặn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 3.4
Hàm số chẵn, hàm số lẻ . . . . . . . . . . . . . . . . . . . . . . . . . . 7 3.5
Hàm số tuần hoàn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 3.6
Hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 3.7
Hàm ngược . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 3.8
Hàm số sơ cấp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 3.9
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 4
Dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 4.1
Dãy số và giới hạn của dãy số . . . . . . . . . . . . . . . . . . . . . . . 19 4.2
Các tiêu chuẩn tồn tại giới hạn . . . . . . . . . . . . . . . . . . . . . . 20 4.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 5
Giới hạn hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 5.1
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 5.2
Các phép toán trên giới hạn . . . . . . . . . . . . . . . . . . . . . . . . 27 5.3
Giới hạn của hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 5.4
Giới hạn vô cùng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 5.5
Các tiêu chuẩn tồn tại giới hạn . . . . . . . . . . . . . . . . . . . . . . 28 5.6
Mối liên hệ giữa giới hạn của dãy số và giới hạn của hàm số . . . . . 29 5.7
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 6
Vô cùng lớn, vô cùng bé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 1 2 MỤC LỤC 6.1
Vô cùng bé (VCB) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 6.2
Vô cùng lớn (VCL) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 6.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 7
Hàm số liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 7.1
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 7.2
Các phép toán số học đối với hàm số liên tục . . . . . . . . . . . . . . 37 7.3
Sự liên tục của hàm ngược . . . . . . . . . . . . . . . . . . . . . . . . . 38 7.4
Sự liên tục của hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . 38 7.5
Các định lý về hàm liên tục . . . . . . . . . . . . . . . . . . . . . . . . 38 7.6
Điểm gián đoạn và phân loại điểm gián đoạn của hàm số . . . . . . . 39 7.7
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 8
Đạo hàm và vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 8.1
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 8.2
Các phép toán trên đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . 43 8.3
Đạo hàm của hàm hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 8.4
Đạo hàm của hàm ngược . . . . . . . . . . . . . . . . . . . . . . . . . . 44 8.5
Đạo hàm của các hàm số sơ cấp cơ bản . . . . . . . . . . . . . . . . . . 44 8.6
Vi phân của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 8.7
Đạo hàm cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 8.8
Vi phân cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 8.9
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
8.10 Đọc thêm: Về khái niệm vi phân . . . . . . . . . . . . . . . . . . . . . 54 9
Các định lý về hàm khả vi và ứng dụng . . . . . . . . . . . . . . . . . . . . . 56 9.1
Các định lý về hàm khả vi . . . . . . . . . . . . . . . . . . . . . . . . . 56 9.2
Các công thức khai triển Taylor, Maclaurin . . . . . . . . . . . . . . . 61 9.3
Quy tắc L’Hospital . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70 9.4
Về một số dạng vô định . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 9.5
Thay tương đương khi có hiệu hai VCB? . . . . . . . . . . . . . . . . . 73 9.6
Hiệu hai VCB tương đương . . . . . . . . . . . . . . . . . . . . . . . . 75 9.7
Ba phương pháp (mới) để tính giới hạn . . . . . . . . . . . . . . . . . . 76 9.8
Về các VCL tiêu biểu . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 9.9
Bài tập ôn tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
10 Các lược đồ khảo sát hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
10.1 Khảo sát và vẽ đồ thị của hàm số y = f (x) . . . . . . . . . . . . . . . . 83
10.2 Khảo sát và vẽ đường cong cho dưới dạng tham số . . . . . . . . . . . 85
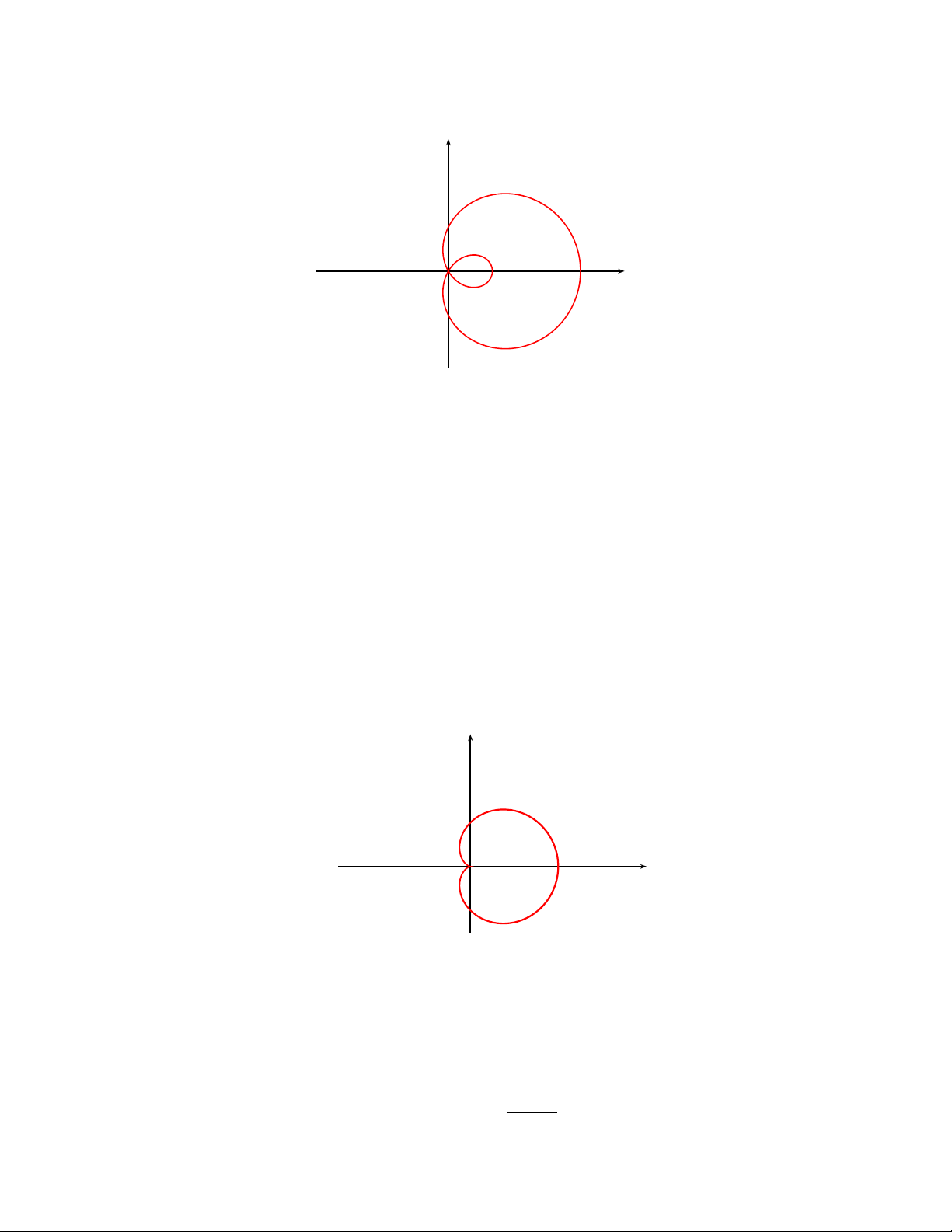
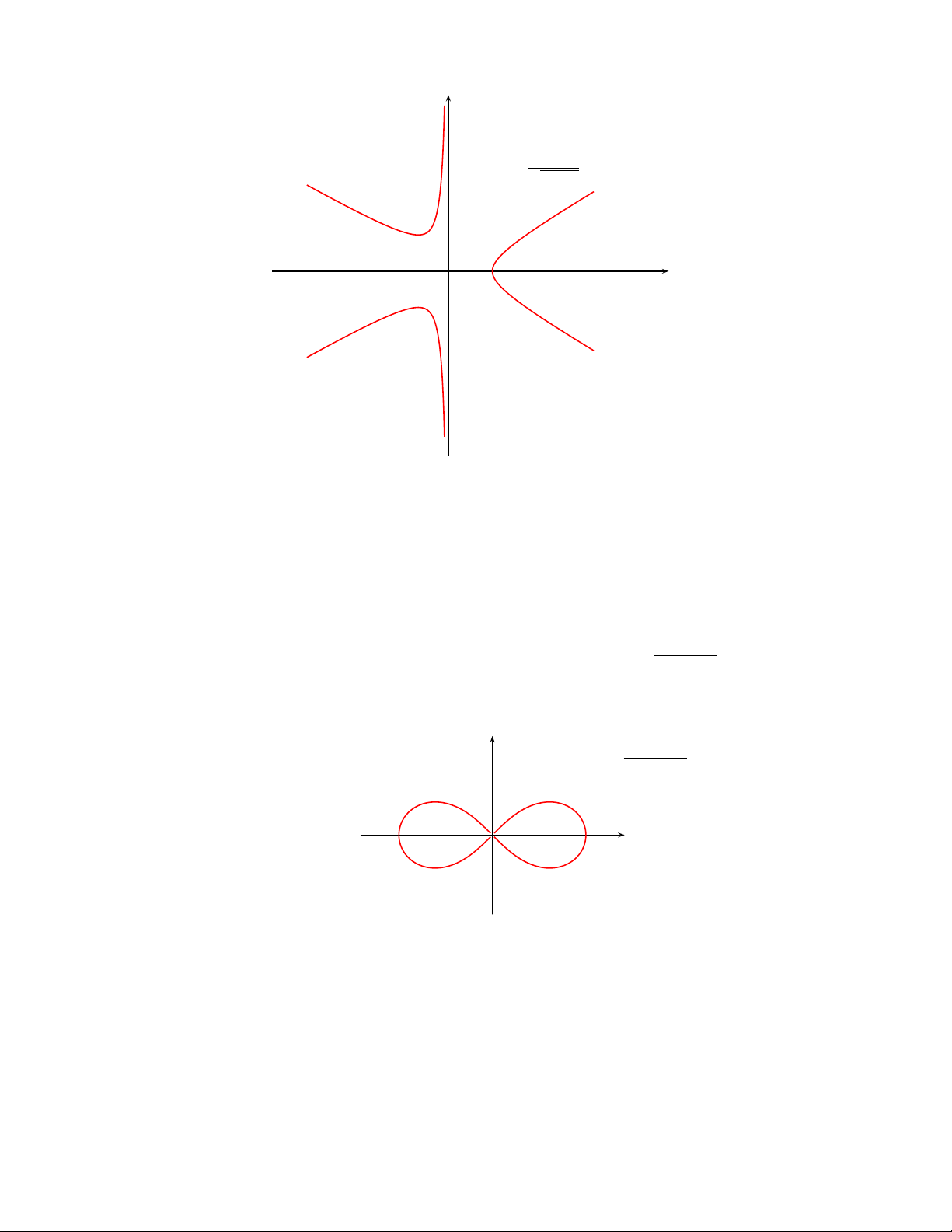
10.3 Khảo sát và vẽ đường cong trong hệ toạ độ cực . . . . . . . . . . . . . 86
10.4 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89 2 MỤC LỤC 3
Chương 2 . Phép tính tích phân một biến số . . . . . . . . . . . . . . . . . 93 1
Tích phân bất định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93 1.1
Nguyên hàm của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . 93 1.2
Các phương pháp tính tích phân bất định . . . . . . . . . . . . . . . . 95 1.3
Tích phân hàm phân thức hữu tỷ . . . . . . . . . . . . . . . . . . . . . 100 1.4
Tích phân hàm lượng giác . . . . . . . . . . . . . . . . . . . . . . . . . 102 1.5
Tích phân các biểu thức vô tỷ . . . . . . . . . . . . . . . . . . . . . . . 104 2
Tích phân xác định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 2.1
Định nghĩa tích phân xác định . . . . . . . . . . . . . . . . . . . . . . 109 2.2
Các tiêu chuẩn khả tích . . . . . . . . . . . . . . . . . . . . . . . . . . 109 2.3
Các tính chất của tích phân xác định . . . . . . . . . . . . . . . . . . . 110 2.4
Tích phân với cận trên thay đổi (hàm tích phân) . . . . . . . . . . . . 111 2.5
Các phương pháp tính tích phân xác định . . . . . . . . . . . . . . . . 112 2.6
Hệ thống bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113 3
Tích phân suy rộng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124 3.1
Tích phân suy rộng với cận vô hạn . . . . . . . . . . . . . . . . . . . . 124 3.2
Tích phân suy rộng của hàm số không bị chặn . . . . . . . . . . . . . 126 3.3
Các tiêu chuẩn hội tụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127 3.4
Tích phân suy rộng hội tụ tuyệt đối và bán hội tụ . . . . . . . . . . . 129 3.5
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130 4
Các ứng dụng của tích phân xác định . . . . . . . . . . . . . . . . . . . . . . . 136 4.1
Tính diện tích hình phằng . . . . . . . . . . . . . . . . . . . . . . . . . 136 4.2
Tính độ dài đường cong phẳng . . . . . . . . . . . . . . . . . . . . . . . 138 4.3
Tính thể tích vật thể . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139 4.4
Tính diện tích mặt tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . 141
Chương 3 . Hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . . . 145 1
Giới hạn của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . . . . . 145 1.1
Giới hạn của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . 145 1.2
Tính liên tục của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . 146 1.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146 2
Đạo hàm và vi phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148 2.1
Đạo hàm riêng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148 2.2
Vi phân toàn phần . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148 2.3
Đạo hàm của hàm số hợp . . . . . . . . . . . . . . . . . . . . . . . . . . 149 2.4
Đạo hàm và vi phân cấp cao . . . . . . . . . . . . . . . . . . . . . . . . 150 2.5
Đạo hàm theo hướng - Gradient . . . . . . . . . . . . . . . . . . . . . . 150 2.6
Hàm ẩn - Đạo hàm của hàm số ẩn . . . . . . . . . . . . . . . . . . . . 152 3 4 MỤC LỤC 2.7
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152 3
Cực trị của hàm số nhiều biến số . . . . . . . . . . . . . . . . . . . . . . . . . 159 3.1
Cực trị tự do . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159 3.2
Cực trị có điều kiện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161 3.3
Giá trị lớn nhất - Giá trị nhỏ nhất . . . . . . . . . . . . . . . . . . . . 163 4 1 CHƯƠNG
HÀM SỐ MỘT BIẾN SỐ (13LT+13BT)
§1. SƠ LƯỢC VỀ CÁC YẾU TỐ LÔGIC; CÁC TẬP SỐ: N, Z, Q, R
1. Phần Lôgic không dạy trực tiếp (phần này Đại số đã dạy) mà chỉ nhắc lại những
phép suy luận cơ bản thông qua bài giảng các nội dung khác nếu thấy cần thiết.
2. Giới thiệu các tập số; cần nói rõ tập Q tuy đã rộng hơn Z nhưng vẫn chưa lấp đầy
trục số còn tập R đã lấp đầy trục số và chứa tất cả các giới hạn của các dãy số hội tụ, ta có bao hàm thức N ⊂ Z ⊂ Q ⊂ R.
§2. TRỊ TUYỆT ĐỐI VÀ TÍNH CHẤT
Nhắc lại định nghĩa và nêu các tính chất sau
• |x| ≥ 0, |x| = 0 ⇐⇒ x = 0, |x + y| ≤ |x| + |y|;
• |x − y| ≥ ||x| − |y|| , |x| ≥ A ⇐⇒ x ≥ A hoặc x ≤ −A
• |x| ≤ B ⇐⇒ −B ≤ x ≤ B. 5 6
Chương 1. Hàm số một biến số (13LT+13BT) §3. HÀM SỐ
3.1 Định nghĩa hàm số
Định nghĩa 1.1. Một hàm số đi từ tập X vào tập Y là một quy tắc cho tương ứng mỗi
phần tử x ∈ X với một và chỉ một phần tử y ∈ Y.
Một hàm số có thể được cho dưới dạng biểu thức giải tích y = f (x), chẳng hạn như hàm số
y = x2. Khi đó, cần phải xác định rõ miền xác định (hay tập xác định), tập hợp tất cả các
phần tử x ∈ X sao cho biểu thức f (x) được xác định, của hàm số.
Tập giá trị của hàm số: là tập tất cả các phần tử y ∈ Y sao cho tồn tại x ∈ X, f (x) = y.
Ví dụ 3.1 (Giữa kì, K61). Tìm tập xác định và tập giá trị của hàm số a) y = arcsin(cos 2x). d) y = arccos(2 sin x). b) y = arcsin(2 cos x). e) y = sin(π cos 3x). c) y = arccos(sin 2x). f) y = cos(π sin 3x).
3.2 Hàm số đơn điệu
• Một hàm số f (x) được gọi là đơn điệu tăng trên khoảng (a, b) nếu:
∀x1, x2 ∈ (a, b), x1 < x2 ⇒ f (x1) < f (x2).
• Một hàm số f (x) được gọi là đơn điệu giảm trên khoảng (a, b) nếu
∀x1, x2 ∈ (a, b), x1 < x2 ⇒ f (x1) > f (x2).
Chú ý 1.1. Trong Bài giảng này chúng ta chỉ quan tâm đến tính đơn điệu của hàm số
trên mỗi khoảng mà hàm số đó xác định. Chẳng hạn như, hàm số f (x) = 1 có f ′(x) = x
− 1 < 0 ∀x ∈ TXĐ = R \ {0} nhưng nếu nói f (x) đơn điệu giảm trên R \ {0} thì sẽ dẫn x2
đến nghịch lý là −1 < 1 nhưng −1 = f (−1) < f (1) = 1. Thay vì đó, ta nói hàm số f (x)
đơn điệu giảm trên mỗi khoảng (−∞, 0) và (0, +∞).
3.3 Hàm số bị chặn
• Một hàm số f (x) được gọi là bị chặn trên nếu tồn tại số M ∈ R sao cho f (x) ≤ M với mọi x ∈ TXĐ. 6 3. Hàm số 7
• Một hàm số f (x) được gọi là bị chặn dưới nếu tồn tại số m ∈ R sao cho f (x) ≥ M với mọi x ∈ TXĐ.
• Một hàm số f (x) được gọi là bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới.
3.4 Hàm số chẵn, hàm số lẻ 
x ∈ TXĐ ⇒ −x ∈ TXĐ
• Một hàm số f (x) được gọi là chẵn nếu f(−x) = f(x).
Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng. 
x ∈ TXĐ ⇒ −x ∈ TXĐ
• Một hàm số f (x) được gọi là lẻ nếu f(−x) = −f(x).
Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Ví dụ 3.2. Chứng minh rằng bất kì hàm số f (x) nào xác định trong một khoảng đối xứng
(−a, a) cũng đều biểu diễn được duy nhất dưới dạng tổng của một hàm số chẵn và một hàm số lẻ.
[Gợi ý] Với mỗi f (x) bất kì ta luôn có 1 1
f (x) = [ f (x) + f (−x)] + [ f (x) − f (−x)] 2 2 | {z } | {z } g(x) h(x)
trong đó g(x) là một hàm số chẵn, còn h(x) là một hàm số lẻ. Các bạn độc giả được khuyến
khích tự chứng minh tính duy nhất của phân tích này. 3.5 Hàm số tuần hoàn
Định nghĩa 1.2. Một hàm số f (x) được gọi là tuần hoàn nếu như tồn tại số thực T > 0 sao cho
f (x) = f (x + T) ∀x ∈ TXĐ .
Ví dụ như các hàm số lượng giác y = sin x, y = cos x, y = tan x, y = cot x đã học ở phổ thông
là các hàm số tuần hoàn. Trong phạm vi Bài giảng này, chúng ta quan tâm chủ yếu là
xem có số T > 0 nào đó thỏa mãn f (x + T) = f (x) mà không đi sâu vào việc tìm chu kỳ (số T > 0 bé nhất).
Các câu hỏi sau đây tuy phát biểu đơn giản (và tưởng chừng như dễ trả lời) nhưng câu
trả lời sẽ rất thú vị: 7 8
Chương 1. Hàm số một biến số (13LT+13BT)
• Tổng (hiệu) của hai hàm số tuần hoàn có tuần hoàn không?
• Tích của hai hàm số tuần hoàn có tuần hoàn không?
• Thương của hai hàm số tuần hoàn có tuần hoàn không?
• Đạo hàm của hàm số tuần hoàn (nếu có) có tuần hoàn không?
• Nếu hàm số F(x) có đạo hàm trên R và F′(x) là một hàm số tuần hoàn thì F(x) có tuần Z x
hoàn không? Nói cách khác, nếu f (x) là một hàm số tuần hoàn thì F(x) = f (t)dt 0 có tuần hoàn không? 3.6 Hàm hợp
Cho hai hàm số f , g. Hàm hợp của f và g, kí hiệu là f ◦ g, là hàm số được định nghĩa bởi ( f ◦ g)(x) = f [g(x)]. 3.7 Hàm ngược
Định nghĩa 1.3. Một hàm số f : X → Y được gọi là ánh xạ 1 − 1 (hay còn gọi là đơn ánh) nếu: x1 6= x2 ⇒ f (x1) 6= f (x2).
Định nghĩa 1.4. Cho f là một đơn ánh với miền xác định A và miền giá trị B. Khi đó hàm
ngược f −1, có miền xác định B và miền giá trị A, được định nghĩa bởi f −1(y) = x ⇔ f (x) = y.
Miền xác định của f = Miền giá trị của f −1
Miền giá trị của f = Miền xác định của f −1
Chú ý 1.2. Đồ thị của hàm ngược đối xứng với đồ thị của hàm y = f (x) qua đường phân
giác của góc phần tư thứ nhất.
Để tìm hàm số ngược của hàm số y = f (x) ta làm như sau: • Viết y = f (x),
• Từ phương trình này giải x theo y, giả sử được x = g(y),
• Đổi vai trò của x và y để được hàm số ngược f −1(x) = g(x). 8 3. Hàm số 9
Ví dụ, tìm hàm ngược của hàm số y = 2x + 3, ta rút x theo y thì được x = y−3, sau đó 2
đổi vai trò của x và y để được hàm ngược là y = x−3. Tuy nhiên, cũng có nhiều khi hàm 2
số không phải là đơn ánh trên toàn trục số R, khi đó chúng ta phải xét hàm số trên các
khoảng mà hàm số đó là đơn ánh và tìm hàm ngược trên các khoảng tương ứng.
Định lý 1.1. Nếu hàm số f (x) đơn điệu tăng (hoặc giảm) trên khoảng (a, b) thì tồn tại
hàm số ngược f −1 của f trên khoảng đó. 3.8 Hàm số sơ cấp
Năm loại hàm số sơ cấp cơ bản
1. Hàm lũy thừa y = xα. TXĐ của hàm số này phụ thuộc vào α.
• Nếu α nguyên dương, ví dụ hàm y = x2, hàm số xác định với mọi x ∈ R,
• Nếu α nguyên âm, ví dụ hàm y = x−2 = 1 , hàm số y = yα = 1 xác định với x2 x−α mọi x ∈ R \ {0}, √
• Nếu α = 1 , p nguyên dương chẵn, ví dụ y = x1/2 =
x, thì hàm số xác định trên p R , ≥0 √
• Nếu α = 1 , nguyên dương lẻ, ví dụ y = x1/3 = 3 x, thì hàm số xác định trên R, p
• Nếu α là số vô tỉ thì quy ước chỉ xét hàm số tại x > 0.
2. Hàm số mũ y = ax (0 < a 6= 1) có tập xác định là R và tập giá trị là R . Hàm này >0
đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1. 3. Làm số logarit y = log (
a x) (0 < a 6= 1), ngược với hàm số mũ, hàm số này có TXĐ là R và tập giá trị là >0
R. Hàm số này đồng biến nếu a > 1 và nghịch biến nếu
0 < a < 1. Nó là hàm số ngược của hàm số mũ, do đó đồ thị của nó đối xứng với đồ
thị của hàm số y = ax qua đường phân giác của góc phần tư thứ nhất. Logarit cơ số
10 của x được kí hiệu là lg x. Logarit cơ số e của x được kí hiệu là ln x. 4. Các hàm lượng giác:
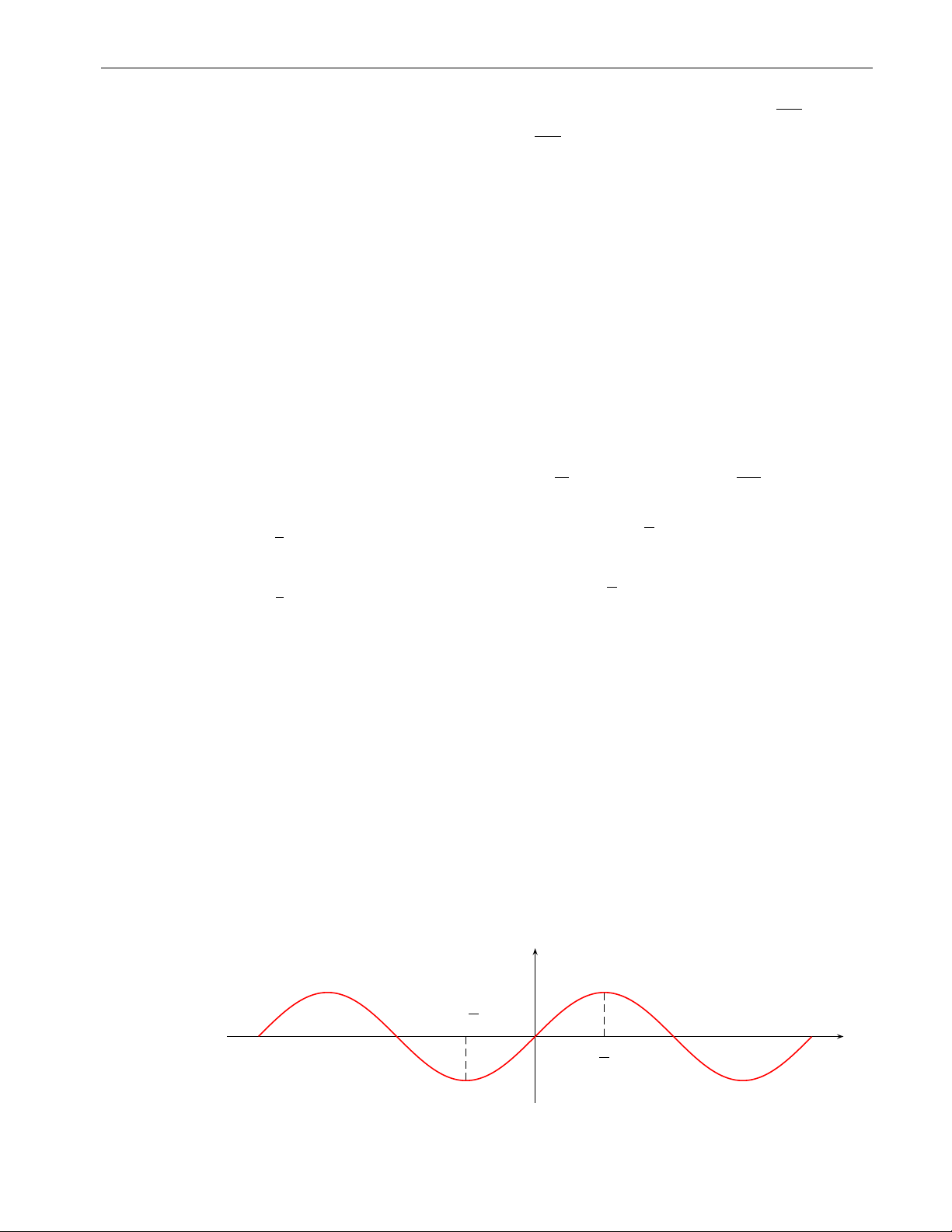
• Hàm số y = sin x xác định ∀x ∈ R, là hàm số lẻ, tuần hoàn chu kì 2π. y y = sin x − π2 O x π 2 9 10
Chương 1. Hàm số một biến số (13LT+13BT)
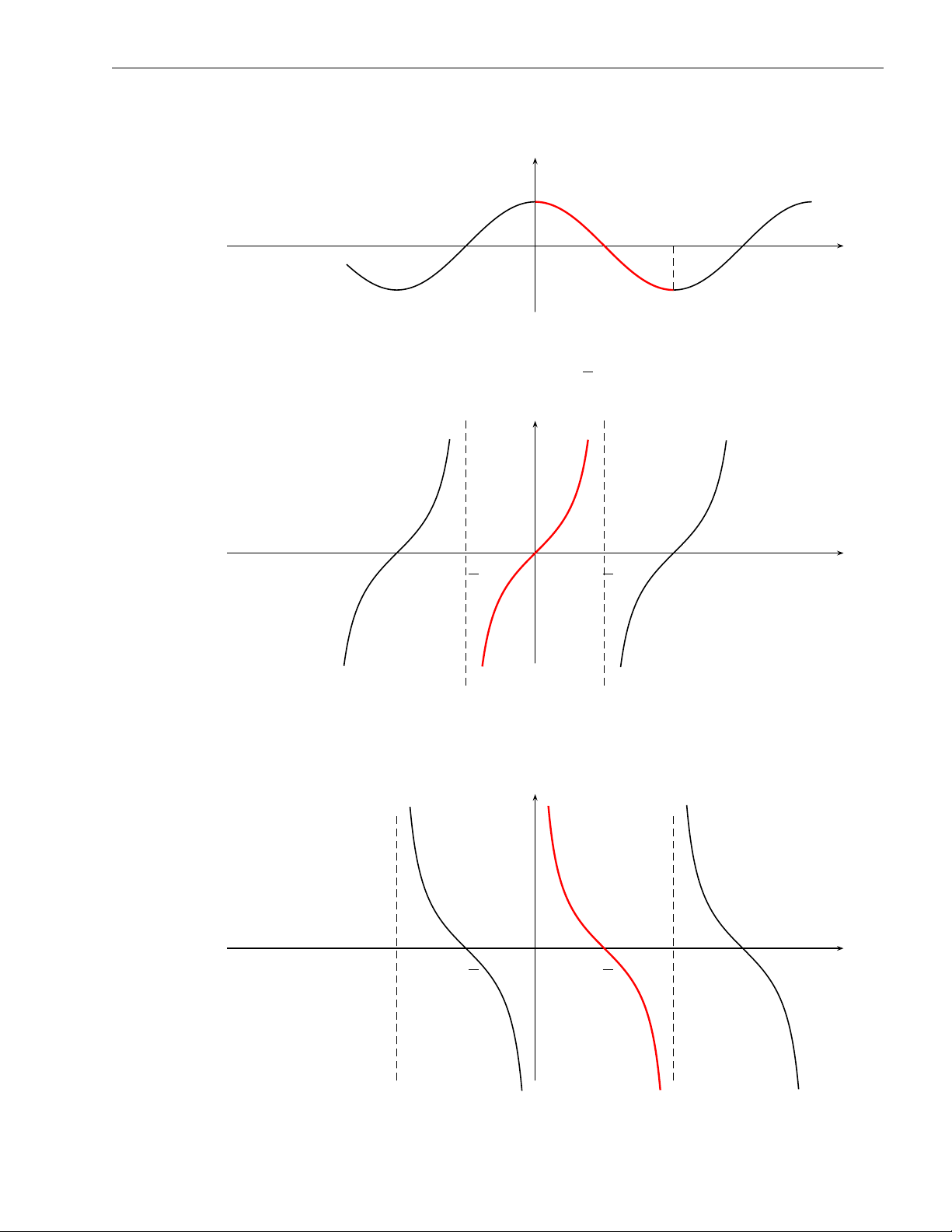
• Hàm số y = cos x xác định ∀x ∈ R, là hàm số chẵn, tuần hoàn chu kì 2π. y
y = cos x, 0 ≤ x ≤ π x O
• Hàm số y = tan x xác định ∀x ∈ R \ {(2k + 1) π , k 2
∈ Z}, là hàm số lẻ, tuần hoàn chu kì π. y O x − π π 2 2
• Hàm số y = cot x xác định ∀x ∈ R \ {kπ, k ∈ Z}, là hàm số lẻ, tuần hoàn chu kì π. y x O − π π 2 2 π 10 3. Hàm số 11
Ví dụ 3.3 (Ngụy biện toán học). Chứng minh rằng 0 = 2. Chứng minh. Ta có p p
cos2 x = 1 − sin2 x ⇒ cos x = 1 − sin2 x ⇒ 1 + cos x = 1 + 1 − sin2 x. Thay p
x = π vào đẳng thức 1 + cos x = 1 + 1 − sin2 x ta được 0 = 2.
5. Các hàm lượng giác ngược:
Muốn tìm hàm ngược của một hàm số, một yêu cầu đặt ra là hàm số đó phải là đơn
ánh. Tuy nhiên, các hàm lượng giác đều là các hàm số tuần hoàn (do đó, không phải
là đơn ánh). Chẳng hạn như, hàm số y = sin x không phải là đơn ánh trên R. Để
vượt qua khó khăn này, người ta hạn chế các hàm số lượng giác trên các khoảng mà
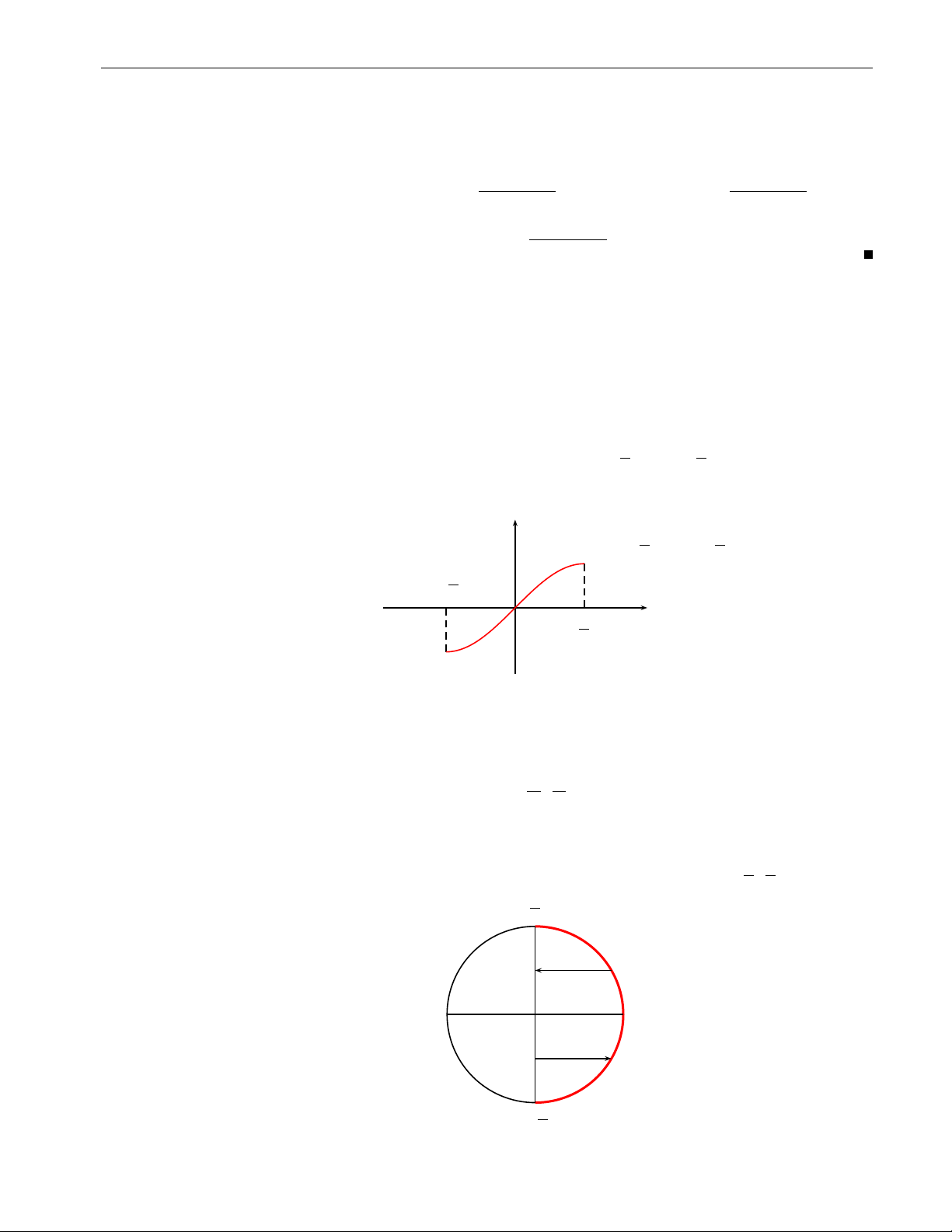
nó là đơn ánh. Chẳng hạn như, hàm số f (x) = sin x, −π là một đơn ánh. 2 ≤ x ≤ π 2 y
y = sin x, − π2 ≤ x ≤ π2 − π2 O x π 2
• Hàm số ngược của hàm số y = sin x, kí hiệu là arcsin x, xác định như sau: h π π i arcsin : [0, 1] → − , 2 2
x 7→ y = arcsin x ⇔ x = sin y Hàm số
y = arcsin x xác định trên [−1, 1], nhận giá trị trên − π , π và là một 2 2 hàm số đơn điệu tăng. π 2 x sin x 0 x arcsin x − π2 11 12
Chương 1. Hàm số một biến số (13LT+13BT)
• Hàm số ngược của hàm số y = cos x, kí hiệu là y = arccos x, được xác định như sau:
arccos : [0, 1] → [0, π]
x 7→ y = arccos x ⇔ x = cos y
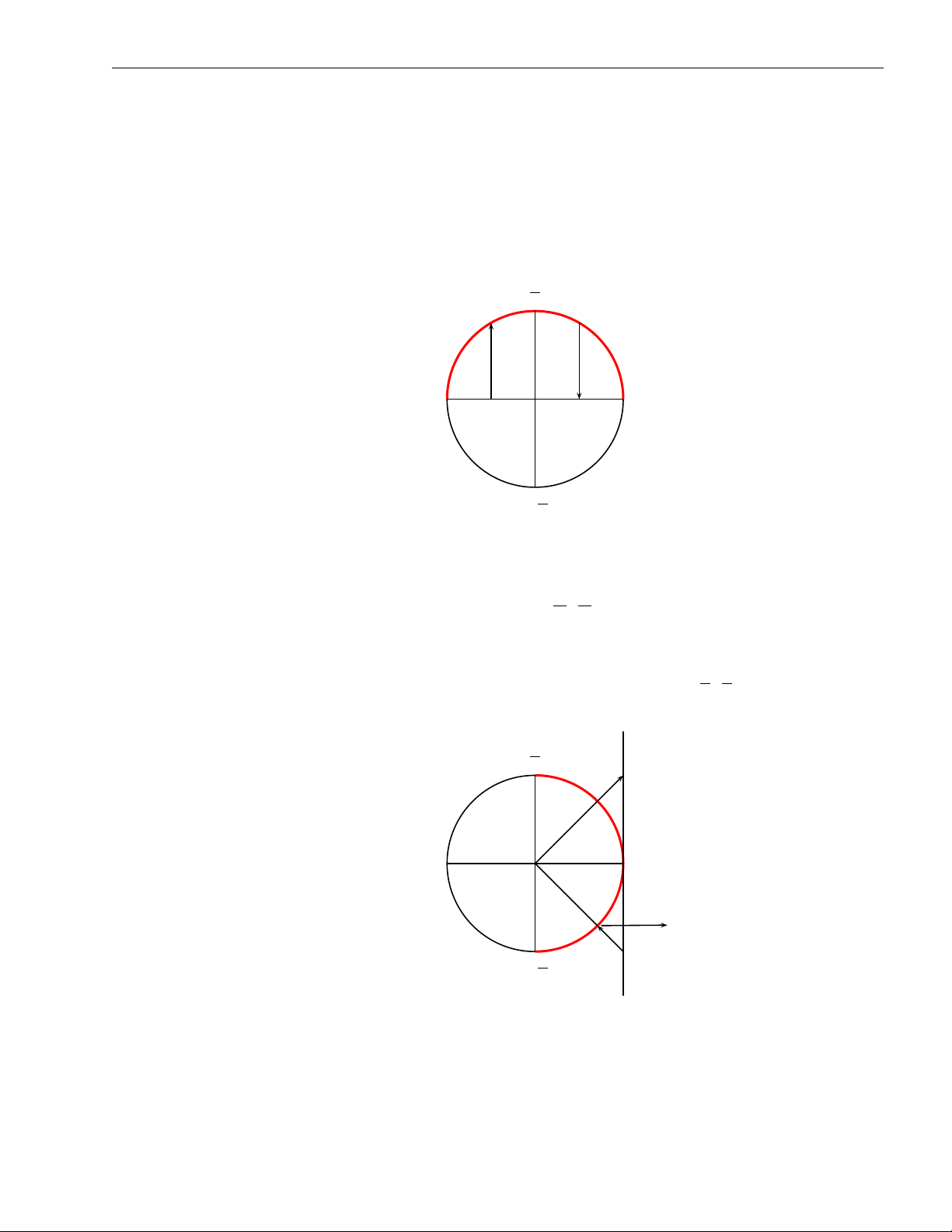
Hàm số y = arccos x xác định trên [−1, 1], nhận giá trị trên [0, π] và là một hàm số đơn điệu giảm. π 2 arccos x x π x cos x 0 − π2
• Hàm số ngược của hàm số y = tan x, kí hiệu là y = arctan x, được xác định như sau: π π
arctan : (−∞, +∞) → − , 2 2
x 7→ y = arctan x ⇔ x = tan y Hàm số
y = arctan x xác định trên R, nhận giá trị trên − π , π và là một hàm 2 2 số đơn điệu tăng. π 2 tan x x 0 arctan x x − π2
• Hàm số ngược của hàm số y = cot x, kí hiệu là y = arccot x, được xác định như sau:
arccot : (−∞, +∞) → (0, π)
x 7→ y = arccot x ⇔ x = cot y 12 3. Hàm số 13
Hàm số y = arccotx xác định trên R, nhận giá trị trên (0, π) và là một hàm số đơn điệu giảm. π x 2 cot x arccot x x π 0 − π2 Hàm số sơ cấp
Người ta gọi hàm số sơ cấp là hàm số được tạo thành bởi một số hữu hạn các phép toán
cộng, trừ, nhân, chia, phép lập hàm số đối với các hàm số sơ cấp cơ bản. Các hàm số sơ cấp
được chia thành hai loại.
• Hàm số đại số: là những hàm số mà khi tính giá trị của nó ta chỉ phải làm một số
hữu hạn các phép toán cộng, trừ, nhân, chia và lũy thừa với số mũ hữu tỉ. Ví dụ: các
đa thức, phân thức hữu tỉ, . . .
• Hàm số siêu việt: là những hàm số sơ cấp nhưng không phải là hàm số đại số, như y = ln x, y = sin x, . . . 3.9 Bài tập
Tìm TXĐ, MGT của hàm số
Bài tập 1.1. Tìm TXĐ của hàm số √ a) p y = 4 lg(tan x), c) x y = , sin πx b) 2x y = arcsin , d) 1 + x y = arccos(2 sin x). [Đáp số]
a) {π/4 + kπ ≤ x < π/2 + kπ, k ∈ Z}, c) {x ≥ 0, x 6∈ Z}, b) {−1/3 ≤ x ≤ 1}, d) {−π + kπ + kπ, k 6 ≤ x ≤ π6 ∈ Z}.
Bài tập 1.2. Tìm miền giá trị của hàm số 13 14
Chương 1. Hàm số một biến số (13LT+13BT) a) x y = lg(1 − 2 cos x) b) y = arcsin lg 10 [Đáp số] a) {−∞ < y ≤ lg 3}
b) {−π/2 ≤ y ≤ π/2} Tìm hàm ngược.
Bài tập 1.3. Tìm hàm ngược của hàm số (trên miền mà hàm số có hàm ngược) a) y = 2x + 3, b) 1 − x 1 y = , c) y = (ex + e−x). 1 + x 2 [Đáp số] a) 1 3 y = x − . 2 2 b) 1 − x y = y = . 1 + x c) Ta có 1 y′ =
(ex − e−x) không xác dịnh dấu, nên hàm số đã cho có thể không phải là 2
một đơn ánh. Trước hết, 1 q q y = (ex + e−x) ⇔ ex = y ± y2 − 1 ⇔ x = ln(y ± y2 − 1). 2 Ta phải xét trên 2 miền:
• Trên miền x > 0, ta có song ánh: (0, +∞) → (1, +∞) 1 x 7→ y = (ex + e−x) 2 q ln(y + y2 − 1) ← y √
Vậy hàm ngược trên miền x > 0 là y = ln(x + x2 − 1), x > 1. √
• Trên miền x < 0, tương tự ta có hàm ngược là y = ln(x − x2 − 1), x > 1.
Ví dụ 3.4 (Giữa kì, K61). Tìm hàm ngược của hàm số sau a) y = x+1 . b) y = x−1 . 2x+1 2x−1
Xét tính chẵn lẻ của hàm số
Bài tập 1.4. Xét tính chẵn lẻ của hàm số 14 3. Hàm số 15 √
a) f (x) = ax + a−x(a > 0) b) f (x) = ln(x + 1 − x2) c) f (x) = sin x + cos x [Đáp số]
a) Hàm số đã cho là hàm số chẵn.
b) Hàm số đã cho là hàm số lẻ.
c) Hàm số đã cho không chẵn, không lẻ.
Ví dụ 3.5 (Giữa kì, K61). Xét tính chẵn lẻ của hàm số a) y = tan(sin x). b) y = sin(tan x).
Ví dụ 3.6. Cho hàm số f (x) xác định và có đạo hàm trên R. Chứng minh rằng
a) nếu f (x) là một hàm số lẻ thì f ′(x) là một hàm số chẵn.
b) nếu f (x) là một hàm số chẵn thì f ′(x) là một hàm số lẻ.
Xét tính tuần hoàn của hàm số
Bài tập 1.5. Xét tính tuần hoàn và chu kì của hàm số sau (nếu có)
a) f (x) = A cos λx + B sin λx, c) f (x) = sin2 x, b) 1 1 f (x) = sin x + sin 2x + sin 3x, d) 2 3 f (x) = sin(x2). Chứng minh.
a) Giả sử T > 0 là một chu kì của hàm số đã cho. Khi đó
f (x + T) = f (x)∀x ∈ R
⇔A cos λ(x + T) + B sin λ(x + T) = A cos λx + B sin λx ∀x ∈ R
⇔A[cos λx − cos λ(x + T)] + B[sin λx − sin λ(x + T)] = 0 ∀x ∈ R −λT λT λT ⇔2 sin [A sin(λx + ) + B cos(λx + )] = 0 ∀x ∈ R 2 2 2 λT ⇔ sin = 0 2 2kπ ⇔T = . λ
Vậy hàm số đã cho tuần hoàn với chu kì 2π T = . |λ|
b) Theo câu a) thì hàm số sin x tuần hoàn với chu kì 2π, hàm số sin 2x tuần hoàn với chu kì 1 1
π, hàm số sin 3x tuần hoàn với chu kì 2π . Vậy f (x) = sin x + sin 2x + sin 3x 3 2 3
tuần hoàn với chu kì T = 2π 15 16
Chương 1. Hàm số một biến số (13LT+13BT) c) 1 − cos 2x f (x) = sin2 x =
tuần hoàn với chu kì T = π 2
d) Giả sử hàm số đã cho tuần hoàn với chu kì T > 0.Khi đó sin(x + T)2 = sin(x2)∀x. √
(a) Cho x = 0⇒T = kπ, k ∈ Z, k > 0. (b) Cho √ x =
π⇒k là số chính phương. Giả sử k = l2, l ∈ Z, l > 0. r (c) Cho π x =
ta suy ra điều mâu thuẫn. 2
Vậy hàm số đã cho không tuần hoàn.
Nhận xét: Muốn chứng minh một hàm số không tuần hoàn, chúng ta có thể sử dụng
phương pháp phản chứng như đã trình bày ở trên. Giả sử hàm số đó tuần hoàn với chu kì
p > 0 sau đó cho một vài giá trị đặc biệt của x để suy ra điều mâu thuẫn. Ngoài phương
pháp phản chứng thì chúng ta cũng có thể sử dụng một số tính chất của hàm số tuần hoàn
để chứng minh. Chẳng hạn như:
• một hàm số tuần hoàn và liên tục thì bị chặn (tại sao?),
• một hàm số tuần hoàn và không phải là hàm hằng thì không tồn tại lim f (x) (tại x→∞ sao?),
• đạo hàm của một hàm số tuần hoàn (nếu có) thì cũng tuần hoàn (tại sao?).
Bài tập 1.6. Chứng minh các hàm số sau không tuần hoàn (a) √ y = cos x + cos x 2, (d) y = cos x2, (b) √ √ y = sin x + sin x 2, (e) y = sin x, (c) √ y = sin x2, (f) y = cos x. √ Chứng minh.
a) Giả sử hàm số y = cos x + cos x 2 tuần hoàn với chu kì T > 0. Khi đó, √ √
cos x + cos x 2 = cos(x + T) + cos(x + T) 2 ∀x ∈ R. Cho √ √
x = 0 ta được 2 = cos T + cos T 2. Vì cos T ≤ 1, cos T 2 ≤ 1 nên   √ cos T = 1,
T = k2π, 0 6= k ∈ N 2 = cos T + cos T 2 ⇔ √ ⇒ √ cos T 2 = 1.
T 2 = l2π, 0 6= l ∈ N.
Khi đó√2 = lk ∈ Q, điều này là vô lý vì√2 là một số vô tỉ. Như vậy, chúng ta đã trả lời
một câu hỏi trong Mục 3.5, rằng tổng của hai hàm số tuần hoàn có thể không phải là 16 3. Hàm số 17
một hàm số tuần hoàn. Hàm số √
f (x) = cos x + cos x 2 là một hàm số hầu tuần hoàn
(almost periodic). Tương tự như vậy, tích của hai hàm số tuần hoàn cũng không phải
là một hàm số tuần hoàn, vì √ √ 1 + 2 1 − 2 √ 2 cos x cos x = cos x + cos x 2. 2 2
Bài tập 1.7. [Giữa kì, K61] Cho f (x), g(x) là các hàm số xác định trên R và tuần hoàn
với chu kì lần lượt là T
là một số hữu tỉ. Chứng minh rằng
1 > 0, T2 > 0. Biết tỉ số T1 T2
f (x) + g(x) và f (x)g(x) cũng là các hàm số tuần hoàn. Các dạng toán khác
Bài tập 1.8. Tìm f (x) biết a) 1 1 x f x + = x2 + , b) f = x2. x x2 1 + x [Đáp số]
a) f (x) = x2 − 2 với |x| ≥ 2. 2 b) x f (x) = ∀x 6= 1. 1 − x
Bài tập 1.9. Cho f (x) = ax + b, f (0) = −2, f (3) = −5. Tìm f (x). [Đáp số] 7 f (x) = x − 2. 3
Bài tập 1.10. Cho f (x) = ax2 + bx + c, f (−2) = 0, f (0) = 1, f (1) = 5. Tìm f (x). [Đáp số] 7 17 f (x) = x2 + x + 1. 6 6 Bài tập 1.11. Cho 1
f (x) = (ax + a−x), a > 0. Chứng minh rằng : 2
f (x + y) + f (x − y) = 2 f (x) f (y).
Bài tập 1.12. Giả sử f (x) + f (y) = f (z). Xác định z nếu: a) f (x) = ax, a 6= 0, c) 1 f (x) = , x 1 + x b) f (x) = arctan x, d) f (x) = lg . 1 − x [Đáp số] 17 18
Chương 1. Hàm số một biến số (13LT+13BT) a) xy z = x + y, c) z = , x + y b) x + y x + y z = , d) z = . 1 − xy 1 + xy 18 4. Dãy số 19 §4. DÃY SỐ
4.1 Dãy số và giới hạn của dãy số
Định nghĩa 1.5. Một dãy số là một hàm số N → R, n 7→ a . Kí hiệu . n {an}n∈N
Một dãy số được gọi là:
• đơn điệu tăng nếu an < an+1∀n, đơn điệu giảm nếu an > an+1∀n.
• bị chặn trên nếu tồn tại số M sao cho an ≤ M ∀n, bị chặn dưới nếu tồn tại số m sao cho an ≥ m ∀n.
Định nghĩa 1.6. Một dãy số {an} được gọi là có giới hạn là L và viết
lim an = L hay an → L khi n → ∞, n→∞ nếu
• (nói một cách nôm na) có thể làm cho các số hạng a gần n
L với một giá trị tùy ý bằng cách chọn n đủ lớn.
• (nói một cách chính xác) với mọi ǫ > 0, tồn tại số tự nhiên N sao cho
nếu n > N thì |an − L| < ǫ.
Hình dung rằng lim an = L nghĩa là với mọi ǫ > 0 thì từ một lúc nào đó toàn bộ số hạng n→+∞ của dãy {a sẽ chui vào trong khoảng n} ( n≥N
L − ǫ, L + ǫ). an, ∀n ≥ N L − ǫ L + ǫ Hình 1.6
Một dãy số {an} có lim an = L hữu hạn được gọi là hội tụ. Ngược lại, nó được gọi là phân n→+∞
kì (nghĩa là lim an = ∞ hoặc là không tồn tại). n→+∞
Định nghĩa 1.7 (Giới hạn vô cùng). Ta nói lim an = +∞ nếu với mọi số thực dương M, n→∞
tồn tại số tự nhiên N sao cho nếu n > N thì an > M.
Hãy phát biểu cho trường hợp lim an = −∞ n→∞ 19 20
Chương 1. Hàm số một biến số (13LT+13BT)
Định lý 1.2 (Các tính chất của giới hạn của dãy số).
• Giới hạn của một dãy số, nếu tồn tại, là duy nhất.
• Mọi dãy số hội tụ đều bị chặn.
Định lý 1.3 (Các phép toán trên giới hạn). Giả sử lim an = A, lim bn = b, ở đó a, b n→+∞ n→+∞
là các số thực hữu hạn. Khi đó:
• Tổng: lim (an + bn) = A + B, n→+∞
• Hiệu: lim (an − bn) = A − B, n→+∞ • Tích: lim (an.bn) = AB, n→+∞
• Thương: lim an = A nếu B 6= 0. n→+∞ bn B
Chú ý 1.3. Các phép toán trên giới hạn sau không thực hiện được, chúng còn được gọi là các dạng vô định: ∞ 0 ∞ − ∞, 0 × ∞, , . ∞ 0
4.2 Các tiêu chuẩn tồn tại giới hạn
Định lý 1.4 (Tiêu chuẩn kẹp). Giả sử i) a với mọi n ≤ bn ≤ cn
n ∈ N hoặc với mọi n ≥ K nào đó, ii) lim an = lim cn = L. n→+∞ n→+∞ Khi đó, lim bn = L. n→+∞
Định lý 1.5 (Tiêu chuẩn đơn điệu bị chặn). Mọi dãy số đơn điệu tăng (đơn điệu giảm)
và bị chặn trên (tương ứng, bị chặn dưới) đều hội tụ. n Ví dụ 4.1. Xét 1 un = 1 + .Chứng minh rằng {u n
n} là một dãy số tăng và bị chặn.
Chứng minh. Áp dụng bất đẳng thức Cauchy ta có : s 1 1 1 n 1 + 1 + + . . . + 1 + ≥ (n + 1) n+1 1 + . n n n | {z } n số hạng 20 4. Dãy số 21 1 n+1 1 n ⇒ 1 + ≥ 1 + . n + 1 n Hơn nữa ta có 1 n n 1 un = 1 + = ∑ Ck n n. nk k=0
k! = 1.2 . . . k ≥ 2k−1 ∀k ≥ 2 1
n.(n − 1) . . . (n − k + 1) 1 1 1 ⇒Ck < n. = . ≤ nk k! nk k! 2k−1 1 1 1 ⇒un < 1 + 1 + + + . . . + < 3. 2 22 2k−1 n
Chú ý 1.4. Giới hạn 1 lim 1 +
là một số vô tỉ, được kí hiệu là e. Nó có giá trị xấp xỉ n→+∞ n 2.71.
Ví dụ 4.2 (Giữa kì, 20173). Xét sự hội tụ và tìm giới hạn (nếu có) của dãy số 1 1 {xn} : x1 > 0, xn+1 = x , n ≥ 1. 2 n + xn
[Lời giải] Từ x1 > 0 ta có xn > 0 với mọi n. 1 1 xn = x ≥ 1. 2 n−1 + xn−1 Do đó, x với mọi n+1 = 1 x n. Như vậy, 2 n + 1 x ≤ xn
{xn} là một dãy số giảm và bị chặn n
dưới nên tồn tại lim xn = a. n→+∞ 1 1 1 1 xn+1 = x ⇒ a = a + ⇒ a = 1. 2 n + xn 2 a Vậy lim xn = 1. n→+∞
Định nghĩa 1.8. Dãy số {an} được gọi là dãy số Cauchy nếu với mọi ǫ > 0, tồn tại số tự
nhiên N sao cho |an − am| < ǫ với mọi m, n > N.
Định lý 1.6 (Tiêu chuẩn Cauchy). Dãy số {an} là hội tụ khi và chỉ khi nó là dãy số Cauchy.
Ví dụ 4.3. Chứng minh rằng dãy số {an} với 1 1 1 an = 1 + + + · · · + 2 3 n
là một dãy số phân kỳ. 21 22
Chương 1. Hàm số một biến số (13LT+13BT)
Ví dụ 4.4 (Ngụy biện toán học). Cho x là một số thực và L = lim xn. Đổi biến số n→+∞ n = m + 1 ta có L = lim
xm+1 = lim x.xm = x. lim xm = xL. m+1→+∞ m→+∞ m→+∞
Vậy L = xL ⇒ L(x − 1) = 0. Nếu x 6= 1 thì L = 0. Nói cách khác, lim xn = 0 ∀x 6= 1. n→+∞
Điều này dẫn đến, chẳng hạn, lim 2n = 0 thật vô lý!. n→+∞
Giải thích tại sao lại dẫn đến mâu thuẫn trên? 4.3 Bài tập
Về bài tập tìm giới hạn của dãy số, về cơ bản cho đến thời điểm hiện tại chúng ta chưa
có nhiều công cụ để xử lý. Chủ yếu vẫn là các phương pháp nhân liên hợp để khử dạng
vô định ở phổ thông, sử dụng tiêu chuẩn đơn điệu bị chặn, tiêu chuẩn kẹp và tiêu chuẩn
Cauchy. Sau này, khi học đến giới hạn của hàm số, các công cụ sẽ phong phú hơn. Khi đó
các bài toán về giới hạn của dãy số có thể đưa về giới hạn của hàm số và tính toán dễ dàng.
Bài tập 1.13. Tìm giới hạn của các dãy số sau: √ √ a) x c) n = n − n2 − n, xn = n + 3 1 − n3, e) sin2 n − cos3 n x . n = n nπ n b) p x d) x sin , n = n(n + a) − n, n = 2 2 [Đáp số] a) 1 b) a c) 0 d) phân kì e) 0 2 2
Bài tập 1.14. Xét dãy số 1 xn = xn−1 + , x x 0 = 1. n−1
a) Chứng minh rằng dãy {xn} không có giới hạn hữu hạn.
b) Chứng minh rằng lim xn = +∞. n→∞ Bài tập 1.15. Cho 1 1 s .Chứng minh rằng n = 1 + + . . . + {s 1! n! n} tăng và bị chặn. Chú ý : lim sn = e. n→+∞ 22 4. Dãy số 23 Bài tập 1.16. Tính 1 + a + . . . + an lim , |a| < 1, |b| < 1. n→+∞ 1 + b + . . . + bn Chứng minh. 1 + a + . . . + an 1 − an+1 1 − b 1 − b lim = lim . = n→+∞ 1 + b + . . . + bn n→+∞ 1 − a 1 − bn+1 1 − a q Bài tập 1.17. Tính p √ lim 2 + 2 + . . . + 2 (n dấu căn). n→+∞ q p √ Chứng minh. Đặt u . Trước hết chứng minh n = 2 + 2 + . . . + 2 ta có u2 = n+ 2 + u 1 n
{un} là một dãy số tăng và bị chặn, 0 ≤ un ≤ 2. Theo tiêu chuẩn đơn điệu bị chặn, {un}
là một dãy số hội tụ. Giả sử lim u , cho
n = a, 0 < a < 2 thì từ phương trình u2 = 2 + un n→∞ n+1 n → ∞ ta có a2 = a + 2 q Vậy p √ a = 2 hay lim 2 + 2 + . . . + 2 = 2 n→+∞ √
Bài tập 1.18. Tính lim (n − n2 − 1) sin n. n→+∞ √ [Gợi ý] sin n
lim (n − n2 − 1) sin n = lim √ = 0 (theo tiêu chuẩn kẹp) n→+∞ n→+∞ n + n2 − 1
Bài tập 1.19. Tính lim [cos(ln n) − cos(ln(n + 1))]. n→+∞ Chứng minh. Ta có ln n + ln(n + 1) ln n − ln(n + 1)
cos(ln n) − cos(ln(n + 1)) = −2 sin . sin 2 2 ln n(n + 1) ln n = −2 sin sin n+1 2 2 nên ln n
0 ≤ |cos(ln n) − cos(ln(n + 1))| ≤ 2 n+1 sin 2 Mặt khác ln n lim sin
n+1 = 0 nên theo nguyên lý giới hạn kẹp n→∞ 2
lim [cos(ln n) − cos(ln(n + 1))] = 0 n→+∞
Bài tập 1.20. Chứng minh rằng n lim = 0. n→+∞ 2n 23 24
Chương 1. Hàm số một biến số (13LT+13BT) [Gợi ý] n(n − 1) n 2 2n = (1 + 1)n > ⇒0 < < . 2 2n n − 1
Dùng nguyên lý kẹp ta có điều phải chứng minh.
Bài tập 1.21. Chứng minh rằng 2n lim = 0. n→+∞ n! [Gợi ý] Ta có 2n 2 2 2 2 2 0 < = . . . . . < 2. ∀n ≥ 2. n! 1 2 3 n n Bài tập 1.22. Tính a) 1 1 n 1 1 n lim + + · · · + b) lim + + · · · + n→+∞ 2 22 2n n→+∞ 3 32 3n [Gợi ý] a. Tính 1 1 3 Sn − S S S S . 2 n⇒ lim n = 2. b. Tính Sn − n⇒ lim n = n→+∞ 3 n→+∞ 4
Bài tập 1.23. Chứng minh rằng √ √
lim n n = 1, lim n a = 1 với mọi a > 0. n→+∞ n→+∞ [Gợi ý] a) Đặt √ n(n − 1) 2
αn = n n − 1⇒n = (1 + αn)n > α2 <
. Áp dụng nguyên lý giới 2 n⇒α2n n − 1 hạn kẹp ta có √ lim α n n = 0. Vậy lim n = 1. n→∞ n→∞ b) Xét √ lim n a. n→+∞ • Nếu a = 1, xong. √ √ √
• Nếu a > 1, 1 ≤ n a ≤ n n ∀n > a⇒ lim n a = 1 n→+∞ 1 √ √
• Nếu a < 1, đặt a′ = ⇒ lim n a′ = 1⇒ lim n a = 1. a n→+∞
Bài tập 1.24. Tính lim x , ở đó ( n xn = 1 n phép chia). n→+∞ 2+ 1 2+···+ 12 [Lời giải] 24 4. Dãy số 25
1) Trước hết ta chứng minh √ √
0 < x2n < −1 + 2 và x2n+1 > −1 + 2. Thật vậy, √ √ Nếu 1 1 1 xn > −1 + 2 thì xn+1 = < √ = √ = −1 + 2. 2 + xn 2 + (−1 + 2) 1 + 2 √ √ Nếu 1 1 1 xn < −1 + 2 thì xn+1 = > √ = √ = −1 + 2. 2 + xn 2 + (−1 + 2) 1 + 2 Như vậy, dãy √
{xn} này có quy luật là, cứ một số hạng nào đó nhỏ hơn −1 + 2 thì số
hạng đứng ngay sau nó lớn hơn √
−1 + 2, và ngược lại. Do đó, 1 √ √ √ x1 = > −1 + 2 ⇒ x 2 ⇒ x 2 ⇒ · · · 2 2 < −1 + 3 > −1 +  √ 
dẫn đến việc 0 < x2n < −1 + 2, √ x2n+1 > −1 + 2.
2) Tiếp theo, ta đi chứng minh dãy {x2n} là một dãy số tăng, thật vậy, 1 1 2 + x x 2n 2n+2 = = = . 2 + x2n+1 2 + 1 5 + 2x 2+x 2n 2n 2 + x √ √ x 2n 2n+2 > x2n ⇔ > x 2 < x 2 5 + 2x
2n ⇔ 2x22n + 4x2n − 2 < 0 ⇔ −1 − 2n < −1 + 2n
Điều này luôn đúng, vì ta đã chứng minh ở trên, rằng dãy các số hạng chẵn thỏa mãn √ x2n < −1 + 2.
Dãy số này tăng và bị chặn trên bởi √
−1 + 2 nên tồn tại lim x2n = a. Phương trình n→+∞ √ x dẫn đến 2n+2 = 2+x2n a = 2+a 2. 5+2x2n 5+a ⇒ a = −1 +
3) Tương tự như vậy, dãy {x2n+1} sẽ là một dãy số giảm. Thật vậy, 1 1 2 + x x 2n+1 2n+3 = = = . 2 + x2n+2 2 + 1 5 + 2x 2+x 2n+1 2n+1 √ √
x2n+3 < x2n+1 ⇔ 2x22n+1 + 4x2n+1 − 2 > 0 ⇔ x2n+1 > −1 + 2 hoặc x2n+1 < −1 − 2
Điều này luôn đúng, vì ta đã chứng minh ở trên, rằng dãy các số hạng lẻ thỏa mãn √ x2n+1 > −1 + 2.
Dãy số này giảm và bị chặn dưới, nên tồn tại giới hạn lim x2n+1 = b. Phương trình n→+∞ √ x dẫn đến 2n+3 = 2+x2n+1 b = 2+b 2. 5+2x2n+1 5+2b ⇒ b = −1 + Kết luận: √ lim xn = −1 + 2. n→+∞ 25 26
Chương 1. Hàm số một biến số (13LT+13BT)
Bài tập 1.25. Dùng tiêu chuẩn Cauchy chứng minh rằng dãy số 1 1 un = 1 + + · · · + 2 n phân kì.
Bài tập 1.26. Chứng minh rằng nếu a lim a 1 + a2 + · · · + an n = a thì lim = a. n→+∞ n→+∞ n
Bài tập 1.27. Chứng minh rằng nếu √
lim an = a, an > 0∀n thì lim n a1a2 . . . an = a. n→+∞ n→+∞ 26
5. Giới hạn hàm số 27
§5. GIỚI HẠN HÀM SỐ 5.1 Định nghĩa
Định nghĩa 1.9. Giả sử rằng hàm số f (x) được xác định tại mọi điểm x ∈ (a, b) \ {x0}. Ta
nói giới hạn của hàm số f (x) khi x tiến đến x bằng 0 L và viết lim f (x) = L x→x0
• (nói một cách nôm na) nếu ta có thể làm cho giá trị của hàm số f (x) gần L với một
giá trị tùy ý bằng cách chọn x đủ gần x . 0
• (nói một cách chính xác) nếu với mọi ǫ > 0, tồn tại số thực δ > 0 sao cho
nếu |x − x0| < δ thì | f (x) − L| < ǫ.
Hình dung rằng lim f (x) = L nghĩa là với mọi ǫ > 0, tồn tại số δ > 0 sao cho đồ thị của x→x0
hàm số trong khoảng (x0 − δ, x0 + δ) sẽ nằm hoàn toàn trong dải (L − ǫ, L + ǫ). y L + ǫ b L − ǫ x0 x O Hình 1.9
Các giới hạn một phía lim = L, lim = L và giới hạn lim f (x) = L được định nghĩa một x→x+ x x→∞ 0 →x− 0 cách tương tự.
Định lý 1.7 (Tính duy nhất của giới hạn). Giới hạn của hàm số lim f (x), nếu tồn tại, x→x0 là duy nhất.
5.2 Các phép toán trên giới hạn
Định lý 1.8 (Các phép toán trên giới hạn). Giả sử lim f (x) = a, lim g(x) = b, ở đó x→x0 x→x0
a, b là các số thực hữu hạn. Khi đó,
• Tổng: lim [ f (x) + g(x)] = a + b, x→x0 27 28
Chương 1. Hàm số một biến số (13LT+13BT)
• Hiệu: lim [ f (x) − g(x)] = a − b, x→x0
• Tích: lim [ f (x)g(x)] = ab, x→x0
• Thương: lim f (x) = a, nếu b 6= 0. x→x g(x) b 0
Chú ý 1.5. Các phép toán trên giới hạn sau không thực hiện được, chúng còn được gọi là các dạng vô định: ∞ 0 ∞ − ∞, 0 × ∞, , . ∞ 0
5.3 Giới hạn của hàm hợp
Nếu có lim u(x) = uo, lim f (u) = f (uo) và có hàm hợp f (u(x)) thì x→x0 u→uo lim f (u(x)) = f (uo). x→x0 Áp dụng lim B(x) ln A(x) lim A(x)B(x) = ex→x0 . x→x0 5.4 Giới hạn vô cùng
Định nghĩa 1.10. Giả sử rằng hàm số f (x) được xác định tại mọi điểm x ∈ (a, b) \ {x0}.
Ta nói giới hạn của hàm số f (x) khi x tiến đến x bằng vô cùng và viết 0 lim f (x) = ∞ x→x0
nếu với mọi số M > 0, tồn tại số thực δ > 0 sao cho
nếu |x − x0| < δ thì | f (x)| > M.
Các giới hạn một phía lim = ∞, lim = ∞ và giới hạn lim f (x) = ∞ được định nghĩa một x→x+ x x→∞ 0 →x− 0 cách tương tự.
5.5 Các tiêu chuẩn tồn tại giới hạn
Định lý 1.9. Nếu f (x) ≤ g(x) với mọi x trong một lân cận nào đó của a, và tồn tại các giới hạn lim f (x), lim g(x) thì x→a x→a lim f (x) ≤ lim g(x). x→a x→a
Hệ quả 1.1 (Tiêu chuẩn kẹp). Nếu f (x) ≤ g(x) ≤ h(x) trong một lân cận nào đó của a,
và tồn tại các giới hạn lim f (x) = lim h(x). Khi đó tồn tại lim g(x), và x→a x→a x→a lim f (x) = lim g(x). x→a x→a 28
5. Giới hạn hàm số 29
5.6 Mối liên hệ giữa giới hạn của dãy số và giới hạn của hàm số
Nhiều bài toán giới hạn của dãy số có thể được chuyển về giới hạn của hàm số và lợi
dụng các công cụ của giới hạn của hàm số để tính toán một cách dễ dàng. Chúng thể hiện qua mối liên hệ sau.
Định lý 1.10. lim f (x) = L khi và chỉ khi với mọi dãy số {x thì n} sao cho lim xn = x0 x→x0 n→+∞ lim f (x và
n) = L, ở đó (chỉ riêng trong Định lý này) x0
L có thể là một số thực hữu hạn n→+∞ hoặc bằng vô cùng.
Chẳng hạn như, muốn chứng minh lim ln n = 0 ta có thể đưa về lim ln x = 0. n→+∞ n x→∞ x 5.7 Bài tập Bài tập 1.28. Tính a) x100 − 2x + 1 0
(xn − an) − nan−1(x − a) 0 lim b) lim x→1 x50 − 2x + 1 0 x→a (x − a)2 0
Phương pháp phân tích đa thức thành nhân tử. Nếu Pn(x0) = Qm(x0) = 0 thì P (x − x P lim n(x) = lim 0).Pn−1(x) = lim n−1(x) . x→x0 Qm(x) x→x0 (x − x0).Qm−1(x) x→x0 Qm−1(x) [Đáp số] a) 49 b) n(n − 1).an−2 24 2
Bài tập 1.29. Tìm giới hạn q √ p √ b) x + x + x lim ( 3 x3 + x2 − 1 − x) (∞ − ∞). a) ∞ x→+∞ lim √ . x→+∞ x + 1 ∞ Chứng minh.
a) Chia cả tử và mẫu cho √x ta được q p √ q p √ x + x + x 1 + 1/x + 1/x3 lim √ = lim √ = 1. x→+∞ x + 1 x→∞ 1 + 1/x
b) Sử dụng phương pháp nhân liên hợp ta được x2 − 1 1 lim ( 3 px3 + x2 − 1 − x) = lim p √ = . x→+∞
x→∞ 3 (x3 + x2 − 1)2 + x 3 x3 + x2 − 1 + x2 3 29 30
Chương 1. Hàm số một biến số (13LT+13BT)
§6. VÔ CÙNG LỚN, VÔ CÙNG BÉ 6.1 Vô cùng bé (VCB)
Định nghĩa 1.11. Hàm số f (x) được gọi là một vô cùng bé (viết tắt là VCB) khi x → a nếu lim f (x) = 0. x→a
Mối liên hệ giữa giới hạn và VCB
lim f (x) = ℓ ⇐⇒ f (x) = ℓ + α(x); x→a
trong đó α(x) là một VCB trong quá trình x → a.
Một số tính chất của VCB
1. Tổng hai VCB (đối với một VCB người ta không quan tâm đến dấu của nó) là một VCB.
2. Tích của VCB với một đại lượng bị chặn là một VCB.
3. Tích các VCB là một VCB.
Chú ý: Thương của hai VCB là một dạng vô định 0. 0 So sánh các VCB
Định nghĩa 1.12 (VCB cùng bậc, tương đương). Giả sử α(x) và β(x) là các VCB khi x → a.
i) Nếu lim α(x) = A 6= 0, ta nói rằng α(x), β(x) là các VCB cùng bậc. x→a β(x)
ii) Đặc biệt, nếu lim α(x) = 1 thì ta nói α(x) và β(x) là các VCB tương đương và viết x→a β(x) α(x) ∼ β(x).
Một số VCB tương đương hay dùng trong quá trình x → 0 ax − 1
• x ∼ sin x ∼ tan x ∼ arcsin x ∼ arctan x ∼ ex − 1 ∼ ∼ ln(1 + x), ln a √ αx
• (1 + x)a − 1 ∼ ax. Đặc biệt, m 1 + αx − 1 ∼ , m 30
6. Vô cùng lớn, vô cùng bé 31 x2 • 1 − cos x ∼ . 2
Định nghĩa 1.13 (VCB bậc cao). Nếu lim α(x) = 0, ta nói rằng α(x) là VCB bậc cao hơn x→a β(x)
β(x) và kí hiệu α(x) = o(β(x)). Định lý 1.11.
a) Hiệu hai VCB tương đương là một VCB bậc cao hơn VCB đó.
b) Tích hai VCB là một VCB bậc cao hơn cả hai VCB đó.
Ứng dụng của VCB để tìm giới hạn
Định lý 1.12 (Quy tắc thay tương đương). Nếu α1(x) ∼ α2(x), β1(x) ∼ β2(x) khi x → a thì α α lim 1(x) = lim 2(x) ,
lim α1(x)γ(x) = lim α2(x)γ(x). x→a β1(x) x→a β2(x) x→a x→a
Định lý 1.13 (Quy tắc ngắt bỏ VCB bậc cao). Nếu α1(x) = o(α2(x)), β1(x) = o(β2(x)) khi x → a thì α α α 1(x) + α2(x) 2(x)
1(x) + α2(x) ∼ α2(x) và lim = lim .
x→a β1(x) + β2(x) x→a β2(x)
Chú ý 1.6. Sai lầm hay mắc: Thay tương đương khi có hiệu hai VCB. Chẳng hạn như, với
VCB α(x) = sin x − tan x + x3 khi x → 0 ta có
i) Thay tương đương α(x) ∼ x3,
ii) Thực tế, α(x) ∼ x3. 2 Thật vậy, sin x − tan x + x3 sin x 1 − 1 cos x − sin x(1 − cos x) 1 lim = 1 + lim = 1 + lim = . x→0 x3 x→0 x3 x→0 x3 cos x 2
Ví dụ 6.1 (Giữa kì, K61). So sánh cặp vô cùng bé sau đây khi x → 0 a) √ α(x) = 3 x2 + x3, β(x) = esin x − 1. b) √ α(x) = 5 x4 + x5, β(x) = etan x − 1. c) √ α(x) = 5 x4 − x5, β(x) = ln(1 + tan x). d) √ α(x) = 3 x2 − x3, β(x) = ln(1 + sin x). e) √ √ α(x) = e x − 1, β(x) = x + x2.
f) α(x) = ex2 − 1, β(x) = x2 + x3. 31 32
Chương 1. Hàm số một biến số (13LT+13BT) 6.2 Vô cùng lớn (VCL)
Định nghĩa 1.14. Hàm số f (x) được gọi là một vô cùng lớn (viết tắt là VCL) khi x → a nếu lim | f (x)| = ∞. x→a
Nghịch đảo của một VCB là một VCL, và ngược lại. So sánh các VCL
Định nghĩa 1.15 (VCL cùng bậc, tương đương). Giả sử α(x) và β(x) là các VCL khi x → a.
i) Nếu lim α(x) = A 6= 0, ta nói rằng α(x), β(x) là các VCL cùng bậc. x→a β(x)
ii) Đặc biệt, nếu lim α(x) = 1 thì ta nói α(x) và β(x) là các VCL tương đương và viết x→a β(x) α(x) ∼ β(x).
Định nghĩa 1.16 (VCL bậc cao). Nếu lim α(x) = ∞, ta nói rằng α(x) là VCL bậc cao hơn x→a β(x) β(x).
Ứng dụng VCL khử dạng ∞ ∞
Định lý 1.14 (Quy tắc thay tương đương). Nếu α1(x) ∼ α2(x), β1(x) ∼ β2(x) là các VCL khi x → a thì α α lim 1(x) = lim 2(x) ,
lim α1(x)γ(x) = lim α2(x)γ(x). x→a β1(x) x→a β2(x) x→a x→a
Định lý 1.15 (Quy tắc ngắt bỏ VCL bậc thấp). Nếu α1(x) là VCL bậc cao hơn α2(x) và
β1(x) là VCL bậc cao hơn β2(x) khi x → a thì α α α 1(x) + α2(x) 1(x)
1(x) + α2(x) ∼ α1(x) và lim = lim .
x→a β1(x) + β2(x) x→a β1(x)
Chú ý 1.7. Còn tồn đọng một số dạng vô định mà phương pháp sử dụng các VCB-VCL
chưa xử lý được, ví dụ x − sin x lim , lim xsin x, . . . x→0 x3 x→0+
Các giới hạn này sẽ được xử lý khi chúng ta học đến công thức L’Hospital và khai triển Maclaurin.
Ví dụ 6.2 (Giữa kì, K61). Tính giới hạn 32
6. Vô cùng lớn, vô cùng bé 33 a) 1−cos x lim ex2−1 . c) lim . ln(1+x2) x→0+ x2+x3 x→0 √ b) x lim e −1 √ . d) lim e2x−1 . x→0+ x+x2 x→0 ln(1−3x) 6.3 Bài tập
Như vậy ngoài các phương pháp phân tích đa thức thành nhân tử và nhân liên
hợp đã trình bày ở trên, bài học hôm nay cung cấp cho chúng ta một công cụ mới để tìm
giới hạn, đó là các quy tắc thay tương đương và ngắt bỏ các VCB bậc cao. Đây có lẽ là một
trong những công cụ rất tốt của Giải tích để tính giới hạn.
Bài tập 1.30. Tìm giới hạn √ √ m p m p a.
1 + αx − n 1 + βx 0
1 + αx. n 1 + βx − 1 0 lim b. lim x→0 x 0 x→0 x 0 Chứng minh. a. √ √ m p p
1 + αx − n 1 + βx m 1 + αx − 1 n 1 + βx − 1 = − x x x Vì √ α β m p 1 + αx − 1 ∼
x, n 1 + βx − 1 ∼ x, nên m n √ m p
1 + αx − n 1 + βx α β lim = − x→0 x m n b. √ √ ! m p p
1 + αx. n 1 + βx − 1 √ n 1 + βx − 1 m 1 + αx − 1 α β lim = lim m 1 + αx. + = + . x→0 x x→0 x x m n Chú ý 1.8.
i) Lưu ý kĩ thuật thêm bớt p
1 ở trong các biểu thức có chứa cos α(x), eα(x) và ln(α(x)), m 1 + α(x).
ii) Với nhiều bài toán nhìn qua tưởng rất phức tạp vì công thức rất cồng kềnh, thực chất
nếu dùng quy tắc thay tương đương và ngắt bỏ các VCB bậc cao thì sẽ thấy rất đơn giản. Ví dụ, tính
sin 2x + arcsin2 x − arctan2 x lim . x→0 3x
Với tử số ta có sin 2x ∼ 2x, arcsin2 x ∼ x2, arctan2 x ∼ x2. Như vậy giới hạn đã cho
bằng 2. Hoặc ví dụ như tính 3
1 − cos x + 2 sin x − sin3 x − x2 + 3x4 lim . x→0
tan3 x − 6 sin2 x + x − 5x3 33 34
Chương 1. Hàm số một biến số (13LT+13BT)
Trông biểu thức này rất phức tạp nhưng thực chất chúng ta có thể nhìn thấy ngay
giới hạn này bằng lim 2sin x = 2 với nhận xét là 2 sin x ∼ 2x là VCB bậc thấp nhất ở x→0 x
tử số và x là VCB bậc thấp nhất ở mẫu số.
Bài tập 1.31. Tìm giới hạn √ √ a) sin x − sin a 0 cos x − 3 cos x 0 lim c) lim x→a x − a 0 x→0 sin2 x 0 1 0 b) √ √ − cos x cos 2x cos 3x lim (sin x + 1 − sin x) d) lim . x→+∞ x→0 1 − cos x 0 [Đáp số] a) cos a b) 0 c) −1 d) 14 12
Bài tập 1.32. Tìm giới hạn x−1 x+1
c) lim [sin(ln(x + 1)) − sin(ln x)] a) x2 − 1 lim x→∞ x→∞ x2 + 1 b) √ 1 √ √ lim (cos x) x (1∞)
d) lim n2( n x − n+1 x), x > 0. x→0+ n→∞ x−1 x+1 Chứng minh.
a) Đây không phải là dạng vô định, x2 − 1 lim = 1. x→∞ x2 + 1 b) Áp dụng công thức lim B(x) ln A(x) lim A(x)B(x) = ex→x0 . Vì x→x0 √ √ √ 1 ln cos x − sin x 1 lim ln cos x x = lim = lim √ = − x→0+ x→0+ x x→0+ 2 x 2 nên √ 1 lim ln cos x x = e− 12 . x→0+ c) Đáp số: 0. 34
6. Vô cùng lớn, vô cùng bé 35 d) √ √
lim n2( n x − n+1 x), x > 0 n→∞ 1 1 = lim n2(x n − x n+1 ) n→∞ 1 1 = lim n2x n+1 (x n(n+1) − 1) n→∞ 1 1 x n(n+1) − 1 1 = lim n2x n+1 . . n→∞ 1 n(n + 1) n(n + 1) 1 n 1 x n(n+1) − 1 = lim .x n+1 . n→∞ n + 1 1 n(n + 1) = ln x So sánh các VCB-VCL. Chú ý 1.9.
i) So sánh 2 VCB: Nếu lim α(x) = 0 thì ta nói α(x) là VCB bậc cao hơn β(x), nhưng x→a β(x)
ii) So sánh 2 VCL: Nếu lim α(x) = ∞ thì ta nói α(x) là VCL bậc cao hơn β(x). x→a β(x) iii) Cùng một biểu thức p √ α(x) = x +
x chẳng hạn, thì nếu trong quá trình x → 0+
thì nó là VCB nên theo quy tắc ngắt bỏ VCB bậc cao, p√ α(x) ∼ x = x1/4, còn nếu
xét trong quá trình x → ∞ thì nó là VCL nên theo quy tắc ngắt bỏ VCL bậc thấp, √ α(x) ∼ x.
Bài tập 1.33. Khi x→0 cặp VCB sau có tương đương không ? q √ α(x) = x +
x và β(x) = esin x − cos x
[Đáp số] β(x) = o(α(x))
Bài tập 1.34. Tìm giới hạn a) 1 lim (1 − 2x) 1 x (1∞), 1 + tan x sin x x→0+ c) lim (1∞), x→0 1 + sin x sin x b) sin x x−sin x lim (sin x)tan x (1∞), d) lim (1∞), x→ π2 x→0 x 35 36
Chương 1. Hàm số một biến số (13LT+13BT) [Gợi ý] Áp dụng lim B(x) ln A(x) lim A(x)B(x) = ex→x0 x→x0 [Đáp số] a) e−2 b) 1 c) 1 d) e
Bài tập 1.35. Tìm giới hạn ax a) eαx − eβx eαx − eβx − xa 0 lim 0 , b) lim 0 , c) lim . 0 x→0 x 0
x→0 sin αx − sin βx 0 x→a x − a
[Gợi ý] Sử dụng phương pháp thay tương đương. [Đáp số] a) α − β b) 1 c) aa(ln a − 1) 36
7. Hàm số liên tục 37
§7. HÀM SỐ LIÊN TỤC 7.1 Định nghĩa
Định nghĩa 1.17. Cho hàm số f (x) xác định trong một lân cận nào đó của x . Nó được 0 gọi là
i) liên tục phải tại x nếu 0 lim = f (x0), x→x+ 0
ii) liên tục trái tại x nếu 0 lim = f (x0), x→x− 0 iii) liên tục tại x nếu 0
lim = f (x0). Nói cách khác, x→x0
∀ε > 0, ∃δ(ε, x0) > 0 : ∀x, |x − x0| < δ ta có | f (x) − f (x0)| < ε.
Từ định nghĩa suy ra hàm số f (x) liên tục tại x khi và chỉ khi nó liên tục phải và liên tục 0 trái tại x . 0
Ví dụ 7.1. Tất cả các hàm số sơ cấp đều liên tục trên tập xác định của chúng.
Ví dụ 7.2 (Giữa kì, K61). Tìm m để hàm số sau liên tục tại x = 1 :   a) (x − m)(x2 + x + 1), nếu x 6= 1, f (x) = 1 + m, nếu x = 1.   b) (x + m)(x2 + x + 1), nếu x 6= 1, f (x) = 1 − m, nếu x = 1.
Định nghĩa 1.18. Hàm số f (x) được gọi là liên tục trên khoảng (a, b) nếu nó liên tục tại
mọi điểm x0 ∈ (a, b). Nó được gọi là liên tục trên đoạn [a, b] nếu nó liên tục tại mọi điểm
x0 ∈ (a, b), đồng thời liên tục phải tại a và liên tục trái tại b.
7.2 Các phép toán số học đối với hàm số liên tục
Định lý 1.16. Giả thiết các hàm số f (x) và g(x) liên tục tại x nào đó. Khi đó các hàm số 0
f (x) ± g(x), f (x)g(x) cũng liên tục tại x . Hàm số f (x) cũng liên tục tại nếu 0 x g(x g(x) 0 0) 6= 0.
Điều tương tự cũng đúng đối với các hàm số liên tục trái (phải) tại x . 0 37 38
Chương 1. Hàm số một biến số (13LT+13BT)
7.3 Sự liên tục của hàm ngược
Định lý 1.17. (Sự liên tục của hàm ngược)
Nếu X là một khoảng, y = f (x) đồng biến (nghịch biến) liên tục trên X. Khi đó có hàm
ngược y = g(x) cũng đồng biến (nghịch biến) và liên tục trên f (X).
Ví dụ: Các hàm số lượng giác ngược là liên tục trên tập xác định của chúng.
7.4 Sự liên tục của hàm hợp
Định lý 1.18. Nếu hàm số f (x) liên tục tại b và lim g(x) = b thì lim f (g(x)) = b. Nói cách x→a x→a khác, lim f (g(x)) = f (lim g(x)) x→a x→a
Hệ quả 1.2. Nếu g(x) liên tục tại a và f (x) liên tục tại g(a) thì hàm số f ◦ g liên tục tại a.
7.5 Các định lý về hàm liên tục
Định lý 1.19. Nếu f (x) liên tục trên khoảng (a, b) mà giá trị f (x0), x0 ∈ (a, b) dương (hay
âm) thì tồn tại một lân cận U(x0) sao cho ∀x ∈ U(x0), f (x) cũng dương hay âm. Hình ảnh hình học.
Định lý 1.20. Nếu f (x) liên tục trên đoạn [a, b] thì nó bị chặn trên đoạn đó. Hình ảnh hình học.
Định lý 1.21. Nếu f (x) liên tục trên đoạn [a, b] thì nó đạt được GTLN, NN trên đoạn này. Hình ảnh hình học.
* Liên tục đều, hình ảnh hình học của liên tục đều.
Định lý 1.22. (Định lý Cantor)
Nếu f (x) liên tục trên [a, b] thì nó liên tục đều trên đó (thay [a, b] bằng khoảng (a, b) thì
định lý không còn đúng). Mô tả hình học.
Định lý 1.23. (Định lý Cauchy)
Nếu f (x) liên tục trên đoạn [a, b] và có f (a). f (b) < 0 thì ∃α ∈ (a, b) để f (α) = 0.
Ví dụ 7.3 (Giữa kì, 20173). Cho hàm số f : [1, 3] → [1, 3] liên tục. Chứng minh rằng tồn tại x .
0 ∈ [1, 3] sao cho f (x0) = x0 38
7. Hàm số liên tục 39
[Lời giải] Xét g(x) = f (x) − x ⇒ g(1) = f (1) − 1 ≥ 0, g(3) = f (3) − 3 ≤ 0. Theo Định lý
Cauchy, phương trình g(x) = 0 có nghiệm x nào đó trong khoảng 0 [1, 3] ⇒ f (x0) = x0.
Hệ quả 1.3. Nếu f (x) liên tục trên đoạn [a, b] , A = f (a) 6= B = f (b) thì nó nhận mọi giá
trị trung gian giữa A và B.
Hệ quả 1.4. Cho f (x) liên tục trên [a, b] , m, M lần lượt là các GTNN, LN của hàm số trên
đoạn này thì [m; M] là tập giá trị của hàm số.
7.6 Điểm gián đoạn và phân loại điểm gián đoạn của hàm số
Định nghĩa 1.19. Nếu hàm số không liên tục tại điểm x thì ta nói nó gián đoạn tại . 0 x0
Hình ảnh hình học: đồ thị không liền nét tại điểm gián đoạn.
Theo định nghĩa, hàm số f (x) liên tục tại x nếu ba điều kiện sau được thỏa mãn: 0
• f (x) xác định tại x , 0 • tồn tại lim f (x), x→x0 • lim f (x) = f (x0). x→x0
Như vậy nếu x là điểm gián đoạn của 0 f (x) thì • hoặc x0 6∈ TXĐ,
• hoặc x0 ∈ TXĐ và 6 ∃ lim f (x), x→x0 • hoặc x theo nghĩa cả
0 ∈ TXĐ và ∃ lim f (x) nhưng lim f (x) 6= f (x0), ở đây x → x0 x→x0 x→x0 hai phía hay một phía.
Nếu x0 6∈ TXĐ của f (x) thì có thể có rất nhiều điểm gián đoạn, nên ta chỉ quan tâm
đến những điểm gián đoạn thuộc tập xác định hay là những điểm đầu mút của khoảng xác định.
Phân loại điểm gián đoạn
Giả sử x là điểm gián đoạn của 0 f (x). 39 40
Chương 1. Hàm số một biến số (13LT+13BT)
1. Điểm gián đoạn loại 1: Nếu ∃
lim f (x) = f x+ và lim f (x) = f x− thì x được gọi là điểm gián đoạn 0 0 0 x→x+ x 0 →x− 0
loại 1 của hàm số f (x). Khi đó, có thể xảy ra hai trường hợp: • Nếu f x+ thì giá trị 0 6= f x− 0 f x+ 0 − f x− 0
gọi là bước nhảy của hàm số.
• Đặc biệt: nếu f x+ = f x− thì x được gọi là điểm gián đoạn bỏ được của 0 0 0
hàm số. Khi đó nếu hàm số chưa xác định tại x thì ta có thể bổ sung thêm giá 0
trị của hàm số tại x để hàm số liên tục tại điểm . Còn nếu hàm số xác định 0 x0
tại điểm x thì ta có thể thay đổi giá trị của hàm số tại điểm này để hàm số liên 0 tục tại x . 0
2. Điểm gián đoạn loại 2:
Nếu x không là điểm gián đoạn loại 1 thì ta nói nó là điểm gián đoạn loại 2. 0
Chú ý 1.10. Với quan điểm xem điểm gián đoạn bỏ được là trường hợp đặc biệt của điểm
gián đoạn loại 1, nếu x là điểm đầu mút của khoảng hay đoạn xác định của 0 f (x), mà có
lim f (x) hoặc lim f (x) hữu hạn thì ta cũng xem x là điểm gián đoạn bỏ được của hàm 0 x→x+ x 0 →x− 0 số.
Ví dụ 7.4 (Giữa kì, K61).
a) Điểm x = π là điểm gián đoạn loại gì của hàm số f (x) = 1 2 1−2tan x .
b) Điểm x = −π là điểm gián đoạn loại gì của hàm số f (x) = 1 2 1−2tan x .
Ví dụ 7.5 (Cuối kì, K61-Viện ĐTQT). Điểm x = 0 là điểm gián đoạn loại gì của hàm số a) π π y = e 2 −arctan 1x . b) y = e 2 −arccot 1x . 7.7 Bài tập
Xét tính liên tục của hàm số. Muốn kiểm tra xem f (x) có liên tục tại x hay không 0
chúng ta đi kiểm tra lim f (x) có bằng f (x0) hay không? Đôi khi phải xét lim f (x) và x→x0 x→x+ 0
lim f (x) nếu biểu thức của f (x) ở hai phía của x được cho dưới các công thức khác nhau. 0 x→x− 0
Thậm chí cũng có khi biểu thức của f (x) ở hai phía của x được cho cùng một công thức 0
nhưng giới hạn trái và giới hạn phải của f (x) tại x vẫn khác nhau. Ví dụ, xét sự liên tục 0   1 của hàm số f (x) = 1−2cot x ,
x 6= 0,. Hàm số này có lim f(x) = 0 và lim f(x) = 1 (tại 1, x = 0 x→0+ x→0−
sao?). Do đó nó liên tục trái tại 0 và không liên tục phải tại 0.
Bài tập 1.36. Tìm a để hàm số liên tục tại x = 0 40
7. Hàm số liên tục 41    1−cos x  a) , nếu x 6= 0 ax2 + bx + 1, nếu x ≥ 0 f (x) = x b) g(x) = a, nếu x = 0. a cos x + b sin x, nếu x < 0. [Đáp số] a) a = 1 b) a = 1 2
Bài tập 1.37. Điểm x = 0 là điểm gián đoạn loại gì của hàm số a) 8 y = , b) sin 1 eax x , c) − ebx 1 − 2cot x y = y = (a 6= b). 1 e x x − 1 [Đáp số] a) Loại I b) Loại II c) Bỏ được
Bài tập 1.38. Xét sự liên tục của các hàm số sau     a) x sin 1 , nếu x 6= 0 sin πx, nếu x vô tỉ f (x) = x c) f (x) = 0, nếu x = 0 0, nếu x hữu tỉ   b) e− 1x2 , nếu x 6= 0 f (x) = 0, nếu x = 0 [Đáp số] a) liên tục b) liên tục c) gián đoạn
Bài tập 1.39. Chứng minh rằng nếu f , g là các hàm số liên tục trên đoạn [a, b] và f (x) =
g(x) với mọi x là số hữu tỉ trong đoạn [a, b] thì f (x) = g(x)∀x ∈ [a, b].
Bài tập 1.40. Chứng minh rằng phương trình x5 − 3x − 1 có ít nhất một nghiệm trong khoảng (1, 2).
Bài tập 1.41. Cho f (x) = ax2 + bx + c, biết 2a + 3b + 6c = 0. Chứng minh rằng f (x) có ít
nhất một nghiệm trong khoảng (0, 1).
Bài tập 1.42. Chứng minh rằng nếu f : [0, 1]→[0, 1] liên tục thì tồn tại x0 ∈ [0, 1] sao cho f (x0) = x0.
Bài tập 1.43. Chứng minh rằng mọi đa thức bậc lẻ với hệ số thực đều có ít nhất một nghiệm thực. 41 42
Chương 1. Hàm số một biến số (13LT+13BT)
§8. ĐẠO HÀM VÀ VI PHÂN 8.1 Định nghĩa
Định nghĩa 1.20. Giới hạn, nếu có, của tỉ số f (x lim 0 + ∆x) − f (x0) ∆x→0 ∆x
được gọi là đạo hàm của hàm số f (x) tại x và được kí hiệu là 0
f ′(x0). Khi đó ta nói hàm số
f (x) có đạo hàm tại x . 0
Nếu quá trình ∆x → 0 trong định nghĩa trên được thay bằng
• ∆x → 0+ thì giới hạn đó được gọi là đạo hàm phải của hàm số f (x) tại x , kí hiệu là 0 f ′(x+). 0
• ∆x → 0− thì giới hạn đó được gọi là đạo hàm trái của hàm số f (x) tại x , kí hiệu là 0 f ′(x−). 0
Đương nhiên, một hàm số có đạo hàm tại x khi và chỉ khi nó có đạo hàm trái và đạo hàm 0 phải tại x . 0 Nếu tồn tại f ′(x
. Tuy nhiên, điều ngược lại không đúng, chẳng
0) thì f (x) liên tục tại x0
hạn như hàm số f (x) = |x| liên tục tại 0 nhưng không có đạo hàm tại đó.
Ví dụ 8.1 (Giữa kì, K61). Tính f ′(0), biết     a) sin x, nếu x ≥ 0, tan x, nếu x ≥ 0, f (x) = b) f (x) = x2 + x, nếu x < 0. −x2 + x, nếu x < 0.
Ví dụ 8.2 (Giữa kì, K61). Hãy chỉ ra một hàm số f (x) xác định trên R, liên tục tại các
điểm x0 = 1, x1 = 2 nhưng không có đạo hàm tại các điểm này.
Ví dụ 8.3 (Giữa kì, K59). Cho hàm số f (x) khả vi tại 1 và biết rằng f (1 + 7x) − f (1 + 2x) lim = 2. x→0 x Tính f ′(1). [Lời giải] Ta có f (1 + 7x) − f (1 + 2x) f (1 + 7x) − f (1) f (1 + 2x) − f (1) lim = lim 7. − 2. x→0 x x→0 7x 2x 2
= 7 f ′(1) − 2 f ′(1) ⇒ f ′(1) = . 5 42
8. Đạo hàm và vi phân 43  
Ví dụ 8.4 (Giữa kì, 20173). Cho hàm số e− 1x , nếu x > 0, f (x) = 0, nếu x = 0. Tính f ′+(0). [Lời giải] Ta có f (x) − f (0) e− 1x f ′+(0) = lim = lim . x→0+ x − 0 x→0+ x Đặt t = 1 t = lim 1 = 0 (L’Hospital) x ⇒ f ′+(0) = lim t→+∞ et t→+∞ et
8.2 Các phép toán trên đạo hàm
Định lý 1.24. Cho u(x) và v(x) là các hàm số có đạo hàm tại x . Khi đó, 0
i) (u ± v)′(x0) = u′(x0) ± v′(x0),
ii) (uv)′(x0) = u′(x0)v(x0) + u(x0)v′(x0), iii) u (x nếu v(x v
0) = u′(x0)v(x0)−u(x0)v′(x0) v2(x 0) 6= 0. 0)
Ví dụ 8.5 (Giữa kì, K61-Viện ĐTQT). Tính đạo hàm của hàm số
a) f (x) = xsin x, 0 < x < π.
d) f (x) = (cos x)x, 0 < x < π. 2 2
b) f (x) = (sin x)x, 0 < x < π.
e) f (x) = (cos x)sin x, 0 < x < π. 2 2
c) f (x) = xcos x, 0 < x < π.
f) f (x) = (sin x)cos x, 0 < x < π. 2 2
8.3 Đạo hàm của hàm hợp
Định lý 1.25. Nếu u có đạo hàm tại x và f có đạo hàm tại u(x) thì hàm số hợp F = f ◦ u có đạo hàm tại x và F′(x) = f ′(u(x)).u′(x).
Ý tưởng chứng minh: ta có ′
u (x0 + ∆x) = u (x0) + u (x0) ∆x + o (∆x)   ′ ′ f [u (x   0 + ∆x)] − f [u (x0)] = f ( uo + u
x0)∆x + o (∆x) − f (x0) = fu (uo) .δy + o δy | {z } δy f [u (x =⇒ lim 0 + ∆x)] − f [u (x0)] ∆x→0 ∆x 43 44
Chương 1. Hàm số một biến số (13LT+13BT)
8.4 Đạo hàm của hàm ngược
Định lý 1.26. Giả thiết i) ′
x = ϕ (y) có đạo hàm tại y và 0 ϕ (y0) 6= 0,
ii) x = ϕ (y) có hàm ngược y = f (x) liên tục tại x0 = ϕ (y0).
Khi đó hàm ngược này có đạo hàm tại điểm ′ 1 x và . 0 f (x0) = ϕ′(y0)
Định lý 1.27. Giả thiết i) ′
x = ϕ(y) có đạo hàm tại y và 0 ϕ (y0) 6= 0,
ii) x = ϕ(y) biến thiên đơn điệu trong lân cận điểm y . 0
Khi đó nó tồn tại hàm ngược y = f (x), hàm ngược này cũng có đạo hàm tại điểm x và 0 ′ 1 f (x . 0) = ϕ′(yo)
Từ đó xây dựng công thức đạo hàm của các hàm số lượng giác ngược.
8.5 Đạo hàm của các hàm số sơ cấp cơ bản
1. (xα)′ = αxα−1 7. (tan x)′ = 1 cos2 x 2. (ax)′ = ax ln a 8. (cot x)′ = − 1 sin2 x 3. (log 9. (arcsin x)′ = 1 √ a x)′ = 1 x ln a 1−x2 4. (ln x)′ = 1 10. (arccos x)′ = − 1 √ x 1−x2 5. (sin x)′ = cos x 11. (arctan x)′ = 1 1+x2 6. (cos x)′ = − sin x 12. (arccot x)′ = − 1 1+x2
8.6 Vi phân của hàm số
Cho hàm số y = f (x) có đạo hàm tại x. Theo định nghĩa của đạo hàm, ′ ∆y f (x + ∆x) − f (x) f (x) = lim = lim . ∆x→0 ∆x ∆x→0 ∆x 44
8. Đạo hàm và vi phân 45 Do đó, ∆y = ′( ∆
f x) + α(∆x), trong đó α(∆x) là một VCB khi ∆x x → 0. Vậy ′
∆y = f (x + ∆x) − f (x) = f (x)∆x + α.∆x. Số hạng ′
α.∆x là một VCB bậc cao hơn ∆x. Do đó, ∆y và f (x)∆x là hai VCB tương đương.
Định nghĩa 1.21. Cho hàm số f (x) xác định trong một lân cận Uǫ(x0). Nếu có ∆ f = A∆x + o(∆x),
ở đó A chỉ phụ thuộc vào x chứ không phụ thuộc vào 0
∆x thì ta nói hàm số f (x) khả vi tại x và biểu thức 0 d f = A∆x
được gọi là vi phân của hàm số f (x) tại điểm x . 0
Mối liên hệ giữa đạo hàm và vi phân
Định lý 1.28. Hàm số f (x) có đạo hàm tại x khi và chỉ khi nó khả vi tại và 0 x0 d f (x0) = f ′(x0)∆x.
Chú ý 1.11. Khái niệm "có đạo hàm" và khái niệm "có vi phân" (hay khả vi) là hai khái
niệm khác nhau. Tuy nhiên, vì tính tương đương giữa hai khái niệm này đối với hàm số
một biến số mà nhiều người hiểu nhầm rằng chúng là một. Trong chương 3 của học phần
Giải tích I này, chúng ta sẽ thấy hai khái niệm này là khác nhau đối với hàm số nhiều biến số.
Xét hàm số y = f (x) = x có d f (x) = dx = 1.∆x. Vì thế với biến số độc lập x ta quy ước viết ′ dx = ∆x và dy = d f (x) = f (x)dx.
Tính bất biến của dạng thức vi phân (cấp 1)
Cho y = f (x) là một hàm số khả vi. Khi đó, ta đã biết nếu x là biến số độc lập thì d f (x) = f ′(x)dx.
Định lý 1.29. Nếu x không phải là một biến số độc lập mà x = x(t) là một hàm số phụ
thuộc vào biến số t thì công thức d f (x) = f ′(x)dx vẫn còn đúng. 45 46
Chương 1. Hàm số một biến số (13LT+13BT)
Chứng minh. Đặt F(t) = f (x(t)), khi đó F′(t) = f ′(x(t))x′(t) và
d f (x(t)) = f ′(x(t))x′(t)dt.
Mặt khác, dx = x′(t)dt nên d f (x) = f ′(x)dx.
Chính vì vậy, tính chất này còn được gọi là tính bất biến của dạng thức vi phân cấp
một. Chú ý rằng tính chất này không còn đúng đối với các dạng thức vi phân cấp cao. Ví dụ 8.6. Tính d x3 − 2x6 − x9. d (x3)
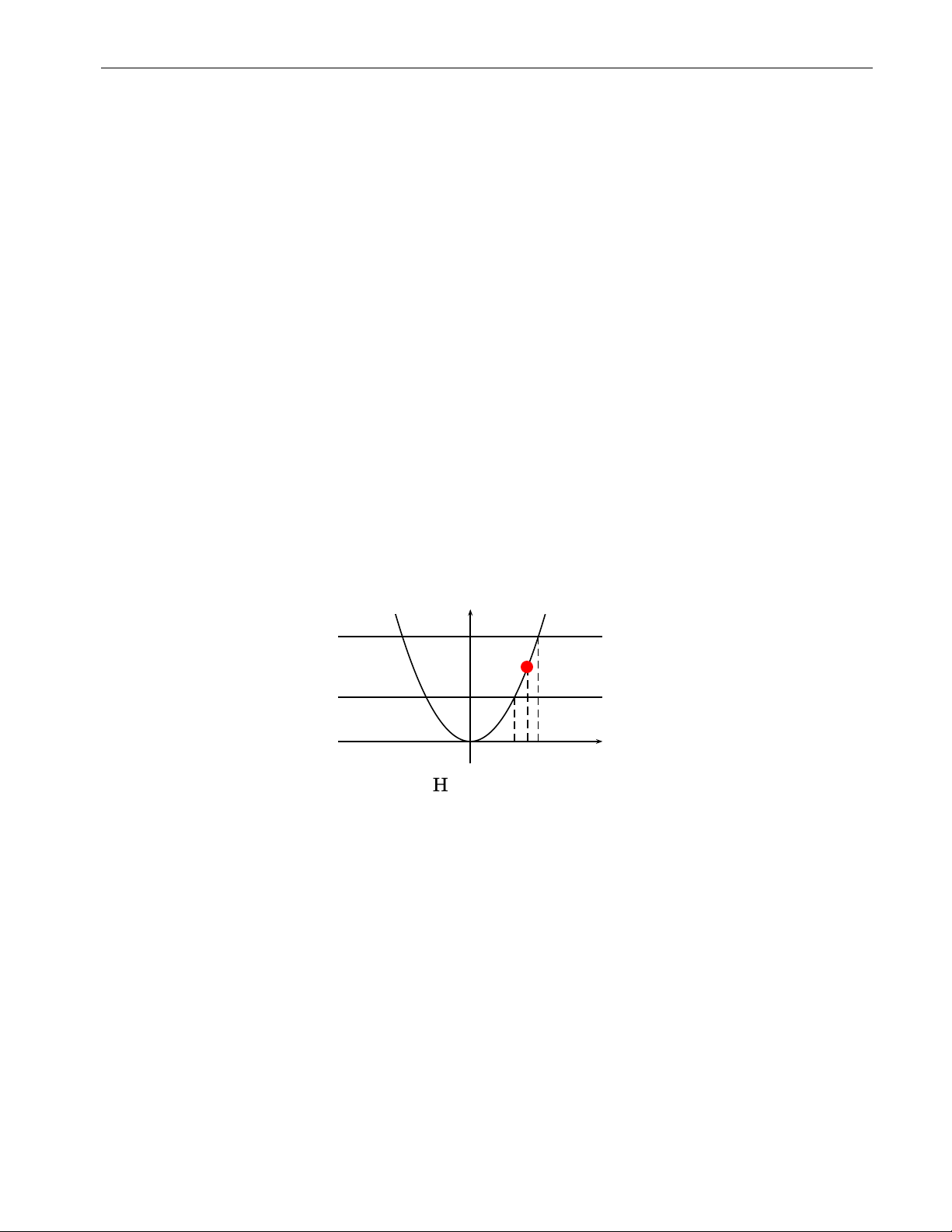
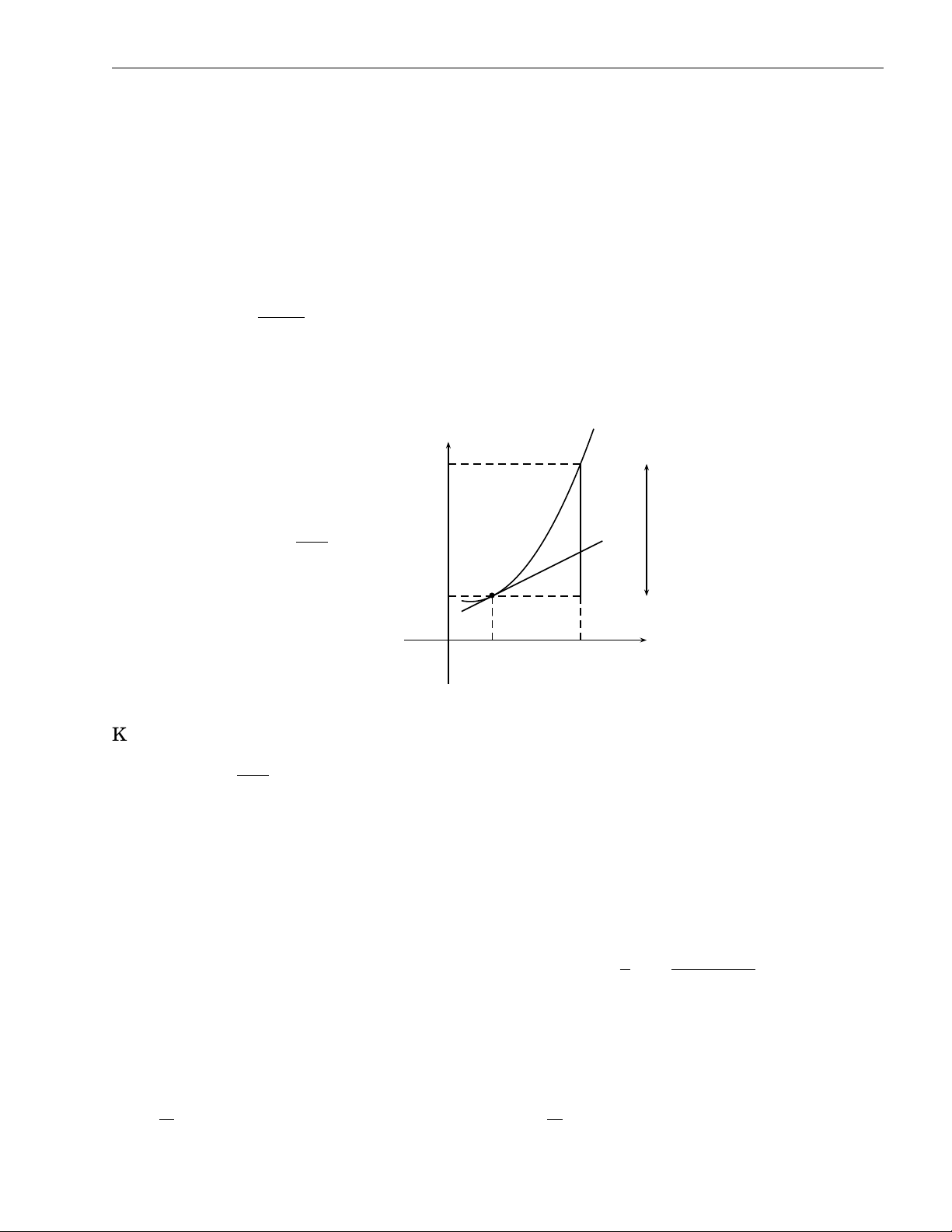
Ý nghĩa hình học của vi phân y y = f (x) yo + ∆y P T ∆y d f (x0) = MT Mo yo b M O x0 x0 + ∆x x
Khi x thay đổi từ x đến 0 x0 + ∆x thì
i) d f (x0) = MT thể hiện sự thay đổi của đường thẳng tiếp tuyến,
ii) ∆y = f (x0 + ∆x) − f (x0) thể hiện sự thay đổi của đường cong y = f (x).
Vi phân của tổng, hiệu, tích, thương u vdu − udv d(u ± v) = du ± dv, d(u.v) = udv + vdu, d = . v v2
Ví dụ 8.7 (Giữa kì, K61). Tìm f ′(x) nếu biết a) d [ f (2016x)] = x2. b) d [ f (2017x)] = x2. dx dx 46
8. Đạo hàm và vi phân 47
Ứng dụng vi phân tính gần đúng
Xuất phát từ công thức ∆ ′
y = f (x + ∆x) − f (x) = f (x)∆x + o(∆x) ta ngắt bỏ phần VCB
bậc cao o(∆x) để được công thức tính gần đúng sau: ′
f (x0 + ∆x) ≈ f (x0) + f (x0)∆x.
Ví dụ 8.8 (Giữa kì, K61). Sử dụng vi phân, tính gần đúng a) √ √ 3 7, 97. b) 3 8, 03.
8.7 Đạo hàm cấp cao
Định nghĩa 1.22. Nếu hàm số ′ ′
y = f (x) có đạo hàm thì y = f (x) gọi là đạo hàm cấp một của f (x).
i) Đạo hàm, nếu có, của đạo hàm cấp một được gọi là đạo hàm cấp hai, kí hiệu là ′′ f (x).
ii) Đạo hàm, nếu có, của đạo hàm cấp n − 1 được gọi là đạo hàm cấp n, kí hiệu là f (n)(x).
Các phép toán trên đạo hàm cấp cao
Định lý 1.30. Cho u, v là các hàm số khả vi đến cấp n. Khi đó, i) (u ± v)(n) = u(n) ± v(n), ii) (Công thức Leibniz) n
(u.v)(n) = ∑ Ckn.u(n−k)v(k). k=0
Ví dụ 8.9. Tính đạo hàm cấp cao của các hàm số sau 1 y = xα, y = , y = sin (ax + b) , x + a
y = cos (ax + b) , y = eax, y = x2 + 1 ex, y = ex sin x.
Đạo hàm cấp cao của một số hàm số cơ bản
1. (xα)(n) = α(α − 1) . . . (α − n + 1)xα−n
2. [(1 + x)α](n) = α(α − 1) . . . (α − n + 1).(1 + x)α−n ( 3. n) 1 = ( 1+x −1)(n). n! (1+x)n+1 ( 4. n) 1 = n! 1−x (1−x)n+1 47 48
Chương 1. Hàm số một biến số (13LT+13BT) 5.
(sin x)(n) = sin x + nπ 2 6.
(cos x)(n) = cos x + nπ 2 7. (ax)(n) = ax. (ln a)n 8. (n − 1)! (ln x)(n) = (−1)n−1. xn
Ví dụ 8.10 (Giữa kì, K61). Tính đạo hàm cấp cao y(10)(0) với a) y(x) = ex2. c) y(x) = arctan x. b) y(x) = e−x2. d) y(x) = arccot x. [Lời giải]
a) Ta có y′(x) = 2xex2 = 2xy. Lấy đạo hàm cấp n hai vế ta được
y(n+1)(x) = (2xy)(n) = 2xy(n)(x) + 2ny(n−1)(x). (Công thức Leibniz)
Thay x = 0 ta được có công thức truy hồi y(n+1)(0) = 2ny(n−1)(0). Do đó,
y(10)(0) = 2.9y(8)(0) = (2.9).(2.7)y(6)(0) = · · · = (2.9)(2.7)(2.5)(2.3)(2.1)y(0)(0) = 30240. b) Tương tự câu a). c) Ta có y′ = 1
1+x2 ⇒ (1 + x2)y′ = 1. Lấy đạo hàm cấp n hai vế ta được n(n − 1)
(1 + x2)y(n+1)(x) + n.2x.y(n)(x) +
.2.y(n−1)(x) = 0. (Công thức Leibniz) 2
Thay x = 0 vào ta được công thức truy hồi
y(n+1)(0) = −n(n − 1)y(n−1)(0). Do đó,
y(10)(0) = −9.8y(8)(0) = (−9.8)(−7.6)y(6)(0) = · · · = (−9.8)(−7.6)(−5.4)(−3.2)y′′(0) = 0 bởi vì, y′ = 1 1+x2 ⇒ y′′(x) = −2x (1+x2)2 ⇒ y′′(0) = 0. d) Tương tự câu c).
Ví dụ 8.11 (Giữa kì, K59). Tính đạo hàm cấp cao y(19)(0) với 48
8. Đạo hàm và vi phân 49 a) y = arcsin x, b) y = arccos x. [Lời giải] a) Ta có 1 p −x y′ = √
⇒ (1 − x2)y′ = 1 − x2 ⇒ (1 − x2)y′′ − 2xy′ = √
⇒ (1 − x2)y′′ − xy′ = 0. 1 − x2 1 − x2
Đạo hàm cấp n hai vế ta được
[(1 − x2)y′′ − xy′](n) = 0 ⇒ (1 − x2)y(n+2) − 2nxy(n+1) − n(n − 1)y(n) − xy(n+1) − ny(n) = 0.
Thay x = 0 vào ta được công thức truy hồi
y(n+2)(0) = n2y(n)(0) ⇒ y(19)(0) = 172y(17)(0) = · · · = (17!!)2y′(0) = (17!!)2. b) Tương tự câu a).
Ví dụ 8.12 (Cuối kì, K60). Tính f (10)(1) với f (x) = x9 ln x.
[Lời giải] Ta xét bài toán tổng quát hơn: tính g(n+1)(x) với g(x) = xn ln x. Nhận xét
i) g′(x) = nxn−1 ln x + xn−1 = nxn−1 ln x + 1n
ii) g′′(x) = n(n − 1)xn−1 ln x + 1 + 1 n−1 n Do đó, 1 1 1 g(n)(x) = n! ln x + + + · · · + 1 2 n n! 10! g(n+1)(x) = ⇒ f (10)(x) = ⇒ f (10)(1) = 10!. x x
Ví dụ 8.13 (Cuối kì, 20152). Cho hàm số f (x) = x . Tính d10 f (0). 1+x3
[Lời giải] Ta có (1 + x3) f (x) = x. Lấy đạo hàm cấp n hai vế ta được n(n − 1) n(n − 1)(n − 2)
(1 + x3) f (n)(x) + n.3x2. f (n−1)(x) + .6x. f (n−2)(x) + .6. f (n−3)(x) = 0. 2 6
Cho x = 0 ta được công thức truy hồi
f (n)(0) = −n(n − 1)(n − 2) f n−3(0). Do đó,
f (10)(0) = −10.9.8. f (7)(0) = (−10.9.8)(−7.6.5)(−4.3.2) f (1)(0) = −10! ⇒ d10 f (0) = −10!dx10.
Ví dụ 8.14 (Giữa kì, K61). Tính đạo hàm cấp cao 49 50
Chương 1. Hàm số một biến số (13LT+13BT) a) (60) 1 . c) (x2 sin 2x)(50). x2−x b) (50) 1 . d) x2+x (x2 cos 2x)(60). 8.8 Vi phân cấp cao
Định nghĩa 1.23. Nếu hàm số ′
y = f (x) khả vi thì dy = f (x)dx gọi là vi phân cấp một của f (x).
i) Vi phân, nếu có, của vi phân cấp một được gọi là vi phân cấp hai, kí hiệu là d2 f (x).
ii) Vi phân, nếu có, của vi phân cấp n − 1 được gọi là vi phân cấp n, kí hiệu là dn f (x).
Biểu thức của vi phân cấp cao
Nếu x là biến số độc lập thì dn f (x) = f (n)(x)dxn.
Vi phân cấp cao không có tính chất bất biến đối với hàm hợp
Ta có d f (x) = f ′(x)dx nên
d2 f (x) = d f ′(x)dx + f ′(x)d2x = f ′′(x)dx2 + f ′(x)d2x.
Ví dụ 8.15. Chứng minh rằng nếu y = x3, x = t2 thì d2y 6= y(2)dx2. 8.9 Bài tập
Bài tập 1.44. Tìm đạo hàm của hàm số   1 − x, khi x < 1   f (x) = (1 − x)(2 − x), khi 1 ≤ x ≤ 2    x − 2, khi x > 2.  
Bài tập 1.45. Với điều kiện nào thì hàm số xn sin 1 , khi x 6= 0 f (x) = x 0, khi x = 0 50
8. Đạo hàm và vi phân 51 a) liên tục tại x = 0, b) khả vi tại x = 0,
c) có đạo hàm liên tục tại x = 0. [Đáp số] a) n > 0, b) n > 1, c) n > 2.
Bài tập 1.46. Chứng minh rằng hàm số f (x) = |x − a|.ϕ(x), trong đó ϕ(x) là một hàm số
liên tục và ϕ(a) 6= 0, không khả vi tại điểm x = a. [Gợi ý]
f ′+(a) = ϕ(a) 6= f ′−(a) = −ϕ(a)
Bài tập 1.47. Tìm vi phân của hàm số a) 1 x 1 x − a y = arctan | (a 6= 0) c) y = ln (a 6= 0) a a 2a x + a √ b) y = arcsin x(a d) y = ln x2 + a a 6= 0) |x + | [Đáp số] a) dx dx dy = c) dy = a2 + x2 x2 − a2 b) dx dx dy = √ .(sign a) d) dy = √ a2 − x2 x2 + a Bài tập 1.48. Tìm a) d d(sin x) I = (x3 − 2x6 − x9), c) K = . d(x3) d(cos x) b) d J = ( sin x ), d(x2) x [Đáp số]
a) I = −3x6 − 4x3 + 1, x 6= 0,
c) K = − cot x, x 6= kπ, k ∈ Z. b) 1 sin x J = cos x − , x 6= 0, 2x2 x
Bài tập 1.49. Tính gần đúng giá trị của biểu thức 51 52
Chương 1. Hàm số một biến số (13LT+13BT) a) r lg 11 b) 2 − 0, 02 7 2 + 0, 02 [Gợi ý] a) Xét 1
f (x) = lg x, x0 = 10, △x = 1, ta có lg 11 ≈ lg 10 + = 1, 043 10 ln 10 r r r b) Cách 1. 2 − 0, 02 4 4 7 = 7 − 1. Xét f (x) = 7 − 1, x 2 + 0, 02 2 + 0, 02 x 0 = 2, △x = 0, 02 Ta có r 4 1 4 −6 −4 1 f (x + △x) = 7 − 1 + 0, 02. .( − 1) 7 . = 1 − 0, 02. . 2 7 2 22 7 q
Cách 2. Xét hàm số f (x) = 7 2−x, với x 2+x 0 = 0, ∆x = 0, 02.
Bài tập 1.50. Tìm đạo hàm cấp cao của các hàm số (a) x2 (c) y = x2e2x, tính y(10). y = , tính y(8). 1 − x (b) 1 + x y = √ , tính y(100). (d) 1 − x y = x2 sin x, tính y(50). [Đáp số] (a) 8! y(8) = , x 6= 1. (1 − x)9 (b) 197! y(100) = √ (399 − x), x < 1. 2100(1 − x)100 1 − x
(c) y(10) = 210e2x x2 + 10x + 45 . 2
(d) y(50) = −x2 sin x + 100x cos x + 2450 sin x.
Bài tập 1.51. Tính đạo hàm cấp n của các hàm số a) x x y = , c) y = √ , x2 − 1 3 1 + x b) 1 y = , d) x2 − 3x + 2 y = eax sin(bx + c). [Đáp số] a) (−1)n 1 1 y(n) = n! + . 2 (x − 1)n+1 (x + 1)n+1 b) 1 1 y(n) = n! − . (1 − x)n+1 (2 − x)n+1 52
8. Đạo hàm và vi phân 53 c) (−1)n−1 3n + 2x y(n) = (1.4 . . . (3n − 5)) , n ≥ 2, x 6= 1. 3n (1 + x)n+ 13
d) Tính y′ rồi dự đoán và chứng minh bằng quy nạp n b a
y(n) = (a2 + b2) 2 eax sin(bx + c + nϕ), ở đó sin ϕ = √ , cos ϕ = √ . a2 + b2 a2 + b2
Bài tập 1.52. Tính đạo hàm cấp n của các hàm số a) 1 e) j) y = , y = sin2 x, y = x cos ax, a + bx f) y = sin3 x, b) 1 y = √ , k) y = x2 cos ax, a + bx g) y = sin ax. sin bx, c) 1 l) y = , y = x2 sin ax, x2 − a2 h) y = sin2 ax. cos bx, d) ax + b a + bx y = , i) m) y = ln . cx + d y = sin4 x + cos4 x, a − bx [Đáp số] a) (−1)n.n!bn y(n) = . (a + bx)n+1 b) (−1)n.(2n − 1)!!bn y(n) = √ . 2n n a + bx " n+1 n+1# c) 1 1 1 (−1)n.n! 1 1 y = = ( − 1 ) nên y(n) = − . x2 − a2 2a x − a x+a 2a x − a x + a d) ax + b a 1 1 1 ad (−1)n.n! y = = + b − ad nên y(n) = b − . cx + d c c c x + d c c n+1 c x + dc e) 1 1 y = sin2 x =
− cos 2x nên y(n) = −2n−1 cos 2x + nπ . 2 2 2 f) y = sin3 x = 3 sin x
sin 3x nên y(n) = 3 sin x + nπ 3n sin 3x + nπ . 4 − 14 4 2 − 14 2
g) y = sin ax. sin bx = 1[cos(a 2 − b)x − cos(a + b)x] nên 1 h nπ i 1 h nπ i
y(n) = (a − b)n cos (a − b)x + − (a + b)n cos (a + b)x + . 2 2 2 2 h) cos bx y = sin2 ax. cos bx =
− 1[cos(2a + b)x + cos(2a − b)x] nên 2 4 1 nπ 1 h nπ i y(n) = bn cos bx + − (2a + b)n cos (2a + b)x + 2 2 4 2 1 h nπ i
− (2a − b)n cos (2a − b)x + . 4 2 53 54
Chương 1. Hàm số một biến số (13LT+13BT) i)
y = sin4 x + cos4 x = 3 + 1 cos 4x nên y(n) = 4n−1 cos 4x + nπ . 4 4 2 j)
y(n) = anx cos ax + nπ + nan−1 cos ax + (n−1)π . 2 2 k)
y(n) = anx2 sin ax + nπ + 2nan−1x sin ax + (n−1)π + n(n ax + (n−2)π . 2 2 − 1)an−2 sin 2 l)
y(n) = anx2 cos ax + nπ + 2nan−1x cos ax + (n−1)π + n(n ax + (n−2)π . 2 2 − 1)an−2 cos 2 m) (n − 1)!bn y(n) =
. [(a + bx)n + (−1)n(a − bx)n] . (a2 − b2x2)n
8.10 Đọc thêm: Về khái niệm vi phân
Vi phân có lẽ là một khái niệm trừu tượng và dễ gây hiểu nhầm nhất trong môn Giải
tích I. Theo sự hiểu biết của tác giả thì có nhiều cách tiếp cận khác nhau đối với phép tính vi phân.
1) Người đầu tiên đưa ra khái niệm vi phân có lẽ là Leibniz, khi ông coi dy là một đại
lượng vô cùng bé thể hiện sự thay đổi của hàm số y = f (x) tương ứng với sự thay đổi
vô cùng bé dx của biến số x, nghĩa là ông định nghĩa dy f ′(x) := . dx
Kí hiệu dy này là kí hiệu của Leibniz cho đạo hàm của hàm số f (x). Mặc dù có nhiều dx
chỉ trích cho kí hiệu này, nó vẫn được dùng cho đến ngày nay. Cũng chú ý thêm rằng,
kí hiệu f ′(x) trên là kí hiệu của d’Alambert.
2) Cauchy là người đã cải tiến ý tưởng của Leibniz và những người đi trước như sau.
Trước hết, ông định nghĩa phép toán đạo hàm f (x + ∆x) − f (x) f ′(x) := lim ∆x→0 ∆x
là giới hạn của tỉ số giữa số gia của hàm số và số gia của đối số khi số gia của đối số
tiến về 0. Sau đó ông định nghĩa vi phân dy = f ′(x)dx,
như một hàm số của hai biến số x và dx, ở đó dx là một biến số mới, có thể lấy giá trị
tùy ý, không nhất thiết phải là một đại lượng VCB như trong kí hiệu của Leibniz.
3) Ngày nay, vi phân được định nghĩa theo lối tiếp cận hiện đại như sau: 54
8. Đạo hàm và vi phân 55
Định nghĩa 1.24. Cho hàm số f (x) có đạo hàm tại x . Ta gọi ánh xạ, kí hiệu là 0 dx f , 0 xác định bởi dx f : R → R, 0 h 7→ f ′(x0)h là vi phân của f tại x . 0
Vậy vi phân của f tại x là một ánh xạ tuyến tính. 0
i) Như vậy, vi phân của hàm số một biến số f (x) là một hàm số d f của hai biến số x và 0 h cho bởi dx f (h) = f ′(x 0 0)h,
ở đó h là một biến số mới có thể nhận giá trị tùy ý.
ii) Kí hiệu Id là ánh xạ đồng nhất, khi đó, dx (Id)(h) = h, hay là d (Id) = Id. 0 x0
iii) Một cách lạm dụng kí hiệu, ta kí hiệu x là ánh xạ đồng nhất x := Id. Khi đó, d nên ta kí hiệu nó là
x x = Id là ánh xạ đồng nhất và không phụ thuộc vào x 0 0
dx. Điều này dẫn đến d trong x f = f ′(x d f và, một 0
0)dx. Đôi khi, người ta bỏ x0 x0
cách lạm dụng, thay x bởi 0
x trong f ′(x0) để có biểu thức cô đọng d f = f ′(x)dx. 55 56
Chương 1. Hàm số một biến số (13LT+13BT)
§9. CÁC ĐỊNH LÝ VỀ HÀM KHẢ VI VÀ ỨNG DỤNG
9.1 Các định lý về hàm khả vi
Định nghĩa 1.25 (Cực trị của hàm số). Cho hàm số f (x) liên tục trên (a, b), ta nói hàm
số đạt cực trị tại điểm x0 ∈ (a, b) nếu ∃U(x0) ⊂ (a, b) sao cho f (x) − f (x0) không đổi dấu ∀x ∈ U(x0) \ {x0}. • Nếu f (x) − f (x .
0) > 0 thì ta nói hàm số đạt cực tiểu tại x0 • Nếu f (x) − f (x .
0) < 0 thì ta nói hàm số đạt cực đại tại x0
Định lý 1.31 (Định lý Fermat). Cho f (x) liên tục trên khoảng (a, b), nếu hàm số đạt cực trị tại điểm ′ x thì
0 ∈ (a, b) và có đạo hàm tại x0 f (x0) = 0.
Chứng minh. Nếu hàm số đạt cực đại tại x thì theo định nghĩa tồn tại một lân cận 0 U(x0)
sao cho f (x) − f (x0) < 0∀x ∈ U(x0). Do đó, với h đủ nhỏ sao cho f (x0 + h) ∈ U(x0) thì f (x0 + h) − f (x0) < 0.
• f ′(x+) = lim f (x0+h)− f (x0) 0 h ≤ 0. h→0+
• f ′(x−) = lim f (x0+h)− f (x0) 0 h ≥ 0. h→0−
Do giả thiết tồn tại f ′(x0) nên f ′(x+) = f ′(x−). Điều này chỉ xảy ra khi 0 0 f ′(x+) = f ′(x−) = 0. 0 0
Ví dụ 9.1 (Giữa kì, K61). Tìm các cực trị của các hàm số
a) y = cos x trong khoảng (0, 2π).
b) y = sin x trong khoảng (0, 2π). 2+sin x 2+cos x
Ví dụ 9.2 (Cuối kì, K61-Viện ĐTQT). Cho f (x) là một hàm số khả vi trên R và thỏa
mãn f ′(2) < λ < f ′(3). Chứng minh rằng tồn tại x0 ∈ (2, 3) sao cho f ′(x0) = λ.
[Lời giải] Xét hàm số g(x) = f (x) − λx. Khi đó,
i) g′(2) = f ′(2) − λ < 0, do đó tồn tại x1 ∈ (2, 3) nào đó sao cho g(x1) < g(2), nếu không thì g(x) − g(2) g′+(2) = lim ≥ 0. x→2+ x − 2
ii) g′(3) = f ′(3) − λ > 0, do đó tồn tại x2 ∈ (2, 3) sao cho g(x2) < g(3), nếu không thì g(x) − g(2) g′−(3) = lim ≤ 0. x→3− x − 3 56
9. Các định lý về hàm khả vi và ứng dụng 57
iii) Do đó, g(x) đạt cực tiểu tại điểm x0 ∈ (2, 3) ⇒ g′(x0) = 0 ⇒ f ′(x0) = λ.
Định lý 1.32 (Định lý Rolle). Nếu hàm số f (x) :
i) Liên tục trong khoảng đóng [a, b],
ii) Có đạo hàm trong khoảng mở (a, b),
iii) thỏa mãn điều kiện f (a) = f (b),
thì tồn tại ít nhất một điểm ′
c ∈ (a, b) sao cho f (c) = 0.
Chứng minh. Do hàm số f (x) liên tục trên [a, b] nên nó đạt GTLN và GTNN trên [a, b]. Ta
chia làm các trường hợp sau:
• Nếu f (x) là hằng số trên [a, b] thì f ′(x) = 0∀x ∈ (a, b).
• Nếu có số x ∈ (a, b) sao cho f (x) > f (a) = f (b) thì GTLN của f (x) sẽ phải đạt được
tại một điểm c nào đó thuộc (a, b) (do nó không đạt GTLN tại hai đầu mút). Khi đó,
theo Định lý Fermat, f ′(c) = 0.
• Nếu có số x ∈ (a, b) sao cho f (x) < f (a) = f (b) thì GTNN của f (x) sẽ phải đạt được
tại một điểm c nào đó thuộc (a, b) (do nó không đạt GTNN tại hai đầu mút). Khi đó,
theo Định lý Fermat, f ′(c) = 0.
Ví dụ 9.3 (Học kì 20163). Cho hàm số f (x) = (x − 1)(x2 − 2)(x2 − 3). Phương trình
f ′(x) = 0 có bao nhiêu nghiệm thực? Giải thích. [Lời giải] Phương trình √ √ √
f (x) = 0 có 5 nghiệm là x = − 3, x = − 2, x = 1, x = 2 và √ x = 3. i) Vì √ √ √ √
f (− 3) = f (− 2) = 0 nên theo Định lý Rolle, tồn tại x1 ∈ (− 3, − 2) sao cho f ′(x1) = 0. ii) Vì √ √
f (− 2) = f (1) = 0 nên theo Định lý Rolle, tồn tại x2 ∈ (− 2, 1) sao cho f ′(x2) = 0. iii) Vì √ √
f (1) = f ( 2) = 0 nên theo Định lý Rolle, tồn tại x2 ∈ (1, 2) sao cho f ′(x3) = 0. iv) Vì √ √ √ √
f ( 2) = f ( 3) = 0 nên theo Định lý Rolle, tồn tại x4 ∈ ( 2, 2) sao cho f ′(x4) = 0.
Vậy phương trình f ′(x) = 0 có ít nhất 4 nghiệm. Mặt khác, f ′(x) là một đa thức bậc bốn,
nên nó có nhiều nhất là bốn nghiệm. Kết luận: phương trình f ′(x) = 0 có đúng 4 nghiệm phân biệt.
Ví dụ 9.4 (Giữa kì, K62). Cho ba số thực a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng 57 58
Chương 1. Hàm số một biến số (13LT+13BT)
a) phương trình 3ax2 + 4bx + 5c = 0 có ít nhất một nghiệm thuộc khoảng (1, +∞).
b) phương trình 2ax2 + 3bx + 4c = 0 có ít nhất một nghiệm thuộc khoảng (1, +∞). [Lời giải]
a) Xét hàm số f (x) = cx5 + bx4 + ax3 thỏa mãn các điều kiện của Định lý Rolle trong khoảng [0, 1]. Do đó, 1 2 1
∃x0 ∈ (0, 1)| f ′(x0) = 5cx40 + 4bx30 + 3ax20 = 0 ⇒ 3a + 4b + 5c = 0. x0 x0
Vậy phương trình 3ax2 + 4bx + 5c = 0 có nghiệm 1x ∈ (1, +∞). 0
b) Xét hàm số f (x) = cx4 + bx3 + ax3 thỏa mãn các điều kiện của Định lý Rolle trong khoảng [0, 1]. Do đó, 1 2 1
∃x0 ∈ (0, 1)| f ′(x0) = 4cx30 + 3bx20 + 2ax0 = 0 ⇒ 2a + 3b + 4c = 0. x0 x0
Vậy phương trình 2ax2 + 3bc + 4c = 0 có nghiệm 1x ∈ (1, +∞). 0 b Z
Ví dụ 9.5 (Cuối kì, K62). Cho f liên tục trên [a, b] và thỏa mãn f (x)dx = 0. Chứng a Z c
minh rằng ∃c ∈ (a, b) sao cho 2017 f (x)dx = f (c). a [Lời giải] Z x Xét hàm số g(x) =
f (t)dt, là một hàm số liên tục trên [a, b], khả vi trên (a, b) và a
g(a) = g(b) = 0. Do đó, hàm số h(x) = e−2017xg(x) cũng là một hàm số liên tục trên [a, b],
khả vi trên (a, b) và h(a) = h(b) = 0. Áp dụng Định lý Rolle với hàm số h(x) trong khoảng [a, b] ta có:
∃c ∈ (a, b) : h′(c) = 0 ⇔ g′(c)e−2017c − 2017e−2017cg(c) = 0 ⇔ g′(c) − 2017g(c) = 0 c c Z Z ⇔ f (c) = 2017 f (t)dt = 2017 f (x)dx. a a
Ví dụ 9.6 (Olympic Toán học sinh viên Toàn quốc 2018 - Bảng B). Giả sử f : [0, 1] → 1 1 Z Z
R là một hàm số khả vi sao cho f (x)dx =
x f (x)dx. Chứng minh rằng tồn tại số 0 0 c ∈ (0, 1) sao cho c Z f (c) = 2018 f (x)dx. 0 58
9. Các định lý về hàm khả vi và ứng dụng 59 x x Z Z Chứng minh. i) Xét hàm số F(x) = x f (t)dt −
t f (t)dt khả vi trên [0, 1] và F(0) = 0 0 x0 Z
F(1) = 0. Theo Định lý Rolle, tồn tại x0 ∈ (0, 1) sao cho F′(x0) = 0 ⇔ f (t)dt = 0. 0 x Z ii) Đặt G(x) = e−2018x
f (t)dt thì G(x) là một hàm số khả vi trên [0, 1] với G(0) = 0
G(x0) = 0. Theo Định lý Rolle, tồn tại c ∈ (0, x0) sao cho c Z G′(c) = 0 ⇔ f (c) = 2018 f (x)dx. 0
Ví dụ 9.7 (Olympic Toán học sinh viên Toàn quốc 2018 - Bảng A). Giả sử f : [0, 1] → 1 1 Z Z
R là một hàm số khả vi sao cho f (x)dx =
x f (x)dx. Chứng minh rằng tồn tại số 0 0 c ∈ (0, 1) sao cho c Z f (c) = 2018 f ′(c) f (x)dx. 0 x x Z Z Chứng minh. i) Xét hàm số F(x) = x f (t)dt −
t f (t)dt khả vi trên [0, 1] và F(0) = 0 0 x0 Z
F(1) = 0. Theo Định lý Rolle, tồn tại x0 ∈ (0, 1) sao cho F′(x0) = 0 ⇔ f (t)dt = 0. 0 x Z ii) Đặt G(x) = e−2018f(x)
f (t)dt thì G(x) là một hàm số khả vi trên [0, 1] với G(0) = 0
G(x0) = 0. Theo Định lý Rolle, tồn tại c ∈ (0, x0) sao cho c Z
G′(c) = 0 ⇔ f (c) = 2018 f ′(c) f (x)dx. 0
Định lý 1.33 (Định lý Lagrange). Nếu hàm số f (x) :
i) Liên tục trong khoảng đóng [a, b],
ii) Có đạo hàm trong khoảng mở (a, b), 59 60
Chương 1. Hàm số một biến số (13LT+13BT)
thì tồn tại ít nhất một điểm ′
c ∈ (a, b) sao cho f (c) = f (b)− f (a). b−a
Chứng minh. Xét hàm số f (b) − f (a) h(x) = f (x) − f (a) − (x − a). b − a
Có thể dễ dàng kiểm chứng h(x) thỏa mãn các điều kiện của Định lý Rolle, do đó tồn tại
c ∈ (a, b) sao cho h′(c) = f ′(c) − f (b)− f (a) = 0. b−a
Ví dụ 9.8 (Giữa kì, K61). Chứng minh các bất đẳng thức sau với 0 < a < b.
a) a−b < arccot b − arccot a < a−b .
b) b−a < arctan b − arctan a < b−a . 1+a2 1+b2 1+b2 1+a2 [Lời giải]
a) Áp dụng Định lý Lagrange với hàm số f (x) = arccot x trong khoảng [a, b] ta có arccot b − arccot a 1 = f ′(c) = − b − a 1 + c2
với c ∈ (a, b) nào đó. Do đó, 1 arccot b − arccot a 1 1 − < = − < − 1 + a2 b − a 1 + c2 1 + b2
dẫn đến điều phải chứng minh. b) Tương tự câu a).
Ví dụ 9.9 (Giữa kì, K59). Cho hàm số f : (0, +∞) → R thỏa mãn f (x) ≤ 1 và f ′′(x) ≥ 0
với mọi x > 0. Chứng minh rằng f ′(x) ≤ 0 với mọi x > 0. [Lời giải]
Giả sử phản chứng, tồn tại x0 > 0 sao cho f ′(x0) > 0.
i) Vì f ′′(x) ≥ 0 nên f ′(x) ≥ f ′(x . 0) với mọi x > x0
ii) Áp dụng Định lý Lagrange cho hàm số f (x) trong khoảng [x0, x] ta có: tồn tại c ∈
(x0, x) sao cho f (x) = f (x0) + f ′(c)(x − x0) ≥ f (x0) + f ′(x0)(x − x0).
iii) Mặt khác, vì f ′(x0) > 0 nên lim f (x0) + f ′(x0)(x − x0) = +∞ ⇒ lim f (x) = +∞, x→+∞ x→+∞
trái với giả thiết f (x) ≤ 1 với mọi x > 0.
Mâu thuẫn này chứng tỏ f ′(x) ≤ 0 với mọi x > 0.
Định lý 1.34 (Định lý Cauchy). Nếu các hàm số f (x), g(x) thỏa mãn các điều kiện: 60
9. Các định lý về hàm khả vi và ứng dụng 61
i) Liên tục trong khoảng đóng [a, b],
ii) Có đạo hàm trong khoảng mở (a, b),
iii) g′(x) không triệt tiêu trong khoảng mở (a, b)
thì tồn tại ít nhất một điểm c ∈ (a, b) sao cho f (b) − f (a) f ′(c) = . g(b) − g(a) g′(c) Chú ý 1.12.
a) Định lý Rolle là trường hợp riêng của định lý Lagrange, định lý La-
grange là trường hợp riêng của định lý Cauchy. Các giả thiết trong các định lý này là cần thiết.
b) Định lý Lagrange còn có một dạng khác, đó là công thức số gia hữu hạn: ′
∆ f = f (x0 + θ∆x) , θ ∈ (0, 1).
9.2 Các công thức khai triển Taylor, Maclaurin
Định lý 1.35. Nếu hàm số f (x)
(i) Có đạo hàm đến cấp n trong khoảng đóng liên tục tại x , 0
(ii) Có đạo hàm đến cấp n + 1 trong lân cận Uǫ(x0),
thì f (x) có thể biểu diễn dưới dạng ′ f (x f (n)(x f (n+1)(c) f (x) = f (x 0) 0) 0) + (x − x (x − x (x − x 1! 0) + · · · + n! 0)n + (n + 1)! 0)n+1,
ở đó c là một số thực nằm giữa x và x nào đó. 0
Nếu x0 = 0 thì công thức sau còn được gọi là công thức Maclaurin: ′ f (0) f (n)(0) f (n+1)(c) f (x) = f (0) + x + · · · + xn + xn+1 (1.1) 1! n! (n + 1)! hay ′ f (0) f (n)(0) f (x) = f (0) + x + · · · + xn + o(xn), (1.2) 1! n!
ở đó o(xn) là một VCB bậc cao hơn xn. 61 62
Chương 1. Hàm số một biến số (13LT+13BT)
Một số khai triển Maclaurin quan trọng
(1) (1 + x)α = 1 + αx + α(α−1) x2 + xn + o(xn) 2
· · · + α(α−1)···(α−n+1) n! (2) 1 = 1 1+x
− x + x2 − · · · + (−1)nxn + o(xn) (3) 1 = 1 + x + x2 + 1−x · · · + xn + o(xn) (4) ex = 1 + x + x2 + + o(xn) 2! · · · + xn n! (5) sin x = x − x3 + x5 + + o(x2n+1) 3! 5! · · · + (−1)n x2n+1 (2n+1)! (6) cos x = 1 − x2 + x4 + + o(x2n) 2! 4! · · · + (−1)n x2n (2n)!
(7) ln(1 + x) = x − x2 + x3 + + o(xn) 2 3 · · · + (−1)n−1 xnn
Các phép toán trên khai triển Maclaurin
Trên khai triển Maclaurin chúng ta có thể thực hiện các phép toán cơ bản sau: cộng,
trừ, nhân, chia, hàm hợp, đạo hàm và tích phân. Các phép toán cộng, trừ, nhân, chia được
thực hiện hệt như cộng, trừ, nhân, chia các đa thức. Cho f (x) = a0 + a1x + a2x2 + a3x3 +
· · · + anxn + · · · và g(x) = b0 + b1x + b2x2 + b3x3 + · · · + bnxn + · · · là các chuỗi Maclaurin hình thức. Khi đó 1. Phép cộng (trừ)
f (x) ± g(x) = (a0 ± b0) + (a1 ± b1)x + (a2 ± b2)x2 + (a3 ± b3)x3 + · · · + (an ± bn)xn + · · · 2. Phép nhân
f (x)g(x) = c0 + c1x + c2x2 + c3x3 + · · · + cnxn + · · · , n +∞ +∞ ở đó c . Chuỗi n = ∑ aibn−i
∑ cnxn còn được gọi là tích chập của hai chuỗi ∑ anxn và i=0 n=0 n=0 +∞ ∑ bnxn. n=0
Ví dụ 9.10. Tìm khai triển Maclaurin của hàm số f (x) = ex sin x.
[Lời giải] Xuất phát từ khai triển Maclaurin của hàm số g(x) = ex x2 xn ex = 1 + x + + · · · + + o(xn) 2! n! và h(x) = sin x x3 x5 sin x = x − +
+ · · · + (−1)n x2n+1 + o(x2n+1) 3! 5! (2n + 1)! 62
9. Các định lý về hàm khả vi và ứng dụng 63 ta có 1 1 ex sin x = x + x2 + − x3 + · · · 2! 3!
Ví dụ 9.11 (Giữa kì, 20173). Cho y = ex sin x. Tính đạo hàm cấp cao y(6)(0).
[Lời giải] Số hạng chứa x6 trong khai triển Maclaurin của y = ex sin x là x3 x5 1 x.(−1)2 x5 + (−1)1 x3 + x = − x6. 5! 3! 3! 5! 90 Do đó, y(6)(0) 1 = − ⇒ y(6)(0) = −8. 6! 90
• Như vậy, nếu chỉ cần tìm một số số hạng đầu tiên trong khai triển Maclarin của
hàm số ex sin x thì có thể dùng phương pháp thực hiện phép nhân này.
• Tuy nhiên, để tìm được số hạng tổng quát thì phương pháp này lại không hiệu
quả. Thay vào đó, ta sẽ đi tính f (n)(x) bằng phương pháp quy nạp như trong Bài tập 1.51d. Từ công thức √ π
f ′(x) = ex(sin x + cos x) = 2ex sin x + , 4 và √ h π π i √ π f ′′(x) = 2ex sin x + + cos x + = ( 2)2ex sin x + 2. 4 4 4 suy ra √ π f (n)(x) = ( 2)nex sin x + n . 4 Do đó, √ ∞ ( 2)n sin nπ ex sin x = ∑ 4 xn. n! n=1
3. Phép chia cũng thực hiện như phép chia đa thức một cách bình thường.
4. Phép lấy hàm hợp. Chúng ta bắt đầu bằng một ví dụ đơn giản sau. Tìm chuỗi Maclau-
rin của hàm số f (x) = sin x2. Muốn tìm chuỗi Maclaurin một cách trực tiếp, ta cần
tính các đạo hàm cấp cao của hàm số f (x) = sin x2 rồi thay vào công thức ′ f (0) f (n)(0) f (x) = f (0) + x + · · · + xn + o(xn). 1! n!
Bằng cách tính các đạo hàm cấp một và cấp hai của f (x): • f ′(x) = 2x cos x2, 63 64
Chương 1. Hàm số một biến số (13LT+13BT)
• f ′′(x) = −4x2 sin x2 + 2 cos x2,
chúng ta thấy rằng quá trình này sẽ rất phức tạp. Chúng ta có một phương pháp
khác. Đó là thực hiện phép đổi biến số, thay x bằng x2 trong khai triển Maclaurin của hàm số x3 x5 sin x = x − +
+ · · · + (−1)n x2n+1 + · · · 3! 5! (2n + 1)! để được x6 x10 sin x2 = x2 − +
+ · · · + (−1)n x2(2n+1) + · · · 3! 5! (2n + 1)!
Bản chất của vấn đề ở đây là chúng ta cần đi tìm khai triển Maclaurin của hàm
số hợp ( f ◦ g)(x) = f (g(x)). Để tìm hiểu sâu thêm về vấn đề này, công thức Faà di
Bruno sau đây giúp chúng ta tính đạo hàm cấp cao của hàm hợp.
Định lý 1.36 (Công thức Faà di Bruno). n! n mj f (g(x))(n) = ∑
· f (m1+···+mn)(g(x)) · ∏ g(j)(x) ,
m1! 1!m1 m2! 2!m2 · · · mn! n!mn j=1
ở đó tổng được lấy trên tất cả các bộ số không âm (m1, . . . , mn) thỏa mãn
1 · m1 + 2 · m2 + 3 · m3 + · · · + n · mn = n. ∞ ∞
Hệ quả 1.5. Cho f (x) = ∑ anxn và g(x) = ∑ bnxn là các chuỗi Maclaurin hình n=0 n=0
thức và b0 = 0. Khi đó, hàm số ( f ◦ g)(x) có chuỗi Maclaurin hình thức là ∞ ∑ cnxn, n=0 ở đó c và 0 = a0 cn = ∑ akbi b · · · b 1 i2 ik i∈Cn và
Cn = {(i1, i2, . . . , ik) : 1 ≤ k ≤ n, i1 + i2 + · · · + ik = n}.
Trường hợp đơn giản nhất, g(x) = xk thì chỉ việc thay x bằng xk trong khai triển
Maclaurin của f (x) để ra khai triển Maclaurin của f (xk) như trong ví dụ hàm số
f (x) = sin(x2) đã nêu ở trên.
5. Phép lấy đạo hàm. Giả sử hàm số f (x) có khai triển Maclaurin là
f (x) = a0 + a1x + a2x2 + a3x3 + · · · + anxn + · · · 64
9. Các định lý về hàm khả vi và ứng dụng 65
Khi đó hàm số f ′(x) có khai triển Maclaurin là
f ′(x) = a1 + 2a2x + 3a3x2 + · · · + nanxn−1 + · · ·
được thực hiện bằng cách lấy đạo hàm của từng thành phần của chuỗi Maclaurin
của hàm f (x). Bạn đọc có thể tự kiểm tra bằng cách lấy đạo hàm chuỗi Maclaurin
của hàm sin x để ra chuỗi Maclaurin của hàm số cos x, hoặc lấy đạo hàm của chuỗi
Maclaurin của hàm số ln(1 + x) để ra chuỗi Maclaurin của hàm số 1 . 1+x
6. Phép lấy tích phân. Cũng tương tự như vậy, giả sử hàm số f (x) có khai triển Maclau- rin là
f (x) = a0 + a1x + a2x2 + a3x3 + · · · + anxn Z x Khi đó hàm số
f (t)dt có khai triển Maclaurin là 0 x Z x2 x3 xn+1 f (t)dt = a0x + a1 + a + · · · + a + · · · 2 2 3 n n + 1 0
được thực hiện bằng cách lấy tích phân của từng thành phần của chuỗi Maclau-
rin của hàm f (x). Chẳng hạn, muốn tìm khai triển Maclaurin của hàm số f (x) =
arctan x, đầu tiên ta tìm chuỗi Maclaurin của hàm số 1
= 1 − x2 + x4 − · · · + (−1)nx2n + · · · , 1 + x2
sau đó ta lấy tích phân hai vế thì được x Z 1 x3 x5 arctan x = dt = x − +
+ · · · + (−1)n x2n+1 + · · · 1 + t2 3 5 2n + 1 0
Ứng dụng của khai triển Maclaurin 1. Tính gần đúng
Ví dụ 9.12. Tính gần đúng số e với sai số nhỏ hơn 0, 0001. Ta có ex = 1 + x + x2 +
+ cn+1 với c là một số thực nào đó nằm giữa 0 và x. 2! · · · + xn n! (n+1)!
Do đó ta xấp xỉ số e bằng 1 1 e ≈ 1 + 1 + + · · · + 2! n!
với sai số mong muốn cn+1 < 1
< 0, 0001. Điều này xảy ra nếu (n + 1)! > 1000 ( ⇔ n+1)! (n+1)! n > 6. Nói cách khác, 1 1 1 1 1 e ≈ 1 + 1 + + + + + . 2! 3! 4! 5! 6! 65 66
Chương 1. Hàm số một biến số (13LT+13BT) 2. Tính giới hạn Ví dụ 9.13. Tính x − sin x lim . x→0 x3
Chứng minh. Dựa vào khai triên Maclaurin của hàm f (x) = sin x ta có x3 sin x = x − + o(x3) 3! nên x3 x3 x − sin x = + o(x3) ∼ + o(x3) 6 6
(theo quy tắc ngắt bỏ VCB bậc cao). Do đó x − sin x 1 lim = . x→0 x3 6
Chú ý 1.13. Khi sử dụng khai triển Maclaurin để tính giới hạn, có thể khai triển
hàm số đến số hạng thích hợp. Chẳng hạn như ở Ví dụ bên trên, mẫu số là x3 nên ta
chỉ khai triển tử số đến số hạng x3, còn phần VCB bậc cao ở phía sau sẽ được ngắt bỏ.
Ví dụ 9.14 (Giữa kì, K61). Tính giới hạn a) ex− 1 b) ex−sin x−cos x lim 1−x . lim . x2 x→0 x2 x→0
Ví dụ 9.15 (Giữa kì, K62). Tìm a, b ∈ R sao cho a) ax+b sin(sin x) lim ax2+b ln(cos x) = 1. b) lim = 1. x→0 x4 x→0 x3 [Lời giải] a) Ta có x2 x4 ln(cos x) = ln 1 − + + o(x4) 2 24 x2 x4 1 x2 x4 2 = − + − − + + o(x4) + o(x4) 2 24 2 2 24 x2 x4 = − − + o(x4). 2 12 Do đó, ax2 + b ln(cos x) a − b x2 x4 + o(x4) 2 − b12 1 = lim = lim ⇒ a = −6, b = −12. x→0 x4 x→0 x4 66
9. Các định lý về hàm khả vi và ứng dụng 67 b) x3 sin(sin x) = sin x − + o(x4) 6 x3 1 x3 3 = x − − x − + o(x4) + o(x4) 6 6 6 x3 = x − + o(x4). 3 Do đó, ax + b sin(sin x) (a + b)x − b x3 + o(x4) 1 = lim = lim 3 ⇒ a = 3, b = −3. x→0 x3 x→0 x3
3. Tính đạo hàm cấp cao f (n)(0).
Ví dụ 9.16 (Giữa kì, K61). Tính đạo hàm cấp cao y(10)(0) với a) y(x) = ex2, c) y(x) = arctan x, b) y(x) = e−x2, d) y(x) = arccot x.
[Lời giải] Ngoài phương pháp dựa vào công thức truy hồi như ở Ví dụ 8.10, ta có thể
dựa vào khai triển Maclaurin.
a) Thay x bởi x2 trong công thức khai triển Maclaurin của ex ta có (x2)2 (x2)3 (x2)n +∞ y(n)(0) ex2 = 1 + x2 + + + · · · + + · · · = ∑ xn. 2! 3! n! n! n=0
So sánh hệ số của x10 ta được y(10)(0) 1 10! = ⇒ y(10)(0) = = 30240. 10! 5! 5! b) Tương tự câu a).
c) Thay x bằng x2 trong khai triển Maclaurin của hàm số f (x) = 1 ta được khai 1+x
triển Maclaurin của hàm số f (x) = 1 như sau: 1+x2 1
= 1 − x2 + x4 − · · · + (−1)nx2n + · · · , 1 + x2
Lấy tích phân hai vế ta được t Z 1 x3 x5 +∞ y(n)(0) arctan x = dt = x − +
+ · · · + (−1)n x2n+1 + · · · = ∑ xn 1 + t2 3 5 2n + 1 n! 0 n=0
So sánh hệ số của x10 hai vế ta được y(10)(0) = 0.
Ví dụ 9.17 (Cuối kì, K62). Tính đạo hàm cấp cao y(10)(0) với 67 68
Chương 1. Hàm số một biến số (13LT+13BT) a) y(x) = sin(x2). b) y(x) = cos(x2). [Lời giải]
a) Thay x bằng x2 trong khai triển Maclaurin của sin x +∞ sin x = ∑ (−1)n x2n+1 (2n + 1)! n=0 ta được +∞ +∞ y(n)(0)
sin(x2) = ∑ (−1)n x2(2n+1) = ∑ xn. (2n + 1)! n! n=0 n=0
So sánh hệ số của x10 hai vế ta được y(10)(0) 1 10! = (−1)2. ⇒ y(10)(0) = = 30240. 10! 5! 5! b) Tương tự câu a).
Ví dụ 9.18 (Giữa kì, K62). Tính đạo hàm cấp cao y(9)(0) với a) f (x) = ln(1 − x + x2). b) g(x) = ln(1 + x + x2). [Lời giải] a) Ta có x6 x9 9 (−1)n−1xn
f (x) = ln(1 − x + x2) = ln(1 + x3) − ln(1 + x) = x3 − + − ∑ + o(x9) 2 3 n n=1
Hệ số của x9 trong khai triển Maclaurin của f (x) bằng f (9)(0) 1 1 2 = − = . 9! 3 9 9 Do đó, f (9)(0) = 2.8! = 80640 b) Tương tự câu a).
Ví dụ 9.19. a) Tìm khai triển Maclaurin của hàm số f (x) = arcsin x.
b) Tính đạo hàm cấp cao arcsin(n)(0) (Giữa kì, K59). [Lời giải] 68
9. Các định lý về hàm khả vi và ứng dụng 69 a) Nhận xét (arcsin x)′ = 1 √
. Trong trường hợp này có lẽ "không có" hoặc "rất 1−x2
khó" để tìm ra công thức tính đạo hàm cấp cao của hàm số arcsin x. Vì vậy, ta
xuất phát từ công thức khai triển Maclaurin của hàm số (1 + x)α ∞
α(α − 1) . . . (α − n + 1) (1 + x)α = ∑ xn. n! n=0
Thay α = −1 ta được 2 1 ∞ −1 . . . ∞ 2 −12 − 1 −12 − (n − 1) (−1)n(2n − 1)!! √ = ∑ xn = ∑ xn. 1 + x n! 2nn! n=0 n=0
Thay x bằng −x2 ta được 1 ∞ (−1)n(2n − 1)!! ∞ (2n − 1)!! (arcsin x)′ = √ = ∑ (−x2)n = ∑ x2n 1 − x2 2nn! (2n)!! n=0 n=0 Do đó x x Z ∞ (2n − 1)!! ∞ (2n − 1)!! Z ∞ (2n − 1)!! x2n+1 arcsin x = ∑ t2ndt = ∑ t2ndt = ∑ . (2n)!! (2n)!! (2n)!! 2n + 1 0 n=0 n=0 0 n=0
b) Dựa vào công thức khai triển Maclaurin của hàm số arcsin x suy ra  arcsin(2n)(0) = 0,
arcsin(2n+1)(0) = [(2n − 1)!!]2.
Ví dụ 9.20 (Cuối kì, 20152). Cho hàm số f (x) = x . Tính d10 f (0). 1+x3
[Lời giải] f (x) = x · 1 , áp dụng công thức Leibniz ta có 1+x3 1 (n) 1 (n−1) f (n)(x) = x · + n. . 1 + x3 1 + x3
Thay x = 0, n = 10 vào ta có f (10)(0) = 10g(9)(0), với g(x) = 1 . 1+x3 Ta có 1 1
= 1 − x + x2 − · · · + (−1)nxn + o(xn) ⇒
= 1 − x3 + (x3)2 − (x3)3 + · · · 1 + x 1 + x3
Từ đó suy ra hệ số của x9 trong khai triển Maclaurin của g(x) = 1 bằng 1+x3 g(9)(0) −1 =
⇒ g(9)(0) = −9! ⇒ f (10)(0) = −10! ⇒ d10 f (0) = −10!dx10 9!
Bài tập 1.53. Tìm khai triển Maclaurin của hàm số f (x) = arccos x.
[Gợi ý] Có thể dựa vào đẳng thức arcsin x + arccos x = π để suy ra khai triển Maclau- 2
rin của hàm số f (x) = arccos x. 69 70
Chương 1. Hàm số một biến số (13LT+13BT) 9.3 Quy tắc L’Hospital
Định lý 1.37 (Quy tắc L’Hospital). Giả thiết
i) Các hàm số f (x), g(x) khả vi trong một lân cận nào đó của điểm x (có thể trừ tại 0 điểm ′ x ) đồng thời 0
g (x) 6= 0 trong lân cận ấy,
ii) lim f (x) = lim g(x) = 0 khử dạng 0 . x→x0 x→x0 0 ′
Khi đó nếu tồn tại lim f (x) = A (có thể hữu hạn hoặc vô hạn) thì lim f(x) = A. x→x g(x) 0 g′ (x) x→x0
Chú ý 1.14. Quy tắc L’Hospital trên vẫn đúng nếu
• thay quá trình x → x bởi một trong các quá trình 0 x → x+, x , x 0 → x− 0 → +∞ hoặc x → −∞.
• thay điều kiện lim f (x) = lim g(x) = 0 bởi x→x0 x→x0
lim f (x) = ∞, lim g(x) = ∞ khử dạng ∞ x→x0 x→x0 ∞
Ý tưởng chứng minh: Chúng ta chứng minh quy tắc L’Hospital cho trường hợp đơn giản, g′(x0) 6= 0. 1. Nếu f (x ta có
0) = g(x0) = 0 thì Với x 6= x0 ′ f (x) f (x) − f (x (Cauchy) f (c) = 0) = , g(x) g(x) − g(x0) g′ (c) c nằm giữa x và x . 0 ′ Khi f (x) x → x thì . Do 0 c → x0 lim = A, suy ra x→x0 g′ (x) ′ f (x) f (c) lim = lim = A. x→x0 g(x) c→x0 g′ (c)
2. Nếu chỉ có lim f (x) = lim g(x) = 0 mà các hàm số chưa chắc đã xác định tại x . Ta 0 x→x0 x→x0 xây dựng    0, x = x0  0, x = x0 F(x) = G(x) =  f (x), x 6= x0, g(x), x 6= x0. 3. Nếu 1 x → ∞, đặt y = . x
Ví dụ 9.21 (Giữa kì, K61). Tính giới hạn 70
9. Các định lý về hàm khả vi và ứng dụng 71 a) lim ln(1+x)−sin x. b) lim e2x−sin2x. x→0 x2 x→0 x2
Ví dụ 9.22. Tính các giới hạn sau: a) x − sin x c) lim , lim xα ln x, x→0 arcsin3 x x→0+ b) ax lim xx, d) lim . x→0+ x→∞ x Chú ý 1.15. f (x)
• Hai qui tắc trên chỉ là điều kiện đủ để tìm lim . g(x) 1 x2 sin Ví dụ như lim
x = 0 theo nguyên lý giới hạn kẹp, nhưng nếu áp dụng quy tắc x→0 sin x
L’Hospital thì sẽ dẫn đến kết quả sai.
• Trong quá trình tìm giới hạn có dạng vô định, nên kết hợp cả thay tương đương với
dùng qui tắc L’Hospital để đạt được hiệu quả tốt nhất.
• Có thể dùng qui tắc L’Hospital nhiều lần.
Chú ý 1.16. Công thức L’Hospital được công bố lần đầu vào năm 1696 trong cuốn sách
Analyse des Infiniment Petits, pour intelligence des lignes courbes của nhà toán học người
Pháp Marquis de l’Hospital (1661-1704), nhưng nó lại được khám phá vào năm 1694 bởi
nhà toán học người Thụy Sỹ John (Johann) Bernoulli (1667-1748). Điều này được giải
thích vì hai nhà toán học có một thỏa thuận lạ kì, rằng Marquis de l’Hospital mua quyền
sở hữu các phát minh của Bernoulli trong một khoảng thời gian nhất định. Bức thư sau
đây của l’Hopital vào ngày 17 tháng 3 năm 1694 đã đề xuất một trong những thỏa thuận
khác thường nhất trong lịch sử khoa học.
"I will be happy to give you a retainer of 300 pounds, beginning with the first of Jan-
uary of this year ... I promise shortly to increase this retainer, which I know is very mod-
est, as soon as my affairs are somewhat straightened out ... I am not so unreasonable as
to demand in return all of your time, but I will ask you to give me at intervals some hours
of your time to work on what I request and also to communicate to me your discoveries, at
the same time asking you not to disclose any of them to others. I ask you even not to send
here to Mr. Varignon or to others any copies of the writings you have left with me; if they
are published, I will not be at all pleased. Answer me regarding all this ..."
9.4 Về một số dạng vô định
Quy tắc L’Hospital, ngoài việc được áp dụng để khử dạng vô định 0, ∞, còn có thể được 0 ∞
dùng để khử các dạng vô định sau: 71 72
Chương 1. Hàm số một biến số (13LT+13BT)
1. Dạng vô định 0 × ∞. Chẳng hạn như muốn tính giới hạn lim f (x)g(x) ta có thể viết x→x0 nó dưới dạng f (x) lim x→x0 1/g(x)
để áp dụng công thức L’Hospital.
Ví dụ 9.23. Tính lim x ln x. x→0+
2. Dạng vô định ∞ − ∞. Để tính các giới hạn này chúng ta đưa phép trừ về dạng phép
thương, chẳng hạn như quy đồng mẫu số, đặt nhân tử chung.
Ví dụ 9.24. Tính lim 1 . x→0 x − 1 sin x
3. Tính các giới hạn có dạng lim A(x)B(x). Đặt f (x) = A(x)B(x) và đi tính x→x0 ln A(x)
lim ln f (x) = lim B(x) ln A(x) = lim x→x0 x→x0 x→x0 1/B(x)
bằng cách áp dụng công thức L’Hospital.
• Nếu lim ln A(x) có dạng 0, nghĩa là x→x 1/B(x) 0 0
lim ln A(x) = 0, lim 1/B(x) = 0. x→x0 x→x0
Khi đó, lim A(x) = 1, lim B(x) = ∞ ta có dạng vô định 1∞. x→x0 x→x0
• Nếu lim ln A(x) có dạng ∞, nghĩa là x→x 1/B(x) ∞ 0
lim ln A(x) = ∞, lim 1/B(x) = ∞. x→x0 x→x0 Khi đó,
– hoặc lim A(x) = 0, lim B(x) = 0 ta có dạng vô định 00, x→x0 x→x0
– hoặc là lim A(x) = ∞, lim B(x) = 0 ta có dạng vô định ∞0. x→x0 x→x0
Chú ý rằng chỉ có ba dạng vô định 00, 1∞, ∞0 cho các giới hạn có dạng lim A(x)B(x). x→x0
Các trường hợp khác hay bị nhầm lẫn sau đây đều không phải là dạng vô định
và có thể tính trực tiếp dựa vào các quy tắc tính giới hạn: 01 = 0, 0+∞ = 0, 0−∞ = +∞, 10 = 1, 11 = 1, ∞1 = ∞, ∞∞ = ∞. 72
9. Các định lý về hàm khả vi và ứng dụng 73
9.5 Thay tương đương khi có hiệu hai VCB?
Đây có lẽ là một câu hỏi thú vị và được rất nhiều bạn đọc quan tâm. Chúng ta bắt đầu
với một ví dụ sau đây.
Ví dụ 9.25 (Câu 6, Đề 4, Giữa kì K61). Tính ex − sin x − cos x lim . x→0 x2 [Lời giải]
Cách 1: Thay tương đương
Cách 2: Dùng quy tắc L’Hospital ex − sin x − cos x lim x→0 x2 ex − sin x − cos x lim
(ex − 1) − sin x + (1 − cos x) x→0 x2 = lim ex x→0 x2 − cos x + sin x = lim x − x + x2 x→0 2x = lim 2 ex + sin x + cos x x→0 x2 = lim 2 1 x→0 = 2 =1.
Trong hai cách giải trên chắc chắn có một cách giải sai, và sai lầm ở đâu? Đây là sai lầm
nhiều người hay mắc phải khi thay tương đương trong các biểu thức có chứa dấu ±.
Chú ý 1.17. Nếu α và
1(x), α2(x), β1(x), β2(x) là các VCB khi x → x0
α1(x) ∼ α2(x), β1(x) ∼ β2(x) thì
• α1(x)β1(x) ∼ α2(x)β2(x)
• lim α1(x) = lim α2(x) x→x β β 0 1(x) x→x0 2(x)
nhưng chưa chắc α1(x) ± β1(x) ∼ α2(x) ± β2(x). Chẳng hạn, sin x ∼ x, tan x ∼ x khi x → 0,
nhưng tan x − sin x ∼ 1x3. 2
Vậy có thay tương đương được trong biểu thức có dấu ± hay không không? Đây là một
câu hỏi rất thú vị. Muốn biết biểu thức α1(x) − β1(x) có tương đương với α2(x) − β2(x) hay
không thì chúng ta quay về Định nghĩa, đi tính lim α1(x)−β1(x). Ta chia làm 4 trường hợp
x→a α2(x)−β2(x) như sau: 1. Nếu α α1(x) α2(x)
1(x) là VCB bậc cao hơn β1(x) thì lim = lim = 0 (theo định nghĩa của x→a β1(x) x→a β2(x) α1(x)
VCB bậc cao). Khi đó lim α1(x)−β1(x) = lim β1(x)−1.β1(x) = 0−1 = 1. Vậy α1(x) − β1(x)
x→a α2(x)−β2(x) x→a α2(x) β2(x) 0−1 β2(x) −1
tương đương với α2(x) − β2(x). 73 74
Chương 1. Hàm số một biến số (13LT+13BT) 2. Nếu β β1(x) β2(x)
1(x) là VCB bậc cao hơn α1(x) thì lim = lim = 0 (theo định nghĩa của x→a α1(x) x→a α2(x) β1(x)
VCB bậc cao). Khi đó lim α1(x)−β1(x) = lim α1(x)−1.α1(x) = 0−1 = 1. Vậy α1(x) − β1(x)
x→a α2(x)−β2(x) x→a β2(x) α2(x) 0−1 α2(x) −1
tương đương với α2(x) − β2(x). 3. Nếu α α1(x)
1(x) và β1(x) là các VCB cùng bậc nhưng không tương đương thì lim = x→a β1(x) α1(x)
A 6= 1. Khi đó lim α1(x)−β1(x) = lim β1(x) −1. β1(x) = A−1 = 1. Vậy α1(x) − β1(x) tương
x→a α2(x)−β2(x) x→a α2(x) β2(x) A−1 β2(x) −1
đương với α2(x) − β2(x). 4. Nếu α α1(x) α1(x)−β1(x)
1(x) và β1(x) là các VCB tương đương thì lim = 1. Khi đó lim = x→a β1(x)
x→a α2(x)−β2(x) α1(x)
lim β1(x) −1. β1(x) = 1−1 là dạng vô định 0 nên không xác định được giới hạn của nó. x→a α2(x) β2(x) 1−1 0 β2(x) −1
5. Nếu α1(x) và β1(x) là các VCB không so sánh được với nhau, thì α1(x) − β1(x) và
α2(x) − β2(x) có thể không so sánh được với nhau.
Kết luận: Nếu α và
1(x), α2(x), β1(x), β2(x) là các VCB khi x → x0
α1(x) ∼ α2(x), β1(x) ∼
β2(x) thì α1(x) − β1(x) ∼ α2(x) − β2(x) ngoại trừ trường hợp α1(x) và β1(x) là các
VCB tương đương hoặc không so sánh được với nhau. Ví dụ, không thay tương
đương được trong biểu thức tan x − sin x vì tan x ∼ sin x, nhưng vẫn thay tương đương
được trong biểu thức tan 2x − sin x ∼ 2x − x = x hoặc sin x − tan2 x ∼ x − x2 ∼ x. Bạn đọc
cần nắm vững điều này, và trong trường hợp không chắc chắn thì tốt nhất nên
tránh thay tương đương trong các biểu thức có chứa dấu cộng và dấu trừ.
Trường hợp α1(x) + β1(x) có tương đương với α2(x) + β2(x) hay không chúng ta lập luận
tương tự. Vẫn thay tương đương được bình thường ngoại trừ trường hợp α1(x) và −β1(x)
là các VCB tương đương hoặc không so sánh được với nhau.
Quay trở lại Ví dụ 9.25 nêu trên thì sai lầm là ở chỗ chúng ta đã thay tương tương
(ex − 1) − sin x ∼ x − x = 0 để dẫn đến (ex − 1) − sin x + (1 − cos x) ∼ x2 . Chúng ta không 2
thực hiện được điều này bởi vì ex − 1 ∼ sin x. Thực tế thì (ex − 1) − sin x là một VCB khi
x → 0 và nếu nhìn vào khai triển Maclaurin của các hàm số ex và sin x thì ta thấy • ex = 1 + x + x2 + o(x2) 2
• sin x = x + o(x2) (số hạng tiếp theo trong khai triển này là − x3 = o(x2)) 3! nên x2 x2 (ex − 1) − sin x = + o(x2) ∼ . 2 2
Cho nên khi thay (ex − 1) − sin x ∼ x − x = 0 nghiễm nhiên chúng ta đã làm mất đi số hạng x2 . 2 74
9. Các định lý về hàm khả vi và ứng dụng 75
Ví dụ 9.26 (Câu 5, Đề 1, Giữa kì K61). Tính ex − cos x − ln(1 + x) lim . x→0 x2
[Gợi ý] Một cách tương tự, hãy chỉ ra rằng với bài tập trên nếu
• thay tương đương ta được kết quả bằng 1 (SAI) 2
• dùng công thức L’Hospital hoặc khai triển Maclaurin ta được kết quả bằng 3 (ĐÚNG). 2
9.6 Hiệu hai VCB tương đương
Trong mục trước, chúng ta biết rằng không thay tương đương được trong biểu thức
α(x) − β(x) nếu α(x) và β(x) là các VCB tương đương. Vậy hiệu của hai VCB tương đương là gì?
Bổ đề 1.1. Hiệu của hai VCB tương đương là một VCB bậc cao hơn cả hai VCB đó.
Chứng minh. Giả sử α(x) ∼ β(x) khi x → x . Khi đó, 0 α(x) − β(x) β(x) lim = 1 − lim = 1 − 1 = 0. x→x0 α(x) x→x0 α(x)
Vậy theo định nghĩa, α(x) − β(x) là một VCB bậc cao hơn α(x).
Ví dụ 9.27 (Một số ví dụ về hiệu hai VCB tương đương). a) x − sin x ∼ x3 h) tan x 6 − arcsin x ∼ x36 b) x − tan x ∼ −x33 i) tan x − arctan x ∼ 2x33 c) x − arcsin x ∼ −x36
j) arcsin x − arctan x ∼ x32 d) x − arctan x ∼ x33 k) x e) − (ex − 1) ∼ − x2 sin x − tan x ∼ − x3 2 2 f) l) sin x − arcsin x ∼ − x3 x − ln(1 + x) ∼ x22 3 g) sin x − arctan x ∼ x3 m) (1 6 − cos x) − x22 ∼ − x4 24
Hiệu hai VCB cùng bậc là một VCB bậc cao hơn cả hai VCB đó, vậy cụ thể, cao hơn là
bậc bằng bao nhiêu? Lấy, chẳng hạn, α(x) = x, ở ví dụ trên ta đã chỉ ra một số hiệu của
hai VCB tương đương "trong tự nhiên", như là x − sin x ∼ x3 cùng bậc với VCB α(x) = x3, 6
còn x − (ex − 1) ∼ −x2 cùng bậc với VCB β(x) = x2 khi x 2
→ 0. Với các VCB tương đương
"nhân tạo" sau đây thì x − β(x) có thể cùng bậc với xa (a > 1) bất kì. Chẳng hạn như muốn
x − β(x) ∼ x2017 thì chỉ cần chọn β(x) = x − x2017. Khi đó,
x ∼ x − x2017 (ngắt bỏ VCB bậc cao), và x − (x − x2017) = x2017 75 76
Chương 1. Hàm số một biến số (13LT+13BT)
9.7 Ba phương pháp (mới) để tính giới hạn
Như vậy đến thời điểm hiện tại chúng ta đã học được ba phương pháp mới để tính giới hạn, đó là
• Phương pháp sử dụng VCB-VCL (thay tương đương, ngắt bỏ),
• Phương pháp dùng khai triển Maclaurin,
• Phương pháp dùng quy tắc L’Hospital.
Mỗi một phương pháp đều có các ưu, nhược điểm riêng và tương ứng với các bài toán đặc
thù. Để so sánh các phương pháp này với nhau, ta minh họa bằng vẽ và 6 Ví dụ sau đây. VD 4 VCB VD 2 VD 1 VD 3 VD 5 VD 6 Maclaurin L’Hospital
Ví dụ 1 (Cả ba phương pháp đều áp dụng được). 1 − cos x lim x→0 ln(1 + x2)
Ví dụ 2 (Sử dụng VCB hoặc khai triển Maclaurin. Không nên dùng L’Hospital). 1 − cos x + x2 − sin x lim
x→0 x + sin2 x + arcsin3 x + arctan4 x
Ví dụ 3 (Sử dụng khai triển Maclaurin hoặc L’Hospital. Không thay tương đương). x − sin x + x3 lim . x→0 x3 76
9. Các định lý về hàm khả vi và ứng dụng 77
Ví dụ 4 (Khai triển Maclaurin. Không thay tương đương (tử số) và L’Hospital). x − sin x − x3 lim . x→0 arcsin(arctan3 x)
Ví dụ 5 (Sử dụng L’Hospital. Không dùng VCB, Maclaurin). ln x lim , hoặc lim xx. x→0+ x x→0+
Ví dụ 6 (Không dùng cả ba phương pháp trên). x − sin x lim . x→+∞ x + cos x [Lời giải] x − sin x 1 − sin x lim = lim x = 1. x→∞ x + cos x x→∞ 1 + cos x x
Chú ý 1.18. Trong quá trình tìm giới hạn của các dạng vô định, nên linh hoạt trong cách
xử lý, có thể kết hợp nhiều phương pháp với nhau để đạt hiệu quả tốt nhất. Chẳng hạn
như trong Ví dụ (4) nêu trên, x − sin x − x3 lim , x→0 arcsin(arctan3 x)
nên sử dụng khai triển Maclaurin ở tử số và thay tương đương ở mẫu số.
9.8 Về các VCL tiêu biểu
Chúng ta đã học về các VCB, VCL, các quy tắc thay tương đương, các quy tắc ngắt bỏ
VCB bậc cao, ngắt bỏ VCL bậc thấp. Tuy nhiên, các bài tập về VCL thường hay bị lãng
quên vì một lý do nào đó. Chúng ta đã học các VCB tương tương hay dùng, nhưng chưa có
nhiều ví dụ về các VCL. Chính vì vậy, mục này sẽ dành riêng để nói về ba VCL tiêu biểu (khi x → +∞), đó là
• Các hàm số mũ với cơ số lớn hơn 1, ví dụ ax (a > 1),
• Các hàm số đa thức, các hàm số là lũy thừa của x, chẳng hạn xn, xα, (α > 0),
• Các hàm số logarit với cơ số lớn hơn 1, như ln x, loga x (a > 1).
Cả ba hàm số này đều tiến ra vô cùng khi x → +∞, tuy nhiên với tốc độ khác nhau. Trong
ba hàm số này thì hàm số mũ (với cơ số lớn hơn 1) là VCL có bậc cao nhất (tiến ra vô cùng
với tốc độ nhanh nhất), sau đó đến các hàm số đa thức, và cuối cùng là các hàm số logarit (với cơ số lớn hơn 1). 77 78
Chương 1. Hàm số một biến số (13LT+13BT)
Hàm số mũ ≻ Hàm số đa thức ≻ Hàm số logarit
Cụ thể, bạn đọc có thể tự chứng minh dễ dàng hai giới hạn sau (bằng cách dùng quy tắc L’Hospital): ax xα lim = ∞, lim
= ∞, ∀a > 1, α > 0. x→+∞ xα x→+∞ loga x Ví dụ 9.28. Tính ln x + x2016 + ex lim . x→+∞ log x + x2017 + 2 2ex  
Áp dụng quy tắc ngắt bỏ VCL bậc thấp ta được, ln x + x2016 + ex ∼ ex, khi x → +∞. log x + x2017 + 2 2ex ∼ 2ex Do đó, ln x + x2016 + ex 1 lim = . x→+∞ log x + x2017 + 2 2 2ex
Bạn đọc sẽ thường xuyên gặp lại các VCL này khi học về Tích phân suy rộng (trong học
phần Giải tích I này) và Chuỗi số (trong học phần Giải tích III, học kì 2).
9.9 Bài tập ôn tập
Bài tập 1.54. Chứng minh rằng phương trình xn + px + q với n nguyên dương không thể
có quá 2 nghiệm thực nếu n chẵn và không thể có quá 3 nghiệm thực nếu n lẻ.
Chứng minh. Xét n chẵn, giả sử phương trình có 3 nghiệm thực x , khi đó tồn 1 < x2 < x3 tại c có
1 ∈ (x1, x2), c2 ∈ (x2, x3) sao cho f ′(c1) = f ′(c2) = 0. Tức là phương trình xn−1 = − p n
2 nghiệm thực, điều này mâu thuẫn do n chẵn.
Xét n lẻ, giả sử phương trình có 4 nghiệm thực x , khi đó theo định lý 1 < x2 < x3 < x4
Rolle, phương trình xn−1 + p = 0 có 3 nghiệm thực, trong khi theo trên ta vừa chứng minh n
thì nó không thể có quá 2 nghiệm thực do n − 1 chẵn.
Bài tập 1.55. Giải thích tại sao công thức Cauchy dạng f (b) − f (a) f ′(c) = không áp g(b) − g(a) g′(c)
dụng được với các hàm số f (x) = x2, g(x) = x3, −1 ≤ x ≤ 1
Bài tập 1.56. Chứng minh các bất đẳng thức
a) | sin x − sin y| ≤ |x − y| b) a − b a a − b < ln < , 0 ≤ b ≤ a. a b b 78
9. Các định lý về hàm khả vi và ứng dụng 79 Chứng minh.
a) Xét hàm số f (t) = sin t, thoả mãn điều kiện của định lý Lagrange
trong khoảng [x, y] bất kì. Khi đó ∃c ∈ [x, y] sao cho
sin x − sin y = f ′(c).(x − y) = cos c.(x − y)⇒| sin x − sin y| ≤ |x − y|
b) Xét hàm số f (x) = ln x, thoả mãn điều kiện của định lý Lagrange trong khoảng [b, a] nên b 1 a a − b
ln a − ln b = f ′(c)(a − b)⇒ ln = (b − a)⇒ ln = a c b c Vậy a − b a a − b < ln < , do b < c < a. a b b
Bài tập 1.57. Tìm giới hạn q (a) p √ tan πx lim x + x + x − x (∞ − ∞), (f) lim 2 ∞ , x→+∞ ∞ x→1− ln(1 − x) (b) x 1 lim − (∞ − ∞), (g) lim xsin x (00), x→1 x − 1 ln x x→0+ 1 (c) e x − cos 1 1 lim x 0 (h) q ,
lim(1 − a tan2 x) xsinx (1∞), x→∞ 0 1 − 1 − 1 x→0 x2 (i) lim(1 − cos x)tanx (00), (d) ex sin x − x(1 + x) lim 0 , x→0 x→0 x3 0 (e) (j)
lim tan πx ln(2 − x) (∞.0), lim (sin x)tan x (1∞). x→1 2 x→ π2 [Gợi ý]
(a) Sử dụng phương pháp nhân liên hợp, đáp số: 1. 2
(b) Quy đồng mẫu số rồi sử dụng công thức L’Hospital, đáp số: 1. 2
(c) Đặt t = 1, sau đó độc giả có thể dùng khai triển Maclaurin hoặc công thức L’Hospital, x đáp số: ∞.
(d) Sử dụng khai triển Maclaurin hoặc công thức L’Hospital, đáp số: 1. 3
(e) Sử dụng trực tiếp công thức L’Hospital (đưa tan πx xuống mẫu số), hoặc đặt t = 1 2 − x
và dùng công thức thay tương đương. đáp số: 2 . π
(f) Sử dụng công thức L’Hospital, đáp số: −∞.
(g) Sử dụng công thức lim A(x)B(x) = elim B(x) ln A(x), đáp số: 1. 79 80
Chương 1. Hàm số một biến số (13LT+13BT)
(h) Sử dụng công thức lim A(x)B(x) = elim B(x) ln A(x), đáp số: e−a.
(i) Sử dụng công thức lim A(x)B(x) = elim B(x) ln A(x), đáp số: 1.
(j) Sử dụng công thức lim A(x)B(x) = elim B(x) ln A(x), đáp số: 1.
Bài tập 1.58. Tính các giới hạn sau h i (a) lim x − x2 ln 1 + 1 , (i) 1 − cos2 x , x→∞ x lim x→0 x sin 2x (b) sin x − x cos x lim 1 1 = , 1 1 x→0 x x − cot x x2 sin x (j) lim − , √ x→0 x ex − 1
(c) lim x−5[sin(sin x) − x. 3 1 − x2], x→0 (k) lim ( 2 arctan x)x, x→+∞ π (d) 1 ex lim[ln(1 + x) x2 − ], (l) arctan x , x→0 x lim x→0 sin x − x (e) cos x − e− x22 ln x lim , (m) lim , x→0 x4 x→0+ 1 + 2 ln(sin x) (f) x − ln(1 + x) sin x − x cos x lim , (n) lim , x→0 x2 x→0 x3 (g) 1 1 sin x − x x2 lim − = , (o) lim √ √ , x→0 x sin x x sin x x→0 1 + x sin x − cos x (h) tan x − x ln(cos ax) lim , (p) lim , a 6= 0, b 6= 0. x→0 x − sin x x→0 ln(cos bx) [Gợi ý] (a) Đáp số: 1.
(h) L’Hospital, đáp số: 2. 2
(b) Khai triển Taylor, đáp số: 1.
(i) L’Hospital, đáp số: 1. 3 2 (c) ĐS: 7 .
(j) Quy đồng mẫu số và L’Hospital, đáp 45 số: 1.
(d) Khai triển Taylor, đáp số: 2 −3. 2 (k) ĐS: e− 2π .
(e) Khai triển Taylor, đáp số: − 1 . 12
(l) L’Hospital, đáp số: ∞.
(f) Khai triển Taylor hoặc L’Hospital, đáp số:
(m) L’Hospital, đáp số: 1. 1 . 2 2
(n) L’Hospital, đáp số: 1.
(g) Khai triển Taylor hoặc L’Hospital, đáp 3 số: 0.
(o) Nhân liên hợp, đáp số: 4. 3 80
9. Các định lý về hàm khả vi và ứng dụng 81
(p) L’Hospital, thay tương đương, đáp số: a2 . b2
Bài tập 1.59. Chứng minh rằng x − sin x lim
tồn tại và bằng 1 nhưng không tính được x→∞ x + cos x bằng quy tắc L’Hospital. Chứng minh. x − sin x 1 − sin x lim = lim x = 1. x→∞ x + cos x x→∞ 1 + cos x x
Nếu áp dụng quy tắc L’Hospital một cách hình thức thì ta có x − sin x 1 − cos x lim = lim x→∞ x + cos x x→∞ 1 − sin x
Tuy nhiên giới hạn ở vế phải không tồn tại, có thể kiểm tra bằng cách chọn 2 dãy xk =
2kπ và yk = π = 2kπ 2
Bài tập 1.60. Tính các giới hạn sau: a) x x lim 2 arctan x , b) lim a1/x+b1/x , a, b > 0. x→∞ π x→∞ 2
Bài tập 1.61. Dùng khai triển Maclaurin để tính các giới hạn sau: √ a) lim 1− 1+x2 cos x ,(1)
b) lim (cosh x−1) ln(1+x)−x3/2. (2) x→0 x(tan x−sinh x) x→0 x(sin x−arcsin x)
Bài tập 1.62. Xác định a, b sao cho biểu thức sau đây có giới hạn hữu hạn khi x→0 1 1 a b x3 − sin3 x(1 + ax + bx2) f (x) = − − − = sin3 x x3 x2 x x3 sin3 x
Chứng minh. Tại lân cận của x = 0, ta có thể viết x3 sin x = x − + o(x3) 3! do đó Mẫu số x3 = x3[x − + o(x3)]3 = x6 + o(x6) 3! và Tử số 1
= x3 − sin3 x(1 + ax + bx2) = x3 − [x3 + ax4 + (b − )x5 + cx6 + o(x6)] 2
ax4 + (b − 1)x5 + cx6 + o(x6) ⇒ f (x) = − 2 x6 + o(x6)
Do đó để tồn tại giới hạn hữu hạn của f (x) khi x→0, ta phải có a = 0, b = 12 (1)sinh x = ex−e−x 2 (2)cosh x = ex+e−x 2 81 82
Chương 1. Hàm số một biến số (13LT+13BT)
Bài tập 1.63. Cho f là một hàm số thực, khả vi trên [a, b] và có đạo hàm f ”(x) trên (a, b),
chứng minh rằng ∀x ∈ (a, b) có thể tìm được ít nhất 1 điểm c ∈ (a, b) sao cho f (b) − f (a) (x − a)(x − b) f (x) − f (a) − (x − a) = f ”(c) b − a 2
Chứng minh. Lấy x0 ∈ (a, b) bất kì. Đặt f (b) − f (a) (x − a)(x − b)
ϕ(x) := f (x) − f (a) − (x − a) − .λ b − a 2
Trong đó λ được xác định bởi điều kiện : f (b) − f (a) (x ϕ(x 0 − a)(x0 − b) 0) = f (x0) − f (a) − (x .λ = 0 b − a 0 − a) − 2
Khi đó ta có ϕ(x0) = ϕ(a) = ϕ(b) = 0
Ta có hàm ϕ liên tục, khả vi trên [a, x0], đo đó ϕ thoả mãn các điều kiện trong định lý
Rolle, suy ra tồn tại c1 ∈ (a, x0) sao cho ϕ′(c1) = 0. Tương tự như thế, tồn tại c2 ∈ (x0, b)
sao cho ϕ′(c2) = 0. Mặt khác, f (b) − f (a) a + b ϕ′(x) = f ′(x) − − λ(x − ) b − a 2
Theo giả thiết, f có đạo hàm cấp 2, do đó ϕ cũng có đạo hàm cấp 2, và ϕ”(c1) = ϕ”(c2) = 0,
nên theo định lý Rolle ta có tồn tại c ∈ (c1, c2) sao cho ϕ”(c) = f ”(c) − λ = 0⇒λ = f ”(c), và ta có : f (b) − f (a) (x − a)(x − b) f (x) − f (a) − (x − a) = f ”(c) b − a 2 82
10. Các lược đồ khảo sát hàm số 83
§10. CÁC LƯỢC ĐỒ KHẢO SÁT HÀM SỐ
10.1 Khảo sát và vẽ đồ thị của hàm số y = f (x)
Mục này học sinh đã được nghiên cứu tương đối kĩ trong chương trình phổ thông nên
chỉ nhấn mạnh cho sinh viên những điểm cần chú ý trong quá trình khảo sát hàm số và
khảo sát một số hàm số khác với chương trình phổ thông như hàm số có chứa căn thức, ... Sơ đồ khảo sát
1. Tìm TXĐ của hàm số, nhận xét tính chẵn, lẻ, tuần hoàn của hàm số (nếu có).
2. Xác định chiều biến thiên: tìm các khoảng tăng, giảm của hàm số.
3. Tìm cực trị (nếu có).
4. Xét tính lồi, lõm (nếu cần thiết), điểm uốn (nếu có).
5. Tìm các tiệm cận của hàm số (nếu có). 6. Lập bảng biến thiên.
7. Tìm một số điểm đặc biệt mà hàm số đi qua (ví dụ như giao điểm với các trục toạ độ,
....) và vẽ đồ thị của hàm số.
Ví dụ 10.1 (Giữa kì, K61). Tìm các cực trị của hàm số sau a) y = 2x . b) y = 2x . x2+2 x2+1
Ví dụ 10.2 (Giữa kì, K59). Tìm các đường tiệm cận của đường cong y = x2 sin 1. x
[Lời giải] TXĐ = R \ {0}. 1 1
0 ≤ x2 sin ≤ x2 ⇒ lim x2 sin = 0 (giới hạn kẹp). x x→0 x
Đường cong không có tiệm cận đứng. 1 sin 1 lim x2 sin = lim x. x = ∞ x→∞ x x→∞ 1 x
Đường cong không có tiệm cận ngang. y sin 1 lim = lim x = 1. x→∞ x x→∞ 1 x 1 1 sin t sin t − t 1
lim (y − x) = lim x x sin − 1 = lim − 1 = lim = 0 đặt t = . x→∞ x→∞ x t→0 t t t→0 t2 x
Đường cong có một tiệm cận xiên là y = x. 83 84
Chương 1. Hàm số một biến số (13LT+13BT)
Ví dụ 10.3. Tìm các tiệm cận xiên của đường cong y = ln(1 + e−2x). [Lời giải] Ta có y y ln(1 + e−2x) −2e−2x lim = 0, a = lim = lim = lim = −2, (L’Hospital). x→+∞ x x→−∞ x x→−∞ x x→−∞ 1 + e−2x
b = lim (y + 2x) = lim ln(1 + e−2x) + 2x = lim ln[(1 + e−2x)e2x] = lim ln(1 + e2x) = 0. x→−∞ x→−∞ x→−∞ x→−∞
Kết luận: y = −2x là tiệm cận xiên của đường cong.
Bài tập 1.64. Khảo sát và vẽ đường cong y = 2−x2 . 1+x4 y x O Hình 1.64 √
Bài tập 1.65. Khảo sát và vẽ đường cong y = 3 x3 − x2 − x + 1. y x O Hình 1.65
Bài tập 1.66. Khảo sát và vẽ đường cong y = x−2 √ . x2+1 84
10. Các lược đồ khảo sát hàm số 85 y x O Hình 1.66
10.2 Khảo sát và vẽ đường cong cho dưới dạng tham số  
Giả sử cần khảo sát và vẽ đường cong cho dưới dạng tham số x = x(t) y = y(t)
1. Tìm TXĐ, nhận xét tính chẵn, lẻ, tuần hoàn của các hàm số x(t), y(t) (nếu có).
2. Xác định chiều biến thiên của các hàm số x(t), y(t) theo biến t bằng cách xét dấu các đạo hàm của nó.
3. Tìm các tiệm cận của đường cong
(a) Tiệm cận đứng: Nếu lim y(t) = ∞ và lim x(t) = x thì là một tiệm 0 x = x0 t→t0(∞) t→t0(∞)
cận đứng của đường cong.
(b) Tiệm cận ngang: Nếu lim x(t) = ∞ và lim y(t) = y thì là một tiệm 0 y = y0 t→t0(∞) t→t0(∞)
cận ngang của đường cong.
(c) Tiệm cận xiên: Nếu lim y(t) = ∞ và lim x(t) = ∞ thì đường cong có thể có t→t0(∞) t→t0(∞) tiệm cận xiên. Nếu y(t) a = lim , b = lim [y(t) − ax(t)] t→t x(t) 0(∞) t→t0(∞)
thì y = ax + b là một tiệm cận xiên của đồ thị hàm số.
4. Để vẽ đường cong được chính xác hơn, ta xác định tiếp tuyến của đường cong tại các
điểm đặc biệt. Hệ số góc của tiếp tuyến của đường cong tại mỗi điểm bằng dy y′ = t dx x′t 85 86
Chương 1. Hàm số một biến số (13LT+13BT)
Ngoài ra có thể khảo sát tính lồi lõm và điểm uốn (nếu cần thiết) bằng cách tính các đạo hàm cấp hai y′ d t d2y x′ y = t = tt”x′t − y′txt” dx2 dx x′3 t
5. Xác định một số điểm đặc biệt mà đồ thị hàm số đi qua và vẽ đồ thị hàm số.
Ví dụ 10.4 (Giữa kì, K61). Tìm các tiệm cận của đường cong cho bởi phương trình tham số     a) x = 2016t x = 2016t 1−t3 b) 1+t3 y = 2016t2 . y = 2016t2 . 1−t3 1+t3  
Bài tập 1.67. Khảo sát và vẽ đường cong x = 2t − t2 y = 3t − t3. y O x Hình 1.67
10.3 Khảo sát và vẽ đường cong trong hệ toạ độ cực
Bài tập 1.68. Khảo sát và vẽ đường cong r = a + b cos ϕ, (0 < a ≤ b). 86
10. Các lược đồ khảo sát hàm số 87 y r = a + b cos ϕ O x Hình 1.68
Bài tập 1.69. Khảo sát và vẽ đường cong r = a (1 + cos ϕ) (a > 0), (đường Cardioid hay
đường hình tim, trường hợp đặc biệt của đường cong trong Bài tập 1.68 với a = b) y a O x 2a −a Hình 1.69
Bài tập 1.70. Khảo sát và vẽ đường cong r = a √ , (a > 0). cos 3ϕ 87 88
Chương 1. Hàm số một biến số (13LT+13BT) y r = a √cos3ϕ O x Hình 1.70
Bài tập 1.71. Khảo sát và vẽ đường cong Lemniscate
(x2 + y2)2 = 2a2(x2 − y2) (a > 0).
Phương trình của đường Lemniscate trong tọa độ cực là p r = a 2 cos 2ϕ. y p r = a 2 cos 2ϕ x O Hình 1.71
Bài tập 1.72. Khảo sát và vẽ đường cong x2 + y22 = 2a2xy (a > 0). (
Tham số hoá đường cong đã cho, đặt
x = r cos ϕ , phương trình đường cong tương đương y = r sin ϕ với r2 = a2 sin 2ϕ. 88
10. Các lược đồ khảo sát hàm số 89 y p r = a sin 2ϕ O x Hình 1.72
Bài tập 1.73. Khảo sát và vẽ đường cong x3 + y3 = axy (a > 0) (Lá Descartes) (
Tham số hoá đường cong đã cho, đặt
x = r cos ϕ , phương trình đường cong tương đương y = r sin ϕ với a sin ϕ cos ϕ
r = sin3 ϕ + cos3 ϕ y 1 2 1 x O 2 Hình 1.73 TCX: y = −x − 13 10.4 Bài tập
Bài tập 1.74. Khảo sát tính đơn điệu của hàm số 89 90
Chương 1. Hàm số một biến số (13LT+13BT) a. y = x3 + x b. y = arctan x − x [Đáp số]
a) hàm số tăng với mọi x
b) hàm số giảm với mọi x
Bài tập 1.75. Chứng minh các bất đẳng thức
a. 2x arctan x ≥ ln(1 + x2) ∀x ∈ R
b. x − x22 ≤ ln(1 + x) ≤ x ∀x ≥ 0 Chứng minh.
a) Xét hàm số f (x) = 2x arctan x − ln(1 + x2)⇒ f ′(x) = 2 arctan x.
• Nếu x ≥ 0, f ′(x) ≥ 0⇒ f (x) ≥ f (0) = 0
• Nếu x ≤ 0, f ′(x) ≤ 0⇒ f (x) ≤ f (0) = 0
b) Tương tự, xét g(x) = x − x22 − ln(1 + x), h(x) = ln(1 + x) − x x2 x g′(x) = − < 0, h′(x) = −
< 0⇒g(x) ≤ g(0) = 0, h(x) ≤ h(0) = 0. 1 + x 1 + x
Bài tập 1.76. Tìm cực trị của hàm số p a) 3x2 + 4x + 4 b) y = x − ln(1 + x) c) y = 3 (1 − x)(x − 2)2 y = x2 + x + 1 Chứng minh. a) y′ = −x(x+2) , y , y (x2+x+1)2 min = y(−2) = 83 max = y(0) = 4. b) y′ = x , y 1+x min = y(0) = 0. √ √ c) 3 (x 3 4 y′ = −1 −2)2 √ + 2 1−x √ = 3 −x √ . 3 3 (1−x)2 3 3 x−2 3 (1−x)2(x−2) 3 √ • Xét x 4 1 = 4 , ta có y ) = 3 min = y( 43 − 3
• Xét x2 = 1, y′ không đổi dấu, hàm số không đạt cực trị tại x2 = 1
• Xét x3 = 2, ta có ymax = y(2) = 0
Bài tập 1.77. Chứng minh các bất đẳng thức sau a) ex > 1 + x ∀x 6= 0
c) tan x > x + x33 ∀0 < x < π2 b) x − x3 < sin x < x 6 ∀x > 0
Bài tập 1.78. Chứng minh rằng với mọi x > 0 ta có 1 x 1 x+1 1 + < e < 1 + x x
Bài tập 1.79. Tính các giới hạn sau 90
10. Các lược đồ khảo sát hàm số 91 h i h √ i (a) lim x − x2 ln(1 + 1) ,
(c) lim x−5 sin(sin x) − x. 3 1 − x2 , x→∞ x x→0 1 ex (b) lim 1 1 , (d) lim ln(1 + x)x2 − . x→0 x x − cot x x→0 x 91 92
Chương 1. Hàm số một biến số (13LT+13BT) 92 2 CHƯƠNG
PHÉP TÍNH TÍCH PHÂN MỘT BIẾN SỐ
§1. TÍCH PHÂN BẤT ĐỊNH
1.1 Nguyên hàm của hàm số
Chương này trình bày về phép tính tích phân, đây là phép toán ngược của phép tính
đạo hàm (vi phân) của hàm số. Nếu ta cho trước một hàm số f (x) thì có tồn tại hay không
một hàm số F(x) có đạo hàm bằng f (x)? Nếu tồn tại, hãy tìm tất cả các hàm số F(x) như vậy.
Định nghĩa 2.26. Hàm số F(x) được gọi là một nguyên hàm của hàm số f (x) trên khoảng
D nếu F′(x) = f (x), ∀x ∈ D hay dF(x) = f (x)dx.
Định lý sau đây nói rằng nguyên hàm của một hàm số cho trước không phải là duy nhất,
nếu biết một nguyên hàm thì ta có thể miêu tả được tất cả các nguyên hàm khác của hàm số đó.
Định lý 2.38. Nếu F(x) là một nguyên hàm của hàm số f (x) trên khoảng D, thì:
• Hàm số F(x) + C cũng là một nguyên hàm của hàm số f (x), với C là một hằng số bất kỳ.
• Ngược lại, mọi nguyên hàm của hàm số f (x) đều viết được dưới dạng F(x) + C, trong đó C là một hằng số.
Như vậy biểu thức F(x) + C biểu diễn tất cả các nguyên hàm của hàm số f (x), mỗi hằng
số C tương ứng cho ta một nguyên hàm. 93 94
Chương 2. Phép tính tích phân một biến số
Định nghĩa 2.27. Tích phân bất định của một hàm số f (x) là họ các nguyên hàm F(x) +
C, với x ∈ D, trong đó C là một nguyên hàm của hàm số f (x) và C là một hằng số bất Z
kỳ. Tích phân bất định của f (x)dx được ký hiệu là
f (x)dx. Biểu thức f (x)dx được gọi là
biểu thức dưới dấu tích phân và hàm số f (x) được gọi là hàm số dưới dấu tích phân. Z Vậy
f (x)dx = F(x) + C, với F(x) là nguyên hàm của f (x).
Các tính chất của tích phân bất định Z ′ Z • f (x)dx = f (x) hay d f (x)dx = f (x)dx Z Z • F′(x)dx = F(x) + C hay dF(x) = F(x) + C Z Z • a f (x)dx = a
f (x)dx (a là hằng số khác 0) Z Z Z • [ f (x) ± g(x)] dx = f (x)dx ± g(x)dx
Hai tính chất cuối cùng là tính chất tuyến tính của tích phân bất định, ta có thể viết chung Z Z Z
[α f (x) + βg(x)] dx = α f (x)dx + β g(x)dx
trong đó α, β là các hằng số không đồng thời bằng 0.
Các công thức tích phân dạng đơn giản Z Z 1)
xαdx = xα+1 + C, (α 7) exdx = ex + C α+1 6= −1) Z 2) dx = ln Z x |x| + C 8) dx = 1 ln a+x + C a2 2a a−x Z Z −x2 3) sin xdx = − cos x + C cos xdx = Z sin x + C 9) dx = 1 arctan x + C x2+a2 a a Z 4) dx = − cot x + C sin2 x Z √ Z 10) dx √ = ln x2 + α 5) dx x + + C = tan x + C x2+α cos2 x Z Z 6) axdx = ax + C, (a > 0, a 11) dx √ = arcsin x + C ln a 6= 1) a2−x2 a Z √ √ 12) a2 − x2dx = 1 x a2 arcsin x + C 2 − x2 + a22 a Z √ h √ √ i 13) x2 + adx = 1 x x2 + a + a ln x2 + a + C 2 x + 94
1. Tích phân bất định 95
1.2 Các phương pháp tính tích phân bất định
1. Phương pháp khai triển
Để tính một tích phân bất kỳ, ta cần sử dụng các phương pháp thích hợp để đưa về
các tích phân đã có trong bảng các công thức tích phân đơn giản ở trên. Một phương
pháp đơn giản là phương pháp khai triển. Phương pháp này dựa trên tính chất tuyến
tính của tích phân bất định: Z Z Z
[α f (x) + βg(x)] dx = α f (x)dx + β g(x)dx
Ta phân tích hàm số dưới dấu tích phân thành tổng (hiệu) của các hàm số đơn giản
mà đã biết được nguyên hàm của chúng, các hằng số được đưa ra bên ngoài dấu tích phân. Z Z Z Ví dụ 1.1. √ 3 5 • (2x x − 3x2)dx = 2 x 2 dx − 3 x2dx = 4 x 2 5 − x3 + C Z Z Z Z • 2 sin x + x3 − 1 dx = 2 sin xdx + x3dx dx = x − x
−2 cos x + x44 − ln |x| + C Z dx Z 1 1 1 • = − dx = − + arctan x + C x2(1 + x2) x2 1 + x2 x
2. Phương pháp biến đổi biểu thức vi phân Z Z Nhận xét: nếu f (x)dx = F(x) + C thì
f (u)du = F(u) + C , trong đó u = u(x) là
một hàm số khả vi liên tục. Ta có thể kiểm tra lại bằng cách đạo hàm hai vế theo x.
Sử dụng tính chất này, ta biến đổi biểu thức dưới dấu tích phân g(x)dx về dạng g(x)dx = f (u(x))u′(x)dx,
trong đó f (x) là một hàm số mà ta dễ dàng tìm được nguyên hàm F(x). Khi đó tích phân cần tính trở thành Z Z Z g(x)dx = f (u(x))u′(x)dx = f (u(x))du = F(u(x)) + C Z
Trong trường hợp đơn giản u(x) = ax + b thì du = adx, do đó nếu f (x)dx = F(x) + C ta suy ra Z 1 f (ax + b)dx = F(ax + b) + C a Z Ví dụ 1.2. (a) sin axdx = −1 cos ax + C a Z (b) eaxdx = eax + C a 95 96
Chương 2. Phép tính tích phân một biến số Z Z (c) esin x cos xdx = esin xd(sin x) = esin x + C Z Z (d) dx =
(1 + tan2 x)d(tan x) = tan3 x + tan x + C cos4 x 3 Z Z (e) √ √ √ 3 x 1 + 3x2dx = 1 1 + 3x2d(1 + 3x2) = 1 1 + 3x2 + C 6 9 (f) Z arccos x arcsin x Z π I = √ dx =
− arcsin x arcsin xd(arcsin x) 1 − x2 2 nên π 1 ⇒ I = arcsin2 x − arcsin3 x + C 4 3
3. Phương pháp đổi biến Z Xét tích phân I =
f (x)dx, trong đó f (x)là một hàm số liên tục. Để tính tích phân
này, ta tìm cách chuyển sang tính tích phân khác của một hàm số khác bằng một
phép đổi biến x = ϕ(t), sao cho biểu thức dưới dấu tích phân đối với biến t có thể tìm
được nguyên hàm một cách đơn giản hơn.
Phép đổi biến thứ nhất:
Đặt x = ϕ(t), trong đó ϕ(t) là một hàm số đơn điệu, và có đạo hàm liên tục. Khi đó ta có Z Z I = f (x)dx =
f [ϕ(t)] ϕ′(t)dt
Giả sử hàm số g(t) = f [ϕ(t)] ϕ′(t) có nguyên hàm là hàm G(t), và t = h(x) là hàm
số ngược của hàm số x = ϕ(t), ta có Z
g(t)dt = G(t) + C ⇒ I = G [h(x)] + C
Phép đổi biến thứ hai:
Đặt t = ψ(x), trong đó ψ(x) là một hàm số có đạo hàm liên tục, và ta viết được hàm
f (x) = g [ψ(x)] ψ′(x). Khi đó ta có Z Z I = f (x)dx =
g [ψ(x)] ψ′(x)dx
Giả sử hàm số g(t) có nguyên hàm là hàm số G(t), ta có I = G [ψ(x)] + C
Chú ý: Khi tính tích phân bất định bằng phương pháp đổi biến số, sau khi tìm được
nguyên hàm theo biến số mới, phải đổi lại thành hàm số của biến số cũ. 96
1. Tích phân bất định 97 Z r
Ví dụ 1.3. (a) Tính tích phân x I1 = dx 2 − x Đặt
x = 2 sin2 t, t ∈ 0, π , ta tính được 2 s r x 2 sin2 t dx = 4 sin t cos tdt, = = tan t 2 − x 2(1 − sin2 t) Suy ra Z r x Z I1 = dx = 4 sin2 tdt = 2t − sin 2t + C 2 − x Đổi lại biến p x, với t = arcsin x , ta thu được 2 Z r r x x p I1 = dx = 2 arcsin − 2x − x2 + C 2 − x 2 Z (b) Tính tích phân e2x I2 = dx ex + 1
Đặt ex = t ⇒ exdx = dt, ta có Z t Z 1 I2 = dt = 1 − dt = t − ln |t + 1| + C t + 1 t + 1
Đổi lại biến x, ta được I2 = ex − ln(ex + 1) + C. Z (c) Tính tích phân dx I3 = √1 + 4x
Đặt t = 2−x ⇒ dt = −2−x ln 2dx, tích phân trở thành Z −dt 1 Z dt 1 p I3 = √ = − √ = − ln(t + t2 + 1) + C t ln 2 1 + t−2 ln 2 t2 + 1 ln 2 Đổi lại biến x, ta có: 1 √ I3 = − ln(2−x + 4−x + 1) + C ln 2
Ví dụ 1.4 (Giữa kì, K61). Tính tích phân Z Z a) xx+1 1 + 1 + ln x dx. b) xx−1 1 + ln x dx. x − 1x
4. Phương pháp tích phân từng phần
Giả sử u = u(x) và v = v(x) là các hàm số có đạo hàm liên tục. Theo quy tắc lấy vi phân Z Z Z d(uv) = udv + vdu ⇒ uv = d(uv) = udv + vdu Suy ra Z Z udv = uv − vdu 97 98
Chương 2. Phép tính tích phân một biến số Z Xét tích phân I =
f (x)dx. Ta cần biểu diễn
f (x)dx = [g(x)h(x)] dx = g(x) [h(x)dx] = udv Z
và áp dụng công thức tích phân từng phần với các hàm số u = g(x), v = h(x)dx. Ta
thường sử dụng phương pháp này khi biểu thức dưới dấu tích phân chứa một trong
các hàm số sau đây: ln x, ax, hàm số lượng giác, hàm số lượng giác ngược. Cụ thể: Z Z Z • Trong các tích phân xnekxdx; xn sin kxdx;
xn cos kxdx , n nguyên dương, ta thường chọn u = xn. Z • Trong các tích phân
xα lnn xdx, α 6= −1 và n nguyên dương, ta thường chọn u = lnn x. Z Z • Trong tích phân xn arctan kxdx;
xn arcsin kxdx, n nguyên dương, ta thường
chọn u = arctan kx hoặc u = arcsin kx; dv = xndx.
Ví dụ 1.5. Tính các tích phân bất định Z Z
(a) I1 = ln xdx = x ln x − dx = x ln x − x + C Z (b) I2 = x2 sin xdx
Đặt u = x2, dv = sin xdx ⇒ v = − cos x, ta được Z I2 = −x2 cos x + 2 x cos xdx
Đặt u = x, dv = cos xdx ⇒ v = sin x, ta được Z
I2 = −x2 cos x + 2 x sin x − sin xdx
= −x2 cos x + 2x sin x + 2 cos x + C Z (c) xexdx I3 = (x + 1)2 Đặt u = xex; dv = dx
; du = (x + 1)exdx, ta được (x+1)2 ⇒ v = − 1 x+1 xex Z xex ex I3 = − + exdx = − + ex + C = + C x + 1 x + 1 x + 1 Z (d) xexdx I4 = √1 + ex Z Đặt √1 + ex = t ⇒ exdx √ = 2dt, ta có I
[ln(t − 1) + ln(t + 1)] dt = 2(t − 1+ex 4 = 2
1) ln(t − 1) + 2(t + 1) ln(t + 1) − 4t + C Đổi lại biến x ta có Z xexdx √ √ √
= 2(x − 2) 1 + ex + 4 ln 1 + 1 + ex − 2x + C 1 + ex 98
1. Tích phân bất định 99 Z (e) x arcsin x I5 = √ dx 1 − x2 Đặt √ u = arcsin x; dv = xdx √ ⇒ du = dx √
; v = − 1 − x2, ta được 1−x2 1−x2 p Z p I5 = − 1 − x2 arcsin x +
dx = − 1 − x2 arcsin x + x + C Z (f) I6 = ex cos 2xdx
Đặt u = cos 2x; dv = exdx ⇒ v = ex; du = −2 sin 2xdx, ta được Z I6 = ex cos 2x + 2 ex sin 2xdx
Đặt u = sin 2x; dv = exdx ⇒ v = ex; du = 2 cos 2xdx, ta được Z
I6 = ex cos 2x + 2 ex sin 2x − 2 ex cos 2xdx
= ex cos 2x + 2ex sin 2x − 4I6 + 5C
Vậy I6 = ex (cos 2x + 2 sin 2x) + C. 5
Ví dụ 1.6 (Giữa kì, K61). Tính tích phân Z Z a) x3 arctan xdx. c) x2 sin 2xdx. Z Z b) x3 arccot xdx. d) x2 cos 2xdx.
Ví dụ 1.7 (Ngụy biện toán học). Chứng minh rằng 0 = 1.
Chứng minh. Xét tích phân Z dx Z 1 I = = d ln x x ln x ln x 1 Z 1 = . ln x − ln xd (tích phân từng phần) ln x ln x Z −1 1 = 1 − ln x. . dx ln2 x x Z dx = 1 − x ln x = 1 + I.
Phương trình I = 1 + I dẫn đến 0 = 1. Sai lầm ở đâu?
Trong các mục sau đây chúng ta sẽ xét tích phân bất định của một số dạng hàm cơ
bản: hàm phân thức hữu tỷ, hàm lượng giác, hàm chứa căn thức; và trình bày một
số phương pháp giải chung đối với tích phân các hàm này. 99 100
Chương 2. Phép tính tích phân một biến số
1.3 Tích phân hàm phân thức hữu tỷ
Định nghĩa 2.28. Một hàm phân thức hữu tỷ là một hàm số có dạng f (x) = P(x) , trong Q(x)
đó P(x), Q(x) là các đa thức của x. Một phân thức hữu tỷ có bậc của đa thức ở tử số nhỏ
hơn bậc của đa thức ở mẫu số là một phân thức hữu tỷ thực sự.
Bằng phép chia đa thức, chia P(x) cho Q(x) ta luôn đưa được một hàm phân thức hữu tỷ về dạng r(x) f (x) = H(x) + Q(x)
trong đó H(x) là đa thức thương, r(x) là phần dư trong phép chia. Khi đó r(x) là một phân Q(x)
thức hữu tỷ thực sự. Nguyên hàm của đa thức được tìm bởi công thức tích phân cơ bản.
Ta sẽ xét việc tìm nguyên hàm của phân thức hữu tỷ còn lại r(x) trong hai trường hợp đặc Q(x)
biệt: mẫu số của phân thức là đa thức bậc nhất hoặc đa thức bậc hai. Trong những trường
hợp mẫu số phức tạp hơn, chúng ta sử dụng phương pháp hệ số bất định để đưa về hai trường hợp trên.
Phương pháp hệ số bất định
Giả sử chúng ta muốn phân tích một phân thức hữu tỷ thực sự P(x) thành tổng (hiệu) Q(x)
của các phân thức hữu tỷ thực sự có mẫu số là đa thức bậc nhất hoặc bậc hai. Trước hết
ta phân tích đa thức ở mẫu số Q(x) thành tích của các đa thức bậc nhất hoặc bậc hai vô nghiệm
Q(x) = (x − α1)a1...(x − αm)am(x2 + p1x + q1)b1...(x2 + pnx + qn)bn trong đó α là các hằng số, là các số nguyên dương, i, pj, qj ai, bj 1 ≤ i ≤ m; 1 ≤ j ≤ n.
• Nếu trong phân tích của Q(x) xuất hiện đơn thức (x − α)a, a là số nguyên dương thì
trong phân tích của phân thức P(x) xuất hiện các hạng tử dạng Ai , trong đó A là Q(x) (x−α)i i hằng số và 1 ≤ i ≤ a.
• Nếu trong phân tích của Q(x) xuất hiện biểu thức (x2 + px + q)b, b là số nguyên
dương thì trong phân tích của phân thức P(x) xuất hiện các hạng tử dạng Bjx+Cj , Q(x) (x2+px+q)j trong đó B là các hằng số và j, Cj 1 ≤ j ≤ b.
Sau khi viết được phân tích của P(x) , ta tìm các hằng số A bằng cách quy đồng mẫu Q(x) i, Bj, Cj
số ở hai vế, rồi đồng nhất hệ số của xn, n ∈ R ở hai vế. Như vậy việc dùng phương pháp hệ
số bất định dẫn chúng ta tới việc tính bốn loại tích phân hữu tỷ cơ bản sau: Z Z I. Adx II. Adx (k ≥ 2) x − a (x − a)k Z Z III. (Mx + N)dx IV. (Mx + N)dx (m ≥ 2) x2 + px + q (x2 + px + q)m trong đó 100
1. Tích phân bất định 101 Z 1. Adx = A ln x−a |x − a| + C Z Z 2. Adx = A(x − a)−kdx = −A + C (x−a)k (k−1)(x−a)k−1 3. Z (Mx + N)dx Z Mt + (N − Mp/2) q = dt (a =
q − p2/4, đổi biến t = x + p/2) x2 + px + q t2 + a2 Z Mtdt Z (N − Mp/2)dt = + t2 + a2 t2 + a2 M 1 t =
ln(t2 + a2) + (N − Mp/2) arctan + C 2 a a M 2N − Mp 2x + p = ln(x2 + px + q) + arctan + C. 2 p p 4q − p2 4q − p2 4. Z (Mx + N)dx Z Mt + (N − Mp/2) q = dt (a =
q − p2/4, đổi biến t = x + p/2) (x2 + px + q)m (t2 + a2)m Z Mtdt Z (N − Mp/2)dt = + (t2 + a2)m (t2 + a2)m Z • Tích phân thứ nhất Mtdt = − M + C. (t2+a2)m 2(m−1)(t2+a2)m−1
• Muốn xử lý tích phân thứ hai ta thực hiện phép đổi biến số lượng giác t = a tan z,   khi đó t2 + a2 = a2 , cos2 z dt = a dz. cos2 z Ta có Z dt Z = a2m−1 cos2m−2 zdz. (t2 + a2)m
Tích phân của hàm lượng giác này sẽ được nghiên cứu kĩ ở phần sau.
Ví dụ 1.8. Tính các tích phân bất định Z a. x4 − x3 + 2x2 − 2x + 1 I1 = dx (x2 + 2)(x − 1) Ta có x4 − x3 + 2x2 − 2x + 1 1 A Bx + C = x + = x + + (x2 + 2)(x − 1) (x2 + 2)(x − 1) x − 1 x2 + 2
Quy đồng mẫu số ở hai vế
3 = (A + B)x2 + (C − B + 2)x − C 101 102
Chương 2. Phép tính tích phân một biến số    A + B = 0 A = 1   
Đồng nhất hệ số của x2, x và hệ số tự do, ta được C − B + 2 = 0 ⇒ B = −1    −C = 1  C = −1 Suy ra x4 − x3 + 2x2 − 2x + 3 1 1 2x 1 = x + − − (x2 + 2)(x − 1) x − 1 2 x2 + 2 x2 + 2 Vậy tích phân bằng x2 ln(x2 + 2) 1 x I = + ln |x − 1| − − √ arctan √ + C 2 2 2 2 Z b. 2x4 + 10x3 + 17x2 + 16x + 5 I2 = dx (x + 1)2(x2 + 2x + 3) Ta viết 2x4 + 10x3 + 17x2 + 16x + 5 2 1 4 = 2 + − − (x + 1)2(x2 + 2x + 3) x + 1 (x + 1)2 x2 + 2x + 3 Suy ra 1 √ x + 1 I = 2x + 2 ln |x + 1| + − 2 2 arctan √ + C x + 1 2
Ví dụ 1.9 (Giữa kì, K61). Tính các tích phân sau Z Z a) 1 dx. c) xdx . x2+2016x (x2+1)(x2+2) Z Z b) 1 dx. d) xdx . x2−2016x (x2+2)(x2+3)
Ví dụ 1.10 (Giữa kì, K61). Tính tích phân Z Z a) x ln(x2 + x + 1)dx. b) x ln(x2 − x + 1)dx.
1.4 Tích phân hàm lượng giác 1. Phương pháp chung Z Xét tích phân
R(sin x, cos x)dx, trong đó hàm dưới dấu tích phân là một biểu thức
hữu tỷ đối với sin x, cos x. Ta có thể sử dụng phép đổi biến tổng quát t = tan t , khi đó 2 2t 1 − t2 2t 2dt sin x = ; cos x = ; tan x = ; dx = 1 + t2 1 + t2 1 − t2 1 + t2
tích phân đang xét được đưa về tích phân của phân thức hữu tỉ của biến t. 102
1. Tích phân bất định 103 Z
Ví dụ 1.11. Tính tích phân sin x − cos x + 2dx 1 + sin x + cos x Ta viết Z sin x − cos x + 2 Z d(1 + sin x + cos x) Z dx dx = − + 2 1 + sin x + cos x 1 + sin x + cos x 1 + sin x + cos x Đặt t = tan x, suy ra 2 Z dx Z dt = = ln |1 + t| + C 1 + sin x + cos x 1 + t
Thay lại biến cũ, ta được Z sin x − cos x + 2 x
dx = − ln |1 + sin x + cos x| + ln 1 + sin x + cos x 1 + tan 2 + C Z 2. Tích phân dạng
sinm x cosn xdx, trong đó m, n là các số nguyên
• Nếu m là số nguyên dương lẻ, ta đặt t = cos x.
• Nếu n là số nguyên dương lẻ, ta đặt t = sin x.
• Nếu m, n là các số nguyên dương chẵn, ta sử dụng công thức hạ bậc: 1 − cos 2x 1 + cos 2x sin2 x = ; cos2 x = 2 2 Z
rồi đưa về tích phân dạng sink 2x cosl 2xdx.
Ví dụ 1.12. Tính các tích phân bất định Z • I1 = sin3 x cos2 xdx
Đặt cos x = t ⇒ − sin xdx = dt ta có Z Z t5 t3 cos5 x cos3 x sin3 x cos2 xdx = (1 − t2)t2(−dt) = − + C = − + C 5 3 5 3 Z • I2 = sin4 x cos2 xdx
Sử dụng công thức hạ bậc ta có Z (1 − cos 2x)2 1 + cos 2x 1 Z I2 = dx =
1 − cos 2x − cos2 2x + cos3 2x dx 4 2 8 Z Z ⇒ I 1+cos 4x 2 = 1 x dx + 1 (1 8 − sin 2x 2 − 2 2 − sin2 2x)d(sin 2x) Vậy ! 1 x sin 2x sin 4x sin 2x sin3 2x ⇒ I2 = − − + − + C 8 2 2 8 2 6 103 104
Chương 2. Phép tính tích phân một biến số
Đối với tích phân I sau khi sử dụng công thức hạ bậc lần thứ nhất ta cũng có 2
thể tiếp tục hạ bậc của biểu thức lượng giác dưới dấu tích phân bởi công thức 3 sin x − sin 3x 3 cos x + cos 3x sin3 x = ; cos3 x = 4 4
Áp dụng vào tích phân I , ta có: 2 1 Z 1 + cos 4x 3 cos 2x + cos 6x I2 = 1 − cos 2x − + dx 8 2 4 1 x sin 2x sin 4x sin 6x = − − + + C 8 2 8 8 24 Z 3. Tích phân
R(sin x, cos x)dx có dạng đặc biệt
• Đặt t = cos x nếu R(− sin x, cos x) = −R(sin x, cos x).
• Đặt t = sin x nếu R(sin x, − cos x) = −R(sin x, cos x).
• Đặt t = tan x nếu R(− sin x, − cos x) = R(sin x, cos x). Z
Ví dụ 1.13. Tính tích phân dx sin x cos4 x
Đặt t = cos x ⇒ dt = − sin xdx, ta có Z dx Z −dt Z 1 1 1 1 = = + + − dt sin x cos4 x (1 − t2)t4 t4 t2 2(t − 1) 2(t + 1) 1 1 1 t − 1 = − − + ln + C 3t3 t 2 t + 1 nên Z dx 1 1 1 1 − cos x = − − + ln + C sin x cos4 x 3 cos x3 cos x 2 1 + cos x
1.5 Tích phân các biểu thức vô tỷ
Xét các tích phân có dạng Z √ • R(x, x2 + α2)dx, Z √ • R(x, x2 − α2)dx, Z √ • R(x, α2 − x2)dx,
trong đó R(u, v) là các hàm số hữu tỷ.
Có hai phương pháp xử lý tích phân các biểu thức hữu tỉ là Phép thế lượng giác và
Phép thế Euler. Ý tưởng của cả hai phương pháp này đều là khử các biểu thức vô tỉ bằng cách: 104
1. Tích phân bất định 105
1. đưa về tích phân của các hàm lượng giác bằng qua phép thế lượng giác,
2. đưa về tích phân của các hàm phân thức hữu tỉ bằng phép thế Euler.
Phép thế lượng giác Z √
• Đặt x = α tan t đối với tích phân R(x, x2 + α2)dx. α α Z √ • Đặt x = hoặc x = đối với tích phân R(x, x2 − α2)dx. cos t sin t Z √
• Đặt x = α sin t hoặc x = α cos t đối với tích phân R(x, α2 − x2)dx. Z Ví dụ 1.14. Tính dx √ . α2−x2   t = arcsin x ,  α 
[Lời giải] Đặt x = α sin t, −π < t < π ta có . 2 2 dx = α cos tdt,     1 √ = 1 . α2−x2 α cos t Z x I = dt = t + C = arcsin + C α Z √ Ví dụ 1.15. Tính α2 − x2dx.   t = arcsin x ,   α
[Lời giải] Đặt x = α sin t, −π ta có . 2 ≤ t ≤ π 2 dx = α cos tdt,  √ 
 α2 − x2 = α cos t. Z Z 1 + cos 2t α2 α2 1 p α2 x I = α2 cos2 tdt = α2 dt = t + sin 2t = x α2 − x2 + arcsin + C. 2 2 4 2 2 α Phép thế Euler √ Z √
• Đặt t = x + x2 + a đối với tích phân
R(x, x2 + a)dx, ở đây a có thể âm hoặc dương,
nghĩa là a = ±α2 đều áp dụng được. Khi đó, √ x x + x2 + a dt dx dt = 1 +√ = √ dx ⇒ = √ , x2 + a x2 + a t x2 + a
và tích phân đã cho được đưa về tích phân của phân thức hữu tỉ. 105 106
Chương 2. Phép tính tích phân một biến số √ Z √
• Đặt α2 − x2 = xt + α đối với tích phân
R(x, α2 − x2)dx,. Khi đó, 2αt
α2 − x2 = (xt + α)2 ⇔ α2 − x2 = x2t2 + 2αxt + α2 ⇔ x = − , 1 + t2
và tích phân đã cho được đưa về tích phân của phân thức hữu tỉ. Z Ví dụ 1.16. Tính dx √ . x2+a √
[Lời giải] Đặt t = x + x2 + a, khi đó dt = dx √ và t x2+a Z dt p I = = ln |t| + C = ln x2 + a t x + + C. Z √ Ví dụ 1.17. Tính x2 + adx.
[Lời giải] Sử dụng công thức tích phân từng phần ta có p Z x2 I = x x2 + a − √ dx x2 + a p Z (x2 + a) − a = x x2 + a − √ dx (2.1) x2 + a p Z 1 = x x2 + a + a √ dx − I. x2 + a Do đó, 1 h p p i I = x x2 + a + a ln x2 + a + C. 2 x +
Nói chung việc tính tích phân của các biểu thức vô tỷ thông thường được đưa về việc
tính bốn loại tích phân cơ bản sau Z 1. dx √ = arcsin x + C. α2−x2 α Z √ √ 2.
α2 − x2dx = 1 x α2 arcsin x + C. 2 − x2 + α22 α Z √ 3. dx √ = ln x2 + a x2+a x + + C. Z √ h √ √ i 4. x2 + adx = 1 x x2 + a + a ln x2 + a + C. 2 x +
Ví dụ 1.18. Tính các tích phân sau Z a) (1 − x2)−32 dx Đặt √
x = sin t, t ∈ − π , π 1 2 2 ⇒ dx = cos tdt, − x2 = cos t, thì Z Z dt (1 − x2)−32 dx =
= tan t + C = tan(arcsin x) + C cos2 t 106
1. Tích phân bất định 107 Z b) dx √ x2 1+x2
Đặt x = tan t ⇒ dx = dt , ta có cos2 t Z dx Z cos tdt 1 1 √ = = − + C = − + C. x2 1 + x2 sin2 t sin t sin(arctan x) Z c) dx √ . x2+x+1 Ta có Z d x + 1 2 1 p I = r = ln x + + x2 + x + 1 + C. 2 2 x + 1 + 3 2 4 Z Tích phân có dạng px+q √ dx ax2+bx+c Viết Z px + q p Z d(ax2 + bx + c) pb Z 1 √ dx = √ + q − √ dx ax2 + bx + c 2a ax2 + bx + c 2a ax2 + bx + c
để đưa về việc tính tích phân của hàm vô tỉ cơ bản. Z Ví dụ 1.19. Tính 4x−1 √ dx. 5−4x−x2 Z Tích phân có dạng dx √ (px+q) ax2+bx+c
Đặt u = 1 để đưa về việc tính tích phân của hàm vô tỉ cơ bản. px+q Z Ví dụ 1.20. Tính dx √ . (1+x) 3+6x+x2 Z
Tính các tích phân có dạng m1/n1 mp/np R x, ax+b , ..., ax+b dx cx+d cx+d r Đặt ax + b k
= t, với k là bội chung nhỏ nhất của n , để đưa tích phân đã cx + d 1, n2, . . . , np
cho về tích phân của phân thức hữu tỉ với biến t. Z q Ví dụ 1.21. Tính x+1 dx. x+2 107 108
Chương 2. Phép tính tích phân một biến số q
[Lời giải] Đặt t = x+1 ta có x = , dx = 2t dt và x+2 −2t2−1 t2−1 (t2−1)2 Z t2 I = 2 dt (t2 − 1)2 1 Z 1 1 1 1 = − + + dt 2 t − 1 t + 1 (t − 1)2 (t + 1)2 1 t − 1 1 1 1 (2.2) = ln − − + C 2 t + 1 2 t − 1 t + 1 q x+1 1 x+2 − 1 = ln + x + 2 + C. 2 q x+1 + 1 x+2 Z Ví dụ 1.22. Tính dx √ √ . x+ 3 x [Gợi ý] Đặt √ √ √ √ √
6 x = t, đáp số I = 2 x − 3 3 x + 6 6 x − 6 ln(1 + 6 x) + C.
Bài tập 2.1. Tính các tích phân sau Z √ Z a) √ x+9 dx, d) dx √ , g) ex + 1dx, x 5 x−1 Z √ Z b) x−1 e) dx , √ dx, √ √ dx 3 h) √ √ , x+1 x− 4 x x+ 3 x Z Z Z c) dx dx √ , f) √√ , i) 3x+2 √ dx. x+ 3 x x−2 x−9 [Đáp số] √ a) Đặt √ √
u = x + 9, I = 2 x + 9 + 3 ln x+9−3 √x+9+3 + C. b) Đặt √ √ √
u = x, I = x − 4 x + 4 ln( x + 1) + C. √ c) Đặt √
u = 3 x, I = 3 ln( 3 x2 + 1) + C. 2 d) Đặt √ 5 √ 5 √ 5 √ √ √ 5 x = u, I = 5 x4 + x3 + x2 + 5 x + ln x + C. 4 3 2 | 5 − 1| e) Đặt √ 12 x = u, 3 √ √ √ 3 12 12 √ 12 12 √ √ √ √ √ I = x2 + x7 + 2 x +
x5 + 3 3 x + 4 4 x + 6 6 x + 12 12 x + 12 ln 12 x˘1 + C. 2 7 5 q f) Đặtp√ √ p√ x − 2 = u, I = 4 x˘2 3 + 8 x˘2 + C. 3 √ g) Đặt√ √
ex + 1 = u, I = 2 ex + 1 − ln 1+ ex+1 √ 1˘ ex+1 + C. h) Đặt √ √ √ √ √
6 x = t, I = 2 x − 3 3 x + 6 6 x − 6 ln(1 + 6 x) + C. i) Đặt√ √
x − 9 = u, I = 2(x − 9)3/2 + 58 x − 9 + C 108
§2. TÍCH PHÂN XÁC ĐỊNH
2.1 Định nghĩa tích phân xác định
Định nghĩa 2.29. Giả sử hàm số f (x) xác định và bị chặn trên [a, b]. Chia [a, b] thành n
khoảng nhỏ [xi, xi+1] bởi phân hoạch a = x0 < x1 < . . . < xn = b. Trong mỗi đoạn [xi, xi+1]
ta chọn điểm ξi ∈ [xi, xi+1] và thành lập biểu thức n−1 S với (2.3) n = ∑ f (ξi) △ xi △ xi = xi+1 − xi i=0
Biểu thức S được gọi là tổng tích phân. Gọi
. Nếu tồn tại giới hạn hữu n λ = max △xi 1≤i≤n
hạn I = lim S không phụ thuộc vào cách chia đoạn n
[a, b] và không phụ thuộc vào cách λ→0 chọn điểm ξ thì i
I được gọi là tích phân xác định của hàm số f (x) trên [a, b] và kí hiệu là Z b
f (x)dx. Trong trường hợp đó ta nói hàm số f (x) khả tích trên [a, b]. a
Chú ý 2.19. Trong định nghĩa trên ta đã xét hàm số f (x) trong khoảng đóng [a, b] tức là Z b Z a
đã giả thiết a < b. Bây giờ nếu b < a ta định nghĩa f (x)dx := − f (x)dx và khi a = b a b Z b ta định nghĩa f (x)dx = 0. a
2.2 Các tiêu chuẩn khả tích
Định lý 2.39. Điều kiện cần và đủ để hàm số bị chặn f (x) khả tích trên [a, b] là lim(S − λ→0 s) = 0, trong đó: n+1 n+1
S = ∑ Mi △ xi, s = ∑ mi △ xi i=1 i=1 Mi = sup f (x), mi = inf f (x) x∈[x x∈[x i,xi+1] i,xi+1]
Áp dụng định lý 2.39 chúng ta có thể chứng minh được các định lý sau:
Định lý 2.40. Nếu f (x) liên tục trên [a, b] thì f (x) khả tích trên [a, b].
Định lý 2.41. Nếu f (x) bị chặn trên [a, b] và có một số điểm gián đoạn trên [a, b] thì f (x) khả tích trên [a, b].
Định lý 2.42. Nếu f (x) bị chặn và đơn điệu trên [a, b] thì f (x) khả tích trên [a, b]. 109 110
Chương 2. Phép tính tích phân một biến số
2.3 Các tính chất của tích phân xác định Z b
Trong các phần tiếp theo sau đây, nếu không có chú thích gì thì khi viết f (x)dx ta a
hiểu là f (x) được giả thiết là khả tích trên [a, b]. • Tính chất 1. b b b Z Z Z
[α f (x) + βg(x)]dx = α f (x)dx + β g(x)dx a a a • Tính chất 2.
Cho 3 khoảng đóng [a, b], [a, c], [b, c], nếu f (x) khả tích trên khoảng có độ dài lớn nhất
thì cũng khả tích trên 2 đoạn còn lại, và b c b Z Z Z f (x)dx = f (x)dx + f (x)dx a a c
• Tính chất 3. Giả thiết a < b. Khi đó: Z b
(i) Nếu f (x) ≥ 0, ∀x ∈ [a, b] thì f (x)dx ≥ 0 a Z b Z b
(ii) Nếu f (x) ≥ g(x)∀x ∈ [a, b] thì f (x)dx ≥ g(x)dx a a
(iii) Nếu f (x) khả tích trên [a, b] thì | f (x)| khả tích trên [a, b] và: b b Z Z f (x)dx ≤ | f (x)|dx a a
(iv) Nếu m ≤ f (x) ≤ M, ∀x ∈ [a, b] thì b Z m(b − a) ≤ f (x)dx ≤ M(b − a) a .
• Tính chất 4.(Định lý trung bình thứ nhất)
Giả sử f (x) khả tích trên [a, b] và m ≤ f (x) ≤ M, ∀x ∈ [a, b], khi đó tồn tại µ sao cho: b Z
f (x)dx = µ(b − a), m ≤ µ ≤ M. a
Đặc biệt, nếu f (x) liên tục trên [a, b] thì tồn tại c ∈ [a, b] sao cho: b Z f (x)dx = f (c)(b − a). a 110
2. Tích phân xác định 111
• Tính chất 5.(Định lý trung bình thứ hai) Giả thiết
(i) f (x) và f (x)g(x) khả tích trên [a, b].
(ii) m ≤ f (x) ≤ M, ∀x ∈ [a, b].
(iii) g(x) không đổi dấu trên [a, b]. Khi đó b b Z Z f (x)g(x)dx = µ g(x)dx, m ≤ µ ≤ M. a a
Đặc biệt nếu f (x) liên tục trên [a, b] thì tồn tại c ∈ [a, b] sao cho: b b Z Z f (x)g(x)dx = f (c) g(x)dx. a a
Ví dụ 2.1 (Cuối kì, K61-Viện ĐTQT). Chứng minh rằng nếu f (x) là một hàm số liên 4 Z
tục trên [3, 4] sao cho f (x) ≥ 0 với mọi x ∈ [3, 4] và
f (x)dx = 0 thì f (x) = 0 với mọi 3 x ∈ [3, 4].
2.4 Tích phân với cận trên thay đổi (hàm tích phân)
Giả sử f (x) là một hàm khả tích trên [a, b], khi đó với mỗi x ∈ [a, b] thì f cũng khả tích x Z
trên [a, x]. Ta xác định hàm số F(x) = f (t)dt. a
Định lý 2.43. (1) Nếu f (t) khả tích trên [a, b] thì F(x) liên tục trên [a, b].
(2) Nếu f liên tục tại x và
0 ∈ [a, b] thì F(x) có đạo hàm tại x0 F′(x0) = f (x0).
Định lý 2.44 (Công thức Newton-Leibniz). Nếu f (x) liên tục trong khoảng đóng [a, b]
và F(x) là một nguyên hàm của f (x) thì b Z f (x)dx = F(b) − F(a). a 111 112
Chương 2. Phép tính tích phân một biến số
2.5 Các phương pháp tính tích phân xác định
1. Sử dụng công thức tích phân từng phần.
Giả sử u(x), v(x) là các hàm số có đạo hàm liên tục trong [a, b]. Khi đó: b b Z Z udv = uv|ba − vdu a a
2. Sử dụng các phép đổi biến số.
Định lý 2.45 (Đổi biến x := ϕ(t)). b Z Xét I =
f (x)dx với f (x) liên tục trong [a, b]. Thực hiện phép đổi biến x = ϕ(t) thoả a mãn 3 điều kiện sau:
(1) ϕ(t) có đạo hàm liên tục trong [a, b].
(2) ϕ(a) = α; ϕ(b) = β.
(3) Khi t biến thiên trong [α, β] từ α đến β thì x = ϕ(t) biến thiên liên tục từ a đến b. Khi đó ta có công thức: b β Z Z f (x)dx =
f [ϕ(t)]ϕ′(t)dt. a α
Định lý 2.46 (Đổi biến t := ϕ(x)). b Z
Giả sử tích phân cần tính có dạng I =
f [ϕ(x)].ϕ′(x)dx. Trong đó ϕ(x) biến thiên a
đơn điệu ngặt và có đạo hàm liên tục trên [a, b]. Khi đó: b ϕ(b) Z Z
f [ϕ(x)].ϕ′(x)dx = f (t)dt. a ϕ(a)
3. Sử dụng các phép truy hồi, quy nạp. 112
2. Tích phân xác định 113 2.6 Hệ thống bài tập
Dạng 1. Tính đạo hàm của hàm tích phân.
Chúng ta có các công thức sau: x Z ′ f (t)dt = f (x) (2.4) a x g(x) Z ′ f (t)dt = f (g(x)).g′(x) (2.5) a x
Công thức 2.4 chúng ta đã biết trong Định lý 2.43, còn công thức 2.5 được suy ra từ công
thức đạo hàm của hàm hợp.
Bài tập 2.1. Tính các đạo hàm: Z y Z y a) d Z x3 et2dt b) d et2dt dt dx dy c) d √ x x dx x2 1+x4 y x Z Z Chứng minh. a) d d et2dt = −
et2dt = −ex2( do y là hằng số) dx dx x y y Z b) d
et2dt = ey2( do x là hằng số) dy x x3 x2 x3 Z Z Z c) d dt d dt d dt −2x 3x2 √ = − √ + √ = √ + √ dx 1 + x4 dx 1 + x4 dx 1 + x4 1 + x8 1 + 12x2 x2 a a
Dạng 2. Tính giới hạn của hàm số dựa vào công thức L’Hospital và đạo hàm của hàm tích phân.
Bài tập 2.2. Tìm giới hạn: sin x x Z √ Z tan tdt (arctan t)2dt a) A = lim 0 b) B = lim 0 √ tan x x→0+ Z √ x→+∞ x2+1 sin tdt 0 113 114
Chương 2. Phép tính tích phân một biến số sin x tan x Z √ Z √ Chứng minh. a) Nhận xét: lim tan tdt = lim
sin tdt = 0 nên áp dụng quy x→0+ x→0+ 0 0 tắc L’Hospital ta có: sin x !′ Z √tantdt ptan(sin x). cos x lim 0 = lim p = 1⇒A = 1 x→0+ tan x !′ Z √ x→0+ sin(tan x). 1 cos2 x sin tdt 0 x Z √ b) Nhận xét: lim (arctan t)2dt = lim
x2 + 1 = ∞ nên áp dụng quy tắc L’Hospital x→+∞ x→+∞ 0 ta có: x !′ Z (arctan t)2dt (arctan x)2 π2 π2 lim 0 √ = ⇒B = x→+∞ x x2 + 1 ′ = lim x→+∞ √ 4 4 x2+1
Dạng 3. Sử dụng công thức tổng tích phân để tính giới hạn của một số dãy số đặc biệt.
Xuất phát từ công thức tính tổng tích phân 2.3 n−1 S với n = ∑ f (ξi) △ xi △ xi = xi+1 − xi i=0
Nếu chúng ta chia đoạn [a, b] thành n khoảng có độ dài bằng nhau bởi phân hoạch a = x thì:
0 < x1 < . . . < xn = b, trong đó xi = a + (b − a) in b − a n−1 Sn = ∑ f (ξ n
i) với ξi ∈ [xi, xi+1] i=0
Khi đó nếu hàm f (x) khả tích trên [a, b], và chọn ξ ta được công thức: i = xi " !# b b − a n−1 b − a Z lim ∑ f a + .i = f (x)dx (2.6) n→∞ n n i=0 a Còn nếu chọn ξ ta được công thức: i = xi+1 " !# b b − a n b − a Z lim ∑ f a + .i = f (x)dx (2.7) n→∞ n n i=1 a 114
2. Tích phân xác định 115
Bài tập 2.3. Dùng định nghĩa và cách tính tích phân xác định, tìm các giới hạn: a) h i A = lim 1 + 1 + 1 + · · · + 1 n→∞ nα nα+β nα+2β nα+(n−1)β q b) q B = lim 1 1 + 1 + 1 + 2 + · · · + p1 + n n→∞ n n n n Chứng minh. a) Viết " # 1 1 1 1 1 A = lim + + + · · · + n→∞ n α α + β α + 2β n n α + (n−1)β n
Áp dụng công thức 2.6 với a = 0, b = 1, f (x) = 1 ta được: α+βx 1 Z 1 1 α + β A = dx = ln α + βx β α 0
Nếu áp dụng công thức 2.7 với a = 0, b = 1, f (x) = 1 ta được: α+βx h 1 1 1 i 1 α + β A′ = lim + + · · · + = A = ln n→∞ nα + β nα + 2β nα + nβ β α
b) Áp dụng công thức 2.7 với √ a = 0, b = 1, f (x) = 1 + x ta được: 1 Z √ 2 √ B = 1 + xdx = (2 2 − 1) 3 0
Nếu áp dụng công thức 2.6 với √ a = 0, b = 1, f (x) = 1 + x ta được: r r ! 1 1 n − 1 2 √ B′ = lim 1 + 1 + + · · · + 1 + = B = (2 2 − 1) n→∞ n n n 3 q
Bài tập 2.4. Tính lim 1 n (2n)! n→∞ n n! q
[Gợi ý] Tính lim ln 1 n (2n)! bằng cách viết biểu thức trong giới hạn dưới dạng tổng n→∞ n n! tích phân.
Dạng 4. Tính tích phân xác định (xem mục 2.5)
Bài tập 2.5. Tính các tích phân 115 116
Chương 2. Phép tính tích phân một biến số Z e a) Z 2 | ln x | (x + 1)dx d) sin2 x cos x dx 1 0 (1+tan2 x)2 Z e Z b) 3 q (x ln x)2dx e) arcsin x dx 1 1+x 0 Z 1 Z π c) 2 (x3 − 2x + 5)e− x2 dx f) cosn x cos nxdx 0 0 [Gợi ý] a) I b) c) a = e2+5 I I 4 b = 5e3−2 27 c = 98 − 144 √e d) 2 Z sin2 x cos x Id = dx (1 + tan2 x)2 0 2 Z = sin2 x. cos x. cos4 xdx 0 2 Z = sin2 x.(1 − sin2 x)d(sin x) 0 sin3(2) 2 sin5(2) sin7(2) = − + 3 5 7 116
2. Tích phân xác định 117 e) 3 Z r x Ie = arcsin dx 1 + x 0 r 3 3 x Z 1 1 1 = x arcsin − x. . . dx 1 + x q q x (x + 1)2 0 1 − x 2 0 1+x x+1 3 √ 1 Z x = π − dx 2 x + 1 0√3 1 Z t = π − .2tdt (đặt √x = t) 2 t2 + 1 0 √3 Z 1 = π − 1 − dt t2 + 1 0 √ h 3i
= π − (t − arctan t)0 4π √ = − 3 3 f) π 2 Z In = cosn x cos nxdx 0 π 2 1 Z = cosn xd sin nx n 0 π 2 1 π 1 Z = 2 cosn x sin nx + sin nx.n. cosn−1 x. sin xdx n 0 n 0 π 2 Z = sin nx. cosn−1 x. sin xdx. 0 117 118
Chương 2. Phép tính tích phân một biến số Suy ra π π 2 Z 2 Z 2In = cosn x cos nxdx + sin nx. cosn−1 x. sin xdx 0 0 π 2 Z = cosn−1 x cos(n − 1)xdx 0 = In−1
Vậy theo phép truy hồi ta có n I 1 n = I . 2 0 = π 2n+1 Bài tập 2.6. Tính π π 2 Z 2 Z a) In = sinn xdx b) Jn = cosn xdx 0 0
Dạng 5. Chứng minh các đẳng thức tích phân
Bài tập 2.7. Chứng minh rằng nếu f (x) liên tục trên [0, 1] thì: Z π Z π Z π Z π a) 2 2 f (sin x)dx = f (sin x)dx b) x f (sin x)dx = π f (cos x)dx. 2 0 0 0 0
[Gợi ý] Đây là bài tập dễ, câu a) đặt t = π2 − x, còn câu b) đặt t = π − x.
Bài tập 2.8. Áp dụng kết quả của bài tập 2.7 hãy chứng minh π π 2 √ √ Z 2 sin x Z cos x π √ √ dx = √ √ dx = sin x + cos x sin x + cos x 4 0 0
Bài tập 2.9. Giả sử f (x) liên tục trên [−a, a](a > 0), hãy chứng minh  a 0
nếu f (x) là hàm số lẻ trên [−a, a] Z   a I = f (x)dx = Z 2 f (x)dx
nếu f (x) là hàm số chẵn trên [−a, a] −a   0
Bài tập 2.10. Cho f (x) liên tục, chẵn trên [−a, a], chứng minh a a Z f (x)dx Z = f (x)dx với 0 ≤ b 6= 1 1 + bx −a 0 Áp dụng tính π π 1 Z 2 2 1 Z 2x cos 2x Z x2 | sin x | I1 = dx, I dx, I dx (x2 + 1)(ex + 1) 2 = 2002x + 2x 3 = 1 + 2x −1 − π2 − π2 118
2. Tích phân xác định 119 b b Z Z
Bài tập 2.11. Chứng minh xm(a + b − x)ndx = xn(a + b − x)mdx a a 1 Z
Áp dụng tính In = x2(1 − x)ndx và chứng minh 0 n 1 1 2 1 ∑ (−1)kCkn. = − + k + 3 n + 1 n + 2 n + 3 k=0
Dạng 6. Chứng minh các bất đẳng thức tích phân
Bài tập 2.12. Cho f (x), g(x) là hai hàm số khả tích trên [a, b]. Khi đó f 2(x), g2(x) cũng
khả tích trên [a, b]. Chứng minh bất đẳng thức sau (a < b) b !2 b ! b ! Z Z Z f (x)g(x)dx ≤ f 2(x)dx . g2(x)dx a a a
(Bất đẳng thức Cauchy-Schwarzt)
Chứng minh. Xét 2 trường hợp: b b Z Z TH1. Nếu f 2(x)dx = g2(x)dx = 0 thì: a a b b b Z Z Z f 2(x) + g2(x) 0 ≤ f (x)g(x)dx ≤ | f (x)g(x)|dx ≤ dx = 0 2 a a a
Khi đó ta có dấu ” = ” xảy ra. b b Z Z
TH2. Nếu ít nhất một trong hai tích phân f 2(x)dx,
g2(x)dx khác 0, không mất tính a a b Z tổng quát ta giả sử f 2(x)dx 6= 0 a b Z
Khi đó [α f (x) + g(x)]2 ≥ 0⇒ [α f (x) + g(x)]2 ≥ 0. Suy ra a b b b Z Z Z f 2(x)dx .α2 + 2 f (x)g(x)dx .α +
g2(x)dx ≥ 0∀α ∈ R (2.8) a a a 119 120
Chương 2. Phép tính tích phân một biến số
Biểu thức ở vế trái là tam thức bậc 2 đối với α nên 2.8 đúng với mọi α ∈ R khi và chỉ khi b !2 b ! b ! Z Z Z △′ = f (x)g(x)dx − f 2(x)dx . g2(x)dx ≤ 0. a a a
Bài tập 2.13 (Cuối kì, K62). Cho hàm số f (x) khả vi liên tục đến cấp hai trên [a, b] và
f (a) = f (b) = 0. Chứng minh rằng  b 2 b b Z Z Z  [ f ′(x)]2dx ≤ [ f (x)]2dx [ f ′′(x)]2dx. a a a Chứng minh. Ta có b b b b Z Z b Z Z [ f ′(x)]2dx =
f ′(x)d f (x) = f (x) f ′(x) − f (x) f ′′(x)dx = − f (x) f ′′(x)dx. a a a a a
Áp dụng bất đẳng thức Cauchy - Schwartz ta có  b 2  b 2 b b Z Z Z Z  [ f ′(x)]2dx = − f (x) f ′′(x)dx ≤ [ f (x)]2dx [ f ′′(x)]2dx. a a a a
Bài tập 2.14 (Cuối kì, K60). Cho hàm số f (x) khả vi liên tục trên [0, 1] và f (0) = 0. 1 1 Z Z
Chứng minh rằng [ f (x)]2dx ≤ 1 [ f ′(x)]2dx. 2 0 0 Chứng minh. Ta có  x 2 x x Z Z Z
f (x)2 = [ f (x) − f (0)]2 =  f ′(t)dt ≤ [ f ′(t)]2dt · 12dt 0 0 0 x 1 1 Z Z Z = x
[ f ′(t)]2dt ≤ x [ f ′(t)]2dt = x [ f ′(x)]2dx. 0 0 0 Do đó, 1 1 1 1 Z Z Z 1 Z [ f (x)]2dx ≤ [ f ′(x)]2dx · xdx = [ f ′(x)]2dx. 2 0 0 0 0
Bài tập 2.14 có thể được mở rộng như sau (với chứng minh hoàn toàn tương tự). 120
2. Tích phân xác định 121
Bài tập 2.15. Cho f là một hàm số khả vi liên tục trên [a, b]. Chứng minh rằng b b Z b − a Z [ f (x) − f (a)]2dx ≤ [ f ′(x)]2dx. 2 a a x Z
Cũng với ý tưởng viết f (x) − f (a) =
f ′(t)dt, bạn đọc có thể chứng minh các kết quả sau. a
Bài tập 2.16. Cho f là một hàm số khả vi liên tục trên [a, b] và f (a) = 0. Chứng minh rằng b b 1 Z Z | f (x)|dx ≤ | f ′(x)|dx. b − a a a [Lời giải] Thật vậy, x x b Z Z Z
| f (x)| = | f (x) − f (a)| = f ′(t)dt ≤ | f ′(t)|dt ≤ | f (t)|dt. a a a Do đó, b b  b  b b Z Z Z Z Z | f (x)|dx ≤  | f (t)|dt dx = (b − a) | f (t)|dt = (b − a) | f (x)|dx. a a a a a
Bài tập 2.17. Cho f là một hàm số khả vi liên tục trên [a, b] và f (a) = 0. Chứng minh rằng b b Z b − a Z | f (x) f ′(x)|dx ≤ [ f ′(x)]2dx. 2 a a x Z
[Lời giải] Ta có f (x) = f (x) − f (a) = f (t)dt nên a x Z
| f (x) f ′(x)| ≤ | f ′(x)| | f ′(t)dt|. a Suy ra b b  x  Z Z Z | f (x) f ′(x)|dx ≤ | f ′(x)| | f ′(t)dt| dx (2.9) a a a 121 122
Chương 2. Phép tính tích phân một biến số   ′ x ′  x 2 Z Z Z x
Vì  | f ′(t)|dt = | f ′(x)| nên   =  | f ′(t)|dt  2| f ′(x)| | f ′(t)dt|. Do đó, a a a b  x   x 2 Z Z 1 Z x=b | f ′(x)|
| f ′(t)dt| dx =  | f ′(t)|dt 2 x=a a a a (2.10)  b 2 b 1 Z b − a Z =  | f ′(x)|dx ≤ | f ′(x)|2dx. 2 2 a a
Từ (2.9) và (2.10) ta có điều phải chứng minh.
Bài tập 2.18. Cho f là một hàm số khả vi liên tục trên [a, b], f (a) = 0 và 0 ≤ f ′(x) ≤ 1 với
mọi x ∈ [a, b]. Chứng minh rằng b  2 Z b b a) Z Z f (x)dx ≥ 1 f (b)2 . 2 − f (a)2, b) [ f (x)]3dx ≤  f (x)dx a a a Chứng minh.
a) Từ giả thiết ta có f (x) là một hàm số đơn điệu không giảm và f (x) ≥
f (a) = 0, ∀x ∈ [a, b]. Do đó,
f (x) ≥ f (x) f ′(x), ∀x ∈ [a, b]. Suy ra b b Z Z 1 b 1 h i f (x)dx ≥ f (x) f ′(x)dx = [ f (x)]2 = f (b)2 − f (a)2 . 2 a 2 a a b) Xét hàm số  x 2 x Z Z F(x) =  f (t)dt − [ f (t)]3dt, x ∈ [a, b]. a a Ta có x  x  Z Z F′(x) = 2 f (x)
f (t)dt − f (x)3 = f (x) 2 f (t)dt − [ f (x)]2 . a a Z x Đặt G(x) = 2 f (t)dt − [ f (x)]2, ta có a
G′(x) = 2 f (x) − 2 f (x) f ′(x) = 2 f (x)(1 − f ′(x)) ≥ 0, ∀x ∈ [a, b]
⇒ G(x) ≥ G(a) = 0, ∀x ∈ [a, b]. b  b 2 Z Z
Từ đó suy ra F′(x) ≥ 0, ∀x ∈ [a, b] ⇒ F(b) ≥ F(a) = 0 ⇒ [ f (x)]3dx ≤  f (x)dx . a a 122
2. Tích phân xác định 123
Bài tập 2.19 (Olympic Toán học Sinh viên Toàn quốc 2018 -Bảng A). Cho f : [a, b] → b Z
R là một hàm số khả vi liên tục sao cho
f (x)dx = 0. Chứng minh rằng a x Z (b − a)2 max f (t)dt ≤ max | f ′(x)|. x∈[a,b] 8 x ∈[a,b] a
[Lời giải] Do f ′(x) liên tục nên tồn tại M = max f ′(x). x∈[a,b] • Đặt x Z (x − a)(x − b) F(x) = f (t)dt + M , x ∈ [a, b]. (2.11) 2 a
Ta có F(a) = F(b) = 0 và F′′(x) = f ′(x) + M ≥ 0, ∀x ∈ [a, b].
• Vì F′′(x) ≥ 0 nên F(x) là hàm lồi trên [a, b], hơn nữa F(a) = F(b) = 0 nên F(x) ≤
0, ∀x ∈ [a, b]. Từ (2.11) ta có x Z (x − a)(b − x) M (x − a) + (b − x) 2 (b − a)2 f (t)dt ≤ M ≤ = M, ∀x ∈ [a, b]. 2 2 2 8 a
• Một cách tương tự, đặt x Z (x − a)(x − b) G(x) = f (t)dt − M , x ∈ [a, b] (2.12) 2 a
sẽ dẫn đến G là một hàm lõm trên [a, b] và bất đẳng thức x Z (b − a)2 f (t)dt ≥ − M, ∀x ∈ [a, b]. 8 a Kết luận: x Z (b − a)2 max f (t)dt ≤ max | f ′(x)|. x∈[a,b] 8 x ∈[a,b] a 123 124
Chương 2. Phép tính tích phân một biến số
§3. TÍCH PHÂN SUY RỘNG
Khi định nghĩa tích phân xác định, chúng ta đã xét các hàm số xác định trên một đoạn
hữu hạn [a, b] và bị chặn trên đoạn đó. Trong phần này chúng ta sẽ mở rộng khái niệm
tích phân, từ đó đưa vào khái niệm tích phân suy rộng với cận vô hạn và tích phân của hàm số không bị chặn.
3.1 Tích phân suy rộng với cận vô hạn
Giả sử f (x) là hàm số xác định trên khoảng [a, +∞)] và khả tích trên mọi đoạn hữu
hạn [a, A] , (a ≤ A < +∞). A Z
Định nghĩa 2.30. Giới hạn của tích phân
f (x)dx khi A → +∞ được gọi là tích phân a
suy rộng của hàm số f (x) trên khoảng [a, +∞) và ký hiệu như sau +∞ A Z Z f (x)dx = lim f (x)dx A→+∞ a a +∞ Z
Nếu giới hạn này tồn tại hữu hạn ta nói tích phân suy rộng
f (x)dx hội tụ. Ngược lại, a
nếu không tồn tại giới hạn này hoặc giới hạn bằng vô cùng ta nói tích phân đó phân kỳ.
Tương tự ta định nghĩa tích phân của một hàm số f (x) trên các khoảng (−∞, a] và
(−∞, +∞) bởi các công thức sau a a +∞ A Z Z Z Z f (x)dx = lim f (x)dx và f (x)dx = lim f (x)dx A→−∞ A→+∞,A′→−∞ −∞ A −∞ A′ Ta có thể viết +∞ +∞ a Z Z Z f (x)dx = f (x)dx + f (x)dx −∞ a −∞
khi hai trong ba tích phân nói trên hội tụ.
Qua các định nghĩa trên ta thấy rằng tích phân suy rộng là giới hạn của tích phân xác
định (hiểu theo nghĩa thông thường) khi cho cận tích phân dần tới vô cùng. Do đó có thể
dùng công thức Leibniz để tính tích phân, sau đó cho cận tiến ra vô cùng. A Z f (x)dx = F(A) − F(a) a 124
3. Tích phân suy rộng 125 kí hiệu F(+∞) = lim F(A) A→∞ thì có thể viết +∞ Z
f (x)dx = F(+∞) − F(a) = F(x)|+∞ a a +∞ Z Ví dụ 3.1. a) Tính tích phân dx x ln x(ln ln x)2 e2 Ta có A A Z dx 1 A Z 1 1 dx 1 = − = − nên ⇒ lim = x ln x(ln ln x)2 ln ln x e2 ln 2 ln ln A A→+∞ x ln x(ln ln x)2 ln 2 e2 e2 Vậy +∞ Z dx 1 = x ln x(ln ln x)2 ln 2 e2 +∞ Z b) Tính tích phân dx (x2 + 1)2 −∞ A Z Trước hết ta tính dx
, đặt x = tan t ⇒ dx = dt = cos2 tdt, (x2+1)2 (1+x2)2 1+tan2 t A′ A arctan A Z dx Z 1 + cos 2t t sin 2t arctan A = dt = + (x2 + 1)2 2 2 4 arctan A′ A′ arctan A′
Khi A → +∞, A′ → −∞ thì arctan A → π; arctan A′ , suy ra 2 → − π2 +∞ π Z dx t sin 2t 2 π = + = (x2 + 1)2 2 4 2 −∞ − π2 0 0 Z Z c) x sin xdx = lim
x sin xdx = lim (−x cos x + sin x)|0 = ( A lim A cos A − sin A) A→−∞ A→−∞ A→−∞ −∞ A
Giới hạn này không tồn tại, do đó tích phân phân kỳ.
d) Xét sự hội tụ của tích phân +∞ Z dx I = xα 1
Tích phân suy rộng I hội tụ khi và chỉ khi α > 1, và phân kỳ khi và chỉ khi α ≤ 1. 125 126
Chương 2. Phép tính tích phân một biến số
3.2 Tích phân suy rộng của hàm số không bị chặn
Giả sử f (x) là hàm số xác định trên khoảng [a, b) và khả tích trên mọi đoạn [a, t], (t < b
bất kỳ), và lim f (x) = ∞. Điểm x = b được gọi là điểm bất thường (điểm kỳ dị) của hàm số x→b f (x). t Z
Định nghĩa 2.31. Giới hạn của tích phân
f (x)dx khi t → b−, được gọi là tích phân suy a
rộng của hàm số f (x) trên khoảng [a, b) và được ký hiệu như sau: b t Z Z f (x)dx = lim f (x)dx t→b− a a
Nếu giới hạn ở vế phải tồn tại, ta nói tích phân suy rộng hội tụ. Ngược lại nếu không tồn
tại giới hạn này hoặc giới hạn bằng vô cùng, ta nói tích phân phân kỳ.
Tương tự ta định nghĩa tích phân suy rộng của hàm số f (x) không bị chặn trên khoảng
(a, b] và (a, b) lần lượt nhận x = a và x = b làm điểm bất thường. b b b t′ Z Z Z Z f (x)dx = lim f (x)dx và f (x)dx = lim f (x)dx t→a+ t→a+,t′→b− a t a t
Đối với tích phân có hai điểm bất thường x = a, x = b, ta có thể viết b c b Z Z Z f (x)dx = f (x)dx + f (x)dx a a c
khi hai trong ba tích phân nói trên hội tụ. 1 Z Ví dụ 3.2.
a) Xét sự hội tụ của tích phân dx √1 − x2 −1 0 0 0 Z dx Z dx π √ = lim √
= lim arcsin x = lim (− arcsin t) = 1 − x2 t→−1 1 − x2 t→−1 t→−1 2 −1 t t 1 1 t Z dx Z dx π √ = lim √
= lim arcsin x = lim arcsin t = 1 − x2 t→1 1 − x2 t→1 t→1 2 0 0 0 nên 1 0 1 Z dx Z dx Z dx √ = √ + √ = π 1 − x2 1 − x2 1 − x2 −1 −1 0 126
3. Tích phân suy rộng 127 1 Z
b) Xét sự hội tụ của tích phân dx I = xα 0
Tích phân suy rộng I hội tụ khi và chỉ khi α < 1, phân kỳ khi và chỉ khi α ≥ 1.
3.3 Các tiêu chuẩn hội tụ
Định lý 2.47 (Tiêu chuẩn so sánh).
1. Cho hai hàm số f (x) và g(x) khả tích trên mọi khoảng hữu hạn [a, A](a ≤ A) và 0 ≤ f (x) ≤ g(x), x ≥ a. Khi đó +∞ +∞ Z Z i) Nếu g(x)dx hội tụ thì f (x)dx hội tụ a a +∞ +∞ Z Z ii) Nếu f (x)dx phân kỳ thì g(x)dx phân kỳ. a a
2. Giả sử f (x) và g(x) là hai hàm số khả tích trên mọi đoạn hữu hạn [a, A](a ≤ A) và +∞ +∞ f (x) Z Z lim
= k(0 < k < +∞). Khi đó các tích phân f (x)dx và g(x)dx hoặc cùng x→+∞ g(x) a a
hội tụ, hoặc cùng phân kỳ.
Hệ quả 2.6. Cho f và g là hai hàm số dương khả tích trên [a, +∞). Khi đó +∞ +∞ Z Z 1. Nếu f (x) lim = 0 và nếu g(x)dx hội tụ thì f (x)dx hội tụ. x→+∞ g(x) a a +∞ +∞ Z Z 2. Nếu f (x) lim = +∞ và nếu g(x)dx phân kì thì f (x)dx phân kì. x→+∞ g(x) a a
Tương tự chúng ta cũng có các tiêu chuẩn hội tụ cho trường hợp tích phân suy rộng của hàm số không bị chặn.
Định lý 2.48 (Tiêu chuẩn so sánh).
1. Cho hai hàm số f (x) và g(x) khả tích trên (a, b] và có cùng điểm bất thường là x = a sao cho
0 ≤ f (x) ≤ g(x), ∀x ∈ (a, b] Khi đó 127 128
Chương 2. Phép tính tích phân một biến số b b Z Z i) Nếu g(x)dx hội tụ thì f (x)dx hội tụ a a b b Z Z ii) Nếu f (x)dx phân kỳ thì g(x)dx phân kỳ a a
2. Giả sử f (x) và g(x) là hai hàm số dương khả tích trên (a, b] và có cùng điểm bất
thường x = a. Nếu tồn tại giới hạn f (x) lim = k(0 < k < +∞) x→a+ g(x) b b Z Z Khi đó các tích phân f (x)dx và
g(x)dx hoặc cùng hội tụ, hoặc cùng phân kỳ. a a
Hệ quả 2.7. Cho f và g là hai hàm số dương khả tích trên (a, b] và có cùng điểm bất thường x = a. Khi đó b b Z Z 1. Nếu f (x) lim = 0 và nếu g(x)dx hội tụ thì f (x)dx hội tụ. x→a+ g(x) a a b b Z Z 2. Nếu f (x) lim = +∞ và nếu g(x)dx phân kì thì f (x)dx phân kì. x→a+ g(x) a a Chú ý:
• Khi xét đến tính chất hội tụ hay phân kì của một tích phân suy rộng, nói chung
chúng ta chỉ "quan tâm" tới dáng điệu của hàm số tại các điểm bất thường.
• Khi sử dụng tiêu chuẩn so sánh chúng ta thường hay so sánh các tích phân suy rộng
đã cho với hai loại tích phân suy rộng sau:  Z +∞ hội tụ nếu a) dx α > 1
I1 = a xα phân kì nếu α ≤ 1 b)   b b Z dx
hội tụ nếu α < 1 Z dx
hội tụ nếu α < 1 I2 = , I′ (x − a)α 2 =
phân kì nếu α ≥ 1
(b − x)α phân kì nếu α ≥ 1 a a
Ví dụ 3.3 (Cuối kì, K61 Viện ĐTQT). Xét sự hội tụ, phân kỳ của tích phân 128
3. Tích phân suy rộng 129 ∞ ∞ Z Z a) (1−cos 2x)dx √ . b) (1−cos 3x)dx √ . x2 ln(1+3 x) x2 ln(1+2 x) 0 0
3.4 Tích phân suy rộng hội tụ tuyệt đối và bán hội tụ +∞ +∞ Z Z Định lý 2.49. 1. Nếu | f (x)|dx hội tụ thì f (x)dx hội tụ a a b +∞ Z Z 2. Nếu
| f (x)|dx (có điểm bất thường là a hoặc b) hội tụ thì f (x)dx cũng hội tụ a a Định nghĩa 2.32. +∞ +∞ +∞ Z Z Z 1. Nếu
| f (x)|dx hội tụ thì ta nói
f (x)dx hội tụ tuyệt đối, còn nếu f (x)dx hội tụ a a a +∞ +∞ Z Z nhưng
| f (x)|dx phân kì thì ta nói | f (x)|dx bán hội tụ. a a b b Z Z 2. Nếu
| f (x)|dx (có điểm bất thường là a hoặc b) hội tụ thì ta nói f (x)dx hội tụ a a b b b Z Z Z tuyệt đối, còn nếu f (x)dx hội tụ nhưng
| f (x)|dx phân kì thì ta nói | f (x)|dx a a a bán hội tụ. Z +∞
Ví dụ 3.4. Chứng minh rằng
cos x hội tụ tuyệt đối. 1 x2 Chứng minh. Ta có cos x 1 , x2 ≤ x2 Z +∞ Z +∞ mà 1 hội tụ nên
cos x hội tụ tuyệt đối. 1 x2 1 x2 Z +∞
Ví dụ 3.5 (Tích phân Dirichlet). Chứng minh rằng sin x là bán hội tụ. x 0 Chứng minh. Ta có +∞ 1 +∞ Z sin x Z sin x Z sin x = + . x x x 0 0 1 129 130
Chương 2. Phép tính tích phân một biến số Z 1 Z 1
sin x thực chất là tích phân xác định vì lim sin x = 1, do đó sin x x x x ∈ R. Vì vậy chỉ cần 0 x→0+ 0 Z +∞ chỉ ra rằng
sin x là hội tụ. Theo công thức tích phân từng phần, x 1 M M M Z sin x cos x M Z cos x cos M Z cos x dx = − + = cos 1 − + dx. x x 1 x2 M x2 1 1 1 Cho M → +∞ ta có +∞ +∞ Z sin x Z cos x dx = cos 1 + dx. x x2 1 1 Z +∞ Z +∞ Z +∞ Mà cos x dx là hội tụ nên
sin x cũng hội tụ. Việc tiếp theo là chỉ ra sin x dx x x 1 x2 1 0 là phân kì. Thật vậy, +∞ (n+1)π π Z +∞ Z +∞ Z sin x sin x sin v dx = ∑ dx = ∑ dv. x x v + nπ 0 n=0 nπ n=0 0 Vì 1 với 0 v+nπ ≥ 1 ( ≤ v ≤ π nên n+1)π π π Z sin v 1 Z 2 dv ≥ sin vdv = . v + nπ (n + 1)π (n + 1)π 0 0 +∞ Z +∞ Mà ∑ 2 là phân kì nên
sin x dx là phân kì theo tiêu chuẩn so sánh. (n+1)π x n=0 0 3.5 Bài tập
Bài tập 2.1. Xét sự hội tụ và tính (trong trường hợp hội tụ) các tích phân sau: Z 0 Z +∞ a) dx xexdx c) −∞ −∞ (x2 + 1)2 Z Z +∞ 1 dx b) d) cos xdx p 0 0 x(1 − x) 0 0 Z Chứng minh. a) xexdx = ex(x − 1) = 1 −∞ −∞ +∞ +∞ Z b) cos xdx = sin x
. Do không tồn tại giới hạn lim sin x nên tích phân đã cho x→+∞ 0 0 phân kì. 130
3. Tích phân suy rộng 131 π +∞ Z Z +∞ 2 Z c) dx dx = 2
. Đặt x = tan t thì I = 2 cos2 tdt = π (x2 + 1)2 2 0 (x2 + 1)2 −∞ 0 1 1 1 Z 2 Z Z d) dx dx dx p = p + p x(1 − x) x(1 − x) x(1 − x) 0 0 1 | {z } 2 I | {z } 1 I2 1
• Xét tích phân I có điểm bất thường là . Mặt 1 x = 0. Khi x → 0, 1 p ∼ √ x(1 − x) x 1 Z khác tích phân dx
√ hội tụ nên I hội tụ. x 1 0 1
• Xét tích phân I có điểm bất thường là . 2 x = 1. Khi x → 1, 1 p ∼ √ x(1 − x) 1 − x 1 Z Mặt khác tích phân dx √ hội tụ nên I hội tụ. 2 1 − x 0 Vậy I = I hội tụ. 1 + I2 b Z
Trong trường hợp tổng quát, muốn tính dx I = ta thực hiện phép đổi p(x − a)(b − x) a biến
x = a cos2 ϕ + b sin2 ϕ
sẽ chuyển I về tích phân xác định π 2 Z I = 2 dϕ = π 0
Bài tập 2.2. Xét sự hội tụ của các tích phân suy rộng sau 1 1 +∞ Z Z √ Z a) dx c) xdx √ e) e−x2 dx tan x−x 1−x4 x2 0 0 1 1 +∞ +∞ Z √ Z Z b) xdx d) ln(1+x)dx f) x2dx esin x−1 x x4−x2+1 0 1 0 Chứng minh.
a) Tích phân đã cho có điểm bất thường là x = 0 và 1 1 1 lim : = x→0 tan x − x x3 3 131 132
Chương 2. Phép tính tích phân một biến số 1 1 Z Z Mặc khác dx phân kì nên dx cũng phân kì. x3 tan x − x 0 0
b) Tích phân đã cho có điểm bất thường là x = 0 và khi x → 0, esin x − 1 ∼ sin x ∼ x nên √ 1 1 √ x 1 Z dx Z xdx ∼ √ . Do √ hội tụ nên cũng hội tụ. esin x − 1 x x esin x − 1 0 0
c) Tích phân đã cho có điểm bất thường là x = và khi x → 1 thì √ √ x x 1 √ = p ∼ √ 1 − x4 (1 − x)(1 + x + x2 + x3) 2 1 − x 1 1 √ Z Z Do dx xdx √ hội tụ nên √ cũng hội tụ. 1 − x 1 − x4 0 0 +∞ +∞ Z Z d) Ta có ln(1 + x) 1 dx ln(1 + x)dx >
với mọi x > e − 1. Mà phân kì nên cũng x x x x 1 1 phân kì. +∞ Z e) Ta có 1 dx
e−x2 < 1 với mọi x > 0 nên e−x2 <
với mọi x > 0. Mặt khác hội tụ nên x2 x2 x2 0 +∞ Z e−x2 dx cũng hội tụ. x2 1 f) Khi 1 x → +∞ thì x2 ∼
nên tích phân đã cho hội tụ. x4 − x2 + 1 x2 +∞ Z Bài tập 2.3. Nếu
f (x)dx hội tụ thì có suy ra được f (x) → 0 khi x → +∞ không? a +∞ Z [Gợi ý]
f (x)dx hội tụ không suy ra được f (x) → 0 khi x → +∞. a +∞ Z Ví dụ như
sin(x2)dx hội tụ (xem bài tập 2.5) nhưng không tồn tại giới hạn lim sin(x2). x→+∞ 0 +∞ Z
Bài tập 2.4. Cho hàm số f (x) liên tục trên [a, +∞) và lim f (x) = A 6= 0. Hỏi f (x)dx x→+∞ a có hội tụ không? 132
3. Tích phân suy rộng 133 +∞ +∞ Z Z [Gợi ý] Theo giả thiết f (x) lim = 1, mà Adx phân kì nên f (x)dx cũng phân x→+∞ A a a kì.
Bài tập 2.5. Xét sự hội tụ của các tích phân suy rộng sau +∞ +∞ Z 1 Z Z a) x2dx sin(x2)dx d) g) p xp−1e−xdx 3 (1 − x2)5 0 0 0 Z +∞ Z π b) 2 1 e−x2dx e) (tan x)pdx Z f (x)dx 0 h) 0 √ , ( f liên tục) 1 − x2 +∞ 1 0 Z Z c) 2 1 − cos dx f) xp−1(1 − x)q−1dx x 1 0 √ Chứng minh.
a) Thực hiện phép đổi biến dt x =
t, dx = √ , đưa tích phân đã cho về 2 t dạng +∞ 1 Z sin tdt I = √ 2 t 0 Ta có thể viết π +∞ +∞ Z 2 sin tdt Z sin tdt Z sin tdt √ = √ + √ t t t 0 0 π | {z } 2 I | {z } 1 I2 Vì sin t
lim √ = 0 nên tích phân I thực chất là tích phân xác định nên hội tụ, do đó chỉ 1 t→0 t cần xét I . 2 +∞ +∞ +∞ +∞ Z sin t Z d(cos t) cos t +∞ Z Z 1 cos t 1 cos t I2 = √ dt = − √ = − √ − dt = − dt t t t π 2 t3/2 2 t3/2 π π 2 π π 2 2 2 2 +∞ Z Vì cos t 1 cos t ≤ nên
dt hội tụ. Vậy ta có I cũng hội tụ và tích phân đã cho 2 t3/2 t3/2 t3/2 π 2 hội tụ. +∞ +∞ Z Z
b) Ta có với x > 1 thì e−x2 < e−x mà
e−xdx = e−1 hội tụ nên e−x2dx cũng hội tụ. 1 0 +∞ Z c) Khi 2 2 2 x → +∞, 1 − cos = 2 sin2 1 ∼ nên 1 − cos dx hội tụ. x x x2 x 1 133 134
Chương 2. Phép tính tích phân một biến số 1 Z d) Khi x2 1 x2dx x → 1, x2 nên p = p ∼ √ p p 3 (1 − x2)5 3 [(1 − x)(1 + x)]5 3 32. 3 (1 − x)5 3 (1 − x2)5 0 hội tụ. Z π
e) Trước hết ta có nhận xét rằng 2 I =
(tan x)pdx có điểm bất thường là x = 0 khi 0 π p < 0 và x = khi p > 0. 2 cos x −p 1
• Nếu p < 0 thì khi x → 0, (tan x)p = ∼
nên I hội tụ nếu −1 < sin x x−p
p < 0 và phân kì nếu p ≤ −1.  p π sin x p sin x 1
• Nếu p > 0 thì khi x → , (tan x)p = =   ∼ 2 cos x  π  π p sin − x − x 2 2
nên I hội tụ nếu 0 < p < 1 và phân kì nếu p ≥ 1. Z π Kết luận:
2 (tan x)pdx hội tụ khi |p| < 1 và phân kì khi |p| ≥ 1. 0
f) Trước hết ta có nhận xét rằng nếu p < 1 thì x = 0 là điểm bất thường, còn nếu q < 1
thì x = 1 là điểm bất thường. Phân tích 1 1 1 Z 2 Z Z I = xp−1(1 − x)q−1dx = xp−1(1 − x)q−1dx + xp−1(1 − x)q−1dx 0 0 1 | {z } 2 I | {z } 1 I2 I chỉ hội tụ khi chỉ hội tụ khi 1
1 − p < 1, nghĩa là p > 0; còn I2 1 − q < 1, nghĩa là
q > 0. Vậy I chỉ hội tụ khi p > 0, q > 0.
g) Nếu p ≥ 1 thì tích phân đã cho chỉ có điểm bất thường tại +∞ và 1 xp+1 lim [xp−1e−x] : = lim = 0 x→+∞ x2 x→+∞ ex Z nên xp−1e−xdx hội tụ. x→+∞
Nếu p < 1 thì x = 0 cũng là một điểm bất thường. Ta có +∞ 1 +∞ Z Z Z xp−1e−xdx = xp−1e−xdx + xp−1e−xdx 0 0 1 | {z } | {z } I1 I2 134
3. Tích phân suy rộng 135 Tích phân I hội tụ khi hội tụ với 1 p > 0 và I2 p bất kì. +∞ Z Vậy
xp−1e−xdx hội tụ nếu p > 0. 0
h) Mặc dù tích phân đã cho là tích phân suy rộng có điểm bất thường là x = 1 nhưng ta
có thể đưa I về tích phân thường bằng cách đổi biến. Đặt x = sin θ, trên [0, c] ta có π 1 c arcsin c Z 2 f (x)dx Z f (x)dx Z Z √ = lim √ = lim f (sin θ)dθ = f (sin θ)dθ 1 − x2 c→1− 1 − x2 c→1− 0 0 0 0
Vì f là một hàm số liên tục trên [0, 1] nên hàm hợp f (sin θ) là một hàm số liên tục và h i bị chặn trên π 0,
và tích phân đã cho là tích phân xác định nên hội tụ. 2
Bài tập 2.6. Tính các tích phân suy rộng sau +∞ +∞ +∞ Z Z Z a) dx e−ax sin bxdx b) e−ax cos bxdx c) 1 + x4 0 0 0 +∞ Z +∞ Chứng minh. a) a sin bx + b cos bx b e−ax sin bxdx = − e−ax = a2 + b2 0 a2 + b2 0 +∞ Z +∞ b) b sin bx − a cos bx b e−ax cos bxdx = e−ax = a2 + b2 0 a2 + b2 0
c) Thực hiện phép đổi biến 1 x = ta có t +∞ +∞ +∞ Z dx Z t2dt Z x2dx I = = = 1 + x4 1 + t4 1 + x4 0 0 0 Do đó 1 +∞ +∞ +∞ +∞ 1 + dx Z dx Z x2dx Z (1 + x2)dx Z x2 2I = + = = 1 + x4 1 + x4 1 + x4 1 0 0 0 0 x2 + x2 Lại đặt 1 z = x − ta được x +∞ 1 Z z 1 z +∞ π I = = √ arctan √ = √ 2 z2 + 2 2 2 2 2 2 −∞ −∞ 135 136
Chương 2. Phép tính tích phân một biến số
§4. CÁC ỨNG DỤNG CỦA TÍCH PHÂN XÁC ĐỊNH
4.1 Tính diện tích hình phằng
1. Trường hợp biên của hình phẳng cho trong hệ toạ độ Descartes (tính diện tích "hình thang cong")  a ≤ x ≤ b     b  Z Nếu y = f (x) S giới hạn bởi thì S = | f (x) − g(x) | dx (2.13)  y = g(x)  a    f , g ∈ C[a, b]  c ≤ y ≤ d     d  Z Nếu x = ϕ(y) S giới hạn bởi thì S =
| ϕ(y) − ψ(y) | dy (2.14)  x = ψ(y)  c  
 ϕ, ψ ∈ [c, d]   a ≤ x ≤ b     t2 y = 0 Z Nếu S giới hạn bởi  thì S =
| ψ(t)ϕ′(t) | dt (2.15)  x = ϕ(t)   t1   y = ψ(t)
Trong đó giả thiết rằng phương trình ϕ(t) = a, ψ(t) = b có nghiệm duy nhất là t và 1, t2
ϕ, ψ, ϕ′ ∈ C[t1, t2].
Ví dụ 4.1 (Cuối kì, K61-Viện ĐTQT). Tính diện tích của miền     a) x + y ≥ 2 x − y ≥ 2 D : b) D : x2 + y2 ≤ 2x. x2 + y2 ≤ 2x.
Bài tập 2.1. Tính diện tích hình phẳng giới hạn bởi:
a) Đường parabol y = x2 + 4 và đường thẳng x − y + 4 = 0.
b) Parabol bậc ba y = x3 và các đường y = x, y = 2x.
c) Đường tròn x2 + y2 = 2x và parabol y2 = x d) Đường y2 = x2 − x4 136
4. Các ứng dụng của tích phân xác định 137 [Gợi ý]
Các câu a), b), c) có thể vẽ hình và tính toán dễ dàng như sau: 1 Z
a) S = [(x + 4) − (x2 + 4)]dx = 16 0 √ 1 2 Z Z
b) S = (2x − x2)dx + (2x − x3)dx = 34 0 2 2 Z √ c) √ S = 2
( 4x − x2) − 2x)dx = 2π − 163 0
d) Trước hết ta có điều kiện 0 ≤ x ≤ 1, và nhận xét rằng nếu M(x, y) ∈ C thì M′(±x, ±y) ∈  0 ≤ x ≤ 1
C . Do đó S = 4S(D), trong đó D là miền giới hạn bởi: √ y = x2 − x4.
Do miền D nằm hoàn toàn trong hình vuông 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, hơn nữa hàm số √ y =
x2 − x4 liên tục, y(0) = y(1) = 0 nên đồ thị của nó trong [0, 1] có hình dáng như hình vẽ dưới đây: y 1 O 1 x 1 Z √
Áp dụng công thức 2.13 ta có S(D) = x2 − x4dx = 1 . 3 ⇒S = 43 0
2. Trường hợp biên của hình phẳng cho trong hệ toạ độ cực (tính diện tích của miền có dạng hình quạt)   ϕ = α     β  Z Nếu ϕ = β 1 S giới hạn bởi thì S = r2(ϕ)dϕ (2.16)  2 r = r( ϕ)  α  
r(ϕ) ∈ C[α, β] 137 138
Chương 2. Phép tính tích phân một biến số
Bài tập 2.2. Tính diện tích hình phẳng giới hạn bởi đường hình tim r2 = a2 cos 2ϕ [Gợi ý] y p r = a cos 2ϕ x O Hình 2.2
Khảo sát và vẽ đồ thị của đường cong trong toạ độ cực và nhận xét tính đối xứng của hình vẽ ta có: π 4 1 Z S = 4S(D) = 4. r2(ϕ)dϕ = a2. 2 0
4.2 Tính độ dài đường cong phẳng
Trường hợp đường cong AB cho bởi phương trình y = f (x)   y = f (x)  b  Z q AB a ≤ x ≤ b thì s = 1 + [ f ′(x)]2 (2.17)    a  f ∈ C1[a, b]
Trường hợp đường cong AB cho bởi phương trình tham số:  x = x(t)      y = y(t)  β  Z q AB α ≤ t ≤ β thì s = [x′(t)]2 + [y′(t)]2dt (2.18)    α  x(t), y(t) ∈ C1[a, b]   
x′2(t) + y′2(t) > 0∀t ∈ [α, β]
Trường hợp đường cong AB cho bởi phương trình trong toạ độ cực:   r = r( ϕ)  β  Z q AB
α ≤ ϕ ≤ β thì s =
r2(ϕ) + r′2(ϕ)dϕ (2.19)    α
r(ϕ) ∈ C1[α, β] 138
4. Các ứng dụng của tích phân xác định 139
Bài tập 2.1. Tính độ dài đường cong
a) y = ln ex+1 khi x biến thiên từ 1 đến 2. ex−1   b) x = a(cos t + ln tan t ) 2
khi t biến thiên từ π đến π. 3 2 y = a sin t Chứng minh. a) Ta có !2 !2 ex ex e2x + 1 1 + y′2(x) = 1 + − = ex + 1 ex − 1 e2x − 1
Nên áp dụng công thức 2.17 ta được: 2 e4 Z e2x + 1 (t=e2x) Z t + 1 e2 + 1 s = dx = = ln e2x − 1 2t(t − 1) e2 1 e2
b) Áp dụng công thức 2.18 ta có π s 2 s cos2 t Z cos2 t 2 x′2(t) + y′2(t) = a2. ⇒s = a dt = a ln √ sin2 t sin2 t 3 π 3
4.3 Tính thể tích vật thể
Trường hợp vật thể được giới hạn bởi một mặt cong và hai mặt phẳng x = a, x = b. Giả
thiết ta biết rằng diện tích S của thiết diện của vật thể khi cắt bởi mặt phẳn x = x là 0
S(x0), và S(x) là hàm số xác định, khả tích trên [a, b]. Khi đó b Z V = S(x)dx (2.20) a
Bài tập 2.1. Tính thể tích của vật thể là phần chung của hai hình trụ x2 + y2 = a2 và y2 + z2 = a2(a > 0).
Lời giải: Do tính đối xứng nên V = 8V′ trong đó V′ = V ∩ {x ≥ 0, y ≥ 0, z ≥ 0}. Một
điểm M(x, 0, 0) ∈ Ox, qua M ta dựng thiết diện của V′ vuông góc với Ox thì được một hình √
vuông có cạnh là a2 − x2, do đó S(x) = a2 − x2. Áp dụng công thức 2.20 ta được a Z 16 V = 8 (a2 − x2)dx = a3 3 0 139 140
Chương 2. Phép tính tích phân một biến số
Bài tập 2.2. Tìm thể tích vật thể giới hạn bởi mặt paraboloit z = 4 − y2, các mặt phẳng
toạ độ và mặt phẳng x = a.
Chứng minh. Sau khi vẽ hình và áp dụng công thức 2.20 ta có: a 2 Z Z 16 16 V = S(x)dx mà S(x) = (4 − y2)dy = nên V = a 3 3 0 0
Tính thể tích vật thể tròn xoay
Trường hợp vật thể là vật thể tròn xoay được tạo thành khi quay hình thang cong   a ≤ x ≤ b   y = 0
quanh trục Ox, trong đó f ∈ C[a, b] thì    y = f (x) b Z V = π f 2(x)dx (2.21) a
Tương tự, nêú vật thể là vật thể tròn xoay được tạo thành khi quay hình thang cong   c ≤ y ≤ d   x = 0
quanh trục Oy, trong đó ϕ ∈ C[c, d] thì    x = ϕ(y) d Z V = π ϕ2(y)dy (2.22) c
Bài tập 2.3. Tính thể tích khối tròn xoay tạo nên khi quay hình giới hạn bởi các đường y = 2x − x2 và y = 0 a) quanh trục Ox một vòng
b) quanh trục Oy một vòng. [Gợi ý]
a) Áp dụng công thức 2.21: 2 Z V = π (2x − x2)dx = 0
b) Áp dụng công thức 2.22: 1 1 Z Z p 2 p 2 V = π 1 + 1 − y dy − π 1 − 1 − y dy 0 0 140
4. Các ứng dụng của tích phân xác định 141
4.4 Tính diện tích mặt tròn xoay   a ≤ x ≤ b  
Cho hình thang cong giới hạn bởi y = 0
với f ∈ C1[a, b]. Quay hình thang cong    y = f (x)
này quanh trục Ox thì ta được một vật thể tròn xoay. Khi đó diện tích xung quanh của vật
thể được tính theo công thức: b Z q S = 2π | f (x) | 1 + f ′2(x)dx (2.23) a   c ≤ y ≤ d  
Tương tự nếu quay hình thang cong x = 0
với ϕ ∈ C1[c, d], quanh trục Oy thì:    x = ϕ(y) d Z q S = 2π | ϕ(y) | 1 + ϕ′2(y)dy (2.24) c
Bài tập 2.1. Tính diện tích mặt tròn xoay tạo nên khi quay các đường sau
a) y = tan x, 0 < x ≤ π quanh trục Ox. 4
b) x2 + y2 = 1 quanh trục Oy(a > b) a2 b2
c) 9y2 = x(3 − x)2, 0 ≤ x ≤ 3 quanh trục Ox. 141 142
Chương 2. Phép tính tích phân một biến số Chứng minh.
a) Áp dụng công thức 2.23 ta có: π 4 Z q S = 2π tan x 1 + (1 + tan2 x)dx 0 1 Z q dt = 2π t 1 + (1 + t2)2. (đặt t = tan x) 1 + t2 0 1 Z p1 + (1 + t2)2 = π .d(t2 + 1) 1 + t2 0 2 √ Z 1 + s2 = π ds (đặt s = 1 + t2) s 1√5 Z 1 = π 1 + du √ u2 − 1 2 ( √ √ √ √ ) 1 h 5 − 1 5 + 1 i = π. 5 − 2 + ln √ − ln √ 2 2 − 1 2 + 1
b) Nhận xét tính đối xứng của miền và áp dụng công thức 2.24 ta có: b s Z a q a y 2 S = 2.2π b2 − y2. 1 + . dy b b pb2 − y2 0 b a Z q = 4π b4 + (a2 − b2)y2dy b 0 b s a p Z b4 = 4π a2 − b2 y2 + dy b a2 − b2 0 b a p Z q b4 = 4π a2 − b2
y2 + βdy( đặt β = ) b a2 − b2 0 b a p 1 h q q i = 4π a2 − b2. y
y2 + β + β ln | y + y2 + β | b 2 0 ! Z q 1 h q q i y2 + βdy = y
y2 + β + β ln | y + y2 + β | 2 c) Trước hết (3 − x)(1 − x) (1 − x)2
9y2 = x(3 − x)2⇒18yy′ = 3(3 − x)(1 − x)⇒y′ = ⇒y′2 = 6y 4x 142
4. Các ứng dụng của tích phân xác định 143
Nên áp dụng công thức 2.23 ta có: 3 √ r 3 Z x(3 − x) (1 − x)2 1 Z S = 2π . 1 + dx = 2π.
(3 − x)(1 + x)dx = 3π. 3 4x 6 0 0
"Nghịch lý sừng Gabriel"   1 ≤ x,  
Cho một vật thể tròn xoay tạo bởi khi xoay miền giới hạn bởi y = 0, quanh trục Ox.    y = 1x
Tính thể tích và diện tích mặt của nó. [Lời giải] Ta có +∞ Z 1 2 V = π dx = π x 1 và +∞ s +∞ Z 1 1 2 Z 1 S = 2π 1 + − dx ≥ 2π dx = +∞. x x2 x 1 1
Như vậy, đây là một vật thể có diện tích mặt bằng +∞, trong khi đó lại có thể tích hữu
hạn. Giả sử bạn có một vật thể như vậy và cần sơn nó.
i) Một mặt, vì diện tích mặt là +∞, bạn cần một lượng vô hạn sơn để sơn nó.
ii) Mặt khác, vì miền giới hạn bởi vật đó có thể tích hữu hạn, bạn có thể đổ đầy nó bằng
một lượng hữu hạn sơn (ở đây là π đơn vị thể tích), và khi đó toàn bộ mặt trong của nó sẽ được sơn.
Một nghịch lý phải không? 143 144
Chương 2. Phép tính tích phân một biến số 144 3 CHƯƠNG
HÀM SỐ NHIỀU BIẾN SỐ
§1. GIỚI HẠN CỦA HÀM SỐ NHIỀU BIẾN SỐ
1.1 Giới hạn của hàm số nhiều biến số
Ta nói rằng dãy điểm {Mn(xn, yn)} dần tới điểm M0(x0, y0) trong R2 và viết Mn → M0 khi n → +∞ nếu lim d(M .
n, M0) = 0 hay nếu xn → x0, yn → y0 n→+∞
Định nghĩa 3.33. Cho hàm số z = f (M) = f (x, y) xác định trong một lân cận V nào đó của điểm M . Ta nói rằng hàm số
0(x0, y0), có thể trừ tại điểm M0
f (x, y) có giới hạn là L khi M dần đến M nếu 0
∀ǫ > 0, ∃δ > 0 : nếu d(M, M0) < δ thì | f (M) − L| < ǫ.
Một cách tương đương, với mọi dãy điểm M ta đều có
n(xn, yn) thuộc lân cận V dần đến M0 lim f (xn, yn) = L. n→+∞ Khi đó ta viết lim f (x, y) = L hay lim f (M) = L. (x,y)→(x0,y0) M→M0
• Khái niệm giới hạn vô hạn cũng được định nghĩa tương tự như đối với hàm số một biến số.
• Các định lý về giới hạn của tổng, hiệu, tích, thương đối với hàm số một biến số cũng
đúng cho hàm số nhiều biến số và được chứng minh tương tự. Nhận xét: 145 146
Chương 3. Hàm số nhiều biến số
• Theo định nghĩa trên, muốn chứng minh sự tồn tại của giới hạn của hàm số nhiều
biến số là việc không dễ vì phải chỉ ra lim f (xn, yn) = l với mọi dãy số {xn → n→+∞
x0}, {yn → y0}. Trong thực hành, muốn tìm giới hạn của hàm số nhiều biến số,
phương pháp chứng minh chủ yếu là đánh giá hàm số, dùng nguyên lý giới hạn kẹp
để đưa về giới hạn của hàm số một biến số.
• Với chiều ngược lại, muốn chứng minh sự không tồn tại giới hạn của hàm số nhiều
biến số, ta chỉ cần chỉ ra tồn tại hai dãy {xn → x0, yn → y0} và {x′n → x0, y′n → y0} sao cho
lim f (xn, yn) 6= lim f (x′n, y′n) n→+∞ n→+∞
hoặc chỉ ra tồn tại hai quá trình (x, y) → (x0, y0) khác nhau mà f (x, y) tiến tới hai giới hạn khác nhau.
1.2 Tính liên tục của hàm số nhiều biến số
• Giả sử hàm số f (M) xác định trong miền D, M là một điểm thuộc 0 D. Ta nói rằng
hàm số f (M) liên tục tại điểm M nếu 0 lim f (M) = f (M0) M→M0
Nếu miền D đóng và M là điểm biên của 0
D thì limM→M f (M) được hiểu là giới hạn 0
của f (M) khi M dần tới M ở bên trong của 0 D.
• Hàm số f (M) được gọi là liên tục trong miền D nếu nó liên tục tại mọi điểm thuộc D.
• Hàm số nhiều biến số liên tục cũng có những tính chất như hàm số một biến số liên
tục. Chẳng hạn, nếu hàm số nhiều biến số liên tục trong một miền đóng, bị chặn thì
nó liên tục đều, bị chặn trong miền ấy, đạt giá trị lớn nhất và giá trị nhỏ nhất trong miền đó. 1.3 Bài tập
Bài tập 3.1. Tìm miền xác định của các hàm số sau a) 1 y − 1 z = c) p z = arcsin x2 + y2 − 1 x b) p z =
(x2 + y2 − 1)(4 − x2 − y2) d) z = px sin y
Bài tập 3.2. Tìm giới hạn (nếu có) của các hàm số sau 146
2. Đạo hàm và vi phân 147 πx a) x2 − y2 b) f (x, y) = (x → 0, y → 0) f (x, y) = sin (x → ∞, y → ∞) x2 + y2 2x + y Chứng minh.
a) Nếu cho (x, y) → (0, 0) theo phương của đường thẳng y = kx thì ta có x2 − k2x2 1 − k2 1 − k2 f (x, kx) = = → khi x → 0 x2 + k2x2 1 + k2 1 + k2
Vậy khi (x, y) → (0, 0 theo những phương khác nhau thì f (x, y) dần tới những giới
hạn khác nhau. Do đó không tồn tại lim f (x, y). (x,y)→(0,0)
b) Nếu cho (x, y) → (∞, ∞) theo phương của đường thẳng y = kx thì ta có πx π π f (x, kx) = sin = sin → sin khi x → 0 2x + kx 2 + k 2 + k
Vậy khi (x, y) → (0, 0 theo những phương khác nhau thì f (x, y) dần tới những giới
hạn khác nhau. Do đó không tồn tại lim f (x, y). (x,y)→(0,0)
Bài tập 3.3. [Cuối kì, K62, GT2, Nhóm ngành 2] Tính các giới hạn a) 2x4 + y4 x4 + 2y4 lim . b) lim . (x,y)→(0,0) x2 + 2y2 (x,y)→(0,0) 2x2 + y2 [Lời giải] Ta có a) 2x4 + y4 2x4 y4 lim = lim + lim = 0 + 0 = 0, (x,y)→(0,0) x2 + 2y2 (x,y)→(0,0) x2 + 2y2 (x,y)→(0,0) x2 + 2y2 do 2x4 y4 0 ≤ ≤ 2x2, 0 ≤
≤ 1y2 và nguyên lý giới hạn kẹp. x2 + 2y2 x2 + 2y2 2 b) x4 + 2y4 x4 2y4 lim = lim + lim = 0 + 0 = 0, (x,y)→(0,0) 2x2 + y2 (x,y)→(0,0) 2x2 + y2 (x,y)→(0,0) 2x2 + y2 do x4 2y4 0 ≤ ≤ 1 x2, 0 ≤
≤ 2y2 và nguyên lý giới hạn kẹp. 2x2 + y2 2 2x2 + y2
Chú ý 3.20. Không nhầm lẫn lim
f (x, y) với các giới hạn lặp lim lim f (x, y) và (x,y)→(x x→x y→y 0,y0) 0 0
lim lim f (x, y). Chẳng hạn như, bạn đọc có thể kiểm tra với hàm số f (x, y) = x2 ta có y→y x2+y2 0 x→x0 i) lim x2 không tồn tại. (x,y)→(0,0) x2+y2 ii) lim lim f (x, y) x2 = 1, x→0 y→0 x2+y2 iii) lim lim x2 = 0. y→0 x→0 x2+y2 147 148
Chương 3. Hàm số nhiều biến số
§2. ĐẠO HÀM VÀ VI PHÂN 2.1 Đạo hàm riêng
• Cho hàm số f (x, y) xác định trong một miền D, điểm M(x , 0, y0) ∈ D. Nếu cho y = y0
hàm số một biến số x 7→ f (x, y
thì đạo hàm đó gọi là
0) có đạo hàm tại điểm x = x0
đạo hàm riêng của f với biến x tại M và được kí hiệu là ∂ f hay ∂ 0 f (x, y). ∂x ∂x ∂ f f (x = lim 0 + △x, y0) − f (x0, y0) ∂x △x→0 △x
• Cho hàm số f (x, y) xác định trong một miền D, điểm M(x , 0, y0) ∈ D. Nếu cho x = x0
hàm số một biến số x 7→ f (x
thì đạo hàm đó gọi là
0, y) có đạo hàm tại điểm y = y0
đạo hàm riêng của f với biến x tại M và được kí hiệu là ∂ f hay ∂ 0 f (x, y). ∂y ∂y ∂ f f (x = lim 0, y0 + △y) − f (x0, y0) ∂y △y→0 △y
Chú ý: Các đạo hàm riêng của các hàm số n biến số (với n ≥ 3) được định nghĩa tương tự.
Khi cần tính đạo hàm riêng của hàm số theo biến số nào, xem như hàm số chỉ phụ thuộc
vào biến đó, còn các biến còn lại là các hằng số và áp dụng các quy tắc tính đạo hàm như hàm số một biến số.
2.2 Vi phân toàn phần
• Cho hàm số z = f (x, y) xác định trong miền D. Lấy các điểm M0(x0, y0) ∈ D, M(x0 +
△x0, y0 + △y0) ∈ D. Biểu thức △ f = f (x0 + △x0, y0 + △y0) − f (x0, y0)(x0, y0) được
gọi là số gia toàn phần của f tại M . Nếu như có thể biểu diễn số gia toàn phần dưới 0 dạng
△ f = A. △ x + B △ y + α △ y + β △ y
trong đó A, B là các hằng số chỉ phụ thuộc x còn , thì ta nói 0, y0
α, β → 0 khi M → M0
hàm số z khả vi tại M , còn biểu thức 0
A. △ x + B △ y + α △ y được gọi là vi phân toàn
phần của z = f (x, y) tại M và được kí hiệu là 0 dz.
Hàm số z = f (x, y) được gọi là khả vi trên miền D nếu nó khả vi tại mọi điểm của miền ấy.
• Đối với hàm số một biến số, sự tồn tại đạo hàm tại điểm x tưong đương với sự khả 0
vi của nó tại x . Đối với hàm số nhiều biến số, sự tồn tại của các đạo hàm riêng tại 0 M
(xem bài tập 3.4). Định lý sau đây cho ta điều
0(x0, y0) chưa đủ để nó khả vi tại M0
kiện đủ để hàm số z = f (x, y) khả vi tại M . 0 148
2. Đạo hàm và vi phân 149
Định lý 3.50. Nếu hàm số f (x, y) có các đạo hàm riêng trong lân cận của M và nếu các 0
đạo hàm riêng đó liên tục tại M thì và 0 f (x, y) khả vi tại M0
dz = f ′x △ x + f ′y △ y
Ví dụ 2.1 (Cuối kì, K61 Viện ĐTQT). Sử dụng vi phân, tính gần đúng a) p(8, 05)2 + (5, 96)2. b) p(6, 05)2 + (7, 96)2.
2.3 Đạo hàm của hàm số hợp
Cho D là một tập hợp trong R2 và các hàm số ϕ
D → ϕ(D) ⊂ R2 f → R
và F = f ◦ ϕ là hàm số hợp của hai hàm số f và ϕ: F(x, y) = f (u(x, y), v(x, y)) Định lý 3.51. Nếu ∂ f
f có các đạo hàm riêng ∂ f ,
liên tục trong ϕ(D) và nếu u, v có các ∂x ∂y
đạo hàm riêng ∂u ∂u ∂v ∂v ∂F , , ,
trong D thì tồn tại các đạo hàm riêng ∂F, và
∂x ∂y ∂x ∂y ∂x ∂y  ∂F ∂ f ∂u ∂ f ∂v   = + ∂x ∂u ∂x ∂v ∂x (3.1) ∂F ∂ f ∂u ∂ f ∂v   = + ∂y ∂u ∂y ∂v ∂y
Công thức 3.1 có thể được viết dưới dạng ma trận như sau  ∂u ∂u ∂F ∂F ∂ f ∂ f   = ∂x ∂y   ∂x ∂y ∂u ∂v  ∂v ∂v  ∂x ∂y trong đó ma trận  ∂u ∂u  ∂x ∂y     ∂v ∂v  ∂x ∂y
được gọi là ma trận Jacobi của ánh xạ ϕ, định thức của ma trận ấy được gọi là định thức
Jacobi của u, v với x, y và được kí hiệu là D(u, v). D(x, y) 149 150
Chương 3. Hàm số nhiều biến số
2.4 Đạo hàm và vi phân cấp cao
• Cho hàm số hai biến số z = f (x, y). Các đạo hàm riêng f ′ là những đạo hàm riêng x, f ′y
cấp một. Các đạo hàm riêng của các đạo hàm riêng cấp một nếu tồn tại được gọi là
những đạo hàm riêng cấp hai. Có bốn đạo hàm riêng cấp hai được kí hiệu như sau:   ∂ ∂ f ∂2 f  ( f ′ =  x)′x = f ” xx =   ∂x ∂x ∂x2    ∂ ∂ f ∂2 f   ( f ′x)′y = f ” xy = = ∂y ∂x ∂y∂x  ∂ ∂ f ∂2 f  ( f ′ =  y)′x = f ” yx =  ∂x ∂y ∂x∂y     ∂ ∂ f ∂2 f  ( f ′ =  y)′y = f ” yy = ∂y ∂y ∂y2
Các đạo hàm riêng của các đạo hàm riêng cấp hai, nếu tồn tại, được gọi là các đạo hàm riêng cấp ba, ...
Định lý 3.52 (Schwarz). Nếu trong một lân cận U nào đó của điểm M0(x0, y0) hàm
số z = f (x, y) có các đạo hàm riêng f ”
và nếu các đạo hàm riêng ấy liên tục tại xy, f ” yx M thì tại . 0 f ”xy = f ”yx M0
• Xét hàm số z = f (x, y), vi phân toàn phần của nó dz = f ′xdx + f ′ydy, nếu tồn tại, cũng
là một hàm số với hai biến số x, y. Vi phân toàn phần của dz, nếu tồn tại, được gọi là
vi phân toàn phần cấp hai của z và được kí hiệu là d2z. Ta có công thức
d2z = f ”xxdx2 + 2 f ”xydxdy + f ”yydy2
Ví dụ 2.2 (Cuối kì, K62, GT2, Nhóm ngành 2). Cho hàm số z = z(x, y) có các đạo hàm  
riêng cấp một liên tục, ở đó x = r cos ϕ, y = r sin ϕ. Chứng minh rằng ∂z 2 ∂z 2 ∂z2 1 ∂z 2 + = + . ∂x ∂y ∂r r2 ∂ϕ
2.5 Đạo hàm theo hướng - Gradient
Định nghĩa 3.34. Cho f (x, y, z) là một hàm số xác định trong một miền D ∈ R3 và ~l =
(l1, l2, l3) là một véctơ đơn vị bất kì trong R3. Giới hạn, nếu có, f (M lim 0 + t~l) − f (M) (3.2) t→0 t 150
2. Đạo hàm và vi phân 151
được gọi là đạo hàm của hàm số f theo hướng~l tại M và được kí hiệu là ∂ f 0 (M0). ∂~l
• Nếu ~l không phải là véc tơ đơn vị thì giới hạn trong công thức 3.2 có thể được thay bằng u(x lim
0 + t cos α, y0 + t cos β, z0 + t cos γ) − u(x0, y0, z0) , t→0 t
trong đó cos α, cos β, cosγ là các cosin chỉ phương của − → l .
• Nếu~l trùng với véctơ đơn vị i của trục Ox thì đạo hàm theo hướng~l chính là đạo hàm
riêng theo biến x của hàm f ∂ f ∂ f (M0) = (M0) ∂~l ∂x
• Vậy đạo hàm riêng theo biến x chính là đạo hàm theo hướng của trục Ox, cũng như
vậy, ∂ f ∂ f ,
là các đạo hàm của f theo hướng của trục Oy và Oz. Định lý sau đây cho ∂y ∂z
ta mối liên hệ giữa đạo hàm theo hướng và đạo hàm riêng:
Định lý 3.53. Nếu hàm số f (x, y, z) khả vi tại điểm M có đạo hàm 0(x0, y0, z0) thì tại M0
theo mọi hướng~l và ta có ∂ f ∂ f ∂ f ∂ f (M0) = (M0) cos α + (M0) cos β + (M0) cos γ ∂~l ∂x ∂y ∂z
trong đó (cos α, cos β, cos γ) là cosin chỉ phương của~l.
Cho f (x, y, z) là hàm số có các đạo hàm riêng tại M0(x0, y0, z0). Người ta gọi gradient của f tại M là véctơ 0 ∂ f ∂ f ∂ f (M (M (M ∂x 0), ∂y 0), ∂z 0)
và được kí hiệu là −−→ grad f (M0).
Định lý 3.54. Nếu − →
l là một véctơ đơn vị và hàm số f (x, y, z) khả vi tại M thì tại đó ta có 0 ∂ f −−→ (M0) = grad f .~l ∂~l
Chú ý: ∂ f (M theo hướng~
0) thể hiện tốc độ biến thiên của hàm số f tại M0 l. Từ công ∂~l thức ∂ f −−→ −−→ −−→ ∂ f (M ~ ta có đạt giá trị lớn nhất
0) = grad f .~l = grad f l . cos grad f ,~l (M0) ∂~l ∂~l bằng −−→ ~ nếu~ grad f l
l có cùng phương với −−−→ grad f . Cụ thể
• Theo hướng ~l, hàm số f tăng nhanh nhất tại M nếu ~ 0
l có cùng phương, cùng hướng với −−−→ grad f .
• Theo hướng~l, hàm số f giảm nhanh nhất tại M nếu~ 0
l có cùng phương, ngược hướng với −−−→ grad f . 151 152
Chương 3. Hàm số nhiều biến số
2.6 Hàm ẩn - Đạo hàm của hàm số ẩn
• Cho phương trình F(x, y) = 0 trong đó F : U → R là một hàm số có các đạo hàm
riêng liên tục trên tập mở U ⊂ R2 và F′y(x0, y0) 6= 0. Khi đó phương trình F(x, y) = 0
xác định một hàm số ẩn y = y(x) trong một lân cận nào đó của x và có đạo hàm 0 F′ y′(x) = − x F′y
• Tương tự, cho phương trình F(x, y, z) = 0 trong đó F : U → R là một hàm số có các
đạo hàm riêng liên tục trên tập mở U ⊂ R3 và F′z(x0, y0, z0) 6= 0. Khi đó phương trình
F(x, y, z) = 0 xác định một hàm số ẩn z = z(x, y) trong một lân cận nào đó của (x0, y0) và có đạo hàm F′ F′y z′ x x = − , z′ F′ y = − z F′z 2.7 Bài tập
Bài tập 3.4. Chứng minh rằng hàm số  xy  nếu (x, y) 6= (0, 0) f (x, y) = x2 + y2 0 nếu (x, y) = (0, 0)
có các đạo hàm riêng tại (0, 0) nhưng không liên tục tại (0, 0) và do đó không khả vi tại (0, 0).
Bài tập 3.5. Tính các đạo hàm riêng của hàm số sau a) p z = ln x + x2 + y2 c) z = xy3 e) u = xyz, (x, y, z > 0) r 1 b) d) x2−y2 z = y2 sin x z = arctan f) x2+y2+z2 y x2+y2 u = e , (x, y, z > 0) Chứng minh. a) 1 + x √ y √ x2+y2 1 x2+y2 z′x = p = p ; z′y = p x + x2 + y2 x2 + y2 x + x2 + y2 b) x x x z′x = y cos ; z′ − x cos . y y = 2y sin y y 152
2. Đạo hàm và vi phân 153 c)
z′x = y3xy3−1; z′y = 3y2 ln x.xy3 d) s ! 1 ∂ x2 − y2 y2 z′x = = x2−y2 p + 1 ∂x x2 + y2 x x4 − y4 x2+y2 s ! 1 ∂ x2 − y2 −y z′y = = x2−y2 p + 1 ∂y x2 + y2 x4 − y4 x2+y2 e)
u′x = yzxyz−1; u′y = xyzzyz−1. ln x; u′z = xyzyz ln y ln x f) 1 −2x 1 1 u′ x2+y2+z2 x2+y2+z2 −2y x2+y2+z2 −2z x = e . ; u′y = e ; u′z = e . (x2 + y2 + z2)2 (x2 + y2 + z2)2 (x2 + y2 + z2)2
Bài tập 3.6. Khảo sát sự liên tục và sự tồn tại, liên tục của các đạo hàm riêng của các hàm số f (x, y) sau  2  nếu a) x arctan y x 6= 0 f (x, y) = x 0 nếu x = 0  x sin y  − y sin x  nếu (x, y) 6= (0, 0) b) f (x, y) = x2 + y2  0 nếu (x, y) = (0, 0) . Chứng minh.
a) Dễ thấy hàm số liên tục với mọi (x, y) 6= (0, y). Xét 2 2 x = 0, vì x arctan y x. arctan y
= 0 = f (0, y) . Vậy f (x, y) x ≤ π 2 |x| nên lim x→0 x liên tục trên R2.
Với x 6= 0 các đạo hàm riêng tồn tại và liên tục: y 2 2x2y2 2x3y z′x = arctan − , z′ x x4 + y4 y = x4 + y4 Xét tại x = 0,     2 0, y = 0  f (h, y) − f (0, y)  h  f ′x (0, y) = lim = arctan =  h→0 h y π , y 2 6= 0    f (0, y + k) − f (0, y)   f ′y (0, y) = lim = lim 0 = 0 k→0 k k→0
Vậy ta thấy f ′x (x, y) liên tục trên R2\ (0, 0) ; f ′y (x, y) liên tục trên R2. 153 154
Chương 3. Hàm số nhiều biến số
b) Hàm số liên tục trên R2\ (0, 0), còn tại (0, 0) thì x sin y − ysinx xy sin y sin x 1 sin y sin x 0 ≤ = − ≤ − x2 + y2 x2 + y2 y x 2 y x nên x sin y − ysinx lim = 0 x→0 x2 + y2 y→0
Vậy f (x, y) liên tục trên R2.
Bài tập 3.7. Giả sử z = y f x2 − y2 , ở đó f là hàm số khả vi. Chứng minh rằng đối với
hàm số z hệ thức sau luôn thoả mãn 1 1 z z′ z′ x x + y y = y2 Chứng minh. Ta có
z′x = y f x2 − y2 .2x, z′y = f x2 − y2 + y. f x2 − y2 . (−2y) nên 1 1 f x2 − y2 z z′ z′ = x x + y y = y y2
Bài tập 3.8. Tìm đạo hàm của hàm số hợp sau đây a) p z = eu2−2v2, u = cos x, v = x2 + y2.
b) z = ln u2 + v2 , u = xy, v = x. y
c) z = arcsin (x − y) , x = 3t, y = 4t3. Chứng minh. a) Ta có (  u′  v′x = x √ x = − sin x ; x2+y2 ; u′y = 0  v′y = y √x2+y2 nên 
z′x = ecos x2−2(x2+y2) [− sin 2x − 4x] .
z′y = ecos x2−2(x2+y2) [−4y] . b) Ta có ( ( u′ v′ x = y x = 1 ; y u′y = x v′y = −x y2 nên 2 2 y4 − 1 z′x = , z′ x y = y (y4 + 1) 154
2. Đạo hàm và vi phân 155 c) Ta có ( x′t = 3 y′t = 12t2 nên 1 z′t = q 3 − 12t2 1 − (x − y)2
Bài tập 3.9. Tìm vi phân toàn phần của các hàm số a) z = sin x2 + y2 c) z = arctan x+y x−y b) z = ln tan y d) u = xy2z x Chứng minh. a) dz = cos x2 + y2 (2xdx + 2ydy) b) 2 xdy − ydx dz = . . sin 2y x2 x c) (x − y) dx + (x + y) dy dz = . (x − y)2 + (x + y)2 d) y2z du = xy2z dx + 2yz ln xdy + y2 ln xdz . x
Bài tập 3.10. Tính gần đúng q √ √ a) A = 3 (1, 02)2 + (0, 05)2
b) B = ln 3 1, 03 + 4 0, 98 − 1 Chứng minh. a) Xét hàm p
f (x, y) = 3 x2 + y2, ∆x = 0, 02; ∆y = 0, 05; x = 1; y = 0. Ta có 1 1 f ′x = 2x; f ′y = 2y 3 (x2 + y2)2/3 3 (x2 + y2)2/3 Khi đó 2
f (1 + ∆x, 0 + ∆y) ≈ f (1, 0) + f ′x (1, 0) ∆x + f ′y (1, 0) ∆y = 1 + .0, 02 + 0.0, 05 = 1, 013. 3 155 156
Chương 3. Hàm số nhiều biến số b) Xét hàm √ √
f (x, y) = ln 3 x + 4 y − 1 ; x = 1; y = 1; ∆x = 0, 03; ∆y = 0, 02 Ta có 1 1 1 1 f ′x = √ √ . ; f ′ √ √ . 3 x + y = 4 y − 1 2 3 3x 3 3 x + 4 y − 1 3y4 Khi đó
f (1 + ∆x, 1 + ∆y) ≈ f (1, 1) + f ′x (1, 1) ∆x + f ′y (1, 1) ∆y 1 1 = 0 + .0, 03 + (−0, 02) = 0, 005. 3 4
Bài tập 3.11. Tìm đạo hàm của các hàm số ẩn xác định bởi các phương trình sau
a) x3y − y3x = a4; tính y′
c) x + y + z = ez; tính z′x, z′y b) arctan x+y = y; tính y′ d) x3 + y3 + z3 a a
− 3xyz = 0, tính z′x, z′y Chứng minh.
a) Xét hàm số ẩn F (x, y) = x3y − y3x − a4 = 0, có F′x = 3x2y − y3; F′y = x3 − 3y2x. Vậy −F′ 3x2y − y3 y′ = x = − F′y x3 − 3y2x  1  a = a F′x = b) Xét hàm số ẩn a2+(x+y)2 F (x, y) = arctan x+y có 1+( x+y )2 a nên a − ya  F′y = a = a2−a2−(x+y)2 a2+(x+y)2 − 1a a(a2+(x+y)2) a y′ = . (x + y)2
c) Xét hàm số ẩn F (x, y, z) = x + y + z − ez có F′x = 1; F′y = 1; F′z = 1 − ez nên −1 −1 z′x = ; z′ 1 − ez y = 1 − ez
d) Xét hàm số ẩn F (x, y) = x3 + y3 + z3 − 3xyz = 0 có F′x = 3x2 − 3yz; F′y = 3y2 − 3xz; F′z = 3z2 − 3xy nên 3yz − 3x2 3xz − 3y2 z′x = ; z′ 3z2 − 3xy x = 3z2 − 3xy
Bài tập 3.12. Cho u = x+z, tính u′
biết rằng z là hàm số ẩn của x, y xác định bởi y+z x, u′y
phương trình z.ez = x.ex + y.ey 156
2. Đạo hàm và vi phân 157   F′  x = − (ex + xex) 
Chứng minh. Xét hàm số F (x, y, z) = zez − xex − yey = 0 có F′ nên y = − (ey + yey)    F′z = ez + zez    1 + ex+xex − (x + z) ex+xex  (1 + z′ ez+zez ez+zez 
x) . (y + z) − (x + z) (z′x) u′ =  x = (y + z)2 (y + z)2 ey+yey  
(x + z) . 1 + z′ − (y + z) z′
(x + z) . 1 + ey+yey − (y + z)  y y ez+zez ez+zez  u′ =  y = (y + z)2 (y + z)2
Bài tập 3.13. Tìm đạo hàm của các hàm số ẩn y(x), z(x) xác định bởi hệ  x + y + z = 0 x2 + y2 + z2 = 1
Chứng minh. Lấy đạo hàm hai vế của các phương trình của hệ ta có  1 + y′x + z′x = 0 2x + 2yy′x + 2zz′x = 0 nên  z − x   y′x = y − z x − y   z′x = y − z
Bài tập 3.14. Phương trình p z2 + 2 = y2 x
− z2, xác định hàm ẩn z = z (x, y). Chứng minh rằng x2z′x + 1z′ y y = 1z   F′  x = − 2  x2 
Chứng minh. Xét hàm số p F (x, y, z) = z2 + 2 y2 F′ nên x − − z2 có y = −y √y2−z2     F′z = 2z + z √y2−z2  2    x2 z′  x =  2z + z √  y2−z2 −y √   y2  −z2 z′   y =  2z + z √y2−z2 Từ đó suy ra z′ x2z′ y x + = 1. y z
Bài tập 3.15. Tính các đạo hàm riêng cấp hai của các hàm số sau 157 158
Chương 3. Hàm số nhiều biến số q a) z = 1 (x2 + y2)3 b) z = x2 ln x2 + y2 c) z = arctan y 3 x Chứng minh. a) Ta có   p 2x 2x2 + y2  z′′ xx = x2 + y2 + x p = p    2 x2 + y2 x2 + y2 p  z′   x = x x2 + y2 p 2y x2 + 2y2 p ⇒ z′′yy = x2 + y2 + y p = p z′y = y x2 + y2   2 x2 + y2 x2 + y2    2xy xy  z′′ =  xy = p p 2 x2 + y2 x2 + y2 b) Ta có  2x 2x (x + y) − x2 z′′ +   xx = 2 ln (x + y) + x2   x + y (x + y)2     z′x = 2x ln (x + y) +  x + y  2x −x2 ⇒ z′′xy = +  x2 x + y (x + y)2   z′  y = x + y    x2   z′′ yy = (x + y)2 c) Ta có  2xy  z′′ 1 −y −y   xx =   (x2 + y2)2 z′ . =   x =   2  1 + y x2 x2 + y2  − x2 + y2 + y.2y y2 − x2 x = 1 1 x ⇒ z′′xy =  z′ =  (x2 + y2)2 (x2 + y2)2  y =   2  1 + y x x2 + y2   −2xy x  z′′  yy = (x2 + y2)2
Bài tập 3.16. Tính vi phân cấp hai của các hàm số sau a) z = xy2 − x2y b) z = 1 2(x2+y2) Chứng minh. a) Ta có
dz = y2 − 2xy dx + 2xy − x2 dy nên
d2z = −2y (dx)2 + 4 (y − x) dxdy+ (2y) (dy)2 b) Ta có dz = x dx + y dy nên 2(x2+y2)2 2(x2+y2)2 y2 − 3x2 4xy x2 − 3y2 d2z = (dx)2 − dxdy + (dy)2 (x2 + y2)3 (x2 + y2)3 (x2 + y2)3 158
3. Cực trị của hàm số nhiều biến số 159
§3. CỰC TRỊ CỦA HÀM SỐ NHIỀU BIẾN SỐ 3.1 Cực trị tự do
Định nghĩa 3.35. Cho hàm số z = f (x, y) xác định trong một miền D và M0(x0, y0) ∈ D.
Ts nói rằng hàm số f (x, y) đạt cực trị tại M nếu với mọi điểm 0
M trong lân cận nào đó của M nhưng khác , hiệu số 0 M0
f (M) − f (M0) có dấu không đổi. • Nếu f (M) − f (M thì
được gọi là cực tiểu
0) > 0 trong một lân cận nào đó của M0 M0 của hàm số f tại M . 0 • Nếu f (M) − f (M thì
được gọi là cực đại
0) < 0 trong một lân cận nào đó của M0 M0 của hàm số f tại M . 0
Trong phần tiếp theo chúng ta sử dụng các kí hiệu sau:
p = f ′x(M), q = fy(M), r = fxx”(M), s = fxy”(M), t = fyy”(M)
Định lý 3.55. Nếu hàm số f (x, y) đạt cực trị tại M và tại đó các đạo hàm riêng p =
f ′x(M), q = fy(M) tồn tại thì các đạo hàm riêng ấy bằng không.
Định lý 3.56. Giả sử hàm số z = f (x, y) có các đạo hàm riêng đến cấp hai liên tục trong
một lân cận nào đó của M ta có 0(x0, y0). Giả sử tại M0 p = q = 0, khi đó
1. Nếu s2 − rt < 0 thì f (x, y) đạt cực trị tại M . Đó là cực tiểu nếu 0
r > 0, là cực đại nếu r < 0.
2. Nếu s2 − rt > 0 thì f (x, y) không đạt cực trị tại M .0
Chú ý: Nếu s2 − rt = 0 thì chưa kết luận được điều gì về điểm M , nó có thể là cực trị, 0
cũng có thể không. Trong trường hợp đó ta sẽ dùng định nghĩa để xét xem M có phải là 0
cực trị hay không bằng cách xét hiệu f (M) − f (M0), nếu nó xác định dấu trong một lân
cận nào đó của M thì nó là cực trị và ngược lại. 0
Ví dụ 3.1 (Cuối kì, K61 Viện ĐTQT). Tìm các cực trị của hàm số a) z = x2 − 2x + arctan(y2). b) z = y2 − 2y + arctan(x2).
Bài tập 3.17. Tìm cực trị của các hàm số sau 159 160
Chương 3. Hàm số nhiều biến số
a) z = x2 + xy + y2 + x − y + 1 c) z = 2x4 + y4 − x2 − 2y2 b) z = x + y − x.ey d) z = x2 + y2 − e−(x2+y2)    p = z′ x = Chứng minh. a) Xét hệ phương trình x = 2x + y + 1 = 0 −1 ⇔ . Vậy
q = z′y = x + 2y − 1 = 0 y = 1
ta có M (−1, 1) là điểm tới hạn duy nhất.
Ta có A = z′′xx(M) = 2; B = z′′xy(M) = 1; C = z′′yy(M) = 2 nên B2 − AC = 1 − 4 = −3 <
0. Vậy hàm số đạt cực trị tại M và do A > 0 nên M là điểm cực tiểu. b) Xét hệ phương trình    p = 1 − ey = 0 x = 1 ⇔ q = 1 − xey = 0 y = 0
Vậy hàm số có điểm tới hạn duy nhất M (1, 0). Ta có A = z′′xx(M) = 0; B = z′′xy(M) =
−1; C = z′′yy(M) = −1 nên B2 − AC = 1 > 0. Hàm số đã cho không có cực trị. c) Xét hệ phương trình    z′   x = 8x3 − 2x x 4x2 − 1 = 0 x = 0 ∨ x = 1 ⇔ ⇔ 2 ∨ x = − 12 z′y = 4y3 − 4y y y2 − 1 = 0
y = 0 ∨ y = 1 ∨ y = −1
Vậy các điểm tới hạn của hàm số là 1 1 M1 (0, 0) ; M2 (0, 1) ; M3 (0, −1) ; M4 , 0 ; M , 1 2 5 2 1 1 1 1 M6 , −1 ; M − , 0 ; M − , 1 ; M − , −1 2 7 2 8 2 9 2
Ta có z′′xx = 24x2 − 2; z′′xy = 0; z′′yy = 12y2 − 4. • Tại M là điểm cực đại
1(0, 0), A = −2; B = 0; C = −4; B2 − AC = −8 < 0 nên M1 với z = 0.
• Tại M2 (0, 1) ; M3 (0, −1) ; A = −2; B = 0; C = 8; B2 − AC = 16 > 0 nên M2, M3
không phải là điểm cực đại với z = 0. • Tại M 1 −1 4 , 0 ; M , 0 ; A = 4; B = 0; C = 2 7 2
−4; B2 − AC = 16 > 0 nên M4, M7
không phải là điểm cực đại với z = 0. • Tại M 1 1 5 , 1 ; M , ; M , 1 ; M , ; A = 4; B = 0; C = 8; B2 2 6 2 −1 8 −12 9 −12 −1 − AC = −32 < 0 nên M
là các điểm cực tiểu với giá trị tại đó là 5, M6, M8, M9 z = −9. 8     d) Xét hệ phương trình
p = z′x = 2x + e−(x2+y2).2x = 0 x = 0 ⇔
q = z′y = 2y + e−(x2+y2).2y = 0 y = 0 160
3. Cực trị của hàm số nhiều biến số 161
Vậy M(0, 0) là điểm tới hạn duy nhất. Xét
z′′xx = 2 + 2.e−(x2+y2) − 4x2.e−(x2+y2) z′′xy = −4xy.e−(x2+y2)
z′′yy = 2 + 2.e−(x2+y2) − 4y2.e−(x2+y2)
Tại M(0, 0) có A = 4; B = 0; C = 4; B2 − AC = −16 < 0; A > 0 nên tại M hàm số đạt cực tiểu.
3.2 Cực trị có điều kiện
Cho tập mở U ⊂ R2 và hàm số f : U → R. Xét bài toán tìm cực trị của hàm số f (x, y)
khi các biến x, y thoả mãn phương trình ϕ(x, y) = 0
Ta nói rằng tại điểm (x0, y0) ∈ U thoả mãn điều kiện ϕ(x0, y0) = 0 hàm f có cực đại tương
đối (tương ứng cực tiểu tương đối) nếu tồn tại một lân cận V ⊂ U sao cho f (x, y) ≤ f (x0, y0)
(tương ứng f (x, y) ≥ f (x0, y0)) với mọi (x, y) ∈ V thoả mãn điều kiện ϕ(x, y) = 0. Điểm
(x0, y0) được gọi là cực trị có điều kiện của hàm số f (x, y), còn điều kiện ϕ(x, y) = 0 được
gọi là điều kiện ràng buộc của bài toán. Nếu trong một lân cận của (x0, y0) từ hệ thức
ϕ(x, y) = 0 ta xác định được hàm số y = y(x) thì rõ ràng (x0, y(x0)) là cực trị địa phương
của hàm số một biến số g(x) = f (x, y(x)). Như vậy, trong trường hợp này bài toán tìm cực
trị ràng buộc được đưa về bài toán tìm cực trị tự do của hàm số một biến số. Ta xét bài toán sau đây
Bài tập 3.18. Tìm cực trị có điều kiện
a) z = 1 + 1 với điều kiện 1 + 1 = 1 x y x2 y2 a2
b) z = x.y với điều kiện x + y = 1 Chứng minh.
a) Đặt x = a ; y = a , ta có 1 + 1 = 1 . Khi đó sin t cos t x2 y2 a2 1 1 sin t cos t z = + = + . x y a a Ta có √ cos t sin t 2 π π 5π z′t = − = sin − t = 0 ⇔ t = ∨ t = a a a 4 4 4 √ Với √ √ t = π ta có x = 2a; y =
2a, hàm số đạt cực tiểu và z 2 . 4 CT = −a √ Với √ √ t = 5π ta có x = 2a; y =
2a, hàm số đạt cực đại và z 2 . 4 − − CĐ = a 161 162
Chương 3. Hàm số nhiều biến số
b) Từ điều kiện x + y = 1 ta suy ra y = 1 − x. Vậy z = xy = x(1 − x). Dễ dàng nhận
thấy hàm số x = x(1 − x) đạt cực đại tại x = 1 và z . 2 CĐ = 14
Tuy nhiên không phải lúc nào cũng tìm được hàm số y = y(x) từ điều kiện ϕ(x, y) = 0. Do
đó bài toán tìm cực trị điều kiện không phải lúc nào cũng đưa được về bài toán tìm cực trị
tự do. Trong trường hợp đó ta dùng phương pháp Lagrange được trình bày dưới đây.
Định lý 3.57 (Điều kiện cần để hàm số đạt cực trị điều kiện). Giả sử U là một tập
mở trong R2, f : U → R và (x0, y0) là điểm cực trị của hàm f với điều kiện ϕ(x, y) = 0.
Hơn nữa giả thiết rằng:
a. Các hàm f (x, y), ϕ(x, y) có các đạo hàm riêng liên tục trong một lân cận của (x0, y0). b. ∂ϕ(x ∂y 0, y0) 6= 0.
Khi đó tồn tại một số λ cùng với
tạo thành nghiệm của hệ phương trình sau (đối với 0 x0, y0 λ, x, y)    ∂φ ∂ f  = 0 
(x, y) + λ ∂ϕ (x, y) = 0    ∂x   ∂x ∂x ∂φ = 0 ⇔
∂ f (x, y) + λ∂ϕ(x, y) = 0 (3.3) ∂y ∂y ∂y     ∂φ   = 0   ϕ(x, y) = 0 ∂λ
với φ(x, y, λ) = f (x, y) + λϕ(x, y) được gọi là hàm Lagrange.
Định lý trên chính là điều kiện cần của cực trị có ràng buộc. Giải hệ phương trình 3.3 ta
sẽ thu được các điểm tới hạn. Giả sử M(x . Ta
0, y0) là một điểm tới hạn ứng với giá trị λ0 có
φ(x, y, λ0) − φ(x0, y0, λ0) = f (x, y) + λ0ϕ(x, y) − f (x0, y0) − λ0ϕ(x0, y0) = f (x, y) − f (x0, y0)
nên nếu M là một điểm cực trị của hàm số φ(x, y, λ0) thì M cũng là điểm cực trị của hàm
số f (x, y) với điều kiện ϕ(x, y) = 0. Muốn xét xem M có phải là điểm cực trị của hàm số
φ(x, y, λ0) hay không ta có thể quay lại sử dụng định lý 3.56 hoặc đi tính vi phân cấp hai ∂2φ ∂2φ ∂2φ
d2φ(x0, y0, λ0) = (x (x (x ∂x2
0, y0, λ0)dx2 + 2 ∂x∂y 0, y0, λ0)dxdy + ∂y2 0, y0, λ0)dy2
trong đó dx và dy liên hệ với nhau bởi hệ thức ∂ϕ ∂ϕ (x (x ∂x
0, y0)dx + ∂y 0, y0)dy = 0 hay ∂ϕ (x0, y0) dy = − ∂x dx ∂ϕ (x ∂y 0, y0) 162
3. Cực trị của hàm số nhiều biến số 163
Thay biểu thức này của dy vào d2φ(x0, y0, λ0) ta có
d2φ(x0, y0, λ0) = G(x0, y0, λ0)dx2 Từ đó suy ra
• Nếu G(x0, y0, λ0) > 0 thì (x0, y0) là điểm cực tiểu có điều kiện.
• Nếu G(x0, y0, λ0) < 0 thì (x0, y0) là điểm cực đại có điều kiện.
Bài tập 3.19. Tìm cực trị có điều kiện của hàm số z = 1 + 1 với điều kiện 1 + 1 = 1 x y x2 y2 a2
Chứng minh. Xét hàm số Lagrange φ(x, y, λ) = 1 + 1 + λ( 1 + 1 ). Từ hệ phương x y x2 y2 − 1 a2 trình  ∂φ   = − 1  ∂x x2 − 2λ x3  ∂φ = ∂y − 1y2 − 2λ y3    ∂φ  = 1 + 1 = 0 ∂λ x2 y2 − 1 a2
ta thu được các điểm tới hạn là √ √ √ √ M , 1(a
2, a 2) ứng với λ1 = − a √ M 2, −a 2) ứng 2 2(−a với λ . Ta có 2 = a √2 ∂2φ ∂2φ ∂2φ 2 6λ 2 6λ d2φ = dx2 + 2 dxdy + dy2 = + dx2 + + dy2 ∂x2 ∂x∂y ∂y2 x3 x4 y3 y4 Từ điều kiện 1 + 1
= 0 suy ra − 2 dx − 2 dy = 0 nên dy = − y3 dx, thay vào biểu thức x2 y2 − 1 a2 x3 y3 x3 d2φ ta có √ √ • Tại M , 2 2
là điểm cực đại có điều 1 d2φ(M1) = −
(dx2 + dy2) = −2 (dx2) < 0 nên M 4a3 4a3 1 kiện. √ √ • Tại M , 2 2
là điểm cực tiểu có điều 2 d2φ(M2) = (dx2 + dy2) = 2 (dx2) > 0 nên M 4a3 4a3 2 kiện.
3.3 Giá trị lớn nhất - Giá trị nhỏ nhất
Giả sử f : A → R là hàm số liên tục trên tập hợp đóng A của R2. Khi đó, f đạt giá trị
lớn nhất và giá trị nhỏ nhất trên A. Để tìm các giá trị này ta hãy tìm giá trị của hàm số
tại tất cả các điểm dừng trong miền A cũng như tại các điểm đạo hàm riêng không tồn tại,
sau đó so sánh các giá trị này với các giá trị của hàm trên biên ∂A của A (tức là ta phải
xét cực trị có điều kiện).
Bài tập 3.20. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số: 163 164
Chương 3. Hàm số nhiều biến số
a) z = x2y(4 − x − y) trong hình tam giác giới hạn bởi các đường x = 0, y = 0, x + y = 6.
b) z = sin x + sin y + sin(x + y) trong hình chữ nhật giới hạn bởi các đường x = 0, x =
π , y = 0, y = π . 2 2 164
Document Outline

Mục lục
Hàm số một biến số (13LT+13BT)
- Sơ lược về các yếu tố Lôgic; các tập số: N,Z,Q,R
- Trị tuyệt đối và tính chất
- Hàm số
  - Định nghĩa hàm số
  - Hàm số đơn điệu
  - Hàm số bị chặn
  - Hàm số chẵn, hàm số lẻ
  - Hàm số tuần hoàn
  - Hàm hợp
  - Hàm ngược
  - Hàm số sơ cấp
  - Bài tập
- Dãy số
  - Dãy số và giới hạn của dãy số
  - Các tiêu chuẩn tồn tại giới hạn
  - Bài tập
- Giới hạn hàm số
  - Định nghĩa
  - Các phép toán trên giới hạn
  - Giới hạn của hàm hợp
  - Giới hạn vô cùng
  - Các tiêu chuẩn tồn tại giới hạn
  - Mối liên hệ giữa giới hạn của dãy số và giới hạn của hàm số
  - Bài tập
- Vô cùng lớn, vô cùng bé
  - Vô cùng bé (VCB)
  - Vô cùng lớn (VCL)
  - Bài tập
- Hàm số liên tục
  - Định nghĩa
  - Các phép toán số học đối với hàm số liên tục
  - Sự liên tục của hàm ngược
  - Sự liên tục của hàm hợp
  - Các định lý về hàm liên tục
  - Điểm gián đoạn và phân loại điểm gián đoạn của hàm số
  - Bài tập
- Đạo hàm và vi phân
  - Định nghĩa
  - Các phép toán trên đạo hàm
  - Đạo hàm của hàm hợp
  - Đạo hàm của hàm ngược
  - Đạo hàm của các hàm số sơ cấp cơ bản
  - Vi phân của hàm số
  - Đạo hàm cấp cao
  - Vi phân cấp cao
  - Bài tập
  - Đọc thêm: Về khái niệm vi phân
- Các định lý về hàm khả vi và ứng dụng
  - Các định lý về hàm khả vi
  - Các công thức khai triển Taylor, Maclaurin
  - Quy tắc L'Hospital
  - Về một số dạng vô định
  - Thay tương đương khi có hiệu hai VCB?
  - Hiệu hai VCB tương đương
  - Ba phương pháp (mới) để tính giới hạn
  - Về các VCL tiêu biểu
  - Bài tập ôn tập
- Các lược đồ khảo sát hàm số
  - Khảo sát và vẽ đồ thị của hàm số y=f(x)
  - Khảo sát và vẽ đường cong cho dưới dạng tham số
  - Khảo sát và vẽ đường cong trong hệ toạ độ cực
  - Bài tập
Phép tính tích phân một biến số
- Tích phân bất định
  - Nguyên hàm của hàm số
  - Các phương pháp tính tích phân bất định
  - Tích phân hàm phân thức hữu tỷ
  - Tích phân hàm lượng giác
  - Tích phân các biểu thức vô tỷ
- Tích phân xác định
  - Định nghĩa tích phân xác định
  - Các tiêu chuẩn khả tích
  - Các tính chất của tích phân xác định
  - Tích phân với cận trên thay đổi (hàm tích phân)
  - Các phương pháp tính tích phân xác định
  - Hệ thống bài tập
- Tích phân suy rộng
  - Tích phân suy rộng với cận vô hạn
  - Tích phân suy rộng của hàm số không bị chặn
  - Các tiêu chuẩn hội tụ
  - Tích phân suy rộng hội tụ tuyệt đối và bán hội tụ
  - Bài tập
- Các ứng dụng của tích phân xác định
  - Tính diện tích hình phằng
  - Tính độ dài đường cong phẳng
  - Tính thể tích vật thể
  - Tính diện tích mặt tròn xoay
Hàm số nhiều biến số
- Giới hạn của hàm số nhiều biến số
  - Giới hạn của hàm số nhiều biến số
  - Tính liên tục của hàm số nhiều biến số
  - Bài tập
- Đạo hàm và vi phân
  - Đạo hàm riêng
  - Vi phân toàn phần
  - Đạo hàm của hàm số hợp
  - Đạo hàm và vi phân cấp cao
  - Đạo hàm theo hướng - Gradient
  - Hàm ẩn - Đạo hàm của hàm số ẩn
  - Bài tập
- Cực trị của hàm số nhiều biến số
  - Cực trị tự do
  - Cực trị có điều kiện
  - Giá trị lớn nhất - Giá trị nhỏ nhất