
Preview text:
Chương 1. HÀM SỐ VÀ ĐỒ THỊ Nguyễn Lê Thi
Trường Đại học Sư phạm Kỹ thuật TP.HCM September 7, 2025
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . 1 Giải tích là gì? 2 Mô hình hóa toán học 3
Một số kiến thức cơ bản 4
Đường thẳng trong mặt phẳng 5 Hàm số và đồ thị 6
Hàm ngược và hàm lượng giác ngược . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 2 / 68 Giải tích là gì? 1. Giải tích là gì?
Giải tích về cơ bản khác với toán học mà bạn đã từng học trước
đây: giải tích ít tĩnh hơn và mang tính động hơn.
Giải tích liên quan đến sự thay đổi và chuyển động; nó nghiên
cứu các đại lượng tiến gần đến những đại lượng khác. Vì lý do
đó, sẽ hữu ích nếu có một cái nhìn tổng quan về môn học trước
khi bắt đầu nghiên cứu chuyên sâu.
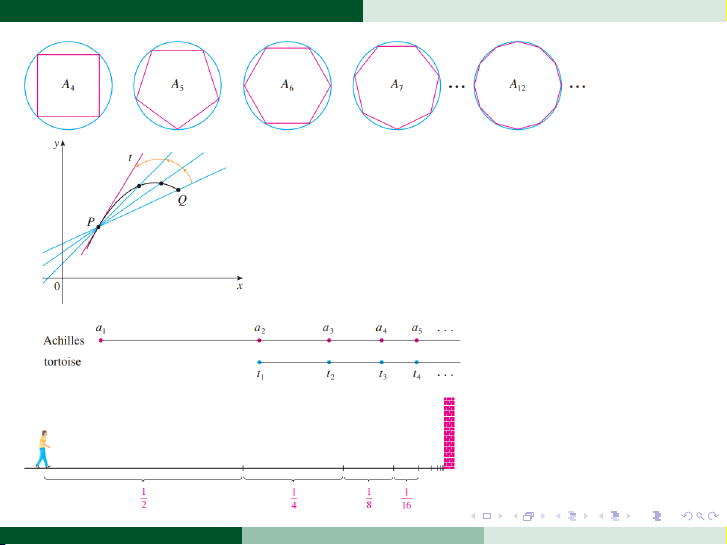
Ở đây, hãy có cái nhìn thoáng qua về một số ý tưởng chính của
giải tích bằng cách chỉ ra cách khái niệm giới hạn xuất hiện khi
chúng ta cố gắng giải quyết nhiều dạng bài toán khác nhau. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 3 / 68 Giải tích là gì? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 4 / 68 Giải tích là gì? 1. Giải tích là gì?
Đột phá trong sự phát triển hai khái niệm trong giải tích là
”Đạo hàm” và ”Tích phân” chính là sự hình thành của một
công cụ toán học mang tên ”giới hạn”.
Giới hạn: là một công cụ toán học nghiên cứu xu hướng của
một hàm số khi biến của nó tiến tới một giá trị nào đó.
Đạo hàm: được định nghĩa như một dạng giới hạn, và đầu tiên,
nó được sử dụng để tính tốc độ thay đổi và hệ số góc của tiếp
tuyến với một đường cong.
Tích phân: được hình thành từ việc lấy giới hạn đặc biệt của một tổng các số hạng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 5 / 68 Mô hình hóa toán học 2. Mô hình hóa toán học
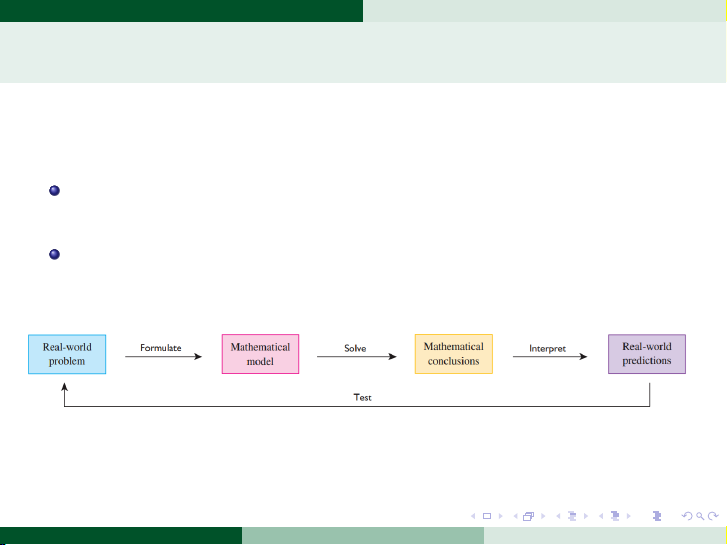
Mô hình toán học của một tình huống thực tế là một hệ thống
các công thức và ngôn ngữ toán học để mô tả tình huống đó.
Quá trình xây dựng mô hình toán học được gọi là mô hình hóa
toán học. Dưới dây là sơ đồ mô tả quá trình xây dựng mô hình toán học. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 6 / 68 Mô hình hóa toán học Mô hình tuyến tính
Khi chúng ta nói rằng y là một hàm số tuyến tính của x, hoặc các
đại lượng x, y có liên quan tuyến tính với nhau, điều đó có nghĩa là đồ
thị của hàm số là một đường thẳng.
Do đó chúng ta có thể sử dụng dạng phương trình đường thẳng theo
hệ số góc và tung độ gốc để viết công thức của hàm số tuyến tính như sau
y = f(x) = mx + b
trong đó m là hệ số góc của đường thẳng và b là tung độ gốc. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 7 / 68 Mô hình hóa toán học Mô hình tuyến tính A
Khi không khí khô di chuyển lên cao, nó giãn nở và lạnh đi. Nếu
nhiệt độ trên mặt đất là 20◦C và nhiệt độ ở độ cao 1 km là
10◦C, hãy biểu diễn nhiệt độ T (tính theo ◦C) như một hàm của
độ cao h (tính bằng km), giả sử mô hình tuyến tính là phù hợp. B
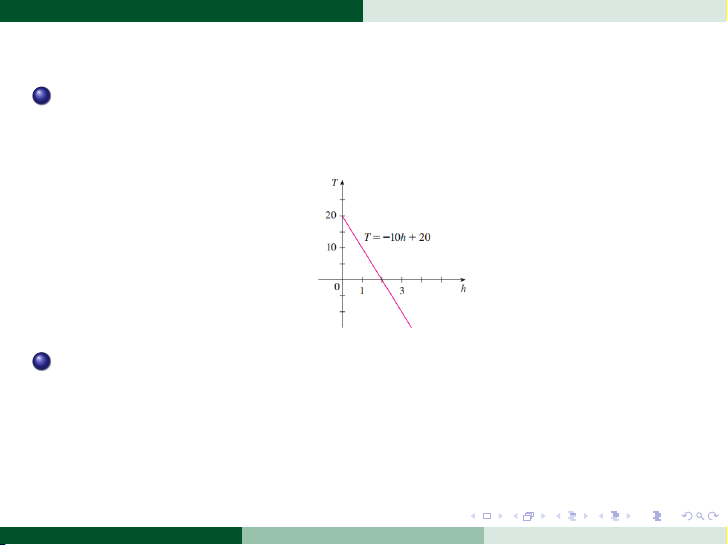
Vẽ đồ thị của hàm số ở câu (A). Hệ số góc (slope) biểu diễn điều gì? C
Nhiệt độ ở độ cao 2.5 km là bao nhiêu? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 8 / 68 Mô hình hóa toán học Mô hình tuyến tính Hướng dẫn giải A
Vì chúng ta giả sử rằng T là một hàm tuyến tính của h, ta có thể viết
T = mh + b
Biết rằng T = 20 khi h = 0, nên
20 = m · 0 + b = b
Nói cách khác, tung độ gốc là b = 20.
Ta cũng được cho rằng T = 10 khi h = 1, nên 10 = m · 1 + 20
m = 10 − 20 = −10
Do đó, hàm tuyến tính cần tìm là
T = −10h + 20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 9 / 68 Mô hình hóa toán học B
Đồ thị được phác họa như hình sau. Hệ số góc là
m = −10◦C/km, và điều này biểu diễn tốc độ thay đổi của nhiệt độ theo độ cao. B
Ở độ cao h = 2.5 km, nhiệt độ là
T = −10(2.5) + 20 = −5◦C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 10 / 68 Mô hình hóa toán học Bài tập vận dụng
Bài tập 1. Một hãng taxi tính giá cước như sau: giá cước cố định là
15.000 đồng, và sau đó tính thêm 12.000 đồng/km. A
Viết hàm số C(d) (đồng) biểu diễn chi phí di chuyển theo quãng đường d (km). B
Tính chi phí khi đi được 5 km. C
Nếu khách chỉ có 75.000 đồng, họ có thể đi tối đa bao nhiêu km?
Bài tập 2. Một cốc nước nóng có nhiệt độ ban đầu 90◦C. Sau khi để
trong phòng, nhiệt độ giảm dần. Sau 10 phút, nhiệt độ còn 70◦C.
Giả sử mô hình tuyến tính là phù hợp. A
Viết hàm số T(t) (tính theo ◦C) biểu diễn nhiệt độ của nước
theo thời gian t (phút). B
Dự đoán nhiệt độ nước sau 20 phút. C . . . . . . . . . . . . . . . . . . . .
Sau bao lâu thì nhiệt độ nước còn 40◦C? . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 11 / 68 Mô hình hóa toán học Hướng dẫn giải Bài 1. A
Vì chi phí cố định là 15.000 và thêm 12.000 cho mỗi km, ta có:
C(d) = 12000d + 15000. B Với d = 5:
C(5) = 12000 · 5 + 15000 = 60000 + 15000 = 75000 (đồng). C
Giải phương trình C(d) = 75000: 12000d + 15000 = 75000 12000d = 60000 ⇒ d = 5.
Vậy khách có thể đi tối đa 5 km. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 12 / 68 Mô hình hóa toán học Hướng dẫn giải Bài 2. A
Giả sử T(t) = mt + b. Biết T(0) = 90 ⇒ b = 90.
Biết T(10) = 70, ta có: 70 − 90 70 = m · 10 + 90 ⇒ m = = −2. 10 Vậy phương trình là:
T(t) = −2t + 90. B Với t = 20:
T(20) = −2 · 20 + 90 = −40 + 90 = 50◦C. C
Giải phương trình T(t) = 40: −2t + 90 = 40
−2t = −50 ⇒ t = 25. . . . . . . . . . . . . . . . . . . . .
Vậy sau 25 phút, nhiệt độ còn 40◦C. . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 13 / 68
Một số kiến thức cơ bản
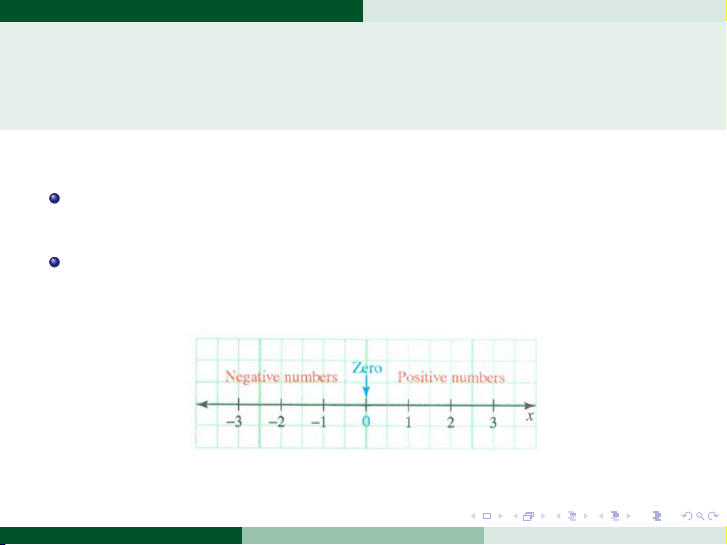
3. Một số kiến thức cơ bản 3.1 Đường thẳng thực
Tập hợp số thực có nhiều tập con như tập số tự nhiên, tập số
nguyên, tập số hữu tỉ, tập số vô tỉ.
Tập hợp số thực được biểu diễn bằng hệ tọa độ một chiều, hay
còn gọi là đường thẳng thực. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 14 / 68
Một số kiến thức cơ bản Các ký hiệu về khoảng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 15 / 68
Một số kiến thức cơ bản
Các tính chất thứ tự của số thực
Với mọi số thực a, b, c, d, ta có:
Định luật ba khả năng (Trichotomy law): Chính xác một trong ba mệnh đề sau là đúng: a < b, a > b, hoặc a = b
Định luật bắc cầu của bất đẳng thức (Transitive law of inequality):
Nếu a < b và b < c, thì a < c.
Định luật cộng của bất đẳng thức (Additive law of inequality):
Nếu a < c và b < d, thì
a + b < c + d
Định luật nhân của bất đẳng thức (Multiplicative law of inequality): Nếu a < b, thì
ac < bc nếu c > 0, và
ac > bc nếu c < 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 16 / 68
Một số kiến thức cơ bản 3.2 Giá trị tuyệt đối 3.2.1 Định nghĩa Definition
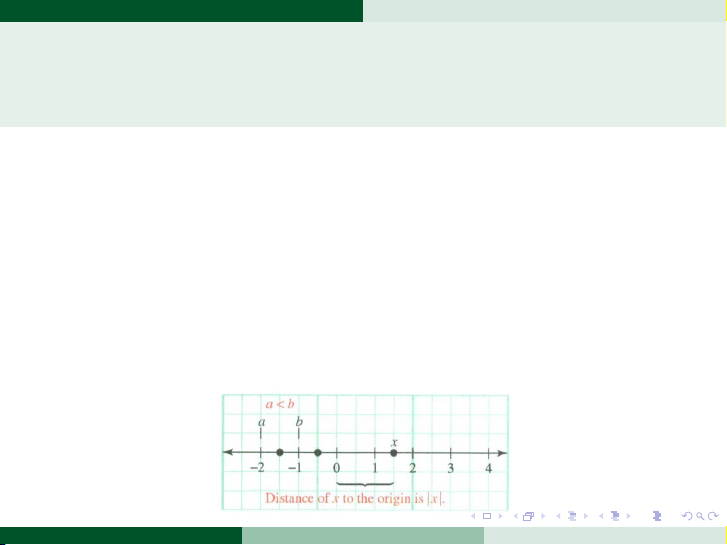
Khoảng cách từ một số thực a bất kỳ đến gốc tọa độ (số 0) là giá trị
tuyệt đối của số đó. Ký hiệu: |a|.
Ví dụ: |7| = 7, | − 9| = 9
Giá trị tuyệt đối của số thực x được xác định bởi x | , x ≥ 0
x| = −x, x < 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 17 / 68
Một số kiến thức cơ bản
3.2.2 Các tính chất của giá trị tuyệt đối
Cho a, b là các số thực: 1 |a| ≥ 0 2 |a| = | − a| 3 |a|2 = a2 4 |ab| = |a||b| a |a| 5 b = |b|, b 6= 0 6 −|a| ≤ a ≤ |a| 7
|a| = b ⇔ a = ±b, b ≥ 0 8
|a| < b ⇔ −b < a < b, b > 0 9
|a| > b ⇔ a > b ∨ a < −b 10
|a + b| ≤ |a| + |b| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 18 / 68
Một số kiến thức cơ bản
3.2.3 Phương trình và bất phương trình chứa giá trị tuyệt đối
Giải các phương trình và bất phương trình sau 1
|x2 − 1| = 8 2
|3x + 5| = x − 1 3
|2x − 1| < 3 4
|x2 − 2| > 14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 19 / 68
Một số kiến thức cơ bản
Giá trị tuyệt đối như một chặn
Giả sử bạn mua một bao xi măng 50 kg. Nó sẽ không cân nặng đúng
50 kg vì việc đo đạc chỉ là xấp xỉ. Một số bao sẽ nặng hơn nhiều
nhất là 0,2 kg so với 50 và một số bao sẽ nhẹ hơn nhiều nhất là 0,2
kg so với 50 kg. Nếu như vậy thì một bao sẽ nặng nhất là 49,8 kg và
nhẹ nhất là 50,2 kg. Hãy phát biểu điều này bằng một bất đẳng thức giá trị tuyệt đối. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nguyễn Lê Thi (Trường Đại học Sư phạm Kỹ thuật TP.HCM)
Chương 1. HÀM SỐ VÀ ĐỒ THỊ September 7, 2025 20 / 68