Chương 1: Mở đầu | Bài giảng môn Phân tích bằng công cụ | Đại học Bách khoa hà nội

CH3320
PHÂN TÍCH BẰNG CÔNG CỤ
Phần 1. Các phương pháp phân tích quang học ..................................................................................... 2
Chương 1. Mở đầu .................................................................................................................................. 2
1.1. Mở đầu ......................................................................................................................................... 2
1.2. Tính chất cơ bản của bức xạ điện từ ............................................................................................ 2
1.2.1. Tính chất sóng của bức xạ điện từ ........................................................................................ 3
1.2.2. Tính chất hạt của bức xạ điện từ .......................................................................................... 5
1.3. Phổ bức xạ điện từ ....................................................................................................................... 5
Chương 2. Phương pháp quang phổ hấp thụ nguyên tử ........................................................................ 6
2.1. Sự hình thành phổ phân tử .......................................................................................................... 6
2.1.1. Sự hấp thụ bức xạ điện từ và sự hình thành các loại phổ hấp thụ phân tử ........................ 6
2.1.2. Phổ hấp thụ ........................................................................................................................... 8
2.2. Định luật cơ bản về hấp thụ bức xạ điện từ ................................................................................ 9
2.2.1. Định luật Lambert-Beer ......................................................................................................... 9
2.2.2. Tính chất cộng tính của độ hấp thụ quang ......................................................................... 11
2.2.3. Các yếu tố làm sai lệch định luật Lambert-Beer ................................................................. 12
2.2.4. Độ chính xác của phép đo độ hấp thụ và phép đo nồng độ ............................................... 13
2.2.5. Điều kiện để tiến hành phân tích đo quang UV-VIS ............................................................ 14
2.3. Các thủ tục thực nghiệm trong phân tích đo quang .................................................................. 15
2.3.1. Phương pháp đường chuẩn ................................................................................................ 15
2.3.2. Phương pháp tính ............................................................................................................... 15
2.3.3. Phương pháp thêm tiêu chuẩn ........................................................................................... 16
2.4. Phương pháp đo quang vi sai .................................................................................................... 16
2.5. Thiết bị quang phổ hấp thụ phân tử .......................................................................................... 18
2.5.1. Sơ đồ thiết bị ....................................................................................................................... 18
2.5.2. Nguồn sáng ......................................................................................................................... 18
2.5.3. Bộ tán sắc: ........................................................................................................................... 19
2.5.4. Cuvet đựng mẫu .................................................................................................................. 22
2.5.5. Detector .............................................................................................................................. 22
2.6. Một số ứng dụng phương pháp đo quang ................................................................................. 23
2.6.1. Phân tích các chất trong hỗn hợp ....................................................................................... 23
2.6.2. Xác định thành phần phức chất trong dung dịch bằng phương pháp dãy đồng phân tử
gam (phương pháp biến thiên liên tục_Continuous Variation) .................................................... 25 1
2.6.3. Xác định thành phần phức chất trong dung dịch bằng phương pháp đường cong bão hòa
(mole-ratio method) ..................................................................................................................... 27
Phần 1. Các phương pháp phân tích quang học
Chương 1. Mở đầu 1.1. Mở đầu
Trước kia, thuật ngữ “quang phổ” đề cập tới một nhánh của khoa học ở đó ánh sáng (đó
là các bức xạ nhìn thấy) được phân giải thành các bước sóng của nó để tạo thành phổ,
được biểu diễn dưới dạng hàm của cường độ bức xạ và bước sóng hoặc tần số. Ngày nay,
ý nghĩa của quang phổ được mở rộng bao gồm việc nghiên cứu không chỉ ở trong vùng
trông thấy mà còn các loại phổ điện từ khác, chẳng hạn như phổ tia X, phổ tử ngoại, hồng
ngoại, sóng viba và radio. Thực tế, việc sử dụng hiện nay mở rộng ý nghĩa của quang phổ
ra hơn cả việc bao gồm các kỹ thuật mà không bao gồm bức xạ điện từ, ví dụ như phổ âm
thanh, phổ khối và phổ điện tử.
Quang phổ đóng một vai trò quan trọng trong sự phát triển lý thuyết nguyên tử hiện đại.
Ngoài ra, các phương pháp phổ hóa cung cấp công cụ sử dụng rộng rãi cho việc dự đoán
cấu trúc của các phần tử phân tử cũng như việc xác định định tính và định lượng các hợp chất vô cơ và hữu cơ.
Chương mở đầu này giới thiệu các tính chất của bức xạ điện từ và sự tương tác đa dạng trong vấn đề này
1.2. Tính chất cơ bản của bức xạ điện từ
Bức xạ điện từ là một dạng năng lượng tồn tại ở rất nhiều dạng hình thức, dạng có thể dễ
dàng nhận ra là ánh sáng vùng trông thấy và bức xạ nhiệt. Biểu hiện ít rõ ràng hơn bao
gồm tia gamma, tia X, tử ngoại, viba, và bức xạ tần số radio. Nhiều tính chất của bức xạ
điện từ là thuận tiện được mô tả bởi mô hình cổ điển dạng sóng hình sin, cái mà được sử
dụng các tham số như bước sóng, tần số, vận tốc và biện độ. Ngược với hiện tượng sóng,
chẳng hạn âm thanh, bức xạ điện từ không đòi hỏi môi trường khi truyền và nó có thể dễ
dàng truyền qua môi trường chân không. 2
Mô hình sóng bị lỗi khi tính tới hiện tượng hấp thụ và phát xạ bức xạ điện từ. Để hiểu các
quá trình này, cần thiết sử dụng mô hình hạt, trong đó bức xạ điện từ được xem như là
một dòng của các hạt rời rạc hay các gói sóng của năng lượng được gọi là photon với
năng lượng của một photon tỉ lệ với tần số của bức xạ. Mô hình kép bức xạ vừa có tính
chất sóng vừa có tính chất hạt không loại trừ lần nhau mà còn bổ sung cho nhau. Thực
tế, mô hình kép được tìm thấy để ứng dụng cho tính chất của các dòng điện tử và các hạt
thứ cấp chẳng hạn như proton và mô hình kép là hoàn toàn hợp lý với cơ chế sóng.
1.2.1. Tính chất sóng của bức xạ điện từ
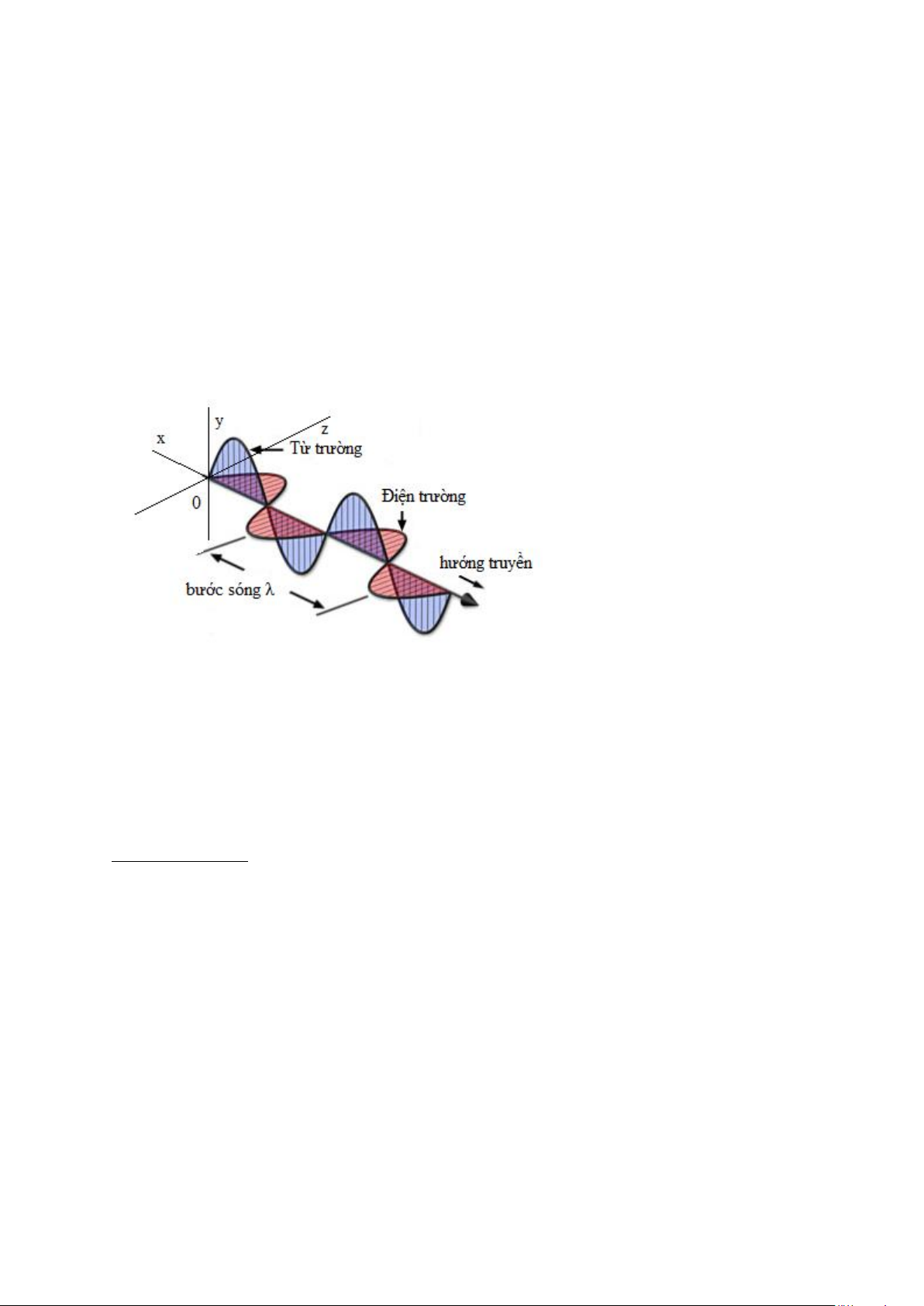
Hình 1-1: Thành phần điện trường và từ trường
Theo mô hình sóng, bức xạ điện từ là những dao động có hai thành phần điện trường và
từ trường làm truyền theo một phương. Các thành phần điện trường và từ trường vuông
góc với nhau và được biểu diễn bằng các sóng phân cực phẳng (hình 1-1). Các tham số sóng:
Cường độ A của sóng hình sin được chỉ trên hình vẽ (1-1) và biểu diễn là độ dài của
vectơ ở cực đại của sóng.
Tần số ν là số dao động mà bức xạ điện từ thực hiện trong một giây.
Bước sóng λ là quãng đường giữa hai điểm cân bằng bất kỳ mà bức xạ điện từ đi qua
(khoảng cách giữa hai cực đại hay cực tiểu).
Vận tốc truyền bức xạ điện từ vi (m/s) là tích số giữa tần số ν và bước sóng λ (tính bằng m): 3 vi = ν λ (1-1)
Vận tốc của bức xạ điện từ phụ thuộc vào thành phần của môi trường mà bức xạ điện từ
đi qua. Chỉ số dưới diễn tả môi trường mà nó truyền qua.
Trong môi trường chân không, vận tốc của bức xạ điện từ trở nên không phụ thuộc vào
bước sóng và nó đạt cực đại. Vận tốc này được ký hiệu là c, và được xác định bằng
2,99792.10-8 m/s. Điều đáng chú ý là vận tốc của bức xạ điện từ trong không khí chỉ
khác rất ít (khoảng 0,03% nhỏ hơn) vận tốc ánh sáng trong chân không. Trong các
trường hợp này phương trình (1-1) có thể viết dưới dạng:
c = ν λ = 3.00.108 m/s = 3,00.1010 cm/s (1-2)
Trong các môi trường khác, vận tốc của bức xạ điện từ bị chậm lại do sự tương tác giữa
trường điện từ của bức xạ và các electron xung quanh các nguyên tử hay phân tử có mặt
trong môi trường. Do tần số của bức xạ là bất biến và cố định bởi nguồn, bước sóng sẽ
phải giảm khi bức xạ từ môi trường chân không sang môi trường khác. Hiệu ứng này
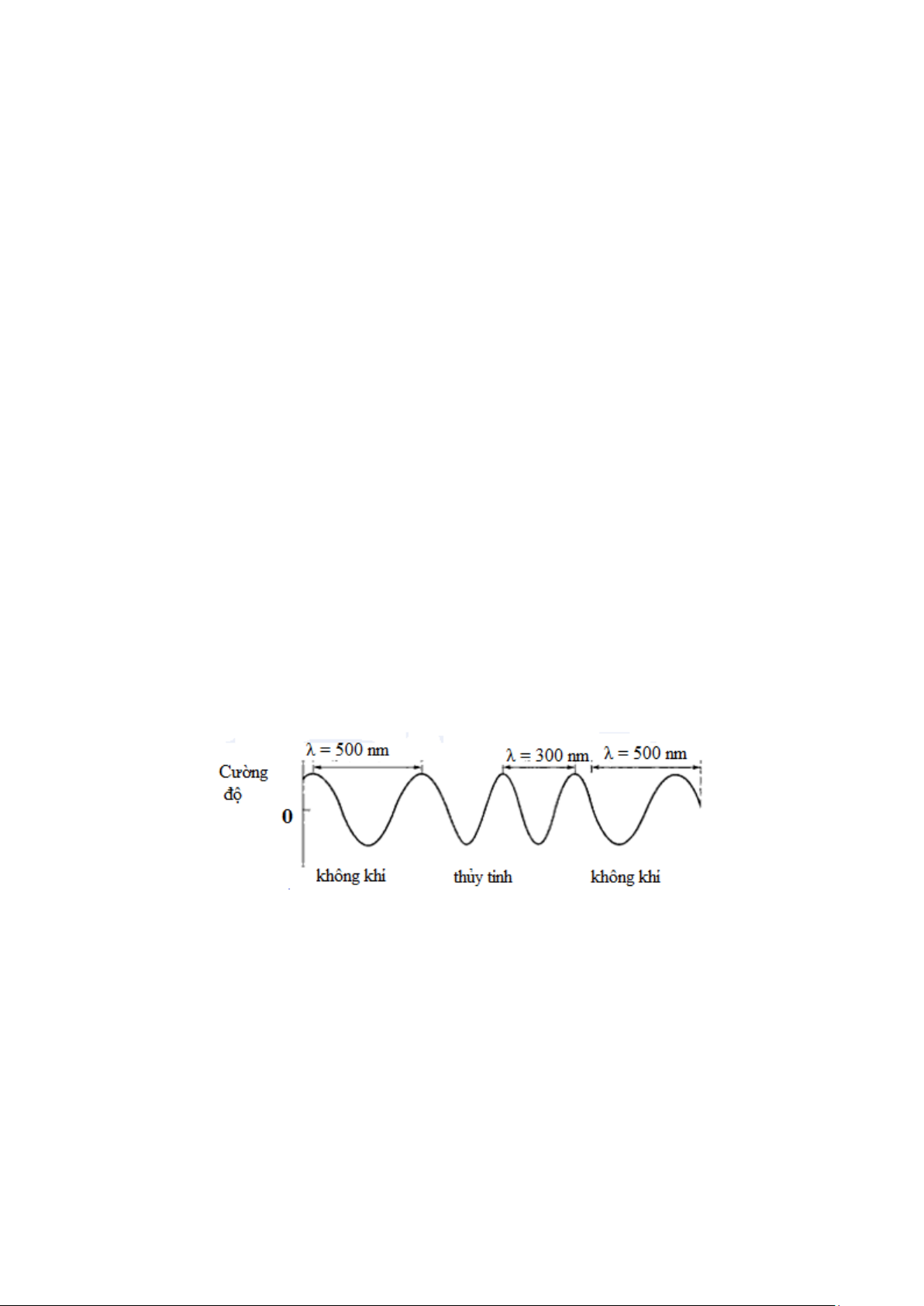
được minh họa ở hình 1-2 cho tia bức xạ ở vùng trông thấy. Chú ý là bước sóng bị ngắn
lại gần 200 nm (hơn 30%) khi đi qua thủy tinh và ngược lại nó lại dài ra khi bức xạ đi tới môi trường không khí.
Hình 1.2. Sự thay đổi bước sóng khi bxđt truyền từ không khí qua thủy tính và truyền trở lại không khí
Số sóng, , được định nghĩa là nghịch đảo của bước sóng (tính bằng đơn vị cm) là một
cách khác để mô tả bức xạ điện từ. Đơn vị của số sóng là cm-1.
Số sóng được sử dụng rộng rãi trong phổ hồng ngoại. Số sóng là một đơn vị thuận tiện,
vì ngược với bước sóng, nó tỉ lệ thuận với tần số (do vậy tỉ lệ với năng lượng) của bức
xạ. Như vậy, ta có thể viết: 4 = k ν (1-3)
ở đây, k là hệ số tỉ lệ, phụ thuộc vào môi trường và về giá trị là nghịch đảo của vận tốc.
Ví dụ: Tính số sóng của tia bức xạ hồng ngoại với bước sóng là 5,00 μm. = = 2000 cm-1
1.2.2. Tính chất hạt của bức xạ điện từ
Năng lượng của photon phụ thuộc vào tần số của bức xạ và được đưa ra dưới dạng: E = hν (1-4)
ở đây h là hằng số Planck (h = 6,63.10-34J.s).
Có thể biểu diễn năng lượng của photon dưới dạng bước sóng và số sóng:
E = = hc (1-5)
Chú ý là số sóng giống như tần số, tỉ lệ thuận với năng lượng.
Ví dụ: Tính năng lượng photon (J) của bức xạ điện từ nếu biết = 2000 cm-1
Áp dụng phương trình (1-5):
E = hc = 6,63.10-34 (J.s) × 3,00.1010 × 2000 cm-1 = 3,98.10-20 (J)
1.3. Phổ bức xạ điện từ
Phổ bức xạ điện từ là quen thuộc với bạn hơn bạn nghĩ. Lò vi sóng, bạn sử dụng để làm
nóng thực phẩm của bạn và điện thoại di động mà bạn sử dụng là một phần của phổ bức
xạ điện từ. Ánh sáng mà đôi mắt của bạn có thể nhìn thấy cũng là một phần của quang
phổ điện từ. Một phần có thể nhìn thấy được của phổ bức xạ điện từ bao gồm các màu
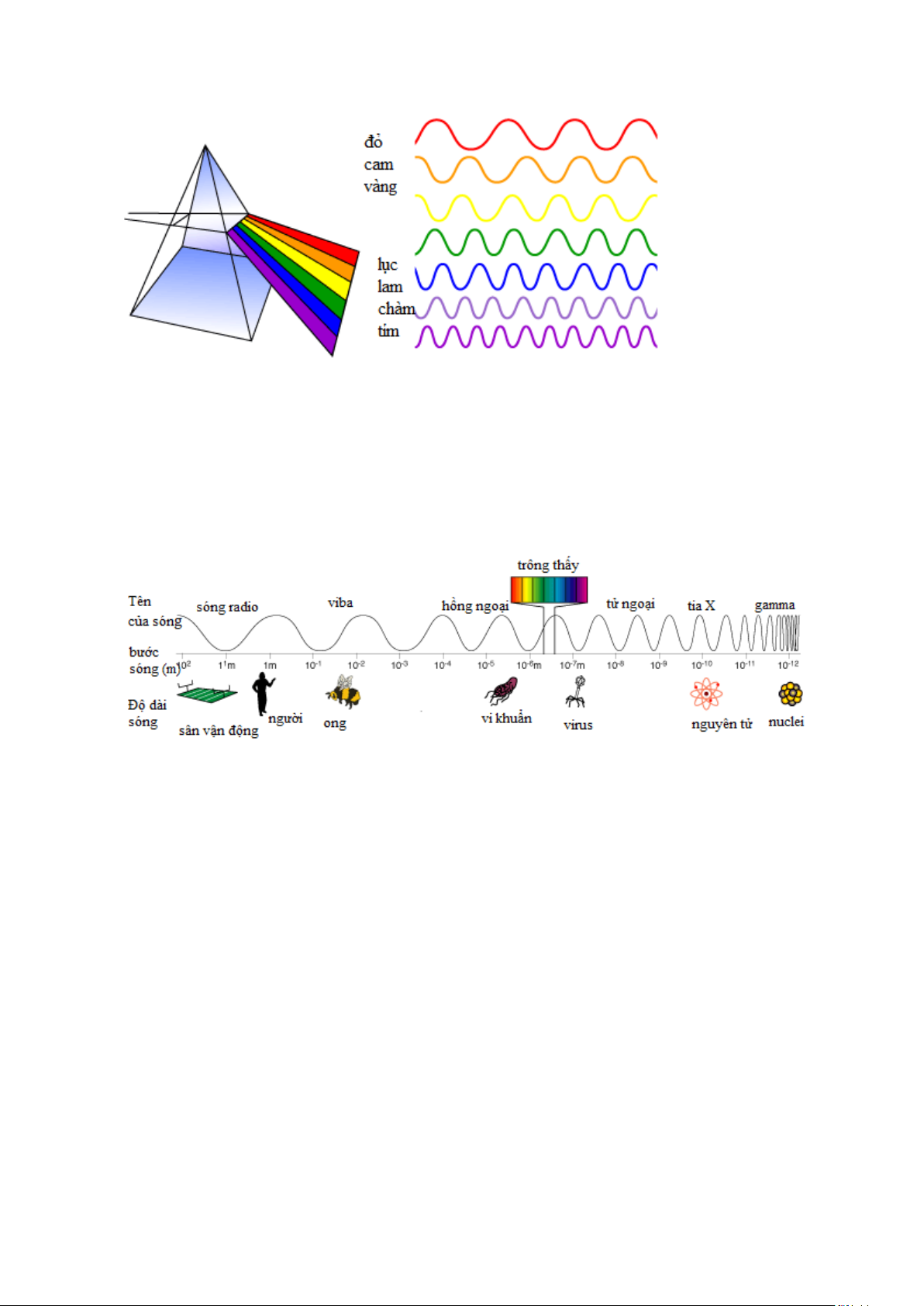
sắc mà chúng ta thấy trong cầu vồng - từ màu đỏ và cam, đến lam, chàm và tím (hình 1- 3). 5
Hình 1-3. Mỗi một màu sắc tương ứng với một bước sóng ánh sáng khác nhau
Các sóng của phổ bức xạ điện từ thay đổi độ dài trong một phạm vi vô cùng rộng, từ
bước sóng dài như kích thước của tòa nhà là sóng radio, đến vô cùng ngắn như hạt nhân
của một nguyên tử là tia γ (hình 1-4).
Hình 1-4.Thang đo bước xạ điện từ
Chương 2. Phương pháp quang phổ hấp thụ nguyên tử
2.1. Sự hình thành phổ phân tử
2.1.1. Sự hấp thụ bức xạ điện từ và sự hình thành các loại phổ hấp thụ phân tử
Một trong những khái niệm quan trọng từ cơ học lượng tử cần thiết cho sự hiểu biết về
sự hấp phụ hay phát xạ phân tử là năng lượng phải được lượng tử hóa. Nói cách khác,
các phân tử có thể tồn tại ở các trạng thái lượng tử cụ thể và mỗi trạng thái lượng tử
được gán một năng lượng. Năng lượng phân tử được lưu giữ có thể coi là tống năng
lượng lưu trữ của ba dạng: quay, dao động và điện tử.
Trong điều kiện bình thường, các phân tử tồn tại ở trạng thái năng lượng thấp nhất
(năng lượng cơ bản). Khi phân tử nhận năng lượng, ví dụ khi phân tử hấp thụ bức xạ 6
điện từ, phân tử có thể chuyển sang mức năng lượng cao hơn ứng với trạng thái kích
thích của phân tử. Phân tử chỉ tồn tại ở trạng thái kích thích trong khoảng thời gian rất
ngắn (10-6-10-9s) và quay trở lại trạng thái cơ bản.
Quá trình phát xạ là quá trình một phân tử chuyển trạng thái lượng tử cao hơn sang
thấp hơn và thoát ra một photon. Quá trình hấp thụ là một quá trình một phân tử
chuyển từ trạng thái lượng tử thấp hơn sang cao hơn và hấp thụ một photon.
Sự thay đổi trạng thái lượng tử của phân tử sẽ dẫn đến sự biến thiên năng lượng ΔE của
phân từ tuân theo định luật Planck. ΔE = Ecao – E thấp = hν (2-1)
Do năng lượng phân tử được lưu giữ dưới ba dạng: quay, dao động và điện tử nên:
ΔE = ΔEquay + ΔEdao động+ ΔEđiện tử (2-2)
Như vậy, do hiện tượng hấp phụ bức xạ điện từ của phân tử gây nên các bước chuyển
năng lượng quay, dao động và điện tử của phân tử và là nguồn gốc của các loại phổ hấp
thụ phân tử mà chúng ta sẽ nghiên cứu ở các chương tiếp theo.
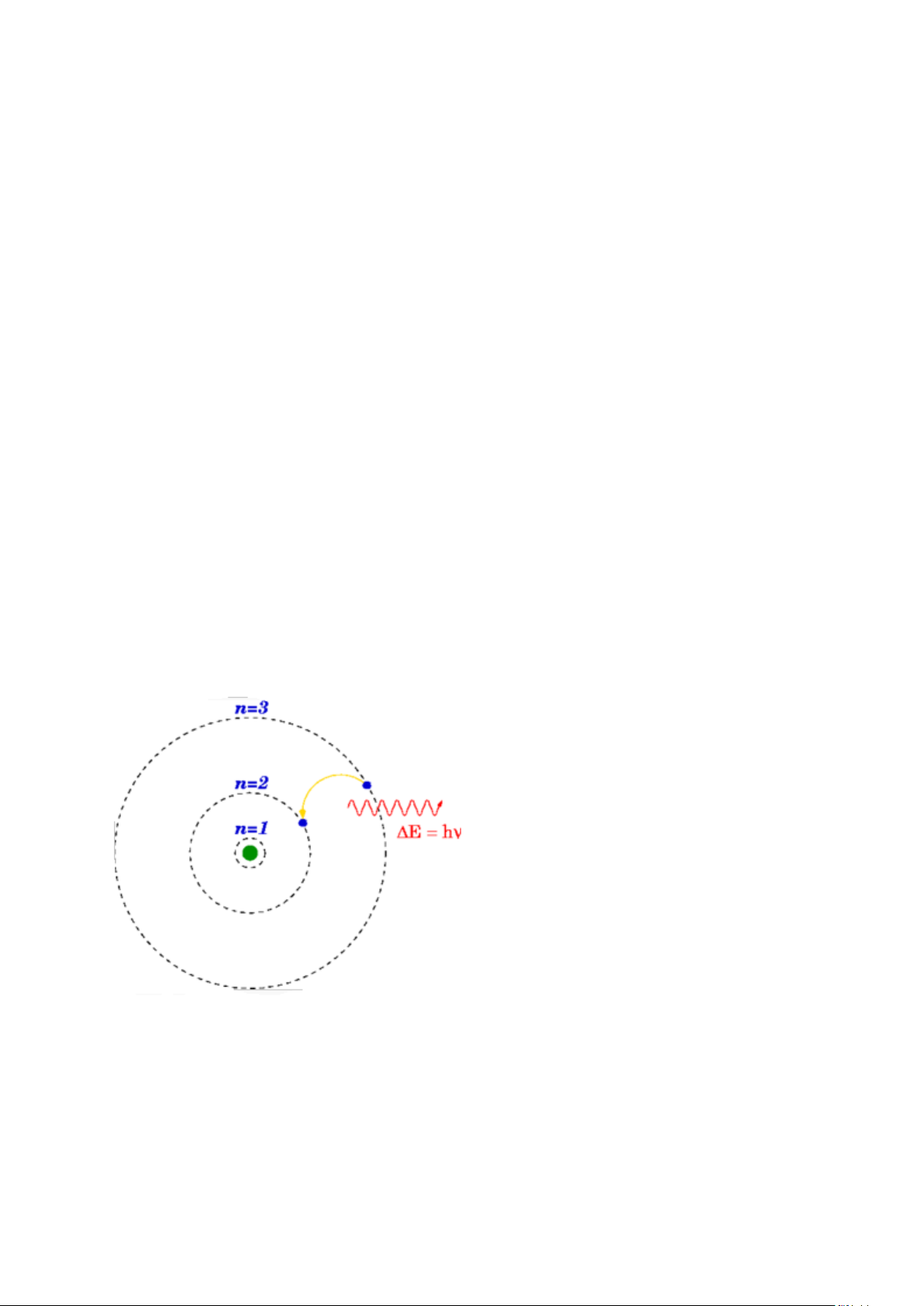
Hình 2-1. Sự dịch chuyển điện tử ở trạng thái năng lượng lượng tử của một nguyên tử tạo ra sự
phát xạ của một photon. 7
2.1.2. Phổ hấp thụ
Phổ hấp thụ mô tả các tính chất hấp thụ của các hạt, nó được biểu diễn ở dạng hàm sự
giảm cường độ tia bức xạ điện từ và bước sóng (hay tần số, hay số sóng). Hai đại lượng
thường được sử dụng để định lượng sự giảm cường độ tia bức xạ điện từ là độ truyền quang và độ hấp thụ.
Độ truyền quang
Ánh sáng đơn sắc (bước sóng λ thuộc miền tử ngoại và trông thấy) có cường độ Io chiếu
qua cuvet đựng mẫu dung dịch có nồng độ C, có bề dày là b, khi ánh sáng đi qua khỏi
cuvet có cường độ là I, một phần ánh sáng bị hấp thụ bởi mẫu bởi vậy I≤Io.
Tỉ số giữa cường độ ánh sáng đi qua mẫu và cường độ ánh sáng ban đầu được gọi là độ truyền quang T T = (2-3)
Bởi vậy, T thay đổi từ 0-1. Phần trăm truyền quang, đơn giản là 100T%, và nó thay đổi tương ứng từ 0-100%.
Độ hấp thụ A được định nghĩa: A = log = -logT (2-4)
- Nếu ánh sáng không bị hấp thụ, I = Io và A = 0
- Nếu 90% ánh sáng bị hấp thụ, 10% đã được truyền quang, khi đó và với tỉ
số này nhận được A = 1
- Nếu chỉ có 1% ánh sáng được truyền quang, A = 2
(Độ hấp thụ A đôi khi còn gọi là mật độ quang – optical density)
Giả sử chúng ta liên tục theo dõi và đo độ hấp thụ của dung dịch nghiên cứu có nồng độ
C khi tăng dần bước sóng tia tới về phía sóng dài và xây dựng nên đồ thị mối quan hệ A-λ
thì đường cong A=f(λ) được gọi là phổ hấp thụ. Đồ thị A=f(λ) thường có dạng hình
chuông úp (hình Gauxơ) (hình 2-2). 8
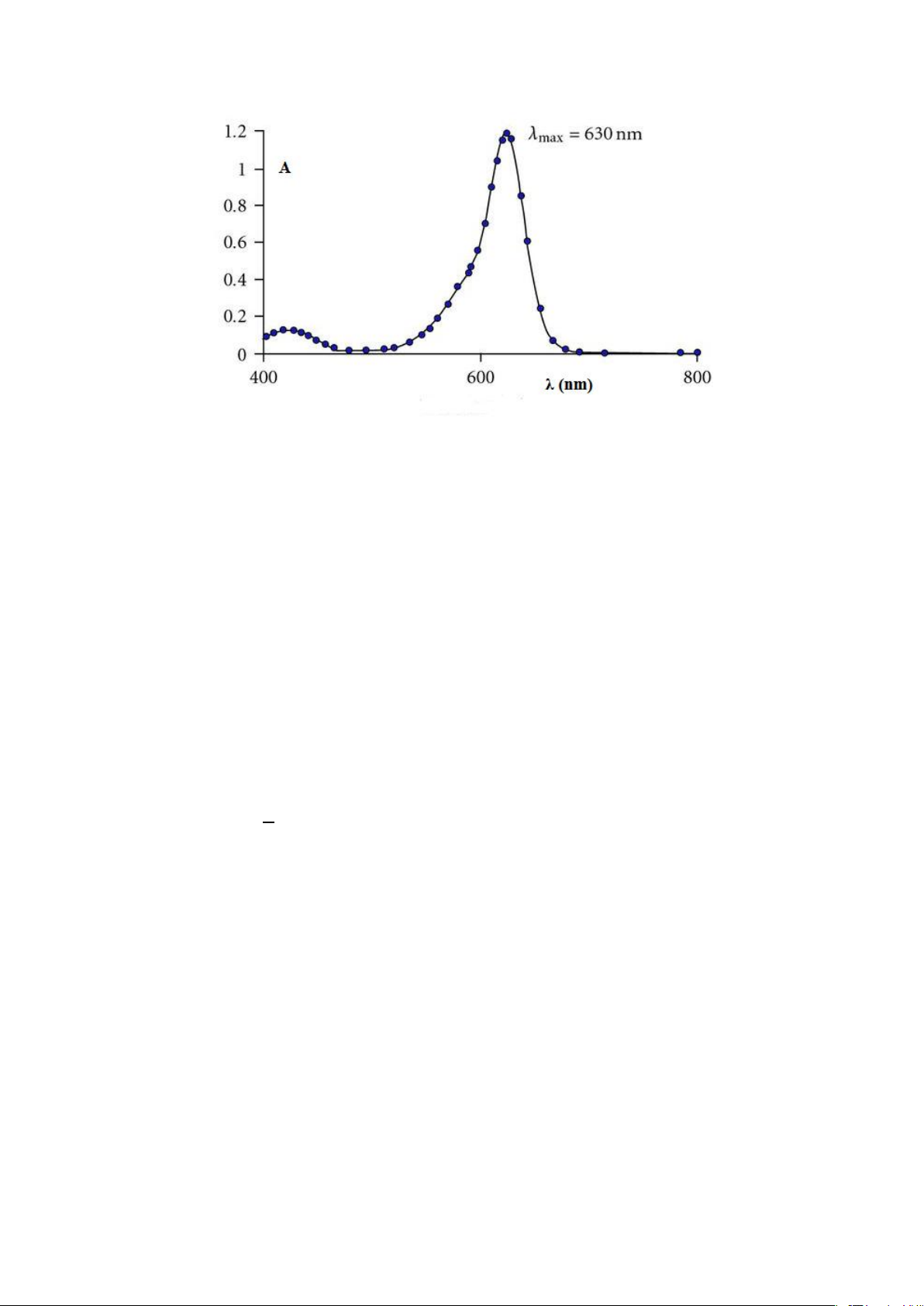
Hình 2-2. Phổ hấp thụ của chất A ở dạng dung dịch
Cực đại Amax ứng với giá trị λmax gọi là cực đại hấp thụ, λmax chỉ phụ thuộc vào bản chất
dung dịch, có thể dùng trong phân tích định tính.
Khi tiến hành phân tích theo phương pháp quang phổ đo quang người ta thường chọn
đo độ hấp thụ A của dung dịch nghiên cứu tại λmax bởi vì việc đo A ở λmax sẽ cho ta kết
quả phân tích có độ nhạy và độ chính xác cao nhất.
2.2. Định luật cơ bản về hấp thụ bức xạ điện từ
2.2.1. Định luật Lambert-Beer
Định luật Lambert – Beer A = εbC = log = –logT (2-5)
Trong đó: Io là cường độ tia tới, I là cường độ ánh sáng đi qua khỏi cuvet (tia ló)
Độ hấp thụ A là một đại lượng không thứ nguyên. Nồng độ của mẫu thường được sử dụng đơn vị
là mol/l. Chiều dày của cuvet đựng mẫu b, thường được mô tả bằng cm. Đại lượng ε gọi là độ hấp
thụ mol (hay còn gọi là hệ số tắt phân tử) và có đơn vị là M–1cm–1, bởi vậy tích số εbC là không
thứ nguyên. Phương trình (2-5) mang tên định luật Bouger – Lambert – Beer.
Trong phân tích đo quang, với dung dịch phân tích xác định, bước sóng tia tới là đơn sắc thì ε là
xác định, người ta luôn có thể chọn b xác định nên định luật hấp thụ ánh sáng có thể viết dưới dạng: A = KC với K= εb = const (2-6) 9
Phương pháp phân tích đo quang định lượng được đặt trên cơ sở phương trình (2-6)
Chứng minh định luật Lambert – Beer
(Để trả lời cho câu hỏi tại sao mối quan hệ giữa độ truyền quang T và nồng độ lại tuân theo mối quan hệ logarit) b
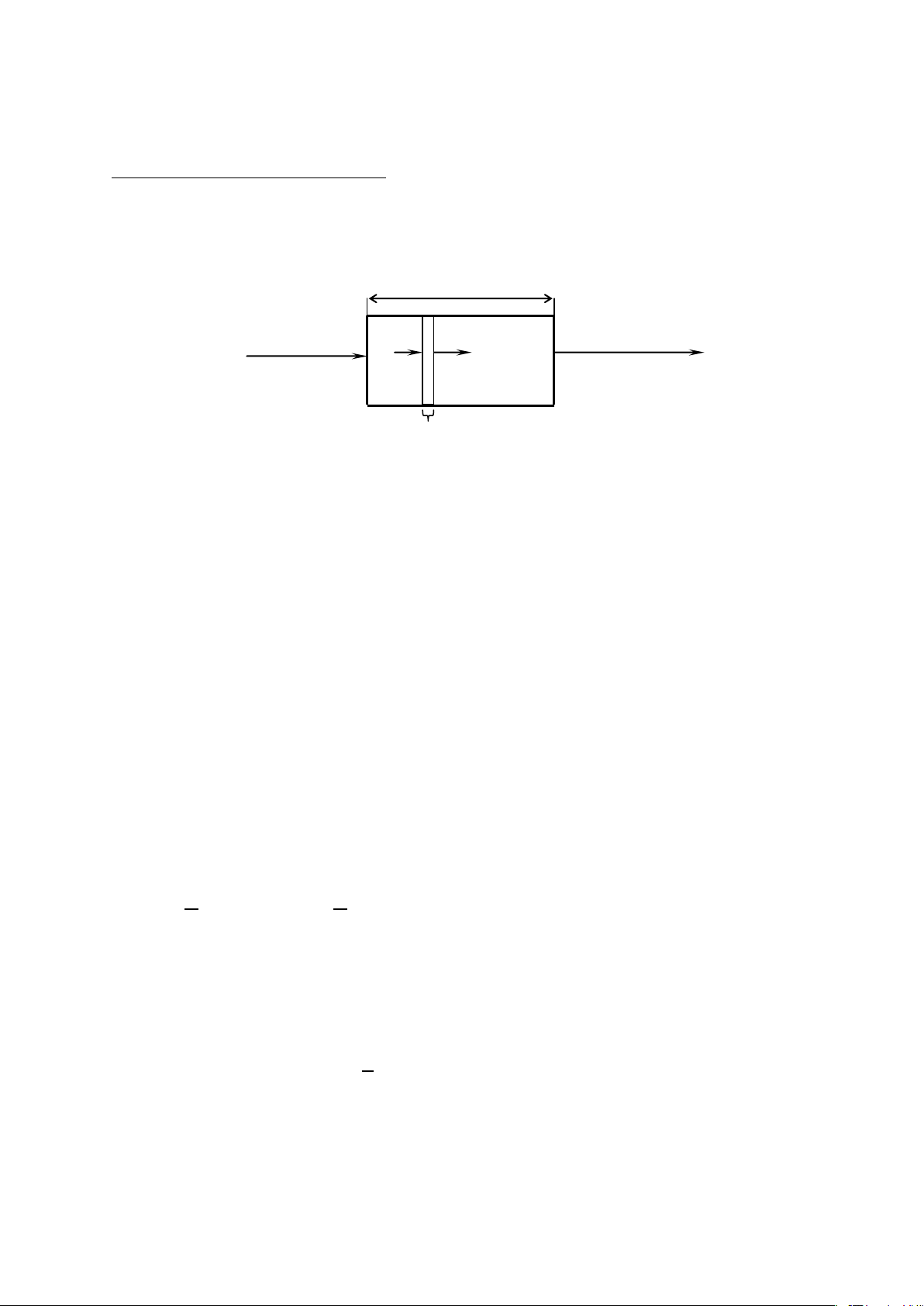
Ánh sáng tới (Io, λ) I I-dI Ánh sáng ló, I C x= 0 dx x=b
Hình 2-3. Chứng minh định luật Bouger – Lambert – Beer
Bằng trực giác ta nhận thấy rằng, khi ánh sáng đi qua dung dịch, ánh sáng bị hấp thụ nhiều hay ít
phụ thuộc vào số phân tử mà nó gặp, mà số phần tử đó lại phụ thuộc quãng đường và nồng độ.
Bây giờ ta sẽ chứng minh bằng toán học.
Chúng ta hãy tưởng tượng chiếu một chùm ánh sáng đơn sắc có cường độ I đi qua một
lớp mỏng của dung dịch có bề dày dx, ánh sáng bị hấp thụ và cường độ của nó giảm đi là –dI. dI = - βICdx (2-7)
ở đây β là hệ số tỉ lệ và dấu âm chỉ sự giảm cường độ I khi x tăng
Biến đổi phương trình (2-7) và lấy tích phân đối với I ta có: ⇿ (2-8)
Giới hạn của tích phân ở đây là I = Io ở x=0 và I = I ở x=b Từ (2-8) đưa tới:
-lnI – (-lnIo) = βbC → = βbC
Cuối cùng, biến đổi ln về lg, sử dụng mối quan hệ lnz = ln(10)(lgz), ta nhận được định
luật Bouger – Lambert – Beer: 10
= bC → = εbC
Độ hấp thụ A Hằng số ε
Đây chính là biểu thức (2-5)
Ví dụ: Tìm độ hấp thụ và truyền quang của dung dịch 0,00240M của một dung dịch có độ
hấp thụ mol ε= 313 M-1cm-1, với bề dày cuvet là b = 1,00 cm Giải: Theo (2-5) ta có:
Độ hấp thụ A = εbC = 313 M-1cm-1 x 1,00 cm x 0,00240M = 0,751
Độ truyền quang T = 10-A = 10-0,751 = 0,177
→ có 17,7% ánh sáng truyền qua dung dịch (ánh sáng ló)
2.2.2. Tính chất cộng tính của độ hấp thụ quang
Giả sử chúng ta chiếu liên tiếp một chùm tia sáng đơn sắc qua hai dung dịch có nồng độ lần lượt
là C1 và C2, độ hấp thụ mol tương ứng là ε1 và ε2.
Ở dung dịch 1 có độ hấp thụ A1 = , ở dung dịch 2 có độ hấp thụ A 2 = Ta có: + = ⇿ A 1 + A2 = A
Như vậy, chúng ta nhận thấy rằng độ hấp thụ có tính chất cộng tính: A = (2-9)
Nói cách khác, nếu có i chất trong cùng một dung dịch hấp thụ một ánh sáng nào đó, độ
hấp thụ sẽ là độ hấp thụ của i chất.
Chúng ta hãy xem xét tính chất này có ý nghĩa thế nào trong phân tích bằng phương pháp quang phổ đo quang.
Nếu một dung dịch gồm chất nghiên cứu và tạp chất thì độ hấp thụ:
Adung dịch = Anghiên cứu + Anền
Trong phân tích đo quang chúng ta chuẩn bị dung dịch trống chứa các tạp chất, có nghĩa là:
Atrống = Anền (do không có mặt ion cần xác định) 11 Và
Anghiên cứu = Adung dịch - Atrống
Như vậy, trong phân tích đo quang bằng việc sử dụng dung dịch trống, giá trị A đo được
sẽ phản ánh đúng nồng độ chất nghiên cứu, nói cách khác phương trình (2-6) được tuân theo chặt chẽ.
2.2.3. Các yếu tố làm sai lệch định luật Lambert-Beer
Định luật Lambert-Beer có thể bị sai lệch do nhiều nguyên nhân vật lý và hóa lý, điều đó
ảnh hưởng đến tính đúng đắn của phương trình (2-5), tức là ảnh hưởng trực tiếp đến độ
chính xác của kết quả phân tích thu được theo phương pháp quang phổ đo quang.
- Tính đơn sắc của ánh sáng tới: Như ta đã biết định luật Lambert-Beer chỉ đúng với bức
xạ điện từ đơn sắc xác định. Nếu ta đo độ hấp thụ của dung dịch bằng một chùm tia đa
sắc thì định luật Lambert-Beer không còn đúng nữa, dẫn đến phá vỡ tính đúng đắn của phương trình (2-5).
- Định luật có thể bị thay đổi với một số điều kiện hóa lý của dung dịch nghiên cứu. Ví dụ,
sự có mặt của ion lạ làm biến dạng các phân tử hấp thụ ánh sáng, làm thay đổi phổ hấp
thụ của chất nghiên cứu.
Khi thay đổi nồng độ chất nghiên cứu làm thay đổi khả năng hấp thụ của các phân tử.
Khi thay đổi nồng độ H+ của dung dịch nghiên cứu có thể làm thay đổi dạng tồn tại của
hợp chất. Ví dụ, với ion CrO42- khi tăng nồng độ [H+] có thể tạo thành ion Cr2O72- theo phản ứng:
2 CrO42- + 2H+ ⇋ Cr2O72- + 2H2O
Làm thay đổi miền bức xạ điện từ bị hấp thụ.
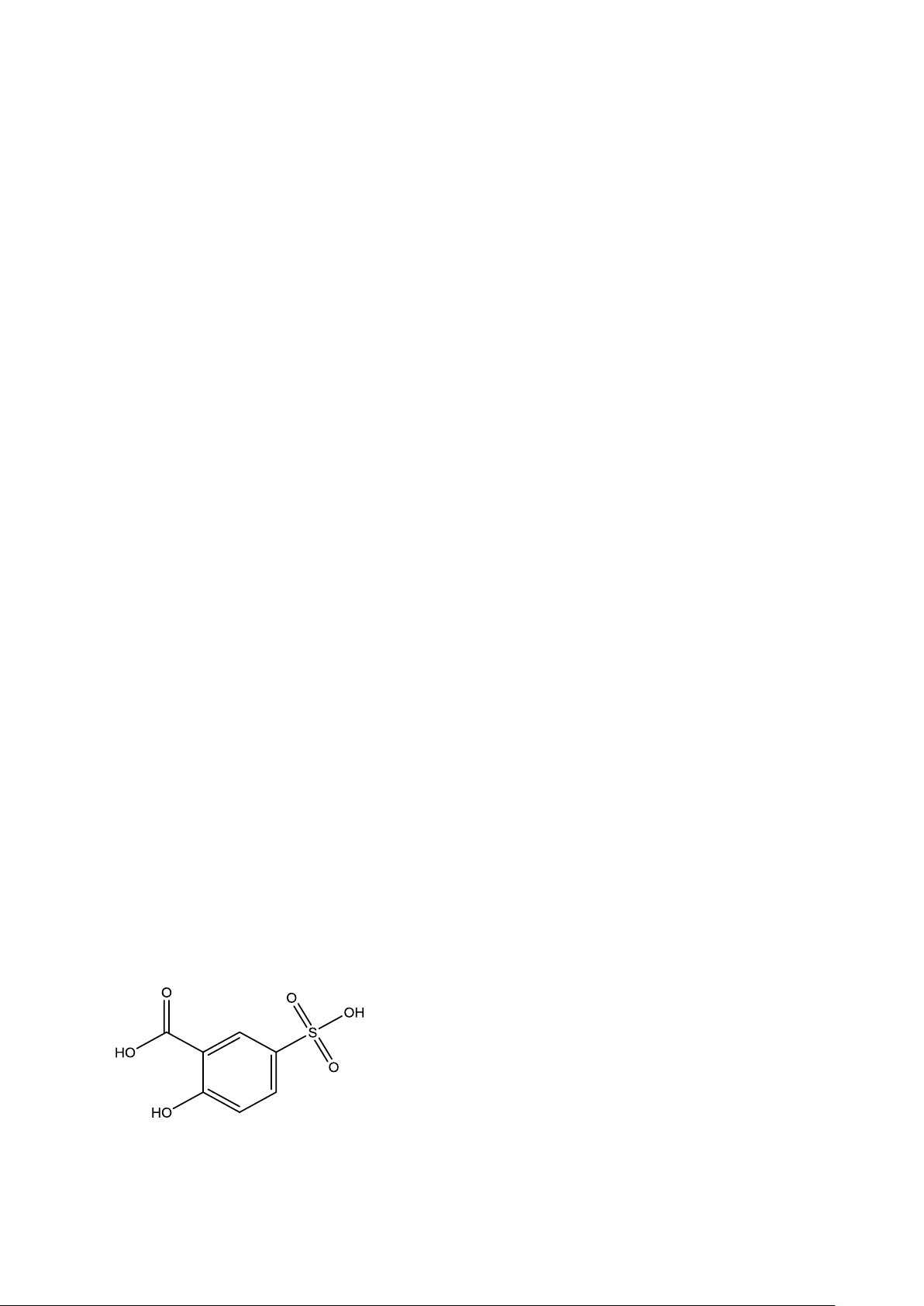
Ví dụ, phức Fe3+ với axit sunphosalysylic tùy thuộc pH mà tạo phức có miền phổ hấp thụ khác nhau. H2Sal (axit sunfosalyxylic) 12
Axit sunfosalyxilic có hai proton ở nhóm cacbonyl và hydroxyl với hằng số phân ly Ka1, Ka2 tương
ứng với sự phân ly của H+ ở nhóm phenolat và caboxylat. Axit sunfosalyxilic tạo phức với Fe3+
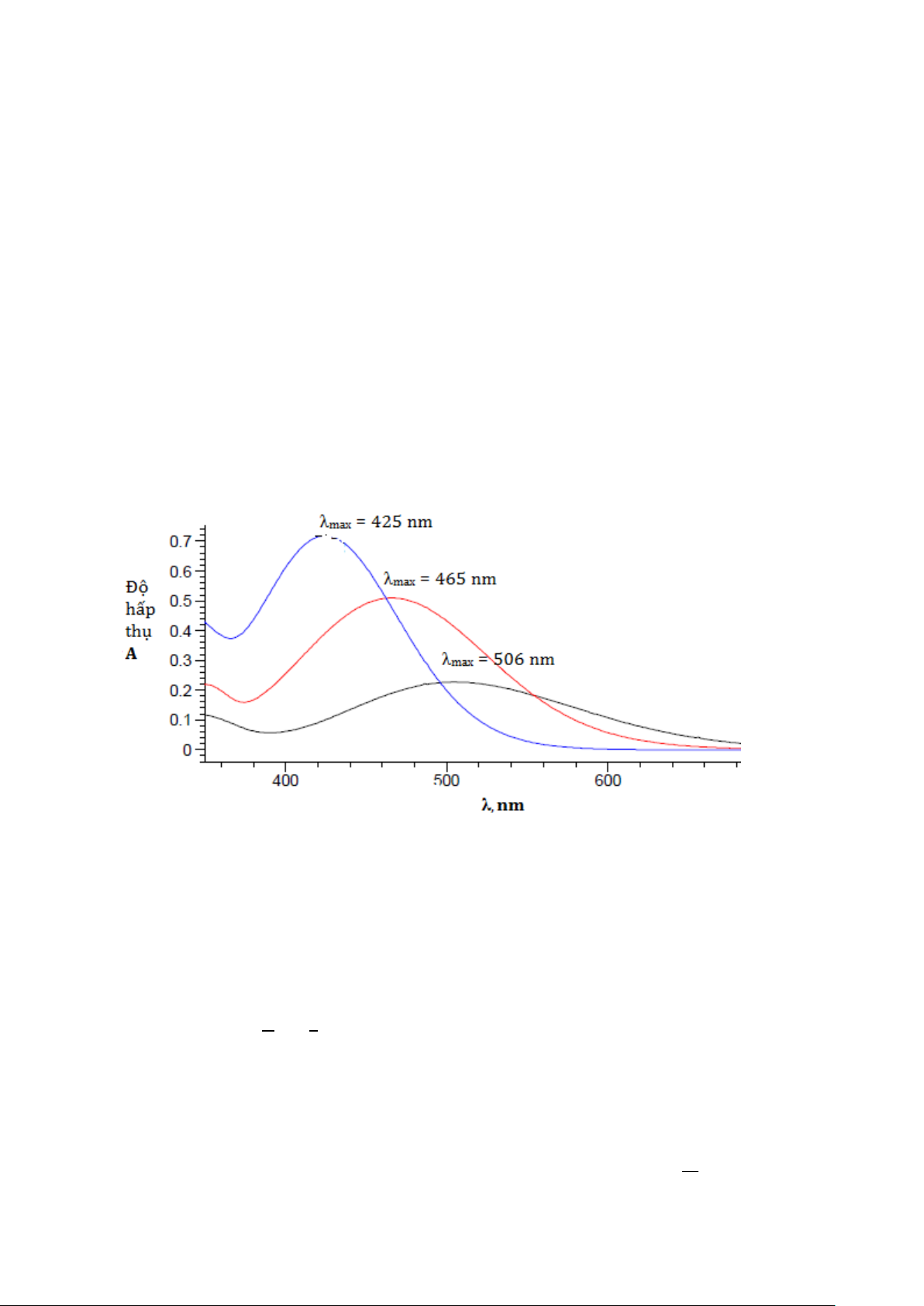
tạo ra các phức mono-, di-and tri- sunfosalyxilat phụ thuộc vào pH môi trường. Fe3+ + H2Sal ⇋ [Fe(Sal)]+ + 2H+ pH = 1-2,5
Màu tím sẫm (λmax = 506nm)
Fe3+ + 2H2Sal ⇋ [Fe(Sal)2]- + 4H+ pH = 4-5
Màu nâu đỏ (λmax = 465nm)
Fe3+ + 3H2Sal ⇋ [Fe(Sal)3]3- + 6H+ pH = 9-10
Màu vàng (λmax = 425nm)
Hình 2-4. Phổ hấp thụ của phức Fe3+ và axit sunfosalyxilic ở các miền pH khác nhau
- Khi thay đổi dung môi có thể làm thay đổi khả năng hấp thụ của chất nghiên cứu, do thay đổi
độ solvat, do đó có thể làm thay đổi khả năng hấp thụ ánh sáng của chất nghiên cứu.
2.2.4. Độ chính xác của phép đo độ hấp thụ và phép đo nồng độ
Từ hệ thức A =log = lg (với T là độ truyền quang có giá trị từ 0-100%), nên với mỗi
máy đo nào đó, với mỗi phép đo độ truyền quang T gây nên sai số dT thì sẽ gây nên các
sai số dA tương ứng khác nhau tùy thuộc dA tương ứng với miền nào của giá trị T đo
được. Mà A lại phụ thuộc tuyến tính với C nên kết quả là cùng với một sai số dT của máy,
tại các miền đo khác nhau có thể gây sai số dC khác nhau và do đó sai số sẽ khác nhau. 13 Ta có: C = = (2-10) Lấy vi phân: dC = (2-11)
Từ (2-10) và (2-11) ta có: =
Chuyển sang gia số hữu hạn ta có: (2-12)
Từ (2-12) ta có thể khảo sát sự biến thiên trong miền giá trị của T (T = 0÷1) với một sai số ΔT cho trước.
Để tìm cực trị ta lấy vi phân phương trình (2-12) theo T với ΔT = const và cực trị xảy ra khi: = = 0
Vì ΔT ≠ 0, nên rõ ràng (lnT+1) = 0. Từ đó lnT = 2,3logT = -1 và –logT = A = 0,435.
Vậy với giá trị độ hấp thụ A = 0,435 thì phép đo sẽ cho giá trị chính xác nhất trong phép
xác định nồng độ C của chất nghiên cứu.
2.2.5. Điều kiện để tiến hành phân tích đo quang UV-VIS
Điều kiện để có thể tiến hành phân tích đo quang là phải tạo được các hợp chất có hiệu
ứng hấp thụ bức xạ điện từ trong miền tử ngoại hoặc trông thấy. Để có hiệu ứng phổ hấp
thụ trong miền trông thấy, thông thường người ta tạo hợp chất màu bằng phản ứng oxy
hóa khử hoặc phản ứng tạo phức. Đối với phản ứng oxy hóa khử trong phân tích đo
quang thường xảy ra thực tế hoàn toàn (ví dụ như phản ứng oxy hóa Mn2+ thành MnO4-).
Đối với các phản ứng tạo phức thì tình hình phức tạp hơn nhiều. Phản ứng tạo phức chịu
ảnh hưởng của nhiều yếu tố: quá trình tạo phức nhiều cấp, H+, hằng số bền.. 14
2.3. Các thủ tục thực nghiệm trong phân tích đo quang
Theo phương trình (2-6) mối quan hệ giữa A và C là tuyến tính. Để xác định nồng độ
trong phương pháp đo quang chúng ta phải xác định hằng số K trong phương trình này.
Có ba cách xác định hằng số K: phương pháp đường chuẩn, phương pháp tính và
phương pháp thêm tiêu chuẩn.
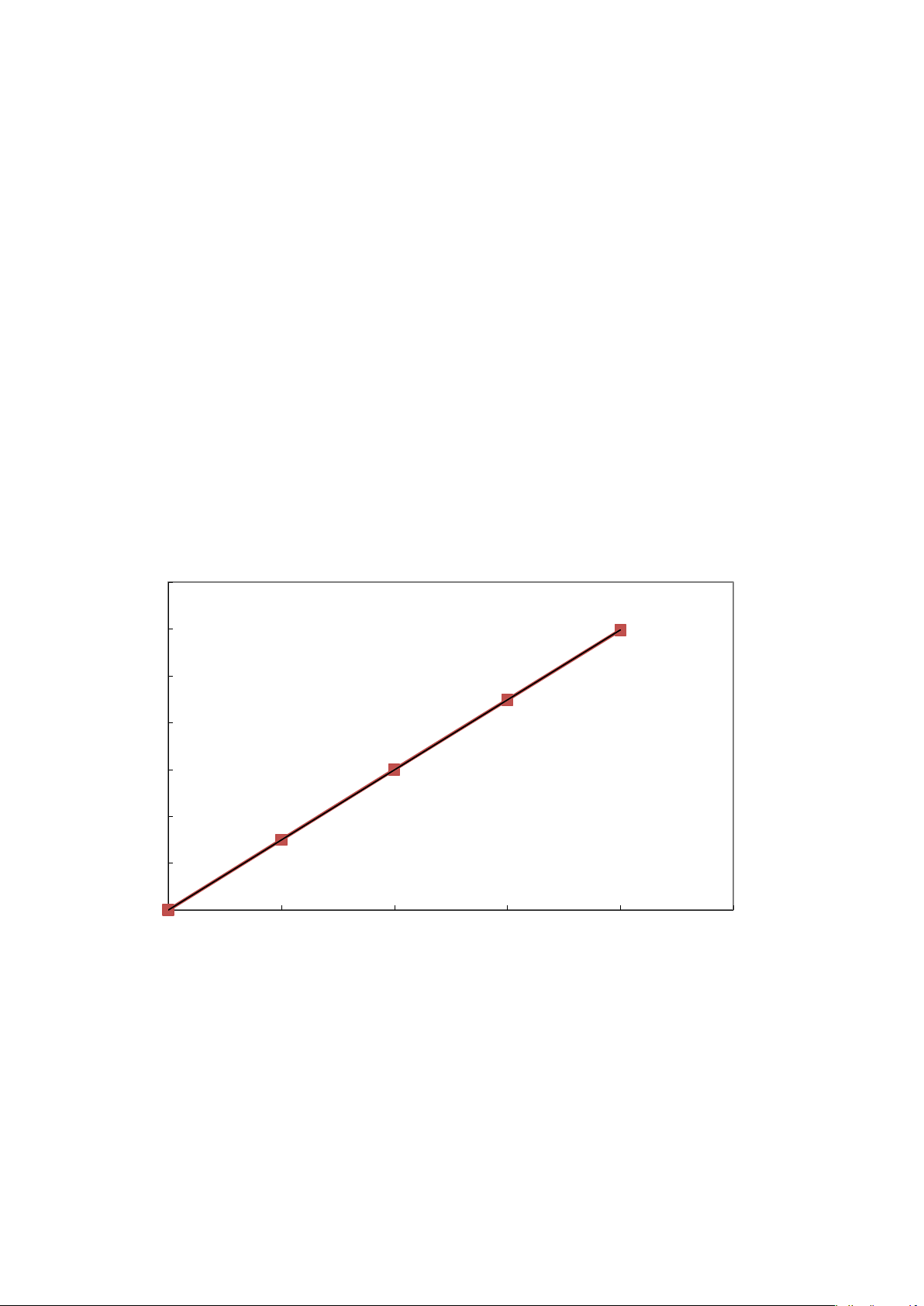
2.3.1. Phương pháp đường chuẩn
Trước hết chúng ta pha chế các dung dịch có nồng độ chính xác C1, C2, C3, . ., xác lập các
điều kiện để tạo các hợp chất có hiệu ứng phổ hấp thụ bức xạ điện từ ở λmax chọn trước.
Đo độ hấp thụ tương ứng A1, A2, A3, . . Mối quan hệ giữa A và C tuân theo định luật
Lambert-Beer, do vậy ta có thể hồi qui các số liệu thực nghiệm rời rạc này về hàm bậc
nhất và hệ số góc của nó chính là hằng số K. 0.700 0.600 y = 1,4963x 0.500 R² = 1 A 0.400 0.300 0.200 0.100 C, mg/l 0.000 0.000 0.100 0.200 0.300 0.400 0.500
Hình 2-4. Phương pháp đường chuẩn
2.3.2. Phương pháp tính
Từ phương trình (2-6) A= ϵbC = KC, với một chất nghiên cứu xác định và b chọn trước
(thường sử dụng cuvet có b = 1,00 cm) và với chất nghiên cứu đủ bền thì việc xác định
nồng độ có thể chỉ cần một mẫu chuẩn có nồng độ biết chính xác là đủ. Vì trong điều kiện
trên thì K sẽ không thay đổi từ thí nghiệm này sang thí nghiệm khác. 15
Chúng ta đo độ hấp thụ Ax của dung dịch mẫu nghiên cứu có nồng độ Cx và độ hấp thụ Ac
dung dịch chuẩn Cc Do có cùng hệ số góc K nên: = C x =
2.3.3. Phương pháp thêm tiêu chuẩn
Tiến hành đo độ hấp thụ của dung dịch nghiên cứu có nồng độ Cx, sau đó thêm một
lượng dung dịch chuẩn vào dung dịch nghiên cứu C1 và đo độ hấp thụ của dung dịch này.
Thường người ta pha chế ít nhất là ba dung dịch, ví dụ Cx, Cx + C1 và Cx +2C1. Mối quan hệ
giữa các số liệu rời rạc là mối quan hệ tuyến tính. Hồi qui các số liệu rời rạc về phương
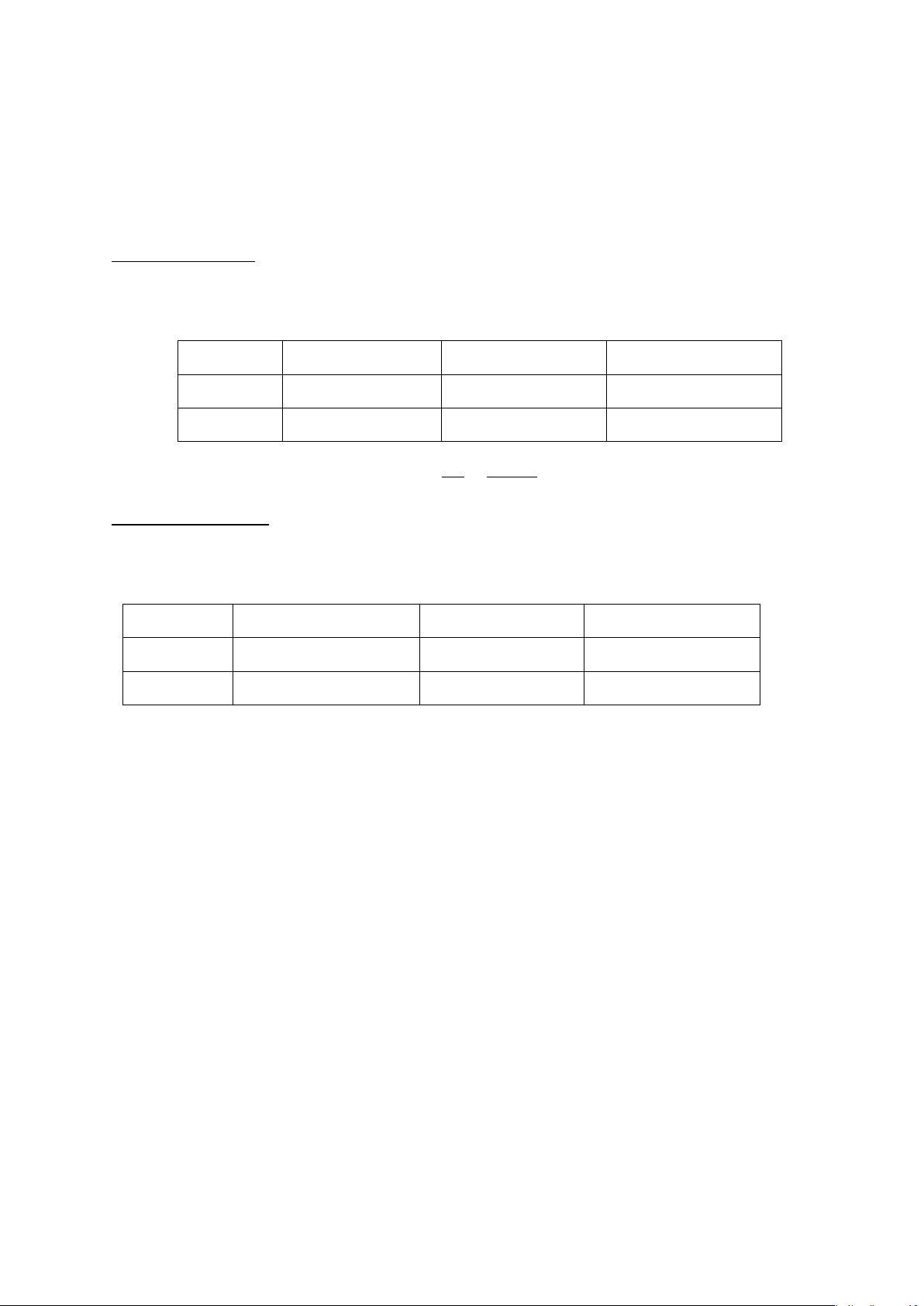
trình bậc nhất, từ đó cho phép chúng ta tính được hệ số góc K. Nồng độ Cx Cx + C1 Cx +2C1 Độ hấp thụ Ax A1 A2
Để phép đo có độ tin cậy cao, thường người ta chọn nồng độ C1 có nồng độ gần bằng Cx.
2.4. Phương pháp đo quang vi sai
Như đã trình bày ở phần 2.5, việc đo độ hấp thụ ở các giá trị A lớn có thể mắc phải sai số
lớn trong việc xác định nồng độ. Với các dung dịch có độ hấp thụ lớn người ta sử dụng
phương pháp đo quang vi sai. Trong phương pháp này độ hấp thụ của dung dịch đo
không phải so với dung môi hoặc dung dịch trống như phương pháp đo quang thường
dùng. Dung dịch so sánh ở đây thường là dung dịch có nồng độ biết trước Css , Css phải
chọn thế nào để độ hấp thụ của nó so với dung môi hoặc dung dịch trống khá lớn nhưng
phải nhỏ hơn độ hấp thụ của dung dịch đo một ít.
Chúng ta có thể xác định nồng độ của chất nghiên cứu sử dụng các thủ tục phân tích như với đo quang thường. Cơ sở phương pháp:
Dung dịch so sánh có nồng độ Css, đo được Ass (qui về 0,000)
Dung dịch phân tích có nồng độ C, đo được A
Khi dung dịch so sánh có nồng độ khác không, giá trị A’ đo được sẽ là hiệu của A-Ass, dựa
trên tính chất cộng tính của độ hấp thụ A’ = A-Ass = ϵb(C-Css) 16
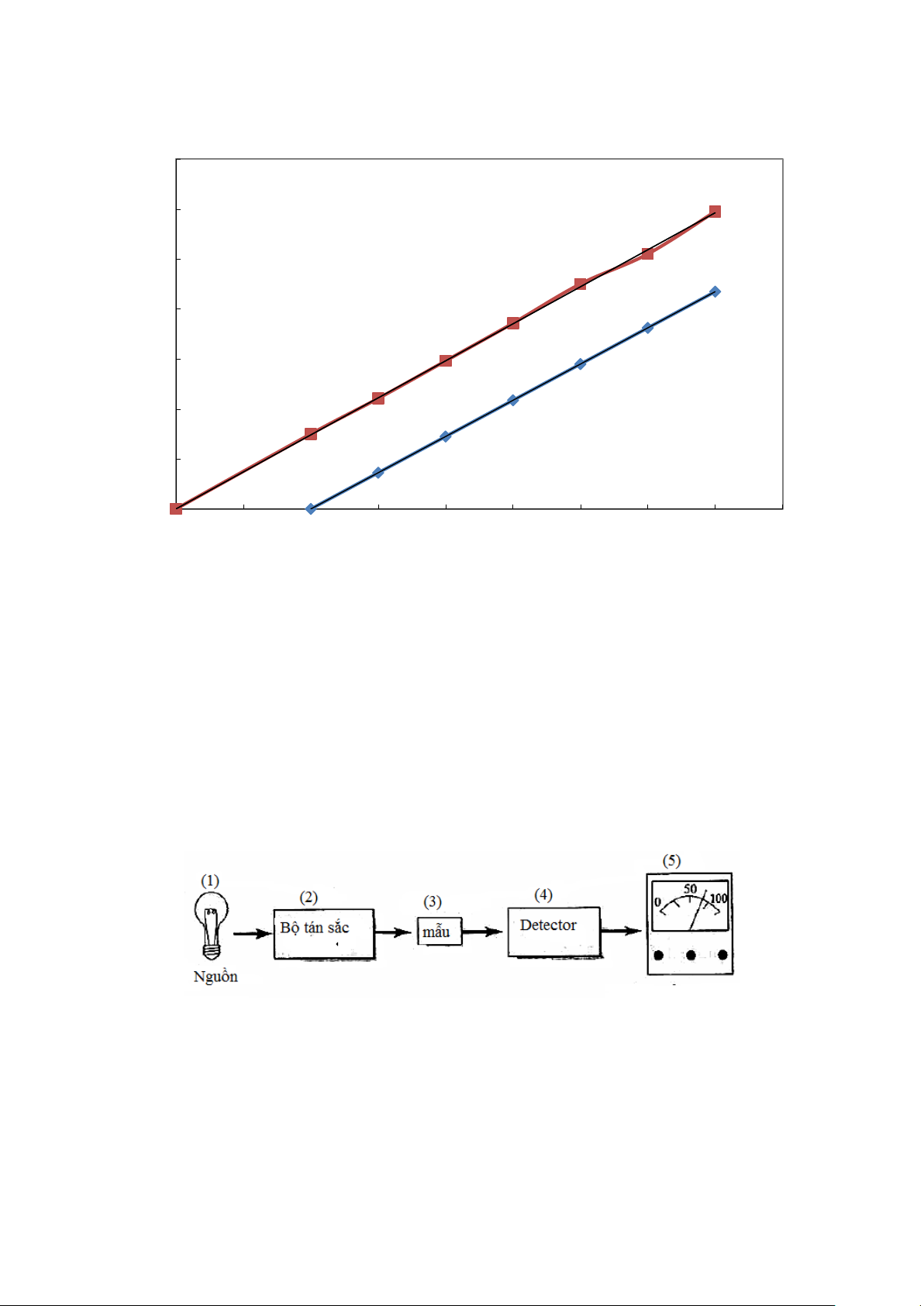
Khi dung dịch phân tích có nồng độ lớn (giá trị A sẽ rất lớn), người ta sử dụng phương
pháp đo quang vi sai nhằm làm giảm giá trị đo A với việc sử dụng dung dịch trống chứa
chất cần phân tích đã biết nồng độ, vì khi đó giá trị đo được sẽ nằm trong khoảng tuyến
tính, tức là hệ thức (2-5) luôn đúng. Phương pháp tính:
Chúng ta cần chuẩn bị dung dịch chuẩn, dung dịch so sánh và dung dịch phân tích Ví dụ: dung dịch chuẩn
dung dịch so sánh dung dịch phân tích Cu2+ Cch Css (Css Cx Độ hấp thụ Ach 0,000 Ax Ta có: = → C x Phương pháp đồ thị:
Chúng ta cần chuẩn bị một dãy dung dịch chuẩn, dung dịch so sánh và dung dịch phân tích
Dãy dung dịch chuẩn dung dịch so sánh dung dịch phân tích Cu2+ Cch1, Cch2, ...Cchi Css (Css Cx
Độ hấp thụ Ach1, Ach2, ... Achi, 0,000 Ax
Đo độ hấp thụ Achi ứng với các dung dịch chuẩn thứ i, dung dịch so sánh được lựa chọn
sao cho nồng độ của nó nhỏ hơn Achi. Xây dựng đồ thị mối quan hệ A-C.
Ta cũng tiến hành đo quang với cùng điều kiện cho dung dịch phân tích có nồng độ Ax với dung dịch so sánh. 17 1.400 1.200 y = 1,4963x R² = 1 1.000 A 0.800 0.600 y = 1,449x - 0,2898 0.400 R² = 1 Đo quang vi sai 0.200 C, mg/l 0.000 0.000 0.100 0.200 0.300 0.400 0.500 0.600 0.700 0.800 0.900
Hình 2-5. Phương pháp đo quang vi sai
Từ đồ thị ta có thể tính được nồng độ của dung dịch nghiên cứu sau khi tiến hành đo độ hấp thụ Ax
2.5. Thiết bị quang phổ hấp thụ phân tử
2.5.1. Sơ đồ thiết bị
Sơ đồ thiết bị quang phổ hấp thụ phân tử được mô tả bằng sơ đồ khối ở hình 2-6 dưới đây:
Hình 2-6. Sơ đồ thiết bị quang phổ hấp thụ phân tử 2.5.2. Nguồn sáng
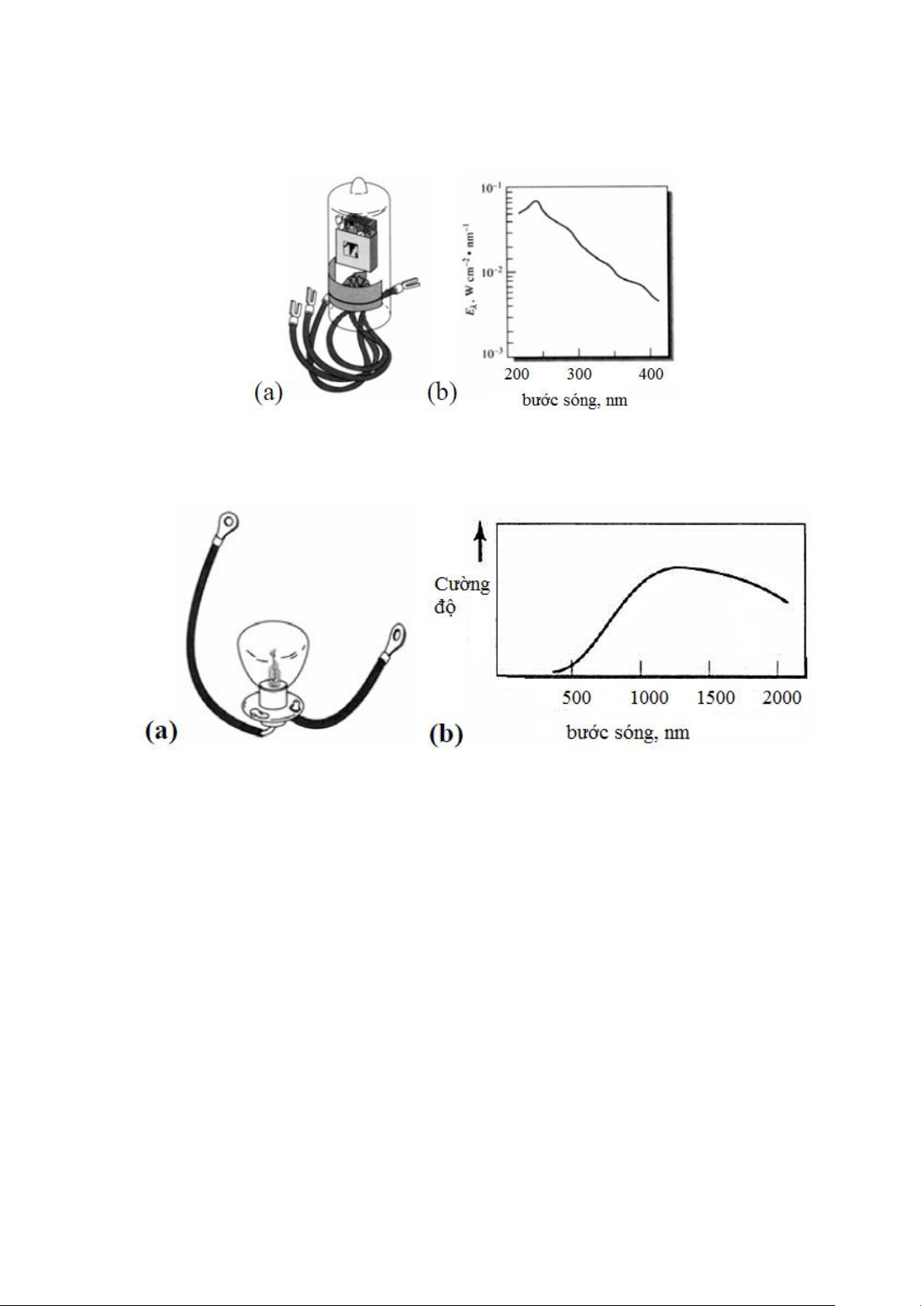
Các loại đèn H2 và D2 cho ánh sáng với bước sóng từ 160-380 nm (hình 2-7)
Đèn sợi đốt vonfram cho ánh sáng từ miền 350-2200 nm (hình 2-8) 18
Các thiết bị UV-VIS hiện đại thường sử dụng cả hai đèn D2 và đèn sợi đốt vonfram cho miền ánh
ổn định từ miền tử ngoại và miền trông thấy.
Hình 2-7. Đèn Deuteri (a) và phổ phát xạ của nó (b)
Hình 2-8. Đèn sợi đốt vonfram (a) và phổ phát xạ của nó (b)
2.5.3. Bộ tán sắc:
Các thiết bị phân tích quang học thường cần đến bộ tán sắc giúp việc phân chia ánh sáng thành
ánh sáng đơn sắc, nó được sử dụng để chất phân tích hấp thụ hay phát xạ. Do vậy, bộ tán sắc
nâng cao cả độ nhạy và độ chọn lọc. Ngoài ra, tính đơn sắc của ánh sáng tới làm tăng tính đúng
đắn của phương trình toán học của định luật Lambert-Beer.
Đầu tiên, cần hiểu rằng không có có bộ tán sắc nào là có khả năng tạo ra bức xạ có bước sóng
đơn sắc. Mặc dù, đầu ra của thiết bị là một miền ánh sáng liên tục được gọi là đám; Các bước
sóng này phân bố ít nhiều đối xứng qua trung tâm của bước sóng danh nghĩa λ1 (nominal wavelength). 19
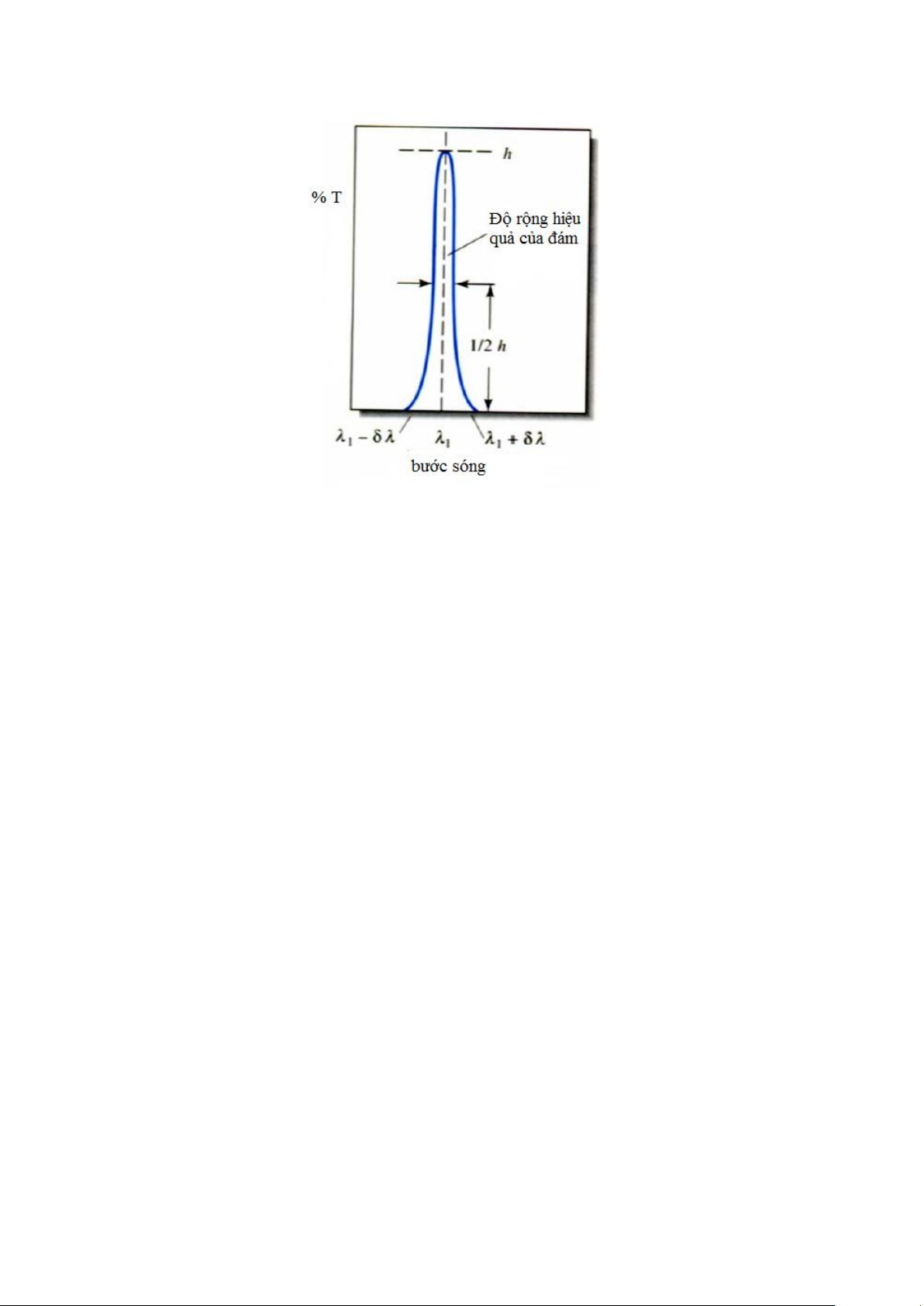
Hình 2-9. Đầu ra của một bộ tán sắc
Như được chỉ ra ở hình 2-9, độ rộng hiệu quả của đám hay còn gọi là độ đơn sắc được định nghĩa
là độ rộng của đám phổ ở chiều cao ½ của chiều cao pic. Độ đơn sắc của bộ tán sắc thay đổi rất
lớn đối với các bộ tán sắc khác khau. Ví dụ, bộ tán sắc có chất lượng cao cho miền trông thấy có
thể cho độ đơn sắc nhỏ hơn 1/10 nm, trong khi đó các bộ lọc trong vùng trông thấy có thể cho
độ đơn sắc tới 200 nm hay lớn hơn.
Cách tử: Hầu hết bộ tán sắc trong các thiết bị phân tích hiện đại là các bản sao cách tử, nhận
được bằng cách đúc từ cách tử chủ. Cách tử chủ là một kính phẳng, được đánh bóng bề mặt và
được chia vạch bằng kim cương. Mặt cắt đứng được phóng đại ở hình 2-9 chỉ cho ta thấy một vài
rãnh. Một cách tử sử dụng cho miền tử ngoại và trông thấy thường chứa từ 300-2000 rãnh/mm.
Cách tử được phủ lớp nhôm để nó có thể phản xạ. Một lớp mỏng SiO2 trên bề mặt nhôm để bảo
vệ kim loại khỏi bị oxy hóa, điều này có thể làm giảm khả năng phản xạ của nó. Khi ánh sáng
được phản xạ từ cách tử, mỗi một rãnh hoạt động như một nguồn bức xạ. Khi các tia sáng liền
kề nhau trong cùng pha, chúng tăng cường lẫn nhau, và khi chúng không cùng một pha, chúng
môt phần hoặc toàn bộ triệt tiêu nhau (hình 2-10). 20