Chương 2: Cấu tạo nguyên tử, hệ thống tuần hoàn | Bài giảng điện tử Hóa 10

CHƯƠNG 2
CẤU TẠO NGUYÊN TỬ
HỆ THỐNG TUẦN HOÀN Nội dung
2.1. Cấu tạo nguyên tử theo cơ học lượng tử
2.1.1.Các luận điểm cơ bản của cơ học lượng tử
2.1.2.Trạng thái electron trong nguyên tử H và ion 1 e
2.1.3.Trạng thái electron trong nguyên tử nhiều electron
2.3. Hệ thống tuần hoàn các nguyên tố hóa học
2.3.1. Định luật tuần hoàn và ý nghĩa
2.3.2. Hệ thống tuần hoàn và cấu trúc electron nguyên tử
2.3.3. Các tính chất của nguyên tố biến đổi tuần hoàn
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT
Lý thuyết cấu tạo nguyên tử hiện đại dựa trên những
ĐL mô tả sự chuyển động của các hạt vi mô. Những
ĐL này là cơ sở của lĩnh vực vật lí mới gọi là cơ học lượng tử (CHLT)
CHLT là một lí thuyết hoàn chỉnh dựa trên cơ sở của
hệ thống nhất quán, hiện đại. Cho đến nay mọi kết
quả tính toán bằng CHLT đều phù hợp với thực nghiệm
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT 3 luận điểm cơ sở của CHLT
Tính chất sóng hạt Nguyên lý bất định
Phương trình sóng
của hạt vi mô Heisenberg Srôđingơ
Dùng khảo sát cấu trúc lớp vỏ e trong nguyên tử
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT
Tính chất sóng - hạt của các hạt vi mô
Tính chất sóng thể hiện qua hiện tượng dao thoa và nhiễu
xạ. AS là những sóng điện từ có tần số dao động (hoặc
bước sóng) xác định được lan truyền với tốc độ C Tính chất sóng
Tính chất hạt thể hiện qua hiện tượng h/ư quang điện và
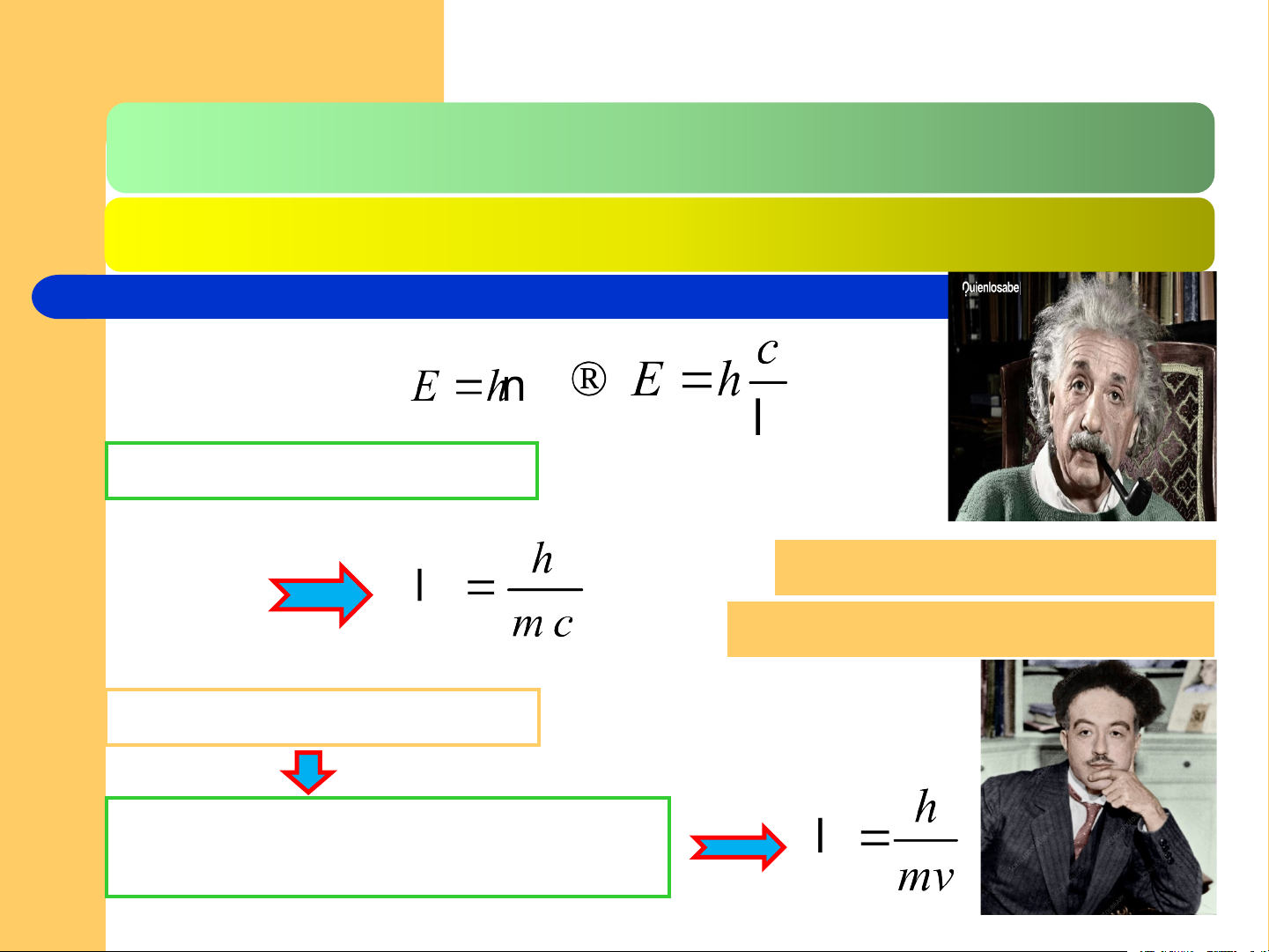
h/ư Compton, do Planck đề xuất, sau này là Anhxtanh: AS
là dòng các hạt vật chất đc gọi là photon (hay quang tử
hoặc lượng tử AS) mà mỗi photon đó có một lượng tử năng lượng
2.1. Cấu tạo nguyên tử theo cơ học LT
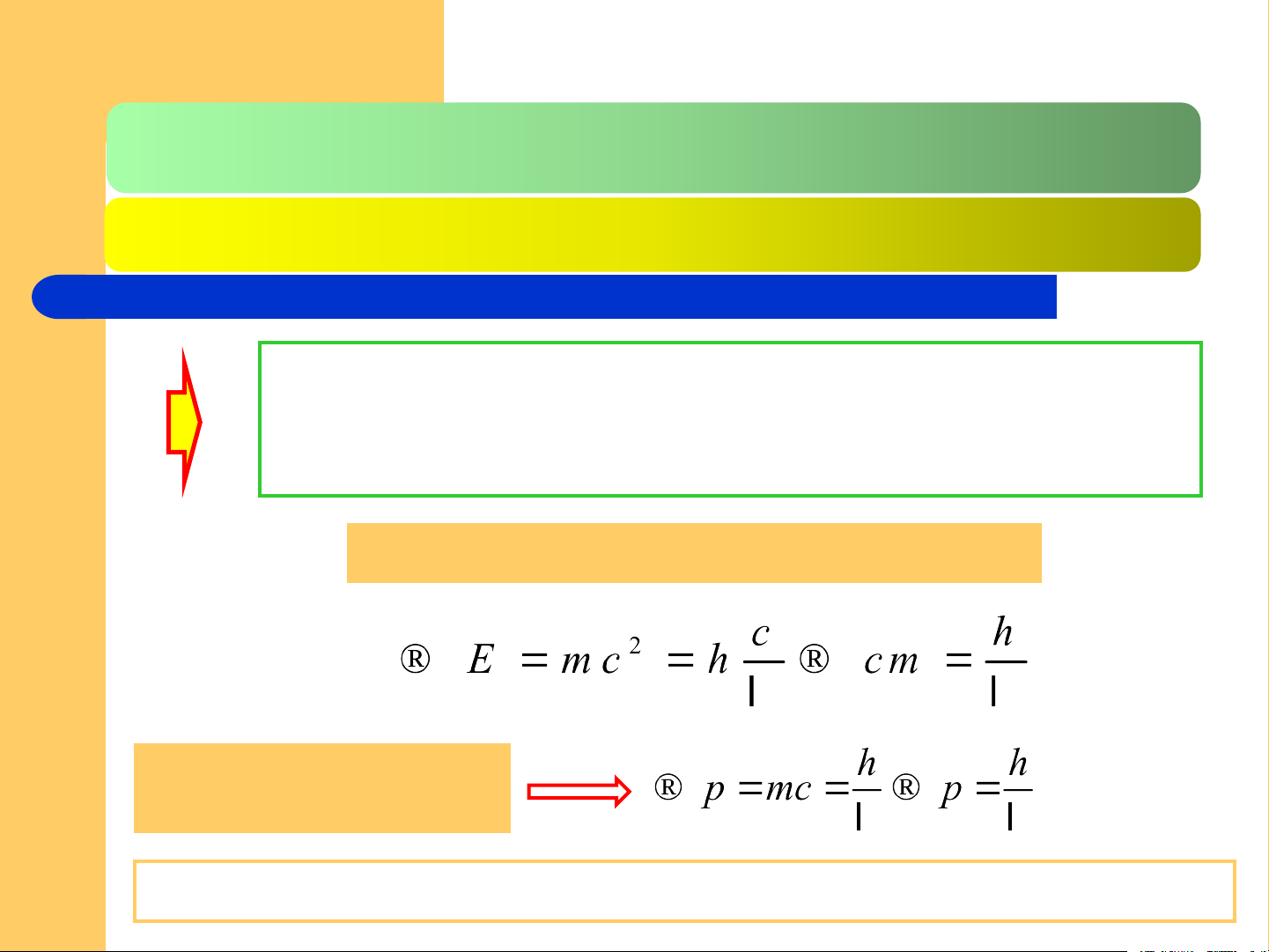
2.1.1. Các luận điểm cơ bản CHLT Theo Anhxtanh: E = mc2
mc – biểu thị tính chất hạt
λ biểu thị t/c sóng của photon Năm 1924, Lui De Broglie
electron cũng như các vật vi mô
khác đều có bản chất sóng – hạt
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT
Nguyên lý bất định Heisenberg
Không thể xác định được đồng thời tọa độ
và tốc độ trong một trạng thái chuyển
động của electron (cũng như vi hạt bất kỳ)
Δv: độ bất định về tốc độ W. Heisenberg
Δx: độ bất định về vị trí 1901-1976
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT
Sự chuyển động của 1 hạt vật chất bất kì đều phải
liên kết với 1 sóng vật chất. Sóng vật chất đó đc gọi
là sóng liên đới với hạt.
Các biểu thức trên cũng có thể viết lại mc chính là xung lượng của photon đang xét
PT trên cũng biểu thị sự thống nhất t/c sóng hạt của ánh sáng
2.1. Cấu tạo nguyên tử theo cơ học LT
Phương trình Srôđingơ
Năm 1926, Srôđingơ đưa ra phương trình
về sau mang tên ông. Đây là những tiên đề
quan trọng bậc nhất của CHLT
Khi một hệ lượng tử ở trạng thái dừng – là trạng thái mà toán
tử Haminton H của hệ ko phụ thuộc tường mình vào thời gian – giữa hàm sóng
mô tả trạng thái của hệ với năng
lượng toàn phần E và toán tử Haminton của hệ
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT
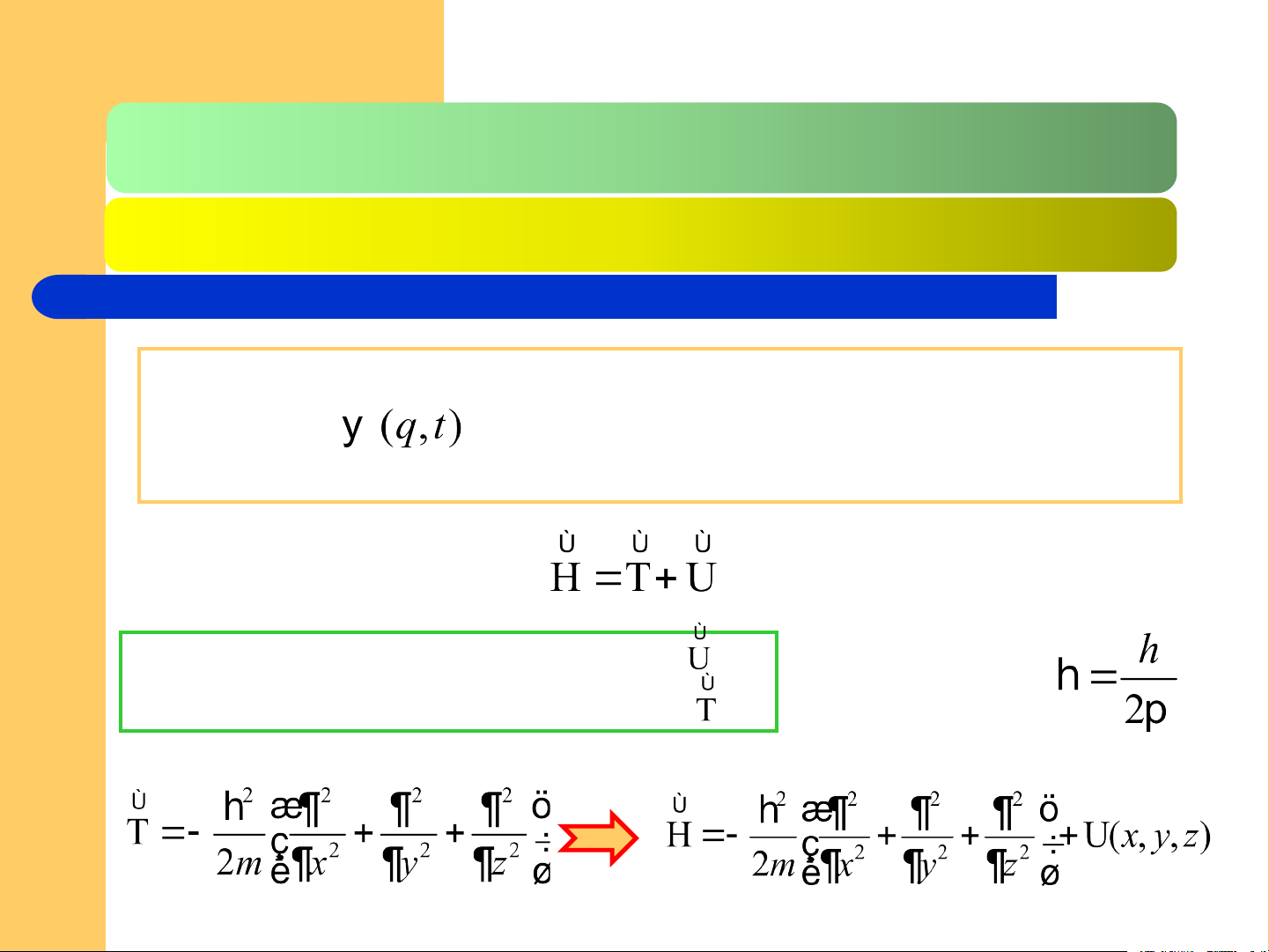
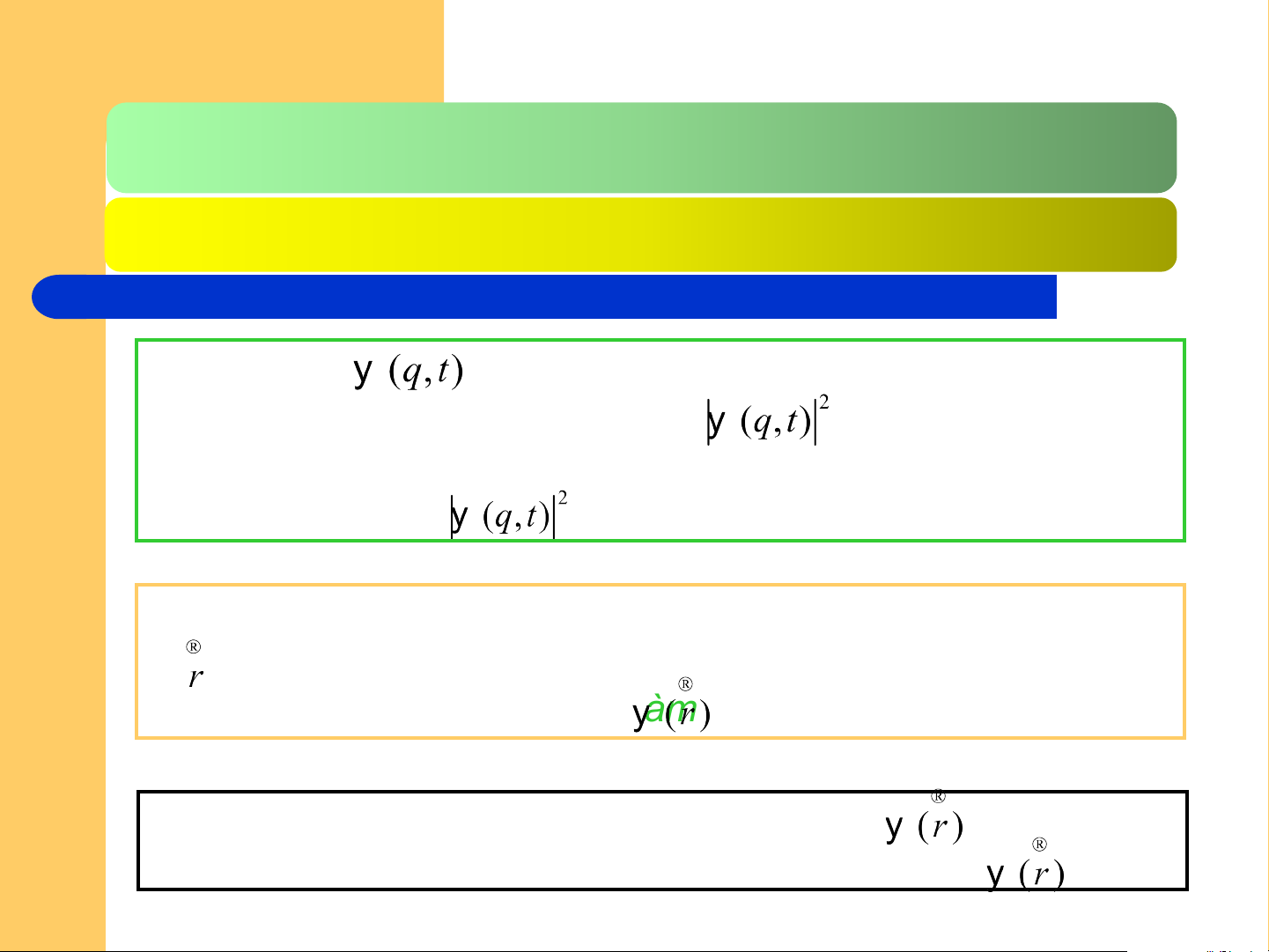
Mỗi trạng thái của hệ lượng tử được mô tả đầy đủ bằng một hàm
- là hàm x/đ của tọa độ khái quát q và
thời gian t – được gọi là hàm sóng hay hàm trạng thái
Thế năng U có tương ứng toán tử
Động năng T có tương ứng toán tử
2.1. Cấu tạo nguyên tử theo cơ học LT
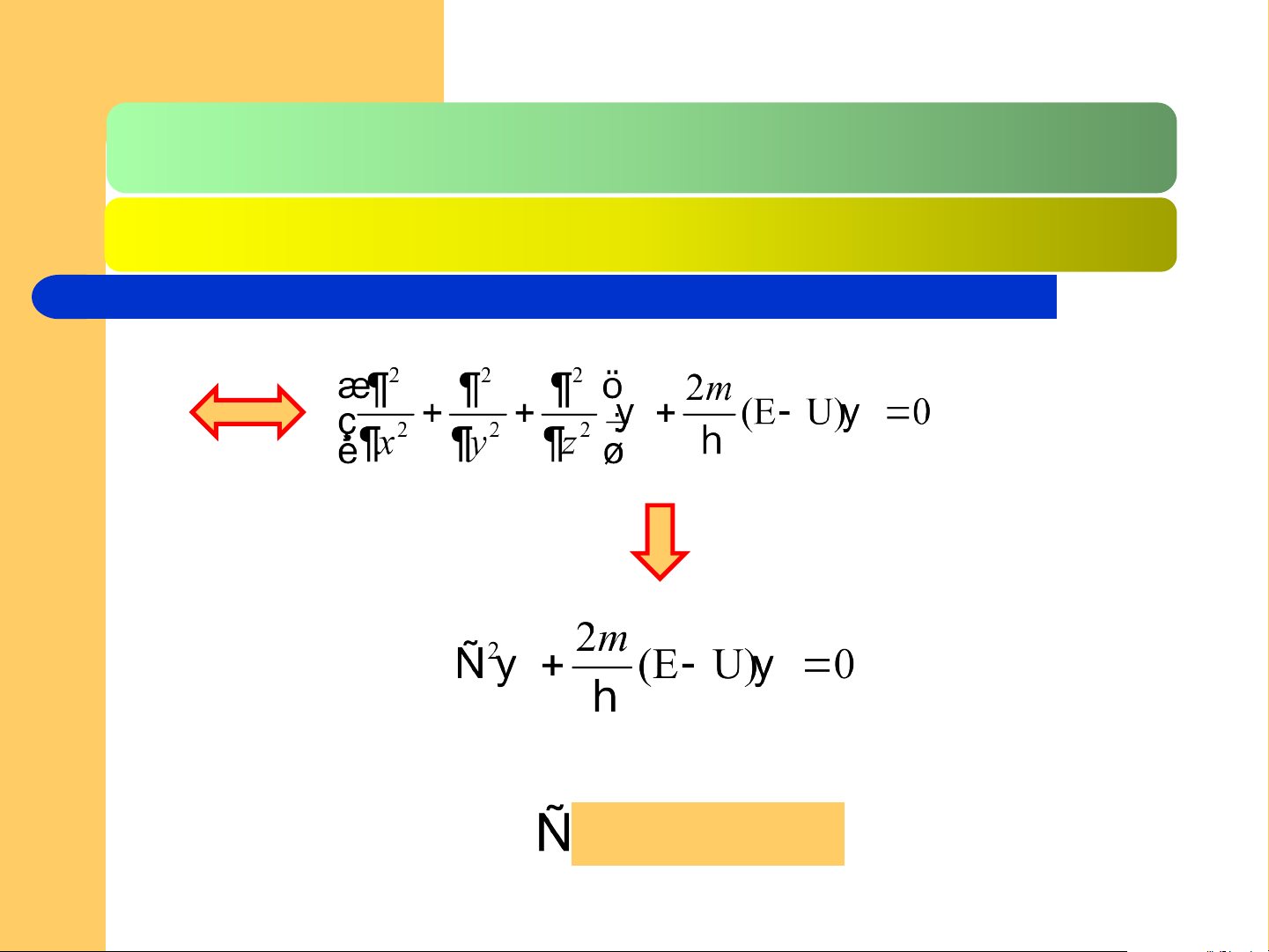
2.1.1. Các luận điểm cơ bản CHLT toán tử laplace
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT Hàm sóng
ko có ý nghĩa vật lí trực tiếp, song bình
phương mô đun của hàm đó - - cho biết xác suất tìm
thấy hệ lượng tử tại 1 điểm trong ko gian có toa độ q ở thời điểm t. Hàm
được gọi là hàm mật độ xác suất
Trong ko gian, vị trí của 1 hệ lượng tử được chỉ bằng tọa
độ (vecto vị trí), do vậy hàm sóng mô tả trạng thái hệ
lượng tử sẽ được kí hiệu là
PT Srodingo là pt hàm riêng trị riêng, trong đó là hàm riêng
của toán tử H, E là trị riêng của H ứng với hàm riêng
2.1. Cấu tạo nguyên tử theo cơ học LT
2.1.1. Các luận điểm cơ bản CHLT
PT Srodingo là PT vi phân tuyến tính cấp 2(hay là pt đạo hàm riêng cấp 2)
Đối với bấc kì hệ lượng tử nào – ion, nguyên tử, phân tử …-
lời giải của PT Srôđingơ cho hệ đó phải bao gồm đồng thời 2
kết quả: hàm riêng
và trị riêng năng lượng toàn phần E
ứng với hàm riêng đó của H
Việc giải PT sóng Srodingo hết sức phức tạp. Bài toán này chỉ có thể
giải chính xác cho chuyển động của 1 hạt vi mô mà thôi, còn đ/v t/h
khác chỉ giải theo pp gần đúng. Tuy nhiên, những kq thu đc qua tính
toán với nhiều hệ nt, pt khác nhau cho thấy phù hợp với thực nghiệm
2.1. Cấu tạo nguyên tử theo cơ học LT
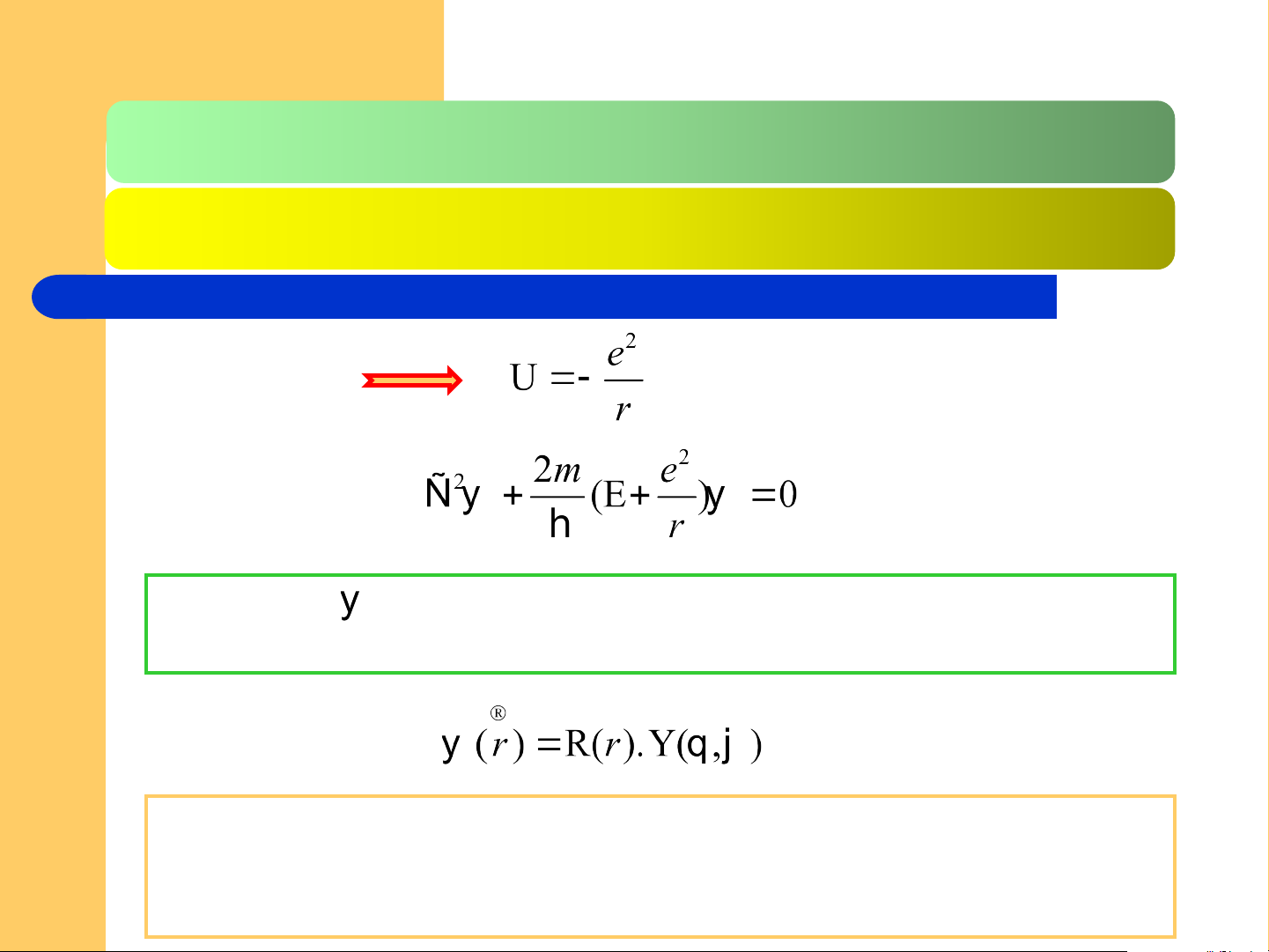
2.2.2. Trạng thái e trong nguyên tử H và ion 1 e Đối với H Hàm sóng
mô tả trạng thái chuyển động của e trong trường
lực đối xứng xuyên tâm đc tách thành tích của 2 phần:
R(r) được gọi là hàm bán kính hay phần xuyên tâm, phụ thuộc
vào 2 tham số n và l; n là số lượng tử chính, l là số lượng tử phụ. Kí hiệu: Rn,l(r).
2.1. Cấu tạo nguyên tử theo cơ học LT
2.2.2. Trạng thái e trong nguyên tử H và ion 1 e
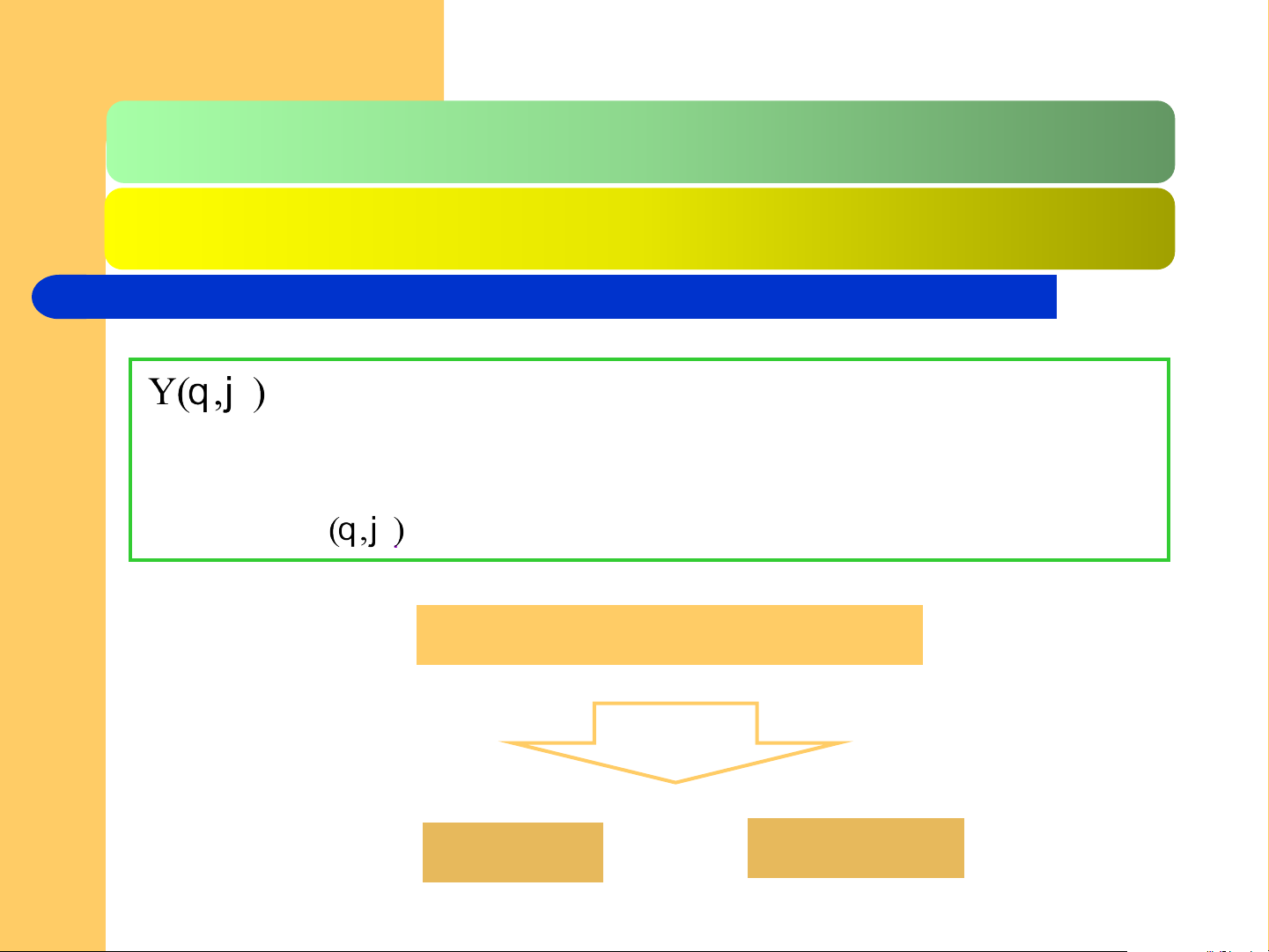
gọi là hàm cầu hay hàm góc. Là hàm riêng của
toán tử mo men động lượng obitan, đó là hàm cầu phụ
thuộc vào số lượng tử phụ l và số lượng tử từ m, nên có kí hiệu là Yl,m .
Giải phương trình Srodingo Trị riêng Hàm riêng
2.1. Cấu tạo nguyên tử theo cơ học LT
2.2.2. Trạng thái e trong nguyên tử H và ion 1 e Trị riêng
Số lượng tử chính n (n = 1;2;3;…,nguyên, dương).
Một giá trị của n có n giá trị l, từ 0 đến (n – 1)
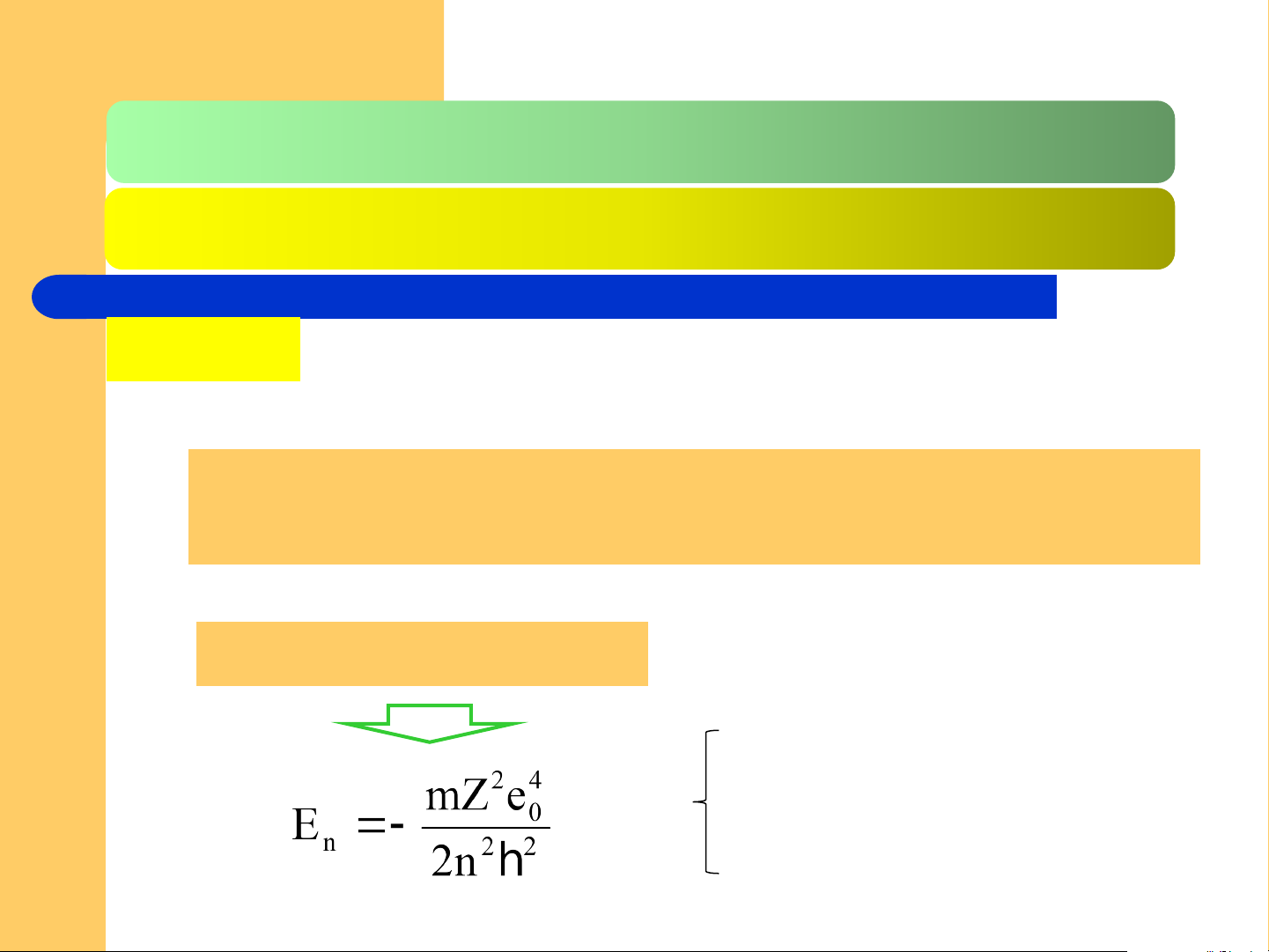
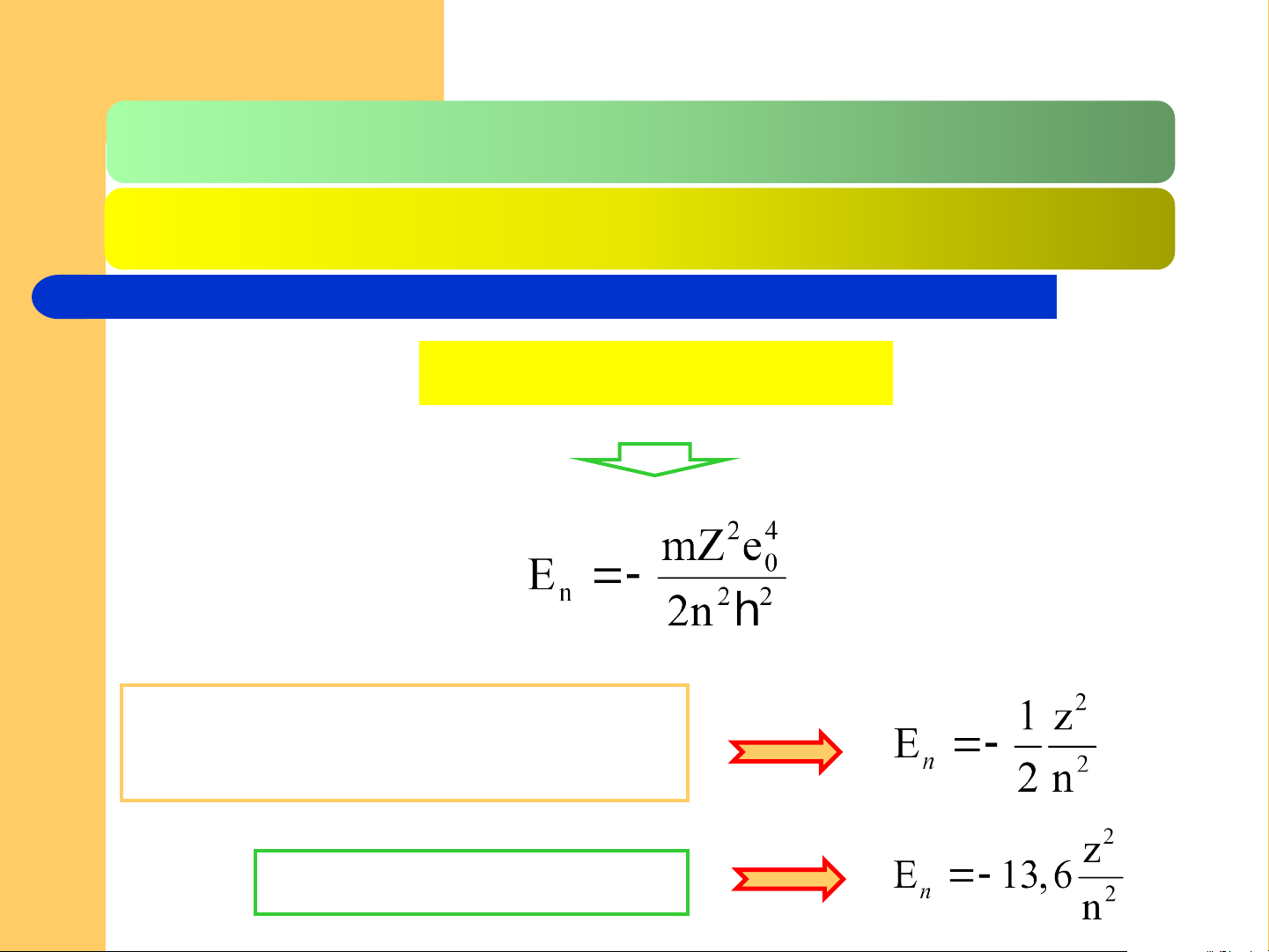
Biểu thức năng lượng m là khối lượng một e e là điện tích cơ sở
Z là điện tích hạt nhân
2.1. Cấu tạo nguyên tử theo cơ học LT
2.2.2. Trạng thái e trong nguyên tử H và ion 1 e
z = 1  nguyên tố xét là H, hệ đó là ng tử H
z = 2  nguyên tố xét là He, hệ đó là He+
z = 3  nguyên tố xét là Li, hệ đó là Li2+
n là số lượng tử chính xác định trạng thái
năng lượng của e trong nguyên tử
2.1. Cấu tạo nguyên tử theo cơ học LT
2.2.2. Trạng thái e trong nguyên tử H và ion 1 e
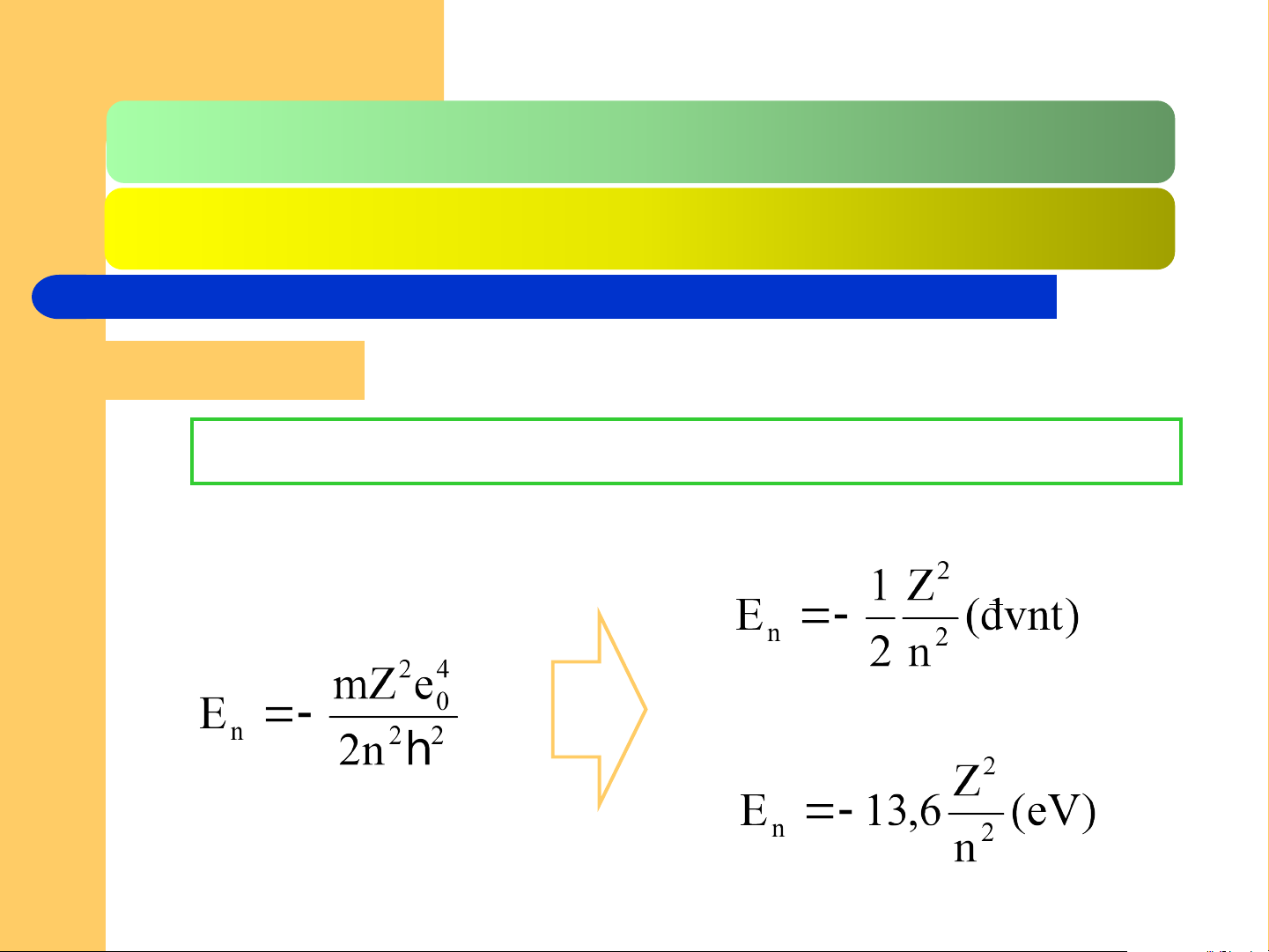
Sự liên hệ giữa E và n
Đối với hệ đơn vị nguyên tử (đvn hay au)
Đối với hệ đơn vị eV
2.1. Cấu tạo nguyên tử theo cơ học LT
2.2.2. Trạng thái e trong nguyên tử H và ion 1 e Bài tập áp dụng
Hãy tính năng lượng ứng với n = 1 cho H, He+, Li2+
2.1. Cấu tạo nguyên tử theo cơ học LT
2.2.2. Trạng thái e trong nguyên tử H và ion 1 e
H : Z = 1 → E1 = - 13,6 eV hay E1 = - 0,5 đvnt
He+ : Z = 2 → E1 = - 54,4 eV hay E1 = - 2 đvnt
Li2+ : Z = 3 → E1 = - 122,4 eV hay E1 = - 4,5 đvnt 1 đvnt = 27,2 eV