lOMoAR cPSD| 40419767 lOMoAR cPSD| 40419767
Chương 2 - Gía trị thời gian của tiền lOMoAR cPSD| 40419767
2.1. Chuỗi thời gian và chuỗi tiền tệ
2.2. Lãi ơn, lãi kép và giá trị tương lai của tiền
2.3. Giá trị hiện tại của tiền
2.4. Một số ứng dụng giá trị thời gian của tiền lOMoAR cPSD| 40419767
Giá trị thời gian của tiền
Tiền có giá trị theo thời gian không? lOMoAR cPSD| 40419767
Giá trị thời gian của tiền
 Khái niệm “giá trị thời gian của tiền có hàm ý nói lên rằng
tiền tệ có giá trị theo thời gian.
 Tiền tệ có giá trị theo thời gian vì:  Yếu tố lạm phát  Tính rủi ro
 Do thuộc tính vận ộng và khả năng sinh lời lOMoAR cPSD| 40419767 Chuỗi thời gian 0 1 2 ........................ n-1 n lOMoAR cPSD| 40419767
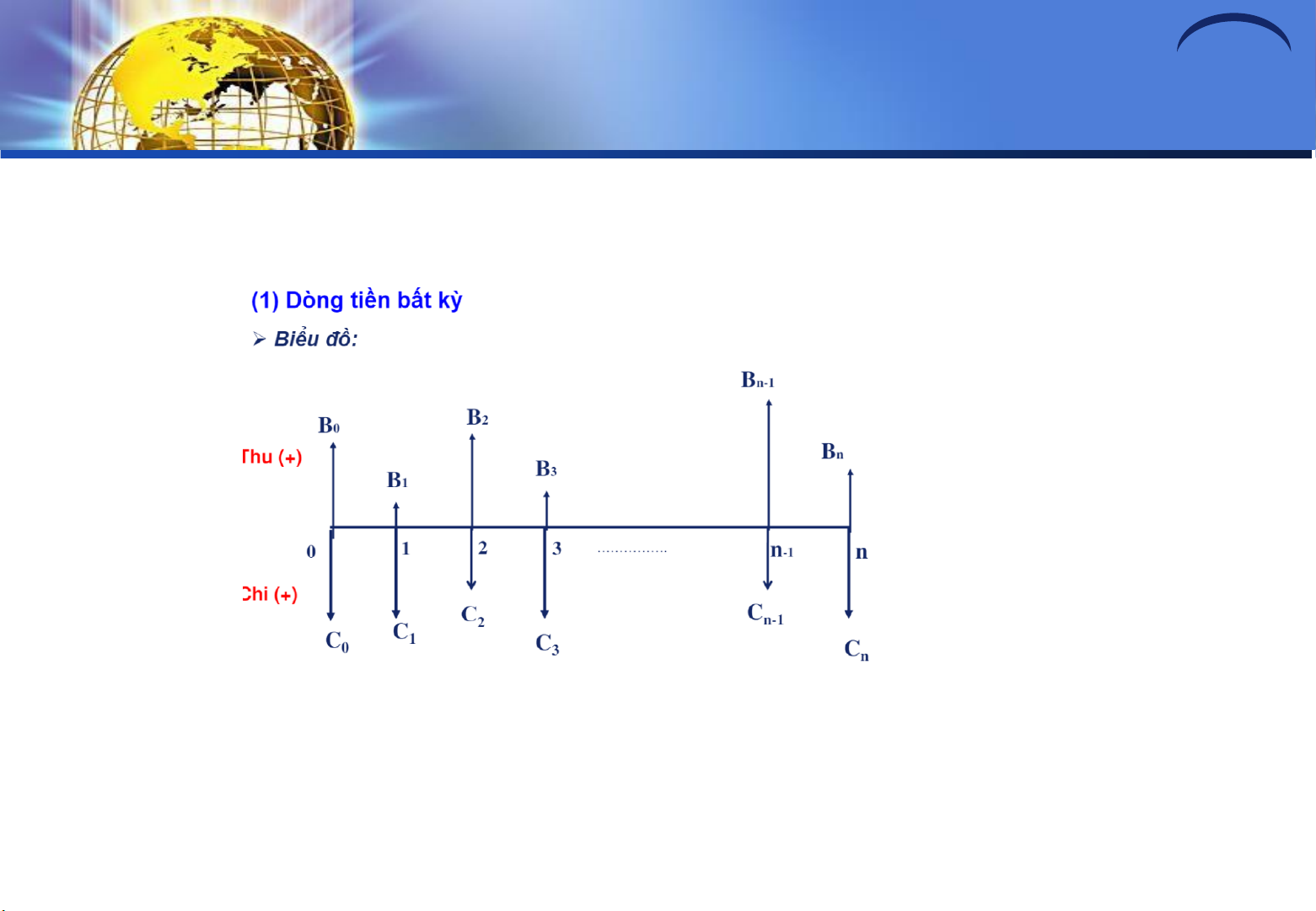
(1) Dòng tiền bất kỳ
Biểu ồ: B n-1 B 2 B 0 Thu (+) B n B 3 B 1 0 ……………. 1 2 3 n -1 n Chi (+) C 2 C n-1 C C 1 0 C 3 C n lOMoAR cPSD| 40419767 Chuỗi tiền tệ lOMoAR cPSD| 40419767 Chuỗi tiền tệ Cuốikỳ Đều Đầukỳ Chuỗi tiền tệ Cuối kỳ Không đều Đầukỳ lOMoAR cPSD| 40419767
Lãi ơn, lãi kép và giá trị tương lai
 Lãi ơn: Là số tiền lãi tính theo số vốn gốc theo một lãi suất nhất định
 Lãi kép: Số thời tiền lãi của kỳ này ược tính dựa trên cơ sở số
tiền lãi của các kỳ trước ó gộp cùng số vốn gốc và một lãi suất nhất định lOMoAR cPSD| 40419767 Giá trị tương lai
Là giá trị ược xác ịnh ở một thời iểm trong tương lai của
một lượng tiền ơn, hoặc một chuỗi tiền tệ nhất ịnh lOMoAR cPSD| 40419767
Giá trị tương lai của một lượng tiền tệ ơn
Là toàn bộ giá trị có thể nhận ược ở một thời iểm trong
tương lai, bao gồm số vốn gốc và toàn bộ tiền lãi có thể
nhận ược tới thời iểm ó lOMoAR cPSD| 40419767
Theo phương pháp tính lãi ơn FV = n V0 (1 r n)
FVn: giá trị tương lai (giá trị ơn) tại thời iểm n Vo : Số vốn gốc
r : lãi suất của một kì ( năm, nửa năm, quý, tháng) n : số kỳ tính lãi lOMoAR cPSD| 40419767
Theo phương pháp tính lãi kép FV = = ´ n
V0 (1+r)n FVn
V0 FVF(r,n)
FVn: giá trị tương lai (giá trị kép) tại thời iểm n
(1+r)n: Thừa số lãi suất tương lai của lượng tiền ơn lOMoAR cPSD| 40419767
Trong công tác QTTC tính theo phương pháp
lãi kép có tầm quan trọng:
1. Khi ra quyết định đầu tư 2. Sử dụng trong việc lượng giá chứng khoán
3. Khi cân nhắc giữa thuê và mua tài sản… lOMoAR cPSD| 40419767
Giá trị tương lai của chuỗi tiền tệ
 Giá trị tương lai của chuỗi tiền tệ chính là tổng giá trị
tương lai của từng khoản tiền CFt xảy ra ở từng thời iểm
khác nhau quy về cùng một mốc tương lai là thời iểm n.
 Ta phải xác ịnh giá trị tương lai của từng khoản CFt và
cộng toàn bộ các giá trị tương lai ó lại với nhau.
Giá trị tương lai của chuỗi tiền tệ ều:
+ Đối với chuỗi tiền tệ cuối kỳ lOMoAR cPSD| 40419767
Giá trị tương lai của chuỗi tiền tệ (1+ −r)n 1 = FVAn CFx =CF FVFA r n( , ) r
FVAn: Giá trị tương lai của chuối tiền tệ ều cuối kì
CF: giá trị khoản tiền ồng nhất ở mỗi thời kì r: lãi
suất một kì n: số thời kì
FVFA(r,n): thừa số lãi suất tương lai của chuỗi tiền tệ ều
+ Đối với chuỗi tiền tệ ều ầu kỳ: lOMoAR cPSD| 40419767
Giá trị tương lai của chuỗi tiền tệ FVAĐ = n CF FVFA r n( , ) (1 r) lOMoAR cPSD| 40419767
Giá trị tương lai của chuỗi tiền tệ
Giá trị tương lai của chuỗi tiền tệ không ều n FV = n CFt (1 r)n t− t=1
FVn: Giá trị tương lai của chuỗi tiền tệ
CFt: Giá trị của khoản tiền ở thời iểm t lOMoAR cPSD| 40419767
Giá trị tương lai của chuỗi tiền tệ r: tỷ lệ chiết khấu n: số kỳ hạn lOMoAR cPSD| 40419767
Giá trị hiện tại của tiền
 Giá trị hiện tại của một lượng tiền ơn 1 PV = FVn (1+r)n PV: Giá trị hiện tại lOMoAR cPSD| 40419767
Giá trị hiện tại của chuỗi tiền tệ
FVn: Giá trị của khoản tiền tại thời iểm n r:
tỷ lệ chiết khấu (tỷ lệ hiện tại hóa) 1
: Hệ số chiết khấu (hệ số hiện tại hóa) (1+r)n
 Giá trị hiện tại của chuỗi tiền tệ ều
+ Đối với chuỗi tiền tệ cuối kỳ
1− +(1 r)−n lOMoAR cPSD| 40419767
Giá trị hiện tại của chuỗi tiền tệ PVA = CF = CF PVFA r n( , ) r
PVA: Giá trị hiện tại của chuỗi tiền tệ ều cuối kỳ
CF: Giá trị khoản tiền ồng nhất ở cuối mỗi thời kỳ
PVFA(r,n): Thừa số lãi suất hiện tại của chuỗi tiền tệ ều
 Đối với chuỗi tiền tệ ầu kỳ lOMoAR cPSD| 40419767
Giá trị hiện tại của chuỗi tiền tệ FVAĐ = n PVA (1 r) FVAĐ = n CF PVFA r n( ; ) (1 r) lOMoAR cPSD| 40419767
Giá trị hiện tại của chuỗi tiền tệ
 Đối với chuỗi tiền tệ vô hạn: 1 PVA =CF r lOMoAR cPSD| 40419767
Giá trị hiện tại của chuỗi tiền tệ
Giá trị hiện tại của chuỗi tiền tệ biến thiên = 1 = PVA n CF n t t CFt PVF r t( , ) t=1
(1+r) t=1 lOMoAR cPSD| 40419767
Cách xác ịnh lãi suất năm
PV: Giá trị tương lai của chuỗi tiền tệ
CFt: Giá trị của khoản tiền ở thời iểm t
r: Tỷ lệ chiết khấu n: số kỳ hạn
Một số ứng dụng giá trị thời gian của tiền
1. Cách xác định lãi suất năm
2. Lập kế hoạch trả tiền lOMoAR cPSD| 40419767
 Tìm lãi suất của khoản tiền có kỳ hạn 1 năm: FV = n PV (1 r)n Khi n=1: r FV −1 PV lOMoAR cPSD| 40419767
Cách xác ịnh lãi suất năm
 Tìm lãi suất thực của khoản tiền có kỳ hạn trên 1 năm FV = n PV (1 r)n FV − r n 1 PV lOMoAR cPSD| 40419767
Cách xác ịnh lãi suất năm
 Tìm lãi suất của khoản tiền có kỳ hạn nhập lãi dưới 1 năm lOMoAR cPSD| 40419767
Cách xác ịnh lãi suất năm r r = + e (1 )m −1 m
m: số lần nhập lãi trong năm
r: lãi suất năm danh nghĩa
r/m: lãi suất của kỳ hạn (6 tháng, quý, tháng…) lOMoAR cPSD| 40419767
Cách xác ịnh lãi suất năm
Tìm lãi suất trả góp
DN phát sinh các trường hợp vay trả góp, hoặc thuê mua
trả góp, mà các khoản tiền vay phải trả ược quy ịnh vào
cuối mỗi thời kỳ với số tiền bằng nhau -> xác ịnh lãi suất
của các hợp ồng tài trợ này ể làm căn cứ cho việc ra các q trả nợ lOMoAR cPSD| 40419767
Lập kế hoạch trả tiền
Lập kế hoạch trả tiền vào cuối mỗi kỳ thanh toán, với số tiền bằng nhau PV CF=
PVFA(r,n)
PV: số tiền tài trợ ban ầu lOMoAR cPSD| 40419767 n: số kỳ thanh toán r: lãi suất tài trợ
CF: số tiền thanh toán cuối mỗi kỳ Ví dụ
Một DN thuê mua một máy dập của một công ty cho
thuê với giá trị 100 tr , lãi suất tài trợ 6%/năm, trả dần
trong thời hạn 4 năm vào cuối mỗi năm. lOMoAR cPSD| 40419767
KH trả tiền vào cuối mỗi kỳ thanh toán Kì Số tiền tài trợ Tiền t.toán Trả lãi Trả nợ gốc Số tiền CK ĐK(1) trong kỳ (2) (3)=(1)*r (4)=(2)-(3) (5)=(1)-(4) 1 100.000.000 28.859.149 6.000.000 22.859.149 77.140.851 2 77.140.851 28.859.149 4.628.451 24.230.698 52.910.153 3 52.910.153 28.859.149 3.174.609 25.684.540 27.225.613 4 27.225.613 28.859.149 1.633.536 27.225.613 0 lOMoAR cPSD| 40419767 Cộng 115.436.596 15.436.596 100.000.000
Lập kế hoạch trả tiền
Lập kế hoạch thanh toán ngay khi hợp ồng có hiệu lực
với số tiền bằng nhau PV CF=
1+PVFA(r,n) lOMoAR cPSD| 40419767 Ví dụ 2
Sử dụng số liệu ví dụ 1. Lập KH trả tiền ngay sau khi
hợp ồng có hiệu lực, với số tiền bằng nhau PV 100.000.000 CF= = = 22.395.914
1+PVFA(r,n) 1+3,4651 lOMoAR cPSD| 40419767
KH trả tiền ngay khi hợp ồng có hiệu
lực với số tiền bằng nhau Kì Số tiền tài trợ Tiền t.toán Trả lãi Trả nợ gốc Số tiền CK ĐK(1) trong kỳ (2) (3)=(1)*r (4)=(2)-(3) (5)=(1)-(4) 0 100.000.000 22.395.914 0 22.395.914 77.604.086 1 77.604.086 22.395.914 4.656.245,1 17.739.668,9 59.864.417,1 2 59.864.417,1 22.395.914 3.591.865 18.804.049 41.060.368,1 lOMoAR cPSD| 40419767 3 41.060.368,1 22.395.914 2.463.622,0 19.932.292 21.128.076,1 4 21.128.076,1 22.395.914 1.267.837,9 21.128.076,1 lOMoAR cPSD| 40419767
 Hàm FV (Future Value)
 Tính giá trị tương lai của một khoản ầu tư có lãi suất cố ịnh trả
theo ịnh kỳ hoặc gửi thêm vào.
 Cú pháp: =FV(rate, nper, pmt, pv, type) Trong ó:
• rate là lãi suất mỗi kỳ
• nper là tổng số kỳ tính lãi
• pmt là số tiền phải trả ều trong mỗi kỳ, nếu bỏ trống thì coi là 0
• pv là giá trị hiện tại của khoản ầu tư, nếu bỏ trống thì coi là 0
• type là hình thức thanh toán. Nếu type = 1 thì thanh toán ầu kỳ,
nếu type = 0 thì thanh toán vào cuối mỗi kỳ (mặc ịnh) lOMoAR cPSD| 40419767
Ứng dụng tính giá trị thời gian của tiền
Ứng dụng tính giá trị thời gian của tiền
 Ví dụ 5: Tính số tiền một người gửi 10.000$ vào ngân hàng và mỗi
năm gửi thêm 200$ với lãi suất 5%/năm (bỏ qua lạm phát) sau 10 năm
 Lưu ý: các khoản khi gửi vào NH ược coi là ầu tư do vậy dòng tiền
này có số âm. Tiền thu về (sau 1 số năm) là dòng tiền dương
Ngược lại, nếu vay tiền từ NH thì khoản vay là khoản tiền dương,
tiền trả NH là dòng tiền âm
 Hàm PV (Present Value) lOMoAR cPSD| 40419767
 Trả về giá trị hiện tại của một khoản đầu tư theo từng kỳ.
 Cú pháp: =PV(rate, nper, pmt, fv, type)
Trong ó: fv là giá trị tương lai của khoản ầu tư và các tham số
khác tương tự như hàm FV.
 Ví dụ 6: Một người muốn có số tiền tiết kiệm 300 ngàn USD sau
năm 10 năm. Hỏi bây giờ người ó phải gửi vào ngân hàng bao
nhiêu? biết lãi suất ngân hàng là 6%/năm (bỏ qua lạm phát) lOMoAR cPSD| 40419767
Ứng dụng tính giá trị thời gian của tiền
Ứng dụng tính giá trị thời gian của tiền  Hàm PMT (Payment)
 Trả về khoản tương ương từng kỳ cho một khoản ầu tư có lãi suất
cố ịnh trả theo ịnh kỳ.
 Cú pháp: =PMT(rate, nper, pv, fv, type)
 Các tham số tương tự như các hàm trên.
 Ví dụ 7: Một người muốn có khoản tiền tiết kiệm 50 triệu ồng sau 5
năm thì người ó phải gửi vào ngân hàng mỗi tháng bao nhiêu tiền?
Biết lãi suất ngân hàng là 8%/năm (bỏ qua lạm phát). lOMoAR cPSD| 40419767
 Hàm IPMT(Interest Payment)
 Tính khoản lãi phải trả trong một khoảng thời gian cho một
khoản ầu tư có lãi suất cố ịnh trả theo ịnh kỳ cố ịnh. Cú pháp:
=IPMT(rate, per, nper, pv, fv, type)  Trong ó:
 rate là lãi suất cố ịnh
 per là khoảng thời gian cần tính lãi
 nper tổng số lần thanh toán
 pv là khoản tiền vay hiện tại
 fv là khoản tiền còn lại khi ến kỳ thanh toán. lOMoAR cPSD| 40419767
Ứng dụng tính giá trị thời gian của tiền
 type là kiểu thanh toán. Nếu type = 1 thì thanh toán ầu kỳ, nếu type
= 0 thì thanh toán vào cuối kỳ (mặc ịnh) lOMoAR cPSD| 40419767
Ứng dụng tính giá trị thời gian của tiền
 Hàm IPMT(Interest Payment)
 Như vậy, thường IPMT (tiền trả lãi) sẽ ược dùng sau khi tính
PMT (tổng tiền trả). Phần chênh lệch giữa 2 ại lượng này chính
là tiền trả gốc (Principal Payment).
 Ví dụ 8: Nếu vay ngân hàng một khoản tiền 1000$ với lãi suất
2%/năm (lãi kép) trong 5 năm thì lượng tiền phải trả mỗi năm là
bao nhiêu? Lượng tiền lãi trả mỗi năm là bao nhiêu? lOMoAR cPSD| 40419767
Ứng dụng tính giá trị thời gian của tiền
 Hàm NPER (Number of PERiod)
 - Trả về số kỳ của một khoản ầu tư trên cơ sở các khoản thanh
toán bằng nhau ịnh kỳ và lãi suất không ổi. - Cú pháp:
=NPER(rate,pmt,pv,[fv],[type]) - Các tham số tương tự như các hàm trên.
 Ví dụ 9: Có một căn hộ bán trả góp theo hình thức sau: Giá trị
của căn hộ là $500,000,000, trả trước 30%, số còn lại ược trả góp
$3,000,000 mỗi tháng (bao gồm cả tiền nợ gốc và lãi), biết lãi suất lOMoAR cPSD| 40419767
Ứng dụng tính giá trị thời gian của tiền
là 8% một năm, vậy bạn phải trả trong bao nhiêu năm thì mới xong?
 Hàm RATE (Interest Rate)
 - Trả về lãi suất theo kỳ hạn của một dòng tiền cố ịnh.
- Cú pháp: =RATE(nper, pmt, pv, [fv], [type], [guess]) -
Các tham số tương tự như các hàm trên.
Ví dụ 10: Ông A quyết ịnh từ 2017 ến 2026, cuối mỗi năm ông sẽ
gửi vào ngân hàng một số tiền không ổi là 100 triệu ồng ể tiết kiệm. lOMoAR cPSD| 40419767
Ứng dụng tính giá trị thời gian của tiền
Biết dự kiến số tiền ông có ược vào cuối năm 2026 là 1,5 tỷ ồng. Lãi
suất tiền gửi của ngân hàng là bao nhiêu? (giả sử lãi suất không ổi qua các năm)