



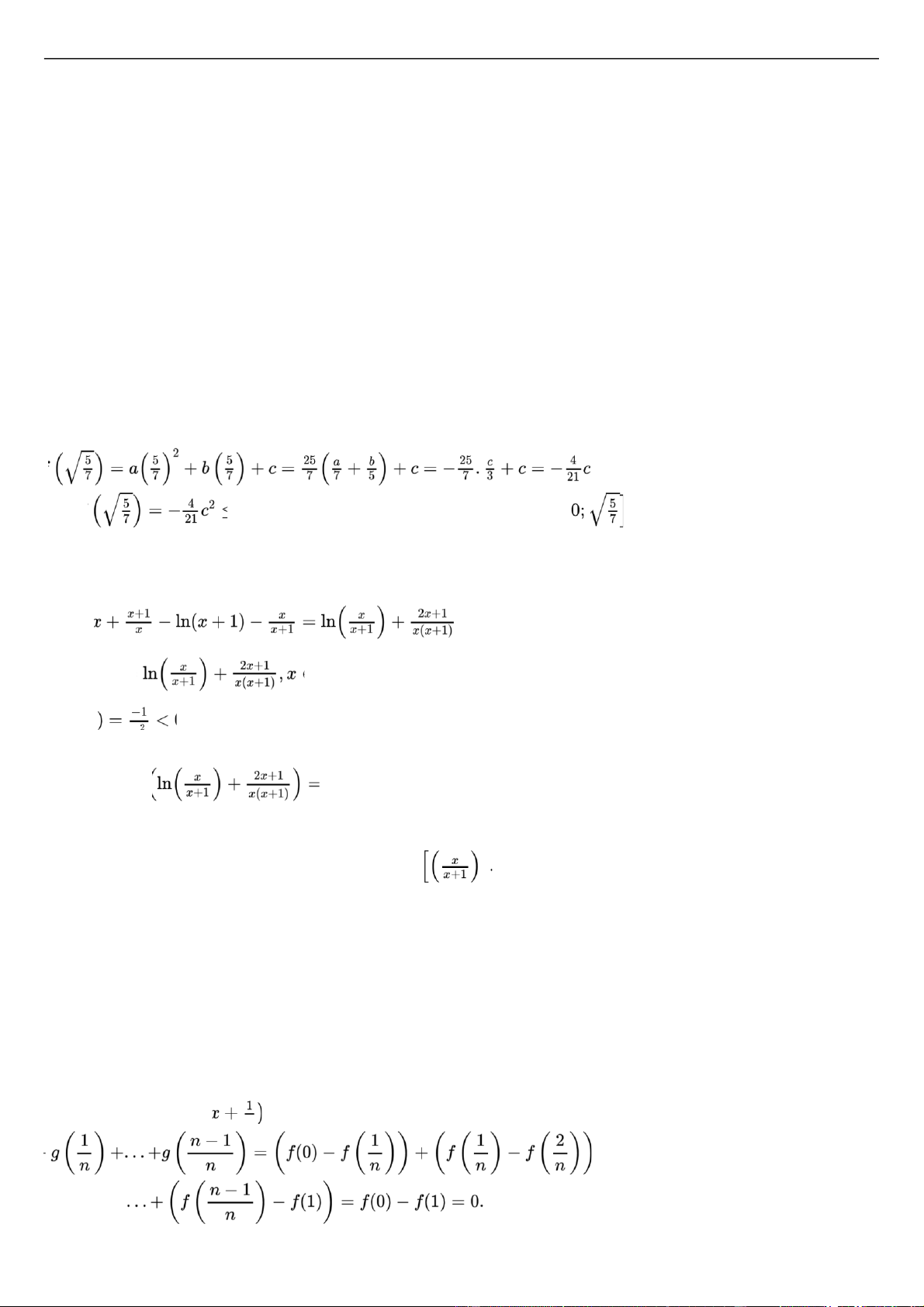

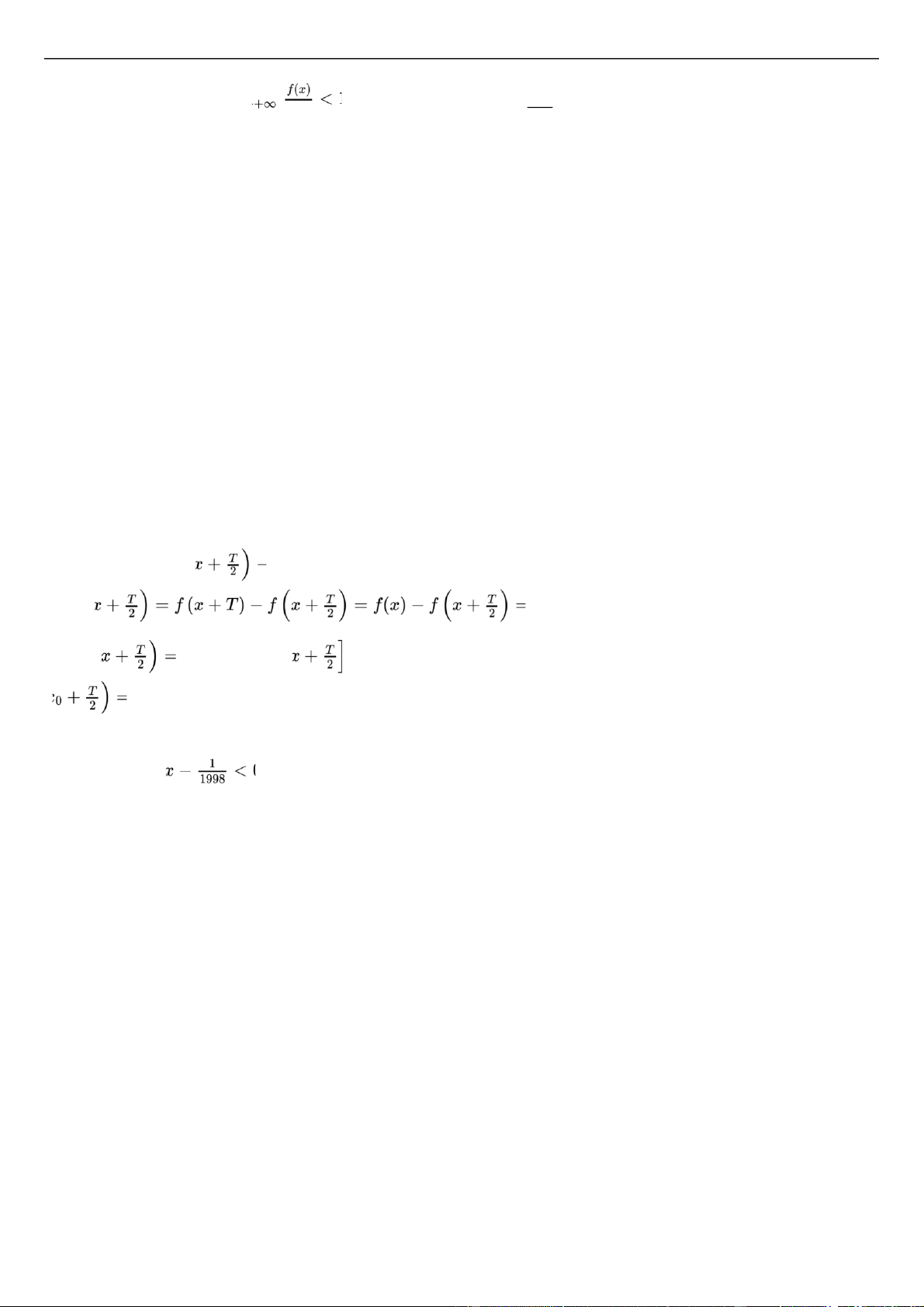




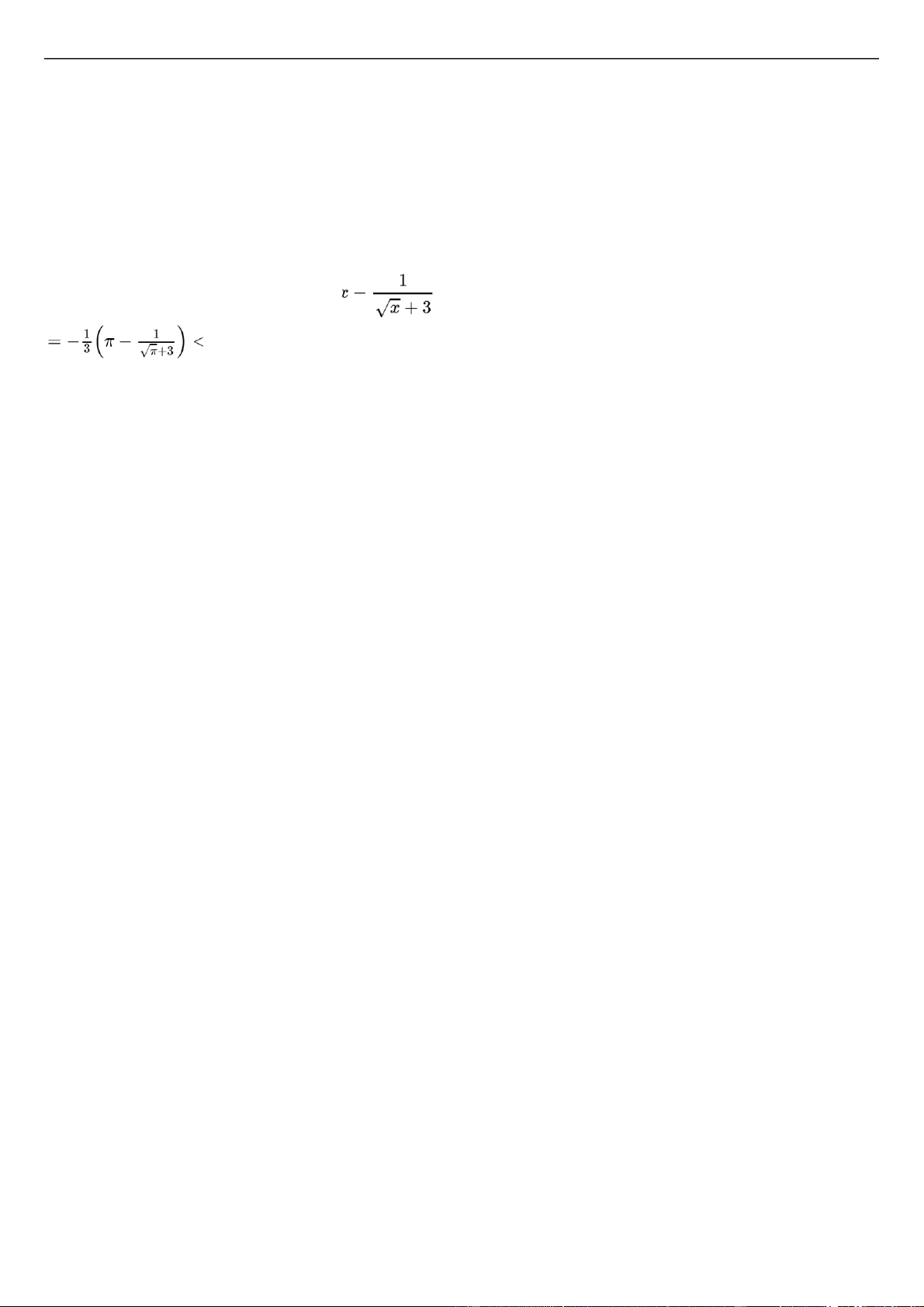
Preview text:
lOMoAR cPSD| 40551442
Họ, tên thí sinh:............................................................................... Trường: ............................................................ a b c
Câu 1 [Q755113955] Chứng minh mọi số thực a,b,c,m (m > 0) thoả mãn + + = 0 thì
m + 2 m + 1 m phương trình ax2
+ bx + c = 0 luôn có nghiệm thực.
Câu 2 [Q708137780] Cho phương trình ax2 + (2b + c)x + 2d + e = 0 có nghiệm không nhỏ hơn 4. Chứng minh phương
trình ax4 + bx3 + cx2 + dx + e = 0 có nghiệm.
Câu 3 [Q858057536] Giả sử phương trình ax2 + (b + c)x + d + e = 0 có nghiệm x0 > 1, chứng minh rằng phương trình
ax4 + bx3 + cx2 + dx + e = 0 có nghiệm.
Câu 4 [Q728838806] Chứng minh rằng các phương trình sau ây có nghiệm : 3x = sinx;2x = x2 + x + 3.
Câu 5 [Q815753151] Chứng minh rằng phương trình x6 − 9x − 8 = 0 có ít nhất hai nghiệm thực. Câu 6
[Q760135806] Chứng minh rằng phương trình x5 + x2 − 8x + 1 = 0 có ít nhất ba nghiệm thực. a b c
Câu 7 [Q358438437] Cho các số thực a,b,c thoả mãn + +
= 0. Chứng minh rằng phương trình 7 5 3
ax4 + bx2 + c = 0 có nghiệm thực.
Câu 8 [Q790476566] Chứng minh rằng phương trình xx+1 = (x + 1)xcó nghiệm thực dương duy nhất.
Câu 9 [Q420545107] Chứng minh rằng mọi a thức bậc lẻ luôn có nghiệm thực.
Câu 10 [Q733118027] Chứng minh rằng một hàm số liên tục và tuần hoàn thì bị chặn.
Câu 11 [Q223515152] Cho f : [0,1] → R là hàm số liên tục sao cho f(0) = f(1). Chứng minh rằng với mọi số nguyên
dương tồn tại n c ∈ [0,1]sao cho f(c) = f (c + 1 n ).
Câu 12 [Q699500449] Cho là hàm liên tục trên f
[0,2]và f(0) = f(2). Chứng minh rằng tồn tại x1 và x2 trong
[0,2] sao cho x2 − x1 = 1 và f(x2) = f(x1).
Câu 13 [Q794221437] Cho hàm số f(x) liên tục và tuần hoàn trên R. Chứng minh rằng phương trình f(x) = f(x + π) luôn có nghiệm thực.
Câu 14 [Q451625243] Cho là hàm liên tục và tuần hoàn trên . Chứng minh rằng tồn tại f R x1 và x2 trong [0,2] sao
cho x2 − x1 = 1 và f(x2) − f(x1) = (f(2) − f(1)).
Câu 15 [Q906359392] Cho a thức P(x) khác 0. Chứng minh rằng phương trình |P(x)| = ex luôn có nghiệm thực.
Câu 16 [Q564177841] Cho f : R → R là hàm liên tục thỏa mãn f(x) = f (x + T),T > 0 với mọi x ∈ R. Chứng minh rằng với
mọi số thực thì phương trình c f(x) = x + c luôn có nghiệm.
Câu 17 [Q054717415] Cho f : R → R là hàm số liên tục và tuần hoàn với chu kỳ bằng . Chứng minh rằng phương1
trình f(x) = f (x + π)luôn có nghiệm.
Câu 18 [Q514473663] Cho f : [0;1] → [0;1] là một hàm liên tục. Chứng minh rằng phương trình =
1có nghiệm duy nhất trên [0;1].
Câu 19 [Q377869946] Cho f : [0,+∞) → [0,+∞) là hàm liên tục thỏa mãn lim
x . Chứng minh rằng tồn tại
x0 ∈ [0,+∞)sao cho f(x0) = x0.
Câu 20 [Q125300100] [Nowak II] Cho các số thực a0 < b0 < a1 < b1 <...< an < bn. Chứng minh rằng mọi n
n nghiệm của a thức P(x) = ∏ (x + ak) + 2 ∏ (x + bk) ều là nghiệm thực. k=0 k=0
Câu 21 [Q713300637] [VMC 2009] Giả sử f,g là các hàm số liên tục trên và thỏa mãn iều kiệnR
f (g(x)) = g(f(x)),∀x ∈ R. / lOMoAR cPSD| 40551442
Chứng minh rằng nếu phương trình f(x) = g(x) không có nghiệm thực thì phương trình f (f(x)) = g(g(x)) cũng không có nghiệm thực.
Câu 22 [Q917651716] Cho f : R → R là hàm liên tục và tuần hoàn với chu kỳ T > 0. Chứng minh rằng tồn tại x0 ∈ R sao cho f (x0 + T2 ) = f(x0).
Câu 23 [Q150636527] [VMC 1998] Cho f(x) liên tục trên [0,1] có f và . Chứng minh
rằng phương trình f(x) = x1997 luôn có ít nhất một nghiệm thuộc (0,1).
Câu 24 [Q755805053] Cho f : R → R là hàm liên tục và nhận giá trị trái dấu. Chứng minh rằng tồn tại cấp số cộng a <
b < c sao cho f(a) + f(b) + f(c) = 0.
Câu 25 [Q571600106] Cho f : R → R là hàm liên tục và nhận giá trị trái dấu trên (0,+∞). Chứng minh rằng tồn tại cấp
số nhân 0 < a < b < c sao cho f(a) + f(b) + f(c) = 0.
Câu 26 [Q655057002] Cho f : R → R thỏa mãn iều kiện |f(a) − f(b)| < |a − b|,∀a,b ∈ R,a ≠ b. Chứng minh rằng nếu f (f (f(0))) = 0 thì f(0) = 0.
Câu 27 [Q493944027] [VMC 1994] Cho hàm số f : [a,b] → [a,b] với a < b và thỏa mãn iều kiện |f(x) −
f(y)| < |x − y|,∀x,y ∈ [a,b],x ≠ y.
Chứng minh rằng phương trình f(x) = x có nghiệm duy nhất thuộc [a,b]. b
Câu 28 [Q700162032] Cho f : [a;b] → Rlà một hàm liên tục thỏa mãn
. Chứng minh rằng với mọi c b
k ∈ (0;1)luôn tồn tại c ∈ (a;b)sao cho .
Câu 29 [Q706346619] [VMC 2001] Chứng minh rằng tồn tại số thực x ∈ (0,1) sao cho 1 t2000 x2001
x∫ (1 + t)(1 + t2)...(1 + t2001) dt = (1 + x)(1 + x2)...(1 + x2001) .
Câu 30 [Q338317355] Cho n ∈ N∗, giả sử là hàm liên tục trên f [0;n] sao cho f(0) = f(n). Chứng minh rằng tồn tại x1
và x2 trong [0;n] sao cho x2 − x1 = 1 và f(x2) = f(x1).
Câu 31 [Q653129164] Cho f,g : [0;1] → R là các hàm liên tục thỏa mãnf(0) = g(1) = 0và f(1) = g(0) = 1.
Chứng minh rằng với mọi số thực dương thì phương trình k f(x) = kg(x)luôn có nghiệm trên [0;1].
Câu 32 [Q565076181] Chứng minh rằng phương trình (1 − x)cosx = sinx luôn có nghiệm thuộc (0,1).
Câu 33 [Q140888708] Cho f : [0;1] → [0;1]là hàm liên tục. Chứng minh rằng tồn tại x0 ∈ [0,1]sao cho f(x0) = x0.
Câu 34 [Q155785943] Cho f,g : [a;b] → R là các hàm liên tục sao cho f(a) < g(a) và f(b) > g(b). Chứng minh rằng tồn
tại x0 ∈ (a;b) sao cho f(x0) = g(x0).
Câu 35 [Q563547150] Cho f : [a;b] → R là hàm liên tục. Chứng minh rằng tồn tại c ∈ [a;b] sao cho mf(a) + nf(b) f(c) =
với mọi số nguyên dương m,n. m + n
Câu 36 [Q373291912] Cho f : R → R là hàm liên tục và limx→+∞ f(x) = +∞. Giả sử tồn tại số thực dương n n ak,k = 1,2,...,n sao cho
.Chứng minh rằng với mọi số thực dương luôn tồn tại số thực dương c n n
bk > ak sao cho ∑ f(bk) = n + c. k=1 / lOMoAR cPSD| 40551442
Câu 37 [Q445327504] Chứng minh rằng với mọi số thực a,b,c thoả mãn 3a + 2b + 6c = 0 thì phương trình atan2x +
btanx + c = 0 luôn có nghiệm thuộc khoảng . π/2
Câu 38 [Q182228846] [VMC 2009] Giả sử liên tục trên f [0; ] và thoả mãn f . Chứng
minh rằng phương trình f(x) = sinx có ít nhất một nghiệm trong khoảng .
Câu 39 [Q259099591] Tìm tất cả các số nguyên dương sao cho mọi hàm liên tục n f : [0;1] → [0;1] thì tồn tại x0 ∈
[0;1]sao cho nf(x0) = (1 − x0)(f(x0) + f(1 − x0))
Câu 40 [Q774825455] [VMC 2005] Cho số dương và hàm số a f(x) có ạo hàm liên tục trên sao cho R f′(x) ≥ a với mọi x ∈ R. Biết rằng
xdx < a. Chứng minh rằng khi ó trên [0, ], phương trình f(x) = 0 có nghiệm duy nhất.
Câu 41 [Q036390693] Cho f : [a;b] → (a;b) là hàm liên tục. Chứng minh rằng với mọi số tự nhiên tồn tại sốn dương và α c ∈ (a;b) sao cho
f(c) + f(c + α)+...+f(c + nα) = (n + 1)(c + nα2 ).
Câu 42 [Q536354744] Cho f : (a;b) → R là hàm liên tục. chứng minh rằng với mọi x1,x2,...,xn ∈ (a;b)luôn tồn 1
tại x0 ∈ (a;b) sao cho f(x0) = (f(x1)+...+f(xn)). n
Câu 43 [Q608393207] Nếu là hàm liên tục trên f [a;b] sao chof , thì tồn tại c ∫ f(x)dx c ∈ (a;b) sao cho f ) =.
Câu 44 [Q377677751] Cho hàm số f(x) = x3 + ax2 + bx + c với { c > 0 . Chứng minh rằng phương a + b + c < −1 trình f(x)
= 0 có 3 nghiệm thực phân biệt.
Câu 45 [Q646766277] Cho là hàm liên tục trên f [−1,1] . Chứng minh rằng tồn tại x0 ∈ [−1,1] sao cho x0f2012(x0) − 2012f(x0) + 2011x0 = 0.
Câu 46 [Q490403402] Cho là hàm liên tục trên f
và . Chứng minh rằng tồn tại số thực c c+1 c ∈ [0,n − 1] sao cho .
Câu 47 [Q305606340] [Mathematical Reflection no.5 2006] Cho f0 là một hàm thực liên tục trên [0;1] với mỗi số nguyên n ≥ 0 xác ịnh f 1 n
dt. Giả sử rằng tồn tại số nguyên dương sao cho k fk(1) = (k+1)! . Chứng
minh rằng tồn tại x0 ∈ R sao cho f0(x0) = x0.
Câu 48 [Q447196319] Cho f(x) khả tích trên [a;b] các số thực k1,k2,...,kn > 0 và các số thực x1,x2,...,xn ∈ [a;b].. Chứng minh rằng tồn tại số c ∈ [a;b] sao cho x1 x2
xn k1 ∫ f(x)dx + k2 ∫ f(x)dx+...+kn ∫ f(x)dx = 0. c c c / lOMoAR cPSD| 40551442
Câu 49 [Q733677737] Chứng minh rằng phương trình x
có nghiệm trên khoảng (0;π).
Câu 50 [Q704007755] Cho các số thực a,b,c thoả mãn a + b + c = 0. Chứng minh rằng phương trình 2ax2 + 3bx + 4c =
0 có ít nhất một nghiệm thuộc khoảng (1;+∞). HƯỚNG DẪN
Câu 1 Xét f(x) = ax2 + bx + c liên tục trên R , ta cóf(0) = c và f (m + 1)2 −c (m + 2)c −c = + = . m (m + 2) Suy ra f(0)f
Ta có iều phải chứng minh.
Câu 2 Kí hiệu f(x) = ax4 + bx3 + cx2 + dx + e.
Giả sử x0 là nghiệm của phương trình bậc hai ã cho, ta có x0 ≥ 4 và ax2
0 + (2b + c)x0 + 2d + e = 0 ⇒ ax d Khi ó f
Theo ịnh lí giá trị trung bình phương trình f(x) = 0 có nghiệm thuộc oạn
. Ta có iều phải chứng minh.
Câu 3 Có ax20 + (b + c)x0 + d + e = 0 ⇔ ax20 + cx0 + e = −(bx0 + d).
Khi ó hàm số f(x) = ax4 + bx3 + cx2 + dx + e liên tục trên vàR f
Theo ịnh lí giá trị trung bình phương trình f(x) = 0 có nghiệm thuộc oạn
. Ta có iều phải chứng minh. Câu 4 a) Xét hàm số f(x) = 3x − sinx liên tục trên R có f − 1 = − 1 < 0 ⇒ f
Do ó phương trình f(x) = 0 có nghiệm thuộc khoảng
. Ta có iều phải chứng minh.
b) Xét hàm số f(x) = 2x − x2 − x − 3 liên tục trên R có f(0) = −2 < 0;f(6) = 19 > 0 ⇒ f(0).f(6) < 0. Do ó phương trình f(x) =
0 có nghiệm thuộc khoảng (0;6). Ta có iều phải chứng minh. ⎪⎧⎨⎪⎩ x→−∞ ⎧⎨⎩ lim f(x).f(0) < 0 lim f(x) = +∞
6 − 9x − 8 liên tục trên R có f(0) = −8 < 0 ⇒ x→−∞ do ó / lOMoAR cPSD| 40551442
Câu 5 Xét hàm số f(x) = x lim f(x).f(0) < 0
lim f(x) = +∞ x→+∞ x→+∞
phương trình f(x) = 0 có các nghiệm thuộc khoảng (−∞;0);(0;+∞). Ta có iều phải chứng minh. ⎧ f(−2) = −11
⎪⎨ ⎨⎩⎪⎧⎪f(−2).f(0) < 0 f(0) = 1
Câu 6 Xét hàm số f(x) = x5 + x2 − 8x + 1 liên tục trên R có ⇒ f(0).f(1) < 0 do ó ó f(1) = −5 ⎪⎩ f(1).f(2) < 0
f(2) = 21 phương trình f(x) = 0 có các
nghiệm thuộc khoảng (−2;0);(0;1);(1;2). Ta có iều phải chứng minh. Câu 7 Xét hàm số f(x) = ax4 + bx2 + c liên tục trên R có f . Do ó f
Vậy phương trình f(x) = 0 có nghiệm thuộc oạn .
Câu 8 Với mọi x > 0. Lấy logarit tự nhiên hai vế của phương trình ta ược : (x + 1)lnx − xln(x + 1) = 0. Xét hàm số
f(x) = (x + 1)lnx − xln(x + 1) liên tục trên khoảng (0,+∞). Ta có f′ . Xét hàm số g . Ta có g′
, nên hàm số g(x) ơn iệu giảm trên khoảng (0,+∞). x Mặt khác ta có
. Vậy g(x) > 0,∀x ∈ (0,+∞). Từ ó suy ra f′(x) > 0,∀x ∈ (0,+∞). Vậy f(x)là hàm ơn
iệu tăng trên khoảng (0,+∞). x
Mặt khác ta có f(1) = −ln2 < 0,limx→+∞ f(x) = limx→+∞ ln = +∞
Theo ịnh lý giá trị trung bình tồn tại x0 ∈ (0;+∞)sao cho f(x0) = 0 và nghiệm này là duy nhất do là hàm ơnf iệu tăng trên (0,+∞). Câu 9 Xét
a thức P(x) = a2n+1x2n+1+...+a1x + a0 (a2n+1 ≠ 0) là một hàm liên tục trên R
có limx→−∞ P(x).limx→+∞
P(x) < 0 do ó phương trình P(x) = 0 luôn có nghiệm.
Câu 10 Thật vậy, giả sử hàm số f(x) liên tục và tuần hoàn với chu kì T. Khi ó ta chỉ cần xét hàm số f(x) trên một chu
kì, chẳng hạn oạn [0;T]. Khi ó trên oạn [0;T] hàm số f(x) luôn có giá trị nhỏ nhất m; giá trị lớn nhất M. Vì vậy ⇒ minR
f(x) = min[0;T] f(x) = m;maxR f(x) = max[0;T] f(x) = M. Tức hàm số bị chặn.
Câu 11 Xét hàm số g
n liên tục trên [0,1]. Ta cần chứng minh tồn tại c ∈ [0,1]sao cho g(c) = 0. Ta có g / lOMoAR cPSD| 40551442
Nếu tồn tại một trong các thừa số trên bằng 0 thì ta có ngay iều phải chứng minh.
Nếu không có thừa số nào bằng 0 khi ó có ít nhất hai thừa số trái dấu nhau giả sử g và g
j. Khi ó g( ni )g( nj ) < 0 suy ra tồn tại c
sao cho g(c) = 0. Bài toán ược chứng minh hoàn toàn.
Câu 12 Ta cần chứng minh tồn tại c ∈ [0,1] sao cho f(c + 1) − f(c) = 0. Xét hàm số g(x) = f (x + 1) − f(x) liên tục trên
[0,2]. Ta có g(0) = f(1) − f(0) và g(1) = f(2) − f(1) = f(0) − f(1).
Suy ra g(0)g(1) = −(f(0) − f(1))2 ≤ 0. Nên tồn tại c ∈ [0,1] sao cho g(c) = 0 tức f (c + 1) = f(c). Bài toán ược chứng minh hoàn toàn.
Câu 13 Vì f(x) liên tục và tuần hoàn trên R nên tồn tại x1,x2 ∈ R|f(x1) = minR f(x);f(x2) = maxR f(x) (xem câu 10).
Xét hàm số g(x) = f(x) − f(x + π) có g(x1) = f(x1) − f(x1 + π) ≤ 0;g(x2) = f(x2) − f(x2 + π) ≥ 0.
Do ó g(x1).g(x2) ≤ 0 iều ó chứng tỏ phương trình g(x) = 0 luôn có nghiệm nằm giữa x1,x2. Ta có iều phải chứng minh.
Câu 14 Ta xét hàm số h liên tục trên .R Ta có h
và ta chứng minh tồn tại x0 ∈ R sao cho g(x0) = f (x0 + 1) − f(x0) = 0 khi ó h và có h
và bài toán ược chứng minh.
Ta xuất phát từ tính tuần hoàn và liên tục của nên tồn tại f
x1,x2 sao cho f(x1) = max f(x) và f(x2) = min f(x). x∈R x∈R
Khi ó g(x) = f (x + 1) − f(x) có g(x1)g(x2) ≤ 0 ⇒tồn tại x0nằm giữa x1,x2sao cho g(x0) = 0 hay f(x0 + 1) = f(x0). Bài toán ược chứng minh hoàn toàn.
Câu 15 Ta viết lại phương trình ã cho thành e−x |P(x)| − 1 = 0.
Ta xét hàm số g(x) = e−x |P(x)| − 1 liên tục trên . Ta có R
limx→+∞ g(x) = 0 và limx→−∞ g(x) = +∞ nên tồn tại x0 ∈ R
sao cho g(x0) = 0 hay |P(x0)| = ex0. Bài toán ược chứng minh hoàn toàn.
Câu 16 Từ giả thiết ề bài suy ra liên tục tuần hoàn với chu kỳ nên bị chặn f T (xem câu 10).
Xét hàm số g(x) = x + c − f(x) liên tục trên R. Ta có limx→+∞ g(x) = +∞và limx→−∞ g(x) = −∞ nên tồn tại x0 ∈ R sao cho
g(x0) = 0 hay f(x0) = x0 + c. Bài toán ược chứng minh hoàn toàn.
Câu 17 Xét hàm số fliên tục trên [−1,1]nên tồn tại a,b ∈ [−1,1] sao cho f(a) = max f(x) và x∈[−1,1]
f(b) = minx∈[−1,1] f(x). Nhưng do tuần hoàn với chu kỳ bằng 1 nên f
f(a) = max f(x)và f(b) = min f(x). x∈R x∈R
Xét hàm số H(x) = f(x) − f (x + π). Ta có H(a) = f(a) − f (a + π) ≥ 0và H(b) = f(b) − f (b + π) ≤ 0. Suy ra H(a)H(b) ≤ 0 nên
tồn tại x0 ∈ [a,b] sao cho H(x0) = 0 tức f(x0) = f (x0 + π). Bài toán ược chứng minh hoàn toàn.
Câu 18 Xét hàm số F
− 1liên tục trên [0;1]. Ta có F(0) = −1 < 0và F
, suy ra F(0).F(1) ≤ 0nên tồn tại x0 ∈ [0;1]sao cho F(x0) = 0, iều này tương ương với
. Nghiệm này là duy nhất vì F ′(x) = 2 − f(x) > 0,∀x ∈ [0;1]. Bài toán ược chứng minh hoàn toàn.
Câu 19 Nếu f(0) = 0 thì ta có ngay iều phải chứng minh.
Nếu f(0) > 0 ta xét hàm số g(x) = f(x) − x liên tục trên [0,+∞). / lOMoAR cPSD| 40551442
Ta có g(0) = f(0) > 0 và do lim a)
x nên tồn tại a > 0sao cho
f(a < 1 tức g(a) = f(a) − a < 0. Suy ra g(0)g(a) <
0 nên tồn tại x0 ∈ (0,a)sao cho g(x0) = 0 hay f(x0) = x0. Bài toán ược chứng minh.
Câu 20 Do P(x) là a thức bậc n + 1 nên sẽ có tối a n + 1 nghiệm. n
Ta có P(−ak) = 2(bk − ak) ∏
(bi − ak) nên P (−ak)cùng dấu với (−1)k. i=0,i≠k n và P(−bk) = (ak − bk) ∏
(ai − bk) nên P (−bk) cùng dấu với (−1)k+1. Suy ra i=0,i≠k
P (−ak)P (−bk) < 0 nên tồn tại ck ∈ (−bk,ak),k = 0,1,...,n sao cho P(ck) = 0 tức a thức P(x) = 0 có ủ n + 1 nghiệm thực phân
biệt. Bài toán ược chứng minh.
Câu 21 Đặt h(x) = f(x) − g(x) là hàm liên tục, theo giả thiết h(x) > 0 hoặc h(x) < 0,∀x ∈ R.
Không mất tính tổng quát, giả sử h(x) > 0,∀x ∈ R. Khi ó h(f(x)) = f (f(x)) − g(f(x)) > 0 Và h(g(x)) = f
(g(x)) − g(g(x)) > 0. Cộng theo vế các bất ẳng thức trên ta ươc h(f(x)) + h(g(x)) = (f (f(x)) − g(g(x))) +
(f (g(x)) − g(f(x))) = f (f(x)) − g(g(x)) > 0.
Tức là phương trình f (f(x)) = g(g(x)) cũng không có nghiệm thực. Ta có iều phải chứng minh.
Câu 22 Xét hàm số g
liên tục trên . Với mỗi số thực R x ∈ R Ta có g . Suy ra g . Suy ra tồn tại x sao cho g(x0) = 0 hay f
. Bài toán ược chứng minh.
Câu 23 Xét hàm số h(x) = f(x) − x1997 liên tục trên [0,1], kết hợp với giả thiết ta có h(0) = f(0) > 0 và
nên tồn tại c ∈ (0,1) sao cho h(c) < 0.
Suy ra h(0)h(c) < 0, và ta có tồn tại số thực x0 ∈ (0,c) ⊂ (0,1) sao cho h(x0) = 0 ⇔ f(x0) = x19970 . Ta có iều phải chứng minh.
Câu 24 Do nhận giá trị trái dấu nên tồn tại f x1,x2 ∈ R sao cho f(x1) < 0 và f(x2) > 0. Nhưng do liên tục nênf tồn tại số
dương δ > 0 ủ nhỏ sao cho f(x) < 0 với mọi x ∈ [x1 − δ,x1 + δ] và f(x) > 0 với mọi x ∈ [x2 − δ,x2 + δ].
Khi ó xét hàm số g(x) = f (x1 − δ + x(x2 − x1)) + f (x1 + x(x2 − x1)) + f (x1 + δ + x(x2 − x1)) liên tục trên R.
Ta có g(0) = f (x1 − δ) + f(x1) + f (x1 + δ) < 0 và g(1) = f (x2 − δ) + f(x2) + f (x2 + δ) > 0 suy ra g(0)g(1) < 0 nên tồn tại x0 ∈
(0,1) sao cho g(x0) = 0 tức f(a) + f(b) + f(c) = 0 với a = x1 − δ + x0 (x2 − x1),b = x1 + x0 (x2 − x1),c = x1 + δ + x0 (x2 − x1). Bài toán ược chứng minh.
Câu 25 Do nhận giá trị trái dấu nên tồn tại f x1,x2 > 0 sao cho f(x1) < 0 và f(x2) > 0. Nhưng do liên tục nênf tồn tại số
dương δ > 0 ủ nhỏ sao cho f(x) < 0 với mọi x ∈ [x1e−δ,x1eδ] và f(x) > 0 với mọi x ∈ [x2e−δ,x2eδ]. / lOMoAR cPSD| 40551442
Khi ó xét hàm số g(x) = f (ex1−δ+x(x2−x1)) + f (ex1+x(x2−x1)) + f (ex1+δ+x(x2−x1)) liên tục trên (0,+∞).
Ta có g(0) = f (ex1−δ) + f(x1) + f (x1 + δ) < 0 và g(1) = f (x2 − δ) + f(x2) + f (x2 + δ) > 0 suy ra g(0)g(1) < 0 nên tồn tại x0 ∈
(0,1) sao cho g(x0) = 0 tức f(a) + f(b) + f(c) = 0 với
a = ex1−δ+x0(x2−x1),b = ex1+x0(x2−x1),c = ex1+δ+x0(x2−x1). Bài toán ược chứng minh.
Câu 26 Điều kiện ề bài tương ương với: |f(a) − f(b)| ≤ |a − b|,∀a,b ∈ R
Dấu bằng xảy ra khi và chỉ khi a = b. Đặt x = f(0),y = f(x)khi ó áp dụng liên tiếp bất ẳng thức trên ta ược
|f(x) − f(y)| ≤ |x − y| = |f(0) − f (f(0))| ≤ |0 − f(0)| = |f(0)| , và
|f(x) − f(y)| ≥ |f (f(x)) − f (f(y))| = |f (f (f(0))) − f (f (f (f(0))))| = |f(0)|.
Do ó tất cả các dấu ẳng thức phải xảy ra và ạt tại khi và chỉ khi f(0) = 0.
Câu 27 Ta có 0 ≤ |f(x) − f(y)| < |x − y| suy ra limx→y |f(x) − f(y)| = 0 nên liên tục trên f [a,b].
Xét hàm số g(x) = f(x) − x liên tục trên [a,b]. Ta có g(a) = f(a) − a ≥ 0và g(b) = f(b) − b ≤ 0 suy ra g(a)g(b) ≤ 0 nên tồn tại
x0 ∈ [a,b] sao cho g(x0) = 0 hay f(x0) = x0. Ta chứng minh x0 là duy nhất. Thật vậy giả sử tồn tại x1 ∈ [a,b],x1 ≠ x0 sao cho
f(x1) = x1 khi ó |x1 − x0| = |f(x1) − f(x0)| < |x1 − x0|. Điều này mẫu thuẫn. Bài toán ược chứng minh. b
Câu 28 Không mất tính tổng quát giả sử . t b Khi ó xét hàm số g
dxlà một hàm liên tục trên [a;b]. Ta có b b b b g
và nên g(a).g(b) < 0. Do ó theo
ịnh lý giá trị trung bình tồn tại c ∈ (a;b)sao cho g(c) = 0, iều này tương ương với c b .
Bài toán ược chứng minh hoàn toàn. 1
Câu 29 Xét hàm số h x t2000 dt x2001 liên tục trên [0,1]. 1 Ta có h t2000 và h(1) = −
< 0 suy ra h(0)h(1) < 0. Nên tồn tại số thực x ∈ (0,1) sao cho h ha y .
Ta có iều phải chứng minh.
Câu 31 Xét hàm số h(x) = f(x) − k.g(x) liên tục trên oạn [0;1] có
h(0) = f(0) − kg(0) = −1;h(1) = f(1) − kg(1) = 1 ⇒ h(0).h(1) = −1 < 0.
Do ó phương trình h(x) = 0 ⇔ f(x) = kg(x) luôn có nghiệm thuộc khoảng (0;1).
Câu 34 Xét hàm số h(x) = f(x) − g(x) liên tục trên oạn [a;b] có / lOMoAR cPSD| 40551442
h(a) = f(a) − g(a) < 0;h(b) = f(b) − g(b) > 0 ⇒ h(a)h(b) < 0 do ó tồn tại x0 ∈ (a;b) sao
cho h(x0) = 0 ⇔ f(x0) = g(x0).
Câu 35 Xét hàm số g(x) = f(x) − mf( a)+ nf(b) m +n
liên tục trên oạn [a;b] có mf(a) + nf(b) n(f(a) − f(b))
⎧⎪ ⎪ ⎪ g(a) = f(a) − = 2 ⎨
m + n m + n ⇒ g(a).g(b) = −
mn(f(a)−f2(b)) ⩽ 0. mf(a) + nf(b) m(f(a) − f(b)) (m+n) ⎪⎩g(b) = f(b) − = − m + n m + n
Do ó tồn tại c ∈ [a;b] sao cho g(c) = 0 ⇔ f(c) = mf( a)+ nf(b) m +n . n n
Câu 36 Xét hàm số g(x) = ∑ f (x + ak) − n − c liên tục trên R. Ta có g và k=1 n
limx→+∞ g(x) = +∞nên tồn tại x0 ∈ (0,+∞) sao cho g(x0) = 0 hay ∑ f (x0 + ak) = n + c. Lúc này các số k=1
bk = x0 + ak là các số thỏa mãn ề bài. Bài toán ược chứng minh. Câu 38 Xét
hàm F(x) = f(x) − sinxliên tục trên . Khi ó: < 1 ⇔ hay Do ó tồn tại c ể F(c) < 0.
Mặt khác F(0) = f(0) > 0, do ó F(0).F(c) < 0 nên tồn tại x
sao cho F(x0) = 0 hay f(x0) = sinx0. Ta có iều phải chứng minh.
Câu 39 Với mọi f : [0;1] → [0;1] nên xét f(x) = x ể tồn tại x0 ∈ [0;1] sao cho nf(x0) = (1 − x0)(f(x0) + f(1 − x0)) ⇒ nx0 = (1
− x0)(x0 + 1 − x0) = 1 − x0 ⇒ n .
Nhưng do n ∈ N∗ nên n = 1.
Ta chứng minh với n = 1 thỏa mãn bài toán.
Thật vậy xét hàm số g(x) = xf(x) − (1 − x)f (1 − x) liên tục trên [0;1] ta có
g(0) = −f(1) và g(1) = f(1) suy ra g(0)g(1) = −(f(1))2 ≤ 0 suy ra tồn tại x0 ∈ [0;1] sao
cho g(x0) = 0 ⇒ f(x0) = (1 −
x0)(f(x0) + f (1 − x0)). Bài toán ược giải quyết hoàn toàn.
Câu 40 Do f′(x) ≥ a > 0 nên tăng trên f
nên ta chỉ cần chứng minh phương trìnhf(x) = 0có nghiệm. Ta có xdx dx
Kết hợp với giả thiết suy ra ⇒ f , và f xdx a ⇒ f(0) < 0. / lOMoAR cPSD| 40551442 Vậy f nên tồn tại x
sao cho f(x0) = 0. Bài toán ược chứng minh hoàn toàn.
Câu 43 Xét hàm số g
dt liên tục trên [a,b] có g(a) = (b − a)f(a)và b g
dx. Kết hợp với giả thiết suy ra g(a)g(b) < 0 nên theo ịnh lý giá trị trung bình tồn tại c ∫ f(x)dx
c ∈ (a,b) sao cho g(c) = 0 hay f
. Bài toán ược chứng minh hoàn toàn. / lOMoAR cPSD| 40551442 VTED.VN|11
BIÊN SOẠN: THẦY ĐẶNG THÀNH NAM – DUY NHẤT
TẠI ⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ x→−∞ ⎧⎪ lim f(x) = −∞ ⇒ ∃x1 < 0|f(x1) < 0 f(0) = c > 0 f(x1)f(0) < 0 Câu 44
Có ⎪ ⎪ ⎪ ⎪⎩⎨⎪ ⇒ ⎨⎩⎪ f(0)f(1) < 0 do ó phương trình f(x) = 0 có 3 f(1) = a + b + c + 1 < 0 lim f(x) =
+∞ ⇒ ∃x2 > 1|f(x2) > 0 f(1)f(x2) < 0 x→+∞
nghiệm lần lượt thuộc các khoảng (x1;0);(0;1);(1;x2).
Câu 45 Xét hàm số g
x liên tục trên [−1,1] . Sử dụng bất ẳng thức Cô si suy ra f (x)+2011 Suy ra g và g f (1)+2011 f (−1)+2011
Suy ra g(−1)g(1) ≤ 0 , theo ịnh lý giá trị trung bình suy ra tồn tại x0 ∈ [−1,1] sao cho g(x0) = 0 hay x0f2012(x0) − 2012f(x0) + 2011x0 = 0. t t+1 t+1
Câu 46 Xét hàm số h(t) = ∫ f(x)dx − ∫ f(x)dx = ∫ f(x)dx liên tục trên [0,n − 1], kếp hợp với giả thiết ta có h 0 1 n−1 0
Nếu tất cả các số hạng ều dương hoặc ều âm thì từ ẳng thức trên dẫn ến iều vô lý, do vậy luôn tồn tại ít nhất hai số
hạng trái dấu suy ra tồn tại h(i)h(j) ≤ 0 với 0 ≤ i ≠ j ≤ n − 1 suy ra tồn tại c ∈ [0,n − 1] sao cho h(c) = 0 c c+1 hay . Ta có iều phải chứng minh.
Câu 47 Ta chứng minh bằng phản chứng. Giả sử ngược lại không tồn tại x0 ∈ Rsao cho f0(x0) = x0 khi ó do g(x) = f0(x)
− x liên tục nên g(x) > 0,∀x ∈ R hoặc g(x) < 0,∀x ∈ R. Không mất tính tổng quát giả sử g(x) > 0,∀x ∈ R. Khi ó f = ⇒ f .
Bằng quy nạp dễ chứng minh ược rằng fn . 1 1 Suy ra f t k k−1 k !
(k+1)! , iều này mẫu thuần với giả thiết dó ó iều giả sử là sai. Tức tồn tại 0 0
x0 ∈ R sao cho f0(x0) = x0. Bài toán ược chứng minh. x1 x2 xn Câu 48 Xét hàm số h . lOMoAR cPSD| 40551442 VTED.VN|12 Ta có
k1h(x1) + k2h(x2)+...+knh(xn) = 0 nên tồn tại các số
1 ≤ i ≠ j ≤ n|kih(xi).kjh(xj) = kikj.h(xi)h(xj) ≤ 0 nên tồn tại c ∈ [a,b] sao cho h(c) = 0 hay x1 x2
xn k1 ∫ f(x)dx + k2 ∫ f(x)dx+...+kn ∫ f(x)dx = 0. c c c
Ta có iều phải chứng minh. Câu 49 Hàm số f liên tục trên oạn [0;π] và f /




