Chương 2: Không gian Vector - Tài liệu tham khảo | Đại học Hoa Sen
Chương 2: Không gian Vector - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả
Môn: Quản trị nhân lực (mn) 152 tài liệu
Trường: Đại học Hoa Sen 4.8 K tài liệu
Tác giả:
Preview text:
Chng II KHÔNG GIAN VECTƠ M U
Trong chng I ta ã thy, nhB nh thc ta ã gi,i >c h) phng
trình Cramer. Song nu chF dùng nh thc nghiên cu vi)c gi,i h)
phng trình tuyn tính t/ng quát (khi m ≠ n ho$c khi m = n nhng nh
thc ca h) phng trình b'ng 0) thì sQ có nhi%u khó khDn, phc tp.
Không gian vect sQ giúp ta v>t qua nh0ng khó khDn y và cCng giúp ta
trình bày lí thuyt h) phng trình tuyn tính m!t cách sáng sa.
trBng Ph/ thông trung h7c ta ã dùng vect nghiên cu hình h7c.
Vect còn >c dùng nghiên cu nhi%u ngành toán h7c khác và c,
nh0ng môn khoa h7c khác nh C h7c, V6t lí, Hoá h7c, a lí, và nhi%u ngành k thu6t.
Nu xét t6p h>p V các vect có chung i m gc O mà ta ã h7c 1
trBng Ph/ thông thì ta thy t6p V cùng v8i phép c!ng hai vect và phép
nhân m!t vect v8i m!t s tho, mãn nh0ng i%u ki)n sau:
1) ( N + P ) + V = N + (P + V ); 2) N + P = P + N ;
3) có vect không 0 tho, mãn i%u ki)n: N + 0 = N ;
4) mGi N có m!t vect i - N tho, mãn i%u ki)n: N + (- N ) = 0 ;
5) r( N + P ) = r N + rP ;
6) (r + s) N = r N + s N ; 7) (rs) N = r(s N ) ;
8) 1. N = N , trong ó r, s, 1 là nh0ng s th4c.
Trong toán h7c và nhi%u khoa h7c khác còn có nh0ng t6p h>p mà các
phn t* ca chúng không ph,i là nh0ng vect hình h7c nh ta v;a nói,
nhng cCng có hai phép toán tho, mãn 8 i%u ki)n nêu trên. Chúng >c
g7i là nh0ng không gian vect.
M#c tiêu ca chng này là trình bày nh ngha không gian vect,
các tính cht ca nó và cu to ca m!t không gian vect, chu:n b cho
vi)c áp d#ng nó vào lí thuyt h) phng trình tuyn tính và vi)c nghiên
cu nó sâu s?c hn trong nh0ng chng sau có th áp d#ng nó nhi%u
hn vào nh0ng b! môn toán h7c khác cCng nh nh0ng lnh v4c khoa h7c khác. Vì th ta cn:
- N?m v0ng nh ngha và các tính cht ca không gian vect, không gian con:
- Hi u rõ r'ng mGi không gian vect >c to thành t; m!t h7 “ti
thi u” nh0ng vect ca không gian mà ta g7i là c s1; bit cách tìm c
s1 và s chi%u ca m!t không gian vect;
- Bit >c mi liên h) gi0a to ! ca cùng m!t vect trong hai c s1 khác nhau.
Trong giáo trình này ta chF xét các không gian vect trên các trBng
s Tuy nhiên nh0ng i%u trình bày sau ây %u úng trong m7i trBng tuH ý.
§1. NH NGHA VÀ CÁC TÍNH CHT ƠN GI,N
1.1. nh ngha
nh ngha. Gi s V là mt tp hp mà các phn t c kí hiu
bi N , P , V ,..., K là mt tr$ng sô. Trên V có mt phép toán gi là phép
cng hai phn t ca V (kí hiu "+") và phép toán th hai gi là phép
nhân mt phn t ca V vi mt s thuc tr$ng K (kí hiu ".").
Tp hp V cùng vi hai phép toán này c gi là mt không gian
vect trên tr$ng K (hay mt K-không gian vect) nên các iu kin sau
c tho mãn $i vi mi N , P , V , ∈ V và mi r, s, 1 ∈ K.
1) ( N + P ) + V = N +( P + V );
2) N + P = P + N ;
3) có mt phn t 0 ∈ V tho mãn iu kin: N + 0 = N ;
4) vi mi N ∈ V có mt phn t, kí hiu bi - N , c!ng thuc V tho
mãn iu kin: N + (- N ) = 0 ;
5) r( N + P ) = r N + r N
6) (r + s) N = r N + s N ;
7) (rs) N = r (s N ) ;
8) 1. N = N .
N ∈ V c gi là mt vect, 0 c gi là vect không, - N c gi
là vect i ca N .
Bn 7c có th dùng nh ngha ca không gian vect ki m chng
r'ng các t6p h>p cho trong các ví d# d8i ây là nh0ng không gian vect.
Ví d 1. T6p h>p V các vect OA , OB , OC ?... chung gc O trong
không gian (mà ta h7c 1 trBng ph/ thông) cùng v8i phép c!ng hai vect
và phép nhân m!t vect v8i m!t s th4c là m!t không gian vect. Nó
>c g7i là không gian vect hình hc.
Ví d 2. MGi trBng K là m!t không gian vect trên K i v8i phép c!ng và phép nhân trên K.
Ví d 3. TrBng s th4c R là m!t không gian vect trên trBng s h0u tF Q.
Ví d 4. TrBng s phc C là m!t không gian vect trên trBng s
th4c R và cCng là m!t không gian vect trên trBng Q.
Ví d 5. Gi, s* K là m!t trBng s, t6p h>p K[x] các a thc ca :n
x v8i h) s trong K, cùng v8i phép c!ng hai a thc và phép nhân a
thc v8i m!t s, là m!t K-không gian vect.
Ví d 6. Kn = K x K x... x K là tích % các ca n phiên b,n K. Trên
Kn xác nh phép c!ng hai phn t* và phép nhân m!t phn t* ca Kn v8i m!t s thu!c K nh sau:
V8i N = (a1, a2,..., an), P = (b1, b2,..., bn) thu!c Kn và s r ∈ K,
(a1, a2,..., an) + (b1, b2,..., bn) = (a1, + b1, a2 + b2, an,..., bn),
r(a1, a2, ..., an) = (ra1, ra2, ..., ran).
Kn là m!t K-không gian vect.
T; ây tr1 i, mGi khi nói n không gian Kn ta hi u r'ng hai phép
toán trong ó ã >c nh ngha nh trên.
T; nh ngha không gian vect ta suy ra ngay m!t s tính cht n gian cua nó.
1.2. Mt s tính cht %n gin
Gi s V là mt K-không gian vect.
1) V ch# có mt vect không 0 duy nht.
2) Vi mi α ∈ V, vect i - α duy nht.
3) Vi mi α ∈ V, -(- α ) = α .
4) Vi α ∈ V và r ∈ K, ρ α = 0 khi và ch# khi r = 0 hoc α = 0 .
5) Vi α ∈ V và r ∈ K, ta có: (-ρα = -(ρ α ) = ρ( α ). Chng minh. 1) Gi, s* 0 và '
0 là nh0ng vect không ca V. Theo i%u ki)n 3)
trong nh ngha, vì 0 là vect không nên 0 + ' 0 = ' 0 . Tng t4, vì ' 0 là vect không nên 0 + ' 0 = 0 . V6y 0 = ' 0 .
2) Gi, s* N ∈ V có nh0ng phn t* i là - N và N' . Theo i%u ki)n 4)
trong nh ngha, N + (- N ) = 0 = N + N . Do ó, áp d#ng các i%u ki)n 1) và 2), ta có :
N = N + 0 = N + [ N + (- N )] = ( N' + N ) + (- N ) = 0 + (- N ) = - N .
3) Vì -(- N ) và N %u là vect i ca - N nên t; 2) suy ra -(- N ) = N . 4) “⇐”
• Nu r = 0 thì theo i%u ki)n 6), ta có:
0 N = (0 + 0) N = 0 N + 0 N .
C!ng -0 N vào v u và v cui ta >c: 0 = 0 N .
• Nu N = 0 thì theo i%u ki)n 5), ta có:
r 0 = r( 0 + 0 ) = r 0 + r 0 .
C!ng -r 0 vào v u và v cui ta >c 0 = r 0 .
“” Gi, s* r N = 0 . Nu r ≠ 0 thì theo i%u ki)n 7) và 8), ta có: 1 1 1
N = 1. N = ( .r) N = ( .r N )= 0 = 0 r r r
5) Vì –(r N ) là vect i ca ra nên nhB tính cht 2), ta chF cn chng
minh (-r) N và r(- N ) %u là vect i ca r N . Ta có:
(-r) N + r N = (-r + r) N = 0 N = 0 ;
r(- N ) + r N = r(- N + N ) = r 0 = 0 .
i%u ó chng t( r'ng (-r) N và r(- N ) %u là vect i ca r N . V6y
(-r) N = -(r N ) = r(- N ).
1.3. Hiu ca hai vect%
nh ngha. α + (-β ) c gi là hiu ca α và β , kí hiu bi α -
β và c là α tr, β .
T; nh ngha này và tính cht ca không gian vect ta suy ra: H) qu,.
1) ρ( α - β ) = p α - c β .
2) (ρ - σ)α = ρα - σα .
Chng minh. Xin dành cho bn 7c. §2. KHÔNG GIAN CON
2.1. nh ngha
nh ngha. Gi s W là mt tp con ca không gian vect V. Nu W
c!ng là mt không gian vect i vi hai phép toán ã cho trong V thì W
c gi là mt không gian con ca V.
Nh v6y mun chng minh t6p con W là m!t không gian con ca
không gian vect V ta ph,i chng t( r'ng các phép ã cho trong V cCng
là các phép toán trong W và ph,i ki m tra r'ng 8 i%u ki)n nêu trong
nh ngha không gian vect %u >c tho, mãn. Song ta sQ thy r'ng chF
cn ki m tra m!t s ít i%u ki)n hn.
2.2. Tính cht "c trưng
nh lí. Gi s V là mt không gian vect trên tr$ng K. W là mt
tp con ca V. Các mnh sau tng ng:
(i) W là mt không gian con ca V.
(ii) W ≠ ∅ và vi mi α , β thuc W, mi r thuc tr$ng K, ta có α
+ β ∈ W, ρα ∈ W.
(iii) W ≠∅ và vi mi α , β thuc W, mi r, s thuc tr$ng K, ta có
rα + σβ ∈ W. Chng minh.
"(i) (ii)": Nu W là m!t không gian con ca không gian vect V
thì W ph,i cha m!t vect 0 ca nó. Do ó W ≠ ∅. Các i%u ki)n còn
li ca (ii) hi n nhiên >c tho, mãn. "(i) (iii)": Hi n nhiên.
"(iii) (i)": Gi, s* các i%u ki)n ca (iii) >c tho, mãn. Khi ó,
v8i N , P thu!c W và r = s = 1 ∈ K, N + P = 1 N + 1P ∈ W;
v8i N ∈ W, r ∈ K, ta có: r N = r N + 0 N ∈ W ;
ngha là các phép toán trong W cCng là hai phép toán trong V. Ta ph,i
ki m tra r'ng 8 i%u ki)n trong nh ngha ca không gian vect %u
>c tho, mãn. Hi n nhiên các i%u ki)n 1), 2), 5), 6), 7), 8) >c tho,
mãn vì hai phép toán trong W chính là hai phép toán ã cho trong V. ChF
còn cn ki m tra các i%u ki)n 3) và 4). Vì W ≠ ∅ nên có m!t N ∈ W.
Theo tính cht ca không gian vect, 0 = 0 N + 0 N , m$t khác, theo gi,
thit 0 N + 0 N ∈ W. Do ó 0 ∈ W. Tng t4, v8i mGi N ∈ W ta %u có
- N = (-1) N + 0 N ∈ W. V6y W là m!t không gian vect trên trBng K và
do ó W là m!t không gian con ca V.
Bn 7c hãy dùng nh lí 2.2 chng minh nh0ng i%u kh9ng nh
trong các ví d# d8i ây:
Ví d 1. V8i mGi không gian vect V, b,n thân V và t6p { 0 } là
nh0ng không gian con ca V.
Chúng >c g7i là nh0ng không gian con tm th$ng ca V.
Ví d 2. T6p Pn g&m a thc 0 và các a thc có b6c bé hn hay b'ng
n ca K[x], (xem ví d# 5, m#c 1.1) là m!t không gian con ca không gian vect K[x].
Ví d 3. Theo ví d# 6), m#c 1.1, v8i n = 4 và K = R là trBng s
th4c, thì R4 là m!t R-không gian vect. T6p W = {(a1, a2, 0, 0}|ai ∈ R) là
m!t không gian con ca không gian R4.
Th6t v6y, ta chng minh cho ví d# 3.
Rõ ràng W ≠ ∅ vì (0, 0, 0, 0) ∈ W. Bây giB v8i N = (a1, a2, 0, 0), P
= (b1, b2, 0, 0) thu!c W và r ∈ R, ta có:
N + P = (a1, a2, 0, 0) + (b1, b2, 0, 0) = (a1 + b1, a2 + b2, 0, 0) ∈ W,
r N = r(a1, a2, 0, 0) = (ra1, ra2, 0, 0) ∈ W.
W tho, mãn i%u ki)n (ii) trong nh lí 2.2. V6y W là m!t không gian con ca R4.
Có nhi%u cách to thành nh0ng không gian con ca m!t không gian vect V.
2.3. T-ng ca nh.ng không gian con
M)nh % và nh ngha. Gi s W %
1, W2,... Wm là nh ng không gian
vect con ca K-không gian vect V. Khi ó: Tp hp W = {α
1 + α 2 + ... + α n| α i ∈ Wi, {1, 2,..., m }} là m t
không gian con ca V.
Không gian này >c g7i là t ng ca m không gian con Wi ã cho và m
c kí hiu bi W1 + W2 +... + Wm hay W . i i=1
Chng minh. Vì 0 ∈ Wi v8i m7i i ∈ {1, 2,..., m} nên 0 = 0 + 0 +
... + 0 ∈ W ; ngha là W ≠ ∅.
V8i N = N 1 + N 2 + .. +am ∈ W, P = P 1+ P 2 +...+ P m ∈ W và r ∈ K,
ta có: N + P = N 1 + N 2 + P 1+ P 2 + ... + P m = ( N 1 + P 1) + ( N 2 + P 2) + .. + ( N m + P m)
Vì N i, P i ∈ Wi và Wi là không gian con ca không gian vect V nên
N i + P i ∈ Wi, r N i ∈ Wi, v8i m7i i ∈ {1, 2,..., m}. Do ó N + P ∈ W, r N ∈ W.
Theo nh lí 2.2, W là m!t không gian con ca V.
2.4. Giao ca nh.ng không gian con
M)nh % và nh ngha. Gi s W %
1, W2,..., Wm là nh ng không gian
vect con ca K-không gian vect V. m Tp hp U = W
i là m t không gian con c a V và c g i là giao i=1
ca m không gian con Wi.
Chng minh. Xin dành cho bn 7c.
T; m!t h) (m!t s hay m!t h7) vect ca không gian V cCng có th
to thành m!t không gian con ca V.
2.5. Không gian sinh b/i mt h vect%
nh lí. Gi s = { N 1, N 2,..., N m} là mt h vect ca K-không
gian vect V. Khi ó tp hp W = {rα ∈ ∈
1 + ρ 2α 2 + ...+ ρ µα µ /r K, v i m i i i {1, 2,..., m}} là
mt không gian con ca V.
W c gi là không gian sinh bi h vect , còn c gi là h sinh ca W.
Chng minh. Rõ ràng W ≠ ∅ vì 0 = N 1 + 0 N 2 + ...+ 0 N m ∈ W.
Gi, s* N , P ∈ W và t ∈ K, ch9ng hn:
T; các i%u ki)n trong nh ngha ca không gian vect, ta suy ra:
Theo nh lí 2.2, W là m!t không gian con ca V.
Chú ý. Không gian sinh b1i m!t vect thBng >c kí hi)u b1i KN .
Nu W là không gian sinh b1i h) vect { N 1, N 2,..., N m} thì W = n KN1. = i 1
Không gian W trên ây sinh b1i m!t h) h0u hn vect. NgBi ta g7i
nó là không gian h%u h"n sinh.
Có nh0ng không gian vect có h) sinh vô hn nhng không có h)
sinh h0u hn nào. Trong giáo trình này ta chF xét các không gian vect có h) sinh h0u hn Ví d 1.
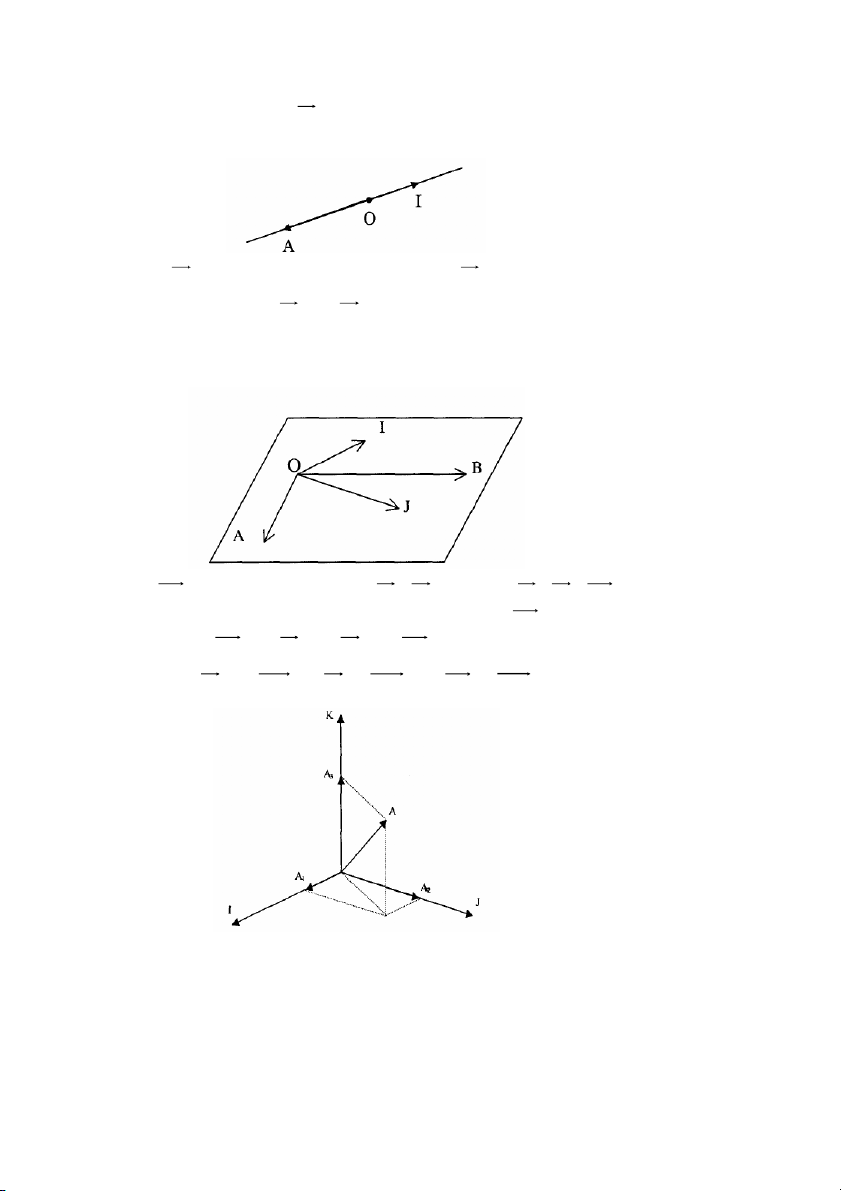
1) Gi, s* V là không gian vect hình h7c trong không gian (xem ví
d# li trong m#c 1.2). OI là m!t vect c nh.
Nu O ≡ I thì t6p U = {r OI | r ∈ R} chF cha vect 0 , là m!t không
gian con tm thBng ca V.
Nu O ≠ I thì t6p U = {r OI | r ∈ R} g&m các vect gc O, n'm trên Bng th9ng OI.
• Gi, s* OJ là vect không cùng phng v8i OI . Khi ó, t6p
W = {r1 OI + r2OJ | r1 ∈ R, r2 ∈ R)
là m!t không gian con ca V g&m các vect,,... n'm trong m$t ph9ng (OIJ).
Gi, s* OK không &ng ph9ng v8i OI , OJ . Th thì { OI , OJ , OK } là
m!t h) sinh ca V. Th6t v6y, nh ta ã bit mGi vect OA trong không
gian %u có dng: OA = r1 OI + r2 OJ + r3 OK . (r1 OI = r1 OA , r OA OA 1 2 OJ = 2 + r3 OK = 3
Ví d 2. Xét không gian vect R4 và không gian con W trong ví d# 3,
m#c 2.2. H) hai vect O = (1, 0, 0, 0), O = (0, 1, 0, 0), ca R4 là m!t h) 1 2 sinh ca W.
chng minh i%u này ta ph,i chng t( r'ng mGi N ∈ W >c bi u
diKn d8i dng N = r1 1O + r2O '
Gi vect trong W có dng N 2 . Bit r ng m
= (a1, a2, 0, 0) ∈ W. Theo phép c!ng và phép nhân v8i m!t s trong R4, ta có:
N = (a1, a2, 0, 0) = (a1, 0, 0, 0) + (0, a2, 0, 0)
= a1(1, 0, 0, 0) + a2(0, 1, 0, 0) = a1 1O + a2O . 2 V6y { 1 O , O } là h) sinh ca W. 2
Ta hãy th* thêm vect W (2, 3, 0, 0) vào h) vect { 1 O , O } và xét 2
không gian con W' sinh b1i h) vect { 1 O , O , W }. MGi N O 2 = a1 1 O + a2 2
+ a W ∈ W’ %u có th vit thành:
ó là m!t vect trong W. Nh v6y, W’ ⊆ W.
Ng>c li, mGi vect P = b1O1 + b2O ∈ W %u có th vit d8i dng 2 P = b1 1
O + b2 O + W . ó là m!t vect thu!c W’. 2
V6y W’ = W; ngha là hai h) {ε, ε2, W } và {ε, ε2, W } %u là h) sinh ca không gian vect W.
M!t câu h(i $t ra là trong m!t h) sinh ca m!t không gian vect có
th có m!t s ti thi u vect sinh ra không gian y hay không? Tr, lBi
ca câu h(i này liên quan n m!t khái ni)m g7i là h) vect !c l6p tuyn tính.
§3. S0 1C LP TUYN TÍNH - S0 PH THU1C TUYN TÍNH
3.1. nh ngha
Gi, s* = { N 1, N 2,..., N m-1, N m} (1)
là m!t h) vect ca K- không gian vect V, (m > 0).
nh ngha 1. Nu N = r
1 α 1 + r2α 2 + ... + rm-1 α m-1 + r1α m thì ta
nói N là mt t hp tuyn tính ca h vect hay N biu th tuyn tính qua m vect ã cho.
nh ngha 2. H vect c gi là ph thuc tuyn tính nu có m s r $ $
1, r2,..., rm-1, rm thu c tr ng K, không
ng th i b ng 0, sao cho
r1α 1 + r2α 2 + ...+ rm-1α m-1 + rmα m = 0 .
nh ngha 3. H vect
c gi là c lp tuyn tính nu nó
không ph thuc tuyn tính; nói cách khác, nu
r1α 1 + r2α 2 + ...+ rm-1α m-1 + rmα m = 0 .
thì r1 = r2 = ... = rm-1 = rm = 0.
Ví d 1. Trong không gian vect, mGi vect khác 0 %u l6p thành
m!t h) vect !c l6p tuyn tính. Th6t v6y, gi, s* N là m!t vect khác 0
trong K-không gian vect V. T; r N = 0 v8i r ~ K, nhB tính cht 4), 1
m#c 1.2, suy ra r = 0; ngha là h) vect { N } !c l6p tuyn tính.
Ví d 2. M7i h) vect cha 0 %u là ph# thu!c tuyn tính. Th6t v6y,
gi, s* { N 1, N 2,..., N m, 0 } là m!t h) vect bt kì ca không gian vect V.
Ch7n r1 = r2 = ...= rm = 0, rm+1 = 1, ta có:
0 N 1 + 0 N 2 + .. +0 N m +1. 0 = 0 .
i%u này chng t( h) ã cho ph# thu!c tuyn tính.
Ví d 3. Trong không gian vect hình h7c V, (xem ví d# 1, m#c 1.1),
ba vect l6p thành m!t h) ph# thu!c tuyn tính khi và chF khi chúng
&ng ph9ng; !c l6p tuyn tính khi và chF khi chúng không &ng ph9ng.
Th6t v6y, OI , OJ , OA ph# thu!c tuyn tính khi và chF khi t&n ti ba
s th4c r1, r2, r3 không &ng thBi b'ng 0 sao cho r1 OI + r2 OJ + r3 OA = r r 0 ; ch9ng hn, r 1 2
3 ≠ 0. Khi ó OA = - OI - OK . i%u này chng t( r r 3 3 ba vect &ng ph9ng.
Ví d 4. Xét không gian vect R4. H) g&m ba vect 1 O = (1, 0, 0, 0),
O2 = (0, 1, 0, 0), N = (2, - 5, 0, 0) là ph# thu!c tuyn tính, còn các h)
vect {O1, O2 }, { O1 , N }, { 2
O , N }!c l6p tuyn tính.
Th6t v6y, N = (2, -5, 0, 0) = (2, 0, 0, 0) + (0, -5, 0, 0)
= 2(1, 0, 0, 0) – (5, 1, 0, 0) = 2 1 O - 5 O2 hay 2 1
O - 5O2 + (-1) N = 0 ; ngha là h) { 1 O , O2 , N } là ph# thu!c
tuyn tính và N bi u th tuyn tính qua O1 , 2 O .
Bây giB ta xét h) vect {O1, N }. Gi, s* r1 1O + r2 N = 0 , ngha là
r1(1, 0, 0, 0) + r2(2, - 5, 0, 0) - (0, 0, 0, 0)
hay (r1, 0, 0, 0) + (2r2, - 5r2, 0, 0) = (r1 + 2r2, - 5r2, 0, 0) = (0, 0, 0, 0). Suy ra:
H) phng trình hai :n r1, r2 này có nghi)m duy nht là r1 = 0, r2 = 0.
V6y h) hai vect {O1 , N } !c l6p tuyn tính.
Bn 7c hãy t4 ki m tra s4 !c l6p tuyn tính ca hai h) { 1 O , O2 }, { O2 , N }.
T; nh ngha suy ra các tính cht sau. 3.2. Các tính cht
Theo nh ngha, hai khái ni)m ph# thu!c tuyn tính và !c l6p tuyn
tính ca h) vect là hai khái ni)m ph nh l-n nhau. Vì th, khái ni)m
này có m!t tính cht gì thì l6p tc suy ra m!t tính cht tng ng ca khái ni)m kia. Tính cht 1.
1) Nu thêm p vect vào mt h vect ph thuc tuyn tính thì c
mt h ph thuc tuyn tính.
2) Nu bt i p vect ca mt h vect c lp tuyn tính thì c
mt h c lp tuyn tính.
Chng minh. 1) Gi, s* h) vect = { N 1, N 2,..., N m-1, N m} ph#
thu!c tuyn tính. Khi ó t&n ti m s s1,..., sm không &ng thBi b'ng 0,
ch9ng hn si ≠ 0, sao cho: Th thì:
Theo nh ngha, h) vect { N 1,..., N i-1 N i, N i+1,..., N m,...,N m+1,...,
N m+p} ph# thu!c tuyn tính.
2) Gi, s* t; h) vect !c l6p tuyn tính b8t i p vect ta >c h)
vect . Nu ph# thu!c tuyn tính thì theo 1), thêm p vect nói trên
vào li >c h) ph# thu!c tuyn tính; trái v8i gi, thit. V6y !c l6p tuyn tính. Tính cht 2.
1) Mt h gm m vect (m > 1) là ph thuc tuyn tính khi và ch# khi
có mt vect ca h c biu th qua các vect còn l"i.
2) Mt h gm m vect (m > 1) là c lp tuyn tính khi và ch# khi
không có mt vect nào ca h c biu th qua các vect còn l"i. Chng minh. 1) "" Gi, s* h) vect
Ca K-không gian vect V là ph# thu!c tuyn tính. Theo nh ngha,
t&n ti m s ri ∈ K, i ∈ {1, 2,..., m) không &ng thBi b'ng 0, ch9ng hn, ri ≠ 0, sao cho:
r1 N 1 + ...+ ri-1 N i-1 + ti+1 N i+1 ... + rm N m = 0 .
Khi ó r1 N 1 = - r1 N 1 -...- ti-1 N i-1 – ri+1 N i+1 - ... - rm0 .
Vì ri ≠ 0 nên t; 9ng thc này suy ra
ngha là N i >c bi u th tuyn tính qua các vect còn li.
“⇐” Gi, s* trong h) vect (1) có vect N i; tho, mãn 9ng thc:
Vì có si = -1 ≠ 0 nên 9ng thc này chng t( h) (1) ph# thu!c tuyn tính. 2) Tr4c tip suy ra t; 1). Tính cht 3.
1) Mt h gm m vect (m > 0) là c lp tuyn tính khi và ch# khi
mi t hp tuyn tính ca h u ch# có mt cách biu th tuyn tính duy nht qua h ó.
2) Mt h gm m vect (m > 0) ca không gian vect V là ph thuc
tuyn tính khi và ch# khi có mt vect ca V biu th tuyn tính c qua
h ó theo hai cách khác nhau.
Chng minh. 1) “” Gi, s* h) vect { N 1, N 2,..., N m} !c l6p tuyn tính và
Nu P còn có cách bi u th tuyn tính
thì (b1 – b’1)N 1 + (b2 - b'2 ) N 2 + ... + (bm – b’m ) N m = 0 .
Vì h) vect gã cho !c l6p tuyn tính nên theo nh ngha, b1 – b’1 =
b2- b'2 = ... = bm – b’m = 0.
Suy ra: b1 = b’1, b2 = b'2 ,..., bm = b’m; ngha là cách bi u th tuyn
tính ca P qua h) vect ã cho là duy nht.
"⇐": Nu mGi t/ h>p tuyn tính ca h) vect { N 1, N 2,..., N m} %u
chF có m!t cách bi u th tuyn tính duy nht thì 0 = 0 N 1 + 0 N 2 + ... +
0 N m cCng là cách bi u th tuyn tính duy nht ca 0 . Do ó, nu 0 = r1 N
+ r2 N 2 + ...+ rm N m thì b?t bu!c r1 = r2 ... = rm = 0. V6y h) vect ã cho !c l6p tuyn tính. 2) Suy ra t; 1). Tính cht 4.
1) Nu thêm vào mt h c lp tuyn tính mt vect không biu th
tuyn tính c qua h y thì c mt h c lp tuyn tính.
2) Nu bt i mt h ph thuc tuyn tính mt vect không biu th
tuyn tính c qua các vect còn l"i thì c mt h ph thuc tuyn tính.
Chng ninh. 1) Gi, s* = { N 1, a2,..., N m-1, N m}là m!t h) vect !c
l6p tuyn tính ca K-không gian vect V. P ∈ V là m!t vect không
bi u th tuyn tính >c qua h) . Ta ph,i chng minh h) vect =
{ N 1, a2,..., N m-1, N m , P } !c l6p tuyn tính. Gi, s* Nu r ≠ 0 thì
trái v8i gi, thit v% P . Do ó r = 0 và r= N 1 +...+ rm N m = 0 vì h) !c
l6p tuyn tính. Suy ra r1 = ... = rm = 0. V6y là h) vect !c l6p tuyn tính. 2) Suy ra ngay t; 1).
Sau khi có khái ni)m v% h) sinh ca m!t không gian vect và h)
vect !c l6p tuyn tính ta nghiên cu cu to ca không gian vect.
§4. CƠ S CA KHÔNG GIAN VECTƠ
Ta nh?c li r'ng, trong giáo trình này ta chF xét các không gian vect
có h) sinh h0u hn (h0u hn sinh) trên trBng s.
4.1. nh ngha
Mt h sinh c lp tuyn tính ca mt không gian vect khác { 0 }
c gi là mt c s ca nó.
Không gian vect { 0 } không có c s1; hay có th nói, s vect trong
c s1 ca không gian { 0 } b'ng 0.
Ví d 1. Trong không gian vect Pn g&m a thc 0 và các a thc
thu!c K[x] v8i b6c bé hn hay b'ng n, h) vect {1, x, x2,..., xn) là m!t c s1.
Th6t v6y, mGi a thc f(x) ∈ Pn %u có dng f(x) = a0 + a1x + a2x2 +...
+ anxn, ai ∈ K, v8i m7i i ∈ {0, 1, 2,..., n). i%u ó chng t( {1, x,
x2,..., xn) là m!t h) sinh ca P n
n. M$t khác, nu a0 + a1x + a2x2 +... + anx
= 0 thì t; nh ngha a thc suy ra a0 = a1 = a2 = ... = an = 0; ngha là {1,
x, x2,..., xn) là h) vect !c l6p tuyn tính. V6y nó là m!t c s1 ca Pn.
Ví d 2. Trong không gian vect R3, h) ba vect 1 O = (1, 0, 0), O2 =
(0, 1, 0), O3 = (0, 0, 1) là m!t c s1; ngBi ta g7i ó là c s chính t&c.
Bn 7c có th chng t( i%u ó.
H) ba vect X 1 = (1, 1, 0), X 2 = (0, 1, 1), X 3 (1, 0, 1) cCng là m!t c s1.
kh9ng nh i%u này ta sQ chng minh h) vect { X 1, X 2, X 3} là
m!t h) sinh ca R3 và !c l6p tuyn tính. Gi, s* N = (a1, a2, a3) là m!t
vect bt kì thu!c R3. Ta tìm ba s r1, r2, r3 ∈ R sao cho N = r1 X 1 + r2 X 2 + r3 X 3 hay sao cho:
Gi,i h) phng trình 3 :n r1, r2, r3 này ta >c nghi)m duy nht
i%u này chng t( { X 1, X 2, X 3} là m!t h) sinh ca R3. M$t khác, vì
ba s r1, r2, r3 >c xác nh duy nht nên mGi N %u có cách bi u th
tuyn tính duy nht qua h) sinh này. Theo tính cht 3, m#c 3.2, h) sinh
này !c l6p tuyn tính. V6y nó là m!t c s1 ca R3.
M!t câu h(i $t ra là mGi không gian vect %u có c s1 hay không?
tr, lBi câu h(i này ta hãy xét mi liên quan gi0a h) sinh và c s1.
4.2. S2 t&n ti ca c% s/
Tr8c ht ta xét b/ % sau v% mi liên quan gi0a h) sinh và c s1
B- $. Nu không gian vect có mt h sinh gm m vect thì svect
ca mi h vect c lp tuyn tính ca nó không vt quá m.
Chng minh. Gi, s* K-không gian vect V có m!t h) sinh = { N 1,
N 2,..., N m}, N ≠ 0 v8i m7i i ∈ {1, 2,..., m) và = { O 1, O 2,..., O n} là m!t
h) vect !c l6p tuyn tính ca V v8i n > m. Vì là m!t h) sinh nên
ε ≠ 0 nên có m!t a1j khác 0, ch9ng hn a11 ≠ 0. Do ó
Thay N 1 trong h) b1i O 1 ta >c h) 1 = { O 1, N 2 ,..., N m}. Gi, s*
P ∈ V P = b1 N 1 + b2 N 2 + ... + bm N m. Th thì
Nh v6y mGi P ∈ V %u bi u th tuyn tính >c qua h) 1; do ó
1 là m!t h) sinh ca V. Nói riêng, O 2 có dng:
Nu tt c, các h) s ca các N i %u b'ng 0 thì O 2 = a21 O 1. Suy ra h)
ph# thu!c tuyn tính; trái v8i gi, thit. Vì th có m!t a2j ≠ 0, V8i j ≠ 1.
Nu cn ta ánh s li các N i gi, thit r'ng a22 ≠ 0. Khi ó
Thay N 2 trong 1 b1i O 2 ta >c h) 2 = { O 1, O 2,..., N m }. L6p lu6n
nh trên, 2 là m!t h) sinh ca V. C tip t#c nh th, ta ln l>t thay m
vect ca h) b1i m vect u tiên ca h) và >c h) sinh m = { O 1,
O 2,..., O m} ca v. Theo gi, thit, n > m nên O m+l ∉ m. Nhng m là h)
sinh ca V nên O m+1 >c bi u th tuyn tính qua h) vect này; trái v8i
gi, thit !c l6p tuyn tính ca h) . V6y n ≤ m.
H qu. S vect trong hai c s ca mt không gian vect bng nhau.
Chng minh. Suy ra ngay t; nh lí trên.
Bây giB ta tr, lBi cho câu h(i $t ra tr8c m#c 4.2.
nh lí 1. Mi K - không gian vect V ≠ {0 } u có c s.
Chng minh. Gi, s* O 1 ≠ 0 là m!t vect thu!c V. Theo ví d# 1, m#c
3.1, h) { O 1} !c l6p tuyn tính. Nu m7i vect ca V %u bi u th tuyn
tính qua h) này thì ó là m!t c s1 ca V. Nu trái li, trong V có O 2
không bi u th tuyn >c qua O 1. Theo tính cht 4, m#c 3.2, h) vect
{ O 1, O 2} !c l6p tuyn tính. Nu h) này không ph,i là m!t c s1 thì
trong V có m!t O 3 không bi u th tuyn tính >c qua h) { O 1, O 2}. Li
theo tính cht 4, m#c 3.2, h) vect { O 1, O 2, O 3} !c l6p tuyn tính. Tip
t#c, b/ sung nh th ta >c nh0ng h) vect !c l6p tuyn tính ca V. Vì
V có m!t h) sinh g&m m vect nào ó (có th ta không bit h) sinh y)
nên theo b/ %, quá trình này ph,i kt thúc 1 vect O n nào ó v8i n ≤ m.
Lúc ó ta >c h) vect
= { O 1, O 2, O 3 ,..., O n}
mà m7i vect ca v %u bi u th tuyn tính >c qua h) . V6y = { O 1,
O 2, O 3 ,..., O n} là m!t c s1 ca V.
H qu. Trong không gian vect, mi h vect c lp tuyn tính bt
kì u có th b sung thành mt c s.
Ý ngha ca nh lí trên ây là dù cho không bit tr8c h) sinh ca
không gian vect ta vJn có th d4ng >c m!t c s1 ca nó. Song khi ã
bit m!t h) sinh ca không gian vect thì nh lí sau ây cho thy có th
ch7n m!t c s1 trong h) sinh này. ó là tr, lBi cho câu h(i $t ra tr8c §3.
nh lí 2. T, mt h sinh ca mt không gian vect khác { 0 } có th
chn ra mt c s.
Chng minh. Cách chng minh nh lí này ging nh cách chng
minh nh lí trên; chF khác 1 chG là áng lQ ta ch7n các vect Q; trong V
thì 1 ây ta ph,i ch7n chúng trong h) sinh ã cho.