Chương 2. Phương pháp phổ hấp thụ phân tử | Bài giảng môn Phân tích bằng công cụ | Đại học Bách khoa hà nội
Năng lượng phân tử được lưu giữ có thể coi là tổng năng lượng lưu trữ của ba dạng. Tài liệu trắc nghiệm môn Phân tích bằng công cụ giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Preview text:
Phần I: Các phương pháp phân tích quang học
Chương 2. Phương pháp phổ hấp thụ phân tử Tran Thi Thuy
Department of Analytical Chemistry
School of Chemical Engineering – Hanoi University of Science and Technology (HUST) Outline
2.1 Sự hình thành phổ phân tử
2.2 Định luật cơ bản về hấp thụ bức xạ điện từ
2.3 Các thủ tục thực nghiệm trong phân tích đo quang
2.4 Phương pháp đo quang vi sai
2.5 Thiết bị quang phổ hấp thụ phân tử
2.6 Một số ứng dụng phương pháp đo quang 2.7 Bài tập 2 HUST SCE 9/22/2020
2.1. Sự hình thành phổ phân tử
2.1.1. Sự hấp thụ bxđt và sự hình thành các loại phổ hấp thụ phân tử
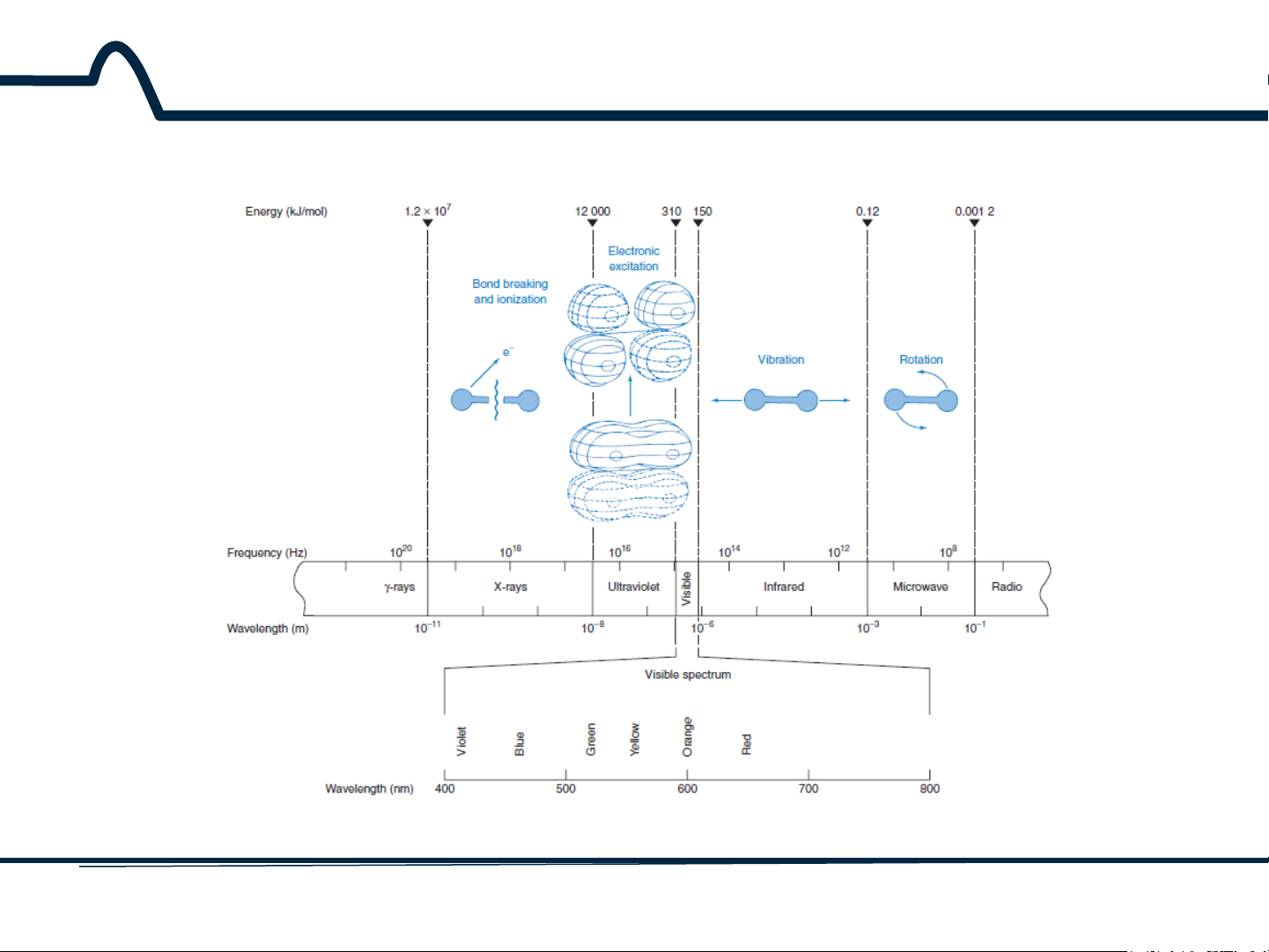
Năng lượng phân tử được lưu giữ có thể coi là tổng năng
lượng lưu trữ của ba dạng: -Quay -Dao động -Điện tử E thấp + hν = Ecao
Phân tử chỉ tồn tại ở trạng thái kích thích trong khoảng thời
gian rất ngắn (10-6-10-9s) và quay trở lại trạng thái cơ bản. 3 HUST SCE
2.1.1. Sự hấp thụ bxđt và sự hình thành các loại phổ hấp thụ phân tử
Điện tử bị kích thích Dao động Quay Bẻ gãy liên kết và ion hóa 4 HUST SCE
2.1.1. Sự hấp thụ bxđt và sự hình thành các
loại phổ hấp thụ phân tử
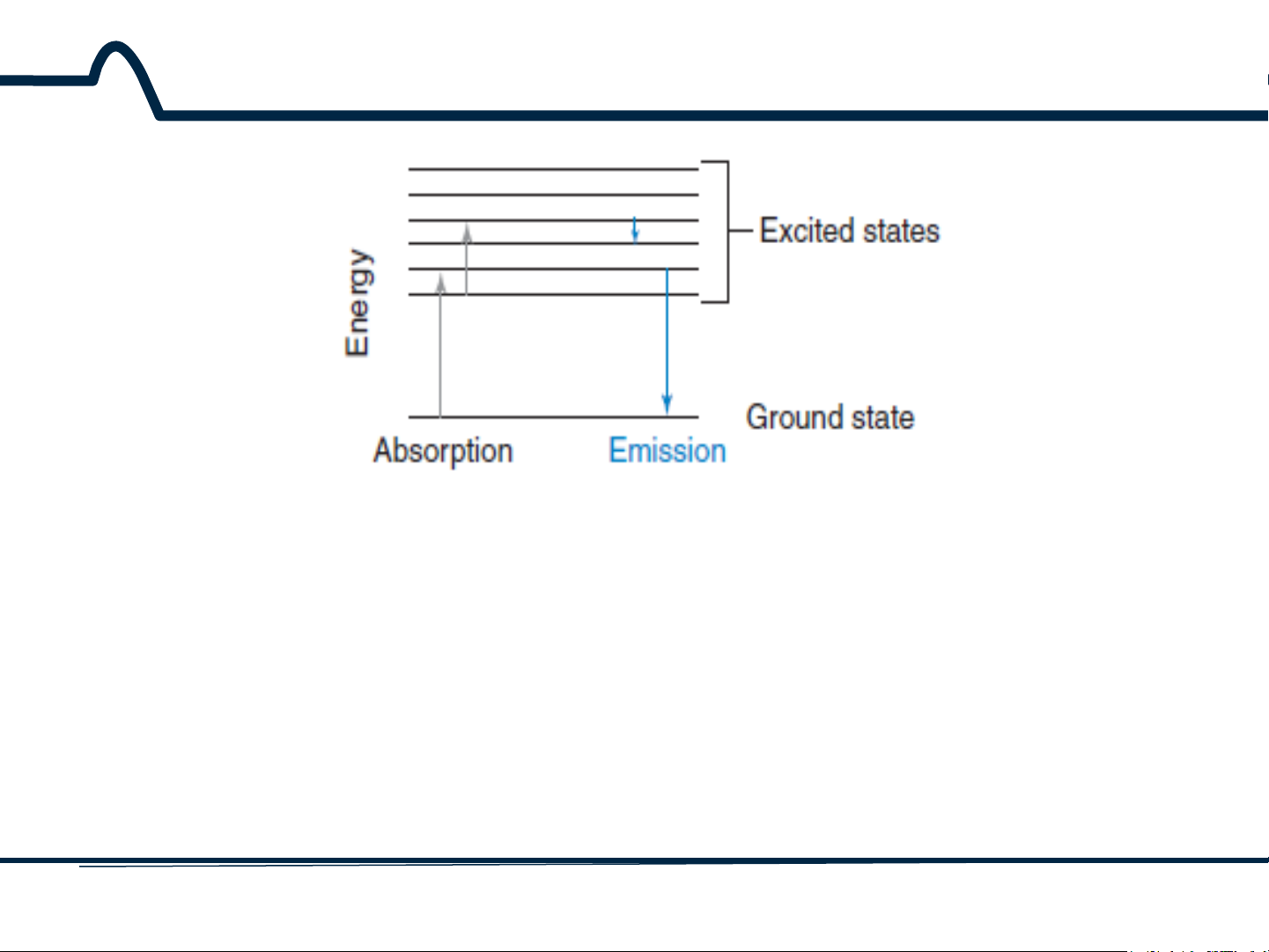
Quá trình phát xạ (Emission) là quá trình một phân tử
chuyển trạng thái lượng tử cao hơn sang thấp hơn và thoát ra một photon.
Quá trình hấp thụ (Absorption) là một quá trình một phân
tử chuyển từ trạng thái lượng tử thấp hơn sang cao hơn và hấp thụ một photon. 5 HUST SCE
2.1.1. Sự hấp thụ bxđt và sự hình thành các loại phổ hấp thụ phân tử
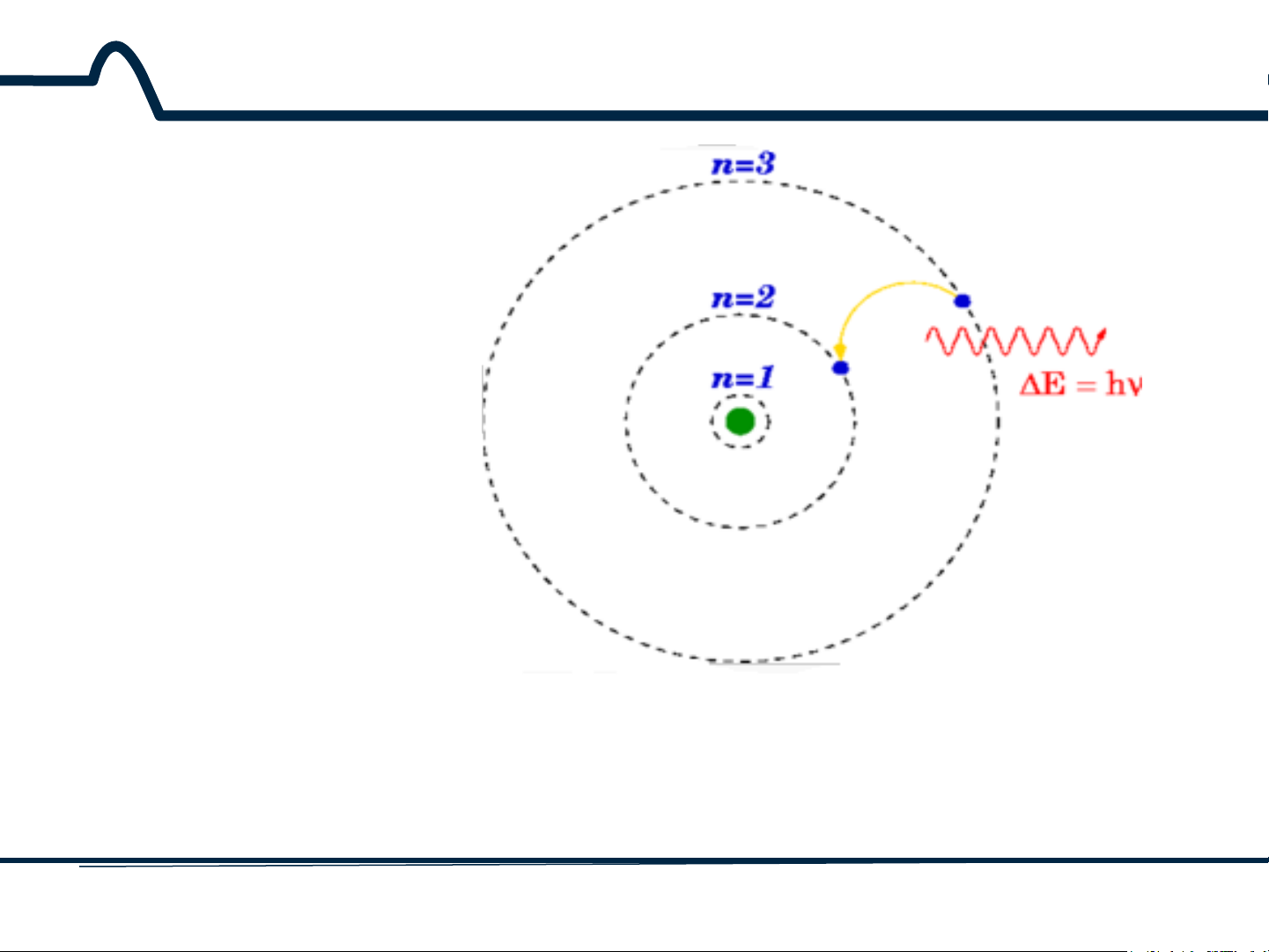
Sự thay đổi trạng thái lượng tử của phân tử sẽ dẫn đến sự
biến thiên năng lượng ΔE của phân từ tuân theo định luật Planck.
ΔE = Ecao – E thấp = hν (2-1)
Do năng lượng phân tử được lưu giữ dưới ba dạng: quay,
dao động và điện tử nên:
ΔE = ΔEquay + ΔEdao động+ ΔEđiện tử (2-2) 6 HUST SCE
2.1.1. Sự hấp thụ bxđt và sự hình thành các loại phổ hấp thụ phân tử
Sự dịch chuyển điện tử ở trạng thái năng lượng lượng tử của một
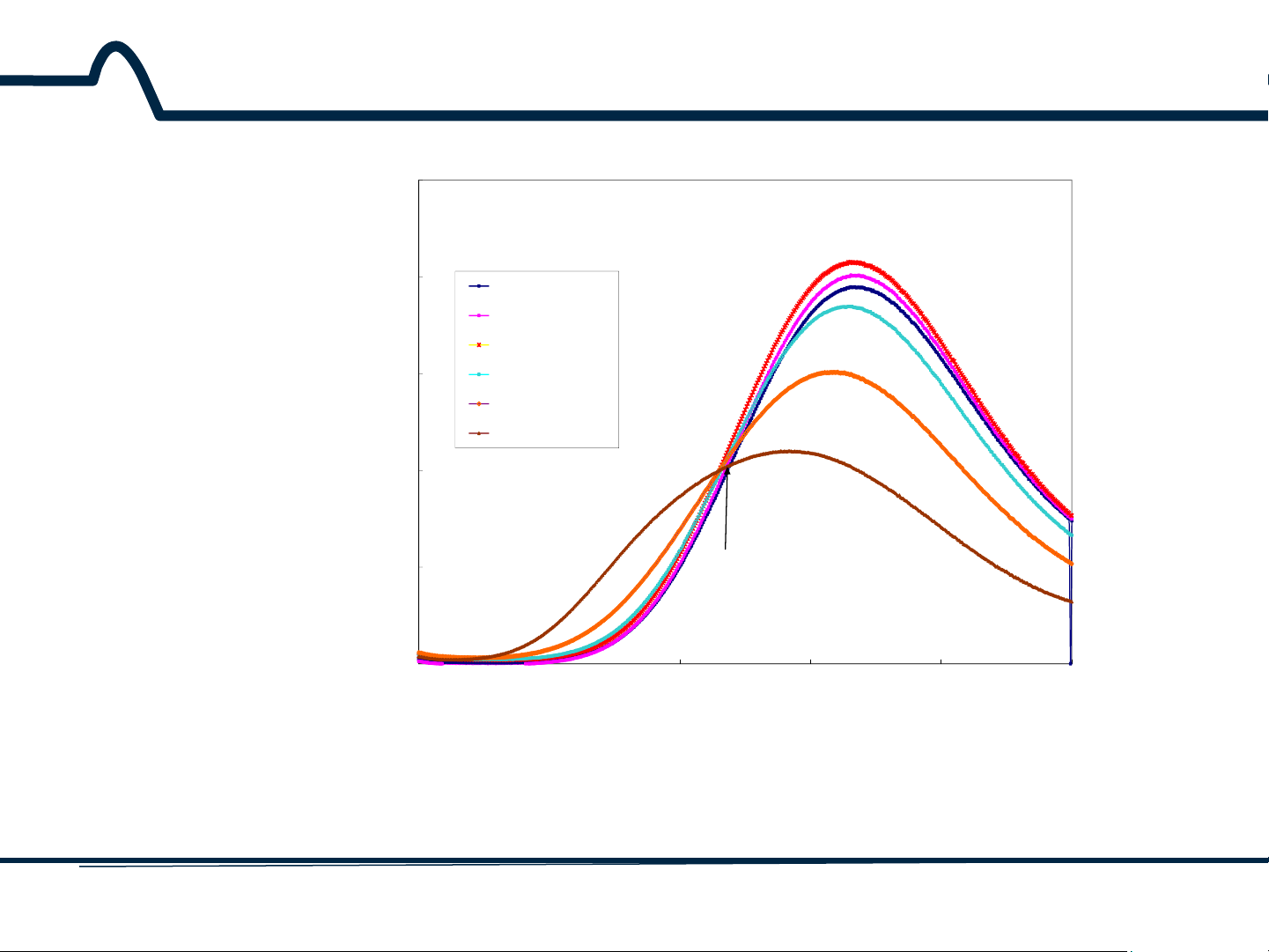
nguyên tử tạo ra sự phát xạ của một photon. 7 HUST SCE 2.1.2. Phổ hấp thụ 0.5 (3) 0.4 (2) (1)_pH=4.10, 730.9nm (1) (2)_pH=5.15, 730.9nm (4) (3)_pH=6.06, 730.9nm (5) 0.3 (4)_pH=7.00, 729.9nm (5)_pH=8.01, 721nm A (6)_pH=9.08, 684.0nm (6) 0.2 isosbestic point 0.1 0 400 500 600 700 800 900 wavelength, nm
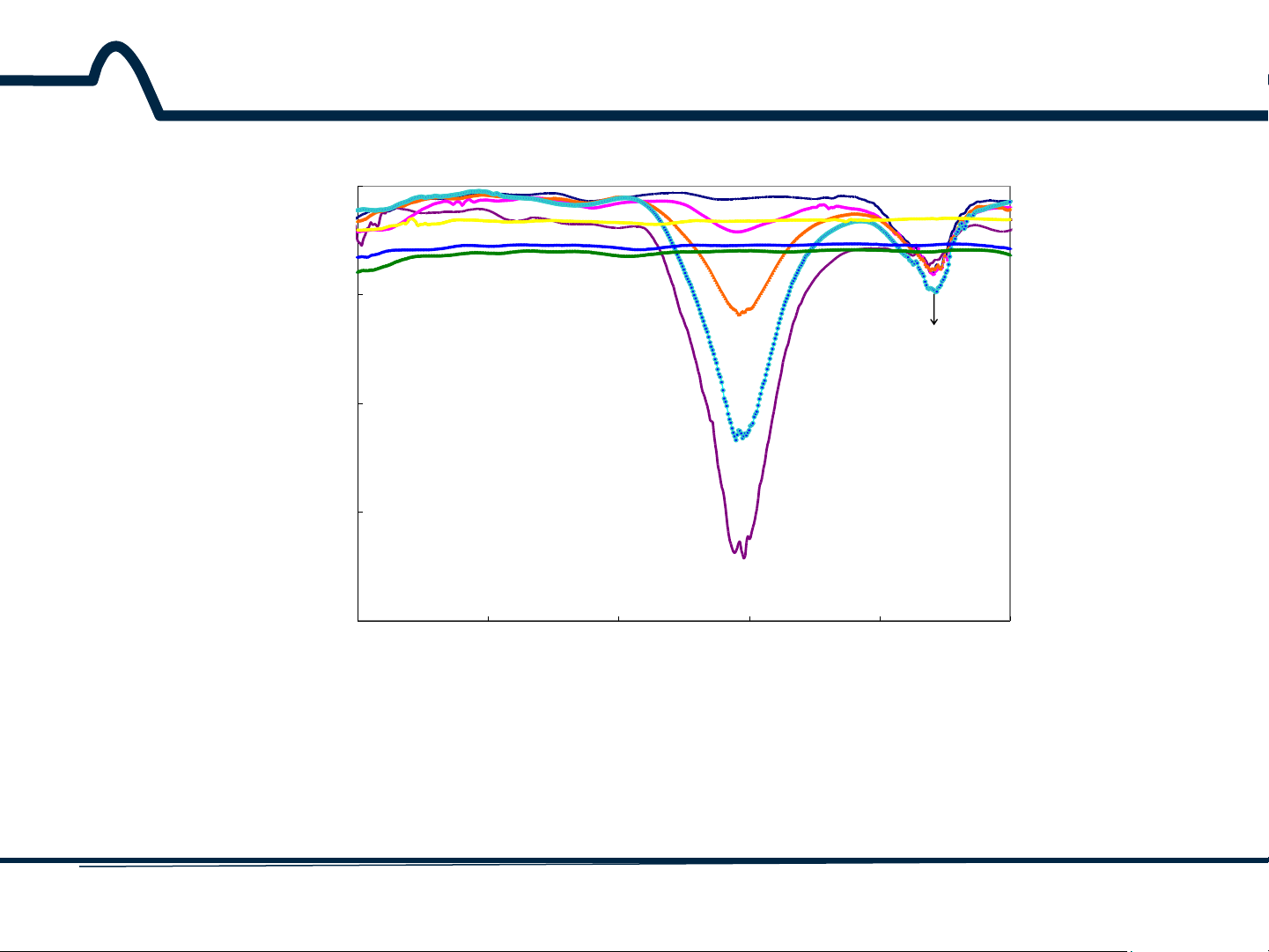
Phổ hấp thụ: mô tả mối quan hệ giữa độ hấp thụ A và bước sóng λ 8 HUST SCE 2.1.2. Phổ hấp thụ 100 (1) (6) (2) (7) (8) 95.5 (3) NaCl T 91 % (4) 86.5 (5) C=O, 1420 cm-1 82 2000 1800 1600 1400 1200 1000 wavelength, cm-1
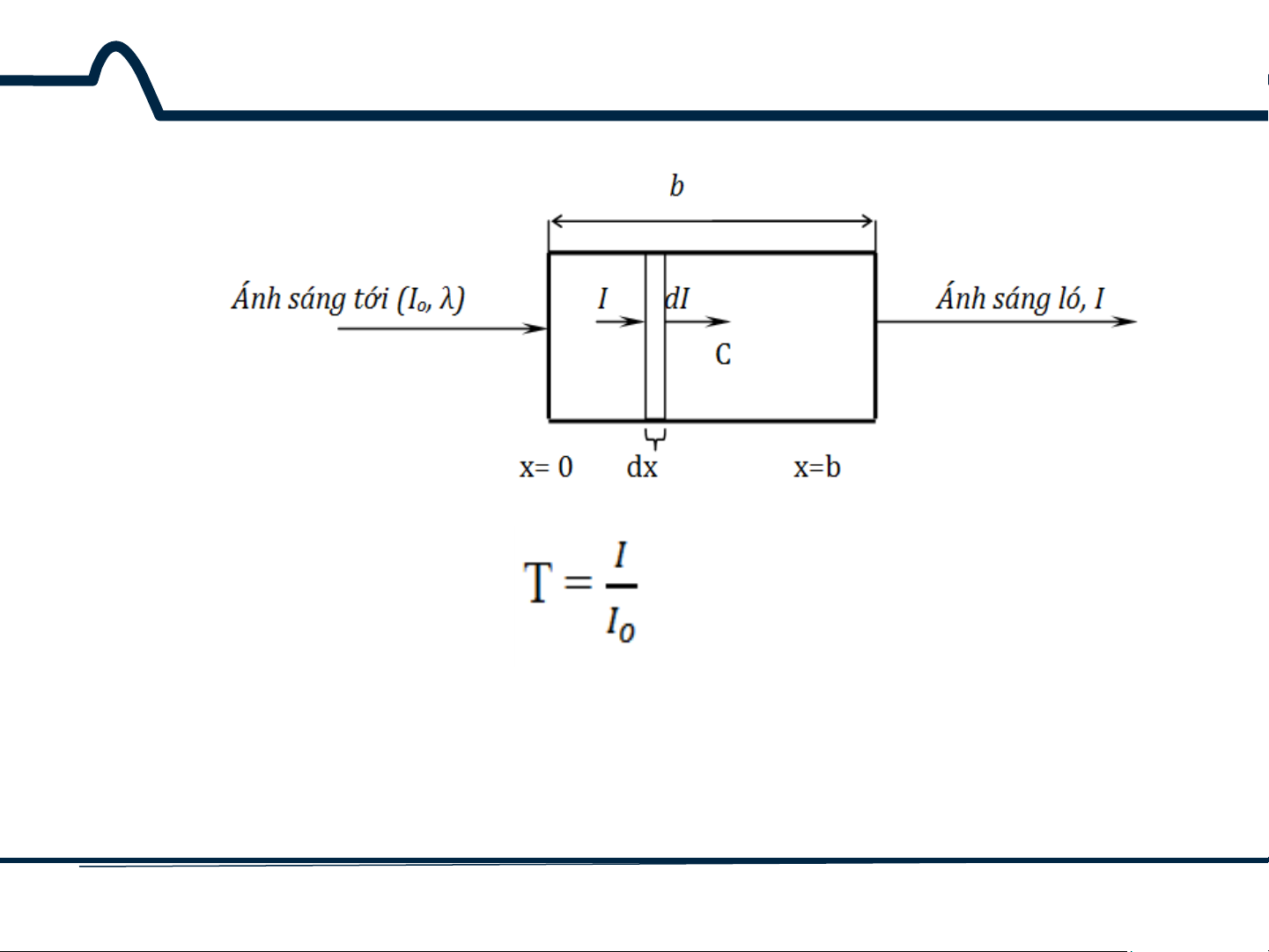
Phổ hấp thụ: mô tả mối quan hệ giữa Phần trăm truyền quang %T và số sóng 9 HUST SCE 2.1.2. Phổ hấp thụ Độ truyền quang T: (2-3)
Bởi vậy, T thay đổi từ 0-1. Phần trăm truyền quang, đơn
giản là 100T%, và nó thay đổi tương ứng từ 0-100%. 10 HUST SCE
2.1.2. Phổ hấp thụ
Độ hấp thụ quang A được định nghĩa: A = log𝐼𝑜 = –logT (2-4) 𝐼
Nếu ánh sáng không bị hấp thụ, I = Io và A = 0
Nếu 90% ánh sáng bị hấp thụ, 10% đã được truyền quang, A = 1
Nếu chỉ có 1% ánh sáng được truyền quang, A = 2
(Độ hấp thụ quang A đôi khi còn gọi là mật độ quang – optical density) 11 HUST SCE
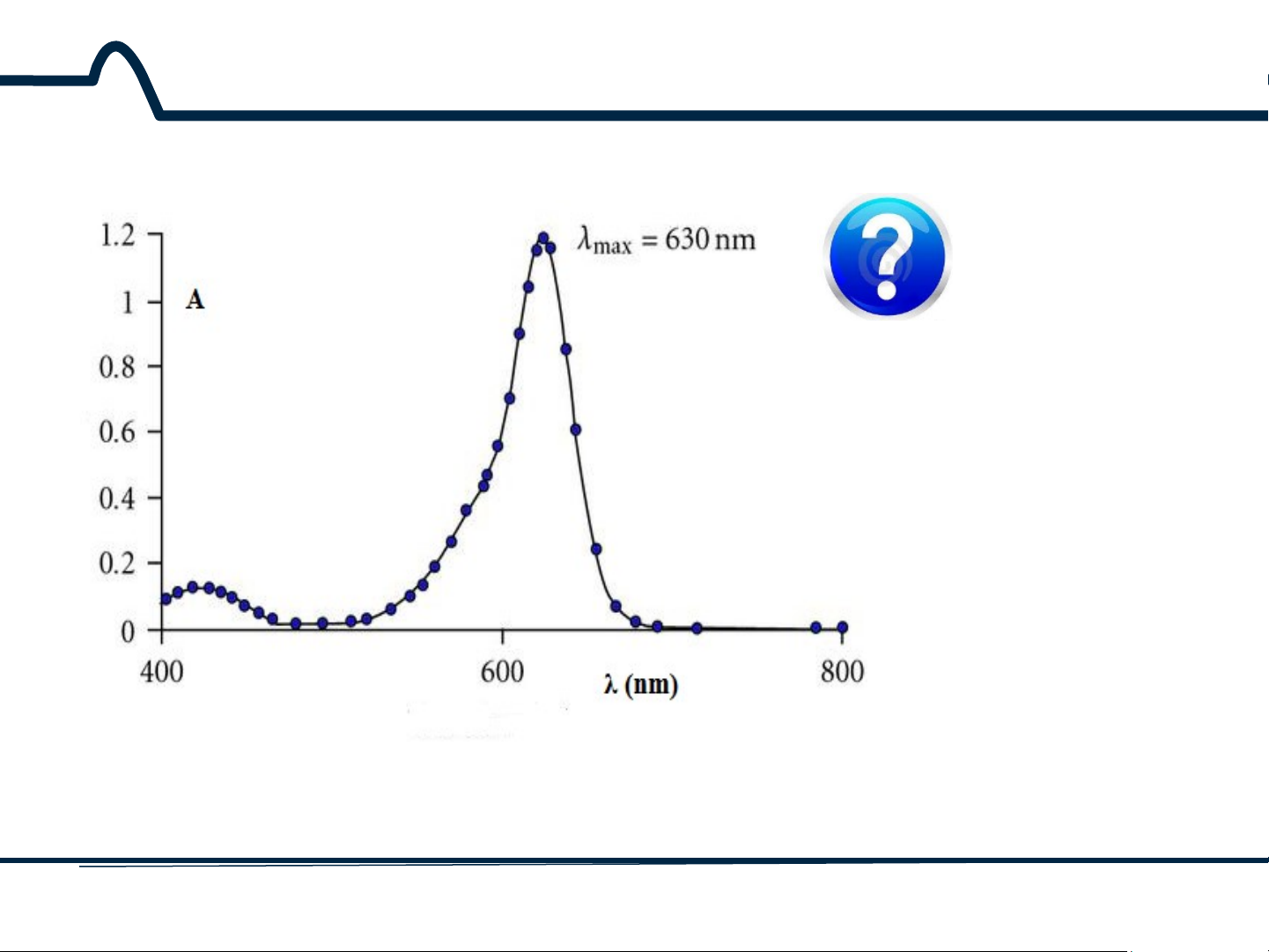
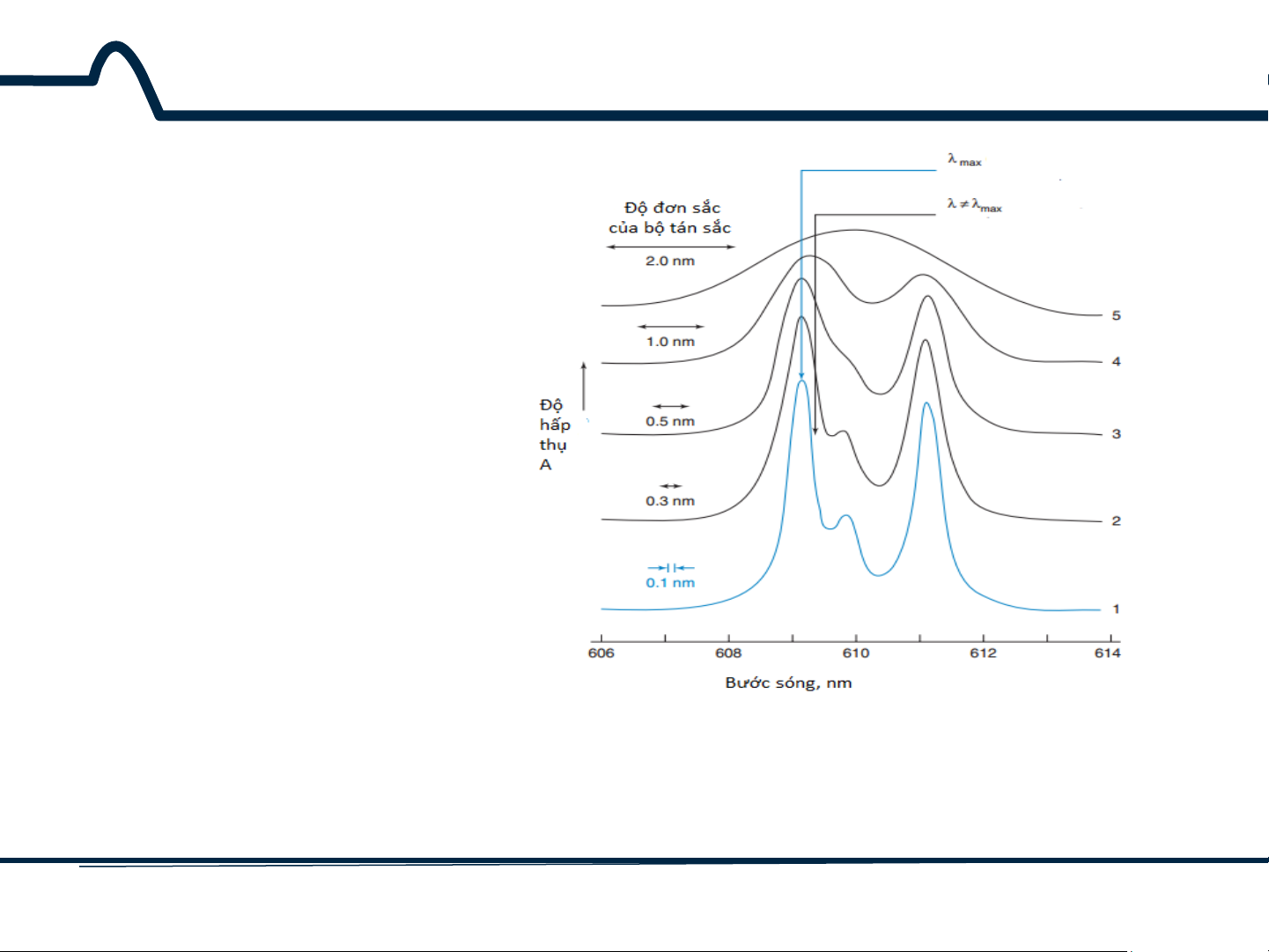
2.1.2. Phổ hấp thụ Tại sao trong phân tích đo quang người ta lựa chọn bước sóng λ là bước sóng tia tới?
Phổ hấp thụ của chất A ở dạng dung dịch 12 HUST SCE
2.1.2. Phổ hấp thụ
Tính đơn sắc của bộ tán sắc càng giảm, dẫn đến sự giảm của độ
hấp thụ của Pr3+ trong tinh thể của một loại vật liệu lazer (yttrium aluminum garnet Y3Al5O12) 13 HUST SCE
2.2. Định luật cơ bản về hấp thụ bức xạ điện từ
2.2.1. Định luật Lambert-Beer
A = εbC = log𝐼𝑜 = –logT (2-5) 𝐼
Độ hấp thụ A là một đại lượng không thứ nguyên. Nồng độ
của mẫu thường được sử dụng đơn vị là mol/l. Chiều dày
của cuvet đựng mẫu b, thường được mô tả bằng cm. Đại
lượng ε gọi là độ hấp thụ mol (hay còn gọi là hệ số tắt phân
tử) và có đơn vị là M-1cm-1, bởi vậy tích số εbC là không thứ nguyên.
Câu hỏi: Nêu ý nghĩa vật lý của ε=? 14 HUST SCE
2.2.1. Định luật Lambert-Beer
Trong phân tích đo quang, với dung dịch phân tích xác định,
bước sóng tia tới là đơn sắc thì ε là xác định, người ta luôn
có thể chọn b xác định nên định luật hấp thụ ánh sáng có thể viết dưới dạng: A = KC với K= εb = const (2-6)
Phương pháp phân tích đo quang định lượng được đặt trên
cơ sở phương trình (2-6) 15 HUST SCE
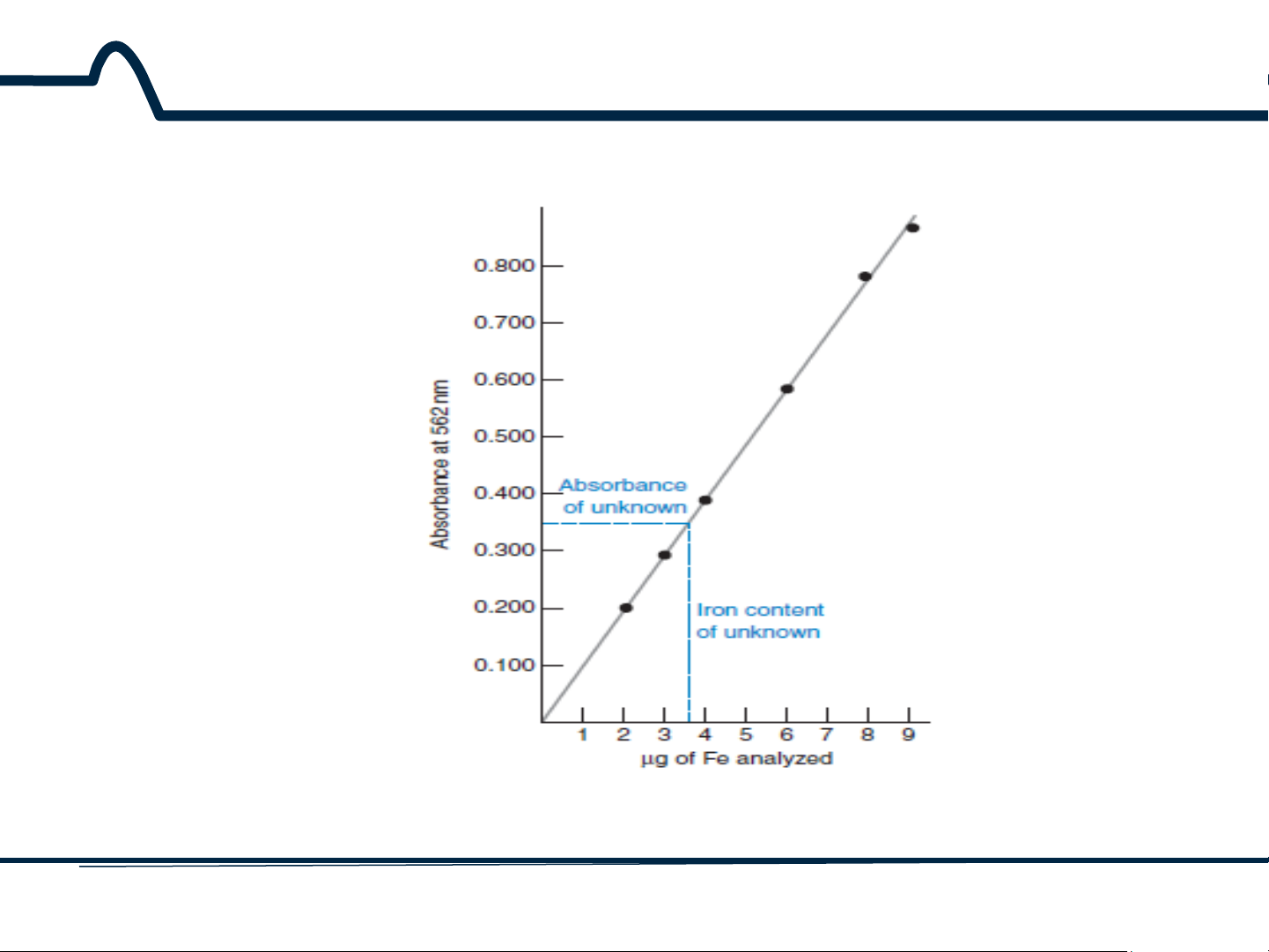
2.2.1. Định luật Lambert-Beer A = KC
Thủ tục đường chuẩn xác định hệ số góc K 16 HUST SCE
2.2.1. Định luật Lambert-Beer
Ví dụ: Tìm độ hấp thụ quang và truyền quang của dung
dịch 0,00240M của một dung dịch có độ hấp thụ mol ε=
313 M –1cm –1, với bề dày cuvet là b = 1,00 cm Giải: Theo (2-5) ta có: Độ hấp thụ:
A = εbC = 313 M –1cm –1 x 1,00 cm x 0,00240M = 0,751
Độ truyền quang T = 10 –A = 10 –0,751 = 0,177
→ có 17,7% ánh sáng truyền qua dung dịch (ánh sáng ló) 17 HUST SCE
2.2.2. Tính chất cộng tính của độ hấp thụ quang
Giả sử chúng ta chiếu liên tiếp một chùm tia sáng đơn sắc
qua hai dung dịch có nồng độ lần lượt là C1 và C2, độ hấp
thụ mol tương ứng là ε1 và ε2.
𝑙𝑜𝑔 𝐼𝑜 + 𝑙𝑜𝑔 𝐼1 = 𝑙𝑜𝑔 𝐼𝑜 × 𝐼1 = 𝑙𝑜𝑔 𝐼𝑜 ⇿ A 𝐼 1 + A2 = A 1 𝐼2 𝐼1 𝐼2 𝐼2 A = 𝑛 𝐴 𝑖=1 𝑖 (2-9) 18 HUST SCE
2.2.2. Các tính chất của độ hấp thụ quang
Nếu một dung dịch gồm chất nghiên cứu và tạp chất thì độ hấp thụ:
Adung dịch = Anghiên cứu + Anền
Trong phân tích đo quang chúng ta chuẩn bị dung dịch
trắng (blank) chứa các tạp chất, có nghĩa là:
Atrắng = Anền (do không có mặt ion cần xác định) Và
Anghiên cứu = Adung dịch– Atrắng
Như vậy, trong phân tích đo quang bằng việc sử dụng
dung dịch trắng, giá trị A đo được sẽ phản ánh đúng
nồng độ chất nghiên cứu, nói cách khác phương trình (2-
6) được tuân theo chặt chẽ. 19 HUST SCE
2.2.3. Các yếu tố làm sai lệch định luật Lambert-Beer
- Tính đơn sắc của ánh sáng tới
- Điều kiện hóa lý của dung dịch nghiên cứu 20 HUST SCE