Chương 2 Vấn đề tài chính trong định giá doanh nghiệp môn Định giá doanh nghiệp | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58457166 CHƯƠNG 2:
NHỮNG VẤN ĐỀ TÀI CHÍNH TRONG ĐỊNH GIÁ DOANH NGHIỆP
Đặng Thị Việt Đức- PTIT Nội dung
Giá trị thời gian của tiền
Tỷ suất sinh lời và rủi ro lOMoAR cPSD| 58457166
Chi phí sử dụng vốn của doanh nghiệp Dòng tiền
Phân tích và dự báo tài chính
Đặng Thị Việt Đức- PTIT
Giá trị thời gian của tiền
Giá trị theo thời gian của tiền Lãi đơn, lãi kép
Giá trị tương lai của tiền lOMoAR cPSD| 58457166
Giá trị hiện tại của tiền Tìm lãi suất tiền vay
Đặng Thị Việt Đức- PTIT
2.1. Giá trị theo thời gian của tiền Khái niệm
Trên góc độ tài chính, đồng tiền ở những thời điểm ở những thời điểm khác
nhau có giá trị khác nhau, do: Cơ hội sử dụng tiền Lạm phát Rủi ro lOMoAR cPSD| 58457166
2.1. Giá trị theo thời gian của tiền
Đồng tiền hiện tại có giá trị hơn đồng tiền trong tương lai.
Dùng giá trị theo thời gian của tiền để:
Quy về giá trị tương đương.
Có thể so sánh với nhau.
Có thể thực hiện các phép toán số học
1. Khái niệm giá trị theo thời gian của tiền
Giá trị theo thời gian của tiền được cụ thể hóa bằng hai khái niệm cơ bản: Giá trị hiện tại. Giá trị tương lai. lOMoAR cPSD| 58457166
3. Giá trị tương lai của tiền
Khái niệm giá trị tương lai
Giá trị tương lai của tiền là giá trị có thể nhận được tại một thời điểm trong
tương lai nếu đầu tư số tiền hiện tại với một tỷ lệ sinh lời nào đó.
Giá trị tương lai bao gồm số vốn gốc và toàn bộ tiền lời tính đến thời điểm tương lai đó.
3. Giá trị tương lai của tiền
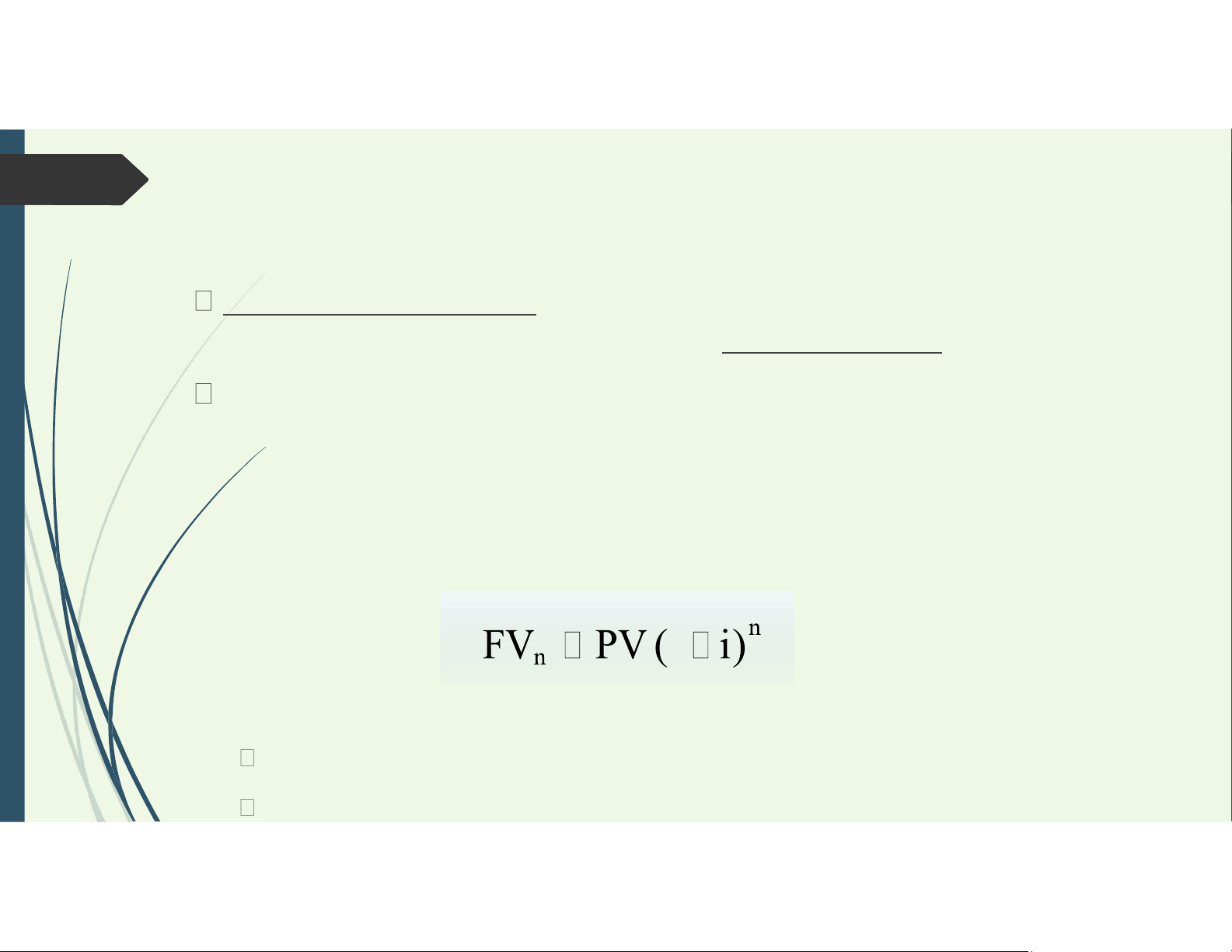
Cách tính giá trị tương lai 1
FVn= giá trị tương lai sau n kỳ hạn
PV= giá trị hiện tại của số tiền gốc ban đầu lOMoAR cPSD| 58457166
i= tỷ lệ lợi tức dự kiến
3. Giá trị tương lai của tiền
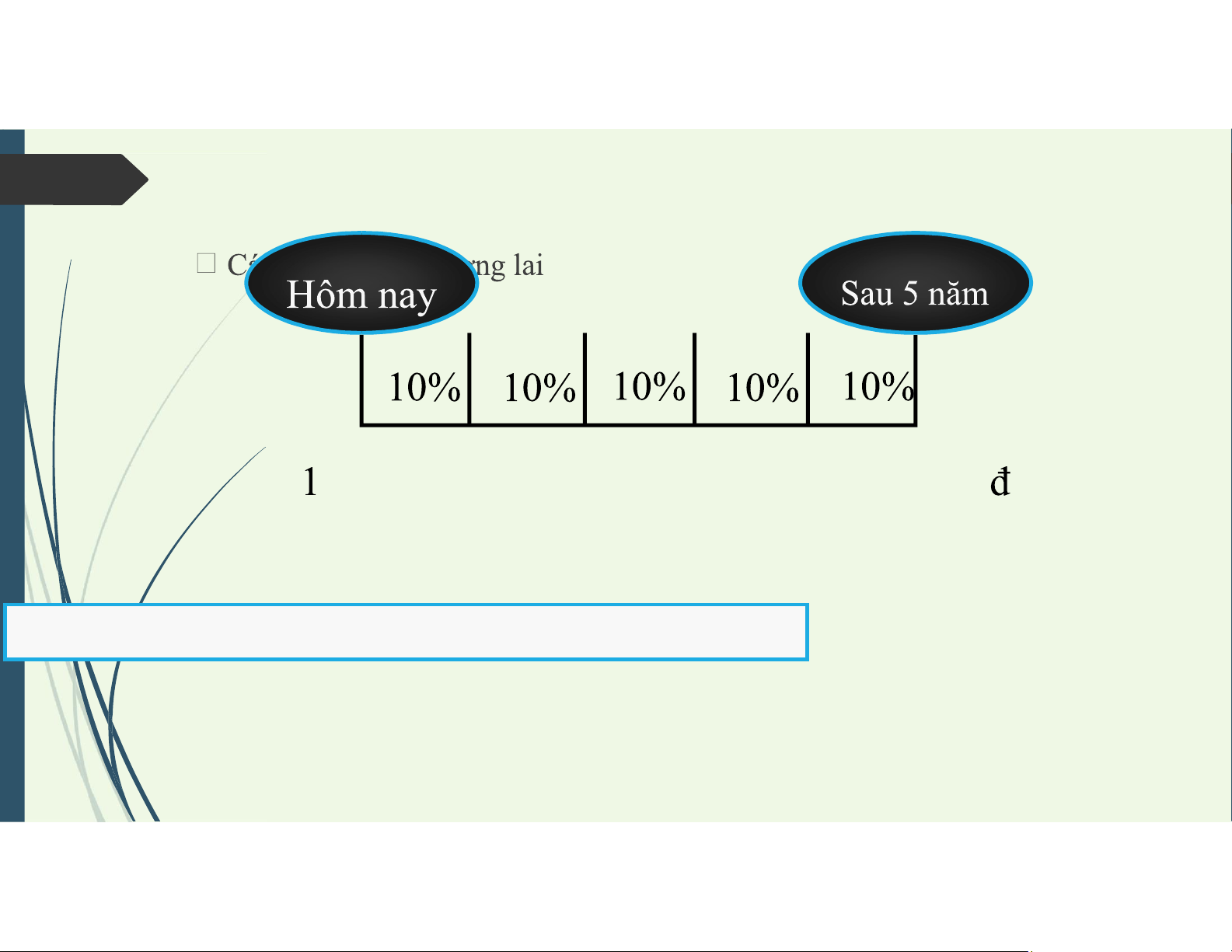
Cách tính giá trị tương lai Ví dụ:
1 triệu đồng hôm nay sẽ có giá trị tương lai là bao nhiêu sau 5 năm nếu lãi
suất đầu tư dự kiến là 10%/năm? lOMoAR cPSD| 58457166
3. Giá trị tương lai của tiền .000.000đ 1.610.510 FVn = PV × (1 + r)n
3. Giá trị tương lai của tiền lOMoAR cPSD| 58457166
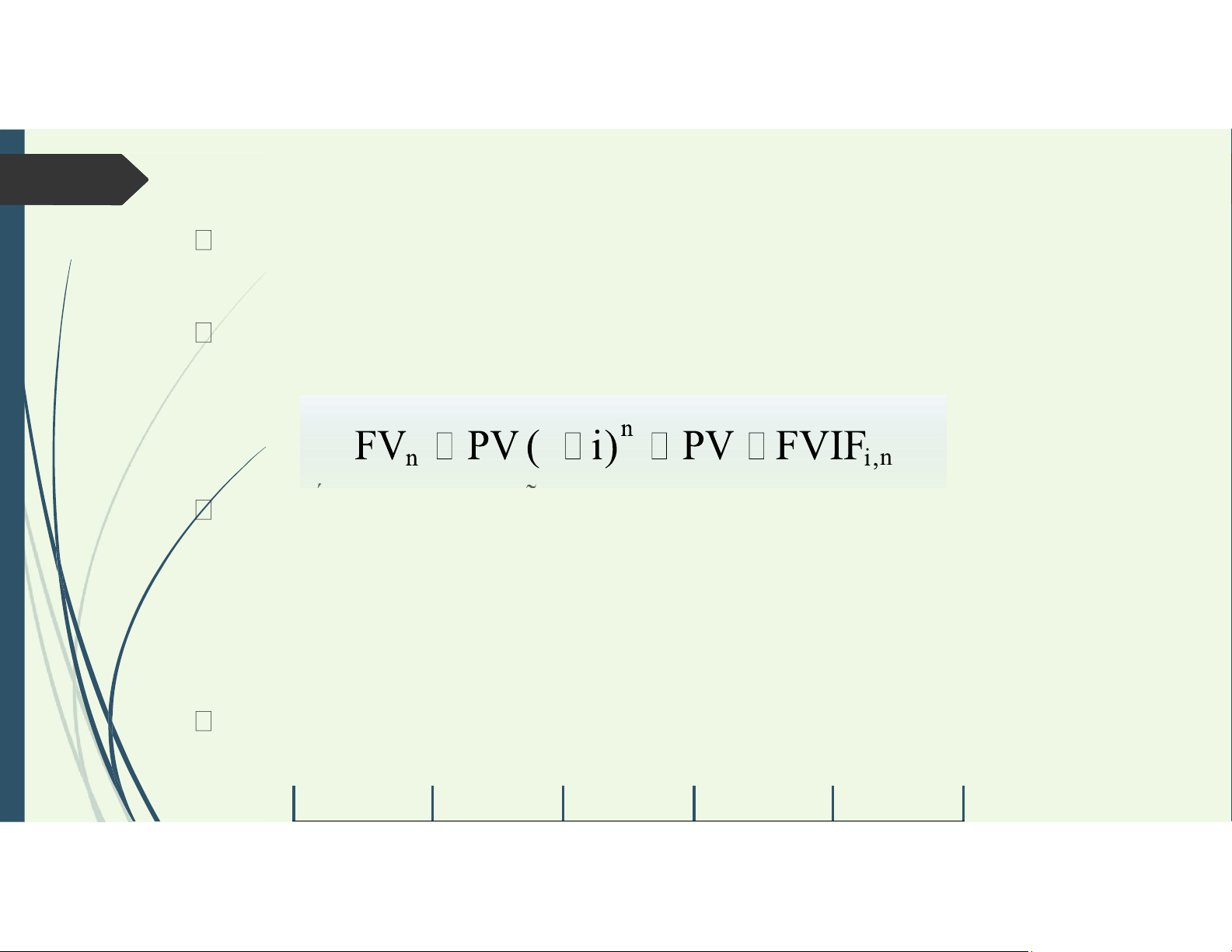
Cách tính giá trị tương lai
(1+i)n : biểu thị giá trị tương lai của 1 đồng sau n kỳ với tỷ lệ lợi tức dự tính
là i (tính theo phương pháp lãi kép)
(1+i)n được gọi là thừa số lãi giá trị tương lai, ký hiệu FVIFi,n (future value interest factor) 1 n
Thừa số này được tính sẵn dạng bảng
3. Giá trị tương lai của tiền Chuỗi tiền tệ
Chuỗi tiền tệ cuối kỳ 0 1 2 3 4 5 lOMoAR cPSD| 58457166 CF1 CF2 CF3 CF4 CF5
Chuỗi tiền tệ đầu kỳ 0 1 2 3 4 5 CF1 CF2 CF3 CF4 CF5
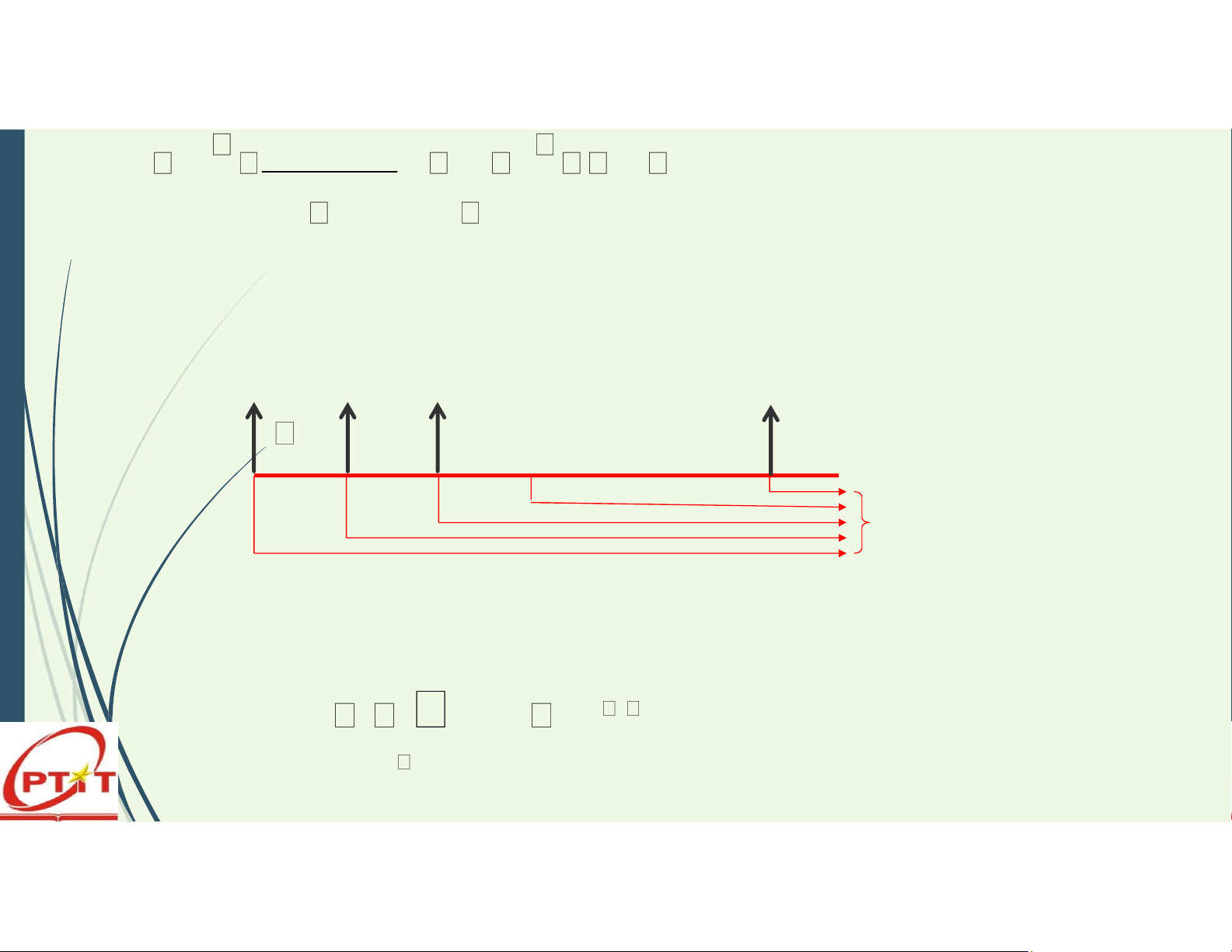
3. Giá trị tương lai của tiền Chuỗi tiền tệ
Chuỗi tiền đều (Annuity) lOMoAR cPSD| 58457166 CF CF CF CF CF Chuỗi tiền không đều CF1 CF2 CF3 CF4 CF5
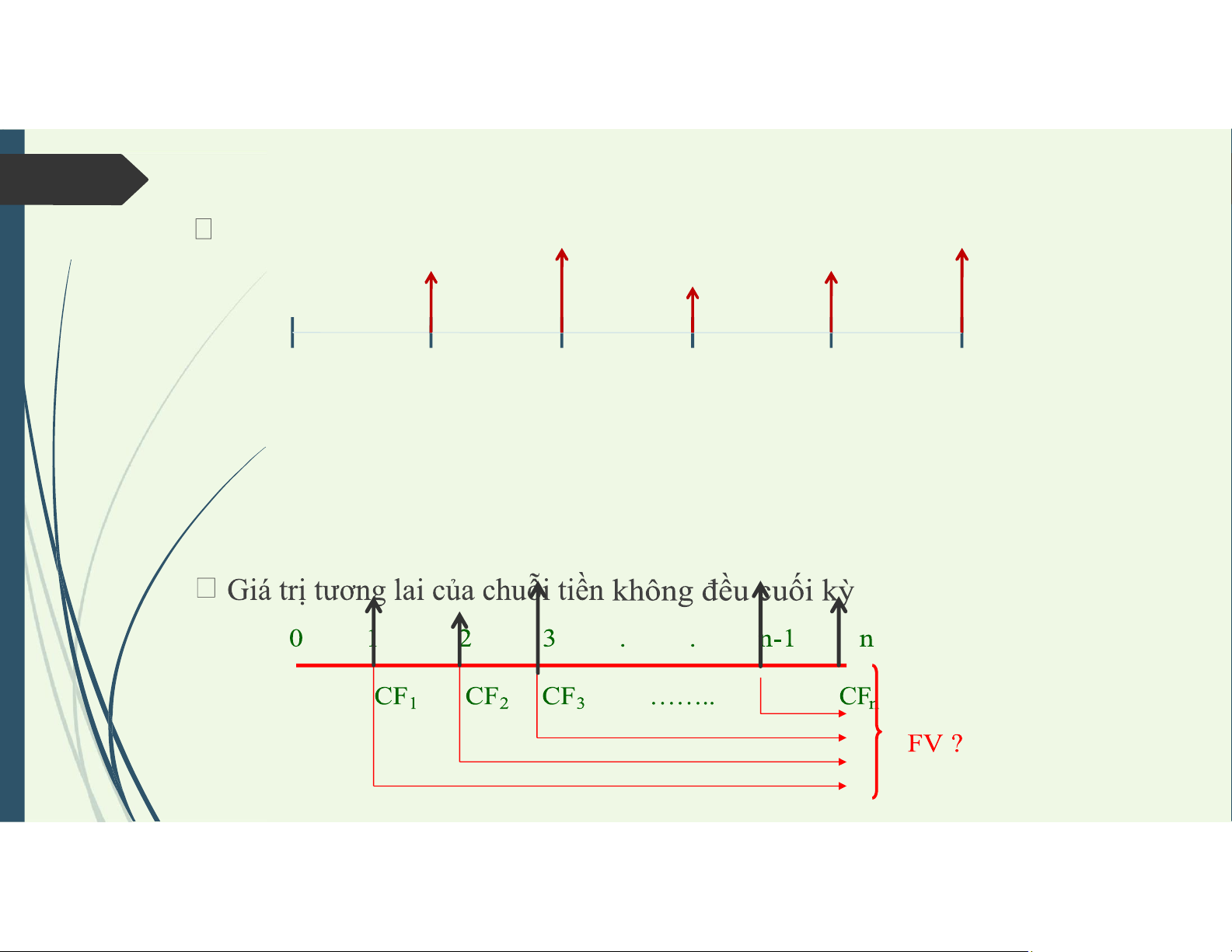
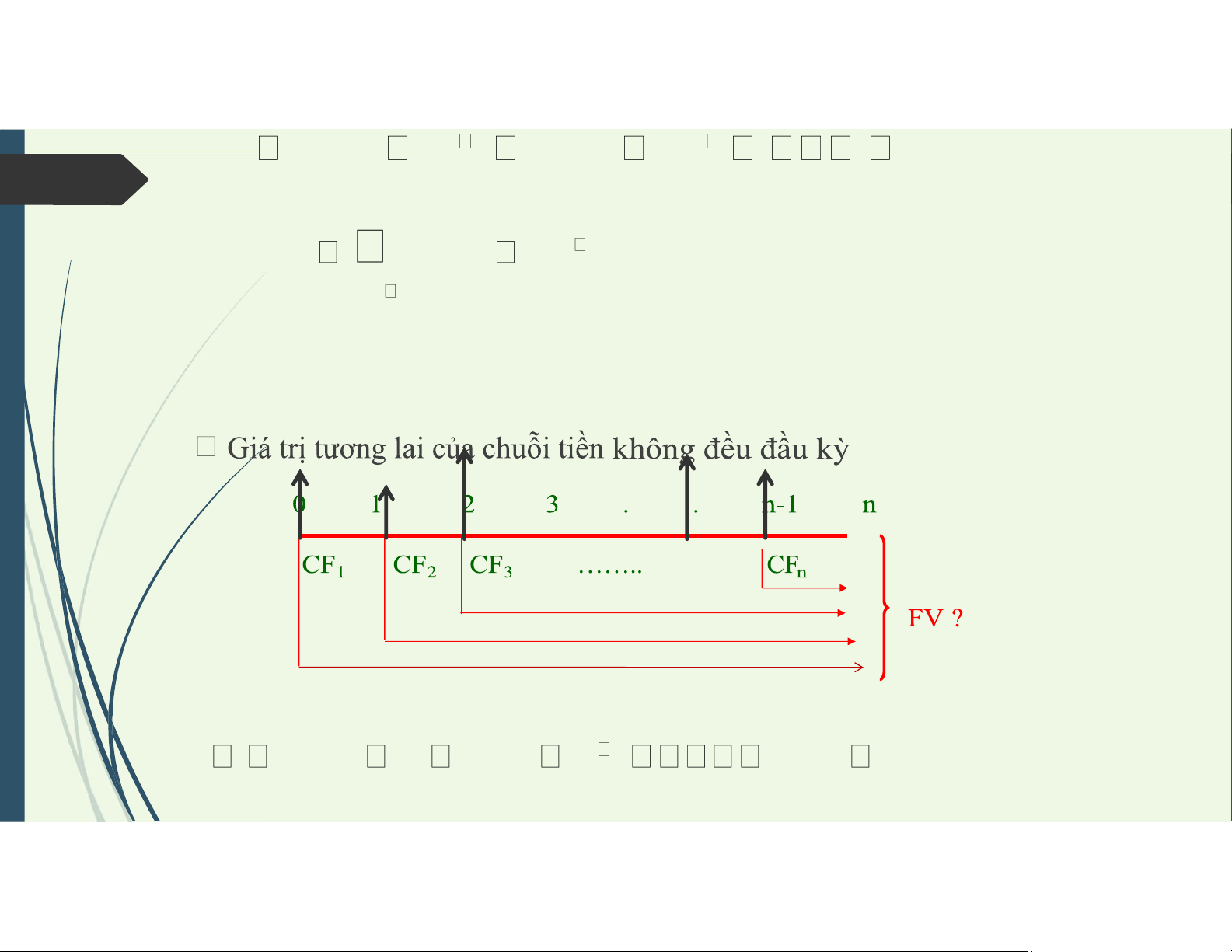
3. Giá trị tương lai của tiền
Chuỗi tiền tệ không đều lOMoAR cPSD| 58457166 FV CF1(1 i)n 1 CF2(1 i)n 2 CFn n FV CF t (1 i) n t t 1
3. Giá trị tương lai của tiền
Chuỗi tiền tệ không đều FV CF1(1 i)n CF2(1 i)n 1 CFn(1 i) lOMoAR cPSD| 58457166 n FV CF t (1 i) n t t 1
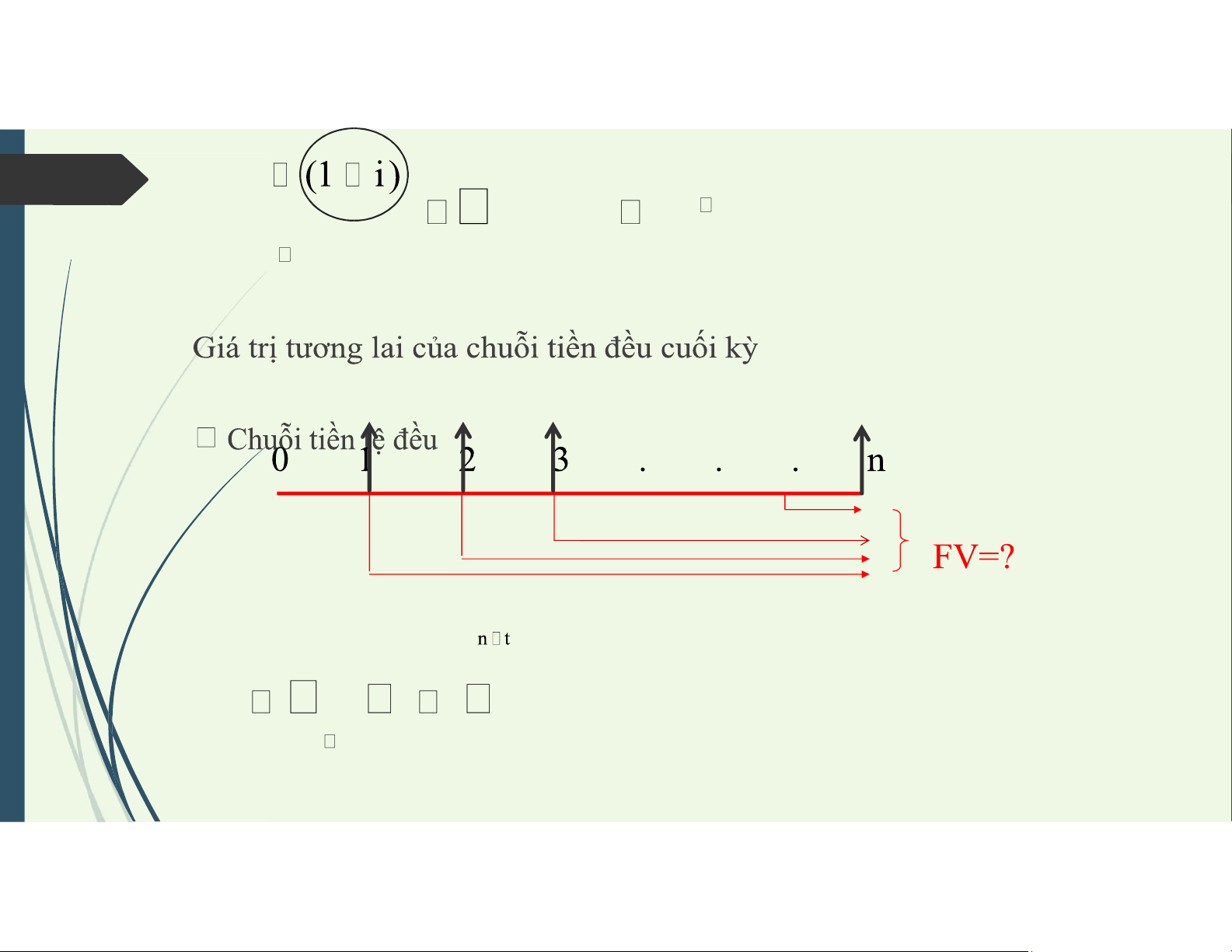
3. Giá trị tương lai của tiền n FV A 1 i FVIFAi,n = hệ số lãi t 1 giá trị tương lai lOMoAR cPSD| 58457166 FV A (1 i)n 1
A FVIFAi,ncủa chuỗi tiền i đều Chuỗi tiền tệ đều
3. Giá trị tương lai của tiền
Giá trị tương lai của chuối tiền đều đầu kỳ 0 1 2 3 . . . n FV/? n FV A(1 i)n t 1 t 1 n lOMoAR cPSD| 58457166 (1 i) 1 FV A (1 i) A FVIFAi,n (1 i) i 1717 Bài tập 1
Tính giá trị tổng cuối cùng của mỗi dòng ngân quỹ vào cuối năm thứ 5 với lãi suất 15%. Cuối năm lOMoAR cPSD| 58457166 Dòng 1 2 3 4 5 ngân quỹ I 200 200 200 200 200 II 600 - 300 - 100 Đặng Thị Việt Đức Bài tập 2
Ông A gửi 15 triệu đồng vào quỹ tiết kiệm với lãi suất 14%. Sau 5 năm, ông A gửi thêm 25
triệu. Ông A sẽ nhận được bao nhiêu tiền vào cuối của: a.
10 năm kể từ ngày gửi khoản tiền đầu tiên? b.
15 năm kể từ ngày gửi khoản tiền đầu tiên? lOMoAR cPSD| 58457166 Đặng Thị Việt Đức
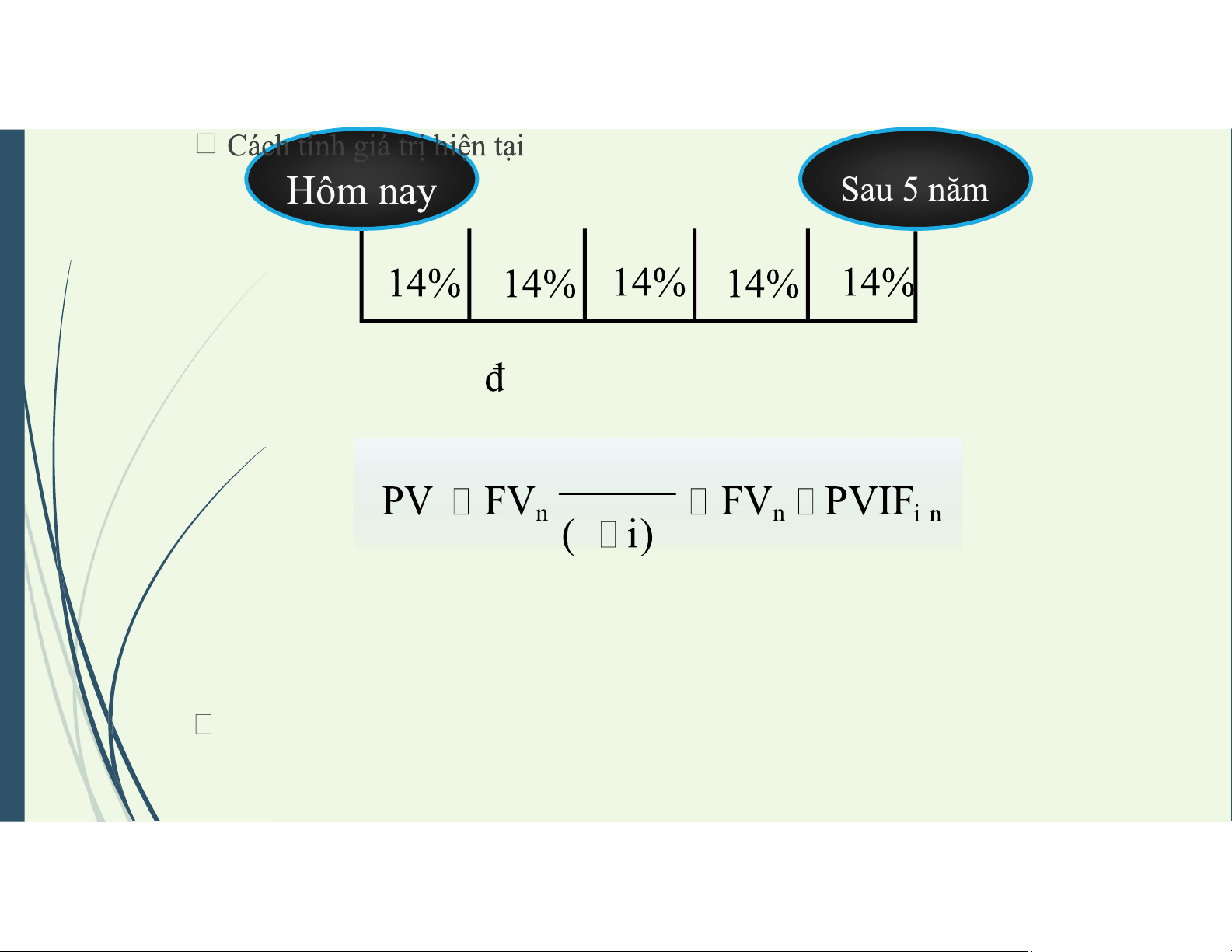
4. Giá trị hiện tại của tiền Khái niệm
Giá trị hiện tại của tiền là giá trị của khoản tiền phát sinh trong tương lai,
được quy đổi về thời điểm hiện tại (thời điểm gốc) theo một tỷ lệ chiết khấu nhất định. lOMoAR cPSD| 58457166
4. Giá trị hiện tại của tiền
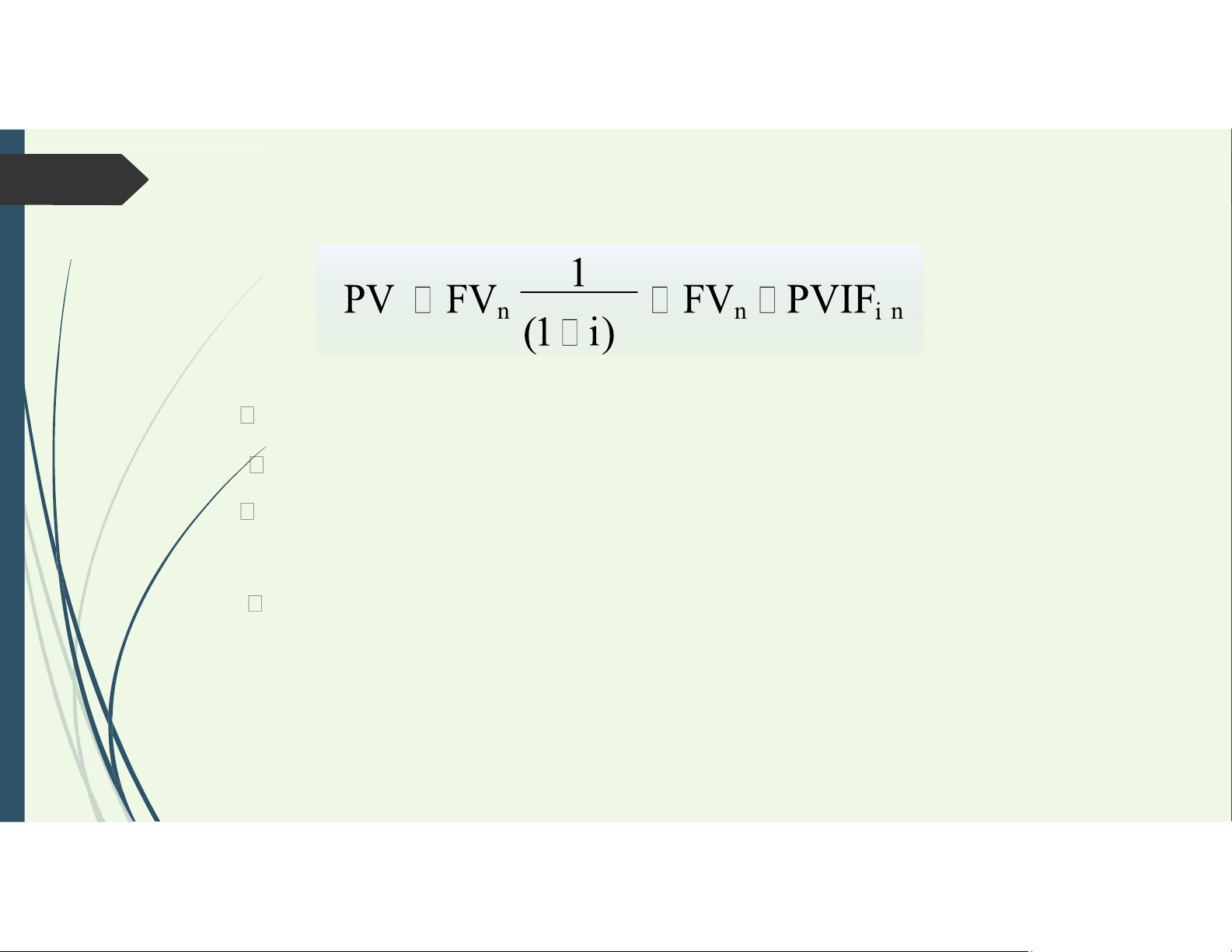
Cách tính giá trị hiện tại n n n ,n
FVn= giá trị tương lai sau n kỳ hạn
PV= giá trị hiện tại của số tiền gốc ban đầu i= tỷ lệ chiết khấu
PVIF i,n = hệ số lãi giá trị hiện tại của tiền
(Present Value Interest Factor)
4. Giá trị hiện tại của tiền lOMoAR cPSD| 58457166
Cách tính giá trị hiện tại Ví dụ:
Một sinh viên đi học đại học và được bố mẹ cho 1 khoản tiền trọn gói từ
năm thứ nhất. Anh ta dự định sẽ mua 1 chiếc xe máy để đi làm khi ra trường.
Thời gian học tập là 5 năm. Giá xe máy dự kiến sẽ là 20.000.000 đ. Lãi suất
ngân hàng là 14%/năm. Hỏi ngay từ năm thứ nhất anh ta phải bỏ riêng ra
khoản tiền là bao nhiêu cho chiếc xe máy?
4. Giá trị hiện tại của tiền lOMoAR cPSD| 58457166 10.388.000 20.000.000đ 1 n n n , 1
4. Giá trị hiện tại của tiền
Giá trị hiện tại của chuỗi tiền đều
Chuỗi tiền đều cuối kỳ 0 1 2 3 . . . n lOMoAR cPSD| 58457166 A A A A PV ? n 1 1 (1 i) n PV A t A A PVIFA t 1 (1 i) i
PVIFAi,n = Hệ số lãi giá trị hiện tại của chuỗi tiền đều
(Present Value Interest Factor of Annuity)
4. Giá trị hiện tại của tiền
Giá trị hiện tại của chuỗi tiền đều
Chuỗi tiền đều đầu kỳ