Chương 3: Kỹ thuật điều chế trong không gian tín hiệu môn Kỹ thuật thông tin vô tuyến | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58737056 Chương 3
KHÔNG GIAN TÍN HIỆU VÀ ĐIỀU CHẾ
3.1. GIỚI THIỆU CHUNG
3.1.1. Các chủ đề được trình bầy trong chương
• Các phương pháp điều chế số
• Các khuôn dạng điều chế số • Không gian tín hiệu
• Đáp ứng của các bô tương quan lên tạp âm
• Bô tách sóng khả giống nhất
• Tính toán xác suất lỗi trong kênh AWGN
• Các kỹ thuật điều chế nhất quán: BPSK, QPSK, M-PSK, MSK, M-ASK và 16-QAM
• Mật độ phổ công suất uả các kỹ thuật điều chế khác nhau
• So sánh các kỹ thuật điều chế 3.1.2. Hướng dẫn
• Học kỹ các tư liệu đựơc trình bầy trong chương
• Tham khảo thêm [2],[3], [8],[9]
3.1.3. Mục đích chương
• Hiểu được các kỹ thuật điều chế số được sử dụng phổ biến nhất trong thông tin vô tuyến số
• Hiểu được phương pháp đánh giá chất lượng đường truyền và băng
thông cần thiết cho từng kỹ thuật điều chế So sánh các kỹ thuật điều chế.
3.2. ĐIỀU CHẾ SỐ
Khi phát một luồng số trên kênh vô tuyến, cần phải điều chế luồng số này
cho một sóng mang (thường là hàm sin). Luồng số có thể là tín hiệu đầu ra của
máy tính hay tiếng nói hoặc hình ảnh đã được số hóa. Trong mọi trường hợp quá
trình điều chế bao gồm khóa chuyển biên độ, tần số hay pha cho sóng mang theo
luồng số vào. Vì vậy tồn tại ba phương pháp điều chế trong truyền dẫn số: điều
chế khóa chuyển biên (ASK: amplitude shift keying), điều chế khóa chuyển tần
số (FSK: frequency shift keying) và điều chế khóa chuyển pha (PSK: phase shift
keying). Có thể coi các phương pháp điều chế này như trường hợp đặc biệt cuả
các phương pháp điều chế biên độ, tần số và pha.
Trong chương này ta sẽ xét các tính năng của các kỹ thuật điều chế số nói
trên: khả năng chống tạp âm, các tính chất phổ và các hạn chế của chúng cũng
như các ứng dụng của chúng và các vấn đề khác. Ta bắt đầu phần này bằng trình lOMoAR cPSD| 58737056
bày tổng quan các khuôn dạng điều chế khác nhau đối với các nhà thiết kế hệ thống số khác nhau.
3.3. CÁC KHUÔN DẠNG ĐIỀU CHẾ SỐ
Điều chế được xem như là quá trình mà trong đó một đặc tính nào đó của
sóng mang được thay đổi theo một sóng điều chế. Chẳng hạn một sóng mang
hàm sin biểu thị theo công thức (3.1) có ba thông số sau đây có thể thay đổi: biên độ, tần số và pha: S(t) = A cos( ct + ) (3.1)
trong đó c = 2 fc là tần số góc của sóng mang, fc là tần số sóng mang còn là pha.
Nếu sử dụng tín hiệu thông tin để thay đổi biên độ A, tần số sóng mang fc
và pha (t) ta được điều biên, điều tần và điều pha tương ứng.
Nếu tín hiệu đưa lên điều chế các thông số nói trên là tín hiệu liên tục thì
ta được trường hợp điều chế tương tự. Nếu tín hiệu điều chế các thông số nói
trên là số thì điều chế được gọi là điều chế số. Trong thông tin số tín hiệu
đưa lên điều chế là một luồng nhị phân hay dạng được mã hóa vào M-mức của
của luồng nhị phân này. Trong trường hợp điều chế số tín hiệu điều chế cũng
làm thay đổi biên độ, tần số, hay pha của sóng mang với các tên gọi tương ứng
là: điều chế khóa chuyển biên (ASK), điều chế khóa chuyển tần (FSK), điều chế
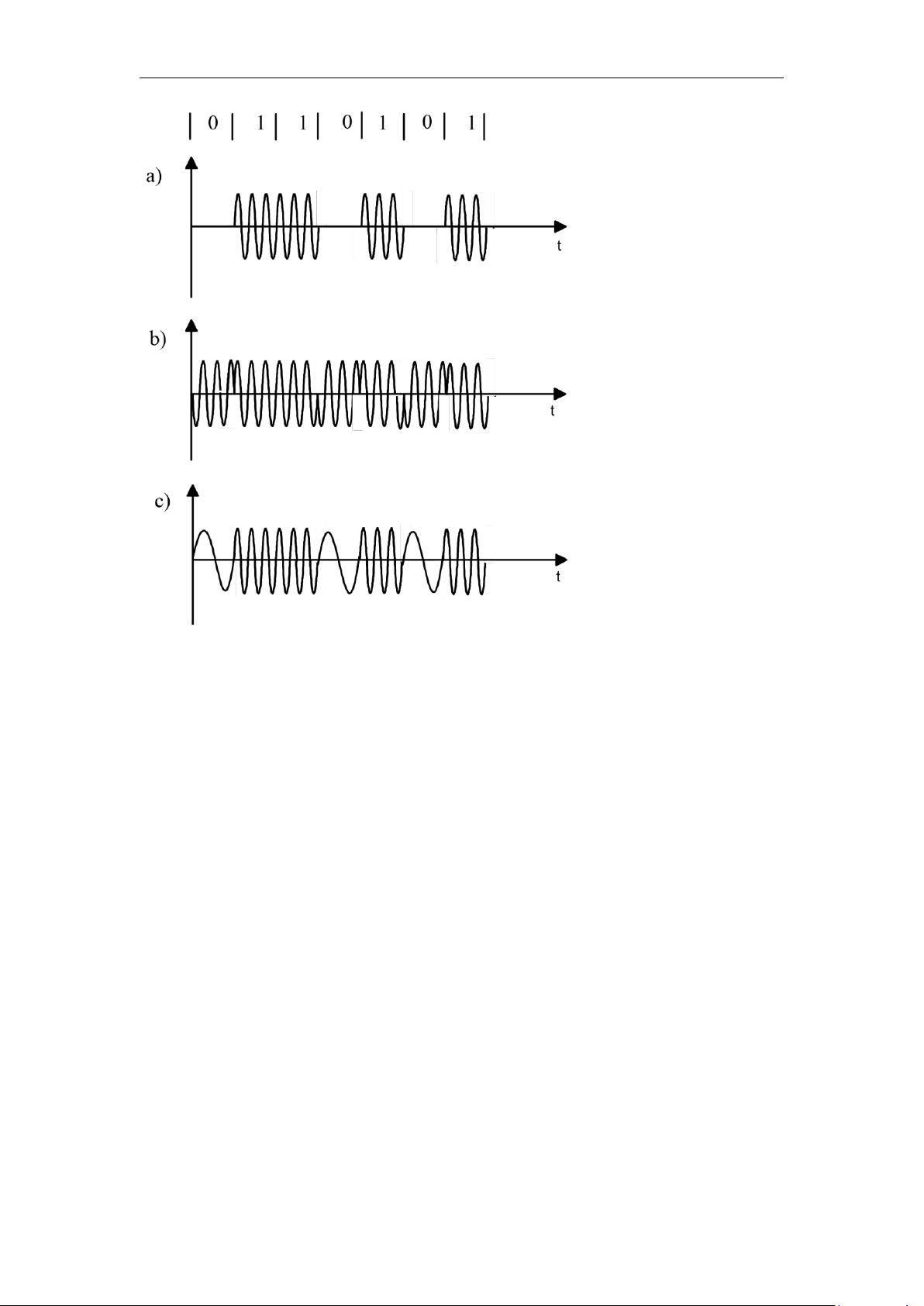
khóa chuyển pha (PSK) (xem thí dụ ở hình 3.1).
Như ta thấy ở hình 3.1, lý tưởng PSK và FSK có hình bao không đổi. Đặc
điểm này cho phép chúng không bị ảnh hưởng của tính phi tuyến thường gập ở
thông tin vi mặt đất số và vệ tinh.số. Vì vậy thường FSK và PSK hay được sử
dụng hơn ASK. Tuy nhiên để có thể tăng dung lượng đường truyền dẫn số khi
băng tần của kênh vô tuyến có hạn người ta sử dụng điều chế khóa chuyển pha
và khoá chuyển biên kết hợp, phương pháp điều chế này được gọi là điều chế
cầu phương hay biên độ vuông góc (QAM: Quadrature Amplitude Modulation).
Trong trường hợp điều chế M trạng thái tổng quát, bộ điều chế tạo ra một
tập hợp M=2m ký hiệu tuỳ theo tổ hợp m bit của luồng số liệu nguồn. Điều chế
nhị phân là trường hợp đặc biệt của điều chế M-trạng thái trong đó M=2.
Trong dạng sóng được vẽ ở hình 3.1, một trong các đặc tính của của sóng
mang (biên độ, tần số hoặc pha) bị điều biến. Như trên đã nói đôi khi cả hai đặc
tính của sóng mang đều thay đổi tạo ra điều chế cầu phương QAM.
Trong thông tin số thuật ngữ tách sóng và giải điều chế thường được sử
dụng hoán đổi cho nhau, mặc dù thuật ngữ giải điều chế nhấn mạnh việc tách tín
hiệu điều chế ra khỏi sóng mang còn tách sóng bao hàm cả quá trình quyết định chọn ký hiệu thu. lOMoAR cPSD| 58737056
Hình 3.1. Các dạng sóng điều chế: a) Khóa chuyển biên độ (ASK); b) Khóa
chuyển pha (PSK); c) Khóa chuyển tần số (FSK).
Giải điều chế ở máy thu có thể thực hiện theo hai dạng: giải điều chế nhất
quán hoặc không nhất quán. Ở dạng giải điều chế nhất quán lý tưởng, bản sao
chính xác sóng mang phát phải có ở máy thu. Nghĩa là máy thu phải biết chính
xác pha chuẩn của sóng mang, trong trường hợp này ta nói máy thu được khóa
pha đến máy phát. Tách sóng tương quan được thực hiện bằng cách thực hiện
tương quan chéo tín hiệu thu được vớí một trong các mẫu nói trên, sau đó thực
hiện quyết định bằng cách so sánh với một mẫu cho trước. Mặt khác ở giải điều
chế không nhất quán không cần thiết phải hiểu biết pha của sóng mang. Vì vậy
độ phức tạp của máy thu được giảm bớt nhưng bù lại là khả năng chống lỗi thấp
hơn so với giải điều chế nhất quán.
Ta thấy rằng tồn tại rất nhiều sơ đồ điều chế/tách sóng dành cho người
thiết kế hệ thống thông tin số để truyền dẫn luồng số trên kênh băng thông. Mỗi
sơ đồ có các ưu nhược điểm riêng của mình. Việc lựa chọn cuối cùng của người
thiết kế phụ thuộc vào: tài nguyên thông tin, công suất phát và độ rộng kênh.
Chẳng hạn việc lựa chọn có thể thiên về sơ đồ phải đảm bảo nhiều mục đích thiết kế dưới đây:
1. Tốc độ số liệu cực đại.
2. Xác suất lỗi ký hiệu cực tiểu.
3. Công suất phát cực tiểu.
4. Độ rộng kênh cực tiểu. lOMoAR cPSD| 58737056
5. Khả năng chống nhiễu cực đại.
6. Mức độ phức tạp của mạch cực tiểu.
Một số các mục tiêu nói trên đối lập với nhau: chẳng hạn mục tiêu (1), (2)
đối lập với mục tiêu (3) và (4). Vì vậy phải lựa chọn một giải pháp dung hòa để
thỏa mãn càng nhiều các mục tiêu nói trên càng tốt.
Ở các phần dưới đây ta sẽ xét các phương pháp điều chế khác nhau sử
dụng thủ tục trực giao Gram-Schimidt để biểu diễn các tín hiệu này vào không gian tín hiệu
3.4. KHÔNG GIAN TÍN HIỆU
Ở thông tin số luồng số điều chế được chia thành các ký hiệu mi, i = 1, 2,
. . ., M trước khi điều chế cho sóng mang để được các tín hiệu si(t). Tập các
sóng mang được điều chế si(t) có thể được trình bầy ở dạng các vectơ trong không
gian tín hiệu theo các quy tắc được trình bầy dưới đây.
Một tập hữu hạn M tín hiệu năng lượng giá trị thực s1(t), s2(t), ....., sM(t)
với mỗi tín hiệu có độ dài T, có thể được trình bầy bằng tổ hợp tuyến tính của N
M hàm trực giao chuẩn cơ sở 1(t), 2(t), ....... , N(t) giá trị thực trong tập tín hiệu như sau: (3.2)
trong đó ma trận thứ nhất trong (3.2) là ma trận hệ số của các tín hiệu trong tập
tín hiệu (đây cũng là ma trận tọa độ của các vectơ điểm tín hiệu trong không gian
tín hiệu), ma trận thứ hai trong (3.2) là ma trận các vectơ đơn vị xác định chiều
của không gian tín hiệu, ma trận trong (3.2) là ma trận các tín hiệu trong tập tín
hiệu, trong đó mỗi tín hiệu sẽ có một điểm tín hiệu trong không gian tín hiệu.
Mỗi tín hiệu si(t) trong tập tín hiệu được xác định như sau: (3.3)
trong đó hệ số khai triển được xác định như sau: (3.4)
trong đó j(t) là hàm trực giao chuẩn xác định vectơ đơn vị của không gian tín hiệu. lOMoAR cPSD| 58737056
Các hàm trực giao chuẩn cơ sở xác định vectơ chuẩn trong không gian tín
hiệu thoả mãn điều kiện sau: (3.5) trong đó (3.6)
được gọi là hàm delta Kronecker.
Tương ứng mỗi tín hiệu trong tập {si(t)} có thể được xác định bằng một
vectơ theo các hệ số của nó như sau: i= 1, 2, . . . , M (3.7)
Vectơ Si được gọi là vectơ tín hiệu. Không gian chứa vectơ này được gọi
là không gian Ơclit N chiều. Ta có thể biểu thị tập các vectơ {Si} này bằng tập
M điểm trong không gian Ơclit N chiều có các trục là 1, 2, . . . , N.. Không gian
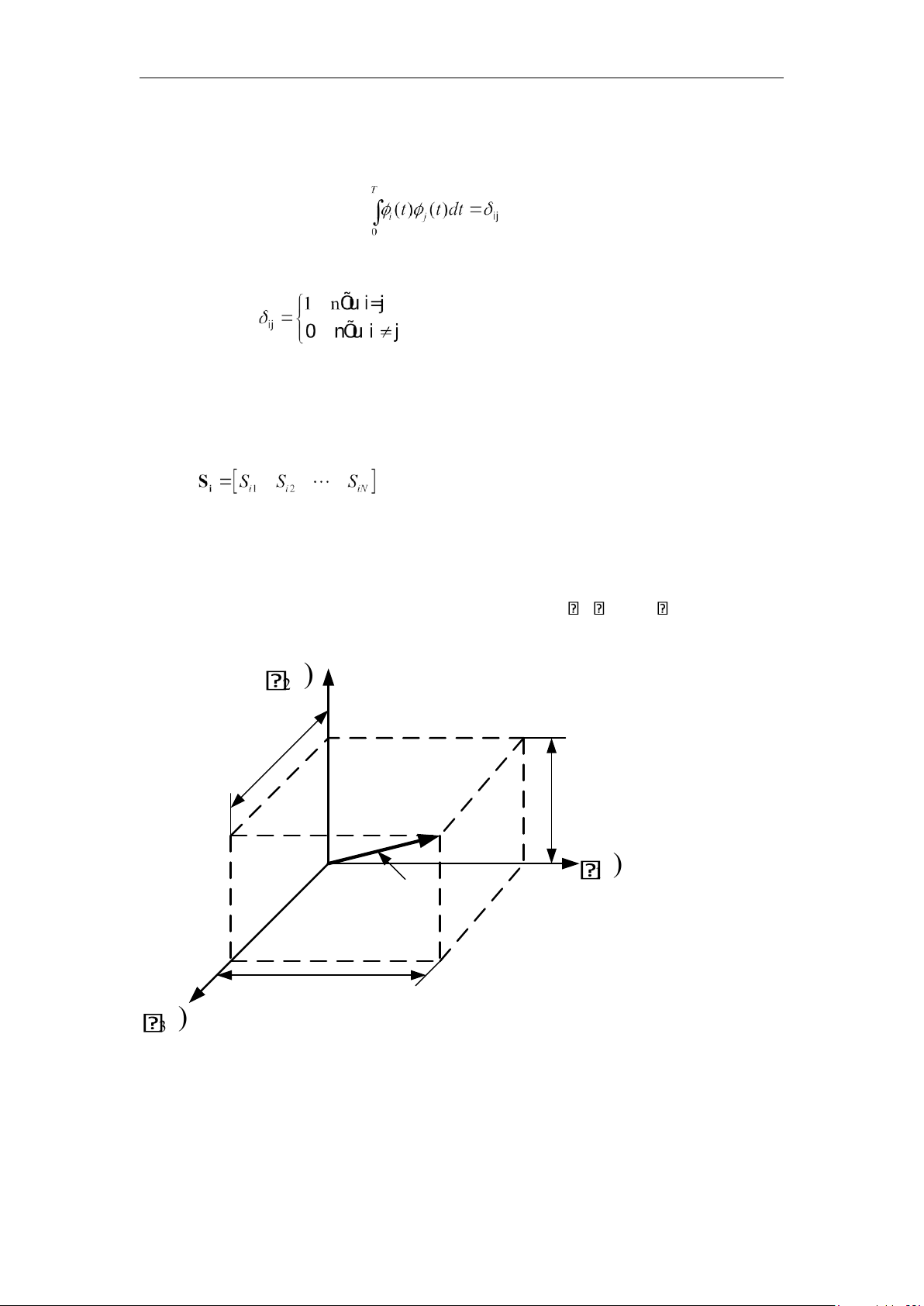
Ơclit N chiều này được gọi là không gian tín hiệu. t Không gian tín hiệu 2 () s i3 s i2 t 1 () Vectơ tín hiệu s i s i1 t 3 ()
Hình 3.2. Không gian vectơ tín hiệu ba chiều
Thí dụ về không gian tín hiệu với N=3 được cho trên hình 3.2.
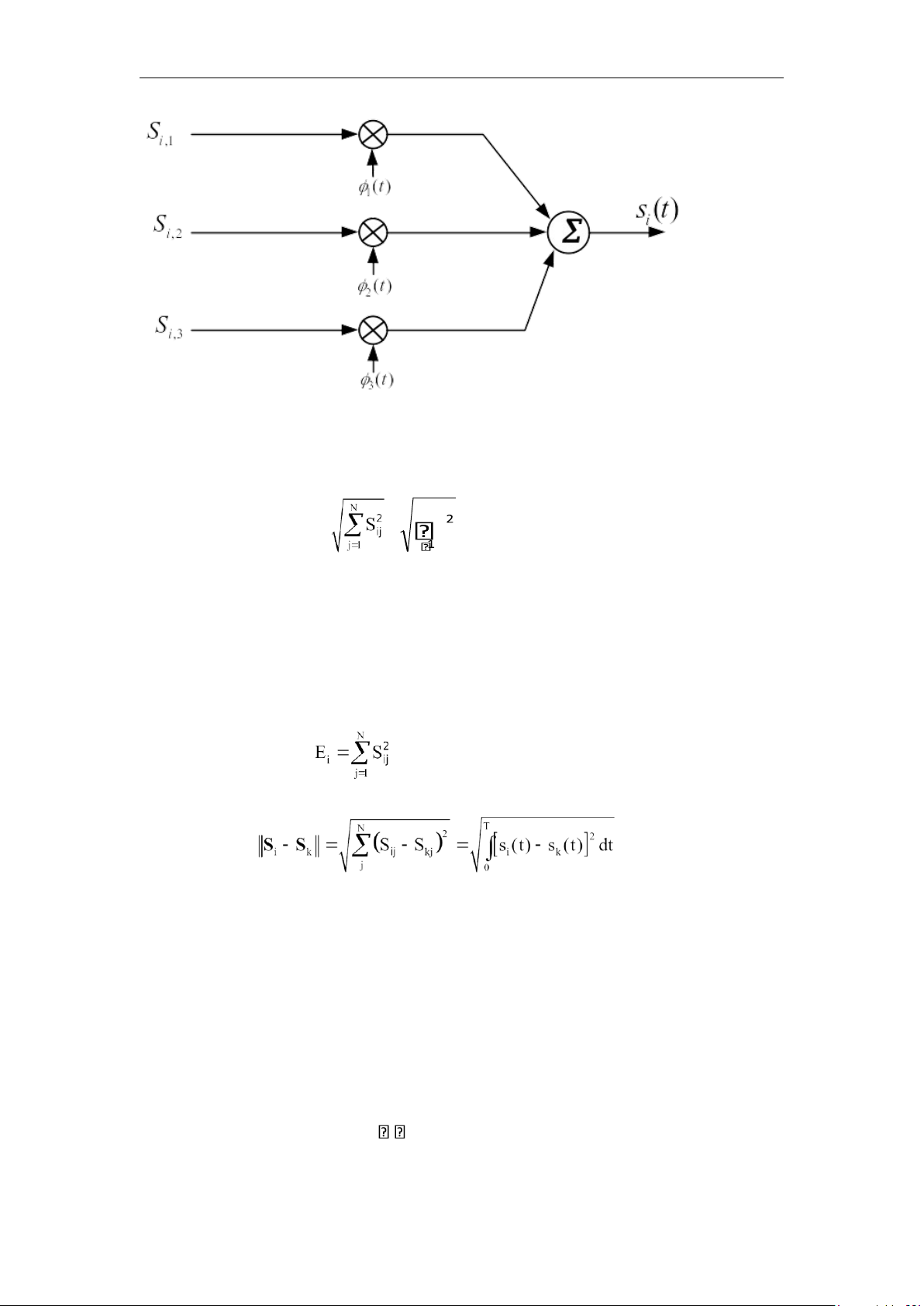
Sơ đồ tạo ra tín hiệu si(t) được cho ở hình 3.3. lOMoAR cPSD| 58737056
Hình 3.3. Tạo tín hiệu truyền dẫn si (t)
Trong không gian tín hiệu ta có thể xác định độ dài vectơ và góc giữa các
vectơ. Độ dài của vectơ xác định như sau: N s ||S j ij i| = (Si.Si)1/2 = (3.8)
Cosin của góc giữa hai vectơ được xác định theo công thức sau: (Si.Sj) /||Si||.||Sj|| (3.9)
Có thể chứng minh rằng năng lượng của mỗi tín hiệu si(t) trong khoảng T
bằng bình phương độ dài vectơ của nó: (3.10)
Khoảng cách Ơclit giữa hai vectơ tín hiệu si và sk được xác định như sau: (3.11)
Nếu hai tín hiệu si(t) và sk(t) trực giao thì:
||Si-Sk| = (Ei +Ek)1/2 (3.12)
3.5. ĐÁP ỨNG CỦA CÁC BỘ TƯƠNG QUAN LÊN TẠP ÂM
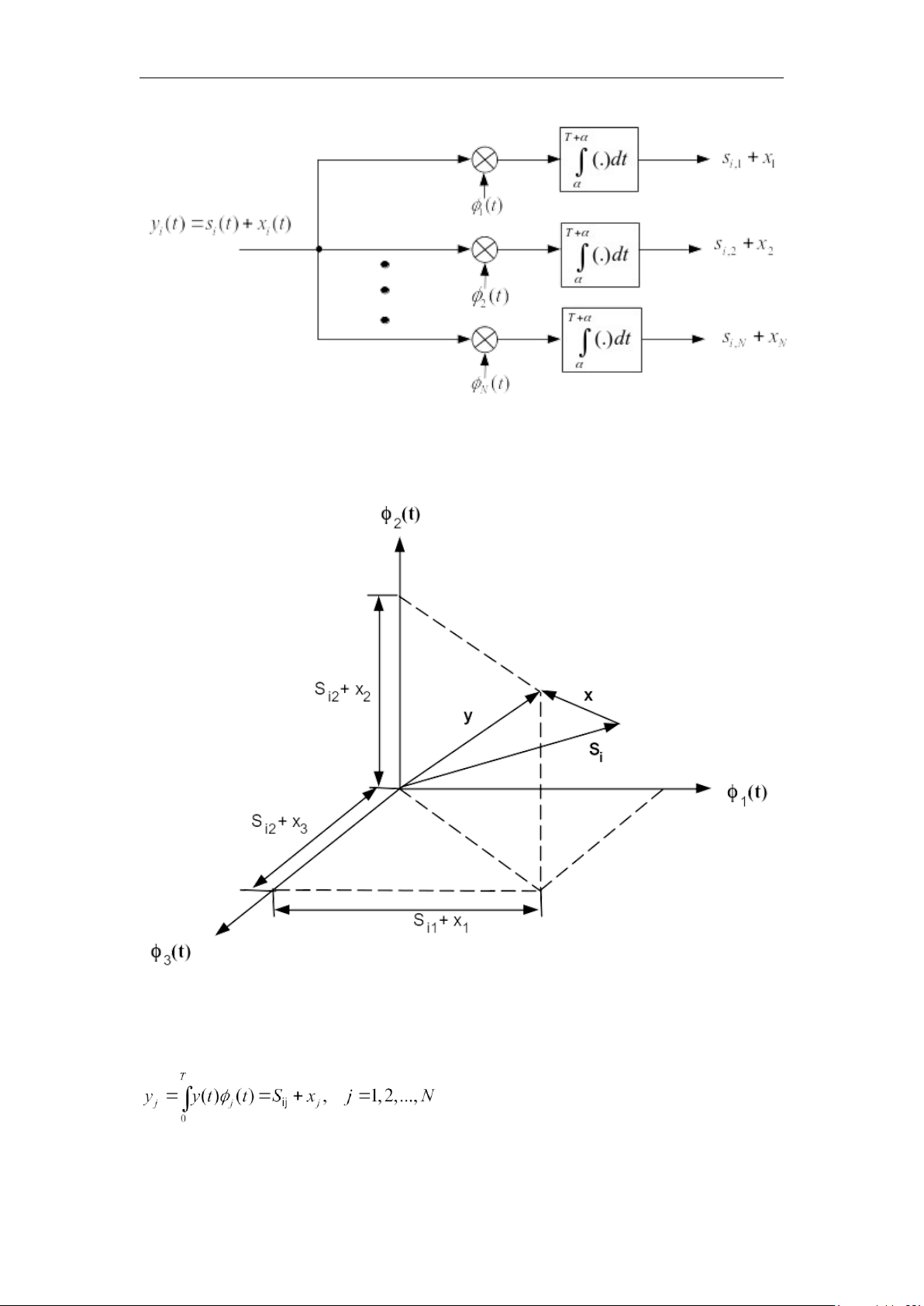
Tín hiệu thu được ở đầu vào của các bộ tương quan (xem hình 3.4) sẽ là
tổng của tín hiệu phát si(t) với tạp âm trắng Gauss trắng cộng x(t): yi(t) = si(t) + x (t) , 0 t T , i = 1, 2, . . . , M (3.13) lOMoAR cPSD| 58737056
Hình 3.4. Tín hiệu đầu ra của bộ tương quan
Ta có thể biểu diễn tín hiệu và tạp âm trong không gian tín hiệu như trên hình 3.5.
Hình 3.5. Biểu diễn tín hiệu và tạp âm trong không gian tín hiệu
Tín hiệu ở đầu ra của các bộ tương quan sẽ là một biến ngẫu nhiên được xác định như sau: (3.14)
trong đó thành phần thứ nhất nhận được từ tín hiệu phát: lOMoAR cPSD| 58737056 (3.15)
Còn thành phần thứ hai là một biến ngẫu nhiên gây ra do tạp âm: T
xj = x t( ) j ( )t dt) (3.16) 0
Do giá trị trung bình của quá trình ngẫu nhiên x(t) bằng không, nên giá trị trung
bình của yj được xác định như sau: lOMoAR cPSD| 58737056
myj = E[yj] = E[Sij + xj ] = Sij (3.17) 2
và phương sai của yj bằng: 2 2 Lưu yj = E[(yj-Sij)2] = E[xj ] (3.18) ý rằng ở các biến
Từ phương trình (3.16) ta được: đổi trên ta sử dung T T công thức 2 sau đây y E x t( ) j j ( )t dt x u ( ) j ( )u du cho hàm 0 0 tương T T quan của E
j ( )tj ( ) ( ) ( )u x t x u dtdu tạp âm trắng: 0 0 T T N0 =
j ( )tj ( )u E x t x u ( ) ( ) dtdu (t 0 0 T T u) =
j ( )tj ( )u x (t u dtdu, ) 0 0 N 0 T T ( )t
j ( ) (u t u dtdu) = j 2 0 0
N0 T 2( )t dt = 2 0 j N Vậy: 2yj 0 đối với mọi j (3.19) x(t,u) = 2
Nếu ta định nghĩa vectơ của N đầu ra bộ tương quan: (3.20)
thì ta có thể viết mật độ xác suất có điều kiện khi phát đi ký hiệu mi và thu được
vectơ y như là tích của N hàm mật độ xác suất thành phần :
(3.21) Vì Yj là một biến ngẫu nhiên Gausơ có trung bình Sịj nên: lOMoAR cPSD| 58737056 (3.22) và: (3.23)
3.6. BỘ TÁCH SÓNG KHẢ GIỐNG NHẤT
Nhiệm vụ của bộ tách sóng khả giống nhất là phải ước tính được ký hiệu
thu m' với xác suất lỗi nhỏ nhất so với ký hiệu được phát mi. Xác suất lỗi ký hiệu
trung bình khi đưa ra quyết định này có thể được biểu diễn đơn giản như sau:
Pe(mi,y) = P(mi không phát | y) =1- P(mi được phát | y) (3.24)
trong đó y là tổng vectơ của tín hiệu được phát và tạp âm.
Để giảm tối đa lỗi, quy tắc quyết định chọn mi như sau:
Quyết m'=mi, nếuP(mi phát | y) P(mk phát | y), cho tất cả k i; k=1,2...,M. (3.25)
Quy tắc quyết định này được gọi là cực đại xác suất hậu định (MAP:
Maximum a Posteriori Probability).
Theo quy tắc Bayes ta có thể viết: Quyết m'=mi nếu pkP(y | mk ) pkfY (y | mk ) hay cực đại khi k=i (3.26) P(y) fY (y)
trong đó pk là xác suất tiền định của việc xuất hiện ký hiệu mk (xác suất phát ký
hiệu mk) còn fY(y) và fY(y | mk) là hàm mật độ xác suất của phát ký hiệu mk và thu y khi phát mk.
Vì P(y) và fY(y) không phụ thuộc vào tín hiệu phát nên ta được: Quyết m'=mi nếu
P(y| mk) hay fY(y|mk) cực đại khi k=i (3.27)
Đây là quy tắc quyết định theo khả năng giống nhất và P(y|mi) hay fY(y| mi)
được gọi là hàm khả năng giống. Nội dung của quy tắc này là bộ tách sóng sẽ lOMoAR cPSD| 58737056
quyết định chọn mi nếu hàm khả năng giống là cực đại. Để tiện lợi hàm khả
năng giống thường được sử dụng ở dạng logrit tự nhiên:
Quyết m'=mi nếu lnP(y|mk) hay lnfY (y|mk) cực đại khi k=i (3.28)
Các hàm lnP(y|mk) và lnfY(y|mk) được gọi là các hàm log khả năng giống
3.7. TÍNH TOÁN XÁC SUẤT LỖI TRUYỀN DẪN TRONG KÊNH
TẠP ÂM GAUSS TRẮNG CỘNG, AWGN
Để tính toán xác suất lỗi ta chia không gian tín hiệu thu thành M vùng {Zi,
i=1,2,....,M}, trong đó Zi là vùng mà ở đó xác suất thu được tín hiệu y khi phát ký hiệu mi lớn nhất :
P(mk được phát | y) = max, khi k = i
Nếu pk là xác suất phát mk thì theo quy tắc Bayes ta có: pkfY (y | mk ) = max khi k = i (3.29) fY (y)
khi coi rằng xác suất phát các ký hiệu mk pk đều như nhau: fY(y|mk) = max, khi k = i (3.30)
Lỗi tín hiệu xẩy ra khi phát đi mi nhưng điểm vectơ của tín hiệu thu y không rơi
vào vùng Zi. Xác suất lỗi ký hiệu trung bình Pe, khi coi rằng xác suất phát các ký hiệu như nhau, bằng: M Pe
P(mi )P(y không nằm trong vùng Zi| mi được phát) i 1 1 M
= M i 1P(y không nằm trong vùng Zi| mi được phát) = = (3.31)
Các sơ đồ điều chế có thể chia thành các sơ đồ điều chế nhất quán và
không nhất quán. Đối với các sơ đồ điều chế nhất quán, sóng mang tại phiá thu
được khôi phục bởi bộ khôi phục sóng mang, còn đối với các sơ đồ không nhất
quán không cần thiết khôi phục sóng mang ở phía thu. Bù lại sơ đồ không nhất lOMoAR cPSD| 58737056
quán thừơng mắc lỗi bit nhiều hơn sơ đồ nhất quán. Trong các phần dưới đây ta
sẽ xét một số sơ đồ điều chế nhất quan thường được sử dụng trong thông tin vi ba số và di động.
3.8. ĐIỀU CHẾ VÀ GIẢI ĐIỀU CHẾ PSK NHỊ PHÂN HAY HAI
TRẠNG THÁI (BPSK) NHẤT QUÁN
Trong một hệ thống điều chế BPSK (Binary phase shift keying điều chế
khóa chuyển pha hai trạng thái) nhất quán cặp các tín hiệu s1(t), s2(t) được sử
dụng để trình bầy các ký hiệu nhị phân 0 và 1 được định nghĩa như sau: (3.32) hay: (3.33a) (3.33b) trong đó :
Tb là độ rộng của một bit , Eb là năng lượng của một bit, (t) là góc pha thay
đổi theo tín hiệu điều chế, 0 là góc pha ban đầu có giá trị không đổi từ 0 đến
2 và không ảnh hưởng lên quá trình phân tích nên ta đặt bằng không, i=1
tương ứng với phát đi ký hiệu 0 và i=2 tương ứng với phát đi ký hiệu 1.
Một cặp sóng mang hàm sin đối pha 1800 như trình bầy ở trên được gọi là
các tín hiệu đối cực.
Từ các phương trình (3.32) và (3.33) ta thấy rằng chỉ có một hàm đơn vị năng lượng cơ sở là: (3.34)
Khi này ta có thể khai triển các tín hiệu s1(t), s2(t) theo 1(t) như sau: (3.35) (3.36)
Vậy hệ thống PSK nhị phân được đặc trưng bởi một không gian tín hiệu
một chiều (N=1) với hai điểm bản tin (M=2) như được vẽ ở hình 3.6. Tọa độ của
các điểm bản tin bằng: (3.37) và: lOMoAR cPSD| 58737056 (3.38)
Điểm bản tin "0" tương ứng s1(t) được đặt ở và điểm bản tin
"1" tương ứng với s2(t) được đặt ở .
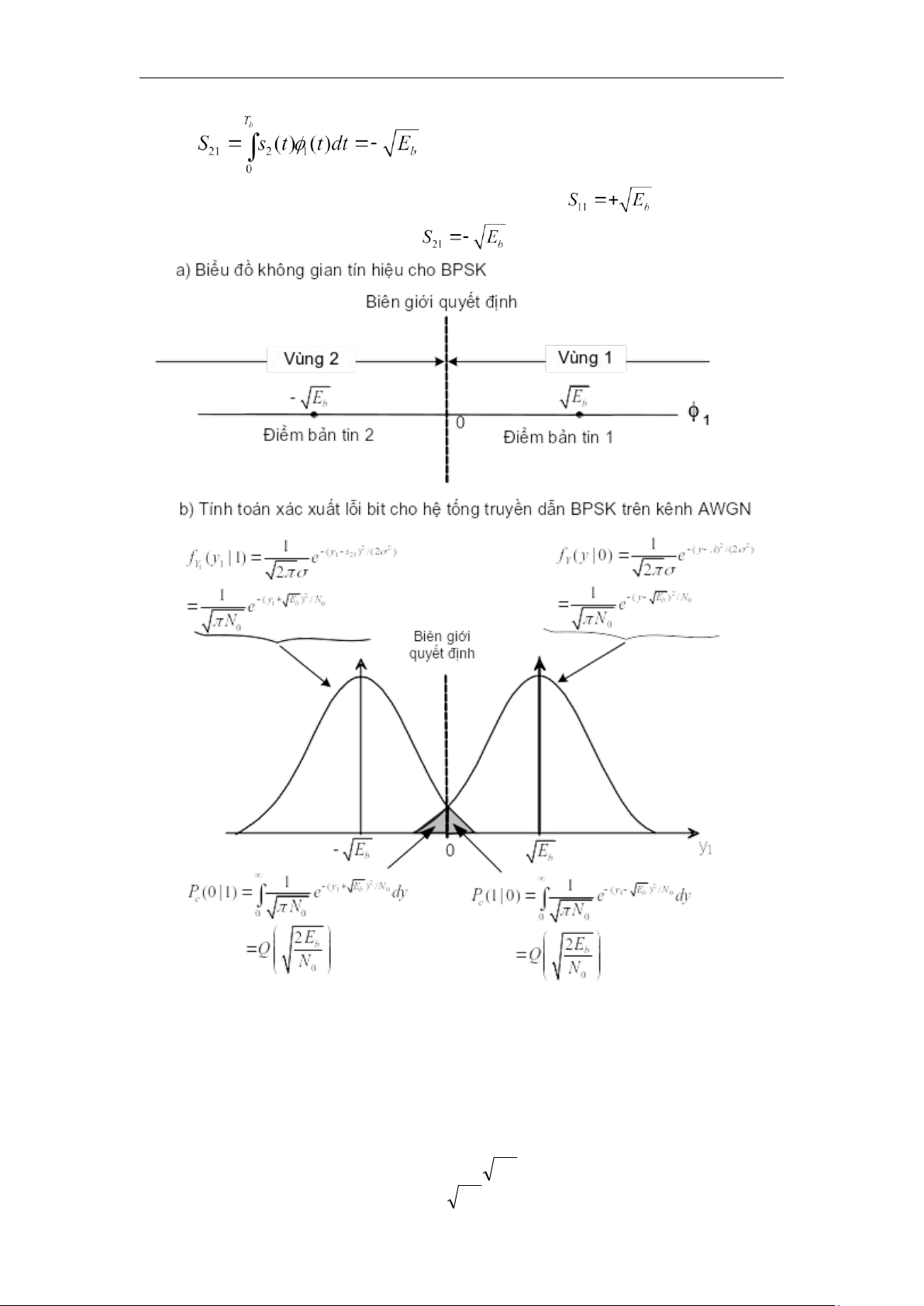
Hình 3.6. a) Biểu đồ không gian tín hiệu cho điều chế BPSK, b) tính toán xác
xuất lỗi bit cho hệ thống truyền dẫn BPSK trên kênh AWGN
Dưới đây ta xét xác xuất lỗi bit cho hệ thống truyền dẫn BPSK trên kênh
AWGN. Quá trình tín toán được mô tả trên hình 3.6b.
Để quyết định tín hiệu thu được là 0 hay 1 ta chia không gian tín hiệu thành hai vùng:
1. Tập hợp các điểm gần điểm bản tin + Eb nhất (tương ứng với "0"): Z1. lOMoAR cPSD| 58737056
2. Tập các điểm gần điểm bản tin - Eb nhất (tương ứng với "1" :Z2 .
Ta thực hiện điều nói trên bằng cách dựng một điểm nằm giữa đường nối
hai điểm bản tin nói trên, sau đó đánh dấu vùng quyết định. Trên hình 3.6 các
vùng quyết định được đánh dấu bằng Z1 và Z2.
Bây giờ quy tắc quyết định là dự đoán tín hiệu là s1(t) hay "0" được phát
nếu tín hiệu thu rơi vào vùng Z1 và là s2(t) hay "1" nếu tín hiệu thu rơi vào vùng
Z2. Tuy nhiên có thể xẩy ra hai quyết định sai. Tín hiệu s2(t) được phát, tuy nhiên
do tác dụng của tạp âm tín hiệu thu rơi vào vùng Z1 và vì thế máy thu quyết định
thiên về s1(t). Ngược lại tín hiệu s1(t) được phát, nhưng do tác dụng của tạp âm
tín hiệu thu rơi vào vùng Z2 và vì thế máy thu quyết định thiên về s2(t).
Để tính toán xác suất gây ra một lỗi của loại 1 ta nhận thấy rằng ở hình
3.6 vùng quyết định liên quan tới s1(t) hay "0" được trình bầy như sau:
Z1 : 0trong đó y1 là đại lượng vô hướng quan trắc như sau: (3.39)
trong đó yi(t) là tín hiệu thu, y1 là hình chiếucủa tín hiệu thu lên trục 1(t), si1 là
tín hiệu phát, x1 là tạp âm AWGN phương sai trung bình không . Ta
có thể rút ra hàm xác suất phân bố xác suất khi ký hiệu 1 hay tín hiệu s2(t) được truyền như sau: 1 é pN0 êë
fY1(y1|1) = expêê- (y s1-N021)2ùúúúû 1 1 2 N exp 0 N0 y1 Eb (3.40) trong đó:
fY1(y1|1) là hàm mật độ xác suất có điều kiện khi phát 1 qua một kênh tạp
âm trắng cộng Gauss lý tưởng (AWGN) thu được y1 , s21 tương ứng với tín
hiệu phát (điều chế) của bit 1.
Xác suất có điều kiện mà máy thu quyết định thiên về ký hiệu 0 khi ký
hiệu 1 được phát sẽ là: (3.41) Đặt lOMoAR cPSD| 58737056 (3.42)
và thay đổi biến tích phân x1 thành z ta có thể viết lại phương trình (3.41) ở dạng sau: (3.43)
trong đó : Q(.) là hàm Q thường được cho ở dạng bảng.
Tương tự ta có thể chỉ ra rằng Pe(1|0), xác suất có điều kiện mà máy thu
quyết định thiên về 1 khi ký hiệu 0 được phát cũng sẽ có cùng giá trị như ở
phương trình (3.43) . Vậy sau khi lấy trung bình cộng các xác suất Pe(0|1) và
Pe(1|0) ta được xác suất lỗi ký hiệu trung bình đối với điều chế nhị phân là : E P b
e= 1/2 Pe(0|1) +1/2 Pe(1|0) = Q 2N 0 (3.44)
Cần lưu ý rằng ở các trường hợp mà không gian tín hiệu được phân chia
đối xứng như ở hình 3.6 thì các xác suất lỗi ký hiệu có điều kiện và xác suất lỗi
ký hiệu trung bình sẽ có cùng giá trị.
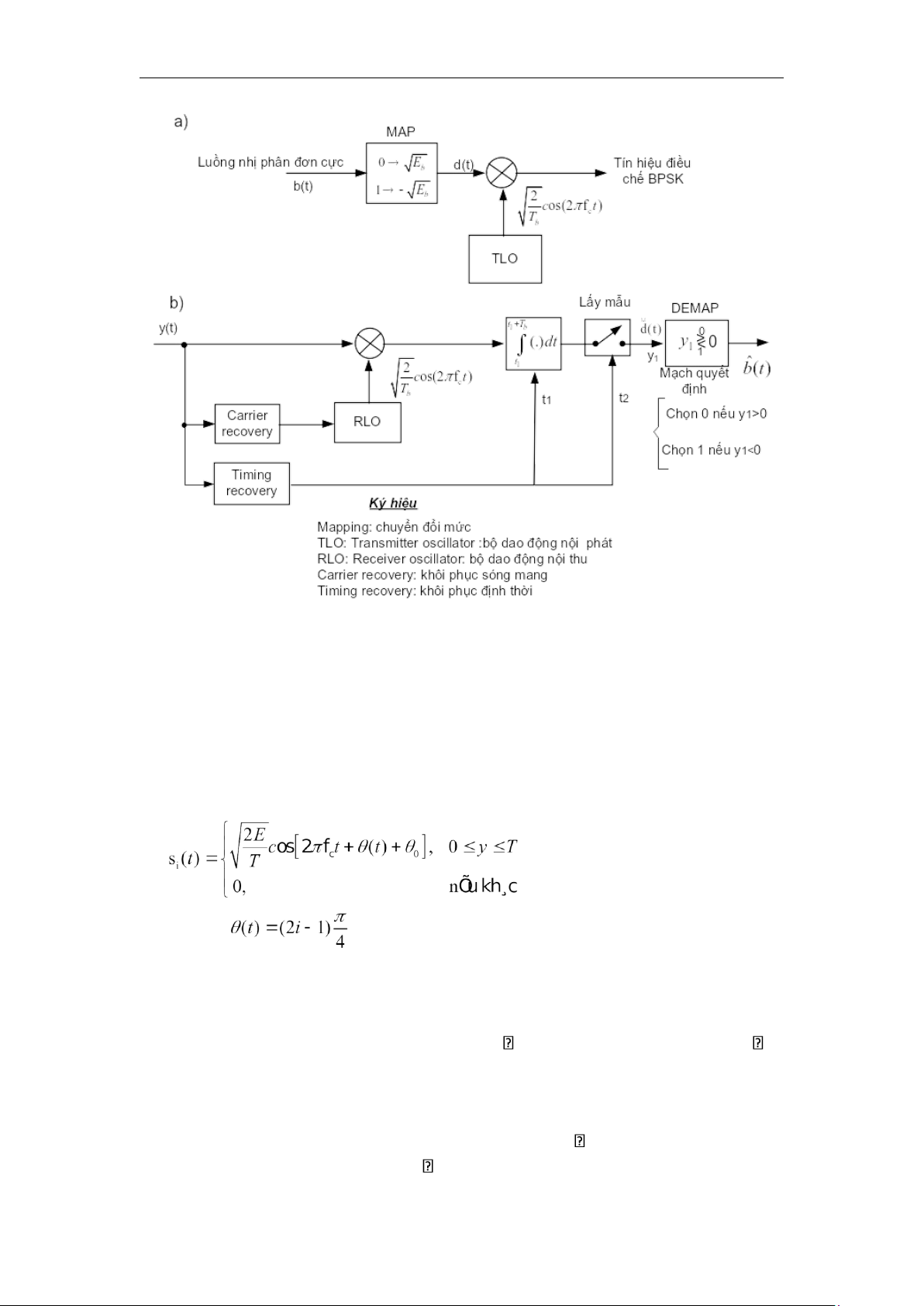
Để tạo ra sóng điều chế BPSK chuỗi bit b(t) đầu vào đơn cực được chuyển
đổi vào dạng lưỡng cực với 1 tương ứng - E và 0 tương ứng + E bằng cách đưa
chuỗi này qua bộ biến đổi mức hay còn gọi là MAP (hình 3.7 a). Dạng tín hiệu
nhị phân này cùng với sóng mang hàm sin đưa đến từ bộ dao động nội phát (TLO:
Transmitter local oscillator) ( 1(t) tần số fc ) được đưa đến bộ điều chế nhân . Ở
đầu ra của bộ điều chế ta nhận được sóng BPSK mong muốn.
Để lấy ra chuỗi bit ban đầu bao gồm các số '1' và '0' (chuỗi này được gọi
là chuỗi ước tính và đựơc ký hiệu là b tˆ( ) ), ta đưa sóng BPSK bị tạp âm y(t)
(ở đầu ra của kênh) đến một bộ tương quan, đồng thời đến bộ này cũng được đưa
tín hiệu nhất quán 1(t) (hình 3.7b) được tạo ra từ bộ dao động nội thu (RLO:
Receiver local oscillator) dựa trên sóng mang nhận được từ bộ khôi phục sóng
mang. Thời điểm khởi đầu tích phân cho một bit được đồng bộ bởi mạch khôi
phục xung định thời. Tín hiệu y1 là ước tính
của chuỗi bit lượng cực d(t)
phía phát được lấy mẫu theo chu kỳ bit (thời điểm lấy mẫu t2 được đồng bộ bởi
bộ định thời) và so sánh với một ngưỡng điện áp 0 Vôn. Nếu y1>0 thì máy thu
quyết định thiên về 0 còn ngược lại nó quyết định thiên về 1. Quá trình này đươc
gọi DEMAP : chuyển đỏi luồng lương cực vào đơn cực lOMoAR cPSD| 58737056
Hình 3.7. Sơ đồ khối máy phát BPSK (a) và máy thu BPSK (b)
3.9. ĐIỀU CHẾ VÀ GIẢI ĐIỀU CHẾ PSK BỐN TRẠNG THÁI HAY
VUÔNG GÓC (QPSK) NHẤT QUÁN
Cũng như ở BPSK điều chế QPSK (Quadrature phase shift keying: khóa
chuyển pha vuông góc) được đặc trưng bởi việc thông tin của luồng số được
truyền đi bằng pha của sóng mang. Ta có thể viết công thức cho sóng mang được điều chế QPSK như sau: (3.45)
trong đó: i = 1,2,3,4 tương ứng với phát đi các ký hiệu hai bit: "00", "01", "11"
và "10"; E là năng lượng tín hiệu phát trên một ký hiệu; T=2Tb là thời gian
của một ký hiệu, fc là tần số sóng mang, (t) là góc pha được điều chế, là góc pha ban đầu.
Mỗi giá trị của pha tương ứng với hai bit duy nhất của được gọi là cặp bit.
Chẳng hạn ta có thể có tập các giá trị pha để biểu diễn tập các cặp bit được mã
hoá Grey như sau: 10, 00, 01 và 11. Góc pha ban đầu 0 có là một hằng số nhận
giá trị bất kỳ trong khoảng 0 đến 2 , vì góc pha này không ảnh hưởng đến quá
trình phân tích nên ta sẽ đặt bằng không lOMoAR cPSD| 58737056
Sử dụng biến đổi lượng giác, ta có thể viết lại phương trình (3.45) vào dạng tương đương như sau: (3.46) Dựa trên
công thức trên ta có thể đưa ra các nhận xét sau:
• Chỉ có hai hàm cơ sở trực giao chuẩn , 1(t) và 2(t) trong biểu thức si (t).
Dạng tương ứng của các 1(t) và 2(t) được định nghĩa như sau: (3.47)
• Mỗi tín hiệu si(t) trong tập tín hiệu và hình chiếu của nó lên các vectơ trực
giao chuẩn được xác định như sau: (3.48)
Kết quả lấy tích phân phương trình (3.48) cho ta bốn điểm bản tin với các
vectơ tương ứng được xác định như sau: (3.49)
Các phần tử của các vectơ tín hiệu: Si1 và Si2 có các giá trị được tổng kết ở
bảng 3.1. Hai cột đầu của bảng cho ta các cặp bit và pha tương ứng của tín hiệu
QPSK, trong đó bit "0" tương ứng với điện áp + E /2, còn bit "1" tương ứng với điện áp - E /2. lOMoAR cPSD| 58737056
Bảng 3.1. Các vectơ ở không gian tín hiệu của QPSK Cặp bit vào Pha của tín hiệu QPSK
Toạ độ của các điểm bản tin 0 t T ( Radian) S i1 S i2 00 /4 + E / + E / 01 3 /4 + E / - E / 11 5 /4 - E / - E / 10 7 /4 - E / + E /
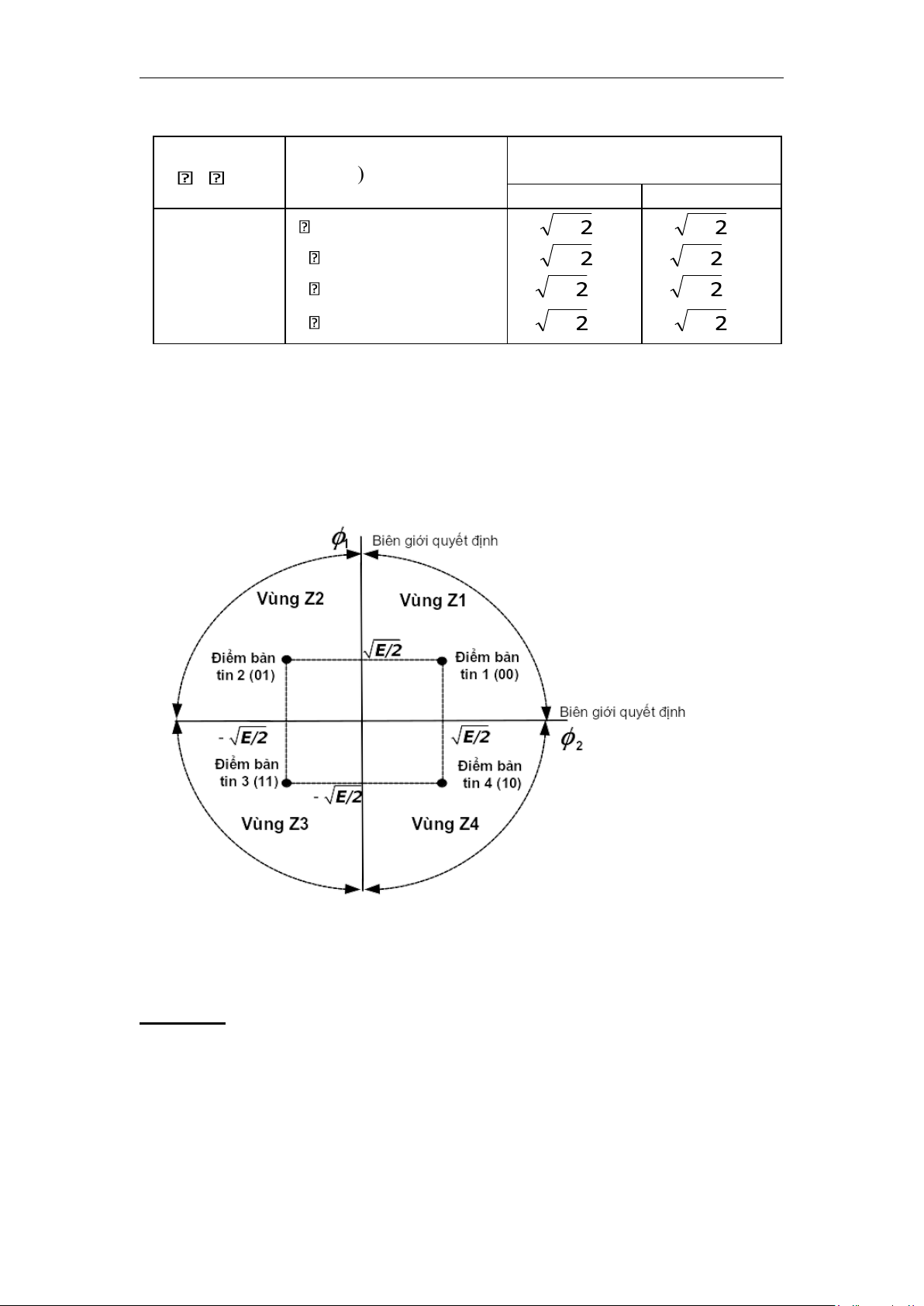
Từ khảo sát ở trên ta thấy một tín hiệu QPSK được đặc trưng bởi một trùm tín
hiệu hai chiều (N=2) và bốn điểm bản tin (M=4) như ở hình 3.8. Các tín hiệu
được sắp xếp trên không gian như theo mã Grey: các tổ hợp bit của hai tian hiệu
liền kế không được khác nhau quá một bit. Đều này đảm bảo rằng tại phía thu
nến một vectơ tín hiệu do tạp âm hoặc nhiễu bị đẩy vảo miền của vectơ tín hiệu
khác thì sẽ chỉ gây ra một bit lỗi.
Hình 3.8. Biểu đồ không gian tín hiệu cho hệ thống QPSK nhất quán Để
hiểu rõ hoạt động của QPSK ta xét thí dụ 3.1 dưới đây. Thí dụ 3.1
Hình 3.9 cho thấy một luồng số đưa lên điều chế QPSK. Chuỗi nhị phân đầu
vào 11000001 được cho ở hình 3.9a. Chuỗi này lại được chia thành hai chuỗi bao
gồm các bit lẻ và các bit chẵn. Hai chuỗi này được biểu thị ở các dòng trên cùng
của các hình 3.9b và 3.9c. Các dạng sóng thể hiện các thành phần đồng pha và
lệch pha vuông góc của QPSK cũng được cho ở các hình 3.9b và 3.9c. Có thể lOMoAR cPSD| 58737056
xét riêng hai dạng sóng này như các thí dụ của một tín hiệu BPSK. Cộng chúng
ta được dạng sóng QPSK ở hình 3.9d.
Lưu ý rằng ở hình vẽ 3.9 lôgic "1" được biến đổi vào mức điện áp - E còn lôgic
"0" được biến đổi vào mức điện áp + E như thường gặp ở sơ đồ thực tế.
Hình 3.9. Quá trình hình thành sóng QPSK. a) Chuỗi nhị phân đầu vào; b)
Các bit lẻ của chuỗi nhị phân đầu vào và dạng sóng BPSK tương ứng; c)
Các bit được đánh số chẵn của chuỗi nhị phân đầu vào và dạng sóng BPSK
tương ứng; d) Dạng sóng QPSK
Để hiểu được nguyên tắc quyết định khi tách sóng chuỗi số liệu phát, ta phân
chia không gian nhớ thành bốn phần như sau:
• Tập hợp của các điểm gần nhất điểm bản tin liên quan với vectơ tín hiệu s1 .
• Tập hợp của các điểm gần nhất điểm bản tin liên quan với vectơ tín hiệu s2 .
• Tập hợp của các điểm gần nhất điểm bản tin liên quan với vectơ tín hiệu s3.
• Tập hợp của các điểm gần nhất điểm bản tin liên quan với vectơ tín hiệu s4 .
Để thực hiện việc phân chia nói trên ta kẻ hai đường vuông góc chia đều hình
vuông nối các điểm bản tin sau đó đánh dấu các vùng tương ứng (hình 3.8). Ta lOMoAR cPSD| 58737056
được vùng quyết định là các góc phần tư có đỉnh trùng với gốc toạ độ. Ở hình
3.8 các vùng này được đánh số là Z1, Z2, Z3 và Z4.
Ta có thể biểu diễn tín hiệu thu được như sau: y(t) = si (t) + x(t) ,
0 t T , i = 1, 2, 3, 4 (3.50) trong đó x(t) là hàm mẫu của
một quá trình tạp âm trắng có giá trị trung bình không và mật độ phổ công suất N0/2.
Vectơ quan trắc y của một máy thu QPSK nhất quán có hai thành phần y1
và y2 được xác định như sau: i = 1, 2, 3, 4 (3.51)
trong đó x1 và x2 là các giá trị mẫu của quá trình ngẫu nhiên có trung bình không và phương sai bằng N0/2.
Vậy y1 và y2 là các giá trị mẫu của các biến ngẫu nhiên Gauss độc lập có
các giá trị trung bình bằng E sin[(2i -1) /4] và E cos[(2i - 1) /4] với phương sai chung bằng N0/2.
Bây giờ quy tắc quyết định chung chỉ đơn giản là đoán s1(t) được phát nếu
điểm tín hiệu thu liên quan đến vectơ y quan trắc rơi vào vùng Z1, đoán s2(t) được
phát nếu điểm tín hiệu thu liên quan đến vectơ y quan trắc rơi vào vùng Z2 v.v...
Sẽ xẩy ra một quyết định sai, khi chẳng hạn tín hiệu s1(t) được phát nhưng tạp
âm x(t) lớn đến mức mà điểm tín hiệu thu rơi ra ngoài vùng Z1.
Sử dụng phương trình (3.31) và lưu ý tính đối xứng của không gian tín hiệu QPSK ta được: (3.52)
Trong đó tích phân tích phân bên phải phương trình (3.52) là xác suất mà
ký hiệu mi hay si(t) rơi đúng vào vùng thu nhận đúng Zi và đây chính là xác
suất thu nhận đúng ký hiệu mi hay tín hiệu si(t).
Ta nhận thấy rằng nhờ tính đối xứng của các vùng quyết định, xác suất
diễn giải điểm tín hiệu thu đúng không phụ thuộc vào tín hiệu nào được phát.
Giả sử ta biết rằng tín hiệu s1(t) được phát. Máy thu sẽ đưa ra một quyết định
đúng nếu điểm tín hiệu thu được trình bầy bởi vectơ quan trắc y nằm trong vùng
Z1 của biểu đồ không gian tín hiệu ở hình 3.10. Vậy đối với một quyết định đúng
khi tín hiệu s1(t) được phát, các thành phần của vectơ quan trắc y : y1 và y2 phải cùng dương (hình 3.10).