Chương 4: Mã hóa kênh kiểm soát lỗi trong hệ thống thông tin số môn Kỹ thuật thông tin vô tuyến | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng Chương 4
MÃ HÓA KÊNH KIỂM SOÁT LỖI
TRONG HỆ THỐNG THÔNG TIN VÔ TUYẾN SỐ
4.1. GIỚI THIỆU CHUNG
4.1.1. Các chủ đề được trình bầy trong chương
• Các phương pháp mã hóa kênh kiểm soát lỗi
• Các mã khối tuyến tính • Các mã xoắn
• Các mã turbo và giải mã MAP 4.1.2. Hướng dẫn
Học kỹ các tư liệu đựơc trình bầy trong chương
Tham khảo thêm [2],[3], [8],[9].
4.1.3. Mục đích chương
• Hiểu nguyên tắc mã hóa kênh kiểm soát lỗi
• Hiểu được hoạt động của các bộ mã hóa kênh kiểm soát lỗi điển hình nhất
trong các hệ thống thông tin vô tuyến hiện đại
• Thiết kế đựơc các bộ mã hóa kênh kiểm soát lỗi đơn giản 4.2. MỞ ĐẦU
Thông thường mã hoá kênh là quá trình xử lý tín hiệu số được thực hiện sau
nguồn tin số và trước điều chế. Một trong các nhiệm vụ của mã hoá kênh là để
kiểm soát lỗi. Mã hoá kênh kiểm soát lỗi là quá trình xử lý tín hiệu số để đảm
bảo truyền dẫn thông tin số tin cậy ở kênh thực tế. Trong phần này chúng ta sẽ
xem xét các kỹ thuật mã hoá để kiểm soát lỗi bằng cách bổ sung cho hệ thống
các ký hiệu dư đến thông tin phát để có thể thực hiện được hai nhiệm vụ ở phía
thu: phát hiện lỗi và sửa lỗi.
Nhiệm vụ của nhà thiết kế hệ thống truyền dẫn số là cung cấp một hệ thống
kinh tế để truyền thông tin từ nơi phát đến nơi nhận ở tốc độ và mức độ tin cậy
mà người sử dụng chấp thuận. Hai thông số quan trọng mà nhà thiết kế có trong
tay khi này là: thông số tín hiệu được phát và băng thông kênh truyền dẫn. Hai
thông số này cùng với mật độ phổ công suất của tạp âm thu xác định tỷ số giữa
năng lượng một bit tín hiệu và mật độ công suất tạp âm, E b/N0. Tỷ số này xác
định đơn trị tỷ số bit lỗi BER (Bit Error Rate) đối với một sơ đồ điều chế cho
trước. Các thiết kế thực tế thường đặt ra một giới hạn giá trị mà ta có thể phân
bổ cho Eb/N0. Trong thực tế tuỳ theo hoàn cảnh ta thường phải sử dụng một sơ
đồ điều chế mà với sơ đồ này không thể đảm bảo chất lượng số liệu. Đối với tỷ lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
số Eb/N0 cố định cách duy nhất để đạt được chất lượng số liệu quy định là sử dụng mã hoá kênh.
Một động cơ thực tiễn khác dẫn đến việc sử dụng mã hoá kênh là để giảm tỷ
số Eb/N0 yêu cầu đối với tỷ số bit lỗi (BER) cố định. Nhờ việc giảm này ta có thể
giảm công suất phát hay giảm giá thành phần cứng chẳng hạn sử dụng anten kích cỡ nhỏ hơn.
Kiểm soát lỗi để đảm bảo sự toàn vẹn của số liệu có thể được thực hiện bằng
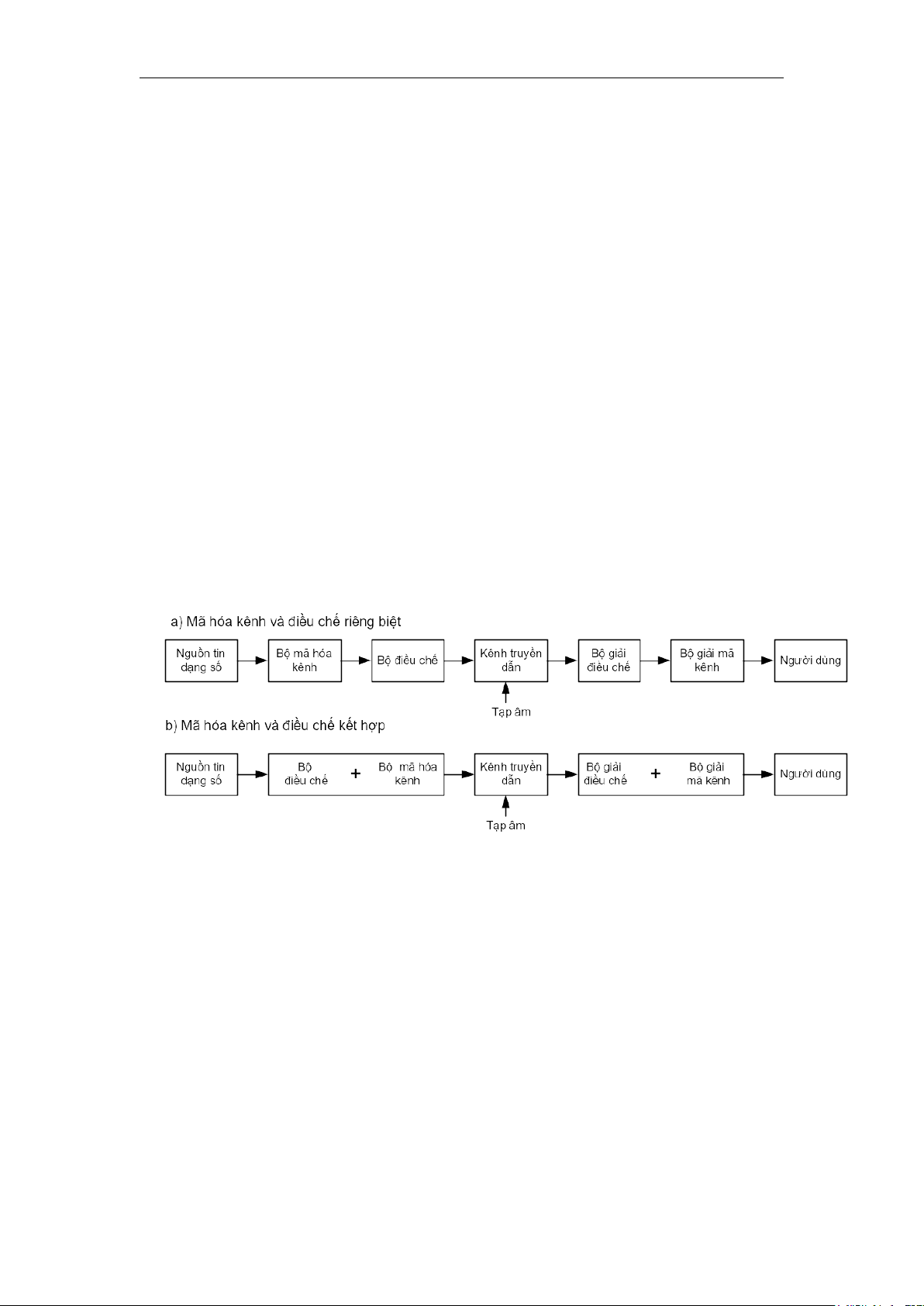
hiệu chỉnh lỗi trước FEC (Forward Error Correction). Hình 4.1a cho thấy mô
hình của một hệ thống thông tin số sử dụng phương pháp này. Bộ mã hoá kênh
nhận các bit của bản tin và bổ sung thêm các bit dư theo một quy tắc được quy
định trước, vì thế tạo ra luồng bit được mã hoá có tốc độ cao hơn. Bộ giải mã sử
dụng các bit dư để quyết định bit nào của bản tin là bit thực tế được phát. Mục
đích của việc kết hợp giữa mã hoá và điều chế (hình 4.1.b) là để giảm thiểu ảnh
hưởng của tạp âm. Nghĩa là giảm thiểu số lỗi giữa đầu vào của bộ mã hoá (lấy
từ nguồn tin) và đầu ra của bộ giải mã kênh (cung cấp cho người sử dụng).
Ngoài FEC còn có một phương pháp khác được gọi là yêu cầu phát lại tự động
(ARQ: Automatic Retransmission Request) cũng được sử dụng để giải quyết vấn
đề kiểm soát lỗi. ARQ sử dụng các bit ký hiệu dư để phát hiện lỗi. Dựa trên kết
quả phát hiện lỗi máy thu yêu cầu phát lại bản tin bị mắc lỗi, vì thế cần phải có một kênh hồi tiếp.
Hình 4.1. Mô hình đơn giản của hệ thống truyền dẫn số. a) Mã hóa và điều
chế kênh riêng biệt; b) Mã hóa kênh và điều chê kết hợp.
Việc bổ sung các bit dư vào bản tin được mã hoá còn dẫn đến việc cần thiết
tăng độ rộng băng thông.
Ngòai ra việc sử dụng mã hoá còn làm tăng tính phức tạp của hệ thống, nhất
là việc thực hiện giải mã kênh ở máy thu. Như vậy các suy xét khi lựa chọn việc
sử dụng mã hoá kênh cần bao hàm cả các cân nhắc về độ rộng băng thông và tính phức tạp.
Từ các vấn đề đã nêu ra ở trên ta có thể phát biểu mục tiêu của mã hoá
kênh kiểm soát lỗi như sau: 1. Phát hiện lỗi:
• Xác đinh đoạn nào của luồng số thu chứa lỗi. Thông báo cho nơi gửi hay nơi nhận về lỗi. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
• Giảm thiểu xác suất không phát hiện lỗi. 2. Sửa lỗi:
• Đạt được sự giảm xác suất lỗi (hay tỷ số bit lỗi, BER) cho tỷ số E b/N0 định trước.
• Đối với xác suất lỗi cho trước giảm giá trị Eb/N0. Lượng giảm được gọi
độ lợi của mã hoá đối với xác suất lỗi .
Các yêu cầu phát hiện và sửa lỗi được xác định trước hết bởi kiểu thông tin
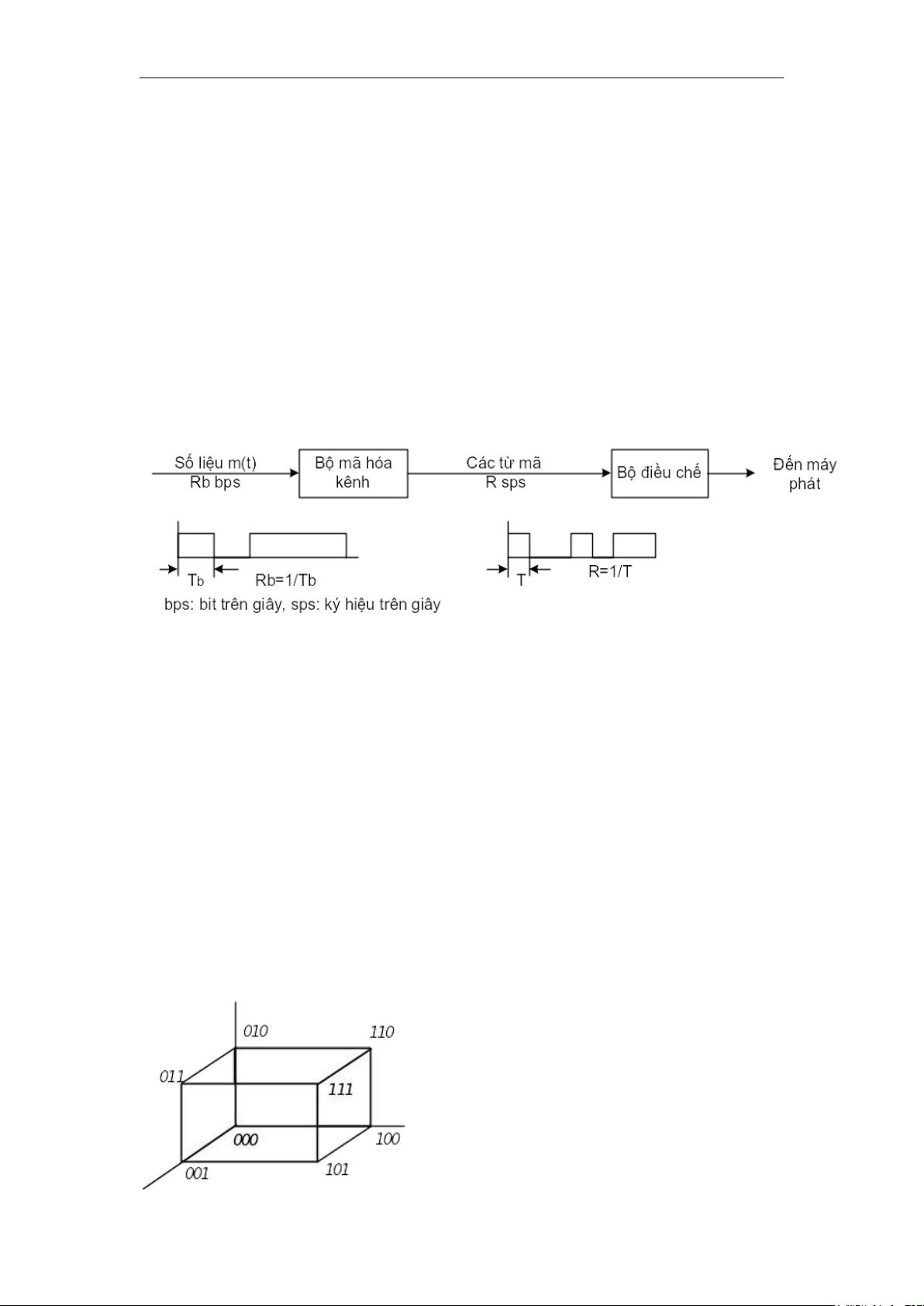
được phát. Sơ đồ khối chức năng của một máy phát sử dụng mã hoá kênh được
cho ở hình 4.2. Từ hình này ta thấy:
• Tốc độ ký hiệu ở đầu ra của bộ mã hoá R luôn luôn lớn hơn tốc độ bit vào Rb..
• Tỷ lệ mã có thể được định nghĩa như sau: Tỷ lệ mã = Rb/R .
Hình 4.2. Sơ đồ khối của máy phát sử dụng mã hóa kênh
4.3. CÁC NGUYÊN TẮC MÃ HÓA KÊNH KIỂM SOÁT LỖI
Ta xét một số nguyên tắc cơ sở để thực hiện mã hoá kênh kiểm soát lỗi. Có
thể phát biểu vấn đề cơ bản khi thực hiện mã hoá kênh này như sau: ta muốn
chuyển đổi m bản tin có thể có vào m từ mã . Các từ mã này phải thỏa mãn các
mục tiêu về phát hiện và sửa lỗi. Chẳng hạn ta xét một bản tin bao gồm 3 bit.
Với 3 bit này có thể có: 23 = 8 bản tin có thể có. Ta muốn thay thế từng bản tin
nói trên bằng một từ mã. Như đã nói ở trên để đạt được điều này ta sử dụng các
bit dư. Khi này các từ mã sẽ dài hơn bản tin tương ứng mã từ đó nó được tạo ra.
Ta có thể phân tích các khả năng phát hiện lỗi và sửa lỗi cuả các mã dư khác
nhau bằng cách trước hết định nghĩa khoảng cách Hamming giữa hai từ mã.
Khoảng cách Hamming giữa hai từ mã bất kỳ có cùng độ dài được định nghĩa là
số vị trí mà ở đó chúng khác nhau. Ta có thể mô tả khoảng cách Hamming này
bằng một không gian nhiều chiều (hình 4.3). lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Hình 4.3. Trình bầy từ mã ba bit ở không gian ba chiều
Giả sử ta có một bản tin nguyên tố bao gồm một số "0" hay một số "1". Khi
bản tin là 0 ta phát đi "000", còn khi nó là "1" ta phát đi "111". Từ hình lập thể ở
hình 4.3 ta thấy khoảng cách giữa hai từ mã đúng nói trên là bằng 3 vì để chuyển
từ một từ mã này sang từ mã khác phải chuyển dịch theo ba cạnh. Bây giờ ta
lại giả thiết rằng bản tin bao gồm ba bit và sử dụng tất cả các tổ hợp bit cuả ba
bit này để truyền bản tin. Từ hình vẽ 4.3 ta thấy tất cảc các đỉnh của hình lập thể
đều được sử dụng để biểu thị các bản tin. Mọi lỗi xẩy ra ở một trong ba bit đều
dẫn đến chuyển vào một đỉnh bên cạnh và sẽ dẫn đến lỗi. Trong trường hợp này
nếu khoảng cách của từ phát và thu là một thì chắc chắn sẽ mắc một lỗi vì từ thu
được là một trong số các bản tin có thể có. Ta cải thiện tình trạng trên bằng cách
tăng khoảng cách. Chẳng hạn các từ mã :
0000, 0011, 0101, 1001, 1010, 1100, 1111 đều có khoảng cách
tối thiều là 2. Đối với bốn từ mã này ta cần một hình không gian có 16 đỉnh để
biểu diễn. Hay tổng quát ta cần một không gian n chiều.
Giả sử xẩy ra một lỗi ở một vị trí của từ mã bốn bit nói trên: ta thu được
1000 chẳng hạn. Máy thu có thể nhận định rằng từ mã này có thể là một trong
hai từ mã gần từ thu nhất : 0000 hay 1010.
Trường hợp này chỉ có thể phát hiện được lỗi chứ không sửa được lỗi. Bây giờ
ta xét các từ mã gồm: 01111, 01000 và 10011. Khoảng cách cực tiểu giữa chúng
bây giờ là 3. Nếu thu được một từ mã 01001 thì một máy thu thông minh có thể
nhận định từ mã được phát phải là 01000 vì đây là từ mã gần với từ thu được
nhất (có khoảng cách nhỏ nhất =1). Bây gìơ giả thiết từ thu được là 01011, máy
thu chỉ có thể nhận định rằng từ phát có thể là một trong hai từ: 01000 và 10011,
vì khoảng cách cuả từ thu với hai từ này đều bằng 2. Vậy trong trường hợp này
máy thu chỉ có thể phát hiện được lỗi chứ không sửa được lỗi. Khi này ta nói
rằng mã trên cho phép phát hiện lỗi kép và sửa lỗi đơn.
Từ các thí dụ trên ta có thể nêu ra công thức chung liên quan đến khoảng cách
Hamming tối thiểu giữa các từ mã và số bit lỗi mà mã cho phép phát hiện và sửa như sau:
* Khả năng phát hiện lỗi: dm = t+1 (4.1) * Khả năng sửa lỗi: dm 2t +1 (4.2)
trong đó dm là khoảng cách Hamming cực tiểu giữa các từ mã có thể có trong tập
mã còn t là số lỗi mã cho phép phát hiện (trường hợp thứ nhất) và sửa (trường hợp hai).
Các mã kênh thường được phân thành hai loại : mã khối tuyến tính và mã xoắn,
dưới đây ta sẽ xét cụ thể hai loại mã này. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
4.4. CÁC MÃ KHỐI TUYẾN TÍNH
Trong loại mã này luồng thông tin được chia thành các khối có độ dài bằng
nhau được gọi là các khối bản tin. Các bit nhận được ở đầu ra của bộ mã hoá
được gọi là từ mã. Các bit dư được bổ sung vào các khối theo một thuật toán
nhất định phụ thuộc vào loại mã được sử dụng, các bit này thường được gọi là
các bit kiểm tra. Các mã khối được xác định bằng ba thông số: độ dài khối bản
tin k, độ dài từ mã n và khoảng cách Hamming cực tiểu dm. Tỷ số r = k/n được
gọi là tỷ lệ mã. Các bit kiểm tra có độ dài n-k. Bộ mà hoá được ký hiệu (n,k).
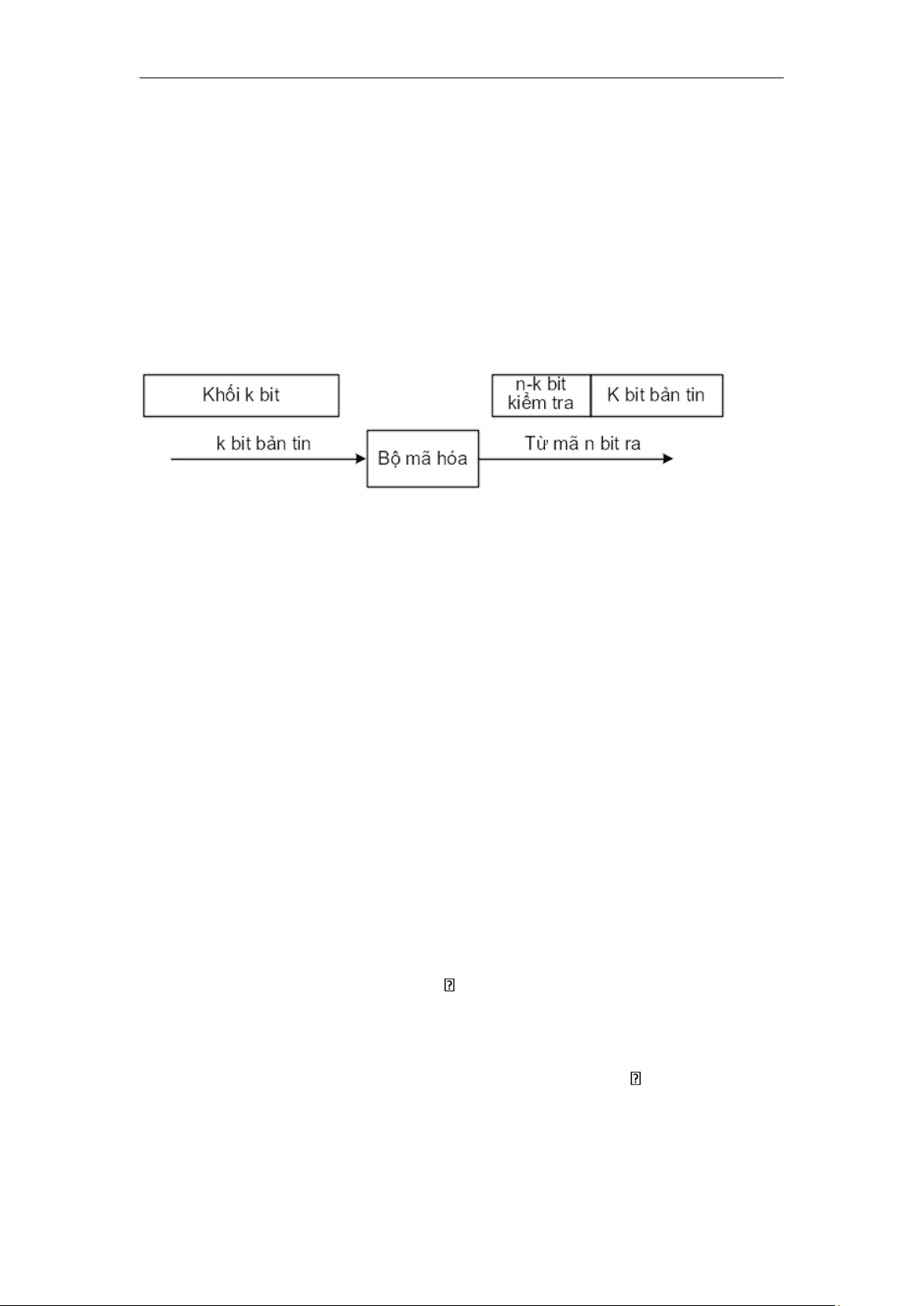
Sơ đồ khối tổng quát của một bộ mã hoá khối tuyến tính được cho ở hình 4.4. .
Hình 4.4 Sơ đồ tổng quát của bộ mã hóa khối
Hoạt động của bộ mã hoá có thể đựơc biểu diễn toán học ở dạng ma trận hay
đa thức. Các ma trận hay các đa thức này được gọi là các ma trận tạo mã hay các đa thức tạo mã.
4.4.1. Ma trận tạo mã
Trong phần này ta sẽ định nghĩa hai ma trận quan trọng cho bộ mã hóa
khối tuyến tính: ma trân tạo mã cho phép xác định từ mã đầu ra và ma trận kiểm
tra chẵn lẻ cho phép kiểm tra từ mã nhận được tại phía thu.
Ta xét cách biểu diễn ma trận tạo mã cho bộ mã hoá khối tuyến tính. Gỉa sử
một khối bản tin k bit : m0, m1, ........, mk-1 được đưa vào bộ mã hoá, đầu ra của
bộ mã hoá cho ta từ mã ở dạng chuỗi bit sau:
b0,b1 ,....., bn-k-1, m0,m1, ......,mk-1
trong đó mj là các bit của khối bản tin, còn bi là các bit kiểm tra, các bit này được
gọi là các bit chẵn lẻ, các bit có chỉ số cao là các bit có nghĩa lớn hơn và được
truyền trứơc. Như vậy đầu vào bộ mã hoá có thể có 2k khối bản tin và tương ứng
ở đầu ra có 2k từ mã được sử dụng trong số 2n từ mã có thể có. Ta có thể biểu
diễn k bit bản tin vào dạng vectơ vơ 1 k sau đây:
m = [m0, m1, ..........,mk-1] (4.3)
Tương tự có thể biểu diễn n-k bit chẵn lẻ vào dạng vectơ 1 (n- k) sau:
b = [b0, b1, ........., bn-k-1] (4.4)
Ta ký hiệu c là vetơ đầu ra của bộ mã hoá như sau: lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
c = [c0, c1, ..........., cn-1] (4.5) trong đó (4.6)
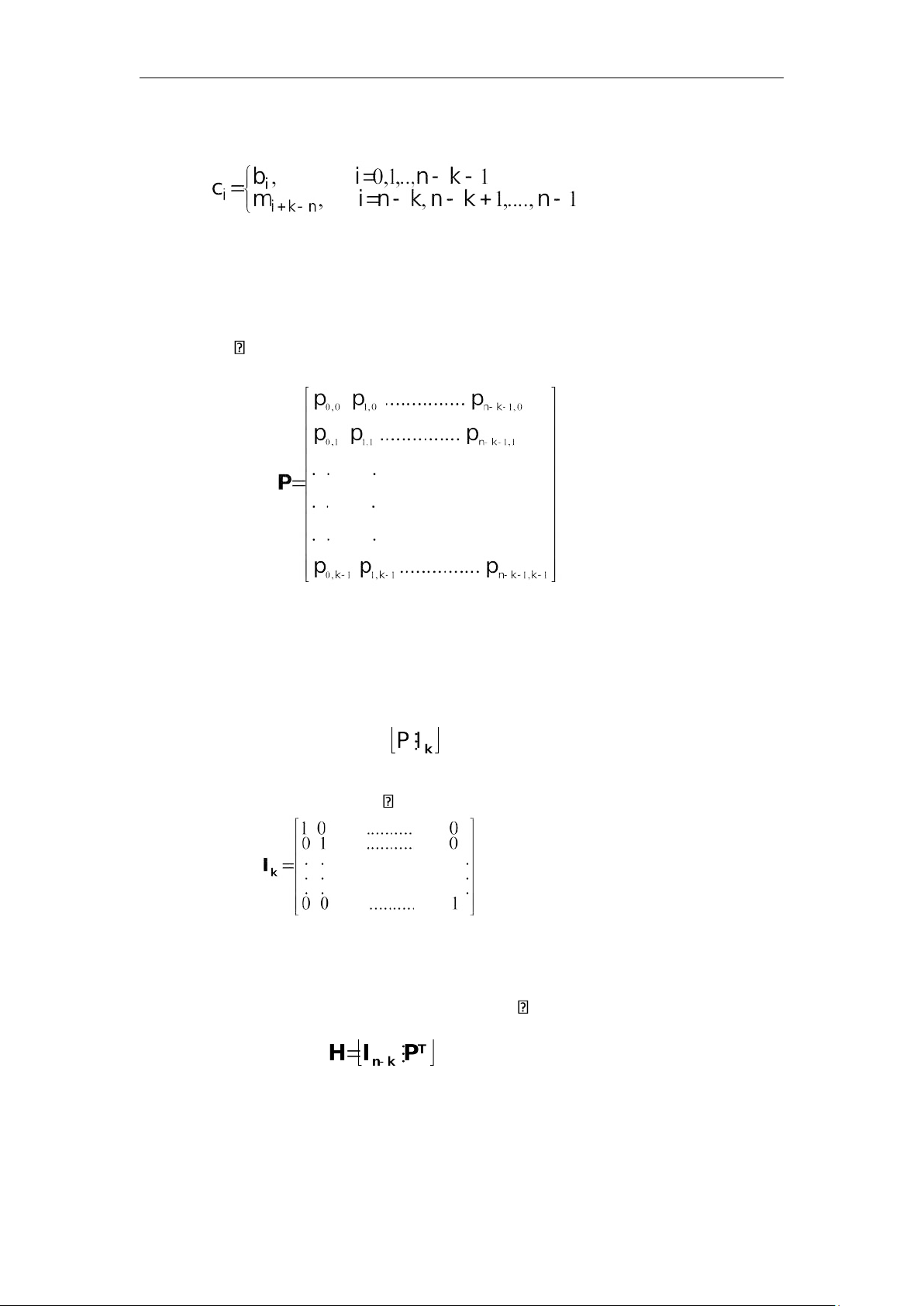
n-k bit chẵn lẻ ở đầu ra của bộ tạo mã được xác định như sau: b = mP (4.7) trong đó P
là ma trận k (n-k) xác định theo công thức sau: (4.8)
với i = 0,1,...,n-k-1 là chỉ số của cột và j = 0,1, ..., k-1 là chỉ số của hàng, pij=0
hoặc 1 tùy thuộc vào việc bi có phụ thuộc vào bit bản tin mi hay không.
Ma trận tạo mã đựơc xác dịnh như sau: G = (4.9)
trong đó Ik là ma trận đơn vị k k: (4.10)
Khi này ma trận từ mã được xác định như sau:
c = mG (4.11)
Ma trận kiểm tra chẵn lẻ H là ma trận (n-k) n được xác định như sau: (4.12)
Trong đó PT là ma trận chuyển vị có kích thước (n-k)xk, nhận được từ P bằng
cách chuyển đổi cột thành hàng. Nhân H với ma trận GT ta được: lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng vì cộng mod 2.
Hay GHT=0. Nhân c trong phương trình (4.11) với HT, ta được:
cHT=mGHT=0 hay HcT=0 (4.13)
Syndrome
Syndrom cho phép xác định từ mã nhận được có bị mắc lỗi hay không và
thậm chí cả mẫu lỗi khi thỏa mãn điều kiện trong phương trình (4.2) Ta xét
quá trình giải mã. Ta ký hiệu y là một vectơ thu được có kích thước là 1 n nhận
được từ việc phát đi vectơ x trên một kênh có tạp âm. Ta biểu diễn vectơ y là
tổng của vectơ thu c và vectơ lỗi e gây ra do tạp âm:
y = c + e (4.13)
Vectơ e được gọi là vectơ lỗi hay mẫu lỗi. Phần tử ei của vectơ này bằng không
nếu phần tử tương ứng của y bằng phần tử tương ứng của c. Ngược lại phần tử
ei bằng 1 nếu phần tử tương ứng của y khác với phần tử tương ứng của c, khi này
xẩy ra một lỗi ở vị trí i. Như vậy với i = 1, 2, ...... , n ta có:
ei = 1 khi một lỗi xẩy ra ở vị trí i ei = 0 khi không có lỗi
Máy thu có nhiệm vụ giải mã vectơ c từ vectơ y thu đươc. Để giải mã người
ta thường tính toán một vectơ 1 (n-k) được gọi là Syndrome. Đặc điểm của
Syndrome là nó chỉ phụ thuộc vào mẫu lỗi.
Syndrome được xác định như sau:
s = y HT (4.15) Syndrome có các
thuộc tính quan trọng sau đây.
Thuộc tính 1: Syndrome chỉ phụ thuộc vào mẫu lỗi chứ không phụ thuộc vào từ mã đựơc phát.
Thuộc tính 2: Tất cả các mẫu lỗi khác nhau nhiều nhất một từ mã đều có cùng Syndrome.
Đối với k bit bản tin ta có 2k vectơ từ mã khác nhau được biểu thị bằng : ci, i=
0,1, 2, 3, .... , 2k-1. Tương ứng đối với một mẫu lỗi e bất kỳ ta có thể định nghiã
2k vectơ ei khác nhau như sau:
ei = e + ci i=0,1, 2, . . ., 2k-1 (4.16) chỉ
khác nhau nhiều nhất một từ mã. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Tập các vectơ {ei , i = 0,1,2,3, ... , 2k-1} theo định nghĩa trên được gọi là Coset
của mã. Nói một cách khác một Coset có đúng 2k phần tử khác nhau nhiều nhất
một từ mã. Số các tổ hợp từ mã có thể có của một mã khối tuyến tính (n,k) là 2n
trong đó chỉ có một bộ 2k từ mã là được sử dụng, vậy tổng số bộ 2k từ mã có thể
có là 2n-k và tương ứng sẽ có 2n-k Coset có thể có (trong đó chỉ có một Coset là
tương ứng với bộ từ mã được sử dụng).
Đối với vectơ y thu được, tính Syndrome s = yHT. Trường hợp mã thu không mác lỗi s=0
Trong tập Coset được đặc trưng bởi Syndrome trên chọn ta mẫu lỗi có xác
suất lớn nhất. Gọi nó và e0. Tính vectơ mã cho đầu ra:
Lưu ý rằng ở số học môđun 2 thì trừ cũng giống như cộng.
Trọng lượng Hamming cực tiểu
Theo định nghĩa thì trọng lượng Hamming của một từ mã là tổng số các vị trí
bit khác không trong từ mã này. Ta cũng có thể coi trọng lượng này là khoảng
cách Hamming giữa một từ mã khác không với từ mã toàn không. Do thuộc tính
của mã khối tuyến tính là tổng (hoặc hiệu) hai từ mã bất kỳ luôn luôn bằng một
từ mã thứ ba cuả mã, nên có thể nói rằng trọng lượng Hamming cực tiểu của các
từ mã khác không của mã khối tuyến tính chính bằng khoảng cách Hamming cực tiểu.
Để kết thúc phần này ta xét thí dụ về mã Hamming. Thí dụ 4.1
Ta xét một họ mã được gọi là mã Hamming có các thông số sau đây: Độ dài từ mã n= 2m -1
Số các bit bản tin k = 2m - m -1
Số các bit chẵn lẻ n - k = m trong đó m 3
Để làm thí dụ ta xét mã Hamming (7,4) có n=7 và k=4 tương ứng với m=3.
Ma trận tạo mã của mã này phải có cấu trúc phù hợp với phương trình (3.13) và có dạng như sau: (4.17)
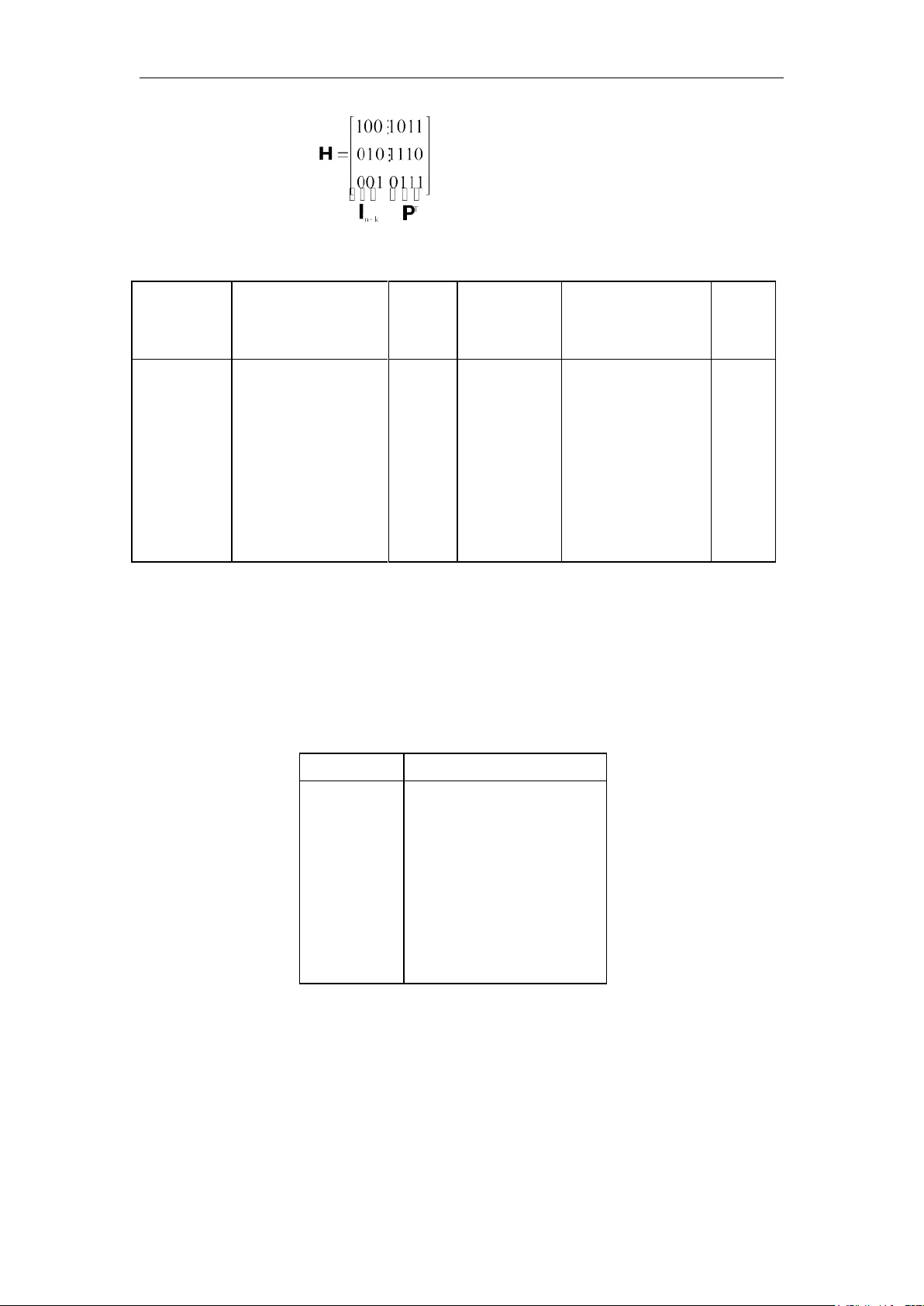
Ma trận kiểm tra chẵn lẻ tương ứng có dạng sau: lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng (4.18)
Các từ mã được tính theo phương trình (4.14) và được cho ở bảng 4.1.
Bảng 4.1 Các từ của mã Hamming (7,4) Bản tin Từ mã Trọng Bản tin Từ mã Trọn lượng g lượng 0000 0000000 0 1000 1101000 3 0001 1010001 3 1001 0111001 4 0010 1110010 4 1010 0011010 3 0011 0100011 3 1011 1001011 4 0100 0110100 3 1100 1011100 4 0101 1100101 4 1101 0001101 3 0110 1000110 3 1110 0101110 4 0111 0010111 4 1111 1111111 7
Từ bảng 4.1 ta thấy trọng lượng nhỏ nhất của các từ mã khác không là 3, vậy
khoảng cách Hamming cực tiểu dmin = 3. Tất nhiên các mã Hamming có thuộc
tính là khoảng cách Hamming cực tiểu luôn luôn bằng 3 không phụ thuộc vào
m. Do dmin = 3 nên từ các phương trình (4.1) và (4.2) ta thấy các mã này chỉ có
thể sửa được một lỗi và phát hiện được hai lỗi. Quan
hệ này cho mã Hamming (7,4) được cho ở bảng 4.2.
Bảng 4.2. Bảng giải mã cho mã Hamming (7,4) Syndrome Mẫu lỗi 000 0000000 100 1000000 010 0100000 001 0010000 110 0001000 011 0000100 111 0000010 101 0000001
4.4.2. Đa thức tạo mã
Trong phần này ta xét việc sử dụng đa thức tạo mã để xây dựng các bộ
tạo mã vòng. Mã vòng là một tập con của mã tuyến tính. Các mã này được xây
dựng trên cơ sở các thanh ghi dịch có hồi tiếp. Một mã được gọi là mã vòng khi
nó thể hiện hai thuộc tính cơ bản sau: 1.
Thuộc tính tuyến tính: tổng của hai từ mã cũng là một từ mã. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng 2.
Thuộc tính vòng: Mọi sự dịch vòng một từ mã sẽ cũng là một từ
mã. Ta có thể biểu diền từ mã là một vectơ n-1 thành phần như sau:
c = (c0, c1 , . . . . , cn-1) (4.19)
Hay ở dạng đa thức bậc (n-1) sau đây:
c = c0 + c1 x+ c2x2 + . . . . + cn-1 xn-1 ( 4.20)
trong đó các hệ số ci = 0/1, và mỗi luỹ thừa của x tương đương với dịch vòng
một bit theo thời gian. Vì thế khi ta nhân đa thức (4.20) với x có nghĩa là dịch
vòng một bit sang phải, vì vậy xn phải bằng 1 và bit ngoài cùng bên phải chuyển
thành bit ngoài cùng bên trái. Quá trình nhân và dịch vòng như vậy thường được biểu diễn như sau:
xc(x) mod (xn - 1) = cn-1 + c0 x + . . . . + cn-2 xn-1 (4.21)
trong đó mod có nghĩa là chia chỉ lấy phần dư.
Tương tự nếu nhân biểu thức (4.21) với x2 , ta được dịch vòng hai bit sang phải như sau:
x2 c(x) mod (xn - 1) = cn-2 + cn-1 x + . . . . . + cn-3xn-1 (4.22)
Một mã vòng (n,k) được đặc tả bởi tập đầy đủ các đa thức bậc (n-1) hay thấp hơn
và nhận một đa thức bậc thấp nhất (n-k) làm thừa số. Thừa số đặc biệt này được
ký hiệu là g(x) và được gọi là đa thức tạo mã của mã này. Đa thức tạo mã g(x)
tương đương với ma trận tạo mã G mà ta đã xét ở phần trước. Đa thức tạo mã
của mã vòng có các thuộc tính sau.
Thuộc tính 1: Đa thức tạo mã của một mã vòng (n,k) là đơn nhất ở ý nghĩa rằng
nó là đa thức từ mã bậc (n-k) cực tiểu duy nhất.
Thuộc tính 2: Mọi bội số của đa thức tạo mã g(x) là một đa thức từ mã mới, xác
định như sau: c(x) = a(x)g(x)mod(xn-1)
trong đó a(x) là một đa thức của x.
Hay: Một đa thức bậc n-1 hay thấp hơn là một đa thức từ mã chỉ và chỉ khi nó
là bội số của g(x).
g(x) là đa thức tạo mã được biểu diễn như sau:
g(x) = g0 + g1x + g2x2 + . . . . . + gn-kxn-k (4.23) trong đó gi={0,1}
Còn m(x) là đa thức của khối bản tin k bit được biểu diễn như sau: m(x)
= m0 + m1x + m2x2 + . . . . . . . + mk-1xk-1 (4.24) lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Giả sử ta được cho một đa thức tạo mã g(x) và phải mã hoá một khối
bản tin (m0, m1, . . . . , mk-1) vào một mã vòng hệ thống vào dạng sau: (4.25)
n-k bit chẵn lẻ k bit bản tin Ta
có thể viết đa thức từ mã như sau:
c= b0+b1x+…+bn-k-1xn-k-1+ m0xn-k+…+ mn-1xn-1 = b(x)+ xn-km(x) (4.26) trong đó:
b(x)= b0+b1x+…+bn-k-1xn-k-1 xn-km(x)= m0xn-k+…+ mn-1xn-1 là đa
thực từ mã được dịch vòng n-k
Ta chia đa thức xn-km(x) cho đa thức tạo mã g(x) và nhận được thương a(x) và
phần dư b(x) như sau: (4.27) hay :
n-k m(x) = a(x)g(x) + b(x) (4.28) trong đó:
a(x) = a0 + a1 x + . . . . . + ak-1 xk-1 (4.29)
và: b(x) = b0 + b1 x + . . . . . + bn-k-1 xn-k-1 (4.30)
Trong số học môđun 2 b(x) = - b(x), nên ta có thể viết lại phương trình (4.26) như sau:
c(x)= b(x) + xn-k m(x) = a(x)g(x) (4.31)
Bậc của phần dư b(x) luôn luôn nhỏ hơn bậc của số chia: n-k. Các hệ số của
phần dư b(x) chính là các bit chẵn lẻ.
Từ phân tích trên ta có thể tổng kết các bước trong quá trình thực hiện mã
hoá cho một mã vòng (n,k) như sau:
1. Nhân đa thức bản tin m(x) với xn-k.
2. Chia xn-k m(x) cho g(x) để được phần dư b(x).
3. Cộng b(x) với xn-km(x) để nhận được đa thức từ mã c(x).
Đa thức tạo mã g(x) và đa thức kiểm tra chẵn lẻ h(x) là các thừa số của đa thức 1 + xn như sau: lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
h(x) g(x) = 1 + xn (4.32) trong đó h(x)
là một đa thức chẵn lẻ định nghĩa như sau: h(x)g(x)mod(xn-1) = 0 (4.33)
hay từ phương trình (4.31), ta có: h(x)c(x)mod(xn-1) = 0 (4.34)
Thuộc tính này cung cấp cho ta cơ sở để chọn đa thức tạo mã hay đa thức kiểm
tra chẵn lẻ. Chẳng hạn ta có thể phát biểu rằng nếu đa thức g(x) là một đa thức
bậc n-k và đồng thời là một thừa số của 1 + xn thì nó là một đa thức tạo mã của
một mã vòng (n,k). Tương tự ta có thể phát biểu rằng nếu h(x) là một đa thức
bậc k và đồng thời là thừa số của 1 + xn thì nó là một đa thức kiểm tra chẵn lẻ
của mã vòng (tuần hoàn) (n,k).
Mọi thừa số của 1 + xn có bậc (n-k) (số các bit chẵn lẻ) đều có thể được
sử dụng như một đa thức tạo mã. Khi giá trị n lớn, đa thức 1 + xn có thể có nhiều
thừa số bậc n-k. Một số trong số này tạo ra các mã vòng tốt còn một số khác lại
tạo ra các mã vòng tồi hơn. Vấn đề tìm ra cách chọn mã vòng tốt là một vấn đề
rất khó mà các nhà bác học đã mất nhiều công nghiên cứu.
Thí dụ 4.2 Các mã Hamming
Để minh hoạ các vấn đề liên quan đến việc trình bầy đa thức cho các mã
vòng ta khảo sát quá trình tạo ra một mã vòng (7,4) cho mã Hamming. Với độ
dài từ mã n = 7, ta thực hiện khai triển đa thức 1 + x7 vào ba đa thức thừa số tối
giản như sau: x7 + 1 = (1 + x)(1 + x2 + x3) (1 + x + x3 )
Đa thức tối giản là đa thức không thể phân chia thành thừa số bằng cách
sử dụng các đa thức có các hệ số là mã cơ số hai. Một đa thức tối giản bậc m
được gọi là đa thức nguyên thuỷ nếu tồn tại quan hệ n = 2m - 1, trong đó n là bậc
của đa thức 1+xn chia hết cho đa thức nguyên thuỷ. Vậy ở thí dụ đang xét ta chỉ
có hai đa thức nguyên thuủy là (1 + x2 + x3) và (1 + x + x3). Giả sử ta chọn: g(x) = 1 + x + x3
làm đa thức tạo mã với bậc bằng số các bit chẵn lẻ, thì đa thức kiểm tra chẵn lẻ sẽ là đa thức sau:
h(x) = (1 + x) (1 + x2 + x3)
= 1 + x + x2 + x4 có bậc bằng số các bit của khối bản tin.
Bây giờ ta sẽ xét các thủ tục tạo mã cho một khối bản tin 1001 bằng cách sử dụng
đa thức tạo mã nói trên. Trước hết ta viết đa thức khối bản tin như sau: m(x) = 1 + x3 lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Nhân đa thức bản tin với xn-k = x3, ta được: x3 (1 + x3) = x3 + x6
Sau đó ta chia tích trên cho đa thức tạo mã để nhận được phần dư b(x).
Ta có thể viết lại kết quả chia trên như sau:
Vậy ta được đa thức của thương và phần dư là: a(x) = x + x3 b(x) = x + x2
Như vậy theo công thức (4.31) ta được đa thức từ mã cần tìm :
c(x) = b(x) + xn-k m(x) = x + x2 + x3 + x6
Kết quả ta được từ mã là: 0111001. Bốn bit bên phải 1001 là các bit của khối bản
tin. Ba bit bên trái là các bit kiểm tra chẵn lẻ. Ta thấy từ mã này giống như một
từ mã có trong bảng 3.1 cho mã Hamming (7,4).
Ta có thể tổng quát hoá kết quả nói trên bằng cách phát biểu rằng mọi mã vòng
được tạo ra bởi một đa thức nguyển thuỷ là một mã Hamming có khoảng cách cực tiều bằng 3.
Sơ đồ bộ mã hoá vòng
Trong phần trước chúng ta đã thấy rằng thủ tục để mã hoá vòng (n,k) bao gồm ba bước sau:
1. Nhân xn-k với đa thức bản tin m(x)
2. Chia tích trên cho đa thức tạo mã g(x).
3, Cộng phần dư b(x) với tích xn-k m(x) để được đa thức từ mã cần tìm. Ba
bước nói trên được thực hiện ở bộ lập mã được cho ở hình 4.5 bao gồm một
thanh ghi dịch (n-k) tầng có mạch hồi tiếp tuyến tính. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Hình 4.5. Bộ tạo mã vòng
Thanh ghi này bao gồm các Flip-Flop hay các phần tử trễ. Các Flip-Flop
này có thể nhận một trong hai trạng thái: 0 hay 1. Một đồng hồ ngoài (không có
ở hình vẽ) thực hiện điều khiển tất cả các Flip-Flop. Ngoài các Flip-Flop, bộ lập
mã lại có một tập hợp các mạch cộng môđun-2 để thực hiện cộng môđun-2 giữa
đầu ra của Flip-Flop với mạch hồi tiếp. Cuối cùng là các bộ nhân để nhân chúng
với nhau. Chẳng hạn nếu gi = 1 thì bộ nhân có nghĩa là "nối trực tiếp", còn nếu
gi = 0 thì bộ nhân có nghĩa là "không nối". Mỗi lần có sườn tăng của xung đồng
hồ, nội dung của thanh ghi dịch lại dịch đi một vị trí theo chiều mũi tên.
Hoạt động của sơ đồ ở hình 4.5 như sau:
1. Đầu tiên các flip-flop được đặt vào không và khoá chuyển mạch CM1 ở
phía trên của sơ đồ ở vị trí đóng mạch, và khoá chuyển mạch ở phía dưới
ở vị trí dưới. k bit bản tin dịch vào kênh và bộ tạo mã tạo ra (n-k) bit chẵn
lẻ trong thanh ghi dịch (nhắc laị rằng các bit chẵn lẻ này có cùng giá trị
như các hệ số của phần dư b(x) ).
2. Sau đó khoá chuyển mạch trên ngắt và khoá chuyển mạch dưới chuyển
vào vị trí trên. Nội dung của thanh ghi dịch được dịch vào kênh.
Thí dụ 4.3. Bộ lập mã vòng Hamming (7,4)
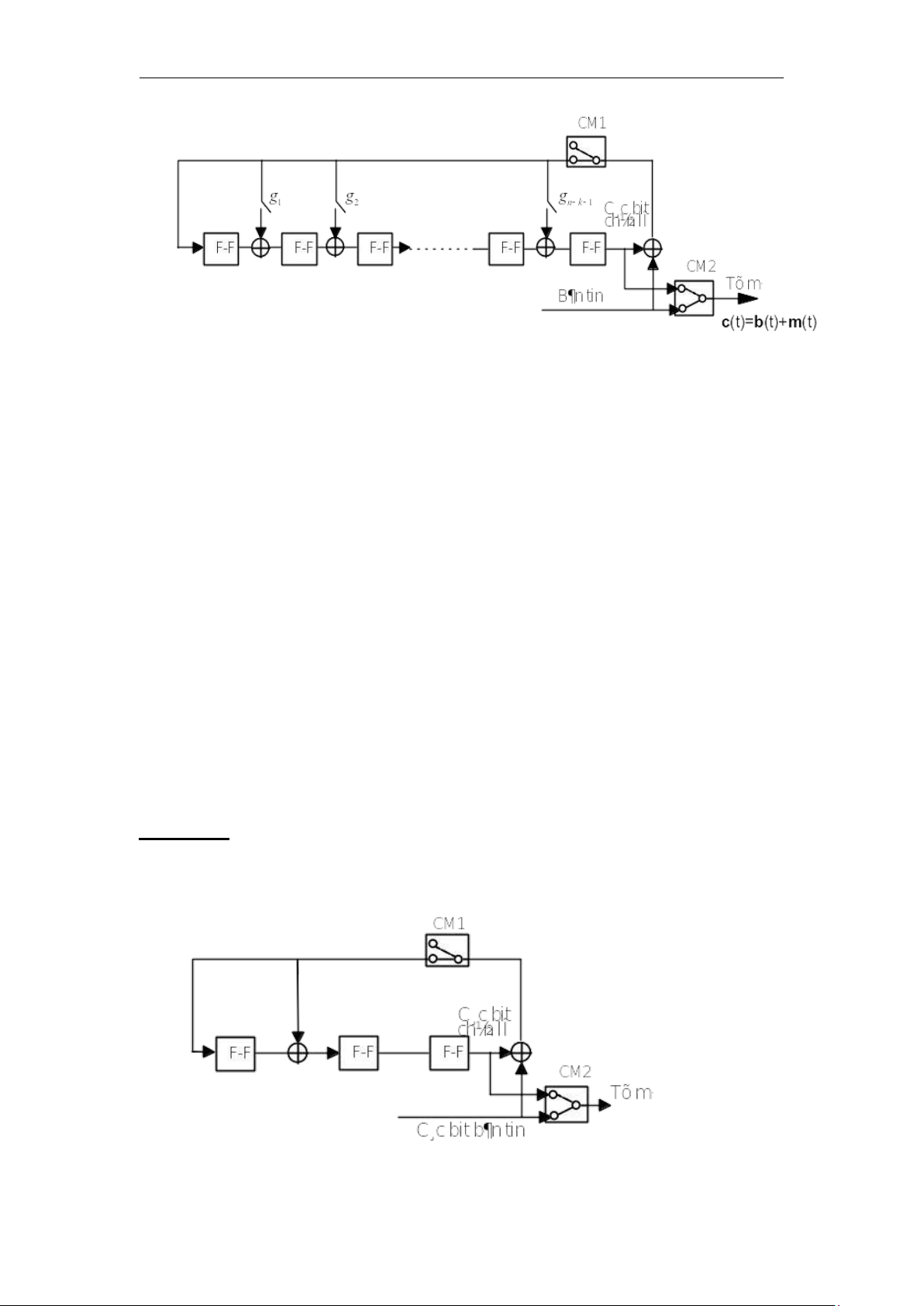
Hình 4.6 cho ta sơ đồ của bộ lập mã để tạo ra mã vòng Hamming (7,4) từ bộ tạo
mã sau: g(x) = 1 + x + x3. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Hình 4.6. Bộ tạo mã vòng (7,4) với g(t) = 1+x+x2
Để mô tả hoạt động của bộ lập mã này ta xét chuỗi bản tin đầu vào là
(1001). Thay đổi nội dung của thanh ghi dịch sau mỗi lần dịch vào một bit thông
tin được cho ở bảng 4.3. Sau bốn lần dịch nội dung của thanh ghi dịch và các bit
chẵn lẻ tương ứng là (011). Vậy nếu gắn các bit này vào các bit bản tin ta được
từ mã (0111001). Kết quả này giống hệt ở thí dụ 4.1.
Bảng 4.3. Nội dung ở thanh ghi dịch thí dụ 4.3 khi bản tin vào (1001)
Dịch Bit vào Nội dung thanh ghi 000 (trạng thái đầu) 1 1 110 2 0 011 3 0 111 4 1 011 Syndrome
Giả thiết từ mã c = (c0, c1, . . . . , cn-1) được truyền trên một kênh
có tạp âm. dẫn đến thu được từ mã y = (y0, y1, . . . . ., yn-1). Bước đầu tiên để giải
mã cho một mã khối tuyến tính là phải tính Syndrome cho từ mã thu. Nếu
Syndrome bằng không thì từ thu không bị lỗi, ngược lại nếu Syndrome khác
không thì từ này bị mác lỗi và cần sửa nó.
Đối với mã vòng ở dạng hệ thống thì có thể tính toán Syndrome dễ dàng.
Giả thiết từ thu được trình bầy ở dạng đa thức sau đây:
y = y0 + y1 x + . . . . . + yn-1 xn-1 (4.35)
Để tính Syndrome ta chia đa thức y(x) cho đa thức tạo mã g(x). Giả sử a(x) là
thương còn s(x) là phần dư của kết quả chia, ta có thể biểu diễn y(x) như sau:
y(x) = a(x) g(x) + s(x) (4.36)
Phần dư s(x) là một đa thức bậc n-k-1 hay thấp hơn. Đa thức này được gọi là đa
thức Syndrome. Nếu đa thức Syndrome s(x) khác không, thì có nghiã là phát
hiện thấy sự có mặt của lỗi truyền dẫn ở từ mã thu được.
Bộ tính toán Syndrome có sơ đồ giống như bộ tạo mã chỉ khác ở chỗ các
bit của từ mã thu được được đưa vào (n-k) tầng của thanh ghi dịch có hồi tiếp từ
phía bên trái (xem hình 4.7). Sau khi các bit cuả từ mã thu đã dịch hết vào thanh
ghi dịch, nội dung của thanh ghi này sẽ xác định syndrome s. Biết được s ta có
thể xác định được mẫu lỗi và đưa ra được quyết định sửa như đã xét ở phần trước. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Hình 4.7. Bộ tính syndrrome
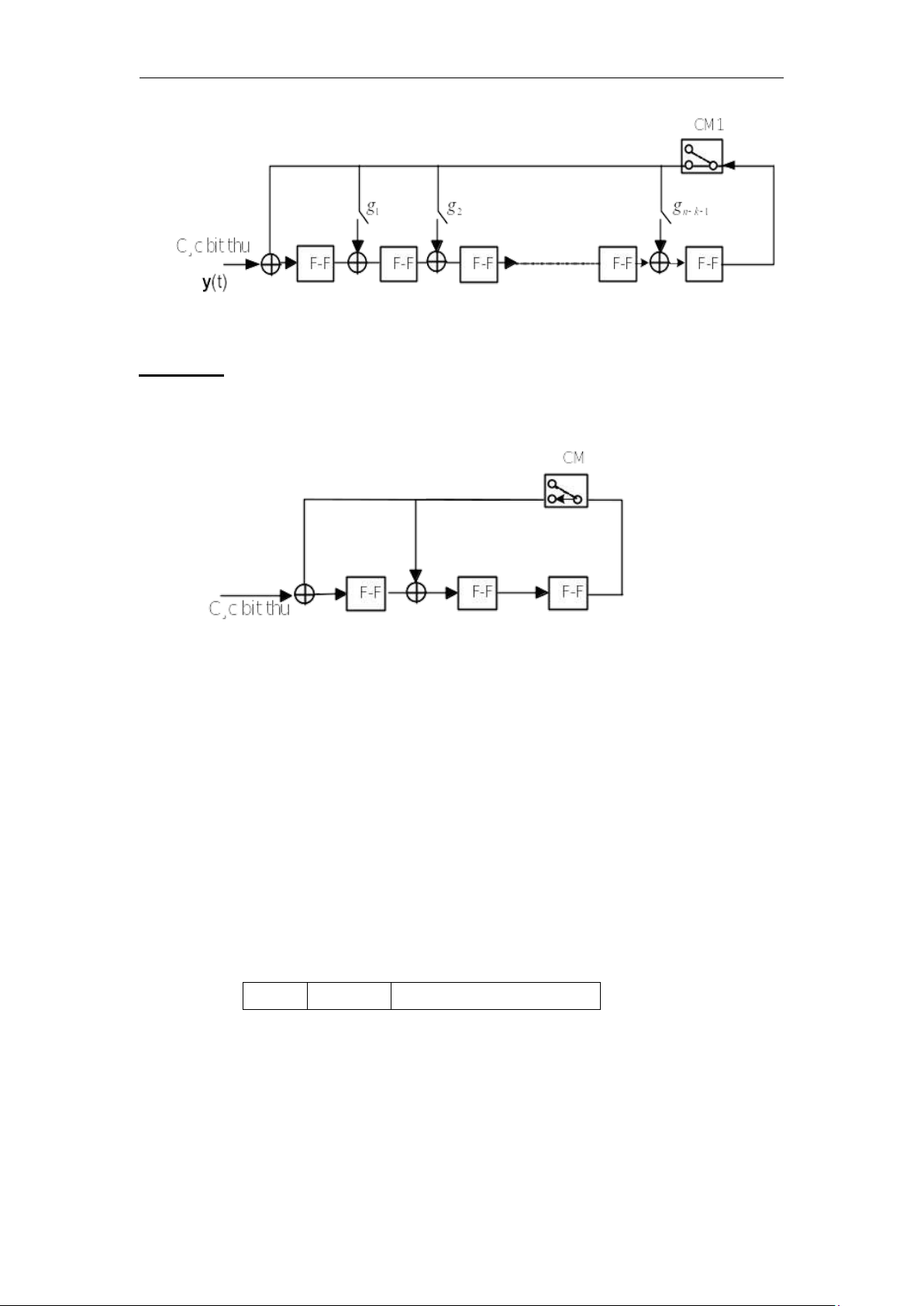
Thí dụ 4.4 Bộ tính syndrome cho mã Hamming vòng (7,4)
Đối với mã Hamming vòng được tạo bởi bộ tạo mã g(x) = 1+x+x3, sơ đồ
tính syndrome được cho ở hình 4.8.
Hình 4.8. Bộ tính syndrom cho mã vòng (7.4) với đa thức g(x)=1+x+x2
Gỉa sử từ mã phát là (0111001) và từ mã thu là (0110001); nghĩa là bit
giữa bị sai. Nội dung thanh ghi dịch của bộ tính syndrome trong trường hợp này được cho ở bảng 4.4.
Bảng 4.4. Nội dung ở bộ tính syndrome ở hình 4.8
khi từ mã thu (0110001)
Dịch Bit vào Nội dung thanh ghi lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng 000 (trạng thái đầu) 1 1 100 2 0 010 3 0 001 4 0 110 5 1 111 6 1 001 7 0 110
Sau bẩy lần dịch syndrome được xác định bằng 110. Vì syndrome khác không từ
mã nhận được bị mắc lỗi. Từ bảng 4.4 ta đựơc mẫu lỗi tương ứng là 0001000,
nghĩa là bit giữa của từ mã bị lỗi. 4.4.3. Mã LDPC
LPDC (Low Density Parity Check: kiểm tra chẵn lẻ mật độ thấp) là một
kỹ thuật mã khối tuyến tính mới cho phép nhận được tốc độ số liêu cực đại gần
với giới hạn của định lý Shannon hơn các mã hiện nay.
Thuật ngữ “mật độ thấp” để biểu thị là có ít phần tử “một” trong các phần
tử của ma trận kiểm tra chẵn lẻ.
LDPC hoạt động trên cơ sở ma trận kiểm tra chẵn lẻ H. Ma trận kiểm tra
chẵn lẻ H của bộ tạo mã LDPC (n,k) với tỷ lệ mã r=k/n có kích thước m n,
trong đó m=n-k. Chẳng hạn ma trận kiểm tra chẵn lẻ của LDPC (10,5) với tỷ lệ
mã r=5/10 có thể có dạng sau: (4.37)
trong đó các cột từ 1 đến 5 thể hiện bản tin, các cột từ 5 đến 10 thể hiện các bit chẵn lẻ.
Bộ mã hóa LDPC được gọi là chính quy nếu số số một trong các cột và
các hàng không đổi và tồn tại quan hệ sau đây giữa số số một trong một hàng
(wr) với số số một trong một cột (wc) như sau: wr=wc(n/m). Trái lại nó được gọi là không chính quy.
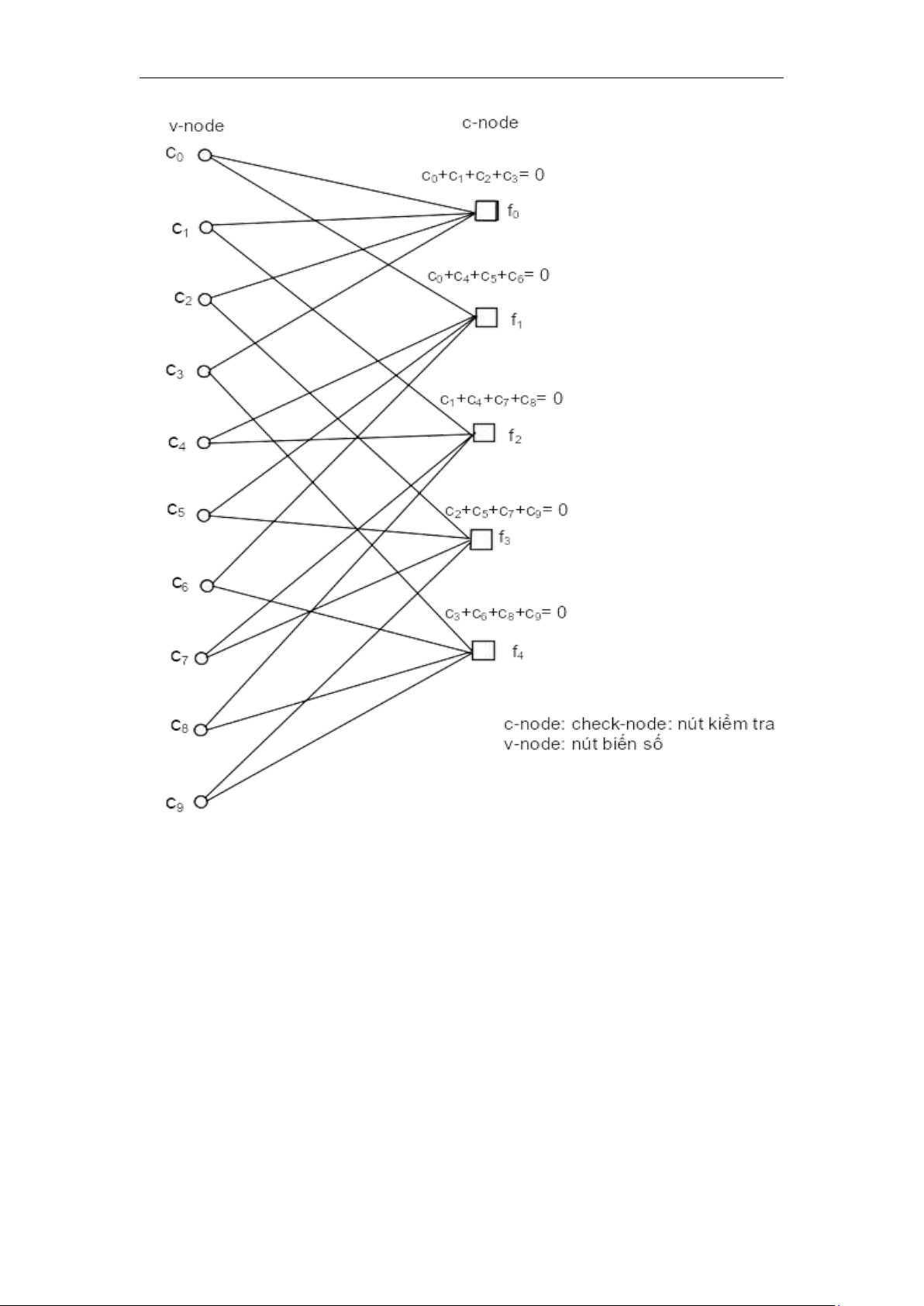
Ma trận chẵn lẻ H có thể được mô tả bằng biểu đồ Tanner mô tả như trên hình 4.9. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Hình 4.9. Biểu đồ Tanner cho mã thí dụ
Xem xét biểu đồ trên hình 4.9 ta thấy rằng các nút v (c0, c1, c2, và c3) được
nối đến các nút c f0 vì tại hàng không của ma trận H các phần từ hi j sau đây khác
không: h00= h01= h02= h03=1. Tương tự đối với các nút c f1, f2, f3 còn lại các phần
tử khác không của các hàng 1,2,3 và 4 của H cũng sẽ được nối đến chúng.
Lưu ý rằng theo phương trình kiểm ta chẵn lẻ (4.13) ta có: HcT=0. Vì thế các giá
trị bit nối đến cùng một nút kiểm tra phải có tổng bằng không. Trong đó c là ma
trận từ mã. Ta cũng có thể đi theo các cột để cấu trúc biểu đồ Tanner. Chẳng hạn,
ta thấy nút v c0 được nối đến các nút c f0 và f1 vì rằng các cột thứ không của H có h00=h10=1.
Giải mã LDCP là một quán trình lặp, trong đó mỗi vòng như sau: Bước
1. ci của các nút v gửi các bit bản tin đến fj của các nút c. Trong bước này ci chỉ có các bit thu yj. lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
Bước 2. fj của các nút c quyết định trả lời cho các nút v nối đến nó. fi coi rằng tất
cả các bản tin này đều đúng trừ bản tin thứ i và tính toán phúc đáp cho c i. Tại
đây, LDCP có thể nhận thấy rằng các bit thu là đúng và kết thúc giải mã nếu tất
cả các phương trình đã được thực hiện
Bước 3. các nút v nhận được các trả lời nói trên từ các nút c và sử dụng thông
tin này để xác định rằng bit thu gốc là bit đúng Bước 4. Trở về bước 2.
Dưới đây ta xét thí dụ về bộ giải mã quyết định cứng cho mã (8,4) LDPC
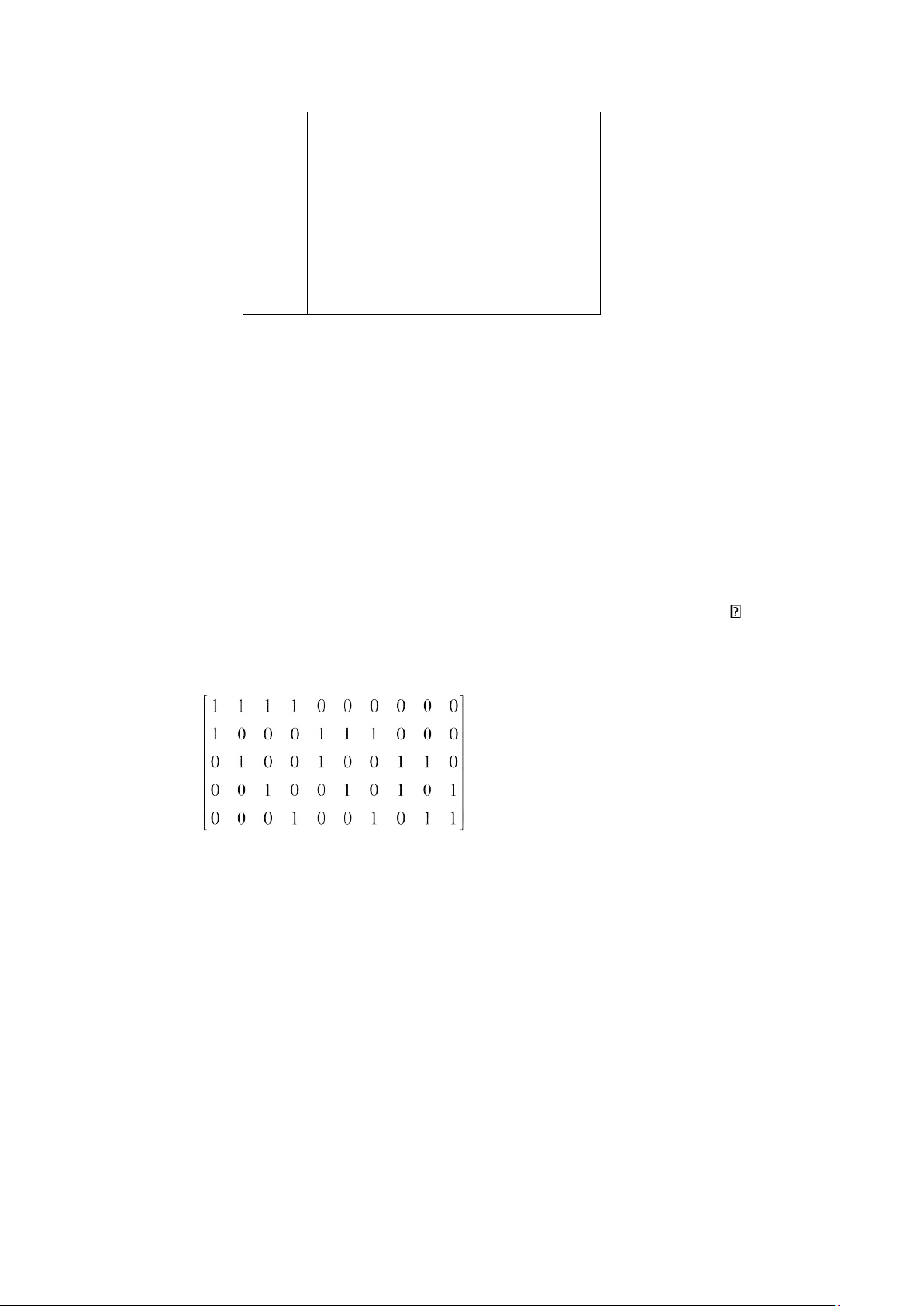
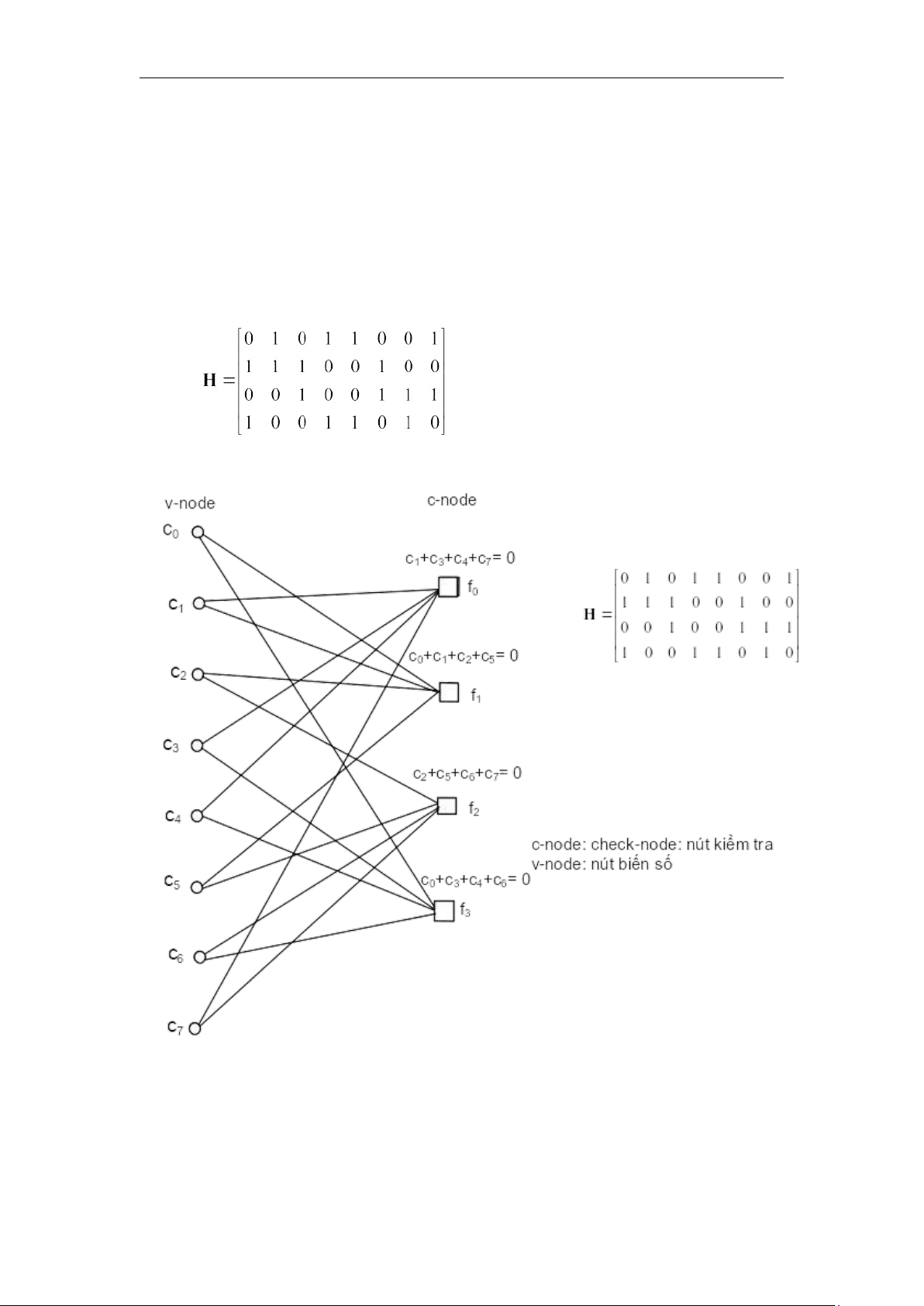
được thể hiện bởi ma trận kiểm tra chẵn lẻ H sau đây: (4.38)
Biểu đồ lưới cho ma trận H trên được thể hiện trên hình 4.10.
Hình 4.10. Biểu đồ cho bộ mã hóa có ma trận kiểm tra theo phương trình 4.38
Giả thiết từ mã được phát là c=[10010101]T. Giả thiết từ mã thu
y=[11010101]T như vậy lỗi tại bit c2. Giải thuật giải mã như sau: lOMoAR cPSD| 58737056 TS. Nguyễn Phạm Anh Dũng
1. Trong bước 1, tất cả các nút bản tin gửi đến nút kiểm tra được nối
vớichúng. Trong trường hợp này bản tin là bit mà chúng tin rằng đúng đối
với chúng. Chẳng hạn nút bản tin c1 nhận được 1 (y1=1), vì thế nó gửi một
bản tin chứa 1 đến các nút kiểm tra f0và f1. Bảng 4.5 minh họa bước này.
2. Trong bước 2, từng nút kiểm tra tính toán trả lời cho các nút bản tinbằng
cách sử dụng các bản tin mà chúng nhận được trong bước 1. Bản tin trả
lời trong trường hợp này là giá trị (0 hay 1) mà nút kiểm tra tin rằng nút
bản tin có được dựa trên bản tin của cac nút bản tin khác được nối đến nó.
Trả lời này được tính toán bằng cách sử dụng các phương trình kiểm tra
chẵn lẻ để buộc tất cả các nút bản tin nối đến nút kiểm tra cộng mod 2
phải bằng không. Chẳng hạn để tính trả lời gửi đi từ nút kiêm tra f0 đến
nút bản tin c1, ta giải phương trinh chẵn lẻ sau:
c1+c3+c4+c7=c1+1+0+1=0 c1=0. Tại điểm này, nếu tất cả các phương trình
tại các nút kiểm tra đều thoả mãn, nghĩa là các giá trị mà các nút kiểm tra
trùng với giá trị mà chúng thu được, thì giải thuật kết thúc. Trái lại chuyển đến bước 3.
3. Trong bước 3, các nút bản tin sử dụng các bản tin mà chúng nhận đượctừ
các nút kiểm tra để quyết định bit tại vị trí của chúng là 0 hay 1 theo quy
tắc đa số. Sau đó các nút gửi quyết định cứng này đến các nút được nối
với chúng. Bảng 4.6 minh họa bước này. Đê làm rõ, ta xét nút bản tin c1.
Nó nhận hai số 0 từ các nút kiểm trâ f1 và f2. Đồng thời nó đã có y1=1, nó
quyết định giá trị đúng là 0. Khi này nó gửi ngược thông tin này trở về
các nút kiểm tra f0 và f1
4. Lặp lại bước 2 hay thực hiện một số lần lặp.
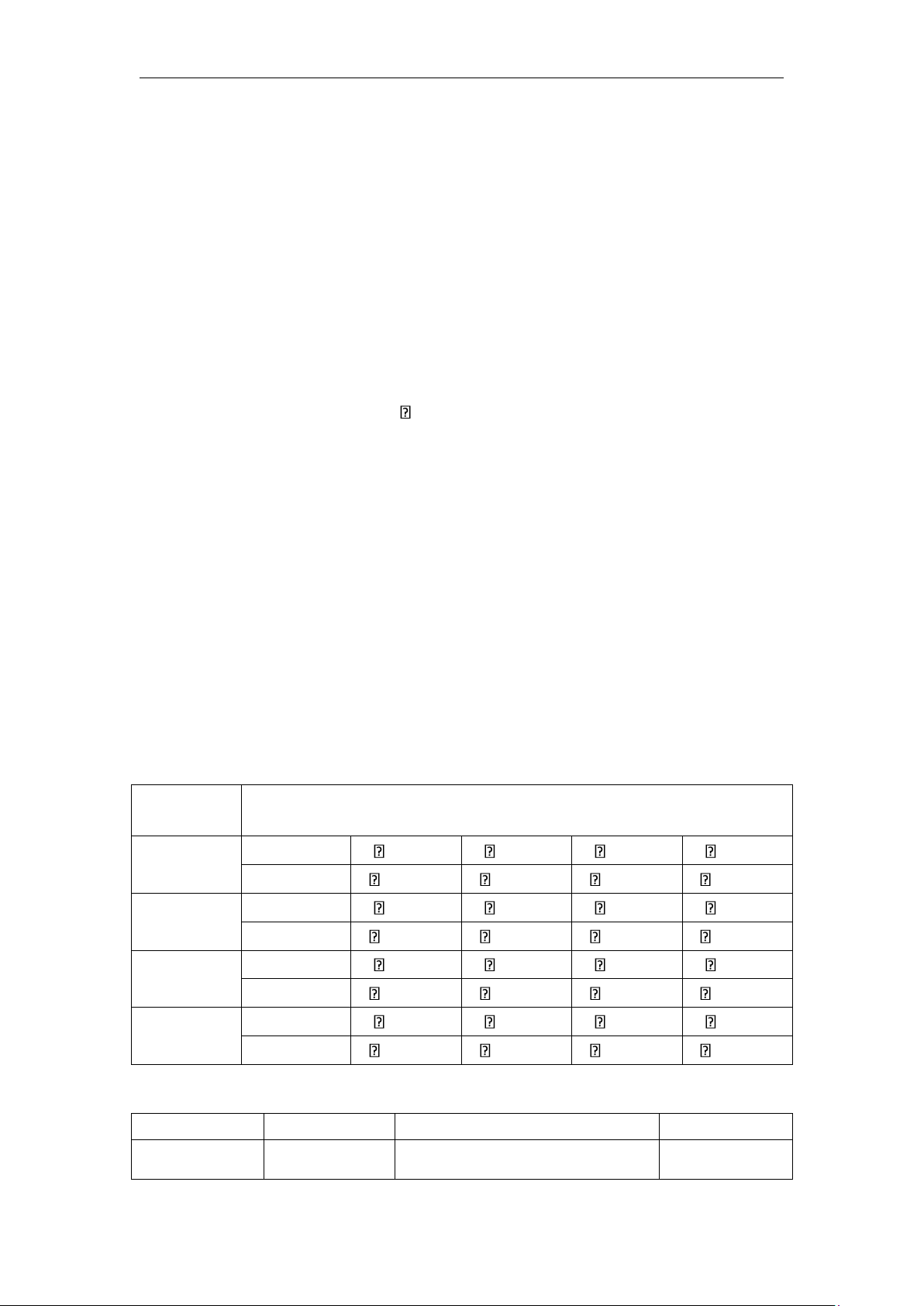
Bảng 4.5 Hoạt động cuả các nút kiểm tra đối với bô giải mã quyết định cứng cho mã trên hình 2 Các nút Các hoạt động kiểm tra f0 Thu c1 1 c3 1 c4 0 c7 1 Phát 0 c1 0 c3 1 c4 0 c7 f1 Thu c0 1 c1 1 c2 0 c5 1 Phát 0 c0 0 c1 1 c2 0 c5 f2 Thu c2 0 c5 1 c6 0 c7 1 Phát 0 c2 1 c5 0 c6 1 c7 f3 Thu c0 1 c3 1 c4 0 c6 0 Phát 1 c0 1 c3 0 c4 0 c6
Bảng 4.6 Quyết định của các nút bản tin đối với bộ giải mã quyết định cứng cho mã trên hình 2. Các nút bản yi
Các bản tin từ các nút kiểm Quyết định tin tra