Chương 4: Một số quy luật phân phối xác xuất thông dụng | Học viện phụ nữ Việt Namất thống kê

Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng Ch−¬ng IV
Mét sè quy luËt ph©n phèi x¸c suÊt th«ng dông
A C¸c quy luËt rêi r¹c
I. Ph©n phèi Bernoulli 1. §Þnh nghÜa
Hµm khèi l−îng x¸c suÊt x
P(X = x) = p (1− p)1−x (x=0, 1) x¸c lËp nªn
mét quy luËt ph©n phèi x¸c suÊt gäi lµ quy luËt Bernoulli (hoÆc ph©n phèi
“0-1”) víi tham sè lµ p ( 0 ≤ p ≤ 1). LuËt ph©n phèi nµy ®−îc ký hiÖu lµ quy luËt A(p) hoÆc B(1; p).
Ghi chó: NÕu trong mét phÐp thö ta chØ cã hai kÕt qu¶ lµ A vµ A víi
P(A) = p th× ®Ó chØ râ cã ®−îc A hay kh«ng ta cã thÓ dïng biÕn ngÉu nhiªn X
tu©n theo quy luËt A(p) ®Ó m« h×nh ho¸ phÐp thö nµy.
Cô thÓ ta cã thÓ ®Æt (X=1) lµ ®−îc A vµ do ®ã P(X =1) = P(A) = p Suy ra
P(X = 0) = P( A ) = 1- p (hoÆc ký hiÖu lµ q) lµ x¸c suÊt kh«ng ®−îc A.
ThÝ dô: Tõ mét chiÕc hép cã chøa M qu¶ cÇu tr¾ng vµ N − M qu¶ cÇu ®en,
ta lÊy ngÉu nhiªn ra 1 qu¶. Gäi X lµ “sè lÇn ®−îc qu¶ cÇu tr¾ng”. Khi ®ã X
cã b¶ng ph©n phèi x¸c suÊt nh− sau: X 0 1 p(x) N − M = N 1− p = q = p N M
VËy hµm khèi l−îng x¸c suÊt cña X cã d¹ng Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 154
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng x 1−x ⎧p q (x = 0,1) p(x) = ⎨ 0 ⎩ (x ≠ 0,1)
Do ®ã X tu©n theo quy luËt A(p) vµ ta ký hiÖu ®iÒu nµy lµ X~A(p) hoÆc X~B(1;p).
2. Kú väng to¸n vµ ph−¬ng sai
§Þnh lý: NÕu X ~B(1;p) th× E(X)=p vµ V(X)=pq Chøng minh a. Ta cã E(X) = x p(x ) = (0)q + (1)p = p ∑ i i i I ∈
b. NÕu dïng c«ng thøc ®Þnh nghÜa ®Ó tÝnh V(X) ta cã: V(X) = ∑[x − E(X)]2 p(x ) 2 2 = (0 − p) q + (1− p) p i i i I ∈ 2 2 = p q + q p = pq(p + q) = pq
NÕu dïng c«ng thøc tÝnh to¸n ®Ó tÝnh V(X) ta cã = −[ ]2 2 V(X) E(X ) E(X) = ∑x p(x ) −[E(X)]2 2 i i i∈I 2 2 2 2 = (
⎡ 0) q +(1) p ⎤ −p = p −p = p(1 −p) = p ⎣ ⎦ q
3. Hµm ®Æc tr−ng §Þnh lý: NÕu X~A(p) th× it g (t) = q + pe x Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 155
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng Chøng minh 1 Ta cã itx g (t) = E ⎡e ⎤ itx it 0 it1 = e p(x) = e q + e p ∑ x ⎣ ⎦ x= 0 it = q + pe
Ghi chó: NÕu dïng hµm ®Æc tr−ng ®Ó tÝnh E(X) vµ V(X) ta cã 1 1 ′ it
E(X) = α = g′(0) = ⎡q + pe ⎤ 1 ⎣ ⎦ t 0 i i = 1 1 it = ⎡ipe ⎤ = ip p ⎣ ⎦ = t= 0 i i 1 1 ′ 2 i E(X ) = α = g′ (0) = ⎡ipe t ⎤ 2 2 2 ⎣ ⎦ t=0 i i 1 1 2 it 2 = ⎡i pe ⎤ = i p p 2 ⎣ ⎦ = 2 t 0 i = i VËy = −[ ]2 2 2 V(X) E(X ) E(X) = p − p = p(1− p) = pq HoÆc lµ 1 ′ 1 ′ −itα it − 1 V(X) = μ = ⎡e (q + pe )⎤ = e ⎡ (q + pe )⎤ 2 2 ⎣ ⎦ itp it ⎣ ⎦ t= 0 i 2 t=0 i 1 ′ 1 ′ − itp it (1− p) = q ⎡ e + pe ⎤ = q ⎡ e− + pe ⎤ 2 ⎣ ⎦ itp itq ⎣ ⎦ t= 0 i 2 t 0 i = 1 1 −itp itq ′ = ⎡−ipqe + ipqe ⎤ = ⎡i p qe− + i q pe ⎤ 2 ⎣ ⎦ 2 2 itp 2 2 itq ⎣ ⎦ t= 0 i 2 t=0 i 1 2 2 2 2 = ⎡i p q + i q p⎤ 2 2 = p q + q p = pq(p + q) = pq 2 ⎣ ⎦ i
II. Ph©n phèi nhÞ thøc 1. §Þnh nghÜa Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 156
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng
Hµm khèi l−îng x¸c suÊt x x n x P(X x) C p q − = = (x = 0, n) x¸c lËp nªn n
mét quy luËt ph©n phèi x¸c suÊt gäi lµ quy luËt nhÞ thøc víi hai tham sè lµ n
vµ p vµ ®−îc ký hiÖu lµ B(n; p).
Së dÜ quy luËt nµy cã tªn gäi nh− ®· nªu v× c¸c x¸c suÊt trong quy luËt
nµy trïng víi c¸c sè h¹ng cña khai triÓn nhÞ thøc sau: n n x x (p+ q) = C p qn−x ∑ n x=0
Ghi chó: Hµm x¸c suÊt nªu trªn chÝnh lµ c«ng thøc Bernoulli. V× vËy biÕn
ngÉu nhiªn X tu©n theo quy luËt B(n; p) th−êng ®−îc dïng ®Ó chØ “sè lÇn
xuÊt hiÖn cña biÕn cè A trong mét l−îc ®å Bernoulli víi hai tham sè lµ n vµ p”.
ThÝ dô 1: NÒu tõ chiÕc hép chøa M qu¶ cÇu tr¾ng vµ N − M qu¶ cÇu ®en ®·
nªu ta lÇn l−ît lÊy ngÉu nhiªn ra n qu¶ theo ph−¬ng thøc cã tr¶ l¹i vµ gäi X lµ
“sè lÇn lÊy ®−îc qu¶ tr¾ng” th× X lµ mét biÕn ngÉu nhiªn tu©n theo quy luËt M (n;p) víi p = . N
ThÝ dô 2: Mét ng−êi b¾n 3 viªn ®¹n ®éc lËp víi nhau vµo mét chiÕc bia víi
x¸c suÊt tróng cña mçi viªn ®Òu lµ 0, 7. Gäi X lµ “Sè viªn tróng bia”.
H·y lËp b¶ng ph©n phèi x¸c suÊt cña X. Bµi gi¶i
NÕu ta coi mçi lÇn b¾n lµ mét phÐp thö th× ë ®©y ta cã 3 phÐp thö ®éc lËp.
Gäi A lµ biÕn cè “Viªn ®¹n tróng bia” th× theo gi¶ thiÕt P(A) ®Òu b»ng 0, 7 ë mçi lÇn b¾n.
VËy ta cã mét l−îc ®å Bernoulli víi n =3, p = 0, 7. Do ®ã X lµ mét biÕn
ngÉu nhiªn tu©n theo quy luËt nhÞ thøc B(3; 0,7). V× thÕ b¶ng ph©n phèi x¸c suÊt cña X nh− sau: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 157
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng X 0 1 2 3 0 0 C (0, 7) (0,3)3 1 1 2 C (0,7) (0,3) 2 2 C (0, 7) (0, 3)1 3 3 0 C (0,7) (0,3) 3 3 3 3 3 = 1 2 = 2 1 = 3 = p(x) (0,3) 3(0, 7) (0,3) 3(0, 7) (0,3) (0,7) = 0,027 = 0,189 = 0,441 = 0,343
Ta thÊy x¸c suÊt trong b¶ng ph©n phèi nµy trïng víi c¸c sè h¹ng cña
khai triÓn nhÞ thøc sau ®©y: 2 3 2 1 1 2
(0,3 + 0,7) = (0,3) + 3(0,3) (0,7) + 3(0,3) (0,7) + (0, 7)3
2. Hµm ®Æc tr−ng cña quy luËt nhÞ thøc vµ mét vµi quan hÖ suy ra tõ
hµm ®Æc tr−ng
a. Hµm ®Æc tr−ng
§Þnh lý: NÕu X~ B(n;p) th× g (t) = (q + pe ) n it x Chøng minh n n Ta cã itx itx itx x x n x g (t) = E ⎡e ⎤ = e P(X = x) = e C p q − x ⎣ ⎦ ∑ ∑ n x= 0 x= 0 n x it x n− x it = C (pe ) q = (pe q) ∑ n + n x= 0
ThÝ dô: NÕu gäi X lµ “sè lÇn ®−îc mÆt sÊp khi tung hai ®ång xu ®èi xøng vµ ⎛ 1 ⎞ ®ång chÊt” th× X~ B 2; ⎜ ⎟ ⎝ 2 ⎠ 2 ⎛ 1 1 ⎞
Do ®ã hµm ®Æc tr−ng cña X lµ it g (t) = + e x ⎜
⎟ . KÕt qu¶ nµy ta còng ®· ⎝ 2 2 ⎠
thu ®−îc trong thÝ dô ë cuèi ch−¬ng trªn. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 158
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng
b. Mèi quan hÖ gi÷a quy luËt A(p) vµ quy luËt B(n;p) §Þnh lý 1 n
NÕu X = ∑ X víi c¸c X ®éc lËp vµ cïng tu©n theo quy luËt A(p) th× X~ k k k=1 B(n; p). Chøng minh
V× c¸c biÕn ngÉu nhiªn X lµ c¸c biÕn ngÉu nhiªn i.i.d víi ph©n phèi k
chung lµ A(p) nªn theo tÝnh chÊt cña hµm ®Æc tr−ng ta cã n n it it n g (t) = g
(t) = ∏ g (t) = ∏ (q+ pe ) = (q + pe ) n x ⎛ ⎞ x k ⎜ X ⎟ ∑ k k=1 k=1 ⎜ ⎟ ⎝ k=1 ⎠
§©y lµ hµm ®Æc tr−ng cña quy luËt B(n; p). V× cã sù t−¬ng øng 1-1 gi÷a
hµm ®Æc tr−ng vµ hµm ph©n phèi nªn ta suy ra X~ B(n; p).
c. Mèi quan hÖ gi÷a quy luËt B( n ;p ) víi k=1, 2, ..., r k §Þnh lý 2 r NÕu X =
X víi c¸c X ®éc lËp vµ tu©n theo B(n ;p ) th× X sÏ tu©n ∑ k k k k 1 = r theo B(n;p) víi n = ∑n k k 1 = Chøng minh
Do c¸c X lµ nh÷ng biÕn ngÉu nhiªn i.i.d nªn t−¬ng tù nh− ë chøng minh k trªn, ta cã: r r r n ∑ k g (t) = g (t) ∏ it n it it n k = (q + pe ) ∏ k 1 = (q + pe ) = = (q + pe ) x xk k=1 k 1 = r víi n = ∑n k k=1 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 159
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng
BiÓu thøc thu ®−îc lµ hµm ®Æc tr−ng cña quy luËt (n;p) nªn ta cã kÕt luËn cña ®Þnh lý.
3. C¸c tham sè ®Æc tr−ng cña quy luËt nhÞ thøc
a. Kú väng to¸n vµ ph−¬ng sai
§Þnh lý: NÕu biÕn ngÉu nhiªn X tu©n theo quy luËt B(n; p) th×: E(X) = np V(X) = npq Chøng minh:
Theo ®Þnh lý 1 võa nªu trªn ta thÊy nÕu X~ B(n; p) th× ta cã thÓ ph©n tÝch n
X = ∑ X víi c¸c X ®éc lËp vµ còng tu©n theo mét quy luËt B(1; p) k k k=1
trong ®ã E(X ) = p vµ V(X ) = pq . k k V× vËy n n n ⎛ ⎞ E(X) = E X = E(X ) = p np ⎜ ∑ ∑ ∑ = k ⎟ k ⎝ ⎠ k=1 k=1 k=1 n n n ⎛ ⎞ V(X) = V X = V(X ) = pq = npq ⎜∑ ∑ ∑ k ⎟ k ⎝ k 1= ⎠ k 1= k 1 = HÖ qu¶
NÕu ký hiÖu f lµ tÇn suÊt xuÊt hiÖn biÕn cè A cÇn xÐt trong mét l−îc ®å X
Bernoulli víi hai tham sè lµ n vµ p th× f = trong ®ã X~ B(n;p). n Tõ ®ã ta cã: ⎛ X⎞ 1 1 E(f ) = E = E(x) = np = p ⎜ ⎟ ⎝ n ⎠ n n ⎛ X ⎞ 1 1 pq V(f ) = V = V(X) = npq = ⎜ ⎟ 2 2 ⎝ n ⎠ n n n Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 160
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng n 1
Ghi chó: NÕu thay X bëi ∑ n X th× f cã d¹ng f = X ∑ k k k 1 = n k 1 =
VËy f còng cã thÓ coi lµ biÕn ngÉu nhiªn trung b×nh (ký hiÖu lµ X ) cña n
biÕn ngÉu nhiªn thµnh phµn X (k = 1, n) víi c¸c ®Æc ®iÓm lµ c¸c X ®éc lËp k k
vµ cïng tu©n theo mét quy luËt A(p).
b. Mèt cña quy luËt nhÞ thøc §Þnh lý:
§èi víi quy luËt B(n;p) th× mèt M lµ mét sè nguyªn d−¬ng tho¶ m·n 0
bÊt ®¼ng thøc kÐp sau: np − q ≤ M ≤ np + p o Chøng minh
Ta ký hiÖu P(X = x) = P (x) (x = 0, n) vµ xÐt diÔn biÕn cña d·y gåm n
(n +1) x¸c suÊt nµy theo x khi n kh«ng ®æi Víi 0 ≤ x ≤ n −1 x+1 x+1 n− ( x+1) P (x + 1) C p q (n − x)p ta cã n n = = (1) x x n x − P (x) C p q (x 1 + )q n n
Khi x t¨ng tõ 0 tíi n-1 th× tö sè gi¶m cßn mÉu sè sÏ t¨ng nªn (1) lµ mét d·y gi¶m. P (1) P (2) P (n) n n n > > ...... > (2) P (0) P (1) P (n −1) n n n
Gi¸ trÞ cña tû sè thø nhÊt lµ P (1) np n = (3) P (0) q n
Gi¸ trÞ cña tû sè cuèi cïng lµ P (n) p n = (4) P (n − 1) nq n Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 161
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng Tõ ®ã ta thÊy: α)NÕu np ≤ q P (1) np Khi Êy n = ≤1 P (0) q n P (1) P (2) P (n) D·y (2) cho ta n n n 1 ≥ > > ..... > P (0) P (1) P (n −1) n n n
Suy ra P (0) ≥ P (1) > P (2) > ..... > P (n) n n n n
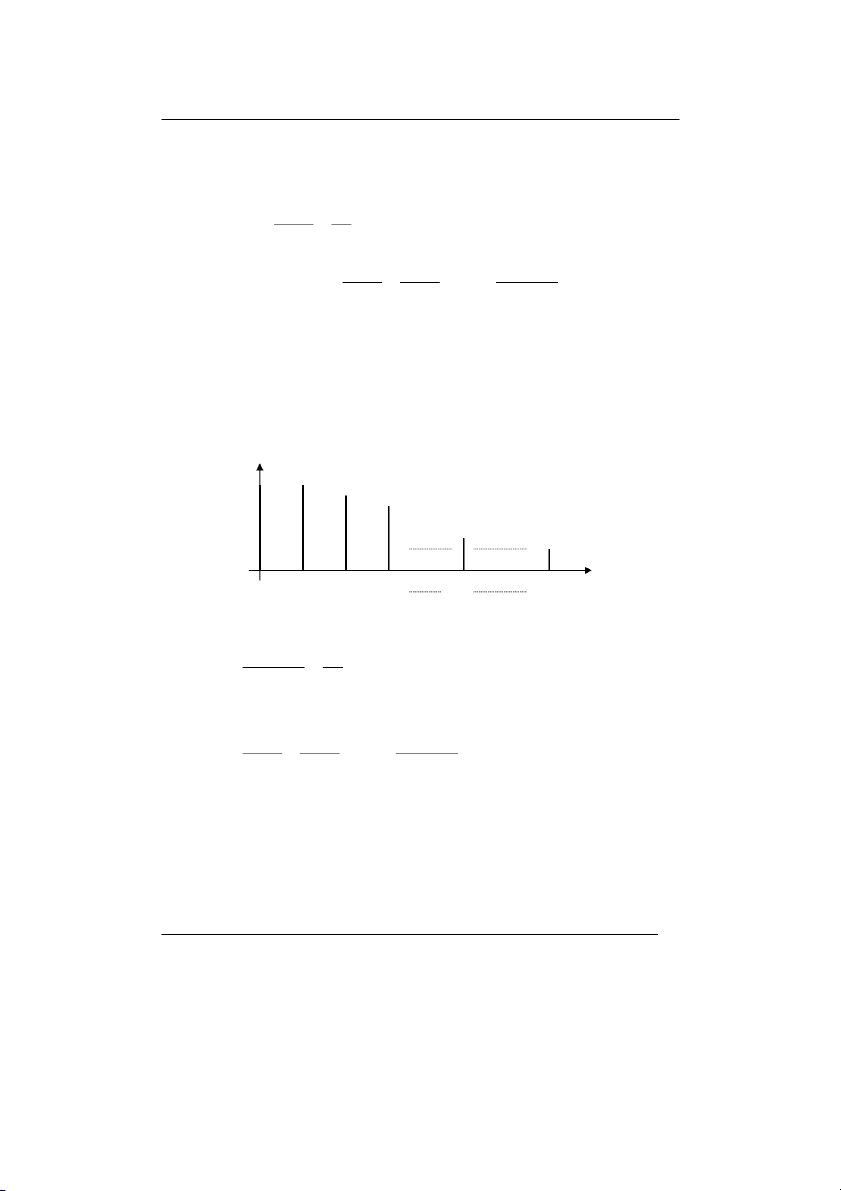
VËy trong tr−êng hîp nµy {P (x) lµ mét d·y ®¬n ®iÖu gi¶m vµ ta cã n } M = 0 vµ M = . 1 0 0 §å thÞ Pn(x) 0 1 2 3 x n ) β NÕu nq ≤ p P (n) p Khi Êy n = ≥1 P (n −1) nq n D·y (2) cho ta P (1) P (2) P (n) n n n > > .....> ≥ 1 P (0) P (1) P (n − 1) n n n Suy ra
P (0) < P (1) < P (2) < ..... < P (n −1) ≤ P (n) n n n n n
VËy trong tr−êng hîp nµy { P (x) lµ mét d·y ®¬n ®iÖu t¨ng vµ ta cã n } M = n −1vµ M = n 0 0 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 162
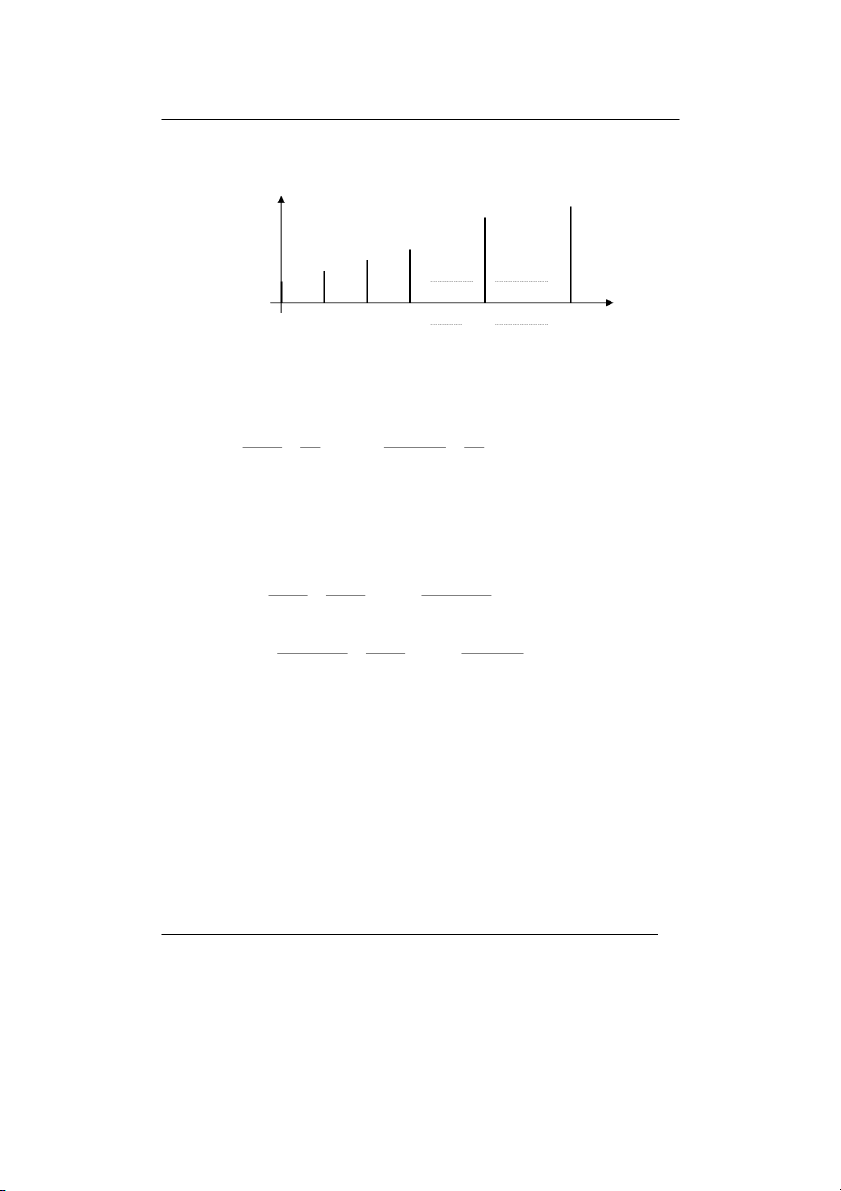
Chương4.Mộtsốquyluậtphânphốixácsuấtthôngdụng §å thÞ Pn(x) 0 1 2 3 n-1 n x
γ) NÕu np > q vµ nq > p Khi Êy P (1) np P (n) p n = >1 vµ n = < 1 P (0) q P (n 1 − ) nq n n
Nh− vËy nÕu x t¨ng th× d·y (2) d¸ng ®iÖu chung lµ gi¶m, nh−ng cã mét sè tû
sè ®Çu tiªn lín h¬n 1 vµ c¸c tû sè sau nhá h¬n 1.
Ta gäi x lµ gi¸ trÞ ph©n chia ranh giíi cho hai lo¹i tû sè nµy, cô thÓ ta cã: 0 P (1) P (2) P (x ) n n n 0 > > ..... > > 1 (5) P (0) P (1) P (x −1) n n n 0 P (x + 1) P (2) P (n) n 0 n n 1 ≥ > > ..... > (6) P (x ) P (1) P (n −1) n 0 n n Tõ (5) ta suy ra
P (0) < P (1) < P (2) < ..... < P (x −1) ≤ P (x ) (7) n n n n 0 n 0 Tõ (6) ta suy ra
P (x ) ≥ P (x +1) > P (x + 2) > ..... > P (n −1) > P (n) (8) n 0 n 0 n 0 n n
VËy xÐt t¹i ®iÓm ranh giíi x ta sÏ cã 0
P (x −1) < P (x ) ≤ P (x +1) n 0 n 0 n 0 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 163