Chương1. Biến ngẫu nhiên và quy luật phân phối xác suất | Học viện phụ nữ Việt Namất thống kê

Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất Ch−¬ng II
BiÕn ngÉu nhiªn vμ quy luËt ph©n phèi x¸c suÊt
A. BiÕn ngÉu nhiªn mét chiÒu
I. §Þnh nghÜa vμ c¸c phÐp to¸n c¬ b¶n 1. §Þnh nghÜa
Cho (Ω, A , P). NÕu X lµ mét ¸nh x¹ ®o ®−îc tõ Ω vµo  th× X ®−îc gäi lµ mét biÕn ngÉu nhiªn
(hoÆc mét ®¹i l−îng ngÉu nhiªn).
Nãi c¸ch kh¸c: X lµ mét hµm sè thùc, h÷u h¹n, x¸c ®Þnh trªn Ω sao cho víi mçi x ∈  th×
{ω ∈ Ω : X (ω ) < } x ∈A . Ghi chó:
§Ó cho gän ta sÏ ký hiÖu (X ∈ S) thay cho {ω ∈ Ω : X (ω ) ∈ } S ch¼ng
h¹n (X ≤ x) = {ω ∈ Ω : X (ω ) ≤ } x . ThÝ dô:
Tung 2 ®ång xu ®èi xøng ®ång chÊt. Gäi X lµ “sè lÇn xuÊt hiÖn mÆt sÊp”. H·y chøng tá X lµ mét biÕn ngÉu nhiªn Bµi gi¶i
a. Ta x©y dùng kh«ng gian x¸c suÊt (Ω, A , P) øng víi phÐp thö nµy. ⎧SS , SN , NS , NN ⎫ Ω = ⎨ ⎬ ⎩ω ,ω , ω , ω 1 2 3 4 ⎭ ⎧∅
⎪⎪⎪⎪⎪{ω , ω , ω , ω 1 } { 2 } { 3 } { 4 } ⎪⎪⎪ A =G(Ω) = ⎨{ω ω , ω ω , ω ω , ω ω , ω ω , ω ω 1 2 } { 1 3 } { 1 4 } { 2 3} { 2 4} { 3 4}
⎪⎪⎪.......... .......... .......... ........... .............. ⎪⎪⎪Ω ⎪⎪⎩ Nh 0 1 2 3 4 4 4
− ta ®· biÕt σ c¸c biÕn cè nµy bao gåm: C + C + C + C + C = 1 ( + ) 1 = 2 = 16 phÇn tö. 4 4 4 4 4
V× tÝnh chÊt ®Òu ®Æn vµ ®èi xøng cña hai ®ång xu nªn ta cã thÓ ®Æt c¸c x¸c suÊt nh− sau: 1
P(ω ) = P(ω ) = P(ω ) = P(ω ) = . 1 2 3 4 4 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 50
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất b. Ta x¸c ®Þnh X
V× X: Ω   nªn miÒn gi¸ trÞ cña nã lµ Im(X) = {0, 1, 2}. PhÐp ¸nh x¹ nµy cã thÓ ®−îc minh häa nh− sau: Ω ω • ω • ω • ω • X 1 2 3 4 R 0 1 2 Tõ ®ã ta thÊy: ⎧∅ ⎪ khi x ≤ 0 ⎪{⎪⎪⎪ω khi 04 } ( ⎪
X < x) ={ω ∈Ω : X (ω ) < } x = ⎨ { ⎪ ω ,ω ,ω khi 1< x ≤ 2 ⎪ 2 3 4 } ⎪⎪Ω ⎪ khi x >2 ⎪⎩
Do tÊt c¶ c¸c tËp hîp viÕt ë vÕ ph¶i ®Òu lµ c¸c tËp thuéc A nªn theo ®Þnh nghÜa X lµ mét biÕn ngÉu nhiªn. NhËn xÐt:
V× X lµ mét ¸nh x¹ tõ Ω vµo R nªn dïng nã ta cã thÓ chuyÓn tõ kh«ng gian mÉu cò sang kh«ng gian
mÉu míi do ®ã cã thÓ chuyÓn c¸c biÕn cè mang néi dung vÒ chÊt thµnh c¸c biÕn cè mang néi dung vÒ
l−îng, cô thÓ lµ c¸c biÕn cè s¬ cÊp thµnh c¸c sè thùc. Ch¼ng h¹n ë kh«ng gian Ω th× biÕn cè {ω , ω } lµ 2 3
biÕn cè cã néi dung “chØ cã 1 lÇn xuÊt hiÖn mÆt sÊp” nh−ng khi chuyÓn sang kh«ng gian míi biÕn cè nµy
t−¬ng ®−¬ng víi biÕn cè “X nhËn gi¸ trÞ 1”.
Dùa trªn x¸c suÊt ®· x©y dùng trªn kh«ng gian cò, nÕu ta x©y dùng ®−îc ®é ®o x¸c suÊt cho kh«ng
gian míi nµy th× c¸c thao t¸c sau nµy sÏ ®¬n gi¶n h¬n vµ lóc ®ã ta cã thÓ trõu xuÊt khái kh«ng gian x¸c suÊt cò.
2. C¸c phÐp to¸n c¬ b¶n víi c¸c biÕn ngÉu nhiªn
a. PhÐp nh©n víi mét sè §Þnh nghÜa:
NÕu X lµ mét hµm sè thùc x¸c ®Þnh trªn Ω vµ C lµ mét h»ng sè thùc th× ta coi CX còng lµ mét hµm
sè thùc mµ víi mçi ω ∈ Ω th× CX sÏ lÊy gi¸ trÞ lµ C.X(ω) tøc lµ CX(ω) = C.X(ω). §Þnh lý:
NÕu X lµ mét biÕn ngÉu nhiªn th× CX còng lµ mét biÕn ngÉu nhiªn. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 51
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất Chøng minh ⎛ x ⎞
§Ó ®¬n gi¶n ta xÐt tr−êng hîp C > 0. Khi ®ã: (CX < x) = ⎜ X <
⎟ ∈ A. Do X lµ biÕn ngÉu nhiªn. ⎝ C ⎠ b. PhÐp céng §Þnh nghÜa:
NÕu X vµ Y lµ hai hµm thùc x¸c ®Þnh trªn Ω th× X + Y còng lµ hµm thùc x¸c ®Þnh trªn Ω sao cho: (X + Y)(ω) = X(ω) + Y(ω). §Þnh lý:
NÕu X vµ Y lµ hai biÕn ngÉu nhiªn th× X + Y còng lµ mét biÕn ngÉu nhiªn. Chøng minh Ta xÐt tËp A = [ ∪ (X < r) Y (
< x - r ]) trong ®ã r ch¹y trªn tËp hîp c¸c sè h÷u tû. Do X lµ mét biÕn ngÉu r
nhiªn nªn (X < r) ∈A, do Y lµ mét biÕn ngÉu nhiªn nªn (Y < x - r)∈A. Tõ ®ã [(X < r)(Y < x - r ] ) ∈A.
Do tËp hîp c¸c sè h÷u tû lµ ®Õm ®−îc nªn ta suy ra A ∈ A.
Ta sÏ chøng minh A = (X + Y < x) vµ tõ ®ã kÕt luËn ®−îc (X + Y) lµ mét biÕn ngÉu nhiªn do (X + Y < x) ∈ A .
α. Tr−íc hÕt ta cã A ⊂ (X + Y < x).
ThËt vËy, ta lÊy ω bÊt kú thuéc A khi ®ã, tån t¹i Ýt nhÊt mét r sao cho ω ∈ [(X < r) ( Y < x - r)] . Do
X vµ Y lµ hai biÕn ngÉu nhiªn ta sÏ cã X(ω) < r vµ Y (ω) < x - r, suy ra: X(ω) + Y (ω) < x. VËy ω ∈ (X + Y < x).
β. Ng−îc l¹i ta còng cã (X + Y < x) ⊂ A .
LÊy ω bÊt kú thuéc (X + Y < x). Khi ®ã (X + Y)(ω) < x, suy ra X(ω) < x - Y(ω).
V× X(ω) vµ x - Y(ω) lµ hai sè thùc nªn ta cã Ýt nhÊt mét sè h÷u tû r sao cho X (ω) < r < x - Y(ω), o o
khi ®ã X(ω) < r vµ Y(ω) < x - r . o o
VËy ω ∈ [(X < r )(Y < x – r )] nh−ng [(X < r )(Y< r – r )] ⊂ A nªn ω ∈ A. 0 0 0 0
c. PhÐp nh©n hai biÕn ngÉu nhiªn §Þnh nghÜa:
TÝch X.Y cña hai hµm sè thùc X vµ Y lµ mét hµm sè thùc sao cho víi mçi ω∈ Ω th× (XY)( ω) = X(ω).Y(ω). §Þnh lý 1:
NÕu X lµ mét biÕn ngÉu nhiªn th× X2 còng lµ mét biÕn ngÉu nhiªn. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 52
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất Chøng minh
NÕu x ≤ 0 th× (X2 < x) = ∅ ∈ A .
NÕu x > 0 th× (X2 < x) = (- x X < < x ) = (X <
x )(X > - x ) . Hai tËp hîp nµy ®Òu thuéc A do
X lµ biÕn ngÉu nhiªn nªn giao cña chóng còng thuéc A . . VËy X2 lµ mét biÕn ngÉu nhiªn. §Þnh lý 2:
NÕu X vµ Y lµ hai biÕn ngÉu nhiªn th× XY còng lµ mét biÕn ngÉu nhiªn. Chøng minh:
Do X vµ Y lµ hai biÕn ngÉu nhiªn nªn X + Y vµ X - Y lµ c¸c biÕn ngÉu nhiªn. (X + Y)2 vµ (X – Y)2 lµ c¸c biÕn ngÉu nhiªn. 1 VËy 2 2
⎡(X Y) (X Y) ⎤ + − − = X.Y ⎢⎣ ⎥ 4 ⎦
còng lµ mét biÕn ngÉu nhiªn.
d. PhÐp chia hai biÕn ngÉu nhiªn §Þnh nghÜa: Th X −¬ng
cña hai hµm thùc X vµ Y x¸c ®Þnh trªn Ω sao cho víi mçi ω ∈ Ω mà Y(ω) ≠ 0 Y th× : X X(ω ) (ω ) = . Y Y(ω ) X
§Þnh lý: NÕu X vµ Y lµ hai biÕn ngÉu nhiªn víi (Y = 0) = ∅ th×
còng lµ mét biÕn ngÉu nhiªn. Y Chøng minh Ta cã thÓ ph©n tÝch ⎛ X ⎞ ⎛ X X ⎜
< x⎟ = ⎜ < x ( ⎞ ⎛ ⎞ ⎟ Y < 0)∪⎜
< x⎟(Y > 0) ⎝ Y ⎠ ⎝ Y ⎠ ⎝ Y ⎠
= (X > xY )(Y < 0)∪(X < xY)(Y > 0).
Do X vµ Y lµ hai biÕn ngÉu nhiªn nªn c¸c tËp (X0) ®Òu thuéc A suy ra
tËp hîp võa viÕt còng thuéc A.
VËy X lµ mét biÕn ngÉu nhiªn. Y
e. Hµm cña biÕn ngÉu nhiªn Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 53
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất
Ta thõa nhËn mÖnh ®Ò sau: “NÕu X lµ mét biÕn ngÉu nhiªn trªn (Ω, A, ,P) vµ G G lµ mét hµm ®o ®−îc
trªn R th× G0 X còng lµ biÕn ngÉu nhiªn trªn (Ω, A, ,P)”.
II. Hμm ph©n phèi x¸c suÊt 1. §Þnh nghÜa
Hµm ph©n phèi x¸c suÊt cña biÕn ngÉu nhiªn X lµ
F (x) = P{ω: X(ω) < x} {x ∈  }. X
Nh− vËy hµm ph©n bè x¸c suÊt lµ sù thu hÑp cña ®é ®o x¸c suÊt P lªn líp c¸c kho¶ng (- ∞, x) cña ®−êng th¼ng thùc  .
Ghi chó: §Ó cho gän ta sÏ ký hiÖu F(x) = P(X < x) ThÝ dô:
Gäi X lµ "sè lÇn xuÊt hiÖn mÆt sÊp khi tung hai ®ång xu ®èi xøng ®ång chÊt". H·y x©y dùng hµm
ph©n phèi x¸c suÊt cña X. Bµi gi¶i
Ta ®· thÊy X lµ mét biÕn ngÉu nhiªn v× ⎧∅ ⎪ v i í x ≤ 0 ⎪{⎪⎪ω v ií 0 ⎪ ≤ 4} ( ⎪ X < x) =⎨ { ⎪ ω ,ω ,ω v i í 1 ⎪ 2 2 3 4} ⎪⎪Ω ⎪ ⎪⎩
lµ c¸c tËp ®Òu thuéc A. Tõ ®ã P ⎧⎪ ( ) ∅ = 0 víi x ≤ 0 ⎪⎪⎪⎪P⎪{ 1 ω = víi 0 < x ≤1 4 } ⎪⎪
F x = P (X < x) 4 ( ) = ⎨ . ⎪P ⎪⎪ { 3 ω , ω , ω = v i í 1 < x ≤ 2 2 3 4 } ⎪⎪ 4 ⎪P ⎪ (Ω) ⎪ =1 víi x > 2 ⎩
Tãm l¹i nÕu trõu xuÊt khái kh«ng gian x¸c suÊt cò ta cã thÓ viÕt biÓu thøc cña F(x) nh− sau: ⎧ 0 ví i x ≤ 0 ⎪ ⎪1 ví i 0 < x ≤ 1 F(x) = P (X < x ) ⎪ = 4 ⎨ . ⎪3 ví i 1 < x ≤ 2 ⎪4 ⎪ ⎩ 1 ví i x > 2 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 54
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất 2. C¸c tÝnh chÊt
TÝnh chÊt 1: 0 ≤ F(x) ≤ 1 víi mäi x. Chøng minh
Do F(x) = P{ω ∈ Ω: X(ω) < x}, mµ 0 ≤ P(A) ≤ 1 víi mäi A ∈ A . Nªn ta suy ra tÝnh chÊt ph¶i chøng minh.
TÝnh chÊt 2: F(x) lµ hµm sè kh«ng gi¶m, cã nghÜa lµ víi mäi x > x ) ) 2 1 th× F(x2 ≥ F(x1 Chøng minh
Do x > x nªn (X < x ) = (X < x )∪(x ≤ X ≤ x ). V× thÕ P(X < x ) = P(X < x ) + P(x ≤ X ≤ x ) 2 1 2 1 1 2 2 1 1 2
(do (X < x )∩(x ≤ X < x ) =∅ ) suy ra F(x ) = F(x ) + P(x ≤ X < x ). 1 1 2 2 1 1 2 Mµ P(x ≤ X < x ) ) 1 2 ≥ 0 nªn F(x2 ≥ F(x1). HÖ qu¶:
Tõ chøng minh trªn ta suy ra P(x ≤ X < x ) = F(x ) 1 2 2 - F(x1). TÝnh chÊt 3:
lim F(x) = 0 vµ lim F(x) = 1. x→ -∞ x → +∞ Chøng minh a. limF(x) = 0 x - → ∞
Do tÝnh chÊt 2 vµ 1 ta thÊy P(x) lµ hµm kh«ng gi¶m vµ bÞ chÆn d−íi nªn nã cã giíi h¹n.
⎧⎪x > x ...> x ...⎫⎪ LÊy d·y {x } (n = , 1 ∞ ) víi 1 2 n ⎪ ⎪ n ⎨ ⎬, ⎪ lim = −∞ ⎪ ⎪⎩ ⎪ x→−∞ ⎭
tøc lµ mét d·y gi¶m tïy ý vµ ®Æt A = {X < x } khi ®ã ta cã: n n A
⎧⎪ ⊃ A ⊃ ... ... ⊃ A ⊃...... 1 2 n ⎪⎪ ∞ ⎨ . l
⎪ im A = ∩ A = ∅ n n ⎪n→∞ ⎪⎪ n ⎩ =1
VËy P( lim A ) = P(∅ ) = 0. n n→ ∞
MÆt kh¸c theo tÝnh chÊt liªn tôc cña ®é ®o x¸c suÊt ta cã : P( lim A ) = lim P(A ) . Do ®ã n n n→ ∞ n→ ∞ lim P(A )= 0 P A = P X < x =
F x . VËy lim F (x ) = 0 . n . Nh−ng: lim ( ) lim ( ) lim ( ) n n →∞ n n n n→∞ n→∞ n→∞ n→∞ Do {x
lµ mét d·y gi¶m lÊy tïy ý nªn ta cã: lim F(x ) = 0 n }(n = , 1 ∞ ) n . n→∞ b. Chøng minh: lim F(x) = 1 n →∞ Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 55
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất
T−¬ng tù lÊy mét d·y t¨ng tïy ý {x sao cho: n }(n = , 1 ∞ ) x
⎧⎪ < x < ...< x < ...⎫⎪ 1 2 n ⎪ ⎪ ⎨ ⎬ . ⎪ lim x = +∞ ⎪ n n ⎪ → ∞ ⎪ ⎪ ⎩ ⎭
Ta ®Æt B = {X < x } khi ®ã: n n
⎧B ⊂ B ⊂ ... ⊂ B ⊂ ... ⎪ 1 2 n ⎨ n . ⎪lim B = B = n ∪ Ω ⎩n →∞ n n =1
Theo tÝnh chÊt liªn tôc cña ®é ®o x¸c suÊt P ta cã: lim P(B ) = P(lim B ) = P(Ω ) = 1 . Nh−ng n n n →∞ n →∞
lim P(B ) = lim P(X < x )= lim F(x ) . n n n n →∞ n→∞ n →∞ VËy lim F(x) = 1. n→∞ Do {x }
lµ mét d·y t¨ng lÊy tïy ý nªn ta kÕt luËn lim F(x) = 1. n (n = , 1 ∞ ) n→+∞ Ghi chó
Hai giíi h¹n nµy sau nµy ta sÏ ký hiÖu gän lµ F(- ∞) = 0 vµ F(+∞) = 1.
TÝnh chÊt 4: Hµm ph©n phèi F(x) liªn tôc bªn tr¸i, cã nghÜa lµ t¹i mäi ®iÓm x ta ®Òu cã 0
lim F (x) = F(x ) . − 0 x x → 0 Chøng minh LÊy mét d·y {x
tïy ý héi tô vÒ x vÒ phÝa bªn tr¸i, tøc lµ n }(n = , 1 ∞ ) 0
⎪⎧x < x < ... < x < ... 1 2 n ⎪⎫ ⎨ ⎬ . ⎪lim x = x n o ⎪ ⎩n →∞ ⎭
⎧C ⊂ C ⊂ ... ⊂ C ⊂ ... ⎧C = X x ⎪ 1 2 n n { < n} Ta ®Æt ⎨ . Khi ®ã ⎨ n ⎩C = {X < x lim C = C = o } ⎪ n ∪ C ⎩n→∞ n n=1 VËy lim P(C = = n ) P( lim C ) P(C) . n n →∞ n → ∞
Nh−ng P(C) = P( X < x ) = F (x ) cßn lim P(C ) = lim P(X < x ) = lim F(x ) . 0 0 n n n n →∞ n→∞ n →∞ VËy lim F(x ) = F(x ). n 0 n →∞ Do {x
lµ mét d·y t¨ng tïy ý héi tô vÒ phÝa tr¸i cña x nªn ta suy ra: F x = F x . n }(n = , 1 ∞ ) 0 lim ( ) ( ) − 0 x→ 0 x Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 56
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất 1 1
Ghi chó: Theo hÖ qu¶ cña tÝnh chÊt 2 ta cã P(x ≤ X < x + ) = F(x + )- F(x). n n 1 ⎡ 1 ⎤
VËy lim P(x ≤ X < x + ) = lim F(x ) - F(x) n → ⎢ + ∞ ⎥ n →∞ n ⎣ n ⎦ = F(x+0) - F(x). ⎛ 1⎞ ⎛ ⎛ 1⎞⎞ MÆt kh¸c lim ⎜ ⎜ ⎟
P⎜⎜ x≤ X < x ⎟ + ⎟ ⎜
⎟ P ⎜lim x≤ X < x+ ⎜ ⎟ ⎟ ⎜ ⎜ ⎟⎟ n→∞ ⎝ n⎠ = n→∞ ⎝ ⎝ n⎠⎟⎠ ∞ ⎡ 1 ⎤
= P ⎢∩(x ≤ X < x + )⎥ ⎢ ⎥ ⎣ = n n 1 ⎦ = P(X = x).
Tõ c¸c kÕt qu¶ trªn ta suy ra:
a. P(X = x) = F(x + 0) - F(x) .
b. Hµm F(x) liªn tôc t¹i x khi vµ chØ khi P(X = x) = 0.
III. BiÕn ngÉu nhiªn rêi r¹c 1. §Þnh nghÜa
BiÕn ngÉu nhiªn X ®−îc gäi lµ rêi r¹c nÕu miÒn gi¸ trÞ cña nã lµ mét tËp h÷u h¹n hoÆc ®Õm ®−îc.
NÕu Im(X) = {x , i ∈ I} víi I =(1, 2, ..., n) hoÆc I = N th× tËp hîp c¸c x¸c suÊt P(X = x ∈ I lËp i) víi i i
thµnh mét quy luËt ph©n phèi x¸c suÊt cña X. Khi ®ã: ⎧ P(x = x ) víi x = x P(X = x) i i = ⎨ ( i ∈ I) 0 víi x ≠ x ⎩ i
®−îc gäi lµ hµm khèi l−îng x¸c suÊt (hoÆc hµm x¸c suÊt) cña biÕn ngÉu nhiªn rêi r¹c X. ⎧ ⎪ (X = x ) = i Ω ∪ Do ⎨ i∈I ,
⎪⎩(X = x ) ∩(X = x ) = Φ ( i≠ j) i j
tøc lµ c¸c biÕn cè (X = x ) (i ∈ I) lËp thµnh mét nhãm ®µy ®ñ nªn ta suy ra i ∑ P(X= x )= 1. i ∈ i I Ghi chó:
§å thÞ cña hµm ph©n phèi F(x) cña mét biÕn ngÉu nhiªn rêi r¹c X sÏ cã d¹ng bËc thang. T¹i c¸c
®iÓm mµ lµ c¸c gi¸ trÞ cã thÓ cã cña X th× ®å thÞ nµy cã b−íc nhÈy. Nh− ta ®· thÊy ë ghi chó trong môc Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 57
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất
trªn, ®é dµi cña b−íc nh¶y chÝnh b»ng x¸c suÊt ®Ó X nhËn gi¸ trÞ t−¬ng øng. Cô thÓ t¹i gi¸ trÞ x th×: i P (X x ) F (x+ = = ) −F (x ) . i i i ThÝ dô:
NÕu X lµ "sè lÇn xuÊt hiÖn mÆt sÊp khi tung hai ®ång xu ®èi xøng vµ ®ång chÊt" th× ta ®· cã biÓu
thøc cña hµm ph©n phèi x¸c suÊt nh− sau: ⎧ 0 v íi x ≤ 0 ⎪ ⎪1 v íi 0 < x ≤ 1 ⎪ F(x) = 4 ⎨ . ⎪3 v íi 1 < x ≤ 2 ⎪4 ⎪ ⎩ 1 v íi > x 2
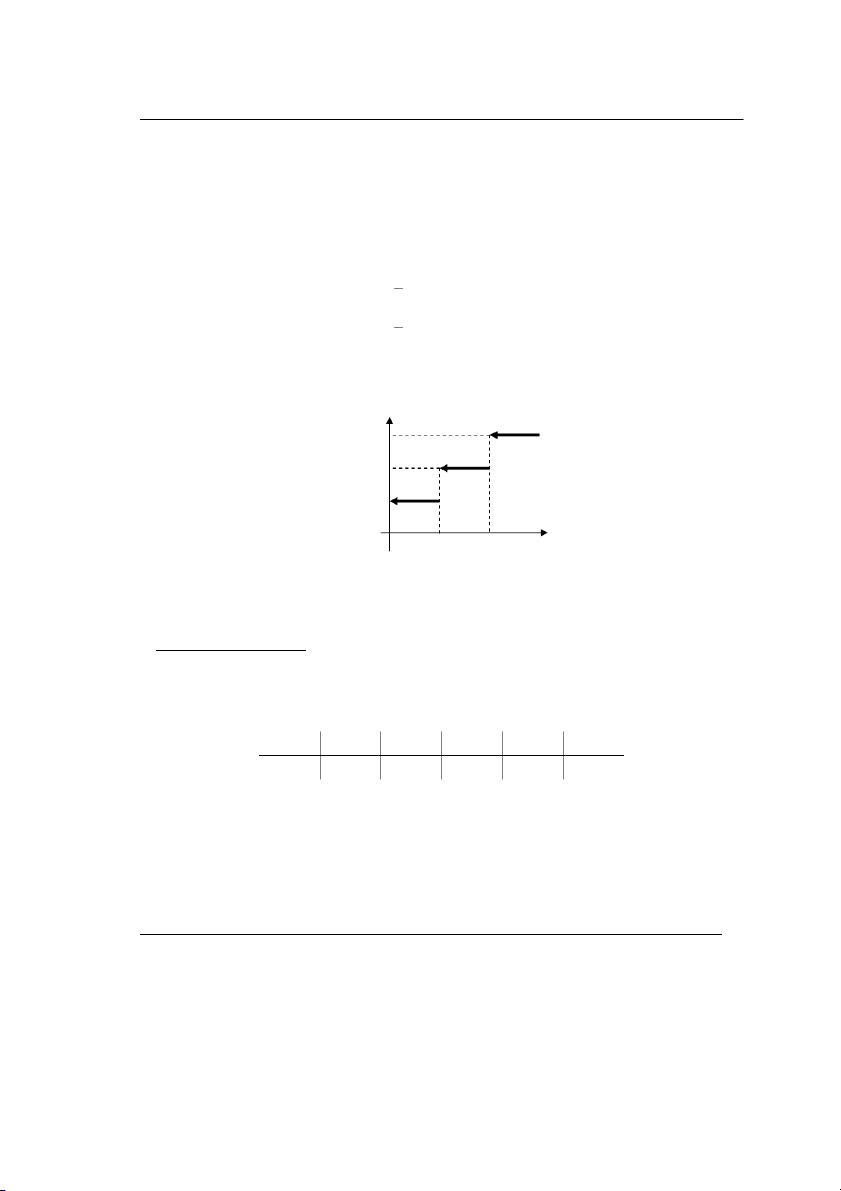
Tõ ®ã ®å thÞ cña hµm nµy cã d¹ng 1 3/ 1/ x 0 1 2
Mòi tªn trªn h×nh nh»m biÓu thÞ gi¸ trÞ cña hµm F(x) t¹i ®iÓm x nµo ®ã lµ øng víi ®é cao cña bËc i
thang d−íi (do tÝnh chÊt liªn tôc cña F(x)).
2. B¶ng ph©n phèi x¸c suÊt
§Ó thùc hiÖn mét c¸ch trùc quan luËt ph©n phèi x¸c suÊt cña mét biÕn ngÉu nhiªn rêi r¹c X, ng−êi ta
th−êng liÖt kª c¸c gi¸ trÞ cã thÓ cã cña X kÌm theo c¸c x¸c suÊt t−¬ng øng ®Ô nhËn mçi gi¸ trÞ cã thÓ cã
®ã trong mét b¶n víi d¹ng sau: X x x ...... x ..... 1 2 i P(x) P(x ) P(x ) ...... P(x ) ..... 1 2 i
B¶ng nµy gäi lµ b¶ng ph©n phèi x¸c suÊt cña X víi 2 ®iÒu kiÖn c¬ b¶n lµ P(x ) ≥ 0 ∈ ⎪⎧ i I ( 1) i ⎨ P(x ) = ∑ 1 ( 2) ⎪⎩ i ∈ i I
Së dÜ cã ®iÒu kiÖn 1 lµ do tÝnh chÊt cña x¸c suÊt, cßn nguyªn nh©n cã ®iÒu kiÖn 2 ®· ®−îc tr×nh bµy ë trªn. ThÝ dô: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 58
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất
H·y lËp b¶ng ph©n phèi x¸c suÊt cña X lµ "sè lÇn xuÊt hiÖn mÆt sÊp khi tung hai ®ång xu ®èi xøng vµ ®ång chÊt". Bµi gi¶i
Ta biÕt c¸c gi¸ trÞ cã thÓ cã cña X lµ
Im(X) = {0, 1, 2} tõ hµm ph©n phèi x¸c suÊt ®· thiÕt lËp ®−îc ta suy ra: + 1 1 P(x = 0) = F(0 ) - F(0) = − 0 = . 4 4 + - 3 1 2 P(x = 0) = F(0 ) - F(0 ) = − = . 4 4 4 3 1 P(x = 2) = F(2+ ) - F(2) = 1 - = . 4 4
VËy b¶ng ph©n phèi x¸c suÊt cña X nh− sau: X 0 1 2 P(X) 1 2 1 4 4 4
Ta thÊy hai ®iÒu kiÖn c¬ b¶n (1) vµ (2) nªu trªn ®−îc tháa m·n. Ghi chó:
Trªn ®©y ta ®· c¨n cø vµo hµm ph©n phèi x¸c suÊt ®Ó thiÕt lËp b¶ng ph©n phèi x¸c suÊt. Ng−îc l¹i tõ
b¶ng ph©n phèi x¸c suÊt ta muèn x©y dùng hµm ph©n phèi x¸c suÊt th× ta thùc hiÖn nh− sau:
a. XÕp c¸c gi¸ trÞ cã thÓ cã cña X theo thø tù t¨ng dÇn.
b. NÕu muèn x¸c ®Þnh gi¸ trÞ cña hµm ph©n phèi t¹i ®iÓm x nµo th× ta céng tÊt c¶ c¸c x¸c suÊt P(x ) i
cña nh÷ng gi¸ trÞ x ë bªn tr¸i ®iÓm x ®ã, tøc lµ i F(x) = ∑ P(x ) . i < xi x
Ch¼ng h¹n, tõ b¶ng ph©n phèi trªn ta x¸c ®Þnh ®−îc: 1 2 3 F 1
( ,5) = P(X < 1,5) = P(X = 0) + P(X = ) 1 = P(0) + P ) 1 ( = + = . 4 4 4 1 2 3 F ) 8 , 1 ( = P(0) + P ) 1 ( = + = . 4 4 4 ---------- -------- --------- 1 2 3 F(2) = P(0) + P ) 1 ( = + = . 4 4 4 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 59
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất 3
Nh− vËy víi mäi x sao cho 1 < x ≤ 2 ta ®Òu cã F(x) = . 4
ThÝ dô 2: Mét ng−êi ph¶i tiÕn hµnh mét thÝ nghiÖm cho tíi khi nµo thµnh c«ng th× th«i. H·y lËp b¶ng
ph©n phèi x¸c suÊt cña sè lÇn ph¶i tiÕn hµnh biÕt r»ng x¸c suÊt thµnh c«ng ë mçi lÇn ®Òu lµ p (0 < p < 1)
vµ c¸c lÇn tiÕn hµnh ®éc lËp víi nhau. Bµi gi¶i
Ta gäi A lµ biÕn cè "ë lÇn tiÕn hµnh thø i ng−êi ®ã thu ®−îc thµnh c«ng" ( i = 1, 2, 3,...) th× i Ω = { A , A A 1 , A 1 A A ,.... . 1 2 2 3 }
Gäi X lµ “sè lÇn ng−êi ®ã ph¶i tiÕn hµnh” th×: Im(X) = {, 1 , 2 , 3 .. } . . Khi ®ã: V× (X = ) 1 = A P(X = ) 1 = P(A ) = 1 nªn p 1 . V× (X = 2) = A1A 2nªn ( P X = 2) = P(A A 1 ) 2 .
Do c¸c lÇn tiÕn hµnh ®éc lËp nªn A1 vµ A lµ hai biÕn cè ®éc lËp. 2 VËy P(x = ) 2 = P(A1 )P(A ) = 1 ( - p)p 2 . ---- ---- ---- --- --- Tæng qu¸t:
V× (X = n) = (A1 A2 A3 .......... A . n 1- A ) nªn n
P(X = n) = P(A1 )P(A2 )P(A3 )...P(An 1- )P(A = 1 . n ) ( - p)n 1- p ----------------- ----------------- ------------------
Tõ ®ã ta cã b¶ng ph©n phèi x¸c suÊt cña X nh− sau: X 1 2 ... n ... P(x) p (1-p)p ... (1-p)n-1p ...
Quy luËt ph©n phèi x¸c suÊt nÇy cã thÓ viÕt gän l¹i lµ ⎧Im(X) = { , 1 , 2 ...., n ... } ⎨ . ⎩P(X = n) = − ( - 1 p) n 1p (n = ,1 ∞)
Ta cã thÓ thÊy hai ®iÒu kiÖn c¬ b¶n (1) vµ (2) ®Òu ®−îc tháa m·n. ThËt vËy:
(1) V× 0 < p < 1 nªn P(X = n) = 1 n 1 − ( - p) p > 0 víi mäi n. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 60
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất ∞ ∞ (2) ∑ P(X = n) = ∑ n −1 1 ( - p)
p . §©y lµ tæng c¸c sè h¹ng cña mét cÊp sè nh©n lïi v« h¹n víi c«ng béi lµ = i 1 i =1 ∞ p p (1 - p), v× thÕ: ∑ n −1 (1- p) p = = =1 . 1- (1 - p) p i=1
IV. BiÕn ngÉu nhiªn liªn tôc tuyÖt ®èi 1. §Þnh nghÜa
BiÕn ngÉu nhiªn X ®−îc gäi lµ liªn tôc tuyÖt ®èi nÕu trªn R cã tån t¹i mét hµm f(u) ≥ 0 sao cho hµm
ph©n phèi x¸c suÊt cña X cã thÓ biÓu diÔn d−íi d¹ng: x F(x) = f(u d ) u - ( ∞ < x < + ) ∞ ∫ . −∞
Ghi chó 1: Khi ®ã hµm f(u) ®−îc gäi lµ hµm mËt ®é x¸c suÊt cña biÕn ngÉu nhiªn X v× dF( ) x ' f ( ) x = F ( ) x = hÇu kh¾p n¬i. dx
Ghi chó 2: NÕu X lµ mét biÕn ngÉu nhiªn liªn tôc th× c¸c gi¸ trÞ cã thÓ cã cña nã lµ kh«ng ®Õm ®−îc, cô
thÓ chóng sÏ lÊp kÝn c¶ mét kho¶ng nµo ®ã (h÷u h¹n hoÆc v« h¹n). Nãi c¸ch kh¸c Im(X) sÏ cã lùc l−îng Continum. ThÝ dô:
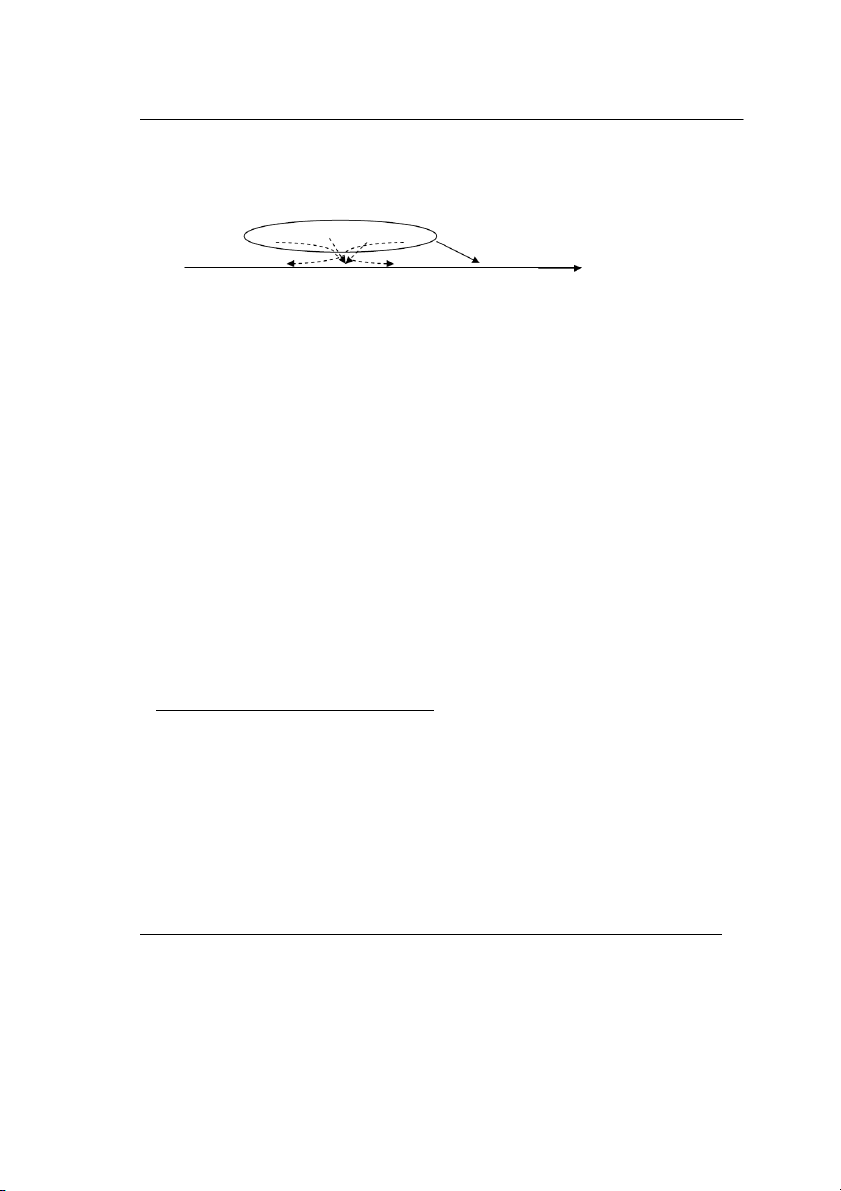
Thùc hiÖn phÐp thö lµ “b¾n mét viªn ®¹n vµo mét chiÕc bia cã t©m lµ 0 vµ b¸n kÝnh lµ R”. NÕu viªn
®¹n tróng bia ë vÞ trÝ nµo th× vÞ trÝ ®ã ®−îc gäi lµ ®iÓm ch¹m cña viªn ®¹n. Gi¶ thiÕt viªn ®¹n lu«n tróng
bia. NÕu gäi X lµ “kho¶ng c¸ch tõ ®iÓm ch¹m cña viªn ®¹n tíi t©m bia” th× X lµ mét biÕn ngÉu nhiªn liªn
tôc trong ®o¹n [0 ; R] v× mäi gi¸ trÞ cña ®o¹n nµy ®Òu lµ gi¸ trÞ cã thÓ cã cña X.
2. Mét sè tÝnh chÊt cña hµm mËt ®é +∞ TÝnh chÊt 1: f(x d ) x = 1 ∫ . −∞ Chøng minh: +∞
f (x)dx = F (+∞)− F (−∞) = 1− 0 = 1 ∫ . −∞ x2 TÝnh chÊt 2: P(x ≤ víi [x ,x ] bÊt kú. 1 x < x 2) = ∫f(x d ) x 1 2 x1 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 61
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất Chøng minh: P(x ≤ x < x ) ) - F(x ) 1 2 = F(x2 1 x 2 x2 = F '(x )dx ∫ = ∫ f(x d ) x. x x 1 1 x1 HÖ qu¶ 1: ( P X = x ) = f ( ) x dx = 0 ∫ 1 x1
VËy x¸c suÊt ®Ó biÕn ngÉu nhiªn liªn tôc X nhËn mét gi¸ trÞ cô thÓ x nµo ®ã lu«n b»ng 0. V× x lµ 1 1
mét gi¸ trÞ bÊt kú cho nªn ta cã thÓ viÕt P(X = x) = 0 víi mäi x. Tõ ®ã ta suy ra:
a. §èi víi biÕn ngÉu nhiªn liªn tôc, ®Ó cã ý nghÜa. Ta ph¶i ®Ò cËp tíi x¸c suÊt ®Ó nã nhËn mét gi¸ trÞ
nµo ®ã n»m trong mét kho¶ng nµo ®Êy.
b. Theo ghi chó b) ë cuèi môc II ta suy ra hµm ph©n phèi x¸c suÊt F(x) cña biÕn ngÉu nhiªn liªn tôc
lµ mét hµm liªn tôc t¹i mäi x.
HÖ qu¶ 2: NÕu X lµ mét biÕn ngÉu nhiªn liªn tôc th× tõ hÖ qu¶ 1 ta thÊy:
P(x ≤ X < x ) = P(x < X ≤ x ) = P(x ≤ X ≤ x ) = P(x < X < x ). 1 2 1 2 1 2 1 2 NhËn xÐt:
T¹i mäi ®iÓm liªn tôc x cña f(x) ta cã: P(x ≤ X < x + d ) x ≈ f (x)dx.
BiÓu thøc f(x)dx gäi lµ mét vi ph©n x¸c suÊ .
t Nã cã vai trß t−¬ng tù nh− hµm khèi l−îng x¸c suÊt p(x)
®èi víi biÕn ngÉu nhiªn rêi r¹c X. Tõ ®ã ta cã hai ®iÒu kiÖn c¬ b¶n t−¬ng tù nh− sau ®èi víi tr−êng hîp
c¸c biÕn ngÉu nhiªn rêi r¹c vµ liªn tôc, cô thÓ: §èi víi hµm p(x) §èi víi hµm f(x) 1) P(x ) ≥ 0 (i∈I) 1) f(x) i ≥ 0 víi mäi x +∞ 2) ∑ P(x ) =1 i 2) f(x d ) x = 1 ∫ ∈ i I −∞
Ng−êi ta chøng minh ®−îc r»ng 1) vµ 2) lµ ®iÒu kiÖn cÇn vµ ®ñ ®Ó mét hµm sè f(x) nµo ®ã trë thµnh
hµm mËt ®é x¸c suÊt cña mét biÕn ngÉu nhiªn liªn tôc X nµo ®Êy. ThÝ dô:
Mét biÕn ngÉu nhiªn liªn tôc X ®−îc gäi lµ tu©n theo quy luËt ph©n phèi mò víi tham sè λ ( λ > 0 )
nÕu hµm mËt ®é x¸c suÊt cña nã cã d¹ng: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 62
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất ⎧ -λx λe víi x > f (x) = 0 ⎨ ⎩0 víi x ≤ 0
a. H·y x¸c ®Þnh hµm ph©n phèi F(x). b. H·y chøng tá r»ng:
P( X > x + x ) = P(X > x ).P(X > x ) víi mäi x , x > 0. 1 2 1 2 1 2
c. Tõ kÕt qu¶ ë c©u b) h·y suy ra r»ng.
P( X > x + x X > x ) = P( X > x ) . 1 2 1 2 Bµi gi¶i x ⎧ -λ 1 - e x víi x > 0 a. Ta cã F(x) = f(u)du = ∫ ⎨ . −∞ ⎩ 0 víi x ≤ 0 b. Tr−íc tiªn ta cã:
P(X > x + x ) = 1- P( X ≤ x + x ) 1 2 1 2
=1- P(X < x + x ) (do X lµ biÕn ngÉu nhiªn liªn tôc). 1 2
Tõ §Þnh nghÜa cña hµm ph©n phèi suy ra:
P( X > x + x ) =1- F (x + x ) 1 2 1 2 - (x x 1 2 ) 1-[1- e λ + = ] - (x x 1 2 ) e λ + = . T−¬ng tù trªn ta cã: - 1 ( ) x P X x e λ > = 1 - 2 ( ) x P X x e λ > = . 2 -λ(x +x ) -λ V× x - x λ 1 2 1 2 e = e e .
nªn ta suy ra ®iÒu ph¶i chøng minh.
c. Tõ §Þnh nghÜa cña x¸c suÊt cã ®iÒu kiÖn ta cã: [
P ( X > x + x )( X > x )] 1 2 1
P(X > x + x X > x ) = . 1 2 1
P( X > x ) 1
P(X > x + x ) Do [
P ( X > x + x )( X > x )] = P( X > x + x ) nªn: 1 2 (
P X > x + x X > x ) = . 1 2 1 1 2 1 2 1 ( P X > x ) 1
Tõ ®ã theo kÕt qu¶ b ta ®−îc: ( P X > x ). ( P X > x ) 1 2 (
P X > x + x X > x ) = = ( P X > x ) . 1 2 1 2 ( P X > x ) 1 Ghi chó: Mét biÕn ngÉu nhiªn X ®−îc gäi lµ "kh«ng cã trÝ nhí" nÕu
P( X > s + t X > t) = P(X > s) víi mäi s, t ≥ 0. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 63
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất
Ch¼ng h¹n nÕu X lµ tuæi thä cña mét lo¹i s¶n phÈm vµ nÕu nã tháa m·n hÖ thøc võa nªu th× cã nghÜa
lµ x¸c suÊt ®Ó nã dïng ®−îc tèi thiÓu (s + t) giê nÕu nh− nã ®· dïng ®−îc t giê còng gièng nh− x¸c suÊt
ta tÝnh ngay tõ ®Çu ®Ó nã dïng ®−îc tèi thiÓu lµ s giê (tøc lµ s¶n phÈm "kh«ng nhí" m×nh ®· tån t¹i ®−îc t giê råi).
Nh− vËy qua kÕt qu¶ trªn ta thÊy nÕu mét biÕn ngÉu nhiªn tu©n theo quy luËt ph©n phèi mò th× ®ã lµ
mét biÕn ngÉu nhiªn "kh«ng cã trÝ nhí". Sau nµy chóng ta sÏ thÊy 1 chÝnh lµ gi¸ trÞ trung b×nh cña X. λ
B. BiÕn ngÉu nhiªn hai chiÒu I. §Þnh nghÜa 1. §Æt vÊn ®Ò
Trong nhiÒu tr−êng hîp chóng ta cÇn xÐt c¸c biÕn ngÉu nhiªn nhËn gi¸ trÞ trong kh«ng gian hai
chiÒu, tøc lµ xÐt c¸c ®iÓm ngÉu nhiªn trªn mÆt ph¼ng.
ThÝ dô: Khi nghiªn cøu ®é ch¹m cña c¸c viªn ®¹n b¾n vµo bia, ta th−êng x¸c ®Þnh vÞ trÝ cña c¸c ®iÓm
ch¹m so víi t©m bia. NÕu lÊy t©m 0 cña bia lµm gèc cña mét hÖ täa ®é vu«ng gãc th× mçi ®iÓm ch¹m M
®−îc x¸c ®Þnh bëi hai täa ®é x vµ y cña nã. V× tr−íc khi b¾n ta kh«ng kh¼ng ®Þnh ®−îc vÞ trÝ cña M nªn
M lµ mét ®iÓm ngÉu nhiªn, do ®ã c¸c täa ®é x vµ y cña nã ®Òu lµ c¸c biÕn ngÉu nhiªn X vµ Y. Nh− vËy
viÖc nghiªn cøu vÞ trÝ cña ®iÓm M dÉn ®Õn viÖc nghiªn cøu ®ång thêi hai biÕn ngÉu nhiªn X vµ Y, tøc lµ
mét hÖ hai biÕn ngÉu nhiªn V = (X , Y) hoÆc cßn gäi lµ mét vÐc t¬ ngÉu nhiªn hai chiÒu. 2. §Þnh nghÜa
Cho kh«ng gian x¸c suÊt (Ω, A, P) vµ hai biÕn ngÉu nhiªn X vµ Y x¸c ®Þnh trªn ®ã. Khi ®ã hÖ V =
(X, Y) ®−îc gäi lµ mét biÕn ngÉu nhiªn hai chiÒu, tøc lµ V lµ mét ¸nh x¹ tõ Ω vµo R2 sao cho víi mçi ω ∈ Ω th× V(ω) = ( X(ω), Y(ω)).
II. Hμm ph©n phèi
1. Hµm ph©n phèi ®ång thêi a. §Þnh nghÜa
Hµm ph©n phèi x¸c suÊt ®ång thêi cña mét biÕn ngÉu nhiªn hai chiÒu
V = (X, Y) ®−îc ®Þnh nghÜa nh− sau: F( , x y) = [ P (X < x)(Y < y)] - ( ∞ < x, y < +∞) . Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 64
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất
Nh− vËy F(x, y) cho ta biÕt l−îng x¸c suÊt −
® îc ph©n cho nh÷ng ®iÓm thuéc h×nh ch÷ nhËt më n − h ë h×nh vÏ d−íi ®©y: y M(x, y) x b. C¸c tÝnh chÊt
T−¬ng tù nh− trong tr−êng hîp mét chiÒu, hµm ph©n phèi x¸c suÊt cña biÕn ngÉu nhiªn hai chiÒu V
= (X, Y) cã c¸c tÝnh chÊt sau:
i. Kh«ng gi¶m ®èi víi mçi ®èi sè, tøc lµ
F(x , y) ≥ F(x , y) nÕu x > x 2 1 2 1 F( ,
x y ) ≥ F(x,y ) nÕu y > y 2 1 2 1
vµ F(x , y ) ≥ F(x ,y ) nÕu x > x > y 2 1 vµ y 2 2 1 1 2 1
ii. Liªn tôc bªn tr¸i ®èi víi mçi ®èi sè.
iii. lim F(x, y) = 1 (hoÆc viÕt gän lµ F(+ , ∞ + ) ∞ = 1 ). x→ +∞ y→+∞ iv. F - ( ,
∞ y) = F(x -,∞) = 0 (hiÓu theo c¸ch viÕt gän nh− trªn).
v. NÕu a < b (i = 1, 2) th× i i P[ a ( ≤ X ≤ b ) a (
≤ y ≤ b )]= F(b , b ) - F(a , b ) - F(b ,a ) + F(a , a ). 1 1 2 2 1 2 1 2 1 2 1 2
§©y lµ x¸c suÊt ®Ó ®iÓm ngÉu nhiªn M (X, Y) r¬i vµo h×nh ch÷ nhËt ⎛ 1 a ≤ x ≤ 1 b ⎞ R ⎜⎜ ⎟⎟. ⎝a2 ≤ y ≤ 2 b ⎠
2. C¸c hµm ph©n phèi biªn
NÕu F(x, y) lµ hµm ph©n phèi x¸c suÊt ®ång thêi cña biÕn ngÉu nhiªn hai chiÒu V = (X, Y) th× c¸c hµm: F( , x + ∞ ) = P(X 1
F(+ ∞, y ) = P(Y < y) = F (y) 2 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 65
Chương1.Biếnngẫunhiênvàquyluậtphânphốixácsuất
lµ c¸c hµm ph©n phèi cña c¸c biÕn ngÉu nhiªn thµnh phÇn t−¬ng øng X vµ Y. C¸c hµm nµy gäi lµ c¸c
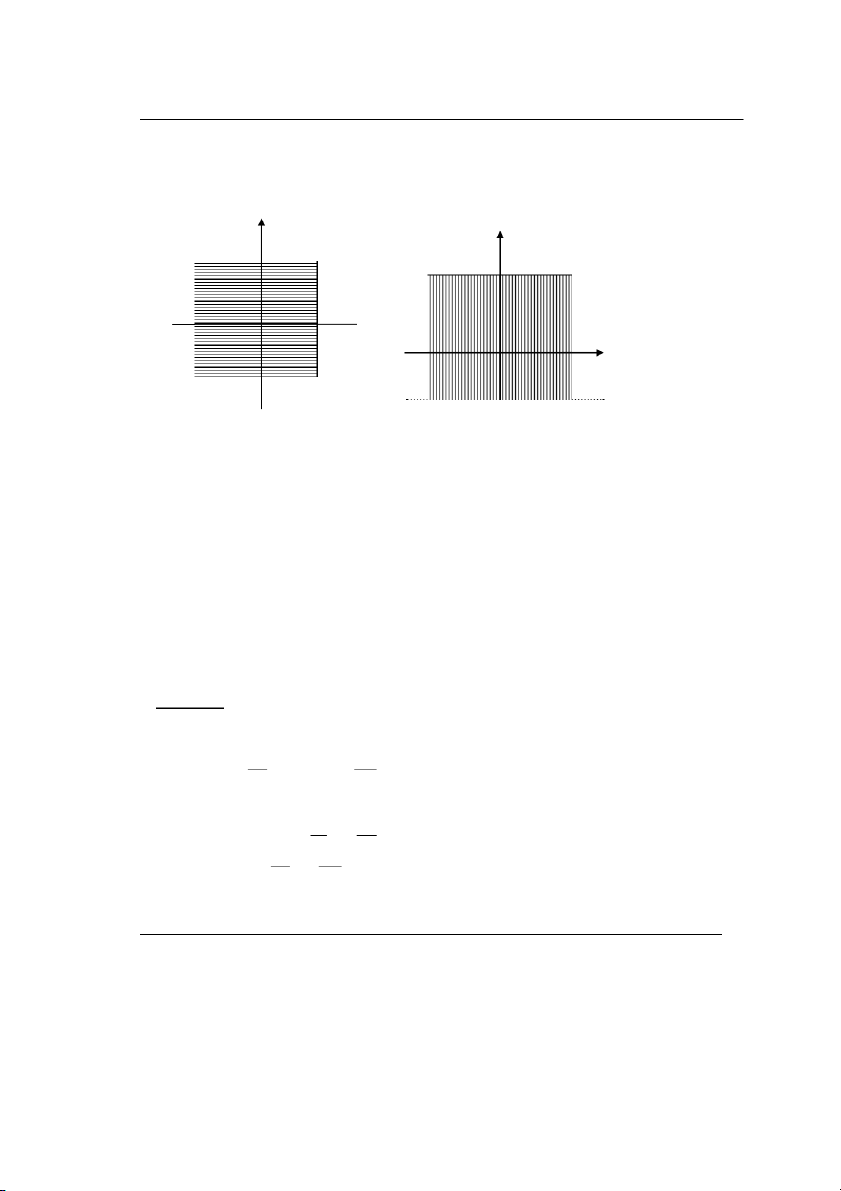
hµm ph©n phèi biªn cña V. §©y lµ lo¹i hµm ph©n phèi mét chiÒu ®· ®−îc xÐt ë phÇn A vµ chóng cho ta
biÕt sù ph©n phèi x¸c suÊt theo chiÒu n»m ngang vµ theo chiÒu th¼ng ®øng, tøc lµ l−îng x¸c suÊt ph©n bè
cho c¸c ®iÓm thuéc vµo c¸c nöa mÆt ph¼ng nh− ë c¸c h×nh vÏ d−íi ®©y. y x o o F (x) = P(X < x) 1 F (y) = P(Y < y) 2
Cho c¸c biÕn ngÉu nhiªn hai chiÒu V = (X, Y) cã hµm ph©n phèi x¸c suÊt nh− sau: ⎧1- e-x - e-y + e-x-y nÕ u x , > y 0 ( F y . x ) = ⎨ . ⎩ 0 nÕu t r¸ il¹i -x ⎧⎪1-e víi x > 0 Khi ®ã ⎪
F (x) = lim F (x, y) =⎨ . 1 y →+∞ ⎪0 v i í x ≤ 0 ⎪⎩
VËy X cã ph©n bè mò víi tham sè λ = 1.
III. BiÕn ngÉu nhiªn hai chiÒu rêi r¹c 1. §Þnh nghÜa
NÕu X vµ Y ®Òu lµ c¸c biÕn ngÉu nhiªn mét chiÒu rêi r¹c th× hÖ V = (X, Y) gäi lµ biÕn ngÉu nhiªn hai chiÒu rêi r¹c.
NÕu {x }(i = 1,n vµ {y } (j =1,m lµ c¸c gi¸ trÞ cã thÓ cã t−¬ng øng cña X vµ Y th× ta sÏ ký hiÖu: j ) i ) [
P ( X = x )(Y = y )] = P(x , y ) = P . i i i i ij C¸c x¸c suÊt P nµy ij
(i = 1,n; j = 1,m) gäi lµ c¸c x¸c suÊt ®ång thêi cña hÖ V= (X, Y). V× c¸c biÕn cè [(X = x )(Y = y )] (i = , 1 n; j = , 1 m) i j
lËp thµnh mét nhãm ®Çy ®ñ (n × m) biÕn cè nªn: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 66