Chương 8. Kiểm định giả thiết thống kê - Xác suất thống kê | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Chương 8. Kiểm định giả thiết thống kê - Xác suất thống kê | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Thông tin:
28 trang 12 tháng trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chương 8. Kiểm định giả thiết thống kê - Xác suất thống kê | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Chương 8. Kiểm định giả thiết thống kê - Xác suất thống kê | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

41 21 lượt tải Tải xuống

Môn: Xác suất thống kê (MAT1011) 33 tài liệu

Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội 537 tài liệu

Thông tin:

28 trang 12 tháng trước

Tác giả:

Profile Mai Nguyệt
1
CHƯƠ Ế ỐNG 8. KIỂM ĐỊNH GIẢ THI T TH NG KÊ
8.1. Ki nh gi giá tr trung bình ểm đị ả thiết về ị
8.2. Ki nh gi t l ểm đị ả thiết về ỷ ệ
8.3. Ki nh gi ểm đị ả thiết cho phương sai
8.4. So sánh hai giá tr ị trung bình
8.5. So sánh hai t l ỷ ệ
8.6. So sánh hai phương sai
8.7. Tiêu chu n phù h p ẩ ợ
2
8.8. Ki p và so sánh nhi u t l ểm tra tính độc lậ ề ỷ ệ
8.9. So sánh nhi u giá tr t nhân t ề ị trung bình: phân tích phương sai mộ ố
Bài 8.1. Kiểm định giả thi giá tr trung bình ết về ị
I. Nguyên lý chung:
Bài toán ki nh gi vào các s u ểm đị ả thiết thống kê là bài toán: căn cứ ố liệ
thống kê c n ph n v m thiầ ải đưa ra kết luậ ề ột giả ết thống kê nào đó mà ta
quan tâm.
Một gi t th t gi t vả thiế ống kê là mộ ả thiế ề phân b xác su t cố ấ ủa tập chính đang
xét. N u phân b xác su g b XÁC SUế ố ất đó được đặc trưn ởi các tham số (như ẤT
(tỷ l ), giá trệ ị trung bình hay phương sai, …), thì giả thiết thống kê là giả thiết
về tham số của phân b ố đó.
Từ nay tr hi u m thi t là m ở đi ta sẽ ể ột giả ế ột giả thiết thống kê, m t quy ộ
tắc dẫn tới quyết định ch p nh n hay bá gi i là mấ ậ c bỏ ả thiết đã nêu gọ ột kiểm
định (test) thống kê.
Giả thiết đưa ra kiểm định đượ đó là giảc ký hiệu H ,
0
thiết mà ta nghi
ngờ. Đối l p v i gi t H . Ch p nh n H H , ậ ớ ả thiết H
0
là đối thiế
1
ấ ậ
0
nghĩa là bác bỏ
1
ngượ ỏc lại, bác b H p nh
0
nghĩa là chấ ận H .
1
Câu hỏi đặt ra là: Chúng ta ch p nh n hay bác b m ng ấ ậ ỏ ột giả thiết bằ
cách nào? Để nh, các nhà th u nhđưa ra quy tắc kiểm đị ống kê đề ất trí với nhau
nguyên lý sau đây:
“Nế ộ ỏu m t biến cố có xác suất rất nh thì trong một phép thử hay một
vài phép th , bi s không x ử ến cố đó ẽ ảy ra”.
Như vậy, chúng ta sẽ bác bỏ H n
0
ếu xuấ ệt hi n biến cố có xác suất nhỏ,
tính trong điề ếu kiện giả thi t H
0
đúng.
Chúng ta sẽ minh h ọa bởi các ví dụ sau:
Ví dụ 1. Gieo m ng ti n 100 l n ta th y xu n m p 60 l n. Ta nghi ột đồ ề ầ ấ ất hiệ ặt sấ ầ
ngờ r ng, xác su t xu t hi n m p l t hi n m t ng ằ ấ ấ ệ ặt sấ ớn hơn xác suất xuấ ệ ặ ửa.
Gọi p là xác su t sất xu t hi n mấ ệ ặ ấp. Khi đó ta có bài toán kiểm định như
sau:
- Giả thiết H
0
: p=1/2
- Đối thi t Hế
1
: p>1/2
2
Ta tính
(60
0
06.0(10
100/5.05.0
5.06.0
100/5.05.0
5.0
100
QPSP
xx
p
028717.0)9.1( Q
Đây là một xác suất nhỏ, mà lại xảy ra trong m n ki nh. V y ta ột lầ ểm đị ậ
bác b H , ch p nh n H . ỏ
0
ấ ậ
1
Ví dụ 2. M c nghiên c u M cho bi t tr em M n ột cuộ ứ ở ỹ ế ẻ ỹ ở độ tuổi đế
trường tiêu thụ trung bình 19.4 OZ sữa 1 ngày (1 OZ=28.35 g).
Trong m t m u ng u nhiên g m 140 tr i ng ộ ẫ ẫ ồ ẻ em ngườ ta tính được lượ
sữa chúng uống trung bình m t ngày là 18.5 OZ vộ ới độ l n là 6.8 ệch tiêu chuẩ
OZ. Điều này có cho phép ta k t lu ng s ế ận là lượ ữa tiêu thụ ít hơn 19.4 OZ hay
không?
Giải
Gọi là lượng s a tiêu th n bài toán ữ ụ trung bình trong 1 ngày. Ta đi đế
kiểm đị ống kê như sau:nh giả thiết th
- Giả thiết H :
0
=19.4
- Đối thi t H : ế
1
<19.4
Giả s H trung bình m u ử
0
đúng, khi đó xác suất để ẫ
5.18X
b ng bao nhiêu? ằ
Do
X
có phân b n (ho p x n) v i k v ng là 19.4 ố chuẩ ặc xấ ỉ chuẩ ớ ỳ ọ và độ
lệch chuẩn là
575.0
140
8.6
n
S
.
Vậy
57.15.18
575.0
4.
195.18
ZPZPXP
.
Xác suất này không nh l ỏ ắm.
Vì vậy ta chưa có đủ cơ sở để bác b gi t H . Nói cách khác, ỏ ả thiế
0
số liệu đã có chưa đủ cơ sở để bác bỏ giả thiết H .
0
Trong khi đưa ra quyết định, chúng ta có thể phạm phải 1 trong 2
loại sai l m sau:ầ
- Sai l i 1: Bác b H ầm loạ ỏ
0
trong khi thực ra H
0
đúng
- Sai l m lo p nh n H c ra Hầ ại 2: Chấ ậ
0
trong khi thự
0
sai.
Sai l m lo m c t án nhầ ại 1, tương tự như sai lầ ủa quan tòa, khi “Kế ầm”
ngườ ội vô t i; còn sai lầm loại 2 tương tự như sai lầm “Tha bổng” kẻ có
tội.
3
Chúng ta mong muốn làm c u c 2 lo i sai lực tiể ả ạ ầm trên, nhưng
khi đó chúng ta phả giá đắi trả t về thời gian, tiền của và công sức.
Hơn nữ ại làm tăng sai lầa, khi ta giảm sai lầm loại này l m loại
kia, và ngược lại.
Trong xã hội văn minh, người ta coi k t án nhế ầm người vô t i là ộ
1 sai l m nghiêm tr m tha b ng k có t ầ ọng hơn so với sai lầ ổ ẻ ội.
Trong bài toán kiểm định cũng vậy, ta coi sai lầm loại 1 là
nghiêm tr m lo sai lọng hơn sai lầ ại 2. Cho nên, người ta cố định trước ầm
loại 1. Xác suất m c sai l m lo i là ắ ầ ại 1 được gọ mức ý nghĩa của tiêu
chuẩn, ký hi u là ệ . Xác su t m c sai l m lo i 2 ký hi u là . Giá tr 1- ấ ắ ầ ạ ệ ị
được gọi là LỰC LƯỢNG của tiêu chuẩ ẩn. Lực lượng của tiêu chu n là
xác su t bác b H khi H ấ ỏ
0 0
sai.
Mức ý n c l c ghĩa ẩn thường đượ của tiêu chu ấy là 0.05; 0.02 hoặ
0.01.
Trong tập các tiêu chu n có cùng m , tiêu chu n nào ẩ ức ý nghĩa ẩ
có xác suất sai l m lo i 2 nh nh c xem là tiêu chu ầ ạ ỏ ất đượ ẩn “tốt nhất”.
Các tiêu chu ng ẩn được đưa ra ở chương này đều đã được chứ
minh ch t ch v m t toán h c là các tiêu chu n t ặ ẽ ề ặ ọ ẩ ốt nhất.
Khi kiểm định thống kê dẫn tới chấp nhận H là m
0
ột quyết định
dè d p nh n H nên hi u là vặt: Chấ ậ
0
, không có nghĩa là H
0
đúng, mà chỉ ể ới
các số u hi bác b H , c n ph i ngh u liệ ện có, không có đủ cơ sở để ỏ
0
ầ ả iên cứ
tiếp.
Các bướ ểm địc cần thiết trong việc giải một bài toán ki nh giả
thiết thống kê như sau:
1.Phát bi u gi ể ả thiết H i thi t H
0
và đố ế
1
2.Chọn tiêu chuẩn (test) th ng kê. ố
3.Định rõ mức ý nghĩa
(xác suất mắc sai l i 1). ầm loạ
4.Ch iọn mi n bác bề ỏ gi ả th ết H
0
.
5.Tính giá tr c a tiêu chu n th ng kê t m ị ủ ẩ ố ừ ẫu quan sát được.
6.Kết luận: Bác b hay ch p nh n gi ỏ ấ ậ ả thiết, tùy thu c vào viộ ệc
giá tr c a tiêu chu n bác b gi t hay không. ị ủ ẩn có rơi vào miề ỏ ả thiế
II. nh gi thi giá tr trung bình: Kiểm đị ả ết về ị
Giả s , X ) là m u ng c rút t bi n ng u nhiên ử (X
1 2
, …, X
n
ẫ ẫu nhiên đượ ừ ế ẫ
chu
ẩn X có EX= , DX= u X không chu n thì n 120).
2
(Nế ẩ
3.A.1. Đố ết hai phía: Xét BTKĐGT i thi
Giả thi ết H
0
:
=
0
Đối thiết H
1
:




0
, v ới mức ý nghĩa
cho trước.
1.N
ếu phương sai
2
= σ
0
2
t đã biế
Bài toán d ng 1: ạ
Các bướ ến hành như sau:c ti
+ B ước 1:
Giả thiết
00
:
H
4
Đối thiết
+ Bước 2: Xác định hàm tiêu chuẩn
0
0
/
x
n
z
+ Bước 3: Xác định mức ý nghĩa α
Do đố ẩn z nên ta tra α/2 phân vịi thiết 2 phía và hàm tiêu chu của phân
phối chuẩn t c, tra b ng ho c Excel: ắ ả ặ
z
α/2
=NORMSINV(1- α/2)
α
10%
5%
2%
1%
z
α/2
1.645
1.96
2.326
2.576
+Bướ ịc 4: Xác đ nh miền bác bỏ
S={(X , X }
1 2
, …, X
n
):|z|>z
α/2
+Bước 5: Dựa vào TB mẫu
x
để tính
n
x
z
/
0
0
+Bước 6: Nếu
|z|>z
α/2
H . thì ta bác bỏ
0
Nếu |z|<=z
α/2
chấp nh n gi ậ ả thiết H .
0
Bài toán dạng 2:
Các bướ ến hành như sau:c ti
+ Bước 1:
Giả thiết
00
:
H
Đối thiết
01
:
H
+ Bướ ác địc 2: X nh hàm tiêu chuẩn
0
/
x
n
z
+ Bước 3: Xác định mức ý nghĩa α
Do đối thiết 1 phía và hàm tiêu chuẩn z nên ta tra α phân vị c a phân phủ ối
chuẩn, tra b ng ho c Excel: ả ặ
z
α
=NORMSINV(1-α)
α
5%
2.5%
2%
1%
0.5%
z
α
1.645
1.96
2.054
2.326
2.576
5
+Bướ ịc 4: Xác đ nh miên bác b ỏ
S={(X , X z>z }
1 2
, …, X
n
):
α
+Bước 5: Dựa vào TB mẫu
x
tính
n
x
z
/
0
0
+Bước 6: Nếu
z>z
α
thì ta bác bỏ H .
0
N
ếu z<=z
α
chấp nh n giậ ả thiết H
0
.
Ví dụ 2. T p chính X có phân ph n v giá trung bình ậ ối chuẩ ới trị chưa biết,
0
=5.2, n=25, TB m u ẫ
56.27x
. V i m =0.05, hãy kiớ ức ý nghĩa ểm
định bài toán sau:
- Giả thiết H :
0
=26
- Đối thi t H : ế
1
≠26.
Giải
Các bướ ến hành như sau:c ti
+ Bước 1:
Giả thiết
26:
0
H
Đối thiết
+ Bước 2: Xác định hàm tiêu chuẩn
25/2.5
26
x
z
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đố ẩn z nên ta tra αi thiết 2 phía và hàm tiêu chu /2 phân vị của phân
phối chuẩn, tra b ng ho ả ặc Excel:
z
α/2
=NORMSINV(1-α/2)=1.96
+Bướ ịc 4: Xác đ nh miên bác bỏ
S={(X , X ): |z|>1.96}
1 2
, …, X
n
+Bước 5: Dựa vào mẫu
6.27x
và
6.1
5/2.5
266.27
/
0
0
n
x
z
+Bước 6:Vì |z|=1.6 <z =1.96, nên ta ch
0.025
ấp nhận giả thiết H
0
.
6
Ví dụ 3. T p chính X có phân ph n v i giá tr g bình ậ ối chuẩ ớ ị trun chưa biết,
0
=5.2, n=25, TB m u ẫ
56.27x
. V i m =0.05, hãy kiớ ức ý nghĩa ểm
định bài toán sau:
- Giả thiết H :
0
=26
- Đối thi t H : ế
1
> 26.
Giải
Các bướ ến hành như sau:c ti
+ Bước 1:
Giả thiết
26:
0
H
Đối thiết
1
: 26H
+ Bước 2: Xác định hàm tiêu chuẩn
25/2.5
26
x
z
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 1 phía và hàm tiêu chuẩn z nên ta tra α phân vị c a phân phủ ối
chuẩn, tra b ng ho c Excel: ả ặ
z
α
=NORMSINV(1- 645 α)=1.
+Bước 4: Xác định miên bác bỏ
S={(X , X ): z>1.645}
1 2
, …, X
n
+Bước 5: Dựa vào mẫu
6.27x
và
6.1
5/2.5
266.27
/
0
0
n
x
z
+Bước 6:Vì z=1.6 <z
0.05
=1.645, nên ta chấp nhận giả thiết H .
0
Bài toán dạng 3:
Các bướ ến hành như sau:c ti
+ Bước 1:
Giả thiết
00
:
H
Đối thiết
01
:
H
+ Bước 2: Xác định hàm tiêu chuẩn
7
n
x
z
/
0
0
+ Bước 3: Xác định mức ý nghĩa α
Do đối thi t 1 phía và hàm tiêu chuế ẩn z nên ta tra α phân vị của phân phối
chuẩn, tra b ng ho c Excel: ả ặ
=NORMSINV(1-α)
+Bướ ịc 4: Xác đ nh miên bác bỏ
S={(X , X ): z<-z }
1 2
, …, X
n α
+Bước 5: Dựa vào mẫu tính
x
và
n
x
z
/
0
0
+Bước 6: Nếu
z< - z
α
H . thì ta bác bỏ
0
N
ếu z=>- z
α
chấp nh n gi ậ ả thiết H
0
.
Ví d
ụ 3. GS X~N( =5.2, n=36, TB m u ,
2
) với chưa biết, ẫ
56.27x
. V i m =0.05, hãy ki nh bài toán sau: ớ ức ý nghĩa ểm đị
- Giả thiết H :
0
=29.64
- Đối thi t H : ế
1
<29.64
Giải
+ Bước 1:
Giả thiết
64.29:
0
H
Đối thiết
64.29:
1
H
+ Bước 2: Xác định hàm tiêu chuẩn
36/2.5
64.29
x
z
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thi t 1 phía và hàm tiêu chuế ẩn z nên ta tra α=0.05 phân v c a phân ị ủ
phối chuẩn, tra b ng ho ả ặc Excel:
=NORMSINV(1-0.05)=1.645
+Bướ ịc 4: Xác đ nh miên bác bỏ
S={(X , X ): z<-1.645}
1 2
, …, X
n
+Bước 5: Dựa vào mẫu tính
56.27x
và
4.2
36/2.5
64.2956.27
/
0
0
n
x
z
8
+Bước 6: Vì z=-2.4 < z =-1.645 nên ta bác b gi t H , ch p nh
α
ỏ ả thiế
0
ấ ận đối
thiết H
1
, nghĩa là chấp nhận giá trị TB μ < 29.64.
2.N
ếu
2
chưa biết:
Trong trường hợp này ta phải giả ế thi t về tính chuẩn của biến ngẫu
nhiên X, c m u nh . ỡ ẫ ỏ hơn 30
Chúng ta có 3 dạng ki nh: ểm đị
Dạng 1. Đối thiết 2 phía
Giả thiết
00
:
H
Đối thiết
Hàm tiêu chu n s d ng ẩ ử ụ ở đây là
.
0
nt
s
x
Với m c ý ta ph c a phân ph i Student n-1 b c t do: ứ nghĩa α ải tra α/2 phân vị ủ ố ậ ự
t
α/2, n-1
.
Nếu tra b ng Excel: t -1). ằ
α/2, n-1
=TINV(α, n
Ví d
ụ 4. GS X~N( , TB m u ,
2
) với chưa biết,
2
chưa biết, n=16 ẫ
56.27x
, s=5.2 . V i m =0.05, hãy ki nh bài toán sau: ớ ức ý nghĩa ểm đị
- Giả thiết H :
0
=26
- Đối thi t H : ế
1
≠26
Giải
+ Bước 1:
Giả thiết
26:
0
H
Đối thiết
+ Bước 2: Xác định hàm tiêu chuẩn
16/2.5
26
x
t
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đố nên ta tra α=0.0i thiết 2 phía và hàm tiêu chuẩn t 25 phân vị của
phân ph Student v i 15 b do, tra b ng ho ối ớ ậc tự ả ặc Excel:
=TINV(0.05,15)=2.13
+Bướ ịc 4: Xác đ nh miên bác bỏ
S={(X , X ): |t|>2.13}
1 2
, …, X
n
9
+Bước 5: Dựa vào mẫu tính
56.27x
và
2.1
16/2.5
2656.27
/
0
ns
x
t
+Bướ ĩc 6: Vì |t|=1.2 < t
α/2,15
=2.13 nên ta chấp nhận giả ế thi t H ngh
0
a là
chấp nh n giá tr =26. ậ ị TB μ
Dạng 2. Đối thiết 1 phía l ớn hơn
Giả thiết
00
:
H
Đối thiết
01
:
H
Ví dụ 5:
GS X~N(
,
2
) với chưa biết,
2
chưa biết, n=16, TB m u ẫ
12.29x
,
s=5.2 . V i m =0.05, hãy ki nh bài toán sau: ớ ức ý nghĩa ểm đị
- Giả thiết H :
0
=26
- Đối thi t H : ế
1
>26
- Giải
+ Bước 1:
- Giả thiết
26:
0
H
- Đối thi t ế
26:
1
H
+ Bước 2: Xác định hàm tiêu chuẩn
16/2.5
26
x
t
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 1 phía và hàm tiêu chuẩn t nên ta tra α=0.05 phân vị của phân
phối Student với 15 b do, tra b ng ho c Excel: ậc tự ả ặ
=TINV(0.10,15)=1.75
+Bướ ịc 4: Xác đ nh miên bác bỏ
S={(X
1
, X ): t>1.75}
2
, …, X
n
10
+Bước 5: Dựa vào mẫu tính
12.29x
và
4.2
16/2.5
2612.29
/
0
ns
x
t
+Bướ ỏc 6: Vì t=2.4 > t
α,15
=1.75 nên ta bác b giả ế thi t H
0
nghĩa là chấp
nhận giá trị TB μ >26.
Dạng 3. Đối thiết 1 phía nh ỏ hơn
Giả thiết
00
:
H
Đối thiết
01
:
H
Ví dụ 6:
GS X~N(
,
2
) với chưa biết,
2
chưa biết, n=16, TB m u ẫ
12.24x
,
s=5.2 . V i m =0.05, hãy ki nh bài toán sau: ớ ức ý nghĩa ểm đị
- Giả thiết H :
0
=26
- Đối thi t H : ế
1
<26
- Giải
+ Bước 1:
- Giả thiết
26:
0
H
- Đối thi t ế
26:
1
H
+ Bước 2: Xác định hàm tiêu chuẩn
16/2.5
26
x
t
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thi t 1 phía và hàm tiêu chuế ẩn t nên ta tra α=0.05 phân vị của phân
phối Student với 15 b do, tra b ng ho c Excel: ậc tự ả ặ
=TINV(0.10,15)=1.75
+Bướ ịc 4: Xác đ nh miên bác bỏ
S={(X , X ): t<-1.75}
1 2
, …, X
n
11
+Bước 5: Dựa vào mẫu tính
12.24x
và
4.2
16/2.5
2612.29
/
0
ns
x
t
+Bướ ỏc 6: Vì t=2.4 > t
α,15
=1.75 nên ta bác b giả ế thi t H
0
nghĩa là chấp
nhận giá trị TB μ >26.
Hàm tiêu chu n s d ng ẩ ử ụ ở đây là
.
0
nt
s
x
- Xuất phát từ mẫu đã cho ta tính
x
, s và
2
.
0
nt
s
x
- Với đã cho, tra bảng phân phối Student với n-1 bậc tự do ta tìm được
t
α/2,n-1
t hừ ệ thức
1,2/1 nn
tTP
, trong đó T
n-1
là biến ngẫu
nhiên Student v i n-1 b do. ớ ậc tự
So sánh t và t :
α/2,n-1
- Nếu
1,2/
n
tt
gi thi t H ta bác bỏ ả ế
0
- Nếu
1,2/
n
tt
p nh n gi thi . ta chấ ậ ả ết H
0
Như vậy miền tiêu chuẩn là:
.:),...,,(
1,2/21
0
ns
x
n
tnXXXS
3.A. 2. Đố ột phía: Xét BTKĐGT Hi thuyết m
0
:
=
0
v i thuyới đố ết
H
1
:
>
0
, v i m ớ ức ý nghĩa
cho trước.
1.N
ếu
2
đã biết
Các bướ ến hành như sau:c ti
- Xuất phát từ mẫu đã cho tính
x
và
n
x
z
/
0
- Tìm giá tr z( b ng sao cho ị ) từ ả ( z())=1-.
So sánh u và u( ):
- Nếu
)(
zz
ta bác bỏ H .
0
12
- Nếu
)(
zz
ta chấp nh n H . ậ
0
Như vậy miền tiêu chuẩn là:
.)(:),...,,(
0
21
znXXXS
x
n
2.N
ếu
2
chưa biết:
Trong trường hợp này ta phải giả thiết về tính chuẩn của biến ngẫu
nhiên X và n<30.
- Xuất phát từ mẫu đã cho ta tính
x
, s và
2
.
0
nt
s
x
- Với đã cho, tra bảng phân phối Student với n-1 bậc tự do ta tìm được
t
α,n-1
t hừ ệ thức
1,1 nn
tTP
, trong là bi n ng u nhiên đó T
n-1
ế ẫ
Student v -1 b do. ới n ậc tự
So sánh t và t :
α,n-1
- Nếu
1,
n
tt
ta bác bỏ gi thi t H ả ế
0
- Nếu
1,
n
tt
ta ch t Hấp nh n gi thiậ ả ế
0
.
Như vậy miền tiêu chuẩn là:
.:),...,,(
1,21
0
n
s
x
n
tnXXXS
Ví d
ụ 4. t, t, n=16, X~N( ). TB m u chưa biế chưa biế ,
2
ẫ
56.27x
,
S =5,2
2 2
. Với m =0.05, hãy ki nh bài toán sau: ức ý nghĩa ểm đị
- Giả thiết H :
0
=26
- t H 26 Đối thiế
1
: >
3. A. 3. Đố ột phía: Xét BTKĐGT Hi thuyết m
0
:
=
0
v i thuyới đố ết
H
1
:
<
0
, v i m ớ ức ý nghĩa
cho trước.
1.N
ếu
2
đã biết
Các bướ ến hành như sau:c ti
- Xuất phát từ mẫu đã cho tính
x
và
n
x
z
/
0
- Tìm giá tr z( b ng sao cho ị ) từ ả ( z())=1-.
So sánh z và z( ):
- Nếu
)(
zz
ta bác bỏ H .
0
- Nếu
)(
zz
ta chấp nh n H . ậ
0
13
Như vậy miền tiêu chuẩn là:
.)(:),...,,(
0
21
znXXXS
x
n
2.N
ếu
2
chưa biết:
Trong trường hợp này ta phải giả ế thi t về tính chuẩn của biến ngẫu
nhiên X và c m u n<30. ỡ ẫ
- Xuất phát từ mẫu đã cho ta tính
x
, s và
2
.
0
nt
s
x
- Với đã cho, tra bảng phân phối Student với n-1 bậc tự do ta tìm được
t
α,n-1
t hừ ệ thức
1,1 nn
tTP
, trong đó T
n-1
là biến ngẫu nhiên
Student v -1 b do. ới n ậc tự
So sánh t và t :
α,n-1
- Nếu
1,
n
tt
ta bác bỏ gi thi t H ả ế
0
- Nếu
1,
n
tt
ta ch t Hấp nh n gi thiậ ả ế
0
.
Như vậy miền tiêu chuẩn là:
.:),...,,(
1,21
0
n
s
x
n
tnXXXS
Bài t p ậ
Giả s ta có m u ng u nhiên c n=10 v i các giá tr m u: ử ẫ ẫ ỡ ớ ị ẫ
6.5; 5; 5.5; 8; 6.5; 10; 10; 8; 6.5; 7
Giả thiết m u t bnn chu n. Hãy ki nh gi t v i mẫ ừ ẩ ểm đị ả thiế ớ ức ý
nghĩa α=5%:
H
0
: µ = 7;
H
1
: µ > 7.
a) Giả s =2; ử đã biết phương sai lý thuyết σ
0
b) Giả thiết chưa biết phương sai.
14
Bài 8.2. Kiểm định giả thi t l ết về ỷ ệ
Giả s , X ) là m u ng ử (X
1 2
, …, X
n
ẫ ẫu nhiên, trong đó:
Acókhôngkhi
Acókhi
X
i
0
1
, p=P(A)
Như vậy, P(X =1)=P(A)=p, P(X -p=q.
i i
=0)=P(A)=1
Khi đó, nếu đặt
n
i
i
pnBmthìXm
1
),(;
Nếu n l n (n 30), và min(m, n- 5, thì ớ m)
XX
n
i
i
nn
m
1
1
, có phân
phối x p xấ ỉ chu n. Lý luẩ ận tương tự tương tự trường hợp 3.A. Ta nhận
được các mi n tiêu chu ki nh gi thuy t H : p=p về ẩn để ểm đị ả ế
0 0
ới các đối
thiết pp
0
, p>p , p<p m
0 0
ức ý nghĩa tương ứng như sau:
)2/(;::
)1(
/
0100
00
0
znSppHvàppH
pp
pnm
)(;::
)1(
/
0100
00
0
znSppHvàppH
pp
pnm
)(;::
)1(
/
0100
00
0
znSppHvàppH
pp
pnm
Ví dụ: p =45%, n=200, m=80, =5%, xem d
0
ự đoán có đúng không?
Giải
+ Bước 1:
- Giả thiết H
0
: p=0.45
- Đối thi t H : pế
1
0.45
+ Bước 2: Vì np
0
=90, và n(1-p
0
)=110 nên ta có hàm tiêu chuẩn:
200/55.0*45.0
45.0
/
00
0
p
nqp
pp
z
15
+ Bướ ới α=0.05 và hàm zc 3: v -tiêu chuẩn ở bước 2, dang BT 1 ta tra
z
α/2
=z
0.025
=1.96.
+ Bước 4:
96.1
)1(
/
00
0
nS
pp
pnm
+ Bước 5:
42.1200
55.045.0
45.0
200
80
x
z
+ Bước 6 : Kiểm tra ta thấy |z|=1.42<z =1.96.
/2
Kết lu t Hận: Ch p nh n gi ấ ậ ả thiế
0
.
Bài 3. Phương pháp p-giá trị
Các k nh ỹ thuật mà ta đã kiểm đị ở các tiết trước được gọi là phương
pháp ki nh truy n th ng. Trong m c này chúng ta sểm đị ề ố ụ ẽ trình bày một phương
pháp khác hi c các nhà th ng kê s d ng khá r ng rãi gện đượ ố ử ụ ộ ọi là phương pháp
p-giá tr . ị
Xét bài toán kiểm định:
- Giả thiết H :
0
=
0
- Đối thi t H : ế
1
<
0
Các s u m u cho ta giá tr c a n, ố liệ ẫ ị ủ
0
xX
và S. Ta mu n ki nh ố ểm đị
xem s H hay không? ố liệu đã cho có cho phép ta bác bỏ
0
Ta lý luận b ng ph n ch ng: Gi s H , ta hãy tính xem xác su ằ ả ứ ả ử
0
là đúng ất để
trung bình mẫu bé hơn hay bằ quan sát đượng giá trị c
0
x
b ng bao nhiêu. ằ
Nếu xác su bác b H , do theo ất này “nhỏ” theo một nghĩa nào đó, ta sẽ ỏ
0
nguyên lý xác su t nh , bi n c y ra trong m t phép th . N u xác ấ ỏ ế ố đó rất ít xả ộ ử ế
suất đó khá “lớn” thì ta không có cơ sở để bác bỏ H .
0
Giá trị c a xác su t này ủ ấ
0
xXPp
(tính trong điều ki n H ệ
0
đúng), được gọi là p-giá trị.
Tương tự, đối với bài toán ki nh: ểm đị
- Giả thiết H :
0
=
0
- Đối thi t H : ế
1
>
0
Thì p-giá tr ị là xác suất
0
xXPp
, tính dưới giả thiết H
0
đúng.
Còn với bài toán ki nh 2 phía: ểm đị
- Giả thiết H :
0
=
0
- Đối thi t H : ế
1

0
Thì p-giá tr ng h p ki nh 2 phía này g -giá tr trong ị trong trườ ợ ểm đị ấp đôi p ị
trườ ợng h p 1 phía, tức là:
16
0
2 xXPp
n u ế
00
xXPxXP
,
và ngược lại:
0
2 xXPp
n u ế
00
xXPxXP
,
p-giá tr ng kê s d ng theo 2 cách. M t s i chị được các nhà thố ử ụ ộ ố ngườ ỉ đơn
thuần tính p-giá tr , còn vi bác b gi thi l nhà ị ệc có ỏ ả ết H
0
hay không thì để ại cho
quản lý t quyự ết định l ấy.
Khi làm như vậy, nhà thống kê có một số ng d hướ ẫn chung như sau:
- Nếu p>0.05, ta không đủ cơ sở để bác b H . ỏ
0
- Nếu 0.01<p<0.05, ta có đủ cơ sở để bác bỏ H .
0
- Nếu p<0.01, ta có m r t m nh, hùng h bác b H . ột cơ sở ấ ạ ồn để ỏ
0
Cách th 2 là s d ng p-giá tr k t h p v i m ứ ử ụ ị ế ợ ớ ức ý nghĩa đã cho.
Ta tính p-giá tr và so sánh nó v : ị ới
Nếu
05.0p
, ta bác b H . ỏ
0
Nếu p> bác b H . Nói cách khác: p-giá tr chính là , ta chưa có cơ sở ỏ
0
ị
mức ý nghĩa thấp nhất mà ta có thể bác bỏ H .
0
Ví dụ 15. T m p h p chính có trung bình i ta lừ ột tậ ợ (chưa biết), ngườ ấy
ra m t mộ ẫu kích thước n=36 và tính được
5040x
và S=780. S ử
dụng phương pháp p-giá trị, hãy kiểm định:
- Giả thiết H :
0
=4700
- Đối thi t H : ế
1
>4700
Mức ý nghĩa =0.02.
Giải. Ta tính p-giá tr ị
5040XP
.
Dưới giả thiết H , vì n=36>30,
0
X
là BNN có x i chu i kấp x phân phỉ ố ẩn vớ ỳ
vọng là 4700 và độ lệch chuẩn là:
130
36
780
n
S
Vậy
)62.2(1)(1504015040
130
47005040
XPXP
= 1-0.9956=0.0044.
Vậy p-giá tr là 0.0044. Giá tr này nh =0.02. V y ta bác b ị ị ỏ hơn mức ý nghĩa ậ ỏ
H
0
và ch p nh n H . ấ ậ
1
Ví dụ 16. T m p h p chính có trung bình i ta lừ ột tậ ợ (chưa biết), ngườ ấy
ra m t m c n=140 ộ ẫu kích thướ và tính được
5.18x
và S=6.8. Với
mức ý nghĩa ểm đị=0.05, hãy ki nh:
17
- Giả thiết H :
0
=19.4
- Đối thi t H : ế
1
<19.4
Giải. Ta tính p-giá tr ị
5.18XP
.
Dưới giả thiết H , vì n=140>30,
0
X
là BNN có x i kấp x phân ph i chu n vỉ ố ẩ ớ ỳ
vọng là 19.4 l ch chu n là: và độ ệ ẩ
575.0
140
8.6
n
S
Vậy
0582.0)57.1()(5.18
575.0
4.
195.18
XP
Vậy p-giá tr là 0.0582. Giá tr này l n =0.05. V y ta không ị ị ớ hơn mức ý nghĩa ậ
có cơ sở bác bỏ H .
0
Ví dụ 19. nh sát giao thông cho r ng 80 i lái xe trên Cơ quan cả ằ % số ngườ
đườ ngường là có bằng lái. Kiểm tra ngẫu nhiên 200 i lái xe, cảnh sát giao thông
th liấy ch có 150 i có b ng lái xe. Sỉ ngườ ằ ố ệu này có ch ng t t l ứ ỏ ỷ ệ người có
bằng lái xe thấp hơn 80% hay không?
Dùng phương pháp p-giá tr v i m =2%. ị ớ ức ý nghĩa
Giải
- Giả thiết H
0
: p=0.8
- Đối thi t Hế
1
: p<0.8
Ta có n=200; m=150; f=150/200=0.75.
Vì np
0
=200x0.6=160>10
n 0>10 (1-p 200x0.2
0
)= =4
Nên f có phân b x p x n v v ng là 0.8 l n là ố ấ ỉ chuẩ ới kỳ ọ và độ ệch chuẩ
028.0
200
2.08.0
200
)1(
00
x
pp
.
Khi đó p-giá tr ị là:
03705.0)786.1()(75.0
028.0
8.075.0
fPp
.
Ta nhận th y p-giá tr l n =0.02. V y ta ch p nh n ấ ị ớ hơn mức ý nghĩa ậ ấ ậ
H
0
. T l i có b ng lái xe thỷ ệ ngườ ằ ực tế là 80%.
Bài 4. Kiểm định gi thi ả ết
về giá tr c a nhi u xác su t ị ủ ề ấ
Giả s B , B là h n c cử
1 2
, …, B
k
ọ các biế ố đôi 1 xung khắc và đầy đủ ủa
không gian m u S c a phép th ng u nhiên E. i xác suẫ ủ ử ẫ Ta quan tâm tớ ất (chưa
biết) của các bi n c B nh là: ế ố
i
, i=1, 2, …, k này. Bài toán kiểm đị
-Giả thiết H : (P(B ), P(B
0 1 2
), …, P(B
k
))=(p
1
, p
2
, …, p
k
).
-Đối thi : (P(Bết H
1 1
), P(B
2
), …, P(B
k
)) (p
1
, p
2
, …, p
k
).
18
Trong đó 0<p
i
<1 và p =1.
1
+p
2
+…+p
k
Tiến hành phép th E n-l p, gi s có n l n x y ra bi n c Bử ần độc lậ ả ử
i
ầ ả ế ố
i
(i=1, 2,
…, k), n
1
+n
2
+…+n
k
=n.
Ta biểu di n k b ng t n s ễ ết quả ởi bả ầ ố sau:
Biến c ố
B
1
B
2
…
B
k
Tổng
Tần s quan sát ố
n
1
n
2
…
n
k
n
Các s ố
ki
npn
ii
,...,2,1,
n s lý thuy u gi được gọi là tầ ố ết. Nế ả
thiết H t s
0
g thì theo luđún ậ ố lớn
i
n
và n x p x nhau.
i
ấ ỉ
Ta sẽ bác b gi t H khi các t n s n s lý thuyỏ ả thiế
0
ầ ố quan sát “khác xa” các tầ ố ết
theo 1 nghĩa nào đó. t đư Khoả ếng cách giữa các tần s quan sát và lý thuyố ợc
đo bở ống kê “Khi ình phương”:i tiêu chuẩn th -b
k
i
n
nn
i
ii
T
1
)(
2
Ta sẽ bác b H khi T l n m n bác b H s có d ng: ỏ
0
ớ ột cách có ý nghĩa. Miề ỏ
0
ẽ ạ
={T>c}, ng s ph thu c mở đây, c là một hằ ố ụ ộ ức đã chọn.
Người ta chứng minh đượ đúng và nếc rằng nếu giả thiết H
0
u các tần số lý
thuyết
kin
i
,...,2,1,5
thì T s i x i ẽ có phân phố ấp x phân phỉ ố
2
với k-1 b do. Tra b ng phân phậc tự ả ối
2
với k-1 b do ta s tìm ậc tự ẽ
được
)(
2
1
k
thỏa mãn:
)}({
2
1k
TP
.
Như vậy
)(
2
1
k
c
là phân v i ị m c a phân phức ủ ố
2
với
k-1 b do. ậc tự
Ví dụ: Gieo 1 con xúc x n. S l n xu n các m c cho b ng ắc 600 lầ ố ầ ất hiệ ặt đượ ởi bả
sau:
1
2
3
4
5
6
Tổng
106
92
97
105
88
112
600
19
Có thể coi con xúc x ng chắc đó là cân đối, đồ ất được không? Mức ý nghĩa là
0.05.
Giải
Tần s lý thuyố ết:
1
2
3
4
5
6
Tổng
100
100
100
100
100
100
600
Tính tiêu chuẩn th ống kê “Khi-bình phương”:
22.4
100
)100112(
100
)10088(
100
)100105(
100
)10097(
100
)10092(
100
)100106(
222
222
T
Tra bảng phân ph ối
0705.
11)05.0()(
2
16
2
1
k
c
So sánh: T=4.22<11.0705
Bài 8.5. Kiểm định giả thi ết về phương sai
20
Giả s ng ng u nhiên có phân b chu n ử X là đại lượ ẫ ố ẩ
N(
,
2
). Tập h p chính p t các gi có th c a X. Xét mợ ở đây là tậ ất cả ả trị ể ủ ột
m
ẫu ng u nhiên c sai m u S là m ng ẫ ỡ n. Như ta đã biết, phương ẫ
2
ột ước lượ
không ch c p h p chính.
ệch cho phương sai
2
ủa tậ ợ
Bây gi ta xét bài toán ki nh gi ờ ểm đị ả thiết:
Trường hợp 1:
-
Giả thiết H :
0
2
=
0
2
-
Đối thi t H : ế
1
2
<
0
2
Tính
2
2
0
( 1)
2
n S
,
2
i Khi bình có phân phố – phương với
n-1 b do. D a vào m , ta tra b ng giá tr ậc tự ự ức ý nghĩa ả ị
)1(
2
1
n
c
.
So sánh T với
)1(
2
1
n
c
, n u: ế
-
)1(
2
1
n
cT
: Bác bỏ H .
0
-
2 2
1
(1 )
n
c
: Chấp nh n H ậ
0.
Trường hợp 2:
-
Giả thiết H :
0
2
=
0
2
-
Đối thi t H : ế
1
2
>
0
2
Tính
2
0
2
)1(
Sn
T
, T có phân ph i Khi i n-1 ố – bình phương vớ
bậc tự do. D a vào m , ta tra b ng giá tr ự ức ý nghĩa ả ị
)(
2
1
n
c
.
So sánh T với
)(
2
1
n
c
, n u: ế
-
)(
2
1
n
cT
: Bác bỏ H .
0
21
-
)(
2
1
n
cT
: Chấp nh n H ậ
0.
Trường hợp 3:
-
Giả thiết H :
0
2
=
0
2
-
Đối thi t H : ế
1
2

0
2
Tính
2
0
2
)1(
Sn
T
, T có phân ph i Khi i n-1 ố – bình phương vớ
bậc tự do. D a vào m , ta tra b ng giá tr ự ức ý nghĩa ả ị
)2/(
)2/1(
2
12
2
11
n
n
c
c
.
So sánh T với
)2/(
)2/1(
2
12
2
11
n
n
c
c
, n u: ế
-
)2/1(
2
11
n
cT
hoặc
)2/(
2
12
n
cT
: Bác bỏ
H
0
.
-
)2/()2/1(
2
12
2
11
nn
cTc
: Chấp
nhận H
0.
22
Ví dụ:
-
Giả thiết H :
0
2
=0.2
2
-
Đối thi t H : ế
1
2
>0.2
2
S=0.3, n=12, =0.2, =5%.
0
Tính
)
05.0(67514.1975.24
2
11
2.0
3.0)112()1(
2
2
2
0
2
xSn
T
Vậy, ta bác b gi thi t H , ỏ ả ế
0
chấp nh t H . ận đối thiế
1
Bài 8.6. So sánh hai giá trị trung bình
Giả s ta có hai m u ng u nhiên ử ẫ ẫ
)...,,,(
1
21 n
XXX
rút ra t bi n ngừ ế ẫu
nhiên XF
1
(x),
)...,,,(
2
21 n
YYY
rút ra từ bi n ng u nhiên Y (y) ế ẫ F
2
Bài toán đặt ra là: ki m tra xem hai m u trên có phể ẫ ải được rút ra từ
một phân phối hay không, t ức là:
)()()()(
2121
xFxFhayxFxF
.
Trong m ục này ta xét bài toán đơn giản hơn là so sánh hai giá trị
EX và EY.
Ký hiệu
DYDX
EYEX
2
2
2
121
,,,
Giả thiết H : t H :
0
1
=
2
, đối thiế
1
1

2.
1.Nếu
2
2
2
1
,
t đã biế
Trong trường hợp này ta cần phải giả thiết ho c X và Y có phân ặ
phối chu n ho c m u n , nẩ ặ ẫ
1 2
đủ lớn (n 30, n 30). Lý lu
1
2
ận tương tự ta
được các miền tiêu chuẩn mức ý nghĩa tương ứng như sau:
2/211210
2
2
2
1
2
1
||;::
zzSHvàH
nn
yx
2/211210
2
2
2
1
2
1
;::
zzSHvàH
nn
yx
23
2/211210
2
2
2
1
2
1
;::
zzSHvàH
nn
yx
Ví d 1. GS t hai t p h p chính có phân b chu n X và Y ta l y hai mụ ừ ậ ợ ố ẩ ấ ẫu
độ ớc lập v i cỡ m ng là n =40 và n =50. Trung bình mẫu tương ứ
1 2
ẫu tính
được là
140,130 yx
.
GS E(X)=
μ
1
(chưa biết)
, biết V(X)=σ
1
2
=80.
GS E(Y)=
μ
2
(chưa biết)
, biết V(Y)=σ
2
2
=100.
Với m nh bài toán : ức ý nghĩa α=1%, kiểm đị
- t H Giả thiế
0
: μ
1
=μ
2
- t H Đối thiế
1
: μ
1
≠μ
2
Giải
Ta có
5
50
100
40
80
140130
T
Với α=1%, ta có u
α/2
=2.576.
Vì |T|=5>2.576, nên ta b gi thi . ác bỏ ả ết H
0
Ví dụ 2. V i m nh gi t sau : ớ ức ý nghĩa α=5% hãy kiểm đị ả thiế
a) - t H Giả thiế
0
: μ
1
=μ
2
- Đối thi t Hế
1
: μ
1
>μ
2
Với số liệu như sau :
256;105;
98;105;32;50
2
2
2
121
yxnn
b) - t H Giả thiế
0
: μ
1
=μ
2
- Đối thi t Hế
1
: μ
1
<μ
2
Với số liệu như sau :
64
;36;25;20;35;25
2
2
2
121
yxnn
Giải
a)
203.2
32
256
50
105
98
105
T
Do T=2.203>u
α
=1.645, nên ta bác b gi thi t H . ỏ ả ế
0
b)
24
77.2
35
64
25
36
2520
T
Do T=-2.77<-z
α
=-1.645, nên ta bác b gi . ỏ ả thiết H
0
2. N u ế
2
2
2
1
,
chưa biết nhưng mẫu l n (n >30, nớ
1 2
>30), trong trường hợp
này ta v n v n d ng test thẫ ậ ụ ống kê như trong phần 1. trong đó các phương sai
chưa biết
2
2
2
1
,
c thay b u: trong T đượ ởi các phương sai mẫ
2
2
2
1
,SS
. Như vậ ống kê đượ đây là: y test th c dùng ở
2
2
2
1
2
1
n
S
n
S
yx
T
Khi n , n nh lý gi i h n trung tâm, T có phân b x p x phân b
1 2
>30 thì theo đị ớ ạ ố ấ ỉ ố
chuẩn t c cho dù X và Y không có phân b chu n. ắ ố ẩ
Ví d ụ 3. Người ta ti n hành m t cu c nghiên c u v ế ộ ộ ứ ề điểm trung bình c a các v n ủ ậ
động viên th dể ục năm 1970 và năm 1995. Một m u gẫ ồm 35 VĐV của năm 1970
có số điểm trung bình là 267 v l ch tiêu chu n là 27. M u g m 40 với độ ệ ẩ ột mẫ ồ ận
độ điểng viên của năm 1995 có số m trung bình là 255 v lới độ ệch tiêu chuẩn là
30. Ki nh xem có s khác nhau hay không gi a hai th h v ng viên ểm đị ự ữ ế ệ ận độ
của năm 1970 và 1995? Mức ý nghĩa α=5%.
Giải
Bài toán ki nh là: ểm đị
- t H Giả thiế
0
: μ
1
=μ
2
- t H Đối thiế
1
: μ
1
≠μ
2
Ta có
823.1
40
2
30
35
2
27
255267
T
Do T=1.823<z =1.96, nên ta ch p nh n H . V kh nh
α/2
ấ ậ
0
ậy không có cơ sở để ẳng đị
có sự khác nhau gi a hai th h v ng viên. ữ ế ệ ận độ
3.Nếu
2
2
2
1
,
t m u nh <30, n <30) chưa biế ẫ ỏ (n
1 2
Trong trường h p này ta ph thi t ợ ải giả ế
25
).
,();,(
2
2
2
1
NYNX
Các bước làm như sau:
- Xuất phát từ hai mẫu đã cho ta tính
22
,,,
yx
ssyx
.
- Tính
21
21
2
21
2
)1
2
(
2
)1
1
(
.
nn
nn
nn
y
sn
x
sn
yx
t
- Với đã cho, tra bả ối Student tìm đượng phân ph c
)2/(
2
21
nn
t
hoặc
)(
2
21
nn
t
. Các mi n tiêu chu ề ẩn như sau:
)2/(;::
2211210
21
nn
ttSHvàH
)(;::
2211210
21
nn
ttSHvàH
)(;::
2211210
21
nn
ttSHvàH
Ví d M ng v i 2 ụ 5. Cơ quan hàng không vụ trụ ỹ (NASA) đã ký hợp đồ ớ
công ty A và B s n xu pin dùng cho v tinh vi n thông. ả ất thử ệ ễ
Dựa trên k t qu c a các pin th nghi m, NASA s quy nh ch n công ế ả ủ ử ệ ẽ ết đị ọ
ty nào làm nhà cung c p pin cho v tinh vi sấ ệ ễn thông. Công ty A đã ản
xuất thử được 10 chi c, có tuế ổi th l ch tiêu ọ trung bình là 4.8 năm và độ ệ
chuẩn là 1.1 năm. Công ty B sản xu t th ấ ử được 12 chi c, v i tu i th trung ế ớ ổ ọ
bình 4.3 năm và độ ẩn là 0.9 năm. lệch tiêu chu
GS r ng tu i th c a pin do A và B cung c p có phân b chu n và ằ ổ ọ ủ ấ ố ẩ
phương sai như nhau. V i m nh xem có s ớ ức ý nghĩa α=1%, kiểm đị ự
khác nhau v i th trung bình c i pin hay không? ề tuổ ọ ủa 2 loạ
Giải
Bài toán ki nh là: ểm đị
- t H Giả thiế
0
: μ
1
=μ
2
26
- t H Đối thiế
1
: μ
1
≠μ
2
Các s ố liệu đã cho như sau:
Công ty A:
1.1;8.4;
10
11
sxn
.
Công ty B:
9.0;3.4;
12
22
syn
.
Phương sai chung của ước lượng là:
99.0
20
8.19
21210
)9.0)(112()1.1)(110(
2
22
s
.
Vậy
174.1
426
.0
5.0
)(99.0
3.48.4
12
1
10
1
T
Tra b ng phân ph i Student 1-0.005 phân v v i 20 b c tả ố ị ớ ậ ự do ta được
2.845.
Do |T|<2.845, nên ta không đủ cơ sở bác bỏ H .
0
4.Khoảng tin c y cho hi u s : ậ ệ ố μ
1
-μ
2
Khi bài toán kiểm định dẫn tới bác bỏ H , ta d
0
ẫn tới bài toán tìm khoảng tin cậy
cho hiệu s . ố μ
1
-μ
2
Trong trường h p ợ
2
2
2
1
,
ng BNN đã biết, có thể chứng minh được rằ
2
2
2
1
2
1
21
)(
nn
yx
T
Có phân b n t ng tin c u s ố chuẩ ắc N(0, 1). Khi đó, khoả ậy γ cho hiệ ố μ
1
-μ
2
là:
2
2
2
1
2
1
2/
nn
uyx
Trong trườ ợng h p
2
2
2
1
,
u l n chưa biết nhưng mẫ ớ
(n
1
, n >30) ta thay
2
2
2
2
1
,
bởi
2
2
2
1
, SS
và nh c kho ng tin c y x p x ận đượ ả ậ ấ ỉ γ:
2
2
2
1
2
1
2/
n
S
n
S
uyx
Và không cần gi thi t 2 t p chính có phân b n. ả ế ậ ố chuẩ
5.Phương pháp so sánh từng cặp:
27
Giả s p g ng ng u nhiên (nói chung phử (X, Y) là một cặ ồm hai đại lượ ẫ ụ thuộc
nhau), v . ới E(X)=μ
1
, E(Y)=μ
2
Chúng ta cần so sánh . μ
1
và μ
2
Xét D=X -Y, khi đó ta đưa BT so sánh về ểm đị BT ki nh về giá trị TB.
Bài 8.7. So sánh hai tỷ l ệ
Xét hai tập h p chính I và II và m i cá th cợ ột đặc tính A nào đó mà mỗ ể ủa hai
tập chính đó thể có hay không. Ta muốn so sánh tỷ lệ cá thể có đặc tính A của
tập chính I với tỷ l cá th c tính A c p chính II. ệ ể có đặ ủa tậ
Giả s u ng u nhiên ử ta có hai mẫ ẫ
)...,,,(
1
21 n
XXX
trong đó
1
1
1111
,1)0(,)1(
n
i
iii
XmpqXPpXP
Và m u ẫ
)...,,,(
2
21 n
YYY
trong đó
2
1
2222
,1)0(,)1(
n
j
jjj
YmpqYPpYP
Giả thiết H : p t H : p
0 1
=p
2
i thiđố ế
1 1
p
2
, p , p
1
>p
2 1
<p
2
Vì EX , EY , DX ), DY ) nên so sánh hai xác su t p , p
i
=p
1 j
=p
2 i
=p
1
(1-p
1 j
=p
2
(1-p
2
ấ
1 2
chính là so sánh hai giá trị trung bình v t. Nới phương sai chưa biế ếu H
0
đúng thì
DX
i
=DY
j
=
2
. Khi đó
).()(
21
11
2
nn
YXD
Ướ ợ
c lư ng của
2
)1.(
21
21
21
21
nn
mm
nn
mm
ĐK áp dụng: m 10 và n - m 10.
1
+m
2
1
+n
2 1
-m
2
Với n , n l n ta x p x phân ph
1 2
đủ ớ ấ ỉ ối
)( YXV
YX
T
b xởi phân phối ấp x ỉ
chuẩn N(0, 1).
Từ đó ta nhận được các tiêu chuẩn mức tương ứng như sau:
.
21
21
21
2121
21
21
2
2
1
1
.
nn
nn
nn
mmnn
nn
mm
n
m
n
m
u
28
Nếu H
0
: p
1
=p
2
, H
1
: p
1
p
2
thì S=|u| u( /2)
Nếu H
0
: p
1
=p
2
, H
1
: p
1
>p
2
thì S=uu()
Nếu H
0
: p
1
=p
2
, H
1
: p
1
<p
2
thì S=u-u()
Ví d 15. Công ty Coca- i ti n s n ph m. V i công thụ cola đang n/c cả ế ả ẩ ớ ức cũ khi
cho 500 ngườ thì có 120 người ưai dùng thử thích. Với công thức mới khi cho
1000 ngườ ời ưa thích. i khác dùng thử thì có 300 ngư
Với m =2%, ki nh xem công th c mức ý nghĩa ểm đị ứ ới đưa vào có làm tăng tỷ
lệ người ưa thích hay không?
Giải
H
0
: p
1
=p
2
, H
1
: p
1
>p
2
.4.2
5001000
50001000
5001000
1203005001000
5001000
120300
500
120
1000
300
21
21
21
2121
21
21
2
2
1
1
..
.
x
nn
nn
nn
mmnn
nn
mm
n
m
n
m
u
u
=u
0.02
=2.054
Do u>u =2.054, nên ta bác b H .
ỏ
0
Giả s X và Y là 2 BNN có phân b n, ử ố chuẩ
),(~
2
11
NX
,
),(~
2
22
NY
,
Chúng ta cần so sánh và d p c a X và Y. μ
1
μ
2
ựa trên 2 mẫu quan sát độc lậ ủ
| 1/28

Tài liệu khác của Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Preview text:

CHƯƠNG 8. KIỂM ĐỊNH GIẢ THIẾT THỐNG KÊ
8.1. Kiểm định giả thiết về giá trị trung bình
8.2. Kiểm định giả thiết về tỷ lệ
8.3. Kiểm định giả thiết cho phương sa i
8.4. So sánh hai giá trị trung bìn h 8.5. So sánh hai tỷ lệ
8.6. So sánh hai phương sai 2  8.7. Tiêu chuẩn phù hợp
8.8. Kiểm tra tính độc lập và so sánh nhiều tỷ lệ
8.9. So sánh nhiều giá trị trung bình: phân tích phương sai một nhân tố
Bài 8.1. Kiểm định giả thiết về giá trị trung bình I. Nguyên lý chung:
Bài toán kiểm định giả thiết thống kê là bài toán: căn cứ vào các số liệu
thống kê cần phải đưa ra kết luận về một giả thiết thống kê nào đó mà ta quan tâm.
Một giả thiết thống kê là một giả thiết về phân bố xác suất của tập chính đang
xét. Nếu phân bố xác suất đó được đặc trưng bởi các tham số (như XÁC SUẤT
(tỷ lệ), giá trị trung bình hay phương sai, …), thì giả thiết thống kê là giả thiết
về tham số của phân bố đó.
Từ nay trở đi ta sẽ hiểu một giả thiết là một giả thiết thống kê, một quy
tắc dẫn tới quyết định chấp nhận hay bác bỏ giả thiết đã nêu gọi là một kiểm định (test) thống kê.
Giả thiết đưa ra kiểm định được ký hiệu H0, đó là giả thiết mà ta nghi
ngờ. Đối lập với giả thiết H0 là đối thiết H1. Chấp nhận H0 nghĩa là bác bỏ H1,
ngược lại, bác bỏ H0 nghĩa là chấp nhận H1.
Câu hỏi đặt ra là: Chúng ta chấp nhận hay bác bỏ một giả thiết bằng
cách nào? Để đưa ra quy tắc kiểm định, các nhà thống kê đều nhất trí với nhau nguyên lý sau đây:
“Nếu một biến cố có xác suất rất nhỏ thì trong một phép thử hay một
vài phép thử, biến cố đó sẽ không xảy ra”.
Như vậy, chúng ta sẽ bác bỏ H0 nếu xuất hiện biến cố có xác suất nhỏ,
tính trong điều kiện giả th ế i t H0 đúng.
Chúng ta sẽ minh họa bởi các ví dụ sau:
Ví dụ 1. Gieo một đồng tiền 100 lần ta thấy xuất hiện mặt sấp 60 lần. Ta nghi
ngờ rằng, xác suất xuất hiện mặt sấp lớn hơn xác suất xuất hiện mặt ngửa.
Gọi p là xác suất xuất hiện mặt sấp. Khi đó ta có bài toán kiểm định như sau: - Giả thiết H0: p=1/2 - Đối thiết H1: p>1/2 1 Ta tính   P S  6  p     P    100  0 5 . 0 6 . 0 5 . 0 (10( 6. 0 0 Q 5 . 0 x 5 . 0 /100 5 . 0 x 5 . 0 /100 0    Q ) 9 . 1 (  0 . 0 28717
Đây là một xác suất nhỏ, mà lại xảy ra trong một lần kiểm định. Vậy ta
bác bỏ H0, chấp nhận H1.
Ví dụ 2. Một cuộc nghiên cứu ở Mỹ cho biết trẻ em Mỹ ở độ tuổi đến
trường tiêu thụ trung bình 19.4 OZ sữa 1 ngày (1 OZ=28.35 g).
Trong một mẫu ngẫu nhiên gồm 140 trẻ em người ta tính được lượng
sữa chúng uống trung bình một ngày là 18.5 OZ với độ lệch tiêu chuẩn là 6.8
OZ. Điều này có cho phép ta kết luận là lượng sữa tiêu thụ ít hơn 19.4 OZ hay không? Giải
Gọi  là lượng sữa tiêu thụ trung bình trong 1 ngày. Ta đi đến bài toán
kiểm định giả thiết thống kê như sau: - Giả thiết H0: =19.4
- Đối thiết H1: <19.4
Giả sử H0 đúng, khi đó xác suất để trung bình mẫu X  18 5 . bằng bao nhiêu?
Do X có phân bố chuẩn (hoặc xấp xỉ chuẩn) với kỳ vọng là 19.4 và độ S 8 . 6   5 . 0 75 lệch chuẩn là n 140 . Vậy  P X  18  5 .   18 5 . 1  9 4 . P Z    P Z   5 . 1 7 5 . 0 75 .
Xác suất này không nhỏ lắm.
Vì vậy ta chưa có đủ cơ sở để bác bỏ giả thiết H0. Nói cách khác,
số liệu đã có chưa đủ cơ sở để bác bỏ giả thiết H0.
Trong khi đưa ra quyết định, chúng ta có thể phạm phải 1 trong 2 loại sai lầm sau:
- Sai lầm loại 1: Bác bỏ H0 trong khi thực ra H0 đúng
- Sai lầm loại 2: Chấp nhận H0 trong khi thực ra H0 sai.
Sai lầm loại 1, tương tự như sai lầm của quan tòa, khi “Kết án nhầm” người vô ộ
t i; còn sai lầm loại 2 tương tự như sai lầm “Tha bổng” kẻ có tội. 2
Chúng ta mong muốn làm cực tiểu cả 2 loại sai lầm trên, nhưng
khi đó chúng ta phải trả giá đắt về thời gian, tiền của và công sức.
Hơn nữa, khi ta giảm sai lầm loại này lại làm tăng sai lầm loại kia, và ngược lại.
Trong xã hội văn minh, người ta coi kết án nhầm người vô tội là
1 sai lầm nghiêm trọng hơn so với sai lầm tha bổng kẻ có tội.
Trong bài toán kiểm định cũng vậy, ta coi sai lầm loại 1 là
nghiêm trọng hơn sai lầm loại 2. Cho nên, người ta cố định trước sai lầm
loại 1. Xác suất mắc sai lầm loại 1 được gọi là mức ý nghĩa của tiêu
chuẩn, ký hiệu là . Xác suất mắc sai lầm loại 2 ký hiệu là . Giá trị 1-
được gọi là LỰC LƯỢNG của tiêu chuẩn. Lực lượng của tiêu chuẩn là
xác suất bác bỏ H0 khi H0 sai .
Mức ý nghĩa  của tiêu chuẩn thường được lấy là 0.05; 0.02 hoặc 0.01.
Trong tập các tiêu chuẩn có cùng mức ý nghĩa , tiêu chuẩn nào
có xác suất sai lầm loại 2 nhỏ nhất được xem là tiêu chuẩn “tốt nhất” .
Các tiêu chuẩn được đưa ra ở chương này đều đã được chứng
minh chặt chẽ về mặt toán học là các tiêu chuẩn tốt nhất.
Khi kiểm định thống kê dẫn tới chấp nhận H0 là một quyết định
dè dặt: Chấp nhận H0, không có nghĩa là H0 đúng, mà chỉ nên hiểu là với
các số liệu hiện có, không có đủ cơ sở để bác bỏ H0, cần phải nghiên cứu tiếp.
Các bước cần thiết trong việc giải một bài toán kiểm định giả thiết thống kê như sau:
1.Phát biểu giả thiết H0 và đối thiết H1
2.Chọn tiêu chuẩn (test) thống kê.
3.Định rõ mức ý nghĩa  (xác suất mắc sai lầm loại 1).
4.Chọn miền bác bỏ giả t i h ết H0.
5.Tính giá trị của tiêu chuẩn thống kê từ mẫu quan sát được.
6.Kết luận: Bác bỏ hay chấp nhận giả thiết, tùy thuộc vào việc
giá trị của tiêu chuẩn có rơi vào miền bác bỏ giả thiết hay không.
II. Kiểm định giả thiết về giá trị trung bình:
Giả sử (X1, X2, …, Xn) là mẫu ngẫu nhiên được rút từ biến ngẫu nhiên
chuẩn X có EX=, DX=2 (Nếu X không chuẩn thì n120). 3.A.1. Đối th ế
i t hai phía: Xét BTKĐGT
Giả thiết H0 : =0
Đối thiết H1: 
 0, với mức ý nghĩa  cho trước.
1.Nếu phương sai 2 = σ 2
0 đã biết Bài toán dạng 1:
Các bước tiến hành như sau: + Bước 1: H :   Giả thiết 0 0 3 H   Đối thiết :  1 0
+ Bước 2: Xác định hàm tiêu chuẩn x 0  z   n 0 /
+ Bước 3: Xác định mức ý nghĩa α
Do đối thiết 2 phía và hàm tiêu chuẩn z nên ta tra α/2 phân vị của phân
phối chuẩn tắc, tra bảng hoặc Excel: zα/2 =NORMSINV(1-α/2) α 10% 5% 2% 1% zα/2 1.645 1.96 2.326 2.576
+Bước 4: Xác định miền bác bỏ
S={(X1, X2, …, Xn):|z|>zα/2} x x z 0  để tín h +Bướ  c 5: Dựa vào TB mẫu / n 0
+Bước 6: Nếu |z|>zα/2 thì ta bác bỏ H0.
Nếu |z|<=zα/2 chấp nhận giả thiết H0.
Bài toán dạng 2:
Các bước tiến hành như sau: + Bước 1: H :   Giả thiết 0 0 H   Đối thiết :  1 0
+ Bước 2: Xác định hàm tiêu chuẩn x z   0/ n
+ Bước 3: Xác định mức ý nghĩa α
Do đối thiết 1 phía và hàm tiêu chuẩn z nên ta tra α phân vị của phân phối
chuẩn, tra bảng hoặc Excel: zα =NORMSINV(1-α) α 5% 2.5% 2% 1% 0.5% zα 1.645 1.96 2.054 2.326 2.576 4
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): z>zα} x0  x z tính  / n
+Bước 5: Dựa vào TB mẫu 0
+Bước 6: Nếu z>zα thì ta bác bỏ H0.
Nếu z<=zα chấp nhận giả thiết H0.
Ví dụ 2. Tập chính X có phân phối chuẩn với giá trị trung bình  chưa biết, 0 x  27 5 . 6 =5.2, n=25, TB mẫu
. Với mức ý nghĩa =0.05, hãy kiểm định bài toán sau: - Giả thiết H0: =26
- Đối thiết H1: ≠26. Giải
Các bước tiến hành như sau: + Bước 1: H :  26 Giả thiết 0   Đối thiết H : 26 1
+ Bước 2: Xác định hàm tiêu chuẩn 26  x z 5.2 / 25
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 2 phía và hàm tiêu chuẩn z nên ta tra α/2 phân vị của phân
phối chuẩn, tra bảng hoặc Excel: zα/2 =NORMSINV(1-α/2)=1.96
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): |z|>1.96} x  27 6 . và +Bước 5: Dựa vào mẫu x0 27 6 . 2  6 z    6 . 1  / 2 . 5 / 5 0 n +Bước 6:Vì |z|=1.6 5
Ví dụ 3. Tập chính X có phân phối chuẩn với giá trị tru g
n bình  chưa biết, 0 x  27 5 . 6 =5.2, n=25, TB mẫu
. Với mức ý nghĩa =0.05, hãy kiểm định bài toán sau: - Giả thiết H0: =26
- Đối thiết H1:  > 26. Giải
Các bước tiến hành như sau: + Bước 1: H :  26 Giả thiết 0   Đối thiết H : 26 1
+ Bước 2: Xác định hàm tiêu chuẩn 26  x z 5.2 / 25
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 1 phía và hàm tiêu chuẩn z nên ta tra α phân vị của phân phối
chuẩn, tra bảng hoặc Excel: zα =NORMSINV(1-α)=1.645
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): z>1.645} x  27 6 . và +Bước 5: Dựa vào mẫu x0 27 6 . 2  6 z    6 . 1  / 2 . 5 / 5 0 n +Bước 6:Vì z=1.6
Bài toán dạng 3:
Các bước tiến hành như sau: + Bước 1: H :   Giả thiết 0 0
Đối thiết H :    1 0
+ Bước 2: Xác định hàm tiêu chuẩn 6 x  z 0  0/ n
+ Bước 3: Xác định mức ý nghĩa α
Do đối thiết 1 phía và hàm tiêu chuẩn z nên ta tra α phân vị của phân phối
chuẩn, tra bảng hoặc Excel: =NORMSINV(1-α)
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): z<-zα} x0  x z và
+Bước 5: Dựa vào mẫu tính  / n 0
+Bước 6: Nếu z< - zα thì ta bác bỏ H0.
Nếu z=>- zα chấp nhận giả thiết H0.
Ví dụ 3. GS X~N(,2) với  chưa biết, =5.2, n=36, TB mẫu x  27 5
. 6 . Với mức ý nghĩa =0.05, hãy kiểm định bài toán sau: - Giả thiết H0: =29.64
- Đối thiết H1: <29.64 Giải + Bước 1: H :  29 6 . 4 Giả thiết 0
Đối thiết H :  29 6 . 4 1
+ Bước 2: Xác định hàm tiêu chuẩn 2 . 9 64  x z 5 2 . / 36
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 1 phía và hàm tiêu chuẩn z nên ta tra α=0.05 phân vị của phân
phối chuẩn, tra bảng hoặc Excel: =NORMSINV(1-0.05)=1.645
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): z<-1.645} x  27 5 . 6 và +Bước 5: Dựa vào mẫu tính x0 27 5 . 629 6 . 4 z     4 . 2  / n 2 . 5 / 36 0 7
+Bước 6: Vì z=-2.4 < zα=-1.645 nên ta bác bỏ giả thiết H0, chấp nhận đối
thiết H1, nghĩa là chấp nhận giá trị TB μ < 29.64.
2.Nếu 2 chưa biết:
Trong trường hợp này ta phải giả th ế
i t về tính chuẩn của biến ngẫu
nhiên X, cỡ mẫu nhỏ hơn 30.
Chúng ta có 3 dạng kiểm định:
Dạng 1. Đối thiết 2 phía H :   Giả thiết 0 0 H   Đối thiết :  1 0 x 0 t n.
Hàm tiêu chuẩn sử dụng ở đây là s
Với mức ý nghĩa α ta phải tra α/2 phân vị của phân phối Student n-1 bậc tự do: tα/2, n-1.
Nếu tra bằng Excel: tα/2, n-1=TINV(α, n-1).
Ví dụ 4. GS X~N(,2) với  chưa biết, 2 chưa biết, n=16, TB mẫu x  27 5
. 6 , s=5.2 . Với mức ý nghĩa =0.05, hãy kiểm định bài toán sau: - Giả thiết H0: =26 - Đối thiết H1: ≠26 Giải + Bước 1: H :  26 Giả thiết 0
Đối thiết H :  26 1
+ Bước 2: Xác định hàm tiêu chuẩn 26  x t 5 2 . / 16
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 2 phía và hàm tiêu chuẩn t nên ta tra α=0.025 phân vị của phân phối S
tudent với 15 bậc tự do, tra bảng hoặc Excel: =TINV(0.05,15)=2.13
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): |t|>2.13} 8 x  27 5 . 6 và +Bước 5: Dựa vào mẫu tính x 0 27 5 . 6 2  6 t    . 1 2 s / n 5 2 . / 16
+Bước 6: Vì |t|=1.2 < tα/2,15=2.13 nên ta chấp nhận giả th ế i t H0 nghĩa là
chấp nhận giá trị TB μ =26.
Dạng 2. Đối thiết 1 phía lớn hơn H :   Giả thiết 0 0
Đối thiết H :    1 0 Ví dụ 5:
GS X~N(,2) với  chưa biết, 2 chưa biết, n=16, TB mẫu x  29 1 . 2 ,
s=5.2 . Với mức ý nghĩa =0.05, hãy kiểm định bài toán sau: - Giả thiết H0: =26
- Đối thiết H1: >26 - Giải + Bước 1: H   - Giả thiết 0 : 26
- Đối thiết H :  26 1
+ Bước 2: Xác định hàm tiêu chuẩn 26  x t . 5 2/ 16
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 1 phía và hàm tiêu chuẩn t nên ta tra α=0.05 phân vị của phân
phối Student với 15 bậc tự do, tra bảng hoặc Excel: =TINV(0.10,15)=1.75
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): t>1.75} 9 x  29 1 . 2 và +Bước 5: Dựa vào mẫu tính x 0 29 1 . 226 t    . 2 4 s / n 5.2 / 16
+Bước 6: Vì t=2.4 > tα,15=1.75 nên ta bác bỏ giả th ế i t H0 nghĩa là chấp
nhận giá trị TB μ >26.
Dạng 3. Đối thiết 1 phía nhỏ hơn H :   Giả thiết 0 0
Đối thiết H :   1 0 Ví dụ 6:
GS X~N(,2) với  chưa biết, 2 chưa biết, n=16, TB mẫu x  24 1 . 2 ,
s=5.2 . Với mức ý nghĩa =0.05, hãy kiểm định bài toán sau: - Giả thiết H0: =26
- Đối thiết H1: <26 - Giải + Bước 1: H   - Giả thiết 0 : 26
- Đối thiết H :   26 1
+ Bước 2: Xác định hàm tiêu chuẩn 26  x t . 5 2/ 16
+ Bước 3: Xác định mức ý nghĩa α=0.05
Do đối thiết 1 phía và hàm tiêu chuẩn t nên ta tra α=0.05 phân vị của phân
phối Student với 15 bậc tự do, tra bảng hoặc Excel: =TINV(0.10,15)=1.75
+Bước 4: Xác định miên bác bỏ
S={(X1, X2, …, Xn): t<-1.75} 10 x  24 1 . 2 và +Bước 5: Dựa vào mẫu tính x 0 29 1 . 226 t    . 2 4 s / n 5.2 / 16
+Bước 6: Vì t=2.4 > tα,15=1.75 nên ta bác bỏ giả th ế i t H0 nghĩa là chấp
nhận giá trị TB μ >26. x 0
Hàm tiêu chuẩn sử dụng ở đây là t n. s x 0
- Xuất phát từ mẫu đã cho ta tính x , s2 và t n. s
- Với  đã cho, tra bảng phân phối Student với n-1 bậc tự do ta tìm được t P T  α/2,n-1 từ hệ thức  t n1 / 2,n     1
, trong đó Tn-1 là biến ngẫu
nhiên Student với n-1 bậc tự do. So sánh t và tα/2,n-1:
- Nếu t t / 2,n 1
 ta bác bỏ giả thiết H0
- Nếu t t / 2,
ta chấp nhận giả thiết H0 . n 1 
Như vậy miền tiêu chuẩn là:  x 0  S X X X n  (  , ,..., ) : t n sn  . 1 2 / 2, 1  
3.A. 2. Đối thuyết một phía: Xét BTKĐGT H0 : =0 với đối thuyết
H1: >0, với mức ý nghĩa   cho trước.
1.Nếu 2 đã biết
Các bước tiến hành như sau: x  z 0 
- Xuất phát từ mẫu đã cho tính x và  / n
- Tìm giá trị z() từ bảng sao cho ( z())=1-. So sánh u và u():
- Nếu z z ( )ta bác bỏ H0. 11
- Nếu z z ( )ta chấp nhận H0.
Như vậy miền tiêu chuẩn là: 
S  ( X , X ,..., Xn ) : x 0  n z( 1 2  ) .
2.Nếu 2 chưa biết:
Trong trường hợp này ta phải giả thiết về tính chuẩn của biến ngẫu nhiên X và n<30. x 0
- Xuất phát từ mẫu đã cho ta tính t n. x , s2 và s
- Với  đã cho, tra bảng phân phối Student với n-1 bậc tự do ta tìm được t P Tt  α,n-1 từ hệ thức
n1 ,n   1
, trong đó Tn-1 là biến ngẫu nhiên Student với - n 1 bậc tự do. So sánh t và tα,n-1:
- Nếu t t ,n 1
 ta bác bỏ giả thiết H0
- Nếu t t ,
ta chấp nhận giả thiết H n 1  0.
Như vậy miền tiêu chuẩn là: 
S  (X , X ,.. , X ) : x 0 n  1 2 t n s , n  . 1
Ví dụ 4.  chưa biết,  chưa biết, n=16, X~N(,2). TB mẫu x  27 5 . 6 ,
S2=5,22 . Với mức ý nghĩa =0.05, hãy kiểm định bài toán sau: - Giả thiết H0: =26
- Đối thiết H1:  > 26
3. A. 3. Đối thuyết một phía: Xét BTKĐGT H0 : =0 với đối thuyết
H1: <0, với mức ý nghĩa   cho trước.
1.Nếu 2 đã biết
Các bước tiến hành như sau: x  z 0 
- Xuất phát từ mẫu đã cho tính x và  / n
- Tìm giá trị z() từ bảng sao cho ( z())=1-. So sánh z và z():
- Nếu z  z( ) ta bác bỏ H0 .
- Nếu z  z( ) ta chấp nhận H0 . 12
Như vậy miền tiêu chuẩn là: 
S  ( X , X ,..., X ) : x 0 n   ( z  1 2 n   ) .
2.Nếu 2 chưa biết:
Trong trường hợp này ta phải giả th ế
i t về tính chuẩn của biến ngẫu
nhiên X và cỡ mẫu n<30. x 0
- Xuất phát từ mẫu đã cho ta tính t n. x , s2 và s
- Với  đã cho, tra bảng phân phối Student với n-1 bậc tự do ta tìm được t P Tt  α,n-1 từ hệ thức  , trong đó T n1 ,n    1 n-1 là biến ngẫu nhiên Student với - n 1 bậc tự do. So sánh t và tα,n-1:
- Nếu t  t ,
ta bác bỏ giả thiết H0 n 1 
- Nếu t  t ,n 1
 ta chấp nhận giả thiết H0 .
Như vậy miền tiêu chuẩn là: 
S  ( X , X ,.. , X ) : x 0 n   1 2 t n s ,  n 1   . Bài tập
Giả sử ta có mẫu ngẫu nhiên cỡ n=10 với các giá trị mẫu:
6.5; 5; 5.5; 8; 6.5; 10; 10; 8; 6.5; 7
Giả thiết mẫu từ bnn chuẩn. Hãy kiểm định giả thiết với mức ý nghĩa α=5%: H0: µ = 7; H1: µ > 7.
a) Giả sử đã biết phương sai lý thuyết σ0=2;
b) Giả thiết chưa biết phương sai. 13
Bài 8.2. Kiểm định giả thiết về tỷ lệ
Giả sử (X1, X2, …, Xn) là mẫu ngẫu nhiên, trong đó: 1 khi có A X  , p=P(A) i  0 khikhôngcó A
Như vậy, P(Xi=1)=P(A)=p, P(Xi=0)=P(A)=1-p=q. n
m   X ; thì m B(n, p) Khi đó, nếu đặt i i1 n m  1  
Nếu n lớn (n30), và min(m, n-m)5, thì X X n n i , có phân i1
phối xấp xỉ chuẩn. Lý luận tương tự tương tự trường hợp 3.A. Ta nhận
được các miền tiêu chuẩn để kiểm định giả thuyết H0 : p=p0 với các đối thiết pp0, p>p0, p
H : p p và H : p p ; m n p 0 S n z  0 0 1 0  / ( / 2 p 1 (  p ) ) 0 0 
H : p p và H : p p ; m n p0 S n z  0 0 1 0  / ( p 1 (  p ) ) 0 0 
H : p p và H : p p ; m n p 0 S n  z  0 0 1 0  / ( ) p 1 (  p )  0 0
Ví dụ: p0=45%, n=200, m=80, =5%, xem dự đoán có đúng không? Giải + Bước 1: - Giả thiết H0: p=0.45 - Đối thiết H1: p0.45
+ Bước 2: Vì np0=90, và n(1-p0)=110 nên ta có hàm tiêu chuẩn:   p p0  p 4 . 0 5 z   p0q0 /n 4 . 0 5 5 . 0 * 5/ 200 14
+ Bước 3: với α=0.05 và hàm z-tiêu chuẩn ở bước 2, dang BT 1 ta tra zα/2=z0.025=1.96. + Bước 4:
S   m/ n 0p n  . 1 9 p 1 (  p )  6 0 0 + Bước 5: 80 4 . 0 5 200 z   200   4 . 1 2 4 . 0 5x 5 . 0 5
+ Bước 6 : Kiểm tra ta thấy |z|=1.42Kết luận: Chấp nhận giả thiết H0.
Bài 3. Phương pháp p-giá trị
Các kỹ thuật mà ta đã kiểm định ở các tiết trước được gọi là phương
pháp kiểm định truyền thống. Trong mục này chúng ta sẽ trình bày một phương
pháp khác hiện được các nhà thống kê sử dụng khá rộng rãi gọi là phương pháp p-giá trị.
Xét bài toán kiểm định: - Giả thiết H0: =0
- Đối thiết H1: <0
Các số liệu mẫu cho ta giá trị của n, X  0
x và S. Ta muốn kiểm định
xem số liệu đã cho có cho phép ta bác bỏ H0 hay không?
Ta lý luận bằng phản chứng: Giả sử H0 là đúng, ta hãy tính xem xác suất để
trung bình mẫu bé hơn hay bằng giá trị quan sát được x0 bằng bao nhiêu.
Nếu xác suất này “nhỏ” theo một nghĩa nào đó, ta sẽ bác bỏ H0, do theo
nguyên lý xác suất nhỏ, biến cố đó rất ít xảy ra trong một phép thử. Nếu xác
suất đó khá “lớn” thì ta không có cơ sở để bác bỏ H0. p   P X  0 x
Giá trị của xác suất này
(tính trong điều kiện H0
đúng), được gọi là p-giá trị.
Tương tự, đối với bài toán kiểm định: - Giả thiết H0: =0
- Đối thiết H1: >0
p PX  0 x
Thì p-giá trị là xác suất
, tính dưới giả thiết H0 đúng.
Còn với bài toán kiểm định 2 phía: - Giả thiết H0: =0
- Đối thiết H1: 0
Thì p-giá trị trong trường hợp kiểm định 2 phía này gấp đôi p-giá trị trong
trường hợp 1 phía, tức là: 15
p  2PX x PX    0
x PX 0 x  0 nếu , và ngược lại:
p  2PX x PX    0
x PX 0 x  0 nếu ,
p-giá trị được các nhà thống kê sử dụng theo 2 cách. Một số người chỉ đơn
thuần tính p-giá trị, còn việc có bác bỏ giả thiết H0 hay không thì để lại cho n hà
quản lý tự quyết định lấy.
Khi làm như vậy, nhà thống kê có một số hướng dẫn chung như sau:
- Nếu p>0.05, ta không đủ cơ sở để bác bỏ H0.
- Nếu 0.01

- Nếu p<0.01, ta có một cơ sở rất mạnh, hùng hồn để bác bỏ H0.
Cách thứ 2 là sử dụng p-giá trị kết hợp với mức ý nghĩa  đã cho.
Ta tính p-giá trị và so sánh nó với :
Nếu p  0.05 , ta bác bỏ H0.
Nếu p>, ta chưa có cơ sở bác bỏ H0. Nói cách khác: p-giá trị chính là
mức ý nghĩa thấp nhất mà ta có thể bác bỏ H0.
Ví dụ 15. Từ một tập hợp chính có trung bình  (chưa biết), người ta lấy
ra một mẫu kích thước n=36 và tính được x  5040và S=780. Sử
dụng phương pháp p-giá trị, hãy kiểm định: - Giả thiết H0: =4700
- Đối thiết H1: >4700 Mức ý nghĩa =0.02.  P X  504  Giải. Ta tính p-giá trị 0 . Dưới giả thiết H X 0, vì n=36>30,
là BNN có xấp xỉ phân phối chuẩn với kỳ
vọng là 4700 và độ lệch chuẩn là: S 780  130 n 36 Vậy  P X  504  0  1  P X  504 
0  1 (50404700) 1 ( 6 . 2 ) 2 130 = 1-0.9956=0.0044.
Vậy p-giá trị là 0.0044. Giá trị này nhỏ hơn mức ý nghĩa =0.02. Vậy ta bác bỏ H0 và chấp nhận H1.
Ví dụ 16. Từ một tập hợp chính có trung bình  (chưa biết), người ta lấy
ra một mẫu kích thước n=140 và tính được x  18 5 . và S=6.8. Với
mức ý nghĩa =0.05, hãy kiểm định: 16 - Giả thiết H0: =19.4
- Đối thiết H1: <19.4 PX 18  Giải. Ta tính p-giá trị 5 . . Dưới giả thiết H X 0, vì n=140>30,
là BNN có xấp xỉ phân phối chuẩn với kỳ
vọng là 19.4 và độ lệch chuẩn là: S 6.8   5 . 0 75 n 140  P X  18  1 . 8 5 1  . 9 4 Vậy 5 .  ( )  (   5 . 1 ) 7  0 . 0 582 . 0 575
Vậy p-giá trị là 0.0582. Giá trị này lớn hơn mức ý nghĩa =0.05. Vậy ta không có cơ sở bác bỏ H0.
Ví dụ 19. Cơ quan cảnh sát giao thông cho rằng 80% số người lái xe trên
đường là có bằng lái. Kiểm tra ngẫu nhiên 200 người lái xe, cảnh sát giao thông
thấy chỉ có 150 người có bằng lái xe. Số liệu này có chứng tỏ tỷ lệ người có
bằng lái xe thấp hơn 80% hay không?
Dùng phương pháp p-giá trị với mức ý nghĩa =2%. Giải - Giả thiết H0: p=0.8 - Đối thiết H1: p<0.8
Ta có n=200; m=150; f=150/200=0.75. Vì np0=200x0.6=160>10 n(1-p0)=200x0.2=40>10
Nên f có phân bố xấp xỉ chuẩn với kỳ vọng là 0.8 và độ lệch chuẩn là p 1 (  p ) 0 0 8 . 0 x 2 . 0   0 . 0 28 200 200 . Khi đó p-giá trị là: p   P f  0 7 . 
5  ( .075 .08 )  (1 7 . 8 ) 6  . 0 03705 028 . 0 .
Ta nhận thấy p-giá trị lớn hơn mức ý nghĩa =0.02. Vậy ta chấp nhận
H0. Tỷ lệ người có bằng lái xe thực tế là 80%.
Bài 4. Kiểm định giả thiết
về giá trị của nhiều xác suất
Giả sử B1, B2, …, Bk là họ các biến cố đôi 1 xung khắc và đầy đủ của
không gian mẫu S của phép thử ngẫu nhiên E. Ta quan tâm tới xác suất (chưa
biết) của các biến cố Bi, i=1, 2, …, k này. Bài toán kiểm định là:
-Giả thiết H0: (P(B1), P(B2), …, P(Bk))=(p1, p2, …, pk).
-Đối thiết H1: (P(B1), P(B2), …, P(Bk))(p1, p2, …, pk). 17
Trong đó 0Tiến hành phép thử E n-lần độc lập, giả sử có ni lần xảy ra biến cố Bi (i=1, 2, …, k), n1+n2+…+nk=n.
Ta biểu diễn kết quả bởi bảng tần số sau: Biến cố B1 B2 … Bk Tổng Tần số quan sát n1 n2 … nk n   ,  ,1 ,2.. , Các số n np i k i i
được gọi là tần số lý thuyết. Nếu giả  n
thiết H0 đúng thì theo luật số lớn
i và ni xấp xỉ nhau.
Ta sẽ bác bỏ giả thiết H0 khi các tần số quan sát “khác xa” các tần số lý thuyết
theo 1 nghĩa nào đó. Khoảng cách giữa các tần số quan sát và lý thuyết được
đo bởi tiêu chuẩn thống kê “Khi-bình phương”:  k 2
T   (n n ) i iini 1
Ta sẽ bác bỏ H0 khi T lớn một cách có ý nghĩa. Miền bác bỏ H0 sẽ có dạng:
={T>c}, ở đây, c là một hằng số phụ thuộc mức  đã chọn.
Người ta chứng minh được rằng nếu giả thiết H0 đúng và nếu các tần số lý  thuyết n  , 5 i  , 1 , 2 . ., k i
thì T sẽ có phân phối xấp xỉ phân phối 2  2 
với k-1 bậc tự do. Tra bảng phân phối
với k-1 bậc tự do ta sẽ tìm 2 k ( ) được 1 thỏa mãn: { P T   2  ( )}  k 1 . 2 c   2  k ( ) Như vậy 1
là phân vị mức  của phân phối với k-1 bậc tự do.
Ví dụ: Gieo 1 con xúc xắc 600 lần. Số lần xuất hiện các mặt được cho bởi bảng sau: 1 2 3 4 5 6 Tổng 106 92 97 105 88 112 600 18
Có thể coi con xúc xắc đó là cân đối, đồng chất được không? Mức ý nghĩa là 0.05. Giải Tần số lý thuyết: 1 2 3 4 5 6 Tổng 100 100 100 100 100 100 600
Tính tiêu chuẩn thống kê “Khi-bình phương”: 1 ( 06 1  00)2 (92 1  00)2 (97 1  00)2 T     100 100 100 1 ( 05 1  00)2 (88 1  00)2 1 ( 12 1  00)2    2 . 4 2 100 100 100 Tra bảng phân phối 2 c   () 2   0 . 0 ( ) 5 11 070 . 5 k 1  6 1  So sánh: T=4.22<11.0705
Bài 8.5. Kiểm định giả thiết về phương sai 19
Giả sử X là đại lượng ngẫu nhiên có phân bố chuẩn
N(, 2). Tập hợp chính ở đây là tập tất cả các giả trị có thể của X. Xét một
mẫu ngẫu nhiên cỡ n. Như ta đã biết, phương sai mẫu S2 là một ước lượng
không chệch cho phương sai 2 của tập hợp chính.
Bây giờ ta xét bài toán kiểm định giả thiết:
Trường hợp 1: - Giả thiết H 2 0: 2=0 - Đối thiết H 2 1: 2<0 2 2 (n 1)S    2  Tính 2  ,
có phân phối Khi – bình phương với 0
n-1 bậc tự do. Dựa vào mức ý nghĩa , ta tra bảng giá trị 2 c  n 1 ( ) 1 . 2 c  n 1 ( ) So sánh T với 1 , nếu: 2
T c  n 1 (  ) - 1 : Bác bỏ H0. 2 2
  c   (1) - n 1  : Chấp nhận H0.
Trường hợp 2: - Giả thiết H 2 0: 2=0 - Đối thiết H 2 1: 2>0 2 (n ) 1 S T   Tính 2  0
, T có phân phối Khi – bình phương với n-1
bậc tự do. Dựa vào mức ý nghĩa , ta tra bảng giá trị 2 c    () n 1 . 2 c    n () So sánh T với 1 , nếu: 2 T c    n 1  ( ) - : Bác bỏ H0. 20 2
T c  n () - 1 : Chấp nhận H0.
Trường hợp 3: - Giả thiết H 2 0: 2=0 - Đối thiết H 2 1: 20 2 (n ) 1 S T   Tính 2  ố – bình phương vớ 0 , T có phân ph i Khi i n-1
bậc tự do. Dựa vào mức ý nghĩa , ta tra bảng giá trị 2 c    n 1 (  / 2) 1 1 2 c   . n  ( / 2) 2 1 2 c  n 1 (   / 2) 1 1  So sánh T với 2 c   , nếu: n   2 1 ( / 2) 2 2
- T c    T c   ( n  / n  1 1 1 ( / ) 2 hoặc ) 2 2 1 : Bác bỏ H0. 2 c   1 (  / ) 2 2
T c   ( / ) 2 - 1 n 1  2 n 1  : Chấp nhận H0. 21 Ví dụ: - Giả thiết H0: 2=0.22
- Đối thiết H1: 2>0.22
S=0.3, n=12, 0=0.2, =5%. Tính (n ) 1 2 S 1 ( 2 ) 1 x 3 . 0 2 T       2 2 2 . 4 75 19 6 . 7514 2 11 ( 0 . 0 ) 5  2 . 0 0
Vậy, ta bác bỏ giả thiết H0, chấp nhận đối thiết H1.
Bài 8.6. So sánh hai giá trị trung bình
Giả sử ta có hai mẫu ngẫu nhiên ( 1
X , X2 ,.. , Xn ) rút ra từ biến ngẫu 1 nhiên XF (Y ,Y ,.. , 1(x), Y ) 1 2
rút ra từ biến ngẫu nhiên YF2(y) 2 n
Bài toán đặt ra là: kiểm tra xem hai mẫu trên có phải được rút ra từ
một phân phối hay không, tức là:
F (x)  F ( ) x hay F ( ) x F ( ) 1 2 1 2 x .
Trong mục này ta xét bài toán đơn giản hơn là so sánh hai giá trị EX và EY. Ký hiệu   ,  2 ,  2 ,  EX EY DX DY 1 2 1 2
Giả thiết H0: 1=2, đối thiết H1: 12. 2 2  , 1.Nếu 1 2 đã biết
Trong trường hợp này ta cần phải giả thiết hoặc X và Y có phân
phối chuẩn hoặc mẫu n1, n2 đủ lớn (n130, n230). Lý luận tương tự ta
được các miền tiêu chuẩn mức ý nghĩa  tương ứng như sau:  x y 
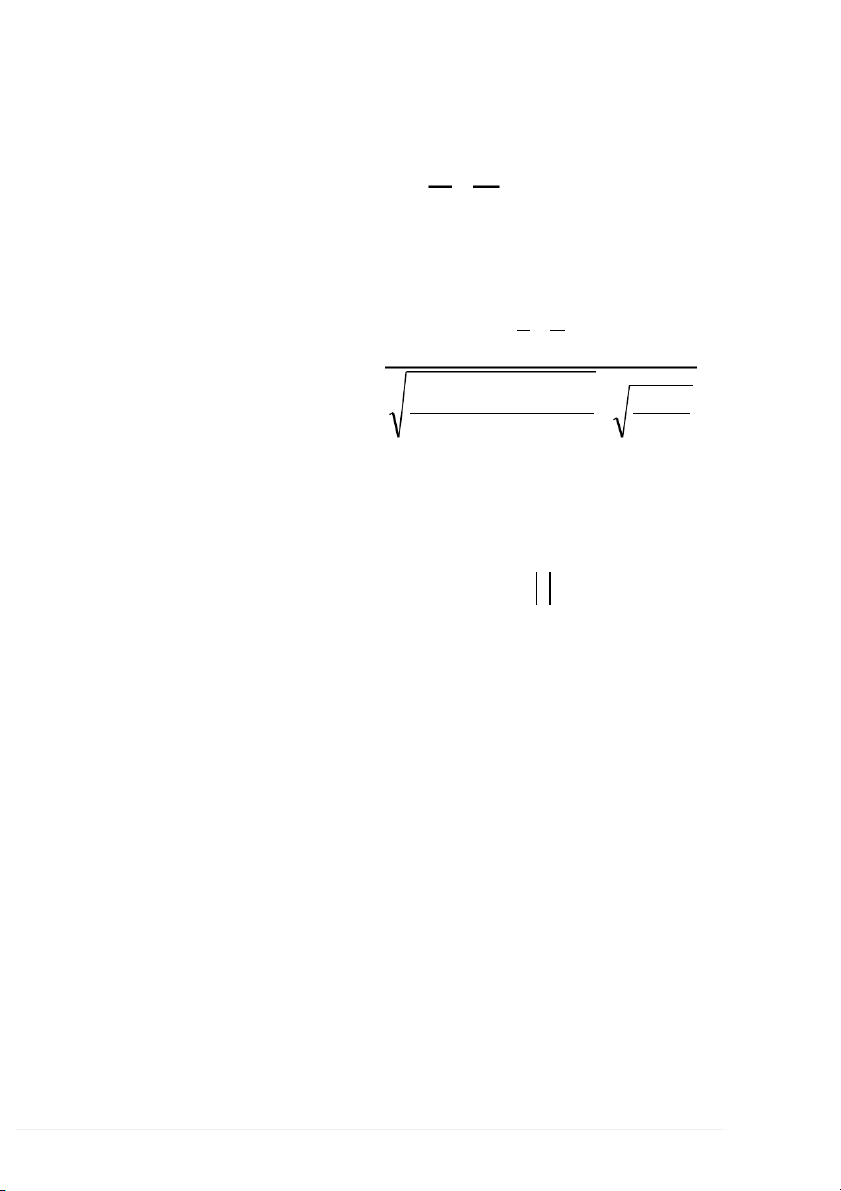
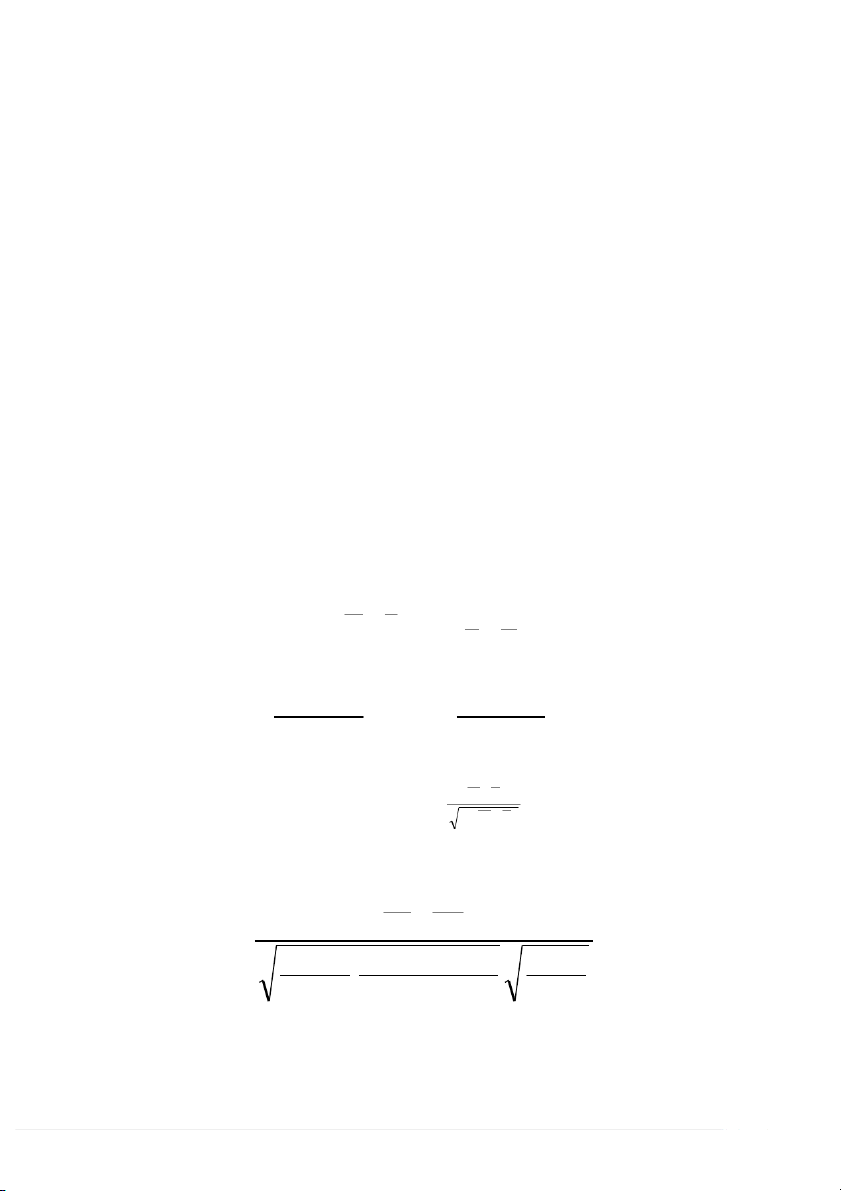
H :   và H :   ; S  | z | 0 1 2 1 1 2    z 2 2  / 2     1  2 n n   1 2   x y 
H :   và H :   ; S  0 1 2 1 1 2 z   z 2 2  / 2   1    2 n n   1 2  22  x y 
H :   và H :   ; S  0 1 2 1 1 2 z   z 2 2  / 2   1 2 n n   1 2 
Ví dụ 1. GS từ hai tập hợp chính có phân bố chuẩn X và Y ta lấy hai mẫu
độc lập với cỡ mẫu tương ứng là n1=40 và n2=50. Trung bình mẫu tính x 13 , 0 y 140 được là . GS E(X)=μ 2
1(chưa biết) , biết V(X)=σ1 =80. GS E(Y)=μ 2
2(chưa biết) , biết V(Y)=σ2 =100.
Với mức ý nghĩa α=1%, kiểm định bài toán : - Giả thiết H0 : μ1=μ2
- Đối thiết H1 : μ1≠μ2 Giải Ta có 130 1  40 T   5  80 100  40 50
Với α=1%, ta có uα/2=2.576.
Vì |T|=5>2.576, nên ta bác bỏ giả thiết H0.
Ví dụ 2. Với mức ý nghĩa α=5% hãy kiểm định giả thiết sau :
a) - Giả thiết H0 : μ1=μ2
- Đối thiết H1 : μ1>μ2 Với số liệu như sau : n n x y      1 5 ; 0 2 3 ; 2 ; 105 9 ; 8 21 ; 105 22 256
b) - Giả thiết H0 : μ1=μ2
- Đối thiết H1 : μ1<μ2 Với số liệu như sau : n 2 ; 5 n 3 ; 5 x 2 ; 0 y 2 ; 5 2  3 ; 6 2  64 1 2 1 2 Giải a) 105 9  8 T   . 2 203 105 256  50 32
Do T=2.203>uα=1.645, nên ta bác bỏ giả thiết H0. b) 23 20 2  5 T    7 . 2 7 36 64  25 35
Do T=-2.77<-zα=-1.645, nên ta bác bỏ giả thiết H0. 2 2  , 2. Nếu 1
2 chưa biết nhưng mẫu lớn (n1>30, n2>30), trong trường hợp
này ta vẫn vận dụng test thống kê như trong phần 1. trong đó các phương sai 2 2  , chưa biết 1
2 trong T được thay bởi các phương sai mẫu: 2 2 S ,
1 S 2 . Như vậy test thống kê được dùng ở đây là: xy T  2 2 1 S S2  1 n n2
Khi n1, n2>30 thì theo định lý giới hạn trung tâm, T có phân bố xấp xỉ phân bố
chuẩn tắc cho dù X và Y không có phân bố chuẩn.
Ví dụ 3. Người ta tiến hành một cuộc nghiên cứu về điểm trung bình của các vận
động viên thể dục năm 1970 và năm 1995. Một mẫu gồm 35 VĐV của năm 1970
có số điểm trung bình là 267 với độ lệch tiêu chuẩn là 27. Một mẫu gồm 40 vận
động viên của năm 1995 có số điểm trung bình là 255 với độ lệch tiêu chuẩn là
30. Kiểm định xem có sự khác nhau hay không giữa hai thế hệ vận động viên
của năm 1970 và 1995? Mức ý nghĩa α=5%. Giải
Bài toán kiểm định là: - Giả thiết H0 : μ1=μ2
- Đối thiết H1 : μ1≠μ2 267 255 T  1.823 2 2 Ta có 27 30  35 40
Do T=1.823có sự khác nhau giữa hai thế hệ vận động viên. 2 2  , 3.Nếu 1
2 chưa biết mẫu nhỏ (n1<30, n2<30)
Trong trường hợp này ta phải giả thiết 24 X N ( , 2
 ); Y N( , 2  ). 1 2 Các bước làm như sau: 2 2
x, y, s , s x y
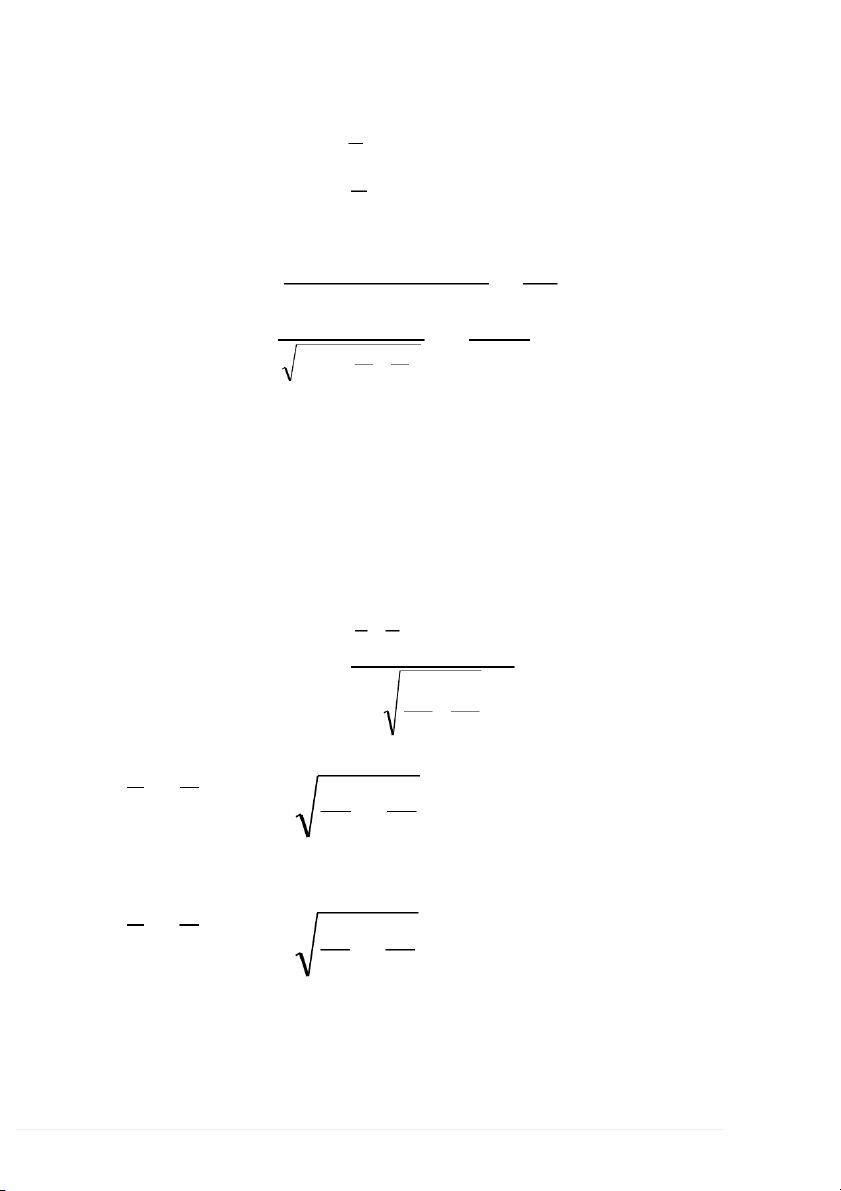
- Xuất phát từ hai mẫu đã cho ta tính . - Tính x y t  2 2 (n 1  ) s ( x 2 n 1  ) 1 sy 1 n n2 . n n 2 1 2 1 n 2 n
- Với  đã cho, tra bảng phân phối Student tìm được t ( / ) 2 n n 2 1 2 hoặc t ( ) n n 2
. Các miền tiêu chuẩn như sau: 1 2
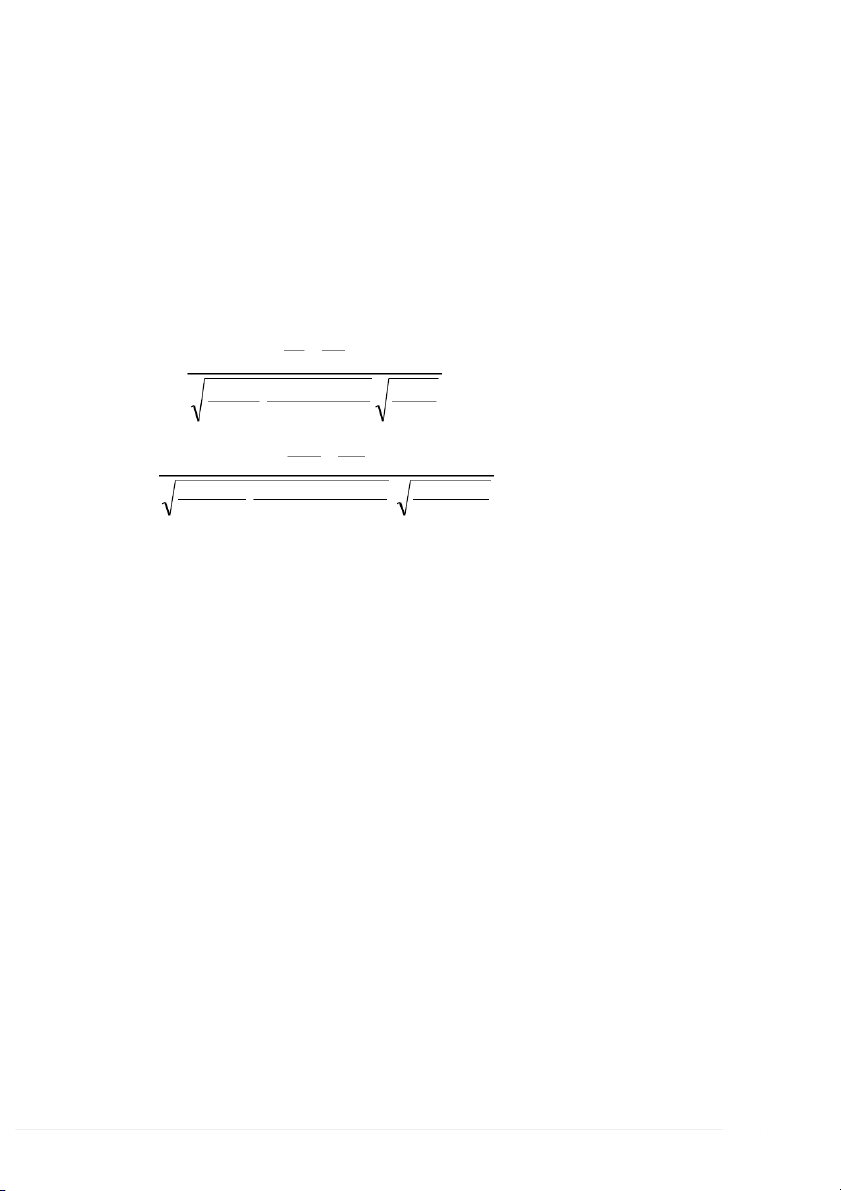
H :   và H :   ; S t t  0 1 2 1 1 2
n n  ( / 2 ) 2 1 2
H :   và H :   ; S t t  0 1 2 1 1 2
n n  (2 ) 1 2
H :   và H :   ; S t  t  0 1 2 1 1 2  n n  ( 2 ) 1 2
Ví dụ 5. Cơ quan hàng không vụ trụ Mỹ (NASA) đã ký hợp đồng với 2
công ty A và B sản xuất thử pin dùng cho vệ tinh viễn thông.
Dựa trên kết quả của các pin thử nghiệm, NASA sẽ quyết định chọn công
ty nào làm nhà cung cấp pin cho vệ tinh viễn thông. Công ty A đã sản
xuất thử được 10 chiếc, có tuổi thọ trung bình là 4.8 năm và độ lệch tiêu
chuẩn là 1.1 năm. Công ty B sản xuất thử được 12 chiếc, với tuổi thọ trung
bình 4.3 năm và độ lệch tiêu chuẩn là 0.9 năm.
GS rằng tuổi thọ của pin do A và B cung cấp có phân bố chuẩn và
phương sai như nhau. Với mức ý nghĩa α=1%, kiểm định xem có sự
khác nhau về tuổi thọ trung bình của 2 loại pin hay không? Giải
Bài toán kiểm định là: - Giả thiết H0 : μ1=μ2 25
- Đối thiết H1 : μ1≠μ2
Các số liệu đã cho như sau: n x s  Công ty A: 1 ; 0 ; 8 . 4 1 . 1 1 1 . n 1 ; 2 y  ; 3 . 4 s  9 . 0 Công ty B: 2 2 .
Phương sai chung của ước lượng là: 2 1 ( 0 ) 1 ( . 1 ) 1 2 1 ( 2 ) 1 ( 9 . 0 )2 19 8 . s    0 9 . 9 10122 20 . 4 8 . 4.3 0.5 T    1 . 1 74 1 1 0 4 . 26 Vậy 0 9 . 9(  ) 10 12
Tra bảng phân phối Student 1-0.005 phân vị với 20 bậc tự do ta được 2.845.
Do |T|<2.845, nên ta không đủ cơ sở bác bỏ H0.
4.Khoảng tin cậy cho hiệu số μ1-μ2:
Khi bài toán kiểm định dẫn tới bác bỏ H0, ta dẫn tới bài toán tìm khoảng tin cậy cho hiệu số μ1-μ2. Trong trường hợp 2 2  , 1
2 đã biết, có thể chứng minh được rằng BNN xy( 1  2) T  2 2 1  2  1 n n2
Có phân bố chuẩn tắc N(0, 1). Khi đó, khoảng tin cậy γ cho hiệu số μ1-μ2 là: 2 2   1 2
x y u   / 2 1 n n2 Trong trường hợp 2 2  , 1
2 chưa biết nhưng mẫu lớn (n 2 2 2 1, n2>30) ta thay  ,  S , 1 2 bởi 2
1 S2 và nhận được khoảng tin cậy xấp xỉ γ: 2 2 1 S S2
x y u   / 2 1 n n2
Và không cần giả thiết 2 tập chính có phân bố chuẩn.
5.Phương pháp so sánh từng cặp: 26
Giả sử (X, Y) là một cặp gồm hai đại lượng ngẫu nhiên (nói chung phụ thuộc
nhau), với E(X)=μ1, E(Y)=μ2.
Chúng ta cần so sánh μ1 và μ2.
Xét D=X-Y, khi đó ta đưa BT so sánh về BT kiểm định về giá trị TB.
Bài 8.7. So sánh hai tỷ lệ
Xét hai tập hợp chính I và II và một đặc tính A nào đó mà mỗi cá thể của hai
tập chính đó thể có hay không. Ta muốn so sánh tỷ lệ cá thể có đặc tính A của
tập chính I với tỷ lệ cá thể có đặc tính A của tập chính II.
Giả sử ta có hai mẫu ngẫu nhiên ( X , X ,.. , X ) 1 2 trong đó 1 n 1 n P(X  )
1  p , P(X  )
0  q  1 p ,m X i 1 i 1 1 1  i i1 Và mẫu (Y , 1 Y , 2 .. , Yn ) trong đó 2 n2 P(Y  )
1  p , P(Y  )
0  q 1 p ,m Y j 2 j 2 2 2  j j 1
Giả thiết H0: p1=p2 đối thiết H1: p1p2, p1>p2, p1Vì EXi=p1, EYj=p2, DXi=p1(1-p1), DYj=p2(1-p2) nên so sánh hai xác suất p1, p2
chính là so sánh hai giá trị trung bình với phương sai chưa biết. Nếu H0 đúng thì DXi=DYj=2. Khi đó 2 1 1
D(X Y )   (  ). 1 n 2 n Ước lượng của 2 1 m  2 m . 1 ( 1 m  2 m  )   1 n 2 n 1 n 2 n
ĐK áp dụng: m1+m2 10 và n1+n2- m1-m210. X Y T
Với n1, n2 đủ lớn ta xấp xỉ phân phối bởi phân phối xấp xỉ V ( X Y  ) chuẩn N(0, 1).
Từ đó ta nhận được các tiêu chuẩn mức  tương ứng như sau: 1 m 2 m  1 n 2 n u  . 1 m  2 m 1 n  2 n  1 m  2 m 1 n  2 . n 1 n  2 n 1 n n2 1 n 2 n 27
Nếu H0: p1=p2, H1: p1p2 thì S=|u|u(/2)
Nếu H0: p1=p2, H1: p1>p2 thì S=uu()
Nếu H0: p1=p2, H1: p1Ví dụ 15. Công ty Coca-cola đang n/c cải tiến sản phẩm. Với công thức cũ khi
cho 500 người dùng thử thì có 120 người ưa thích. Với công thức mới khi cho
1000 người khác dùng thử thì có 300 ng ời ư ưa thích.
Với mức ý nghĩa =2%, kiểm định xem công thức mới đưa vào có làm tăng tỷ
lệ người ưa thích hay không? Giải H0: p1=p2, H1: p1>p2 1 m 2  m 1 n 2 u n 1
m m2 n1n 2 1 m m 2 1 n  2 . n 1 n  2 n 1 n  2 n 1 n 2 n 300 120  1000 500   . 2 . 4 300 1  20 1000500300120 10005000 . . 1000500 1000500 1000x500 u=u0.02=2.054
Do u>u=2.054, nên ta bác bỏ H0. 2 X N  
Giả sử X và Y là 2 BNN có phân bố chuẩn, ~ ( 1, 1 ) , Y ~ N ( , 2  ) 2 2 ,
Chúng ta cần so sánh μ1 và μ2 dựa trên 2 mẫu quan sát độc lập của X và Y. 28