
lOMoARcPSD|40651217
lOMoARcPSD|40651217
CHƯƠNG 1. XÁC SUẤT VÀ CÁC PHÉP TÍNH VỀ XÁC SUẤT
Tóm tắt nội dung:
• Phép thử và các loại biến cố.
• Khái niệm xác suất (quan điểm cổ điển, quan điểm thống kê) Nguyên lý
xác suất lớn và nhỏ. Mối quan hệ giữa các biến cố
• Các định lý và công thức xác suất.
Xác suất có điều kiện và công thức nhân xác suất.
Công thức cộng xác suất.
Công thức xác suất của hai biến cố đối lập Công thức Bernoulli.
Công thức xác suất đầy đủ và công thức Bayes.
1. Phép thử và các loại biến cố
1.1 Phép thử và biến cố
a. Phép thử (Experiment)
Việc thực hiện một nhóm các điều kiện cơ bản để quan sát một hiện tượng
nào đó được gọi là một phép thử.
Trong thực tế có hai loại phép thử:
+ Phép thử không ngẫu nhiên: là phép thử mà khi bắt đầu tiến hành thực
hiện ta đã biết kết quả sẽ xảy ra.
Ví dụ: Khi làm phép thử cho dung dịch muối và axit tác dụng với nhau, ta đã
biết thu được muối mới và axit mới.
+ Phép thử ngẫu nhiên: là phép thử mà khi bắt đầu tiến hành thực hiện ta
không biết được kết quả nào sẽ xảy ra.
Ví dụ: Cho ấp 10 quả trứng vịt, ta không biết được có mấy con vịt sẽ nở ra.
Trồng 20 cây non, sẽ có bao nhiêu cây sống sót và phát triển.
Ở môn học này, chúng ta chỉ nghiên cứu những phép thử ngẫu nhiên. Để cho
ngắn gọn: từ đây trở đi ta gọi phép thử ngẫu nhiên là phép thử.
b. Biến cố (Event)
Hiện tượng, sự việc có thể xảy ra trong kết quả của phép thử được gọi là
biến cố.
Ví dụ: Sự việc nhận được muối mới và axit mới là biến cố, sự việc có 8 con
vịt con nở ra là một biến cố, sự việc có 7 con vịt con nở ra là một biến cố, … hay
20 cây non đều sống là một biến cố.

lOMoARcPSD|40651217
1.2 Các loại biến cố
Trong thực tế ta có thể gặp các loại biến cố sau đây:
a) Biến cố chắc chắn (Certain event)
Biến cố chắc chắn là biến cố nhất định phải xảy ra trong kết quả của một
phép thử. Ta thường ký hiệu biến cố chắc chắn là U.
Ví dụ:
1. Khi thực hiện phép thử: Tung một con xúc xắc, gọi U là biến cố “Xúc
xắcxuất hiện mặt có số chấm nhỏ hơn hoặc bằng sáu và lớn hơn hoặc bằng 1”
thì U là biến cố chắc chắn.
2. Gọi U là biến cố “Nước sôi ở nhiệt độ 100
0
C, dưới áp suất 1 atm” thì
U là một biến cố chắc chắn.
b) Biến cố không thể có (Imposible event)
Biến cố không thể có là biến cố không thể xảy ra trong kết quả của phép
thử. Biến cố không thể có được ký hiệu là V.
Ví dụ:
1. Khi tung một con xúc xắc. Gọi V là biến cố “Xuất hiện mặt 7 chấm”,
V làbiến cố không thể có.
2. Biến cố nước sôi ở nhiệt độ 50
0
C, với áp suất 1 atm là biến cố không
thể có.
c) Biến cố ngẫu nhiên (Random event)
Biến cố ngẫu nhiên là biến cố có thể xảy ra hoặc không xảy ra khi thực hiện
phép thử. Các biến cố ngẫu nhiên thường được ký hiệu là A, B, C hoặc là A
1
, A
2
,
A
3
, … Ví
dụ:
1. Bắn một viên đạn vào bia thì việc bắn súng là phép thử còn viên đạn
trúngbia (hay trượt bia) là biến cố ngẫu nhiên. Ta ký hiệu A là biến cố “Bắn
trúng”, B là biến cố “Bắn trượt”.
2. Tung một con xúc xắc khi chơi cá ngựa là một phép thử, còn việc lật
lênmặt nào đó là biến cố ngẫu nhiên. Ta có thể gọi A
i
là biến cố “Mặt i chấm
được lật lên”, (i=1..6).
3. Từ một lô sản phẩm gồm chính phẩm và phế phẩm. Người ta lấy
ngẫunhiên một sản phẩm: việc lấy sản phẩm là một phép thử, còn lấy được
chính phẩm (hay phế phẩm) là biến cố ngẫu nhiên. Ta có thể gọi A là biến cố
“Lấy được chính phẩm”, B là biến cố “Lấy được phế phẩm”.
4. Một người mua một tờ vé số là một phép thử. Các biến cố A- “Vé số
đótrúng độc đắc”, B- “Vé số trúng giải nhất”, C- “Vé số không trúng giải nào”
là những biến cố ngẫu nhiên. Biến cố U - “Vé số đó hoặc trúng giải, hoặc

lOMoARcPSD|40651217
không trúng giải” là biến cố chắc chắn. Biến cố V - “Vé số đó vừa trúng giải
nhất vừa không trúng giải nào” là biến cố không thể có.
Như vậy, ta thấy rằng: một biến cố chỉ có thể xảy ra khi phép thử gắn liền
với nó được thực hiện. Trong thực tế, biến cố ngẫu nhiên là loại biến cố thường
gặp hơn cả.
2. Xác suất và các định nghĩa về xác suất
Các biến cố ngẫu nhiên có đặc điểm chung là có thể xảy ra, có thể không xảy ra
sau khi thực hiện phép thử. Khi phép thử chưa thực hiện xong ta không thể biết
chắc chắn là biến cố ngẫu nhiên mà ta quan tâm có xảy ra hay không. Tuy nhiên, ta
vẫn cảm nhận được rằng biến cố này dễ xảy ra hơn, còn biến cố kia khó xảy ra hơn.
Nói một cách khác, khả năng xảy ra của mỗi biến cố ngẫu nhiên nói chung là khác
nhau. Ta muốn lượng hóa hay là tìm cách đo khả năng xảy ra của mỗi biến cố bởi
một con số. Con số đó được gọi là xác suất của biến cố.
2.1 Khái niệm xác suất (Probability)
Xác suất của biến cố A là một số thực, thể hiện khả năng khách quan xảy ra
biến cố A hoặc tỉ lệ xuất hiện biến cố A trong một tập hợp các kết quả của phép
thử. Kí hiệu là P(A).
Vấn đề đặt ra là, với mỗi biến cố A đã cho, làm thế nào để xác định P(A)? Các
nhà toán học đã nghiên cứu và đưa ra một số định nghĩa khác nhau về xác suất.
Dưới đây ta sẽ giới thiệu hai định nghĩa về xác suất.
2.2 Định nghĩa xác suất theo quan điểm cổ điển
a. Bài toán: Trong một lớp có 10 học sinh nam và 20 học sinh nữ. Người ta
chọn ngẫu nhiên một em vào đội tình nguyện. Tính xác suất chọn được học sinh
nữ?
Việc chọn một em bất kỳ từ 30 em là một phép thử. Trong phép thử này ai
cũng có khả năng được chọn như nhau. Như vậy, có 30 trường hợp có thể xảy ra.
Người ta gọi đây là 30 trường hợp đồng khả năng của phép thử.
Gọi A là biến cố “Chọn được học sinh nữ”. Ta cần tính xác suất của biến cố
A. Biến cố A xảy ra nếu ta chọn được 1 trong 20 em nữ, tức là có 20 trường hợp để
biến cố A xảy ra. Người ta gọi đây là 20 trường hợp thuận lợi cho biến cố A. Tỉ số
20 được lấy làm số đo khả năng xảy ra biến cố A, hay xác suất của biến cố A
là 30
P(A) = 20 2 30
3 .
Nếu gọi B là biến cố “Chọn được học sinh nam” thì P(B)
= 10 1
30 3 .

lOMoARcPSD|40651217
b. Định nghĩa: Xác suất của biến cố A là tỉ số giữa số trường thuận lợi cho
biến cố A và số các trường hợp đồng khả năng của phép thử.
m
Ký hiệu P(A) =
n
Ở đó, m là số trường thuận lợi cho biến cố A và n là số các trường hợp đồng
khả năng của phép thử.
c. Tính chất
1. Xác suất của biến cố ngẫu nhiên là một số dương nhỏ hơn 1: Nếu A là biến
cố ngẫu nhiên thì:
0 < P(A) <1.
2. Xác suất của biến cố chắc chắn bằng 1.
P(U) = 1
3. Xác suất của biến cố không thể có bằng 0. P(V) = 0
Như vậy, nếu B là một biến cố bất kỳ thì 0 ≤ P(B) ≤ 1.
Chú ý rằng: một biến cố có xác suất bằng 1 chưa chắc đã biến cố chắc chắn và
biến cố có xác suất bằng 0 chưa chắc là biến cố không thể có.
d. Các phương pháp tính xác suất theo quan điểm cổ điển
1. Phương pháp suy luận đơn giản: Thường dùng trong các bài toán mà
phép thử có ít trường hợp xảy ra.
Ví dụ 1: Từ ba số 3, 5, 6 thiết lập các số có hai chữ số, tính xác suất được các số
có hai chữ số giống nhau.
Giải
Các số thiết lập được là: 33, 35, 36, 53, 55, 56, 63, 65, 66. Số các trường hợp
đồng khả năng của phép thử ta có thể đếm được n = 9. Gọi A là biến cố “Được số
có hai chữ số giống nhau”. Số trường hợp thuận lợi cho biến cố A là m = 3.3 1
Vậy P(A) =
9 3
Ví dụ 2: Từ 1 hộp có bi đỏ và 5 bi trắng có kích thước như nhau.
Ta lấy ngẫu nhiên 1 bi, tính xác suất lấy được bi trắng?
Giải
Khi thực hiện phép thử lấy một bi từ hộp có 15 bi, đơn giản ta có thể đếm được
số trường hợp đồng khả năng của phép thử là n= 15. Gọi A là biến cố “Lấy được bi
trắng”. Số trường hợp thuận lợi cho biến cố A là m = 5.
Khi đó xác suất để lấy được bi trắng là P(A) = 5 1
15
3
2. Phương pháp dùng công thức giải tích tổ hợp: Thường dùng trong các bài
toán mà phép thử có nhiều trường hợp phức tạp xảy ra.
10

lOMoARcPSD|40651217
Nhắc lại công thức giải tích tổ hợp
a. Hoán vị: Số hoán vị của n phần tử là số cách đổi chỗ n phần tử đó
P
n
= n!
b. Tổ hợp: Số tổ hợp chập k của n phần tử là số cách lấy k phần tử từ
tập n phần tử, tập con k phần tử không sắp thứ tự.
Ck n! n
(n k)!.k!
c. Chỉnh hợp: Số chỉnh hợp chập k của n phần tử là số cách lấy k phần
tử từ tập n phần tử, tập con k phần tử được sắp thứ tự (mỗi phần tử có mặt một
lần).
Ak n! n
(n k)!
d. Chỉnh hợp lặp: Số chỉnh hợp lặp chập k của n phần tử là số cách lấy
k phần tử từ tập n phần tử, tập con k phần tử được sắp thứ tự (mỗi phần tử có
mặt nhiều
lần).
Ank nk
e. Quy tắc cộng: Nếu
Có n
1
cách chọn sự việc 1;
Có n
2
cách chọn sự việc 2;
…
Có n
k
cách chọn sự việc k;
Thì có n
1
+ n
2
+ … + n
k
cách chọn 1 sự việc nào đó.
Ví dụ : Một người có 3 áo trắng, 2 áo xanh, 1 áo vàng và người này cần
chọn 1 áo để mặc. Người đó có 3+2+1 = 6 cách chọn được 1 áo. f. Quy tắc
nhân: Nếu
Có n
1
cách chọn sự việc 1;
Có n
2
cách chọn sự việc 2;
…
Có n
k
cách chọn sự việc k;
Thì có n
1
.n
2
…n
k
cách chọn đồng thời k sự việc.
Ví dụ: Từ Hà Nội đi thành phố Hạ Long có 3 cách đi: ô tô, tàu hỏa, xe máy.
Từ thành phố Hạ Long ra vịnh có 2 cách: tàu thủy và ca nô. Du khách có 3.2 = 6
cách để đi từ Hà Nội ra vịnh Hạ Long.
Ví dụ 3: Một bàn dài có 5 ghế. Có bao nhiều cách để xếp 5 người A, B, C, D,
E ngồi vào bàn sao cho:
+ 5 người ngồi tùy ý?
+ C ngồi chính giữa?

lOMoARcPSD|40651217
+ A và B ngồi hai đầu bàn?
Giải
+ Số cách xếp 5 người vào 5 chỗ là số hoán vị của 5. Có 5! = 120 cách để 5
người ngồi tùy ý.
+ Xếp C ngồi chính giữa chỉ có 1 cách, đồng thời xếp 4 người còn lại vào 4
chỗ có 4! cách. Áp dụng quy tắc nhân ta có 4! = 24 cách để C ngồi chính giữa.
+ Xếp A và B có 2 cách, đồng thời xếp 3 người còn lại vào 3 chỗ có 3!
cách.
Có 2.3! =12 cách để A và B ngồi hai đầu bàn.
Ví dụ 4: Bốn người vào rút tiền ở ngân hàng có ba máy ATM. Có bao nhiêu
cách để:
+ 4 người vào tùy ý?
+ 2 người vào máy số 1?
+ Có hai người cùng một máy?
Giải
+ Số cách để 4 người vào tùy ý là số cách chọn 4 phần tử từ 3 phần tử, 4 phần
tử được sắp thứ tự và mỗi phần tử được chọn nhiều lần nên có A
3
4
3
4 81 cách.
+
Để chọn 2 người có C
2
cách, đồng thời với mỗi cách đó 2 người còn lại 6
4
chọn tùy ý 2 máy: số 2 và số 3, vậy có 2! = 2 cách.
Áp dụng quy tắc nhân, ta có:
6.2 =12 cách để 2 người vào máy số 1.
+ Để chia 4 người thành nhóm 2 người có: C
2
cách, với mỗi cách chia đó
6
4 ta có 2 nhóm. Các nhóm
sẽ chọn 2 trong 3 máy (không được lặp lại), nên có: A
3
2
6 cách. Vậy có: 6.6
= 36 cách để 2 người vào cùng một máy.
Ví dụ 5: Một lô sản phẩm có 10 sản phẩm, trong đó có 8 chính phẩm và 2 phế
phẩm. Lấy ngẫu nhiên một lần từ lô sản phẩm đó ra 3 sản phẩm, tính xác suất để:
a) Cả 3 sản phẩm lấy ra đều là chính phẩm.
b) Trong 3 sản phẩm lấy ra có 2 chính phẩm.
Giải
a) Gọi A là biến cố “Lấy được 3 chính phẩm”.
Số trường hợp đồng khả năng của phép thử là n =
10
120
C3

lOMoARcPSD|40651217
Số trường hợp thuận lợi cho biến cố A xảy ra là m =
C
38
56
Do đó
P(A) 56 7
120
15

lOMoARcPSD|40651217
b) Gọi B là biến cố “Trong ba sản phẩm lấy ra có 2 chính phẩm”, số kết quả
thuận lợi cho B xảy ra là: m C
1
2
. 56
= C8 2
P(B) 7
Do đó
.
15
Ví dụ 6: Xếp ngẫu nhiên bảy người lên chín toa tàu. Tính xác suất để:
a) Bảy người lên cùng toa đầu?
b) Bảy người lên cùng một toa?
c) Bảy người lên bảy toa đầu?
d) Bảy người lên bảy toa khác nhau?
Giải
Phép thử là việc chọn tùy ý 7 toa tàu từ 9 toa. Số các trường hợp đồng khả năng
của phép thử là n = A
9
7
9
7
.
a) Gọi A là biến cố “Bảy người cùng lên toa đầu”. Chỉ có 1 trường hợp
để biến
1
cố A xảy ra hay m = 1. Ta có P(A) = .
97
b) Gọi B là biến cố “Bảy người lên cùng một toa”. Có 9 trường hợp để
biến cốB xảy ra hay m = 9. Ta có P(B) = 9 1
7 6.
9 9
c) Gọi C là biến cố “Bảy người lên bảy toa đầu”. Có 7! trường hợp để
biến cố
C xảy ra hay m = 7!= 5040. Ta có P(C) = 5040
.
97 7
d) Gọi D là biến cố “Bảy người lên bảy toa khác nhau”. Có A
9
trường hợp để
biến cố D xảy ra hay m =1814407
181440. Ta có P(D) = 0,0379.
Nhận xét A

lOMoARcPSD|40651217
9 97
• Ưu điểm: Định nghĩa theo quan điểm cổ điển của xác suất đơn giản,
dễ hiểu, dễ tính toán, không cần làm phép thử.
• Hạn chế: Định nghĩa này chỉ áp dụng được khi số tất cả các trường
hợp đồng khả năng của phép thử là một số hữu hạn.
Để khắc phục hạn chế của định nghĩa xác suất theo quan điểm cổ điển, các
nhà toán học đưa ra định nghĩa sau đây.
2.3 Định nghĩa xác suất theo quan điểm thống kê
a) Định nghĩa tần suất: Tần suất xuất hiện biến cố A trong n phép thử là tỷ số
giữa số phép thử trong đó biến cố A xuất hiện và tổng số phép thử được thực hiện.
Nếu ký hiệu số phép thử là n, số lần xuất hiện biến cố A là k, tần suất xuất hiện k
biến cố A là:
f (A) . (k được gọi là tần số xuất hiện biến cố A) n
Cùng với khái niệm xác suất, tần suất là một trong những khái niệm cơ bản của
lý thuyết xác suất.
Ví dụ 7: Khi khảo sát ngẫu nhiên 50 sinh viên người ta phát hiện ra 10 sinh viên
đi làm thêm. Nếu gọi B là biến cố “Xuất hiện sinh viên đi làm thêm” thì tần suất
xuất hiện sinh viên đi làm thêm trong số 50 SV được khảo sát là: f (B)
10
1
50 5
Ví dụ 8: Để nghiên cứu khả năng xuất hiện mặt sấp khi tung một đồng xu, ba
người tiến hành tung đồng xu nhiều lần và thu được kết quả cho ở bảng dưới đây
(A là biến cố “Xuất hiện mặt sấp”):
Từ kết quả các lần thử trên, ta thấy khi số phép thử tăng lên, tần suất xuất hiện
mặt sấp tiến dần đến 0,5 là xác suất xuất hiện mặt sấp khi tung đồng xu. Vậy tần
suất tiến dần đến xác suất khi số phép thử tăng dần đến vô hạn. Từ đó ta có định
nghĩa thống kê về xác suất:
b) Định nghĩa xác suất
!
"#
$%
&'()
*++,,
',,+&
'(-*
-,'*
*,,..
,/&,-,'
,/&,*+(
,/&,,&'

lOMoARcPSD|40651217
Khi số phép thử tăng lên vô hạn, tần suất xuất hiện biến cố A tiến dần đến một
số xác định được gọi là xác suất của biến cố đó. Hay nói cách khác, xác suất là
giới hạn của tần suất khi số phép thử tăng lên vô hạn:
k
P(A)= lim
n n
Nhận xét:
+ Ưu điểm: Định nghĩa theo quan điểm thống kê về xác suất có ưu điểm lớn là
nó không đòi hỏi những điều kiện áp dụng như đối với định nghĩa cổ điển. Nó
hoàn toàn dựa trên các quan sát thực tế để làm cơ sở kết luận về xác suất xảy ra của
một biến cố.
+ Hạn chế: Trong thực tế không thể tiến hành vô hạn phép thử nên việc tính
toán chính xác là không thể. Đối với số phép thử đủ lớn ta có thể lấy xác suất xấp
xỉ bằng tần suất:
k
P(A) n
1. Nguyên lý xác suất lớn và xác suất nhỏ
1.1 Nguyên lý xác suất nhỏ
Qua thực nghiệm và quan sát thực tế, người ta thấy rằng các biến cố có xác suất
nhỏ sẽ không xảy ra khi ta thực hiện một phép thử hay một vài phép thử. Từ đó ta
thừa nhận nguyên lý sau:
“Nếu một biến cố có xác suất rất nhỏ thì thực tế có thể cho rằng trong một phép
thử, biến cố đó sẽ không xảy ra”
1.2 Nguyên lý xác suất lớn
“Nếu một biến cố có xác suất gần bằng 1 thì thực tế có thể cho rằng trong một
phép thử, biến cố đó sẽ xảy ra”
Việc quy định một mức xác suất thế nào được cho là lớn và thế nào được cho là
nhỏ sẽ tùy thuộc vào từng trường hợp cụ thể. Chẳng hạn, xác suất để một máy bay
có sự cố khi cất cánh bằng 0,01 là rất lớn, nhưng xác suất một chuyến tàu muộn
giờ bằng 0,01 là rất nhỏ.
2. Mối quan hệ giữa các biến cố
2.1 Hai biến cố tương đương
Định nghĩa 1
Hai biến cố A và B được gọi là tương đương (hay bằng nhau), ký hiệu A = B,
nếu biến cố A xảy ra thì biến cố B cũng xảy ra và ngược lại trong kết quả của một
phép thử.

lOMoARcPSD|40651217
(A=B) (A xảy ra B xảy ra)
Ví dụ 9: Hộp có 6 bi đỏ, 2 bi xanh, lấy ngẫu nhiên ra 2 bi. Gọi A là biến cố
“Lấy được 1 bi đỏ” và B là biến cố “Lấy được 1 bi xanh”. Ta có A và B là 2 biến
cố tương đương: A = B.
2.2 Tổng của các biến cố
Định nghĩa 2
Tổng của hai biến cố: A và B, ký hiệu A + B (hay AB), là biến cố mà nó xảy
khi và chỉ khi ít nhất một trong hai biến cố A, B xảy ra trong kết quả của phép thử.
(A+B xảy ra) (Hoặc A xảy ra, hoặc B xảy ra, hoặc cả A và B xảy ra)
Ví dụ 10: Chọn ngẫu nhiên từ 2 lớp: A và B mỗi lớp 1 sinh viên. Gọi A là biến
cố “Chọn từ lớp A được bạn nam”, B là biến cố “ Chọn từ lớp B được bạn nam” và
C là biến cố “Chọn được sinh viên nam”.
Rõ ràng biến cố C xảy ra khi có ít nhất một trong hai biến cố A và B xảy ra,
biến cố C là tổng của 2 biến cố A và B. Vậy C = A + B.
Ví dụ 11: Tung một con xúc xắc, gọi A là biến cố “Xuất hiện mặt 1 chấm”, B là
biến cố “Xuất hiện mặt 2 chấm”, C là biến cố “Xuất hiện mặt không quá 2 chấm”.
Biến cố C xảy ra nếu biến cố A hoặc B xảy ra nên C = A + B.
Định nghĩa 3 n n
Tổng của n biến cố: A
1
, A
2
,.., A
n
, ký hiệu A
1
+ A
2
+…+ A
n
= A
i
(hay A
i
),
i1 i1 là biến
cố mà nó xảy ra khi và chỉ khi có ít nhất một trong n biến cố đó xảy ra trong kết
quả của phép thử.
n
( A
i
xảy ra) ⇔ (1 hoặc 2 hoặc 3 , … , hoặc n biến cố xảy ra).
i1
Ví dụ 12: Một trường có 10 em học sinh đi thi học sinh giỏi. Gọi A
i
là biến cố
“Học sinh thứ i đoạt giải”, A là biến cố “Trường có học sinh đoạt giải”. Biến cố A
xảy ra khi và chỉ khi có ít nhất 1 trong 10 em đoạt giải. Vậy biến cố A là tổng của
10 biến cố A
1
, A
2
,.., A
10.
Ta có A = A
1
+ A
2
+ …+ A
10
.
2.3 Biến cố tích
Định
nghĩa 4
Tích của hai biến cố A và B, ký hiệu A.B (hay AB), là biến cố mà nó xảy ra khi
và chỉ khi cả A và B cùng xảy ra trong kết quả của phép thử.

lOMoARcPSD|40651217
(A.B xảy ra) (A x⇔ ảy ra và B xảy ra)
Ví dụ 13: Hai lớp D8 và D9 đều có sinh viên quê Thái Bình. Chọn ngẫu nhiên
mỗi lớp 1 sinh viên. Gọi A là biến cố “Chọn được sinh viên quê Thái Bình ở lớp
D8”, B là biến cố “Chọn được sinh viên quê Thái Bình ở lớp D9”, C là biến cố “Cả
hai sinh viên được chọn đều quê Thái Bình”. Rõ ràng C xảy ra khi và chỉ khi cả A
và B cùng xảy ra. Vậy C = A.B.
Ví dụ 14: Một sinh viên chỉ phải thi 2 môn Tin và Toán, gọi A là biến cố “Sinh
viên thi đạt môn Tin”, B là biến cố “Sinh viên thi đạt môn Toán”, C là biến cố
“Sinh viên không trượt môn nào”. Biến cố C xảy ra nếu biến cố A và B cùng xảy
ra nên C = A.B. Định nghĩa 5
n
Tích của n biến cố: A
1
, A
2
,.., A
n
, ký hiệu A
1
.A
2
.... A
n
=
n
A
i
(hay A
i
) , là biến
i1 i1 cố mà nó xảy
ra khi và chỉ khi tất cả n biến cố ấy đồng thời xảy ra trong kết quả của phép
thử.
n
( A
i
xảy ra) (⇔ A
1
xảy ra, A
2
xảy ra, … và A
n
xảy ra)
i1
Ví dụ 15: Xét phép thử lấy ngẫu nhiên: lần lượt ra 4 viên bi từ hộp có 10 viên bi
(trong đó có 6 viên bi màu trắng). Gọi A
i
là biến cố “Lần thứ i lấy được viên bi
trắng”, (i = 1..4). Gọi A là biến cố “Lấy được 4 viên bi trắng”. Ta thấy A xảy ra khi
và chỉ khi cả 4 biến cố A
1
, A
2
, A
3
, A
4
đồng thời xảy ra. Vậy: A= A
1
.A
2
.A
3
. A
4
2.4 Biến cố xung khắc
Định nghĩa 6
Hai biến cố A và B được gọi là xung khắc nhau nếu chúng không đồng thời xảy
ra trong một phép thử.
(A và B xung khắc) ⇔ A.B = V.
Ví dụ 16: Xét phép thử chọn ngẫu nhiên 1 sinh viên trong lớp chỉ có 2 giới:
nam và nữ. Gọi A là biến cố “Sinh viên được chọn là nam” và B là biến cố “Sinh
viên được chọn là nữ” thì A và B là hai biến cố xung khắc vì chúng không thể cùng
xảy ra trong kết quả của phép thử.
Ví dụ 17: Tung một đồng xu, gọi A là biến cố “Xuất hiện mặt sấp”, B là biến cố
“Xuất hiện mặt ngửa”. Biến cố A và B không thể cùng xảy ra trong kết quả của
phép thử nên chúng là 2 biến cố xung khắc.

lOMoARcPSD|40651217
Định nghĩa 7
Nhóm n biến cố: A
1
, A
2
,.., A
n
được gọi là xung khắc từng đôi nếu hai biến cố bất
kỳ trong n biến cố này xung khắc với nhau.
(A
1
, A
2
,.., A
n
xung khắc từng đôi) (⇔ A
i
.A
j
=V với mọi i ≠ j)
Ví dụ 18: Tung một con xúc xắc. Gọi A
i
là biến cố “Xúc xắc xuất hiện mặt i
chấm”, (i =1..6). Khi đó, nhóm biến cố: A
1
, A
2
,.., A
6
xung khắc từng đôi.
2.5 Biến cố đối
lập Định nghĩa 8
Hai biến cố được gọi là đối lập nhau nếu chúng xung khắc và trong kết quả của
phép thử, nhất thiết phải xảy ra một trong hai biến cố đó.
Biến cố đối lập của biến cố A được ký hiệu là A .
A A U;
A.A V.
Ví dụ 19: Khi tung một con xúc xắc. Gọi A là biến cố “Xuất hiện mặt chẵn” và
A là biến cố “Xuất hiện mặt lẻ”. Biến cố A và A không cùng xảy ra nên chúng
xung khắc và trong kết quả của phép thử phải xảy ra A hoặc A . Rõ ràng A và A là
hai biến cố đối lập nhau.
Ví dụ 20: Phép thử tung một đồng xu có thể xảy ra một trong hai biến cố
A“Được mặt sấp” và A - “Được mặt ngửa”. Hai biến cố A và A đối lập nhau.
Chú ý: Hai biến cố đối lập thì xung khắc nhưng hai biến cố xung khắc thì chưa
chắc đối lập.
Ví dụ 21: Tung một con xúc xắc. Gọi A
i
là biến cố “Xúc xắc xuất hiện mặt i
chấm”, (i =1..6). Biến cố A
1
và A
3
xung khắc nhưng trong kết quả của một phép
thử có thể không xảy ra hai biến cố này nên chúng không đối lập.
Ví dụ 22: Một sinh viên thi ba môn Toán, Anh, Tin. Gọi:
A là biến cố “Sinh viên thi đạt môn Toán”;
B là biến cố “Sinh viên thi đạt môn Anh”;
C là biến cố “Sinh viên thi đạt môn Tin”;Hãy biểu diễn các biến cố sau qua ba
biến cố trên: a) Sinh viên đó chỉ đạt môn Toán?
b) Sinh viên đó thi đạt một môn?
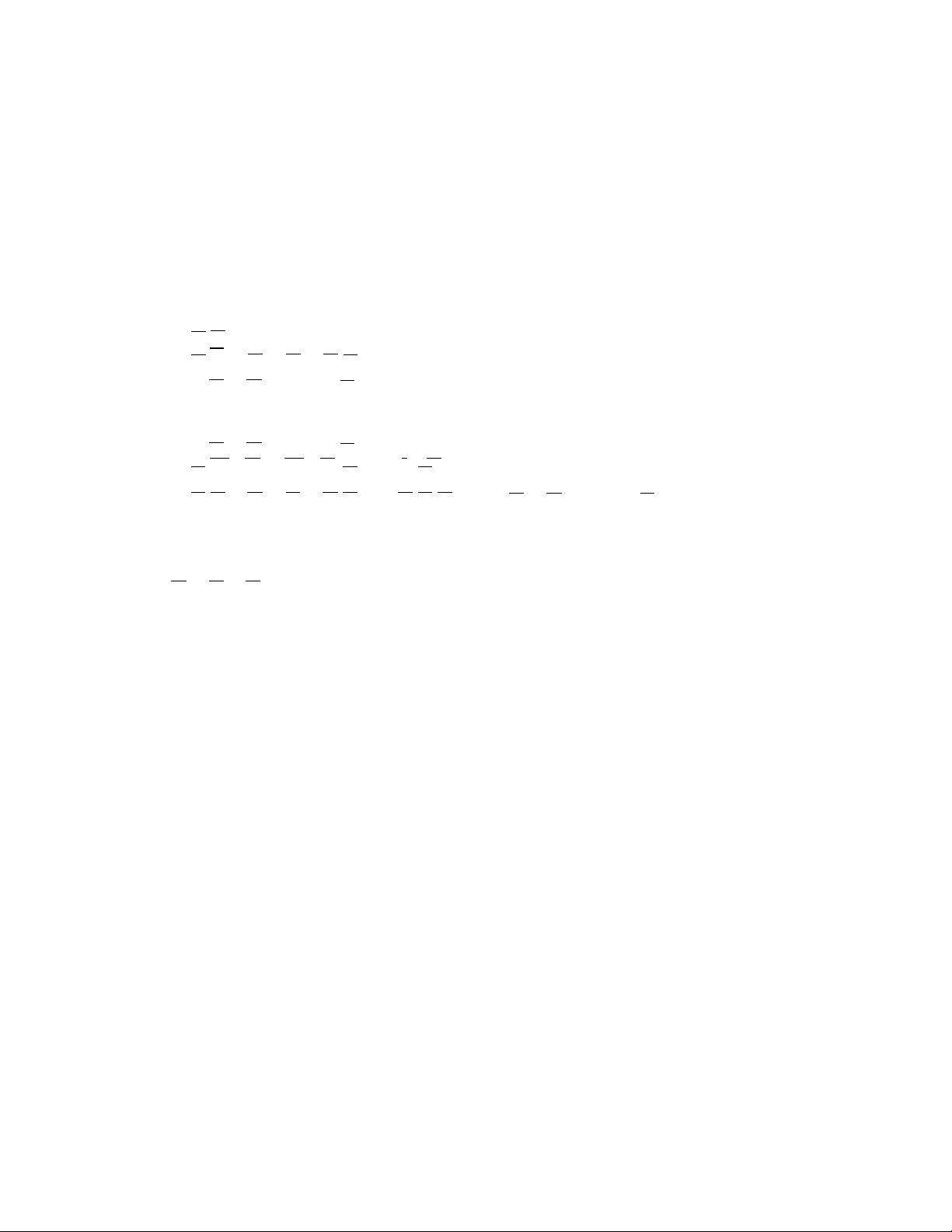
lOMoARcPSD|40651217
c) Sinh viên đó thi đạt hai môn?
d) Sinh viên đó thi đạt ít nhất một môn?
e) Sinh viên đó thi đạt ít nhất hai môn?
f) Sinh viên đó thi đạt nhiều nhất một môn?
g) Sinh viên đó thi đạt không quá hai môn?
h) Sinh viên đó có môn không đạt?
i) Sinh viên đó thi đạt bốn môn?
Giải
a) A.B.C
b) A.B.C A.B.C A.B.C
c) A.B.C A.B.C A.B.C
d) A+B+C
e) A.B.C A.B.C A.B.C+A.B.C
f) A.B.C A.B.C A.B.C A.B.C
g) A.B.C A.B.C A.B.C A.B.C + A.B.C A.B.C A.B.C 0
12022
h) A B C
i) V.
2.6 Biến cố độc
lập Định nghĩa 9
Hai biến cố A và B được gọi là độc lập với nhau, nếu sự xảy ra hay không xảy
ra của biến cố nào trong chúng đều không ảnh hưởng đến khả năng xảy ra của
biến cố còn lại.
Hai biến cố không độc lập được gọi là hai biến cố phụ thuộc.
Ví dụ 23: Trong phép thử tung hai đồng xu, gọi A là biến cố “Xu thứ nhất sấp”,
B là biến cố “Xu thứ hai sấp”. Ta có A và B là hai biến cố độc lập.
Định nghĩa 10
Nhóm n biến cố (n ≥ 3) A
1
, A
2,
…, A
n
được gọi là độc lập toàn phần nếu mỗi biến
cố đều độc lập với một tổ hợp bất kỳ các biến cố còn lại.
A
2
độc lập với A
1
;
A
3
độc lập với A
1
A
2
;

lOMoARcPSD|40651217
…
A
n
độc lập với A
1
A
2
…A
n-1
Ví dụ 24: Mười xạ thủ thi bắn súng, gọi A
i
là biến cố “Xạ thủ thứ i bắn trúng”.
Vì mỗi xạ thủ bắn trúng hay trượt thì không ảnh hưởng đến những người còn lại
nên nhóm 10 biến cố A
1
, A
2
, …, A
10
là độc lập toàn phần. Chú ý: Nếu hai biến cố
A và B độc lập thì:
Cặp biến cố A và B cũng độc lập
Cặp biến cố A và B cũng độc lập
Cặp biến cố A và B cũng độc lập
2.7 Nhóm biến cố đầy đủ
Định nghĩa 11
Các biến cố A
1
, A
2
, …, A
n
được gọi là nhóm biến cố đầy đủ nếu chúng xung
khắc từng đôi và tổng của chúng là biến cố chắc chắn.
Nói cách khác, trong kết quả của phép thử có một và chỉ một biến cố trong n
biến cố đó xảy ra.
A
i
.A
j
V, i j
n A U
i1 i
Ví dụ 25: Xét phép thử tung một con xúc xắc. Gọi A
i
(i = 1..6) là biến cố “Xuất
hiện mặt i chấm”. Các biến cố A
1
, A
2
, …, A
6
tạo nên một nhóm các biến cố đầy đủ
vì chúng xung khắc từng đôi một và tổng của 6 biến cố đó là biến cố chắc chắn: U
= A
1
+ A
2
+ …+ A
6
.
Ví dụ 26: Một nhà máy có ba phân xưởng I, II, III sản xuất cùng một loại sản
phẩm. Trong lô sản phẩm của nhà máy, người ta lấy ngẫu nhiên một sản phẩm. Gọi
A là biến cố “Lấy được sản phẩm của phân xưởng I”, B là biến cố “Lấy được sản
phẩm của phân xưởng II”, C là biến cố “Lấy được sản phẩm của phân xưởng III”.
Ta có ba biến cố A, B, C là nhóm biến cố đầy đủ.
Chú ý: Hai biến cố đối lập A và A luôn tạo thành nhóm biến cố đầy đủ.
2.8 Một số tính chất của các phép toán
1) Tính giao hoán: A + B = B + A và A.B =B.A

lOMoARcPSD|40651217
2) Tính kết hợp: A+ (B+C) = (A+B) +C và A.(B.C) = (A.B).C 3) Tính
phân phối: A.(B+C) = A.B +A.C và A+(B.C)= (A+B).(A + C) 4) A+ A
= A; A.A =A;
22
2
2= A.
3. Các định lý và công thức xác suất
3.1 Định lý nhân xác suất
3.1.1 Xác suất có điều kiện: Cho A, B là hai biến cố tùy ý. Giả sử B đã xảy ra
rồi. Khi đó xác suất của biến cố A được tính trong điều kiện biết biến cố B đã xảy
ra được gọi là xác suất có điều kiện của A trong điều kiện B đã xảy ra, ký hiệu là
P(A/B).
Ví dụ 27: Cho một hộp kín có 6 quả cầu đỏ và 4 quả cầu xanh. Người ta lấy
ngẫu nhiên lần lượt 2 quả theo phương thức không hoàn lại. Tính xác suất để lần
thứ hai lấy được cầu đỏ, nếu biết lần thứ nhất đã lấy được cầu đỏ?
Giải
Gọi A là biến cố “Lần thứ hai lấy được cầu đỏ”, B là biến cố “Lần thứ nhất lấy
được cầu đỏ”. Ta cần tìm P(A/B).
Sau khi lấy lần thứ nhất (biến cố B đã xảy ra) trong hộp còn lại 9 quả cầu, trong
5
đó 5 cầu đỏ nên P(A/B) = .
9
3.1.2 Định lý 1: Xác suất của tích hai biến cố A và B bằng tích xác suất của một
trong hai biến cố đó với xác suất có điều kiện của biến cố còn lại:
P(A.B) = P(A).P(B/A) = P(B).P(A/B) (1.1)
Chứng minh: Giả sử phép thử có n trường hợp đồng khả năng, có thể xảy ra
m
A
trường hợp thuận lợi cho biến cố A, m
B
trường hợp thuận lợi cho biến cố B. Vì
A và B là hai biến cố bất kì, do đó nói chung sẽ có k trường hợp thuận lợi cho cả A
và B đồng thời xảy ra. Theo định nghĩa cổ điển của xác suất ta có:
k m
P(A.B) = ; P(A) =
A
n n
Ta đi tính P(B/A).
Với điều kiện biến cố A đã xảy ra, nên số trường hợp đồng khả năng
của phép thử đối với biến B là m
A
, số kết quả thuận lợi cho B là k. Do đó: k
P(B/A) = m
A
Như vậy: P(A.B) = k m A k
P(A).P(B / A)
.
n n m
A

lOMoARcPSD|40651217
Vì vai trò của hai biến cố A và B như nhau. Bằng cách chứng minh tương tự
ta được: P(A.B) = P(B).P(A/B)♦
Ví dụ 28: Trong hộp có 10 thẻ cào, trong đó có 3 thẻ trúng thưởng. Người ta
rút thăm lần lượt hai thẻ. Tính xác suất để cả hai thẻ đều trúng thưởng?
Giải
Gọi A là biến cố “Thẻ đầu trúng thưởng”, B là biến cố “Thẻ thứ hai trúng
thưởng”, C là biến cố “Cả 2 thẻ đều trúng thưởng”. Ta có C = A.B.
Vì P(A) có thể tính được ngay nên ta sử dụng công thức P(A.B) = P(A).P(B/A).
Khi rút thăm lần đầu thì trong hộp có 10 thẻ, trong đó có 3 thẻ trúng thưởng
3
nên P(A) =
Khi biến cố A đã xảy ra thì còn lại 9 thẻ, trong đó có 2 thẻ trúng thưởng. Do
2
đó: P(B/A) = .
9
Từ đó ta có: P(C) = P(A.B) = P(A).P(B/A) = 3 2 1
10 . 9
15 .
Ví dụ 29: Một ứng viên tham gia thi tuyển vào công ty H phải qua 2 vòng,
nếu cả hai vòng đều đạt thì ứng viên được nhận vào làm. Biết rằng khả năng vượt
qua vòng 1 của người này là 96%, và khả năng vượt qua vòng 2 của người này sau
khi qua vòng 1 là 83%. Hãy tính xác suất để ứng viên này được nhận?
Giải
Gọi A là biến cố “Ứng viên vượt qua vòng 1”, B là biên cố “Ứng viên vượt
qua vòng 2”, C là biến cố “Ứng viên được nhận”. Ta có C = A.B.
P(C) = P(A). P(B/A) = 0,96.0,83 = 0,7968.
Định lý 2: Xác suất của tích n biến cố bằng tích xác suất của các biến cố đó,
trong đó xác suất của mỗi biến cố tiếp sau đều được tính với điều kiện tất cả các
biến cố trước đó đã xảy ra:
P(A
1
.A
2
… A
n
) = P(A
1
).P(A
2
/A
1
).P(A
3
/A
1
.A
2
)…P(A
n
/A
1
.A
2
…A
n-1
). (1.2) Công
thức này được chứng minh bằng quy nạp.
Hệ quả 1:
Xác suất của tích hai biến cố độc lập bằng tích xác suất của các biến cố đó:
P(A.B) = P(A).P(B). (1.3)
Chứng minh: Nếu hai biến cố A và B độc lập thì P(A/B) = P(A) và P(B/A)
= P(B). Thay vào công thứ của định lý nhân xác suất ta có P(A.B) = P(A).P(B).
Hệ quả 2:
Xác suất của tích n biến cố độc lập toàn phần bằng tích xác suất của các biến
cố đó:
lOMoARcPSD|40651217
P(A
1
.A
2
… A
n
) = P(A
1
).P(A
2
) … P(A
n
) (1.4)
Chứng minh: Theo định nghĩa 10, nhóm biến cố A
1
.A
2
… A
n
độc lập toàn
phần thì:
P(A
2
/A
1
) = P(A
2
),
P(A
3
/A
1
.A
2
) = P(A
3
)
…
P(A
n
/A
1
.A
2
…A
n-1
) = P(A
n
)
Nên P(A
1
.A
2
… A
n
) = P(A
1
).P(A
2
) … P(A
n
).
Ví dụ 30: Một thủ kho có chùm gồm 20 chìa khóa có bề ngoài giống hệt
nhau, trong đó chỉ có 2 chiếc mở được khóa kho. Anh ta thử ngẫu nhiên từng chìa
(chìa nào không đúng thì bỏ ra). Tính xác suất anh này mở được khóa kho ở lần
thử thứ ba.
Giải
Gọi A
i
là biến cố “Chọn được đúng chìa khóa ở lần thứ i”, khi đó A
i
là biến
cố “Chọn không đúng chìa khóa ở lần thứ i”, i = 1..20.
Gọi A là biến cố “Mở được khóa kho ở lần thử thứ ba”, khi đó A= A
1
.A
2
.A
3
Theo công thức (1.2) ta có:
P( A1.A2 .A3 ) = P(A18 1 ).P(A2 / A1 )17. P(A 3 / A1.A2 ) .2
Với P( A ) ; / A ) ; / A .A ) .
P(A P(A
1 20 2 1 19 3 1 2 18
Vậy xác suất anh này mở được khóa kho ở lần thử thứ ba là:
P(A .A .A )2
18 .17 .
17
.
1
3
2
20 19 18 190
Ví dụ 31: Một xưởng dệt có ba máy: dệt vải, dệt sợi, dệt len hoạt động độc
lập. Xác suất để các máy dệt bị hỏng trong tháng lần lượt là: 0,02; 0,03; 0,05. Tính
xác suất để trong tháng có cả ba máy cùng bị hỏng?
Giải
Gọi A là biến cố “Trong tháng máy dệt vải
hỏng”, B là biến cố “Trong tháng máy dệt sợi

lOMoARcPSD|40651217
hỏng”, C là biến cố “Trong tháng máy dệt len
hỏng”.
Ta có:
P(A) = 0,02; P(B) = 0,03; P(C) = 0,05.
Gọi D là biến cố “Trong tháng có cả ba máy cùng bị hỏng”. Ta có D=A.B.C.
Vì ba máy hoạt độc độc lập nên ba biến cố A, B, C độc lập toàn phần.
Theo công thức (1.4), ta có xác suất để trong tháng có cả ba máy cùng bị hỏng là:
P(D) = P(A).P(B).P(C) = 0,02.0,03.0,05 = 0,00003.
5.2 Định lý cộng xác suất
Định lý 1: Xác suất của tổng hai biến cố A và B bằng tổng xác suất của hai biến
cố thành phần trừ đi xác suất của tích hai biến cố đó:
P(A+B) = P(A) + P(B) – P(A.B). (1.5)
Chứng minh: Giả sử phép thử có n trường hợp đồng khả năng, có thể xảy ra m
A
trường hợp thuận lợi cho biến cố A, m
B
trường hợp thuận lợi cho biến cố B. Vì A
và B là hai biến cố bất kì, do đó nói chung sẽ có k trường hợp thuận lợi cho cả A
và B đồng thời xảy ra. Gọi m
A+B
là số trường hợp thuận lới cho biến cố A+B. Ta có
m
A+B
= m
A
+ m
B
– k.
Theo định nghĩa cổ điển của xác suất ta có:
P(A+B) = mAB mA mB k mA mB k P(A) P(B) P(A.B)
n n n n n
Tương tự, ta chứng minh được định lý công xác suất đối với 3 biến cố.
Định lý 2: Xác suất của tổng ba biến cố A, B, C được tính bởi công thức sau:
P(A+B+C) = P(A) + P(B) + P(C) – P(A.B) – P(A.C) – P(B.C) + P(A.B.C) (1.6)
Ví dụ 32: Theo thống kê trung bình một năm 365 ngày có 65 ngày mưa to, 40
ngày gió lớn, 25 ngày có bão (mưa to và gió lớn). Chọn ngẫu nhiên một ngày trong
năm, tính xác suất ngày đó có thời tiết bất thường (mưa to hoặc gió lớn)?
Giải
Gọi A là biến cố “Chọn ngày mưa to”, B là biến cố “Chọn ngày gió lớn”, C là
biến cố “Chọn ngày có thời tiết bất thường”. Ta có: C = A + B.
P(A) = 65 ; P(B) 40 ; P(A.B) 25
365 365 365.
Hai biến cố A và B không xung khắc vì có ngày vừa mưa to, vừa gió lớn. Áp
dụng công thức (1.5):

lOMoARcPSD|40651217
P(C) = P(A+B) = P(A) + P(B) – P(A.B) = 65
36540
25 36580
0,219.
365
365
Ví dụ 33: Hai người chơi ném bóng vào rổ. Khả năng trúng của người thứ nhất
là 0,7. Khả năng trúng của người thứ hai là 0,6. Mỗi người ném 1 quả, tính xác suất
có bóng trúng rổ?
Giải
Gọi A là biến cố “Người thứ nhất ném trúng rổ”, B là biến cố “Người thứ hai
ném trúng rổ”.
Ta có P(A) = 0,7 và P(B) = 0,6.
A và B là 2 biến cố độc lập.
Gọi C là biến cố “Có bóng trúng rổ”.
C xảy ra nếu ít nhất 1 người ném trúng rổ nên C= A+B.
Theo định lý cộng xác suất ta có:
P(C) = P(A+B) = P(A) + P(B) – P(A.B) = 0,7 + 0,6 – 0,7.0,6 = 0,88.
Hệ quả 1: Nếu hai biến cố A và B xung khắc thì:
P(A+B) = P(A) + P(B) (1.7)
Chứng minh: Nếu hai biến cố A và B xung khắc thì A.B = V nên P(A.B) =
P(V) = 0. Thay vào công thức (1.5) của định lý trên ta có:
P(A+B) = P(A) + P(B).
Ví dụ 34: Trong hộp có 6 bút bi xanh và 4 bút bi đen. Lấy ngẫu nhiên một lần
hai bút từ hộp. Tính xác suất được ít nhất một bút xanh?
Giải
Gọi A
i
là biến cố “Lấy được i bút xanh”, i = 0, 1, 2 và B là biến cố “Lấy được ít
nhất một bút xanh”. Ta có B = A
1
+ A
2
.
Hai biến cố A
1
và A
2
xung khắc vì trong phép thử trên chỉ xảy ra một trong ba
trường hợp A
0
, A
1
hoặc A
2
, vậy:
P(B) = P(A
1
+ A
2
) = P(A
1
) + P(A
2
)
Ta có P(A1) = C .C 61
1 4
C
10
2
24
120 0,2
C2
và P(A
2
) = C
26
30
0,25.
120
10
Do đó P(B) = 0,2 + 0,25 = 0,45
Hệ quả 2: Nếu n biến cố A
1
, A
2
, …, A
n
xung khắc với nhau từng đôi thì xác
suất của tổng n biến cố đó bằng tổng n xác suất của các biến cố thành phần:
n n
P(A
i
) P(A
i
(1.8)
Bấm Tải xuống để xem toàn bộ.




